Prerpints.org logo
Preprint
Article

Efficient Neural Networks on the Edge with FPGAs by Optimizing an Adaptive Activation Function

Altmetrics

Downloads

131

Views

63

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

18 January 2024

Posted:

19 January 2024

You are already at the latest version

Alerts
Abstract
The implementation of neural networks (NN) on edge devices enables local processing of wireless data but faces challenges such as high computational complexity and memory requirements when deep neural networks (DNN) are used. Shallow neural networks customized for specific problems are more efficient, requiring fewer resources, and resulting in a lower latency solution. An additional benefit of the smaller network size is that it is suitable for real-time processing on edge devices. The main concern with shallow neural networks is their accuracy performance compared to DNNs. In this paper, we demonstrate that a customized adaptive activation function (AAF) can meet the accuracy of a DNN. We designed an efficient FPGA implementation for a customized segmented spline curve neural network (SSCNN) structure to replace the traditional fixed activation function with an AAF. We compared our SSCNN with different neural network structures such as real-valued time delay neural network (RVTDNN), augmented real-valued time delay neural network (ARVTDNN), and deep neural networks with different parameters. Our proposed SSCNN implementation uses 40% fewer hardware resources and no Block RAMS compared to the DNN with similar accuracy. We experimentally validate this computationally efficient and memory-saving FPGA implementation of SSCNN for digital predistortion of RF power amplifiers using the AMD/Xilinx RFSoC ZCU111. The implemented solution uses less than 3% of the available resources. The solution also enables an increase of the clock frequency to 221.12 MHz, allowing the transmission of wide bandwidth signals.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Wireless communications is an important area in edge computing and a growing application area for FPGAs. Machine learning is increasingly used in wireless applications and as a result, compact and accurate implementations on FPGA are in demand. For edge processing, consuming few resources and delivering low latency is important. This paper addresses the issue of machine learning applied to Digital Predistortion (DPD), an important application in wireless communications. Power Amplifiers (PAs) are required for the transmission of radio frequency signals, and DPD improves the linear operation of transmitted signals, which is essential to avoiding interference in wireless communication. Operators would like to run their PAs in the most power-efficient mode possible; however, these modes typically cause the PA to introduce more non-linear distortion to the signal.
DPD introduces nonlinear behavior which is the inverse of that caused by the PA. FPGAs can be effective in implementing DPD, especially just before the RF front end where signals are transmitted and received. Coefficients for DPD need to be determined such that the particular implementation best linearizes the PAs under the current operating conditions, which may change over time. By implementing DPD at the edge we can respond quickly to these current operating conditions. By using few resources on the FPGA, other front-end processing can be combined with DPD for wireless receivers and transmitters. We implement DPD on an AMD/Xilinx RFSoC which integrates the RF frontend with FPGA fabric to demonstrate the ability to quickly respond to current operating conditions by changing DPD coefficients with very little hardware overhead.
Neural networks have been applied to DPD, including real-valued time delay neural networks (RVTDNN) [1]. More recent neural network structures for DPD [2,3] have targeted enhanced dynamic range performance at the cost of increased network size, additional parameters, and long training times. Recently, CNNs have been applied to DPD [4,5,6]. However, these network structures have even more network parameters resulting in greater computational complexity and longer training times. This is evident from observing the resource requirements for FPGA implementation of CNNs for image classification [7]. In general, network structures with fewer parameters require shorter training times and are more suitable for systems with resource limitations on edge devices, however, they must still be capable of delivering the required performance.
Most prior work in neural networks, for DPD and for other applications, make use of fixed activation functions. These lose accuracy when modeling non-linear functions, such as is required in DPD, during training. To increase accuracy, the common solution is to increase the size of the neural network model. In this paper we focus on an alternative approach, namely using an activation function that can be adapted during training.
For inference, which is frequently implemented in hardware, non-linear activation functions such as tanh and sigmoid are common. These models are not implemented directly but rather approximated using piece-wise linear approximations or multiple order based approximations. These approximations cause the model to lose accuracy. At the same time, approximation based hardware solutions increase costs in terms of resource usage while slowing the speed, as further elaborated in Section 2.
An adaptive activation function can better fit the nonlinear model during training compared to a fixed model, and this reduces training loss [8,9]. This network structure and training strategy has been used in prior research [10,11,12]. However, there is little research that explores the hardware efficiency in implementing adaptive activation functions. This is the focus of this research.
In this work, we present a complexity-reduced and resource-saving, adaptive activation function based Segmented Spline Curve Neural Network (SSCNN) implementation for DPD and validate its operation on an AMD/Xilinx RFSoC platform. The SSCNN employs an adaptive activation function that can be better tailored for the objective of linearizing the PA while greatly reducing the hardware resources needed on the FPGA.
The contributions of this work are:
  • The first FPGA implementation of an adaptive activation function (AAF) based neural network for regression.
  • An adaptive activation function applied to Digital Predistortion and implemented in FPGA hardware.
  • An optimized segmented spline curve layer that has been designed with the target hardware in mind to provide an implementation true to the mathematical basis of the segmented spline curve layer.
  • Results show that the implementation of the AAF for DPD using the SSCNN is capable of effective linearization while consuming minimal resources.
  • A thorough comparison of different neural network structures and their FPGA implementations that compares performance and resources used. The comparison shows that the SSCNN has similar performance to a Deep Neural Network (DNN) while using far fewer hardware resources.
The rest of this paper is organized as follows. Related research on activation functions is discussed in Section 2. Section 3 provides background on DPD and introduces different neural network models and activation functions used. In Section 4 we describe our hardware design and implementation. Results are presented in Section 5, including a comparison of different approaches with respect to performance and resource usage. Finally, we present conclusions and future work.

2. Related Work on Activation Functions

A major contribution of this research is the implementation of an adaptive activation function on an FPGA for regression. Currently, most neural networks that target regression problems use fixed activation functions such as tanh and sigmoid. Despite the increased model size caused by the accuracy limitation of fixed activation functions, the hardware implementation for those functions is expensive to achieve functions such as e x and 1 / x , and the latency is high. The majority of traditional activation functions are implemented based on piecewise linear and one piecewise second-order approximation. The DCT interpolation-based tanh function, which was implemented on FPGA with minimal error, requires 21 Look Up Tables (LUTs) for an 8-bit output as per Abdelsalam et al. (2017) [13]. Si et al. (2020) [14] proposed a hardware-friendly D-ReLU, but it is only suitable for classification problems and not regression. Ngah et al. (2016) [15] designed a differential lookup table-based sigmoid function with limited accuracy. Gao et al. (2020) [16] designed a better sigmoid function on FPGA for regression problems, but it operates at a slow speed. Xie et al. (2020) [17] implemented a twofold LUT-based tanh function, but it comes at a high cost on hardware. [18] describes a generic model for three types of non-linear traditional activation functions based on a piecewise linear model. Pasca et al. (2018) [19] present several floating-point architectures for sigmoid and tanh functions and evaluate the impact of the activation function on both the area and latency of RNN performance. They highlighted that the hardware area and latency can be significantly reduced if the tanh/sigmoid activation function is directly implemented. All of the above works implementations are only improving the accuracy between training and inference and aiming at reducing hardware cost during inference, but the activation function also influences the size of the neural network during training, which in turn has implications for the hardware requirements during inference.
In [8,9,11], it has been shown that adaptive activation functions allow the networks to estimate a more accurate solution by training the activation function parameters during the training process. Meanwhile, the hardware-based investigation of AAF has received less attention. [20] implemented an adaptive ReLU activation function, but for a image classification problem. So in this paper, we explore the accuracy and hardware efficiency of an AAF in detail.

3. Materials & Methods: DPD Coefficient Learning and Neural Network Structures

3.1. DPD

The concept of Digital Predistortion (DPD) is to place a predistorter before a power amplifier(PA) in order to linearize the amplifier’s nonlinear behavior before transmitting signals in wireless communication. Ideally, when cascading the predistorter and PA, the output of the PA becomes linear as the predistorter behaves as the inverse of the PA.
AMD/Xilinx has some hardware with DPD directly available on their FPGAs, specifically the RFSoC DFE, illustrating the importance of this application [21]. They implement the memory polynomial structure [22] for single input/single output PAs. Neural networks have an inherent parallel structure and are naturally suited to multiple PAs [23,24]. Many researchers are investigating NNs for DPD as NNs are more adaptable than the memory polynomial approach, due to the ability to take advantage of additional inputs such as input signal magnitude or temperature. This is increasingly important for 5G and 6G scenarios. In this paper, we investigate efficient implementations of such DPD solutions that could be incorporated into hardware blocks in the future.

3.2. Direct Learning and Indirect Learning Architectures

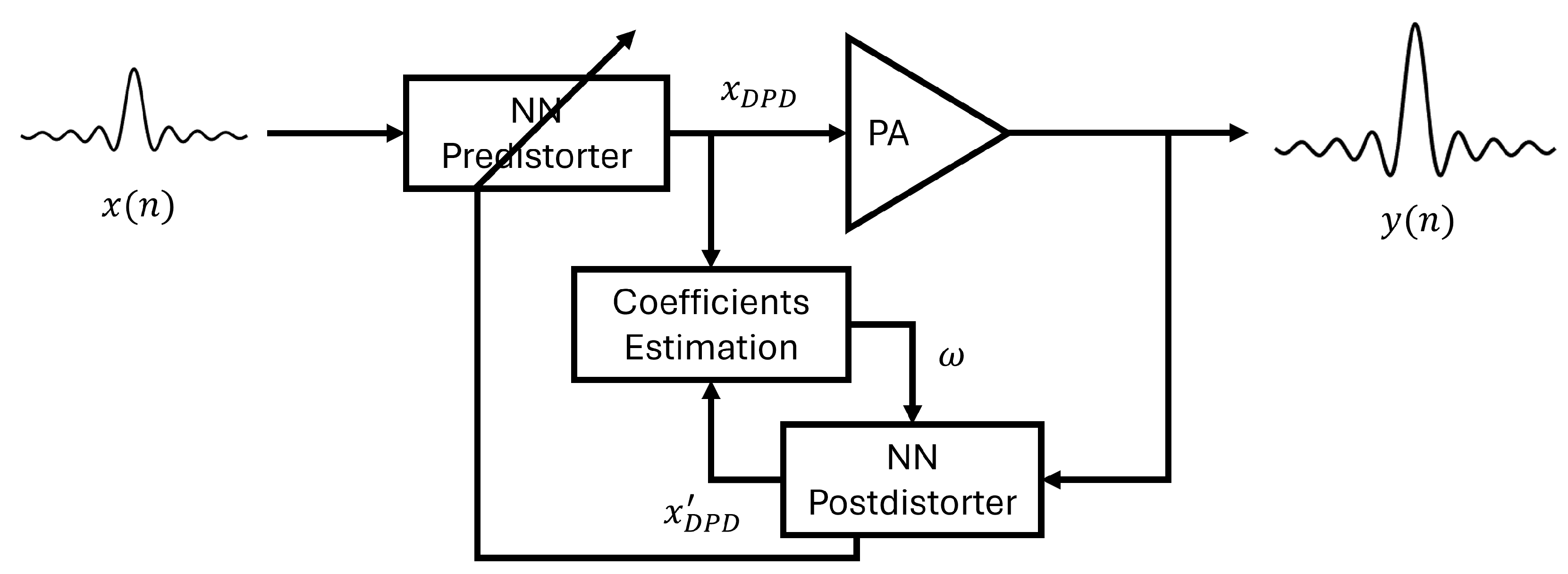
As learning the characteristics of the PA is the key to generating the predisorter, the Direct Learning Architecture (DLA) and Indirect Learning Architecture (ILA) [25,26,27] are two commonly used architectures for identifying the coefficients of DPD. The DLA firstly trains a PA model based on the PA’s input and output, then inverts this model to implement a predisorter. In ILA, a postdistorter is trained as an inverse nonlinear PA model and then the coefficients are copied to the predistorter to achieve digital predistortion (DPD). Because of its good performance and straightforward implementation, we adopt the ILA structure combined with different neural network models to estimate the parameters of DPD, as shown in Figure 1.

3.3. Real-Valued Time-Delay Neural Network

RVTDNN [1,28] is one of the most commonly used neural network structures for DPD and PA behavioral modeling. RVTDNN takes a complex signal’s in-phase (I) and quadrature (Q) components as two sets of real-valued inputs to the neural network and makes use of delay taps to incorporate memory effects in the PA model. One of its variants, Augmented Real-Valued Time-Delay Neural Network (ARVTDNN) [29], improves DPD performance by introducing envelope terms as additional inputs to the RVTDNN. These two commonly used neural network structures involve nonlinear activation functions which increase computational complexity and cost when implemented in hardware.

3.4. Segmented Spline Curve Neural Network

The SSCNN structure, an enhancement of the original RVTDNN structure, was first presented in [30]. This new structure significantly cuts down the number of necessary coefficients. It avoids the need for bias coefficients in the neurons of the hidden layer and incorporates the envelope terms directly at the output layer. Meanwhile, SSCNN employs an adaptive activation function that can be tuned during the neural network training process. This gives SSCNN an edge over other RVTDNNs for several reasons. Since the adaptive activation function substitutes a piecewise linear approximation in place of a non-linear activation function, such as the hyperbolic tangent activation function, it provides better accuracy while reducing computational complexity in both the training and inference phases. In this study, we have designed an FPGA-based SSCNN structure based on a hardware-oriented, mathematical simplification that simplifies the calculation steps of the adaptive activation function. This design reduces hardware complexity and conserves resources in comparison to the commonly used nonlinear activation functions found in other structures while maintaining accuracy.

3.5. Deep Neural Networks

Deep neural networks (DNNs) have also been utilized in DPD research [4,31]. DNNs, which are built with more than three layers, can sometimes offer superior accuracy compared to shallow neural networks due to their increased layer count. As demonstrated in [4], a DPD application using a DNN can outperform a shallow neural network, albeit at a significant hardware resource cost. Given that hardware implementations of DPD typically occur on edge devices and are thus constrained, DNNs may not be the best choice when solving DPD. The implementation of large and complex DNNs can be hindered by factors such as requirements for memory bandwidth and buffer size, which are needed for coefficient access during the inference phase, and are limited on edge devices. Recent efforts have been made to choose the best DNN structures for PA linearization [31] but these approaches still result in substantial hardware expenses to achieve the desired level of accuracy.
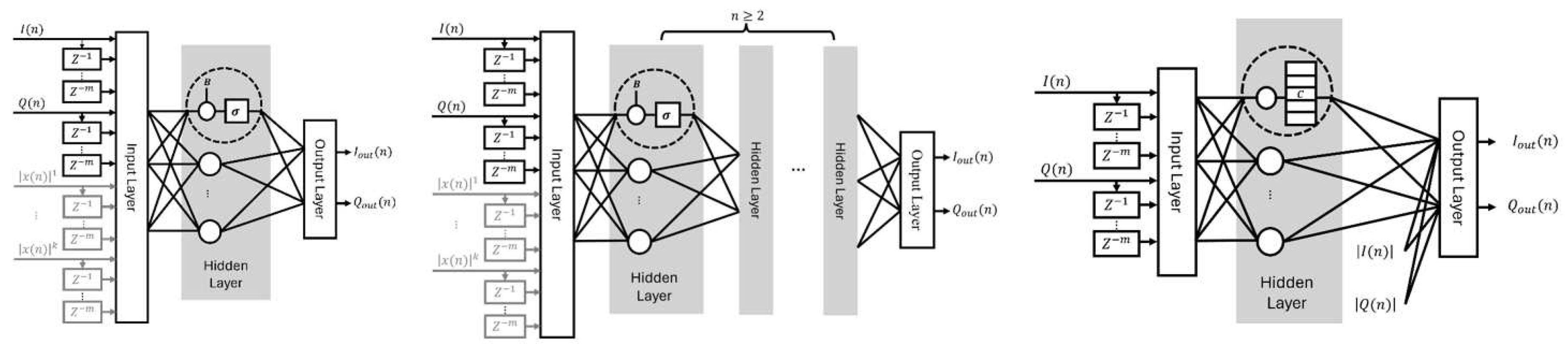
In this paper, we compare our SSCNN implementation with other network structures including RVTDNN, ARVTDNN, and DNNs that utilize fully connected layers, specifically in the context of FPGA implementation. The four different neural network structures are shown in Figure 2.

3.6. Activation Functions

3.6.1. Problems of Traditional Activation Functions

While a number of architecture optimizations for neural networks such as pruning have been the focus of studies for hardware implementations [32,33], activation functions that are used in neural networks have received far less attention. Some commonly used activation functions are nonlinear which makes FPGA implementation challenging. We list the most popular activation functions in Table 1 along with the segmented spline activation function presented here. For most nonlinear activation functions such as sigmoid or tanh, direct implementation based on their definition is inefficient as the division and exponential operations will cost a large amount of resources and increase the computational delay. Usually, a solution for a nonlinear function’s digital implementation is a piece-wise linear approximation. In [34,35], the sigmoid activation functions are broken down into linear segments with acceptable accuracy loss and are implemented using Look Up Tables (LUTs). One problem with these solutions is that using sigmoid or tanh functions to fit the nonlinear function inherently sacrifices accuracy, and using linear segments to mimic sigmoid or tanh functions will increase accuracy loss. Prior research has demonstrated that fixed activation functions based on linear segment approximation have a minimal impact on classification problems [36]. However, in the context of regression problems, accuracy is a crucial requirement. At the same time, the hardware cost in realizing these functions is still high.

3.6.2. Adaptive Activation Functions

In contrast, adaptive activation functions are a unique class of activation functions whose parameters are trainable and can adapt their shape and amplitude to the target dataset. Consequently, AAF has better learning capabilities than fixed activation functions as it improves greatly the convergence rate as well as the solution accuracy [8,9]. The segmented spline activation function1 which is an AAF proposed in a previous paper [30] is defined as:
f ( x ) = ( C [ i + 1 ] − C [ i ] ) ( ( x + 1 ) Δ − i ) + C [ i ]
where C is a trainable coefficient array that has length L, Δ = ( L − 1 ) / 2 is the inverse of the x-axis width of a spline segment, and i is the segment index which can be calculated by:
i ( x ) = f l o o r ( ( x + 1 ) Δ )
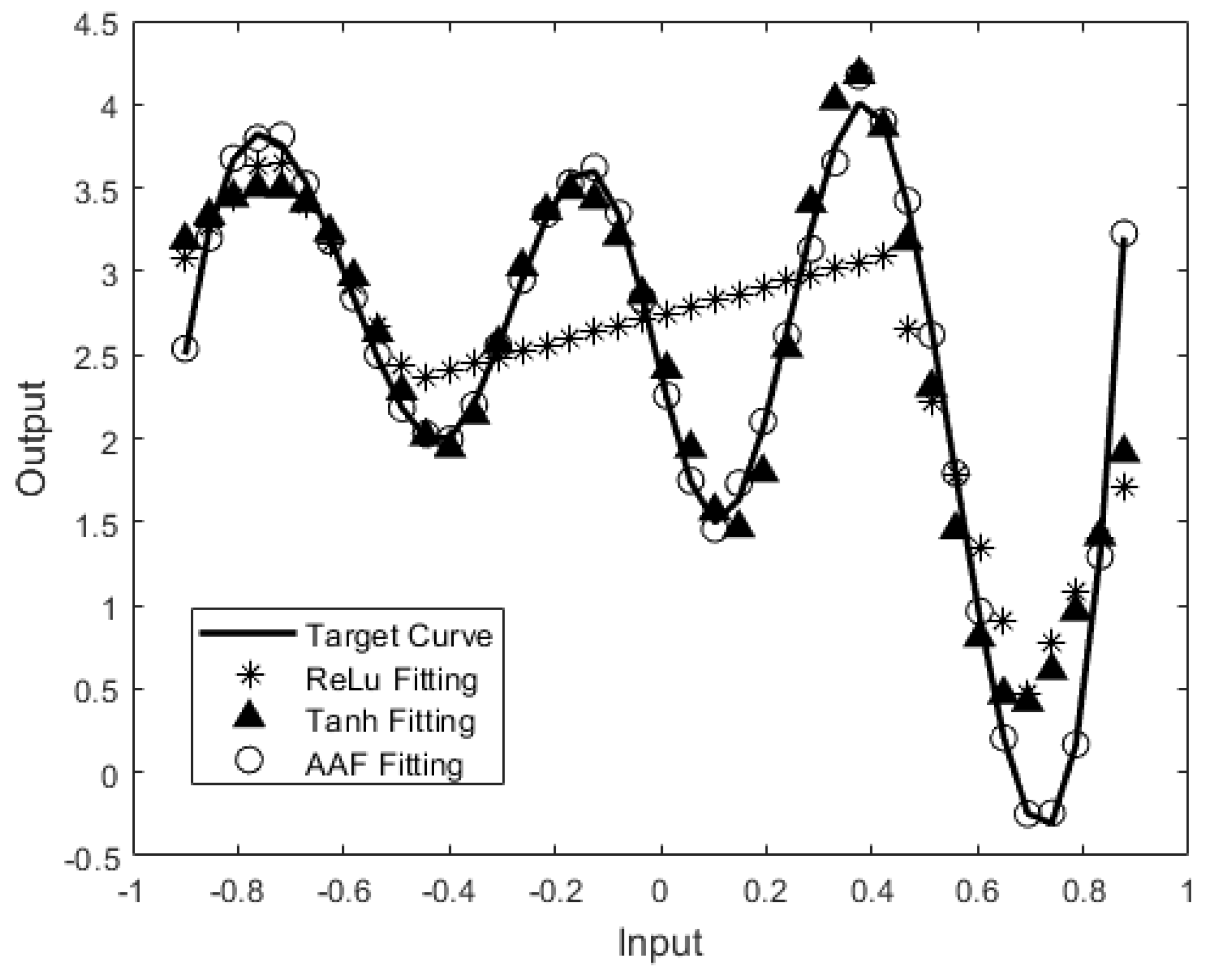
This AAF directly implements the nonlinear function required by the neural network during training so that it achieves a better accuracy compared to other activation functions. In Figure 3, we evaluated the performance of a segmented spline activation function based on 9 neurons (represented by circles) against the performance of a hyperbolic tangent activation function and ReLU activation function both based on 9 neurons (represented by triangles and stars). All were used to model a nonlinear function (represented by a black line) in double precision floating point. Under the same settings for training, the results indicate that the AAF provides the best fit to the nonlinear function compared to the other traditional activation functions. The hyperbolic tangent function (tanh) has worse accuracy at the tops and bottoms of the target curve, while ReLU does not really follow the curve. This demonstrates that an adaptive activation function can be a more efficient solution for solving regression problems. As the merits of AAF, have been laid out in relation to training the network parameters, the hardware efficiency in inference is the next step to achieving an efficient neural network on the edge.
A previous paper [30] proved the AAF-based SSCNN structure worked on DPD implemented in software and demonstrated its computational efficiency. To fully exploit the hardware efficiency of the segmented spline activation function, we designed the SSCNN hardware structures based on the previously presented mathematical algorithm and optimized it to achieve high quality DPD for a PA while minimizing the amount of hardware required.

4. Hardware Design and Implementation

While previous studies have explored various algorithmic approaches to optimize the structure of neural networks for DPD, few have actually implemented these strategies in hardware. Moreover, there is a lack of discussion of efficient implementations of the adaptive activation functions used in these networks. Given that non-linear activation functions involve complex exponential and division computations, their hardware implementation is significantly more challenging than their linear counterparts. The challenge of fitting a neural network onto an edge device often comes down to trade-offs between accuracy, performance, and hardware cost due to resource limitations. In our study, we carefully designed the SSCNN at the circuit level based on its mathematical function. We also implemented various neural network structures to evaluate their DPD performance and compared the associated hardware costs among these with the SSCNN.

4.1. SSCNN Model Analysis

Compared to the RVTDNN based structures, the SSCNN structure does not need bias terms and eliminates nonlinear calculations which save hardware resources on implementation.
The configurable segmented spline activation function defined in Eq. 1 can be achieved by the following steps:
Step 1: 
Choose the coefficient array length L;
Step 2: 
Calculate the inverse of the x-axis width of a single segment Δ = ( L − 1 ) / 2 ;
Step 3: 
Find the coefficient index i ( x ) = ⌊ ( x + 1 ) Δ ⌋ ;
Step 4: 
Access coefficients C [ i + 1 ] and C [ i ] ;
Step 5: 
Achieve the activation function f ( x ) = ( C [ i + 1 ] − C [ i ] ) ( ( x + 1 ) Δ − i ) + C [ i ] .
The resolution of the segmented spline activation function is determined by the first and second steps; it is flexible and can be adjusted during the training phase. The hardware improvements arise in the implementation of Step 3 to Step 5. The coefficient index i calculated in Step 3 falls in the range between 1 and L which is always larger than zero. Comparing the index i calculation function (Eq. 2) to the second multiplicand in Step 5, which is ( ( x + 1 ) Δ − i ) , we notice that the second multiplicand is actually the fractional part of ( x + 1 ) Δ while the index i is the integral part of it. Based on this observation, we can simply split the integer and fractional part of the output of ( x + 1 ) Δ to efficiently achieve the activation function. Another thing to note is that the multiplication between ( x + 1 ) and Δ is only a shifting operation if we choose the segment length L wisely.

4.2. SSC Layer Structure

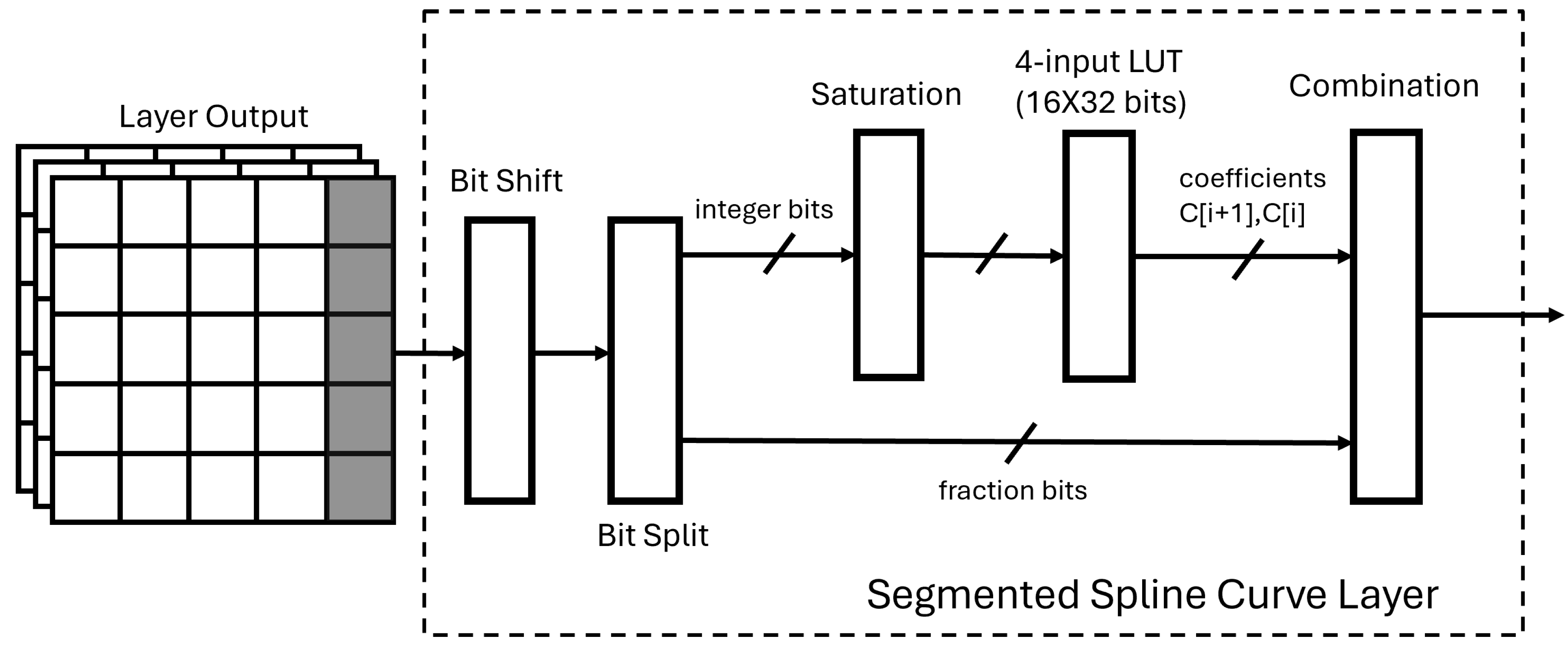
The only hidden layer of the SSCNN is the segmented spline curve (SSC) layer. Based on the mathematical analysis in the previous section, the segmented spline curve layer design can be divided into several small blocks. The block diagram of the SSC layer architecture is shown in Figure 4. The output of the previous layer is presented as the input matrix. The Bit Shift block is used to multiply the input matrix by Δ defined in Eq. 1. During the training phase, we choose the coefficient array length L to be a power of 2 plus 1 so that the Δ value will become a power of 2, and the multiplication can therefore be achieved by bit shifting. After shifting, a Bit Split block is used for parallel processing of Step 3 and Step 5 from Section 4.1. The bits of the integer part from the shifting block are used as the address for the LUT-based distributed memory which contains the 32-bit wide coefficients. As the LUT-based distributed memory size is limited by the segment length L which was decided during the training phase, the integral part of ( x + 1 ) Δ should not exceed the memory address. Thus, those integers are truncated in the saturation block to prevent memory access overflow. For example, in our case, we choose the coefficient array length L to be 9 which means the integer bits after the saturation block are 4 bits to access the memory address between 0 to 2 4 . After saturation, the trainable coefficients in the memory are read while the bits of the fraction are sent to the combination block for calculation. Finally, the combination block combines all the parts needed to achieve the spline activation function. The output of the segmented spline cure layer will be passed to the output layer of the SSCNN shown in Figure 2.

4.3. Saturation

To prevent memory access overflow, the integer part from the bit split block needs to fall into the range from 1 to L. The saturation process divides the input into three cases: Case 1, when the input is larger or equal to segment length L, it turns the output value into L − 1 ; Case 2, when the input is smaller than 1, it outputs the value 1, Case 3, when the input is between 1 and L, it outputs the original value. Meanwhile, by adding this saturation step, the design improves the hardware efficiency by saving unnecessary decoding processes for LUT-based memory access as the integer after saturation is the address for the memory. For other LUT based nonlinear activation functions, the integer part cannot directly be used to access the memory so the decoding process is necessary for those functions, and the hardware cost is consequently increased.

4.4. Systolic Processing

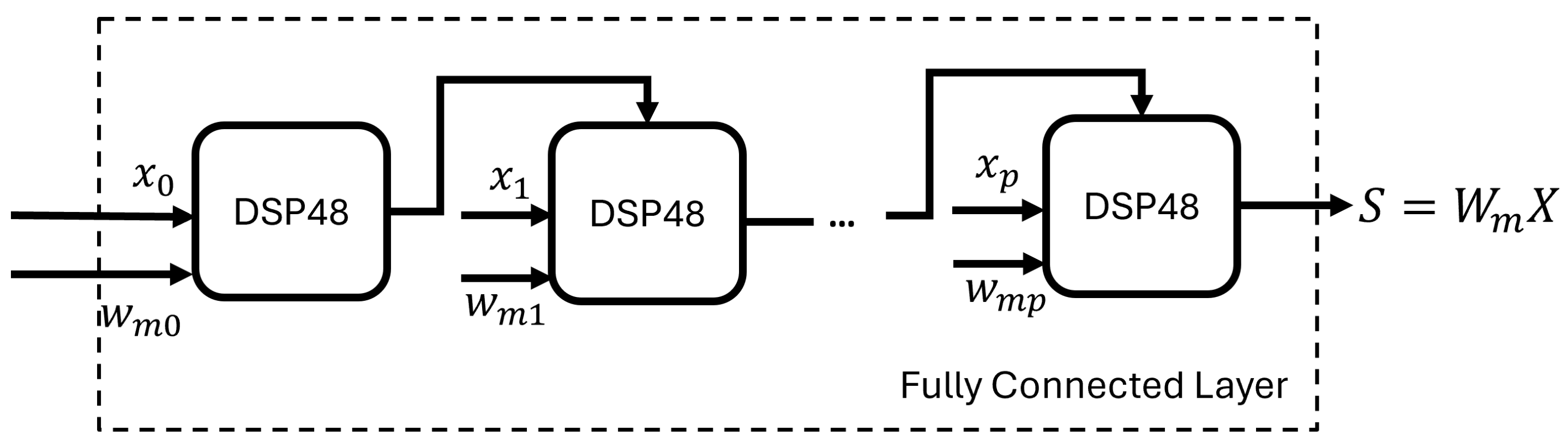
Besides the SSC layer, the other layers (input layer and output layer) only include linear operations (weighted multiplications and additions). To process data efficiently, the neuron structure in these other layers makes use of the DSP48 slices available in the FPGA fabric. Each neuron in fully connected layers needs to sum all output from the previous layer after they are multiplied by the weights. If the design processes all the multiplications in parallel and then adds the results, it will introduce idle time for the adders while increasing the delay between the multipliers and the adders. The optimal solution for this issue is to apply systolic processing for each layer. Figure 5 shows that in a layer, the inputs after are multiplied by the corresponding weights and accumulated in sequence to be fed into the activation function block efficiently.

4.5. Implementation

As mentioned earlier, a lot of fixed activation function based neural network structures have been proposed and optimized in previous research, but few AAFs have been implemented in hardware, so data concerning their implementation efficiency is lacking. In this research, we implement five different network architectures with two different activation functions in FPGA hardware: the hyperbolic tangent activation function-based RVTDNN and ARVTDNN structures, two hyperbolic tangent activation function-based fully connected deep neural networks, and the segmented spline activation function-based SSCNN structure. The purpose of these implementations is to compare different activation function based neural networks in DPD performance and in their hardware efficiency.

4.5.1. Parameters

To ensure a fair comparison, we standardized the architecture of all shallow neural networks (RVTDNN, ARVTDNN, and SSCNN) to consist of one input layer, one hidden layer, and one output layer. In contrast, the two deep neural networks feature four to five layers, comprising one input layer, one output layer, and two to three fully connected hidden layers. This approach aims to evaluate diverse neural network structures within a similar framework. Specifically, the number of neurons in the input layer matches that of the first hidden layer. In all shallow neural networks, the number of hidden layer neurons was fixed at 9. Additionally, ARVTDNN incorporated a first-order envelope term. For SSCNN, we established a segment length L equal to 9, chosen because L − 1 corresponds to a power of 2. For the deep neural networks, we configured the count of neurons in the hidden layers to be ( 9 , 4 ) and ( 9 , 4 , 4 ) for the two respective networks. Across all structural variations, the output layer consistently comprised 2 neurons. In each of the neural networks, we establish a memory depth of 2. The hyperbolic tangent activation function was applied in all hidden layers of both RVTDNN, ARVTDNN, and DNNs.
As the goal of training is to obtain an inverse PA model, in each DPD training iteration, the input of the PA will be the training target, and the output of the PA model will be fed into the next DPD training iteration. When the minimum error or a preset number of DPD training iterations is reached, the trained coefficients will be stored for DPD implementation. The whole training procedure finishes in 2 DPD training iterations. Both training and inference data contain 25600 samples collected from the experimental setup. For the inference phase, all data are presented based on 32 bit word length fixed point with 1 sign bit and 26 fraction bits. All fully connected layers in these five neural networks are implemented in the same systolic structure mentioned in Section 4.4 for fair comparison. For implementing the hyperbolic tangent activation function, 32 bit width by 300 units LUT is used.

5. Results and Discussion

5.1. Experimental Setup

We conducted a performance assessment of digital pre-distortion using five distinct neural networks (discussed in Section 3) on the AMD/Xilinx RFSoC ZCU111 FPGA board [37]. This board is equipped with the Zynq UltraScale+ RFSoC ZCU28DR device, which offers high direct RF sampling rates. It utilizes 8 12-bit ADCs with a maximum rate of 4.096 GSPS and 8 14-bit DACs with a maximum rate of 6.554 GSPS. The programmable logic fabric of the device comprises 4272 DSP slices, 930K system logic cells, and 60.5 Mb memory. In addition to the FPGA fabric, this system-on-chip (SoC) also incorporates a full Arm processing subsystem, forming a heterogeneous compute architecture. The device is equipped with 4 GB of Programmable Logic (PL) DDR4 memory and 4 GB of Processing System (PS) DDR4 memory. We connected the XM500 RFMC balun transformer add-on card to the device via its expansion connectors to establish a complete software-defined radio (SDR) chain.
The experiment testbench consists of an AMD/Xilinx RFSoC ZCU111 board with an NXP AFSC5G37D37 Doherty PA and a linear driver stage PA NXP BGA7210. The transmit signal sent from the DAC goes through the driver PA and the test PA, then goes back to the ADC through a 40dB attenuator chain as shown in Figure 6. A 40MHz bandwidth OFDM waveform, commonly used in LTE and 4G/5G standards, is transmitted at a center frequency of 3.8 GHz. The transmit signal sent from the host computer goes through the Processor System (PS) side DDR4 memory and then is stored in the external DDR4 on the Programmable Logic (PL) side. On the PL side, the DPD models with synchronization block are applied to predistort the signal and then store the preprocessed signal back in the memory. The RF front end DAC will transmit the signal by reading DDR4 memory repeatedly. After the signal passes through the power amplifiers, the PAs’ outputs will be written back to the PS and read by the host computer. The offline training for DPD is carried out with the Deep Learning Toolbox in MATLAB R2023a. DPD IPs are constructed in Simulink and then translated to Verilog using the MATLAB HDL Coder. The entire synthesis and implementation process is completed in Vivado 2020.1.

5.2. DPD Performance

In power amplifier linearization, three key performance metrics are typically used: Normalized Mean Square Error (NMSE), Adjacent Channel Power Ratio (ACPR), and Error Vector Magnitude (EVM). NMSE quantifies the in-band distortion at the PA’s output. ACPR, on the other hand, quantifies the relative power that leaks into neighboring frequency channels due to the PA’s nonlinearity, which helps evaluate the level of interference a signal from that transmitter may cause to other signals in adjacent frequency bands. Lastly, EVM is used to measure the discrepancy between the ideal and actual signal, providing an assessment of the quality of the transmitted signal.
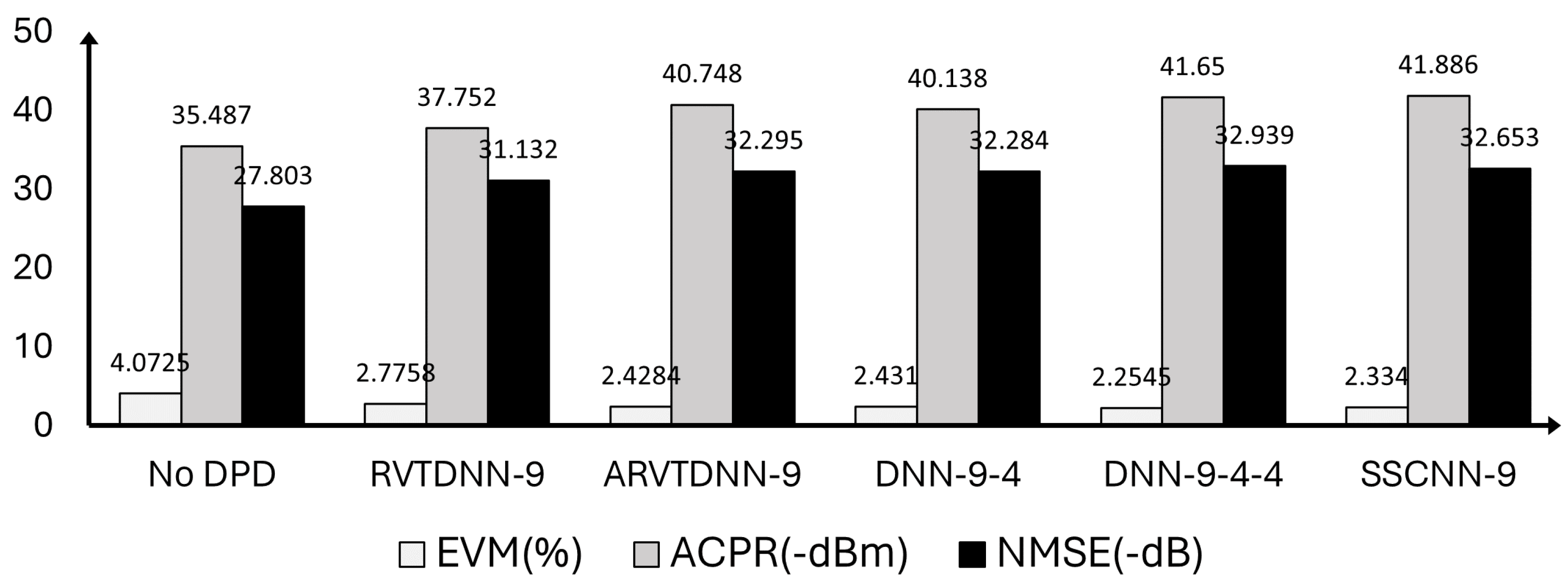
Table 2 presents the DPD performance across various neural network model structures. The number in each model name represents the number of neurons in the hidden layer(s). Among the similar architectures, RVTDNN and ARVTDNN, the latter requires more coefficients due to its inclusion of additional linear inputs. However, ARVTDNN exhibits slightly superior performance compared to RVTDNN. In comparison to ARVTDNN, the DNN provides no improvement by introducing one layer with a very small number of neurons but requires 30 more coefficients. The DNN with three hidden layers increased the performance compared to ARVTDNN at the cost of 50 extra coefficients. SSCNN, on the other hand, attains a performance level comparable to the ARVTDNN and three hidden layer DNN models while utilizing a similar number of coefficients as RVTDNN. As shown in Figure 7, compared to the PA output without DPD, RVTDNN with merely 9 hidden neurons exhibits the poorest performance, while SSCNN with an equivalent number of hidden neurons delivers the best performance. It should be noticed that for a fair comparison of hardware utilization later, these neural network models were intentionally set with similar parameters.
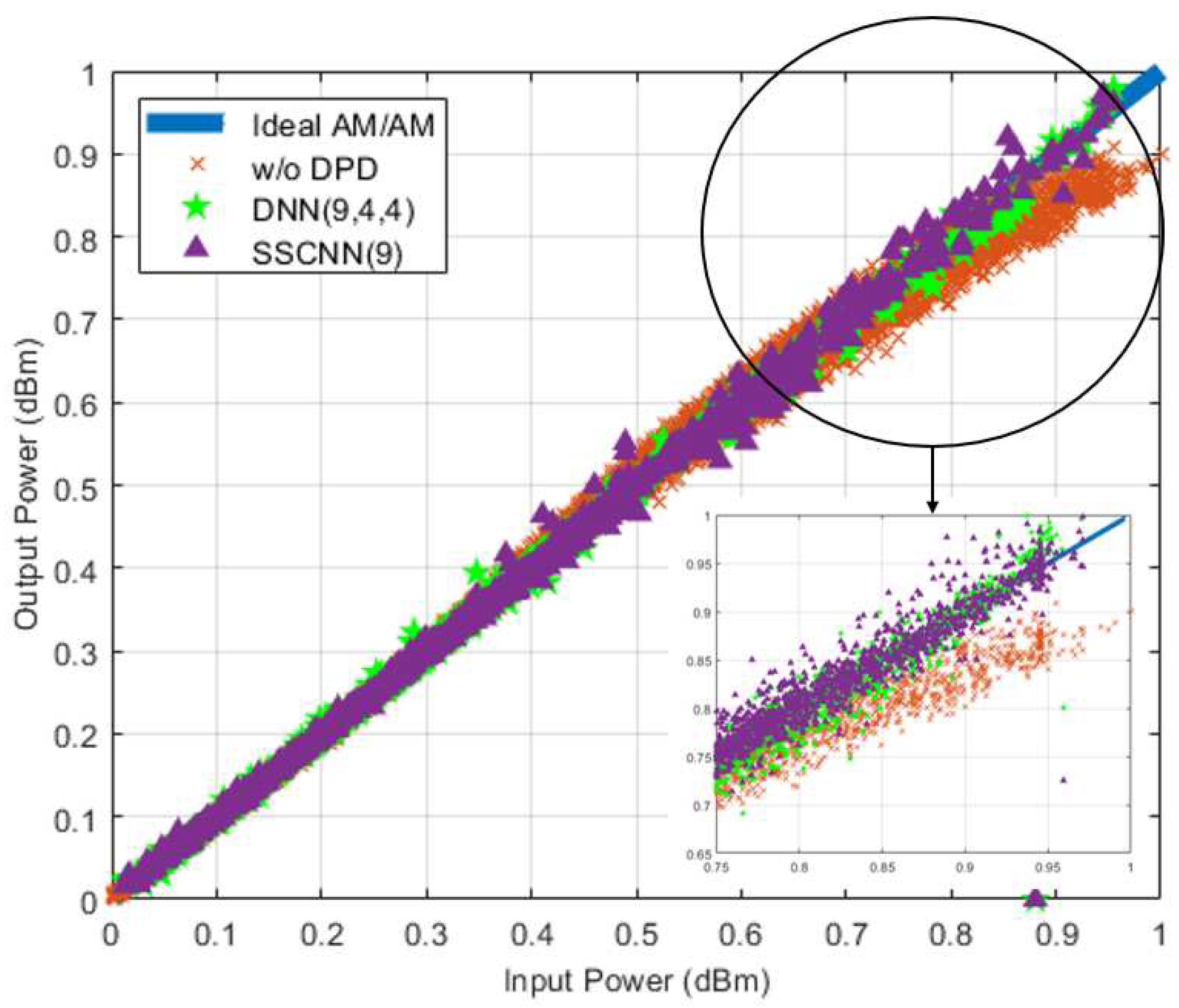
In Figure 8, we show the AM/AM curves based on SSCNN and 3-hidden layer DNN. The AM/AM curve represents how the amplitude of the output signal changes as a function of the amplitude of the input signal. The in-band linearization performance of both neural network based DPD is compared with the PA’s performance without DPD. The blue line signifies the ideal linear output of the PA, while the red “x” line depicts the actual behavior of the PA without DPD. The green star and purple triangles represent the performance of the 3-hidden layer DNN-based DPD and SSCNN-based DPD. It shows that the two neural network-based DPDs have successfully corrected the PA’s nonlinear behavior, as both the green star and purple triangles form a straight line close to the ideal output of the PA. The SSCNN performs comparable in-band linearization to 3-hidden layer DNN.
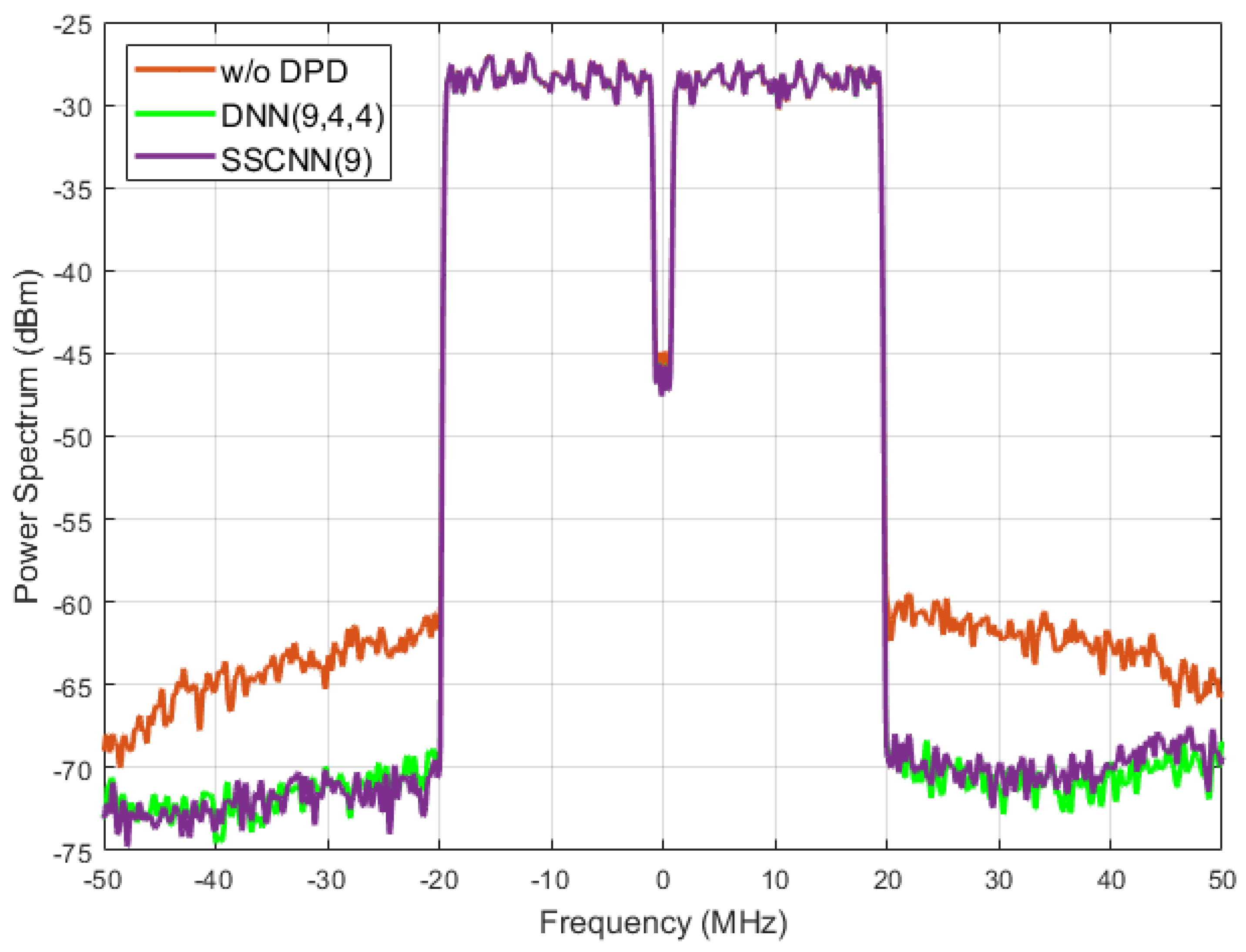
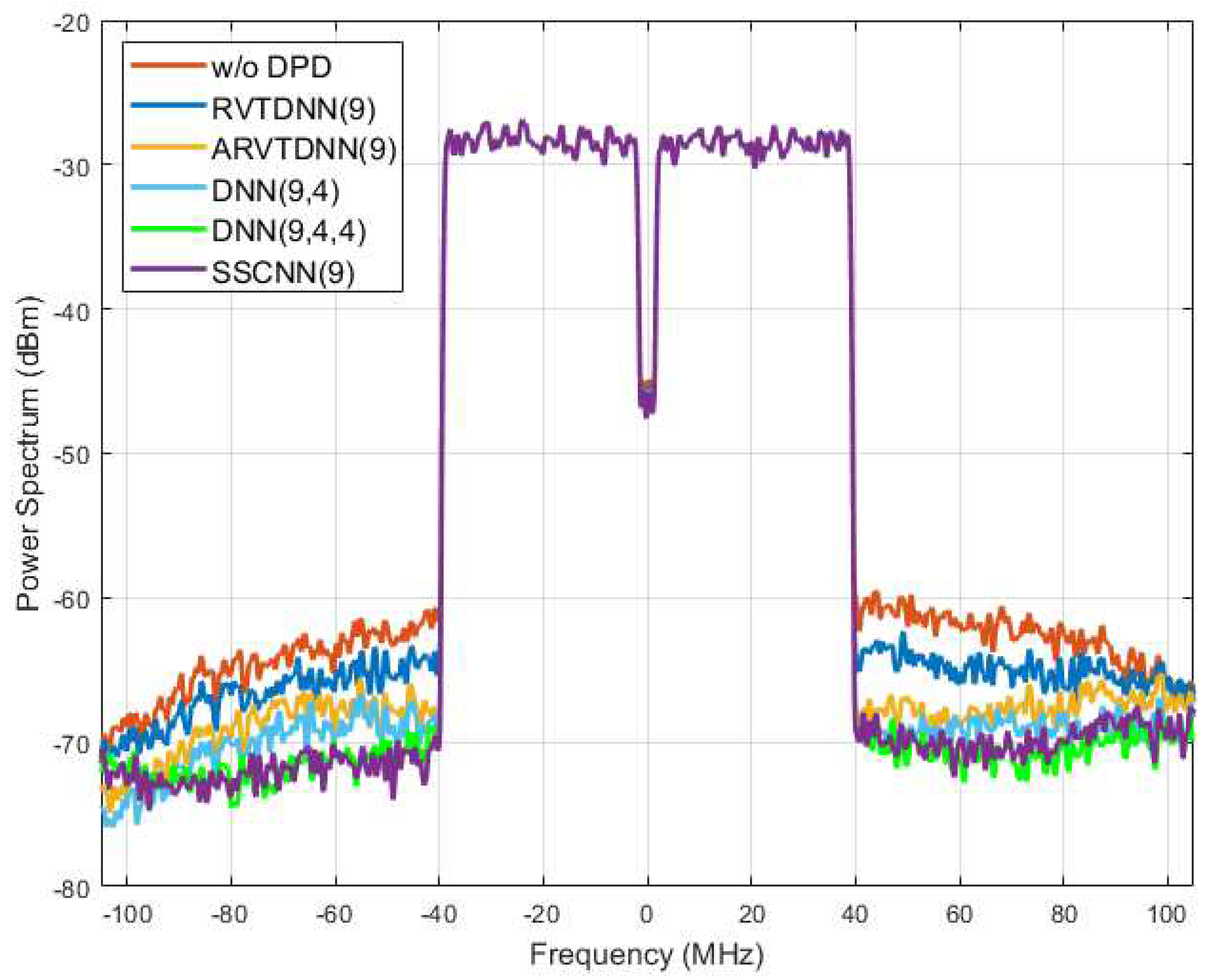
Figure 9 shows the two DPD’s out-of-band linearization performance. The power spectrum refers to the distribution of power into frequency components composing that signal. Ideally, the power should be focused on the transmitted signal’s baseband. The PA’s nonlinear performance will lead to an increase in power beyond the baseband range and leak power to a neighbor channel to cause interference. As the orange line indicates here, outside of the bandwidth of the transmitted signal, the power is above -70dBm. This line indicates the signal transmitted after the PA, without Digital DPD. The green and purple lines, showing 3-hidden layer DNN and SSCNN performances, represent that the transmitted signal’s shoulders are notably reduced compared to the transmitted signal without predistortion. This reduction signifies a decrease in the risk of the PA-transmitted signal interfering with adjacent channels when employing NN-based DPD. Once again, the SSCNN and the DNN with three hidden layers produce a similar degree of out-of-band linearization. Figure 10 presented all five models’ spectrum performance.
From an effective DPD perspective, these results show that with a fixed activation function, DNN is not always the best solution as in a similar structure, comparing DNN(9,4,4) with SSCNN(9). DNN requires the most coefficients while only offering limited performance improvements. On the other hand, comparing SSCNN(9) with DNN(9,4), shows that with an adaptive activation function, the model can significantly reduce the depth of neural networks while having great accuracy. This emphasizes the importance of developing a hardware efficient adaptive function based model for neural network implementation on edge devices.

5.3. Resource Utilization

Table 3 shows resource utilization for the different DPD models explored in this paper. The first thing to note is that the deep neural network requires the most hardware resources. Combined with its performance (see Table 2), we find that DNN has limited efficiency for DPD implementation on edge devices not only because of its expensive computational cost but also because of its slow speed. The delay that caused the slow speed is not only from increased layer numbers but also from the latency to access the coefficients stored in BRAM for nonlinear activation functions. On the other hand, SSCNN has a similar number of coefficients as RVTDNN but the best performance as shown in Table 2, while using similar hardware resources needed for RVTDNN. Compared to RVTDNN’s cost, SSCNN doesn’t require any BRAMs. This is due to the fact that we replaced complicated nonlinear activation functions with an optimized adaptive activation function which significantly reduces memory cost. Specifically, SSCNN(9) uses 32% less slice LUTs, 42% less FFs, 100% less BRAMs and 41% less DSPs compared to DNN(9,4,4). Meanwhile, by eliminating the latency to access the BRAM and using optimized systolic processing, the speed of SSCNN has been increased by 117% compared to DNN models. RVTDNN costs less resources than ARVTDNN but scarifies the accuracy. ARVTDNN which obtains the second-best performance among shallow neural networks, has comparable performance to DNN while still costing less than DNN. Among all the different models, SSCNN provides the most efficient hardware solution as it has the fastest speed, and the least hardware cost while reaching a similar level of DPD performance compared to DNN models.

6. Conclusions and Future Work

Applying neural networks on the edge where they can be used to directly process transmitted and received signals is a growing area in FPGA implementations for wireless communications. Efficient neural networks that are hardware friendly can achieve both high performance and low hardware usage, freeing the FPGA to implement other functions. Digital predistortion is a critical technique to remove nonlinear distortion from wireless signals. FPGAs offer an ideal platform to implement the predistorter in these real-time communication systems. Deep Neural Network based predistorters have been proposed; however, they typically require large amounts of hardware resources to be realized. In this work, an implementation of an adaptive activation function based shallow neural network with a very small footprint in FPGA fabric compared to other fixed activation function based approaches has been detailed. The final implementation demonstrates the substantial reduction of resources required for the SSCNN compared to previous techniques as well as the comparable performance from a communications perspective. This reduction in required hardware means more programmable logic resources are available for additional functions such as signal interpolation, filtering, error correction, modulation, and encoding, such as non-orthogonal multiple access (NOMA) for 6G. In future research, we plan to build an online NN-based DPD system that includes both training and inference on the edge. As compared with 5G, 6G is expected to provide ten times lower latency which requires a faster and more adaptive DPD real-time system for more complicated dynamic scenarios.

Acknowledgments

This work was supported in part by MathWorks. This publication has emanated from research conducted with the financial support of Science Foundation Ireland under grant numbers 18/CRT/6222 and 13/RC/2077_P2.

References

  1. Boumaiza, S.; Mkadem, F. Wideband RF power amplifier predistortion using real-valued time-delay neural networks. 2009 European Microwave Conference (EuMC). IEEE, 2009, pp. 1449–1452.
  2. Zhang, Y.; Li, Y.; Liu, F.; Zhu, A. Vector decomposition based time-delay neural network behavioral model for digital predistortion of RF power amplifiers. IEEE Access 2019, 7, 91559–91568. [Google Scholar] [CrossRef]
  3. Li, H.; Zhang, Y.; Li, G.; Liu, F. Vector decomposed long short-term memory model for behavioral modeling and digital predistortion for wideband RF power amplifiers. IEEE Access 2020, 8, 63780–63789. [Google Scholar] [CrossRef]
  4. Hongyo, R.; Egashira, Y.; Hone, T.M.; Yamaguchi, K. Deep neural network-based digital predistorter for Doherty power amplifiers. IEEE Microwave and Wireless Components Letters 2019, 29, 146–148. [Google Scholar] [CrossRef]
  5. Jung, S.; Kim, Y.; Woo, Y.; Lee, C. A two-step approach for DLA-based digital predistortion using an integrated neural network. Signal Processing 2020, 177, 107736. [Google Scholar] [CrossRef]
  6. Liu, Z.; Hu, X.; Xu, L.; Wang, W.; Ghannouchi, F.M. Low computational complexity digital predistortion based on convolutional neural network for wideband power amplifiers. IEEE Transactions on Circuits and Systems II: Express Briefs 2021, 69, 1702–1706. [Google Scholar] [CrossRef]
  7. Liu, Z.; Dou, Y.; Jiang, J.; Wang, Q.; Chow, P. An FPGA-based processor for training convolutional neural networks. 2017 International Conference on Field Programmable Technology (ICFPT). IEEE, 2017, pp. 207–210.
  8. Jagtap, A.D.; Kawaguchi, K.; Karniadakis, G.E. Adaptive activation functions accelerate convergence in deep and physics-informed neural networks. Journal of Computational Physics 2020, 404, 109136. [Google Scholar] [CrossRef]
  9. Lau, M.M.; Lim, K.H. Review of adaptive activation function in deep neural network. 2018 IEEE-EMBS Conference on Biomedical Engineering and Sciences (IECBES). IEEE, 2018, pp. 686–690.
  10. Jagtap, A.D.; Shin, Y.; Kawaguchi, K.; Karniadakis, G.E. Deep Kronecker neural networks: A general framework for neural networks with adaptive activation functions. Neurocomputing 2022, 468, 165–180. [Google Scholar] [CrossRef]
  11. Qian, S.; Liu, H.; Liu, C.; Wu, S.; San Wong, H. Adaptive activation functions in convolutional neural networks. Neurocomputing 2018, 272, 204–212. [Google Scholar] [CrossRef]
  12. Özbay, Y.; Tezel, G. A new method for classification of ECG arrhythmias using neural network with adaptive activation function. Digital Signal Processing 2010, 20, 1040–1049. [Google Scholar] [CrossRef]
  13. Abdelsalam, A.M.; Langlois, J.P.; Cheriet, F. A configurable FPGA implementation of the tanh function using DCT interpolation. 2017 IEEE 25th annual international symposium on field-programmable custom computing machines (FCCM). IEEE, 2017, pp. 168–171.
  14. Si, J.; Harris, S.L.; Yfantis, E.; others. Neural networks on an FPGA and hardware-friendly activation functions. Journal of Computer and Communications 2020, 8, 251. [Google Scholar] [CrossRef]
  15. Ngah, S.; Bakar, R.A.; Embong, A.; Razali, S.; others. Two-steps implementation of sigmoid function for artificial neural network in field programmable gate array. ARPN J. Eng. Appl. Sci 2016, 7, 4882–4888. [Google Scholar]
  16. Gao, Y.; Luan, F.; Pan, J.; Li, X.; He, Y. Fpga-based implementation of stochastic configuration networks for regression prediction. Sensors 2020, 20, 4191. [Google Scholar] [CrossRef]
  17. Xie, Y.; Raj, A.N.J.; Hu, Z.; Huang, S.; Fan, Z.; Joler, M. A twofold lookup table architecture for efficient approximation of activation functions. IEEE Transactions on Very Large Scale Integration (VLSI) Systems 2020, 28, 2540–2550. [Google Scholar] [CrossRef]
  18. Al-Rikabi, H.M.; Al-Ja’afari, M.A.; Ali, A.H.; Abdulwahed, S.H. Generic model implementation of deep neural network activation functions using GWO-optimized SCPWL model on FPGA. Microprocessors and Microsystems 2020, 77, 103141. [Google Scholar] [CrossRef]
  19. Pasca, B.; Langhammer, M. Activation function architectures for FPGAs. 2018 28th International Conference on Field Programmable Logic and Applications (FPL). IEEE, 2018, pp. 43–437.
  20. Liu, S.; Fan, H.; Luk, W. Accelerating fully spectral CNNs with adaptive activation functions on FPGA. 2021 Design, Automation & Test in Europe Conference & Exhibition (DATE). IEEE, 2021, pp. 1530–1535.
  21. AMD. Xilinx RFSoC DFE. https://www.xilinx.com/products/silicon-devices/soc/rfsoc/zynq-ultrascale-plus-rfsoc-dfe.html.
  22. Morgan, D.; Ma, Z.; Kim, J.; Zierdt, M.; Pastalan, J. A Generalized Memory Polynomial Model for Digital Predistortion of RF Power Amplifiers. IEEE Trans. on Signal Process 2006, 54, 3852–3860. [Google Scholar] [CrossRef]
  23. Vaicaitis, A.; Hu, A.; Dooley, J. Direct Input-to-Output Neural Network for Efficient Digital Predistortion of MIMO Transmitters. 2021 51tst European Microwave Conference, EuMC 2021 2021.
  24. Jiang, Y.; Vaicaitis, A.; Leeser, M.; Dooley, J. Neural Network on the Edge: Efficient and Low Cost FPGA Implementation of Digital Predistortion in MIMO Systems. 2023 Design, Automation & Test in Europe Conference & Exhibition (DATE). IEEE, 2023, pp. 1–2.
  25. Braithwaite, R.N. A comparison of indirect learning and closed loop estimators used in digital predistortion of power amplifiers. 2015 IEEE MTT-S International Microwave Symposium. IEEE, 2015, pp. 1–4.
  26. Hesami, S.; Dooley, J.; Farrell, R. ; others. Digital predistorter in crosstalk compensation of MIMO transmitters. 2016 27th Irish Signals and Systems Conference (ISSC). IEEE, 2016, pp. 1–5.
  27. Abi Hussein, M.; Bohara, V.A.; Venard, O. On the system level convergence of ILA and DLA for digital predistortion. 2012 International Symposium on Wireless Communication Systems (ISWCS). IEEE, 2012, pp. 870–874.
  28. Liu, T.; Boumaiza, S.; Ghannouchi, F.M. Dynamic behavioral modeling of 3G power amplifiers using real-valued time-delay neural networks. IEEE Transactions on Microwave Theory and Techniques 2004, 52, 1025–1033. [Google Scholar] [CrossRef]
  29. Wang, D.; Aziz, M.; Helaoui, M.; Ghannouchi, F.M. Augmented real-valued time-delay neural network for compensation of distortions and impairments in wireless transmitters. IEEE Transactions on Neural Networks and Learning Systems 2018, 30, 242–254. [Google Scholar] [CrossRef] [PubMed]
  30. Vaicaitis, A.; Dooley, J. Segmented Spline Curve Neural Network for Low Latency Digital Predistortion of RF Power Amplifiers. IEEE Transactions on Microwave Theory and Techniques 2022, 70, 4910–4915. [Google Scholar] [CrossRef]
  31. Fawzy, A.; Sun, S.; Lim, T.J.; Guo, Y.X. An Efficient Deep Neural Network Structure for RF Power Amplifier Linearization. 2021 IEEE Global Communications Conference (GLOBECOM). IEEE, 2021, pp. 1–6.
  32. Blott, M.; Preußer, T.B.; Fraser, N.J.; Gambardella, G.; O’brien, K.; Umuroglu, Y.; Leeser, M.; Vissers, K. FINN-R: An end-to-end deep-learning framework for fast exploration of quantized neural networks. ACM Transactions on Reconfigurable Technology and Systems (TRETS) 2018, 11, 1–23. [Google Scholar] [CrossRef]
  33. Sun, M.; Zhao, P.; Gungor, M.; Pedram, M.; Leeser, M.; Lin, X. 3D CNN acceleration on FPGA using hardware-aware pruning. 2020 57th ACM/IEEE Design Automation Conference (DAC). IEEE, 2020, pp. 1–6.
  34. Zhang, M.; Vassiliadis, S.; Delgado-Frias, J.G. Sigmoid generators for neural computing using piecewise approximations. IEEE transactions on Computers 1996, 45, 1045–1049. [Google Scholar] [CrossRef]
  35. Tatas, K.; Gemenaris, M. High-Performance and Low-Cost Approximation of ANN Sigmoid Activation Functions on FPGAs. 2023 12th International Conference on Modern Circuits and Systems Technologies (MOCAST). IEEE, 2023, pp. 1–4.
  36. Decherchi, S.; Gastaldo, P.; Leoncini, A.; Zunino, R. Efficient digital implementation of extreme learning machines for classification. IEEE Transactions on Circuits and Systems II: Express Briefs 2012, 59, 496–500. [Google Scholar] [CrossRef]
  37. Xilinx. ZCU111 Evaluation Board User Guide, 2023. UG1271 (v1.4).
1
Segmented spline is also the term used in image processing which is not related to the activation function.
Preprints 96786 g001
Figure 1. NN-based Indirect Learning Architecture
Figure 1. NN-based Indirect Learning Architecture
Preprints 96786 g001
Preprints 96786 g002
Figure 2. Different Neural Networks: (left)(A)RVTDNN (grey), (middle) DNN, (right) SSCNN
Figure 2. Different Neural Networks: (left)(A)RVTDNN (grey), (middle) DNN, (right) SSCNN
Preprints 96786 g002
Preprints 96786 g003
Figure 3. Segmented Spline Activation Function vs. Hyperbolic Tangent Activation Function vs. ReLU Activation Function Performance to Mimic a Nonlinear Line
Figure 3. Segmented Spline Activation Function vs. Hyperbolic Tangent Activation Function vs. ReLU Activation Function Performance to Mimic a Nonlinear Line
Preprints 96786 g003
Preprints 96786 g004
Figure 4. Segmented Spline Curve Layer Structure
Figure 4. Segmented Spline Curve Layer Structure
Preprints 96786 g004
Preprints 96786 g005
Figure 5. Systolic Processing for Fully Connected Layer. x p is the input vector of the layer, w m p is the weight vector, and the output of each DSP48 slice is one of the addends for next slice.
Figure 5. Systolic Processing for Fully Connected Layer. x p is the input vector of the layer, w m p is the weight vector, and the output of each DSP48 slice is one of the addends for next slice.
Preprints 96786 g005
Preprints 96786 g006
Figure 6. Experimental Setup (AMD/Xilinx RFSoC ZCU111 board, XM500 RFMC balun board, NXP AFSC5G37D37 Doherty PA (test PA), PA NXP BGA7210 (driver PA), a 40dB attenuator chain)
Figure 6. Experimental Setup (AMD/Xilinx RFSoC ZCU111 board, XM500 RFMC balun board, NXP AFSC5G37D37 Doherty PA (test PA), PA NXP BGA7210 (driver PA), a 40dB attenuator chain)
Preprints 96786 g006
Preprints 96786 g007
Figure 7. Different Neural Network based DPD Results. Comparing five neural network based DPDs in terms of performance with regards to EVM (white), ACPR (grey) and NMSE (black).
Figure 7. Different Neural Network based DPD Results. Comparing five neural network based DPDs in terms of performance with regards to EVM (white), ACPR (grey) and NMSE (black).
Preprints 96786 g007
Preprints 96786 g008
Figure 8. AM/AM Curve. 2-hidden layer based DNNs vs. SSCNN in-band performance. Zooing into the nonlinear range shows the PA’s performance after DNN(9,4,4) (green star) and SSCNN(9) (purple triangle) are close to the ideal PA’s AM/AM curve (blue line) compared to the PA’s performance w/o DPD (orange cross).
Figure 8. AM/AM Curve. 2-hidden layer based DNNs vs. SSCNN in-band performance. Zooing into the nonlinear range shows the PA’s performance after DNN(9,4,4) (green star) and SSCNN(9) (purple triangle) are close to the ideal PA’s AM/AM curve (blue line) compared to the PA’s performance w/o DPD (orange cross).
Preprints 96786 g008
Preprints 96786 g009
Figure 9. Spectrum Performance Improvement. At least 8dBm power drop between the original PA output (orange line) and the two neural network based DPD outputs (green and purple lines).
Figure 9. Spectrum Performance Improvement. At least 8dBm power drop between the original PA output (orange line) and the two neural network based DPD outputs (green and purple lines).
Preprints 96786 g009
Preprints 96786 g010
Figure 10. Spectrum Performance of Five Neural Networks.RVTDNN(9) reduces only 4dBm while both DNN(9,4,4) and SSCNN(9) reduce at least 8 dBm.
Figure 10. Spectrum Performance of Five Neural Networks.RVTDNN(9) reduces only 4dBm while both DNN(9,4,4) and SSCNN(9) reduce at least 8 dBm.
Preprints 96786 g010
Table 1. Commonly Used Activation Functions and Segmented Spline Activation Function
Table 1. Commonly Used Activation Functions and Segmented Spline Activation Function
Activation Function Definition
ReLu f ( x ) = m a x ( 0 , x )
Sigmoid f ( x ) = 1 1 + e − x
Hyperbolic Tangent f ( x ) = e x − e − x e x + e − x
Segmented Spline f ( x ) = ( C [ i + 1 ] − C [ i ] ) ( ( x + 1 ) Δ − i ) + C [ i ]
Table 2. Linearity Performance for Different Neural Networks
Table 2. Linearity Performance for Different Neural Networks
Model # Coefficients EVM(%) ACPR(dBm) NMSE(dB)
No DPD - 4.0725 -35.487 -27.803
RVTDNN(9) 83 2.7758 -37.752 -31.132
ARVTDNN(9) 110 2.4284 -40.748 -32.295
DNN(9,4) 140 2.4310 -40.138 -32.284
DNN(9,4,4) 160 2.2545 -41.650 -32.939
SSCNN(9) 85 2.3340 -41.886 -32.653
Table 3. Resource Utilization for Different Neural Networks
Table 3. Resource Utilization for Different Neural Networks
Model Slice LUTs FFs BRAMs DSPs Clock
Speed(MHz)
RVTDNN(9) 6123 (1.44%) 7880 (0.93%) 4.5 (0.42%) 90 (2.11%) 118.73
ARVTDNN(9) 7289 (1.71%) 10935 (1.29%) 4.5 (0.42%) 117 (2.74%) 116.71
DNN(9,4) 9355 (2.2%) 12425 (1.46%) 6 (0.56%) 152 (3.56%) 102.25
DNN(9,4,4) 12080 (2.84%) 14072 (1.65%) 8 (0.74%) 184 (4.31%) 100.68
SSCNN(9) 8258 (1.94%) 8084 (0.95%) 0 (0%) 108 (2.53%) 221.12
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated