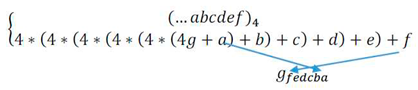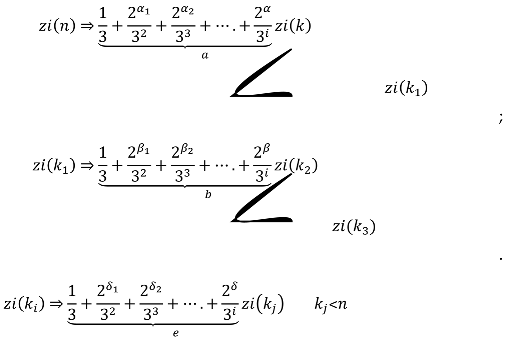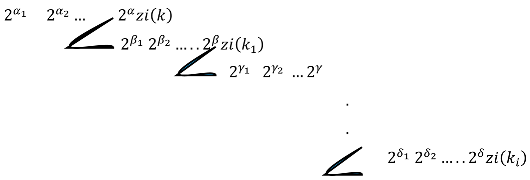Introduction
Choose a natural number. If the current number is
even, divide it by 2, and if it is odd, multiply it by three and add one. The
Collatz conjecture says when you proceed with these two rules again and again,
you reach 1; no matter which positive number has been chosen to start the
sequence. It is named after the mathematician Lothar Collatz, who introduced
the idea in 1937, two years after receiving his doctorate [1].J.Lagarias provided a useful survey of the
subject[2]. collatz conjecture is a very
famous problem in mathematics, and has not yet been completely solved. This
conjecture is also known as Kakutani`s problem, the 3x+1 problem, the Ulam
conjecture, the Thwaites conjecture, Hasse’s algorithm, and the Syracuse
problem [3][4]. The Collatz conjecture has
been checked up to 268 for all positive numbers by 2020 [5]. The nearest proof of conjecture has been posted
by Dr. Terence Tao who shows that conjecture is “almost” true for “almost “all
numbers [6]. This paper presents a simple,
complete elementary proof for collatz conjecture. I use a new method and some
new symbols in this article which will be explained later. This proof is based
on a diagram that is the result of two rules and will be present in second
part.
1.
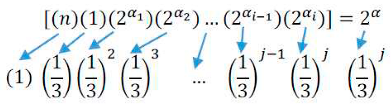
1.1. Definition of base ⅓
We say that a natural number is converted into
when there are powers of 2, so that the following
relationship exists between n and them:
The base is
and its digits are powers of 2.Here, we actually
express n to powers of 2 and 3. Same as above, we say that n is converted into
if there are powers of 2 and 3, so that we have:
And so on. Here, is the base, and the digits are the product of
powers of 2 and 3.We have similar definitions for other bases. For , the digits are the product of powers of primes
smaller than n.
1.2.
different ways of writing n when it is converted into.
When n is converted into base . We show it in 3 ways:
1.2.b.
As
a pyramid fraction:
such as pyramid fraction in the beginning of this article.
1.2.c.As a finite
series, we called
or
.
We can continue
:
When we continue
after some terms, each term becomes a quadruple the previous term. These terms of
are called calm terms or calm zone.The first terms of
that aren’t regular are called hailstone terms or hailstone zone of
.For example:
1.3.
The series has been written according to the collatz sequence called
.
But With a few algebraic changes in ,so that numerators of terms remain powers of 2 we can obtain different for a natural number.
We can write or as an equation between powers of 2, 3, and n :
For zi(n) if:
Then: .4
1.4.a. definition of
The set of powers of 2 that are numerators of terms in
, is called numbers of
, and we indicate it with
For example:
1.4.b. Definition ofThe set of powers of 2 obtain from dividing each numerator of any term by the numerator of the previous term is called jump numbers of
, and we show them with
,
In the calm zone, all of jump numbers are 4. contains 20 and the negative powers of 2, but only has positive powers of 2,and the smallest jump number in is 2.
Here is the difference between
:
Therefore:
2. Rule 1(algebraic rule):
Reducing zi(n) to zi(k) so that k<n using algebraic rule of obtaining zi(n) from Initial terms of are important for obtaining from them . In some numbers, with a few algebraic changes, we can obtain zi(m) from .
In some numbers that we couldn’t obtain from directly, we need to continue n according to collatz sequence to reach a right number such as m with suitable initial terms in so that we can obtain from it; however, for reducing n last terms of after initial terms must end with a smaller number than n.
In general, there is a path for each n to reducing zi(n). This path contains
For reducing n, we have to choose the correct path so that the last line of the path after the initial terms ends with a number smaller than n, and the initial terms of each line during the path have to be suitable for obtaining zi(m) from of that line.
In general, with basic algebraic rules for these series, we can obtain zi(n) from or or, or even sometimes from which depends on n. From all the basic algebraic rules of such series, we only use obtaining zi(n) from in the Zi3-diagram and consider it as Rule Number 1.
3. Rule 2(arithmetic rule)
Every natural number can be converted into base-4, and we write it as;
In other form: Rule number 2 (arithmetic rule) says that the more two numbers are similar in base-4, The more they have similar first terms in their co(n), and this is provable by the rules of divisibility easily.
Lemma 1. if:
Then:
Proof: Suppose
we can write:
Proof of rule 2:
When we have two different numbers that are similar in base 4, such as and that are common in some digits according to lemma 1, we see that they have similar digits in base 4 even when they are converted to 3n+1. Divisibility by 2 for the last terms in 3n+1 in two numbers is same, and initial sentences have enough 4 for divisibility by 2. This makes similar initial terms in co(n) for two numbers.
For example:
They are common in six terms in their co(n). We can consider these two numbers as members of this branch:
For convenience in writing, we indicate this branch as .
In general, for these numbers:
We show with g(4) or g, and their common part as index of g.
indicate a set of numbers (not a specific number), that produce with replacing g with {0,1, 2, …}.
4. the zi3-diagram and Description of zi3-diagram
we have described two rules:
In the zi3-diagram, according to rule 2, we categorize natural numbers into different branches by the modularity of 4. The more we proceed with branching, the more numbers in branches become similar to their own co(n), so we continue to reach suitable branches whose numbers have enough common terms in their co(n), and then, with the help of rule 1, we reduce zi(n) to zi(k) so that k˂n in each branch. In other words, we continue categorize numbers according to the modularity 4 until we reach the branches whose numbers have the same path to reducing zi of them to zi of a smaller number. The path includes horizontal and vertical movements, and the path for each branch in this diagram isn’t unique. Number of branches in this diagram is finite. We use this diagram to prove zi-existence theorem or theorem A and also collatz conjecture. This diagram will be presented in second part of article.
When we categorize numbers according to the modularity of four numbers that have the same path placed in the same branch, we can find a path for each branch to reduce zi(n)’s.
However, you can make the zi-diagram shorter if you accept 0 and 1 in numerators of zi(n) and accept all algebraic rules of such series as Rule Number 1.
Here is the first page of branching numbers at the beginning of the zi-diagram in two forms below. For convenience, I will use the second form in the second part of the article. After that, it will be continued to reach the branches that have a suitable path for reducing zi(n) to zi(k) provided that k˂n. The branches are finite in this tree-diagram.
In some branches, when we continue n according to collatz sequence, we reach k, where k˂n. for example g1, g3300, g3302, g32101211, ….
In some branches, we can obtain zi(n) from zi() directly, such as: g3321,g3323,g3301,….
But in some branches, we need to choose a complicated path, include horizontal and vertical movements to reach the right number such as k, so that has two conditions:
a. We should be able to obtain zi() from with algebraic changes in the initial terms of .
b. after these initial terms reaches a number smaller than n.
Furthermore, we must be able to obtain zi(
) from
by a few algebraic changes in initial terms of
during the path in any line. In general, we have such path:
We can indicate this path according to jump numbers:
The story of branch g33…3 is different, which I will explain in second part of the article. The second part of the article contains zi3-diagram. In the zi-diagram, we will show the path of every branch and the numbers in any branch will be reduced to a smaller number.
5. Theorem(A)
Zi3-existence-theorem, which is a weak form of collatz theorem:
There is zi(n) for every natural number; in other words, all natural numbers can be converted into .
Proof:
In the zi3-diagram, we have categorized numbers into different branches according to modularity of 4, and we continue branching until we reach branches whose numbers are enough similar in base-4, then we have reduced zi(n) to zi(k) by a path so that k˂n in each branch. With the zi3-diagram, we can obtain zi(n) for every n. First, we should determine n belongs to which branch of diagram, and in that branch, we reduce zi(n) to zi (k) so that k ˂n. Now k belongs to another branch in the zi3-diagram, and we can reduce k to a smaller number. By continuing this process again and again, we reach 1, and we find zi(n) for all the natural numbers. This proves theorem A.
6. Converting ziʼs of n to each other
According to the theorem (A), for every n, we have:
We close zi(n), in the second term:
We can obtain
) from the zi-diagram. In this series, with desire r, we change the second term and consequently other terms aftermath, and we have a different zi for n. Here we choose and close the second term in the original zi. We can close the other terms and obtain a different zi of n. In general, for term i:
In fact, with different r, the path of zi(n) changes, and we can obtain different zi for n.
7. Collatz theorem proof
In the zi-diagram for every n we have:
With equation (v), we can write every zi of n [especially co(n)], such as:
That zi(q)𝛜 zi-diagram.
Actually, you can use the branches in the zi-diagram as elements to make any zi, even co(n), from them.
According to theorem A, we know
, therefore:
If co(n) don’t end with co(1) then there is a zi(m) in the zi-diagram don’t end with 1 and theorem(A) must be false.
8. Conclusion
In this paper, we proved collatz conjecture only with two simple rules. We actually used a relationship between co(n) and modularity of 4.
With two rules, we make the zi3-diagram that it shows all natural numbers can be converted into . In part 2, we will represent the zi3-diagram. This led to a proof of collatz conjecture.
This method can be used for:
other bases such as: 1/5 ,1/7, ….
other forms of collatz problem’s generalizations. We can even, arrange a similar diagram for negative integer.
You can write the zi5-diagram which could be easier than zi3-diagram, or the zi-diagrams for other bases: zi7, zi11, ….
But writing the zin-diagram is time-consuming.
Acknowledgements
I dedicate my research to my parents. I would like to thank my nephew Mehrdad Ghassabi, who introduced me to this problem several years ago. I am also very grateful to Dr. Mehdi Nasri, the Research Deputy of Azad University of Khomeinishahr, who helped me to publish this article.
References
- O’connor.J.J. ;Robertson,E.F.(2006).”Lothar Collatz”.St Andrews University School of Mathematics and Statistics,Scotland.
- Lagarias,Jeffrey C. (1985). “The 3x+1 problem and its generalizations”. The American Mathematical Monthly. 92 (1): 323. [CrossRef]
- Maddux,Cleborne D.Johnson,D.Lamont(1997).Logo:A Retrospective.New York:Haworth Press.P.160.ISBN 0-7890-0374-0.
- According to Lagarias(1985),p.4,the name “Syracuse problem” was proposed by Hasse in the 1950s,during a visit to Syracuse University.
- Barina, David (2020).” Convergence verification of the Collatz problem.” The Jornal of Supercomputing. 77 (3): 26812688. [CrossRef]
- Terence Tao. Almost all orbits of the collatz map attain almost bounded values. 2019. URL https://arxiv.org/pdf/1909.03562.pdf. Published directly to arXiv with arXiv ID 1909.03562. [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).