Prerpints.org logo
Preprint
Article

Random Convolutional Kernel Transform with Empirical Mode Decomposition for Medium Voltage Insulator Classification based on Ultrasound Sensor

Altmetrics

Downloads

94

Views

33

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

19 January 2024

Posted:

22 January 2024

You are already at the latest version

Alerts
Abstract
The electrical energy supply relies on the satisfactory operation of insulators. The ultrasound recorded from insulators in different conditions has a time series output, which can be used to classify faulty insulators. The random convolutional kernel transform (Rocket) algorithms use convolutional filters to extract various features from time series data. This paper proposes the combination of Rocket algorithms, machine learning classifiers, and empirical mode decomposition (EMD) methods, such as complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN), empirical wavelet transform (EWT), and variational mode decomposition (VMD). The results show that the EMD methods combined with MiniRocket, significantly improve the accuracy of logistic regression in insulator fault diagnosis. The proposed strategy achieves respectively an accuracy of 0.992 using CEEMDAN, 0.995 with EWT, and 0.980 with VMD. These results highlight the potential of incorporating EMD methods in insulator failure detection models to enhance the safety and dependability of power systems.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Electrical power grids form the backbone of modern society, and their components’ effective management and maintenance are of paramount importance [1]. Insulators play a critical role in ensuring the stability and reliability of these grids, as they serve as both mechanical supports for the wires and electrical potential insulation [2]. A degradation in an insulator’s characteristics can have severe consequences, leading to disruptive discharges, system failures, and compromised network dependability [3]. Therefore, it is crucial to develop robust and accurate methods for monitoring and assessing the performance of insulators [4].
Inspections of the electrical system using radio frequency-based techniques are increasingly being applied by power utilities since before a fault occurs, partial discharges can emit light or noise that humans have difficulty identifying [5]. For this purpose, specific equipment such as ultraviolet cameras, infrared cameras, and ultrasound detectors are used [6]. Therefore, when there is a higher probability of failure, the maintenance team can take action in advance, improving the reliability of the electrical network [7].
Based on the ultrasound, analyzing time series data captured from the insulators during the inspections becomes a promising avenue for fault detection [8]. Ultrasound-based techniques have proven effective in identifying various insulator faults, providing valuable insights into their condition, and allowing for timely maintenance and replacement [9]. However, the accurate classification of these time series data remains a challenge. The major advantage of using ultrasound compared to leakage current detection [10], for example, is that the ultrasound does not need to be in direct contact with the network; thus, inspections can be performed with greater speed and less risk for the technical team [11].
Time series classification is a task that involves predicting a categorical label for a given time series dataset. This data is a sequence of observations collected over time. Time series classification aims to learn a model that can classify new time series based on past observations. Recent advances in time series classification methods have opened new possibilities for addressing this issue [12]. The accuracy and effectiveness of time series classification methods have recently undergone several types of substantial developments based on statistical models [13], machine learning [14], and deep learning [15] approaches. In particular, the random convolutional kernel transform (Rocket) algorithms [16], including MiniRocket [17] and MultiRocket [18], has gained considerable attention from researchers due to their ability to efficiently and accurately process time series data.
Rocket is a kernel-based approach that uses random Fourier features to map data from time series into a feature space of high dimensionality. MiniRocket is a lightweight version of Rocket. MiniRocket is a faster and more memory-efficient method than Rocket, given that it only takes a small portion of the random Fourier features toward account. Despite each time point being represented by many variables, MultiRocket is a variant of MiniRocket capable of handling multivariate time series classification challenges. Intending to generate a shared feature representation for the multivariate time series, MultiRocket implements an innovative multivariate feature mapping technique that integrates the outputs from several univariate MiniRocket classifiers [19].
This paper proposes a novel approach combining Rocket algorithms with machine learning classifiers to enhance insulator time series classification accuracy and efficacy based on ultrasound data. The contributions of this research are summarized below:
(i) An efficient classification framework that combines the advantages of Rocket approaches and machine learning models for time series classification of medium voltage insulators is proposed, increasing classification accuracy and generalization capabilities.
(ii) The impact of integrating empirical mode decomposition methods with the proposed framework demonstrates significant improvements in classification accuracy.
(iii) Several classification algorithms are comprehensively compared to provide a benchmark for performance evaluation. This comparison will help engineers select the most appropriate method for their specific insulator classification task, considering classification accuracy versus model complexity.
The remainder of the work proceeds as follows: The related works are briefly approached in Section 2. The description of the classification problem is detailed in Section 3. The fundamentals of the evaluated methods and the proposed approach are explained in Section 4. Section 5 discusses the classifier designs regarding performance evaluation and result analysis, while Section 6 provides the main conclusions and suggestions for further research.

2. Related works

Several authors have explored the application of time series for identifying and predicting insulator failures [20]. Klaar et al. [21] used the empirical wavelet transform for denoising in a hypertuned long short-term memory (LSTM) framework to fault prediction in insulators considering a sequence-to-sequence problem. In this case, the prediction was regarding leakage current, similar to the method presented by Sopelsa Neto et al. [22] and Medeiros et al. [23], where several models were explored for this task.
Concerning evaluating the time series for predicting the increase of faults in the power supply system, Branco et al. [24] presented a study of the number of faults over the year. The failures can be related to climatic variations. Depending on the season, more failures can happen, especially in this study, where there is a rainy season, increasing the probability of failure [25]. A highlight that was presented in this research was the use of the wavelet transform to mitigate the impact of unrepresentative variations. This technique can be used in chaotic time series, such as ultrasound, which is studied to detect failures by power utilities [26].
Especially using ultrasound to classify the condition of the insulators of medium voltage power grids, Stefenon et al. [27] proposed using the echo state network. They showed that identifying a specific condition, such as drilling, is easier than performing multiclassification. They have highlighted that the broken and drilling insulators have more partial discharges than contaminated or clean insulators, been possible to have results of classification with over 99% accuracy when these conditions are evaluated. In this evaluation, the echo state network was more promising than the support-vector machine (SVM) or multilayer perceptron.
Ferreira et al. [28] proposed a method for calculating electrical insulator pollution using ultrasonic noise. The audio was reduced using the spectral subband centroid energy vectors algorithm before input into an artificial neural network that can distinguish between different degrees of pollution. Their method was applied to process ultrasonic sounds from different electrical equipment given to multiple forms of pollution. In [29] the contamination of insulators is evaluated using deep learning.
The problem of interpreting leakage current measurements for overhead insulator condition monitoring due to the intermittent harmonic content of the supply voltage was dealt by Ghosh et al. [30]. To monitor leakage current in the presence of voltage harmonics, the study suggested applying the instant value of the time integral of the leakage current as a low sensitivity parameter. The study demonstrated that changes in system voltage’s harmonic content significantly impact the harmonic properties of leakage current. The suggested measuring method has been tested and validated using experimental data that was captured in the lab and integrated into an online measurement tool that has been evaluated in the lab.
The problem of appropriately simulating the flashover phenomena in contaminated insulators was approached by Belhouchet et al. [31], which is made more challenging by the complexity of determining the arc constants generated in dry bands when the electrical voltage goes beyond critical levels. Using data from artificially contaminated insulator experiments, the authors suggest a strategy for optimization based on genetic algorithms and artificial neural networks (ANN) to identify the arc constants and dielectric properties of the surface. The research, which used a generalized pollution flashover model, observed that the inverse connection of flashover voltage and leakage current was validated by the optimized mathematical model’s realistic simulation of the experimental data.
A method for predicting line trip defects in power systems that combine support vector machine and LSTM networks was suggested by Zhang et al. [32]. The suggested approach addresses the shortcomings of existing approaches based on activities taken to preserve relays and electrical components. In order to acquire the final prediction results, the support-vector machine is used for classification and the LSTM networks are employed to capture the temporal aspects of multi-sourced data. The LSTM is well-indicated for time series with high nonlinearities [33] and it can be further improved by using the attention mechanism [34].
You only look once (YOLO) deep learning neural network model using the unmanned aerial vehicle has been presented in the work of Sadykova et al. [35] as an effective technique for detecting high voltage insulators. The purpose is to provide a real-time classification of insulator conditions while avoiding expensive manual inspections involving traveling across a wide area in adverse weather. The technique uses a training set size of 56,000 image samples and data augmentation to prevent overfitting. The experimental findings show how well the proposed method works for accurately determining insulators and assessing their surface conditions for the presence of ice, snow, and water through different classifiers. Also, in [36] and in [37] a hybrid version of YOLO is proposed for inspections of the power grids.
To automate visual inspection tasks, Prates et al. [38] suggested applying convolutional neural networks to recognize flaws and different insulators in overhead power distribution lines (OPDLs). More than 2,500 photos obtained from a studio and a realistic OPDL are used to train the model. Multi-task learning was also employed to enhance fault detection performance by predicting the insulator class. Also based on images, in [39] a new hybrid method is proposed, which combines object detection to convolutional neural networks (CNNs) for classification.
Polisetty et al. [40] concentrated on the significance of keeping a close watch on outside insulation systems to preserve the integrity of substations and overhead transmission and distribution lines. The study used an ANN and a commercial acoustic sensor to classify electrical discharge patterns in external insulating systems. The ANN then expanded to incorporate three different types of flaws on outdoor ceramic insulators and distinguished between five frequent discharges of electricity produced under controlled settings. The investigation successfully identified approximately 85% of controlled samples.
Intending to monitor the condition of equipment for high-voltage power stations, Mitiche et al. [41] addressed using bispectrum representations as complex input features in complex-valued deep CNNs. This approach achieved excellent classification accuracy for discharge signals. An automated inspection system that uses computer vision to gauge erosion in silicone rubber samples was presented by Ibrahim et al. [42]. Using the IEC-60587 (International Electrotechnical Commission) standard to describe failure, the system was intended to classify samples into one of three groups based on the level of erosion. The suggested system compared the performance of ANNs, applying feature extraction methods and pre-processing approaches.
A new method for insulator condition monitoring based on meteorological and environmental information was suggested by De Santos and Sanz-Bobi [43]. The method combined the random under-sampling technique to estimate important condition indicators with an adaptive boosting algorithm (RUSBoost). The proposed method was compared with other algorithms at France’s 245 kV test station. The findings indicate that RUSBoost outperformed the competitors’ algorithms, rating high for the estimation of insulator conditions. Advanced hybrid methods are been applied by several researchers [44,45,46], and the idea of combining techniques helps the model by using the advantages of more than one approach.
A knowledge-based optimization approach to deal with the challenge of determining the optimal process settings for manufacturing medium voltage insulators was proposed by Kong et al. [47]. Their method utilized historical approximations produced in the optimization process to enhance the accuracy of the gradient estimates and to adjust the size of the iteration step. Their approach reduced the cost and improved quality control efficiency for insulators, which is crucial for their efficient production and confident operation. Models based on the ensemble approach are promising considering that usually the need less computational effort compared to deep learning [48].
A novel model based on feature pyramid neural networks and adaptive threshold algorithm with line detection, image rotation, and vertical projection data applied to insulators fault detection in transmission lines was proposed by Zhao et al. [49]. Singh et al. [50] presented an evaluation of infrared thermal images, their method computes several features from the segmented region of interest and utilizes a Gaussian kernel SVM to classify the insulator faults. A robust methodology based on deep learning and uncertainty detection for automatic insulator fault inspection using aerial images was approached by Dai [51]. The bounding box prediction was improved, and the detection robustness was enhanced using the predicted uncertainty scores.
The adoption of deep learning algorithms for condition monitoring of high voltage equipment in electrical power systems was reviewed in Mantach et al. [52]. Contrasting conventional machine learning approaches, deep learning combines feature extraction with the learning stage and uses raw data as input. This paper included contemporary research on deep learning approaches for monitoring high-voltage equipment, including gas-insulated switchgear, transformers, cables, rotating machines, and outside insulators.
A novel approach for monitoring pollutant insulator discharge mode in high voltage lines by combining auditory emission signals with a one-dimensional convolutional neural network structure (1D-CNN) was provided by Hao et al. [53]. The procedure includes data collection in a lab accompanied by using 1D-CNN to reduce the dimensionality of the signal samples and extract features. With a recognition rate of over 99.84%, the model successfully replaces the need for human data preparation in conventional monitoring approaches and may be used to carry out monitoring tasks for pollution insulator discharge mode.
A CNN bidirectional LSTM named CNN-Bi-LSTM neural network design with hyperparameters optimization to classify leakage current levels according to sequential weather factors and insulator data was evaluated in Nguyen et al. [54]. The CNN-Bi-LSTM was employed in real-time monitoring services to improve the operations of the TaiPower electric utility in Taiwan. On the other hand, a CNN-LSTM neural network with hyperparameter tuning for categorizing leakage/discharge current on a web-based service was evaluated by Tham and Cho [55]. Leakage current surge and weather data are input parameters in four different models to predict leakage current classification.
The study of ultrasound has been explored by several authors [56,57,58,59], and can be applied for classification, as presented in this paper. Considering an experiment in medium voltage, the ultrasound equipment is employed to define insulator patterns under different conditions, as will be explained in detail in the next section.

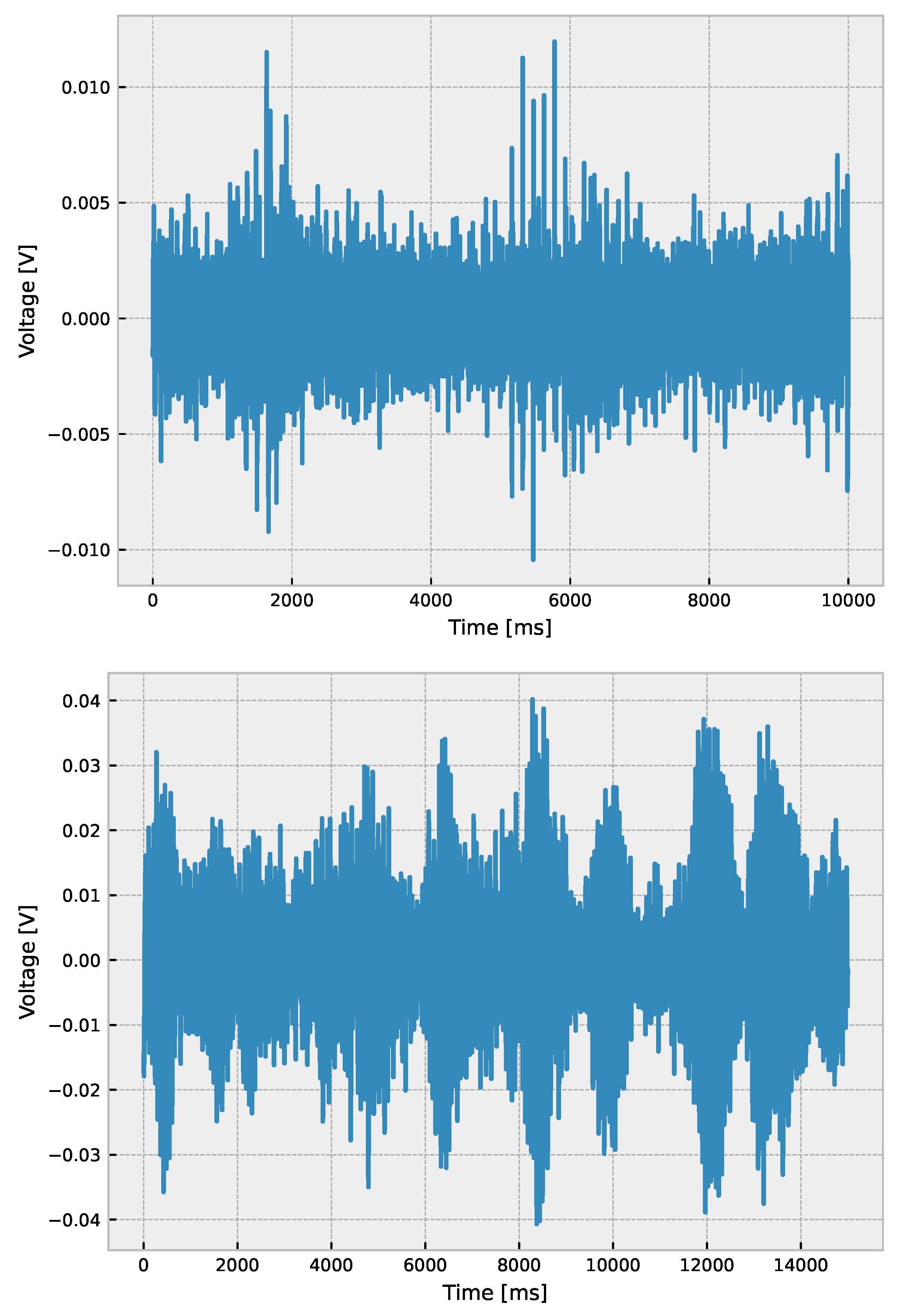
3. Insulators Ultrasound Measurement

This section provides a detailed account of the classification problem and explains the experiment performed in the high-voltage laboratory presented in Figure 1. The experiment involves applying a voltage of 7.95 kV phase-to-ground to the insulators, equivalent to 13.8 kV phase-to-phase in the power system, the electrical potential used in the considered distribution branch located in southern Brazil.
This paper considered three conditions: an insulator in good condition, an artificially contaminated insulator, and a drilled insulator. The insulators are pin-type profiles, class 15 kV, from the Germer manufacturer. These insulator profiles are commonly installed in conventional distribution power grids in rural southern Brazil, exposed to organic contamination from unpaved roads, and saline contamination when close to the coast [60].
To simulate drilling caused by lightning, a perforation was performed on the top of insulators using a bench drill. Figure 1A presents the top view of the drilling, and Figure 1B shows the bottom view, where the fixation pin is attached. This problem is hardly found in the distribution grid because the perforations can be underneath the mooring. Perforation is more common in polymeric insulators, where the temperature required for carbonization is lower than in glass insulators [61].
The contamination over the insulator surface is an issue that increases the conductivity of the surface, leading to a higher leakage current and possible flashovers [62]. The flashovers occur mainly in bad weather conditions, making it challenging to identify the exact location of the fault during inspections. When lightning strikes the electrical power grid, perforations or boundary discharges might occur, resulting in a higher risk of irreversible failures, in which corrective maintenance is required [63].
To simulate the contamination on the insulators, the solid layer procedure given by NBR 10621/2017 (Brazilian Standard: High-voltage insulators to be used in alternating current systems - artificial pollution tests) was followed, based on IEC/507 (Artificial pollution tests on high-voltage insulators to be used in alternating current systems). The contaminants considered were kaolin and sodium chloride. The NBR 10621/2017 standard determines the tolerable performance of porcelain or glass insulators for outdoor applications [64].
The experiment was conducted inside an acrylic chamber since the ultrasound detector is sensitive to capturing noise from external sources. The ultrasound detector was set at a distance of 0.4 m from the insulators (see Figure 2), and it recorded noise signals with a maximum frequency of 500 kHz; this distance was fixed for comparative purposes. In the distribution grids, the operator may face scenarios with varying relief that may result in a greater need for measurement. The difficulty in reaching the grid is one of the significant challenges in inspecting power distribution networks by the electric utility company [65].
To mitigate the interference from partial discharges coming from the mooring of the insulator, the fixing was done with non-conductive materials [66]. The chamber held two insulators affixed, and voltage was applied to these insulators while the ground had an equal reference. The ground was attached only to the insulator under evaluation to prevent one insulator from affecting the other. An M500 model from Petterson recorded the ultrasonic signal. The conductivity of the water used to spray the samples during the experiment was 56 kg/m3, which corresponds to a medium-high contamination level according to IEC-507.
Considering partial discharge typically occurs over the frequency range from 10 kHz to 210 kHz, a comprehensive assessment of more than 50 times the base frequency ensures that all frequencies beyond 10 kHz are captured under a single wave cycle. Besides the 500 kHz frequency rate, to ensure that the signal has been properly recorded for a sufficient time length, the data log was held for 50 seconds. After the signal was saved, a total of 1 × 10 5 records were considered for a comprehensive assessment. Figure 3 presents an example of the signal recorded by the ultrasound equipment.

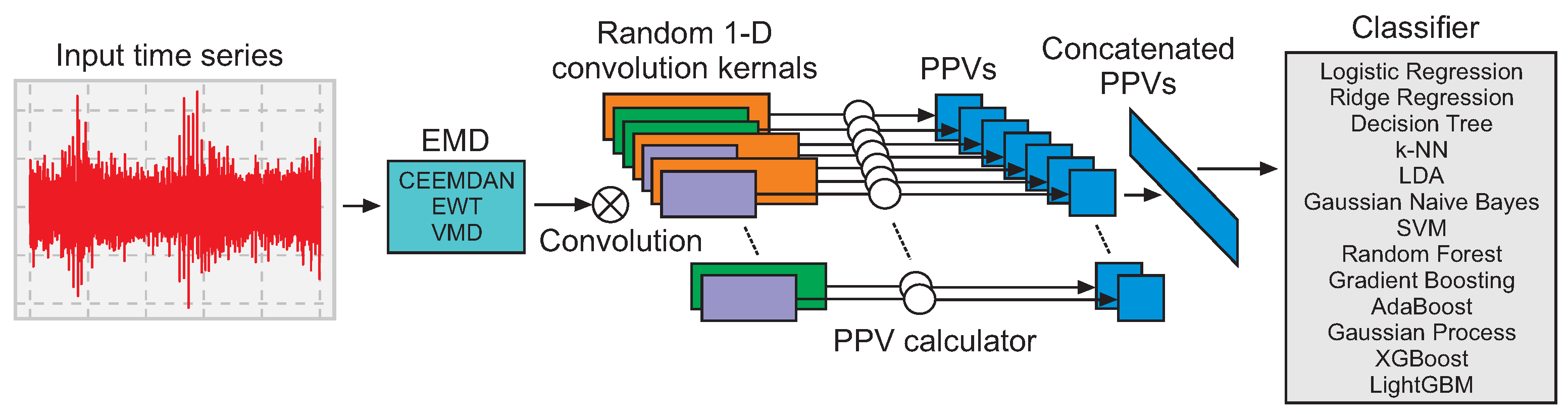
4. Methodology

The model proposed in this paper combines empirical mode decomposition methods with random convolutional kernel transform models and state-of-the-art classifiers to obtain a hybrid architecture, presented in Figure 4, which is explained in this section. The input signal is based on a time series measured by ultrasound during high-voltage experiments considering insulators under different conditions, as explained in the previous section.
A time series is a sequence of points of information collected over time, typically at fixed intervals. The classification of time series is related to the development of models to classify time series data into predetermined categories based on their patterns and characteristics over time. The Rocket [16], MiniRocket [17], and MultiRocket [18] are algorithms that have been widely evaluated recently for time series classification tasks.
The fundamental concept of Rocket methods is obtaining features from time series data and employing those features to train a classifier. These models use convolutional kernels to transform the time series data into features, which are then used for classification [67]. Given a time series x = x 1 , x 2 , … , x T , these algorithms compute features such as the maximum value (Max) and the proportion of positive values (PPV) for each of the k convolutional kernels. The convolutional operation for a kernel ϕ = ϕ 1 , ϕ 2 , … , ϕ m can be expressed as:
z i = ( x ∗ ϕ ) i = ∑ j = 1 m x i + j − 1 ϕ j ,
where ∗ denotes the convolutional operation, z i is the output of the convolution, and m is the kernel length. The Max and PPV features are computed as follows:
Max = max 1 ≤ i ≤ T − m + 1 z i ,
PPV = 1 T − m + 1 ∑ i = 1 T − m + 1 1 ( z i > 0 ) ,
where 1 ( · ) is the indicator function. The extracted features are then used to train a linear classifier for time series classification.
MiniRocket distinguishes itself from Rocket by computing features using a fixed set of k convolutional kernels with a shorter kernel length, resulting in greater computational efficiency and refining the convolutional process by introducing alterations to the kernels [68]. The MiniRocket transform calculates the Max and PPV features for each k fixed convolutional kernel. By leveraging a fixed set of kernels with shorter kernel lengths, MiniRocket significantly diminishes the computational effort while retaining competitive performance in time series classification tasks [69].
The MultiRocket algorithm extends the Rocket framework by incorporating multiple pooling operators and transformations to enhance the diversity of the generated features. MultiRocket employs first-order differences to transform the primary input series, thereby creating an alternative representation and processing the raw input series. Both representations undergo the application of convolutions, and the processing of convolution outputs is executed using four distinct pooling operators. The integration of additional procedures expands the range of features and improves the algorithm’s overall performance [18].

4.1. Empirical Mode Decomposition

For time series decomposition, feature extraction, and noise reduction the empirical mode decomposition (EMD) methods are applied [70]. The variations of the EMD include the complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) [71], empirical wavelet transform (EWT) [72], and variational mode decomposition (VMD) [73]. These methods are advanced signal processing techniques that aim to decompose a given time series into a finite set of components, each representing an intrinsic mode function (IMF) [74] or oscillatory mode.
EMD is a data-driven method that decomposes non-linear time series in a set of IMFs [75]. The main idea behind EMD is the so-called sifting process, which iteratively extracts IMFs by identifying local extrema and fitting envelopes using cubic spline interpolation. Given a time series x ( t ) , the sifting process begins with the identification of all the local maxima and minima. Next, the upper and lower envelopes are created by the interpolation of the local maxima and minima employing cubic spline interpolation. The mean of the envelopes is then calculated as follows:
m ( t ) = 1 2 ( e upper ( t ) + e lower ( t ) ) ,
where e upper ( t ) is the upper envelope and the e lower ( t ) is the lower envelope [76].
The difference between the original signal and the mean is considered a candidate IMF:
c ( t ) = x ( t ) − m ( t ) ,
and this process is repeated on the IMF until it meets the predefined stopping criterion. Then, it is applied to the residual signal until all IMFs are extracted.
The EWT involves the decomposition of a given signal in oscillatory modes having varying scales and frequencies [77]. The EWT algorithm produces a collection of n non-linear functions known as IMFs from the signal x ( t ) and a wavelet mother function ψ ( t ) . The process for generating these IMFs is outlined in Algorithm 1.
Algorithm 1:EWT
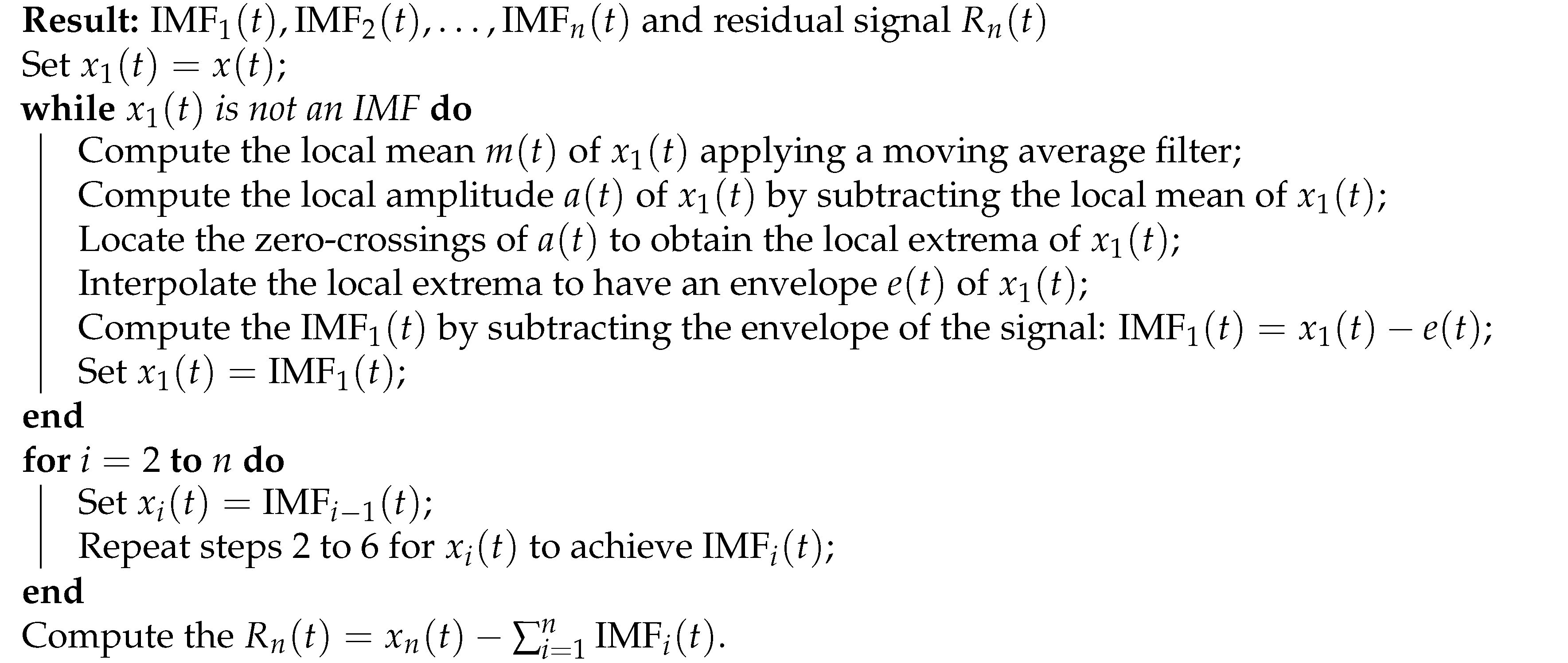Preprints 96873 i001
Once the set of IMFs is obtained, EWT employs a Fourier transform to each IMF to produce a set of n spectrograms, that are utilized to visualize the time-frequency information of the signal [78]. The EWT has the following expression:
x ( t ) = ∑ i = 1 n IMF i ( t ) + R n ( t ) IMF i ( t ) = ∫ x ( τ ) h i ( τ − t ) d τ
where h i ( τ ) is the ith filter set as the convolution of the scaling function φ ( t ) and the ψ ( t ) is scaled by a factor of 2 i :
h i ( τ ) = 2 i φ ( 2 i τ ) ψ ( 2 i τ ) .
The EWT combines the concepts of EMD and wavelet transform. The main idea of EWT is to decompose the signal in a set of oscillatory modes using an adaptive filter bank. The filter bank is designed based on the signal’s time-frequency content, estimated by the continuous wavelet transform [79]. The EWT decomposition is given by:
x ( t ) = ∑ i = 1 N w i ( t ) + r ( t ) ,
where w i ( t ) are the wavelet components, N is the number of modes, and r ( t ) is the residual.
VMD is another decomposition technique that formulates the extraction of IMFs as a constrained variational problem. VMD decomposes the time series in a set of band-limited IMFs by minimizing the cost function that balances the compactness of the frequency spectrum and the smoothness of the time-domain signal [80]. The VMD optimization problem can be written as:
min u k ( t ) , ω k ∑ k = 1 K ∫ ∂ t u k ( t ) 1 + j ω k t 2 d t
s . t . x ( t ) = ∑ k = 1 K u k ( t )
where u k ( t ) are the mode functions, K is the number of modes, and ω k are the center frequencies of the modes.

4.2. Classification Methods

To evaluate the effectiveness of Rocket methods, including MiniRocket and MultiRocket, for classifying faults in insulators, a comprehensive analysis is conducted by combining these algorithms with various classifiers mentioned above. This experimental design aims to determine the best-suited combination of Rocket techniques and classification methods, ultimately enhancing insulator fault detection accuracy.
Logistic Regression: Logistic regression, a prevalent linear technique employed for classification, utilizes a logistic function to model the probability of a specific class or event [81]. The following equation represents the logistic function:
P ( y = 1 | x ) = 1 1 + e − ( β 0 + β 1 x )
Ridge Regression: Ridge regression, also known as Tikhonov regularization, is a linear regression technique incorporating an L 2 regularization term to address the issue of multicollinearity and improve the generalization of the model [82]. It is particularly useful when there are highly correlated features. The objective function for ridge regression can be written as follows:
L ( w , b ) = ∑ i = 1 n ( y i − ( w T x i + b ) ) 2 + λ | w | 2
where w is the weight vector, b is the bias term, y i and x i are the true label and the feature vector for the i-th instance, respectively, and λ is the regularization parameter that controls the trade-off between model complexity and the goodness of fit. The regularization term, λ | w | 2 , discourages the model from assigning large weights to the features, leading to a more stable and robust solution.
Decision Tree: Decision tree classifier, a non-parametric, hierarchical model, recursively partitions the input space into discrete regions according to feature values. The decision rules are derived by minimizing the impurity of the resultant nodes, which can be quantified utilizing metrics such as Gini impurity or entropy [83].
The architecture of the classifier is built in the form of a tree structure where each internal node represents a feature or attribute, each branch represents a decision rule, and each leaf node represents a class label or a decision. According to Mishra et al. [84], the architecture can be further improved by using clustering techniques.
k-NN: The k-nearest neighbors (k-NN) classifier, a non-parametric, instance-based learning algorithm, classifies novel instances based on the majority class of their k nearest neighbors. The distance metric and the value of k are crucial to the algorithm’s performance. Since it is a classification problem, employing an odd k is more advantageous, thus avoiding draws [85]. For this task, the weighted mode is denoted by:
γ t = arg max c ∈ Y ∑ i = 1 k ω i I ( c , γ i )
where,
ω i = 1 d ( x t , x i ) ,
I ( a , b ) returns 1 if a = b [86]. Given that γ i is the class of the x i example associated with the ω i weight, and c is the class with the best-weighted mode. To calculate the neighbors the Euclidean, cosine, correlation, chebychev, city block, spearman, standardized Euclidean, Minkowski, and Mahalanobis distances methods can be applied [87].
LDA: Linear discriminant analysis (LDA), a technique utilized for dimensionality reduction and classification, identifies the linear combination of features that optimally separates distinct classes by maximizing the dispersion between classes and minimizing the dispersion within a class [88]:
J ( w ) = w T S B w w T S W w
where S B and S W represent the between-class and within-class scatter matrix respectively.
Gaussian Naive Bayes: Gaussian Naive Bayes is a classification algorithm that is based on Bayes’ theorem [89], assuming the features are conditionally independent and follow a Gaussian distribution:
P ( A | B ) = P ( B | A ) P ( A ) P ( B )
where A and B are events or variables. The Gaussian Naive Bayes assumes that the features in the dataset are normally distributed and that they are independent of each other.
SVM: The support vector machine (SVM) classifier, endeavors to identify the optimal separating hyperplane between classes [90]. Its performance is governed by the kernel function and regularization parameter C:
min w , b , ξ 1 2 w T w + C ∑ i = 1 n ξ i
s . t . y i ( w T x i + b ) ≥ 1 − ξ i
ξ i ≥ 0 .
Random Forest: An ensemble learning methodology constructs multiple decision trees and amalgamates their outputs via majority voting [91]. The operator regulates the number of trees (T) and their maximum depth. Let X be the set of input features and Y be the set of output classes. The random forest classifier consists of T decision trees, h t ( x ) t = 1 T , each grown to a maximum depth. Each tree is created by a randomly sampled subset of the train data, typically with replacement (i.e., bootstrapped samples), and a random subset of input features at each split. The random forest classifier is given in the following definition:
H ( x ) = arg max c ∈ Y ∑ t = 1 T I ( c , h t ( x ) ) ,
where H ( x ) represents the final classification, again I ( a , b ) returns 1 if a = b , and 0 otherwise, and h t ( x ) is the output of the t-th decision tree for input x.
Gradient Boosting: The gradient boosting classifier, an ensemble learning technique, sequentially builds weak learners, with each learner rectifying the errors committed by the preceding one [92]:
F m ( x ) = F m − 1 ( x ) + ρ m h m ( x )
where F m ( x ) denotes the boosted model at step m, h m ( x ) signifies the weak learner, and ρ m represents the step size. The gradient boosting method has also been utilized for prediction by various authors [93,94,95].
AdaBoost: Adaptive boosting (AdaBoost) classifier, an adaptive boosting technique, combines weak learners to form a robust classifier, with each learner weighted based on its accuracy [96]. The algorithm updates the weights of the training instances at each iteration, assigning greater importance to misclassified instances:
D t + 1 ( i ) = D t ( i ) e − α t y i h t ( x i ) Z t
where D t ( i ) is the weight of instance i at iteration t, h t ( x i ) is the prediction, y i is the true label, α t is the weight of the weak learner, and Z t is the normalization factor.
Gaussian Process: Gaussian process classifier, a Bayesian, non-parametric model, employs a Gaussian process prior over the function space and yields probabilistic classification results [97]. It is determined by a mean m ( x ) and a covariance function k ( x , x ′ ) :
f ( x ) ∼ GP ( m ( x ) , k ( x , x ′ ) )
XGBoost: The extreme gradient boosting (XGBoost) algorithm is a highly efficient and scalable tree-based ensemble learning model, designed for both classification and forecasting problems [98]. It is an extension of the gradient boosting algorithm, employing advanced regularization techniques to improve the model’s generalization and control overfitting. XGBoost optimizes the following objective function:
L ( ϕ ) = ∑ i = 1 n l ( y i , y ^ i ) + ∑ j = 1 K Ω ( f j )
where ϕ represents the model parameters, l ( y i , y ^ i ) denotes the loss function comparing the true label y i and the forecasted label y ^ i , and Ω ( f j ) is the regularization term for the j-th tree. The regularization term comprises the tree complexity, measured by the number of leaves T, and the L 2 -norm of the leaf scores w:
Ω ( f ) = γ T + 1 2 λ | w | 2
The algorithm employs second-order gradient information (Hessian) and the first-order gradient for updating the model, making the learning process more accurate and faster. Furthermore, it utilizes column block and sparsity-aware techniques to efficiently handle sparse data and parallelize the tree construction process, enabling it to tackle large-scale datasets efficiently [99].
LightGBM: The light gradient boosting method (LightGBM), a boosting framework, leverages tree-based learning algorithms and is designed to be efficient and scalable for large datasets [100]. It adopts gradient-based one-side sampling and exclusive feature bundling to expedite training and diminish memory usage.
In the next section, the results of the application of the proposed method are presented, initially the results of using different classifiers considering window sizes of 10, 50, and 100 records are presented. Then, the incorporation of Rocket, MiniRocket, and MultiRocket models with 10, 50, and 100-time steps are evaluated. And finally, the use of EMB methods to reduce noise that is not significant is evaluated.

5. Results

In the experiments presented in this section, it is utilized a k-fold cross-validation methodology to evaluate the performance of the models, in particular, the k is equal to five. Cross-validation is a widely used technique to estimate the predictive performance of a model; in particular, 5-fold cross-validation involves splitting the dataset into five equal-sized partitions. Four partitions are used for training the model for each fold, and the remaining partition is utilized for testing. This procedure is repeated five times such that each fold serves as the test set exactly once. The resulting accuracy scores from each fold are then averaged to estimate the model’s accuracy The default scikit-learn [101] parameters were employed in all the classification algorithms.
The performance of various algorithms for fault detection in insulators is evaluated using three different time window sizes, namely WS10, WS50, and WS100. Table 1 presents the accuracy results of 14 algorithms, including logistic regression, ridge regression, decision tree, k-NN, LDA, Gaussian Naive Bayes, SVM, random forest, gradient boosting, AdaBoost, Gaussian process, XGBoost, LightGBM, and CatBoost. The results indicate a clear trend regarding the time window size and the overall performance of the algorithms, with the critical difference diagram shown in Figure 5.
From Table 1 it is evident that tree-based methods, such as decision tree, random forest, gradient boosting, AdaBoost, XGBoost, LightGBM, and CatBoost, exhibit superior performance compared to other algorithms, as can be further seen in Figure 6. CatBoost, LightGBM, and gradient boosting show the highest accuracies in WS50 and WS100 time windows, particularly strong results. Moreover, the table demonstrates that the accuracy of the algorithms generally improves as the time window size increases from WS10 to WS100. This observation suggests that longer time windows provide more information for the algorithms to identify the patterns and relationships between the features, resulting in improved performance. For instance, CatBoost’s accuracy increases from 0.8842 ± 0.0658 in WS10 to 0.95 ± 0.0459 in WS100, highlighting the significance of using longer time windows for fault detection in insulators.
Table 2, Table 3, and Table 4 present the results of different machine learning algorithms applied to insulator fault detection when using Rocket, MiniRocket, and MultiRocket data transforms for three different time windows, WS10, WS50, and WS100, respectively. These transforms have been applied to enhance the time-series data and improve the performance of the algorithms. A notable outcome of these transformations is the improvement in accuracy across all algorithms, particularly in the case of linear algorithms.
Upon applying the Rocket, MiniRocket, and MultiRocket transforms, linear algorithms such as logistic regression, ridge regression, and LDA exhibit a substantial increase in their accuracy, as can be observed in the tables. These improvements can be attributed to the transforms’ ability to capture better the underlying patterns in the data, which allows linear algorithms to leverage this information and perform more effectively.
For instance, in Table 2, the accuracy of logistic regression increases from 0.7552 ± 0.0353 with Rocket to 0.8465 ± 0.06 with MultiRocket. In contrast, the accuracy of ridge regression increases from 0.6762 ± 0.0462 with Rocket to 0.8068 ± 0.0447 with MultiRocket. Similarly, in Table 3, logistic regression and ridge regression exhibit high accuracy of 0.955 ± 0.0395 and 0.9533 ± 0.036 with Rocket, respectively. These results suggest that the use of data transforms boosts the performance of linear algorithms, enabling them to compete with more complex models.
It is essential to note that the algorithm’s performance still improves as the time window size increases, consistent with the earlier observation in Table 1. This trend is evident across all three tables, reinforcing the importance of considering longer time windows when applying these algorithms to insulator fault detection.

5.1. Empirical Mode Decomposition

Table 5 presents the logistic regression results applied to fault detection in insulators with the MiniRocket transform for a window size of 100 (WS100), and further explores the impact of combining the MiniRocket transform with three different EMB methods: EWT, CEEMDAM, and VMD. The purpose of applying these EMB methods before the MiniRocket transform is to explore if the predictions can be further improved.
When these EMB methods are applied in conjunction with MiniRocket, the accuracy of logistic regression significantly improves compared to using the MiniRocket transform alone. This improvement can be attributed to the ability of EMB methods to decompose the time series into different components, thereby highlighting the underlying patterns and structures in the data that may not be easily captured by the MiniRocket transform.
For example, when using the EWT method, the accuracy of logistic regression increases from 0.9783 ± 0.0194 without EMB to 0.995 ± 0.0067 with EWT. Similarly, the accuracy of logistic regression improves to 0.9917 ± 0.0105 with CEENDAM and 0.98 ± 0.0187 with VMD. Figure 7 presents the critical difference diagram comparing the methods. These results indicate that applying EMB methods before the MiniRocket transform enhances the performance of logistic regression by providing a more refined representation of the data.

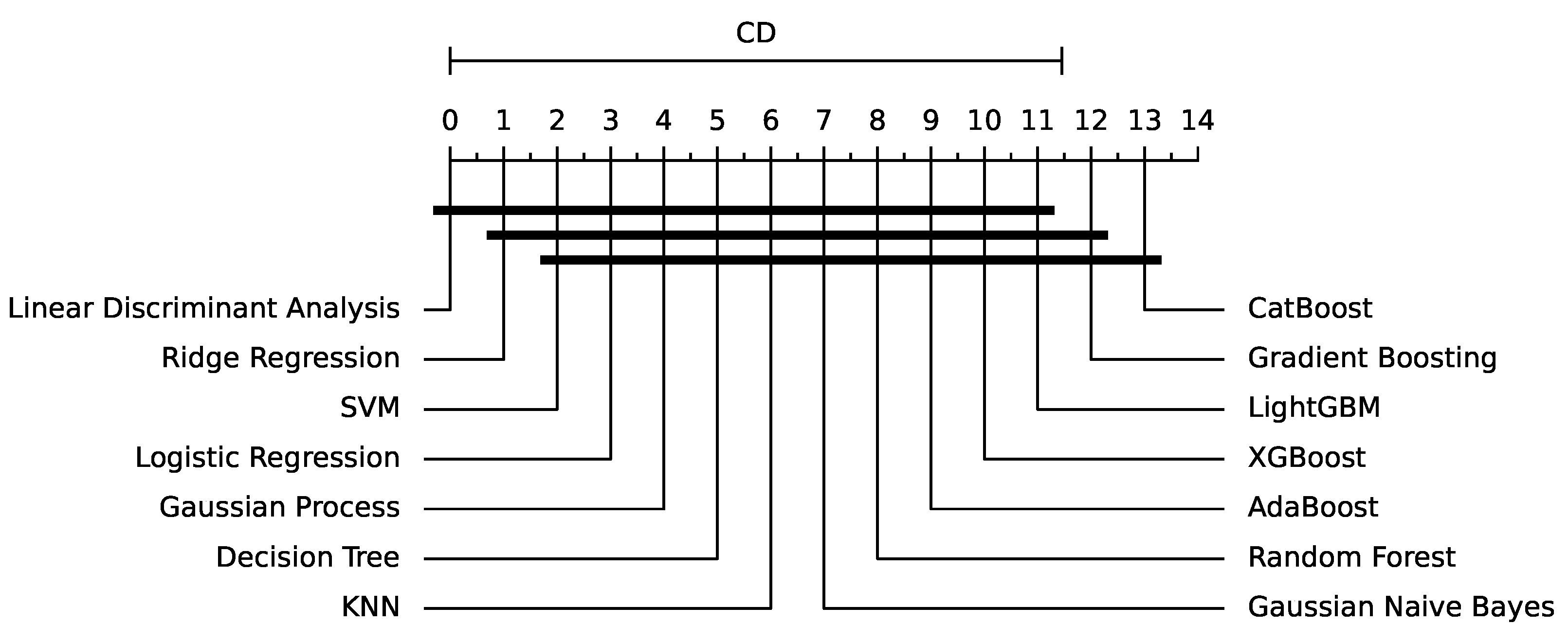
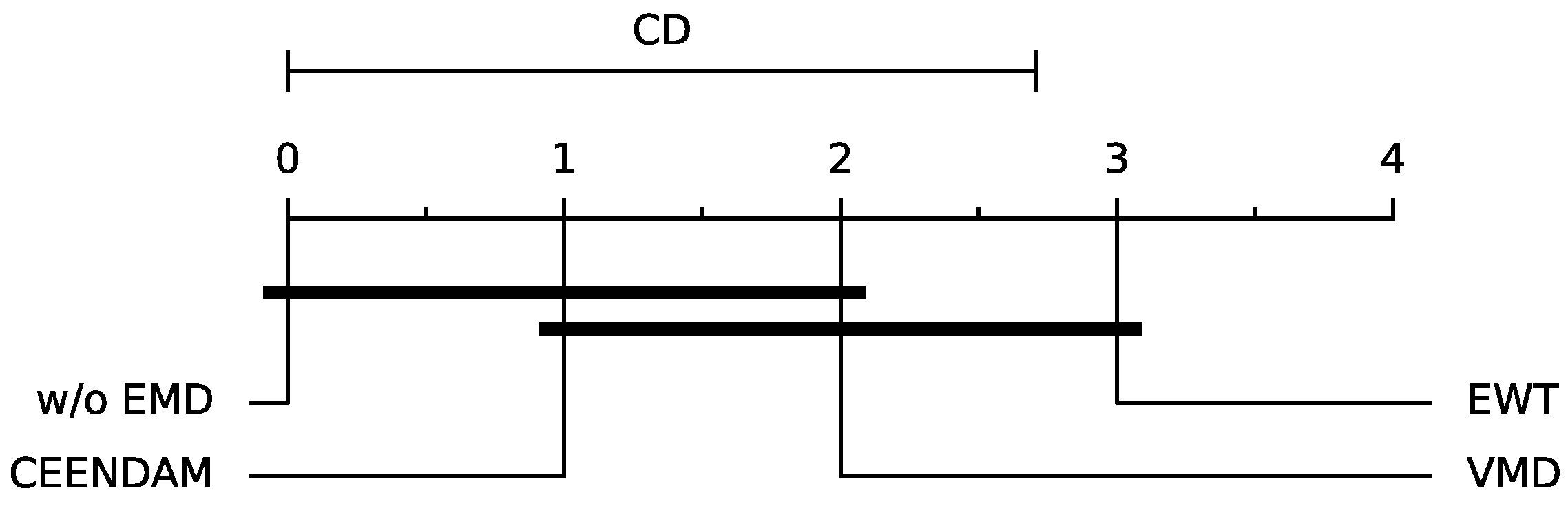
5.2. Discussion

The findings in the preceding subsections offer insightful information on how various machine learning techniques for defect detection perform. The study of these results can aid the selection of acceptable methodologies and techniques for fault detection in insulators, notably the effects of time window size and data transforms. The performance of the models was constantly enhanced by increasing the temporal window size. Longer time windows give the algorithms more information to find patterns and connections between features, improving insulator defect identification.
According to this study, adopting larger time windows should be favored in practical applications to improve the precision of defect detection models. The advantages of extended periods must be weighed against the additional computational expenses. The amount of data being processed and the complexity of the models grow as the time window size grows. More extended training periods and increased computational demands may result from this. Therefore, when choosing the time window size for insulator fault detection, practitioners should carefully consider the trade-offs between the improvements in accuracy and the extra computational resources needed.
The results show that tree-based approaches, considering random forests, decision trees, gradient boosting, AdaBoost, XGBoost, and LightGBM consistently outperform other algorithms in insulator fault detection. These techniques offer great accuracy when identifying insulator faults and are particularly good at managing non-linear connections between features. This shows that tree-based approaches should be the best options for insulator failure detection jobs. However, tree-based methods might be more prone to overfitting than other algorithms, mainly when working with small datasets. Pruning is one regularization approach that should be used to decrease overfitting risks and preserve model generalizability.
Logistic regression, ridge regression, and LDA perform much better when Rocket, MiniRocket, and MultiRocket data transforms are used. These modifications allow linear algorithms to take advantage of the information and perform better, even competing with more complicated models, by capturing more underlying patterns in the data. This result suggests that data transforms can be a useful preprocessing step in real-world applications, especially when using linear algorithms for insulator fault detection. Engineers may simplify their models by using these transforms while maintaining excellent fault detection accuracy.
Further, the results indicate that combining EMD methods and MiniRocket transform enhances the performance of logistic regression by providing a more refined representation of the data. This suggests that using EMD methods can improve fault detection capabilities when used in conjunction with rocket-like algorithms. The following guidelines it can be given for insulator failure detection using ultrasound signals in light of the study’s findings:
  • Consider the trade-offs with computational resources and training timeframes carefully when using longer time windows to increase the fault detection models’ accuracy.
  • Consider tree-based algorithms for insulator failure detection, such as CatBoost, LightGBM, and gradient boosting, while being cautious of overfitting concerns and using regularization techniques as necessary. To improve the efficiency of linear algorithms and potentially reduce model complexity while retaining high accuracy, use data transforms like Rocket, MiniRocket, or MultiRocket.
  • Employ EMD methods to enhance the performance of less complex regression methods by providing a more refined representation of the data and improving fault detection capabilities.
By using these suggestions, engineers can create more successful insulator failure detection models that improve the dependability and safety of electrical power systems. The next section presents the final remarks and suggestions for future work. The conclusions will be related to the applicability of ultrasound, the best structure to classify the time series, and what can be accomplished with the ultrasound equipment in future projects.

6. Conclusion and future directions of research

Using ultrasound as a decision-making support tool during inspections of the electrical power grid combined with deep learning proves to be promising since the proposed model achieves acceptable classification results. A significant advantage of using this equipment is that it is not necessary to measure contact with the electrical potential, reducing the risk to the operator and improving flexibility in inspecting the distribution power grid.
The findings indicate that tree-based methods, such as decision tree, random forest, gradient boosting, AdaBoost, XGBoost, and LightGBM generally outperform other algorithms in terms of accuracy. Longer time windows (e.g., WS100) resulted in improved performance across all algorithms, suggesting that larger windows provide more information for pattern identification. Additionally, the application of Rocket, MiniRocket, and MultiRocket data transforms led to a significant increase in accuracy for linear algorithms such as logistic regression, ridge regression, and linear discriminant analysis. This improvement can be attributed to the transforms’ ability to capture the underlying patterns in the data better, enabling linear algorithms to perform more effectively.
In future work, it is promising to evaluate the development of an embedded system to perform the inspections based on the model presented in this paper. The evaluated model has a low computational effort in the test phase, making its application in an embedded system an interesting solution to be explored, besides the test performed with the aid of a personal computer.

Author Contributions

Writing—original draft, A.C.R.K.; writing—review and editing, software, methodology, validation, L.O.S.; writing—review and editing, V.C.M.; supervision, L.d.S.C. All authors have read and agreed to the published version of the manuscript.

Funding

The authors Mariani and Coelho thank the National Council of Scientific and Technologic Development of Brazil — CNPq (Grants number: 314389/2023-7-PQ, 313169/2023-3-PQ, 407453/2023-7-Universal, and 442176/2023-6-Peci), and Fundação Araucária PRONEX Grant 042/2018 for its financial support of this work. The author Seman thanks the National Council of Scientific and Technologic Development of Brazil — CNPq (Grant number: 308361/2022-9).

Informed Consent Statement

Not applicable.

Data Availability Statement

It can be provided upon request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Salem, A.A.; Lau, K.Y.; Ishak, M.T.; Abdul-Malek, Z.; Al-Gailani, S.A.; Al-Ameri, S.M.; Mohammed, A.; Alashbi, A.A.S.; Ghoneim, S.S.M. Monitoring porcelain insulator condition based on leakage current characteristics. Materials 2022, 15, 6370. [Google Scholar] [CrossRef]
  2. Ibrahim, A.; Dalbah, A.; Abualsaud, A.; Tariq, U.; El-Hag, A. Application of machine learning to evaluate insulator surface erosion. IEEE Transactions on Instrumentation and Measurement 2020, 69, 314–316. [Google Scholar] [CrossRef]
  3. Stefenon, S.F.; Yow, K.C.; Nied, A.; Meyer, L.H. Classification of distribution power grid structures using inception v3 deep neural network. Electrical Engineering 2022, 104, 4557–4569. [Google Scholar] [CrossRef]
  4. Yang, D.; Cao, B.; Li, Z.; Yang, L.; Wu, Y. On-line monitoring, data analysis for electrolytic corrosion of ±800 kV high voltage direct current insulators. International Journal of Electrical Power & Energy Systems 2021, 131, 107097. [Google Scholar] [CrossRef]
  5. Ilomuanya, C.; Nekahi, A.; Farokhi, S. A study of the cleansing effect of precipitation and wind on polluted outdoor high voltage glass cap and pin insulator. IEEE Access 2022, 10, 20669–20676. [Google Scholar] [CrossRef]
  6. Stefenon, S.F.; Oliveira, J.R.; Coelho, A.S.; Meyer, L.H. Diagnostic of insulators of conventional grid through LabVIEW analysis of FFT signal generated from ultrasound detector. IEEE Latin America Transactions 2017, 15, 884–889. [Google Scholar] [CrossRef]
  7. Corso, M.P.; Stefenon, S.F.; Singh, G.; Matsuo, M.V.; Perez, F.L.; Leithardt, V.R.Q. Evaluation of visible contamination on power grid insulators using convolutional neural networks. Electrical Engineering 2023, 105, 3881–3894. [Google Scholar] [CrossRef]
  8. Stefenon, S.F.; Seman, L.O.; Sopelsa Neto, N.F.; Meyer, L.H.; Mariani, V.C.; Coelho, L.d.S. Group method of data handling using Christiano-Fitzgerald random walk filter for insulator fault prediction. Sensors 2023, 23, 6118. [Google Scholar] [CrossRef]
  9. Wang, H.; Cheng, L.; Liao, R.; Zhang, S.; Yang, L. Nonlinear ultrasonic nondestructive detection and modelling of kissing defects in high voltage composite insulators. IEEE Transactions on Dielectrics and Electrical Insulation 2020, 27, 924–931. [Google Scholar] [CrossRef]
  10. Salem, A.A.; Lau, K.Y.; Rahiman, W.; Abdul-Malek, Z.; Al-Gailani, S.A.; Rahman, R.A.; Al-Ameri, S. Leakage current characteristics in estimating insulator reliability: Experimental investigation and analysis. Scientific Reports 2022, 12, 14974. [Google Scholar] [CrossRef]
  11. Stefenon, S.F.; Singh, G.; Souza, B.J.; Freire, R.Z.; Yow, K.C. Optimized hybrid YOLOu-Quasi-ProtoPNet for insulators classification. IET Generation, Transmission & Distribution 2023, 17, 3501–3511. [Google Scholar] [CrossRef]
  12. Salem, A.A.; Lau, K.Y.; Abdul-Malek, Z.; Al-Gailani, S.A.; Tan, C.W. Flashover voltage of porcelain insulator under various pollution distributions: Experiment and modeling. Electric Power Systems Research 2022, 208, 107867. [Google Scholar] [CrossRef]
  13. Abanda, A.; Mori, U.; Lozano, J.A. A review on distance based time series classification. Data Mining and Knowledge Discovery 2019, 33, 378–412. [Google Scholar] [CrossRef]
  14. Faouzi, J. Time series classification: A review of algorithms and implementations. Machine Learning (Emerging Trends and Applications) 2022, 1, 1–34. [Google Scholar]
  15. Ismail Fawaz, H.; Forestier, G.; Weber, J.; Idoumghar, L.; Muller, P.A. Deep learning for time series classification: A review. Data mining and knowledge discovery 2019, 33, 917–963. [Google Scholar] [CrossRef]
  16. Dempster, A.; Petitjean, F.; Webb, G.I. ROCKET: Exceptionally fast and accurate time series classification using random convolutional kernels. Data Mining and Knowledge Discovery 2020, 34, 1454–1495. [Google Scholar] [CrossRef]
  17. Dempster, A.; Schmidt, D.F.; Webb, G.I. Minirocket: A very fast (almost) deterministic transform for time series classification. Conference on Knowledge Discovery & Data Mining, 2021, Vol. 27, pp. 248–257. [CrossRef]
  18. Tan, C.W.; Dempster, A.; Bergmeir, C.; Webb, G.I. MultiRocket: Multiple pooling operators and transformations for fast and effective time series classification. Data Mining and Knowledge Discovery 2022, 36, 1623–1646. [Google Scholar] [CrossRef]
  19. Yin, X.; Liu, F.; Cai, R.; Yang, X.; Zhang, X.; Ning, M.; Shen, S. Research on seismic signal analysis based on machine learning. Applied Sciences 2022, 12, 8389. [Google Scholar] [CrossRef]
  20. Stefenon, S.F.; Branco, N.W.; Nied, A.; Bertol, D.W.; Finardi, E.C.; Sartori, A.; Meyer, L.H.; Grebogi, R.B. Analysis of training techniques of ANN for classification of insulators in electrical power systems. IET Generation, Transmission & Distribution 2020, 14, 1591–1597. [Google Scholar] [CrossRef]
  21. Klaar, A.C.R.; Stefenon, S.F.; Seman, L.O.; Mariani, V.C.; Coelho, L.d.S. Optimized EWT-Seq2Seq-LSTM with attention mechanism to insulators fault prediction. Sensors 2023, 23, 3202. [Google Scholar] [CrossRef]
  22. Sopelsa Neto, N.F.; Stefenon, S.F.; Meyer, L.H.; Ovejero, R.G.; Leithardt, V.R.Q. Fault prediction based on leakage current in contaminated insulators using enhanced time series forecasting models. Sensors 2022, 22, 6121. [Google Scholar] [CrossRef]
  23. Medeiros, A.; Sartori, A.; Stefenon, S.F.; Meyer, L.H.; Nied, A. Comparison of artificial intelligence techniques to failure prediction in contaminated insulators based on leakage current. Journal of Intelligent & Fuzzy Systems 2022, 42, 3285–3298. [Google Scholar] [CrossRef]
  24. Branco, N.W.; Cavalca, M.S.M.; Stefenon, S.F.; Leithardt, V.R.Q. Wavelet LSTM for fault forecasting in electrical power grids. Sensors 2022, 22, 8323. [Google Scholar] [CrossRef]
  25. Seman, L.O.; Stefenon, S.F.; Mariani, V.C.; Coelho, L.S. Ensemble learning methods using the Hodrick–Prescott filter for fault forecasting in insulators of the electrical power grids. International Journal of Electrical Power & Energy Systems 2023, 152, 109269. [Google Scholar] [CrossRef]
  26. Stefenon, S.F.; Ribeiro, M.H.D.M.; Nied, A.; Mariani, V.C.; Coelho, L.D.S.; Leithardt, V.R.Q.; Silva, L.A.; Seman, L.O. Hybrid Wavelet Stacking Ensemble Model for Insulators Contamination Forecasting. IEEE Access 2021, 9, 66387–66397. [Google Scholar] [CrossRef]
  27. Stefenon, S.F.; Seman, L.O.; Sopelsa Neto, N.F.; Meyer, L.H.; Nied, A.; Yow, K.C. Echo state network applied for classification of medium voltage insulators. International Journal of Electrical Power & Energy Systems 2022, 134, 107336. [Google Scholar] [CrossRef]
  28. Ferreira, T.V.; Germano, A.D.; da Costa, E.G. Ultrasound and artificial intelligence applied to the pollution estimation in insulations. IEEE Transactions on Power Delivery 2012, 27, 583–589. [Google Scholar] [CrossRef]
  29. Stefenon, S.F.; Freire, R.Z.; Meyer, L.H.; Corso, M.P.; Sartori, A.; Nied, A.; Klaar, A.C.R.; Yow, K.C. Fault detection in insulators based on ultrasonic signal processing using a hybrid deep learning technique. IET Science, Measurement & Technology 2020, 14, 953–961. [Google Scholar] [CrossRef]
  30. Ghosh, R.; Chatterjee, B.; Chakravorti, S. A novel leakage current index for the field monitoring of overhead insulators under harmonic voltage. IEEE Transactions on Industrial Electronics 2018, 65, 1568–1576. [Google Scholar] [CrossRef]
  31. Belhouchet, K.; Bayadi, A.; Bendib, M.E. Artificial neural networks (ANN) and genetic algorithm modeling and identification of arc parameter in insulators flashover voltage and leakage current. International Conference on Electrical Engineering (ICEE), 2015, Vol. 4, pp. 1–6. [CrossRef]
  32. Zhang, S.; Wang, Y.; Liu, M.; Bao, Z. Data-based line trip fault prediction in power systems using LSTM networks and SVM. IEEE Access 2018, 6, 7675–7686. [Google Scholar] [CrossRef]
  33. Fernandes, F.; Stefenon, S.F.; Seman, L.O.; Nied, A.; Ferreira, F.C.S.; Subtil, M.C.M.; Klaar, A.C.R.; Leithardt, V.R.Q. Long short-term memory stacking model to predict the number of cases and deaths caused by COVID-19. Journal of Intelligent & Fuzzy Systems 2022, 6, 6221–6234. [Google Scholar] [CrossRef]
  34. Stefenon, S.F.; Seman, L.O.; Aquino, L.S.; dos Santos Coelho, L. Wavelet-Seq2Seq-LSTM with attention for time series forecasting of level of dams in hydroelectric power plants. Energy 2023, 274, 127350. [Google Scholar] [CrossRef]
  35. Sadykova, D.; Pernebayeva, D.; Bagheri, M.; James, A. IN-YOLO: Real-time detection of outdoor high voltage insulators using UAV imaging. IEEE Transactions on Power Delivery 2020, 35, 1599–1601. [Google Scholar] [CrossRef]
  36. Singh, G.; Stefenon, S.F.; Yow, K.C. Interpretable visual transmission lines inspections using pseudo-prototypical part network. Machine Vision and Applications 2023, 34, 41. [Google Scholar] [CrossRef]
  37. Souza, B.J.; Stefenon, S.F.; Singh, G.; Freire, R.Z. Hybrid-YOLO for classification of insulators defects in transmission lines based on UAV. International Journal of Electrical Power & Energy Systems 2023, 148, 108982. [Google Scholar] [CrossRef]
  38. Prates, R.M.; Cruz, R.; Marotta, A.P.; Ramos, R.P.; Simas Filho, E.F.; Cardoso, J.S. Insulator visual non-conformity detection in overhead power distribution lines using deep learning. Computers & Electrical Engineering 2019, 78, 343–355. [Google Scholar] [CrossRef]
  39. Stefenon, S.F.; Singh, G.; Yow, K.C.; Cimatti, A. Semi-ProtoPNet deep neural network for the classification of defective power grid distribution structures. Sensors 2022, 22, 4859. [Google Scholar] [CrossRef]
  40. Polisetty, S.; El-Hag, A.; Jayram, S. Classification of common discharges in outdoor insulation using acoustic signals and artificial neural network. High Voltage 2019, 4, 333–338. [Google Scholar] [CrossRef]
  41. Mitiche, I.; Jenkins, M.D.; Boreham, P.; Nesbitt, A.; Morison, G. Deep complex neural network learning for high-voltage insulation fault classification from complex bispectrum representation. European Signal Processing Conference; IEEE,, 2019; Vol. 27, pp. 1–5. [CrossRef]
  42. Ibrahim, A.; Dalbah, A.; Abualsaud, A.; Tariq, U.; El-Hag, A. Application of machine learning to evaluate insulator surface erosion. IEEE Transactions on Instrumentation and Measurement 2020, 69, 314–316. [Google Scholar] [CrossRef]
  43. De Santos, H.; Sanz-Bobi, M.A. A machine learning approach for condition monitoring of high voltage insulators in polluted environments. Electric Power Systems Research 2023, 220, 109340. [Google Scholar] [CrossRef]
  44. Stefenon, S.F.; Seman, L.O.; Mariani, V.C.; Coelho, L.S. Aggregating prophet and seasonal trend decomposition for time series forecasting of Italian electricity spot prices. Energies 2023, 16, 1371. [Google Scholar] [CrossRef]
  45. Stefenon, S.F.; Kasburg, C.; Freire, R.Z.; Silva Ferreira, F.C.; Bertol, D.W.; Nied, A. Photovoltaic power forecasting using wavelet neuro-fuzzy for active solar trackers. Journal of Intelligent & Fuzzy Systems 2021, 40, 1083–1096. [Google Scholar] [CrossRef]
  46. Stefenon, S.F.; Kasburg, C.; Nied, A.; Klaar, A.C.R.; Ferreira, F.C.S.; Branco, N.W. Hybrid deep learning for power generation forecasting in active solar trackers. IET Generation, Transmission & Distribution 2020, 14, 5667–5674. [Google Scholar] [CrossRef]
  47. Kong, X.; Guo, J.; Zheng, D.; Zhang, J.; Fu, W. Quality control for medium voltage insulator via a knowledge-informed SPSA based on historical gradient approximations. Processes 2020, 8, 146. [Google Scholar] [CrossRef]
  48. Klaar, A.C.R.; Stefenon, S.F.; Seman, L.O.; Mariani, V.C.; Coelho, L.S. Structure optimization of ensemble learning methods and seasonal decomposition approaches to energy price forecasting in Latin America: A case study about Mexico. Energies 2023, 16, 3184. [Google Scholar] [CrossRef]
  49. Zhao, W.; Xu, M.; Cheng, X.; Zhao, Z. An insulator in transmission lines recognition and fault detection model based on improved faster RCNN. IEEE Transactions on Instrumentation and Measurement 2021, 70, 1–8. [Google Scholar] [CrossRef]
  50. Singh, L.; Alam, A.; Kumar, K.V.; Kumar, D.; Kumar, P.; Jaffery, Z.A. Design of thermal imaging-based health condition monitoring and early fault detection technique for porcelain insulators using Machine learning. Environmental Technology & Innovation 2021, 24, 102000. [Google Scholar] [CrossRef]
  51. Dai, Z. Uncertainty-aware accurate insulator fault detection based on an improved YOLOX model. Energy Reports 2022, 8, 12809–12821. [Google Scholar] [CrossRef]
  52. Mantach, S.; Lutfi, A.; Moradi Tavasani, H.; Ashraf, A.; El-Hag, A.; Kordi, B. Deep learning in high voltage engineering: A literature review. Energies 2022, 15, 5005. [Google Scholar] [CrossRef]
  53. Hao, L.; Zhenhua, L.; Ziyi, C.; Xingxin, C.; Xu, Y. Insulator fouling monitoring based on acoustic signal and one-dimensional convolutional neural network. Frontiers in Energy Research 2023, 10, 43–50. [Google Scholar]
  54. Nguyen, T.P.; Yeh, C.T.; Cho, M.Y.; Chang, C.L.; Chen, M.J. Convolutional neural network bidirectional long short-term memory to online classify the distribution insulator leakage currents. Electric Power Systems Research 2022, 208, 107923. [Google Scholar] [CrossRef]
  55. Thanh, P.N.; Cho, M.Y. Online leakage current classification using convolutional neural network long short-term memory for high voltage insulators on web-based service. Electric Power Systems Research 2023, 216, 109065. [Google Scholar] [CrossRef]
  56. Sajjadi, B.; Asaithambi, P.; Raman, A.A.A.; Ibrahim, S. Hybrid nero-fuzzy methods for estimation of ultrasound and mechanically stirring Influences on biodiesel synthesis through transesterification. Measurement 2017, 103, 62–76. [Google Scholar] [CrossRef]
  57. Pisani, P.; Greco, A.; Conversano, F.; Renna, M.D.; Casciaro, E.; Quarta, L.; Costanza, D.; Muratore, M.; Casciaro, S. A quantitative ultrasound approach to estimate bone fragility: A first comparison with dual X-ray absorptiometry. Measurement 2017, 101, 243–249. [Google Scholar] [CrossRef]
  58. Pisani, P.; Conversano, F.; Chiriacò, F.; Quarta, E.; Quarta, L.; Muratore, M.; Lay-Ekuakille, A.; Casciaro, S. Estimation of femoral neck bone mineral density by ultrasound scanning: Preliminary results and feasibility. Measurement 2016, 94, 480–486. [Google Scholar] [CrossRef]
  59. Greco, A.; Pisani, P.; Conversano, F.; Soloperto, G.; Renna, M.D.; Muratore, M.; Casciaro, S. Ultrasound fragility Score: An innovative approach for the assessment of bone fragility. Measurement 2017, 101, 236–242. [Google Scholar] [CrossRef]
  60. Stefenon, S.F.; Furtado Neto, C.S.; Coelho, T.S.; Nied, A.; Yamaguchi, C.K.; Yow, K.C. Particle swarm optimization for design of insulators of distribution power system based on finite element method. Electrical Engineering 2022, 104, 615–622. [Google Scholar] [CrossRef]
  61. Stefenon, S.F.; Americo, J.P.; Meyer, L.H.; Grebogi, R.B.; Nied, A. Analysis of the electric field in porcelain pin-type insulators via finite elements software. IEEE Latin America Transactions 2018, 16, 2505–2512. [Google Scholar] [CrossRef]
  62. Sopelsa Neto, N.F.; Stefenon, S.F.; Meyer, L.H.; Bruns, R.; Nied, A.; Seman, L.O.; Gonzalez, G.V.; Leithardt, V.R.Q.; Yow, K.C. A study of multilayer perceptron networks applied to classification of ceramic insulators using ultrasound. Applied Sciences 2021, 11, 1592. [Google Scholar] [CrossRef]
  63. Stefenon, S.F.; Bruns, R.; Sartori, A.; Meyer, L.H.; Ovejero, R.G.; Leithardt, V.R.Q. Analysis of the ultrasonic signal in polymeric contaminated insulators through ensemble learning methods. IEEE Access 2022, 10, 33980–33991. [Google Scholar] [CrossRef]
  64. Stefenon, S.F.; Seman, L.O.; Pavan, B.A.; Ovejero, R.G.; Leithardt, V.R.Q. Optimal design of electrical power distribution grid spacers using finite element method. IET Generation, Transmission & Distribution 2022, 16, 1865–1876. [Google Scholar] [CrossRef]
  65. Stefenon, S.F.; Corso, M.P.; Nied, A.; Perez, F.L.; Yow, K.C.; Gonzalez, G.V.; Leithardt, V.R.Q. Classification of insulators using neural network based on computer vision. IET Generation, Transmission & Distribution 2021, 16, 1096–1107. [Google Scholar] [CrossRef]
  66. Stefenon, S.F.; Silva, M.C.; Bertol, D.W.; Meyer, L.H.; Nied, A. Fault diagnosis of insulators from ultrasound detection using neural networks. Journal of Intelligent & Fuzzy Systems 2019, 37, 6655–6664. [Google Scholar] [CrossRef]
  67. Middlehurst, M.; Large, J.; Flynn, M.; Lines, J.; Bostrom, A.; Bagnall, A. HIVE-COTE 2.0: A new meta ensemble for time series classification. Machine Learning 2021, 110, 3211–3243. [Google Scholar] [CrossRef]
  68. Pantiskas, L.; Verstoep, K.; Hoogendoorn, M.; Bal, H. Taking ROCKET on an efficiency mission: Multivariate time series classification with LightWaveS. International Conference on Distributed Computing in Sensor Systems (DCOSS), 2022, Vol. 18, pp. 149–152. [CrossRef]
  69. Bondugula, R.K.; Udgata, S.K.; Sivangi, K.B. A novel deep learning architecture and MINIROCKET feature extraction method for human activity recognition using ECG, PPG and inertial sensor dataset. Applied Intelligence 2022, 1–26. [Google Scholar] [CrossRef]
  70. Thangarajoo, R.G.; Reaz, M.B.I.; Srivastava, G.; Haque, F.; Ali, S.H.M.; Bakar, A.A.A.; Bhuiyan, M.A.S. Machine learning-based epileptic seizure detection methods using wavelet and EMD-based decomposition techniques: A review. Sensors 2021, 21, 8485. [Google Scholar] [CrossRef]
  71. Yao, L.; Pan, Z. A new method based CEEMDAN for removal of baseline wander and powerline interference in ECG signals. Optik 2020, 223, 165566. [Google Scholar] [CrossRef]
  72. Anuragi, A.; Sisodia, D.S.; Pachori, R.B. Epileptic-seizure classification using phase-space representation of FBSE-EWT based EEG sub-band signals and ensemble learners. Biomedical Signal Processing and Control 2022, 71, 103138. [Google Scholar] [CrossRef]
  73. Ding, J.; Xiao, D.; Li, X. Gear fault diagnosis based on genetic mutation particle swarm optimization VMD and probabilistic neural network algorithm. IEEE Access 2020, 8, 18456–18474. [Google Scholar] [CrossRef]
  74. Smith, J.R.; Al-Badrawi, M.H.; Kirsch, N.J. An Optimized De-Noising Scheme Based on the Null Hypothesis of Intrinsic Mode Functions. IEEE Signal Processing Letters 2019, 26, 1232–1236. [Google Scholar] [CrossRef]
  75. Liu, S.; Sun, Y.; Zhang, L.; Su, P. Fault diagnosis of shipboard medium-voltage DC power system based on machine learning. International Journal of Electrical Power & Energy Systems 2021, 124, 106399. [Google Scholar] [CrossRef]
  76. Yamasaki, M.; Freire, R.Z.; Seman, L.O.; Stefenon, S.F.; Mariani, V.C.; dos Santos Coelho, L. Optimized hybrid ensemble learning approaches applied to very short-term load forecasting. International Journal of Electrical Power & Energy Systems 2024, 155, 109579. [Google Scholar] [CrossRef]
  77. Wang, X.; Zhang, F.; Wei, X.; Gao, J.; Guo, L.; Wang, Y. Fault location of flexible grounding distribution system based on multivariate modes and kurtosis calibration. International Journal of Electrical Power & Energy Systems 2023, 150, 109108. [Google Scholar] [CrossRef]
  78. Liu, Y.; Yuan, D.; Gong, Z.; Jin, T.; Mohamed, M.A. Adaptive spectral trend based optimized EWT for monitoring the parameters of multiple power quality disturbances. International Journal of Electrical Power & Energy Systems 2023, 146, 108797. [Google Scholar] [CrossRef]
  79. Cheng, H.; Ding, X.; Zhou, W.; Ding, R. A hybrid electricity price forecasting model with Bayesian optimization for German energy exchange. International Journal of Electrical Power & Energy Systems 2019, 110, 653–666. [Google Scholar] [CrossRef]
  80. Wang, X.; Gao, X.; Liu, Y.; Wang, R.; Ma, N.; Qu, M. Bi-level decision matrix based fault location method for multi-branch offshore wind farm transmission lines. International Journal of Electrical Power & Energy Systems 2022, 141, 108137. [Google Scholar] [CrossRef]
  81. Campos, F.S.; Assis, F.A.; Leite da Silva, A.M.; Coelho, A.J.; Moura, R.A.; Schroeder, M.A.O. Reliability evaluation of composite generation and transmission systems via binary logistic regression and parallel processing. International Journal of Electrical Power & Energy Systems 2022, 142, 108380. [Google Scholar] [CrossRef]
  82. Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
  83. Kumar Mohanty, S.; Swetapadma, A.; Kumar Nayak, P.; Malik, O.P. Decision tree approach for fault detection in a TCSC compensated line during power swing. International Journal of Electrical Power & Energy Systems 2023, 146, 108758. [Google Scholar] [CrossRef]
  84. Mishra, S.; Mallick, P.K.; Tripathy, H.K.; Bhoi, A.K.; González-Briones, A. Performance evaluation of a proposed machine learning model for chronic disease datasets using an integrated attribute evaluator and an improved decision tree classifier. Applied Sciences 2020, 10, 8137. [Google Scholar] [CrossRef]
  85. Tripoppoom, S.; Ma, X.; Yong, R.; Wu, J.; Yu, W.; Sepehrnoori, K.; Miao, J.; Li, N. Assisted history matching in shale gas well using multiple-proxy-based Markov chain Monte Carlo algorithm: The comparison of K-nearest neighbors and neural networks as proxy model. Fuel 2020, 262, 116563. [Google Scholar] [CrossRef]
  86. Zhang, S.; Li, X.; Zong, M.; Zhu, X.; Wang, R. Efficient k-NN classification With different numbers of nearest neighbors. IEEE Transactions on Neural Networks and Learning Systems 2018, 29, 1774–1785. [Google Scholar] [CrossRef] [PubMed]
  87. Corso, M.P.; Perez, F.L.; Stefenon, S.F.; Yow, K.C.; García Ovejero, R.; Leithardt, V.R.Q. Classification of contaminated insulators using k-nearest neighbors based on computer vision. Computers 2021, 10, 112. [Google Scholar] [CrossRef]
  88. Ali, L.; Zhu, C.; Zhang, Z.; Liu, Y. Automated detection of Parkinson’s disease based on multiple types of sustained phonations using linear discriminant analysis and genetically optimized neural network. IEEE Journal of Translational Engineering in Health and Medicine 2019, 7, 1–10. [Google Scholar] [CrossRef] [PubMed]
  89. Jayachitra, S.; Prasanth, A. Multi-feature analysis for automated brain stroke classification using weighted Gaussian naïve Bayes classifier. Journal of Circuits, Systems and Computers 2021, 30, 2150178. [Google Scholar] [CrossRef]
  90. Yılmaz, A.; Küçüker, A.; Bayrak, G.; Ertekin, D.; Shafie-Khah, M.; Guerrero, J.M. An improved automated PQD classification method for distributed generators with hybrid SVM-based approach using un-decimated wavelet transform. International Journal of Electrical Power & Energy Systems 2022, 136, 107763. [Google Scholar] [CrossRef]
  91. Samantaray, S. Ensemble decision trees for high impedance fault detection in power distribution network. International Journal of Electrical Power & Energy Systems 2012, 43, 1048–1055. [Google Scholar] [CrossRef]
  92. Khan, M.S.I.; Islam, N.; Uddin, J.; Islam, S.; Nasir, M.K. Water quality prediction and classification based on principal component regression and gradient boosting classifier approach. Journal of King Saud University-Computer and Information Sciences 2022, 34, 4773–4781. [Google Scholar] [CrossRef]
  93. Hou, H.; Zhang, Z.; Yu, J.; Wei, R.; Huang, Y.; Li, X. Damage prediction of 10 kV power towers in distribution network under typhoon disaster based on data-driven model. International Journal of Electrical Power & Energy Systems 2022, 142, 108307. [Google Scholar] [CrossRef]
  94. Hou, H.; Chen, X.; Li, M.; Zhu, L.; Huang, Y.; Yu, J. Prediction of user outage under typhoon disaster based on multi-algorithm Stacking integration. International Journal of Electrical Power & Energy Systems 2021, 131, 107123. [Google Scholar] [CrossRef]
  95. Xuan, W.; Shouxiang, W.; Qianyu, Z.; Shaomin, W.; Liwei, F. A multi-energy load prediction model based on deep multi-task learning and ensemble approach for regional integrated energy systems. International Journal of Electrical Power & Energy Systems 2021, 126, 106583. [Google Scholar] [CrossRef]
  96. Hu, G.; Yin, C.; Wan, M.; Zhang, Y.; Fang, Y. Recognition of diseased Pinus trees in UAV images using deep learning and AdaBoost classifier. Biosystems Engineering 2020, 194, 138–151. [Google Scholar] [CrossRef]
  97. Xiao, G.; Cheng, Q.; Zhang, C. Detecting travel modes Using rule-based classification system and Gaussian process classifier. IEEE Access 2019, 7, 116741–116752. [Google Scholar] [CrossRef]
  98. Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. International Conference on Knowledge Discovery and Data Mining; ACM: New York, USA, 2016. [Google Scholar] [CrossRef]
  99. Dong, W.; Huang, Y.; Lehane, B.; Ma, G. XGBoost algorithm-based prediction of concrete electrical resistivity for structural health monitoring. Automation in Construction 2020, 114, 103155. [Google Scholar] [CrossRef]
  100. Fang, H.; Xiao, J.W.; Wang, Y.W. A machine learning-based detection framework against intermittent electricity theft attack. International Journal of Electrical Power & Energy Systems 2023, 150, 109075. [Google Scholar] [CrossRef]
  101. Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; Vanderplas, J.; Passos, A.; Cournapeau, D.; Brucher, M.; Perrot, M.; Duchesnay, E. Scikit-learn: Machine Learning in Python. Journal of Machine Learning Research 2011, 12, 2825–2830. [Google Scholar]
Preprints 96873 g001
Figure 1. Insulator drilled with a bench drill to simulate a perforation caused by an electric discharge: A) Top view; B) Bottom view.
Figure 1. Insulator drilled with a bench drill to simulate a perforation caused by an electric discharge: A) Top view; B) Bottom view.
Preprints 96873 g001
Preprints 96873 g002
Figure 2. High-voltage applied experiment under controlled conditions.
Figure 2. High-voltage applied experiment under controlled conditions.
Preprints 96873 g002
Preprints 96873 g003
Figure 3. Ultrasound recorded signal: (a) normal; (b) fault.
Figure 3. Ultrasound recorded signal: (a) normal; (b) fault.
Preprints 96873 g003
Preprints 96873 g004
Figure 4. Architecture of the proposed model.
Figure 4. Architecture of the proposed model.
Preprints 96873 g004
Preprints 96873 g005
Figure 5. Critical Difference Diagram for the results of Table 1.
Figure 5. Critical Difference Diagram for the results of Table 1.
Preprints 96873 g005
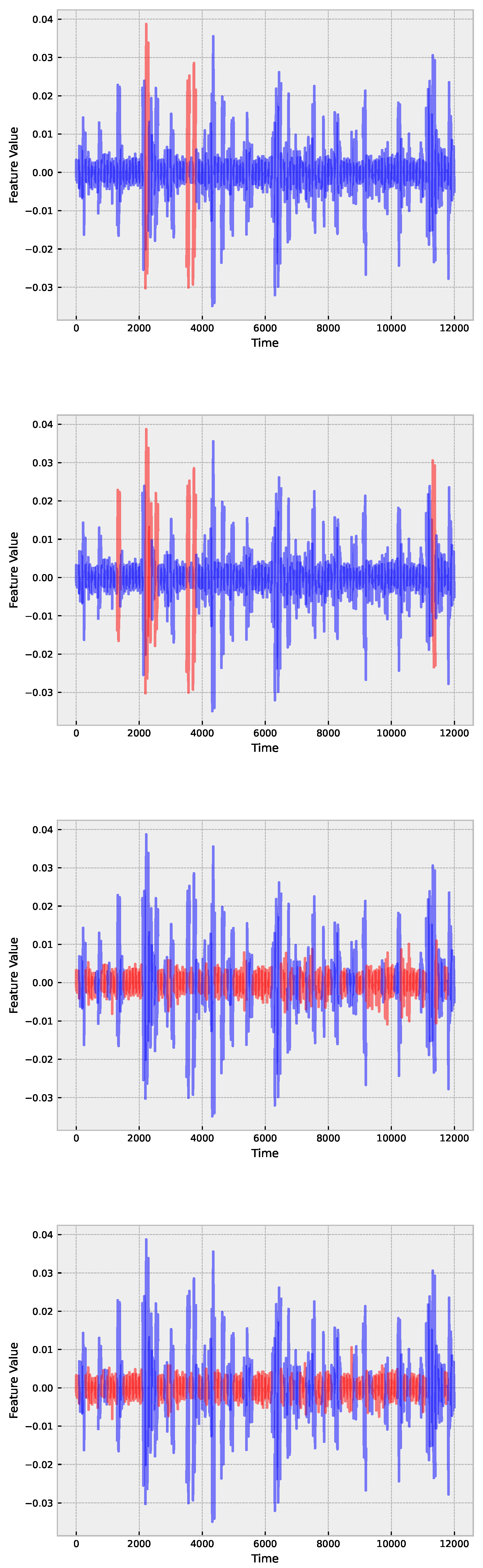
Preprints 96873 g006
Figure 6. Classification for a time window of 100 for (a) Logistic Regression; (b) Ridge Regression; (c) Decision Tree; (d) XGBoost. Blue indicates normal operation conditions, while red indicates a fault.
Figure 6. Classification for a time window of 100 for (a) Logistic Regression; (b) Ridge Regression; (c) Decision Tree; (d) XGBoost. Blue indicates normal operation conditions, while red indicates a fault.
Preprints 96873 g006
Preprints 96873 g007
Figure 7. Diagram of Critical Difference for the results of Table 5.
Figure 7. Diagram of Critical Difference for the results of Table 5.
Preprints 96873 g007
Table 1. Accuracy of different methods for windows size of 10, 50 and 100.
Table 1. Accuracy of different methods for windows size of 10, 50 and 100.
Model WS10 WS50 WS100
Logistic Regression 0.5193 ± 0.0395 0.5167 ± 0.0325 0.5683 ± 0.0436
Ridge Regression 0.4923 ± 0.0134 0.5158 ± 0.0308 0.58 ± 0.041
Decision Tree 0.849 ± 0.0832 0.8658 ± 0.0789 0.8283 ± 0.0759
k-NN 0.8762 ± 0.0713 0.9025 ± 0.0748 0.85 ± 0.1182
LDA 0.4858 ± 0.0147 0.495 ± 0.0286 0.525 ± 0.0247
Gaussian Naive Bayes 0.8428 ± 0.0927 0.9133 ± 0.0746 0.9283 ± 0.0586
SVM 0.5343 ± 0.0379 0.5283 ± 0.0263 0.53 ± 0.0306
Random Forest 0.8672 ± 0.0815 0.9225 ± 0.0621 0.925 ± 0.0548
Gradient Boosting 0.8792± 0.0694 0.9433± 0.0439 0.9433 ± 0.0464
AdaBoost 0.8693 ± 0.07 0.9258 ± 0.0504 0.9317 ± 0.0593
Gaussian Process 0.6085 ± 0.0811 0.6342 ± 0.0564 0.615 ± 0.0883
XGBoost 0.8753 ± 0.0691 0.9417 ± 0.0484 0.935 ± 0.0539
LightGBM 0.8732 ± 0.0695 0.94 ± 0.0467 0.95± 0.0431
Table 2. Accuracy of different methods with different rockets methods for a window size of 10-time steps.
Table 2. Accuracy of different methods with different rockets methods for a window size of 10-time steps.
Model Rocket MiniRocket MultiRocket
Logistic Regression 0.7552 ± 0.0353 0.8453 ± 0.068 0.8465 ± 0.06
Ridge Regression 0.6762 ± 0.0462 0.7943 ± 0.0518 0.8068 ± 0.0447
Decision Tree 0.7427 ± 0.0617 0.8635 ± 0.0687 0.8687 ± 0.064
k-NN 0.7375 ± 0.0387 0.8488 ± 0.0729 0.8623 ± 0.0676
LDA 0.6048 ± 0.0635 0.7832 ± 0.0421 D.N.C. *
Gaussian Naive Bayes 0.7615 ± 0.0515 0.8253 ± 0.0926 0.8342 ± 0.0894
SVM 0.6968 ± 0.0438 0.8257 ± 0.0647 0.8413 ± 0.0583
Random Forest 0.762 ± 0.0553 0.8788 ± 0.0659 0.882 ± 0.0676
Gradient Boosting 0.7735 ± 0.0543 0.8837± 0.0655 0.8873± 0.0632
AdaBoost 0.7452 ± 0.0544 0.8678 ± 0.0695 0.8715 ± 0.0639
XGBoost 0.7623 ± 0.0472 0.8785 ± 0.0687 0.8823 ± 0.0638
LightGBM 0.7713 ± 0.0482 0.8832 ± 0.067 0.8873± 0.0622
* Did not converge (D.N.C.).
Table 3. Accuracy of different rocket methods with a window size of 50-time steps.
Table 3. Accuracy of different rocket methods with a window size of 50-time steps.
Model Rocket MiniRocket MultiRocket
Logistic Regression 0.955± 0.0395 0.955± 0.0395 0.955 ± 0.0384
Ridge Regression 0.9533 ± 0.036 0.9533 ± 0.036 0.9508 ± 0.0389
Decision Tree 0.9258 ± 0.0551 0.9342 ± 0.0468 0.9367 ± 0.0511
k-NN 0.9483 ± 0.0427 0.9483 ± 0.0427 0.9433 ± 0.043
LDA 0.9533 ± 0.0361 0.9533 ± 0.0361 0.9492 ± 0.0418
Gaussian Naive Bayes 0.9308 ± 0.0491 0.9308 ± 0.0491 0.9283 ± 0.0502
SVM 0.9525 ± 0.0398 0.9525 ± 0.0398 0.9525 ± 0.0368
Random Forest 0.9483 ± 0.0459 0.9508 ± 0.0461 0.9483 ± 0.0402
Gradient Boosting 0.9517 ± 0.042 0.9483 ± 0.0452 0.9492 ± 0.0414
AdaBoost 0.9475 ± 0.0416 0.9475 ± 0.0416 0.955 ± 0.0349
Gaussian Process 0.9367 ± 0.0509 0.9367 ± 0.0509 D.N.C. *
XGBoost 0.9475 ± 0.044 0.9475 ± 0.044 0.9575 ± 0.0339
LightGBM 0.9542 ± 0.0365 0.9542 ± 0.0365 0.9592± 0.0309
* Did not converge (D.N.C.).
Table 4. Accuracy of different methods with different rockets methods for a window size of 100-time steps.
Table 4. Accuracy of different methods with different rockets methods for a window size of 100-time steps.
Model Rocket MiniRocket MultiRocket
Logistic Regression 0.9783± 0.0194 0.9783± 0.0194 0.9733 ± 0.0249
Ridge Regression 0.9767 ± 0.0193 0.9767 ± 0.0193 0.9717 ± 0.034
Decision Tree 0.9633 ± 0.0323 0.9667 ± 0.0316 0.97 ± 0.0282
k-NN 0.9567 ± 0.037 0.9567 ± 0.037 0.9683 ± 0.0309
LDA 0.97 ± 0.0261 0.97 ± 0.0261 0.975 ± 0.0247
Gaussian Naive Bayes 0.945 ± 0.0515 0.945 ± 0.0515 0.9483 ± 0.0392
SVM 0.9783 ± 0.018 0.9783± 0.018 0.9717 ± 0.0277
Random Forest 0.9717 ± 0.0314 0.9767 ± 0.0244 0.9733 ± 0.0309
Gradient Boosting 0.9683 ± 0.0271 0.97 ± 0.0251 0.9717 ± 0.0245
AdaBoost 0.9783± 0.0201 0.9733 ± 0.0295 0.965 ± 0.0399
Gaussian Process 0.96 ± 0.0363 0.96 ± 0.0363 D.N.C. *
XGBoost 0.9767 ± 0.0249 0.9767 ± 0.0249 0.975± 0.0228
LightGBM 0.9767 ± 0.022 0.9767 ± 0.022 0.965 ± 0.0429
* Did not converge (D.N.C.).
Table 5. Results for logistic regression considering different window sizes and EMB.
Table 5. Results for logistic regression considering different window sizes and EMB.
Accuracy
Window Size W/o EMB EWT CEENDAM VMD
10 0.8487 ± 0.0711 0.9757 ± 0.0177 0.9192 ± 0.129 0.9677 ± 0.0267
50 0.9583 ± 0.0333 0.9883 ± 0.0116 0.98 ± 0.0278 0.9767 ± 0.0187
100 0.9783 ± 0.0194 0.995 ± 0.0067 0.9917 ± 0.0105 0.98 ± 0.0187
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated