Unified Classical Thermodynamics: Primacy of Dissymmetry over Free Energy

Preprint

Article

Unified Classical Thermodynamics: Primacy of Dissymmetry over Free Energy

Altmetrics

Downloads

110

Views

Comments

A peer-reviewed article of this preprint also exists.

Lin-shu Wang^*

This version is not peer-reviewed

Submitted:

19 January 2024

Posted:

22 January 2024

You are already at the latest version

Alerts

Abstract

In thermodynamic theory, free energy (i.e., available energy) is the concept facilitating the combined applications of the theory’s two fundamental laws, the first and the second laws of thermodynamics. The critical step was taken by Kelvin, then by Helmholtz and Gibbs— that in natural processes, free energy dissipates spontaneously. With the formulation of the second law of entropy growth, this may be referred to as the dissymmetry proposition manifested in the spontaneous increase of system/environment-entropy towards equilibrium. Because of Kelvin’s pre-entropy-law formulation of free energy, our concept of free energy is still defined, energy-centrally, as body’s internal energy or enthalpy, subtracted by energy that is not available within a framework on the premise of primacy of energy, in which free energy dissipates spontaneously and universally. This primacy of energy is called into question because the driving force to cause a system’s change is the purview of the second law. This paper makes a case for an engineering thermodynamics framework, instead, to be based on the premise of the primacy of dissymmetry over free energy. With Gibbsian thermodynamics undergirded with dissymmetry proposition and engineering thermodynamics with the dissymmetry premise, the two branches of thermodynamics are unified to become classical thermodynamics.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction: Free Energy vs. Nature’s Dissymmetry

The theory of thermodynamics is based on a set of four laws of thermodynamics: the zeroth law of thermodynamics defining temperature, the first law of thermodynamics of energy conservation, the second law of thermodynamics of inexorable entropy growth, and the third law of thermodynamics defining the absolute entropy value. While the theory is incomplete with the absence of any one of the four laws, it may be said that the two principal laws of the set are the first law and the second law and that the core content of the theory and its applications are the combined applications of the theory’s two principal laws.

In the formative years of thermodynamics of 1850 to 1855, [1] the focus was on the combined application of the two laws for treating the interactive relationship between heat and work in terms of energy. The defining problem of thermodynamics was the motive power of heat. For this reason, Thomson (Kelvin) invented the concept of available energy, i.e., in the interactions between heat work, total energy is conserved but available energy dissipates ([2]: 511-514; see also [¹]: Appendix II, especially [page five]). In the title of paper [²], Thomson talked about the dissipation of mechanical energy, but he clearly was referring to the dissipation of mechanical energy and available energy:

Significantly, he made it clear, by writing “When heat is diffused by conduction, there is a dissipation of mechanical energy” and “the mechanical effect stated in Carnot’s Theory to be absolutely lost by conduction,” that the universal dissipation of mechanical energy meant the universal dissipation of available energy. Heat energy or high temperature thermal internal energy is one form of available energy. [3: 5]

That Kelvin invented the concept of available energy without a clear conception of entropy and the fact that he should be credited as the sole originator of the concept was also made clear by Maxwell:

Thomson, the last but not the least of the three great founders [Clausius, Rankine, and Thomson], does not even consecrate a symbol to denote the entropy, but he was the first to clearly define the intrinsic energy of a body, and to him alone are due the ideas and definitions of the available energy and the dissipation of [available] energy. [4]

Between 1854 and 1865, Clausius developed his entropy theorem, which he referred to initially as the second fundamental theorem (the equivalence theorem of heat and work as the first fundamental theorem). The development culminated in 1865 in the formal introduction of entropy as a new thermodynamic variable, and the formulation of the entropy law as the second law of thermodynamics.

With the introduction of entropy, we have the complete set of thermodynamic variables: pressure, volume, temperature, internal energy, and entropy. The focus of the combined application of the two laws shifted from engineering and engineered processes of heat and work to physics/chemistry and spontaneous natural processes driven by thermodynamic potentials. As Vemulapalli noted,

Massieu [1869] and Gibbs [1873] steered thermodynamics in a radically different direction. Their idea was to find characteristic functions, called thermodynamic potentials, for a system and relate all thermodynamic properties of the system to these functions. Thermodynamic processes between system and surroundings are viewed as consequences of changes in thermodynamic potentials within the system, while in earlier theories the properties of a system were defined by its interaction with the surroundings. Massieu and Gibbs were perhaps the first to consider entropy as a property of the system rather than as energy unavailable for work on the surroundings [5].

In Sects. 2 and 3 of the paper, an outline of this new focus on physics and chemistry is given representing the outcome to a successful and elegant Gibbsian equilibrium thermodynamics. In Sect. 3, some details are provided to describe the spontaneous tendency of systems towards equilibrium as manifestation of the second law. This has been referred to as Nature’s Dissymmetry in a book on The Second Law by Atkins. [6] Dissymmetry and its manifestation into chaos are the theme of the book [⁶]: The Second Law, in its Ch. 3, talks about the natural tendency of “collapsing into chaos”; the “potency of chaos” that “the central theme of our discussion so far is that chaos can be constructive” in Ch. 5; and “constructive chaos” and “patterns of chaos” in Chaps. 8 and 9.

In Sects. 4, 5, and 6, the paper continues the tread of the theory core as the combined applications of the theory’s two principal laws returning to its original engineering focus, i.e., engineering thermodynamics. A critical evaluation is carried out. This evaluation exposes a structural problem of engineering thermodynamics. In contrast to the success of equilibrium thermodynamics, the paper identifies a deficiency in engineering thermodynamics: the deficiency will be referred to as engineering thermodynamics of entropy pessimism in another writing project by the author. Within the present paper’s scope, the deficiency is characterized in Sect. 7.2 to be inadequacy in the understanding within the framework of the energy conversion doctrine of “reversibility,” a concept of central importance ever since Carnot invented the concept.

The paper begins with the suggestion that the Kelvin project of combining the first law and the second law without the benefit of the mature second law is destined to be a defective project. Sects. 2 and 3 record that the success of Gibbsian equilibrium thermodynamics is crucially due to the fact that it is a theoretical system of inferences (in terms of “states” or “properties” as the fundamental constructs of the theory) centered on the entropy law. Deriving from this observation, the lesson is that it is necessity to transforming engineering thermodynamics to be the same kind of system: the thesis of the paper is that the dissymmetry proposition of equilibrium thermodynamics—the second law of thermodynamics and its direct inference that a system has the spontaneous tendency towards equilibrium characterized in terms of the maximization of total entropy—should be generalized to be the foundation (to be referred to as the dissymmetry premise) of the WHOLE thermodynamics; under the “old stereos [stereotypes]” (Marshall McLuhan, Dec. 30, 2011) of viewing heat as the driving force of steam engines, the foundational question in this generalization is what the real driving force of the irreversible world is. (An expanded version of the thesis is found at the end of Sect. 7, Sect, 7.3.)

In one sense, the paper transforms engineering thermodynamics into a theoretical system by translating the verbal “chaos can be constructive” assertion of The Second Law [⁶] into a quantitative theoretical system of classical thermodynamics unifying the two branches of equilibrium and engineering thermodynamics.

2. Combined Statement of the First and Second Laws

Let us start with the first law,

d U = δ Q - δ W

(1)

where U is the internal energy of the system, Q the heat added to the system, and W the work produced by the system. At this point, it is useful to introduce the concepts of reversibility, internal reversibility, and quasi-staticity ([7: Sect, 6,5], see Figure 1, which is reproduced from [⁷]).

Between 1854 and 1865, Clausius formulated the second law first by expressing entropy, S, to heat added to the system,

d S = {(\frac{δ Q}{T})}_{R e v}

(2)

And the second law itself as,

S_{f i n a l} - S_{i n i t i a l} \geq 0

(3)

Similarly, for reversible processes, the work produced by the system is

δ W = p d V

where p is the pressure of the system and V the volume of the system. Substitution of

δ W

and

δ Q

(Eq. (2)) into Eq. (1) yields, for reversible processes,

d U = T d S - p d V

, the combined statement of the first law and the second law.

The condition of reversibility in (2) is a severe limitation to the equation rendering it useless: If no real process can be truly reversible, how can we apply (2) for determining the value of entropy? In an attempt to answer the question, the classical (Caratheodory) formalism introduced the quasi-static process interpretation of

d U = T d S - p d V

, and Landsberg noted, in the formalism, “the concept of reversible processes, which plays an essential role in many expositions of thermodynamics, is not required in the present approach” [8].

As noted in A Treatise [⁷], Sects. 6.2 and 6.7, classical formalism is correct in pointing out that reversibility is too restrictive a condition for defining entropy. Classical formalism is mistaken, however, in replacing reversibility with quasi-staticity. An argument is made in A Treatise (Sect. 6.7) that quasi-staticity in the classical formalism,

{(δ Q)}_{Q u a s i} = T d S

(4)

is in fact Internal Reversibility,

{(δ Q)}_{I R} = T d S

(5)

The so called “quasi-static work and quasi-static heat” expressions should be “internal reversibility work and heat” expressions,

{(δ W)}_{I R} = p d V

and (5).

That is to say, referring to Figure 1, reversibility, the condition for the definition of entropy in accordance with Clausius, is the sufficient condition for the definition of entropy; while quasi-staticity is the necessary condition; and internal reversibility, IR, is the necessary and sufficient condition. Correspondingly, of the four equations,

d U = δ Q - δ W

(1)

d U = δ Q - p d V

(6)

d U = T d S - δ W

(7)

d U = T d S - p d V

(8)

Eq. (1) always holds because it is the first law expression, while eq. (6) and eq. (7) hold only under IR condition when “internal reversibility work” and “internal reversibility heat” apply respectively.

Let us turn our attention to eq. (8),

d U = T d S - p d V

(8)

Even though A treatise [⁷] refutes Classical Formalism’s replacement of reversibility with quasi-staticity for the definition of entropy, the innovation of Classical Formalism of quasi-staticity is of fundamental importance. Its introduction answers the question, “If no real process can be truly reversible, how can we determine the value of entropy without relying on eq. (2)?” It turns out that we don’t need eq. (2) nor eq. (5) because of the availability of eq. (8), which holds under the condition of quasi-staticity: for the expression being a differential form of a relation among thermodynamic state functions of U, T, S, p, and V, the values of which depend on states independent of the specific paths of the system approaching the states. We may consider a functional relation of U as a function of S and V.

Callen calls this functional relation a fundamental relation, [9]

U = U (S, V)

(9)

Partial derivatives of which are identified as,

T = T (S, V) = {(\frac{\partial U}{\partial S})}_{V}

(10)

p = p (S, V) = - {(\frac{\partial U}{\partial V})}_{S}

(11)

The validity of relations (8), (9), (10), and (11) is quasi-staticity.

In sum, as A Treatise concludes, “A reversible machine remains the best or natural approach to start the consideration of the concept of entropy” [⁷: 152]; once the introduction is made, “classical formalism is correct in pointing out that reversibility is a too restrictive condition or defining entropy,” but the proposed condition for entropy definition, quasi-staticity, “is in fact internal reversibility,” the condition for internal reversibility work and internal reversibility heat; the importance of the proposed quasi-staticity lies not for serving as the condition for defining entropy but stead for enabling the value determination of entropy through establishing the quasi-staticity validity for the set of the fundamental relation, (9), its associated partial derivatives, (10) and (11), and the differential form of the fundamental relation, (8).

For an example of the value determination of entropy without involving the direct use of the entropy definition of (2) or (5), one finds, for instance, the application of equation (16) in paper [⁵].

For highlighting the pivotal role quasi-staticity validity plays as the foundation of Classical Formalism, I propose to call the fundamental relation, Eq. (9), the Gibbs-Carathéodory fundamental relation, and Eq. (8) the Gibbs-Carathéodory equation.

3. Method of Potentials: Nature’s Dissymmetry

The Gibbs- Carathéodory fundamental relation is a canonical relationship of one canonical form. We refer to

U = U (S, V)

as the energy representation of the fundamental relation [⁹: 28, 41]. Correspondingly,

S = S (U, V)

is referred to as the entropy representation of the fundamental relation [⁹: 41].

“It is an inference naturally suggested by the general increase of entropy which accompanies the changes occurring in any isolated material system that when the entropy has reached a maximum, the system will be in a state of equilibrium,” noted Gibbs [10]. Consider an example of isolated composite system consisting of a subsystem⁽¹⁾ and a subsystem⁽²⁾, details of which are found in Callen [⁹: Chapter 2]. The entropic fundamental relation is,

S = S^{(1)} (U^{(1)}, V^{(1)}) + S^{(2)} (U^{(2)}, V^{(2)})

(12)

(12) is subject to the restriction of the closure conditions

U^{(1)} + U^{(2)} = c o n s t a n t

(13)

V^{(1)} + V^{(2)} = c o n s t a n t

(14)

Assume that such a system initially exists at

{T^{(1)}}_{i n i} > {T^{(2)}}_{i n i}

and

{p^{(1)}}_{i n i} > {p^{(2)}}_{i n i}

. And assume that the wall separating the two subsystems that has kept the system at its initial state are replaced by a diathermal and movable wall at a given time. The system will spontaneously move towards thermodynamic equilibrium in accordance with the entropy law corresponding to a state of maximum entropy. That is,

d S_{e q u i l i} = 0

(15)

Substitution of (12) into (15) yields,

\begin{matrix} 0 = d S_{e q u i l i} = d {S^{(1)}}_{e q u i l i} + d {S^{(2)}}_{e q u i l i} = \\ [{(\frac{\partial S^{(1)}}{\partial U^{(1)}})}_{V^{(1)}} d U^{(1)} + {(\frac{\partial S^{(1)}}{\partial V^{(1)}})}_{U^{(1)}} d V^{(1)}] + [{(\frac{\partial S^{(2)}}{\partial U^{(2)}})}_{V^{(2)}} d U^{(2)} + {(\frac{\partial S^{(2)}}{\partial V^{(2)}})}_{U^{(2)}} d V^{(2)}] \end{matrix}

(16)

Note that the definition of temperature,

{(\frac{\partial S^{(1)}}{\partial U^{(1)}})}_{V^{(1)}} = \frac{1}{T^{(1)}}

, and of pressure, (11), therefore,

{(\frac{\partial S^{(1)}}{\partial V^{(1)}})}_{U^{(1)}} = \frac{p^{(1)}}{T^{(1)}}

. It follows,

0 = \frac{1}{T^{(1)}} d U^{(1)} + \frac{1}{T^{(2)}} d U^{(2)} + \frac{p^{(1)}}{T^{(1)}} d V^{(1)} + \frac{p^{(2)}}{T^{(2)}} d V^{(2)}

In view of the closure conditions,

d U^{(2)} = - d U^{(1)}

and

d V^{(2)} = - d V^{(1)}

, we find,

0 = (\frac{1}{T^{(1)}} - \frac{1}{T^{(2)}}) d U^{(1)} + (\frac{p^{(1)}}{T^{(1)}} - \frac{p^{(2)}}{T^{(2)}}) d V^{(1)}

(17)

That is,

d S_{e q u i l i} = 0

\Rightarrow

{T^{(1)}}_{e q u i l i} = {T^{(2)}}_{e q u i l i}

(18)

and

{p^{(1)}}_{e q u i l i} = {p^{(2)}}_{e q u i l i}

(19)

“Massieu [1869] and Gibbs [1873] steered thermodynamics in a radically different direction.” In this move, as Callen noted, the formulation of thermodynamics “features states, rather than processes as fundamental constructs” [⁹: viii of First edition]. Rather than the motive power of heat, the defining problem of thermodynamics became the existence of spontaneity towards equilibrium and what defines the condition of equilibrium: the existence of spontaneous direction or dissymmetric direction is the direct outcome of the entropy law, Eq. (3), and the condition defining equilibrium of maximum entropy over the constraint of constant system U and system V is an immediate inference derived from the law, Eq. (15).

Variables that can be controlled and measured experimentally are p, V, and T. The first law introduces the variable U, with the introduction one can express U as a function of the set of any two of the variables p, V, and T, e.g.,

U = U (p, V)

U = U (p, T)

. These are examples of equations of state. Their determination is described in Chapter 7 of Callen [⁹: Ch. 7] in terms of the application of Maxwell Relations, which are inference of (the mixed partial derivatives of) the fundamental relation, which in turn is the direct outcome of the introduction of the variable entropy. The concept of the fundamental relation, i.e., that the canonical set of U, S, and V, plays a central role in thermodynamic theory.

Another way to describe the fundamental relation is that it is an equation of state with special status. Note that the derivatives of which give rise to the set of Eqs. (10) and (11), which individually are also equations of state but without the special status. That is, knowledge of a fundamental relation constitutes the knowledge of the complete set of the derived set of equations of state, thus the complete knowledge of the thermodynamic properties of a system. Whereas a single equation of state in the set does not constitute complete knowledge of the thermodynamic properties of the system.

We can expand the significance of the fundamental relation,

U = U (S, V)

, by replacing one or both independent variable(s) with alterative(s) that can be controlled or is(are) particularly convenient in certain types of problems. For instance, replacing

(S, V)

with

(T, V)

. However, the relation of

U (T, V)

will not preserve the “complete knowledge”:

U (T, V)

is not a fundamental equation of state as

U (S, V)

is. One needs to find the Legendre transformation of U, which in the case of

S \to T

replacement is the Helmholtz function,

A_{H}

[⁹: Sects. 5-2 and 5-3],

A_{H} = A_{H} (T, V) = U - T S

(20)

d A_{H} = - S d T - p d V

(21)

A_{H} (T^{r}, V)

is the fundamental equation of state (fundamental relation) of an isothermal composite system in interaction with an isothermal heat reservoir at

T^{r}

. Consider next the replacement of

(S, V)

with

(S, p)

. The Legendre transformation of U, in this case, is enthalpy, H [⁹: Sects. 5-2 and 5-3],

H = H (S, p) = U + p V

(22)

d H = T d S + V d p

(23)

H (S, p^{r})

is the fundamental equation of state of a composite system in interaction with a constant pressure reservoir. Consider further the Legendre transformation of H replacing

(S, p)

with

(T, p)

. The Legendre transformation of H in this case is,

G = G (T, p) = U + p V - T S

(24)

d G = - S d T + V d p

(25)

G (T^{r}, p^{r})

is the fundamental equation of state of a chemical composite system in interaction with a constant temperature, constant pressure reservoir.

Returning to the consideration of the fundamental relation,

A_{H} (T, V)

. Consider an isothermal composite system consisting of subsystems

V^{(1)}

and

V^{(2)}

, which are subject to the constraint of

V^{(1)} + V^{(2)} = c o n s t

. The system is kept at constant temperature due to interaction with a heat reservoir/bath. Such a system is not an isolated system. But the totality of the composite system and the isothermal heat bath is, i.e., the combined system in total is an isolated system. For the COMBINED system of the composite system and the isothermal heat bath, therefore, Eq. (15) takes the form,

d_{e q u i} (S + S^{r}) = 0

(26)

where

S^{r}

is the entropy of the heat bath (reservoir), which is kept at a constant temperature of

T^{r}

. We may write (26) as

T^{r} d_{e q u i} (S + S^{r}) = 0

(26)

Since

V^{(1)} + V^{(2)} = c o n s t

implies

δ W = 0

, and that

δ Q = - δ Q^{r}

, with a heat bath remaining at constant

T^{r}

in which heat transmission approximates a reversible heat transmission,

δ Q^{r} = T^{r} d S^{r}

—we have the following, in accordance with the first law,

d U = δ Q + 0 = - δ Q^{r} = - T^{r} d S^{r},

Substitution of

d S^{r} = - \frac{d U}{T^{r}}

into (26) yields,

T^{r} d_{e q u i} (S + S^{r}) = T^{r} d_{e q u i} S + T^{r} d_{e q u i} S^{r} = T^{r} d_{e q u i} S - d_{e q u i} U = - d_{e q u i} (U - T^{r} S) = 0

(27)

Since the extreme of entropy is a maximum of

S + S^{r}

, (27) represents an equilibrium condition of minimum of

U - T^{r} S

, i.e., the equilibrium condition of minimum of the Helmholtz function,

A_{H} (T^{r}, V)

. The Helmholtz function of the composite system is, in view of (21), and

d T = 0

and

V^{(1)} + V^{(2)} = c o n s t

d ({A_{H}}^{(1)} + {A_{H}}^{(2)}) = - p^{(1)} d V^{(1)} - p^{(2)} d V^{(2)} = [- p^{(1)} + p^{(2)}] d V^{(1)}

At equilibrium, therefore,

d ({A_{H}}^{(1)} + {A_{H}}^{(2)}) = - [{p^{(1)}}_{e q u i} + {p^{(2)}}_{e q u i}] d V^{(1)} = 0

That is,

{p^{(1)}}_{e q u i} = {p^{(2)}}_{e q u i}

(28)

Consider next the case of a composite system kept at a constant pressure,

p^{r}

, consisting of subsystems

T^{(1)}

and

T^{(2)}

. This part of discussion is further clarified by limiting the consideration to that of an isolated composite system,

H (T^{(1)}, p^{r}) + H (T^{(2)}, p^{r}) = H^{(1)} + H^{(2)} = c o n s t

(29)

Interaction of such an isolated system does not change the entropy of the reservoir with which it interacts. Therefore, (26) reduces to

d_{e q u i} S = 0

. It follows from

d S = \frac{1}{T} d H - \frac{V}{T} d p = \frac{1}{T} d H

d S = d S^{(1)} + d S^{(2)} = \frac{1}{T^{(1)}} d H^{(1)} + \frac{1}{T^{(2)}} d H^{(2)} = (\frac{1}{T^{(1)}} - \frac{1}{T^{(2)}}) d H^{(1)}

It follows,

0 = d_{e q u i} S = {(\frac{1}{T^{(1)}} - \frac{1}{T^{(2)}})}_{e q u i} d H^{(1)}

, therefore,

{T^{(1)}}_{e q u i} = {T^{(2)}}_{e q u i}

(30)

We now consider the third alternate thermodynamic potential of

G = G (T, p) = U + p V - T S

. In order to consider this case as a composite system, we need to generalize our investigation to that of multiple component systems that are chemically active, the Gibbs function of which is,

G (T, p, N_{1}, N_{2}, \dots, N_{r}) = U + p V - T S = H - T S

(31)

Which means that

U (S, V, N_{1}, N_{2}, \dots, N_{r})

, and

d U = T d S - p d V + \sum_{j = 1}^{r} μ_{j} d N_{j}

, [⁹: Ch.2 and Sect. 6-4] correspondingly,

d G = - S d T^{r} + V d p^{r} + \sum_{j = 1}^{r} μ_{j} d N_{j} = \sum_{j = 1}^{r} μ_{j} d N_{j}

(32)

The original form of (26) applies in this case,

T^{r} d_{e q u i} (S + S^{r}) = 0

(26)

The first law leads to,

d U = δ Q - p d V

, which in view of

δ Q = - δ Q^{r} = - T^{r} d S^{r}

becomes,

d U = - T^{r} d S^{r} - p^{r} d V

That is,

0 = T^{r} d_{e q u i} (S + S^{r}) = - d_{e q u i} (H - T^{r} S) = d_{e q u i} G

(33)

We may write (32) by introducing the stoichiometric coefficients defined as,

\frac{d N_{1}}{ν_{1}} = \frac{d N_{2}}{ν_{2}} = \frac{d N_{3}}{ν_{3}} = \dots \equiv d \tilde{N}

(34)

(32) becomes,

d G = \sum_{j = 1}^{r} μ_{j} d N_{j} = d \tilde{N} \sum_{j = 1}^{r} ν_{j} μ_{j}

The equilibrium condition (33) becomes, therefore,

\sum_{j = 1}^{r} ν_{j} μ_{j} = 0

(35)

The direct inference of the second law of thermodynamics that a system has the spontaneous tendency towards equilibrium characterized in terms of the maximization of total entropy of the system and its interacting surroundings (for isolated systems that will be the entropy of the system counted by itself) is the dissymmetry proposition of thermodynamics. One of the three cases considered in this section has the option of dealing with chemical changes and the other dealing exclusively with chemical changes. For these two cases, (27) and (33), the Helmholtz function,

U - T^{r} S

, and the Gibbs function,

H - T^{r} S

, introduced the concept of free energy—which supplants the old idea of affinity (the concept in accordance with the thermal theory of affinity) as the true measure of what drives chemical changes.

4. Kelvin and the Creation of Energy Physics: Free Energy

Whether as the Helmholtz function and the Gibbs function, or as Helmholtz free energy and Gibbs free energy, the former’s are examples of the concept used as affinity that relates irreversible chemical reactions to entropy increase, whereas the latter’s as examples of the concept used in connection with equilibrium states and reversible processes producing mechanical energy [11]: 111]—which was the topic of thermodynamics in its formative years, to which we return in this section and the next section.

In the period of 1840-1851, William Thomson (Kelvin) with his years’ interaction with Joule, finally, becoming convinced of Joule’s claim of interconversion between heat and work as described by Smith:

… while THOMSON sees JOULE as asserting and supporting a framework of mutual convertibility he still does not himself believe that a satisfactory demonstration of the conversion of heat into work by experiment has been given. Nonetheless, THOMSON now... "considers it certain that the fact has only to be tried to be established experimentally, having been convinced of the mutual convertibility of the agencies by Mr. Joule’s able arguments." [²: 174-200 (1851)] So THOMSON has in effect come to accept JOULE’S conceptual framework before he has been convinced by actual experiments of the validity of the conversion of heat into work. While little of this discussion appears in the Introduction as published in 1851, THOMSON there sums up his position, having rejected heat as having a substantial nature, and holding heat to be instead "a dynamical form of mechanical effect" wherein... "there must be an equivalence between mechanical work and heat, as between cause and effect" ([¹]: 268).

The 1851 paper was the culmination of Thomson’s skepticism and critical evaluation of the competing ideas of Carnot’s and Joule’s, both ideas having elements that are convincing in themselves but also the same or other elements that are contradictory with each other. “A fuller appreciation of the conceptual problems and subtleties in Thomson’s thought” can be found in Thomson’s draft of the 1851 paper, which is documented and reproduced in the Appendix II of Ref [¹]: Text of William Thomson’s Preliminary Draft for the "Dynamical Theory of Heat".

As Harman wrote,

In an address to the British Association in 1854, Thomson declared that Joule’s discovery of the conversion of heat into work had ’led to the greatest reform that physical science had experienced since the days of Newton’, the development of energy physics. In his introductory lecture at Glasgow in 1846, Thomson had argued that physics was to be based on the laws of dynamics, physics being the science of force. By 1851 energy had become, in his view, the primary concept on which physics was to be based [¹²].

Among the 19^th century scientists Thomson was the most important holdout from embracing heat-work convertibility throughout 1840s. By 1851, however, he came to accept “equivalence between mechanical work and heat” as interpreted to be allowing conversion of heat into work. From that point onward, he became the greatest champion of the energy-central view of physics.

The fact that he “has in effect come to accept Joule’s conceptual framework before he has been convinced by actual experiments of the validity of the conversion of heat into work,” however, remained true. From 1851 to 1855, Thomson’s research has progressed to formulate a conceptual framework of his own. It is a theoretical framework, rather than a framework based on the empirical evidence of an actual experiment. It is a framework based on the core idea that there are two fundamental laws of thermodynamics. We shall call this, because there cannot be a complete theory of thermodynamics without the concept of entropy while Thomson’s second fundamental law was formulated without using the concept of entropy, not the thermo-dynamics framework but Thomson’s energy physics framework.

The key step of this development was the 1852 Thomson paper ([²]: 511-514), in which he wrote, “The object of the present communication is to call attention to the remarkable consequences which follow from Carnot’s proposition, that there is an absolute waste of mechanical energy available to man when heat is allowed to pass from one body to another at a lower temperature, by any means not fulfilling his criterion of a ‘perfect thermo-dynamic engine,’ established, on a new foundation, in the dynamical theory of heat. As it is most certain that Creative Power alone can either call into existence or annihilate mechanical energy, the ‘waste’ referred to cannot be annihilation, but must be some transformation of energy.” Here, he reasoned that since the first law holds no energy can be annihilated, the second law derived from Carnot’s proposition infers that the waste of mechanical energy must be some transformation of energy—which as he argued in the draft of the 1851 paper ([¹]: Appendix II, especially [page five]) is the dissipative transformation of available energy.

This was how Thomson formulated his second law of thermodynamics as well as, in a single stroke, pointed out the combined application of the two laws of thermodynamics in terms of the conservation of energy (energy cannot be annihilated) and the dissipation of available energy. Later, Helmholtz and Gibbs adopted the concept of spontaneous dissipation of Helmholtz free energy and Gibbs free energy. Note, however, Helmholtz and Gibbs were interested in problems of physics and chemistry, not transformations between heat and work in both directions. The production of mechanical energy, which is the purview of engineering, is what Kelvin was interested in. Kelvin ended the barely four-page paper ([²]: 511-514) with three general conclusions, the second of which is:

Figure 2. General Conclusion 2 of Thomson’s 1852 paper [²:511-514].

Unlike Helmholtz and Gibbs, who dealt with the application of the entropy law rather than the formulation of the law, Thomson (Kelvin) in this paper is “back to thinking directly about the Second Law, and he’s cut through the technicalities, and is stating the Second Law in everyday terms,” noted Stephen Wolfram [13]. It is significant that, in the way that he talked about “the control of man sources of power which if the opportunity of turning them to his own account had been made use of might have been rendered available” ([¹]: Appendix II, especially [page six), Thomson realized that he was dealing with an atypical law of nature, not one of objectivity (without a model of observers) of mathematical paradigm. Wolfram may be on to something in his search for new paradigms in the case of the second law, as “a story of the interplay between underlying computational irreducibility and our nature as computationally bounded observers” [14]. Eddington in 1929 anticipated explicitly the view of the second law being an atypical law of nature: “The question whether the second law of thermodynamics and other statistical laws are mathematical deduction from the primary laws…is difficult to answer; but I think it is generally considered that there is an unbridgeable hiatus. At the bottom of all the questions settled by second law there is an elusive conception of ‘a priori probability of states of the world’ which involves an essentially different attitude to knowledge from that presupposed in the construction of the scheme of primary law” [15: Ch. 4].

Even with his intuition about the unique nature of the second law, three-quarters century before Eddington and one and three-quarters century before Wolfram, Thomson in 1852 was not able to transcend the construction of the second law, explicitly, beyond the presupposed scheme of primary law of inexorability. He was obligated to treat the dissipation of available energy as inexorable, not only spontaneously but also universally— “any restoration of mechanical energy, without more than an equivalent of dissipation, is impossible.” As the key part of the free energy principle, Thomson stated the general conclusions simply as one of “unargued statements” [16: 94] as a law of nature of energy physics.

The principle of universal dissipation of free energy is best characterized as a “self-evident proposition” [⁷: Sect. 4.7]. As a self-evident proposition, it has been supremely influential in the thermodynamic thought of every student of thermodynamics equal to the “supreme position among the laws of Nature” [¹⁵: Ch. 4] of the entropy law. Except, as Uffink told the story, this is not how Planck viewed the matter:

If someone can be said to have codified the second law, and given it its definitive classical formulation, that someone is Max Planck. His Vorlesungen ¨uber Thermodynamik went through eleven successive editions between 1897 and 1966 and represent the authoritative exposition of thermodynamics par excellence for the first half of this century [the 20^th century] … Planck puts the second law, the concepts of entropy and irreversibility at the very centre of thermodynamics. For him, the second law says that for all processes taking place in nature the total entropy of all systems involved increases, or, in a limiting case, remains constant … Increase of entropy is therefore a necessary and sufficient criterion for irreversibility. Before Planck’s work there were also alternative views. We have seen that Kelvin attributed irreversibility to processes involving special forms of energy conversion. This view on irreversibility, which focuses on the ‘dissipation’ or ‘degradation’ of energy instead of an increase in entropy was still in use at the beginning of the century…Planck’s work extinguished these views, by pointing out that mixing processes are irreversible even though there is no energy being converted or degraded [¹⁶: 42-43].

In Planck’s own words:

The real meaning of the second law has frequently been looked for in a “dissipation of energy”… [But] there are irreversible processes in which the final and initial states show exactly the same form of energy … They occur only for the reason that they lead to an appreciable increase of the entropy. ([¹⁷: 103–104)

Details of the example are found in [⁷: Sect. 5.10], of how mechanical energy can be restored in a reversible process involving no change in forms-of-energy of an oxygen-nitrogen mixture: since both elements of which remain at the same temperature. In a nutshell, universal dissipation of free energy as a law of nature is not tenable.

“Energy makes the world go ‘round” is nonsensical [18]. Free energy makes the world go ‘round is a much-improved statement. But the doctrine undergirding the statement, the energy-conversion doctrine, is based on the proposition of universal dissipation of free energy. The self-evident proposition of universal dissipation of free energy has been falsified: free energy dissipates spontaneously not universally. It is ironic that Thomson was the most persistent voice skeptical about the validity of the conversion of heat into mechanical energy, then became the very person who turned that skepticism on its head to assert, without proof, the universal dissipation of free energy, the assertion defining the doctrine of the interconversion of heat and mechanical energy. In actuality, Thomson’s original skepticism shows that he had the right intuition.

5. Heat and Disorganized Energy, “Energy” as the Ability to Cause Change?

Mechanical energy can be defined as the ability to do work. When the invention of steam engines demonstrated that heat is associated with the production of work and the discovery of the equivalence theorem by Mayer and Joule established that heat is a form of energy, disorganized energy (see [19]), this definition of mechanical energy was carried over to be the definition of energy (all energy including the heat energy): energy is “the capacity for doing work” [20].

It should be noted: “Before the discovery [of disorganized energy], the science of mechanics did not need an independent definition of energy. While mechanical energy of a system was indeed the capacity of the system for doing work, the mechanical-energy framework was an alternative to the force framework, an option for the science of motion. The discovery of the motive power of heat made it a necessity to introduce the concept of energy that comprises of heat energy and mechanical energies for the science of motion and heat. The resulting energy-centric, energy physics is completely different from mechanics. Both the meaning and the role of energy are now different” [21: 9/24]. Disorganized energy, which is of the central role in the science of motion and heat, has a very different meaning from the mechanical sciences notion of energy. Unlike mechanical energy, “the newly discovered disorganized energy cannot be fully used to do work. Energy physics and orthodox thermodynamics, therefore, ‘have been applying thermodynamics in the context of the pre-industrial mechanical sciences.’ That means: the common ‘energy’ view inherited from the equivalence of heat and work is a mischaracterization of the NWCJ [Newcomen, Watt, Carnot, Joule] discovery. The real discovery is the discovery—in accordance with the concept of reversible-like compensation—of the production of work to be derived/compensated from ‘transformations of natural direction’ found in fuels and in renewables, not of the production of work to be derived from energy found in fuels” [¹⁹: 27/31].

The rest of the paper below will explicate this last statement.

Before the theory was applied to spontaneous natural processes driven by thermodynamic potentials, thermodynamics was in its formative years a theory dealing with heat and work. For those applications, the theory was based on two fundamental theorems, the first fundamental theorem of the equivalence of heat and work and the second fundamental theorem of the equivalence of transformations (the transformation of heat to work, and the transformation of heat at a higher temperature to a lower temperature) [22: Abstract]. Clausius began the development of the second fundamental theorem in 1854 with his Fourth Memoir [23: 111-135] This was the real beginning of Clausius’ transformation of Carnot’s idea into the precise statement of the second law of thermodynamics. Xue and Guo noted,

…the idea of equivalence of transformations is difficult to grasp and is not even mentioned in most thermodynamics textbooks. However, the equivalence of transformations is, we think, of momentous significance for the second law of thermodynamics, as with the equivalence of work and heat for the first law of thermodynamics [²²: 4/9] …

Clausius himself regarded “Theorem of the equivalence of the transformation of heat to work, and the transformation of heat at a higher temperature to a lower temperature”, rather than “Heat can never pass from a colder to a warmer body without some other change”, as the statement of the second law of thermodynamics … [which] is the real Clausius Statement of the second law of thermodynamics [²²: Abstract]

That “the idea of equivalence of transformations is not even mentioned in most thermo-dynamics textbooks” is most unfortunate and probably the main reason why the second law is poorly understood.

We shall now consider the problem of the transformation of heat into mechanical energy comparing the nuances of its meaning between Thomson (the late Thomson in his energy physics stage) and Carnot/Clausius. First of all, we adopt the word, transformation, as a general sense while the word, conversion, as a special kind of transformation: as Clausius in his Eighth Memoir wrote, “… the difference which exists between the transfer of heat from a warmer to a colder body, and that from a colder to a warmer one; the former may, but the latter cannot, take place of itself. This difference between the two kinds of transmission being assumed from the commencement, it can be proved that an exactly corresponding difference must exist between the conversion of work into heat, and the transformation of heat into work” ([²³: 290], underlines added). That is, conversion is transformation that can take place by itself: conversion of work into heat can take place by itself whereas transformation of heat into work “can only take place in such a manner as to be compensated by simultaneously occurring positive transformation” ([²²: 364]; “compensated” and “compensation” are the terms Clausius used in his second fundamental theorem; “positive transformations” are defined as transformations that take place without compensation such as conversion).

The standard interpretation of the NWCJ discovery is the discovery of heat as a form of energy, which in the form of high temperature heat can be converted into mechanical energy. Let us consider an amount of heat

Q_{1}

at a temperature

T_{1}

. Assume the availability of a heat reservoir at a temperature

T_{2}

. According to Thomson,

Q_{1}

at a temperature

T_{1}

can be inputted into a Carnot Cycle, the operation of which necessarily discharges a minimum amount of heat,

Q_{2}

, equal to

Q_{2} = T_{2} \cdot (\frac{Q_{1}}{T_{1}})

(36)

Therefore, the maximum work derivable from

Q_{1}

W_{R e v e r s i b l e} = Q_{1} - Q_{2} = Q_{1} \cdot (1 - \frac{T_{2}}{T_{1}})

(37)

In talking about “can only take place in such a manner as to be compensated by simultaneously occurring positive transformation,” Clausius framed the problem by asking what the necessary element(s) in this picture are. It is obvious that they are “

Q_{1}

at a temperature

T_{1}

” and the “heat reservoir.” The real question, more precisely, is what are the roles these elements, “

Q_{1}

at a temperature

T_{1}

” and the "heat reservoir” play? The latter question, the role of the "heat reservoir,” is the crucial one because one cannot address the role of “

Q_{1}

at a temperature

T_{1}

” without also addressing the role of the heat reservoir at

T_{2}

: as Carnot stated, “Heat alone is not sufficient to give birth to the impelling power: it is necessary that there should also be cold [the heat reservoir at

T_{2}

as the heat sink]; without it, the heat would be useless.”

In presenting the Second Fundamental Theorem, Clausius explicated this argument on the essential role of transmission of heat at a higher temperature at

T_{1}

to a lower temperature at

T_{2}

in this picture of transformations in nature [²³: 111-145]. In the body of his work, Clausius generalized Carnot’s attribution to transmission of heat, as causation of transformations, to that of the idea of compensation. While the First Law serves as the closure condition for all transformations in nature, it is the second fundamental theorem (the Second Law) that provides the driving force, the compensation [²³: 118, 248, 290, 364], for enabling a system’s transformations in negative, i.e., unnatural direction. For a system’s positive (i.e., spontaneous) transformations, the second law began as the law that dictates the direction of these transformations. Therefore, the driving force to cause a system’s change, whether they are in unnatural direction or spontaneous—i.e., what makes the world go ‘round—is the purview of the second law.

The context of this discussion is that first law serves as the closure condition for all transformations. The remaining issue is then, “from where the energy of the work comes?” This is answered by Clausius with his invention of a six-stage cycle, which is updated in [²¹], called the Carnot-Clausius cycle of the Carnot engine. It is reproduced here as Figure 3,

Figure 3 depicts the Carnot-Clausius cycle, 1’-2’-3-4-5-6-1’: in which,

dotted 4-5 and 2’-3 are adiabatic steps, linking isotherm $T_{1}$ and isotherm $T_{2}$ ,
isotherms 3-4 and 5-7-6 represent heat transmission of $Q_{1}$ from $T_{1}$ to $T_{2}$ , noting the assumed availability of a heat reservoir/sink at $T_{0}$ which is infinitesimally colder than $T_{2}$
adiabatic 6-1’ represents adiabatic cooling over an infinitesimal temperature-difference so that $T_{1^{'}}$ infinitesimally colder than the temperature of the heat reservoir/sink at $T_{0}$
isotherm $T_{1^{'}}$ - $T_{2^{'}}$ represents the extraction of heat $Q^{t_{2}}$ from the $T_{0}$ heat reservoir.

The notation of

Q^{t_{2}}

is explained in [¹⁹: Figure 3 and Figure 7].

Q^{t_{2}}

can be shown to equal to

Q_{1} - Q_{2} = W_{R e v e r s i b l e}

, detail of which can be found in [¹⁹] and [²¹]. By demarcating precisely heat transmission as the driving force of the Carnot engine, the Carnot-Clausius cycle shows that the energy of the work comes from the heat extracted from the

T_{0}

heat reservoir. It is indisputable that Carnot/Clausius’ account of how work is derived from disorganized energy is superior. It is the account that is coherent whereas the energy conversion doctrine account, one that is based on the proposition of universal dissipation of free energy, can become illogical and self-contradictory. Thomson’s erstwhile skepticism about the validity of the conversion of heat into mechanical energy was justified! In the next section, we return to the main thesis of the paper, the primacy of dissymmetric tendency towards equilibrium (including that of heat transmission) and shall see that the Carnot/Clausius entropy/heat-extraction framework is also, in many cases, the only account for explaining what causes changes in the Universe.

6. Reversible Processes Approaching the Extremes of Thermodynamic Potentials

The success of Carnot/Clausius’ account emphasizing the demarcated heat transmission as the entropic driving force suggests that problems of engineering thermodynamics can be treated with the same systematic approach like the problems of equilibrium thermodynamics. Here we consider two examples corresponding to two of the three alternative thermodynamic potentials in Sect. 3.

The Helmholtz function may be expressed for multicomponent reactive systems as

A_{H} = A_{H} (T, V, N_{1}, N_{2}, \dots) = U - T S

(38)

Application of the Helmholtz function in the general form of (38) will be commented, indirectly, in Sect. 7.2; in the meantime, we consider in this section the application of which to pure substance of ideal gas.

Consider a composite system made of two subsystems, subsystem⁽¹⁾ and subsystem⁽²⁾, each is filled with

N

kmol of an ideal gas. Given the following assumptions:

A heat reservoir (bath) at temperature $T^{r}$
Subsystem⁽¹⁾ initially at ${p^{(1)}}_{i n i}$ , ${V^{(1)}}_{i n i}$ and $T^{(1)} = T^{r}$
Subsystem⁽²⁾ initially at ${p^{(2)}}_{i n i}$ , ${V^{(2)}}_{i n i}$ and $T^{(2)} = T^{(1)} = T^{r}$
${V^{(2)}}_{i n i} = 5 {V^{(1)}}_{i n i}$ ; it follows that the total system volume is

V = {V^{(1)}}_{i n i} + {V^{(2)}}_{i n i} = 6 {V^{(1)}}_{i n i}

That is, we consider the composite system to undergo an isothermal process from its initial state subject to the closure condition,

V^{(1)} + V^{(2)} = 6 {V^{(1)}}_{i n i}

(39)

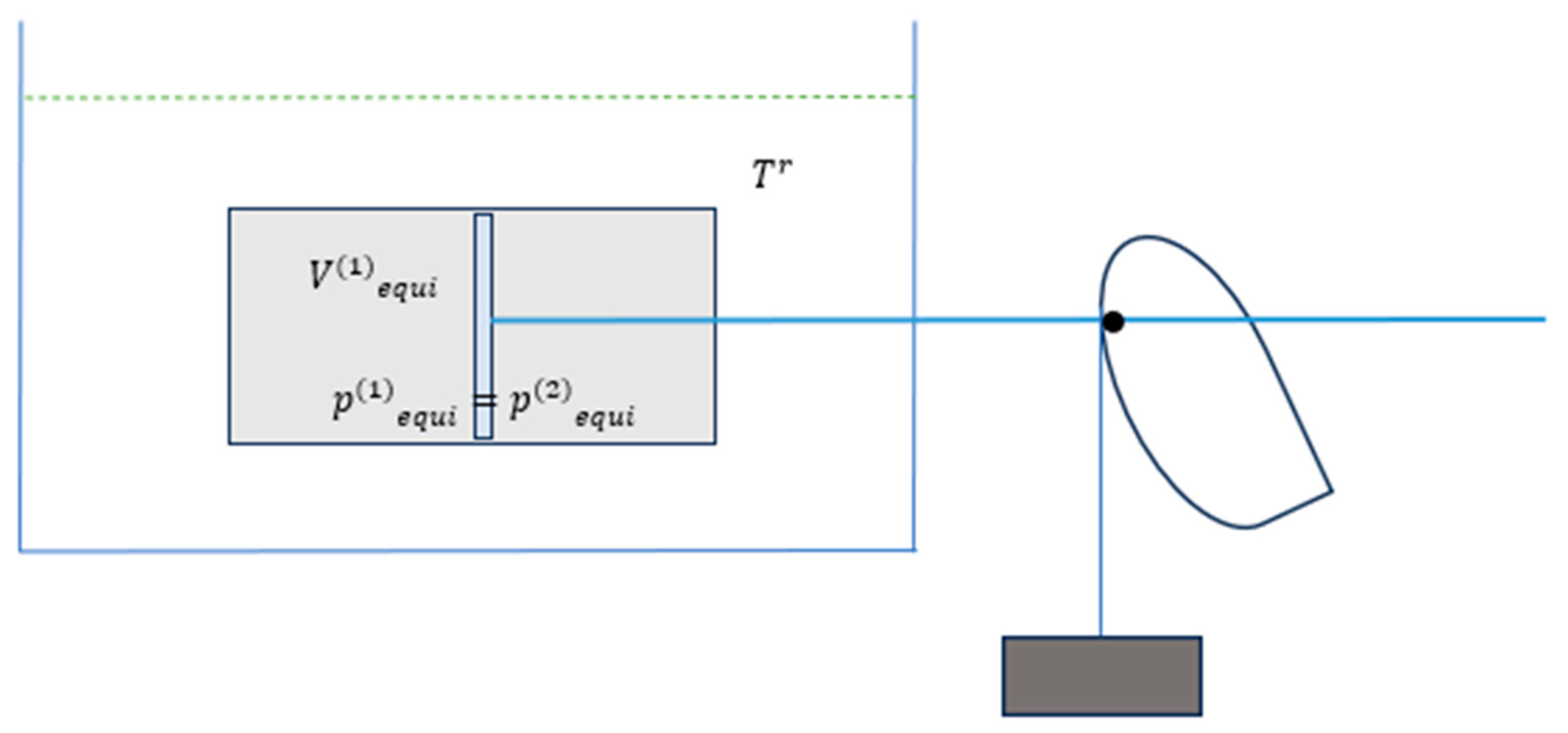
The arrangement of the system, a heat bath it interacts with, and the mechanical arrangement schematically are shown in Figure 4.

The initial pressures of the two subsystems are

{p^{(1)}}_{i n i} = \frac{N ℛ T^{r}}{{V^{(1)}}_{i n i}}

{p^{(2)}}_{i n i} = \frac{N ℛ T^{r}}{{V^{(2)}}_{i n i}} = \frac{N ℛ T^{r}}{5 {V^{(1)}}_{i n i}} = (\frac{1}{5}) \cdot {p^{(1)}}_{i n i}

Difference in

{p^{(1)}}_{i n i}

and

{p^{(2)}}_{i n i}

is balanced by the torque-force exerted by the weight-cam through the piston-rod. Figure 4 and Figure 5 (below) schematically suggest that throughout the isothermal process of the piston moving rightward, the difference in

p^{(1)}

and

p^{(2)}

resulting in force on the piston to the right is balanced with the weight induced force transmitted through the piston-rod to the left. This nearly balancing suggests the process, as shown below, being sufficiently slow for heat transmission from the bath to gases in the subsystems to take place—so that the two subsystems to remaining isothermal at

T^{r}

. The isothermal process with subsystem⁽¹⁾ expanding from its initial volume to its final volume reversibly, therefore, results in work as shown (where the final equilibrium state is given by (28) corresponding with

{V^{(1)}}_{f i n a l} = {V^{(2)}}_{f i n a l}

as shown in Figure 5),

W_{r e v} = \int_{{V^{(1)}}_{i n i}}^{3 {V^{(1)}}_{i n i}} (p^{(1)} - p^{(2)}) d V^{(1)}

In view of the closure condition (39), it becomes,

\begin{array}{l} = N ℛ T^{r} \int_{{V^{(1)}}_{i n i}}^{3 {V^{(1)}}_{i n i}} (\frac{1}{V^{(1)}} - \frac{1}{6 {V^{(1)}}_{i n i} - V^{(1)}}) d V^{(1)} \\ = N ℛ T^{r} (l n \frac{3 {V^{(1)}}_{i n i}}{{V^{(1)}}_{i n i}} + l n \frac{3 {V^{(1)}}_{i n i}}{5 {V^{(1)}}_{i n i}}) = 0.588 N ℛ T^{r} \end{array}

(40)

Figure 5. The composite system together with a heat bath of Figure 4 at the final equilibrium state of the WHOLE.

Note that this reversible isothermal process results in the entropy increase of the composite system,

S_{f i n a l} - S_{i n i} = Δ S^{(1)} + Δ S^{(2)} = N ℛ l n \frac{3 {V^{(1)}}_{i n i}}{{V^{(1)}}_{i n i}} + N ℛ l n \frac{3 {V^{(1)}}_{i n i}}{5 {V^{(1)}}_{i n i}}

Which is exactly what the heat bath decreases in entropy so that the combined WHOLE “composite system and heat bath” experiences no change in entropy—corresponding to the heat bath gives out heat of the amount

W_{r e v} = T^{r} {(S_{f i n a l} - S_{i n i})}_{C o m S y s t e m}

(41)

to the composite system during the reversible isothermal process. That is, energy of the reversible work

W_{r e v}

comes from heat of the heat bath; heat is 100% transformed into work in the reversible manifestation of nature’s dissymmetry.

A comment on the meaning of “free” is found in the “Thermodynamic free energy” page of Wikipedia, in which it writes, “This expression [of Helmholtz free energy

A_{H} = U - T S

] has commonly been interpreted to mean that work is extracted from the internal energy U while TS represents energy not available to perform work.” While this is a serviceable interpretation of decreases in the Helmholtz function and the Gibbs function as free energy and free enthalpy, respectively, (more on this in Sect. 7.2) it is nonsensical for the ideal gas example here. For ideal gases in the two subsystems,

Δ U

= 0. Instead of being “energy not available to perform work,”

T^{r} {(S_{f i n a l} - S_{i n i})}_{C o m S y s t e m}

is precisely the heat corresponding with ALL the work being produced. Rather than being waste heat (the rejected heat) in accordance with the energy conversion doctrine, heat in the heat bath is the source of heat for the work.

Consider next the example of a composite system kept at a constant pressure,

p^{r}

, consisting of subsystems

T^{(1)}

and

T^{(2)}

. This part of discussion is further clarified by limiting the consideration to that of an isolated composite system,

H (T^{(1)}, p^{r}) + H (T^{(2)}, p^{r}) = H^{(1)} + H^{(2)} = c o n s t

(29)

We assume a specific such a composite system: an isolated composite system of two subsystems of thermal-mass blocks: block X and block Y [X is aluminum (

c_{p X} = 0.900 \frac{k J}{k g \cdot K}

) with

m_{X}

= 0.5 kg, and Y is copper (

c_{p Y} = 0.386 \frac{k J}{k g \cdot K}

) with

m_{Y}

= 1 kg], which are, initially, at

T^{(1)} =

100^oC and

T^{(2)} =

500^oC, respectively (Figure 6, left). The blocks are brought together in thermal contact, triggering a spontaneous heat transfer process to a final state of 557.84 K (

{284.69}^{o} C

, Figure 6, right), with a corresponding entropy growth of 0.054949 kJ/K (reproduced from [³]; see also A Treatise [⁷:206-210] for details).

Figure 7 depicts the same system undergoing a reversible event. We stress that the reversible event in the present case, depicted in Figure 7, are defined in terms of the same set of initial state and final state of the spontaneous event of Figure 6. The reversible event is depicted in two phases; a heat reservoir is used in the second phase.

Phase One is an isentropic process brought about by a Carnot heat engine leading the composite thermal system to a uniform temperature of 522.4 K (

{249.2}^{o} C

). That is, the system arrives at a uniform temperature lower than the final temperature of the spontaneous event at 557.8 K.

To bring the uniform-temperature system back to the final temperature of the spontaneous thermal event, it is necessary to use a heat reservoir in Phase Two (a Phase Two in two stages) in an arrangement shown in Figure 7 on the right—where shows, in the first stage, a Carnot heat engine operating between a cold thermal system and heat reservoir to bring the temperature of the system to the temperature of the reservoir. In the second stage, the power produced by the Carnot heat engine is then applied to drive a Carnot heat pump to bring the system to the same final state of the spontaneous event. The reservoir temperature chosen here corresponds to the condition that the Carnot heat engine output is exactly equal to the required Carnot heat pump input.

Examples of other reservoir temperatures are given in A Treatise [⁷: 206-210] to demonstrate the general validity that, for a given dissymmetry driven force as exemplified in the three examples -- Figure 3 as a special case of Clausius’ six-stage cycles; the example of Figs. 4 and 5; and the example of Figure 7—the amount of heat extracted from the heat reservoir (heat source) is propositional to the temperature of the reservoir.

Note that in Figure 6, there is neither heat exchange nor work exchange involved between the isolated system and its surroundings. In comparison with Figure 6, the overall process in Figure 7 involves a system work exchange in Phase One of 29.67 kJ and a system heat exchange with the heat reservoir in Phase Two. Energy balancing requires the two exchange values to be equal; i.e., heat extracted during Phase Two exactly equals work output during Phase One: work output is in fact derived from heat extracted from the heat reservoir, i.e.,

W_{r e v} = T_{r e s} \cdot {(Δ S)}_{s p o n} = 539.9 \times 0.054949 = 29.667

(42)

Carnot/Clausius’ account of how work is derived from disorganized energy is shown in this section to link nature’s dissymmetry manifested in spontaneous processes (Sect. 3) with reversible harnessing of which for doing work (this section), providing unification of equilibrium thermodynamics and engineering thermodynamics. The energy conversion doctrine has never provided such unification nor a “mechanism” for reversible work; the Carnot/Clausius account is the only account that provides the mechanism for reversible energy transformations [⁷: Sect. 10.4] with a common thread: the energy of work coming from heat extracted from heat reservoir driven by the entropy growth of nature’s dissymmetry.

7. The Dissymmetry Premise

7.1. Primacy of Dissymmetry over Free Energy, an Epistemological Issue

There are two lessons associated with the discovery of heat as disorganized energy, the first fundamental theorem and the second fundamental theorem. The first fundamental theorem teaches that heat and work are equivalent as measured in energy and that heat is a form of energy. The second fundamental theorem teaches that heat as disorganized energy is a new kind of phenomenon from mechanical phenomena of reversible nature. In coexistence with mechanical reversible processes,

(i) there is another kind of processes (to be called transformations) that, in distinction from mechanical reversible processes, are processes manifesting nature’s preferred direction, i.e., nature’s dissymmetry;

(ii) one additional detail in association with dissymmetry is that each type of the new processes, to adopt the terms of Cropper [24], can be divided into “processes or transformations of natural direction” and “processes or transformations of unnatural direction”;

(iii) another is the notion of “compensation” or “compensated,” and that an uncompensated process of unnatural direction of the new kind of processes can never occur;

(iv) an additional comment: whereas a mechanical reversible universe allows the conception of a “block-universe,” a deterministic and unchanged universe, a dissymmetric universe allows the conception of transformations in a changing universe.

In short, there are the lesson of energy and the lesson of dissymmetry. While both lessons, i.e., both the first fundamental theorem and the first law and the second fundamental theorem and the second law, are indispensable, the precise roles of the two theorems/laws in the theoretical structure of thermodynamics are subtle issue—for similar reason that the concept of energy is subtle [25]. The treatment of how to combine the two may begin with a premise that supposes the primacy of one of the two lessons over the other as an epistemological presupposition, steppingstone that forms the theoretical argument’s structure and impacts on the kind of conclusions possible—even though the two laws’ status as inexorable laws of nature is never in question.

We already have the example of a premise in the energy conversion doctrine, the principal legacy of Thomson [26], which asserts the primacy of energy over dissymmetry, undergirding the orthodoxy of engineering thermodynamics today. That the “expression

A_{H} = U - T S

has commonly been interpreted to mean that work is extracted from the internal energy U while TS represents energy not available to perform work” represents the premise of primacy of energy over dissymmetry.

The energy conversion doctrine places thermodynamics at home with standard branches of physics that are associated with the causal understanding of what Zwier referred to as the “Consensus View of Physical Causation” (CVPC) [27]. This causal understanding may be described as causality exhibited as “constant conjunction” and “invariable succession” in causal laws of equations of motion in physics. That is, physics describes systems in terms of “an autonomous model of dynamics.” As Zwier wrote, “The completely autonomous evolutions of isolated systems that are familiar from physical theories in which we have complete equations of motion are somewhat foreign to thermodynamic theorizing. This is because we do not have a complete equation of motion for thermodynamic systems” [²⁷: 149] What Zwier perceives something unfamiliar and new in thermodynamics theorizing, however, is not shared by most thermodynamicists. The nonexistence hypothesis of equation-of-motion for energy conversion processes was made earlier by the author in an unpublished Report [28], an earlier submitted paper version of which was reviewed/rejected by leading thermodynamicists (including Gyftopoulos, who signed his review of the submitted paper). One unnamed reviewer simply asserted, “the equation of the change (motion) exists for energy conversion processes.” The reviewers in this instance expressed the orthodox view of physical sciences.

This is an example of Marshall McLuhan’s “old stereotypes” habit [29] in the age of new discovery or invention. As Ulanowicz noted,

Whenever a new tool emerged within an endeavor, practitioners tended to use it in the context of previous habits and remained blind for a while to its full potential. His [McLuhan’s] example was IBM, which saw its purpose as the manufacture of business machines. It wasn’t until its leaders realized they were in the business of processing information that the enterprise began to take off [30].

Our example here is the discovery of equivalence of heat and work, i.e., correlation of heat and work. But correlation is not necessarily causation. The discovery is encapsulated fully by the dualistic lessons of energy and dissymmetry, of which energy and CVPC are the previous habits thinking carried over from conceptualization in the reversible world of physics while dissymmetry is the discovery in the new irreversible world, the essence of which is captured by interventionist conceptualization.

We may surmise that orthodox engineering thermodynamics follows the orthodoxy of CVPC, thus, if one question CVPC, one may question orthodox engineering thermodynamics. This is exactly what Zwier did in making the case of interventionist causation, a theory of causation by the philosopher James Woodward [31]. In her thesis, she wrote,

Yet CVPC relies entirely on an autonomous model of dynamics in which everything about the evolution of a system can be predicted purely by knowledge of its beginning state and its internal dynamical rules. For a theory such as thermodynamics, where we have no fully-developed autonomous dynamics, CVPC is wholly inadequate…

I have argued in this chapter that interventionist reasoning is evident not only of the process of discovery of thermodynamic theory, but in the very structure of the theory itself. We can see the interventionist underpinnings in the Clausius submanifold that forms the skeleton of thermodynamic theory and in the “driving forces” which turn out to be interventionist causes of their respective conjugate variables. Interventionist causal claims, in which one variable is said to cause another in a given context, can be formulated and assessed quite naturally using standard “textbook” thermodynamic language and explanations. [²⁷: 158]

In view of Zwier’s philosophical argument and the thermodynamics investigation of this paper, we make the case for supplanting the premise of the primacy of energy with the premise of primacy of dissymmetry over free energy: the structure of thermodynamic theory outlined in this paper is the most important result from the new premise, the missing interventionist conceptualization, instead of the energy conceptualization, may be the deeper reason why Clausius’ “idea of equivalence of transformations is difficult to grasp and is not even mentioned in most thermodynamics textbooks.” The new premise will lead to conclusions, including those drawn from the Carnot/Clausius account, that are radically different from conventional conclusions drawn from the energy conversion doctrine account (see summary of which in Sect. 7.3 and Sect. 8).

7.2. Helmholtz Free Energy and Gibbs Free Enthalpy; Entropy Growth Potentials

Coopersmith referred to “the conflict between Carnot and Joule” as Thomson’s problem [²⁵: 284]. With his second fundamental theorem [²³: 111–135] as the more precise version of Carnot’s theory, Clausius in 1854 succeeded in coming to the resolution of Thomson’s problem [²⁵: 284]. I call this the Carnot·Clausius account. Clausius’ 1854 Fourth Memoir then led to the development by Gibbs the Gibbsian equilibrium thermodynamics [¹⁰]. It is the equilibrium thermodynamics based on the Gibbs-Carathéodory fundamental relation and the Gibbs-Carathéodory equation that provides the most satisfactory CORE theoretical structure of thermodynamics. This paper is an attempt to achieve unification of the Carnot·Clausius account and equilibrium thermodynamics on the bedrock of this core. Sect. 6 is one element of this project. Note that the Carnot/Clausius account is in terms of heat and work and dissymmetry in the account is in terms of transmission of heat, whereas dissymmetry in the equilibrium thermodynamics account is in terms of thermodynamic potentials. There is a disconnect in our treatment of the complete project. The disconnect can be filled by investigating the dissymmetry in the two thermodynamic potentials, Helmholtz free energy and Gibbs free enthalpy, manifested as heat release transformation.

In the context of multicomponent reactive systems, the Helmholtz free energy,

A_{H} = A_{H} (T, V, N_{1}, N_{2}, \dots) = U - T S

, and the Gibbs free enthalpy,

G = G (T, p, N_{1}, N_{2}, \dots) = H - T S

, can be interpreted similarly: the former represents a body’s internal energy (e.g., as released as heat in combustion taking place in a bomb calorimeter), subtracted by energy that is not available, and the latter represents a body’s enthalpy (e.g., as released as heat in combustion taking place in a isobaric combustion chamber), subtracted by enthalpy that is not available. For our purpose here, we shall use the latter example for discussion.

First of all, it is possible to consider the latter example in the same manner as the two examples in Sect. 6, the reversible manifestation of entropy growth as driving force for useful work. The detail can be found in a 1992 paper [32]. Here a summary of the discussion is reproduced: Consider a mixture of 1

k m o l

C O

and ½

k m o l

O_{2}

. A reversible “combustion” heat engine may be constructed along the same lines as a Carnot heat engine. It also consists of four steps (see Figure 8): an isentropic compression,

R O

→ 1; an isothermal process at peak temperature, 1 → 2 → 3; an isentropic expansion, 3 → 4; and finally, an isothermal heat transfer process at

T_{0}

, 4 → P0. This final isothermal process will be a heat rejection process if (

S_{R 0} - S_{P 0}

) is positive, or a heat absorption process if (

S_{R 0} - S_{P 0}

) is negative. Instead of combustion step, the key step of the reversible engine cycle is the isothermal processes at peak temperature, 1 → 2 → 3 (see also Figure 10 of [³²] for examples of different peak temperatures).

The isothermal process at peak temperature is made up of two phases (see. 3 of [³²]). After separating each component of the mixture (

C O, O_{2}

) through corresponding semipermeable membranes into individual manifolds (mixture at 1 becoming components at 1(a), 1(b), …), each component undergoes an isothermal expansion, 1 (a) → 2(a), 1(b) → 2(b), … (the first phase). This is followed by a reversible heat release reaction process (the second phase): components at 2(a), 2(b), … are collected through semipermeable membranes into a Van’t Hoff reaction box where reversible reaction takes place, releasing heat and producing an equilibrium mixture at “3.” Note that pressure

p_{3}

at state 3 is selected on the condition of

S_{3} = S_{1} (= S_{R 0}

). (Note that even though point 3 and point 1 overlap each other in the figure, they represent different pressures.) In that case, heat released in the reaction box exactly matches the heat required for maintaining the isothermal expansion processes of the two individual components.

This arrangement transfers the chemical affinity “released” reversibly in 2 → 3 to the enhancement of mechanical spontaneity manifested as isothermal expansions in 1 → 2. Note that heat rejection (area under P0→R0, see Figure 10 of [³²]), therefore the thermal efficiency of the reversible heat engine, is independent of the peak temperature

T_{1}

. It is noted that a reversible combustion heat engine operating with different peak operating temperatures as shown in Figure 10 of [³²] produces the same useful work equal to Gibbs free energy since the heat rejection remains the same.

In this sense, “Gibbs free enthalpy” corresponds to the situation that, of the “combustion heat” released in a spontaneous event, only a minimum amount of heat has to be theoretically subtracted (in fact, if the (

S_{R 0} - S_{P 0}

) of another mixture is negative we’ll have a situation of heat addition instead of subtraction). So, we should be talking about this “work,” which equals the maximum amount of heat that can be extracted, as derived from “available heat,” (see p. 28, lines 18-20).

From these previous examples, whether it is the Carnot-Clausius cycle, or the two examples in Sect. 6, or the example of Figure 8, the logical name for the work obtained reversibly should be available or free heat that nature’s dissymmetry makes them possible. Only, when irreversible steps are involved intrinsically in the practice of producing work, the use of free energy or free enthalpy makes some kind of sense, as we shall discuss.

The practice of combustion technology is intrinsically irreversible; the technology led to the invention of steam engines and Carnot’s theoretical investigation. Consider the schematic diagram of Figure 9, in which a combustion chamber is depicted. The figure is in reference to Figure 3 and Figure 8: combustion process of a reactant mixture at

T_{0}

and

p_{0}

enters the chamber with enthalpy

H_{R 0} .

The mixture is transformed into the burned product at

T_{a d i a b}

with enthalpy

H_{P} (T_{a d i a b}) = H_{R 0}

. These notations are consistent with those in Figure 8. Heat transmission takes place in the chamber from burned product to the working fluid of the Carnot heat engine—with working fluid of state “3” entering the chamber with an operating temperature designed at

T_{p e a k} = T_{1}

. The working fluid receives heat,

Q_{1}

, corresponding to step 3 → 4. The exiting working fluid of state “4” enters the adiabatic expander of the Carnot engine at state “4”. These notations are consistent with those in Figure 3.

Heat added to the Carnot engine,

Q_{1}

, depends on the design selection of the working-fluid peak temperature,

T_{p e a k} = T_{1}

Q_{1} = H_{P} (T_{a d i a b}) - H_{P} (T_{1}) = H_{R 0} - H_{P} (T_{1})

(43)

The selection of the peak temperature is a critical design factor: a too high temperature lowers

Q_{1}

for the Carnot heat engine while a too low peak temperature lowers the thermal efficiency of the Carnot engine. Both combustion irreversibility and a poor design selection of peak temperature impact significantly on the end performance result of work production. However, these considerations are not the present focus of the paper, which addresses the teaching of the Carnot cycle and the Carnot-Clausius cycle.

We train on the role of heat reservoir for the operation of Carnot cycle, particularly on the impact of the heat reservoir temperature on the efficiency of the Carnot cycle. The “real value of the Carnot cycle” is often described this way, “Thermal efficiency increases with an increase in the average temperature at which heat is supplied to the system or with a decrease in the average temperature at which heat is rejected from the system,” wrote Cengel and Boles in the textbook Thermodynamics, an Engineering Approach Sixth Edition [33]. We ask in what roles the heat reservoir plays in leading to the conclusion that a decrease in the average temperature at which heat is rejected from the system causes greater fraction of

Q_{1}

to be transformed into work.

Demarcation of heat transmission as the driving force of the Carnot engine in accordance with the Carnot-Clausius cycle can be generalized. The demarcated treatment of high temperature heat-energy

Q_{1}

as a “driving force” of

Q_{1}

heat transmitted from

T_{1}

T_{2}

, can be generalized to the consideration of a “driving force” in association with a source-system, whether it is a composite system considered in Sect. 6 (two such systems considered there: Eq.(41) and Eq.(42)) or the example immediately below in this subsection. We referred to, in this generalization, the “driving force” as Entropy Growth Potential, EGP. [⁷: Sects. 8.3 to 8.5] The value of EGP is determined by the total entropy growth or entropy production of the source-system and the environment the system interacts with (referred to as “source-system”

+

“the environment-reservoir”

= u n i v e r s e

{(Δ_{G r o w t h} S)}_{u n i v e r s e} = {(Δ S)}_{s y s} + {(Δ S)}_{r e s e r v}

(44)

That is,

{(Δ_{G} S)}_{u n i v e r s e}

is the total entropy growth of universe in a spontaneous event. Correspondingly, there is a reversible event. It has been argued in [⁷] that the two events define a set of infinite possibilities (the set is referred to as Poincare Range) that share “a property common to all possibilities” ([34], also see [⁷: 197]). By letting,

{(Δ_{G r o w t h} S)}_{u n i v e r s e} = {(Δ_{P o t e n t i a l} S)}_{P o i n R a n g e} \equiv E G P

(45)

and naming it Entropy Growth Potential, we acknowledge EGP to be the common property of all possibilities within the set of a Poincare Range.

While the entropy growth of each event is different from other events, every event in the set has the same entropy growth potential, which represents the maximum (potential) useful work of each and every event in the set, corresponding to,

W_{m a x} (= W_{r e v - e v e n t}) = T_{r e s} \cdot (Δ_{p} S)_{PoinRange} = T_{r e s} \cdot E G P

(46)

The actual useful work produced by each specific event is less than the maximum useful work of a specific value in association with the specific entropy growth.

For the case of the Carnot-Clausius cycle, (46) takes the form,

W_{r e v - e v e n t} = T_{0} \cdot E G P (T_{0})

(47)

Note that in this case

E G P (T_{0})

, in accordance with (45), is a function of

T_{0} (= T_{2})

, and equals to

E G P (T_{0}) = \frac{- Q_{1}}{T_{1}} + \frac{Q_{1}}{T_{2}} = \frac{- Q_{1}}{T_{1}} + \frac{Q_{1}}{T_{0}}

(48)

It follows that

W_{r e v - e v e n t}

is,

W_{r e v - e v e n t} = T_{0} \cdot \frac{- Q_{1}}{T_{1}} + \frac{Q_{1}}{T_{0}} = Q_{1} (1 - \frac{T_{0}}{T_{1}})

(37)

Instead of looking at

Q_{1} (1 - \frac{T_{0}}{T_{1}}),

demarcation identifies the dual roles the heat reservoir plays, as a heat sink for the EGP driving force and as a heat source-reservoir for the heat extraction mechanism made possible by the driving force. Reason for the decrease in heat rejected from the Carnot-Clausius cycle in association with lower heat reservoir temperature is the combined result of a stronger increase in EGP, the driving force in (37)

\frac{- Q_{1}}{T_{1}} + \frac{Q_{1}}{T_{0}}

, and a proportional decrease in extracted heat resulted from lower heat reservoir temperature

T_{0}

in (37) and (47)—rather than that a lower heat reservoir temperature favors the heat extraction process.

Now we consider the direct application (sans heat exchange as shown in Figure 9) of burned product derived from combustion of a reactant mixture at adiabatic flame temperature with enthalpy

H_{P} (T_{a d i a b}) = H_{R 0}

. Instead of discharging the burned product at a designed value of peak temperature as implied in Figure 9 for heat to be added to the Carnot cycle at approximately constant peak temperature, the burned product is designed to discharge ideally at

T_{0}

, the surroundings temperature. This can be done either as an “internal combustion heat engine” with fuel-air-reactant/burned-product as the working fluid, or as an “external combustion engine” with a fluid other than the fuel-air-reactant/burned-product, e.g., steam, as the working fluid. In the latter case, the idealization of a cycle is defined by the minimization of heat transmission irreversibility by keeping the temperature difference between burned product and working fluid small.

Because the burned product is designed to discharge ideally at

T_{0}

, this case represents the more effective combustion application of fossil fuel. In this case,

E G P (T_{0})

, in accordance with (45), becomes, in view of (44),

E G P (T_{0}) = {(Δ S)}_{s y s} + {(Δ S)}_{r e s e r v} = (S_{P 0} - S_{P} (T_{a d i a b}, p_{0})) + \frac{(H_{P} (T_{a d i a b}, p_{0}) - H_{P 0})}{T_{0}}

(49)

Correspondingly,

W_{r e v - e v e n t} = T_{0} \cdot E G P (T_{0}) = (H_{P} (T_{a d i a b}, p_{0}) - H_{P 0}) - T_{0} (S_{P} (T_{a d i a b}, p_{0}) - S_{P 0})

(50)

As it has been noted, the logical name for the work obtained reversibly should be available or free heat. The use of free energy or free enthalpy makes some kind of sense only when irreversible steps are involved in the practice of producing work, such as combustion, whether it is internal combustion or external combustion. Eq. (50) shows, of the enthalpy released by combustion,

H_{P} (T_{a d i a b}, p_{0}) - H_{P 0} = H_{R 0} - H_{P 0}

, a minimum fraction of which is not available, therefore, must be subtracted from the released enthalpy. For the reversible example of Gibbs “free enthalpy,”

(H_{R 0} - H_{P 0}) - T_{0} (S_{R 0} - S_{P 0})

, calling

T_{0} (S_{R 0} - S_{P 0})

unavailable can be problematic since the term may be negligible or even negative (in the latter case, enthalpy is to be added to the release enthalpy rather than to be subtracted). In the case involving irreversible steps, irreversibility ensures the amount of enthalpy to be subtracted to be significant. It is useful to call the “released enthalpy subtracted by a sizable unavailable fraction” free flame enthalpy, the word flame serving to remind us of the context of irreversible combustion involved in its meaning.

Thermodynamics began with a focus on the relation between heat and work and with Carnot’s innovation of investigating this relation in terms of reversible processes. Analysis in this paper and particularly in this subsection suggests, however, that this historical background of thermodynamics contains, by linking heat and the discussion of reversibility so closely, a misleading notion of the true nature of reversibility. Any discussion of heat necessitates involvement of heat release that is intrinsically irreversible. “Reversible” use of heat, such as Carnot cycle or the Carnot-Clausius cycle, only idealizes the part involving heat transmission, leaving the irreversible heat release hidden from consideration.

True reversibility for the whole processes is represented by examples in Sect. 6 and the example of Figure 8. These are examples that require no heat sink or sizable heat sink. For the example of Figure 8, due to the reaction being driven by infinitesimal affinity rather than large affinity of typical combustion reactions, the required heat sink, if any, is of moderate size. For the examples in Sect. 6, these are examples of pure spontaneity, EGP of which is independent of

T_{0}

because

{(Δ_{G r o w t h} S)}_{u n i v e r s e} (= {(Δ S)}_{s y s})

requires no heat discharging to the surrounding. No heat sink is required.

In these latter cases, the heat reservoir serves solely as a heat-source, with the whole processes requiring no heat sink. It follows that the temperature of a heat-source reservoir can be any arbitrarily one,

T_{X}

, because EGP is not dependent of

T_{X}

W_{r e v - e v e n t} = T_{X} \cdot E G P

(51)

For these examples, referring

T_{X} \cdot E G P

as available or free energy is misleading. Instead, it should be referred to as

a v a i l a b l e h e a t

In addition to examples in Sect. 6 and the example of Figure 8, the application of renewables is examples requiring no sizable heat sink. The reversible realization of all these cases represents “transformations of heat into work” in which heat extraction from the surroundings, rather than heat discharge into which, is the dominant mechanism. The real lesson of the equivalence of heat and work is the requirement of heat reservoir for serving as a heat-source, whereas a heat reservoir serving as a sizable heat sink is the result of fossil fuel combustion practices rather than the result of physics as the consequence of the equivalence theorem. Demand of a sizable heat sink is an option, resulted from the technological choice, rather than a necessity, in accordance with physics.

Calling heat discharged to heat sink waste heat may be misleading, [35] but the necessity of sizable heat-sink for the disposal of heat manifests irreversibility involved in heat release in fire. The teaching that the equivalence theorem demands, cumulatively, prodigious production of heat to be disposed represents both an incorrect scientific interpretation of the theorem and a mistakenly pessimistic fate facing the Anthropocene with mankind indoctrinated by the Prometheus myth of fire necessitating the planetary environment as a heat sink.

7.3. The Dissymmetry Premise, the Driving Force of the Irreversible World

Cropper, the chemist and historian of physics, made the observation on Thomson,

In his discursive way, Thomson touched on every one of the major problems of thermodynamics. But except for his temperature scale and interpretation of the energy concept, his work is not found in today’s textbook version of thermodynamics. Although he ranks with Clausius and Gibbs among thermodynamicists, his legacy is more limited than theirs. The comparison with Clausius is striking. These two, of about the same age, and both in possession of the Carnot legacy, had the same thermodynamic concerns. Yet it was the Clausius thermodynamic scheme, based on the two concepts of energy and entropy and their laws, that impressed Gibbs … left no doubt about the conceptual foundations of his theories, and gave Gibbs the requisite clues to put together the scheme we see today in thermodynamics texts. [36: 90]

It is true that in physics and chemistry the textbook version of thermodynamics follows the scheme of Clausius and Gibbs. But Thomson’s legacy on engineering thermodynamics and technology is supreme as evidenced by the unchallenged acceptance of the theory of exergy, which is based on the universal dissipation of free energy or exergy (a proposition that is shown to be falsified in Sect. 4). Other highlights of Thomson’s legacy are these widely accepted truisms: Joule’s assertion of conversion of heat to work (which Thomson initially hesitated to accept); heat cannot be 100% converted into mechanical energy; the notion that “free energy makes the world go ‘round.” In a nutshell, the legacy of the energy premise that the free-energy portion of disorganized energy is the driving force causing changes/transformations in nature.

But that legacy is directly challenged by Clausius’ second fundamental theorem, which Clausius stated in the 1865 Ninth Memoir as,

The second fundamental theorem, in the form which I have given to it, asserts that all transformations occurring in nature may take place in a certain direction, which I have assumed as positive, by themselves, that is, without compensation; but that in the opposite, and consequently negative direction, they can only take place in such a manner as to be compensated by simultaneously occurring positive transformations {²³: 364].

Examples of positive transformations, which can be called conversions since they are transformations that take place by themselves, are heat transmission from high temperature to low temperature; dissipative conversion of work into heat; reaction of reactant into product. The opposite of “dissipative conversion of work into heat” is the “transformation of heat into work,” as asserted by Joule and advocated by the post-1850 Thomson. But missing from this general “understanding” is the precise nature of these transformations: such negative transformations, without being “compensated by simultaneously occurring positive transformations.” are impossible in accordance with the second fundamental theorem. It is positive transformations that cause (autonomously or interventionistically) changes in nature, whether they are spontaneous changes (autonomously) or changes of negative transformation kind (interventionistically), i.e., all processes in the irreversible world, possible. The second fundamental theorem, the bedrock of the second law [²²], transmutes the discovery of heat by NWCJ, the disorganized form of energy, into the discovery of dissymmetry of spontaneous transformations. That is the dissymmetry premise, the primacy of dissymmetry over free energy, which asserts dissymmetry manifested by entropy growth to be the real driving force of the irreversible world—in which real transformations happen and are made to happen.

Some notable clarifications/comments that can be drawn from the dissymmetry premise are:

The deceptive association of high temperature heat as an “energy driving force” of a Carnot engine is due to the fact that entropy growth potentials, EGPs, in these cases requires a heat sink for the disposal of heat released at high temperature: other examples, especially of pure spontaneity kind, in the paper make it clear that that situation is a manifestation of one kind of entropy growth rather than an intrinsic feature of every EGP; the universal feature of harnessing dissymmetry manifested by entropy growth is heat extraction instead of heat disposal.
The second law asserts the inexorable increase of entropy, but the law—the premise emphasizes—does not directly or automatically assert the inexorable change of any other variable. Some examples of common misconceptions are found in the present paper.
That includes that processes towards equilibrium are spontaneous but not inexorable (i.e., universal), i.e., an assertion of dissymmetry is not that of unidirectionality (unidirectional means processes opposite to that of unidirectional is not possible, while dissymmetry in processes towards equilibrium allows processes moving away from equilibrium only that they must be made to happen interventionistically).
A related point to Point 3 should be emphasized that far-from-equilibrium is the precondition for extracting free energy. There has been a lot of talk about extracting free energy, including the advocation of acceleration in extracting free energy by techno-optimists. Without safeguarding the Far·From·Equilibrium precondition, the accelerating extraction of free energy as advocated by techno-optimists will kill the goose that lays the golden eggs.

Discussion in more detail in reference to Points 3 to 4 will be given in another venue, a hint of which is found in Sect. 8.

8. Afterword

The discovery of irreversible world is encapsulated by the dualistic lessons of energy and dissymmetry. Orthodox thermodynamics begins with the premise of primacy of energy over dissymmetry, which represents an epistemological choice of the first fundamental theorem and CVPC ranked ahead of the second fundamental theorem and the interventionist causation it requires. This choice is in keeping with the “previous habits,” orthodox “autonomous evolutions” conceptualization of the mechanical world while dissymmetry is the new discovery of the new world, the essence of which can be captured only by interventionist conceptualization. Only with dissymmetry and interventionist conceptualization can the discovery of the irreversible world, the incorrect explication of which gave rise to the problematic Anthropocene, reach its full potential transcending the Anthropocene.

This paper argues for the primacy of the second fundamental theorem in the formulation of Unified Classical Thermodynamics. The formulation begins with the Carnot/Clausius account of Thomson’s problem, in acknowledging the extraordinary insight of Thomson expressed in the draft of the Dynamical theory of heat paper ([²: 174-200; see [¹]: Appendix II, especially “page five”) and the 1852 Universal dissipation of mechanical energy paper ([²]: 511-514). To this day, the idea that although energy can never be destroyed in a system, it can be wasted or dissipated with the maximum amount of waste given as work output in a reversible operation has been the lesson taught to generations of engineers. Though the case is made here for the second fundamental theorem providing much better solution guidance to reversible operation, we cannot overestimate the role Thomson’s problem played in setting off the processes of problem solving.

It is in this spirit that I suggest another question or thinking out loud by Thomson, referred to as a new Thomson’s problem, to be a source for productive future problem solving. This is in reference to the following, from Wikiquote, [37] quote by William Thomson,

It is conceivable that animal life might have the attribute of using the heat of surrounding matter, at its natural temperature, as a source of energy for mechanical effect . . . . The influence of animal or vegetable life on matter is infinitely beyond the range of any scientific enquiry hitherto entered on. Its power of directing the motions of moving particles, in the demonstrated daily miracle of our human free-will, and in the growth of generation after generation of plants from a single seed, are infinitely different from any possible result of the fortuitous concurrence of atoms.

We have argued for the superiority of the Carnot/Clausius account for Thomson’s problem. And throughout the paper we showed examples—the Carnot-Clausius cycle, Figure 3; the example in Figs. 4 and 5; the example in Figs. 6 and 7; the reversible manifestation of Gibbs “available heat” in Figure 8; and the example manifesting the “approximately” reversible “free flame enthalpy” as shown in Eq. (50)—all these examples demonstrate heat extraction as the dominant mechanism for effectively harnessing the driving force of the irreversible world. Of the five examples, three of them, from the second to the fourth, represent the application of classical thermodynamics within the framework of Clausius and Gibbs showing extraction of “heat of surrounding matter, at its natural temperature, as a source of energy for mechanical effect.” We may refer to these accounts, rather than being miraculous mechanisms or some kind of probability based statistical mechanics mechanism, as the Carnot/Clausius/Gibbs account for the new Thomson’s problem—the classical thermodynamics-based, interventionist, heat extraction mechanism account.

“Just as the Industrial Revolution once generated change in many fields in the 19^th century,” wrote the architect James Wines, “so too the information revolution…serves as a conceptual model in the 21^st century for a new approach to architecture and design…” [38]. I argue for the following for providing even better context for “architecture [and economic activities] to become truly green” [³⁸]: just as the Carnot/Clausius account generated the prodigious progress for mankind during the Anthropocene, the Carnot/Clausius/Gibbs account will serve as a scientific/technological foundation for bringing about coexistence of mankind and the planetary environment at far from equilibrium, a Gaian state of the Earth, for mankind continuing its striving in its home.

References

Smith C W (1977) “William Thomson and the Creation of Thermodynamics: 1840-1855,” Archive for History of Exact Sciences 16: 231–288.
Thomson W (Lord Kelvin) (1911) Mathematical and Physical Papers of William Thomson 1:1–571. Cambridge Univ Press.
Wang L-S (2022) “Triadic relations in thermodynamics,” Energy Conversion and Management: X 15 100233.
Maxwell JC. Tait’s Thermodynamics II. Nature 17 (Feb. 7, 1878):278–280.
Vemulapalli G K (2012) “Thermodynamics in chemistry,” Philosophy of Chemistry (2012 Elsevier B.V.-- North Holland).
Atkins P (1984) The Second Law (Scientific American Library).
Wang L-S (2019) A Treatise of Heat and Energy (Springer, Dec. 7, 2019).
Landsberg PT (1961) Thermodynamics. (Interscience, New York [p. 94]).
Callen H (1985; first edition, 1960) Thermodynamics and an Introduction to Thermostatistics (2^nd edition, Wiley).
Gibbs J W (1878) “On the equilibrium of heterogeneous substances,” in the collection of The Scientific Papers of J W Gibbs, Vol. 1: Thermodynamics: 354-371 (Dover Publications, New York, 1961).
Kondepudi D and Prigogine I (1998) Modern Thermodynamics: From Heat Engines to Dissipative Structures (Wiley): The exact quote is found on p. 111: This change in the Gibbs free energy, called the ‘Gibbs free energy of reaction,’ is related to affinity A by a simple negative sign, but there is a fundamental conceptual difference between the two: affinity is a concept that relates irreversible chemical reactions to entropy, whereas Gibbs free energy is primarily used in connection with equilibrium states and reversible processes.
Harman, P M (1982). Energy, Force, and Matter: The Conceptual Development of Nineteenth-Century Physics (Cambridge Univ. Press).
How Did We Get Here? The Tangled History of the Second Law of Thermodynamics—Stephen Wolfram Writings.
Computational Foundations for the Second Law of Thermodynamics—Stephen Wolfram Writings.
Eddington A (1928) The Nature of the Physical World (The Macmillan Co.).
Uffink J (2001) “Bluff your way in the Second Law of Thermodynamics,”.
Planck M (1969) Treatise on Thermodynamics, 3rd edition. (Dover, New York).
Rovelli C (2018) The Order of Time (Riverhead Books, New York).
Wang L-S (2022) “Clausius’ thermodynamics, a theory of motive power from disorganized energy” Qeios ID: G43182.3. [CrossRef]
California Energy Commission, Energy Glossary: Energy Glossary (Ica.gov).
Wang L-S (2022) “The Thomson-Clausius synthesis revisited: Why “conversion” of heat to work is a misnomer?” Qeios ID: 0FII5E. [CrossRef]
Xue T-W and Guo Z-Y (2019) “What Is the Real Clausius Statement of the Second Law of Thermodynamics?” Entropy 2019, 21, 926. [CrossRef]
Clausius, R. The Mechanical Theory of Heat, with Its Applications to the Steam-Engine and to the Physical Properties of Bodies. John van Voorst: London, UK, 1867; pp. 1-374: (Fourth Memoir, 111–135; Sixth Memoir, 215–256; Ninth Memoir, 327–374).
Cropper W H (1986) “Rudolf Clausius and the road to entropy,” Am. J. Phys. 54 (12): 1068-1074.
Coopersmith J (2015) Energy, the Subtle Concept.
Baldwin M, Sobotka A, and Clough M P () “Conceptualizing Energy: Conservation of Mechanical Energy and the Introduction of Potential Energy”. https://www.storybehindthescience.org/how-science-works.
Zwier K R (2014) “Interventionist causation in physical science,” Doctoral Thesis (University of Pittsburgh, HPS).
Wang L-S (1992) “The nonexistence hypothesis of equation-of-motion for energy conversion processes,” CEAS Technical Report 632 (June 19, 1992).
Marshall McLuhan: Old Versus New Assumptions. Marshall McLuhan: Old Versus New Assumptions (fs.blog).
Ulanowicz R E (2021). “Socio-Ecological Networks: A Lens That Focuses Beyond Physics,” Front. Ecol. Evol. Vol. 26 February 2021 | https://doi.org/10.3389/fevo.2021.643122: 1-8. [CrossRef]
Woodward J (2003) Making Things Happen: A Theory of Causal Explanation. Oxford University Press (Lakatos Award winner, 2005).
Wang L-S, Jeng Y-L, Wang A C (1992) “Reflections on heat engines: the operational analysis of isothermal combustion,” AES-Vol. 27/HTD-Vol. 228, Thermodynamics and the Design, Analysis, and improvement of Energy Systems (ASME 1992).
Cengel Y A and Boles M A (2008) Thermodynamics, an Engineering Approach, Sixth Edition (McGraw-Hill).
Poincaré H (1913) Science and Hypothesis. The Science Press, Lancaster, PA (pp. 122–123).
Kostic M (2024) “2024 Key Reflections on the 1824 Sadi Carnot’s “Réflexions,” Ver. 1.07 UPDATED PDF * .
Cropper W H (2001) Great Physicists: The Life and Times of Leading Physicists from Galileo to Hawking (Oxford).
William Thomson - Wikiquote. As quoted in The Life of Lord Kelvin (1910), by Silvanus Phillips, Volume 2, (2005 edition, p.1093).
Wines J. (2000) Green Architecture (TASCHEN [May 1, 2000]).

Figure 1. Venn diagram of the conditions of reversibility, internal reversibility (IR), and quasi-staticity.

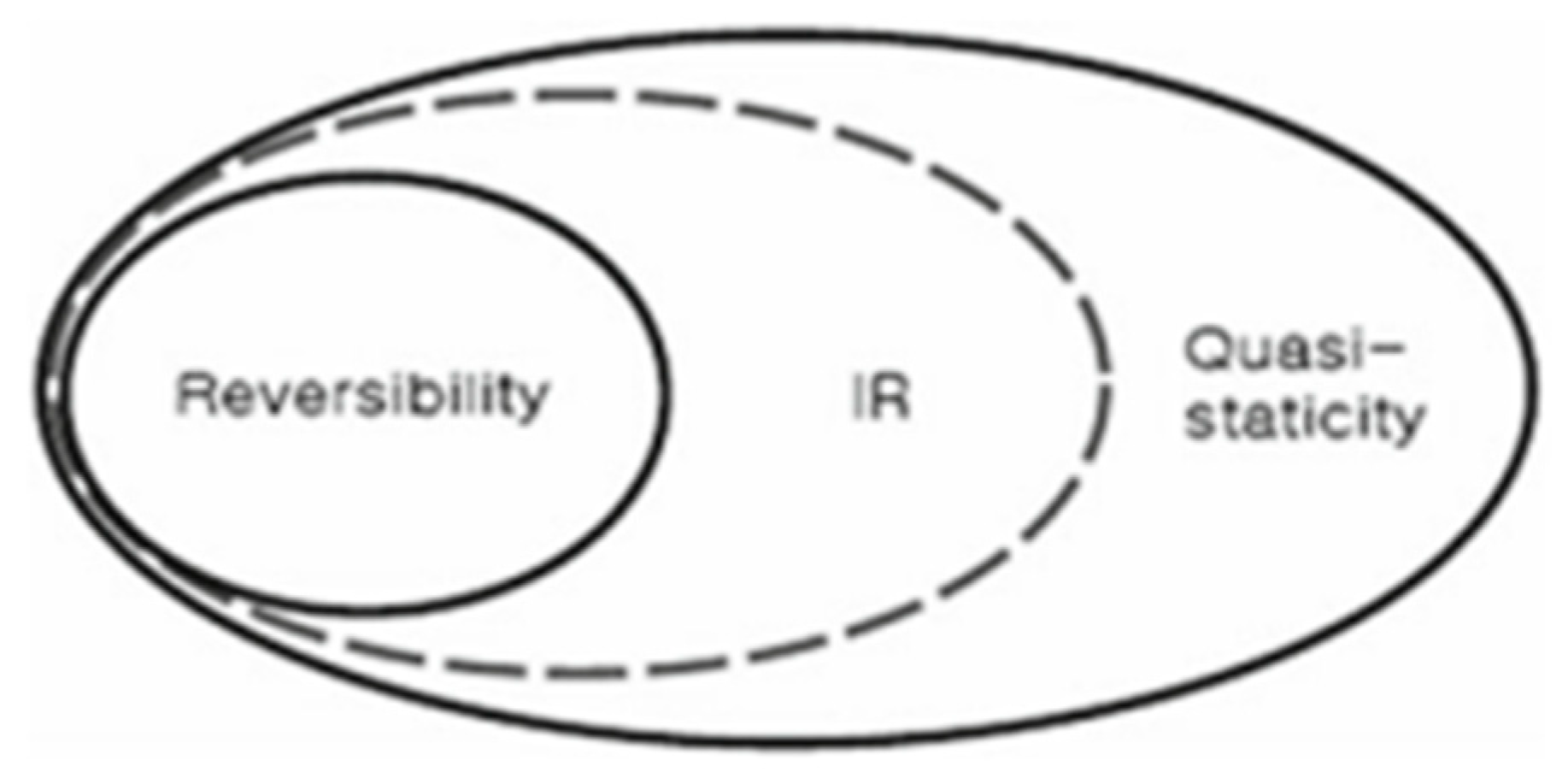
Figure 3. The Carnot-Clausius cycle of the Carnot engine, in which a

T_{0}

-heat-reservoir doubles as a heat sink for heat transmission which drives the process and as a heat reservoir from which the work (measured by area 3-4-5-7[2’]-3) comes. Note that

T_{2} (T_{5} = T_{6})

is infinitesimally higher than

T_{0}

, which is infinitesimally higher than

T_{1^{'}} (= T_{2^{'}})

Figure 3. The Carnot-Clausius cycle of the Carnot engine, in which a

T_{0}

-heat-reservoir doubles as a heat sink for heat transmission which drives the process and as a heat reservoir from which the work (measured by area 3-4-5-7[2’]-3) comes. Note that

T_{2} (T_{5} = T_{6})

is infinitesimally higher than

T_{0}

, which is infinitesimally higher than

T_{1^{'}} (= T_{2^{'}})

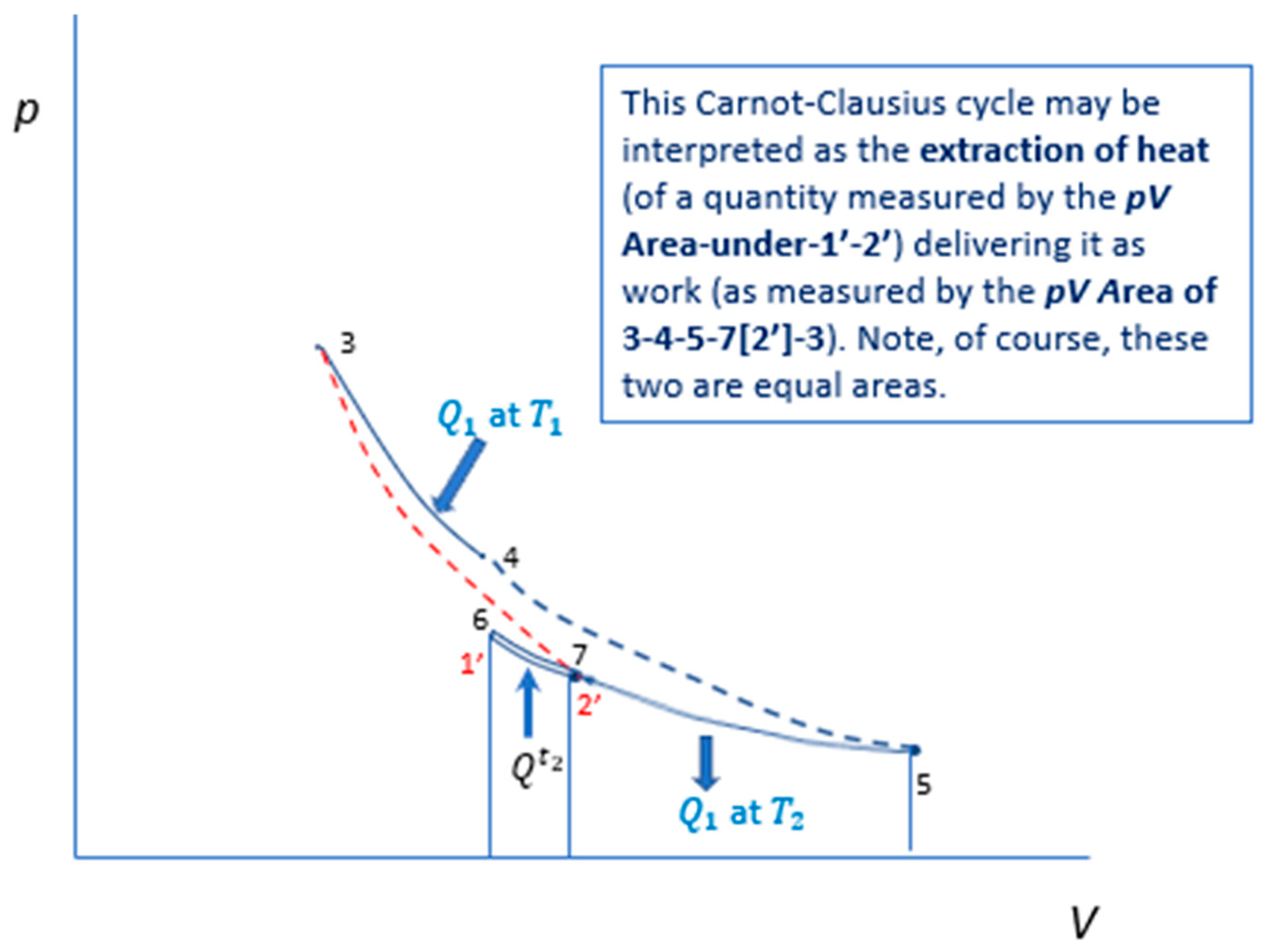
Figure 4. A composite system together with a heat bath, the composite system being at its initial state.

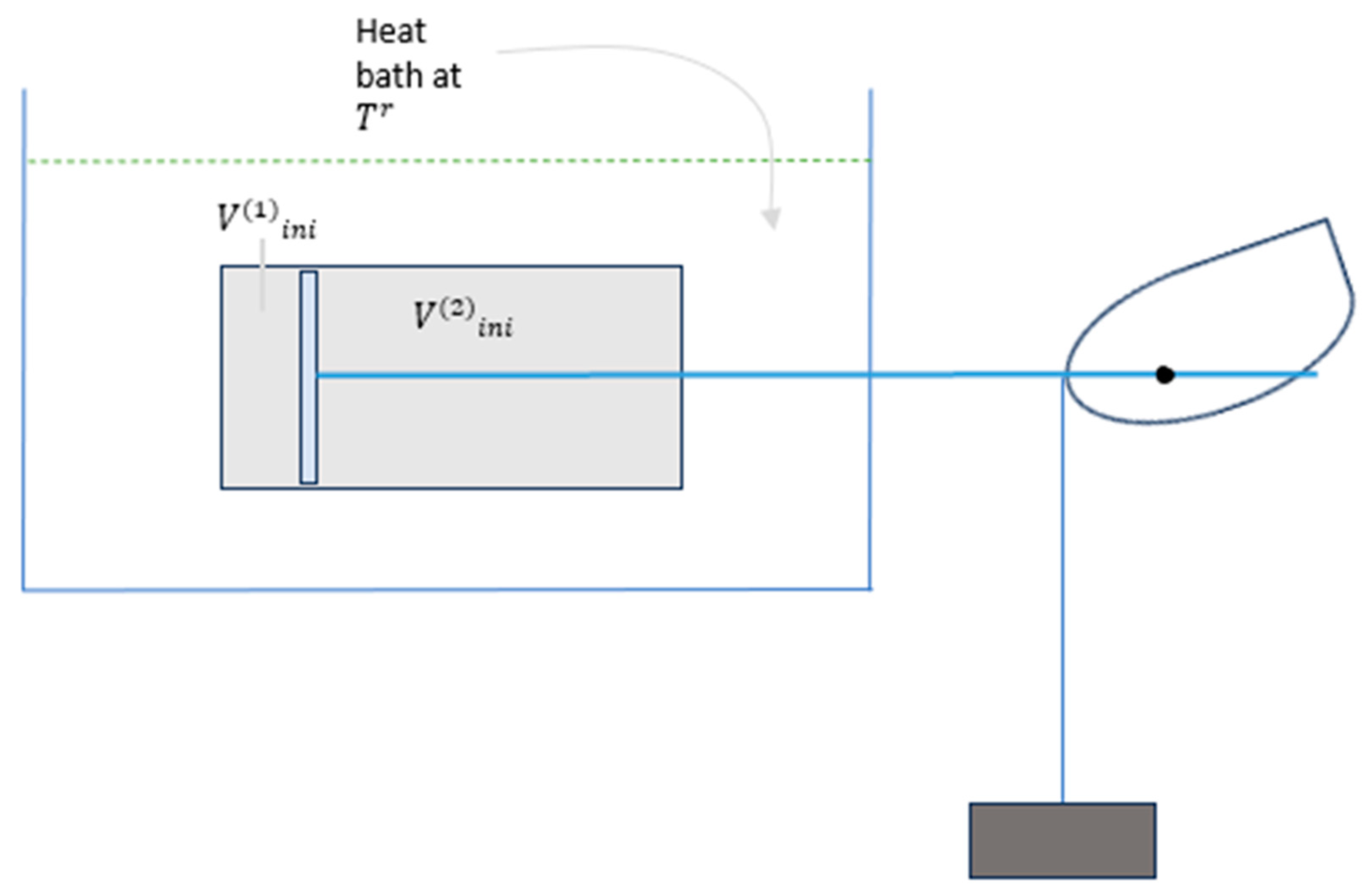
Figure 6. Spontaneous thermal event of two blocks approaching internal thermal equilibrium.

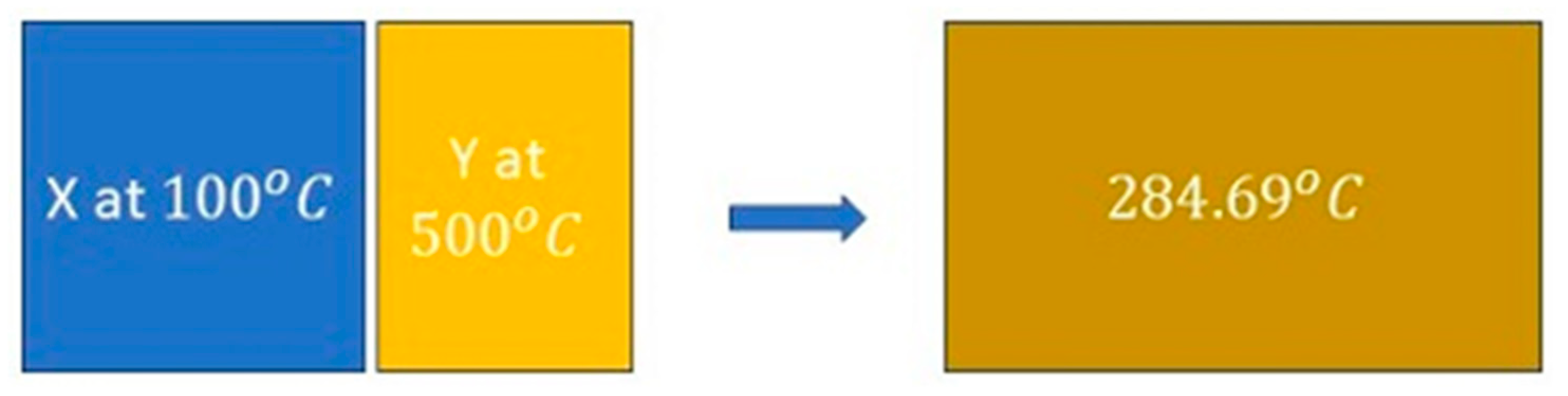
Figure 7. Reversible event in two phases: The end result is that the two phases together are equivalent to the “extraction of heat” in Phase Two for the “production of work” in Phase One of an amount,

W_{r e v} = 539.9 \cdot 0.0549

W_{r e v} = 539.9 \cdot 0.0549

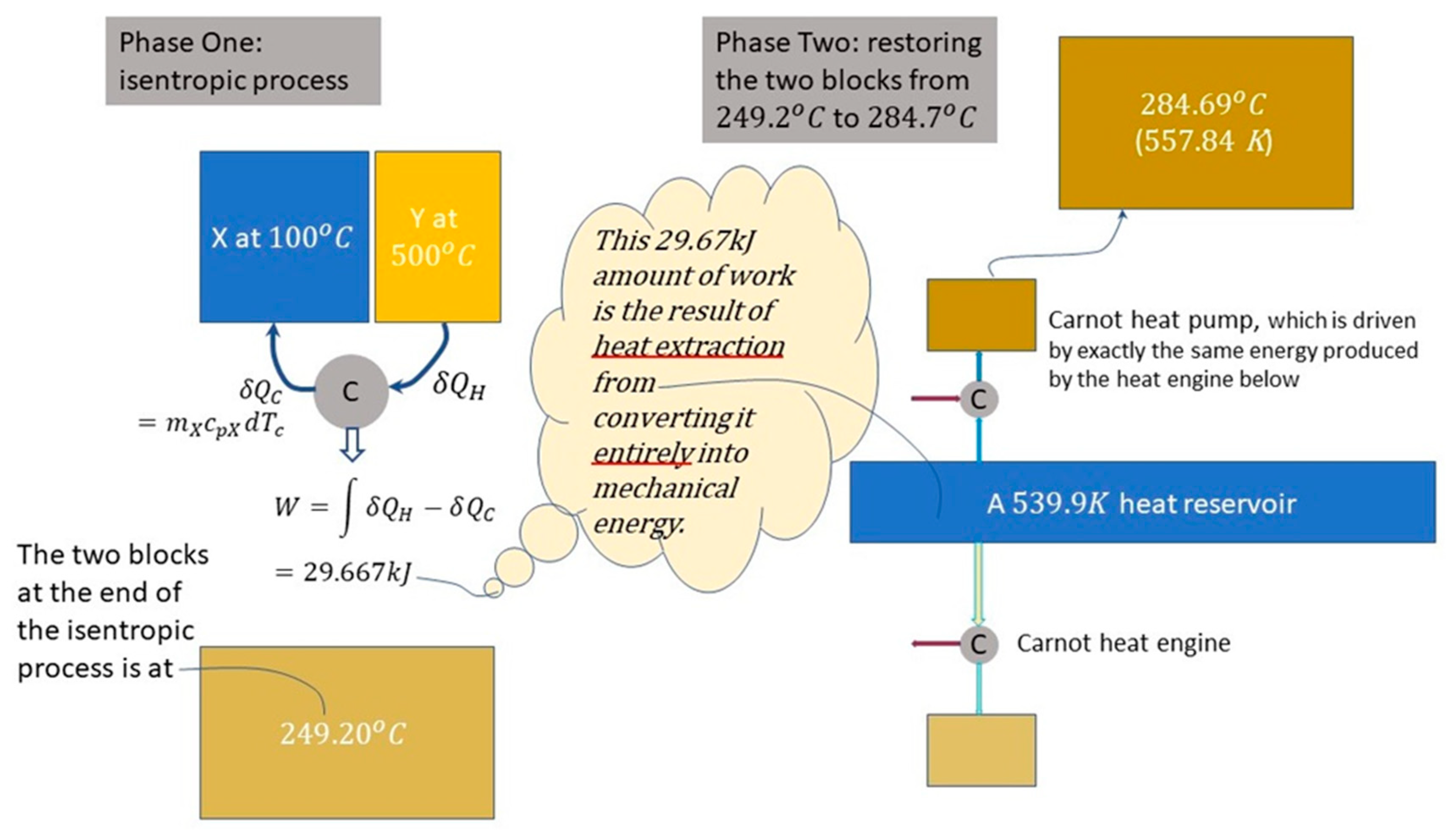
Figure 8. The reversible manifestation of Gibbs free enthalpy or free heat.

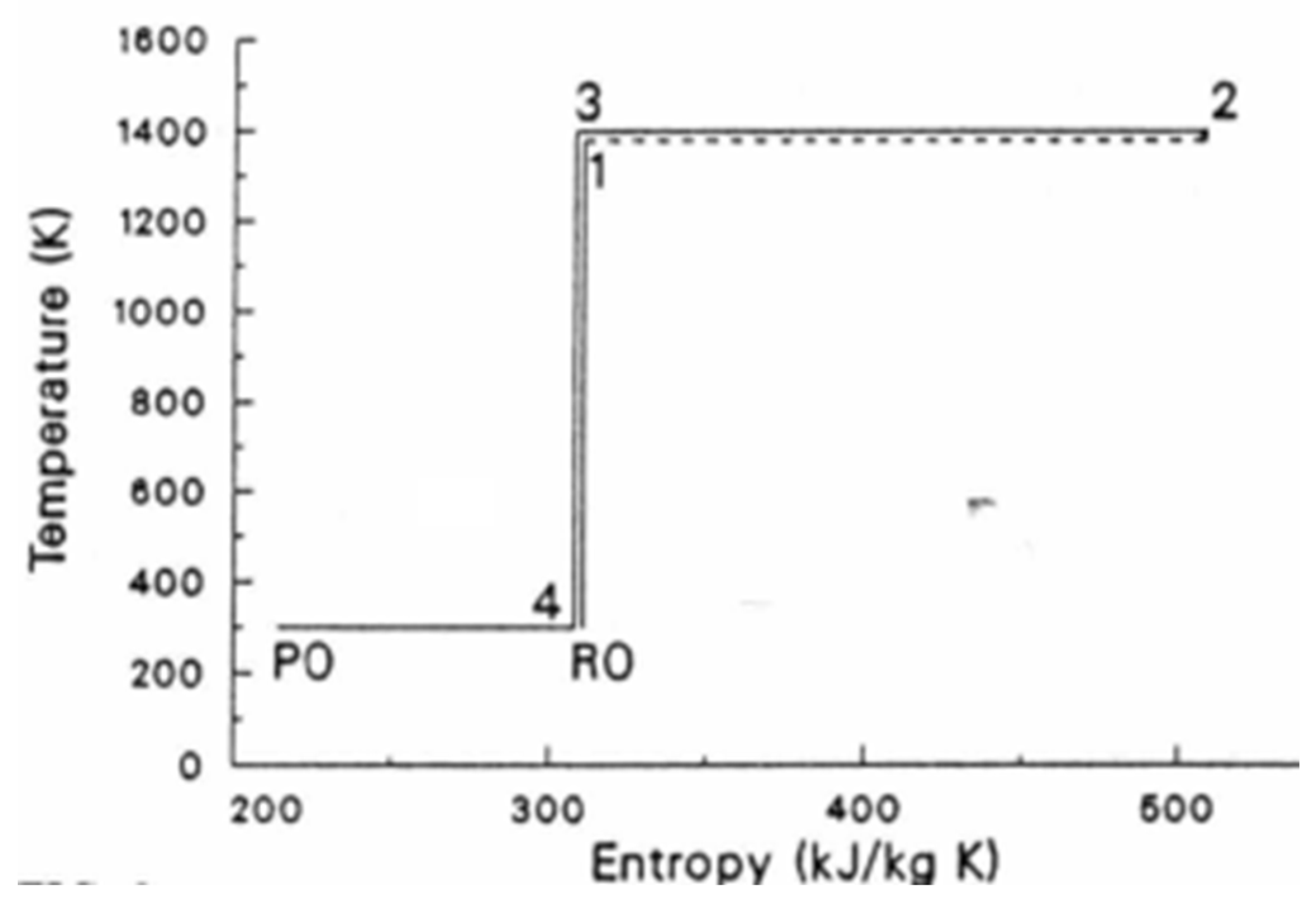
Figure 9. A combustion chamber for feeding a Carnot engine’s isothermal heat addition.

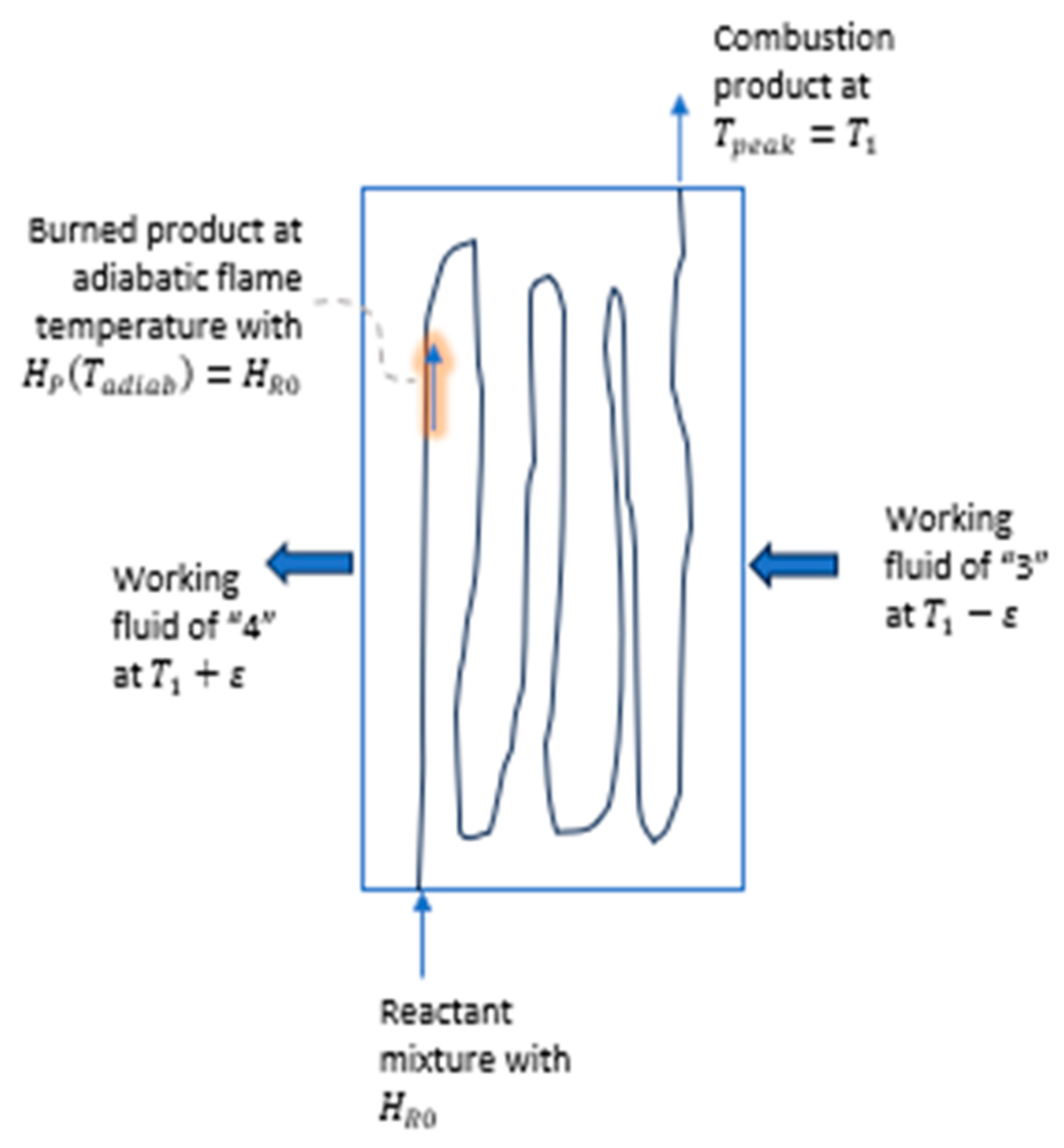
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Unified Classical Thermodynamics: Primacy of Dissymmetry over Free Energy

Abstract

1. Introduction: Free Energy vs. Nature’s Dissymmetry

2. Combined Statement of the First and Second Laws

3. Method of Potentials: Nature’s Dissymmetry

4. Kelvin and the Creation of Energy Physics: Free Energy

5. Heat and Disorganized Energy, “Energy” as the Ability to Cause Change?

6. Reversible Processes Approaching the Extremes of Thermodynamic Potentials

7. The Dissymmetry Premise

7.1. Primacy of Dissymmetry over Free Energy, an Epistemological Issue

7.2. Helmholtz Free Energy and Gibbs Free Enthalpy; Entropy Growth Potentials

7.3. The Dissymmetry Premise, the Driving Force of the Irreversible World

8. Afterword

References

MDPI Initiatives

Important Links

Subscribe