Preprint
Article
CMARL: A Multi-agent Deep Reinforcement Learning Model with Emphasis on Communication Content
Altmetrics
Downloads
151
Views
71
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
22 January 2024
Posted:
22 January 2024
You are already at the latest version
Alerts
Abstract
In recent years, the viability of employing multi-agent reinforcement learning technology for adaptive traffic signal control has been extensively validated. However, owing to restricted communication among agents and the partial observability of the traffic environment, the process of mapping road network states to actions encounters numerous challenges. To address this problem, this paper proposes a multi-agent deep reinforcement learning model with an emphasis on communication content (CMARL). The model decouples the complex relationships between multi-signal agents through centralized training and decentralized execution. Specifically, we first pass the traffic state through an improved deep neural network to achieve the extraction of high-dimensional semantic information and the learning of the communication matrix. Then the agents selectively interact with each other based on the learned communication matrix and generate the final state features. Finally, the features are inputted to the QMIX network to achieve the final action selection. We compare the CMARL model with 6 other baseline algorithms in real traffic networks. The results show that CMARL can significantly reduce vehicle congestion, and run stably in various scenarios.
Keywords:
Subject: Engineering - Transportation Science and Technology
1. Introduction
With the rapid development of urban motorization, there has been a serious imbalance between the traffic demand and supply. Traffic congestion has become a major traffic problem faced by most cities, and its environmental, social, and economic consequences are well documented [1,2,3]. Adaptive traffic signal control (ATSC) is one of the effective means to solve traffic congestion. It balances the traffic flow in the road network by coordinating the timing scheme of traffic lights in the control area, so as to reduce the number of stops, delay time, and energy consumption. Promoting the development of traffic control systems is of great significance for giving full play to the traffic benefits of the road system, mitigating environmental pollution, and assisting the sustainable development of the traffic system.
In recent years, machine learning methods have been widely used in various fields as a new artificial intelligence technology [4,5,6,7]. In the reinforcement learning (RL) based control framework, the traffic signal control system no longer relies on heuristic assumptions and equations but learns to optimize the signal control strategy through continuous trial and error through real-time interaction with the road network. Therefore, compared with traditional traffic control methods, RL signal control methods can usually achieve better control effects [8,9,10]. Early RL-based models solve traffic signal control problems by querying q-tables that record traffic state, actions, and rewards [11,12]. This is easy to implement in environments with relatively simple traffic conditions, but the processing method will occupy a large amount of storage space in a relatively complex traffic environment. In this regard, some scholars choose to use q-network to fit q-table, apply deep learning (DL) to enhance the ability of RL-based algorithms to cope with complex environments, and propose the deep reinforcement learning (DRL) algorithm [13]. Since then, a large number of studies have used DRL algorithms to solve TSC problems, and have achieved good results in practice [14,15,16,17].
However, for signal control of multiple intersections within a certain area (the collaborative control task under a multi-agent system), the partial observability of the traffic environment makes the mapping from road network state to actions face many challenges [18]. Communication collaboration between intersections has become an important link that cannot be ignored in effective regional signal control, and the multi-agent reinforcement learning (MARL) algorithm has gradually become one of the most promising methods in large-scale traffic signal control (TSC) [19,20,21]. According to the collaborative method, MARL-based control methods can be divided into two types: centralized control methods and distributed control methods.
In the centralized control method, all signal lights (agents) in the road network are controlled by a unified central controller. Each agent passes the observed local traffic state to the central controller, and the central controller uses a deep network (DNN) to fit the joint action function value performs action sampling from the corresponding policy network, and then sends it to each agent for execution. The centralized method combines the information of all agents and implies a communication and coordination mechanism between agents, so it is easier to obtain the global optimal solution. However, action decisions also need to be made after the traffic state statistics of all agents are completed, and the strategy formulation speed is relatively slow. In addition, as the number of agents increases, the action space and state space of the algorithm will grow exponentially [11]. Therefore, in large-scale TSC, the centralized learning paradigm is generally not used to avoid the "curse of dimensionality" problem. The distributed control method assumes that the agent is in a stable environmental state and regards other agents as part of the environment. Each agent optimizes its own strategy in the direction of maximizing global reward based on its own observations, so the scalability of distributed control methods is relatively good. However, the independent learning method also makes the distributed control method more likely to fall into local optimality [22].
In order to solve this problem, most scholars have incorporated the communication mechanism into the TSC model framework to achieve better control effects. Specifically, communication mechanisms can be mainly divided into two types: "explicit" communication and "implicit" communication [23,24]. The core of explicit communication is to explore how intelligent agents communicate. Among them, the selection of communication objects can be achieved through heuristic frameworks [25,26] and gating mechanisms [27]; the adjustment of communication content and time is based on DL methods such as attention mechanisms [18,28], recurrent neural networks [29], and graph neural networks [30,31,32]. Implicit communication mainly affects the behavioral strategy formulation of the signal agent through value function decomposition and centralized value function [20,23,33,34,35]. Most implicit communication MARL frameworks use the centralized-training decentralized-execution (CTDE) learning paradigm, which allows agents to use global (road network) information for centralized learning during the training phase. After the training is completed, each agent can complete the selection of action execution only through its own observation and local information interaction, which greatly reduces communication overhead while ensuring agent communication cooperation.
In this article, we use the adjustment plan of signal timing as optimization variables, with the goal of minimizing the average vehicle delay in the road network, and design a multi-agent deep reinforcement learning model considering communication content based on QMIX [33], namely CMARL. This model combines two communication mechanisms and belongs to the distributed control method under the CTDE paradigm. The contributions of the present study lie in:
1. A MARL model that considers communication content is proposed to solve the regional TSC problem. This model decouples the complex relationships among multi-signal agents through the CTDE paradigm and uses a modified DNN network to realize the mining and selective transmission of traffic flow features. It enriches the information content while reducing the communication overhead caused by the increase in information.
2. We design several comparison experiments using traffic data sets from the real world, and prove the advantages of CMARL in regional traffic signal control tasks by comparing with six baseline methods including the fixed signal control model and other five advanced DRL control models.
The remainder of the article is organized as follows. Section 2 reviews related research on traffic signal control based on DRL. Section 3 introduces the definition of the problem and the CMARL algorithm framework proposed in this paper. Experiments and performance evaluation are presented in Section 4. Finally, we conclude our work and future prospects in Section 5.
2. Literature Review
2.1. Single-agent Deep Reinforcement Learning in Traffic Signal Control
The setting of single-agent reinforcement learning mainly consists of two parts: the agent and the environment. The essence of the model is a Markov decision process, called MDP, which is represented by a 5-tuple containing environmental state, action, state transition function, reward, and reward discount coefficient, that is, . DRL algorithms based on single agents are mostly applied to traffic control problems at isolated intersections. Researchers usually conduct specific research around the two directions of intersection environment feature extraction and model structure improvement. Ma et al. [29] used historical traffic state as a time series image sequence, mining the spatiotemporal feature information in traffic flow data based on the combined structure of convolutional neural layers and LSTM, and achieved final signal control through the actor-critic framework. Li et al. [36] constructed an adaptive control method for isolated intersection signal control using signal phase and duration as actions and minimizing the average waiting time of vehicles as the goal. Yazdani et al. [37] considered pedestrian travel needs and established a traffic signal adaptive control method based on DRL to minimize delays for total intersection users (vehicle flow and pedestrian flow). Bouktif et al. [38] considered both discrete and continuous decision-making, and used the intersection phase and duration as optimization variables to propose a parameterized deep q-network architecture. Similarly, Ducrocq et al. [39] proposed a new DQN model for signal control in a traffic environment where intelligent connected vehicles and ordinary vehicles mix, and adjusted the model architecture and hyperparameters through partial discrete traffic state coding and delay-based reward functions.
2.2. Multi-agent Deep Reinforcement Learning in Traffic Signal Control
There are at least two agents in a multi-agent system, and there is usually a certain relationship between the agents, such as cooperation, competition, or both competition and cooperation. The collaborative control problem of multi-signalized intersections is generally a multi-agent control problem under a cooperative relationship, and the traffic lights in the road network are regarded as intelligent agents. Since the sensors carried by each agent only cover a small part of the overall environment in actual situations, the signal control model based on multi-agent is usually described as a decentralized partially observable Markov decision process (DEC-POMDP). This process can be represented by the seven-tuple of . Among them, represents the local observation received by the agent, and is the observation function. During the training process of the network, each agent learns the control strategy of traffic signals through continuous interaction with the environment to achieve the purpose of alleviating traffic congestion. However, from the perspective of each agent, the environment is unstable, which is not conducive to convergence. In order to increase the stability of training, the communication interaction between agents has gradually become a key issue that researchers pay attention to.
Wang et al. [12] extracted the state representation of the road network environment through the k-nearest neighbor algorithm and stabilized the model based on spatial discount rewards. Zhu et al. [17] designed a dynamic interaction mechanism based on the attention mechanism to promote information interaction between agents. On this basis, they used a generalized network to process joint information and used ridge regression to update network parameters. Li et al. [40] proposed a knowledge-sharing deep deterministic policy gradient (DDPG) model, in which each agent has access to the state set collected by all agents. Yang et al. [41] constructed an RL framework that considers multi-agent mutual information. They measured the correlation between input states and output information through mutual information and optimized the overall model based on mutual information. Wu et al. [22] and Chen et al. [42] both used LSTM to alleviate the instability of local observable states in the environment. On this basis, Wu used a DDPG framework of centralized training and distributed execution to share environmental parameters, and Chen realized communication and collaboration between agents based on the value decomposition-based QMIX network.
However, to apply these methods to actual engineering, communication limitations such as bandwidth availability are still unavoidable and important issues [43]. The communication network not only brings more useful feature information, but also increases the overall communication overhead of the model to a certain extent. Therefore, how to limit additional communication overhead while maintaining cooperation is still a major challenge facing the road network TSC problem.
3. Methodology
3.1. Problem Definition
In CMARL, the traffic light in the road network is regarded as independent agent , and each agent obtains state that characterize the current environment based on sensor observations within the respective intersection range. The detailed definitions are as follows:
State: For each agent, the traffic state of the intersection consists of the number of vehicles in each lane, the number of queuing vehicles in each lane, and the current phase number of the traffic light. Among them, represents the number of entrance lanes at the intersection n, and is the set of lanes at all intersections in the road network. The global state is the set obtained by splicing the traffic states of each agent.
Action: The phase sequence of the signalized intersection is fixed. Action is set to the adjustment of the current green light phase, that is, whether to switch the current phase to the next phase: indicates a switch to the next phase, and indicates that the current phase is maintained. In addition, we set the maximum and minimum green light time and the constraint rules of the yellow phase that must be implemented to convert the phase to ensure the reasonable passage of traffic flow.
Reward: Select the distance delay as the parameter to construct the reward function:
3.2. Model Structure
Figure 1 shows the network framework of the CMARL model. As shown in the figure, the model consists of three modules: information processing, feature mining, and action value function fitting. Among them, the information processing module simulates the traffic flow in the actual road network through the simulation of urban mobility (SUMO) and obtains the state parameters for subsequent network training. The feature mining module is mainly composed of an improved DNN network. The input information of the network is the initial state of each agent at time t and the action of the previous moment (the action in the initial state defaults to 0). The output is the corresponding feature matrix and the communication matrix . Based on communication signals, each agent can selectively communicate with other agents in the road network to obtain the final state characteristic matrix . The action value function fitting network is consistent with the QMIX network. The overall network is mainly composed of the local action value function network (red box network) and the joint action value function network (green box network). The local action value function network belongs to the recurrent neural network (RNN). The input and output of the network are the final feature matrix of each agent and the action value function value of each action respectively. Based on , each agent uses a greedy strategy to select the optimal action suitable for the current environment to act on the environment. The environment then moves to the next state and returns the reward value under the group of joint actions .
The joint action value function network also uses a neural network structure, consisting of a yellow parameter generation network and a purple inference network. The difference is that the weights and biases of the inference network are generated by the parameter generation neural network. At time t, the parameter generation network accepts the global state and generates weights and biases. On this basis, the inference network receives the action function values of all agents, and assigns the weights and biases generated by the generation network to its own network, thereby inferring the joint action function value . During the training process of the network, based on the joint action value function and reward function of the extracted data, we can calculate the loss function and update the parameters of the network.
3.3. Feature Extraction Module
The main framework of the feature extraction module is a modified DNN. Specifically, we use GRU to replace a hidden layer in the DNN network to better extract features. As shown in Eqs. (2)-(5), the features carrying traffic flow information and the historical action are first mapped to a higher-dimensional vector space to obtain richer semantic information. Then based on the GRU network, we mine the temporal features in the historical data, and obtain the final feature matrix and communication matrix through two multi-layer perceptron structures with a single hidden layer.
where the parameters with W and b as variables are the trainable weights and biases in the network respectively; and are the hidden states at t time and t-1 time respectively, ; and are nonlinear activation functions, which can enhance the representation ability and learning ability of the network; is a rounding function that can return the operation result rounded according to the specified number of decimal places.
On this basis, each agent realizes communication and interaction with each other based on the communication matrix. Taking the signal agent n as an example, the communication information corresponding to agent n is located in the n row of the communication matrix , that is, . This is an -dimension bull vector, which is a binary vector composed of 0 and 1. If (the bit in ), agent n will refer to the environmental information of the agent to select an action; otherwise, the environment information of agent number will be ignored. The above process can be expressed by Eqs. (7)-(8):
where is the feature matrix that contains information about other agents, .
To facilitate subsequent calculations, we use a fully connected layer to change the dimension of and add it to the state vector to generate the final state feature . Eqs. (9)-(11) also take agent n as an example to illustrate the flow of information during the generation of final state features.
3.4. Action_value Function Fitting Module
The composition of the action value function fitting network has been introduced in Section 3.1 , so this section mainly shows the specific equations corresponding to the module, as well as the detailed meaning of the parameters in it. Eqs. (12)-(14) show the RNN network, that is, the local value function fitting network. The input of the network is the feature matrix of all signal agents, and the output is the action function value corresponding to each action in the action set of the signal light agent.
where the parameters with w and b as variables are the trainable weights and biases in the network; the definition of 、、 are also consistent with the above, .
The calculation of the joint action function value requires the optimal local action function value as input. In order to implement distributed control under global optimal conditions, the joint action value function and the local value function need to have the same monotonicity, which means the action that can maximize the joint action value function should be equivalent to the local optimal action set:
where the is used to take parameters (set) of the function and return the action label corresponding to the maximum value of the action value function; 、… are the action value function of road network and signal intersection respectively; 、… are the historical actions of road network and signal intersection respectively.
The QMIX network converts the above equation into the constraint condition shown in Eq. (16), and satisfies the constraint by restricting the weights and in the joint action value function network (making their values positive).
- This section may be divided by subheadings. It should provide a concise and precise description of the experimental results, their interpretation, as well as the experimental conclusions that can be drawn.
In summary, the joint action function value of the road network can be calculated by the following equation:
where is the action function value under greedy strategy selection.
3.5. Model Update
The update method of CMARL is similar to that of traditional DQN. Both use TD error to calculate the loss function and use the backpropagation algorithm to update network parameters. This process involves two networks: the evaluation network and the target network. The two network structures are identical, as shown in Figure 1, but the input and output information of the two networks are different. The evaluation network takes the features and historical actions in state s as input and outputs the actual joint action function value . The target network takes the features and historical actions of the road network in state as input and calculates the target (expected) action function value . The difference between the output contents of the two networks constitutes the TD error in state s:
where R is the reward value in state s; is the action function value corresponding to all actions of the target network, .
It can be seen from the above that the calculation of TD error requires knowing the road network state s at the current moment, the actual joint action taken a, the road network state after taking the action, the reward R returned by reaching the state , and the actual joint actions in history proceed below. Therefore, the calculation of TD error is not real-time, but is performed after a certain amount of experience has been accumulated. On this basis, the loss function is expressed as follows:
where represents the b-th experience in a batch of extracted experiences; B represents the number of extracted experiences.
In summary, the update process of the CMARL framework has the following expression:

4. Experiments
4.1. Experimental Setup
4.1.1. Simulation Setting
Based on the real data sets collected from the actual road network in Fushun City, China, we use SUMO to build a simulation platform and implement model optimization and information interaction through application program interfaces. The road network simulation environment is shown in Figure 2. The range of the detectors we arrange in each entrance road is 100 meters, and the range of the detectors in the exit road is 80 meters. For four-way intersections, we use a four-phase signal control scheme of east-west straight, east-west left, south-north straight, and south-north left. For three-way intersections, such as intersections 1, 2, and 7, the signal phase sequence is east-west straight, east/west left, and south/north straight. The duration of the yellow light phase is set to 2 seconds.
In addition, to determine the optimal parameters of the model, we pre-trained the network with the traffic configuration shown in Table 2. For the test phase, we refer to the traffic load of the real data set to set the OD matrix of traffic flow distribution during peak hours (6:30-8:30) and off-peak hours (14:00-16:00), as shown in Figure 3.
Table 1.
Traffic volume statistics of the real-world dataset.
| Stage | Duration (s) | Arrival rate (veh/300s) | |||
|---|---|---|---|---|---|
| Mean | SD | Max | Min | ||
| Off-peak hours | 0-7200 | 103.55 | 15.15 | 139 | 89 |
| Peak hours | 7200-14400 | 177.20 | 48.92 | 255 | 132 |
4.1.2. Training Parameters Setting
The duration of each round of training of the CMARL model is 3600s. The parameter settings during the training process are shown in Table 3. The values of these parameters are the results of multiple experiments.
4.1.3. Baseline
(1) FixedTime: A traditional signal control method in which the signal lights run a fixed timing scheme.
(2) DQN: A centralized control method in which all intersections are controlled by the same agent. The agent directly fits the joint action value function based on the global environmental state, and then selects the optimal joint action.
(3) IQL: A distributed control method, each intersection is equipped with independent intelligent agents, and there is no additional information interaction between the intelligent agents. Each agent optimizes its control strategy in the direction of maximizing global returns based on the global environmental state.
(4) DDQNPER: A communication-free distributed control method that defines state and reward functions simply and directly, and fits the action value function through Double DQN with experience playback function.
(5) QPLEX: Each intersection is controlled by an independent agent, and the action value function of each agent is decomposed into a state value function and an advantage value function. The agent realizes the calculation of joint action values based on the multi-head attention mechanism, and ensures the consistency of global and local optimality by constraining the value range of the advantage value function. It is a distributed control method with implicit communication.
(6) MN_Light: This method uses bidirectional LSTM to mine the temporal characteristics of historical traffic flow status and action information. It is a distributed control method for explicit communication.This section may be divided by subheadings. It should provide a concise and precise description of the experimental results, their interpretation, as well as the experimental conclusions that can be drawn.
4.2. Experimental Results
4.2.1. Comparative Experiment
This section shows the control effects of each baseline method and the CMARL model and further analyzes and discusses the reasons for the above results. As shown in Table 3, we select three indicators: queue length, waiting time, and travel time to evaluate the model effect. Among them, the queue length and waiting time are respectively equal to the average queue length and queue time of each intersection entrance lane during the simulation period, and the travel time is the average time required for all vehicles in the road network to complete the scheduled trip. As can be seen from the table, various types of DRL algorithms have better control effects than the FixedTime algorithm. In order to further compare and demonstrate the control effects of various algorithms, we plot the differences in various evaluation indicators between the above six DRL algorithms and the FixedTime algorithm into a clustered column chart as shown in Figure 4. It can be seen that compared with basic distributed control methods, such as IQL and DDQNPER, the centralized control method based on DQN obviously has better control effects. DQN converged at the 82nd generation, while IQN and DDQNPER converged at the 127th and 131st generation respectively. This is in line with our inference, that is, the centralized method that collects all information implies a communication and collaboration mechanism between agents, and can easily obtain the global optimal solution. However, the basic distributed control method is more likely to fall into local optimality due to the lack of information interaction between agents.
QPLEX and MN_Light belong to the distributed control methods of implicit communication and explicit communication respectively. The former adds global state information during the training process and realizes information interconnection by decomposing the global rewards according to their respective contributions. The latter uses bidirectional LSTM to contact context information to achieve temporal feature extraction in complex environments and enrich the state information that the agent can receive. Compared with the previous two distributed methods, both have improved to a certain extent in various evaluation indicators: taking peak hours as an example, compared with DDQNPER, the queue length of QPLEX was reduced by 17.09%, and the waiting time was reduced by 8.53%, the travel time was reduced by 2.16%. MN_Light's queue length was reduced by 20.86%, the waiting time was reduced by 6.01%, and the travel time was reduced by 2.75%.
The CMARL model established in this article combines two communication methods: implicit communication and explicit communication. It uses an improved DNN to realize the mining and selective transmission of high-dimensional features of traffic flow. While enriching information content, it reduces communication overhead and has better control effects. Compared with the optimal method MN_Light among the baseline methods, CMARL's queue length during peak hours was reduced by 9.12%, the waiting time was reduced by 7.67%, and the travel time was reduced by 3.31%; the queue length during off-peak hours was reduced 5.43%, the waiting time decreased by 2.72%, and the travel time decreased by 3.83%.
4.2.2. Ablation experiment
To further explore the effectiveness of the proposed feature extraction module, we designed an ablation experiment as shown below. Figure 5 shows the degree of improvement in each evaluation index of the QMIX and CMARL compared to the MN_Light algorithm. It can be seen that after removing the feature extraction module, the model control effect drops significantly. This phenomenon is especially obvious during peak hours. During peak hours, CMARL's queue length and queuing time were reduced by 9.73% and 5.64% respectively compared to QMIX; while during off-peak hours, compared to QMIX, CMARL's queue length and queuing time were reduced by 8.87% and 4.47% respectively. This is because there are many vehicles in the road network during peak hours, and the spatiotemporal relationship between traffic flows is relatively complex. At this time, relying only on the status information directly obtained by the detector, the agent cannot obtain enough environmental information to determine the optimal action.
5. Discussion
This paper designs a multi-agent deep reinforcement learning model with an emphasis on communication content to solve the signal control problem of road networks. In order to alleviate the instability of model learning caused by local observable states, we use a modified DNN network to excavate and selectively share nonlinear features in traffic flow data, enriching the information content and reducing the communication overhead caused by the increase of information. Using real data sets, we conduct a comparative analysis between CMARL and six advanced traffic signal control methods, and come to the following conclusions:
(1) CMARL can operate stably in a variety of scenarios and has good control effects. Compared with the optimal method MN_Light among the baseline methods, CMARL's queue length during peak hours was reduced by 9.12%, the average waiting time was reduced by 7.67%, and the average travel time was reduced by 3.31%; the queue length during off-peak hours was reduced 5.43%, the average waiting time decreased by 2.72%, and the average travel time decreased by 3.83%.
(2) In relatively complex traffic environments, further extraction of high-dimensional nonlinear features helps the agent select optimal actions. After adding the feature extraction module, the model control effect of QMIX was greatly improved, and the queue length and average waiting time during peak hours were reduced by 9.73% and 5.64% respectively.
In future work, we will further expand the scale of the road network and explore the applicability of different types of MARL in large-scale road network signal control problems.
Author Contributions
Conceptualization, Ande Chang; methodology and validation, Yuting Ji; writing—original draft preparation, Chunguang Wang; writing—review and editing, Yiming Bie.
Funding
This research was supported by the plan project of Department of Science and Technol-ogy, Jilin Province, China [grant number 20230508048RC].
References
- Zhao, D.; Dai, Y.; Zhang, Z. Computational intelligence in urban traffic signal control: A survey. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews) 2011, 42, 485–494. [Google Scholar] [CrossRef]
- Cong, Y.; Wang, H.; Bie, Y.; Wu, J. Double-battery configuration method for electric bus operation in cold regions. Transportation Research Part E: Logistics and Transportation Review 2023, 180, 103362. [Google Scholar] [CrossRef]
- Bie, Y.; Liu, Y.; Li, S.; Wang, L. HVAC operation planning for electric bus trips based on chance-constrained programming. Energy 2022, 258, 124807. [Google Scholar] [CrossRef]
- Mao, F.; Li, Z.; Li, L. A comparison of deep reinforcement learning models for isolated traffic signal control. IEEE Intelligent Transportation Systems Magazine 2022, 15, 160–180. [Google Scholar] [CrossRef]
- Osman, M.; He, J.; Mokbal, F. M. M.; Zhu, N.; Qureshi, S. Ml-lgbm: A machine learning model based on light gradient boosting machine for the detection of version number attacks in rpl-based networks. IEEE Access 2021, 9, 83654–83665. [Google Scholar] [CrossRef]
- Jiang, X.; Zhang, J.; Wang, B. Energy-efficient driving for adaptive traffic signal control environment via explainable reinforcement learning. Applied Sciences 2022, 12, 5380. [Google Scholar] [CrossRef]
- Liu, Y.; Jia, R.; Ye, J.; Qu, X. How machine learning informs ride-hailing services: A survey. Communications in Transportation Research 2022, 2, 100075. [Google Scholar] [CrossRef]
- Peng, B.; Keskin, M. F.; Kulcsár, B.; Wymeersch, H. Connected autonomous vehicles for improving mixed traffic efficiency in unsignalized intersections with deep reinforcement learning. Communications in Transportation Research 2021, 1, 100017. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, Z.; LaClair, T. J.; Wang, C.; Shao, Y.; Yuan, J. A Novel Deep Reinforcement Learning Approach to Traffic Signal Control with Connected Vehicles. Applied Sciences 2023, 13, 2750. [Google Scholar] [CrossRef]
- Wang, H.; Zhu, J.; Gu, B. Model-Based Deep Reinforcement Learning with Traffic Inference for Traffic Signal Control. Applied Sciences 2023, 13, 4010. [Google Scholar] [CrossRef]
- Chu, T.; Wang, J.; Codecà, L.; Li, Z. Multi-agent deep reinforcement learning for large-scale traffic signal control. IEEE Transactions on Intelligent Transportation Systems 2019, 21, 1086–1095. [Google Scholar] [CrossRef]
- Wang, T.; Cao, J.; Hussain, A. Adaptive Traffic Signal Control for large-scale scenario with Cooperative Group-based Multi-agent reinforcement learning. Transportation research part C: emerging technologies 2021, 125, 103046. [Google Scholar] [CrossRef]
- Mannion, P.; Duggan, J.; Howley, E. An experimental review of reinforcement learning algorithms for adaptive traffic signal control. Autonomic road transport support systems 2016, 47–66. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A. A.; Veness, J.; Bellemare, M. G.; Graves, A.; Riedmiller, M.; Fidjeland, A. K.; Ostrovski, G. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Haydari, A.; Yılmaz, Y. Deep reinforcement learning for intelligent transportation systems: A survey. IEEE Transactions on Intelligent Transportation Systems. 2020, 23, 11–32. [Google Scholar] [CrossRef]
- Liang, X.; Du, X.; Wang, G.; Han, Z. A deep reinforcement learning network for traffic light cycle control. IEEE Transactions on Vehicular Technology 2019, 68, 1243–1253. [Google Scholar] [CrossRef]
- Zhu, R.; Li, L.; Wu, S.; Lv, P.; Li, Y.; Xu, M. Multi-agent broad reinforcement learning for intelligent traffic light control. Information Sciences 2023, 619, 509–525. [Google Scholar] [CrossRef]
- Han, Y.; Wang, M.; Leclercq, L. Leveraging reinforcement learning for dynamic traffic control: A survey and challenges for field implementation. Communications in Transportation Research 2023, 3, 100104. [Google Scholar] [CrossRef]
- Joo, H.; Lim, Y. Intelligent traffic signal phase distribution system using deep Q-network. Applied Sciences 2022, 12, 425. [Google Scholar] [CrossRef]
- Wan, J.; Wang, C.; Bie, Y. Optimal Traffic Control for a Tandem Intersection With Improved Lane Assignments at Presignals. IEEE Intelligent Transportation Systems Magazine 2023. [Google Scholar] [CrossRef]
- Liu, Y.; Lyu, C.; Zhang, Y.; Liu, Z.; Yu, W.; Qu, X. DeepTSP: Deep traffic state prediction model based on large-scale empirical data. Communications in transportation research 2021, 1, 100012. [Google Scholar] [CrossRef]
- Wu, T.; Zhou, P.; Liu, K.; Yuan, Y.; Wang, X.; Huang, H.; Wu, D. O. Multi-agent deep reinforcement learning for urban traffic light control in vehicular networks. IEEE Transactions on Vehicular Technology 2020, 69, 8243–8256. [Google Scholar] [CrossRef]
- Zhuang, H.; Lei, C.; Chen, Y.; Tan, X. Cooperative Decision-Making for Mixed Traffic at an Unsignalized Intersection Based on Multi-Agent Reinforcement Learning. Applied Sciences 2023, 13, 5018. [Google Scholar] [CrossRef]
- Kővári, B.; Szőke, L.; Bécsi, T.; Aradi, S.; Gáspár, P. Traffic signal control via reinforcement learning for reducing global vehicle emission. Sustainability 2021, 13, 11254. [Google Scholar] [CrossRef]
- Lin, Z.; Gao, K.; Wu, N.; Suganthan, P. N. Scheduling Eight-Phase Urban Traffic Light Problems via Ensemble Meta-Heuristics and Q-Learning Based Local Search. IEEE Transactions on Intelligent Transportation Systems 2023, 24, 14414–14426. [Google Scholar] [CrossRef]
- Olayode, I. O.; Tartibu, L. K.; Okwu, M. O.; Severino, A. Comparative traffic flow prediction of a heuristic ANN model and a hybrid ANN-PSO model in the traffic flow modelling of vehicles at a four-way signalized road intersection. Sustainability 2021, 13, 10704. [Google Scholar] [CrossRef]
- Hussain, B.; Afzal, M. K.; Ahmad, S.; Mostafa, A. M. Intelligent traffic flow prediction using optimized GRU model. IEEE Access 2021, 9, 100736–100746. [Google Scholar] [CrossRef]
- Wang, M.; Wu, L.; Li, M.; Wu, D.; Shi, X.; Ma, C. Meta-learning based spatial-temporal graph attention network for traffic signal control. Knowledge-based systems 2022, 250, 109166. [Google Scholar] [CrossRef]
- Ma, D.; Zhou, B.; Song, X.; Dai, H. A deep reinforcement learning approach to traffic signal control with temporal traffic pattern mining. IEEE Transactions on Intelligent Transportation Systems 2021, 23, 11789–11800. [Google Scholar] [CrossRef]
- Yoon, J.; Ahn, K.; Park, J.; Yeo, H. Transferable traffic signal control: Reinforcement learning with graph centric state representation. Transportation Research Part C: Emerging Technologies 2021, 130, 103321. [Google Scholar] [CrossRef]
- Yan, L.; Zhu, L.; Song, K.; Yuan, Z.; Yan, Y.; Tang, Y.; Peng, C. Graph cooperation deep reinforcement learning for ecological urban traffic signal control. Applied Intelligence 2023, 53, 6248–6265. [Google Scholar] [CrossRef]
- Xu, M.; Di, Y.; Ding, H.; Zhu, Z.; Chen, X.; Yang, H. AGNP: Network-wide short-term probabilistic traffic speed prediction and imputation. Communications in Transportation Research 2023, 3, 100099. [Google Scholar] [CrossRef]
- Rashid, T.; Samvelyan, M.; De Witt, C. S.; Farquhar, G.; Foerster, J.; Whiteson, S. Monotonic value function factorisation for deep multi-agent reinforcement learning. The Journal of Machine Learning Research 2020, 21, 7234–7284. [Google Scholar]
- Wang, J.; Ren, Z.; Liu, T.; Yu, Y.; Zhang, C. Qplex: Duplex dueling multi-agent q-learning. arXiv preprint, arXiv:2008.01062 2020.
- Ji, J.; Bie, Y.; Wang, L. Optimal electric bus fleet scheduling for a route with charging facility sharing. Transportation Research Part C: Emerging Technologies 2023, 147, 104010. [Google Scholar] [CrossRef]
- Li, D.; Wu, J.; Xu, M.; Wang, Z.; Hu, K. Adaptive traffic signal control model on intersections based on deep reinforcement learning. Journal of Advanced Transportation 2020, 2020, 1–14. [Google Scholar] [CrossRef]
- Yazdani, M.; Sarvi, M.; Bagloee, S. A.; Nassir, N.; Price, J.; Parineh, H. Intelligent vehicle pedestrian light (IVPL): A deep reinforcement learning approach for traffic signal control. Transportation research part C: emerging technologies 2023, 149, 103991. [Google Scholar] [CrossRef]
- Bouktif, S.; Cheniki, A.; Ouni, A. Traffic signal control using hybrid action space deep reinforcement learning. Sensors 2021, 21, 2302. [Google Scholar] [CrossRef]
- Ducrocq, R.; Farhi, N. Deep reinforcement Q-learning for intelligent traffic signal control with partial detection. International Journal of Intelligent Transportation Systems Research 2023, 21, 192–206. [Google Scholar] [CrossRef]
- Li, Z.; Yu, H.; Zhang, G.; Dong, S.; Xu, C.-Z. Network-wide traffic signal control optimization using a multi-agent deep reinforcement learning. Transportation Research Part C: Emerging Technologies 2021, 125, 103059. [Google Scholar] [CrossRef]
- Yang, S. Hierarchical graph multi-agent reinforcement learning for traffic signal control. Information Sciences 2023, 634, 55–72. [Google Scholar] [CrossRef]
- Chen, X.; Xiong, G.; Lv, Y.; Chen, Y.; Song, B.; Wang, F.-Y. A Collaborative Communication-Qmix Approach for Large-scale Networked Traffic Signal Control. In Proceedings of the 2021 IEEE International Intelligent Transportation Systems Conference (ITSC), Indianapolis, USA, 9-22 September 2021; pp. 3450–3455. [Google Scholar]
- Bokade, R.; Jin, X.; Amato, C. Multi-Agent Reinforcement Learning Based on Representational Communication for Large-Scale Traffic Signal Control. IEEE Access 2023, 11, 47646–47658. [Google Scholar] [CrossRef]
Figure 1.
Network framework of the CMARL.
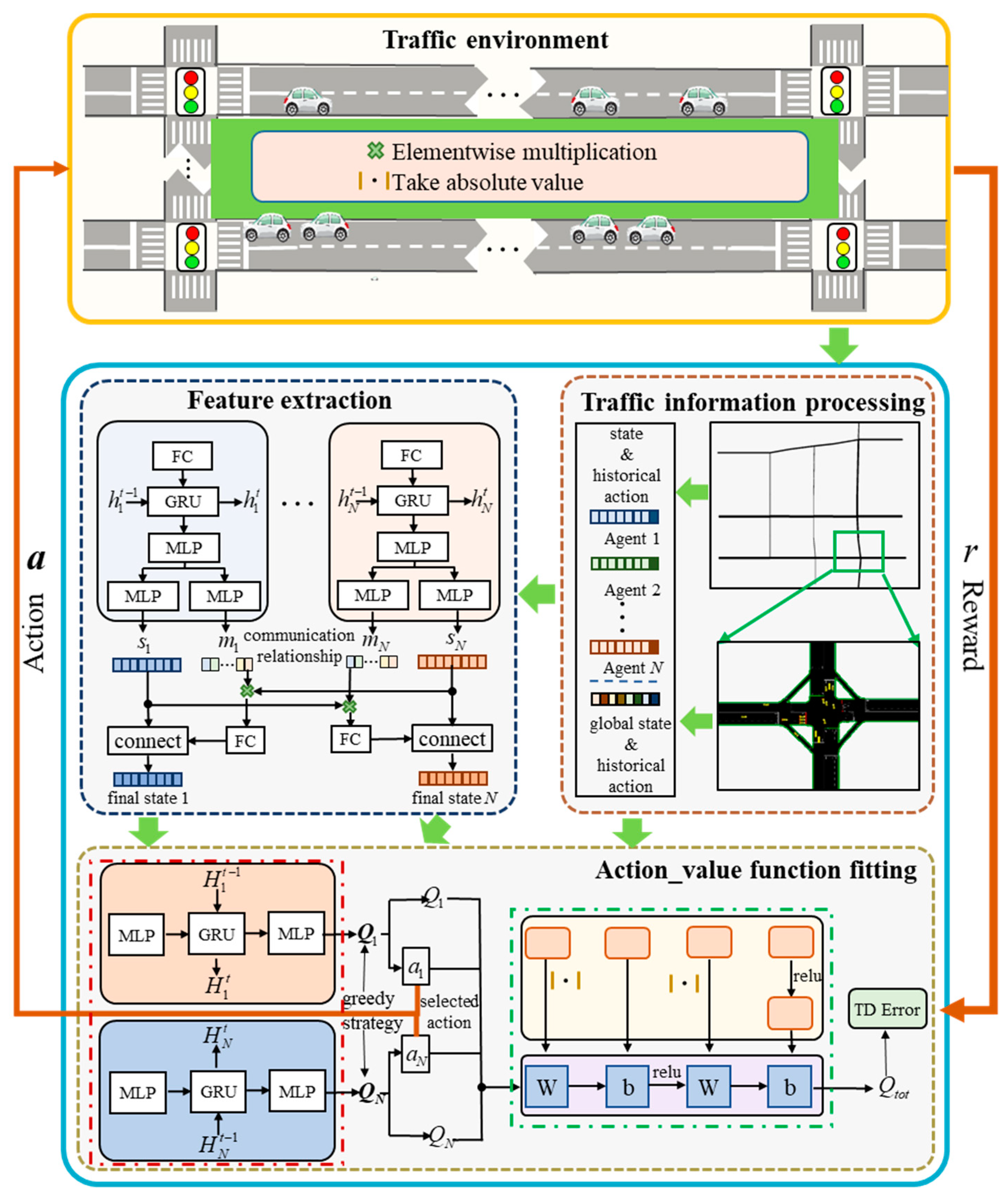
Figure 2.
Schematic diagram of road network simulation environment.
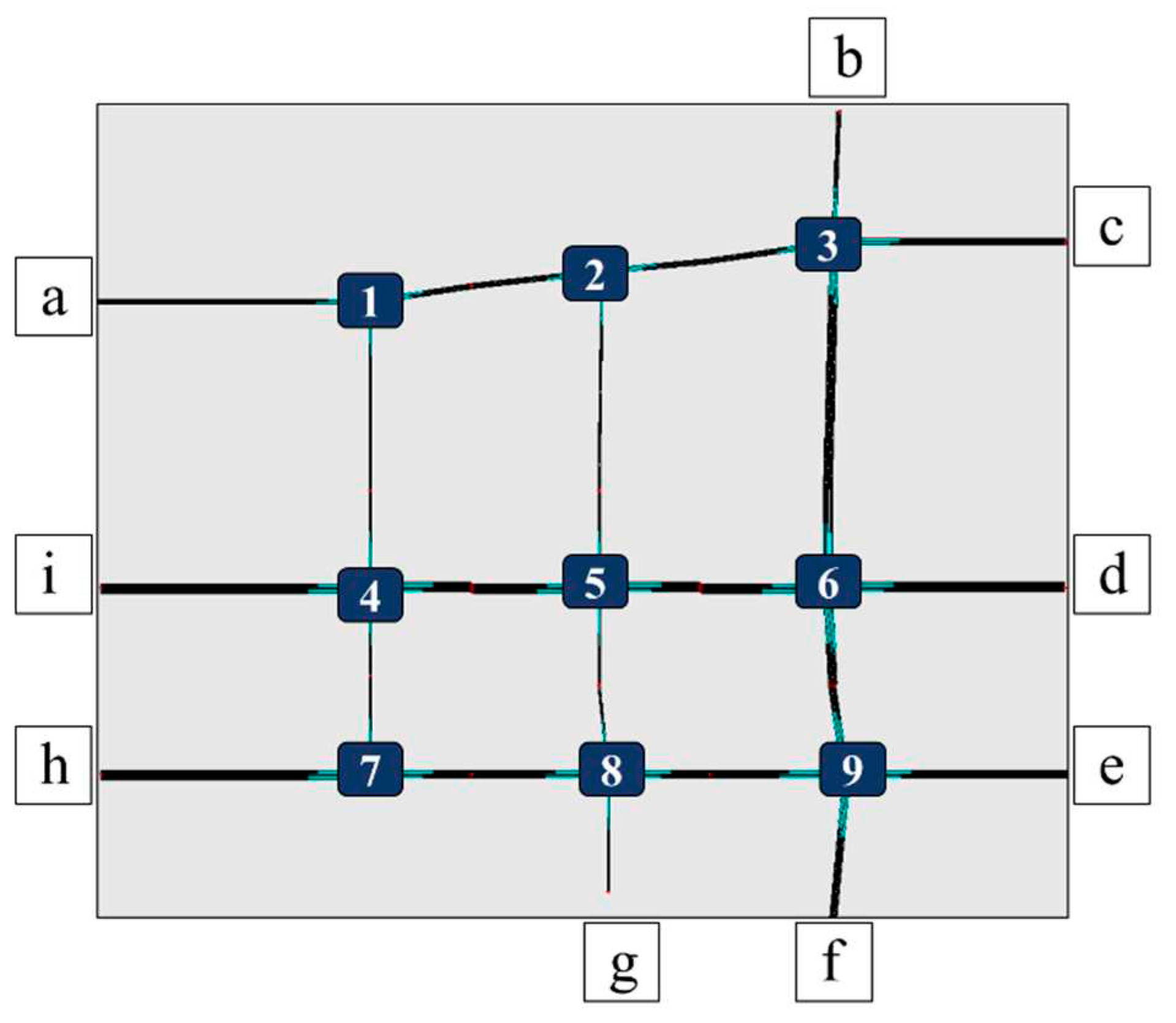
Figure 3.
Traffic flow distribution during the test phase. (a) Traffic flow distribution of off-peak hours; (b) Traffic flow distribution of peak hours.
Figure 3.
Traffic flow distribution during the test phase. (a) Traffic flow distribution of off-peak hours; (b) Traffic flow distribution of peak hours.
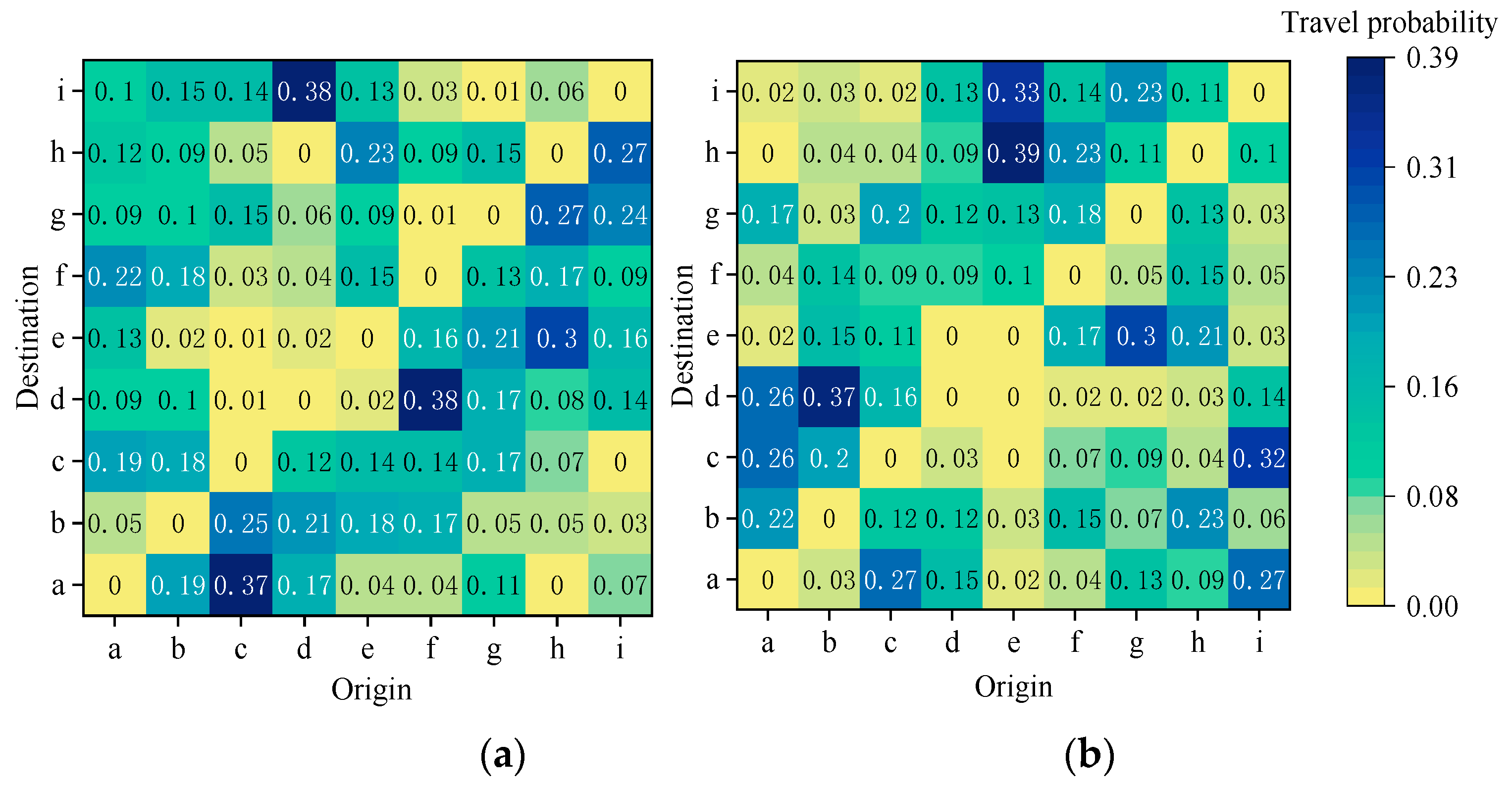
Figure 4.
Change diagram of various evaluation indicators of the DRL algorithms relative to the FixedTime method. (a) Change diagram of peak hours; (b) Change diagram of off-peak hours.
Figure 4.
Change diagram of various evaluation indicators of the DRL algorithms relative to the FixedTime method. (a) Change diagram of peak hours; (b) Change diagram of off-peak hours.
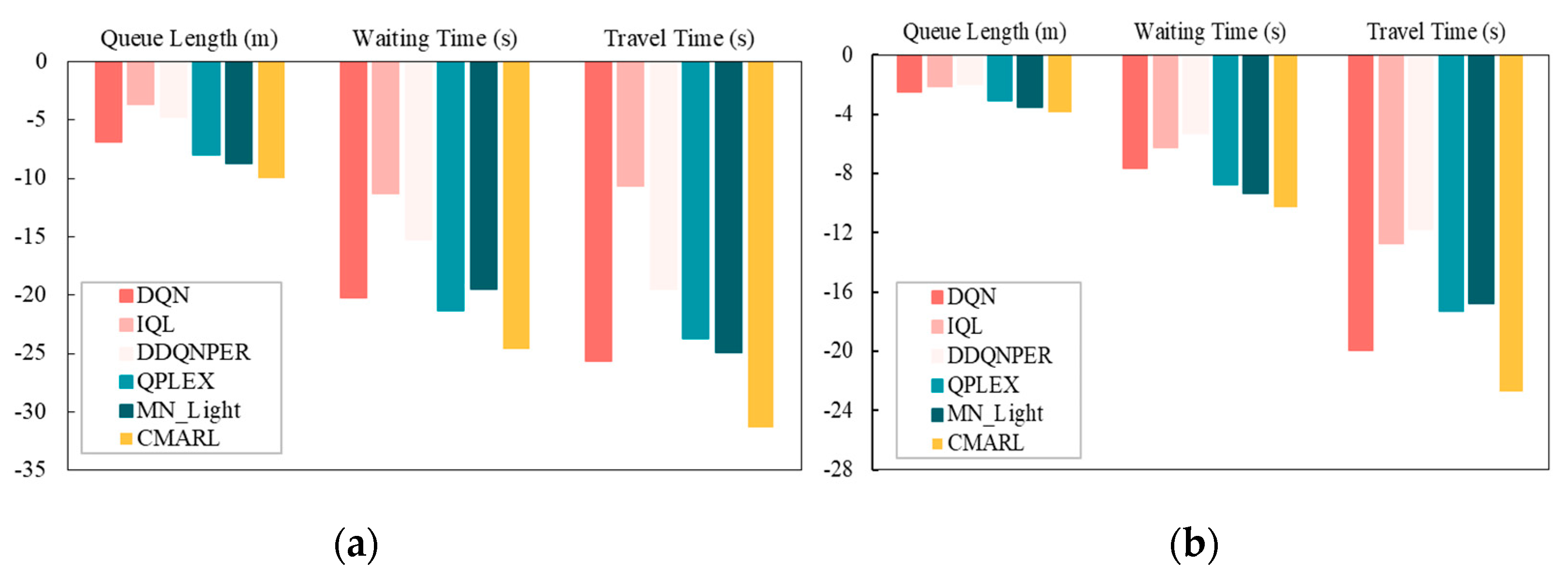
Figure 5.
Comparison of QMIX and CMARL model effects. QMIX is the network framework of CMARL after stripping off the feature extraction module. (a) Comparison of peak hours; (b) Comparison of off-peak hours.
Figure 5.
Comparison of QMIX and CMARL model effects. QMIX is the network framework of CMARL after stripping off the feature extraction module. (a) Comparison of peak hours; (b) Comparison of off-peak hours.
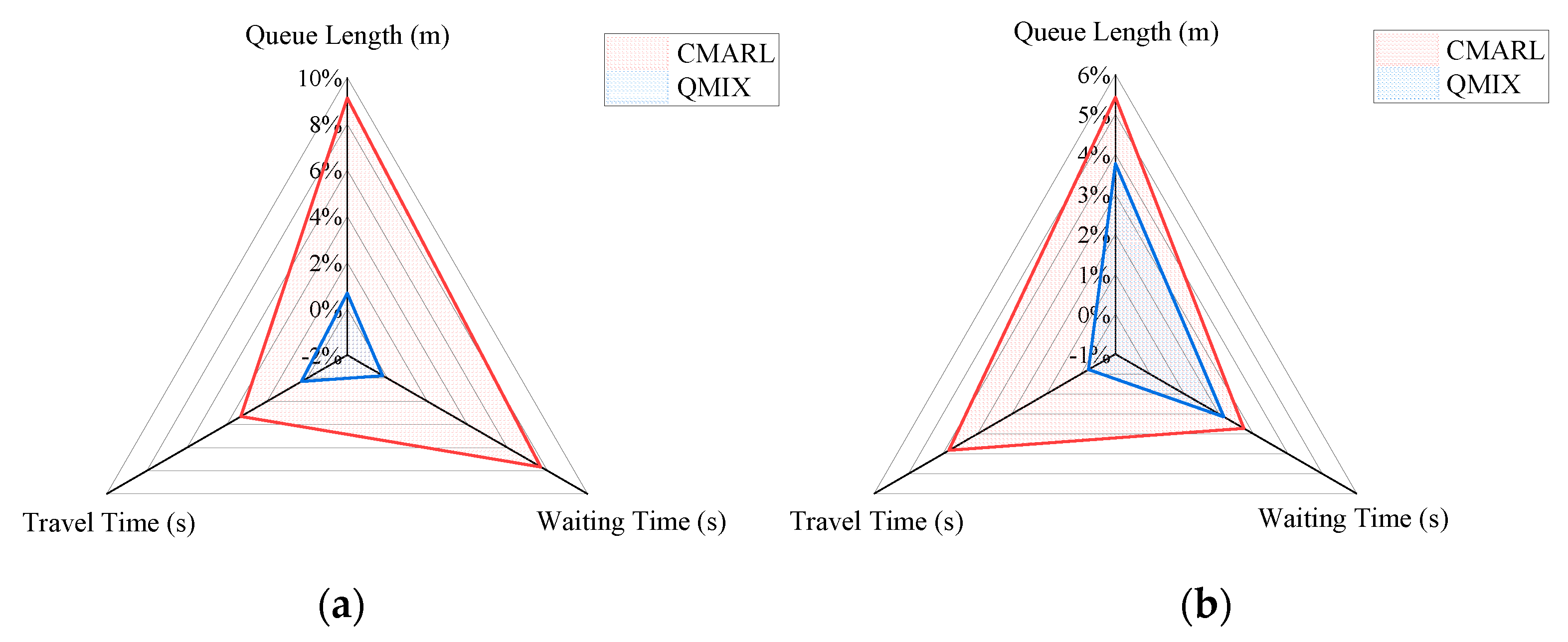
Table 2.
Model parameter value.
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| B | 32 | greedy probability | 0.95-0.01 |
| 0.95 | initial learning rate lr | 0.001 | |
| M | 1000 | 16 | |
| K | 200 | 32 | |
| T | 300 | 32 | |
| p | 10 | 64 |
Table 3.
Comparison of control performance of baseline methods.
| Model | Peak hours | Off-peak hours | ||||
|---|---|---|---|---|---|---|
| Queue length (m) | Waiting time (s) | Travel time (s) | Queue length (m) | Waiting time (s) | Travel time (s) | |
| FixedTime | 23.59 | 86.35 | 218.80 | 10.15 | 44.35 | 173.80 |
| DQN | 16.75 | 66.11 | 193.13 | 7.69 | 36.70 | 153.90 |
| IQL | 19.98 | 75.11 | 208.19 | 8.07 | 38.10 | 161.05 |
| DDQNPER | 18.84 | 71.11 | 199.36 | 8.19 | 39.06 | 162.05 |
| QPLEX | 15.62 | 65.04 | 195.05 | 7.09 | 35.65 | 156.49 |
| MN_Light | 14.91 | 66.83 | 193.88 | 6.63 | 35.02 | 157.05 |
| CMARL | 13.55 | 61.71 | 187.47 | 6.27 | 34.06 | 151.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







