The Physics of the Thermodynamic Entropy

Preprint

Article

The Physics of the Thermodynamic Entropy

Altmetrics

Downloads

201

Views

Comments

David Sands^*

This version is not peer-reviewed

Submitted:

17 April 2024

Posted:

18 April 2024

You are already at the latest version

Alerts

Abstract

The historical idea of entropy as a property of a body has been reviewed and shown to arise from Clausius’s view of heat as motion. This view of heat, being intermediate between the now defunct idea of heat as substance and the modern view that heat represents an exchange of energy, implied that a body contains a definite quantity of heat. Heat, and therefore entropy, was thus considered a property of a body. These ideas led Clausius to develop his famous inequality and the idea that entropy always increases in irreversible, non-cyclic processes. In this paper, the notion of the entropy as a property of a body is examined in detail. A physical meaning is attached to the thermodynamic entropy by showing that a change in the function Q/T can be understood as representing a change in the number of ways that energy can be distributed among the degrees of freedom active in the system at any given temperature. The idea is illustrated with reference to solids and simple liquids. It is shown that the total thermodynamic entropy is, in general, less than the Boltzmann entropy, except for the case of a monatomic classical ideal gas in which the number of degrees of freedom is independent of temperature. Finally, entropy as a state function is discussed. It is argued that this is entirely mathematical in nature and that the entropy of a state represented in p-V space is not equivalent to a physical property of a physical system in the same thermodynamic state.

Keywords:

Subject: Physical Sciences - Thermodynamics

1. Introduction

Entropy is perhaps one of the most enigmatic concepts in physics. Whereas we can attach a clear meaning to the various forms of statistical entropy, the underlying physics of the thermodynamic entropy has presented a mystery since the foundations of the concept, with the mathematical expression for the change in the thermodynamic entropy,

d S = \frac{d Q}{T}

, affording no insight. Those properties that we do attach to the thermodynamic entropy, such as, for example, that it is an extensive property of a body that increases in irreversible processes, should more properly be considered assumptions, as there is no firm empirical evidence to support them.

Take, for example, the notion of entropy as a property of matter. The function we identify now as entropy is evident in Carnot’s analysis of a heat engine and there it is associated firmly with the transfer of heat from a reservoir. However, Carnot developed his theory using the idea of heat as caloric, the invisible, indestructible substance that was believed to permeate matter. Clausius reworked Carnot’s theory in his famous paper of 1850 [1] to take into account the then emerging idea of heat as motion. It is not commonly appreciated, however, that this was an intermediate view of heat. It superceded the theory of caloric but came before the modern theory of heat as energy which is exchanged between bodies at different temperatures and which contributes to the total internal energy via the First law. It is this author’s belief that failure to appreciate this has led directly to a failure to appreciate the flaws in the concept of entropy.

By way of example, Tyndall [2] set out the theory of heat as motion in his book of 1865, “Heat: a mode of motion”, which was in print for over 40 years and into the 20^th century in at least six editions. On page 29, Tyndall describes the effect of rapid compression of air by a piston and states that, “… heat is developed by compression of air.” Whether there is heat flow or not depends on whether the compression is adiabatic or not, but Tyndall explicitly refers to development, rather than the flow, of heat. An adiabatic compression would have the effect of raising the temperature and Tyndall’s statement would very likely be interpreted from a modern perspective as an old-fashioned, somewhat cumbersome way of saying this. However, this is not the meaning intended by Tyndall. On page 25, when discussing the nature of heat, Tyndall refers to two competing theories: the material view of heat as substance and the dynamical, or mechanical view in which heat is, “… a condition of matter, namely a motion of its ultimate particles”. There are two important aspects to this statement. First, heat is a property of matter. Secondly, Tyndall’s reference to heat being produced by compression should be taken literally: the kinetic energy of the constituent particles, and therefore, by Tyndall’s definition, the heat, is increased by the act of compressing the gas.

Clausius was working within the same theoretical framework. The function he later came to call the entropy of a body was derived in his Sixth Memoir, first published in 1862 [3]. It contained three variables, H, T and Z, defined as, respectively, the actual heat in a body, the absolute temperature and the disregation. Clausius claimed that H was proportional to T and may be understood as the total kinetic energy, or, according to the dynamical theory, the heat of the constituent particles as explained by Tyndall. He explained the disgregation in 1866 as, “… a quantity completely determined by the actual condition of the body, and independent of the way in which the body arrived at that condition.” [4]. Neither the actual heat nor the disgregation are concepts accepted within modern thermodynamics, but Clausius’s concept of entropy is still very much accepted and it is worth considering briefly his thinking [3] in order to assess the ramifications for modern thermodynamics.

Clausius was interested in what he called, “internal work”, by which he meant the work done on or by a particle by the inter-particle forces exerted by its neighbours. His whole purpose for developing the disgregation was to look at internal work through its effect on heat because in the mechanical theory, heat is converted to work and vice versa within the gas as a particle moves either against or in the direction of the inter-particle forces. In Clausius’s mind, this was essentially the same as the conversion of heat into so-called “external” work by a heat engine. This latter was summarized by a single equation which gave the sum of transformations, to use Clausius’s term, around a closed cycle of operations as:

\oint \frac{d Q}{T} \geq 0

(1)

The equality applies to reversible cycles, but in modern thermodynamics the sign of the inequality is reversed because the modern definition of positive heat is different from that used by Clausius. Therefore, we regard the sum as being less than or equal to zero. Clausius later changed his notation to accord with the modern view, but his original inequality is important because he based his thinking on that. Clausius actively sought an equivalent inequality for a single process in which heat is converted to internal work.

Clausius described the increase of disgregation as “the action by means of which heat performs work” [ref 3 , p227], and substituted the quantity TdZ for dW in what was essentially the First Law. However, TdZ also contained the internal work, but field energies were implicitly contained within the internal energy. Clausius split the latter so that a change in the internal energy was decomposed into a change in the kinetic energy, or what he called “actual heat”, and the internal work, or the field energies. As he described in 1866 [4], disgregation “serves to express the total quantity of work which heat can do when the particles of the body undergo changes of arrangement at different temperatures”. Therefore, he wrote, for reversible changes in which a quantity of heat, dQ, is exchanged with the exterior,

d Q + d H + T d Z = 0

(2)

Notwithstanding the difficulty that one of these terms must implicitly be negative, this is essentially an expression for the conservation of energy. However, conservation of energy was not part of Clausius’s thinking. He was more concerned with reversibility and the notion of disgregation seemed to him to afford the possibility of reversible changes simply because the separation of particles could be reversed by a reverse operation. It mattered not that the process by which the separation was reversed might itself be irreversible because of his view that the disgregation represents the work that the heat can do. This led Clausius to state explicitly [ref 3, p223] that “the law does not speak of the work which heat does, but of the work which it can do.” The emphasis is Clausius’s own.

The work that heat can do is simply the reversible work, pdV, and the change TdZ therefore comprised the internal work and pdV. For an irreversible process in which dW<pdV,

d Q + d H + T d Z > 0

(3)

This was the inequality that Clausius sought and which in his view unified cyclic and non-cyclic processes. The change in entropy of a body over a large change in volume is simply,

∆ S = \int \frac{d H}{T} + \int d Z \geq \int \frac{d Q}{T}

(4)

This is essentially the origin of the well known inequality of irreversible thermodynamics.

Three things immediately follow from Clausius’s definition of entropy in equation (4).

H, Z and T are all properties of a body in a given state, so entropy must also be a property of a body;
Entropy can increase through changes in H arising from internal work;
Entropy can increase in irreversible work processes arising from changes in TdZ.

What is perhaps not so obvious is that it also violates energy conservation, as is most easily demonstrated with the free expansion of gases into a vacuum. In an ideal gas there are no interparticle forces and therefore

d H \equiv d U

. Equations (3) and (4) together give the change in entropy as

∆ S = \int \frac{p d V}{T}

(5)

As T remains unchanged throughout the expansion, it follows that

T ∆ S = \int p d V

. This accords with the modern view. However, pdV is a work term and there is no work done in the free expansion. Neither is there any change in the internal energy, which also means that there is no heat flow. If entropy is a property of a body, then some quantity, TΔS, with the units of energy is changing in a way that is inconsistent with the First Law of thermodynamics.

A similar inconsistency can be identified with the chemical potential, as described by the author in a recent conference presentation [5]. This raises the question as to whether entropy should be considered a property of a body, despite a long-standing acceptance of entropy as a property of matter within non-equilibrium thermodynamics. In that presentation, the author also presented an analysis of the entropy of a solid using silicon as an example. Looking at the entropy of a solid has the advantage that changes in volume can generally be ignored, leaving only the thermal component of entropy due to the exchange of heat. Moreover, it is the author’s experience that comparisons between the thermodynamic and statistical entropy are only ever made with reference to the classical ideal gas and solids therefore present something of a challenge.

Silicon was chosen in that presentation simply because of the author’s long familiarity with the material, but it presented a feature which, at first sight, is puzzling, given the accepted picture of the thermodynamics of solids. The Dulong-Petit law holds that the heat capacity at high temperatures should be 3Nk_B and this is imposed as the upper limit of the integral in the Debye theory of the specific heat, but in silicon the heat capacity exceeds this by some way. However, the data used in [5] relates to the constant-pressure heat capacity, whereas both the Dulong-Petit law and the Debye theory of the specific heat relate only to the vibrational energy in the solid. The Dulong-Petit law reflects the classical notion that there are six degrees of freedom per atom whilst the Debye theory explicitly excludes any expansion by being restricted to constant volume. This condition is necessary because relaxation of the lattice would alter the quantized levels within the solid and would complicate considerably the theoretical treatment of the quantized vibrations over the whole temperature range. Nonetheless, data was presented in [5] for the constant-volume heat capacity of silicon which suggested that the high temperature heat capacity would exceed the Dulong-Petit limit as well as the Debye limit. Although the data was limited to the temperature range 0<T<800K, it had already reached 25 J mol^-1 K^-1, which is equivalent to 3N_Ak, at that higher temperature and showed no sign of levelling out.

Whether there is an issue with the Debye theory and the Dulong-Petit law is of secondary importance here. The concern here is to examine the relationship between the thermodynamic entropy, which requires the total internal energy, and the distribution of that energy among the degrees of freedom. Unlike a gas, the difference between the constant-volume and constant pressure heat capacities derives not from the work done against the external pressure, though there will be a very small contribution from that, but from the work done against the internal cohesive forces. The work done against these forces represents energy that remains within the solid and therefore has to be considered in the calculation of the total entropy. It is shown here with reference to several metals chosen at random that the average number of active degrees of freedom can be evaluated by a simple means. In addition, the theory of active degrees of freedom presented in [5] is extended to include simple liquids. Before doing so, however, it is necessary to clarify the nature of entropy. The preceding discussion has raised the question as to whether it is a property of a body or not, but in calculating the total entropy of a solid, it is necessary to integrate both dU and dU/T over the whole temperature range from absolute zero to the temperature of interest. Arguably, these are both properties of a solid at a given temperature, or at least they can be treated as such, so in order to put the results of this analysis into context in the light of the preceding discussion, it is necessary to try to answer the question of whether entropy can legitimately be considered a property of a body.

This is done via an exploration of the chemical potential in a classical ideal gas using a geometrical interpretation. It is not always explicit in the teaching of thermodynamics, but entropy is often associated with mass. This is explicit in the treatment by Planck [6], who, following Clausius, defined the entropy of unit mass of a gas. It is also a fundamental assumption of irreversible, non-equilibrium thermodynamics, as set down by DeGroot and Mazur [7]. These authors defined the total entropy as the integral of the product of the entropy per unit mass and the density over the entire volume of the system under consideration. This would imply that in an ideal gas, in which the only mass present comes from the particles that comprise the gas, the entropy should change if the number of particles changes. Even if the association of entropy with mass is disputed, and it is not clear to this author in what intrinsic property of matter entropy resides, there can be no dispute that entropy is regarded as a function of the extensive variables of a system [8,9]. The number of particles, the internal energy and the volume comprise the extensive parameters and so entropy should change if the number of particles changes. It is difficult to imagine how a solid can be regarded as an open system in which the number of particles can vary and an ideal gas provides a much better system for considering the chemical potential. In [5], a difficulty around the chemical potential in a classical ideal gas was identified, but no solution was provided. The simplicity of the analysis afforded by the geometrical approach adopted in this paper allows a definite conclusion and implication to emerge which will be supported by the analysis of the entropy of solids.

2. The Chemical Potential in a Classical Ideal Gas

Suppose an ideal gas containing N₀ particles in a volume V at temperature T₀ and further suppose that we can add or extract a small number of particles, dN, and that the volume, V, is allowed to change so that the system remains at the same temperature and pressure. The precise details of how this might be done need not be specified in detail, but we can imagine a particle reservoir at the same temperature connected to the system which will allow a small number of particles to be either added or subtracted from the system. Figure 1 shows the linear variation of U with temperature for three different values of particle number: N₊>N₀>N_-.

As might be expected, increasing the number of particles increases U, whilst decreasing the number of particles decreases U. If particles are added, the entropy increases according to the well-known Gibbs relation,

T d S = d U + p d V - μ d N

(6)

Equation (6) can readily be derived from the assumption that the entropy, S(U,V,N), is a function of U, V and N. Partial differentiation of S with respect to each of the extensive variables leads directly to equation (6) upon substitution of the appropriate relations:

{(\frac{\partial S}{\partial U})}_{V, N} = \frac{1}{T} {(\frac{\partial S}{\partial V})}_{U, N} = \frac{p}{T} {(\frac{\partial S}{\partial N})}_{U, V} = - \frac{μ}{T}

(7)

Suppose that the system is compressed isothermally to its initial volume. The work done is pdV and the entropy decreases so that the final value for the increase in entropy caused by adding particles at the same volume is simply,

T d S = d U - μ d N

(8)

However, from Figure 1, the change in internal energy is due only to the extra particles and is:

∆ U = \frac{3}{2} (N_{+} - N_{0}) k T

(9)

Writing ϵ as the average energy per particle,

\frac{3}{2} k T

, then,

T d S = (ϵ - μ) d N

(10)

This is problematic because the only energy change in the system is given by

d U = ϵ d N

, so either μ=0 or μ=ϵ are the only two values possible that are consistent with energy conservation. Any other value 0<μ< ϵ implies that there is some property of the gas, TdS, which has the units of energy, that is changing in a way that is not consistent with the actual energy changes. It will be demonstrated that in fact, the value of μ is contrary to expectation. On the face of it, μ=0 implies that entropy doesn’t change with the addition of particles, but nonetheless a change in TdS occurs. On the other hand, μ=ϵ appears to imply that entropy changes upon the addition of particles, but TdS=0. In order to resolve this apparent paradox, the geometric analysis of Figure 1 is extended.

Entropy is usually defined to be a function of U, V and N and the chemical potential is defined by equation (7), namely

{(\frac{\partial S}{\partial N})}_{U, V} = - (\frac{μ}{T})

As Figure 1 shows, however, it is not possible to change N and keep U constant without changing the temperature. Figure 2 shows the sequence of physical operations required to fulfil the conditions for the partial differential to hold.

The number of particles must be changed at constant volume and the system either cooled or heated according to whether particles are added or subtracted. Assuming particles are added, the internal energy needs to change by,

∆ U = \frac{3}{2} N_{+} k ∆ T = \frac{3}{2} (N_{0} + ∆ N) k ∆ T

(11)

N_{0} ≫ ∆ N

this reduces to

∆ U = \frac{3}{2} N_{0} k ∆ T

(12)

In the limit

∆ U \to d U

, the entropy change is simply,

d S = \frac{d U}{T} = \frac{3}{2} N_{0} k \frac{d T}{T}

(13)

The entropy change can be expressed as a function of dN by first manipulating equations (9) and (12) to connect dN and dT:

d T = \frac{d U}{\frac{3}{2} N_{0} k} = \frac{\frac{3}{2} T_{0} k d N}{\frac{3}{2} N_{0} k} = \frac{T_{0} d N}{N_{0}}

(14)

The subscript can be dropped as this only indicates the starting state. In addition, this relationship has been derived using only the magnitudes evident in Figure 2. The requirement that U must be kept constant means that T must decrease if N is increased and vice versa. Therefore,

d T = - \frac{T}{N} d N

(15)

Writing the entropy in terms of the heat capacity, we have:

d S = C_{V} \frac{d T}{T} = - \frac{3}{2} N k \frac{d N}{N} = - \frac{3}{2} k d N

(16)

As dS is the entropy change required to maintain constant U, we can write:

{(\frac{\partial S}{\partial N})}_{U, V} = - \frac{3}{2} k

(17)

Comparison with equation (10) yields,

μ = \frac{3}{2} k T

(18)

Substitution back into equation (10) yields total entropy change of zero for the addition of particles at constant volume and temperature.

It could be argued that this assumption is implicit in the analysis. The only entropy change that has been considered is that which occurs when the system is cooled. The fact that this leads to an expression for the chemical potential that in turn confirms an entropy change of zero on the addition of particles is consistent, but not conclusive. The alternative is to put μ=0 in equation (10) and to consider the consequences. There would then be an increase in entropy of

\frac{3}{2} k d N

upon the addition of particles. The rest of the analysis remains the same. The system still has to be cooled to maintain constant U and this would decrease the entropy by the same amount, leading to a total entropy change of zero. From equation (7), μ=0. Again, consistent but not conclusive.

As described earlier, both of these outcomes appear to be somewhat paradoxical. On the one hand, there is no entropy is attached to the particles themselves, meaning that entropy does not increase when particles are added, yet a non-zero value of the chemical potential ensues. On the other hand, if entropy is attached to the particles and entropy increases, the chemical potential comes out as zero. However, there is no real paradox. U and N are not independent of each other and in order to maintain a constant U as N is varied means that some other operation has to be conducted. The chemical potential reflects this.

The question then arises as to which one is correct. Entropy enters thermodynamics through the flow of heat and there is no logical reason to assume it is a property of a body. However, if entropy is a property of a body, heat can be supplied at constant temperature in an isothermal expansion and its entropy correspondingly increased, but the circumstances leading to μ=0 investigated above imply an entropy of

\frac{3}{2} k

per particle in an ideal gas, which is independent of temperature. The product TS at any temperature would simply equal the internal energy, which is inconsistent with the known facts. It would mean, for example, that the Helmholtz free energy is zero and that the Gibbs free energy is simply pV. On the other hand, if no entropy is attached to the particles themselves the physical meaning of the Helmholz function is unclear, but the very fact that it can be defined and is non-zero suggests that entropy is not attached to the particles themselves.

The essential difficulty is that we do not have a microscopic understanding of thermodynamic entropy. The assumption that statistical entropy is identical to thermodynamic entropy is just that: an assumption. Although Boltzmann derived an expression for an ideal gas which was identical to the mathematical form of the thermodynamic entropy using what later came to be known as the Shannon information entropy, it is by no means clear that this mathematical identicality extends to physical equivalence or that is in fact general. In [5], the author presented an analysis of solids in which he concluded that the Boltzmann and thermodynamic entropies are not generally identical, but the analysis was restricted to a single solid, silicon. In the following, this analysis is extended to include other solids and whilst the number of materials considered is small, it shows that silicon is not unique in its properties, which appear to contradict the known theories on the specific heat. Moreover, the analysis is extended to simple liquids arising when such solids are taken beyond their melting point.

3. Entropy in Complex Systems: an Examination of Solids

The connection between thermodynamic entropy and degrees of freedom has been established for the classical ideal gas [10] via physical interpretation of the function,

T^{\frac{C_{v}}{k}}

, which arises because the dimensionless change in entropy at constant volume in a system with constant-volume heat capacity C_v is,

d S = \frac{C_{v}}{k T} d T = \frac{C_{v}}{k} d l n T

(19)

The restriction to constant volume is important because in an ideal gas the quantity

\frac{C_{v}}{k} = \frac{3 N}{2}

is the number of degrees of freedom. Comparison with the Boltzmann entropy,

k l n W

yields

{W = T}^{\frac{C_{v}}{k}}

, which has been interpreted as the total number of ways of arranging the energy among the degrees of freedom in the system. This interpretation arises from the property of the Maxwellian distribution that it is the product of three independent Gaussian distributions of the velocity in each of the x, y and z directions. It was argued that each particle has access to, in effect,

T^{\frac{1}{2}}

velocity states in each of the three directions, making a total of

T^{\frac{3 N}{2}}

states for N particles across the three dimensions.

The restriction to constant volume is important as it means that no energy is supplied to the system to do work against the external pressure and any energy that is supplied is distributed among the degrees of freedom. In a solid, a small amount of work is done against the external pressure as a solid expands, but the volume change is usually so small that this contribution to the heat supplied can be neglected. Therefore, the main difference between the constant-volume and constant-pressure heat capacities arises predominantly from work done against the internal cohesive forces. Unlike in a gas, therefore, the excess heat supplied at constant pressure over that supplied at constant volume remains within the solid and the heat supplied at constant pressure is equivalent to the change in internal energy of a solid. Therefore, use of the constant-volume heat capacity in the calculation of the total thermodynamic entropy would under-estimate the total entropy. In consequence, the change in entropy in equation (19) has to be modified to include the constant-pressure heat capacity and as this is dependent on temperature, it must be included in the integration over the temperature range.

Unlike in an ideal gas, the active degrees of freedom within a solid are not so readily identifiable. The heat capacity of a solid can be understood as arising from the excitation of quantized oscillations of the lattice, as described first by Einstein and later by Debye. The Debye model itself is strictly a constant-volume heat capacity, as the quantised levels are assumed to remain unchanged over the entire temperature range of interest, but relaxation of the lattice would not allow for this. Even without this difficulty, the Debye model does not lend itself to an identification of activated degrees of freedom. At high temperatures, the heat capacity is assumed to approach the Dulong-Petit limit of

3 N k_{B}

, which is imposed as an upper limit and corresponds to the classical model of six degrees of freedom per atom, with the kinetic and potential energies each characterised by three degrees of freedom. At very low temperatures, the heat capacity varies as T³ and the heat capacity tends to zero as T tends to zero. Whereas in the classical view of a solid, the energy of the oscillation can steadily decrease simply through a reduction in the amplitude, the energy of a quantized oscillator cannot be continuously reduced. The fact of a decrease in heat capacity means that vibrational energy is partitioned among fewer and fewer atoms as the temperature is lowered, thereby implying that degrees of freedom are de-activated. Quantifying this, or the inverse, the activation of degrees of freedom as the temperature is raised, is the difficulty.

The phonon spectrum of a crystalline solid always contains so-called “acoustic mode” vibrations, regardless of the solid. Despite its name, the frequency of the phonons can extend into GHz and beyond at the edge of the Brillouin zone, where the wave vector

k = \frac{π}{a}

, with a being the lattice spacing. Close to the centre of the Brillouin zone the frequency tends to zero at very small wavevectors and these acoustic mode phonons represent travelling waves with relatively long wavelengths moving at the velocity of sound. These are the modes that are excited at very low temperatures and for which the solid acts as a continuum [11]. Therefore, these vibrations do not correspond to the classical picture of atoms vibrating randomly relative to their neighbours, for which there are six degrees of freedom, but constitute a collective motion of a large number of atoms. The average energy per atom is probably very small and it is not clear just how many effective degrees of freedom are active. By contrast, at the edge of the Brillouin zone,

\frac{\partial ω}{\partial k} \approx 0

, meaning that the group velocity is close to, or could even be, zero. These are not travelling waves but isolated vibrations. Some materials also contain higher frequency phonon modes, called optical mode phonons because the frequency extends into the THz and beyond and the phonons themselves can be excited by optical radiation.

The detailed phonon structure for any given solid can be quite complex and the Debye theory, being general in nature, does not take this detail into account. Rather, it represents the internal energy as the integral over a continuous range of phonon frequencies with populations given by Bose-Einstein statistics and an arbitrary cut off for the upper frequency [11]. The specific heat is then derived from the variation of internal energy with temperature. Despite the wide acceptance of the Debye theory, it is also recognised that it does not constitute a complete description of the specific heats. Instead of the T² dependence of the specific heat derived by Einstein at very low temperatures, the Debye model gives

c_{v} \propto T^{3}

. All this is well known and forms the staple of undergraduate courses in this topic, but what is perhaps not so well known is that, according to Blackman [ref 11, p24], “The experimental evidence for the existence of a T³ region is, on the whole, weak…”. Moreover, the Debye theory gives rise to a single characteristic temperature, the Debye temperature, for a given solid which should define the heat capacity over the whole temperature range, but in fact does not. Low temperature heat capacities generally require a different Debye temperature from high temperature values.

This discussion of the inadequacies of the Debye model is important because, whilst it shows that in general the heat capacity of a solid can be understood as arising form the excitation of quantized oscillations, a complete, accurate and general picture is not available. Moreover, in practice, the high temperature specific heats of solids often exceeds 3Nk_B, making the quantification of the number of active degrees of freedom even more difficult. This deviation might possibly be explained by the difference between the constant-volume and constant-pressure heat capacities, but in [5] the author presented data for the molar heat capacity of silicon over the whole temperature range from 0K to the melting point [12]. Close to the melting point (1687K) the constant-pressure heat capacity is 28.93 J mol^-1 K^-1, which, assuming ½k_BT per degree of freedom, is equivalent to 7 degrees of freedom per atom. However, data for the constant-volume heat capacity [13] was also presented which showed that C_v is already 25 J mol^-1 K^-1 at 800K. This equates to six degrees of freedom per atom (3N_Ak_B, N_A being Avogadro’s number corresponds to 24.9 J mol^-1 K^-1), but as data is available only up to 800K [13] it is not clear whether the constant-volume heat capacity continues to increase with temperature, thereby exceeding 3N_Ak_B, or flattens off. Clearly, the constant-pressure heat capacity does not directly represent the active degrees of freedom because there is no classical theory which allows for 7 degrees of freedom per atom, but the constant-volume heat capacity does not properly account for the total change in internal energy and hence the entropy change. This means that the function

T^{\frac{C_{v}}{k}}

, which gives the number of ways of distributing the energy among the degrees of freedom in an ideal gas, has no directly comparable meaning in a solid, even allowing for a change from C_v to C_p.

Nonetheless, we can suppose that there exists at any given temperature β(T) active degrees of freedom, each associated with an average of ½k_BT of energy. Then, for one mole of substance, the internal energy can be written as,

U = β (T) (\frac{1}{2} k_{B} T)

(20)

The meaning of this is perhaps not immediately apparent, but it is equivalent to taking an average heat capacity. For simplicity, let

{T_{B} = k}_{B} T

(21)

T_{B}

has the units of Joules, but it can be considered a temperature if we effectively rescale the absolute temperature so that

k_{B} = 1 .

If the molar heat capacity at constant volume is

c_{m}

, then for 1 mole,

d U = \frac{c_{m}}{k_{B}} d (k_{B} T) = c_{m k} {d T}_{B}

(22)

By definition, the internal energy at some value of

T_{B} = T_{B 1}

is,

U (T_{B 1}) = \int_{0}^{T_{B 1}} c_{m k} {d T}_{B}

(23)

It follows that

\frac{U (T_{B 1})}{T_{B 1}} = \frac{1}{T_{B 1}} \int_{0}^{T_{B 1}} c_{m k} {d T}_{B} = 〈c_{m k}〉

(24)

The angular brackets denote an average. Therefore

U (T_{B 1}) = 2 〈c_{m k}〉 (\frac{1}{2} T_{B 1})

(25)

This is equivalent to the geometrical transformation indicated in Figure 3a,b.

By comparison with equation (22),

2 〈c_{m k}〉 = β (T_{B})

(26)

By definition, for simple solids for which the heat capacity increases with temperature,

〈c_{m k}〉 \leq c_{m k}

, so we can expect the number of active degrees of freedom to be less than would be indicated by the heat capacity alone. Making use of equations (22) and (26) together, we have,

c_{m k} = \frac{\partial U}{\partial T_{B}} = \frac{1}{2} (β (T_{B}) + T_{B} \frac{\partial β (T_{B})}{\partial T_{B}})

(27)

It follows that,

β (T_{B}) {= 2 c}_{m k} - T_{B} \frac{\partial β (T_{B})}{\partial T_{B}}

(28)

In other words, for a heat capacity that varies with temperature, the effective number of degrees of freedom is less than twice the dimensionless heat capacity, becoming equal only when all the degrees of freedom have been activated and

\frac{\partial β (T_{B})}{\partial T_{B}} = 0

. This is true regardless of the system, whether solid, liquid or gas. It should be noted, however, that equation (27) does not account for latent heat and therefore implies a restriction to the solid state or at least to ideal systems in which phase changes do not occur. This includes phase changes within the solid state and therefore implies a simple solid, such as one that is described by the Debye theory of the heat capacity over the entire temperature range to melting.

Figure 4a shows the reduced heat capacity of five such solids based on the constant pressure heat capacity. As discussed in relation to equation (19), the heat capacity at constant pressure gives the internal energy. Included in Figure 4a is data for silicon and, for comparison, germanium as a similar semiconducting material, though the available data is restricted in its temperature range [14]. The reduced heat capacity is the dimensionless heat capacity of equation (22) normalized to Avogadro’s number and a reduced heat capacity of 3 would therefore correspond to the classical Dulong-Petit limit of a molar heat capacity of 3N_Ak_B. In all cases, the reduced heat capacity exceeds 3 at a temperature close to the Debye temperature, which might well be a consequence of using the constant-pressure rather than the constant-volume heat capacity. Figure 4b shows the mean reduced heat capacity (equation (24)) of the four solids for which heat capacity data down to T=0 is readily available.

There is nothing particular about the elements represented in Figure 4 other than that they have moderate to low melting points. They were chosen because an internet search produced a complete range of data for each of the three metals, aluminium [15], indium [16] and lead [17]. It is noticeable that, with the exception of lead, all four have a mean reduced heat capacity below three. Even for lead, the discrepancy is less than 3%, with the maximum value being 3.08. Arblaster claims an accuracy of 0.1% in his data for temperatures exceeding 210K [17], so it is not clear what the cause of this excess might be. Figure 4a shows very clearly, however, that the heat capacity is not a direct representation of the active degrees of freedom. By definition, from equations (20) and (26), the mean heat capacity is a direct representation of the number of effective degrees of freedom and it is clear that even up to the melting point, the small excess with lead notwithstanding, there is less than 3k_BT of energy associated with each constituent atom.

The mean heat capacity can now be used to attach a physical meaning to the thermodynamic entropy. From equation (20), the change in internal energy is,

d U = \frac{1}{2} β (T_{B}) d T_{B} + \frac{1}{2} T_{B} d β (T_{B})

(29)

Under the assumption that the internal energy is partitioned equally among active degrees of freedom, the change in internal energy comprises two components: the change in the average energy among the degrees of freedom already activated and the distribution of some the additional energy into newly activated degrees of freedom, each of which contains an average energy

\frac{1}{2} T_{B}

. Both of these terms contribute to the entropy. However, as the change in internal energy is written in terms of T_B, it is necessary to divide the entropy by k_B to give the dimensionless quantity,

\frac{d S}{k_{B}} = \frac{d U}{T_{B}}

(30)

Upon substitution of equation (29), the dimensionless entropy change is,

\frac{d S}{k_{B}} = \frac{β (T)}{2} \frac{d T}{T} + \frac{1}{2} d β (T)

(31)

Here we make use of the fact that

\frac{d T_{B}}{T_{B}} = \frac{k_{B} d T}{k_{B} T} = \frac{d T}{T}

(32)

It is notable that the change in entropy is still given as a function of the absolute temperature in Kelvins, which allows for a ready interpretation in terms of the active degrees of freedom, as expressed in equation (33) below.

The first term on the right in equation (31) can be interpreted as the change in the function

W = T^{\frac{β}{2}}

, which has already been defined for a classical ideal gas as the number of arrangements by direct comparison of the thermodynamic entropy and Boltzmann’s entropy [10]. Straightforward differentiation of lnW with respect to lnT yields

\frac{d W}{W} = \frac{β}{2} \frac{d T}{T} = d \ln W

(33)

The change in thermodynamic entropy therefore represents the fractional change in the number of arrangements or, equivalently, the change in the Boltzmann entropy, plus the addition of new degrees of freedom. Integrating equation (31) by parts to get the total entropy at some temperature T₁, we find,

\frac{S}{k} = \int_{0}^{T_{1}} \frac{β (T)}{2} \frac{d T}{T} + \frac{1}{2} \int_{0}^{β (T_{1})} d β (T) = {[\frac{β (T)}{2} \ln T]}_{0}^{T_{1}} - \frac{1}{2} \int_{0}^{β (T_{1})} \ln T d β (T) + \frac{1}{2} \int_{0}^{β (T_{1})} d β (T)

(34)

T = 0

\ln T \to - \infty

, but

β (T) = 0

and the lower limit is also zero. Therefore,

\frac{S}{k} = \frac{β (T_{1})}{2} \ln T_{1} - \frac{1}{2} \int_{0}^{β (T_{1})} (\ln T - 1) d β (T)

(35)

The first term on the RHS is recognizable as the Boltzmann entropy,

\ln W = \frac{β}{2} \ln T

. In the second term on the RHS,

\ln T

is a positive number for T>1, and greater than unity for

T \geq e = 2.718

. Therefore, for systems in which the heat capacity varies with temperature the thermodynamic entropy at any given temperature above approximately 3K is less than the Boltzmann entropy for the simple reason that the number of arrangements at any given temperature depends only on the number of degrees of freedom active at that temperature, whereas the thermodynamic entropy, being given by an integral over all temperature, accounts for the fact that the number of degrees of freedom have changed over the temperature range. This relationship is illustrated in Figure 5.

4. Extension to simple liquids and gases

The preceding treatment can be generalized by writing the internal energy as,

U (T_{B 2}) = U_{0} (T_{B 1}) + \int_{T_{B 1}}^{T_{B 2}} c_{m k} {d T}_{B}

(36)

Rearranging slightly,

U (T_{B 2}) - U_{0} (T_{B 1}) = ∆ U = \int_{T_{B 1}}^{T_{B 2}} c_{m k} {d T}_{B}

(37)

The average heat capacity over the temperature range T_B1 to T_B2 can be defined by dividing through by the temperature difference,

\frac{∆ U}{(T_{B 2} - T_{B 1})} = \frac{1}{(T_{B 2} - T_{B 1})} \int_{T_{B 1}}^{T_{B 2}} c_{m k} {d T}_{B}

(38)

This gives the change in internal energy as,

\frac{∆ U}{(T_{B 2} - T_{B 1})} = 〈c_{m, k}〉

(39)

Rewriting,

∆ U = 〈c_{m, k}〉 {∆ T}_{B}

(40)

If T_B1=0, ΔU=U and ΔT_B=T_B, recovering the preceding formulation. The similarity is revealed by a similar geometric interpretation to Figure 3b, as shown in Figure 6.

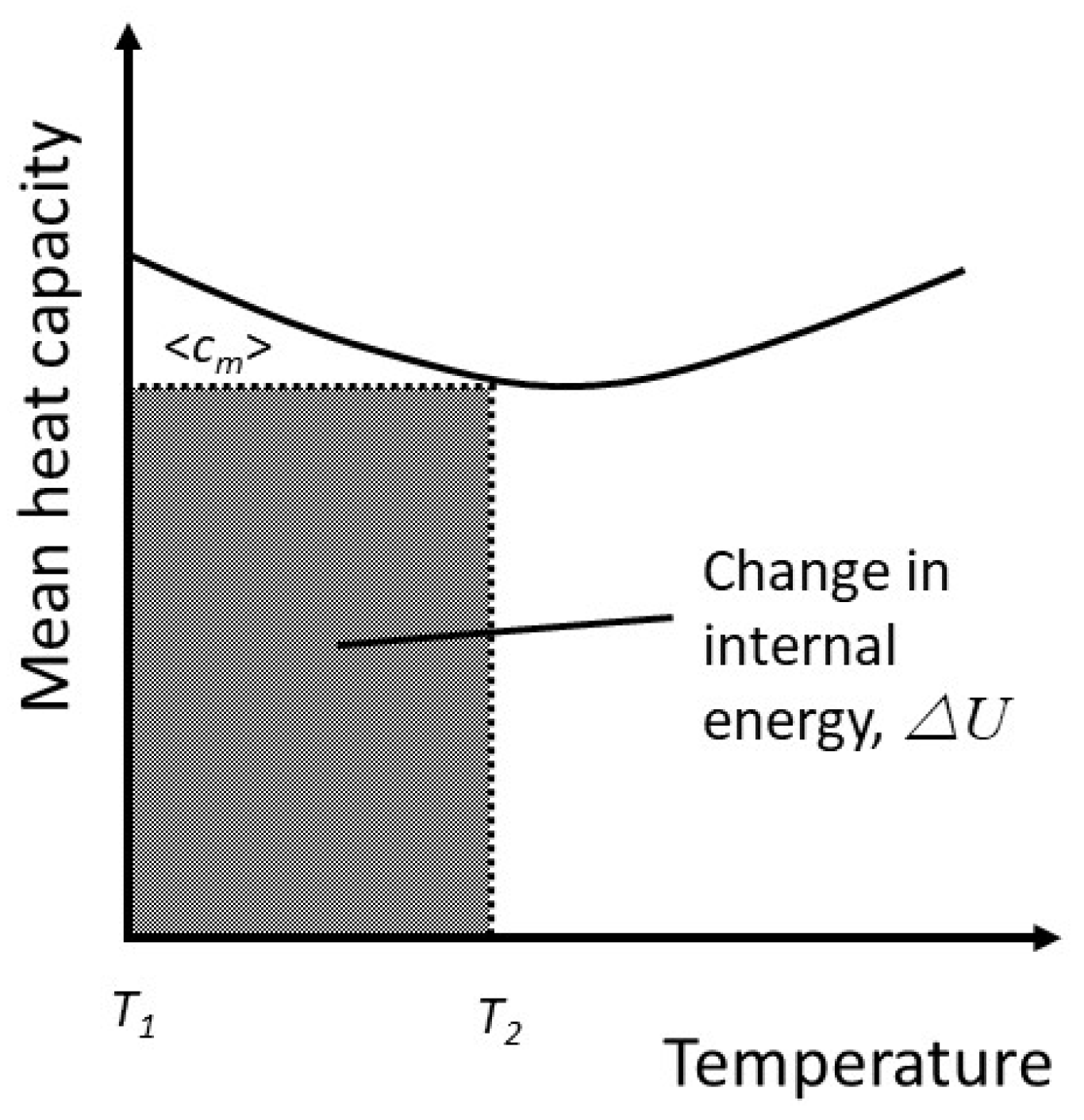
The advantage of this approach is that it allows for phase changes by looking only at the change in the internal energy within, say, the liquid phase, or the vapour phase. By way of example, consider lead vapour. Arblaster [17] gives the constant pressure heat capacity of lead as a function of temperature for all phases: solid, liquid and both monatomic and diatomic vapour. The data for vapour covers the temperature range from well below melting, 298.15K, to well above boiling, 2400 K. The monatomic vapour has a constant-pressure heat capacity of 20.786 J mol^-1 K^-1, corresponding to 3 degrees of freedom, up to approximately 700K, whereupon it begins to increase steadily, reaching 28.174 J mol^-1 K^-1 at 2400K. Quite clearly, the vapour over the solid is acting like an ideal gas. Whatever degrees of freedom characterized the atoms as part of a solid and whatever energy has been absorbed in order to liberate the atoms from the solid are irrelevant to both the degrees of freedom and the kinetic energy in the vapour phase, the latter being simply the thermal energy.

Suppose we have 1 mole of vapour which has been created at some temperature T_B1. Expanding equation (39), and substituting

〈c_{m, k}〉 = \frac{β (T_{B 2})}{2}

, we have, at some higher temperature T_B,

U (T_{B}) = U (T_{B 1}) - {\frac{β (T_{B})}{2} T}_{B 1} + {\frac{β (T_{B})}{2} T}_{B}

(41)

This admits to a simple physical interpretation.

U (T_{B 1})

is the total energy supplied to create the vapour, which has an effective thermal energy

{\frac{β (T_{B})}{2} T}_{B 1}

at this temperature and

{\frac{β (T_{B})}{2} T}_{B}

is the effective thermal energy at T_B. Unlike the case of a solid, it is not so obvious that for either a vapour or a liquid, the mean dimensionless heat capacity has the same physical interpretation as the active number of degrees of freedom. However, it has been argued that the active number of degrees of freedom following a phase change is entirely independent of the number of degrees of freedom preceding the phase change, and if, say, a vapour were to behave like an ideal gas with a constant heat capacity between the vapourisation point and some arbitrary higher temperature, then

〈c_{m, k}〉

averaged over that temperature range would be exactly equal to half the number of degrees of freedom. It follows that, in general, if the heat capacity varies with temperature

〈c_{m, k}〉

must represent some quantity that reduces to

\frac{β}{2}

in this limiting case and it seems reasonable to assume that equation (26) holds in this case also. It would also be reasonable to assume that the same applies to a liquid, not least because the internal energy can effectively be expressed as a function of absolute temperature via equation (41).

The change in entropy can be derived from equation (41) as,

\frac{d S}{k_{B}} = \frac{d U}{T_{B}} = \frac{1}{2} (T_{B} - T_{B 1}) \frac{d β}{T_{B}} + \frac{β}{2} \frac{{d T}_{B}}{T_{B}}

(42)

The last term on the right is recognizable as the change in the Boltzmann entropy and the first term on the right tends to

\frac{1}{2} d β

as T_B increases. For

T_{B} ≫ T_{B 1}

equation (42) reduces to equation (31). It follows from the preceding argument that the total entropy change in either the liquid or vapour phase will be less than the Boltzmann entropy at the higher temperature for positive changes in β. If β decreases, as illustrated in Figure 6, the thermodynamic entropy might well exceed the Boltzmann entropy.

5. Discussion and Conclusions

This paper opened with a historical analysis of the development of the concept of entropy by Clausius and showed how his ideas violate energy conservation for irreversible processes. There was, nonetheless, a compelling logic to his arguments. Clausius’s belief that heat was a property of a body, which was the prevailing view at that time, meant that some property of the body must have changed during an isothermal expansion. As the internal energy remains unchanged, and in an ideal gas this was equivalent to Clausius’s idea of the heat content, it followed that the change must be bound up with the separation of the particles. In a real gas subject to inter-particle forces, a change in volume will affect the potential energy of the particles and with it the kinetic energy, which Clausius believed corresponded to heat. However, heat is no longer defined as motion and therefore no longer regarded as a property of a body. Instead, it represents an exchange of energy, but the concept of entropy was not revised in the light of this change. Logically, entropy,

\frac{δ Q}{T}

, should more properly be associated with a transfer of heat, δQ.

It has been shown that applying this constraint to the entropy change consequent upon the addition of particles to an ideal gas leads to a non-zero value of the chemical potential owing to the fact that an exchange of energy with the exterior must occur in order to maintain a constant internal energy within the system, but this example also illustrates one of the difficulties in interpreting the concept of entropy. It is a derived quantity which is not susceptible to empirical observation and mathematical consistency is not sufficient. In this analysis of the chemical potential, a different assumption about the energy attached to particles leads to a different value of the chemical potential, but one which is also consistent with the initial assumption. In order to decide which is correct, it is necessary to go beyond these arguments and look at the wider picture. In this paper, this has been attempted by trying to attach a physical meaning to the change in entropy of a solid as an example of a system with temperature-dependent heat capacity. This follows work by the author in 2008 [10] that showed that the apparent entropy of a classical ideal gas can be described by the distribution of energy over the available states, which were defined to be

T^{\frac{1}{2}}

per degree of freedom.

This arises from the normal distribution of energy within each classical degree of freedom, whether related to kinetic or potential energy. The variance is related to the thermal energy and depends on T, meaning that the standard deviation, and with it the width of the distribution, depends on

T^{\frac{1}{2}}

. In this paper, the temperature has effectively been rescaled and in this view the number of states depends on

T_{B}^{\frac{1}{2}} = \sqrt{k_{B} T}

. The spacing between states then varies with

m^{- \frac{1}{2}}

for velocity states. Were the same reasoning to be applied to systems which oscillate harmonically, the spacing between states would be

k_{e f f}^{- \frac{1}{2}}

, where k_eff is the effective spring constant. In principle, this should allow the theory to be applied to solids, but there are difficulties. Even though the heat capacity is derived from quantized oscillations, it is generally assumed that this is equivalent in the high temperature limit to the classical picture and that the number of degrees of freedom is 6 per atom, as given by the Dulong-Petit law. The present work has shown that this picture is too simple for two main reasons. First, the theory of quantized oscillations is restricted to constant volume and takes no account of lattice expansion, which requires work to be done against the internal cohesive forces. It has been argued, therefore, that the total internal energy is effectively given by the constant-pressure heat capacity rather than the constant-volume heat capacity and the constant pressure heat capacity appears to exceed 6 degrees of freedom per atom by some way, even at moderate temperatures. Secondly, there is no direct relationship between the lattice vibrations and the degrees of freedom. However, it is possible to derive an average heat capacity which is equivalent to the number of degrees of freedom.

Having defined the effective number of degrees of freedom, the change in thermodynamic entropy upon constant volume heating has been shown to be directly related to the change in the number of ways of distributing the increased internal energy among the active degrees of freedom. This then brings the interpretation of the thermodynamic entropy in solids in line with the interpretation for the classical ideal gas. It has been shown in consequence that the total thermodynamic entropy of a solid at any given temperature is less than the corresponding Boltzmann entropy, which gives only the number of ways of distributing energy among the degrees of freedom active at a given temperature and takes no account of the thermal history. The treatment has been extended to include phase changes from liquid to solid and again the argument is made that the thermodynamic entropy of a liquid at any given temperature is different from the Boltzmann entropy. It might even exceed the Boltzmann entropy as the effective number of degrees of freedom will decrease with temperature in line with a decrease in the heat capacity, which is very common in simple liquids [18].

This shows that the Boltzmann and thermodynamic entropies are not generally equivalent, despite the widespread assumption to the contrary. It is the authors experience over many years of teaching statistical mechanics that no example other than the classical ideal gas is ever presented in text books in order to demonstrate this equivalence, but the present work shows that this is a special case. The heat capacity of a monatomic gas is independent of temperature and is related directly to the degrees of freedom in the system. Mathematically, the thermodynamic and Boltzmann entropies are equivalent in this case. However, it is generally assumed that this mathematical equivalence symbolizes a physical equivalence and that, generally, thermodynamic entropy is explained by a statistical description. The argument here is that the general connection between the two entropies lies in the change in thermodynamic entropy and the change in the distribution of energy among the degrees of freedom.

The physical bases of the two types of entropy are different and there is no reason why the two should be equivalent under all circumstances. Thermodynamic entropy derives from the flow of heat and its connection to work and internal energy via the First Law. Specifically, the existence of an integrating factor, 1/T, converts a path-dependent integral into an exact integral. The volume dependence of the entropy arises because in an isothermal work process, heat flows in order to maintain the internal energy at a given value. The statistical entropy, on the other hand, is a dimensionless, general property of probability distributions and as such need bear no relation to thermodynamics. In the case of an ideal gas, however, the probability distribution of the phase of the particles leads to an expression for the entropy identical to the thermodynamic entropy except for Boltzmann’s constant [10]. Despite this mathematical similarity, differences between these two emerge in the Gibbs paradox, however. This arises when two identical volumes containing identical amounts of an ideal gas separated by a removable partition are allowed to mix after the partition is removed. Thermodynamically, the entropy appears to be extensive in as much as it would require twice the internal energy, and hence twice the heat, to achieve a given temperature for twice the number of particles. Therefore, the total entropy is assumed to be unchanged upon removal of the partition, but the statistical entropy increases because the particles have access to a greater volume and hence there is a greater uncertainty over the position of the particles.

The increase in statistical entropy is entirely consistent with information theory, but not with the assumption that the statistical and thermodynamic entropies are both mathematically and physically equivalent. A proper discussion of the Gibbs paradox is not possible in this article, but the fact that papers continue to be published, and even a recent special issue of the journal Entropy has been devoted to it [19], suggests that here is no unique solution. Quite possibly, the paradox is insoluble. The conventional solution is to treat particles of the same gas as indistinguishable and alter the partition function by dividing through by N!. This has the effect of making the statistical entropy extensive, but the partition function itself is derived from the probability over the phase, which is a proper probability distribution in so far as it is normalized. Simply dividing through by N! destroys this normalization and is therefore not consistent with a proper statistical treatment of the entropy. Moreover, although treating like particles as indistinguishable appears to solve the paradox, it means that if the particles on either side of the partition are distinguishable, by for example having two different gases A and B, the entropy increases on removal of the partition. This is often described as the entropy of mixing, but in fact has nothing to do with mixing. Expansion of gas A into the volume occupied by B yields the same increase in entropy whether B is present or not and likewise with the expansion of B into the volume occupied by A. An increase in entropy implies that the entropy of distinguishable particles is additive whereas the entropy of indistinguishable particles is not. The obvious question is, Why? Unfortunately, there is no obvious answer.

These and other issues are discussed more fully in the special issue [19], but it is clear that the apparent resolution of one difficulty simply leads to another and doesn’t resolve the essential difficulty that thermodynamic entropy appears to be different from statistical entropy. The equation of state of an ideal gas contains no information about the identity of the particles, such as its mass or chemical nature, so thermodynamically, indistinguishability does not matter. In a mixture of ideal gases, the total pressure is the sum of the partial pressures and the heat capacity is the sum of the separate heat capacities. The amount of work done by a given number of particles does not depend on the type of particle doing the work, nor does the heat required to change the temperature by a given amount either at constant pressure or constant volume. It matters not, therefore, whether the gas comprises a single species or several. If a mixture behaves in all respects like an ideal gas, the identity of the particles is irrelevant in the calculation of the entropy change from one state to another.

The present work has suggested that the Boltzmann and thermodynamic entropies are not equivalent. As the Boltzmann entropy is a special case of the Shannon information entropy in the case of a uniform probability distribution for the access to each state, this also implies that the Shannon information entropy and thermodynamic entropy are not the same. Even in the case of a classical ideal gas, where the Shannon entropy of the probability distribution over the phase agrees with the apparent thermodynamic entropy and in turn the Boltzmann entropy, the equivalence is only mathematical. The Shannon information entropy can by regarded as a property of a state in so far as the probability distributions over both components of phase space, the real space and the momentum space, are determined by the thermodynamic state, but only the distribution over momentum space given by the Maxwellian distribution can be said to have any thermodynamic significance. Even then, it is not general. It is restricted to an ideal, monatomic gas in which the particles have translational kinetic energy only. For a diatomic molecule, or indeed any polyatomic molecule, in which vibrational and rotational degrees of freedom are activated with changes in temperature, or in which a phase change from liquid to gas might occur, the arguments presented in this paper will apply. The statistical entropy at any given temperature will be given by the distribution of energy over the active degrees of freedom and will therefore be different from the thermodynamic entropy, which, being given by an integral over the whole temperature range, must include the effect of activating additional degrees of freedom as well as any phase changes.

The difficulty with regarding thermodynamic entropy as a property of a body lies in the association of entropy with volume in a gas. The Gibbs paradox arises because the statistical entropy changes as the total volume available to the particles changes, but the thermodynamic entropy, being regarded as extensive, does not. However, the association of thermodynamic entropy with volume is responsible for the idea that entropy increases in an irreversible process, such as a free expansion. As described earlier, this must imply that something with the units of energy increases in a way that is inconsistent with energy conservation as expressed in the First law. Moreover, it follows that if entropy is a property of a body then it must also change if the number of particles changes. This association between matter and entropy is expressed, in the case of a gas, through the chemical potential, but for the entropy to change with the addition of particles, as argued in the discussion of equation (10), it is necessary to associate some energy with the particles themselves that is not the average energy per particle and which also lies outside the domain of the First Law. This can be seen explicitly in the approach to the chemical potential taken by Buchdahl [20], for example, who derived the chemical potential from the Gibbs free energy and accounted for this energy within the work;

d W = p d V - \sum_{i = 1}^{z} μ_{i} d N

This makes it clear that the chemical potential has the units of energy per particle and if the chemical potential is different from the average thermal energy of the particles, there must be some energy attached to the particles themselves which is not the thermal energy. However, it is questionable whether particles really do work in any meaningful sense. Particles added from a reservoir at the same temperature as the system of interest will carry with them thermal energy, but only thermal energy. Whilst this will change the total internal energy of the composite system of original and added particles, it will not change the internal energy of the system of original particles. Therefore, there is neither heat flow nor work done.

On of the reasons why entropy is believed to be a property of a body is the fact that it is a state function. The argument here is that this is no more than a mathematical property of thermodynamic phase space. It arises purely from the differential geometry of ideal trajectories between states represented in phase space. The end points of these trajectories are states defined by particular values of p and V, and therefore T, and any path independent integral between any two states must, by definition, be a function only of the two states at the ends of the trajectories. However, that is not equivalent to assuming that this is equivalent to a physical property of a physical system in same thermodynamic state. The trajectories merely define the amount of heat that would have to be exchanged with a reservoir, or series of reservoirs, in order to execute such a trajectory, which, by definition, is reversible. However, real physical processes are unlikely to be reversible [21] and if so, they cannot be represented as trajectories in p-V space.

Nonetheless, the fact the entropy is a state function means that it is possible to calculate the entropy of the end state of an irreversible process, but the question then arises as to what it represents. It cannot represent the heat exchanged with a reservoir because TdS>dQ in such a process, but if we suppose that the entropy corresponds to a physical property that increases in an irreversible process, we are entitled to ask, What is increasing? What is the cause? What is the mechanism? What is the physical effect? We know the answer to none of these questions and the finding in this paper that the statistical entropy is not generally the same as the thermodynamic entropy means that we cannot fall back on an “explanation” from statistical physics. All we can say for certain is that if entropy is a physical property that increases in an irreversible process, it is necessary to suppose the existence of some form of energy associated with matter that is not revealed by kinetic theory and which lies outside classical conservation laws. It is precisely the effect of separating entropy from the exchange of heat that brings about a conflict with energy conservation as expressed in the First Law. The inescapable conclusion is that entropy is not a physical property. It is inextricably associated with heat flow. As a state function, it is a mathematical property of differential geometry thermodynamic phase space, but it is not to be confused with a property of a body in the same thermodynamic state.

To summarise, it has been argued that the notion that entropy is a property of a body derives from Clausius’s conception of heat as a property of a body and that, logically, it should be associated with an exchange of heat. It has been argued in consequence that:

the total thermodynamic entropy has no physical meaning;
the connection between thermodynamic entropy and statistical entropy lies in the change in entropy: a change in internal energy can be understood as giving rise to a change in the distribution of energy among the degrees of freedom as well as the activation of new degrees of freedom where relevant;
the notion of entropy as a state function does not, and should not, imply that entropy is a property of a body in a given thermodynamic state. Rather, it arises from the differential geometry of thermodynamic phase space.

Funding

This research has been conducted by the author independently and without any funding from any organisation.

Conflicts of Interest

The author declares no conflicts of interest in the preparation or publication of this manuscript.

References

Clausius, R. 1867. On The Moving Force Of Heat And The Laws Of Heat Which May Be Deduced Therefrom, in The Mechanical Theory of Heat, with its applications to the steam engine and to the physical properties of bodies, Ed. T. Archer Hirst, John van Voorst, London, pp14-69.
Originally published in 1863, a reprinted version is available at: Tyndall, J. 2014. Heat Considered as a Mode of Motion: Being a Course of Twelve Lectures Delivered at the Royal Institution of Great Britain in the Season of 1862, Cambridge University Press, ISBN 9781107239449. [CrossRef]
Clausius, R. 1867. On The Application Of The Equivalence Of Transformations To Interior Work, in The Mechanical Theory of Heat, with its applications to the steam engine and to the physical properties of bodies, Ed. T. Archer Hirst, John van Voorst, London, pp215-250.
Clausius, R. On the determination of the Disgregation of a Body and on the True Capacity For Heat, Phil. Mag. 1866, 31, 29. [Google Scholar]
Sands, D 2022. The Problem of Entropy in the Teaching of Thermodynamics, presented at the International Conference FFP16, Istanbul, May 23-26, 2022, Proceedings to be presented in the book series: Springer Proceedings in Physics (SPPHY, volume 392). [CrossRef]
Planck, M. 1905. Treatise on Thermodynamics, 3^rd Edn, Dover Publications Inc.
de Groot, S. R. and Mazur, P. 1984. Non-equilibrium thermodynamics, Dover Publications (New York).
Callen, H. B. 1960. Thermodynamics: an introduction to the physical theories of equilibrium thermostatics and irreversible thermodynamics, Wiley (New York), p24.
Landsberg P. T. 1961, Thermodynamics, Interscience Publishers, p152.
Sands, D. Thermodynamic entropy and the accessible states of some simple systems. European Journal of Physics 2007, 29, 129–135. [Google Scholar] [CrossRef]
Blackman, M. The Theory Of The Specific Heat Of Solids. Rep. Prog. Phys. 1941, 8, 11. [Google Scholar] [CrossRef]
Desai, P. Thermodynamic Properties of Iron and Silicon. Journal of Physical and Chemical Reference Data 1986, 15, 967–983. [Google Scholar] [CrossRef]
Wei, S.; Li, C.; Chou, M. Ab initio calculation of thermodynamic properties of silicon. Physical Review B 1994, 50, 14587–14590. [Google Scholar] [CrossRef]
Crouch, R.K.; Fripp, A.L.; Debnam, W.J.; Taylor, R.E.; Groot, H. Thermophysical Properties of Germanium for Thermal Analysis of Growth From the Melt. MRS Online Proceedings Library 1981, 9, 657–663. [Google Scholar] [CrossRef]
Kozyrev, Nikolay V., and Vladimir V. Gordeev. 2022. "Thermodynamic Properties and Equation of State for Solid and Liquid Aluminum" Metals 12, no. 8: 1346. [CrossRef]
Khvan, A.V.; Konstantinova, N.; Uspenskaya, I.A.; Dinsdale, A.T.; Druzhinina, A.I.; Ivanov, A. and Bajenova, I. 2022. A description of the thermodynamic properties of pure indium in the solid and liquid states from 0 K, Calphad, 79, 102484, ISSN 0364-5916. [CrossRef]
Arblaster, J.W. 2012. Thermodynamic properties of lead, Calphad, 39, 47-53, ISSN 0364-5916. [CrossRef]
Schirmacher, Walter; Bryk, Taras and Ruocco, Giancarlo, 2022. Comment on “Explaining the specific heat of liquids based on instantaneous normal modes”, Phys. Rev. E 106, 066101. [CrossRef]
https://www.mdpi.com/journal/entropy/special_issues/gibbs_paradox#info.
Buchdahl, H. A. 1966. The Concepts of Classical Thermodynamics, Cambridge University Press.
Norton, J. D. The Impossible Process: Thermodynamic Reversibility, Studies In History and Philosophy of Science Part B Studies In History and Philosophy of Modern Physics 55. [CrossRef]

Figure 1. The dependence of internal energy on temperature for a classical ideal gas. Three different particle numbers are illustrated, with N₊>N₀>N_-.

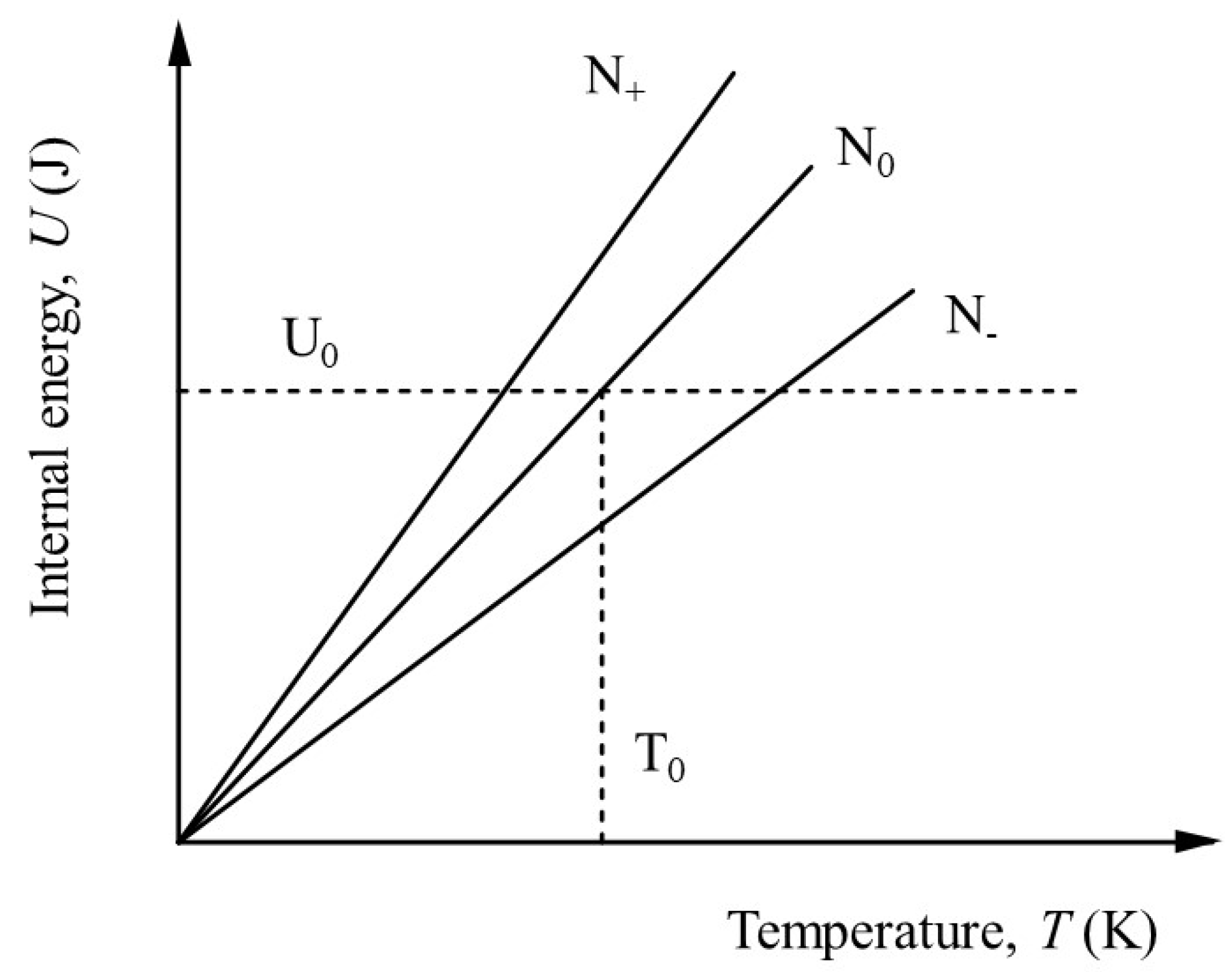
Figure 2. The sequence of operations required to maintain constant internal energy. Particles can be added or subtracted at constant temperature, thereby changing the internal energy (a), so the system has to be either cooled or heated to restore the internal energy to its initial value (b).

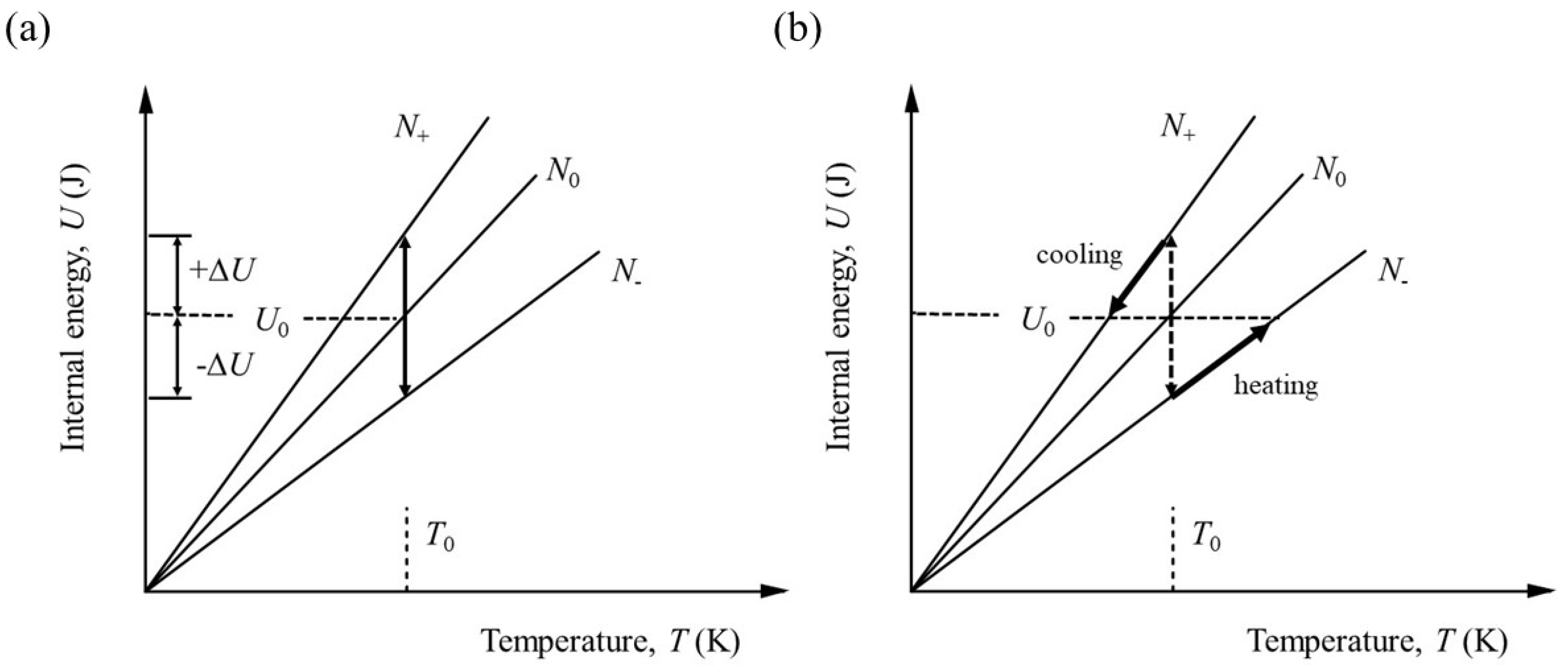
Figure 3. A schematic representation of the change in geometric interpretation of the internal energy from an area under a curve (a), corresponding to equation (23), to the area of a simple rectangle (b), corresponding to equation (25).

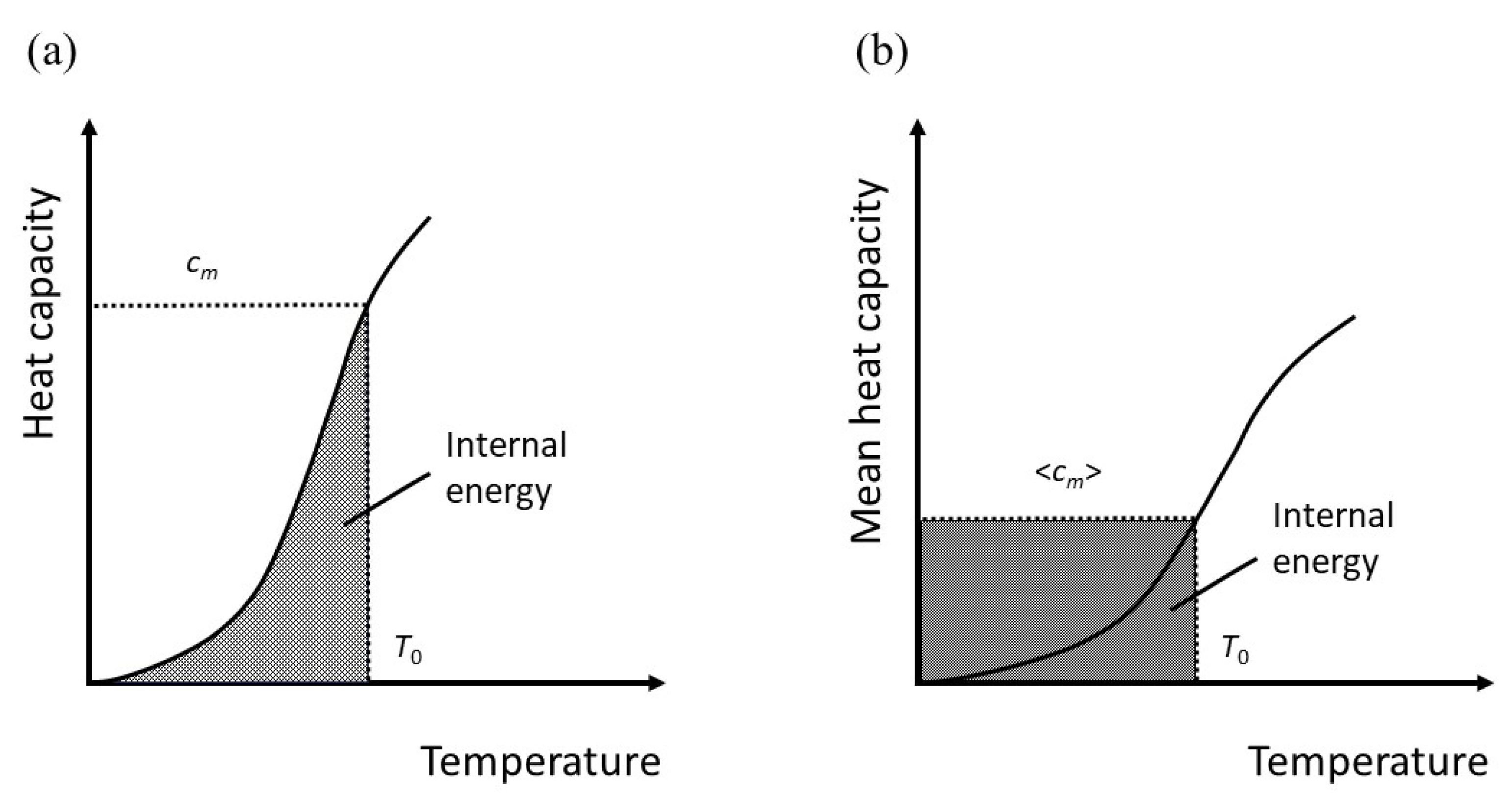
Figure 4. The specific heat of three different metals, In [16], Al [15], Pb[17] and Si [12] from 0K to their respective melting points. The specific heat of Ge [14] is shown over a limited range of temperature range, but including the melting point, for direct comparison with silicon. Figure 4b shows the mean reduced heat capacity, which is effectively half the number of active degrees freedom per atom, for each of the materials in (a).

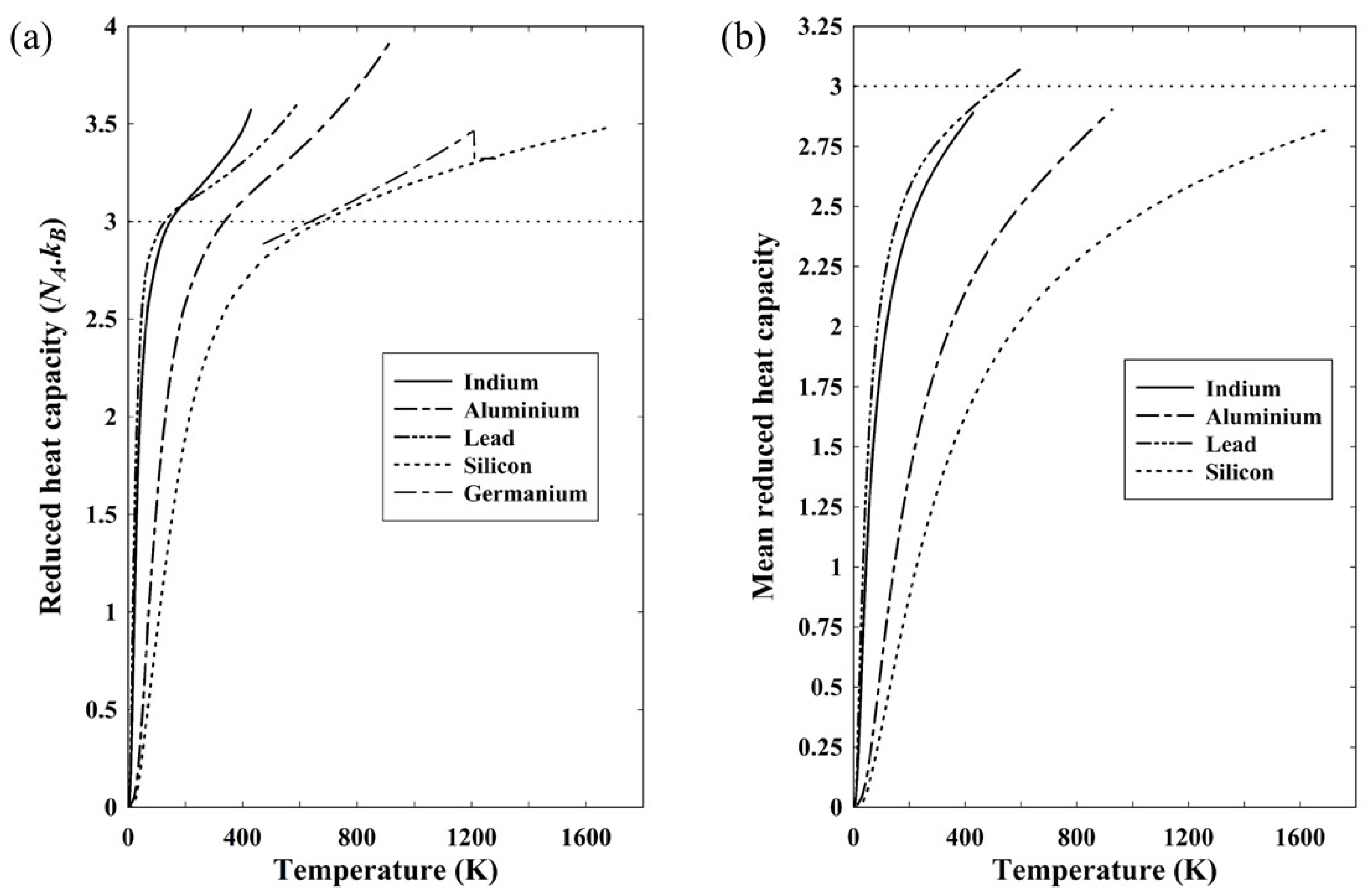
Figure 5. A geometric representation of equation (35), with

〈c_{m k}〉 = \frac{β}{2}

. The Boltzmann entropy is simply the area of the rectangle defined by the value of

〈c_{m k}〉

at any given value of

\ln T

except for a very small contribution corresponding to T<1, or ln T <0. The thermodynamic entropy is given by the unshaded area and is seen to be equal to the Boltzmann entropy when ln T=1.

Figure 5. A geometric representation of equation (35), with

〈c_{m k}〉 = \frac{β}{2}

. The Boltzmann entropy is simply the area of the rectangle defined by the value of

〈c_{m k}〉

at any given value of

\ln T

except for a very small contribution corresponding to T<1, or ln T <0. The thermodynamic entropy is given by the unshaded area and is seen to be equal to the Boltzmann entropy when ln T=1.

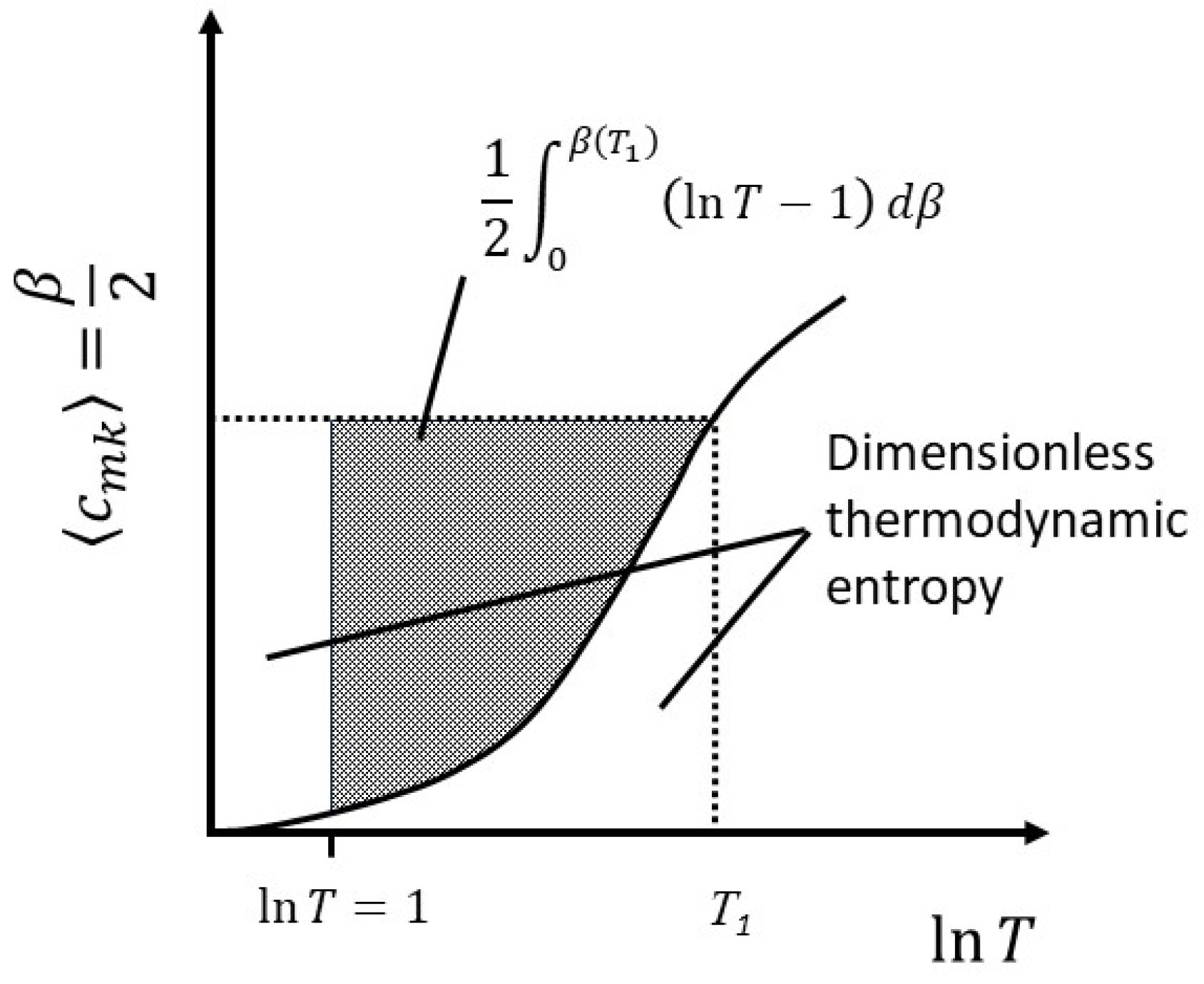
Figure 6. The geometric representation of equation (40). Note that the molar heat capacity has not been made dimensionless, for direct comparison with Figure 3(b). The shape of the

〈c_{m}〉

curve is intended to reflect the properties typical of simple liquids. It is well known that the heat capacity decreases with increasing temperature before rising again [18].

Figure 6. The geometric representation of equation (40). Note that the molar heat capacity has not been made dimensionless, for direct comparison with Figure 3(b). The shape of the

〈c_{m}〉

curve is intended to reflect the properties typical of simple liquids. It is well known that the heat capacity decreases with increasing temperature before rising again [18].

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

The Physics of the Thermodynamic Entropy

Abstract

1. Introduction

2. The Chemical Potential in a Classical Ideal Gas

3. Entropy in Complex Systems: an Examination of Solids

4. Extension to simple liquids and gases

5. Discussion and Conclusions

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe