Prerpints.org logo
Preprint
Review

Survey on AI Applications for Product Quality Control and Predictive Maintenance in Industry 4.0

Altmetrics

Downloads

186

Views

121

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

22 January 2024

Posted:

23 January 2024

You are already at the latest version

Alerts
Abstract
Recent technological advancements such as IoT and Big Data have granted industries extensive access to data, opening up new opportunities for integrating Artificial Intelligence (AI) across various applications to enhance production processes. We can cite two critical areas where AI can play a key role in industry such as product quality control and predictive maintenance. This paper presents a survey of AI applications in the domain of Industry 4.0, with a specific focus on product quality control and predictive maintenance. Experiments were conducted using two datasets, incorporating different machine learning and deep learning models from the literature. Furthermore, this paper provides an overview of the AI solution development approach for product quality control and predictive maintenance. This approach includes several key steps, such as data collection, data analysis, model development, model explanation, and model deployment.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

The industrial sector and its actors have always been in a state of continuous evolution, primarily driven by competitiveness and a desire for efficiency gains. The fourth industrial revolution emerged in response to rapid technological advances. This has led to a series of innovative practices known today as Industry 4.0. The objective of this transformation is to create an interconnected system where automated means of production are able to communicate with each other, as well as with humans through message exchanges [1]. Technologies such as Internet of Things (IoT), Cloud Computing, and Big Data play a crucial role in driving this intelligent production [1]. As a result of automating and monitoring production processes through these technologies, large amounts of data have been made available [2]. This data availability opens up opportunities for the use of Data Analysis and AI to create various applications aimed at improving production processes. These applications have great potential to further automate and revolutionize applications in supply chain optimization [3], energy management [4], product quality control [5], and predictive maintenance [6,7].
Product quality control plays an essential role in manufacturing, as the main goal of most industries is to deliver high-quality products to their customers. Defective products detected at the end of the production can not be commercialized and could lead to significant revenue losses. Detecting signs of defects as soon as they appear on the production lines is crucial to avoid significant losses. Constant maintenance that ensures the quality of the equipments and machines is also very important for the manufacturing process. Addressing equipment failure post-incident prolongs production downtime and creates significant costs. A more efficient method involves adopting a preventive strategy to anticipate failures before they occur. Predictive maintenance is a preventive measure that employs machine condition data to anticipate equipment failures. [6].
Statistical Process Control (SPC) has been used to monitor production processes [8]. It enables proactive measures to prevent defects and deviations, supporting a joint optimization of maintenance and quality [9]. Control charts are used in SPC to monitor variations in production efficiency, and detect potential deviations from established quality standards [10]. However, the analysis of these charts is complex and requires significant statistical knowledge [10]. The integration of AI can further enhance the capabilities of SPC by having a deeper understanding of the data. Industry 4.0 enables data collection through sensors distributed on production lines, and machines are now capable of recording data during the production cycle. This data can then be analyzed and used to train AI models to enhance manufacturing defect detection and machine failure prediction.
Research on the usage of AI for the enhancement of product quality control and predictive maintenance has been done. This paper presents a general overview as well as an experimental comparative study of existing approaches on two datasets. Furthermore, we provide an overview of the approach for developing AI solutions for these two applications.
We begin with a review of AI applications for product quality control and predictive maintenance in section 2. In section 3, we present an experimental study on two datasets, one related to product quality control and another to predictive maintenance. Finally, section 4 focuses on providing an overview on the process of development of these AI solutions.

2. Literature Review

This section reviews the current applications of AI in product quality control and predictive maintenance, focusing on suitable data types and exploring various Machine Learning (ML) and Deep Learning (DL) techniques proposed in the literature.

2.1. Product Quality Control

Product quality management plays a fundamental role in the manufacturing process. It not only ensures conformity with standards during product commercialization, but also establishes customer trust. There are many studies done about the usage of AI for product quality control using, and they can be categorized into two distinct categories. Defect Detection, and Defect Prediction.

2.1.1. Defect Detection

It is a critical stage of the QC process in order to decide whether a product should be approved or rejected. The work that has been done in this field, gives significant attention to automatic defect inspection using Computer Vision (CV) to examine produced parts. Recent studies have primarily relied on images of the product for visual defect identification. The annotation of images obtained from both defective and non-defective parts is a fundamental requirement for training good AI models. Examples of defects detected from images using AI include electronics connectors defects [11], background texture defects [12], and surface defects [13,14].

2.1.2. Defect Prediction

Defect prediction involves monitoring the production process to predict the quality of the produced parts. The quality of the product is strongly influenced by process parameters. The majority of the work present in the literature focuses on using process parameters along with the outcomes of quality inspections to develop AI prediction models. The data used in these works typically consist of numerical data recorded from sensors placed on the production lines during the manufacturing process. Examples of this category include porosity detection in aluminum wheels [15] and geometrical defects in extruded tubes [16]. Several works are specifically related to plastic injection molding [5,17,18,19].

2.2. Predictive Maintenance

Maintenance plays a crucial role in the industry by ensuring the proper functioning of machines. Predictive maintenance [20] involves predicting when a machine is likely to experience a failure. This strategy relies on data analysis techniques and AI to predict machine failures. By using data related to the operating conditions of the machines, AI models can be employed to identify anomalies and determine when maintenance is necessary. Many studies have focused on predictive maintenance using AI in the literature. They can be categorized into Failure Prediction and Remaining Useful Life (RUL) prediction.
Failure prediction focuses on identifying imminent failures, while RUL prediction determines the remaining time before a failure occurs.

2.2.1. Failure Prediction

Failure prediction consists of real-time monitoring of machine conditions using sensor data and employing AI models to detect signs of future failure. Several research studies on failure prediction have been proposed, using numerical data and time-series data collected from IoT sensors associated with machine operating conditions. The data should represent the dynamic behavior and machine conditions over time during its operational phase. Numerical data can provide insights into the quantitative aspects of machine performance, while time-series data enable the analysis of temporal patterns to identify trends and anomalies preceding equipment failure. For example, [21] predicts machine component failures using telemetry measurements, maintenance history, and machine specifications. [22] employed time-series data to predict tool wear, gearbox, and bearing faults. [23] focused on predicting failures in rotating machines by analyzing vibration signals. [24] predicted the degradation of cutting tools.

2.2.2. Remaining Useful Life Prediction

It allows for estimating the remaining operating time of machines before a failure or breakdown occurs. Knowing the remaining useful life of equipments helps in the effective planning of maintenance operations. Two major categories of data are frequently employed in the literature, numerical data and time series data. For instance, [25] predicts the RUL of rolling element bearings and milling cutters, using time series data related to their operating conditions. [26] for example, forecasted the RUL of plastic injection machines using numerical sensor data. Several works including [27,28,29,30,31] employ the C-MAPSS [32] time series dataset to predict the RUL of turbofan engines.

2.3. AI Models for Product Quality Control and Predictive Maintenance

In this section, we present existing Machine Learning and Deep Learning method that focus on data used in product quality control and predictive maintenance.

2.3.1. Machine Learning Methods

Machine learning is a branch of AI that enables computers to learn from data in order to acquire decision making capabilities, and perform tasks without human intervention [33]. ML models are trained on a set of examples known as training data, in order to be able to make predictions on newer never before seen data.
To predict defects and failures in manufacturing, the data used for model development should cover both normal conditions and instances of failures or defects. Various ML algorithms have been proposed in the literature in order to create these models :
  • Support Vector Machine: It is an ML technique commonly employed for classification and regression tasks [34]. In classification, SVM creates hyperplanes to effectively separate different classes using support vectors [34]. In regression, the objective is to identify a function that closely matches data points within a defined margin [34]. SVM was employed in various studies including predicting part quality in plastic injection [5], identifying defects in laser additive manufacturing [35], predicting tool wear during milling operations [24], and estimating the RUL of machine components [36].
  • K-Nearest Neighbors: [37] is a machine learning technique used for classification and regression tasks. To classify a new data point, the algorithm looks at the K closest data points from the training set and assigns the majority class among those neighbors to the new data point [37]. For regression, it predicts the value based on the average of the K nearest data points values [37]. It does not require training but its performance can be affected by the chosen K value and distance metric. in [38] KNN was used for fabric defect detection based on features extracted from thermal camera images . In the context of additive manufacturing quality control, KNN demonstrated effective porosity prediction, as presented in [39]. The effectiveness of KNN was also highlighted in [40], a comparative study on predictive maintenance.
  • Naive Bayes: [41] is a probabilistic machine learning algorithm that relies on Bayes’ theorem. It assumes feature independence given the class label. The algorithm calculates probabilities for a data point belonging to each class, and predicts the class with the highest probability. Naive Bayes can also be used for regression tasks [42]. The Naive Bayes algorithm combined with Particle Swarm Optimization (PSO) [43] in [44] effectively detected product defects. In [45], a Naive Bayes approach using vibration signals successfully identified specific bearing faults.
  • Regression (Linear and Logistic): Linear regression [46] is an ML algorithm that searches for a linear relationship between input features and the target variable by fitting a straight line to the data points. The effectiveness of this algorithm depends on the linearity assumption of the data. Logistic regression [47] on the other hand, is used for classification by calculating the probability of belonging to a class using a logistic function that produces values between 0 and 1. In [48], a logistic regression model is proposed for predicting product quality in the rolling process. Linear regression is applied in [49] to forecast machine failure in a turbine generator for maintenance scheduling in oil and gas platforms. The study in [50] employs Multiple Linear Regression (MLR) [51] to estimate the RUL of bearings based on vibration data.
  • Decision Tree: [52] is an ML technique used for both classification and regression tasks. It constructs a model in the form of a tree where each internal node represents a feature and each leaf node represents a class or a predicted value. It recursively splits the data based on the feature that provides the best separation at each node up to a certain stopping criterion. In [53], the authors used a J48 decision tree model to predict part quality in the injection molding process. The study in [54] employed Decision Trees in combination with a genetic algorithm to predict the RUL of an aircraft air conditioning system.
  • Ensemble Learning: [55] is a category of machine learning techniques that combines predictions from multiple models to predict the target variable. Predictions are often combined using voting for classification tasks and averaging for numerical value prediction. There are different ensemble methods such as bagging, XGBoost [56], Random Forest [57], and Gradient Boosting Machine [58]. XGBoost successfully predicts manufacturing defects in [15,18]. In [59], a Gradient Boosting model is suggested for predicting steel product quality. In predictive maintenance, Random Forest models are used to predict the RUL of machines in [26,60].

2.3.2. Deep Learning Models

Deep learning is an advanced approach that uses artificial neural networks with multiple interconnected layers of neurons [61]. It is particularly effective for processing large amounts of data and can handle both structured and unstructured data [62]. There are different proposed architectures of neural networks, each adapted to particular types of data. We will present in this section different architectures that have been proposed for product quality control and predictive maintenance in the literature.
  • Multi-Layer Perceptron: MLP [63] models are the most well-known deep learning models. MLP consists of interconnected layers of neurons. Neurons in intermediate layers assign weights to inputs from the previous layer, sum them with a bias, and apply an activation function. The last layer gives the output value depending on the nature of the problem, whether it is a classification or regression task. The study in [19] applied MLP in an online defect detection system for the injection molding process. In [31], MLP was employed to predict the RUL of aircraft turbofan engines. MLP model demonstrated strong performance in predicting machine component failures in [21].
  • Convolutional Neural network: Convolutional Neural Network (CNN) [64] is a widely employed DL method for image processing such as image classification, object detection, and image segmentation. Its key component, the convolutional layer, uses filters to detect patterns in input images through convolutions. CNNs can learn features automatically without the need for manual features extraction. It is common in the literature to use Transfer Learning, which involves taking a pre-trained CNN model on one task and adapting it to a new, similar task. Many pre-trained model architectures have been proposed [65]. In [12] a CNN was used for background texture-based defect detection. In [13], a modified YOLO [66] transformed into a fully convolutional model, was introduced for real-time surface defect detection in steel strips. The work in [14] reviews and presents other examples of defect detection in images of products. Regarding predictive maintenance, [29,67] applied CNNs to predict RUL.
  • Recurrent Neural Network: an RNN [68] is a type of network introduced to process sequential data such as time series data or text. RNNs take an ordered sequence of data as input to predict one or more output values. They are designed to extract important information from sequential data and use it for prediction. There are different types of RNN architectures including vanilla RNN [68], Long Short-Term Memory (LSTM) networks [69], and Gated Recurrent Units (GRU)[70]. [71] proposed an approach to predict the RUL of aircraft engines using a basic LSTM model. The study in [22] demonstrates the effectiveness of a system based on a Gated Recurrent Unit (GRU) model for predicting tool wear, gearbox faults, and bearing faults.
  • Generative Adversarial Network: a GAN [72] is a type of deep artificial network that enables the generation of synthetic data from a given real dataset. This model primarily consists of two components: a generator and a discriminator, each with a specific role during the model training process. The generator transforms a random noise vector into synthetic data that resembles the original dataset. On the other hand, the discriminator is used to differentiate between the synthetic and real sample, by classifying them accordingly. A steel surface defect detection method utilizing GANs was introduced in [73]. Works such as [74,75,76] propose approaches using GANs for predicting the RUL of machines using data extracted from multiple sensors.
  • Autoencoder: It [77] is an artificial neural network consisting of two main components: the encoder and the decoder. The encoder processes input data and transforms it into a lower-dimensional encoded representation within a latent space. The decoder performs the inverse operation by taking the encoded representation and decoding it to reconstruct the original data. Its role is to recreate a version of the initial input as close as possible. The main objective of the autoencoder is to minimize the difference between the input data and the reconstructed data. An autoencoder-based model is used in [17] for quality prediction in the injection molding process. The study in [78] proposed a deep learning model composed of a Variational Autoencoder (VAE) [79] and a Recurrent Neural Network (RNN) for predicting the RUL of machines. The VAE is used to reduce the dimensionality of the data and extract features from sensor data, while the RNN is used for RUL prediction.
  • Transformer: It [80] was initially created for natural language processing tasks such as language translation and text summarization. Similar to Autoencoders, Transformers mainly consist of two parts: an encoder and a decoder, both composed of multiple layers of self-attention and feed-forward neural networks. The transformer is designed to learn to produce outputs by focusing only on relevant information extracted from the input data using the attention mechanism. Recently, several studies have explored the application of Transformers in other tasks, such as image processing [81] and time series data analysis [82]. Transformers enable parallel processing of data, overcoming the sequential processing limitations of RNNs [83]. Studies like [84] [85] have used Transformers for surface defect detection. In addition, a system employing the Transformer was proposed for predicting RUL of Li-ion batteries in [86].

2.4. Conclusion and Discussion

After taking a look over the current State-of-the-art, we remark that models based on CNNs have been widely used to detect defects from images of products in the literature. These models appear to be well-suited for image processing. Other models based on GANs and Transformers have also recently emerged for defect detection. ML approaches such as SVMs and KNN have also been explored, but these models require prior feature extraction from images. Defect detection can assist operators in conducting quality control at the end of production. However, Computer Vision techniques can only be applied to visible surface defects and can not identify non-visual surface defects. Unfortunately, Other performance related quality criteria should be considered because quality is not just about external appearance.
In the literature, defect prediction from process data is carried out using structured numerical data. Many studies employ classical ML with Ensemble Learning, as it can provide better performance by combining predictions from multiple models, instead of a single one. Algorithms such as XGBoost, Gradient Boosting, and Random Forest are among the most commonly used. In other studies that use a DL approach, MLP models were employed as they are suitable for structured data.
Data used in predictive maintenance typically consist of numerical data or multivariate time series. That kind of data is generally related to the operating conditions of the machines. In terms of numerical data, commonly used methods include Ensemble Learning (XGBoost, Random Forest, Gradient Boosting) and MLP. For time series data, existing approaches often use RNN models. Other recent approaches suggest the use of Transformer models. AI-based Predictive Maintenance approaches have demonstrated to be quite effective in the literature, whether for predicting machine failure or RUL.
Despite the advancements in the application of AI for product quality control and predictive maintenance, we have identified some limitations in existing works in the literature:
  • Data Imbalance: It is a prevalent challenge in applying AI to predictive maintenance and product quality control. Machine failure instances and defective product examples, are often rare compared to normal cases, resulting in imbalanced datasets. AI models are designed to minimize overall error rates and may perform well on normal cases, but struggle with predicting machine failures and identifying defects. Various techniques [87] have been employed to address this issue, but data imbalance remains a significant challenge for AI applications in many fields.
  • Explainability and Interpretability: Some traditional machine learning models, such as decision trees, are by default explainable. However, more complex models like ensemble and deep learning models are not inherently explainable. Deep learning models are often viewed as complex black-box models, presenting a challenge in understanding decision-making processes and the internal logic. This opacity may cause regulatory compliance issues regarding the accountability and transparency of their decisions. Explainability and interpretability techniques [88] should be applied to establish confidence in the decision of the model. Furthermore, these techniques can help identify the root causes of a product defect or a machine failure. A better understanding of these causes could aid in optimizing the production process by adjusting parameters related to these incidents. Most of the existing studies on product quality control and predictive maintenance did not address the explainability of the proposed solutions.
  • Real-time Detection Instead of Prediction: Most of the works predict equipment failure at the time of prediction rather than in future states. These approaches perform real-time failure detection rather than making a prediction. A reliable predictive maintenance system should be capable of predicting future failures based on the current state, equipment history, and other information related to the environmental conditions of the equipment.
  • Domain Dependency and the Need for Industry-Specific Datasets: Domain dependence is one of the main challenges of applying AI for predictive maintenance and product quality control. It can be observed in the literature that the field of predictive maintenance is not only relevant to the manufacturing industry but also to other sectors. Public datasets like C-MAPSS [32] and PHM08 [89] have been used to evaluate predictive maintenance proposals, but these datasets are not specifically related to the manufacturing industry. It is challenging to ensure that the proposed approaches will be effective when applied to real-world cases in industry. Transfer learning [90] techniques allow adapting a model built in one domain to another, but the input data of the model could not be the same. Domain dependence is a persistent issue in the application of AI in industry, and this can impact the performance of the model. A model may perform well on benchmarking data but exhibit very poor performance in a real-world industrial application.
  • Overlooking Component Interactions: The degradation of one component may be linked to other components, further complicating the identification of failure causes. Failing to account for these interactions can lead to inaccurate failure predictions. It is crucial to monitor the overall machine state and consider interactions between components in the design of AI models for predictive maintenance.
  • Single-quality Criterion Consideration: One limitation of existing works on defect prediction is that they typically focus on a single quality criterion. To establish an effective quality control system, the dataset should include data from partial quality inspections that address all relevant criteria. Sources of defects may differ across various quality criteria, introducing an additional challenge in the application of AI for predicting manufacturing defects.

3. Experimental Study

In this section, we conducted an experimental study using two real industrial datasets: one related to predicting product quality in the plastic injection process and another related to predicting machine component failures. We selected these datasets because they originate from real-world industry cases.

3.1. Evaluation metrics

In both datasets, we have a categorical target, which indicates a classification problem. Therefore, we chose to use precision, recall, and F-score as metrics [91], which are among the most commonly used measures in the literature for evaluating models in a class prediction problem.
  • Precision: measures the proportion of correctly predicted instances among those predicted as positive [91].
    Precision = True Positives True Positives + False Positives
  • Recall: evaluates the proportion of correctly predicted positive instances among all truly positive instances [91].
    Recall = True Positives True Positives + False Negatives
  • F-score: combines precision and recall into a single measure allowing the assessment of balance between the two [91].
    F - score = 2 × Precision × Recall Precision + Recall

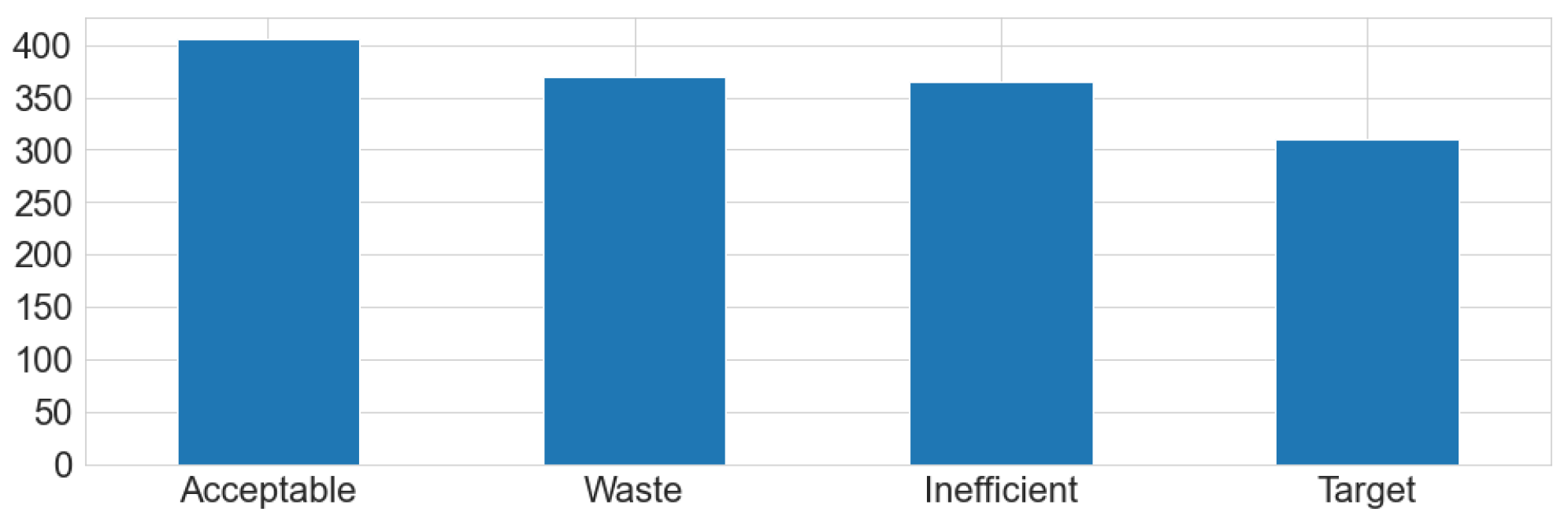
3.2. Quality Prediction in Plastic Injection

This experimental study is about quality prediction in plastic injection molding process. The data was collected from sensors in the injection machine during the production of plastic road lenses [92]. The dataset comprises 1451 records and consists of 13 process parameters, including the temperature of the melted material, mold temperature, filling time, plasticizing time, cycle time, closing force, peak closing force value, peak torque value, average torque value, peak back pressure value, peak injection pressure value, screw position at the end of holding pressure, and injection volume. In addition to these parameters, the dataset contains an attribute indicating the quality of the lenses. Authors in [92] have defined four quality classes based on the standard "UNI EN 13201-2:2016" for lenses in motorized roads. According to this standard, the general uniformity U 0 of the lens should be greater than 0.4 [92]. Samples with U 0 less than 0.4 are categorized as "Waste" (Class 1) and should be discarded for not meeting the standard. Those with a uniformity between 0.4 and 0.45 are labeled as "Acceptable" (Class 2), meeting the standard but falling short of the company’s higher quality target. "Target" (Class 3) includes samples with a uniformity between 0.45 and 0.5, considered optimal. Samples with U 0 greater than 0.5 are labeled as "Inefficient" (Class 4) and should be avoided, as producing lenses with such uniformity exceeds standard requirements. The class distribution in the dataset is illustrated in Figure 1, which shows that the dataset is quite balanced.
We conducted a performance comparison of various ML and DL models. We selected a set of models commonly employed in quality control applications for numerical data. The set of models includes SVM, Logistic Regression, Decision Tree, Random Forest, XGBoost, KNN, Naive Bayes, and MLP. Time series models like recurrent neural networks were not applicable in this study due to the absence of timestamp information in the dataset.
We divided the dataset into a training set, a validation set, and a test set, and the size of each subset is presented in Table 1. Figure 2 illustrates the class distribution within each subset of the data.
The validation set is employed to control overfitting during the training of the MLP model. To ensure a fair comparison of models, machine learning models were trained exclusively on the training set.
The results of the performance evaluation for various models on the test set are presented in Table 2. Each model was fine-tuned by adjusting hyperparameters manually. The results show that ensemble models present good performances in terms of precision, recall, and F1-score. Random Forest shows the best scores for all performance metrics and is also the top-performing model identified by the authors in [92]. Following Random Forest, MLP demonstrates a value of 0.95 for all three metrics, followed by XGBoost, Gradient Boosting, and Extra Trees. The random forest was configured with 100 decision trees. The architecture of the MLP model is presented in Table 3.
Models such as KNN and Decision Tree also show good F-score values of 0.91, while the remaining models SVM, Naive Bayes, and Logistic Regression present lower performances. It can be assumed that these models are simpler and struggle to identify complex relationships among different features in the dataset.
Figure 3 illustrates the confusion matrix for Random Forest and MLP. It shows that the two models are able to effectively determine the quality of the parts with only seven misclassified parts for Random Forest and 15 misclassified parts for MLP. The result indicates that a well-balanced dataset contributes to achieving high-performing models.

3.3. Machine Component Failure Prediction

The objective of this use case is to predict machine component failures based on real-time data collected from the machine and its operating conditions. This allows for anticipating failures before they occur and planning maintenance operations in advance.
The dataset used in this section, provided by Microsoft [93], includes detailed information related to the operational conditions of 100 machines in an anonymous industrial process. The dataset was also used in the work of [21] where the authors proposed a prediction of failures for four machine components. The dataset consists of five distinct data sources [21]:
  • Telemetry: includes measurements of machine pressure, vibration, rotation, and voltage.
  • Errors: log of recorded machine errors.
  • Machine: provides machine characteristics such as age and model.
  • Maintenance: contains the history of all machine component replacements.
  • Failures: information on the history of failed component replacements.
The initial dataset comprises 876,100 records of telemetry measured at hourly intervals. The date and time are rounded to the nearest hour for errors, maintenance, and failures data.
Since we have five data sources, it is necessary to gather the different data sources to create features that can best describe the health condition of a machine at a given time. For this purpose, we applied the same feature engineering techniques used in [21] to merge the different data sources. To achieve this, additional information was extracted from the initial data sources to enrich the dataset [21]. The means and standard deviations of telemetry measurements over the previous 3 hours and 24 hours were computed to create a short-term and long-term history of telemetry data. This allows for better anticipation of failures and provides an early warning in case of a failure [21]. The "errors" data source helped determine the number of errors of each type in the last 24 hours for each machine [21]. From the "maintenance" data source, the number of days elapsed since the last component replacement was calculated [21]. The "Failures" data source was used to create the label. Records within a 24-hour window preceding the replacement of a failed component were labeled with the corresponding component name (comp1, comp2, comp3, or comp4), while other records were labeled as "None" [21]. A more detailed description of the applied feature engineering process can be found in [21].
After the feature engineering, the final dataset comprises 290,642 records with 29 features, including machine information such as the machine identifier (machineID), age, and the model of the machine; 3-hour and 24-hour rolling measurements for voltage, rotation rate, pressure, and vibration; error counts during the last 24 hours for different error types; time since the last replacement for each component; and a ’datetime’ column indicating the registration of each record at regular three-hour intervals.
We compared multiple ML and DL models by evaluating them on the same test set. As the dataset includes a "datetime" column indicating the timestamp of the data, we incorporated recurrent neural networks that take a sequence of records as input. To achieve this, we selected a sequence length of eight records to analyze information over the past 24 hours. The class of the last record in the sequence is considered as the sequence class. To avoid overlaps, sequences containing a record corresponding to a failure were excluded if the last record had a ’none’ class. We excluded these records along with the first seven records for each machine from the test set used for the evaluation of models that take one record at a time. This ensures a fair comparison between models handling a single record and those handling a sequence of eight records.
To develop models, we first divided the data into train, validation, and test sets. To achieve this, we followed the same partitioning as presented in [21]. The records until 08/31/2015 1:00:00 are used as the training set to train the model. Those between 01/09/2015 1:00:00 and 31/10/2015 1:00:00 serve as the validation set, and those starting from 01/11/2015 1:00:00 are reserved to compose the test set.
Table 4 presents the number of records for each subset for both RNN models and other models. The difference in the number of records between RNN models and other models is a result of using sequences of eight records specifically as input for RNN models.
Figure 4 and Figure 5 depict the distribution of classes in the training, validation, and test subsets for the two cases. We can observe that subsets have similar class distributions which indicates a good data partitioning. Class distributions in those subsets are also similar to that of the intial dataset.
Table 5 presents the performance results of the different models used in our experiment. Fine-tuning of hyperparameters for each model was performed manually. We can observe that SVM, Ensemble models (Random Forest, XGBoost, Gradient Boosting, Extra Trees), and DL models (MLP, SimpleRNN, LSTM, GRU) all demonstrated high performance with an F-score exceeding 0.95. XGBoost and GRU outperform other models with an F-score of 0.98, followed Random Forest with an F-score of 0.97. The architecture of the GRU model is presented in Table 6. The XGBoost model is set up with 70 estimators and the Random Forest model is configured with 100 estimators.
The confusion matrices for these three models are shown in Figure 6. We can observe that the primary sources of prediction errors are associated with the prediction of failure for components 1 and 3. The results obtained confirm that Ensemble Learning models could give good results for failure prediction with a numerical dataset. On the other hand, recurrent neural networks could capture relevant information in a time series for failure prediction.

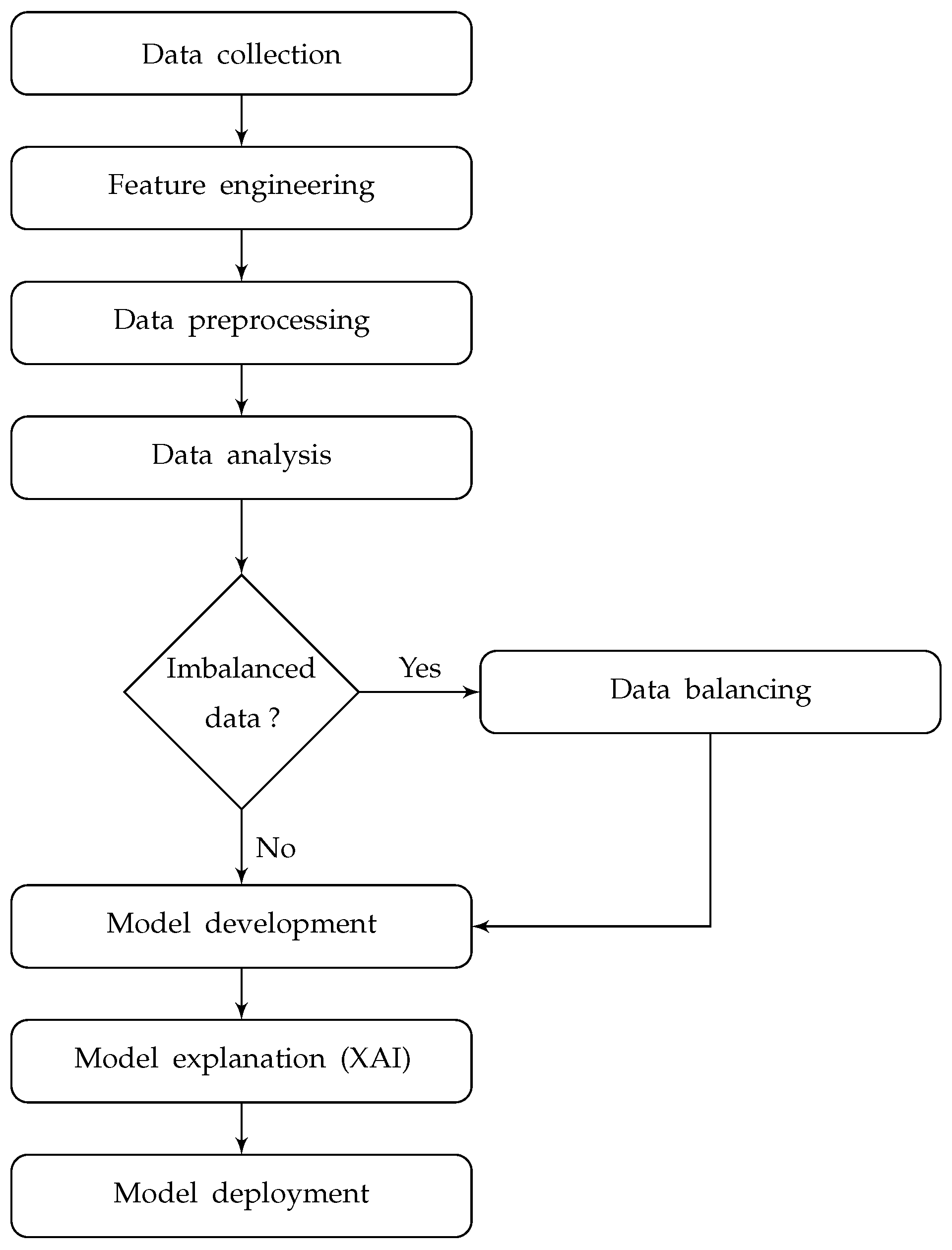
4. AI Solution Development for Product Quality Control and Predictive Maintenance

In this section, we will present an overview of AI solution development approach for product quality control and predictive maintenance, building upon the studies conducted in the previous sections. The approach takes into consideration the limitations identified in existing works, specifically addressing data imbalance and the explainability of AI models.
This comprehensive approach encompasses data collection, feature engineering, data preprocessing, data analysis, model development, model explanation, and model deployment. The entire process is summarized in Figure 7.

4.1. Data Collection and Feature Engineering

To develop a data-driven quality control and predictive maintenance system, the first step is data collection. Subsequently, it is essential to aggregate data from various sources through feature engineering, creating a dataset that accurately represents the addressed problem. During the data collection process, data annotation should also be performed. The goal is to provide the model with the most relevant information for detecting and predicting manufacturing defects and machine failures.

4.2. Data Preprocessing

Before developing an AI model, data preprocessing plays a critical role in cleaning and preparing the data. It involves several essential steps, such as removing missing, incorrect or outlier values, as well as duplicates, ensuring that the data used is consistent and reliable. Additionally, feature selection plays a significant role in reducing the dimensionality of the dataset. Some features may have little influence on the decision of the model and could potentially degrade its performance. Feature selection methods [94] can help choose the most informative features for the model. Furthermore, data can be measured on different scales or units, potentially leading to biases in the model. Data normalization [95] enables scaling the data to a common range using techniques such Min-Max normalization, Z-score normalization and Decimal scaling normalization. This allows models to treat the data fairly and avoid biases caused by measurement differences.

4.3. Data Analysis

Data analysis is an important step to better understand data and identify patterns, trends, and relationships between features that can be useful in model development. Data visualization is a commonly used technique to graphically represent data and provide an overview. Graphs like variation plots, histograms, scatter plots, and box plots are often used to explore features and relationships between variables. Correlation analysis [96] can also assist in identifying highly correlated features and removing them by retaining only a representative single feature. Data imbalance is also an important point to analyze. It is necessary to check if the data classes are evenly distributed. Significant data imbalance could lead to model performance issues as it may be biased towards the majority classes. In such cases, resampling techniques or synthetic data generation can be used to balance the classes and improve model performance.

4.4. Model Development

Model development involves splitting the preprocessed data into training set, validation set, and test set. The training set is used to train the model by searching for the best configuration. The validation set serves to identify overfitting during the training process, while the test set is employed to assess the model’s performance on unseen data. This enables an evaluation of the ability of the model to generalize to new data and measure its real-world performance. Often, the best model type and configuration for a given problem are not known in advance. Developing a quality control and predictive maintenance system requires testing different models. A step of selecting the best-performing models is then performed based on appropriate evaluation metrics. The goal is to develop models capable of accurately predicting manufacturing defects and machine failures.

4.5. Model Explanation

After developing models, it is important to ensure confidence in their decisions for them to be accepted by industry professionals. Some models, like most traditional machine learning models, are by default explainable. However, more complex models like deep learning models require the use of explainability techniques. These techniques enable the explanation of model decisions in a way that makes them comprehensible to humans. The principle of these methods is to identify the most important parameters in the input data during model prediction. Explainability techniques help find out why defects or failures happen. Understanding these reasons can improve how machines are used, cut down on failures, and reduce the number of defective products. Various explainability techniques [88] are available in the literature. The selection of the appropriate technique depends on both the type of data and the nature of the model.

4.6. Model Deployment

The final step of the solution involves deploying the models on the production lines. The deployment of AI models in the industry typically occurs on local servers or in Cloud Computing. However, these solutions can lead to latency issues, resulting in a delay between the request for data and receiving the data. This delay can be critical for applications such as quality control and predictive maintenance, where real-time predictions are essential. An alternative to these solutions is Edge AI [97], which involves deploying AI models on embedded resources in production lines to bring sensors closer for data processing. This approach allows for real-time prediction of equipment status without the need to transmit data to a remote server. However, deploying AI models in Edge AI also presents significant challenges concerning resource limitations and the need for lighter AI models. It is imperative to compress and optimize to ensure the deployment of models on resource-constrained edge devices.

5. Conclusions

In this work, we have presented a review of existing research on data-driven product quality control and predictive maintenance using AI. Product quality control facilitates the early detection and prediction of manufacturing defects on production lines. Predictive maintenance allows to predict equipment failures before they occur. Several solutions were published to address these two applications using different AI approaches and demonstrate their performances. However, we have observed that there are gaps that need to be researched in future works, notably addressing data imbalances in industry, incorporating model explanation techniques for validation and confidence in decision-making, and exploring approach that combine different types of data to enhance performance. Additionally, we have presented an overview of an approach that includes the various steps required for developing an AI solution for the two applications presented in this paper, taking into account notable limitations of existing approaches, such as data imbalance and model explanation.

Acknowledgments

This work was supported by Service Public de Wallonie Recherche under grant n° 2010235 – ARIAC by DIGITALWALLONIA4.AI

Abbreviations

The following abbreviations are used in this manuscript:
AI Artificial Intelligence
IoT Internet of Things
SPC Statistical Process Control
ML Machine Learning
DL Deep Learning
QC QUality Control
CV Computer Vision
RUL Remaining Useful Life
C-MAPSS Commercial Modular Aero-Propulsion System Simulation
SVM Support Vector Machine
KNN K Nearest Neighbors
MLR Multiple Linear Regression
MLP Multilayer Perceptron
CNN Convolutional Neural Network
RNN Recurrent Neural Network
LSTM Long Short-term Memory
GRU Gated Recurrent Unit
GAN Generative Adversarial Network
VAE Variational Autoencoder

References

  1. Moeuf, A.; Lamouri, S.; Pellerin, R.; Tamayo-Giraldo, S.; Tobon-Valencia, E.; Eburdy, R. Identification of critical success factors, risks and opportunities of Industry 4.0 in SMEs. International Journal of Production Research 2020, 58, 1384–1400. [Google Scholar] [CrossRef]
  2. Kotsiopoulos, T.; Sarigiannidis, P.; Ioannidis, D.; Tzovaras, D. Machine learning and deep learning in smart manufacturing: The smart grid paradigm. Computer Science Review 2021, 40, 100341. [Google Scholar] [CrossRef]
  3. Dash, R.; McMurtrey, M.; Rebman, C.; Kar, U.K. Application of artificial intelligence in automation of supply chain management. Journal of Strategic Innovation and Sustainability 2019, 14, 43–53. [Google Scholar]
  4. Laayati, O.; Bouzi, M.; Chebak, A. Smart energy management: Energy consumption metering, monitoring and prediction for mining industry. 2020 IEEE 2nd International Conference on Electronics, Control, Optimization and Computer Science (ICECOCS). IEEE, 2020, pp. 1–5.
  5. Silva, B.; Sousa, J.; Alenya, G. Machine learning methods for quality prediction in thermoplastics injection molding. 2021 International Conference on Electrical, Computer and Energy Technologies (ICECET). IEEE, 2021, pp. 1–6.
  6. Abidi, M.H.; Mohammed, M.K.; Alkhalefah, H. Predictive maintenance planning for industry 4.0 using machine learning for sustainable manufacturing. Sustainability 2022, 14, 3387. [Google Scholar] [CrossRef]
  7. Colantonio, L.; Equeter, L.; Dehombreux, P.; Ducobu, F. A systematic literature review of cutting tool wear monitoring in turning by using artificial intelligence techniques. Machines 2021, 9, 351. [Google Scholar] [CrossRef]
  8. Oakland, J.; Oakland, J.S. Statistical process control; Routledge, 2007. [Google Scholar]
  9. Dutoit, C.; Dehombreux, P.; Lorphèvre, E.R.; Equeter, L. Statistical process control and maintenance policies for continuous production systems subjected to different failure impact models: literature review. Procedia CIRP 2019, 86, 55–60. [Google Scholar] [CrossRef]
  10. Ramezani, J.; Jassbi, J. Quality 4.0 in action: smart hybrid fault diagnosis system in plaster production. Processes 2020, 8, 634. [Google Scholar] [CrossRef]
  11. Wang, K.J.; Fan-Jiang, H.; Lee, Y.X. A multiple-stage defect detection model by convolutional neural network. Computers & Industrial Engineering 2022, 168, 108096. [Google Scholar]
  12. Wang, T.; Chen, Y.; Qiao, M.; Snoussi, H. A fast and robust convolutional neural network-based defect detection model in product quality control. The International Journal of Advanced Manufacturing Technology 2018, 94, 3465–3471. [Google Scholar] [CrossRef]
  13. Li, J.; Su, Z.; Geng, J.; Yin, Y. Real-time detection of steel strip surface defects based on improved yolo detection network. IFAC-PapersOnLine 2018, 51, 76–81. [Google Scholar] [CrossRef]
  14. Chen, Y.; Ding, Y.; Zhao, F.; Zhang, E.; Wu, Z.; Shao, L. Surface defect detection methods for industrial products: A review. Applied Sciences 2021, 11, 7657. [Google Scholar] [CrossRef]
  15. Uyan, T.Ç.; Otto, K.; Silva, M.S.; Vilaça, P.; Armakan, E. Industry 4.0 foundry data management and supervised machine learning in low-pressure die casting quality improvement. International Journal of Metalcasting 2022, 1–16. [Google Scholar] [CrossRef]
  16. García, V.; Sánchez, J.S.; Rodríguez-Picón, L.A.; Méndez-González, L.C.; Ochoa-Domínguez, H.d.J. Using regression models for predicting the product quality in a tubing extrusion process. Journal of Intelligent Manufacturing 2019, 30, 2535–2544. [Google Scholar] [CrossRef]
  17. Jung, H.; Jeon, J.; Choi, D.; Park, J.Y. Application of machine learning techniques in injection molding quality prediction: Implications on sustainable manufacturing industry. Sustainability 2021, 13, 4120. [Google Scholar] [CrossRef]
  18. Obregon, J.; Hong, J.; Jung, J.Y. Rule-based explanations based on ensemble machine learning for detecting sink mark defects in the injection moulding process. Journal of Manufacturing Systems 2021, 60, 392–405. [Google Scholar] [CrossRef]
  19. Chen, J.C.; Guo, G.; Wang, W.N. Artificial neural network-based online defect detection system with in-mold temperature and pressure sensors for high precision injection molding. The International Journal of Advanced Manufacturing Technology 2020, 110, 2023–2033. [Google Scholar] [CrossRef]
  20. Mobley, R.K. An introduction to predictive maintenance; Elsevier, 2002. [Google Scholar]
  21. Cardoso, D.; Ferreira, L. Application of predictive maintenance concepts using artificial intelligence tools. Applied Sciences 2020, 11, 18. [Google Scholar] [CrossRef]
  22. Zhao, R.; Wang, D.; Yan, R.; Mao, K.; Shen, F.; Wang, J. Machine health monitoring using local feature-based gated recurrent unit networks. IEEE Transactions on Industrial Electronics 2017, 65, 1539–1548. [Google Scholar] [CrossRef]
  23. Janssens, O.; Slavkovikj, V.; Vervisch, B.; Stockman, K.; Loccufier, M.; Verstockt, S.; Van de Walle, R.; Van Hoecke, S. Convolutional neural network based fault detection for rotating machinery. Journal of Sound and Vibration 377. [CrossRef]
  24. Lee, W.J.; Wu, H.; Yun, H.; Kim, H.; Jun, M.B.; Sutherland, J.W. Predictive maintenance of machine tool systems using artificial intelligence techniques applied to machine condition data. Procedia Cirp 2019, 80, 506–511. [Google Scholar] [CrossRef]
  25. Wang, B.; Lei, Y.; Yan, T.; Li, N.; Guo, L. Recurrent convolutional neural network: A new framework for remaining useful life prediction of machinery. Neurocomputing 2020, 379, 117–129. [Google Scholar] [CrossRef]
  26. ASLANTAŞ, G.; ÖZSARAÇ, M.; RUMELLİ, M.; ALAYGUT, T.; BAKIRLI, G.; BIRANT, D. Prediction of Remaining Useful Life for Plastic Injection Molding Machines Using Artificial Intelligence Methods. Journal of Artificial Intelligence and Data Science 2, 8–15.
  27. CEYLAN, U.; Yakup, G. Siamese Inception Time Network for Remaining Useful Life Estimation. Journal of Artificial Intelligence and Data Science 1, 165–175.
  28. Ellefsen, A.L.; Ushakov, S.; Æsøy, V.; Zhang, H. Validation of data-driven labeling approaches using a novel deep network structure for remaining useful life predictions. IEEE Access 2019, 7, 71563–71575. [Google Scholar] [CrossRef]
  29. Li, H.; Zhao, W.; Zhang, Y.; Zio, E. Remaining useful life prediction using multi-scale deep convolutional neural network. Applied Soft Computing 2020, 89, 106113. [Google Scholar] [CrossRef]
  30. Chen, Z.; Wu, M.; Zhao, R.; Guretno, F.; Yan, R.; Li, X. Machine remaining useful life prediction via an attention-based deep learning approach. IEEE Transactions on Industrial Electronics 2020, 68, 2521–2531. [Google Scholar] [CrossRef]
  31. Kang, Z.; Catal, C.; Tekinerdogan, B. Remaining useful life (RUL) prediction of equipment in production lines using artificial neural networks. Sensors 2021, 21, 932. [Google Scholar] [CrossRef]
  32. Ramasso, E.; Saxena, A. Performance Benchmarking and Analysis of Prognostic Methods for CMAPSS Datasets. International Journal of Prognostics and Health Management 2014, 5, 1–15. [Google Scholar] [CrossRef]
  33. Nozari, H.; Sadeghi, M.E.; others. Artificial intelligence and Machine Learning for Real-world problems (A survey). International Journal of Innovation in Engineering 2021, 1, 38–47. [Google Scholar]
  34. Gunn, S.R.; others. Support vector machines for classification and regression. ISIS technical report 1998, 14, 5–16. [Google Scholar]
  35. Liu, T.; Huang, L.; Chen, B. Real-time defect detection of laser additive manufacturing based on support vector machine. Journal of Physics: Conference Series. IOP Publishing, 2019, Vol. 1213, p. 052043. [CrossRef]
  36. Huang, H.Z.; Wang, H.K.; Li, Y.F.; Zhang, L.; Liu, Z. Support vector machine based estimation of remaining useful life: current research status and future trends. Journal of Mechanical Science and Technology 2015, 29, 151–163. [Google Scholar] [CrossRef]
  37. Kramer, O.; Kramer, O. K-nearest neighbors. Dimensionality reduction with unsupervised nearest neighbors 2013, pp. 13–23.
  38. Yıldız, K.; Buldu, A.; Demetgul, M. A thermal-based defect classification method in textile fabrics with K-nearest neighbor algorithm. Journal of Industrial Textiles 2016, 45, 780–795. [Google Scholar] [CrossRef]
  39. Khanzadeh, M.; Chowdhury, S.; Marufuzzaman, M.; Tschopp, M.A.; Bian, L. Porosity prediction: Supervised-learning of thermal history for direct laser deposition. Journal of manufacturing systems 2018, 47, 69–82. [Google Scholar] [CrossRef]
  40. Ouadah, A.; Zemmouchi-Ghomari, L.; Salhi, N. Selecting an appropriate supervised machine learning algorithm for predictive maintenance. The International Journal of Advanced Manufacturing Technology 2022, 119, 4277–4301. [Google Scholar] [CrossRef]
  41. Rish, I.; others. An empirical study of the naive Bayes classifier. IJCAI 2001 workshop on empirical methods in artificial intelligence, 2001, Vol. 3, pp. 41–46.
  42. Frank, E.; Trigg, L.; Holmes, G.; Witten, I.H. Naive Bayes for regression. Machine Learning 2000, 41, 5–25. [Google Scholar] [CrossRef]
  43. Shami, T.M.; El-Saleh, A.A.; Alswaitti, M.; Al-Tashi, Q.; Summakieh, M.A.; Mirjalili, S. Particle swarm optimization: A comprehensive survey. IEEE Access 2022, 10, 10031–10061. [Google Scholar] [CrossRef]
  44. Romli, I.; Pardamean, T.; Butsianto, S.; Wiyatno, T.N.; bin Mohamad, E. Naive bayes algorithm implementation based on particle swarm optimization in analyzing the defect product. Journal of Physics: Conference Series. IOP Publishing, 2021, Vol. 1845, p. 012020. [CrossRef]
  45. Zhang, N.; Wu, L.; Yang, J.; Guan, Y. Naive bayes bearing fault diagnosis based on enhanced independence of data. Sensors 2018, 18, 463. [Google Scholar] [CrossRef]
  46. Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to linear regression analysis; John Wiley & Sons, 2021. [Google Scholar]
  47. Stoltzfus, J.C. Logistic regression: a brief primer. Academic emergency medicine 2011, 18, 1099–1104. [Google Scholar] [CrossRef]
  48. Jin, R.; Li, J.; Shi, J. Quality prediction and control in rolling processes using logistic regression. Transactions of NAMRI/SME 2007, 35, 113–120. [Google Scholar]
  49. Akhir, E.A.P.; Ayuni, N. Predictive analytics of machine failure using linear regression on KNIME platform. 2021 5th International Conference on Artificial Intelligence and Virtual Reality (AIVR), 2021, pp. 59–64.
  50. Zhao, M.; Tang, B.; Tan, Q. Bearing remaining useful life estimation based on time–frequency representation and supervised dimensionality reduction. Measurement 2016, 86, 41–55. [Google Scholar] [CrossRef]
  51. Uyanık, G.K.; Güler, N. A study on multiple linear regression analysis. Procedia-Social and Behavioral Sciences 2013, 106, 234–240. [Google Scholar] [CrossRef]
  52. Kotsiantis, S.B. Decision trees: a recent overview. Artificial Intelligence Review 2013, 39, 261–283. [Google Scholar] [CrossRef]
  53. Ogorodnyk, O.; Lyngstad, O.V.; Larsen, M.; Wang, K.; Martinsen, K. Application of machine learning methods for prediction of parts quality in thermoplastics injection molding. International workshop of advanced manufacturing and automation. Springer, 2018, pp. 237–244.
  54. Gerdes, M.; Galar, D.; Scholz, D. Genetic algorithms and decision trees for condition monitoring and prognosis of A320 aircraft air conditioning. Insight-Non-Destructive Testing and Condition Monitoring 2017, 59, 424–433. [Google Scholar] [CrossRef]
  55. Dietterich, T.G. Ensemble methods in machine learning. Multiple Classifier Systems: First International Workshop, MCS 2000 Cagliari, Italy, June 21–23, 2000 Proceedings 1. Springer, 2000, pp. 1–15.
  56. Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining, 2016, pp. 785–794.
  57. Breiman, L. Random forests. Machine learning 2001, 45, 5–32. [Google Scholar] [CrossRef]
  58. Natekin, A.; Knoll, A. Gradient boosting machines, a tutorial. Frontiers in neurorobotics 2013, 7, 21. [Google Scholar] [CrossRef] [PubMed]
  59. Takalo-Mattila, J.; Heiskanen, M.; Kyllönen, V.; Määttä, L.; Bogdanoff, A. Explainable Steel Quality Prediction System Based on Gradient Boosting Decision Trees. IEEE Access 2022. [Google Scholar] [CrossRef]
  60. Ayvaz, S.; Alpay, K. Predictive maintenance system for production lines in manufacturing: A machine learning approach using IoT data in real-time. Expert Systems with Applications 2021, 173, 114598. [Google Scholar] [CrossRef]
  61. Hao, X.; Zhang, G.; Ma, S. Deep learning. International Journal of Semantic Computing 2016, 10, 417–439. [Google Scholar] [CrossRef]
  62. Dey, L.; Meisheri, H.; Verma, I. Predictive Analytics with Structured and Unstructured data-a Deep Learning based Approach. IEEE Intell. Informatics Bull. 2017, 18, 27–34. [Google Scholar]
  63. Taud, H.; Mas, J. Multilayer perceptron (MLP). Geomatic approaches for modeling land change scenarios 2018, pp. 451–455.
  64. Bhatt, D.; Patel, C.; Talsania, H.; Patel, J.; Vaghela, R.; Pandya, S.; Modi, K.; Ghayvat, H. CNN variants for computer vision: history, architecture, application, challenges and future scope. Electronics 2021, 10, 2470. [Google Scholar] [CrossRef]
  65. Ribani, R.; Marengoni, M. A survey of transfer learning for convolutional neural networks. 2019 32nd SIBGRAPI conference on graphics, patterns and images tutorials (SIBGRAPI-T). IEEE, 2019, pp. 47–57.
  66. Shafiee, M.J.; Chywl, B.; Li, F.; Wong, A. Fast YOLO: A fast you only look once system for real-time embedded object detection in video. arXiv preprint arXiv:1709.05943 2017.
  67. Sateesh Babu, G.; Zhao, P.; Li, X.L. Deep convolutional neural network based regression approach for estimation of remaining useful life. Database Systems for Advanced Applications: 21st International Conference, DASFAA 2016, Dallas, TX, USA, April 16-19, 2016, Proceedings, Part I 21. Springer, 2016, pp. 214–228.
  68. Medsker, L.R.; Jain, L. Recurrent neural networks. Design and Applications 2001, 5, 64–67. [Google Scholar]
  69. Staudemeyer, R.C.; Morris, E.R. Understanding LSTM–a tutorial into long short-term memory recurrent neural networks. arXiv preprint arXiv:1909.09586 2019.
  70. Dey, R.; Salem, F.M. Gate-variants of gated recurrent unit (GRU) neural networks. 2017 IEEE 60th international midwest symposium on circuits and systems (MWSCAS). IEEE, 2017, pp. 1597–1600.
  71. Wu, Y.; Yuan, M.; Dong, S.; Lin, L.; Liu, Y. Remaining useful life estimation of engineered systems using vanilla LSTM neural networks. Neurocomputing 2018, 275, 167–179. [Google Scholar] [CrossRef]
  72. Creswell, A.; White, T.; Dumoulin, V.; Arulkumaran, K.; Sengupta, B.; Bharath, A.A. Generative adversarial networks: An overview. IEEE signal processing magazine 2018, 35, 53–65. [Google Scholar] [CrossRef]
  73. Liu, K.; Li, A.; Wen, X.; Chen, H.; Yang, P. Steel surface defect detection using GAN and one-class classifier. 2019 25th international conference on automation and computing (icac). IEEE, 2019, pp. 1–6.
  74. Verstraete, D.; Droguett, E.; Modarres, M. A deep adversarial approach based on multi-sensor fusion for semi-supervised remaining useful life prognostics. Sensors 2019, 20, 176. [Google Scholar] [CrossRef] [PubMed]
  75. Li, X.; Zhang, W.; Ma, H.; Luo, Z.; Li, X. Data alignments in machinery remaining useful life prediction using deep adversarial neural networks. Knowledge-Based Systems 2020, 197, 105843. [Google Scholar] [CrossRef]
  76. Khan, S.A.; Prosvirin, A.E.; Kim, J.M. Towards bearing health prognosis using generative adversarial networks: Modeling bearing degradation. 2018 International Conference on Advancements in Computational Sciences (ICACS). IEEE, 2018, pp. 1–6.
  77. Bank, D.; Koenigstein, N.; Giryes, R. Autoencoders. arXiv preprint arXiv:2003.05991 2020.
  78. Su, C.; Li, L.; Wen, Z. Remaining useful life prediction via a variational autoencoder and a time-window-based sequence neural network. Quality and Reliability Engineering International 2020, 36, 1639–1656. [Google Scholar] [CrossRef]
  79. Doersch, C. Tutorial on variational autoencoders. arXiv preprint arXiv:1606.05908 2016.
  80. Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Advances in neural information processing systems 2017, 30. [Google Scholar]
  81. Khan, S.; Naseer, M.; Hayat, M.; Zamir, S.W.; Khan, F.S.; Shah, M. Transformers in vision: A survey. ACM computing surveys (CSUR) 2022, 54, 1–41. [Google Scholar] [CrossRef]
  82. Wen, Q.; Zhou, T.; Zhang, C.; Chen, W.; Ma, Z.; Yan, J.; Sun, L. Transformers in time series: A survey. arXiv preprint arXiv:2202.07125 2022.
  83. Zaheer, M.; Guruganesh, G.; Dubey, K.A.; Ainslie, J.; Alberti, C.; Ontanon, S.; Pham, P.; Ravula, A.; Wang, Q.; Yang, L.; others. Big bird: Transformers for longer sequences. Advances in neural information processing systems 2020, 33, 17283–17297. [Google Scholar]
  84. Wang, J.; Xu, G.; Yan, F.; Wang, J.; Wang, Z. Defect transformer: An efficient hybrid transformer architecture for surface defect detection. Measurement 2023, 211, 112614. [Google Scholar] [CrossRef]
  85. Shang, H.; Sun, C.; Liu, J.; Chen, X.; Yan, R. Defect-aware transformer network for intelligent visual surface defect detection. Advanced Engineering Informatics 2023, 55, 101882. [Google Scholar] [CrossRef]
  86. Chen, D.; Hong, W.; Zhou, X. Transformer network for remaining useful life prediction of lithium-ion batteries. Ieee Access 2022, 10, 19621–19628. [Google Scholar] [CrossRef]
  87. Johnson, J.M.; Khoshgoftaar, T.M. Survey on deep learning with class imbalance. Journal of Big Data 2019, 6, 1–54. [Google Scholar] [CrossRef]
  88. Linardatos, P.; Papastefanopoulos, V.; Kotsiantis, S. Explainable ai: A review of machine learning interpretability methods. Entropy 2020, 23, 18. [Google Scholar] [CrossRef] [PubMed]
  89. Saxena, A.; Goebel, K. PHM08 challenge data set, NASA AMES prognostics data repository. Moffett Field, CA, Tech. Rep 2008. [Google Scholar]
  90. Zhuang, F.; Qi, Z.; Duan, K.; Xi, D.; Zhu, Y.; Zhu, H.; Xiong, H.; He, Q. A comprehensive survey on transfer learning. Proceedings of the IEEE 2020, 109, 43–76. [Google Scholar] [CrossRef]
  91. Vujović, Ž.; others. Classification model evaluation metrics. International Journal of Advanced Computer Science and Applications 2021, 12, 599–606. [Google Scholar] [CrossRef]
  92. Polenta, A.; Tomassini, S.; Falcionelli, N.; Contardo, P.; Dragoni, A.F.; Sernani, P. A Comparison of Machine Learning Techniques for the Quality Classification of Molded Products. Information 2022, 13, 272. [Google Scholar] [CrossRef]
  93. Microsoft. Predictive Maintenance Modelling Guide. 2018. https://github.com/ashishpatel26/Predictive_Maintenance_using_Machine-Learning_Microsoft_Casestudy/tree/master/data (Consulted on March 23, 2023).
  94. Li, J.; Cheng, K.; Wang, S.; Morstatter, F.; Trevino, R.P.; Tang, J.; Liu, H. Feature selection: A data perspective. ACM computing surveys (CSUR) 2017, 50, 1–45. [Google Scholar] [CrossRef]
  95. Patro, S.; Sahu, K.K. Normalization: A preprocessing stage. arXiv preprint arXiv:1503.06462 2015.
  96. Gogtay, N.J.; Thatte, U.M. Principles of correlation analysis. Journal of the Association of Physicians of India 2017, 65, 78–81. [Google Scholar] [PubMed]
  97. Li, E.; Zeng, L.; Zhou, Z.; Chen, X. Edge AI: On-demand accelerating deep neural network inference via edge computing. IEEE Transactions on Wireless Communications 2019, 19, 447–457. [Google Scholar] [CrossRef]
Preprints 97006 g001
Figure 1. Class distribution in the road lens dataset.
Figure 1. Class distribution in the road lens dataset.
Preprints 97006 g001
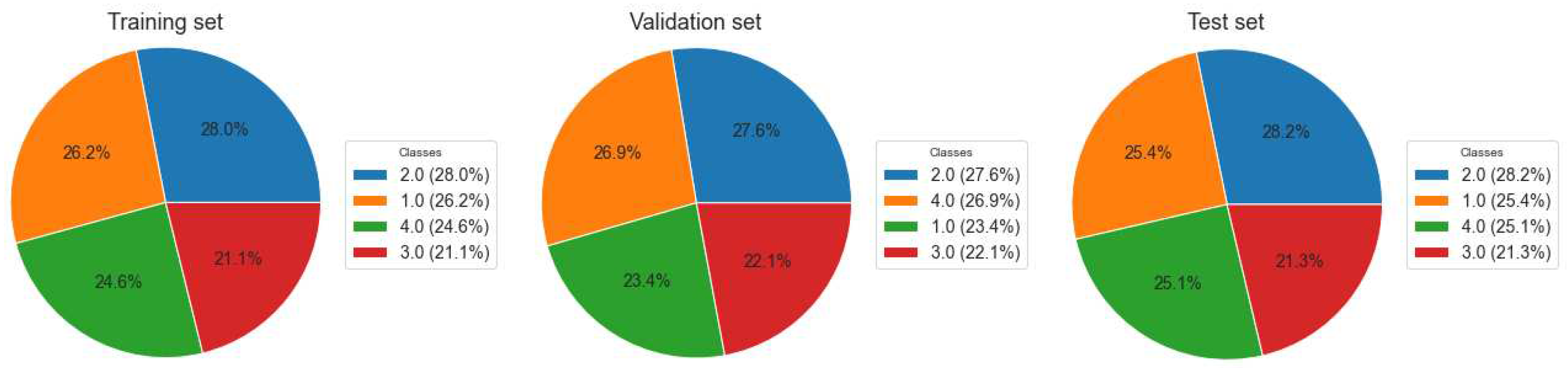
Preprints 97006 g002
Figure 2. Class distribution in the training, validation, and test sets: road lense dataset.
Figure 2. Class distribution in the training, validation, and test sets: road lense dataset.
Preprints 97006 g002
Preprints 97006 g003
Figure 3. Confusion matrices of Random Forest and MLP: road lens quality prediction.
Figure 3. Confusion matrices of Random Forest and MLP: road lens quality prediction.
Preprints 97006 g003
Preprints 97006 g004
Figure 4. Class distribution in the training, validation, and test sets for RNN models.
Figure 4. Class distribution in the training, validation, and test sets for RNN models.
Preprints 97006 g004
Preprints 97006 g005
Figure 5. Class distribution in the training, validation, and test sets for other models.
Figure 5. Class distribution in the training, validation, and test sets for other models.
Preprints 97006 g005
Preprints 97006 g006
Figure 6. Confusion matrices of Random Forest XGBoost and GRU: component failure prediction.
Figure 6. Confusion matrices of Random Forest XGBoost and GRU: component failure prediction.
Preprints 97006 g006
Preprints 97006 g007
Figure 7. AI solution development approach for product quality control and predictive maintenance.
Figure 7. AI solution development approach for product quality control and predictive maintenance.
Preprints 97006 g007
Table 1. Number of records in each subset of the road lens dataset.
Table 1. Number of records in each subset of the road lens dataset.
Data Partition Size
Training set 870
Validation set 290
Test set 291
Total 1451
Table 2. Performance of models on the test set: road lens quality prediction.
Table 2. Performance of models on the test set: road lens quality prediction.
Model Precision Recall F1-Score
SVM 0.87 0.86 0.86
Naive Bayes 0.85 0.83 0.83
KNN 0.92 0.91 0.91
Logistic Regression 0.80 0.79 0.79
Decision Tree 0.91 0.91 0.91
Random Forest 0.98 0.98 0.98
XGBoost 0.94 0.93 0.93
Gradient Boosting 0.95 0.94 0.94
Extra Trees 0.94 0.93 0.93
MLP 0.95 0.95 0.95
Table 3. MLP model architecture summary: road lens quality prediction.
Table 3. MLP model architecture summary: road lens quality prediction.
Layer (type) Output Shape Param #
dense (Dense) (None, 80) 1120
dense_1 (Dense) (None, 50) 4050
dropout (Dropout) (None, 50) 0
dense_2 (Dense) (None, 4) 204
Total params: 5,374
Trainable params: 5,374
Non-trainable params: 0
Table 4. Data partitioning for component failure prediction: RNN models vs. Other models.
Table 4. Data partitioning for component failure prediction: RNN models vs. Other models.
Data partition Size (RNN models) Size (Other models)
Training set 189517 193528
Validation set 46346 47804
Test set 47047 47047
Total 281910 288379
Table 5. Performance of models on the test set: component failure prediction.
Table 5. Performance of models on the test set: component failure prediction.
Model Precision Recall F1-Score
SVM 0.95 0.96 0.96
Naive Bayes 0.61 0.95 0.71
KNN 0.59 0.34 0.39
Logistic Regression 0.93 0.84 0.88
Decision Tree 0.99 0.94 0.96
Random Forest 0.99 0.96 0.97
XGBoost 0.99 0.97 0.98
Gradient Boosting 0.98 0.76 0.77
Extra Trees 0.98 0.95 0.96
MLP 0.96 0.97 0.96
SimpleRNN 0.98 0.94 0.96
LSTM 0.98 0.95 0.96
GRU 0.99 0.97 0.98
Table 6. GRU model Architecture summary: component failure prediction
Table 6. GRU model Architecture summary: component failure prediction
Layer (Type) Output Shape Param #
gru (GRU) (None, 56) 14,784
dense (Dense) (None, 5) 285
Total params: 15,069
Trainable params: 15,069
Non-trainable params: 0
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated