Preprint
Article
Squeezing Droplet Formation in a Flow-Focusing Micro Cross-Junction
Altmetrics
Downloads
93
Views
34
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
22 January 2024
Posted:
23 January 2024
You are already at the latest version
Alerts
Abstract
Motivated by the increasing need of optimised micro-devices for droplets production in medical and biological applications, this paper introduces an integrated approach for the study of the liquid-liquid droplet creation in flow-focusing micro cross-junctions. The micro-junction considered is characterised by a restriction of the channels cross-sections in the junction, which has the function of focusing the flow in the region of the droplet formation. The problem is studied numerically in OpenFOAM environment and validated by the comparison with experimental results obtained by high-speed camera images and micro-PIV measurements. The analysis of the forces acting on the dispersed phase during the droplet formation and the diameter of the droplets obtained numerically are considered for the development of a model of the droplet breakup under the squeezing regime. On the basis of energy balancing during the breakup, a relation between interfacial tension, the size of the cross-sections in the junction, and the time interval needed for droplet creation is obtained, which yields a novel correlation between the dimensionless length of the droplet and the dimensionless flow rate. This correlation is general and can be used to predict the droplet diameters produced by similar micro-junctions with different aspect ratios and extended to different geometries of flow-focusing micro-junctions.
Keywords:
Subject: Engineering - Other
1. Introduction
In the last years, the proliferation of micro-fabrication technologies has provided a broad range of microfluidic applications in engineering. Micro-droplet technology has proven to be a promising and flexible platform for microfluidic functions, such as the production of mono-disperse particles, droplets, bubbles, foams and emulsions with precise control of components and sizes, which can give advancement in chemical, pharmacological, medical and industrial applications. Many microfluidic devices have been designed to generate uniform droplets, including geometry-dominated devices, flow-focusing devices, T-junctions, and co-flowing devices. However, the mechanism of droplet formation in micro-junctions is not yet fully understood. The two-phase flow characteristics are determined by flow conditions, fluids properties and geometry of the micro-device. The first key parameter in the control of the diameter of droplets created within a micro-junction is the flow rate ratio, i.e. the ratio between the flow rate of the dispersed phase to the flow rate of the continue phase [1]. Other key parameters are the geometry of the junction and the properties of the two fluids, such as the capillary number or the viscosity ratio [2]. Several micro-junction geometries are presented in the literature, such as the most studied micro T-junctions [3] and the micro cross-junctions [4]. For these devices, the dependence of the two-phase flow patterns by the flow rate ratio has been shown [5] and correlations have been provided between the droplet diameter to important key parameters, such as the flow rate ratio and the capillary number [6]. The mechanism of droplet formation, called droplet breakup has been largely studied since two decades in the micro-scale. Different mechanisms have been identified, such as squeezing, dripping and jetting [7]. By studying the underlying mechanisms in the droplet breakup, some scaling laws have been established, to predict the size of droplets produced in micro-junctions. However, more experimental data are needed to generalise the results. Based on statistical analysis of a large number of available literature data, Steegmans et al. [8] have shown that none of the scaling models, which are developed to predict droplet formation in a microfluidic T-junction, is general enough to describe the original data and data from other literature sources. Numerical approaches can be complementary to experimental investigation, if validated and integrated with the experimental measurements. The aim of this work is the prediction of the droplet generation in a micro cross-junction under the squeezing regime. The real micro-device considered has a restriction in the junction, i.e. the diameter of the micro-channels in the junction is smaller than the diameters of the micro-channels out of the junction. The dynamics of the droplet creation within the micro-junction is studied numerically by means of a VOF based code in OpenFOAM environment. The simulation results are compared with experimental data obtained on the real cross-junction by means of images obtained by a high-speed camera and micro-PIV measurements. The numerical results are used to build a model for the prediction of the droplet diameter, based on energy balancing during the breakup. A relation between interfacial tension, size of neck cross-section, and the time interval needed for droplet creation is obtained. By this approach, droplet diameters are predicted. The results obtained by the model are in a very good agreement with the the validated numerical simulations. This study can provide useful information for understanding micro-droplet dynamics, providing a basis for optimal design of multi-phase microfluidic devices.
2. Materials and methods
The micro-junction geometry considered for the numerical simulations refers to a real micro-device manufactured by Dolomite Microfluidics, shown in Figure 1 (top). The junction connects four micro-channels with a stadium-shaped cross-section, as shown in Figure 1 (bottom), with a restriction in the junction.
The channel width is m, while the channel depth is m. At the junction, the restriction has width m and depth m. The channel aspect ratio is , while the aspect ratio in the junction is . The restriction ratio, defined as the ratio between the channel width at the restriction and the channel width is . For the numerical simulations, a computational domain, shown in Figure 2 has been built, characterised by three inlet branches with length m, and one outlet branch with length m. The ratios between the inlet and outlet branches and the hydraulic diameter of the channels, m, are and respectively. A polyhedral mesh has been built, Figure 2 (bottom) shows the volume (in m3) of the cells, where the red zones at the three inlets are characterised by larger grid elements, while the outlet region is characterized by smaller elements, with a refinement in the junction where the breakup phenomena occurs, the total number of elements is about 5 milions.
The solver used to perform the numerical simulations is the interFoam solver provided by the opensource code OpenFOAM. This is a solver for two incompressible, isothermal and immiscible fluids, based on a VOF (volume of fluid) phase-fraction-based interface capturing approach.The equations solved are the continuity equation,
and the Navier-Stokes equation,
plus an additional equation to capture the interface between the fluids, the advection of the scalar quantity ,
The field is used to distinguish the two fluids and is defined as
To solve these equations, the MULES (multi-dimensional limiter for explicit solution ) algorithm is used in order to guarantee the boundness of the solution and obtain more smeared interfaces. The last term of the right hand side of Eq. 3 is the so-called compression term, which is not negligible only at the interface between the two fluids . In this term is present the relative velocity defined as:
For micro-fluidic applications, can be taken equal to 1 [10]. In Eq. 2 the source term is used to estimate the surface tension forces by means of the Continuum Surface Force (CSF) model, which gives
where is the curvature, evaluated starting from the volume fraction ,
The dispersed phase is water, with density = 998 kg/m3 and viscosity = 8.788 m2/s. The continuous phase is oil, with density = 950 kg/m3 and viscosity = 1.900 m2/s.
The dispersed phase enters from the channel along the x-axis and the continuous phase enters from the two channels along the z-axis. The dispersed phase flow rate has been varied in the range ml/h, while the continuous phase flow rate has been fixed to ml/h. The regime is laminar, as the Reynolds number calculated for the dispersed phase is and ranges from 0.5 to 6. The capillary number for the dispersed phase, ranges from 0.00005 to 0.0006, where N/m is the surface tension between the two fluids [6]. The capillary number for the continuous phase is . Then, the regime for droplet creation is the squeezing regime, for all the cases in these ranges [6].
Five meshes have been built to check the grid convergence. The convergence has been proven by comparing the velocity and the diameter of the droplets as a function of the number of elements, as shown by Figure 3.
3. Validation of the numerical simulations
A schematic and a picture of the experimental apparatus used in this work are shown in Figure 4. Two syringe pumps (Harvard Instruments PHD 400) were used to control the flow rates of the two working fluids. The pumps were connected to the microfluidic-chip with the micro-junction (Dolomite Microfluidics) which was placed over an inverted microscope (Nikon Eclipse TE2000-U) and observed through a 10× objective lens. High-speed video recordings of the droplets in the microfluidic device were taken using a high-speed camera (Olympus I-Speed I). The illumination was provided by a high-power LED powered by DC current. The shapes and dimensions of the droplets were determined by a custom-made image processing code developed in the Python environment. The two-dimensional velocity field in the mid-plane of the dispersed phase was measured utilizing the micro-PIV technique [11]. For these measurements, polystyrene micro-spheres with a diameter of 1.19 m and a density of 1050 kg/m3 were inserted at low concentration in the dispersed phase and used as a passive tracer. The micro-PIV analysis was performed using the open-source library DefocusTracker in the MATLAB environment [12].
In order to validate the simulations, the dimensions of the droplets obtained numerically were compared with the dimensions of the droplets obtained experimentally for the same working conditions. A qualitative comparison is presented in Figure 5 for three different values of the dimensionless flow rates showing an excellent agreement between numerical results and experiments (with a maximum estimated error of 5 %). Moreover, the dynamics of the breakup phenomena in the experiments was compared with the results of the simulations. Figure 6 shows the 3D shapes of the interface colored with the velocity magnitude, to highlight the zone where the acceleration is higher, and compared with the corresponding picture in the experiments. The comparison shows that the simulations can accurately predict the drop geometries observed in the experiment, with an error on the time needed for breakup of about 5.3 %.
Finally, a comparison between the experimental and simulated velocity field in the mid-plane of the dispersed phase was performed. Figure 7 shows the velocity vector map obtained by the numerical simulations (left), together with the velocity vector map obtained by micro-PIV analysis (right), which has been mirrored. The vectors show a vortex in the thread nose, which is well known for droplets moving in two-phase flows [5]. The position and the dimensions of the vortexes obtained by the numerical simulation are in agreement with those obtained by the micro-PIV measurements. Also the velocity magnitude of the analysed fields is in agreement. In summary, we can conclude that the numerical simulations are in good agreement with the experiments both for the prediction of the dynamics of the droplet formation and for the velocity distribution.
4. Interface dynamics during droplet breakup
The dynamics of the droplet during the breakup is analysed in this section, starting from the case with a dimensionless flow rate , defined as , equal to 0.08 and and increasing the dispersed phase flow rate. During the breakup, three stages can be observed. In a first phase, called filling stage, the dispersed phase evolves as a thread which starts with a hemispherical shape, then the thread increases with the shape of a cylinder with a rounded front end which we will call the thread nose. In the second phase, called necking, the thread starts to be squeezed while the thread nose position moves along the junction. The final phase is the pinch-off, when the neck thickness decreases quickly until the thread surface breaks and the droplet is created. Figure 8 shows the thread interface at four time instants equally spaced from to s, during the first two phases.
The thread at the final instant is also shown in the figure (right) to show the point P1, which represents the position of the thread nose, and the point P2, which represents the position of the neck. Figure 9 shows the evolution in time of P1 (left) and the evolution in time of the thickness of the neck (right) (2P2) as a function of the dimensionless time.
The dimensionless time has been obtained by dividing the time by the time interval between a droplet detachment and the successive droplet detachment. The figure (left) shows that the filling and necking phases last for most of the total time, while P1 increases slowly until , (black dots), while for it increases faster. The figure (right) also shows that the neck thickness decreases slowly for and drops very quickly for . The first time interval corresponds to the filling and necking phases, while the second one characterise the pinch-off stage. Figure 10 shows the evolution of the thread interface with time, from the first instant where the neck starts to be visible until the last time instant before the breakup. The dimensionless time has been obtained in this case dividing by the time duration of the necking stage.
The figure shows that during the necking phase, the squeezing of the thread in the neck is slow and the diameter of the thread can be assumed as a constant for a large time interval before the pinch-off phase. Similar trends can be shown at different flow rate ratios, as shown in Figure 11.
In the Figure 11, the evolution of P1 and P2 are shown for = [0.08, 0.15, 0.25, 0.35, 0.65]. The figure shows that P1 increases proportionally to , in the necking phase, while the neck thickness P2 does not depend on , i.e. the neck collapses with the same trend in all the cases. This can suggest that the duration of the breakup is an key-parameter of the droplet creation process. During the breakup phenomena, the main forces acting on the drop are shear-stress at the interface and the pressure differences between the two phases. In the squeezing regime the effect of the pressure build-up is the most important [7], because the thread can occlude the micro-channel in the junction, then the pressure in the continuous phase increases, breaking the interface. To investigate this phenomena, the pressure difference between the phases is plotted along the interface during the process, as shown in Figure 12. The plot is made in polar coordinates, where the angle 0 is on the thread nose and the angle 180 is on the inlet section.
In Figure 12, the red dashed lines indicates the position of the restriction in the micro-junction. The figure shows that, when the thread occupies a large portion of the channel, the pressure difference increases, while it decreases when the forming drop has already crossed the restriction in the junction. In a similar way it is possible to describe the shear-stress acting on the thread surface, as shown by Figure 13 for the same time instant as those shown in Figure 12. The plot is made in polar coordinates, where the angle 0 is on the thread nose and the angle 180 is on the inlet section.
Figure 13 shows that the shear is higher when the thread occupies the restriction in the first time instants, as the continuous flow rate reaches the maximum velocity due to the reduction on the cross section. Then, the shear decreases when the cross-section free for continuous phase passage increases. Figure 13 and Figure 13 show that the shear stress is lower than the pressure difference between the phases for all the time instants considered.
5. Model of the droplet formation
The length of the droplets obtained by the simulations in function of the flow rate ratio are reported in Table 1. In the table, indicates the flow rate ratio and is the dimensionless length of the droplet.
Many papers in the literature show linear correlation between and for T-junctions [13,14] and cross-junctions [15]. By fitting the dimensionless length obtained by the simulations we obtain the following relation
with an average error about 1.3%.
In order to find a model which supports this trend the dynamics of the droplet formation can be considered, following the approach shown in [16] for predicting the time interval which involves the necking stage. The approach is applied to the entire necking stage, as it affects the the final droplet size more than the filling stage, as shown by [17]. The control volume considered in this approach is shown in Figure 14.
The control volume is a cylinder containing the volume of the thread at the beginning of the necking stage, as shown by the figure. This region is inside the restriction in the junction. The final droplet volume is assumed to be given by the product of the dispersed phase volume flow rate multiplied by the time lapse between the beginning of the necking phase and the pinch-off. The droplets created in the junction show a circular shape by the high-speed camera images which record the the droplets on a plane containing the direction of the flow, as shown in Figure 5. This means that the volume of the created droplet is a sphere in the case a droplet diameter (that we will call length of the droplet ) smaller than the height of the channel H, and is a cylinder if . Then, the volume of the droplet is if , or if . Assuming that the time interval between the beginning of the droplet creation and the time instant when the droplet detaches from the thread is , the volume of the droplet is
where is the dispersed volume flow rate and is the volume of the thread at the end of the filling stage, i.e. at the beginning of the necking stage, that is the stage described by the modelling in this section. Then, the length of the droplet after the detachment can be obtained by the dispersed phase volume flow rate
The time interval for the droplet creation during the necking stage can be obtained by the energy balance approach introduced by [16]. The surface tension energy stored in the thread before the droplet detachment is balanced by the energy difference between the inlet and the outlet sections in the control volume after the droplet detachment,
where is the surface tension between the two phases, is the surface of the droplet in the region of the neck approximated by a cylinder with radius r and length l, and is its mass. If and are the pressure in the continuous and dispersed phase respectively, and is the velocity of the droplet after the detachment, on the right of the equation we have the energy of the droplet after creation. Equation 11 can be rewritten as
and considering that one obtains the velocity of the dispersed phase:
Assuming that then one obtains
Substituting equation 14 in equation 10 one obtains
Dividing the droplet length by the width of the junction and rewriting the equation in a dimensionless form one obtains
where is the Weber number referred to the continuous phase in the junction and is the superficial velocity of the continuous phase in the junction. In equation is a constant with and is obtained by the initial volume of the thread. Equation 5 is in a very good agreement with the measurements, as shown by Figure 15.
In the figure, the dimensionless length of the droplets obtained by the numerical simulations are shown by the symbols, while the continuous line refers to the results obtained by Eq. 8 and the dashed line represents the linear fit 5. The error between the numerical results and the Eq. 5 is less than 1%, showing a better fit with respect to the linear correlation. This result is in agreement with what has been shown by [16,18]. The dependence on the Weber number evaluated in the junction emphasises the influence of the restriction of the junction which forces the continuous phase to flow at a higher velocity in the region of the neck. Similar results have been shown by Liu et al. [19] for cross-junctions where the two channels carrying the continuous phase have a smaller width with respect to the central channel for the dispersed phase inlet. This results can be extended to micro cross-junctions with restriction and flow-focusing device, showing to be potentially used for optimal design of micro-machines for particles and droplets manipulation.
6. Conclusions
The dynamics of the droplet formation in a micro cross-junction with a restriction has been studied by an integrated approach between CFD simulations in the OpenFOAM environment, experimental measurements, and an up-scaled model of the droplet breakup. The results of the simulations have been validated by a comparison with experimental measurements by means of high-speed camera images of the droplets and velocity measurements in the dispersed phase by micro-PIV. By the numerical simulations, the forces acting on the dispersed phase during the droplet formation and the droplets diameters have been obtained for different dimensionless flow rates. These results have been used for the development of a model of the droplet breakup under the squeezing regime, and a novel correlation between the dimensionless length of the droplet and the dimensionless flow rate has been obtained. These results can be generalised to similar flow-focusing cross-junctions, showing that the methodology introduced in this paper can be used for the optimization and control of droplets production in microfluidics applications.
Author Contributions
Conceptualization, F.A.,B.P.,M.R. and G.L.M.; methodology, F.A.,B.P.,M.R. and G.L.M. software, F.A, B.P. and M.R.; validation, F.A., M.R.; formal analysis, F.A.,B.P.,M.R. and G.L.M.; investigation, F.A., B.P.; resources, B.P.,G.L.M.; data curation, A.F. and M.R.; writing—original draft preparation, A.F. and B.P.; writing—review and editing, F.A.,B.P.,M.R. and G.L.M. ; visualization, A.F.; supervision, B.P., M.R. and G.L.M.; project administration, B.P. and G.L.M.; funding acquisition, B.P. and G.L.M:. All authors have read and agreed to the published version of the manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CFD | Computational fluid dynamics |
| PIV | Particle image velocimetry |
References
- Garstecki, P.; Stone, H.A.; Whitesides, G.M. Mechanism for Flow-Rate Controlled Breakup in Confined Geometries: A Route to Monodisperse Emulsions. Physical Review Letters 2005, 94, 164501. [Google Scholar] [CrossRef] [PubMed]
- Xi, H.; Guo, W.; Leniart, M.; Chong, Z.Z.; Tan, S.H. AC electric field induced droplet deformation in a microfluidic T-junction. Lab Chip 2016. [Google Scholar] [CrossRef] [PubMed]
- Guillot, P.; Colin, A. Stability of parallel flows in a microchannel after a T junction. Phys. Rev. E 2005, 72, 066301. [Google Scholar] [CrossRef] [PubMed]
- Tan, S.H.; Nguyen, N.T.; Yobas, L.; Kang, T.G. Formation and manipulation of ferrofluid droplets at a microfluidic T-junction. Journal of Micromechanics and Microengineering 2010, 20, 045004. [Google Scholar] [CrossRef]
- Xiong, Q.; Chen, Z.; Li, S.; Wang, Y.; XU, J. Micro-PIV measurement and CFD simulation of flow field and swirling strength during droplet formation process in a coaxial microchannel. Chemical Engineering Science 2018, 185, 157–167. [Google Scholar] [CrossRef]
- Rostami, B.; Morini, G. Experimental characterisation of a micro cross-juntion as generator of Newtonian and non-Newtonian droplets in silicone oil flow at low Capillary numbers. Experimental Thermal and Fluid Science 2019, 103, 191–200. [Google Scholar] [CrossRef]
- DE MENECH, M.; GARSTECKI, P.; JOUSSE, F.; STONE, H.A. Transition from squeezing to dripping in a microfluidic T-shaped junction. Journal of Fluid Mechanics 2008, 595, 141–161. [Google Scholar] [CrossRef]
- Steegmans, M.; Schroën, K.; Boom, R. Generalised insights in droplet formation at T-junctions through statistical analysis. Chemical Engineering Science 2009, 64, 3042–3050. [Google Scholar] [CrossRef]
- Dolomite microfluidics: https://www.dolomite-microfluidics.com/.
- Chen, Q.; Jingkun, L.; Song, Y.; Christopher, D.; Li, X. Modeling of Newtonian droplet formation in power-law non-Newtonian fluids in a flow-focusing device. Heat and Mass Transfer 2020, 56. [Google Scholar] [CrossRef]
- Lindken, R.; Rossi, M.; Große, S.; Westerweel, J. Micro-particle image velocimetry (μPIV): recent developments, applications, and guidelines. Lab on a Chip 2009, 9, 2551–2567. [Google Scholar] [CrossRef] [PubMed]
- Barnkob, R.; Rossi, M. DefocusTracker: A Modular Toolbox for Defocusing-based, Single-Camera, 3D Particle Tracking. Journal of Open Research Software 2021, 9, 22. [Google Scholar] [CrossRef]
- Garstecki, P.; Fuerstman, M.J.; Stone, H.A.; Whitesides, G.M. Formation of droplets and bubbles in a microfluidic T-junction—scaling and mechanism of break-up. Lab on a Chip 2006, 6, 437. [Google Scholar] [CrossRef] [PubMed]
- Rostami, B.; Morini, G. Generation of Newtonian and non-Newtonian droplets in silicone oil flow by means of a micro cross-junction. International Journal of Multiphase Flow 2018, 105. [Google Scholar] [CrossRef]
- Yu, W.; Liu, X.; Zhao, Y.; Chen, Y. Droplet generation hydrodynamics in the microfluidic cross-junction with different junction angles. Chemical Engineering Science 2019, 203, 259–284. [Google Scholar] [CrossRef]
- Maurya, T.; Dutta, S. Pinch-off dynamics of droplet formation in microchannel flow. Chemical Engineering Science 2023, 282, 119296. [Google Scholar] [CrossRef]
- Z., L.; Y., M.; X., W.; Y., P.; Y., R.; D., L. Experimental and theoretical studies on neck thinning dynamics of droplets in cross junction microchannels. Experimental thermal and fluid science 2022, 139, 110739. [Google Scholar] [CrossRef]
- Loizou, K.; Wong, V.L.; Hewakandamby, B. Examining the Effect of Flow Rate Ratio on Droplet Generation and Regime Transition in a Microfluidic T-Junction at Constant Capillary Numbers. Inventions 2018, 3. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, Y. Droplet formation in microfluidic cross-junctions. Physics of Fluids 2011, 23, 082101. [Google Scholar] [CrossRef]
Figure 1.
Dolomite cross-junction chip (top) [9]. Channel section (bottom, left) and restriction section (bottom, right).
Figure 1.
Dolomite cross-junction chip (top) [9]. Channel section (bottom, left) and restriction section (bottom, right).
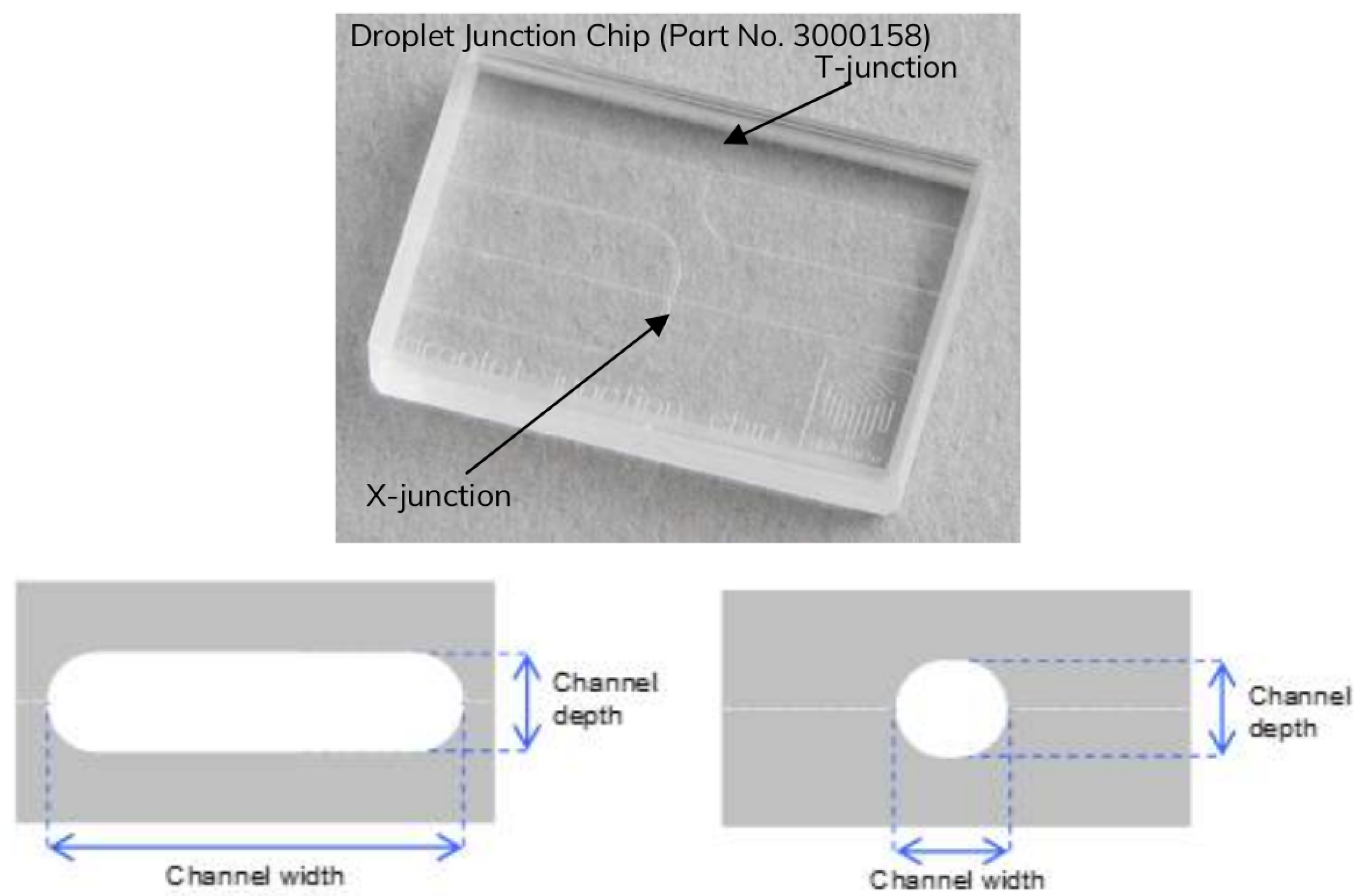
Figure 2.
Computational domain (top). Top view of the polyhedral mesh (bottom)
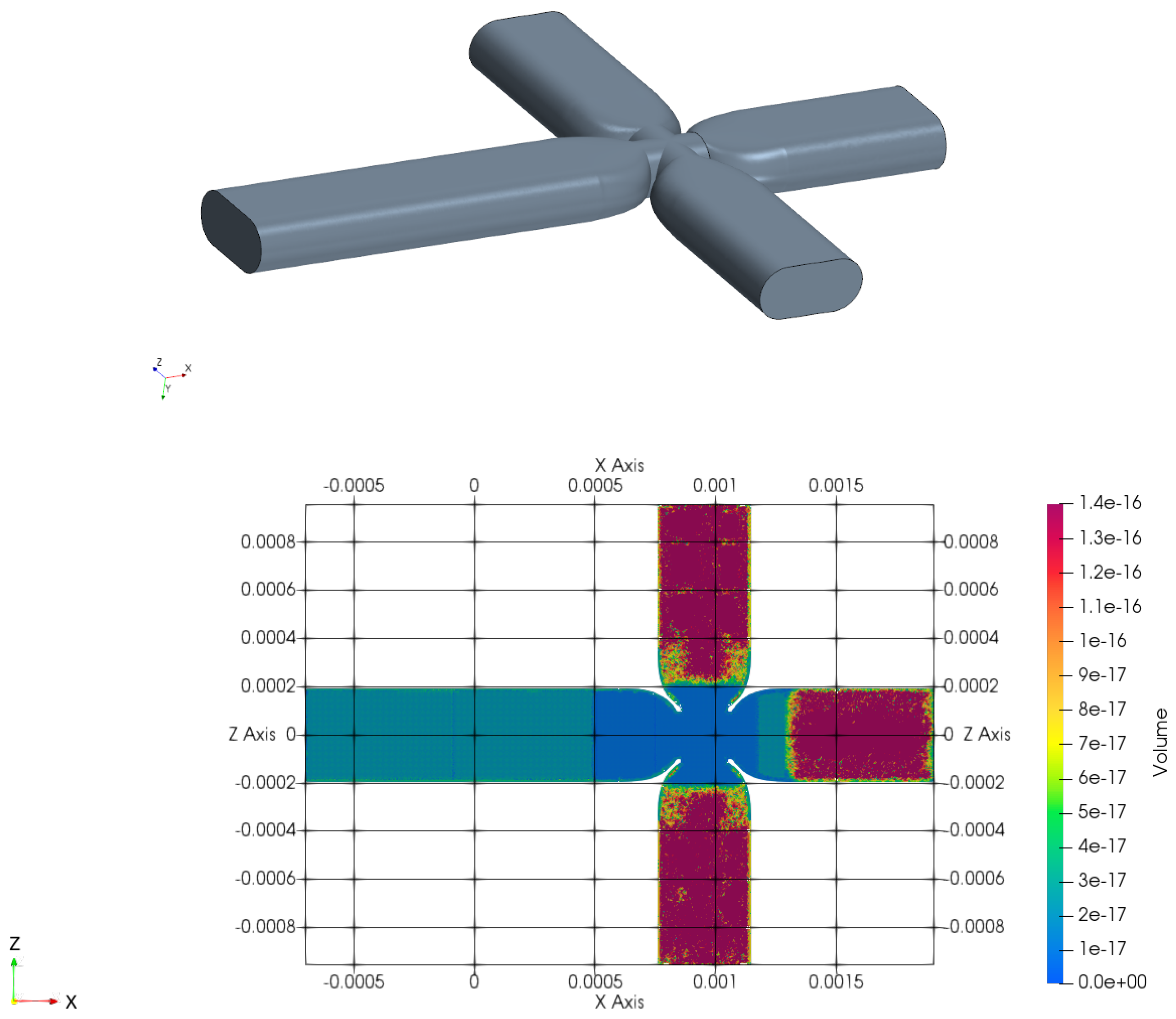
Figure 3.
(a) Radius of the droplet; (b) Velocity of the droplet
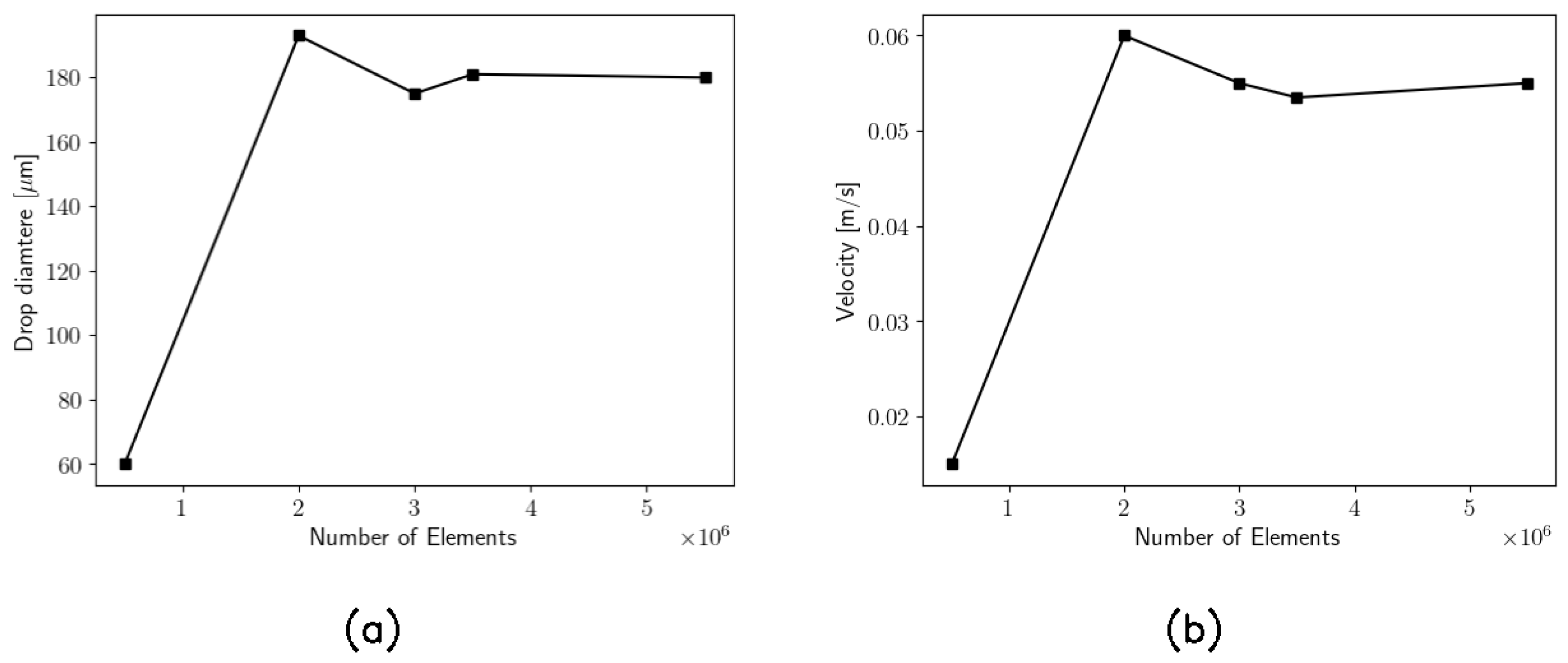
Figure 4.
(a) Schematic and (b) picture of the experimental apparatus consisting of two syringe pumps (1) to control the flow rates of the working fluids, the microfluidic device (2) placed on an inverted microscope (3) connected to a high-speed camera (4).
Figure 4.
(a) Schematic and (b) picture of the experimental apparatus consisting of two syringe pumps (1) to control the flow rates of the working fluids, the microfluidic device (2) placed on an inverted microscope (3) connected to a high-speed camera (4).
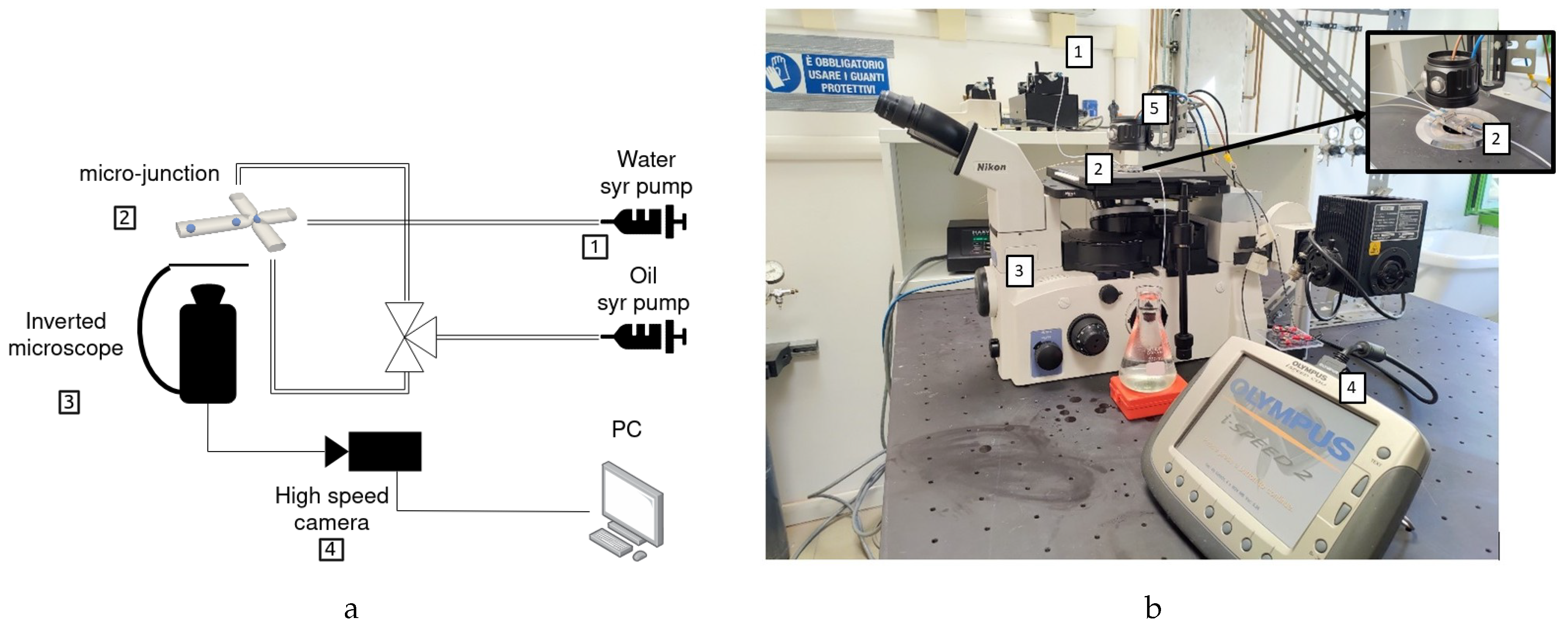
Figure 5.
Superposition between the interface obtained numerically (red dots) and the images of the drops for different dimensionless flow rates
Figure 5.
Superposition between the interface obtained numerically (red dots) and the images of the drops for different dimensionless flow rates

Figure 6.
Comparison of the break-down
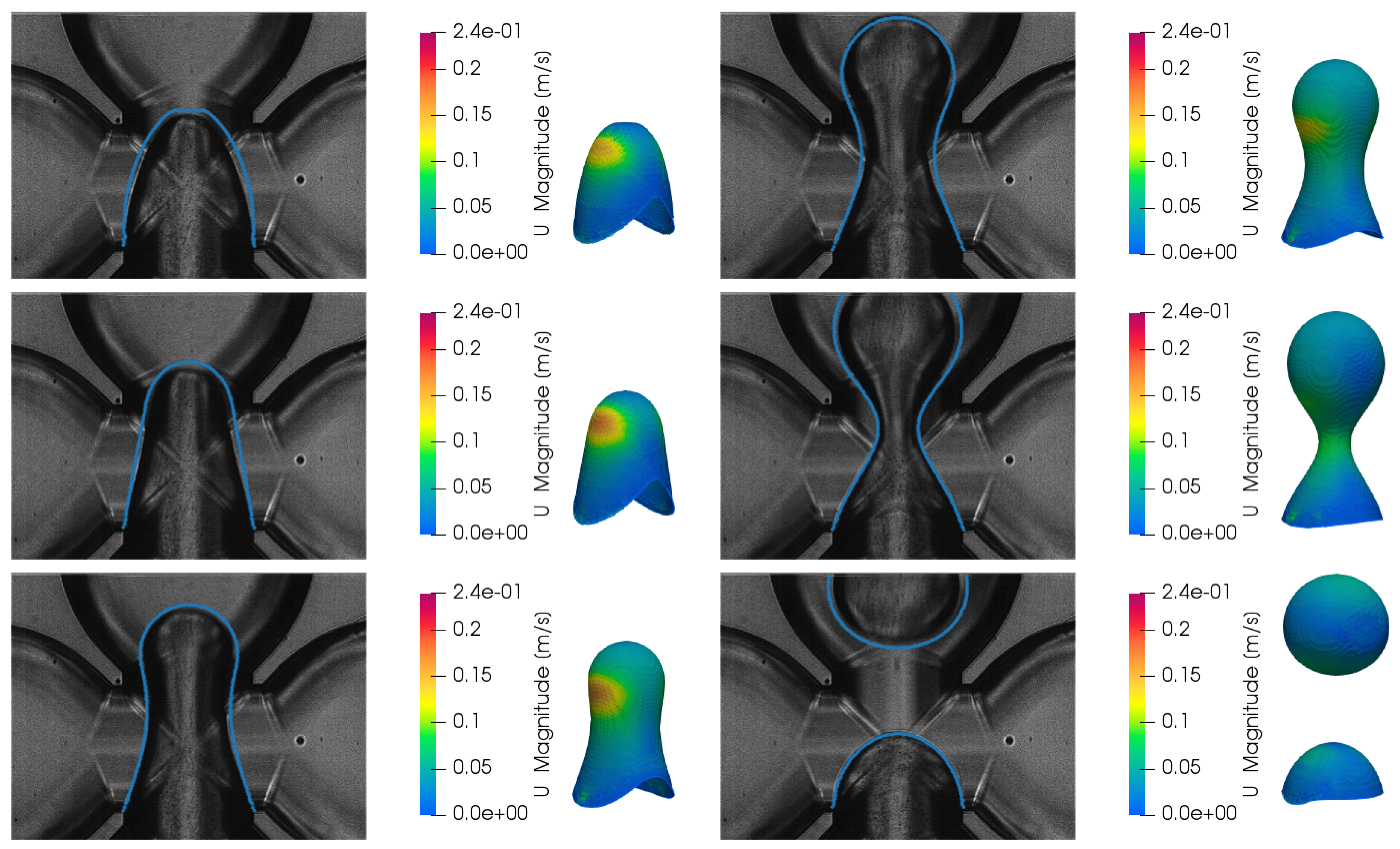
Figure 7.
Comparison between the velocity vectors obtained by the numerical simulation (left) and the velocity vectors obtained by the micro-PIV analysis (right) in different instants.
Figure 7.
Comparison between the velocity vectors obtained by the numerical simulation (left) and the velocity vectors obtained by the micro-PIV analysis (right) in different instants.
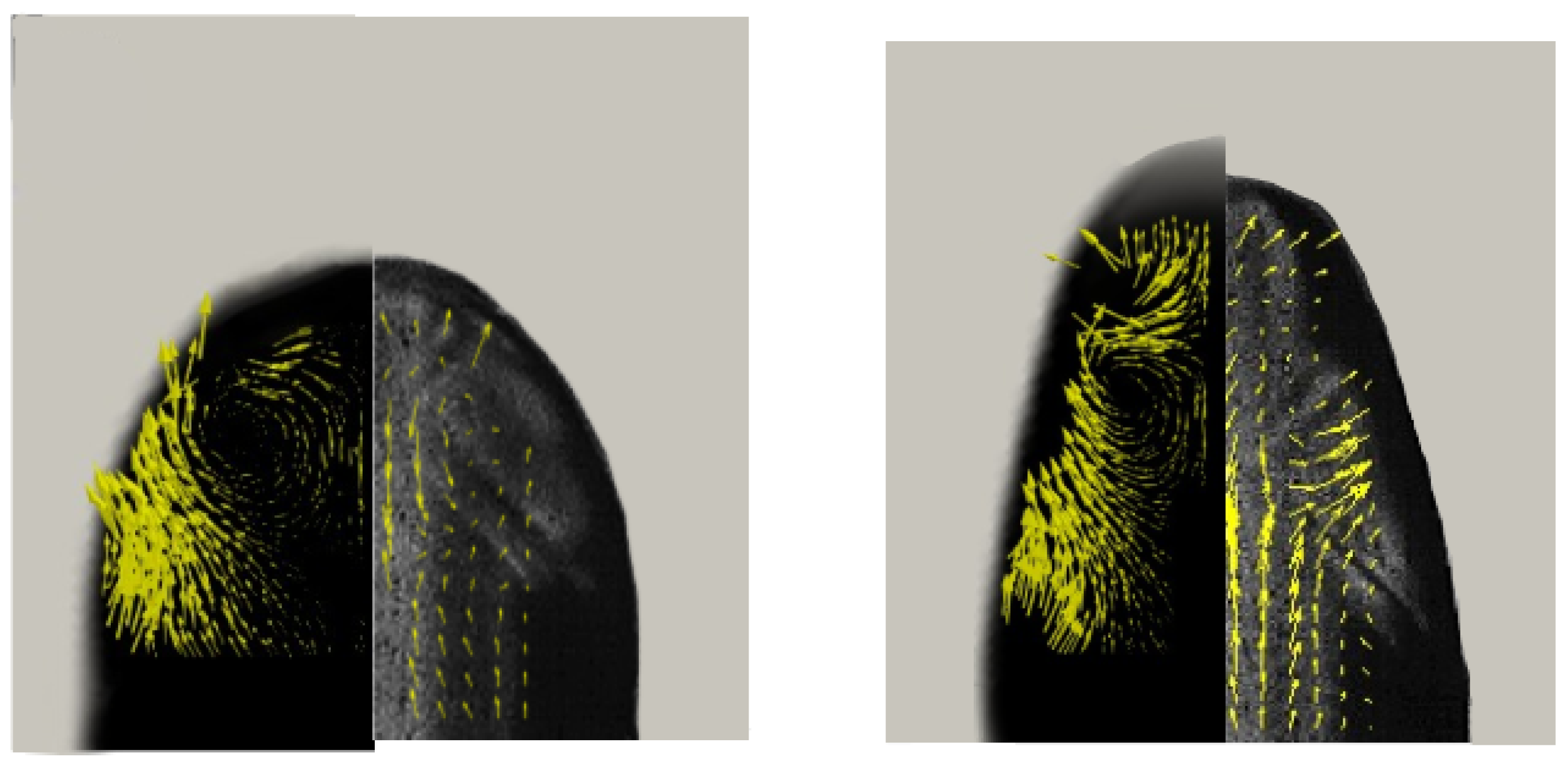
Figure 8.
Thread interface at four time instants with s (left) and final thread interface (right).
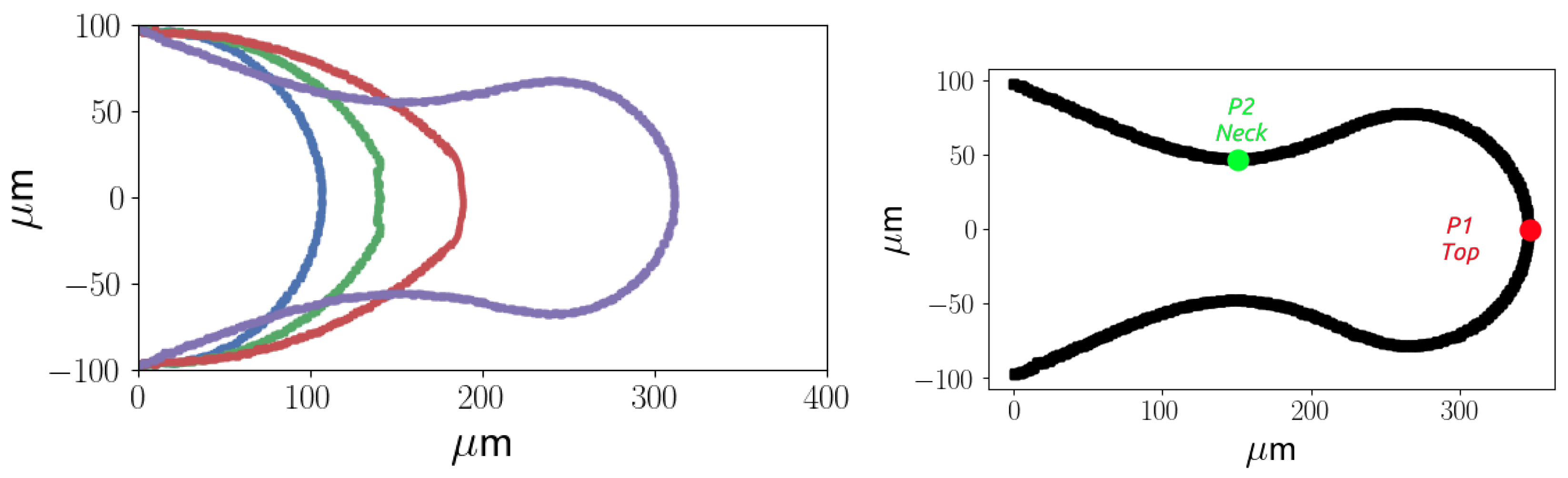
Figure 9.
Evolution of the length of the evolving droplet in time (left) and evolution of the neck thickness (right).
Figure 9.
Evolution of the length of the evolving droplet in time (left) and evolution of the neck thickness (right).
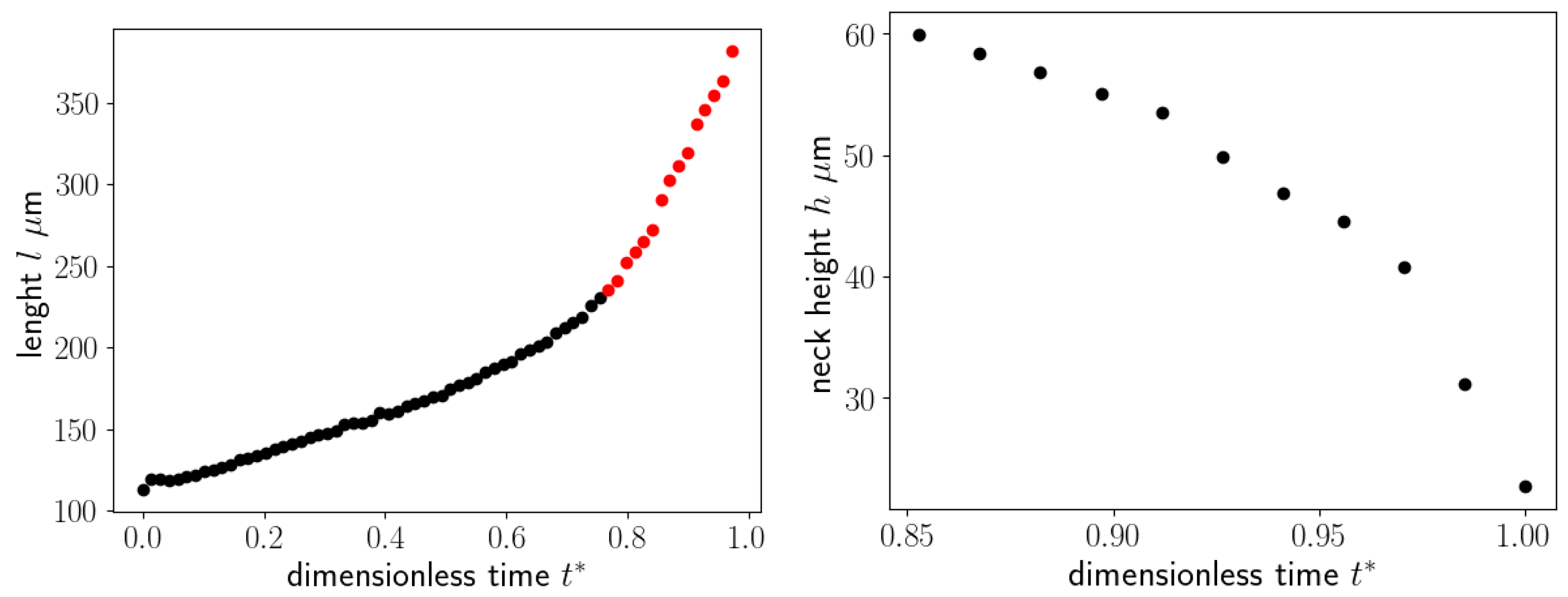
Figure 10.
Evolution of the droplet with time. The two red lines refer to the position of point P1 and point P2, the two black lines represent the position of the restriction in the junction.
Figure 10.
Evolution of the droplet with time. The two red lines refer to the position of point P1 and point P2, the two black lines represent the position of the restriction in the junction.
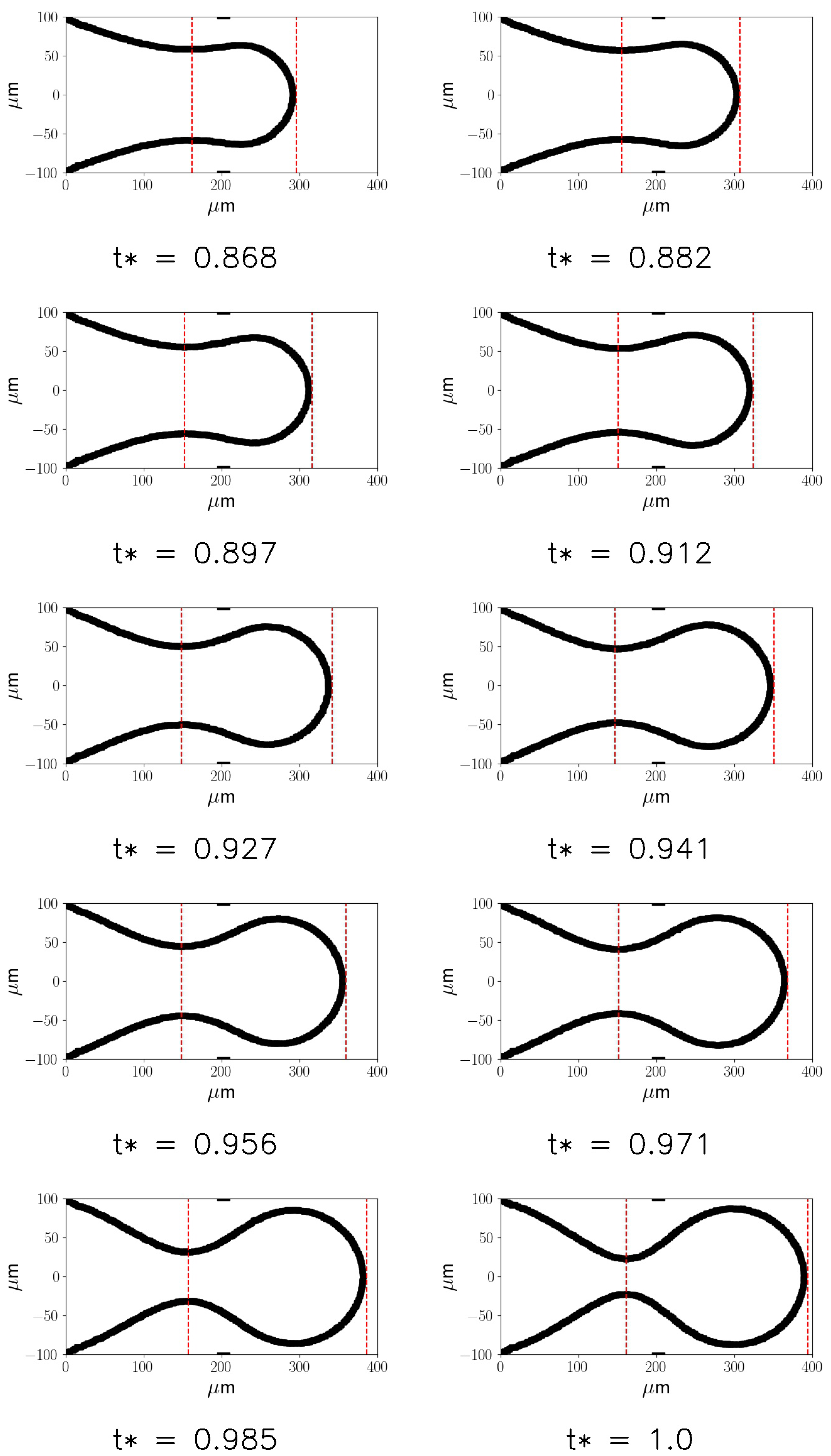
Figure 11.
Evolution of the length of the thread (P1) (left) and neck thickness P2 (right) versus time for flow rates.
Figure 11.
Evolution of the length of the thread (P1) (left) and neck thickness P2 (right) versus time for flow rates.
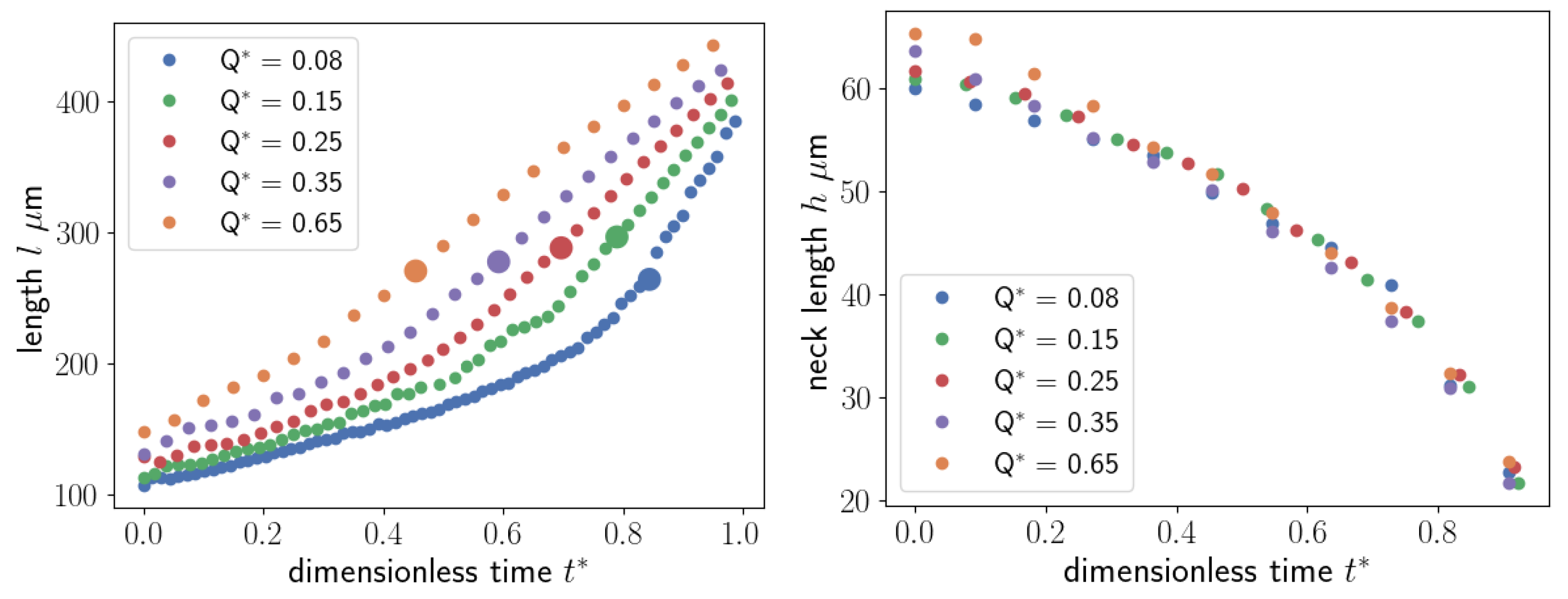
Figure 12.
Pressure difference between the phases along the droplet surface during the breakup.
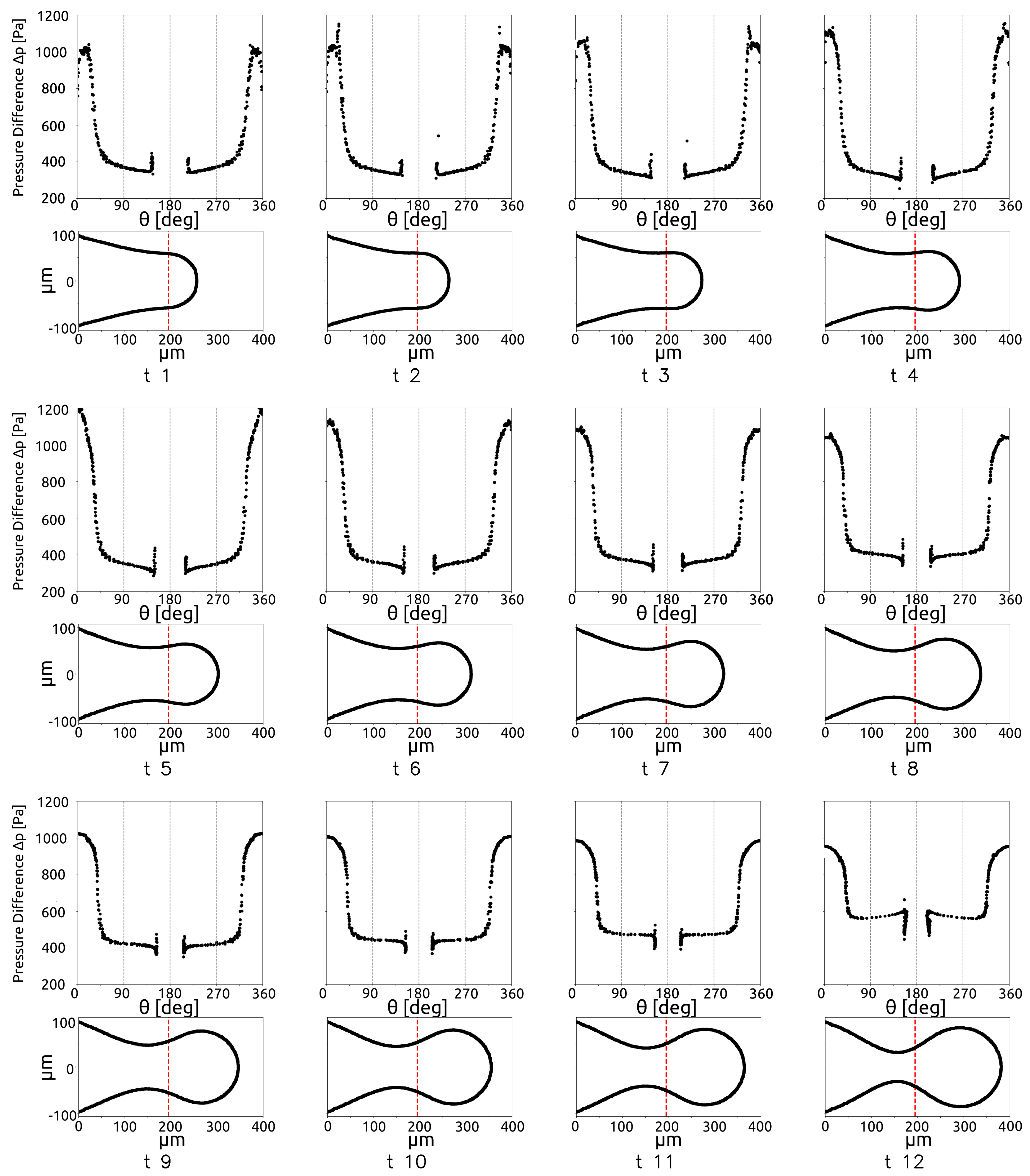
Figure 13.
Shear-stress evolution along the drop during the breakup.
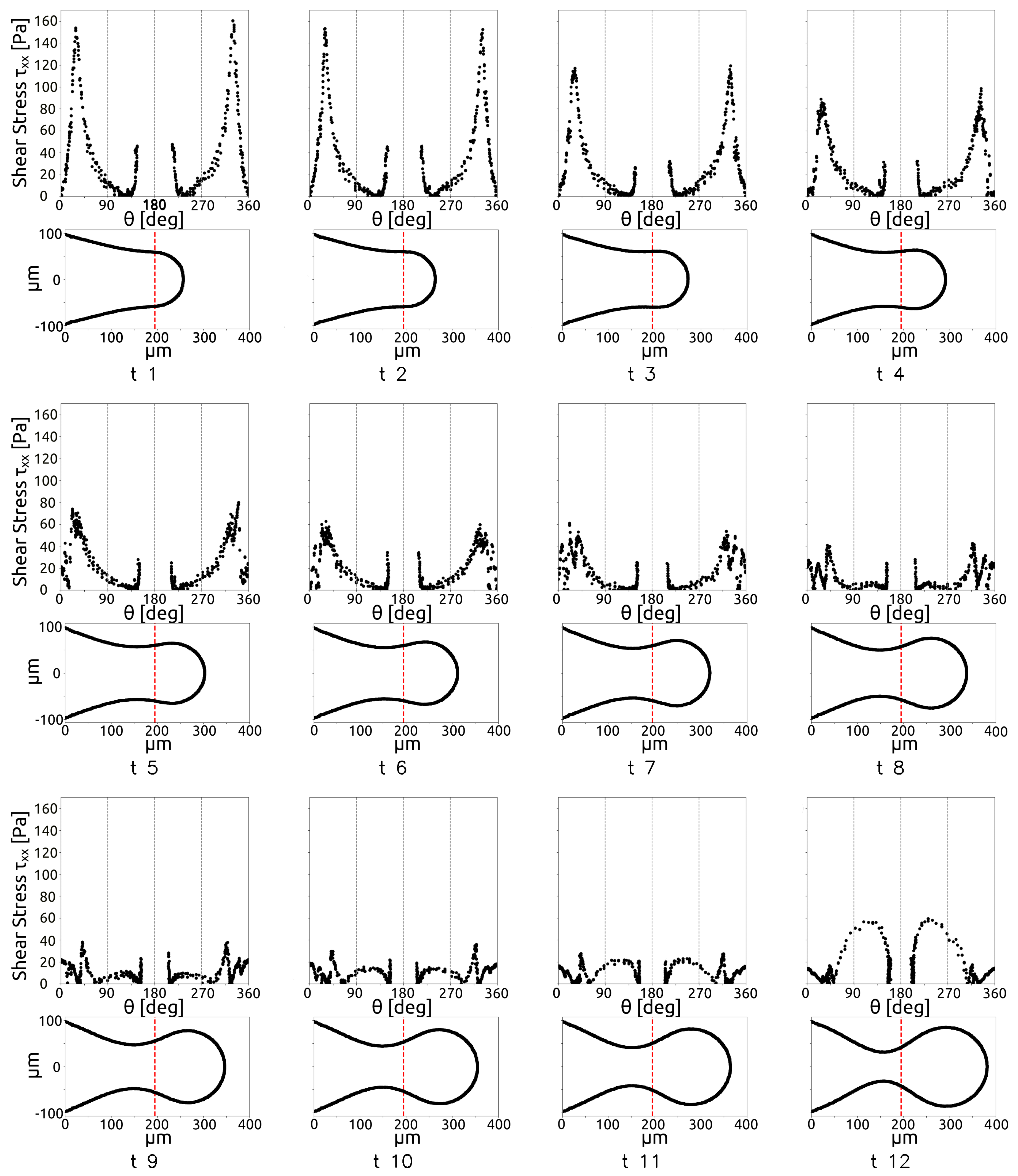
Figure 14.
Control volume considered for the energy balance.
Figure 15.
Dimensionless droplet length versus dimensionless dispersed volume flow rate. Simbols refer to experimental results, continue line refers to Eq. 5 and dashed line refers to Eq. 8
Figure 15.
Dimensionless droplet length versus dimensionless dispersed volume flow rate. Simbols refer to experimental results, continue line refers to Eq. 5 and dashed line refers to Eq. 8
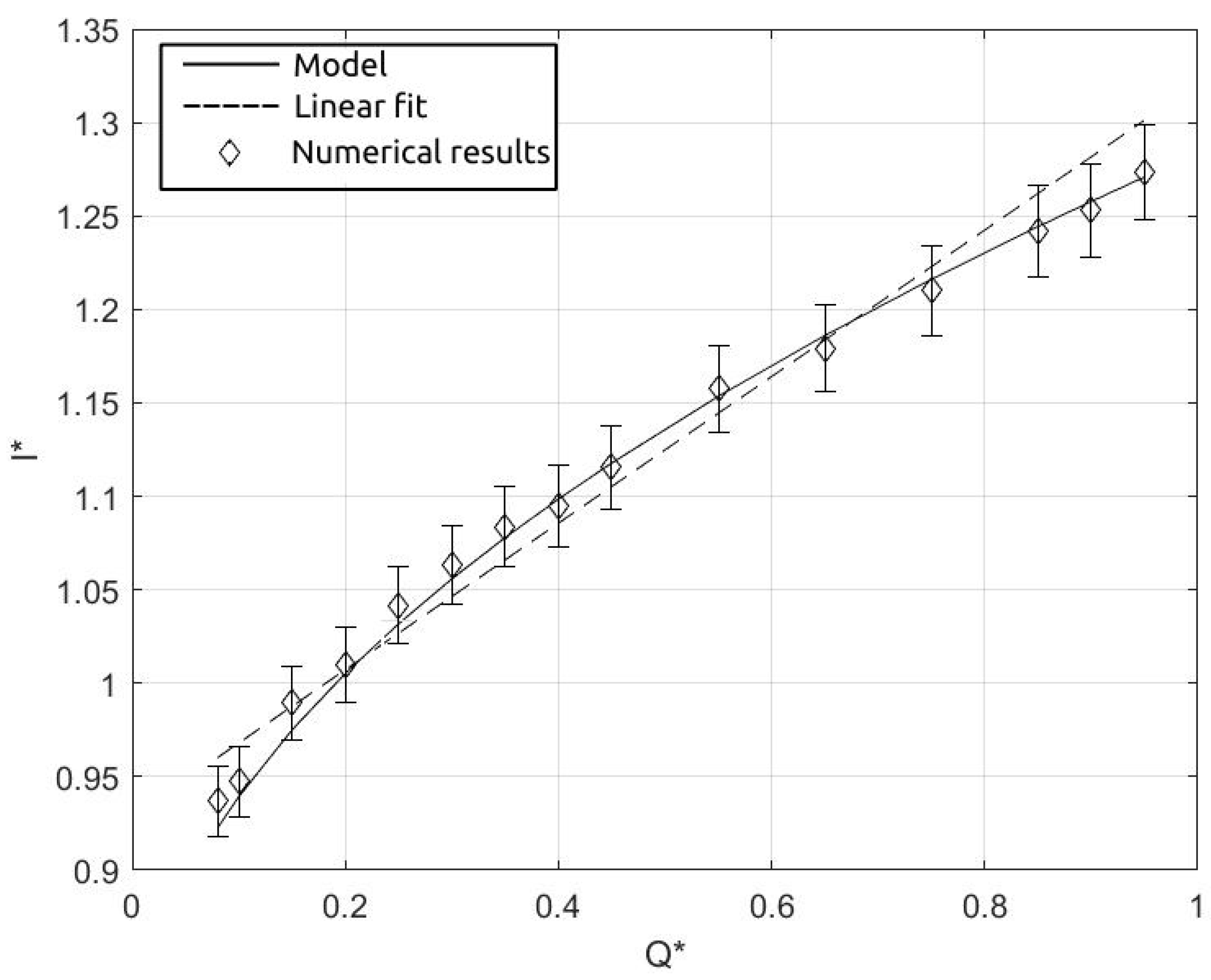
Table 1.
Drop length in function of
| sim. | Q* | drop length l [m] | |
|---|---|---|---|
| 1 | 0.08 | 178 | 0.913 |
| 2 | 0.10 | 180 | 0.923 |
| 3 | 0.15 | 188 | 0.964 |
| 4 | 0.20 | 192 | 0.984 |
| 5 | 0.25 | 198 | 1.015 |
| 6 | 0.30 | 202 | 1.036 |
| 7 | 0.35 | 206 | 1.056 |
| 8 | 0.40 | 208 | 1.067 |
| 9 | 0.45 | 212 | 1.087 |
| 10 | 0.55 | 222 | 1.128 |
| 11 | 0.65 | 224 | 1.149 |
| 12 | 0.75 | 230 | 1.179 |
| 13 | 0.85 | 236 | 1.210 |
| 14 | 0.90 | 238 | 1.221 |
| 15 | 0.95 | 242 | 1.241 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated









