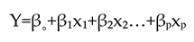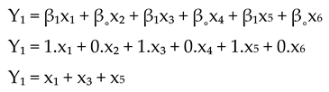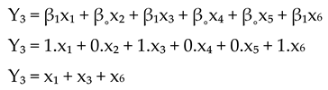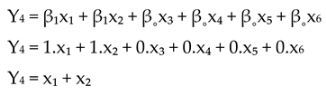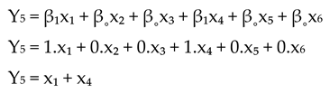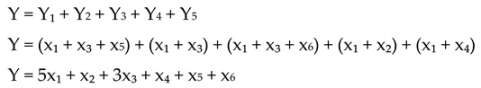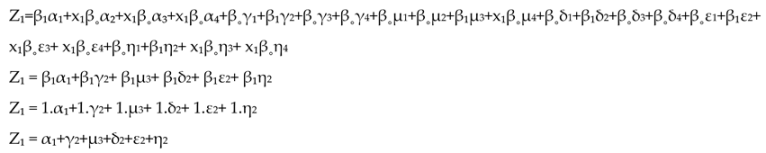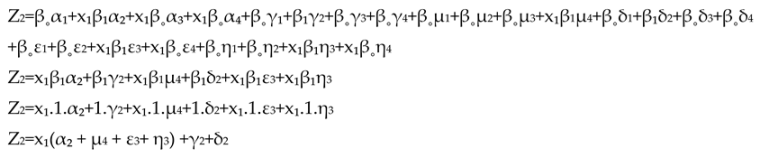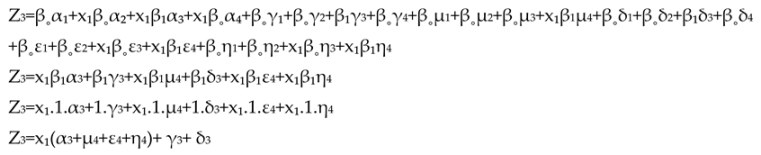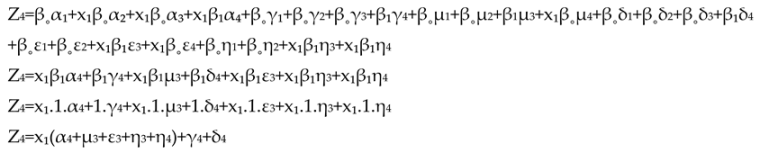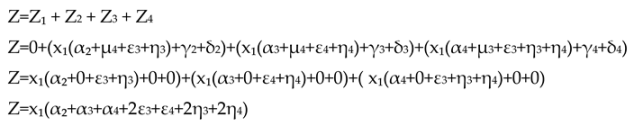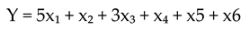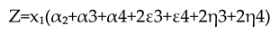Prerpints.org logo
Preprint
Article

Quantitative Descriptive Decision-Making: Mathematical Models for Bearing Wear Lifetime Stage Diagnosis in Vibration Analysis

Altmetrics

Downloads

96

Views

58

Comments

0

This version is not peer-reviewed

Predictive Analytics and Fault Diagnosis of Machines with Machine Learning Techniques

Submitted:

24 January 2024

Posted:

24 January 2024

You are already at the latest version

Alerts
Abstract
In the evolving landscape of vibration analysis, the integration of machine learning technologies for semi-automated analytical processes presents challenges in establishing clear cause-and-effect relationships in decision-making formulas. This research addresses this gap by exploring analytical diagnosis through residual signals, enabling the identification of anomalies and underperformance in machinery. Vibration signature analysis, focusing on distinctive vibration patterns, proves instrumental in detecting bearing defects and optimizing maintenance for enhanced operational efficiency and safety. Mathematical modeling, particularly worst-case analysis, provides a structured framework for decision-making under uncertainty. The research employs descriptive methods to analyze bearing wear data, transforming it into quantitative data for multiple regression equations. The derived equations reveal the dominance of harmonics in determining bearing wear stages, with PeakVue and overall vibration further indicating damage progression. The findings emphasize the significance of harmonic detection and high-frequency vibration analysis in predicting bearing health, offering a comprehensive approach to enhance machinery reliability. The study concludes with practical recommendations for bearing damage diagnosis based on the developed mathematical models, providing valuable insights for predictive maintenance strategies.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

Evolving landscape of vibration analysis, machine learning technologies are gaining traction for their potential to enable semi-automated analytical processes (Ghazali et al, 2021). However, a critical examination reveals a significant challenge: the foundational formulas guiding decision-making often lack a clear cause-and-effect relationship, deviating from empirical realities observed in field conditions (Fischhoff et al, 2020). For example, while machine learning algorithms may generate predictions about impending machinery failures, the absence of a definitive cause-effect linkage undermines the interpretive and predictive robustness of such models (Leukel et al, 2021). This gap between algorithmic outputs and empirical data not only compromises the reliability of analysis outcomes but also highlights the imperative for developing causally grounded mathematical frameworks in the domain of vibration analysis (Hosni et al, 2020).
Analytical diagnosis relies on inconsistencies between actual process behavior and its expected behavior, exhibited in signals called residuals (Kinnaert, 2003). These discrepancies manifest as residual signals, which capture the deviations from expected patterns (Pierce et al, 1986). By analyzing these residuals, analysts can pinpoint areas where the system may be underperforming or exhibiting anomalies (Hashemi et al, 2019). This method offers a quantitative approach to diagnostics, allowing for objective evaluations of bearing wear (Cui et al, 2016). Understanding these inconsistencies is crucial for predictive maintenance and enhancing system reliability (Wang et al, 2020). Thus, analytical diagnosis serves as a pivotal tool in ensuring operational efficiency and reliability (Su, 2010).
Vibration signature analysis effectively detects and locates even small bearing defects, improving maintenance and safety in rotating machines (Azeez et al, 2014). This method capitalizes on the unique vibration patterns emitted by machines, which are indicative of specific fault types (Saxena et al, 2016). By detecting these subtle signatures, technicians can preemptively address issues before they escalate, thereby prolonging the lifespan of the equipment (McFadden et al, 2000). Additionally, the early identification of defects contributes significantly to bolstering safety measures, minimizing the risk of catastrophic failures (Plante et al, 2015). In essence, vibration signature analysis plays a pivotal role in optimizing both operational efficiency and equipment longevity (Dai et al, 2008).
Mathematical modeling is crucial for decision-making under severe uncertainty, with worst-case analysis being particularly important (Sniedovich, 2007). It offers a structured framework to evaluate various scenarios and outcomes, aiding stakeholders in making informed choices amidst ambiguity (Badiru et al, 2013). Within this realm, worst-case analysis emerges as a critical component, emphasizing the examination of scenarios with the most adverse implications. By focusing on worst-case scenarios, decision-makers can develop strategies that are resilient to extreme conditions, thereby mitigating potential risks (Beyerer et al, 2016). In essence, mathematical modeling, complemented by worst-case analysis, enhances the robustness and reliability of decision-making under conditions of severe uncertainty.

2. Materials and Methods

Descriptive research focuses on describing a phenomenon and its characteristics, often using observation and survey tools, and is often analyzed quantitatively to determine relationships (Nassaji, 2015). The bearing wear descriptive data in this study is sourced from secondary data obtained from the Vibration Analysis Training Course (Mobius, 2016). The descriptive data on bearing wear includes Ball Pass Frequency Inner race (BPFI), Ball Pass Frequency Outer race (BPFO), Ball Spin Frequency (BSF), Fundamental Train Frequency (FTF), and Rotating Looseness (RL).
Table 1. This is a table of rolling element bearing defect frequency (Mobius, 2016).
Table 1. This is a table of rolling element bearing defect frequency (Mobius, 2016).
Bearing Defect Frequencies Spectrum Pattern Data
Harmonic Position 1st Peak Sideband
Ball Pass Frequency Inner Race (BPFI) Yes Non-Synchronous 1xTS*
Ball Pass Frequency Outer Race (BPFO) Yes Non-Synchronous -
Ball Spin Frequency (BSF) Yes Non-Synchronous FTF
(0.3xTS – 0.5xTS)
Fundamental Train Frequency (FTF) Yes Sub-Synchronous -
Rotating Looseness (RL) Yes 1xTS* -
* TS = Turning Speed.
Bearing defect frequencies is a critical parameter for monitoring bearing health and performance (El-Thalji et al, 2015). BPFI, or Ball Pass Frequency Inner race, is the frequency at which the rolling elements in a bearing pass over the inner race (Cole et al, 2002). BPFO stands for Ball Pass Frequency Outer race. It refers to the frequency at which the balls or rolling elements in a bearing pass over the outer race of the bearing assembly (Hou et al, 2019). Ball Spin Frequency (BSF) is the frequency at which the rolling elements in a bearing rotate around their own axis.
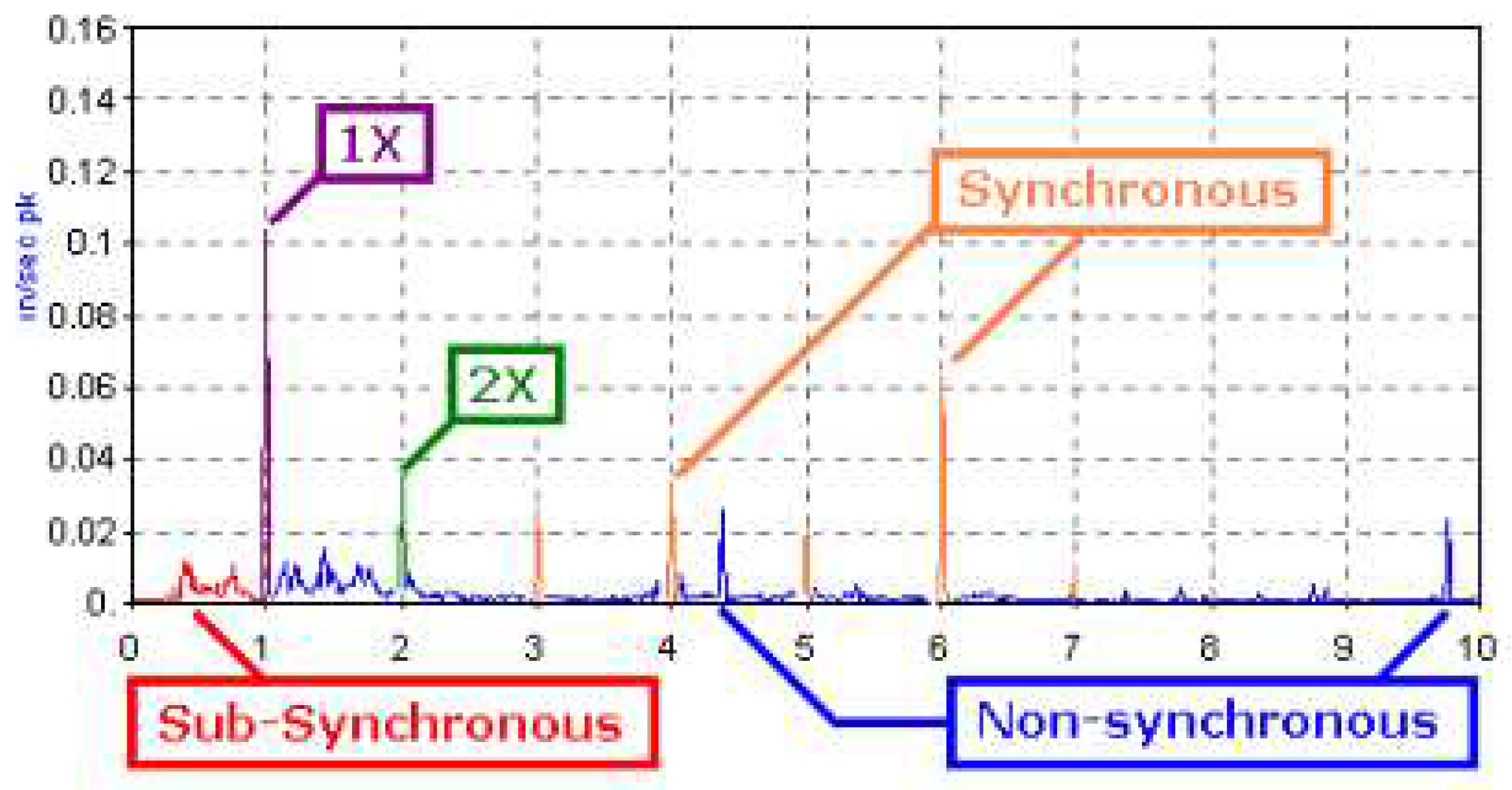
Preprints 97179 g001
Figure 1. Spectral energy can be categorized into one of three groups (Mobius, 2016).
Figure 1. Spectral energy can be categorized into one of three groups (Mobius, 2016).
Preprints 97179 g001
In the realm of vibration analysis, understanding the distinctions between sub-synchronous, synchronous, and non-synchronous harmonics in spectrum readings is pivotal for accurate diagnostics (Fong et al, 2020). Sub-synchronous harmonics occur at frequencies below the fundamental, often linked to mechanical issues like (FTF) Fundamental Train Frequency (Mobius, 2016). Synchronous harmonics align precisely with the running speed of the machine and are typically associated with (RL) Rotating Looseness (Mobius, 2016). On the other hand, non-synchronous harmonics are indicative of issues unrelated to machine running speed, encompassing BPFI, BPFO, BSF (Mobius, 2016). This nuanced understanding of harmonic types enhances the diagnostic precision of vibration analysis, enabling practitioners to decipher distinct machinery issues accurately (Veselovska et al, 2020). Anomalies signal is potential issues bearing wear (Jin et al, 2016). Monitoring allows for early detection of defects, enabling timely interventions to prevent catastrophic failures (Machado et al, 2015). Understanding and analyzing bearing defect frequencies is essential for effective predictive maintenance strategies (Ali et al, 2015).
This descriptive bearing wear vibration data will be modeled into quantitative data to describe a phenomenon and its characteristics, so that it can explain a relationship pattern. After that the data is converted into a multiple regression equation. Multiple linear regression is a method used to quantify the relationship between predictor variables and the dependent variable in a statistical study (Hawkins, 2004).
Preprints 97179 i001
Explanation:
  • Y = predicted or expected value of the dependent variable
  • x1 − xp = distinct independent or predictor variables
  • β˳ = value of Y when all of the independent variables (X1 through Xp) are equal to zero
  • β1-βp = estimated regression coefficients
If used in descriptive for bearing wear data.
  • Y1 = BPFI
  • Y2 = BPFO
  • Y3 = BSF
  • Y4 = FTF
  • Y5 = RL
  • Y = Bearing Wear
  • x1 = Harmonic
  • x2 = Position 1st peak (Sub-synchronous)
  • x3 = Position 1st peak (Non-synchronous)
  • x4 = Position 1st peak (1xTurning Speed)
  • x5 = Sideband Spacing Frequency (1xTurning Speed)
  • x6 = Sideband Spacing Frequency FTF (0.3xTS - 0.5xTS)
  • β1 = 1 = Yes
  • β0 = 0 = No
Ball Pass Frequency Inner Race (BPFI)
Preprints 97179 i002
Ball Pass Frequency Outer Race (BPFO)
Preprints 97179 i003
Ball Spin Frequency (BSF)
Preprints 97179 i004
Fundamental Train Frequency (FTF)
Preprints 97179 i005
Rotating Looseness (RL)
Preprints 97179 i006
The onset of bearing wear hinges on specific conditions within the vibration spectrum, particularly concerning Rolling Element Bearing Frequency Defects (REFD). According to established literature, when an REFD emerges, it must coincide with a harmonic condition—whether sub-synchronous, synchronous, or non-synchronous—to signify impending bearing wear (Jain et al, 2021). Notably, the appearance of side bands alongside these harmonics remains variable; they may manifest or remain absent without negating the diagnostic significance of the primary harmonic detection (Yang et al, 2020). For instance, the detection of a synchronous harmonic in the presence of an REFD could signal an early stage of bearing wear, even in the absence of accompanying side bands. This nuanced understanding underscores the multifaceted nature of vibration analysis in predicting bearing health, necessitating a comprehensive evaluation of harmonic conditions and their associated phenomena (Alves et al, 2021).
Bearing Wear
Preprints 97179 i007
From this multiple regression formula will show the relationship pattern and forms the basis for decision making regarding bearing life stages, by grouping them into stages one, two, three, or four (Mobius, 2016).
Preprints 97179 g002
Figure 2. Four stages of bearing lifetime (Mobius, 2016).
Figure 2. Four stages of bearing lifetime (Mobius, 2016).
Preprints 97179 g002
Stage one represents the initial phase in the bearing’s lifetime condition, detectable solely at ultra-high frequencies through the employment of ultrasound-based PdM technology (Lu et al, 2009). It exhibits subtle symptoms, characterized by normal noise and normal temperature (Baruffaldi et al, 2020). Ultrasound measurements indicate an increased spike in energy, yet overall vibration values remain normal (Pribil et al, 2019). Recommendations suggest that the equipment can still operate normally, with a remaining lifetime of 10% to 20% of the L10 or 1 to 2 years (Mobius, 2016). So it can be said that when the bearing is still in stage one, potential failure has not yet occurred.
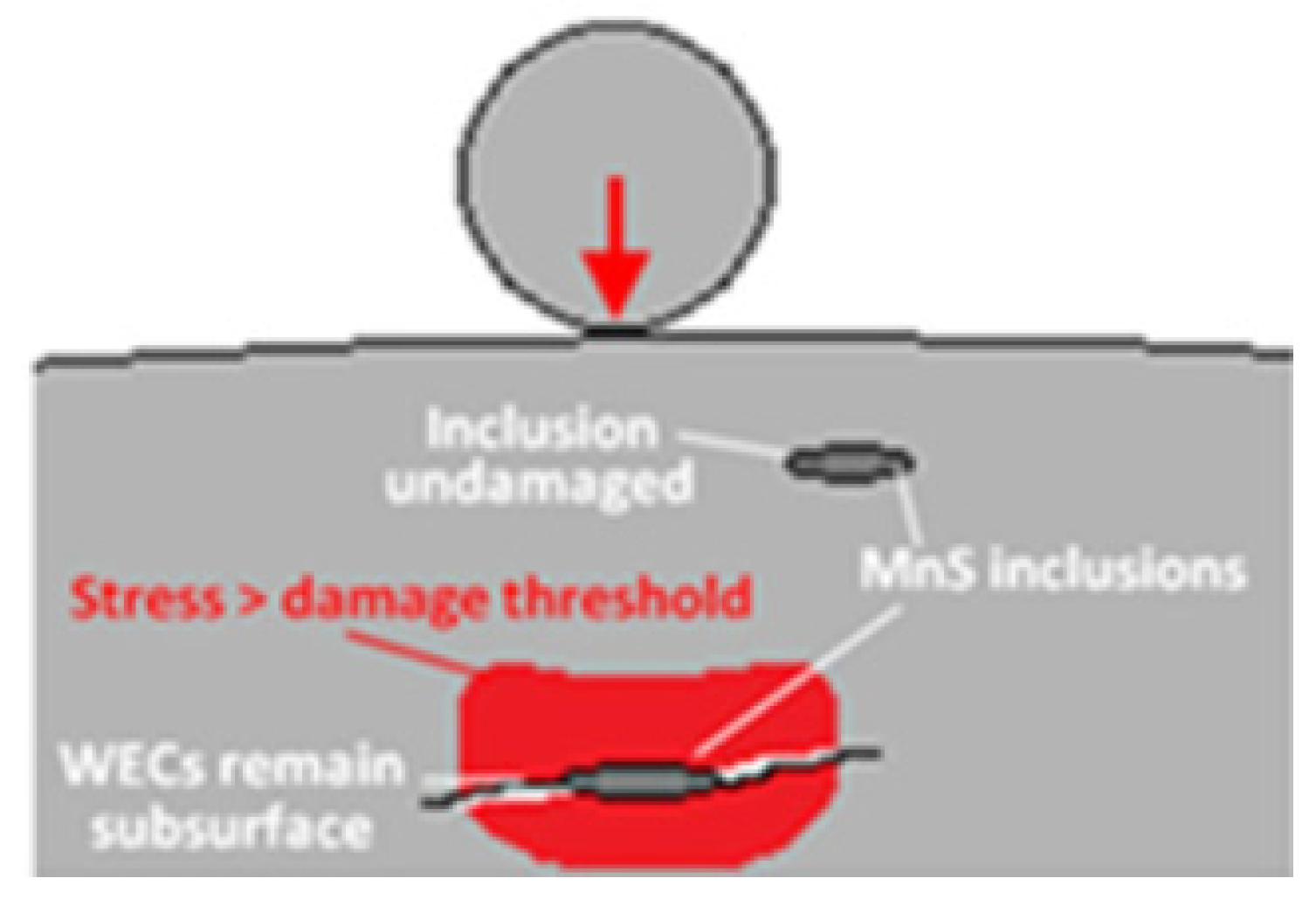
Stage two represents stress wave or subsurface dagame in intermediate phase in the bearing’s lifetime condition, detectable at ultra-high frequencies and now accessible through PdM technologies such as ultrasound and high-frequency vibration analysis, including enveloping or PeakVue (Darlow et al, 1976). Characterized by a slight increase in noise levels and normal temperatures, this stage is marked by a sharp rise in spike energy during ultrasound measurements. While overall vibration (RMS) values slight rise, the PeakVue values exhibit an increase (Degrande et al, 2004). Recommendations at this point suggest initiating plans for bearing replacement, with a remaining lifetime of 5% to 10% of the L10 or 6 months to 1 year (Mobius, 2016). So it can be said that when the bearing is stage two, potential failure already occurred.
Preprints 97179 g003
Figure 3. Stress wave or sub surface damage (Bruce et al, 2018).
Figure 3. Stress wave or sub surface damage (Bruce et al, 2018).
Preprints 97179 g003
Stage three signifies an advanced phase in the bearing’s lifetime condition, detectable at low frequencies through vibration analysis, commonly known as spectrum velocity (Nistane et al, 2016). This stage is marked by an audible increase in noise levels, a slight rise in temperature, and a notable increase in overall vibration (RMS) values. Frequencies associated with the bearing, such as FTF, BPFI, BPFO, and BSF, become clearly evident in the spectrum velocity, where harmonics and sidebands are prominently visible (Isranuri et al, 2020). Recommendations at this stage suggest the need for bearing replacement, with a remaining lifetime < 5% of the L10 or < 6 months (Mobius, 2016).
Stage four signifies the final phase in the bearing’s lifetime condition, where bearing frequencies are detected in a random broadband manner through vibration analysis (Nistane et al, 2016). Characterized by a distinct increase in noise levels with a highly varied rhythm, there is a drastic rise in temperature. The overall vibration (RMS) values sometimes increase and other times decrease, the latter due to the formation of new ball bearing grooves inside the bearing. Frequencies associated with the bearing, such as FTF, BPFI, BPFO, and BSF, are clearly visible in the spectrum velocity, with harmonics and sidebands prominently evident. Recommendations at this critical stage emphasize the immediate need for bearing replacement, with a remaining lifetime <1% of the L10 or < 1 month (Mobius, 2016).
If used in descriptive for bearing lifetime data.
  • Z1 = Stage One. Detected using ultrasound technology.
  • Z2 = Stage Two. Detected using Vibration technology.
  • Z3 = Stage Three. Detected using Vibration technology.
  • Z4 = Stage Four. Detected using Vibration technology.
  • Z = Bearing Lifetime
  • α1 = Bearing Ultrasonic Frequency (without harmonic spectrum or only noise floor). Detected using Ultrasound technology.
  • α2 = Appear Harmonic spectrum Bearing Natural Frequency / stress wave / subsurface damage. Detected using Vibration technology.
  • α3 = Defect Harmonic spectrum Bearing Natural Frequency. Detected using Vibration technology.
  • α4 = Random Broadband Harmonic spectrum Bearing Natural Frequency. Detected using Vibration technology.
  • γ1 = low in noise sound. Detected using human hearing.
  • γ2 = normal in noise sound. Detected using human hearing.
  • γ3 = slight rise in noise sound. Detected using human hearing.
  • γ4 = drastic in noise sound. Detected using human hearing.
  • μ1 = low in noise sound. Detected using ultrasound technology.
  • μ2 = normal in noise sound. Detected using ultrasound technology.
  • μ3 = slight rise in noise sound. Detected using ultrasound technology.
  • μ4 = drastic with harmonic spectrum in noise sound. Detected using ultrasound technology.
  • δ1 = low in temperature. Detected using IR Thermography technology.
  • δ2 = normal in temperature. Detected using IR Thermography technology.
  • δ3 = slight rise in temperature. Detected using IR Thermography technology.
  • δ4 = drastic rise in temperature. Detected using IR Thermography technology.
  • ε1 = low in high frequency vibration (peakvue). Detected using Vibration technology.
  • ε2 = normal in high frequency vibration (peakvue). Detected using Vibration technology.
  • ε3 = slight rise in harmonic spectrum high frequency vibration (peakvue). Detected using Vibration technology.
  • ε4 = drastic rise in harmonic spectrum high frequency vibration (peakvue). Detected using Vibration technology.
  • η1 = low in overall vibration. Detected using Vibration technology.
  • η2 = normal in overall vibration. Detected using Vibration technology.
  • η3 = slight rise in harmonic spectrum overall vibration. Detected using Vibration technology.
  • η4 = drastic rise in harmonic spectrum overall vibration. Detected using Vibration technology.
  • β1 = 1 = Yes
  • β0 = 0 = No
Bearing Stage One (remaining lifetime 1 – 2 years)
Preprints 97179 i008
Bearing Stage Two (remaining lifetime 6 months - 1 years)
Preprints 97179 i009
Bearing Stage Three (remaining lifetime < 6 months)
Preprints 97179 i010
Bearing Stage Four (remaining lifetime < 1 month)
Preprints 97179 i011
Assuming that the observations on the bearing only use vibration monitoring technology and bearing lifetime stage one is normal condition, then.
  • Z1 = 0
  • α1 = 0
  • γ1,γ2,γ3,γ4 = 0
  • μ1,μ2,μ3,μ4 = 0
  • δ1,δ2,δ3,δ4 = 0
Bearing Lifetime
Preprints 97179 i012

3. Results

The outcomes derived from multiple regression mathematical models offer pivotal insights into bearing wear conditions (Campbell, 2014).
Preprints 97179 i013
Notably, empirical findings underscore that a coefficient value of 5 consistently correlates with the presence of harmonics, serving as a reliable indicator of potential bearing degradation. Additionally, a coefficient value of 3 emerges as significant, highlighting the appearance of non-synchronous harmonics as the next dominant factor in bearing health assessment. For example, if a vibration analysis yields a coefficient of 5 for harmonics and 3 for non-synchronous components, it suggests a heightened risk of bearing wear, warranting immediate attention. This quantitative approach enhances the diagnostic accuracy of vibration analysis, emphasizing the critical role of regression modeling in prognosticating machinery health.
The outcomes derived from multiple regression mathematical models offer pivotal insights into bearing lifetime stage.
Preprints 97179 i014
From the mathematical model utilizing multiple regressions above, it is evident that in determining the remaining lifetime of the bearing from stages 2 to 4, the dominant factor is the harmonic denoted by X1. It is observed that all variables for validation need to be multiplied by X1 (harmonic) first, indicating that the first sign of bearing damage is the emergence of harmonics in the vibration spectrum. Following this, there is a slight rise in PeakVue represented by ε3, signifying that PeakVue (high-frequency vibration) also plays a significant role in determining the bearing’s level of damage for the first time. Furthermore, there is a slight rise in overall vibration denoted by η3 and a drastic rise in overall vibration represented by η4, both serving as evidence that higher vibration values correlate with increased bearing damage or a diminishing remaining lifetime, indicating the bearing has progressed to stages 3 and 4.

4. Conclusions

The conclusion of the research process using Quantitative Descriptive Decision-Making using Mathematical Models for Bearing Wear Lifetime Stage Diagnosis in Vibration Analysis can be concluded that:
  • If a bearing is already damaged, the first step is to examine the presence of harmonic patterns, followed by substantiating and determining the nature of these patterns, whether they are sub-synchronous, synchronous, or non-synchronou.
  • Bearing has entered the initial stage of bearing damage or the bearing is at stage 2 is the appearance of an increase in peakvue or high frequency vibration.
  • The more damaged a bearing is, the overall vibration value will increase, indicating that the bearing is at stage 3 and stage 4.

References

  1. Ghazali, M., & Rahiman, W. (2021). Vibration Analysis for Machine Monitoring and Diagnosis: A Systematic Review. Shock and Vibration. [CrossRef]
  2. Fischhoff, B., & Broomell, S. (2020). Judgment and Decision Making.. Annual review of psychology. [CrossRef]
  3. Leukel, J., González, J., & Riekert, M. (2021). Adoption of machine learning technology for failure prediction in industrial maintenance: A systematic review. Journal of Manufacturing Systems. [CrossRef]
  4. Hosni, H., & Vulpiani, A. (2020). Random thoughts about Complexity, Data and Models. ArXiv, abs/2005.04729. [CrossRef]
  5. Kinnaert, M. (2003). Fault diagnosis based on analytical models for linear and nonlinear systems - a tutorial. IFAC Proceedings Volumes, 36, 37-50. [CrossRef]
  6. Pierce, D., & Schafer, D. (1986). Residuals in Generalized Linear Models. Journal of the American Statistical Association, 81, 977-986. [CrossRef]
  7. Hashemi, N., German, E., Ramirez, J., & Ruths, J. (2019). Filtering Approaches for Dealing with Noise in Anomaly Detection. 2019 IEEE 58th Conference on Decision and Control (CDC), 5356-5361. [CrossRef]
  8. Cui, L., Zhang, Y., Zhang, F., Zhang, J., & Lee, S. (2016). Vibration response mechanism of faulty outer race rolling element bearings for quantitative analysis. Journal of Sound and Vibration, 364, 67-76. [CrossRef]
  9. Wang, J., Liang, Y., Zheng, Y., Gao, R., & Zhang, F. (2020). An integrated fault diagnosis and prognosis approach for predictive maintenance of wind turbine bearing with limited samples. Renewable Energy, 145, 642-650. [CrossRef]
  10. Su, W., Wang, F., Zhu, H., Zhang, Z., & Guo, Z. (2010). Rolling element bearing faults diagnosis based on optimal Morlet wavelet filter and autocorrelation enhancement. Mechanical Systems and Signal Processing, 24, 1458-1472. [CrossRef]
  11. Azeez, N., & Alex, A. (2014). Detection of rolling element bearing defects by vibration signature analysis: A review. 2014 Annual International Conference on Emerging Research Areas: Magnetics, Machines and Drives (AICERA/iCMMD), 1-5. [CrossRef]
  12. Saxena, M., Bannet, O., Gupta, M., & Rajoria, R. (2016). Bearing Fault Monitoring Using CWT Based Vibration Signature. Procedia Engineering, 144, 234-241. [CrossRef]
  13. McFadden, P., & Toozhy, M. (2000). Application of synchronous averaging to vibration monitoring of rolling element bearings. Mechanical Systems and Signal Processing, 14, 891-906. [CrossRef]
  14. Plante, T., Nejadpak, A., & Yang, C. (2015). Faults detection and failures prediction using vibration analysis. 2015 IEEE AUTOTESTCON, 227-231. [CrossRef]
  15. Dai, J., Chen, C., Xu, X., & Hu, P. (2008). Condition monitoring on complex machinery for predictive maintenance and process control. 2008 IEEE International Conference on Systems, Man and Cybernetics, 3595-3600. [CrossRef]
  16. Sniedovich, M. (2007). The Art and Science of Modeling Decision-Making Under Severe Uncertainty. , 1, 111-136. [CrossRef]
  17. Badiru, A., & Osisanya, S. (2013). Project Management for the Oil and Gas Industry: A World System Approach. [CrossRef]
  18. Beyerer, J., & Geisler, J. (2016). A Framework for a Uniform Quantitative Description of Risk with Respect to Safety and Security. European Journal for Security Research, 1, 135-150. [CrossRef]
  19. Nassaji, H. (2015). Qualitative and descriptive research: Data type versus data analysis. Language Teaching Research, 19, 129 - 132. [CrossRef]
  20. Mobius Institute (2016). Vibration Analysis Course Training. learn@mobiusinstitute.com. 13, 1 – 59. Available online at: www.mobiusinstitute.com.
  21. Hawkins, D. (2004). The Problem of Overfitting. Journal of chemical information and computer sciences, 44 1, 1-12. [CrossRef]
  22. Cole, M., Keogh, P., & Burrows, C. (2002). The Dynamic Behavior of a Rolling Element Auxiliary Bearing Following Rotor Impact. Journal of Tribology-transactions of The Asme, 124, 406-413. [CrossRef]
  23. El-Thalji, I., & Jantunen, E. (2015). A summary of fault modelling and predictive health monitoring of rolling element bearings. Mechanical Systems and Signal Processing, 60, 252-272. [CrossRef]
  24. Jin, X., Sun, Y., Que, Z., Wang, Y., & Chow, T. (2016). Anomaly Detection and Fault Prognosis for Bearings. IEEE Transactions on Instrumentation and Measurement, 65, 2046-2054. [CrossRef]
  25. Machado, T., & Cavalca, K. (2015). Modeling of hydrodynamic bearing wear in rotor-bearing systems. Mechanics Research Communications, 69, 15-23. [CrossRef]
  26. Ali, J., Chebel-Morello, B., Saidi, L., Malinowski, S., & Fnaiech, F. (2015). Accurate bearing remaining useful life prediction based on Weibull distribution and artificial neural network. Mechanical Systems and Signal Processing, 56, 150-172. [CrossRef]
  27. Hou, G., & Lee, C. (2019). Estimation of the Defect Width on the Outer Race of a Rolling Element Bearing under Time-Varying Speed Conditions. Shock and Vibration. [CrossRef]
  28. Fong, S., Harmouche, J., Narasimhan, S., & Antoni, J. (2020). Mean Shift Clustering-Based Analysis of Nonstationary Vibration Signals for Machinery Diagnostics. IEEE Transactions on Instrumentation and Measurement, 69, 4056-4066. [CrossRef]
  29. Veselovska, N., Shargorodskiy, S., Bratslavets, B., & Yalina, O. (2020). RESEARCH OF FEATURES OF DEVELOPMENT OF BEARING DEFECTS ON THE BASIS OF WAVELET ANALYSIS. ENGINEERING, ENERGY, TRANSPORT AIC. [CrossRef]
  30. Jain, P., & Bhosle, S. (2021). Frequency Spectrum Analysis of Various Defects in Rolling Element Bearings Used in Heavy Load and High Speed Machinery. Techno-Societal 2020. [CrossRef]
  31. Yang, Y., Liu, C., Jiang, D., & Behdinan, K. (2020). Nonlinear vibration signatures for localized fault of rolling element bearing in rotor-bearing-casing system. International Journal of Mechanical Sciences. [CrossRef]
  32. Alves, D., Fieux, G., Machado, T., Keogh, P., & Cavalca, K. (2021). A parametric model to identify hydrodynamic bearing wear at a single rotating speed. Tribology International, 153, 106640. [CrossRef]
  33. Campbell, M. (2014). Time Series Regression. , 1-6. [CrossRef]
  34. Lu, B., Durocher, D., & Stemper, P. (2009). Predictive maintenance techniques. IEEE Industry Applications Magazine, 15. [CrossRef]
  35. Baruffaldi, F., Mecca, R., Stea, S., Beraudi, A., Bordini, B., Amabile, M., Sudanese, A., & Toni, A. (2020). Squeaking and other noises in patients with ceramic-on-ceramic total hip arthroplasty. HIP International, 30, 438 - 445. [CrossRef]
  36. Pribil, J., Přibilová, A., & Frollo, I. (2019). Analysis of the Influence of Different Settings of Scan Sequence Parameters on Vibration and Noise Generated in the Open-Air MRI Scanning Area †. Sensors (Basel, Switzerland), 19. [CrossRef]
  37. Darlow, M., Shinaishin, O., & Winn, L. (1976). High-frequency acoustic signals for condition monitoring. Journal of the Acoustical Society of America, 60. [CrossRef]
  38. Degrande, G., Schevenels, M., Chatterjee, P., Velde, W., Hölscher, P., Hopman, V., Wang, A., & Dadkah, N. (2004). Vibrations due to a test train at variable speeds in a deep bored tunnel embedded in London clay. Journal of Sound and Vibration, 293, 626-644. [CrossRef]
  39. Nistane, V., & Harsha, S. (2016). Failure Evaluation of Ball Bearing for Prognostics. Procedia Technology, 23, 179-186. [CrossRef]
  40. , S., Isranuri, I., & , S. (2020). Bearing Damage Detection using Support Vector Machine. IOP Conference Series: Materials Science and Engineering, 851. [CrossRef]
  41. Nistane, V., & Harsha, S. (2016). Failure Evaluation of Ball Bearing for Prognostics. Procedia Technology, 23, 179-186. [CrossRef]
  42. T. Bruce, H. Long, & R. S. Dwyer-Joyce (2018). Threshold Maps for Inclusion-Initiated Micro-Cracks and White Etching Areas in Bearing Steel: The Role of Impact Loading and Surface Sliding. Tribology Letters (2018) 66:111. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated