Preprint
Article
Controlling the Collective Behaviors of Ultrasound-Driven Nanomotors by Frequency Regulation
Altmetrics
Downloads
102
Views
26
Comments
0
A peer-reviewed article of this preprint also exists.
supplementary.zip (51.36MB )
This version is not peer-reviewed
Submitted:
23 January 2024
Posted:
25 January 2024
You are already at the latest version
Alerts
Abstract
Controlling the collective behavior of micro/nanomotors with ultrasound may enable new functionality in robotic, medicine and other engineering disciplines. Currently, various collective behaviors of nanomotors, such as assembly, reconfiguration and disassembly, have been explored by using acoustic fields with a fixed frequency, while regulating their collective behaviors by varying the ultrasound frequency still remains challenging. In this work, we design an ultrasound manipulation methodology allowing nanomotors to exhibit different collective behaviors by regulating the applied ultrasound frequency. This work has important implications for design of artificial actuated nanomotors and optimize their performances.
Keywords:
Subject: Physical Sciences - Applied Physics
1. Introduction
Micro/nano motors, tiny devices converting external energy into motion and force, have gained attention for applications in micro/nanofabrication, environmental remediation, and biomedicine [1,2,3,4,5,6,7,8,9,10,11]. Collective behavior, a common occurrence in nature, involves cooperative actions such as aggregation and transportation in ant colonies, as well as collective defense and offensive behaviors in African hyenas [12]. Inspired by these natural phenomena, researchers have developed micro/nanomotors with diverse driving forces to collaboratively tackle complex tasks. Over the years, various energy sources, including magnetic force [13,14,15,16,17,18,19], gradient energy [1,3,20,21,22,23,24], and ultrasonic energy [25,26,27,28,29,30,31,32,33], have been employed to power these motors. Ultrasonic energy, in particular, is promising due to its non-invasive nature, causing no harm to organisms, and its ability to operate without physical contact.
In current research, scientists actively manipulate the collective behavior of micro/nanomotors by regulating transducer activation or controlling the intensity of ultrasonic energy [28]. For example, Xiao Long Lu’s group influences the aggregation or dispersion of micro/nanomotor collectives through precise control of transducer activation [29]. Similarly, Ze Sheng Li’s group observed micro/nanomotors exhibiting dynamic self-organization, forming intricate flower-like clusters when exposed to a 720kHz acoustic frequency [30]. Although specific ultrasound frequencies have been applied to drive various micro/nanomotors [31,33], there has been limited research on controlling their collective behavior by controlling ultrasound frequencies. Regulating ultrasound frequency holds the potential to introduce a wider range of patterns in micro/nanomotor collective behavior and create continuous variations in motion. As of now, effectively controlling the collective behavior of micro/nanomotors through ultrasound frequency adjustments remains unresolved.
In current research, scientists actively manipulate the collective behavior of micro/nanomotors by regulating transducer activation or controlling the intensity of ultrasonic energy [28]. For example, Xiao Long Lu’s group influences the aggregation or dispersion of micro/nanomotor collectives through precise control of transducer activation [29]. Similarly, Ze Sheng Li’s group observed micro/nanomotors exhibiting dynamic self-organization, forming intricate flower-like clusters when exposed to a 720kHz acoustic frequency [30]. Although specific ultrasound frequencies have been applied to drive various micro/nanomotors [31,33], there has been limited research on controlling their collective behavior by controlling ultrasound frequencies. Regulating ultrasound frequency holds the potential to introduce a wider range of patterns in micro/nanomotor collective behavior and create continuous variations in motion. As of now, effectively controlling the collective behavior of micro/nanomotors through ultrasound frequency adjustments remains unresolved.
In this study, we conducted experiments in which nanomotors demonstrated distinct collective behaviors through the continuous modulation of ultrasound frequencies. The nanomotors composed of GaOOH with a rod-shaped morphology are capable of autonomous assembly into different patterns, reconfiguration and disassembly by continuously changing the frequency of applied ultrasonic field. The collective behaviors include clustering together, moving in stripe-like formations, and vortex-shaped rotation. Experimental results and FEM simulations demonstrates that the secondary ultrasonic waves at the interface between solids and liquids lead to the formation of complex acoustic pressure fields and microfluidic patterns, causing these collective behaviors. This work offers valuable insights that could pave the way for the development of next-generation ultrasonically controlled micromotors and their integration into various applications.
2. Materials and Methods
Gallium was purchased from Dongguan Huatai Metal Materials Technology Co., Ltd, other chemicals used in experiments were from Hubei Zechuan Technology Co., Ltd, Deionized water was obtained from YA·ZD·5 water distiller from Shanghai Baolan Experimental Instrument Manufacturing Co., Ltd. The piezoelectric transducer which produces the ultrasound waves (PZT5 disc, 20mm in diameter, 0.5mm in thickness) was attached to the bottom center of the glass. The continuous ultrasound sine wave was applied via a piezoelectric transducer, through a Tektronix AFG3102C dual channel arbitrary waveform generator, in connection to a FPA301 power amplifier. All experiments were observed in a two-dimensional plane near the bottom surface and recorded at room temperature by an inverted optical microscope (Zeiss Axio BA600 microscope with 10x, 20x, 50x, and 100x objectives) using a Photometrics ModelGP-550H CCD camera. The electrical signal was monitored using a 60 MHz Tektronix TDS1002 storage oscilloscope.
3. Results and Discussion
The nanomotors were fabricated by ultrasonic treating Gallium at 40 ℃ for 30 minutes, as schematically illustrated in Figure 1a. Figure 1b presents the near-infrared absorption (NIR) spectrum of the resulting nanomotors. The NIR spectrum reveals that the transverse peak (λT) of nanomotors is found at 980 nm, while the longitudinal NIR peak (λL) is at 1200 nm. Scanning electron microscopy (SEM) and transmission electron microscopy (TEM) (Figure 1c-f) are employed to image and evaluate the nanostructures of the nanomotors. Figures 1c-e illustrate that most nanomotors exhibit a rod-shaped structure, with only a small portion appearing as irregular shapes. These rod-shaped nanomotors, with some small shape asymmetries, have been determined to have a length of 150±10 nm and a diameter of 100±10 nm. The high magnification SEM image in Figure 1d provides a detailed view of a single rod-shaped nanomotor. The surface structure of a rod-shaped nanomotor is characterized by High-Resolution Transmission Electron Microscope (HRTEM) in Figure 1f, displaying lattice fringes that confirm the crystal nature of these GaOOH nanomotors (Figure S1). Energy Dispersive Spectroscopy (EDS) was employed for the analysis of the nanomotors’ composition. As depicted in EDS mapping (Figure 1g-h), gallium and oxygen elements are evenly distributed on the nanorod. To further investigate the valence states of gallium elements in nanomotors, X-ray photoelectron spectroscopy (XPS) analysis was carried out. The XPS survey scans (Figure 1i) show that all gallium in the nanomotor exhibits trivalent behavior, indicating complete oxidation of gallium elements in the nanomotors. X-ray diffraction (XRD) studies were performed to identify the composition and purity of the nanomotors, revealing that the chemical composition is GaOOH, a typical form of gallium oxide formed when gallium undergoes oxidation in water (Figure 1j).
We tested the collective performance of these nanomotors under different input ultrasound frequencies. Experiments were conducted using a homemade ultrasonic manipulation platform, as illustrated in Figure 2a. It integrates a signal generator for customizable frequency signals, a power amplifier, and a homemade ultrasonic platform (cell width: 5.2mm, length: 5.8mm, height: 260μm). Videos were taken with an optical microscope (ocular lenses: 10x, objective lenses: 20x~100x). The observed collective behaviors can be broadly categorized into three distinct patterns: stripe-like chains, vortex-shaped patterns, and relatively stable clusters. As seen in Figure 2c, d, nanomotors gathered into small clusters, and forming a vortex-shaped pattern at a 1.3 MHz ultrasonic field frequency (Video S1, Part 1) with very fast in-plane rotations. While at a driving frequency of 1.4 MHz, these nanomotors form parallel stripes with fast rotations along the axis of the stripes. Representative observations of this stripe-like pattern are shown in Figure 2e, f (taken form Video S1, Part 2). Interestingly, tuning the frequency away from these frequency range (for example, frequency = 2.8MHz), these nanomotors aggregated progressively (Figure 2g, h, Video S1, Part 3). Turing off the acoustic field caused the nanomotors redispersing into a suspension uniformly (Video S1, Part 3). Obviously, varying the frequency could lead to the transformation between these collective patterns. As demonstrated in Video S2, tuning the frequency from 2.4 MHz to 2.6 MHz shifted the nanomotors’ collective behavior from stripe-like chains to vortex-shaped rotation. When the frequency changes from 2.6 MHz to 2.8 MHz, the nanomotors aggregated progressively. The transformation behaviors are summarized briefly in Figure 2b. As seen, the nanomotors exhibited alternating motion between stripe-like chains and vortex-shaped patterns in the 1 MHz-2.6 MHz range, transforming into clusters in the frequency range from 2.6 MHz to 2.8 MHz.
The collective behaviors of these nanomotors are highly influenced by the geometric parameters of the sample cell and the applied ultrasound frequency. In our experiment, the ultrasonic platform consists of several layers: the bottom transducer, covered by a glass slide for a smooth surface; a micro-water cell (5.8mm length, 5.2mm width, 260μm height) enclosed with tape (Biaxially oriented polypropylene film, BOPP); and a top glass slide to reflect ultrasonic waves (Figure 3a). The bottom transducer generates continuous ultrasonic waves along the z-axis in isotropic elastic media (for example, in water and tape). While at the edge of the cell, interaction-induced secondary waves arise due to the non-uniformity of the medium, as depicted in Figure 3b. Different densities of the liquid and the wall (composed of adhesive tape) cause different velocities and wavelengths. As a consequence, oscillation coupling between the wall and water generates ultrasonic waves along the x-axis and y-axis with the same frequency. The in-plane waves continuously reflect within the x-o-y plane of the cell (Figure 3c). It is well-known that the stripe-like chains’ pattern, regardless of their direction, is usually considered to be the results of collecting nanomotors at the nodes of ultrasonic standing waves, and the motion of the nanomotors are driven by the acoustic pressure fields [25]. Thus, changing the frequency alters the position of in-plane wave nodes, which induces different collective behaviors of the nanomotors.
To illustrate the critical role of the ultrasound frequency in achieving different patterns, we further carefully compared the collective behaviors of nanomotors in ultrasonic field with frequency from 1.5 to 1.7 MHz. When the frequency is set at 1.7 MHz (Figure 3d, corresponding to Video S3), standing ultrasound waves exclusively exist along the x-axis, with their trajectory parallel to the y-o-z plane. Consequently, nanomotors are observed displaying stripe-like patterns parallel to the y-axis while simultaneously spinning around their own axis that generally considered to be due to the interference of traveling waves along the z-axis. However, a slight deviation away from the resonant frequency (1.6 MHz) dramatically decreased the intensity of standing waves in the cell, and thus only traveling waves can be observed in x-o-y plane. In this state, the microfluidic field generated by the disturbance of these traveling waves induces nanomotors to exhibit a vortex-shaped collective behavior (Figure 3e). As the input frequency decreases to 1.5 MHz, the standing waves forms along the y-axis. At certain frequencies, the nanomotors formed the stripe-like aggregates that parallel the x-axis within seconds, as shown in Figure 3f and the corresponding Video S3. Such transformation indicates that the aggregation of these nanomotors into defined pattern can be attributed to the distribution of acoustic pressure fields in the cell.
From theoretical model of ultrasound [32], the conditions for forming standing waves in an enclosed space can be represented by
Here, s represents the characteristic length of ultrasonic wave transmission, and c denotes the speed of sound in the medium. In our experiment, c corresponds to the speed of sound in deionized water, specifically c = 1492m/s, and thus the conditions for the formation of standing waves for in-plane and out-of-plane waves can be calculated using equation (1) as follows:
The ultrasonic waves continuously reflected and superimposed in the square cell, leading to the formation of complex acoustic pressure fields and microfluidic patterns, thereby resulting in the diverse collective behavior of nanomotors.
To further investigate this mechanism, we simulated the acoustic pressure field using a multi-physics field simulation approach based on the finite element method. (see supporting materials for more details). Figures 3g illustrates the two-dimensional acoustic pressure field distribution within the x-o-y plane of cells at a resonant frequency of 1.7 MHz, in which standing wave planes parallel to the y-o-z plane. This is consistent with our observation (Figure 3 d). Figure 3 h displays the acoustic pressure field with a frequency of 1.6 MHz, in which standing waves are not observed. At that frequency, nanomotors were trapped by traveling waves along the y-axis and x-axis simultaneously, and thus autonomously assembling into many small vortices that rotate together in a synchronized manner, as illustrated Figure 3e. Figure 3i depicts the acoustic pressure field with a frequency of 1.5 MHz, similar to that in 1.7 MHz except the direction of the stripes.
It is crucial to emphasize that these simulated results were limited to the x-o-y plane. Because the ultrasound manipulation platform used here has a very small vertical scale (260μm), the minimum frequency for standing waves in z direction waves is significantly higher than the minimum frequency for in-plane (x-o-y plane) waves (~2.86 MHz). When the ultrasound frequency gets close to 2.86 MHz, out-of-plane waves propagate along the z-axis and are reflected back from the cover glass giving rise to a standing wave. At this state, the nanomotors levitated into the nodal plane, forming small clusters. The origin of the levitation force is generally attributed to the primary acoustic radiation force exerted on the nanomotors by sound propagation perpendicular to the substrate [25]. A slight deviation away from 2.86 MHz caused the nanomotors redisperse into a suspension, as illustrated in supporting video 1, Part 3.
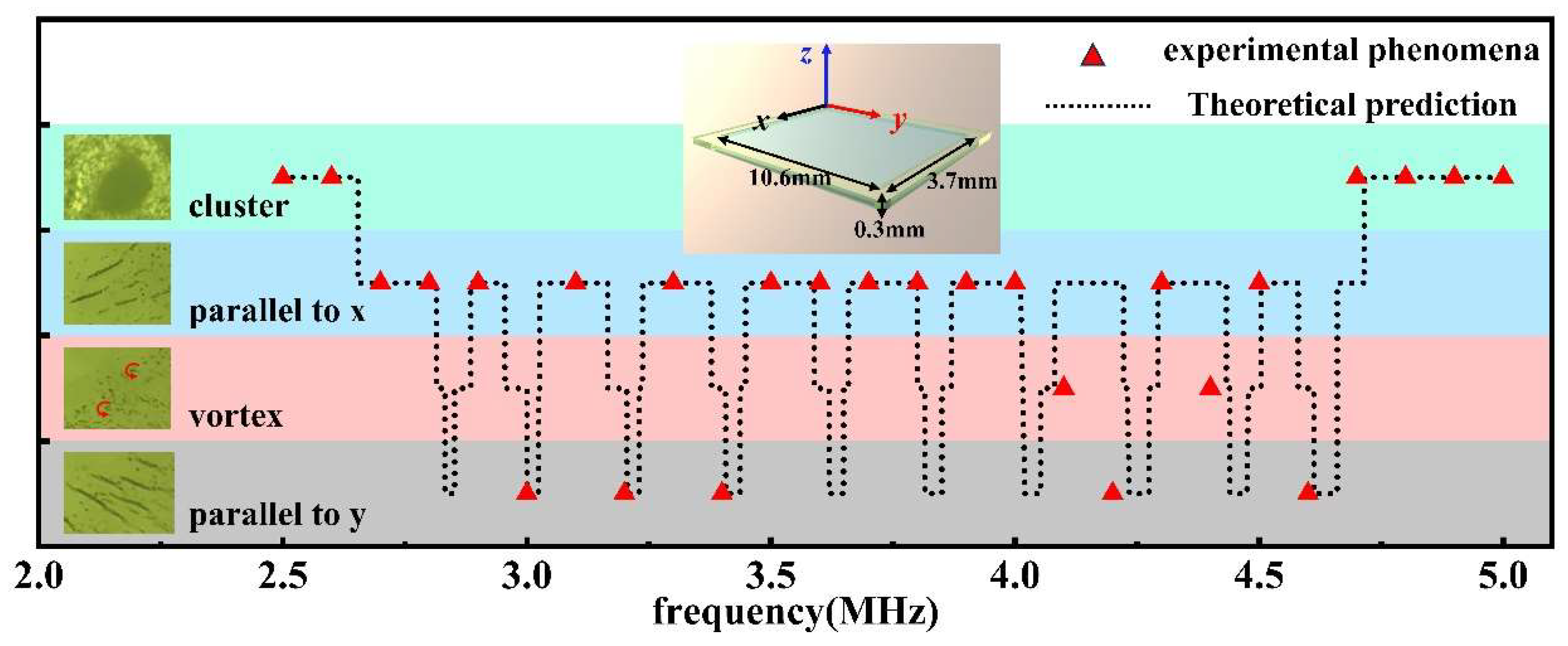
As we mentioned above, this mechanism discussed above allows us to change the collective behaviors of the nanomotors by independently adjusting the geometric parameters of the sample cells. To further investigate this mechanism, we fabricated another sample cell with dimensions of 3.7mm width in the x-direction, 10.6mm length in the y-direction, and 0.3mm height in the z-direction. It is easy to predict the collective behaviors of nanomotors in such a cell. Figure 4 shows the theoretical predication and experimental results. As expected, the experimental results show a high degree of conformity with the predicted phenomena. When the frequency is adjusted to approximately 2.48 MHz or 4.96 MHz, standing waves manifest in the vertical direction, giving rise to observed clustering phenomena. Besides, both stripe-like and vortex- shaped patterns were effectively observed by tuning the ultrasound frequency in the range from 2.48 MHz to 4.96 MHz. Because the configuration of our transduce and cell are not yet optimized, it seems reasonable to conclude that more collective patterns will be possible in different sample cell with more complex geometries.
4. Conclusions
In conclusion, we have presented a general approach to control the collective behavior of ultrasound-driven nanomotors by tuning the ultrasound frequency. The GaOOH nanomotors are capable of autonomous assembly, reconfiguration and disassembly in response to changes in applied frequency of ultrasound field in a square sample cell. It was demonstrated that the secondary ultrasonic waves produced from the edge of sample cell led to the formation of complex acoustic pressure fields and microfluidic patterns that causes these collective behaviors. In contrast to commonly used methods that involve adjusting the intensity of ultrasound with a fixed frequency, the reported method demonstrates greater flexibility, offering different collective behavior patterns and enabling precise control of nanomotor movement across a broader range of frequencies. It not only offers fresh perspectives for the innovation of ultrasound manipulation platforms but also has the potential to inspire the development of diverse ultrasound-driven micro/nanomotors for accomplishing more intricate tasks.
Supplementary Materials
The following supporting information can be downloaded at: Preprints.org, Video S1: Three distinct collective behaviors of nanomotors in ultrasonic field with different frequencies. Video S2: The transformation of collective behavior between different patterns. Video S2: Changing the direction of stripe-like patterns from the x-axis direction to the y-axis direction.
Author Contributions
Conceptualization—Z.Z. and J.C.1; Data curation—Z.Z.; formal analysis—Z.Z. and J.C.1; funding acquisition—J.C.2; investigation—G.Z. and S.G.; methodology—Y.L. and M.L.; software—Z.Z. and Y.L.; supervision—M.L.; writing original draft—Z.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Natural Science Foundation of China (NSFC), grant number 51501102, the Natural Science Foundation of Hubei Province (grant number 2018CFB161 and 2019CFB194).
Acknowledgments
Dr. Zhihong Zhao and Jie Chen contributed equally to this work. The authors wish to thank Analysis and Testing Center, CTGU for SEM measuring assistance.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, D.L.; Gao, C.Y.; Si, T.Y.; Li, Z.S.; Guo, B.; He, Q. Near-infrared light propelled motion of needlelike liquid metal nanoswimmers. Colloid. Surface. A. 2021, 661, 125865. [Google Scholar] [CrossRef]
- Wang, Y.X.; Kuai, Y.B.; Zhang, G.Q.; Zhang, H.R.; Cong, J.W.; Xu, Y.L.; Yi, L.Z.; Liu, M.; Liu, Y.M. Electric-field-guided 3D manipulation of liquid metal microfleas. Soft. Materials. 2022, 20, 129–139. [Google Scholar] [CrossRef]
- Zhang, J.H.; Laskar, A.; Song, J.Q.; Shklyaev, O.E.; Mou, F.Z.; Guan, J.G.; Balazs, A.C.; Sen, A. Light-Powered, Fuel-Free Oscillation, Migration, and Reversible Manipulation of Multiple Cargo Types by Micromotor Swarms. ACS Nano 2023, 17, 251–262. [Google Scholar] [CrossRef] [PubMed]
- Wu, F.Y.; Yang, D.C.; Huang, X.F.; Yi, L.Z.; Liu, Y.M.; Pan, L.Q. Ultrafast Bubble-Propelled and Magnetic-Field-Navigated Porous Catalytic Janus Micromotor. J. Nanosci. Nanotechnol. 2019, 19, 4154–4159. [Google Scholar] [CrossRef] [PubMed]
- Li, J.W.; Tan, W.H. A Single DNA Molecule Nanomotor. Nano. Lett. 2002, 2, 315–318. [Google Scholar] [CrossRef]
- Orozco, J.; Allan, C.; Cheng, G.Z.; Sattayasamitsathit, S.; Gao, W.; Feng, X.M.; Shen, T.F.; Wang, J. Molecularly Imprinted Polymer-Based Catalytic Micromotors for Selective Protein Transport. J. Am. Chem. Soc. 2013, 135, 5336–5339. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.B.; Zhao, J.N.; Zhao, Z.H.; Chen, K.X.; Li, P.S.; Cong, J.W.; Pan, L.Q.; Liu, M.; Liu, Y.M. Cooperative behavior of miniature magnetic swimmers in uniform magnetic fields. Appl. Phys. Express 2023, 16, 067001. [Google Scholar] [CrossRef]
- Wang, D.L.; Gao, C.Y.; Wang, W.; Sun, M.M.; Guo, B.; Xie, H.; He, Q. Shape-Transformable, Fusible Rodlike Swimming Liquid Metal Nanomachine. ACS Nano. 2018, 12, 10212–10220. [Google Scholar] [CrossRef] [PubMed]
- Li, J.X.; Li, T.L.; Xu, L.T.; Kiristi, M.; Liu, W.J.; Wu, Z.G.; Wang, J. Magneto−Acoustic Hybrid Nanomotor. Nano. Lett. 2015, 15, 4814–4821. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.M.; Ge, D.Q.; Cong, J.W.; Piao, H.G.; Huang, X.F.; Xu, Y.L.; Lu, G.D.; Pan, L.Q.; Liu, M. Magnetically Powered Annelid-Worm-Like Microswimmers. Small. 2018, 14, 1704546. [Google Scholar] [CrossRef]
- Liu, T.Y.; Xie, L.; Zeng, J.; Yan, M.; Qiu, B.L.; Wang, X.Y.; Zhou, S.; Zhang, X.; Zeng, H.; Liang, Q.R.; He, Y.J.; Liang, K.; Liu, J.; Velliou, E.; Jiang, L.; Kong, B. Interfacial Superassembly of Light-Responsive Mechanism-Switchable Nanomotors with Tunable Mobility and Directionality. ACS Appl. Mater. Interfaces. 2022, 14, 15517–15528. [Google Scholar] [CrossRef] [PubMed]
- Giardina, I. Animal Behaviour. Anim. Behav. 2011, 82, 608. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, G.Q.; Feng, Y.B.; Kuai, Y.B.; Chen, K.X.; Cong, J.W.; Piao, H.G.; Liu, Y.M.; Pan, L.Q. Highly Efficient Magnetic Propulsion of NiFe Nanorod-Based Miniature Swimmers in Three Dimensions. ACS Appl. Mater. Interfaces. 2021, 13, 58898–58907. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Wang, Y.X.; Kuai, Y.B.; Cong, J.W.; Xu, Y.L.; Piao, H.G.; Pan, L.Q.; Liu, Y.M. Magnetically Powered Shape-Transformable Liquid Metal Micromotors. Small. 2019, 15, 1905446. [Google Scholar] [CrossRef]
- Li, J.J.; He, X.L.; Jiang, H.D.; Xing, Y.; Fu, B.; Hu, C.Z. Enhanced and Robust Directional Propulsion of Light-Activated Janus Micromotors by Magnetic Spinning and the Magnus Effect. ACS Appl. Mater. Interfaces. 2022, 14, 36027–36037. [Google Scholar] [CrossRef] [PubMed]
- Li, S.S.; Liu, D.; Hu, Y.P.; Su, Z.J.; Zhang, X.N.; Guo, R.R.; Li, D.; Lu, Y. Soft Magnetic Microrobot Doped with Porous Silica for StabilityEnhanced Multimodal Locomotion in a Nonideal Environment. ACS Appl. Mater. Interfaces. 2022, 14, 10856–10874. [Google Scholar] [CrossRef] [PubMed]
- Song, S.J.; Mayorga-Martinez, C.C.; Jan, V.; Markéta, C.; Tomáš, R.; Pumera, M. Precisely Navigated Biobot Swarms of Bacteria Magnetospirillum magneticum for Water Decontamination. ACS Appl. Mater. Interfaces. 2023, 15, 7023–7029. [Google Scholar] [CrossRef] [PubMed]
- Kichatov, B.; Korshunov, A.; Sudakov, V.; Petrov, O.; Gubernov, V.; Korshunova, E.; Kolobov, A.; Kiverin, A. Magnetic Nanomotors in Emulsions for Locomotion of Microdroplets. ACS Appl. Mater. Interfaces. 2022, 14, 10976–10986. [Google Scholar] [CrossRef] [PubMed]
- Li, N.; Huang, G.W.; Liu, Y.; Qu, C.B.; Li, M.; Xiao, H.M. Performance Deficiency Improvement of CNT-Based Strain Sensors by Magnetic-Induced Patterning. ACS Appl. Mater. Interfaces. 2023, 15, 5774–5786. [Google Scholar] [CrossRef]
- Huang, T.; Li, B.; Wang, H.; Granick, S. Molecules, the Ultimate Nanomotor: Linking Chemical Reaction Intermediates to their Molecular Diffusivity. ACS Nano. 2021, 15, 14947–14953. [Google Scholar] [CrossRef]
- Liu, R.; Sen, A. Autonomous Nanomotor Based on CopperPlatinum Segmented Nanobattery. J. Am. Chem. Soc. 2011, 133, 20064–20067. [Google Scholar] [CrossRef] [PubMed]
- Mou, F.Z.; Li, X.F.; Xie, Q.; Zhang, J.H.; Xiong, K.; Xu, L.L.; Guan, J.G. Active Micromotor Systems Built from Passive Particles with Biomimetic Predator−Prey Interactions. ACS Nano. 2020, 14, 406–414. [Google Scholar] [CrossRef] [PubMed]
- Karshalev, E.; Berta, E.D.; Wang, J. Micromotors for “Chemistry-on-the-Fly”. J. Am. Chem. Soc. 2018, 140, 3810–3820. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.H.; Xiong, Z.; Liu, M.; Li, X.M.; Zheng, J.; Zhan, X.J.; Ding, W.T.; Chen, J.N.; Li, X.C.; Li, X.D.; Feng, S.P.; Tang, J.Y. Rational Design of Reversible Redox Shuttle for Highly Efficient Light-Driven Microswimmer. ACS Nano. 2020, 14, 3272–3280. [Google Scholar] [CrossRef]
- Wang, W.; Castro, L.A.; Hoyos, M.; Mallouk, T.E. Autonomous Motion of Metallic Microrods Propelled by Ultrasound. ACS Nano. 2021, 6, 6122–6132. [Google Scholar] [CrossRef]
- Garcia-Gradilla, V.; Orozco, J.; Sattayasamitsathit, S.; Soto, F.; Kuralay, F.; Pourazary, A.; Katzenberg, A.; Gao, W.; Shen, Y.F.; Wang, J. Functionalized Ultrasound-Propelled Magnetically Guided Nanomotors: Toward Practical Biomedical Applications. ACS Nano. 2021, 7, 9232–9240. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, S.; Wang, W.; Bai, L.J.; Gentekos, D.T.; Hoyos, M.; Mallouk, T.E. Density and Shape Effects in the Acoustic Propulsion of Bimetallic Nanorod Motors. ACS Nano. 2016, 10, 4763–4769. [Google Scholar] [CrossRef]
- Xu, T.L.; Soto, F.; Gao, W.; Dong, R.F.; Garcia-Gradilla, V.; Ernesto, M.; Zhang, X.J.; Wang, J. Reversible Swarming and Separation of Self-Propelled Chemically Powered Nanomotors under Acoustic Fields. J. Am. Chem. Soc. 2015, 137, 2163–2166. [Google Scholar] [CrossRef]
- Lu, X.L.; Wei, Y.; Ou, H.; Zhao, C.; Shi, L.K.; Liu, W.J. Universal Control for Micromotor Swarms with a Hybrid Sonoelectrode. Small. 2021, 17, 2104516. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.S.; Zhang, H.Y.; Wang, D.L.; Gao, C.Y.; Sun, M.M.; Wu, Z.G.; He, Q. Reconfigurable Assembly of Active Liquid Metal Colloidal Cluster. Angew. Chem. 2020, 132, 1–6. [Google Scholar]
- Gao, Q.; Yang, Z.; Zhu, R.T.; Wang, J.P.; Xu, P.Z.; Liu, J.Y.; Chen, X.W.; Yan, Z.Y.; Peng, Y.X.; Wang, Y.P.; Zheng, H.R.; Cai, F.Y.; Wang, W. Ultrasonic Steering Wheels: Turning Micromotors by Localized Acoustic Microstreaming. ACS Nano. 2023, 17, 4729–4739. [Google Scholar] [CrossRef] [PubMed]
- Athanassiadis, A.G.; Ma, Z.C.; Moreno-Gomez, N.; Melde, K.; Choi, E.; Goyal, R.; Fischer, P. Ultrasound-Responsive Systems as Components for Smart Materials. Chem. Rev. 2022, 122, 5165–5208. [Google Scholar] [CrossRef] [PubMed]
- Zhou, C.; Zhao, L.L.; Wei, M.S.; Wang, W. Twists and Turns of Orbiting and Spinning Metallic Microparticles Powered by Megahertz Ultrasound. ACS Nano. 2017, 11, 12668–12676. [Google Scholar] [CrossRef] [PubMed]
Figure 1.
Preparation and characterization of rod-shaped nanomotors. (a): Scheme of the fabrication of Ga-based nanomotors. (b): Absorption spectrum of the prepared nanomotors. (c-d): SEM image (scale bar: 100 nm) and (e) TEM image of nanomotors (scale bar: 200 nm). (f): High-resolution TEM image of a single nanomotor (scale bar: 10 nm). (g-h): EDX mapping images showing the distribution of Ga and O elements in a single nanomotor (scale bar: 100 nm). Inset: the corresponding SEM image (scale bar: 100 nm). (i): XPS spectrum and (j): XRD pattern of the nanomotors.
Figure 1.
Preparation and characterization of rod-shaped nanomotors. (a): Scheme of the fabrication of Ga-based nanomotors. (b): Absorption spectrum of the prepared nanomotors. (c-d): SEM image (scale bar: 100 nm) and (e) TEM image of nanomotors (scale bar: 200 nm). (f): High-resolution TEM image of a single nanomotor (scale bar: 10 nm). (g-h): EDX mapping images showing the distribution of Ga and O elements in a single nanomotor (scale bar: 100 nm). Inset: the corresponding SEM image (scale bar: 100 nm). (i): XPS spectrum and (j): XRD pattern of the nanomotors.
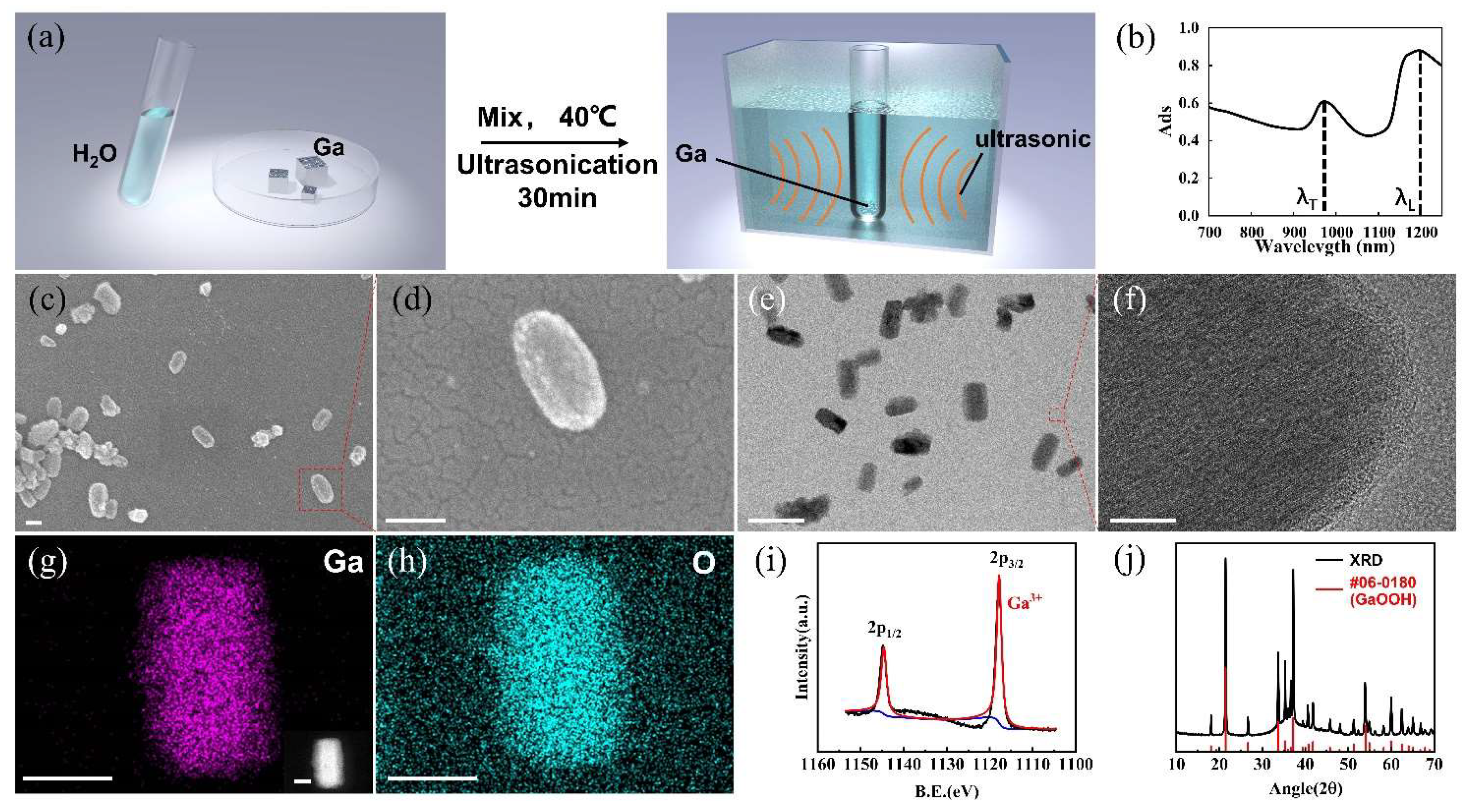
Figure 2.
The collective behaviors of the GaOOH nanometers under the ultrasonic field with different frequencies. (a): Scheme of the experimental setup. The ultrasonic platform consisting of a signal generator, a power amplifier, the ultrasonic platform, and a microscope for observation. (b) The collective behavior of nanomotors varying with the ultrasound frequency. Schematic diagrams (c, e, g) and experimental results (d, f, h) of three patterns of collective behavior. (d): Nanomotors exhibit a vortex-shaped pattern at an ultrasound frequency of 1.3 MHz; Scale bar: 20 µm. (f): Nanomotors exhibit stripe-like chains at a frequency of 1.4 MHz; Scale bar: 10 µm. (h): Nanomotors exhibit a cluster pattern at an ultrasound frequency of 2.8 MHz; Scale bar: 100 µm.
Figure 2.
The collective behaviors of the GaOOH nanometers under the ultrasonic field with different frequencies. (a): Scheme of the experimental setup. The ultrasonic platform consisting of a signal generator, a power amplifier, the ultrasonic platform, and a microscope for observation. (b) The collective behavior of nanomotors varying with the ultrasound frequency. Schematic diagrams (c, e, g) and experimental results (d, f, h) of three patterns of collective behavior. (d): Nanomotors exhibit a vortex-shaped pattern at an ultrasound frequency of 1.3 MHz; Scale bar: 20 µm. (f): Nanomotors exhibit stripe-like chains at a frequency of 1.4 MHz; Scale bar: 10 µm. (h): Nanomotors exhibit a cluster pattern at an ultrasound frequency of 2.8 MHz; Scale bar: 100 µm.
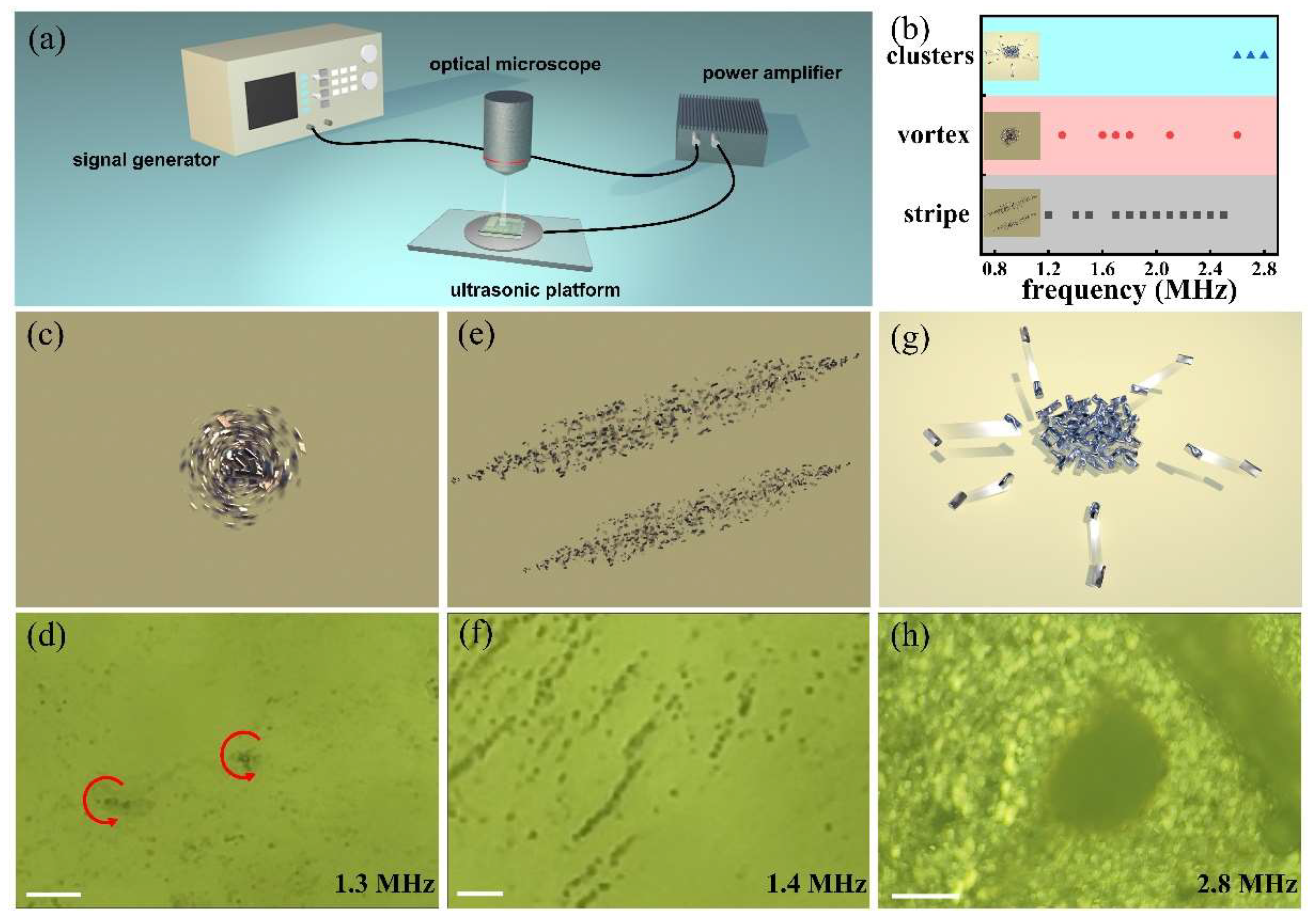
Figure 3.
Propagation characteristics of ultrasonic waves and acoustic pressure field distribution within the ultrasonic manipulation platform at different frequencies. (a): The ultrasonic manipulation platform is composed of a substrate glass, transducer, microfluidic cell, and cover glass. (b): The ultrasonic waves in the vertical direction generate secondary waves in the horizontal direction at the solid-liquid interface. (c): Schematic diagram of a microfluidic cell with dimensions of 5.2mm × 5.8mm × 0.26mm. (d-f): The corresponding collective behaviors at ultrasound frequencies of 1.7 MHz, 1.6 MHz, and 1.5 MHz; Scale bar: 50 µm; Corresponding to Video S3. (g-i): Simulation diagrams of the acoustic pressure field in the horizontal plane at frequencies of 1.7 MHz, 1.6 MHz, and 1.5 MHz.
Figure 3.
Propagation characteristics of ultrasonic waves and acoustic pressure field distribution within the ultrasonic manipulation platform at different frequencies. (a): The ultrasonic manipulation platform is composed of a substrate glass, transducer, microfluidic cell, and cover glass. (b): The ultrasonic waves in the vertical direction generate secondary waves in the horizontal direction at the solid-liquid interface. (c): Schematic diagram of a microfluidic cell with dimensions of 5.2mm × 5.8mm × 0.26mm. (d-f): The corresponding collective behaviors at ultrasound frequencies of 1.7 MHz, 1.6 MHz, and 1.5 MHz; Scale bar: 50 µm; Corresponding to Video S3. (g-i): Simulation diagrams of the acoustic pressure field in the horizontal plane at frequencies of 1.7 MHz, 1.6 MHz, and 1.5 MHz.
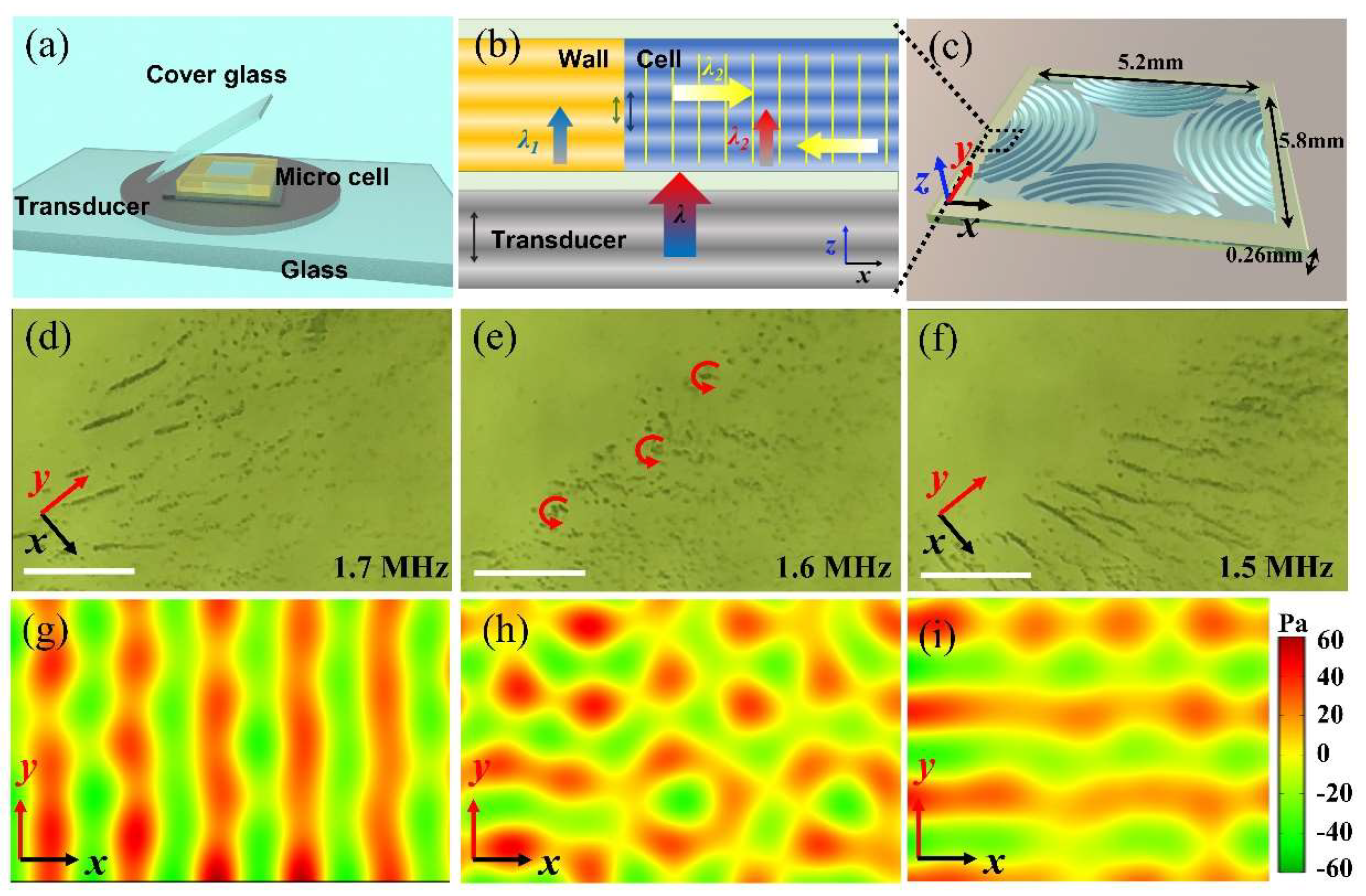
Figure 4.
Predicted and observed collective behavior patterns of nanomotors at different frequencies. The predicted collective behavior of nanomotors at different ultrasound frequencies is represented by black dashed lines, while the experimentally observed phenomena are denoted by red dots. Inset: Schematic diagram of a cell with dimensions 3.7mm × 10.6mm × 0.3mm.
Figure 4.
Predicted and observed collective behavior patterns of nanomotors at different frequencies. The predicted collective behavior of nanomotors at different ultrasound frequencies is represented by black dashed lines, while the experimentally observed phenomena are denoted by red dots. Inset: Schematic diagram of a cell with dimensions 3.7mm × 10.6mm × 0.3mm.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated




