Design and Modeling of Hardware Kit for QKD Education of Engineering Students and Communication Engineers

The paper discusses the design and modeling of a simple and illustrative hardware kit for teaching the basics of quantum cryptography to engineering students. The novel solution differs from those already on the market in that it is focused on familiarising trainees with the physical principles of quantum key distribution, as well as with the basics of mathematical formalism in quantum mechanics. This is achieved by using a minimally sufficient set of optical elements with a simple mathematical description in the Jones formalism. This composition of the kit is targeted mostly at engineering students and does not require advanced training in physics as a prerequisite. The configurable architecture of the hardware educational kit contributes to the deeper involvement of students. By independently changing the modular configuration of the system, students can conduct experiments that were not directly provided by the developers. For instance, students can assess the impact of choosing the basic settings of phase retarders on the course of a man-in-the-middle attack. The proposed amount of mathematical and informational support, as well as ready-made formal models, is sufficient to reasonably put forward hypotheses for experimental verification and interpret the obtained empirical data. At this moment, the hardware kit is being replicated, distributed and successfully applied at universities and companies in the communications industry. The accumulated experience of educational use testifies to the high efficiency of the kit as a tool for basic QKD training for people without prior knowledge of quantum mechanics. A discrete event model simulating the operation of the hardware kit is implemented in the non-commercial modeling software CPN Tools and is openly distributed.

Keywords:

Subject: Computer Science and Mathematics - Security Systems

1. Introduction

Quantum information technologies, and quantum computing in particular, have been developing rapidly in recent decades. [1] For this reason, cryptographic schemes with asymmetric encryption, which became classic in the 1980s, are expected to lose relevance in the next few decades. The well-known quantum Shore algorithm is able to provide exponential acceleration for solving problems of factorization, discrete logarithm and discrete logarithm on elliptic curves, which compromise almost all currently actively used public key cryptographic schemes as well as electronic signatures. [2,3] Either reliance on the wider use of symmetric cryptographic schemes or the development of asymmetric encryption protocols based on new mathematical principles, such as error-based learning or lattice-based cryptography, are considered possible solutions. [3,4]

It should be noted, however, that cryptographic attacks on symmetric encryption schemes will also be affected by the emergence of quantum computers. In particular, the use of quantum search in an unordered data storage, known as Grover's algorithm, makes it possible to significantly (O(n^1/2) versus O(n) for classical algorithms) speed up key searching. [3] Nonetheless, it is possible to counter this emerging advantage for the attacker by doubling the length of the encryption key. [5] The long-standing tendency toward the gradual increase of telecommunications devices computing capabilities leaves an inexhaustible potential to strengthen keys by this mean. [6] For this reason, even in the context of the predicted leap in quantum computing, attacks on symmetric cryptographic schemes will not become practical in the coming decades. [5,6]

The main problem in the practical application of symmetric cryptographic systems has always been and still is the requirement to share a common secret between both parties in information exchange. The only way to produce a shared secret that is simultaneously secure and practically feasible is based on the physical principles of quantum mechanics. Quantum key distribution (QKD) has been developed since the 1980s and is currently becoming an integral and critical element of the security infrastructure of real-world communication systems. [7] In the near future, we can expect a further increase in the coverage of quantum networks and an increase in their criticality, up to the emergence of a global quantum telecommunications network Qinternet predicted in [8].

Despite the recent advances, the introduction of QKD systems into the existing telecommunications infrastructure is associated with a multitude of challenges, such as technological [9,10,11,12], organizational and economic [13,14]. One of the important challenges for upscaling quantum networks today remains the lack of human resources capable of effectively running the quantum communications infrastructure. Due to a lack of sufficient training in the field of theoretical physics, the operation principles of QKD systems are often counterintuitive and difficult for specialists in classical communication systems to understand. Lacking a thorough understanding of the physical foundations behind the quantum protocols and the inherent drawbacks associated with their implementation can be considered a factor that could affect the security of networks negatively. [10]

The problem described above in a broader context has been labelled the "quantum skills gap" and is considered an urgent challenge in a number of global and national programs for the development of quantum telecommunications. [15,16,17] The issue is exacerbated by the fact that current telecommunications engineers typically do not receive adequate training in quantum theory to comprehend the physical principles of quantum information systems. Recent years have seen an increase in academic efforts focused on addressing the quantum skills gap, with the primary goal of transforming engineering and technological education at the university level. [18,19] Despite the necessity for such an approach to shape the future personnel landscape, its implementation will affect the industry only after a fair amount of time. A possible auxiliary solution, suitable for the field of quantum cryptography, would be focused ad-hoc training in the field of QKD for already enrolled students and current telecommunications engineers. This article studies recently developed educational technologies targeted at familiarizing various target groups with the principles of the QKD as well as hardware QKD educational kits available on the market.

From our perspective, the range of QKD educational solutions is not complete for two reasons. On the one hand, the majority of the training materials focus merely on the logical side of the implementation of the basic QKD protocols, which is clearly separate from the physical information transmission over a quantum channel. On the other hand, the remainder of the training and research kits for the QKD are compact but functional systems, requiring extensive theoretical training to operate effectively.

In this article, we propose an educational solution that, on the one hand, allows one to conveniently and systematically familiarize themselves with the physical principles of QKD and the mathematical formalism used to describe quantum optical systems and does not rely on complex mathematics and quantum mechanics. We consider this solution primarily a tool for the initial training of current telecommunications engineers, as well as engineering students, prior to practicing with more detailed QKD hardware. The experimental operation of the training kit in practical conditions has proven its efficiency for training and certification exams for telecommunications engineers without prior experience with quantum information systems.

The remainder of the paper is organized as follows. The next section briefly summarizes the logical basics of the QKD (using the example of BB84), discusses the educational technologies associated with the QKD training, and reviews a few well-known hardware QKD kits available on the market. The third section provides a functional diagram of our hardware kit as well as a simple, yet sufficient, formal description of its components based on Jones calculus. The fourth section presents a mathematical justification for the selection of phase retarders consisting of sequentially placed half-wave and quarter-wave plates, as well as describes the key design features of the hardware kit. The fifth section discusses the competitive features of our solution and shares the experience of its practical application in real-world cases. In the concluding section, we address the prospects for further development of our solution as well as the problem of QKD education in general.

2. Related Work

Specialized literature notes that despite all the accomplishments and undisputable success of quantum theory over the past hundred years, it is still characterized by exceptional conceptual complexity and is considered as a difficult thing to understand. [20,21,22,23] The systematic study of quantum mechanics is usually done at the university level in a set of special science disciplines, and is rarely done outside of them. This is becoming an urgent problem due to the drastic increase in the applied value of quantum mechanics observed in recent decades.

The current progress in the field of quantum computing, since its first practical instantiation in the late 1990s, has given impetus to the unprecedented development of quantum and post-quantum cryptography. [24] At this moment, QKD systems are already in the phase of extensive introduction into the current communication infrastructure. The rate and efficacy of the QKD system application are contingent upon the proficiency of the engineering personnel accountable for the general operation of communication systems. Eliminating the gap in the competencies of telecommunications engineers in the field of quantum mechanics is a pressing problem that requires a comprehensive approach to its solution. One of the key aspects of its solution is the development of new educational technologies applicable to training both students and practitioners.

2.1. BB84 QKD Protocol

The first BB84 QKD protocol was proposed by Bennett and Brassard in 1984 in [25]. To date, it is the most widely used both in practical applications [26] and in educational ones [27]. The advantage of the BB84 protocol is the relative simplicity of the underlying formal model. A detailed description of the protocol and the details of its practical implementation can be found in [28]. Further, we provide only the basic information essential to describe and reproduce the physical transmission of quantum states with polarization encoding.

The protocol uses four different quantum states of photon polarization. Further, these states are provisionally designated as follows

horizontal polarization ∣H⟩;
vertical polarization ∣V⟩;
diagonal polarization ∣D⟩;
anti-diagonal polarization ∣A⟩.

These states are mutually orthogonal within a pair (∣H⟩ and ∣V⟩, ∣D⟩ and ∣A⟩), conveying that they can be reliably distinguished when selecting the correct analyzer. Each of the two analyzers used in the protocol is characterized by a basis (HV or DA), which determines the quantum states that can be reliably distinguished with it. The four operational polarization states are selected in a way that makes it impossible to distinguish the orthogonal states within other pair when an incorrect analyzer is used. That is, for instance, a transmitted photon in state ∣H⟩ is equally likely to be registered with the analyzer DA as a photon in state ∣D⟩ or as a photon in state ∣A⟩. The last feature, in combination with the quantum no-cloning theorem, is the physical mechanism that ensures the security of data transmission. [25]

The transmission of photons via a quantum communication channel is the capital stage in the key distribution. A binary value is assigned to each of the polarization states of the received photons, for instance, ∣H⟩ and ∣D⟩ can be registered as 0, and ∣V⟩ and ∣A⟩ as 1. The transmitting side (Alice) sends a photon to the receiving side (Bob) in one of four possible polarization states. The choice of four states implies that Alice chooses both the binary value and the basis of the analyzer, which Bob should register the photon with. It is assumed that the state of the transmitted photon is randomly selected by the sender. In his turn, Bob is independent of Alice and randomly selects one of the two analyzers and registers the polarization state of the received photon. Depending on the choice of the state of the transmitted photon by Alice and the choice of the analyzer by Bob, various situations are possible, as shown in Table 1. Those accepted bits in which the bases of Alice and Bob coincide are known to both participants of the exchange and will be used further to produce the key material.

It should be noted that after the transmission of photons via the quantum channel, the data exchange within the instance of the protocol does not end. The generation of the key material requires a subsequent message exchange over the classical communication channel. In particular, in order to sift through the bits in which the bases do not comply, both parties are having to share with a peer the information regarding the bases they have chosen. Several more messages are used to estimate the bit error rate in the sifted bits and reconcile the key material. There is no interest in the content of messages transmitted over the classical channel and accompanying data processing in the framework of this paper. [26,29]

2.2. QKD Education

Over the last few years, educational technologies aimed at honing students' quantum skills have been intensively developed. The key trends in quantum education are the high interactivity of educational materials and their visual clarity, which are required to reach an expanding audience of trainees. To attain interactivity, both specially designed virtual environments [30,31,32] and physical kits are used [33,34,35,36]. Research papers consider QKD as the main subject of study [31,32,35,36] and as a demonstration of a real-world application of quantum mechanics, that is being studied in a broader context [20,37,38]. A significant number of research is devoted to introducing the concepts of quantum mechanics to an audience without a sufficient background in theoretical physics, including high school students [20,31,35,36,38,39]. Nevertheless, some educational solutions are targeted at a broader set of professionals, including those specializing in telecommunications and information security. [27,30,37]

Primarily, the BB84 protocol or its variants are used in the reviewed studies. In almost all cases, the formal aspect of the protocol (such as the choice of bases or message processing) remains unchanged. The physical aspect of the protocol, namely the information exchange over a quantum channel, could be implemented at different levels of detail. Thus, in [20] and [31,32] there was no intention to reproduce the photon exchange in a physically accurate way. In [37], somewhat simplified but physically accurate reproductions of real QKD systems are used. Intermediate solutions that imitate single photons with short light pulses are also widely presented. [33,35,36] Despite the fact that, for obvious physical reasons, no cloning could not be reproduced for such signals, it can be reproduced schematically or with a software in a lab kit. In [35], violations of this physical principle are used to demonstrate a side channel attack. The works [34,38] use commercially available QKD emulators, which are discussed further.

Along with the BB84 protocol, the E91 protocol [40], based on the effect of quantum entanglement, is a popular educational implement. In case of E91 kits, the cryptographic system usually serves as a visual demonstration for the Einstein-Podolsky-Rosen paradox. [30] As with BB84, both virtual solutions [30] and more physically accurate kits with beta barium borate crystals are available. [39]

We consider hardware kits imitating single photons with light pulses to be the most practical solution to the problem of the basic preparation of specialists for their subsequent training with more detailed QKD systems. An important prerequisite for such a conclusion was the fact that the physical operation of such a hardware can be adequately described using mathematical formalism, which is widely used in other engineering disciplines and is so familiar to trainees.

2.3. Hardware Educational Kits

The range of hardware kits available on the market, designed specifically for QKD education, is limited at this time. As we have noted above, for this reason, virtual emulators and fully functional equipment are widely used for training purposes.

The problem with the virtual solutions is that all physical processes are mathematically modeled, often not in the most physically accurate way. At the same time, software visualization of physical light transmission is not always graphical and clear, since it is considered mostly an addition to the formal description of the system. The description itself is based on the notation of quantum mechanics and is comprehensible only to a restricted audience with a background in theoretical physics.

Hardware solutions based on telecommunication equipment usually utilize optical fiber lines and operate at wavelengths beyond the visible spectrum. The latter has a negative impact on the clarity of physical transmission for the audience. Due to the complexity of the full-featured practical QKD equipment, in the educational settings it is often considered a black box by trainees, so it does not make an efficient supplementary material to the basic training. From our perspective, such a class of hardware is absolutely essential at the stage of honing practical skills for operating QKD systems, but it is redundant and ineffective at the stage of mastering the physical basics of quantum cryptography.

Rare exceptions that differ from the above-mentioned classes of education kits are represented by the following solutions:

EKPQC Quantum Cryptography Educational Kit by S-Fifteen Instruments [41],
quED-QKD by qutools [42]
QC Analogy Demonstration Kit by ThorLabs [43].

ThorLabs kit uses pulses of visible light to simulate single photons in data exchange over a quantum channel. It makes physics somewhat simplified but easy to comprehend and also makes data transmission easy to follow. Another feature of the solution is that it is based on manual configuration of optical components within the provided hardware set. On the one hand, this makes solutions flexible and potentially fitting to a wide variety of educational tasks, however, on the other hand, it requires qualified educators to design training activities and demonstration settings. The latter somewhat limits its applicability to dedicated university courses.

The qutools kits differ from the ThorLabs kits in that they have software-controlled actuators that allow one to automatically configure optical components for a basic set of training or demonstration scenarios. Other features of this solution are that it reproduces physical processes with very high accuracy and is able to produce entangled photon pairs. These merits make quED-QKD one of the best commercially available educational kits that could be applied to academic research in the field of quantum cryptography. Nonetheless, the control tools and visualization tools are geared towards specialists and thus pose a challenge for untrained students.

The S-Fifteen Instruments kit, as well as ThorLabs kit, simulates single photons with visible light pulses. At the same time, just like quED-QHD, it has the means to automate the configuration of optical components. A unique feature of the solution is that the classical channel is physically implemented as an infrared interface within the hardware. This kit physically models data exchange outside the initial photon exchange phase. That level of detail makes the solution restricted to the simulation of the BB84 protocol. There is also no possibility of arranging changes to the set of states of polarization used in exchange via the optical channel.

Figure 1. Commercially available hardware kits for QKD education: (a) EKPQC Quantum Cryptography Educational Kit [41]; (b) quED-QKD [42]; (c) ThorLabs QC Analogy Demonstration Kit [43].

3. Materials and Methods

When creating the educational kit, we elected a variant that simulates the transmission of photons by light pulses (such as the QC Analogy Demonstration Kit or EKPQC Quantum Cryptography Educational Kit). To manipulate the polarization, we used an optical system of two wave plates proposed in [44]. Similar yet less complex hardware solutions were designed and studied in [35,36] and [33]. Our QKD kit physically simulates the quantum channel of protocols with polarization encoding.

The light pulses are formed by a monochromatic laser and propagate freely in the air. The probability of bit error (BER) close to zero under normal operating conditions due to the small distance between the laser and the photoreceivers and the excessive pulse energy. Since the hardware has a training purpose, it cannot be considered a full-fledged QKD system. The optical pulses are not secure from interception by an attacker using a translucent mirror, as well as from other basic attacks. [45] The way the kit is designed allows one to simulate the impact of an active of passive attack, as well as signal contamination within the optical path.

3.1. Functional Diagram of the Hardware Kit

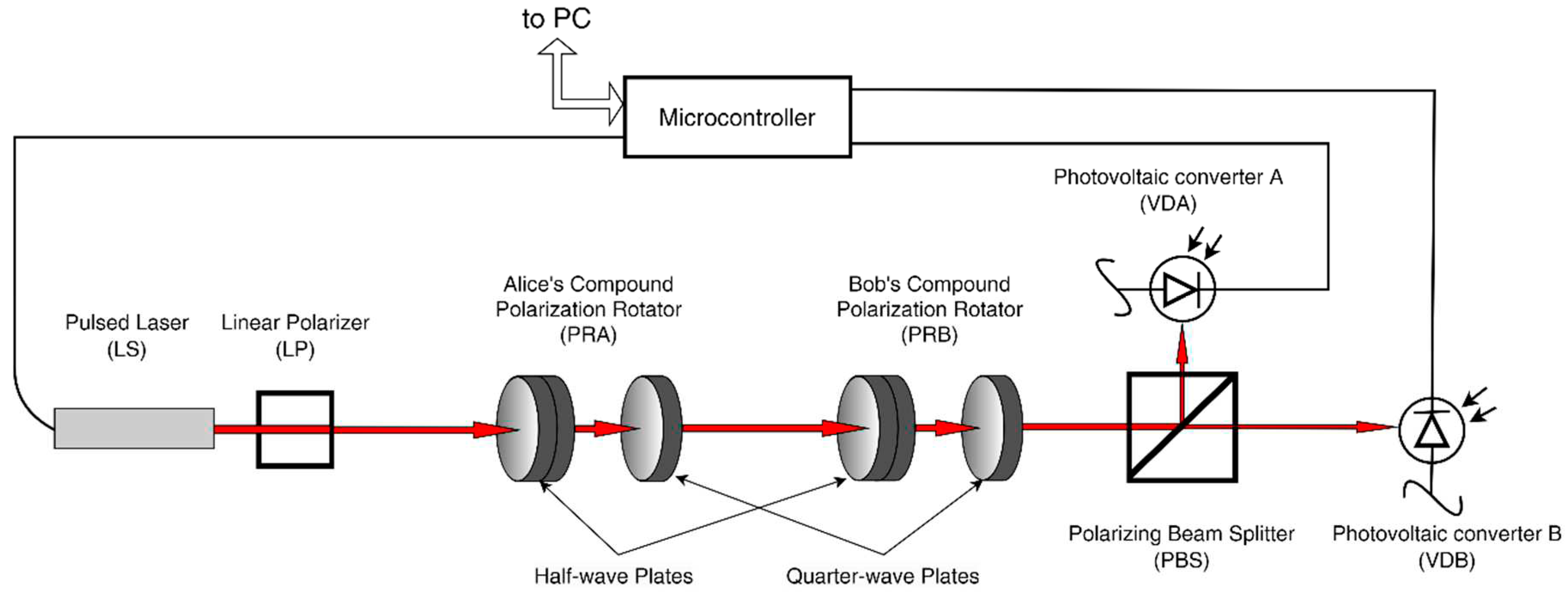
A functional diagram of the hardware is shown in Figure 2. In the two-party configuration, the kit is composed of two nonidentical modules. Alice's module includes a laser with a linear polarizer (LP) and polarization rotator (PRA). Bob's module includes an identical polarization rotator (PRB), a polarization beam splitter (PBS), two diode detectors (VDA, VDA) in photovoltaic mode. The polarization rotators consist of two wave plates used as phase retarders. The receiver and transmitter are controlled by a shared microcontroller, which also performs the interfaces function to a personal computer. The microcontroller initiates the emission of the laser pulses, manipulates both polarization rotators and registers the electrical voltage on the receiver's photodiode. When additional modules are introduced into the kit, for instance, one that simulates an active attack (Eva module), it has a separate microcontroller that is linked to the primary one.

3.2. Jones Calculus

Jones calculus is a convenient mathematical tool that is used to formally define the principles of optical signal transformation in an optical transmission channel. The foundation of this mathematical approach was proposed by R. Clark Jones in back in 1941 and since is being actively developed. [46,47,48] Currently it is applied in quantum cryptography [49] and beyond it [47,48,50]. To date, its numerous extensions and generalizations are suggested as for light beams with inhomogeneous polarization [47], or for vortex beam transformations [48].

We elected to use Jones calculus because of its relative simplicity, which makes the entry threshold minimal for students. Classical Jones calculus is exclusively based on matrix algebra and the formal analogy between complex numbers and planar rotating vectors. Such mathematical concepts are widely used in various branches of engineering, in particular in electrical engineering, control theory and communication theory, and are familiar to enrollees.

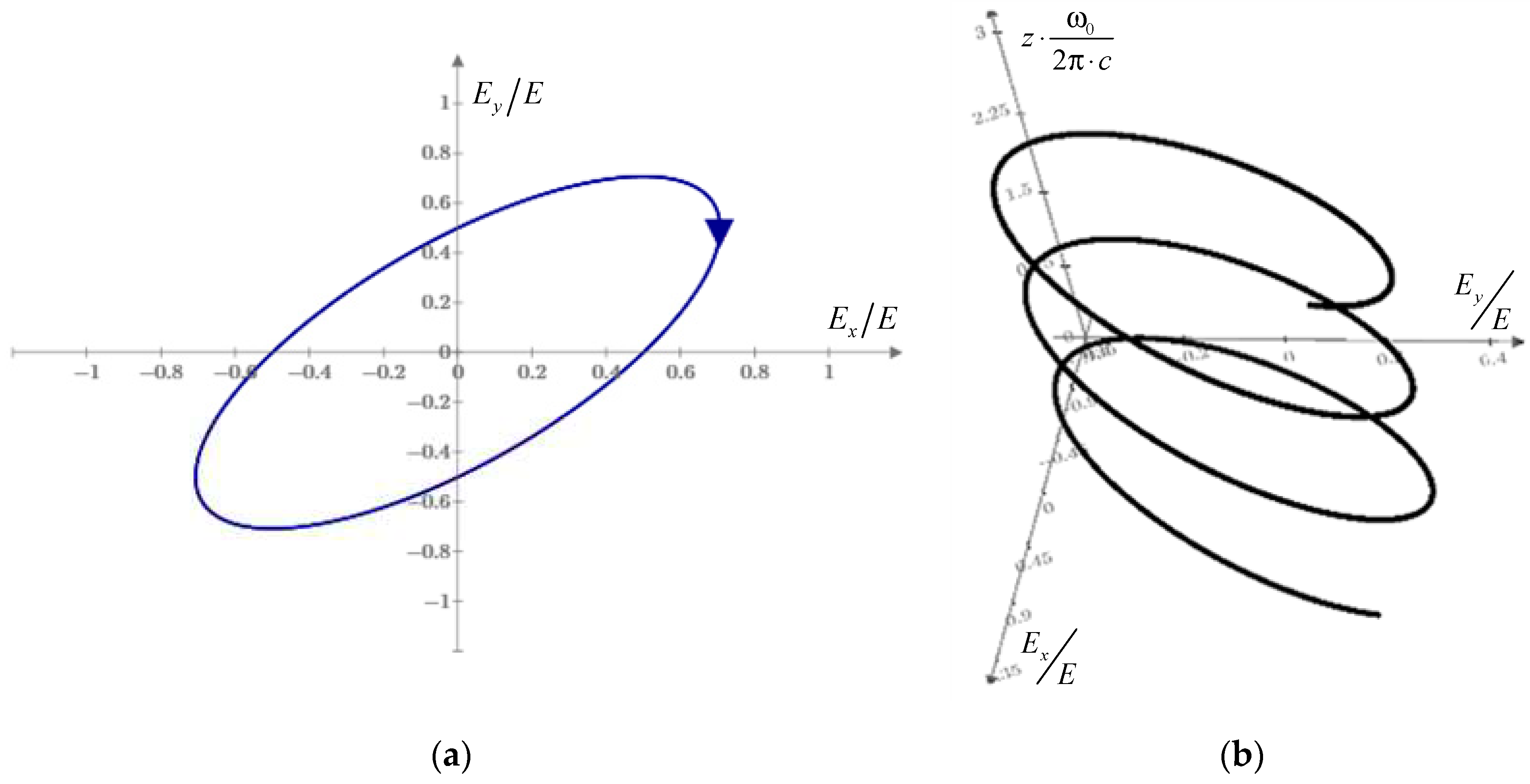
Widely known that light is a transverse electromagnetic wave. Considering monochromatic wave, that means, the vector of the electric field E(t,z) with incrementing time t draws some closed shape in a plane z = z₀ perpendicular to the direction of wave propagation. The shape of this drawn planar figure is uniquely determined by the intensity level of light and its polarization. [50] For demonstration, the spatial trajectory drawn by the vector E and the corresponding projection shape onto the transverse plane is shown in Figure 3.

Formally, a monochromatic light wave that propagates in the positive direction along the z axis can be defined as [51]

E (t, z) = (\begin{matrix} E_{x} \cdot e^{i \cdot φ_{x}} \cdot e^{i \cdot (\frac{ω_{0}}{c} \cdot z - ω_{0} \cdot t)} \\ \begin{array}{l} E_{y} \cdot e^{i \cdot φ_{y}} \cdot e^{i \cdot (\frac{ω_{0}}{c} \cdot z - ω_{0} \cdot t)} \\ 0 \end{array} \end{matrix}),

(1)

where E_x, E_y are components of the electric field vector in a transverse plane; φ_x, φ_y are the initial phase shifts of the components; ω₀ is the wave frequency; с the speed of light.

The third dimensional coordinate in (1) is trivial and of no interest for further consideration. Having excluded it, we transform (1) to the form

E (t, z) = E \cdot e^{i \cdot (φ - ω_{0} \cdot t)} (\begin{matrix} \cos (α) \\ \sin (α) \cdot e^{i \cdot Δ φ} \end{matrix}) e^{i \cdot (\frac{ω_{0}}{c} \cdot z)},

(2)

where

E_{x} = \cos (α) \cdot E, E_{y} = \sin (α) \cdot E, φ_{x} = φ, φ_{y} = φ + Δ φ .

The last multiplier in (2) is accountable for the spatial distribution of the oscillations. To formally define polarization, it is enough to consider an arbitrary point on the trajectory, as z = 0. For simplicity of notation, we will also omit the multiplier e^–ω0t. Then (2) will take the following form

E = E \cdot e^{i \cdot φ} (\begin{matrix} \cos (α) \\ \sin (α) \cdot e^{i \cdot Δ φ} \end{matrix}) .

(3)

The last two-dimensional multiplier in (3) is fully responsible for the polarization state of the wave and is named the Jones vector (J). [51] It is obvious that in the proposed form, the Jones vector has a unit metric

|J|

= 1. In this case, the intensity of light I is exclusively determined through the amplitude of the electric field E

I \propto E^{2},

where symbol ∝ denotes proportionality.

The coordinates of the Jones vector are associated with two invariant and extrinsic (relatively to the hardware) principle states of polarization (PSP). Since PSPs form a basis in two-dimensional space, any arbitrary Jones vector can be represented as a linear combination of PSPs

J (α, Δ φ) = (\begin{matrix} \cos (α) \\ \sin (α) \cdot e^{i \cdot Δ φ} \end{matrix}) = \cos (α) \cdot J_{X} + \sin (α) \cdot e^{i \cdot Δ φ} \cdot J_{Y},

(4)

J_{X} = (\begin{matrix} 1 \\ 0 \end{matrix}), J_{Y} = (\begin{matrix} 0 \\ 1 \end{matrix}) .

where J_X, J_Y are mutually orthogonal PSPs.

All basic optical transformations according to the Jones formalism are specified as multiplying the transfer function of the TF_A transformation by the input electrical field vector E_in defined by (3)

E_{out} = T F_{A} \times E_{in},

(5)

T F_{A} = k_{A} \cdot M_{A},

(6)

where k_A is the scalar complex-valued factor; M_A is the complex-valued Jones matrix.

As far as the proposed kit uses polarization states for encoding, for the sake of simplicity of a formal description, we further neglect alterations in intensity and phase shift within the optical channel. Therefore, instead of (5), we will use

J_{o u t} = M_{A} \times J_{i n},

where J_in, J_out are the states of polarization of the input and output optical signals, respectively.

The sequence of consecutive transformations of the polarization state, which are described by the series of Jones matrices M_A, M_B, M_C can be represented by one equivalent transformation with the matrix M_E

M_{E} = M_{C} \times M_{B} \times M_{A} .

(7)

All optical transformations used in Figure 2 could be divided into two classes: polarization filtration and polarization alteration without introducing attenuation. In the latter case, the M_P transformation matrix is unitary and satisfies the following equation

M_{P}^{†} \times M_{P} = U,

(8)

where symbol † denotes matrix conjugate transpose; U is the identity matrix.

The transfer functions of the basic optical components are well known and described, for example, in [51]. In further sections, only the components that used in our solution are discussed in the needed details.

3.3. Bases in Polarization Encoding

As we have addressed before, protocol BB84 with polarization encoding requires discriminating four states of polarization ∣H⟩, ∣V⟩, ∣D⟩, ∣A⟩ which constitute two bases (HV, DA) which are not orthogonal one to another.

Let us assume that the "horizontal" polarization state ∣H⟩ is described by the arbitrary Jones vector

| H 〉 = J_{H} = (\begin{matrix} \cos (α) \\ \sin (α) \cdot e^{i \cdot Δ φ} \end{matrix}) .

In this case, the befitting "vertical" polarization ∣V⟩ can be determined with the condition of vectors orthogonality

〈 V | H 〉 = J_{V}^{†} \times J_{H} = 0 .

So we have

| V 〉 = J_{V} = (\begin{matrix} - \sin (α) \\ \cos (α) \cdot e^{i \cdot Δ φ} \end{matrix}) .

An appropriate non-orthogonal basis constituted of "diagonal" ∣D⟩ and "antidiagonal" ∣A⟩ polarizations can be made based on the following equality

| 〈 D | H 〉 | = | 〈 D | V 〉 | = | 〈 A | H 〉 | = | 〈 A | V 〉 | = \frac{1}{\sqrt{2}} .

(9)

According to (9), the modules of all projections of the vectors J_D and J_A on the vectors J_H and J_V are numerically equal. This means that the corresponding complex values of the projections are the coordinates of the vectors J_D, J_A in the basis of the vectors J_H, J_V. That is, up to a complex scalar multiplier with a single module, representable as

| D 〉 = \frac{1}{\sqrt{2}} \cdot | H 〉 + \frac{1}{\sqrt{2}} \cdot e^{i \cdot Q_{D}} \cdot | V 〉, | A 〉 = \frac{1}{\sqrt{2}} \cdot | H 〉 + \frac{1}{\sqrt{2}} \cdot e^{i \cdot Q_{A}} \cdot | V 〉,

(10)

where Q_D, Q_A are real values. In order for ∣D⟩, ∣A⟩ to form a basis, it is sufficient and required that the representation of ∣D⟩, ∣A⟩ in the basis of ∣H⟩, ∣V⟩ are linearly independent. This means that condition Q_A = Q_D ± π must be true. Since any of the bases formed in this way is equally fitting, we are free to assume that Q_D = 0 for simplicity. In this case, (10) will take the form

| D 〉 = \frac{1}{\sqrt{2}} \cdot | H 〉 + \frac{1}{\sqrt{2}} \cdot | V 〉, | A 〉 = \frac{1}{\sqrt{2}} \cdot | H 〉 - \frac{1}{\sqrt{2}} \cdot | V 〉 .

(11)

Before proceeding to the definition of optical components and corresponding transformations in the Jones formalism, it is essential to focus on the properties of polarization rotators which alter states of polarization without introducing attenuation to the signal. As we have already noted, the matrix M_P of such transformations satisfies (8), therefore, its columns are orthogonal vectors. [51] That means that for PSPs J_X, J_Y

J_{Y}^{'} \times J_{X}^{'} = 0,

(12)

J_{X}^{'} = M_{P} \times J_{X}, J_{Y}^{'} = M_{P} \times J_{Y} .

Using the linearity of matrix multiplication, as well as (12) and (4), we can easily show that the transformations of polarization rotators preserve the mutual relation between the polarization states represented at their inputs. Thus, the use of a polarizer to mutually orthogonal states ∣H⟩, ∣V⟩ will result in another pair of mutually orthogonal states ∣H′⟩, ∣V′⟩. In the same way, that kind of transformation will preserve ratios defined in (11) for all four possible states ∣H′⟩, ∣V′⟩, ∣D′⟩, ∣A’⟩.

3.4. Optical Components

The kit uses a linear polarizer (LP), a PBS, half-wave plates (HW), quarter-wave plates (QW). A formal description of these components introduced further.

3.4.1. Linear Polarizer

An LP is an optical filtering device capable of passing the polarization component that is parallel to its optical axis and completely absorbing the orthogonal component. [51] For this reason, the state of polarization of the optical signal at the output of an LP is determined exclusively by the properties of the component itself and does not depend on the state of polarization of the input signal

J_{O U T} = (\begin{matrix} \cos (θ) \\ \sin (θ) \end{matrix}), \forall J_{I N},

where θ is the angle between the axis of transmission in LP and the PSP J_X.

The light intensity at the output is dependent on both the input polarization and output polarization. The complex attentuation rate is defined as the projection of J_OUT on J_IN

k_{L P} = J_{I N}^{†} \times J_{O U T} .

(13)

Considering (4), we transform (13) to

k_{L P} = \cos (θ) \cdot \cos (α) + \sin (θ) \cdot \sin (α) \cdot (\cos (Δ φ) + i \cdot \sin (Δ φ)) .

(14)

If we bind the PSP J_X to the transmission axis of LP so (J_OUT = J_X), then (14) will be written as

k_{L P} = \cos (α) .

(15)

The LP in the scheme in Figure 2 is used to get rid of the possible deviation of the polarization state of the light at the LS output. To estimate the pulse intensity I₀ after LP one can take pulse intensity produced by LS as I_LS and multiply by with (15)

I_{0} = k_{L P} \cdot I_{L S} .

3.4.2. Polarizing Beam Splitter

The PBS partially transmits and partially reflects the light incident on it. The ratio between the intensity of transmitted and reflected beams is determined by the polarization of the incident light. Formally, this component can be defined as a pair of LPs placed on parallel branches in data flow diagram. The transmission axes of the LPs are mutually orthogonal. Therefore, the PBS physically decomposes the input Jones vector J_IN into the basis of linear polarizations J^A_OUT, J^B_OUT

J_{O U T}^{A} = (\begin{matrix} \cos (θ) \\ \sin (θ) \end{matrix}), J_{O U T}^{B} = (\begin{matrix} - \sin (θ) \\ \cos (θ) \end{matrix}),

where θ is the angle between the transmission axis and PSP J_X. The corresponding attenuation rates are defined by

k_{P B S}^{A} = \cos (θ) \cdot \cos (α) + \sin (θ) \cdot \sin (α) \cdot (\cos (Δ φ) + i \cdot \sin (Δ φ)), k_{O U T}^{B} = - \sin (θ) \cdot \cos (α) + \cos (θ) \cdot \sin (α) \cdot (\cos (Δ φ) + i \cdot \sin (Δ φ)) .

(16)

If we place PBS in a way that its axis transmission axis coincides with the transmission axis of the LP, so J^A_OUT = J_X, J^B_OUT = J_Y, then (16) will be written as

k_{P B S}^{A} = \cos (α), k_{O U T}^{B} = \sin (α) \cdot (\cos (Δ φ) + i \cdot \sin (Δ φ)) .

(17)

3.4.3. Half-Wave Plate

A HW plate is used to alter the polarization state without changing the intensity of the signal itself. Here and after, we neglect the optical losses that appear due to reflection from the surface of the plates' material. Structurally, HW plate is a thin piece of birefringence material. The difference in refractive indices associated with the two orthogonal axes within the plate introduces the phase shift between the orthogonal components of the electric field. The latter leads to an alteration in the state of polarization of the light on the backside of the plate.

The thickness of the HW plate is selected in such a way that the phase shift between the light components polarized along the fast and slow axes of the element is equal to π.

The transfer function of the HW plate is defined by the Jones matrix [51]

H W (θ) = (\begin{matrix} \cos (2 \cdot θ) & \sin (2 \cdot θ) \\ \sin (2 \cdot θ) & - \cos (2 \cdot θ) \end{matrix}),

(18)

where θ is the angle between the fast axis of the plate and PSP J_X.

Regardless of θ, the matrix (18) satisfies (8) and is unitary. Assuming that the light at the front side of the plate is linearly polarized and its state of polarization is defined by J_IN, then the light at backside of the plate will also be linearly polarized, so

J_{O U T} = H W (θ) \times J_{I N} = (\begin{matrix} \cos (2 \cdot θ) & \sin (2 \cdot θ) \\ \sin (2 \cdot θ) & - \cos (2 \cdot θ) \end{matrix}) \times (\begin{matrix} \cos (α) \\ \sin (α) \end{matrix}),

J_{O U T} = (\begin{matrix} \cos (2 \cdot θ - α) \\ \sin (2 \cdot θ - α) \end{matrix}) = (\begin{matrix} \cos (α + 2 (θ - α)) \\ \sin (α + 2 (θ - α)) \end{matrix}) .

(19)

3.4.4. Quarter-Wave Plate

A QW plate does not differ much from a HW plate in its design or principle of operation. The only essential difference is that the plate thickness is selected in such a way that the phase shift between the light components polarized along the fast and slow axes of the element is π/2. That normally means that QW plate is about two times thinner than HW plate. The transfer function of a QW plate without considering a complex scalar is defined as [51]

Q W (θ) = (\begin{matrix} \cos^{2} (θ) + i \cdot \sin^{2} (θ) & (1 - i) \cdot \sin (θ) \cdot \cos (θ) \\ (1 - i) \cdot \sin (θ) \cdot \cos (θ) & i \cdot \cos^{2} (θ) + \sin^{2} (θ) \end{matrix}),

(20)

where θ is the angle between the fast axis of the plate and PSP J_X. Matrix (20) satisfies (8) and is unitary.

3.5. Simulation of Detectors

To simulate the behavior of photon detectors in real-world system, we have used a pair of diodes in photovoltaic mode (VDA and VDB in Figure 2). The energy of the light pulse after the PBS falls on two photodiodes and is converted into an electric voltage by means of a transimpedance amplifier. [52] The operating point of the photovoltaic output characteristic of the converters is selected in such a way as to ensure the linear dependence between the voltage V and the intensity I of the received light pulse

V = k_{D} \cdot I .

Let us assume that the light intensity at the PBS is I_PBS, so we can estimate the voltage V^A, V^B at the output of photovoltaic converters

V^{A} = k_{D} \cdot {| k_{P B S}^{A} |}^{2} \cdot I_{P B S}, V^{B} = k_{D} \cdot {| k_{P B S}^{B} |}^{2} \cdot I_{P B S} .

(21)

Considering (17), we then transform (21)

V^{A} = k_{D} \cdot \cos {(α)}^{2} \cdot I_{P B S}, V^{B} = k_{D} \cdot \sin {(α)}^{2} \cdot I_{P B S} .

(22)

The voltages V^A, V^B are supplied to analog-to-digital converters (ADCs) of the microcontroller. Further, the following simple algorithm is used to determine the active detector:

uniformly distributed U(0,1) real value R is randomly generated;
detector A is considered active when the following condition is true

$R \leq \frac{V^{A}}{k_{D} \cdot I_{0}};$
detector B is considered active when the opposite condition is true

$R \geq 1 - \frac{V^{B}}{k_{D} \cdot I_{0}} .$

In terms introduced in Table 1, the triggering of detector A can be considered the registration of a zero bit. Similarly, the triggering of detector B is the registration of a unit bit. From the equations above, it is easy to show that

P (A) = \cos {(α)}^{2} \cdot \frac{I_{P B S}}{I_{0}}, P (B) = \sin {(α)}^{2} \cdot \frac{I_{P B S}}{I_{0}} .

(23)

The last multiplier in (23) in the logic of the analogy can be interpreted as the probability of "photon loss". The difference between I_PBS and I₀ may be due, for example, to the presence of an eavesdropper in the channel executing a passive attack with a semitransparent mirror. In this scenario, the voltage value k_D·I₀ can be measured prior to the introduction of the attacker into the model. In different cases, an alternative way to get the denominator k_D·I₀ = V^A+V^B can be applied.

4. Modeling and Designing

This section discusses the principles of manipulating the states of polarization with compound polarization rotators (PRA and PRB). In addition, we describe some essential aspects of the hardware design of the kit and, in particular, the positioning technique for wave plates. The final part of the section presents the virtual implementation of the described model in the CPN Tools simulation environment.

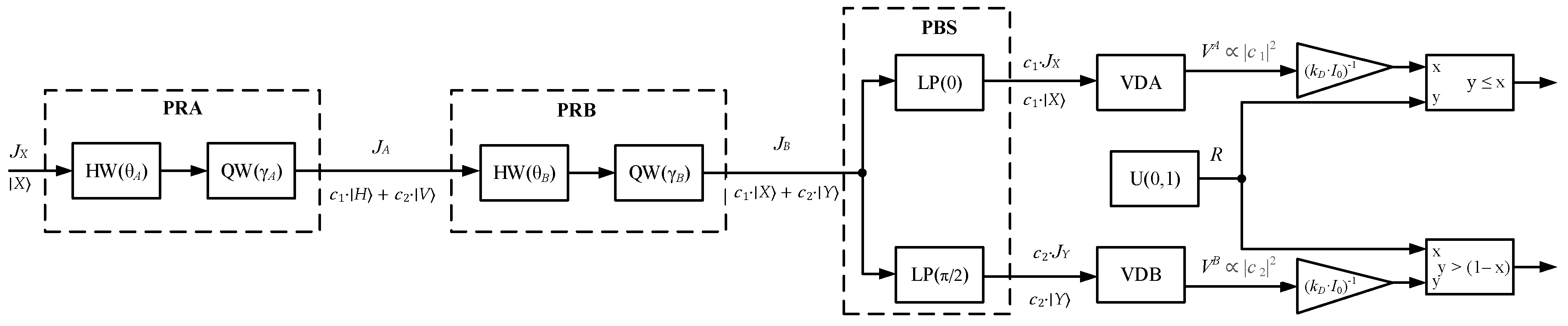
4.1. Flow Diagram

Figure 4 shows a data flow diagram that uses the notation introduced in the previous section. The PRA manipulates the polarization state of the transmitted light pulse. The LS signal is sent to the PRA via an LP, and its state of polarization always corresponds to one of the PSPs. Within the compound rotator PRA, there are two wave plates with electrical drives and angular position sensors each. Both HW and QW plates are controlled independently. So the polarization of Alice's signal is set by positioning the HW and QW within PRA at angles θ_A, γ_A correspondingly. Similarly, the choice of the Bob's basis is made by rotating the PRB plates at angles θ_B, γ_B. Then the signal is decomposed by PBS into the PSP basis and converted to electrical voltage by VDA, VDB. Depending on the rising at the output of the converters, the microcontroller registers one of the detectors as active.

The control of the angular position of the plates during the transmission session, that is, generating the setpoints for electrical drives, is carried out by the microcontroller in automatic mode or guided mode. The principal configuration, including the selection of polarization bases, is done by the user via software on a personal computer.

4.2. Compound Rotators Transfer Function

The compound polarization rotators on the receiving and transmitting sides are comprised of half-wave and quarter-wave plates sequentially placed in the path of light. According to (7), the rotators transfer function can be defined as

P R (θ, γ) = Q W (γ) \times H W (θ) .

(24)

Since the states of polarization of the light at the frontside of PRA and at the backside of PRB are unchanged and therefore bound to the PSPs, so it shall be

P R (θ_{B}, γ_{B}) \times P R (θ_{A}, γ_{A}) = U,

(25)

where θ_A, γ_A are angular positions of HW and QW plates at transmitting side; θ_B, γ_B are angular positions of HW and QW plates at receiving side.

As long as matrices (18) and (20) are both unitary, so are their products. Therefore, for (25) we have

P R {(θ, γ)}^{†} = P R {(θ, γ)}^{- 1} .

In order to get the angular positions of the plates required to inverse the transformation, let us make the equation

P R (θ + Δ θ, γ + Δ γ) = P R {(θ, γ)}^{†},

(26)

where ∆θ, ∆γ are extra rotations of HW and QW plates respectively.

Taking (26), we can produce a system of four equations by equating the corresponding elements of the matrices. Using the symbolic processor of the Mathcad Prime 5 for trigonometric transformations, one can verify that ∆θ = π/2, ∆γ = 2·(θ-γ)+π/2 turn (25) into an identity.

Thus, in order to ensure (25), one only needs to select

θ_{B} = θ_{A} + π / 2, γ_{B} = γ_{A} + 2 \cdot (θ_{A} - γ_{A}) + π / 2, \forall θ_{A}, γ_{A} .

(27)

4.3. Managing Bases in BB84

The implementation of the BB84 protocol with polarization encoding requires the choice of one of the four polarization states by Alice and the choice of one of the two bases by Bob. In our scheme, phase rotators are used to manipulate polarizations on both sides.

4.3.1. Manipulations with Rotator on Alice’s Side

State of polarization J_A of the light at the input of the optical channel is defined as

J_{A} = Q W (γ_{A}) \times H W (θ_{A}) \times J_{X} .

Assuming θ_A = θ₀, γ_A = γ₀ we consider

| H 〉 = Q W (γ_{0}) \times H W (θ_{0}) \times J_{X} .

Therefore, considering (19), equation for ∣V⟩ takes form

| V 〉 = Q W (γ_{0}) \times H W (θ_{0} + π / 4) \times J_{X} .

In the same fashion, we define ∣D⟩ and ∣A⟩

| D 〉 = Q W (γ_{0}) \times H W (θ_{0} + π / 8) \times J_{X},

| A 〉 = Q W (γ_{0}) \times H W (θ_{0} - π / 8) \times J_{X} .

The set of angular positions θ_A, γ_A applicable to use in BB84 is presented in Table 2.

4.3.2. Manipulations with Rotator on Bob’s Side

In order to set receiver’s analyzer to HV basis we can use (27) considering that θ_A = θ₀, γ_A = γ₀.

θ_{B} = θ_{0} + π / 2, γ_{B} = γ_{0} + 2 \cdot (θ_{0} - γ_{0}) + π / 2 .

Similarly, to set analyzer to DA we use (27) considering θ_A = θ₀ + π/4, γ_A = γ₀

θ_{B} = θ_{0} + 5 π / 8, γ_{B} = γ_{0} + 2 \cdot (θ_{0} - γ_{0}) + 3 π / 4 .

Angular positions θ_B, γ_B for use in BB84 are presented in Table 2.

4.3.3. Polarization Basses in Optical Path

The proposed scheme allows one to vary the polarization states of the light transmitted to the optical channel. In general, with the few exceptions discussed below, those states of polarization are elliptical. Proper operation of the optical channel requires consensus between parties regarding the base angular positions θ₀, γ₀. Manageable non-elliptical polarization states are presented in Table 3.

The method of manipulating the polarization state in Table 2 does not allow the use of linear bases. However, this option could be applied with the proposed compound rotators. To do this, one should select the angular positions according to Table 4. In the table below, α is the angle between the polarization state ∣H⟩ and the PSP.

4.4. Hardware Implementation

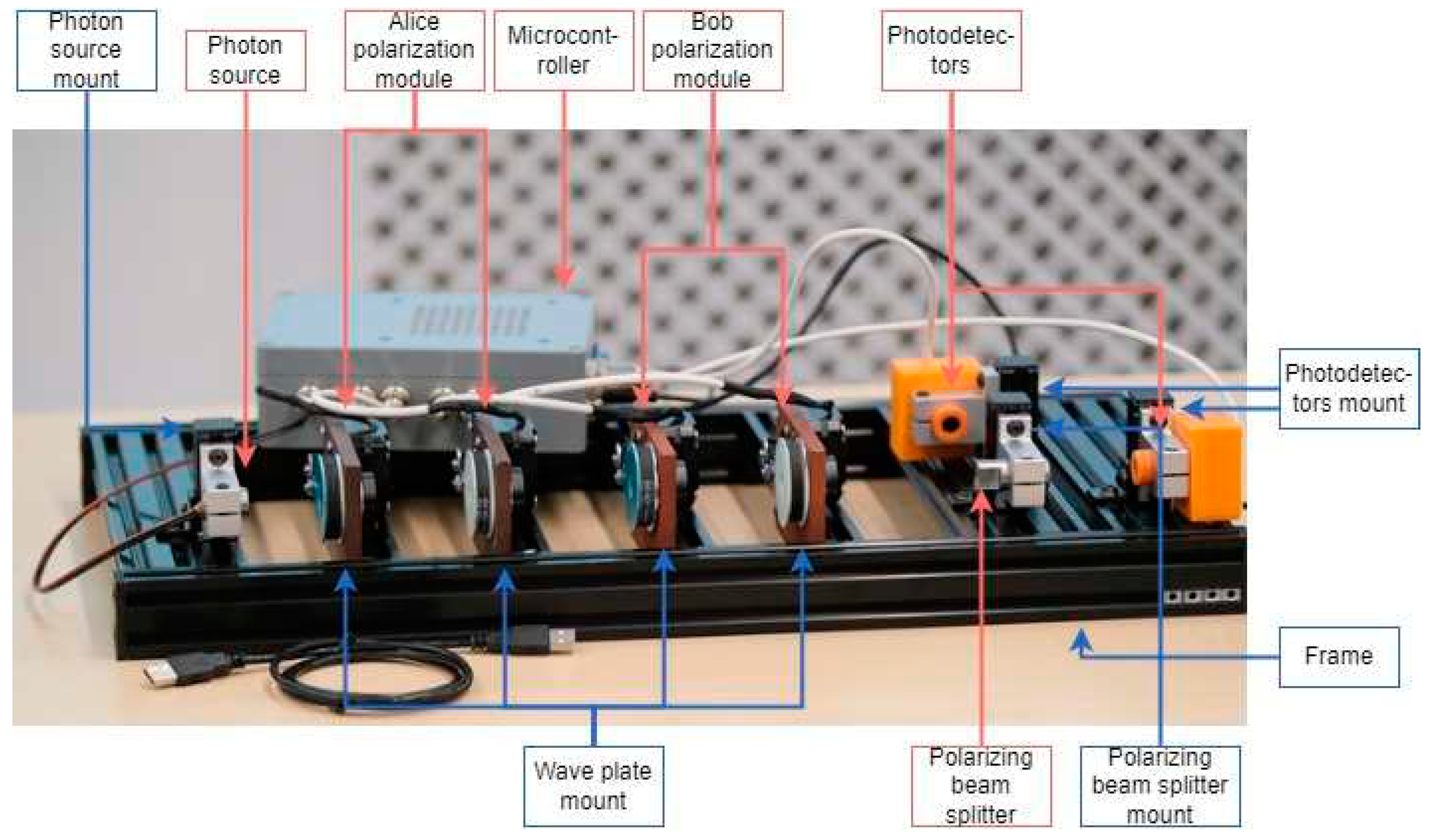
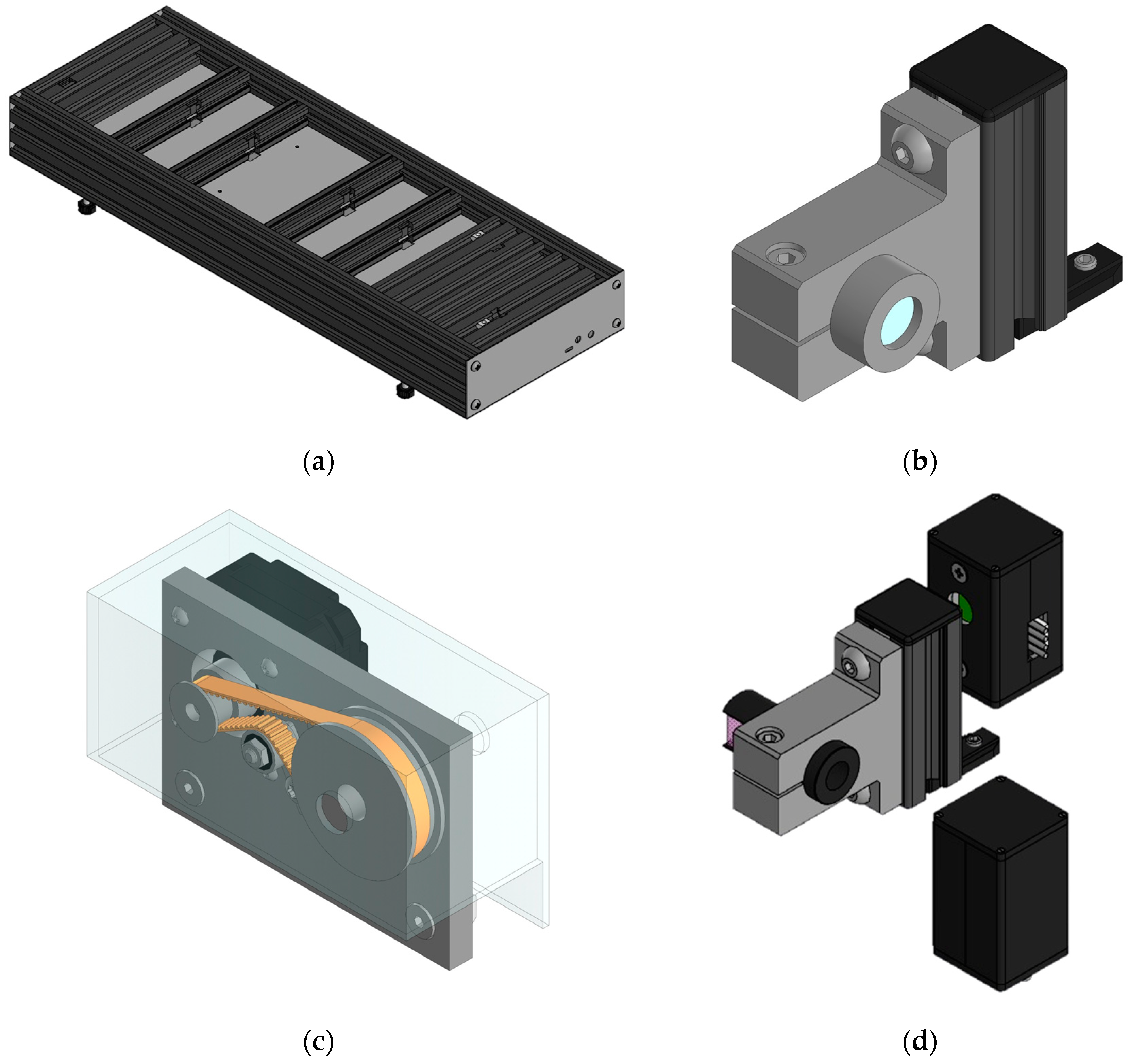
The assembled hardware educational QKD kit is in Figure 5.

We developed the hardware, pursuing several criteria that are essential for its practical operation. One of those criteria was the ability to keep the kit in a near-operational state during transportation. It implies that the kit can be run out of the box without lengthy assembly, tuning and testing. The latter is important because it eliminates the necessity for a qualified specialist to prepare the kit on the spot, this task can be easily solved by a regular user.

With this in mind, we designed a solid frame to apply a rigid fixation to the optical components and preserve the optical axis by this means. The frame is built with metal railings and supplementary metal stiffeners to maintain an original shape under the pressure. To attach optical components conveniently and reliably to the frame with bolt clamps, we designed stiffened mounts with original construction. The frame design is shown in Figure 6a.

For greater clarity of the optical transmission taking place, we decided to use a light monochromatic source operating in pulse mode (pulse width of 120 ms) at a wavelength of 523 nm (green light). To avoid potential injuries in a classroom environment, we chose a compact, low-power laser (up to 5 mW). To neglect the effect of the non-polarized component of the emitted light on photodetectors and to make the solution robust to accidental rotations of the source, we placed an additional liner polarizer on it. The design of the mount for the light source is shown in Figure 6b.

Polarization encoding in QKD is executed by manipulating the angular positions of the wave plates in the compound polarization rotators. An individual control circuits, comprised of stepper motors and encoders, are used to set an angular position for each of the four plates. Stepper motors provide the accuracy of angular positioning up to 0.3 degrees. The design of the mount for the wave plates is shown in Figure 6c. The microcontroller takes the setpoint for each plate and their current positions and then renders tasks for each of the motors. The setpoints are determined by the mode of operation or selected by the user via the operator station, that is, a dedicated PC. Such an architecture provides ease of operation on the one hand and, on the other hand, diversion and flexibility in choosing the states of polarization used for encoding. These features distinguish our solution from many analogues on the market.

In order to streamline the preparation of the kit for operation after its transportation, we have introduced a special initialization algorithm into the software of the operator station. Our observations have shown that during the relocation, the angular offset between the plates' optical axes and the sensors' initial position is not always preserved. The initialization algorithm is triggered at the first start and automatically updates the offset and stores it in the long-term memory for future use. The algorithm utilizes exclusively optical channel and does not require any input from the user.

A PBS and a pair of photodetectors are used to detect the state of polarization of the received light pulse. The exact position of the PBS on the optical axis of the kit, as well as the relative position of the PBS and the photodetectors, are critical for the accuracy of operation. In order to ensure this, we have designed a mount for these elements that makes their relative displacement virtually impossible. The mounts for the PBS and the photodetectors in shown in Figure 6d.

The PC is responsible for the interaction between a user and the hardware. All subsequent phases of data processing included in the QKD protocol of choice are performed by the special software installed on the PC. Data exchange over a classical channel is emulated virtually within the software.

The overall dimensions of the frame were chosen in such a way as to leave the possibility of including an extra module in the kit. These modules could imitate a passive or an active attacker. We are currently finalizing design of the supplementary modules and studying the methods of their seamless integration into the hardware kit. In the future, the proposed stand will allow not only to teach the basics of QKD, but also to demonstrate how attacks on such systems occur and how can they be countered.

4.5. Discrete-Event Model

As a supplement to the hardware kit, we have designed its software models. We have used this virtual kit both for educational purposes and as a prototyping tool while designing a hardware kit. For external use, we offer a discrete event model created in the openly distributed CPN Tools environment.

The CPN Tools modeling software is licensed under the GNU General Public License v. 2 and is available for free download on [53]. This tool is designed for discrete event modeling in the notation of colored Petri nets. [54] The Standard Meta Language (SML) is used as the main programming language. So the modeling environment combines imperative and declarative development paradigms that makes it a lite, but effective tool to animate data flow diagrams. [53] This software package has found academic recognition as a visual and simple tool for formal modeling of telecommunications [55,56] and computing systems [57,58]. The merit of CPN Tools is the bulk of open documentation provided by the developers. Beside the information, the software features a configurable subsystem for automated distribution and assessment of student assignments.

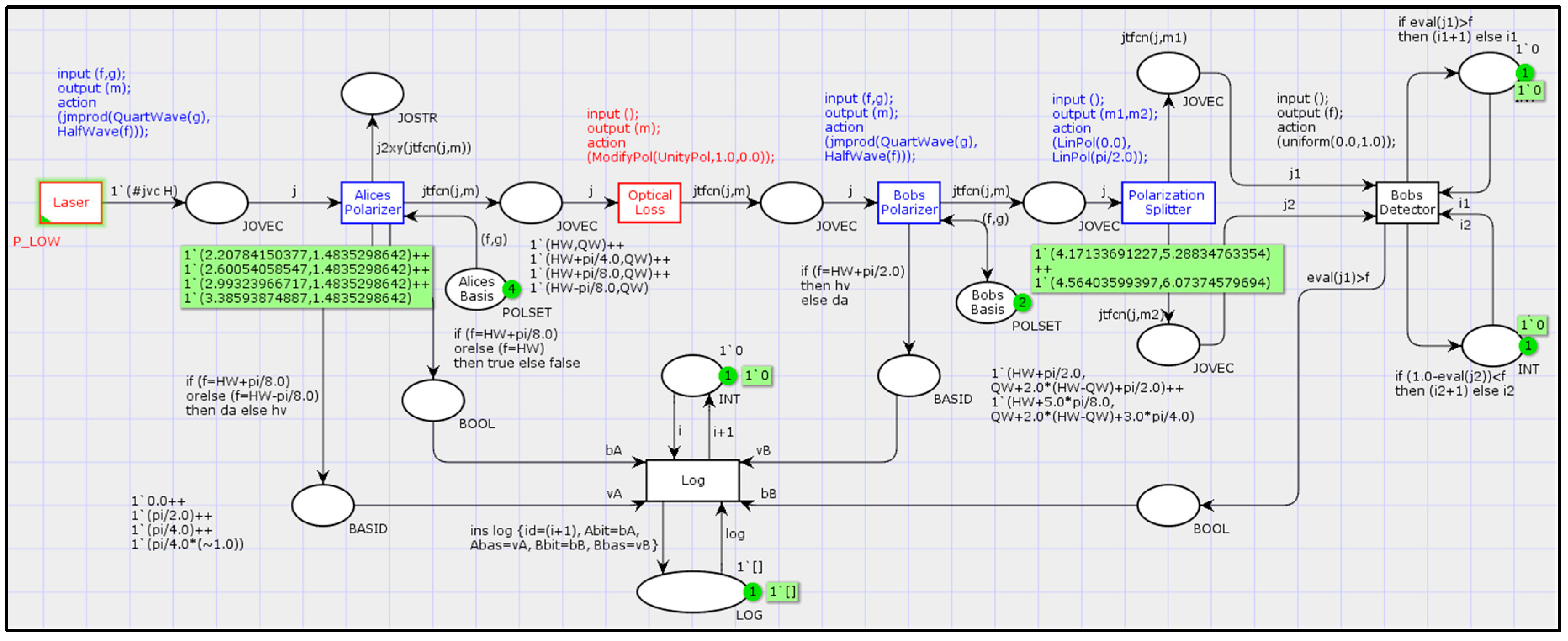
The model in CPN Tools is shown in Figure 7. The Petri graph on the canvas indicates the signal transformations according to the data flow diagram in Figure 4. The featured model is capable of logging data and leaves an opportunity for exporting it. The mathematical transformations described in section 3 are implemented as functions in the SML language and included in the model. With a basic understanding of the Petri nets and a familiarity with SML, the user can make changes to the virtual, for example, introduce Eve into the transmission channel.

5. Discussion

Our proposed solution has such merits as visual clarity of depicting the transmission via optical channel, adequacy and simplicity of physical analogy, robustness of the design and ease of use, as well as flexibility in training and demonstration scenarios. We believe that this kit has the qualities needed to create an interactive educational environment for basic QKD training of communication engineers without any background in quantum mechanics. Our experience of its application in the field indicates that in this role it is able to effectively replace more expensive and advanced QKD systems, the use of which is more beneficial at subsequent stages of training.

5.1. Field Experience

As we have discussed above, the kit is dedicated to the training of future specialists in the fields of information security and quantum communication. At this moment, the kit is actively used for teaching the theoretical basis and core practical skills of QKD to the students with a major in information security at our university. The hardware solution was introduced into the laboratory workshop in spring 2023 and has since been used as a part of practical training. More than 40 students specializing in information security in telecommunications have been trained there. The results of the final exams of students who used this kit for training indicated a significant increase in academic credentials relative to past students. According to our survey conducted among the students who successfully passed the exam, "insufficient training in natural sciences" was noted as a key problem by only 4 people (compared to 13 last year).

Excluding major university-level educational programs, we are also developing advanced training courses in the field of quantum communications for telecommunication engineering practitioners. Those courses are being designed to utilize the proposed kit. Trial executions of individual disciplines focused on the practice with the QKD hardware have proven that no prior training in quantum mechanics or theoretical physics is required for enrollees. In the following few years, we plan to start QKD training courses for various target groups of practitioners.

Based on the national educational standard, we have developed a set of performance assessment materials for verifying the qualifications of QKD specialists. The set included practical tasks, some of which can be performed using the proposed kit. The assessment materials could be used by personnel departments of industry organizations to independently confirm the qualifications of university graduates and other job applicants for positions related to quantum communications.

Our solution was chosen by the community of professionals in the fields of information security and telecommunications to be applied as a tool in the project of establishing a nation-wide exam for independent assessment of quantum communications specialists. In the course of the project, examination hubs have been established at several leading universities in the country. Those hubs were institutionalized as subordinates of the center for qualification assessment of the council for professional qualifications in the fields of telecommunications, postal communications and radio engineering. To date, a series of pilot exams have been held, which were attended by about 50 people. The pilot phase of the project has been acknowledged as successful and is planned to continue in the future.

5.2. Availability of the Software Model

The up-to-date version of the CPN Tools model is available for free download via the ResearchGate social network [59]. Further updating of the model is planned in the context of the development of the project, and in the context of the introducing CPN IDE as a successor to CPN Tools. We will be grateful if you leave a link to this article if you elect to use the model in your work and find it satisfactory. The CPN Tools software for opening the model can be freely downloaded from the official website [53].

6. Conclusions

Analysis of the trends in the development of quantum information technologies demonstrates that in the coming years, the quantum skills gap will remain relevant at the national and global levels. Quantum communications are by far the most widely adopted quantum information technology. The high rate of introduction of QKD systems into existing communication infrastructure is justified by the expectations of a leap in quantum computing in the near future. Advances in quantum computing will likely threaten existing asymmetric cryptographic systems, and this challenge is needs to be addressed beforehand. To date, the application of QKD in symmetric cryptographic systems seems to be the most practical response to the challenge from quantum computers. However, despite the clear progress in quantum communications over the last five years, the wide introduction of QKD into the practice accents the existing quantum skills gap.

One of the possible ways to solve this problem, at least in quantum communications, is the retraining of telecommunication practitioners. However, since they usually lack any background in quantum mechanics or theoretical physics, their training in QKD makes a non-trivial task. New educational technologies should be developed and aimed at teaching a theoretical base of quantum mechanics and providing a learning environment to practice skills of operating QKD systems to the trainees without prior knowledge in the field. The QKD education kits already available on the market do not always fit this purpose in the best possible way. We see their main problem in the fact that they are not meet the right balance between the complexity of the solution and the accuracy of representation of quantum transmission. In the most cases, educational kits lean towards complexity and constitute virtually full-functional systems, suitable for limited industrial use. Those solutions are difficult for untrained enrollees to master and therefore not efficient for a basic training.

We proposed a new hardware education QKD kit, that uses optical analogy to demonstrate and study the basics of quantum communications. The merits of our solution are the high detail of the simulation of the physical transmission process, with the relative simplicity of its formal description. The mathematical formalism of our solution is Jones calculus, which is based on mathematical concepts that are familiar to telecommunications engineers. To familiarize the audience with the mathematical model of the kit, we created it in the free distributed discrete event modeling environment CPN Tools.

When designing the hardware of the kit, we prioritized its reliability, safety, convenience, and ease of use. The software is primarily focused on fully automated configuring the optical system on the first run after its relocation. However, we also incorporate computer-aid managing the hardware in educational and demonstration scenarios into the capabilities of the software. The rightness of the choice of our design priorities was later confirmed during the operation of the kit.

The proposed kit has successfully passed practical testing in various educational tasks. We used it to carry out practical classes within the framework of a few university courses, delivered for information security students. Our experience indicated that using of the kit leads to improved academic performance and partly eliminates the lack of training in fundamental physics among students. At the national level, our solution was selected to be a hardware tool in a pilot project for the instituting of certification exams for QKD specialists. The kit proven itself worth during a few dozens of exam sessions, held in several universities across the country. The pilot project in general was also designated as a success.

Thus, the field experience confirmed that our solution meets the requirements that we set for it at the design stage. In the future, we plan to broaden the range of the hardware component by providing modules that simulate attacks. In addition, we are readying new educational technologies focused specifically at extra QKD training of practicing telecommunications engineers.

Author Contributions

Conceptualization, A.S. and A.T.; methodology, V.F. and D.B.; software, V.F. and A.T.; validation, A.T., D.B. and V.F.; formal analysis, V.F.; investigation, A.T.; resources, A.S.; data curation, D.B.; writing—original draft preparation, V.F. and A.T.; writing—review and editing, V.F. and A.S.; visualization, A.T.; supervision, A.S.; project administration, D.B. and A.S.; funding acquisition, A.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Ministry of Science and Higher Education of the Russian Federation within the framework of scientific projects carried out by teams of research laboratories of educational institutions of higher education subordinate to the Ministry of Science and Higher Education of the Russian Federation, project number FEWM-2020-0042. This research was funded by the Ministry of Science and Higher Education of the Russian Federation within the framework of scientific projects carried out by teams of research laboratories of educational institutions of higher education subordinate to the Ministry of Science and Higher Education of the Russian Federation, project number FEWM-2020-0042.

Data Availability Statement

Mathematical formalism applied to justify the design of the kit is implemented as a model in CPN Tools and can be freely downloaded for verification. Particular details regarding hardware implementation could be provided after reasonable request via email.

Acknowledgments

We want to express our deep appreciation and gratitude to our collaborators from Infotecs Academy (https://academy.infotecs.ru/), Tomsk branch for sharing their invaluable expertise in practical QKD and for a sustained discussion on quantum skills shortage in Russia and worldwide. We also thank our industrial partners from the center for qualification assessment of the council for professional qualification in the fields of telecommunications, mail services and radio technics (COK SPK Svyazi, https://spksvyaz.ru/cok-mas) for providing us with the field data of application of our kit in real-world educational setting and their constructive feedback.

Conflicts of Interest

The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

Khan, F.S.; La Torre, D. Quantum information technology and innovation: a brief history, current state and future perspectives for business and management. Technol. Anal. Strateg. Manag. 2021, 33, 1281–1289. [Google Scholar] [CrossRef]
Aumasson, J.P. The impact of quantum computing on cryptography. Comput. Fraud Secur. 2017, 2017, 8–11. [Google Scholar] [CrossRef]
Bavdekar, R.; Chopde, E.J.; Bhatia, A.; Tiwari, K.; Daniel, S.J.; Atul Post Quantum Cryptography: Techniques, Challenges, Standardization, and Directions for Future Research Available online: http://arxiv.org/abs/2202.02826.
Dam, D.T.; Tran, T.H.; Hoang, V.P.; Pham, C.K.; Hoang, T.T. A Survey of Post-Quantum Cryptography: Start of a New Race. Cryptography 2023, 7, 1–18. [Google Scholar] [CrossRef]
Mina, M.-Z.; Simion, E. Information Security in the Quantum Era. Threats to modern cryptography: Grover’s algorithm. Cryptol. ePrint Arch. 2021, 1–12. [Google Scholar]
Horpenyuk, A.; Opirskyy, I.; Vorobets, P. Analysis of Problems and Prospects of Implementation of Post-Quantum Cryptographic Algorithms. CEUR Workshop Proc. 2023, 3504, 39–49. [Google Scholar]
Yao, C.Y.; Hsia, W.C. An Indoor Positioning System Based on the Dual-Channel Passive RFID Technology. IEEE Sens. J. 2018, 18, 4654–4663. [Google Scholar] [CrossRef]
Hua, C.; Zhao, K.; Dong, D.; Zheng, Z.; Yu, C.; Zhang, Y.; Zhao, T. Multipath map method for TDOA based indoor reverse positioning system with improved chan-taylor algorithm. Sensors (Switzerland) 2020, 20, 1–14. [Google Scholar] [CrossRef]
Lee, Y.S.; Chien, H. Te; Tsai, W.N. Using random bit authentication to defend IEEE 802.11 DoS attacks. J. Inf. Sci. Eng. 2009, 25, 1485–1500. [Google Scholar] [CrossRef]
Scarani, V.; Kurtsiefer, C. The black paper of quantum cryptography: Real implementation problems. Theor. Comput. Sci. 2014, 560, 27–32. [Google Scholar] [CrossRef]
Zhang, Q.; Xu, F.; Chen, Y.-A.; Peng, C.-Z.; Pan, J.-W. Large scale quantum key distribution: challenges and solutions. Opt. Express 2018, 26, 24260. [Google Scholar] [CrossRef]
Bogdanov, Y.I.; Fastovets, D. V; Bantysh, B.I.; Chernyavskii, A.Y.; Semenikhin, I.A.; Bogdanova, N.A.; Katamadze, K.G.; Kuznetsov, Y.A.; Kokin, A.A.; Lukichev, V.F. Methods for analysing the quality of the element base of quantum information technologies. Quantum Electron. 2018, 48, 1016–1022. [Google Scholar] [CrossRef]
Stanley, M.; Gui, Y.; Unnikrishnan, D.; Hall, S.R.G.; Fatadin, I. Recent Progress in Quantum Key Distribution Network Deployments and Standards. J. Phys. Conf. Ser. 2022, 2416. [Google Scholar] [CrossRef]
Al Natsheh, A.; Gbadegeshin, S.A.; Rimpiläinen, A.; Imamovic-Tokalic, I.; Zambrano, A. Identifying the Challenges in Commercializing High Technology: A Case Study. Technol. Innov. Manag. Rev. 2015, 5, 26–36. [Google Scholar] [CrossRef]
Kaur, M.; Venegas-Gomez, A. Defining the quantum workforce landscape: a review of global quantum education initiatives. Opt. Eng. 2022, 61, 1–33. [Google Scholar] [CrossRef]
Velu, C.; Putra, F.; Geurtsen, E.; Norman, K.; Noble, C. Adoption of Quantum Technologies and Business Model Innovation; 2022.
IQM State of Quantum 2022 Report; 2022.
Vishwakarma, S.; D, S.; Ganguly, S.; Morapakula, S.N. A Universal Quantum Technology Education Program. arXiv:2305.15959 2023.
Hasanovic, M.; Panayiotou, C.; Silberman, D.; Stimers, P.; Merzbacher, C. Quantum technician skills and competencies for the emerging Quantum 2.0 industry. Opt. Eng. 2022, 61, 1–17. [Google Scholar] [CrossRef]
Carreño, M.J.; Sepúlveda, J.; Tecpan, S.; Hernández, C.; Herrera, F. An instrument-free demonstration of quantum key distribution for high-school students. Phys. Educ. 2019, 54. [Google Scholar] [CrossRef]
Özcan, Ö.; Didiş, N.; Taşar, M.F. Students’ conceptual difficulties in quantum mechanics: Potential well problems. Hacettepe Egit. Derg. 2009, 36, 169–180. [Google Scholar]
Singh, C.; Marshman, E. Review of student difficulties in upper-level quantum mechanics. Phys. Rev. Spec. Top. - Phys. Educ. Res. 2015, 11, 1–25. [Google Scholar] [CrossRef]
Katamadze, K.G.; Pashchenko, A.V.; Romanova, A.V.; Kulik, S.P. Generation and Application of Broadband Biphoton Fields (Brief Review). Opt. Lasers Phys. 2022, 115, 581–595. [Google Scholar] [CrossRef]
Pathan, A.K. Simulation Technologies in Networking and Communications; 2014; ISBN 9781439881576.
Bennett, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. Theor. Comput. Sci. 2014, 560, 7–11. [Google Scholar] [CrossRef]
Pereira, M.; Currás-Lorenzo, G.; Navarrete, Á.; Mizutani, A.; Kato, G.; Curty, M.; Tamaki, K. Modified BB84 quantum key distribution protocol robust to source imperfections. Phys. Rev. Res. 2023, 5, 1–24. [Google Scholar] [CrossRef]
Verma, P.K.; El Rifai, M.; Chan, K.W.C. Quantum Key Distribution: An Introduction With Exercises; 2019; ISBN 9783030739904.
Applied Quantum Cryptography; Kollmitzer, C., Pivk, M., Eds.; Springer, 2013; ISBN 9780333227794.
Winiarczyk, P.; Zabierowski, W. BB84 analysis of operation and practical considerations and implementations of quantum key distribution systems. 2011 11th Int. Conf. - Exp. Des. Appl. CAD Syst. Microelectron. CADSM 2011 2011, 23–26.
Åkerberg, E.; Åsgrim, E. Developing an educational tool for simulations of quantum key distribution systems, KTH Royal Institute of Technology, 2023.
Kohnle, A.; Rizzoli, A. Interactive simulations for quantum key distribution. Eur. J. Phys. 2017, 38. [Google Scholar] [CrossRef]
Devore, S.; Singh, C. Interactive learning tutorial on quantum key distribution. Phys. Rev. Phys. Educ. Res. 2020, 16, 1–17. [Google Scholar] [CrossRef]
Camargo, A.L.P.; Pereira, L.O.; Balthazar, W.F.; Huguenin, J.A.O. Simulação do protocolo BB84 de criptografia quântica utilizando um feixe laser intenso. Rev. Bras. Ensino Fis. 2017, 39. [Google Scholar] [CrossRef]
Frank, R.I.; Grant, K.A.; Harris, A.L.; Colton, D.; Dickinson, F.; Frank, R.I.; Johnson, D.; Colton, D. An IS Undergraduate Course Module on Quantum Key Distribution. Inf. Syst. Educ. J. 2005, 3. [Google Scholar]
Utama, A.N.; Lee, J.; Seidler, M.A. A hands-on quantum cryptography workshop for pre-university students. Am. J. Phys. 2020, 88, 1094–1102. [Google Scholar] [CrossRef]
Bloom, Y.; Fields, I.; Maslennikov, A.; Rozenman, G.G. Quantum Cryptography—A Simplified Undergraduate Experiment and Simulation. Phys. 2022, 4, 104–123. [Google Scholar] [CrossRef]
Fedorov, A.K.; Kanapin, A.A.; Kurochkin, V.L.; Kurochkin, Y. V.; Losev, A. V.; Miller, A. V.; Pashinskiy, I.O.; Rodimin, V.E.; Sokolov, A.S. Educational Potential of Quantum Cryptography and Its Experimental Modular Realization. Proc. Sci. Conf. “Research Dev. - 2016” 2018, 83–91. [Google Scholar] [CrossRef]
Akdemir, Z.G.; Menekse, M.; Hosseini, M.; Nandi, A.; Furuya, K. For Your Eyes Only: Introducing Quantum Key Distribution to High School Students. Sci. Teach. 2021, 88. [Google Scholar]
Bista, A.; Sharma, B.; Galvez, E.J. A demonstration of quantum key distribution with entangled photons for the undergraduate laboratory. Am. J. Phys. 2021, 89, 111–120. [Google Scholar] [CrossRef]
Ekert, A.K. Quantum Cryptography and Bell’s Theorem. 1992, 413–418. [CrossRef]
S-Fifteen Instruments Pte. Ltd. Educational Kit: Programmable Quantum Cryptography Available online: https://cdn.shopify.com/s/files/1/0092/6485/7152/files/EKPQC_Assembly_and_Installation_Manual_v1.2_ebook.pdf?v=1688977202.
Qutools quED: The Entanglement Demonstrator Hardware Available online: https://www.qutools.com/files/quED/qutools_quED_Datasheet.pdf.
ThorLabs Quantum Cryptography Demonstration Kit Available online: https://lenlasers.ru/upload/iblock/2c5/EDU_QCRY1_M-Manual.LLS.pdf.
Katamadze, K. Demonstrative Simulator of QKD System (RU 2795245) 2021.
Sabani, M.; Savvas, I.; Poulakis, D.; Makris, G. Quantum Key Distribution: Basic Protocols and Threats. ACM Int. Conf. Proceeding Ser. 2022, 383–388. [Google Scholar] [CrossRef]
Gutiérrez-Vega, J.C. The field of values of Jones matrices: Classification and special cases. Proc. R. Soc. A Math. Phys. Eng. Sci. 2020, 476. [Google Scholar] [CrossRef]
Matsuo, S. Matrix calculus for axially symmetric polarized beam. Opt. Express 2011, 19, 12815. [Google Scholar] [CrossRef]
Kuan, W.-H.; Lin, K.-H.; Wang, C.-W.; Hung, N.-H. Generalized Jones Calculus for Vortex, Vector, and Vortex-Vector Beam Transformations Available online: http://arxiv.org/abs/2103.13779.
Fan-Yuan, G.J.; Chen, W.; Lu, F.Y.; Yin, Z.Q.; Wang, S.; Guo, G.C.; Han, Z.F. A universal simulating framework for quantum key distribution systems. Sci. China Inf. Sci. 2020, 63, 1–16. [Google Scholar] [CrossRef]
Menzel, C.; Rockstuhl, C.; Lederer, F. Advanced Jones calculus for the classification of periodic metamaterials. Phys. Rev. A - At. Mol. Opt. Phys. 2010, 82, 1–9. [Google Scholar] [CrossRef]
Collett, E. Field Guide to Polarization; SPIE Press, 2005; ISBN 9780819458681.
Wei, Y.; Lehmann, T.; Silvestri, L.; Wang, H.; Ladouceur, F. Photodiode working in zero-mode: detecting light power change with DC rejection and AC amplification. Opt. Express 2021, 29, 18915. [Google Scholar] [CrossRef] [PubMed]
Westergaard, M.; Verbeek, E. CPN Tools official website Available online: https://cpntools.org/2018/01/16/download/.
Jensen, K.; Kristensen, L.M. Coloured Petri Nets; Springer: Berlin, 2009; ISBN 9783642002830. [Google Scholar]
Zaitsev, D.A.; Shmeleva, T.R. A Parametric Colored Petri Net Model of a Switched Network. Int. J. Commun. Netw. Syst. Sci. 2011, 04, 65–76. [Google Scholar] [CrossRef]
Zhou, W.; Dague, P.; Liu, L.; Ye, L.; Zaïdi, F.; Petri, A.C.; Based, N.; Zhou, W.; Dague, P.; Liu, L.; et al. A Coloured Petri Nets Based Attack Tolerance Framework. In Proceedings of the 27th Asia-Pacific Software Engineering Conference (APSEC 2020); IEEE: Singapore; 2021. [Google Scholar]
Faerman, V.; Voevodin, K.; Avramchuk, V. Case of Discrete-Event Simulation of the Simple Sensor Node with CPN Tools. In Proceedings of the International Siberian Conference on Control and Communications (SIBCON); 2022; pp. 1–9. [Google Scholar]
Zhu, L.; Tong, W.; Cheng, B. CPN tools’ application in verification of parallel programs. Commun. Comput. Inf. Sci. 2010, 105 CCIS, 137–143. [Google Scholar] [CrossRef]
Faerman, V.A. Model of QKD with polarization encoding (CPN Tools) Available online: https://www.researchgate.net/publication/376650885_vk_072?channel=doi&linkId=6582c01b0bb2c7472bf9c394&showFulltext=true.

Figure 2. Functional diagram of the proposed hardware educational kit.

Figure 3. Elliptically polarized monochromatic electromagnetic wave, which is defined by the Jones vector J (α, ∆f), α = π/4, ∆f = π/4: (a) projection of the electric field on a transverse plain (z = z₀); (b) section of spatial trajectory of the electric field (t = t₀).

Figure 4. Data flow diagram of the kit.

Figure 5. Proposed hardware QKD kit: Alice’s and Bob’s modules are present.

Figure 6. 3D design sketches of the key assembly parts of the hardware kit created in KOMPAS-3D: (a) metallic frame; (b) mount for the light source; (c) mount for the waveplate with a stepper motor and an angular position sensor; (d) mounts for the PBS and photodetectors.

Figure 7. Discrete-event model of the kit in the CPN Tools.

Table 1. Possible scenarios for data transmitted and received via quantum channel in BB84.

Alice’s Choice	Bob’s Choice	Received State	Received Bit	Bases Compliance
∣H⟩ (0 в HV)	HV	∣H⟩	0	OK
∣H⟩ (0 в HV)	DA	∣D⟩ or ∣A⟩	0 or 1	X
∣V⟩ (1 в HV)	HV	∣V⟩	1	OK
∣V⟩ (1 в HV)	DA	∣D⟩ or ∣A⟩	0 or 1	X
∣D⟩ (0 в DA)	HV	∣H⟩ or ∣V⟩	0 or 1	X
∣D⟩ (0 в DA)	DA	∣D⟩	0	OK
∣A⟩ (1 в DA)	HV	∣H⟩ or ∣V⟩	0 or 1	X
∣A⟩ (1 в DA)	DA	∣A⟩	1	OK

Table 2. Angular positions of plates for BB84 (encoding with elliptical polarization states).

Alice’s Choice	Bob’s Choice	Alice’s Plates Positions	Bob’s Plates Positions	Active Detector
∣H⟩	HV	θ_A = θ₀, γ_A = γ₀	θ_B = θ₀ + π/2, γ_B = γ₀ + 2·(θ₀ – γ₀) + π/2	A
∣V⟩		θ_A = θ₀ + π/4, γ_A = γ₀		B
∣D⟩		θ_A = θ₀ + π/8, γ_A = γ₀		A or B
∣A⟩		θ_A = θ₀ – π/8, γ_A = γ₀		A or B
∣H⟩	DA	θ_A = θ₀, γ_A = γ₀	θ_B = θ₀ + 5π/8, γ_B = γ₀ + 2·(θ₀ – γ₀) + 3π/4	A or B
∣V⟩		θ_A = θ₀ + π/4, γ_A = γ₀		A or B
∣D⟩		θ_A = θ₀ + π/8, γ_A = γ₀		A
∣A⟩		θ_A = θ₀ – π/8, γ_A = γ₀		B

Table 3. Non-elliptical bases achievable with plates positions in Table 2.

Base HV	Base DA	States of polarization	θ₀	γ₀
linear	circular	$\| H 〉 = (\begin{matrix} \cos (α) \\ \sin (α) \end{matrix}), \| V 〉 = (\begin{matrix} - \sin (α) \\ \cos (α) \end{matrix}),$ $\| D 〉 = (\begin{matrix} \cos (π / 4) \\ \sin (π / 4) \cdot e^{i \cdot π / 2} \end{matrix}), \| V 〉 = (\begin{matrix} - \sin (π / 4) \\ \cos (π / 4) \cdot e^{i \cdot π / 2} \end{matrix}),$	α	2α
circular	linear	$\| H 〉 = (\begin{matrix} - \sin (π / 4) \\ \cos (π / 4) \cdot e^{i \cdot π / 2} \end{matrix}), \| V 〉 = (\begin{matrix} \cos (π / 4) \\ \sin (π / 4) \cdot e^{i \cdot π / 2} \end{matrix}), .$ $\| D 〉 = (\begin{matrix} - \sin (α) \\ \cos (α) \end{matrix}), \| A 〉 = (\begin{matrix} \cos (α) \\ \sin (α) \end{matrix})$	α	2α+π/4

Table 4. Plates positions for BB84 implementation (encoding with linear polarization states).

Alice’s Choice	Bob’s Choice	Alice’s Plates Positions	Bob’s Plates Positions	Active Detector
∣H⟩	HV	θ_A = α, γ_A = 2α	θ_B = α + π/2, γ_B = 0	A
∣V⟩		θ_A = α + π/4, γ_A = 2α + π/2		B
∣D⟩		θ_A = α + π/8, γ_A = 2α + π/4		A or B
∣A⟩		θ_A = α – π/8, γ_A = 2α – π/4		A or B
∣H⟩	DA	θ_A = α, γ_A = 2α	θ_B = α + 5π/8, γ_B = 0	A or B
∣V⟩		θ_A = α + π/4, γ_A = 2α + π/2		A or B
∣D⟩		θ_A = α + π/8, γ_A = 2α + π/4		A
∣A⟩		θ_A = α – π/8, γ_A = 2α – π/4		B

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer