Provably secure ECC-based anonymous authentication and key Agreement for IoT

Preprint

Article

Provably secure ECC-based anonymous authentication and key Agreement for IoT

Altmetrics

Downloads

128

Views

Comments

A peer-reviewed article of this preprint also exists.

Shunfang Hu^*

Shaoping Jiang,Qing Miao,Fan Yang,Weihong Zhou,Peng Duan

Shunfang Hu^*

Shaoping Jiang,Qing Miao,Fan Yang,Weihong Zhou,Peng Duan

This version is not peer-reviewed

Submitted:

23 January 2024

Posted:

25 January 2024

You are already at the latest version

Alerts

Abstract

With the rise of the Internet of Things (IoT), maintaining data confidentiality and protecting user privacy have become increasingly challenging. End devices in IoT are often deployed in unattended environments and connected to open networks, which can make them vulnerable to physical tampering and other security attacks. Different authentication key agreement (AKA) schemes have been validated to date, but most schemes do not cover the necessary security features or are incompatible with resource-constrained end devices. Besides, their security proofs have been performed under the real-or-random model, which is not guaranteed to be secure in real applications. To reduce the weaknesses, we present an AKA protocol for end devices and servers. The proposal leverages the ECC-based key exchange mechanism and one-way hash function-based message authentication method to achieve mutual authentication, user anonymity, and forward security. Formal security proof of the proposed scheme is performed under the standard model with the elliptic curve encryption computational assumptions, and an automatic formal verification was performed with ProVerif. Further, the performance comparison verifies that our scheme reduces computation and communication costs while providing improved security features.

Keywords:

Subject: Computer Science and Mathematics - Security Systems

1. Introduction

Thanks to advances in chipset production and embedding technologies, sensors and actuators (referred to as end devices) are pervasive in the Internet of Things (IoT), being integrated into intelligent agriculture, smart grid, telemedicine, smart home, intelligent manufacturing, and many other fields to collect and disseminate the data [1]. According to the latest estimates, there will be 83 billion IoT connections by 2024 [2]. In IoT applications, the collected and transmitted data is susceptible and critical. Besides, privacy is another crucial issue, especially regarding user data such as consumption habits, location, and communication activities [3,4]. To ensure security, authentication key agreement (AKA) schemes for IoT applications have been widely investigated, which offer mutual authentication and privacy protection and ensure confidentiality, integrity, and non-repudiation of data transmissions based on the negotiated session keys [5]. End devices are often linked to open networks and deployed in unattended environments with limited computation, communication, and storage capabilities. As a result, implementing mutual authentication and key agreement between end devices and servers to sustain efficiency is a critical challenge.

1.1. Related work

Over the last few years, numerous AKA solutions have been developed for IoT applications. The symmetric cryptography-based AKA protocols [6,7,8,9] have the advantages of low computational complexity and high efficiency. On the other hand, such schemes necessitate the sharing of key parameters between end devices beforehand or each device transferring its key to the server. It is unrealistic for numerous end devices and burdens the servers significantly. Physical Unclonable Function (PUF) is a promising lightweight hardware security primitive that has been adopted by many IoT AKA protocols [10,11,12]. In these schemes, each individual participant should record one or more Challenge-Response Pairs (CRPs) of its PUF with the registration server beforehand. When a registered device, Alice, wants to communicate with another registered device, Bob, it can only do so with the assistance of the server, which results in a lack of flexibility and efficiency. In contrast, the asymmetric cryptography-based AKA schemes requiring fewer restrictions have attracted increasing attention [13]. Elliptic Curve Cryptography (ECC) provides smaller key sizes than other asymmetric algorithms with the same security [14,15], which makes it introduced in IoT AKA protocols.

Until now, numerous IoT AKA protocols based on ECC have been developed. In 2015, a bilinear pairing-based AKA protocol for wireless body area networks (WBAN) was put forward by Wang et al. [16], which requires a high computational overhead. They claimed that this scheme could achieve absolute anonymity, perfect forward security (PFS), and overcome the weaknesses of previous schemes. After analysis, it was found that the session key could be captured after temporary session information disclosure. In addition, Wu et al. [17] pointed out that the protocol is incapable of withstanding impersonation (IM) attacks. And then, they proposed an enhanced version for WBANs. However, the enhanced scheme also uses bilinear pairing and suffers from ephemeral secret leakage (ESL) attacks. Seo et al. [18] introduced an AKA scheme for dynamic WSNs. Later, Saeed et al. [19] point out that the scheme [18] could not provide PFS; then they proposed a scheme for establishing an authenticated key between WSNs and cloud servers. Whereas, the proposal [19] is also not resistant to ESL attacks and cannot provide user anonymity. In 2020, an AKA scheme for IoT was introduced by Fang et al. [20]. In this scheme, heterogeneous-type IoT smart devices are deployed based on a trust model. Regrettably, their solution requires higher computational and communication costs and is susceptible to ESL attacks [21]. In the same year, Dariush et al. [22] introduced an AKA protocol for smart grid (SG) that covers available problems such as ESL attacks and private key leakage attacks. Unfortunately, in [22], the trusted authority (TA) is able to masquerade as a smart meter to agree on session keys with the server provider. Moreover, the scheme needs more computational and communication costs for the bilinear pairing computation.

Recently, Srinivas et al. [23] designed an anonymous AKA protocol with Schnorr’s signature. Later, Baruah et al. [24] demonstrated the scheme [23] is prone to MIM attacks and IM attacks. Crypt-analysis showcases that the protocol [23] is also vulnerable to key escrow problems and ESL attacks. Yang et al. [25] stated that Shen et al.’s scheme [26] suffers from MIM attacks and key compromise impersonation (KCI) attacks and is incapable of providing PFS, and then introduced an enhanced cloud-based scheme. Unfortunately, the enhanced scheme has key escrow problems and is incapable of providing user anonymity. Chaudhry et al. [27] present an AKA scheme for SG using ECC and symmetric encryption. Unfortunately, this scheme [27] has key escrow problems and suffers from MIM attacks. Hajian et al. [28] examined the deficiencies of four existing AKA schemes and then proposed an improved device-to-device AKA scheme in the IoT. However, the improved scheme suffers from MIM attacks and KCI attacks and is incapable of affording PFS. In 2023, Chen et al. [29] presented an AKA scheme for industrial control systems. However, the solution requires high computation and communication costs, suffers from ESL attacks, and cannot afford PFS.

1.2. Related formal security model

In 1993, Bellare et al. [30] put forward the first formal security model for the AKA scheme, the BR model, which is resistant to known-key attacks and IM attacks. Later, the BR model was modified by Blake-Wilson et al. [31] by introducing long-term private key corruption attacks. In 2001, Canetti et al. [32] proposed the CK model, which covers attacks on ephemeral private keys and intermediate result leakage. All these models attempt to cover the essential safety and performance attributes required. In 2007, LaMacchia et al. [33,34] introduced a remarkably strong security model, the extended CK model (eCK model), which incorporates weak PFS and KCI attacks.

1.3. Motivation and contributions

To summarize, previous ECC-based AKA schemes suffer from more or less vulnerabilities, i.e., failure to provide user anonymity [19,25], PFS [18,23,28,29] and vulnerability to specific attacks [16,17,18,19,20,22,23,25,27,28,29]. Next, high computational and communication costs eliminate the suitability of some solutions for resource-limited IoT [10,16,17,20,22,29]. Besides, their security proofs are performed in the Real-or-Random (RoR) model [22,23], which is weak perfect forward secrecy and discounts compromised impersonation attacks [33,34,35]. It is attractive to design an efficient AKA scheme for IoT and provide security proof under the standard model and eCK model.

We proposed an AKA scheme with the ECC-based message exchange mechanism and the one-way hash function message authentication technique. During registration, the TA only possesses part of the entity’s private key, solving the key escrow issues. The protocol encrypts entity identities dynamically with random numbers and transmits them anonymously from session to session.

The paper’s contributions can be summarized as follows:

(1) Cryptanalysis of the previous scheme reveals the security issues and vulnerabilities.

(2) A secure-enhanced AKA protocol for IoT has been presented. Its security is formally proved under the standard model and eCK model with the elliptic curve encryption computational assumptions and automatically verified with ProVerif.

(3) The proposed protocol has better security features with lower communication and computational overheads than existing schemes.

1.4. Roadmap

The paper is structured as follows: Section 2 provides a review of the network model and the basics of elliptic curve encryption. In Section 3, we analyze a related AKA scheme. We then describe an improved ECC-based AKA protocol in Section 4. In Section 5, Section 6, Section 7, and Section 8, we present our security analysis and performance comparison. Finally, we conclude the paper in Section 9.

2. PRELIMINARIES

The following preliminaries and symbols are used to explain and analyze the schemes.

2.1. Network Model

A typical IoT application is shown in Figure 1. It mainly involves three main components: end devices, routers, and servers. The end devices may be sensors, actuators, cell phones, etc. Routers include gateway nodes, base stations, and routers for relaying and passing messages. In addition, servers are in charge of managing devices and assigning security parameters.

An IoT system consists of many low-power, resource-limited end devices placed in unattended or open environments and typically connected to open networks. Through these terminal devices, real-time monitoring and control can be implemented remotely. The end sensors collect real-time data such as agricultural environment parameters, power consumption, biomedical data, and machine conditions and then send the data to remote servers. The servers receive and store the collected data, then extract and evaluate the data to provide the appropriate control measures. The actuators carry out control commands that are received from the server.

2.2. Elliptic curve encryption mathematical problems

Let

q > 3

be a big prime number,

E (a, b)

denote a non-singular elliptic curve over a finite field

F_{q}

, G be a cyclic group of prime order p as big as q, and P be a generator point [36]. Hence:

Definition 1. Elliptic curve discrete logarithm (ECDL) problem: For the given points X and

a X

, where

X \in G

and

a \in Z_{q}^{*}

, it is computationally intractable to find a.

Definition 2. Elliptic curve Diffie-Hellman (ECDH) problem: For the given points

a X, b X \in G

, where

X \in G

and

a, b \in Z_{q}^{*}

, finding point

a b X

is computationally intractable.

2.3. Symbols

Symbols for the schemes are cataloged in Table 1.

3. Security analysis of Srinivas et al.’s scheme

Baruah et al. [24] point out that the scheme [23] is insure of MIM attacks and IM attacks. Cryptanalysis shows that the protocol [23] also suffers from key escrow issues and ESL attacks. Figure 2 and Figure 3 demonstrate the scheme’s registration and authentication & key agreement phases.

3.1. Key escrow problem

As shown in Figure 2, TA generates the private keys of

S M_{i}

and

S P_{j}

with Schnorr’s signature.

T A

calculates

T_{S M_{i}} = t_{S M_{i}} \cdot P

and

M_{S M_{i}} = t_{S M_{i}} + h (T_{S M_{i}}

∥ I D_{S M_{i}}) \cdot t (mod q)

for

S M_{i}

, and also

T_{S P_{j}} = t_{S P_{j}} \cdot P

P_{S P_{j}} = t_{S P_{j}} + h (T_{S P_{j}} ∥ I D_{S P_{j}}) \cdot t (mod q)

for

S P_{j}

. Then the long-term private secrets,

T_{S M_{i}}

M_{S M_{i}}

T_{S P_{j}}

, and

P_{S P_{j}}

, are known to him/her.

3.2. No resistance to ESL attacks

An AKA protocol is designed to resist an ESL attack, meaning that even if all the session-specific information of the entities in a session is compromised, the secrecy of the session key would remain uncompromised. As shown in Figure 3, once the ephemeral secrets

r_{i}

and

r_{j}

are compromised,

A

can compromise the session key

S K_{i j}

S K_{j i}

by the following steps:

A1:

A

obtains the messages

M S G_{1} = {R_{i}, T S_{i}}

M S G_{2} = {R_{j}, V_{j}, T_{S P_{j}}, T S_{j}}

and

M S G_{3} = {B_{i}, C_{i}, T S_{i}^{'}}

by eavesdropping via the open channels;

A2:

A

extracts

T S_{i}, T_{S P_{j}}, T S_{j}, B_{i}

and

T S_{i}^{'}

from the messages, then

A

calculates

S_{i} = h (r_{i} ∥ T S_{i}) \cdot (T_{S P_{j}} + h (T_{S P_{j}} ∥ I D_{S P_{j}}) \cdot T_{p u b})

;

A3: For

S_{i} = S_{j}

A

gets

(I D_{S M_{i}} ∥ T_{S M_{i}}) = B_{i} \oplus h (S_{i} ∥ T S_{i}^{'})

then calculates

U_{j} = h (r_{j} ∥ T S_{j}) \cdot (T_{S M_{i}} + h (T_{S M_{i}} ∥ I D_{S M_{i}}) \cdot T_{p u b})

A4: For

A_{i} = U_{j}

A

calculates

S K_{i j} = h (A_{i} ∥ S_{i} ∥ I D_{S M_{i}} ∥ I D_{S P_{j}})

4. The proposed protocol

The proposal involves three phases: initialization, registration, and authentication & key agreement. To begin, TA generates and releases parameters for the system during the initialization phase. In the registration phase, each end device

S_{s}

or server

S P_{s p}

acquires its private key and both parties’ public key with the assistance of

T A

. Ultimately,

S_{s}

and

S P_{s p}

will authenticate each other and negotiate a session key.

4.1. Initialization phase

TA generates and releases parameters for the system as follows:

TA1: TA selects an elliptic curve

E (a, b)

over finite field

F_{q}

with a base point P;

TA2: Then TA picks

h (\cdot)

as the collision-resistant one-way hash function;

TA3: TA issues

{(E (a, b), p, q, P, h (\cdot)}

publicly.

4.2. Registration phase

As shown in Figure 4. Taking the registration of the server

S P

as an example, the processes are as follows:

R1: Firstly, SP chooses a random

r_{s p} \in Z_{q}^{*}

and its identifier

I D_{s p} \in Z_{q}^{*}

and computes

R_{s p} = r_{s p} \cdot P

. Then SP transmits a registration request,

{I D_{s p}, R_{s p}}

, to TA securely.

R2: In response, First, TA chooses

r_{t a}^{s p} \in Z_{q}^{*}

randomly to calculate the public key of

S P

P K_{s p} = R_{s p} + r_{t a}^{s p} \cdot P

. Next, TA sends

{P K_{s p}, r_{t a}^{s p}, I D_{s}, P K_{s}}

to SP via a secure channel.

R3: In response,

S P

takes

r_{t a}^{s p}

as part of its private key and gets its private key,

k_{s p} = ((r_{s p} + r_{t a}^{s p}) mod q)

. Then SP checks whether

P K_{s p} ? = k_{s p} \cdot P

; if it holds, then SP computes

W S_{s} = k_{s p} \cdot P K_{s}

and stores

(I D_{s p}, k_{s p}, P K_{s p}, I D_{s}, W S_{s})

Similarly, S stores

(I D_{s}, k_{s}, P K_{s}, I D_{s p}, W S_{s p})

after registration. When a new end device,

S^{'}

, joins and registers the system, TA sends

{I D_{S^{'}}, P K_{S^{'}}}

to SP securely.

4.3. Authentication and key agreement phase

S_{s}

and

S P_{s p}

will authenticate each other and negotiate a session key, as shown in Figure 5.

S1: S first picks

x_{s} \in Z_{q}^{*}

randomly and generates a timestamp

T_{s}

. Next, S calculates

A_{s} = x_{s} \cdot P K_{s}

and

B_{s} = x_{s} \cdot W S_{s p}

. Third, S encrypts

I D_{s}

E I D_{s} = I D_{s} \oplus B_{s}

and gets a verifier

V_{s} = h (W S_{s p} ∥ T_{s} ∥ I D_{s} ∥ B_{s})

. Finally, S transmits

{A_{s}, E I D_{s}, T_{s}, V_{s}}

S P

SP1: Upon receiving the above message,

S P

first examines its freshness against the timestamp

T_{s}

. Next, SP calculates

B_{s p} = k_{s p} \cdot A_{s}

to decrypt

I D_{s} = E I D_{s} \oplus B_{s p}

. Thus, SP gains S’s verifier and validates the equation of

V_{s} = ? h (W S_{s} ∥ T_{s} ∥ I D_{s} ∥ B_{s p})

to assure the integrity of the incoming message and the validity of S.

SP2: Firstly,

S P

selects

x_{s p}

randomly and obtains a timestamp

T_{s p}

. Secondly, SP calculates

A_{s p} = x_{s p} \cdot P K_{s p}

and

C_{s p} = x_{s p} \cdot B_{s p}

. SP get the session key as

S S K_{s p} = h (I D_{s} ∥ I D_{s p} ∥ B_{s p} ∥ C_{s p})

. Third, SP figures out a verifier:

V_{s p} = h (W S_{s} ∥ T_{s p} ∥ I D_{s p} ∥ S S K_{s p})

. and transmits

{A_{s p}, T_{s p}, V_{s p}

} to S.

S2: On receiving the message, S first examines its freshness against

T_{s p}

. Next, S calculates

C_{s} = (x_{s} k_{s} mod q) \cdot A_{s p}

to get the session key,

S S K_{s} = h (I D_{s} ∥ I D_{s p} ∥ B_{s} ∥ C_{s})

. Thus, S gains SP’s verifier and validates the equation of

V_{s p} = ? h (W S_{s p} ∥ T_{s p} ∥ I D_{s p} ∥ S S K_{s})

to assure the integrity of the incoming message and the validity of SP.

5. Formal Proof

The eCK security model [33,34,35] has been employed for the security proof.

5.1. Security model

Participants. There are n participants in the proposed protocol

P

, which are uniformly denoted by the set

F = {F_{1}, . . ., F_{n}}

, and each participant may have i instances (oracles) involved in distinct, possibly concurrent executions of

P

, where n and i are polynomial numbers.

Sessions. Let

\prod_{i, j}^{m}

denote the mth protocol session running between entity

F_{i}

and intended partner entity

F_{j}

. A session

\prod_{i, j}^{m}

is accepted if it has computed a session key

S K_{i, j}^{m}

, with a session identifier of

s i d_{i, j}^{m} = (I D_{i}, I D_{j}, X_{i}, X_{j})

, where

X_{i}

is the outgoing information of

F_{i}

and

X_{j}

is the outgoing information of

F_{j}

Adversary. The adversary

A

has complete control of the communicating network. Namely,

A

is able to eavesdrop on, alter, ascertain, and inject communication messages. In addition,

A

can have knowledge of the system’s master secret keys, the participants’ long-term private keys, and ephemeral secrets.

A

allows replacing the participants’ public keys.

A

can interact with

\prod_{i, j}^{m}

with the following Oracle queries:

(1)

E S R e v e a l (\prod_{i, j}^{m})

A

can obtain the ephemeral secrets of

F_{i}

with the query.

(2)

P K R e p l a c e (I D_{i})

A

replaces the public key of

F_{i}

using this query.

(3)

P K R e v e a l (I D_{i})

A

is available with this query for the public key of

F_{i}

(4)

S K R e v e a l (I D_{i})

. By running the query,

A

is able to get the long-term private keys of

F_{i}

while the public key of

F_{i}

has not yet been replaced.

(5)

S S K R e v e a l (\prod_{i, j}^{m})

. Returns ⊥ if session

\prod_{i, j}^{m}

was not accepted. If not, it returns the session key that

\prod_{i, j}^{m}

holds.

(6)

S e n d (\prod_{i, j}^{m}, M)

A

represents

F_{j}

sending the message M to

F_{i}

in session

\prod_{i, j}^{m}

then receiving a reply from

F_{i}

according to

P

(7)

T e s t (\prod_{i, j}^{m})

. The query does not simulate the adversary’s ability, but it simulates the indistinguishability between real session keys and random keys. Input session

\prod_{i, j}^{m}

must be fresh. As a challenger,

C

, toss a coin

b \in {0, 1}

. If

b = 0

C

returns the session key held by

\prod_{i, j}^{m}

; if

b = 1

C

returns a random key from the distribution of the session key.

Matching session. If

\prod_{i, j}^{m}

and

\prod_{j, i}^{n}

have the same session

s i d

, then

\prod_{j, i}^{n}

is said to be a matching session for

\prod_{i, j}^{m}

Freshness. Let

\prod_{i, j}^{m}

denote an accepted session between honest participants

F_{i}

and

F_{j}

\prod_{i, j}^{m}

and

\prod_{j, i}^{n}

are matching sessions.

\prod_{i, j}^{m}

is fresh if all the following conditions do not hold:

(1)

A

issues

S S K R e v e a l (\prod_{i, j}^{m})

S S K R e v e a l (\prod_{j, i}^{n})

queries if

\prod_{j, i}^{n}

exists.

(2) The matching session

\prod_{j, i}^{n}

exists.

A

makes

S K R e v e a l (I D_{i})

and

E S R e v e a l (\prod_{i, j}^{m})

queries, or

S K R e v e a l (I D_{j})

and

E S R e v e a l (\prod_{j, i}^{n})

queries.

(3) The matching session

\prod_{j, i}^{n}

does not exist.

A

makes

S K R e v e a l (I D_{i})

and

E S R e v e a l (\prod_{i, j}^{m})

, or

S K R e v e a l (I D_{j})

queries.

A game simulates the security of an AKA protocol. In the game,

A

can issue multiple queries in any order.

A

can issue the

T e s t (\prod_{i, j}^{m})

query only once for a fresh session

\prod_{i, j}^{s}

. Next, a coin

b \in {0, 1}

is flipped by

C

. When the game ends,

A

will guess the value of b as

b^{'}

. If

b^{'} = b

and the test session

\prod_{i, j}^{m}

is still fresh, then

A

wins the game. The advantage of

A

to win the game is defined as

A d v_{A K A} (A) = |Pr [b^{'} = b] - \frac{1}{2}|

eCK Security. To ensure the security of the AKA protocol in the eCK model, the following conditions must be met:

(1) If both parties complete a matching session, they will calculate the same session key, unless the probability is negligible.

(2) For any polynomial-time adversary

A

, the advantage in breaking the AKA protocol,

A d v_{A K A} (A)

, must be negligible.

5.2. Formal security analysis

At first, three empty lists are created to hold the query and the corresponding answers.

L: input-output pairs of the hash function. Instead of being randomly chosen by

C

, the real hash function computes the outputs. To complete the safety proof,

C

needs to record the mapping between the inputs and outputs.

L_{U}

: Tuple

(I D_{i}, k_{i}, P K_{i})

for storing the queries-answers of

P K R e v e a l (I D_{i})

P K R e p l a c e (I D_{i})

, and

S K R e v e a l (I D_{i})

L_{w}

: Tuple

(I D_{i}, I D_{j}, s, x_{i}, x_{j})

for storing the queries-answers of

E S R e v e a l (\prod_{i, j}^{s})

To continue, it is essential to clarify a few fundamental configurations. Suppose that

A

is activating no more than

n_{1}

honest parties, and each party is engaged in no more than

n_{2}

sessions. Assume that

A

selects the

\prod_{I, J}^{S}

as the test session.

A

can distinguish a test session key from a random string in the three ways below:

A1. Guessing.

A

guesses the session key correctly.

A2. Key replication.

A

creates a mismatched session that has the same session key as

\prod_{I, J}^{S}

. So

A

is able to fetch the session key by querying the mismatched session.

A3. Forging. The value of

h (I D_{i} ∥ I D_{j} ∥ B_{i} ∥ C_{i})

is computed at some point by

A

Theorem 1. Since the

ECDL

ECDH

problem is intractable, the advantage of

A

against the AKA scheme in the eCK model is negligible.

Proof. Since the session key

S S K_{i} \in Z_{q}^{*}

, there is only a

\frac{1}{q - 1}

chance of guessing the correct

S S K_{i}

in the guessing attack.

The hash function should yield the same results for different input values in order to prevent the key replication attack. The probability of success of a key duplication attack is negligible.

The analysis of the forging attack is shown below.

Consider the tuple

(P, u_{1} P, u_{1} u_{2} P, v_{1} P, v_{1} v_{2} P)

as an example of the

ECDH

problem, in which the ephemeral keys

x_{s}

and

x_{s p}

are denoted by

u_{2}

and

v_{2}

, and the long-term keys

k_{s}

and

k_{s p}

are represented by

u_{1}

and

v_{1}

. If

A

is successful in forging attack with non-negligible probability,

ECDH (u_{1} u_{2} P, v_{1} P) = u_{1} u_{2} v_{1} v_{1} P

and

ECDH (u_{1} u_{2} P, v_{1} v_{2} P) = u_{1} u_{2} v_{1} v_{1} P

can be computed by

C

using

A

First,

C

creates a test session

\prod_{I, J}^{S}

by randomly selecting

S \in {1, n_{2}}

and

I, J \in {1, n_{1}} (I \neq J)

. Therefore,

C

has no higher chance of correctly guessing the test session

\prod_{I, J}^{S}

than

\frac{1}{n_{1}^{2} \cdot n_{2}}

. Let

\prod_{J, I}^{E}

be the matching session of

\prod_{I, J}^{S}

. There are six complementary events to consider, as shown in Table 2.

At least one event in the set,

{E 1 \land A 3, E 2 \land A 3, E 3 \land A 3, E 4 \land A 3, E 5 \land A 3, E 6 \land A 3}

, happens with non-negligible probability if

A

succeeds in faking attack with non-negligible probability.

5.2.1. Analysis of E1

1) Setup.

C

sends

(E (a, b), p, q, P, P, h (\cdot))

to the

A

2) Query.

A

will query the public key before an identity is used in any other queries, and all queries are different.

C

answers the queries issued by

A

as follows:

(1) $P K R e v e a l (I D_{i})$ .

A

submits an identity

I D_{i}

C

picks at random

k_{i} \in Z_{q}^{*}

, computes

P K_{i} = k_{i} \cdot P

, then returns

P K_{i}

and adds

(I D_{i}, k_{i}, P K_{i})

to the list

L_{U}

(2) $P K R e p l a c e (I D_{i})$ .

A

submits a tuple

P K_{i}^{'} = k_{i}^{'} \cdot P

for

I D_{i}

C

replaces

P K_{i}

with

P K_{i}^{'}

, and update

(I D_{i}, k_{i}, P K_{i})

with

(I D_{i}, *, K_{i}^{'})

in the list

L_{U}

, where ∗ can be the secret value

k_{i}^{'}

or be the symbol ⊥.

(3) $S K R e v e a l (I D_{i})$ .

A

submits an identity

I D_{i}

C

looks up

(I D_{i}, k_{i}, P K_{i})

in the list

L_{U}

and returns

k_{i}

. If

A

has replaced the public key

P K_{i}

and has not submitted a new one,

C

will refuse to respond.

(4) $E S R e v e a l (\prod_{i, j}^{m})$ .

A

submits a session

\prod_{i, j}^{s}

, then

C

processes as follows:

If $\prod_{i, j}^{s} = \prod_{I, J}^{S}$ or $\prod_{i, j}^{s} = \prod_{J, I}^{E}$ , then $C$ fails and stops.
If not, $C$ selects $x_{i}, x_{j} \in Z_{q}^{*}$ at random and appends $(I D_{i}, I D_{j}, s, x_{i}, x_{j})$ to $L_{W}$ .

(5) $S S K R e v e a l (\prod_{i, j}^{m})$ .

A

submits a session

\prod_{i, j}^{s}

, and

C

processes as follows: If

A

has replaced the public key

P K_{i}

(or

P K_{j}

) and did not submit the new secret value

P K_{i}^{'}

(or

P K_{j}^{'}

), then

C

may refuse to reply, else

$C a s e 1 :$ If $\prod_{i, j}^{s} = \prod_{I, J}^{S}$ or $\prod_{i, j}^{s} = \prod_{J, I}^{E}$ , then $C$ fails and stops.
$C a s e 2 :$ If $A$ has made $E S R e v e a l (\prod_{i, j}^{m})$ for $\prod_{i, j}^{s}, C$ will look up $(I D_{i}, I D_{j}, s, x_{i}, x_{j})$ in $L_{W}$ , $(I D_{i}, k_{i}, P K_{i})$ , or $(I D_{j}, k_{j}, P K_{j})$ in $L_{U}$ , then figures out the session key according to the AKA scheme.
$C a s e 3 :$ Else, $C$ selects $x_{i}, x_{j} \in Z_{q}^{*}$ at random and appends $(I D_{i}, I D_{j}, s, x_{i}, x_{j})$ to $L_{W}$ , then proceeds as in case 2.

(6) $S e n d (\prod_{i, j}^{s}, M)$ .

C

will answer the query as below.

If $(\prod_{i, j}^{s}, M) = (\prod_{I, J}^{S}, ⊥)$ , $C$ looks up $(I D_{I}, k_{I}, P K_{I})$ in $L_{U}$ and then returns $k_{I} u_{2} P$ .
If $(\prod_{i, j}^{s}, M) = (\prod_{J, I}^{E}, ⊥)$ , $C$ looks up $(I D_{J}, k_{J}, P K_{J})$ in $L_{U}$ and then returns $k_{I} v_{2} P$ .
If $\prod_{i, j}^{s} \neq \prod_{I, J}^{S}$ and $\prod_{i, j}^{s} \neq \prod_{J, I}^{E}$ , $C$ looks up $(I D_{i}, k_{i}, P K_{i})$ in $L_{U}$ and processes as follows:

·

If $A$ has made $E S R e v e a l (\prod_{i, j}^{m})$ for $\prod_{i, j}^{s}$ , $C$ looks up $(I D_{i}, I D_{j}, s, x_{i}, x_{j})$ in $L_{W}$ , then computes and returns $A_{i}$ .

·

If not, $C$ randomly selects $x_{i}, x_{j} \in Z_{q}^{*}$ and calculates and returns $A_{i}$ , then appends $(I D_{i}, I D_{j}, s, x_{i}, x_{j})$ to $L_{W}$ .
If $M = (A_{j}, *)$ , $C$ accepts $\prod_{i, j}^{s} \neq \prod_{I, J}^{S}$ .

(7) $T e s t (\prod_{i, j}^{s})$ . If the public key

P K_{i}

(or

P K_{j}

) had been replaced with

k_{i}^{'}

(or

k_{j}^{'})

A

would have had to commit the new secret value

k_{i}^{'}

(or

k_{j}^{'})

C

; since

C

is unable to generate the session key if he does not know the secret values for

I D_{i}

and

I D_{j}

. The responses of

C

T e s t (\prod_{i, j}^{s})

are as follows:

If $\prod_{i, j}^{s} \neq \prod_{I, J}^{S}, C$ fails and stops.
If $\prod_{i, j}^{s} = \prod_{I, J}^{S}$ , $C$ randomly chooses $S S K_{i} \in Z_{q}^{*}$ and sends it back to $A$ .

3) Solve ECDH problems. To win the game by forging attack,

A

would have to calculate

h (I D_{I} ∥ I D_{J} ∥ B_{I} ∥ C_{I})

, where

B_{I} = k_{J} k_{I} u_{2} P

and

D_{I} = k_{J} k_{I} u_{2} v_{2} P

C

finds

k_{I}

and

k_{J}

L_{U}

and computes

B_{I}

and

D_{I}

by solving the

ECDH

problem.

4) Probability. If it is possible for

C

to properly guess the test session

\prod_{I, J}^{S}

C

will not fail in the query phase. Thus,

C

is able to calculate

B_{I} = ECDH (k_{J} P, k_{I} u_{2} P)

and

D_{I} = ECDH (k_{J} v_{2} P, k_{I} u_{2} P)

with probability

\frac{1}{n_{1}^{2} n_{2}} A d v_{A K A} (A)

, if

A

wins in the game with advantage

A d v_{A K A} (A)

5.2.2. Analysis of E2

(1) Setup. Same as that in the analysis of E1.

(2) Query.

C

responds to the queries from

A

as those in the analysis of E1 except for the

P K R e v e a l (I D_{i})

S K R e v e a l (I D_{i})

E S R e v e a l (\prod_{i, j}^{m})

and

S e n d (\prod_{i, j}^{s}, M)

(1) $P K R e v e a l (I D_{i})$ .

A

submits an identity

I D_{k}

C

will respond to the query as follows:

If $I D_{k} = I D_{J}$ , $A$ computes $K_{J} = v_{1} P$ , returns $v_{1} P$ , and adds $(I D_{J}, ⊥, v_{1} P)$ to the list $L_{U}$ .
If not, C randomly selects $k_{k} \in Z_{q}^{*}$ and calculates $P K_{k} = k_{k} P$ , then returns $P K_{k}$ and adds $(I D_{k}, k_{k}, P K_{k})$ in $L_{U}$ .

(2) $S K R e v e a l (I D_{i})$ . If

I D_{i} = I D_{J}

C

will fail and stop. If not,

C

looks up

(I D_{i}, k_{i}, P K_{i})

L_{U}

and returns

k_{i}

(3) $E S R e v e a l (\prod_{i, j}^{m})$ .

C

will respond to the query as follows:

If $\prod_{i, j}^{s} = \prod_{I, J}^{S}$ or $\prod_{i, j}^{s} = \prod_{J, I}^{E}$ , $C$ randomly chooses $x_{J} \in Z_{q}^{*}$ and returns $(⊥, x_{J})$ , then appends $(I D_{J}, I D_{J}, s, ⊥, x_{J})$ to $L_{W}$ .
If not, $C$ randomly chooses $x_{i}, x_{j} \in Z_{q}^{*}$ and returns $(x_{i}, x_{j})$ , then appends $(I D_{i}, I D_{j}, s, x_{i}, x_{j})$ to $L_{W}$ .

(4) $S e n d (\prod_{i, j}^{s}, M)$ .

C

will respond to the query as follows:

If $(\prod_{i, j}^{s}, M) = (\prod_{I, J}^{S}, ⊥)$ , $C$ looks up $(I D_{I}, k_{I}, P K_{I})$ in $L_{U}$ and returns $(k_{1} u_{2} P)$ .
If $(\prod_{i, j}^{s}, M) = (\prod_{J, I}^{E}, ⊥)$ , $C$ looks up $(I D_{J}, ⊥, v_{1} P)$ in $L_{U}$ , and $(I D_{I}, I D_{J}, S, ⊥, x_{J})$ in $L_{W}$ , then sends $(v_{1} x_{J} P)$ back.
Otherwise, same analysis as E1.

3) Solve ECDH problems. To win the game by forging attack,

C

must compute

h (I D_{I} ∥ I D_{J} ∥ B_{I} ∥ C_{I})

, where

B_{I} = k_{J} k_{I} u_{2} P

and

C_{I} = k_{I} u_{2} v_{1} x_{J} P

C

finds

k_{I}

in the list

L_{U}

and

(⊥, x_{J})

in the list

L_{W}

to compute

B_{I}

and

C_{I}

by solving

ECDH

problems.

4) Probability. If it is possible for

C

to properly guess the test session

\prod_{I, J}^{S}

C

will not fail in the query phase. Thus,

C

is able to calculate

B_{I} = ECDH (k_{J} P, k_{I} u_{2} P)

and

D_{I} = ECDH (v_{1} x_{J} P, k_{I} u_{2} P)

with the same probability as E1 winning the game.

5.2.3. Analysis of E3

C

can swap

I D_{I}

and

I D_{J}

in E3 and then carry out the analysis of E2.

5.2.4. Analysis of E4

(1) Setup. Same as that in the analysis of E1.

(2) Query. The responses of

C

to the queries from

A

are the same as in E1, except for

P K R e v e a l (I D_{i})

S K R e v e a l (I D_{i})

E S R e v e a l (\prod_{i, j}^{m})

S K R e v e a l (I D_{i})

, and

S e n d (\prod_{i, j}^{s}, M)

queries.

(1) $P K R e v e a l (I D_{i})$ .

A

submits an identity

I D_{k}

C

process as follows:

If $I D_{k} = I D_{I}$ , $C$ computes $K_{I} = u_{1} P$ , then returns $u_{1} P$ and appends $(I D_{I}, ⊥, u_{1} P)$ to $L_{U}$ .
If $I D_{k} = I D_{J}$ , $C$ computes $K_{J} = v_{1} P$ , then returns $v_{1} P$ and appends $(I D_{J}, ⊥, v_{1} P)$ to $L_{U}$ .
Else, C chooses $k_{k} \in Z_{q}^{*}$ randomly and calculates $K_{k} = k_{k} P$ , then returns $K_{k}$ and adds $(I D_{k}, k_{k}, K_{k})$ in $L_{U}$ .

(2) $S K R e v e a l (I D_{i})$ . If

I D_{i} = I D_{I}

I D_{i} = I D_{J}

, then

C

fails and stops. If not, C looks up

(I D_{i}, k_{i}, K_{i})

L_{U}

and returns

k_{i}

(3) $E S R e v e a l (\prod_{i, j}^{m})$ .

A

submits a session

\prod_{i, j}^{s}

C

randomly chooses

x_{i}, x_{j} \in Z_{q}^{*}

and returns

(x_{i}, x_{j})

, then appends

(I D_{i}, I D_{j}, s, x_{i}, x_{j})

L_{W}

(4) $S e n d (\prod_{i, j}^{s}, M)$ .

C

finds

(I D_{i}, k_{i}, K_{i})

in the list

L_{U}

, then responds to queries as follows:

If $(\prod_{i, j}^{s}, M) = (\prod_{I, J}^{S}, ⊥)$ , $C$ performs as follows:

·

If $A$ has made $E S R e v e a l (\prod_{i, j}^{m})$ for $\prod_{i, j}^{s}$ , $C$ looks up $(I D_{i}, I D_{j}, s, x_{i}, x_{j})$ in $L_{W}$ and returns $(u_{1} x_{i} P)$ .

·

If $A$ has made $E S R e v e a l (\prod_{j, i}^{m})$ for $\prod_{j, i}^{s}$ , $C$ looks up $(I D_{i}, I D_{j}, s, x_{i}, x_{j})$ in $L_{W}$ and returns $(v_{1} x_{j} P)$ .

·

Else, $C$ randomly chooses $x_{i}, x_{j} \in Z_{q}^{*}$ and returns $A_{i}$ , then appends $(I D_{i}, I D_{j}, s, x_{i}, x_{j})$ to $L_{W}$ .
$M = (A_{j}, *), C$ accepts the session.

3) Solve ECDH problems. To win the game by forging attack,

C

must compute

h (I D_{I} ∥ I D_{J} ∥ B_{I} ∥ D_{I})

, where

B_{I} = u_{1} v_{1} x_{I} P

and

D_{I} = u_{1} x_{I} v_{1} x_{J} P

C

looks up

(I D_{i}, I D_{j}, s, x_{i}, x_{j})

L_{W}

to compute

B_{I}

and

D_{I}

by solving

{ECDH}_{1}

and

{ECDH}_{2}

problems.

4) Probability. If it is possible for

C

to properly guess the test session

\prod_{I, J}^{S}

C

will not fail in the query phase. Thus,

C

is able to calculate

B_{I} = {ECDH}_{1} (v_{1} P, u_{1} x_{I} P)

and

D_{I} = {ECDH}_{2} (u_{1} x_{I} P, v_{1} x_{J} P)

with the same probability as E1 winning the game.

5.2.5. Analysis of E5

In E2, there is a matching session

\prod_{J, I}^{E}

for the test session

\prod_{I, J}^{S}

, whereas in E5, there isn’t a matching session for

\prod_{I, J}^{S}

. Therefore, the analysis for E5 is similar to that of E2.

5.2.6. Analysis of E6

In E4, there is a matching session

\prod_{J, I}^{E}

for the test session

\prod_{I, J}^{S}

. However, in E6, there is no matching session for

\prod_{I, J}^{S}

. Therefore, the analysis of E6 is similar to that of E4. ▪

6. Descriptive Security analysis

6.1. Anonymity

In this scheme,

I D_{s}

and

I D_{s p}

are masked before being transmitted during the authentication process and change dynamically from session to session with the choice of the temporary random numbers

x_{s}

and

x_{s p}

A

is incapable of retrieving and tracing the identity from the transmitted messages. That is, the proposal guarantees anonymity.

6.2. Mutual Authentication

During authenticating, S verifies

S P

by checking the correctness of

V_{s p}

. For

V_{s p} = h (W S_{s} ∥ T_{s p} ∥ I D_{s p} ∥ S S K_{s p})

, where

S S K_{s p} = x_{s p} \cdot B_{s p} = k_{s p} x_{s p} \cdot A_{s}

V_{s p}

cannot be figured out without long-term secrets

k_{s p}

S P

. Similarly,

S P

verifies S by checking

V_{s}

6.3. ESL attack resistance

Resistant to ESL attacks means

A

is unable to figure out the session key in spite of knowing ephemeral secrets,

x_{s}

and

x_{s p}

. For

S S K_{s} = H (I D_{s} ∥ I D_{s p} ∥ B_{s} ∥ C_{s})

, where

C_{s} = (x_{s} k_{s} mod q) \cdot A_{s p} = (x_{s p} k_{s p} mod q) \cdot A_{s}

, even if

x_{s}

and

x_{s p}

are revealed,

A

cannot figure out

S S K_{s}

because they do not know the long-term secrets

k_{s}

and

k_{s p}

. Similarly, if

A

knows the short-term secrets

x_{s}

and

x_{s p}

, then he/she cannot calculate

S S K_{s p}

6.4. Impersonation attacks resistance

Firstly, we analyze the S impersonation attack. If

A

tries to impersonate S to generate the message

{A_{s}, E I D_{s}, T_{s}, V_{s}

} to make

S P

believe that the message is legitimate and generated by S,

A

cannot generate valid information and impersonate S in polynomial time without knowing parameters such as

k_{s}

and

x_{s}

6.5. IoT nodes capture attack resistance

Some IoT end devices are placed in unattended environments and may be physically captured by an adversary. Thus, their credentials,

{I D_{s}, k_{s}, P K_{s}, I D_{s p}, W s_{s p}}

, can be easily extracted by

A

can easily extract their credentials,

{I D_{s}, k_{s}, P K_{s}, I D_{s p}, W s_{s p}}

. The credentials for different end devices in the proposed scheme are different. Therefore, this will only lead to session key leakage between the captured

S_{s}

and the server

S P

, but not between the un-corrupted end device

S_{s}^{'}

and the server

S P

. This implies that the proposal can withstand IoT node capture attacks.

6.6. KCI attack resistance

Resistance against KCI attacks refers to the inability of

A

to impersonate another legitimate participant, Bob, to authenticate with Alice after Alice’s long-term private key disclosure. Suppose

A

learns the long-term key,

k_{s}

, of the end device S and wants to impersonate

S P

to produce

{A_{s p}, T_{s p}, V_{s p}

} to convince S that the message is legitimate and generated by

S P

. For

V_{s p} = h (W S_{s} ∥ T_{s p} ∥ I D_{s p} ∥ S S K_{s p})

, where

C_{s p} = x_{s p} \cdot B_{s p} = k_{s p} x_{s p} \cdot A_{s}

, and

k_{s p}

has not been compromised,

A

cannot impersonate server

S P

to perform authentication and key agreement with S. Similarly,

A

cannot carry out KCI attacks against

S P

7. Automatic formal verification

The security of the proposal is formally validated with ProVerif [5]. Table 3 illustrates the codes of S, where

s c h s

is a secret channel used for S’s registration, and

c h

is a public channel used for S and

S P

authentication. Based on the following results, it can be concluded that both the authentication process and the session key are secure from adversary attacks.

Here are the results of queries in Proverif:

1): RESULT inj-event(endAuthS)==>inj-event(startAuthS) is true.
2): RESULT inj-event(endAuthSP)==>inj-event(startAuthSP) is true.
3): RESULT inj-event(endAuthSP)==>inj-event(endAuthS) is true.
4): RESULT inj-event(endAuthS)==>inj-event(endAuthSP) is true.
5): RESULT not attacker(SSKs[]) is true.
6): RESULT not attacker(SSKsp[]) is true.
7): RESULT not attacker(ks[]) is true.
8): RESULT not attacker(ksp[]) is true.

8. Performance comparison

8.1. Communication Cost

According to [22,37], Suppose

G_{1}

is an additive cyclic group with order

q_{1}

G_{2}

is a multiplicative cyclic group with order q. The bilinear map is defined as

e : G_{1} \times G_{1} \to G_{2}

. In addition, it is assumed that the lengths of an identifier (ID), a hash output (H), a timestamp (TS), and a random number (R) are 64, 128, 32, and 128 bits, respectively. Table 4 indicates the proposed scheme has the lowest communication overhead during authentication.

8.2. Computation Cost

According to He et al.’s [37], Table 5 shows the run-time of the relevant encryption operation on a

S a m s u n g G a l a x y S 5

. Table 6 displays the runtime of each scheme during authentication. It is evident that the proposed scheme requires the least computational overhead.

8.3. Performance Comparison

The results of the comparison between the proposal and related schemes [22,23,25,27,28,29] in terms of security are shown in Table 7. Compared to the existing schemes, the proposed protocol provides better security and functionality; e.g., it is resistant to attacks such as IM, MIM, and ESL while providing anonymity and PFS without key escrow issues.

9. Conclusion

To begin, we analyze previous ECC-based AKA proposals and show that they are vulnerable to known attacks, failing to meet specific security goals. In addition, these schemes have been verified for security in the RoM model. It is widely recognized that cryptographic schemes proven secure in the RoM model may not necessarily provide the same level of security when implemented in real-world systems. Furthermore, We propose a security-enhanced AKA protocol for IoT devices to connect to servers. The security of the proposed scheme is rigorously proved under the eCK model with the elliptic curve encryption computational assumptions, and ProVerif verifies the session key confidentiality and authentication properties. Furthermore, the proposed protocol provides stronger security features at a lower computational and communication cost.

Author Contributions

Conceptualization, S.H., S.J. and Q.M.; methodology, S.H. and F.Y.; software, W.Z.; validation, S.H. and P.D.; formal analysis, S.H. and S.J..; investigation, S.H., S.J. and Q.M.; resources, S.H.; data curation, Q.M.; writing—original draft preparation, S.H.and F.Y.; writing—review and editing, S.H., S.J., Q.M., F.Y., W.Z. and P.D.; visualization, S.H.; supervision, S.H.; project administration, S.H.; funding acquisition, S.H. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported in part by the Natural Science Foundation of China (No. 62072319).

References

Tedeschi, P.; Sciancalepore, S.; Eliyan, A.; Di Pietro, R. LiKe: Lightweight Certificateless Key Agreement for Secure IoT Communications. IEEE Internet of Things Journal 2020, 7, 621–638. [Google Scholar] [CrossRef]
Whitepaper, J.R. IoT The Internet of Transformation 2020. [Online]. https://www.juniperresearch.com/whitepapers/iot-the-internet-of-transformation-2020. Accessed: July 14, 2022.
Nicanfar, H.; Hosseininezhad, S.; TalebiFard, P.; Leung, V.C. Robust privacy-preserving authentication scheme for communication between Electric Vehicle as Power Energy Storage and power stations. 2013 IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), 2013, pp. 55–60. [CrossRef]
Showkat, D.; Som, S.; Khatri, S.K.; Ahluwalia, A.S. Security Implications in IoT using Authentication and Access Control. 2018 7th International Conference on Reliability, Infocom Technologies and Optimization (Trends and Future Directions) (ICRITO), 2018, pp. 689–694. [CrossRef]
Zheng, Y.; Hu, S.; Wei, L.; Chen, Y.; Wang, H.; Yang, Y.; Li, Y.; Xu, B.; Huang, W.; Chen, L. Design and Analysis of a Security-Enhanced Three-Party Authenticated Key Agreement Protocol Based on Chaotic Maps. IEEE Access 2020, 8, 66150–66162. [Google Scholar] [CrossRef]
Wong, K.; Zheng, Y.; Cao, J.; Wang, S. A dynamic user authentication scheme for wireless sensor networks. IEEE International Conference on Sensor Networks, Ubiquitous, and Trustworthy Computing (SUTC’06), 2006, Vol. 1, pp. 8 pp.–. [CrossRef]
Wu, D.; Zhou, C. Fault-Tolerant and Scalable Key Management for Smart Grid. IEEE Transactions on Smart Grid 2011, 2, 375–381. [Google Scholar] [CrossRef]
He, D.; Zeadally, S.; Kumar, N.; Lee, J. Anonymous authentication for wireless body area networks with provable security. IEEE Systems Journal 2016. [Google Scholar] [CrossRef]
Gope, P.; Amin, R.; Hafizul Islam, S.; Kumar, N.; Bhalla, V.K. Lightweight and privacy-preserving RFID authentication scheme for distributed IoT infrastructure with secure localization services for smart city environment. Future Generation Computer Systems 2018, 83, 629–637. [Google Scholar] [CrossRef]
Aman, M.N.; Sikdar, B. ATT-Auth: A Hybrid Protocol for Industrial IoT Attestation With Authentication. IEEE Internet of Things Journal 2018, 5, 5119–5131. [Google Scholar] [CrossRef]
Chatterjee, U.; Govindan, V.; Sadhukhan, R.; Mukhopadhyay, D.; Chakraborty, R.S.; Mahata, D.; Prabhu, M.M. Building PUF Based Authentication and Key Exchange Protocol for IoT Without Explicit CRPs in Verifier Database. IEEE Transactions on Dependable and Secure Computing 2019, 16, 424–437. [Google Scholar] [CrossRef]
Gope, P.; Lee, J.; Quek, T.Q.S. Lightweight and Practical Anonymous Authentication Protocol for RFID Systems Using Physically Unclonable Functions. IEEE Transactions on Information Forensics and Security 2018, 13, 2831–2843. [Google Scholar] [CrossRef]
Imam, R.; Areeb, Q.M.; Alturki, A.; Anwer, F. Systematic and Critical Review of RSA Based Public Key Cryptographic Schemes: Past and Present Status. IEEE Access 2021, 9, 155949–155976. [Google Scholar] [CrossRef]
Hankerson, D.; Menezes, A.J.; Vanstone, S. Guide to Elliptic Curve Cryptography; Springer-Verlag: Berlin, Heidelberg, 2003. [Google Scholar]
Gura Nils, Patel Arun, W.A.; etc. Comparing Elliptic Curve Cryptography and RSA on 8-bit CPUs. Cryptographic Hardware and Embedded Systems - CHES 2004; Springer Berlin Heidelberg: Berlin, Heidelberg, 2004; pp. 119–132.
Wang, C.; Zhang, Y. New Authentication Scheme for Wireless Body Area Networks Using the Bilinear Pairing. Journal of Medical Systems 2015, 39, 136. [Google Scholar] [CrossRef]
Wu, L.; Zhang, Y.; Li, L.; Shen, J. Efficient and Anonymous Authentication Scheme for Wireless Body Area Networks. Journal of Medical Systems 2016, 40, 134. [Google Scholar] [CrossRef] [PubMed]
Seo, S.H.; Won, J.; Sultana, S.; Bertino, E. Effective Key Management in Dynamic Wireless Sensor Networks. IEEE Transactions on Information Forensics & Security 2017. [Google Scholar]
Saeed, M.E.; Liu, Q.Y.; Tian, G.; Gao, B.; Li, F. AKAIoTs: Authenticated Key Agreement for Internet of Things. Wirel. Netw. 2019, 25, 3081–3101. [Google Scholar] [CrossRef]
Fang, D.; Qian, Y.; Hu, R.Q. A Flexible and Efficient Authentication and Secure Data Transmission Scheme for IoT Applications. IEEE Internet of Things Journal 2020, 7, 3474–3484. [Google Scholar] [CrossRef]
Maurya, A.K.; Das, A.K.; Jamal, S.S.; Giri, D. Secure user authentication mechanism for IoT-enabled Wireless Sensor Networks based on multiple Bloom filters. Journal of Systems Architecture 2021, 120, 102296. [Google Scholar] [CrossRef]
Abbasinezhad-Mood, D.; Ostad-Sharif, A.; Nikooghadam, M.; Mazinani, S.M. A Secure and Efficient Key Establishment Scheme for Communications of Smart Meters and Service Providers in Smart Grid. IEEE Transactions on Industrial Informatics 2020, 16, 1495–1502. [Google Scholar] [CrossRef]
Srinivas, J.; Das, A.K.; Li, X.; Khan, M.K.; Jo, M. Designing Anonymous Signature-Based Authenticated Key Exchange Scheme for Internet of Things-Enabled Smart Grid Systems. IEEE Transactions on Industrial Informatics 2021, 17, 4425–4436. [Google Scholar] [CrossRef]
Baruah, B.; Dhal, S. An Authenticated Key Agreement Scheme for Secure Communication in Smart Grid. 2021 International Conference on COMmunication Systems NETworkS (COMSNETS), 2021, pp. 447–455. [CrossRef]
Yang, X.; Yi, X.; Nepal, S.; Khalil, I.; Huang, X.; Shen, J. Efficient and Anonymous Authentication for Healthcare Service With Cloud Based WBANs. IEEE Transactions on Services Computing 2022, 15, 2728–2741. [Google Scholar] [CrossRef]
Shen, J.; Gui, Z.; Ji, S.; Shen, J.; Tan, H.; Tang, Y. Cloud-aided lightweight certificateless authentication protocol with anonymity for wireless body area networks. Journal of Network and Computer Applications 2018, 106, 117–123. [Google Scholar] [CrossRef]
Chaudhry, S.A.; Nebhan, J.; Yahya, K.; Al-Turjman, F. A Privacy Enhanced Authentication Scheme for Securing Smart Grid Infrastructure. IEEE Transactions on Industrial Informatics 2022, 18, 5000–5006. [Google Scholar] [CrossRef]
Hajian, R.; Haghighat, A.; Erfani, S. A Secure Anonymous D2D Mutual Authentication and Key Agreement Protocol for IoT. Internet of Things 2022, 18, 100493. [Google Scholar] [CrossRef]
Chen, Y.; Yin, F.; Hu, S.; Sun, L.; Li, Y.; Xing, B.; Chen, L.; Guo, B. ECC-Based Authenticated Key Agreement Protocol for Industrial Control System. IEEE Internet of Things Journal 2023, 10, 4688–4697. [Google Scholar] [CrossRef]
Bellare, M.; Rogaway, P. Entity Authentication and Key Distribution. In Advances in Cryptology — CRYPTO’ 93; Springer Berlin Heidelberg: Berlin, Heidelberg, 1994; Vol. 773, Lecture Notes in Computer Science, pp. 232–249. [Google Scholar]
Blake-Wilson, S.; Johnson, D.; Menezes, A. Key agreement protocols and their security analysis. CRYPTOGRAPHY AND CODING, PROCEEDINGS; Springer Nature: BERLIN, 1997; Vol. 1355, pp. 30–45.
Canetti, R.; Krawczyk, H. Analysis of Key-Exchange Protocols and Their Use for Building Secure Channels. In ADVANCES IN CRYPTOLOGY-EUROCRYPT 2001, PROCEEDINGS; Springer Berlin Heidelberg: Berlin, Heidelberg, 2001; Vol. 2045, Lecture Notes in Computer Science, pp. 453–474.
Sun, H.; Wen, Q.; Zhang, H.; Jin, Z. A strongly secure identity-based authenticated key agreement protocol without pairings under the GDH assumption. Security and Communication Networks 2015, 8, 3167–3179. [Google Scholar] [CrossRef]
Deng, L.; Gao, R. Certificateless two-party authenticated key agreement scheme for smart grid. Information Sciences 2021, 543, 143–156. [Google Scholar] [CrossRef]
LaMacchia, B.; Lauter, K.; Mityagin, A. Stronger Security of Authenticated Key Exchange. Proceedings of the 1st International Conference on Provable Security; Springer-Verlag: Berlin, Heidelberg, 2007; ProvSec’07, p. 1–16.
Hu, S.; Chen, Y.; Zheng, Y.; Xing, B.; Li, Y.; Zhang, L.; Chen, L. Provably Secure ECC-Based Authentication and Key Agreement Scheme for Advanced Metering Infrastructure in the Smart Grid. IEEE Transactions on Industrial Informatics 2023, 19, 5985–5994. [Google Scholar] [CrossRef]
He, D.; Wang, H.; Khan, M.K.; Wang, L. Lightweight anonymous key distribution scheme for smart grid using elliptic curve cryptography. IET Communications 2016, 10, 1795–1802, [https://ietresearch.onlinelibrary.wiley.com/doi/pdf/10.1049/iet-com.2016.0091]. [Google Scholar] [CrossRef]

Figure 1. Network model

Figure 2. Registration processes of Srinivas et al.’s scheme

Figure 3. Authentication and key agreement of Srinivas et al.’s scheme

Figure 4. Registration processes of the proposed scheme

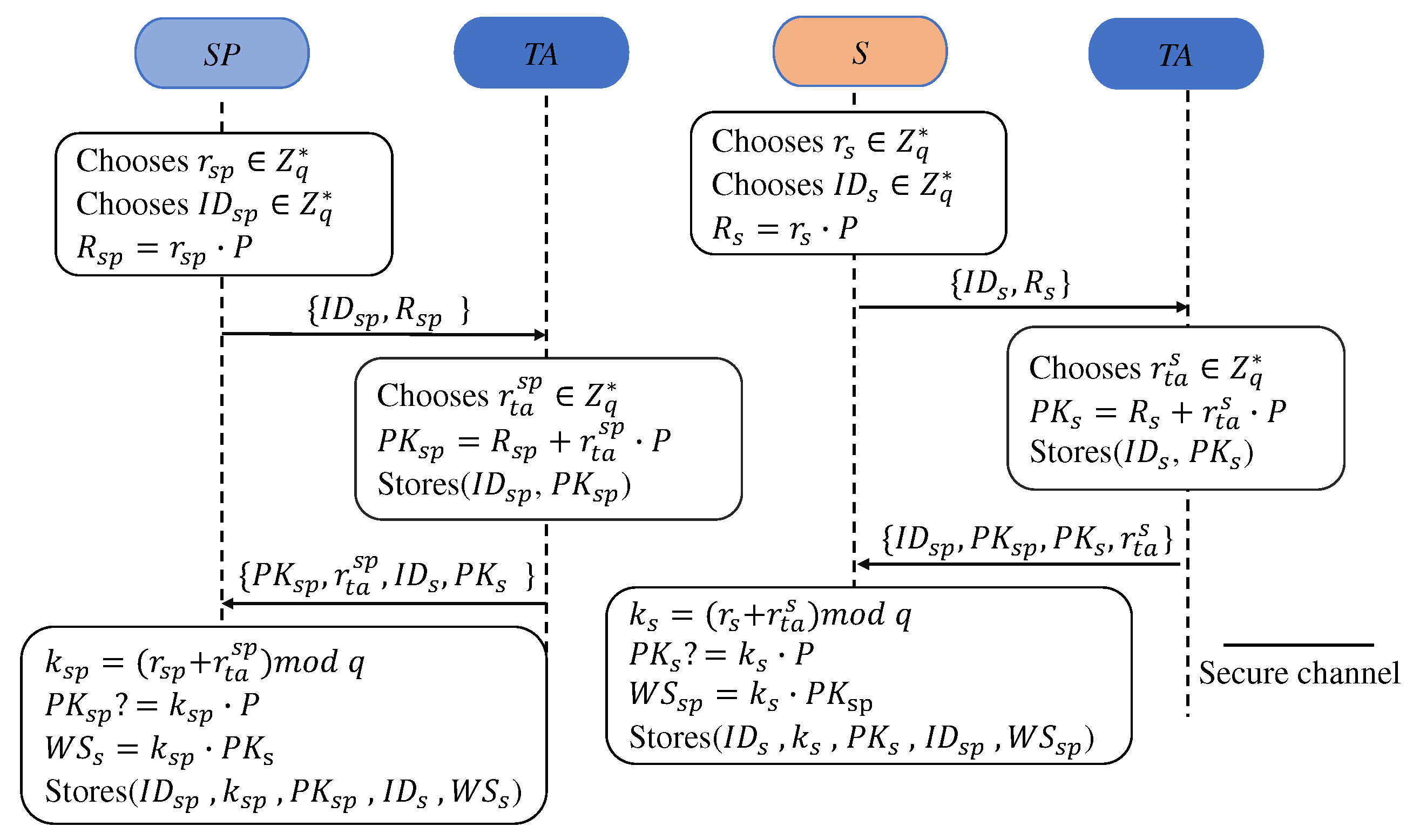
Figure 5. Authentication and key agreement of proposed protocol

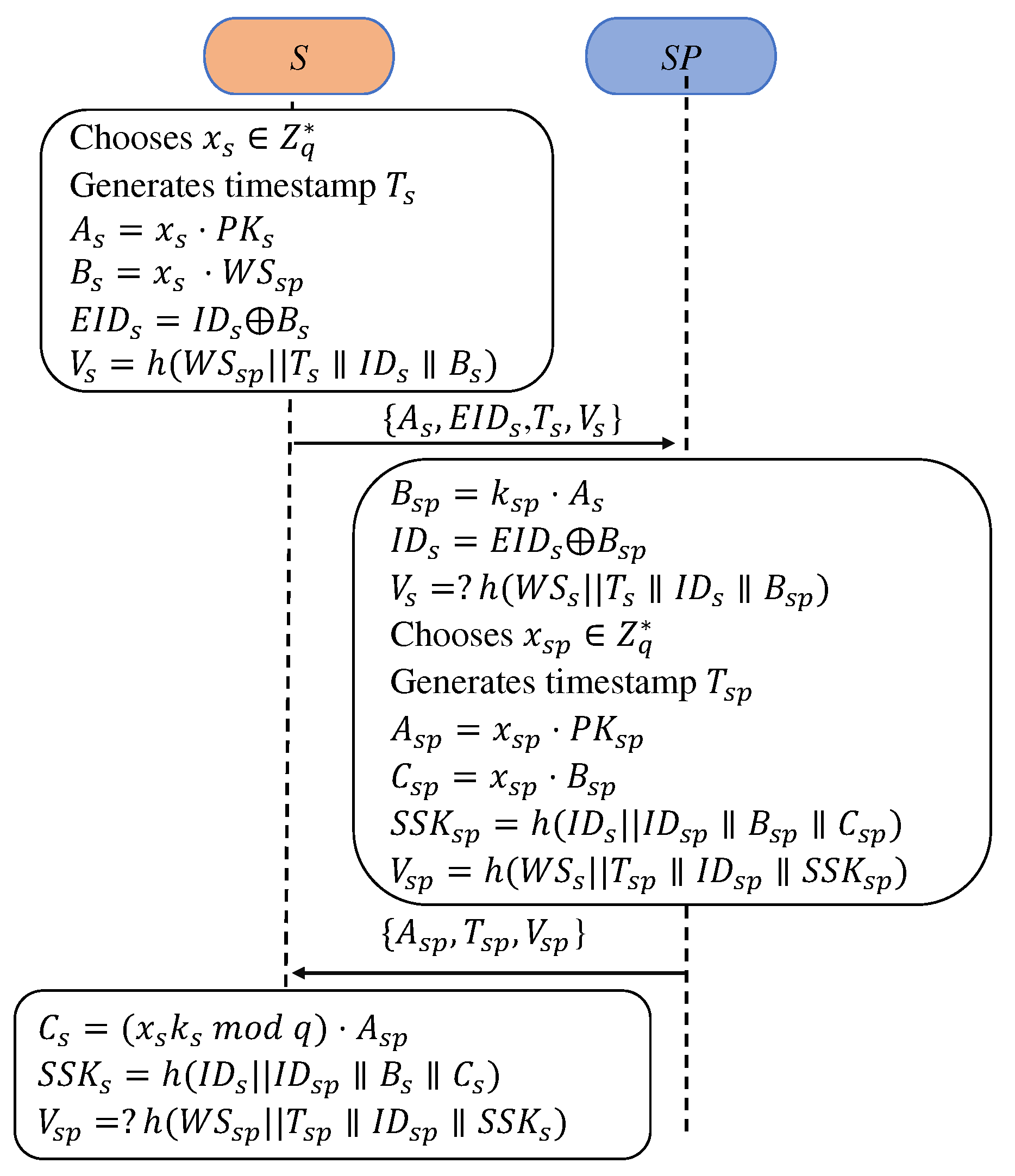
Table 1. Symbols for the schemes


Notation	Description
$T A$ , $K G C$	Trust Anchor, Key Generation Center
$A, C$	Adversary, Challenger
$S P_{j}, I D_{S P_{j}}$	$j^{t h}$ service provider and its identity
$S M_{i}, I D_{S M_{i}}$	$i^{t h}$ smart meter and its identity
$E_{q} (a, b)$	A non-singular elliptic curve
P	A base point of $E_{q} (a, b)$
$t, T_{p u b}$	Private-public key pair of $T A$ [23]
$S K_{i j}, S S K_{i}$	Session key
$\oplus, ∥$	Bitwise XOR and concatenation operations
$T S, T$	Timestamps
$Δ T$	Maximum transmission delay
$h (\cdot)$	One-way hash functions
$S, S P$	End device, Server
$k / K$	Private/public key of a entity

Table 2. Complementary events


	E1	E2	E3	E4	E5	E6
$\prod_{J, I}^{E}$					×	×
Ephemeral secret keys of $I D_{I} (u_{2})$	×	×			×
Ephemeral secret keys of $I D_{J} (v_{2})$	×		×
Secret value of $I D_{I} (u_{1})$			×	×		×
Secret value of $I D_{I} (v_{1})$		×		×	×	×

×: the session does not exit or

A

does not obtain the parameter.

Table 3. Codes for end device S

let S=

new rs:bitstring;

let Rs= Mul(rs, P) in

out (schs, (IDs, Rs));

in (schs, (vIDsp:bitstring,vPKsp: bitstring, vPKs: bitstring,vrtas:bitstring));

let ks=add (rs, vrtas) in

let PKs=Mul (ks, P) in

if PKs=vPKs then

let WSsp= Mul (ks, vPKsp) in

(

event startAuthsp;

let As=Mul(xs,PKs) in

let Bs=Mul(xs, WSsp) in

let EIDs = xor (IDs, Bs) in

new TSeeds:bitstring;

let Ts=generate_Timeline(TSeeds) in

let Vs = Hash(con (con (con (WSsp, Ts), IDs),Bs))in

out (ch, (As, EIDs, Ts, Vs));

in (ch, (vAsp: bitstring, vTsp: bitstring, vVsp:bitstring));

let Cs=Mul (mul (xs, ks), vAsp) in

let SSKs = Hash(con (con (con (IDs,IDsp), Bs), Cs)) in

let Vsp=Hash(con (con (con (WSsp,vTsp),IDsp), SSKs)) in

if Vsp=vVsp then

event endAuths;

Table 4. Communication cost


Scheme	End device	Server	Total
[22]	$2 G + G 1 + H + T S + I D = 2016$	$G + H + T S = 544$	2560
[23]	$2 G + H + 2 T S + I D = 1024$	$2 G + H + T S = 928$	1952
[25]	$2 G + 2 H + T S = 1056$	$G + H + T S = 512$	1568
[27]	$G + H + R + 2 T S + I D = 832$	$G + H + 2 T S + I D = 640$	1472
[28]	$G + 2 H + T S = 672$	$G + 2 H + I D = 704$	1376
[29]	$3 G + 2 H + I D = 1472$	$3 G + H + I D = 1344$	2816
Ours	$G + H + T S + I D = 608$	$G + H + T S = 544$	1152

Table 5. Run-time of related operations


Notation	Operation	Time (ms)
$T_{b p}$	Bilinear pairing	$32.713$
$T_{h}$	Hash function	$0.006$
$T_{p m 1}$	Point multiplication in G1	$13.405$
$T_{p a 1}$	Point addition in G1	$0.56$
$T_{e x p 2}$	Exponentiation in G2	$2.249$
$T_{s}$	Symmetric encryption	$0.012$
$T_{p a}$	ECC point addition	$0.014$
$T_{p m}$	ECC point multiplication	$3.352$

Table 6. Computation cost


Scheme	End device	Server	Total
[22]	$2 T_{p m 1} + T_{p a 1} + T_{e x p 2} + 4 T_{p m} + T_{p a} + 6 T_{h} = 43.077$	$T_{p b} + 4 T_{p m} + T_{p a} + 5 T_{h} = 46.165$	89.242
[23]	$4 T_{p m} + T_{p a} + 7 T_{h} = 13.464$	$4 T_{p m} + T_{p a} + 7 T_{h} = 13.464$	26.982
[25]	$3 T_{p m} + 4 T_{h} = 10.08$	$3 T_{p m} + 2 T_{p a} + 5 T_{h} = 13.466$	23.546
[27]	$3 T_{p m} + 2 T_{s} + 4 T_{h} = 10.104$	$4 T_{p m} + 3 T_{s} + 4 T_{h} = 13.468$	23.572
[28]	$4 T_{p m} + 7 T_{h} = 13.45$	$4 T_{p m} 7 T_{h} = 13.45$	26.9
[29]	$7 T_{p m} + 2 T_{p a} + 5 T_{h} = 23.522$	$7 T_{p m} + 2 T_{p a} + 5 T_{h} = 23.522$	47.044
Ours	$3 T_{p m} + 3 T_{h} = 10.074$	$3 T_{p m} + 3 T_{h} = 10.074$	20.148

Table 7. Performance Comparison

Scheme

SF1

SF2

SF3

SF4

SF5

SF6

SF7

SF8

SF9

SF10

SF11

SF12

[22]

√

[23]

√

[25]

√

[27]

√

[28]

√

[29]

√

Ours

√

SF1: IM attack resistance; SF2: MIM attack resistance; SF3: Mutual authentication without the help of RC; SF4: ESL attack resistance; SF5: KCI attack; SF6: IoT nodes capture attack resistance; SF7: Anonymity; SF8: Unknown key share attack resistance; SF9: Perfect forward secrecy; SF10: Formal security proof; SF11: Replay attack resistance; SF12: No key escrow issue; √: Secure or supportive ×: Insecure or unsupported.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Provably secure ECC-based anonymous authentication and key Agreement for IoT

Abstract

1. Introduction

1.1. Related work

1.2. Related formal security model

1.3. Motivation and contributions

1.4. Roadmap

2. PRELIMINARIES

2.1. Network Model

2.2. Elliptic curve encryption mathematical problems

2.3. Symbols

3. Security analysis of Srinivas et al.’s scheme

3.1. Key escrow problem

3.2. No resistance to ESL attacks

4. The proposed protocol

4.1. Initialization phase

4.2. Registration phase

4.3. Authentication and key agreement phase

5. Formal Proof

5.1. Security model

5.2. Formal security analysis

5.2.1. Analysis of E1

5.2.2. Analysis of E2

5.2.3. Analysis of E3

5.2.4. Analysis of E4

5.2.5. Analysis of E5

5.2.6. Analysis of E6

6. Descriptive Security analysis

6.1. Anonymity

6.2. Mutual Authentication

6.3. ESL attack resistance

6.4. Impersonation attacks resistance

6.5. IoT nodes capture attack resistance

6.6. KCI attack resistance

7. Automatic formal verification

8. Performance comparison

8.1. Communication Cost

8.2. Computation Cost

8.3. Performance Comparison

9. Conclusion

Author Contributions

Funding

References

MDPI Initiatives

Important Links

Subscribe