Prerpints.org logo
Preprint
Review

Inertial Propulsion Devices: A Review

Altmetrics

Downloads

255

Views

256

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

25 January 2024

Posted:

26 January 2024

You are already at the latest version

Alerts
Abstract
The use of the Google Scholar produces about 278 hits on the term ‘‘inertial propulsion.’’ If patents are also included, the number of hits increases to 536. This paper discusses, in a critical way, some characteristic aspects of this controversial topic. The review starts with the halteres of athletes in the Olympic games of ancient times and then continues with some typical devices which were developed or/and patented from the second fourth of the twentieth century till today.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

The origin of the term “inertial propulsion” is not clear. Some of the early scientific papers mentioning this term around mid-1960s are [1,2]. In 1977, this term was already included as an entry in a technical encyclopedia [3] but was restricted to the experimental works by Professor Eric Laithwaite [4]. We could say that inertial propulsion typically refers to a hypothetical concept where a propulsion system generates thrust without expelling mass or propellant. It is widely accepted that such concepts often fall into the realm of speculative or fringe ideas and may lack scientific validation or consensus. A paper that demonstrates that an inertia propelled device under dry friction moves in the opposite direction than the same device under viscous friction is [5].
Despite this unfavorable point of view of this controversial term, there are also many useful applications of inertial propulsion which will be discussed in this review paper. Interestingly, this idea has attracted the interest of many practicians, as well as of many serious researchers of high academic background, including persons coming from aerospace industry or academia who have granted a considerable number of patents (e.g., [6] among many others).
The motivation of the researchers on inertial propulsion is multiple. Some of them had found a supposed way to break the physical laws thus to achieve action-without-reaction and thus to increase the efficiency of machines. Others have found an alternative way to move heavy objects by vibrations without actual lifting thus saving energy costs (e.g., [7,8,9,10,11]). Also, gyroscopes have been used for harvesting energy from waves [12,13].
Concerning space applications, the tendency of researchers to replace the fuel-consuming rockets for interstellar space travels is also a particular topic of high importance for the future of the mankind. Some of the alternatives have been reported in [14,15]. And because the supply of new inventive ideas was plentiful and pressing (more than three applications per day), in the year 2006 NASA decided to release a report to discourage new inventors [16].
Nevertheless, although the topic of inertial propulsion does not seem to provide a practical means for space propulsion by itself (it is useful for navigation [17,18] and attitude control [19] though), it is interesting to write down the course the human mind has followed so far and dreamed a better future. This review also offers a global approach to future researchers of this kind.
The structure of the paper is as follows. Section 2 refers to ancient times. Section 3 discusses the progress in the 20th century, while section 4 continues with the 21rst century. Section 5 refers to the involved mechanics in inertial drives, and section 6 is a thorough discussion in which additional breakthrough methods are also mentioned.

2. Ancient Times and Fictional References

As previously was mentioned, there are several reasons for this kind of research. If we begin from the ancient times, Greek athletes used hand-held weights (called “halteres”, see Figure 1) aiming at extending the distance travelled in the Olympic long jump [20]. It is hypothesized that as far as the athlete is into the air, the conservation of momentum is the reason that he may control the horizontal motion by lowering the inertial mass ([21,22] and papers therein).
In a chronological sequence, the second written record exists in one of the stories regarding Baron Münchhausen, a fictional German nobleman created by the writer Rudolf Erich Raspe in his 1785 book. Münchhausen is trapped on his horse into a lake of mud, and he tries to pull his hair to give his body a boost to escape (Figure 2) [23]. Of course, in the real world this is not possible because the pulling force is internal thus the center of mass cannot move. Nevertheless, it is a case for reflection as to whether release is possible.

3. Inventions in the Twentieth Century

3.1. Rotating Masses

Since the second fourth of twentieth century a lot of “inertial drives” have been developed and some of them were patented. The main idea is that unidirectional thrust may be caused by contra-rotating eccentric masses (the assembly is called inertial drive) which are attached to a vehicle or a cart. The need of two masses (even number in general) is related to the cancelation of the forces in the vertical (undesirable) direction of vehicle’s motion.
The first official record is probably the patent by the Italian Professor Marco Todeschini (1933) [24], in which the drive consists of two contra-rotating masses moving on a three-dimensional curve thus offering a net thrust and motion of the vehicle (i.e., toward the vertical axis on Earth’s surface shown in Figure 3).
Thirty-five years later, the American citizen Norman Dean proposed a different setup and claimed that it could assist space travels (Figure 4) [25,26]. The topic has kept researchers from the civilian and military sector busy, therefore a lot of favorable publications are available. [27,28,29,30,31,32].
A few years later (in 1963), the “Dean drive” was rejected for the first time in a scientific paper by Professor Stepanov [33] (Figure 5) while later references on the same issue from Russian academics (already mentioned) are [7,8].
The abovementioned negative comments did not influence the Italian Professor Alfio Di Bella who came back by extending the ideas of his compatriot Marco Todeschini [24], first by filling a patent in May 1967 [34] and fifteen months later (August 1968) presenting an experimental prototype accompanied with theoretical results [35]. Briefly, with respect to Figure 6, the motor 1 turns frame 4, carrying axle 9, counterweight 11 and bevel gear 10, which meshes with the fixed bevel gear 14. This causes the out-of-balance shown mass m to follow the eight-shaped locus, known to mathematicians as the Viviani’s curve, or Viviani’s window (see, [36]). Similar differential mechanisms for ornithopters were later reported by [37].
According to [38] as well as additional sources, in the year 1936, the Russian engineer Vladimir Tolchin (an engineer and head of the design office at Perm’s Dzerzhinsky Machine Plant) had invented, described, and engineered a mechanism he dubbed the “inertioid”. It was a cart on which one or two loads were moved about — one slower, the other faster — by means of a spring motor. The cart itself then moved in an uneven fashion, even though no power was transmitted to the wheels. What is most interesting in the story of the inertioid (and its numerous variations) is the ontological interpretation of its principle of motion. Tolchin believed his cart moved without propulsion (there was no transmission mechanism from the motor to the wheels), arguing at the same time that it functioned “in accordance with the laws of a full mechanical process”, some aspects of which he interpreted in a new way [39]. However, the Perm designer’s intemperate followers, responding to critics who pointed out that the movement of Tolchin’s cart violated the law of conservation of momentum, made the dizzying conclusion that the inertioid challenged existing physical laws. A new physics was needed to explain its motion. By the time Tolchin published his book in the late 1960s (first edition), the “natural” objects of this other physics had, in fact, been in evidence for some time. For the demonstration of an experimental prototype the reader is addressed to [40].
The fact that the use of vibrational methods was a favorite subject of Eastern scientists is confirmed by [7,8,9,10,26], as well as the numerous bibliographic references cited in the works of the Bulgarian Professor Ivan Lukanov, whose second language was Russian (see, section 4.2).
From the above discussion it becomes evident that the “Dean-drive” which appeared in USA in late 1950s and caused much ‘noise’, was not a local event, but an issue that had kept inventors busy some years earlier, at least in Italy and Russia. It is worthy to mention that in mid-1960s the concept of propulsion without wheels was also an attractive topic in United Kingdom to Professor Eric Laithwaite but was based mostly on electromagnetic considerations [41] (first printed in 1966).

3.2. Gyroscopes and Spinning Wheels

Apart from the unidirectional thrust caused by contra-rotating eccentric masses, there are several experiments performed on gyroscopes. It has been written in [42] that Professor Eric Laithwaite was an able communicator and made many television appearances including those of his Royal Institution Christmas Lectures to young people in 1966 and 1974. The latter of these made much of the surprising properties of the gyroscope. In his 1974 lectures, Laithwaite suggested that Newton’s laws of motion could not account for the behaviour of gyroscopes and that they could be used as a means of reactionless propulsion. The members of the Royal Institution rejected his ideas and his lectures were not published at the time, a first for the Royal Institution. His lectures were subsequently published independently as Engineer Through The Looking-Glass and also on the Royal Institution website [43].
At almost the same time, another scientific attempt to study rotating gyroscopes is due to Bruce De Palma (1935-1997), who was working at MIT as a lecturer in Photographic Science in the Laboratory of Dr. Harold Edgerton and directed 3-D color photographic research for Dr. Edwin Land of Polaroid Corporation [44]. Based on photographic experiments since 1974 until his untimely death in October 1977, he claimed to have measured a delay in a falling gyro or an increase of its upper level in an oblique shoot [45,46,47].
Thirteen years after De Palma’s experiments, Hayasaka and Takeuchi measured a weight reduction of gyros when rotating in the right direction (spin vector pointing downward) [48]; they showed that the higher the gyro revolutions per minute the higher the weight loss. This finding was disputed by many others [49,50,51,52,53,54,55]. However, it is not perhaps widely known that Hayasaka insisted to his findings and eight years later he cooperated with three other coworkers and presented again similar measurements when the rotating gyro falls from a height [56] (unfortunately, the volume in which this paper belongs has been withdrawn from the electronic version of the Journal; so the interested reader has to ask for a hard copy in a library). In contrast, in a later paper Luo et al. [57] report that:
“…the differential acceleration between a rotating mechanical gyroscope and a nonrotating one was directly measured by using a double free-fall interferometer, and no apparent differential acceleration has been observed at the relative level of 2×10-6. It means that the equivalence principle is still valid for rotating extended bodies, i.e., the spin-gravity interaction between the extended bodies has not been observed at this level. Also, to the limit of our experimental sensitivity, there is no observed asymmetrical effect or antigravity of the rotating gyroscopes as reported by Hayasaka et al. [48]”.
Moreover, the last paper in favour of Hayasaka’s theory is [58], and probably those by professor Dmitriev [59,60] (closely related papers by the same author are [61,62,63]). Recently, it has been shown that within the context of Newtonian mechanics a possible explanation for the decrease of the observed gravitational acceleration may be the change in the inclination of the gyroscope [64].
One of the latest paper concerning gyroscopes, and particular Laithwaite’s experiments is probably due to the British physicist Wayte [65] who reported a weight loss of 8 percent (it is noted that this loss has been calculated as a time integral of measured impulse of the reaction force). This finding was later disputed by Lőrincz and Tajmar [66]. In addition, the mechanics of Laithwaite’s engine have been studied until recently by Provatidis [67,68] and this issue will be discussed later in the present paper (see section 4.3).

4. Progress in the Twenty-First Century

4.1. Theoretical Contributions

In the turn to the twentieth-first century a lot of questions regarding ‘gravity control’ had not been answered, thus at least three projects were running simultaneously.
The first is Project Greenglow (The Quest for Gravity Control), which started in the mid-1990s, and has run officially under management of the mathematician Ron Evans at BAE (British Aerospace) [69,70,71,72,73].
For the second project, called GRASP (Gravity Research for Advanced Space Propulsion), it has been written that took place at Boeing Co. although the company said that did not spent money on that [73,74,75]. The latter is related with Eugene Podkletov for sure but not much info is available in the public domain [76].
Regarding the third project, in 1996, a team of (USA) government, university and industry researchers proposed a program to seek the ultimate breakthroughs in space transportation: propulsion that requires no propellant mass, propulsion that can approach and, if possible, circumvent light speed, and breakthrough methods of energy production to power such devices [77]. In the period 1996-2004, NASA funded the Breakthrough Physics Program, managed by Marc Millis (open access reports are [77,78,79]), and the very final report was documented in a book of 740 pages [80].
Within the context of the abovementioned NASA’s project, it was concluded that the ‘mechanical antigravity’ is impossible thus a particular report was released in December 2006 to prevent future inventors from disturbing them [16].
Despite the suggestions by NASA, the USA Patent Office continued to grant patents related to the term “antigravity” or other closely related ones. An internet search in Google Patents in January 2024 shows about 10,000 entries on the word “antigravity”, 7,777 entries for the word “gravity control”, 17 entries for the word “antigravity propulsion” and another 18 entries for the word “reactionless propulsion”. Considering that more than 20 alternative principles of physics can be used to achieve propulsion (as has been documented in [80,81]), of which one such methodology is the inertial propulsion, it becomes evident that this review paper cannot cover the whole topic. Instead of this, the present paper restricts to the use of masses and gyroscopes and occasionally refers to other methods only when it makes sense.
As already mentioned, the conventional Dean-drive consists of two contra-rotating out-of-balance masses (eccentrics) thus each mass traces out a complete closed circular path, when the cart is still immobile. As a result, as the mass rotates the impulse of the inertial (centripetal) force given in the upper half of this circle is cancelled by the impulse of the lower half of the same circle. To restore this shortcoming and break the symmetry (upper equals lower), some inventors have tried to modify the lower part (see, e.g., Hoshino [82] and Figure 7) or to introduce a secondary motion on the articulation of the rotating masses on the vehicle or to modify the ideally symmetric shape of the curve [83,84] thus causing a sort of time delay (as they claim).
Another way to modify the symmetrical shape of the circle traced by the two contra-rotating masses is as follows. A patent filled in October 2008 [85], smoothly modifies the lower part of the circular path of the rotating masses, using a special differential mechanism was explained in [86,87]. In more detail, the rotating masses trace a figure-eight-shaped path (the symbol of infinity, ∞) which is also inscribed into a half-spherical surface. This configuration (i) preserves the motion of the rotating masses in the upper part (either above or below the center of the sphere) and (ii) allows for the orientation of the axis of symmetry (of the said half-spherical surface) toward the desired direction of motion. But although this setup introduces a sort of asymmetry, it is obvious that after every 360 degrees of rotation (at angular velocity ω 1 ) the masses always take the same initial position thus the time integral of the inertial force over a period vanishes. To overcome this shortcoming, the axis of symmetry of the said half-spherical surface is subject to a second rotation (at angular velocity ω 2 ) thus fully breaking the symmetry except of the case that its angular velocity is a multiple of the angular velocity of the contra-rotating masses (i.e., ω 2 = k ω 1 , where k is an integer number) (for details, see [87]). Nevertheless, despite the title of that paper, and even though it is unlikely that two upper points of the traced curve will be at the same altitude (height) on the vertical z -axis, during the almost chaotic motion of each rotating mass there will always two successive points along the curve (say the first point is the local lowest the next will be the local highest) at which the horizontal velocity component will both vanish (see, Figure 8). In conclusion, despite the title of [87], within the context of Newtonian mechanics, it is not possible to continuously obtain net thrust.
It has been widely written that the most simplistic way to break the symmetry is to force the rods of the rotating masses to trace a circular arc of only 180 degrees, like car wiper blades. However, a mechanical study reveals vanishing impulse per period thus null net thrust (see, Appendix A).
Another idea has come from the axial impact of an elastic beam (Figure 9). It is well-known from the theory of elasticity, that when a Heaviside axial force F is exerted on an elastic bar it takes some time until the elastic wave reaches the fixation and then the reaction force becomes double (i.e., equal to 2 F ) and remains constant during the half period [88]. This fact is not against Newton’s third law (action equals to reaction) because the total impulse is preserved (see, Figure 9b). Based on this observation, it was though that the rectification of the axial force would be possible if the beam was rotating with a period equal to the period of the elastic wave. The initial thought was that the dead time-interval in which the reaction force vanishes could correspond to positions of the beam below the horizontal line passing through the articulation point O, thus when the reaction force becomes non-zero then the beam would be found in the upper half space and would be pushed upwards. Unfortunately, this supposed “brilliant” idea did not work for the following two reasons: (i) because the reaction force is internal to the system and (ii) because a Coriolis force cancels it action. And since the Coriolis force does not exist in electromagnetics, a mechanical model of the Dean drive was compared with a Tesla-like electromagnetically based model [89] (a paper approved by Boeing Co.). In other words, both models, i.e. the mechanical Dean drive (based on circular track) and the electromagnetic model showed null thrust. A report describing the atmosphere of a relevant Conference meeting, with the eyes of a specialized journalist, is [90].
The reader may easily find many Internet (e.g., YouTube) movies in which a black box swims or jumps up by itself or a cart moves aided by a sort of inertial drive. In other words, the inertial propulsion is an experimental fact, but its limits had not been explored, or at least had not been published until the end of the first decade of 2000. The only “scientific” work is that of Davis [30] in which a ‘fourth law of motion’ is proposed (in addition to the three ones by Isaac Newton). On the other hand, one may still find a lot of (pseudo-scientific) explanations that have been posted to the Internet.
To the best of our understanding, till the end of the twentieth century the literature was reduced to rather the description of existing patents and/or qualitative characteristics of them [91,92,93,94]. In the beginning a the 21rst century (2006), a PhD thesis focusing on some existing inertial propulsion patents, without encouraging results on the possibility of net thrust, was defended [95]. Another relevant paper is [96].
To show the capabilities of the conventional Dean-drive (let us call it so) operating into the air, Provatidis [97,98,99,100] published his first four papers considering that the rotating masses track circular curves (the simplest case). To make robust conclusions, several formulations were applied such as (i) decomposition of the mechanical system into free body-diagrams and further application of Newton’s laws, (ii) study of the center of mass, (iii) application of Lagrange equations, and (iv) conservation of linear momentum. Obviously, all these four approaches have led to the same result, which for ‘motion in the air’ is as follows:
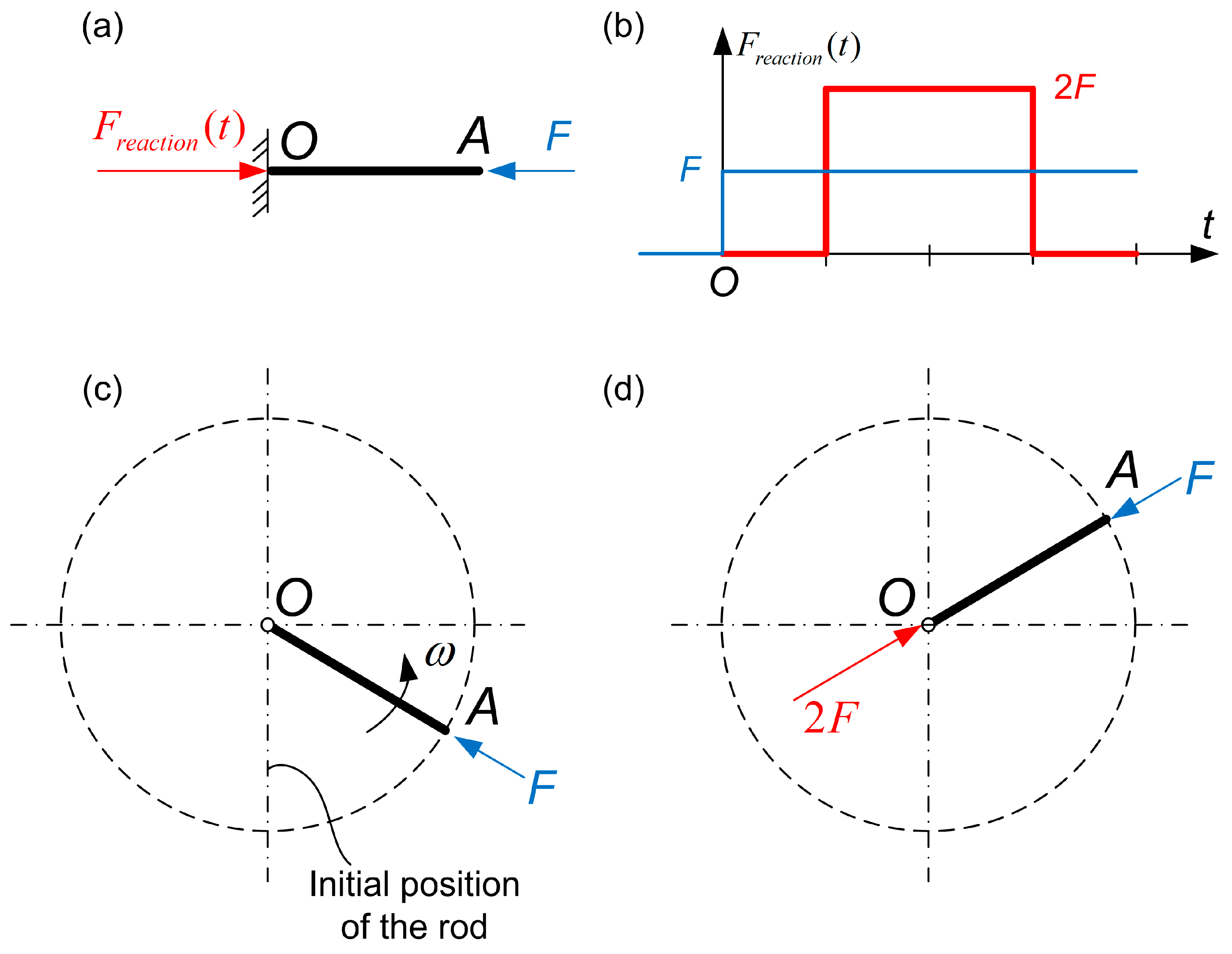
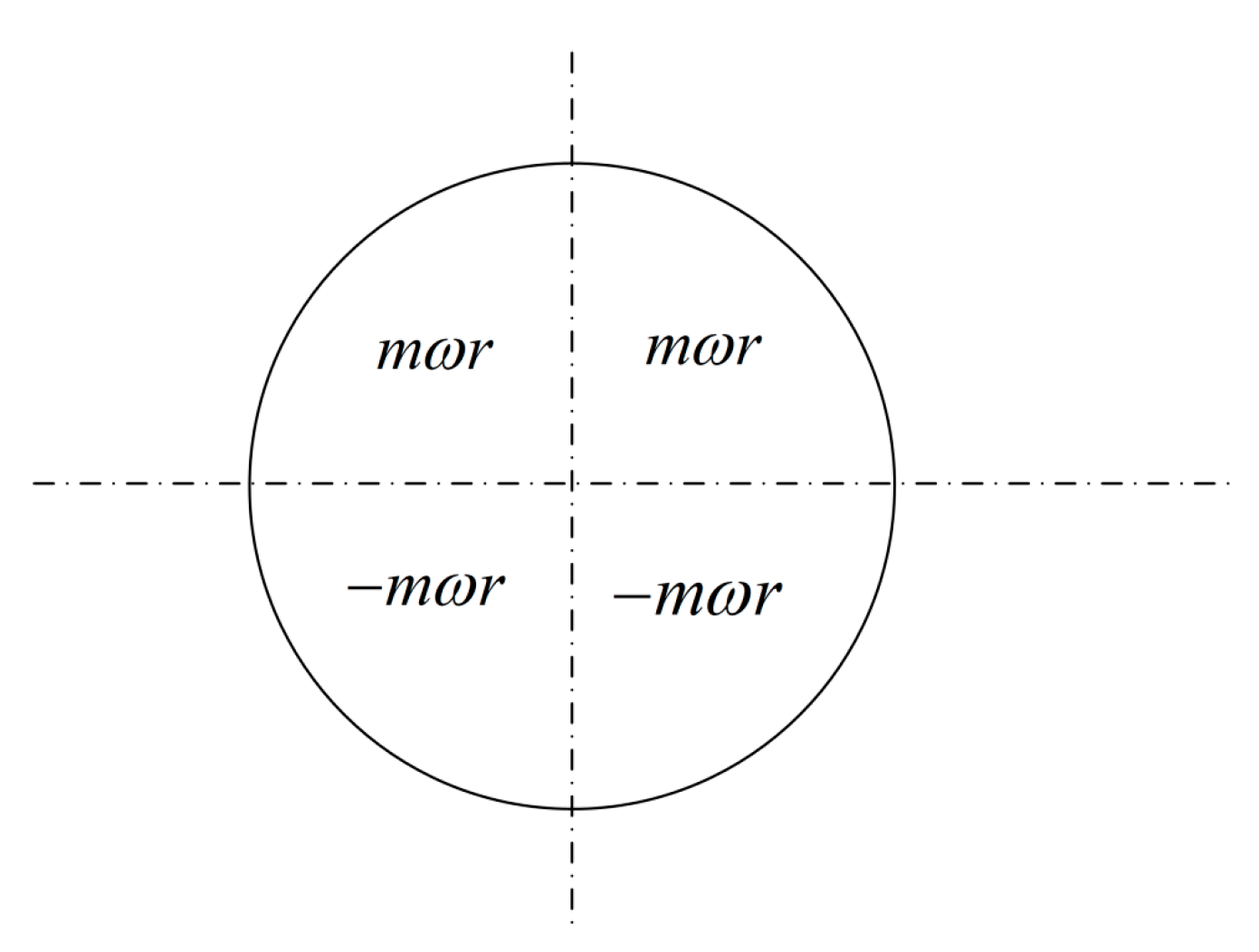
  • An inertial drive attached to a vehicle or cart, which initially lies on the ground, causes alternating (sinusoidal) support forces on it. For an immobilized vehicle, the total linear momentum of the contra-rotating masses varies in time and its temporal derivative equals to the vertical support force (ground reaction exerted on the vehicle or cart). For the continuous motion of the contra-rotating masses at a constant angular velocity , external energy is generally required to withstand the friction loses [97].
  • When the magnitude of the constant angular velocity, ω 0 , is adequately high, the vehicle (cart) can perform a vertical jump. This happens because in the upward motion of the rotating masses (i) the reaction force is higher than the weight, and (ii) the center of mass of the system (cart + rotating masses) has an adequately large initial velocity which allows for a vertical shoot.
  • An alternative explanation for the motion of the vehicle due to the attached inertial drive is as follows. In the beginning the rotating masses of the inertial drive possess a certain linear momentum P 0 toward the vertical z -axis. When the orientation of the connecting rods (radii of out-of-balance masses) becomes vertical, the velocity vectors of these masses become horizontal thus the linear momentum of the rotating masses vanishes. If -for example- the angular velocity is high, the change of linear momentum per revolution ( M g Δ t ) is a small percentage of the total initial value, thus practically the linear momentum of the system is preserved. Due to the said conservation of linear momentum in the vertical z -axis, the lost momentum is undertaken by the vehicle. But since after 90 degrees the connecting rods will become horizontal with peak velocities, the instantaneous velocity of the vehicle vanishes, and so on.
  • Obviously, if no extra energy is transmitted to the inertial drive, the initial angular velocity of the rotating masses cannot be preserved at a constant value ω 0 but again the vehicle can jump [98].
  • The maximum height the mechanical system “vehicle + drive” can reach depends on the initial velocity of the center of mass of this system.
  • The initial velocity of the center of mass occurs when the two connecting rods to which the masses are attached are found on a horizontal position and at the same time the ground suddenly opens like the cover of a well. Then, the conservation of the linear momentum toward the vertical axis is ensured [98]. Again, it should become clear that while the vehicle stands on the ground the linear momentum is not preserved.
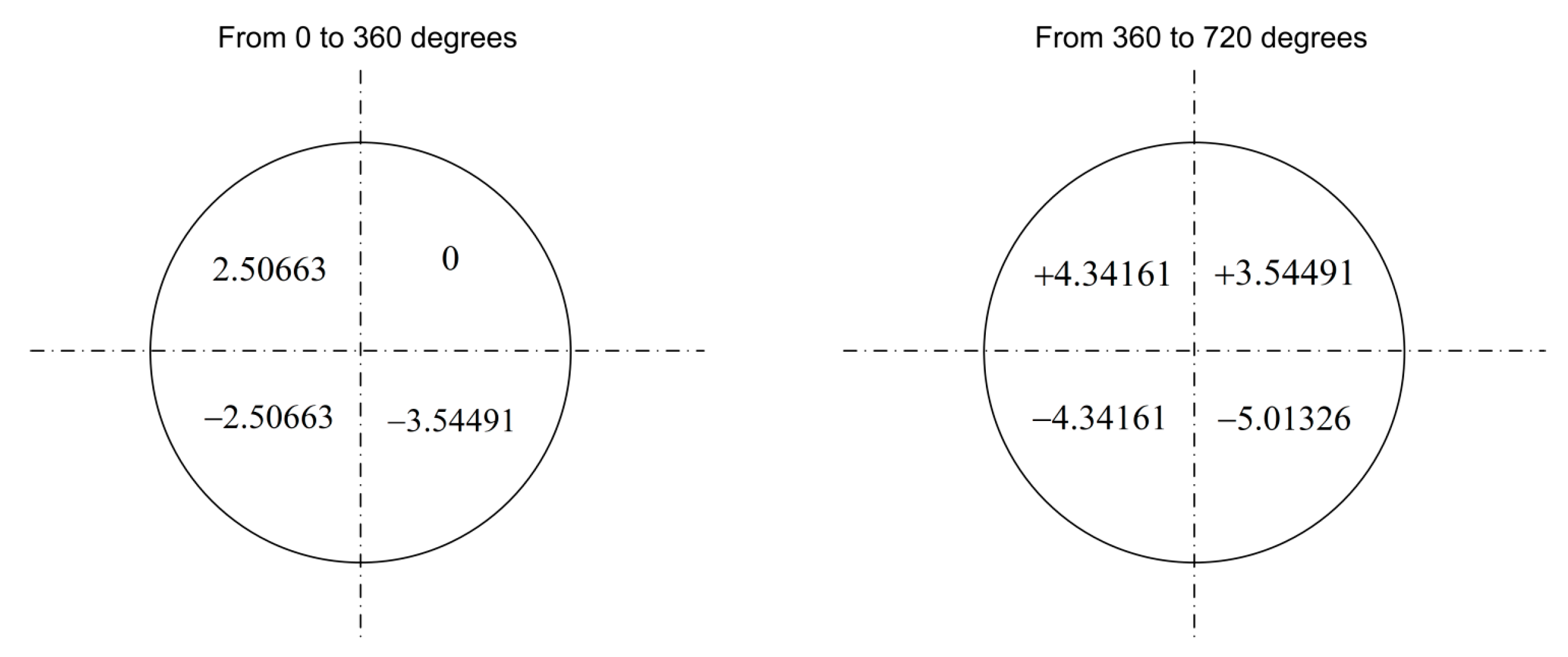
  • Depending on the level of the initial velocity, the vehicle may elevate following an oscillating mode with the rods having performed usually a lot of revolutions, until the center of mass takes a zero value. Then the vehicle starts falling, again elevate following an oscillating mode until it takes its initial velocity in the opposite direction.
  • During an extremely short time interval, it is possible to keep the vehicle immobile into the air. This phase ends when the rods which carry the rotating masses become vertical, thus the denominator of a closed-form expression vanishes, and the fraction becomes infinite [97].
  • In some sense, the sinusoidal support forces are very similar to those exerted on the ground by a spring-mass system [100]. To better understand this issue, note that when the topic of oscillations is presented in high-schools or colleges, teachers say that the oscillation is the projection of a moving material point on a circle determined by the extreme positions of that oscillation.
  • Therefore, the center of mass of the system performs a vertical shoot, but also an oblique shoot is possible [98].
From the above conclusions, one may understand that an inertial drive practically offers the initial velocity to the center of mass (as far as the vehicle presses the ground), which velocity could be alternatively given through a catapult. In conclusion, within the context of inertial propulsion the inertial drive practically replaces the catapult.
Now, the above observation can justify the ‘peculiar’ behaviour of an untransparent box within which an inertial drive exists, i.e. that the said ‘magic’ box may perform an unexpected upward jump, vertical or oblique, or even to climb an inclined plane. The only condition is that when the box is left to move or fall, the connecting bars (carrying the rotating masses) must be close to the horizontal direction to ensure linear momentum in the upward vertical z -direction.
Similar conclusions may be derived for a floating object on water. Since the influence of the gravity is indirect (it affects only the weight), the difference with the previous case is that now a water resistance appears, depending on Reynolds number. The boat travels a certain distance on the water and when it reaches a maximum distance from the starting point it practically stops (it performs a slight oscillation). A publication dedicated on this issue is [101] accompanied with some movies.
Of major practical importance is the motion on the ground. Typical cases are the possible motion of a washing machine or the motion from the bumper of a mobile cellphone. In general, the inertial drive induces centripetal forces which may overcome the static friction thus causing motion. This is a rather old story which has been applied to vibrational transportation [7,8,9,10,11], and to micro- and nano-robots [102,103,104,105,106,107]. Later, the concept of Dean drive (although not clearly mentioned therein) was applied to the modeling and control of micro-robotic systems by Vartholomeos and Papadopoulos [108,109]. Quite independently, the theoretical capability of Dean drive to perform motion of a vehicle has been further elucidated by Provatidis [110,111] and a particular study for an alternative figure-eight shaped drive was reported in [112]. Also, a state-of-the-art report until 2011, including more propulsive methods than those by inertial drives, is [113,114].
In August 2015, Mike Gamble, a senior electrical engineer at Boeing Co., presented a released paper regarding the history of Boeing (CMG) Control Moment Gyros [115]. His presentation was mainly a non-technical pictorial history of Boeing’s CMG work, which started back in the 1960s and continued into the 1990s. He got involved with it in 1995 when he took over operations of the (GN&C) Guidance, Navigation and Controls lab at the Boeing Kent (WA) Space Center. This lab and the building that housed it were badly damaged in the 2001 Seattle earthquake and later demolished. The pictures in his presentation show many of the different types of test articles built and used along with some of the lab facilities.
In the same Conference Mike Gamble presented a second paper [116], from which the extracted chart of Figure 10 shows the sawtooth input torquing rate waveshape (scissoring) for generating the pulsed output force. He has claimed that torquing fast in one direction and slow in the other, generates a pulsed (average) output force which is similar in waveshape to that of the examples based on rotating masses.
Remaining within the field of gyroscopes, a remarkable work is that by Alexander Dmitriev, a former professor at the University of Saint Peterburg in the laboratory of Optics, who has shown that a horizontally spinning rotor loses more weight the faster it spins [59,60,61,62,63]. Based on these experiments as well as of those by V.N. Samokhvalov [117,118], the American mathematician Dennis Allen, Jr., has been highly influenced thus he has developed a new theory according to which Newton’s Second Law has to be revised by modifying the mass to its updated form:
m r = m { 1 − [ C ( | a | | s | cos 2 α ) ] + K [ C ( | a | | s | cos 2 α ) ] 2 } ,
where C , K are experimentally determined constants, α is an angle in degrees, | a | is the magnitude of the acceleration vector and | s | is the magnitude of the surge vector (i.e. s = d a / d t ). Details may be found in a Chapter of his revised book jointly with the senior lecturer Jeremy Dunning-Davies [119].
Until now the review has reduced to rotating masses and gyroscopes. Since the friction causes a fast decay in both, there are some patents introducing the concept of the pendulum in which the decay is much smaller [120]. A particular patent of the talented inventor Mr. Veljko Milkovic in which an inclined pendulum could offer inertial propulsion to a cart was studied by Allen and Provatidis [121]. The latter study was based on mechanics and computer methods that had been previously developed and documented in [122,123].

4.2. Practical Applications

Ivan Loukanov’s devices: Before his retirement he was a professor of mechanical engineering at the University of Botswana (South Africa) and Sofia (Bulgaria). Although he worked independently, the knowledge of the Russian language assisted him to criticize and improve the design solutions he dealt with, as reflected by the references cited in his papers. In brief, he has designed and get manufactured many inertial propulsion devices, initially for agricultural applications. Later, he studied mobile wheeled robots intended for inspections and observations of air ducts or any other restricted environments where human do not have a direct access (e.g., dangerous military, chemical or radiation sites, such as nuclear power stations, chemical reactors etc.). In the last works the vibration-driven robot consists of a shaker and a chassis. The latter is mounted on wheels furnished with one-way clutch bearings build into the wheels hubs thus only forward motion of the chassis is allowed. Through a DC motor the robot is propelled by the resonance vibrations created by the shaker’s rotating masses, which generate propulsive impulses transmitted to the chassis. Typical devices are shown in Figure 11. The interested reader may also consult [124,125,126,127] and papers therein.

4.3. Other Patents and Broadcasts

Since the period of “Dean drive”, a lot of somehow relevant patents have appeared (see, Hoshino [82], Cook [128], Thornson [129], Foster [130], Robertson [131], Chung [132], Tanner [133], Farral [134], among others) and have attracted the interest of technicians and scientists, mostly in the United States of America (USA), perhaps because this attempt is also encouraged by established scholars such as [135,136].
Furthermore, it has also even occupied educational television programs such as the German Chanel 2 (Zweiter Deutsche Fernsehen: ZDF), in which the Austrian mechanical engineer Johann Klimpfinger has participated on February 26, 2012, in a 30 minutes-documentary on oscillating devices and applications such as toys [137].
In Austria, there are relevant publications (e.g., Hilscher [138]) and YouTube videos such as (Gyro Precession Drive) [139].
In the United Kingdom the influence of Eric Laithwaite is still alive. The author has been recently informed that William Stoney, owner of the “Thermo Inertial Research” company, with background aircraft prototyping and business jet flying, has met Eric Laithwaite and Bill Dawson in the late 1990s and have kept up an ongoing discussion with Bill Dawson who kindly gave him most of their experimental gyroscopes including the 14 kg gyro that featured in the BBC documentary. Since then, he has done many thousands of hours testing different configurations and measuring them. Currently he has filled a relevant patent [140] in which an existing prototype is described.
But the most difficult-to-review information is coming from Russia, where (because of the language) it is not at all easy to distinguish science from pseudo-science. On this issue the author tries to remain neutral. For the sake of completeness, we will not avoid the temptation to expand the review a little beyond the narrow margins of inertial propulsion, but in no case can we fully cover the subject. As was mentioned in the beginning, the Russian academicians used inertial propulsion for practical reasons such as motion of heavy objects by vibrational techniques [7,8,9,10]. Nevertheless, they denied the capability of Dean’s drive to be useful for space applications [33]. They did the same with their compatriot Vladimir Tolchin who introduced the term “inertiod” [39].
As previously said, due to the Russian language, it is not an easy task to overview the topic in a complete way, but it seems that tens of unexplainable microscopic and macroscopic effects in natural sciences and especially in physics and biology have been revealed and investigated. It should be emphasized that a large part of these phenomena was demonstrated by objects having spin or angular momentum. Probably the first researcher who experimentally detected the unusual effects associated with torsion was professor Myshkin of the Russian physical-chemical society [141], who at the end of the nineteenth century conducted a series of experiments using scales. These experiments were successfully repeated in the 1960s by professor N.A.Kozyrev [142,143] and V.V.Nasonov and later by V.S.Belyaev, S.P.Mikhailov, A.G.Parkhomov and others. For more details, the interested reader can consult an Internet website [144], while an opposing reference for the more recent activities of this “School” is [145]. Recent out-of-stream works are (Linevich and Ezshov [146], Kouznetsov [147], as well as Ventura & Shipov [148] among others).
According to the Russian NTV correspondent Vladislav Sorokin [149], in April 2, 2006, members of the ‘Suburban Institute of Space Systems’ invented the engine called ‘gravitsapu («гравицапу»)’, which, according to the creators, can accelerate to infinity; their final wish is to send it into space. However, the Russian Academy of Sciences did not recognize the theory underlying the creation of this invention. Later, in 2009, details were reported by the newpaper “Pravda” [150]. For more relevant information the interested reader can consult Internet resources such as [151,152].
In China, the use of shaking masses has been explored for sure in terrestrial applications (Zhao et al. [153,154,155]), while publications refer to novel electromagnetic drives as well [156].

5. A Critical Note on the Involved Mechanics in Inertial Drives

According to the Newtons Second Law in mechanics, the sum of the external forces to a system of masses (concentrated or not) equals to the total mass times the acceleration of the center of mass. The proof of this law is based on (i) the separate use of Newton’s second law on each mass of the system and (ii) on the assumption of Newtons Third Law (action = reaction). The reader may refer to Halliday [157] (pp. 59-61) as well as to Casey [158,159].
Despite the above established laws, there are many who believe that these laws are not always applicable, especially when the component bodies are rotating. This is mostly supported by experiences coming from the mechanical behaviour of the gyroscope [4,41,42,43,48,56,160,161]. The purpose of this paper is not to deal with this issue, which may be performed in the context of a journal of physics such as [162]. Nevertheless, we reduce to a particular issue for which there are many records in Internet and has kept busy a few of researchers. For example, based on a record from the book of Gutsche [163] p. 109, regarding measurements on a three-bar mechanism (a similar analogue is also described in [164]), an investigator (with background in mathematics) has calculated a nonvanishing impulse thus he concludes that net thrust is produced [165]. And since it is very difficult for me to convince someone in his ‘terrain of thinking’, in the present paper I slightly change the terms of discussion dealing with another, much easier topic to be understood by the medium reader.
We start with the well-known mathematical physics aiming at deriving the d’Alembert (fictitious inertial) force toward the vertical y -direction. At the initial time t = 0 , the radius associated to the mass m is assumed to be at the horizontal position (θ = 0) and then rotates in the counterclockwise direction. Therefore, the y -coordinate of the imbalance with respect to its center of rotation at rest is given by y = r sin θ where θ is the polar angle, whence we obtain that the second derivative with respect to the time is
y ¨ = r θ ¨ cos θ − r θ ˙ 2 sin θ
Therefore, the component of the inertial force in the vertical y -direction will be:
F y = − m y ¨ = − m ( r θ ¨ cos θ − r θ ˙ 2 sin θ )
Then, considering the gravitational force the total force in the y -direction will be given by
( F y ) T O T A L = F y − m g = − m y ¨ = − m ( r θ ¨ cos θ − r θ ˙ 2 sin θ + g )
Newton’s second law is written as:
( F y ) T O T A L = d P y d t
By integrating Eq. (4) in time t , we obtain a formula for the vertical component P y of the linear momentum:
P y ( t ) = P y 0 + ∫ 0 t [ F y ( t ) ] T O T A L d τ
Note that the integral in Eq. (5) is the so-called ‘impulse’.
I. Constant angular velocity
First, we start with the trivial case of a constant angular velocity ω = θ ˙ = def d θ / d t = ω 0 , and a constant radius r (the track is an ideal circle). Obviously, then it will be θ ¨ = 0 and the angular velocity is associated to a constant period T so as ω = 2 π / T . Below we shall see that the time integral of the vertical force component F y = − m y ¨ (i.e., not including the term – m g ) is equal and opposite in the upper and lower halves of the circle on which the imbalance m moves.
In more detail, in the first quadrant (upper right) the impulse (i.e., the integral of the force over time) will be:
I 1 = ∫ 0 T / 4 F y d t = − m r ∫ 0 T / 4 ( θ ¨ cos θ − θ ˙ 2 sin θ ) d t = m r ω 2 ∫ 0 T / 4 ( sin ω t ) d t = ⏞ ( ω T = 2 π ) − m r ω 2 [ cos ( ω t ) ω ] 0 T / 4 = m r ω ,
Similarly, in the second quadrant (upper left) the impulse will be:
I 2 = ∫ T / 4 T / 2 F y d t = m r ω 2 ∫ T / 4 T / 2 ( sin ω t ) d t = − m r ω 2 [ cos ( ω t ) ω ] T / 4 T / 2 = m r ω ,
Similarly, in the third quadrant (lower left) the impulse will be:
I 3 = ∫ T / 2 3 T / 4 F y d t = m r ω 2 ∫ T / 2 3 T / 4 ( sin ω t ) d t = − m r ω 2 [ cos ( ω t ) ω ] T / 2 3 T / 4 = − m r ω ,
Finally, in the fourth quadrant (lower right) the impulse will be:
I 4 = ∫ 3 T / 4 T F y d t = m r ω 2 ∫ 3 T / 4 T ( sin ω t ) d t = − [ cos ( ω t ) ω ] 3 T / 4 Τ = − m r ω .
The results are illustrated in Figure 12, where one may observe equal positive impulses in the two top quadrants and negative ones in the two bottom ones. Therefore, the total upward impulse is equal and opposite of the downward one. In simple words, “the net impulse is zero” thus the so-called thrust vanishes. The latter implies the conservation of linear momentum P y ( t ) in the y -direction (see, Eq.(5)).
At this point the reader may understand why most inventors try to make the integral I = ∫ 0 T F y ( t ) d τ in Eq. (5) be different than zero after a whole revolution of the imbalances. To achieve this, they say that we need either a variation of the radius r (e.g. to be different in the lower part of the track, as for example in Figure 7 referring to Hoshino [82]) or to modify the angular velocity ω thus offering greater values in the upper part of the track, if possible.
Below we study a particular case in which the impulse per revolution (period) is non-zero. Instead of developing an exotic setup as those exposed in the various patents, we merely assume a constant radius r , while the angular velocity ω increases linearly in terms of time as
ω = a t ,
where a is a constant, and t is the time. If we assume that at the initial time t = 0 the rods are horizontal thus θ 0 = θ ( 0 ) = 0 , the polar angle θ ( t ) will be given by
θ ( t ) = 1 2 a t 2 ,
thus the elapsed time can be expressed in terms of the travelled polar angle as
t = 2 θ a
Here, a difficulty arises about the time interval [ 0 , T ] over which the integral of the impulse I = ∫ 0 T F y ( t ) d τ will be performed. Since the only period is geometrically determined by the repeated revolutions, a reasonable choice is to consider a full revolution, from θ =0 to θ = 2 π . In the general case, the impulse between the initial θ i and the final position θ f includes both terms (centripetal and tangential terms) and after the substitution d t = d θ / ω it takes the final form:
I = m r ∫ θ i θ f ( ω sin θ − ω ˙ ω cos θ ) d θ ,
Again, it is repeated that the gravitational acceleration has not been considered.
After the substitution of Eqs. (7) to (9) into (10), the latter becomes:
I = m r a ∫ θ i θ f ( 2 θ sin θ − 1 2 θ cos θ ) d θ ,
Using the latest version of the Wolfram/Alpha (MATHEMATICA®) software, the analytical expression of the integral in Eq. (11) is very complicated as it includes the incomplete gamma function Γ ( a , x ) . Nevertheless, for specific limits the numerical value of this integral is available. In conclusion, for the first revolution of 360 degrees starting from the horizontal direction, the incremental impulse is given in Figure 13.
One may observe that for every 360 degrees the total impulse is different than zero and particularly it is negative because the bottom values are higher than those of the top values. Obviously, if we change the direction of rotation the signs are reversed.
Another remark is that if we start measuring the polar angle from a different position of the connecting rods, for example from the vertical position ( θ = π / 2 ), combining both graphs of Figure 13 it is easy to see that the total impulse per 180 degrees vanishes. This is due to Eq. (4) according to which the change of linear momentum in the y -direction between θ and θ + π equals to the impulse. In more detail, since at the ends of the polar angle intervals [ − π / 2 , π / 2 ] and [ π / 2 , 3 π / 2 ] the vertical velocity components vanish (because the velocity vector is in the horizontal direction) the change of the linear momentum is Δ P y = 0 − 0 = 0 , 0 . In other words, whatever the shape of the curve (circular or not) and whatever the function of the angular velocity ω ( t ) is, the passing through the upper and the lowest points, where the velocity components are horizontal, dictates the zeroing of the change of the linear momentum thus the zeroing of the impulse between any two halves per 180 degrees.

6. Discussion

In his paper against the claim of Dean drive, Professor Stepanov [33] begins his introduction as follows: “In 1907, the famous Russian scientist V.L. Rirpichev, speaking about people who spent their energy on creating perpetual motion machines, indicated that “. . . and now every professor of mechanics constantly has to deal with the inventors of such chimeras. From my personal experience, I must say that these are almost always respectable persons, conscientiously devoted to the idea, but carried away by it so much that they are absolutely deaf to the arguments of reason. They are not affected, not only by verbal, logical proofs, but even by such strong proofs, which the products of their ingenuity present to them with their complete inertia”. …Here we are already dealing with material that is interesting not for mechanics, but for psychology”.
The counterargument to the above concept is that we should perhaps “let all the birds sing” (metaphorically), because in such a difficult technical issue the final solution (if indeed there is one) will perhaps be given by some unconventional researcher, as for example the Wright brothers were (December 17, 1903) while everyone in USA expected that it would be given by the renowned late Professor Langley. At some point in their lives, when insurmountable obstacles are met, many people go through states of inner searching and transcendence [166,167] with the final purpose to draw strength from within themselves.
In the previous sections of the present paper, it was shown that since the third decade of the twentieth century a lot of scientists and practitioners all-over the world conceived the concept of the inertial propulsion and most of them believed that they discovered a propulsive means without reaction. Since the most experimental prototypes concerned with terrestrial devices, the apparent explanation for their propulsive capability was attributed to the friction of the ground, similarly to the friction induced when a person walks.
It was made clear that within the context of Newtonian mechanics it is not possible that a vehicle can perform unlimited motion by virtue of an inertial drive. In brief, the inertial drive offers an initial velocity at the center of mass of the mechanical system “vehicle + drive” thus it acts as a catapult. This initial velocity is based on the fix support of the vehicle which assists the development of a large support (reaction) force, as exactly happens when a spring-mass system is highly compressed on the ground (without being glued on it). In either case when the center of mass reaches its upper position, we need again the assistance of a support to resist the reaction force, and so on. This event is like the motion of a monkey on a tree, which jumps higher and higher, caught by the branches that are at different heights on a tree.
To make a breakthrough in alternative propulsion it is necessary to find a case in which the physical laws break. For example, the Newton’s third law states that action equals reaction but this is not always exact. For example, when two charged particles move along two skew straight lines (not intersected and non-parallel), the electromagnetic (Lorentz) force are equal in magnitude but vertical in orientation thus we talk about “weak formulation” of Newton’s third law [168]. Although this mismatch gives advantage to electromagnetics (in addition to the fact that the operating frequencies are much higher than those of the mechanical parts), the comparative study [89] revealed null net thrust.
The imagination of many researchers and inventors has been fired by strange phenomena such as the ‘magical’ support of an aluminum triangle in the air; such a case has been fully attributed to the existence of ionized air [169,170]. Other peculiar phenomena such as the Indian rope trick (where a rope rise is caused by sounds) have been analyzed by eminent scientists [171,172,173]. Also, the unexpected behaviour of Laithwaite’s experiment has been analyzed experimentally [174,175] and theoretically [67,68] as well. Closely related is the work by Sheheitli [176,177].
For a thorough description of gravity-controlled (‘antigravity’) systems the reader is addressed to [178,179], among others.
As also happened with the Michelson–Morley experiment that positively supported the General Theory of Relativity (GTR), the analogous testbed to justify whether the eternal laws of Nature can be (or have been) bypassed (or broken) is the “gyroscope” [180]. There are many scientists who claim that have discovered an issue on the gyroscope which contrasts with Newton’s laws [181,182].
Regarding the peculiar and controversial behaviour of the gyroscope, it was also shown that the easiness of the experimenter to rise it is because the axle of the spinning wheel performs precession thus the hand operates as an articulation (pin) and not as a fixed point (clamp). The latter allows for a normal force distribution of the forces in the bicepts and tricepts muscles otherwise the torque at a supposed stiff articulation would lead to unsufferable loads [67]. The topic has been discussed in [183,184] but we believe that the physical units have caused confusion. A re-examination of the rotation frequency for the hands of the experimenter shows that the unit of ‘minutes’ (min) had been confused with the units of ‘seconds’ (s) and therefore it had been understood that the pivot was rotated at a quite different frequency than what the axle of the gyroscope does. It is worthy to add that while the gyroscope may be easily risen it is very difficult to stop it when falling at the second half of a period thus a null resultant occurs. As previously mentioned, experimental studies on the rise and fall of a gyroscope in Laithwaite’s experiment are [174,175].
Regarding the supposed inertial propulsion in satellites mentioned in [115], it is true that the change of the position of the gyroscopes plays a significant role in the orientation thus attitude control may be performed without additional small rockets, as shown in Appendix B. Nevertheless, this is quite different than saying that a net thrust may be produced, and the latter needs additional explanation, in general.
Therefore, when the vehicle is on the ground, by consuming energy it is possible to accelerate the connecting rods of the inertial device that to produce linear momentum. The associated instantaneous change of linear momentum over time equals to the reaction force, from the ground to the vehicle. This means that in the relevant oscillation of the supporting force, if the amplitude happens to be sufficiently large the vehicle may perform a jump of which the maximum travelled distance depends on the initial velocity of the center of mass. Having said this it is crucial to understand that at the end of this cycle (from the ground to the upper position) there is no ground to resist, thus the supporting force cannot be exerted for a second time. The latter is the most critical issue that should be understood. Of course, if someone invents a viable way to offer support to allow the development of the supporting (reaction) forces, then everything will be correct.
To continue the discussion, there is no apparent way to exert a reaction force to an object in vacuum. In general, a sort of external means is required. For example, it has been written that the release of air from a balloon could assist [100] but then we use the action-reaction principle like the shoot of a gun. There are two ways to take energy and perform the difficult job. The first is to harvest energy from the air somehow, and he second is to receive energy from the cosmic environment (cosmic radiation, ionized air, magnetic energy, etc). In other words, whatever one may invent, the motion of the center of mass requires an external force (Newton’s Second Law).
Having said this, it possible to apply the principle of the inertial forces in the water. Therefore, when the floating or submerged object reaches the longest position where the center of mass obtains a zero velocity, the surrounding water could probably somehow operate to offer an instantaneous artificial fixation to be possible the rotating bars be almost vertical to the desired direction of motion at the time of departure.
When the object is in the space the gravity is less or does not exist but again the initial velocity for an object (say on the Mon’s surface) could be alternatively achieved using a catapult. But, again, the principle of inertial propulsion could be implemented. For example, in a MSc thesis in Sweden [185] and a PhD thesis at Cornell University [186] it has been proposed to use a gyroscopic drive of cubic shape, so it can move on the surface of Mars [187,188,189], of course by exploiting the friction.
A similar inertial cube consisting of gyroscopes was also developed in Switzerland [190].
At this point the interested reader may attend a 16-minute video which covers a broad spectrum of inertial propulsion [191], a gyroscopic precession powered car [192], and a cart powered by two contra-rotating oscillating gyroscopes [193].
It is also worth mentioning that some inventors, for several reasons, do not insist to the usefulness of inertial systems as propulsive systems but present them as educational toys [164] to point out the peculiar properties of the gyroscopes. I still remember the experimental setup of my professor in physics Evangelos Anastassakis [194] who was demonstrating, in his (auditorium) lectures, a miniature gyroscope climbing an inclined plane.
In other words, although the direct use of the inertial propulsion cannot be used because, unlike the internal combustion engine (ICE), in every period the impulse of inertial forces vanishes, we may take advantage of the surrounding environment either in the form of the friction or a more exotic manner which is open for further research.
During the last years the focus of the research returns to gyroscopes [195,196,197,198] or to asymmetric fields [199], while an out-of-stream book is [200].
All the above discussion was restricted in the framework of Newtonian mechanics. If for a while we leave the engines and focus on the space, at least during the last 50 years it is well known that there is a discrepancy between observed galaxies rotation curves and the prediction using the known laws of orbital kinematics. Here, it is not the proper place to discuss about Modified Newtonian Dynamics (MoND) valid for galaxies but we restrict to mention the work by Dr. Mike McCulloch, a lecturer in geometics at Plymouth University (U.K.). McCulloch has developed a theory of Quantized Inertia (QI) [201], formerly known with the acronym MiHsC [202], which explains the effect and how it could help with human space travel [202]. This theory has been used to explain the weight loss which has been reported in the famous Podkletnov’s experiments of rotating superconductive materials [203].
As previously mentioned, there are more than twenty physical principles on which breakthrough propulsion (such as electric propulsion [204], inertia modification, space drive: sails and fields, negative matter propulsion, electromagnetic techniques, mechanical techniques, spacetime modification/gravity control, quantum approaches to gravity control, brute fast, spacetime modification for faster-than-light, quantum nonlocality for faster-than-light information, quantum vacuum energy conversion, novel nuclear processes, etc) might be possible [80,81]. One of them is based to General Relativity according to which when a mass is closed to a rapidly rotating ring, not only a centripetal but also an axial force is induced [205,206]. On the same direction there are some newer thoughts on the frame-dragging effect by Tajmar [207] which were later extended by Millis [208]. But the most striking publication is probably that describing the theory by Wisdom [209] according to which “…Therefore, it is indeed possible to swim in spacetime. Translation in space can be accomplished merely by cyclic changes in shape, without thrust or external forces. The curvature of spacetime is very slight, so the ability to swim in spacetime is unlikely to lead to new propulsion devices. For a meter-sized object performing meter-sized deformations at the surface of the Earth, the displacement is of order 10-23 m. Nevertheless, the effect is interesting as a matter of principle. You cannot lift yourself by pulling on your bootstraps, but you can lift yourself by kicking your heels.”.
The above claim gives much hope to inventors who can still dream. For example, one could claim that if the eight-shaped motion of the contra-rotating masses (or circulating fluid) such as those in the setup described in [87,112] is combined with a revolution of the whole system under the prism of GRT [206], small axial forces could be developed, as has been explained by Forward [205]. Who could a-priori deny that the frame-dragging effect in conjunction with a resonance between these two rotations is abandoned to offer promising results to interstellar space propulsion?

7. Conclusions

This paper is a critical review of many human attempts to create thrust by consuming energy but without expelling material from a vehicle, merely by rotating masses. It was clearly shown that while the shoot of an apparently stationary object is possible without using a catapult, the repetition of the same cycle is impossible unless an external force is somehow exerted from the environment to the mechanical system. For a better performance, this has to be done near the end of the motion cycle. This happens because whatever the setup is, the curve on which the rotating masses move will continuously have extrema (or saddle) points at which the vertical velocity components vanish. Therefore, the temporal integral of the inertial forces (i.e., the impulse) per cycle between these two saddle points vanishes, and hence it is not possible to create net thrust within every such period (from peak-to-peak point). This exactly is what we call conservation of linear momentum. It was also shown that for a satellite where only the angular (not the linear) momentum is preserved, the motion of the rotating masses causes small displacements of the satellite and no displacement for the system’s center of mass which continues ideally to move on a circle of constant radius. In contrast, it is possible to use inertial masses and gyroscopes to change the orientation of the satellite thus avoiding the use of small-scale liquid rockets, a fact which is well known as attitude control. Having said this, it should eventually become clear that (within the context of Newtonian mechanics) the replacement of the thrust of small-scale rockets by inertial propulsion, does not mean that that the moving masses produce net thrust. This happens because the center of mass does not move unless an external force is applied to it.

Appendix A. Contra-Rotating Wipers

Let us consider two contra-rotating masses at the ends of rigid rods of length r , which are moving like car wipers (see, Figure A1). This means that the masses start from the horizontal position (A1 and B2) at a zero velocity and after a rotation of 180 degrees take again the horizontal position (A2 and B1) at zero velocity. Obviously, the period consists of two half-rotations for each mass (see, Figure A1). Even though each mass moves only above the center of the associated circle, the time integral of the vertical inertial component F y (i.e., the impulse I y ) vanishes in each half period (rotation by 180 degrees), because the change of the linear momentum (at A1-A2 and B1-B2) is zero, as a difference of zero values at the ends.
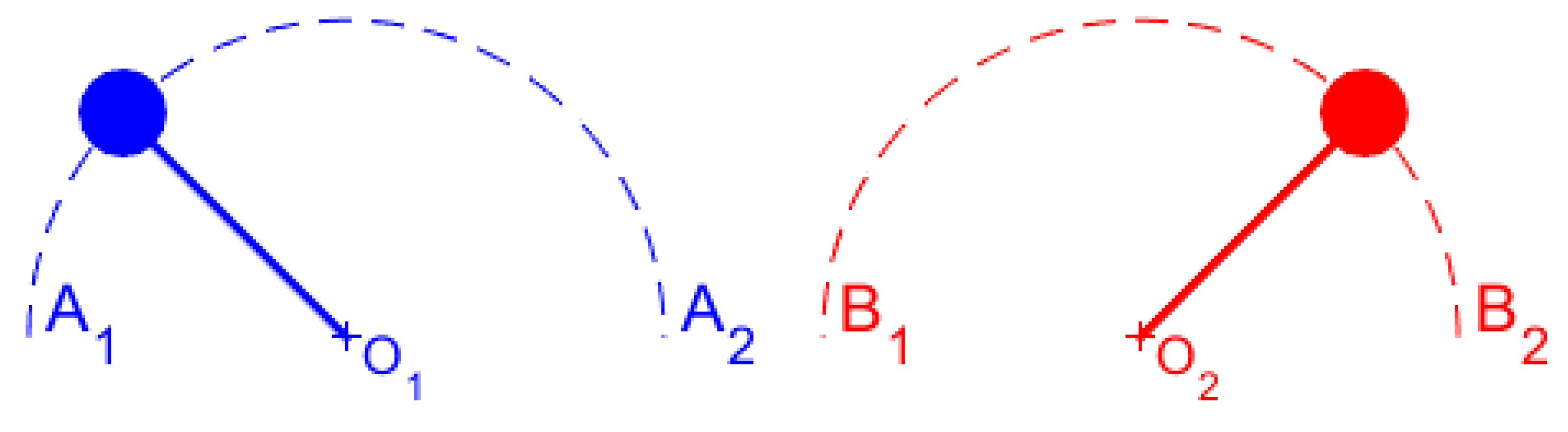
Preprints 97285 g0a1
Figure A1. Motion of two contra-rotating masses in the upper plane (from A1-to-A2 and at the same time from B2-to-B1, and vice versa).
Figure A1. Motion of two contra-rotating masses in the upper plane (from A1-to-A2 and at the same time from B2-to-B1, and vice versa).
Preprints 97285 g0a1

Appendix B. Radial Displacement of a Satellite

Let us consider a satellite of mass m s which is in orbit around the Earth at height h , thus moving on an (assumed) ideal circle of radius R = R E + h with R E denoting the Earth’s radius. It is well known that the measure v s of the velocity of the satellite (a vector tangent to the assumed circular orbit) is given by:
v s = ( G M E R ) 1 / 2
where G is the gravitational constant, and M E is Earth’s mass.
Let us now assume that, by consuming an amount of energy, a mechanical component such as a dual gyroscope changes it orientation thus moves radially by distance L (or, for example, an astronaut of the satellite raises his two contra-rotating arms-forearms-hands by length L , which is very close to the setup shown in [193] in the horizontal direction though). Then we wish to determine the new position h ’ of the center of mass of the satellite, measured from Earth’s surface.
The conservation of the angular momentum with respect to the Earth’s center implies:
m s v s ( R E + h ) = m s v ′ s ( R E + h ′ ) ,
hence
v s ( R E + h ) = v ′ s ( R E + h ′ ) ,
Substituting (B-1) into (B-2), one time for the radius R = R E + h and another time for R ' = R E + h ' , we eventually obtain:
h = h ' ,
Equation (B-3) shows that the center of mass of the satellite along the radius of the circular orbit will always remain at the same height h above Earth’s surface.

References

  1. Potier, O.N.R. The cancellation of gravity. Electronics and Power 1965, 11(3), 111. [Google Scholar] [CrossRef]
  2. Farrall. A.W. An Inertial Propulsion System. Transactions of the ASAE 1966, 9(4), 0586–0587. [CrossRef]
  3. Hancock R. (Ed.). Entry: “PROPULSION inertial”, In: The Illustrated Encyclopedia of Science and Technology: HOW IT WORKS, Marshall Cavendish Ltd, New York & London, 1977 (Vol. 14, 1874-1877). https://archive.org/details/howitworksillust14ralp/page/1874/mode/2up?q=inertial.
  4. Walgate, R. Eric Laithwaite defies Newton. New Scientist 1974, 14 November, p470. [Google Scholar]
  5. Engel, A.B.; Stiebitz, P.H. The cybernetics of inertial propulsion. Kybernetes 2009, 38(1/2), 141–157. [Google Scholar] [CrossRef]
  6. Fiala, H.E.; Fiala, J.E.; Fiala, J.-A. Inertial Propulsion Device to Move an Object up and Down. Patent No.: US 8.066,226 B2, Date of Patent: Nov. 29, 2011 YouTube: Harvey Fiala - Inertial Propulsion with ONLY 1 Moving Part, Extraordinary Technology Conference 2007: https://www.youtube.com/watch?v=RdxZEGPUSLI&ab_channel=TeslaTech.
  7. Goncharevich, I.F. Dynamics of vibrational transportation. Nauka, Moscow (1972); p. 244 [in Russian].
  8. Blekhman I.I., “Vibrational Mechanics: Nonlinear dynamic effects, General approach, Applications”, World Scientific, Singapore, 2000 (p.15 and p.19).
  9. Kononenko, V. O., Vibrating Systems with a Limited Power Supply. Iliffe Books Ltd: London, 1969, p.24 (in English). Translated from Russian: V. O. Kononenko, Oscillatory Systems with Limited Excitation. Moscow, Nauka, 1964.
  10. Blekhman, I.I. Synchronization in Science and Technology. ASME Press: New York, 1988 (in English, translated from Russian 1981).
  11. Majewski. T. Vibratory Forces and Synchronization in Physical Systems. Ingeniería Mecánica Tecnología y Desarrollo 2013, 4(4), 119–128.
  12. Chen, L.; Pei, Z.; Tang, Z. Maximum power control of gyroscopic wave energy converter, E3S Web Conf. 2019, 118 02022. [CrossRef]
  13. Townsend, N.; Shenoi, A. A gyroscopic wave energy recovery system for marine vessels. IEEE J. Oceanic Eng. 2012, 37(2), 271–80. [Google Scholar] [CrossRef]
  14. Tajmar M. Advanced Space Propulsion Systems. Springer: New York-Wien, 2002.
  15. Bruno, C.; Accettura, A.G. (Eds.) Advanced propulsion systems and technologies: Today to 2020, Volume 223 Progress in Astronautics and Aeronautics, American Institute of Aeronautics and Astronautics, Virginia, 2008.
  16. Millis, M.G.; Thomas, N.E. Responding to Mechanical Antigravity, NASA/TM-2006-214390, AIAA-2006-4913, December 2006. Available at: http://gltrs.grc.nasa.gov/reports/2006/TM-2006-214390.pdf.
  17. ElSheimy, N.; Youssef, A. Inertial sensors technologies for navigation applications: state of the art and future trends Satellite Navigation 2020, 1 Article number 2. [CrossRef]
  18. Lawerance, A. Modern Inertial Technologies: Navigation, Guidance and Control. Springer: New York, 1992.
  19. Rimrott, F.P.J. Introductory Attitude Dynamics. Springer: New York, 1989.
  20. Minetti, A.E.; Ardigó, L.P. Halteres used in ancient Olympic long jump. Nature 2002, 420, 141–142. [Google Scholar] [CrossRef] [PubMed]
  21. Provatidis, C.G. Simplified biomechanics for a possible explanation of the ancient Greek long jump using halteres. Universal Journal of Engineering Science 2013, 1(1), 5–16. [Google Scholar] [CrossRef]
  22. Provatidis, C.G. On the maximum length of standing long jump using halters. International Journal Multidisciplinary Research and Studies 2018, 1(3), 153–169. [Google Scholar]
  23. Citizendium: http://en.citizendium.org/wiki/Reactionless_propulsion.
  24. Todeschini M. Motore a forza propulsive centrifuga alimentato ad acqua dissociate con variazione di velocita graduale automatic. Regno d’Italia, Ministero delle Corporazioni, Brevetto Industriale No. 312496, 17 November 1933 (see the first two pages of the patent at the website www.circolotodeschini.com).
  25. Dean N.L. System for converting rotary motion into unidirectional motion. US Patent 2,886,976, May 19, 1959.
  26. Dean, N.L. Variable oscillator system. US Patent 3,182,517, May 11, 1965.
  27. Campbell, J., Jr. The Space Drive Problem. Astounding Science Fact and Fiction, 19 June; 83–106.
  28. Dempewolff, R.F. Engine with Built-in Wings,” Popular Mechanics, Sept. 1961, 131–134 and 264-266.
  29. Burridge, G. Toward Antigravity,” Rosicrucian Digest, Vol. XL, April 1962, 136–139.
  30. Davis, W.O. The Fourth Law of Motion, Analog 69(3): 83-104 (May 1962). Extract is available at: http://www.rexresearch.com/dean/davis4.htm.
  31. Stine, G.H. Detesters, Phasers and Dean Drives,” Analog, June 1976, 75.
  32. Campbell, J.W. (1962) - Interview by Fred Lerner: https://www.youtube.com/watch?v=SC-o9z-E010&ab_channel=FANACFanHistory.
  33. Stepanov, G.Yu. , “Why is it impossible to have ‘Dean’s Apparatus’?,” Jour. Priroda, vol. 7, 1963, pp. 85-91 (in Russian).
  34. Di Bella, A. Apparatus for imparting motion to a body, US Patent 3,404,854 (filed on May 5, 1967 and granted on Oct. 8, 1968).
  35. Di Bella, A. On propulsive effects of a rotating mass. In: R. D. Cooper, and S. W. Doroff (Eds.), Proceedings Seventh Symposium Naval Hydrodynamics, August 25-30, 1968, Rome, Italy (Office of Naval Research -Department of The Navy, Arlington, Va.), pp. 1373-1396.
  36. Online: https://en.wikipedia.org/wiki/Viviani%27s_curve.
  37. Therriault, C. Wing movement for ornithopters and apparatus of the like, US Patent No. 6,227,483 B1, May 8, 2001.
  38. Kuchinov, E. Quesalid’s Knots: A Guide to the Soviet Union’s Esoteric Research Institutes. https://sreda.v-a-c.org/en/read-01.
  39. Tolchin, V.N. Sily inertsii kak istochnik postupatel’nogo dvizheniia (Perm: Permskoe knizhnoe izdatel’stvo, 1977). Translation: Forces of inertia as a source of translational motion.
  40. Tolchin Drive-Short Original Film Copy: https://www.youtube.com/watch?v=DOXoaYs790M&ab_channel=stclairtechrd https://www.youtube.com/watch?
  41. Laithwaite, E.R. Propulsion without wheels, 2nd edition. English Universities Press: London, 1970.
  42. Wikipedia: https://en.wikipedia.org/wiki/Eric_Laithwaite.
  43. Laithwaite, E.R. The engineer through the looking glass | The Royal Institution: Science Lives Here. Retrieved 7 January 2024. (https://www.rigb.org/explore-science/explore/video/engineer-through-looking-glass-looking-glass-house-1974).
  44. Bruce De Palma: https://en-academic.com/dic.nsf/enwiki/1876830. 1876.
  45. DePalma, B. The Tuning Fork Experiment, In: R.L. Dione, 1976 (ISBN 553-02723-150); see also: http://www.brucedepalma.com/n-machine/spinning-ball-experiment/.
  46. http://rexresearch.com/depalma2/depalm.htm.
  47. https://depalma.pairsite.com/gyrodrop.html.
  48. Hayasaka, H.; Takeuchi, S. Anomalous weight reduction on a gyroscope’s right rotations around the vertical axis on the earth. Physical Review Letters 1989, 63(25), 2701–2704. [Google Scholar] [CrossRef]
  49. Adelberger, E.G. Science correspondence on paper by Hayasaka & Takeuchi. Nature 1990, 345, 121. [Google Scholar]
  50. Faller, J. E.; Hollander, W.J.; Nelson, P.G.; McHugh, M.P. Gyroscope-weighing experiment with a null result. Phys Rev Lett 1990, 64, 825–826. [Google Scholar] [CrossRef] [PubMed]
  51. MacCallum, M. Does a spinning mass really lose weight? New Scientist 1990, N1704, 30. [Google Scholar]
  52. Nitschke, J.M.; Wilmarth, P.A. Null result for the weight change of a spinning gyroscope. Phys Rev Lett 1990, 64, 2115–2116. [Google Scholar] [CrossRef] [PubMed]
  53. Quinn, T.J.; Picard, A. The mass of spinning rotors: no dependence on speed or sense of rotation. Nature 1990, 343, 732–735. [Google Scholar] [CrossRef]
  54. Salter, S.H. Good vibrations for physics. Nature 1990, 343, 509–510. [Google Scholar] [CrossRef]
  55. Imanishi, A.; Maruyama, K.; Midorikawa, S.; Morimoto, T. Observation against the weight-reduction of spinning gyroscopes. Journal of the Physical Society of Japan 1991, 60, 1150–1152. [Google Scholar] [CrossRef]
  56. Hayasaka, H.; Tanaka, H.; Hashida, T.; Chubachi, T.; Sugiyama, T. Possibility for the existence of anti-gravity: evidence from a free-fall experiment using a spinning gyro. Speculations in Science and Technology 1997, 20, 173–181. [Google Scholar]
  57. Luo, J.; Nie, Y.X.; Zhang, Y.Z.; Zhou, Z.B. Null result for violation of the equivalence principle with the free-fall rotating gyroscopes, Phys. Rev. D 2002, 65, 042005. [Google Scholar] [CrossRef]
  58. Labeysh, V.G. Experiments on Asymmetrical Mechanics. Galilean Electrodynamics 2000, 11, 8–11. [Google Scholar]
  59. Dmitriev A., L. and Snegov V. S.. Measurements of mass: the weighing of a mechanical gyroscope with horizontal and vertical orientation of the spin axis. Measurement Techniques 2001, 44(8), 831–833, (Translated from Izmeritel’naya Tekhnika, No. 8, pp. 33–35, August, 2001. Original article submitted April 3, 2001). [Google Scholar] [CrossRef]
  60. Dmitriev A., L. Frequency Dependence of Rotor’s Free Falling Acceleration and Inequality of Inertial and Gravity Masse. January 2011, arXiv:1101.4678 [pdf].
  61. Dmitriev, A.L.; Snegov, V.S. Measurements of mass: the weighing of a mechanical gyroscope with horizontal and vertical orientation of the spin axis. Measurement Techniques 2001, 44, 831–833. [Google Scholar] [CrossRef]
  62. Dmitriev, A.L. Physical substantiation of an opportunity of artificial change of body weight. Physics Procedia 2012, 38, 150–163. [Google Scholar] [CrossRef]
  63. Dmitriev, A.L. Prospects of high-frequency gravimetry. International Journal of Circuits, Systems and Signal Processing 2015, 9, 275–280, Online at: https://www.inase.org/library/2015/vienna/bypaper/APNE/APNE-37.pdf. [Google Scholar]
  64. Provatidis, C.G. Free fall of a symmetrical gyroscope in vacuum. European Journal of Physics 2021, 42, 065011. [Google Scholar] [CrossRef]
  65. Wayte, R. The phenomenon of weight-reduction of a spinning wheel. Meccanica 2007, 42, 359–364. [Google Scholar] [CrossRef]
  66. Lőrincz, I.; Tajmar, M. Identification of error sources in high precision weight measurements of gyroscopes. Measurement 2015, 73, 453–461. [Google Scholar] [CrossRef]
  67. Provatidis, Forced precession in a spinning wheel supported on a rotating pivot, Mechanics Research Communications 2013, 52, 46– 51. [CrossRef]
  68. Provatidis, C.G. Forced precession of a gyroscope with application to the Laithwaite’s engine. European Journal of Physics 2021, 42(3). [Google Scholar] [CrossRef]
  69. Allen, J.E. Quest for a novel force: a possible revolution in aerospace. Progress in Aerospace Sciences 2003, 39(1), 1–60. [Google Scholar] [CrossRef]
  70. Meek, J. BAe’s anti-gravity research braves X-Files ridicule. The Guardian, Mon 27 Mar 2000. Online: https://www.theguardian.com/science/2000/mar/27/uknews.
  71. Anonymous. Project Greenglow and the battle with gravity. News, 23 March 2016, https://www.bbc.com/news/magazine-35861334. See als, https://www.documentaryarea.com/video/Project%20Greenglow%20The%20Quest%20for%20Gravity%20Control/.
  72. Interview from Ron Evans: https://www.youtube.com/watch?v=BwI7Ij-5cMA&ab_channel=TimVentura.
  73. Anonymous. Science Does The Impossible: February 2003 Cover Story. Popular Mechanics. https://archive.ph/20070930015205/http://www.popularmechanics.com/science/research/1282281.html?page=3.
  74. Anonymous, Boeing Internal Report Looks At Propellentless Propulsion, https://www.spacedaily.com/news/rocketscience-02t.html.
  75. BBC-News, Boeing tries to defy gravity. Monday, 29 July, 2002. http://news.bbc.co.uk/2/hi/science/nature/2157975.stm.
  76. Wikipedia: Eugene Podkletnov. https://en.wikipedia.org/wiki/Eugene_Podkletnov#cite_note-8.
  77. Millis, M.G. Breakthrough Propulsion Physics Research Program. NASA Technical Memorandum 107381. December 199.
  78. Millis, M.G. NASA breakthrough propulsion physics program. Acta Astronautica 1999, 44(2-4), 175–182. [Google Scholar] [CrossRef]
  79. Millis, M.G. Assessing Potential Propulsion Breakthroughs. Annuals of New York Academy of Sciences 2005, 1065, 441–461. [Google Scholar] [CrossRef] [PubMed]
  80. Millis, M.G.; Davis, E.W. Frontiers of Propulsion Science. American Institute of Aeronautics and Astronautics Inc.: Reston, VA, 2009.
  81. Millis, M.G. Progress in revolutionary propulsion physics, Paper IAC-10-C4.8.7. In: Proceedings 61st International Astronautical Congress, Prague CZ, 2010.
  82. Hoshino M., U.S. Patent for “Propulsion apparatus using centrifugal force,” No. 20050139022 (Filed 7 Jan. 2004; Published: 30 June 2005).
  83. Hampton, S.M., From Dean Drives and Davis Mechanics: Inertial Propulsion and the Manipulation of Time in Symmetrical Systems ©, Ebook, Apple Communications, London Mills, Illinois, 2007, 2011 (ISBN 518 373).
  84. Hampton, S.M. Asymmetric Impulse Drive. AIAA 2022-4391. ASCEND 2022 (24-26 October 2022, Las Vegas, Nevada & Online). Session: Frontiers in Deep Space Propulsion. View Video Presentation. [CrossRef]
  85. Tsiriggakis, V.Th.; Provatidis C.G.; Frigas S. U.S. Patent Application for an “Antigravity Mechanism,” No. 61/110,307, filed 31 Oct. 2008.
  86. Provatidis, C.G.; Tsiriggakis, V.T. A new concept and design aspects of an ‘antigravity’ propulsion mechanism based on inertial forces. Proceedings of 46th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Nashville, TN, 25-28 July 2010 (Paper AIAA 2010-6684).
  87. Provatidis, C.G. A device that can produce net impulse using rotating masses. Engineering 2020, 2(8), 648–657. [Google Scholar] [CrossRef]
  88. Pipes, L.A.; Harville, L.R. Applied mathematics for engineers and physicists, 3rd ed. McGraw-Hill: New York, 1981, pp. 494–496.
  89. Provatidis, C.G.; Gamble, M.A. Support forces in a synchronized rotating spring-mass system and its electromagnetic equivalent. International Journal of Applied Electromagnetics and Mechanics 2013, 41(3), 313–333. [Google Scholar] [CrossRef]
  90. Manning, J. Space, Propulsion & Energy Sciences International Forum-A Journalist’s Notes, Infinite Energy (May/June) 2012, May-June, Issue 103, 18-23.
  91. Valone, T. Inertial Propulsion: Concept and Experiment, Part I, Proc. IECEC, 1993.
  92. Valone, T. Inertial Propulsion: Concept and Experiment, Part II, Intersociety Energy Conversion Engineering Conference (07 August 1994 - 12 August 1994, Monterey, CA, U.S.A), AIAA-94-4167-CP, pp. 1484-1489. [CrossRef]
  93. Valone, T.; Cox, J. Inertial Propulsion: Patent Collection. Integrity Research Institute: Washington, D.C., 2008.
  94. Valone, T.F. Eric Laithwaite Report: Gyromagnetic Engineering Genius – Publications, Inventions & News Clips (IRI PR-02-005), Integrity Research Institute: Beltsville, MD, December, 2006.
  95. Almesallmy, M. Experimental and Analytical Investigation of Inertial Propulsion Mechanisms and Motion Simulation of Rigid-Multi-Body Mechanical Systems. PhD Dissertation. University of Rhode Island, 2006.
  96. Guiad, D.; Nilvetti, F.; Pappalardo, C.M. Dry Friction Influence on Cart Pendulum Dynamics. International Journal of Mechanics 2009, 3(2), 31–38. [Google Scholar]
  97. Provatidis, C.G. Some issues on inertia propulsion mechanisms using two contra-rotating masses. Theory of Mechanisms and Machines 2010, 8(1), 34–41, Download from: http://tmm.spbstu.ru/15/Provatidis_15.pdf. [Google Scholar]
  98. Provatidis, C.G. A study of the mechanics of an oscillating mechanism, International Journal of Mechanics 2011, 5(4), 263-274. Online at: https://www.naun.org/main/NAUN/mechanics/17-093.pdf.
  99. Provatidis, C.G. An overview of the mechanics of oscillating mechanisms. American Journal of Mechanical Engineering 2013, 1(3), 58–65. [Google Scholar] [CrossRef]
  100. Provatidis, C.G. Repeated vibrational motion using an inertial drive. Vibration and Acoustics Research Journal 2019, 1(1). Online: https://www.cansrg.com/journals/varj/2019/70.pdf.
  101. Provatidis, C.G. On the inertial propulsion of floating objects using contra-rotating masses. Mechanics Research Communications 2014, 62, 117–122. [Google Scholar] [CrossRef]
  102. Ikuta, K., Aritomi, S. and Kabashima, T. Tiny silent linear cybernetic actuator driven by piezoelectric device with electromagnetic clamp. [1992] Proceedings IEEE Micro Electro Mechanical Systems, Travemunde, Germany, 1992, pp. 232-237. [CrossRef]
  103. Aoyama, H., Iwata, F. and Sasaki, A. Desktop flexible manufacturing system by movable miniature robots-miniature robots with micro tool and sensor. Proceedings of 1995 IEEE International Conference on Robotics and Automation, Nagoya, Japan, 1995, pp. 660-665 vol.1. [CrossRef]
  104. Zesch, W.; Buchi, R.; Codourey, A.; Siegwart, R. Inertial Drives for Micro- and Nanorobots: Two Novel Mechanisms. Proc. SPIE Microrobotics and Micromechanical Systems, Philadelphia, USA, pp. 80-88, 18 October 1995. [CrossRef]
  105. Buchi, R.; Zesch, W.; Codourey, A.; Siegwart, R. Inertial Drives for Micro- and Nanorobots: Analytical Study. Proc. SPIE Vol. 2593, p. 89-97, Microrobotics and Micromechanical Systems, 1995. [CrossRef]
  106. Yoshikawa, H.; Kagiwada, T.; Harada, H.; Mimura, M. Improvement of Propulsion Mechanism Based on the Inertial Force. In: F. Kimura and K. Horio (Eds.), Towards Synthesis of Micro-/Nano-Systems. Springer: London, 2007, pp. 333-334.
  107. Ju, J.; Wang, Q.; Zhang, K. Design and analysis of a novel micro-robot driving platform. Proc IMechE-Part C: Journal of Mechanical Engineering Science 2019, 233, 3849–3857. [Google Scholar] [CrossRef]
  108. Vatholomeos, P.; Papadopoulos, E. Dynamics, design and simulation of a novel micro-robotic platform employing vibration micro-actuators. ASME Journal of Dynamic Systems, Measurement and Control 2006, 128, 122–133. [Google Scholar] [CrossRef]
  109. Vartholomeos, P.; Papadopoulos, E. Analysis and experiments on the force capabilities of centripetal-force-actuated microrobotic platforms. IEEE Transactions on Robotics 2008, 24, 588–599. [Google Scholar] [CrossRef]
  110. Provatidis, C.G. Design of a propulsion cycle for endless sliding on frictional ground using rotating masses. Universal Journal of Mechanical Engineering 2014, 2 (2), 35 – 43. [CrossRef]
  111. Provatidis, C.G. Mechanics of Dean drive on frictional ground, Journal of Mechanical Design and Vibration 2014, 1(1), 10-19. Online at: https://pubs.sciepub.com/jmdv/1/1/3/index.html. [CrossRef]
  112. Provatidis, C.G. Unidirectional motion using rotating masses along figure-eight-shaped trajectories, Journal of the Brazilian Society of Mechanical Sciences and Engineering 2015, 37(1), 397–409. [CrossRef]
  113. Provatidis, C.G. Progress in an Antigravity Mechanism using Inertial Masses. Proceedings Space, Propulsion & Energy Sciences International Forum (SPESIF-2011) [CR-ROM], presented on March 15-17, 2011, University of Maryland, College Park, MD, USA.
  114. Provatidis, C.G. Older and contemporary attempts for inertial propulsion. The General Science Journal, 14 November 2011. Online: http://gsjournal.net/Science-Journals/Essays/View/3772.
  115. Gamble, M. History of Boeing Control Moment Gyros (CMG). Presentation in Seventh International Conference On Future Energy (COFE7), July 30 – August 1, 2015, Embassy Suites, Albuquerque New Mexico (Boeing 15-00051-EOT).
  116. Gamble, M. Linear Propulsion. Presentation in Seventh International Conference On Future Energy (COFE7), July 30 – August 1, 2015, Embassy Suites, Albuquerque New Mexico.
  117. Samokhvalov, V.N. Research on, and Measurement of, Force Effects During Mass-Dynamic Interaction. Galilean Electrodynamics & GED East 2015, 26, 3–11. [Google Scholar]
  118. Samokhvalov, V.N. Non-electromagnetic force interaction in presence of rotating masses in vacuum. International Journal of Unconventional Science 2016, Issue E1, 68-80. http://www.unconv-science.org/en/e1/samokhvalov/. /.
  119. Allen, D.P. Jr.; Dunning-Davies, J. Neo-Newtonian Mechanics with Extension to Relativistic Velocities; Part 1: Non-Radiative Effects, 18 th Ed., Kindle Direct Publishing, 2023. Part 1.
  120. Milković, V. Gravitational Machines: from Leonardo da Vinci to the latest discoveries. Veljko Milkovic Research & Development Center: Novi Sad, Serbia, 2013 (ISBN 978-86-88883-03-0).
  121. Allen, D.P.; Provatidis, C.G. Inclined large-angle pendulum may produce endless linear motion of a cart when friction is negligible. WSEAS Transactions on Applied and Theoretical Mechanics 2022, 17, Art. #23, p.184-197. Online: https://wseas.com/journals/mechanics/2022/a465111-016(2022).pdf. [CrossRef]
  122. Provatidis, C. Teaching the Fixed Spinning Top Using Four Alternative Formulations. WSEAS Transactions on Advances in Engineering Education 2021, 18, 80–95. [Google Scholar] [CrossRef]
  123. Provatidis, C.G. Revisiting the Spinning Top. International Journal of Materials and Mechanical Engineering 2012, 1, 71–88, Online at: https://www.academia.edu/27516500/Revisiting_the_Spinning_Top. [Google Scholar]
  124. Loukanov, I.A. Vibration Propulsion of a Mobile Robot. IOSR Journal of Mechanical and Civil Engineering 2015, 12, 23–33, www.iosrjournals.org. Online: https://www.academia.edu/65248904/Vibration_Propulsion_of_a_Mobile_Robot. [Google Scholar]
  125. Loukanov, I.A. Application of Inertial Forces for generating Unidirectional Motion. Proceedings of the Scientific Conference of University of Rousse 2014, 53(2). Online https://www.researchgate.net/publication/314067949_Application_of_Inertial_Forces_for_Generating_Unidirectional_Motion.
  126. Loukanov, I.A.; Uziak, J. Upon Improving the Prediction of the Flow Rate of Sonic Pump. International Journal of Engineering Research and Applications 2013, 3, 393–398, Online: https://www.ijera.com/papers/Vol3_issue1/BF31393398.pdf. [Google Scholar]
  127. Lukanov, I.A.; Vitliemov, V.G.; Ivanov, I.V. Dynamics of a Mobile Mechanical System with Vibration Propulsion (VibroBot). International Journal of Research in Engineering and Science (IJRES) 2016, 4, 44–51. [Google Scholar]
  128. Cook, R.L. Device for Conversion of Centrifugal Force to Linear Force and Motion, US Patent 4,238,968, granted December 16, 1980.
  129. Thornson, B.R. Apparatus for developing a propulsion force. United States Patent No. 4,631,971 (Filed: 25.05.84; Awarded: 30.12.1986).
  130. Foster, R.E. Converting rotary motion into unidirectional motion. United States Patent No. 3653269, 1972.
  131. Robertson, D.B. Propulsion method and apparatus utilizing centrifugal force. World Intellectual Property Organization (WIPO), Number WO 01/46584 A3, 28 June 2001.
  132. Chung, T.B. Internal propulsion apparatus of closed system using a Coriolis force. International Patent WO 03/087574 A1, 23 (Filing date: 08 April 2003; Publication date: 23 October 2003).
  133. Tanner, M.A. Resonant Maglev Centrifugal Propulsion. United States Patent Application US 2007/0079663 A1 (Filed: 12 Aug. 2006; Published: 12 Apr. 2007).
  134. Farrall, A.W. (1966), “Inertial propulsion device”, United States Patent No. US3266233A (associated to reference [2]).
  135. Robertson, G.A.; Murad, P.A.; Davis, E. New Frontiers in Space Propulsion Sciences. Energy and Conversion Management 2008, 49, 436–452. [Google Scholar] [CrossRef]
  136. Robertson, G.A.; Webb, D.W. The Death of Rocket Science in the 21st Century. Physics Procedia 2011, 20, 319–330. [Google Scholar] [CrossRef]
  137. Die Schwunge Maschine: http://www.zdf.de/ZDFmediathek/hauptnavigation/startseite/#/beitrag/video/1573468/Die-Schwung-Maschine.
  138. Hilscher, G. Trägheit der Masse mobilisiert die Energietechnik: Mit dem findigen Johann Klimpfinger auf Entdeckungstour durch Archive und seine experimentelle Welt. NET-Journal 2011, 16(3/4), 46-50. Online: http://www.borderlands.de/net_pdf/NET0311S46-50.pdf.
  139. Anonymous, Kreisel Präzessions Antrieb (Gyro Precession Drive), Online at: https://www.youtube.com/watch?v=nstIIZZadAM&ab_channel=gyro2012.
  140. Stoney, W. Method of propulsion. Irish Patent Application. IE 20190160 A2. Date of Publication of Application: 03.08.2022 Journal No. 2469.
  141. Myshkin, N.P. “Dvizheniye tela, nakhod yashegosya v potoke luchistoi energii.” //Zhyrnal Russkogo fiziko-himicheskogo obshestva, 1906, v.3, p.149. (Russian) (“The movement of object placed in the radiant energy flow.”).
  142. Kozyrev, N.A. “Prichinnaya ili nesimmetrichnaya mekhanika v lineinom priblizhenii.”, Pulkovo, GAO AN SSSR, 1958, 90 p. (Russian) (“Causal or asymmetrical mechanics in linear approximation.”).
  143. Kozyrev, N.A. “On the possibility of experimental investigation of the properties of time.” //Time in science and philosophy, Prague, 1971, p.111-132.
  144. http://shipov.com/science.html; http://shipov.com/gennady-i-shipov/.
  145. Wikipedia: https://en.wikipedia.org/wiki/Torsion_field_(pseudoscience).
  146. Linevich, E.I.; Ezshov, A.F. The inertial motor. New Energy Technologies 2004, 3, 12–15. [Google Scholar]
  147. Kouznetsov, D. Support of non-traditional concepts. Far East Journal of Mechanical Engineering and Physics 2010, 1, 1–6, Online: https://www.pphmj.com/abstract/5076.htm. [Google Scholar]
  148. Tim Ventura & Dr. Gennady Shipov, Inertial Propulsion in Russia: Dr. Gennady Shipov on Torsion Physics & Inertial Propulsion, Interview to American Antigravity.Com, 2012, pp. 1-8 (http://shipov.com/files/200506_news09.pdf; http://einsteinandtesla.com/files/200506_news09.pdf).
  149. V. Sorokin: http://www.ntv.ru/novosti/84720/video.
  150. Alex Naumov. Russian scientists test perpetual motion machine in space. PRAVDA Newspaper, 14.04.2009. Accessed on 22nd January 2024: http://english.pravda.ru/science/tech/14-04-2009/107399-russian_scientists-0. /.
  151. Wikipedia: https://en.citizendium.org/wiki/Valery_Menshikov.
  152. Wikipedia: http://en.wikipedia.org/wiki/Yubileiny.
  153. Zhao, C.; Zhu, H.; Zhang, Y. Synchronization of two coupled exciters in a vibrating system of spatial motion. Acta Mechanica Sinica 2010, 26, 477–493. [Google Scholar] [CrossRef]
  154. Zhao, C.; Zhang, Y.; Wen, B. Synchronisation and general dynamic symmetry of a vibrating system with two exciters rotating in opposite directions. Chin Phys B 2010, 19, 030305-1-7. [Google Scholar] [CrossRef]
  155. Chen, X.; Liu, J.; Li, L. Dynamics of the Vibration System Driven by Three Homodromy Eccentric Rotors Using Control Synchronization, Appl. Sci. 2021, 11. [Google Scholar] [CrossRef]
  156. Hambling, D. EmDrive: China’s radical new space drive, Wired 06.02.2013 (https://www.wired.co.uk/article/emdrive-and-cold-fusion).
  157. Halliday, D.; Resnick, R. Physics. Wiley: NY, International Edition, pp.59-61, 1966.
  158. Casey, J. Geometrical derivation of Lagrange’s equations for a system of particles. American Journal of Physics 1994, 62, 836–847. [Google Scholar] [CrossRef]
  159. Casey, J. Applying the principle of angular momentum to constrained systems of point masses. American Journal of Physics 2014, 82, 165–168. [Google Scholar] [CrossRef]
  160. Laithwaite E 1994 Heretics BBC2 Television London; plus private demonstrations and Imperial College Christmas Lectures available in internet (e.g. http://youtube.com/watch?v&tnqx3d; KnNUTOxHoto), Accessed 04.04.2020.
  161. Laithwaite, E.; Dawson, W. Propulsion System. US Patent No. 5,860,317 (grant Jan.1999).
  162. Pinheiro, M.J. On Newton’s third law and its symmetry-breaking effects. Physica Scripta 2010, 84(5), 055004. [Google Scholar] [CrossRef]
  163. Gutsche, G.J. Inertial Propulsion; and you thought you knew everything about physics. CreateSpace Independent Publishing Platform (November 26, 2018).
  164. Gutsche, G.J. Device for efficient self -contained inertial vehicular propulsion. United States Patent, Patent No .: US 9,995,284 B1, Date of Patent : Jun . 12 , 2018.
  165. Allen D.P., Jr. Foundations of Gutschian Mechanics: Part 1: Basics. Kindle Direct Publishing; 6th edition (November 29, 2019).
  166. Provatidis, C.G. A Review on Antigravity, Levitation, Resonance, and Devices Inspired by the Ouroboros Serpent. The Rose+Croix Journal 2012, 9, 18–47, Online at: https://www.academia.edu/download/50150834/vol9_18_47_provatidis.pdf. [Google Scholar]
  167. Manning, J. Escape from Gravity: Is the Ancient Promise of Freedom from the Pull of Earth Alive and Well at NASA and Elsewhere? In: J. Douglas Kenyon (Ed.), Forbidden Science: From Ancient Technologies to Free Energy, Chapter 13.
  168. Gerjuoy, E. On Newton’s third law and the conservation of momentum. American Journal of Physics 1949, 17, 477–482. [Google Scholar] [CrossRef]
  169. Martins, A.A.; Pinheiro, M.J. On the nature of the propulsive force of asymmetric capacitors in the atmosphere. Physics Procedia 2011, 20, 103–111. [Google Scholar] [CrossRef]
  170. Martins, A.A.; Pinheiro, M.J. On the nature of the propulsive force of asymmetric capacitors in a vacuum. Physics Procedia 2011, 20, 112–119. [Google Scholar] [CrossRef]
  171. Stephenson A 1908 XX. On induced stability London Edinburgh Dublin Phil. Mag. J. Sci. 15 233–6.
  172. Kapitsa, P.L. Dynamic stability of the pendulum when the point of suspension is oscillating. J. Exp. Theor. Phys. 1951, 21, 588–597. (in Russian). [Google Scholar]
  173. Blekhman I I, Dresig H and Shishkina E 2004 On the theory of the Indian magic rope Selected Topics in Vibrational Mechanics ed I I Blekhman (Singapore: World Scientific) pp 139–49. W.
  174. Cross R 2014 Laithwaite’s heavy spinning disk demonstration Phys. Teach. 52 349.
  175. Davidowsky P and Rogers M 2015 Debunking a video on YouTube as an authentic research experience Phys. Teach. 53 304–6.
  176. Sheheitli, H. On the dynamics of a spinning top under high-frequency excitation: part I—pivot point under vertical harmonic vibration. Nonlinear Dyn 2017, 90, 765–779. [Google Scholar] [CrossRef]
  177. Sheheitli, H. 2017 On the dynamics of a spinning top under high-frequency excitation. Part II: pivot point under horizontal harmonic vibration Nonlinear Dyn. 2017, 90, 2269–2276. [Google Scholar] [CrossRef]
  178. LaViolette, P.A. Secrets of Antigravity Propulsion: Tesla, UFOs, and Classified Aerospace Technology. Bear & Company: Rochester, Vermont, 2008.
  179. Childress, D.H. The Antigravity Handbook, 3rd edn. Adventures Unlimited Press: Kampton-Illinois, 2010.
  180. Passaro, V.M.N.; Cuccovillo, A.; Vaiani, L.; De Carlo, M; Campanella, C.E. Gyroscope technology and applications: a review in the industrial perspective. Sensors 2017, 17(10), 2284. [CrossRef] [PubMed]
  181. Usubamatov, R. Theory of Gyroscopic Effects for Rotating Objects: Gyroscopic Effects and Applications. Springer: Cham, 2020. [CrossRef]
  182. Shipov, G. Four-dimensional gyroscope, demonstrating the violation of the momentum conservation law during the absolute electic collision with the wall. US20040166482A1, United States, Application filed on 2001-02-15.
  183. Solomon, B.T. An introduction to gravity modification: A guide to using Laithwaite’s and Podkletnov’s experiments and the physics of forces for empirical results, 2nd ed. Universal-Publishers: Boca Raton, 2012 [Chapter 5: The Laithwaite Effect, pp. 67-81, as well as §14.5 (pp. 309-315) and §14.6 (pp. 315-326)].
  184. Solomon, B.T. Gravitational acceleration without mass and noninertia fields. Physics Essays 2011, 24, 327–337. [Google Scholar] [CrossRef]
  185. Bjerke, E.; Pehrsson, B. Development of a Nonlinear Mechatronic Cube: The Jumping and Balancing Cube. Master of Science Thesis, Department of Signal and Systems, Division of Automatic control, Automation and Mechatronics, Chalmers University of Technology, Gothenburg, Sweden 2016.
  186. Elliott, D.S. Momentum Control Systems and their Application in Robotic Systems. PhD thesis, Cornell University, December 2019.
  187. Elliott, D.S.; Peck, M.; Nesnas, I.A.D. Optimal Solution for Torque Capability of Control Moment Gyroscopes. Proc. IEEE Aerospace Conference, Big Sky, MT, USA, 2019, pp. 1-17. [CrossRef]
  188. Elliott, D.S.; Peck, M.A. Dynamics and Control of Polyhedral Surface Robots with Control Moment Gyroscopes, Proc. AIAA Guidance, Navigation, and Control Conference, 9 - 13 January 2017. Grapevine, Texas, AIAA 2017-1050, Session: Spacecraft Robotics. [CrossRef]
  189. CMG-rover: NASA has supported researchers in Cornell University to develop technologies to use it for locomotion purposes (say) in Mars: https://www.spacecraftresearch.com/cmg-rover; https://www.nasa.gov/directorates/spacetech/strg/nstrf2016/Polyhedral_Rover/.
  190. M. Gajamohan, M. Merz, I. Thommen, and R. D’Andrea, The Cubli: a cube that can jump up, balance, and ‘walk’, In: Proc. IROS (Algavre, Portugal), pp. 3722-3727, October 2012.
  191. NASA’s Helical Engine and Other Reactionless Drives: https://www.youtube.com/watch?v=yNro9yiVZno&t=3s&ab_channel=PhysicsUnsimplified.
  192. Gyroscopic Precession Powered Car: https://www.youtube.com/watch?v=zOGlHC56Brs&t=4s&ab_channel=anisotropicplus (accompanied by 12 more movies).
  193. YouTube: Falcon Space Demonstrates Gyroscopic Propellentless Propulsion (Part 2): https://www.youtube.com/watch?v=OPPnmAFcPiw&ab_channel=CharlieC.
  194. Raptis, Y.; Kourouklis, G.A. A Tribute to the Work of the Late Professor Evangelos Anastassakis (1938-2000). physica status solidi (b) 2001, 223, 1–13. [Google Scholar] [CrossRef]
  195. Ünker, F.; Çuvalci, O. Gyroscopic inertial thruster (GIT), In: U.E.Solmaz, N, Kaya, and F. Ozturk, Proceedings 9th International Automotive Technologies Congress, OTEKON 2018, pp. 686-695.
  196. Gerocs, A.; Gillich, G.-R.; Nedelcu, D.; Korka, Z.-I. A multibody inertial propulsion drive with symmetrically placed balls rotating on eccentric trajectories. Symmetry 2020, 12, 1422. [Google Scholar] [CrossRef]
  197. Gerocs, A.; Korka, Z.-I.; Biró, I.; Cojocaru, V. Analytical investigation of an inertial propulsion system using rotating masses. J. Phys.: Conf. Ser. 1426 012031 (2020).
  198. Gerocs, A.; Korka, Z.-I; Biró, I.; Cojocaru, V. Analytical investigation of an inertial propulsion system using rotating masses. Journal of Physics: Conference Series, vol. 1426 012031. International Conference on Applied Sciences 9–11 May 2019, Hunedoara, Romania. [CrossRef]
  199. Sprenger, A.R.; Scholz; C., Ldov, A. et al. Inertial self-propelled particles in anisotropic environments. Commun Phys 6, 301 (2023). [CrossRef]
  200. Frolov, A.V. italic>New Aerospace Technologies. Independent Publisher: St.-Petersburg, Russia, 2017 (ISBN 978-5-7679-3883-4).
  201. McCulloch, M.E. Low-acceleration dwarf galaxies as tests of quantised inertia. Astrophys Space Sci 2017, 362: 57. [CrossRef]
  202. McCulloch, M.E. Physics from the edge: a new cosmological model for inertia. World Scientific: Singapore, 2014.
  203. McCulloch, M.E. Can the Podkletnov effect be explained by quantised inertia? Physics Procedia 2011, 20, 134–139. [Google Scholar] [CrossRef]
  204. Goebel, D.M.; Katz, I. Fundamentals of Electric Propulsion: Ion and Hall Thrusters. Wiley: New Jersey, 2008.
  205. Forward, R. L. Guidelines to Antigravity. American Journal of Physics 1963, 31, 166–170. [Google Scholar] [CrossRef]
  206. Mashhoon, B.; Hehl, F.W.; Theiss, D.S. On the gravitational effects of rotating masses: The Thirring-Lense papers. General Relativity and Gravitation 1984, 16, 711–750. [Google Scholar] [CrossRef]
  207. Tajmar, M. Homopolar artificial gravity generator based on frame-dragging. Acta Astronautica 2010, 66((9-10)), 1297–1301. [Google Scholar] [CrossRef]
  208. Millis, M.G. Inertial frames and breakthrough propulsion physics. Acta Astronautica 2017, 138, 85–94. [Google Scholar] [CrossRef]
  209. Wisdom, J. Swimming in spacetime: motion by cyclic changes in body shape. Science 2023, 299(5614), 1865–1869. [Google Scholar] [CrossRef]
Preprints 97285 g001
Figure 1. Halteres used in athletic games in ancient Greece, National Archaeological Museum, Athens (from https://en.wikipedia.org/wiki/Halteres_(ancient_Greece))
Figure 1. Halteres used in athletic games in ancient Greece, National Archaeological Museum, Athens (from https://en.wikipedia.org/wiki/Halteres_(ancient_Greece))
Preprints 97285 g001
Preprints 97285 g002
Figure 2. Baron Münchhausen uses support-less propulsion to get out from the swamp by pulling himself up by his hair (source: [23]).
Figure 2. Baron Münchhausen uses support-less propulsion to get out from the swamp by pulling himself up by his hair (source: [23]).
Preprints 97285 g002
Preprints 97285 g003
Figure 3. Extract from Todeschini’s patent [24]. (source: https://www.circolotodeschini.com/brevetto-provatidis/).
Figure 3. Extract from Todeschini’s patent [24]. (source: https://www.circolotodeschini.com/brevetto-provatidis/).
Preprints 97285 g003
Preprints 97285 g004
Figure 4. Dean drive (source: https://en.wikipedia.org/wiki/Dean_drive).
Figure 4. Dean drive (source: https://en.wikipedia.org/wiki/Dean_drive).
Preprints 97285 g004
Preprints 97285 g005
Figure 5. The front page of the paper by Professor Stepanov [33] regarding Dean drive.
Figure 5. The front page of the paper by Professor Stepanov [33] regarding Dean drive.
Preprints 97285 g005
Figure 6. The Di Bella mechanism [34]. (source: http://perpetualmotion21.blogspot.com/2014/07/the-todeschinidi-bella-device-part-i.html).
Preprints 97285 g006
Preprints 97285 g007
Figure 7. One way to modify the lower radius in the path of the eccentric masses (from Hoshino [82]).
Figure 7. One way to modify the lower radius in the path of the eccentric masses (from Hoshino [82]).
Preprints 97285 g007
Preprints 97285 g008
Figure 8. The concept of the eight-shaped drive [85,86,87] (artwork by S. Frigas).
Figure 8. The concept of the eight-shaped drive [85,86,87] (artwork by S. Frigas).
Preprints 97285 g008
Preprints 97285 g009
Figure 9. The concept of the rotating elastic rod under an impact force (a) immobile rod, (b) reaction force, (c) first halve, (d) second halve of period.
Figure 9. The concept of the rotating elastic rod under an impact force (a) immobile rod, (b) reaction force, (c) first halve, (d) second halve of period.
Preprints 97285 g009
Preprints 97285 g010
Figure 10. The average thrust produced by the gyro scissor operation (from [116] with permission).
Figure 10. The average thrust produced by the gyro scissor operation (from [116] with permission).
Preprints 97285 g010
Preprints 97285 g011
Figure 11. Devices based on professor Loukanov’s activity (inertial pumps and inertial driven vehicle) (from [124,125,126,127]).
Figure 11. Devices based on professor Loukanov’s activity (inertial pumps and inertial driven vehicle) (from [124,125,126,127]).
Preprints 97285 g011
Preprints 97285 g012
Figure 12. Incremental impulse in the four quadrants (constant angular velocity).
Figure 12. Incremental impulse in the four quadrants (constant angular velocity).
Preprints 97285 g012
Preprints 97285 g013
Figure 13. Incremental impulse in the four quadrants (linearly increasing angular velocity), times the factor m r a .
Figure 13. Incremental impulse in the four quadrants (linearly increasing angular velocity), times the factor m r a .
Preprints 97285 g013
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated