Prerpints.org logo
Preprint
Article

Chondrogenic Cancer Grading by combining Machine and Deep Learning with Raman Spectra of Histopathological Tissues

Altmetrics

Downloads

240

Views

90

Comments

0

This version is not peer-reviewed

Submitted:

13 May 2024

Posted:

14 May 2024

Read the latest preprint version here

Alerts
Abstract
Raman spectroscopy (RS) turns out to be a promising tool for cancer di- agnosis. In particular, in the last years several studies have demonstrated how the diagnostic performances of Raman Spectroscopy can be significantly improved by employing Machine Learning (ML) algorithms for the interpre- tation of Raman-based data. In line with these findings, in this paper, we demonstrated how RS coupled with ML allowed to accurately distinguish the three grades of Chondrosarcoma and to distinguish Chondrosarcoma and a benign counterpart called Enchondroma. We obtained such results by ana- lyzing a dataset composed of a relatively small number of Raman spectra, collected in a previous study. Such spectra were acquired from micromet- ric tissue sections with a Confocal Raman Microscope. In particular, we tested the classification performances of a Support Vector Machine and a Random Forest Classifier, as representative of Machine Learning, and two versions of the Multi-Layer Perceptron, as representative of Deep Learning (DL). These models showed excellent classification performances, especially those belonging to DL, with accuracy reaching 99.7%. This outcome makes the aforementioned models a promising route for future improvements of di- agnostic devices focused on detecting bone cancerous tissues. In addition, we highlighted how the ML models studied resulted in slightly worse classifi- cation performances in comparison to DL. Alongside the diagnostic purpose, the aforementioned approach allowed to identify characteristic molecules, i. e. amino acids, nucleic acids and bioapatites, relevant for the obtainment of the final diagnostic response, through the analysis of the so-called Per- mutation Feature Importance. Permutation Feature Importance could hence represent a promising parameter for the understanding of the biochemical processes on the basis of the tumor progression. In turn, the spectral bands highlighted by Permutation Feature Importance could represent precious in- dicators in the attempt to restrict the spectral acquisition to specific Raman bands. This last objective could help to reduce the amount of experimental data needed to obtain an accurate final grading outcome, with consequent reduction of the computational cost.
Keywords: 
Subject: Physical Sciences  -   Biophysics
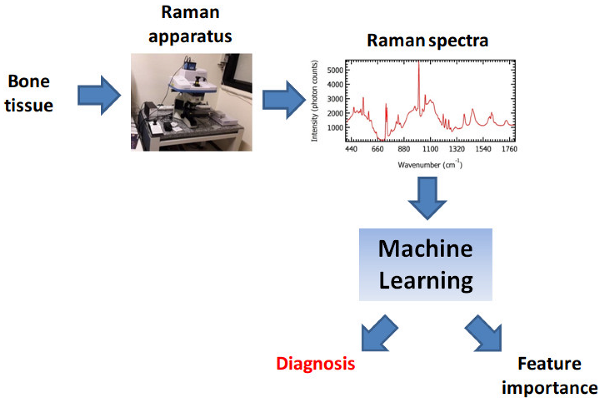
Graphical abstract
Preprints 106395 i001
Highlights
  • Raman spectroscopy combined with Machine Learning and Deep Learning is able to detect Chondrosarcoma and Enchondroma from bone tissues with accuracy larger than 99%.
  • Machine Learning and Deep Learning highlighted the Raman bands associated to biomolecular groups, particularly relevant to distinguish between tissues corresponding to different malignant degrees.

1. Introduction

Chondrosarcoma (CS) turns out to be the second most common form of primary bone tumor worldwide, with almost seven cases per million people registered every year [1]. In the continuous effort to introduce effective and minimally invasive therapies, the ability to grade CS and to distinguish this form of bone cancer from healthy tissues and/or benign tumors, such as Enchondroma (EC), represents a crucial factor. The common protocol for the diagnosis of CS is based on an initial examination of radiological and/or Magnetic Resonance (MRI) images, followed by the histopathological analysis of a tissue biopsy. One of the drawbacks of this procedure is represented by the frequent discrepancies between the response of pre- and post-surgical histopathological analysis, mainly due to the presence of tissue inhomogeneities within the same tumor mass. This last feature also determines the presence of not well-defined tumor margins, undoubtedly affecting the outcome of the surgical therapies. As previously demonstrated [2], the presence of not removed tumor margins represents a concrete risk factor, increasing the probability of recurrence and thus decreasing the 5-year survival rate. Setups for image-guided surgery, e.g., Computed Tomography (CT) and MRI, were introduced to help the surgeon in maximizing the size of the excised tumor mass by preserving the surrounding healthy tissues. Despite the progress of these techniques, they still show weaknesses. In particular, CT is based on the use of ionizing radiation, with possible side effects for the patient and/or the operator. Furthermore, MRI employs intense magnetic fields, not suitable for patients with metallic devices implanted within the body. Among the imaging techniques, we also mention the Ultrasonographic (US) analysis. However, this technique is not yet considered a reliable solution, since it suffers from problems in the detection of soft tissues characterizing bone metastasis [3]. Finally, nuclear medicine, such as Positron Emission Tomography (PET), represents an interesting solution, since it potentially provides additional information about metabolism and drug activity. Despite the large values of sensitivity and specificity in detecting tumor masses, nuclear medicine is characterized by small spatial resolution. This feature pushed the researchers to couple such technique to other approaches, such as MRI [4].
Raman Spectroscopy (RS) represents a promising, easy-to-use, and low-cost solution to respond to the aforementioned needs [5,6,7]. RS is based on the measurement of the so-called Raman effect [8], i. e. a light scattering phenomenon produced by the interaction between a beam of photons and virtual molecular energy levels [9]. The difference between the wavelengths of the scattered and the incident photons is strongly correlated to the chemical properties of the molecular target that determined the scattering. Therefore, by performing a spectral analysis of the radiation scattered by a sample of interest, it is possible to retrieve detailed information about the chemical composition of the target under investigation [10]. Since the Raman effect doesn’t involve the interaction between photons and well-defined electronic energy levels, the technique is intrinsically not subject to non-radiative relaxation phenomena, possible source of sample cooling and consequent degradation. This feature makes RS particularly suitable to in vivo applications, e.g., for intra-operative cancer detection, aimed at estimating the tumor margins. Unlike the conventional histopathological analysis, requiring staining procedures to bring out the characteristic features of the tissues under investigation, RS is a label-free approach, i. e. applicable directly to the tissue with no preliminary treatments.
Despite the aforementioned strengths, RS presents two main limitations for its application in cancer diagnosis: first of all, the low acquisition speed could represent a relevant obstacle if diagnostic times of fractions of seconds are needed, e.g., in intraoperative cancer detection. In addition, the presence of a large amount of information characterizing a single Raman spectrum dramatically increases the difficulties in the visual interpretation of Raman spectra. This last issue assumes particular significance in the study of biological tissues, often characterized by complex chemical composition. This class of samples is characterized by frequent cases of subtle molecular differences between tissues corresponding to different diseases affecting the same type of organ, often associated with partially overlapped Raman bands.
In this sense, the employment of Machine Learning (ML) algorithms to interpret Raman-derived experimental data could represent a powerful solution to retrieve the information of interest in times compatible with the final use requirements [11,12,13]. In particular, Several works [14,15,16,17] showed how RS in combination with ML allows to detect malignant tissues in timescales of minutes or even seconds, being a potential help in the intraoperative estimation of the tumor margins.
Analogously, recently, RS has been applied to chondrogenic tumor classification with excellent classification performances, by employing either classical ML or algorithms belonging to the sub-field of ML called Deep Learning (DL) [6,18,19]. Such investigations demonstrated the effectiveness of such algorithms in systematically interpreting Raman-derived experimental data for the diagnosis of bone tumors. This finding represents an advantage over the analysis of stained tissue sections, requiring expert pathologists to express an ultimate diagnosis. In addition, the high level of detail of such an approach could potentially detect sub-types or sub-stages of a disease, intermediate to the conventionally accepted ones, e.g., the three different grades of CS. This outcome could represent a breakthrough toward an accurate oncological diagnosis and, therefore, the planning of personalized therapies.
In this paper, we explored the ability of ML and DL models to perform an accurate diagnosis of CS and EC from Raman-based data, collected from ex-vivo tissues. Our analysis was focused either on the problem of distinguishing CS from EC or on assigning a correct grade to the CS cases. The results demonstrated the effectiveness of ML and Deep Learning (DL) models in identifying the aforementioned CS tumor, with classification accuracy reaching 99.7%. This analysis of the Permutation Feature Importance (PFI) allowed to identify Raman spectral components, relevant for the classification process. In particular, the analysis of PFI potentially represents an important tool in the attempt to restrict the spectral range, to reduce the acquisition time and the computational cost of the classification phase.

2. Materials and Methods

2.1. Samples

The study involved ten patients, treated in 2018 in the Azienda Ospedaliero Universitaria Pisana, Pisa, Italy. Among the examined patients, three of which corresponded to the diagnosis of EC, three to CS of grade 1 (G1), two to CS of grade 2 (G2) and two to CS of grade 3 (G3).
Further details about the patients’ cohort are available in reference [6]. The resulting bone-excised tissues were subjected to formalin-fixing and paraffin-embedding, without decalcification. Two tissue sections of thickness 5- μ m were obtained from the resulting excised masses for each patient. After being deposited on a glass slide, commonly employed in microscopy, the paraffin was removed through immersion in two baths of xylene for 10 min. Then, the residuals of formalin were removed by rinsing in Polybutylene succinate (PBS). One of the aforementioned two sections was stained with Hematoxylin and Eosin (H&E) for the following histopathological examination. This procedure allowed to assign a label to the resulting Raman spectra and therefore to employ ML in a supervised fashion. The other tissue section was not subjected to staining and it was employed for the acquisition of Raman spectra. The employment of not stained tissues for the acquisition of Raman spectra allowed to minimize the contribution to the resulting signal attributable to the sample fluorescence.

2.2. Raman Apparatus and Data Pre-Processing

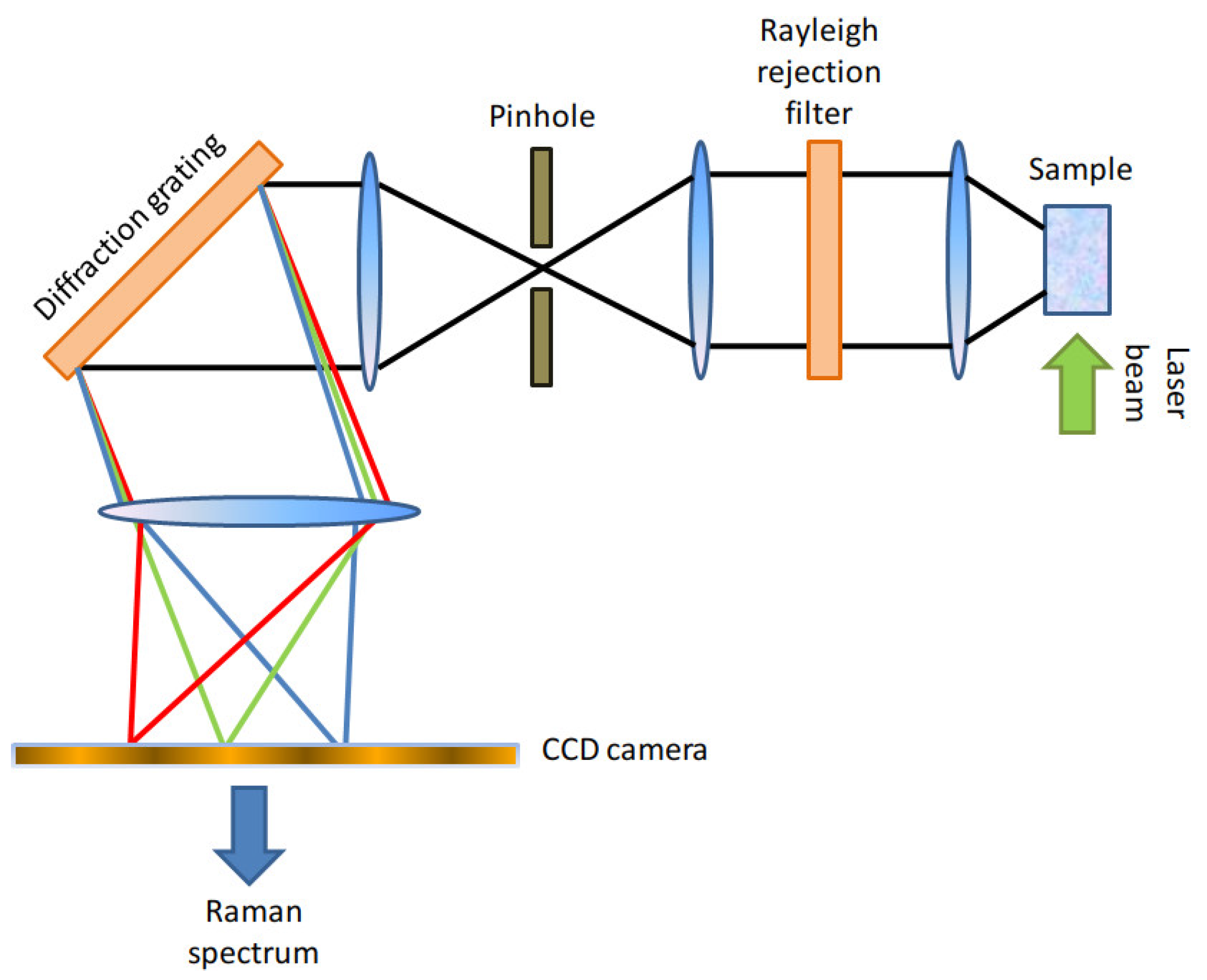
Here, we will provide only a brief description of the Raman apparatus employed in this paper and of the pre-processing operations carried out on the resulting spectra. Further details are available in [6]. The Raman setup employed in this work was a Thermo Fisher Scientific DXR2xi [20] Confocal Raman Microscope, whose setup is schematically represented in Figure 1. The Raman setup was equipped with a 532 nm laser, whose power was set within the range between 5-10 mW, representing a right compromise between the need to avoid tissue damage and to achieve an adequate signal-to-noise ratio.
The back-scattered photons were collected with a 100 × objective and the out-of-focus components of the detected light were suppressed through an aperture (pinhole) of diameter 25 μ m . A 1200 gr/mm diffraction grating allowed to separate the spectral components from the detected light. We reported a schematic representation of the Raman setup in Figure 1. Each spectrum was collected with 10 accumulations and an acquisition time of 0.2 s for each accumulation. The resulting Raman spectra had a spectral resolution of ∼ 2 cm − 1 and they were defined within the spectral interval between 400 and 1800 cm − 1 . 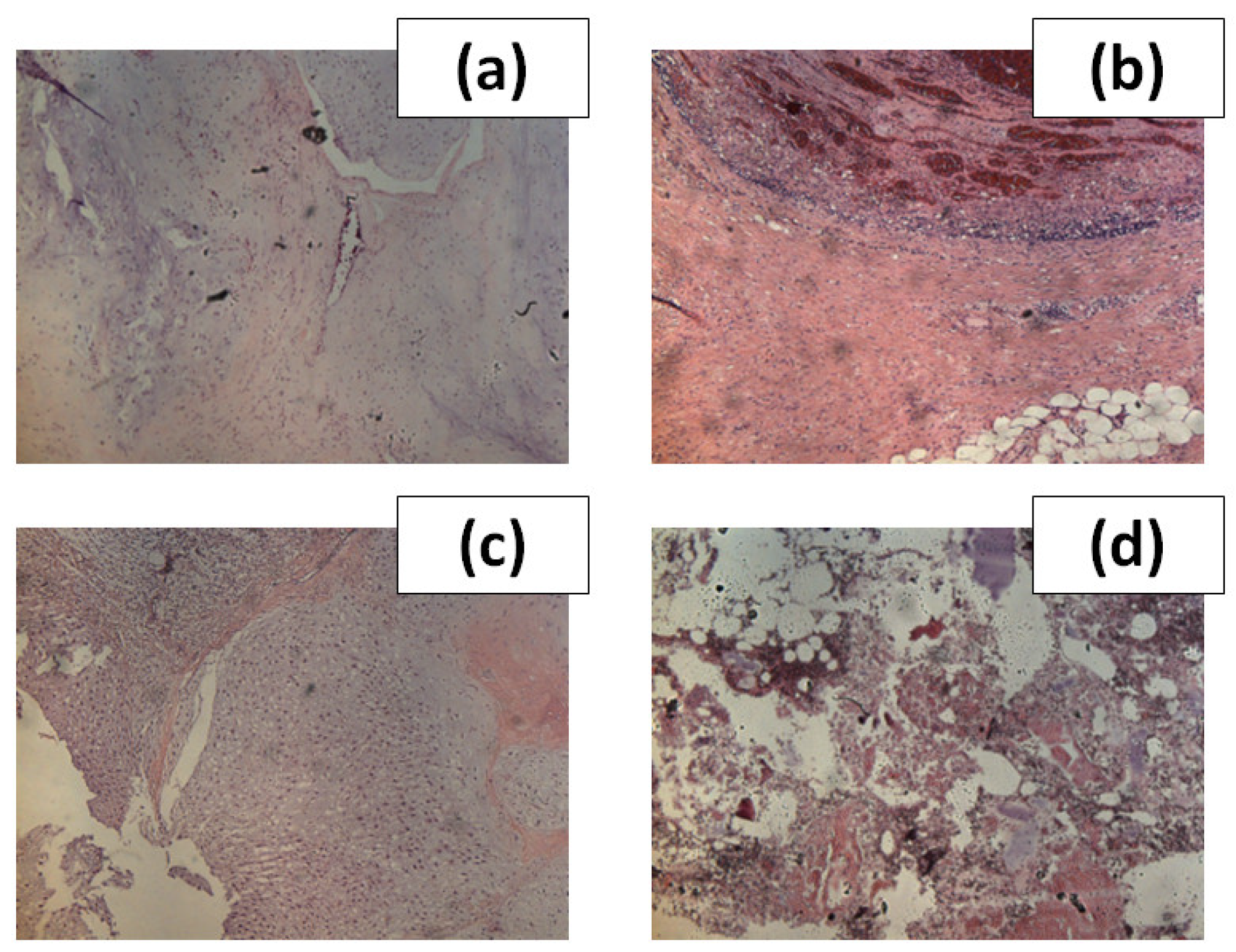In Figure 2, we showed images of H&E stained sections associated to the four types of tissue examined in this work.
The spectra were collected in grids of pixel resolution 4 μ m × 4 μ m , within the portions of unstained samples. The final dataset included N s = 400 spectra, 80 spectra for EC, 80 for G1, 84 for G2 and 93 for G3. We applied a baseline subtraction algorithm to the raw Raman spectra through the tool Omnicxi, integrated into the application controlling the CRM. We carried out this operation by subtracting a 5th-order polynomial. Then, we referred the spectra to the minimum signal. We didn’t normalize the spectra, to exploit the additional information of the absolute signal intensity for the following ML and DL classification routines.

2.3. Data Analysis

In the following, we will represent the Raman data as couples { ( x i , y i ) } , i = 1 , . . . , N s , where x i ∈ R N p is a vector storing the Raman intensities within a single spectrum, while y i represents the value of the label associated to the i-th spectrum. The spectrum x i can be also viewed as the i-th row of a matrix X of size N s × N p .
As stated in the Introduction section, the main objective of this work was to employ RS in combination with ML to classify bone tissue. In particular, we focused our attention on three distinct classification problems:
  • The problem of distinguishing EC and CS (EC-CS);
  • The problem of distinguishing G1, G2 and G3 (G1-G2-G3);
  • The problem of distinguishing EC, G1, G2 and G3 (EC-G1-G2-G3).
To this aim, we employed three ML protocols:
  • Random Forest Classifier (RFC): this non-linear ML algorithm is based on building decision trees by training them on datasets obtained by bootstrap-sampling spectra from the initial dataset. The result of this procedure is a “forest”, whose prediction is based on the majority of the responses of the trees belonging to it. In our analysis, we adopted a forest of 4000 trees, to minimize the so-called out-of-bag error [21];
  • Multi-Layer Perceptron (MLPC): in this investigation, this simple DL algorithm consisted of a single hidden layer with 900 neurons. We introduce non-linearity through a ReLU activation function. We carried out the training either with the ADAM [22] or with the L-BFGS-B [23] solvers, with an upper limit of 600 iterations. In the following, we will refer to the aforementioned DL models as MLPC(ADAM) and MLPC(L-BFGS-B), respectively;
  • Support Vector Machine (SVM): this ML algorithm is aimed at determining the so-called maximum-margin hyperplane, separating the vectors { x i } corresponding to different values of the label [24]. The general equation of a hyperplane can be written as
    w T x − b = 0 ,
    where w is a vector normal to the hyperplane and b is a real constant. According to the linear version of SVM, the classification is performed by solving the following minimum problem:
    min w , b w T w
    with the constraint y i ( w T x i + b ) ≥ 1 ∀ i = 1 , … , N s . Despite the introduction of non-linear and more advanced versions of this algorithm, we adopted the original linear version as representative of a linear ML model, intending to compare the resulting performances with the aforementioned non-linear ML routines;
We assessed the performances of the ML models mentioned before through a 5-fold Cross Validation, in terms of Sensitivity (S), Specificity ( S P ) and Accuracy (A), widely employed in medicine.
One of the purposes of this work was the search for the Raman bands associated with biomolecules (collagen components, DNA, lipids, hydroxyapatite, etc.). These findings could allow to understand the biochemical processes behind the occurrence of such diseases and, on the other hand, to reduce the amplitude of the spectral region employed for the acquisition. In the framework of ML and DL, this problem is referred to as the assessment of the Feature Importance (FI). In turn, we adopted the so-called Permutation Feature Importance (PFI) [25,26,27]. Consider an ML or DL model M, previously trained on the dataset represented by the matrix X. Let s be a generic score, assessing the performance of M on a test dataset X ′ . Suppose to calculate the parameter s j , representing the aforementioned score, on the dataset X ′ after a permutation of the elements of the j-th column. The basic idea behind the definition of PFI is that, if s j ∼ s , the spectral component corresponding to the j-th column of X ′ can be considered irrelevant for the classification. The PFI associated to the j-th spectral component is defined as
P F I j = s − 1 K ∑ l K s l , j .
in this definition, X ′ is subjected to K permutations of the j-th column, and s l , j represents the score obtained at the l-th permutation. By definition, the larger P F I j , the larger the importance of the j-th spectral component. Despite RFC provides an intrinsic definition of FI, based on the ability of a single feature to increase the “purity” of the classification domains [28], the use of PFI allowed to compare the FI of different ML models and to reinforce our considerations about the relevant chemical compounds in the biochemical processes at the origin of the diseases under interest. Hence, we calculated the PFI associated with the prediction accuracy ( s ≡ A ), on a X ′ dataset obtained by randomly selecting spectra from X, with a proportion of 20% with respect to the total number of spectra. We chose this proportion in line with the 5-fold cross-validation adopted. In addition, we chose K = 5 .
All the calculations were carried out through a hybrid script, obtained by customizing an Orange Data Mining script with Python codes [26].

3. Results and Discussion

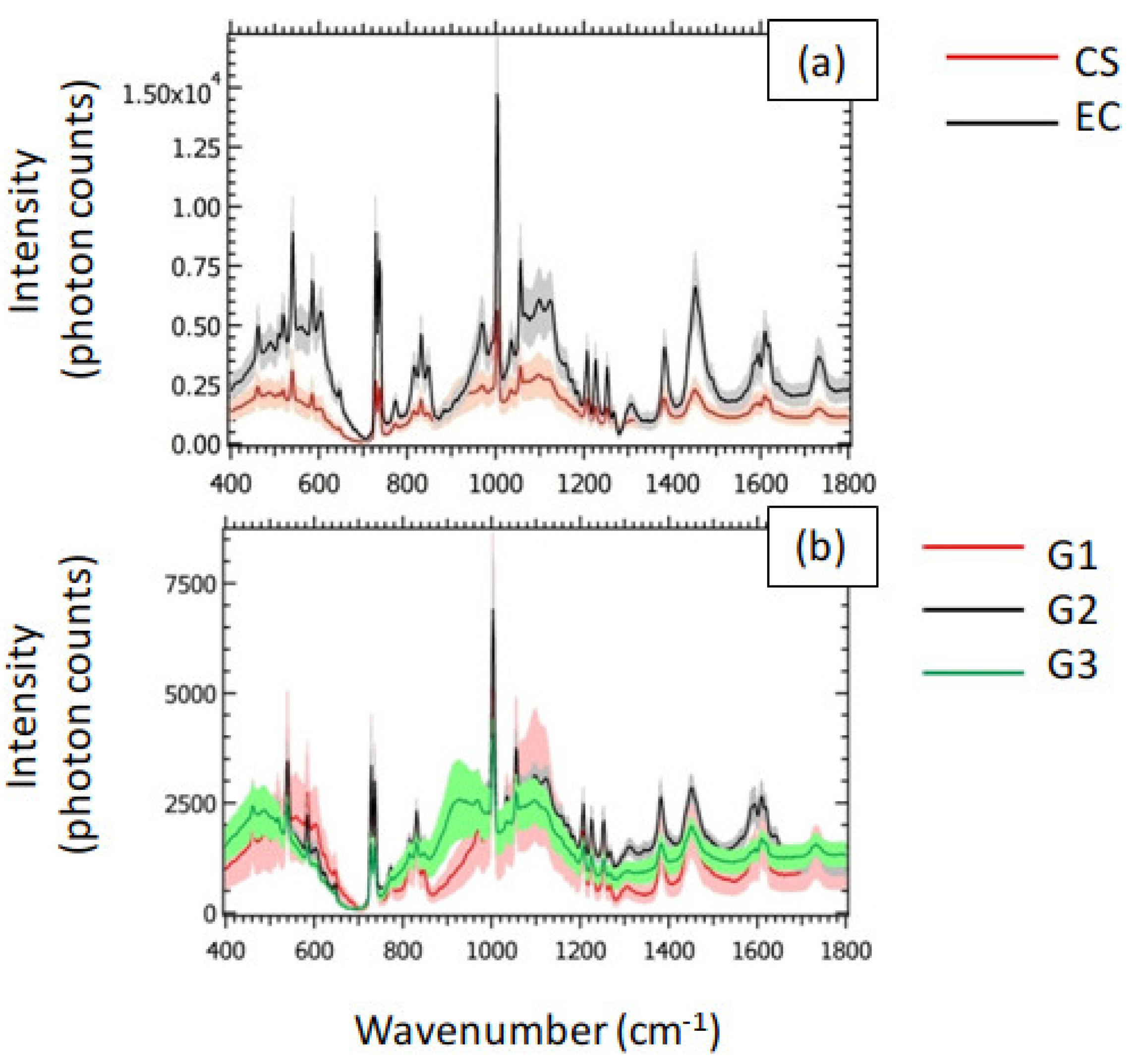
In Figure 3 (a), we showed the averaged spectra associated with CS and EC. The shaded areas represent the related standard deviation. The corresponding peak assignments are reported in Table 1. The general behavior of the averaged spectra highlighted a decrease in the Raman signal of CS with respect to EC. In particular, we qualitatively observed the largest differences between CS and EC in the Raman intensities in the following spectral bands: the most intense peak ( ∼ 1003 cm − 1 ) is attributed to Phenylalanine (Phe), recognized as a strongly Raman-active molecule [29]. Phe is a precursor of several amino acids, such as Tyrosine, represented by the peaks at 815, 1172 and 1207 cm − 1 . Tyrosine was previously recognized as an amino acid regulating the production and activity of osteoclasts [30] The presence of Phe is testified also by the peak at 1609 cm − 1 . We attributed the two narrow peaks at ∼ 729 cm − 1 to carbonates that, alongside bioapatites (604, 849, 1035, 1057 and 1098 cm − 1 ), represent one of the most abundant inorganic components of the bone tissue. Other relevant spectral components can be found in the peaks at 830 and 1453 cm − 1 , assigned to proline (collagen) and CH 2 wagging, respectively.
The small standard deviation in comparison to the average Raman spectra observed for the CS class in Figure 3 (a) resulted in small differences between the averaged Raman spectra of G1, G2 and G3, as shown in Figure 3 (b). However, the peak of Phe qualitatively highlighted the largest differences between the three grades of CS. This last feature makes the peak of Phe a promising candidate for the grading of CS.
In view of the employment of the collected Raman spectra to classify the analyzed tissues, we emphasize that the apparent macroscopic difference in the signal intensity of CS and EC observed in Figure 3 (a) is not necessarily sufficient to perform an accurate classification based on the sole visual interpretation of the Raman spectra. We stress that the shaded areas associated with the mean spectra represent the standard deviation. For this reason, CS and EC could have a superposition region in the intensity domain, due to Raman spectra corresponding to the tails of the related intensity distributions, possible source of misclassification problems. In this case, the employment of ML algorithms allowed to rely on additional information, provided by the spectral components, in a systematic and efficient fashion.
In Table 2, we resumed the performances of the ML and DL models for the examined classification problems. In particular, we averaged the Accuracy A, the Sensitivity S and the Specificity S P over the 5 folds and over the values of the label. The most evident result highlighted is the substantial difference between the performances of the linear SVM with respect to the other models, for all the classification problems considered. This feature revealed how non-linearities in the definition of the models resulted in enhanced classification performances, with relative uncertainties of ∼ 10 − 3 % , indicating a negligible overfitting. As expected, the simplest binary classification problem EC-CS led to the maximum performances, i. e. A = ( 99.7 ± 0.1 ) % , S = ( 99.7 ± 0.1 ) % and S P = ( 99.0 ± 0.1 ) % , reached with MLPC(ADAM). This result is in line with previous works about the Raman-based detection of CS and EC [6,18,19]. On the other hand, the classification problem EC-G1-G2-G3 resulted in the minimum classification accuracy, with the maximum value of A = ( 97.6 ± 0.1 ) % obtained with MLPC(ADAM). In conclusion, the tested routines showed excellent classification performances, making the technique a promising candidate for future applications in the diagnosis and grading of CS.
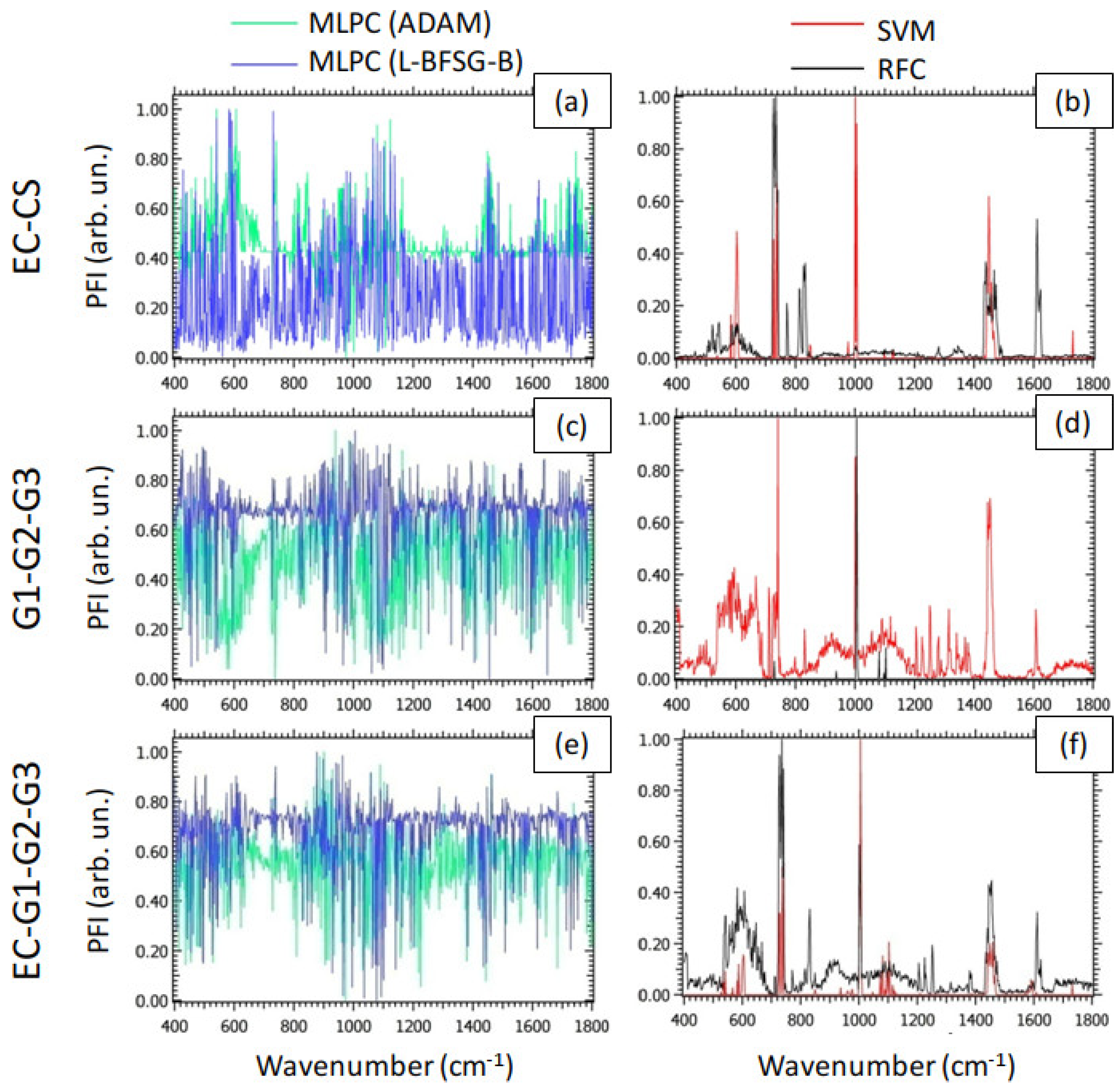
Figure 4 reports the PFI associated with the prediction accuracy for the models examined as a function of wavenumber, for all the classification problems of interest. In particular, we normalized PFI through the MinMax rule [59], to highlight the spectral components corresponding to the maximum PFI. We emphasize that the PFI provides a measure of the relevance of a spectral component in detecting the values of the label. In this sense, the behavior of PFI for MLPC (Figure 4 (a), (c) and (e)), characterized by the presence of a large number of peaks of similar intensities, indicated that the DL models studied rely on a large number of spectral components to reach the aforementioned classification performances. This trend is probably the result of the strongly non-linear nature of MLPC. On the other hand, the PFI of SVM and RFC, represented in Figure 4 (b), (d) and (f), showed a small number of well-definite peaks in comparison to MLPC. Therefore, despite SVM and RFC showed worse classification performances than the DL models, they are potentially capable of providing more information about the biochemical mechanisms on the basis of the malignant degree under interest. In particular, by observing the Figure 4 (b), we detected a peak of PFI at ∼ 602 cm − 1 , exhibiting large feature importance either for SVM or for RFC. As shown in Table 1, this peak is attributable to phosphate groups (P-O bending) associated with hydroxyapatite. This result is in line with previous investigations, attributing the growing presence of bioapatites to the production of calcifications [60]. To conclude the analysis of PFI for the G1-G2-G3 classification problem, we mention also the peaks related to SVM and located at ∼ 730 and ∼ 1449 cm − 1 . These spectral components can be attributed to DNA and CH 2 bending, respectively. These findings suggested differences in EC and CS attributable to cell proliferation. Analogously, the peak of Phe ( ∼ 1003 cm − 1 ) observed either for SVM or for RFC in Figure 4 (d) suggested relevant differences between different grades of CS in the content of this molecule. Finally, as expected, in the classification problem EC-G1-G2-G3, the behavior of the PFI (Figure 4 (f)) appeared to be intermediate between the PFI in the EC-CS and the G1-G2-G3 classification problems.

4. Conclusions and Future Perspectives

Chondrosarcoma and the classification of its various degrees of malignancy has recently become a case study for the application of Raman spectroscopy in oncology. In this investigation, we tested the ability of different ML and DL routines to accurately discriminate between CS and EC from a Raman-based experimental dataset, on which several multivariate statistical approaches have already achieved good classification performances [6], or DL algorithms based on wavelet transform [18], as well as topology machine learning [19].
The classifiers used in this paper allowed to achieve two main objectives. First of all, we observed how the MLPC(ADAM) classifier was able to distinguish CS and EC with an accuracy reaching 99.7% and to distinguish the specific grades of CS with an accuracy reaching 99.2%. In addition, the aforementioned DL algorithm was able to distinguish the three grades of CS and EC within a single-stage process, with an accuracy reaching 97.6%. This outcome highlighted the technique as a promising route for future applications in the intra-operative diagnosis of bone cancer, to correctly estimate the tumor margins. Furthermore, the analysis of PFI highlighted that, despite the worse classification performances of RFC and SVM in comparison to MLPC, they offer the capability to detect characteristic tissue components (proline, DNA, bioapatites), particularly relevant for the grading. In particular, according to this analysis, Raman bands associated with bioapatites turned out to be the most relevant in the distinction between CS and EC. On the other hand, Phenylalanine (Phe) turned out to be the most relevant amino acid in grading CS.
The main limitation associated with our analysis is represented by the employment of a relatively small statistical sample, either in terms of the number of patients or the number of collected Raman spectra. Therefore, the results generated by our analysis have to be considered an exploratory investigation, representing the basis for further analysis relying on more statistically significant and larger RS-based datasets. Furthermore, as already described in the Introduction section, the richness of information within a single Raman spectrum complicates the data interpretation, requiring the employment of ML or DL to retrieve the information of interest. This operation often requires high computational cost and/or long computational times. This issue may represent a problem, especially for the implementation of such technology on engineered probes for real-time intra-operative diagnosis, where diagnostic times of seconds or fractions of seconds are strongly required.
To achieve such challenging objectives, further efforts have to be devoted, distributed on multiple routes: first of all, to test ML or DL routines on specific Raman bands, such as the Raman bands corresponding to the peaks of PFI, to assess the ratio between the computational time needed to obtain the response and the classification performances; in turn, to realize cost-effective and powerful hardware, able to speed up the calculation; to operate on the software, by implementing the classification routines in high-performance computing codes.

List of symbols and abbreviations

Abbreviation/Symbol Definition
CS Chondrosarcoma
EC Enchondroma
MRI Magnetic Resonance Imaging
CT Computed Tomography
US Ultrasonography
PET Positron Emission Tomography
RS Raman Spectroscopy
ML Machine Learning
CRM Confocal Raman Microscopy
DL Deep Learning
ECM ExtraCellular Matrix
G1 Chondrosarcoma (grade 1)
G2 Chondrosarcoma (grade 2)
G3 Chondrosarcoma (grade 3)
PBS Polybutylene succinate
H&E Hematoxylin & Eosin
x i i-th Raman spectrum
y i Value of the label y for the i-th Raman spectrum
X Training dataset matrix
X ′ Test dataset matrix
N s Number of Raman spectra
N p Number of points of a single Raman spectrum
EC-CS Classification problem (values of the label: EC and CS)
G1-G2-G3 Classification problem (values of the label: G1, G2 and G3)
EC-G1-G2-G3 Classification problem (values of the label: EC, G1, G2 and G3)
SVM Linear Support Vector Machine
RFC Random Forest Classifier
MLPC(ADAM) Multi-Layer Perceptron (ADAM solver)
MLPC(L-BFSG-B) Multi-Layer Perceptron (L-BFSG-B solver)
FI Feature Importance
PFI Permutation Feature Importance
Phe Phenylalanine

Author Contributions

Conceptualization, G.L. and M.D.; methodology, G.L.; software, G.L.; validation, G.L. and M.D.; experimental investigation, M.D.; resources, M.D.; data curation, M.D.; original draft preparation, G.L.; review and editing, G.L.; supervision, M.D.; project administration, M.D.; funding acquisition, M.D. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Regione Toscana through the TELEMO Project under 146 Grant Ricerca Salute 2018.

Institutional Review Board Statement

The study was approved by the local Ethical Committee Comitato Etico Regionale per la Sperimentazione Clinica della Regione Toscana, Sezione AREA VASTA NORD OVEST (protocol number 14249). An informed consent was collected from all patients. For study participation of patients under the age of 18 years, a specific informed consent from a parent has been acquired (mod. C2; protocol number 14249). All the experiments were carried out in accordance with Good Clinical Practice (GCP) and with the ethical principles of the Declaration of Helsinki.

Informed Consent Statement

Ten patients affected by primary chondrogenic tumors of the skeleton were enrolled in this study. All patients were diagnosed and treated at our Institution, Azienda Ospedaliera Universitaria Pisana, Pisa, in 2018.

Data Availability Statement

The request for data sets, both raw and processed data, generated during the present study can be agreed and made directly to the corresponding author.

Acknowledgments

The authors wish to thank Dr. R. Gaeta and Prof. A. Franchi, from Azienda Ospedaliera Universitaria Pisana, for useful support. The NanoBioTLab CNR-IBF is warmly acknowledged.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Weinschenk, R.C.; Wang, W.L.; Lewis, V.O. Chondrosarcoma. JAAOS-Journal of the American Academy of Orthopaedic Surgeons 2021, 29, 553–562. [Google Scholar] [CrossRef]
  2. Stevenson, J.D.; Laitinen, M.K.; Parry, M.C.; Sumathi, V.; Grimer, R.J.; Jeys, L.M. The role of surgical margins in chondrosarcoma. European Journal of Surgical Oncology 2018, 44, 1412–1418. [Google Scholar] [CrossRef] [PubMed]
  3. Bäuerle, T.; Komljenovic, D.; Berger, M.R.; Semmler, W. Multi-modal imaging of angiogenesis in a nude rat model of breast cancer bone metastasis using magnetic resonance imaging, volumetric computed tomography and ultrasound. JoVE (Journal of Visualized Experiments) 2012, e4178. [Google Scholar]
  4. Fernandes, R.S.; dos Santos Ferreira, D.; de Aguiar Ferreira, C.; Giammarile, F.; Rubello, D.; de Barros, A.L.B. Development of imaging probes for bone cancer in animal models. A systematic review. Biomedicine & Pharmacotherapy 2016, 83, 1253–1264. [Google Scholar]
  5. Lieppo, L.; Toyras, J.; Saarakkala, S. Vibrational spectroscopy of articular cartilage. Applied Spectroscopy Reviews 2017, 52, 249–266. [Google Scholar]
  6. D’Acunto, M.; Gaeta, R.; Capanna, R.; Franchi, A. Contribution of Raman spectroscopy to diagnosis and grading of chondrogenic tumors. Scientific Reports 2020, 10. [Google Scholar] [CrossRef] [PubMed]
  7. Shi, L.; Fung, A.A.; Zhou, A. Advances in stimulated Raman scattering imaging for tissues and animals. Quantitative Imaging in Medicine and Surgery 2021, 11, 1078–11101. [Google Scholar] [CrossRef] [PubMed]
  8. Raman, C.V.; Krishnan, K.S. A new type of secondary radiation. Nature 1928, 121, 501–502. [Google Scholar] [CrossRef]
  9. Cialla-May, D.; Schmitt, M.; Popp, J. Theoretical principles of Raman spectroscopy. Physical Sciences Reviews 2019, 4, 20170040. [Google Scholar] [CrossRef]
  10. Jones, R.R.; Hooper, D.C.; Zhang, L.; Wolverson, D.; Valev, V.K. Raman techniques: fundamentals and frontiers. Nanoscale research letters 2019, 14, 1–34. [Google Scholar] [CrossRef]
  11. Blake, N.; Gaifulina, R.; Griffin, L.D.; Bell, I.M.; Thomas, G.T. Machine Learning of Raman Spectroscopy Data for Classifying Cancers: A Review of the Recent Literature. Diagnostics 2022, 12. [Google Scholar] [CrossRef]
  12. Lazzini, G.; D’Acunto, M. Grading of Melanoma Tissues by Raman MicroSpectroscopy. Engineering Proceedings 2023, 51, 10. [Google Scholar]
  13. Manganelli Conforti, P.; Lazzini, G.; Russo, P.; D’Acunto, M. Raman Spectroscopy and AI Applications in Cancer Grading: An Overview. IEEE Access 2024, 12, 54816–54852. [Google Scholar] [CrossRef]
  14. Jabarkheel, R.; Ho, C.S.; Rodrigues, A.J.; Jin, M.C.; Parker, J.J.; Mensah-Brown, K.; Yecies, D.; Grant, G.A. Rapid intraoperative diagnosis of pediatric brain tumors using Raman spectroscopy: A machine learning approach. Neuro-Oncology Advances 2022, 4, vdac118. [Google Scholar] [CrossRef]
  15. Jelke, F.; Mirizzi, G.; Borgmann, F.K.; Husch, A.; Slimani, R.; Klamminger, G.G.; Klein, K.; Mombaerts, L.; Gérardy, J.J.; Mittelbronn, M.; et al. Intraoperative discrimination of native meningioma and dura mater by Raman spectroscopy. Scientific Reports 2021, 11, 23583. [Google Scholar] [CrossRef]
  16. Riva, M.; Sciortino, T.; Secoli, R.; D’Amico, E.; Moccia, S.; Fernandes, B.; Conti Nibali, M.; Gay, L.; Rossi, M.; De Momi, E.; et al. Glioma biopsies classification using Raman spectroscopy and machine learning models on fresh tissue samples. Cancers 2021, 13, 1073. [Google Scholar] [CrossRef] [PubMed]
  17. Li, Z.; Li, Z.; Chen, Q.; Zhang, J.; Dunham, M.E.; McWhorter, A.J.; Feng, J.M.; Li, Y.; Yao, S.; Xu, J. Machine-learning-assisted spontaneous Raman spectroscopy classification and feature extraction for the diagnosis of human laryngeal cancer. Computers in biology and medicine 2022, 146, 105617. [Google Scholar] [CrossRef] [PubMed]
  18. Manganelli Conforti, P.; D’Acunto, M.; Russo, P. Deep Learning for Chondrogenic Tumor Classification through Wavelet Transform of Raman Spectra. Sensors 2022, 22. [Google Scholar] [CrossRef]
  19. Conti, F.; D’Acunto, M.; Caudai, C.; Colantonio, S.; Gaeta, R.; Moroni, D.; Pascali, M.A. Raman spectroscopy and topological machine learning for cancer grading. Scientific Reports 2023, 13. [Google Scholar] [CrossRef]
  20. Rzhevskii, A. The recent advances in Raman microscopy and imaging techniques for biosensors. Biosensors 2019, 9, 25. [Google Scholar] [CrossRef]
  21. Fawagreh, K.; Gaber, M.M.; Elyan, E. Random forests: from early developments to recent advancements. Systems Science & Control Engineering: An Open Access Journal 2014, 2, 602–609. [Google Scholar]
  22. Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980 2014.
  23. Zhu, C.; Byrd, R.H.; Lu, P.; Nocedal, J. Algorithm 778: L-BFGS-B: Fortran subroutines for large-scale bound-constrained optimization. ACM Transactions on mathematical software (TOMS) 1997, 23, 550–560. [Google Scholar] [CrossRef]
  24. Kecman, V. Support vector machines–an introduction. In Support vector machines: theory and applications; Springer, 2005; pp. 1–47.
  25. Altmann, A.; Toloşi, L.; Sander, O.; Lengauer, T. Permutation importance: a corrected feature importance measure. Bioinformatics 2010, 26, 1340–1347. [Google Scholar] [CrossRef]
  26. Demšar, J.; Curk, T.; Erjavec, A.; Gorup, Č.; Hočevar, T.; Milutinovič, M.; Možina, M.; Polajnar, M.; Toplak, M.; Starič, A.; et al. Orange: data mining toolbox in Python. the Journal of machine Learning research 2013, 14, 2349–2353. [Google Scholar]
  27. Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. the Journal of machine Learning research 2011, 12, 2825–2830. [Google Scholar]
  28. James, G.; Witten, D.; Hastie, T.; Tibshirani, R.; et al. An introduction to statistical learning; Vol. 112, Springer, 2013.
  29. Hernández, B.; Pflüger, F.; Kruglik, S.G.; Ghomi, M. Characteristic Raman lines of phenylalanine analyzed by a multiconformational approach. Journal of Raman Spectroscopy 2013, 44, 827–833. [Google Scholar] [CrossRef]
  30. Shalev, M.; Elson, A. The roles of protein tyrosine phosphatases in bone-resorbing osteoclasts. Biochimica Et Biophysica Acta (BBA)-Molecular Cell Research 2019, 1866, 114–123. [Google Scholar] [CrossRef] [PubMed]
  31. Pathmanapan, S.; Poon, R.; De Renshaw, T.B.; Nadesan, P.; Nakagawa, M.; Seesankar, G.A.; Loe, A.K.H.; Zhang, H.H.; Guinovart, J.J.; Duran, J.; et al. Mutant IDH regulates glycogen metabolism from early cartilage development to malignant chondrosarcoma formation. Cell Reports 2023, 42. [Google Scholar] [CrossRef] [PubMed]
  32. Movasaghi, Z.; Rehman, S.; Rehman, I.U. Raman spectroscopy of biological tissues. Applied Spectroscopy Reviews 2007, 42, 493–541. [Google Scholar] [CrossRef]
  33. Rehman, I.; Smith, R.; Hench, L.; Bonfield, W. FT-Raman spectroscopic analysis of natural bones and their comparison with bioactive glasses and hydroxyapatite. In Bioceramics; Elsevier, 1994; pp. 79–84.
  34. Buchwald, T.; Niciejewski, K.; Kozielski, M.; Szybowicz, M.; Siatkowski, M.; Krauss, H. Identifying compositional and structural changes in spongy and subchondral bone from the hip joints of patients with osteoarthritis using Raman spectroscopy. Journal of biomedical optics 2012, 17, 017007–017007. [Google Scholar] [CrossRef]
  35. Errassifi, F.; Sarda, S.; Barroug, A.; Legrouri, A.; Sfihi, H.; Rey, C. Infrared, Raman and NMR investigations of risedronate adsorption on nanocrystalline apatites. Journal of colloid and interface science 2014, 420, 101–111. [Google Scholar] [CrossRef] [PubMed]
  36. Gunasekaran, S.; Anbalagan, G.; Pandi, S. Raman and infrared spectra of carbonates of calcite structure. Journal of Raman Spectroscopy: An International Journal for Original Work in all Aspects of Raman Spectroscopy, Including Higher Order Processes, and also Brillouin and Rayleigh Scattering 2006, 37, 892–899. [Google Scholar] [CrossRef]
  37. Dippel, B.; Mueller, R.T.; Pingsmann, A.; Schrader, B. Composition, constitution, and interaction of bone with hydroxyapatite coatings determined by FT Raman microscopy. Biospectroscopy 1998, 4, 403–412. [Google Scholar] [CrossRef]
  38. Gaifulina, R.; Nunn, A.D.; Draper, E.R.; Strachan, R.K.; Blake, N.; Firth, S.; Thomas, G.M.; McMillan, P.F.; Dudhia, J. Intra-operative Raman spectroscopy and ex vivo Raman mapping for assessment of cartilage degradation. Clinical Spectroscopy 2021, 3, 100012. [Google Scholar] [CrossRef]
  39. Freeman, J.; Wopenka, B.; Silva, M.; Pasteris, J. Raman spectroscopic detection of changes in bioapatite in mouse femora as a function of age and in vitro fluoride treatment. Calcified tissue international 2001, 68. [Google Scholar] [CrossRef] [PubMed]
  40. Khan, A.F.; Awais, M.; Khan, A.S.; Tabassum, S.; Chaudhry, A.A.; Rehman, I.U. Raman spectroscopy of natural bone and synthetic apatites. Applied spectroscopy reviews 2013, 48, 329–355. [Google Scholar] [CrossRef]
  41. Mandair, G.S.; Morris, M.D. Contributions of Raman spectroscopy to the understanding of bone strength. BoneKEy reports 2015, 4. [Google Scholar] [CrossRef] [PubMed]
  42. Kozielski, M.; Buchwald, T.; Szybowicz, M.; Błaszczak, Z.; Piotrowski, A.; Ciesielczyk, B. Determination of composition and structure of spongy bone tissue in human head of femur by Raman spectral mapping. Journal of Materials Science: Materials in Medicine 2011, 22, 1653–1661. [Google Scholar] [CrossRef]
  43. Mangialardo, S.; Cottignoli, V.; Cavarretta, E.; Salvador, L.; Postorino, P.; Maras, A. Pathological biominerals: Raman and infrared studies of bioapatite deposits in human heart valves. Applied Spectroscopy 2012, 66, 1121–1127. [Google Scholar] [CrossRef]
  44. Timchenko, E.; Zherdeva, L.; Timchenko, P.; Volova, L.; Ponomareva, U. Detailed analysis of the structural changes of bone matrix during the demineralization process using Raman spectroscopy. Physics Procedia 2015, 73, 221–227. [Google Scholar] [CrossRef]
  45. Li, J.; Li, J.; Wang, H.; Chen, Y.; Qin, J.; Zeng, H.; Wang, K.; Wang, S. Microscopic Raman illustrating antitumor enhancement effects by the combination drugs of γ-secretase inhibitor and cisplatin on osteosarcoma cells. Journal of Biophotonics 2022, 15, e202200189. [Google Scholar] [CrossRef]
  46. Woess, C.; Unterberger, S.H.; Roider, C.; Ritsch-Marte, M.; Pemberger, N.; Cemper-Kiesslich, J.; Hatzer-Grubwieser, P.; Parson, W.; Pallua, J.D. Assessing various Infrared (IR) microscopic imaging techniques for post-mortem interval evaluation of human skeletal remains. PLoS One 2017, 12, e0174552. [Google Scholar] [CrossRef]
  47. Lau, C.P.; Ma, W.; Law, K.Y.; Lacambra, M.D.; Wong, K.C.; Lee, C.W.; Lee, O.K.; Dou, Q.; Kumta, S.M. Development of deep learning algorithms to discriminate giant cell tumors of bone from adjacent normal tissues by confocal Raman spectroscopy. Analyst 2022, 147, 1425–1439. [Google Scholar] [CrossRef]
  48. Bautista-González, S.; González, N.J.C.; Campos-Ordoñez, T.; Elías, M.A.A.; Pedroza-Montero, M.R.; Beas-Zárate, C.; Gudiño-Cabrera, G. Raman spectroscopy to assess the differentiation of bone marrow mesenchymal stem cells into a glial phenotype. Regenerative Therapy 2023, 24, 528–535. [Google Scholar] [CrossRef]
  49. Wang, S.; Liang, Z.; Gong, Y.; Yin, Y.; Wang, K.; He, Q.; Wang, Z.; Bai, J. Confocal raman microspectral imaging of ex vivo human spinal cord tissue. Journal of Photochemistry and Photobiology B: Biology 2016, 163, 177–184. [Google Scholar] [CrossRef]
  50. Pavlou, E.; Zhang, X.; Wang, J.; Kourkoumelis, N. Raman spectroscopy for the assessment of osteoarthritis. Annals of Joint 2018, 3. [Google Scholar] [CrossRef]
  51. Gamsjaeger, S.; Klaushofer, K.; Paschalis, E.P. Raman analysis of proteoglycans simultaneously in bone and cartilage. Journal of Raman Spectroscopy 2014, 45, 794–800. [Google Scholar] [CrossRef]
  52. Souza, R.A.d.; Jerônimo, D.P.; Gouvêa, H.A.; Xavier, M.; Souza, M.T.d.; Miranda, H.; Tosato, M.G.; Martin, A.A.; Ribeiro, W. Fourier-transform Raman spectroscopy study of the ovariectomized rat model of osteoporosis. The Open Bone Journal 2010, 2. [Google Scholar] [CrossRef]
  53. Olsztynska-Janus, S.; Gasior-Glogowska, M.; Szymborska-Malek, K.; Komorowska, M.; Witkiewicz, W.; Pezowicz, C.; Szotek, S.; Kobielarz, M. Spectroscopic techniques in the study of human tissues and their components. Part II: Raman spectroscopy. Acta Bioeng. Biomech 2012, 14, 121–133. [Google Scholar]
  54. Gautam, R.; Ahmed, R.; Haugen, E.; Unal, M.; Fitzgerald, S.; Uppuganti, S.; Mahadevan-Jansen, A.; Nyman, J.S. Assessment of spatially offset Raman spectroscopy to detect differences in bone matrix quality. Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy 2023, 303, 123240. [Google Scholar] [CrossRef]
  55. Ciubuc, J.D.; Manciu, M.; Maran, A.; Yaszemski, M.J.; Sundin, E.M.; Bennet, K.E.; Manciu, F.S. Raman spectroscopic and microscopic analysis for monitoring renal osteodystrophy signatures. Biosensors 2018, 8, 38. [Google Scholar] [CrossRef] [PubMed]
  56. Cavalu, S.; Pînzaru, S.C.; Peica, N.; Damian, G.; Kiefer, W. Adsorption behavior of hyaluronidase onto silver nanoparticles and PMMA bone substitute. Journal Of Optoelectronics And Advanced Materials 2007, 9, 686. [Google Scholar]
  57. Castorina, F.; Masi, U.; Giorgini, E.; Mori, L.; Tafuri, M.A.; Notarstefano, V. Evidence for Mild Diagenesis in Archaeological Human Bones from the Fewet Necropolis (SW Libya): New Insights and Implications from ATR–FTIR Spectroscopy. Applied Sciences 2023, 13, 687. [Google Scholar] [CrossRef]
  58. Hędzelek, W.; Marcinkowska, A.; Domka, L.; Wachowiak, R. Infrared spectroscopic identification of chosen dental materials and natural teeth. Acta Physica Polonica A 2008, 114, 471–484. [Google Scholar] [CrossRef]
  59. Gautam, R.; Vanga, S.; Ariese, F.; Umapathy, S. Review of multidimensional data processing approaches for Raman and infrared spectroscopy. EPJ Techniques and Instrumentation 2015, 2, 1–38. [Google Scholar] [CrossRef]
  60. Campanacci, D.A.; Scoccianti, g.; Franchi, A.; Roselli, G.; Beltrami, G.; Ippolito, M.; Caff, G.; Frenos, F.; Capanna, R. Surgical treatment of central grade I chondrosarcoma of the appendicular skeleton. J. Orthop. Traumatol. 2013, 14, 101–107. [Google Scholar] [CrossRef]
Preprints 106395 g001
Figure 1. Schematic representation of a Confocal Raman Microscope, equipped with a Rayleigh rejection filter, a pinhole, a high-resolution diffraction grating and an electron multiplied CDD camera as a detector.
Figure 1. Schematic representation of a Confocal Raman Microscope, equipped with a Rayleigh rejection filter, a pinhole, a high-resolution diffraction grating and an electron multiplied CDD camera as a detector.
Preprints 106395 g001
Preprints 106395 g002
Figure 2. (a) image of a stained histological section of tissue corresponding to G1; (b) image of a stained histological section of tissue corresponding to G2; (c) image of a stained histological section of tissue corresponding to G3; (d) image of a stained histological section of a tissue corresponding to EC. The images of the histological sections were obtained with a magnification of 20 × .
Figure 2. (a) image of a stained histological section of tissue corresponding to G1; (b) image of a stained histological section of tissue corresponding to G2; (c) image of a stained histological section of tissue corresponding to G3; (d) image of a stained histological section of a tissue corresponding to EC. The images of the histological sections were obtained with a magnification of 20 × .
Preprints 106395 g002
Preprints 106395 g003
Figure 3. (a) Averaged Raman spectra of CS and EC; (b) averaged spectra of G1, G2 and G3. The shaded areas represent the standard deviation.
Figure 3. (a) Averaged Raman spectra of CS and EC; (b) averaged spectra of G1, G2 and G3. The shaded areas represent the standard deviation.
Preprints 106395 g003
Preprints 106395 g004
Figure 4. (a) PFI for MLPC(ADAM) and MLPC(L-BFSG-B) in the classification problem EC-CS; (b) PFI for SVM and RFC in the classification problem EC-CS; (c) PFI for MLPC(ADAM) and MLPC(L-BFSG-B) in the classification problem G1-G2-G3; (d) PFI for SVM and RFC in the classification problem G1-G2-G3; (e) PFI for MLPC(ADAM) and MLPC(L-BFSG-B) in the classification problem EC-G1-G2-G3; (f) PFI for SVM and RFC in the classification problem EC-G1-G2-G3. The PFI signals were normalized with the MinMax rule.
Figure 4. (a) PFI for MLPC(ADAM) and MLPC(L-BFSG-B) in the classification problem EC-CS; (b) PFI for SVM and RFC in the classification problem EC-CS; (c) PFI for MLPC(ADAM) and MLPC(L-BFSG-B) in the classification problem G1-G2-G3; (d) PFI for SVM and RFC in the classification problem G1-G2-G3; (e) PFI for MLPC(ADAM) and MLPC(L-BFSG-B) in the classification problem EC-G1-G2-G3; (f) PFI for SVM and RFC in the classification problem EC-G1-G2-G3. The PFI signals were normalized with the MinMax rule.
Preprints 106395 g004
Table 1. Raman peaks of the analyzed samples within the range between 400 and 1800 cm − 1 and corresponding peak interpretation. [6].
Table 1. Raman peaks of the analyzed samples within the range between 400 and 1800 cm − 1 and corresponding peak interpretation. [6].
Wavenumber ( cm − 1 ) Interpretation Reference
490 Glycogen  [31]
519 Phosphatidylinositol  [32]
540 Amminoacid cysteine  [32]
584 Phosphate (bend) peak  [33]
604 Phosphate (minerals)  [34]
646 C-P vibrations  [35]
729 Carbonates  [36]
773 Hydroxyapatite  [37]
815 Proline, Hydroxyproline, Tyrosine, ν 2 PO 2 − stretching of nucleic acids  [32]
831 Collagen  [38]
849 Apatite  [39]
971 Tricalcium phosphate  [40]
1003 Phenylalanine  [41]
1035 Apatite  [42]
1057 ν 3 − PO 4 3 − (Apatite)  [43]
1098 ν 1 − CO 3 2 − (Hydroxyapatite)  [44]
1123 C-N (Proteins)  [32]
1159 C-C/C-N stretching (Proteins)  [32]
1172 Tyrosine  [45]
1185 Carbohydrates  [46]
1207 Hydroxyproline, tyrosine  [47]
1227 Nucleic acids  [48]
1253 Amide III  [49]
1267 Amide III, lipids  [32]
1307 Amide III, lipids  [50]
1383 N-acetyl-glucosamine  [51]
1453 CH 2 wagging  [52]
1489 Guanine  [53]
1595 Amide I  [54]
1609 Amide I, Phenylalanine  [55]
1619 Amide I (aggregates)  [56]
1639 Proteins, collagen  [57]
1731 Ester group  [58]
Table 2. Accuracy A, Sensitivity S and Specificity S P , averaged over the 5 folds and over the values of the label.
Table 2. Accuracy A, Sensitivity S and Specificity S P , averaged over the 5 folds and over the values of the label.
Classification problem Model A ( ± 0.1 % ) S ( ± 0.1 % ) S P ( ± 0.1 % )
EC-CS SVM 78.9 78.9 79.7
EC-CS RFC 98.5 98.5 97.0
EC-CS MLPC(ADAM) 99.7 99.7 99.0
EC-CS MLPC(L-BFSG-B) 99.1 99.1 97.1
G1-G2-G3 SVM 75.9 75.9 87.4
G1-G2-G3 RFC 99.2 99.2 99.6
G1-G2-G3 MLPC(ADAM) 99.2 99.2 96.6
G1-G2-G3 MLPC(L-BFSG-B) 99.2 99.2 99.6
EC-G1-G2-G3 SVM 76.6 76.6 92.4
EC-G1-G2-G3 RFC 97.3 97.3 99.1
EC-G1-G2-G3 MLPC(ADAM) 97.6 97.6 99.2
EC-G1-G2-G3 MLPC(L-BFSG-B) 97.3 97.3 99.1
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated