Preprint
Article
Chondrogenic Cancer Grading by combining Machine and Deep Learning with Raman Spectra of Histopathological Tissues
Altmetrics
Downloads
238
Views
90
Comments
0
This version is not peer-reviewed
Submitted:
09 August 2024
Posted:
09 August 2024
You are already at the latest version
Alerts
Abstract
The present paper explored the possibility of discriminating between different malignant degrees of Chondrosarcoma (CS), a diffused bone tumor, and Enchondroma (EC), its benign version, through an approach based on the coupling between Confocal Raman Microscopy (CRM) and Machine Learning (ML) techniques. Recently, Raman Spectroscopy has proven to be a powerful tool for a complete grading of CS by distinguishing between grade 1, 2 and 3, and to distinguish CS from EC. In this paper, we tested some models, belonging either to ML or to the sub-type called Deep Learning (DL), showing excellent classification performances, especially the DL algorithms, with classification accuracy approaching to 100%, making the models promising for future implementations of Raman spectroscopy when applied to oncology diagnosis. In turn, we highlighted how some proper ML models result in worse classification performances but better resolution of specific chemical target compounds, possible candidate to become malignant markers, with relevant implication for a correct diagnosis.
Keywords:
Subject: Physical Sciences - Biophysics
1. Introduction
Chondrosarcoma (CS) turns out to be the second most common form of primary bone tumor worldwide, with almost seven cases per million people registered every year [1]. In the continuous effort to introduce effective and minimally invasive therapies, the ability to grade CS and to distinguish this form of bone cancer from healthy tissues and/or benign tumors, such as Enchondroma (EC), represents a crucial factor. The common protocol for the diagnosis of CS is based on an initial examination of radiological and/or Magnetic Resonance (MRI) images, followed by the histopathological analysis of a tissue biopsy. One of the drawbacks of this procedure is represented by the frequent discrepancies between the response of pre- and post-surgical histopathological analysis, mainly due to the presence of tissue inhomogeneities within the same tumor mass. This last feature also determines the presence of not well-defined tumor margins, undoubtedly affecting the outcome of the surgical therapies. As previously demonstrated [2], the presence of not removed tumor margins represents a concrete risk factor, increasing the probability of recurrence and thus decreasing the 5-year survival rate. Setups for image-guided surgery, e.g. Computed Tomography (CT) and MRI were introduced to help the surgeon in maximizing the size of the excised tumor mass by preserving the surrounding healthy tissues. Despite the progress of these techniques, they still show weaknesses. In particular, CT is based on the use of ionizing radiation, with possible side effects for the patient and/or the operator. Furthermore, MRI employs intense magnetic fields, not suitable for patients with metallic devices implanted within the body. Among the imaging techniques, we also mention the Ultrasonographic (US) analysis. However, this technique is not yet considered a reliable solution, since it suffers from problems in the detection of soft tissues characterizing bone metastasis [3]. Finally, nuclear medicine, such as Positron Emission Tomography (PET), represents an interesting solution, since it potentially provides additional information about metabolism and drug activity. Despite the large values of sensitivity and specificity in detecting tumor masses, nuclear medicine is characterized by small spatial resolution. This feature pushed the researchers to couple such techniques to other approaches, such as MRI [4].
In the last two decades, RS demonstrated to be a promising, easy-to-use, and low-cost solution to respond to the aforementioned needs [5,6,7]. RS is based on the measurement of the so-called Raman effect [8], i.e. a light scattering phenomenon produced by the interaction between a beam of photons and virtual molecular energy levels [9]. The difference between the wavelengths of the scattered and the incident photons is strongly correlated to the chemical properties of the molecular target that determined the scattering. Therefore, by performing a spectral analysis of the radiation scattered by a sample of interest, it is possible to retrieve detailed information about the chemical composition of the target under investigation [10]. Since the Raman effect doesn’t involve the interaction between photons and well-defined electronic energy levels, the technique is intrinsically not subject to non-radiative relaxation phenomena, possible source of sample cooling and consequent degradation. This feature makes RS particularly suitable to in vivo applications, e.g. for intra-operative cancer detection, aimed at estimating the tumor margins. Unlike the conventional histopathological analysis, requiring staining procedures to bring out the characteristic features of the tissues under investigation, RS is a label-free approach, i.e. applicable directly to the tissue with no preliminary treatments.
Despite the aforementioned strengths, RS presents two main limitations for its application in cancer diagnosis: first of all, the low acquisition speed could represent a relevant obstacle if diagnostic times of fractions of seconds are needed, e.g. in intraoperative cancer detection. In addition, the presence of a large amount of information characterizing a single Raman spectrum dramatically increases the difficulties in the visual interpretation of Raman spectra. This last issue assumes particular significance in the study of biological tissues, often characterized by complex chemical composition. This class of samples is characterized by frequent cases of subtle molecular differences between tissues corresponding to different diseases affecting the same type of organ, often associated with partially overlapped Raman bands.
In this sense, the employment of ML algorithms to interpret Raman-derived experimental data could represent a powerful solution to retrieve the information of interest in times compatible with the final use requirements [11,12,13]. In particular, Several works [14,15,16,17] showed how RS in combination with ML allows to detect malignant tissues in timescales of minutes or even seconds, being a potential help in the intraoperative estimation of the tumor margins.
Analogously, recently, RS has been applied to chondrogenic tumor classification with excellent classification performances, by employing either classical ML or algorithms belonging to the sub-field of ML known as DL [6,18,19]. Such investigations demonstrated the effectiveness of such algorithms in systematically interpreting Raman-derived experimental data for the diagnosis of bone tumors. This finding represents an advantage over the analysis of stained tissue sections, requiring expert pathologists to express an ultimate diagnosis. In addition, the high level of detail of such an approach could potentially detect sub-types or sub-stages of a disease, intermediate to the conventionally accepted ones, e.g. the three different grades of CS. This outcome could represent a breakthrough toward an accurate oncological diagnosis and, therefore, the planning of personalized therapies.
In this paper, we improved the ability of ML and DL models to perform an accurate diagnosis of CS and EC from Raman-based data, collected from ex-vivo tissues, managing the dataset originally collected in [6]. Our analysis was focused either on the basic problem of distinguishing CS from EC (or on assigning a correct grade to the CS cases), either on the crucial question to identify the most relevant Raman bands of any malignat degree. About the first question, the results demonstrated the effectiveness of ML and DL models in identifying the aforementioned CS tumor, with classification accuracy reaching 99.7%. But much more relevant, the method for the identification of the RBI, i.e., the Raman bands evidencing the degree of malignancy of tissues under investigation, basically inspired by Permutation Feature Importance [20], allowed to identify Raman spectral components, more relevant to the classification process. Such results represent the most original contribution of our paper. This is because the analysis of RBI potentially represents an important tool in the attempt to restrict the spectral range, to reduce the acquisition time and the computational cost of the classification phase.
2. Materials and Methods
2.1. Samples
The study involved ten patients, treated in 2018 in the Azienda Ospedaliero Universitaria Pisana, Pisa, Italy. Among the examined patients, three of which corresponded to the diagnosis of EC, three to CS of grade 1 (G1), two to CS of grade 2 (G2), and two to CS of grade 3 (G3).
Further details about the patients’ cohort are available in reference [6]. The resulting bone-excised tissues were subjected to formalin-fixing and paraffin-embedding, without decalcification. Two tissue sections of thickness 5 μm were obtained from the resulting excised masses for each patient. After being deposited on a glass slide, commonly employed in microscopy, the paraffin was removed through immersion in two baths of xylene for 10 min. Then, the residuals of formalin were removed by rinsing in Polybutylene succinate (PBS). One of the aforementioned two sections was stained with Hematoxylin and Eosin (H&E) for the following histopathological examination. This procedure allowed to assign a label to the resulting Raman spectra and therefore to employ ML in a supervised fashion. The other tissue section was not subjected to staining and it was employed for the acquisition of Raman spectra. The employment of not stained tissues for the acquisition of Raman spectra allowed to minimize the contribution to the resulting signal attributable to the sample fluorescence.
2.2. Raman Apparatus and Data Pre-Processing
Here, we will provide only a brief description of the Raman apparatus employed in this paper and of the pre-processing operations carried out on the resulting spectra. Further details are available in [6]. The Raman setup employed in this work was a Thermo Fisher Scientific DXR2xi [21] Confocal Raman Microscope, whose setup is schematically represented in Figure 1. The Raman setup was equipped with a 532 nm laser, whose power was set within the range between 5-10 mW, representing a right compromise between the need to avoid tissue damage and to achieve an adequate signal-to-noise ratio.
The back-scattered photons were collected with a 100× objective and the out-of-focus components of the detected light were suppressed through an aperture (pinhole) of diameter 25 μm. A 1200 gr/mm diffraction grating allowed to separate the spectral components from the detected light. We reported a schematic representation of the Raman setup in Figure 1. Each spectrum was collected with 10 accumulations and an acquisition time of 0.2 s for each accumulation. The resulting Raman spectra had a spectral resolution of ~2 cm−1 and they were defined within the spectral interval between 400 and 1800 cm−1. In Figure 2, we showed images of H&E stained sections associated with the four types of tissue examined in this work.
Figure 1.
Schematic representation of a Confocal Raman Microscope, equipped with a Rayleigh rejection filter, a pinhole, a high-resolution diffraction grating, and an electron multiplied CDD camera as a detector.
Figure 1.
Schematic representation of a Confocal Raman Microscope, equipped with a Rayleigh rejection filter, a pinhole, a high-resolution diffraction grating, and an electron multiplied CDD camera as a detector.
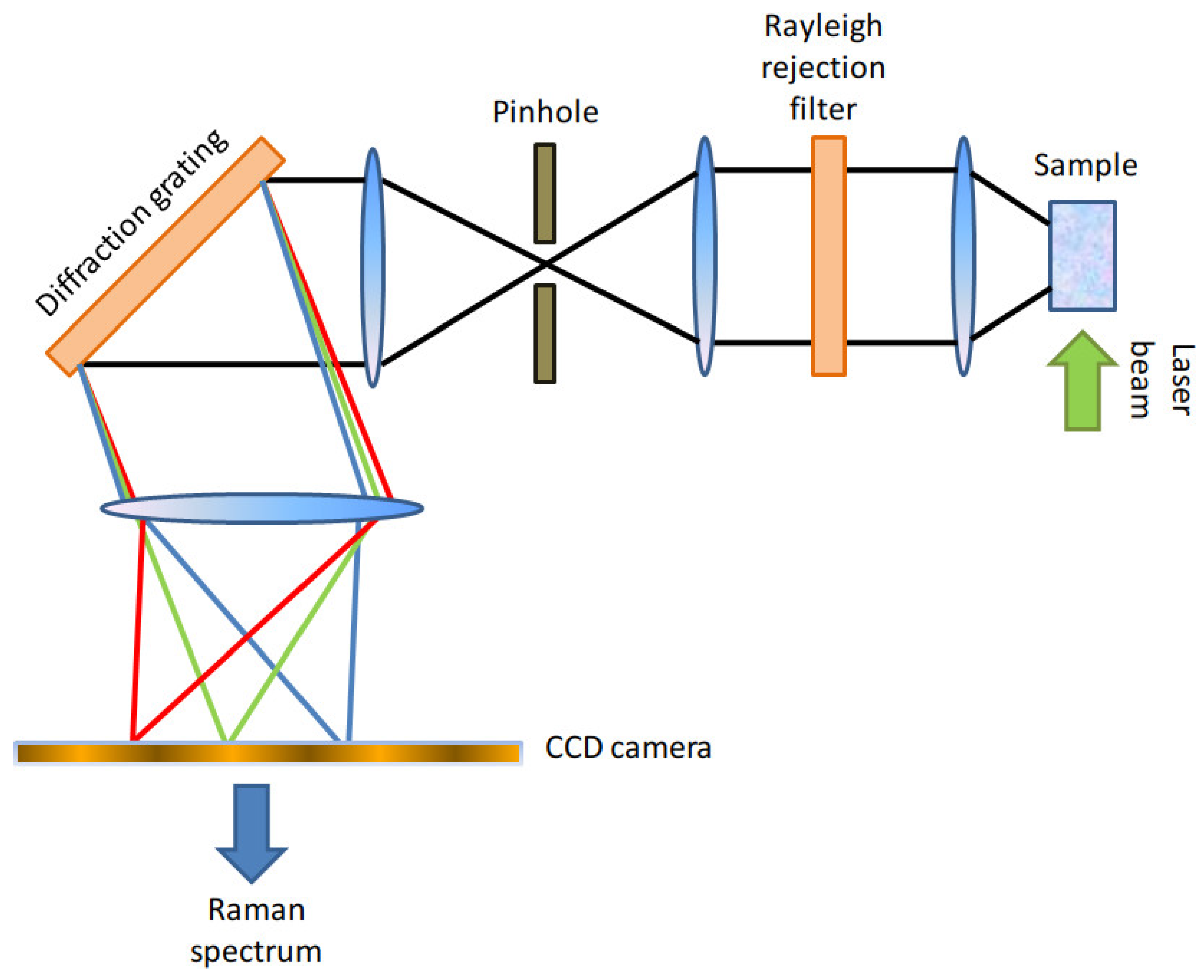
Figure 2.
(a) image of a stained histological section of tissue corresponding to G1; (b) image of a stained histological section of tissue corresponding to G2; (c) image of a stained histological section of tissue corresponding to G3; (d) image of a stained histological section of a tissue corresponding to EC. The images of the histological sections were obtained with a magnification of 20×.
Figure 2.
(a) image of a stained histological section of tissue corresponding to G1; (b) image of a stained histological section of tissue corresponding to G2; (c) image of a stained histological section of tissue corresponding to G3; (d) image of a stained histological section of a tissue corresponding to EC. The images of the histological sections were obtained with a magnification of 20×.

The spectra were collected in grids of pixel resolution 4 μm × 4 μm, within the portions of unstained samples. The final dataset included = 400 spectra, 80 spectra for EC, 80 for G1, 84 for G2, and 93 for G3. We applied a baseline subtraction algorithm to the raw Raman spectra through the tool Omnicxi, integrated into the application controlling the CRM. We carried out this operation by subtracting a 5th-order polynomial. Then, we referred the spectra to the minimum signal. We didn’t normalize the spectra, to exploit the additional information of the absolute signal intensity for the following ML and DL classification routines.
2.3. Data Analysis
In the following, we will represent a single Raman spectrum as a vector x of dimension . In the supervised learning framework, a discrete variable y, called label, assuming, is associated with x. As stated before, we will have a set , with , representing all the available instances. The instances can be conveniently conceived as the rows of a matrix X of size .
As stated in the Introduction section, the main objective of this work was to employ RS in combination with ML to classify bone tissue. In particular, we focused our attention on three distinct classification problems:
- The problem of distinguishing EC and CS (EC-CS). In this case, y can assume the values EC and CS;
- The problem of distinguishing G1, G2 and G3 (G1-G2-G3). In this case, y can assume the values G1, G2 and G3;
- The problem of distinguishing EC, G1, G2 and G3 (EC-G1-G2-G3). In this case, y can assume the values EC, G1, G2 and G3.
To this aim, we employed three ML protocols:
-
Support Vector Machine (SVM): this ML was originally conceived to find the hyperplane that correctly separates the clouds in the space of dimension corresponding to the different values of y. Let the equation of the hyperplane, where w is an -dimensional vector normal to the hyperplane, b a real number, and · denotes the scalar product. In the version of SVM implemented in this work, the parameters related to w and b were optimized by solving the following bound minimum problem:In this equation denotes the Euclidean norm of w. In addition, C, here fixed to 0.4, represents a regularization parameter accounting for the penalty related to the presence of outliers, i.e. instances. Finally, the parameters , here fixed to 0.8, are variables aimed at relaxing the constraints [22]. Despite more advanced versions of SVM, conceived to separate the classes of interest through hyper curves more complex than a hyperplane, we adopted the classical linear kernel as representative of a linear model and to compare it with more complex ML classifiers;
- Random Forest Classifier (RFC): RFC is a “bagging” ML routine, building the classifier as an ensemble, or forest, of decisional trees. A single tree is built from an ensemble of Raman spectra obtained through a procedure called bootstrap sampling. This selection procedure is aimed at selecting spectra, with the possibility of repeated spectra within the resulting dataset. Then, k spectral components, with are randomly selected to build each node of a single tree. Among the previously selected spectral components, the best one is selected according to its capability to discriminate the values of the label y. In this paper, we adopted Gini’s index as the parameter quantifying this ability. The growth of each tree was stopped when a perfect separation of the spectra belonging to the training dataset was obtained. The final RFC classifier contained 4000 trees, considered a good solution to obtain small levels of overfitting and small out-of-bag error [23]. The response of the entire classifier is thus given by the majority of the prediction of its trees.
- Multi-Layer Perceptron (MLPC): in this investigation, this simple DL algorithm consisted of a single hidden layer with 400 neurons and zero bias. The hidden layer is followed by an activation layer employing a ReLU activation function. We carried out the training either with the ADAM [24] or with the L-BFGS-B [25] solvers, with an upper limit of 600 iterations. In the following, we will refer to the aforementioned DL models as MLPC(ADAM) and MLPC(L-BFGS-B), respectively;
We assessed the performances of the ML models mentioned before through a 5-fold Cross Validation, in terms of Sensitivity (S), Specificity (), and Accuracy (A), widely employed in medicine. IN particular, in the following, we will refer to S, , and A as quantities averaged over the values of the label y and over the folds of the Cross-Validation.
One of the purposes of this work was the search for the Raman components associated with molecules relevant to the classification process. By definition, these molecules can be considered biomarkers of the diseases under investigation. In particular, the search of cancer biomarkers could provide interesting information about the biochemical processes behind the occurrence of such diseases. Furthermore, this analysis could help to reduce the amplitude of the spectral region needed to reach a reliable diagnosis. This perspective could have important consequences in terms of the future implementation of this technology in simple and low-cost engineered devices. To this aim, we adopted the so-called Raman Band Identification (RBI), inspired by the so-called Permutation Feature Importance (PFI) [20,26,27]. Consider an ML or DL model M, previously trained on the dataset represented by the matrix X. Let s be a generic score, assessing the performance of M on a test dataset . Suppose to calculate the parameter , representing the aforementioned score, on the dataset after a permutation of the elements of the j-th column. The basic idea behind the definition of RBI is that, if , the spectral component corresponding to the j-th column of can be considered irrelevant for the classification. The RBI associated to the j-th spectral component is defined as
in this definition, is subjected to K permutations of the j-th column, and represents the score obtained at the l-th permutation. By definition, the larger , the larger the importance of the j-th spectral component. Despite RFC providing an intrinsic definition of Feature Importance, based on the ability of a single feature to increase the “purity” of the classification domains [28], the use of RBI allowed to compare the results of different ML models directly and to reinforce our considerations about the relevant chemical compounds in the biochemical processes at the origin of the diseases under interest. Hence, we calculated the RBI associated with the prediction accuracy (), on a dataset obtained by randomly selecting spectra from X, with a proportion of 20% with respect to the total number of spectra. We chose this proportion in line with the 5-fold cross-validation adopted. In addition, we chose .
All the calculations were carried out through a hybrid script, obtained by customizing an Orange Data Mining script with Python codes [26].
3. Results and Discussion
In Figure 3a, we showed the averaged spectra associated with CS and EC. The shaded areas represent the related standard deviation. The corresponding peak assignments are reported in Table 1. The general behavior of the averaged spectra highlighted a decrease in the Raman signal of CS with respect to EC. In particular, we qualitatively observed the largest differences between CS and EC in the Raman intensities in the following spectral bands: the most intense peak (~1003 cm−1) is attributed to Phenylalanine (Phe), recognized as a strongly Raman-active molecule [29]. Phe is a precursor of several amino acids, such as Tyrosine, represented by the peaks at 815, 1172 and 1207 cm−1. Tyrosine was previously recognized as an amino acid regulating the production and activity of osteoclasts [30] The presence of Phe is testified also by the peak at 1609 cm−1. We attributed the two narrow peaks at ~729 cm−1 to carbonates that, alongside bioapatites (604, 849, 1035, 1057 and 1098 cm−1), represent one of the most abundant inorganic components of the bone tissue. Other relevant spectral components can be found in the peaks at 830 and 1453 cm−1, assigned to proline (collagen) and wagging, respectively.
The small standard deviation in comparison to the average Raman spectra observed for the CS class in Figure 3a resulted in small differences between the averaged Raman spectra of G1, G2 and G3, as shown in Figure 3b. However, the peak of Phe qualitatively highlighted the largest differences between the three grades of CS. This last feature makes the peak of Phe a promising candidate for the grading of CS.
In view of the employment of the collected Raman spectra to classify the analyzed tissues, we emphasize that the apparent macroscopic difference in the signal intensity of CS and EC observed in Figure 3a is not necessarily sufficient to perform an accurate classification based on the sole visual interpretation of the Raman spectra. We stress that the shaded areas associated with the mean spectra represent the standard deviation. For this reason, CS and EC could have a superposition region in the intensity domain, due to Raman spectra corresponding to the tails of the related intensity distributions, possible source of misclassification problems. In this case, the employment of ML algorithms allowed to rely on additional information, provided by the spectral components, in a systematic and efficient fashion.
In Table 2, we resumed the performances of the ML and DL models for the examined classification problems. In particular, we averaged the Accuracy A, the Sensitivity S and the Specificity over the 5 folds and over the values of the label. The most evident result highlighted is the substantial difference between the performances of the linear SVM with respect to the other models, for all the classification problems considered. This feature revealed how non-linearities in the definition of the models resulted in enhanced classification performances, with relative uncertainties of , indicating a negligible overfitting. As expected, the simplest binary classification problem EC-CS led to the maximum performances, i.e. , and , reached with MLPC(ADAM). This result is in line with previous works about the Raman-based detection of CS and EC [6,18,19]. On the other hand, the classification problem EC-G1-G2-G3 resulted in the minimum classification accuracy, with the maximum value of obtained with MLPC(ADAM). In conclusion, the tested routines showed excellent classification performances, making the technique a promising candidate for future applications in the diagnosis and grading of CS.
Figure 4 reports the RBI associated with the prediction accuracy for the models examined as a function of wavenumber, for all the classification problems of interest. In particular, we normalized RBI through the MinMax rule [59], to highlight the spectral components corresponding to the maximum RBI. We emphasize that the RBI provides a measure of the relevance of a spectral component in detecting the values of the label. In this sense, the behavior of RBI for MLPC (Figure 4a,c,e), characterized by the presence of a large number of peaks of similar intensities, indicated that the DL models studied rely on a large number of spectral components to reach the aforementioned classification performances. This trend is probably the result of the strongly non-linear nature of MLPC. On the other hand, the RBI of SVM and RFC, represented in Figure 4b,d,f, showed a small number of well-definite peaks in comparison to MLPC. Therefore, despite SVM and RFC showing worse classification performances than the DL models, they are potentially capable of providing more information about the biochemical mechanisms on the basis of the malignant degree under interest. In particular, by observing the Figure 4b, we detected a peak of RBI at ~602 cm−1, exhibiting large feature importance either for SVM or for RFC. As shown in Table 1, this peak is attributable to phosphate groups (P-O bending) associated with hydroxyapatite. This result is in line with previous investigations, attributing the growing presence of bioapatites to the production of calcifications [60]. To conclude the analysis of RBI for the G1-G2-G3 classification problem, we mention also the peaks related to SVM and located at ~ 730 and ~1449 cm−1. These spectral components can be attributed to DNA and bending, respectively. These findings suggested differences in EC and CS attributable to cell proliferation. Analogously, the peak of Phe (~1003 cm−1) observed either for SVM or for RFC in Figure 4d suggested relevant differences between different grades of CS in the content of this molecule. Finally, as expected, in the classification problem EC-G1-G2-G3, the behavior of the PFI (Figure 4f) appeared to be intermediate between the PFI in the EC-CS and the G1-G2-G3 classification problems.
4. Conclusions and Future Perspectives
Chondrosarcoma and the classification of its various degrees of malignancy has recently become a case study for the application of Raman spectroscopy in oncology. In this investigation, we tested the ability of different ML and DL routines to accurately discriminate between CS and EC, as well as the identification of the most relevant Raman bands associated to any specific malignat degree.
The classifiers used in this paper allowed to achieve two main objectives. First of all, we observed how the MLPC(ADAM) classifier was able to distinguish CS and EC with an accuracy reaching 99.7% and to distinguish the specific grades of CS with an accuracy reaching 99.2%. Hence, the aforementioned DL algorithm was able to distinguish the three grades of CS and EC within a single-stage process, with an accuracy reaching 97.6%. This outcome highlighted the technique as a promising route for future applications in the intra-operative diagnosis of bone cancer, to correctly estimate the tumor margins. Furthermore, in comparison to MLPC, SVM and RFC achieved worse classification performances. However, the analysis of RBI revealed that SVM and RFC rely on a smaller number of spectral components in comparison to MLPC to reach the aforementioned classification performances. This feature results in two important consequences: first of all, the spectral components maximizing the RBI of SVM and RFC potentially indicated the presence of biomarkers (proline, DNA, bioapatites) for the diseases under investigation. In particular, according to this analysis, Raman bands associated with bioapatites turned out to be the most relevant in the distinction between CS and EC. On the other hand, Phenylalanine (Phe) turned out to be the most relevant amino acid in grading CS. Secondly, these findings suggest the possibility to restrict the spectral interval on the bands maximizing RBI, with negligible loss of the classification performances. In view of future implementations of this technology in engineered devices, the perspective of restricting the spectral interval needed for accurate and robust diagnosis undoubtedly represents an advantage, either in terms of acquisition speed or of cost of the hardware.
The main limitation associated with our analysis is represented by the employment of a relatively small statistical sample, either in terms of the number of patients or the number of collected Raman spectra. In general, the employment of datasets where the number of features of each instance is similar or larger than the number of instances available is traditionally associated with the occurrence of overfitting. Despite in this work we observed a negligible level of overfitting, further investigations have to be carried out in order to further monitor the robustness of the models. For this reason, the results generated by our analysis have to be considered an exploratory investigation, representing the basis for further studies relying on more statistically significant and larger RS-based datasets.
In general, further efforts have to be devoted, distributed on multiple routes: primarily, to test ML or DL routines on specific Raman bands, such as the Raman bands corresponding to the peaks of RBI, to assess the ratio between the computational time needed to obtain the response and the classification performances; therefore, to realize cost-effective and powerful hardware, able to speed up the calculation; to operate on the software, by implementing the classification routines in high-performance computing codes.
Author Contributions
Conceptualization, G.L. and M.D.; methodology, G.L.; software, G.L.; validation, G.L. and M.D.; experimental investigation, M.D.; resources, M.D.; data curation, M.D.; writing—original draft preparation, G.L.; writing—review and editing, G.L.; supervision, M.D.; project administration, M.D.; funding acquisition, M.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Regione Toscana through the TELEMO Project under 146 Grant Ricerca Salute 2018.
Institutional Review Board Statement
The study was approved by the local Ethical Committee Comitato Etico Regionale per la Sperimentazione Clinica della Regione Toscana, Sezione AREA VASTA NORD OVEST (protocol number 14249). An informed consent was collected from all patients. For study participation of patients under the age of 18 years, a specific informed consent from a parent has been acquired (mod. C2; protocol number 14249). All the experiments were carried out in accordance with Good Clinical Practice (GCP) and with the ethical principles of the Declaration of Helsinki.
Informed Consent Statement
Ten patients affected by primary chondrogenic tumors of the skeleton were enrolled in this study. All patients were diagnosed and treated at our Institution, Azienda Ospedaliera Universitaria Pisana, Pisa, in 2018.
Data Availability Statement
The request for data sets, both raw and processed data, generated during the present study can be agreed and made directly to the corresponding author.
Acknowledgments
The authors wish to thank Dr. R. Gaeta and Prof. A. Franchi, from Azienda Ospedaliera Universitaria Pisana, for useful support. The NanoBioTLab CNR-IBF is warmly acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations and Symbols
The following abbreviations are used in this manuscript:
| Abbreviation/Symbol | Definition |
| CS | Chondrosarcoma |
| EC | Enchondroma |
| MRI | Magnetic Resonance Imaging |
| CT | Computed Tomography |
| US | Ultrasonography |
| PET | Positron Emission Tomography |
| RS | Raman Spectroscopy |
| ML | Machine Learning |
| CRM | Confocal Raman Microscopy |
| DL | Deep Learning |
| ECM | ExtraCellular Matrix |
| G1 | Chondrosarcoma (grade 1) |
| G2 | Chondrosarcoma (grade 2) |
| G3 | Chondrosarcoma (grade 3) |
| PBS | Polybutylene succinate |
| H&E | Hematoxylin & Eosin |
| i-th Raman spectrum | |
| Value of the label y for the i-th Raman spectrum | |
| X | Training dataset matrix |
| Test dataset matrix | |
| Number of Raman spectra | |
| Number of points of a single Raman spectrum | |
| EC-CS | Classification problem (values of the label: EC and CS) |
| G1-G2-G3 | Classification problem (values of the label: G1, G2 and G3) |
| EC-G1-G2-G3 | Classification problem (values of the label: EC, G1, G2 and G3) |
| SVM | Linear Support Vector Machine |
| RFC | Random Forest Classifier |
| MLPC(ADAM) | Multi-Layer Perceptron (ADAM solver) |
| MLPC(L-BFSG-B) | Multi-Layer Perceptron (L-BFSG-B solver) |
| FI | Feature Importance |
| PFI | Permutation Feature Importance |
| RBI | Raman Band Identification |
| Phe | Phenylalanine |
References
- Weinschenk, R.C.; Wang, W.L.; Lewis, V.O. Chondrosarcoma. JAAOS-Journal of the American Academy of Orthopaedic Surgeons 2021, 29, 553–562. [Google Scholar] [CrossRef] [PubMed]
- Stevenson, J.D.; Laitinen, M.K.; Parry, M.C.; Sumathi, V.; Grimer, R.J.; Jeys, L.M. The role of surgical margins in chondrosarcoma. European Journal of Surgical Oncology 2018, 44, 1412–1418. [Google Scholar] [CrossRef] [PubMed]
- Bäuerle, T.; Komljenovic, D.; Berger, M.R.; Semmler, W. Multi-modal imaging of angiogenesis in a nude rat model of breast cancer bone metastasis using magnetic resonance imaging, volumetric computed tomography and ultrasound. JoVE (Journal of Visualized Experiments) 2012, e4178. [Google Scholar] [CrossRef]
- Fernandes, R.S.; dos Santos Ferreira, D.; de Aguiar Ferreira, C.; Giammarile, F.; Rubello, D.; de Barros, A.L.B. Development of imaging probes for bone cancer in animal models. A systematic review. Biomedicine & Pharmacotherapy 2016, 83, 1253–1264. [Google Scholar] [CrossRef]
- Lieppo, L.; Toyras, J.; Saarakkala, S. Vibrational spectroscopy of articular cartilage. Applied Spectroscopy Reviews 2017, 52, 249–266. [Google Scholar] [CrossRef]
- D’Acunto, M.; Gaeta, R.; Capanna, R.; Franchi, A. Contribution of Raman spectroscopy to diagnosis and grading of chondrogenic tumors. Scientific Reports 2020, 10. [Google Scholar] [CrossRef] [PubMed]
- Shi, L.; Fung, A.A.; Zhou, A. Advances in stimulated Raman scattering imaging for tissues and animals. Quantitative Imaging in Medicine and Surgery 2021, 11, 1078–11101. [Google Scholar] [CrossRef]
- Raman, C.V.; Krishnan, K.S. A new type of secondary radiation. Nature 1928, 121, 501–502. [Google Scholar] [CrossRef]
- Cialla-May, D.; Schmitt, M.; Popp, J. Theoretical principles of Raman spectroscopy. Physical Sciences Reviews 2019, 4, 20170040. [Google Scholar] [CrossRef]
- Jones, R.R.; Hooper, D.C.; Zhang, L.; Wolverson, D.; Valev, V.K. Raman techniques: fundamentals and frontiers. Nanoscale research letters 2019, 14, 1–34. [Google Scholar] [CrossRef]
- Blake, N.; Gaifulina, R.; Griffin, L.D.; Bell, I.M.; Thomas, G.T. Machine Learning of Raman Spectroscopy Data for Classifying Cancers: A Review of the Recent Literature. Diagnostics 2022, 12, 1491. [Google Scholar] [CrossRef] [PubMed]
- Lazzini, G.; D’Acunto, M. Grading of Melanoma Tissues by Raman MicroSpectroscopy. Engineering Proceedings 2023, 51, 10. [Google Scholar] [CrossRef]
- Manganelli Conforti, P.; Lazzini, G.; Russo, P.; D’Acunto, M. Raman Spectroscopy and AI Applications in Cancer Grading: An Overview. IEEE Access 2024, 12, 54816–54852. [Google Scholar] [CrossRef]
- Jabarkheel, R.; Ho, C.S.; Rodrigues, A.J.; Jin, M.C.; Parker, J.J.; Mensah-Brown, K.; Yecies, D.; Grant, G.A. Rapid intraoperative diagnosis of pediatric brain tumors using Raman spectroscopy: A machine learning approach. Neuro-Oncology Advances 2022, 4, vdac118. [Google Scholar] [CrossRef]
- Jelke, F.; Mirizzi, G.; Borgmann, F.K.; Husch, A.; Slimani, R.; Klamminger, G.G.; Klein, K.; Mombaerts, L.; Gérardy, J.J.; Mittelbronn, M.; et al. Intraoperative discrimination of native meningioma and dura mater by Raman spectroscopy. Scientific Reports 2021, 11, 23583. [Google Scholar] [CrossRef] [PubMed]
- Riva, M.; Sciortino, T.; Secoli, R.; D’Amico, E.; Moccia, S.; Fernandes, B.; Conti Nibali, M.; Gay, L.; Rossi, M.; De Momi, E.; et al. Glioma biopsies classification using Raman spectroscopy and machine learning models on fresh tissue samples. Cancers 2021, 13, 1073. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Li, Z.; Chen, Q.; Zhang, J.; Dunham, M.E.; McWhorter, A.J.; Feng, J.M.; Li, Y.; Yao, S.; Xu, J. Machine-learning-assisted spontaneous Raman spectroscopy classification and feature extraction for the diagnosis of human laryngeal cancer. Computers in biology and medicine 2022, 146, 105617. [Google Scholar] [CrossRef] [PubMed]
- Manganelli Conforti, P.; D’Acunto, M.; Russo, P. Deep Learning for Chondrogenic Tumor Classification through Wavelet Transform of Raman Spectra. Sensors 2022, 22, 7492. [Google Scholar] [CrossRef]
- Conti, F.; D’Acunto, M.; Caudai, C.; Colantonio, S.; Gaeta, R.; Moroni, D.; Pascali, M.A. Raman spectroscopy and topological machine learning for cancer grading. Scientific Reports 2023, 13. [Google Scholar] [CrossRef]
- Altmann, A.; Toloşi, L.; Sander, O.; Lengauer, T. Permutation importance: a corrected feature importance measure. Bioinformatics 2010, 26, 1340–1347. [Google Scholar] [CrossRef]
- Rzhevskii, A. The recent advances in Raman microscopy and imaging techniques for biosensors. Biosensors 2019, 9, 25. [Google Scholar] [CrossRef]
- Kecman, V. Support vector machines–an introduction. In Support vector machines: theory and applications; Springer, 2005; pp. 1–47. [Google Scholar] [CrossRef]
- Shahhosseini, M.; Hu, G. Improved weighted random forest for classification problems. Progress in Intelligent Decision Science: Proceeding of IDS 2020. Springer, 2021; pp. 42–56. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar] [CrossRef]
- Zhu, C.; Byrd, R.H.; Lu, P.; Nocedal, J. Algorithm 778: L-BFGS-B: Fortran subroutines for large-scale bound-constrained optimization. ACM Transactions on mathematical software (TOMS) 1997, 23, 550–560. [Google Scholar] [CrossRef]
- Demšar, J.; Curk, T.; Erjavec, A.; Gorup, Č.; Hočevar, T.; Milutinovič, M.; Možina, M.; Polajnar, M.; Toplak, M.; Starič, A.; et al. Orange: data mining toolbox in Python. the Journal of machine Learning research 2013, 14, 2349–2353. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. the Journal of machine Learning research 2011, 12, 2825–2830. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R.; et al. An introduction to statistical learning; Springer, 2013; Volume 112. [Google Scholar]
- Hernández, B.; Pflüger, F.; Kruglik, S.G.; Ghomi, M. Characteristic Raman lines of phenylalanine analyzed by a multiconformational approach. Journal of Raman Spectroscopy 2013, 44, 827–833. [Google Scholar] [CrossRef]
- Shalev, M.; Elson, A. The roles of protein tyrosine phosphatases in bone-resorbing osteoclasts. Biochimica Et Biophysica Acta (BBA)-Molecular Cell Research 2019, 1866, 114–123. [Google Scholar] [CrossRef]
- Pathmanapan, S.; Poon, R.; De Renshaw, T.B.; Nadesan, P.; Nakagawa, M.; Seesankar, G.A.; Loe, A.K.H.; Zhang, H.H.; Guinovart, J.J.; Duran, J.; et al. Mutant IDH regulates glycogen metabolism from early cartilage development to malignant chondrosarcoma formation. Cell Reports 2023, 42. [Google Scholar] [CrossRef]
- Movasaghi, Z.; Rehman, S.; Rehman, I.U. Raman spectroscopy of biological tissues. Applied Spectroscopy Reviews 2007, 42, 493–541. [Google Scholar] [CrossRef]
- Rehman, I.; Smith, R.; Hench, L.; Bonfield, W. FT-Raman spectroscopic analysis of natural bones and their comparison with bioactive glasses and hydroxyapatite. In Bioceramics; Elsevier, 1994; pp. 79–84. [Google Scholar] [CrossRef]
- Buchwald, T.; Niciejewski, K.; Kozielski, M.; Szybowicz, M.; Siatkowski, M.; Krauss, H. Identifying compositional and structural changes in spongy and subchondral bone from the hip joints of patients with osteoarthritis using Raman spectroscopy. Journal of biomedical optics 2012, 17, 017007. [Google Scholar] [CrossRef] [PubMed]
- Errassifi, F.; Sarda, S.; Barroug, A.; Legrouri, A.; Sfihi, H.; Rey, C. Infrared, Raman and NMR investigations of risedronate adsorption on nanocrystalline apatites. Journal of colloid and interface science 2014, 420, 101–111. [Google Scholar] [CrossRef]
- Gunasekaran, S.; Anbalagan, G.; Pandi, S. Raman and infrared spectra of carbonates of calcite structure. Journal of Raman Spectroscopy: An International Journal for Original Work in all Aspects of Raman Spectroscopy, Including Higher Order Processes, and also Brillouin and Rayleigh Scattering 2006, 37, 892–899. [Google Scholar] [CrossRef]
- Dippel, B.; Mueller, R.T.; Pingsmann, A.; Schrader, B. Composition, constitution, and interaction of bone with hydroxyapatite coatings determined by FT Raman microscopy. Biospectroscopy 1998, 4, 403–412. [Google Scholar] [CrossRef]
- Gaifulina, R.; Nunn, A.D.; Draper, E.R.; Strachan, R.K.; Blake, N.; Firth, S.; Thomas, G.M.; McMillan, P.F.; Dudhia, J. Intra-operative Raman spectroscopy and ex vivo Raman mapping for assessment of cartilage degradation. Clinical Spectroscopy 2021, 3, 100012. [Google Scholar] [CrossRef]
- Freeman, J.; Wopenka, B.; Silva, M.; Pasteris, J. Raman spectroscopic detection of changes in bioapatite in mouse femora as a function of age and in vitro fluoride treatment. Calcified tissue international 2001, 68. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.F.; Awais, M.; Khan, A.S.; Tabassum, S.; Chaudhry, A.A.; Rehman, I.U. Raman spectroscopy of natural bone and synthetic apatites. Applied spectroscopy reviews 2013, 48, 329–355. [Google Scholar] [CrossRef]
- Mandair, G.S.; Morris, M.D. Contributions of Raman spectroscopy to the understanding of bone strength. BoneKEy reports 2015, 4. [Google Scholar] [CrossRef]
- Kozielski, M.; Buchwald, T.; Szybowicz, M.; Błaszczak, Z.; Piotrowski, A.; Ciesielczyk, B. Determination of composition and structure of spongy bone tissue in human head of femur by Raman spectral mapping. Journal of Materials Science: Materials in Medicine 2011, 22, 1653–1661. [Google Scholar] [CrossRef]
- Mangialardo, S.; Cottignoli, V.; Cavarretta, E.; Salvador, L.; Postorino, P.; Maras, A. Pathological biominerals: Raman and infrared studies of bioapatite deposits in human heart valves. Applied Spectroscopy 2012, 66, 1121–1127. [Google Scholar] [CrossRef]
- Timchenko, E.; Zherdeva, L.; Timchenko, P.; Volova, L.; Ponomareva, U. Detailed analysis of the structural changes of bone matrix during the demineralization process using Raman spectroscopy. Physics Procedia 2015, 73, 221–227. [Google Scholar] [CrossRef]
- Li, J.; Li, J.; Wang, H.; Chen, Y.; Qin, J.; Zeng, H.; Wang, K.; Wang, S. Microscopic Raman illustrating antitumor enhancement effects by the combination drugs of γ-secretase inhibitor and cisplatin on osteosarcoma cells. Journal of Biophotonics 2022, 15, e202200189. [Google Scholar] [CrossRef]
- Woess, C.; Unterberger, S.H.; Roider, C.; Ritsch-Marte, M.; Pemberger, N.; Cemper-Kiesslich, J.; Hatzer-Grubwieser, P.; Parson, W.; Pallua, J.D. Assessing various Infrared (IR) microscopic imaging techniques for post-mortem interval evaluation of human skeletal remains. PLoS One 2017, 12, e0174552. [Google Scholar] [CrossRef] [PubMed]
- Lau, C.P.; Ma, W.; Law, K.Y.; Lacambra, M.D.; Wong, K.C.; Lee, C.W.; Lee, O.K.; Dou, Q.; Kumta, S.M. Development of deep learning algorithms to discriminate giant cell tumors of bone from adjacent normal tissues by confocal Raman spectroscopy. Analyst 2022, 147, 1425–1439. [Google Scholar] [CrossRef]
- Bautista-González, S.; González, N.J.C.; Campos-Ordoñez, T.; Elías, M.A.A.; Pedroza-Montero, M.R.; Beas-Zárate, C.; Gudiño-Cabrera, G. Raman spectroscopy to assess the differentiation of bone marrow mesenchymal stem cells into a glial phenotype. Regenerative Therapy 2023, 24, 528–535. [Google Scholar] [CrossRef]
- Wang, S.; Liang, Z.; Gong, Y.; Yin, Y.; Wang, K.; He, Q.; Wang, Z.; Bai, J. Confocal raman microspectral imaging of ex vivo human spinal cord tissue. Journal of Photochemistry and Photobiology B: Biology 2016, 163, 177–184. [Google Scholar] [CrossRef] [PubMed]
- Pavlou, E.; Zhang, X.; Wang, J.; Kourkoumelis, N. Raman spectroscopy for the assessment of osteoarthritis. Annals of Joint 2018, 3. [Google Scholar] [CrossRef]
- Gamsjaeger, S.; Klaushofer, K.; Paschalis, E.P. Raman analysis of proteoglycans simultaneously in bone and cartilage. Journal of Raman Spectroscopy 2014, 45, 794–800. [Google Scholar] [CrossRef]
- Souza, R.A.d.; Jerônimo, D.P.; Gouvêa, H.A.; Xavier, M.; Souza, M.T.d.; Miranda, H.; Tosato, M.G.; Martin, A.A.; Ribeiro, W. Fourier-transform Raman spectroscopy study of the ovariectomized rat model of osteoporosis. The Open Bone Journal 2010, 2. [Google Scholar] [CrossRef]
- Olsztynska-Janus, S.; Gasior-Glogowska, M.; Szymborska-Malek, K.; Komorowska, M.; Witkiewicz, W.; Pezowicz, C.; Szotek, S.; Kobielarz, M. Spectroscopic techniques in the study of human tissues and their components. Part II: Raman spectroscopy. Acta Bioeng. Biomech 2012, 14, 121–133. [Google Scholar]
- Gautam, R.; Ahmed, R.; Haugen, E.; Unal, M.; Fitzgerald, S.; Uppuganti, S.; Mahadevan-Jansen, A.; Nyman, J.S. Assessment of spatially offset Raman spectroscopy to detect differences in bone matrix quality. Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy 2023, 303, 123240. [Google Scholar] [CrossRef] [PubMed]
- Ciubuc, J.D.; Manciu, M.; Maran, A.; Yaszemski, M.J.; Sundin, E.M.; Bennet, K.E.; Manciu, F.S. Raman spectroscopic and microscopic analysis for monitoring renal osteodystrophy signatures. Biosensors 2018, 8, 38. [Google Scholar] [CrossRef] [PubMed]
- Cavalu, S.; Pînzaru, S.C.; Peica, N.; Damian, G.; Kiefer, W. Adsorption behavior of hyaluronidase onto silver nanoparticles and PMMA bone substitute. Journal Of Optoelectronics And Advanced Materials 2007, 9, 686. [Google Scholar]
- Castorina, F.; Masi, U.; Giorgini, E.; Mori, L.; Tafuri, M.A.; Notarstefano, V. Evidence for Mild Diagenesis in Archaeological Human Bones from the Fewet Necropolis (SW Libya): New Insights and Implications from ATR–FTIR Spectroscopy. Applied Sciences 2023, 13, 687. [Google Scholar] [CrossRef]
- Hędzelek, W.; Marcinkowska, A.; Domka, L.; Wachowiak, R. Infrared spectroscopic identification of chosen dental materials and natural teeth. Acta Physica Polonica A 2008, 114, 471–484. [Google Scholar] [CrossRef]
- Gautam, R.; Vanga, S.; Ariese, F.; Umapathy, S. Review of multidimensional data processing approaches for Raman and infrared spectroscopy. EPJ Techniques and Instrumentation 2015, 2, 1–38. [Google Scholar] [CrossRef]
- Campanacci, D.A.; Scoccianti, g.; Franchi, A.; Roselli, G.; Beltrami, G.; Ippolito, M.; Caff, G.; Frenos, F.; Capanna, R. Surgical treatment of central grade I chondrosarcoma of the appendicular skeleton. J. Orthop. Traumatol. 2013, 14, 101–107. [Google Scholar] [CrossRef]
Figure 3.
(a) Averaged Raman spectra of CS and EC; (b) averaged spectra of G1, G2 and G3. The shaded areas represent the standard deviation.
Figure 3.
(a) Averaged Raman spectra of CS and EC; (b) averaged spectra of G1, G2 and G3. The shaded areas represent the standard deviation.
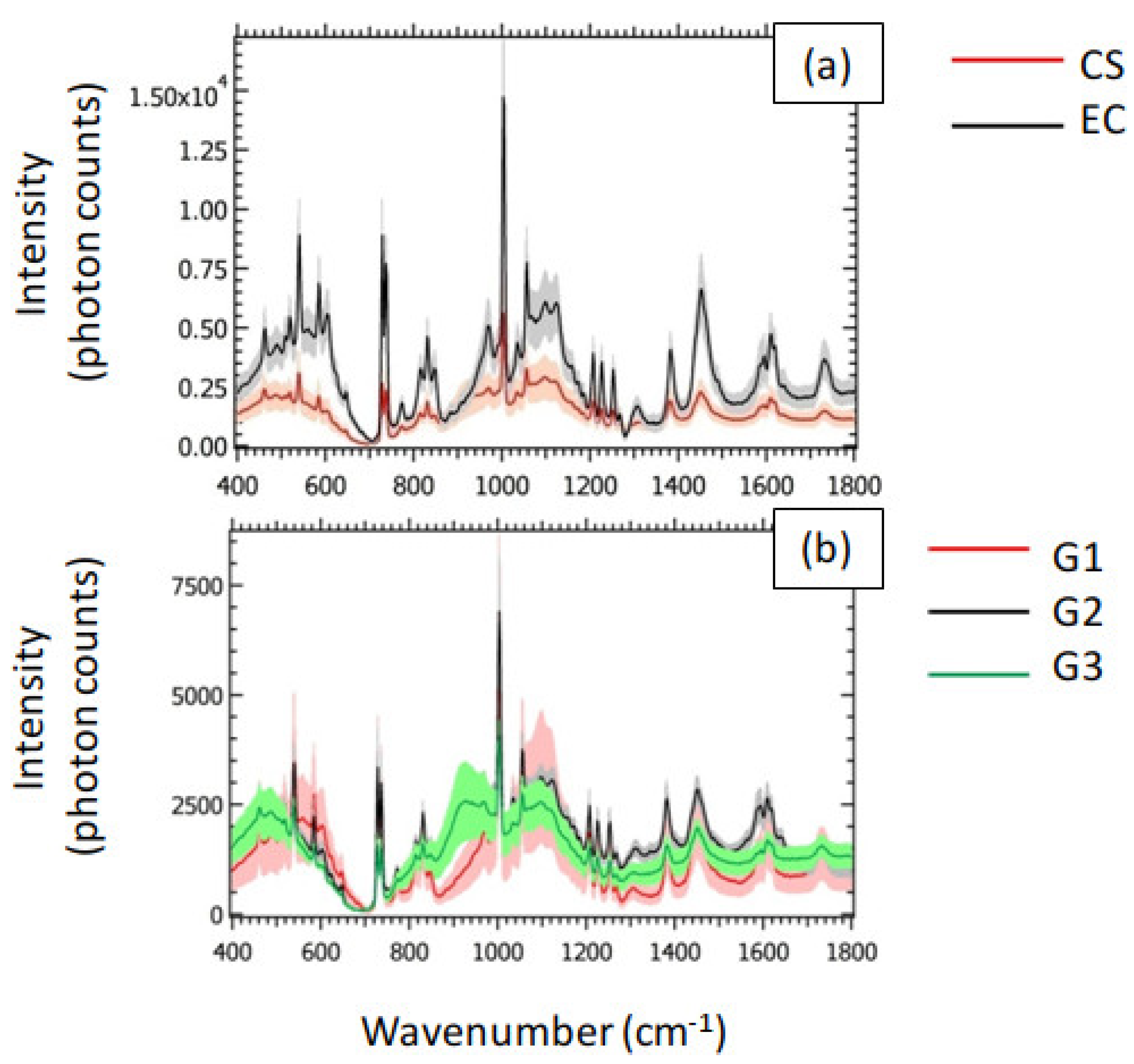
Figure 4.
(a) RBI for MLPC(ADAM) and MLPC(L-BFSG-B) in the classification problem EC-CS as a function of the wavenumber; (b) RBI for SVM and RFC in the classification problem EC-CS as a function of the wavenumber; (c) RBI for MLPC(ADAM) and MLPC(L-BFSG-B) in the classification problem G1-G2-G3 as a function of the wavenumber; (d) RBI for SVM and RFC in the classification problem G1-G2-G3 as a function of the wavenumber; (e) RBI for MLPC(ADAM) and MLPC(L-BFSG-B) in the classification problem EC-G1-G2-G3 as a function of the wavenumber; (f) RBI for SVM and RFC in the classification problem EC-G1-G2-G3 as a function of the wavenumber. We normalized RBI with the MinMax rule.
Figure 4.
(a) RBI for MLPC(ADAM) and MLPC(L-BFSG-B) in the classification problem EC-CS as a function of the wavenumber; (b) RBI for SVM and RFC in the classification problem EC-CS as a function of the wavenumber; (c) RBI for MLPC(ADAM) and MLPC(L-BFSG-B) in the classification problem G1-G2-G3 as a function of the wavenumber; (d) RBI for SVM and RFC in the classification problem G1-G2-G3 as a function of the wavenumber; (e) RBI for MLPC(ADAM) and MLPC(L-BFSG-B) in the classification problem EC-G1-G2-G3 as a function of the wavenumber; (f) RBI for SVM and RFC in the classification problem EC-G1-G2-G3 as a function of the wavenumber. We normalized RBI with the MinMax rule.
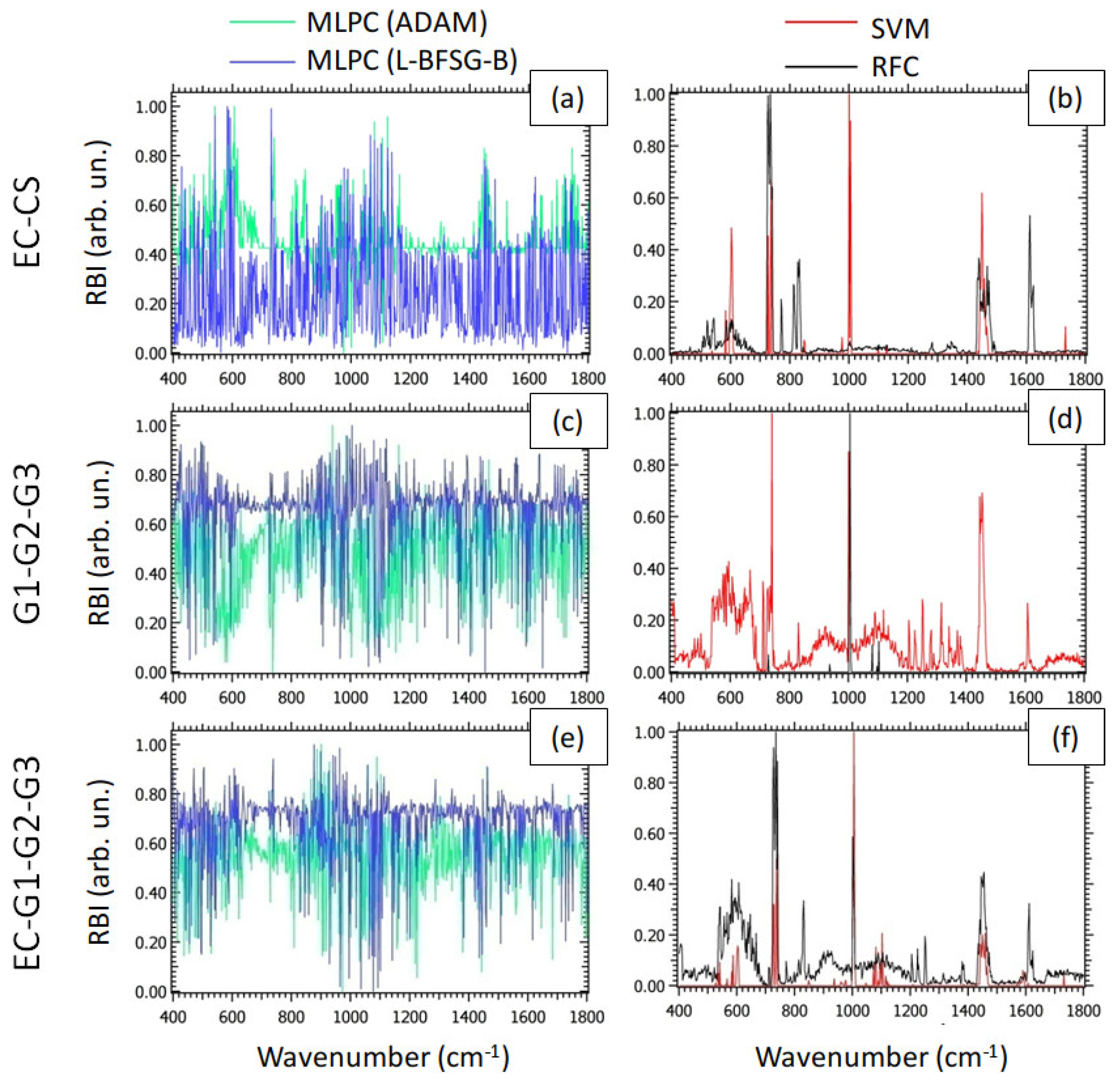
Table 1.
Raman peaks of the analyzed samples within the range between 400 and 1800 cm−1 and corresponding peak interpretation [6].
Table 1.
Raman peaks of the analyzed samples within the range between 400 and 1800 cm−1 and corresponding peak interpretation [6].
| Wavenumber (cm−1) | Interpretation | Reference |
|---|---|---|
| 490 | Glycogen | [31] |
| 519 | Phosphatidylinositol | [32] |
| 540 | Amminoacid cysteine | [32] |
| 584 | Phosphate (bend) peak | [33] |
| 604 | Phosphate (minerals) | [34] |
| 646 | C-P vibrations | [35] |
| 729 | Carbonates | [36] |
| 773 | Hydroxyapatite | [37] |
| 815 | Proline, Hydroxyproline, Tyrosine, stretching of nucleic acids | [32] |
| 831 | Collagen | [38] |
| 849 | Apatite | [39] |
| 971 | Tricalcium phosphate | [40] |
| 1003 | Phenylalanine | [41] |
| 1035 | Apatite | [42] |
| 1057 | (Apatite) | [43] |
| 1098 | (Hydroxyapatite) | [44] |
| 1123 | C-N (Proteins) | [32] |
| 1159 | C-C/C-N stretching (Proteins) | [32] |
| 1172 | Tyrosine | [45] |
| 1185 | Carbohydrates | [46] |
| 1207 | Hydroxyproline, tyrosine | [47] |
| 1227 | Nucleic acids | [48] |
| 1253 | Amide III | [49] |
| 1267 | Amide III, lipids | [32] |
| 1307 | Amide III, lipids | [50] |
| 1383 | N-acetyl-glucosamine | [51] |
| 1453 | wagging | [52] |
| 1489 | Guanine | [53] |
| 1595 | Amide I | [54] |
| 1609 | Amide I, Phenylalanine | [55] |
| 1619 | Amide I (aggregates) | [56] |
| 1639 | Proteins, collagen | [57] |
| 1731 | Ester group | [58] |
Table 2.
Accuracy A, Sensitivity S, and Specificity , averaged over the 5 folds and over the values of the label and related to the four classifiers examined.
Table 2.
Accuracy A, Sensitivity S, and Specificity , averaged over the 5 folds and over the values of the label and related to the four classifiers examined.
| Classification problem | Model | |||
|---|---|---|---|---|
| EC-CS | SVM | 78.9 | 78.9 | 79.7 |
| EC-CS | RFC | 98.5 | 98.5 | 97.0 |
| EC-CS | MLPC(ADAM) | 99.7 | 99.7 | 99.0 |
| EC-CS | MLPC(L-BFSG-B) | 99.1 | 99.1 | 97.1 |
| G1-G2-G3 | SVM | 75.9 | 75.9 | 87.4 |
| G1-G2-G3 | RFC | 99.2 | 99.2 | 99.6 |
| G1-G2-G3 | MLPC(ADAM) | 99.2 | 99.2 | 96.6 |
| G1-G2-G3 | MLPC(L-BFSG-B) | 99.2 | 99.2 | 99.6 |
| EC-G1-G2-G3 | SVM | 76.6 | 76.6 | 92.4 |
| EC-G1-G2-G3 | RFC | 97.3 | 97.3 | 99.1 |
| EC-G1-G2-G3 | MLPC(ADAM) | 97.6 | 97.6 | 99.2 |
| EC-G1-G2-G3 | MLPC(L-BFSG-B) | 97.3 | 97.3 | 99.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






