Prerpints.org logo
Preprint
Article

How Much Cosmic Time Does It Take for a Star to Collapse Forming a Black Hole?

Altmetrics

Downloads

170

Views

35

Comments

0

This version is not peer-reviewed

Submitted:

06 February 2024

Posted:

07 February 2024

You are already at the latest version

Alerts
Abstract
The concept of a black hole is examined through a historical lens, emphasizing the distinctions between its mathematical definition and the observed phenomena in the cosmos. An essential point of contention is highlighted, the challenge of reconciling the ultimate state of gravitational collapse, conceptualized as a black hole with its associated future event horizon, with the vast age of the universe as measured in cosmic time. The work delves into the evolution of black hole theories, tracing their development from the early mathematical solutions, such as the Schwarzschild solution, to the contemporary understanding shaped by contributions from Hawking and Penrose. The complex interplay between mathematical descriptions and observational realities is explored, shedding light on the difficulties inherent in merging theoretical concepts with astrophysical observations. A particular focus is placed on the discrepancy between the theoretical formation of a black hole and the seemingly infinite cosmic time required for the collapse process according to the seminal work of Oppenheimer and Snyder. This apparent incongruity raises questions about the nature of objects labeled as black holes in astrophysics and prompts a critical examination of how observational data align with theoretical predictions. In essence, this exploration underscores the need for a nuanced and critical analysis of the concept of black holes, considering the intricate interplay between theoretical constructs and empirical observations within the framework of General Relativity.
Keywords: 
Subject: Physical Sciences  -   Mathematical Physics

1. Introduction

Over the past 70 years, astronomers have made significant strides in the detection and understanding of black holes, marking key milestones in our exploration of the cosmos. One of the groundbreaking discoveries was in 1964 with the identification of Cygnus X-1, a binary system containing a black hole. Within our Milky Way galaxy, the gravitational center harbors a supermassive black hole known as Sagittarius A*. This object was first detected in 1974 and has been a focal point for studying the dynamics of stars in its vicinity.
In 2019, the gravitational-wave detectors LIGO and Virgo made history by capturing signals from the most massive gravitational-wave source observed to date. This cosmic event was attributed to a binary black hole merger, unleashing gravitational waves equivalent to the energy of eight suns (see for instance [1]).
Simultaneously, the Event Horizon Telescope (EHT) collaboration [2] unveiled an unprecedented achievement – the first-ever image of a black hole. This groundbreaking image, located at the center of the galaxy M87, provided a visually compelling confirmation of the existence of black holes, aligning, "in principle", with theoretical predictions.
Recent advancements have extended our understanding of black holes to the early universe, with the discovery of black holes formed within the first few hundred million years after the Planck time [3]. The James Webb Space Telescope played a crucial role in identifying an ancient black hole in the galaxy GM-z11 [4].
While these discoveries captivate both the scientific community and the general public, a critical question arises: Do these observed black holes align with the theoretical objects described by the mathematical solutions of General Relativity?
In order to provide reasonable answers to this kind of questions, this work aims to delve into the historical evolution of the concept of black holes, tracing its development from the Schwarzschild solution to our current understanding. Special attention will be given to the period from 1917 to the mid-sixties when Hawking and Penrose [5] introduced the concept of a mathematical black hole, leading to a profound comprehension of its dynamic structure.
In parallel, cosmologists, drawing inspiration from the pioneering work of Oppenheimer and Snyder [6], have sought to unravel the ultimate fate of a collapsing star. Their theoretical results suggest that the collapse may not culminate in the formation of a black hole within a finite cosmic time, the time scale used to depict the entire history of the universe. This prompts a need to clarify the nature of the objects referred to as black holes in astrophysics.
For this reason, it seems essential to critically examine the relationship between observations, astrophysical ideas, and the pure mathematical solutions of General Relativity. An analogy can be drawn with the concept of the Big Bang, which, though a mathematical singularity in Einstein’s equations, is sometimes inaccurately portrayed as a literal explosion at the beginning of the universe. For example, in Carl Sagan’s renowned program "Cosmos," he frequently portrayed the beginning of the universe as a colossal explosion, a depiction that lacks a scientific foundation when viewed through the lens of General Relativity (Recall that Albert Einstein himself emphasized that for large energy densities, his equations lose their meaningful interpretation [7]). Expanding on this notion, the portrayal of the Big Bang as a dramatic explosion stems more from a desire to convey a captivating narrative than a precise representation of scientific principles. In fact, the term "Big Bang" itself was initially coined, during a radio broadcast in 1949, as a somewhat dismissive label by the astronomer Fred Hoyle who favored his steady-state model over the evolving universe proposed by the theoretical physicist and astronomer Georges Lemaître, where he proposed that the universe expanded from a "Primeval Atom" [8]. In fact, as Dirac explained in [9], Lemaître’s proposal was that the universe started from a single super-radioactive atom with an extremely large mass, which decayed in a very abrupt manner, breaking into fragments, each fragment into still smaller pieces. In Lemaître’s own words:
We need a fireworks theory of evolution. The last two thousand million years are slow evolution: they are ashes and smoke of bright but very rapid fireworks.
Note that in this sentence, the figurative use of the term "fireworks" has led to persistent misunderstandings, perpetuated to this day by popular narratives, portraying the beginning of the universe as an explosion of matter localized in outer space. However, in a more enlightening manner, he wrote in [10]:
If the world has begun with a single quantum, the notions of space and time would altogether fail to have any sense at the beginning and would only begin to get some sensible meaning when the original quantum would have been divided in a sufficient number of quanta. If this suggestion is correct, the beginning of the world happened a little before the beginning of space and time. Such a beginning of the world is far enough from the present order of nature to be not at all repugnant.
It is clear that the current understanding of the Big Bang has significantly evolved, particularly with the introduction of the inflationary paradigm [12]. The majority of cosmologists now accept that a classical depiction of the universe is only feasible at GUT scales, at which point an accelerated expansion is driven by a scalar field known as the inflaton. Following inflation, the universe undergoes a process of reheating, either through the energy released by the inflaton or through gravitational particle production, in order to align with the hot Friedmann universe.
All in all, it seems to me that this serves as a pertinent example, illustrating the need for a meticulous and critical analysis of the physical concept of black holes.

2. The Big Bang Singularity and the Cosmic Evolution of the Whole Universe

In cosmology, the so-called "Cosmological Principle" is assumed, stating that the spatial distribution of matter in the universe is homogeneous and isotropic when viewed on a large enough scale. Thus, on large scales, it is possible to assume that the entire universe is filled with several homogeneous fluids and fields. To foliate the manifold (the spacetime), the time used is that of an observer co-moving with these components, known as cosmic time.
The metric that delineates this foliation and serves to describe the evolution of the universe is the Friedmann-Lemaître-Roberson-Walker (FLRW) metric. The simplest one is the flat FLRW metric, corresponding to a spatially flat universe, and is given by: d s 2 = − d t 2 + a 2 ( t ) d x i d x i , where t is the cosmic time, and a ( t ) the scale factor.
In this case, the field equations of General Relativity (GR), named Friedmann and conservation equations [11], take the form
H 2 = ρ 3 M p l 2 and ρ ˙ = − 3 H ( ρ + p ) ,
where M p l represents the reduced Planck mass, H denotes the Hubble rate, ρ signifies the energy density, and p represents the pressure. To solve these equations, an Equation of State (EoS) p = p ( ρ ) is required, establishing a relationship between pressure and energy density. The most straightforward EoS is the linear form p = w ρ , where w > − 1 . This choice leads to the following solution:
H ( t ) = 2 3 ( 1 + w ) t and ρ ( t ) = 4 M p l 2 3 ( 1 + w ) 2 t 2 .
The solution (2) diverges at t = 0 , leading to the "Big Bang singularity." This is, of course, a mathematical singularity that only reflects the breakdown of General Relativity (GR) at high energy densities. In Einstein’s words (see page 76 of [7]):
The theoretical doubts are based on the fact that for the time of the beginning of the expansion the metric becomes singular and the density, ρ, becomes infinite. In this connection the following should be noted: The present theory of relativity is based on a division of physical reality into a metric field (gravitation) on the one hand, and into and electromagnetic field and matter on the other hand. In reality space will probably be of a uniform character and the present theory be valid only as a limiting case. For large densities of the field and of matter, the field equations and even the field variables which enter into them will have no real significance. One may not therefore assume the validity of the equations for very high density of field and of matter, and one may not conclude that the "beginning of expansion" must means a singularity in the mathematical sense. All we have to realize is that the equations may not be continued over such regions. This consideration does, however, not alter the fact that the "beginning of the world" really constitutes a beginning, from the point of view of the development of the now existing stars and systems of stars, at which those stars and systems of stars did not yet exist as individual entities.
Therefore, what this mathematical singularity signals is that for a cosmic time very close to t = 0 , the field equations of GR are not valid to classically depict the universe. In this sense, is generally assumed that GR describes the universe for scales bellow the Planck’s one. This idea is clearly state by A. Guth in [12] when he wrote:
The standard model has a singularity which is conventionally taken to be at time t = 0 . As t → 0 , the temperature T → ∞ . Thus, no initial-value problem can be defined at t = 0 . However, when T is of the order of the Planck mass ( m p l ≅ 1.22 × 10 19 GeV) or greater, the equations of the standard model are undoubtedly meaningless, since quantum gravitational effects are expected to become essential. Thus, within the scope of our knowledge, it is sensible to begin the hot big bang scenario at some temperature T 0 which is comfortably below m p l ; let us say T 0 = 10 17 GeV. At this time one can take the description of the universe as a set of initial conditions, and the equations of motion then describe the subsequent evolution. Of course, the equation of state for matter at these temperatures is not really known, but one can make various hypotheses and pursue the consequences.
Therefore, following Guth, and taking into account the relation T M e V ∼ 1 t s e c , where the temperature is in MeV and the time in seconds. T 0 = 10 7 GeV correspond approximately to a cosmic time around t 0 = 10 − 40 s e c ≅ 2 × 10 3 t p l , which can be taken as a minimal time where the classical evolution of the universe can be safely depicted by GR.
Finally, it is important to stress that one can continue back in time, for t < t 0 , the evolution of the universe but using a new theory where General Relativity, as Einstein believed, is a limiting case (see Section 3.4 of [13]). There are some ideas to build up this extension of GR, for example, introducing quantum effects as in semi-classical gravity taking into account the vacuum energy density of massless conformally coupled fields (see, for instance, [14,15]) or loop quantum gravity [16], or modifying the Hilbert-Einstein action as in f ( R ) gravity [17,18].

3. The Schwarzschild metric

Based on Einstein’s calculation of the Perihelion motion of Mercury [19], where Einstein used approximations of second order to determine the Christoffel symbols, soon after the presentation of the final covariant equations of General Relativity in 1915, K. Schwarzschild published his famous solution to the GR equations [20].
Starting with the assumptions made by Einstein in [19] about the form of the metric and using unimodular gravity (recall that Einstein presented, for the first time -though it was incorrect in the general case but correct for a trace-less stress-energy tensor and thus correct in the vacuum case- his covariant field equations for gravity in unimodular form at the Prussian Academy of Science on November 4, 1915 [21]), Schwarzschild began with a metric in Cartesian coordinates ( x , y , z ) of the form:
d s 2 = − F ( r ) d t 2 + G ( r ) ( d x 2 + d y 2 + d z 2 ) + H ( r ) ( x d x + y d y + z d z ) 2 ,
where r = x 2 + y 2 + z 2 , and the undetermined functions have to satisfy lim r → ∞ F ( r ) = lim r → ∞ G ( r ) = 1 and lim r → ∞ H ( r ) = 0 .
After making a change to polar coordinates x = r sin θ cos ϕ , y = r sin θ sin ϕ and z = r cos θ , the metric becomes
d s 2 = − F ( r ) d t 2 + ( G ( r ) + r 2 H ( r ) ) d r 2 + r 2 G ( r ) ( d θ 2 + sin 2 θ d ϕ 2 ) .
In order to continue working in unimodular gravity, Schwarzschild introduced the new coordinates
x 1 = r 3 3 , x 2 = − cos θ , x 3 = ϕ , x 4 = t ,
obtaining the metric
d s 2 = − f 4 ( x 1 ) d x 4 2 + f 1 ( x 1 ) d x 1 2 + f 2 ( x 1 ) d x 2 2 1 − x 2 2 + f 3 ( x 1 ) ( 1 − x 2 2 ) d x 3 2 ,
where the new undetermined functions f i , which have to satisfy f 1 f 2 f 3 f 4 = 1 , are related with the older ones by:
f 4 = F , f 1 = G r 4 + H r 2 , f 2 = f 3 = r 2 G .
After imposing the vacuum field equations, Schwarzschild obtained:
f 2 = f 3 = ( 3 x 1 + σ ) 2 / 3 , f 4 = 1 − α ( 3 x 1 + σ ) − 1 / 3 , f 1 = ( 3 x 1 + σ ) − 4 / 3 1 − α ( 3 x 1 + σ ) − 1 / 3 ,
where α and σ are positive constants of integration.
We can see that f 1 is singular at x 1 = 1 3 ( α 3 − σ ) . Then, assuming that the field is produced by a point particle situated in the origin of coordinates, to move the discontinuity to the origin r = 0 , one has to take σ = α 3 , and thus,
f 1 = 1 R α 4 ( r ) 1 − α R α ( r ) − 1 , f 2 = f 3 = R α 2 ( r ) , f 4 = 1 − α R α ( r ) ,
with R α ( r ) = R ( α 3 , r ) where R 3 ( σ , r ) = r 3 + σ .
The final form of the metric becomes:
d s 2 = − 1 − α R α ( r ) d t 2 + 1 − α R α ( r ) − 1 d R α 2 ( r ) + R α 2 ( r ) ( d θ 2 + sin 2 θ d ϕ 2 ) ,
or in terms of the polar coordinates
d s 2 = − 1 − α ( r 3 + α 3 ) 1 / 3 d t 2 + r 4 ( r 3 + α 3 ) 4 / 3 1 − α ( r 3 + α 3 ) 1 / 3 − 1 d r 2 + ( r 3 + α 3 ) 2 / 3 ( d θ 2 + sin 2 θ d ϕ 2 ) .
At the end of his work, Schwarzschild obtained the equation of motion of a planet in the equatorial plane θ = π / 2
d x d ϕ 2 = 1 − h + h α x − x 2 + α x 3 ,
where x = 1 / R and h is a constant of integration, and shown that approximately coincide with the one used by Einstein in [19] to calculate the advance of the Perihelion of Mercury.
Now, to identify the parameter α we use the week limit approximation g t t ≅ 1 + 2 Φ , where Φ = − G M r is the Newtonian potential corresponding with an star with mass M, for r > r 0 , being r 0 the radius of the star. So, we have
α ≅ 2 M G ( r 3 + α 3 ) 1 / 3 r ⟹ α ≅ 2 M G 1 − ( 2 M G ) 3 r 3 − 1 / 3 ≅ 2 M G ,
where we have assumed that r 0 ≫ 2 M G .
This effectively holds in our solar system because the radius of the Sun is approximately r 0 ≅ 7 × 10 5 Km, and 2 M G ≅ 3 Km. So, since α is a constant of integration, from the weak approximation, we can state that its value is α = 2 M G .
What is important to realize from the metric (11) is that the only singularity appears at the origin of coordinates r = 0 .

3.1. Hilbert’s derivation

Looking at (8), we can see that the solutions depend on two parameters. As we have previously discussed, Schwarzschild chose the relation σ = α 3 in order to move the singularity of f 1 to the origin of coordinates r = 0 . However, one can make other choices; for example, σ = 0 . In that case, we will have:
f 2 = f 3 = r 2 , f 4 = 1 − α r , f 1 = r − 4 1 − α r − 1 ,
and consequently, the metric for a point particle situated at the origin of coordinates becomes:
d s 2 = − 1 − α r d t 2 + 1 − α r − 1 d r 2 + r 2 ( d θ 2 + sin 2 θ d ϕ 2 ) f o r r > 0 ,
which was derived by D. Hilbert [22] (and also by Droste [23]). It is commonly named the "Schwarzschild metric," but one has to realize that this is not the metric obtained by Schwarzschild.
In that case, the weak limit leads exactly to α = r s = 2 M G , which is the so-called Schwarzschild radius.
In fact, Hilbert’s derivation is a little different:
Writing R 3 ( r ) = r 3 + σ , and now σ is not fixed as in the Schwarzschild choice. Then, one can define the new radial variable
r * = r G ( r ) = f 2 ( r ) = ( 2 x 1 + σ ) 1 / 3 = ( r 3 + σ ) 1 / 3 = R ( σ , r ) .
Now, recall that using Schwarzschild calculation, if σ is not fixed, the metric becomes
d s 2 = − 1 − α R ( σ , r ) d t 2 + 1 − α R ( σ , r ) − 1 d R 2 ( σ , r ) + R 2 ( σ , r ) ( d θ 2 + sin 2 θ d ϕ 2 ) ,
that is,
d s 2 = − 1 − α r * d t 2 + 1 − α r * − 1 d r * 2 + r * 2 ( d θ 2 + sin 2 θ d ϕ 2 ) , w i t h r * > σ ,
and of course, choosing σ = 0 one gets (15) with r * = r > 0 .
Remark 3.1
It is interesting to note that in [24], Einstein, in order to show that it is physically impossible for a static spherically symmetric star to have a radius less than the Schwarzschild one, uses the "isotropic" form of Hilbert’s metric (15), obtained for the first time by Weyl in [25]:
d s 2 = − 1 − μ 2 r ˜ 1 + μ 2 r ˜ 2 d t 2 + 1 + μ 2 r ˜ 4 d r ˜ 2 + r ˜ 2 ( d θ 2 + sin 2 θ d ϕ 2 ) ,
obtained with the change of variable r = r ˜ 1 + μ 2 r ˜ 2 with μ = α / 2 .
In addition, dealing with the flat FLRW spacetime, McVittie obtained the following metric [26] (see also [27]):
d s 2 = − 1 − μ 2 a ( t ) r ˜ 1 + μ 2 a ( t ) r ˜ 2 d t 2 + 1 + μ 2 a ( t ) r ˜ 4 a 2 ( t ) d r ˜ 2 + r ˜ 2 ( d θ 2 + sin 2 θ d ϕ 2 ) ,
once again with μ = α / 2 .
Therefore, it seems that the difference between the metrics (10) and (15) is the different choice of the parameter σ . Schwarzschild’s choice was σ = α 3 and Hilbert’s choice was σ = 0 .
At this point, it is important to note that Hilbert’s metric is not stationary for 0 < r < α , which entails some difficulties in its interpretation, as clearly pointed out in [28,29]. For example, the singularity r = 0 is a space-like surface, and, more interestingly, the trajectory of light moving in a radial direction satisfies:
t − t 0 = r − r 0 + α ln r − α r 0 − α .
So, when r 0 approaches α , the time taken for the signal emitted from r 0 at time t 0 goes to infinity. Thus, as pointed out in [29], none of the laws describing the behavior of r ≅ α are, in principle, testable by observers (including those on Earth) far away from r = α .
The majority consensus was and is the use of Hilbert’s metric to depict spacetime around a spherically symmetric star. However, there are few authors (see, for instance, [30,31,32]) who nowadays claim that the original Schwarzschild metric (10) is the correct one to depict the metric originated by a spherically symmetric star. In fact, in 1922, Brillouin wrote the Schwarzschild metric as follows [33]:
d s 2 = − r ¯ r ¯ + α d t 2 + r ¯ + α r ¯ d r ¯ 2 + ( r ¯ + α ) 2 ( d θ 2 + sin 2 θ d ϕ 2 ) , with r ¯ > 0 ,
where r ¯ = R α ( r ) − α , and argued that the only singularity appears at r ¯ = 0 , and it is nonsensical to extend the metric to − α < r ¯ < 0 because, in that case, the metric is not static.
However, the general consensus is that the point r = 0 in the Schwarzschild metric ( r ¯ = 0 in the expression provided by Brillouin) corresponds to r = α in the Hilbert’s metric (15), which is valid for r > 0 . Therefore, the general consensus is that the metric generated by a point mass or a star with a radius less than the Schwarzschild radius r s = 2 M G is the Hilbert’s one that has a coordinate singularity at r = r s . This can be seen using Eddington–Finkelstein coordinates, i.e., defining t ′ = t − α ln | r α − 1 | , which leads to the metric [34]:
d s 2 = − 1 − α r d t ′ 2 + 1 + α r d r 2 − 2 α r d t ′ d r + r 2 ( d θ 2 + sin 2 θ d ϕ 2 ) ,
and a true singularity at r = 0 . This fact can also seen using Lemaître coordinates: [35]
d τ = d t + α r 1 − α r − 1 d r and d ρ = d t + r α 1 − α r − 1 d r ,
which leads to the metric
d s 2 = − d τ 2 + α r d ρ 2 + r 2 ( d θ 2 + sin 2 θ d ϕ 2 ) ,
with r = 3 α 2 ( ρ − τ ) 2 / 3 .
On the other hand, a maximal extension of the Hilbert metric can be done using the so-called Kruskal–Szekeres coordinates, defined implicitly by [36]:
r α − 1 e r / α = X 2 − T 2 and t = α ln X + T X − T ,
and leading to the metric
d s 2 = 4 α 3 r e − r / α ( − d T 2 + d X 2 ) + r 2 ( d θ 2 + sin 2 θ d ϕ 2 ) .
A synchronous system of coordinates with metric
d s 2 = − d τ 2 + 3 2 α ( R − τ ) − 2 / 3 d R 2 + 3 α 2 ( R − τ ) 4 / 3 ( d θ 2 + sin 2 θ d ϕ 2 ) ,
is obtained when one performs the change of co-ordinates [37]
τ = t + 2 α 3 r α 3 / 2 + 2 α r α + α ln 1 − 2 1 + r α R = t + 2 α r α + α ln 1 − 2 1 + r α .
We see the simple relation r = 3 α 2 ( R − τ ) 2 / 3 , which shows that the straight line R − τ = 2 α 3 correspond to r = α and t = + ∞ .
Four final remarks are in order:
  • All the different change of coordinates (Eddington-Finkelstein, Lemaître, Kruskall-Szekeres and synchronous) are singular at r = α , sending the time t (the one of the external observer) to + ∞ .
  • Once again, I emphasize the general consensus. Examining the Schwarzschild metric (10), it becomes apparent that the point r = 0 actually corresponds to a sphere of radius α . Therefore, this metric can be extended for − α < r ≤ 0 , yielding a metric entirely equivalent to Hilbert’s, with the caveat that, in Schwarzschild coordinates, r = 0 corresponds to r = α in Hilbert’s coordinates.
  • We can observe that the parameter σ is spurious when examining the metric (17). Here, we can choose σ > α 3 , and as a result, the metric exhibits no singularities for r ≥ 0 , including r = 0 . Therefore, in this scenario, the metric can be extended to r > − σ 1 / 3 , creating an equivalent metric to Hilbert’s.
  • In classical mechanics, the conservation of energy in a central gravitational field yields
    E = 1 2 m v 2 − α m 2 r ,
    thus, the minimum radius, R, of a star from which nothing can escape (in our units c = 1 ) is given by
    0 = 1 2 m − α m 2 R ⟹ R = α ,
    which is the Schwarzschild radius. Therefore, it seems natural for it to also appear in General Relativity, as it does in Hilbert’s metric.
    In addition, the geodesic equation for a radial in-falling observer, in terms of the proper time (the derivatives are with respect the proper time), is:
    r ¨ = − α 2 r 2 ,
    which "coincides" with the Newtonian law. And for E = 0 , has the solution τ = 2 3 α ( r 0 3 / 2 − r 3 / 2 ) with initial condition r ( 0 ) = r 0 . So, the observer enters in the Schwarzschild radius in a finite proper time τ α = 2 3 α ( r 0 3 / 2 − α 3 / 2 ) . But, with an infinite time t, because
    t = 2 3 α r ( τ ) ( 3 α + r ( τ ) ) − r 0 ( 3 α + r 0 ) + 2 α ln ( r ( τ ) − α ) ( r 0 + α ) ( r ( τ ) + α ) ( r 0 − α ) ,
    with r ( τ ) = r 0 3 / 2 − 3 α 2 τ 2 / 3 .
    On the contrary, for the Schwarzschild metric, one gets:
    r ¨ = − α r 2 2 ( r 3 + α 3 ) 4 / 3 ⟺ E = 1 2 m r ˙ 2 − α m 2 ( r 3 + α 3 ) 1 / 3 ,
    which is completely different from Newton’s law. One only has to check that at the origin r = 0 , the acceleration vanishes. In fact, the free falling observer enters in the region − α < r ≤ 0 .

3.2. Mathematical black holes

One can imagine a black hole as "a region of spacetime from which no signal can escape to infinity." However, this definition does not seem satisfactory because infinity is not part of the spacetime. For this reason, mathematically speaking, it is interesting to make a conformal compactification of the spacetime.
What happens is that to achieve this goal, a theory applying differential topology to GR was developed [5,38,39]. The theory contains a lot of definitions and concepts that one can see in Hawking & Ellis’s book [40] (In fact, Hawking qualifies his book as highly technical and unreadable for the layperson). Here, because this is not the goal of this work, I only present the concept of a mathematical black hole and its future event horizon without entering into the technical details (see also [41] for a not too technical review).
We start with a Lorentzian manifold ( M , g ) where g is the geometry on it. Then, it is said that the spacetime ( M ˜ , g ˜ ) is a conformal completion of it when there exists an embedding ϕ : M → M ˜ , such that ϕ ( M ) = M ˜ ∖ ∂ M ˜ satisfying:
  • There is an smooth function Ω : M ˜ → R + such that ϕ * g ˜ = ( ϕ * Ω ) 2 g , where ϕ * is the pull-back of ϕ .
  • On ∂ M ˜ we have Ω = 0 and d Ω = 0 .
  • The image of every inextendible null geodesic in M has to end points on ∂ M ˜ .
The boundary ∂ M ˜ is a null hypersurface comprised of two disconnected pieces, future null infinity  J + and past null infinity J − , the collections of future and past (respectively) endpoints in M ˜ provided by the image of in-extensible null geodesics in M .
A black hole can be defined in M ˜ as follows:
B = M ˜ ∖ J − ( J + ) ,
where J − ( U ) denotes the causal past of the subset U, the set of points of M ˜ that causally precedes the points of U, i.e., all the points for which there exists past causal curves, non space-like, connecting them with the points of U. Having this definition, the future event horizon is H + = ∂ B .
As a simple example we start with the Kruskal-Szekeres coordinates, and we use null coordinates
U = arctan T + X and V = arctan T − X ,
to obtain the metric
d s 2 = 4 α 3 r cos 2 ( U ) cos 2 ( V ) e − r / α d U d V + r 2 ( d θ 2 + sin 2 θ d ϕ 2 ) ,
where now
− π 2 < U , V < π 2 and − π < U + V < π .
We see that for constant angular coordinates, the metric d s 2 is conformally related to d U d V . Therefore, in this case, the future event horizon H + corresponds to the line of 2-spheres V = 0 with 0 < U < π / 2 , which, in Hilbert coordinates, corresponds to r = α and t = + ∞ (see, for instance, the figure 2 of [42]).
What is important to stress here is that these mathematical objects are treated globally, and even more so when dealing with gravitational collapse. To form a black hole, the surface of the star enters the future event horizon. In the case of the Hilbert metric, it enters when t = + ∞ , although in a finite time with other coordinates, for example in Eddington-Finkelstein coordinates, that extend to infinity the time of an outer observer (see, for instance, the Figure 2 in [43]). In the next section, I will discuss, based on recent studies, the physical last stage of the gravitational collapse of a star and its relation with mathematical black holes.
Another mathematical aspect is the study of singularities in General Relativity, which can be examined in terms of causal geodesic incompleteness, which is generally considered more robust that to identify some divergent curvature invariant [44]. In this sense, one can imagine the fate of a traveler approaching a singularity: the traveller will disappear from our world in a finite time. The time-reversal situation will describe the creation of the Universe: things suddenly appeared from nowhere a finite time ago. Thus, one can realize the existence of singularities whenever there are travelers which disappear, or materialize, abruptly. Of course, this indicates a break down of GR close to that times.
To establish singularity theorems that demonstrate the geodesic incompleteness of spacetime, one requires concepts such as Cauchy and trapped surfaces or energy conditions [45,46] (see also the self-contained review [47]). An example of such theorems is:
Theorem: 
(Penrose). A space-time ( M , g ) cannot be future null geodesically complete if:
  • R c ( N , N ) ≥ 0 for all null vectors N. Equivalently, in terms of the stress-energy tensor, T ( N , N ) > 0 .
  • There is a non-compact Cauchy hypersurface Σ in M .
  • There is an achronal closed future trapped surface S in M ,
where R c denotes the Ricci tensor.
Here it is important to realize that such theorems do not provide any description of the behavior of spacetime near the singularity. Specifically, they do not assert that there is a curvature invariant that blows up at the singularity, nor do they suggest that an entire set of observers within a future trapped region will experience singular behavior in the future [48].
Furthermore, it is crucial to consider Hawking’s perspective. Specifically, in the introduction of [49], the author asserts:
The theorems in this and the earlier papers probably indicate, not that singularities actually occur in the universe, but that General Relativity breaks down. One would expect it to break down anyway in very strong fields when quantum effects become important.
In a most compelling and convincing manner, Senovilla recently asserts in [45]:
Sometimes the Penrose theorem is interpreted as definite proof that black holes form in gravitational collapse. This is incorrect and the actual fact is much more subtle. The assumption of the existence of a trapped sphere does not state anything about the formation of black holes, rather it uncovers (some of) what happens inside black holes once they are formed!..... Therefore, Penrose’s theorem informs us of what happens beyond the event horizon of black holes. It is a result about the interior of black holes telling us that, if they form, inside them there will probably be closed trapped surfaces and, therefore, incompleteness of the spacetime will follow (classically and under certain conditions).
From my viewpoint, this assertion highlights the subtle distinction between the idealized mathematical object appearing in Penrose’s theorems and the astrophysical objects detected in nature. While Penrose’s theorems assume the existence of a mathematical black hole, the goal of cosmologists is to ascertain whether gravitational collapse does indeed lead to this final stage of a black hole. This is the subject of discussion in Section 4.

3.3. Some comments about Hilbert’s metric

I would like to note that some comments made by authors who reject Hilbert’s metric in favor of the Schwarzschild one sometimes appear controversial and, from my viewpoint, do not contribute to arriving at a consensus within the scientific community. Let me explain, for example, in the English translation of the original Schwarzschild paper [20], in the foreword the authors assert about the Schwarzschild metric:
It is regular in the whole space-time, with the only exception of the origin of the spatial co-ordinates; consequently, it leaves no room for the science fiction of the black holes. (In the centuries of the decline of the Roman Empire people said: “Graecum est, non legitur”...)
In a similar manner in [31], the author states at the end of the abstract: Thus, the Kruskal-Fronsdal black hole is merely an artifact of Hilbert’s error. In the same way in the introduction of [32] it is stated that:
The orthodox concepts of gravitational collapse and the black hole owe their existence to a confusion as to the true nature of the r-parameter in the metric tensor for the gravitational field.
It seems to me that such aggressive claims against the work done over decades by many researchers can only result in the rejection of the arguments put forth by those authors, especially considering the arguments in favor of the Hilbert metric presented above.
However, there are more positive attitudes, such as the one expressed by McVittie in [50], suggesting that there is no way of asserting, with some analogy to Newtonian theory, that two black holes could collide or that a black hole could be a component of a binary system. Similarly, Weinberg states in [51]:
However, it is not known whether a real massive star will actually develop a trapped surface [for the Hilbert metric are two-spheres with r = 2 M G and t constant], or merely explode into fragments with small enough mass to form stable neutron stars or white dwarfs.
Dirac (see [52]) believed that the interior of the Schwarzschild radius was non-physical and could not be produced by point-mass particles. Instead, he believed that the Schwarzschild radius was a natural boundary to space and tried to build a theory with pulsating particles with a radius greater than the Schwarzschild one.
It is also worth mention that the abstract of Kerr’s latest paper is very illuminating. In this paper, the author asserts [53]:
There is no proof that black holes contain singularities when they are generated by real physical bodies. Roger Penrose claimed sixty years ago that trapped surfaces inevitably lead to light rays of finite affine length (FALL’s). Penrose and Stephen Hawking then asserted that these must end in actual singularities. When they could not prove this they decreed it to be self evident. It is shown that there are counterexamples through every point in the Kerr metric. These are asymptotic to at least one event horizon and do not end in singularities.
To end, what is interesting is that authors such as Weyl or Droste denied the validity of Hilbert’s metric for r < α in their papers. In addition, we will never know Schwarzschild’s opinion because unfortunately, he died before the publication of Hilbert’s metric.

4. Gravitational Collapse

In 1939, Oppenheimer and Snyder published their seminal work on gravitational collapse, where they considered a simplified model, specifically a non-rotating, pressure-less, spherically symmetric star [6]. In this work, the authors established a relationship between the coordinates of a distant static observer and those of a co-moving observer with the matter. Although the relationship is somewhat complicated (in the exterior of the star, the relationship is essentially the one given by (29)), here we focus on the hypersurfaces t = + ∞ and r = α in coordinates (29):
t = + ∞ ⟺ τ = R − 2 3 α when R ≥ R R b − α 3 2 3 − R R b 4 / 3 3 / 2 when R < R b ,
and
r = α ⟺ τ = R − 2 3 α when R ≥ R R b 1 − 2 α 3 R when R < R b ,
where R b denotes the radius of the star in co-moving co-ordinates.
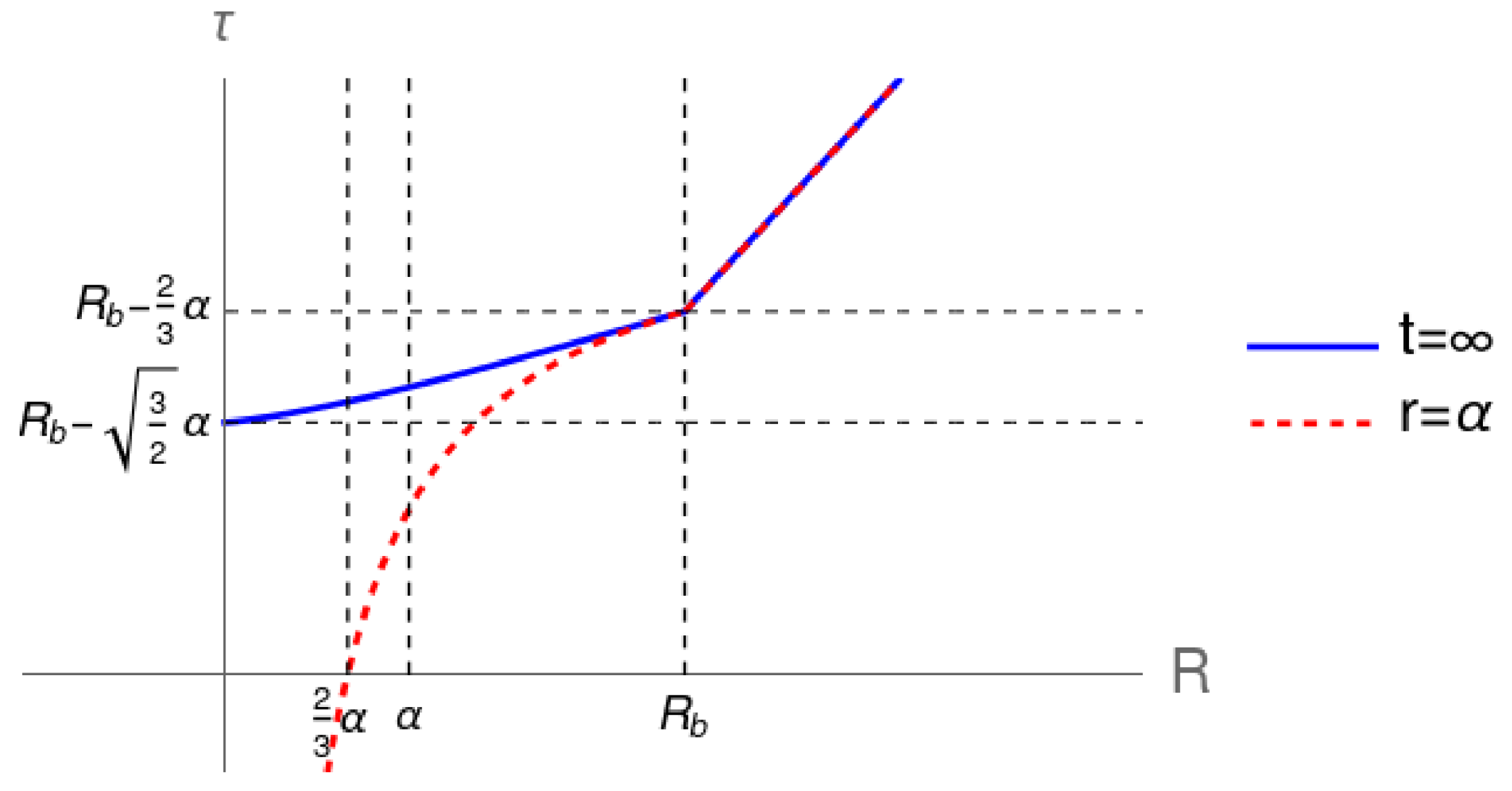
A crucial observation is made: for an external observer, the time it takes for the surface of the star to enter the Schwarzschild radius is infinite, in contrast to the time experienced by a co-moving observer. This difference can be easily seen from (39) and (40), where both curves intersect at the point ( R , τ ) = R b , R b − 2 3 α . Additionally, the event horizon is given by τ = R − 2 3 α for R ≥ R b , corresponding to t = + ∞ and r = α (see Figure 1).
Initially termed the formation of a "frozen star" until the mid-sixties, this phenomenon was later renamed a "black hole," first by J. A. Wheeler, but from a different perspective—that of a co-moving observer. From this viewpoint, a black hole forms in a finite time, leading to an extensive body of literature exploring its structure. For instance, using semi-classical gravity, S. Hawking demonstrated that black holes radiate similarly to a black bodies and eventually evaporate [54]. Moreover, this radiation depends on only a few parameters of the black hole, such as its mass or charge, giving rise to the well-known "information paradox" [55]. This paradox revolves around the contention that information about the initial state of the black hole (specifics of its formation) would be lost, violating its deterministic evolution. The information paradox has sparked a significant debate within the physics community (see, for instance, [56]) and underscores the challenges of reconciling quantum mechanics with general relativity to formulate a quantum theory of gravity.
Concluding the discussion on the quantum theory of black holes, it is noteworthy to mention Hawking’s recent work against firewalls [57]—a proposal aimed at resolving the information paradox [58]. In this work, Hawking argues that assuming quantum gravity is CPT invariant rules out remnants, event horizons, and firewalls.
Next, I return to classical and semi-classical collapse. Several authors argue against the formation of the event horizon. Allow me to cite some of them: Mitra [59] advocates for "Eternally Collapsing Objects" instead of the usual black holes. In [60], Mazur and Mottola introduce the idea of a gravastar, a kind of condensed star. Quasi black holes (objects that are close to forming an event horizon but do not form it) are studied in [61]. Situations where gravitational collapse might lead first to a regular black hole, which could dynamically evolve into a horizonless ultra-compact star, are considered in [62]. Minimally Modified Gravity (MMG) is used in [63] to study gravitational collapse. Since in MMG, four-dimensional diffeomorphism invariance is replaced by spatial diffeomorphism invariance, the theory has a preferred time slicing that should be regular. This is crucial because when dealing with MMG, the standard Schwarzschild-type foliation of a static and spherically symmetric metric is ill-defined at the horizon, and thus the corresponding solution is physically singular, while in General Relativity, it is simply a coordinate singularity. In [63], the authors construct solutions where the final state of the collapse occurs at infinite time t, where t corresponds to the temporal foliation (the physically preferred foliation) of a distant observer. The use of semi-classical gravity is done in [64,65], taking into account the vacuum expectation value of a regularization of the stress-energy tensor. The authors show that the back-reaction generates solutions describing ultra-compact fluid spheres with a negative mass interior, leading to regular static stars with mass M and radius R surpassing the Buchdahl limit M < 32 π 9 R M p l 2 .
Contrary to this view of the collapse in ultra-compact objects sometimes termed as "black stars" [66,67], as far as I know, few authors advocate for the gravitational formation of black holes. For example, in [68,69], the authors argue that, for an external observer, in the problem of gravitational collapse, the star can fall across the Schwarzschild radius within a finite time, forming a black hole. In addition, the matter fallen into the black hole can never arrive at the center, and thus, the gravitational singularity does not exist in the physical universe. Strictly speaking, what those authors explain is not the formation of a mathematical black hole because, as explained above, the formation of this structure requires the formation of a future event horizon, which happens, at least for a symmetric non-rotating star, at time t = + ∞ for a faraway observer.
Finally, it is important to emphasize the significance of the "separation of scales." I believe this is crucial, and it seems to me that sometimes this factor is not taken seriously into account. For instance, in cosmology, when dealing with the entire universe on a global scale, one studies it on average using the Friedmann-Lemaître-Robertson-Walker metric. It assumes that spacetime is foliated for t > t p l (as I already discussed, GR is assumed to work well for scales lower than the Planck’s one) with spatial hypersurfaces with t = constant where t is the cosmic time. However, when dealing with black holes, the scale is many orders smaller. One can think that to observe a black hole in the entire universe, one has to use a microscope, or in more mathematical language, it seems that black holes are defined in a small local chart of the manifold.
What happens is that sometimes the study of black holes and their formation as gravitational collapse is examined globally, and researchers seek a geodesically complete spacetime to depict the gravitational collapse.
Then, from the viewpoint of an observer far from the black hole and moving with the fluid that, on average, models the universe, and thus, using cosmic time (recall that in cosmic time the "age of the universe," as understood as the time from the beginning of its classical description around 10 − 40 s e c . up to now, is approximately 1 / H 0 which is of the order of 14 billion years), one can argue that the cosmic time it takes for the boundary of the star to reach the Schwarzschild radius is infinite. However, for an infalling observer whose proper time is finite, it is a different story. In fact, this is consistently the viewpoint employed when authors depict the formation of a black hole (as seen, for instance, in the iconic picture in Penrose’s seminal work ’Gravitational collapse and space-time singularities’ [70]).
From the perspective of the global spacetime, one assumes that, on average, the FLRW metric works, and one can argue that, for a typical equation of state of the fluid filling the universe, the manifold is geodesically complete, at least in the future, using cosmic time.
Therefore, the question is how to reconcile the fact that globally the manifold may be geodesically complete using cosmic time, but when dealing locally with gravitational collapse, it seems that it is not. Equivalently, given the evidence of black holes, how long does it take, in cosmic time, to form a black hole via gravitational collapse?
It seems to me that this question can only be answered realizing the difference between a mathematical back hole and a physical black hole (some heavily dense compact object eternally collapsing -in terms of the cosmic time- similar to a "black star").
To conclude, let me cite some viewpoints, about the concept of black hole, of different scientists quoted in [71]:
  • Sean Gryb: The existence of [a classical event horizon] just does not seem to be a verifiable hypothesis.
  • Carlo Rovelli: The classic conception of a horizon is probably a very useless definition, because it assumes we can compute the future of real black holes, and we cannot.
  • Beatrice Bonga: Ideally the definition used in Quantum Gravity reduces to the one in classical General Relativity in the limit ℏ goes to zero. . . . But since no one agrees on what a good theory of quantum gravity is (not even which principles it should satisfy), I don’t think anyone agrees on what a black hole is in quantum gravity.
  • Don Marolf: In practice we do not really care whether an object is ‘precisely’ a black hole. It is enough to know that it acts approximately like a black hole for some finite amount of time. . . . [This is] something that we can observe and test.
  • Carlo Rovelli: Today ‘black hole’ means those objects we see in the sky, like for example Sagittarius A*.
  • Robert Wald: I have no idea why there should be any controversy of any kind about the definition of a black hole. There is a precise, clear definition in the context of asymptotically flat spacetimes, [an event horizon]. . . . I don’t see this as any different than what occurs everywhere else in physics, where one can give precise definitions for idealized cases but these are not achievable/measurable in the real world.
  • Domenico Giulini: It is tempting but conceptually problematic to think of black holes as objects in space, things that can move and be pushed around. They are simply not quasi-localised lumps of any sort of ‘matter’ that occupies [spacetime] ‘points’.
  • William Unruh: A black hole is a region which cannot communicate with the outside world for a long time (where ‘long time’ depends on what I am interested in).
  • Ramesh Narayan: A black hole is a compact body of mass greater than 4 Solar masses—the physicists have shown us there is nothing else it can be.
  • Avi Loeb: A black hole is the ultimate prison: once you check in, you can never get out.
  • Ramesh Narayan: For all intents and purposes we are at future null infinity with respect to Sagittarius A*.
  • Shing-Tung Yau: We [mathematicians] view a black hole to be a natural singularityfor the Einstein equation, a singularity shielded by a membrane [i.e., a horizon].
  • Gerard ’t Hooft: A black hole is the solution of Einstein’s field equations for gravity without matter, which you get after all matter that made up a heavy object such as one or more stars, implodes due to its own weight.

5. Conclusions

The concept of black holes and their formation remains a subject of ongoing scientific research and debate, with differing viewpoints among various scientists spanning across multiple disciplines, from theoretical physicists grappling with the intricacies of General Relativity to astrophysicists scrutinizing observational data from telescopes across the electromagnetic spectrum.
Some cosmologists propose the existence of a final stage resembling a dense object referred to as a "black star", an "eternally collapsing star," or a "gravastar", suggesting alternative endpoints to stellar collapse. These objects share certain properties with mathematical black holes, prompting discussions on their classification and observational signatures. In contrast, others tend to align more closely with the idealized mathematical definition of a black hole, which includes the concept of a future event horizon, emphasizing the role of singularities and event horizons in defining black holes within the framework of General Relativity.
When addressing the question of whether detected black holes exhibit the same nature as predicted by mathematical solutions of General Relativity and if they can form through the collapse of a star, providing a definitive answer proves challenging. The formation of an event horizon, as described by GR, would theoretically require an infinite cosmic time, whereas the age of our universe, measured in cosmic time, is estimated to be around 14 billion years.
Of course, one can argue that for an observer co-moving with the collapsing star, the time required for the formation of a mathematical black hole is finite but infinite in terms of cosmic time, which is the time used to describe the history of the universe. Therefore, it seems impossible for the formation of an event horizon and thus a mathematical black hole at the present age of the universe.
In more mathematical terms, on a large enough scale, we know that the universe is well-defined by the FLRW metric, meaning we can foliate our Lorentz manifold in terms of cosmic time with hyper-surfaces t = c o n s t a n t , at least for t > 10 3 t p l , where GR works well to depict the evolution of the whole universe.
However, the formation of a physical black hole, which is a local object (many orders smaller than the whole universe), is always studied in GR as a global phenomenon. This involves the existence of a collapsing star surrounded by a vacuum. In this idealized scenario, the formation of a mathematical black hole theoretically requires an infinite amount of cosmic time. Thinking ’à la Mach’, the gravitational collapse is influenced by all the matter filling the universe. On average, this matter contributes to the Lorentz manifold, giving an FLRW structure, which foliates in slices of constant time (the time of a co-moving observer with respect to the whole mass). This allows us to adopt a preferred time frame: cosmic time. As we have already discussed, the formation of such an idealized object (a collapsing star surrounded by vacuum in the entire Lorentz manifold) necessitates an infinite amount of cosmic time.
A more cautious response suggests that the objects detected in the cosmos, potentially formed in the early universe, exhibit characteristics similar to idealized mathematical black holes, raising questions about the precise nature of their formation and properties. Therefore, it can be reasonably stated that while these detected black holes closely resemble their mathematical counterparts in many aspects, including their gravitational behavior and observational signatures, they may not conform precisely to the predictions of Einstein’s field equations, indicating the need for further investigation and refinement of our understanding of these enigmatic cosmic phenomena.
This perspective parallels the understanding of the Big Bang as the beginning of our classical universe according to General Relativity, rather than the mathematical singularity described by the Friedmann equations. In this sense, any mathematical singularity is considered a manifestation of the limitations of Einstein’s field equations at high scales, such as the Planck scale.
It is also worth noting that there may be alternative ways in which black holes could have formed, unrelated to gravitational collapse. In such cases, it would be possible for them to possess the exact nature predicted by GR. However, it appears that this alternative hypothesis is not extensively explored in the current literature.
In closing, it is worth reflecting on Einstein’s perspective:
At this point an enigma presents itself which in all ages has agitated inquiring minds. How can it be that mathematics, being after all a product of human thought which is independent of experience, is so admirably appropriate to the objects of reality? Is human reason, then, without experience, merely by taking thought, able to fathom the properties of real things?
In my opinion the answer to this question is, briefly, this:—As far as the laws of mathematics refer to reality, they are not certain; and as far as they are certain, they do not refer to reality [72].
What sharply contrasts with Hilbert’s mathematical viewpoint:
Although in my opinion only regular solutions of the fundamental equations of physics immediately represent the reality, nevertheless just the solutions with non regular points are an important mathematical tool for approximating characteristic regular solutions - and in this sense, according to the procedure of Einstein and Schwarzschild, the interval [His interval (15)], not regular for r = 0 and for r = α , must be considered as expression of the gravitation of a mass distributed with central symmetry in the surroundings of the origin [22,30].

Acknowledgments

This work is supported by the Spanish grant PID2021-123903NB-I00 funded by MCIN/AEI/10.13039/501100011033 and by “ERDF A way of making Europe”.

References

  1. Isi, M. Recent LIGO-Virgo discoveries. Mod. Phys. Lett. 2021, A36. [Google Scholar] [CrossRef]
  2. The Event Horizon Telescope Collaboration. First M87 Event Horizon Telescope Results. VIII. Magnetic Field Structure near The Event Horizon, The Astrophysical Journal Letters 2021, 910, 1.
  3. Inayoshi, K.; Visbal, E.; Haiman, Z. The Assembly of the First Massive Black Holes. ARA & A 2020, 58, 27–97. [Google Scholar]
  4. Maiolino, R.; et al. A small and vigorous black hole in the early Universe. Nature 2024. [Google Scholar] [CrossRef] [PubMed]
  5. Hawking, S.W.; Penrose, R. The singularities of the gravitational collapse. Proc. Roy. Soc. Lond. 1970, A314, 520–548. [Google Scholar]
  6. Oppenheimer, J.R.; Snyder, H. On Continued Gravitational Contraction. Phys. Rev. 1939, 56, 455–459. [Google Scholar] [CrossRef]
  7. Einstein, E. The Meaning of Relativity, 5th ed.; Princeton University press: Princeton, New Jersey, USA, 1921. [Google Scholar]
  8. Lemaître, G. The Evolution of the Universe: Discussion. Nature 1931, 128, 699–701. [Google Scholar] [CrossRef]
  9. Dirac, P.A.M. The scientific work of Georges Lemaître; Pontificia Academia Scientiarum, Vol II, N 11: 1-20 (1968).
  10. Lemaître, G. The beginning of the world from the point of view of quantum theory. Nature 2011, 127, 706, reproduced as a Golden Oldie and Editorial Note by J.-P. Luminet, Gen. Rel. Grav. 43(10),2911 (2011). [Google Scholar] [CrossRef]
  11. Friedmann, A. Über die Krümmung des Raumes. Z. Phys. 1999, 10, 377–386, General Relativity and Gravitation 31 (12): 1991–2000 (1999).. [Google Scholar] [CrossRef]
  12. Guth, A.H. Inflationary universe: A possible solution to the horizon and flatness problems. Phys. Rev. 1981, D23, 347–356. [Google Scholar] [CrossRef]
  13. Elizalde, E. Einstein, Barcelona, Symmetry & Cosmology: The Birth of an Equation for the Universe. Symmetry 2023, 15, 1470. [Google Scholar]
  14. Fischetti, M.V.; Hartle, J.B.; Hu, B.L. Quantum Effects in the Early Universe. 1. Influence of Trace Anomalies on Homogeneous, Isotropic, Classical Geometries. Phys. Rev. 1979, D20, 1757–1771. [Google Scholar] [CrossRef]
  15. Starobinsky, A.A. A new type of isotropic cosmological models without singularity. Phys. Lett. 1980, 99–102. [Google Scholar] [CrossRef]
  16. Ashtekar, A.; Bianchi, E. A Short Review of Loop Quantum Gravity. Rep. Prog. Phys. 2021, 84, 042001. [Google Scholar] [CrossRef] [PubMed]
  17. De Felice, A.; Tsujikawa, S. f(R) theories. Living Rev. Rel. 2010, 13, 3. [Google Scholar]
  18. Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified Gravity Theories on a Nutshell: Inflation, Bounce and Late-time Evolution. Phys. Rept. 2017, 692, 1–104. [Google Scholar]
  19. Einstein, A. Explanation of the Perihelion Motion of Mercury from the General Theory of Relativity. Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin, Phys.-Math.: Klasse, 1916; pp. 189-196. Translated by Brian Doyle and reprinted from "A Source Book in Astronomy and Astrophysics", 1900-1975 edited by Kenneth R. Lang and Owen Gingerich.
  20. K. Schwarzschild (translation and foreword by S.Antoci and A.Loinger), On the gravitational field of a mass point according to Einstein’s theory, Sitzungsber.Preuss.Akad.Wiss.Berlin (Math.Phys.): 1916; pp. 189-196. arXiv:physics/9905030.
  21. Einstein, A. On the General Theory of Relativity, Plenary Session of November 4, 1915. Published in: Königlich Preußische Akademie der Wissenschaften. Sitzungsberichte: 1915; pp. 778-786. 4 November.
  22. D. Hilbert, Nachr. Ges. Wiss. Göttingen, Math. Phys. Kl. 53 (1917).
  23. Droste, J. The field of a single centre in Einstein’s theory of gravitation, and the motion of a particle in that field. Proc. K. Ned. Akad. Wet., Ser. A 1917, 19, 197. [Google Scholar] [CrossRef]
  24. Einstein, E. On a Stationary System With Spherical Symmetry Consisting of Many Gravitating Masses. The Annals of Mathematics 1939, 40, 922–936. [Google Scholar] [CrossRef]
  25. Weyl, H. On the Theory of Gravitation, Ann. Phys. 1917, 54, 117. [Google Scholar]
  26. McVittie, G.C. The mass-particle in an expanding universe. Monthly Notices of the Royal Astronomical Society 1933, 93, 325–339. [Google Scholar] [CrossRef]
  27. Kaloper, N.; Kleban, M.; Martin, D. McVittie’s Legacy: Black Holes in an Expanding Universe. Phys. Rev. 2010, D81. [Google Scholar] [CrossRef]
  28. Doran, R.; Lobo, F.S.N.; Crawford, P. Interior of a Schwarzschild black hole revisited. Found. Phys. 2008, 38, 160–187. [Google Scholar] [CrossRef]
  29. Narlikar, J.V.; Padmanabhan, T. The Schwarzschild solution: Some conceptual difficulties. Found. Phys. 1988, 18, 659–668. [Google Scholar] [CrossRef]
  30. Antoci, S. David Hilbert and the origin of the "Schwarzschild solution". arXiv:physics/0310104.
  31. Abrams, L.S. Black Holes: The Legacy of Hilbert’s Error. Can. J. Phys. 1989, 67, 919. [Google Scholar] [CrossRef]
  32. Crothers, S.J. On the general solution to Einstein’s vacuum field and its implications for relativistic degeneracy. Progress in Physics 2005, 1, 68–73. [Google Scholar]
  33. Brillouin, M. Les points singuliers de l’univers d’Einstein. Journ. Phys. Radium 1923, 23, 43. [Google Scholar] [CrossRef]
  34. Eddington, A.S. A Comparison of Whitehead’s and Einstein’s Formulae. Nature 1924, 113, 2832. [Google Scholar] [CrossRef]
  35. Lemaître, G. L’Univers en expansion. Annales de la Société Scientifique de Bruxelles 1933, A53, 51–85. [Google Scholar]
  36. Wald, R. General Relativity, University of Chicago Press: 1984.
  37. Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields, 4th ed.; Elsevier: Amsterdam, The Netherlands, 1980. [Google Scholar]
  38. Penrose, R. Singularities and time-asymmetry. General Relativity: An Einstein Centenary Survey; Hawking, S.W., Israel, W., Eds.; Cambridge University Press: Cambridge, UK, 1979; pp. 581–638. [Google Scholar]
  39. Penrose, R. Techniques of Differential Topology in Relativity. SIAM 1972. [Google Scholar]
  40. Hawking, S.W.; Ellis, G.F.R. The large scale structure of space-time. Cambridge Monograph on Mathematical Physics 1973. [Google Scholar]
  41. Landsman, K. Singularities, black holes, and cosmic censorship: A tribute to Roger Penrose. arXiv 2021. [Google Scholar] [CrossRef]
  42. Sato, T.; Maeda, H.; Harada, T. Conformally Schwarzschild cosmological black holes. Class. Quant. Grav. 2022, 39, 215011. [Google Scholar] [CrossRef]
  43. Hawking, S.W. The event horizon, In From Black Holes, eds. Dewitt and Dewitt, Gordon and Breach (1973).
  44. Senovilla, J.M.M.; Garfinkle, D. The 1965 Penrose singularity theorem. Class. Quantum Grav. 2015, 32, 124008. [Google Scholar] [CrossRef]
  45. Senovilla, J.M.M. A critical appraisal of the singularity theorems. arXiv 2021. [Google Scholar] [CrossRef] [PubMed]
  46. Steinbauer, R. The singularity theorems of General Relativity and their low regularity extensions. arXiv 2022. [Google Scholar] [CrossRef] [PubMed]
  47. Senovilla, J.M.M. Singularity Theorems and Their Consequences. GERG 1998, 30, 701–848. [Google Scholar] [CrossRef]
  48. Barceló, C.; Carballo-Rubio, R.; Garay, L.J. Where does the physics of extreme gravitational collapse reside? Universe 2016, 2, 7. [Google Scholar] [CrossRef]
  49. Hawking, S.H. The occurrence of singularities in cosmology. III. Causality and singularities. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences 1967, 300, 187–201. [Google Scholar]
  50. MacVittie, G.C. Laplace’s alleged ’Black Hole’. Observatory 1978, 98, 272. [Google Scholar]
  51. Weinberg, S. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity; John Wiley & Sons, Inc: Hoboken, NJ, USA, 1972. [Google Scholar]
  52. Dirac, P.A.M. Particles of finite size in the gravitational field. Proc. Roy. Soc. London. 1962, A270, 354. [Google Scholar]
  53. Kerr, R.P. Do Black Holes have Singularities? arXiv 2023, arXiv:2312.00841. [Google Scholar]
  54. Hawking, S.W. Particle creation by black holes. Communications in Mathematical Physics 1974, 43, 199–220. [Google Scholar] [CrossRef]
  55. Hawking, S.W. Breakdown of predictability in gravitational collapse. Physical Review 1976, D14, 2460–2473. [Google Scholar]
  56. Susskind, L. The Black Hole War: My Battle with Stephen Hawking to Make the World Safe for Quantum Mechanics; Little Brown and Company: 2008.
  57. Hawking, S.W. Information Preservation and Weather Forecasting for Black Holes. arXiv 2014, arXiv:1401.5761. [Google Scholar]
  58. Almheiri, A.; Marolf, D.; Polchinski, J.; Sully, J. Black Holes: Complementarity or Firewalls? J. High Energy Phys. 2013, 2, 062. [Google Scholar] [CrossRef]
  59. Mitra, A. Non-occurrence of trapped surfaces and Black Holes in spherical gravitational collapse: An abridged version. Found. Phys. Lett. 2002, 13, 543, On the Final State of Spherical Gravitational Collapse, Found. Phys. Lett. 2002, 15, 439. arXiv:astro-ph/0207056.. [Google Scholar] [CrossRef]
  60. Mazur, P.O.; Mottola, E. Gravitational vacuum condensate stars. Proc. Nat. Acad. Sci. 2023, 111, 9545, Gravitational Condensate Stars: An Alternative to Black Holes, Universe 2023 9, 88. arXiv:gr-qc/0109035.. [Google Scholar] [CrossRef]
  61. Bronnikov, K.A.; Zaslavskii, O.B. Quasi-black holes: general features and purely field configurations. Mod. Phys. Lett. 2015, A30, 1550154. [Google Scholar] [CrossRef]
  62. Carballo-Rubio, R.; Filippo, F.D.; Liberati, S.; Visser, M. A connection between regular black holes and horizonless ultracompact stars. JHEP 2023, 08, 046, Singularity-free gravitational collapse: From regular black holes to horizonless objects. 2023. arXiv:2302.00028.. [Google Scholar] [CrossRef]
  63. Felice, A.D.; Maeda, K.; Mukohyama, S.; Pookkillath, M.C. Gravitational collapse and formation of a black hole in a type II minimally modified gravity theory. arXiv 2022, arXiv:2211.14760. [Google Scholar] [CrossRef]
  64. Arrechea, J.; Barceló, C.; Carballo-Rubio, R.; Garay, L.J. Ultracompact horizonless objects in order-reduced semiclassical gravity. arXiv 2023, arXiv:2310.12668. [Google Scholar]
  65. Barceló, C.; Boyanov, V.; Carballo-Rubio, R.; Garay, L.J. Classical mass inflation versus semiclassical inner horizon inflation. Phys. Rev. 2022, D106, 124006. [Google Scholar] [CrossRef]
  66. Barceló, C.; Liberati, S.; Sonego, S.; Visser, M. Black Stars, Not Black Holes; Scientific American: 2009; pp.39-45.
  67. Vachaspati, T. Black Stars and Gamma Ray Bursts. arXiv 2007, arXiv:0706.1203. [Google Scholar]
  68. Zhang, S.-N. On the Solution to the "Frozen Star" Paradox, Nature of Astrophysical Black Holes, non-Existence of Gravitational Singularity in the Physical Universe and Applicability of the Birkhoff’s Theorem. Int.J.Mod.Phys. 2011, D20, 1891–1899. [Google Scholar] [CrossRef]
  69. Liu, Y.; Zhang, S.N. Exact solutions for shells collapsing towards a pre-existing black hole. Physics Letters 2009, B679, 88. [Google Scholar] [CrossRef]
  70. Penrose, R. Gravitational collapse and space-time singularities. Physical Review Letters 1965, 14, 57–59. [Google Scholar] [CrossRef]
  71. Curiel, E. The Many Definitions of a Black Hole. Nature Astronomy 2019, 3, 27–34. [Google Scholar] [CrossRef]
  72. Einstein, A. Geometrie und Erfahrung; Julius Springer: Berlin, Germany, 1921. [Google Scholar]
Preprints 98341 g001
Figure 1. Plot with hyper-surfaces corresponding to the Schwarzschild radius and t = ∞ , for the Oppenheimer-Snyder model.
Figure 1. Plot with hyper-surfaces corresponding to the Schwarzschild radius and t = ∞ , for the Oppenheimer-Snyder model.
Preprints 98341 g001
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated