The theory of relativity provides us with a theory of objective spacetime, in which the transformation from the coordinates of one observer to the coordinates of another observer, the physical quantities are like the geometry of spacetime, the transformation of coordinates is covariant, and the basic physical equations are like the geometry of spacetime, keeping the formal structure unchanged. According to this, we further hold that: after defining the physical meaning of the space-time geometry, the physical law is equivalent to the space-time geometry law, and the particle and field are equivalent to the structure of their internal space-time. An interesting phenomenon is that people generally take an intuitive and one-sided view of space-time understanding, that is, only space-time coordinates are regarded as space-time. Modern theory shows that the coordinate transformation is also the movement behavior of space-time, we should not only consider the reading of the clock and the scale as space-time, but also consider the group of space-time transformations as space-time. Coordinates and coordinate transformation groups should be regarded as space-time, they are two representations of space-time, the former focuses on the length and direction of space-time such as the external property, while the latter expresses the symmetry of space-time such as the intrinsic property. In addition, a quantum system also shows that there is a strong correlation (entanglement) between time and space and that time and space will periodically transform each other. The behavior of objective spacetime is actually a set of several fundamental properties, and modern theory shows that the set of these properties constitutes a group. The aforementioned space-time coordinate based on the observer's intuition is actually the mark or event of space-time, which is actually a mapping of real numbers. The linear space constructed by the field of real numbers is the representation space: the Minkowski space $M^4$. The elements of this space form a group under the addition operation, and any one of them is the vector representation or spatial representation of space-time. Spacetime transformation, on the other hand, is a matrix group representation of spacetime on $M^4$ space. All symmetries of spacetime are spontaneous behaviors of objective spacetime and should be regarded as intrinsic properties of spacetime. Spacetime and symmetry are inseparable, so the symmetry group of spacetime is also spacetime. After group mapping, the space-time symmetry group also describes space-time, so we call all these symmetry groups collectively the space-time group G. In $M^4$ space, a basic space-time group composed of 10 kinds of motion behaviors of space-time that satisfy isomorphism is Poincare group (non-homogeneous Lorentz group) $PO\left(\mathrm{1,3}\right)$, i.e. $G_p=PO\left(\mathrm{1,3}\right)$. This space-time group is the semi-direct product of the space-time rotation group, i.e. the homogeneous Lorentz group S$O\left(\mathrm{1,3}\right)$, and the space-time translation group $P^{\mathrm{1,3}}$: $G_p=P^{\mathrm{1,3}}⋉SO\left(\mathrm{1,3}\right)$, and the space $M^4$ can be seen as a coset of the space-time group and its subgroups: $M^4=PO\left(\mathrm{1,3}\right)/SO\left(\mathrm{1,3}\right)$, which means that the group representation space is still generated by the group. Since elementary particles are constructed from their internal spacetime, in this case the spacetime group is mapped to a unitary group with corresponding unitary representations, and the spacetime representation space is mapped to the Hilbert space H, any element of which is also a vector representation of spacetime and is called a state vector. In particle physics, space-time groups are represented as gauge groups on which the standard model of particle physics is built, and the generators of space-time groups are represented as operant groups and generate phase Spaces, which are mapped to physically observable in a certain way. Therefore, we can point out more generally: after giving the physical properties of space-time geometric quantities, the motion characteristics of space-time are equivalent to the motion characteristics of physics, space-time coordinates, physical quantities, quantum wave functions, space-time degrees of freedom and the generated space are all derived from objective space-time, and the physical system is a combination of objective space-time.

In special relativity, the metric describing the four-dimensional space-time continuum is: ${ds}^2={dx}^2+{dy}^2+{dz}^2-c^2{dt}^2$, giving this quadratic invariant transformation group the name Lorentz group. Due to the particularity of the time dimension in this quadratic form, it can be expressed as the rotation group of the rotation imaginary Angle between space-time, or the rotation group of time is the imaginary axis, so its transformation group is also called the pseudo-rotation group. Considering a two-dimensional case, a general transformation that leaves $x^2-c^2{t}^2$ unchanged is:

The set of the above transformation matrices is a two-dimensional representation of the pseudo-rotation group. By substitution: $\left(x,ct\right)\to (x,ict)$, then the group that holds $x^2-c^2{t}^2=x^2+{\left(ict\right)}^2$ unchanged is the SO(2) group, whose general transformation is: This is the two-dimensional rotation of time as an imaginary number. Giving $\alpha =i\varphi$ in equation (1) gives the same transformation relationship as in equation (2) :

When time takes real coordinates, the transformation matrix of virtual rotation Angle is called Lorentz boost. According to our point of view, time should be regarded as a real existence, and the above-mentioned rotation of space-time should be regarded as a real rotation, then the internal time of the physical system should be an imaginary number, and the invariance of $d{s}^2$ shows that this rotation transforms time and space into each other. The above transformation matrix describes a representation of the Lorentz group, a subgroup of the spacetime group, in a complex two-dimensional spacetime, and the intrinsic spacetime of a physical system should be represented as a complex number in the appropriate representation space. Taking the observer's space as a representation space is based on the coordinate or coordinate difference of spacetime, which is an external property of spacetime, where time is usually expressed as a real number and is positive definite. In the observer coordinates, we have established various motion equations and field equations, including the Schrödinger equation. All the time in these equations is based on the observer's time, and in most cases, only the length of time is included as a feature. Observer time comes from the marking of events, and in fact, the behavior of this marking (measurement) maps the objective spacetime of complex numbers to a real number. For a classical mechanical system, the correlation between time and space is very weak, and sometimes time in classical mechanics can be separated from space-time as an independent parameter, but for a quantum mechanical system, time and space are highly correlated, and the objective feature that time is an imaginary number will appear. The representation space of the internal space-time of matter must be replaced by the Hilbert space with complex structure, and the Schrödinger equation describes the evolution of the internal space-time of matter from the perspective of observer coordinates (external space-time), in which the internal space-time is a complex number[1].

In the previous article[2], we made a space-time interpretation of the wave function: the real part and imaginary part of the wave function are respectively interrelated space waves and time waves. The complex wave function represents a space-time quantum unit entangled with time and space, which is a description of a space-time feature of matter or elementary particles. The wave functions distributed in space share time, clock synchronization and have corresponding conserved quantum numbers. The space-time interpretation of the wave function reveals the nature of time. We cannot "see" time in space, but we can feel time because time is an imaginary number, which is associated with space in the form of an imaginary number. The physical meaning expressed by time with the imaginary number unit i is: It not only indicates the particularity of time that is different from space, but also indicates that time can be entangled with space in a non-localized way. Quantum is not a point in space but a subregion in space-time. In this subregion, time waves and space waves form an entangled region (the distribution of wave function). This is reflected in the collapse of the wave function when measuring or interacting and the global integration and normalization of the wave function in the relevant quantum operations. Replacing the probability amplitude in space with the space-time amplitude can give a physical explanation of the collapse of the wave function, but the probability cannot. In fact, if the quantum particle is understood as a point in all processes, then it is inevitable to make a statistical probabilistic interpretation of the quantum wave function, which is actually a semi-classical interpretation of the quantum without abandoning the concept of particle points. One of the wonderful reasons why the probabilistic interpretation can be effective is that the space-time amplitude of a quantum is equivalent to the probability amplitude. On the other hand, the mathematical rotation characteristic of the imaginary number unit i corresponds to the unitary evolution of the wave function that physically describes a phase change, which means that a quantum time and space will transform each other, and this fundamental law of space-time transformation reveals the so-called " the First Cause" problem. The above two aspects ultimately come down to the indivisibility of time and space, which constitutes matter within a specific range, and we must express time as an imaginary number in order to be fully expressed. In statistical physics, replacing real time with imaginary time is called Wick rotation, and the introduction of imaginary numbers implies the introduction of non-localized quantum correlations. An important symbol of the transition from a quantum mechanical system to a classical mechanical system is that $i\hslash \to 0$ of the classical system, as a macroscopic inertial system constructed by the combination of quantum space-time, changes phase Angles rapidly in finite time t due to $\mathrm{L}/\hslash \to \infty$ in $e^{iS/\hslash }=e^{iLt/\hslash }$, which represents the transformation of space-time. The wave function propagating along any path makes space-time rapidly transform into each other, and the system becomes a mixture of space-time, which makes the wave property no longer obvious, and the coordinate transformation appears as the change of space-time length caused by the mutual transformation of time and space, and the correlation between time and space is only expressed in the constant four-dimensional interval. On the other hand, when $i\hslash \to 0$, the Schrödinger equation and the Dirac equation fail, the commutation relation of quantum operators becomes a classical relation, and the quantum effect of the whole system is no longer obvious. In this case, the space-time group does not need to consider the quantum characteristics. In addition, for a classical macroscopic system, the wave effect will be further weakened due to the collapse of the wave function due to frequent spontaneous interactions within the matter. However, for the microscopic system constructed by space-time, especially the elementary particles, $\mathrm{L}/\hslash$ is a finite number, so the phase angle changes slowly, and the continuous mutual transformation process between space-time and the non-local correlation between space-time will appear. The most appropriate way to express this entanglement of space-time is to express time as an imaginary number. To represent a quantum as a whole is to represent it as a complex number. In modern theory, the background space-time of the observer and matter is regarded as a four-dimensional Riemann manifold $\{M^4,g_{\mu ,\nu }\}$, the internal space-time of matter is regarded as the fiber bundles distributed on the base manifold $M^4$ where the observer resides, and the internal space-time structure group of the matter field and the interaction field is the gauge group. The base manifold and the Lie algebra of the gauge group together form fiber bundles, and the cross section of the fiber bundles projection map of space-time geometry is represented as a physically meaningful field: scalar field, vector field, spinor field, tensor field, etc., wherein the interaction field and matter field correspond to the principal bundles and associated bundles respectively, and the wave functions of the interaction field and matter field are described by a space-time fiber of the principal bundles and the associated bundles respectively. The space-time structure group of one-dimensional fiber bundles is $G_{em}=U\left(1\right)$, which describes the electromagnetic interaction. The space-time group of two-dimensional fiber bundles: $G_w=SU\left(2\right)$, which describes the weak interaction; The space-time structure group of three-dimensional fiber bundles is $G_s=SU\left(3\right)$, which describes the strong interaction. The group of space-time structures that unites the three standard models of interactions is the direct product of the three gauge groups: $G_{sm}=U\left(1\right)\otimes SU\left(2\right)\otimes SU\left(3\right)$. From this, we can see that all physical quantities, including the wave function, are a representation of the geometry of space-time inside matter. For example, when space-time is expressed as a wave function, the internal space-time of the Dirac spinor field $\psi ={({\psi }_1,{\psi }_2,{\psi }_3,{\psi }_4)}^T$ can be regarded as a 4-dimensional complex space $C^4$, and the wave function of x point on $M^4$ is a mapping: $\psi ：M^4\to M^4\times C_x^4，\forall x\in M^4$. For the Standard Model, the N-dimensional special unitary group describes N fermions, and the $(N^2-1)$-dimensional Lie algebra describes bosons. Field particles are irreducible unitary representations of the space-time group, that is, they are all represented as rotating state vectors in Hilbert space. Both the wave function and the Hilbert space have space-time properties. A point on the complex plane corresponding to any phase Angle of the state vector should be regarded as a space-time point in the space of bundles. The arbitrariness of the selection of the initial phase Angle corresponds to the arbitrariness of the selection of the space-time reference point. Therefore, we can think of special relativity as the space-time relativity principle expressed in Minkowski space and gauge invariance as the space-time relativity principle expressed in Hilbert space, and the space-time relativity principle does not change with the mapping of space.

Since the wave function, like other physical quantities, is a representation of space-time fibers, the continuous distribution of fiber bundles on the base manifold allows the four-dimensional space-time continuum to be described as a continuum of wave functions, with the Hilbert space embedded at every point in space-time on the $M^4$ manifold and the wave function ψ having any representation.According to the Feynman path integral principle, the wave function of any space-time point is the initial amplitude and initial phase determined by the initial wave function of all other space-time points on the manifold along infinite paths with the action $S\left[x\right]$ as the following functional integral: Since the wave function on each path can be regarded as a vector in H-space, the above integral is equivalent to the sum of all vectors, and the resulting vector must be a wave function in terms of the universal action S: The universal action S satisfies all space-time symmetries at this point. The action may be selected as follows: The integrable functional is Einstein-Hilbert, QED, GWS, QED, Dirac, and Klein-Gordon action densities, each of which determines a quantum correlation governed by time waves in equation (4). The field equation corresponding to the action can be derived from the principle of minimum action δS=0. It is noted that equation (4) is a representation of the transformation of space and time at any point on the $M^4$ manifold by the phase Angle φ=S/ℏ, so δφ=0 means that the universal field equation is the constraint of the transformation of space and time or the description of the law of the transformation of space and time. In addition, equation (4) also shows that at any point on the $M^4$ manifold, even the vacuum without matter or radiation, there are gravitational wave functions governed by the curvature of spacetime. These wave functions that evolve over time constitute the background spacetime of the universe, and the corresponding action is determined by the curvature R of spacetime: $S_G=\kappa \int R{\sqrt{-g}d}^{4}x$, if at time t the space scale of the universe is $a\left(t\right)$ and the mean curvature of spacetime is $R(t)$, then there is a gravity-dependent wave function ${\psi }_G$ that fills the whole universe satisfying the following equation: Because the curvature of spacetime is related to all matter, it is difficult to imagine the existence of a graviton filled with a total spacetime manifold, which means that it is confusing to understand gravity in terms of forces, which behave locally as a scalar and are quantized in a way such as formula (4). The background space-time of the universe is the gravitational connection of all matter, and a strictly flat space-time does not really exist.

To sum up, elementary particles and fields are space-time structures of complex manifolds, and the inherent property of space-time is group symmetry, so the group operation of space-time groups corresponds to some interaction in nature. For example, the space-time group defines a binary operation between two group elements that corresponds to the interaction between space-time, which contains the physical nature of the measurement and interaction, one of the most important interactions is the conjugate interaction between wave functions: ${\psi }^{*}\psi$, when measuring a Schrödinger system, the collapse of the wave function is described by the well-known equation ${\partial }_t{(\psi }^{*}\psi )=i\hslash \nabla ·{(\psi }^{*}\nabla \psi -\psi \nabla {\psi }^{*})/2m$, which also has an equation for measuring a Dirac system or other quantum systems. In this case, the wave function is a group element of the space-time group. As the basic space-time group in Minkowski space, the 10 generative elements of Poincare group give rise to the freedom and extensibility of space-time rotation and space-time translation. We think that matter is classified according to the 10 degrees of freedom of its internal spacetime, with 3 spatial rotation and 3 boost degrees of freedom generating visible matter, 3 spatial translation degrees of freedom generating dark energy, and 1 time translation degree of freedom generating dark matter. The general Poincare transformation can be expressed as: the group element of the corresponding space-time group is expressed as: In the above formula, $J^{\mu \nu }$ and $P^{\mu }$ are the group generators, ${\omega }_{\mu \nu }$ and $a_{\mu }$ are the space-time degrees of freedom corresponding to the generators. After the generator is defined as an observable physical quantity, the space-time group has the physical properties of matter, so that each term of the above equation represents the evolution and physical properties of a space-time unit. Since the above equations are induced based on the observer of matter, they are a basic description of the interaction field acting on matter. According to the space-time interpretation of the wave function, the quantum mechanical rules expressed by the above equation are also a representation of the internal quantized space-time of the interacting field in H-space. In order to simply describe the types of matter formed by the space-time degrees of freedom, we take the 10 kinds of quantized space-time units described by equation (7) and their conjugations as the basic units of space-time, and propose the principle of quantum space-time degrees of freedom aggregation, although this principle does not conform to the current research paradigm of physics and does not have specific operational details. But our aim is not to describe every elementary particle in detail, but to show by a reduced representation that the fundamental space-time geometry defines the basic types of matter that are made up of physical properties. First, note that each term to the right of equation (7) clearly has conjugate symmetries $G^{†}G=I, {\mathit{J}}^{†}=\mathit{J}, {\mathit{K}}^{†}=\mathit{K}, {\mathit{P}}^{†}=\mathit{P}$, and since both the field and equation have conjugate symmetries that make it impossible for the observer to distinguish bosons and their antiparticles, the interacting field particles without rest mass have no composite structure in the free state. The conjugate symmetry of its internal spacetime is its inversion symmetry. The 10 generators are reduced as follows: $\mathbf{J}\to \circlearrowright$, where the corresponding state is $\exp \left(-i\mathit{\theta }·\mathit{J}\right)=(\circlearrowright )$ and its inversion state is $\exp \left(i\mathit{\theta }·\mathit{J}\right)=(\circlearrowleft )={(\circlearrowright )}^{\mathbf{*}}$, where they represent the degrees of freedom of rotation $\pm \mathit{\theta }$ of space, which generates the angular momentum and magnetic properties of matter; $\mathit{K}\to \curvearrowleft$, corresponding state $\exp \left(-i\mathit{\varphi }·\mathit{K}\right)=(\curvearrowleft )$, and its inverse state $\exp \left(i\mathit{\varphi }·\mathit{K}\right)=(\curvearrowright )={(\curvearrowleft )}^{*}$, which represent the Lorentz boost, i.e. the degrees of freedom in spacetime rotation$\pm \mathit{\varphi }$, which generates the angular momentum and electromagnetic properties of matter; In a similar way, the spatial component of the third term on the right of equation (7) is reduced to: $\exp \left(-i\mathit{a}·\mathit{p}\right)=(\to ), \mathit{p}=-i\hslash \nabla$, and its inverse state is: $\exp \left(i\mathit{a}·\mathit{p}\right)=\left(\leftarrow \right)={(\to )}^{*}$, they represent the freedom of space translation $\pm \mathit{a}$, which generates the momentum of matter; The time components are reduced to $\exp \left(-i\tau ·E\right)=(⇢), E=i\hslash {\partial }_t$ and its inversion state is $\exp \left(i\tau ·E\right)=(⇠)$=${(⇢)}^{*}$, where they represent the degrees of freedom of time translation ±τ, which describes the energy of matter. There is a correspondence between the electromagnetic field and space-time: $(\mathit{A},i\varphi )\iff (\mathit{a},i\tau )$, thus it is inferred that the interaction field of the charged particle is space-time rotation, so the photon field is represented by: $(\gamma :\curvearrowleft )$, and the strong interacting gluon field is represented by: $\left(g^{\alpha }:\curvearrowleft \right), 1\le \alpha \le 8$. Secondly, the Higgs scalar boson that gives the weak interaction field mass and zero spin is represented by: $\left(H:⇢\right)$, the neutral Z boson is represented by: $(Z:\circlearrowright \bowtie ⇢)$, and the charged W boson is represented by: $(W^{+}:\curvearrowleft \bowtie ⇢) , (W^{-}:\curvearrowright \bowtie ⇠)$. Since the matter field particles have rest mass, their internal space-time must be some composite structure of the space-time basic unit expressed by formula (7), each space-time basic unit has energy, and their composite structure makes the matter field particles have rest mass. Considering that the matter field has a corresponding antimatter field, the internal space-time structure of the matter field should be the same as that of the antimatter field before evolution, and its initial structure corresponds to a unit of the space-time group under a certain parameter, so we represent the matter field by the aggregation of the interaction field and its inversion degrees of freedom. The interaction field between the charged particles is a space-time rotation, and the conjugate aggregation of this degree of freedom forms an indissoluble charged fermion and is expressed as: $(\curvearrowleft )\oplus (\curvearrowright )=(\curvearrowleft \bowtie \curvearrowright )$，the internal space-time reduction of an electron is expressed as:$({\mathrm{e}}^{-}:\curvearrowleft \bowtie \curvearrowright ),({\mathrm{e}}^{+}:\curvearrowright \bowtie \curvearrowleft )$，the internal space-time reduction of quarks is expressed as:$(\mathrm{u}:\curvearrowleft \bowtie \curvearrowright ),(\mathrm{d}:\curvearrowright \bowtie \curvearrowleft )$，the spinor field with left-handed spin and right-handed spin is reduced to: $\mathsf{\psi }={[{(\curvearrowleft \bowtie \curvearrowright )}_{\mathrm{R}},{(\curvearrowleft \bowtie \curvearrowright )}_{\mathrm{L}},{(\curvearrowright \bowtie \curvearrowleft )}_{\mathrm{R}},{(\curvearrowright \bowtie \curvearrowleft )}_{\mathrm{L}}]}^{\mathrm{T}}$.Space rotation conjugate aggregate is expressed as:$\left(\circlearrowright \right)\oplus (\circlearrowleft )=(\circlearrowright \bowtie \circlearrowleft )$，it makes up the internal space-time degrees of freedom of electrically neutral spin particles like neutrinos, the internal space-time of neutrinos is reduced to:$(\upsilon :\circlearrowright \bowtie \circlearrowleft ), \left(\overline{\upsilon }:\circlearrowleft \bowtie \circlearrowright \right)$. Conjugate aggregation of spatial translation: $\left(\to \right)\oplus (\leftarrow )=(\to \bowtie \leftarrow )$, the freedom of space-time inside dark energy is described: $(DE:\to \bowtie \leftarrow )$. Conjugate aggregation of time translation: $\left(⇢\right)\oplus (⇠)=(⇢\bowtie ⇠)$, describing the internal space-time degrees of freedom of the dark matter field: $\left(DM:⇢\bowtie ⇠\right)$. If the universe starts from a singularity without space scale, then it must start from the one DOF of time translation, that is, the universe starts from the only symmetry -- time inversion symmetry. Considering the entangled nature of time, it is assumed that the universe begins with a huge number of entangled time translation units, i.e.,${\oplus }_{i=1}^N{(⇢\bowtie ⇠)}_i$, N is a huge number, each unit corresponds to a quantized energy, and the sum of the energies corresponding to all translation operators is the total energy of the universe. These operators start the evolution of the cosmic time scale, which is also consistent with our common sense, because all matter operates in the time dimension. After that, some of the time translation degrees of freedom are derived into other degrees of freedom and energy is conserved, and the entanglement between the derived degrees of freedom is maintained through the space-time curvature R, and this unbreakable space-time entanglement is called gravity. Two points need to be emphasized here: first, time and space always abide by the law of mutual transformation, even after it is derived into other space-time quantum modes, time and space still periodically transform each other in a way of entanglement, which means that they always have to be expressed in the form of a wave function; The basic property of space-time entanglement comes from the entanglement of time, so space-time entanglement contains the essence of quantum entanglement, but for independent quantum without quantum entanglement, its internal space-time is still entangled, and gravitational entanglement is included in the space-time entanglement described in formula (4). The derivation of time translation degrees of freedom to other degrees of freedom is expressed as: $\left(⇢\right)\Rightarrow \left(\curvearrowleft \right),\left(\circlearrowright \right),\left(\to \right)$. Due to the high energy state of the universe, some space-time degrees of freedom and their derived degrees of freedom are aggregated, and all kinds of matter formed so far are divided into visible matter, dark energy and dark matter. These substances then undergo general aggregation with non-fixed combinations of degrees of freedom such as spatial translation and spatial rotation, providing their external space-time properties such as external momentum and angular momentum. Therefore, we reduce the space-time freedom inside various substances to:

Visible matter: $(\circlearrowright \bowtie \circlearrowleft )\oplus (\curvearrowleft \bowtie \curvearrowright )\oplus (\circlearrowright )\oplus \left(\curvearrowleft \right)\oplus \left(\to \right)\cdots ,\mathit{a}\mathit{l}\mathit{l}\in \left(⇢\right)\mathit{o}\mathit{r}(⇠)$;

Dark matter: $(⇢\bowtie ⇠)\oplus (\circlearrowright )\oplus \left(\curvearrowleft \right)\oplus \left(\to \right)\cdots ,\mathit{a}\mathit{l}\mathit{l}\in \left(⇢\right)\mathit{o}\mathit{r}(⇠)$;

Dark Energy: $(\to \bowtie \leftarrow )\oplus (\circlearrowright )\oplus \left(\curvearrowleft \right)\oplus \left(\to \right)\cdots ,\mathit{a}\mathit{l}\mathit{l}\in \left(⇢\right)\mathit{o}\mathit{r}(⇠)$.

Dark energy decay: $(\to \bowtie \leftarrow )\Rightarrow \left(\to \right)+\left(\leftarrow \right)$, dark energy decays into kinetic energy, causing the momentum of other matter in the universe to increase, making the universe expand. This decay will lead to the decay process of visible matter beyond the influence of the standard model, which can be verified by observing the decay anomaly of visible matter[3].

The above analysis shows that dark matter and dark energy obey Poincare symmetry, and they can be described as the vector field of the third term on the right of equation (7). Since this vector field shows isotropy, it can be expressed as the derivative of the scalar field. One scheme of this attempt is to add a covariant derivative of the scalar field φ to the right end of the Einstein field equation[4]： in this equation, the covariant differential of the scalar field represents dark matter and dark energy. Since their energy is positively definite, they affect the geometry of space-time in the same way as the energy-momentum tensor of ordinary matter, and the decay of dark energy may be an intrinsic mechanism for the expansion of the universe.

The matter field at the base manifold where the observer lives is a cross section of the associated bundles, the wave function is the mapping of the internal spacetime of matter on the base manifold, there are spacetime degrees of freedom inside the elementary particles, and the inversion symmetry of the observer spacetime cannot cover the internal spacetime symmetry properties. Since we interpret the electromagnetic field, spin, and charge as the internal spacetime of matter, it is inevitable that the symmetry of the electromagnetic field and charge is determined by the symmetry of their internal spacetime, through the following analysis we show that the conjugate symmetry $𝒞$ of charges is actually the internal time inversion symmetry $\mathcal{T}i$ of charged particles: $\mathcal{C}=\mathcal{T}i$. It has been pointed out above that the time of the field equation is based on the observer time, that is, the external time of matter, and the imaginary part of the wave function represents time, therefore, the equation satisfied after the conjugate of the wave function (imaginary part becomes negative) is the inverse equation of the time of quantum mapping to the outside, and the conjugate treatment of the wave function, Schrodinger equation or Dirac equation means the inversion of the mapping time. Consider the Dirac equation and conjugate equation of a charged spinor particle moving in the electrostatic field $V_{\left(\mathit{X}\right)}$: Here, $x_{\mu }=\left(x,y,z,it\right),c=\hslash =1$, and T represents the transpose of the matrix. There exists a 4-4 matrix $\mathcal{T}$ and its inverse matrix ${\mathcal{T}}^{-1}$, and the following conditions are met: The conjugate equation (10) returns to equation (9) through the transformation of equation (11), which is actually the inversion of the external time of spinor particles. According to the aforementioned degrees of freedom aggregation model, the reduction is expressed as: $\mathcal{T}\left(\curvearrowleft \bowtie \curvearrowright \right)={\left(\curvearrowleft \bowtie \curvearrowright \right)}^{*}$. We believe that the matrix that can express the freedom of time inside the charge is γ₄, which is derived from the Hamiltonian of the Dirac equation: $H=c\mathit{\alpha }·\mathit{p}+m{c}^2\beta$. The value ${\gamma }_4=\beta =\pm 1$ gives the charge a DOF independent of external time, which can be seen to be valid even when the charge is at rest. When ${\gamma }_4=-1$, the time inside the charge is reversed and the polarity of the charge changes, the corresponding so-called negative energy state should be interpreted as a positive energy time inversion state. In fact, the energy and mass of antimatter observed in the laboratory are actually positive definite, and its gravitational effect is the same as that of ordinary matter[5]. The transformation that can express the inversion of internal time of charges is the charge conjugation transformation $𝒞$ in QFT, which has a 4-4 matrix $\mathcal{C}$ and its inverse matrix ${\mathcal{C}}^{-1}$, satisfying the following conditions: By transforming eq. (12), eq. (10) can be obtained as follows: Eq. (13) reverts to the form of eq. (9) except that charge e changes polarity, so we think that the conjugate symmetry of charge is equivalent to the inverse symmetry of the internal time of charge, expressed by the DOF aggregation symbol: $\mathcal{C}\left(e^{-}:\curvearrowleft \bowtie \curvearrowright \right)={\mathcal{T}}_i\left(e^{-}:\curvearrowleft \bowtie \curvearrowright \right)=\left(e^{+}:\curvearrowright \bowtie \curvearrowleft \right)$, which means that the charge of the internal time and mapped to the external joint inversion.

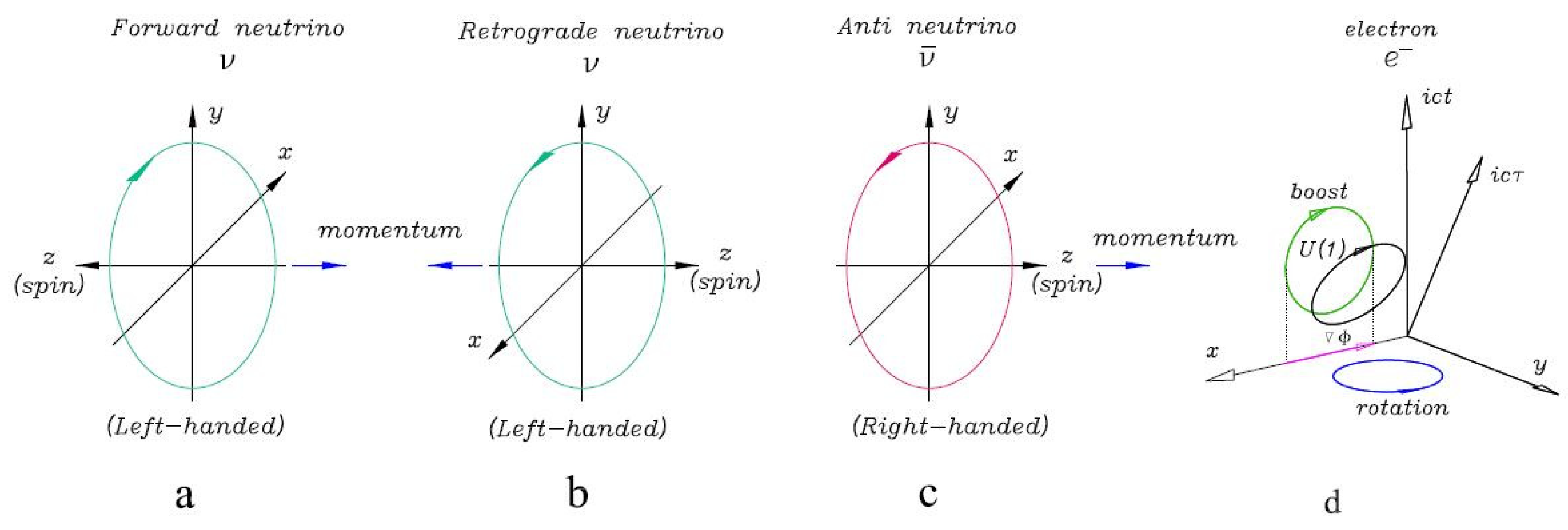
In the following, we make a brief analysis of the spin orientation of spinor matter using the internal space-time freedom of matter. Fig. 1 shows the projection mapping of the internal spacetime rotation of neutrinos ν, antineutrino $\overline{\nu }$ and electron $e^{-}$ to the external coordinates. As a neutrino ν aggregated by the mutually conjugate spatial rotation DOF, we are always able to align the inner spatial rotation plane of the neutrino to the x-y plane of the outer coordinates as shown in Fig. 1.a. According to the definition of angular momentum, the spin axis of the neutrino must be in the z direction, assuming that we observe that the neutrino is left-handed, then the spin z direction is opposite to the direction of the momentum p, that is, a forward moving neutrino has a negative spin on the p axis.

If we reverse the space of a forward moving neutrino into a regressive neutrino with the same observer perspective, we should pay special attention to the fact that this situation appears inconsistent with the "mirror image" result, because the neutrino's spin constraint is in its internal plane determined by the two spatial directions x and y, and the plane will flip when reversed, as shown in Figure 1.b. A retroactive neutrino is equivalent to rotating the coordinate frame in Figure 1.a around the y axis by 180°, and the internal z axis of the neutrino is reversed with the x axis, so the neutrino's left spin chirality will remain unchanged, and its spin direction will still be given according to the definition of angular momentum, and cannot only refer to the direction of the rotation arrow, in fact, only the projection of the spin in the momentum direction is observable. From this, it can be seen that neutrinos are aggregated by conjugated space rotation degrees of freedom, and space rotation is a constraint on two spatial directions. Unless time is reversed, neutrinos can only take one spin direction, which may be the inherent mechanism of non conservation of neutrino parity. When time is reversed, the motion directions of Figures 1.a and 1.b are reversed, as shown in Fig. 1.c, and the spins of all antineutrinos $\overline{\nu }$ become right-handed. For charged particles, because their internal spacetime is a spacetime rotation of one-dimensional space plus one-dimensional time, there is only one spatial direction constraint, as shown in Fig. 1.d. If the constrained spatial direction of a spinor particle with internal space-time U(1) is aligned with the observer coordinate x, taking into account the relative motion of internal space-time and observer space-time, there is an Angle difference between the internal time axis icτ and the observer time axis ict, and the spatial rotation direction projected onto the observer x-y plane determines the spin direction. The direction of the boost (spacetime rotation) projected onto the observer's x-ict plane determines the charge polarity, and the internal spatial axes of the charged spinor, y' and z' are not constrained, so the spin can have two directions.

Based on the above analysis of the freedom of space-time inside the charge and neutrino, it can be concluded that when the internal space-time of the spinor field is projected into the outer space, the spatial rotation shown corresponds to the magnetic properties of the matter, and the spacetime rotation shown corresponds to the electromagnetic properties of the matter.

The above principle of space-time freedom aggregation is only a tentative reduction. Because the mechanism of quantum space-time aggregation inherent in matter is not clear, some degrees of freedom can be exchanged with each other, that is, the aggregation is not fixed, for example, the spatial translation degree of freedom that generates momentum. There are also some aggregations at high energy levels to form structurally unstable matter particles with decay properties, etc., so we are only proposing an enlightening view here. In QFT, the spinor field can be directly described as the representation of Poincare group. Two spinor wave functions are used to form the field freedom of the tensor field, for example, $\overline{\varphi }\psi$ constitutes the scalar,$i{\overline{\varphi }\gamma }_{\mu }\psi$ constitutes the vector, $\overline{\varphi }{\sigma }_{\mu \upsilon }\psi$ constitutes the second-order antisymmetric tensor, etc. A precise description of all elementary particles in terms of the degree of freedom of space-time inside matter remains to be studied further.

The basic point we want to express in this article is that spacetime is not only the background that provides the movement and change of matter, it is also the fundamental element of the structure of matter. Matter is the geometric structure of spacetime. The flowing spacetime always appears as a group property, and the spacetime group of visible matter is represented as a gauge group. This means that the particle physics standard model that unifies the three basic interactions in nature is the internal spacetime representation of matter. On the other hand, in general relativity, the material energy momentum tensor at the right end of the gravitational field equation is equal to the spacetime structure at the left end of the equation, and the physical properties of matter are equivalent to the geometry of spacetime, so the quantization of matter particles and fields also means the quantization of spacetime, and the theory describing matter will be unified with the theory describing spacetime. Tracing the invariance of physical laws to the symmetry of spacetime is undoubtedly one of the important discoveries of modern physics. Of course, any description of objective matter cannot replace itself. However, based on the belief that the laws of the universe follow the principles of knowability and logical simplicity, the author proposes a preliminary viewpoint in this article, with the aim of developing a more comprehensive theory about matter and spacetime in the future.