Prerpints.org logo
Preprint
Article

Info-Geometric Analysis of the Dynamics of Parthasarathian Transient Solution of M/M/1 Queue Manifold with Info-Geometric Applications to Machine Learning

Altmetrics

Downloads

76

Views

15

Comments

0

This version is not peer-reviewed

Submitted:

26 January 2024

Posted:

29 January 2024

You are already at the latest version

Alerts
Abstract
The current study characterizes the transient M/M/1 queue manifold info-geometrically, through devising Fisher Information matrix(FIM) and its inverse(IFIM). Additionally, the impact of stability on the existence of IFIM and explore the geodesic equations of motion has been revealed. More potentially, the paper discusses some info-geometric applications to Machine Learning are highlighted. Closing remarks with some challenging open problems combined with the next phase of research are given.
Keywords: 
Subject: Computer Science and Mathematics  -   Applied Mathematics

1. Introduction

Numerous study areas, including statistical sciences, have extensively used IG [1]. In other words, the goal of IG is to use statistics to apply the methods of differential geometry (DG), which indicates the major goal of IG is to use stochastic processes and probability theoretic in the applications of methodologies of non-Euclidean geometry.
A manifold is a topological finite-dimensional Cartesian space,   ℝ n , in which an infinite-dimensional manifold exists[2]. Additionally, IG supports SMs’ descriptions that are based on intuitive reasoning. One might have a greater understanding of the crucial significance of IG[3,4].
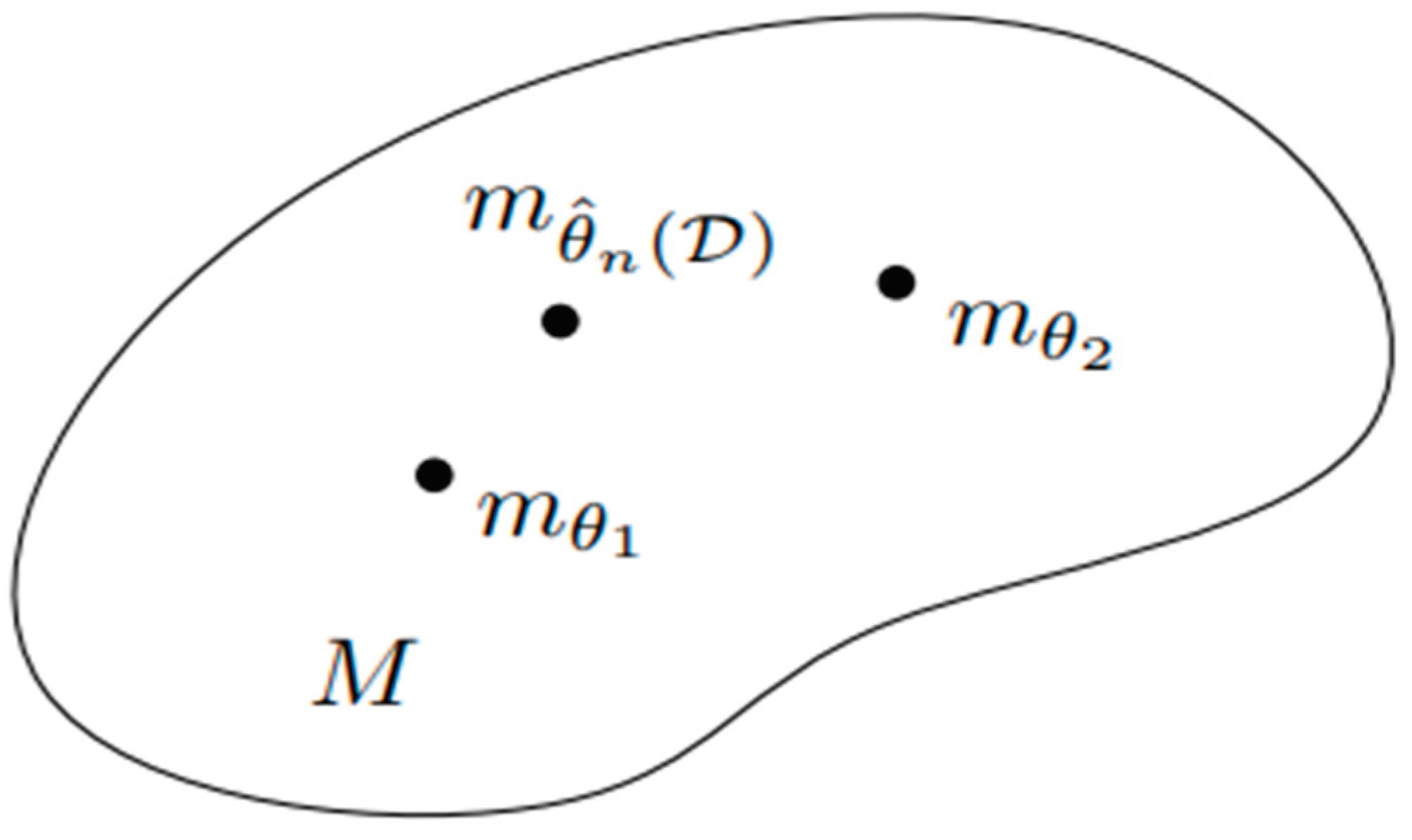
Parametrization of a Statistical Manifold (SM) is visualized by Figure 1 [4].
According to the literature, a paper by[5] examined info-geometrically the stable M/D/1 queue based on queue length routes ‘characteristics, was the real motivator for the current study.
The main deliverables of this paper are described below.
  • The discovery of the FIM and its inverse for the transient M/M/ 1 queue.
  • Revealing the new discovery of the geodesic equations of motion of the coordinates of the transient M/M/ 1 queue.
  • In the context of the research paper, a novel α-connection [6] is introduced, which maps each coordinate to a value.
  • Highlighting potential IG applications to ML.
The remainder of the paper is divided into the following sections: Preliminary IG definitions are given in Section II. The transient M/M/1 QM’s FIM and it IFIM are introduced in Section III. While Section IV gives the Information Geometric Equations of Motion (IMEs) for the coordinates of the transient M/M/1 QM. Section V addresses IG applications to ML. Section VI wraps up the paper and provides some challenging open problems combined with further research.

2. Main IG Definitions

1 Statistical Manifold (SM)
M = { p ( x , θ ) | θ ϵ Θ } is called an SM[7]if x is a random variable in sample space X and p ( x , θ ) is the probability density function, which satisfies certain regular conditions. Here, θ = ( θ 1 , θ 2 , .. , θ n ) ϵ Θ is an n-dimensional vector in some open subset Θ ⊂ ℝ n , and θ can be viewed as the coordinates on manifold M.
2 Potential Function
The potential function Ψ ( θ ) [7] is the distinguished negative function of the coordinates alone of ℒ ( x ; θ ) = l n ( p ( x ; θ ) ) )
3 Fisher’s Information Matrix(FIM)
FIM, namely [ g i j ] reads as:
[ g i j ] = [ ∂ 2 ∂ θ i ∂ θ j ( Ψ ( θ ) ) ] ,   i , j = 1 , 2 , .. , n
with respect to natural coordinates.
4 IFIM
Given the FIM, the inverse matrix of [ g i j ] is defined by[7]
  [ g i j ] = ( [ g   i j ] )   ) − 1 = a d j [ g i j ] Δ ,   Δ = det [ g i j ]  
5  α -Connection
For each α ϵ ℝ ,   the α (or ∇ ( α ) )-connection [6] is the torsion-free affine connection with components:
Γ i j , k ( α ) = ( 1 − α 2 ) ( ∂ i ∂ j ∂ k ( Ψ ( θ ) ) )
where Ψ ( θ ) is the potential function and ∂ i = ∂ ∂ θ i .
6 Geodesic equations of motion
(1)The geodesic equations of manifold M with coordinate system θ = ( θ 1 , θ 2 , .. , θ n ) read as [7]
d 2 θ k d t 2 + Γ i j k ( 0 ) ( d θ i d t ) ( d θ j d t ) = 0 , i , j = 1 , 2 , … , n ,   Γ i j k ( α ) = Γ i j , s ( α ) g s k
By the above definition, the geodesic equations are interpreted physically as the information geometric equations of motion , shortly (IGEMs), or the relativistic equations of motion (REMs) , or the Riemannian equations of motion. At this stage, the current study provides a ground- breaking discovery of the IG analysis of transient queueuing systems in comparison to that of non-time dependent queueing systems, namely IG analysis of stable queues[8,9].

3. Fim And IFIM of the Transient M/M/1QM

A single-channel model with exponential inter-arrival times, service times, and FIFO queue discipline is the simplest probabilistic queueing model that can be addressed analytically. In queueing theory, this is referred to as the M/M/1 queue [10].
Based on the introduction of the function, Parthasarathy[10] suggested a straightforward method for the transient solution of the M/M/1 system to read as
  p n ( t ) = ρ p 0 ( t ) e − ( λ + μ ) t [ ∑ m = 1 n r m ( t ) + e ( λ + μ ) t ]   ,   n = 0 , 1 , 2 , … .  
where λ   stands for the mean rate per unit time at which arrival instants occur, μ is the mean rate of service time, ρ = λ ( t ) μ ( t ) defines the traffic intensity or utilization factor,
r n ( t ) = (   μ β 2 n − a 1 ( 1 − δ 0 a 1 ) [ I n − a 1 ( β 1 t ) − I n + a 1 ( β 1 t ) ] +
λ β 2 n − 1 − a 1 ( I n + 1 − a 1 ( β 1 t ) − I n − 1 − a 1 ( β 1 t ) ) )
with   β 1 = 2 λ μ   ,   β 2 = 2 λ μ , I n ( x ) [19] is the modified Bessel function and
p 0 ( t ) = ∫ 0 t r 1 e − ( λ + μ ) y d y + δ 0 a 1
Theorem 1.
The underlying queue of (5) has:
(i) FIM reads as
[ g i j ] = [ a b c b 0 h c h l ]  
where
a = 1 ρ 2 − 1 ( 1 − ρ ) 2
b = t  
c = ρ . ρ 2 + ρ . ( 1 − ρ ) 2 + t μ . + μ ρ .
h = ( 1 + ρ ) + t ρ .
l = (   ρ .2 − ρ ρ .. ρ 2 + ρ .2 + ( 1 − ρ ) ρ .. ( 1 − ρ ) 2 +
( ( 1 + ρ ) t μ .. + μ + 2 ρ . μ . + 2 μ ρ . + 2 ρ μ . + μ t ρ .. )
Δ = d e t ( [ g i j ] ) = ( a ( − h 2 ) − b ( b l − c h ) + c ( b h ) )  
Provided that, . refers to the temporal derivative  d d t .
(ii) [ g i j ] reads as
  [ g i j ] = a d j [ g i j ] Δ = [ A B L B E F L F H ]
where
A = ( − h 2 ) Δ
B = ( c h − b l ) Δ
L = ( b h ) Δ
E = ( a l − c 2 ) Δ
F = ( b c − a h ) Δ
H = ( − b 2 ) Δ
Proof. 
(i) Following (5), we have:
ℒ ( x ; θ ) = l n ( p n ( x ; θ ) ) = ( l n ( ρ p 0 ( t ) e − ( λ + μ ) t ) +
l n ( ρ p 0 ( t ) e − ( λ + μ ) t [ ∑ m = 1 n r m ( t ) + e ( λ + μ ) t ]   )  
θ = ( θ 1 ,   θ 2 , θ 3 ) = ( ρ , μ , t )  
We have
Ψ ( θ ) = − l n ( ρ ) − l n ( 1 − ρ ) + μ ( 1 + ρ ) t ,  
p 0 ( t ) = 1 − ρ
Thus,
∂ 1 = ∂ Ψ ∂ ρ = − 1 ρ + 1 ( 1 − ρ ) + μ t ,   ∂ 2 = ∂ Ψ ∂ μ = ( 1 + ρ ) t ,   ∂ 3 = ∂ Ψ ∂ t = − ρ . ρ + ρ . ( 1 − ρ ) + ( 1 + ρ ) t μ .   + μ ( 1 + ρ ) + μ t ρ .
∂ 1 ∂ 1 = 1 ρ 2 − 1 ( 1 − ρ ) 2  
∂ 1 ∂ 2 = ∂ 2 ∂ 1 = t  
∂ 2 ∂ 2 = 0
∂ 1 ∂ 3 = ρ . ρ 2 + ρ . ( 1 − ρ ) 2 + t μ . + μ ρ . = ∂ 3 ∂ 1
∂ 2 ∂ 3 = ( 1 + ρ ) + t ρ . = ∂ 3 ∂ 2
∂ 3 ∂ 3 = ( ρ .2 − ρ ρ .. ρ 2 + ρ .2 + ( 1 − ρ ) ρ .. ( 1 − ρ ) 2 +
( 1 + ρ ) t μ .. + μ + 2 ρ . μ . + 2 μ ρ . + 2 ρ μ . + μ t ρ .. )
Therefore, the Fisher Information Matrix, FIM, is obtained (c.f., (7)).
[ g i j ] reads as:
[ g i j ] = [ g i j ] − 1 = a d j [ g i j ] Δ = T r a n s p o s e ( C o v [ g i j ] ) Δ =
1 Δ t r a n s p o s e ( C o v [ a b c b 0 h c h l ] )
= [ ( − h 2 ) ( c h − b l ) ( b h ) ( c h − b l ) ( a l − c 2 ) ( b c − a h ) ( b h ) ( b c − a h ) ( − b 2 ) ]
Thus,
[ g i j ] = 1 Δ t r a n s p o s e ( C o v [ ( − h 2 ) ( c h − b l ) ( b h ) ( c h − b l ) ( a l − c 2 ) ( b c − a h ) ( b h ) ( b c − a h ) ( − b 2 ) ] ) = [ A B L B E F L F H ]
as requested,
It is notable that FIM should satisfy the symmetry requirement.
In what follows, the components of α   (or ∇ ( α ) )- connection are obtained. These calculated expressions are needed to obtain the corresponding Geodesic Equations (GEs) of the parametric coordinates of M/M/1 QM.
From (3), the reader can check that
Γ 11 , 1 ( α ) = − ( 1 − α ) ( 1 ( 1 − ρ ) 3 + 1 ρ 3 )
0 = Γ 22 , 2 ( α ) = Γ 12 , 2 ( α ) = Γ 22 , 1 ( α ) = Γ 21 , 2 ( α ) = Γ 11 , 2 ( α ) = Γ 12 , 1 ( α ) = Γ 21 , 1 ( α ) = Γ 22 , 3 ( α ) = Γ 23 , 2 ( α ) =   Γ 32 , 2 ( α )
Γ 31 , 1 ( α ) = ( 1 − α ) ρ . ( 1 ( 1 − ρ ) 3 − 1 ρ 3 )
Γ 13 , 1 ( α ) = Γ 11 , 3 ( α ) = (   1 − α ) ρ . ( 1 ( 1 − ρ ) 3 − 1 ρ 3 )
Γ 13 , 2 ( α ) = Γ 12 , 3 ( α ) = ( 1 − α ) 2
Γ 13 , 3 ( α ) = ( 1 − α ) 2 [ ρ .. ρ 2 + ρ .. ( 1 − ρ ) 2 + 2 ρ .2 ( 1 − ρ ) 3 + t μ .. + 2 μ . ]  
Γ 23 , 1 ( α ) = Γ 21 , 3 ( α ) = ( 1 − α ) ρ . 2
Γ 23 , 3 ( α ) = ( 1 − α ) ( 1 + 2 ρ . + t ρ .. ) 2
Γ 31 , 2 ( α ) = Γ 32 , 1 ( α ) = ( 1 − α ) 2
Engaging the same procedure, the remaining components can be determined.

4. The IGMES of the Coordinates of the Transient M/M/1 QM

A. The  I M E s  of the  s e r v e r   u t i l i z a t i o n    coordinate,  ρ    of the transient M/M/1 QM
The IMEs corresponding to the arrival   rate   coordinate, ρ   of the transient M/M/1 QM are:
d 2 θ 1 d t 2 + Γ i j 1 ( 0 ) ( d θ i d t ) ( d θ j d t ) = 0 , i , j = 1 , 2 , 3
Now, we are in a situation of trying to find the path of motion of family of families of IMEs corresponding to the server utilization coordinate, ρ .
[ d 2 ρ d t 2 + [ L 2 + L ρ . 2 ] ( d ρ d t ) ( d μ d t )   + [ 1 2 ( 2 A ρ . ( 1 ( 1 − ρ ) 3 − 1 ρ 3 ) +   B + L [ ρ .. ρ 2 + ρ .. ( 1 − ρ ) 2 + 2 ρ .2 ( 1 − ρ ) 3 + t μ .. + 2 μ . ] ) +
1 2 ( 2 A ρ . ( 1 ( 1 − ρ ) 3 − 1 ρ 3 ) + B +   ( ρ ρ .. − 2 ρ .2 ρ 3 + 2 ρ .2 + ( 1 − ρ ) ρ .. ( 1 − ρ ) 3 +
t μ .. + ρ . μ . + μ . + μ ρ .. L ) ) ] ( d ρ d t ) ( d t d t ) + [ ρ . L ( 1 ( 1 − ρ ) 3 − 1 ρ 3 ) ] ( d ρ d t ) 2 +
[ 1 2 ( A ρ . + B ( 1 + 2 ρ . + t ρ .. ) ) + 1 2 ( A   + ( ρ . + t ρ .. ) L ) ] ( d μ d t ) ( d t d t ) +
  [   1 2 ( (   ρ ρ .. − 2 ρ .2 ρ 3 + 2 ρ .2 + ( 1 − ρ ) ρ .. ( 1 − ρ ) 3 + t μ .. + ρ . μ . + μ . + μ ρ .. ) A + ( ρ . + t ρ .. ) B + [ ( ρ . ρ .. − ρ ρ … ) ρ − 2 ρ . ( ρ .2 − ρ ρ .. ) ρ 3 + ( ρ . ρ .. + ( 1 − ρ ) ρ … ) ( 1 − ρ ) + 2 ρ . ( ρ .2 + ( 1 − ρ ) ρ .. ) ( 1 − ρ ) 3 +
( 1 + ρ ) t μ ... + ( 1 + ρ ) μ .. + 3 ρ . μ .. + μ . + 2 ρ .. μ . + 2 μ ρ .. +
4 μ . ρ . + 2 ρ μ .. + μ t ρ ... + μ ρ .. + μ . t ρ .. ] L ) ]   ( d t d t ) 2 ] = 0
It can be verified that one of the closed form solutions of (40) is determined by the paths of motion:
ρ ( t ) = c o n s t a n t , μ ( t ) = c o n s t a n t  
such that
ρ ∈ ( 0 , 1 ) ,   μ > 1  
B. The  I M E s  of the  M e a n   s e r v i c e   R a t e  coordinate,  μ    of the transient M/M/1 QM
The IMEs of μ   , of the transient M/M/1 QM are
d 2 θ 2 d t 2 + Γ i j 1 ( 0 ) ( d θ i d t ) ( d θ j d t ) = 0 , i , j = 1 , 2 , 3
Now, we are in a situation of trying to find the path of motion of family of families of IMEs corresponding to the mean service rate, μ .
[ d 2 μ d t 2 + [ F 2 + F ρ . 2 ] ( d ρ d t ) ( d μ d t )   + [ 1 2 ( 2 B ρ . ( 1 ( 1 − ρ ) 3 − 1 ρ 3 ) + E + F [ ρ .. ρ 2 + ρ .. ( 1 − ρ ) 2 + 2 ρ .2 ( 1 − ρ ) 3 + t μ .. + 2 μ . ] ) +
1 2 ( 2 B ρ . ( 1 ( 1 − ρ ) 3 − 1 ρ 3 ) + E +   ( ρ ρ .. − 2 ρ .2 ρ 3 + 2 ρ .2 + ( 1 − ρ ) ρ .. ( 1 − ρ ) 3 + t μ ..
+ ρ . μ . + μ . + μ ρ .. )   F ) ] ( d μ d t ) ( d t d t ) + [ ρ . ( 1 ( 1 − ρ ) 3 − 1 ρ 3 ) F ] ( d ρ d t ) 2 +
[ 1 2 ( B ρ . + E ( 1 + 2 ρ . + t ρ .. ) ) + 1 2 ( B   + ( ρ . + t ρ .. ) F ) ] ( d ρ d t ) ( d t d t ) +
  [   1 2 ( (   ρ ρ .. − 2 ρ .2 ρ 3 + 2 ρ .2 + ( 1 − ρ ) ρ .. ( 1 − ρ ) 3 + t μ .. + ρ . μ . + μ . + μ ρ .. ) B +
( ρ . + t ρ .. ) E + [ ( ρ . ρ .. − ρ ρ … ) ρ − 2 ρ . ( ρ .2 − ρ ρ .. ) ρ 3 + ( ρ . ρ .. + ( 1 − ρ ) ρ … ) ( 1 − ρ ) + 2 ρ . ( ρ .2 + ( 1 − ρ ) ρ .. ) ( 1 − ρ ) 3 +
( 1 + ρ ) t μ ... + ( 1 + ρ ) μ .. + 3 ρ . μ .. + μ . + 2 ρ .. μ . + 2 μ ρ .. + 4 μ . ρ . + 2 ρ μ .. + μ t ρ ... + μ ρ .. + μ . t ρ .. ] F   )   ]   ( d t d t ) 2 ] = 0
Let ρ = constant ,   then   ( 42 ) reduces   to  
[ d 2 μ d t 2 + [ 1 2 (   E + F [ t μ .. + 2 μ . ] ) + E +   ( t μ .. + μ . )   F ) ] ( d μ d t ) + [   1 2 ( (   t μ .. + μ . ) B +
[ ( 1 + ρ ) t μ ... + ( 1 + ρ ) μ .. + μ . + 2 ρ μ .. ] F   )   ]   ] = 0
Δ = d e t ( [ g i j ] ) =
( ( 1 ρ 2 − 1 ( 1 − ρ ) 2 ) ( − ( ( 1 + ρ ) ) 2 ) − ( t 2 [ ( ( 1 + ρ ) t μ .. + μ + 2 ρ μ . ] ) )
B = ( t μ . ( 1 − ρ ) − t [ ( ( 1 + ρ ) t μ .. + μ ] ) Δ =
( t μ . ( 1 − ρ ) − t [ ( ( 1 + ρ ) t μ .. + μ ] ) ( ( 1 ρ 2 − 1 ( 1 − ρ ) 2 ) ( − ( ( 1 + ρ ) ) 2 ) − ( t 2 [ ( ( 1 + ρ ) t μ .. + μ + 2 ρ μ . ] ) )  
E = ( a l − c 2 ) Δ =
( ( 1 ρ 2 − 1 ( 1 − ρ ) 2 ) [   ( ( 1 + ρ ) t μ .. + μ + 2 ρ μ . ] − ( t μ . ) 2 ) ( ( 1 ρ 2 − 1 ( 1 − ρ ) 2 ) ( − ( ( 1 + ρ ) ) 2 ) − ( t 2 [ ( ( 1 + ρ ) t μ .. + μ + 2 ρ μ . ] ) )
F = ( b c − a h ) Δ = ( t ( t μ . ) − ( 1 ρ 2 − 1 ( 1 − ρ ) 2 ) ( 1 + ρ ) ) ( ( 1 ρ 2 − 1 ( 1 − ρ ) 2 ) ( − ( ( 1 + ρ ) ) 2 ) − ( t 2 [ ( ( 1 + ρ ) t μ .. + μ + 2 ρ μ . ] ) )
Thus,
[ d 2 μ d t 2 + [ 1 2   ( ( 1 ρ 2 − 1 1 − ρ 2 ) [   ( 1 + ρ t μ . . + μ + 2 ρ μ . ] − t μ . 2 ) 1 ρ 2 − 1 1 − ρ 2 − 1 + ρ 2 − t 2 [ ( 1 + ρ t μ . . + μ + 2 ρ μ . ] + ( t ( t μ . ) − ( 1 ρ 2 − 1 1 − ρ 2 ) 1 + ρ ) ( 1 ρ 2 − 1 ( 1 − ρ ) 2 ) − ( 1 + ρ ) 2 − t 2 [ ( 1 + ρ t μ . . + μ + 2 ρ μ . ] t μ . . + 2 μ . +
( t ( t μ . ) − ( 1 ρ 2 − 1 ( 1 − ρ ) 2 ) ( 1 + ρ ) ) ( ( 1 ρ 2 − 1 ( 1 − ρ ) 2 ) ( − ( ( 1 + ρ ) ) 2 ) − ( t 2 [ ( ( 1 + ρ ) t μ .. + μ + 2 ρ μ . ] ) ) +
  ( t μ .. + μ . )   ( t ( t μ . ) − ( 1 ρ 2 − 1 ( 1 − ρ ) 2 ) ( 1 + ρ ) ) ( ( 1 ρ 2 − 1 ( 1 − ρ ) 2 ) ( − ( ( 1 + ρ ) ) 2 ) − ( t 2 [ ( ( 1 + ρ ) t μ .. + μ + 2 ρ μ . ] ) ) ) ] ( d μ d t ) + [   1 2 ( (   t μ .. + μ . ) ( t μ . ( 1 − ρ ) − t [ ( ( 1 + ρ ) t μ .. + μ ] ) ( ( 1 ρ 2 − 1 ( 1 − ρ ) 2 ) ( − ( ( 1 + ρ ) ) 2 ) − ( t 2 [ ( ( 1 + ρ ) t μ .. + μ + 2 ρ μ . ] ) ) +
[ ( 1 + ρ ) t μ … + ( 1 + ρ ) μ .. + μ . + 2 ρ μ .. ] ( t ( t μ . ) − ( 1 ρ 2 − 1 ( 1 − ρ ) 2 ) ( 1 + ρ ) ) ( ( 1 ρ 2 − 1 ( 1 − ρ ) 2 ) ( − ( ( 1 + ρ ) ) 2 ) − ( t 2 [ ( ( 1 + ρ ) t μ .. + μ + 2 ρ μ . ] ) ) )   ]   ] = 0
It is obvious that for arbitrary constant values of ρ , μ , we have a closed form solution for (48). As time becomes sufficiently large, i.e., t → ∞ , (48) reduces to
[ 3 μ .. 2 − 3 μ .2 2 ( 1 + ρ ) − μ . μ ... μ .. ] = 0
We propose the closed form solution, μ = 2 γ t ( 1 + γ t ) ,   for some arbitrary non-zero constant γ . substituting in (49) implies:
18 γ 3 + 6 γ 2 ( 1 + γ t ) ( 1 + ρ ) + 6 γ 4 = 0
As t → ∞ , γ = 0 , 0 , 0 , − 3 . The only accepted value is γ = − 3 , μ = 6 t ( 3 t − 1 ) ,   which tends to the value μ = 2 as t → ∞ .
C. The  I M E s  of the  t e m p o r a l   coordinate,  t  of the transient M/M/1 QM
Engaging a similar lengthy mathematical manipulation, it can be verified that the IMEs of the temporal coordinate, t of the transient M/M/1 QM, as time reaches infinity and for a constant server utilization will have a closed form solution that is characterized by the family of families of temporal curves:
μ ( t ) = ζ 1 + ζ 2 t + ζ 3 t 2
for some arbitrary non-zero constants ζ 1 , ζ 2 , ζ 3 ,   ζ 1 > 1

5. IG Applications to ML

Stochastic gradient descent is a popular optimisation approach in ML that seeks to determine which direction of descent is the steepest within a parameter space of probability distributions. Amari[3] created the natural gradient, which is superior to the ordinary gradient since it more accurately captures this direction. Furthermore, even with gradient descent, FIM can be used to calculate the predicted change in output about parameter changes. Artificial neural networks (ANNs) are functions with multiple parameters that map input vectors to output vectors. They are widely applied in regression, computer vision, and speech processing. ANNs can be trained through supervised learning, where a training set of input-output pairs is used, or through unsupervised learning, which does not require a training set. The back-propagation algorithm efficiently computes the gradient descent by determining the contribution of each parameter to the error. Overfitting, a common issue in ANNs, can be mitigated by techniques such as using a validation set, early stopping, data augmentation, and dropout[11].
In reinforcement learning(RL) [12], when an agent needs to prepare for unknown tasks, one approach is unsupervised skill discovery. These algorithms learn a set of policies without using a reward function and are like representation learning algorithms in supervised learning. While prior work has shown that these methods can accelerate downstream tasks, our analysis reveals that they do not learn skills that are optimal for every possible reward function. However, the distribution over skills can provide an optimal initialization that minimizes regret against adversarially chosen reward functions, assuming a specific adaptation procedure. Notably, understanding which state marginals are achievable is crucial for analyzing the behavior of unsupervised skill learning algorithms[12] and their relevance to state-dependent reward functions. The set of achievable state marginal distributions can be characterized by a set of linear equations or by a complementary description based on a specific property. This alternative perspective provides insights into the relationship between learned skills and downstream tasks in reinforcement learning.
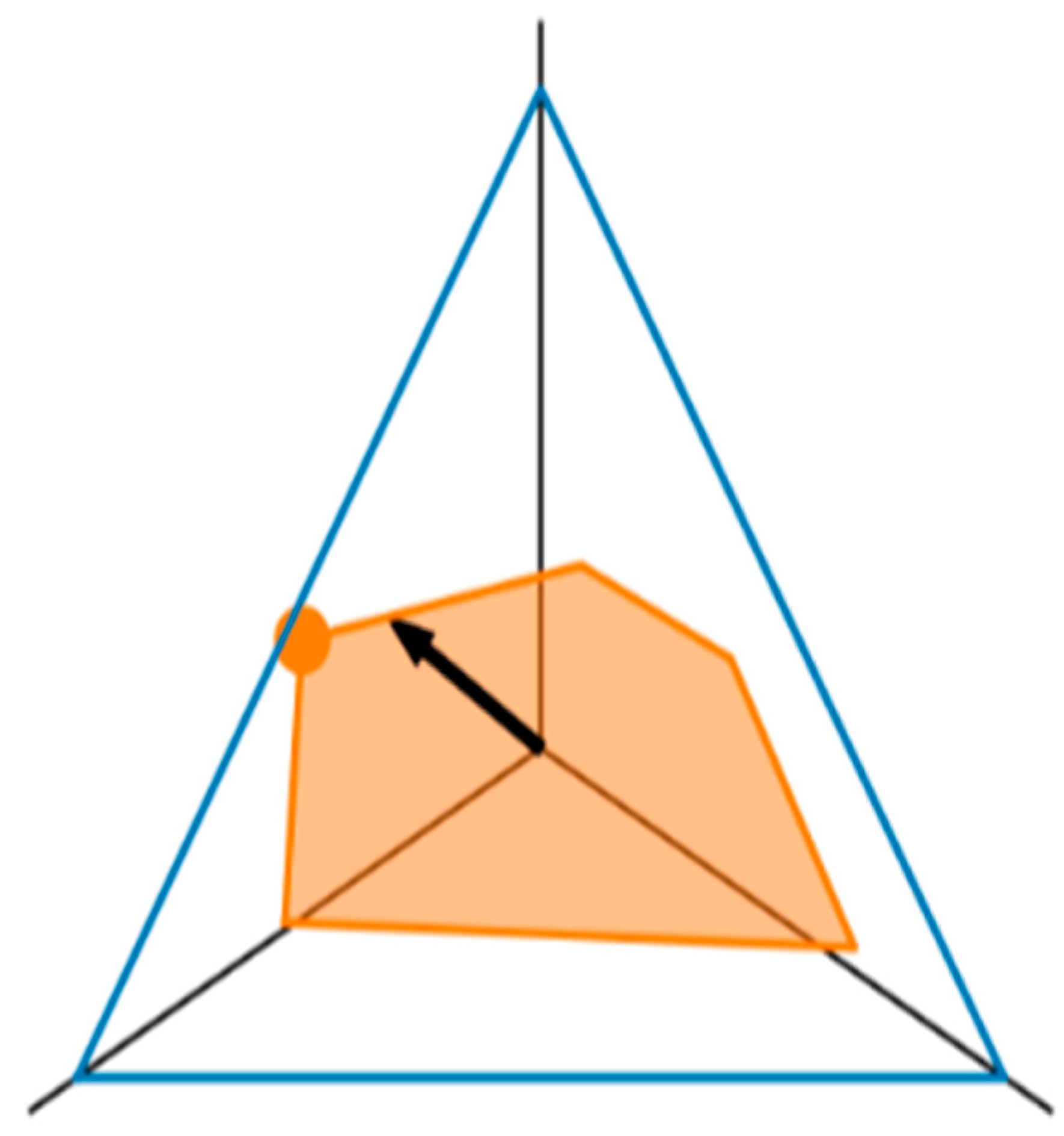
So, if we have a set of possible state distributions, any combination of those distributions within the convex hull is also possible. This means that there exists a policy that can achieve any state distribution within that convex hull. By taking the convex hull of the state distributions of all deterministic policies, we can obtain the set of all possible state distributions, which is referred to as a polytope. Each vertex of the polytope represents a deterministic policy, and any policy’s state distribution can be expressed as a combination of the state distributions at the vertices, as visualized by Figure 2.
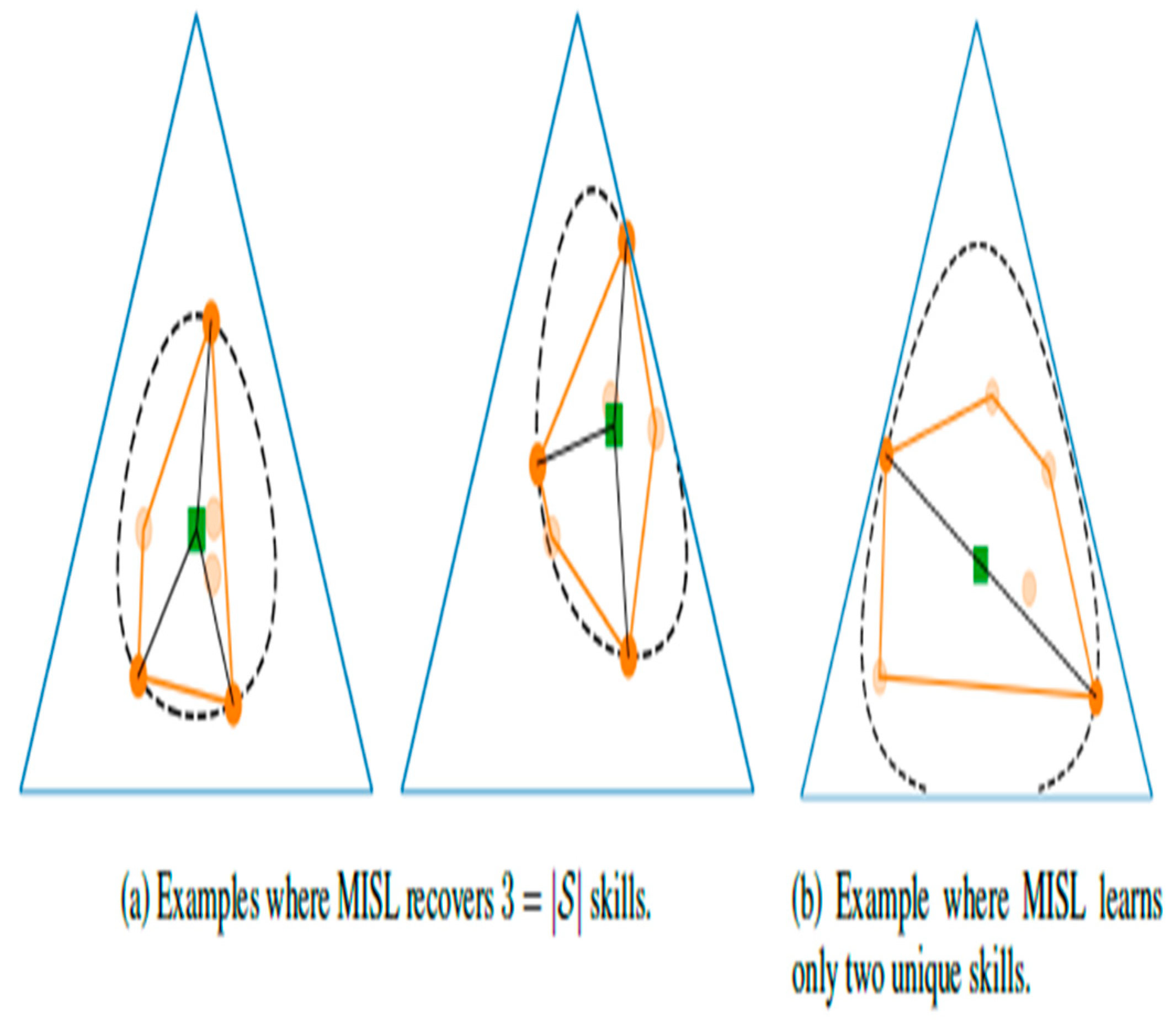
The analysis of where the skills learned by Mutual Information-based Skill Learning (MISL) are positioned on the state marginal polytope, which has motivated [12] to undertake this analysis by examining the mutual information objective and dissecting it to understand how the learned skills align with the polytope. In the context of skill learning[12], maximizing mutual information is equivalent to minimizing the maximum difference between a prior distribution over states (represented by a green square) and any possible state distribution.
This concept, known as information geometry, helps optimize skill learning algorithms by assigning higher probabilities to policies with state distributions that deviate further from the average state distribution. The goal is to find skills that are as distinct as possible from each other and from the average state distribution. Most importantly, the opaque circles represent the skills discovered by the Mutual Information Skill Learning (MISL) algorithm.
The dashed line represents state marginals that are equidistant from the green square, indicating an equal divergence from the prior distribution over states. This visualization helps illustrate the relationship between the skills learned by MISL and their distribution in relation to the average state distribution. This is illustrated by Figure 3.
Reliable detection of out-of-distribution (OOD) samples[13] is crucial for ensuring the safety of modern machine learning systems. The work of [13] introduced IGEOOD, an effective method that can detect OOD samples using any pre-trained neural network, regardless of the level of access to the ML model. By leveraging the geodesic distance between data distributions, IGEOOD combines confidence scores from the neural network’s logits outputs and learned features to achieve superior performance compared to other state-of-the-art methods across different network architectures and datasets[13].
The authors [13] introduced the concept of IG and derived a metric based on the Fisher-Rao distance to measure the mismatch between probability density functions of a pre-trained neural classifier. Experimental results demonstrate that IGEOOD performs competitively with state-of-the-art methods in different setups, including black-box and grey-box scenarios, and achieves improved performance on various benchmarks.
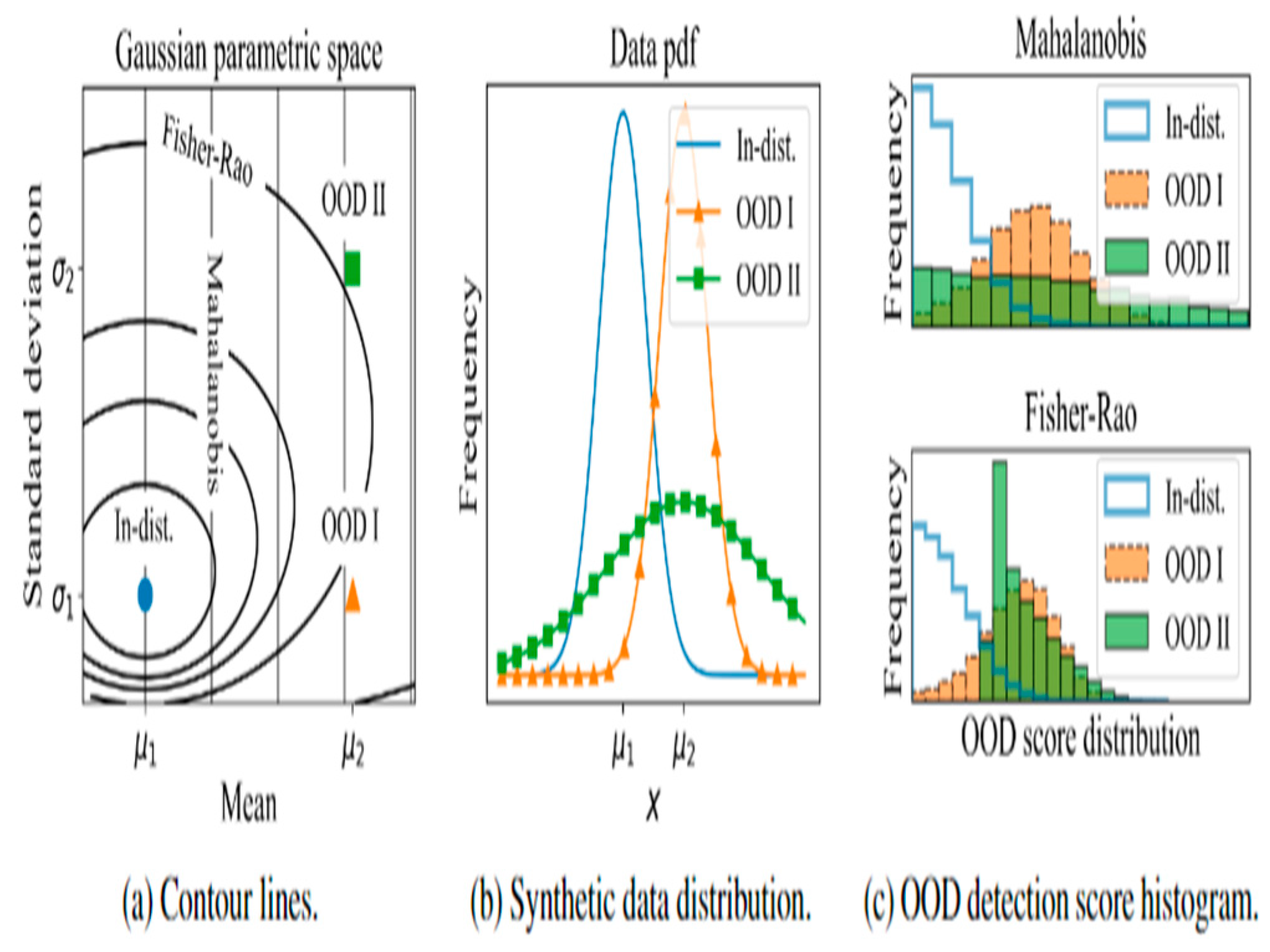
Figure 4 showcases a comparison between Fisher-Rao and Mahalanobis distances for distinguishing between 1D Gaussian distributions in the context of out-of-distribution (OOD) detection. It highlights the motivation to use the Fisher-Rao metric, which measures the dissimilarity between probability models, as it shows better performance in distinguishing between in-distribution and OOD samples compared to other distance-based approaches.
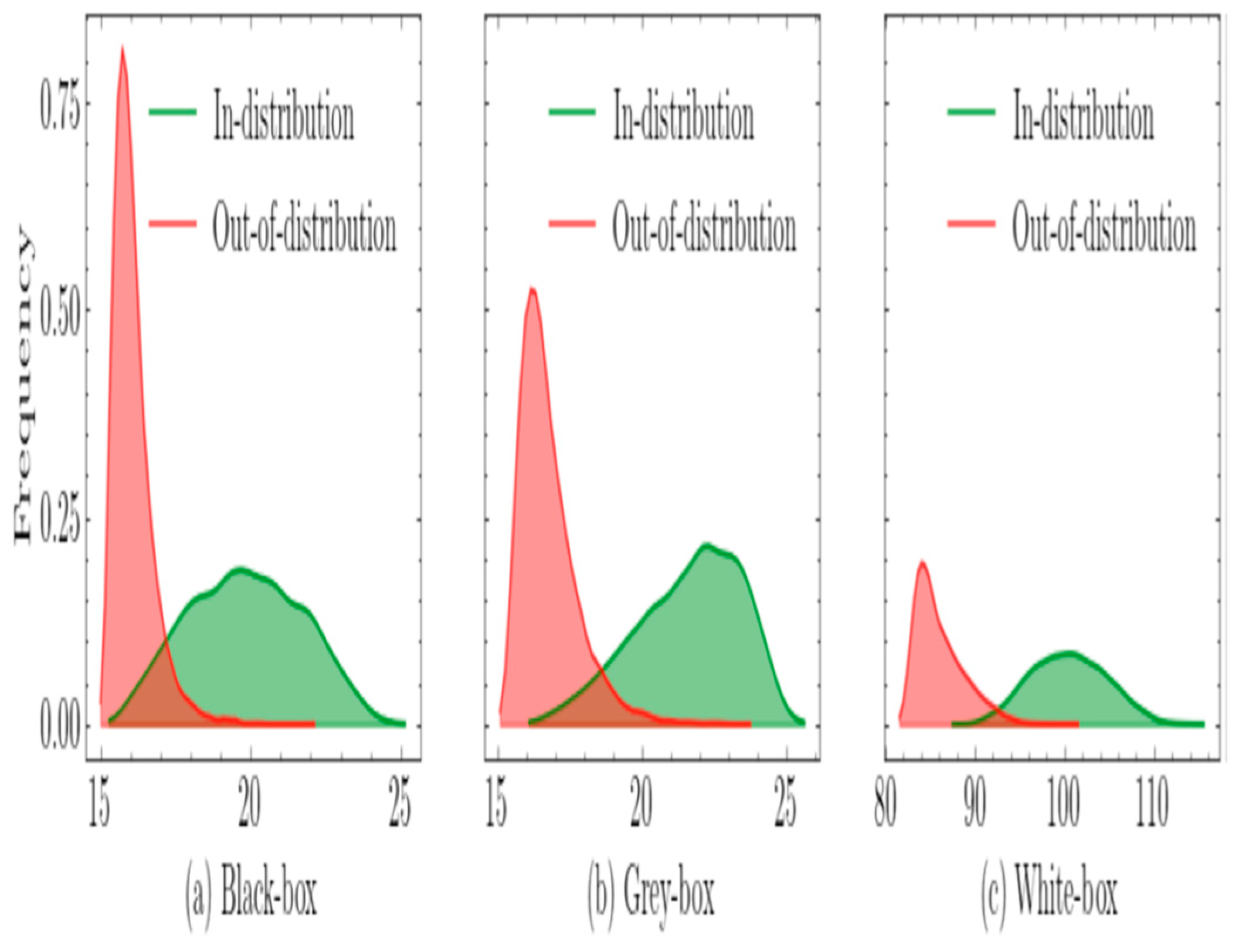
In the context of the experiment, the authors [13]compared three different settings for out-of-distribution (OOD) detection. They use a unified metric, but with different formulations based on the type of distribution. For the deep neural network (DNN) outputs, they use the softmax posterior probability distribution, while for the intermediate layers, they employ a model based on diagonal Gaussian probability density functions (pdfs). This unified framework combines a single distance measure for both the softmax outputs and the latent features of the neural network, contributing to the separation of in-distribution and OOD samples, as illustrated in Figure 5.

6. Conclusion, Open Problems and Future Work

This study offers a revolutionary info-geometrics of transient M / M / 1 QM. For this queue, FIM and IFIM are established. The geodesic equations of motion for the queue’s coordinates are determined. More potentially, some IG applications to ML are provided.
Here are some challenging open problems to be addressed:
Open problem One:
According to the analysis in [12], a simplified model of skill learning algorithms that treated policy parameters and latent codes as a single representation, with different skills having distinct parameter sets was employed. However, practical implementations of skill learning algorithms are less flexible, which can alter the shape of the state marginal polytope.
This limited flexibility may lead to incomplete representation of certain state distributions, resulting in gaps or divisions in the polytope. It is yet to be determined if these practical implementations learn fewer unique skills and how these limitations impact the average state distribution, which is a really challenging open problem.
Open problem Two:
Following the derivation of the potential function, PF
Ψ ( θ ) = − l n ( ρ ) − l n ( 1 − ρ ) + μ ( 1 + ρ ) t ,   p 0 ( t ) = 1 − ρ
Is the process of finding the threshold of PF based on its parameters decidable? The problem is still open.
Open problem Three:
Having discovered PF (c.f., (21)), is it feasible to examine its algebraic properties as well as doing the same for its inverse, if it exists? This is a challenging open problem, yet unsolved so far.
Open problem Four :
The discovery of Revolutionary relativistic connections with the investigated transient queue is still unsolvable problem, for example finding the corresponding Gaussian, Ricci, Scalar and Einesteinian tensors for the transient M/M/1 QM.
The frontiers are open for unlimited explorations.
The next phase of research includes answering the above open research problems and exploring more new avenues of IG applications to other scientific disciplines. More importantly, the possibility of employing Riemannian Geometric (RG) analysis, and the Theory of Relativity (TR) to the analysis of the dynamics of transient queues.

References

  1. A. Mageed, Y. Zhou, Y. Liu and Q. Zhang, “Towards a Revolutionary Info-Geometric Control Theory with Potential Applications of Fokker Planck Kolmogorov(FPK) Equation to System Control, Modelling and Simulation,” 2023 28th International Conference on Automation and Computing (ICAC), Birmingham, United Kingdom,2023,pp.1-6. [CrossRef]
  2. Z. Skoda, Z., 2019, available online at https://ncatlab.org/nlab/show/information+geometry.
  3. A. Mageed, Q. Zhang, T. C. Akinci, M. Yilmaz and M. S. Sidhu, “Towards Abel Prize: The Generalized Brownian Motion Manifold’s Fisher Information Matrix With Info-Geometric Applications to Energy Works,” 2022 Global Energy Conference (GEC), Batman, Turkey, 2022, pp. 379-384. [CrossRef]
  4. A. Mageed, X. Yin, Y. Liu and Q. Zhang, “Z(a,b) of the Stable Five-Dimensional M/G/1 Queue Manifold Formalism’s Info- Geometric Structure with Potential Info-Geometric Applications to Human Computer Collaborations and Digital Twins,” 2023 28th International Conference on Automation and Computing (ICAC), Birmingham, United Kingdom, 2023, pp. 1-6. [CrossRef]
  5. K. Nakagawa, “The geometry of M/D/1 queues on Large Deviation,” International Transactions of Operational Research, vol. 9, 2002.
  6. C.T. J. Dodson, “Topics in Information Geometry,” University of Manchester, 2005, Available online on http://eprints.maths.manchester.ac.uk/131/1/InfoGeom.pdf.
  7. L. Peg, H. Sun, and J. Jiu, 2007, “The Geometric Structure of the Pareto Distribution, ” Boletin de la Asociación Matemática Venezolana, vol. XIV, no.1, 2007.
  8. A. Mageed and D. D. Kouvatsos, “Information Geometric Structure of Stable M/G/1 Queue Manifold and its Matrix Exponential,” Proceedings of the 35th UK Performance Engineering Workshop, School of Computing, University of Leeds, Edited by Karim Djemame, 2019, p. 123-135. [Online] at: https://sites.google.com/view/ukpew2019/home.
  9. I.A.Mageed and D. D. Kouvatsos, “ The Impact of Information Geometry on the Analysis of the Stable M/G/1 Queue Manifold,” In Proceedings of the 10th International Conference on Operations Research and Enterprise Systems - ICORES, ISBN 978-989-758- 485-5, vol. 1, 2021, p. 153-160. [CrossRef]
  10. [10] P. R. Parthasarathy, “A transient solution to an M /M /1 queue: a simple approach,” Adv. Appl. Prob., vol. 19, 1987, p. 997-998.
  11. I. A. Mageed and Q. Zhang, “Information Geometry? Exercises de Styles,” electronic Journal of Computer Science and Information Technology, vol. 8, no. 1, 2022, p. 9-14.
  12. B. Eysenbach, R. Salakhutdinov, and S. Levine S, “The information geometry of unsupervised reinforcement learning,” arXiv preprint arXiv:2110.02719, 2021.
  13. E. D. Gomes, et al, “Igeood: An information geometry approach to out-of-distribution detection,” arXiv preprint arXiv:2203.07798,2022.
Preprints 97452 g001
Figure 1. SM’s parametrization [3].
Figure 1. SM’s parametrization [3].
Preprints 97452 g001
Preprints 97452 g002
Figure 2. We can represent reward functions as vectors starting from the origin. The objective of maximizing expected return is equivalent to maximizing the dot product between the state marginal distribution and the reward vector. This visualization helps us understand how different reward-maximizing policies are related to the state marginal polytope and provides insights into the relationship between state-dependent reward functions and the optimal policies[12].
Figure 2. We can represent reward functions as vectors starting from the origin. The objective of maximizing expected return is equivalent to maximizing the dot product between the state marginal distribution and the reward vector. This visualization helps us understand how different reward-maximizing policies are related to the state marginal polytope and provides insights into the relationship between state-dependent reward functions and the optimal policies[12].
Preprints 97452 g002
Preprints 97452 g003
Figure 3. Skill Learning’s IG [12].
Figure 3. Skill Learning’s IG [12].
Preprints 97452 g003
Preprints 97452 g004
Figure 4. Portraying the reason behind using Fisher-Rao OOD detection[13].
Figure 4. Portraying the reason behind using Fisher-Rao OOD detection[13].
Preprints 97452 g004
Preprints 97452 g005
Figure 5. The probability distributions of the IGEOOD score, which is a metric used for out-of-distribution (OOD) detection. The distributions are shown for three different settings, specifically for a pre-trained DenseNet model on CIFAR-10 dataset, considering both in-distribution and OOD data from TinyImageNet (downsampled). This analysis helps evaluate the effectiveness of the IGEOOD score in distinguishing between in-distribution and OOD samples[13].
Figure 5. The probability distributions of the IGEOOD score, which is a metric used for out-of-distribution (OOD) detection. The distributions are shown for three different settings, specifically for a pre-trained DenseNet model on CIFAR-10 dataset, considering both in-distribution and OOD data from TinyImageNet (downsampled). This analysis helps evaluate the effectiveness of the IGEOOD score in distinguishing between in-distribution and OOD samples[13].
Preprints 97452 g005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated