Preprint
Article
Continuous Multi-utility Representations of Preorders and the Chipman Approach
Altmetrics
Downloads
61
Views
21
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
29 January 2024
Posted:
30 January 2024
You are already at the latest version
Alerts
Abstract
Chipman contends, in stark contrast to the conventional view, that utility is not a real number but a vector and is inherently lexicographic in nature. According to these views, it will be proved that, for every preordered topological space (X,≾,t), the assumption t to be finer than the order topology t≾ on (X,t), i.e. t⊇t≾, and the assumption the quotient topology t∣∼≾ that is defined on the preordered set (X∣∼,≾∣∼) of indifference classes of ≾ to be Hausdorff imply that a cardinal number κ and a (complete) preorder ≲ on {0,1}κ that is coarser than the lexicographical ordering ≤lex on {0,1}κ, i.e. ≤lex⊂≲, can be chosen in such a way that there exists a continuous order-embedding ϑ:(X,≾,t)⟶({0,1}κ,≲,t≤lex). This theorem will be compared with a theorem that, in particular, describes necessary and sufficient conditions for ≾ to have a continuous multi-utility representation.
Keywords:
Subject: Computer Science and Mathematics - Mathematics
MSC: 62H05; 62H12; 62H20
1. Introduction
The first author attended and presented a contribution at an international conference which took place in Essen (Germany) in October 1997. It was the case of a very impressive conference, which concerned Mathematical Utility Theory and brought together economists, mathematicians, and psychologists. In that occasion, the first author known personally, for the first time, Professor Gerhard Herden, an extremely fertile and intelligent mathematician, who was the principal organizer of the conference. Professor Herden personally compiled the list of all the invited speakers (there were no contributed talks). Professor Herden, who became a frequent coauthor of the first author, passed away on January 30, 2019. His enthusiasm remains unforgettable, as well as his capacity to formulate problems and to furnish extremely sharp definitions and axiomatizations. His work inspired the present contribution. In addition, the first author met in Essen Professor Chipman, who was also an invited speaker. He was a very kind person, whose contribution was invasive.
1.1. The Chipman approach
Let be some arbitrarily chosen non-empty preordered set. Using as the codomain of a utility function (order-preserving function) on is of almost universal practice in mathematical utility theory. But, as it has been shown by many illustrating examples in Herden and Mehta [1], there are cogent economic (and mathematical) reasons for not insisting on real-valued utility representations. In order to approach the general (continuous) utility representation problem we, therefore, follow in a first step the views of Chipman. Chipman explicitly and wittingly studies utility functions with values in a set of lexicographically ordered transfinite sequences of length equal to an ordinal number . Indeed, in an elegant paper Chipman [2] contends, in stark contrast to the conventional view, that utility is not a real number but a vector and is inherently lexicographic in nature. Chipman also says that the concept of utility as a vector is easier to understand than that of utility as a real number.
In the same paper, he argues that, even if there is a real-valued utility function, it is preferable from an economic point of view to use a utility representation of the commodity space (which always exists) into a Dedekind-complete chain of transfinite sequences of length , where is an appropriately chosen ordinal number and is the lexicographic ordering on . In addition, Chipman [3] argues that insisting or requiring on a real-valued utility representation implies the commodity space to have a countable order-dense subset. But countability as such does not have any intuitive appeal from an economic point of view.
In order to now mathematically approximate the Chipman approach, let be an arbitrarily chosen preordered set. We denote, for every point , by the set of all points such that and by the set of all points such that . In addition, we still note that is for every point the set of all points such that and for every point the set of all points such that . Then the order topology on X is the coarsest topology on X for which the sets and are open. In order to avoid artificial and superfluous considerations we assume for the moment to be a Hausdorff topology on . Recall that ∼ is the indifference relation associated to the preorder ≾ on X (i.e., for all points , is equivalent to the assertion that and ). For underlining the importance of this assumption and for later use, we still notice that, in case that contains at least two elements, the following necessary conditions for to be Hausdorff hold. For the sake of brevity the straightforward proofs of these conditions may be omitted. Nevertheless, the reader should notice that the validity of condition LR is based upon the validity of condition SB.
SB: In order for to be Hausdorff it is necessary that the sets and where x runs through X constitute a subbasis of .
LR: In order for to be Hausdorff it is necessary that for all points and the validity of the following implication holds for all and for all :
In Lemma 2 it will be proved that in case ≾ to be semi-closed, i.e. and are closed subsets of for every , the validity of the conditions SB and LR already implies to be Hausdorff. The general case, however, is difficult. No simple solution can be expected.
Let us proceed by considering an ordinal number . Then the triplet is the preordered topological space that consists of the lexicographically ordered set endowed with its order topology . Now we set , i.e. is the cardinality of the set of indifference classes of ≾, and consider the particular triplet . As it is at least implicitly well-known, there exists a natural order-embedding . But for some arbitrarily chosen topology t on that is finer than , in general, there exists no order preserving function such that the composition is continuous. The reader may notice that this observation principally excludes the existence of some continuous order-embedding . Therefore, using a construction that is due to Beardon [4], an effort has been made in coarsening to some preorder ≲ in such a way that the indifference classes of ≲ are (in some sense) smallest possible closed intervals of with respect to the property of guaranteeing a continuous order-embedding . This is the content of Theorem 1.
In the literature various Dedekind-complete chains have been considered for possibly being appropriate codomains of a utility function (cf. the papers that are quoted in Herden and Mehta [1]).
In order to examine these possible codomains of a utility function more closely, let be fixed chosen and an order-embedding. Let, furthermore, run through the class of all ordinal numbers. Then the universal character of as codomain of a utility function is underlined by the observation that there exist an ordinal number and order-embeddings and such that the following diagram commutes
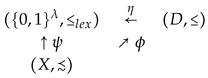
Moreover, (total) preorders on D and on and order-embeddings
and
can be chosen in such a way that the compositions
and
are continuous and the following diagram commutes
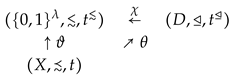
These are the contents of Theorem 2.
1.2. The continuous multi-utility representation theorem
In this section we want to compare the Chipman approach to mathematical utility theory with the standard real-valued approach to mathematical utility theory.
We, thus, choose a preordered topological space the topology t of which is finer than . Then the reader may recall that ≾ is said to have a continuous multi-utility representation if there exists a family of increasing and continuous functions such that
or, equivalently, if there exists for every pair such that some continuous and increasing function such that .
In addition, the reader may recall that ≾ is said to be closed if ≾ is a closed subset of with respect to the product topology on that is induced by t.
We recall that multi-utility representations were introduced by Levin [5]. A full study of this kind of representation, compatible with nontotal preorders, was provided by Evren and Ok [6], after a seminal paper by Ok [7]. Contributions in this topic were presented by Minguzzi [8,9] and Pivato [10]. Very interesting applications to expected utility theory are due to Dubra et al. [11], Evren [12], and Galaabaatar and Karni [13]. We just mention that continuous representations of interval orders by a pair of functions were axiomatized by Bosi et al. [14]. Hack et al. [15] in a very recent paper studied the classification of preordered spaces in terms of their possible multi-utility representations.
With help of this notation we shall prove that the assumption to be Hausdorff guarantees the equivalence of the assertions ≾ to admit a continuous multi-utility representation, ≾ to be semi-closed and ≾ to be closed (cf. Theorem 3).
Let, for the moment, be the cardinality of the set of all pairs such that . Then we arbitrarily choose a bijective function in order to consider the direct sum of ordered topological spaces .
We proceed by assuming to be Hausdorff and ≾ to satisfy the equivalent assertions of Theorem 3, which, in particular, means that ≾ admits a continuous multi-utility representation. Let now be the direct sum of preordered topological spaces . Since ≾ has a continuous multi-utility representation, the definition of implies the existence of a continuous order-preserving function . This in the same way simple as obvious consideration already clarifies the relation of the multi-utility approach for representing a preorder with the Richter-Peleg approach for representing a preorder (cf. Herden [16], Peleg [17] and Evren and Ok [7]).
We recall that a Richter-Peleg representation (or utility function, or else order-preserving function) of a preordered set is a real-valued function u on X which is order-preserving (i.e., u is increasing and, for all points , implies that ).
Let, finally, and . Then an application of Theorem 2 (cf. the last paragraph of section 1.1) guarantees the existence of a continuous order-embedding
and of a continuous order-embedding
such that the following diagram commutes
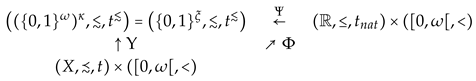
In this way the Chipman approach as well as the multi-utility approach and the Richter-Peleg approach for representing a preorder have been combined (cf. Theorem 4).
2. On an order-embedding theorem of Chipman-type
Let in the remainder of this section some preordered topological space the topology t of which is finer than the order topology be chosen in such a way that the quotient topology that is defined on the set of indifference classes of ≾ is Hausdorff. Then it is the first aim of this section to prove and to comment on the following theorem.
Theorem 1.
The following assertions hold:
(i) There exists some cardinal number κ for which there exists an order-embedding .
(ii) There exists some cardinal number κ and a (complete) preorder ≲ on that is coarser than for which there exists a continuous order-embedding .
Proof. 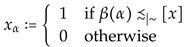
The validity of assertion (i) is (at least implicitly) well known. It holds without assuming to be a Hausdorff-space. Nevertheless we must repeat its proof here in order to preparing the proof of assertion (ii). Let, therefore, be the cardinality of . Then we arbitrarily choose some bijective function in order to define the desired order-embedding by identifying for every with the tuple that is defined by setting
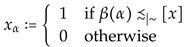
for all ordinal numbers . Since for every point and every point the validity of the equivalence holds it follows that is an order-embedding.
In order to now verify assertion (ii) let S be an arbitrary subset of . Then a lacuna of S is a non-degenerate (non-trivial) interval of that is disjoint from S and has an upper and lower bound in S. A gap of S is a maximal lacuna. Although ≾ is not necessarily complete it is easily to be seen that the inclusion would imply the continuity of considered as a function if would not have any gaps of the form or , i.e. half-closed half-open or half-open half-closed gaps (cf. Beardon [1]). But in order to eliminate these gaps a difficulty appears. Indeed, let be a net that converges to some point . Then it may happen that or that .
This means that a (crucial) gap to be eliminated in order to guarantee continuity of at x is of the form
or
or
or
But, of course, there may exist another net that converges to x. It, thus, follows that a possibility to eliminate these (crucial) gaps only exists if
or
in case that
and that
in case that
i.e. the precise form of the (crucial) gaps must be independent of the considered net that converges to x. In order to guarantee independence of (crucial) gaps from particularly chosen nets that converge to x the assumption to be a Hausdorff-topology is needed (cf. Example 1). Indeed, if is Hausdorff independence of (crucial) gaps from particularly considered nets that converge to x follows by distinguishing between four different cases (cf. the above described possibilities of (crucial) gaps) each of which can be done by applying always the same indirect argument that is based upon condition SB and the definition of applied to the equations . Since this argument is routine and obvious in nature it may be omitted for the sake of brevity. The independence of (crucial) gaps from particularly chosen nets that converge to x allows us to now proceed by considering the collection of all half-closed half-open and all half-open half-closed gaps of . In accordance with Beardon [1] we define as follows an equivalence relation ∼ on with respect to . If and are adjacent gaps of then is an equivalence class of ∼. In addition, if and respectively are gaps that do not belong to pairs of adjacent gaps of then and respectively define the corresponding equivalence classes of ∼. All the other equivalence classes of ∼ are defined to be singletons. Since the equivalence classes of ∼ are closed intervals of we may define the desired preorder ≲ on that is coarser than by setting
for all and all . Since for all and all the inequality implies that it follows that ≲, actually, is coarser than . Hence, we now consider the (continuous) identity-function . Furthermore, the definition of ∼ implies that the image of the composition
of the functions and has with respect to ≲ neither half-closed half-open nor half-open half-closed gaps.
Since is an order-embedding we, therefore, may conclude that is a continuous order-embedding. This last observation finishes the proof of the theorem. □
Example 1.
Let X be the real unit interval . Then we endow X with the order
It follows that which means that is not Hausdorff. Let be the order-embedding that has been described in Theorem 1. Then we may conclude that the nets (sequences) and converge with respect to to 1 but that .
Let ORD be the class of ordinal numbers. As it already has been outlined to some degree in the last paragraph of section 1.1 we now prove a theorem that underlines the universal character of the class of chains.
Theorem 2. 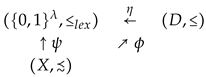
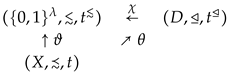
Let be an order-embedding of into the Dedekind-complete chain . Then the following assertions hold:
(i) There exist some ordinal number λ and order-embeddings
and
such that the following diagram commutes
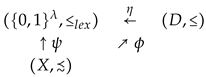
(ii) In addition to assertion (i) (total) preorders on D and and order-embeddings
and
can be chosen in such a way that the compositions
and
are continuous and the following diagram commutes
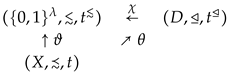
Proof. 
Of course, we may assume without loss of generality that . In order to now verify assertion (i) we first notice the validity of the equivalences (**) which mean that
for all points and . Let be the maximum of and and an arbitrarily chosen bijective function. Then the equivalences (**) imply in combination with condition LR the existence of an order-embedding that is defined by identifying for every with the tuple 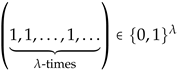 , if . Let, therefore, . Then we must at first verify that the subsequent definition is independent of the particular chosen point such that . This means that we must prove that the equation implies that . Indeed, if then the equivalences (**) allow us to conclude that and . Hence, it follows that assumptions of condition LR are satisfied which implies that . Let, consequently, some such that be arbitrarily chosen. Then we may identify with the tuple that is defined by setting
for all ordinal numbers (cf. the definition of in the proof of Theorem 1). Of course, also the order-embedding has to be defined in the same way, i.e. by identifying for every with the tuple that is defined by setting
, if . Let, therefore, . Then we must at first verify that the subsequent definition is independent of the particular chosen point such that . This means that we must prove that the equation implies that . Indeed, if then the equivalences (**) allow us to conclude that and . Hence, it follows that assumptions of condition LR are satisfied which implies that . Let, consequently, some such that be arbitrarily chosen. Then we may identify with the tuple that is defined by setting
for all ordinal numbers (cf. the definition of in the proof of Theorem 1). Of course, also the order-embedding has to be defined in the same way, i.e. by identifying for every with the tuple that is defined by setting
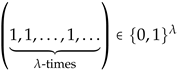 , if . Let, therefore, . Then we must at first verify that the subsequent definition is independent of the particular chosen point such that . This means that we must prove that the equation implies that . Indeed, if then the equivalences (**) allow us to conclude that and . Hence, it follows that assumptions of condition LR are satisfied which implies that . Let, consequently, some such that be arbitrarily chosen. Then we may identify with the tuple that is defined by setting
, if . Let, therefore, . Then we must at first verify that the subsequent definition is independent of the particular chosen point such that . This means that we must prove that the equation implies that . Indeed, if then the equivalences (**) allow us to conclude that and . Hence, it follows that assumptions of condition LR are satisfied which implies that . Let, consequently, some such that be arbitrarily chosen. Then we may identify with the tuple that is defined by setting
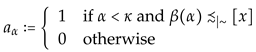
for every ordinal number . The definitions of the order-embeddings and imply that which proves assertion (i).
In order to prove the validity of assertion (ii) we use the notation that has been introduced in the proof of assertion (ii) of Theorem 1. Then we apply the arguments that have been used in the proof of assertion (ii) of Theorem1 in order to verify that the image of the order-embedding neither has half-closed half-open nor half-open half-closed gaps. The proof of assertion (i) implies that is an order-isomorphism. Hence, the validity of the following implications that will be abbreviated by (*) holds:
If the crucial gap I of is the image of some half-closed half-open or some halfopen half-closed interval J then J is a crucial gap of . And, conversely:
If the crucial gap J of is the image of some half-closed half-open or some half-open half-closed interval I then I is a crucial gap of .
In particular, we may conclude that the crucial gaps of are independent from particularly chosen converging nets. Hence, we may apply the Beardon construction that has been described in the proof of assertion (ii) of Theorem 1 in order to define a preorder ⊴ on D that is coarser than ≤ in such a way that neither the image of the order-embedding nor the image of the order-embedding has any half-closed half-open or half-open half closed gaps. Hence, the validity of the implications (*) allows us to conclude that the compositions , and are continuous (cf. the proof of assertion (ii) of Theorem 1). In addition, the validity of assertion (i) guarantees that , which finishes the proof of the theorem. □
3. On a relation of the Chipman approach with the continuous multi-utility representation problem of preorders
Let be an arbitrarily chosen topological space. In the focus of this section is the problem of determining (characterizing) all preorders ≾ on X the order topology of which is coarser than t that admit a continuous multi-utility representation. It is well known (cf, for instance, Bosi and Herden [3]) that the assumption ≾ to admit a continuous multi-utility representation implies that ≾ must be closed and, therefore, also semi-closed. Hence, the following lemmas provide a first important step towards a complete solution of the just mentioned characterization problem. As in the proof of Theorem 2 throughout this section we may assume without loss of generality that .
In order to proceed let us denote for every point by the set of all points such that . This notation allows us to verify the validity of the following lemma.
Lemma 1.
Let be arbitrarily chosen. Then ≾ satisfies the following conditions:
HD: Let ≾ have a continuous multi-utility representation. Then is a Hausdorff space.
OC: Let be a Hausdorff space and let ≾ be closed. Then is open (and closed) for every point that is maximal with respect to .
Proof. HD: Let ≾ have a continuous multi-utility representation and let and be arbitrarily chosen points such that . Then there exists a continuous and increasing function such that . Hence, the desired conclusion follows.
OC: Let be a maximal element of , which means that . Then the assumption to be Hausdorff implies with help of condition SB that . Hence, we may distinguish between the cases to have a maximal element and to have no maximal element. Let us, therefore, assume at first that to have a maximal element m. Then the interval is empty. This means, in particular, that there exists no net of points that converges to y. Hence, the set must be closed and we may conclude that is open and closed. We, thus, proceed by showing that both sets as well as are open and closed. In order to verify these properties of and respectively it suffices to prove that is closed and that is open. Let, therefore, in a first step some point be arbitrarily chosen. Then we have to show that . We, thus, consider some net of points that converges to p. Since ≾ is closed and for all it follows that and it remains to verify that the equivalence can be excluded. Indeed, if then the just proved property of to be open (and closed) implies that there exists some index such that for all that are at least as great as . This contradiction implies that must be closed. For later use, in particular in the proof of Theorem 3, we abbreviate this conclusion by (*). Since is open and is open it follows in a second step that is open, which completes the discussion of the case to have a maximal element. We now still must think of the situation to coincide with . Let, in this situation, be some sub-chain of such that Because of (*) we may assume without loss of generality to be not open (and closed). We, thus, may arbitrarily choose some point in order then consider some net of points that converges to y. Because of the maximality of y with respect to it follows that for every there exist points and such that . Indeed, otherwise the definition of implies that is the meet of two open intervals and, thus, open (and closed), which contradicts our assumption to not being open (and closed). This argument will be abbreviated it by (M). But this consideration allows us to conclude that for every point the set is an open neighborhood of y. Hence, it follows for every point that is open (and closed), which still was to be shown. □
As it already has been announced in the introduction we now characterize those semiclosed preorders ≾ on for which is Hausdorff.
Lemma 2.
Let ≾ be semi-closed. Then in order for to be Hausdorff it is necessary and sufficient that ≾ satisfies the conditions SB and LR.
Proof.
As it already has been mentioned in the introduction the validity of the conditions SB and LR are necessary in order to guarantee to be Hausdorff. Hence, we may concentrate on the sufficiency part of the lemma. In order to verify that the assumption ≾ to be semi-closed implies in combination with validity of the conditions SB and LR that is a Hausdorff topology on we notice at first that condition SB is equivalent to condition LU which states that for every point at least one of the sets or is not empty. Let now points and such that be arbitrarily chosen. Then the cases and are possible. Therefore, we have to distinguish between these possible cases.
Case 1: . In this situation we distinguish between two more cases.
Case 1.1: There exist points and such that the interval is empty and . In this case is an open set that contains y and is an open set that contains x. Therefore, the equation settles 1.1.
Case 1.2: The closed interval does not contain any jump. In this situation there exists some point such that . Hence and respectively are disjoint open sets that contain y and x respectively.
Case 2: . In this situation condition LU implies that the lemma will be shown if the cases or successfully have been handled. Since both cases can be settled by completely analogous arguments it suffices to concentrate on the case to be not empty. The inequality implies with help of condition LR that there exists some such that in case that or that there exist points and such that in case that . Since ≾ is semi-closed it, thus, follows that and respectively or and respectively are disjoint open sets that contain the point x and the point y respectively, which still was to be shown. □
It is well known that a closed preorder ≾ on X is semi-closed. On the other side, however, a semi-closed preorder, in general, is not closed. Indeed, in Bosi and Herden [2, Theorem 2.2] very restrictive necessary and sufficient conditions for a semi-closed preorder to be closed have been presented. Because of this theorem it is somewhat surprising that the following proposition holds, which surely is worth to be stated separately.
Proposition 1.
Let be Hausdorff and let ≾ be semi-closed. Then ≾ is closed.
Proof.
In order to verify the proposition we must show that for any two points and such that there exist (open) neighborhoods U of x and V of y such that for every point and every point the relation holds. Indeed, having proved the existence of U and V it follows that and we are done. An analysis of the proof of Lemma 2 allows us to concentrate on the case that also the relation holds and that neither nor is empty. Let us, therefore, assume in contrast that every open neighborhood of x and every open neighborhood of y that is disjoint from contains points and respectively such that . In order to proceed we set and . Since is Hausdorff we may conclude that and . Then we distinguish between the cases as well as to be open and closed, to be open and closed and to only be closed, to only be closed and to be open and closed and as well as to only be closed. The case as well as to be open and closed is trivial. Indeed, in this case we may set and . The remaining three cases can be done by analogous arguments. Hence, we may concentrate without loss of generality on the case as well as to only be closed. Let now in every interval and every interval points and such that be arbitrarily chosen. Then we may assume without loss of generality that for all intervals such that or that for all intervals such that and that for all intervals such that or that for all intervals such that . The symmetry of the cases to be considered now allows us to concentrate on the case for all intervals such that and for all intervals such that and on the case for all intervals such that and for all intervals such that . Since ≾ is assumed to be semi-closed it follows in the first case that which means that and, thus, contradicts our assumption x to be not smaller or equivalent to y. The assumptions of the second case imply that But ≾ is semi-closed. Hence, we may conclude that the smallest closed increasing set that contains is . It, thus, follows that which again implies that and, therefore, contradicts the relation . This conclusion, finally, proves the validity of the proposition. □
In combination with Lemma 1, Lemma 2 and Proposition 1, the following theorem now presents a complete solution of the characterization problem that is in focus of this section and, in this way, (in opinion of the authors) also allows an interesting comparison of the Chipman approach on the one side and the real-valued approach on the other side to mathematical utility theory (cf. Theorem 4).
Theorem 3.
Let be a preordered topological space the topology t of which is finer than the order topology . Then the following assertions are equivalent:
(i)≾ admits a continuous multi-utility representation.
(ii) is Hausdorff and ≾ is closed.
(iii) is Hausdorff and ≾ is semi-closed.
Proof. (i) ⇒ (ii): It already has been mentioned above that a preorder ≾ that admits a continuous multi-utility representation must be closed. Therefore, Lemma 1 guarantees the validity of the implication (i) ⇒ (ii)".
(ii) ⇒ (iii): Since a closed preorder ≾ is semi-closed nothing has to be proved.
(iii) ⇒ (ii): Proposition 1.
(ii) ⇒ (i): Let assertion (ii) be valid and let points and such that be arbitrarily chosen. Then we must prove that there exists some continuous and increasing function such that . In order to verify the existence of we distinguish between the cases y to be contained in and y to be contained in .
Case 1:. In this case we must distinguish between the situations y being a maximal element of and y to not being a maximal element of. In the first situation we may apply property OC in order to setting
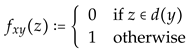
for all . In the second situation, i.e. y is not maximal element of there exists some point such that . Of course, u may be a maximal element of . In this case, however, we may apply the argument that has been applied in the first situation. Hence, we may assume without loss of generality that there exist points and such that . We proceed by assuming at first that v and, thus, also u is contained in . We abbreviate this assumption by (**). In addition, we assume both (open) intervals and to be empty. These assumptions imply that there does not exist any open interval of that contains u and is completely contained in . Hence, there cannot exist any net of points that converges to u, which implies that the set of all points the indifference classes of which are different from must be closed. This means that we now may apply the conclusion that in the proof of Lemma 1 has been abbreviated by (*) in order to conclude that is open and closed. Since both points u and v are contained in these considerations, finally, allow us to define the desired continuous and increasing function by setting
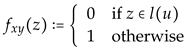
for all . In addition, the above considerations imply that for the moment we may assume without loss of generality that there exist no points , and such that and both intervals and are empty. With help of this assumption we now verify that the preordered set is not scattered. Indeed, the assumption implies by complete induction, each induction step of which may be settled by some straightforward indirect argument that contains some order-dense subset, i.e. a subset that does not contain any jumps, or that the set that is ordered by setting or for all intervals and is order-dense. Let be the real unit interval. Then our considerations allow us to conclude that in any case there exists an order-embedding . We, thus, proceed by showing that for all rationals and such that the inclusion holds. Since ≾ is closed and, therefore, also semi-closed it follows that . The validity of the strong inequality , thus, implies the desired inclusions . These considerations imply that the assumptions of Peleg’s Theorem (cf. Peleg [10]) are satisfied or, equivalently, that the family is a (decreasing) separable system in the sense of Herden [8]. Peleg’s theorem or Theorem 4.1 in Herden [8], therefore, implies the existence of some continuous and increasing function such that and . Let us abbreviate these arguments by (***). In order to finish the first case we still must consider the situation v to be not contained in , i.e. the situation v to be contained in . Of course, it is possible that , which means that also . In this situation, however, is an open and closed subset of X. Hence, we may define the desired continuous and increasing function by setting
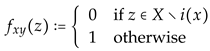
for all . These considerations now allow us to assume that but and . Since it already has been shown that we may assume without loss of generality that at least one of the (open) intervals or is not empty we first briefly discuss the case the case to be not empty. In this case, however, we may apply the arguments that have been summarized by (***) in order to guarantee the existence of some continuous and increasing function such that and . Hence, we now may assume that the (open) interval is not empty. In this situation reiteration of the just used argument in combination with an analysis of the arguments that have been summarized by (***) imply that there exists some net of points that converges to u. We now proceed by applying an indirect argument. This means precisely that we assume for all indexes each point to be contained in . Since ≾ is a closed preorder this assumption allows us to conclude, however, that , which contradicts our assumption u to be an element of . This contradiction guarantees the existence of some point such that . Since now the same situation is given as has been described in (**). This reduction to assumption (**), finally, settles the first case.
Case 2: In this case we distinguish between the sub-case to coincide with and the sub-case to be properly contained in . But since the sub-case to coincide with already has been discussed in the second part of the first case we only have to consider that strong inclusion . Here also the arguments having been used in discussing the first case apply. Indeed, let in this sub-case some point be arbitrarily chosen. Then or . If then the situation is given and we may apply the arguments having been used above when discussing the situation . If then the inclusion implies and we may apply the arguments that already have been applied when considering the last part of the first case in order to also handle this situation. This last conclusion completes the proof of the theorem. □
In the second section of this paper the universal character of the Chipman approach to mathematical utility has been demonstrated (cf. Theorem 1 and Theorem 2). Concentrating on continuous multi-utility representation in Theorem 3, however, it could be shown that the Chipman approach, at least formally, is not as far away from the real-valued approach as it seems at first sight. Therefore, we now still discuss the relations between the Chipman approach, the continuous multi-utility approach and the Richter-Peleg approach to mathematical utility theory in more detail (cf. sub-section 1.2 of the introduction). The relation between the Chipman approach and the continuous multi-utility approach can be described by combining Theorems 1 and Theorem 2 in order to state the following theorem.
Theorem 4.
Let, ≾ be a semi-closed that is defined on some topological space , and let us assume, in addition that is Hausdorff and that the order topology is coarser than t. Then the following assertions hold:
(i) There exists some cardinal number κ and a preorder ≲ on that is coarser than for which there exists a continuous order-embedding ;
(ii) ≾ admits a continuous multi-utility representation.
Proof. 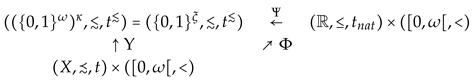
Let now be the cardinality of the set of all pairs such that . Then we consider the direct sum of ordered topological spaces as well as the direct sum of preordered topological spaces . As it already has been shown in sub-section 1.2 of the introduction it follows that there exists a continuous order-preserving function . This consideration already clarifies the relation of the continuous multi-utility approach for representing a preorder with the Richter-Peleg approach for representing a preorder (cf. Evren and Ok [7]). Let, finally, and . Then Theorem 2 implies the existence of a continuous order-embedding
and of a continuous order-embedding
such that the following diagram commutes
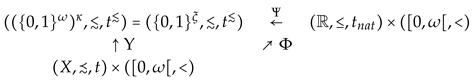
□
This last theorem completely clarifies the relations between the Chipman-approach, the continuous multi-utility approach and the Richter-Peleg approach to mathematical utility theory (cf. sub-section 1.2 of the introduction).
4. Conclusion
The Chipman-approach to mathematical utility theory, on the one hand, and the continuous multi-utility approach, on the other hand, chiefly is in the focus of this paper. Indeed, it has been shown in the second and in the third section of this paper that both approaches to mathematical utility theory are not as far away from each other as it seems at first sight. In sub-section 1.2 of the introduction and in Theorem 4 the (formal) relations of these approaches to mathematical utility theory still have been combined with the usual Richter-Peleg approach to mathematical utility theory in order to describe and visualize in this way the intimate relations that exist between these generally used approaches.
Author Contributions
Conceptualization, G.B.; methodology, M.Z.; supervision, R.D. All authors have read and agreed to the published version of the manuscript.
Funding
Not applicable.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Herden, G. , Mehta, G.B. The Debreu Gap Lemma and some generalizations. J. Math. Econom. 2004, 40, 747–769. [Google Scholar] [CrossRef]
- Chipman, J.S. The foundations of utility. Econometrica 1960, 28, 193–224. [Google Scholar] [CrossRef]
- Chipman, J.S. On the lexicographic representations of preference orderings. In Preference, Utility and Demand, Chipman, J.S., Hurwicz, L., Richter, M., Sonnenschein, H.F. (eds),, Harcourt Brace and Jovano-vich, New York (1971), pp. 276-288.
- Beardon, A.F. Debreu’s Gap Theorem. Economic Theory 1992, 2, 150–152. [Google Scholar] [CrossRef]
- Levin, V.L. A continuous utility theorem for closed preorders on a σ-compact metrizable space. Soviet Mathematics Doklady 1983, 28, 715–718. [Google Scholar]
- Evren, O. , Ok, E.A. On the multi-utility representation of preference relations. J. Math. Econom. 2011, 47, 554–563. [Google Scholar] [CrossRef]
- Ok, E.A. Utility representation of an incomplete preference relation. J. Econom. Theory 2002, 104, 429–449. [Google Scholar] [CrossRef]
- Minguzzi, E. Topological conditions for the representation of preorders by continuous utilities, Appl. Gen. Topol. 2012, 13, 81–89. [Google Scholar]
- Minguzzi, E. Normally Preordered Spaces and Utilities. Order 2013, 30, 137–150. [Google Scholar] [CrossRef]
- Pivato, M. Multiutility representations for incomplete difference preorders, Math. Social Sci. 2013, 66, 196–220. [Google Scholar] [CrossRef]
- Dubra, J. , Maccheroni, F., Ok, E.A. Expected utility theory without the completeness axiom. J. Econom. Theory 2004, 115, 118–133. [Google Scholar] [CrossRef]
- Evren, O. On the existence of expected multi-utility representations. Econom. Theory 2008, 35, 575–592. [Google Scholar] [CrossRef]
- Galaabaatar, T. , Karni, E. Expected multi-utility representations. Math. Social Sci. 2012, 64, 242–246. [Google Scholar] [CrossRef]
- Bosi, G. , Estevan, A., utiérrez García, J., Induráin, E. Continuous representability of interval orders: The topological compatibility setting. Internat. J. Uncertain. Fuzziness Knowledge-Based Systems 2015, 2, 345–365. [Google Scholar] [CrossRef]
- Hack, P. , Braun, D.A., Gottwald, S. The classification of preordered spaces in terms of monotones: complexity and optimization. Theory and Decision 2023, 94, 693–720. [Google Scholar] [CrossRef]
- Herden, G. On the existence of utility functions. Math. Social Sci. 1989, 17, 297–313. [Google Scholar] [CrossRef]
- Peleg, B. Utility functions for partially ordered topological spaces. Econometrica 1970, 38, 93–96. [Google Scholar] [CrossRef]
- Bosi, G. , Herden, G. Continuous multi-utility representations of preorders. J. Math. Econom. 2012, 48, 212–218. [Google Scholar] [CrossRef]
- Bosi, G. , Herden, G. On continuous multi-utility representations of semi-closed and closed preorders. Math. Social Sci. 2016, 69, 20–29. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





