1. Introduction
Wave propagation in most dynamic systems is dependent on the energy of the system and the boundary conditions. Investigating these effects through the resonant states in driven oscillation systems allows for advanced applications across a myriad of fields, e.g., seismology [
1], quantum billiards [
2], and nanomechanics [
3,
4]. Such advancements lead to greater insights into oscillatory systems in general and can be applied across all scales.
In this study we analyse the experimentally measured resonant states of Chladni plates and by considering a standing wave emanating from the centre of the plate, the excitation frequency and the geometry of the spatial boundaries, we theoretically determine the nodal line patterns.
Nodal line patterns formed by the excitation of a thin plate are one of the most extensively studied wave systems, yet our understanding of them remains incomplete. Although predictions of the resonant modes can be made utilising approximation methods, this does not yield exact solutions that can deepen our understanding of the system dynamics.
In 1787, building on the observations of Galileo and Hooke, the musician and physicist Ernst Chladni demonstrated the various modes of vibration on a rigid surface [
5,
6,
7]. These nodal patterns are now known as Chladni patterns or Chladni Figures and the plates that are used as a rigid surface are known as Chladni plates.
Through the centuries the type of surface and vibrating particle has taken many forms: from a brass plate and its shavings excited by a chisel [
8]; a glass plate and flour excited by a violin bow string [
9]; a metal plate and sand excited by a violin bow string [
5]; a metal plate and sand excited by a block of high density carbon dioxide [
10,
11,
12,
13]; to a drum membrane and quartz sand excited by singing through a pipe [
14].
The modern Chladni experiments are conducted using an electronically controlled mechanical oscillator which drives the plate at specific frequencies. The main difference being the accuracy of the driving frequency and the position of the driving source, which for the modern experiments is typically the central position of the plate as opposed to the original experiments which were generally driven by vibrating the edge of the plate. This difference in position alters the boundary conditions and hence the nodal line patterns.
To theoretically determine the nodal line patterns, several different forms and solutions of the wave equation have been used (e.g., Helmholtz , Bernoulli etc.). For example, Kirchhoff [
15,
16] determined the vibration modes of a circular plate by considering the effects of deformation and stresses in a vibrating plate. This was then extended to the square plate for the case of free edges [
16] and then for the case of clamped edges [
16,
17]. However, as noted by Wah [
18], it is near impossible to simulate the case of ‘clamped edges in the laboratory and moreover plates generally behave as if they have boundary conditions between the theoretical ‘simple support and ‘clamped edge conditions.
In any case, the response of the square plate was deemed of such a variable nature that to determine an exact solution requires approximate or numerical procedures (e.g., Greens function method, Ritz method, finite element analysis etc.). In fact, exact solutions are only available for a few cases such as the circular plate which can be expressed in terms of the Bessel functions [
19].
For more complex boundary conditions, the experimentally observed resonant modes do not correspond to theoretically determined eigenmodes, therefore, as noted by Tuan et al. [
20], they should instead be solved from the inhomogeneous Helmholtz equation.
Furthermore, as first noted by Waller [
13,
19,
21,
22], due to the effects of degeneracy and damping, the nodal line patterns at higher frequencies consist of two or more compounded nodes which need to be accounted for by different methods. This forming of the resonant mode by a superposition of numerous degenerate eigenmodes, or nearly degenerate eigenmodes, is also referred to as mode mixing, e.g., [
23] and references therein.
To date, the most successful method in the analysis of nodal line patterns is that of the inhomogeneous Helmholtz equation. For example, utilising the Green’s function, Tuan et al. [
24] solves the inhomogeneous Helmholtz equation and finds the response function for a vibrating wave on a thin plate as a function of the driving wave number, where the wave numbers are determined from the maximum entropy states. Thus, by substituting the theoretically determined wave numbers into the derived response function the resonant modes can be calculated and the experimental nodal line patterns successfully reconstructed for both the square and equilateral triangle plates [
20,
23,
24,
25,
26,
27].
Other approaches have been successful, for example, instead of using the usual numerical approaches, Amore [
28] finds solutions to the Helmholtz equation (both homogeneous and inhomogeneous) by using the little sinc method [
28,
29,
30]. Utilising this method, he obtains a discretisation of a finite region of space in the 2D plane, and successfully calculates the modes of vibration for membranes of arbitrary shapes. However, this approach has not yet been applied to nodal line patterns on Chladni plates.
In any case, these approaches require approximation methods and techniques that do not necessarily translate across more complex boundary conditions. In this paper we present a simple model that considers the response function in terms of the geometry of the spatial boundaries, and is thus potentially applicable for all boundary conditions.
2. Resonant Mode Chladni Patterns
Each Chladni plate, depending on the material it is made of, its size and shape, will have resonant modes i.e., frequencies at which standing waves are formed. Before we can investigate the behaviour of these modes, we need to determine the resonant frequencies. This can be done by investigating the impedance of the mechanical oscillator as a function of frequency.
2.1. Impedance experiment to determine resonant modes
Following the work of Tuan et al. [
23] we determine the resonant mode frequencies by measuring the impedance of the mechanical wave driver, with and without a plate attached.
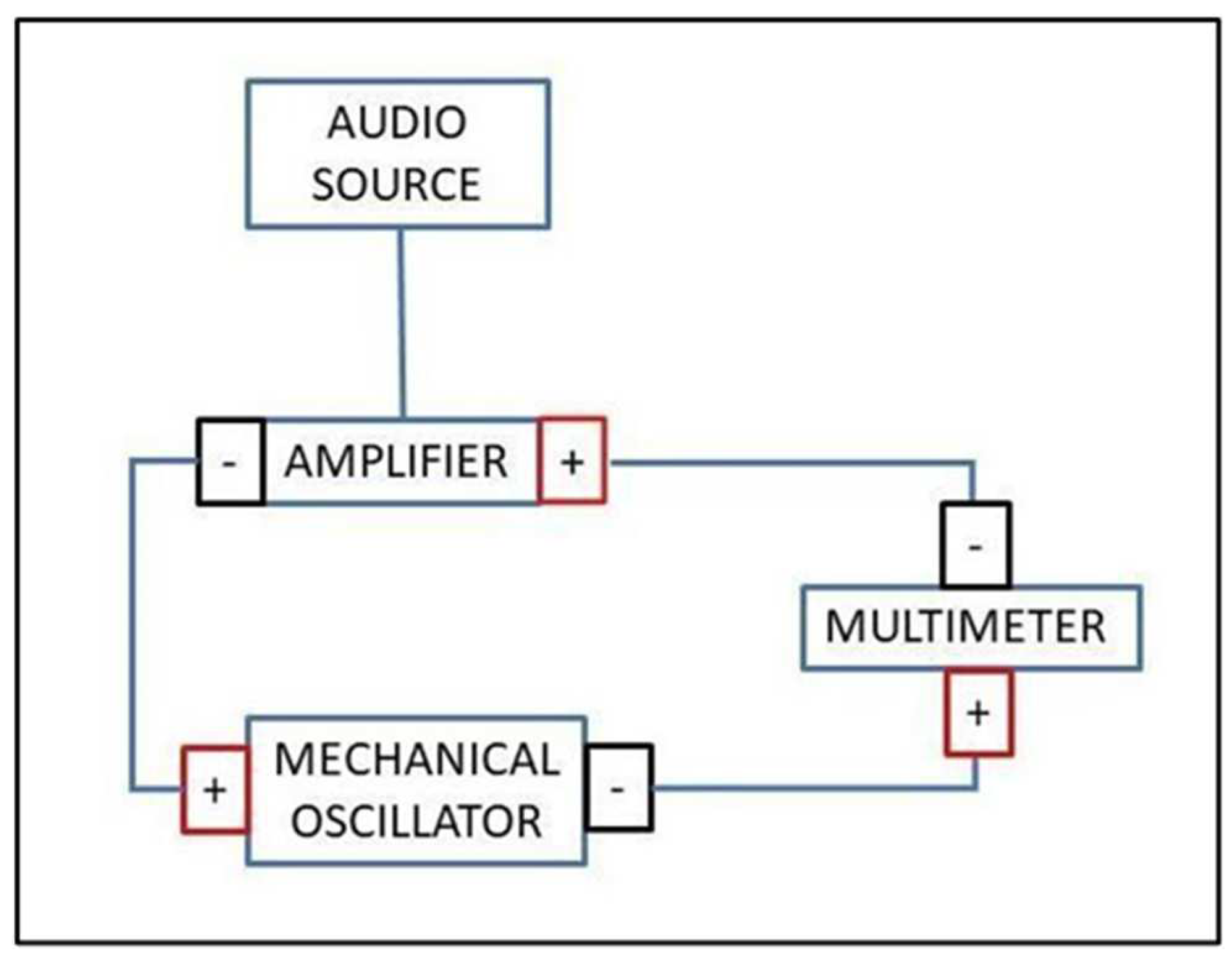
The setup of the experiment is shown in
Figure 1. A 20W Thomann TA50 Amplifier was connected in series with a PASCO Mechanical Wave Driver and a GDM 8342 Multimeter. The mechanical wave driver was driven by the amplifier at ~30% via a Max/MSP patch that generated a sinusoidal wave over the frequency range 20–2000 Hz. The multimeter took measurements of the AC voltage every second over a period of ~20 minutes, giving a resolution of ~1.6 Hz. These measurements were initially carried out with no plate attached to the mechanical wave driver. Subsequent measurements were then taken for a total of ten plates of the following shape and dimensions: circle of diameter 18 cm, and 24 cm; triangle of side 18 cm, and 24 cm; square of side 18 cm, and 24 cm; pentagon of side 9.5 cm, and 14.5 cm; hexagon of side 9 cm and 12 cm. The plates were made of acrylic with a thickness of 2 mm, resulting in a thickness to size ratio ≪0.1 for all plates.
In each case, the impedance, Zf , was calculated as a function of frequency from the variable voltage output, Vf , and the base current, I, via the formula Zf = Vf /I.
The effective impedance was then determined by subtracting the impedance found in the case where no plate was attached from the impedance found when the plate was attached.
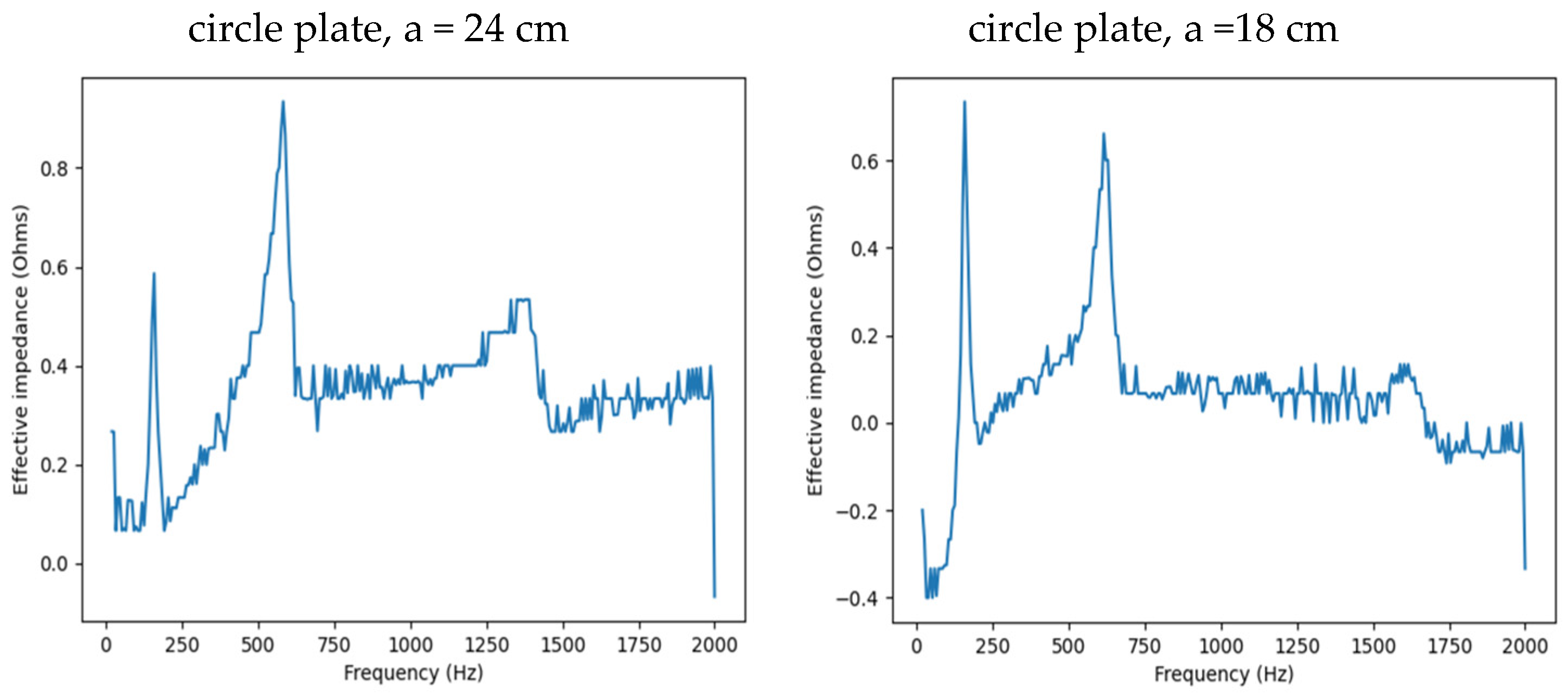
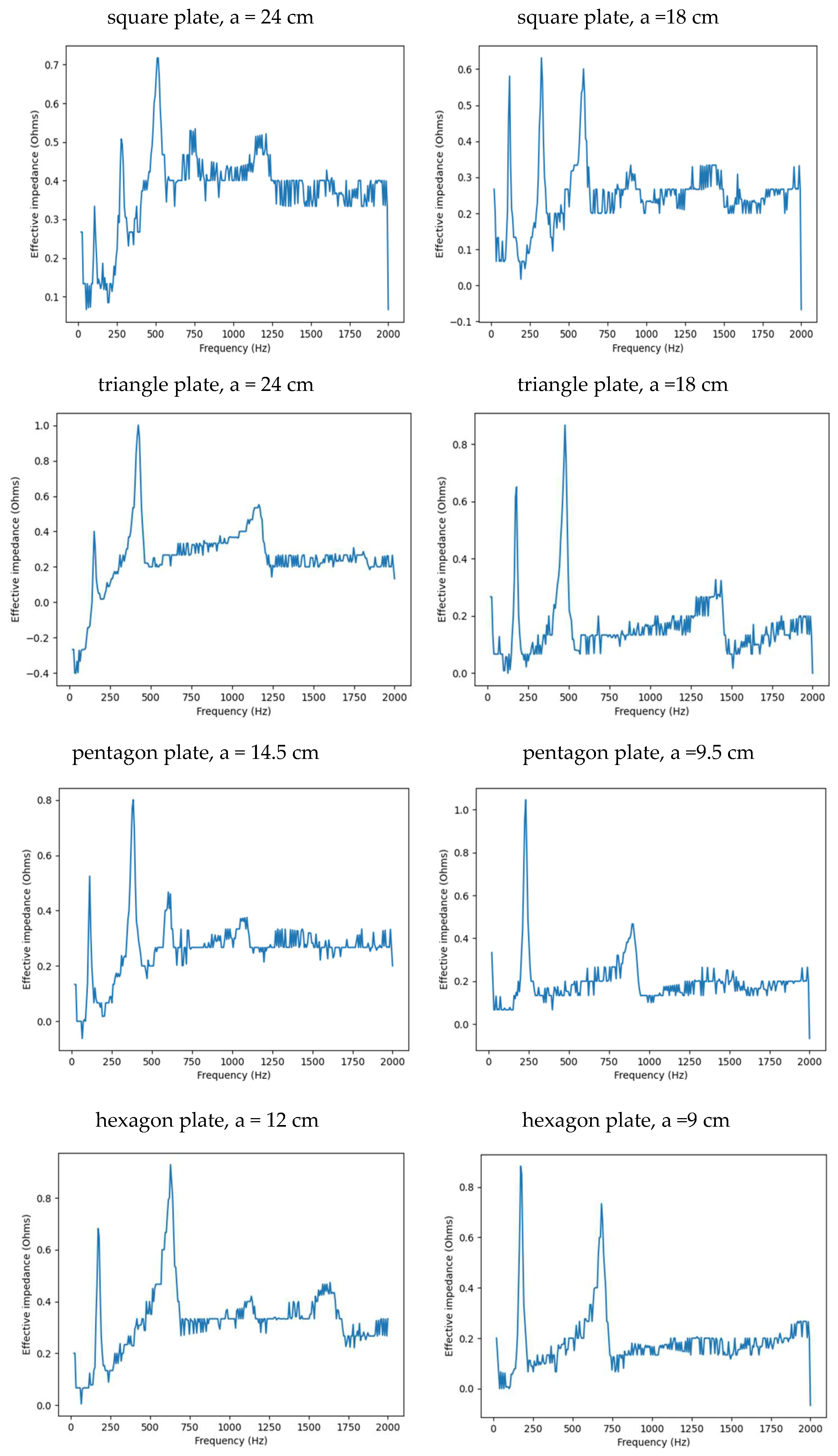
Figure 2A-E show the results for each plate, where the impedance is shown as a function of frequency and the peaks indicate the resonant frequencies in each case. The resonant frequencies found from the impedance peaks are shown in
Table 1.
2.2. Impedance experiment to determine resonant modes
Following the setup shown in
Figure 1, we investigated the patterns formed at the resonant frequencies determined from the impedance analysis (see
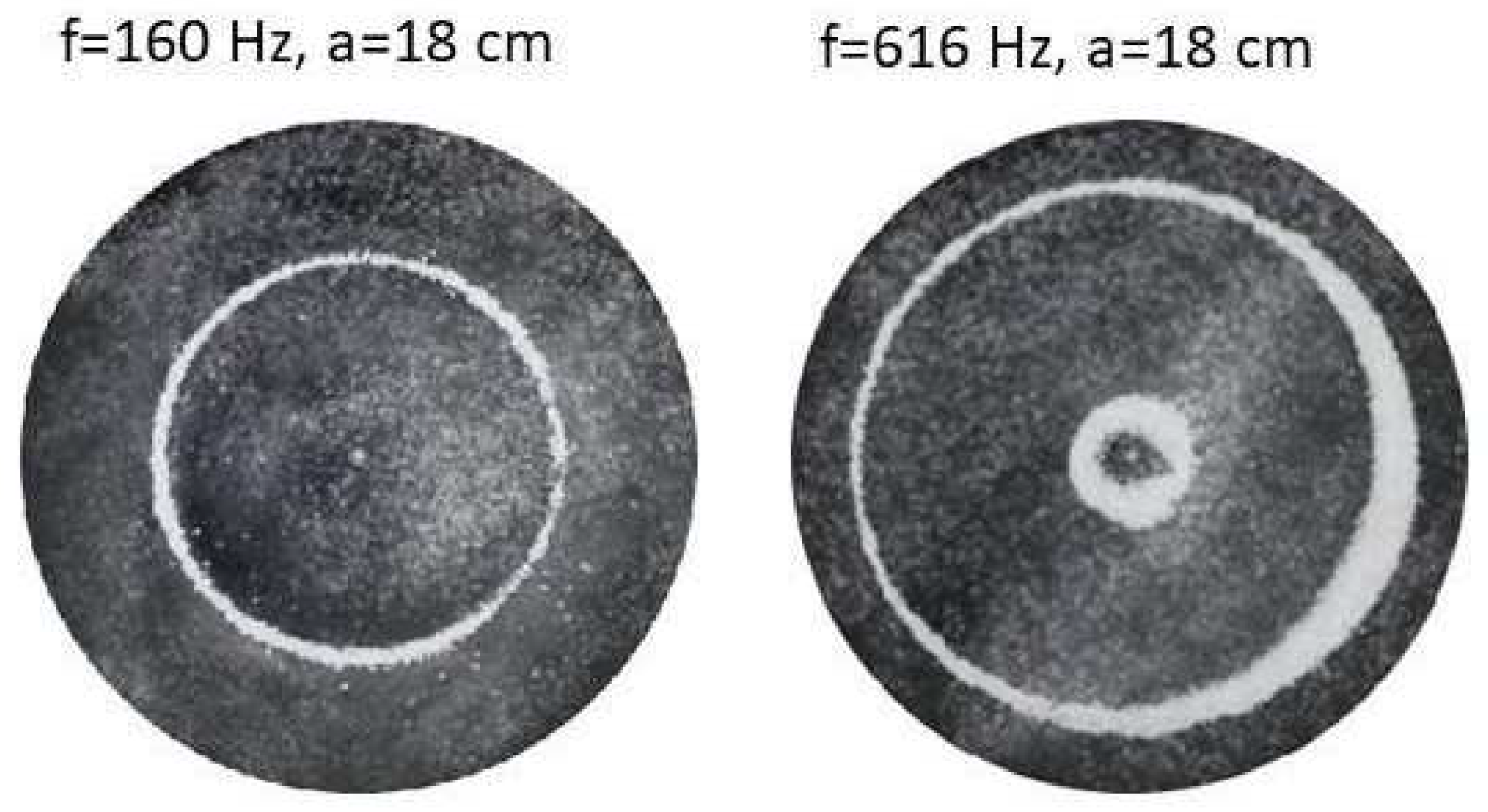
Section 2.1). For each of the 10 plates, a sand sprinkler was used to completely cover the plate with sand. Once the desired frequency was set, more sand is added as necessary, ensuring optimum pattern formation. To record pattern formation a Canon EOS 5D Mark IV Camera, with a Canon 100 mm macro lens, is mounted parallel to the Chladni plates. The recordings were taken in video mode, with the aperture set at F2.8, the shutter speed set to 1/50, and the ISO set at 25600.
Figure 3,
Figure 4,
Figure 5,
Figure 6,
Figure 7,
Figure 8,
Figure 9,
Figure 10,
Figure 11 and
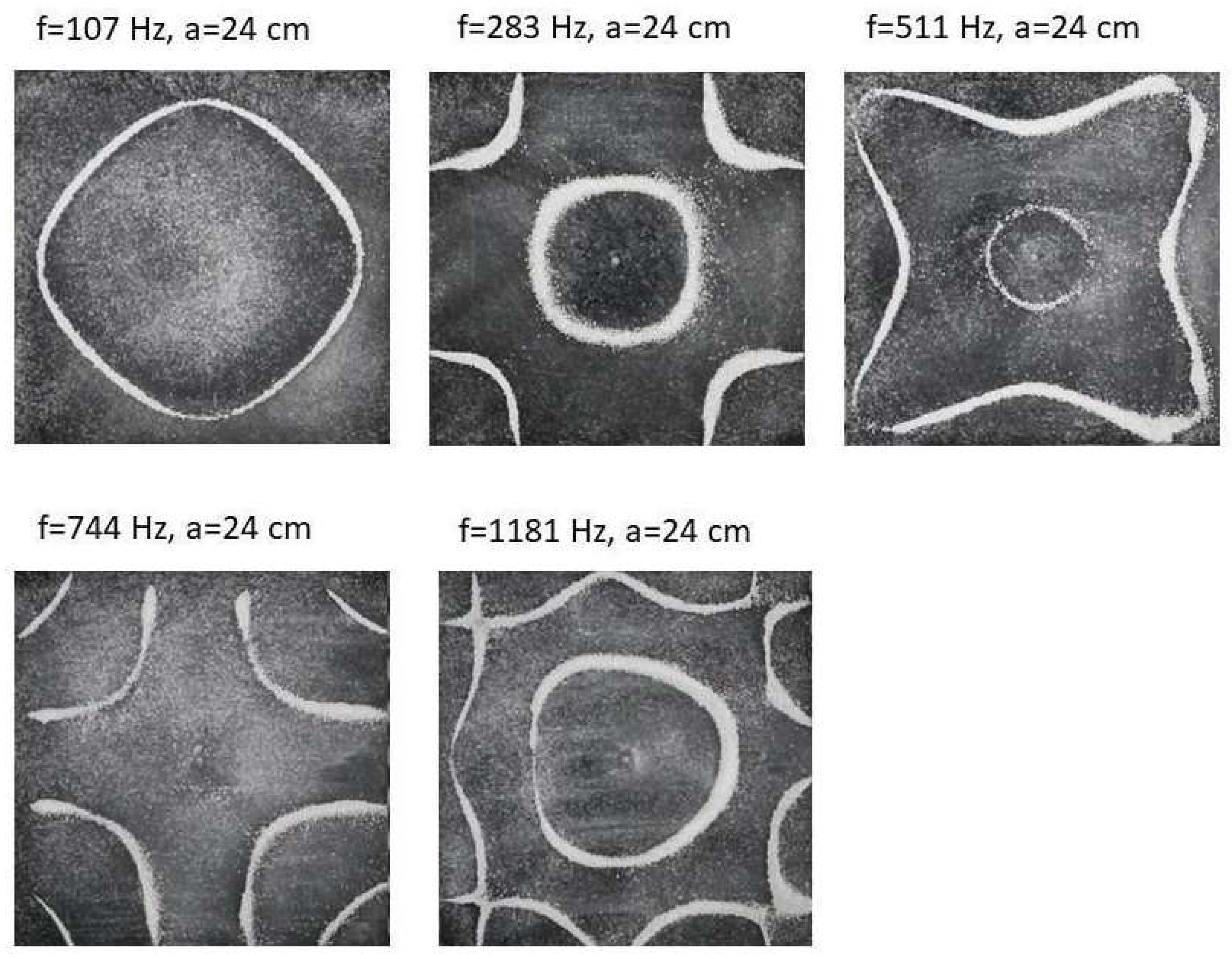
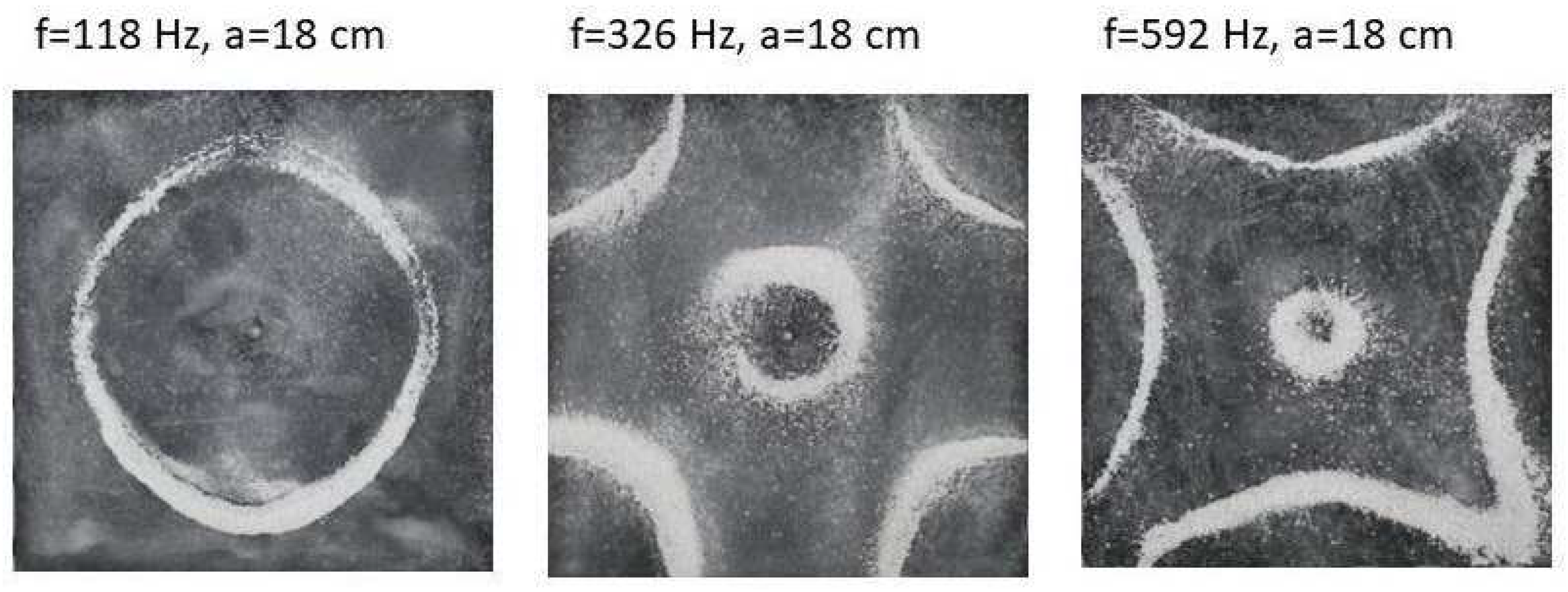
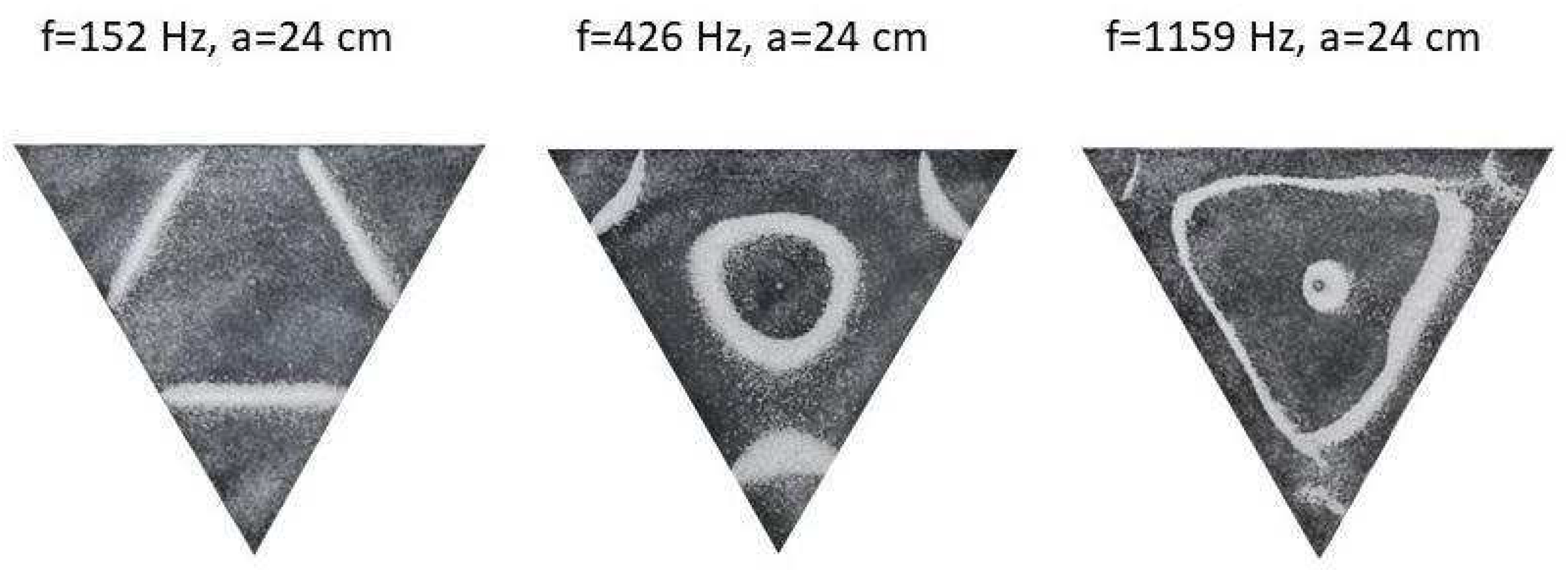
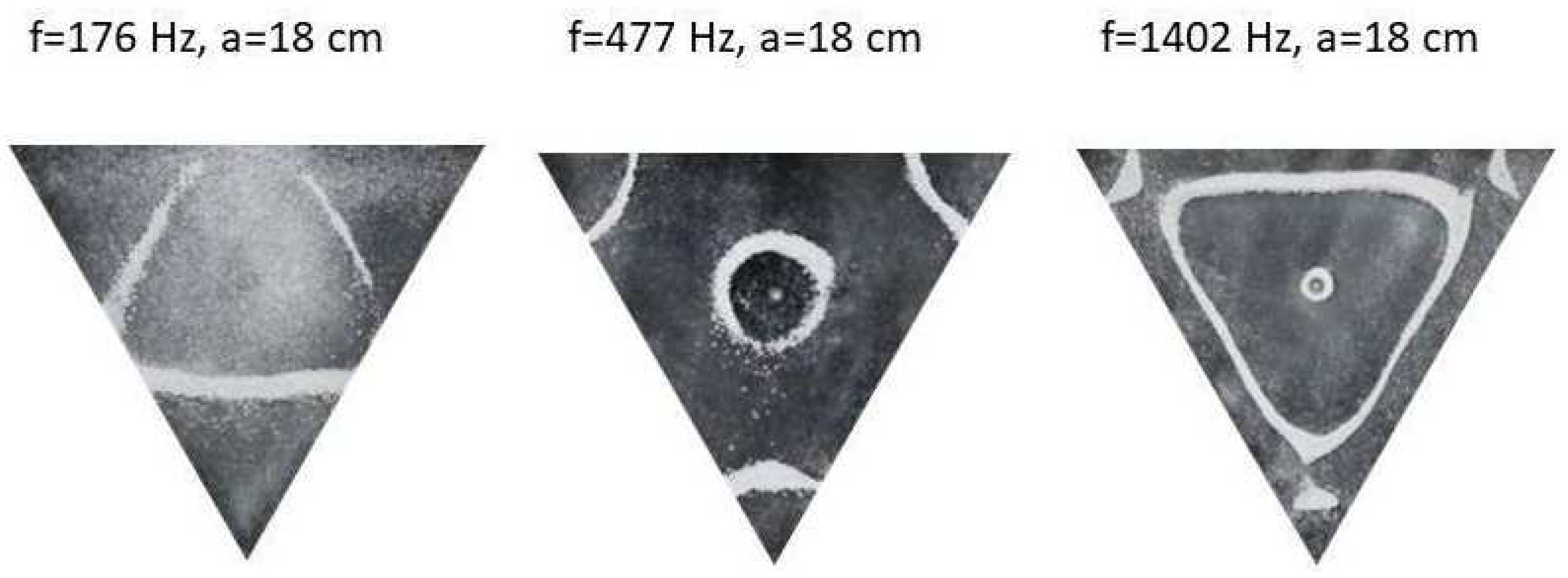
Figure 12 shows the resulting resonant frequency pattern formations, also referred to as nodal line patterns, for each of the 10 plates. As expected, the number of nodal line patterns increases with increasing frequency and for the polygonal plates the degree of complexity also increases with frequency. The same pattern morphology is exhibited in both the larger sized plates and the smaller sized plates but is generally exhibited at a higher frequency in the smaller sized plates. This observed difference in frequency between the larger and the smaller plates increases with increasing modes, i.e., the number of nodal lines.
3. Theoretical Determination of The Nodal Line Patterns
To theoretically recreate the nodal line patterns, we consider a simple wave equation for a standing wave.
Let
z represent the variable amplitude of the wave as it propagates up and down,
here z1 is the outward wave; z2 is the reflected wave; zr is the resultant wave; A is the amplitude; ω is the angular frequency; and ϕ is the phase difference between the outward and reflected wave.
The nodal points, where the sand collects, corresponds to the points of zero displacement, also described as maximum entropy states [
27], and can therefore be found by setting
zr in Eq. (3) to equal 0, i.e.,
we can then assume that,
giving,
and thus the time it takes for the wave to get to a given point is given as,
If the wave is reflected and is oscillating at the resonant frequency of the system, then there is no phase difference between the waves, so ϕ = 0 and a standing wave is formed, i.e., a resonant mode.
At specific frequencies, Chladni plates are known to exhibit coherent patterns referred to as Chladni Figures, or nodal line patterns. These nodal line patterns consist of nodal points which, like in Eq. (4), can be expressed in terms of time,
In polar coordinates (r, θ, φ) at zr = 0, φ = π/2 (note the polar coordinate φ is not the same as the phase difference ϕ defined earlier). We can therefore assume that r only exists in the x, y plane which physically represents the spatial dimension of the plate.
If we then consider the spatial dimension of the plate in terms of time, we can define
r as,
and we can then also set the boundary condition in terms of time as,
where Lθ is the spatial dimension given as a function of θ; t is the time it takes for the wave to traverse the distance Lθ; and v is the velocity of the wave.
Note, the velocity of a sound wave is ~ 340 ms
-1 in air at average room temperature, ~ 1500 ms
-1 in water and for solids is given as
, where
is the Young’s Modulus given in pascals (Pa);
σ(
ε) is a measure of stress;
ε is a measure of strain; and
ρ is the density. However, in the case of the Chladni plate we are not interested in the velocity of the sound wave. Instead, we are interested in the velocity of the mechanical wave which lifts the sand grains up and down which can be given as
v =
λf. For a circular plate of known diameter, the wavelength, and hence velocity, can be determined from the observed nodal line patterns. For the circular plate, the resulting velocity as a function of frequency was thus found to be,
This is in good agreement with the observations by Tuan et al. [
23] and was subsequently used to determine the velocity for each of the plates.
The plate is also subject to forces that will influence wave propagation and the motion of the sand particles. The thickness to size ratio of the plate is ≪0.1, so we can therefore assume the response function to be variable in the
x,
y plane (
r,
θ plane) and negligible in the
z plane (
φ plane). To account for this, we can include a response function,
FR, such that,
3.1. Circular Chladni plate
To begin with we will take the example of a Chladni plate with one boundary condition, i.e., a circular plate.
For the case of a circular plate, which behaves symmetrically across the shape (i.e., the variability is constant with respect to
θ), we can define
FR as a simple coefficient, which we call
C, see
Table 2 for the list of coefficients. Note in each case the coefficient was first determined by manually adjusting the value until the theoretical nodal line patterns match those of the experiment. This was done visually and also using a fitting function which adjusts the coefficients according to the fit.
From Eq. (8) and by setting the boundary condition in terms of
L =
a/2 , where
a is the diameter of the circular plate, and the velocity
v, as determined from the experimental analysis, we recreate the nodal line patterns in a good approximation with the experimental results, see
Figure 13 and
Figure 14. All equations and boundary conditions were implemented using a custom software application created in Python.
It is interesting to note that, depending on the position of the nodal line relative to the plate centre, we see lesser or greater effects of the response function. For example, at a critical closeness to the centre we see a greater response function. Then as we move further away from the centre of the plate we see a smaller response function, until reaching a critical distance away from the centre, where we again see almost zero response function. For a specific plate this is clearly expressed in the value of the
C coefficient, which increases with increasing frequency and decreases with increasing number of nodal lines (see
Table 2 for the full list of coefficients).
3.2. Square Chladni plate
As with the circular plate we expect the nodal points to be shifted due to the response function of the plate. However, as we are dealing with a polygon, we must also take into consideration the variability of
L, which for any n-sided polygon varies with respect to the angle with the primary axis,
θ. Thus, for a square plate, the minimum length from the centre is given as
where
a is the length of one side and thus
Lθ varies as,
The response function FR, for the square plate, or any other polygon, will thus depend on the variability in the length of the plate, with respect to the centre, θ, as well as the distance from the centre, r.
To investigate this further, and as a first approximation, we set the response function in the form of a trigonometric function, e.g., a rose function,
where n is the number of sides of the polygon, so for the square plate n = 4.
From Eqn. (8), and by setting
FR as given by Eq. (11), the boundary condition in terms of
Lθ as given by Eq. (10), and the velocity
v, as given by Eq. (7), we recreate the nodal line patterns in a good approximation with the experimental results. See
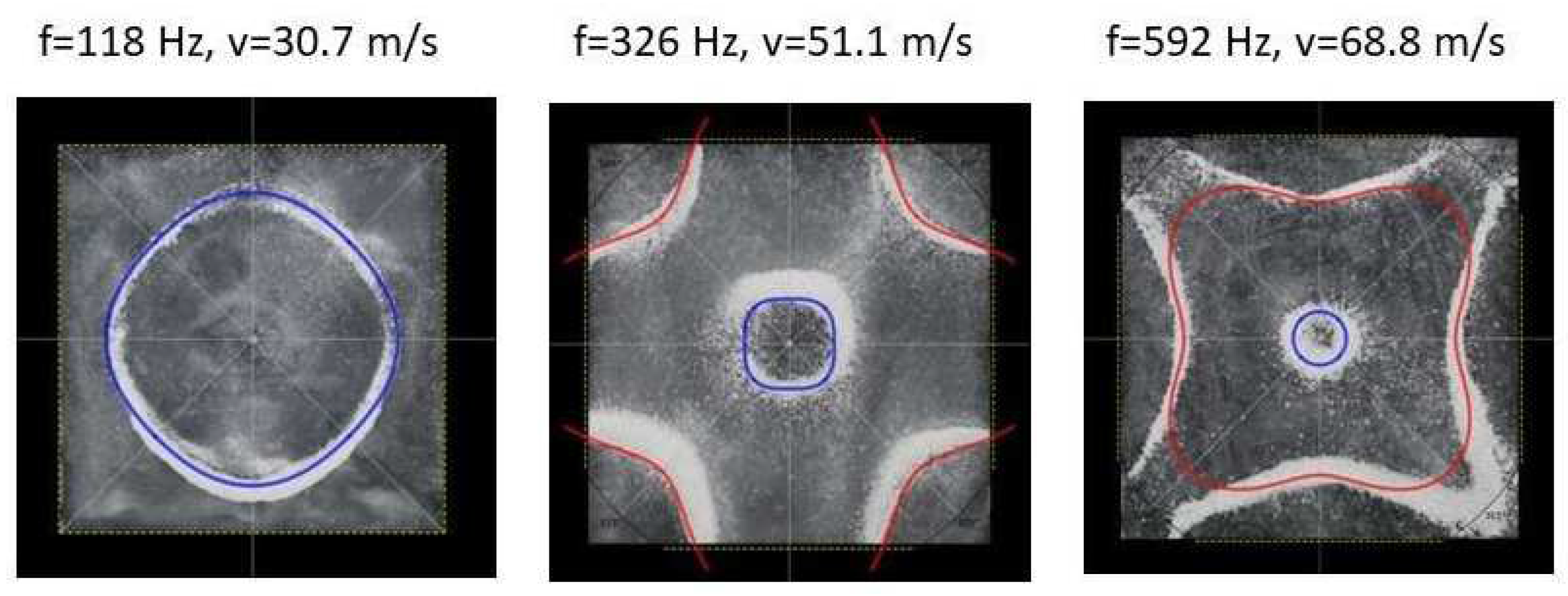
Figure 15 and
Figure 16.
It is interesting to note that, depending on the position of the nodal line relative to the plate centre, we see lesser or greater effects of the response function variability. For example, at a critical closeness to the centre we see no variability in the response function, and it acts in the same way as you would see for a circular plate. Then as we move further away it exhibits more variability, until reaching a critical distance away from the centre where again we again see no variability in the response function. For a specific plate this is clearly expressed in the value of the
A coefficient, which appears to oscillate between positive and negative values with the increasing number of nodal lines. As well like the circular plate the value of the
C coefficient increases with increasing frequency, for a specific nodal line (defined as
Cr), and decreases with increasing number of nodal lines, for a specific frequency (see
Table 2 for the full list of coefficients). For the higher frequencies we can see the beginnings of mode mixing, not yet fully effecting. As we move into increasingly higher frequencies this will be more evident.
3.3. Triangular Chladni plate
As with the square plate we must also take into consideration the variability of
L with respect to
θ. Thus, for a triangular plate, the minimum length from the centre is given as,
where
a is the length of one side and thus
Lθ varies as,
From Eq. (8), by setting
FR as given by Eq. (11) with
n = 3, the boundary condition in terms of
Lθ as given by Eq. (13), and the velocity
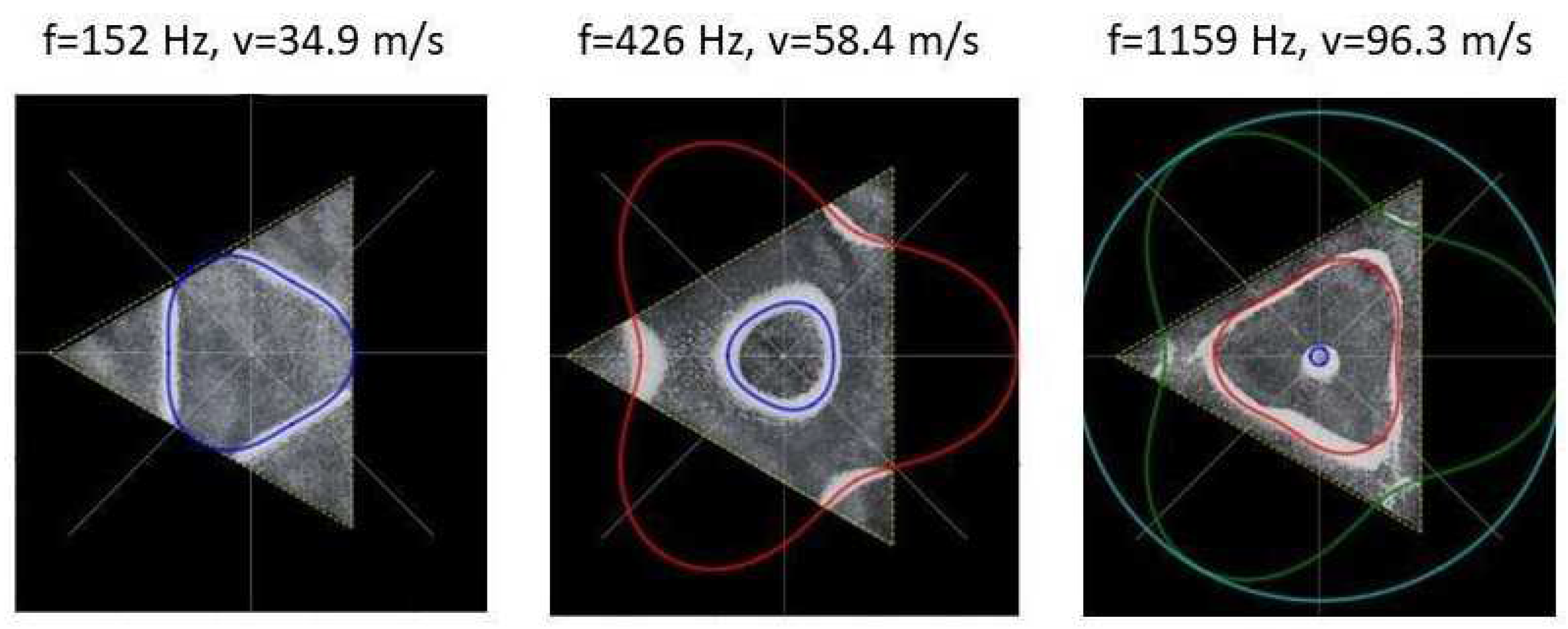
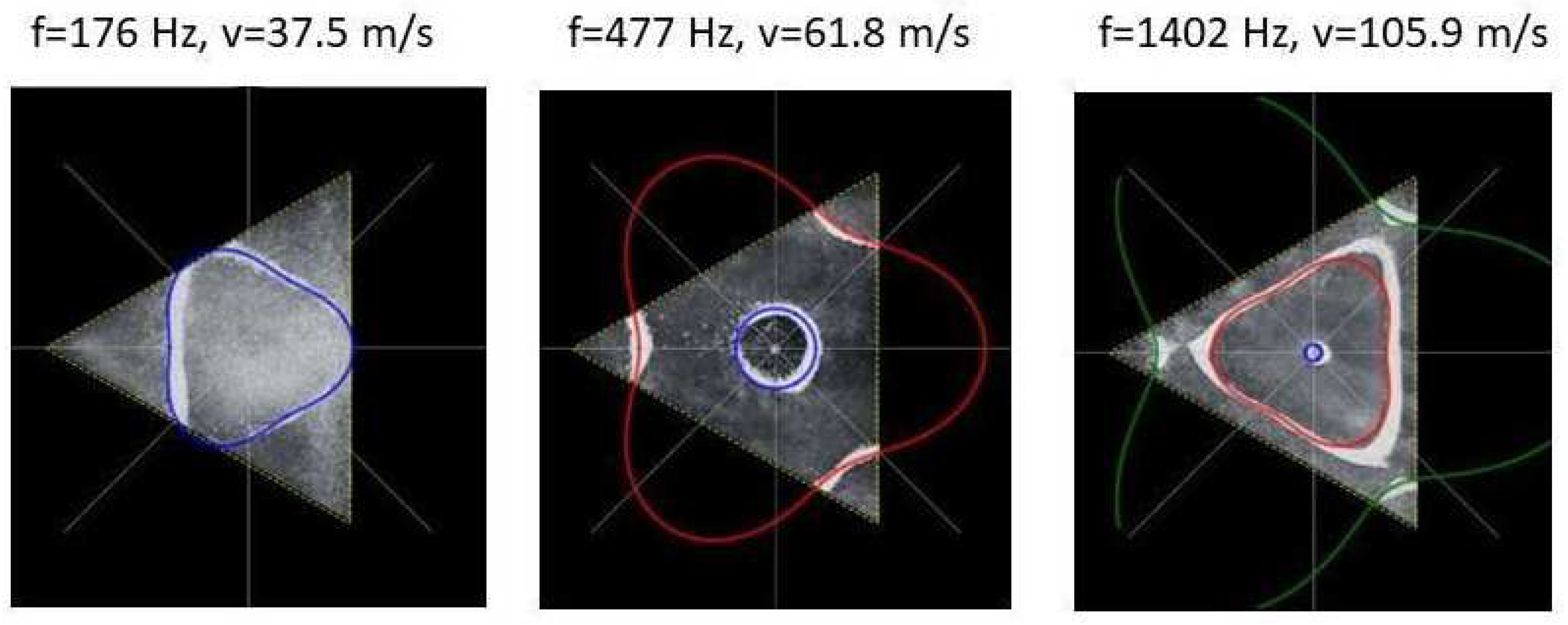
v, as determined from the experimental analysis, as given by Eq. (7), we recreate the nodal line patterns in a good approximation with the experimental results. See
Figure 17 and
Figure 18.
It is interesting to note that, again, like the square plate we see the same progression of pattern complexity, with the value of the coefficients following a similar relationship to that of both the circle and the square plate.
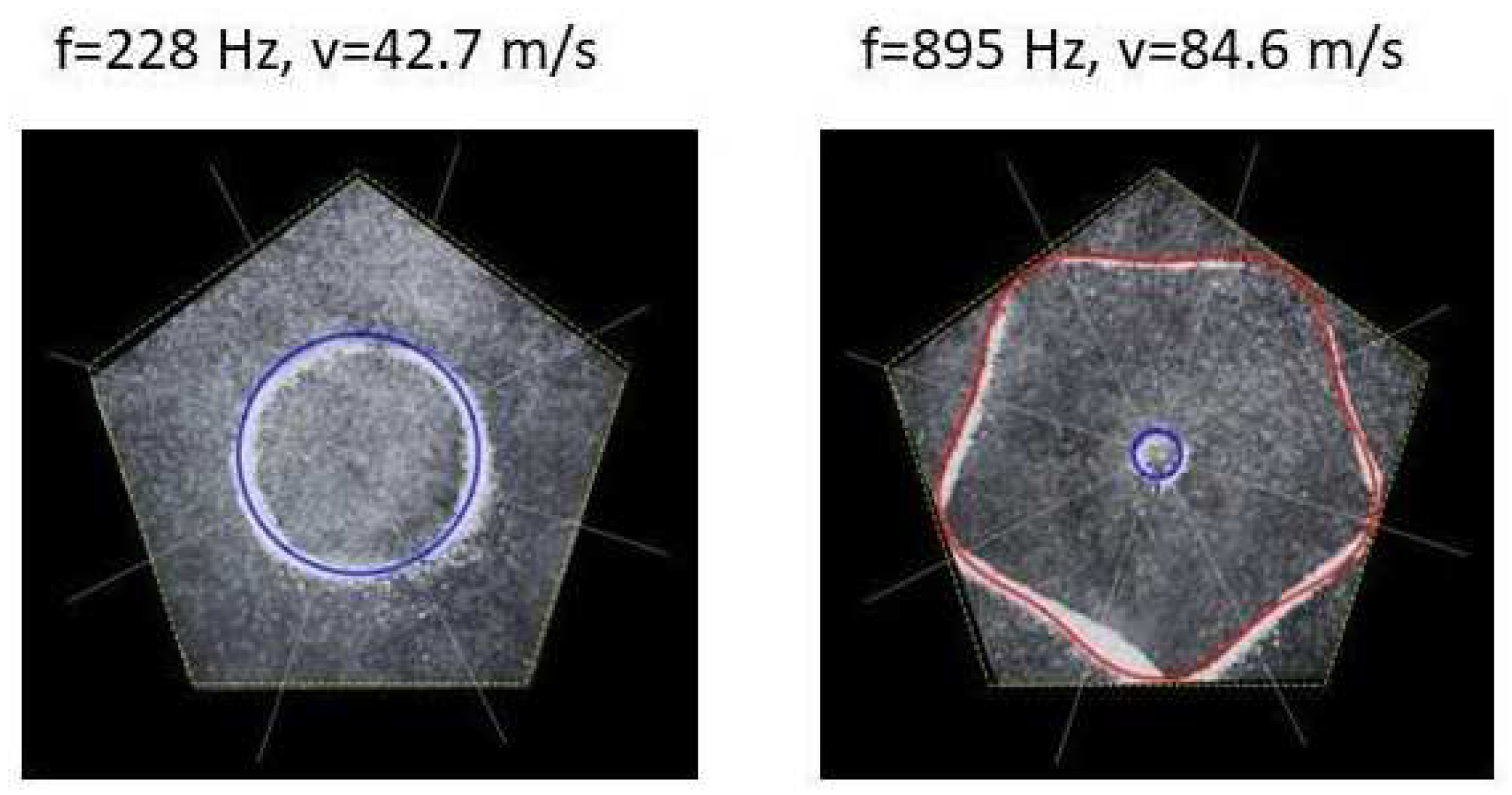
3.4. Pentagon Chladni plate
As with the other polygon plates we must also take into consideration the variability of
L with respect to
θ. Thus, for a pentagon plate, the minimum length from the centre is given as,
where
a is the length of one side and thus
Lθ varies as,
From Eq. (8), by setting
FR as given by Eq. (11) with
n = 5, the boundary condition in terms of
Lθ as given by Eq. (15), and the velocity
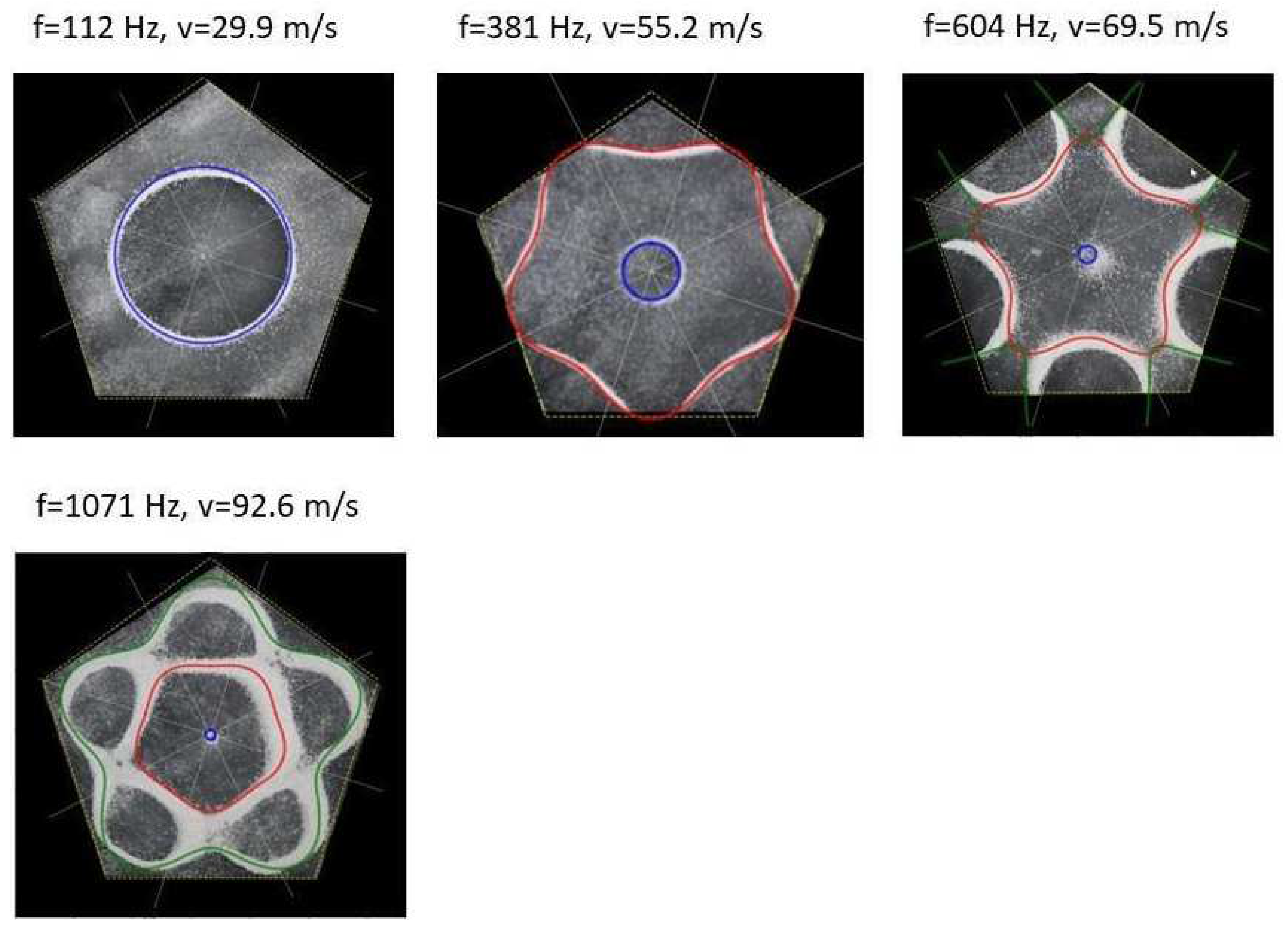
v, as given by Eq. (7), we recreate the nodal line patterns in a good approximation with the experimental results. See
Figure 19 and
Figure 20.
It is interesting to note that, again, like the other polygon plates we see the same progression of pattern complexity, with the value of the coefficients following a similar relationship to that of both the circle and the other polygon plates.
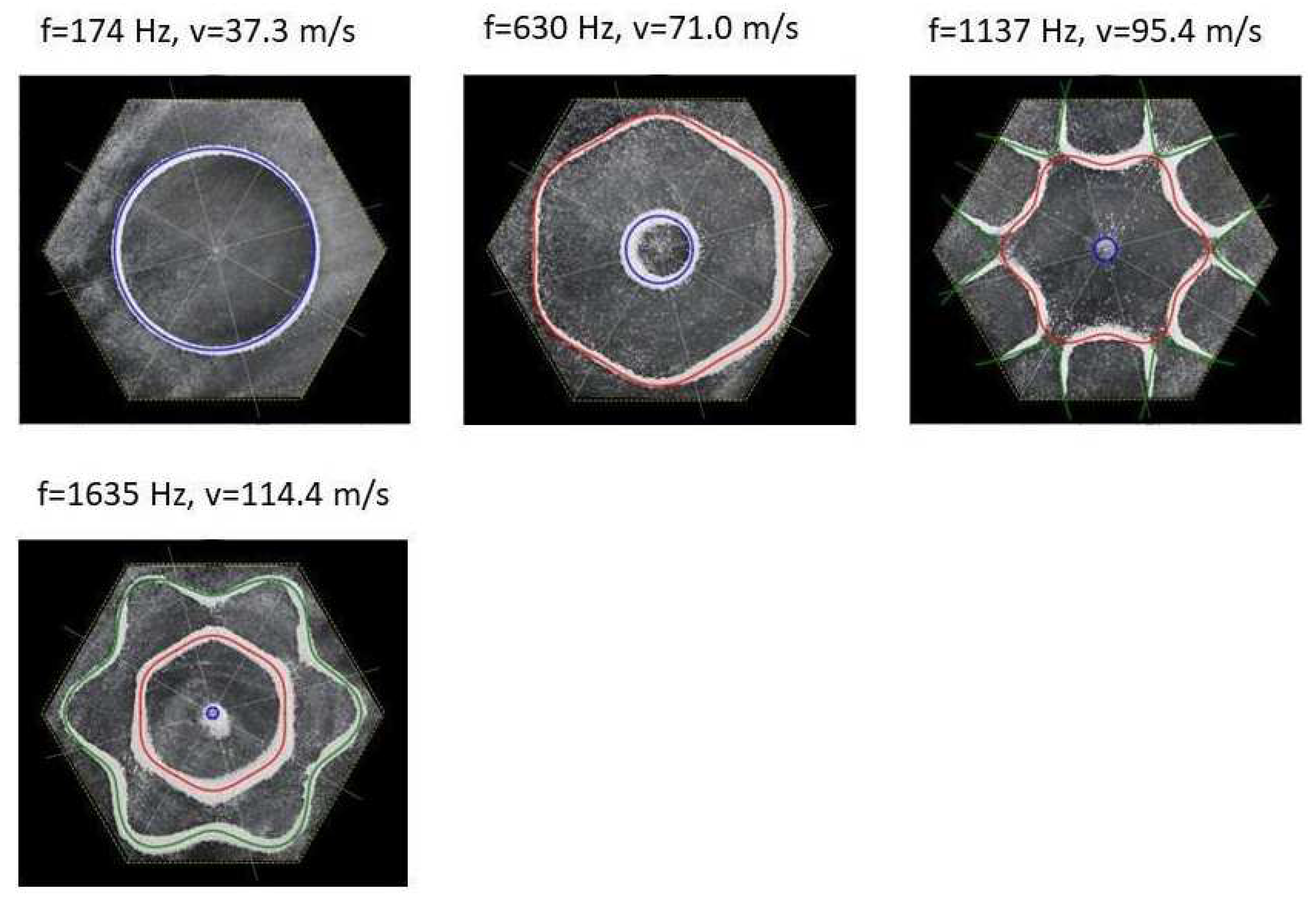
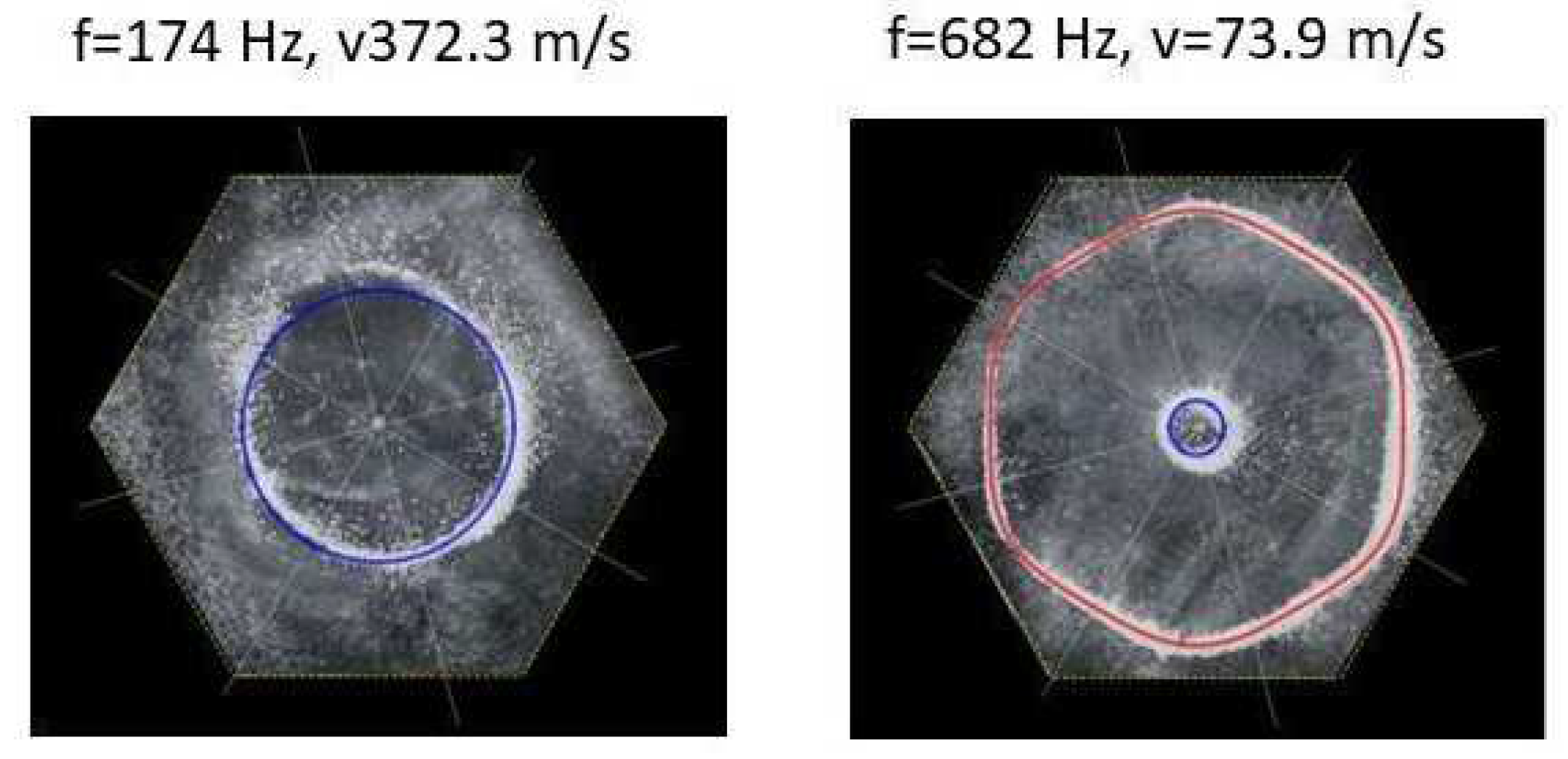
3.5. Hexagon Chladni plate
Again, as with the other polygon plates we must also take into consideration the variability of
L with respect to
θ. Thus, for a hexagon plate, the minimum length from the centre is given as,
where
a is the length of one side and thus
Lθ varies as,
From Eq. (8), by setting
FR as given by Eq. (11) with
n = 6, the boundary condition in terms of
Lθ as given by Eq. (17), and the velocity
v, as given by Eqn. (7), we recreate the nodal line patterns in a good approximation with the experimental results. See
Figure 21 and
Figure 22.
It is interesting to note that, again, like the other polygon plates we see the same progression of pattern complexity, with the value of the coefficients following a similar relationship to that of both the circle and the other polygon plates.
4. Summary
In this paper we analyse the experimentally measured resonant states of 10 different shaped and sized Chladni plates and present a simple model that considers a response function in terms of the geometry of the spatial boundaries.
Depending on the position of the nodal line relative to the plate centre, we see lesser or greater effects of the response function. For example, at a critical closeness to the centre we see a greater response function. Then as we move further away from the centre of the plate we see a smaller response function, until reaching a critical distance away from the centre, where we again see almost zero response function. For the polygon plates, these effects extend to the variability within nodal lines, where at a critical closeness to the centre we see no variability in the response function, and it acts in the same way as you would see for a circular plate. Then as we move further away it exhibits more variability, until reaching a critical distance away from the centre where again we see no variability in the response function. This behaviour is expected, as at a critical point the boundary effects become either negligible or significant.
For all plates, circular and polygonal, the value of the C coefficients, for a specific nodal line (defined as Cr), increases with increasing frequency and for a specific frequency, decreases with increasing number of nodal lines. For the polygonal plates the value of the A coefficient, for a specific nodal line (defined as Ar) appears to oscillate between positive and negative values (or between higher and lower values), tending to zero as the frequency increases. As well, for a specific frequency, the A coefficient decreases with increasing number of nodal lines. However, there are a couple of exceptions to this relationship, especially at the higher frequencies (e.g., the hexagon a = 12 cm, f = 1635 Hz; and the pentagon a = 14.5cm, f = 1071 Hz), and this is most likely due to the effects of mode mixing. With the range of frequencies investigated in this study, we can only see the beginnings of mode mixing, which will become more evident as we investigate increasingly higher frequencies. For these effects to be accounted for and a quantitative relationship to be made, more investigations yielding a larger data set are required and will be done in a future study.
It is obvious that, for a non-idealized system, the resonance modes will not equate with the eigenmodes of the wave equation. This is the result of the response function of the plate, which causes a shift and hence a discrepancy between the eigenmodes and the resonant modes. As well the boundary conditions and restrictions will result in mode mixing, resulting in further deviations from the eigenmodes. However, the results presented here show that these deviations are not the result of inhomogeneity and are rather a coherent geometrical effect that determines the response function. This is not only evident from the symmetry of the nodal line patterns, but also from the simplistic method presented to reconstruct the nodal patterns.
This study considers a finite range of frequencies and plate geometries and presents a simple model that has been shown to successfully recreate the nodal line patterns to a first approximation. However, more data is needed so that quantitative analysis can define the coefficients as a function of the driving frequency and boundary conditions and as well include the effects of mode mixing at higher frequencies. We envision the development of this model to its full predictive capacity is achievable and has huge potential for a wide range of applications. For example, with a model that defines the coefficients, the resonant modes could be determined for more complex and asymmetric boundary conditions. This could then be applied to different types of mediums as well as different points of excitation, multiple points of excitation and extended to higher dimensions. Compared with more approximate methods, this simple model has the potential to improve both accuracy and efficiency, as well as deepening our understanding of system dynamics. Further investigations are therefore needed to extend this model to a broader range of frequencies, mediums and more complex plate geometries.
Author Contributions
Conceptualization, Amira val Baker, Mate Csanad and Ia Mgvdliashvili; Data curation, Nicolas Fellas and Nour Atassi; Formal analysis, Amira val Baker and Ia Mgvdliashvili; Funding acquisition, Paul Oomen; Investigation, Amira val Baker; Methodology, Amira val Baker and Mate Csanad; Project administration, Paul Oomen; Resources, Nicolas Fellas, Nour Atassi and Ia Mgvdliashvili; Software, Ia Mgvdliashvili; Supervision, Paul Oomen; Validation, Mate Csanad and Ia Mgvdliashvili; Visualization, Ia Mgvdliashvili and Paul Oomen; Writing – original draft, Amira val Baker and Nour Atassi; Writing – review & editing, Amira val Baker, Mate Csanad and Paul Oomen.
References
- Flores, J. Nodal patterns in the seismic response of sedimentary valleys. The European Physical Journal Special Topics 2007, 145, 63–75. [Google Scholar] [CrossRef]
- Schaadt, K.; Kudrolli, A. Experimental investigation of universal parametric correlators using a vibrating plate. Physical Review E 1999, 60, R3479–R3482. [Google Scholar] [CrossRef] [PubMed]
- Dorrestijn, M.; Bietsch, A.; Açıkalın, T.; Raman, A.; Hegner, M.; Meyer, E.; Gerber, C. Chladni Figures Revisited Based on Nanomechanics. Physical Review Letters 2007, 98, 026102. [Google Scholar] [CrossRef] [PubMed]
- Chakram, S.; Patil, Y.S.; Chang, L.; Vengalattore, M. Dissipation in Ultrahigh Quality Factor SiN Membrane Resonators. Physical Review Letters 2014, 112, 127201. [Google Scholar] [CrossRef] [PubMed]
- Chladni, E.F.F. Entdeckungen uber die Theorie des Klanges; Weidmanns Erben und Reich: Leipzig, 1787. [Google Scholar]
- Chladni, E.F.F. Die Akustik; Breitkopf und Härtel: Leipzig, 1802. [Google Scholar]
- Chladni, E.F.F. Neue Beitruge zur Akustik; Breitkopf und Härtel: Leipzig, 1817. [Google Scholar]
- Galilei, G. Dialogues Concerning Two New Sciences; Macmillan. Translated by Henry Crew and Alfonso de Salvio.: London, 1914; pp. 209–221. [Google Scholar]
- Andrade, E.N.D.C. Wilkins Lecture - Robert Hooke. Proceedings of the Royal Society of London. Series B - Biological Sciences 1997, 137, 153–187. [Google Scholar] [CrossRef]
- Waller, M.D. Vibrations produced in bodies by contact with solid carbon dioxide. Proceedings of the Physical Society 1933, 45, 101–116. [Google Scholar] [CrossRef]
- Waller, M.D. The production of sounds from heated metals by contact with ice and other substances. Proceedings of the Physical Society 1934, 46, 116–123. [Google Scholar] [CrossRef]
- Waller, M.D. The production of chladni figures by means of solid carbon dioxide. Part 1: bars and other metal bodies. Proceedings of the Physical Society 1937, 49, 522–531. [Google Scholar] [CrossRef]
- Waller, M.D. Vibrations of free circular plates. Part 3: A study of Chladni’s original figures. Proceedings of the Physical Society 1938, 50, 83–86. [Google Scholar] [CrossRef]
- H. Jenny. CYMATICS - A Study of Wave Phenomena and Vibration. Volume 1 (1967) & Volume 2 (1974); Macromedia Press: Newmarket, NH, USA, 2001. [Google Scholar]
- Kirchhoff, G. Über das Gleichgewicht und die Bewegung einer elastischen Scheibe. Journal für die reine und angewandte Mathematik 1850, 40, 51–88. [Google Scholar] [CrossRef]
- Rayleigh, J.W.S. Chapter 10. Vibrations of Plates. In The Theory of Sound, vol. 1, Rayleigh, J.W.S., Ed.; Macmillan and Co.: London, 1877; pp. 203–326.
- Timoshenko, S. Vibration Problems in Engineering, 3rd ed.; D. Van Nostrand Company, Inc.: Princeton, New Jersey, 1961. [Google Scholar]
- Wah, T. Vibration of Circular Plates. Journal of Acoustical Society of America 1962, 34, 275–281. [Google Scholar] [CrossRef]
- Waller, M.D. Vibrations of free circular plates. Part 2: Compounded normal modes. Proceedings of the Physical Society 1938, 50, 77–82. [Google Scholar] [CrossRef]
- Tuan, P.H.; Wen, C.P.; Yu, Y.T.; Liang, H.C.; Huang, K.F.; Chen, Y.F. Exploring the distinction between experimental resonant modes and theoretical eigenmodes: From vibrating plates to laser cavities. Physical Review E 2014, 89. [Google Scholar] [CrossRef]
- Waller, M.D. Vibrations of free square plates: part I. Normal vibrating modes. Proceedings of the Physical Society 1939, 51, 831–844. [Google Scholar] [CrossRef]
- Waller, M.D. Vibrations of free square plates: part II, compounded normal modes. Proceedings of the Physical Society 1940, 52, 452–455. [Google Scholar] [CrossRef]
- Tuan, P.H.; Wen, C.P.; Chiang, P.Y.; Yu, Y.T.; Liang, H.C.; Huang, K.F.; Chen, Y.F. Exploring the resonant vibration of thin plates: Reconstruction of Chladni patterns and determination of resonant wave numbers. The Journal of the Acoustical Society of America 2015, 137, 2113–2123. [Google Scholar] [CrossRef]
- Tuan, P.H.; Tung, J.C.; Liang, H.C.; Chiang, P.Y.; Huang, K.F.; Chen, Y.F. Resolving the formation of modern Chladni figures. EPL (Europhysics Letters) 2015, 111. [Google Scholar] [CrossRef]
- Tuan, P.H.; Liang, H.C.; Tung, J.C.; Chiang, P.Y.; Huang, K.F.; Chen, Y.F. Manifesting the evolution of eigenstates from quantum billiards to singular billiards in the strongly coupled limit with a truncated basis by using RLC networks. Physical Review E 2015, 92, 062906. [Google Scholar] [CrossRef]
- Tuan, P.H.; Lai, Y.H.; Wen, C.P.; Huang, K.F.; Chen, Y.F. Point-driven modern Chladni figures with symmetry breaking. Scientific Reports 2018, 8, 10844. [Google Scholar] [CrossRef]
- Shu, Y.-H.; Tseng, Y.-C.; Lai, Y.-H.; Yu, Y.-T.; Huang, K.-F.; Chen, Y.-F. Exploring the Origin of Maximum Entropy States Relevant to Resonant Modes in Modern Chladni Plates. Entropy 2022, 24. [Google Scholar] [CrossRef]
- Amore, P. Solving the Helmholtz equation for membranes of arbitrary shape: numerical results. Journal of Physics A: Mathematical and Theoretical 2008, 41. [Google Scholar] [CrossRef]
- Amore, P.; Cervantes, M.; Fernández, F.M. Variational collocation on finite intervals. Journal of Physics A: Mathematical and Theoretical 2007, 40, 13047–13062. [Google Scholar] [CrossRef]
- Amore, P. Alternative representation for nonlocal operators and path integrals. Physical Review A 2007, 75. [Google Scholar] [CrossRef]
Figure 1.
Schematic of experimental setup.
Figure 1.
Schematic of experimental setup.
Figure 2.
Plots of the effective impedance of a mechanical oscillator with a plate attached shown as a function of frequency for the following plates: A: large circle, small circle; B: large square, small square; C: large triangle, small triangle; D: large pentagon, small pentagon; E: large hexagon, small hexagon. The peaks indicate the resonance frequencies which are listed in
Table 1 below.
Figure 2.
Plots of the effective impedance of a mechanical oscillator with a plate attached shown as a function of frequency for the following plates: A: large circle, small circle; B: large square, small square; C: large triangle, small triangle; D: large pentagon, small pentagon; E: large hexagon, small hexagon. The peaks indicate the resonance frequencies which are listed in
Table 1 below.
Figure 3.
Nodal line patterns observed in the larger circular plate, a = 24 cm.
Figure 3.
Nodal line patterns observed in the larger circular plate, a = 24 cm.
Figure 4.
Nodal line patterns observed in the smaller circular plate, a = 18 cm.
Figure 4.
Nodal line patterns observed in the smaller circular plate, a = 18 cm.
Figure 5.
Nodal line patterns observed in the larger square plate, a = 24 cm.
Figure 5.
Nodal line patterns observed in the larger square plate, a = 24 cm.
Figure 6.
Nodal line patterns observed in the smaller square plate, a = 18 cm.
Figure 6.
Nodal line patterns observed in the smaller square plate, a = 18 cm.
Figure 7.
Nodal line patterns observed in the larger triangle plate, a = 24 cm.
Figure 7.
Nodal line patterns observed in the larger triangle plate, a = 24 cm.
Figure 8.
Nodal line patterns observed in the smaller triangle plate, a = 18 cm.
Figure 8.
Nodal line patterns observed in the smaller triangle plate, a = 18 cm.
Figure 9.
Nodal line patterns observed in the larger pentagon plate, a = 14.5 cm.
Figure 9.
Nodal line patterns observed in the larger pentagon plate, a = 14.5 cm.
Figure 10.
Nodal line patterns observed in the smaller pentagon plate, a = 9.5 cm.
Figure 10.
Nodal line patterns observed in the smaller pentagon plate, a = 9.5 cm.
Figure 11.
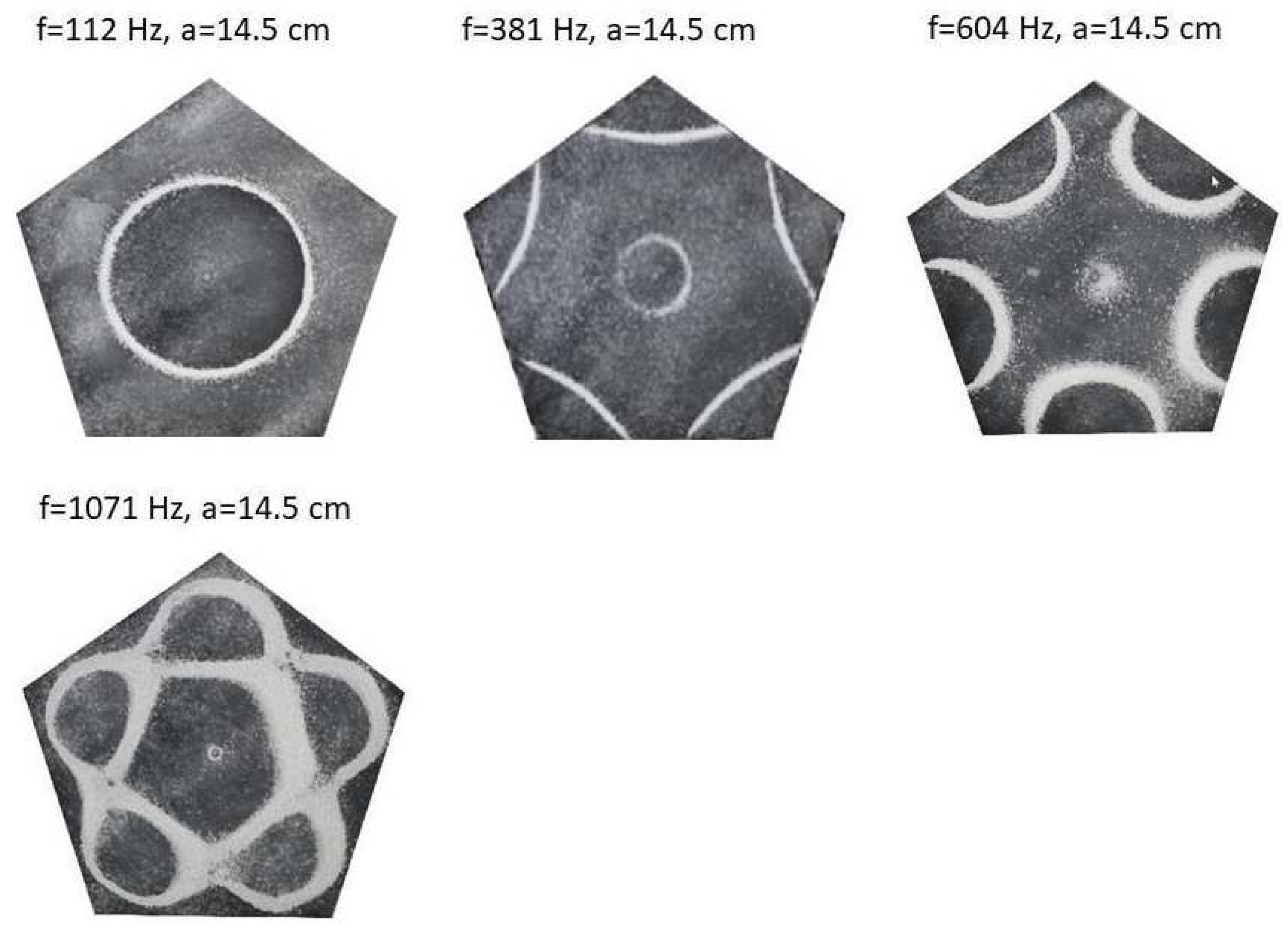
Nodal line patterns observed in the larger pentagon plate, a = 14.5 cm.
Figure 11.
Nodal line patterns observed in the larger pentagon plate, a = 14.5 cm.
Figure 12.
Nodal line patterns observed in the smaller hexagon plate, a = 9 cm.
Figure 12.
Nodal line patterns observed in the smaller hexagon plate, a = 9 cm.
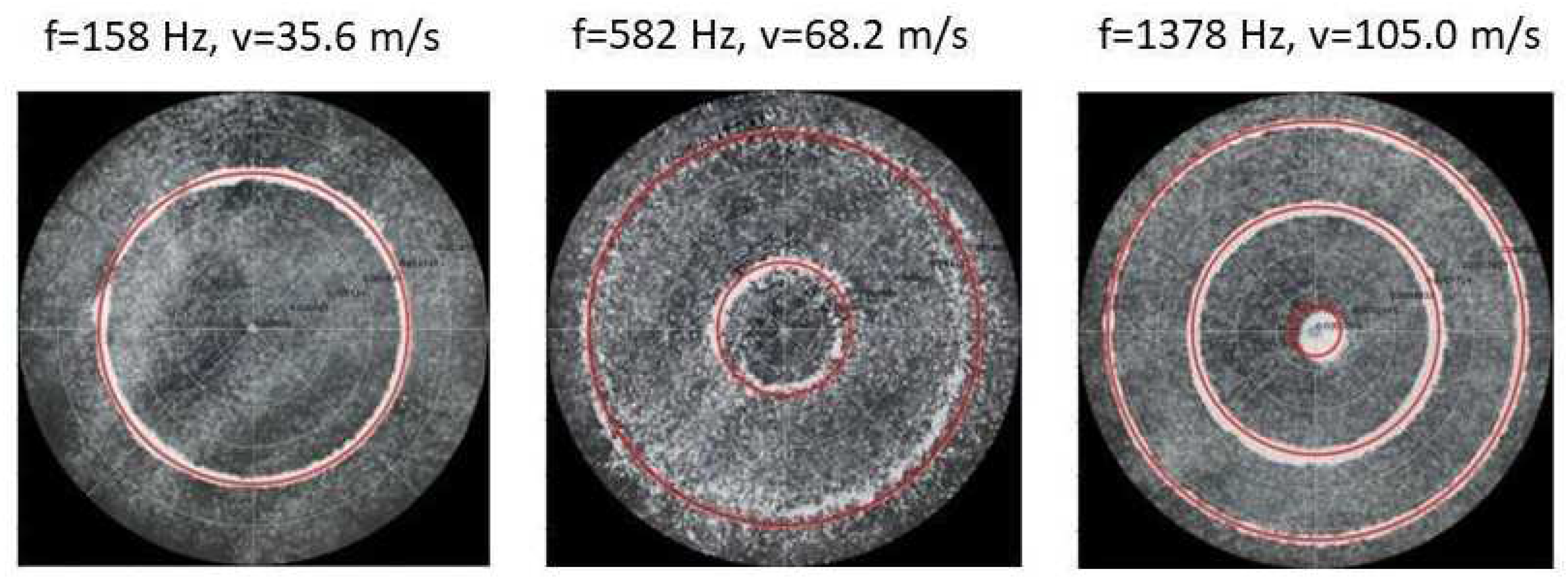
Figure 13.
Simulation of nodal line patterns for the larger circular plate, a = 24 cm.
Figure 13.
Simulation of nodal line patterns for the larger circular plate, a = 24 cm.
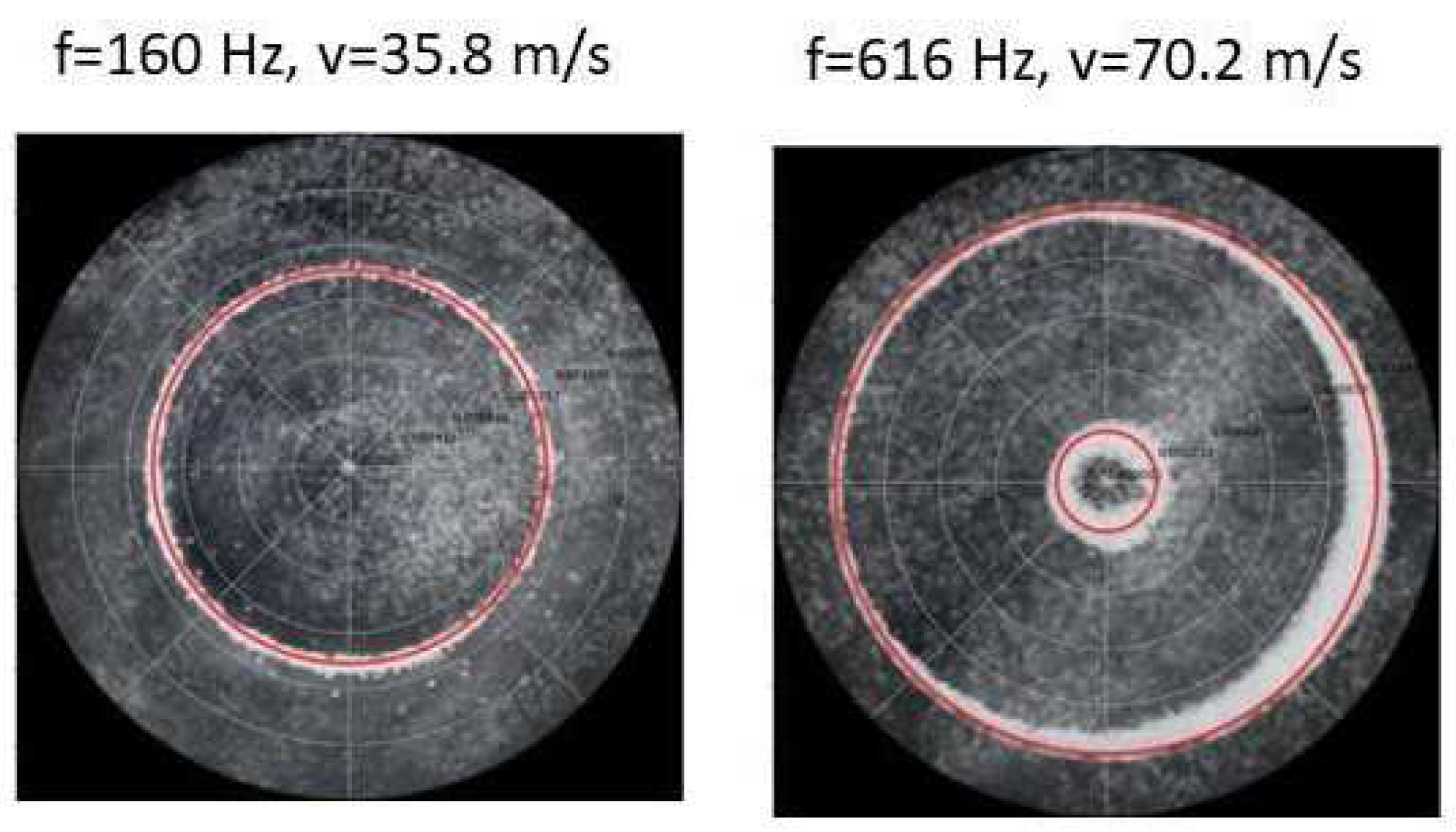
Figure 14.
Simulation of nodal line patterns for the smaller circular plate, a = 18 cm.
Figure 14.
Simulation of nodal line patterns for the smaller circular plate, a = 18 cm.
Figure 15.
Simulation of nodal line patterns for the larger square plate, a = 24 cm.
Figure 15.
Simulation of nodal line patterns for the larger square plate, a = 24 cm.
Figure 16.
Simulation of nodal line patterns for the smaller square plate, a = 18 cm.
Figure 16.
Simulation of nodal line patterns for the smaller square plate, a = 18 cm.
Figure 17.
Simulation of nodal line patterns for the larger triangle plate, a = 24 cm.
Figure 17.
Simulation of nodal line patterns for the larger triangle plate, a = 24 cm.
Figure 18.
Simulation of nodal line patterns for the smaller triangle plate, a = 18 cm.
Figure 18.
Simulation of nodal line patterns for the smaller triangle plate, a = 18 cm.
Figure 19.
Simulation of nodal line patterns for the larger pentagon plate, a = 14.5 cm.
Figure 19.
Simulation of nodal line patterns for the larger pentagon plate, a = 14.5 cm.
Figure 20.
Simulation of nodal line patterns for the smaller pentagon plate, a = 9.5 cm.
Figure 20.
Simulation of nodal line patterns for the smaller pentagon plate, a = 9.5 cm.
Figure 21.
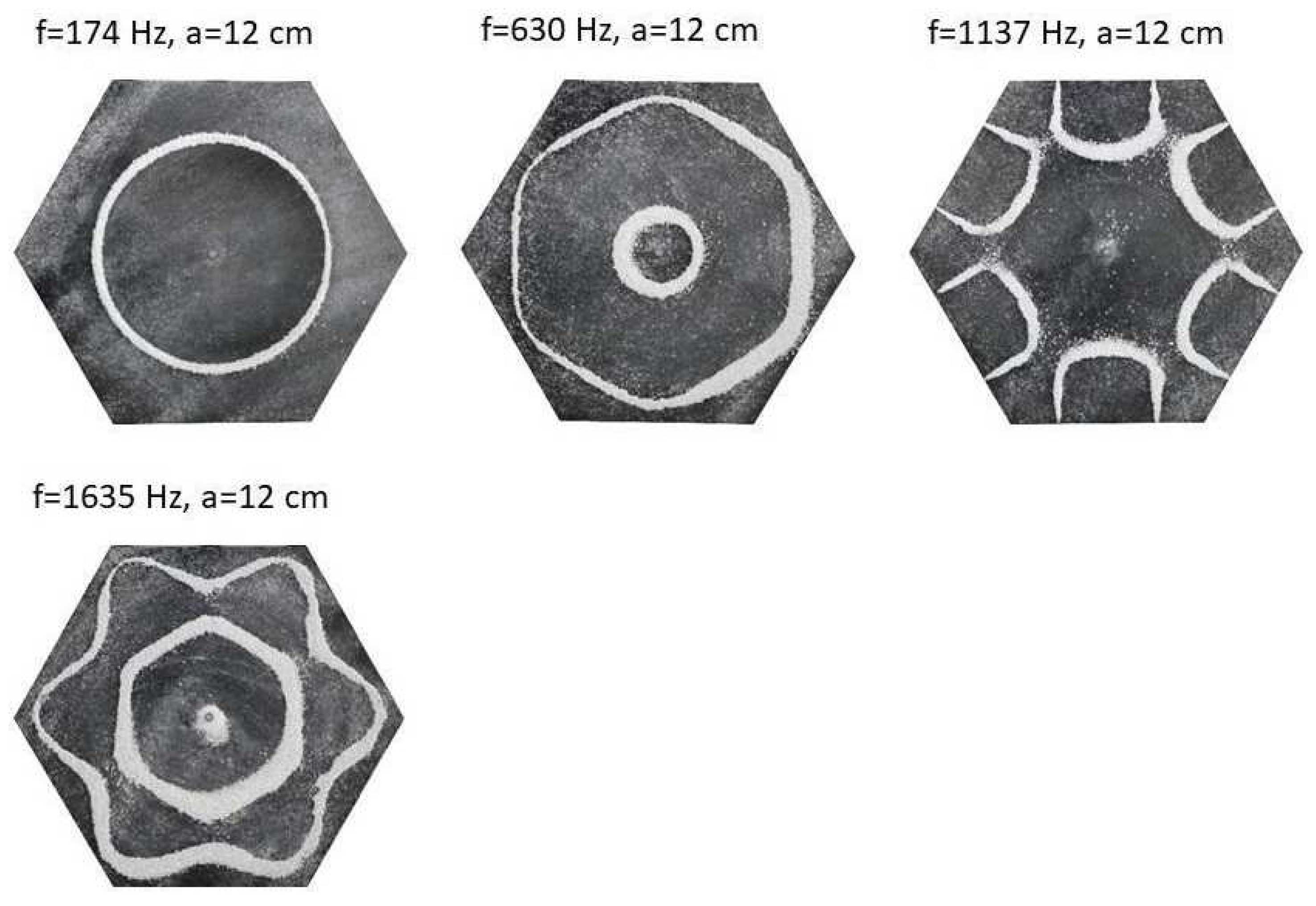
Simulation of nodal line patterns for the larger hexagon plate, a = 12 cm.
Figure 21.
Simulation of nodal line patterns for the larger hexagon plate, a = 12 cm.
Figure 22.
Simulation of nodal line patterns for the smaller hexagon plate, a = 9 cm.
Figure 22.
Simulation of nodal line patterns for the smaller hexagon plate, a = 9 cm.
Table 1.
Resonant frequencies (Hz) found from the impedance peaks for each of the 10 plates.
Table 1.
Resonant frequencies (Hz) found from the impedance peaks for each of the 10 plates.
| shape |
circle |
square |
triangle |
pentagon |
hexagon |
| size (cm) |
24 |
18 |
24 |
18 |
24 |
18 |
14.5 |
9.5 |
12 |
9 |
| 1 |
158 |
160 |
107 |
118 |
152 |
176 |
112 |
228 |
174 |
174 |
| 2 |
582 |
616 |
283 |
326 |
426 |
477 |
381 |
895 |
630 |
682 |
| 3 |
1378 |
|
511 |
592 |
1159 |
1402 |
604 |
|
1137 |
|
| 4 |
|
|
744 |
|
|
|
1071 |
|
1635 |
|
| 5 |
|
|
1181 |
|
|
|
|
|
|
|
Table 2.
Coefficients, A and C, of the response function for each of the 10 plates for each frequency.
Table 2.
Coefficients, A and C, of the response function for each of the 10 plates for each frequency.
| |
|
|
coefficients |
shape
(cm) |
frequency (Hz) |
velocity (m/s) |
A1 |
A2 |
A3 |
A4 |
C1 |
C2 |
C3 |
C4 |
|
| circle 24 |
158 |
35.6 |
|
|
|
|
0.95 |
|
|
|
|
| |
582 |
68.2 |
|
|
|
|
1.35 |
1 |
|
|
|
| |
1378 |
105.0 |
|
|
|
|
2.1 |
1.15 |
0.75 |
|
|
| circle 18 |
160 |
35.8 |
|
|
|
|
1.65 |
|
|
|
|
| |
616 |
70.2 |
|
|
|
|
2.4 |
2.25 |
|
|
|
| square 24 |
107 |
29.3 |
-0.1 |
|
|
|
0.95 |
|
|
|
|
| |
283 |
47.6 |
0.05 |
-1.85 |
|
|
1.25 |
0.6 |
|
|
|
| |
511 |
63.9 |
0 |
1.7 |
|
|
1.6 |
0.7 |
|
|
|
| |
744 |
77.1 |
0 |
-1.2 |
-1.3 |
|
2.7 |
1.1 |
0 |
|
|
| |
1181 |
97.2 |
0 |
0.2 |
-0.55 |
-5.8 |
2.7 |
1.45 |
1.35 |
-3.65 |
|
| square 18 |
118 |
30.7 |
-0.05 |
|
|
|
1.55 |
|
|
|
|
| |
326 |
51.1 |
0 |
-0.9 |
|
|
2.3 |
2.2 |
|
|
|
| |
592 |
68.8 |
0 |
0.6 |
|
|
2.5 |
2.4 |
|
|
|
| triangle 24 |
152 |
34.9 |
-0.2 |
|
|
|
1.4 |
|
|
|
|
| |
426 |
58.4 |
0.1 |
-1.4 |
|
|
1.6 |
0.8 |
|
|
|
| |
1159 |
96.3 |
0 |
0.7 |
-2.3 |
|
2.7 |
1.6 |
-0.8 |
|
|
| triangle 18 |
176 |
37.5 |
-0.2 |
|
|
|
1.75 |
|
|
|
|
| |
477 |
61.8 |
0 |
-0.95 |
|
|
2.15 |
2 |
|
|
|
| |
1402 |
105.9 |
0 |
0.6 |
-2.8 |
|
2.8 |
2.6 |
0 |
|
|
| pentagon 14.5 |
112 |
29.9 |
0 |
|
|
|
1.7 |
|
|
|
|
| |
381 |
55.2 |
0 |
-0.4 |
|
|
2.3 |
2.3 |
|
|
|
| |
604 |
69.5 |
0 |
0.7 |
-2.9 |
|
2.8 |
2.4 |
2 |
|
|
| |
1071 |
92.6 |
0 |
-0.2 |
1.1 |
|
2.9 |
2.6 |
2.6 |
|
|
| pentagon 9.5 |
228 |
42.7 |
0 |
|
|
|
2 |
|
|
|
|
| |
895 |
84.6 |
0 |
-0.3 |
|
|
2.7 |
2.35 |
|
|
|
| hexagon 12 |
174 |
37.3 |
0 |
|
|
|
1.1 |
|
|
|
|
| |
630 |
71.0 |
0 |
-2 |
|
|
1.85 |
1.25 |
|
|
|
| |
1137 |
95.4 |
0 |
0.5 |
-2.5 |
|
2.55 |
1.4 |
1.3 |
|
|
| |
1635 |
114.4 |
0 |
-0.15 |
1 |
|
2.8 |
1.6 |
1.1 |
|
|
| hexagon 9 |
174 |
37.3 |
0 |
|
|
|
1.9 |
|
|
|
|
| |
682 |
73.9 |
0 |
-0.1 |
|
|
2.65 |
2.45 |
|
|
|
|
Disclaimer/Publishers Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).