Preprint
Article
Influence of the Gain-Bandwidth of the Front-End Amplifier on the Performance of a QEPAS Sensor
Altmetrics
Downloads
74
Views
22
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
30 January 2024
Posted:
31 January 2024
You are already at the latest version
Alerts
Abstract
The quartz tuning fork used as an acoustic sensor in Quartz-Enhanced Photo-Acoustic Spectroscopy gas detection systems is usually read-out by means of a transimpedance preamplifier, based on a low-noise operational amplifier closed in a feedback loop. The gain-bandwidth product of the operational amplifier used in the circuit is a key parameter which must be properly chosen to guarantee that the circuit works as expected. Here we demonstrate that, if the value of this parameter is not sufficiently large, the response of the preamplifier exhibits a peak at a frequency which does not coincide with the series resonant frequency of the quartz tuning fork. If this peak frequency is selected for modulating the laser bias current and is also used as reference frequency of the lock-in amplifier, a penalty results in terms of signal to noise ratio at the output of the QEPAS sensor. This worsens the performance of the gas sensing system in terms of ultimate detection limits. We show that this happens when the front-end preamplifier of the quartz tuning fork is based on some amplifier models that are typically used for such application, both when the integration time of the lock-in amplifier filter is long, to boost noise rejection, and when it is short, in order to comply with a relevant measurement rate.
Keywords:
Subject: Engineering - Electrical and Electronic Engineering
1. Introduction
In gas detection systems based on the Quartz-Enhanced Photo-Acoustic Spectroscopy technique (QEPAS), the resonance properties of a Quartz Tuning Fork (QTF) are exploited to enhance the electric signal resulting from the interaction between a modulated laser source and the target gas [1,2,3,4]. As shown in the schematic diagram of Figure 1, the intensity of a laser source of suitable wavelength, chosen accordingly to the absorption line of the molecules to be detected, is modulated at a given frequency f0. Non-radiative, periodic relaxation processes of the gas molecules, excited by the modulated laser light, generate sound waves that are efficiently transformed into electric signals by means of the QTF, if the laser modulation frequency is tuned to the resonant frequency fs of the crystal or one its sub-harmonics. A lock-in amplifier (LIA) is used to demodulate the signal generated by the QTF and produces a DC output voltage proportional to its amplitude, which, in turns, is proportional to the concentration of the target gas. The QEPAS technique has been proven to be very sensitive and reliable, enabling sub-ppm and even sub-ppb minimum detection limits [5,6,7].
Since the Q factor of typical QTFs used in QEPAS sensors is very high, with an order of magnitude of several thousands [8], the frequency of the laser modulation signal and the lock-in reference frequency must be carefully selected, to fully exploit the resonance properties of the QTF and maximize the signal-to-noise ratio (SNR) of the sensor.
Although voltage-mode front-end preamplifiers for the QTF have been proposed in the literature [9,10,11,12], the most common circuit configuration for interfacing the QTF is still the classic transimpedance preamplifier (TIA), schematically represented in Figure 2 [13,14,15,16].
If the loop gain of the circuit in Figure 2 is large enough, the inverting input terminal of the operational amplifier (OPAMP) can be considered a virtual ground. This makes the current signal IQTF generated by the QTF independent of parasitic components, such as the input capacitance of the OPAMP CIN. Furthermore, the current IF which flows in the feedback resistor RF is equal to IQTF, thus the output signal VOUT depends only on the characteristics of the piezoelectric sensor and on the value of RF:
The response of the TIA exhibits a sharp peak at the series resonant frequency fS of the QTF, which as a consequence, is the most suitable operating frequency for the QEPAS sensor. The value of this frequency is usually identified using the same TIA, by disconnecting from ground the QTF terminal, applying a sinusoidal voltage signal to this terminal and scanning the frequency around the expected value of fS , until the peak amplitude of VOUT is reached [17].
As already pointed out, the ideal behavior of the circuit described above is strictly related to the presence of the virtual ground at the inverting input of the OPAMP, which, in turns, is effective only if the loop gain of the feedback loop is much larger than unity. Usually, in order to guarantee that this condition is fulfilled, it is deemed sufficient to use an OPAMP with a gain-bandwidth product (GBW) much higher than the operating frequency. For instance, in case of a classic QTF with fS=32.768 kHz, often low-noise OPAMPs with GBW of a few MHz have been used [9,10,12]. In this work, we demonstrate that, due to the behavior of the QTF around its resonant frequency, much larger values of the GBW are needed to guarantee a good virtual ground for the TIA at these frequencies. In case an amplifier with an insufficient bandwidth is used, some undesirable phenomena occur. First, the peak frequency of the circuit response fpeak is no more located at the intrinsic fS of the QTF, but is shifted to lower frequencies, thus the characterization procedure described above is no more able to provide the intrinsic resonance frequency of the piezoelectric sensor. Moreover, some contributions to the total output noise are strongly affected by the missing virtual ground and, as a consequence, the operating frequency where the maximum SNR is obtained can be different from the frequency fpeak. Thus, in this case, the characterization procedure is no more able to provide the optimal value for the operating frequency of the QEPAS sensor. In any case, it will be shown that the SNR performance obtained are sub-optimal, if compared to the ones that it is possible to achieve if an OPAMP with the same noise characteristics but a much larger GBW is used.
2. TIA Loop Gain as a Function of the OPAMP Gain-Bandwidth Product
To study the frequency response of the TIA shown in Figure 2, the QTF can be the described by means of the classic Butterworth-Van Dyke model, with a sinusoidal voltage source Vin inserted in series with the motional arm, composed by RP, CS and L, as represented in Figure 3. Here, Vin represents the electric signal generated by the QTF when the sensor is excited by an acoustic stimulus, due to the piezoelectric effect. In Figure 3 the QTF model is coupled to the TIA, where the resistor RF sets the closed loop gain of the circuit, CF accounts for the parasitic capacitance in parallel to the feedback resistor and CIN is the input capacitance of the OPAMP.
A typical set of values for the passive components of the circuit in Figure 3 is reported in Table 1. With these parameters, the series resonant frequency of the QTF is 32.768 kHz and its Q factor is about 104. A conservative value of 50fF has been assumed for the parasitic capacitance CF associated to a surface mount resistor [18]. A large value of RF has been considered, to reduce the contribution of the feedback resistor to the total equivalent input noise of the circuit [19]. In the following, these parameter values will be used for all the simulations, except the input capacitance of the OPAMP, which depends on the specific considered device.
If the loop gain of the circuit in Figure 3 is very large, so that the inverting terminal of the OPAMP can be considered a good virtual ground, the total capacitance CP+CIN=CPTOT is short circuited and does not give any contribution to the transfer function H(jω)=VOUT/VIN of the circuit. The modulus squared of this transfer function is expressed as follows [19]:
where . Since at this frequency the reactances of L and CS are equal and opposite, they cancel each other and the function |H(jω)|2 exhibits a peak:
Note that CF has been neglected in equations (2) and (3), since ωZ=1/(RFCF) is much higher than . We conclude that the most suitable operation frequency for the QEPAS system is the series resonant frequency of the QTF, where the response of the circuit to an acoustic excitation is maximized.
As already pointed out, equations (2) and (3) hold true only if the loop gain T of the circuit is much greater than unity. Thus, it is important to evaluate this parameter around the series resonant frequency of the QTF, in order to understand the conditions which must be fulfilled to validate the above analysis. The transfer function T(s), can be obtained by multiplying the differential gain of the OPAMP ADM(s) by the voltage divider formed by the impedance of the QTF, ZQTF, and the feedback impedance RF//(1/sCF):
The following expression is obtained, neglecting CS and CF with respect to CPTOT:
Typically, ADM(s) is a single-pole transfer function with a very low cut-off frequency f0, due to OPAMP internal compensation. For frequencies higher than the cut-off, the differential gain of the OPAMP can be expressed as a function of the frequency as follows:
where A0 is the DC gain of the amplifier and GWB=A0⋅ω0 is its gain-bandwidth product. The transfer function of equation (5) contains a zero at ωZ, due to the presence of the small capacitance CF, which makes acceptable the phase margin of the circuit.
If, for instance we use the OP27 [10], an OPAMP with a gain-bandwidth product of about 8 MHz, the result of a broadband SPICE simulation of the magnitude of the loop gain |T(jω)| as a function of the frequency is shown in Figure 4.
Figure 4 has been generated by simulating 1000 point per decade and, as a consequence, the effects of the QTF resonance, confined in a very narrow band around 32.768 kHz, are barely visible. Instead, the main singularities of T(s), i.e., the dominant pole of the OPAMP at f0≅4 Hz, a low frequency pole at f1≅1/(2πRFCPTOT)≅1.8 kHz and the zero at fZ=1/(2πRFCF)≅318 kHz are clearly visible. We can conclude that, due to the presence of the low frequency poles located at f0 and f1, the magnitude of the loop gain around fS is slightly more than 20 dB, despite the GBW of the OPAMP is about two orders of magnitude larger than the QTF resonant frequency.
Let us consider now what happens in correspondence of the frequency fS, which should be the optimal operating frequency for the QEPAS sensor. Here, the motional branch of the QTF reaches its minimum impedance and can be replaced by the only resistor RP. With the typical values of the parameters we are considering, the frequency 1/(2πRPCPTOT)≅180 kHz is quite large as compared to fS, so we can neglect the capacitance CPTOT in parallel with RP. Thus, the loop gain at fS is simply evaluated as:
Equation (6) states that the value of |T(jωS)| is obtained by multiplying the gain of the OPAMP at the resonant frequency of the QTF by the ratio RP/RF, which is very small in typical cases, as our one. For instance, if we use the OP27, |T(jωS)| results to be around 2.3 and the inverting input terminal of the OPAMP cannot be considered a good virtual ground at all. This invalidates equations (2) and (3). An OPAMP with a GBW at least an order of magnitude higher would be needed to have a TIA with a behavior closer to the ideal one.
SPICE simulations of the TIA confirm this result. Figure 5 shows the amplitude of the loop gain of the circuit as a function of the frequency in a narrow band around the resonant frequency of the QTF. The value of |T(jωS)| results to be around 2, very close to the above estimation.
The low value of the loop gain will cause deviations of the TIA response with respect to the ideal one. In turn, this modified behavior affects the choice of the optimal operating frequency for the application of the QEPAS technique, as will be discussed in the next section.
3. Closed-Loop Response of the TIA coupled to the QTF
With a very low value of the loop gain |T(jωS)|, the analysis of the closed-loop behavior of the circuit in Figure 3 cannot be carried out considering the presence of the virtual ground. The finite value of the OPAMP gain around the resonant frequency of the QTF must be necessarily taken into account. To study the circuit, we can apply Miller’s theorem [20] to the feedback impedance ZF, composed by the parallel of the resistor RF and the parasitic capacitor CF. According to this theorem, an equivalent circuit of the TIA is created by replacing ZF with an impedance ZM1, placed between the inverting input of the OPAMP and ground, and an impedance ZM2, connected between the OPAMP output node and ground:
Due to the very low output impedance of the OPAMP, ZM2 cannot affect the behavior of the circuit and can be omitted. Instead, for what concerns ZM1, there are two contributions ZMR and ZMC in parallel, coming from RF and CF, respectively. According to equation (6), ZMR(jω) is expressed as follows:
and can be considered as the parallel of the resistor RF with an inductor LEQ= RF/GBW.
The contribution of the parasitic capacitance to the input Miller’s impedance is the following:
ZMC can be considered the parallel of the capacitance CF with a resistor REQ=1/CFGBW. With the typical values of the parameters shown in Table 1, using the OP27 (GBW≅2π⋅8x106), we obtain LEQ≅0.2 H and REQ≅400 kΩ. Figure 6 shows the equivalent circuit of the TIA after the application of Miller’s theorem.
Note that CF << CPTOT and RF>>REQ can be neglected. Moreover, the resonant frequencies of the circuit in Figure 6 are poorly affected by the resistors RP and REQ, thus, in order to find their location, it is sufficient to consider the simplified circuit shown in Figure 7.
The resonant frequency of the parallel LEQ-CPTOT is placed at:
quite higher than fS. As a consequence, around fS, this network exhibits an inductive behavior, which slightly shifts the peak of the transfer function |H(jω)| with respect to the expected value fS. In fact, since around fS the parallel LEQ-CPTOT is equivalent to a frequency-dependent inductor LX(ω), the transfer function of the circuit in Figure 7 is the following:
and its peak is located at the frequency fpeak, lower than the series resonant frequency of the QTF:
Of course, the complete transfer function H(jω)=VOUT/VIN of the circuit in Figure 7 is obtained by multiplying V-/VIN by the open loop gain of the OPAMP ADM(jω).
The shift of the peak frequency towards lower values, expressed by equation (11), is confirmed by SPICE simulations of the TIA. Figure 8 shows the behavior of the modulus of the transfer function H(jω) for three different OPAMPs, listed in Table 2 together with their gain-bandwidth products and the peak frequency fpeak obtained in simulation.
Table 2 shows that, in case the large bandwidth OPAMP AD8067 is used, the peak frequency of the TIA response coincides with the resonant frequency of the QTF as expected. Instead, with the other two OPAMP models, the shift of fpeak with respect to fS is apparent and is more pronounced for the slowest OPAMP, the TL071. This shift, of about 0.9 Hz and 1.8 Hz for the OP27 and the TL071 respectively, can be significant in terms of performance of the QEPAS sensor. Note that, if an external sine wave is applied to the QTF coupled to the TIA for the identification of the optimal operating frequency of the QEPAS sensor, as described in the Introduction, the result of the procedure will be always fpeak, different from fS, in case a too slow OPAMP is used, such as the OP27 or the TL071.
4. Effects of the Limited GBW on the TIA Output Noise
To assess the performance of the TIA used as a front-end for the QTF in a QEPAS sensor, it is mandatory to study the signal-to-noise ratio (SNR) obtained at its output. The main noise sources in the circuit of Figure 6 are the thermal noise of the resistors RP and RF, vn_rp and in_rf respectively, and the equivalent input noise sources of the OPAMP, vn_op and in_op, as represented in Figure 9.
The total power spectral density of the output noise Sn_out is obtained by summing the contributions given by the power spectral densities of the noise sources in Figure 9, weighted by the corresponding transfer functions:
where
and k is the Boltzmann constant and T the absolute temperature.
If the gain-bandwidth product of the OPAMP is large enough and its inverting input terminal can be considered a good virtual ground, |H(jω)|2 is given by equation (2), |Hf(jω)|2≅RF2, and
where and [19].
A comparison between the results obtained with SPICE simulations and the analytical model confirms the validity of equations (2) and (12). Figure 10 shows the modulus of the TIA transfer function |H(jω)|, whereas Figure 11 displays the total output noise power spectral density of the circuit Sn_out(ω), when the AD8067 is used, in which case the OPAMP inverting input can be considered a good virtual ground. In the analytical model, the values of the equivalent input noise sources of the OPAMP, in_op = 0.6 fA/√Hz and vn_op = 6.6 nV/√Hz, have been derived from its data-sheet. The parameters of the QTF model are the same reported in Table 1. The analytical model just slightly overestimates the results provided by SPICE simulations, but the frequency fpeak coincides exactly with the series resonant frequency of the QTF fS=32768 Hz, as expected.
If an OPAMP with a low GBW is used in the TIA, the noise transfer functions which appear in equation (12) are affected by the missing virtual ground at the inverting input of the OPAMP, exactly as happens to |H(jω)|. If, for instance we consider the OP27 and an OPAMP with the same input equivalent noise sources and the same input capacitance CIN, but much larger GBW, we will observe a different frequency behavior of all the noise contributions in equation (12). Figure 12 shows a comparison between the total output noise power spectral density Sn_out of the TIA realized using the OP27 and the same OPAMP, but with an increased GBW, obtained by inserting an ideal voltage amplifier with gain equal to 20 into the feedback loop of the TIA, at the output of the OPAMP (see Figure 13).
It is apparent from Figure 12 that the behavior of Sn_out as a function of frequency is completely different in the two cases, which differ only in the GBW of the OPAMP. In particular, as illustrated by Figure 14, the transfer function Hf(jω) is strongly affected by the absence of a good virtual ground, as well as the contributions to the total output noise due to the equivalent input current noise of the OPAMP and the feedback resistor.
As a consequence, also the behavior of the SNR at the output of the QEPAS sensor will be dependent on the GBW of the OPAMP used in the LIA, other than by its noise performance.
5. Evaluation of the SNR and Effects of the Limited GBW
For the evaluation of the SNR at the output of the QEPAS sensor, the function of the LIA can be considered equivalent to a band-pass filter with narrow bandwidth BW, centered at its reference frequency fREF [19,21]. Thus, assuming a unity amplitude for the input signal VIN, the SNR at the output of the LIA can be defined as follows:
where Vn_out is the rms value of the output noise, ωREF=2πfREF and
is the response of a biquadratic band-pass filter with center frequency fREF and bandwidth BW=ωREF/Qfilt, used to simulate the LIA function.
If we want to enhance noise rejection, the bandwidth of the LIA filter must be extremely narrow, i.e. the LIA integration time must be very large. As a consequence, in practice, the squared rms output noise Vn_out(ωREF)2 is proportional to the noise power spectral density Sn_out(ωREF) [10], and the SNR can be expressed as:
Notice that, in equation (14), the ratios |Hf(jωREF)|2/|H(jωREF)|2 and |Hvn_op(jωREF)|2/|H(jωREF)|2 are independent on the GBW of the OPAMP used in the TIA. In other words, if the loop gain of the circuit is increased by adding a gain stage in the feedback loop, as done to obtain Figure 12 and Figure 14, these ratios are unaffected, due to the linearity of the system. Thus, equation (14) states that the dependence of the SNR on the LIA reference frequency fREF is not affected by the GBW of the OPAMP.
Extensive SPICE simulations have been carried out to support this conclusion. A band-pass filter with BW=0.1 Hz has been cascaded to the same TIAs, based on the OPAMP OP27, used to reproduce Figure 12 and Figure 13. The SNR at the filter output, expressed by equation (13), has been simulated, by varying the center frequency of the filter by steps of 0.1 Hz around the resonance of the QTF, in the interval from 32758 Hz to 32776 Hz.
Figure 15 shows the behavior of the SNR, obtained with and without boosting the GBW of the OPAMP by means of an ideal voltage amplifier with gain 20. As expected, the increase of the loop gain of the TIA does not affect too much the behavior of the SNR and, in particular, does not modifies the value of the reference frequency corresponding to the peak of the SNR, which remains almost coincident with the series resonant frequency of the QTF, fS. This means that the optimal operating frequency for the QEPAS sensor is fS, which is different from fpeak, i.e. the frequency where the peak of the signal is obtained, in case the OP27 is used for the TIA. As a consequence, if the QEPAS sensor is operated at the frequency fpeak, an appreciable penalty in terms of SNR results, as highlighted in Figure 15. Thus, we can conclude that, for very long integration time of the LIA, the use of a TIA realized with an OPAMP with limited GBW, like the OP27 or the TL071, leads to a nonoptimal choice of the operating frequency of the QEPAS sensor.
Since the shift of fpeak with respect to fS increases for decreasing values of GBW, using an OPAMP such as the TL071 (GBW=3 MHz) would result in larger penalties in terms of SNR, if the chosen operating frequency of the QEPAS sensor is fpeak instead of fS.
When we need to increase the rate of the measurements, the bandwidth of the LIA filter must be increased as well. The noise power spectral density is integrated in a larger bandwidth around the LIA reference frequency and the peak of the SNR at the LIA output tends to move close to the peak frequency of the signal fpeak, thus the choice of the operating frequency of the QEPAS sensor is near to the optimal one. Nevertheless, the maximum SNR achievable is well below the one that can be obtained keeping the same noise performance of the OPAMP but increasing its GBW, so that the optimal operating frequency and the signal peak frequency fpeak both coincide with fS. This is illustrated in Figure 16, where the simulated behavior of the SNR as a function of the LIA reference frequency is shown for a filter bandwidth of 3 Hz and a TIA based on the OPAMP OP27, with and without boosting of the loop gain.
If the sheer OP27 is used, the frequency corresponding to the peak of the SNR is fmax=32768.2 Hz, very close to fpeak=32768.1 Hz, but the maximum value of the SNR is about 9.2e6, which is less than the value that is possible to achieve when the GBW is increased by a factor of 20, equal to about 9.8e6. So, also in this case, the best performance that is possible to achieve with the QEPAS sensor is once again limited by the small GBW of the OPAMP used in the TIA.
6. Conclusions
The analog front-end of the QTF, in a typical QEPAS sensor, is a transimpedance amplifier realized with a low-noise OPAMP. We have shown that, even though the gain-bandwidth of the OPAMP is two order of magnitude larger than the series resonant frequency of the QTF, this can be insufficient to guarantee that the preamplifier works as expected in terms of closed loop behavior, due to the remarkable attenuation introduced in the loop gain of the circuit by the QTF around its series resonant frequency fS. The effect of the low value of the loop gain around fS is a shift of the frequency fpeak corresponding to the peak of the TIA output signal with respect to the expected value fS. As a consequence, in this case fpeak ≠ fS is chosen as reference frequency for the LIA. When the LIA filter is very selective, in order to reject the noise as much as possible and increase the sensitivity of the QEPAS sensor, this turns out to be a wrong choice, since the operating frequency corresponding to the maximum value of the SNR at the LIA output is fS, not fpeak. On the other hand, when the integration time of the LIA is decreased, to increase the measurement rate, the choice of fpeak as QEPAS operating frequency is correct, but the maximum achievable value of the SNR is lower than the one which can be obtained using in the TIA an OPAMP with the same noise performance, but with much larger GBW. In conclusion, the OPAMP must be selected not only considering its noise characteristics, but also a GBW sufficiently high to guarantee a large value of the TIA loop gain. In this respect, OPAMPs with higher GBW are needed especially in case the quality factor of the QTF is very large, which corresponds to low values of the resistance Rp, and the TIA feedback resistor is increased, to reduce its noise contribution and increase the closed loop gain of the circuit.
Author Contributions
Conceptualization, C.M.; methodology, L.L.; validation, C.M., and G.M.; formal analysis, C.M, L.L. and G.M.; investigation, L.L. and G.M.; visualization, L.L. and G.M.; writing—original draft preparation, C.M.; writing—review and editing, C.M, L.L and G.M.; supervision, C.M.; funding acquisition, C.M. All authors have read and agreed to the published version of the manuscript.
Funding
All authors acknowledge funding from the European Union’s Horizon 2020 research and innovation program under grant agreement No. 101016956 PASSEPARTOUT, in the context of the Photonics Public Private Partnership.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kosterev, A.A.; Bakhirkin, Y.A.; Curl, R.F.; Tittel, F.K. Quartz-enhanced photoacoustic spectroscopy. Opt. Lett. 2002, 27, 1902–1904. [Google Scholar] [CrossRef] [PubMed]
- Kosterev, A.A.; Tittel, F.K.; Serebryakov, D.V.; Malinovsky, A.L.; Morozov, I.V. Applications of quartz tuning forks in spectroscopic gas sensing. Rev. Sci. Instrum. 2005, 76, 043105. [Google Scholar] [CrossRef]
- Ma, Y. Review of Recent Advances in QEPAS-Based Trace Gas Sensing. Appl. Sci. 2018, 8, 1822. [Google Scholar] [CrossRef]
- Yin, X.; Gao, M.; Miao, R.; Zhang, L.; Zhang, X.; Liu, L.; Shao, X.; Tittel, F.K. Near-infrared laser photoacoustic gas sensor for simultaneous detection of CO and H2S. Opt. Express. 2021, 29, 34258. [Google Scholar] [CrossRef] [PubMed]
- Menduni, G.; Zifarelli, A.; Kniazeva, E.; Dello Russo, S.; Ranieri, A.C.; Ranieri, E.; Patimisco, P.; Sampaolo, A.; Giglio, M.; Manassero, F.; Dinuccio, E.; Provolo, G.; Wu, H.; Lei, D.; Spagnolo, V. Measurement of methane, nitrous oxide and ammonia in atmosphere with a compact quartz-enhanced photoacoustic sensor. Sens. and Actuators B: Chem. 2023, 375, 132953. [Google Scholar] [CrossRef]
- H. Lin, H. Zheng, B.A.Z. Montano, H. Wu, M. Giglio, A. Sampaolo, P. Patimisco, W. Zhu, Y. Zhong, L. Dong, R. Kan, J. Yu, V. Spagnolo. Ppb-level gas detection using on-beam quartz-enhanced photoacoustic spectroscopy based on a 28 kHz tuning fork. Photoacoustics 2022, 25, 100321. [CrossRef] [PubMed]
- M. Yang, Z. Wang, H. Sun, M. Hu, P.T. Yeung, Q. Nie, S. Liu, N. Akikusa, W. Ren, Highly sensitive QEPAS sensor for sub-ppb N2O detection using a compact butterfly-packaged quantum cascade laser. Appl. Phys. B, 2024, 30, 6. [CrossRef]
- Lin, H.; Liu, Y.; Lin, L.; Zhu, W.; Zhou, X.; Zhong, Y.; Giglio, M.; Sampaolo, A.; Patimisco, P.; Tittel, F.K.; Yu, J.; Spagnolo, V.; Zheng, H. Application of standard and custom quartz tuning forks for quartz-enhanced photoacoustic spectroscopy gas sensing. Appl. Spectr. Rev. 2022, 57, 1–23. [Google Scholar] [CrossRef]
- Menduni, G.; Sampaolo, A.; Patimisco, P.; Giglio, M.; Dello Russo, S.; Zifarelli, A.; Elefante, A.; Wieczorek, P.Z.; Starecki, T.; Passaro, V.M.N.; Tittel, F.K.; Spagnolo, V. Front-End Amplifiers for Tuning Forks in Quartz Enhanced PhotoAcoustic Spectroscopy. Appl. Sci. 2020, 10, 2947. [Google Scholar] [CrossRef]
- Wieczorek, P.Z.; Starecki, T.; Tittel, F.K. Improving the signal to noise ratio of QTF preamplifiers dedicated for QEPAS applications. Appl. Sci. 2020, 10, 4105. [Google Scholar] [CrossRef]
- Winkowski, M.; Stacewicz, T. Low noise, open-source QEPAS system with instrumentation amplifier. Sci. Rep. 2019, 9, 7–12. [Google Scholar] [CrossRef] [PubMed]
- Starecki, T.; Wieczorek, P.Z. A High Sensitivity Preamplifier for Quartz Tuning Forks in QEPAS (Quartz Enhanced PhotoAcoustic Spectroscopy) Applications. Sensors 2017, 17, 2528. [Google Scholar] [CrossRef] [PubMed]
- Yi Xie, Yixin Zhang, Dehua Zhu, Xiaojing Chen, Juncheng Lu, Jie Shao, Compact QEPAS CO2 sensor system using a quartz tuning fork-embedded and in-plane configuration. Opt. & Laser Techn., 2023, 159, 109018. [CrossRef]
- B. Li, G. Menduni, M. Giglio, P. Patimisco, A. Sampaolo, A. Zifarelli, H. Wu, T. Wei, V. Spagnolo, L. Dong, Quartz-enhanced photoacoustic spectroscopy (QEPAS) and Beat Frequency-QEPAS techniques for air pollutants detection: A comparison in terms of sensitivity and acquisition time. Photoacoustics, 2023, 31, 100479. [CrossRef]
- Zhang, Q. , Chang, J., Wang, Z., Wang F., Jiang F., Wang M., SNR Improvement of QEPAS System by Preamplifier Circuit Optimization and Frequency Locked Technique. Photonic Sensors, 2018, 8, 127–133. [Google Scholar] [CrossRef]
- P. Breitegger, B. Schweighofer, H. Wegleiter, M. Knoll, B. Lang, A. Bergmann, Towards low-cost QEPAS sensors for nitrogen dioxide detection. Photoacoustics, 2020, 18, 100169. [CrossRef] [PubMed]
- Rousseau, R.; Maurin, N.; Trzpil, W.; Bahriz, M.; Vicet, A. Quartz Tuning Fork Resonance Tracking and application in Quartz Enhanced Photoacoustics Spectroscopy. Sensors 2019, 19, 5565. [Google Scholar] [CrossRef] [PubMed]
- Vishay Intertechnology, Frequency Response of Thin Film Chip Resistors, Technical Note, Revision 04-Feb-09. Available online: https://www.vishay.com/docs/49427/vse-tn00.pdf.
- M. Di Gioia, G. Menduni, A, Zifarelli, A. Sampaolo, P. Patimisco, M. Giglio, C. Marzocca, V. Spagnolo, Study of the effect of the low-pass filter time constant on the noise level of Quartz Enhanced Photoacoustic Spectroscopy sensors, In Proceedings of SPIE – Quantum Sensing and Nano Electronics and Photonics XIX, San Francisco, California (USA), 29 January 2023. [CrossRef]
- A.S. Sedra, K.C. Smith. Microelectronic Circuits, 6th ed.; Oxford University Press: Oxford, UK, 2009; pp. 727–731. [Google Scholar]
- M. Di Gioia, L. Lombardi, C. Marzocca, G. Matarrese, G. Menduni, P. Patimisco, V. Spagnolo, Signal-to-Noise Ratio Analysis for the Voltage-Mode Read-Out of Quartz Tuning Forks in QEPAS Applications. Micromachines 2023, 14, 619. [CrossRef] [PubMed]
Figure 1.
Simplified block diagram of a QEPAS sensor.
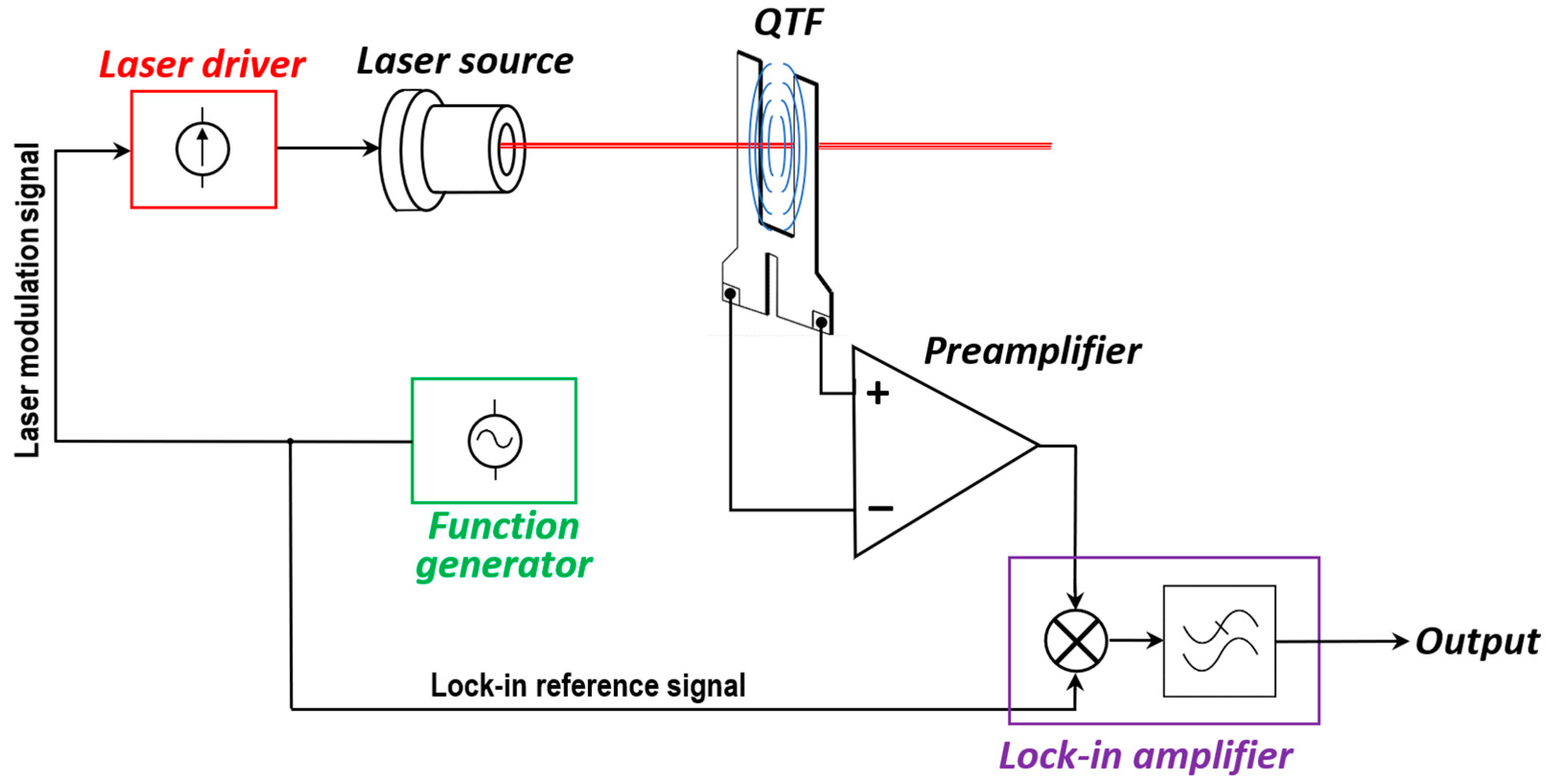
Figure 2.
QTF read-out by means of a transimpedance preamplifier.
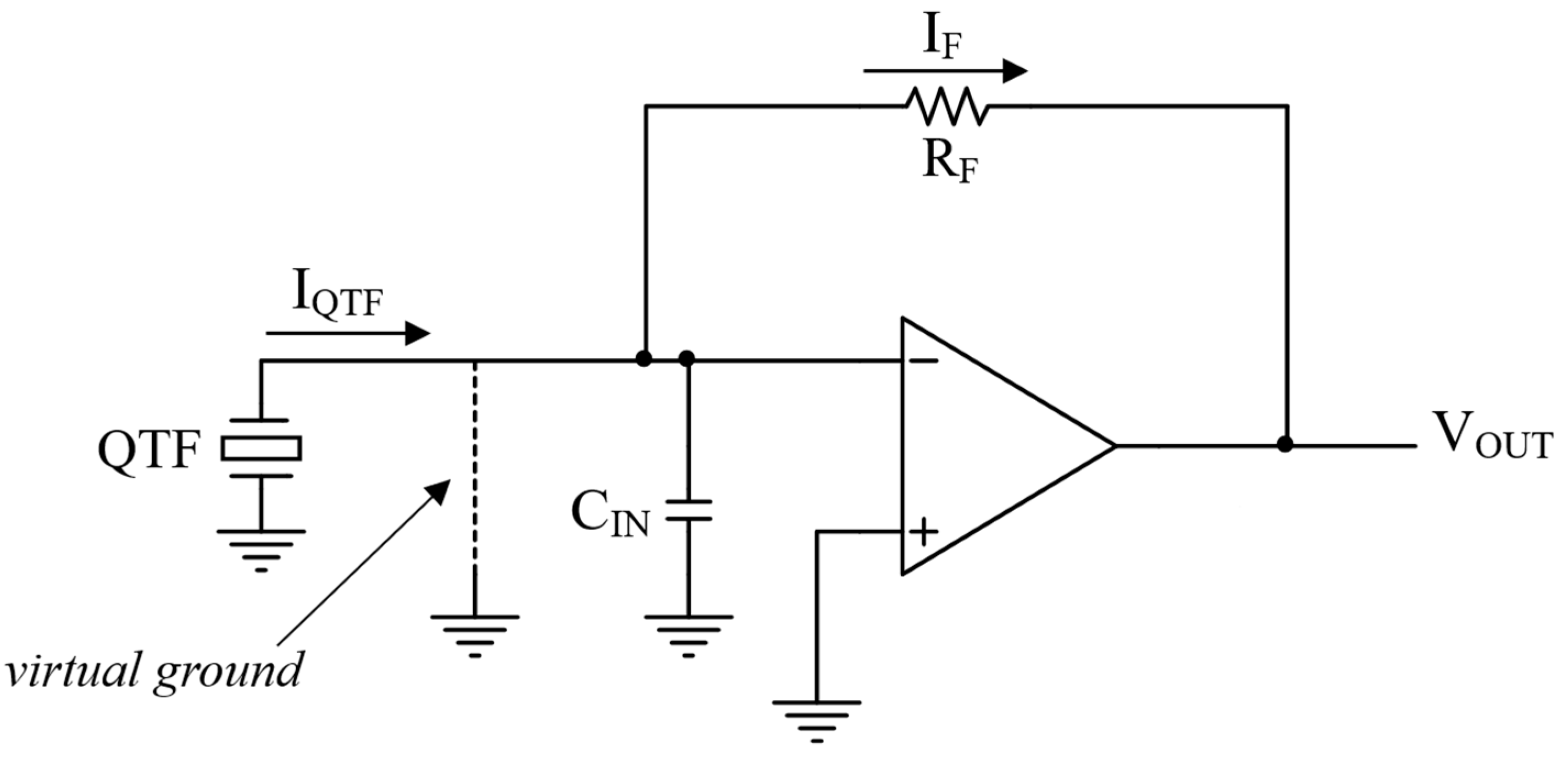
Figure 3.
Butterworth-Van Dyke model of the QTF coupled to the TIA.
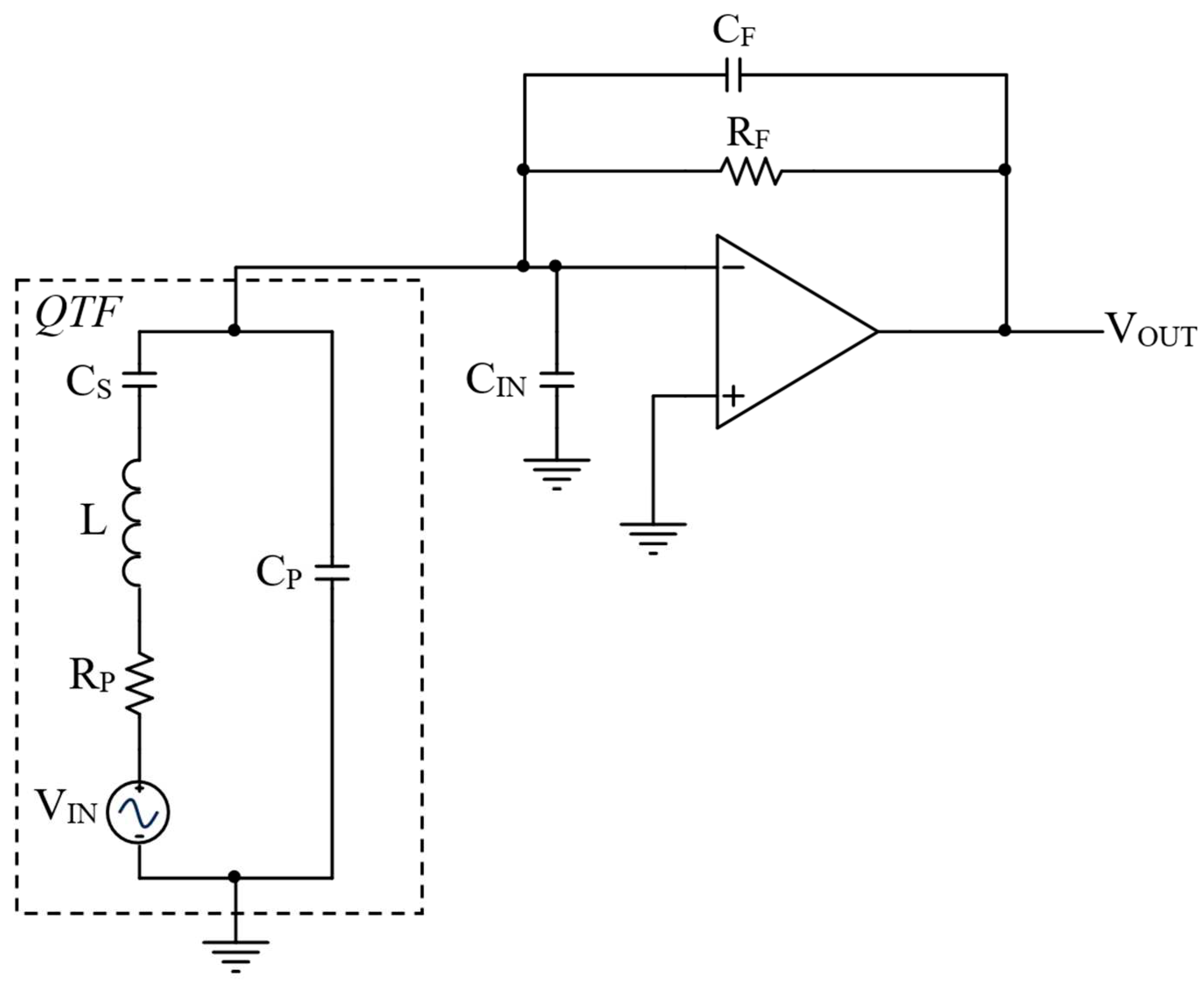
Figure 4.
SPICE simulation of the loop gain of the TIA in Figure 2, with the OPAMP OP27.
Figure 4.
SPICE simulation of the loop gain of the TIA in Figure 2, with the OPAMP OP27.
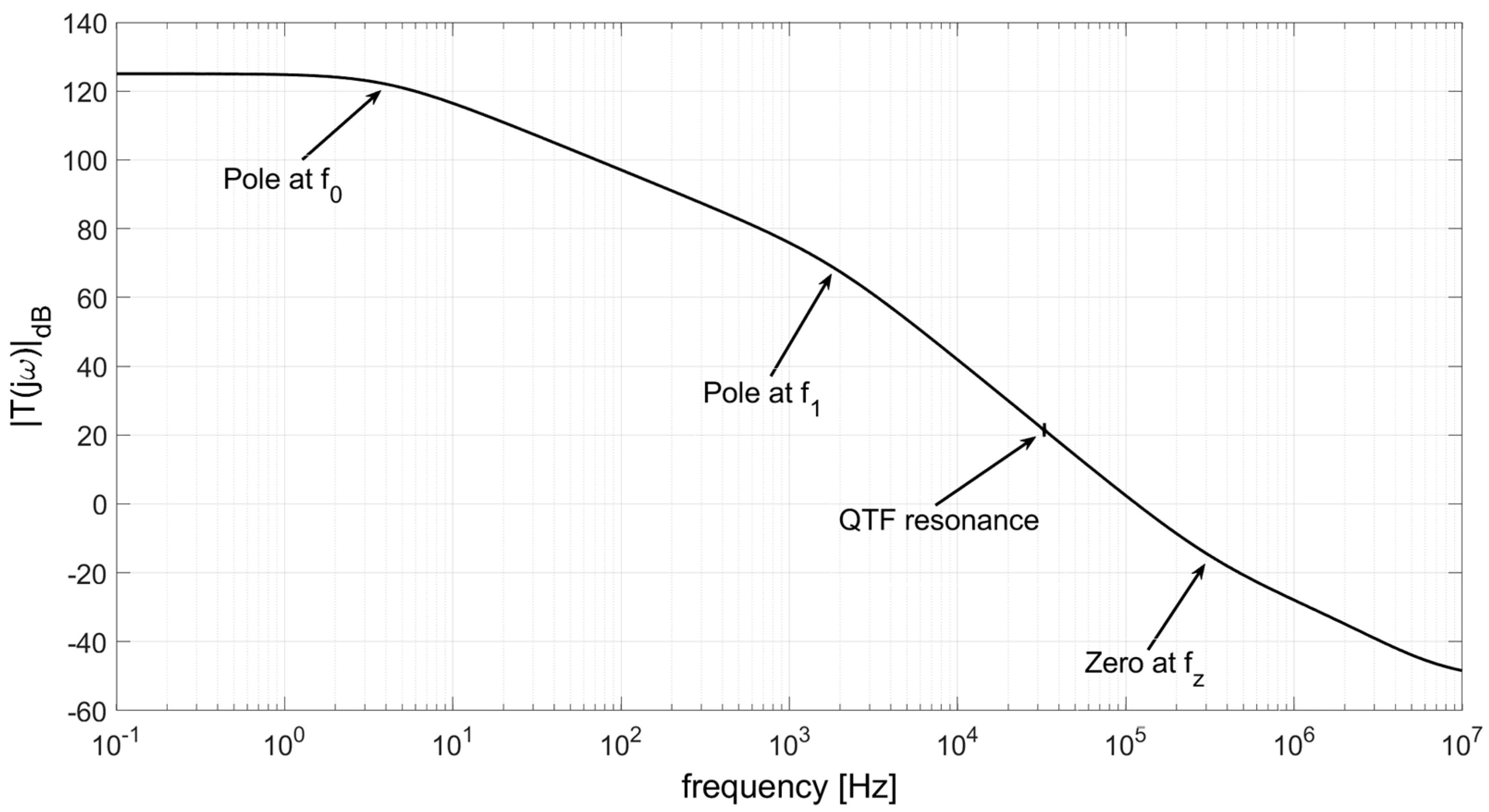
Figure 5.
Detail of the frequency behavior of |T(jω)| around the resonant frequency of the QTF, for the TIA based on the OP27 OPAMP.
Figure 5.
Detail of the frequency behavior of |T(jω)| around the resonant frequency of the QTF, for the TIA based on the OP27 OPAMP.
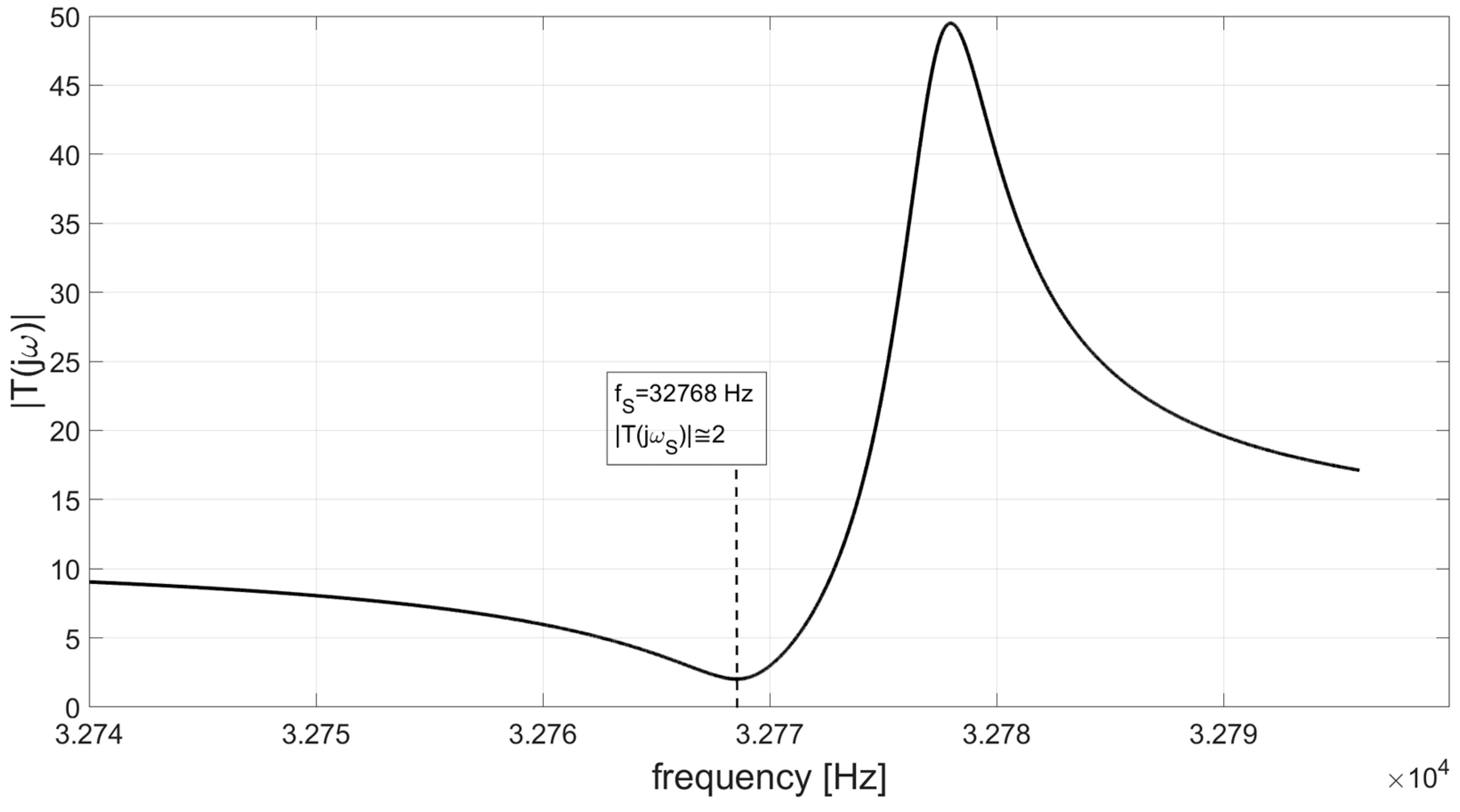
Figure 6.
Equivalent circuit of the TIA after the application of Miller’s theorem to the feedback impedance.
Figure 6.
Equivalent circuit of the TIA after the application of Miller’s theorem to the feedback impedance.
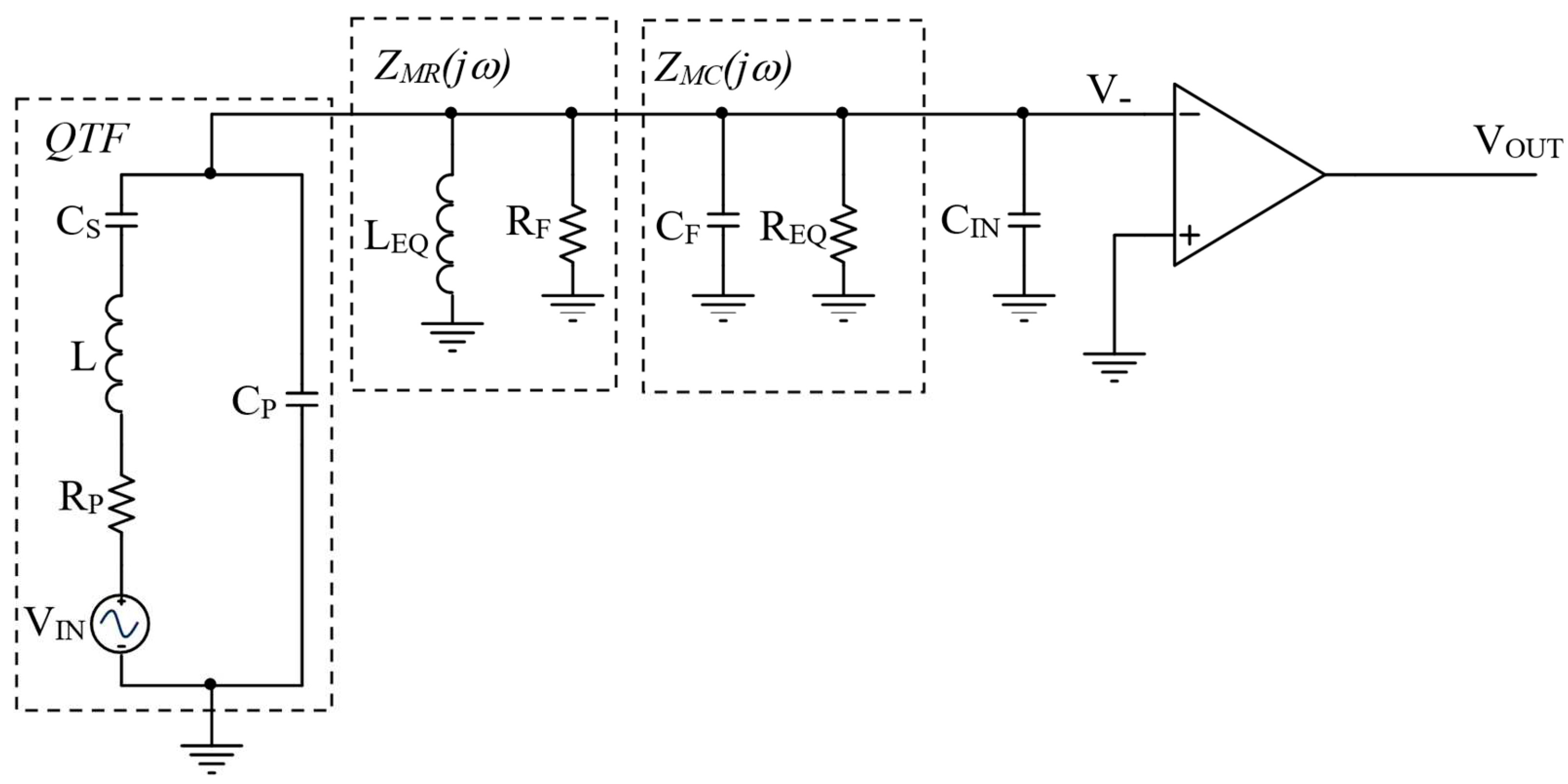
Figure 7.
Simplified circuit for the evaluation of the resonant frequencies of the circuit in Figure 6.
Figure 7.
Simplified circuit for the evaluation of the resonant frequencies of the circuit in Figure 6.
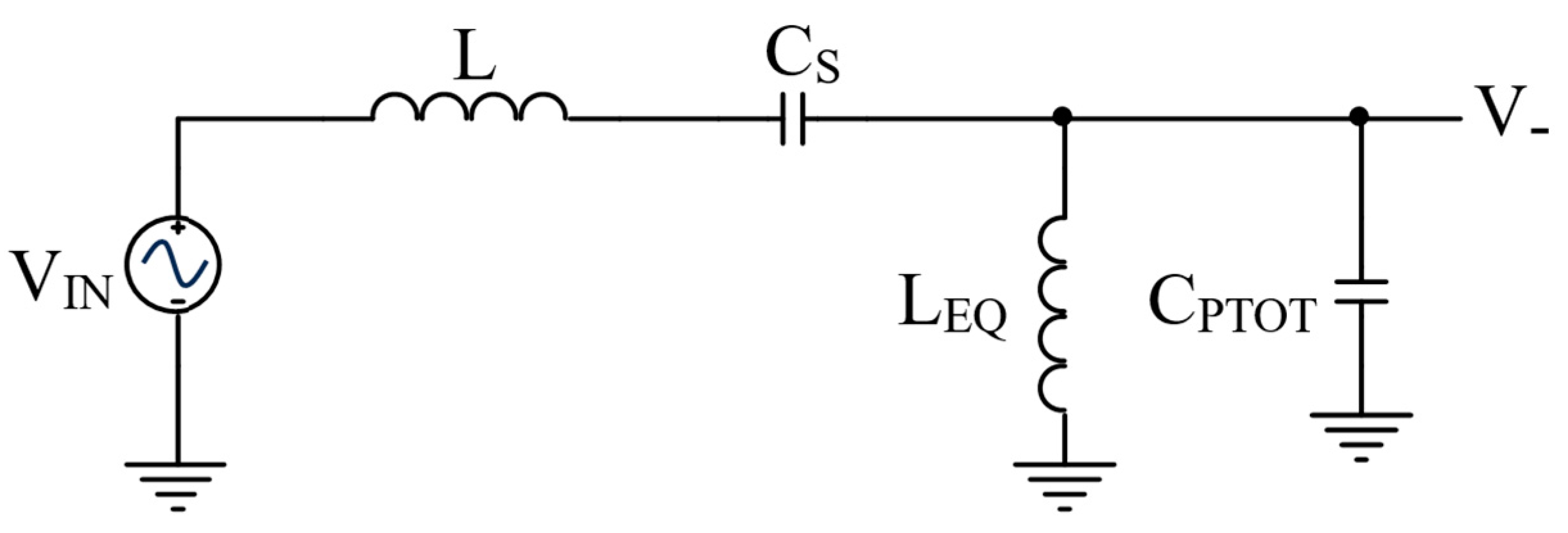
Figure 8.
Frequency response of the TIA realized with three different OPAMPs.
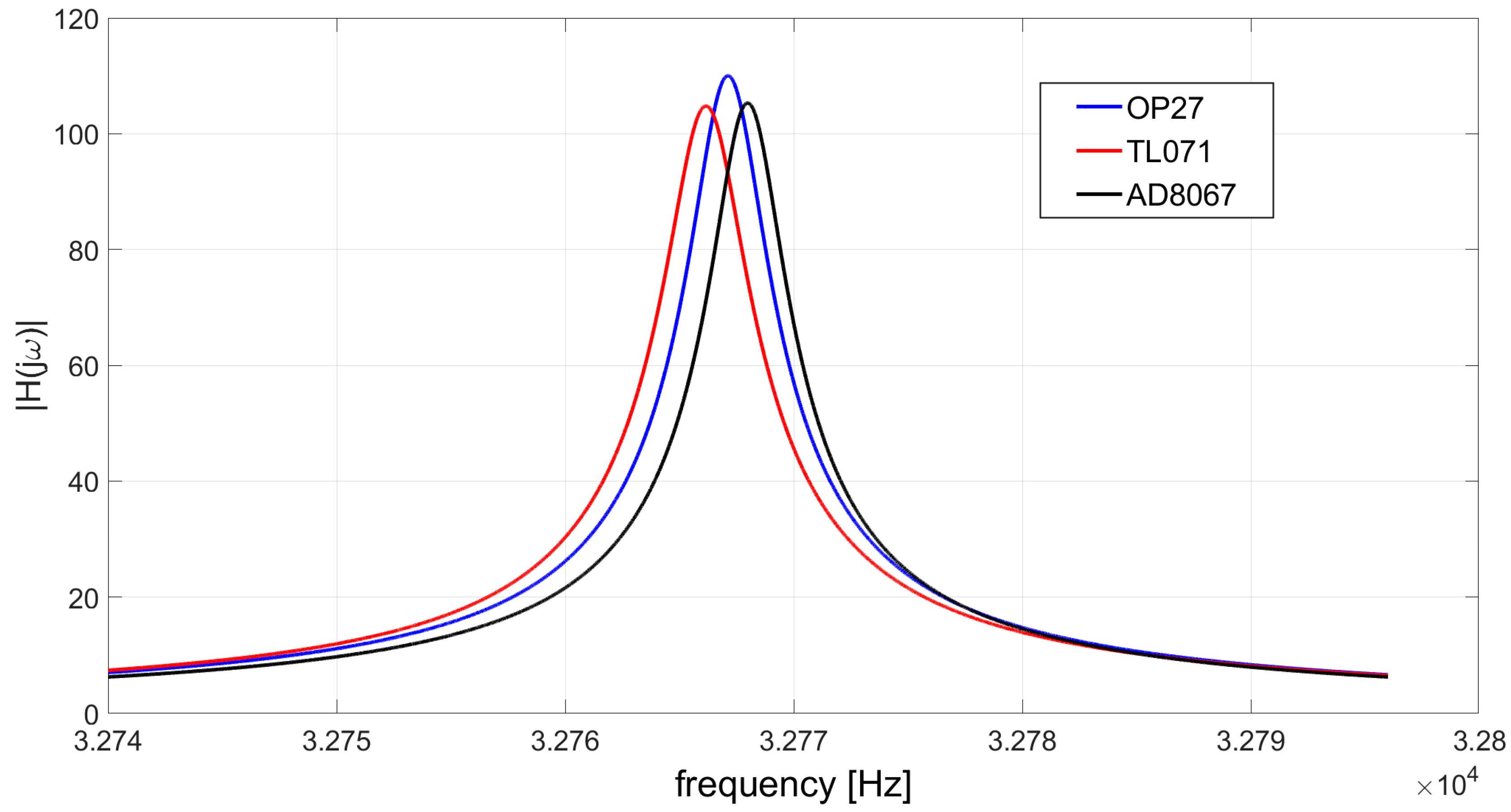
Figure 9.
Main noise sources in the TIA.
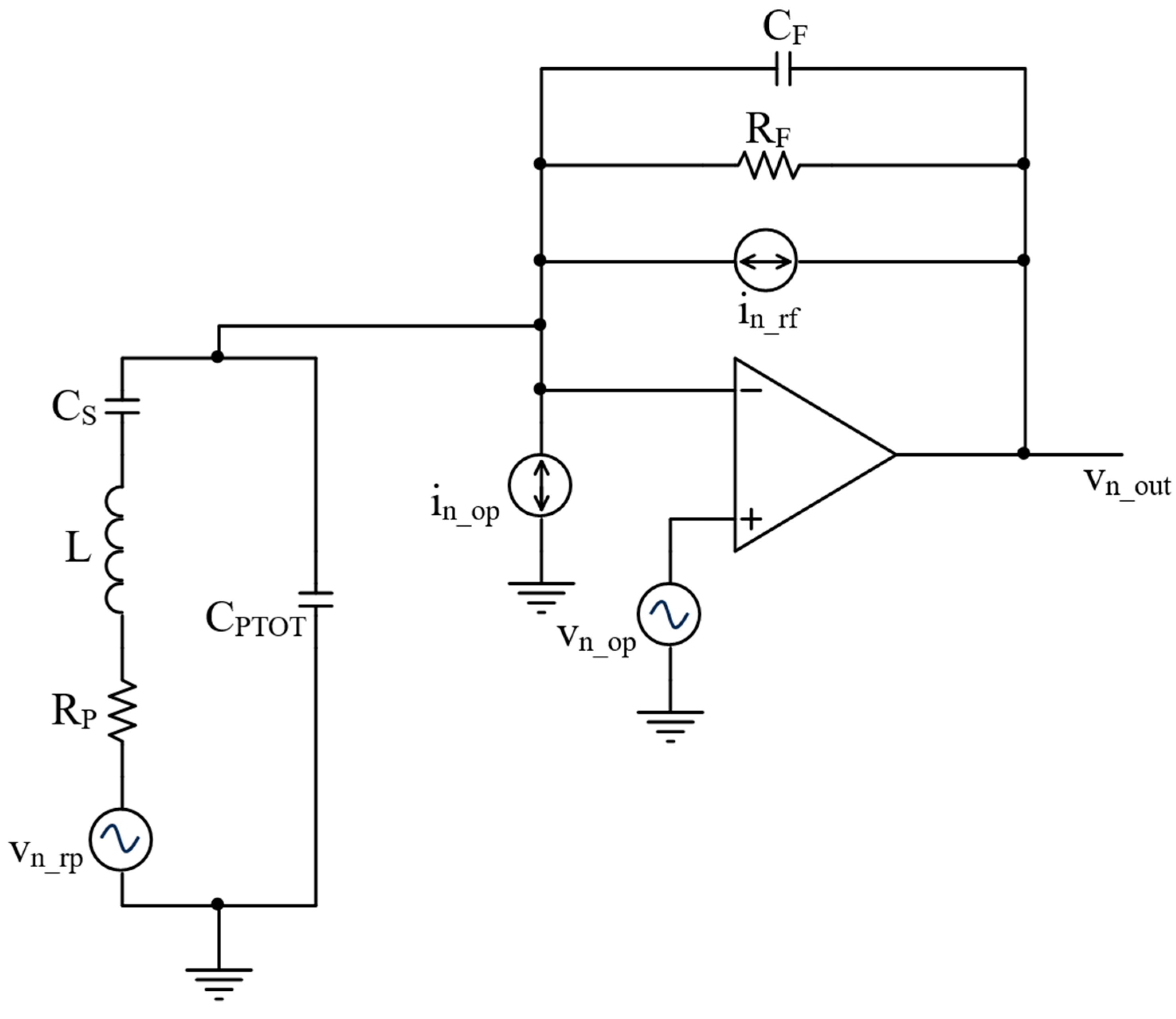
Figure 10.
TIA realized with the AD8067: modulus of the transfer function |H(jω)| obtained with SPICE simulations and equation (2).
Figure 10.
TIA realized with the AD8067: modulus of the transfer function |H(jω)| obtained with SPICE simulations and equation (2).
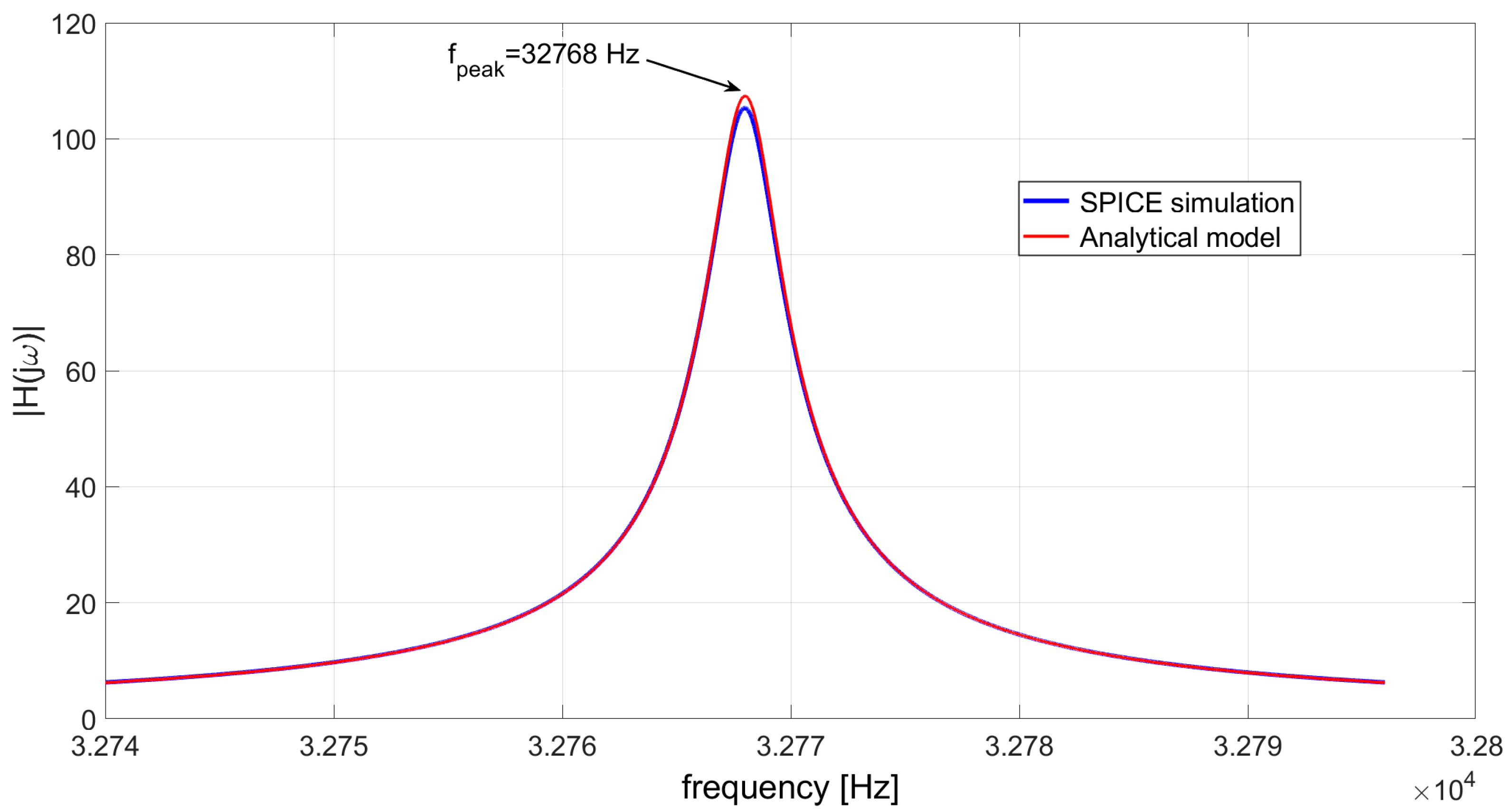
Figure 11.
TIA realized with the AD8067: total output noise power density obtained with SPICE simulations and equation (12).
Figure 11.
TIA realized with the AD8067: total output noise power density obtained with SPICE simulations and equation (12).
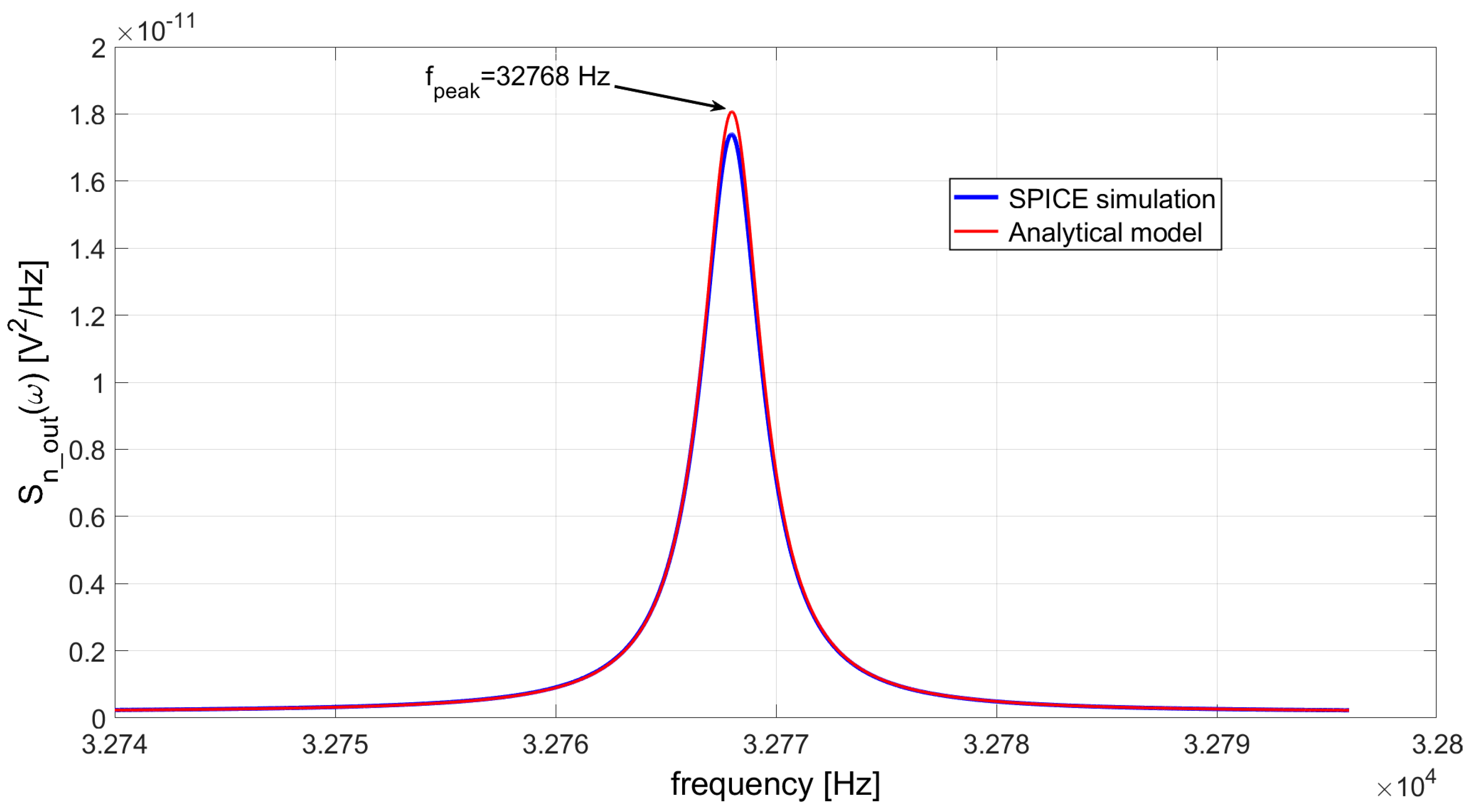
Figure 12.
Comparison between the output noise power spectral densities of the TIA realized with the OP27 and with the same OPAMP, but with loop gain increased by a factor of 20, by means of an ideal voltage amplifier inserted in the feedback loop.
Figure 12.
Comparison between the output noise power spectral densities of the TIA realized with the OP27 and with the same OPAMP, but with loop gain increased by a factor of 20, by means of an ideal voltage amplifier inserted in the feedback loop.
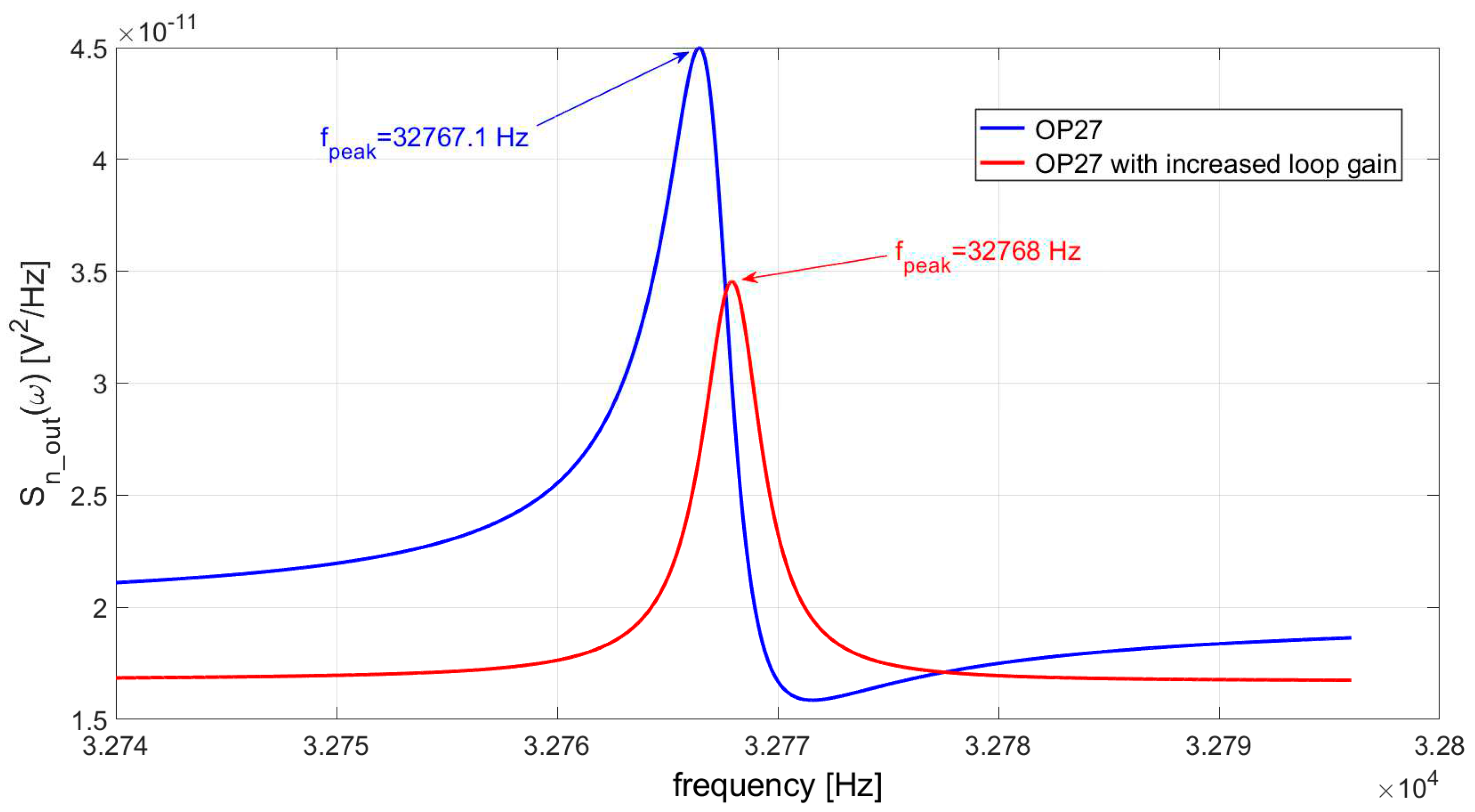
Figure 13.
Increasing the loop gain of the TIA based on the OP27, by inserting an ideal voltage amplifier in the feedback loop.
Figure 13.
Increasing the loop gain of the TIA based on the OP27, by inserting an ideal voltage amplifier in the feedback loop.
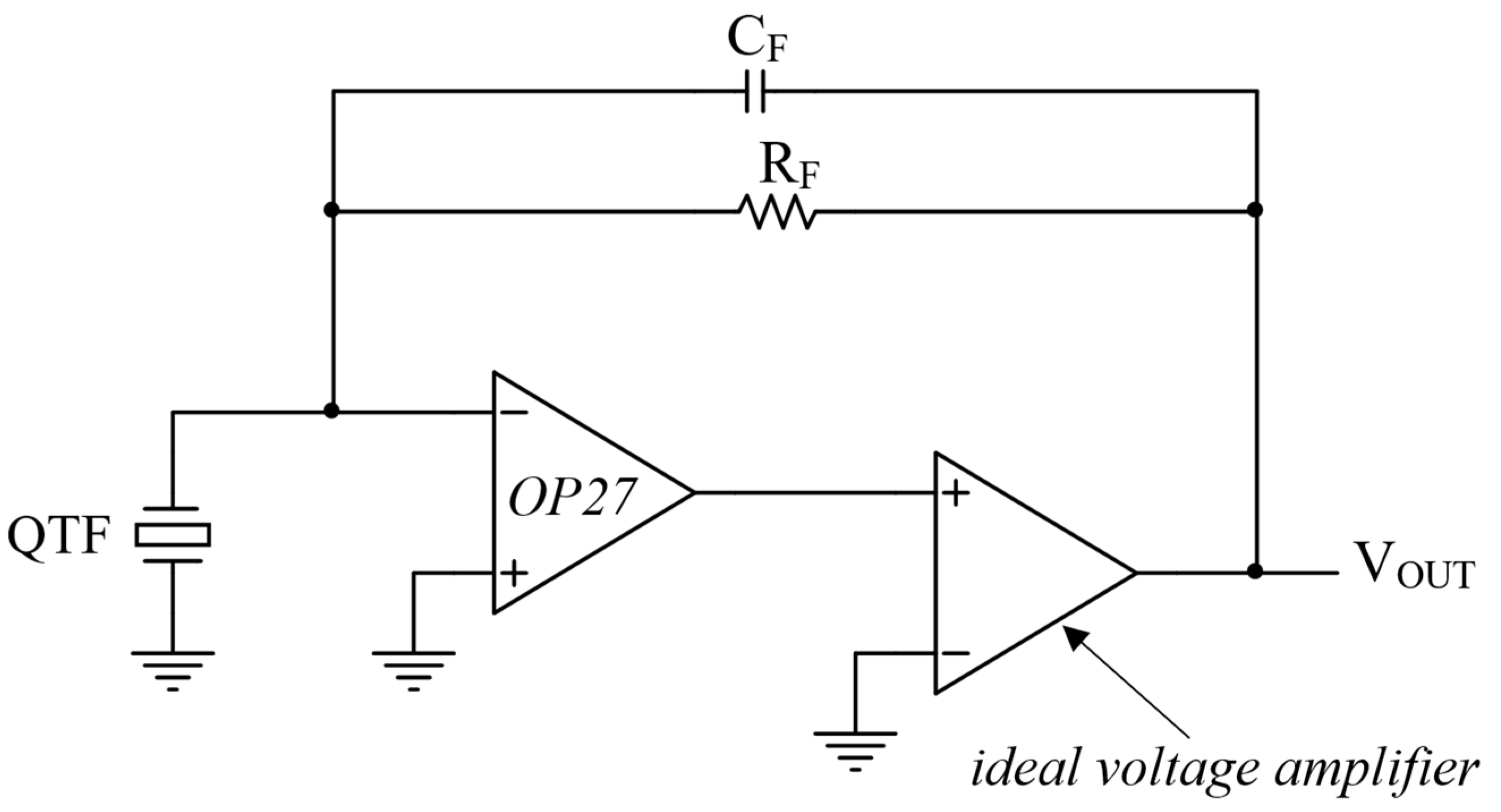
Figure 14.
Comparison between the modulus of the transfer function Hf(jω) of the TIA realized with the OP27 and with the same OPAMP, but with loop gain increased by a factor of 20.
Figure 14.
Comparison between the modulus of the transfer function Hf(jω) of the TIA realized with the OP27 and with the same OPAMP, but with loop gain increased by a factor of 20.
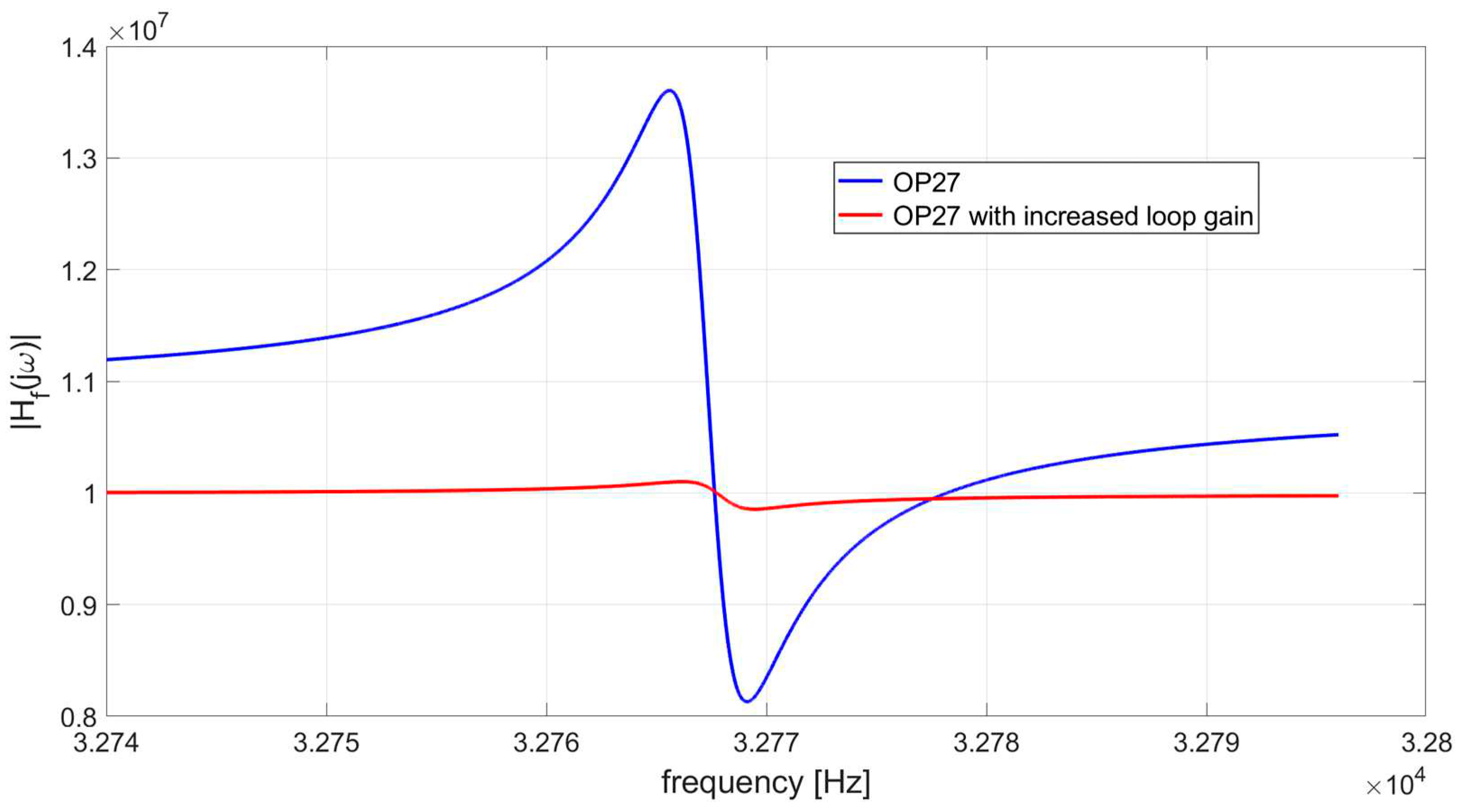
Figure 15.
SNR at the LIA output as a function of the LIA reference frequency: LIA filter bandwidth BW=0.1 Hz, TIA realized with the OP27 and with the same OPAMP, but with loop gain increased by a factor of 20.
Figure 15.
SNR at the LIA output as a function of the LIA reference frequency: LIA filter bandwidth BW=0.1 Hz, TIA realized with the OP27 and with the same OPAMP, but with loop gain increased by a factor of 20.
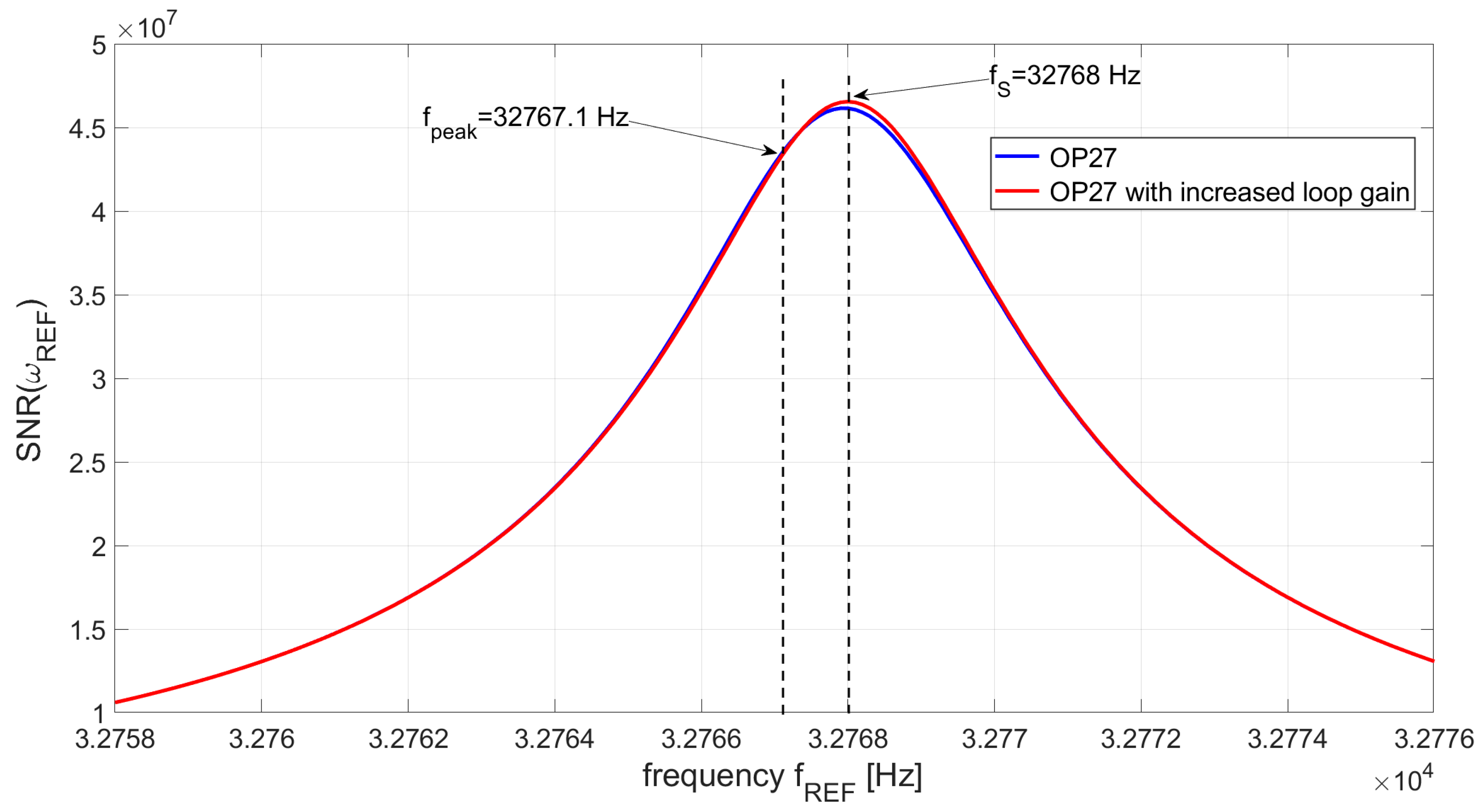
Figure 16.
SNR at the LIA output as a function of the LIA reference frequency: LIA filter bandwidth BW=3 Hz, TIA realized with the OP27 and with the same OPAMP, but with loop gain increased by a factor of 20.
Figure 16.
SNR at the LIA output as a function of the LIA reference frequency: LIA filter bandwidth BW=3 Hz, TIA realized with the OP27 and with the same OPAMP, but with loop gain increased by a factor of 20.
Table 1.
Values of the passive components of the circuit in Figure 2.
Table 1.
Values of the passive components of the circuit in Figure 2.
| Parameter | Value |
|---|---|
| Cp | 5 pF |
| CS | 5.2424 fF |
| L | 4.50 kH |
| Rp | 92.65 kΩ |
| Cin | 4 pF |
| RF | 10 MΩ |
| CF | 50 fF |
Table 2.
OPAMP models used for the SPICE simulations.
| OPAMP | Gain-Bandwidth Product [MHz] | Peak Frequency fpeak [Hz] |
|---|---|---|
| OP27 | 8 | 32767.1 |
| TL071 | 3 | 32766.2 |
| AD8067 | 300 | 32768.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






