Prerpints.org logo
Preprint
Article

Smith-Watson-Topper Parameter in Partial Slip Bimodal Oscillations of Axisymmetric Elastic Contacts of Similar Materials: Influence of Load Protocol and Profile Geometry

Altmetrics

Downloads

64

Views

14

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

31 January 2024

Posted:

31 January 2024

You are already at the latest version

Alerts
Abstract
Based on a very fast numerical procedure for the determination of the subsurface stress field beneath frictional contacts of axisymmetric elastic bodies under arbitrary 2D oblique loading, the contact mechanical influences of loading parameters and contact profile geometry on the Smith-Watson-Topper (SWT) fatigue crack initiation parameter in elastic fretting contacts with superimposed normal and tangential oscillations are studied in detail. The efficiency of the stress calculation allows for a comprehensive physical analysis of the multi-dimensional parameter space of influencing variables. It is found that a superimposed normal oscillation of the contact can significantly increase or decrease the SWT parameter, depending on the initial phase difference and frequency ratio between the normal and tangential oscillation. Written in proper non-dimensional variables, the rounded flat punch always exhibits smaller values of the SWT parameter, compared to a full paraboloid with the same curvature, while the truncated paraboloid exhibits larger values. A small superimposed profile waviness also significantly increased or decreased the SWT parameter, depending on the amplitude and wave length of the waviness. While both the load protocol and the profile geometry can significantly alter the SWT parameter, the coupling between both influencing factors is weak.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

Mechanical contacts that are subject to small oscillations often suffer from various forms of damage, which are summarized under the term "fretting", and which can significantly decrease the lifetime or performance of the contacting materials and bodies. Depending on the characteristic extent of the stick and slip zones in the contact during the oscillation, it is common to distinguish different "fretting regimes" [1], mainly the partial slip and the sliding regime.
The two main damage phenomena associated with fretting are fretting wear and fretting fatigue. While the dominant damage mode in the partial slip regime often is fretting fatigue, the sliding regime mostly suffers from fretting wear. Nevertheless, both phenomena interact with each, and a numerical routine for the life prediction of a fretting contact should account for both wear and fatigue ([2,3,4]). However, doing so in a rigorous way – especially considering that, in the partial slip regime, the wear debris material will act as a "third body" in the contact – has proven to be extremely difficult [5].
The amount of influencing mechanisms and governing parameters in fretting is vast. Some of these have a contact mechanical origin, while others are of a more general tribological (physico-chemical) nature. One of the almost strictly contact mechanical aspects of fretting is the fatigue crack initiation due to the intricate, multiaxial, and rapidly changing stress field beneath the frictional contact under complex cyclic loading [6]. For the prediction of fatigue crack nucleation, there are different well-established mechanical frameworks [7]. One of the most common approaches are critical plane parameters [8], like the Smith-Watson-Topper (SWT, [9]) parameter.
Based on the SWT parameter (or similar critical plane approaches), different aspects of the fatigue crack initiation problem in fretting have already been analyzed numerically and experimentally in the literature. In that regard, especially in the past decade, a lot of research interest was dedicated to the impact of the loading protocol and the contact profile geometry on crack initiation, as these are influence factors that can be controlled more or less easily in design and construction of fretting contacts. With respect to the loading protocol, the influences of out-of-phase loading [10] and phase difference ([11,12]), as well as more complex cyclic loading paths ([13,14]) were studied. On the other hand, regarding the influence of the surface geometry on crack initiation, the overall contact geometry [15] and macroscopically worn profiles [16], as well as the surface microgeometry [17], surface pit treatment [18] and machined surface texture [19] have been considered.
Most of the aforementioned numerical studies are based on the Finite-Element-Method (FEM). While the FEM, due to its flexibility with respect to the physical modelling, can account for a wide variety of mechanisms and phenomena in a specific fretting contact – und thus achieves good predictive power under sufficiently well-defined circumstances – its demands for computational power and calculation time often make large parameter studies for the comprehensive analysis of different influencing factors unfeasible.
One solution to this problem consists in the application of data science and machine learning approaches, e.g., artificial neural networks [20]. These, however, sacrifice the aspiration of a physical description and understanding of the system, for the purpose of a robust prediction of only a few concrete output variables, e.g., the fatigue life.
Another approach may be the reduction and simplification of the physical modelling: If the model description of the system is simple enough – so that the numerical solution of the resulting system of equations can be executed sufficiently fast to allow for a comprehensive analysis of a large parameter space – one is able to get a broad and deep physical understanding of the reduced model. While the results of such a reduced model, in most cases, won’t achieve a very high quantitatively predictive power, they can provide a broad, physically-based set of ideas, which parameter combinations can be worthwhile to analyze deeper with a more elaborate modelling, e.g., based on the FEM.
The latter approach shall be pursued in the present work. As was pointed out above, fretting fatigue crack initiation is mainly due to the complex oscillating mechanical stress field beneath a frictional contact under cyclic tangential (or multimodal) loading. For the elastic frictional contact of smooth, convex, axisymmetric bodies (this characterization constitutes the aforementioned model reduction), very recently an extremely efficient procedure has been suggested for the determination of the subsurface stress state beneath the frictional contact under arbitrary 2D oblique loading [21], which reduces the problem of calculating the subsurface stresses to the evaluation of elementary one-dimensional integrals. Once the subsurface stress state is known, the critical plane parameters for the prediction of fatigue crack initiation can be determined easily, allowing for the very fast analysis of a specific set of geometrical and loading parameters.
Based on this procedure, in the present manuscript, the influence of the loading protocol and the contact profile geometry on the SWT parameter in partial slip bimodal oscillations of axisymmetric elastic contacts is theoretically studied. That shall provide general insights into the coupled (contact mechanical) dependencies of fretting fatigue life on these two classes of input parameters, i.e., load and geometry.
The remainder of the manuscript is structured as follows: In Section 2, the analyzed problem is formulated in a physically rigorous form. After that, in Section 3, the semi-analytical and numerical procedures for the solution of the contact problem and the determination of the subsurface stress state, as well as the fatigue crack initiation criterion, are described in detail. Section 4 presents the obtained numerical results with respect for the influence of load and profile geoemtry on the SWT parameter. A discussion of the results finishes the manuscript.

2. Problem Statement

Let us consider the contact of axisymmetric elastic bodies, made of linear, isotropic, homogeneous materials that are elastically similar to each other (to avoid elastic coupling between the normal and tangential contact problems), i.e., whose shear moduli G i and Poisson ratios ν i (at least, approximately) satisfy the relation
1 − 2 ν 1 G 1 = 1 − 2 ν 2 G 2 .
Moreover, the bodies shall also obey the restrictions of the half-space approximation; in that case, the contact between the two elastic bodies is equivalent to the one between an elastic half-space, having the effective moduli
E * = 1 − ν 1 2 G 1 + 1 − ν 2 2 G 2 − 1 and G * = 1 − 2 ν 1 4 G 1 + 1 − 2 ν 2 4 G 2 − 1 ,
and a rigid indenter having the axisymmetric profile z = f ( r ) , with the polar radius r in the contact plane and the contact normal direction z; f is given by the gap between the contacting surfaces in the instant of first contact. Microscopic surface roughness is neglected
We will consider different profile functions f; specifically, the paraboloid (i.e., the axisymmetric Hertzian contact),
f ( r ) = r 2 2 R ,
with the curvature radius R; the cylindrical rounded flat punch,
f ( r ) = ( r − b ) 2 2 R H ( r − b )
with the radius b of the flat face of the punch, the curvature radius R of the rounded edge, and the Heaviside step function H; the truncated paraboloid
f ( r ) = r 2 − b 2 2 R H ( r − b ) ,
and the paraboloid with superimposed small waviness,
f ( r ) = r 2 2 R + h 1 − cos 2 π r λ ,
with the amplitude h and wave length λ of the waviness. The analyzed contact problems are shown schematicallyin Figure 1.
The contacts shall be subject to displacement-controlled bimodal harmonic oscillations; that is to say, the indentation depth δ as a function of the time t shall be
δ ( t ) = δ 0 + δ A sin ω 1 t + ψ ,
with the average indentation depth δ 0 , the amplitude δ A and angular frequency ω 1 of the normal oscillation, and a phase angle ψ ; moreover, for the macroscopic relative tangential displacement between the contacting bodies, u,
u ( t ) = u A sin ω 2 t ,
with the amplitude u A and angular frequency ω 2 of the tangential oscillation.
Note that in the literature recently also variable amplitude fretting oscillations have been considered ([22,23]). This would in principle be possible to analyze within the framework described in the present manuscript, but would too significantly extent the relevant parameter space.
The tangential contact problem with friction shall be solved within the framework of the Cattaneo-Mindlin approximation ([24,25]), specifically:
  • validity of a local Amontons-Coulomb friction law between normal and frictional surface tractions, with a globally constant coefficient of friction μ
  • neglect of the lateral (i.e., orthogonal to the loading plane) elastic surface displacements – which would slightly violate the isotropy of the friction law
Munisamy et al. [26] compared the Cattaneo-Mindlin approximate theory to a rigorous numerical contact solution for the frictional Hertzian contact under shear load, and found that the error of the approximation in terms of the contact tractions is generally small.
We are interested in the Smith-Watson-Topper (SWT, [9]) multiaxial fatigue crack initiation parameter due to the oscillating subsurface stress and deformation fields. It belongs to the group of critical plane criteria of (fretting) fatigue crack initiation [7]; that is to say, it evaluates a certain characteristic scalar quantity of the intricate time-evolution of the subsurface stress and deformation fields in each material plane at a specific material point. The plane with the highest value of the scalar quantity is deemed critical, i.e., most prone to crack nucleation.
In the case of the SWT parameter, the scalar quantity is given by the product of the maximum normal stress σ n max and the normal strain amplitude Δ ε n / 2 in the specific plane,
swt = σ n max Δ ε n 2 max ,
where the upper index "max" of the stress and the strain amplitude are to be understood over one (stationary) oscillation cycle; the lower index "max" indicates maximizing with respect to the orientation of the plane [27]. The SWT parameter is thus defined for every material point with the cartesian coordinates ( x , y , z ) ; we will be interested only in the maximum value of the field,
SWT = max swt ( x , y , z ) ,
which can be connected to the specimen lifetime (measured in oscillation cycles to initiate a crack of given length) [8]. In that regard, it has to be kept in mind, that, because of the highly localized character of the contact stress fields – and therefore, too, the SWT parameter – such a strictly local version of the crack initiation criterion will provide very conservative lifetime estimates [6]. To obtain better lifetime predictions, the local field of the parameter can either be averaged over a certain volume [28], or evaluated at a certain critical distance [29] from the strictly local maximum. Both the averaging volume and the critical distance depend on the specifics of the fretting contact, e.g., the material pairing. As the present work doesn’t aim for concrete lifetime predictions – but rather aspires to analyze the behavior of the criterion (9) under different contact mechanical conditions – and therefore chracteristics like the concrete material pairing aren’t specified, we will use a local formulation of the SWT parameter. However, theoretically speaking, the averaged or critical distance formulations can easily be obtained from the local field, as well.
Final it should be noted, that very recently also the crack orientation prediction within the SWT framework has been significantly improved, based on the critical direction method [30].

3. Methods

In this section, the semi-analytical and numerical procedures for the solution of the problem formulated above are described. First, the contact solver, which is based on the method of dimensionality reduction (MDR), is detailed. After that, the determination of the subsurface stress fields and the SWT parameter are discussed.

3.1. Contact Solution

There are different formalisms for the solution of the axisymmetric tangential contact problem with friction under arbitrary 2D oblique loading, within the framework of the Cattaneo-Mindlin approximation; namely, Jäger’s algorithm [31], the method of memory diagrams (MMD, [32]), and the method of dimensionality reduction (MDR, [33,34]). All these are equivalent to each other, and can, in fact, be "translated" into one another. Depending on the specific task which is to be executed, all methods have their own advantages and disadvantages. To solve the problem at hand, for reasons that will become clear below, the most efficient and direct approach is the MDR.
Within the framework of MDR, the contact between axisymmetric elastic bodies is mapped exactly onto an equivalent contact between a rigid plane profile g and a one-dimensional foundation of independent linear springs. Sketches of the original three-dimensional contact and the equivalent contact within MDR are shown in Figure 2.
For the mapping procedure to be exact, the MDR profile g must correspond to the relation between indentation depth δ and contact radius a in the original axisymmetric system. Hence ([34], p. 7),
g ( ξ ) = | ξ | ∫ 0 | ξ | f ′ ( r ) d r ξ 2 − r 2 ,
where the prime denotes the derivative.
Moreover, the spring elements of the elastic foundation must have normal and tangential values of line stiffness according to ([34], p. 131)
d k N = E * d ξ , d k x = G * d ξ ,
with the effective moduli defined in Eq. (2), and the spacing d ξ between the elastic elements.
For the exact mapping of the tangential contact problem with friction, the spring elements only have to obey a local Amontons-Coulomb friction law with the same coefficient of friction as in the original system ([34], p. 132).
If these mapping rules are implemented and evaluated according to the given load protocol – in our case, given by Eqs. (7) and (8) – the relationships between the macroscopic displacements ( δ and u), contact forces ( F N and F x ), as well as the radii of the contact and the inner stick zone (a and c) in the MDR model will exactly match the ones in the original three-dimensional system, for arbitrary 2D oblique loading of the contact ([35], p. 102).
Moreover, the MDR solution of the contact problem allows for a very fast determination of the subsurface elastic stress fields for the original contact, as will be discussed below.

3.2. Subsurface Stress Fields and SWT Parameter

The determination of the subsurface stress field is based on the understanding of the partial slip tangential contact as a superposition of incremental rigid translations of circular contact domains – which originally stems from Mossakovski [36] and later Jäger [37] – and this superposition’s very close relationship to the MDR contact solution.
Suppose, the original axisymmetric bodies are brought into contact over a circular contact area with the radius ξ , and two remote points of the bodies on the axis of symmetry are moved to one another by an incremental indentation depth d δ . Then, the two bodies will experience an increment of the contact pressure p of ([34], p. 12)
d p ( r ; ξ ) = E * π d δ ξ 2 − r 2 , r < ξ ,
which corresponds to the pressure under the incremental indentation by a rigid cylindrical flat punch with the radius ξ . Similarly, if two remote points on the axis of symmetry are moved relative to one another in the tangential direction by an incremental displacement d u (without slip and without tilting), the bodies will experience incremental tangential surface tractions ([34], p. 137)
d q ( r ; ξ ) = G * π d u ξ 2 − r 2 , r < ξ .
The subsurface stress fields due to the surface tractions (13) and (14) have been very recently determined analytically and in closed form by the author [21].
As the tangential contact with friction under 2D oblique loading can be thought of as a specific series of incremental (normal and tangential) rigid translations of circular contact domains with varying radius ξ , the corresponding subsurface elastic stress field can be superimposed from the "basic" fields that originate from the surface tractions (13) and (14).
Hence, the subsurface stress field due to the normal contact load is given by [21]
σ j k norm ( x , y , z ; a ) = ∫ 0 a σ j k ( 1 ) ( x , y , z ; ξ ) δ ′ ( ξ ) d ξ ,
where σ j k ( 1 ) denotes the stress field due to the unit indentation by a rigid cylindrical flat punch (which is known explicitly). The subsurface stress field due to the tangential contact load is analogously given by [21]
σ j k tan g ( x , y , z ; a ) = ∫ 0 a σ j k ( 2 ) ( x , y , z ; ξ ) u ′ ( ξ ) d ξ ,
where σ j k ( 2 ) denotes the stress field due to the (rigid) unit tangential displacement without slip of a circular contact domain (which is also known explicitly).
However, what are the correct "histories" of rigid translations, δ ( ξ ) and u ( ξ ) – which are required for the evaluation of the superposition integrals (15) and (16) – to reproduce the contact configuration of the partial slip contact under oblique loading?
As it turns out, these are directly "encoded" in the MDR solution to the contact problem. Let the normal and tangential displacements of the spring elements in the MDR model be w MDR ( ξ , t ) and u MDR ( ξ , t ) , respectively. These displacements can be calculated very easily based on the MDR rules described in the previous subsection. Any of the spring elements at position ξ corresponds to a rigid cylindrical flat punch with radius ξ in the original system. Therefore, the histories of rigid translations can be calculated from the MDR displacements according to
δ ( ξ , t ) = w MDR ( ξ = 0 , t ) − w MDR ( ξ , t ) ,
and
u ( ξ , t ) = u MDR ( ξ = 0 , t ) − u MDR ( ξ , t ) .
The problem of determining the subsurface stress fields has thus been reduced to the (numerical) calculation of the elementary one-dimensional integrals (15) and (16). Once the stress fields are known, it is easy to implement a numerical routine for the evaluation of the definitions (9) and (10) for the SWT parameter.

4. Results

4.1. Scaling Laws

The characteristic scale of the SWT parameter is the scale of the elastic energy density,
SWT 0 = E * ε 0 2 = E * δ 0 R ,
with the characteristic deformation scale in an axisymmetric Hertzian contact, ε 0 = δ 0 / R .
Dimensional analysis and numerical solutions of the problem stated in Section 2 show that the SWT parameter, normalized for its characteristic scale (19), will only depend on a few non-dimensional parameters, specifically
s = SWT SWT 0 = s ν , μ , δ A δ 0 , ω 2 ω 1 , G * u A μ E * δ 0 , ψ , κ i .
Here, κ i denote the non-dimensional parameters for the characterization of the profile geometry, which wil be detailed in Section 4.3.
It should be noted that the dependencies of the non-dimensional SWT parameter on the friction coefficient and the non-dimensional tangential oscillation amplitude, G * u A / ( μ E * δ 0 ) , are rather elementary (increasing these parameters with all others held constant increases s), and shall not occupy us further. The dependence on Poisson’s ratio is intricate, but very weak. Therefore, the remaining dependencies, that will be analyzed in the following, are the ones on the normalized normal oscillation amplitude, δ A / δ 0 , the frequency ratio between tangential and normal oscillation, ω 2 / ω 1 , the (initial) phase difference ψ , and the profile parameters κ i .
Unless stated otherwise explicitly, the simulations used the fixed non-dimensional parameters listed in Table 1.
It should be pointed out, that for basically all simulations the critical point (with the maximum SWT parameter) was in the contact surface, in the plane y = 0 , and well outside the region of permanent stick. The orientation of the critical plane was always close to perpendicular into the material (i.e., the normal vector of the critical plane pointed in the tangential x-direction). This is in agreement with respective experimental data in the literature [7].

4.2. Influence of Load Parameters in Parabolic Contact

First, let us analyze in-detail the influence of the bimodal loading protocol parameters δ A / δ 0 (normalized amplitude of normal oscillation), ω 2 / ω 1 (frequency ratio between tangential and normal oscillation) and ψ (phase angle between normal and tangential oscillation at the beginning of the stationary cycle), on the non-dimensional SWT parameter in a parabolic contact.
In the case of oscillations with the same frequency ( ω 2 = ω 1 ), the remaining function s = s ( δ A / δ 0 , ψ ) could, in theory, be demonstrated comprehensively in a countour diagram. However, this presentation would be hard to read; therefore, in Figure 3, the normalized SWT parameter is shown as a function of the phase angle ψ for different values of the normal oscillation amplitude.
Without normal oscillation, there would, of course, be no dependence on the phase angle. Therefore, for small normal oscillation amplitudes, the curves in Figure 3 are almost constant. Expectedly, for large normal oscillations, the dependence on the phase angle increases, and turns out to be actually very relevant, as for δ A / δ 0 = 8 / 9 , the maximum and minimum values of the SWT parameter, as a function of the phase angle, differ by almost the factor of Two!
Moreover, there is a very interesting effect with regard to the coupled dependencies on the frequency ratio and the phase angle, which is shown in Figure 4. There, the normalized SWT parameter is shown as a function of the phase angle for different frequency ratios, and small (A, left) or large normal oscillations (B, right).
The variation of the crack initiation criterion with the phase angle seems to be most prominent for frequency ratios of 1/4, 1/2 and 3/2; other values were tested, but showed little influence on the SWT parameter; probably, because the cycle duration of the full stationary cycle is very long for less commensurate frequencies, and thus the precise form of the loading protocol becomes less relevant, as normal and tangential contact configurations become statistically less correlated. Also, there seems to be a periodicity in the function s = s ( ψ ) , whose period length decreases with increasing frequency of the tangential oscillation.
Once again, all effects are amplified for larger amplitudes of the normal oscillation.

4.3. Influence of Profile Geometry

Let us now turn our attention to the influence of the contact profile geometry on the crack initiation criterion.

4.3.1. Rounded Flat Punch and Truncated Paraboloid

In the popular case of the cylindrical flat punch with rounded corners – the contact profile was given in Eq. (4) – the only governing profile parameter in the non-dimensional formulation (20) is the ratio between the radius b of the flat face of the punch, and the Hertzian contact radius a H = R δ 0 . Note that the curvature radius R of the rounded corners also enters the scale SWT 0 of the SWT parameter in Eq. (19); that is to say, if the curvature radius is reduced, the scale of the crack initiation criterion (and accordingly, the criterion itself) increases; the limit R → 0 corresponds to the sharp flat punch, which will be extremely prone to crack nucleation, due to the oscillating stress singularity at the edge of the punch.
For the truncated paraboloid with the profile given in Eq. (5), once again, the only influencing profile parameter in the non-dimensional formulation is the ratio between the radius b of the indenter’s flat face, and the Hertzian contact radius
In Figure 5, the normalized maximum SWT parameter is shown for the same-frequency bimodal contact oscillation, as a function of the phase angle ψ , for different values of the normalized radius of the punch face, b / a H , for the rounded flat punch (A, left) and the truncated paraboloid (B, right).
Obviously, in these cases, the dependence on the profile geometry is rather simple: For increasing values of b / a H , the normalized SWT parameter globally and monotonously decreases for the rounded flat punch, and increases for the truncated paraboloid.
Also there seems to be only a very weak coupling between the profile geometry as an influencing factor, and the loading protocol – especially for the rounded punch, for which this coupling is basically negligible – as the curves for different profile parameters differ only slightly in their dependence on the loading protocol (i.e., in the case of Figure 5, the phase angle). This phenomenon is highlighted again in Figure 6, showing the normalized SWT parameter for the different-frequency oscillation of a rounded flat punch, as a function of the normalized radius of the punch face b / a H , for different values of the frequency ratio between tangential and normal oscillation, for a phase angle ψ = 0 (A, left) and a phase angle ψ = π (B, right).
Interestingly, no coupling between profile and loading influences can be detected in Figure 6, as all curves exhibit exactly the same decreasing behavior; the influence of the loading protocol on the crack initiation criterion for the rounded flat punch seems to be the same as for the paraboloid, which was discussed in-detail in Section 4.2.

4.3.2. Paraboloid with Small Waviness

An intriguing problem is the question, whether a small waviness influences the crack initiation criterion. As it turns out, there are two non-dimensional parameters to characterize the waviness, as given in the profile function (6): the normalized waviness amplitude h / δ 0 , and the normalized wave length λ / h R . Note that for the contact area to remain compact (which is a necessary prerequisite for the contact solution within the MDR), the wave length has to be large enough; this has been checked in the simulations.
In Figure 7, the normalized maximum SWT parameter for the same-frequency bimodal contact oscillation are shown as a function of the waviness amplitude, for different values of the normalized wave length; for small (A, left), or large (B, right) normal oscillations.
It is apparent that even a very small waviness can have a significant impact, especially the waviness amplitude. In that regard, it is interesting that this impact is only slightly affected by the normal oscillation, as both diagrams in Figure 7, qualitatively and quantitatively, show quite similar behavior. Another notheworthy effect are the oscillations of the crack initiation parameter for small waviness amplitudes, which decrease in period length and amplitude, as the waviness amplitude decreases.
To analyze the coupling between the influencing variables of contact profile and load protocol for this indenter type, in Figure 8 the normalized SWT parameter for the different-frequency oscillation is shown, as a function of the normalized waviness amplitude h / δ 0 , for different values of the frequency ratio between tangential and normal oscillation, for a phase angle ψ = 0 (A, left) and a phase angle ψ = π (B, right).
As was the case also for the paraboloid without waviness, the most significant difference in the SWT parameter for different phase angles appears for a frequency ratio of ω 2 / ω 1 = 1 / 2 . Moreover, there seems to be weak coupling between the profile and load influences, as all curves in Figure 8 quantitatively are quite distinct from each other, but qualitatively all exhibit similar trends.

5. Discussion

As was laid out in the Introduction, the obtained results are not necessarily intended as quantitative predictions of fretting fatigue life, but shall give a comprehensive understanding of the coupled contact mechanical influences of loading and profile geometry on the SWT parameter – which is a very valid indicator for possible fatigue crack initiation – in elastic fretting contacts. Various interesting trends and ideas have been identified, which are worthwhile to analyze deeper with physically more flexible numerical procedures, e.g., the FEM.
The calculations have been performed within the framework of several simplifying model assumptions, that should be kept in mind when applying the results to real engineering contacts, most prominently linear elasticity, the validity of a local-global Amontons-Coulomb friction law and the neglect of microscopic surface roughness. In that regard, it should be noted that the influences of both plasticity [38] and an unstable friction law [39] on fretting fatigue crack initiation have already been considered in the literature.
A very desirable extension of the proposed formalism, which remains for future work, is the inclusion of bulk stress (which is also necessary to propagate nucleated fatigue cracks from the vicinity of the contact into the bulk material) into the calculation of the subsurface stress fields, as was already done successfully very recently for plane fretting contacts [40].

Funding

This research was funded by the German Research Foundation under the project number PO 810/66-1.

Institutional Review Board Statement

Not applicable.

Conflicts of Interest

The author declares no conflict of interest.

References

  1. Vingsbo, O.; Söderberg, S. On fretting maps. Wear 1988, 126, 131–147. [Google Scholar] [CrossRef]
  2. Madge, J.J.; Leen, S.B.; Shipway, P.H. The critical role of fretting wear in the analysis of fretting fatigue. Wear 2007, 263, 542–551. [Google Scholar] [CrossRef]
  3. Llavori, I.; Zabala, A.; Urchegui, M.A.; Tato, W.; Gómez, X. A coupled crack initiation and propagation numerical procedure for combined fretting wear and fretting fatigue lifetime assessment. Theoretical and Applied Fracture Mechanics 2019, 101, 294–305. [Google Scholar] [CrossRef]
  4. Wang, S.; Yue, T.; Wang, D.; Wahab, M.A. Effect of wear debris on fretting fatigue crack initiation. Friction 2022, 10, 927–943. [Google Scholar] [CrossRef]
  5. Zhu, T.; Shipway, P.H.; Sun, W. The dependence of wear rate on wear scar size in fretting; the role of debris (third body) expulsion from the contact. Wear 2019, 440-441, 203081. [Google Scholar] [CrossRef]
  6. Araújo, J.A.; Nowell, D.; Vivacqua, R.C. The use of multiaxial fatigue models to predict fretting fatigue life of components subjected to different contact stress fields. Fatigue and Fracture of Engineering Materials and Structures 2004, 27, 967–978. [Google Scholar] [CrossRef]
  7. Bhatti, N.A.; Wahab, M.A. Fretting fatigue crack nucleation: A review. Tribology International 2018, 121, 121–138. [Google Scholar] [CrossRef]
  8. Szolwinski, M.P.; Farris, T.N. Mechanics of fretting fatigue crack formation. Wear 1996, 198, 93–107. [Google Scholar] [CrossRef]
  9. Smith, K.N.; Watson, P.; Topper, T.H. A Stress-Strain Function for the Fatigue of Metals. Journal of Materials 1970, 5, 767–778. [Google Scholar]
  10. Bhatti, N.A.; Wahab, M.A. A numerical investigation on critical plane orientation and initiation lifetimes in fretting fatigue under out of phase loading conditions. Tribology International 2017, 115, 307–318. [Google Scholar] [CrossRef]
  11. Hojjati-Talemi, R.; Wahab, M.A.; De Baets, P. Finite element simulation of phase difference effects on fretting fatigue crack nucleation behaviour. Proceedings of the Institution of Mechanical Engineers Part J: Journal of Engineering Tribology 2014, 228, 470–479. [Google Scholar] [CrossRef]
  12. Li, X.; et al. The effect of phase difference and stiffness ratio on fretting fatigue behavior under variable normal load conditions. Proceedings of the Institution of Mechanical Engineers Part C: Journal of Mechanical Engineering Science 2022, 236, 9095–9108. [Google Scholar] [CrossRef]
  13. Li, X.; Yang, J.; Li, M.; Zuo, Z. An investigation on fretting fatigue mechanism under complex cyclic loading conditions. International Journal of Fatigue 2016, 88, 227–235. [Google Scholar] [CrossRef]
  14. Blades, L.E.; Truelove, J.P.J.; Paynter, R.J.H.; Hills, D.A. Experimental investigation of the effects of load path on the life of fretting fatigue contacts. Tribology International 2023, 188, 108858. [Google Scholar] [CrossRef]
  15. Majzoobi, G.H.; Abbasi, F. On the Effect of Contact Geometry on Fretting Fatigue Life Under Cyclic Contact Loading. Tribology Letters 2017, 65, 125. [Google Scholar] [CrossRef]
  16. Willert, E. Influence of Wear Profile Geometry on Critical Plane Fatigue Crack Initiation Criteria in Plane and Axisymmetric Elastic Fretting Contacts. Frontiers in Mechanical Engineering 2022, 8, 904282. [Google Scholar] [CrossRef]
  17. Song, Y.; et al. Numerical simulation of the effect of surface microgeometry and residual stress on conformal contact fretting fatigue crack initiation behaviour. Fatigue and Fracture of Engineering Materials and Structures 2023, 46, 2798–2815. [Google Scholar] [CrossRef]
  18. Deng, Q.; Yin, X.; Wahab, M.A. The Effect of Surface Pit Treatment on Fretting Fatigue Crack Initiation. Computers, Materials and Continua 2021, 66, 659–673. [Google Scholar] [CrossRef]
  19. Gu, H.; et al. Effect of machined surface texture on fretting crack nucleation under radial loading in conformal contact. Tribology International 2021, 153, 106575. [Google Scholar] [CrossRef]
  20. Wang, C.; et al. Artificial neural network combined with damage parameters to predict fretting fatigue crack initiation lifetime. Tribology International 2022, 175, 107854. [Google Scholar] [CrossRef]
  21. Willert, E. Elastic Stress Field beneath a Sticking Circular Contact under Tangential Load. Solids 2024, 5, 14–28. [Google Scholar] [CrossRef]
  22. Kouanga, C.T.; et al. A variable amplitude fretting fatigue life estimation technique: Formulation and experimental validation. Tribology International 2023, 178, 108055. [Google Scholar] [CrossRef]
  23. Pinto, A.L.; Cardoso, R.A.; Talemi, R.; Araújo, J.A. Fretting fatigue under variable amplitude loading considering partial and gross slip regimes: Numerical analysis. Tribology International 2020, 146, 106199. [Google Scholar] [CrossRef]
  24. Cattaneo, C. Sul Contatto di due Corpore Elastici: Distribuzione degli sforzi. Rendiconti dell’ Academi Nazionale dei Lincei 1938, 27, 342–348,434–436,474–478. [Google Scholar]
  25. Mindlin, R.D. Compliance of Elastic Bodies in Contact. Journal of Applied Mechanics 1949, 16, 259–268. [Google Scholar] [CrossRef]
  26. Munisamy, R.L.; Hills, D.A.; Nowell, D. Static Axisymmetric Hertzian Contacts Subject to Shearing Forces. Journal of Applied Mechanics 1994, 61, 278–283. [Google Scholar] [CrossRef]
  27. Socie, D. Multiaxial Fatigue Damage Models. Journal of Engineering Materials and Technology 1987, 109, 293–298. [Google Scholar] [CrossRef]
  28. Bhatti, N.A.; Pereira, K.; Wahab, M.A. Effect of stress gradient and quadrant averaging on fretting fatigue crack initiation angle and life. Tribology International 2019, 131, 212–221. [Google Scholar] [CrossRef]
  29. Zabala, A.; et al. On the use of the theory of critical distances with mesh control for fretting fatigue lifetime assessment. Tribology International 2020, 142, 105985. [Google Scholar] [CrossRef]
  30. Pinto, A.L.; Cardoso, R.A.; Talemi, R.; Araújo, J.A. Early crack orientation prediction methods under fretting fatigue loading including wear effects. International Journal of Fatigue 2022, 161, 106893. [Google Scholar] [CrossRef]
  31. Jäger, J. Elastic contact of equal spheres under oblique forces. Archive of Applied Mechanics 1993, 63, 402–412. [Google Scholar] [CrossRef]
  32. Aleshin, V.; Bou Matar, O.; Van Den Abeele, K. Method of memory diagrams for mechanical frictional contacts subject to arbitrary 2D loading. International Journal of Solids and Structures 2015, 60-61, 84–95. [Google Scholar] [CrossRef]
  33. Popov, V.L.; Heß, M. Method of Dimensionality Reduction in Contact Mechanics and Friction; Springer-Verlag: Berlin Heidelberg, 2015. [Google Scholar]
  34. Popov, V.L.; Heß, M.; Willert, E. Handbook of Contact Mechanics – Exact Solutions of Axisymmetric Contact Problems; Springer-Verlag: Berlin, Heidelberg, 2019. [Google Scholar]
  35. Willert, E. Stoßprobleme in Physik, Technik und Medizin - Grundlagen und Anwendungen; Springer-Verlag: Berlin, 2020. [Google Scholar]
  36. Mossakovskij, V.I. Compression of Elastic Bodies under Conditions of Adhesion (Axisymmetric Case). PMM Journal of Applied Mathematics and Mechanics 1963, 27, 630–643. [Google Scholar] [CrossRef]
  37. Jäger, J. Axi-symmetric bodies of equal material under torsion or shift. Archive of Applied Mechanics 1995, 65, 478–487. [Google Scholar] [CrossRef]
  38. Gandiolle, C.; Fouvry, S.; Charkaluk, E. Lifetime prediction methodology for variable fretting fatigue loading: Plasticity effect. International Journal of Fatigue 2016, 92, 531–547. [Google Scholar] [CrossRef]
  39. Hintikka, J.; Mäntylä, A.; Vaara, J.; Frondelius, T.; Lehtovaara, A. Stable and unstable friction in fretting contacts. Tribology International 2019, 131, 73–82. [Google Scholar] [CrossRef]
  40. Truelove, J.P.J.; Blades, L.E.; Hills, D.A.; Paynter, R.J.H. Frictional half plane contacts subject to varying normal load and bulk tension under various load paths with application to fretting fatigue experiments. Tribology International 2023, 185, 108563. [Google Scholar] [CrossRef]
Preprints 97782 g001
Figure 1. Schematic representation of the considered contact profiles. A: Paraboloid B: Flat punch with rounded corners C: Truncated paraboloid D: Paraboloid with small waviness
Figure 1. Schematic representation of the considered contact profiles. A: Paraboloid B: Flat punch with rounded corners C: Truncated paraboloid D: Paraboloid with small waviness
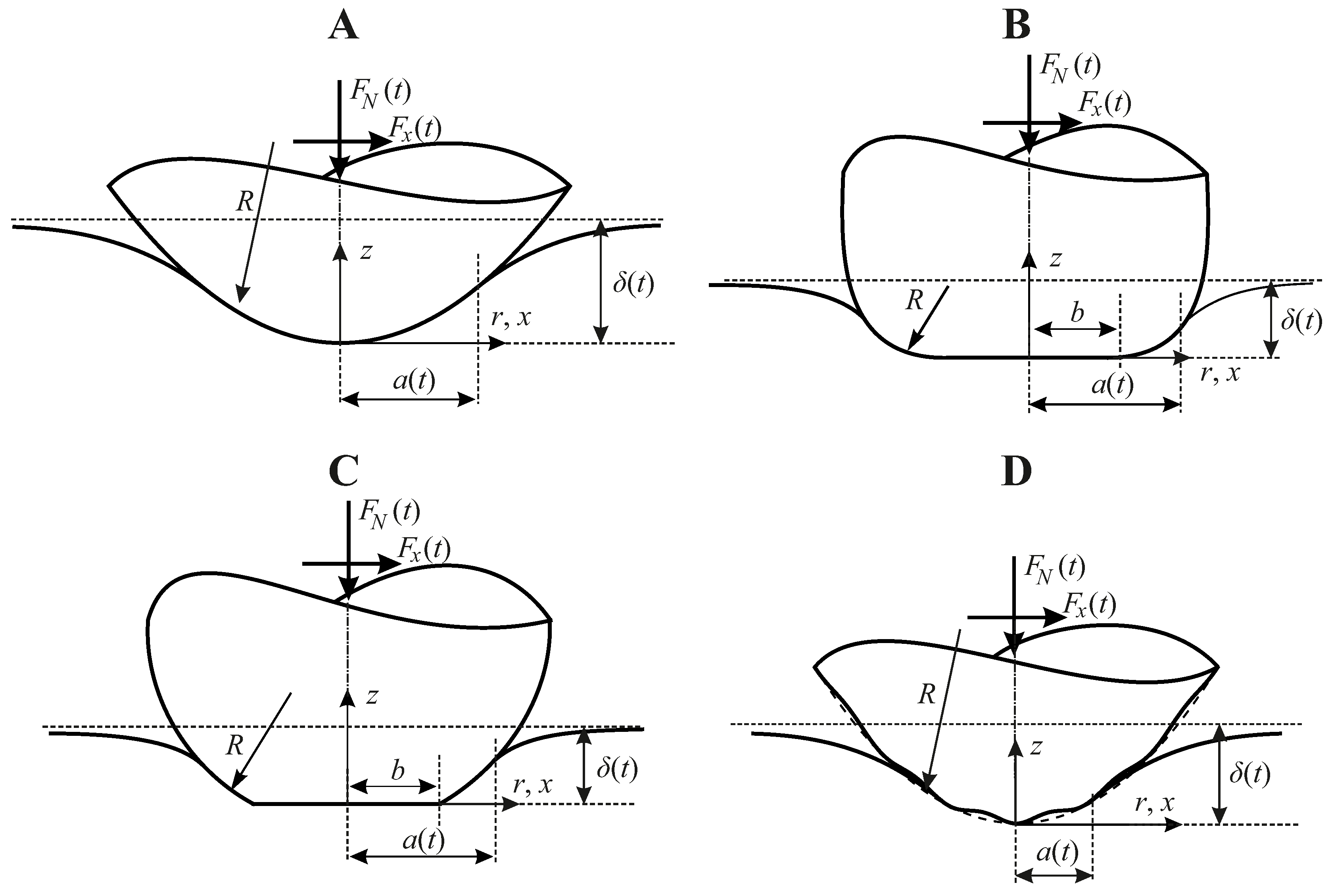
Preprints 97782 g001
Preprints 97782 g002
Figure 2. A: Original axially symmetric tangential contact problem between a rigid indenter with the profile f ( r ) and an elastic half-space B: Equivalent problem within the MDR.
Figure 2. A: Original axially symmetric tangential contact problem between a rigid indenter with the profile f ( r ) and an elastic half-space B: Equivalent problem within the MDR.
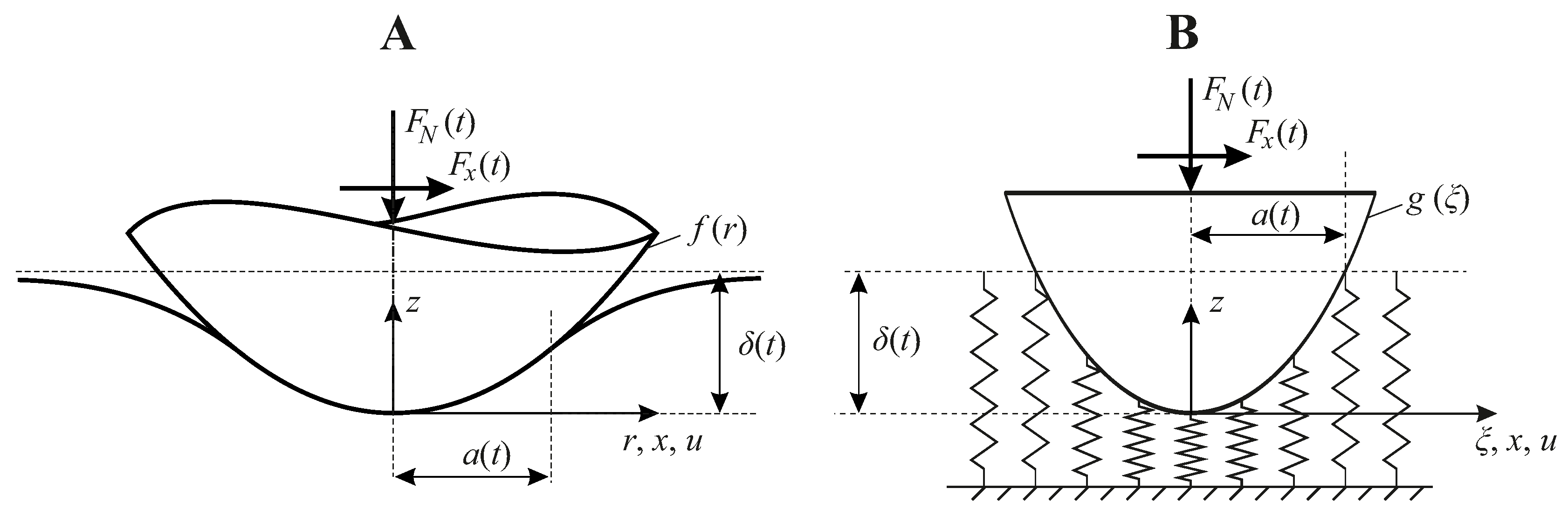
Preprints 97782 g002
Preprints 97782 g003
Figure 3. Normalized maximum SWT parameter for the same-frequency bimodal contact oscillation between a paraboloid and a flat, as a function of the phase angle ψ , for different values of the normal oscillation amplitude.
Figure 3. Normalized maximum SWT parameter for the same-frequency bimodal contact oscillation between a paraboloid and a flat, as a function of the phase angle ψ , for different values of the normal oscillation amplitude.
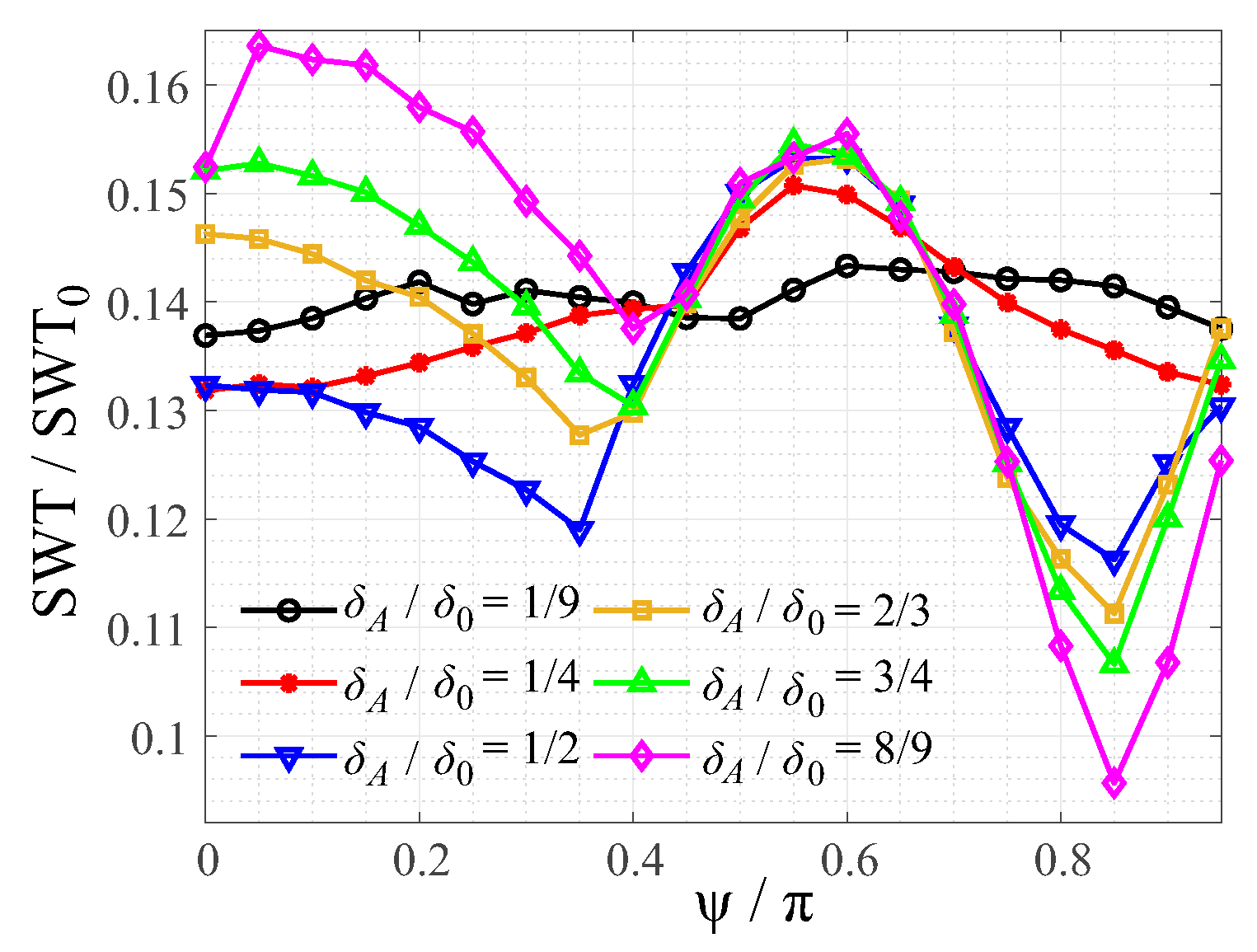
Preprints 97782 g003
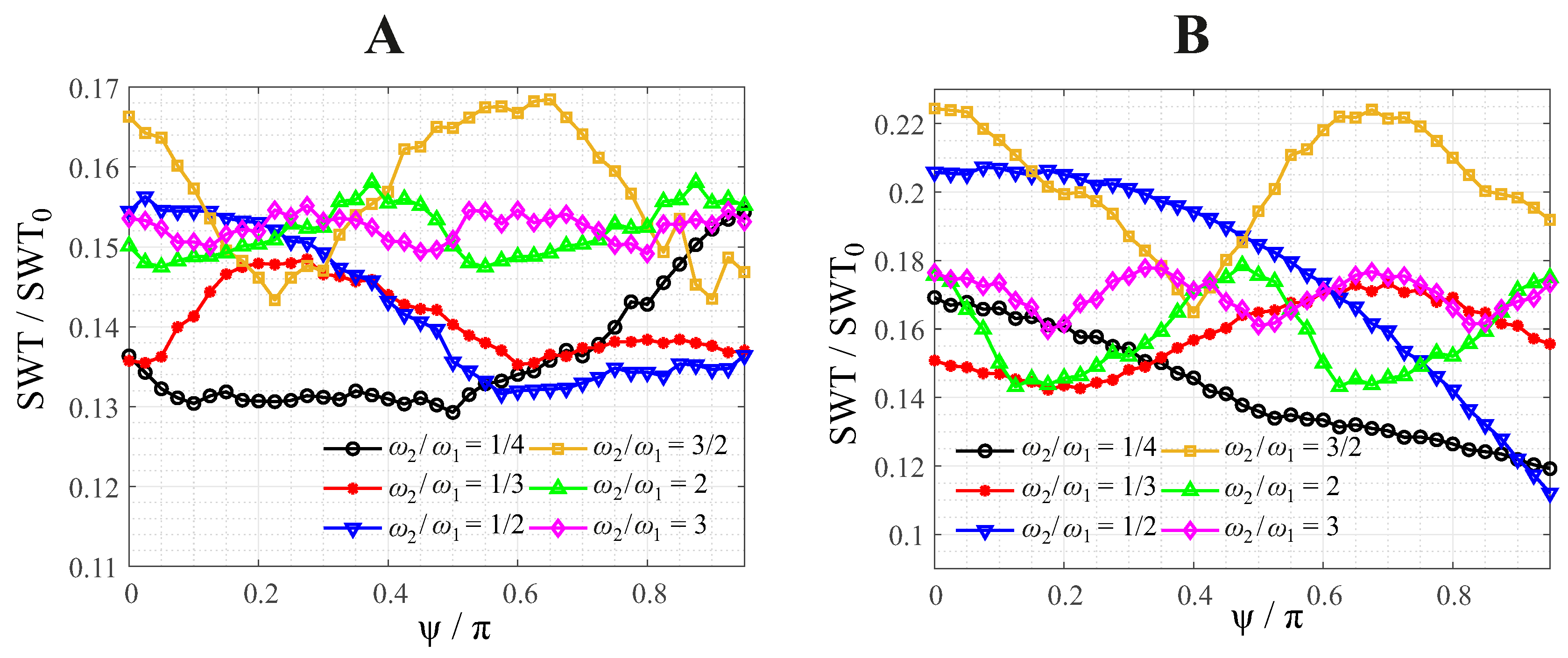
Preprints 97782 g004
Figure 4. Normalized maximum SWT parameter for the different-frequency bimodal contact oscillation between a paraboloid and a flat, as a function of the phase angle ψ , for different values of the frequency ratio. A: δ A = 0.25 δ 0 B: δ A = 0.75 δ 0 .
Figure 4. Normalized maximum SWT parameter for the different-frequency bimodal contact oscillation between a paraboloid and a flat, as a function of the phase angle ψ , for different values of the frequency ratio. A: δ A = 0.25 δ 0 B: δ A = 0.75 δ 0 .
Preprints 97782 g004
Preprints 97782 g005
Figure 5. Normalized maximum SWT parameter for the same-frequency bimodal contact oscillation between a flat face indenter and a flat, as a function of the phase angle ψ , for different values of the radius of the punch face. A: rounded flat punch B: truncated paraboloid
Figure 5. Normalized maximum SWT parameter for the same-frequency bimodal contact oscillation between a flat face indenter and a flat, as a function of the phase angle ψ , for different values of the radius of the punch face. A: rounded flat punch B: truncated paraboloid
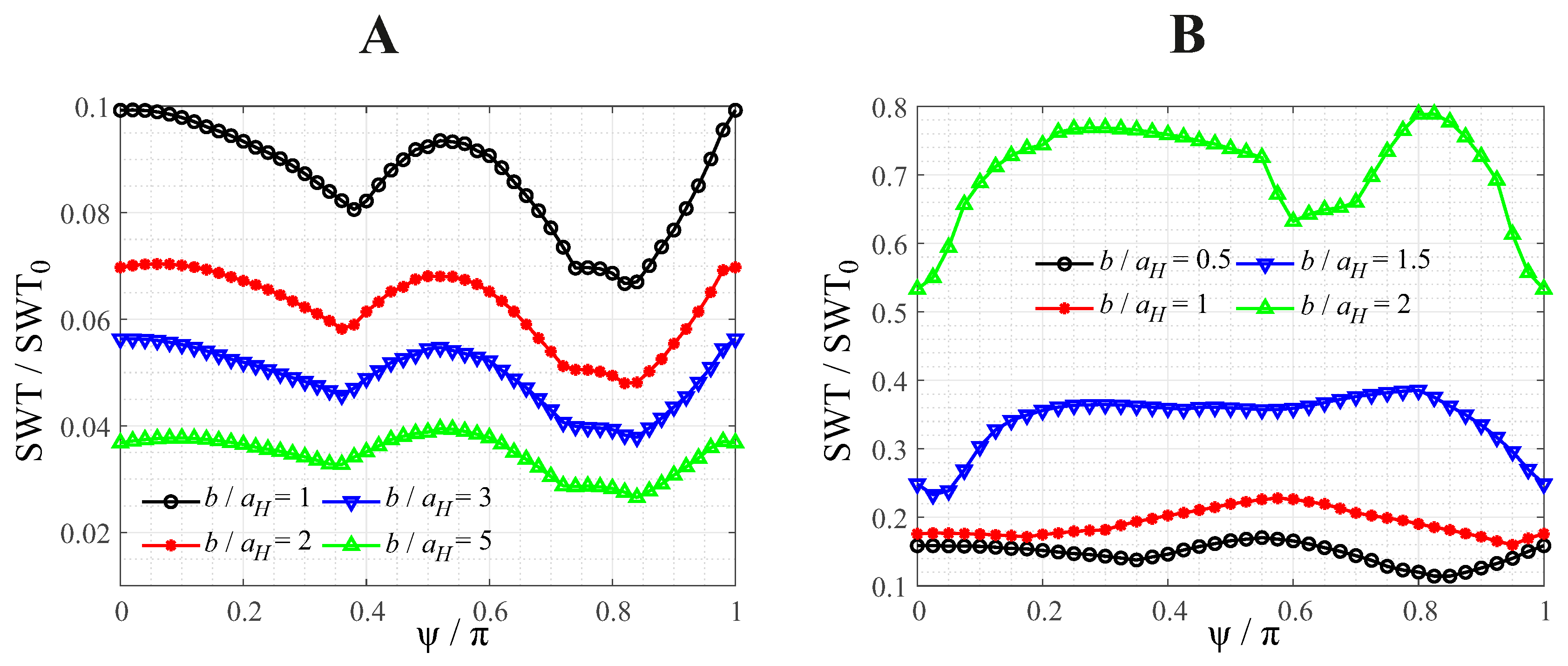
Preprints 97782 g005
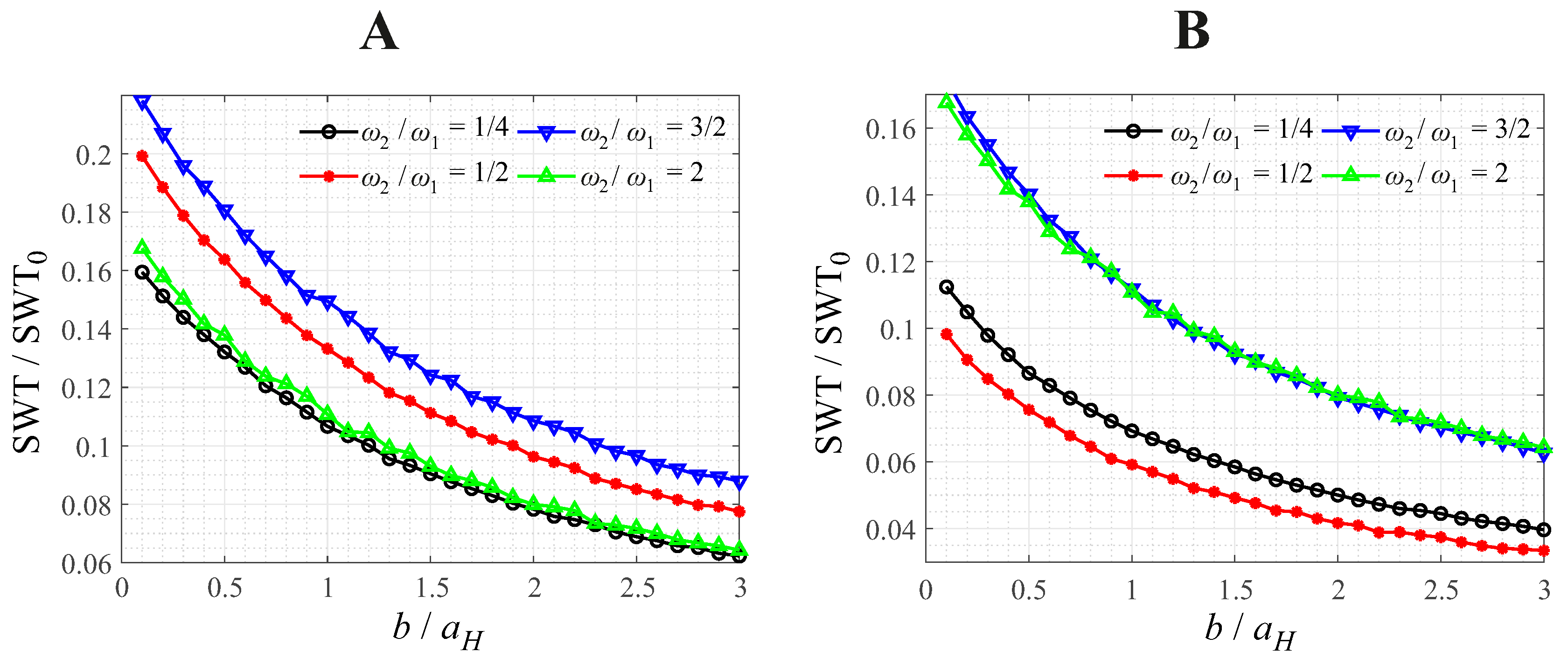
Preprints 97782 g006
Figure 6. Normalized maximum SWT parameter for the different-frequency bimodal contact oscillation between a rounded flat punch and a flat, as a function of the normalized radius of the punch face b / a H , for different values of the frequency ratio between tangential and normal oscillation. A: phase angle ψ = 0  B: phase angle ψ = π .
Figure 6. Normalized maximum SWT parameter for the different-frequency bimodal contact oscillation between a rounded flat punch and a flat, as a function of the normalized radius of the punch face b / a H , for different values of the frequency ratio between tangential and normal oscillation. A: phase angle ψ = 0  B: phase angle ψ = π .
Preprints 97782 g006
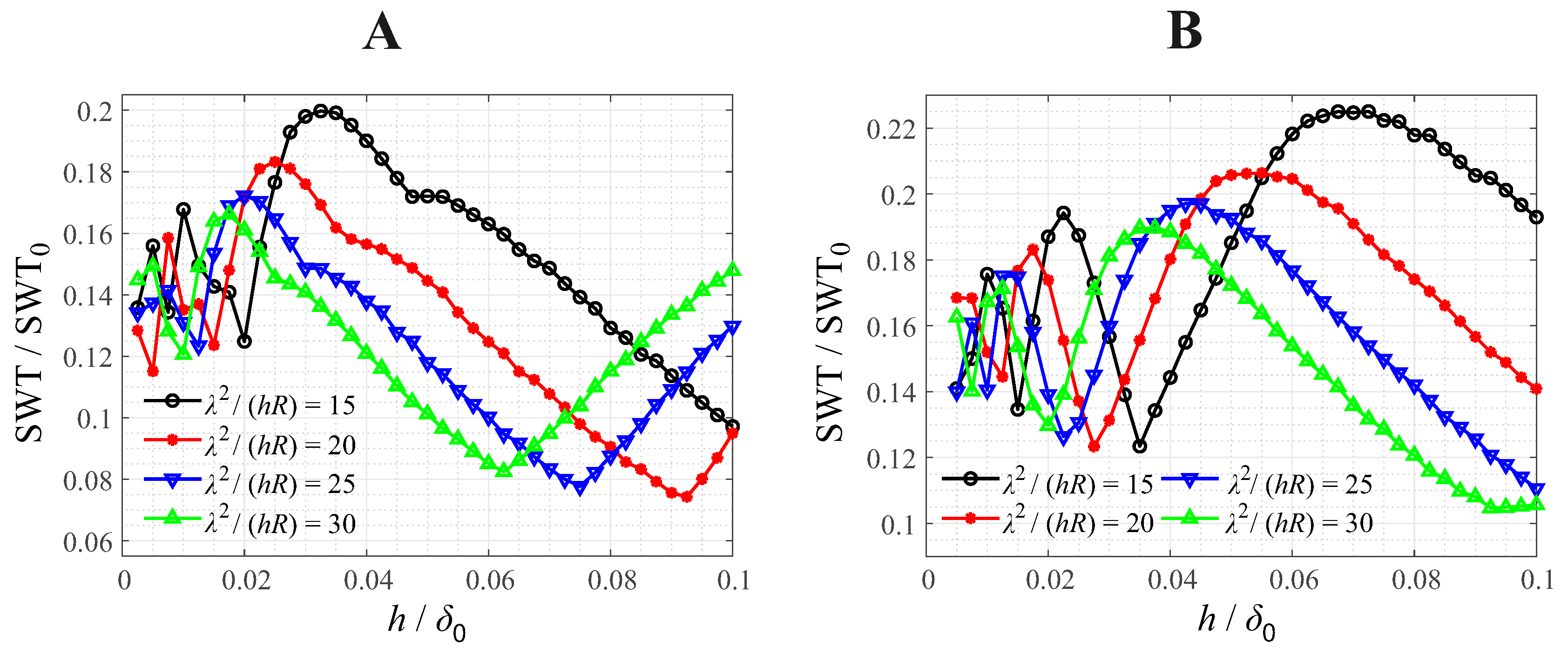
Preprints 97782 g007
Figure 7. Normalized maximum SWT parameter for the same-frequency bimodal contact oscillation between a paraboloid with small waviness and a flat, as a function of the normalized waviness amplitude, for different values of the normalized wave length; A: for δ A = 0.25 δ 0  B: for δ A = 0.75 δ 0
Figure 7. Normalized maximum SWT parameter for the same-frequency bimodal contact oscillation between a paraboloid with small waviness and a flat, as a function of the normalized waviness amplitude, for different values of the normalized wave length; A: for δ A = 0.25 δ 0  B: for δ A = 0.75 δ 0
Preprints 97782 g007
Preprints 97782 g008
Figure 8. Normalized maximum SWT parameter for the different-frequency bimodal contact oscillation between a paraboloid with small waviness with λ 2 = 20 h R and a flat, as a function of the normalized waviness amplitude, for different values of the frequency ratio between tangential and normal oscillation. A: phase angle ψ = 0  B: phase angle ψ = π
Figure 8. Normalized maximum SWT parameter for the different-frequency bimodal contact oscillation between a paraboloid with small waviness with λ 2 = 20 h R and a flat, as a function of the normalized waviness amplitude, for different values of the frequency ratio between tangential and normal oscillation. A: phase angle ψ = 0  B: phase angle ψ = π
Preprints 97782 g008
Table 1. List of used fixed non-dimensional parameters for the simulations (unless stated otherwise in the text).
Table 1. List of used fixed non-dimensional parameters for the simulations (unless stated otherwise in the text).
Parameter ν μ δ A δ 0 ω 2 ω 1 G * u A μ E * δ 0 ψ
Value 0.3 0.3 3/4 1 5/6 0
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated