Preprint
Review
Experimental Linear and Nonlinear Vibration Methods for the Structural Health Monitoring (SHM) of Polymer-Matrix Composites (PMC): A Literature Review
Altmetrics
Downloads
101
Views
40
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
31 January 2024
Posted:
01 February 2024
You are already at the latest version
Alerts
Abstract
The goal of this article is to provide a review of the experimental techniques and procedures using vibration methods for the Structural Health Monitoring (SHM) of Polymer-Matrix Composites (PMC). It aims to be a guide for any researchers to carry out vibration experiments. The linear methods are first introduced. But as PMC is a complex material, these classic methods showed some limits, such as low accuracy for small damages, and a high environmental dependency. This is why the nonlinear methods are secondly studied, considering that the complexity of PMC induces a nonlinear behavior of the structure after damage occurrence. The different damage mechanisms are well explained in order to evaluate the potential of each vibration method to detect them.
Keywords:
Subject: Engineering - Mechanical Engineering
1. Introduction
Nowadays, the use of PMCs in industrial sectors, such as aeronautics and automotive, is sharply increasing, thanks to their high mechanical properties, low weight, high resistance to corrosion environments, … [1,2,3,4,5,6,7,8,9,10], permitting them to challenge classical materials like metals. PMCs are made of fiber and matrix. The combination and the variation of fraction or orientation of fibers make it a complex, heterogeneous and anisotropic material, which complicates its damage mechanisms. This is why measuring and understanding them as well as evaluating their severity on the structure is important to ensure the continuity of services. This is known as Structural Health Monitoring (SHM). The concept of SHM brought these four steps [11]: (i) detect damage in the structure; (ii) localize it; (iii) quantify its severity and qualify it; (iv) give a conclusion regarding the service life of the structure.
Many Non-Destructive Testing (NDT) techniques are available for SHM purposes [12], such as Ultrasonic Testing (UT) [13,14], Acoustic Emission (AE) [15,16], Digital Image Correlation (DIC)[17,18], X-Ray tomography [19,20], Infrared thermography [21], Vibration analysis and others. As in the literature, many reviews focused on the numerical aspect of vibration analysis, this review focuses on the experimental vibration methods applied to the PMC materials. They are divided into two parts: the linear and the nonlinear methods. Given the anisotropy and the heterogeneous aspects of PMCs, it turns out that the detection and quantification of their damage mechanisms are more relevant using nonlinear vibration methods [22]. As this review aims to be a guide for the different experimental vibration methods, the equipment and devices used for each method, as well as the damages studied in the literature will be described in detail.
This article is divided as follows. The first part introduces the PMCs: their composition, the different kind of architecture and their principal damage mechanisms which can occur. The second part describes the methods, the equipment used in the literature for experimental linear and nonlinear vibration analysis, and the damage specificities.
2. Reminder about PMCs and Their Damage Mechanisms
A composite is a structural material that combines two different components. One is the matrix and the other is the reinforcement. There exist several types of composites depending on the used constituents: the Ceramic-Matrix Composites (CMC), the Metal-Matrix Composites (MMC) and the PMC. This article only focuses on the PMC.
2.1. Composition and Structure of PMC
In PMC, the reinforcing part is made of continuous or short fibers and the matrix is made of polymers such as thermoplastic or thermoset resins [6,23]. The volume or the orientation of the fibers, the number of layers, the different possible structures and the different possible constituents expand the possibilities in the creation of PMC. A list of possible constituents of PMCs is given in Table 1.
The common structures made of PMC are the laminates and the sandwiches, both are shown in Figure 1. The laminated composite consists of the assembly of several plies with different fiber orientations, while the sandwich is made of two thin skins joined with an adhesive to a core, the skin is made of laminates and the core is made of a thick low-strength material which can be foam material (polyurethane, …), honeycombs, and others. The layers of laminates can either be made of unidirectional, short or woven fibers [24]. The woven fabric consists of the interlacing of warp and weft fibers, with a specific pattern (plain, satin, twill, …).
Recently, many 3D woven composites have been developed for particular applications (aerospace and defense domains) and some studies about their mechanical properties have been proposed [25].
2.2. Damage Mechanisms
In PMC service life, four main damage mechanisms can cause structure failure: matrix cracking, fiber breaking, delamination, and fiber-matrix interfacial debonding. They can be observed in Figure 2. In general, damage starts with very small matrix cracking (microcracks) and the three other mechanisms will be induced from this start, resulting in a combination of them. On a laboratory scale, these damages can be artificially generated: fiber-breakage can be made from fiber cutting before the manufacturing step, delamination can be introduced by inserting Teflon or foreign film between 2 plies, ... In service, impact damage is common and it results in the same damage mechanisms. The more forceful the impact, the more the structure is damaged. In reference [26], a clarification is made on the characteristic failure mechanisms of PMC. In Figure 3 we can observe the evolution of damages during a tensile test.
2.2.1. Matrix Cracking
The first step in the damage process is the microscopic matrix cracks consisting of the breaking of the resin. They have two forms: transverse or longitudinal. The transverse ones propagate perpendicular to the direction of the mechanical load, whereas the longitudinal ones follow the direction of the loading. Therefore, the two forms depend on the type of applied mechanical stress (tensile, compression, shear or bending, etc.) and the orientation of the fibers within the composite material. With increasing stress, these cracks will progressively propagate and reach the fibers. At this step, the damage process will either be stopped or will continue with the propagation of the cracks in a less energetic way, which corresponds to the interface between the fiber and the matrix. This will lead to fiber-matrix debonding.
2.2.2. Fiber-Matrix Interfacial Debonding
Fiber-matrix interfacial debonding usually happens when the cohesion of the fiber-matrix is lower than the shear strength of the matrix or when the adherence fiber-matrix is weak. The matrix crack induces debonding without fiber breaking. The number of debonding will increase while the stress increases.
As the matrix cracks and the debonding will propagate, the interlaminar cracks will occur and the load will progressively increase on the fibers, resulting in delamination and the fibers breaking.
2.2.3. Delamination or Interlaminar Cracking
Delamination [29] concerns the laminated composites. It consists of the separation between two successive plies. Delamination can be internal or near-surface. It can grow and extend its area, then it will lead to the failure of the laminated. It can be considered one of the most severe damages for laminate composite materials
2.2.4. Fiber Breaking
Fiber breaking is also one of the main reasons for PMC structure failure, when the stress reaches the fracture strength of the fiber, it will break. It usually happens when the stress direction is similar to the orientation of the fiber.
The final failure of the PMC material is a combination and an accumulation of these various damage mechanisms.
3. Vibration Methods
The vibration of a structure provides a lot of information regarding its physical properties, which motivates its use as a damage indicator [30,31,32,33,34,35,36,37,38]. A focus on the modes of vibration (how the structure vibrates at specific frequencies) of the structure is given, this is called modal analysis. How to perform it, is first introduced to have the basis to understand the linear and nonlinear techniques.
3.1. Modal Analysis
A brief and nice introduction to modal analysis is given in [39]. In dynamic analysis like vibration one, we have to introduce: the system that excites the structure (actuator) and all equipment necessary (input equipment), the system that catches the information (sensor), and the equipment that processes the output data and displays results (output equipment), the system which holds the structure and all additional setup and equipment.
3.1.1. Fixation Setup
To perform vibration analysis, there exist several ways of fixing the structure according to the boundary conditions we are looking for. The classical one is to suspend the structure, with elastic wires or threads, to obtain free-free boundary conditions. This will isolate the dynamic response of the structure. Other can be the cantilever configuration with the free-clamped condition (one edge clamped) or putting the structure on absorbing foam. These three configurations can be seen in Figure 4. Some researchers also used the clamped-clamped configuration to perform their analysis. As the vibrations of bridges are often investigated, another method consists of laying the structure on several supports, it can be one support for each edge or even some support in the middle of the structure.
3.1.2. Actuators and Sensors
The classical modal analysis is performed with an impact hammer and accelerometers [40]. The hammer has a force sensor to record the input force. For repeatability purposes, it can be replaced by a shaker, which permits to apply different kinds of excitation: white noise, sweep signals, … It needs a generator and an amplifier to provide an electrical signal. The hammer test is the easiest to perform, it will provide a global view of the vibration of the structure, it is often used as a first test to obtain the natural frequencies and their damping ratios. Exciting the structure with white noise will give similar results. Once these parameters are obtained, a lot of researchers use different signals: harmonic signal, sweep-sine signal, … with the intention of focusing on specific modes or working on a large frequency band.
Different actuators and sensors have been used in [41,42], to make modal analyses and identify natural frequencies. The actuators were an impact hammer, a loudspeaker, a fan, and an in-situ PVDF piezoelectric transducer (Polyvinylidene fluoride). PVDF and a loudspeaker were used with a white noise generator and piezo-amplifier (the output of the amplifier was 500V to excite the PVDF), and the accelerometer and the PVDF received the output signal. These articles present a lot of possibilities to perform modal analysis. The setup necessary to excite with PVDF is given in Figure 5. The SQV 1/500 piezo amplifier is necessary to provide the 500V at the PVDF.
Piezoelectric transducers deform when they are receiving an electrical signal, which creates vibration, and inversely emit voltage signal while stress is applied to them (this is known as the piezoelectric effects) [43,44]. There exist several piezoelectric transducers, such as PVDF, PZT - piezoceramic (Lead Zirconate Titanate), MFC (Macro Fiber Composite), and PFC (Piezoelectric Fiber Composite). They have all been used for modal analysis in literature, where they are mostly surface-bonded, but researchers investigated the possibility of the in-situ transducers [12,45,46,47,48]. They can be used as actuators and sensors, but PZT needs a lower amplitude of excitation to excite the structure (20 – 100 V for PZT against 500V for PVDF), this is why PZT are often used as actuators and PVDF as sensors. Table 2 presents a non-exhaustive list of equipment used for modal analysis.
3.1.3. Data Processing
The response from the sensors usually goes into an analyzer which directly gives the needed information: Frequency Response Function (FRF)[49], Auto power function [50], Coherence and Spectrum. There exist several analyzers, such as Simcenter Testlab (also called LMS Testlab). Without an analyzer, data from the sensors has to be processed to obtain the information that we are looking for, it exists plenty of data processing techniques, the most famous is the Fast Fourier Transform (FFT) to obtain output in the frequency domain. Some tools, for example Matlab® software or Python libraries, also allow extracting such information from the output signal [51].
Some new tools, such as BeagleBoneBlack or Rasberry cards, propose low and small acquisition systems that permit to easily implement them on operational structures.
3.1.4. Sensors Placement
In modal analysis, the placement of the sensors is very important to get the highest amplitude of the response possible or even to get a response. Apart from the LV, the accelerometer and the piezoelectric sensors need optimal placement. There exist several techniques and algorithms to optimize it [52,53,54]. The easiest way is to make a complete modal analysis of the structure, experimentally with a LV or even numerically, and to observe the mode shapes, in order to see the displacement or the strain field in the structure. Indeed, the accelerometers catch the acceleration of the structure at a single point, which is directly linked to the velocity and then the displacement. On the other hand, piezoelectric transducers catch the stress applied to them, which is directly linked to the strain. Accelerometers and piezoelectric transducers do not give the optimal signal at the same position. An example is given in Figure 6, there is the displacement field of the first four modes of vibration of a free plate, the accelerometers should not be placed in the blue area in order to record as much acceleration as possible. Obviously, for a free plate, the highest displacement will be on its edge (red area). In Figure 7, we can see the optimal placement obtained for a set of accelerometers and PVDF transducers, using Effective Independence (EI) method, based on the maximum kinetic energy [42].
3.2. Linear Vibration Methods
3.2.1. Natural Frequencies
The natural frequencies of a structure are the frequencies where the structure will tend to vibrate, after applying an external force. Using these frequencies to excite the structure will introduce the effect of resonance which creates a higher amplitude of vibration. They are directly linked to the mass and stiffness of the structure, as well as its boundary condition. This is what pushed many researchers to use them as damage indicators. Indeed, the damage will create a loss of stiffness, which induces a decrease in natural frequencies (Figure 8). Moreover, this technique is one of the cheapest and easiest to perform. In a review published in 1996 [55], it is indicated that the first one to use natural frequency loss as a damage indicator was Lifshitz [56] in 1969.
In [57], the change of the first natural frequency in E-glass/epoxy laminated composite plates with 2 different dimensions (13x6cm² and 19x6cm²) and 3 stacking sequences ([90/90/90/90]°, [0/0/0/0]° and [0/90/0/90]°), with a cantilever configuration (Figure 9) was investigated. Damage was introduced by cutting the inner fibers in two locations: in the middle and at the root of the structure (which plies is unknown). The fiber cutting dimension was 2.1x1 cm² and 3.1x1cm². PZT transducers have been used to excite the plate but also to catch the output signal. An oscillating voltage with different amplitudes was transmitted to the actuator (from 40 to 80V) and the output was displayed on a sensing unit. The frequency was manually varied from 0 to 40 Hz until a sharp increase in the sensing voltage was observed. The frequency of this increase corresponded to the first natural frequency of the structure. The frequency decreased (1.5 to 4Hz for the smaller plate and 0.3 to 1Hz for the larger plate) when the structure was damaged for the [90/90/90/90] stacking sequence. However, this was not the case for the other stratifications, due to the high stiffness in the [0/90/0/90] sequence.
In [58,59], two kinds of inner piezoelectric transducers MFC and PFC have been used in glass/epoxy laminate and sandwich beams in a cantilever configuration. Different severities of delamination (10/20/30/40/50/60 % of the area of the structure) and crack (2/3/7/14/20/27/34 % of the length of the structure) were created in laminates (300x32x21mm3) and only delamination between core and skin (10/30/45/60/75% of the area of the structure) in the sandwich material (300x32x14mm3). The excitation was introduced by displacing the tip of the beam by 0.5 inches and the transducers caught the vibration of the structure. Here the change of the first two natural frequencies was investigated. The frequencies decreased when the severity of damage increased, the decrease is almost linear and slow, which means no clear distinction is possible before a large amount of damage (20% for the delamination and 15% for the crack of the laminates and 60% for the sandwiches), which means the small damage cannot be detected. The loss of natural frequency is higher in the laminated composite.
In [60], PZTs have been surface-bonded and used as actuators and sensors, on a graphite/epoxy [90/+45/-45/0]° plate (250x50x1mm3) clamped at one end. The natural frequencies of six modes of vibration were used for several types of damage: a 6.4 mm diameter hole in the center, matrix cracks induced by fatigue testing and mallet hit, and delamination (8%) made of Teflon strip and cut. A signal generator was used to transmit the voltage to the PZT and a LV was used to compare with the results from PZT. Clear distinctions about frequency loss for any type of damage, from LV or PZT, were not possible.
In [61,62], experimentation was conducted on a plate (305x244x2.16mm3) made of 8 plies of carbon/epoxy stack in [0]s. To isolate the dynamical response, the plate was suspended with wires. An impact hammer made the structure vibrate and the signal from surface-bonded MFCs and accelerometers was caught, then it was processed in a data acquisition LMS system and displayed on a PC analyzer interface Testlab. Results were difficult to analyze and no real distinctions between undamaged and damaged structures (made from hole and impact – no information is given regarding the dimensions of damages) were observable. For this reason, the authors used different metrics that compared healthy and damaged signals (see FRF section).
The effects of damage on natural frequencies of the first three modes have been investigated, on glass/epoxy laminate (200x30x8mm3) [63] and sandwiches (250x40x26mm3) [64,65] with PVC foam core and glass/epoxy skin, on a cantilever configuration. The damages were debonding between the core and skin for the sandwich (from 20 to 180 mm of debonding by 20 mm step) and fatigue induced for the laminate. The structure was excited with a shaker and a power amplifier, and the vibration was sensed with an accelerometer. The excitation signal was a swept-sine around bending mode frequency with an amplitude of 50 mV. The natural frequency decreased with damage severity and the higher mode seemed more influenced by this severity (Figure 10). In these references, the change of natural frequency was studied and investigated, especially, the loss factor and the nonlinear elastic and dissipative parameters. These magnitudes will be introduced later.
Through these articles, detecting damages from the variation of natural frequencies seems efficient only when damage is already consequent. However, when damage is small (< 20%), this technique showed some limits. Table 3 gives additional bibliographical references using this method. Nowadays, it is less and less used, because of its high sensitivity to environmental effects, like temperature or boundary conditions.
3.2.2. Mode Shapes
The mode shapes correspond to the displacement of a structure for a particular natural frequency (a particular mode). The simplest example is the vibration of a fixed string, for each mode, there will be nodes (fixed part) and antinodes (maximum displacement) (Figure 11).
The first thing is to obtain the mode shapes of the structure, so it is necessary to perform a modal analysis that takes the vibration measurements at several locations. This means having a network of sensors, moving excitation location and sensor position [39,72], or scanning the structure with a LV.
Several techniques are existed using modal shapes to detect and localize damage: the most classical ones are the Mode Shape Displacement difference (MSD) or the use of assurance criteria such as Modal Assurance Criterion (MAC) [73] and criteria derived from it, such as Co-Ordinate MAC (COMAC) and others …[74]. Damage indexes derived from these criteria can also be used such as the Mode Shape Damage Index (MSDI).
The MAC [75] is the main statistical tool regarding mode shapes, it compares two sets of modal vectors using this formula:
where φs and φr are the modal vectors. MAC will be close to one if there exists a linear relationship between 2 modes (if the vectors have a similar way of moving), otherwise, it will be close to zero (Figure 12). In other words, MAC can detect which modes will be affected by the damage. A MAC can have similar modal vectors even for an intact structure, this is why reference of MAC from the intact structure is necessary to detect the variation. The MAC is also commonly used to see the coherence between experimental and numerical vibration analysis.
In [76], the modal parameters of a hemp fiber/epoxy resin plate (150x150x5mm3) in a free-free condition were used to detect six damage scenarios: cut of a layer with different sizes and positions (20x20, 15x15, 10x10mm2 in the center and 20x10mm2 on the edge), cut of 2 layers (10x10mm2) and 3 layers (10x10mm2). The classical impact hammer/accelerometer combination was used to perform the modal analysis (Figure 13). A grid of 6x6 was created on the plate to acquire 36 data points through the roving hammer method [72]. The MAC and COMAC confusion matrixes between intact plates were created, in order to have a reference of both matrixes without damage. Then, it was made between the intact and the six damaged plates and both detected damage occurrence in the structure. Moreover, the COMAC has higher sensitivity to small damage than MAC.
In [77], COMAC was used to detect and localize damage in a helicopter composite blade made of glass fiber-reinforced plastic with a honeycomb (Figure 14). The structure was suspended to obtain a free-free condition for modal analysis. The actuator was an electrodynamic shaker implemented with a burst random signal and the sensors were accelerometers positioned on 55 localizations. “Fake” damage was introduced by adding an extra mass of 300 g at one location, the goal of the study was to localize this mass. The modal analysis was performed for both intact and damaged blades. The COMAC detected the presence of damage very close to the exact position.
Two derivations of MAC: PrMAC and WECoMAC have been used in [78], on composite plates, made of carbon/epoxy. Damage was introduced from a drop-weight impact test and then compression after the impact test has been made, in order to determine the compressive residual strength of the structure. The mode shapes were obtained from the roving hammer test at 25 different locations and damage indicators were calculated at each damage step, and PrMAC showed the highest sensitivity regarding damage detection.
To summarize, using changes in modes shape to detect and localize damage has been used by many researchers, however, there exist many techniques and damage indicators, and the classical ones are MAC and COMAC. In [74], a large list of such criteria derived from MAC is given. This technique shows good results in many studies, however, it needs a lot of sensors or heavy measurement processes to acquire the modal deformation accurately. There exist several vibration methods derived from the mode shapes, such as the mode shapes curvature and the modal strain energy, this is why this is common to see articles using several and comparing them.
Table 4.
Other articles about the experimental use of mode shapes for SHM.
| Method | Structure | Fixation | Input | Output | Damage | Description | Ref |
|---|---|---|---|---|---|---|---|
| MSC | T-stiffened panels of carbon/epoxy | Elastic bands | Shaker (sinusoidal wave (0 – 10 kHz)) | LV | Delamination (PTFE Film) Porosity |
Change in mode shape displacement between damaged and intact structures was not the best indicator of damage presence | [79] |
| MSC and mode shape slope change | Carbon/epoxy laminated plate | Suspended with 2 cotton strings | Impulse hammer | Accelerometer | Surface and penetrated crack | The experimental results were not able to detect crack location using both methods (Mode Shape Displacement and Slope Change) | [80,81] |
| Gapped-Smoothing Method (GSM) | E-glass/epoxy laminated beam | Cantilever configuration | PZT (Continuous-sweep sine 140V) Power amplifier |
LV (PSV 400 SLV) and PVDF | 3 delaminations (Teflon insertion), impact damage and saw-cut | GSM is able to localize damage through LV or a network of PVDF | [82] |
3.2.3. Mode Shape Curvature
The mode shape curvature is the second derivative of the mode shapes. It can be calculated from the central difference method as [83,84]:
where φij is the jth mode shape of the measurement point i and h is the distance between points i+1 and i-1.
The first thing usually made is to determine the difference of mode shape curvatures (named as Mode Shape Curvature criterion (MSC)), between intact and damaged structures:
The largest value will give the location of the damage (Figure 15). As for the mode shapes method, the main disadvantage is the number of sensors needed to obtain the most accurate results.
Damage indicators have been derived from the MSC. The classical thing is to normalize the MSC (NMSC) and then the Normalized Curvature Damage Factor (NCDF) [85]:
There exist a lot of possible damage indexes such as Modal Curvature Change Rate (MCI) and Curvature Mode Difference (CMD).
Modal curvatures have been used in [86], in order to detect damage in glass/epoxy plates in a cantilever configuration. The modal analysis was performed with 10x5 localization for the PCB impact hammer and a PCB accelerometer was fixed on the end of the plate. The damage was a crack made from a 1mm thick blade, positioned at 10% of the length of the structure close to the fixed end. NCDF detected well the damage position.
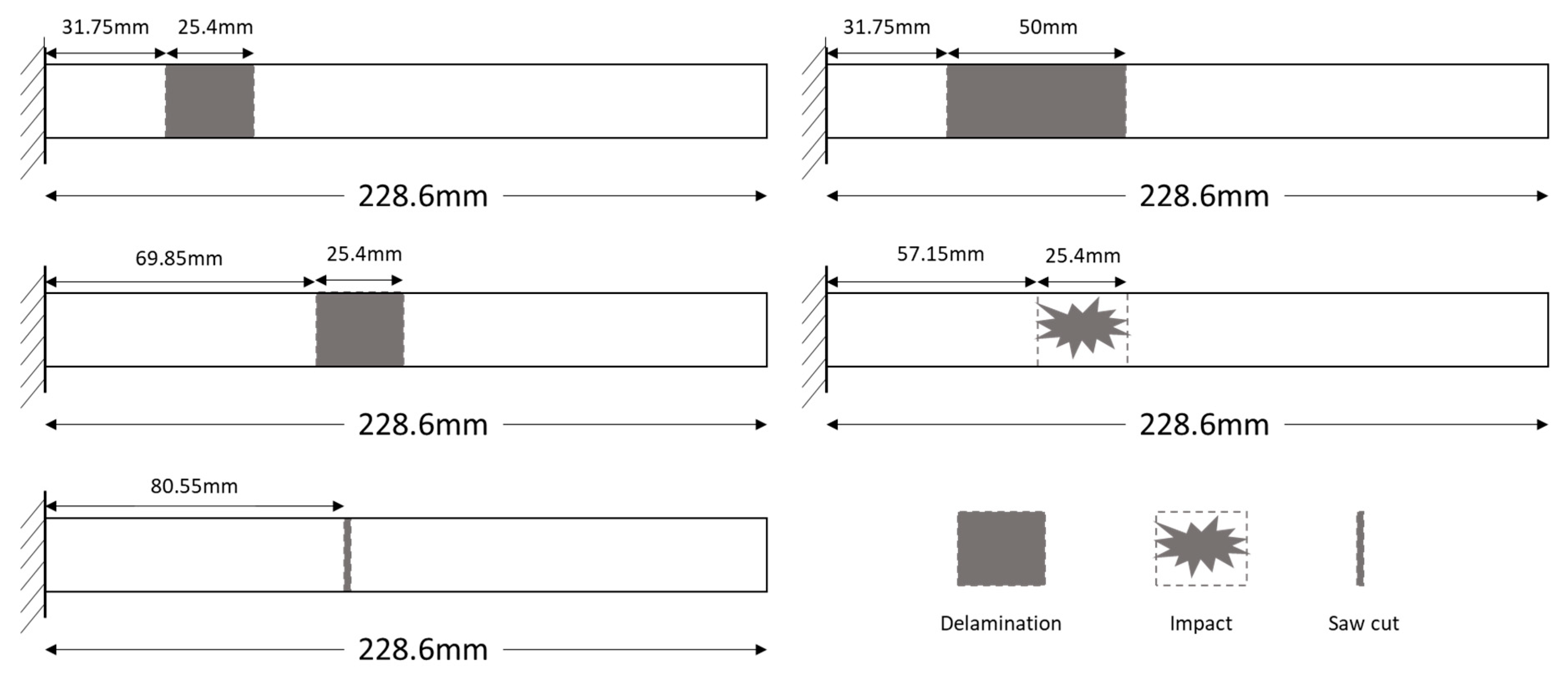
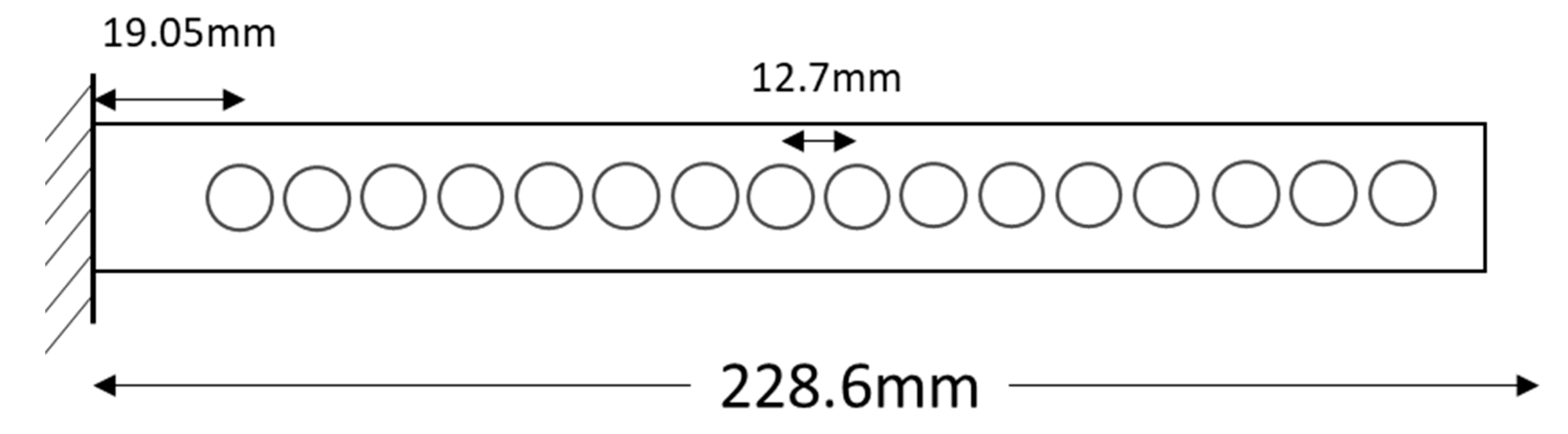
In [87,88], the modal shape curvature was tested on a carbon/epoxy beam (241.3x25.4x1.76mm3) in a cantilever configuration, damaged from different sources: an impact, a saw-cut notch and three different types of delamination (Figure 16). The modal analysis was performed using PZT or impact hammer as actuators and 16 PVDF as sensors, all surface-bonded (Figure 17). Both NCDF and the DI were used to localize damage, these methods were efficient for 3 damage scenarios: the saw cut, the impact and the delamination far from the fixed end, but the conclusion that more sensors are necessary for the 2 other damage scenarios was made: the two delaminations closed to the fixed end.
Table 5.
Other articles about the experimental use of mode shapes curvature for SHM.
| Method | Structure | Fixation | Input | Output | Damage | Description | Ref |
|---|---|---|---|---|---|---|---|
| MSC | T-stiffened panels of carbon/epoxy | Elastic bands | Shaker (sinusoidal wave (0 – 10 kHz)) | LV | Delamination (PTFE Film) Porosity |
MSC showed that it can detect delamination accurately, but porosity was not detectable | [79] |
| MCI and CMD | Carbon/epoxy laminated beam | Cantilever configuration | Modal hammer | Accelerometer | Delamination (Teflon patch) | CMD showed higher sensitivity than MCI to localize damage | [89] |
| MSC | Carbon/epoxy beams | Suspended on a frame | Shaker (periodic chirp) Impulse hammer |
LV | Delamination and crack | The damage was identified efficiently by the MSC | [90] |
3.2.4. Modal Strain Energy
Modal Strain Energy (MSE) is the energy that is stored in the structure for each mode of vibration. According to [91,92], the MSE methods are more sensitive to SHM than the natural frequencies and mode shapes. Many articles used this method on offshore platform structures.
In [93], the ways of calculating MSE for a beam and a plate are given. A review of MSE-based methods for SHM is made on [94]. Four groups were introduced: Damage Indexes (DI) such as Stubbs’ DI (SDI) or MSE Decomposition (MSED), Modal Strain Energy Chance (MSEC), Cross-Modal Strain energy (CMSE), and others. In this review, the methods, their calculations and an experimental study using them were presented. Moreover, a lot of other methods derived from MSE can be found in the literature.
Several articles [95,96,97] used the MSE method on several composite structures, for example in [95] on a carbon/epoxy plain-woven laminate (310x222x2.2mm3), the damage was a surface crack (16x1mm2) made from a knife located in the middle of the small dotted area in Figure 18. First, a tensile test was made to determine the mechanical properties of the material. The modal analysis was performed with an impact hammer and an accelerometer fixed on the plate (Figure 18). The total (Uk) and sub-region (delimited by the grid – Uk,ij) strain energies induced by mode shapes for healthy and damaged plates were calculated from plate formulation. From these equations, the fractional energies (Fk,ij) for healthy and damaged (*) plates, and the damage index (βij) and its normalization (Zij) for each sub-region, were calculated as follows:
where and are the mean and standard deviation. This damage index was able to localize it accurately after using at least 3 modes of vibration, by creating a map of DI on the (x,y) position.
The same helicopter blade [77,98] as with the COMAC method previously discussed (Figure 14), has been used, the “fake” damage was a mass adding. The modal analysis was performed with an impact hammer and shaker, with a burst random signal, the sensors were 55 accelerometers. The method used to calculate strain energy is based on a Euler-Bernoulli beam and used the modal shape curvature. These calculations are similar to the previous one of the plates. The main goal is to calculate a damage index. The modal strain energy methods showed higher sensitivity than COMAC and were able to detect and localize damage, with a high value on a XY map.
Table 6.
Other articles about the experimental use of modal strain energy for SHM.
| Method | Structure | Fixation | Input | Output | Damage | Description | Ref |
|---|---|---|---|---|---|---|---|
| MSEC | Carbon/epoxy laminated plate | Suspended with 2 cotton strings | Impulse hammer | Accelerometer | Surface and penetrated crack | MSEC was able to locate both types of damage | [80] |
| MSE and Differential Quadrature (DQM) | Carbon/epoxy laminated plate | Suspended with 2 cotton strings | Impulse hammer | Accelerometer | Surface and penetrated crack | For MSE peaks are present around the location of damage, but some also occur at other positions, this is why the DQM is implemented and very good results were obtained with it | [81] |
| MSEC | E-glass/epoxy laminated beam | Cantilever configuration | PZT (sweep sine 140V)Power amplifier | LV (PSV 400 SLV) and PVDF | 3 delaminations (Teflon insertion), impact damage and saw-cut | Strain energy detected well the location of damage, except for special cases with some doubt caused by other high-value | [82] |
| MSECR | E-glass/epoxy skin and PVC foam for sandwich beams | Cantilever configuration | Electrodynamic shaker | Accelerometer | Debonding + remove face (Teflon sheet) | MSECR correctly located damage for single and multiple damage cases | [99] |
3.2.5. Modal Flexibility
The modal flexibility method (MFM or MF) is another kind of damage detection technique, which seems more sensitive than others and needs less experimental data. The modal flexibility is defined as a matrix:
where fi is the i-th natural frequency and {X}i is the mass normalized mode shape vectors. What is interesting to observe using MFM is the flexibility difference between undamaged and damaged structures:
The highest value of variation will give the location of the damage (Figure 19).
In [100], the MF was also compared to other methods previously seen (Figure 20). In this experiment, the MF seemed the most accurate SHM method.
In [101], the MF and a derivate damage indicator (MDI) have been used on a carbon fiber bi-directional corrugated sandwich panel, with the dimensions 200x200x15mm3. A grid of 9x9 points was created on the surface, in order to obtain the vibration at different locations and localize the damages. They created 2 debonding (1.2% of total area) and 3 core damage (0.3% of total volume of the core) cases, with single and multiple damage cases. The vibration analysis was performed by suspending the plate and with two accelerometers and an impact hammer, an LMS signal analyzer stored all the output and input data of the first four modes of vibration. The MF only was not able to clearly distinguish the damage location, as several peaks with similar amplitude were observable. These peaks also occurred in the MDI, but the peak closed to the damaged area had a higher value, which avoids the fake damage detection of the MF. They concluded that the new MDI is efficient in detecting single and multiple damages in composite structures.
3.2.6. Damping
Damping corresponds to the energy of dissipation of material. In [102], a review of the use of damping for SHM is provided. According to this article, the change in damping has higher sensitivity than natural frequencies or mode shapes to detect damage, but research is still in progress. The simplest analysis of damping is the difference in damping between intact and damaged structures, usually, it will be higher when the structure is damaged and it shows higher sensibility than the change in natural frequency (Figure 21). Damage identification using damping can either be linear or nonlinear.
In modal analysis, the damping ratio is mostly calculated from the -3dB method (or half-power bandwidth) (Figure 23) in the frequency domain, but time domain and time-frequency domain methods are also found in the literature. In the time domain, the most frequent method used is the logarithmic decrement [103] and, in the time-frequency domain, the use of analyzing wavelets such as the Gabor wavelet is necessary [104]. There exist several quantities to define damping, you can find them in Figure 22. Damping to detect damage is also used with a Damage Index and it is often mixed with other methods such as modal shape, natural frequencies, modal strain energy, …
In [62], in addition to compare natural frequency, a comparison of the difference in damping between damaged and intact carbon/epoxy plates was made, in a free-free configuration from impact hammer excitation and two accelerometer sensors. Two damages were studied: one impact damage and one hole (unknown diameter) both in the center of the plate. No specific pattern in the difference in damping ratio was detectable.
In [63,64,65] the effects of damage on loss factors have also been investigated, on the laminated and sandwich composite with delamination and fiber cutting, it was shown that the loss factor increased with damage severity (Figure 24).
In [105,106], a method was developed, using damping mixed with Plane Shape Function (PSF) to localize damage, the name is Damping Damage Indicator (DaDI). It was tested on a woven carbon/phenolic plate damaged from impacts and quasi-static pressure. The structure was suspended with two nylon strings to obtain a free-free configuration. The DaDI needs modal strain shapes and modal damping factors, to localize damage. The excitation was made with an electromagnetic shaker and a multisite excitation force, the sensor was LV at four different points. The PSF for mode n and DaDI at coordinate (i,j) is calculated as:
where and are the strain in both directions, is the difference in damping ratio between damaged and intact structures. In this article, DaDI seems to well determine the location of both damages. Adding mass to the structure with transducers may decrease the accuracy of this method. In [107], similar experiments were made on carbon/epoxy plates. Several indexes have been used, such as Multiparameter Damage Indicator (MuDI) which is created from two others: the DaDI and the frequency damage indicator (FreDI), to localize the damage. A weighting function has been introduced to emphasize the role of FreDI or DaDI in the computation of MuDI, this weighting function showed the importance of the correct localization of damage.
3.2.7. Frequency Response Function Metrics
Comparing the FRF of intact and damaged structures can be a way to detect damage [108]. Several damage indicators based on FRF have been introduced in literature [61] such as the Frequency Domain Assurance Criterion (FDAC) [109] or the Frequency Response Assurance Criterion (FRAC) [110].
In [61,62,111], the metrics introduced were tested on a carbon/epoxy plate suspended in a free-free configuration, the sensors were accelerometers and MFC, and the actuator was an impact hammer. The plates were damaged by a central hole and an impact (dimensions are unknown). The change of natural frequencies was not sufficient to detect damage, but the metrics gave interesting results, it seemed that metrics using more than one sensor gave higher sensitivity.
3.2.8. Transmittance or Transmissibility Function (TF)
TF is a technique to determine the localization of the damage, it is built from the ratio of the vibration response of the structure at two separate locations and the location of the input force. It is often written as .
where x is the displacement at i and j location, where the force is applied on k. TF can also be calculated from the velocity of the structure instead of displacement. Then detecting damage is made with a damage indicator on a frequency range [ω1; ω2], which compares the TF for healthy (h) and damaged (d) structures.
A review of TF is given in [112]. This technique is mostly used numerically, but with a network of sensors or a LV this can be used experimentally. One issue of this method is the selection of the frequency range to obtain accurate results. As we can see in Figure 25, damage on paths 2-3 can be detected with the frequency range [0,39] but not with the range [0,300]. Usually, the upper value of the range is chosen as the first natural frequency of the structure. The position of the input force will also have a strong influence on the result.
To summarize, in the review, they said that the perfect localization of the damage is possible when the damage is located next to the input force localization, or by choosing the correct frequency band, which means the global vibration of the structure has to be known.
In [113], TF has been used on a cantilever fiberglass beam (112x1.18x0.635cm3) with a PZT actuator and accelerometers or PZT patches as sensors (Figure 26). The PZT actuator was excited with a random noise signal coming out of an amplifier. It was shown that using an impact hammer and shaker as actuators did not give nice repeatability of the experimentation, but the PZT actuator gave correct repeatability. Translational and curvature TF have been investigated. The damage was created by bonding a steel plate (5.08x5.08x0.635cm3) to the beam, between path 1-2. The translational and curvature TF showed efficiency in localizing moderate damage, the curvature one seemed more accurate while the frequency range was higher (10 – 20 kHz), and a very high-frequency range did not allow detecting damage and the curvature TF seemed more sensitive for small damage.
In [114], the modal analysis of a wind turbine blade made of fiberglass in a free-free boundary condition has been made. PZT patches have been used with a periodic chirp signal at 200V as an actuator and an LV as the sensor. The damage was introduced as “fake” damage by clamping a steel plate (8.5”x6.2”x0.75”) near one edge, closed to the path 11-15. The damage indicator of the TF indicated the correct location for the “fake” damage (Figure 27), this damage indicator should be near 0 for the healthy structure and healthy paths.
In [115], two models based on transmittance function were created and studied, the first one using only one transmittance model for the healthy state named “single transmittance model” (STM) and the second one using several transmittances models, the “multiple transmittance models” (MTM). Both models were based on a data-based response-only methodology using the autoregressive with exogenous (ARX). The study was using 29 composite beams made of carbon fiber in unidirectional or woven fabrics. The damage was introduced in the middle of two beams with an impact hammer at 5 and 15J. The modal analysis was performed in a cantilever configuration with a shaker as an actuator and two accelerometers. The STM-scheme detected most of the damage, but it gave some false alarms and failed to detect some damage, on the other hand, the MTM-scheme was able to detect all damage cases without false alarms.
3.2.9. Wavelet Transforms
In vibration analysis, the Wavelet Transform (WT) has been used a lot to process the vibration data coming from various sensors. The principle relies on dividing a time-series signal into a set of sub-signals (wavelets) and extracting data from these sub-signals. There exist different kinds of Wavelet such as Daubechies and Symlet. A review of WT is given in [116].
In [117], small delamination (0.11%, 0.167% and 0.22% of the total surface) of glass/epoxy plates (360x250x4mm3) with piezoelectric transducers (1 actuator and 4 sensors) were studied. The signals were decomposed for each sensor into 16 sub-signals with Daubechies Wavelet and a damage indicator was introduced, for intact and damaged structures, based on the energy of these sub-signals, then by setting a threshold of this damage indicator. The conclusion that using a threshold of 20% with WT helps to detect small delamination of an area superior to 0.12% of the total area of the structure. In Table 7, it is possible to see the damage indicator calculated for each sub-wavelets. If one of the sixteen sub-wavelet damage indicators is higher than the threshold, authors considered the delamination detected (grey cells).
3.3. Nonlinear Vibration Methods
As the damage mechanisms in a composite structure are complexes, the tendency nowadays is to focus on nonlinear vibration methods, as they give the opportunity to increase accuracy and detect smaller damages. Most of these methods consider that the damage of the composite structure will induce nonlinearity, caused by some microcracks, delaminations between layers or fiber breakages. As an indication, opening and closing consecutive phases of a matrix cracking can generate a non-linear response.
This behavior has been investigated in many studies, and some nonlinear methods have emerged. Some of them cross the boundary between ultrasonic and vibration fields, but they are still introduced to see the possibilities and the potential setup needed. Moreover, as these methods are less used than linear ones, the number of experimental studies focused on PMC materials is smaller.
3.2.1. Single Frequency Excitation (SFE) and Sub-/Super-Harmonics Generation
By definition, a harmonic is a multiple of a fundamental frequency (which is the harmonic n°1). Sub- and super-harmonics are ratios of this harmonic, the sub-harmonics are , and super-harmonics are n x f (with f the harmonic). The damage detection technique relies on the fact that by exciting the structure through a harmonic signal, the response will only show this harmonic for an intact structure, and will show super-harmonics (or higher harmonics) and sub-harmonics of smaller amplitude for a damaged structure (Figure 28).
Some authors highlighted the fact that better results can be obtained using a frequency of excitation corresponding to a ratio of a natural frequency: ½, 2 …. Higher amplitude of sub- and super-harmonic can be observed. But a lot of them used ultrasonic frequency.
The nonlinearities can also be observed as distortions in the time-domain response (Figure 29). It can be velocity, acceleration or voltage signal distortions. Phase portrait: velocity vs displacement or acceleration vs velocity graphs can be made. The phase portrait should not show any distortions for an intact structure (circle or ellipse), while it should show some for a damaged structure (Figure 30).
In [118], three different methods to detect damages in carbon/epoxy laminate plates (200x200x2.08mm3) have been investigated, the structure was suspended freely with thin wires and the damages were introduced by inserting Teflon sheets located under the 4th plies from the surface (Figure 31), which created delamination (35x35, 40x40 and 45x45 mm2). One of these methods was the SFE, five piezoelectric transducers were used: one as an actuator and four as sensors, they were bonded onto the surface. From the actuator, the plate was excited with a sinusoidal wave of 120 V and with a frequency varying from 20 to 100 kHz. The additional equipment was a generator, a power amplifier and an oscilloscope. Higher harmonics in the damage cases were observable. Some frequencies (20-40 kHz) have higher sensitivity, which means the choice of the best one is important. A damage indicator based on the amplitude of harmonics was defined to easily detect damage.
In [120], the SFE methods have been tested on a PMC plate embedded with an in-situ PVDF sensor and a shaker actuator, an accelerometer sensor was also used to validate the effectiveness of the PVDF. Three natural frequencies were chosen for excitation purposes, and two ratios of them (1/2 and 1/3), which gives six tested frequency. The excitation was a sinus with an amplitude of 1V. Several plates with different damages (delamination (35x35mm2), fiber cutting (70mm) and holes (from 1.5 to 10 mm diameter)) were tested (Figure 32). The comparison of the amplitude of the sub- and super-harmonics was used as a damage indicator and showed sensitivity to detect all the introduced damages.
A similar technique has been used in [121], named Second-harmonic generation, on a carbon/epoxy plate damaged from impact (at low (18 mm length) and high (32 mm length) energy) or 2 Teflon-FEP (5x5x0.012 or 10x10x0.012mm3) insertion (Figure 33). The excitation was introduced from an in-situ PZT with a sweep signal and a frequency band from 20 to 500 kHz. The goal was to determine which frequencies show the higher amplitudes of the output signal, these frequencies became the input frequencies of the tests. Then a signal with different amplitude from 60 to 100 V has been sent and vibration from an acoustic sensor on the surface was measured. A second harmonic generation was observable for the damaged plate. Similar experimentation with a LV has been made, in order to see if the chosen frequency was correct. In [122] damage localization method was created, it is based on the amplitude of the second harmonic generation and a network of surface-bonded PZTs. A nonlinear parameter is calculated, as (A2fs and Afs are the amplitudes of the 2nd and the 1st harmonics; Lij is the distance of the path), for every path of the network (actuator/sensor path), the one with the highest value of this parameter becomes the ‘damaged path’ and a map can be created to visualize the expected localization. This method showed nice results to localize damage with an error from 4 mm to 22 mm.
Another technique, quite similar to the SFE, has been used in [118] with the same equipment as the SFE method. Instead of using a harmonic signal, this one uses a sweep signal excitation, and the higher-harmonics band will be observed for a damaged structure (Figure 34).
Table 8 summarizes other studies that have used the SFE method for the SHM of PMC materials.
3.3.2. Frequency Shifts from Different Excitation Amplitude
This technique consists of finding the natural frequencies of an intact and damaged structure for several amplitudes of excitation (for example from 0.1 to 1V every 0.1V step). The frequency will be the same for an intact structure while a loss of frequency will be observed for a damaged structure (Figure 35). The classical linear frequency shift can be observed between intact and damaged structures, but only the slop of decreasing frequency is used.
In [63,64,65], this method has been used, on the same equipment as previously seen. A small frequency shift was present for intact beams and a big one for damaged beams. By using the elastic nonlinear parameter:
(f and f0 are the current and the initial frequencies, ε is the strain), it was shown a higher sensitivity of it compared to the linear natural frequency change (Figure 36). It reduces linearly as a function of the excitation amplitude.
Another name for this method is the single-mode nonlinear resonance ultrasound (NRUS). In [126], several low-velocity impact damages (10 J with different sizes of impactors) were detected in carbon/epoxy plates. The excitation was a sweep signal around the 1st bending natural frequency, several experimentations were made by varying the amplitude of excitation. To visualize the delamination area (between 2.9 and 3.9 cm2), a C-scan was used, then the delamination area function of the nonlinear parameter α showed that this parameter is highly sensitive to damage area (Figure 37). In [127] the limits of the techniques in the previous article have been investigated. A clamped carbon/epoxy plate was used, with a speaker and an accelerometer. To investigate the influence of the clamping system on this method, the clamping setup was two steel plates with a torque system. By modifying the torque value, a frequency shift that increased while the torque value increased was observable, this directly means that the presence of a frequency shift is not only caused by damage, but also by boundary conditions. This phenomenon can give false alarms about damage detection or hide them. For this, special care has to be taken when using it.
In [128], the “fast dynamic” and “slow dynamic” were investigated, on concrete and composite materials. The fast dynamic is the successive measurement of resonant curves with different amplitudes of excitation, without time between two excitations to avoid the material to relax. The slow dynamic starts with the highest excitation and is kept for several minutes to “condition” the material. Then, the excitation is stopped allowing the material to relax. To follow this relaxation, a low excitation amplitude is introduced into the material, which permits following the evolution of the resonant curve in time. In this thesis, it is shown that the phenomenon of frequency shifts from different excitation amplitudes is induced by the conditioning and relaxing phenomena of the material. The fast dynamic on PMC was studied, by focusing around the 6th bending mode with a frequency of 16.685 kHz and an amplitude varying from 10 to 100 mV amplified with a 52-dB gain. PZT patches as actuator and sensor were used, and low damages with a 3-point bending test were gradually introduced in four steps. Then, with the same equipment, the slow dynamic has been studied by using the 100-mV excitation, the conditioning process was first analyzed, and by letting the structure relax, the times of conditioning and relaxation were analyzed. By focusing on the time of relaxation, it was shown that this is a promising damage indicator for SHM, it seems that the damaged structure will have a lower natural frequency (linear method) but also that the damaged structure will relax to an initial frequency slower than an intact structure (Figure 38).
In [120], in addition to the SFE method, the NLR was also performed with the same configuration, damages and equipment (Figure 32). Six natural frequencies have been chosen for the excitation. The fiber cutting showed the biggest sensitivity in this method, with a big frequency shift for two tested modes, the delaminations showed a small sensitivity for one mode while the holes showed sensitivity on five modes, with increasing frequency shift according to the increasing diameter of the hole.
Table 9 presents other studies using frequency shifts from different amplitudes excitation method for the SHM of the PMC materials.
3.3.3. Vibro-Acoustic Modulation – VAM
The VAM methods may be beyond the scope of this article because some of the excitation frequencies used are in the ultrasonic field (ultrasound starts around 15~20 kHz). However, this is an interesting technique. It consists of exciting the structure with a pumping signal having a low frequency and applying a probing signal simultaneously with a high frequency, both excitations are harmonic signals. The nonlinearities caused by damage will induce super-harmonics of the pumping signal frequency (similar to the SFE method) and sub- and super-harmonics made of both ‘frequencies’ modulation (also called sidebands) (Figure 39). This technique can have several names regarding the frequencies used: vibroacoustic modulation, Vibro-ultrasonic, … If pumping and probing frequencies are both very high, it will enter the ultrasonic field more than the vibration one. In most cases, the pumping frequency corresponds to the natural frequency of the structure while the probing frequency is much higher (ultrasound). The reference [132] gives a small overview of this technique.
A lot of articles used the amplitude of this sideband as a damage indicator by comparing them with the sidebands of an intact structure (which should be very low). A similar technique is the Impact Modulation, this one uses an impact as the pumping excitation and an actuator as probing excitation. Wave distortions in the time domain (velocity, acceleration, voltage) can also be observed performing VAM methods.
Some researchers name it, the Nonlinear Wave Modulation Technique (NWMS). In [126], NWMS was used, with two natural frequencies of carbon/epoxy plate (200 Hz and 2245 Hz), damage in the plate was introduced by low-velocity impact, and the excitation of the structure was made with a loudspeaker. Unfortunately, we do not have information about the sensing equipment (the accelerometer is the most commonly used). The results clearly showed the super-harmonics after the pumping frequency and the sidebands around the probing frequency for the damaged structure. When the damage severity is elevated, the sideband amplitude is higher.
In [133], the VAM method was used with two in-situ PZT as actuators and one acoustic sensor on the surface of a carbon/epoxy plate, the setup was the same as with the SFE method. One PZT was excited with a harmonic signal at 18kHz and another one at 192 kHz (these values were obtained after finding the best combination that generates higher modulation). Sidebands were observable only for the damaged plates and they confirmed this with LV experimentation. In [127], the limits of VAM methods were also investigated, the same configuration as previously seen with the SFE method was used, the carbon/epoxy plate clamped between two steel plates with different torque values. Higher harmonics and sidebands for undamaged structures were observable, the higher the torque value, the higher the amplitude of harmonics and sidebands. This means that false damage detection can happen while performing this method, we should be careful about the boundary condition.
As we have seen through these articles, the choice of the best combination of frequencies is important to increase the accuracy of the method. This is why in [134], this choice has been investigated through several experimentations on carbon/epoxy plates with impact damage. First, a classical modal analysis with an electromagnetic shaker using white noise and LV has been made, in order to choose the best natural frequencies for the VAM method. Secondly, the high-frequency sinusoidal signal with a piezoelectric transducer and the low-frequency signal with the electromagnetic shaker were sent to the structure. The two natural frequencies previously determined were used for the low-frequency excitation while Local Defect Resonance (LDR - [135,136,137]) and a random high frequency were used for the probing signal. The results obtained from an LV showed that the combination with higher sensitivity is to use a natural frequency corresponding to a mode with an out-of-plane motion as a pumping signal and the LDR as a probing signal.
In [118] the vibration was introduced with PZT in a carbon/epoxy plate with delamination created from Teflon-FEP insertion. The pumping signal had a 5 kHz frequency and the probing signal had a 100 kHz frequency. Then the pumping and the probing frequency were changed sequentially, in order to evaluate the influence of each frequency, a damage index calculated from the amplitude of the sidebands was used.
In [138,139], this technique was investigated with surface bonded PZTs, and especially its limitations. On a carbon/epoxy plate, with impact damage in a cantilever configuration, the clamping conditions affected the amplitude of sidebands, for undamaged structures, as previously seen, but also for damaged structures. Similarly, with a lot of articles, the sidebands happened around the probing frequency, for damaged cases, but also undamaged cases. Then, the observation that the amplitude of fundamental increases, while clamping force is increasing for undamaged plates, was made, and it is the reverse for the damaged ones. Otherwise, the amplitude of sidebands decreases while the clamping force increases for undamaged plates, and it is the reverse for damaged ones (Figure 40).
In [140], the same structure as in [125,141], the skin-stiffener composite one has been used with the VAM method, this structure was damaged by impact testing, which mainly created delamination. A shaker was used to introduce the pumping signal with a frequency of 1455 Hz and a piezoelectric diaphragm to introduce the probing one with a frequency of 50 kHz, then the vibration was caught by an LV. By using a Hilbert Transform, instantaneous amplitude and frequency were obtained and used to plot them over time. Two damage indicators represented by the peak-to-peak value of the signal were used and their distributions over the length of the structure showed that the instantaneous amplitude has high sensitivity in the area of the damage, this is not the case for instantaneous frequency.
In [142,143], both probing and pumping signals have been sent to the same actuator, which is an interesting way of using this technique.
Table 10 presents other studies using the VAM method for the SHM purposes of PMC materials.
3.3.4. Damping
According to [102], damping can also have nonlinear features, one is called the instantaneous damping coefficient, and the other nonlinear damping parameter.
The instantaneous damping coefficient is determined from Continuous Wavelet Transform (CWT) on the vibration response of the structure, it was created to show the variation of damping over time. The instantaneous amplitude and phase are extracted from the CWT to create the instantaneous damping coefficient h0.
where A is the instantaneous amplitude and ω is the damped angular frequency, with their first derivative.
The nonlinear damping parameter αQ, also known as the dissipative nonlinear parameter, can be found with the same method as “frequency shift with different amplitude of excitation”, indeed, the dissipative parameter can be calculated from [63,64].
where Q is the loss quality factor (1/loss factor), Q0 is the loss of quality factor for the first low amplitude and ε is the strain.
In [63,64], the dissipative parameter has been used to evaluate its sensibility to damage against the classical loss factor. The configuration was the same as for the elastic parameter on the sandwich and laminate. It was found a higher sensibility of this dissipative nonlinear parameter over the linear one (Figure 41). This behavior has also been investigated in [131] where the dissipative parameter showed a high sensitivity for damaged cases.
3.4. Summary of the Vibration Methods and Decision Tree
Many methods have been presented, and most of the researchers investigated several of them in their articles. For example, the natural frequencies shift is often combined with the damping ratio and the modes shape methods: modes shapes, modes shape curvature, modal strain energy, and modal flexibility (as in Figure 20). These three methods linked to modes shape need only to be calculated, it would not be wise not to use them. In addition, in all the methods, a general overview of the vibration of the structure over a large frequency band is needed. From this result, the natural frequencies and the damping ratio only have to be detected and calculated, this is why they are always used as a first reference. In nonlinear methods, the sub- and super-harmonics generation induced by damage is also often investigated through SFE and VAM in the same articles. Indeed, the techniques are a bit different, but the phenomena observed are similar. These two techniques are both vibro-ultrasonic methods, where the frequencies used for excitation can either correspond to the modes of vibration or ultrasonic wave, but both showed that they can be used within the vibration field efficiently.
4. Conclusions
An important amount of techniques, about the main methods of vibration analysis for SHM, have been presented in this article, with a focus on PMC materials. The goal of this review was to study the techniques, used equipment and configurations, as well as their effectiveness and, for some techniques, their drawbacks and limitations. But also, the different damage mechanisms detected or not, with these techniques, which permits to select the best method according to the studied damage.
Firstly, the classical linear methods have been introduced, even though they are considered insufficient to detect small and complex damage in the composite structures, and secondly, the nonlinear methods have shown interesting capacities in the last few years in detecting and locating damage with nonlinear behavior of the structure. The nonlinear methods are still in development, and nowadays there already exist three main techniques which can easily be used to perform SHM of PMC: the SFE, the VAM and the nonlinear resonance.
In the introduction, the concept of SHM has been presented, and from the cited articles, it is clear that the step of qualifying the damage mechanism is not yet well-developed in vibration analysis, whereas detection and localization are possible through several techniques. In addition, most of them investigated the presence of damage on laboratory-scale composite structures. This is important to take into consideration that the transposition to the operational scale still needs improvement and development.
As vibration analysis showed interesting results but is still influenced a lot by boundary conditions and external factors, the current researches focus on combining the results of several vibration methods, but also, with other NDT results (such as AE, US, …), in order to obtain a more robust conclusion about SHM. Indeed, a large range of NDT exists, which allows combining them and obtaining different information about the damaged structure. The next step will be the use of Artificial Intelligence (AI) algorithms for the combination, in order to visualize similar patterns, induced by the different types of damage, through all of these techniques. This will help to avoid fake detection/localization and to increase accuracy in the SHM process, with the goal of qualifying the damage mechanisms efficiently.
Author Contributions
Conceptualization, W.H., Z.A. and L.D.; methodology, W.H., Z.A. and L.D.; formal analysis, W.H. and L.D.; investigation, W.H. and L.D.; data curation, L.D.; writing—original draft preparation, W.H. and L.D.; writing—review and editing, W.H., Z.A. and L.D.; supervision, W.H. Z.A. and L.D.; project administration, W.H and Z.A.; funding acquisition, W.H. All authors have read and agreed to the published version of the manuscript.
Funding
The authors would like to thank the “Ministère de l’Enseignement Supérieur et de la Recherche” of France for funding this work as part of the doctoral thesis of Loan Dolbachian.
Data Availability Statement
The raw/processed data required to reproduce these findings cannot be shared at this time as the data also forms part of an ongoing study.
Conflicts of Interest
The authors declare no conflict of interest.
Glossary
| AE | Acoustic Emission |
| BVID | Barely Visible Impact Damage |
| CFRP | Carbon-Fiber Reinforced Polymer |
| CMC | Ceramic-Matrix Composite |
| DaDI | Damping Damage Indicator |
| DI | Damage Indicator |
| DIC | Digital Image Correlation |
| FEP | Fluorinated Ethylene Propylene |
| FFT | Fast Fourier Transform |
| FRF | Frequency Response Function |
| GFRP | Glass-Fiber Reinforced Polymer |
| LDR | Local Defect Resonance |
| LV | Laser Vibrometer |
| MAC | Modal Assurance Criterion |
| MF | Modal Flexibility |
| MFC | Macro-Fiber Composite |
| MMC | Metal-Matrix Composite |
| MSC | Modal Shape Curvature |
| MSD | Modal Shape Displacement |
| MSE | Modal Strain Energy |
| NDT | Non-Destructive Techniques |
| NWMS | Nonlinear Wave Modulation Technique |
| PFC | Piezo-Fiber Composite |
| PM | Process Monitoring |
| PMC | Polymer-Matrix Composite |
| PSF | Plane Shape Function |
| PVC | PolyVinyl Chloride |
| PVDF | Polyvinylidene Fluoride |
| PZT | Lead Zirconate Titanate |
| SFE | Single Frequency Excitation |
| SHM | Structural Health Monitoring |
| SWP | Sweep Signal Excitation |
| TF | Transmittance or Transmissibility Function |
| UT | Ultrasonic Testing |
| VAM | Vibro-Acoustic Modulation |
References
- Harizi, W.; Chaki, S.; Bourse, G.; Ourak, M. Mechanical Damage Characterization of Glass Fiber-Reinforced Polymer Laminates by Ultrasonic Maps. Compos B Eng 2015, 70, 131–137. [Google Scholar] [CrossRef]
- Harizi, W.; Chaki, S.; Bourse, G.; Ourak, M. Mechanical Damage Assessment of Polymer-Matrix Composites Using Active Infrared Thermography. Compos B Eng 2014, 66, 204–209. [Google Scholar] [CrossRef]
- Harizi, W.; Chaki, S.; Bourse, G.; Ourak, M. Mechanical Damage Assessment of Glass Fiber-Reinforced Polymer Composites Using Passive Infrared Thermography. Compos B Eng 2014, 59, 74–79. [Google Scholar] [CrossRef]
- Saba, N.; Jawaid, M. A Review on Thermomechanical Properties of Polymers and Fibers Reinforced Polymer Composites. Journal of Industrial and Engineering Chemistry 2018, 67, 1–11. [Google Scholar] [CrossRef]
- Al-Haik, M.S.; Hussaini, M.Y.; Garmestani, H. Prediction of Nonlinear Viscoelastic Behavior of Polymeric Composites Using an Artificial Neural Network. Int J Plast 2006, 22, 1367–1392. [Google Scholar] [CrossRef]
- Sajan, S.; Philip Selvaraj, D. A Review on Polymer Matrix Composite Materials and Their Applications. Mater Today Proc 2021, 47, 5493–5498. [Google Scholar] [CrossRef]
- Jia, Z.; Li, T.; Chiang, F. pen; Wang, L. An Experimental Investigation of the Temperature Effect on the Mechanics of Carbon Fiber Reinforced Polymer Composites. Compos Sci Technol 2018, 154, 53–63. [Google Scholar] [CrossRef]
- Indra Reddy, M.; Vijaya Kumar Raju, P.; Bhargava, N.R.M.R. Experimental Investigation on the Mechanical and Thermal Properties of Sprouts Center Stem (Asian Palmyra) Fiber Reinforced Polymer Composites. Mater Today Proc 2018, 5, 7808–7817. [Google Scholar] [CrossRef]
- Colombo, C.; Vergani, L.; Burman, M. Static and Fatigue Characterisation of New Basalt Fibre Reinforced Composites. Compos Struct 2012, 94, 1165–1174. [Google Scholar] [CrossRef]
- Harizi, W.; Chaki, S.; Ourak, M.; Harizi, W.; Chaki, S.; Bourse, G.; Ourak, M. Characterization of the Damage Mechanisms in Polymer Composite Materials by Ultrasonic Waves, Acoustic Emission and Infrared Thermography. In Proceedings of the ECCM15; ECCM15: Venice, 2012.
- Rytter, A. Vibrational Based Inspection of Civil Engineering Structures. Fracture and Dynamics, 1993; Vol. R9314 No. 44. [Google Scholar]
- Tuloup, C.; Harizi, W.; Aboura, Z.; Meyer, Y.; Khellil, K.; Lachat, R. On the Use of In-Situ Piezoelectric Sensors for the Manufacturing and Structural Health Monitoring of Polymer-Matrix Composites: A Literature Review. Compos Struct 2019, 215, 127–149. [Google Scholar] [CrossRef]
- Bastianini, F.; di Tommaso, A.; Pascale, G. Ultrasonic Non-Destructive Assessment of Bonding Defects in Composite Structural Strengthenings. Compos Struct 2001, 53, 463–467. [Google Scholar] [CrossRef]
- Aymerich, F.; Meili, S. Ultrasonic Evaluation of Matrix Damage in Impacted Composite Laminates. Compos B Eng 2000, 31, 1–6. [Google Scholar] [CrossRef]
- Bourchak, M.; Farrow, I.R.; Bond, I.P.; Rowland, C.W.; Menan, F. Acoustic Emission Energy as a Fatigue Damage Parameter for CFRP Composites. Int J Fatigue 2007, 29, 457–470. [Google Scholar] [CrossRef]
- Harizi, W.; Chaki, S.; Bourse, G.; Ourak, M. Damage Mechanisms Assessment of Glass Fiber-Reinforced Polymer (GFRP) Composites Using Multivariable Analysis Methods Applied to Acoustic Emission Data. Compos Struct 2022, 289, 115470. [Google Scholar] [CrossRef]
- Erwin Hack; Pramod Rastogi Optical Methods for Solid Mechanics; Wiley, 2012.
- McCormick, N.; Lord, J. Digital Image Correlation. Materials Today 2010, 13, 52–54. [Google Scholar] [CrossRef]
- Schilling, P.J.; Karedla, B.P.R.; Tatiparthi, A.K.; Verges, M.A.; Herrington, P.D. X-Ray Computed Microtomography of Internal Damage in Fiber Reinforced Polymer Matrix Composites. Compos Sci Technol 2005, 65, 2071–2078. [Google Scholar] [CrossRef]
- Wang, L.B.; Frost, J.D.; Voyiadjis, G.Z.; Harman, T.P. Quantification of Damage Parameters Using X-Ray Tomography Images. Mechanics of Materials 2003, 35, 777–790. [Google Scholar] [CrossRef]
- G. Gaussorgues, S.C. Infrared Thermography; Springer, 1993, Ed.; 1994.
- Hassani, S.; Mousavi, M.; Gandomi, A.H. Structural Health Monitoring in Composite Structures: A Comprehensive Review. Sensors 2021, 22, 153. [Google Scholar] [CrossRef]
- Akay, M. An Introduction to Polymer-Matrix Composites; Bookboon, 2015; ISBN 9788740309805.
- Mohan Kumar, S.; Raghavendra Ravikiran, K.; Govindaraju, H.K. Development of E-Glass Woven Fabric / Polyester Resin Polymer Matrix Composite and Study of Mechanical Properties. Mater Today Proc 2018, 5, 13367–13374. [Google Scholar] [CrossRef]
- Tableau, N.; Aboura, Z.; Khellil, K.; Laurin, F.; Schneider, J. Multiaxial Loading on a 3D Woven Carbon Fiber Reinforced Plastic Composite Using Tensile-Torsion Tests: Identification of the First Damage Envelope and Associated Damage Mechanisms. Compos Struct 2019, 227. [Google Scholar] [CrossRef]
- Talreja, R. PMC Failure Mechanisms. Comprehensive Composite Materials II 2017, 107–117. [Google Scholar] [CrossRef]
- E. Greenhalgh Defects and Damage and Their Role in the Failure of Polymer Composites. Failure Analysis and Fractography of Polymer Composites 2009, 356–440. [CrossRef]
- Duchene, P.; Chaki, S.; Ayadi, A.; Krawczak, P. A Review of Non-Destructive Techniques Used for Mechanical Damage Assessment in Polymer Composites. J Mater Sci 2018, 53, 7915–7938. [Google Scholar] [CrossRef]
- Bolotin, V. Mechanics of Delaminations in Laminate Composite Structures. Mechanics of Composite Materials 2001, 37. [Google Scholar] [CrossRef]
- Gomes, G.F.; Mendez, Y.A.D.; da Silva Lopes Alexandrino, P.; da Cunha, S.S.; Ancelotti, A.C. A Review of Vibration Based Inverse Methods for Damage Detection and Identification in Mechanical Structures Using Optimization Algorithms and ANN. Archives of Computational Methods in Engineering 2019, 26, 883–897. [Google Scholar] [CrossRef]
- Bovsunovsky, A.; Surace, C. Non-Linearities in the Vibrations of Elastic Structures with a Closing Crack: A State of the Art Review. Mech Syst Signal Process 2015, 62, 129–148. [Google Scholar] [CrossRef]
- He, M.; Zhang, Z.; Ramakrishnan, K.R. Delamination Identification for FRP Composites with Emphasis on Frequency-Based Vibration Monitoring-a Review. SDHM Structural Durability and Health Monitoring 2018, 12, 213–256. [Google Scholar] [CrossRef]
- Hou, R.; Xia, Y. Review on the New Development of Vibration-Based Damage Identification for Civil Engineering Structures: 2010–2019. J Sound Vib 2021, 491. [Google Scholar] [CrossRef]
- Montalvão, D.; Maia, N.M.M.; Ribeiro, A.M.R. A Review of Vibration-Based Structural Health Monitoring with Special Emphasis on Composite Materials. Shock and Vibration Digest 2006, 38, 295–324. [Google Scholar] [CrossRef]
- Montalvão, D.; Maia, N.M.M.; Ribeiro, A.M.R. A Review of Vibration-Based Structural Health Monitoring with Special Emphasis on Composite Materials. Shock and Vibration Digest 2006, 38, 295–324. [Google Scholar] [CrossRef]
- Sinou, J.-J. A Review of Damage Detection and Health Monitoring of Mechanical Systems from Changes in the Measurement of Linear and Non-Linear Vibrations; 2013.
- Worden, K.; Farrar, C.R.; Haywood, J.; Todd, M. A Review of Nonlinear Dynamics Applications to Structural Health Monitoring. Struct Control Health Monit 2008, 15, 540–567. [Google Scholar] [CrossRef]
- Fan, W.; Qiao, P. Vibration-Based Damage Identification Methods: A Review and Comparative Study. Struct Health Monit 2011, 10, 83–111. [Google Scholar] [CrossRef]
- Avitabile, P. Sound & Vibration Magazine. 2001,.
- Kranjc, T.; Slavić, J.; Boltežar, M. A Comparison of Strain and Classic Experimental Modal Analysis. JVC/Journal of Vibration and Control 2016, 22, 371–381. [Google Scholar] [CrossRef]
- Cugnoni, J.; Guzman, E.; Cugnoni, J.; Gmür, T. Use of PVDF Transducers as Actuators for Operational Modal Analysis on Composite Samples. In Proceedings of the ICCE21; 2013.
- Guzman, E.; Cugnoni, J.; Gmur, T. Monitoring of Composite Structures Using a Network of Integrated PVDF Film Transducers. Smart Mater Struct 2015, 24. [Google Scholar] [CrossRef]
- Xin, Y.; Sun, H.; Tian, H.; Guo, C.; Li, X.; Wang, S.; Wang, C. The Use of Polyvinylidene Fluoride (PVDF) Films as Sensors for Vibration Measurement: A Brief Review. Ferroelectrics 2016, 502, 28–42. [Google Scholar] [CrossRef]
- Bregar, T.; Starc, B.; Čepon, G.; Boltežar, M. On the Use of PVDF Sensors for Experimental Modal Analysis. In Proceedings of the Conference Proceedings of the Society for Experimental Mechanics Series; Springer, 2021; pp. 279–281. [Google Scholar]
- Tuloup, C.; Harizi, W.; Aboura, Z.; Meyer, Y.; Ade, B.; Khellil, K. Detection of the Key Steps during Liquid Resin Infusion Manufacturing of a Polymer-Matrix Composite Using an in-Situ Piezoelectric Sensor. Mater Today Commun 2020, 24, 101077. [Google Scholar] [CrossRef]
- Janeliukstis, R.; Mironovs, D. Smart Composite Structures with Embedded Sensors for Load and Damage Monitoring – A Review. Mechanics of Composite Materials 2021, 57, 131–152. [Google Scholar] [CrossRef]
- Paradies, R.; Ruge, M. In Situ Fabrication of Active Fibre Reinforced Structures with Integrated Piezoelectric Actuators. Smart Mater. Struct. 2000, 9. [Google Scholar] [CrossRef]
- Kovalovs, A.; Wesolowski, M.; Barkanov, E.; Gluhihs, S. Application of Macro-Fiber Composite (MFC) as a Piezoelectric Actuator. Vibromechanical journal of vibroengineering 2009, 11. [Google Scholar]
- Siemens Company What Is a Frequency Response Function (FRF)? Available online: https://community.sw.siemens.com/s/article/what-is-a-frequency-response-function-frf (accessed on 11 March 2022).
- Siemens company Autopower Function. Available online: https://community.sw.siemens.com/s/article/the-autopower-function-demystified (accessed on 11 March 2022).
- Baptiste Chomette MIMO Modal Parameters Identification in Frequency Domain - File Exchange - MATLAB Central. Available online: https://fr.mathworks.com/matlabcentral/fileexchange/82380-mimo-modal-parameters-identification-in-frequency-domain (accessed on 11 April 2022).
- An, H.; Youn, B.D.; Kim, H.S. A Methodology for Sensor Number and Placement Optimization for Vibration-Based Damage Detection of Composite Structures under Model Uncertainty. Compos Struct 2022, 279. [Google Scholar] [CrossRef]
- Mallardo, V.; Aliabadi, M.H. Optimal Sensor Placement for Structural, Damage and Impact Identification: A Review. SDHM Structural Durability and Health Monitoring 2014, 9, 287–323. [Google Scholar] [CrossRef]
- Ferreira Gomes, G.; SimõesSim, S.; da Cunha Jr, S.; da Silva Lopes Alexandrino, P.; Silva de Sousa, B.; Carlos Ancelotti Jr, A. Sensor Placement Optimization Applied to Laminated Composite Plates under Vibration. Structural and Multidisciplinary Optimization 2022, 58, 2099–2118. [Google Scholar] [CrossRef]
- Doebling, S.W.; F.C.R.; P.M.B.; S.D.W. Damage Identification and Health Monitoring of Structural and Mechanical Systems from Changes in Their Vibration Characteristics: A Literature Review. The shock and vibration digest 1996, 30. [CrossRef]
- Lifshitz, J.M.; Rotem, A. Determination of Reinforcement Unbonding of Composites by a Vibration Technique. Journal of Composite material 2016, 3. [Google Scholar] [CrossRef]
- Kuriakose, V.M.; Sreehari, V.M. Experimental Investigation on the Enhancement of Vibration and Flutter Characteristics of Damaged Composite Plates Using Piezoelectric Patches. Compos Struct 2021, 275, 114518. [Google Scholar] [CrossRef]
- Prasad Konka, H. Embedded Piezoelectric Fiber Composite Sensors for Applications in Composite Structures (Thesis Report). Louisiana State University and Agricultural and Mechanical College: Bâton-Rouge, 2011. [Google Scholar]
- Konka, H.P.; Wahab, M.A.; Lian, K. On Mechanical Properties of Composite Sandwich Structures with Embedded Piezoelectric Fiber Composite Sensors. Journal of Engineering Materials and Technology, Transactions of the ASME 2012, 134. [Google Scholar] [CrossRef]
- Kessler, S.S.; Spearing, S.M. In-Situ Sensor-Based Damage Detection of Composite Materials for Structural Health Monitoring. In Proceedings of the Collection of Technical Papers - AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference; American Inst. Aeronautics and Astronautics Inc., 2002; Vol. 4; pp. 2706–2716. [Google Scholar]
- De Medeiros, R.; Sartorato, M.; Tita, V.; De Medeiros, R.; Sartorato, M.; Vandepitte, D.; Tita, V. SHM of Composite Plates: Vibration Based Method by Using PZT Sensors.; Proceedings of ISMA2014, 2014.
- de Medeiros, R.; Sartorato, M.; Marques, F.D.; Tita, V.; De, R.; Murilo, M.; Flávio, S.; Marques, D.; Vandepitte, D. Vibration-Based Damage Identification Applied for Composite Plate: Experimental Analyses. In Proceedings of the COBEM 2013; 2013.
- Idriss, M.; El Mahi, A. Linear and Nonlinear Resonant Techniques for Characterizing Cyclic Fatigue Damage in Composite Laminate. Compos B Eng 2018, 142, 36–46. [Google Scholar] [CrossRef]
- Idriss, M.; El Mahi, A.; El Guerjouma, R. Characterization of Sandwich Beams with Debonding by Linear and Nonlinear Vibration Method. Compos Struct 2015, 120, 200–207. [Google Scholar] [CrossRef]
- El Mahi, A.; Idriss, M.; Assarar, M.; El Guerjouma, R.; Dazel, O. Effets de l’endommagement Sur Le Comportement Vibratoire Des Matériaux Sandwichs Endommagés. In Proceedings of the 19ème Congrès Français de Mécanique; 2009.
- Tracy, J.J.; Manager, S.; Pardoen, G.C. Effect of Delamination on the Natural Frequencies of Composite Laminates. J Compos Mater 1989, 23. [Google Scholar] [CrossRef]
- Ghoshal, A.; Chattopadhyay, A.; Schulz, M.J.; Thornburgh, R.; Waldron, K. Experimental Investigation of Damage Detection in Composite Material Structures Using a Laser Vibrometer and Piezoelectric Actuators. J Intell Mater Syst Struct 2003, 14, 521–537. [Google Scholar] [CrossRef]
- Okafor, A.C.; Chandrashekhara, K.; Jiang, Y.P. Delamination Prediction in Composite Beams with Built-in Piezoelectric Devices Using Modal Analysis and Neural Network. Smart Mater. Struct. 1996, 5, 338–347. [Google Scholar] [CrossRef]
- Islam, A.S.; Craig, K.C. Damage Detection in Composite Structures Using Piezoelectric Materials. Smart Mater. Struct. 1994, 3, 318–328. [Google Scholar] [CrossRef]
- Hou, J.P.; Jeronimidis, G. Vibration of Delaminated Thin Composite Plates. Compos Part A Appl Sci Manuf 1999, 30, 989–995. [Google Scholar] [CrossRef]
- Lakhdar, M.; Mohammed, D.; Boudjemâa, L.; Rabiâ, A.; Bachir, M. Damages Detection in a Composite Structure by Vibration Analysis. Energy Procedia 2013, 36, 888–897. [Google Scholar] [CrossRef]
- Siemens Company Modal Tips: Roving Hammer versus Roving Accelerometer. Available online: https://community.sw.siemens.com/s/article/modal-tips-roving-hammer-versus-roving-accelerometer (accessed on 7 March 2022).
- Pastor, M.; Binda, M.; Harčarik, T. Modal Assurance Criterion. Procedia Eng 2012, 48, 543–548. [Google Scholar] [CrossRef]
- Allemang, R.J. The Modal Assurance Criterion (MAC): Twenty Years of Use and Abuse. Sound & Vibration 2003, 37, 14–23. [Google Scholar]
- Siemens Company Modal Assurance Criterion (MAC). Available online: https://community.sw.siemens.com/s/article/modal-assurance-criterion-mac (accessed on 4 March 2022).
- Patil, S.; Mallikarjuna Reddy, D. Damage Identification in Hemp Fiber (Cannabis Sativa) Reinforced Composite Plates Using MAC and COMAC Correlation Methods: Experimental Study. Journal of Natural Fibers 2020. [Google Scholar] [CrossRef]
- dos Santos, F.L.M.; Peeters, B.; van der Auweraer, H.; Góes, L.C.S.; Desmet, W. Vibration-Based Damage Detection for a Composite Helicopter Main Rotor Blade. Case Studies in Mechanical Systems and Signal Processing 2016, 3, 22–27. [Google Scholar] [CrossRef]
- Pérez, M.A.; Gil, L.; Oller, S. Impact Damage Identification in Composite Laminates Using Vibration Testing. Compos Struct 2014, 108, 267–276. [Google Scholar] [CrossRef]
- Herman, A.P.; Orifici, A.C.; Mouritz, A.P. Vibration Modal Analysis of Defects in Composite T-Stiffened Panels. Compos Struct 2013, 104, 34–42. [Google Scholar] [CrossRef]
- Hu, H.; Wang, B.-T.; Su, J.-S. Application of Modal Analysis to Damage Detection in Composite Laminates. In Proceedings of the ESDA04; Manchester, UK, 2004.
- Hu, H.; Wang, B.T.; Lee, C.H.; Su, J.S. Damage Detection of Surface Cracks in Composite Laminates Using Modal Analysis and Strain Energy Method. Compos Struct 2006, 74, 399–405. [Google Scholar] [CrossRef]
- Qiao, P.; Lestari, W.; Shah, M.G.; Wang, J. Dynamics-Based Damage Detection of Composite Laminated Beams Using Contact and Noncontact Measurement Systems. J Compos Mater 2007, 41, 1217–1252. [Google Scholar] [CrossRef]
- Sampaio, R.P.C.; Maia, N.M.M.; Silva, J.M.M. Damage Detection Using the Frequency-Response-Function Curvature Method. J Sound Vib 1999, 226, 1029–1042. [Google Scholar] [CrossRef]
- Pandey, A.K.; Biswas, M.; Samman, M.M. Damage Detection from Changes in Curvature Mode Shapes. J Sound Vib 1991, 145, 321–332. [Google Scholar] [CrossRef]
- Radzieński, M.; Krawczuk, M.; Palacz, M. Improvement of Damage Detection Methods Based on Experimental Modal Parameters. Mech Syst Signal Process 2011, 25, 2169–2190. [Google Scholar] [CrossRef]
- Govindasamy, M.; Kamalakannan, G.; Kesavan, C.; Meenashisundaram, G.K. Damage Detection in Glass/Epoxy Laminated Composite Plates Using Modal Curvature for Structural Health Monitoring Applications. Journal of Composites Science 2020, 4. [Google Scholar] [CrossRef]
- Lestari, W.; Qiao, P.; Hanagud, S. Curvature Mode Shape-Based Damage Assessment of Carbon/Epoxy Composite Beams. J Intell Mater Syst Struct 2007, 18, 189–208. [Google Scholar] [CrossRef]
- Hamey, C.S.; Lestari, W.; Qiao, P.; Song, G. Experimental Damage Identification of Carbon/Epoxy Composite Beams Using Curvature Mode Shapes. Struct Health Monit 2004, 3, 333–353. [Google Scholar] [CrossRef]
- He, M.; Yang, T.; Du, Y. Nondestructive Identification of Composite Beams Damage Based on the Curvature Mode Difference. Compos Struct 2017, 176, 178–186. [Google Scholar] [CrossRef]
- Mohammad Mehdizadeh Curvature Mode Shape Analyses of Damage in Structures (Thesis Report), School of Aerospace, Mechanical & Manufacturing Engineering College of Science, Engineering and Technology: Bundoora, 2009.
- Sazonov, E.; Klinkhachorn, P. Optimal Spatial Sampling Interval for Damage Detection by Curvature or Strain Energy Mode Shapes. J Sound Vib 2005, 285, 783–801. [Google Scholar] [CrossRef]
- Cha, Y.J.; Buyukozturk, O. Structural Damage Detection Using Modal Strain Energy and Hybrid Multiobjective Optimization. Computer-Aided Civil and Infrastructure Engineering 2015, 30, 347–358. [Google Scholar] [CrossRef]
- Eraky, A.; Anwar, A.M.; Saad, A.; Abdo, A. Damage Detection of Flexural Structural Systems Using Damage Index Method - Experimental Approach. Alexandria Engineering Journal 2015, 54, 497–507. [Google Scholar] [CrossRef]
- Wang, S.; Xu, M. Modal Strain Energy-Based Structural Damage Identification: A Review and Comparative Study. Structural Engineering International 2019, 29, 234–248. [Google Scholar] [CrossRef]
- Hu, H.; Wang, J. Damage Detection of a Woven Fabric Composite Laminate Using a Modal Strain Energy Method. Eng Struct 2009, 31, 1042–1055. [Google Scholar] [CrossRef]
- Hu, H.; Wang, B.T.; Lee, C.H.; Su, J.S. Damage Detection of Surface Cracks in Composite Laminates Using Modal Analysis and Strain Energy Method. Compos Struct 2006, 74, 399–405. [Google Scholar] [CrossRef]
- Hu, H.; Lee, C.H.; Wu, C.B.; Lu, W.J. Detection of Matrix Cracks in Composite Laminates by Using the Modal Strain Energy Method. Mechanics of composite materials 2010, 46. [Google Scholar] [CrossRef]
- dos Santos, F.L.M.; Peeters, B.; van der Auweraer, H.; Góes, L.C.S. Modal Strain Energy Based Damage Detection Applied to a Full Scale Composite Helicopter Blade. In Proceedings of the Key Engineering Materials; Trans Tech Publications Ltd, 2013; Vol. 569–570, pp. 457–464.
- Kumar, M.; Shenoi, R.A.; Cox, S.J. Experimental Validation of Modal Strain Energies Based Damage Identification Method for a Composite Sandwich Beam. Compos Sci Technol 2009, 69, 1635–1643. [Google Scholar] [CrossRef]
- Meng, F.; Yu, J.; Alaluf, D.; Mokrani, B.; Preumont, A. Modal Analysis and Damage Detection for Suspension Bridges: A Numerical and Experimental Investigation. Smart Struct Syst 2019, 23, 15–29. [Google Scholar]
- Yang, J.S.; Liu, Z. da; Schmidt, R.; Schröder, K.U.; Ma, L.; Wu, L.Z. Vibration-Based Damage Diagnosis of Composite Sandwich Panels with Bi-Directional Corrugated Lattice Cores. Compos Part A Appl Sci Manuf 2020, 131. [Google Scholar] [CrossRef]
- Cao, M.S.; Sha, G.G.; Gao, Y.F.; Ostachowicz, W. Structural Damage Identification Using Damping: A Compendium of Uses and Features. Smart Mater Struct 2017, 26. [Google Scholar] [CrossRef]
- Inman, D.J. Engineering Vibration; Pearson education limited, 1994; ISBN 978-0-13-287169-3.
- Slavič, J.; Simonovski, I.; Boltežar, M. Damping Identification Using a Continuous Wavelet Transform: Application to Real Data. J Sound Vib 2003, 262, 291–307. [Google Scholar] [CrossRef]
- Montalvão, D.; Ribeiro, A.M.R.; Duarte-Silva, J. A Method for the Localization of Damage in a CFRP Plate Using Damping. Mech Syst Signal Process 2009, 23, 1846–1854. [Google Scholar] [CrossRef]
- Montalvão, D.; Ribeiro, A.M.R.; Duarte-Silva, J.A.B. Experimental Assessment of a Modal-Based Multi-Parameter Method for Locating Damage in Composite Laminates. Exp Mech 2011, 51, 1473–1488. [Google Scholar] [CrossRef]
- Montalvão, D.; Karanatsis, D.; Ribeiro, A.M.; Arina, J.; Baxter, R. An Experimental Study on the Evolution of Modal Damping with Damage in Carbon Fiber Laminates. J Compos Mater 2015, 49, 2403–2413. [Google Scholar] [CrossRef]
- Kessler, S.S.; Spearing, S.M.; Atalla, M.J.; Cesnik, C.E.S.; Soutis, C. Damage Detection in Composite Materials Using Frequency Response Methods. Composites: Part B 2002, 33, 87–95. [Google Scholar] [CrossRef]
- Sampaio, R.P.C.; Maia, N.M.M.; Silva, J.M.M. The Frequency Domain Assurance Criterion as a Tool for Damage Detection. Key Eng Mater 2003, 245–246, 69–76. [Google Scholar] [CrossRef]
- Chen, A. Frequency Response Assurance Criterion and Applications to Model Correlation of Body Structures. SAE Technical Papers 2003. [Google Scholar] [CrossRef]
- de Medeiros, R. Development of a Criterion for Predicting Residual Strength of Composite Structures Damaged by Impact Loading (Thesis Report). Mechanical Engineering, University of Sao Paulo –USP Sao Carlos School of engineering: Sao Paulo, 2016.
- Chesné, S.; Deraemaeker, A. Damage Localization Using Transmissibility Functions: A Critical Review. Mech Syst Signal Process 2013, 38, 569–584. [Google Scholar] [CrossRef]
- Zhang, H.; Schulz, M.J.; Ferguson, F.; Pai, P.F. Structural Health Monitoring Using Transmittance Functions. Mech Syst Signal Process 1999, 13, 765–787. [Google Scholar] [CrossRef]
- Sundaresan, M.; Ferguson, F.; Pai, P.; Sundaresan, M.J.; Schulz, M.J.; Hill, J.; Wheater, E.A.; Ferguson, F.; Pai, P.F. Damage Detection on a Wind Turbine Blade Section. In Proceedings of the The international Society for Optical Engineering; 1999.
- Poulimenos, A.G.; Sakellariou, J.S. A Transmittance-Based Methodology for Damage Detection under Uncertainty: An Application to a Set of Composite Beams with Manufacturing Variability Subject to Impact Damage and Varying Operating Conditions. Struct Health Monit 2019, 18, 318–333. [Google Scholar] [CrossRef]
- Lin, C.-; Liu A Tutorial of the Wavelet Transform; 2010;
- Yan, Y.J.; Yam, L.H. Detection of Delamination Damage in Composite Plates Using Energy Spectrum of Structural Dynamic Responses Decomposed by Wavelet Analysis. Comput Struct 2004, 82, 347–358. [Google Scholar] [CrossRef]
- Singh, A.K. Detection of Defects in Composite Laminates with Vibro-Ultrasonic Methods (Thesis Report), National University of Singapore: Singapore, 2019.
- Andreaus, U.; Baragatti, P. Experimental Damage Detection of Cracked Beams by Using Nonlinear Characteristics of Forced Response. Mech Syst Signal Process 2012, 31, 382–404. [Google Scholar] [CrossRef]
- Dolbachian, L.; Harizi, W.; Aboura, Z. Structural Health Monitoring (SHM) Study of Polymer Matrix Composite (PMC) Materials Using Nonlinear Vibration Methods Based on Embedded Piezoelectric Transducers. Sensors 2023, 23. [Google Scholar] [CrossRef]
- Andreades, C.; Ciampa, F. CFRP Composites with Embedded PZT Transducers for Nonlinear Ultrasonic Inspection of Space Structures. In Proceedings of the EWSHM2018; 2018.
- Andreades, C.; Malfense Fierro, G.P.; Meo, M. A Nonlinear Ultrasonic SHM Method for Impact Damage Localisation in Composite Panels Using a Sparse Array of Piezoelectric PZT Transducers. Ultrasonics 2020, 108. [Google Scholar] [CrossRef]
- Polimeno, U.; Meo, M.; Almond, D.P. Smart Nonlinear Acoustic Based Structural Health Monitoring System. CIMTEC 2008 - Proceedings of the 3rd International Conference on Smart Materials, Structures and Systems - Emboding Intelligence in Structures and Integrated Systems 2008, 56, 426–434. [Google Scholar] [CrossRef]
- Loi, G.; Porcu, M.C.; Aymerich, F. Impact Damage Detection in Composite Beams by Analysis of Non-Linearity under Pulse Excitation. Journal of Composites Science 2021, 5. [Google Scholar] [CrossRef]
- Ooijevaar, T.H.; Rogge, M.D.; Loendersloot, R.; Warnet, L.L.; Akkerman, R.; Tinga, T. Nonlinear Dynamic Behavior of an Impact Damaged Composite Skin-Stiffener Structure. J Sound Vib 2015, 353, 243–258. [Google Scholar] [CrossRef]
- Meo, M.; Polimeno, U.; Zumpano, G. Detecting Damage in Composite Material Using Nonlinear Elastic Wave Spectroscopy Methods. Applied Composite Materials 2008, 15, 115–126. [Google Scholar] [CrossRef]
- Polimeno, U.; Meo, M. Understanding the Effect of Boundary Conditions on Damage Identification Process When Using Nonlinear Elastic Wave Spectroscopy Methods. Int J Non Linear Mech 2008, 43, 187. [Google Scholar] [CrossRef]
- Bentahar, M. Nonlinear Acoustics: Application to Ultrasonic Characterisation of Damage in Heterogeneous Materials and Remaining Life Determination (Thesis Report), INSA Lyon: Lyon, 2005.
- Wei, Q.; Zhu, L.; Zhu, J.; Zhuo, L.; Hao, W.; Xie, W. Characterization of Impact Fatigue Damage in CFRP Composites Using Nonlinear Acoustic Resonance Method. Compos Struct 2020, 253. [Google Scholar] [CrossRef]
- van den Abeele, K.E.A.; Sutin, A.; Carmeliet, J.; Johnson, P.A. Micro-Damage Diagnostics Using Nonlinear Elastic Wave Spectroscopy (NEWS). NDT and E International 2001, 34, 239–248. [Google Scholar] [CrossRef]
- Novak, A.; Bentahar, M.; Tournat, V.; el Guerjouma, R.; Simon, L. Nonlinear Acoustic Characterization of Micro-Damaged Materials through Higher Harmonic Resonance Analysis. NDT and E International 2012, 45, 1–8. [Google Scholar] [CrossRef]
- Pieczonka, L.; Klepka, A.; Martowicz, A.; Staszewski, W.J. Nonlinear Vibroacoustic Wave Modulations for Structural Damage Detection: An Overview. Optical Engineering 2015, 55, 011005. [Google Scholar] [CrossRef]
- Andreades, C.; Malfense Fierro, G.P.; Meo, M.; Ciampa, F. Nonlinear Ultrasonic Inspection of Smart Carbon Fibre Reinforced Plastic Composites with Embedded Piezoelectric Lead Zirconate Titanate Transducers for Space Applications. J Intell Mater Syst Struct 2019, 30, 2995–3007. [Google Scholar] [CrossRef]
- Klepka, A.; Pieczonka, L.; Staszewski, W.J.; Aymerich, F. Impact Damage Detection in Laminated Composites by Non-Linear Vibro-Acoustic Wave Modulations. Compos B Eng 2014, 65, 99–108. [Google Scholar] [CrossRef]
- Adebahr, W.; Solodov, I.; Rahammer, M.; Gulnizkij, N.; Kreutzbruck, M. Local Defect Resonance for Sensitive Non-Destructive Testing. In Proceedings of the AIP Conference Proceedings; American Institute of Physics Inc., February 10 2016; Vol. 1706.
- Solodov, I.; Bai, J.; Bekgulyan, S.; Busse, G. A Local Defect Resonance to Enhance Acoustic Wave-Defect Interaction in Ultrasonic Nondestructive Evaluation. Appl Phys Lett 2011, 99. [Google Scholar] [CrossRef]
- Solodov, I.; Bai, J.; Bekgulyan, S.; Busse, G. A Local Defect Resonance to Enhance Wave-Defect Interaction in Nonlinear Spectroscopy and Ultrasonic Thermography. In Proceedings of the World Conference on Nondestructive Testing; Durban, South Africa, 2012.
- Aymerich, F.; Staszewski, W.J. Impact Damage Detection in Composite Laminates Using Nonlinear Acoustics. In Proceedings of the Composites Part A: Applied Science and Manufacturing; September 2010; Vol. 41, pp. 1084–1092.
- Aymerich, F.; Staszewski, W.J. Experimental Study of Impact-Damage Detection in Composite Laminates Using a Cross-Modulation Vibro-Acoustic Technique. Struct Health Monit 2010, 9, 541–553. [Google Scholar] [CrossRef]
- Ooijevaar, T.H.; Loendersloot, R.; Rogge, M.D.; Akkerman, R.; Tinga, T. Vibro-Acoustic Modulation Based Damage Identification in a Composite Skin-Stiffener Structure. Struct Health Monit 2016, 15. [Google Scholar] [CrossRef]
- Ooijevaar, T.H.; Loendersloot, R.; Warnet, L.L.; de Boer, A.; Akkerman, R. Vibration Based Structural Health Monitoring of a Composite T-Beam. Compos Struct 2010, 92, 2007–2015. [Google Scholar] [CrossRef]
- Chen, B.Y.; Soh, S.K.; Lee, H.P.; Tay, T.E.; Tan, V.B.C. A Vibro-Acoustic Modulation Method for the Detection of Delamination and Kissing Bond in Composites. J Compos Mater 2016, 50, 3089–3104. [Google Scholar] [CrossRef]
- Prevorovsky, Z.; Krofta, J.; Kober, J.; Chlada, M.; Kirchner, A. Non-Linear Ultrasonic Spectroscopy of 3D Printed Metallic Samples. Insight: Non-Destructive Testing and Condition Monitoring 2019, 61, 157–161. [Google Scholar] [CrossRef]
- Loi, G.; Uras, N.; Porcu, M.C.; Aymerich, F. Damage Detection in Composite Materials by Flexural Dynamic Excitation and Accelerometer-Based Acquisition. IOP Conf Ser Mater Sci Eng 2022, 1214, 012007. [Google Scholar] [CrossRef]
- Kim, S.; Adams, D.E.; Sohn, H.; Rodriguez-Rivera, G.; Myrent, N.; Bond, R.; Vitek, J.; Carr, S.; Grama, A.; Meyer, J.J. Crack Detection Technique for Operating Wind Turbine Blades Using Vibro-Acoustic Modulation. Struct Health Monit 2014, 13, 660–670. [Google Scholar] [CrossRef]
Figure 1.
Laminated (left) and sandwich composite (right).
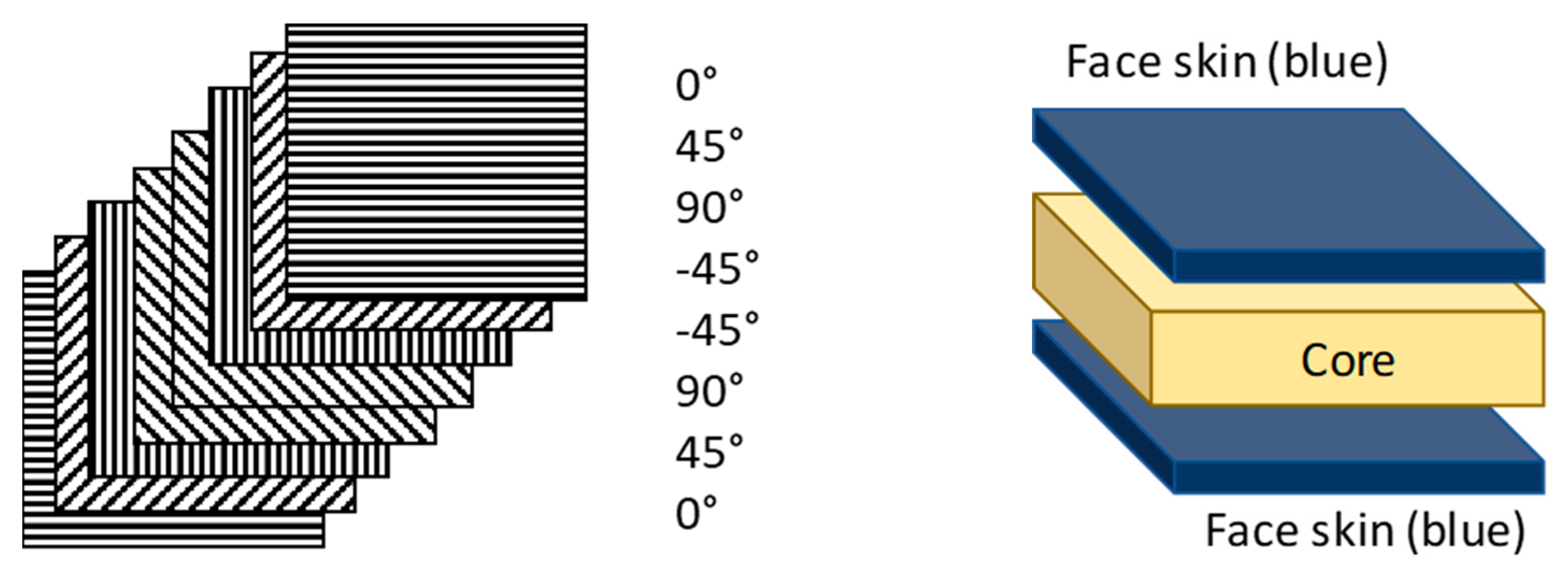
Figure 2.
Impact damage mechanisms in composite laminate (adapted from [27]).
Figure 2.
Impact damage mechanisms in composite laminate (adapted from [27]).
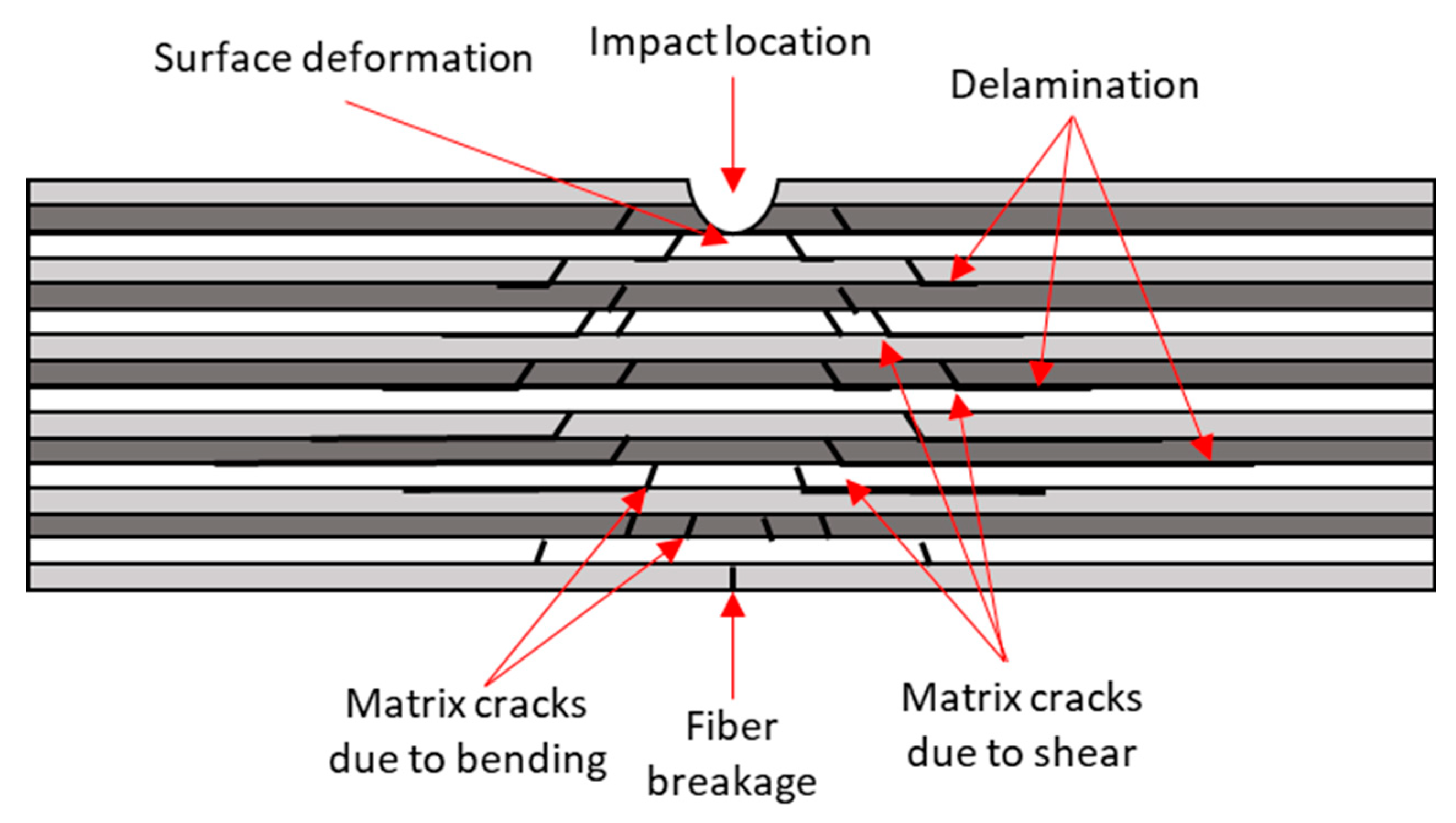
Figure 3.
Evolution of damage in composite laminate (adapted from [28]).
Figure 3.
Evolution of damage in composite laminate (adapted from [28]).
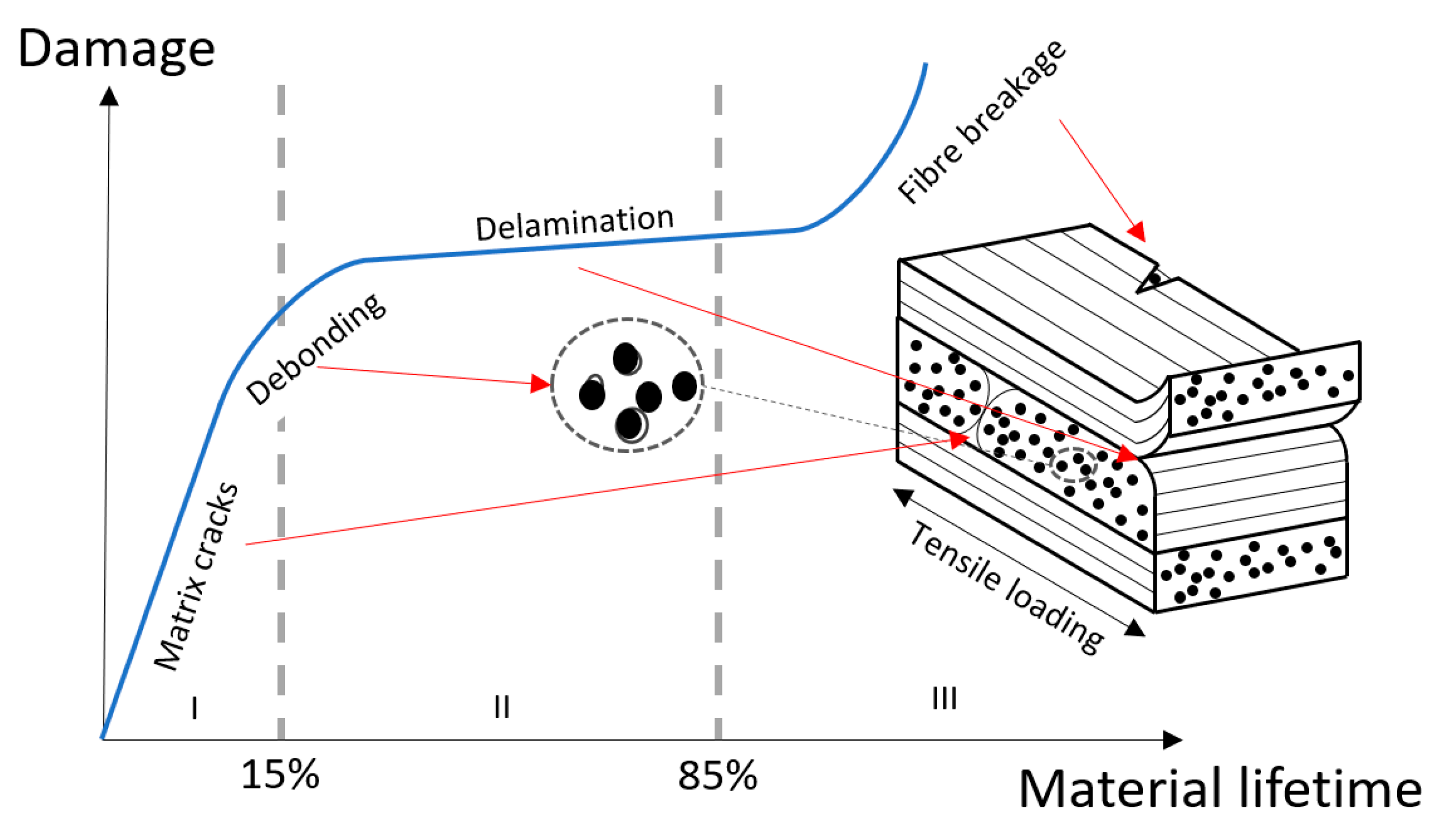
Figure 4.
Schematic of different fixation setup: suspended with wire (a), clamped in cantilever configuration (b) and isolated with foam (c).
Figure 4.
Schematic of different fixation setup: suspended with wire (a), clamped in cantilever configuration (b) and isolated with foam (c).
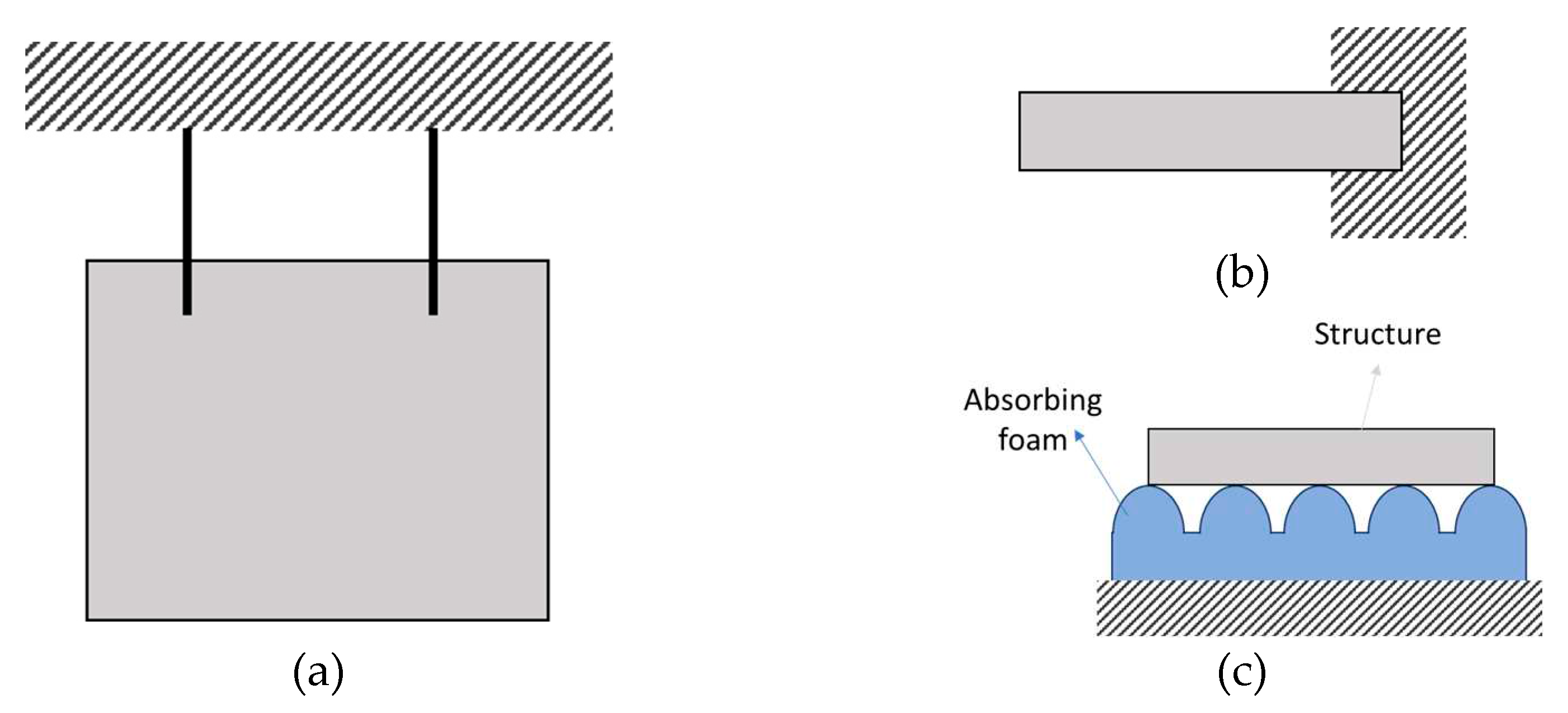
Figure 5.
Setup vibration analysis with PVDF as actuator (adapted from [41]).
Figure 5.
Setup vibration analysis with PVDF as actuator (adapted from [41]).
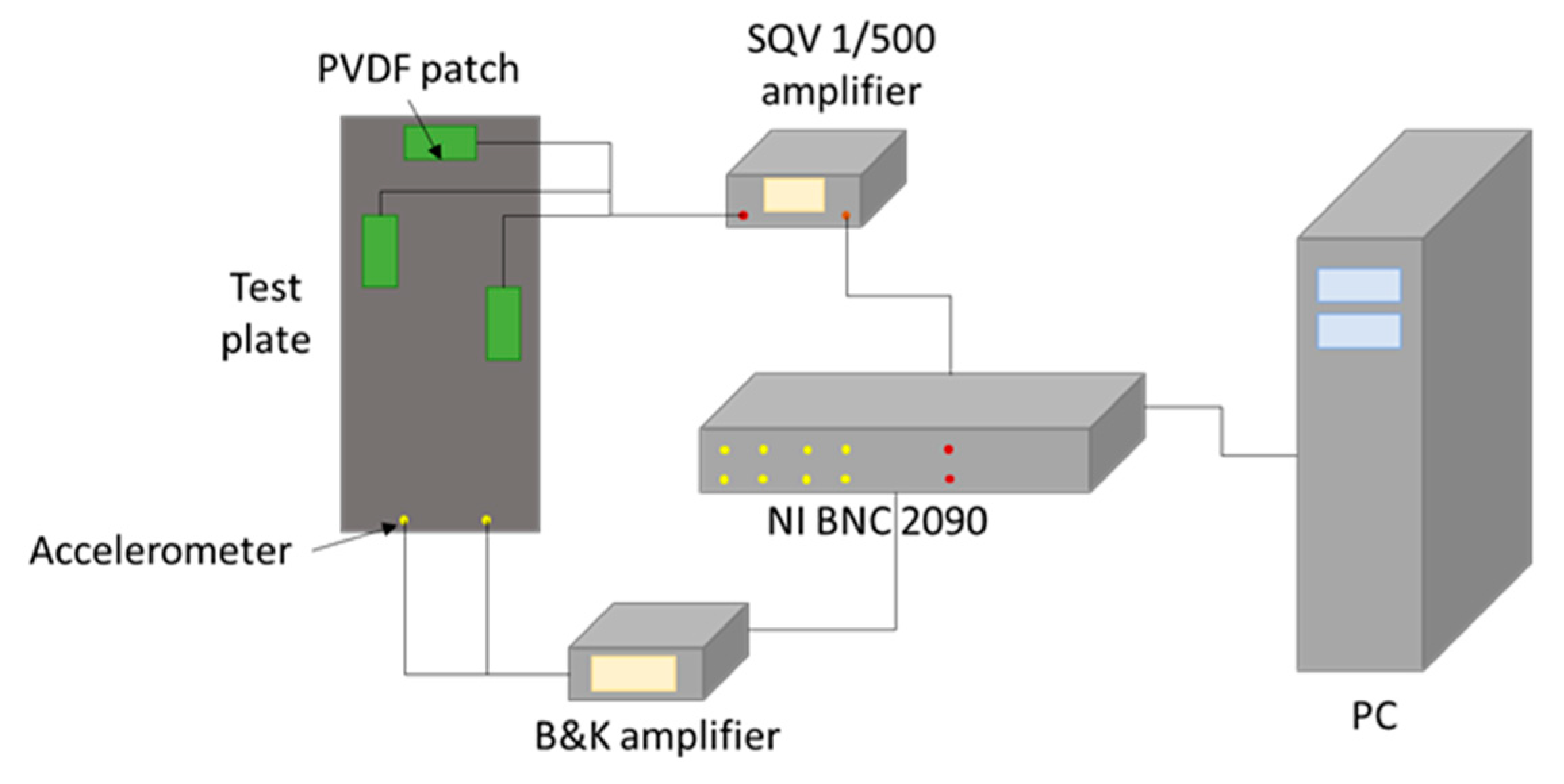
Figure 6.
Four first modes of vibration of a free-free plate (displacement is shown).

Figure 7.
Optimal placement obtained from the Effective Independence (EI) for 3 accelerometers (left) and 3 PVDFs (right) (adapted from [42]).
Figure 7.
Optimal placement obtained from the Effective Independence (EI) for 3 accelerometers (left) and 3 PVDFs (right) (adapted from [42]).

Figure 8.
Natural frequency shift induced by damage.
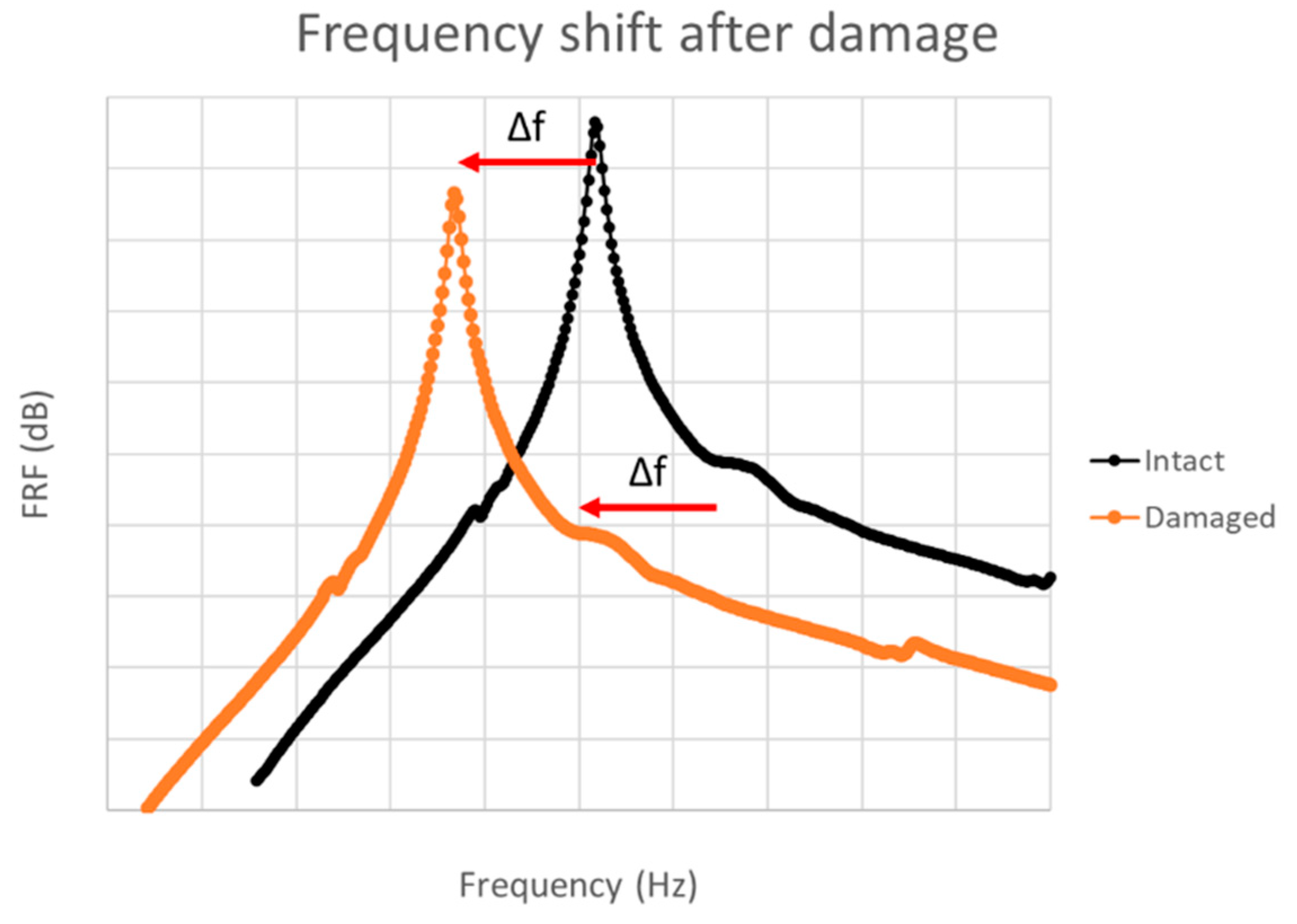
Figure 9.
Schematic experimental cantilever setup: middle damage (adapted from [57]).
Figure 9.
Schematic experimental cantilever setup: middle damage (adapted from [57]).
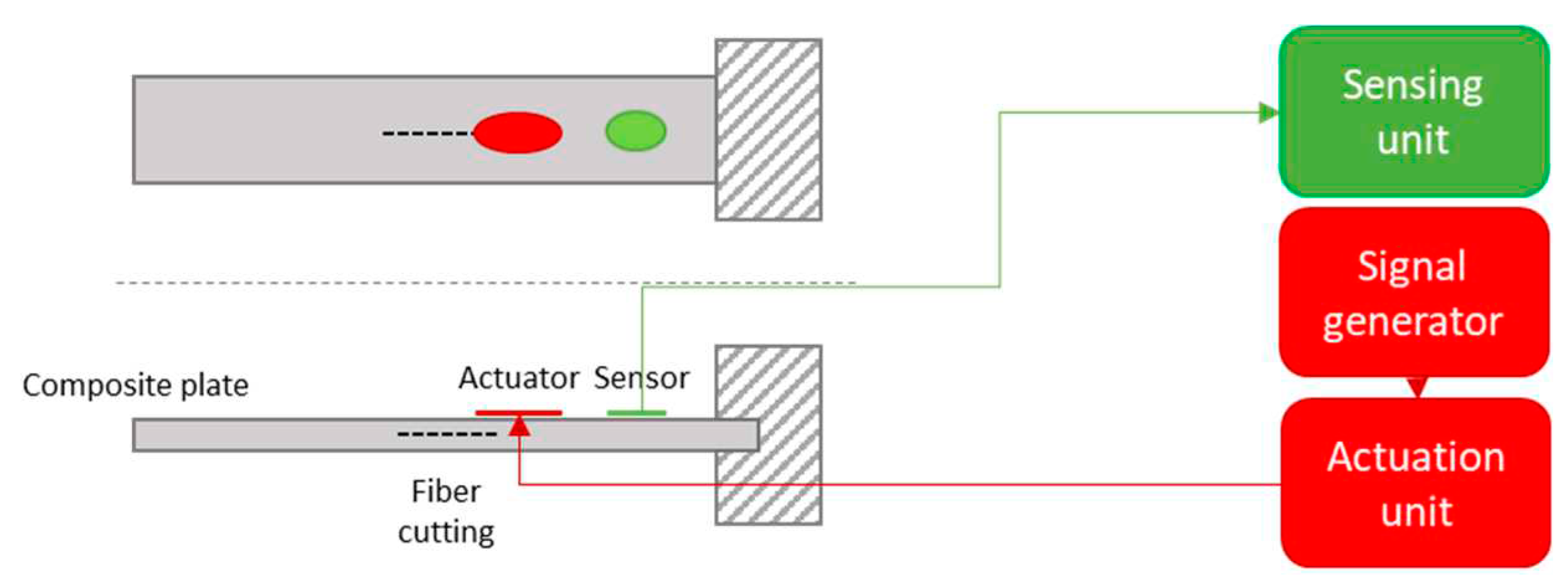
Figure 10.
Loss of natural frequency with increase of damage severity for sandwiches (a)(adapted from [64,65]) and laminate (b) (adapted from [63]).
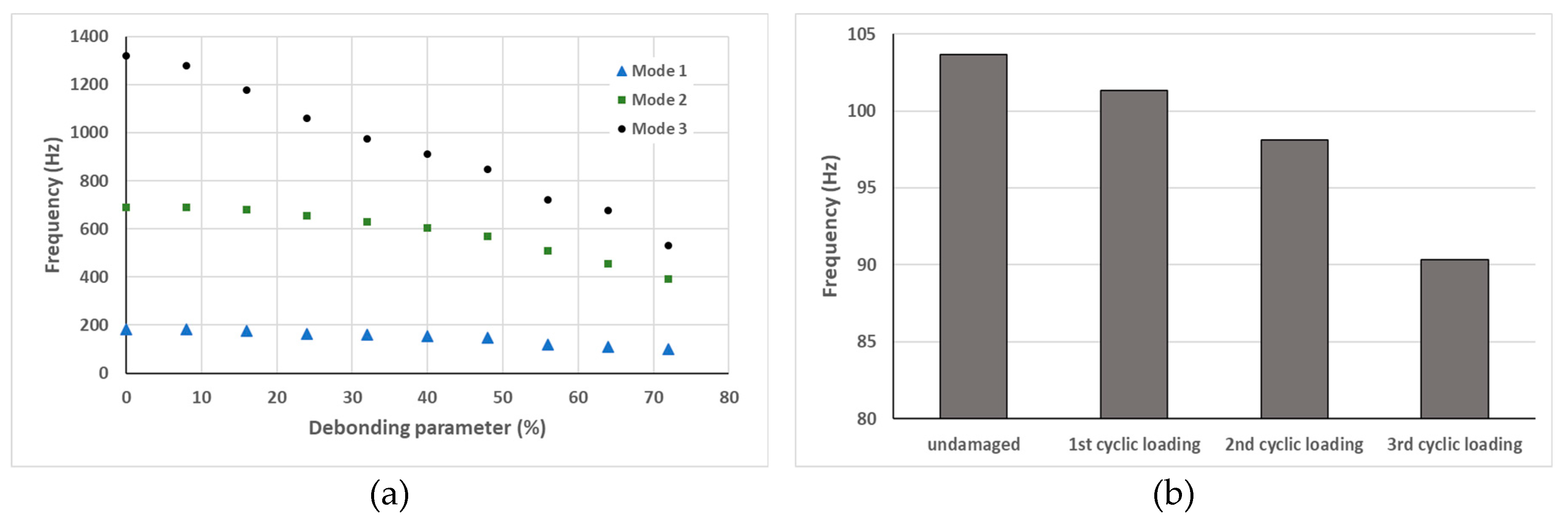
Figure 11.
Two first modes of vibration of a fixed string.
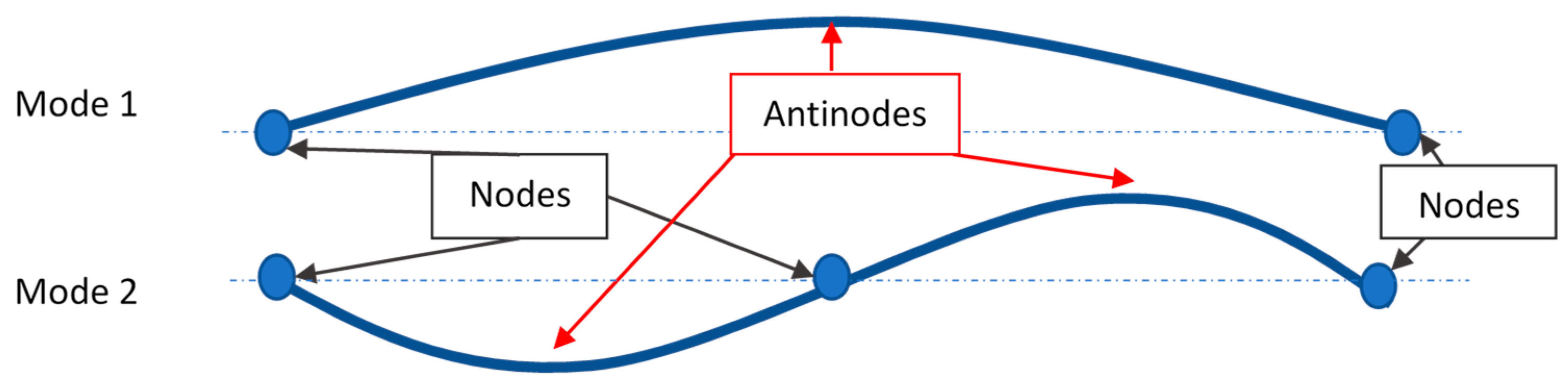
Figure 12.
Typical MAC: No similar way of moving of the modes (a) and some modes with a similar way of moving (b).
Figure 12.
Typical MAC: No similar way of moving of the modes (a) and some modes with a similar way of moving (b).
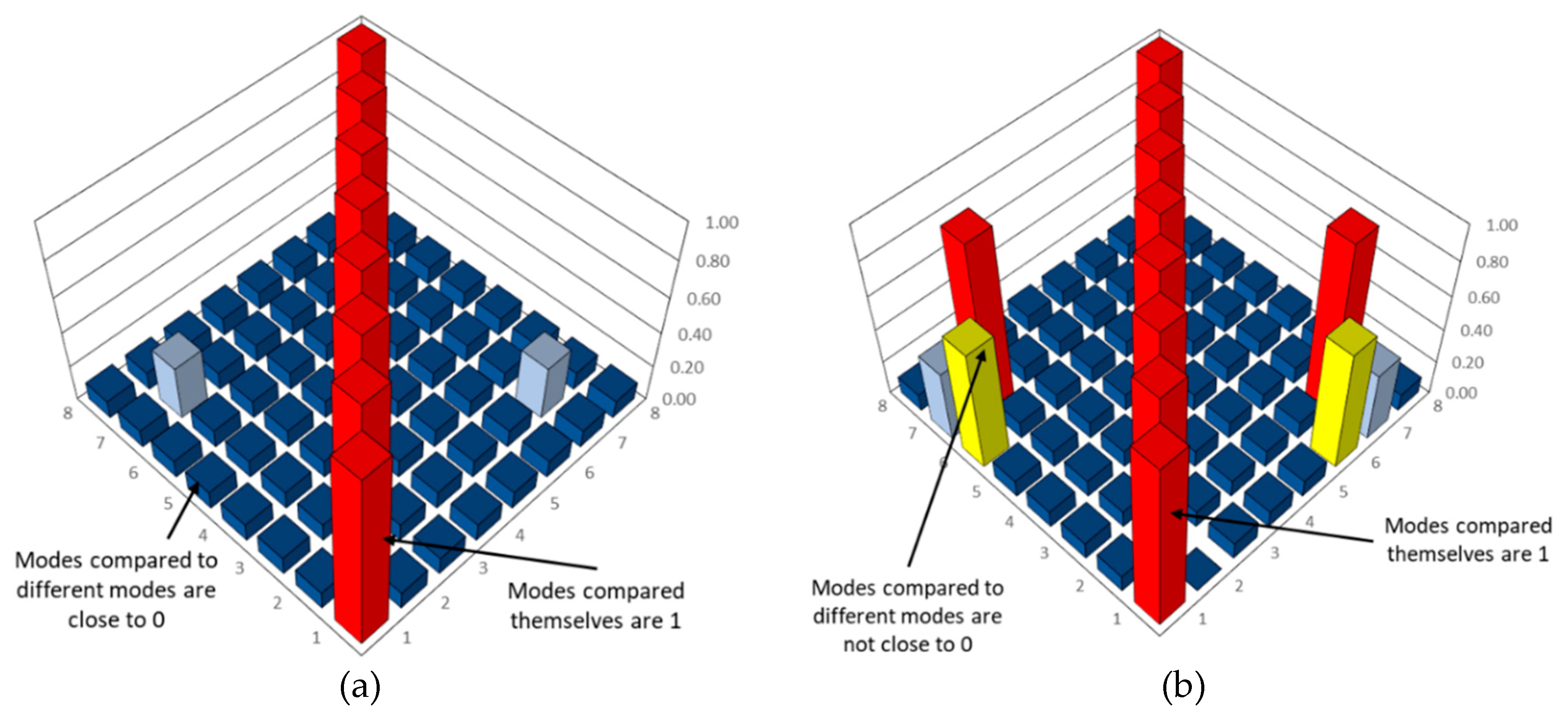
Figure 13.
Schematic of the experimental setup (adapted from [76]).
Figure 13.
Schematic of the experimental setup (adapted from [76]).
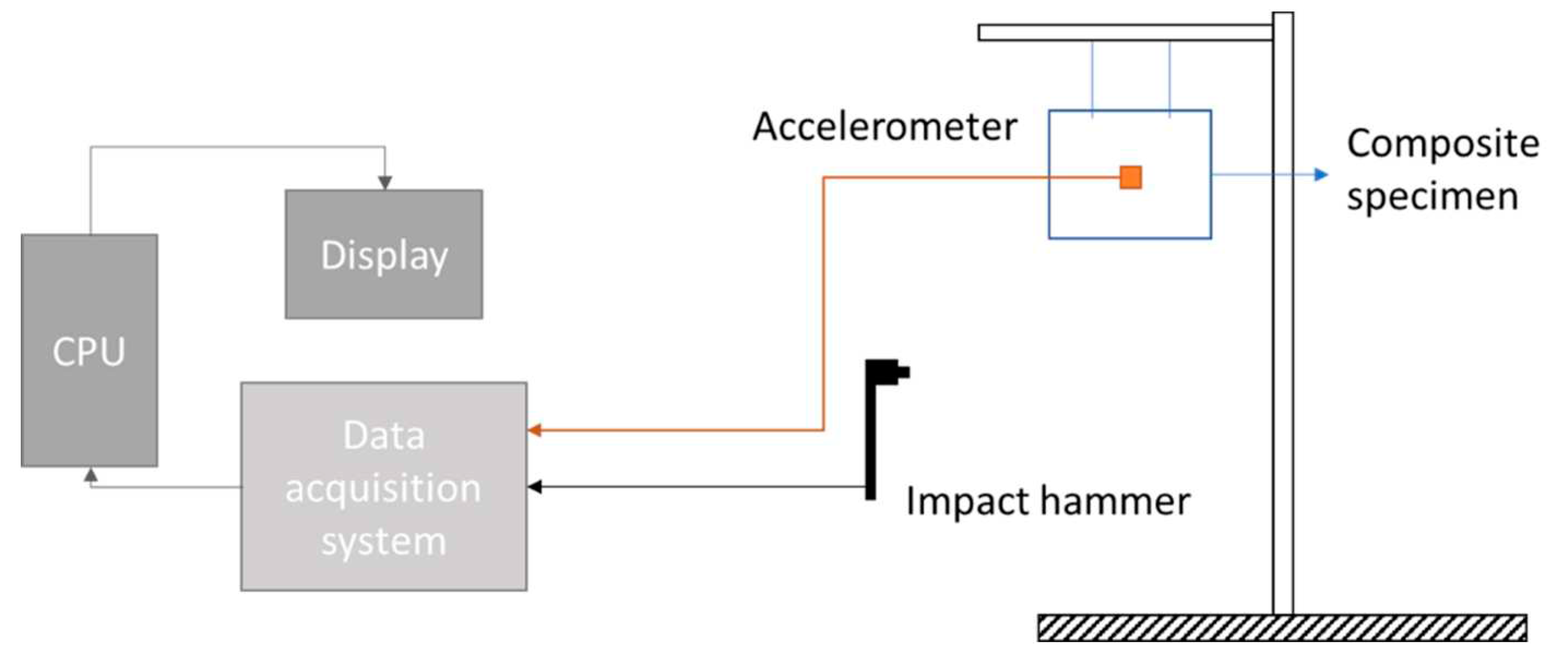
Figure 14.
Helicopter blade made of composite suspended with wires (adapted from [77]).
Figure 14.
Helicopter blade made of composite suspended with wires (adapted from [77]).
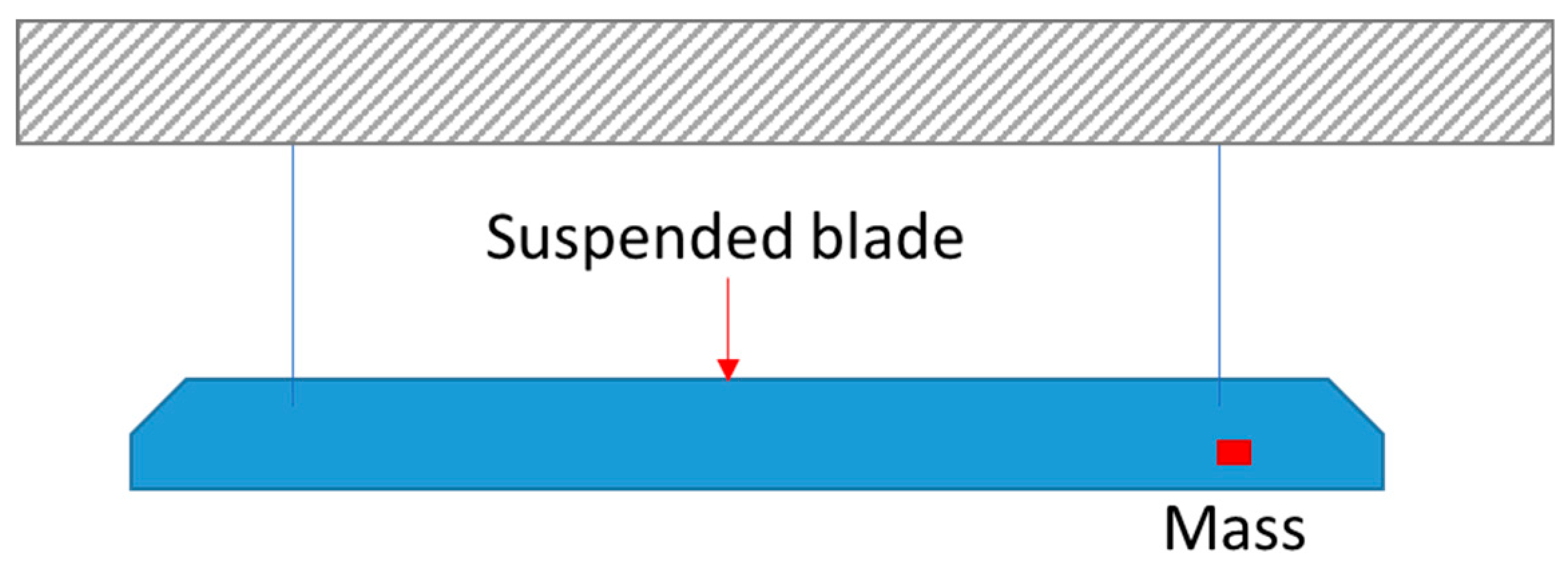
Figure 15.
Example of MSC for a different level of damage - Damage at the red arrow.

Figure 18.
Woven laminate and the grid of measured points for global and local testing (adapted from [95]).
Figure 18.
Woven laminate and the grid of measured points for global and local testing (adapted from [95]).

Figure 19.
Example of flexibility change for different levels of damage - Damage at red arrow.
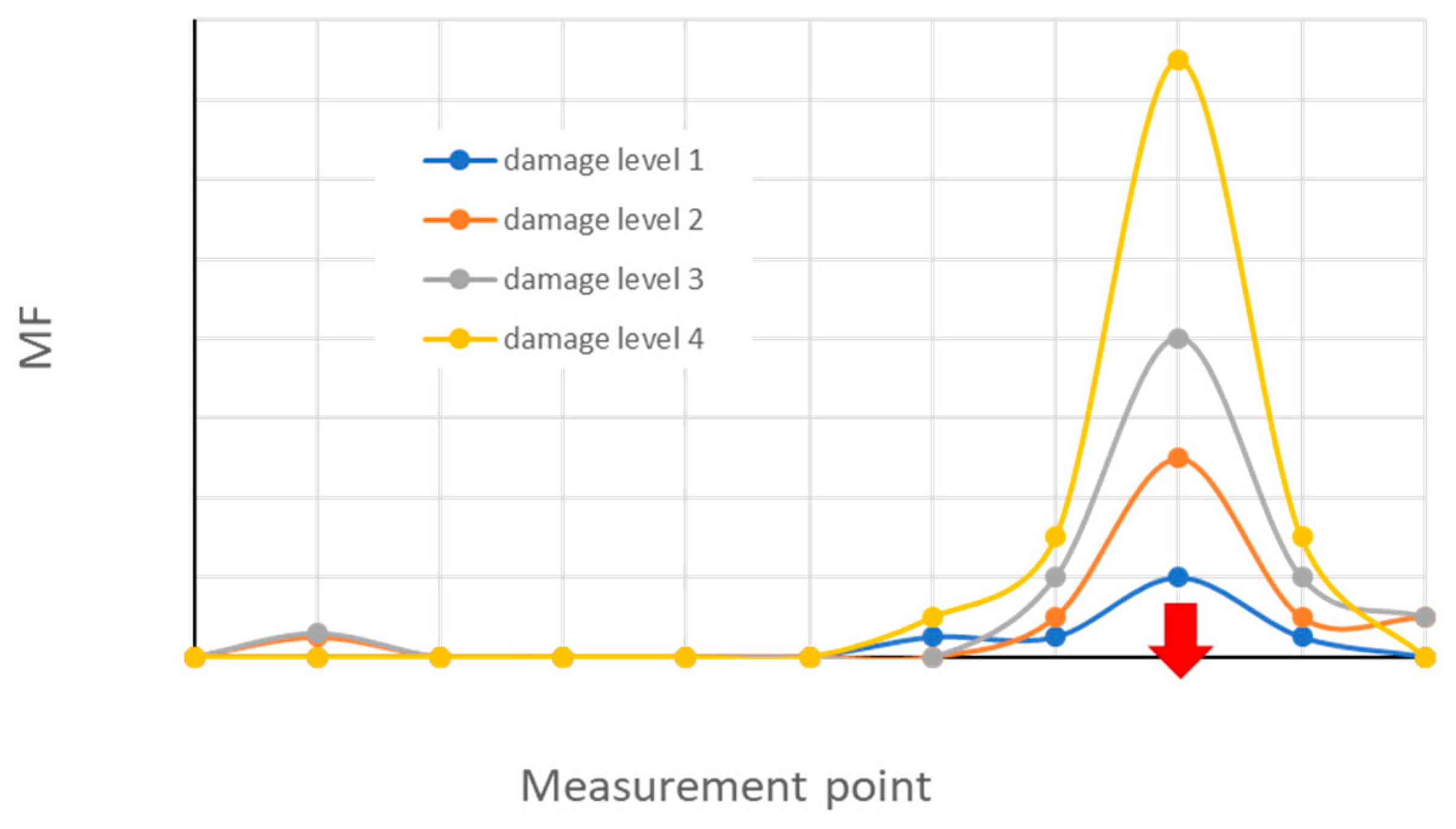
Figure 20.
Comparison of MF with mode shapes, curvature and strain energy methods on locating the different damage scenarios (adapted from [100]).
Figure 20.
Comparison of MF with mode shapes, curvature and strain energy methods on locating the different damage scenarios (adapted from [100]).
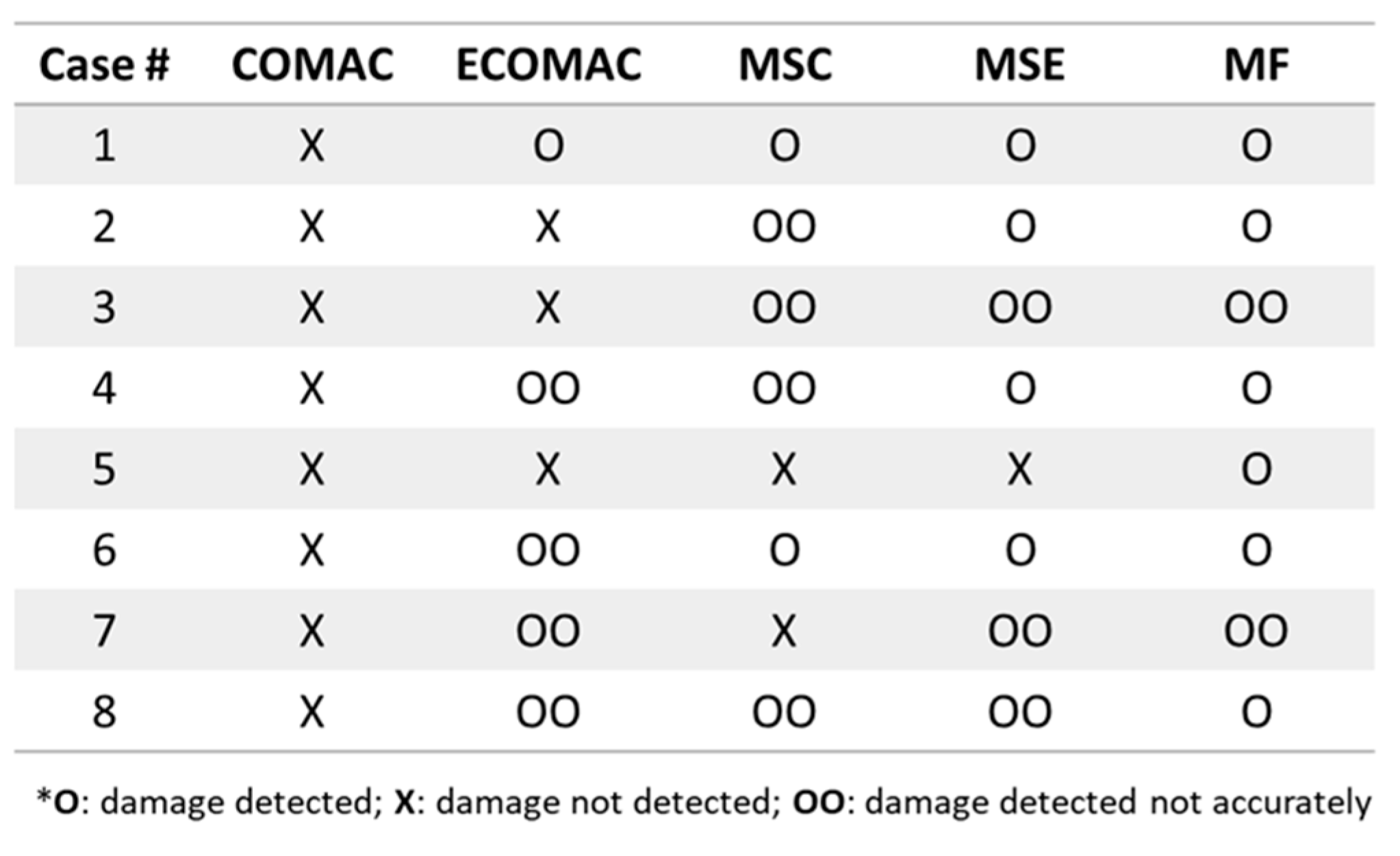
Figure 21.
Difference of sensibility between damping and natural frequency methods (adapted from [102]).
Figure 21.
Difference of sensibility between damping and natural frequency methods (adapted from [102]).
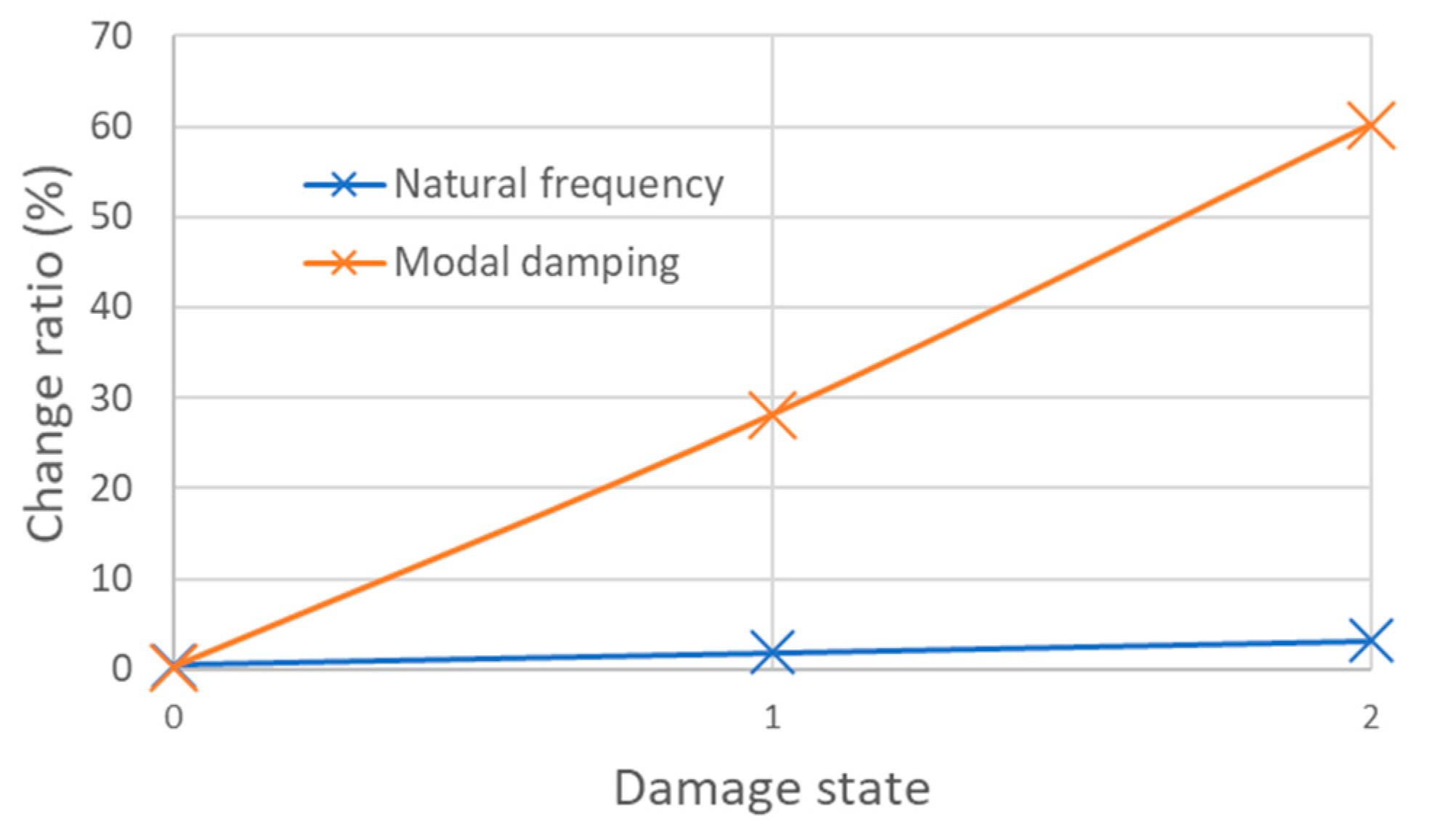
Figure 22.
Different damping quantities.
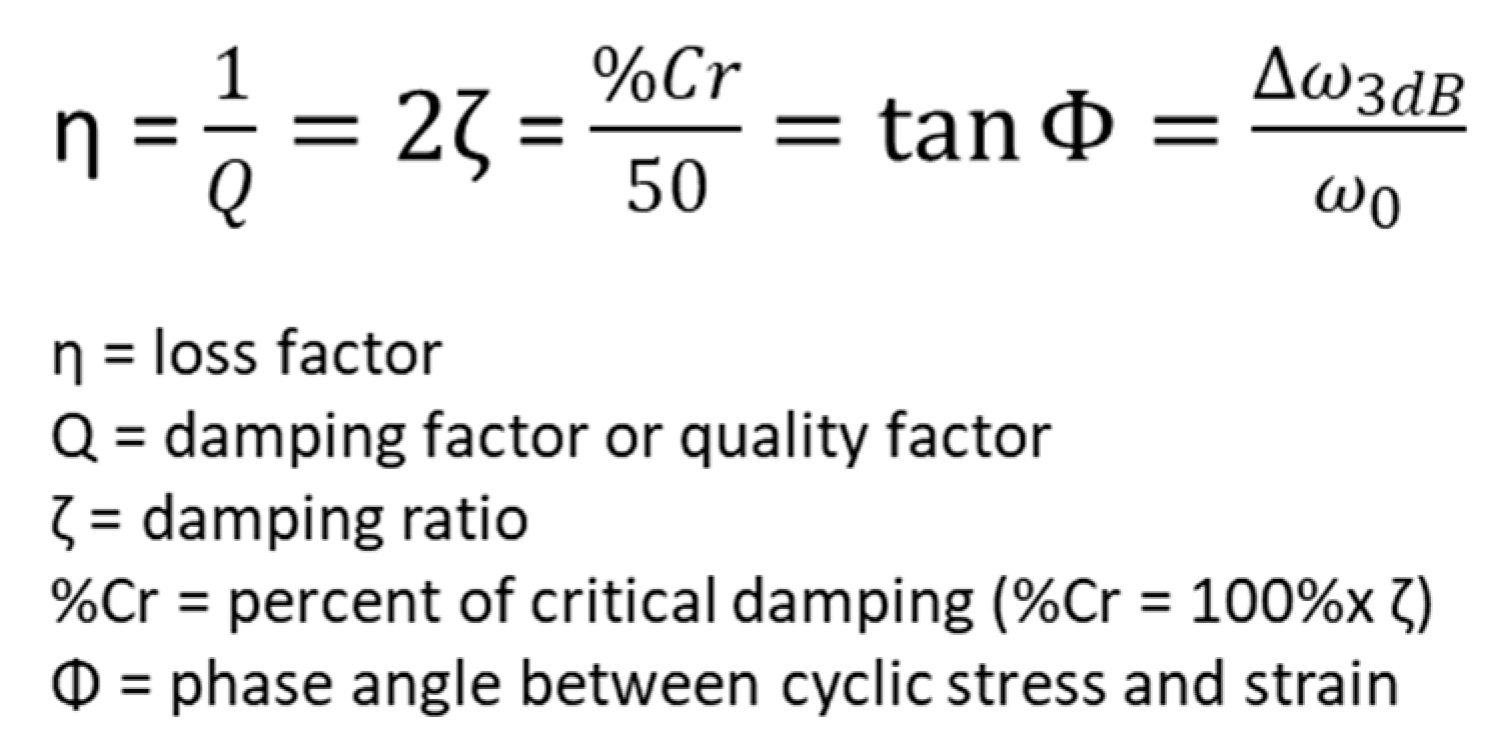
Figure 23.
-3dB method.

Figure 24.
Loss factor increase with the increase of damage severity for the sandwich (a) (adapted from [64,65]) and laminate (b) (adapted from [63]).
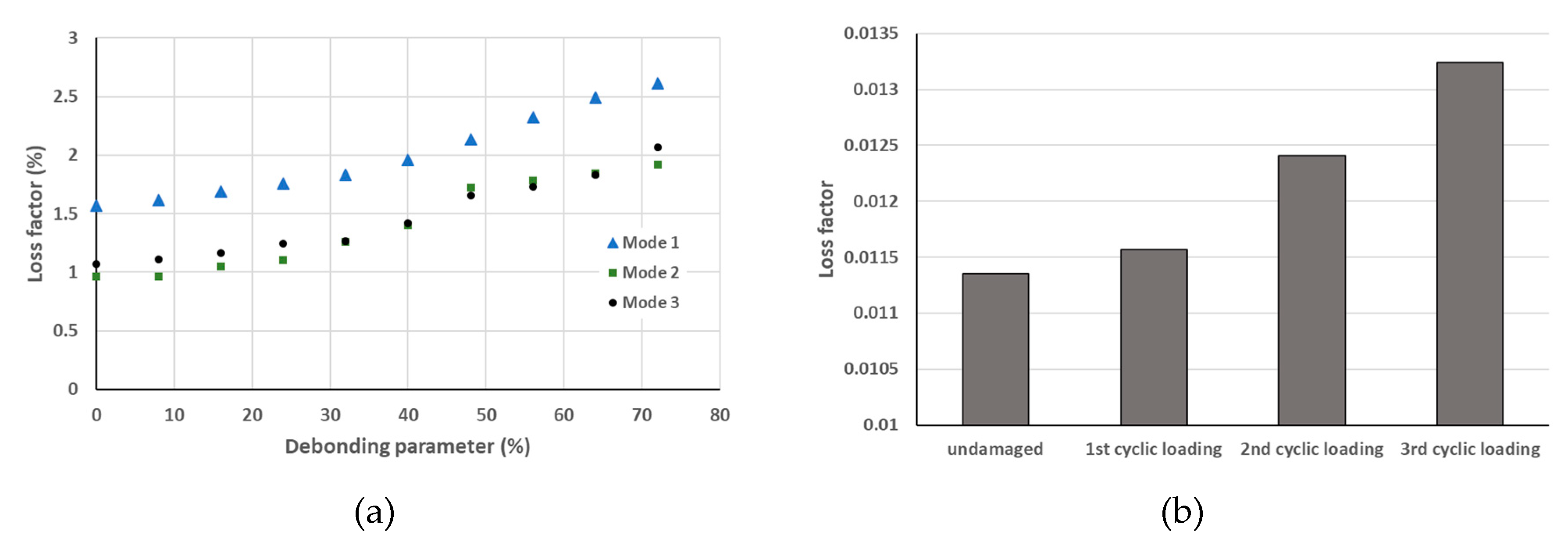
Figure 25.
Damage indicator of TF for different frequency ranges, damage on path 2-3 (adapted from [112]).
Figure 25.
Damage indicator of TF for different frequency ranges, damage on path 2-3 (adapted from [112]).
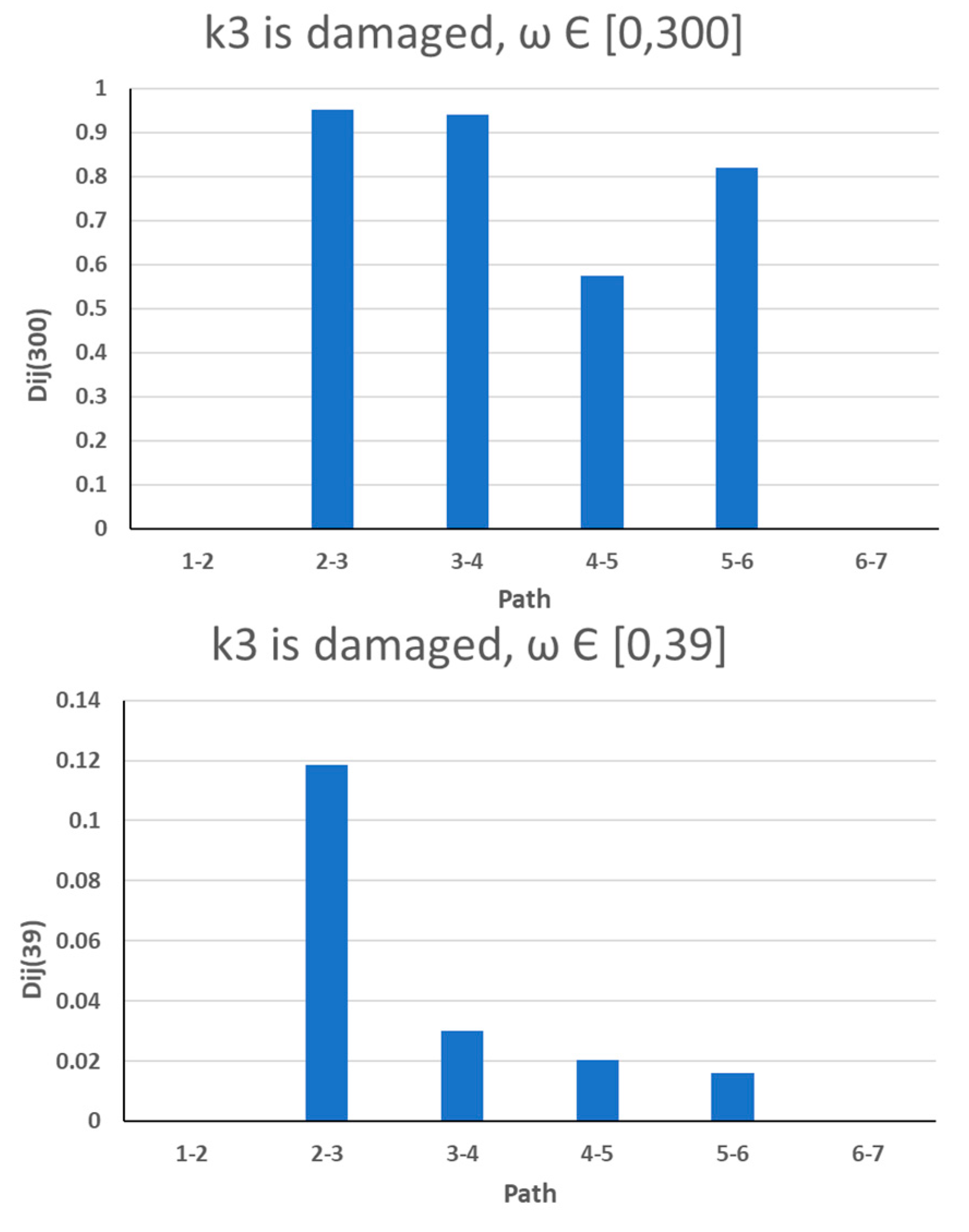
Figure 26.
Experimental setup of the cantilever fiberglass beam with 8 accelerometers and one PZT actuator (adapted from [113]).
Figure 26.
Experimental setup of the cantilever fiberglass beam with 8 accelerometers and one PZT actuator (adapted from [113]).
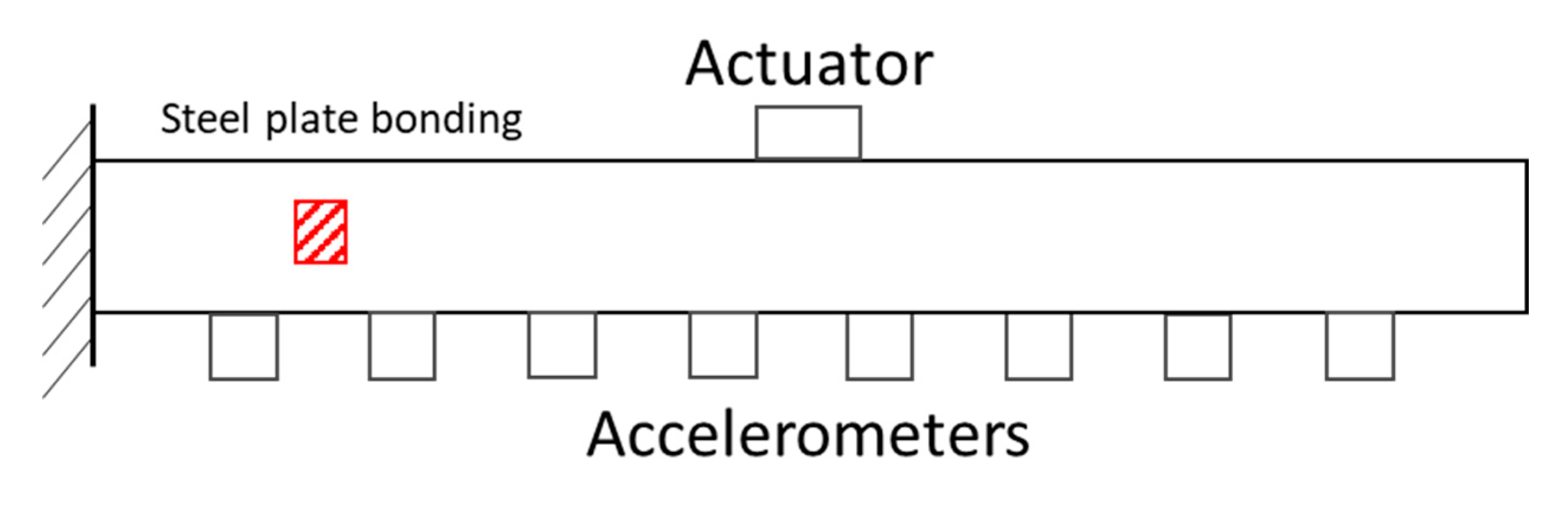
Figure 27.
TF variance DI, damage between path 11-15 (adapted from [114]).
Figure 27.
TF variance DI, damage between path 11-15 (adapted from [114]).
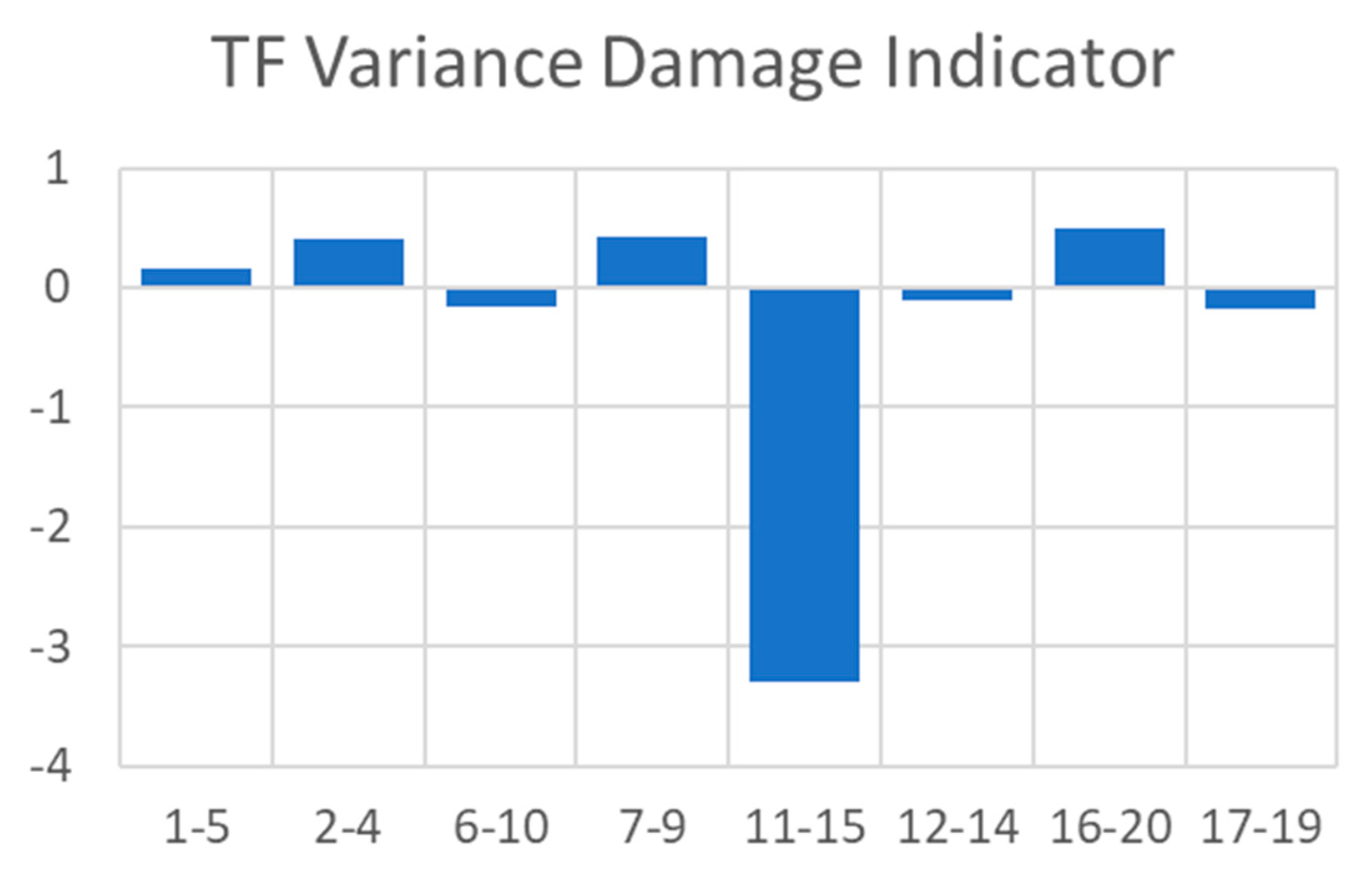
Figure 28.
Schematic of the SFE method of (adapted from [118]).
Figure 28.
Schematic of the SFE method of (adapted from [118]).
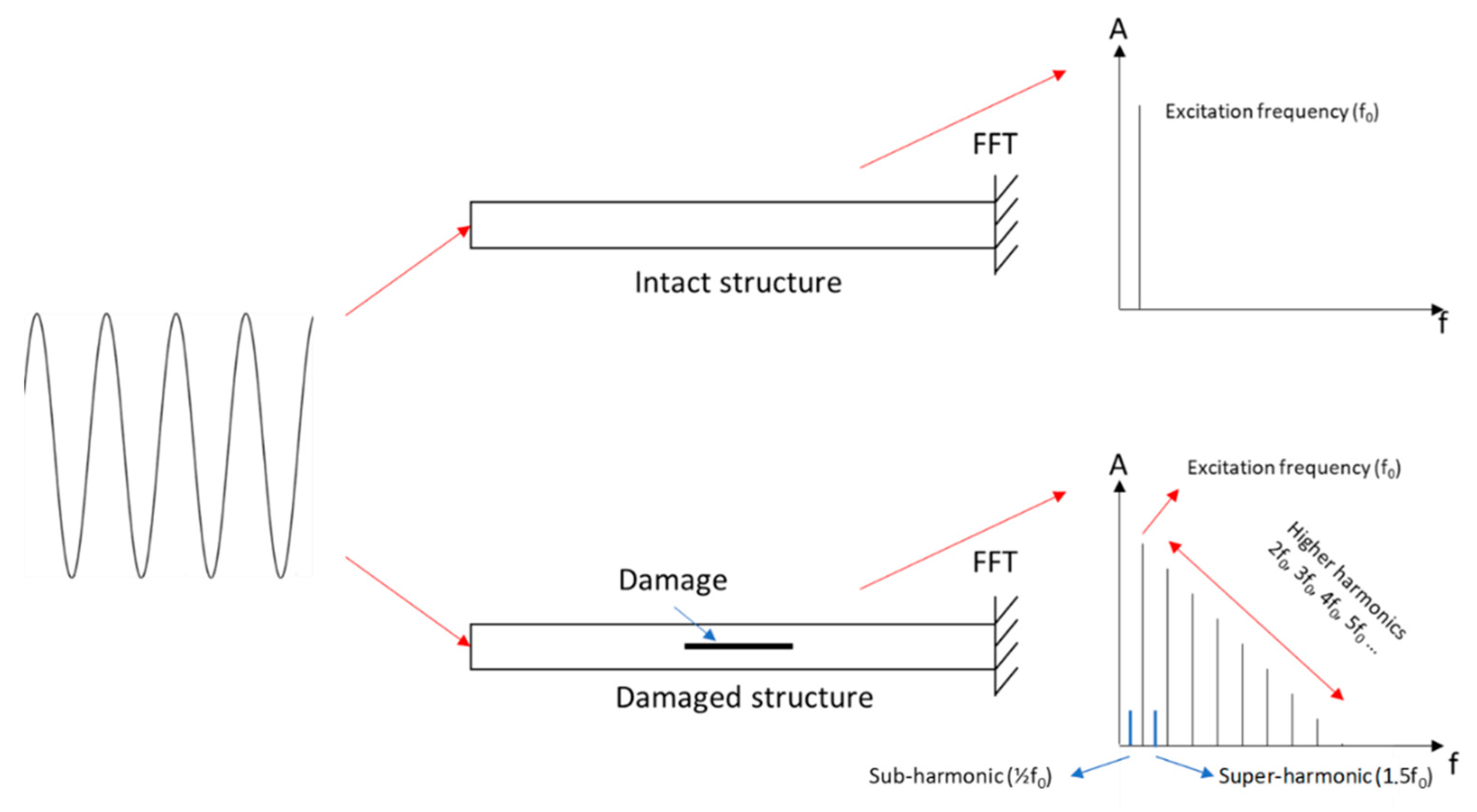
Figure 29.
Time-domain signal of the voltage of the structure under a harmonic signal excitation – intact (a) and damaged (b) structures.
Figure 29.
Time-domain signal of the voltage of the structure under a harmonic signal excitation – intact (a) and damaged (b) structures.
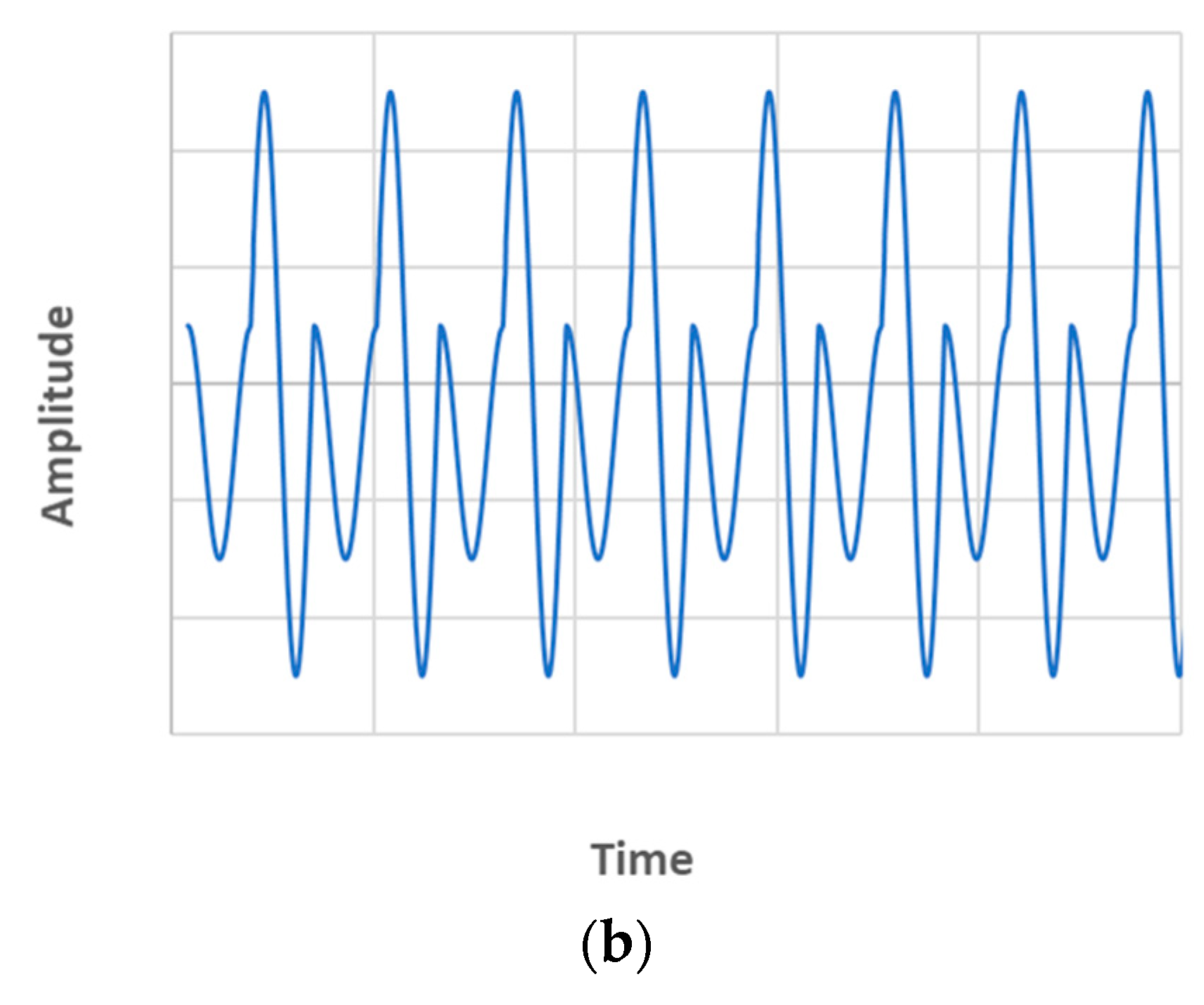
Figure 30.
Phase portrait: velocity vs displacement for intact (a) and damaged (b) structures (adapted from [119]).
Figure 30.
Phase portrait: velocity vs displacement for intact (a) and damaged (b) structures (adapted from [119]).

Figure 31.
Composite plate with 5 PZT transducers and 2 delaminations (adapted from [118]).
Figure 31.
Composite plate with 5 PZT transducers and 2 delaminations (adapted from [118]).

Figure 32.
PMC plate used to perform the nonlinear vibration analysis. Delamination is introduced in the center of the plate. PVDF and accelerometer are used as sensors [120].
Figure 32.
PMC plate used to perform the nonlinear vibration analysis. Delamination is introduced in the center of the plate. PVDF and accelerometer are used as sensors [120].

Figure 33.
Specimen and damage specification (adapted from [121]).
Figure 33.
Specimen and damage specification (adapted from [121]).
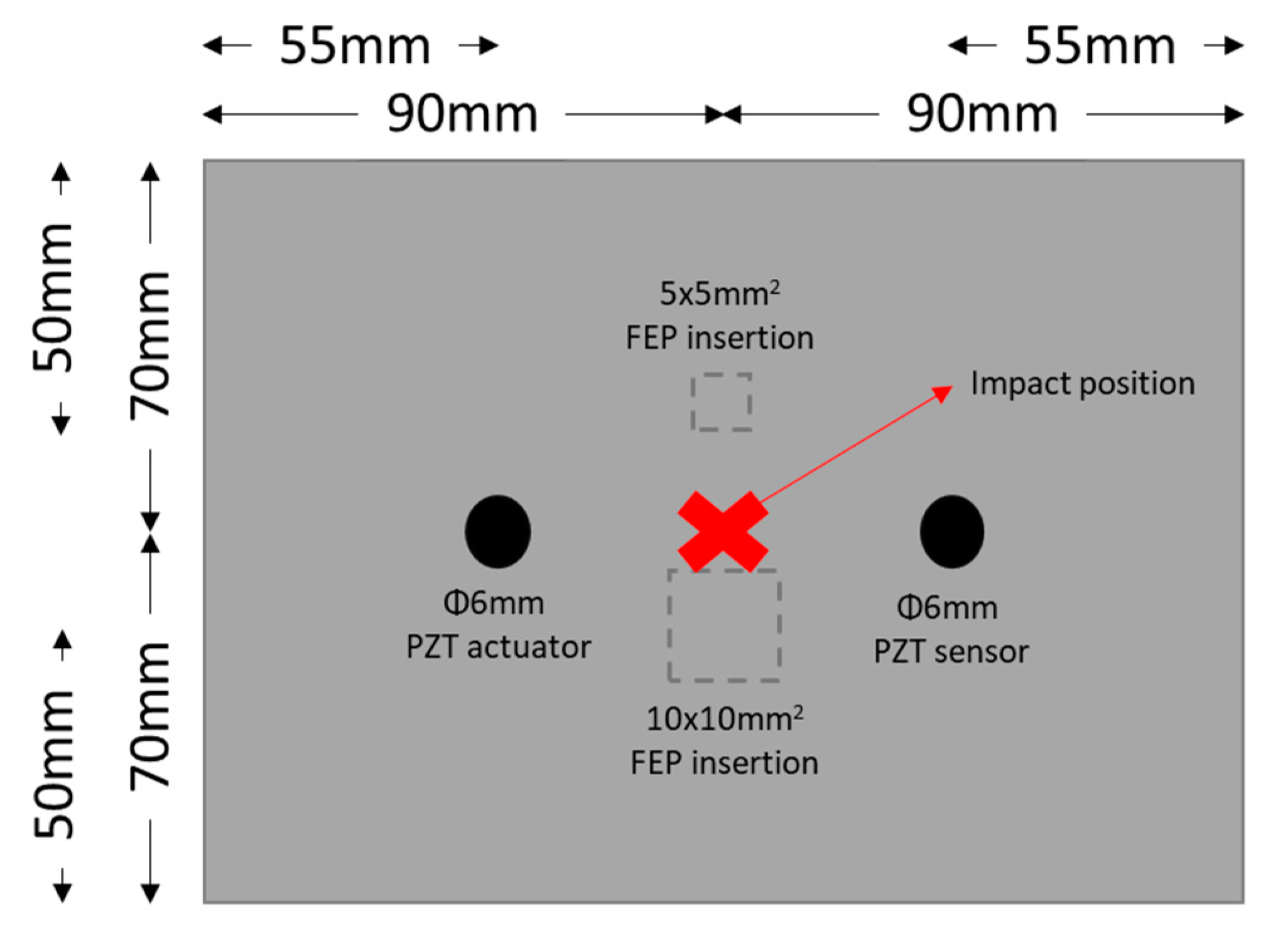
Figure 34.
Schematic of the SWP method (adapted from [118]).
Figure 34.
Schematic of the SWP method (adapted from [118]).
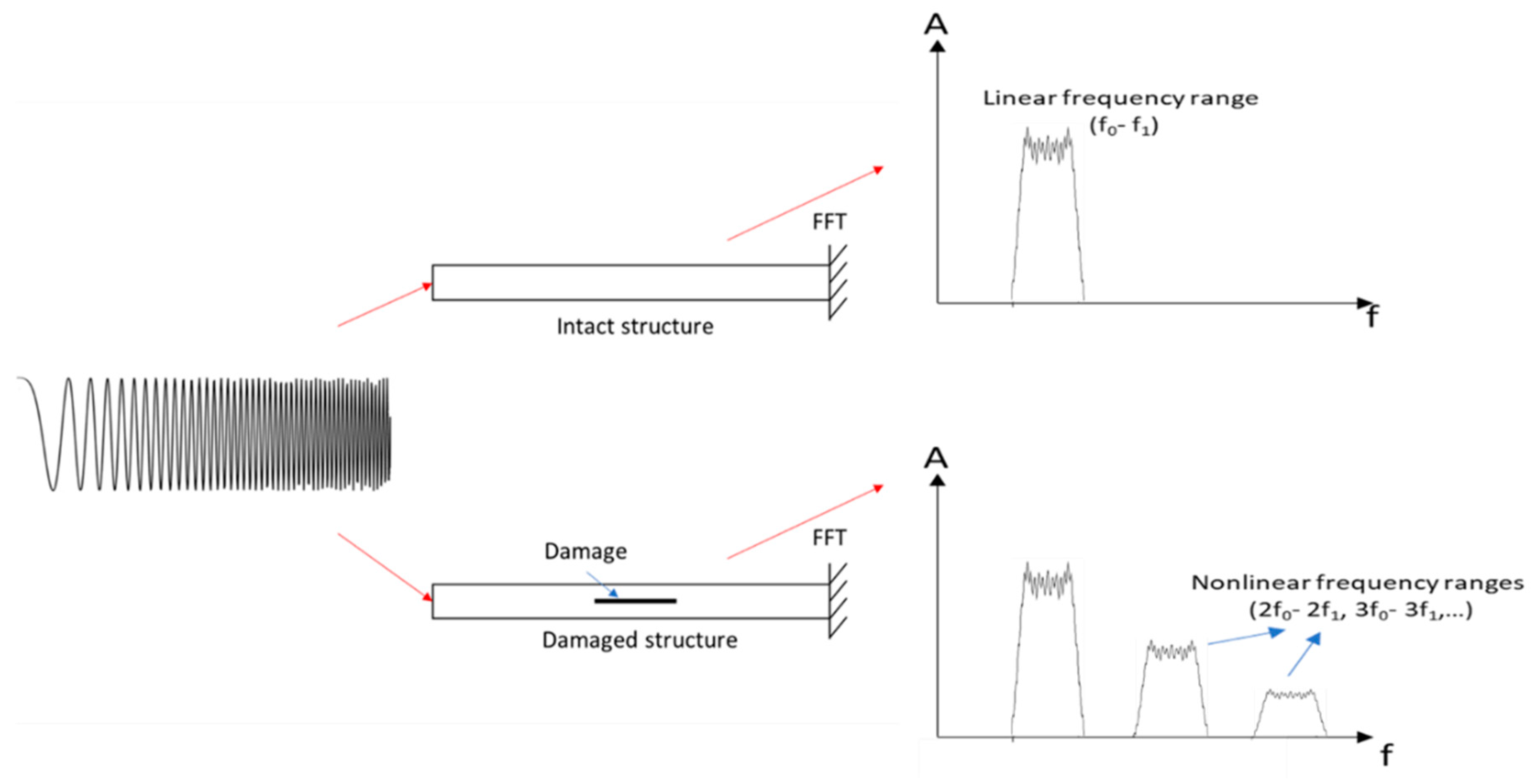
Figure 35.
Frequency shift for several amplitudes of excitation for intact (a) and damaged (b) structure.
Figure 35.
Frequency shift for several amplitudes of excitation for intact (a) and damaged (b) structure.
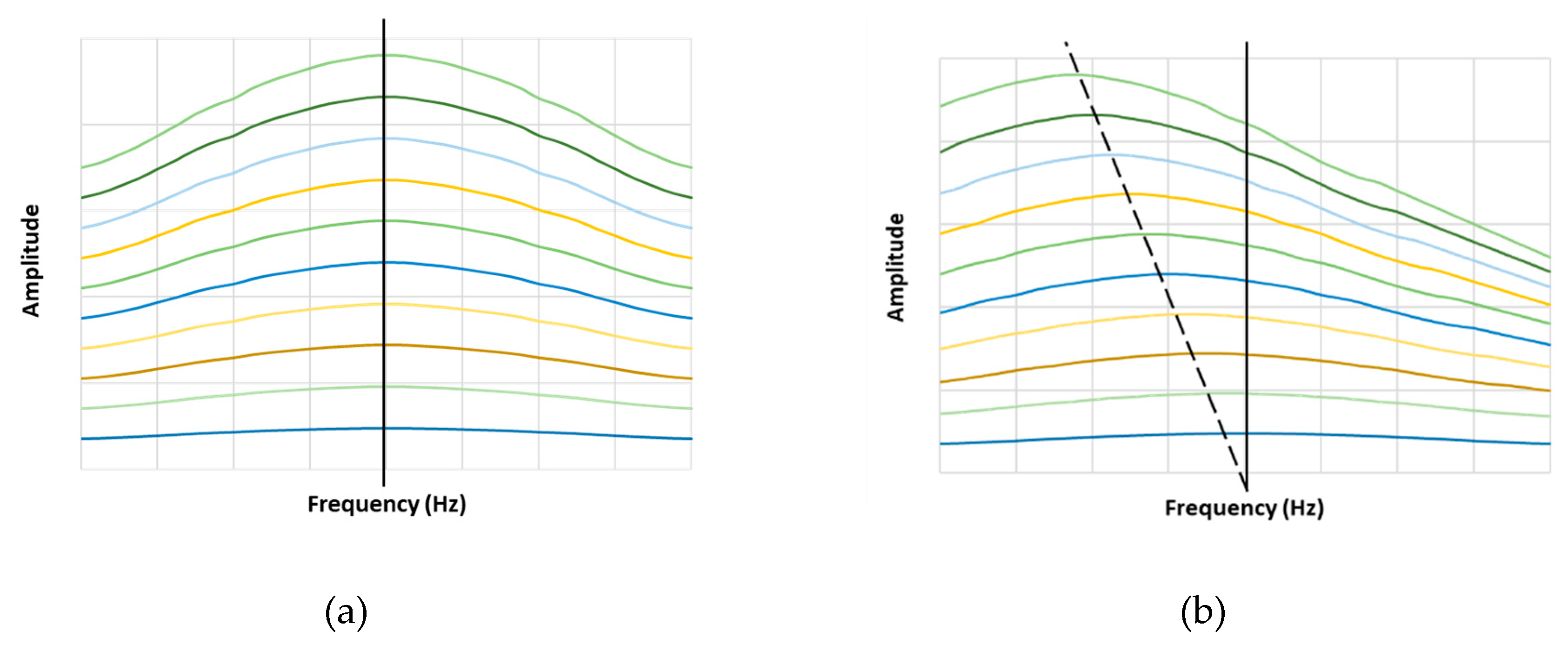
Figure 36.
Nonlinear elastic parameter sensibility against the linear frequency loss parameter: debonding on sandwich (a) (adapted from [64]) and fatigue damage induced on laminate (b) (adapted from [63]).
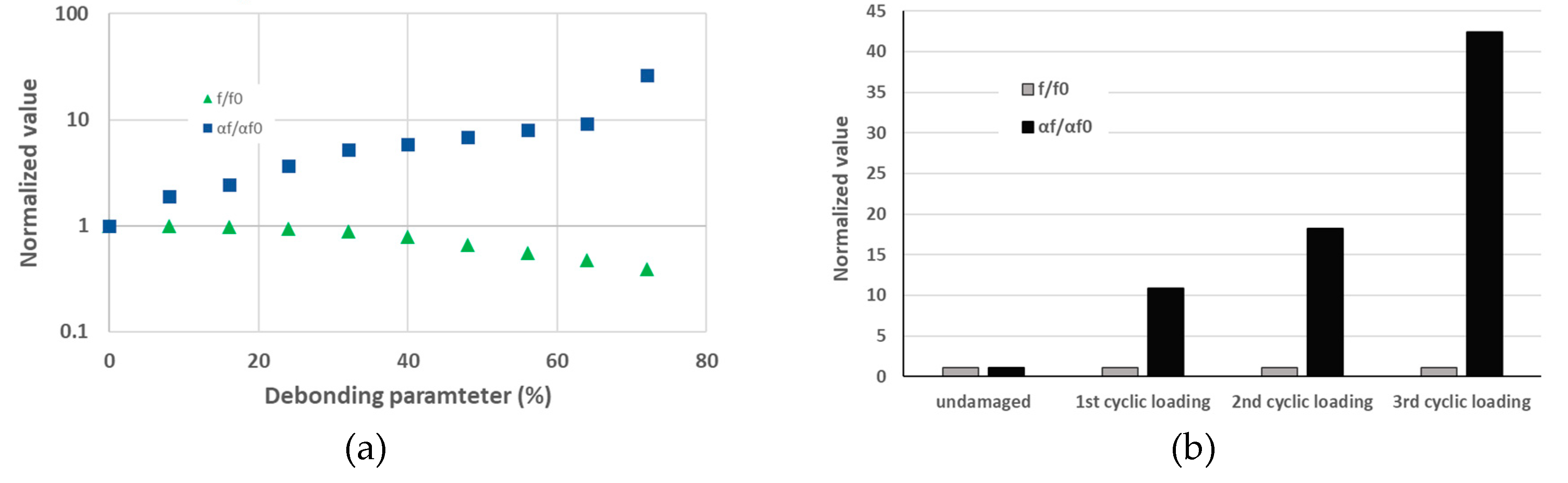
Figure 37.
Delamination area function of the nonlinear parameter (adapted from [126]).
Figure 37.
Delamination area function of the nonlinear parameter (adapted from [126]).
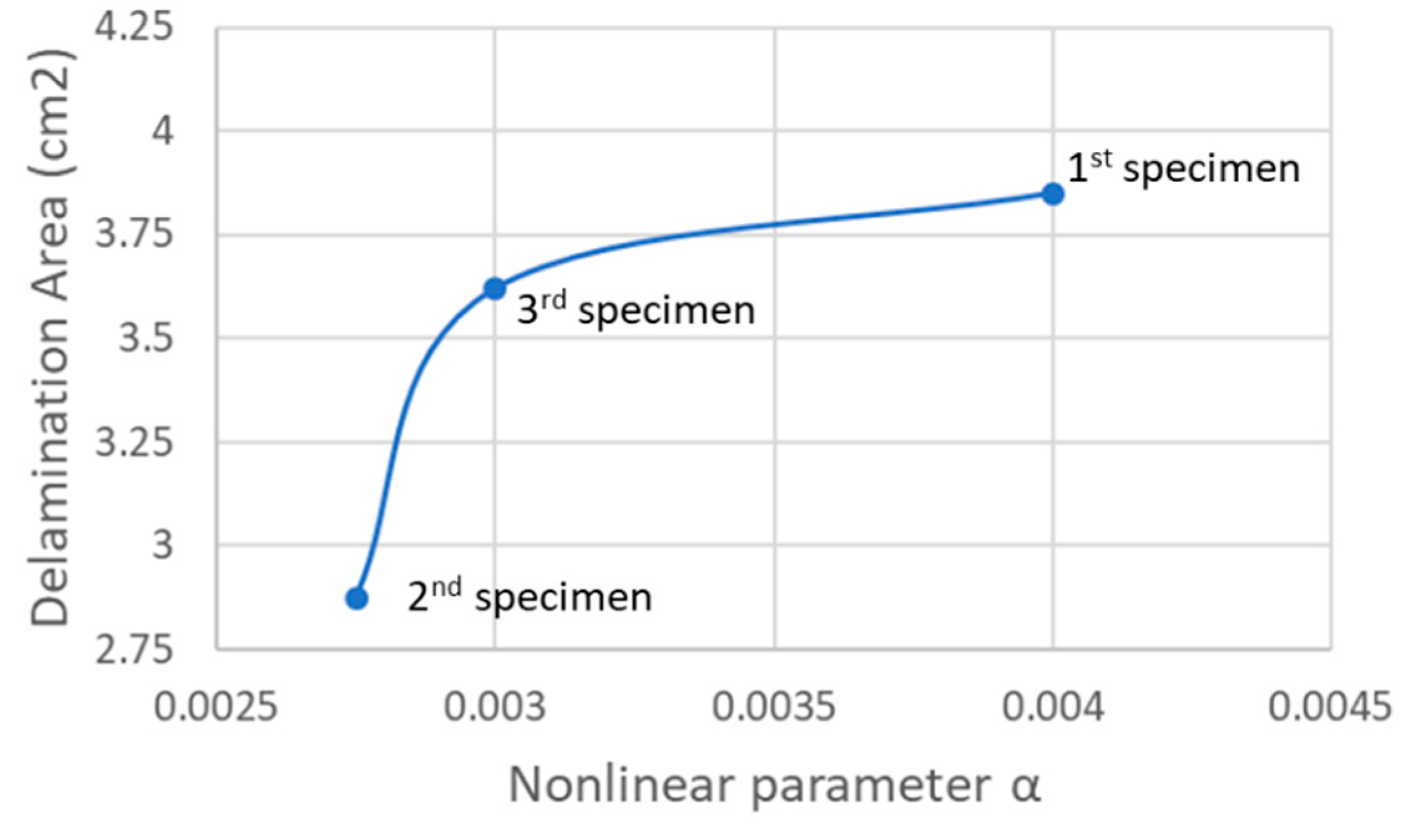
Figure 38.
Time of relaxation of 4 damage levels of a PMC structure (adapted from [128]).
Figure 38.
Time of relaxation of 4 damage levels of a PMC structure (adapted from [128]).

Figure 39.
Schematic of the VAM method (adapted from [118]).
Figure 39.
Schematic of the VAM method (adapted from [118]).
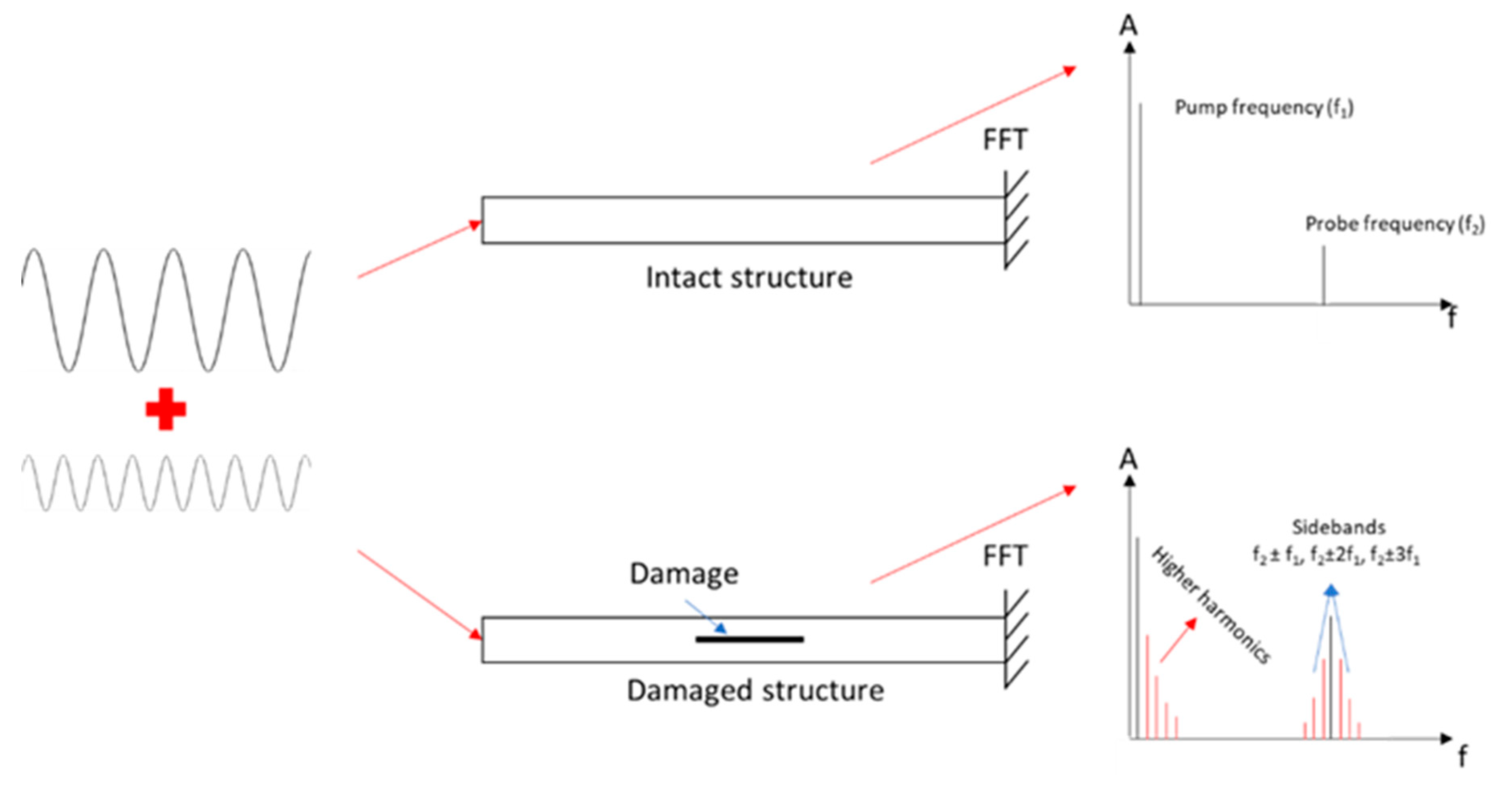
Figure 40.
Effect of increasing clamping force on fundamental and sidebands amplitude, for the undamaged and damaged plate (adapted from [138]).
Figure 40.
Effect of increasing clamping force on fundamental and sidebands amplitude, for the undamaged and damaged plate (adapted from [138]).
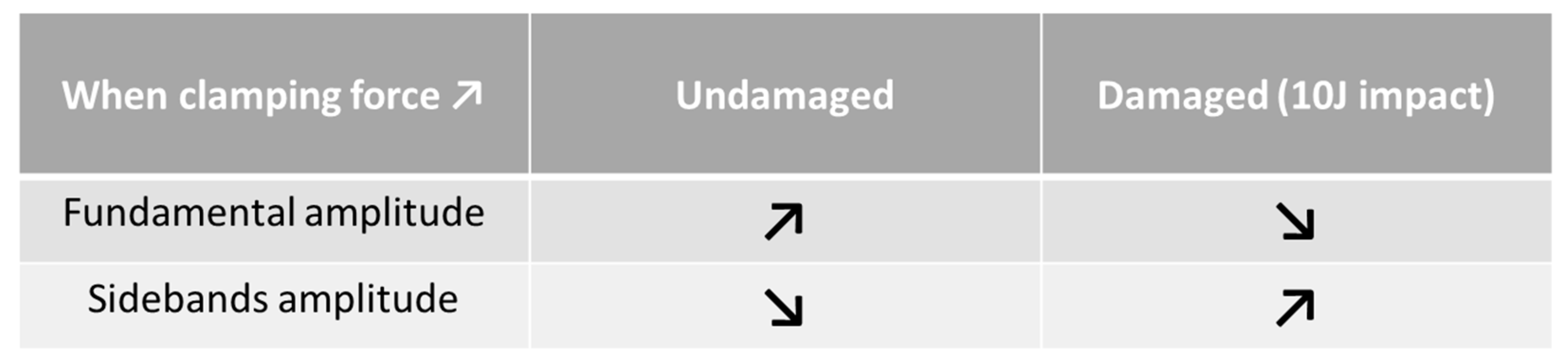
Figure 41.
Nonlinear dissipative parameter sensibility against the linear loss factor parameter: debonding on a sandwich (a) (adapted from [64]) and fatigue damage induced on the laminate (b) (adapted from [63]).
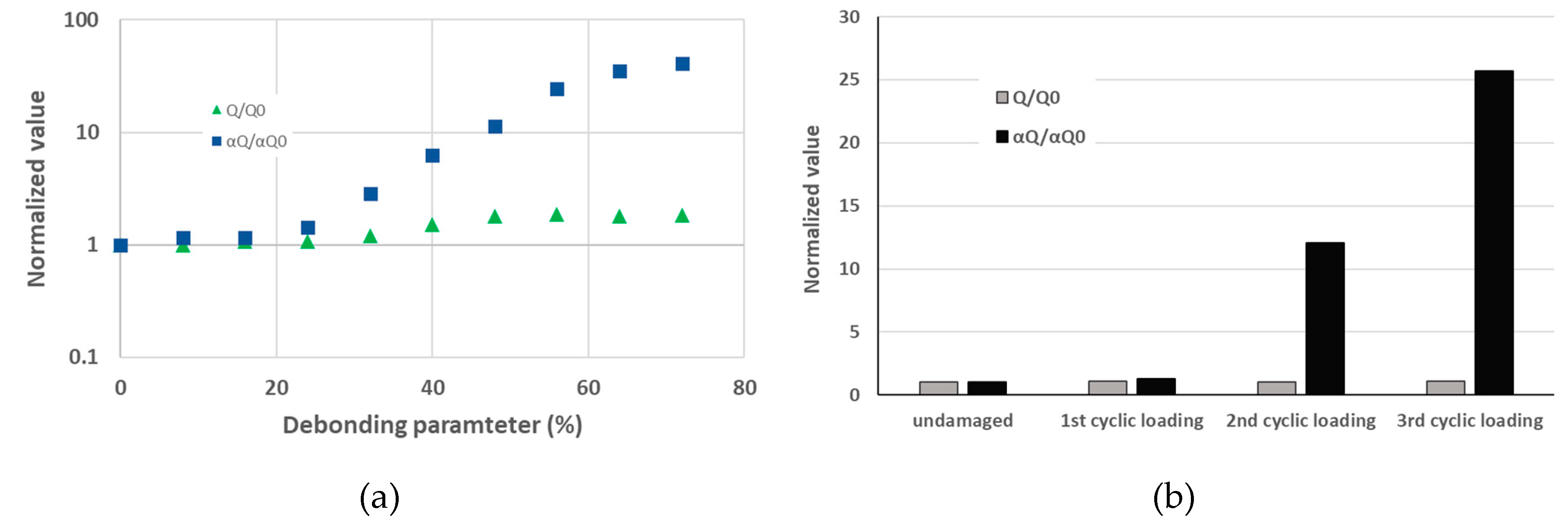
Figure 42.
Decision tree of vibration methods for specific damage in PMC structure.
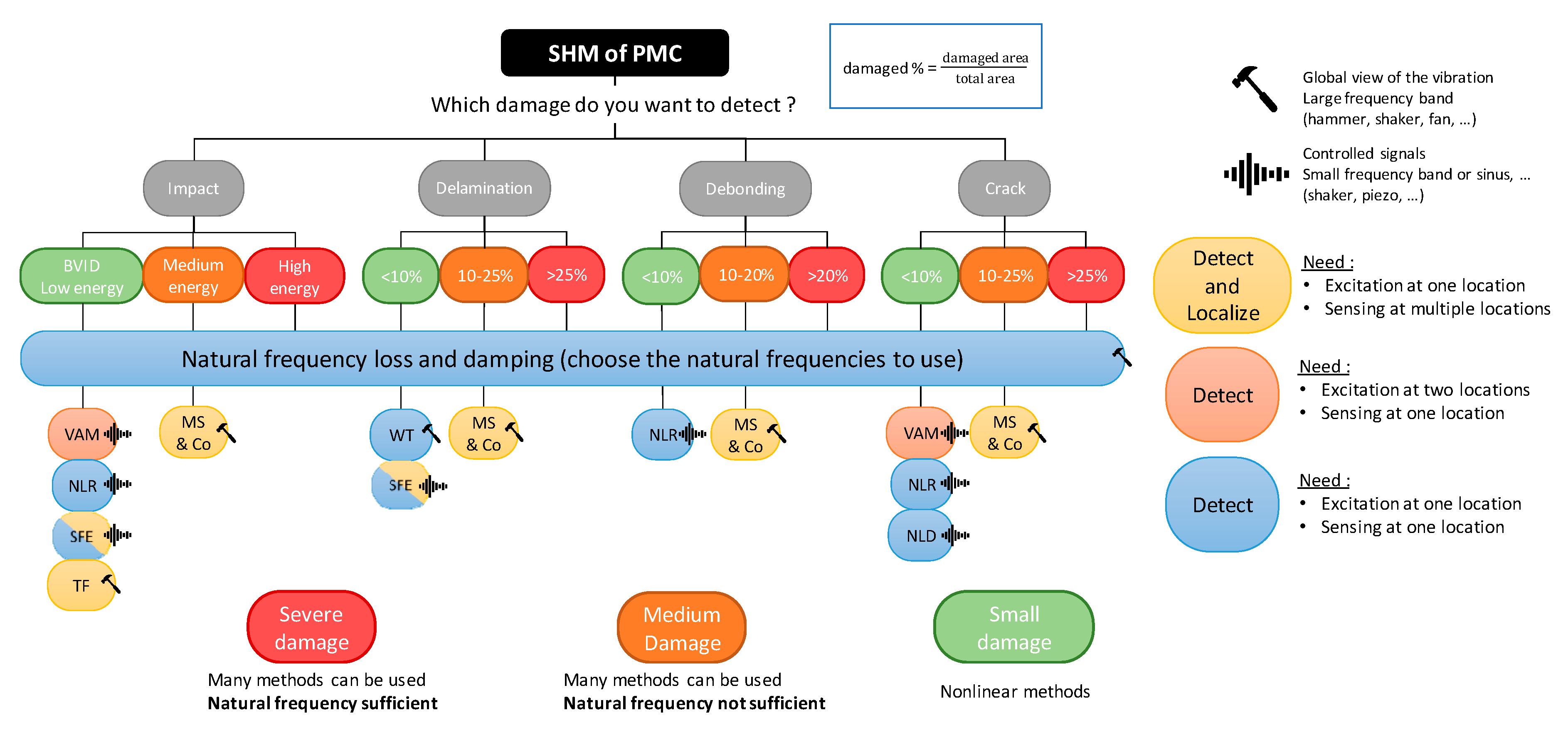
Table 1.
PMCs composition.
| Reinforcement (fiber) | Matrix (polymer) | |
| Thermoplastics | Thermosets | |
|
|
|
Table 2.
List of possible equipment for modal analysis.
| Equipment | Additional Equipment | Details | |
|---|---|---|---|
| Fixation | Foam Wire Clamping system Fixed-fixed |
“ | “ |
| Input | Impact hammer Manual action Fan |
“ | “ |
| Shaker Loudspeaker |
Generator – Amplifier | “ | |
| PZT | Generator – Piezo amplifier |
40-100V out of the amplifier | |
| PVDF | 500V out of the amplifier | ||
| MFC | Generator | “ | |
| Output | Accelerometer Laser Vibrometer (LV) Piezoelectric sensors |
Analyzer and PC Oscilloscope |
“ |
Table 3.
Other articles about the experimental use of natural frequency shift for SHM.
| Structure | Fixation | Input | Output | Damage | Description | Ref |
|---|---|---|---|---|---|---|
| Graphite/epoxy laminated plate | Fixed in V-blocks | Accelerometers | Delamination (Fluorinated Ethylene Propylene (FEP) patches) | 4 first natural frequencies have been used to observe that delamination has effects on the frequency loss, 1/3 of the area of the specimen will lead to 20% of max defect | [66] | |
| Carbon/cyanate laminated plate | Cantilever configuration | Surface bonded bimorph PZT patch actuator QP25N (150V) Agilient 33120A waveform generator CX Quickpack Amplifier |
LV | Delamination (plastic film) | Natural frequencies are used to identify delamination in composite plates, a small loss of natural frequencies is observed, especially for higher modes (20% of decrease) | [67] |
| Glass/epoxy laminated beam | Cantilever configuration | Impact hammer G1195 PZT bonded patch (sine sweep signal) Amplifier |
PVDF bonded patch Analyzer (HP35665A) |
Delamination (Teflon patches) | Natural frequencies shift induced by delamination is used to feed a NN, the natural frequencies became lower when the structure is damaged | [68] |
| Carbon and Kevlar/epoxy laminated beam | Cantilever configuration | Impact hammer PZT |
Accelerometer PZT |
Delamination (FEP patches) | Natural frequencies decrease is observable for the damaged structure, for both PZT and accelerometer sensors | [69] |
| Circular glass/epoxy laminated plate | Suspended with 3 flexibles | Loudspeaker Oscillator and amplifier |
Accelerometer Oscilloscope |
Delamination (impact 45J) | Natural frequencies tend to decrease when the delamination area gets bigger and bigger, for mode 1 and 6, the natural frequency increase after reaching a delamination area (probably induced by a local change of the geometry) | [70] |
| Glass/polyester laminated beam | Suspended by flexible | Impact hammer | Accelerometer Analyzer |
Crack | Natural frequencies tend to decrease when the crack size increases, and some modes seemed more influenced by this damage | [71] |
Table 7.
DI results for 3 different delamination and 16 sub-wavelets: the threshold at 20% [117].
Table 7.
DI results for 3 different delamination and 16 sub-wavelets: the threshold at 20% [117].
| Delamination area of the total area | ||||
|---|---|---|---|---|
| 0.11% | 0.167% | 0.22% | ||
| Sub-Wavelets | 0 | 1.703 | 2.491 | 0.908 |
| 1 | 8.053 | 6.078 | 21.32 | |
| 2 | 0.403 | 3.718 | -1.005 | |
| 3 | -0.634 | 2.197 | -1.818 | |
| 4 | -14.10 | -45.38 | -6.603 | |
| 5 | 12.83 | 5.221 | 36.42 | |
| 6 | 0.395 | 1.546 | 3.626 | |
| 7 | 6.811 | 5.449 | 17.76 | |
| 8 | 0.961 | 3.068 | -2.736 | |
| 9 | 3.575 | -0.045 | 8.691 | |
| 10 | 0.561 | 4.663 | -1.279 | |
| 11 | 0.165 | 1.226 | -2.389 | |
| 12 | -12.30 | -31.87 | -8.129 | |
| 13 | 3.143 | -2.751 | 17.04 | |
| 14 | 0.412 | 4.026 | -1.193 | |
| 15 | 0.602 | 3.390 | 0.225 | |
Table 8.
Others articles about Single Frequency Excitation for SHM of PMC materials.
| Method | Structure | Fixation | Input | Output | Damage | Description | Ref |
|---|---|---|---|---|---|---|---|
| Higher harmonics | Carbon/epoxy laminated plates | - | Signal generator Power amplifier Periodic signal |
Accelerometer | Barely Visible Impact Damage (BVID) | Higher harmonics are observable and their amplitudes get bigger with higher damage severity | [123] |
| Damage indicator based on the amplitude of higher harmonics | Carbon/epoxy laminated beam | Suspended with nylon cords | PI PL055.31 – piezo actuator Harmonic excitation – 6 V – 1580, 2860 and 3915 Hz |
PZT Oscilloscope |
Impact damage | The first thing observed is that the response of the sensor is a linear function of the excitation amplitude for the intact structure, and this is not the case for the damaged ones. The damage index for the first frequency detected clearly the damage presence, but it was not the case for the two other frequencies. This is why they used a damage index combining all the frequencies. |
[124] |
|
Sub- and super-harmonics Velocity and acceleration distortions Phase portraits |
Skin-stiffener composite structure | Freely suspended by elastic wire | Electromechanical shaker Single tone harmonic excitation signal – 4th bending mode frequency – at different amplitude of excitation |
LV | Damaged from impact testing (delamination) | Super-harmonics were present for the damaged structure. Velocity, acceleration and also phase portrait showed distortion in the time-domain for damaged structure. Link between the motion of the structure and the distortions have been made. Opening and closing phases did not give high distortions, but the contact phase gave these distortions. |
[125] |
Table 9.
Other articles about Frequency shifts from the different amplitudes of excitation methods for SHM.
Table 9.
Other articles about Frequency shifts from the different amplitudes of excitation methods for SHM.
| Structure | Fixation | Input | Output | Damage | Description | Ref |
|---|---|---|---|---|---|---|
| CFRP laminated plate | Support by foam | Waveform generator Amplifier Speaker – 100 Hz sweep signal around resonance frequencies – from 1.05 to 1.3 V (0.05 V step) |
Accelerometer | Pendulum impact damage (repeated) | An obvious frequency shift is observable with increasing excitation amplitude. The damage indicator used in this article increased with the increase of the damage. | [129] |
| Rectangular beam of fibre-cemented slate | Suspended with nylon wires | Function generator Speaker Excited at the lowest flexural resonance mode at different amplitude |
Accelerometer Labview |
Hydrothermal shocks | The micro-cracks, induced by the hydrothermal shocks, clearly exhibited nonlinear behavior in the vibration response of the structure, with a frequency shift increasing with the damage severity. | [130] |
|
Steel-TiC composite beams Glass rods Polymer based beams |
PZT or electromagnetic shaker Swept-sine signal – around bending mode frequencies - from 1 to 10 V |
Accelerometer | Damage from tensile test | The classical nonlinear frequency shift gave nice results, but it was also combined with the harmonic-generation method which showed higher sensitivity. | [131] |
Table 10.
Other articles about the VAM method for SHM.
| Structure | Fixation | Input | Frequencies | Output | Damage | Description | Ref |
|---|---|---|---|---|---|---|---|
| Carbon/epoxy laminated beam | Glued on an aluminum stud linked to the rod of the shaker | Pump:
|
Pump: 155, 282 and 494 HzProbe: 6710 and 7180 Hz | Accelerometer | Delamination and fiber break (Impact damage at 1.8 and 2.4 J) | VAM clearly detected damage occurrence in composite beam, but the accuracy of it depends on the choice of the pumping and probing frequenciesThe lowest pumping frequency showed higher performance | [144] |
| Carbon-reinforced fiberglass wind turbin | On service | Pump:
|
Pump:3.1, 6.2, 9.4 Hz400 HzProbe: 5-10 kHz | MFC | Crack | VAM can be used while the turbine is rotating, and can detect the presence of damage, the sidebands for damage cases were higher than for healthy structure, but it still showed high sidebands for healthy structure | [145] |
Table 11.
Linear vibration methods for SHM (Detected Size represents the minimum percentage of the detected damaged area divided by the total area).
Table 11.
Linear vibration methods for SHM (Detected Size represents the minimum percentage of the detected damaged area divided by the total area).
| Technique | What is needed? | How to? | Drawbacks | Damage | Detected Size |
|---|---|---|---|---|---|
| Natural frequencies shift | The vibration of the structure in the frequency domain for a large frequency range is needed, to evaluate the natural frequencies. | Send a white noise or a sweep signal with a large frequency band. Compare the natural frequencies of intact and damaged structures. |
Only big damages are detectable. It can be influenced by some external conditions: temperature, boundary conditions... Some modes show a higher shift, which means several modes have to be tested. |
Delamination | > 20% |
| Crack | >20% | ||||
| Impact | X | ||||
| Fiber cutting | X | ||||
| Debonding | >16% | ||||
| Modes shape (MS) | The vibration of the structure in the frequency domain for a large frequency range and at several locations is needed, to record the mode shapes. | With LV, a network of sensors or a roving input method, displacement at several locations can be obtained. Several criteria comparing intact and damaged structures can be used: MAC, CoMAC, ECoMAC, PrMAC, … |
A large number of sensors or heavy processes are needed. | Delamination | > 10% |
| Crack | >10% | ||||
| Impact | >10% | ||||
| Layer cutting | >0.4% | ||||
| Mode shape curvature | The modes shape. | Several criteria comparing intact and damaged structures can be used: MSC, NMSC, NCDF, … | Crack | >27.7% | |
| Surface cut | >7% | ||||
| Debonding | >10% | ||||
| Modal strain energy | The modes shape. | Several criteria comparing intact and damaged structures can be used: MSEC, MSED, CMSE, … | Delamination | >11% | |
| Surface cut | >11% | ||||
| Impact | >11% | ||||
| Modal flexibility | The modes shape. | Check the flexibility change. | Debonding | >1.2% | |
| Core | >0.3% | ||||
| Damping | The vibration of the structure is needed, and the damping can be obtained with several techniques, but the most classical one is the -3dB method. | Send a white noise or a sweep signal with a large frequency band. Compare the damping parameter of intact and damaged structures. |
Mainly influenced by operational factors and uncertainty in the damping characterization. | Delamination | >48% |
| Fatigue | 3rd cycle | ||||
| Impact | BVID | ||||
| FRF | Input and output are needed to build the FRF. |
Some metrics can be used to observe differences in the FRF of intact and damaged structures for a large frequency range. |
Impact | ||
| Hole | |||||
| TF | The displacements or velocities at several locations of the structure for the same input are needed. |
A ratio of two displacements or velocities has to be made, and a damage indicator is calculated from this ratio. | A large number of sensors or heavy processes are needed. | Bonding steel plate | >20% |
| Impact | >5J | ||||
| WT | Vibration output in the time domain. | General vibration of the structure is needed, and the time domain signal should be divided into several sub-signals, to compare each sub-signal energy. | Extra processing is needed, and the correct choice of wavelets should be made. | Delamination | >0.12% |
Table 12.
Nonlinear vibration methods for SHM (Detected Size represents the minimum percentage of the detected damaged area divided by the total area).
Table 12.
Nonlinear vibration methods for SHM (Detected Size represents the minimum percentage of the detected damaged area divided by the total area).
| Technique | What is needed? | How to? | Drawbacks | Damage | Detected Size |
|---|---|---|---|---|---|
| SFE | Global knowledge of the vibration of the structure, to choose the best frequency for the harmonic signal excitation. | Compare damaged and intact structures through distortions in time-domain and phase portraits, sub- and super-harmonics, and damage indicators. |
Small peaks can be hidden in the noise, in operational detection. | Impact | BVID (>7J) |
| Delamination | >3% | ||||
| Nonlinear resonance (NLR) and damping | Global knowledge of the vibration of the structure, to choose the natural frequencies used for this technique: with a harmonic or a sweep signal around these frequencies. | Compare the resonance curves obtained from different amplitudes of excitation for damaged and intact structures. Use nonlinear elastic and dissipative parameters as damage indicators. | A lot of tests have to be made to obtain the resonance curves (10 in general) for 1 natural frequency. The frequency shift is also influenced by the boundary condition. |
Debonding | >8% |
| Fatigue crack | 1st cycle | ||||
| Impact | BVID (10 J and 2400 times 3 J) | ||||
| VAM | Global knowledge of the vibration of the structure, to choose the best frequency of excitation for pumping signal and in some cases also for probing one. | Compare the occurrence of super-harmonics and sidebands between damaged and intact structures. Damage indicators based on their amplitude are also used. | This method is influenced a lot by the boundary conditions, so special care should be made with VAM. | Impact | BVID (>1.8 J) |
| Crack | |||||
| Nonlinear Damping (NLD) | Time-frequency domain signal is needed in order to perform the CWT. | Extract the instantaneous amplitude and phase of the response, to calculate the instantaneous damping. Compare the variation of it between intact and damaged structures. |
Post-processing techniques (CWT) have to be used to obtain the instantaneous parameters which are necessary for the damping calculation. | Delamination | >32% |
| Fatigue crack | 2nd cycle |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated