1. Introduction

2. Literature review

3. Data and Methodology

3.1. Data

We collect daily data on TUNINDEX returns amid the COVID-19 pandemic. The period spans from January 2d, 2020 to December, 30^th 2022, making a total of 755 observations, omitting nontrading days. Since the objective is to analyze the impact of the sanitary crisis on the Tunisian stock return volatility, we gather data on the number of cases (total, new, and death) and on the government intervention to limit the spread of the virus (see Table 1 for details).

Table 1. Data definitions.

Table 1. Data definitions.

Variable	Symbol	Definition	Source
TUNINDEX	tun	The daily closing price of the Tunisian market index	https://www.investing.com/indices/tunindex-historical-data
Total cases	total_cases	Cumulative number of the confirmed cases due to COVID-19	Our World in Data https://ourworldindata.org/coronavirus/country/tunisia
Total deaths	total_death	Cumulative number of the confirmed death cases due to COVID-19
New cases	new_cases	Total number of the new confirmed cases due to COVID-19
New deaths	new_death	Total number of new confirmed death cases due to COVID-19
Rate of confirmed cases	cases_rate	News cases/Total cases	Calculus
Rate of deaths	death_rate	Death cases/Total deaths	Calculus
Stringency index	stringency_index	Ranges from 0 to 100, where higher values indicate stricter government policies and restrictions in response to the COVID-19 pandemic.	Oxford COVID-19 Government Response Tracker (OxCGRT) https://github.com/OxCGRT/covid-policy-dataset
Containment health index	containement_health_index	Typically ranges from 0 to 100, where higher values indicate better virus containment.
Economic policy index	economic_policy_index	Ranges from 0 to 100, where higher values indicate a more accommodative economic policy stance and lower values indicate a more restrictive stance.
Government response index	government_response_index	Ranges between 0 and 100. A higher score means a better country’s response to the pandemic.
WTI crude oil price	wti_price	Crude oil price (United States)	Energy Information Administration database https://www.eia.gov/dnav/pet/pet_pri_spt_s1_d.htm
School closing	s1	Sub-indicator 1 of the stringency index	Oxford COVID-19 Government Response Tracker (OxCGRT) https://github.com/OxCGRT/covid-policy-dataset
Workplace closing	s2	Sub-indicator 2 of the stringency index
Cancel public events	s3	Sub-indicator 3 of the stringency index
Restrictions on public gatherings	s4	Subindicator 4 of the stringency index
Closures of public transport	s5	Sub-indicator 5 of the stringency index
Stay-at-home requirements	s6	Sub-indicator 6 of the stringency index
Restrictions on internal movements	s7	Subindicator 7 of the stringency index
International travel control	s8	Sub-indicator 8 of the stringency index
Public information gatherings	s9	Subindicator 9 of the stringency index

Source: The Author.

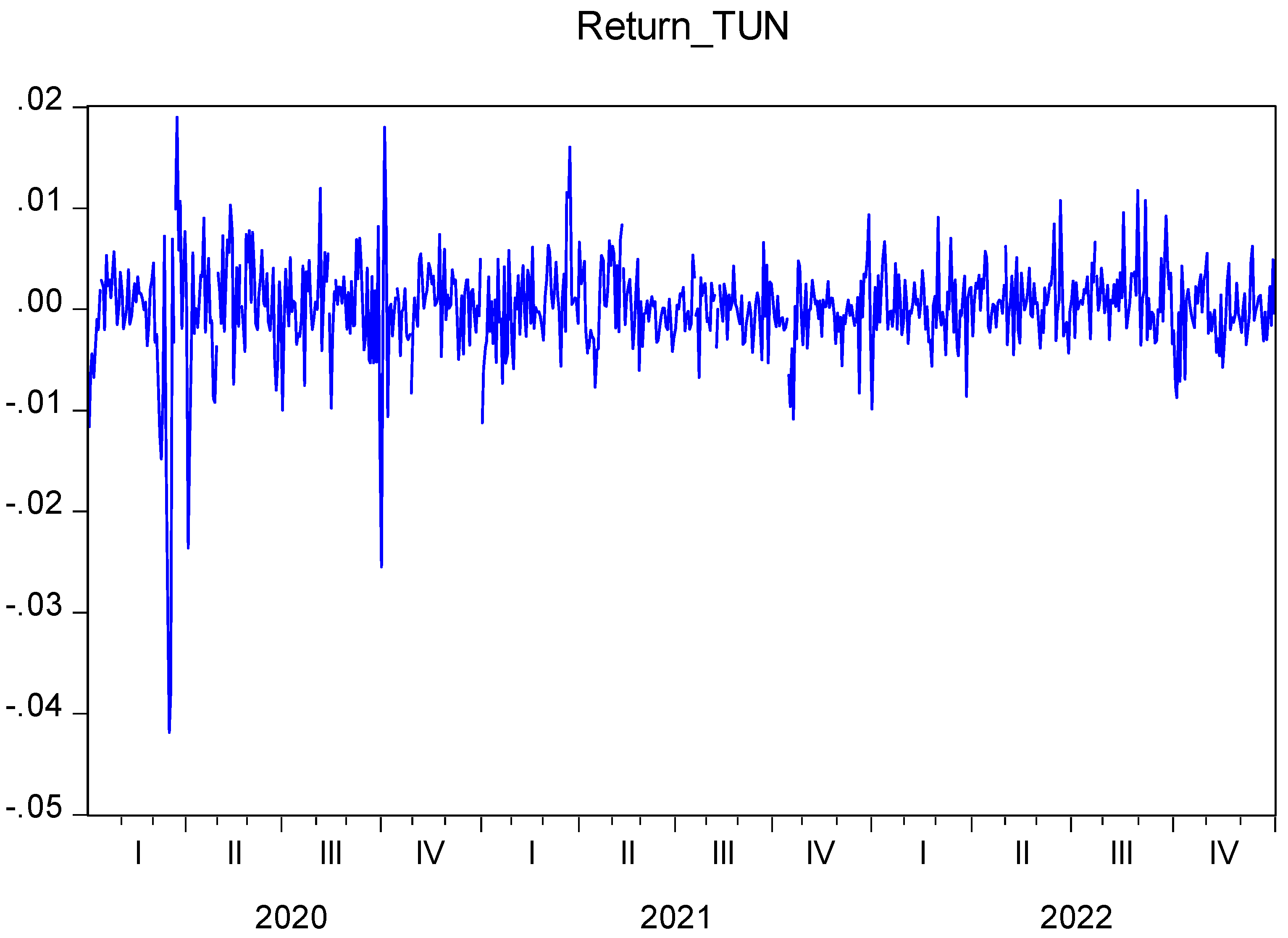
Descriptive statistics of the above variables are displayed in Table 2. The TUNINDEX exhibits a mean return of 0.000150, indicating a generally modest performance. Figure 1 illustrates a compelling narrative of diminishing returns in TUNINDEX, particularly during the challenging times of the COVID-19 era. The total number of COVID-19 cases and deaths, with means of 551,839.1 and 16,432.85 respectively, reflects the significant impact of the pandemic on public health. The stringency index, with a mean of 49.03363, suggests varying degrees of government measures. Interestingly, the containment health index, economic support index, and government response index do not seem to strongly influence market volatility. The skewness values, particularly for TUNINDEX, indicate a negatively skewed distribution, and the kurtosis values suggest heavy tails in the distribution.

Table 2. Descriptive statistics of the variables.

Table 2. Descriptive statistics of the variables.

	RETURN_TUN	TOTAL_CASES	TOTAL_DEATHS	STRINGENCY_INDEX	S1	S2	S3	S4	S5	S6	S7	S8	S9	CONTAINMENT_HEALTH_INDEX	ECONOMIC_SUPPORT_INDEX	GOVERNMENT_RESPONSE_INDEX	WTI_OIL_RETURN
Mean	0.000150	551839.1	16432.85	49.03363	1.034043	1.144681	1.597163	3.262411	0.307801	0.808511	0.639716	1.876596	1.846809	50.28391	46.84397	49.85403	0.001816
Median	0.000339	603981.0	21941.00	45.31000	1.000000	1.000000	2.000000	4.000000	0.000000	0.000000	0.000000	2.000000	2.000000	49.96000	50.00000	48.80000	0.002294
Maximum	0.018974	1147571.	29284.00	90.74000	3.000000	3.000000	2.000000	4.000000	2.000000	2.000000	2.000000	4.000000	2.000000	77.74000	75.00000	77.40000	0.425832
Minimum	-0.041859	1.000000	3.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	-0.281382
Std. Dev.	0.004802	444625.6	11959.82	21.88917	1.017728	0.804146	0.757157	1.546832	0.603267	0.967621	0.918936	1.122006	0.490616	18.04488	25.69635	17.32935	0.045112
Skewness	-2.203420	0.060338	-0.263656	-0.119352	0.546806	0.438110	-1.480724	-1.632203	1.799000	0.390066	0.772150	0.298314	-3.148689	-1.074264	-0.287851	-1.055407	1.353766
Kurtosis	20.12168	1.393214	1.331061	2.671155	2.097217	2.843062	3.384040	3.672980	4.993379	1.183648	1.632938	2.231494	11.52594	4.109855	1.785051	4.541901	29.12992
Jarque-Bera	9181.807	72.04800	83.47809	4.850368	59.07326	23.27648	261.9562	326.3342	497.0006	114.7899	124.9530	27.80539	3300.243	171.7835	53.09627	200.7193	20271.78
Probability	0.000000	0.000000	0.000000	0.088462	0.000000	0.000009	0.000000	0.000000	0.000000	0.000000	0.000000	0.000001	0.000000	0.000000	0.000000	0.000000	0.000000
Sum	0.105709	3.68E+08	10747083	34568.71	729.0000	807.0000	1126.000	2300.000	217.0000	570.0000	451.0000	1323.000	1302.000	35450.16	33025.00	35147.09	1.280245
Sum Sq. Dev.	0.016235	1.31E+14	9.34E+10	337311.6	729.1830	455.2426	403.5943	1684.454	256.2071	659.1489	594.4879	886.2638	169.4553	229234.8	464852.8	211415.7	1.432724
Observations	705	666	654	705	705	705	705	705	705	705	705	705	705	705	705	705	705

Source: The Author.

Figure 1. Evolution of TUNINDEX stock return (02/01/2020-30/12/2022). Source: The Author.

Figure 1. Evolution of TUNINDEX stock return (02/01/2020-30/12/2022). Source: The Author.

3.2. Methodology

The assessment of volatility has mandated the application of models within the Autoregressive Conditional Heteroskedasticity (ARCH) framework in the realm of financial literature. Originating with the seminal ARCH model introduced by Engle (1982), subsequent advancements have been made, encompassing the development of models such as Generalized ARCH (GARCH), GARCH-in-mean, Quadratic GARCH, and Threshold GARCH, among others.

The stock return is calculated following previous related literature using this formula:

$$R_t=\mathrm{L}\mathrm{n}(\frac{P_t}{P_{t-1}})$$

where $P_t\mathrm{a}\mathrm{n}\mathrm{d}{P}_{t-1}$ are the stock market indices of the Tunisian Stock Exchange at times t and t-1, respectively. Ln is the natural logarithm.

The logarithm transformation serves as a technique to induce stationarity in variables by mitigating trends and seasonality within time series data. Consequently, Augmented Dickey-Fuller (ADF) and Phillips-Perron (PP) tests are conducted to verify the attainment of stationarity in the level of returns. The associated results are available in Table 3.

The autoregressive (AR) (p) or autoregressive moving average (ARMA) (p, q) structures are commonly integrated as explanatory elements within the conditional mean equation of Generalized Autoregressive Conditional Heteroskedasticity (GARCH) models for the dependent variable. Following Insaidoo et al. (2021), an advantageous feature of the GARCH model lies in its adaptability to include explanatory variables and dummy variables in both the conditional mean and variance equations, thereby accommodating the specific objectives of the study. Hence, we incorporate each of the COVID-19 variables and the government intervention controls in both the mean equation and the variance equation, separately to capture the effect of the pandemic on the Tunisian stock return and volatility. Our econometric modeling is essentially based on Fakhfekh et al. (2023). However, we distinguish from their study by including specific controls related to the sanitary crisis instead of separating pre-crisis and during-crisis periods. Thus, we estimate the following GARCH family models.

Table 3. Results of ARCH/GARCH family models for the TUNINDEX volatility and oil volatility.

Table 3. Results of ARCH/GARCH family models for the TUNINDEX volatility and oil volatility.

Panel A: Stock return volatility
Model	ARCH(1), constant	ARCH(1), AR(1)	ARCH(1), MA(1)	ARCH(1), ARMA(1,1)	GARCH(1,1), constant	GARCH(1,1), AR(1)	GARCH(1,1), MA(1)	GARCH(1,1), ARMA(1,1)
AIC	-8.248105	-8.283928	-8.274759	-8.281654	-8.332585	-8.376225	-8.365392	-8.378094
SC	-8.229721	-8.259390	-8.250246	-8.250982	-8.308073	-8.345553	-8.334751	-8.341287
Model	EGARCH(1,1), constant	EGARCH(1,1), AR(1)	EGARCH(1,1), MA(1)	EGARCH(1,1), ARMA(1,1)	TGARCH(1,1), constant	TGARCH(1,1), AR(1)	TGARCH(1,1), MA(1)	TGARCH(1,1), ARMA(1,1)
AIC	-8.323690	-8.369747	-8.358517	-8.369772	-8.330636	-8.374358	-8.363444	-8.376183
SC	-8.293050	-8.332940	-8.321748	-8.326830	-8.299996	-8.337551	-8.326675	-8.333242
Panel B: WTI oil volatility
Model	ARCH(1), constant	ARCH(1), AR(1)	ARCH(1), MA(1)	ARCH(1), ARMA(1,1)	GARCH(1,1), constant	GARCH(1,1), AR(1)	GARCH(1,1), MA(1)	GARCH(1,1), ARMA(1,1)
AIC	-3.856832	-3.990224	-4.003052	-4.000366	-4.272393	-4.269562	-4.269562	-4.257070
SC	-3.837436	-3.964362	-3.977190	-3.968039	-4.246531	-4.237234	-4.237235	-4.231253
	EGARCH(1,1), constant	EGARCH(1,1), AR(1)	EGARCH(1,1), MA(1)	EGARCH(1,1), ARMA(1,1)	TGARCH(1,1), constant	TGARCH(1,1), AR(1)	TGARCH(1,1), MA(1)	TGARCH(1,1), ARMA(1,1)
AIC	-4.278102	-4.275790	-4.275864	-3.344925	-4.292975	-4.290166	-4.290171	-4.287428
SC	-4.245774	-4.236997	-4.237071	-3.299666	-4.260648	-4.251373	-4.251377	-4.242170

Source: The Author.

3.2.1. ARCH

The ARCH model characterizes the variance of a time series, particularly in situations involving dynamic and potentially volatile variance. It was introduced by Engle (1982). While ARCH models can potentially depict a slowly escalating variance trend over time, their primary application lies in scenarios featuring brief episodes of heightened variation. It is worth noting that situations involving a gradual increase in both variance and mean level may be more effectively addressed by transforming the variable.

The mean equation is written as follows:

$$R_t=\alpha +\sum _{i=1}^p{\beta }_i{R}_{t-i}+\sum _{i=1}^q{\theta }_i{\epsilon }_{t-i}+{\epsilon }_t$$

The choice between AR(1), MA(1), and ARMA(1,1) is made based on the conventional information criteria (Aikake, Schwarz) for which the value is minimized.

Our estimations show that AR(1) is the preferred one.

The conditional variance equation is defined as:

$${\sigma }_t^2=a_0+\sum _{i=1}^p{a}_i{\epsilon }_{t-i}^2$$

where $a_0>0,a_i>0$. This model is known as the linear ARCH(p). In financial data analysis, the model captures the phenomenon of volatility clustering, wherein significant (insignificant) price changes tend to be succeeded by other substantial (moderate) price changes, but with an unpredictable direction. To streamline the model and guarantee a consistently diminishing impact of more distant shocks, a makeshift linearly declining lag structure was frequently enforced in many early applications of the model (see Bollerslev et al., 1992; Bollerslev and Mikkelsen, 1996).

3.2.2. GARCH

Bollerslev’s GARCH model (1986) is the most widely used model for estimating volatility. volatility. GARCH models have had great success in the literature due to their simple specification and ease of interpretation.

The conditional variance equation is defined as:

$${\sigma }_t^2=a_0+\sum _{i=1}^p{a}_i{\epsilon }_{t-i}^2+\sum _{j=1}^q{b}_j{\sigma }_{t-j}^2$$

where $a_0>0,a_i>0,b_j>0$. For a GARCH(1,1), the constraint  $a_1+b_1$< 1 implies that the unconditional variance of the ε yield series is finite and that the conditional variance ${\sigma }_t^2$ evolves. It also provides the necessary and sufficient for the stochastic process ${\sigma }_t$; t ∈ Z to be a unique process strictly stationary with E(${\sigma }_t^2$) < ∞.

Two key properties can be noted from the above equation. First, a high value of ${\epsilon }_{t-1}^2$ or ${\sigma }_{t-1}^2$ gives rise to a high value of ${\sigma }_t^2$ and this generates the volatility clustering that is common in time series. Second, the tail distribution is thicker than that of a normal distribution (see Mestiri, 2022).

3.2.4. EGARCH

This model is suggested by Nelson (1991) to account for leverage effects. It is an asymmetric Exponential GARCH specification that distinguishes between “good” and “bad” news on volatility.

The conditional volatility equation is given by:

$$Ln{\sigma }_t^2=a_0+\sum _{i=1}^p{a}_i\frac{\left|{\epsilon }_{t-i}\right|+{\delta }_i{\epsilon }_{t-i}}{{\sigma }_{t-i}}+\sum _{j=1}^q{b}_{j}Ln{\sigma }_{t-j}^2$$

If there is "good" news, ${\epsilon }_{t-i}>0$ and the total effect is given by $(1+{\delta }_i){\epsilon }_{t-i}$. If there is "bad" news, ${\epsilon }_{t-i}<0$, and the total effect is given by $(1-{\delta }_i){\epsilon }_{t-i}$. “Bad” news is likely to have a more pronounced impact on volatility and ${\delta }_i$ is expected to be negative.

3.2.5. GJR-GARCH

Another version of an asymmetric GARCH model with leverage effects is the Threshold GARCH specification, called also GJR-GARCH. The conditional volatility is given by:

$${\sigma }_t^2=a_0+\sum _{i=1}^p{a}_i{\epsilon }_{t-i}^2+\sum _{i=1}^p{\gamma }_i{S}_{t-i}{\epsilon }_{t-i}^2+\sum _{j=1}^q{b}_j{\sigma }_{t-j}^2$$

With

$$S_{t-i}=\left\{\begin{array}{c}1if{\epsilon }_{t-i}<0\\ 0if{\epsilon }_{t-i}>0\end{array}\right.$$

When ${\epsilon }_{t-i}>0$, the total effect is given by $a_i{\epsilon }_{t-i}^2$. If ${\epsilon }_{t-i}<0$, the total effect is given by $\left(a_i+{\gamma }_i\right){\epsilon }_{t-i}^2$. The coefficient ${\gamma }_i$ is expected to be positive so that “bad” news has a larger impact on volatility.

The best-fit model is chosen based on Akaike (AIC) and Schwarz (SC) information criteria for which the value is minimized.

According to Bera and Higgins (1993), the most applied financial work shows that GARCH (1,1) provides a flexible and parsimonious approximation of the conditional variance dynamics and is capable of representing the majority of financial series. Therefore, p=1 and q=1 are applied for all GARCH family models to be estimated.

Before estimating ARCH-type models, we need to test for the presence of ARCH(q) effects. We rely on the Lagrange Multiplier (LM) test. We reject the null hypothesis of no ARCH effects (F-statistic=342.0031, p-value=0.000; Obs*R²=235.6154, p-value=0.000).

To know what a combination of variables is to be included in the regression we provide the pairwise correlation matrix (see supplemental file for details).

4. Results and discussion

4.1. Impact of COVID-19 announcements and government intervention on TUNINDEX stock return volatility

Table 3 shows that GJR-GARCH is the preferred one as the conventional information criteria exhibit the lowest values. To examine the impact of COVID-19 announcements and the government intervention variables, we regress the conditional stock return variance that results from the GJR-GARCH(1,1), AR(1) model on the variables of interest and a set of controls (see Ibrahim et al., 2020; Bakry et al., 2022):

$${VOL}_t=\alpha +{\beta }_1{CR}_t+{\beta }_2{DR}_t+{\beta }_2{GII}_t+{\beta }_1{Oil\_VOL}_t+{\mu }_t$$

where CR: cases_rate, DR: death_rate, GRI: Government intervention index (this includes stringency_index, containment_health_index, economic_support_index, government_response_index, and subindicators of the stringency index (s1 to s9), Oil_Vol: Conditional WTI oil volatility from GJR-GARCH(1,1) with a constant.

To handle the multicollinearity issue, we include the government intervention indicators separately. Further, we control for autocorrelation and heteroscedasticity by estimating the equation with the Newey-West method. Results are available in Table 4 and Table 5. We re-estimate the variants of the equations while skipping for the cases_rate variable. All results duplicate mostly the ones in Table 4 and Table 5, except that death_rate becomes statistically significant (see Table 6 and Table 7).

According to Kamal and Wohar (2023), "Considering global market integration (Solnik, 1974) and to remove misspecification error, [..]. We also lagged the independent variables by one period to examine the slow response of the market. Slow response supports the underreaction hypothesis, which suggests investors adjust slowly to new information.". We replicate the output while considering the variables of interest and controls lagged with one period (see Table 8, Table 9, Table 10 and Table 11).

The observed incidence of confirmed cases and mortality rates exhibit a positive association with heightened volatility in the TUNINDEX in addition to the WTI conditional volatility. Moreover, there exists a positive correlation between the stringency index and volatility in the Tunisian stock market. Conversely, the indices about containment health economic support and government response do not manifest a discernible impact on market volatility. Those observations can be attributed to increased uncertainty and economic impacts. Rising cases make investors cautious, leading to market fluctuations. Stringent government measures, reflected in the stringency index, also correlate positively with market volatility, indicating economic repercussions. However, indices related to health economic support and government response show no significant impact on volatility, suggesting that other factors may be more influential in shaping the Tunisian stock market.

Table 4. Effect of COVID-19 announcements and government intervention on TUNINDEX volatility.

Table 4. Effect of COVID-19 announcements and government intervention on TUNINDEX volatility.

Eq Name:	EQ01	EQ02	EQ03	EQ04
C	0.000011	0.000011	0.000011	0.000011
	[10.9061]***	[11.0044]***	[11.6222]***	[11.3206]***
CASES_RATE	0.000359	0.000358	0.000389	0.000366
	[3.3678]***	[3.3480]***	[3.2211]***	[3.2644]***
DEATH_RATE	0.000049	0.000053	0.000010	0.000037
	[0.7213]	[0.7701]	[0.1111]	[0.4705]
CONDVAR_WTI	0.001224	0.001220	0.001185	0.001219
	[2.3954]**	[2.3831]**	[2.3961]**	[2.3998]**
DSTRINGENCYINDEX	0.000001
	[0.9286]
DCONTAINMENTHEALTHINDEX		0.000001
		[0.7738]
DECONOMICSUPPORTINDEX			0.000001
			[1.2960]
DGOVERNMENTRESPONSEINDEX				0.000001
				[0.9220]
Observations:	654	654	654	654
R-squared:	0.4811	0.4794	0.4907	0.4823
F-statistic:	150.4010	149.4343	156.3274	151.1775
Prob(F-stat):	0.0000	0.0000	0.0000	0.0000

Note: *, **, *** significant at 10%, 5% and 1%, respectively. Source: The Author.

Table 5. Effect of stringency index sub-indicators on TUNINDEX volatility.

Table 5. Effect of stringency index sub-indicators on TUNINDEX volatility.

Eq Name:	EQ01	EQ02	EQ03	EQ04	EQ05	EQ06	EQ07	EQ08	EQ09
C	0.000011	0.000011	0.000011	0.000011	0.000011	0.000011	0.000011	0.000011	0.000011
	[10.4573]***	[10.8456]***	[10.3587]***	[17.3295]***	[10.6964]***	[11.0051]***	[10.7373]***	[10.4448]***	[10.4588]***
CASES_RATE	0.000348	0.000355	0.000346	0.000367	0.000353	0.000368	0.000345	0.000348	0.000348
	[3.4899]***	[3.4638]***	[3.5209]***	[10.9008]**	[3.4494]***	[3.3898]***	[3.3523]***	[3.5048]***	[3.4969]***
DEATH_RATE	0.000077	0.000058	0.000075	0.000024	0.000068	0.000041	0.000082	0.000076	0.000076
	[1.3980]	[0.9628]	[1.3625]	[0.9679]	[1.1819]	[0.6740]	[1.3229]	[1.3816]	[1.3822]
CONDVAR_WTI	0.001212	0.001233	0.001221	0.001232	0.001209	0.001203	0.001213	0.001213	0.001213
	[2.3589]**	[2.4250]**	[2.3817]**	[8.2596]***	[2.3672]**	[2.3704]**	[2.3559]**	[2.3603]**	[2.3588]**
D(S1)	-0.000002
	[-0.7363]
D(S2)		0.000008
		[1.0688]
D(S3)			0.000005
			[0.6859]
D(S4)				0.000011
				[4.5894]***
D(S5)					0.000007
					[0.8645]
D(S6)						0.000016
						[1.6222]
D(S7)							-0.000002
							[-0.3753]
D(S8)								-0.000002
								[-0.7549]
D(S9)									0.000004
									[4.7152]***
Observations:	654	654	654	654	654	654	654	654	654
R-squared:	0.4766	0.4808	0.4773	0.4928	0.4777	0.4938	0.4767	0.4764	0.4764
F-statistic:	147.7157	150.2575	148.1492	157.6232	148.3977	158.2759	147.8009	147.6410	147.6070
Prob(F-stat):	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000

Note: *, **, *** significant at 10%, 5% and 1%, respectively. Source: The Author.

Table 6. Effect of COVID-19 announcements and government intervention on TUNINDEX volatility, excluding cases_rate.

Table 6. Effect of COVID-19 announcements and government intervention on TUNINDEX volatility, excluding cases_rate.

Eq Name:	EQ01	EQ02	EQ03	EQ04	EQ05
C	0.000012	0.000012	0.000012	0.000012	0.000012
	[10.9188]***	[10.7714]***	[11.0068]***	[11.7608]***	[11.1964]***
DEATH_RATE	0.000226	0.000217	0.000221	0.000212	0.000218
	[4.7771]***	[4.4689]***	[4.3267]***	[3.4279]***	[3.9955]***
CONDVAR_WTI	0.001680	0.001692	0.001686	0.001689	0.001689
	[2.0681]**	[2.0647]**	[2.0570]**	[2.0576]**	[2.0545]**
DSTRINGENCYINDEX		0.000000
		[0.6286]
DCONTAINMENTHEALTHINDEX			0.000000
			[0.3755]
DECONOMICSUPPORTINDEX				0.000000
				[0.8845]
DGOVERNMENTRESPONSEINDEX					0.000000
					[0.5446]
Observations:	654	654	654	654	654
R-squared:	0.3916	0.3923	0.3916	0.3928	0.3919
F-statistic:	139.4355	139.8593	139.4782	140.1365	139.6133
Prob(F-stat):	0.0000	0.0000	0.0000	0.0000	0.0000

: *, **, *** significant at 10%, 5% and 1%, respectively. Source: The Author.

Table 7. Effect of stringency index sub-indicators on conditional stock return volatility, excluding cases_rate.

Table 7. Effect of stringency index sub-indicators on conditional stock return volatility, excluding cases_rate.

Eq Name:	EQ01	EQ02	EQ03	EQ04	EQ05	EQ06	EQ07	EQ08	EQ09
C	0.000012	0.000012	0.000012	0.000012	0.000012	0.000012	0.000012	0.000012	0.000012
	[10.9181]***	[11.0699]***	[10.8839]***	[11.1801]***	[11.0729]***	[10.9574]***	[11.1625]***	[10.9210]***	[10.9188]***
DEATH_RATE	0.000227	0.000216	0.000223	0.000195	0.000225	0.000207	0.000238	0.000226	0.000226
	[4.8043]***	[4.3602]***	[5.0099]***	[3.8221]***	[4.5418]***	[4.3190]***	[4.6804]***	[4.7765]***	[4.7771]***
CONDVAR_WTI	0.001679	0.001700	0.001689	0.001712	0.001681	0.001693	0.001668	0.001681	0.001680
	[2.0665]**	[2.0838]**	[2.0807]**	[2.0813]**	[2.0665]**	[2.0689]**	[2.0528]**	[2.0688]**	[2.0681]**
D(S1)	-0.000002
	[-0.8260]
D(S2)		0.000005
		[1.0467]
D(S3)			0.000008
			[0.8771]
D(S4)				0.000008
				[1.5721]
D(S5)					0.000001
					[0.3585]
D(S6)						0.000012
						[1.5046]
D(S7)							-0.000006
							[-1.6216]
D(S8)								-0.000001
								[-0.3842]
D(S9)									0.000006
									[6.3409]***
Observations:	654	654	654	654	654	654	654	654	654
R-squared:	0.3920	0.3933	0.3939	0.3999	0.3915	0.4004	0.3948	0.3915	0.3916
F-statistic:	139.6728	140.4515	140.8341	144.3825	139.3918	144.7011	141.3569	139.3879	139.4355
Prob(F-stat):	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000

Note: *, **, *** significant at 10%, 5% and 1%, respectively. Source: The Author.

Table 8. Effect of lagged COVID-19 announcements and government intervention on conditional stock return volatility.

Table 8. Effect of lagged COVID-19 announcements and government intervention on conditional stock return volatility.

Eq Name:	EQ01	EQ02	EQ03	EQ04	EQ05
C	0.000011	0.000011	0.000011	0.000011	0.000011
	[12.7748]***	[12.5856]***	[12.7677]***	[13.5131]***	[12.9403]***
CASES_RATE(-1)	0.000286	0.000298	0.000296	0.000300	0.000301
	[2.9352]***	[2.8389]**	[2.8335]***	[2.8340]***	[2.7877]***
DEATH_RATE(-1)	0.000093	0.000064	0.000070	0.000069	0.000061
	[1.8091]	[0.9606]	[1.0295]	[0.7853]	[0.7971]
CONDVAR_WTI(-1)	0.001005	0.001017	0.001013	0.000996	0.001011
	[2.2048]**	[2.2664]**	[2.2434]**	[2.2277]**	[2.2419]**
DSTRINGENCYINDEX(-1)		0.000001
		[0.9800]
DCONTAINMENTHEALTHINDEX(-1)			0.000001
			[0.8861]
DECONOMICSUPPORTINDEX(-1)				0.000000
				[0.6285]
DGOVERNMENTRESPONSEINDEX(-1)					0.000001
					[0.9491]
Observations:	653	653	653	653	653
R-squared:	0.4440	0.4499	0.4475	0.4459	0.4484
F-statistic:	129.3621	132.4748	131.2354	130.3794	131.6918
Prob(F-stat):	0.0000	0.0000	0.0000	0.0000	0.0000

Note: *, **, *** significant at 10%, 5% and 1%, respectively. Source: The Author.

Table 9. Effect of lagged stringency index sub-indicators on TUNINDEX volatility.

Table 9. Effect of lagged stringency index sub-indicators on TUNINDEX volatility.

Eq Name:	EQ01	EQ02	EQ03	EQ04	EQ05	EQ06	EQ07	EQ08	EQ09
C	0.000011	0.000011	0.000011	0.000011	0.000011	0.000011	0.000011	0.000011	0.000011
	[12.7748]***	[12.4731]***	[12.4731]***	[19.4073]***	[12.9331]***	[13.1147]***	[13.1060]***	[12.7608]***	[12.7727]***
CASES_RATE(-1)	0.000286	0.000278	0.000278	0.000308	0.000288	0.000297	0.000276	0.000286	0.000286
	[2.9352]***	[3.0439]***	[3.0439]***	[9.7976]**	[2.9264]**	[2.9031]***	[2.8274]***	[2.9395]**	[2.9380]**
DEATH_RATE(-1)	0.000093	0.000090	0.000090	0.000031	0.000089	0.000073	0.000110	0.000092	0.000092
	[1.8091]	[1.8281]	[1.8281]	[1.3184]	[1.5830]	[1.1912]	[1.8552]	[1.8018]	[1.8017]
CONDVAR_WTI(-1)	0.001005	0.001035	0.001035	0.001029	0.001005	0.001001	0.001005	0.001006	0.001006
	[2.2048]**	[2.3250]*	[2.3250]**	[7.3751]***	[2.2097]**	[2.2029]**	[2.2010]**	[2.2054]**	[2.2049]**
DS1(-1)	-0.000001
	[-0.4926]
DS2(-1)		0.000016
		[1.1974]
DS3(-1)			0.000016
			[1.1974]
DS4(-1)				0.000013
				[5.8101]***
DS5(-1)					0.000002
					[0.4818]
DS6(-1)						0.000009
						[1.4857]
DS7(-1)							-0.000007
							[-1.4505]
DS8(-1)								0.000000
								[0.0492]
DS9(-1)									0.000004
									[5.3218]***
Observations:	653	653	653	653	653	653	653	653	653
R-squared:	0.4440	0.4571	0.4571	0.4714	0.4441	0.4501	0.4483	0.4439	0.4439
F-statistic:	129.3621	136.3843	136.3843	144.4733	129.4049	132.6088	131.6345	129.2985	129.3374
Prob(F-stat):	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000

Note: *, **, *** significant at 10%, 5% and 1%, respectively. Source: The Author.

Table 10. Effect of lagged COVID-19 announcements and government intervention on TUNINDEX volatility, excluding cases_rate.

Table 10. Effect of lagged COVID-19 announcements and government intervention on TUNINDEX volatility, excluding cases_rate.

Eq Name:	EQ01	EQ02	EQ03	EQ04	EQ05
C	0.000012	0.000012	0.000012	0.000012	0.000012
	[12.4786]***	[11.6893]***	[12.0227]***	[13.4926]***	[12.1689]***
CASES_RATE(-1)
DEATH_RATE(-1)	0.000216	0.000203	0.000209	0.000225	0.000210
	[3.3319]***	[3.3824]***	[3.3369]***	[2.8312]***	[3.2388]***
DSTRINGENCYINDEX(-1)		0.000000
		[0.6574]
CONDVAR_WTI(-1)	0.001389	0.001405	0.001398	0.001385	0.001396
	[2.0659]**	[2.0877]**	[2.0750]**	[2.0566]**	[2.0696]**
DCONTAINMENTHEALTHINDEX(-1)			0.000000
			[0.4969]
DECONOMICSUPPORTINDEX(-1)				-0.000000
DGOVERNMENTRESPONSEINDEX(-1)					0.000000
					[0.4215]
Observations:	653	653	653	653	653
R-squared:	0.3757	0.3772	0.3759	0.3762	0.3757
F-statistic:	130.2065	130.9974	130.3240	130.4563	130.1818
Prob(F-stat):	0.0000	0.0000	0.0000	0.0000	0.0000

Note: *, **, *** significant at 10%, 5% and 1%, respectively. Source: The Author.

Table 11. Effect of lagged stringency index sub-indicators on TUNINDEX volatility, excluding cases_rate.

Table 11. Effect of lagged stringency index sub-indicators on TUNINDEX volatility, excluding cases_rate.

Eq Name:	EQ01	EQ02	EQ03	EQ04	EQ05	EQ06	EQ07	EQ08	EQ09
C	0.000012	0.000012	0.000012	0.000012	0.000012	0.000012	0.000012	0.000012	0.000012
	[12.4786]***	[12.4489]***	[12.4489]***	[11.8281]***	[12.6835]***	[12.5178]***	[12.9708]***	[12.4828]***	[12.4783]***
CASES_RATE(-1)
DEATH_RATE(-1)	0.000216	0.000208	0.000208	0.000174	0.000217	0.000207	0.000235	0.000215	0.000215
	[3.3319]***	[3.7286]***	[3.7286]***	[2.8572]***	[3.2616]***	[3.1008]***	[3.4991]***	[3.3297]***	[3.3299]***
CONDVAR_WTI(-1)	0.001389	0.001412	0.001412	0.001432	0.001390	0.001396	0.001370	0.001390	0.001390
	[2.0659]**	[2.1157]**	[2.1157]**	[2.1208]**	[2.0670]**	[2.0679]**	[2.0482]**	[2.0679]**	[2.0676]**
DS1(-1)	-0.000002
	[-0.5970]
DS2(-1)		0.000018
		[1.2257]
DS3(-1)			0.000018
			[1.2257]
DS4(-1)				0.000010
				[1.3438]
DS5(-1)					-0.000002
					[-0.5121]
DS6(-1)						0.000005
						[1.0782]
DS7(-1)							-0.000010
							[-2.5152]**
DS8(-1)								0.000001
								[0.3804]
DS9(-1)									0.000005
									[6.2728]***
Observations:	653	653	653	653	653	653	653	653	653
R-squared:	0.3757	0.3927	0.3927	0.3931	0.3756	0.3775	0.3855	0.3755	0.3756
F-statistic:	130.2065	139.9066	139.9066	140.1240	130.1326	131.2005	135.7357	130.0510	130.1076
Prob(F-stat):	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000

Note: *, **, *** significant at 10%, 5% and 1%, respectively. Source: The Author.

4.2. Wavelet coherence analysis

Wavelet coherence analysis is a method used to investigate the relationship between two-time series in both the time and frequency domains. It is particularly useful for exploring the coherence between signals that vary in time and is well suited to handle series with both stationary and non-stationary properties. Then, we can explore the coherence or synchronization between two signals across different scales and time intervals, making it a valuable tool in the analysis of complex and dynamic relationships between time-varying processes (see Torrence and Webster, 1998; Grinsted et al., 2004; Liu et al., 2007, Cazelles et al., 2008; Rouyer et al., 2008, Veleda et al., 2012).

Bias-corrected wavelet analysis refines traditional methods by mitigating edge effects and leakage issues associated with finite-length time series. This approach provides more accurate estimates of wavelet coefficients, enhances statistical inference, and improves the interpretability of time-frequency characteristics. It is particularly valuable for handling challenges related to discreteness and non-stationarity in signals, offering a robust tool for understanding the dynamics of time-varying processes. In this part, we follow this approach (e.g., Dhanya and Gupta, 2014; Hosseini et al., 2023).

The mathematical expressions provided will be based on Tissaoui et al. (2021), Tissaoui et al. (2022), and Li et al. (2022). A wavelet is a function Ψ(.) that can be either real-valued or complex-valued, and it meets the criterion of being square-integrable.

A wavelet is characterized as a compact or small-sized wave if

$${\mathsf{\Psi }}_{l,d}\left(t\right)=\frac{1}{\sqrt{d}}\mathsf{\Psi }(\frac{t-l}{d})$$

where $\frac{1}{\sqrt{d}}$ is the normalization factor, such that $‖{\mathsf{\Psi }}_{l,d}\left(t\right)‖=1$, $l$ stands for the location parameter, providing the exact position of the wavelet, and $d$ denotes the scale dilatation parameter of the wavelet.

The cross-wavelet technique can break down the $x(t)$ function initially and subsequently reconstruct it such that

$$x\left(t\right)=\frac{1}{C_W}{\int }_0^{\infty }\left[{\int }_{-\infty }^{\infty }{W}_x\left(l,s\right){\mathsf{\Psi }}_{l,d}\left(t\right)dl\right]\frac{dd}{d^2},d>0$$

The process involves projecting a particular wavelet to achieve the desired outcome. The primary goal of wavelet coherence is to calculate localized correlations within a time-frequency domain across a series. We have

$$R^2\left(l,d\right)=\frac{{\left|S(s^{-1}(W_{mn}(l,d)\right|}^2}{S\left(s^{-1}\left({\left|W_m\left(l,d\right)\right|}^2\right).s^{-1}\left({\left|W_n\left(l,d\right)\right|}^2\right)\right)}$$

The given expression is assessed using the absolute smooth cross-wavelet value. $R^2\left(l,d\right)$ is very similar to the correlation coefficient between two signals $m$ and $n$.

• approaches zero, it indicates a weak correlation between $m$ and $n$, whereas a value close to 1 signifies a strong correlation between the two variables.

The phase discrepancy serves as an indicator of the timing variation between oscillations in two variables about their frequency. The analysis of this phase difference involves examining the orientation of arrows depicted in wavelet coherence graphs. More precisely, the identification of the lead-lag relationship between two-time series is made by observing the directional alignment of arrows. When arrows point in the right direction, it signifies the in-phase alignment of the two signals, whereas leftward-pointing arrows indicate an anti-phase alignment.

The horizontal axis of the graph displays time, while the vertical axis depicts frequency, with higher scales corresponding to lower frequencies. The wavelet coherence identifies regions in time-frequency space where two-time series co-vary. Significantly related areas are represented by warmer colors (red), indicating a strong interrelation, whereas colder colors (blue) signify lower dependence between the series. Cold regions outside the significant areas indicate time and frequencies where there is no dependence in the series. In the wavelet coherence plots, arrows indicate lead/lag phase relations between the examined series. A zero-phase difference denotes that the two-time series move together at a particular scale. Arrows pointing to the right (left) indicate in-phase (anti-phase) relationships between the time series.

Globally, the COVID-19 virus persisted in causing anxiety, uncertainty, and distress in Tunisia. This situation heightened volatility in financial markets and led to liquidity challenges. The Tunisian stock market was not exempt from the profound effects of the COVID-19 outbreak, as evidenced by the ratios of confirmed cases and death cases, respectively (see Figure 2 and Figure 3).

Figure 2. WAVELET TRANSFORM COHERENCE: Tunisian Stock return volatility versus COVID-19 cases rate. Notes: The black contour shows where the spectrum is significantly different from red noise at the 5% level. The lighter shade represents the cone of influence, marking high-power areas and indicating autocorrelation of wavelet power at each scale. The horizontal axis represents time from March 3rd, 2020, to December 30, 2022, and the vertical axis denotes scale bands with daily frequency. Arrows to the right (left) indicate in-phase (out-of-phase) relationships, meaning a positive (negative) connection. If arrows move right and up (down), the first variable "m" (Cases rate) drives (follows), while if arrows move left and up (down), variable "n" (TUNINDEX volatility) leads (lags). This visualization helps understand the dynamic relationships between variables. Source: The Author.

Figure 2. WAVELET TRANSFORM COHERENCE: Tunisian Stock return volatility versus COVID-19 cases rate. Notes: The black contour shows where the spectrum is significantly different from red noise at the 5% level. The lighter shade represents the cone of influence, marking high-power areas and indicating autocorrelation of wavelet power at each scale. The horizontal axis represents time from March 3rd, 2020, to December 30, 2022, and the vertical axis denotes scale bands with daily frequency. Arrows to the right (left) indicate in-phase (out-of-phase) relationships, meaning a positive (negative) connection. If arrows move right and up (down), the first variable "m" (Cases rate) drives (follows), while if arrows move left and up (down), variable "n" (TUNINDEX volatility) leads (lags). This visualization helps understand the dynamic relationships between variables. Source: The Author.

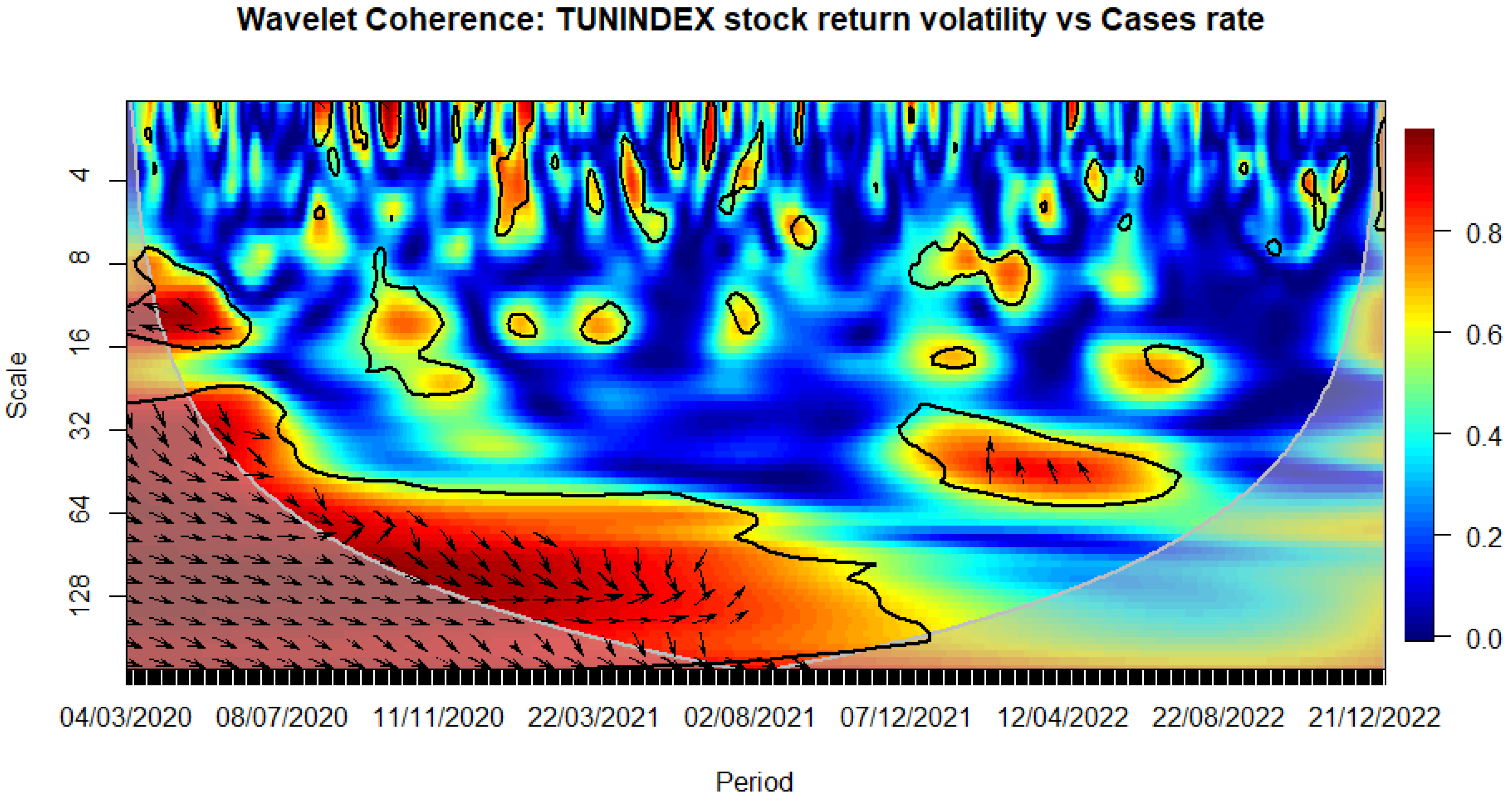
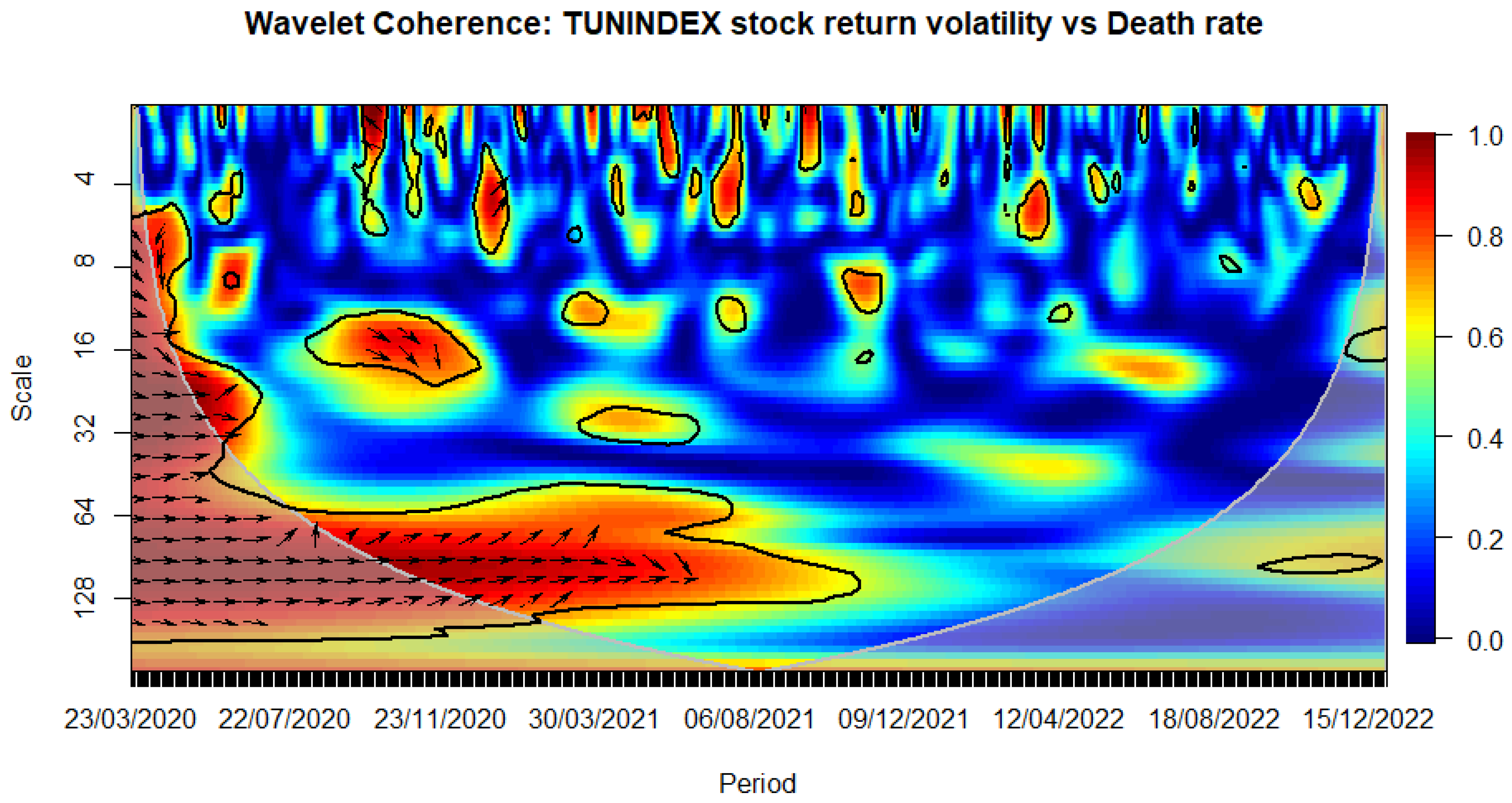
Figure 3. WAVELET TRANSFORM COHERENCE: Tunisian stock Return volatility versus COVID-19 death rate. Notes: The black contour identifies areas where the spectrum is statistically significant at the 5% level compared to red noise. The lighter shade designates the cone of influence, outlining high-power regions. Time, ranging from March 23rd, 2020, to December 30, 2022, is represented on the horizontal axis, while the vertical axis denotes scale bands with daily frequency. Source: The Author.

Figure 3. WAVELET TRANSFORM COHERENCE: Tunisian stock Return volatility versus COVID-19 death rate. Notes: The black contour identifies areas where the spectrum is statistically significant at the 5% level compared to red noise. The lighter shade designates the cone of influence, outlining high-power regions. Time, ranging from March 23rd, 2020, to December 30, 2022, is represented on the horizontal axis, while the vertical axis denotes scale bands with daily frequency. Source: The Author.

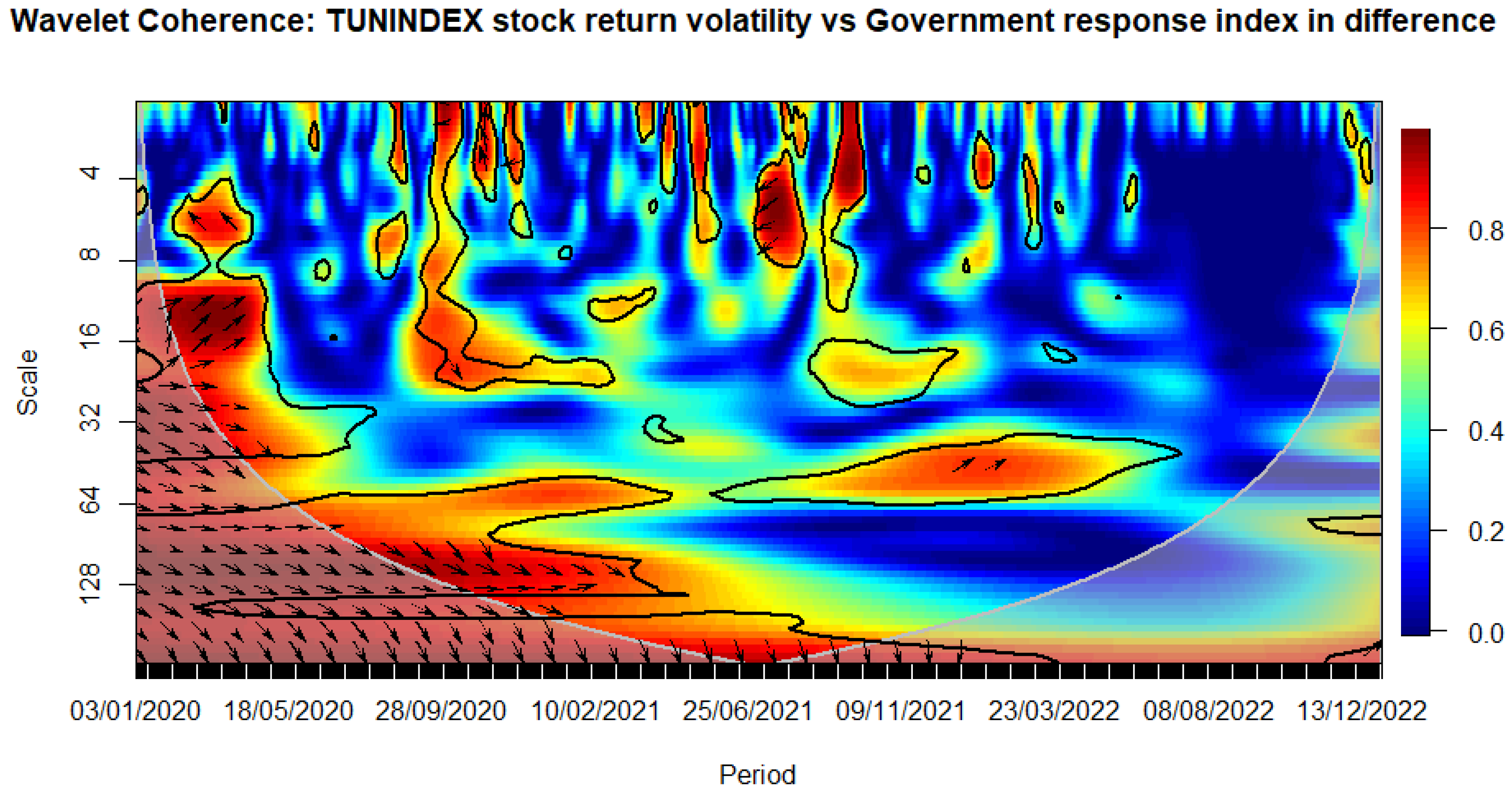
Among the government intervention metrics, the stringency index, the containment health index, and government response indices seem to affect the most stock market volatility during the COVID-19 times, while the economic support index had a neglected impact in the same period (see Figure 4, Figure 5, Figure 6 and Figure 7), confirming partially our previous results (see Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10 and Table 11).

Now, we decompose the stringency index into sub-indices. Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16 display the correlations between TUNINDEX stock market volatility and each of the nine-stringency index sub-indicators.

Figure 4. WAVELET TRANSFORM COHERENCE: Tunisian stock return volatility versus Stringency index. Notes: The black contour identifies areas where the spectrum is statistically significant at the 5% level compared to red noise. The lighter shade designates the cone of influence, outlining high-power regions. Time, ranging from January 3rd, 2020, to December 30, 2022, is represented on the horizontal axis, while the vertical axis denotes scale bands with daily frequency. Source: The Author.

Figure 4. WAVELET TRANSFORM COHERENCE: Tunisian stock return volatility versus Stringency index. Notes: The black contour identifies areas where the spectrum is statistically significant at the 5% level compared to red noise. The lighter shade designates the cone of influence, outlining high-power regions. Time, ranging from January 3rd, 2020, to December 30, 2022, is represented on the horizontal axis, while the vertical axis denotes scale bands with daily frequency. Source: The Author.

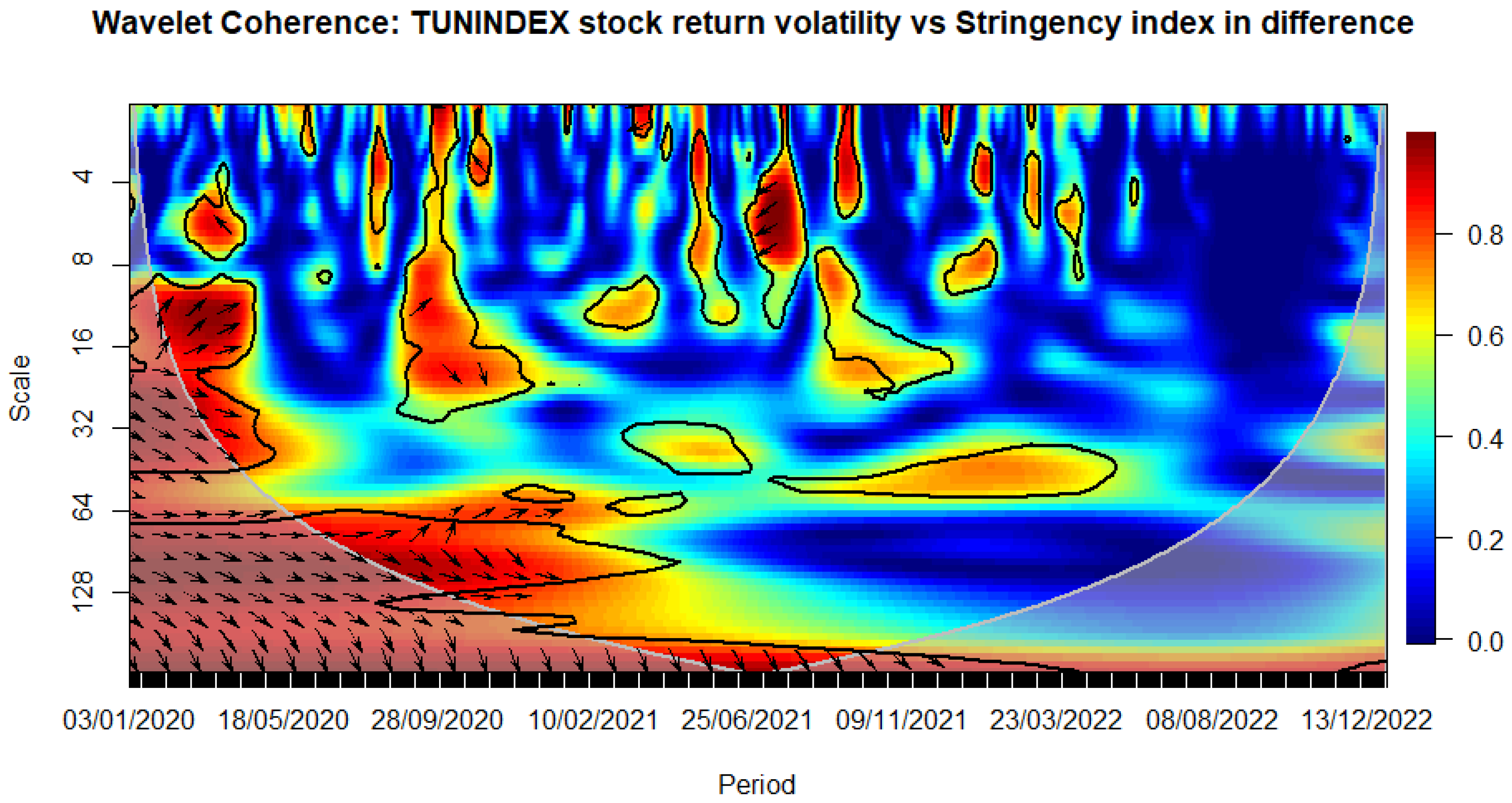
Figure 5. WAVELET TRANSFORM COHERENCE: Tunisian stock return volatility versus Containment health index. Notes: The black contour identifies areas where the spectrum is statistically significant at the 5% level compared to red noise. The lighter shade designates the cone of influence, outlining high-power regions. Time, ranging from January 3rd, 2020, to December 30, 2022, is represented on the horizontal axis, while the vertical axis denotes scale bands with daily frequency. Source: The Author.

Figure 5. WAVELET TRANSFORM COHERENCE: Tunisian stock return volatility versus Containment health index. Notes: The black contour identifies areas where the spectrum is statistically significant at the 5% level compared to red noise. The lighter shade designates the cone of influence, outlining high-power regions. Time, ranging from January 3rd, 2020, to December 30, 2022, is represented on the horizontal axis, while the vertical axis denotes scale bands with daily frequency. Source: The Author.

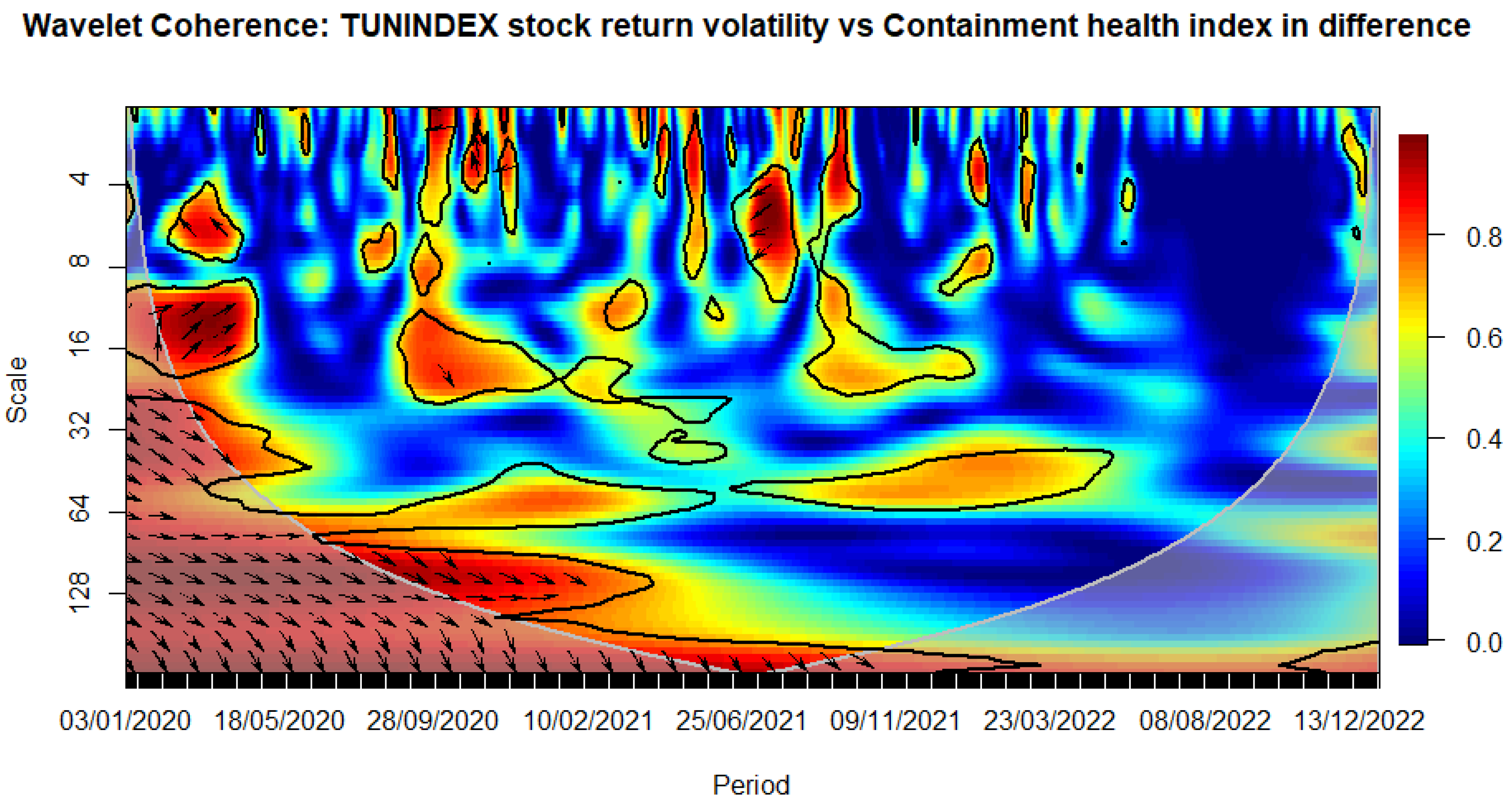
Figure 6. WAVELET TRANSFORM COHERENCE: Tunisian stock return volatility versus Economic support index. Notes: The black contour identifies areas where the spectrum is statistically significant at the 5% level compared to red noise. The lighter shade designates the cone of influence, outlining high-power regions. Time, ranging from January 3rd, 2020, to December 30, 2022, is represented on the horizontal axis, while the vertical axis denotes scale bands with daily frequency. Source: The Author.

Figure 6. WAVELET TRANSFORM COHERENCE: Tunisian stock return volatility versus Economic support index. Notes: The black contour identifies areas where the spectrum is statistically significant at the 5% level compared to red noise. The lighter shade designates the cone of influence, outlining high-power regions. Time, ranging from January 3rd, 2020, to December 30, 2022, is represented on the horizontal axis, while the vertical axis denotes scale bands with daily frequency. Source: The Author.

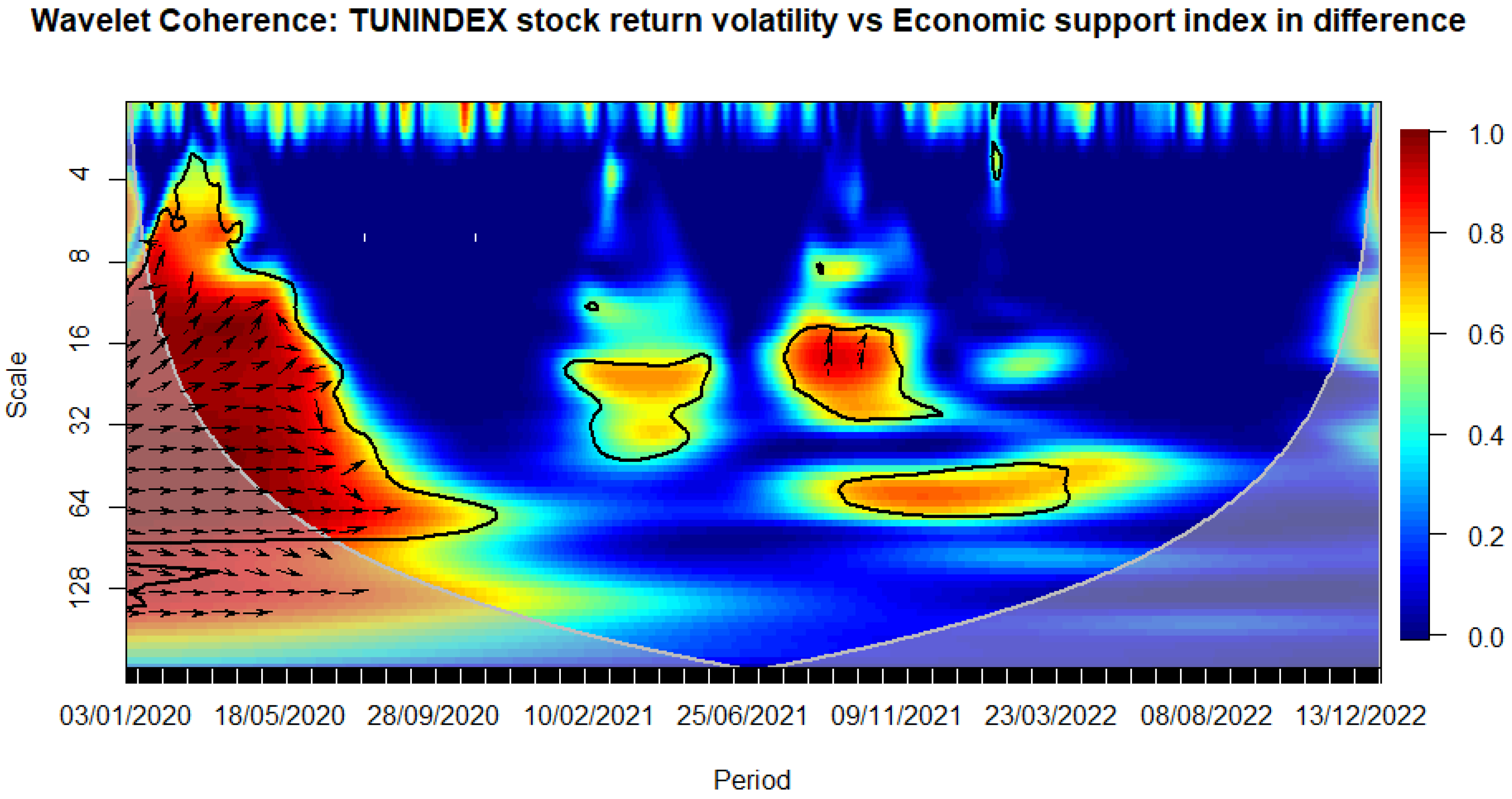
Figure 7. Tunisian stock return volatility versus government response index. Notes: The black contour identifies areas where the spectrum is statistically significant at the 5% level compared to red noise. The lighter shade designates the cone of influence, outlining high-power regions. Time, ranging from January 3rd, 2020, to December 30, 2022, is represented on the horizontal axis, while the vertical axis denotes scale bands with daily frequency. Source: The Author.

Figure 7. Tunisian stock return volatility versus government response index. Notes: The black contour identifies areas where the spectrum is statistically significant at the 5% level compared to red noise. The lighter shade designates the cone of influence, outlining high-power regions. Time, ranging from January 3rd, 2020, to December 30, 2022, is represented on the horizontal axis, while the vertical axis denotes scale bands with daily frequency. Source: The Author.

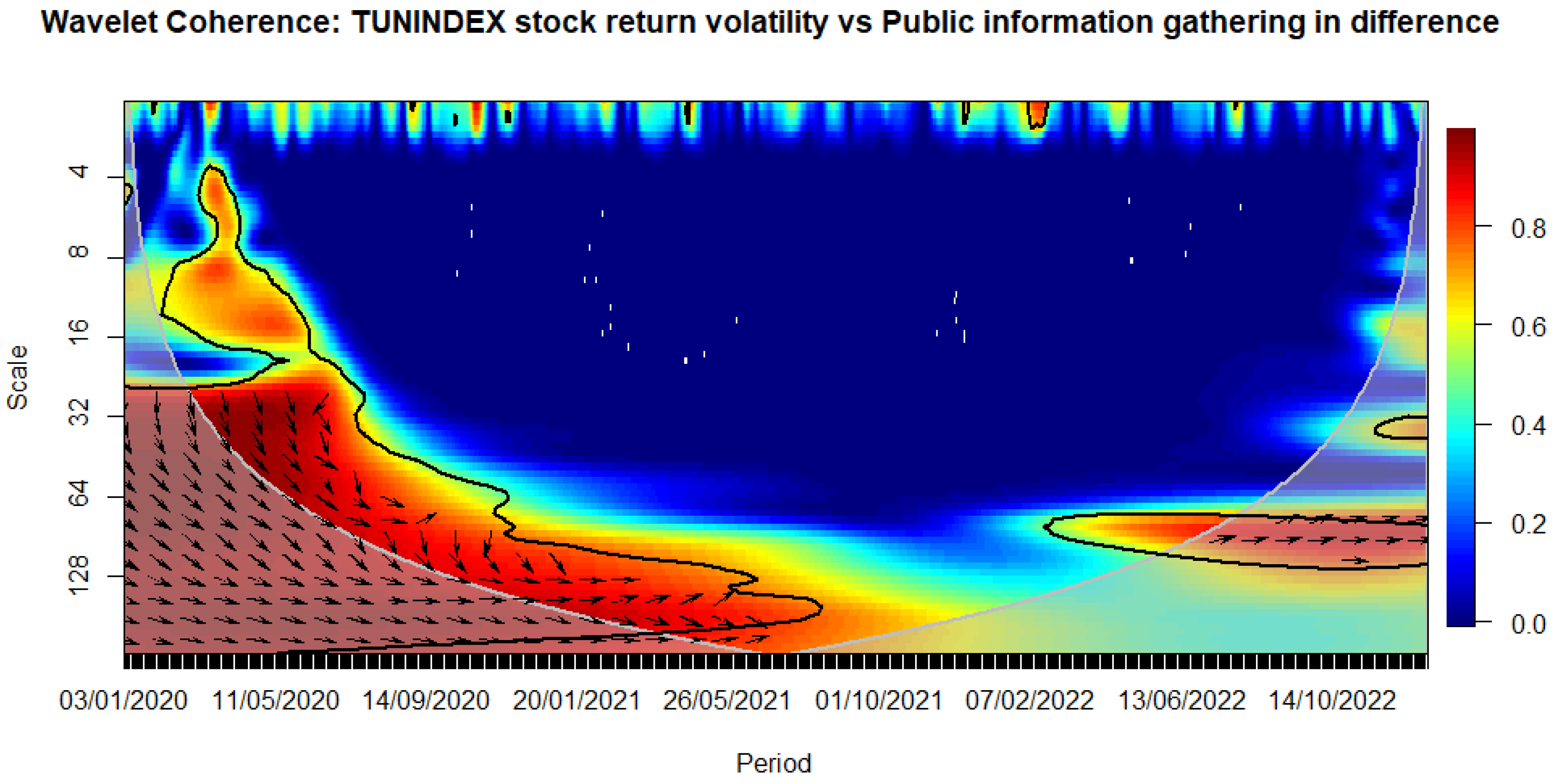
We observe that the closure of schools immediately influences volatility during the sanitary crisis (see Figure 8). Similarly, workplace closures exhibit an immediate impact, persisting over a medium-term horizon (see Figure 9). The cancellation of public events appears to have a notable and enduring impact over a longer-term horizon, as evidenced by a relatively high correlation with stock market volatility that persists beyond the COVID-19 period (see Figure 10). This pattern is evident when considering the stringency subindex related to restrictions on public gatherings (see Figure 11). Restrictions on public gatherings seem to impact conditional volatility over a short-term horizon (see Figure 12). Stay-at-home requirements distinctly impact volatility over short to medium-term horizons (see Figure 13). Restrictions on internal movements have an immediate impact on volatility triggered by the pandemic (see Figure 14). Control measures on international travel affect volatility over a medium-term horizon, with the effect extending post-COVID (see Figure 15). The gathering of public information influences volatility in the long run (see Figure 16).

The observed impact of various stringency measures on market volatility during the COVID-19 crisis holds significant implications for policymaking. Measures such as school closures and workplace shutdowns immediately contribute to volatility during the sanitary crisis, necessitating swift and targeted interventions to stabilize financial markets. Notably, workplace closures exhibit a sustained impact over a medium-term horizon, underscoring the importance of measures to counter prolonged market uncertainties. Public event cancellations demonstrate a lasting influence, emphasizing the need for strategies to manage and recover from enduring economic disruptions. The stringency subindex related to restrictions on public gatherings affects conditional volatility over a short-term horizon, requiring a delicate balance in policymaking to ensure public health measures without causing prolonged market disruptions. Stay-at-home requirements distinctly impact volatility over short to medium-term horizons, necessitating adaptive financial measures. Internal movement restrictions trigger an immediate market response, highlighting the importance of swift financial interventions. International travel control affects volatility over a medium-term horizon, prompting policymakers to consider strategies supporting industries reliant on international travel and trade. Lastly, the influence of public information gathering on long-term volatility underscores the importance of transparent communication for maintaining market stability. Policymakers can leverage these insights to design targeted interventions addressing both immediate and prolonged economic implications during crises.

Figure 8. WAVELET TRANSFORM COHERENCE: Tunisian stock return versus School closing index. Notes: The black contour identifies areas where the spectrum is statistically significant at the 5% level compared to red noise. The lighter shade designates the cone of influence, outlining high-power regions. Time, ranging from January 3rd, 2020, to December 30, 2022, is represented on the horizontal axis, while the vertical axis denotes scale bands with daily frequency. Source: The Author.

Figure 8. WAVELET TRANSFORM COHERENCE: Tunisian stock return versus School closing index. Notes: The black contour identifies areas where the spectrum is statistically significant at the 5% level compared to red noise. The lighter shade designates the cone of influence, outlining high-power regions. Time, ranging from January 3rd, 2020, to December 30, 2022, is represented on the horizontal axis, while the vertical axis denotes scale bands with daily frequency. Source: The Author.

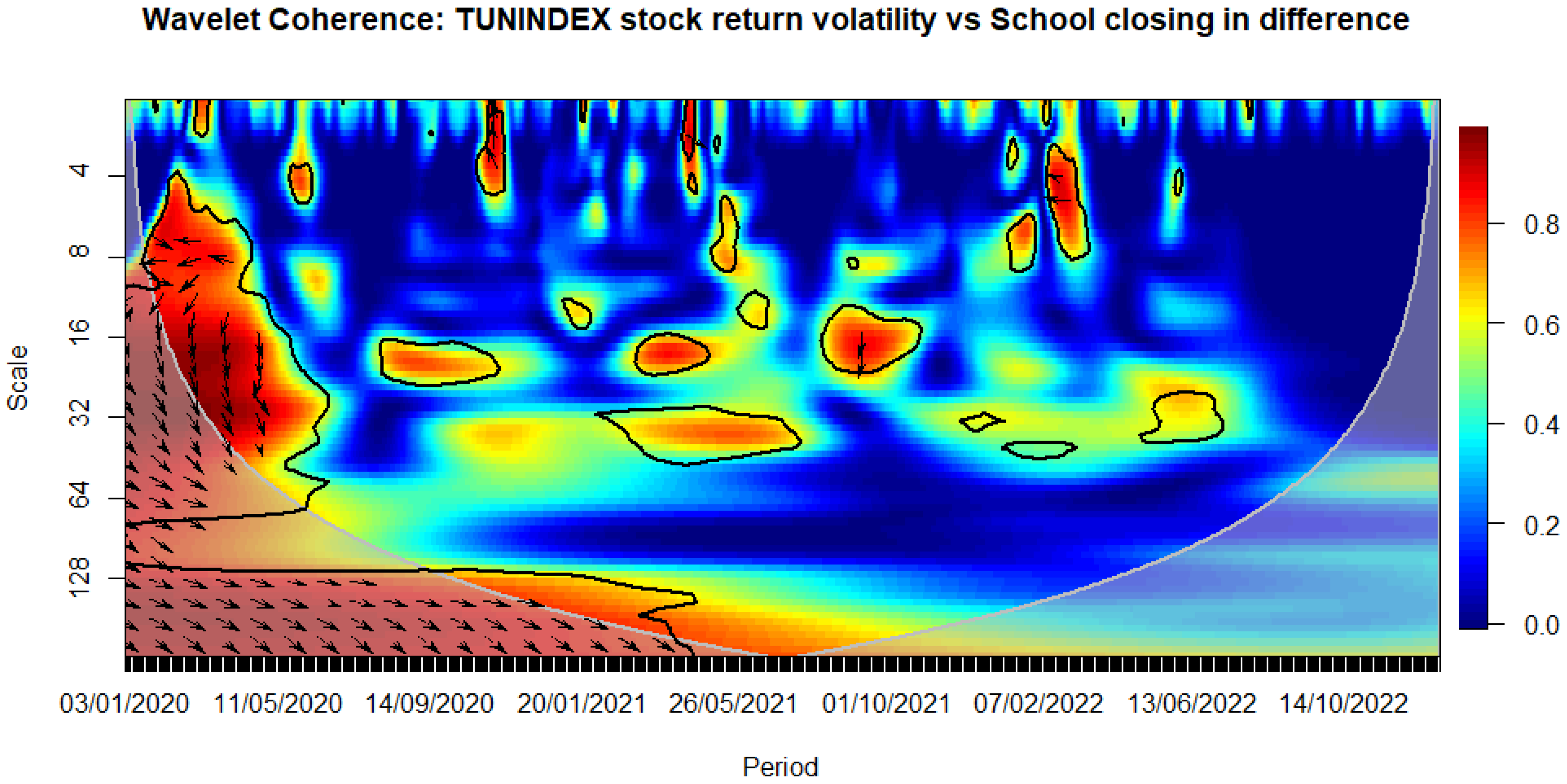
Figure 9. WAVELET TRANSFORM COHERENCE: Tunisian stock return versus Workplace closing. Notes: The black contour identifies areas where the spectrum is statistically significant at the 5% level compared to red noise. The lighter shade designates the cone of influence, outlining high-power regions. Time, ranging from January 3rd, 2020, to December 30, 2022, is represented on the horizontal axis, while the vertical axis denotes scale bands with daily frequency. Source: The Author.

Figure 9. WAVELET TRANSFORM COHERENCE: Tunisian stock return versus Workplace closing. Notes: The black contour identifies areas where the spectrum is statistically significant at the 5% level compared to red noise. The lighter shade designates the cone of influence, outlining high-power regions. Time, ranging from January 3rd, 2020, to December 30, 2022, is represented on the horizontal axis, while the vertical axis denotes scale bands with daily frequency. Source: The Author.

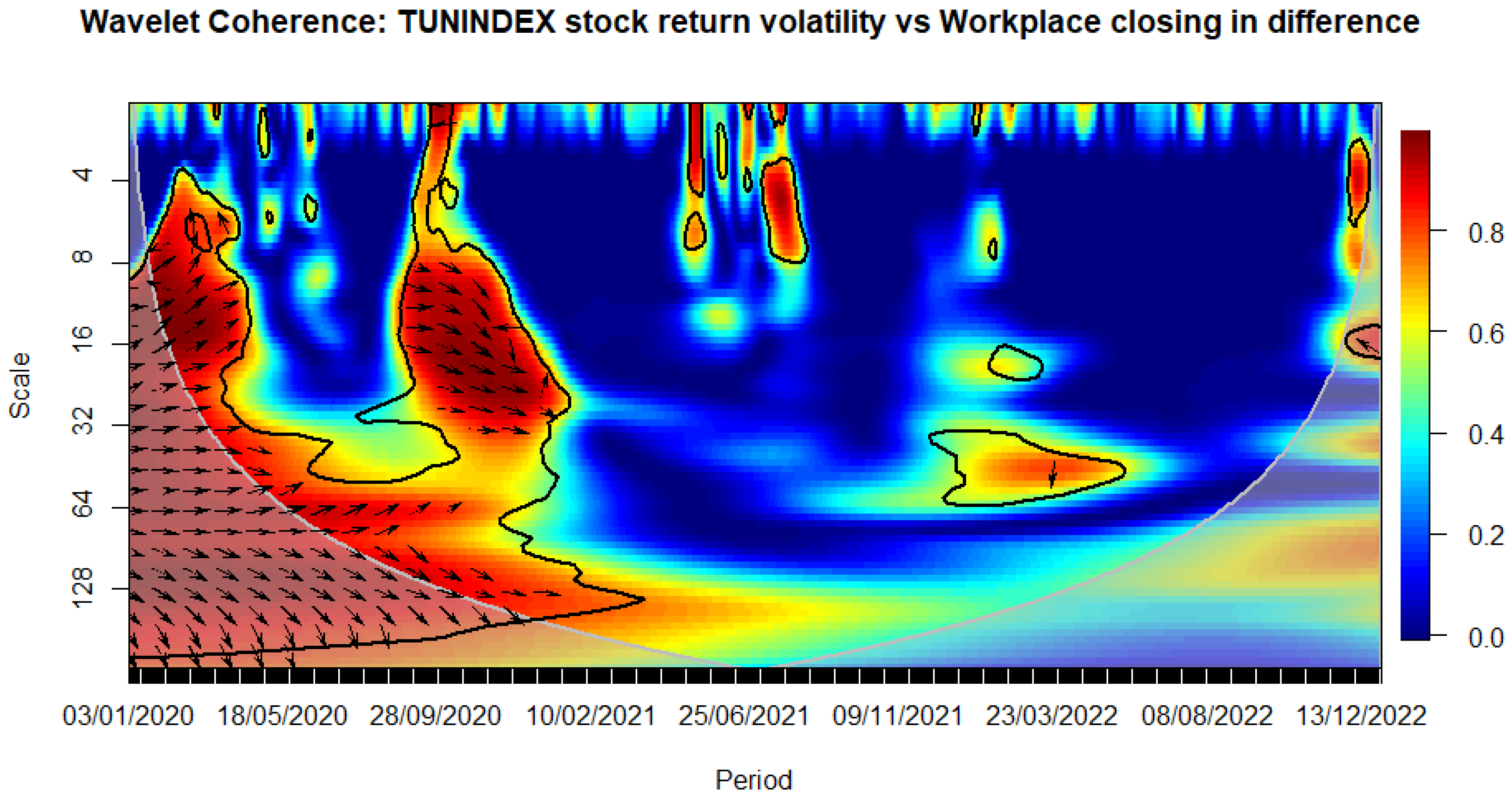
Figure 10. WAVELET TRANSFORM COHERENCE: Tunisian stock return versus Public events canceling. Notes: The black contour identifies areas where the spectrum is statistically significant at the 5% level compared to red noise. The lighter shade designates the cone of influence, outlining high-power regions. Time, ranging from January 3rd, 2020, to December 30, 2022, is represented on the horizontal axis, while the vertical axis denotes scale bands with daily frequency. Source: The Author.

Figure 10. WAVELET TRANSFORM COHERENCE: Tunisian stock return versus Public events canceling. Notes: The black contour identifies areas where the spectrum is statistically significant at the 5% level compared to red noise. The lighter shade designates the cone of influence, outlining high-power regions. Time, ranging from January 3rd, 2020, to December 30, 2022, is represented on the horizontal axis, while the vertical axis denotes scale bands with daily frequency. Source: The Author.

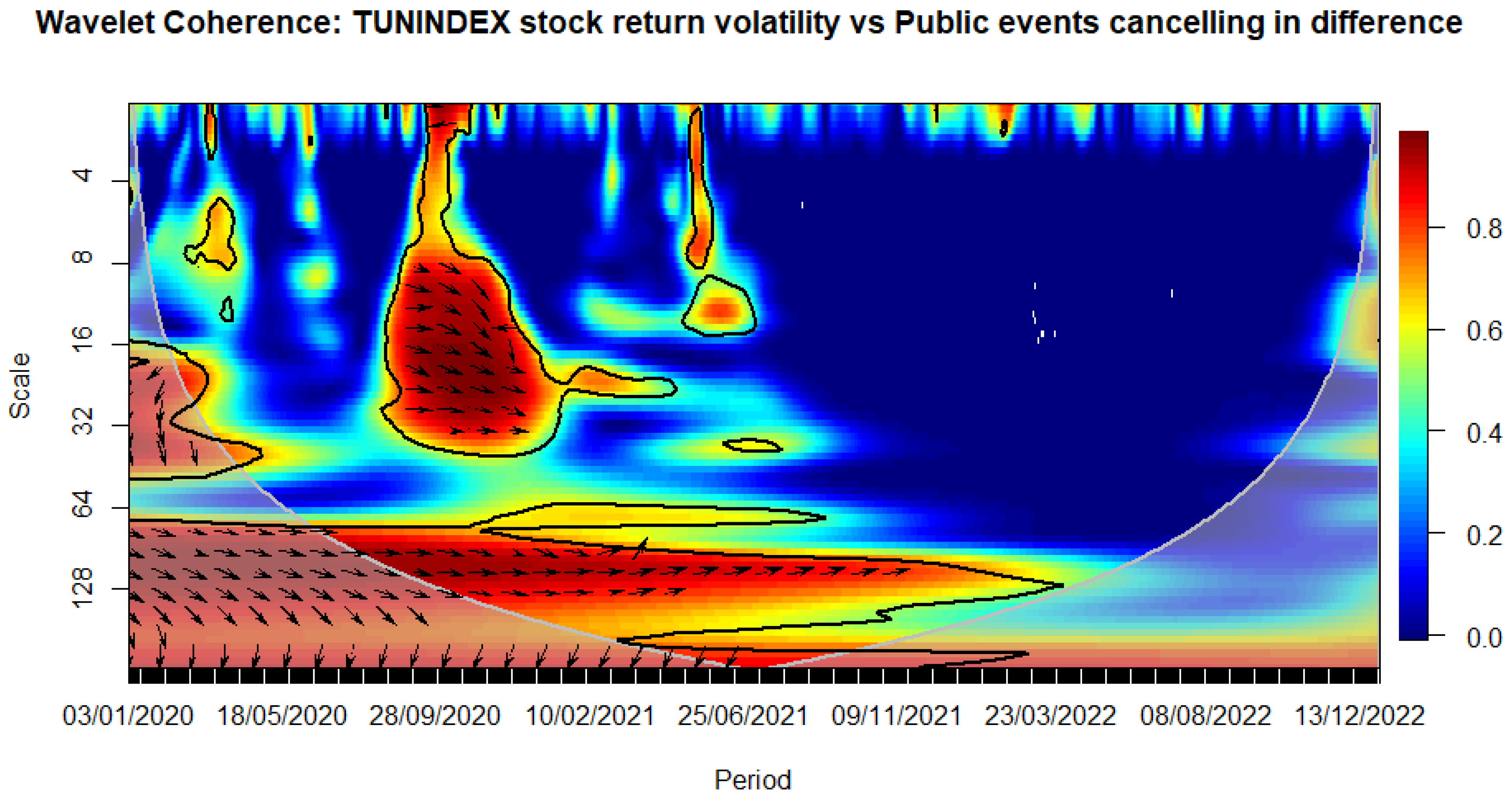
Figure 11. WAVELET TRANSFORM COHERENCE: Tunisian stock return versus Public gathering restrictions. Notes: The black contour identifies areas where the spectrum is statistically significant at the 5% level compared to red noise. The lighter shade designates the cone of influence, outlining high-power regions. Time, ranging from January 3rd, 2020, to December 30, 2022, is represented on the horizontal axis, while the vertical axis denotes scale bands with daily frequency. Source: The Author.

Figure 11. WAVELET TRANSFORM COHERENCE: Tunisian stock return versus Public gathering restrictions. Notes: The black contour identifies areas where the spectrum is statistically significant at the 5% level compared to red noise. The lighter shade designates the cone of influence, outlining high-power regions. Time, ranging from January 3rd, 2020, to December 30, 2022, is represented on the horizontal axis, while the vertical axis denotes scale bands with daily frequency. Source: The Author.

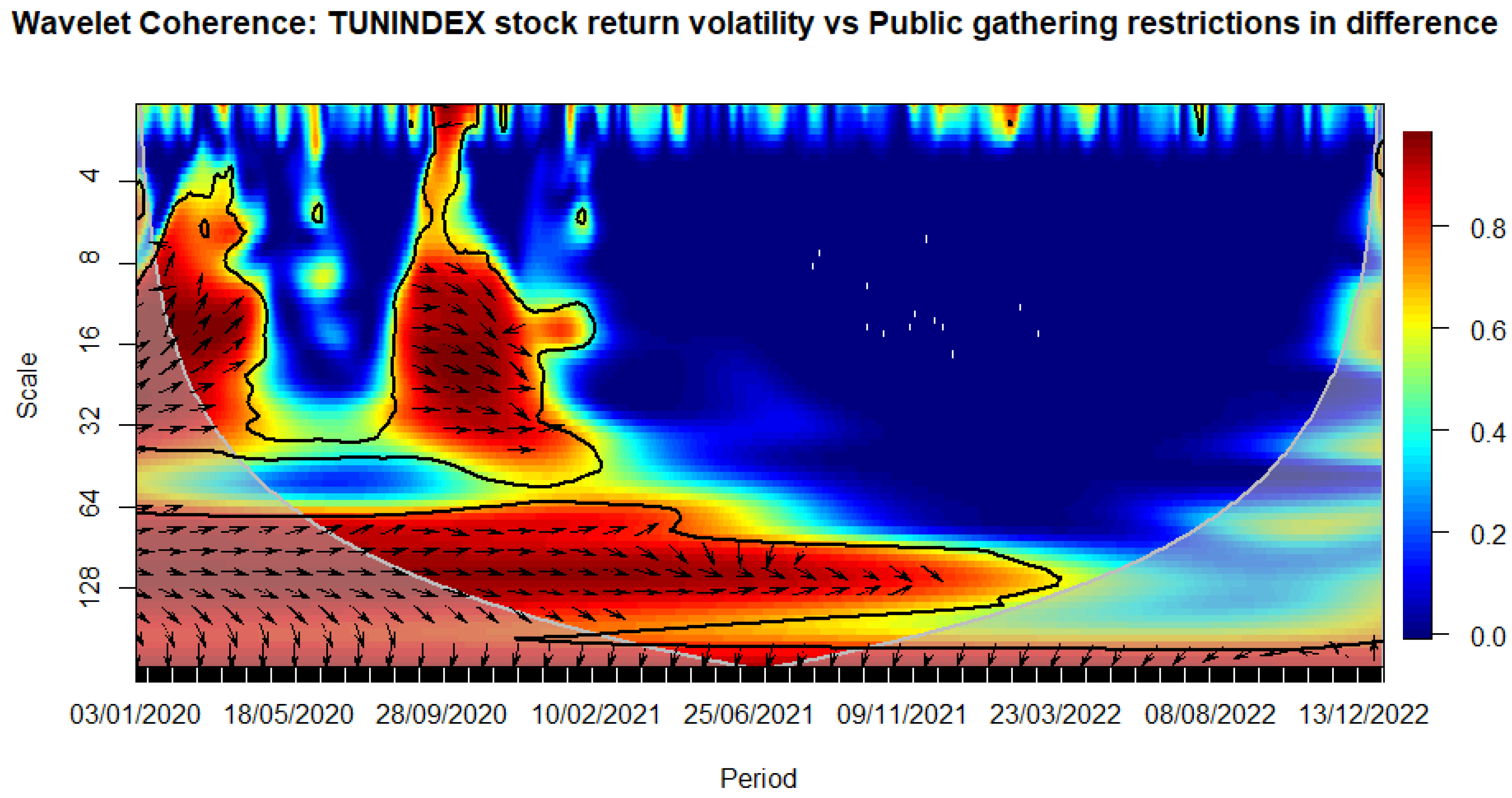
Figure 12. WAVELET TRANSFORM COHERENCE: Tunisian stock return versus Public transport closure. Notes: The black contour identifies areas where the spectrum is statistically significant at the 5% level compared to red noise. The lighter shade designates the cone of influence, outlining high-power regions. Time, ranging from January 3rd, 2020, to December 30, 2022, is represented on the horizontal axis, while the vertical axis denotes scale bands with daily frequency. Source: The Author.

Figure 12. WAVELET TRANSFORM COHERENCE: Tunisian stock return versus Public transport closure. Notes: The black contour identifies areas where the spectrum is statistically significant at the 5% level compared to red noise. The lighter shade designates the cone of influence, outlining high-power regions. Time, ranging from January 3rd, 2020, to December 30, 2022, is represented on the horizontal axis, while the vertical axis denotes scale bands with daily frequency. Source: The Author.

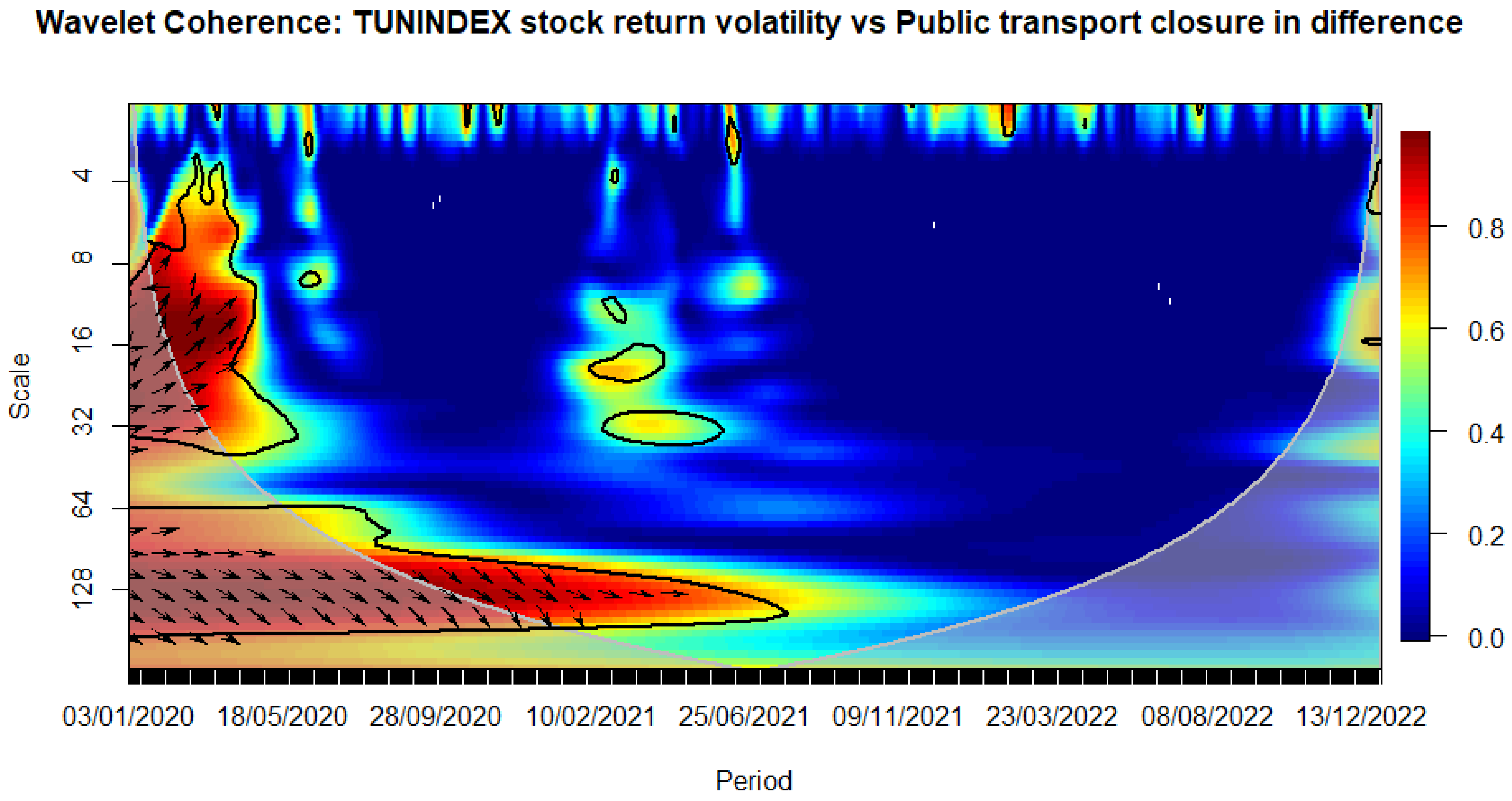
Figure 13. WAVELET TRANSFORM COHERENCE: Tunisian stock return versus Stay-at-home requirements. Notes: The black contour identifies areas where the spectrum is statistically significant at the 5% level compared to red noise. The lighter shade designates the cone of influence, outlining high-power regions. Time, ranging from January 3rd, 2020, to December 30, 2022, is represented on the horizontal axis, while the vertical axis denotes scale bands with daily frequency. Source: The Author.

Figure 13. WAVELET TRANSFORM COHERENCE: Tunisian stock return versus Stay-at-home requirements. Notes: The black contour identifies areas where the spectrum is statistically significant at the 5% level compared to red noise. The lighter shade designates the cone of influence, outlining high-power regions. Time, ranging from January 3rd, 2020, to December 30, 2022, is represented on the horizontal axis, while the vertical axis denotes scale bands with daily frequency. Source: The Author.

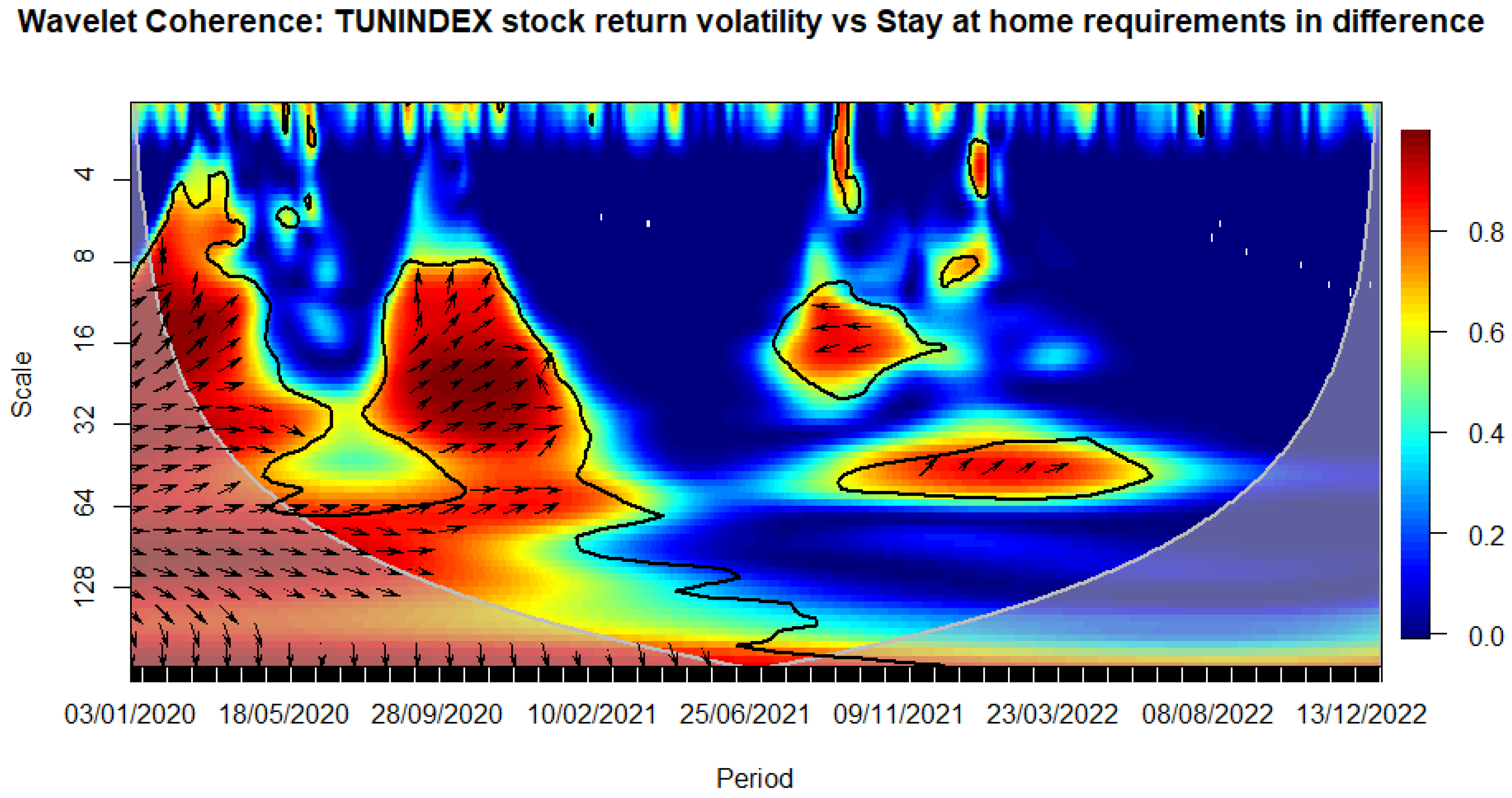
Figure 14. WAVELET TRANSFORM COHERENCE: Tunisian stock return versus Internal movements restrictions Notes: The black contour identifies areas where the spectrum is statistically significant at the 5% level compared to red noise. The lighter shade designates the cone of influence, outlining high-power regions. Time, ranging from January 3rd, 2020, to December 30, 2022, is represented on the horizontal axis, while the vertical axis denotes scale bands with daily frequency. Source: The Author.

Figure 14. WAVELET TRANSFORM COHERENCE: Tunisian stock return versus Internal movements restrictions Notes: The black contour identifies areas where the spectrum is statistically significant at the 5% level compared to red noise. The lighter shade designates the cone of influence, outlining high-power regions. Time, ranging from January 3rd, 2020, to December 30, 2022, is represented on the horizontal axis, while the vertical axis denotes scale bands with daily frequency. Source: The Author.

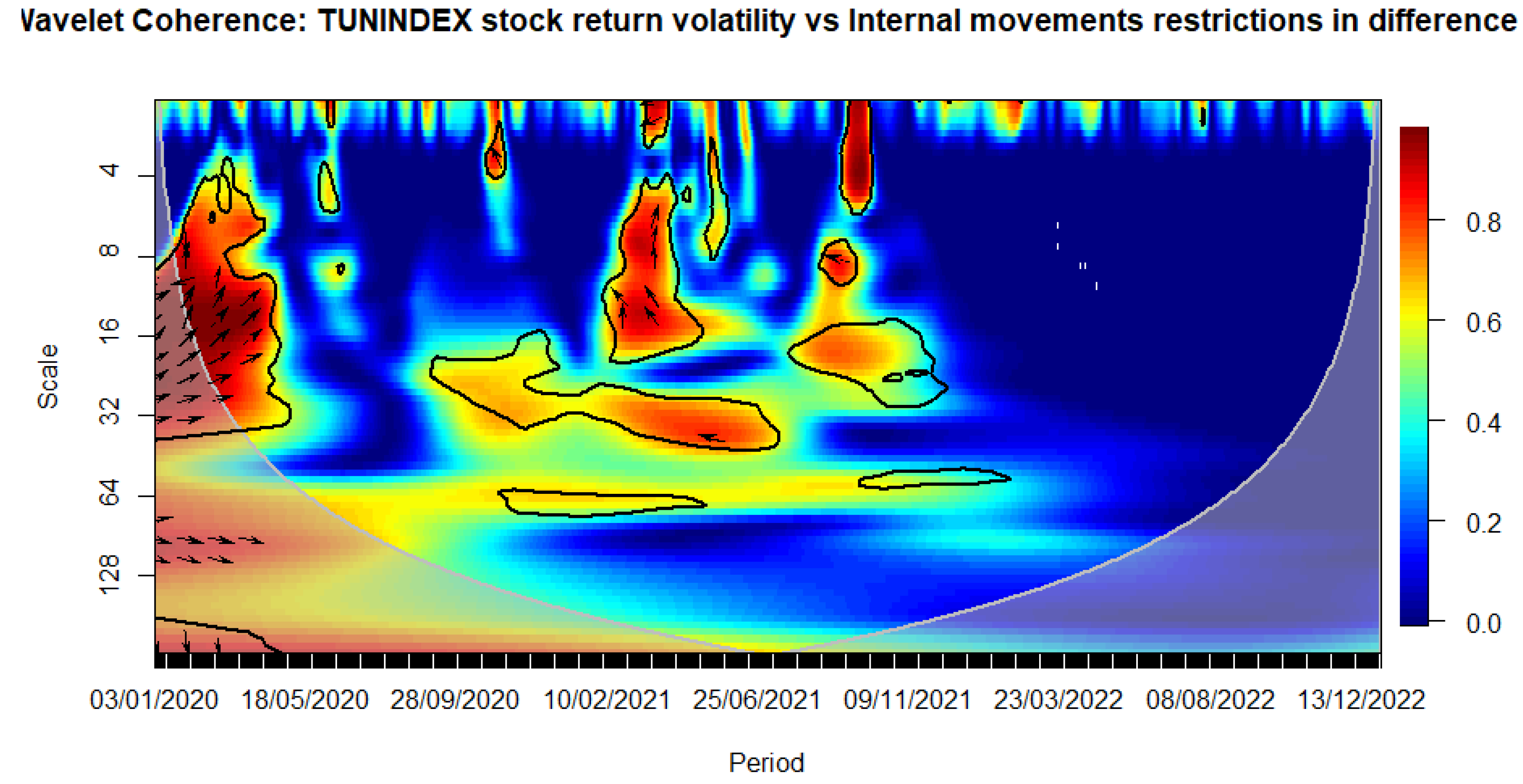
Figure 15. WAVELET TRANSFORM COHERENCE: Tunisian stock return versus International travel control. Notes: The black contour identifies areas where the spectrum is statistically significant at the 5% level compared to red noise. The lighter shade designates the cone of influence, outlining high-power regions. Time, ranging from January 3rd, 2020, to December 30, 2022, is represented on the horizontal axis, while the vertical axis denotes scale bands with daily frequency. Source: The Author.

Figure 15. WAVELET TRANSFORM COHERENCE: Tunisian stock return versus International travel control. Notes: The black contour identifies areas where the spectrum is statistically significant at the 5% level compared to red noise. The lighter shade designates the cone of influence, outlining high-power regions. Time, ranging from January 3rd, 2020, to December 30, 2022, is represented on the horizontal axis, while the vertical axis denotes scale bands with daily frequency. Source: The Author.

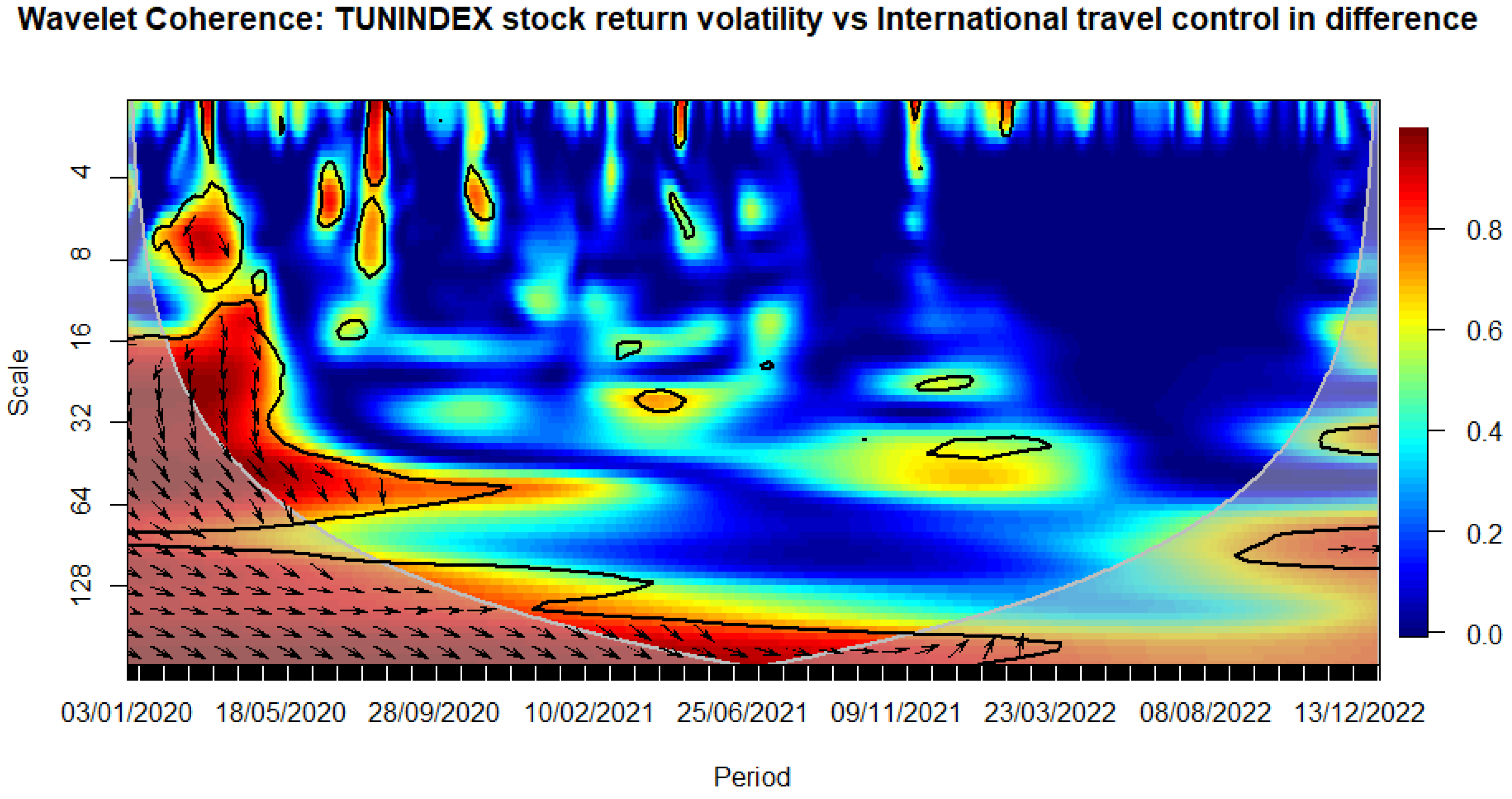
Figure 16. WAVELET TRANSFORM COHERENCE: Tunisian stock return versus Public information gathering. Notes: The black contour identifies areas where the spectrum is statistically significant at the 5% level compared to red noise. The lighter shade designates the cone of influence, outlining high-power regions. Time, ranging from January 3rd, 2020, to December 30, 2022, is represented on the horizontal axis, while the vertical axis denotes scale bands with daily frequency. Source: The Author.

Figure 16. WAVELET TRANSFORM COHERENCE: Tunisian stock return versus Public information gathering. Notes: The black contour identifies areas where the spectrum is statistically significant at the 5% level compared to red noise. The lighter shade designates the cone of influence, outlining high-power regions. Time, ranging from January 3rd, 2020, to December 30, 2022, is represented on the horizontal axis, while the vertical axis denotes scale bands with daily frequency. Source: The Author.

4.3. Impact of uncertainty on the TUNINDEX stock return volatility using ARDL

The earlier COVID-19 and government intervention metrics serve as indicators of the broader economic and health landscape, influencing investor confidence and risk perceptions. However, the uncertainty surrounding COVID-19 has a notable impact on stock market volatility. The dataset comprises daily values of Economic Policy Uncertainty (EPU), the Infectious Disease EMV Tracker (IDEMV), Implied Volatility (VIX), and US Equity Market Uncertainty (EMU). The development of EPU and IDEMV was initiated by Baker et al. (2016, 2019). Quoting Tissaoui et al. (2022, p. 4), EPU quantifies the number of articles in major newspapers covering news related to the economy, uncertainty, monetary and trade policies, and financial regulation in the US (https://www.policyuncertainty.com/us_monthly.html). IDEMV (https://www.policyuncertainty.com/infectious_EMV.html). Additionally, the VIX is the implied volatility index of the Chicago Board Options Exchange. We gather data on EMU from the Federal Reserve Bank of St. Louis https://fred.stlouisfed.org/series/WLEMUINDXD. Unit root and Johansen tests indicate that the variables are I(0) and I(1) and cointegrated (see Table 12 and Table 13, respectively). We adjust coefficients to the White estimator as only heteroscedasticity is detected when analyzing residuals that remain uncorrelated and stable according to the Ramsey test (not shown for tractable reasons but available upon request). All variables, except EPU, have both positive long and short-term effects on Tunisian stock market volatility (see Table 14). This could be due to factors like the stronger influence of local economic conditions, political stability, and industry-specific dynamics on TUNINDEX volatility. At the same time, the findings emphasize the importance of monitoring not only domestic factors but also global economic and health-related developments to anticipate and navigate volatility in the Tunisian stock market.

Table 12. Unit root test results.

Table 12. Unit root test results.

UNIT ROOT TEST TABLE (PP)
	At Level
		CONDVAR_TUN	EMU	EPU	IMEDV	VIX
With Constant	t-Statistic	-5.8831	-17.7598	-9.9104	-16.6159	-3.8380
	Prob.	0.0000	0.0000	0.0000	0.0000	0.0027
		***	***	***	***	***
With Constant & Trend	t-Statistic	-6.0788	-18.5316	-12.8521	-17.9677	-4.0035
	Prob.	0.0000	0.0000	0.0000	0.0000	0.0090
		***	***	***	***	***
Without Constant & Trend	t-Statistic	-4.9680	-8.6348	-2.8802	-6.0788	-1.0620
	Prob.	0.0000	0.0000	0.0039	0.0000	0.2607
		***	***	***	***	n0
	At First Difference
		d(CONDVAR_TUN)	d(EMU)	d(EPU)	d(IMEDV)	d(VIX)
With Constant	t-Statistic	-23.6448	-325.2894	-72.6030	-104.2793	-34.4302
	Prob.	0.0000	0.0001	0.0001	0.0001	0.0000
		***	***	***	***	***
With Constant & Trend	t-Statistic	-23.6141	-321.7941	-72.7563	-105.3697	-34.4139
	Prob.	0.0000	0.0001	0.0001	0.0001	0.0000
		***	***	***	***	***
Without Constant & Trend	t-Statistic	-23.6785	-330.9807	-72.6602	-104.4676	-34.4538
	Prob.	0.0000	0.0001	0.0001	0.0001	0.0000
		***	***	***	***	***
UNIT ROOT TEST TABLE (ADF)
	At Level
		CONDVAR_TUN	EMU	EPU	IMEDV	VIX
With Constant	t-Statistic	-6.6410	-4.9317	-2.9816	-4.5133	-3.5374
	Prob.	0.0000	0.0000	0.0371	0.0002	0.0073
		***	***	**	***	***
With Constant & Trend	t-Statistic	-6.9345	-5.2977	-3.8321	-5.2213	-3.6962
	Prob.	0.0000	0.0001	0.0154	0.0001	0.0232
		***	***	**	***	**
Without Constant & Trend	t-Statistic	-5.5114	-2.2028	-1.4589	-2.1077	-0.9997
	Prob.	0.0000	0.0267	0.1352	0.0338	0.2850
		***	**	n0	**	n0
	At First Difference
		d(CONDVAR_TUN)	d(EMU)	d(EPU)	d(IMEDV)	d(VIX)
With Constant	t-Statistic	-12.8719	-17.3275	-20.8561	-21.3098	-14.0249
	Prob.	0.0000	0.0000	0.0000	0.0000	0.0000
		***	***	***	***	***
With Constant & Trend	t-Statistic	-12.8629	-17.3155	-20.8449	-21.2986	-14.0230
	Prob.	0.0000	0.0000	0.0000	0.0000	0.0000
		***	***	***	***	***
Without Constant & Trend	t-Statistic	-12.8813	-17.3398	-20.8711	-21.3238	-14.0341
	Prob.	0.0000	0.0000	0.0000	0.0000	0.0000
		***	***	***	***	***

* MacKinnon (1996) one-sided p-values.

Table 13. Johansen cointegration test.

Table 13. Johansen cointegration test.

Date: 01/12/24 Time: 16:39
Sample (adjusted): 1/10/2020 12/30/2022
Included observations: 693 after adjustments
Trend assumption: Linear deterministic trend
Series: EMU EPU VIX IMEDV CONDVAR_TUN
Lags interval (in first differences): 1 to 4
Unrestricted Cointegration Rank Test (Trace)
Hypothesized		Trace	0.05
No. of CE(s)	Eigenvalue	Statistic	Critical Value	Prob.**
None *	0.159673	287.2357	69.81889	0.0001
At most 1 *	0.087501	166.6788	47.85613	0.0000
At most 2 *	0.074215	103.2221	29.79707	0.0000
At most 3 *	0.048996	49.78261	15.49471	0.0000
At most 4 *	0.021368	14.96863	3.841466	0.0001
Trace test indicates 5 cointegrating eqn(s) at the 0.05 level
* denotes rejection of the hypothesis at the 0.05 level
** MacKinnon-Haug-Michelis (1999) p-values

Table 14. Long-run and short-run results of ARDL.

Table 14. Long-run and short-run results of ARDL.

Using EPU and VIX	Levels Equation
	Case 2: Restricted Constant and No Trend
	Variable	Coefficient	Std. Error	t-Statistic	Prob.
	EPU	-1.10E-08	2.72E-08	-0.406081	0.6848
	VIX	2.44E-06	9.45E-07	2.576858	0.0102
	C	-4.02E-05	1.99E-05	-2.022307	0.0435
	EC = CONDVAR_TUN - (-0.0000*EPU + 0.0000*VIX -0.0000 )
	F-Bounds Test		Null Hypothesis: No levels of relationship
	Test Statistic	Value	Signif.	I(0)	I(1)
				Asymptotic: n=1000
	F-statistic	20.22501	10%	2.63	3.35
	k	2	5%	3.1	3.87
			2.5%	3.55	4.38
			1%	4.13	5
	ECM Regression
	Case 2: Restricted Constant and No Trend
	Variable	Coefficient	Std. Error	t-Statistic	Prob.
	D(CONDVAR_TUN(-1))	0.305200	0.036072	8.460905	0.0000
	D(CONDVAR_TUN(-2))	0.163597	0.037889	4.317848	0.0000
	D(CONDVAR_TUN(-3))	-0.135407	0.038054	-3.558262	0.0004
	D(CONDVAR_TUN(-4))	0.042966	0.036567	1.174983	0.2404
	D(CONDVAR_TUN(-5))	0.156755	0.036535	4.290596	0.0000
	D(CONDVAR_TUN(-6))	-0.064229	0.036672	-1.751465	0.0803
	D(VIX)	4.99E-07	1.75E-07	2.846085	0.0046
	D(VIX(-1))	5.59E-07	1.83E-07	3.060780	0.0023
	CointEq(-1)*	-0.214080	0.023749	-9.014119	0.0000
Using EMU + VIX	Levels Equation
	Case 2: Restricted Constant and No Trend
	Variable	Coefficient	Std. Error	t-Statistic	Prob.
	EMU	1.02E-07	5.16E-08	1.982838	0.0478
	VIX	1.33E-06	5.94E-07	2.233982	0.0258
	C	-2.63E-05	1.49E-05	-1.769359	0.0773
	EC = CONDVAR_TUN - (0.0000*EMU + 0.0000*VIX -0.0000 )
	F-Bounds Test		Null Hypothesis: No levels relationship
	Test Statistic	Value	Signif.	I(0)	I(1)
				Asymptotic: n=1000
	F-statistic	16.68016	10%	2.63	3.35
	k	2	5%	3.1	3.87
			2.5%	3.55	4.38
			1%	4.13	5
	ECM Regression
	Case 2: Restricted Constant and No Trend
	Variable	Coefficient	Std. Error	t-Statistic	Prob.
	D(CONDVAR_TUN(-1))	0.280360	0.037720	7.432660	0.0000
	D(CONDVAR_TUN(-2))	0.169588	0.039402	4.303995	0.0000
	D(CONDVAR_TUN(-3))	-0.147548	0.039403	-3.744638	0.0002
	D(CONDVAR_TUN(-4))	0.033769	0.037466	0.901324	0.3677
	D(CONDVAR_TUN(-5))	0.153700	0.037312	4.119377	0.0000
	D(CONDVAR_TUN(-6))	-0.080614	0.037319	-2.160150	0.0311
	D(EMU)	-5.65E-09	6.22E-09	-0.908323	0.3640
	D(EMU(-1))	-2.82E-08	7.75E-09	-3.638482	0.0003
	D(EMU(-2))	-2.49E-08	8.39E-09	-2.968032	0.0031
	D(EMU(-3))	-3.79E-08	8.57E-09	-4.418311	0.0000
	D(EMU(-4))	-2.99E-08	8.34E-09	-3.587680	0.0004
	D(EMU(-5))	-3.58E-09	7.60E-09	-0.471456	0.6375
	D(EMU(-6))	1.44E-08	6.23E-09	2.315235	0.0209
	D(VIX)	4.39E-07	1.75E-07	2.513163	0.0122
	D(VIX(-1))	7.64E-07	1.87E-07	4.091321	0.0000
	D(VIX(-2))	3.64E-07	1.88E-07	1.933189	0.0536
	D(VIX(-3))	4.45E-07	1.89E-07	2.355937	0.0188
	D(VIX(-4))	2.90E-07	1.90E-07	1.523589	0.1281
	D(VIX(-5))	2.81E-07	1.89E-07	1.489922	0.1367
	D(VIX(-6))	4.49E-07	1.80E-07	2.488358	0.0131
	CointEq(-1)*	-0.208323	0.025447	-8.186456	0.0000
Using IDEMV + VIX	Levels Equation
	Case 2: Restricted Constant and No Trend
	Variable	Coefficient	Std. Error	t-Statistic	Prob.
	IMEDV	7.74E-07	3.47E-07	2.230579	0.0260
	VIX	1.56E-06	6.78E-07	2.293725	0.0221
	C	-3.15E-05	1.69E-05	-1.860152	0.0633
	EC = CONDVAR_TUN - (0.0000*IMEDV + 0.0000*VIX -0.0000 )
	F-Bounds Test		Null Hypothesis: No levels relationship
	Test Statistic	Value	Signif.	I(0)	I(1)
				Asymptotic: n=1000
	F-statistic	16.16596	10%	2.63	3.35
	k	2	5%	3.1	3.87
			2.5%	3.55	4.38
			1%	4.13	5
	ECM Regression
	Case 2: Restricted Constant and No Trend
	Variable	Coefficient	Std. Error	t-Statistic	Prob.
	D(CONDVAR_TUN(-1))	0.294640	0.038541	7.644852	0.0000
	D(CONDVAR_TUN(-2))	0.156728	0.040128	3.905726	0.0001
	D(CONDVAR_TUN(-3))	-0.148119	0.039993	-3.703629	0.0002
	D(CONDVAR_TUN(-4))	0.032052	0.037988	0.843737	0.3991
	D(CONDVAR_TUN(-5))	0.149479	0.037947	3.939136	0.0001
	D(CONDVAR_TUN(-6))	-0.066308	0.037763	-1.755902	0.0796
	D(IMEDV)	4.17E-08	6.49E-08	0.642959	0.5205
	D(IDEMV(-1))	-1.54E-07	8.11E-08	-1.893384	0.0587
	D(IDEMV(-2))	-1.26E-07	8.97E-08	-1.409433	0.1592
	D(IDEMV(-3))	-1.98E-07	9.24E-08	-2.139318	0.0328
	D(IDEMV(-4))	-1.67E-07	8.99E-08	-1.854306	0.0641
	D(IDEMV(-5))	-5.06E-08	8.15E-08	-0.620560	0.5351
	D(IDEMV(-6))	1.28E-07	6.64E-08	1.925914	0.0545
	D(VIX)	4.08E-07	1.81E-07	2.259421	0.0242
	D(VIX(-1))	7.04E-07	1.95E-07	3.607629	0.0003
	D(VIX(-2))	3.73E-07	1.98E-07	1.889694	0.0592
	D(VIX(-3))	3.89E-07	1.98E-07	1.966048	0.0497
	D(VIX(-4))	1.44E-07	1.99E-07	0.724840	0.4688
	D(VIX(-5))	2.50E-07	1.94E-07	1.290037	0.1975
	D(VIX(-6))	4.65E-07	1.84E-07	2.522034	0.0119
	CointEq(-1)*	-0.212775	0.026401	-8.059500	0.0000

5. Conclusion

6. Policy Implications

References

1. Akinlaso, M. I., Robbana, A., & Mohamed, N. (2022). Volatility transmission within financial markets during the COVID-19 pandemic: are faith-based investors well off in Tunisia?. Journal of Islamic Accounting and Business Research, 13(1), 98-113. [CrossRef]
2. Albulescu, C. T. (2021). COVID-19 and the United States financial markets’ volatility. Finance research letters, 38, 101699. [CrossRef]
3. Alqahtani, A., Wither, M. J., Dong, Z., & Goodwin, K. R. (2020). Impact of news-based equity market volatility on international stock markets. Journal of Applied Economics, 23(1), 224-234. [CrossRef]
4. Asgharian, H., Christiansen, C., & Hou, A. J. (2023). The effect of uncertainty on stock market volatility and correlation. Journal of Banking & Finance, 106929. [CrossRef]
5. Baek, S., Mohanty, S. K., & Glambosky, M. (2020). COVID-19 and stock market volatility: An industry level analysis. Finance research letters, 37, 101748. [CrossRef]
6. Baker, S. R., Bloom, N., & Davis, S. J. (2016). Measuring economic policy uncertainty. The quarterly journal of economics, 131(4), 1593-1636. [CrossRef]
7. Baker, S. R., Bloom, N., Davis, S. J., & Kost, K. J. (2019). Policy news and stock market volatility (No. w25720). National Bureau of Economic Research. Available online: https://www.nber.org/papers/w25720.
8. Bera, A. K., & Higgins, M. L. (1993). ARCH models: properties, estimation and testing. Journal of economic surveys, 7(4), 305-366. [CrossRef]
9. Binder, J. J., & Merges, M. J. (2001). Stock market volatility and economic factors. Review of Quantitative Finance and Accounting, 17, 5-26. https://link.springer.com/article/10.1023/A:1011207919894.
10. Biu, G. S., & Kusuma, P. K. (2023). Stock Market Volatility Analysis During the Global Financial Crisis: Literature Review. Riwayat: Educational Journal of History and Humanities, 6(4), 2510-2520. Available online: https://jurnal.usk.ac.id/riwayat/article/view/34539.
11. Bollerslev, T. (1986). Generalized autoregressive conditional heteroskedasticity. Journal of econometrics, 31(3), 307-327. [CrossRef]
12. Bollerslev, T., & Mikkelsen, H. O. (1996). Modeling and pricing long memory in stock market volatility. Journal of econometrics, 73(1), 151-184. [CrossRef]
13. Bollerslev, T., Chou, R. Y., & Kroner, K. F. (1992). ARCH modeling in finance: A review of the theory and empirical evidence. Journal of econometrics, 52(1-2), 5-59. [CrossRef]
14. Bora, D., & Basistha, D. (2021). The outbreak of COVID-19 pandemic and its impact on stock market volatility: Evidence from a worst-affected economy. Journal of Public Affairs, 21(4), e2623. [CrossRef]
15. Cazelles, B., Chavez, M., Berteaux, D., Ménard, F., Vik, J. O., Jenouvrier, S., & Stenseth, N. C. (2008). Wavelet analysis of ecological time series. Oecologia, 156, 287-304. [CrossRef]
16. Chaudhary, R., Bakhshi, P., & Gupta, H. (2020). Volatility in international stock markets: An empirical study during COVID-19. Journal of Risk and Financial Management, 13(9), 208. [CrossRef]
17. Chowdhury, E. K., Dhar, B. K., & Stasi, A. (2022). Volatility of the US stock market and business strategy during COVID-19. Business Strategy & Development, 5(4), 350-360. [CrossRef]
18. Dhanya, C. T., & Gupta, A. (2014). Improved bias correction method using wavelet decomposition. Int J Civil Eng Res, 5(1), 1-8.
19. Dhingra, B., Batra, S., Aggarwal, V., Yadav, M., & Kumar, P. (2023). Stock market volatility: a systematic review. Journal of Modelling in Management. [CrossRef]
20. Endri, E., Aipama, W., & Septiano, R. (2021). Stock price volatility during the COVID-19 pandemic: The GARCH model. Investment Management & Financial Innovations, 18(4), 12. Available online: https://pdfs.semanticscholar.org/5a95/11cd49f467a2dfd2924cd4d4ee165aa417ca.pdf.
21. Engle, R. F. (1982). Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econometrica: Journal of the econometric society, 987-1007. [CrossRef]
22. Erdem, O. (2020). Freedom and stock market performance during COVID-19 outbreak. Finance Research Letters, 36, 101671. [CrossRef]
23. Fakhfekh, M., Jeribi, A., & Ben Salem, M. (2023). Volatility dynamics of the Tunisian stock market before and during the COVID-19 outbreak: Evidence from the GARCH family models. International Journal of Finance & Economics, 28(2), 1653-1666. [CrossRef]
24. Gao, X., Ren, Y., & Umar, M. (2022). To what extent does COVID-19 drive stock market volatility? A comparison between the US and China. Economic Research-Ekonomska Istraživanja, 35(1), 1686-1706. [CrossRef]
25. Gherghina, Ș. C., Armeanu, D. Ș., & Joldeș, C. C. (2021). COVID-19 pandemic and Romanian stock market volatility: A GARCH approach. Journal of Risk and Financial Management, 14(8), 341. [CrossRef]
26. Grinsted, A., Moore, J. C., & Jevrejeva, S. (2004). Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear processes in geophysics, 11(5/6), 561-566. [CrossRef]
27. Hewamana, R., Siriwardhane, D., & Rathnayake, A. (2022). Determinants of Stock Price Volatility: A Literature Review. Available online: http://dr.lib.sjp.ac.lk/handle/123456789/12689.
28. Hosseini Baghanam, A., Nourani, V., Norouzi, E., Vakili, A. T., & Gökçekuş, H. (2023). Application of Wavelet Transform for Bias Correction and Predictor Screening of Climate Data. Sustainability, 15(21), 15209. [CrossRef]
29. Hussain, S., Murthy, K. V., & Singh, A. (2019). Stock market volatility: A review of the empirical literature. IUJ Journal of Management, 7(01). Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3418148.
30. Insaidoo, M., Arthur, L., Amoako, S., & Andoh, F. K. (2021). Stock market performance and COVID-19 pandemic: evidence from a developing economy. Journal of Chinese Economic and Foreign Trade Studies, 14(1), 60-73. [CrossRef]
31. Izzeldin, M., Muradoğlu, Y. G., Pappas, V., & Sivaprasad, S. (2021). The impact of COVID-19 on G7 stock markets volatility: Evidence from a ST-HAR model. International Review of Financial Analysis, 74, 101671. [CrossRef]
32. Jeribi, A., Fakhfekh, M., & Jarboui, A. (2015). Tunisian revolution and stock market volatility: evidence from FIEGARCH model. Managerial Finance, 41(10), 1112-1135. [CrossRef]
33. Kamal, J. B., & Wohar, M. (2023). Heterogenous responses of stock markets to covid related news and sentiments: Evidence from the 1st year of pandemic. International Economics, 173, 68-85. [CrossRef]
34. Kusumahadi, T. A., & Permana, F. C. (2021). Impact of COVID-19 on global stock market volatility. Journal of Economic Integration, 36(1), 20-45. Available online: https://www.jstor.org/stable/26985574.
35. Li, T., Ma, F., Zhang, X., & Zhang, Y. (2020). Economic policy uncertainty and the Chinese stock market volatility: Novel evidence. Economic Modelling, 87, 24-33. [CrossRef]
36. Li, W., Chien, F., Waqas Kamran, H., Aldeehani, T. M., Sadiq, M., Nguyen, V. C., & Taghizadeh-Hesary, F. (2022). The nexus between COVID-19 fear and stock market volatility. Economic research-Ekonomska istraživanja, 35(1), 1765-1785. Available online: https://hrcak.srce.hr/file/435909.
37. Liu, Y., San Liang, X., & Weisberg, R. H. (2007). Rectification of the bias in the wavelet power spectrum. Journal of Atmospheric and Oceanic Technology, 24(12), 2093-2102. [CrossRef]
38. Mazur, M., Dang, M., & Vega, M. (2021). COVID-19 and the march 2020 stock market crash. Evidence from S&P1500. Finance research letters, 38, 101690. [CrossRef]
39. Mazzucato, M., & Semmler, W. (2002). The determinants of stock price volatility: An industry study. Nonlinear Dynamics, Psychology, and life Sciences, 6, 197-216. [CrossRef]
40. Megaritis, A., Vlastakis, N., & Triantafyllou, A. (2021). Stock market volatility and jumps in times of uncertainty. Journal of International Money and Finance, 113, 102355. [CrossRef]
41. Mestiri, S. (2022). Modeling the volatility of Bitcoin returns using Nonparametric GARCH models. Journal of Academic Finance, 13(1), 2-16. [CrossRef]
42. Nelson, D. B. (1991). Conditional heteroskedasticity in asset returns: A new approach. Econometrica: Journal of the econometric society, 347-370. [CrossRef]
43. Nikmanesh, L., & Nor, A. H. S. M. (2016). Macroeconomic determinants of stock market volatility: An empirical study of Malaysia and Indonesia. Asian Academy of Management Journal, 21(1), 161. Available online: https://www.academia.edu/download/87514331/aamj21012016_8.pdf.
44. Onali, E. (2020). COVID-19 and stock market volatility. Available at SSRN 3571453. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3573622.
45. Papadamou, S., Fassas, A., Kenourgios, D., & Dimitriou, D. (2020). Direct and indirect effects of COVID-19 pandemic on implied stock market volatility: Evidence from panel data analysis. Available online: https://mpra.ub.uni-muenchen.de/100020/.
46. Rouyer, T., Fromentin, J. M., Stenseth, N. C., & Cazelles, B. (2008). Analysing multiple time series and extending significance testing in wavelet analysis. Marine ecology progress series, 359, 11-23. [CrossRef]
47. Sadiq, M., Hsu, C. C., Zhang, Y., & Chien, F. (2021). COVID-19 fear and volatility index movements: empirical insights from ASEAN stock markets. Environmental Science and Pollution Research, 28, 67167-67184. [CrossRef]
48. Solnik, B. H. (1974). An equilibrium model of the international capital market. Journal of economic theory, 8(4), 500-524. [CrossRef]
49. Su, Z., Fang, T., & Yin, L. (2019). Understanding stock market volatility: What is the role of US uncertainty?. The North American Journal of Economics and Finance, 48, 582-590. [CrossRef]
50. Tissaoui, K., Hkiri, B., Talbi, M., Alghassab, W., & Alfreahat, K. I. (2021). Market volatility and illiquidity during the COVID-19 outbreak: Evidence from the Saudi stock exchange through the wavelet coherence approaches. The North American Journal of Economics and Finance, 58, 101521. [CrossRef]
51. Tissaoui, K., Hkiri, B., Zaghdoudi, T., & Azibi, J. (2022). Illiquidity, Uncertainty Indices, and COVID-19 Outbreak Conditions: Empirical Evidence from the US Financial Market. Complexity. Available online: https://downloads.hindawi.com/journals/complexity/2022/2818633.pdf.
52. Torrence, C., & Webster, P. J. (1998). The annual cycle of persistence in the El Nño/Southern Oscillation. Quarterly Journal of the Royal Meteorological Society, 124(550), 1985-2004. [CrossRef]
53. Uddin, M., Chowdhury, A., Anderson, K., & Chaudhuri, K. (2021). The effect of COVID–19 pandemic on global stock market volatility: Can economic strength help to manage the uncertainty?. Journal of Business Research, 128, 31-44. [CrossRef]
54. Veleda, D., Montagne, R., & Araujo, M. (2012). Cross-wavelet bias corrected by normalizing scales. Journal of Atmospheric and Oceanic Technology, 29(9), 1401-1408. [CrossRef]
55. Yousef, I. (2020). Spillover of COVID-19: Impact on stock market volatility. International Journal of Psychosocial Rehabilitation, 24(6), 18069-18081.