The Interplay Between Tunneling and Parity Violation in Chiral Molecules

1. Introduction

Classical mechanics was developed in 1687 by Isaac Newton in his famous book Philosophiae Naturalis Principia Mathematica [1]. In the subsequent 200 years, it was used to theoretically interpret all known physical phenomena. In 1900, a set of discoveries related to the nature of light, molecules, and atoms, led Max Planck to introduce a new way to describe the world: quantum mechanics (reviewed in [2]). Subsequently, Erwin Schrödinger introduced in 1926 the wave nature of matter [3], where a quantum wave function describes the state of a physical system following the famous Schrödinger equation

$$i\hslash \frac{\partial }{\partial t}|\psi \left(t\right)\rangle =\widehat{H}|\psi \left(t\right)\rangle ,$$

(1)

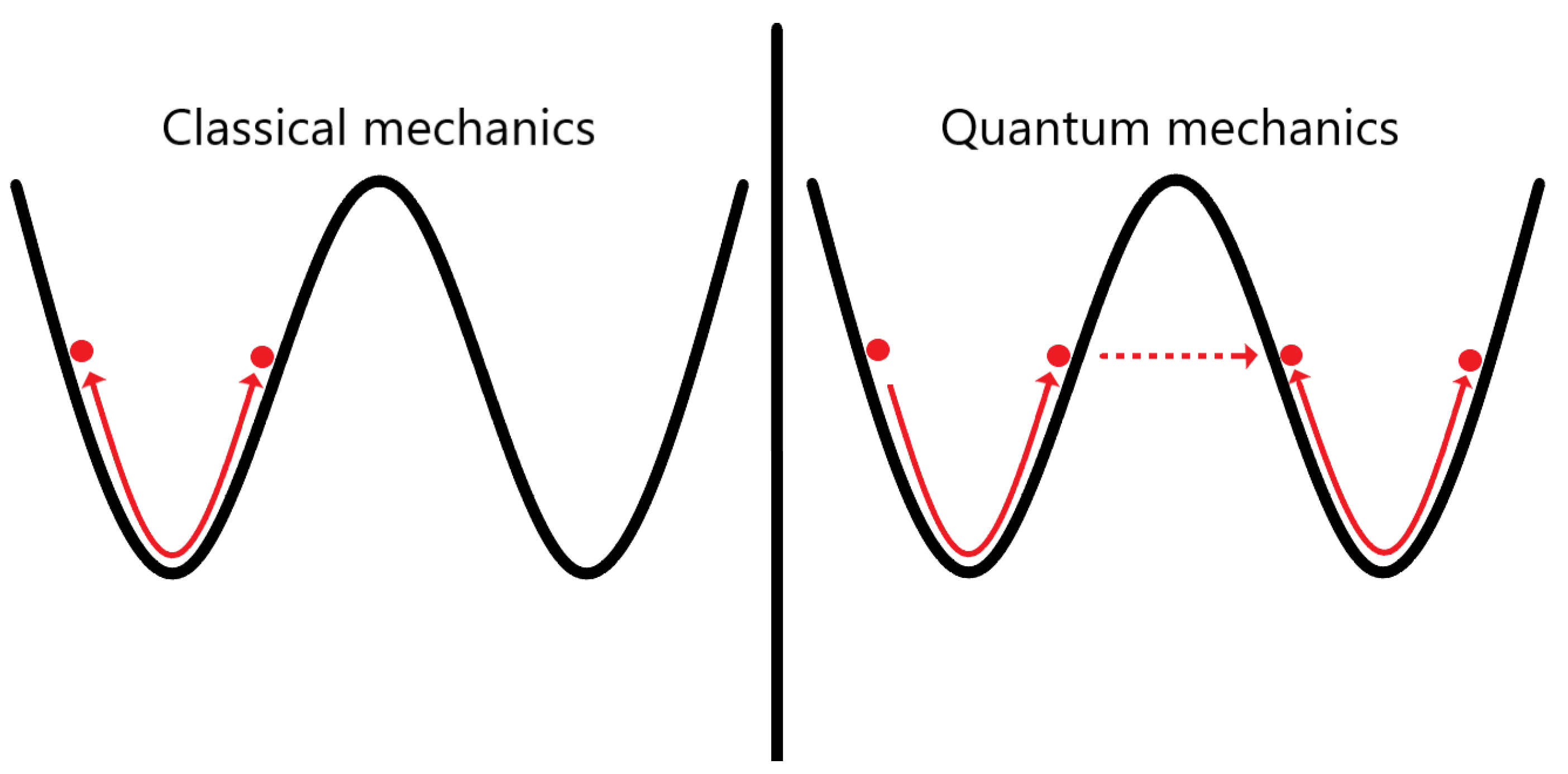
creating a probabilistic way to observe the world. This probabilistic treatment gave place to one of the less intuitive and most important discoveries of all time: quantum tunneling (reviewed in [4]). Quantum tunneling is an effect where a particle can go through a potential barrier, in contrast with classical mechanics, where the particle must overcome this barrier possessing enough energy to do it. It can be seen graphically in Figure 1.

In 1927, the German physicist Freidrich Hund [5,6], applied the Schrödinger equation (1) to understand the behavior of chiral molecules, obtaining that the tunneling has consequences on it, as we will see later. The term “chiral” was first introduced by Lord Kelvin in 1901 [7] to design all geometric structures or groups of points whose reflections in a plane mirror can not be superimposed with itself. He called the two possible forms of those geometric structures “enantiomers”. Later, it was discovered that the fundamental symmetry that interconverts the enantiomers is the parity symmetry (the symmetry through a point of inversion), not the reflection as Lord Kelvin stated [8], acquiring parity processes great importance in the context of chiral molecules, specially the parity-violating ones, as we will see along the manuscript.

Parity-violating processes were derived from the prediction by Lee and Yang [9], in which they postulated that parity can be violated in weak interactions, being the unique fundamental force capable of producing that behavior. That prediction was confirmed one year later by Wu et. al.[10].

The fact that the weak force violates parity made physicists to ask at what scales parity-violating effects could be present. The first answer came from Bouchiat and Bouchiat [11], by observing spontaneous optical activity of Bismuth atomic vapors, revealing effects of weak interactions in the atomic scale. After this important experiment was performed [12], Wood and coworkers discovered the nuclear anapole moment of Cesium [13], with is a different signal of parity violation, by improving low-temperature and high-resolution spectroscopic techniques. Therefore, parity violation was initially observed in elementary particles, and then in more complex systems like nuclei and atoms. If we continue considering more complex systems, we reach the molecular scale. Thus, one could ask if does it make sense to relate parity violation with molecular physics

As we have briefly commented in this introduction, there is an interesting interplay between chiral molecules, quantum tunneling and parity violation, which will be developed along the manuscript.

Specifically, this work is organized as follows: In Section 2 we introduce a simple quantum treatment of chiral molecules and its relation with the tunneling time. In Section 3 we add parity-violation to our description of chiral molecules, showing that there could exist an energy difference between the L and R enantiomers (PVED). In Section 4 we give some examples of parity-violating interactions, focusing on the electroweak force. In Section 5 we briefly review how the PVED can be calculated using simple or more sophisticated methods. In Section 6 we mention some experiments devoted to detecting the PVED. Finally, Section 7 provides the conclusions of the present work.

2. Introduction to molecular chirality

The process of converting an L chiral molecule to its enantiomer, R, can be represented by the movement of an effective mass in an energy potential $V\left(q\right)$ which is function of a generalized coordinate, q [14]. If we use the time-independent Schrödinger, we can obtain the eigenfunctions, ${\varphi }_k\left(q\right)$, and eigenvalues (energies), $E_k$, of the stationary states

$$\begin{array}{cc}\hfill \widehat{H}=\widehat{T}+V\left(q\right)=& -\frac{{\hslash }^2}{2m}{\nabla }^2+V\left(q\right)\end{array}$$

(2)

$$\begin{array}{cc}\hfill \widehat{H}{\varphi }_k\left(q\right)=& E_k{\varphi }_k\left(q\right),\end{array}$$

(3)

where $\widehat{T}$ is the kinetic energy, the potential energy is given by $V\left(q\right)$, and $\widehat{H}$ is the Hamiltonian operator.

In quantum mechanics, it is well known that the probability of the system to be in a determinate state can be expressed as

$$P_k\left(q\right)={\left|{\varphi }_k\left(q\right)\right|}^2.$$

(4)

Interestingly, Hund applied the time-dependent Schrödinger equation (1) to the study of chiral molecules, with emphasis on the stereomutation process between left and right states, which at this time was only thought to be a consequence of quantum tunneling. The time-dependent Schrödinger equation can be expressed as

$$i\hslash \frac{\partial \psi (q,t)}{\partial t}=\widehat{H}\psi (q,t),$$

(5)

and its general solution is

$$\psi (q,t)=\sum _{k=1}^{\infty }{c}_k{\varphi }_k\left(q\right)exp\{-i{E}_{k}t/\hslash \},$$

(6)

where $c_k$ are complex coefficients.

As a first toy model, chiral molecules can be represented with only two states, related to the two possible chiralities, left-handed and right-handed. Taking into account these two lowest energy states, the solution of the Ec. (5) is

$$\psi (q,t)=c_{+}|+\rangle exp\{-i{E}_{+}t/\hslash \}+c_{-}|-\rangle exp\{-i{E}_{-}t/\hslash \},$$

(7)

where we denote as $|+\rangle$ and $|-\rangle$ the time-independent Hamiltonian eigenstates.

With this in mind, the probability density can be expressed as

$$P(q,t)={\left|\psi (q,t)\right|}^2=\frac{1}{2}{\left||+\rangle +|-\rangle exp\{-i\delta t/\hslash \}\right|}^2,$$

(8)

where we choose that in the initial time, the probability of finding both enantiomers is the same, so $c_{+}=c_{-}=\frac{1}{\sqrt{2}}$, and we define $\delta =E_{+}-E_{-}$. This result suggests that the system is located in the states $|+\rangle$ or $|-\rangle$ with a probability of

$$\begin{array}{cccc}\hfill P_{-}\left(t\right)=& {sin}^2(\delta t/\hslash ),\hfill & \hfill P_{+}\left(t\right)=& {cos}^2(\delta t/\hslash ),\hfill \end{array}$$

(9)

therefore, the $|+\rangle$ and $|-\rangle$ states will oscillate with a period given by

$$\tau =\frac{\hslash }{\delta }.$$

(10)

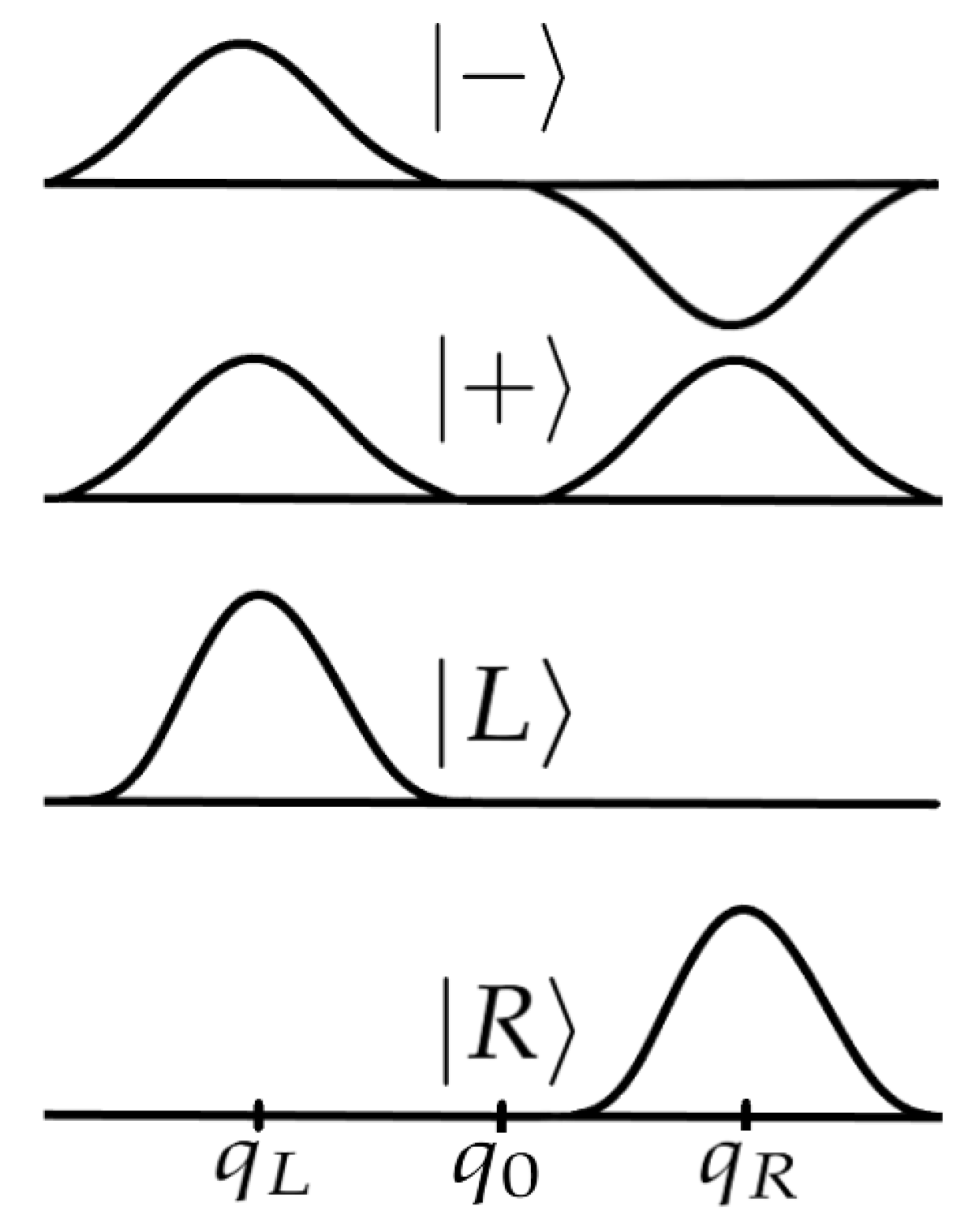
At this point, some comments are in order. It is well-known that chiral states are interconverted by the parity operator. The time-independent Hamiltonian eigenfunction $|+\rangle$ and $|-\rangle$ are also eigenfunctions of the parity operator ($\widehat{P}|\pm \rangle =\pm |\pm \rangle$), but they have definite parity and, therefore, they can not represent chiral molecules. As a consequence, we have to define a different algebraic base which can be used to represent chiral molecules.

The condition which has to be fullfilled is

$$\begin{array}{cccc}\hfill \widehat{P}|L\rangle =& |R\rangle ,\hfill & \hfill \widehat{P}|R\rangle =& |L\rangle ,\hfill \end{array}$$

(11)

where we call $|L\rangle$ and $|R\rangle$ the states representing the L and R enantiomers. These states can be represented as

$$\begin{array}{cc}\hfill |L\rangle =& \frac{1}{\sqrt{2}}(|+\rangle +|-\rangle )\end{array}$$

(12)

$$\begin{array}{cc}\hfill |R\rangle =& \frac{1}{\sqrt{2}}(|+\rangle -|-\rangle ),\end{array}$$

(13)

which are called chiral states or chiral base (see Figure 2)). These states are no eigenstates of the Hamiltonian, being delocalized and having no defined energy (so it is necessary to work using the average of the energy). With this in mind, it is easy to reach an expression similar to Eq. (10), and conclude that chiral molecules undergo an oscillating motion between L and R enantiomers, with a period of

$${\tau }_{LR}=\frac{\hslash }{2\delta }.$$

(14)

With this in mind, we would like to remark that Hund performed two important considerations. First, he realized that although the energies $E_{+}$ and $E_{-}$ were not enough to exceed the potential barrier $V\left(q\right)$, the transition between enantiomers could be observed, which is impossible in classical mechanics. This fact was the origin of the recognized tunneling effect in molecular physics, as we mentioned in the introduction. The second consideration is related to what is known as “Hund’s paradox" [6], as pointed out by Harris and Stodolsky in [15]. This paradox refers to the stability of some molecules in one specific enantiomeric state (e.g. CHFClBr, amino acids, and sugars), which is in principle impossible because there must be a periodic transition between enantiomers, in agreement with Eq. (14). This paradox can be solved by the introduction of a new concept into our model: parity violation.

3. Parity violation

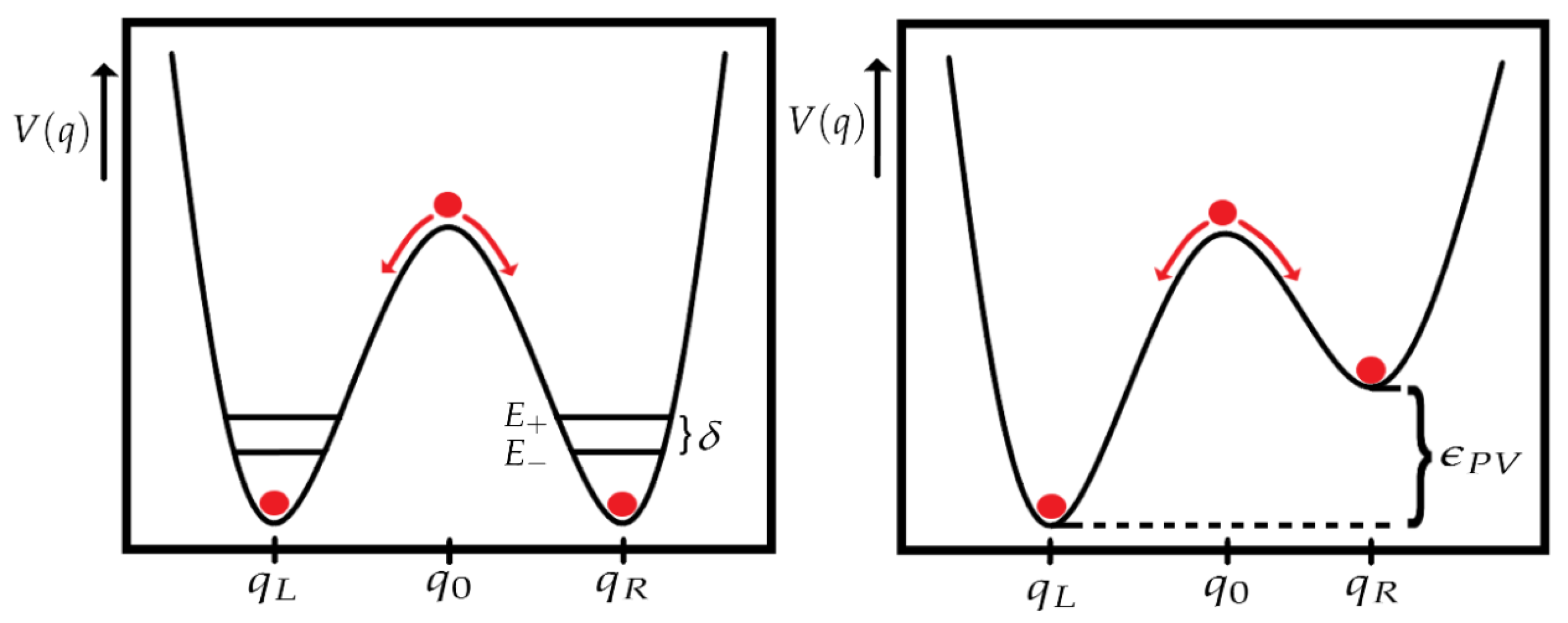
We have described chiral molecules in a two-state system without parity violation, described as a symmetric double well. We can now add parity violation to our model, which can be represented by a asymmetric double well, modifying the Hamiltonian [15], which is expressed as

$$\widehat{H}={\widehat{H}}^0+{\widehat{H}}^{PV}=\left(\begin{array}{cc}{E}_0& \delta \\ \delta & E_0\end{array}\right)+\left(\begin{array}{cc}-{ϵ}_{PV}& 0\\ 0& {ϵ}_{PV}\end{array}\right),$$

(15)

where ${\widehat{H}}_{PV}$ is the parity-violating term of the Hamiltonian ($\widehat{P}{H}^{PV}{\widehat{P}}^{-1}=-H^{PV}$), allowing the breakdown of the enantiomer degeneration. Besides, $E_0$, $\delta$ and ${ϵ}_{PV}$ are defined as

$$\begin{array}{cccccc}\hfill E_0=& \frac{H_{LL}+H_{RR}}{2},\hfill & \hfill \delta =& H_{RL},\hfill & \hfill {ϵ}_{PV}& =\frac{H_{LL}-H_{RR}}{2},\hfill \end{array}$$

(16)

where we used the notation $H_{XY}=\langle X|H|Y\rangle$. The $\delta$ parameter is defined in the previous section, and it is related to the height of the potential well and the tunneling time ($\delta =E_{+}-E_{-}$), and ${ϵ}_{PV}$ is related to the energy difference between the two potential wells. The ${ϵ}_{PV}$ parameter is also known as PVED (Parity Violation Energy Difference) and represents the energy difference between the L and the R enantiomers (see Figure 3)).

We will define $|A\rangle ,|B\rangle$ as the eigenstates of the Hamiltonian (15). It is remarkable that $|A\rangle ,|B\rangle$ are different from the definite parity states $|+\rangle$ and $|-\rangle$, and they can be expressed in function of the chiral states as [16,17]

$$\left(\begin{array}{c}|A\rangle \\ |B\rangle \end{array}\right)=\left(\begin{array}{cc}sin\theta & cos\theta \\ cos\theta & -sin\theta \end{array}\right)\left(\begin{array}{c}|L\rangle \\ |R\rangle \end{array}\right),$$

(17)

where $\theta$ is the mixing angle and can be obtained as

$$tan2\theta =\frac{2H_{RL}}{H_{LL}-H_{RR}}=\frac{\delta }{{ϵ}_{PV}}.$$

(18)

The energies of the system are now given by the eigenstates of the Hamiltonian (17) and they are

$$E_{AB}=E_0\mp \Delta ,$$

(19)

with

$$\begin{array}{c}\hfill \Delta \equiv \sqrt{{ϵ}_{PV}^2+{\delta }^2}.\end{array}$$

(20)

It is interesting to calculate the probability of a chiral molecule being located in its left or right state. For that, we have to express the wave function in the chiral base, obtaining

$$|\psi \left(t\right)\rangle =c_L\left(t\right)|L\rangle +c_R\left(t\right)|R\rangle .$$

(21)

The evolution of $c_L\left(t\right)$ and $c_R\left(t\right)$ will be determined by the time-dependent Schrödinger equation (1):

$$i\hslash {\partial }_t\left(\begin{array}{c}{c}_L\left(t\right)\\ c_R\left(t\right)\end{array}\right)=\left(\begin{array}{cc}{E}_0-{ϵ}_{PV}& \delta \\ \delta & E_0+{ϵ}_{PV}\end{array}\right)\left(\begin{array}{c}{c}_L\left(t\right)\\ c_R\left(t\right)\end{array}\right).$$

(22)

If we suppose that $E_0=0$, $c_L\left(0\right)=1$ and $c_R\left(0\right)=0$, we obtain

$$\begin{array}{cc}\hfill c_L\left(t\right)=& cos\left(\frac{\Delta }{\hslash }t\right)-\frac{iϵ}{\Delta }sin\left(\frac{\Delta }{\hslash }t\right),\end{array}$$

(23)

$$\begin{array}{cc}\hfill c_R\left(t\right)=& -\frac{i\delta }{\Delta }sin\left(\frac{\Delta }{\hslash }t\right),\end{array}$$

(24)

being $|c_L\left(t\right){|}^2$ and $|c_R\left(t\right){|}^2$ the probability of the wave function to be in the $|L\rangle$ or $|R\rangle$ states, respectively. At this point, it is necessary to remark two specific cases [16,17]:

Case 1, $\theta \to 0$:

This case implies that ${ϵ}_{PV}\gg \delta$ ($tan2\theta \to 0$) tending the energy eigenstates to be the chiral states

$$\begin{array}{cccc}\hfill |A\rangle \to & |L\rangle ,\hfill & \hfill |B\rangle \to & |R\rangle .\hfill \end{array}$$

(25)

As we know, the states $|A\rangle$ and $|B\rangle$ are eigenstates of the Hamiltonian (17), therefore they are localized states. In this particular case, the $|L\rangle$ and $|R\rangle$ states are also localized, being the chiral molecule stable in one of the two possible enantiomers. According to (23), $|c_L\left(t\right){|}^2=1$, being the chiral molecule stable in the L state, solving the aforementioned Hund’s paradox, as pointed out by Harris and Stodolsky [15].

Case 2, $\theta \to \pi /4$:

This case implies that ${ϵ}_{PV}\ll \delta$ ($tan2\theta \to \infty$), making sense to recover the non-parity violating case. If we use the Eq. (17), and we impose $\theta =\pi /4$, we obtain the equations (12) and (13), resulting in

$$\begin{array}{cccc}\hfill |A\rangle & =|+\rangle ,\hfill & \hfill |B\rangle & =|-\rangle .\hfill \end{array}$$

(26)

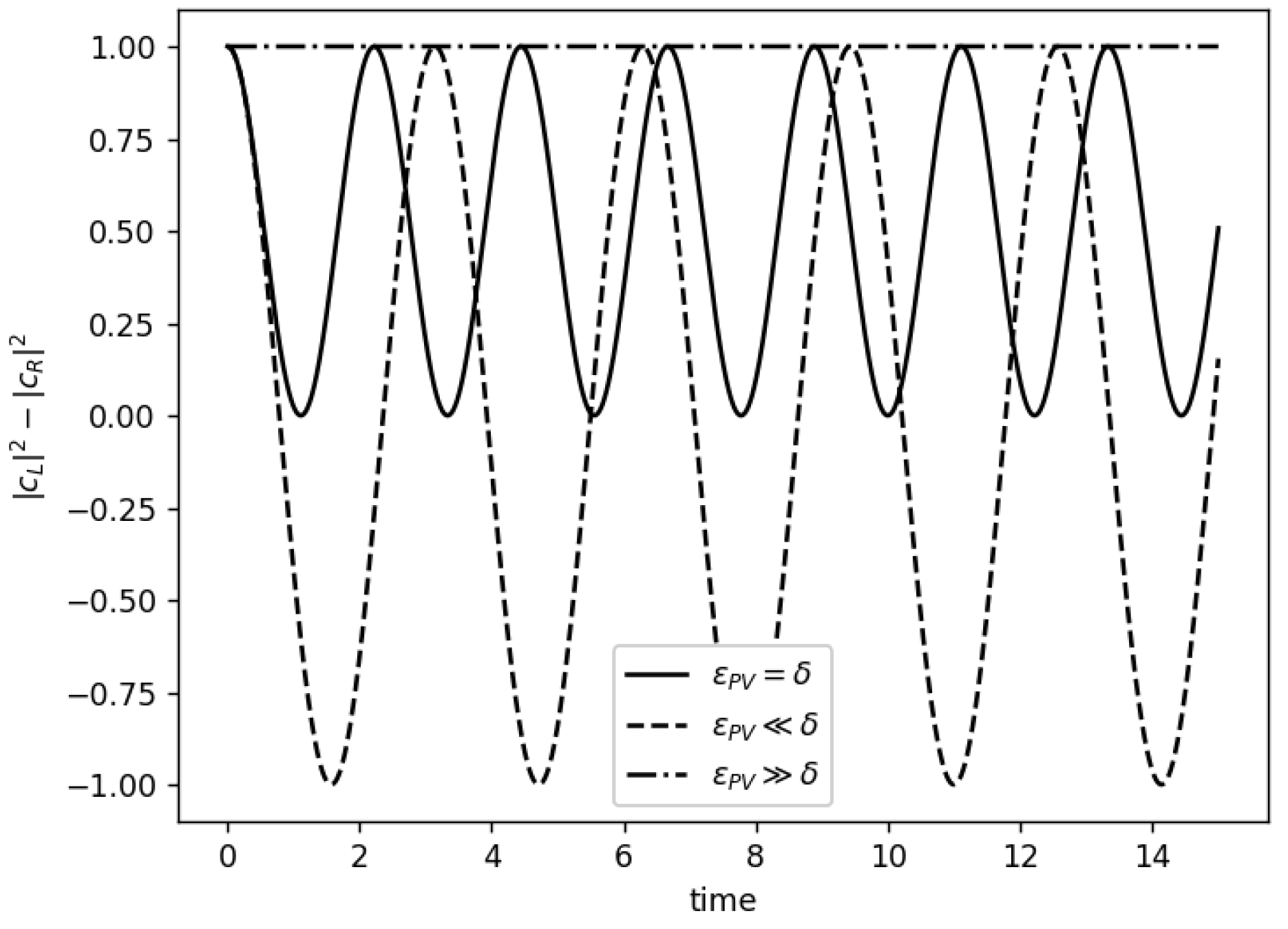
As the eigenstates of the Hamiltonian $\widehat{H}$ (15) are equal to the eigenstates of ${\widehat{H}}_0$, we can conclude that there is no parity violation in this case. Both cases can be better understood with the help of Figure 4.

At this point, some comments are in order. As we have seen, if parity violation affects our system, there could be an energy difference between enantiomers ${ϵ}_{PV}$. In the other case, enantiomers are degenerate (${ϵ}_{PV}=0$). This behavior can be seen algebraically as follows:

Without parity violation

We already know the expressions for $|L\rangle$ and $|R\rangle$ without parity violation:

$$\begin{array}{cc}\hfill |L\rangle =& \frac{1}{\sqrt{2}}(|+\rangle +|-\rangle )\end{array}$$

(27)

$$\begin{array}{cc}\hfill |R\rangle =& \frac{1}{\sqrt{2}}(|+\rangle -|-\rangle ).\end{array}$$

(28)

With this in mind, we can perform the next development

$$\begin{array}{cc}\hfill E_L=\langle L|\widehat{H}|L\rangle =& \frac{1}{2}(\langle +|+\langle -|)\widehat{H}(|+\rangle +|-\rangle )=\frac{1}{2}(\langle +|\widehat{H}|+\rangle +\langle -|\widehat{H}|-\rangle )=\frac{1}{2}(E_{+}+E_{-})\\ \hfill E_R=\langle R|\widehat{H}|R\rangle =& \frac{1}{2}(\langle +|-\langle -|)\widehat{H}(|+\rangle -|-\rangle )=\frac{1}{2}(\langle +|\widehat{H}|+\rangle +\langle -|\widehat{H}|-\rangle )=\frac{1}{2}(E_{+}+E_{-}),\end{array}$$

where we defined $\langle +|\widehat{H}|+\rangle =E_{+},\langle -|\widehat{H}|-\rangle =E_{-}$. Therefore we have shown that $E_L=E_R$ (${ϵ}_{PV}=0$), confirming the enantiomer degeneration in the absence of parity violation.

With parity violation

In a parity-violating context, the chiral states can be represented in function of the Hamiltonian eigenstates as:

$$\begin{array}{cc}\hfill |L\rangle =& sin\theta |A\rangle +cos\theta |B\rangle \end{array}$$

(29)

$$\begin{array}{cc}\hfill |R\rangle =& cos\theta |A\rangle -sin\theta |B\rangle .\end{array}$$

(30)

A process similar to the previous one can be performed:

$$\begin{array}{cc}\hfill E_L=\langle L|\widehat{H}|L\rangle =& \frac{1}{2}(cos\theta \langle A|+sin\theta \langle B|)\widehat{H}(cos\theta |A\rangle +sin\theta |B\rangle )=\frac{1}{2}({cos}^2\theta E_A+{sin}^2\theta E_B)\\ \hfill E_R=\langle R|\widehat{H}|R\rangle =& \frac{1}{2}(sin\theta \langle A|-cos\theta \langle B|)\widehat{H}(sin\theta |A\rangle -cos\theta |B\rangle )=\frac{1}{2}({sin}^2\theta E_A+{cos}^2\theta E_B).\end{array}$$

If we use Eq. (19) and taking $E_0=0$, we obtain

$$\begin{array}{cc}\hfill E_L=& -\frac{1}{2}\Delta ({cos}^2\theta -{sin}^2\theta )\\ \hfill E_R=& \frac{1}{2}\Delta ({cos}^2\theta -{sin}^2\theta ).\end{array}$$

Therefore, the energy of the enantiomers is not the same ($E_L=-E_R\to {ϵ}_{PV}=2E_L$) unless for $\theta =\frac{\pi }{4}\pm n\frac{\pi }{2}$∀n∈$\mathbb{N}$ where ${ϵ}_{PV}=0$.

In this section we have shown how parity violation can affect the Hamiltonian, changing its eigenstates and eigenvalues (energies) resulting sometimes in the apparent stability of chiral molecules. Therefore, an evident relationship between chiral molecules and PVED emerges, as well as with tunneling, being two principal concepts of study in the context of chiral molecules. Although tunneling is well-known theoretically and experimentally, there is still interest in applying novel theories in this framework, like instanton calculations [18]. On the contrary, the PVED has not yet been detected, its relationship with molecular chirality constituting one of the most intriguing problems of [19]. Before going into a brief review on theory and experiments designed to study parity violation in chiral molecules, we will give a bird’s eye view of the type of interactions which can show a parity-violating behavior.

4. Parity-violating interactions

As it was said before, the weak interaction is the unique fundamental force capable of producing parity violation in the SMPP. Despite that, there are other relevant theories beyond the SMPP that can violate parity, like axion interactions or modified gravity theories, which we would like to mention briefly.

The Axion is a particle not include in the SMPP, being a dark matter candidate (see [20] for a recent review). A parity-violating electron-nucleon interaction mediated by an axion was proposed by Moody and Wilczek [21] and is given by

$$H_{ax}=\left(g_s^N{g}_p^e\right)\frac{{\overrightarrow{\sigma }}_e·\overrightarrow{r}}{8\pi m_e}\left(\frac{m_{\varphi }}{r}+\frac{1}{r^2}\right)e^{-m_{\varphi }r},$$

(31)

where $c=\hslash =1$, $g_s^N$ is the scalar coupling constant of the axion to a nucleon, $g_p^e$ is the pseudoscalar coupling constant to the electron, $\overrightarrow{r}$ represents the separation vector between the electron and the nucleon, and $m_{\varphi }$ is the mass of the axion. We would like to remark that the parity-violating behavior of some axion interactions makes them an interesting way to study PVED in chiral molecules [22].

Other different parity violating mechanisms can be included in gravity. As commented in [23], Leitner and Okubo were the first who pioneered this idea[24]. After their proposal, Hari Dass wrote a parity-violating gravitational potential of the form (c = 1) [25]

$$V^{Grav}\left(r\right)=GM\left({\alpha }_1\frac{\overrightarrow{s}·\overrightarrow{r}}{r^3}+\frac{\overrightarrow{s}·\overrightarrow{v}}{r^2}+\frac{\overrightarrow{s}\times \overrightarrow{r}·\overrightarrow{v}}{r^3}\right),$$

(32)

where M represents the mass of the gravitating object, $\overrightarrow{r}$ is the separation vector from that mass to the test particle, whose spin and velocity are given by $\overrightarrow{s}$ and $\overrightarrow{v}$, respectively.

Another relevant proposal is the Chern-Simons (CS) theory for gravity [26], extending general relativity by considering not only the Einstein tensor but also the C-tensor [27] and an extra pseudoscalar field (a field which violates parity).

Although there are other relevant theories, in thefollowing lines we will only consider electroweak interactions, which are routinely included in quantum chemistry calculations to study the PVED in chiral molecules.

4.1. Electroweak interaction

At the beginning of the discovery of the weak force, it was believed that it dependeded on charge transference (charged currents). Subsequently, in some attempts to unify weak and electromagnetic forces [28,29,30], a new type of interaction emerged, based on weak neutral currents, which were capable of producing observable effects of parity violation in atoms [11,31]. With this in mind and knowing that molecules are essentially made by nucleons and electrons, we can use Quantum Field Theory and Feynman’s rules propose a Hamiltonian that could produce PVED in chiral molecules. This Hamiltonian represents the interaction between electrons and nucleons of the chiral molecule, mediated by a $Z^0$ boson (the propagator of the weak neutral current), and can be expressed as

$$H_{NC}=\frac{G_F}{\sqrt{2}}:\overline{N}\left(x\right){\gamma }^{\mu }(V^N-A^N{\gamma }^5)N\left(x\right)\overline{e}\left(x\right){\gamma }_{\mu }(V^e-A^e{\gamma }_5)e\left(x\right):,$$

(33)

where the notation $:X:$ refers to the normal ordering of the X operators, $G_F$ is the Fermi constant, ${\gamma }^{\mu }$ are the Dirac matrices which satisfy $\{{\gamma }^{\mu },{\gamma }^{\nu }\}=2{\eta }^{\mu \nu }$ ( ${\eta }^{\mu \nu }$ is the Minkowskian metric with signature $(-,+,+,+)$), $\overline{\psi }\equiv {\psi }^{†}{\gamma }^0$ is Dirac adjoint, $A^e$, $A^N$, $V^e$, and $V^N$ are coupling constants, $e(t,\overrightarrow{x})$ and $N(t,\overrightarrow{x})$ are the electron and nucleon fields respectively.

For simplicity, the study of PVED is usually done in a non-relativistic regime, leading to the non-relativistic electron-nucleon interaction Hamiltonian [11,32,33]:

$$H_{NC}=\frac{G_F}{4\sqrt{2}}\sum _j\sum _i{Q}_{W_j}\{{\overrightarrow{p}}_i·{\overrightarrow{\sigma }}_i,\delta (\overrightarrow{r_j}-{\overrightarrow{r}}_i)\},$$

(34)

where $\overrightarrow{p}$ and $\overrightarrow{\sigma }$ are the momentum and spin of the electrons, $\rho$ is the nucleon density and the index i and j refers to a summation over electrons and nucleons respectively. Additionally, the weak charge, $Q_W$, is given by

$$Q_W=(1-4{sin}^2{\theta }_W)Z-N,$$

(35)

where ${\theta }_W$ is the Weinberg angle and N and Z are the number of neutrons and protons respectively.

In order to understand why the Hamiltonian (34) is used in the context of chiral molecules, we need to make some clarifications. On one hand, polar vectors violate parity as well as rotations do, while axial vectors get a minus sign under rotations. On the other hand, pseudoscalars violate parity and respect rotations, and scalars respect both of these symmetries. Concerning time inversion, time-odd and time-even refer to the violation or not of this symmetry.

Now, let us note that there are only two non-scalar terms in the Hamiltonian (34). The first one is the momentum of the electrons $\overrightarrow{p}$, which is a time-odd polar vector, and the second one is the spin of the electron $\overrightarrow{\sigma }$, which is a time-odd axial vector. This results in a time-even pseudoscalar behavior of the Hamiltonian (34), violating parity while respecting time inversion. Importantly, these time-even pseudoscalars are used to define true chirality, which leads to the possibility of producing PVED in chiral molecules (if the Hamiltonian also violates time inversion, it is defined as false chirality, and can not produce PVED in chiral molecules) [34,35,36,37].

5. Calculations of PVED

Although the Hamiltonian (34) violates parity, there is still a problem in calculating the PVED. In the non-relativistic approximation, the molecular wave function is always real, while the parity-violating part of the Hamiltonian (34) is purely imaginary. This led to a zero expectation value for $H_{NC}$ over the molecular wave function. There are two possible solutions to this problem. The first one is to implement a parity-odd perturbation operator into a fully relativistic four-component Dirac-Hartree-Fock framework treatment of the parity-violating energy differences in chiral molecules [38]. The second one is to maintain a non-relativistic regime, adding a spin-orbit coupling to give a first-order correction to the wave function [39]. That spin-orbit coupling can be written as

$$V^{SO}=\frac{1}{4}{\alpha }^2\sum _i({\mathbf{E}}_i\times p_i)·{\sigma }_i,$$

(36)

where $\alpha$ is the fine-structure constant and ${\mathbf{E}}_i$ is the electric field seen by an electron i. Then, the ground state ${\psi }_0$ is perturbed as

$${\psi }_0\to {\psi }_0+\sum _n\frac{\langle n|V^{SO}|n\rangle }{E_0-E_n}{\psi }_n,$$

(37)

resulting in a term for the PVED different from 0, which is

$$\Delta E_{PV}=\sum _n\frac{\langle 0|H^{EW}|n\rangle \langle n|V^{SO}|0\rangle }{E_0-E_n}+C.C.$$

(38)

At this point, an estimation of the PVED can be done. In one way, this estimation was performed in a work by Bouchiat and Bouchiat [11]. In that work, they stated that, for dominant heavy atoms with atomic number Z, the $H^{EW}$ part of the Eq. (38) is of order $G{Z}^3\alpha$. By the other way, from atomic theory, we know that the $V^{SO}$ part of Eq. (38) is of order $Z^2{\alpha }^2$. With these considerations in mind, we can estimate that

$$\Delta E_{PV}\approx G{\alpha }^3{Z}^5,$$

(39)

which shows that the higher Z, the higher the PVED. The Eq. (39) is usually known as $Z^5$ scaling law, and it was used in numerical calculous in different works [40,41].

Although nowadays there are diffferent methodologies based on different levels for the theory employed, we would like to remarkable the CIS-RHF formalism [42,43], a formalism that emerged from critically analyzing calculations of electroweak quantum chemistry. This formalism is a perturbation-theory mixture of the ground RHF (restricted Hartree-Fock) with the CIS (configuration interaction singles) excited states. Using this approach, the authors found that the PVED in chiral molecules has essentially a tensor character

$${ϵ}_{PV}={ϵ}_{PV}^{i,j}={ϵ}_{PV}^{xx}+{ϵ}_{PV}^{yy}+{ϵ}_{PV}^{zz},$$

(40)

which transforms as a polar vector in its first index and as an axial vector in its second index, being this tensor a pseudoscalar. With this method in mind, they calculated ${ϵ}_{PV}$ in typical chiral molecules, obtaining a PVED up to two orders of magnitude higher than reported using other methodologies. Please note that these enhancement has been confirmed by other groups in subsequent years [44,45,46,47].

Finally, we would like to remark that there are other interesting methods to mention. For example, if we want to study parity-violating potentials in chiral molecules with light nuclei, an interesting way is using the Breit-Pauli approximation [48]. If molecules involving heavy atoms are considered, the Dirac-Fock theory does a nice job [45,47,49].

6. Experiments searching the PVED

It is remarkable that, although the search for PVEDs has been an exhaustive work, it has not been detected yet, due to the high sensibility needed in the experiments. Up to this date, in our opinion, there are two promising experiments whose purpose is the detection of PVED in chiral molecules. One of them is located in Zürich, based on a proposal made by Quack in 1986 [50] and the other one emerged in Paris in 1999 [51] (see [14] if more information is required). As an incomplete list, we would like to remark other experimental approaches working on parity-violating effects on chiral molecules [52,53,54,55,56,57,58,59,60,61,62,63] (see [64,65] for more information about other experiments). Here we will briefly comment on the Zürich and Paris proposals.

Firstly we will expose the Zürich experiment, mainly developed before 1986 by Quack’s group [50]. They use excited energy levels of achiral molecules with well-defined parity which connect both enantiomers by radiative electric dipole transition moments. They prepare coherent superpositions of parity-defined states in the fundamental state using those energy levels, following the temporal evolution of the molecular parity. From this, ${ϵ}_{PV}$ can be obtained directly, which is the objective of the experiment (see section 4.2 of the review [14] for more detailed information). Recently, they have achieved an experimental sensitivity (using $N{H}^3$) of ${ϵ}_{PV}=100aeV$ [66]. Such values have been found theoretically in chiral molecules with lighter nuclei than sulfur and chlorine [67,68,69], so maybe such data can be of great interest to future experiments.

The other experiment was proposed by Letokhov in 1975 [70,71] in Paris. This experiment tries to measure the differences in the high-resolution spectrum in separate L and R enantiomers, which can have a transition frequency ${\nu }_L$, ${\nu }_R$ for specific transitions. The energy difference between two molecular levels can be expressed in function of the transition frequency as

$${ϵ}_{PV}^{*}-{ϵ}_{PV}=h({\nu }_R-{\nu }_L).$$

(41)

Recently, the group of the Laboratoire de Physique des Lasers in Paris achieved a sensitivity of $\frac{\Delta {\nu }^{PV}}{\nu }\approx {10}^{-13}$. Even more, it is expected that, for specific molecules composed of Ruthenium (Ru) and Osmium (Os) atoms, that measurement could be of the order of $\frac{\Delta {\nu }^{PV}}{\nu }\approx {10}^{-14}$ [72]. Therefore, we think we are close to observing the PVED in chiral molecules.

7. Discussion and conclusions

After concluding this brief review, we would like to mention possible extensions to study the interplay between tunneling and parity violation in chiral molecules. Once it is accepted that physical systems do no exist in isolation, and given that decoherence is an ubicuous feature of nature, it seems mandatory to include interactions between the chiral molecule under consideration and its surroundings. In this sense, some techniques of Caldeira-Leggett type were imported into the problem of stereomutation of chiral molecules, including parity violation effects [73]. The main message one can get from these works is the following: in general, although the medium usually acts as some kind of dissipator [74,75], there are some cases where an enhancement of parity-violating effects due to the medium can occur [73]. In this sense, we think that it would be interesting to treat chiral molecules as a open system by combining high-level theoretical descriptions of both the molecule, the surroundings and their interaction. Perhaps the medium can take a protagonic role in order to enhance or diminish the PVED.

Along this manuscript, we have briefly reviewed the interplay between parity violation and quantum tunneling in the context of chiral molecules. Firstly, we have given a more theoretical point of view to finally end with a brief experimental overview.

By using a simple quantum treatment to describe chiral molecules as a two-level system, and after defining a good algebraic base to describe chiral molecules, the necessity of introducing quantum tunneling between the L and R enantiomers emerged. Interestingly, the tunneling time is inversely proportional to the energy difference between the time-independent Hamiltonian eigenfunctions with definite parity, $|+\rangle$ and $|-\rangle$, represented as $\delta$ in the manuscript. Subsequently, we have added parity violation as an essential ingrediant of our model, which gives place to an energy difference between the L and R enantiomers, the so-called parity-violating energy difference (PVED). The introduction of this new parameter changes the probability of the chiral molecule to be in the L or R states, resulting in the apparent stability of one of the possible enantiomers of a chiral molecule when the PVED is substantially higher than $\delta$. That is, when parity violation overcomes the tunneling effects, a possible solution to the "Hund’s paradox" emerges.

Along the rest of the manuscript, we mentioned possible parity-violating interactions, like axion interactions or modified gravity theories, focusing on electroweak interactions. Specifically, we commented on the electron-nucleon interaction mediated by weak neutral currents as it is the most used way to study the PVED in chiral molecules. Although we have a well established parity-violating Hamiltonian, calculating the PVED is difficult task. Different methods and approximations have been proposed based on different levels of the theory employed. We have remarked some of them as the $Z^5$ scaling law, the CIS-RHF formalism, the Breit-Pauli approximation, and the Dirac-Fock theory. Finally, we have commented on some experimental searches of the PVED, noticing that important progresses have been made along the last sixty years. Therefore, we think that we are finally close detect the PVED in chiral molecules.