Prerpints.org logo
Preprint
Article

Models of Protocells Undergoing Asymmetrical Division

Altmetrics

Downloads

123

Views

34

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

01 February 2024

Posted:

02 February 2024

You are already at the latest version

Alerts
Abstract
The conditions which allow sustained growth of a protocell population are investigated in the case of asymmetrical division. The results are compared to those of previous studies concerning models of symmetrical division, where synchronization (between duplication of the genetic material and fission of the lipid container) was found under a variety of different assumptions about the kinetic equations and about the place where molecular replication takes place. Such synchronization allows a sustained proliferation of the protocell population. In the asymmetrical case there can be no true synchronization, since the time to duplication may depend upon the initial size, but we introduce a notion of homogeneous growth which actually allows sustained reproduction of a population of protocells. We first analyze Surface Reaction Models, defined in the text, and we show that in many cases they undergo homogeneous growth under the same kinetic laws which lead to synchronization in the symmetrical case. This is the case also for Internal Reaction Models (IRMs), which however require a deeper understanding of what homogeneous growth actually means, as discussed below.
Keywords: 
Subject: Computer Science and Mathematics  -   Mathematical and Computational Biology

1. Introduction

The process of cell division (fission) is extremely important both for unicellular species, where it provides the mechanism of proliferation, and for multicellular organisms, where it is active not only during embryo growth to full adult size, but also during the whole lifetime of an individual, assuring proper renewal of its cells.
Cell fission is usually preceded by duplication of its genetic material, to assure that every daughter cell gets a full copy (a remarkable exception being the generation of germ cells in those species which undergo sexual reproduction). While present-day cells host sophisticated control mechanisms which assure that fission does not start before DNA duplication has occurred [1], it is highly unlikely that such control mechanisms were in place in the early days of primordial protocells.
Protocells are entities that resemble in some way, but are much simpler than, present-day cells1. Many different hypotheses have been proposed, concerning their “architectures” as well as their chemical compositions and the relevant kinds of physical and chemical processes which take place. A key property should of course be their capability to grow and to reproduce, giving rise to daughter protocells which resemble their parents. It is fair to say that, while several interesting intermediate results have been obtained [2,3,4], full-fledged protocells, able to continuously generate several successive generations, have not yet been achieved. Given the time and cost of actual wet experiments, mathematical and computational models are extremely important to indicate directions of research and to test the suitability of the different proposals. While they cannot substitute laboratory experiments, they can be of great help in identifying the main strengths and weaknesses of the different proposals, and in pointing out major problems which need to be addressed [5,6,7].
There is an interesting class of supramolecular structures, i.e. lipid vesicles, which do actually exist and which are spontaneously formed under a broad set of conditions, in aqueous solutions of amphiphiles [8,9,10,11,12]. Such lipid vesicles (sometimes called liposomes) resemble cells in that their aqueous interior is surrounded by an approximately spherical membrane, which is composed by a lipid bilayer, similar to those found in cells and in some cellular compartments. If further lipids are supplied, the size of vesicles can grow and, under some experimental conditions, their splitting has been observed [2,13,14,15,16]. The resemblance of this process to cell fission is probably the main reason why vesicles have been proposed as the starting point of most hypothesized protocell architectures.
In this paper we will indeed consider broad classes of mathematical and computational models of protocells, all based upon lipid vesicles which will be assumed to spontaneously undergo fission when they reach a certain size. Moreover, it will be assumed that each protocell hosts some chemicals (“replicators”) which are able to collectively self-replicate, and that some of these replicators also increase the rate of growth of the vesicle lipid membrane (e.g. by catalyzing the synthesis of its amphiphiles2). For simplicity, we consider a single type of lipid in aqueous environments, so the replicators determine the identity (i.e. the properties) of the protocell: their set (or a subset) can be loosely regarded as its “protogenetic material”.
Two different processes take place in these vesicles, i.e. (i) cell reproduction by fission and (ii) duplication of the genetic material. One major problem is indeed that of assuring that the two processes take place at the same pace. If cell reproduction were much faster than duplication, the genetic material would be increasingly diluted through generations, while in the opposite case its quantity would continue to increase and accumulate in cells. In both cases no sustainable growth of a population of protocells would take place.
If we do not want to introduce unlikely hypotheses about the existence from the very beginning of sophisticated control mechanisms, we are led to raise the key question of whether the synchronization of these two processes might have spontaneously emerged in early (proto)life. In our previous works, briefly recalled in Section 2, we used simplified mathematical and computational models (which will be collectively referred to as here as Symmetrical Division Models) to show that this may indeed be the case under a surprisingly wide set of different hypotheses. The rates of the two processes (reproduction of the protocell and duplication of its protogenetic material) tend to a common value generation after generation, without resorting to any specific evolutionary mechanism, provided that they are coupled. We referred to this tendency as synchronization of the two processes, and we showed that it is robust with respect to different types of random fluctuations.
In these models, the dynamics of a protocell between its birth and its fission is ruled by ordinary first-order differential equations, which allow us to compute the relationship between the initial quantities of replicators X at successive generations, i.e. the discrete map which relates X(k+1) to X(k). Since the size of the mother cell when splitting takes place is fixed, as well as the initial size of the newborns, the various generations differ only in the initial values of the replicators. Therefore, in order to prove synchronization, it suffices to prove that as k grows the quantities of replicators (and therefore the lifetime of each generation) tend to constant values. In many interesting cases this can indeed be analytically demonstrated, in other cases this can be verified by numerical simulations.
The situation seems reasonably well understood in the case of symmetrical division, and here below we summarize in section 2 the main results of these previous studies. However, different phenomena have also been observed in real vesicles, which may sometimes give rise to offsprings of largely different sizes [17]. In this paper we will consider the case where a protocell splits in two daughters of different sizes, using models similar to those which had been previously applied to the case of symmetrical division. We will consider both Surface Reaction Models (SRMs), where the replicators are found in the lipid membrane, and Internal Reaction Models (IRMs), where they inhabit the internal aqueous phase. These models are quite abstract (for example, replicators are defined by their kinetic equations, without any explicit reference to their chemical identity) so they can represent several different more specific models.
When the offsprings are born different, the issue can no longer that of synchronization since, in general, they will mature (i.e. reach the critical size for division) at different times. Sustainable growth through generations will take place if the daughters are similar to how their parents were, when they were born. We will refer to this situation as homogeneous growth: synchronization implies homogeneous growth, but homogeneous growth can be achieved even without synchronization of the two processes. In order to claim that a generation is similar to the previous one, it may be requested that, at splitting time, the chemical compositions of the cells be the same. Since we assume that there is a single type of lipids, and that the size of splitting is the same, the chemical composition of a cell is determined by the total quantities of different replicators. We therefore observe homogeneous growth if these quantities are the same at the end of successive generations. For reasons which will be detailed in sections 4, it will actually be required that the ratios of the quantities of different types of replicators be the same in different protocells.
We are of course aware that evolution requires that changes can intervene between generations. The kind of abstract models described here and in the previous works on synchronization are based on deterministic differential equations among a fixed set of replicators and lipids, so there is no explicit room for true evolution, which requires the introduction of further rules (e.g., those for the creation of new chemical species). We had also previously shown how this can be done, proving that synchronization can be observed in stochastic evolving models, in the case of symmetrical division [18,19,20,21]. We suppose that homogeneous growth will also be observed in the case of evolution under asymmetrical division, but these studies lie beyond the scope of this paper.
The purpose of this paper is indeed to study under which conditions homogeneous growth can take place when the daughter cells are of different sizes. In order to do so, we will consider the case of a population which repeatedly undergoes the same kind of asymmetrical division, looking for the possible emergence of a sustainable pattern of protocells. In the simpler case of symmetrical division with synchronization, the time interval between successive fissions tends to a common value, so the population size doubles at each interval, undergoing exponential growth. In asymmetrical division, the duplication time is a function of the initial quantities of lipids (C) and of replicators (X1…Xq): while the initial and final quantities of lipids are the same for every protocell that has the same size, the initial compositions of replicators may depend upon their previous histories, so different protocells can duplicate at different times. Each splitting event gives rise to a small protocell and to a large one, while of course the mother disappears: therefore, the total number of protocells increases by one. As the population size grows, the time interval between two successive splitting events tends to shrink, thus increasing the overall growth rate of the population.
We performed various types of simulations, starting in each case from a single protocell of size  and a given quantity of replicators. The above-mentioned unbounded growth of the population size is of course unrealistic, since the scarcity of some resource will sooner or later prevent any further growth. In order to analyze the long-time behavior of the system, we took the simple approach of imposing a limit to the total number of protocells: when a new splitting would lead to exceed (by one) the limit, the two newborns are added to the existing population, and a randomly chosen protocell is removed – thus keeping their total number constant. We report here results based on this method, although we have also performed different types of simulations, e.g. following a single lineage through generations, which confirm the main conclusions. Note that the populations are renewed, but there is no selection pressure, since the removal is performed randomly, with uniform distribution.
In section 3 we will introduce the model of asymmetrical division in SRMs, and we will first analyze the case of a single self-replicator, whose proliferation is described by a linear differential equation. Autocatalysis is however quite rare, therefore we will also consider the case when more replicators interact linearly, so that self-replication is a collective rather than individual property. We will also analyze some nonlinear cases. It will be shown (perhaps unexpectedly) that in all these cases the behavior under asymmetrical division is strikingly similar to that of its symmetrical counterpart, in the sense that homogeneous growth is observed in those cases where synchronization is observed in symmetrical models.
In section 4 we then study asymmetrical division in models where reactions take place in the aqueous interior of the protocell, paying particular attention to the important case of two replicators catalyzing each other’s synthesis. It will be seen that in such IRMs some differences are observed with respect to symmetrical division, and they will be stressed.
The results will be discussed in section 5, where also indications for further work will be presented.

2. Symmetrical Division Models

We will quickly summarize the classes of models which have been used to describe symmetrical division, and the most important known results about synchronization, which are important to understand the properties of the asymmetrical cases. No new results will be presented in this section. To the best of our knowledge, the importance of synchronization was first observed [22] in the case of the so-called Los Alamos bug model [23,24,25,26], which was based on a number of specific hypotheses about the protocell architectures and the chemical properties of the replicators. Shortly after, it was shown [27], that the same properties might hold in more general cases, by introducing a new class of abstract models, amenable to analytical treatment or to numerical simulation. In a series of papers, it was shown that synchronization can be found in several cases, and that it is robust with respect to different changes [20,27,28,29,30]. These results have also been discussed in depth in a book [21].
As described in Section 1, protocells are assumed to be spherical, and to undergo duplication when they reach a critical size θ, giving rise to two equal daughter cells. There is a single type of lipids and, while there may be different types of replicators, for the sake of simplicity, we will first consider the case of a single (self)replicator. Let C be the total quantity of membrane lipids, and let X be the total quantity of replicator; then a protocell grows in time according to two ordinary differential equations:
C ˙ = f C , X X ˙ = g C , X
where a dot denotes time derivative. Let S be the surface area and let δ be its (constant) width, then the volume of the lipid membrane is Vm=Sδ. Since we assume spherical protocells, S also determines the total volume of the protocell, i.e. its size. Moreover, if lipid density ρ is constant, the total quantity of membrane lipid C is equal to Sδρ. Therefore the critical size is associated to a specific value of C, so we assume that splitting takes place when C=θ.
The growth of both X and C depends also on the availability of suitable precursors, which is given for granted here (i.e. they are buffered). Other assumptions are also necessary to arrive at Eq.1, they are discussed at length in [27] and in [21] and will not be further analyzed here. From now on, in this section we will concentrate on Surface Reaction Models, where the replicators are found in the membrane. Let us assume that X linearly catalyzes its own production and also the growth of the membrane from suitable precursors. In this case Eqs.1 become3
C ˙ = α X X ˙ = η X
Observing that Q(t)≡ηC(t)−αX(t) is constant during the continuous growth described by Eq.2, and observing that in each generation the initial and final sizes are θ/2 and θ, one straightforwardly derives a relationship between the initial values of the replicator quantity in successive generations:
X k + 1 = X k + D 2 ;   D = θ η 2 α
By taking the limit k→∞ one gets Xk→D; since the initial values of X become constant, so does also the duplication time ΔTk:
Δ T k → 1 η l n 2
Synchronization is thus proven. Using a similar method, it can also be analytically proven if dX/dt follows a nonlinear power law, i.e. when the kinetic equations are:
C ˙ = α X X ˙ = η C ν − 1 X ν
provided that ν<2.
As it has been observed, autocatalysis is quite rare, therefore it is interesting to consider cases where more replicators are involved. Let X → denote the quantities of the q types of replicators X1 …Xq and let the kinetic equations be:
C ˙ = α → · X → X ˙ = M X →
The long-time behavior of the system is ruled by the eigenvalue with the largest real part (λ1) of the q*q matrix M. If the matrix M is nonnegative (all its entries are ≥0) and non-null (at least one entry is ≠0), then the Perron theorem guarantees that λ1 is positive and admits a nonnegative eigenvector (whose components specify the long-term quantities of the various replicators). In this case synchronization is guaranteed, a conclusion which also holds if there are some negative diagonal terms. The discussion of cases with negative nondiagonal terms requires more care, but a satisfactory physical interpretation can also be given, as extensively discussed in [21,28,29].
This is how far we can go with analytical methods. We can however investigate by simulations also different cases of one or several interacting replicators, and we find that synchronization is widespread. It is not achieved in the case of nonlinear quadratic interactions, but this result is structurally unstable: if a lower order term (e.g. linear) is added, then synchronization takes place even when there are quadratic terms. In some cases λ1 is complex, and synchronization takes place between quantities that oscillate in time. We also tested some kinetic equations which are known to give rise to chaotic behavior but, when replicators are coupled to the splitting of their lipid containers, synchronization is again observed [30].
Apart from changes in the kinetic equations, synchronizations has also been observed when the full geometry of the vesicle is taken into account, when the membrane itself is composed by replicators (as for example in GARD models [31,32]) and when the splitting threshold is subject to random fluctuations. Synchronization is robust with respect to these perturbations.
Stochasticity can play a major role when the number of specimens of a type of replicator is very small, as it may easily happen when a new type is discovered: in these cases the deterministic kinetic equations used so far, based on the law of mass action, may be inadequate, and they should be substituted by stochastic equations. We have also analyzed this type of equations, showing that synchronization may also take place (e.g. when there is a so-called RAF set of replicators [20,33,34]) but a thorough discussion of these cases lies beyond the purpose of this paper.
The other major class of models which will be considered are those where the replicators are solutes in the internal liquid phase, which are also able to catalyze the growth of the container from buffered precursors (indeed, most protocell models assume that the key reactions take place inside the protocell, rather than in the membrane). Like in the SRM case, we will assume homogeneous distribution of the replicators inside the protocell, which implies their infinitely fast diffusion rate in water, and unlimited buffered availability of precursors, which implies also infinite transmembrane diffusion rate (hypotheses which can be and have been relaxed in Symmetrical Division Models) [28].
Assuming that both the growth of the container C and the rate of self-replication are linear functions of the concentration of X, the equations of the IRMs turn out to be the same as those for SRMs, i.e. Eq.5 (which is the same as Eq.2 in the case of a single replicator). The observed phenomena are therefore the same as those of the SRMs.
In the case of nonlinear models, the equations are no longer the same. Let us consider the case of first order reactions, which involve a single type of reactant: according to the law of mass action, when precursors are always available, the reaction rate (equal to the rate of change of [X]=X/Vi, where Vi is the internal volume) is proportional to [X]. The total number of events in unit time is proportional to [X]Vi, i.e. to the internal quantity X. This is why in the linear case the equations are the same as those of SRMs.
But in second-order reactions, the rate of encounters per unit volume is proportional to [X]2 = X2/Vi2 and therefore the total number of encounters is X2/Vi. If we assume that the internal volume is proportional to S3/2, and therefore to C3/2, then the equations become:
C ˙ = α X X ˙ = η C 3 2 X 2
Despite this difference, the results concerning synchronization still follow the same pattern as those for IRMs, as detailed in [21,28]. A remarkable difference with respect to SRMs is that in this case some internal material is lost (see the following section 4 for details).

3. Asymmetrical division in Surface Reaction Models

The notions of SRM and IRM concern the architecture of a protocell, and they can of course be applied also to the study of asymmetrical replication. The continuous growth phase of SRMs is described by the same equations as those of the previous section, while the splitting may give rise to two different daughters. As in the case of symmetrical division, we will assume that no lipids are lost, so the total volume of the membranes of the two daughters equals that of their “mother”. Since the width δ of the membrane is constant, this also implies that the total surface is constant, which in turn (assuming uniform concentration) implies that also the total quantity C is conserved in splitting4. Just like in the models of section 2, C=Sδρ and the condition for splitting is C=θ.
In asymmetrical division, one daughter gets a fraction ω of the total membrane lipids, i.e. ωθ [35]. Replicators are homogeneously dissolved in these lipids, therefore that protocell will also get the same fraction of replicators, i.e. ωXfin where Xfin is the total quantity of X in the mother protocell at splitting time. The other daughter will then inherit (1- ω)θ lipids and (1-ω)Xfin replicators.
In the case of symmetrical division, we had written equations using quantities of replicators in a protocell. But here each division gives rise to a large and to a small protocell, and using concentrations, as is usually done in chemistry, turns out to be convenient. Note that the splitting threshold is fixed irrespective of the initial size, therefore concentrations at splitting time are simply proportional to quantities.
We performed several simulations of protocell populations. For reasons highlighted in section 1, all these populations start from the asymmetrical division of a mother protocell; the fraction ω is the same at every generation so the impact of its value can be determined (but see section 5 for a preliminary discussion about the case of a variable threshold). There is a limit Nmax on the maximum number of protocells in the system, so after a transient their total number remains constant (as discussed in section 1, old protocells are removed randomly - with uniform distribution - to avoid exceeding that number). When that number has been reached, a generation is defined to be equal to Nmax individual splitting events (i.e. the minimum number which might allow complete renewal of the population).
There are only two possible initial sizes, ωθ or (1- ω)θ, but the initial concentrations [Xinitial] of replicators may differ, depending upon their different histories. Lifetime of protocells might also be different since they also depend upon [Xinitial].
Transients may depend upon initial values, so we will show below results concerning the distribution of the relevant variables after some generations have elapsed since the division of the first protocell (and since reaching the maximum number of protocells Nmax).
Let us first consider the case of a single linear replicator, whose continuous growth is described by Eq. 2. The first interesting observation is that the final concentration tends to a constant value, the same for every protocell, which depends upon the values of the ratio ηθ/α like in the case of symmetrical division (section 2). There are now two lifetimes, one for the protocells which were born small, and one for those which were born large. It is interesting that, after 75 generations, the values of the final concentration [Xfin] and of the lifetime Tduplication are the same, irrespective of the value of the concentration of the progenitor cell (provided of course that the other parameters are kept fixed), as shown in Figure 1.
One can observe that the concentration at the beginning of a new generation is the same as the concentration of the previous one just before splitting, so the initial concentration of one daughter, Xinitial/Cinitial is:
X i n i t i a l C i n i t i a l = ξ X f i n , p r e v i o u s ξ θ = X f i n , p r e v i o u s C f i n
Where ξ=ω for one daughter, ξ=(1-ω) for the other one, and Xfin,previous refers to the previous generation. Since the final concentration becomes constant, so do also the (equal) concentrations of the two daughters. In SRMs, after an initial transient, all the initial and final concentrations take the same value, and it has been observed in simulations that they also remain constant during the continuous growth phases. Indeed, concentrations tend to the value X/C=η/α, which makes their time derivatives vanish since
d d t X C = η X C − α X C 2
Also note that in the long term the sum of final concentrations of replicators in the two daughters is equal to the same sum at the previous generation, thus allowing homogeneous growth.
A major observation is that the case of a single linear replicator is one of homogeneous growth – it behaves in a way similar to that of symmetrical division, where there is synchronization. As it is obvious (also checked by simulation) the same also applies to the case of several linear replicators, where the eigenvalue with the largest real part and its eigenvector(s) determine the outcome.
Moreover, also in the simulated cases of nonlinear replicator kinetics one observes a similar parallelism between the behaviors of the two types of models. Note that in the case of a power law, when d[X]/dt is proportional to [X]ν, we see homogeneous growth as long as ν<2 (see Figure 2).
The overall conclusion of these studies is that asymmetrical SRMs behave much like Symmetrical Division Models: they lead to homogeneous growth in those cases where there was synchronization, thus allowing the growth of a population of protocells which, after a transient, maintain their features. Of course, mutations have not yet been considered in the studies described in this paper.
It is also interesting to explore how the variables depend upon the degree of asymmetry, related to the fraction ω. The larger protocells reach the splitting threshold sooner than the smaller ones, and in Figure 3 it is shown how the difference between the duplication times increases as asymmetry increases (linear case).

4. Asymmetrical division in Internal Reaction Models

In this case the replicators are dissolved in the internal water phase; as in the previous case, splitting is achieved by partitioning the membrane between the two daughters, without any loss of lipids. Since for simplicity we assume that both the mother’s and the daughters’ shapes are spherical then, for every protocell, the volume V is related to the quantity of membrane lipids C by:
V C = 4 3 π δ 3 C ρ π δ 3 − 1 3 − 1 2 3 ~ 1 6 π δ 3 1 ρ π δ 3 3 2 C 3 2 = k C 3 2
where k is a constant. The last expression is valid when the membrane width δ is small, and we see that in this case the Volume scales as C3/2. When the membrane reaches the value C=θ (so V(C)= kθ3/2) the cell is divided in two fractions whose membranes are proportional to ω and to (1-ω); therefore the corresponding volumes are proportional to ω3/2 and to (1- ω)3/2. The volume concentration of replicators in the daughters is homogeneous, so the quantities of replicators are proportional to their volumes.
As in section 3, let ξ be equal to ω for one daughter protocell and to (1-ω) for the other one: then in both cases the relevant concentration, X/V, obeys the equation:
X i n i t i a l V i n i t i a l = ξ 3 / 2 X f i n , p r e v i o u s ( ξ θ ) 3 / 2 = X f i n , p r e v i o u s V f i n
which is identical to Eq.8. If the asymptotic Xfin were the same in different generations, we would come to the same conclusions as in the previous section, but this is not the case. In the case of the linear self-replicator (described by the same Eq. 2), after several generations have passed, we continue to observe a distribution of different final values, contrary to what was observed in SRMs. This distribution (see Figure 4) seems to approach a constant non-obvious shape, where the final values tend to cluster in two groups, with a narrow gap in between.
A bimodal distribution is observed also in duplication times (Figure 5) thus showing that the two groups are formed, as it should be expected, from protocells born either small or large (small ones take a longer time to reach the threshold for splitting).
The presence of two different duplication times involves an interesting consequence. In our simulations, whenever a “mother” protocell M reaches its critical size, it gives rise to two daughters, a large and a small one, which take the place of both the mother and of another randomly chosen protocell (R): M and R disappear from the population, while a large and a small cell are added. If M is small and R is large, or vice versa, the fraction of large and small protocells remains the same. If M and R are both large then the total number of small cells increases, and the number of large ones decreases, while the opposite happens if M and R are both small. But large cells have shorter lifetimes, i.e. they die faster than small ones, so the chosen “mother” is more likely to be a large protocell. This leads to an unbalance between the two populations: in the case of a mature population, the number difference between the two types in the population, which is related to their lifetimes, increases as the degree of asymmetry (i.e. the value of |ω -1/2|) increases (as shown in Figure 9), and that it.
While we have so far examined static pictures taken at a given generation, or at most comparisons between pictures taken at different times, in the following Figure 7 we follow the value of the final concentration [Xfin] through successive generations, starting from the very beginning. As generations pass, stories can become blurred. Remember that at each splitting there is one large and one small daughter. If we always follow the large daughter of the large daughter of the large daughter of the mother, we can see what happens to a “pure” lineage. As it can be seen, the final concentrations become constant in this case. They also become constant in the case of a pure small lineage. If we show at each cell division the final concentration of a randomly chosen daughter, we see that the values oscillate (since the choice is random) but the oscillations do not take place only between the two pure values (Figure 7). This is again a consequence of the fact that in IRMs there is a distribution of final concentration values.
The above results (Figure 7) show that the total number of replicators in the two daughter protocells, born at different times, can differ from twice the value of the mother – a phenomenon which was not present in SRMs. Indeed, it is the average value of the replicator quantity which doubles, but the differences among generations give rise to oscillations.
Similar oscillations are also observed in the case of several linearly interacting replicators. Since the continuous equations are the same as those of SRMs, the ELRP and its eigenvectors play similar roles in IRMs. We show below the simulation of a two-replicators case, whose kinetic equations are:
d C d t = α X d X d t = k 11 X + k 12 Y d Y d t = k 21 X + k 22 Y
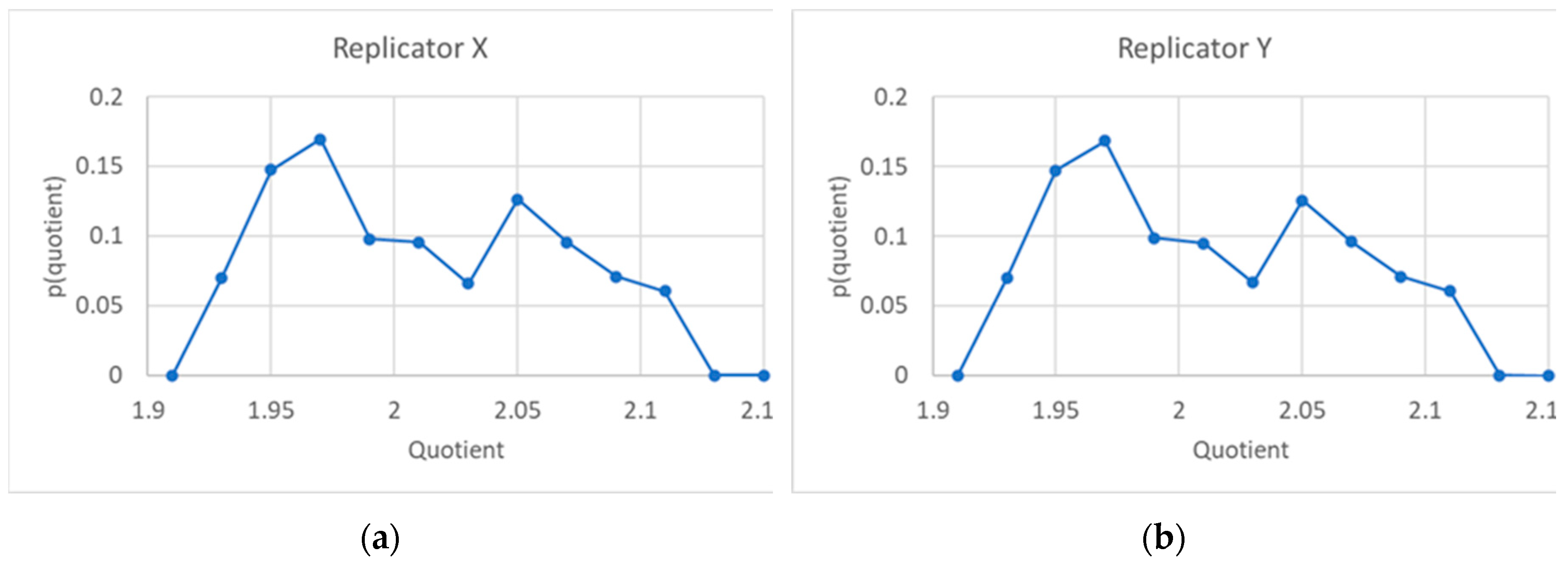
The ratios R between the sum of final quantities of the two kinds of replicators, X and Y, in the daughter protocells, and the corresponding quantity in the mother may differ. We show in Figure 8 the distribution of these ratios, with 2 as the average value.
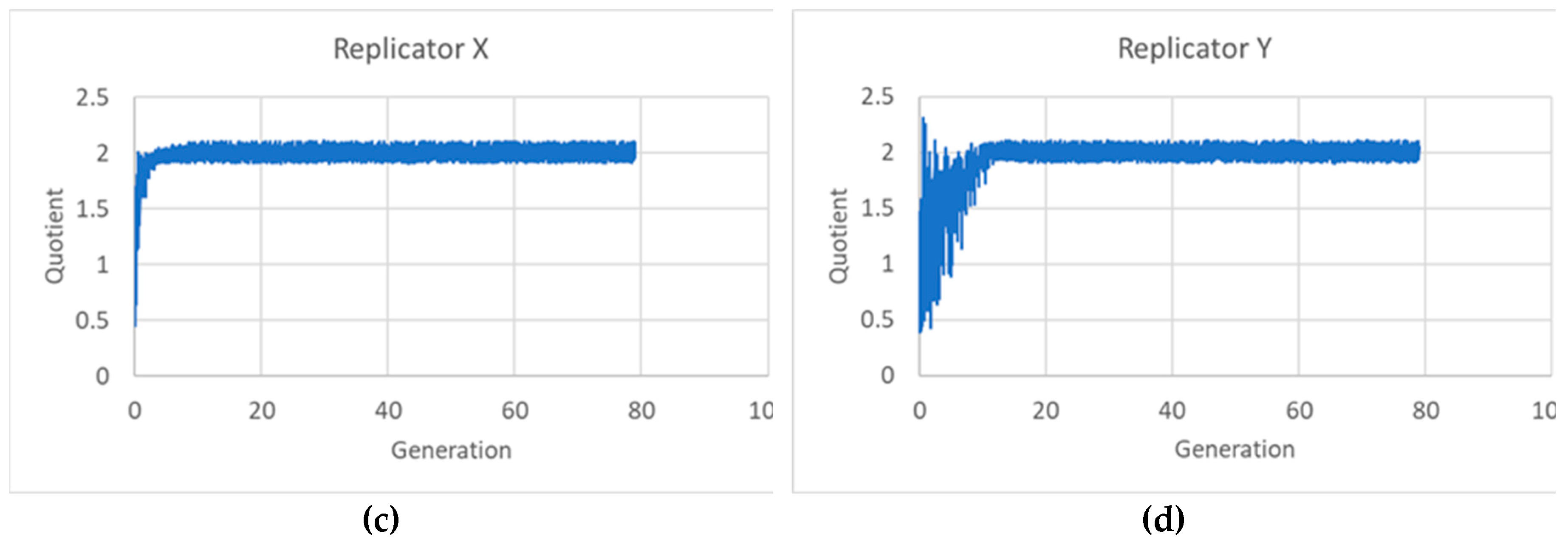
The fact that the average value of the ratio R between the quantities is not always 2 does not make sustained growth impossible, since the constancy of its average value suffices to guarantee the maintenance of the protogenetic material. The identity of a protocell with several different replicators is rather associated to its chemical composition, which is directly related to the ratio between the quantities of the two replicators (or to the sets of ratios in the case of more than two replicators) rather than to the ratio R between total quantities in daughters and mother. And it is impressive to see how, at the time of division in a (mature) population, notwithstanding the oscillations of the various variables, this ratio is exactly the same, up to an impressive number of significant digits, for every protocell (Figure 9a). The relative composition of the protogenetic material remains the same, so homogeneous growth actually takes place in the model.
Figure 9b looks identical to Figure 9a: this surprising property will be commented in the final section 5.
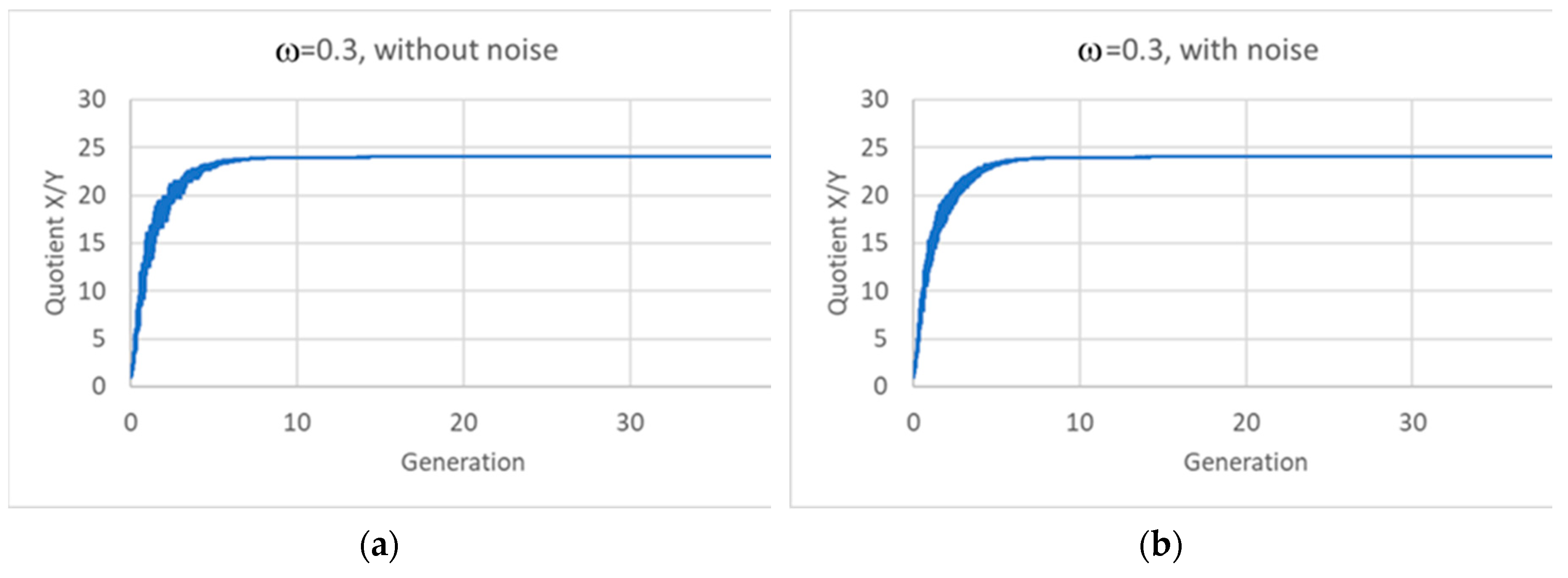
Preprints 97909 g009
Figure 9. Ratio X/Y with the passing of generations, two linear replicators: (a) noise-free asymmetric division, ω=0.3; (b) asymmetric division with noise (ω=0.3±0.1, with uniform distribution). In both plots the quotient reaches exactly the ratio present in the eigenvector of the system (k11=5e-3; k12=2e-6; k21=2e-4; k22=2e-4; ratio= 24.0002).
Figure 9. Ratio X/Y with the passing of generations, two linear replicators: (a) noise-free asymmetric division, ω=0.3; (b) asymmetric division with noise (ω=0.3±0.1, with uniform distribution). In both plots the quotient reaches exactly the ratio present in the eigenvector of the system (k11=5e-3; k12=2e-6; k21=2e-4; k22=2e-4; ratio= 24.0002).
Preprints 97909 g009

5. Conclusions

The main conclusions of the studies just described is that, in those models which have been analyzed, sustainable growth of a population of protocells can be observed under a broad set of conditions. In particular, when the kinetic equations for the replicators and for their coupling to the growth of the lipid container lead to synchronization in models with symmetrical division, we have found homogenous growth under asymmetrical division.
This is particularly clear in the case of Surface Reaction Models. We stress that this result is not trivial, since the lifetime (i.e. the time interval from their birth to their splitting) of those protocells which are born small is larger than that of their larger “sisters”. In the case of linear replicators, after a transient has died out, the pairs of newborn protocells tend to be equal in successive generations. This is a consequence of the fact that the concentration of replicators at division times tend to become equal – exactly as it happens in the case of symmetrical division.
In the case of asymmetrical division of IRMs, these equalities no longer hold. As we have seen, the initial concentration of replicators in pairs of newborn protocells can be different from that of their parent, even after many generations, so that quantities of replicators are not identical in successive generations. However, we have argued that the chemical identity of a protocell is not related to the volume concentration of the replicators, but rather to their ratios, and we have shown that this ratio tends to be remarkably constant in every protocell of a population.
An important question concerns the robustness of these results with respect to random fluctuations in the sizes of the daughter protocells. Fission and budding processes can be affected by several uncontrolled variables, so it may be unrealistic to assume that division takes always place at a given critical size. This point needs to be addressed an a wider and more complete future study, but we have analyzed the case of two linear replicators (Eq. 12), supposing that splitting gives rise to a large and to a small protocell, with ω chosen at random, with uniform probability, in the interval [0.2,0.4]. The results are shown in Figure 9b, which looks the same as its counterpart with fixed value ω=0.30. Homogeneous growth is maintained also when size fluctuations are taken into account.
These results have been achieved in the case of linear kinetic equations, and they still need to be analyzed under more general assumptions. We have also successfully explored some nonlinear cases, anyway the possibility of homogeneous growth needs to be verified in a broader set of cases. We expect that, as it happened in the case of synchronization in symmetrical division, extensive simulations will confirm this result. In any case, this paper demonstrates its validity under a wide set of interesting hypotheses.
A final word of caution concerns the fact that the duplication process described here is quite different from that of present-day cells. In this latter case, not only there are effective controls which guarantee that the genetic material has been duplicated before fission, but the whole process of DNA duplication is made in such a way as to generate, with high probability, macromolecules which are identical to those of the parent. It seems unlikely that such a process emerged all at once. The mechanisms described in this paper, where molecules proliferate under kinetic equations, are plausible for protocells at the dawn of life, but they must have been overtaken at some time to generate those which are at work nowadays. And understanding this takeover (possibly a new Major Transition in evolution) is an open fascinating problem.

Author Contributions

Conceptualization, M.V., E.A. and R.S.; methodology, M.V., E.A. and R.S; software, M.V. and E.A.; validation, M.V. and E.A.; investigation, M.V. and R.S.; data curation, M.V. and E.A.; writing—original draft preparation, M.V. and R.S.; writing—review and editing, M.V., E.A. and R.S; visualization, M.V and E.A.; supervision, M.V. and R.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research was partially funded by Università degli Studi di Modena e Reggio Emilia (FAR2023 project of the Department of Physics, Informatics and Mathematics).

Acknowledgments

MV and RS gratefully thank Stuart Kauffman for several important discussions about protocells.

Conflicts of Interest

The authors declare no conflicts of interest.

Notes

1
Besides their possible role in the origin of life from abiotic material, the interest in protocells is related also to their possible application in different domains (e.g. drug synthesis and delivery, remediation of polluted sites, etc.)
2
As it is often the case, we will often use the term lipid as a synonym of amphiphiles: lipids with a polar head are indeed the best-known examples of amphiphilic molecules
3
In the following, time is measured in arbitrary units; the absolute quantities in kilograms; lengths in meters; concentrations in kg/liter. The units of measurement of the other entities (for example, those of parameters) are consistently derived
4
Note that, since we assume that there is a single type of lipids, using different units (e.g. mass or moles or number of molecules) to measure this quantity does not make any conceptual difference, since they are all related to each other by constant multiplicative coefficients

References

  1. Alberts, B.; Johnson, A.; Lewis, J.; Morgan, D.; Raff, M.; Roberts, K.; Walter, P. Molecular Biology of the Cell; Garland Science: New York, NY, USA, 2014.
  2. Luisi, P.L. The emergence of life: from chemical origins to synthetic biology; Cambridge University Press: New York, USA, 2007.
  3. Rasmussen, S.; Bedau, M.A.; Chen, L.; Deamer, D.; Krakauer, D.C.; Packard, N.H.; Stadler, P.F. Protocells; MIT Press: Cambridge, Massachusetts, USA, 2008.
  4. Rasmussen, S.; Constantinescu, A.; Svaneborg, C. Generating minimal living systems from non-living materials and increasing their evolutionary abilities. Philos. Trans. R. Soc. Lond. B. 2016, 371, 20150440. [CrossRef]
  5. Gánti, T. Chemoton Theory: theory of living systems; Kluwer Academic & Plenum Publishers: New York, NY, USA, 2003.
  6. Kaneko, K. Life: An Introduction to Complex Systems Biology; Springer: Berlin, Germany, 2006.
  7. Mavelli, F.; Ruiz-Mirazo K. Stochastic simulations of minimal self-reproducing cellular systems. Philos. Trans. R. Soc. Lond. B. Biol. Sci. 2007, 362, 1789–1802. [CrossRef]
  8. Israelachvili, J.N.; Mitchell, D.J.; Ninham, B.W. Theory of self-assembly of hydrocarbon amphiphiles into micelles and bilayers. J. Chem. Soc. Faraday Trans. 2 1976, 72, 1525. [CrossRef]
  9. Israelachvili, J.N.; Mitchell, D.J.; Ninham, B.W. Theory of self-assembly of lipid bilayers and vesicles. Biochim. Biophys. Acta. 1977, 470, 185–201. [CrossRef]
  10. Sakuma, Y.; Imai, M.; Stano, P.; Mavelli, F. From vesicles to protocells: the roles of amphiphilic molecules. Life 2015, 5, 651–675.
  11. Szostak, J.W.; Bartel, D.P.; Luisi, P.L. Synthesizing life. Nature 2001, 409, 387–390.
  12. Walde, P.; Umakoshi, H.; Stano, P.; Mavelli, F. Emergent properties arising from the assembly of amphiphiles. Artificial vesicle membranes as reaction promoters and regulators. Chem. Commun. 2014, 50, 10177–10197. [CrossRef]
  13. Hanczyc, M.M.; Szostak, J.W. Replicating vesicles as models of primitive cell growth and division. Curr. Opin. Chem. Biol. 2004, 8, 660–664. [CrossRef]
  14. Terasawa, H.; Nishimura, K.; Suzuki, H.; Matsuura, T.; Yomo, T. Coupling of the fusion and budding of giant phospholipid vesicles containing macromolecules. Proc. Natl. Acad. Sci. 2012, 109, 5942–5947. [CrossRef]
  15. Svetina, S. Vesicle budding and the origin of cellular life. ChemPhysChem 2009, 10, 2769–2776. [CrossRef]
  16. Svetina, S. Cellular life could have emerged from properties of vesicles. Orig. Life Evol. Biosph. 2012, 42, 483–486. [CrossRef]
  17. Miele, Y.; Holló, G.; Lagzi, I.; Rossi, F. Shape Deformation, Budding and Division of Giant Vesicles and Artificial Cells: A Review. Life 2022, 12, 841. [CrossRef]
  18. Filisetti, A.; Serra, R.; Carletti, T.; Poli, I.; Villani, M. Synchronization phenomena in protocell models. Biophys. Rev. Lett. 2008, 3, 325–342. [CrossRef]
  19. Serra, R., Filisetti, A., Villani, M. et al. A stochastic model of catalytic reaction networks in protocells. Nat Comput 2014, 13, 367–377. [CrossRef]
  20. Villani, M.; Filisetti, A.; Graudenzi, A.; Damiani, C.; Carletti, T.; Serra, R. Growth and division in a dynamic protocell model. Life 2014, 4, 837–864. [CrossRef]
  21. Serra R.; Villani M. Modelling Protocells; Springer Science+Business Media BV: Dordrecht, Netherlands, 2017.
  22. Munteanu, A.; Attolini, C.S.O.; Rasmussen, S.; Ziock, H.; Solé, R.V. Generic Darwinian selection in catalytic protocell assemblies. Philos. Trans. R. Soc. Lond. B. Biol. Sci. 2007, 362, 1847–1855. [CrossRef]
  23. Rasmussen, S.; Chen, L.; Nilsson, M.; Abe, S. Bridging nonliving and living matter. Artif. Life 2003, 9, 269–316. [CrossRef]
  24. Rasmussen, S.; Chen, L.; Deamer, D.; Krakauer, D.C.; Packard, N.H.; Stadler, P.F.; Bedau, M.A. Transitions from nonliving to living matter. Science 2004a, 303, 963–965. [CrossRef]
  25. Rasmussen, S.; Chen, L.; Stadler, B.M.R.; Stadler, P.F. Photo-organism kinetics: evolutionary dynamics of lipid aggregates with genes and metabolism. Orig. Life Evol. Biosph 2004b, 34, 171–180. [CrossRef]
  26. McCaskill, J.S.; Packard, N.H.; Rasmussen, S.; Bedau, M.A. Evolutionary self-organization in complex fluids. Philos. Trans. R. Soc. Lond. B. Biol. Sci. 2007, 362, 1763–1779. [CrossRef]
  27. Serra, R.; Carletti, T.; Poli, I. Synchronization phenomena in surface-reaction models of protocells. Artif. Life 2007, 13, 123–138. [CrossRef]
  28. Carletti, T.; Serra, R.; Poli, I.; Villani, M.; Filisetti, A. Sufficient conditions for emergent synchronization in protocell models. J. Theor. Biol. 2008, 254, 741–751. [CrossRef]
  29. Filisetti, A.; Serra, R.; Carletti, T.; Poli, I.; Villani, M. Synchronization phenomena in protocell models. Biophys. Rev. Lett. 2008, 3, 325–342. [CrossRef]
  30. Filisetti, A.; Serra, R.; Carletti, T.; Villani, M.; Poli, I. Non-linear protocell models: synchronization and chaos. Eur. Phys. J. B. 2010, 77, 249–256. [CrossRef]
  31. Segré, D.; Lancet, D.; Kedem, O.; Pilpel, Y. Graded Autocatalysis Replication Domain (GARD): kinetic analysis of self-replication in mutually catalytic sets. Orig. Life Evol. Biosph. 1998, 28, 501– 514. [CrossRef]
  32. Segré, D.; Ben-Eli, D.; Deamer, D.W.; Lancet, D. The lipid world. Orig. Life Evol. Biosph. 2001, 31, 119–145.
  33. Hordijk, W.; Steel, M. Detecting autocatalytic, self-sustaining sets in chemical reaction systems. J. Theor. Biol. 2004, 227, 451–461. [CrossRef]
  34. Hordijk, W.; Hein, J.; Steel, M. Autocatalytic sets and the origin of life. Entropy 2010, 12, 1733–1742. [CrossRef]
  35. Musa, M.; Villani, M.; Serra, R. Simulating Populations of Protocells with Uneven Division. In: Pelillo, M., Poli, I., Roli, A., Serra, R., Slanzi, D., Villani, M. (eds) Artificial Life and Evolutionary Computation. WIVACE 2017. 2018 Communications in Computer and Information Science, vol 830. Springer, Cham.
Preprints 97909 g001
Figure 1. Final concentration of X (a) and duplication times (b) at the 75th generation (15,000 duplications in a population of 200 individuals, asymmetrical division, ω=0.4). The X axis reports the X concentration values of the initial generation. In this figure, α=0.05, η=0.002, θ=2.70E-16
Figure 1. Final concentration of X (a) and duplication times (b) at the 75th generation (15,000 duplications in a population of 200 individuals, asymmetrical division, ω=0.4). The X axis reports the X concentration values of the initial generation. In this figure, α=0.05, η=0.002, θ=2.70E-16
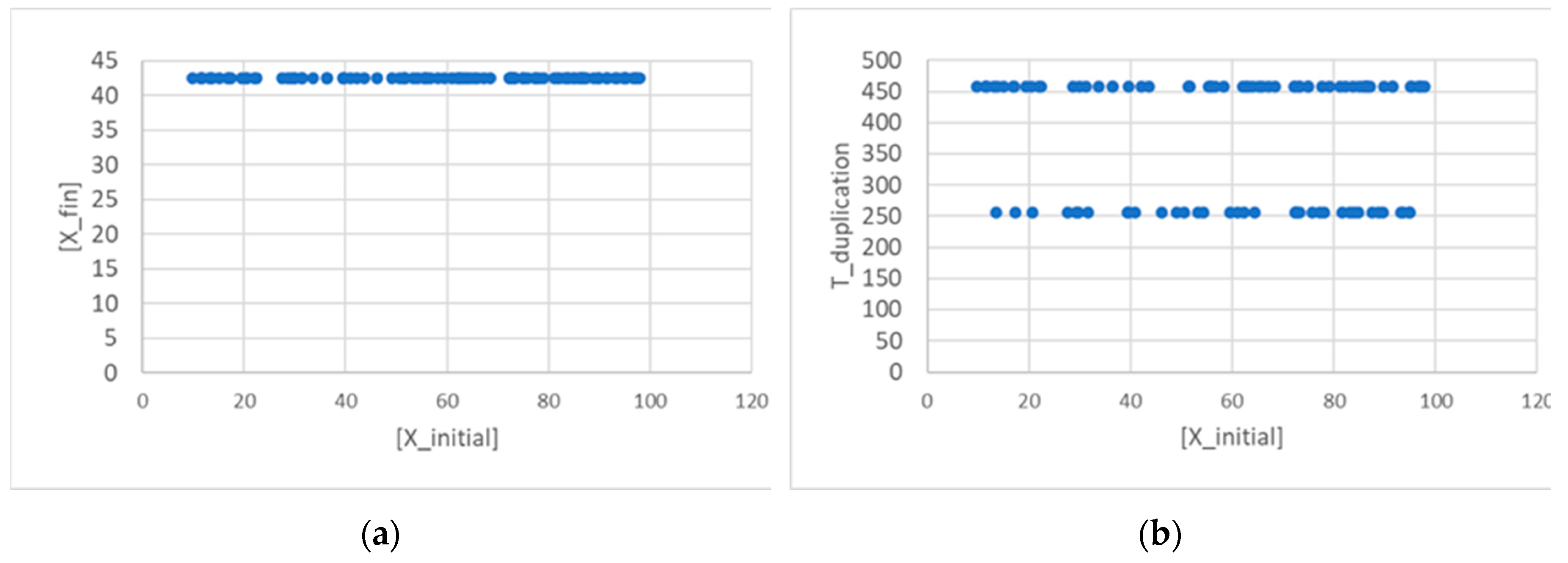
Preprints 97909 g001
Preprints 97909 g002
Figure 2. Duplication times Tduplication and replicator concentration at duplication time [Xfin] of a stable population, as ν varies.
Figure 2. Duplication times Tduplication and replicator concentration at duplication time [Xfin] of a stable population, as ν varies.
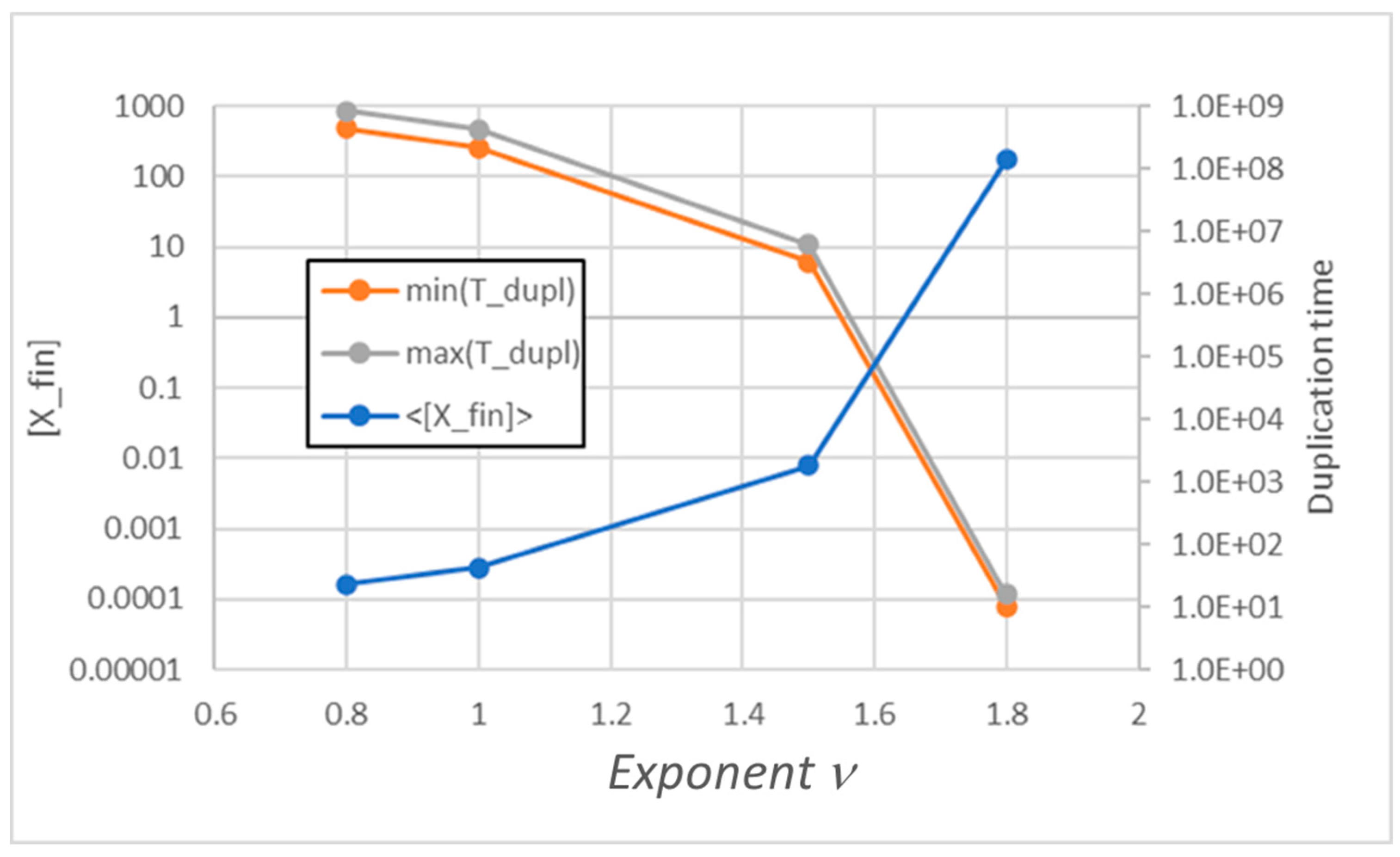
Preprints 97909 g002
Preprints 97909 g003
Figure 3. Duplication times Tduplication (of a stable population – here is the 75th generation) as asymmetry varies: the duplication times of "born small" and "born large" protocells are shown. Values on the x-axis show the fraction of lipids inherited by the smaller protocell.
Figure 3. Duplication times Tduplication (of a stable population – here is the 75th generation) as asymmetry varies: the duplication times of "born small" and "born large" protocells are shown. Values on the x-axis show the fraction of lipids inherited by the smaller protocell.
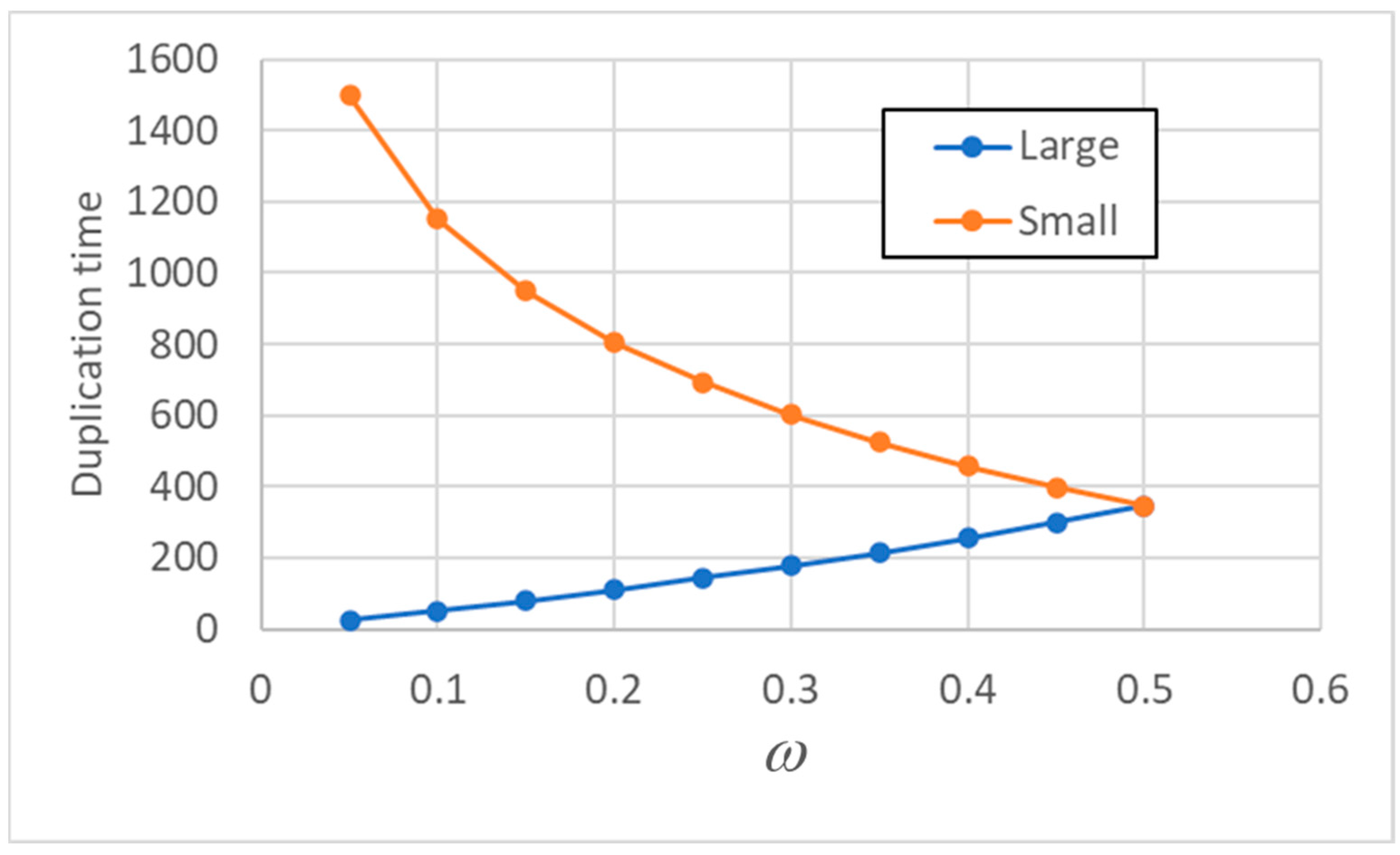
Preprints 97909 g003
Preprints 97909 g004
Figure 4. (a) Distribution of concentration of a linear replicator X at the 75th generation (15,000 duplications in a population of 200 individuals, asymmetrical division, ω=0.4). (b) The same at the 150th generation (30,000 duplications in a population of 200 individuals). (c) The same, computed on two samples of 10 generations, showing that the shape of the distributions is basically constant in time.
Figure 4. (a) Distribution of concentration of a linear replicator X at the 75th generation (15,000 duplications in a population of 200 individuals, asymmetrical division, ω=0.4). (b) The same at the 150th generation (30,000 duplications in a population of 200 individuals). (c) The same, computed on two samples of 10 generations, showing that the shape of the distributions is basically constant in time.
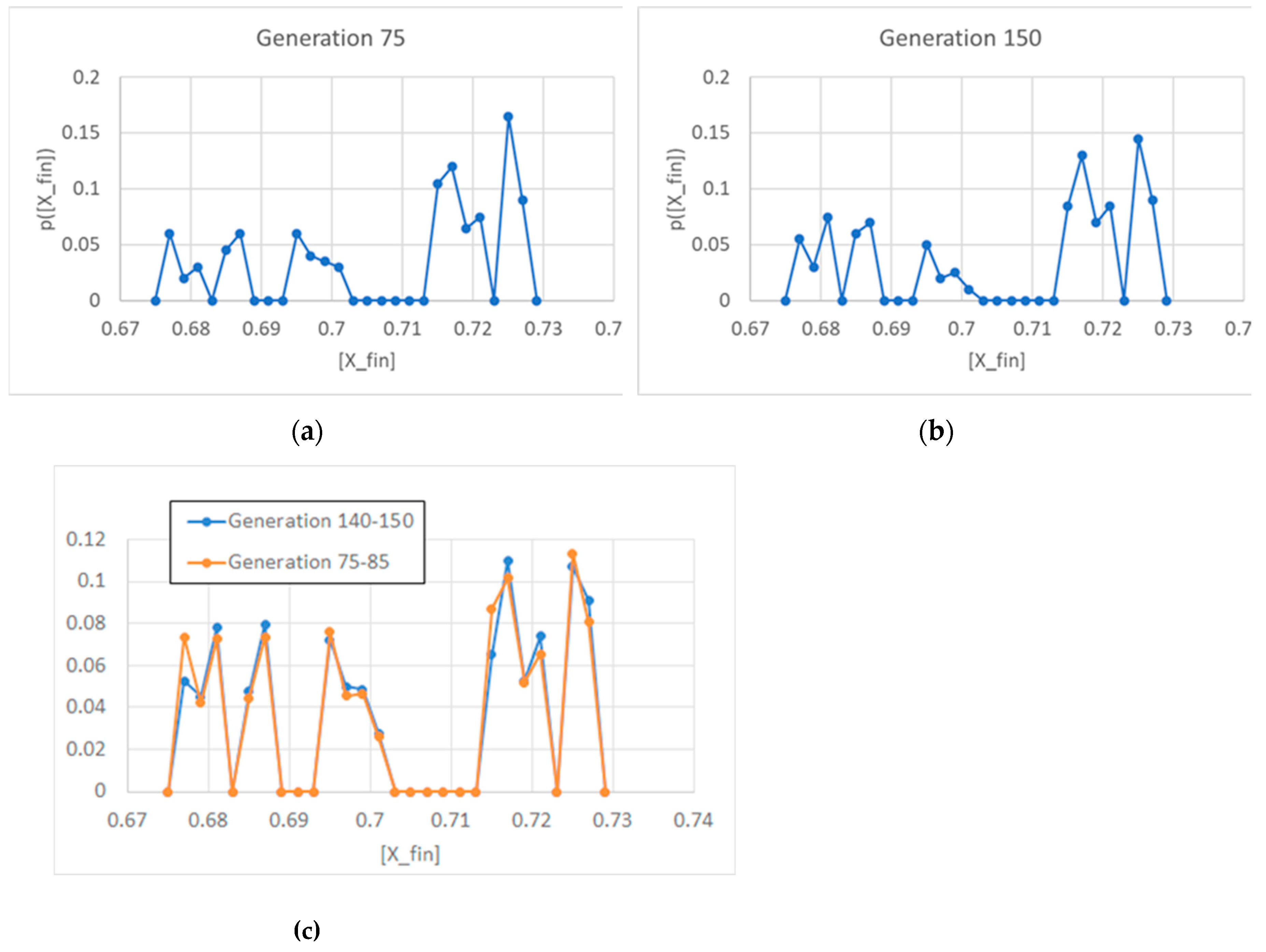
Preprints 97909 g004
Preprints 97909 g005
Figure 5. Duplication time at the 75th generation (15,000 duplications in a population of 200 individuals, asymmetrical division, ω=0.4). We have highlighted in different colors two groups, corresponding to the duplication times of protocells born large (small duplication times) and protocells born small (large duplication times).
Figure 5. Duplication time at the 75th generation (15,000 duplications in a population of 200 individuals, asymmetrical division, ω=0.4). We have highlighted in different colors two groups, corresponding to the duplication times of protocells born large (small duplication times) and protocells born small (large duplication times).
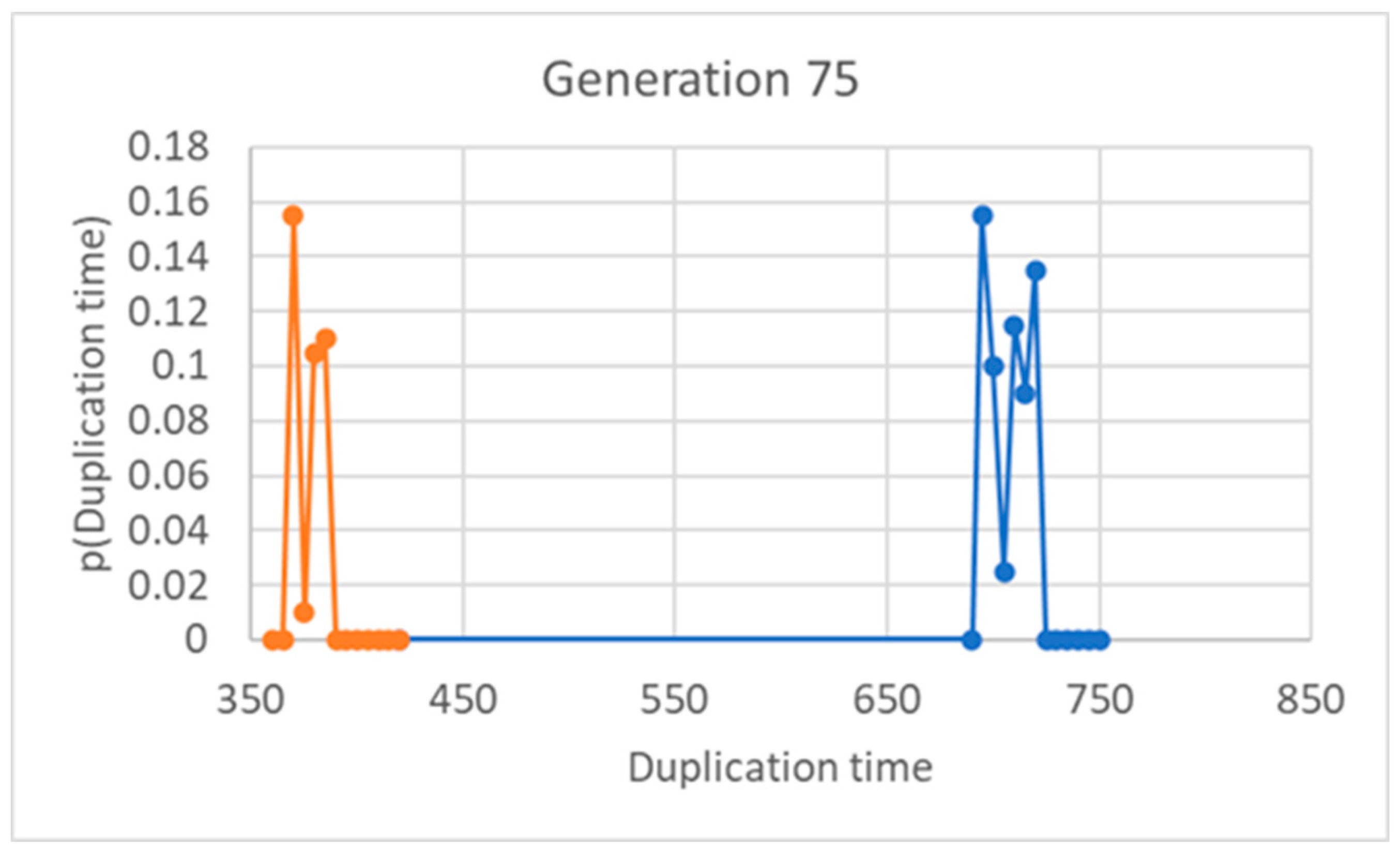
Preprints 97909 g005
Preprints 97909 g006
Figure 6. Number of “small” protocells as asymmetry varies: population of 200 protocells, 75th generation. The fraction of lipids inherited by the smaller descendant (i.e. ω) is shown on the x-axis.
Figure 6. Number of “small” protocells as asymmetry varies: population of 200 protocells, 75th generation. The fraction of lipids inherited by the smaller descendant (i.e. ω) is shown on the x-axis.
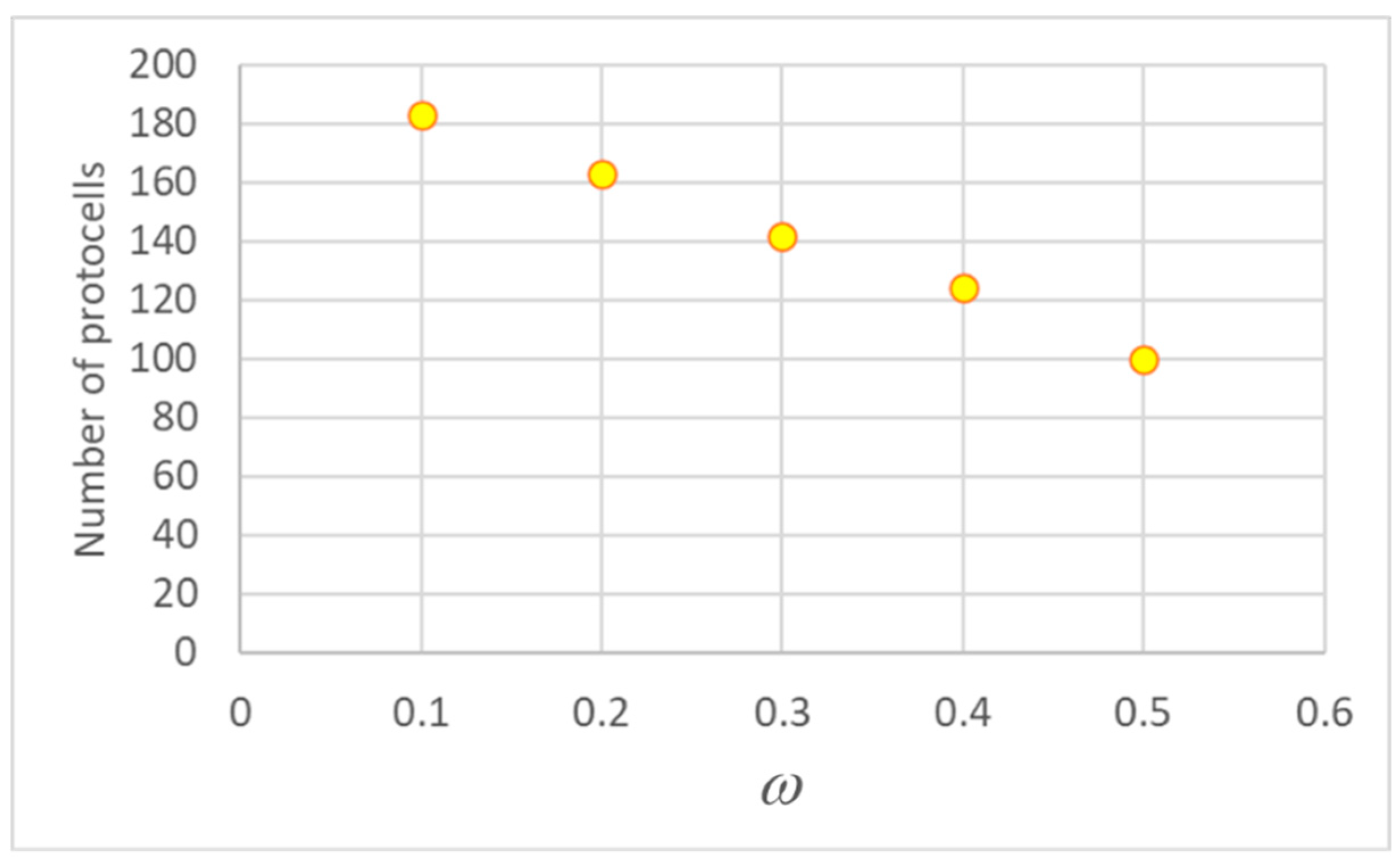
Preprints 97909 g006
Preprints 97909 g007
Figure 7. (a) Final concentration of X across generations, for the pure “large protocells only” and the pure “small protocells only” lineages (in the insert a magnification in linear scale). (b) Final concentration of X across generations of the two pure lineages, and of a lineage in which at each duplication only one randomly chosen protocell was followed. It can be noted that the concentration of protocells belonging to this "mixed" lineage, as the generations vary, varies between the extremes constituted by the concentrations of the "pure" lineage.
Figure 7. (a) Final concentration of X across generations, for the pure “large protocells only” and the pure “small protocells only” lineages (in the insert a magnification in linear scale). (b) Final concentration of X across generations of the two pure lineages, and of a lineage in which at each duplication only one randomly chosen protocell was followed. It can be noted that the concentration of protocells belonging to this "mixed" lineage, as the generations vary, varies between the extremes constituted by the concentrations of the "pure" lineage.
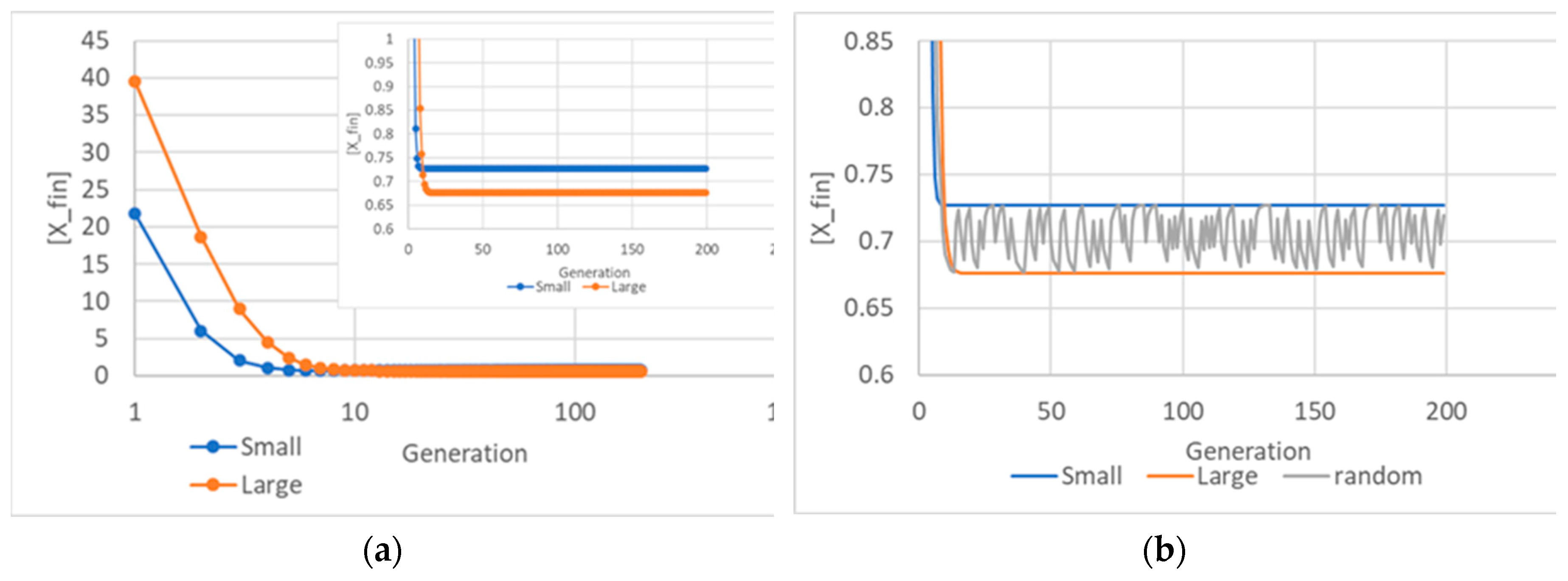
Preprints 97909 g007
Preprints 97909 g008aPreprints 97909 g008b
Figure 8. (a) Distribution of the ratio between the sum of the quantities of X of two "sister" protocells and the quantity of replicator X of the "mother" protocell, at the 75th generation. (b) The same, for the Y replicator. (c) Time trend of the ratio for the X replicator. (d) Time trend of the ratio for the Y replicator. In each protocell in (c) and (d) the ratio between the quantities of replicators is given by the corresponding ratios in the eigenvalue of the system.
Figure 8. (a) Distribution of the ratio between the sum of the quantities of X of two "sister" protocells and the quantity of replicator X of the "mother" protocell, at the 75th generation. (b) The same, for the Y replicator. (c) Time trend of the ratio for the X replicator. (d) Time trend of the ratio for the Y replicator. In each protocell in (c) and (d) the ratio between the quantities of replicators is given by the corresponding ratios in the eigenvalue of the system.
Preprints 97909 g008aPreprints 97909 g008b
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated