Prerpints.org logo
Preprint
Article

TFCD-Net: Target and False Alarm Collaborative Detection Network for Infrared Imagery

This version is not peer-reviewed.

Submitted:

18 January 2024

Posted:

02 February 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
Infrared small target detection (ISTD) plays a crucial role in both civilian and military applications. The detection of small targets against dense cluttered backgrounds remains a challenging task, requiring the collaboration of false alarm source elimination and target detection. Existing approaches primarily focus on modeling targets while often neglecting false alarm sources. To address this limitation, we propose a Target and False Alarm Collaborative Detection Network to leverage the information provided by false alarm sources and the background. Firstly, we introduce a False Alarm Source Estimation Block (FEB) that estimates potential interferences present in the background by extracting features on multiple scales and employing stepwise upsampling for feature fusion. Subsequently, we propose a framework that employs multiple FEBs to eliminate false alarm sources across multiple scales. Finally, a Target Segmentation Block (TSB) is introduced to accurately segment the targets to produce the final detection result. Experiments on public datasets demonstrate that, compared to other methods, our model achieves high accuracy in segmenting targets while being able to extract false alarm sources which can be used for further studies.
Keywords: 
Subject: 
Computer Science and Mathematics  -   Computer Vision and Graphics

1. Introduction

Infrared Searching and Tracking (IRST) systems play a crucial role in contemporary aerospace and military operations, leveraging the emitted or reflected infrared radiation from objects to detect, track, and identify targets [1,2,3,4,5,6]. The capability to discern targets of interest based on their infrared signatures is pivotal in environments where visual detection is impaired or infeasible due to various constraints such as distance, camouflage, or adverse weather conditions [7,8].
The detection of small infrared targets, defined by their limited size—often under 9×9 pixels or constituting less than 0.15% of the field of view—poses a significant challenge in IRST applications [9]. These targets are characterized by their minimal texture and shape information, making them difficult to distinguish from complex backgrounds that include terrain, artificial structures, and clouds [10,11,12,13,14]. These backgrounds often reflect solar radiation that can create false alarms with patterns akin to those of the intended targets, as shown in Figure 1, in which, as the scenes become more complex, an increasing number of false alarm sources appear, resulting in the targets being less salient.
Infrared small target detection algorithms can be broadly categorized into two approaches: multi-frame-based and single-frame-based [15]. Multi-frame-based methods detect targets by exploiting the relative motion between targets and background across frames [16,17,18,19,20,21], assuming a relatively static background and necessitating the accumulation of information over multiple frames to pinpoint the target’s location. However, there is a pressing need for rapid target detection in practical scenes [22]. Moreover, multi-frame approaches can employ single-frame methods to extract candidate targets in each frame [23], making single-frame detection methods a focal point of research in the field of infrared small target detection.
Single-frame detection methods diverge into two categories: non-deep learning and deep learning approaches. The non-deep learning methods encompass background suppression techniques, which seek to isolate the target region by subtracting an estimated background from the input image [24]; target enhancement methods, which employ calculations of local contrast and saliency to search or amplify the target region [25,26,27,28,29,30]; image structure-based methods, which assume a mathematical model of low-rank background and sparse targets within the infrared image, solving for the target region through optimization techniques [31,32,33,34]; and classifier-based methods, which function by extracting potential target regions and their features, and subsequently classifying those features to identify true targets [35,36]. These methods rely on a priori knowledge to model infrared small targets. However, their effectiveness is often compromised in complex scenes where accurately discerning between targets and false alarms becomes problematic.
On the other hand, deep learning-based methods automate feature extraction for targets using deep neural networks (DNN). In this context, detection networks regress target bounding boxes to approximate the location of small targets [37,38], while semantic segmentation networks treat small target detection as a semantic segmentation problem [39,40], performing pixel-level segmentation to accurately delineate the target area. The latter approach is becoming increasingly prevalent in research due to its potential for precise small target region identification [41], heralding a promising direction for future advancements in the domain.
Deep learning-based methods have made remarkable advancements in infrared small target detection in recent years [42,43,44,45,46,47,48]. However, a significant limitation of these methods is their primary focus on modeling targets while often neglecting the modeling of false alarm sources. This oversight becomes particularly critical in real-world infrared small target detection applications, where detecting small targets against densely cluttered backgrounds necessitates the collaborative elimination of false alarm sources and target detection. Moreover, infrared small target detection is a risk-sensitive task that demands interpretability in the employed methods. To address these challenges, we propose the Target and False Alarm Collaborative Detection Network for Infrared Imagery. This network leverages specialized False Alarm Source Estimation Blocks (FEB) to estimate false alarm sources while incorporating a target segment block (TSB) to accurately detect infrared small targets on the false alarm source suppressed result. By combining these two components, the proposed TFCD-Net aims to improve the overall effectiveness and interpretability of infrared small target detection systems.
The major contributions of this research can be summarized as follows:
(1)
We propose a novel framework that synergistically models both targets with TSB and false alarm sources with FEBs. This dual-focus approach is designed to handle the complexities of dense cluttered backgrounds, as well as remaining interpretable.
(2)
We propose a specialized FEB for estimating potential false alarm sources. By incorporating multiple FEBs in the framework, false alarm sources are estimated and eliminated on a multi-scale, block-wise basis. This approach not only improves the accuracy of our method but also facilitates small target detection for other existing techniques.
(3)
Extensive experiments on public datasets validated the effectiveness of our model compared to other state-of-the-art approaches. Alongside the accurate detection of targets, our model stands out with its ability to produce multi-scale false alarm source estimation results. These estimations are not merely byproducts but are valuable datasets in their own right, offering rich material for further research and development in the field.
The remainder of this paper is structured as follows: Section 2 delineates the proposed TFCD-Net, starting with an exploration of related works, then a detailed description of FEB, the overall framework, and the loss function. Section 3 reports on the experimental validation, including setup, ablation studies, and comparative analysis. Section 4 concludes with a summary of our findings and implications for future work.

2. Related Works

In recent years, infrared small target detection in the presence of dense clutter has emerged as a significant challenge in the field of image processing and computer vision. Traditional detection methods [49,50] often represent infrared images using Equation (1):
f D ( x , y ) = f T ( x , y ) + f B ( x , y ) + f N ( x , y ) ,
where f D , f T , f B , f N and ( x , y ) denote the original image, the target image, the background image, the noise, and the pixel location, respectively. This representation suggests that an infrared image can be expressed as a superimposition of three components: the target image, the background image, and the noise image.
Traditional non-deep learning methods for infrared small target detection, such as the Top-Hat algorithm [51,52], focus on background suppression. These algorithms typically employ morphological operations like opening to remove smaller objects and estimate the background. The target response is then obtained by subtracting the estimated background from the original image. This approach subdivides target detection into background suppression and target segmentation.
In methods based on image structure, it is commonly assumed that the background of an infrared image is low-rank and the small target is sparse [53,54,55]. Through the establishment of constraint equations for the background and target, mathematical optimization methods are exploited to separate the image into these two components.
These techniques not only detect small targets but also consider background information. This allows for adaptation to different scenes in infrared imaging by modeling the background and enables the retrieval of targets that were mistakenly classified as background through subsequent methods.
Inspired by these approaches, we employ a multi-stage neural network to mimic the process of separating the background from the targets in infrared images. Our method initiates with background suppression followed by target segmentation, effectively detecting small infrared targets. This design focuses on background clutter and noise, which not only improves detection performance but also endows the network with a certain level of interpretability.

3. Proposed Method

3.1. False Alarm Source Estimation Block

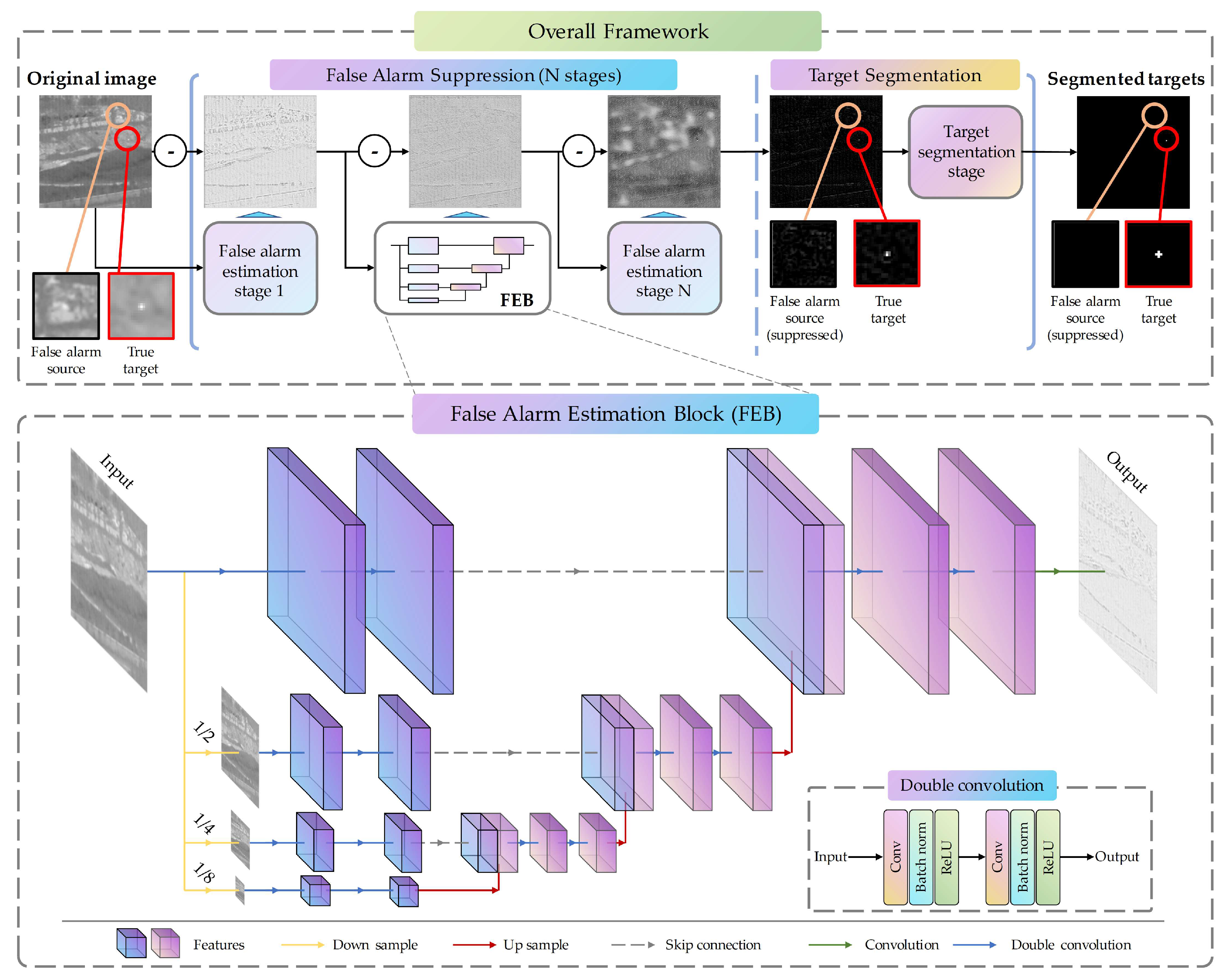
The False Alarm Source Estimation Block (FEB) is an integral component of the proposed TFCD-Net framework, designed to accurately estimate the background and noise components, which are the primary sources of false alarms. As delineated in Equation (1), the estimation of these false alarm sources effectively involves the subtraction of the target component from the background. Given the small size of infrared small targets, this estimation process is comparable to an image denoising network that specifically targets the removal of small objects from the image.
Typically, denoising networks employ stacked convolutional layers or UNet-like multiscale encoder-decoder architectures [56,57]. The multiscale structures are particularly beneficial as they capture a broader range of background patterns, thereby facilitating a more comprehensive estimation. To this end, we propose a multiscale architecture for modeling false alarm sources, as depicted in the lower part of Figure 2.
Within the FEB, the original image is first downsampled by 1 / 2 , 1 / 4 , and 1 / 8 , resulting in a total of 4 scales of input images as follows.
O pool , k = MaxPool 2 ( k − 1 ) I FEB ,
where O pool , k is the downsampled image of the k-th scale, k = 2 , 3 , … , n . I FEB is the input of FEB. MaxPool 2 ( k − 1 ) performs max pooling of factor 2 ( k − 1 ) .
Subsequently, two double convolution operations are performed on each scale, forming the encoder component of the network. The double convolution block is depicted in the bottom-right corner in Figure 2, consisting of two sets of convolutional layers, batch normalization layers, and ReLU activations. The formula is as follows:
O dc = ReLU BN Conv 3 × 3 ReLU BN Conv 3 × 3 ( I dc ) ,
where O d c and I d c are the output and input of the double convolution block.
The decoder component of the network uses a UNet-like decoder structure for progressive upsampling and feature fusion: for each scale, upsampling by a factor of 2 is initially performed, followed by feature concatenation with the previous level. The formula is as follows:
I de = O k ⊕ Up 2 × bilinear ( O k + 1 ) ,
where O k and O k + 1 are the k and (k+1)-th scale, k = 1 , 2 , … , n − 1 . ⊕ represents the concatenation operation. Up 2 × bilinear indicates bilinear upsampling by a factor of 2.
The concatenated feature is then forwarded through two double-convolution operations. This upward feature fusion continues until the original image size is reached, and the output image is obtained through a single convolution operation. The block uses max-pooling for downsampling, bilateral filter for upsampling, and 3 × 3 sized 64-channel convolution kernels for all double convolution operations, except for the input and output, resulting in a single-channel feature map. There is no activation function used after the final convolution layer, for activations between blocks are placed in false alarm subtraction as in Equation (6), which will be describe in the following subsection.

3.2. Overall Framework

The overall framework of the proposed TFCD-Net is depicted in the upper section of Figure 2. It is designed to suppress false alarm sources in a multi-stage process before segmenting the target, which is critical for eliminating potential interferences. 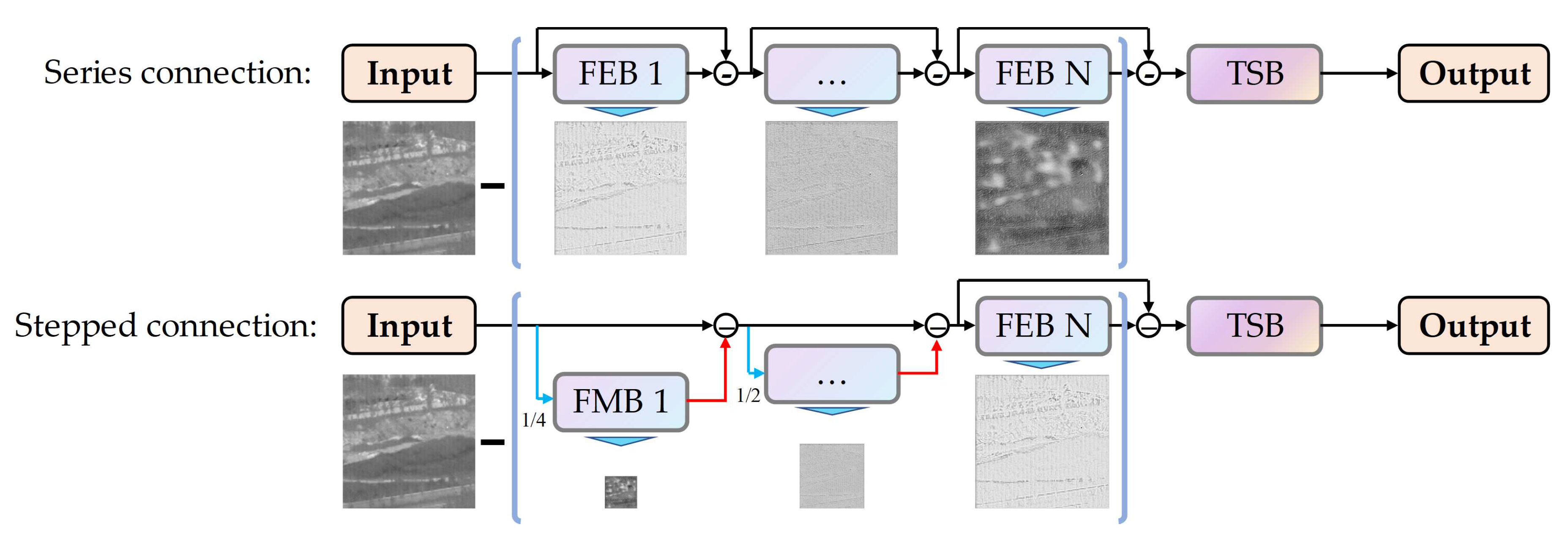This suppression is achieved through the implementation of multiple False Alarm Source Estimation Blocks (FEBs), each functioning as a residual block [58] where the input is subtracted by its output, serving as the input for the subsequent blocks. Although the number of these suppression stages can be varied, practical tests have shown that 2 to 3 stages are usually sufficient to meet the requirements of subsequent high-performance target segmentation, a series connection configuration of the blocks is illustrated in the upper section of Figure 3.
To accommodate larger image sizes and infrared small targets of greater areas, we explored an alternative multi-scale, multi-stage structure. An example is depicted in the lower section of Figure 3, three FEBs operate at different scales: 1/4, 1/2, and the original scale. The formula of this configuration is as follows:
O FEB k = Up 2 ( n − k ) × bilinear FEB MaxPool 2 ( n − k ) ( I FEB k ) ,
where Up x bilinear is factor x bilinear upsampling, MaxPool x is factor x max pooling, k = 1 , 2 , … , n − 1 , n is the number of FEBs. This design strategy is aimed at enabling the network to suppress false alarms progressively from coarse to fine levels. In this framework, the output of each FEB is upsampled back to the original scale before it is subtracted by the output of the previous stage, ensuring that no original image information is lost during the downsampling process.
The role of the FEB is to suppress false alarm sources to a certain extent, and it does not precisely extract the shape of the target. To accurately segregate the target from the original image, which has had false alarm sources mitigated, a semantic segmentation network is employed as the segmentation head. While there are various choices for the segmentation head, we utilize the same architecture as FEB for the TSB, but the output of the block is processed through a Sigmoid activation function to ensure pixel output values are confined between 0 and 1. Unlike the TSB outputs, FEBs do not restrict their outputs with an activation function. Instead, false alarm subtraction is performed using a ReLU activation function to constrain negative values. The overall process is shown in Equation (6):
O 1 = ReLU FEB 1 I 1 O k = ReLU O k − 1 − FEB k O k − 1 , k = 2 , 3 , … , n O final = Sigmoid O n − TSB O n
where I 1 is the original image, O k is the output of the k-th stage, FEB k is the k-th FEB with aforementioned downsampling and upsampling if in stepped connection as in Equation (5), O final is the final target segmentation result.

3.3. Loss Function

In the field of infrared small target detection, the commonly used loss function is the soft Intersection over Union (IoU) loss function [59], which is a loss function based on IoU. IoU is a common evaluation metric for image segmentation tasks, used to measure the overlap between predicted and ground truth segmentations, defined as the ratio of the intersection of the prediction and the ground truth to their union. However, since IoU is non-differentiable, it is hard to use directly as a loss function in the training process of deep learning models. Instead, a variant of IoU, the soft IoU, is used to design the loss function. Soft IoU is a differentiable approximation of IoU and is defined in Equation (7):
L S I ( P , Y ) = 1 − ∑ i = 1 N P i · Y i + ε ∑ i = 1 N P i + ∑ i = 1 N Y i − ∑ i = 1 N P i · Y i + ε ,
where P and Y respectively denote the predicted output of the network and the ground truth, ε represents the smoothing factor, and N indicates the total number of samples. The incorporation of the smoothing factor is a common strategy to prevent the denominator of the loss function, which includes division, from becoming zero. To ensure that the inclusion of the smoothing factor does not significantly affect the actual loss value, ε is typically chosen to be very small.
The soft IoU loss function has several advantages in infrared small target segmentation. Due to the nature of IoU computation, a loss based on IoU independently calculates the loss function for each pixel, compared to mean squared error (MSE) and cross-entropy (CE) losses, and considers the spatial arrangement of pixels, placing greater emphasis on accurately locating targets. Additionally, in infrared small target segmentation tasks, the number of background class pixels far exceeds that of target class pixels, leading to class imbalance. IoU-based calculations directly reduce the impact of imbalance and can improve network IoU performance.
However, in practical applications, the soft IoU loss function also has limitations, such as the maximizing of the IoU may not necessarily result in clear edges. To address unclear edges, a weighted binary cross-entropy (WBCE) loss function designed for single-class small target segmentation is formulated as in Equation (8):
L W B C E ( P , Y , W ) = − 1 N ∑ i = 1 N W i [ Y i · log ( P i ) + ( 1 − Y i ) · log ( 1 − P i ) ] ,
where P and Y respectively denote the predicted output of the network and the ground truth, W represents the weight map, and N indicates the total number of samples. The weights W are applied on a per-pixel basis to the Binary Cross-Entropy (BCE) loss, an approach that serves to emphasize specific regions. The weights are designed as Equation (9):
W = D ( C ( Y ) , E ) ,
where C represents the Canny edge detection operator, D denotes the morphological dilation operation, and E is a square structural element measuring 2 × 2 .
The total loss function of this method is as given in Equation (10):
L ( P , Y , W ) = L S I ( P , Y ) + α L W B C E ( P , Y , W ) ,
where α is the weight coefficient.
The idea behind the loss function design is to use the soft IoU function as the core and improve the performance of the loss function through edge loss to achieve stable segmentation of small targets.

4. Experiments

4.1. Settings

In the experiments, two public datasets were utilized: the NUAA-SIRST dataset [39] and the NUDT-SIRST dataset [47]. The NUAA-SIRST dataset comprises 427 images, while the NUDT-SIRST dataset contains 1327 training images. These images encompass a variety of typical infrared scenes, including clouds, sea surfaces, urban environments, and ground scenes, relevant for both terrestrial and aerial infrared detection tasks. The resolution of all images in the datasets is 256 × 256 pixels. The datasets were divided evenly into training and testing sets, with a split ratio of 50%.
The performance of the algorithms and networks was assessed using several evaluation metrics. The probability of detection ( P d ), false alarm rate ( F a ), intersection over union ( I o U ) and Receiver Operation Characteristics (ROC) were the key metrics adopted for evaluation. The definitions of these metrics are as follows.
Probability of detection ( P d ): Measures the ability of detecting true targets on target level. Defined as the ratio of the number of correctly detected targets over true targets as follows:
P d = T c o r r e c t T A l l ,
where T c o r r e c t is the number of correctly detected targets, and T A l l is the number of true targets. Higher score indicates better detection capability.
False alarm rate ( F a ): Measures the rate of falsely detected pixels on pixel level. Defined as the ratio of false positive pixels over all pixels as follows:
F a = P f a l s e P A l l ,
where P f a l s e is the number of falsely detected pixels, and P A l l is the number of all pixels. Lower score indicates fewer false positive detection.
Intersection over union ( I o U ): Measures the accuracy of detection on pixel level. Defined as the area of overlap between the predicted and the ground truth targets divided by the area of the union of them as follows:
I o U = A I A U ,
where A I is the area of intersection, and A U is the area of union. Higher score indicates higher accuracy segmenting the targets.
Receiver Operation Characteristics (ROC): Measures the robustness of detection. Demonstrates as the curve of false positive rate (FPR) to true positive rate (TPR). Higher area under the curve (AUC) indicates better robustness.
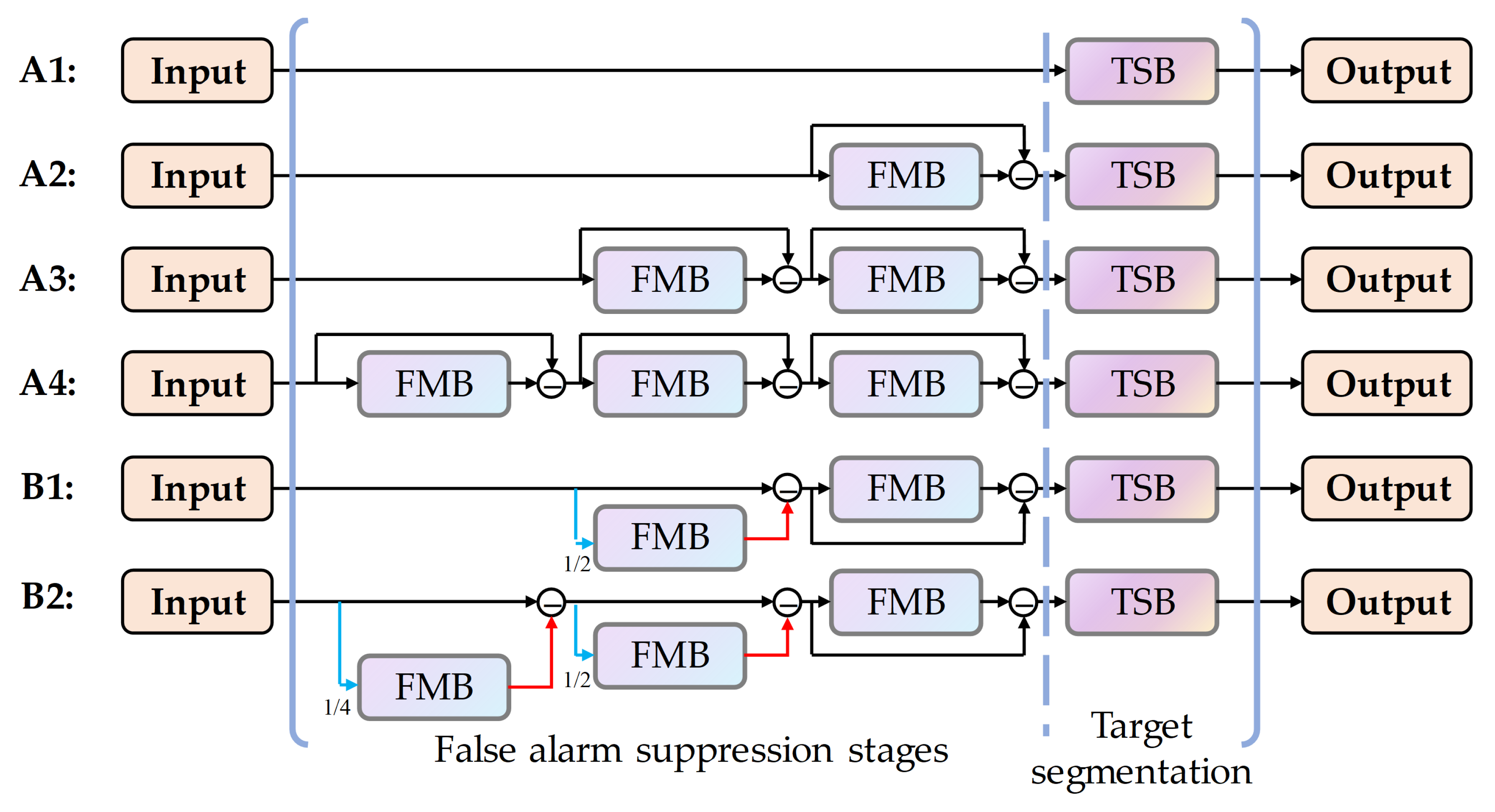
For the model setup, the network structures displayed in Figure 6 were employed in ablation study, structure A3 in Figure 6 was employed in comparative experiments. Regarding the loss function, the coefficient α was set to 0 during the initial 50 training epochs and was adjusted to 0.2 thereafter. The optimization algorithm used was Adaptive Moment Estimation (ADAM). The initial learning rate was set at 0.001 and scheduled to decay by a factor of 0.1 every 50 epochs. The training regimen spanned 200 epochs with a batch size of 8.
Illustrative samples from the datasets are showcased in Figure 4 and Figure 5, providing visual context to the types of infrared images used in the experiments.

4.2. Ablation Experiments

Initially, the overall framework of the network was subjected to ablation testing, involving six different structural configurations as demonstrated in Figure 6. Within these figures, Type-A networks are represented in a serial connection, composed of 0, 1, 2, or 3 FEBs coupled with a single TSB. Type-B networks feature a stair-step connection consisting of either 2 or 3 FEBs and a single TSB. The intent behind these experiments was to identify the optimal number of stages for background suppression and to examine the effectiveness of the stair-step connection approach.
The six aforementioned network structures were trained and tested on two distinct datasets: NUAA-SIRST and NUDT-SIRST. The outcomes of these trials are presented in Table 1.
The results outlined in Table 1 indicate that employing a stair-step connection (Type-B networks) does not enhance network performance. Contrarily, an increase in the number of stages correlated with a decline in performance metrics, a trend that was particularly pronounced with the NUDT-SIRST dataset. This dataset typically features smaller targets, and it is hypothesized that the Type-B network’s upsampling and downsampling procedures might introduce disturbances to the edge characteristics of these targets.
Conversely, for Type-A networks, the inclusion of two FEBs yielded optimal performance. Further expansion of block quantity did not translate to improvements in network capability. Consequently, the network structure A3 was selected for comparative testing in this chapter based on these findings.

4.3. False Alarm Source Estimation Capability

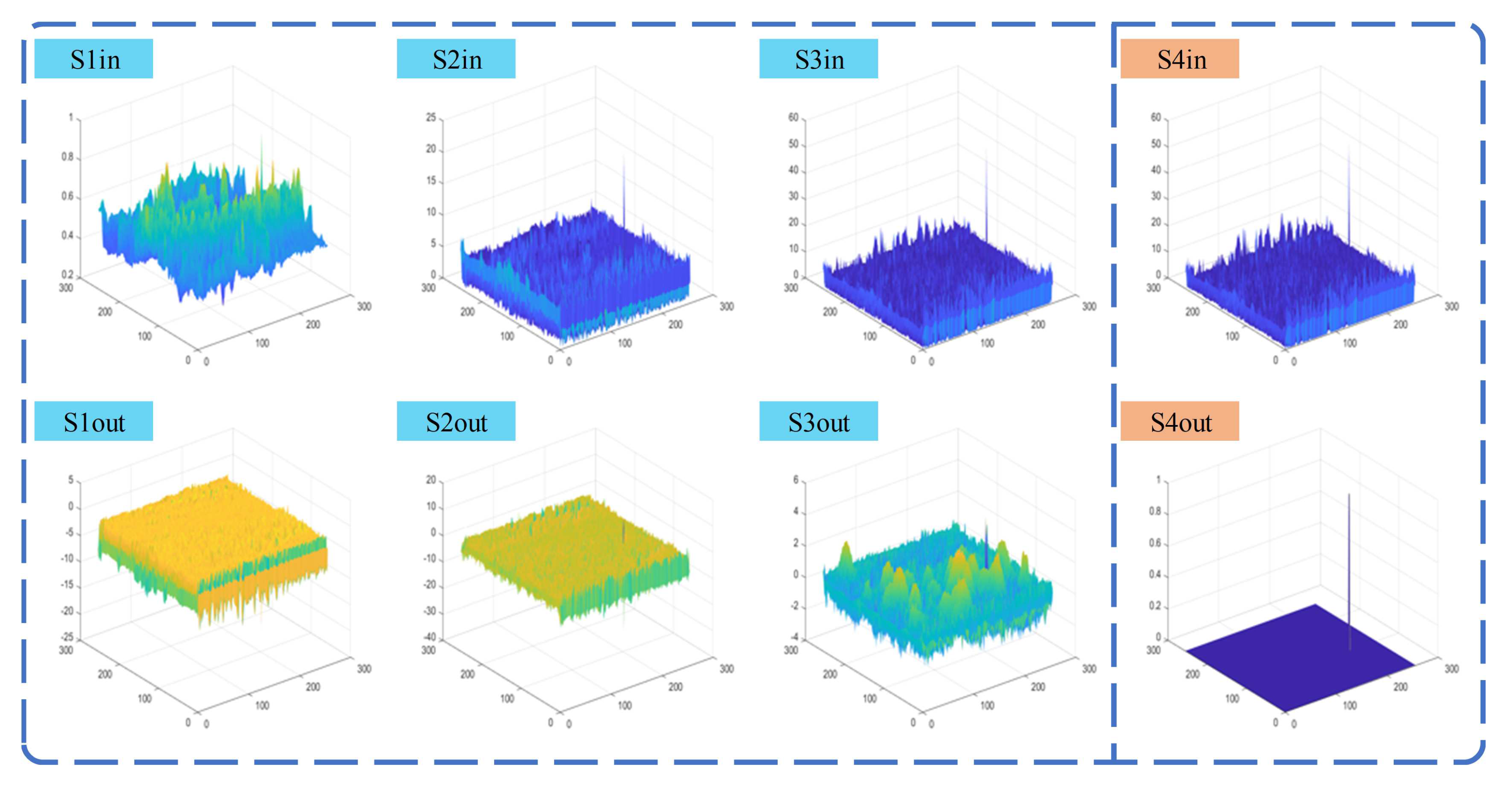
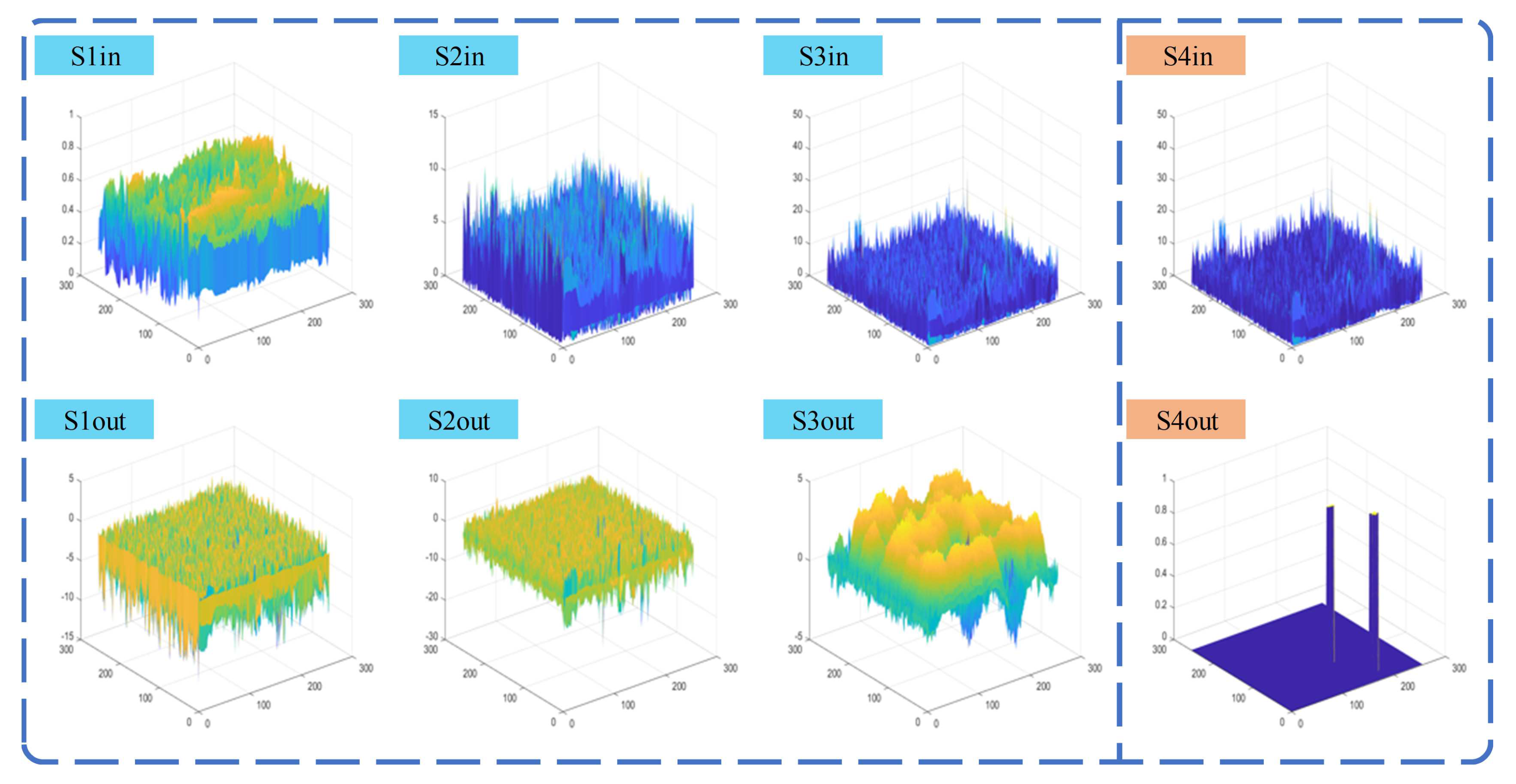
A series of ablation experiments were conducted to validate the false alarm source estimation capabilities of the proposed model. For an in-depth analysis, the A4 structure was chosen due to its comprehensive and intuitive stage-wise presentation. The model’s input and output at eight different stages, as illustrated in Figure 7, were examined. These stages include the network input, equivalent to the original image (S1in), and the network output (S4out).
The experiments were performed on multiple scenes, with results depicted in Figure 8, Figure 9, Figure 10 and Figure 11. Figure 8 and Figure 10 exhibit two dense clutter scenes selected from the NUDT-SIRST dataset. In these figures, the first row demonstrates the inputs at each stage, while the second row shows the corresponding outputs, with red circles indicating the regions of interest, i.e., the targets. The 3D schematic diagrams of these scenes are respectively presented in Figure 9 and Figure 11.
Analyzing Figure 8 and Figure 10, it is evident that the false alarm sources are progressively suppressed from S1in to S4in; meanwhile, the target regions are preserved. This is manifested by the gradual dimming of non-target edge areas, making the target more prominent and easier for the final TSB to process. Outputs from S1out to S3out correspond to outputs from the FEB. It was observed that the suppression of false alarm sources progresses from fine to coarse and from high frequency to low frequency. This indicates that each stage of the network estimates and suppresses the most prominent non-target edge areas. By the S3 stage, as most high-frequency areas are already suppressed, the FEB begins estimating the low-frequency fluctuations of the background. It is crucial to note that the FEBs do not suppress the target area at any stage, as evidenced by S1out, S2out, and S3out, ensuring that the target is preserved and becomes increasingly prominent. This characteristic is particularly apparent in the S2in, S3in, and S4in schematic illustrations of Figure 9.
In summary, the testing of the network with the A4 structure confirmed that each FEB could correctly estimate false alarm sources as anticipated. Through the subtraction process defined by Equation (6), the model effectively suppresses false alarm sources in a stage-wise manner. Consequently, false alarm sources are diminished, targets are preserved, and correct segmentation is achieved by the final TSB.

4.4. Comparative Experiments

The proposed TFCD-Net was evaluated through a series of experiments and compared against nine contemporary algorithms. The competing methods encompass optimization-based approaches such as NRAM [53], PSTNN [54], and SRWS [55], as well as DNN models including ACM [39], ALCNet [46], RDIAN [42], UNet [60], ISTDUNet [48], and DNANet [47].
For the non-DNN methods, the original parameters from their respective publications were employed. The DNN models were trained using the ADAM optimizer with a batch size of 8, an initial learning rate of 0.001 for 200 epochs, and a learning rate decay by a factor of 0.1 every 50 epochs. Soft IoU loss was used for training the comparative DNN models.
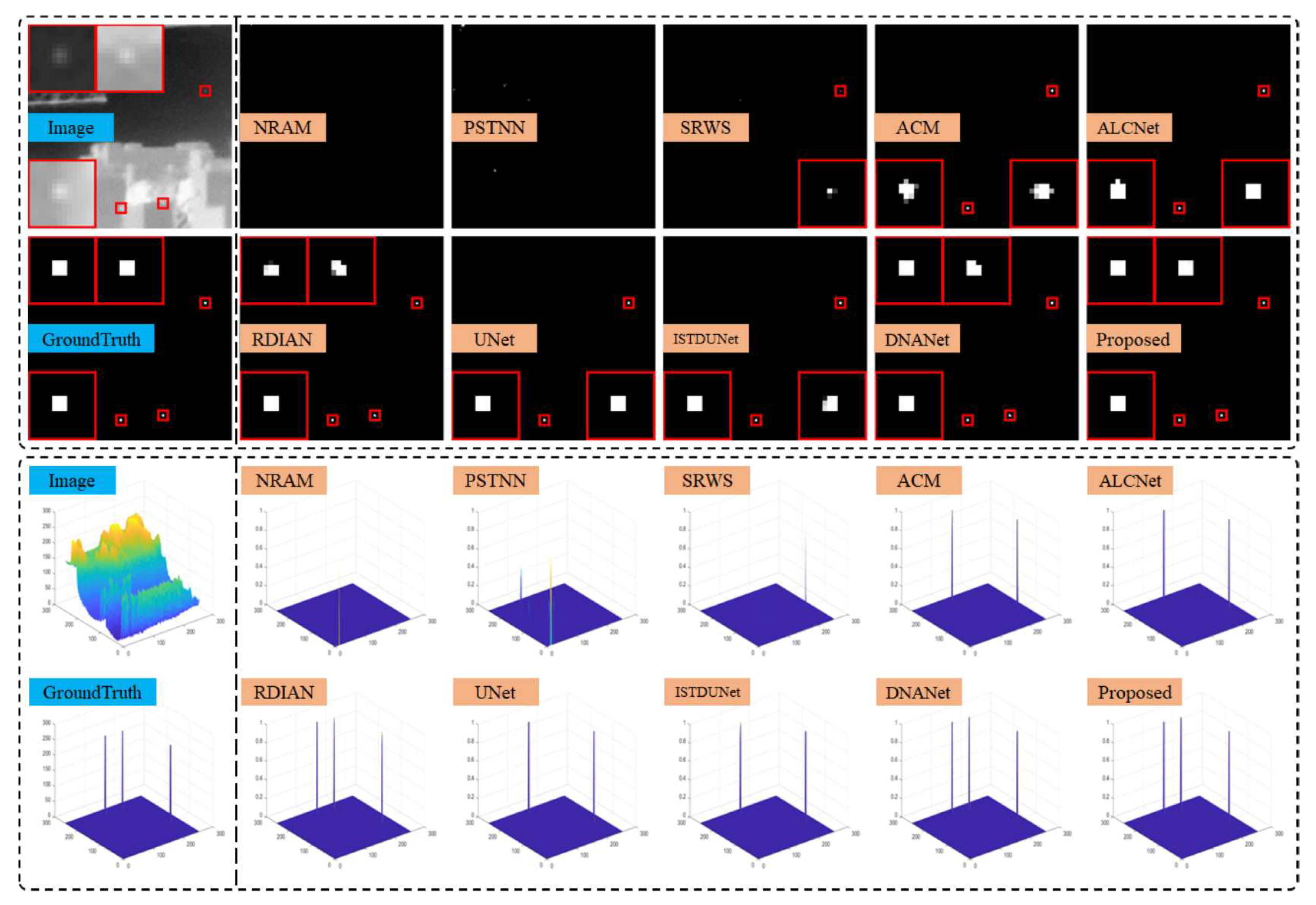
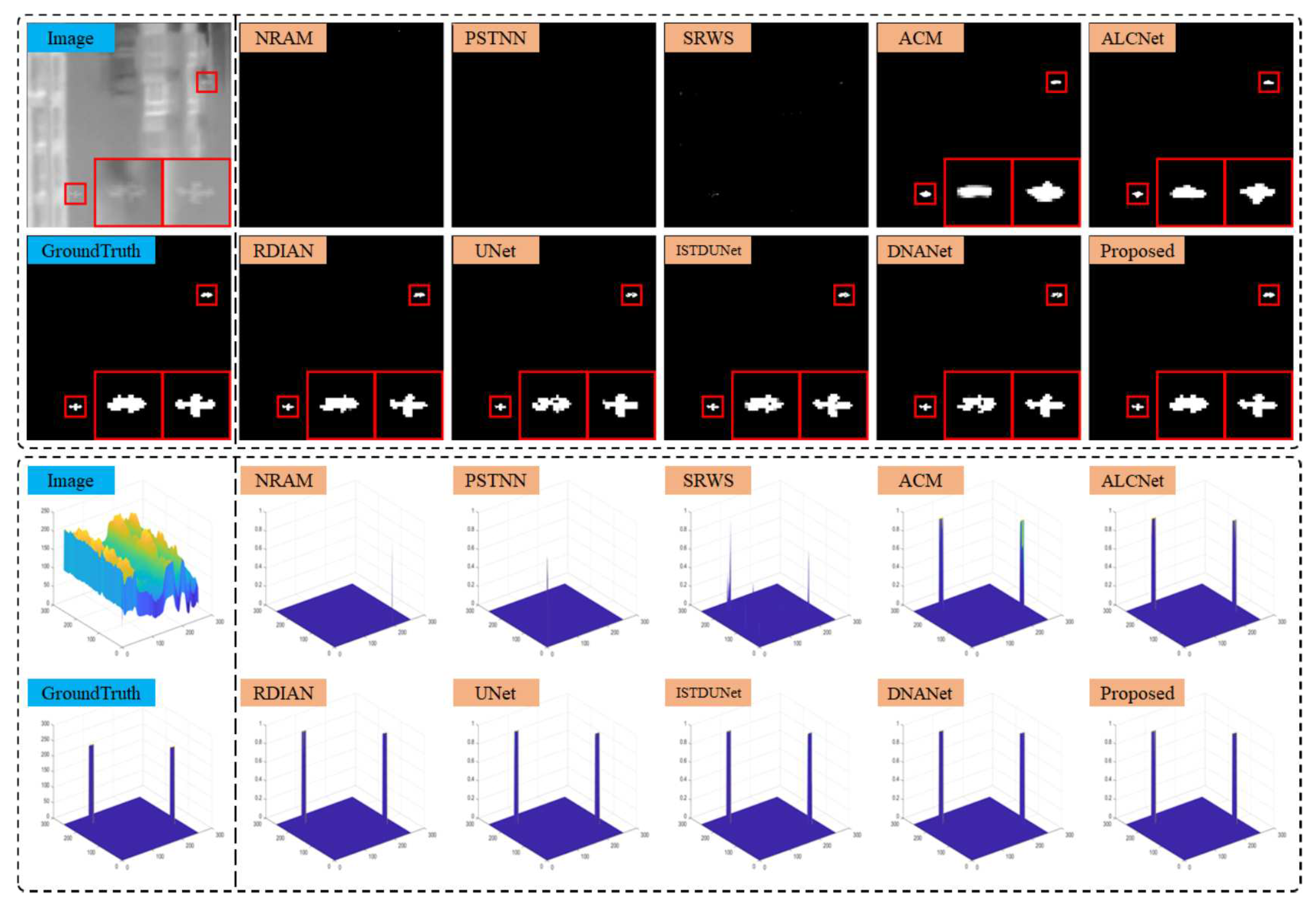
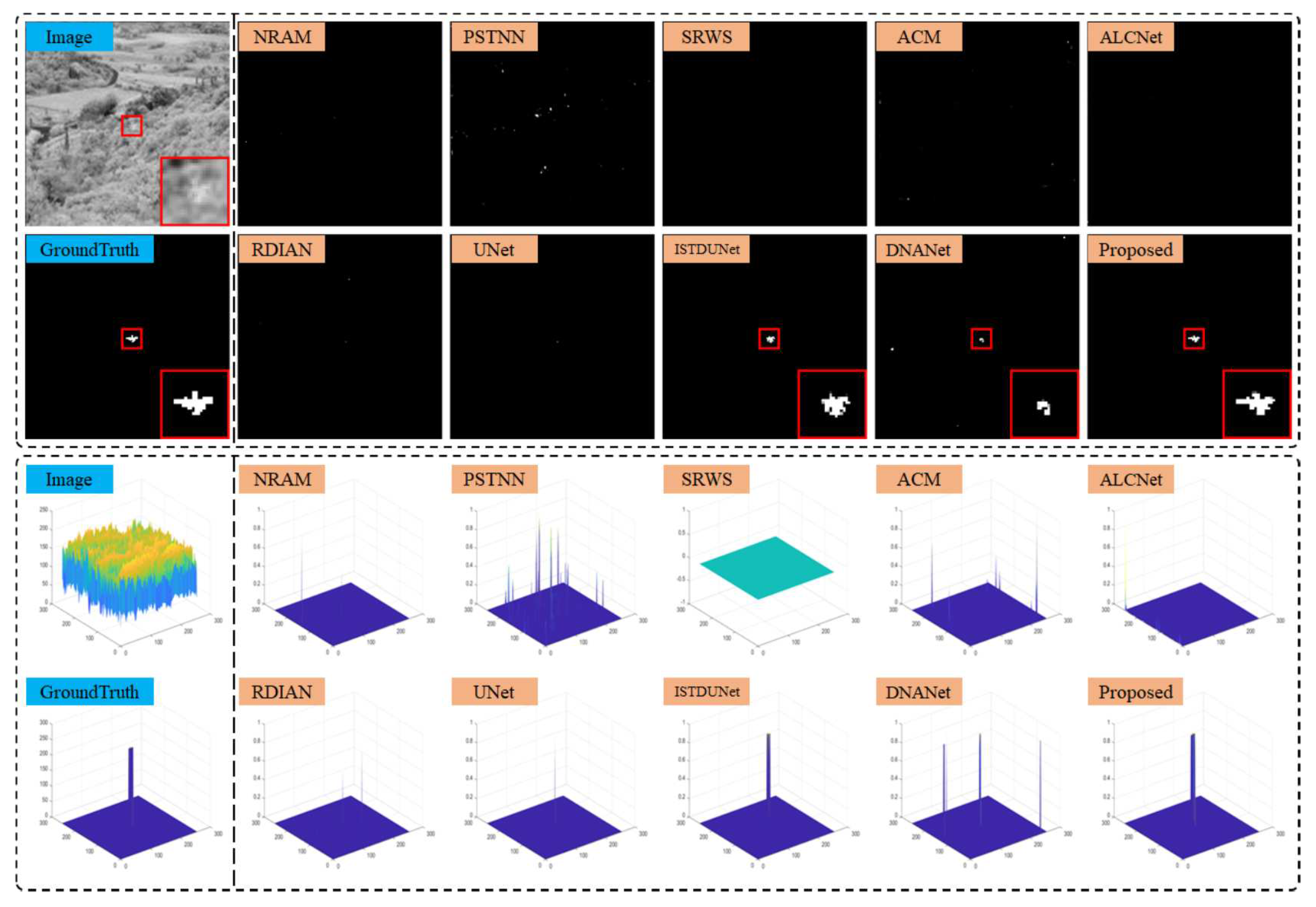
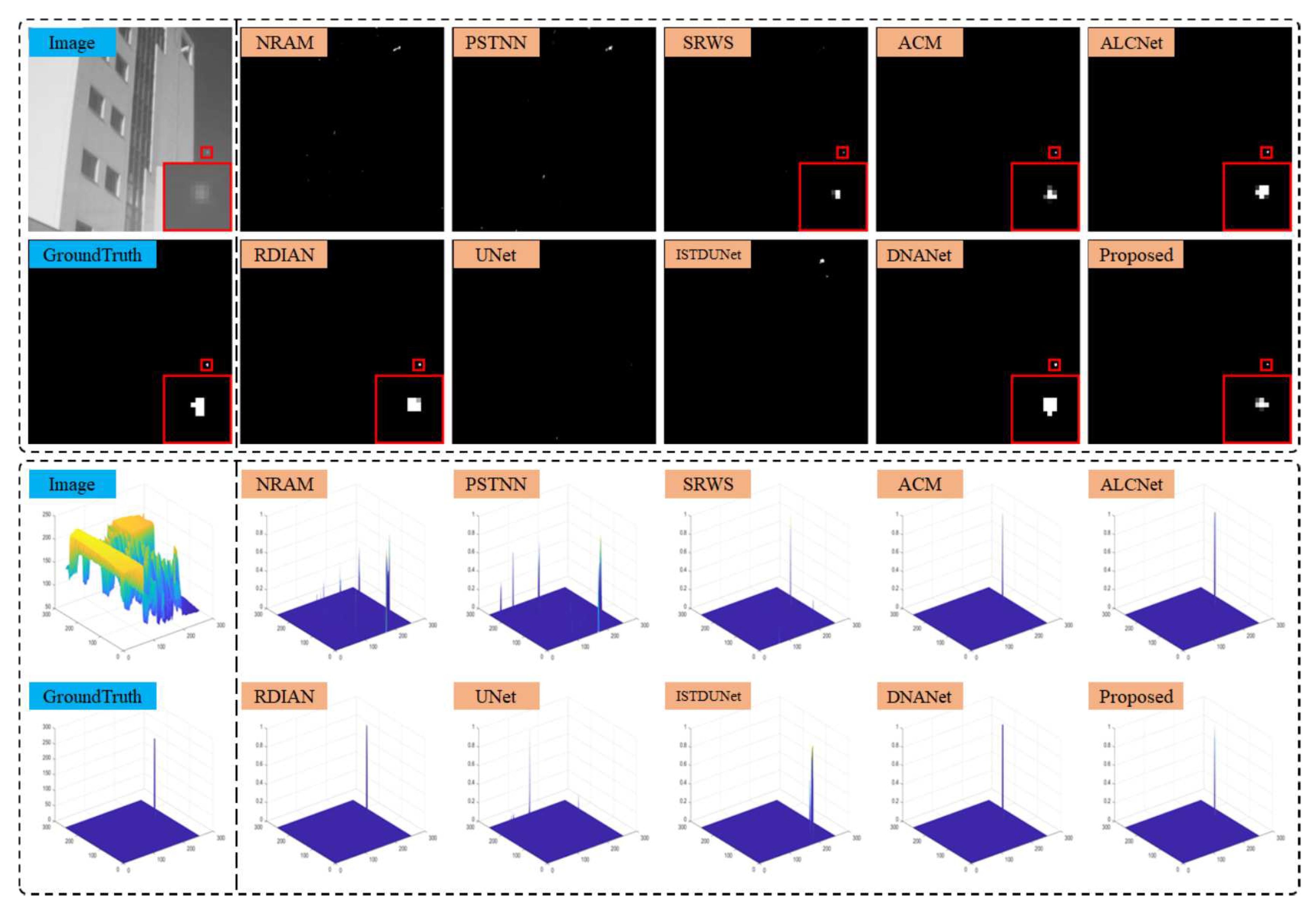
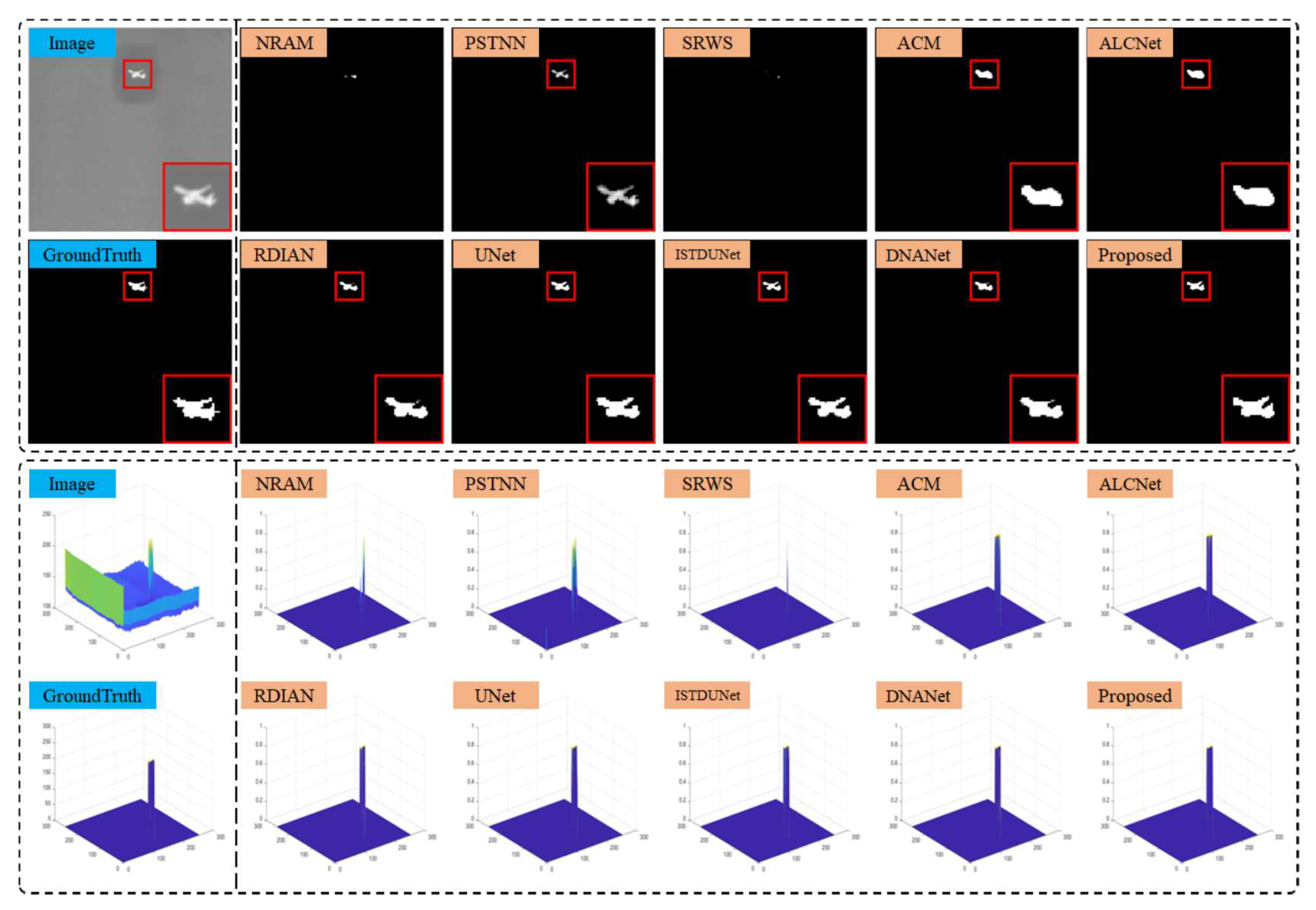
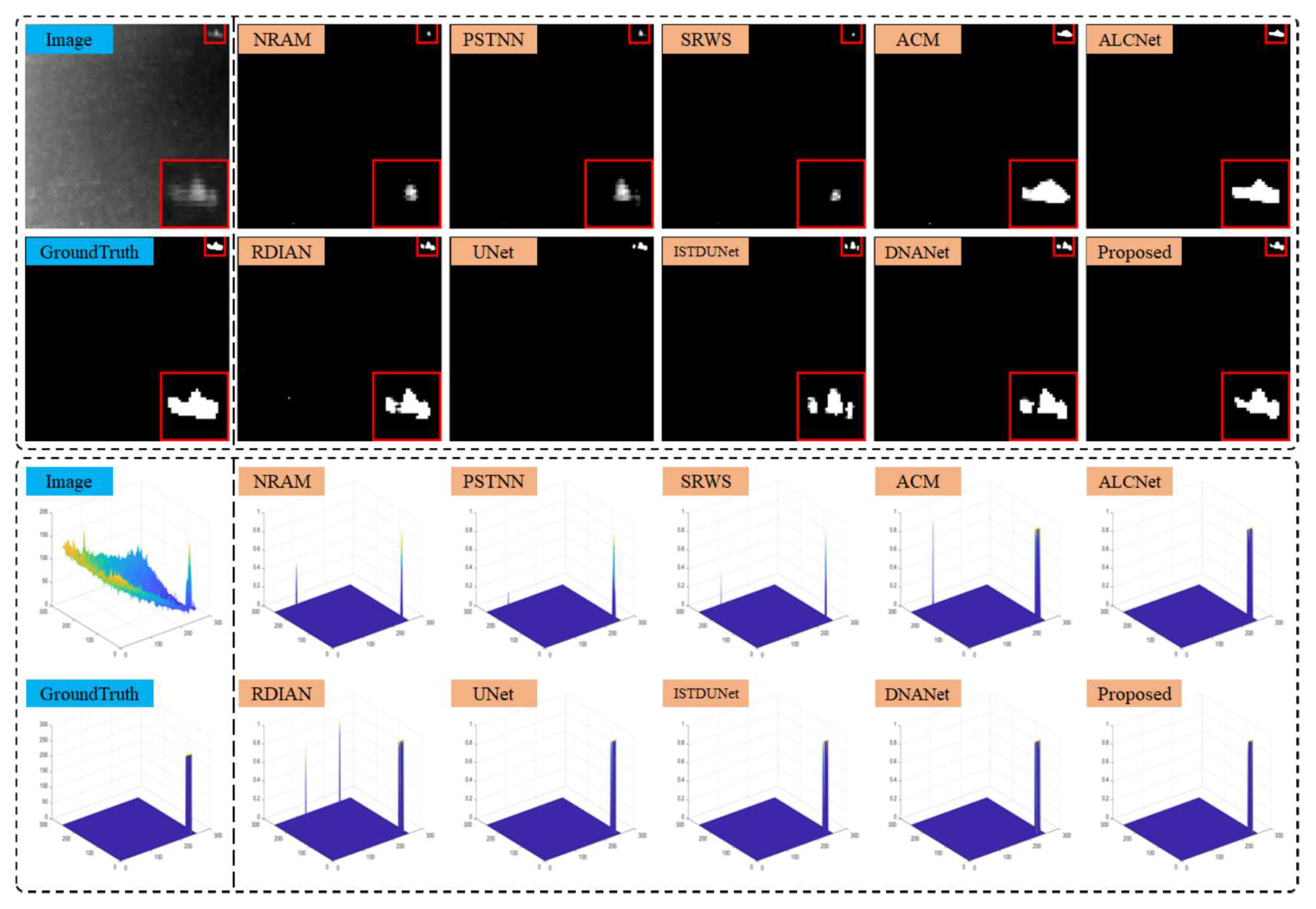
The performance of the proposed TFCD-Net and the comparison methods was demonstrated on six representative scenes from NUAA-SIRST and NUDT-SIRST datasets. The output results and 3D visualizations for these scenes are depicted in Figure 12 to Figure 17. It was observed that in scenes 1 to 5, the three non-DNN methods failed to detect some targets, highlighting the insufficient stability of model-driven approaches in complex environments. This was particularly evident when the assumptions of sparsity for targets and low rank for backgrounds were violated, such as in cluttered scenes and scenes with larger targets. Figure 14 showcases a complex scene where most comparison algorithms failed to detect the target. While the ISTDUNet and DNANet models detected the target, they lacked precision in segmentation. However, the proposed model was capable of accurately segmenting the target. In Figure 16, larger targets posed a challenge for models like ACM and ALCNet, which produced imprecise contours and thus could not discern target details. In Figure 17, RDIAN, UNet, ISTDUNet, and DNANet segmented the single target into multiple parts, potentially affecting precise localization and subsequent identification in practical applications; for instance, UNet’s detection was more than three pixels away from the true center of the target, which is significant given the small size of the targets. The proposed TFCD-Net performed well across all six scenes, especially on the more complex NUDT-SIRST dataset, as shown in Figure 12 to Figure 14.
For a quantitative assessment, Table 2 and Table 3 present the comparative test results of the proposed TFCD-Net and other methods on the NUAA-SIRST and NUDT-SIRST datasets, respectively.
From Table 2 and Table 3, we observe that for P d value, the proposed TFCD-Net achieved the highest on the NUDT-SIRST dataset, and the second-best on the NUAA-SIRST dataset, comparable to the performance of DNANet, confirming its effectiveness in detecting small targets alongside the leading algorithms.
For the I o U score, the model achieved the highest on the NUDT-SIRST dataset, and reached the second-best I o U score, trailing behind the RDIAN model which demonstrates a slightly more precise target segmentation in that particular case. The RDIAN model, with its MPCM-inspired convolutional kernel design, showed limited generalizability on the NUDT-SIRST dataset where the proposed TFCD-Net maintains its strong performance.
Regarding the F a metric, the proposed TFCD-Net outperformed all other DNN approaches on both datasets, demonstrating its superior capability in suppressing false alarms. It is important to note that the SRWS algorithm, while not a DNN-based approach, showed a significantly lower F a score, which may be attributed to its lower I o U and P d values, suggesting a tendency to output smaller target-responsive areas, which can be also inferred from results in Figure 12 to Figure 17.
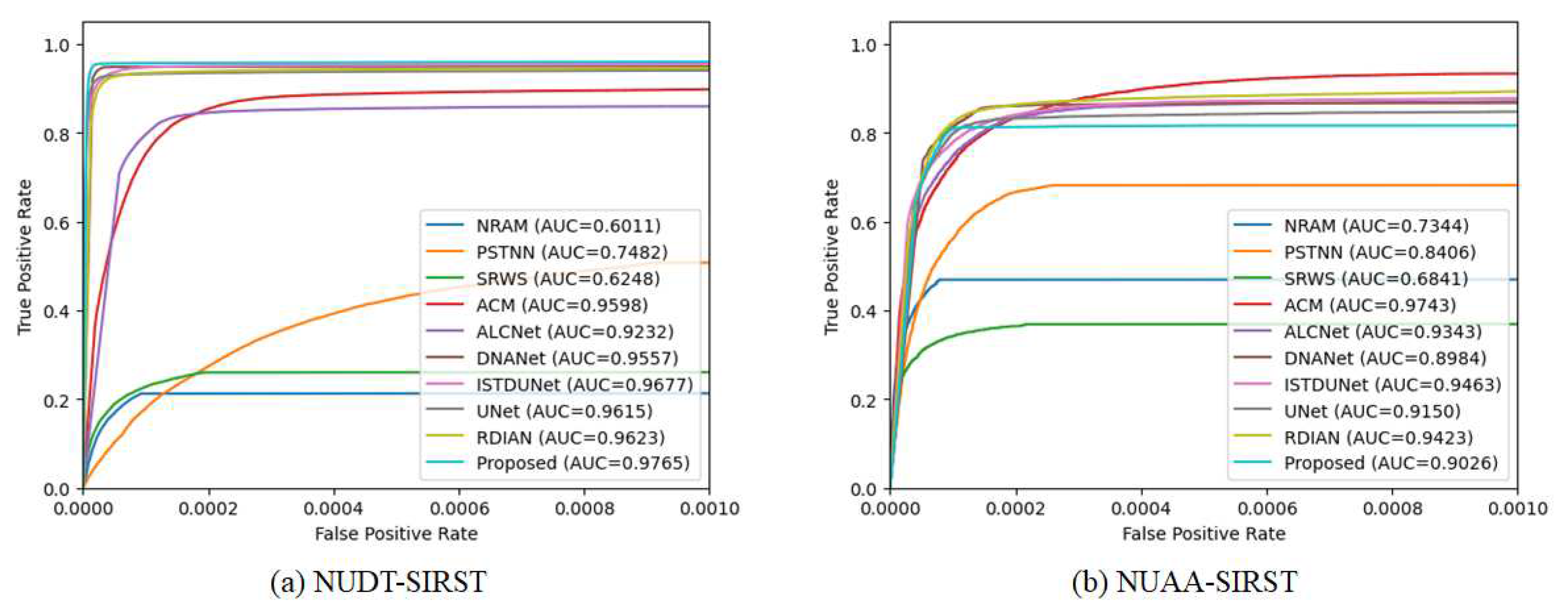
The robustness of the algorithms was further analyzed by plotting the ROC curves shown in Figure 18 and calculating the AUC values as presented in Table 2 and Table 3. The proposed TFCD-Net achieved the best score on the NUDT-SIRST dataset and showcased competitive AUC scores among DNN approaches on the NUAA-SIRST dataset. A high AUC value suggests effective clutter suppression and a strong target response, which is indicative of the proposed TFCD-Net’s stable target segmentation capabilities.
Further analysis of Table 2, Table 3, and Figure 18 indicates that the performance of DNN-based methods significantly exceeds that of non-DNN approaches in all metrics except the Fa value. Non-DNN model-driven algorithms are constrained by the need to manually model small target features, applying constraints such as shape or sparsity and extracting specific components from images. While such designs do not rely on large datasets, they are limited in their scope due to their modeling bias. In contrast, convolutional DNNs learn features that minimize the loss function through the backpropagation algorithm, facilitated by appropriate loss function settings. The proposed TFCD-Net, leveraging the FEB for progressive false alarm suppression combined with a precise TSB, achieves correct target detection and precise segmentation across various conditions.
Further analysis of Table 2, Table 3, and Figure 18 suggests that, in comparison to non-DNN approaches, DNN-based methods generally provide superior performance across most metrics. Non-DNN model-driven algorithms rely on manual modeling of small target features, which imposes constraints such as shape or sparsity and necessitates the extraction of specific image components. These designs do not depend on large datasets for training but suffer from a modeling bias that limits their generalizability. In contrast, DNNs like TFCD-Net utilize convolutional architectures to learn discriminative features through backpropagation, which is enhanced by the use of well-designed loss functions. The TFCD-Net, in particular, effectively combines the FEB and the TSB to achieve precise target detection and segmentation, significantly outperforming non-DNN algorithms in terms of I o U , P d and AUC.
For evaluation on complexity, Table 4 illustrates comparison of DNN models on 2 datasets. The experiments were performed on an RTX 3090 GPU using Python. Our model exhibited a medium number of parameters compared to the other models investigated. Notably, the inference speed of our model was 4.203 milliseconds per image and registered training durations of 3.9463 seconds per epoch on the NUAA-SIRST dataset and 12.4757 seconds per epoch on the NUDT-SIRST dataset. Though our approach did not surpass the speed of ACM, ALCNet, and RDIAN, it significantly outpaced models such as UNet, ISTDUNet, and DNANet in both training and inference times. These results highlight that our model achieves high performance with comparatively modest parameter count, making it suitable for real-time applications due to its fast inference time.
In summary, the proposed TFCD-Net demonstrates superior detection and segmentation capabilities for small infrared targets in complex scenes, outperforming both traditional optimization-based methods and contemporary DNN models in performance metrics. The comprehensive experimental evaluation showcases the robustness and generalizability of the proposed TFCD-Net across different datasets, establishing its potential for practical deployment in real-world infrared small target detection applications.

5. Conclusion

In this study, we introduced the Target and False Alarm Collaborative Detection Network for Infrared Imagery. Our model confronts the challenge of dense clutter and false alarms in infrared imaging by synergistically employing specialized FEBs alongside a TSB. The dual focus of this model on both target recognition and false alarm suppression represents a step forward in the field, combining interpretability with high performance.
The experimental results have demonstrated that compared with other state-of-the-art methods, our model performs best and second-best results in terms of I o U , P d and AUC, and low F a among the DNN approaches. The incorporation of FEBs leads to a reduction in false positives by a multi-scale, block-wise approach to false alarm source estimation, not only improves the detection capabilities of our network but the extracted false alarm source estimations also enriches the potential for further advancements in the field, providing valuable data for subsequent research.
Despite these advancements, our model does exhibit certain limitations that should be acknowledged: Owing to the multi-stage design, the model encompasses a larger number of parameters compared to light-weight models, which results in a longer training time, also while FEBs are designed to suppress false alarms effectively, there are instances where they may suppress actual targets.
Further research could explore the refinement of the architecture for better accuracy and interpretability, as well as the application of our model to other types of datasets or the integration of additional sensory data to enhance detection capabilities.

Author Contributions

Conceptualization, S.C.; methodology, S.C.; validation, S.C., Z.L. and J.D.; formal analysis, S.C.; data collection, S.C.; writing—original draft preparation, S.C.; writing—review and editing, Z.L. and Y.H.; visualization, Z.L.; supervision, Z.P.; project administration, Z.P.; funding acquisition, Z.P. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported in part by the Natural Science Foundation of Sichuan Province of China under Grant 2022NSFSC40574 and Grant 2023NSFSC0508, and in part by the National Natural Science Foundation of China under Grant 61775030 and Grant 61571096.

Data Availability Statement

Publicly available datasets were analyzed in this study. NUAA-SIRST dataset can be found here: https://github.com/YimianDai/sirst, NUDT-SIRST dataset can be found here: https://github.com/YeRen123455/Infrared-Small-Target-Detection.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Li, M.H.; Peng, L.B.; Chen, Y.P.; Huang, S.Q.; Qin, F.Y.; Peng, Z.M. Mask Sparse Representation Based on Semantic Features for Thermal Infrared Target Tracking. Remote Sensing 2019, 11, 22. [Google Scholar] [CrossRef]
  2. Peng, L.B.; Zhang, T.F.; Huang, S.Q.; Pu, T.; Liu, Y.H.; Lv, Y.X.; Zheng, Y.C.; Peng, Z.M. Infrared small-target detection based on multi-directional multi-scale high-boost response. Optical Review 2019, 26, 568–582. [Google Scholar] [CrossRef]
  3. Li, M.H.; Peng, L.B.; Wu, T.F.; Peng, Z.M. A Bottom-Up and Top-Down Integration Framework for Online Object Tracking. Ieee Transactions on Multimedia 2021, 23, 105–119. [Google Scholar] [CrossRef]
  4. Zhu, Q.; Zhu, S.Y.; Liu, G.H.; Peng, Z.M. Infrared Small Target Detection Using Local Feature-Based Density Peaks Searching. Ieee Geoscience and Remote Sensing Letters 2022, 19, 5. [Google Scholar] [CrossRef]
  5. Han, Y.Q.; Liao, J.W.; Lu, T.S.; Pu, T.; Peng, Z.M. KCPNet: Knowledge-Driven Context Perception Networks for Ship Detection in Infrared Imagery. Ieee Transactions on Geoscience and Remote Sensing 2023, 61, 19. [Google Scholar] [CrossRef]
  6. Kou, R.K.; Wang, C.P.; Peng, Z.M.; Zhao, Z.H.; Chen, Y.H.; Han, J.H.; Huang, F.Y.; Yu, Y.; Fu, Q. Infrared small target segmentation networks: A survey. Pattern Recognition 2023, 143, 25. [Google Scholar] [CrossRef]
  7. Rawat, S.S.; Verma, S.K.; Kumar, Y. Review on recent development in infrared small target detection algorithms. International Conference on Computational Intelligence and Data Science (ICCIDS); Elsevier Science Bv: AMSTERDAM, 2020. [Google Scholar] [CrossRef]
  8. Li, X.; Wang, J.; Li, M.H.; Peng, Z.M.; Liu, X.R. Investigating Detectability of Infrared Radiation Based on Image Evaluation for Engine Flame. Entropy 2019, 21, 10. [Google Scholar] [CrossRef]
  9. Wang, X.Y.; Peng, Z.M.; Kong, D.H.; He, Y.M. Infrared Dim and Small Target Detection Based on Stable Multisubspace Learning in Heterogeneous Scene. Ieee Transactions on Geoscience and Remote Sensing 2017, 55, 5481–5493. [Google Scholar] [CrossRef]
  10. Liu, Y.H.; Peng, Z.M.; Huang, S.Q.; Wang, Z.R.; Pu, T. River detection using LBP and morphology in infrared image. 9th International Symposium on Advanced Optical Manufacturing and Testing Technologies (AOMATT) - Optoelectronic Materials and Devices for Sensing and Imaging; Proceedings of SPIE; Spie-Int Soc Optical Engineering: BELLINGHAM, 2019; Volume 10843. [Google Scholar] [CrossRef]
  11. Yang, C.P.; Kong, X.; Cao, Z.Y.; Peng, Z.M. Cirrus Detection Based on Tensor Multi-Mode Expansion Sum Nuclear Norm in Infrared Imagery. Ieee Access 2020, 8, 149963–149983. [Google Scholar] [CrossRef]
  12. Lyu, Y.X.; Peng, L.B.; Pu, T.; Yang, C.P.; Wang, J.; Peng, Z.M. Cirrus Detection Based on RPCA and Fractal Dictionary Learning in Infrared imagery. Remote Sensing 2020, 12, 25. [Google Scholar] [CrossRef]
  13. Xiao, S.Y.; Peng, Z.M.; Li, F.S. Infrared Cirrus Detection Using Non-Convex Rank Surrogates for Spatial-Temporal Tensor. Remote Sensing 2023, 15, 21. [Google Scholar] [CrossRef]
  14. Gao, Z.; Yin, J.; Luo, J.; Li, W.; Peng, Z. Multidirectional Graph Learning-Based Infrared Cirrus Detection With Local Texture Features. IEEE Transactions on Geoscience and Remote Sensing 2023, 61, 1–20. [Google Scholar] [CrossRef]
  15. Kong, X.; Yang, C.P.; Cao, S.Y.; Li, C.H.; Peng, Z.M. Infrared Small Target Detection via Nonconvex Tensor Fibered Rank Approximation. Ieee Transactions on Geoscience and Remote Sensing 2022, 60, 21. [Google Scholar] [CrossRef]
  16. Fan, X.S.; Xu, Z.Y.; Zhang, J.L.; Huang, Y.M.; Peng, Z.M.; Wei, Z.R.; Guo, H.W. Dim small target detection based on high-order cumulant of motion estimation. Infrared Physics & Technology 2019, 99, 86–101. [Google Scholar] [CrossRef]
  17. Hu, Y.X.; Ma, Y.P.; Pan, Z.X.; Liu, Y.H. Infrared Dim and Small Target Detection from Complex Scenes via Multi-Frame Spatial-Temporal Patch-Tensor Model. Remote Sensing 2022, 14, 36. [Google Scholar] [CrossRef]
  18. Wang, G.; Tao, B.; Kong, X.; Peng, Z. Infrared Small Target Detection Using Nonoverlapping Patch Spatial–Temporal Tensor Factorization With Capped Nuclear Norm Regularization. IEEE Transactions on Geoscience and Remote Sensing 2022, 60, 1–17. [Google Scholar] [CrossRef]
  19. Wang, Y.; Cao, L.H.; Su, K.K.; Dai, D.; Li, N.; Wu, D. Infrared Moving Small Target Detection Based on Space-Time Combination in Complex Scenes. Remote Sensing 2023, 15, 25. [Google Scholar] [CrossRef]
  20. Yi, H.Y.; Yang, C.P.; Qie, R.C.; Liao, J.W.; Wu, F.Y.; Pu, T.; Peng, Z.M. Spatial-Temporal Tensor Ring Norm Regularization for Infrared Small Target Detection. Ieee Geoscience and Remote Sensing Letters 2023, 20, 5. [Google Scholar] [CrossRef]
  21. Wu, F.Y.; Yu, H.; Liu, A.R.; Luo, J.H.; Peng, Z.M. Infrared Small Target Detection Using Spatiotemporal 4-D Tensor Train and Ring Unfolding. Ieee Transactions on Geoscience and Remote Sensing 2023, 61, 22. [Google Scholar] [CrossRef]
  22. Kou, R.K.; Wang, C.P.; Yu, Y.; Peng, Z.M.; Yang, M.B.; Huang, F.Y.; Fu, Q. LW-IRSTNet: Lightweight Infrared Small Target Segmentation Network and Application Deployment. Ieee Transactions on Geoscience and Remote Sensing 2023, 61, 13. [Google Scholar] [CrossRef]
  23. Ding, L.H.; Xu, X.; Cao, Y.; Zhai, G.T.; Yang, F.; Qian, L. Detection and tracking of infrared small target by jointly using SSD and pipeline filter. Digital Signal Processing 2021, 110, 9. [Google Scholar] [CrossRef]
  24. Huang, S.Q.; Liu, Y.H.; He, Y.M.; Zhang, T.F.; Peng, Z.M. Structure-Adaptive Clutter Suppression for Infrared Small Target Detection: Chain-Growth Filtering. Remote Sensing 2020, 12, 22. [Google Scholar] [CrossRef]
  25. Huang, S.Q.; Peng, Z.M.; Wang, Z.R.; Wang, X.Y.; Li, M.H. Infrared Small Target Detection by Density Peaks Searching and Maximum-Gray Region Growing. Ieee Geoscience and Remote Sensing Letters 2019, 16, 1919–1923. [Google Scholar] [CrossRef]
  26. Guan, X.; Peng, Z.; Huang, S.; Chen, Y. Gaussian Scale-Space Enhanced Local Contrast Measure for Small Infrared Target Detection. IEEE Geoscience and Remote Sensing Letters 2020, 17, 327–331. [Google Scholar] [CrossRef]
  27. Qi, S.X.; Xu, G.J.; Mou, Z.Y.; Huang, D.Y.; Zheng, X.L. A fast-saliency method for real-time infrared small target detection. Infrared Physics & Technology 2016, 77, 440–450. [Google Scholar] [CrossRef]
  28. Chen, C.L.P.; Li, H.; Wei, Y.T.; Xia, T.; Tang, Y.Y. A Local Contrast Method for Small Infrared Target Detection. Ieee Transactions on Geoscience and Remote Sensing 2014, 52, 574–581. [Google Scholar] [CrossRef]
  29. Han, J.H.; Moradi, S.; Faramarzi, I.; Zhang, H.H.; Zhao, Q.; Zhang, X.J.; Li, N. Infrared Small Target Detection Based on the Weighted Strengthened Local Contrast Measure. Ieee Geoscience and Remote Sensing Letters 2021, 18, 1670–1674. [Google Scholar] [CrossRef]
  30. Lu, R.T.; Yang, X.G.; Li, W.P.; Fan, J.W.; Li, D.L.; Jing, X. Robust Infrared Small Target Detection via Multidirectional Derivative-Based Weighted Contrast Measure. Ieee Geoscience and Remote Sensing Letters 2022, 19, 5. [Google Scholar] [CrossRef]
  31. Gao, C.Q.; Meng, D.Y.; Yang, Y.; Wang, Y.T.; Zhou, X.F.; Hauptmann, A.G. Infrared Patch-Image Model for Small Target Detection in a Single Image. Ieee Transactions on Image Processing 2013, 22, 4996–5009. [Google Scholar] [CrossRef]
  32. Zhang, T.F.; Wu, H.; Liu, Y.H.; Peng, L.B.; Yang, C.P.; Peng, Z.M. Infrared Small Target Detection Based on Non-Convex Optimization with Lp-Norm Constraint. Remote Sensing 2019, 11, 30. [Google Scholar] [CrossRef]
  33. Guan, X.W.; Zhang, L.D.; Huang, S.Q.; Peng, Z.M. Infrared Small Target Detection via Non-Convex Tensor Rank Surrogate Joint Local Contrast Energy. Remote Sensing 2020, 12, 31. [Google Scholar] [CrossRef]
  34. Cao, Z.; Kong, X.; Zhu, Q.; Cao, S.; Peng, Z. Infrared dim target detection via mode-k1k2 extension tensor tubal rank under complex ocean environment. ISPRS Journal of Photogrammetry and Remote Sensing 2021, 181, 167–190. [Google Scholar] [CrossRef]
  35. Bi, Y.G.; Bai, X.Z.; Jin, T.; Guo, S. Multiple Feature Analysis for Infrared Small Target Detection. Ieee Geoscience and Remote Sensing Letters 2017, 14, 1333–1337. [Google Scholar] [CrossRef]
  36. Cao, S.Y.; Deng, J.K.; Luo, J.H.; Li, Z.; Hu, J.S.; Peng, Z.M. Local Convergence Index-Based Infrared Small Target Detection against Complex Scenes. Remote Sensing 2023, 15, 18. [Google Scholar] [CrossRef]
  37. Li, S.S.; Li, Y.J.; Li, Y.; Li, M.J.; Xu, X.R. YOLO-FIRI: Improved YOLOv5 for Infrared Image Object Detection. Ieee Access 2021, 9, 141861–141875. [Google Scholar] [CrossRef]
  38. Ma, J.Y.; Tang, L.F.; Xu, M.L.; Zhang, H.; Xiao, G.B. STDFusionNet: An Infrared and Visible Image Fusion Network Based on Salient Target Detection. Ieee Transactions on Instrumentation and Measurement 2021, 70, 13. [Google Scholar] [CrossRef]
  39. Dai, Y.M.; Wu, Y.Q.; Zhou, F.; Barnard, K.; Ieee. Asymmetric Contextual Modulation for Infrared Small Target Detection. IEEE Winter Conference on Applications of Computer Vision (WACV); Ieee Computer Soc: LOS ALAMITOS, 2021. IEEE Winter Conference on Applications of Computer Vision 2021, 949–958. [Google Scholar] [CrossRef]
  40. Kou, R.; Wang, C.; Yu, Y.; Peng, Z.; Huang, F.; Fu, Q. Infrared Small Target Tracking Algorithm via Segmentation Network and Multistrategy Fusion. IEEE Transactions on Geoscience and Remote Sensing 2023, 61, 1–12. [Google Scholar] [CrossRef]
  41. Han, Y.Q.; Yang, X.Y.; Pu, T.; Peng, Z.M. Fine-Grained Recognition for Oriented Ship Against Complex Scenes in Optical Remote Sensing Images. Ieee Transactions on Geoscience and Remote Sensing 2022, 60, 18. [Google Scholar] [CrossRef]
  42. Sun, H.; Bai, J.X.; Yang, F.; Bai, X.Z. Receptive-Field and Direction Induced Attention Network for Infrared Dim Small Target Detection With a Large-Scale Dataset IRDST. Ieee Transactions on Geoscience and Remote Sensing 2023, 61, 13. [Google Scholar] [CrossRef]
  43. Hou, Q.Y.; Wang, Z.P.; Tan, F.J.; Zhao, Y.; Zheng, H.L.; Zhang, W. RISTDnet: Robust Infrared Small Target Detection Network. Ieee Geoscience and Remote Sensing Letters 2022, 19, 5. [Google Scholar] [CrossRef]
  44. Zhang, T.F.; Li, L.; Cao, S.Y.; Pu, T.; Peng, Z.M. Attention-Guided Pyramid Context Networks for Detecting Infrared Small Target Under Complex Background. Ieee Transactions on Aerospace and Electronic Systems 2023, 59, 4250–4261. [Google Scholar] [CrossRef]
  45. Wang, H.; Zhou, L.P.; Wang, L.; Ieee. Miss Detection vs. False Alarm: Adversarial Learning for Small Object Segmentation in Infrared Images. IEEE/CVF International Conference on Computer Vision (ICCV); Ieee: NEW YORK, 2019. IEEE International Conference on Computer Vision 2019, 8508–8517. [Google Scholar] [CrossRef]
  46. Dai, Y.M.; Wu, Y.Q.; Zhou, F.; Barnard, K. Attentional Local Contrast Networks for Infrared Small Target Detection. Ieee Transactions on Geoscience and Remote Sensing 2021, 59, 9813–9824. [Google Scholar] [CrossRef]
  47. Li, B.Y.; Xiao, C.; Wang, L.G.; Wang, Y.Q.; Lin, Z.P.; Li, M.; An, W.; Guo, Y.L. Dense Nested Attention Network for Infrared Small Target Detection. Ieee Transactions on Image Processing 2023, 32, 1745–1758. [Google Scholar] [CrossRef] [PubMed]
  48. Hou, Q.Y.; Zhang, L.W.; Tan, F.J.; Xi, Y.Y.; Zheng, H.L.; Li, N. ISTDU-Net: Infrared Small-Target Detection U-Net. Ieee Geoscience and Remote Sensing Letters 2022, 19, 5. [Google Scholar] [CrossRef]
  49. Wang, X.Y.; Peng, Z.M.; Kong, D.H.; Zhang, P.; He, Y.M. Infrared dim target detection based on total variation regularization and principal component pursuit. Image and Vision Computing 2017, 63, 1–9. [Google Scholar] [CrossRef]
  50. Liu, Y.; Peng, Z.M. Infrared Small Target Detection Based on Resampling-Guided Image Model. Ieee Geoscience and Remote Sensing Letters 2022, 19, 5. [Google Scholar] [CrossRef]
  51. Deng, L.Z.; Zhu, H.; Zhou, Q.; Li, Y.S. Adaptive top-hat filter based on quantum genetic algorithm for infrared small target detection. Multimedia Tools and Applications 2018, 77, 10539–10551. [Google Scholar] [CrossRef]
  52. Bai, X.Z.; Zhou, F.G. Analysis of new top-hat transformation and the application for infrared dim small target detection. Pattern Recognition 2010, 43, 2145–2156. [Google Scholar] [CrossRef]
  53. Zhang, L.D.; Peng, L.B.; Zhang, T.F.; Cao, S.Y.; Peng, Z.M. Infrared Small Target Detection via Non-Convex Rank Approximation Minimization Joint l(2,1) Norm. Remote Sensing 2018, 10, 26. [Google Scholar] [CrossRef]
  54. Zhang, L.D.; Peng, Z.M. Infrared Small Target Detection Based on Partial Sum of the Tensor Nuclear Norm. Remote Sensing 2019, 11, 34. [Google Scholar] [CrossRef]
  55. Zhang, T.F.; Peng, Z.M.; Wu, H.; He, Y.M.; Li, C.H.; Yang, C.P. Infrared small target detection via self-regularized weighted sparse model. Neurocomputing 2021, 420, 124–148. [Google Scholar] [CrossRef]
  56. Zhang, K.; Zuo, W.M.; Chen, Y.J.; Meng, D.Y.; Zhang, L. Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising. Ieee Transactions on Image Processing 2017, 26, 3142–3155. [Google Scholar] [CrossRef]
  57. Tripathi, P.C.; Bag, S. CNN-DMRI: A Convolutional Neural Network for Denoising of Magnetic Resonance Images. Pattern Recognition Letters 2020, 135, 57–63. [Google Scholar] [CrossRef]
  58. He, K.M.; Zhang, X.Y.; Ren, S.Q.; Sun, J.; Ieee. Deep Residual Learning for Image Recognition. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR); Ieee: NEW YORK, 2016. In IEEE Conference on Computer Vision and Pattern Recognition; Ieee: NEW YORK, 2016; pp. 770–778. [Google Scholar] [CrossRef]
  59. Rahman, M.A.; Wang, Y. Optimizing Intersection-Over-Union in Deep Neural Networks for Image Segmentation. Advances in Visual Computing; Springer International Publishing: Cham, 2016; pp. 234–244. [Google Scholar]
  60. Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. 18th International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI); Springer International Publishing Ag: CHAM, 2015. [Google Scholar] [CrossRef]
Preprints 96705 g001
Figure 1. Images (1) to (4) depict four scenes with backgrounds ranging from simple to complex. Row (a) shows the original images, row (b) displays the results processed by the Top-Hat algorithm. It is evident that as the scenes become more complex, an increasing number of false alarm sources appear, resulting in the targets being less salient.
Figure 1. Images (1) to (4) depict four scenes with backgrounds ranging from simple to complex. Row (a) shows the original images, row (b) displays the results processed by the Top-Hat algorithm. It is evident that as the scenes become more complex, an increasing number of false alarm sources appear, resulting in the targets being less salient.
Preprints 96705 g001
Preprints 96705 g002
Figure 2. Architecture of the proposed TFCD-Net consisting of two main stages. In false alarm suppression stage, multiple FEBs are employed to estimate false alarm sources stepwisely. The false alarm subtracted result is input into target segmentation stage to detect the targets. The lower section depicts the false alarm estimation block (FEB).
Figure 2. Architecture of the proposed TFCD-Net consisting of two main stages. In false alarm suppression stage, multiple FEBs are employed to estimate false alarm sources stepwisely. The false alarm subtracted result is input into target segmentation stage to detect the targets. The lower section depicts the false alarm estimation block (FEB).
Preprints 96705 g002
Preprints 96705 g003
Figure 3. Overall framework utilizing different connection configurations. The upper section shows the series configuration with 3 FEBs, the lower section shows the stepped configuration with 3 FEBs. The number of FEBs can be adjusted according to requirements.
Figure 3. Overall framework utilizing different connection configurations. The upper section shows the series configuration with 3 FEBs, the lower section shows the stepped configuration with 3 FEBs. The number of FEBs can be adjusted according to requirements.
Preprints 96705 g003
Preprints 96705 g004
Figure 4. Sample images of NUAA-SIRST dataset.
Figure 4. Sample images of NUAA-SIRST dataset.
Preprints 96705 g004
Preprints 96705 g005
Figure 5. Sample images of NUDT-SIRST dataset.
Figure 5. Sample images of NUDT-SIRST dataset.
Preprints 96705 g005
Preprints 96705 g006
Figure 6. Structural configurations of overall framework used in ablation experiments.
Figure 6. Structural configurations of overall framework used in ablation experiments.
Preprints 96705 g006
Preprints 96705 g007
Figure 7. The sampling points of outputs of each blocks.
Figure 7. The sampling points of outputs of each blocks.
Preprints 96705 g007
Preprints 96705 g008
Figure 8. Inputs and outputs of each blocks on scenes 1.
Figure 8. Inputs and outputs of each blocks on scenes 1.
Preprints 96705 g008
Preprints 96705 g009
Figure 9. 3D visualization of inputs and outputs of each blocks on scenes 1.
Figure 9. 3D visualization of inputs and outputs of each blocks on scenes 1.
Preprints 96705 g009
Preprints 96705 g010
Figure 10. Inputs and outputs of each blocks on scenes 2.
Figure 10. Inputs and outputs of each blocks on scenes 2.
Preprints 96705 g010
Preprints 96705 g011
Figure 11. 3D visualization of inputs and outputs of each blocks on scenes 2.
Figure 11. 3D visualization of inputs and outputs of each blocks on scenes 2.
Preprints 96705 g011
Preprints 96705 g012
Figure 12. Results and 3D visualizations of different methods on scenes 1. The red boxes identify the target area and zoom in for display.
Figure 12. Results and 3D visualizations of different methods on scenes 1. The red boxes identify the target area and zoom in for display.
Preprints 96705 g012
Preprints 96705 g013
Figure 13. Results and 3D visualizations of different methods on scenes 2. The red boxes identify the target area and zoom in for display.
Figure 13. Results and 3D visualizations of different methods on scenes 2. The red boxes identify the target area and zoom in for display.
Preprints 96705 g013
Preprints 96705 g014
Figure 14. Results and 3D visualizations of different methods on scenes 3. The red boxes identify the target area and zoom in for display.
Figure 14. Results and 3D visualizations of different methods on scenes 3. The red boxes identify the target area and zoom in for display.
Preprints 96705 g014
Preprints 96705 g015
Figure 15. Results and 3D visualizations of different methods on scenes 4. The red boxes identify the target area and zoom in for display.
Figure 15. Results and 3D visualizations of different methods on scenes 4. The red boxes identify the target area and zoom in for display.
Preprints 96705 g015
Preprints 96705 g016
Figure 16. Results and 3D visualizations of different methods on scenes 5. The red boxes identify the target area and zoom in for display.
Figure 16. Results and 3D visualizations of different methods on scenes 5. The red boxes identify the target area and zoom in for display.
Preprints 96705 g016
Preprints 96705 g017
Figure 17. Results and 3D visualizations of different methods on scenes 6. The red boxes identify the target area and zoom in for display.
Figure 17. Results and 3D visualizations of different methods on scenes 6. The red boxes identify the target area and zoom in for display.
Preprints 96705 g017
Preprints 96705 g018
Figure 18. ROC curves of different methods on 2 datasets.
Figure 18. ROC curves of different methods on 2 datasets.
Preprints 96705 g018
Table 1. Ablation results of different structures on 2 datasets.
Table 1. Ablation results of different structures on 2 datasets.
NUAA-SIRST NUDT-SIRST
Structure I o U ( × 10 − 2 ) P d ( × 10 − 2 ) F a ( × 10 − 6 ) I o U ( × 10 − 2 ) P d ( × 10 − 2 ) F a ( × 10 − 6 )
A1 65.49 92.02 88.9 78.23 90.79 41.09
A2 67.13 94.3 108.94 91.19 97.04 18.67
A3 68.65 94.30 103.52 92.66 97.46 16.63
A4 66.95 93.92 104.45 92.43 97.88 17.61
B1 62.06 91.63 120.15 75.11 93.76 68.85
B2 58.86 95.06 148.97 54.34 84.34 149.49
Table 2. Results achieved on NUDT-SIRST dataset.
Table 2. Results achieved on NUDT-SIRST dataset.
Method I o U ( × 10 − 2 ) P d ( × 10 − 2 ) F a ( × 10 − 6 ) AUC ( × 10 − 2 )
NRAM 11.4 58.52 23.45 60.11
PSTNN 21.69 68.04 214.06 74.82
SRWS 8.69 66.35 9.27 62.48
ACM 67.65 95.77 138.66 95.98
ALCNet 69.93 94.92 118.29 92.32
RDIAN 86.93 97.25 41.05 95.57
UNet 89.84 96.4 19.89 96.77
ISTDUNet 89.73 97.88 29.76 96.15
DNANet 91.63 97.46 22.74 96.23
Proposed 92.66 97.99 16.63 97.65
Table 3. Results achieved on NUAA-SIRST dataset.
Table 3. Results achieved on NUAA-SIRST dataset.
Method I o U ( × 10 − 2 ) P d ( × 10 − 2 ) F a ( × 10 − 6 ) AUC ( × 10 − 2 )
NRAM 26.17 81.75 10.27 73.44
PSTNN 41.69 84.79 56.22 84.06
SRWS 12.36 84.79 4.00 68.41
ACM 63.49 92.78 113.08 97.43
ALCNet 64.52 93.54 117.79 93.43
RDIAN 70.46 93.54 95.89 94.23
UNet 68.28 93.16 98.39 91.50
ISTDUNet 66.66 92.78 104.24 94.63
DNANet 69.23 93.16 104.38 89.84
Proposed 69.38 93.16 91.82 90.26
Table 4. Comparison of complexity of DNN models on 2 datasets.
Table 4. Comparison of complexity of DNN models on 2 datasets.
Method Params( × 10 6 ) Inference (ms) Training on NUAA(s/epoch) Training on NUDT(s/epoch)
ACM 0.3978 3.905 1.5274 4.5036
ALCNet 0.4270 3.894 1.4335 4.7769
RDIAN 0.2166 2.757 2.6016 8.2245
UNet 34.5259 2.116 4.1787 13.0852
ISTDUNet 2.7519 13.489 6.4446 18.6608
DNANet 4.6966 15.819 8.4540 26.3606
Proposed 1.4501 4.203 3.9463 12.4757
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated