Prerpints.org logo
Preprint
Article

Female Teens and Young Adults with Mental Illness Who Are Autistic: How Common Is It and Why Is It Important?

Altmetrics

Downloads

335

Views

388

Comments

0

This version is not peer-reviewed

Submitted:

22 February 2024

Posted:

22 February 2024

You are already at the latest version

Alerts
Abstract
New information suggests female autistic spectrum disorder (ASD) is much more common than previously thought, with a likely prevalence of 6% and with 80% undiagnosed at the age of 18. ASD then becomes a common comorbidity of female mental illness with nearly one in five women who develop a mental illness being autistic. ASD has heretofore been regarded as a pediatric condition and though now thought to be life long it is still not well recognized by adult health services. Most mental illness first presents in the teens and early twenties. Comorbid ASD is more difficult to diagnose due to diagnostic overshadowing, and ASD comorbidity maks the mental illness more severe and mor difficult to treat. Recognized ASD is readily treatable with an approach sympathetic to neurodiversity. Improving the pathway from adolescence to adulthood by increasing knowledge of autism in adult health services would dramatically improve female mental health at surprisingly little extra cost. It is low hanging fruit in a very fraught area of healthcare. This paper will examine the extent of the problem. It will explore solutions and quantify the gains of appropriate therapy.
Keywords: 
Subject: Public Health and Healthcare  -   Public Health and Health Services

1. Introduction.

1.1. The Importance of autism spectrum disorder (ASD) as a mental health comorbidity in adolescent girls and young women.

There is extensive qualitative information that female ASD is considerably commoner than current estimates (Section 1.2). Recent quantitative information suggests it is at least as common as in males [1] and possibly even more common over the life span [2]. There is also information demonstrating that ASD may be comorbid with most mental health conditions [3] and this is not well recognized by adult mental health services (Section 1.4). If the ASD diagnosis is made, 75% are first diagnosed with another condition and the ASD diagnosis may be delayed 8 years [4]. This makes these conditions more difficult to manage in psychosis [5], anorexia nervosa [6,7,8,9], and anxiety and depression [10,11], with increased risk of suicide [12]. It is well documented that therapy in ASD has to be tailored to the neurodiverse mind or it will not succeed (Section 3.3). There has only been one published numerical estimate of bias-free female ASD prevalence [2]. If this estimate of 6% is correct then clinical reasoning about female ASD needs a new frame of reference. It would be the key to unlocking a great deal of epidemiological information in female adolescent and adult mental illness, and could lead to practical solutions to improve management of these comorbid conditions.
This paper aims to use Bayes’ theorem [13] to calculate the components of the comorbid landscape to assess their overall quantitative importance. The independent variables will be derived from extant literature and the author’s clinical practice.
The format of the study is a population analogy of a clinical case: diagnosis, therapy and prognosis. In each step methods and results will be described. The paper is then an exercise in quantitative induction and risk management. The problem with testing a hypothesis by deductive reasoning is that in an observational study information supporting an alternative hypothesis tends to be discounted [14,15], particularly if alternative explanations are deemed to be rare. The starting point of this paper is the observation that female autism is not rare, and so its importance needs to be explored. The focus will be on cis-gender adolescent girls and young women. Specific problems for transgender individuals will not be examined. The reason is this introduces an added layer of complexity to the definition and quantification of female mental illness (MI). Transgender ASD with comorbid mental illness is an extremely important area, and likely fairly common. It deserves its own study.

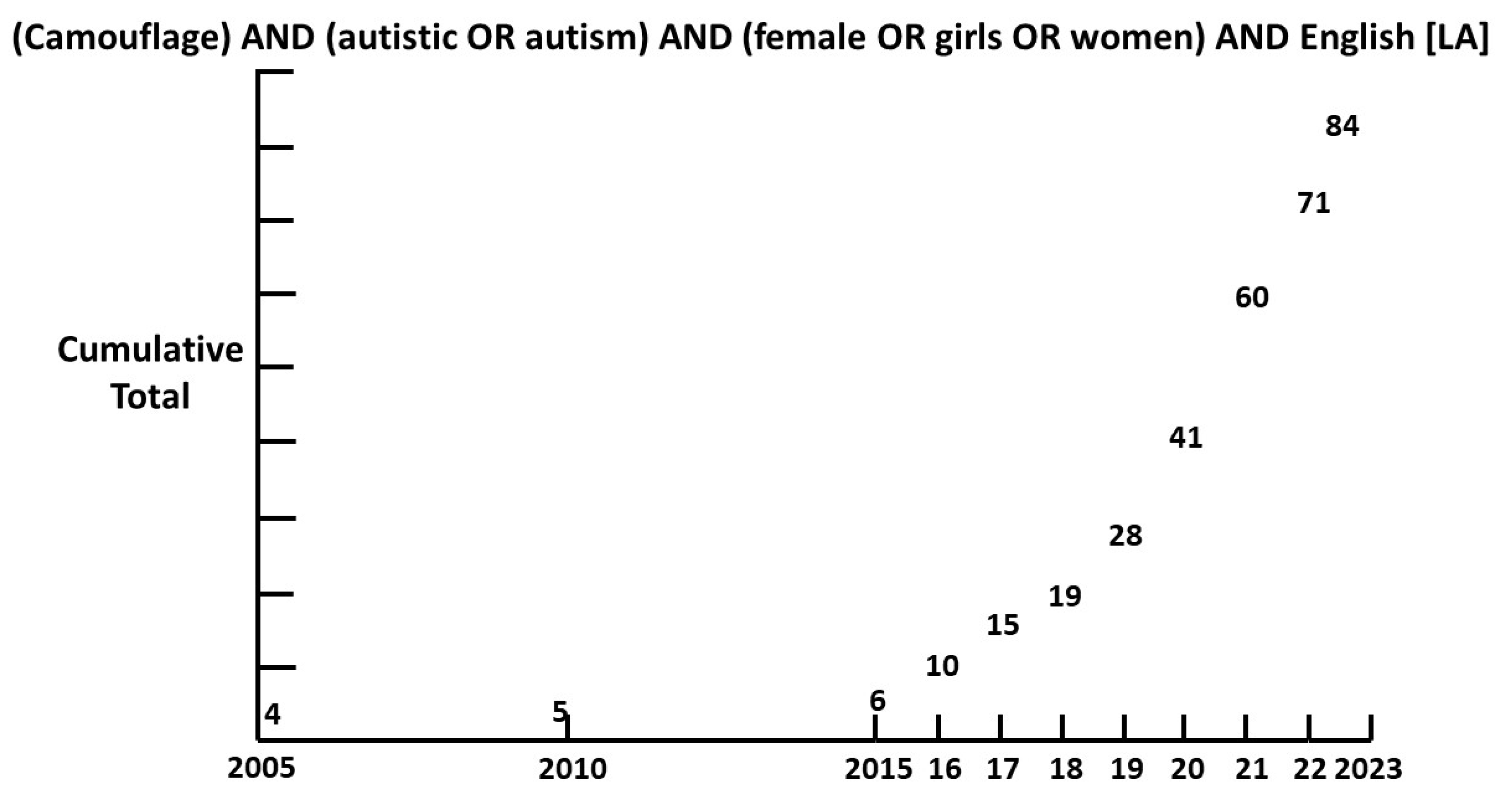
1.2. Camouflage.

The prevalence of female ASD, P(ASD), has generally been reported as around 0.01, or 1% of the female population. This is now believed to be underestimated (Section 1.6). There appears to be a female phenotype not well recognized [16] and a significant feature is female camouflage, now well described qualitatively [17,18] and with quantitative estimations of about 90% of ASD females [2,18,19]. Though camouflaging was first described by Wing in 1981 [20], it is only since 2015 that interest has grown dramatically (Figure 1). With such a high proportion of individuals camouflaging it is not surprising that a minority of females are recognized [2], let alone diagnosed. From a young age autistic girls strive to “fit in” with their neurotypical peers, at great psychological cost [21]. The key to successful management is the acceptance of their neurodiversity, and the tragic irony is they are so good at hiding it.
Camouflage in ASD is part of a larger problem in female neuroscience. There is a large gender bias where for example only 0.5% of brain imaging articles have considered factors specific to women, such as postpartum depression [22].

1.3. Neurodiversity.

The concept of neurodiversity was first proposed in 1999 by Singer [23]. The basic premise is difference, not innate disability. While some may be disabled, as within the neurotypical majority as well, the problem is that the dominant societal paradigm does not suit neurodiverse people. The root cause of most of the problems is a lack of mutual understanding, characterized as the double empathy problem [24]. The implications for management are simple but profound. Neurotypicals, both therapists and contacts of all degrees of intimacy, need to understand the mutual misunderstanding and allow for it. Neurodiverse individuals need to do the same, but as “aliens on Earth” have to make extra adjustments. Society as a whole is not going to understand and the neurodiverse are going to often have to adjust. One might say: “learn to camouflage well when necessary but learn strategies to minimize the pressure. Then make your excuses and leave”.
The aim of therapy is not to “cure” the individual. Autistic spectrum conditions (ASC) and ASD can usefully be seen as different, with the disorder as a subset of the condition [2]. The aim is to minimize the disorder element and manage in society. An ASC is permanent and not a pathology, but an ASC individual who has significant problems coping in a pervasive neurotypical environment, with or without a comorbid illness, has a disorder and requires assistance to cope successfully. Obviously understanding that ASD is present is required to manage it and professional assistance is required for comorbid mental illness. About 80% of autistic females have a comorbid mental health condition (Section 2.2). The comorbid illness often presents during the transition period to adult care (Section 2.2) and the transition is often poorly managed [25,26]. The pathological element of ASD usually has a comorbidity as the major driver [27] and the analysis of this problem is the overall purpose of this paper.

1.4. ASD and Attention Deficit Hyperactivity Disorder (ADHD).

Within neurodiversity there is generally believed to be a polythetic taxon, which is a shared pattern of features that need neither to be universal nor constant among members of a class. The class includes ASD and ADHD. There is a continuous field of clinical characteristics which are best managed without worrying about a precise categorical diagnosis. This naturally leads to a multidisciplinary approach of environmental adjustment, education of the neurodiverse and the neurotypical, talking therapies and medication, all tailored to the individual. To tease out the elements requires careful listening to the individual and then delivering therapy that they are comfortable with. For autistic management in particular a top down approach will not work [13]. The distinction between ASD and ADHD is complicated by many ADHD features being also explained by features of ASD [28]. In a continuous field there will be a high degree of diagnostic overshadowing and relative weighting of features is a work in progress. Since ADHD, like ASD, is not necessarily seen as a mental illness, a rate of comorbidity will not be considered in this paper. The possibility of cryptic ASD should always be considered when ADHD is diagnosed, in particular in female inattentive ADD.

1.5. Guidelines and ASD.

On the other side of the pediatric/adult divide mental health services do not appear to have appreciated the potential importance of ASD as a comorbidity in mental illness (MI), especially in females. This may also apply to transition guidelines. There are a growing number of papers considering the relationship but these are generally coming from an ASD focus, and invariably conclude adult mental health services need to pay more attention to ASD. The lack of diffusion across the barrier is likely due to not appreciating either the frequency or the severity of the ASD/MI interaction. The product of frequency and severity is the way risk is quantified. The literature on the severity of the relation again comes from an ASD focus, and the lack of a quantified P(ASD) until recently, together with female camouflage, have hidden the frequency. We will examine a selection of papers and guidelines that demonstrate aspects of the problem.
1 National Institute for Health and Care Excellence (NICE) Guideline in 2022 [29]. Depression in Adults: treatment and management. Listed as comorbidities: bipolar disorder, PTSD, anxiety. If there are language or communication difficulties eg autism, the guideline is linked to the NICE Autism guideline, but does not mention female camouflage possibly hiding comorbid ASD. The assumption appears to be that ASD has been recognized. If not, very good understanding of female ASD would be needed. The language and communication in female ASD can appear satisfactory, and the pathway would be difficult to navigate for a general practitioner/primary care physician.
2 An adolescent depression primary care screen in 2018 did not mention ASD among mental health risk factors [30].
3 A study of treatment resistant depression in primary care in 2018 [31] did not mention the possibility of comorbid ASD, though it did generate a response which did so [32].
4 A 2021 paper on postpartum depression and psychosis [33] examined the prevalence of neurodevelopmental disorders in the children but not in the mothers.
5 It has been suggested [34] pediatricians have a role to play in reducing perinatal mortality and notes some do screen for maternal depression. ASD is not mentioned. We would add that this is an area where pediatric expertise could indeed be very useful if looking for it became routine, perhaps in partnership with midwives [35] aware of both depression and ASD (Section 2.2 and Section 3.5).
6 A study [36] characterizing treatment-resistant anorexia nervosa (TRAN) from 2000 to 2016 in patients aged 17 and upwards was published in 2021. It did not mention ASD but did speculate that TRAN might be a different concept warranting additional research. There is qualitative information to support this [25,37].
7 The American Psychiatric Association 2023 Guideline [38] for treating eating disorders lists other psychiatric disorders that should be particularly sought. ASD is not among them.
8 A 2023 paper [39] on difficult to treat bipolar disorder mentioned ADHD, but not ASD.
9 A discussion of treatment resistance in mental illness [40] lists autism being misdiagnosed as schizophrenia but does not list schizophrenia spectrum disorder as being comorbid with ASD.
10 A 2023 paper [41] listing comorbidities of borderline personality disorder (BPD) quotes BPD as a comorbidity of 37.7% of ADHD but does not list ASD.
The obvious conclusion is that knowledge possessed by ASD focused practitioners, generally but not solely on the pediatric side of the divide, is not reaching our adult colleagues. If indeed the risk of undiagnosed ASD is much higher than currently believed, it becomes essential to manage it. It is to the elements of this risk assessment we will now turn.

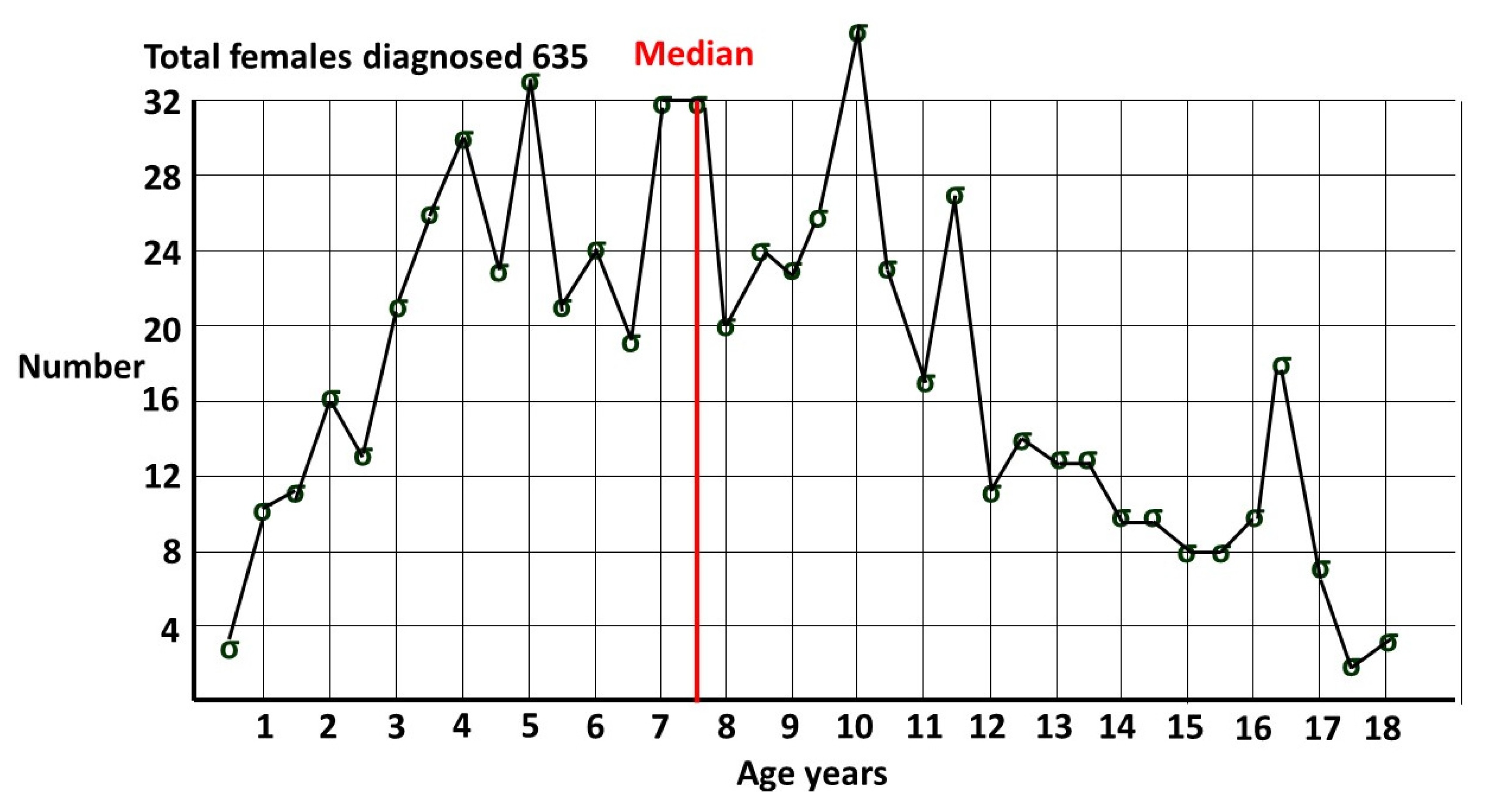
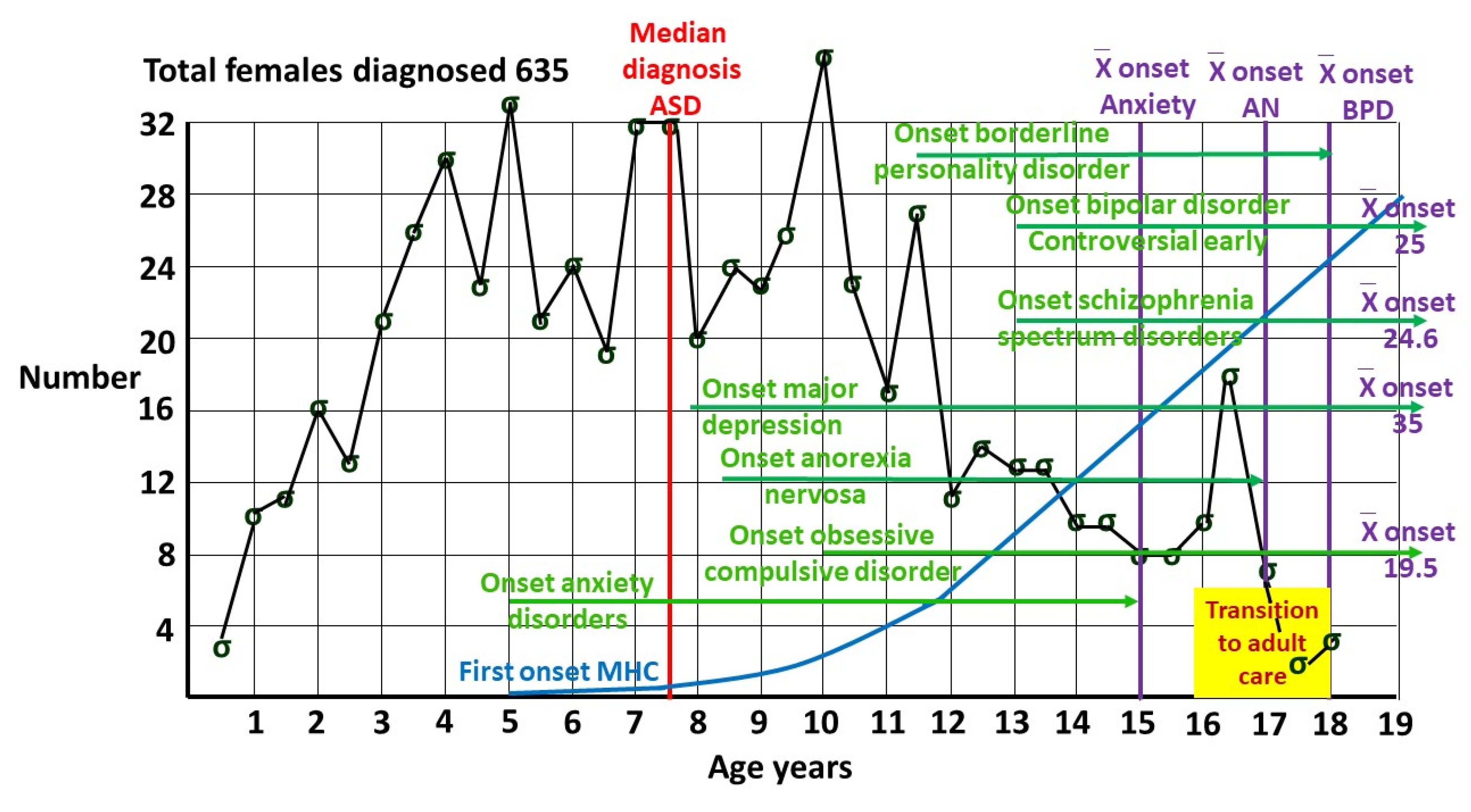
1.3. Prevalence of female ASD.

We can only rely on a measurement of female ASD prevalence P(ASD) if we are sure that all ASD patients in the measured population have been recognized and diagnosed. Initial recognition appears to be the major problem rather than diagnostic bias [2]. Community professionals do miss girls on diagnosis [2] but at a fairly low rate compared to research studies. A recent study [42] showed a “leaky pipeline” in the comparison of the male to female odds ratio (MFOR) for the community versus research diagnosis of females. The research standard was the Autism Diagnostic Observation Schedule (ADOS) module 4. The MFOR for community databases of referred patients (males 9192 females 5768) was 1.594. The MFOR for research ADOS assessments (189 males and 25 females) was 7.56. In my referred community specialist clinic [2] (1052 males 659 females) the MFOR was 1.596. The ADOS relies on an observation protocol and it is difficult not to believe that camouflage was a serious confounding factor. The Centers for Disease Control (CDC) prevalence [43] for ASD at 8 years of age is often incorrectly referenced as the prevalence of ASD. The age qualification is often omitted when cited. In any cohort the overall prevalence must be greater as cases accumulate after this age, as demonstrated in Figure 2 from my pediatric clinic showing females diagnosed by me [2], all with a known date of diagnosis. Median age of diagnosis was 7 years 6 months. At 8 years only around half the pediatric age diagnoses in females have been made.
Reliable recognition of ASD and subsequent accurate calculation of P(ASD) will occur in a population which has:
  • Focused experienced observers. This population is ASD siblings recognized by their carers due to their prior experience of the condition [1,2].
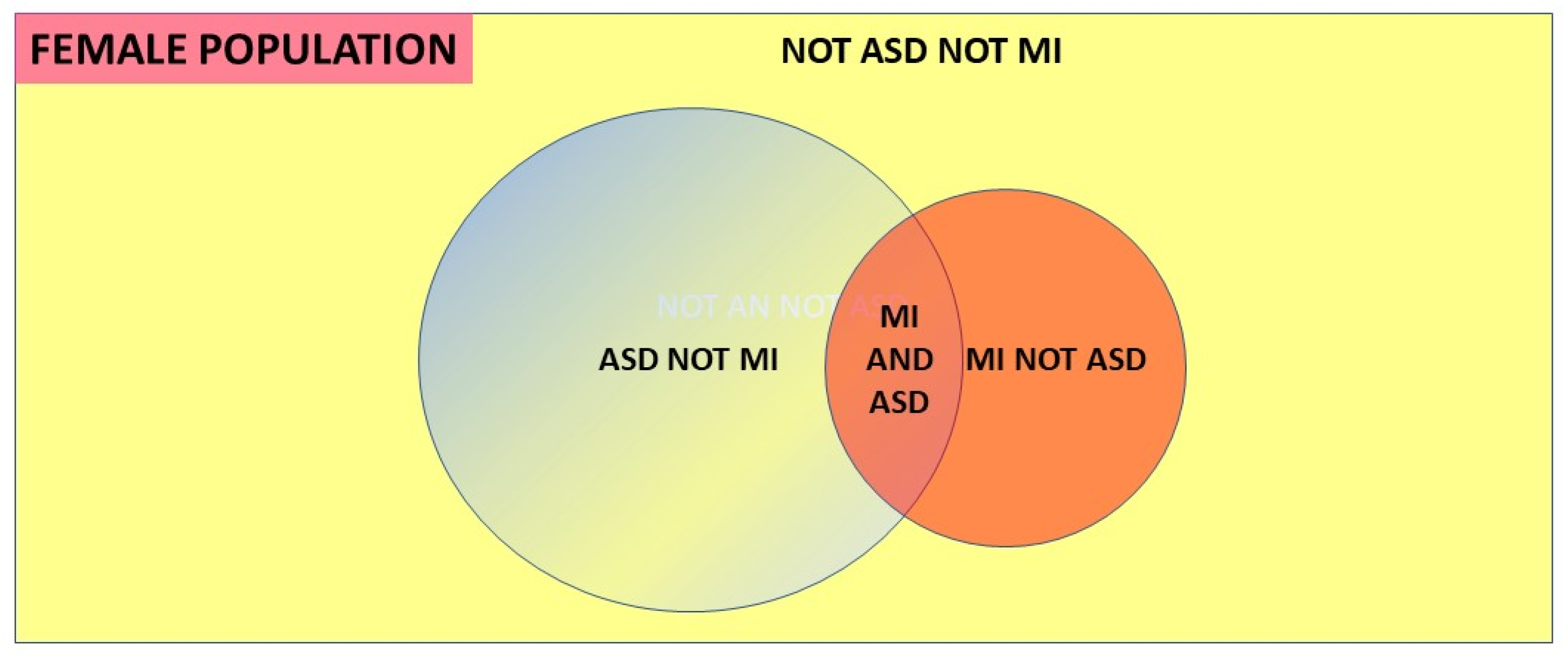
  • A discrete comorbid mental illness population (MI) with a known prevalence, with a diagnosed ASD population where the comorbid MI proportion is known, and where ASD in the MI population is carefully looked for. It will be reliably diagnosed because the major bias is initially recognizing that ASD must be sought, rather than in the diagnostic process itself [2].
  • A total population with a discrete population of diagnosed ASD where there is an easily recognized comorbidity and the proportion of the comorbid condition in that ASD population is known, together with the prevalence of the comorbid condition in the balance of the population without ASD [13] eg the Danish [44] and Swedish [45] national registers including ASD and anorexia nervosa (AN).
In (1) the bias in ascertaining probands can be calculated and the true P(ASD) found [2]. In (2) and (3) P(ASD) can be found by using versions of Bayes’ theorem [2,13]. The biases are accounted for in (2) and (3) because they have populations where ASD has already been diagnosed or reliably sought. These methods gave 14 results with a median value of 6.0% with interquartile range (IQR) of 1.5, first quartile Q1 5.9 and third quartile Q3 7.4 and range of 4.8-9.4.

1.6. Conditional probability and Bayes’ theorem.

Charles Lutwidge Dodgson, nom de plume Lewis Carroll, was a mathematics don at Oxford University. He may have hoped to instill logic in his readers (Figure 3) [46]. A worthy endeavor, but he failed (Section 3.2).
“… you should say what you mean,” the March Hare went on.
“I do,” Alice hastily replied; “at least—at least I mean what I say—that’s the same thing, you know.”
“Not the same thing a bit!” said the Hatter. “You might just as well say that ‘I see what I eat’ is the same thing as ‘I eat what I see’!”
“You might just as well say,” added the March Hare, “that ‘I like what I get’ is the same thing as ‘I get what I like’!”
“You might just as well say,” added the Dormouse, who seemed to be talking in his sleep, “that ‘I breathe when I sleep’ is the same thing as ‘I sleep when I breathe’!”
Text by Lewis Carroll, Illustration by Sir John TennielLike Alice, it remains very common not to understand conditional probability. The (not so mad) Hatter, March Hare and Dormouse know that a conditional statement is not commutative and must not be transposed. Conditional probability is a subset with the same rule and its relevance is as follows:
Mental illness given ASD. Bad. It is hard to manage because it is more complex than the mental illness alone. The therapist may lack the necessary skills, but knows ASD is present and can refer for expert help.
ASD given mental illness. Much worse. The usually undiagnosed ASD with comorbid mental illness (MI) may be intractable to therapy and the therapist does not know why, and the person they refer to will probably not know either.
The Dormouse gets it. They are not the same! Accordingly in Section 2.2 we will calculate the prevalence of ASD in each mental illness, and show how common and clinically significant it is given the high but unrecognized population prevalence of female ASD.
Bayes’ theorem (Figure 4) visually represents the equation for population prevalences (P condition A) and (P condition B) and the relative proportions of each condition comorbid with the other, the conditional probabilities P(A given condition B) and P(B given condition A). Then:
P(ASD|MI) x P(MI) = P(MI|ASD) x P(ASD)

2. Methods and results.

2.1. Context.

For ASD and comorbid MI, the prevalence of the comorbid condition P(MI) is generally known, and also one of the conditional probabilities. This is usually P(MI|ASD) because female ASD is cryptic, but here ASD must have been diagnosed. If there is a representative diagnosed ASD population then P(MI|ASD) may be determined. Because it is cryptic the proportion of ASD as a comorbidity in a mental illness has usually not been established and P(ASD|MI) is unknown. The key then for the management of intractable mental illnesses in females due to comorbid ASD is finding the crucial P(ASD|MI). P(ASD) must be established so Bayes’ theorem can be used. While the overall theme of this paper is supported by the qualitative information, P(ASD) is needed to assess the true extent of the problem and focus the clinical and bureaucratic mind. Three methods to do so were employed using the 3 reliable recognition methods listed in Section 1.6.
Method (1) [2] calculated biases and adjusted published biased estimates of P(ASD).
Method (2) [2,13] used P(ASD|MI), P(MI) and P(MI|ASD) in Bayes’ theorem:
P(ASD) = P(ASD|MI) x P(MI)/P(MI|ASD)
Method (3) [13] used the mathematical equivalence of a hazard ratio and a likelihood ratio (LR) [13], and employed a more visible comorbid mental illness (anorexia nervosa) as a “test” for ASD using the odds version of Bayes’ theorem. We can then generalize to other mental illnesses:
Odds (ASD) = Odds (ASD|MI)/LR
where the LR is P(MI|ASD)/P(MI|not ASD).
These methods yielded a median P(ASD) of 0.060 as detailed in Section 1.6. With this prevalence value of 6.0% for female ASD we can now reverse the process and depending on the reported variables, calculate the proportion of females, P(ASD|MI), who have comorbid ASD with their diagnosed mental illness. There are 3 possible ways to find the result:
  • P(ASD|MI) may have been directly measured. For the reasons described this is uncommon.
  • It is relatively common to find values for P(MI|ASD) because in the adolescent literature it has long been known comorbid mental illness is common in this ASD population. In the adult literature researchers with a primary ASD focus are now assessing for comorbidities. Bayes’ theorem can be used if we know P(MI|ASD), P(ASD) and P(MI).
  • If a hazard ratio is available:
Odds (ASD|MI) = Odds (ASD) x P(MI|ASD)/P(MI|not ASD)

2.2. P(ASD|MI) for selected mental illnesses in adolescents and young adults.

With these methods we can now calculate the proportion of ASD given different mental illnesses. The range of values for some of these conditions are wide, and recent and reasonably conservative data have been used where available. Precise values are not critical. The aim of this paper study is to set a frame of reference to establish the clinical importance of the relationship P(ASD|MI). Figure 5 shows indicative timing of onset of comorbid illnesses in females to put the results in context. Half of all individuals with a mental health disorder have their onset by 18 years, and 62.5% by age 25 [47]. Mental illness is a problem for the young, emphasizing the importance of an informed transition to adult services.
1.
Anorexia nervosa (AN).
There is reasonable current agreement [48,49] on a range of about 0.20 to 0.30 for P(ASD|AN). A value of 0.25 was used to calculate P(ASD) [13].
Margari et al. [50] give P(AN|ASD) of 0.068 compared to the published value [13] of 0.083. With the same values [13] for P(ASD|AN) of 0.25 and P(AN) of 0.02 this gives P(ASD) of 0.074. This is the third quartile value of the published median estimate of 0.060 and independently corroborates the estimated P(ASD).
2.
Schizophrenia spectrum disorder (SSD).
Published values for P(ASD|SSD) vary widely, likely due to significant diagnostic overshadowing, but the upper estimates are about 0.5 [51,52,53]. Overall P(SSD) is about 1% with a male:female ratio of 1.4:1 [52,53,54] giving a female P(SSD) of 0.0083. If we take P(SSD|ASD) to be 0.06 [55] then by Bayes’ theorem with P(ASD) of 0.06:
P(ASD|SSD) = 0.06 x 0.06/0.0083
= 0.434
This suggests values of up to 0.5 or 50% are plausible. This is supported by the shared genetics of SSD and ASD [56].
3.
Borderline personality disorder (BPD).
The value is uncertain with many overlapping features and uncertainty about the age when the diagnosis should be considered but 14.6% [57] is widely referenced giving P(ASD|BPD) of 0.146. This value was used to calculate a P(ASD) of 0.060 [2].
4.
Bipolar disorder (BP).
A cohort study of 267 young adult females with ASD were matched with 534 referents and the hazard ratio for BP in ASD ie P(BP|ASD)/P(BP|not ASD) was 5.85 [58]. Given P(ASD) of 0.060, by method (3) this gives P(ASD|BP) of 0.272 or 27.2%.
5.
Depression (DP).
Kirsch et al. [58] gave a hazard ratio for depression-related diagnoses of 2.28 which gives P(ASD|DP) of 12.7%. Pezzimenti et al. [59] for adolescents gave P(DP|ASD) of 0.202 and P(DP) of 0.084. With (P(ASD) of 0.060 this gives P(ASD|DP) of 0.144 or 14.4%. Hudson [60] gave an effective lifetime hazard ratio of ~4 giving P(ASD|DP) of 0.203 or 20.3% consistent with the cumulative incidence of depression increasing with age.
6.
Anxiety disorders (ANX)
Kirsch et al. [58] gave a hazard ratio for anxiety-related diagnoses of 2.91 which gives P(ASD|ANX) of 15.7%. Croen et al. [61] gave data for anxiety related diagnoses in adults, allowing calculation of a hazard ratio of 3.22 which gives a P(ASD|ANX) of 0.170 or 17.0%
7.
Obsessive compulsive disorder (OCD)
From a UK mental health trust study [62] of females aged 4-17: females with OCD + ASD (121), OCD (522), ASD (1625). Then P(ASD|OCD) is 121/522 ie 0.2318 or 23.2%. This paper also gives P(OCD|ASD) of 0.0745. With a female OCD prevalence of 0.015 [63] Bayes’ theorem gives a P(ASD) of 0.047, another independent measure of the high prevalence of female ASD. The relatively young age range may explain the value at the low end of the overall calculated range of P(ASD).
8.
Social anxiety disorder (SA)
Values vary for P(SA|ASD) but are generally high. If we use an indicative value of 0.45 with a lifetime P(SA) of 0.103 [64] then with P(ASD) of 0.060 we find a P(ASD|SA) of 0.262 or 26.2%. This is higher than the estimate for anxiety-related diagnoses but this is not surprising given that social communication is the major problem in ASD. The conclusion overall is that ASD is common in anxiety disorders.
9.
Perinatal depression (PND).
Pohl et al. [65] found a postnatal depression rate P(PND|ASD) in autistic women of 60%. This was potentially signaled by an antenatal rate of 40%. Luca et al. in a 2017 study [66] found a postnatal rate in pregnancy, P(PND), of 11.5%. Then we find:
P(ASD|PND) = P(PND|ASD) x P(ASD)/P(PND)
= 0.60 x 0.060/0.115
= 0.313
The likelihood of autism in postnatal depression may be a shocking 31.3%. Two thirds of these mothers will have antenatal depression [65] and it is essential to make neurodiversity friendly arrangements to ease the stress of birthing for autistic mothers [35].
10.
Post traumatic stress disorder (PTSD)
PTSD is experienced by 10-12% of women [67]. There is not a precise figure for female P(PTSD|ASD) but a lifetime figure may be as high as 60% [68]. Then we find:
P(ASD|PTSD) = P(PTSD|ASD) x P(ASD)/P(PTSD)
= 0.60 x 0.06/0.12
= 0.30
Considering the stresses that autistic women have to cope with [17] it is not surprising that up to 30% of women with PTSD may be autistic and will need to be diagnosed so the PTSD is not perpetuated by inappropriate therapy.
11.
Any mental health disorder (MI)
Nyrenius et al. [69] give P(ASD|MI) as 18.9%. Studies of P(MI|ASD) are quite heterogeneous. LeCavalier et al. [70] gives any externalizing disorder as 80.9% and any internalizing disorder as 43.6%. Lever et al. [71] give 79% with no gender breakdown but female rates are typically higher than male rates. If we take 80% as representative then with the National Institute of Mental Health [72] 2021 value for female P(MI) of 0.272 and P(ASD) of 0.060 we obtain P(ASD|MI) of 0.176 or 17.6%. These values are less than for some individual conditions because it is common with ASD to have multiple mental health comorbidities [73]. The overall magnitude of P(ASD|MI) however reinforces the primary thesis that female ASD is being routinely missed in female mental illness. Between one in six and one in five women with mental illness are autistic.
The outcome of the calculations of the proportion of women with comorbid ASD in mental illness are summarized in Table 1. The Bayes’ calculation can done by the probability equation:
P(ASD|MI) = P(MI|ASD) x P(ASD)/ P(MI)
or the odds equation:
Odds (ASD|MI) = Odds (ASD) x Likelihood Ratio
where the likelihood ratio is P(MI|ASD)/P(MI|not ASD). This is mathematically equivalent to the hazard ratio which is commonly reported as the ratio of the proportion of a mental illness comorbid with ASD to the prevalence of the mental illness in the rest of the relevant population without ASD [58,60,61]. This is providing the presence of comorbid ASD does not alter the proportion of the MI diagnosed. If it is not altered the accuracy of the proportion of the MI diagnosis in each population (ASD and not ASD) is not critical since a systematic error in diagnosis will be cancelled when deriving the ratio.

2.3. Attempted suicide.

The rate of completed suicide is of no immediate clinical value since it is too late for intervention. Attempted suicide however, while not a categorical mental illness, is a serious indicator of an underlying problem [12]. A Danish registry study by Kolves et al. [74] showed a marked increase in attempted suicide (AS) in female ASD, P(AS|ASD), compared to the non-ASD population, P(AS|not ASD). The comparison gave a likelihood ratio of 6.0. By the odds form of Bayes’ theorem this gave P(ASD|AS) of 0.277 or 27.7%. The clinician in practice has to first assess the patient by how they present, and then consider the variables that need to be diagnosed and managed. This prevalence strongly suggests seeking ASD is essential in female attempted suicide, with tailored prevention strategies [74]. If the presence of ASD is recognized in attempted suicide in treatment resistant depression the knowledge is of itself therapeutic [11]. The American Psychiatric Association’s clinical review journal suggests ADHD as a risk factor for suicide but does not list ASD [75].

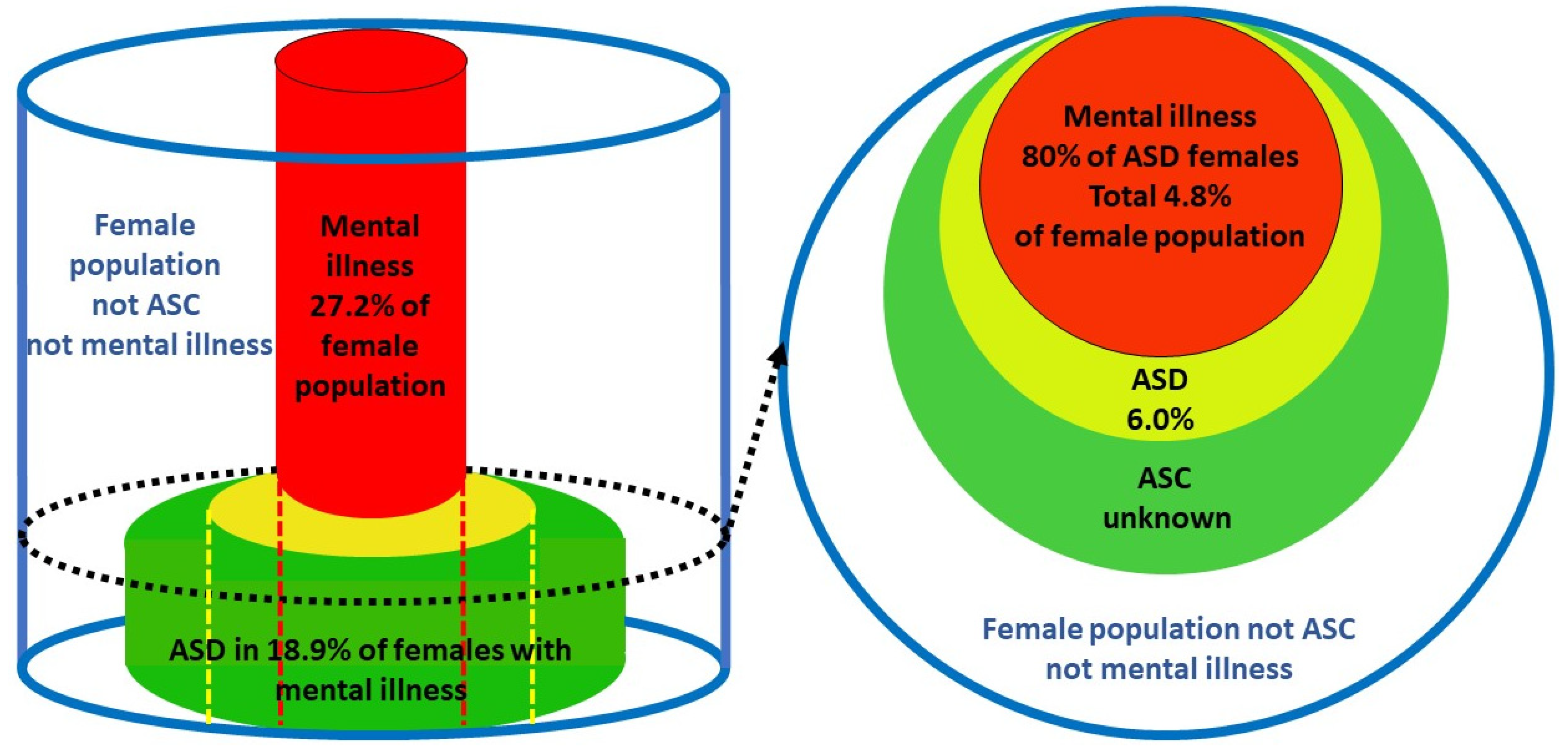
2.4. Validation of the female prevalence value for P(ASD).

We can use the data from Figure 6 which summarizes the relation of autism and mental illness in the female population to obtain another independent value for P(ASD) using Bayes’ theorem:
P(ASD) = P(ASD|MI) x P(MI)/P(MI|ASD)
= 0.189 x 0.272/0.80
= 0.064
Figure 6 summarizes the relation of autism and mental illness in the female population.
In addition to the 14 values already determined [13] we can add 0.047, 0.064 and 0.074 found in Section 2.2. The median value of P(ASD) is then 0.060, with Q1 0.057, Q3 0.074, IQR 0.017, range 0.047-0.094, number of values 17.
For individual mental illnesses, values for P(MI|ASD) and P(MI) are quite variable due to heterogeneous populations, different diagnostic methods and diagnostic overshadowing. Average values for individual comorbid illness P(MI|ASD) and mental illness P(MI) are going to be very different due to the natural variation in prevalence of the different mental illnesses. The degree in which they are comorbid with ASD is going to vary, and there are different degrees and combinations of multiple comorbidities in individual patients. All these variables are integrated in the values of P(MI|ASD), P(ASD|MI) and P(MI) for overall female mental illness shown in Figure 6. The value of P(ASD) derived from the data for overall mental illness was 0.064. The mean for the other 16 measurements of P(ASD) was 0.064. This suggests the median of 6.0% and mean of 6.4% for the prevalence of female ASD are plausible.

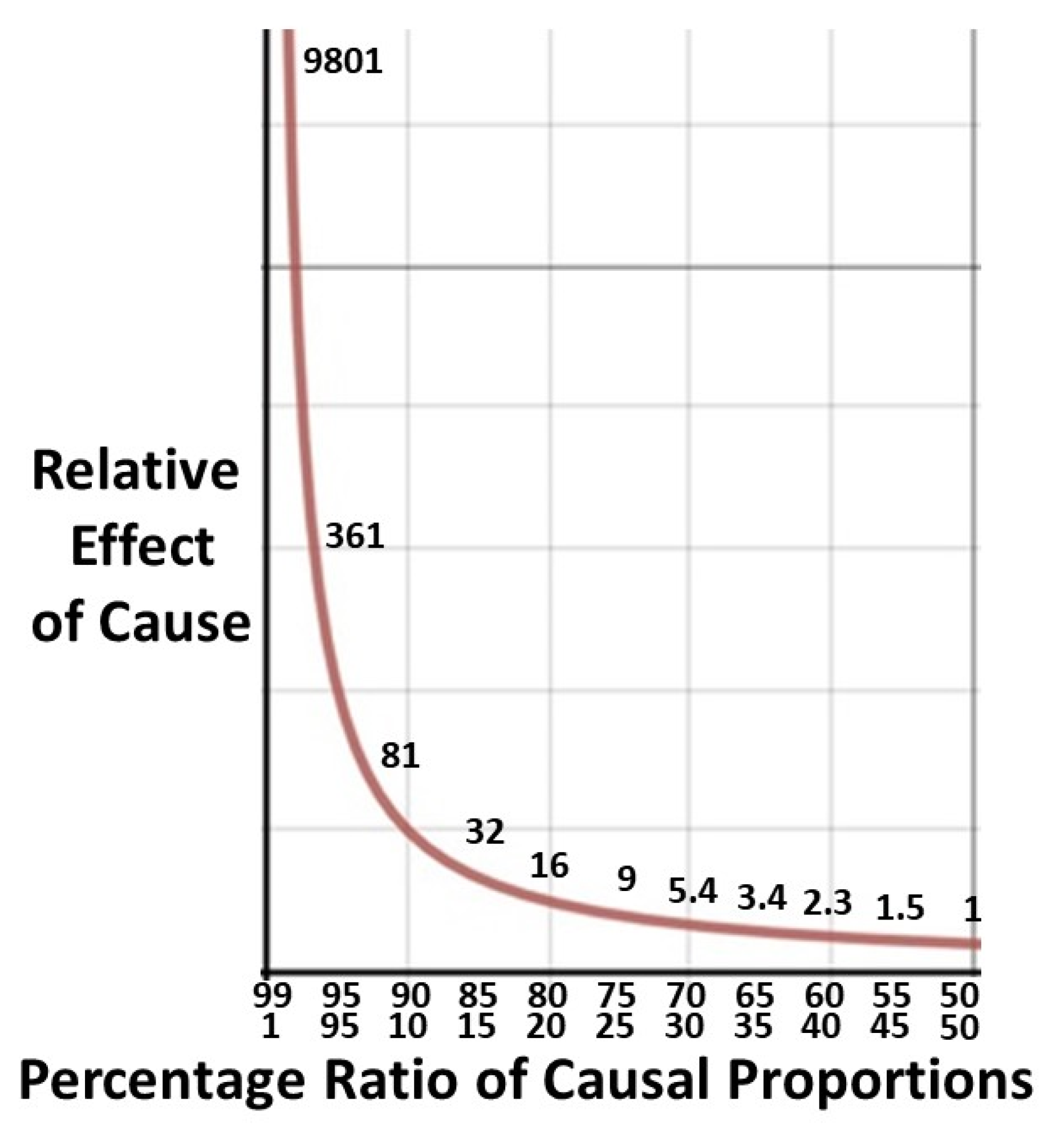
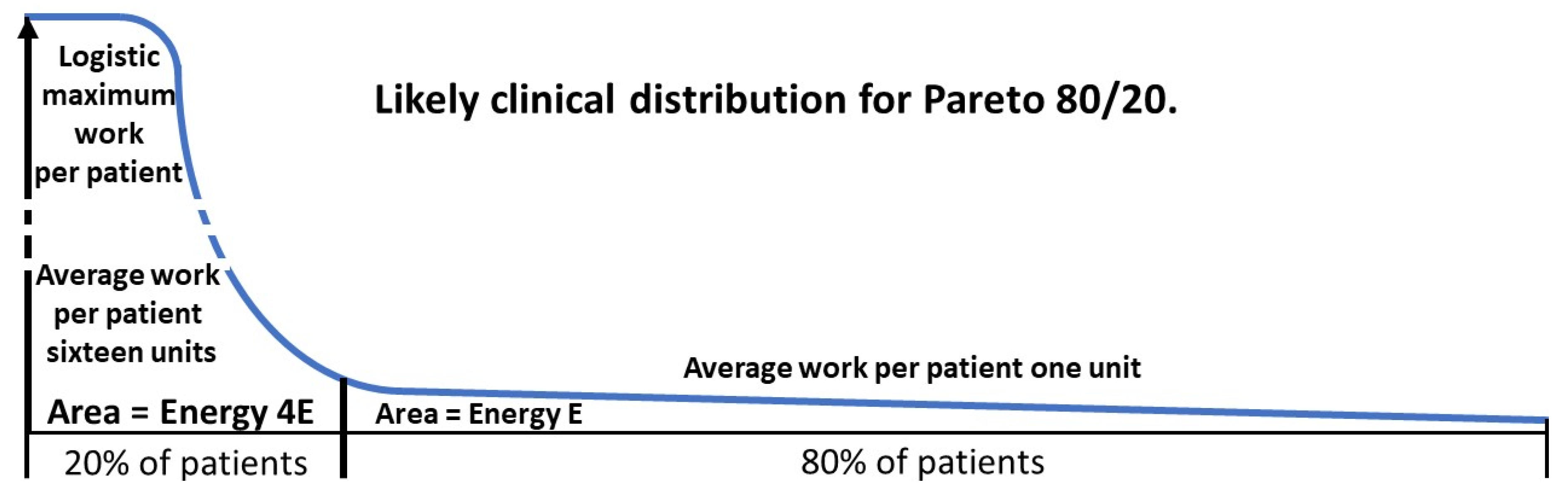
2.5. Degree of benefit: Pareto calculations.

2.5.1. The Pareto principle in health.

The Pareto principle is commonly called the 80/20 rule where 20% of the cause leads to 80% of the effect. While the variable strength of a particular cause will be a continuous power function, the division into 2 parts comparing the effect of the average of the strongest 20% of the cause to the average of the remaining 80% is a useful simplification. There may be multiple causes depending on the scenario but for the effect of ASD on female mental health we will consider ASD as a single cause. In mental health financial cost is a useful measure but is not necessarily the limiting variable. This is often a lack of trained staff poorly distributed in the population. A useful analogy for the drivers is the first law of thermodynamics. The amount of energy remains constant but can be moved around to do work. We will define a unit of energy as what is necessary to do the work to deliver a unit of service to an average patient in the less difficult group. This could equate to funding or performing a service. The two proportions do not have to be 80/20 and do not even have to add up to 100%. The Pareto principle is a useful simplification which seems to have wide application. We will now analyse why this might be so and apply it to health management.

2.5.2. Derivation of Pareto formulae.

The aim is to derive formulae to estimate the gain in system efficiency of management by treating the ASD of comorbid mental health patients in a manner empathetic to neurodiversity.
To examine the general case of the relation of 2 causal proportions let the higher patient proportion with the weaker average effect be p and the lower patient proportion with the stronger average effect be q. Proportion p of the patients requires proportion q of the energy so an average patient in group p uses q/p energy. An average patient in group q uses proportion p/q energy. Then the energy cost ratio of the average high work patient in group q to the average low work patient in group p is (p/q)/(q/p) or (p/q)2.
For the 80/20 rule the relative effect will be 16/1 (Figure 7). The Pareto principle is said to be an empirical rule but in biology there is a plausible reason why it is rarely higher, say 90/10. Due to the exponential nature of cause and effect for delivery of a costly labor intensive biological service there will be a logistical upper limit to the ratio. The absolute ceiling will be the most intensive inpatient care possible or its clinical equivalent in the system of interest. There is evidence intense limited medical services do obey the 80/20 ratio [39,76,77,78] and the p2/q2 ratio of 16/1 for the difficult 20% to the easier 80% reflects the logistic ceiling. The likely patient work distribution for a ratio of 80/20 is shown in Figure 8. Focusing on the needs of the high risk group is intuitively sensible but can be seen as inequitable if large numbers of patients get no care at all. We will show how to quantify its dramatic positive effect on the whole health system.
If we assume the energy cost of the service is the sum of the costs of individual consultations then the energy cost of the visits of the high work group q is:
q x p2/q2
p2/q
The energy cost of the visits of the low work group p is p x 1.
Total energy cost in groups p and q in units of the work per average patient in group p is:
p2/q + p
(p2 + pq)/q
p(p + q)/q (1)
In a typical current reasonably well functioning health system the limiting variable will be staff availability. Group q will have been triaged for treatment but there will be a long waiting list for inclusion in the less severely affected group p. Since ASD makes MI more difficult to treat, the comorbid patients will be distributed preferentially into the higher work group q. In calculating a formula for the distribution of the comorbid ASD patients in the entire p + q patients with a mental illness we will assume that on average the patients without ASD in each group, p and q, will require the same range of energy input as those with ASD. With overall P(ASD|MI) of nearly 20% it is likely that most of the patients in group q will have ASD. ASD should however be sought when assessing all MI patients since the patients in group p will also benefit. ASD does have continuous traits [79] which will be distributed over a number of further patients in both groups. These patients will also benefit from an empathetic approach to neurodiversity and contribute an extra unmeasured benefit to the final outcome.
We then start with p + q patients with a mental illness (MI):
Each group q patient needs p2/q2 units of work. Each group p patient needs one unit of work.
Let the proportion P(ASD|MI) with comorbid ASD be m.
Then the number of patients with ASD is m(p + q).
Let the proportions of patients with ASD in groups p and q be s/(r + s) and r/(r + s).
Then the total work required by ASD patients in group q is p2/q2 x m(p + q) x r/(r + s).
Then the total work required by ASD patients in group p is 1 x m(p + q) x s/(r + s).
Total work required for all comorbid ASD patients is:
p2/q2 x m(p + q) x r/(r + s) + 1 x m(p + q) x s/(r + s)
m(p +q) (p2r + q2s)/q2(r + s)
Let the fractional efficiency gain by treating ASD patients in an empathetic neurodiverse manner be e and assume this fraction applies at all degrees of severity. Then reduction in work needed (= energy saved) in units required to treat group p patients is:
em(p +q) (p2r + q2s)/q2(r + s) formula (2)
This energy can be used to service an extra em(p +q) (p2r + q2s)/ q2(r + s) patients in the low work category p providing there is no removal of energy from the system. The rule should be a guide to the redistribution of resources, not a way to reduce them. The exercise demonstrates that identifying ASD, especially in group q, gives a considerable positive opportunity dividend for therapy, where the clinical need far exceeds the resources.

2.5.3. A worked example.

We can use data from anorexia nervosa and overall female mental illness to derive an indicative overall energy benefit. The 80/20 rule does appear to approximately apply for AN. About 20% are refractory to treatment [80]. P(ASD|AN) is about 25% [13]. It is known that this group is more difficult to treat than AN alone [6,7,9,37,81]. Successful treatments for this group are being found (Section 3.2). A study [82] has shown managing diagnosed inpatient AN/ASD patients accounting for their neurodiversity saves 32.2% cost per patient. Then an indicative e is 0.322. We have 2 values for P(ASD|MI), 0.189 [69] and 0.176 (Section 2.2). The mean 0.1825 for m is also quite close to 20% and most comorbid patients are likely to be in Pareto group q. A reasonable starting point then for an indicative efficiency dividend would be with both p/q and r/s being 80/20.
Then energy saved in group p patient equivalents by formula (2) is:
0.322 x 0.1825 x 100(803 + 203)/202(100)
= 76.4
We have nearly doubled the number of low work patients treatable in female mental illness, where a proportion is comorbid with ASD, by recognizing the ASD and managing it appropriately. This is the substantial result of diagnosing a common unrecognized but treatable comorbidity (ASD) which caused significant management problems in the initial diagnosed mental illness. We might stretch the energy analogy to the second law of thermodynamics. We have reduced the entropy of the open system by improving efficiency and increasing order in the disordered minds of the patients by transforming ASD to ASC.

2.5.4. Downstream effects.

If a treatment gain is achieved there will be a major positive ripple effect due to significant improvement in personal, family and societal problems associated with unrecognized and undertreated mental illness. The ratio of direct treatment cost to overall societal cost for mental illness has been estimated to be about 4.7 [83]. We then find the total useful societal energy gain (“heat” loss foregone) is:
4.7em(p +q) (p2r + q2s)/q2(r + s)
For every 100 patients (p + q) we would divert enough energy to treat an extra 359 group p patients, though in practice most of the energy would be potential, appropriately preventing adverse consequences in the downstream community.
As an example of downstream savings Luca [66] found the average cost of an untreated postnatal depression mother/child dyad from conception to 5 years post-partum was $31,800. P(ASD|PND) from Section 2.2 is 0.313 so 31.3% of these dyads would be complicated by ASD. The societal ripple effect would give an extended average cost of 4.7 x 31,800 or $149,460 per dyad. We can calculate the overall savings achieved by screening for maternal ASD in the antenatal period. Assume the costs of no treatment have a Pareto distribution and let the low initial average cost for the mother/child dyad in group p over 5 years be z. The total cost of the patients p + q by formula (1) is:
zp(p + q)/q
The average dyad cost including ripple effect over 5 years is:
zp(p + q)/q(p + q)
zp/q
zp/q = 149,460
The proportion of patients with ASD is high at 31.3%. A realistic Pareto distribution would be p/q of 70/30. Then the low average extended cost z is $64,054. The therapeutic effect of a diagnosis for mother is probably going to be quite high. The child would also be assessed as having an increased probability of ASD, and if diagnosed would receive early intervention, so aiming for a 50% saving (e = 0.5) for comorbid dyads would probably be conservative. The proportion of ASD patients in group q is likely to be very high, say r/s in groups q and p respectively of 90/10 then by formula (2) cost saving as multiples of z is:
0.5 x 0.313 x 100(702 x 90 + 302 x 10)/(302 x 100)
76.685
Then total 5 year cost saving is $64,054 x76.685 ie $4,911,981 for every p + q patients, giving % saving:
100 x 4,911,981/14,946,000
32.9%
$49,120 per dyad.
The substantial overall saving across all dyads is because most of the ASD/PND dyads are in the high cost Pareto group q.
A 2023 paper on new screening recommendations for PND [84] describes PND as the leading cause of overall and preventable maternal mortality. This will obviously cause severe downstream effects. The paper lists several comorbid mental illnesses but does not mention autism.

3. Discussion.

3.1. Stumbling blocks.

In adults identification is not made and services are not accessed [85]. Neurotypical people tend to have less positive first impressions of autistic people [86], most commonly because they appear awkward and lacking in empathy. Health workers are not necessarily immune [6]. ASD should be considered a possible underlying condition in adult psychiatry. There is no easy way of ruling out ASD in this population [87,88]. For anxiety and depression more session time is needed. More medication is used in the ASD comorbid group implying unresponsiveness to talk therapy or more complexity [89].
Malik-Soni et al. [26] find transition to adult ASD services has the following multiple problems:
  • Services are accessed by only 1/5 of autistic youth.
  • About 70% of pediatricians do not support youth during the transition process and >50% of families lack information on how to proceed.
  • Little is still known about the effects of comorbid MI. Adult physicians need to monitor ongoing symptoms of ASD-which can intensify and diminish-to guide diagnosis and treatment choices.
  • Specific barriers include a shortage of health care services, poor physician knowledge, cost of services, lack of family and individual knowledge, stigma and language barriers.
We would add that language here refers to non-native speaking patients, and not double empathy problems with lack of mutual understanding in one’s “native” language.

3.2. A final word on conditional probability.

When searching on the internet for relevant ASD/mental illness conditional probabilities it was routinely found that the data were randomly transposed, or if the probability was unknown the transposed probability was reported. Truly useful information would be that no result could be found, rather than the ambiguous and confusing wrong information. This can potentially have unfortunate consequences. The proportion of female patients with anorexia nervosa believed to be autistic is well established to be about 20-30% [48,49] but this information is often given under a heading of the likelihood of developing AN if you are autistic. This could lead an autistic teenage girl to incorrectly believe she has a high chance of developing AN, the mental illness with the highest mortality [90], and only a 20% chance of complete recovery [91]. With a high level of anxiety and depression to deal with already this would not be helpful. The real likelihood is about 8% [13]. We can also surmise that the future is much more hopeful with the new information on the different causes of the comorbid AN [6,25,37] and the improved outcome with therapy recognizing neurodiversity [82]. Ironically the problem here is the unrecognized P(AN|ASD), the reverse of the usually unknown P((ASD|MI). The Dormouse, awakening from a 158 year hibernation, would no doubt be mortified to find that understanding of the logic has progressed not a whit. It needs to be continually reinforced [92].

3.3. Effective therapy.

The key to effective therapy is understanding neurodiversity. The key concept is that neurodiverse and neurotypical are just different ways of thinking. Neurodiverse is not inferior and only disabling due to mutual misunderstanding in an overwhelmingly neurotypical environment. Understanding neurodiversity is critical for helping autistic adults cope in all walks of life including health [93]. The World Health Organization definition of Health requires “a state of complete physical, mental and social wellbeing [94] …” This applies to both neurotypes. ASD does not meet the definition of health, but the definition should be accepted for ASC (Section 1.3). The neurodiverse minority is going to struggle in a predominantly neurotypical world so assistance must be twofold; to optimize social adaptation to that environment, but also to treat comorbid mental illness in a manner empathetic to neurodiversity. A healthy outcome does not however require conversion to a neurotypical mental state. Neurodiversity recognizes that disability needs attention, but also recognizes that in particular areas the neurodiverse can have great strengths [95], which can be empowering and thereby, if necessary, therapeutic. A recent Delphi study of management of comorbid ASD and anorexia nervosa emphasized the need to manage the individual in the context of ASD and that treatment goals should not aim to change autistic behaviors [96].
Rules for empathetic therapy include:
  • Recognize the centrality of the double empathy problem [97]. There are variations in empathy in autistic people and some can be quite empathetic [98].
  • Recognize that autistic people are often more deliberative and less intuitive than neurotypical individuals [99].
  • Cognitive behavior therapy can be adapted to the core features of ASD [100].
  • In designing therapy improvements researchers with lived experience of autism should be involved [101]. We would add autistic clinicians, patients and parents.
  • Specific areas for therapists listed by Gilmore et al. include [102]:
    • Be a change agent in the mental health workplace.
    • Make thoughtful language choices.
    • Individualize treatment.
    • Leverage patient strengths.
    • Agree on practical goals to navigate life situations.
We would add that a necessary corollary to individualizing treatment is individual treatment. Autistic people are often uncomfortable in a group and trying to stretch therapist resources is pointless if the therapy will not work.

3.4. The art of the possible.

We must trust that responsible governments will adopt a utilitarian approach and generally provide services doing the most good for the greatest number. To do this they require an evidence base, in particular if the service has received little attention in the past. “If you can’t measure it, you can’t manage it” is not strictly true [103], but if you want evidence-based policy it helps to provide quantitative evidence, otherwise governments have a tendency to find policy-based evidence [104], and the Dormouse will tell you that policy based on evidence and evidence based on policy are definitely not commutative.
If governments have evidence they tend to apply risk management. ASD is common in young women with mental health issues, a population at risk. The commonly occurring ASD increases the severity of their condition, and so the risk, the product of frequency and severity of outcome, is high. Since female ASD is cryptic the obvious next step is a screening process. There are effective screening mechanisms which can be incorporated in normal care [35] once the possibility of ASD has been recognized [2]. There is a clear road map for effective therapy (Section 3.3) and it is cost-effective (Section 2.5).
The neglect of female ASD in adult mental health has been due to inertia in knowledge transfer. There is no obvious political issue, and the solution lies within the health field itself. As the Pareto examination indicates, it is possible to achieve a significant improvement in mental health coverage without extra cost. If the knowledge is transferred the stumbling block will be training extra practitioners and getting them to go to the regions, but you have to start somewhere, and the following section shows how difficulties may be overcome with a bit of silo demolition.

3.5. It takes a village.

It takes a village to provide a safe, healthy environment for children [105]. The African proverb “It takes a village to raise a child” conveys the message that it takes many cooperating people to provide complete childcare. Two elements relevant to health are social connectedness where different agencies can cooperate, and the breaking down of siloes within the complex agencies of health delivery. This is much easier to achieve in…a village. Three examples follow from my own personal experience of rural pediatric practice. During a period as the sole pediatrician serving a rural population of about 50,000, about a third of my patients were seen for behavior problems alone and a further quarter had physical illnesses complicated by behavior problems. It was essential and not too difficult to get to know teachers, guidance officers, principals and education bureaucrats operating in the local provincial area. This was crucial for effective management of ASD, which was also my task to diagnose. It was easier to have a personal relationship with the local child protection service and have more influence in their decisions as the only pediatrician on their team. Health is notorious for siloes, but a common interest in preventing birthing disasters and ensuring optimal outcomes for mothers and babies led to a close working relationship with the local midwives. Considering the new knowledge regarding perinatal depression (Section 2.2), if midwives were screening for maternal ASD [35] a logical step forward would be to use local pediatric expertise to at least informally assess mothers. This would in turn improve the downstream pediatric care of the children. There is no reason why this could not extend to antenatal care. This would assist mothers during delivery with an autism friendly approach [35,106]. Even an informal diagnosis can be very therapeutic and would likely decrease the degree of depression. There is still likely to be a problem with allied health access ie psychology, speech therapy and occupational therapy, but there is evidence that telehealth is not inferior to face-to-face therapy [107]. Counterintuitively non-acute care delivered in a rural setting can often be superior to that in larger centers due to better interdisciplinary communication. It is also not fun transporting autistic children and adolescents to and from distant appointments. The value of a short and relatively relaxed drive to a free and available carpark should not be underestimated. Parents and patients love local care.

3.6. The long view.

There are too many stresses facing young people today. The year 2100 is often chosen to date catastrophic features of global heating. These outcomes, while scientifically well informed, are only predictions, but for teenage girls one realization is absolutely certain (Figure 9):
“If I decide to have a future family, in 2100 my kids will be the same age as my grandma is now, and I might still be around as well.”
World-wide or jurisdiction-wide stresses are beyond easy control, but managing the interacting effects of comorbid ASD is quite feasible at health service level with current techniques.
Financial resources and mental health therapist numbers are quite inadequate, and appropriate attention will free up therapy time to deal with more patients and reduce their intractable problems.
A recurring theme among patients and their parents is “they did not listen to me”. The mother of one of my patients said: “We have to learn to think aspie.” We all, especially if neurotypical, have to get better at listening, empathizing with the different mindset, and managing the problems but celebrating the benefits of neurodiversity [108].

4. Limitations

The experience of adult women in struggling to get a diagnosis of ASD and the evidence for extensive female camouflage makes it certain that the prevalence must be significantly higher than generally reported but there remains only the one bias-free estimate of 6%. When Bayes’ theorem is used with reliable estimates of mental illness prevalence in diagnosed ASD populations, it turns out that there is quite a lot of corroborating data. However estimates of P(MI|ASD) are heterogeneous with diagnostic overshadowing. Estimates of P(MI) are also heterogeneous with differing values due to diagnostic variation and the prevalence being different at different ages. Current results should be seen as indicative but it does seem likely that overall up to one in five women with a mental illness is autistic and this is not generally being managed.

5. Future Directions.

Refinement of diagnostic criteria will help quantify prevalence estimates.
Recent rapid advances in knowledge about female autism should help break down the transition barrier.
More work is needed to continue to improve talking therapies in mental illness with ASD.
Funding should follow quantitation of the risk of comorbid ASD to female mental health.
More examples of savings by managing comorbid ASD are needed.
The Pareto principle can be refined to quantify efficiency gains. Government tends to fund programs with evidence of success.

6. Conclusions.

  • The prevalence of ASD in female mental illness is high and ASD must be diligently sought both prior to and after the transition to adult care.
  • The solution to facilitating this transition lies within the health system in terms of establishing the extent of the problem and transmitting the information.
  • The overall risk in extent and severity of outcome is much higher than generally believed.
  • Necessary funding eventually follows convincing evidence.
  • Effective therapy is quite feasible. A lot of energy is being wasted on ineffective therapy due to the lack of an ASD diagnosis. That wasted energy can be redirected to effective modes of management with a consequent large positive effect on the relevant system.
  • The key to effective diagnosis and therapy is listening, understanding and empathizing with neurodiverse individuals.
  • The overall improvement in female mental health and prevention of the downstream effects of mental illness will be substantial.

Funding

The research received no external funding.

Institutional Review Board Statement

The data pertinent to the study was abstracted from peer reviewed published articles referenced in the text. It is completely deidentified and there are no ethical issues.

Institutional Review Board Statement

The data pertinent to the study was abstracted from peer reviewed published articles referenced in the text. It is completely deidentified and there are no ethical issues.

Informed Consent Statement

Not applicable.

Conflicts of Interest

The author declares no conflict of interest.

References

  1. Burrows, C.A.; Grzadzinski, R.L.; Donovan, K.; Stallworthy, I.C.; Rutsohn, J.; St. John, T.; Marrus, N.; Parish-Morris, J.; MacIntyre, L.; Hampton, J.; Botteron, K.N.; Dager, S.R.; Hazlett, H.C.; Pandey, J.S.; Shen, M.D,; Estes, A.M.; Pruett Jr., J.R.; Schultz, R.T.; Zwaigenbaum, L.; Truong, K.N.; Piven, J.; Elison, J.T. A data-driven approach in an unbiased sample reveals equivalent sex ratio of autism spectrum disorder–associated impairment in early childhood. Biol. Psychiatry. 2022; 92:654–662. [CrossRef]
  2. McCrossin, R. Finding the true number of females with autistic spectrum disorder by estimating the biases in initial recognition and clinical diagnosis. Children. 2022; 9:272. [CrossRef]
  3. Rodgaard, E-M.; Jensen, K.; Miskowiak, K.W.; Mottron L. Autism comorbidities show elevated female-to-male odds ratios and are associated with the age of first autism diagnosis. Acta Psychiatr. Scand. 2021; 144:475–486. [CrossRef]
  4. Gesi, C.; Migliarese, G.; Torriero, S.; Capellazzi, M.; Omboni, A.C.; Cerveri, G.; Mencacci, C. Gender differences in misdiagnosis and delayed diagnosis among adults with autism spectrum disorder with no language or intellectual disability. Brain Sci. 2021; 11:912. [CrossRef]
  5. Downs, J.M.; Lehler, S.; Dean, H.; Sears, N.; Patel, R.; Shetty, H.; Simonoff, E.; Hotopf, M.; Ford, T.J.; Diaz-Caneja, C.M.; Arango, C.; MacCabe, J.H.; Hayes, R.D.; Pina-Camacho, L. The association between comorbid autism spectrum disorders and antipsychotic treatment failure in early-onset psychosis: a historical cohort using electronic health records. J. Clin. Psychiatry. 2017; 78:e1233-e1241. [CrossRef]
  6. Kinnaird, E.; Norton, C.; Tchanturia, K. Clinicians’ views on working with anorexia nervosa and autism spectrum disorder comorbidity: a qualitative study. BMC Psychiatry. 2017; 17:292. [CrossRef]
  7. Kinnaird, E.; Oakley, M.; Lawrence, V.; Shergill, S.; Tchanturia, K. A peer interview qualitative study exploring support for carers of people with comorbid autism and eating disorders. J. Eat. Disord. 2021; 9:42. [CrossRef]
  8. Leppanen, J.; Sedgewick, F.; Halls D.; Tchanturia K. Autism and anorexia nervosa: Longitudinal prediction of eating disorder outcomes. Front. Psychiatry. 2022; 13:985867. [CrossRef]
  9. Nazar, B.P.; Peynenburg, V.; Rhind, C.; Hibbs, R.; Schmidt, U.; Gowers, S.; Macdonald, P.; Goddard, E.; Todd, G.; Micali, N.; Treasure J. An examination of the clinical outcomes of adolescents and young adults with broad autism spectrum traits and autism spectrum disorder and anorexia nervosa: a multi centre study. Int. J. Eat. Disord. 2018; 51:174–179. [CrossRef]
  10. El Baou, C.; Bell, G.; Saunders. R.; Buckman, J.E.J.; Mandy, W.; Dagnan, D.; O’Nions, E.; Pender, R.; Clements, H.; Pilling, S.; Richards, M.; John, A.; Stott, J. Effectiveness of primary care services for treating depression and anxiety in autistic adults in England: a retrospective, matched, observational cohort study of national health-care records. Lancet Psychiatry. 2023; 10: 944–54. [CrossRef]
  11. Secci, I.; Petigas, L.; Cuenod, A.; Klauser, P.; Kapp, C.; Novatti, A.; Armando, M. Case report: treatment-resistant depression, multiple trauma exposure and suicidality in an adolescent female with previously undiagnosed autism spectrum disorder. Front. Psychiatry. 2023; 14:1151293. [CrossRef]
  12. Cassidy, S.A.; Gould, K.; Townsend, E.; Pelton M.; Robertson, A.E.; Rodgers J. Is camouflaging autistic traits associated with suicidal thoughts and behaviours? Expanding the interpersonal psychological theory of suicide in an undergraduate student sample. J. Autism Dev. Disord. 2020; 50:3638–3648. [CrossRef]
  13. McCrossin, R. Finding the proportion of females with autistic spectrum disorder who develop anorexia nervosa, the true prevalence of female ASD and its clinical significance. Children. 2023; 1:272. [CrossRef]
  14. Yanai, I.; Lercher M. A hypothesis is a liability. Genome Biology. 2020; 21:231. [CrossRef]
  15. Hernan, M.A.; Greenland S. Why stating hypotheses in grant applications is unnecessary. JAMA. 2024; E1-E2. [CrossRef]
  16. Harmens, M.; Sedgewick, F.; Hobson, H. Autistic women’s diagnostic experiences: interactions with identity and impacts on well-being. Women’s Health. 2022; 18:1–11. [CrossRef]
  17. Bargiela, S.; Steward, R.; Mandy, W. The experiences of late-diagnosed women with autism spectrum conditions: an investigation of the female autism phenotype. J. Autism Dev. Disord. 2016; 46:3281–3294. [CrossRef]
  18. Hull, L.; Petrides, K.V.; Allison, C.; Smith, P.; Baron-Cohen, S.; Lai, M.C.; Mandy W. “Putting on my Best normal”: social camouflaging in adults with autism spectrum conditions. J. Autism Dev. Disord. 2017; 47:2519–2534. [CrossRef]
  19. Zubia, A.G.; y Carrillo Saucedo, I.C. Exploración del enmascaramiento en mujeres autistas y la presencia de sintomatología ansiosa y depresiva. Ehquidad. International Welfare Policies and Social Work Journal. 2023; 20:99-110. [CrossRef]
  20. Wing, L. Sex ratios in early childhood autism and related conditions. Psychiatry Research. 1981; 5:129-137. [CrossRef]
  21. Cage, E.; Troxell-Whitman, Z. Understanding the reasons, contexts and costs of camouflaging for autistic adults. J. Autism Dev. Disord. 2019; 49:1899–1911. [CrossRef]
  22. Jacobs, E.G. Bridging the neuroscience gender divide. Nature. 2023; 623:667. [CrossRef]
  23. Singer, J. ”why can’t you be normal for once in your life?” From a problem with no name to the emergence of a new category of difference. In: Corker M, French S. (eds). Disability Discourse. Buckingham, UK: Open University Press; 1999; 59-67.
  24. Mitchell, P.; Sheppard, E.; Cassidy S. Autism and the double empathy problem: implications for development and mental health. British Journal of Developmental Psychology. 2021; 39:1–18. [CrossRef]
  25. Babb, C.; Brede, J.; Jones, C.R.G.; Elliott, M.; Zanker, C.; Tchanturia, K.; Serpell, L.; Mandy, W.; Fox, J.R.E. ‘It’s not that they don’t want to access the support . . . it’s the impact of the autism’: The experience of eating disorder services from the perspective of autistic women, parents and healthcare professionals. Autism. 2021; 25:1409–1421. [CrossRef]
  26. Malik-Soni, N.; Shaker, A.; Luck, H.; Mullin, A.E.; Wiley, R.E.; Lewis, M.E.S.; Fuentes, J.; Frazier, TW. Tackling healthcare access barriers for individuals with autism from diagnosis to adulthood. Pediatric Research. 2022; 91:1028–1035. [CrossRef]
  27. Bernard, S.; Grosjean, B.; Caravallah, L. Neurodiversity and early autism. JAMA Pediatr. 2022; 176:1272-1273. [CrossRef]
  28. Hours, C.; Recasens, C.; Baleyte J-M. ASD and ADHD comorbidity: what are we talking about? Front. Psychiatry. 2022; 13:837424. [CrossRef]
  29. NICE guidelines 2022. www.nice.org.u,k/guidance/ng222. Accessed 01 November 2023.
  30. Zuckerbrot, R.A.; Cheung, A.; Jensen, P.S.; Stein, R.E.K.; Laraque D. Guidelines for adolescent depression in primary care (GLAD-PC): Part I. Practice preparation, identification, assessment, and initial management. Pediatrics. 2018; 141: e20174081. [CrossRef]
  31. Wiles, N.; Taylor, A.; Turner, N.; Barnes, M.; Campbell, J.; Lewis, G.; Morrison, J.; Peters, T.J.; Thomas, L.; Turner, K.; Kessler, D. Management of treatment-resistant depression in primary care: a mixed-methods study. Br. J. Gen. Pract. 2018; e673-e681. [CrossRef]
  32. White, M.J. Treatment-resistant depression: consider autism. Br. J. Gen. Pract. 2019; 14. [CrossRef]
  33. Chen, M-H. Postpartum depression and psychosis and subsequent severe mental illness in mothers and neurodevelopmental disorders in children. J. Clin. Psychiatry. 2021; 82:20m13735. [CrossRef]
  34. Scott, K.; Gregory, E.F.; Burrus, H.H. Addressing Maternal Mortality in the US—A Pediatrics Responsibility. JAMA. 2023; 329:1819-1820. [CrossRef]
  35. Fox, D. Exploring how health inequalities can be addressed through autism training and understanding in maternity services. MIDIRS Midwifery Digest. 2022; 32:279-282.
  36. Smith, S.; Woodside DB. Characterizing Treatment-Resistant Anorexia Nervosa. Front. Psychiatry. 2021; 11:542206. [CrossRef]
  37. Brede, J.; Babb, C.; Jones, C.; Elliott, M.; Zanker, C.; Tchanturia, K.; Serpell, L.; Fox, J.; Mandy, W, “For me, the anorexia is just a symptom, and the cause is the autism”: investigating restrictive eating disorders in autistic women. J. Autism Dev. Disord. 2020; 50:4280–4296. [CrossRef]
  38. Crone, C.; Fochtmann, L.J.; Attia, E.; Boland, R.; Escobar, J.; Formari, V.; Golden, N.; Guarda, A.; Jackson-Triche, M.; Manzo, L.; Mascolo, M.; Pierce, K.; Riddle, M.; Seritan, A.; Uniacke, B.; Zucker, N.; Yager, J.; Craig, T.; Hong, S-H.; Medicus J. The American Psychiatric Association practice guideline for the treatment of patients with eating disorders. Am. J. Psychiatry. 2023; 180:167-171. [CrossRef]
  39. Suran, M. Treating bipolar disorder is notoriously difficult, but research underway could lead to new options. JAMA. 2023; E1-E4. [CrossRef]
  40. Howes, O.D.; Thase, M.E.; Pillinger T. Treatment resistance in psychiatry: state of the art and new directions. Molecular Psychiatry. 2022; 27:58–72. [CrossRef]
  41. Leichsenring, F. Borderline personality disorder. A review. JAMA. 2023; 329:670-679. [CrossRef]
  42. D’Mello, A.M.; Frosch, I.R.; Li, C.E.; Cardinaux, A.L.; Gabrieli, J.D.E. Exclusion of females in autism research: empirical evidence for a “leaky” recruitment-to-research pipeline. Autism Research. 2022; 15:1929–1940. [CrossRef]
  43. Maenner, M.J.; Warren, Z.; Williams, A,R.; Amoakahene, E.; Bakian, A.V.; Bilder, DA. et al. Prevalence and characteristics of autism spectrum disorder among children aged 8 years: autism and developmental disabilities monitoring network, 11 sites, United States, 2020. MMWR Surveill. Summ. 2023; 72(2):1-14. [CrossRef]
  44. Koch, S.V.; Larsen, J.T.; Mouridsen, S.E.; Bentz, M.; Petersen, L.V.; Bulik, C.; Mortensen, P.B.; Plessen, K.J. Autism spectrum disorder in individuals with anorexia nervosa and in their first- and second-degree relatives: Danish nationwide register-based cohort-study. Br. J. Psychiatry. 2015; 206:401–407. [CrossRef]
  45. Martini, M.I.; Kuja-Halkola, R.; Butwicka. A.; Du Rietz, E.; D’Onofri, B.M.; Happé, F.; Kanina, A.; Larsson, H.; Lundström, S.; Martin, J.; Rosenqvist, M.A.; Lichtenstein, P.; Taylor, M.J. Sex differences in mental health problems and psychiatric hospitalization in autistic young adults. JAMA Psychiatry. 2022; 79:1188-1198. [CrossRef]
  46. Carroll, L. Alice’s Adventures in Wonderland. 1st ed. London: Macmillan and Co; 1866.
  47. Solmi, M.; Radua, J.; Olivola, M.; Croce, E.; Soardo, L.; de Pablo, G.S.; Shin, J.I.; Kirkbride, J.B.; Jones, P.; Kim, J.H.; Kim, J.Y.; Carvalho, A.F.; Seeman, M.V.; Correll, C.U.; Fusar-Poli, P. Age at onset of mental disorders worldwide: large-scale metaanalysis of 192 epidemiological studies. Molecular Psychiatry. 2022; 27:281–295. [CrossRef]
  48. Westwood, H.; Tchanturia K. Autism spectrum disorder in anorexia nervosa: an updated literature review. Curr. Psychiatry Rep. 2017; 19:41. [CrossRef]
  49. Pruccoli, J.; Solari, A.; Terenzi, L.; Malaspina, E.; Angotti, M.; Pignataro, V.; Gualandi, P.; Sacrato, L.; Cordelli, D.M.; Franzoni, E, Parmeggiani, A. Autism spectrum disorder and anorexia nervosa: an Italian prospective study. Ital. J. Pediatr. 2021; 47:59. [CrossRef]
  50. Margari, L.; Palumbi, R.; Peschechera, A.; Craig, F.; de Giambattista, C.; Ventura, P.; Margari, F. Sex-gender comparisons in comorbidities of children and adolescents with high functioning autism spectrum disorder. Front. Psychiatry. 2019; 10:159. [CrossRef]
  51. Rapoport, J.; Chavez, A.; Greenstein, D.; Addington A.; Gogtay N. Autism spectrum disorders and childhood onset schizophrenia: clinical and biological contributions to a relationship revisited. J. Am. Acad. Child Adolesc. Psychiatry. 2009: 48:10-16. [CrossRef]
  52. Kincaid, D.L.; Doris, M.; Shannon, C.; Mulholland, M. What is the prevalence of autism spectrum disorder and ASD traits in psychosis? A systematic review, Psychiatry Research. 2017; 250:99-105. [CrossRef]
  53. Zheng, Z.; Zheng, P.; Zou X. Association between schizophrenia and autism spectrum disorder: a systematic review and meta-analysis. Autism Res. 2018; 11:1110-1119. [CrossRef]
  54. Li, X.; Zhou, W.; Yi, Z. A glimpse of gender differences in schizophrenia. General Psychiatry. 2022; 35:e100823. [CrossRef]
  55. Marin, J.L.; Rodriguez-Franco, M.A.; Chugani, V,M.; Maganto, M.M.; Villoria, E.D.; Bedia RC. Prevalence of schizophrenia disorders in average-IQ adults with autism-spectrum disorders: a meta-analysis. J. Autism Dev. Disord. 2018; 48:239-250. [CrossRef]
  56. Rees, E.; Creeth, H.D.J.; Hwu, H-G.; Chen, W.J.; Tsuang, M.; Glatt, S.J.; Rey, R.; Kirov, G.; Walters, J.T.R.; Holmans, P.; Owen, M.J.; O’Donovan, M.C. Schizophrenia, autism spectrum disorder sand developmental disorders share specific disruptive coding mutations. Nature Communications. 2021; 1-9. [CrossRef]
  57. Hofvander, B.; Delorme, R.; Chaste, P.; Nydén, A.; Wentz, E.; Ståhlberg, O.; Herbrecht, E.; Stopin, A.; Anckarsäter, H.; Gillberg, C.; Rastam, M.; Leboyer M. Psychiatric and psychosocial problems in adults with normal-intelligence autism spectrum disorders. BMC Psychiatry 2009; 9:35. [CrossRef]
  58. Kirsch, A.C.; Huebner, A.R.S.; Mehta, S.Q.; Howie, F.R.; Weaver, A.L.; Myers, S.M.; Voigt, R.G.; Katusic, S.K. Association of comorbid mood and anxiety disorders with autism spectrum disorder. JAMA Pediatr. 2020; 174:63-70. [CrossRef]
  59. Pezzimenti, F.; Han, G.T.; Vasa, R.A.; Gotham K. Depression in youth with autism spectrum disorder. Child Adolesc. Psychiatr. Clin. N. Am. 2019; 28:397–409. [CrossRef]
  60. Hudson, C.C.; Hall, L.; Harkness, K.L. Prevalence of depressive disorders in individuals with autism spectrum disorder: a meta-analysis. J. Abnorm. Child Psychol. 2019; 47:165-175. [CrossRef]
  61. Croen, L.; Zerbo, O.; Qian, Y.; Massolo, M.L.; Rich, S.; Sidney, S.; Kripke C. The health status of adults on the autistic spectrum. Autism. 2015; 19:814-823. [CrossRef]
  62. Martin, A.F.; Jassi, A.; Cullen, A.E.; Broadbent, M.; Downs, J.; Krebs G. Co-occurring obsessive–compulsive disorder and autism spectrum disorder in young people: prevalence, clinical characteristics and outcomes. European Child Adolescent Psychiatry. 2020; 29:1603–1611. [CrossRef]
  63. Fawcett, E.J.; Power, H.; Fawcett, J.M. Women are at greater risk of OCD than men: a meta-analytic review of OCD prevalence worldwide. J. Clin. Psychiatry. 2020; 23:19r13085. [CrossRef]
  64. McLean, C.P.; Asnaani, A.; Litz, B.T.; Hofmann, S.G. Gender differences in anxiety disorders: prevalence, course of Illness, comorbidity and burden of illness. J. Psychiatr. Res. 2011; 45: 1027–1035. [CrossRef]
  65. Pohl, A.L.; Crockford, S.K.; Blakemore, M.C.; Allison, C.; Baron-Cohen, S. A comparative study of autistic and nonautistic women’s experience of motherhood. Molecular Autism. 2020; 11:3. [CrossRef]
  66. Luca, D.L.; Margiotta, C.; Staatz, C.; Garlow, E.; Christensen, A.; Zivin, K. Financial toll of untreated perinatal mood and anxiety disorders among 2017 births in the United States. Am. J. Public Health. 2020; 110:888–896. [CrossRef]
  67. Olff, M. Sex and gender differences in post-traumatic stress disorder: an update. European Journal of Psychotraumatology. 2017; 8:sup4, 1351204. [CrossRef]
  68. Rumball, F.; Happe, F.; Grey N. Experience of trauma and PTSD symptoms in autistic adults: risk of PTSD development following DSM-5 and non-DSM-5 traumatic life events. Autism Res. 2020; 13:2122-2132. [CrossRef]
  69. Nyrenius, J.; Eberhard, J.; Ghaziuddin, M.; Gillberg, C.; Billstedt, E. Prevalence of Autism Spectrum Disorders in Adult Outpatient Psychiatry. J. Autism Dev. Disord. 2021; 52:3769-3779. [CrossRef]
  70. LeCavalier, L.; McCracken, C.E.; Aman, M.G.; McDougle, C.J.; McCracken, J.; Tierney, E.; Smith, T.; Johnson, C.; King, B.; Handen, B.; Swiezy, N.B.; Arnold, L.E.; Bearss, K.; Vitiello, B.; Scahill, L. An exploration of concomitant psychiatric disorders in children with autism spectrum disorder. Comprehensive Psychiatry. 2019; 88:57–64. [CrossRef]
  71. Lever, A.G.; Geurts, H.M. Psychiatric co-occurring symptoms and disorders in young, middle-aged, and older adults with autism spectrum disorder. J. Autism Dev. Disord. 2016; 46:1916–1930. [CrossRef]
  72. National Institute of Mental Health: Statistics 2021. https://www.nimh.nih.gov/health/statistics. Accessed 01 November 2023.
  73. Kalb, L.G.; Contractor, A.; Engel C. Advancing Collaborative Care for Autistic Children and Adolescents. JAMA Pediatrics. 2023; 177:1125-1126. [CrossRef]
  74. Kolves, K.; Fitzgerald, C.; Nordentoft, M.; Wood, S.J.; Erlangsen, A. Assessment of suicidal behaviors among individuals with autism spectrum disorder in Denmark. JAMA Network Open. 2021; 4:e2033565. [CrossRef]
  75. Ryan, E.P.; Oquendo, M.A. Suicide risk assessment and prevention: Challenges and opportunities. Focus (Am. Psychiatr. Publ.). 2020; 18:88-99. [CrossRef]
  76. Krieg, C.; Hudon, C.; Chouinard, M-C.; Dufour, I. Individual predictors of frequent emergency department use: a scoping review. BMC Health Services Research. 2016; 16:594. [CrossRef]
  77. Naoum,V.; Kyriopoulos, D.; Charonis, A.; Athanasakis, K. Kyriopoulos, J. The Pareto principle (“80−20 rule”) in healthcare services in Greece PHS82. Value In Health. 2016; 19:A618. [CrossRef]
  78. Hardtstock, F.; Knapp, R.; Maywald, U.; Wilke, T. Health care spending and the Pareto principle -the minority that causes the majority. Value in Health 2020; PM;U8, S604.
  79. Bralten, J.; van Hulzen, K.L.; Martens, M.B, Galesloot, T.L.; Arias Vasquez, A.; Kiemeney, L.A.; Buitelaar, J.K.; Muntjewerff, J.W.; Franke, B.; Poelmans, G. Autism spectrum disorders and autistic traits share genetics and biology. Molecular Psychiatry. 2018; 23:1205–1212. [CrossRef]
  80. Karazewska, D.; Cleintuar, P.; Oudijn, M.; Lok, A, van Elburg, A.; Denys, D.; Mocking R. Efficacy and safety of deep brain stimulation for treatment refractory anorexia nervosa: a systematic review and metaanalysis. Translational Psychiatry. 2022: 12:333. [CrossRef]
  81. Babb, C.; Brede, J.; Jones, C.R.G.; Serpell, L.; Mandy, W.; Fox J. A comparison of the eating disorder service experiences of autistic and non-autistic women in the UK. European Eating Disorders Review. 2022; 30:616–627. [CrossRef]
  82. Tchanturia, K.; Dandil, Y.; Li, Z.; Smith, K.; Leslie, M.; Byford, S. A novel approach for autism spectrum condition patients with eating disorders: analysis of treatment cost savings. Eur. Eat. Disorders Rev. 2020; 1–5. [CrossRef]
  83. Taylor, H.L.; Menachemi, N.; Gilbert, A.; Chaudhary, J.; Blackburn, J. Economic burden associated with untreated mental illness in Indiana. JAMA Health Forum. 2023; 4:e233535. [CrossRef]
  84. Moore Simas, T.A.; Whelan, A.; Byatt N. Postpartum depression-new screening recommendations and treatments. JAMA. 2023; E1-E2. [CrossRef]
  85. O’Nions, E.; Petersen, I.; Buckman, J.E.J.; Charlton, R.; Cooper, C.; Corbett, A.; Happé, F.; Manthorpe, J.; Richards, M.; Saunders, R.; Zanker, C.; Mandy, W.; Stott, J. Autism in England: assessing underdiagnosis in a population based cohort study of prospectively collected primary care data. The Lancet Regional Health – Europe. 2023; 29: 100626. [CrossRef]
  86. Alkhaldi, R.S.; Sheppard. E.; Burdett, E.; Mitchell, P. Do neurotypical people like or dislike autistic people? Autism In Adulthood. 2021; 3:275-279. [CrossRef]
  87. Ribolsi, M.; Nastro, F.; Pelle, M.; Medici, C.; Sacchetto, S.; Lisi, G.; Riccioni, A.; Siracusano, M.; Mazzone, L.; Di Lorenzo, G. Recognizing Psychosis in Autism Spectrum Disorder. Front. Psychiatry. 2022; 13:768586. [CrossRef]
  88. Nyrenius, J.; Eberhard, J.; Ghaziuddin, M.; Gillberg, C.; Billstedt, E. The ‘lost generation” in adult psychiatry: psychiatric, neurodevelopmental and sociodemographic characteristics of psychiatric patients with autism unrecognized in childhood. B. J. Psych. Open. 2023; 9:e89. [CrossRef]
  89. Maddox, B.B.; Gaus, V.L. Community mental health services for autistic adults: good news and bad news. Autism In Adulthood. 2019; 1. [CrossRef]
  90. Auger, N.; Potter, B.J.; Ukah, U.V.; Low, N.; Israel, M.; Steiger, H.; Healey-Profitos, J.; Paradis, G. Anorexia and the long-term risk of mortality in women. World Psychiatry. 2021; 20:448-449. [CrossRef]
  91. Accurso, E.C.; Sim, L.; Muhlheim, L.; Lebow, J. Parents know best: caregiver perspectives on eating disorder recovery. Int. J. Eat. Dis. 2019; 53:1252-1260. [CrossRef]
  92. Hicks, T.; Buckleton, J.; Castella, V.; Evett, I.; Jackson, G. A logical framework for forensic DNA Interpretation. Genes. 2022; 13:957. [CrossRef]
  93. Doyle, N. Neurodiversity at work: a biopsychosocial model and the impact on working adults. British Medical Bulletin. 2020; 135:108–125. [CrossRef]
  94. Lewis DM. WHO definition of health remains fit for purpose. BMJ. 2011; 343:d5357. [CrossRef]
  95. Pellicano, E.; den Houting, J. Annual Research Review; Shifting from ‘normal science’ to neurodiversity in autism science. J. Child Psychology Psychiatry. 2021; 63:381-396. [CrossRef]
  96. Field, S.L.; Fox, J.R.E.; Jones, C.R.G.; Williams, M.O. “Work WITH us”: a Delphi study about improving eating disorder treatment for autistic women with anorexia nervosa. J. Eat. Disord. 2023; 11:17. [CrossRef]
  97. López, B. Commentary on autism and the double-empathy problem: implications for development and mental health. Br. J. Dev. Psychol. 2022; 40:368–370. [CrossRef]
  98. Hume, R.; Burgess H. ‘‘I’m human after all’’: autism, trauma, and affective empathy. Autism In Adulthood. 2021; 3:221-229. [CrossRef]
  99. Brosnan, M.; Ashwin, C. Thinking, fast and slow on the autism spectrum. Autism. 2023; 27:1245–1255. [CrossRef]
  100. Spain, D.; Happé, F. How to optimise cognitive behaviour therapy (CBT) for people with autism spectrum disorders (ASD): a Delphi study. Journal of Rational-Emotive & Cognitive-Behavior Therapy. 2020; 38:184–208. [CrossRef]
  101. Riches, S.; Hammond, N.; Bianco, M.; Fialho, C.; Acland, J. Adapting cognitive behaviour therapy for adults with autism: a lived experience-led consultation with specialist psychological therapists. The Cognitive Behaviour Therapist. 2023; 16:e13, page 1-12. [CrossRef]
  102. Gilmore, D.; Longo, A.; Krantz, M.; Radford, D.; Hand, B.N. Five ways providers can improve mental healthcare for autistic adults: a review of mental healthcare use, barriers to care, and evidence-based recommendations. Current Psychiatry Reports. 2022; 24:565–571. [CrossRef]
  103. Berenson, R.A. If you can’t measure performance, can you improve it? JAMA Forum. 2016; 315:645-646. [CrossRef]
  104. Marmot, M. Evidence based policy or policy based evidence? BMJ. 2004; 328:906-907. [CrossRef]
  105. Reupert, A.; Straussner, S.L.; Weimand, B.; Maybery, D. It takes a village to raise a child: understanding and expanding the concept of the “Village”. Front. Public Health. 2022; 10:756066. [CrossRef]
  106. King, S.L. How do maternity services support autistic women and birthing people now? What improvements could be made to help autistic people who are pregnant and giving birth and the staff who support them? MIDIRS Midwifery Digest. 2022; 32:283-288.
  107. de Nocker, Y.L.; Toolan, C.K. Using telehealth to provide interventions for children with ASD: a systematic review. Rev. J. Autism Dev. Disord. 2023; 10:82–112. [CrossRef]
  108. Pellicano, E.; Heyworth M. The foundations of autistic flourishing. Curr. Psychiatry Rep. 2023; 25:419-427. [CrossRef]
Preprints 99582 g001
Figure 1. Cumulative total from Pubmed search for camouflage papers 26 June 2023.
Figure 1. Cumulative total from Pubmed search for camouflage papers 26 June 2023.
Preprints 99582 g001
Preprints 99582 g002
Figure 2. Age at diagnosis of female ASD in a community referred pediatric clinic.
Figure 2. Age at diagnosis of female ASD in a community referred pediatric clinic.
Preprints 99582 g002
Preprints 99582 g003
Figure 3. From A Mad Tea Party: Alice’s Adventures in Wonderland.
Figure 3. From A Mad Tea Party: Alice’s Adventures in Wonderland.
Preprints 99582 g003
Preprints 99582 g004
Figure 4. Venn diagram of Bayes’ theorem for ASD and mental illness (MI).
Figure 4. Venn diagram of Bayes’ theorem for ASD and mental illness (MI).
Preprints 99582 g004
Preprints 99582 g005
Figure 5. Indicative first and mean onset of mental illnesses in the pediatric age group.
Figure 5. Indicative first and mean onset of mental illnesses in the pediatric age group.
Preprints 99582 g005
Preprints 99582 g006
Figure 6. Three dimensional Euler diagram and cross section of female population prevalences.
Figure 6. Three dimensional Euler diagram and cross section of female population prevalences.
Preprints 99582 g006
Preprints 99582 g007
Figure 7. Curve of Cause and Effect.
Figure 7. Curve of Cause and Effect.
Preprints 99582 g007
Preprints 99582 g008
Figure 8. Work per patient distribution.
Figure 8. Work per patient distribution.
Preprints 99582 g008
Preprints 99582 g009
Figure 9. Indicative Proportions for Mood Disorders and ASD.
Figure 9. Indicative Proportions for Mood Disorders and ASD.
Preprints 99582 g009
Table 1. Summary of P(ASD|MI) values.
Table 1. Summary of P(ASD|MI) values.
Condition P(ASD|MI) References Given value or Bayes’ calculation
Anorexia Nervosa 0.2-0.3 48 Given
0.23 49 Given
Schizophrenia Spectrum D 0.43 2,52,53,54,55 Bayes’ probability
Borderline Personality D 0.146 57 Given
Bipolar Disorder 0.272 13,58 Bayes’ odds
Depression 0.127 13,58 Bayes’ odds
0.144 13,59 Bayes’ probability
0.203 13,60 Bayes’ odds
Anxiety Disorders 0.157 13,58 Bayes’ odds
0.170 13,61 Bayes’ odds
Obsessive Compulsive D 0.232 62 Given
Social Anxiety D 0.262 2,64 Bayes’ probability
Postnatal Depression 0.313 2,65,66 Bayes’ probability
Post Traumatic Stress D 0.30 2,67,68 Bayes’ probability
Any Mental Illness 0.189 69 Given
0.176 2,70-72 Bayes’ probability
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated