Prerpints.org logo
Preprint
Article

Optimization and Performance Analysis of CAT Method for DNA Sequence Similarity Searching and Alignment

Altmetrics

Downloads

158

Views

51

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

18 February 2024

Posted:

19 February 2024

You are already at the latest version

Alerts
Abstract
Bioinformatics is a rapidly developing field enabling scientific experiments through computer models and simulations. Considering the vast databases of biological data available, it is ex-tremely important to develop efficient methods and algorithms for their processing. Sequence comparison is the best method for studying the evolutionary interaction between genes. It is based on alignment – the process of arranging two or more sequences to achieve the maximum level of identity and degree of similarity. The paper presents a new version of the algorithm for pairwise DNA sequences alignment, based on a new method called CAT, where a dependency with a previous match and the closes neighbor are taken in consideration to increase uniqueness of the CAT profile and to reduce possible collisions, i.e. two or more sequence having same CAT profiles. This makes proposed algorithm suitable for finding exact match of a concrete DNA se-quence in a big set of DNA data faster. The generation of CAT profiles is made once before data has been uploaded to the database, allowing the profiles to be used as metadata for the sequenc-es. It consists of an algorithm to calculate a CAT profile against the selected reference sequences and an algorithm to compare two sequences based on the calculated CAT profiles. Improve-ments in generation of the CAT profiles, are detailed described in the paper. Block scheme, pseudo code tables and figures were updated according to the proposed new version and ex-perimental results. Experiments have been carried out with the new version of the method and different datasets to align DNA sequences based on the CAT method. New experimental results in terms of collisions, speed, and efficiency of the proposed solutions are presented. Experiments related to the performance comparison with Needleman-Wunsch were re-executed with the new version of the algorithm to confirm that we have the same performance. An analysis of the per-formance of the proposed CAT based algorithm against Knuth–Morris–Pratt algorithm, which has a complexity of O(n) and is one of the most widely used for searching biological data, was performed. The impact of prior matching dependencies on uniqueness for generated CAT pro-files is investigated. The analysis of the experimental results obtained by sequence alignment shows a small deviation of the proposed algorithm based on the CAT method, which can be ig-nored if this deviation is acceptable at the expense of performance. The time efficiency of the CAT algorithm remains constant, regardless of the length of the sequences. Therefore, the ad-vantage of the proposed method is its fast processing in the alignment of large sequences, for which the execution of the exact algorithms takes a long time. The example code realization of the CAT Method, under the protection of the GNU General Public License v3.0, can be accessed on GitHub at: https://github.com/HristoS/CATSequenceAnalysis.
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Science

1. Introduction

The development of technologies for generating biological data - sequencers that generate genetic data - leads to the accumulation of a large volume of data. We are witnessing an explosion in the amount of data available in bioinformatics due to the rapid progress of high-throughput sequencing projects. An unprecedented amount of data is generated daily, containing clinical reports, genome sequences, gene expression profiles, biomedical literature reports, medical images, and sensor data. For example, the European Bioinformatics Institute maintains approximately 390 petabytes of raw storage data—gene, protein, and small molecule data [1]. With this exponential data growth, applications for the analysis of multiple biological data, such as sequence alignment, assembly of the genome, single nucleotide polymorphism detection and genome-wide association studies. Many of these applications have several characteristics in common: 1) the massive amount of data that is generated in sequencing centers; 2) extremely long processing time, for example the genome assembly tool SOAPdenovo [2] takes several days consuming hundreds of GB of memory to complete the construction of a single human genome; and 3) application dependency - in order to obtain the final result from which useful knowledge can be extracted, it is necessary to perform various processing steps, resulting in significant costs added due to data transmission.
In biology, it is necessary to understand how similar two sequences are to each other, for example sequences of amino acids making up a protein molecule or sequences of nucleic acids in a DNA molecule. In bioinformatics, a computer model is built of the DNA molecule, which is represented as a string of four-letter alphabets, and of the protein molecule, which is represented as a string of 20-letter alphabets. The nucleotide or protein sequences being compared are usually represented as rows in a matrix. Gaps are inserted between residues so that identical or similar characters are arranged in consecutive columns.
Sequence comparison is the best method for studying the evolutionary interaction between genes. It is based on alignment - the process of aligning two or more sequences to achieve the maximum level of identity (for evaluation purposes), degree of similarity and possibility of homology. Sequence alignment algorithms are used to compare and search DNA or protein databases. They have become one of the most powerful techniques to help determine the biological functions of a given gene or the protein it encodes. The main stream of searchable information in such a database is in the form of raw nucleotide or protein sequence. Therefore, to obtain information about a new biological sequence, one of the first steps is to compare it with a group of already known ones contained in a database. The results often suggest functional, structural, or evolutionary analogs between the sequences.
A critical aspect of biological data processing involves identifying homologous sequences in databases. Although algorithms like Needleman-Wunsch [3], Smith-Waterman [4] and Knuth-Morris-Pratt [5] accurately measure similarity between two sequences, applying them to large datasets is time-consuming. To expedite searches in substantial databases, researchers employ heuristic methods and algorithms, which, while accelerating search times, may compromise result quality. FASTA, a software package for DNA and protein sequence alignment, introduces heuristic methods for querying entire databases. BLAST, a widely used sequence search tool [6,7], employs a faster heuristic algorithm than optimal alignment approaches, enhancing search efficiency without sacrificing sensitivity.
A metaheuristic method for multiple sequence alignment involves generating a favorite sequence, serving as a benchmark for comparing all other sequences in the database [8]. Challenges arise applying this approach, when introducing new data or removing existing records:
  • When data changes, the favorite sequence requires recalculation.
  • Re-comparing each database sequence with the updated favorite sequence consumes computational time and resources.
  • Each database has a distinct favorite sequence, complicating the merging of databases, particularly in extensive datasets with diverse structures and access methods.

1.1. Proposed Research Objectives

In seeking to enhance existing heuristic algorithms, our research aims to introduce improvements in three key areas:

1.1.1. Constant Favorite Sequence:

We aim to devise a method for establishing a constant favorite sequence, independent of the data in the database, ensuring that it remains unchanged even when the database undergoes modifications. This approach seeks to provide stability in sequence alignment, mitigating the need for frequent recalculations of the favorite sequence.

1.1.2. Minimizing Comparisons with Favorite Sequence:

Our research endeavors to reduce the number of comparisons with the favorite sequence during the database search. Typically, each sequence involves a complex comparison algorithm against the favorite sequence. By optimizing this process, we intend to enhance the efficiency of the alignment process, making it more resource effective.

1.1.3. Unification of Sequence Favorites across Databases:

To address challenges in database merging, we propose a unified approach to sequence favorites. This involves developing a method to unify sequence favorites for all databases, ensuring compatibility and coherence in large-scale data scenarios. This unification aims to streamline the management and analysis of biological data across diverse databases.

1.2. Research Purpose and Methodology

The overarching purpose of this research is to introduce a novel algorithm for pairwise DNA sequence alignment. Our approach leverages a new, efficient, and unified method for DNA sequence alignment, employing the trilateration method. The primary goal is to offer solutions to three fundamental issues in biological sequence alignment:
(1) Constant Favorite Sequence: Introduce a methodology to create a stable and constant favorite sequence, reducing the need for frequent recalculations.
(2) Reduced Comparisons with Favorite Sequence: Develop strategies to minimize the number of comparisons with the favorite sequence during the alignment process, enhancing computational efficiency.
(3) Unified Favorite Sequences: Propose a method to unify favorite sequences across all databases, providing a standardized approach to sequence alignment in diverse data environments.
Through this comprehensive approach, we aim to contribute to the advancement of bioinformatics methodologies, addressing key challenges in DNA sequence alignment. The research included in this article is an extension of the research presented in [9].
The paper introduces an enhanced version of the CAT algorithm for pairwise DNA sequence alignment, incorporating novel elements that consider dependencies on previous matches and proximity to the closest neighbor. These adjustments aim to augment the distinctiveness of the CAT profiles and minimize potential collisions, where two or more sequences share identical CAT profiles. Such advancements render the revised algorithm more efficient for accurately identifying exact matches within extensive DNA datasets quickly. The improvements made to the CAT profile generation process are elaborated. Changes are in the first stage of the calculation of the CAT profiles, and they do not affect the second stage, which is the actual comparison.
New results from the same experiments are exposed. With the new version, all experiments related to the examination of collisions are re-executed; no collisions are found, and some of the figures in the original article became redundant and were removed. Block scheme, pseudocode, tables, and figures are updated according to the proposed new version and experimental results. Additionally, the paper presents experimental results derived from applying this updated version of the CAT method across various datasets for DNA sequence alignment.
The following sections of the research will delve into the specific methodologies, results, and conclusions related to each of these proposed improvements.

2. Materials and Methods

2.1. Methods and Alorithms for Sequence Alignment

String alignment algorithms are widely used in bioinformatics to compare DNA sequences. The pattern of a particular DNA sequence in the form of a character string is compared or searched against other sequences to find similarity [10]. Thus, the pattern is matched to the large amount of DNA sequences, which are sometimes very complex and not easy to extract. In order to obtain a result or matching pattern with greater accuracy, algorithms such as Knuth-Morris-Pratt, Boyer-Moore, Brute Force, Rabin-Karp [11] and other algorithms are used.
A number of studies have been conducted on string matching algorithms, including exact matching and approximate string matching [12,13]. Their complexity is compared using DNA datasets to find the appropriate algorithm with high temporal quality and accuracy. Global alignment is a form of global optimization where the alignment spans the entire length of the sequences being examined. Local alignment identifies similar regions in long sequences that are generally too different.
In the field of bioinformatics, two main groups of algorithms are used to align pairs of sequences: exact algorithms and approximate (heuristic-based) algorithms [14]. The exact algorithms are based on the dynamic programming methodology [15,16]. Such are Needleman-Wunsch and Smith-Waterman algorithms. FASTA [17,18] and BLAST are heuristic-based algorithms and are more widely used because they offer faster computational performance. The challenge in performing sequence alignment from biological data is the trade-off between accuracy and efficiency. Needleman-Wunsch and Smith-Waterman algorithms tend to be very computationally complex, but they manage to find the optimal arrangement between pairs of sequences.
Needleman-Wunsch algorithm provides a method for finding an optimal global alignment of two sequences, so it cannot be used to detect local regions of high similarity. This algorithm tries to reach the maximum of matches and the minimum of mismatches (gaps) when comparing protein or nucleotide sequences. It is based on the method of dynamic programming and guarantees the calculation of the maximum order.
Smith-Waterman algorithm implements local sequence alignment. Instead of aligning the entire length of the two sequences, this algorithm finds the region with the highest similarity. Its purpose is to identify similar regions between strings, nucleotides and proteins. This technology is potentially more applicable due to the fact that the ends of proteins are in most cases less conserved compared to the middle regions, resulting in higher mutation, deletion and insertion rates at the ends of the protein. Smith-Waterman algorithm allows to align proteins that can be quite different without having to align their ends. Smith-Waterman algorithm is a basic algorithm based on dynamic programming and provides high accuracy. The time complexity of this algorithm for comparing two sequences is O(MN), where M and N are the lengths of the two sequences being compared. As the database of genetic biological sequences grows exponentially, the complexity relevant to real applications is O(kMN), where k represents the growth of the volume of genetic databases.
The first developed and implemented popular heuristic algorithm for database similarity search is FASTA, which can be used for rapid comparison of protein or nucleotide sequences. The FASTA algorithm is most commonly used to search biological sequence databases. The short identical sections in the two sequences are located. A sequence of multiple matching regions that are observed in the same order in both sequences is used as the starting point for dynamic programming algorithm ordering. This algorithm achieves a high level of similarity search accuracy and high speed due to the use of a word matching model. The goal is to find a potential match before starting the time-consuming optimized search. The trade-off between speed and accuracy is governed by a parameter that determines the size of the word. The FASTA algorithm does not search for every word match, but instead searches for segments containing several adjacent matches. These segments are compared using a heuristic method to determine the segment with the best score.
The BLAST algorithm is perhaps the most widely used tool that has been developed for bioinformatics research purposes. It is also heuristic-based and is used to search for homologous sequences. Sequences that have k-fold matches are found in the database using the BLAST algorithm. BLAST creates a look-up table of all substrings of the given input length contained in the input sequence, as well as similar "neighboring" substrings. It is used to compare sequences with biological information, both for sequences containing amino acids of different proteins and for sequences containing nucleotides of DNA. The BLAST algorithm compares a given sequence to a database of sequences.
Different variants of the BLAST algorithm have been developed to accommodate different types of sequence alignment (MEGABLAST, PSIBLAST). As the volume of nucleotide and protein sequence databases increases, it is imperative to compare, search and analyze the data using parallel algorithms and high-performance computers. Several parallel versions of the BLAST alignment and search algorithm have been developed. mpiBLAST uses the database segmentation strategy. It can be used on different types of computer clusters and supercomputers. It is very popular among bioinformatics scientists in need of a high-throughput BLAST algorithm. Many scientists have reported experimental results of their research works using parallel implementations of the BLAST package [19,20,21,22,23].
However, even parallel execution of sequence alignment algorithms faces limitations on hardware systems [24,25,26]. A novel approach for sequence comparison is proposed by defining a heuristic pairwise alignment inside the database environment [27]. This method takes advantage of the benefits provided by the database management system and presents a way to use similarities in datasets to speed up the alignment algorithm. Deep learning models are also used to predict miRNA binding site [28]. An interpretation technique called imputation sequence alignment has been reported for miRNA target site prediction models that can interpret deep learning models on a two-dimensional representation of miRNA and putative target sequence. Another technique for detecting the similarity of DNA sequences is to define a generalized string editing distance that allows the addition or deletion of entire motifs in addition to single nucleotide edits. A dynamic programming implementation is developed for computing this distance between sequences [29].

2.2. Method for DNA Sequence Alignmment Based on Trilateration

Finding a beginning point, or benchmark, against which the other data in the database can be compared is at the core of the concept of a favorite sequence. Alternatively, if we were to approach the problem mathematically, sequence favorite could be represented as a function of N unknowns (in the context of DNA, the unknowns being the 4 bases adenine, thymine, guanine, and cytosine), and the remaining database entries could then be represented once more as functions of the same variables. In this scenario, the distance between each individual sequence and the preferred sequence would be represented by the similarity comparison. In other words, determine the relationship between a point defined by the favorite sequence function and a point described by the sequence function.
A point is generated somewhere in the center of the cloud of points that is used as a reference (sequence favorite) when comparing to a set of points (the database entries) because there is no coordinate system. However, if a coordinate system or three or more reference points are found, it would be possible to use trilateration or elementary analytical geometry to determine the positions of the points relative to one another, which would reflect the degree to which the database records match one another. Moreover, to do away with the requirement for favorite computation sequence.
A novel approach, known as the CAT method (named after the first letter of the defined constant benchmarks C, A, and T), has been introduced for aligning DNA sequences, utilizing the trilateration technique [30]. This method establishes three consistent reference points for trilateration application, resulting in a steadfast reference sequence. This sequence, comprising C-benchmark, A-benchmark, and T-benchmark, remains constant regardless of alterations in the database content.
Key point establishing the reference benchmark are:
-
For A-benchmark and T- benchmark, we should never have matching position and base. On this way base from processed DNA could match on index and base on A or T, but not both.
-
For C-benchmark, we want index and base of 25% of A-benchmark and 25% of T-benchmark to match on C-benchmark.
  • ACGTACGTACGTACGTACGTACGTACGTACGTACGTAC....... –   A-Benchmark
  • GTACGTACGTACGTACGTACGTACGTACGTACGTACGT…… –   T- Benchmark
  • AGTCAGTCAGTCAGTCAGTCAGTCAGTCAGTCAGTCAG....... –   C- Benchmark
Once the three constant benchmarks for applying trilateration are established, issue (1) is eliminated. Constant sequence favorite – i.e. independent of the records in the database and to remain the same when the data set is changed.
Since the constant benchmark sequences are determined (i.e. they do not depend on either the data or their count), this allows comparisons to be made at the very beginning - when the sequences are uploaded into the database, and this is metadata information accompanying each sequence. This way, sequences won’t need to be compared during lookup (which is the slowest operation), but instead only the metadata information generated during the upload will be compared.
By establishing the benchmark sequences, issue (3) unification of favorite sequences for all databases is also eliminated. There are now unified sequences that are standardized for all databases using the described alignment algorithm. When two sequences have the same profiles, this means that they have regions with the same alignment, and one hundred percent complete matching of one sequence on the other can be expected.
For the evaluation of two sequences, it is necessary to calculate the distance of the segment S1S2 in Figure 1.
  S 1 S 2 = A D 1 − A D 2 2   + h 1 − h 2 2  
For now, ∆AS1T is considered, then analogous calculations and reasoning are per- formed for AS2T. What is known about ∆AS1T is the sides AT = |1|, AS1 = distance from S1 to A-benchmark (it is known), S1T = distance from S1 to T-benchmark. Use the cosine theorem to find ∡TAC, then side AD1:
  S 1 T 2 = A S 1 2 + A T 2 − 2 . A S 1 . A T . cos ⁡ α 1
  cos ⁡ α 1 = A S 1 2 + A T 2 − S 1 T 2 2 . A S 1 . A T
  A D 1 = A S 1 . cos ⁡ α 1
  h 1 = A S 1 2 − ( A S 1 . c o s ⁡ ( α 1 ) ) 2
The calculations for triangle AS2T are analogous. After substituting the values found, a value for S1S2 is obtained.
  S 1 S 2 = A D 1 − A D 2 2   + h 1 − h 2 2  
The smaller value obtained for the intercept, the greater the probability of a complete match, expressed as a percentage. This allows the database to be quickly searched for sequences with a certain percentage of similarity, which can later be aligned and compared with more accurate algorithms such as Needleman-Wunsch or Smith-Waterman.
It is possible to occur collisions in such proposed DNA sequence alignment method based on trilateration, i.e.:
  • More than one sequence of the same length to get the same values for AD and h:
    • Due to the nature of benchmark sequences and the fact that the real sequence projects at most a quarter of the bases onto the benchmark, i.e. with benchmark ACGT and projection of G at the second position, there are no matches, and no value is accumulated for match rate.
  • During S1S2 calculation, the same values are obtained:
    • Because of statistical errors accumulated when calculating AD and h.
    • Because of rounding in calculations due to the range of data types, this cannot be avoided even with the use of more precise types.
To minimize collisions, the precision in calculations for AD and h should be increased by adding the dependency on neighboring bases. Like in local alignment, when the current base of the benchmark sequence does not match the current base of the real sequence, additional points can be added or subtracted, depending on whether a neighboring base match is. After Needleman-Wunsch alignment, the places where the bases do not match appear as gaps “_” positions and are given different points accordingly.
A similar principle can be applied in the proposed method. If a base and index match is given value of 1. If there is a mismatch, a neighboring base from the benchmark sequence is checked and given a value of 0.6 or 0.4 depending on how far the neighbor is, i.e. when there is match with the left or right base from the benchmark then give 0.6, when is the far – 0.4. If we define baseDistance array for near matches it will looks like: [0, 0.6, 0.4, 0.6]. Left and right neighbors are with indexes 1 and 3, 0 index is for exact match and index 2 is the far neighbor.
Example of benchmark ACGT base at position 2 G
  • ACGT
  • XGXX
G at position 2 corresponds to C from the benchmark sequence and instead of 0 a match value of 0.6 can be given because it is adjacent to the right and in Needleman- Wunsch ordering it has the following alignment:
  • ACG_T
  • X_GXX
In this way, the precision of AD and h calculation is increased, the accumulation of statistical errors is reduced 1., thus reducing collisions 2. After finding a suitable sequence in the base, one with a minimum value for S1S2, a more accurate alignment algorithm can be applied. The comparison calculations in the direction calculate the CAT of two sections proposed in the presented method with a constant complexity that makes it to be applied as a first step suitable in the FASTA algorithm as well as for multiple alignments such as ClustalW.
Add dependency with a previous match and current position to increase uniqueness of the CAT profile. Like in positional numeral system contribution of a digit to the value of a number is the value of the digit multiplied by a factor determined by the position of the digit. It is needed something like this to be done here but considering the average length of the sequence exact same approach cannot be used. Instead, when a previous exact or near match is detected, a sum of current maximum theoretical sequence of matches is tracked, will be increased. The ratio of current maximum theoretical sequence of matches to current index will be added to the sum of previous matches, and this will be considered as kind of a bonus points. All given bonuses from previous matches must be tracked as well, since they are need in a later stage to correct the distances, so that a tringle can be formed. To be able to apply method of trilateration calculated distances should ensure that in any conditions a triangle can be formed. I.e. the sum of any two sides must be greater than the third one.

2.3. An Algorithm for Pairwise DNA Sequences Alignment Based on the Proposed CAT Method

The algorithm for pairwise DNA sequences alignment based on the proposed alignment method can be divided into two stages. The first stage is the calculation of a CAT profile against the selected benchmark sequences. This stage is the slowest operation in CAT method but is done only once. For each of the benchmarks, the profile of the input sequence is calculated to create a complete CAT profile of the input sequence (Figure 2 and Figure 3).
This operation is performed once during the entry of the sequence into the database, and the outcome is stored as additional information associated with the sequence. This stage of the algorithm exhibits linear complexity, denoted as O(n).
The second stage involves a comparison against the previously calculated CAT profiles (Figure 4). This operation is carried out iteratively when assessing the similarity of two or more sequences from the database. The DNA sequence alignment algorithm based on the CAT method maintains a constant complexity of O(21), making it highly efficient and easily implementable on computing machines. This characteristic significantly reduces the time required for searching large databases. To further enhance database speed, the algorithm can be parallelized by employing multiple threads for comparing against the computed CAT profiles. Additionally, it is feasible to set similarity limits for the search results, allowing the algorithm to consider not only exact matches but also similarities within defined limits.
For improvement of accuracy of CAT in terms of precisely detecting the rate of similarities of sequences, we could change stage 2 of the algorithm, to work with the areas of the triangles with vertexes points from the corresponding benchmark of the CAT profile (D and h from fig1). We could use Sutherland–Hodgman algorithm to identify overlapping area of the compared profiles, then compute the area of the resulting convex polygon. Ratio of resulting area to the minimal from the two profiles' area should give us theoretical optimal alignment. This will slowdown stage 2 but will keep is complexity as O(const). This enhancement will be explored in some of the upcoming research.

2.4. Implementation of the Proposed Method CAT for Sequences Alignment

The aim of the experiments is to empirically assess the efficacy of the developed algorithm based on the proposed CAT method for DNA sequence alignment. To achieve this goal, a program implementation has been developed using the C# programming language, and the class diagram is depicted in Figure 5.
  • Benchmark: Base class serving as an abstraction for representing benchmark sequences.
  • BenchmarkRepo: Repository containing predefined benchmark sequences.
  • BenchmarkProfile: Abstraction for plotting a DNA sequence against a benchmark sequence, calculating base parameters for the CAT comparison method such as Cos, D, H.
  • CatProfile: Abstraction representing a DNA sequence with pre-calculated parameters for each benchmark sequence from the CAT method.

3. Results

The proposed new method for DNA sequences alignment, called CAT, based on the trilateration method, is experimentally verified. Three constant benchmarks have been established for the application of trilateration, which creates a constant favorite sequence - i.e., independent of the records in the database and remains the same when the set is changed.
Since the benchmark sequences established are constant (i.e., they do not depend either on the data or on their number), this allows the comparisons to be made at the very beginning – when the sequences are uploaded into database and this to be metadata information, accompanying each sequence. In this way, there is no need to compare sequences during lookup (the slowest operation), but instead only the metadata generated when the data is entered is compared.
A new algorithm for DNA sequences alignment based on proposed CAT method is designed, consisting of an algorithm for calculating a CAT profile against the selected benchmark sequences and an algorithm for comparing two sequences, based on the calculated CAT profiles. Implementation steps, inputs and outputs are defined.

3.1. Collision Analysis

To assess the reliability of the CAT method, it is essential to explore the potential for collisions across the entire combination space, encompassing all permutations for a given sequence length. This prompts an inquiry into the uniqueness of the CAT profiles and the impact of accumulating statistical errors on the method's reliability. To address this, all conceivable permutations of sequences with lengths 10, 11, 12, 13, and 15 were systematically generated (refer to Table 1, DNA length column).
For each set, a sample of 1000 sequences were randomly selected and compared against the entire set. The count was made to determine how many of these sequences, after comparison with CAT, yielded a 100% match result (refer to Table 1, Average Collisions column). The collision rate is computed by dividing the total number of permutations (refer to Table 1, Total permutations column) for a sequence of a specific length by the instances of Average Collisions where CAT resulted in a 100% match (1).
From the table above can be observed that with the proposed implementation of CAT there is no collisions found for the examined lengths. This makes CAT very reliable to find exact sequence match among sequences with equal length.

3.2. Performance Analysis

To assess the speed of CAT profile comparisons, an experiment was conducted. One hundred sequences of varying lengths (100, 1000, 10000, and 50000) were generated. CAT profiles were pre-calculated for these sequences. Subsequently, the CAT profiles, along with the Needleman-Wunsch and Knuth–Morris–Pratt algorithms, were compared against each sequence individually. The execution time for each comparison was recorded, and the average results are presented in Table 2.
Table 2 indicates that the comparison times with CAT profiles are consistently close and do not vary based on the sequence's size. In contrast, the comparison time with the Needleman-Wunsch algorithm exhibits exponential growth as the sequence length increases (refer to Figure 6).
Comparison with Knuth–Morris–Pratt algorithm, which is with complexity of O(n), shows the advantage of CAT for searching of exact match of sequences (Figure 7). Here we should point out that with Knuth–Morris–Pratt we could only identify occurrence of subsequence in bigger or equal sequence. We cannot use this method for identifying of similarities.

4. Discussion

The proposed CAT method has been experimentally verified. Three constant benchmarks have been established for the application of trilateration, which creates a constant favorite sequence that is independent of the records in the database and remains the same when the set is changed. Since the benchmark sequences established are constant (i.e., they do not depend either on the data or on their number), this allows comparisons to be made at the very beginning, when the sequences are uploaded into the database, and this is metadata information accompanying each sequence. In this way, there is no need to compare sequences during lookup (the slowest operation), but instead only the metadata generated when the data is entered is compared.
CAT methodology is designed to prepare input data, to extract and cache (algorithm for calculating a CAT profile against the selected benchmark sequences), and evaluate similarity based on pregenerated data. Implementation steps, inputs, and outputs are defined. CAT profiles generation is done once during the data upload, which allows the pro-files to be used as accompanying metadata information for the sequences. Search comparisons with the CAT method are minimized and have a constant O(24) algorithm complexity, which helps optimize searches in large biological datasets and makes it suitable for implementation as a first step in more refined algorithms like FASTA. Based on the CAT profiles, sequences can be organized into a hierarchical storage structure to be used as a database for biological data storage in search-optimized systems.
This new version of CAT, build on trilateration method, improve the old one in the degree of collisions and is as fast. The generation of CAT profiles is done once data is entered into the database, allowing the profiles to be used as metadata for the sequences. A dependency with a previous match and the closest neighbor is taken into consideration to increase the uniqueness of the CAT profile and to reduce possible collisions, i.e., two or more sequences having the same CAT profile. This makes the proposed algorithm suitable for finding the exact match of a concrete DNA sequence in a large set of DNA data.
Changes are in the first stage of the calculation of the CAT profiles, and they do not affect the second stage, which is the actual comparison. With the new version, all experiments related to the examination of collisions were re-executed; no collisions were found, and some of the figures in the original article became redundant and were removed. In this paper, new results from the same experiments are exposed. Block scheme, pseudocode, tables, and figures were updated according to the proposed new version and experimental results.
The analysis of the experimental results obtained by sequence alignment shows a small deviation of the proposed algorithm based on the CAT method, which can be ignored if this deviation is acceptable at the expense of performance. The execution time of the Needleman-Wunsch algorithm increases as the length of the sequences increases. The time efficiency of the CAT algorithm remains constant, regardless of the length of the sequences. Therefore, the advantage of the proposed method is its fast processing in the alignment of large sequences, for which the execution of the exact algorithms takes a long time. Experiments have been carried out with different datasets for DNA sequence alignment using the triplet-based CAT method. Experiments related to the performance comparison with Needleman-Wunsch were re-executed with the new version of the algorithm to confirm that we have the same performance as the version presented on the conference paper. And we also added a performance comparison of the algorithm for pairwise DNA sequence alignment based on trilateration against Knuth-Morris-Pratt, which has a complexity of O(n) and is one of the most widely used for searching biological data. The results of the new experiments are represented in a table and in graphical formats for better understanding and as evidence of the advantages of the proposed modifications.

5. Conclusion

The approach of precomputing metadata and applying the trilateration principle provides a solution to the problem of slow alignment and similarity searching of biological data. Modification of the benchmark sequences and the way how the profiles are calculated and how they are compared results on the output of the comparison. This makes the approach adjustable to desired level of accuracy. The experiments underscore the efficiency of the proposed algorithm and its potential to significantly speed up the process of DNA sequence alignment by leveraging the refined CAT profiles. The updated algorithm promises to be a valuable tool in bioinformatics, offering a faster and more reliable mean for processing the vast and growing repositories of genetic data.

Author Contributions

Conceptualization, V.G. and Y.Y.; methodology, V.G..; software, H.S.; validation, H.S.; formal analysis, H.S.; investigation, V.G. and H.S.; resources, V.G. and H.S.; writing—original draft preparation, V.G. and H.S.; writing—review and editing, V.G. and H.S .; visualization, H.S.; supervision, V.G.; project administration, V.G.; funding acquisition, V.G. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the European Union-NextGenerationEU, through the National Recovery and Resilience Plan of the Republic of Bulgaria, project № BG-RRP-2.004-0005.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. EMBL’s European Bioinformatics Institute (EMBL-EBI), Available online:. Available online: https://www.ebi.ac.uk/about/our-impact (accessed on 31 November 2023).
  2. Luo, R., Liu, B., Xie, Y. et al. SOAPdenovo2: an empirically improved memory-efficient short-read de novo assembler. GigaSci 2012, 1, 18. [CrossRef]
  3. Needleman, S.B.; Wunsch, C.D. A general method applicable to the search for similarities in the amino acid sequence of two proteins. Journal of Molecular Biology 1970;48:443–453. [CrossRef]
  4. Smith, T.F.; Waterman M.S. Identification of common molecular subsequences. J. Mol. Biol. 1981;147:195–197. [CrossRef]
  5. Regnier, M. Knuth-Morris-Pratt algorithm: An analysis. In: Kreczmar, A., Mirkowska, G. (eds) Mathematical Foundations of Computer Science, Lecture Notes in Computer Science 1989, vol 379. Springer. [CrossRef]
  6. Altschul, S.F.; Gish, W.; Miller, W.; Myers, E.W.; Lipman D.J. Basic local alignment search tool. J. Mol. Biol. 1990;215:403–410. [CrossRef]
  7. Altschul, S.; et al. Gapped BLAST and PSIBLAST: a new generation of protein database search programs. Nucleic Acids Research 1997, 25, 3389–3402. [Google Scholar] [CrossRef] [PubMed]
  8. Borovska, P.; Gancheva, V.; Landzhev, N. Massively parallel algorithm for multiple biological sequences alignment. Proceeding of 36th IEEE International Conference on Telecommunications and Signal Processing 2013, pp. 638-642. [CrossRef]
  9. Gancheva, V.; Stoev, H. An algorithm for pairwise DNA sequences alignment. Bioinformatics and Biomedical Engineering. IWBBIO 2023. Lecture Notes in Computer Science 2023, vol 13919. Springer, Cham. [Google Scholar] [CrossRef]
  10. Liu, Y.; Yan, Y.; Ren, J.; Marshall, S. Sequence similarity alignment algorithm in bioinformatics: techniques and challenges. In: Ren, J. et al. Advances in Brain Inspired Cognitive Systems. Lecture Notes in Computer Science 2020, vol 11691. Springer, Cham. [CrossRef]
  11. Karp, R.M.; Rabin, M.O. Efficient randomized pattern-matching algorithms. IBM J. Res. Dev. 1987;31:249–260. [CrossRef]
  12. Harde, P. Comparative study of string matching algorithms for DNA dataset. International Journal of Computer Sciences and Engineering 2018, 6. [CrossRef]
  13. Tun, N.; Thin, M. Comparison of three pattern matching algorithms using DNA Sequences. International Journal of Scientific Engineering and technology Research 2014, 3, 6916–6920. [Google Scholar]
  14. Chao, J.; Tang, F.; Xu L. Developments in algorithms for sequence alignment: a review. Biomolecules. 2022 Apr 6;12(4):546. [CrossRef]
  15. Spouge, J.L. Speeding up dynamic programming algorithms for finding optimal lattice paths. SIAM J. Appl. Math. 1989;49:1552–1566. [CrossRef]
  16. Zhang, F.; Qiao, X. Z.; Liu, Z. Y. A parallel Smith-Waterman algorithm based on divide and conquer, Proceedings of the Fifth International Conference on Algorithms and Architectures for Parallel Processing ICA3PP 2002. [CrossRef]
  17. Lipman, D.J.; Pearson, W.R. Rapid and sensitive protein similarity searches. Science. 1985;227:1435–1441. [CrossRef]
  18. Pearson, W.R.; Lipman D.J. Improved tools for biological sequence comparison. Proc. Natl. Acad. Sci. USA. 1988 ;85:2444–2448. [CrossRef]
  19. Braun, R.; et al. Three complementary approaches to parallelization of local BLAST service on workstation clusters. Fifth International Conference on Parallel Computing Technologies (PaCT). Lecture Notes in Computer Science (LNCS) 1999, 1662. [Google Scholar]
  20. Costa, R.; Lifschitz, S. Database allocation strategies for parallel BLAST evaluation on clusters Distributed Parallel Databases 2003, 13, 99–127.
  21. Oehmen, C.; Nieplocha, J. ScalaBLAST: A scalable implementation of BLAST for high-performance data-intensive bioinformatics analysis. IEEE Transactions on Parallel and Distributed Systems 2006, 17, 740–749. [Google Scholar] [CrossRef]
  22. Thorsen, O.; Jiang, K.; Peters, A.; Smith, B.; Lin, H.; Feng, W.; Sosa, C. Parallel genomic sequence-search on a massively parallel system. ACM International Conference on Computing Frontiers 2007, New York, USA. [Google Scholar]
  23. Lin, H.; et al. Massively parallel genomic sequence search on the Blue Gene/P architecture. In Proceedings of the ACM/IEEE conference on Supercomputing, 2008.
  24. Farrar, M. Striped Smith-Waterman speeds database searches six times over other SIMD implementations. Bioinformatics 2007, 23, 156–161. [Google Scholar] [CrossRef] [PubMed]
  25. Sathe S.R.; Shrimankar, D.D. Parallelizing and analyzing the behavior of sequence alignment algorithm on a cluster of workstations for large datasets, Int. J. Comput. Appl. 2013, vol. 74, no. 21, pp. 1-13.
  26. Kaur, K.; Chakraborty, S.; Gupta, M.K. Accelerating Smith-Waterman algorithm for faster sequence alignment using graphical processing unit, Phys.: Conf. Ser. 2022, 2161 012028. [CrossRef]
  27. Lipták, P.; Kiss, A.; Szalai-Gindl, J.M. Heuristic pairwise alignment in database environments. Genes 2022, 13, 2005. [Google Scholar] [CrossRef] [PubMed]
  28. Grešová, K.; Vaculík, O.; Alexiou, P. Using attribution sequence alignment to interpret deep learning models for miRNA binding site prediction. Biology 2023, 12, 369. [Google Scholar] [CrossRef] [PubMed]
  29. Petty, T.; Hannig, J.; Huszar, T.I.; Iyer, H. A New string edit distance and applications. Algorithms 2022, 15, 242. [Google Scholar] [CrossRef]
  30. Gancheva, V.; Stoev, H. DNA sequence alignment method based on trilateration. Bioinformatics and Biomedical Engineering, Lecture Notes in Computer Science 2019, vol. 11466, Springer, Cham, pp. 271-283. [CrossRef]
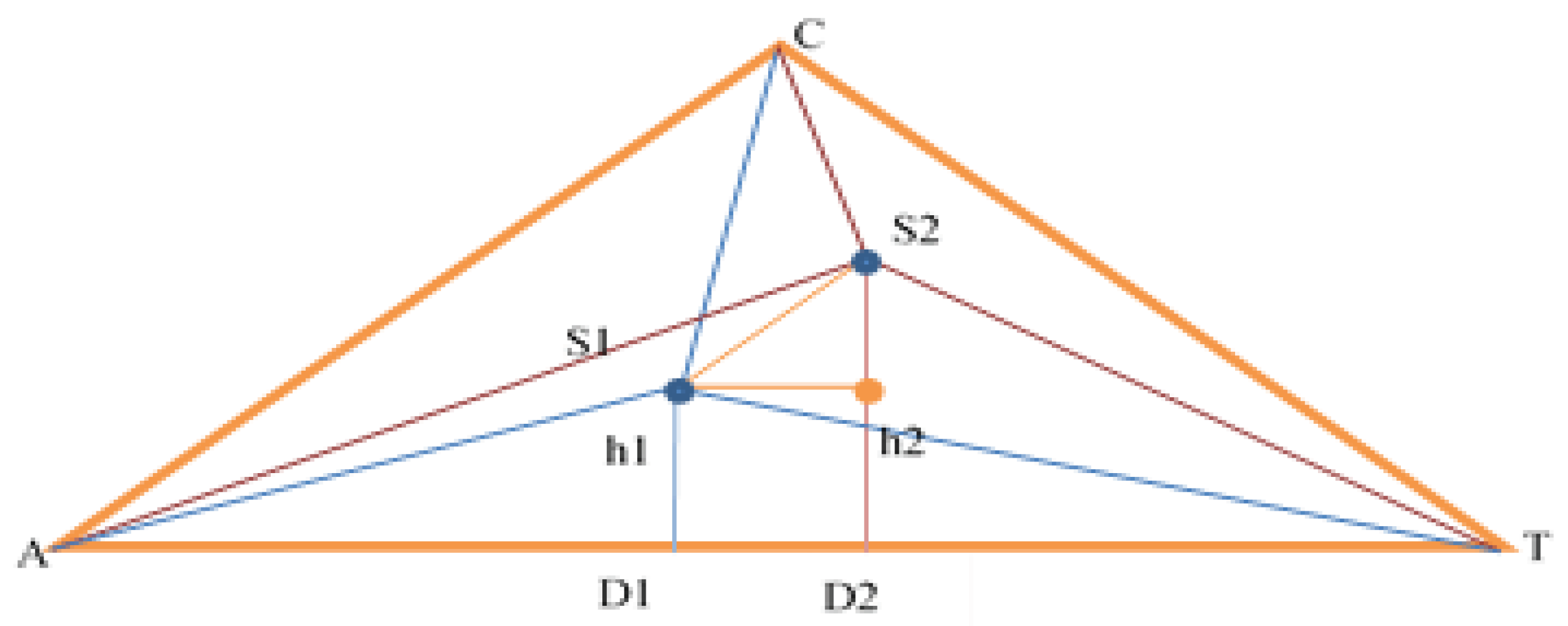
Preprints 99202 g001
Figure 1. Calculation of the distance between two profiles.
Figure 1. Calculation of the distance between two profiles.
Preprints 99202 g001
Preprints 99202 g002
Figure 2. Algorithm for calculation of CAT profile against the selected benchmark sequences.
Figure 2. Algorithm for calculation of CAT profile against the selected benchmark sequences.
Preprints 99202 g002
Preprints 99202 g003
Figure 3. Block diagram of an algorithm for calculating a sequence profile against a benchmark.
Figure 3. Block diagram of an algorithm for calculating a sequence profile against a benchmark.
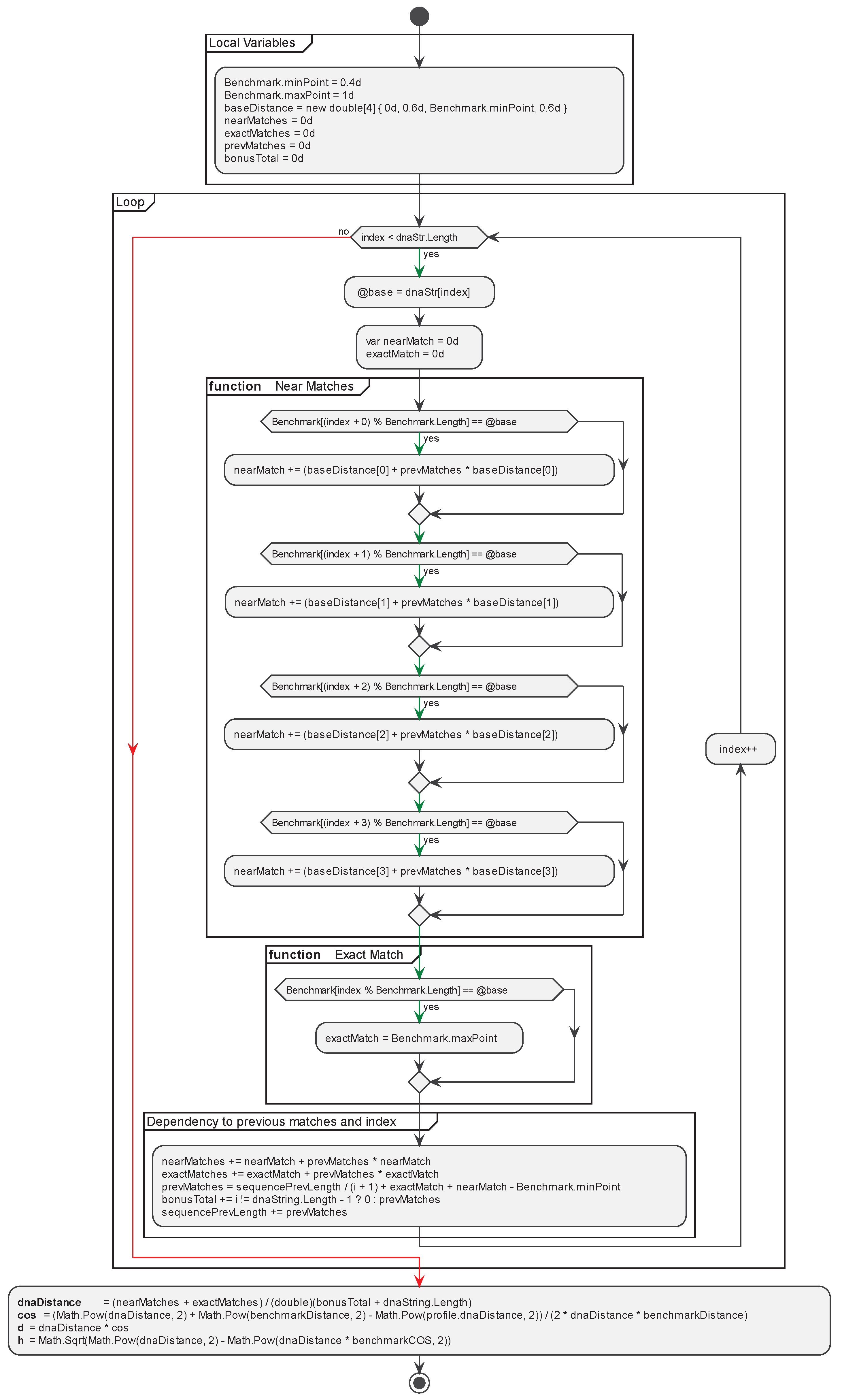
Preprints 99202 g003
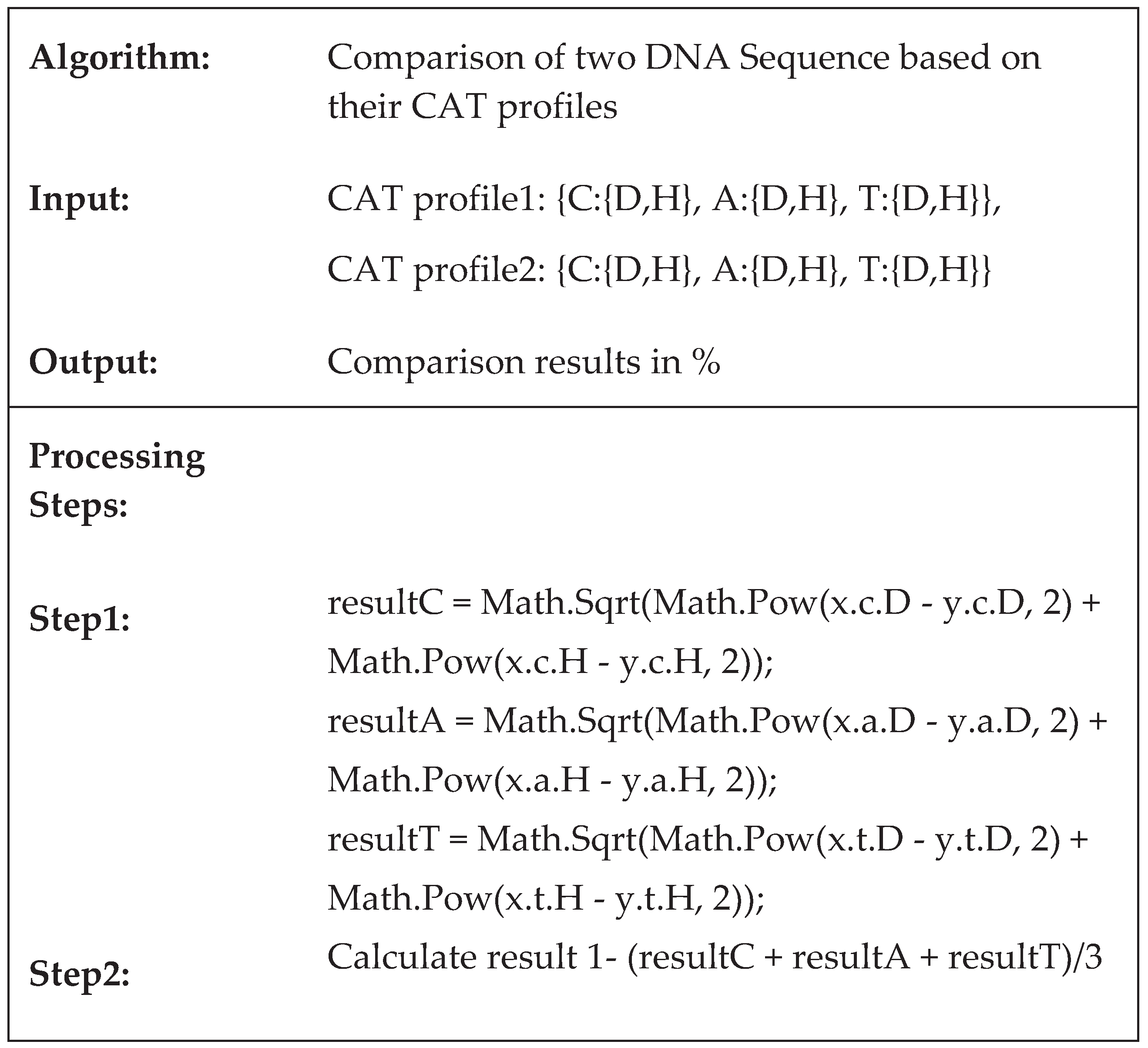
Preprints 99202 g004
Figure 4. Algorithm for comparing two sequences, based on the calculated CAT profiles.
Figure 4. Algorithm for comparing two sequences, based on the calculated CAT profiles.
Preprints 99202 g004
Preprints 99202 g005
Figure 5. Class diagram of the algorithm implementation based on the CAT method for sequence alignment.
Figure 5. Class diagram of the algorithm implementation based on the CAT method for sequence alignment.
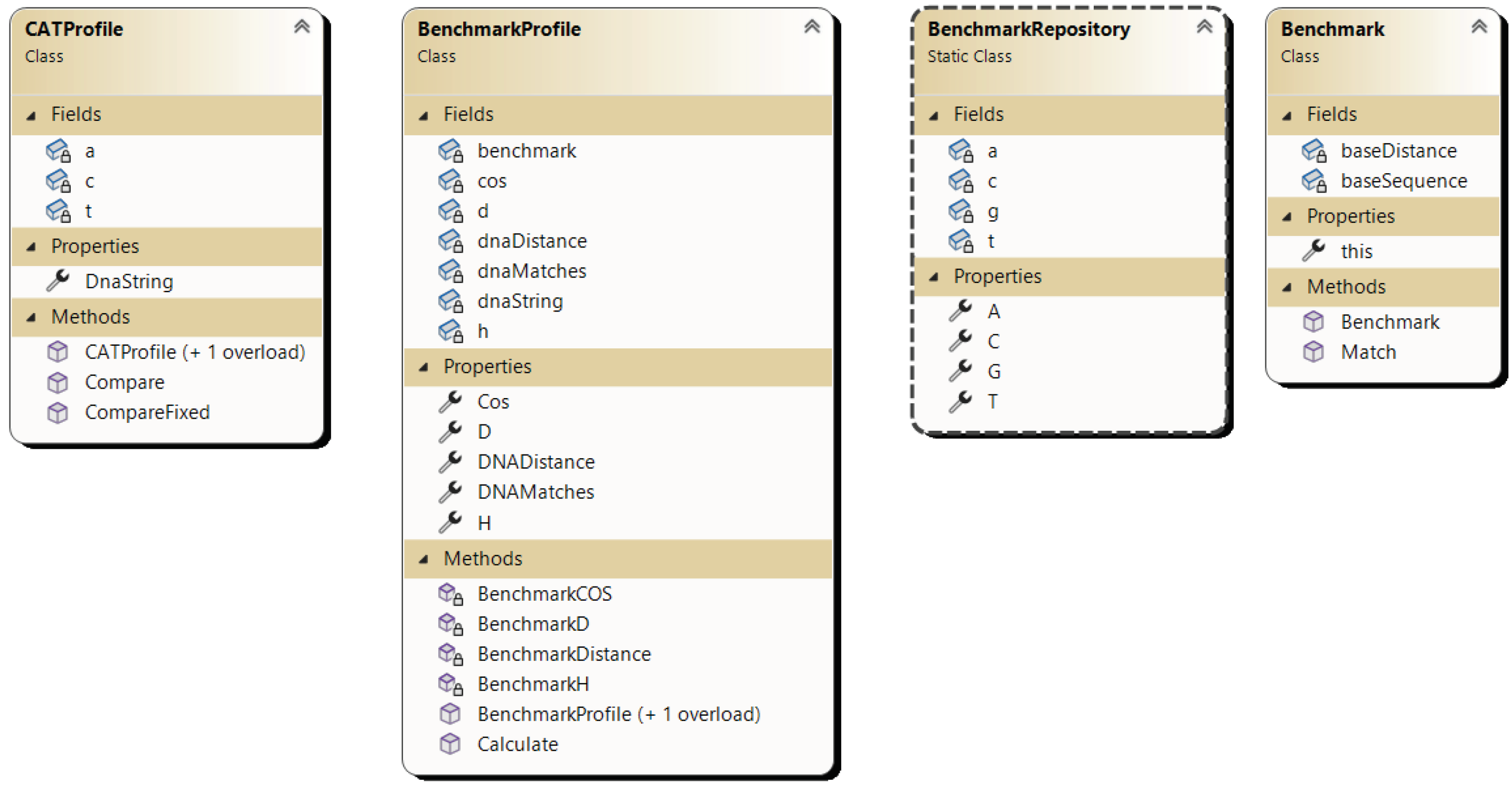
Preprints 99202 g005
Preprints 99202 g006
Figure 6. Performance comparison using CAT profiles and Needleman-Wunsch.
Figure 6. Performance comparison using CAT profiles and Needleman-Wunsch.
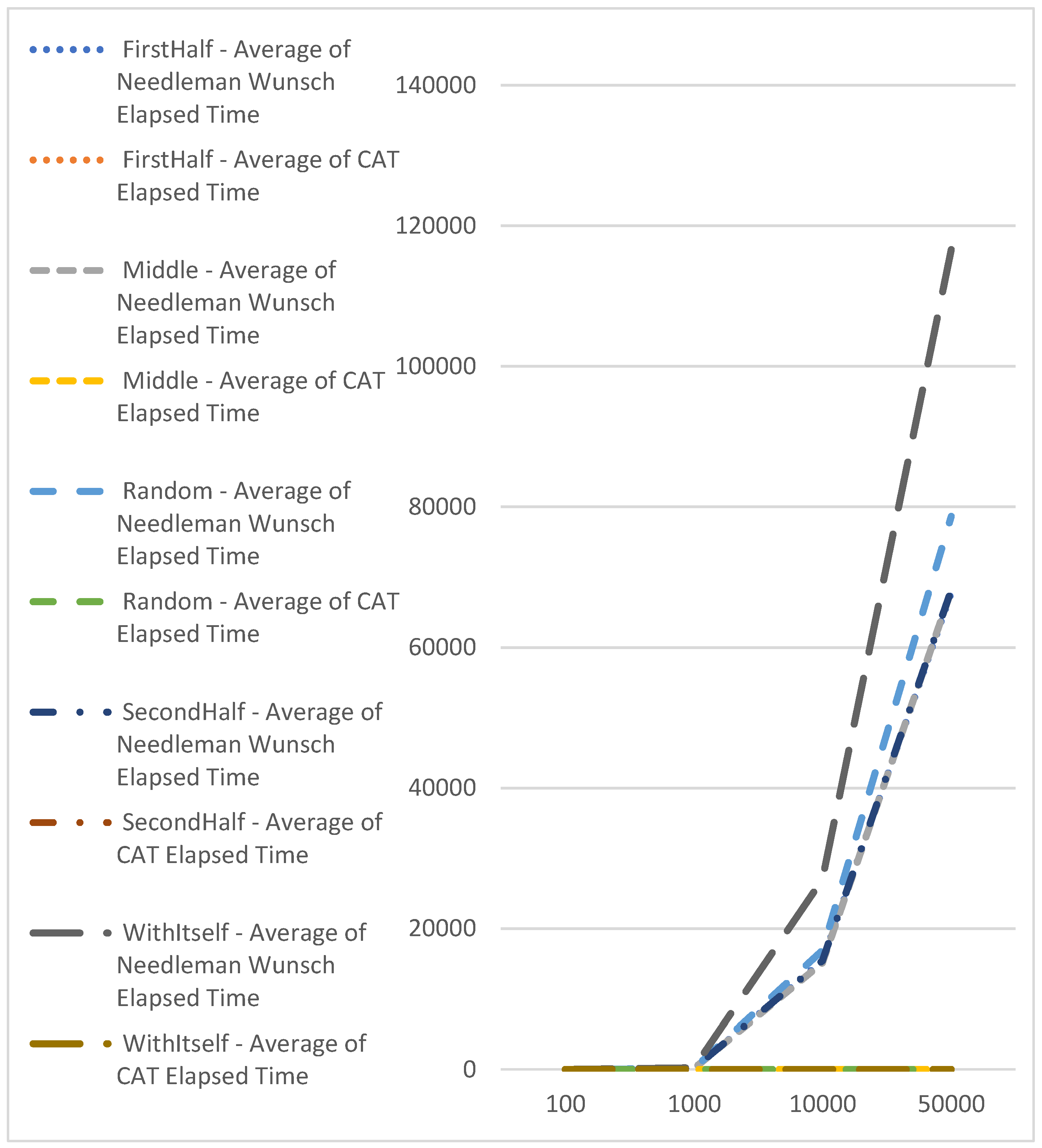
Preprints 99202 g006
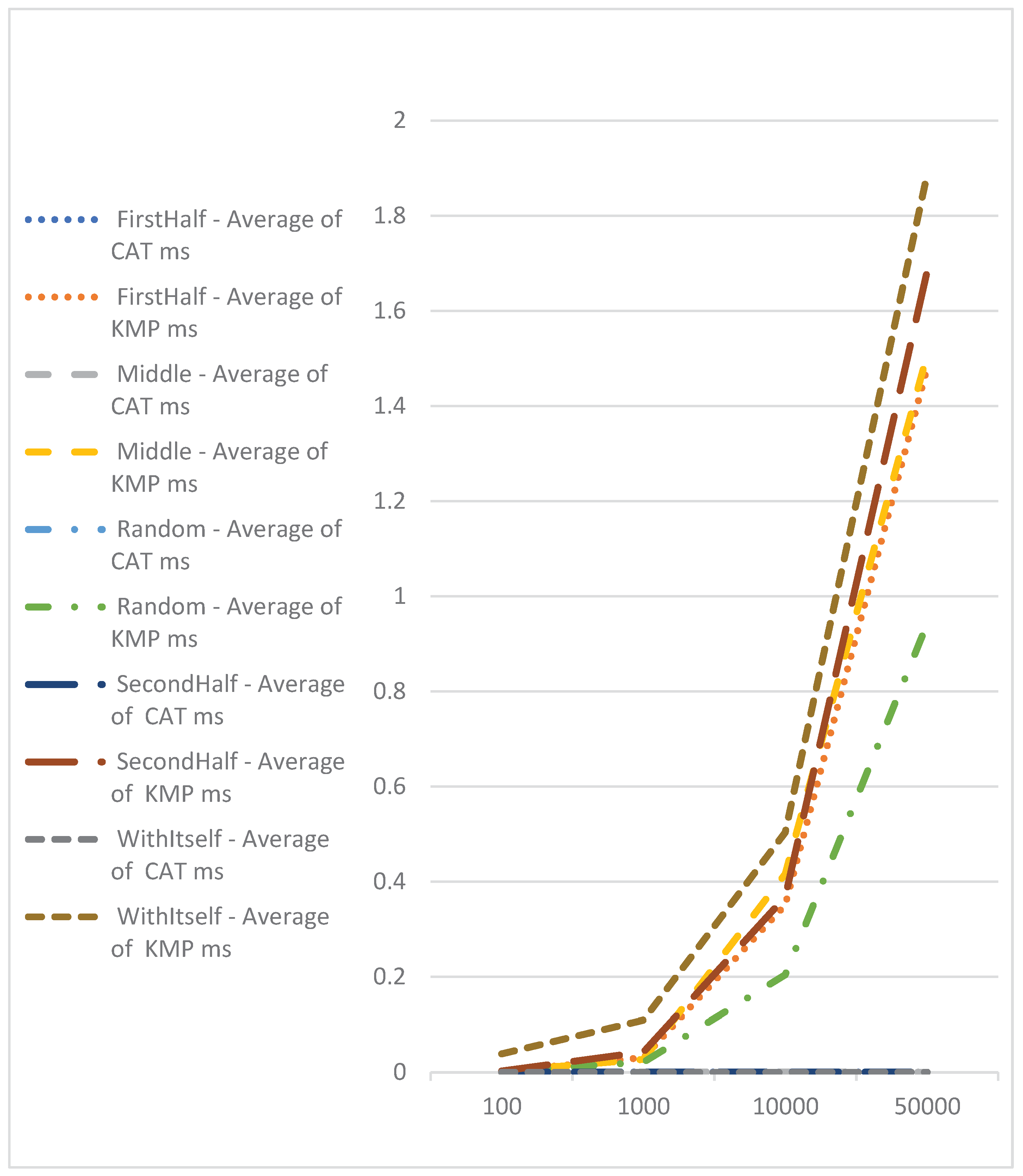
Preprints 99202 g007
Figure 7. Performance comparison using CAT profiles and Knuth–Morris–Pratt.
Figure 7. Performance comparison using CAT profiles and Knuth–Morris–Pratt.
Preprints 99202 g007
Table 1. Collision comparison results.
Table 1. Collision comparison results.
DNA length Average Collisions Total permutations Rate of collision‰ 0 - 1000
10 1 1048576 NaN
11 1 4194304 NaN
12 1 16777216 NaN
13 1 67108864 NaN
15 1 1073741824 NaN
Table 2. Performance of CAT and Needleman-Wunsch comparisons.
Table 2. Performance of CAT and Needleman-Wunsch comparisons.
Average of CAT Elapsed Time
DNA Length FirstHalf Middle Random SecondHalf WithItself
100 0.0004025 0.000396 0.0004144 0.0003975 0.000254
1000 0.000466 0.0004495 0.0005036 0.0004555 0.0003
10000 0.0007015 0.000644 0.0007408 0.0006945 0.00036
50000 0.0003645 0.0003805 0.0003788 0.000356 0.000388
Average of Needleman Wunsch Elapsed Time
FirstHalf Middle Random SecondHalf WithItself
100 0.810224833 0.8224725 0.875811143 0.807499499 1.59419
1000 137.5561462 137.9288827 148.2296519 136.8088905 238.639932
10000 15351.73013 15130.27244 16907.69611 15416.20968 26981.14435
50000 67806.26151 68099.07336 78652.58283 68162.06354 116611.3085
Average of Knuth–Morris–Pratt Elapsed Time
FirstHalf Middle Random SecondHalf WithItself
100 0.002494 0.002726 0.0018664 0.002865 0.038884
1000 0.0312275 0.0270915 0.0212584 0.043221 0.109476
10000 0.350831 0.416332 0.2042432 0.368386 0.503456
50000 1.4803245 1.507671 0.9423872 1.683394 1.88701
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated