Submitted:
02 February 2024
Posted:
05 February 2024
You are already at the latest version
Abstract
Keywords:
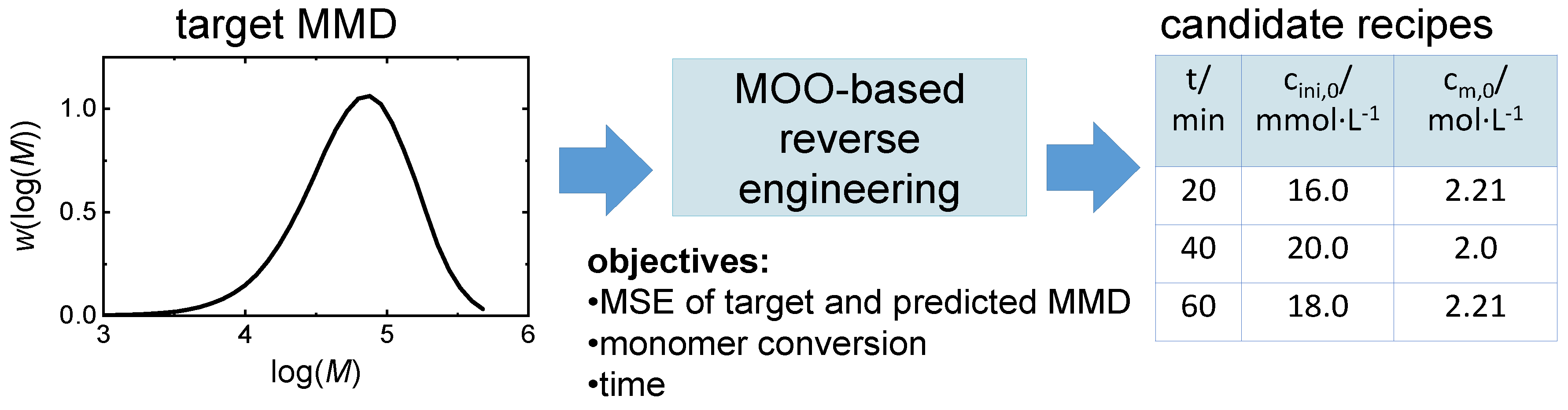
1. Introduction
2. Reverse Engineering Modeling Approach
2.1. Model Development
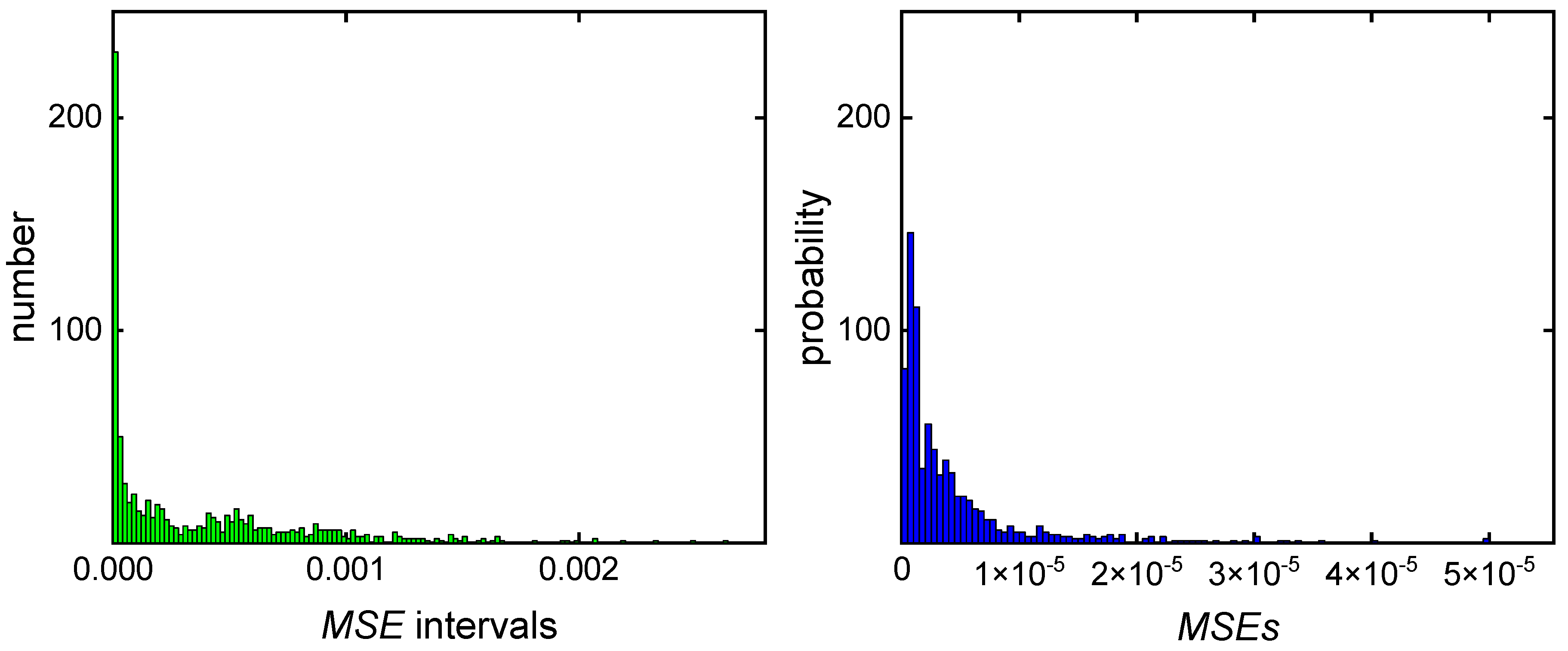
2.2. Data acquisition and Processing
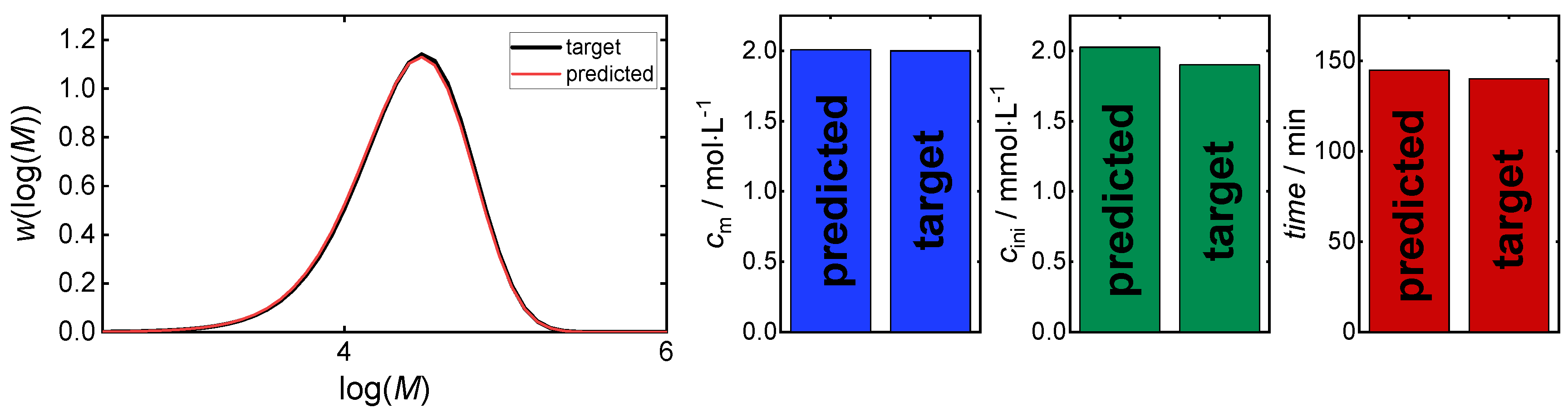
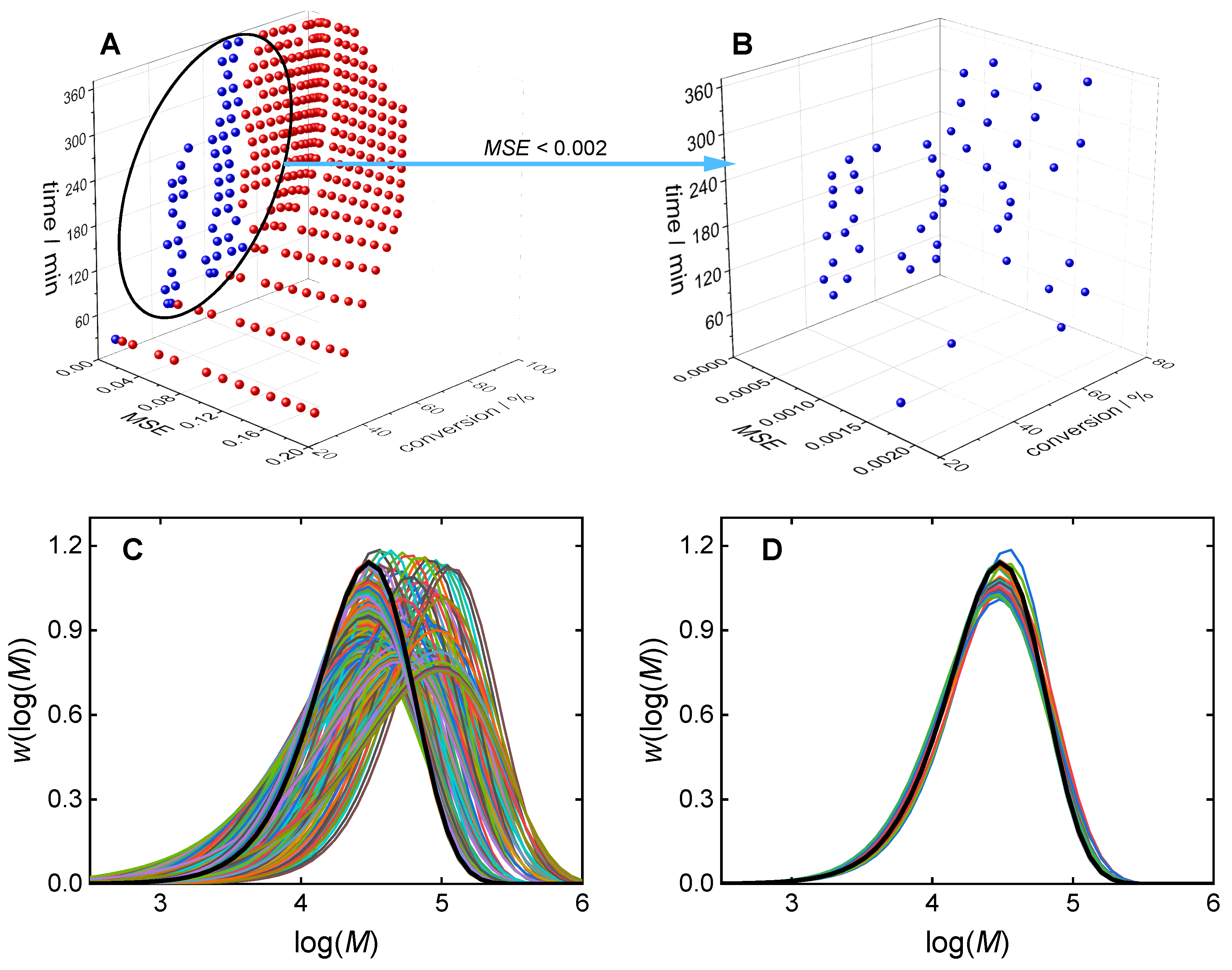
3. Results and Discussion
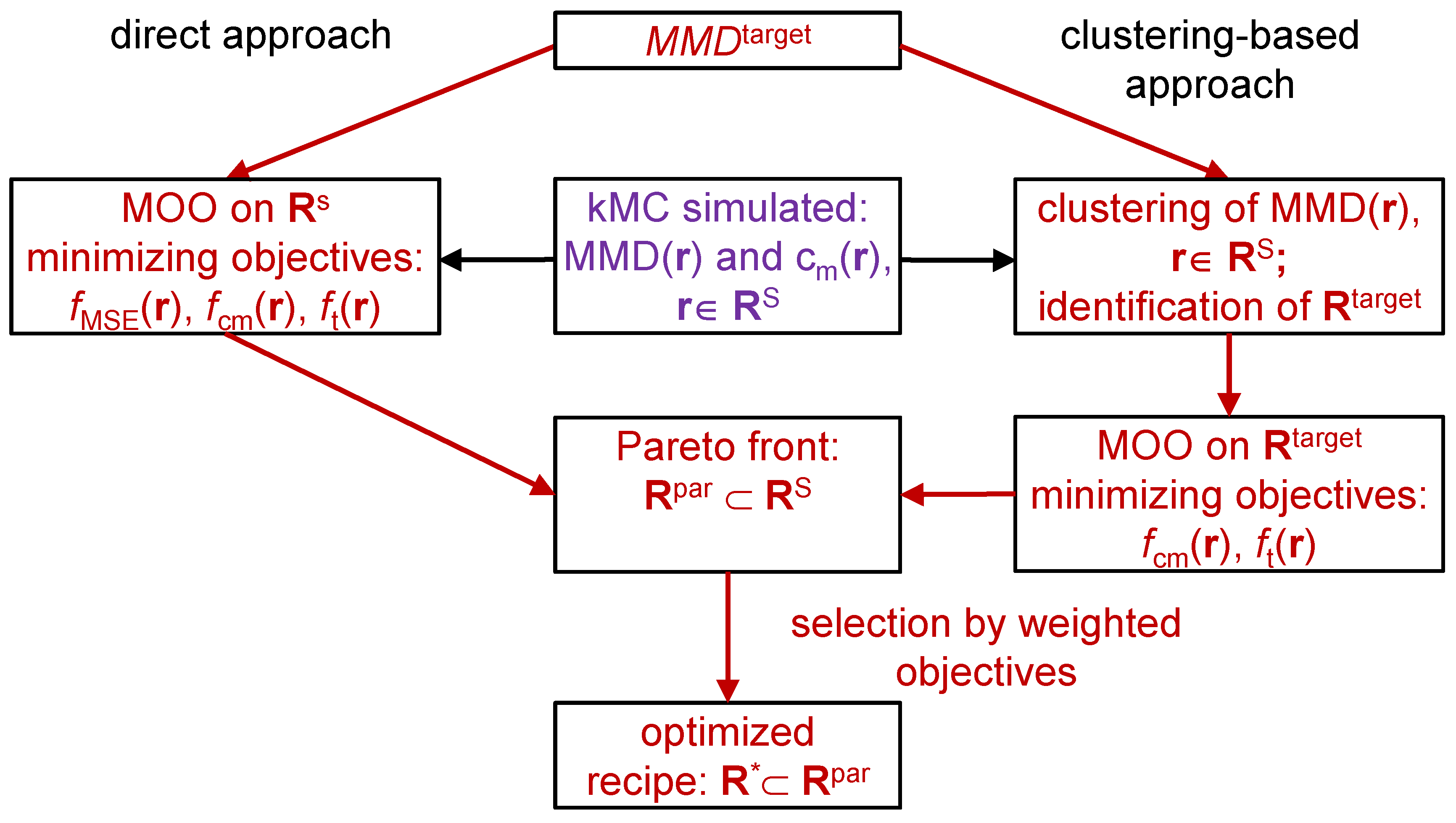
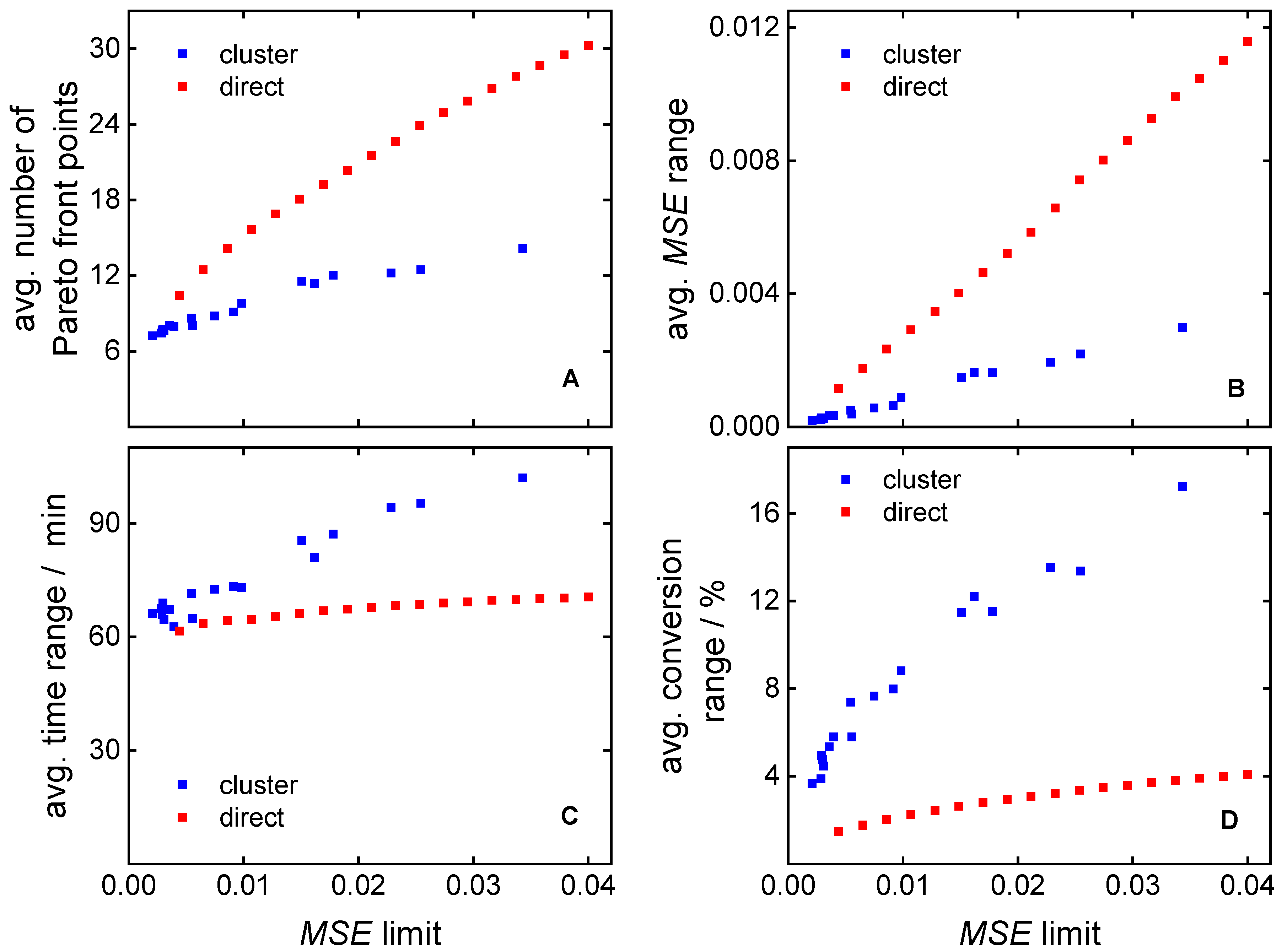
3.1. Direct Pareto Optimization
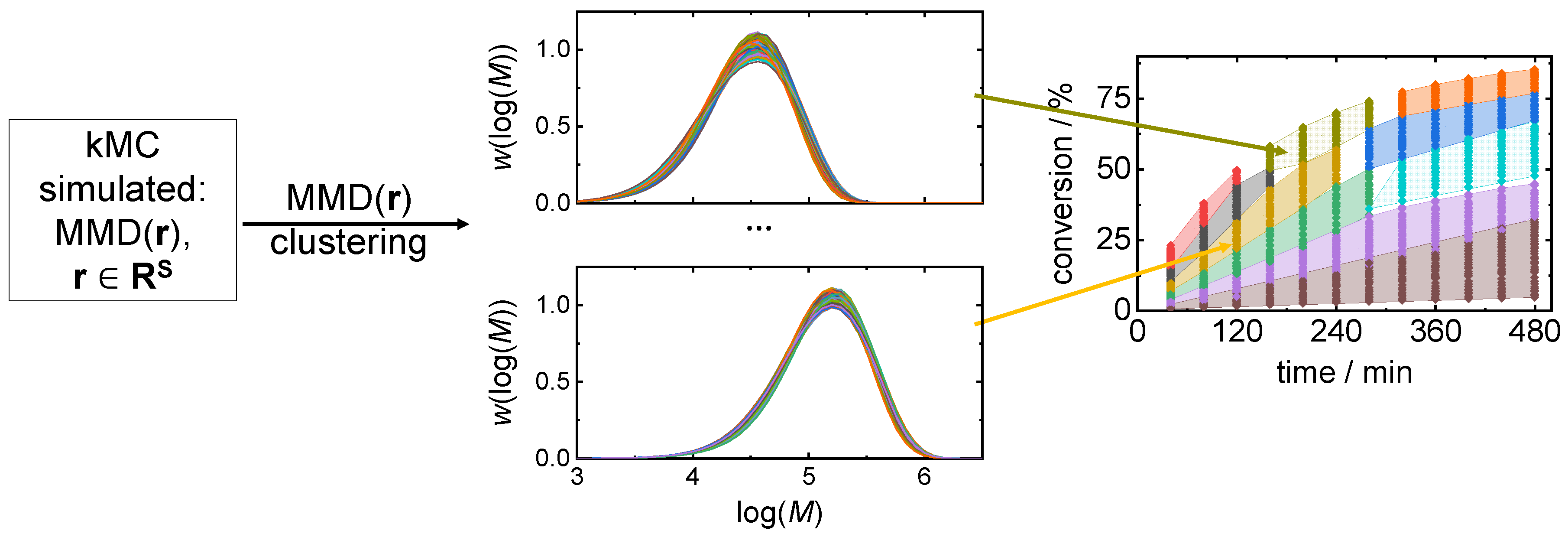
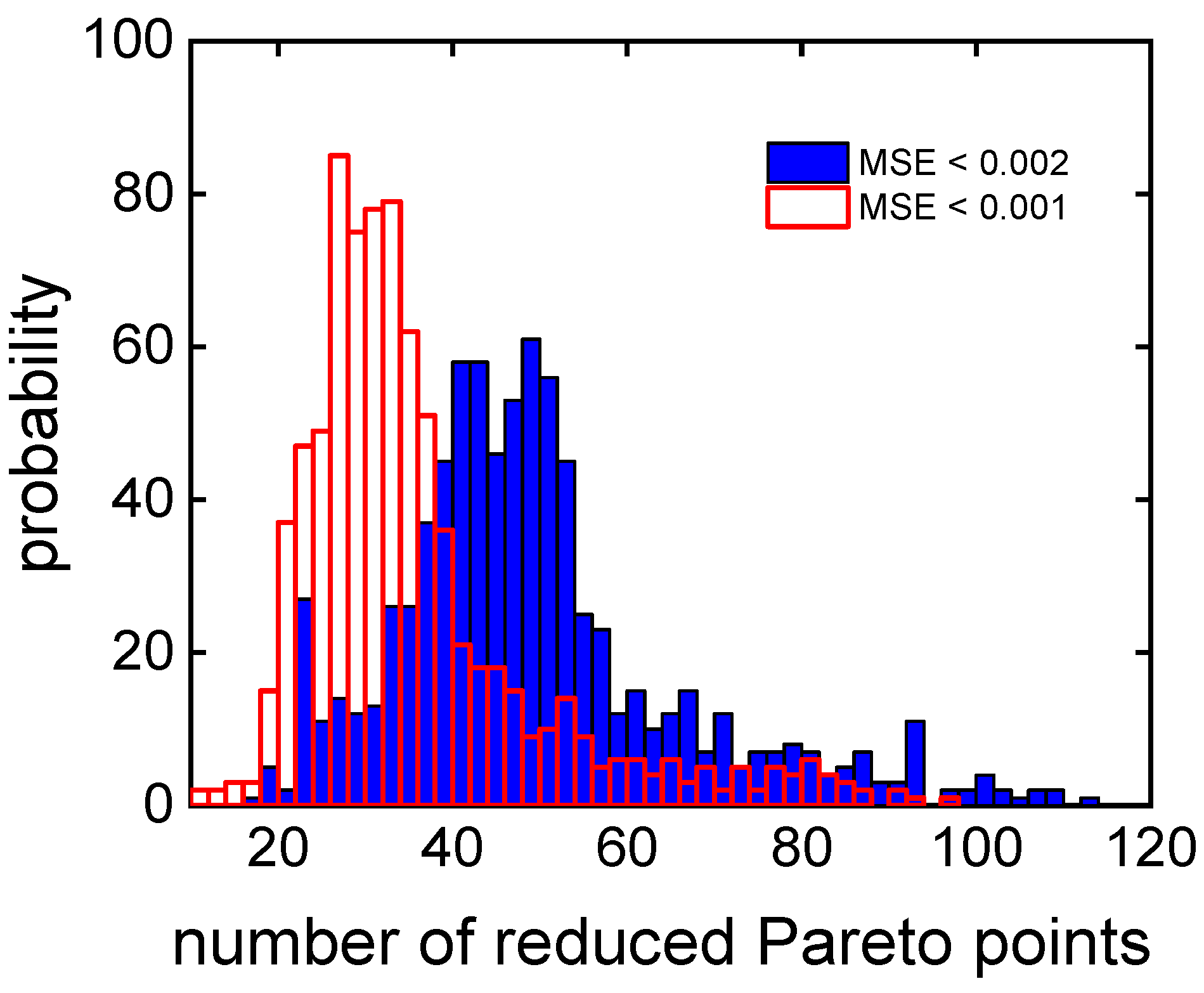
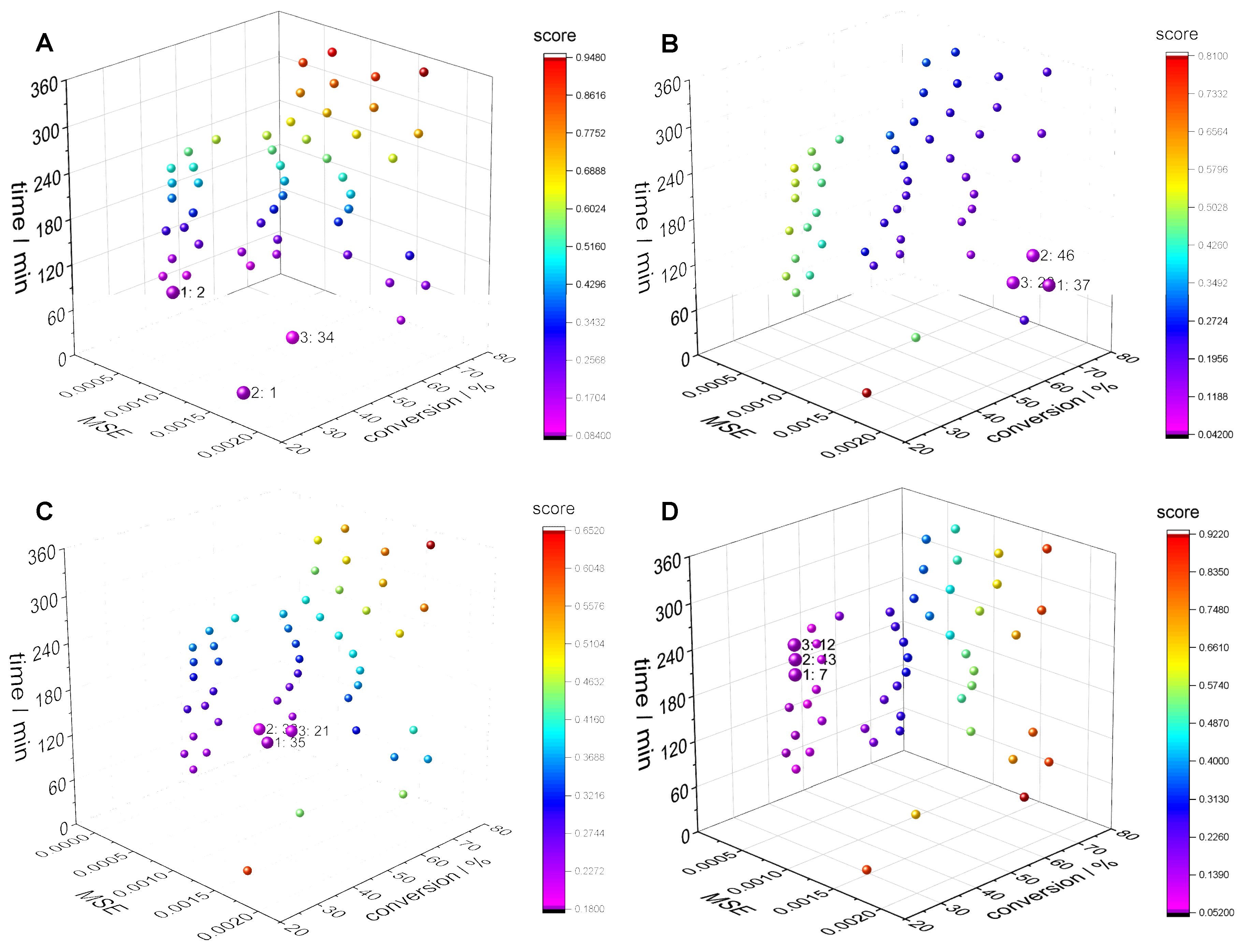
3.2. Clustering Supported Pareto Optimization
4. Conclusions and Outlook
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ballard, N.; Asua, J.M. Radical polymerization of acrylic monomers: An overview. Prog. Polym. Sci. 2018, 79, 40–60. [Google Scholar] [CrossRef]
- Meszena, Z.G.; Johnson, A.F. Modelling and simulation of polymerisation processes. Comput. Chem. Eng. 1999, 23, 375–378. [Google Scholar] [CrossRef]
- Saldívar-Guerra, E. Numerical Techniques for the Solution of the Molecular Weight Distribution in Polymerization Mechanisms, State of the Art. Macromol. React. Eng. 2020, 14, 2000010. [Google Scholar] [CrossRef]
- Gómez-Reguera, J.A.; Vivaldo-Lima, E.; Gabriel, V.A.; Dubé, M.A. Modeling of the Free Radical Copolymerization Kinetics of n-Butyl Acrylate, Methyl Methacrylate and 2-Ethylhexyl Acrylate Using PREDICI®. Processes 2019, 7, 395. [Google Scholar] [CrossRef]
- Trigilio, A.D.; Marien, Y.W.; Van Steenberge, P.H.M.; D’hooge, D.R. Gillespie-Driven kinetic Monte Carlo Algorithms to Model Events for Bulk or Solution (Bio)Chemical Systems Containing Elemental and Distributed Species. Ind. Eng. Chem. Res. 2020, 59, 18357–18386. [Google Scholar] [CrossRef]
- Peikert, P.; Pflug, K.M.; Busch, M. Modeling of High-Pressure Ethene Homo- and Copolymerization. Chem. Ing. Tech. 2019, 91, 673–677. [Google Scholar] [CrossRef]
- Trigilio, A.D.; Marien, Y.W.; Van Steenberge, P.H.M.; D’hooge, D.R. Toward an Automated Convergence Tool for Kinetic Monte Carlo Simulation of Conversion, Distributions, and Their Averages in Non-dispersed Phase Linear Chain-Growth Polymerization. Ind. Eng. Chem. Res. 2023, 62, 2583–2593. [Google Scholar] [CrossRef]
- Brandão, A.L.T.; Soares, J.B.P.; Pinto, J.C.; Alberton, A.L. When Polymer Reaction Engineers Play Dice: Applications of Monte Carlo Models in PRE. Macromol. React. Eng. 2015, 9, 141–185. [Google Scholar] [CrossRef]
- Mohammadi, Y.; Saeb, M.R.; Penlidis, A.; Jabbari, E.; J Stadler, F.; Zinck, P.; Matyjaszewski, K. Intelligent Machine Learning: Tailor-Making Macromolecules. Polymers 2019, 11, 579. [Google Scholar] [CrossRef]
- Mohammadi, Y.; Penlidis, A. Polymerization Data Mining: A Perspective. Adv. Theory Simul. 2019, 2, 1800144. [Google Scholar] [CrossRef]
- Fiosina, J.; Sievers, P.; Drache, M.; Beuermann, S. Polymer reaction engineering meets explainable machine learning. Comput. Chem. Eng. 2023, 177, 108356. [Google Scholar] [CrossRef]
- Spyromitros-Xioufis, E.; Tsoumakas, G.; Groves, W.; Vlahavas, I. Multi-target regression via input space expansion: treating targets as inputs. Mach. Learn. 2016, 104, 55–98. [Google Scholar] [CrossRef]
- Ngatchou, P.; Zarei, A.; El-Sharkawi, A. Pareto Multi Objective Optimization. In Proceedings of the 13th International Conference on Intelligent Systems Application to Power Systems, 2005. 13th International Conference on, Intelligent Systems Application to Power Systems, Arlington, Virginia, USA, 06–10 Nov. 2005; IEEE / Institute of Electrical and Electronics Engineers Incorporated. 2005; pp. 84–91, ISBN 1-59975-174-7. [Google Scholar]
- Gunantara, N. A review of multi-objective optimization: Methods and its applications. Cogent Eng. 2018, 5, 1502242. [Google Scholar] [CrossRef]
- Doumpos, M.; Zopounidis, C. Multi-objective optimization models in finance and investments. J. Glob. Optim. 2020, 76, 243–244. [Google Scholar] [CrossRef]
- Gupta, S.; Haq, A.; Ali, I.; Sarkar, B. Significance of multi-objective optimization in logistics problem for multi-product supply chain network under the intuitionistic fuzzy environment. Complex Intell. Syst. 2021, 7, 2119–2139. [Google Scholar] [CrossRef]
- Bhaskar, V.; Gupta, S.K.; Ray, A.K. APPLICATIONS OF MULTIOBJECTIVE OPTIMIZATION IN CHEMICAL ENGINEERING. Rev. Chem. Eng. 2000, 16, 1–54. [Google Scholar] [CrossRef]
- Murugan, C.; Subbaian, S. Multi-Objective Optimization for Enhanced Ethanol Production during Whey Fermentation. In 2022 International Conference on Power, Energy, Control and Transmission Systems (ICPECTS), Chennai, India, 08–09 Dec. 2022; IEEE, 2022; pp 1–7, ISBN 978-1-6654-6275-4.
- Fiandaca, G.; Fraga, E.S.; Brandani, S. A multi-objective genetic algorithm for the design of pressure swing adsorption. Eng. Optim. 2009, 41, 833–854. [Google Scholar] [CrossRef]
- Ganesan, T.; Elamvazuthi, I.; Ku Shaari, K.Z.; Vasant, P. Swarm intelligence and gravitational search algorithm for multi-objective optimization of synthesis gas production. Appl. Energy 2013, 103, 368–374. [Google Scholar] [CrossRef]
- Charoenpanich, T.; Anantawaraskul, S.; Soares, J.B.P. Using Artificial Intelligence Techniques to Design Ethylene/1-Olefin Copolymers. Macromol. Theory Simul. 2020, 29, 2000048. [Google Scholar] [CrossRef]
- Dragoi, E.N.; Curteanu, S. The use of differential evolution algorithm for solving chemical engineering problems. Rev. Chem. Eng. 2016, 32, 149–180. [Google Scholar] [CrossRef]
- Fernandes, F.A.N.; Lona, L.M. Neural network applications in polymerization processes. Braz. J. Chem. Eng. 2005, 22, 401–418. [Google Scholar] [CrossRef]
- Konak, A.; Coit, D.W.; Smith, A.E. Multi-objective optimization using genetic algorithms: A tutorial. Reliab. Eng. Syst. Saf. 2006, 91, 992–1007. [Google Scholar] [CrossRef]
- Marler, R.T.; Arora, J.S. The weighted sum method for multi-objective optimization: new insights. Struct. Multidisc. Optim. 2010, 41, 853–862. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A K-Means Clustering Algorithm. Appl. Stat. 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Nielsen, F.; Nock, R.; Amari, S. On Clustering Histograms with k-Means by Using Mixed α-Divergences. Entropy 2014, 16, 3273–3301. [Google Scholar] [CrossRef]
- Henderson, K.; Gallagher, B.; Eliassi-Rad, T. EP-MEANS: An Efficient Nonparametric Clustering of Empirical Probability Distributions. In Proceedings of the 30th Annual ACM Symposium on Applied Computing. SAC 2015: Symposium on Applied Computing, Salamanca Spain, 13–17 Apr. 2015; Wainwright, R.L., Corchado, J.M., Bechini, A., Hong, J., Eds.; ACM: New York, NY, USA, 2015; pp 893–900, ISBN 9781450331968.
- Banerjee, A.; Merugu, S.; Dhillon, I.S.; Ghosh, J. Clustering with Bregman Divergences. J. Mach. Learn. Res. 2005, 6, 1705–1749. [Google Scholar]
- Drache, M.; Drache, G. Simulating Controlled Radical Polymerizations with mcPolymer—A Monte Carlo Approach. Polymers 2012, 4, 1416–1442. [Google Scholar] [CrossRef]
- Feuerpfeil, A.; Drache, M.; Jantke, L.-A.; Melchin, T.; Rodríguez-Fernández, J.; Beuermann, S. Modeling Semi-Batch Vinyl Acetate Polymerization Processes. Ind. Eng. Chem. Res. 2021, 60, 18256–18267. [Google Scholar] [CrossRef]
- Mätzig, J.; Drache, M.; Drache, G.; Beuermann, S. Kinetic Monte Carlo Simulations as a Tool for Unraveling the Impact of Solvent and Temperature on Polymer Topology for Self-Initiated Butyl Acrylate Radical Polymerizations at High Temperatures. Macromol. Theory Simul. 2023, 32, 2300007. [Google Scholar] [CrossRef]

| variables | description | restrictions |
| cm,0 | initial monomer concentration | cm,0(min) ≤ cm,0 ≤ cm,0(max) |
| cini,0 | initial initiator concentration | cini,0(min) ≤ cini,0 ≤ cini,0(max) |
| t | reaction time | tmin ≤ t ≤ tmax |
| r=[cm,0, cini,0, t] | initial recipe |
| objectives | description |
| fMSE(r)= | minimal MSE, where MMD(r) is simulated |
| fcm(r)= | minimal relative monomer concentration |
| ft(r) = t | minimal reaction time (directly from r) |
| IDs of the best recipe | 1 | 34 | 35 | 46 | 20 | 33 | ||
| wi | time focus (A) | wi | conversion focus (B) | |||||
| cm,0 / mol∙L−1 | 2.0 | 2.21 | 2.21 | 2.21 | 2.43 | 2.21 | ||
| cini,0 / mmol∙L−1 | 20 | 20 | 20 | 8.4 | 16.1 | 10.5 | ||
| time / min | 0.9 | 20 | 40 | 60 | 0.19 | 120 | 80 | 100 |
| MSE /∙10−3 | 0.05 | 1.63 | 1.37 | 0.35 | 0.01 | 1.72 | 1.58 | 1.16 |
| conversion / % | 0.05 | 25.9 | 46.6 | 61.8 | 0.8 | 71.3 | 69.6 | 68.7 |
| IDs of the best recipe | 35 | 32 | 21 | 43 | 12 | 0 | ||
| wi | equal weights (C) | wi | MSE focus (D) | |||||
| cm,0 / mol∙L−1 | 2.21 | 2.21 | 2.21 | 2.0 | 2.0 | 2.0 | ||
| cini,0 / mmol∙L−1 | 20.0 | 10.5 | 13.0 | 12.4 | 10.0 | 8.5 | ||
| time / min | 1/3 | 60 | 80 | 80 | 0.01 | 180 | 200 | 60 |
| MSE / ∙10−5 | 1/3 | 35 | 31 | 54 | 0.9 | 0.086 | 0.032 | 0.64 |
| conversion / % | 1/3 | 61.8 | 60.2 | 64.4 | 0.09 | 48.3 | 48.2 | 45.1 |
| objective weights | cand. ID | cm,0 / mol∙L−1 |
cini,0 / mmol∙L−1 |
time / min |
MSE / 10−3 |
conversion / % |
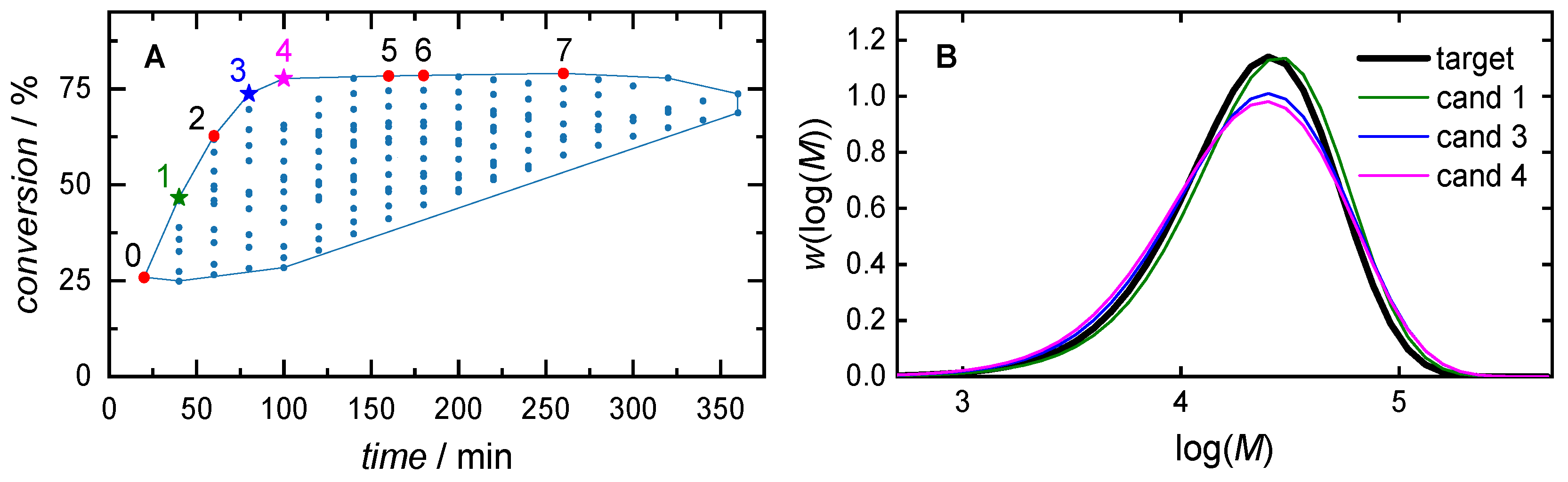
| 0 | 2.00 | 20.0 | 20 | 1.63 | 25.9 | |
| time focus: (wcm = 0.2, wt = 0.8) |
1 | 2.21 | 20.0 | 40 | 1.37 | 46.6 |
| 2 | 2.43 | 20.0 | 60 | 1.94 | 62.7 | |
| equal weights: (wcm = 0.5, wt = 0.5) |
3 | 2.43 | 20.0 | 80 | 1.81 | 73.7 |
| conversion focus: (wcm = 0.8, wt = 0.2) |
4 | 2.43 | 16.1 | 100 | 2.61 | 77.7 |
| 5 | 2.43 | 6.86 | 160 | 2.79 | 78.3 | |
| 6 | 2.43 | 5.54 | 180 | 2.83 | 78.5 | |
| 7 | 2.43 | 2.91 | 260 | 2.98 | 79.0 |
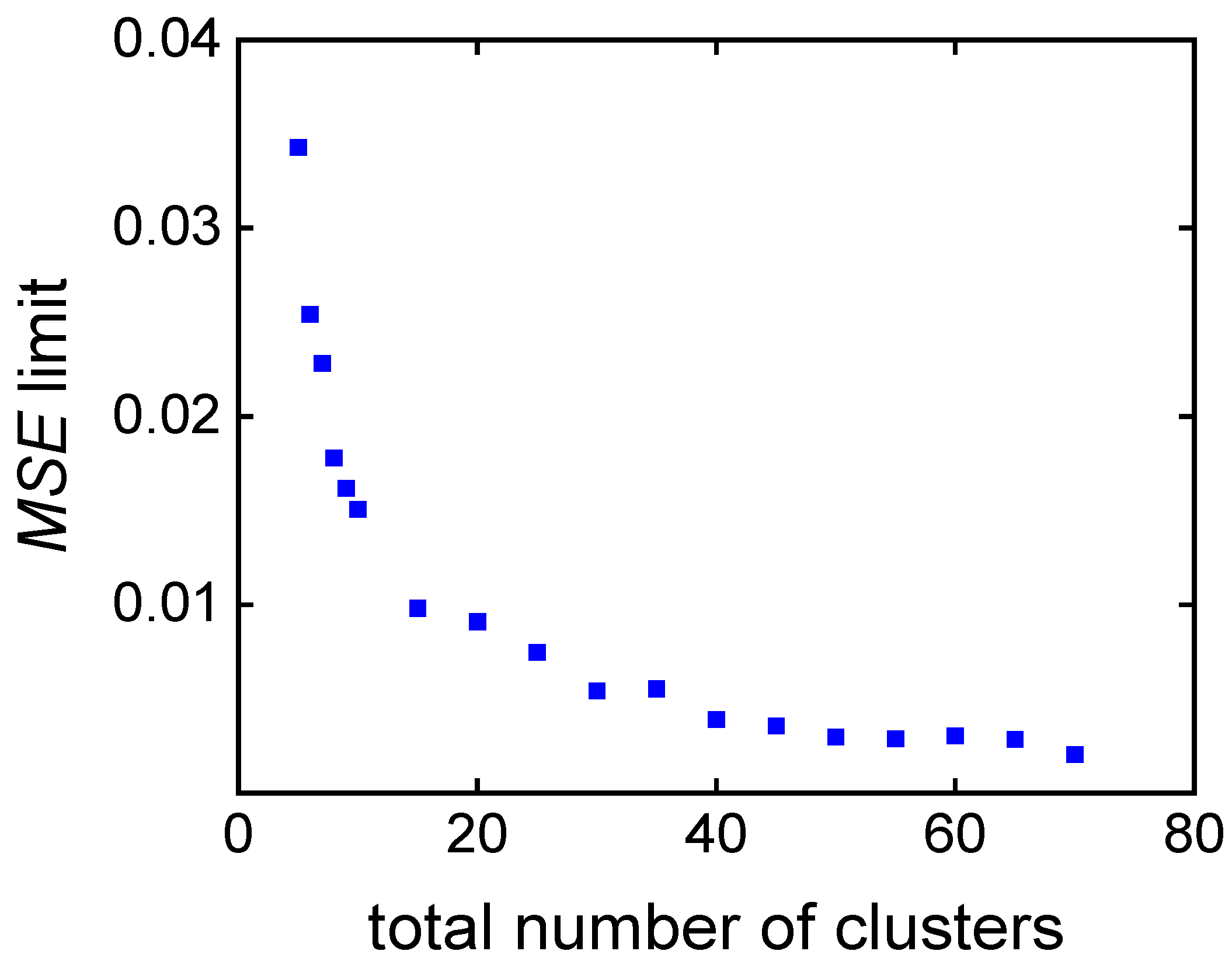
| Number of clusters | 20 | 40 | 60 | |
| cand. ID/ | 3 | 2 | 1 | |
| property | wi | |||
| cm,0 / mol∙L−1 | 3.50 | 3.07 | 2.86 | |
| cini,0 / mmol∙L−1 | 13.0 | 20.0 | 20.0 | |
| time / min | 0.5 | 60.0 | 40.0 | 20.0 |
| MSE /∙10-3 | 3.04 | 0.32 | 0.03 | |
| conversion / % | 0.5 | 58.2 | 49.2 | 27.0 |
| score (wt = 0.5, wcm = 0.5) | 0.50 | 0.39 | 0.50 | |
| score (wMSE = 1/3, wcm = 1/3, wt = 1/3) | 0.67 | 0.30 | 0.33 |
| approach | direct | clustering supported approach | ||||
| 20 clusters | 40 clusters | 60 clusters | 80 clusters | 100 clusters | ||
| execution time, s | 679 | 56 | 25 | 18 | 14 | 12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





