Information geometry (IG) has been widely applied in many research fields such as statistical inference, stochastic control, and neural networks .In other words, IG aims to apply the techniques of differential geometry (DG) to statistics. This means that IG’s main idea is to apply methods and techniques of non-Euclidean geometry to stochastic processes and probability theories. IG indicates that the use of Euclidian geometry technique is useful to think of a family of probability distributions as a statistical manifold (SM). Moreover, IG has been adopted for the study of statistical manifolds (SMs), where the geometric metrics gave a new description of the probability density function which plays an important role in SM and can be regarded as the coordinate system.

A manifold is a topological finite dimensional Cartesian space, ${\mathbb{R}}^n$, where one has an infinite-dimensional manifold. ${\mathbb{R}}^{n }$ could be described merely as topological space (may be defined as a set of points, along with a set of neighbourhoods for each point, satisfying a set of axioms relating points and neighbourhoods). In addition, IG supports reasoning intuitively the description of SMs. Note that although figures can be visualised (i.e., plotted in coordinate charts), they should be thought of as purely abstract figures, namely, geometric figures. One may have a higher level of appreciation of the significant importance of IG. In Figure 1, the parameter inference$\widehat{\theta }$of a model from data can be interpreted as a decision-making problem: One has to decide which parameter of a family of models $M={\left\{m_{\theta }\right\}}_{\theta ϵ\mathsf{\Theta }}$ suits “best’’ the data, where $\mathsf{\Theta }$ is the set of parameters {${\theta }_1,{\theta }_2,..,{\theta }_n\}$ of the probability density function of the distributionof the geometric manifold. IG provides a differential-geometric manifold structure$M$ that is useful for developing decision rules.

In this paper, a study is undertaken of the geometric structure of the Generalized Brownian Motion Manifold (GBM) as well as finding its information matrix exponential (IME). The (IME) is a matrix on square matrices analogous to the ordinary exponential function. Furthermore, the Lorenzian Dynamics for (GBM) is devised.

It is used to solve systems of linear differential equations. In addition to that, the matrix exponential plays a crucial role in the theory of Lie groups. To our knowledge, the current paper is the first ever to revolutionize classic Brownian Motion Theory (BMT) by devising the Info-Geometric analysis of (GBM).

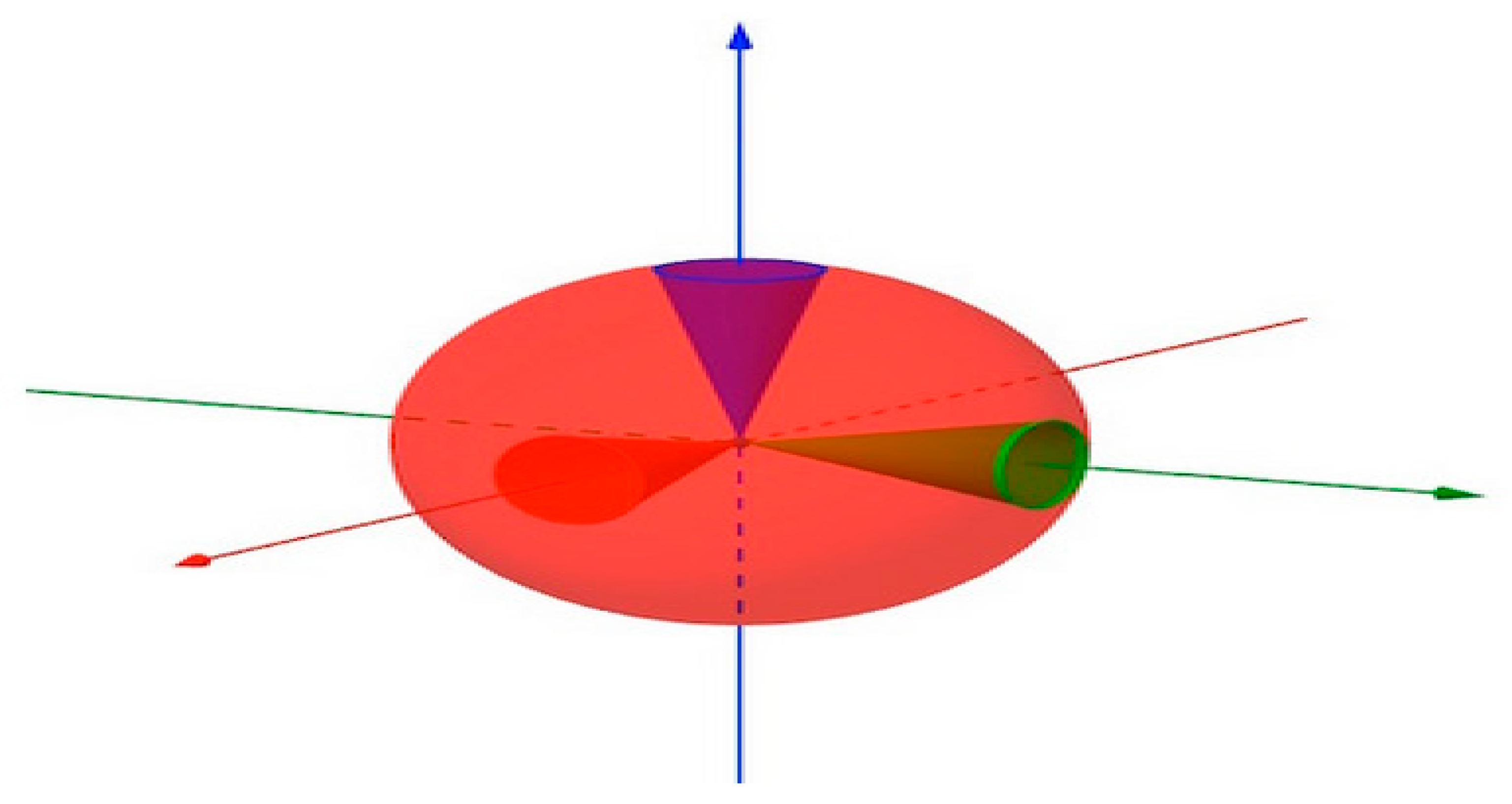
In this context, by analogy to information theory (IT), the geometric approach adopted in this paper enables the study of invariance and equivariance of figures in a coordinate-free approach (n.b., by equivariance as a concept, it is meant when there is a group acting on a pair of spaces and there is a map from functions on one to the functions on the other. In the context of this paper, Ricci curvature measures the deviation of the Riemannian metric (RM) from the standard Euclidean metric (EM) and how scalar curvature measures the deviation in the volume of a geodesic ball from the volume of an Euclidean ball of the same radius (c.f., Figure 2).

Geodesics are the analogue of straight lines in Euclidean space and possess many of the same properties as straight lines. In Einstein’s classical concept of General Relativity(GR), objects travel on a geodesic in curved space-time, which extremises the proper time between two points. Hence, the same mathematics describes both the geometry of curved spaces and the geometry of space-time. Moreover, a “straight line on a curved surface” is called a geodesic, which minimizes the distance between 2 points. In IG, the Fisher information metric (FIM) is a particular Riemannian metric (RM), which can be defined on a smooth statistical manifold (i.e., a smooth manifold whose points are probability measures defined on a common probability space). It can be used to calculate the informational difference between measurements. The FIM measures closeness of the shape between two distribution functions, it is also proportional to the amount of information that the distribution function contains about the parameter of the probability density function of the SM.

Einstein first gave a rigorous and accurate description of diffusion in simple physical systems. This description can be understood in the Eulerian framework as satisfying the diffusion equation with a constant diffusion coefficient, and in the Lagrangian framework as Brownian motion; a continuous stochastic process with stationary, independent, Gaussian increments, $X\left(t\right)-X\left(s\right), t>s >0,$of variance ${\delta }^2(t-s)$. In recent years several diffusive phenomena that do not fit neatly into Einstein’s framework have been discovered, and these sorts of diffusion have been collectively described as being anomalous. Examples of these phenomena include diffusion in cytoplasm and confined nanofilms, the motion of albatrosses and sharks, diffusion of polymers and dispersion in the geophysical subsurface among many others. One of the hallmarks of classical diffusion (i.e., diffusion which is described by Brownian motion and the diffusion equation with constant diffusion coefficient) is that the mean square displacement grows linearly in time.

Anomalous diffusion processes frequently do not exhibit this behaviour with a power-law mean square displacement often appearing. We should point out, however, that many diffusive processes with linear mean square displacement still are anomalous. A diverse set of models have been constructed to describe the behaviour of anomalous diffusion phenomena. These models include continuous time random walk, Lévy motion, fractional Brownian motion, and many others These models frequently have power-law mean square displacements or heavy tails. In the Lagrangian framework, they can be understood to differ from Brownian motion by having interdependent, non-stationary, or non-Gaussian increments (or some combination of the three).

The Boltzmann-Gibbs entropy can be derived by assuming that the four Shannon- Khinchin axioms hold.

For a set of discrete states, the Tsallis entropy is: where $p\left(n\right)$ is the probability of being in the $n^{th}$ state. In the limit $q\to 1$, the Tsallis entropy reduces to the Boltzmann-Gibbs entropy. Assuming that the Tsallis entropy is the appropriate entropy for the system under examination, the value of q that produces an extensive entropy can be determined by examining the volume of phase space (the space of all possible system states) as a function of the system size. For example, in a classical statistical mechanical setting the system size is determined by the number of particles and the phase space volume is given by the set of all possible position and momenta coordinates (${\mathsf{\Omega }}^N\times R^{3N}$) where $\mathsf{\Omega }$ is the box within the particles within $\mathsf{\Omega }$.

For a continuous random variable$X$, the Tsallis entropy of $X$ is: where $f_X\left(x\right)$ is the probability density function of $X.$(In a dimensional system, an issue of dimensional consistency arises $–$ the 1 in the integral in equation (1.2) have different units. However, this issue is not essential, because the 1 is a carry-over from the discrete entropy so that a system without ant randomness (one of the $p\left(n\right)=1)$has zero. Shifting $H_q\left(X\right)$ by a constant has no impact on the employed maximum entropy).

Random variables following a q-Gaussian distribution are maximum Tsallis entropy distributions subject to holding various statistics constant (e.g., the second moment or the second q-moment). Note, however, that for fixed second moment, a q-Gaussian random variable maximizes $H_{2-q}$ rather than $H_q$. The maximum entropy properties make the q-Gaussian distribution in the context of the Tsallis entropy the analogue of the Gaussian distribution in the context of the Boltzmann-Gibbs entropy. The probability density function for a q-Gaussian is given by where is called the q-exponential, $C_q$ is a normalization constant, and $\beta >0$ is a scale parameter. In the range of extensive values of the information theoretic parameter $q$, $1<q<3$, the q-Gaussian distribution is a rescaled version of the Student’s $t$ –distribution with $\nu = \frac{3-q}{q-1}$ degrees of freedom. The scaling is such that the distributions are the same if $\beta = \frac{\nu +1}{2\nu }= \frac{1}{3-q}$. It is notable to state that the extensive values assigned to the information theoretic parameter q justifies the physical interpretation of Brownian Motion.

Focussing on this range, will utilize a representation of the Student’s t-distribution for a key part of the analysis below.

Consider the stochastic differential equation: where$B\left(t\right)$ is a Brownian motion, and D is a random variable that is independent of $B\left(t\right).$Here the stochastic differential equation is regarded as being conditioned on D. If the probability density function, $f_D\left(x\right)$, of D is given by then D is a constant, and the distribution of the displacement due to diffusion, $X\left(t\right)-X\left(0\right)-\nu t$, is a Gaussian (note that the Gaussian distribution maximizes the Boltzmann-Gibbs entropy). This naturally leads to the question of whether there are distributions of D that would make the distribution of $X\left(t\right)-X\left(0\right)-\nu t$ maximize the Tsallis entropy. We will answer this question in the affirmative and explicitly construct the appropriate distribution for D.

Suppose that: where$V\sim {\chi }^2\left(\nu \right)$ is a chi-squared distribution with $\nu$ degrees of freedom and $\sim$ denotes that two random variables have the same distribution. Then the distribution of $X\left(t\right)-X\left(0\right)-\nu t$ takes the form where Z is a standard normal random variable. At this point, we note that a Student’s t-distribution takes the form $\frac{Z}{\raisebox{1ex}{$V$}\!\left/ \!\raisebox{-1ex}{$\nu $}\right.}$ where Z is a standard normal distribution and $V$ is a chi-squared distribution with ν degrees of freedom. Therefore, the right-hand side of equation (1.9) is a rescaled (by a factor $\sqrt{D_{0}t}$) Student’s t-distribution, or, in other words, a q-Gaussian. Hence, the distribution of $X\left(t\right)-X\left(0\right)-\nu t$ maximizes the Tsallis entropy.

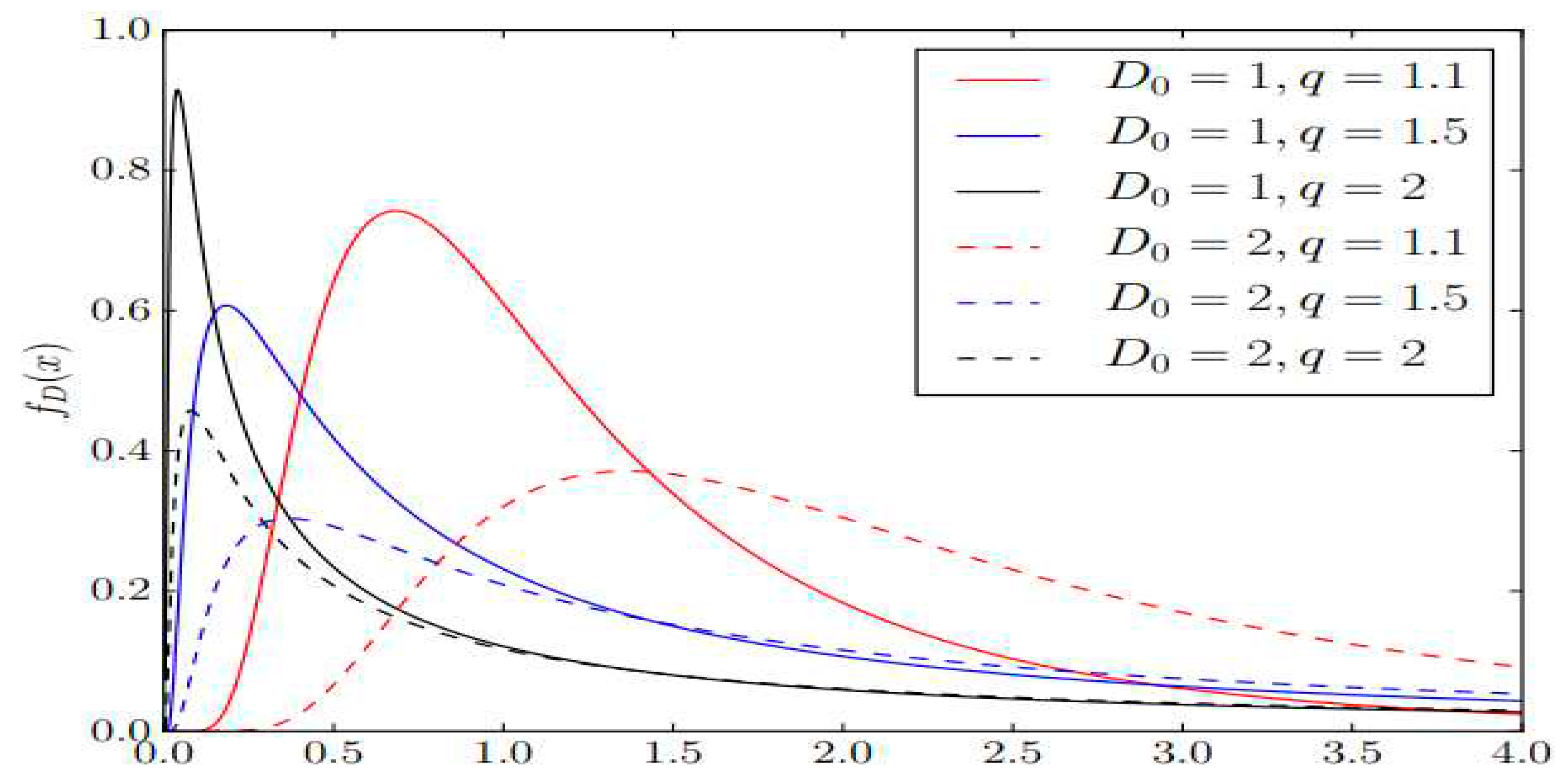
By changing variables in equation (1.7), we obtain the probability density function for D: This equation can be recast in terms of q by recalling that $= \frac{3-q}{q-1}$ . Figure 3 shows several plots of $f_D\left(x\right).$Note that in the limit as $q\to 1^{+}$(or equivalently, $\nu$ → ∞), $f_D\left(x\right)$ → $\delta (x-D_0)$, so that equation (1.6) is satisfied in the limit. Therefore, classical advection-dispersion is recovered in the limit as $q\to 1^{+}$ for equation (1.5). This is to be expected, since $q\to 1$corresponds to the classical Boltzmann-Gibbs entropy, and classical advection-dispersion maximizes the Boltzmann-Gibbs entropy.

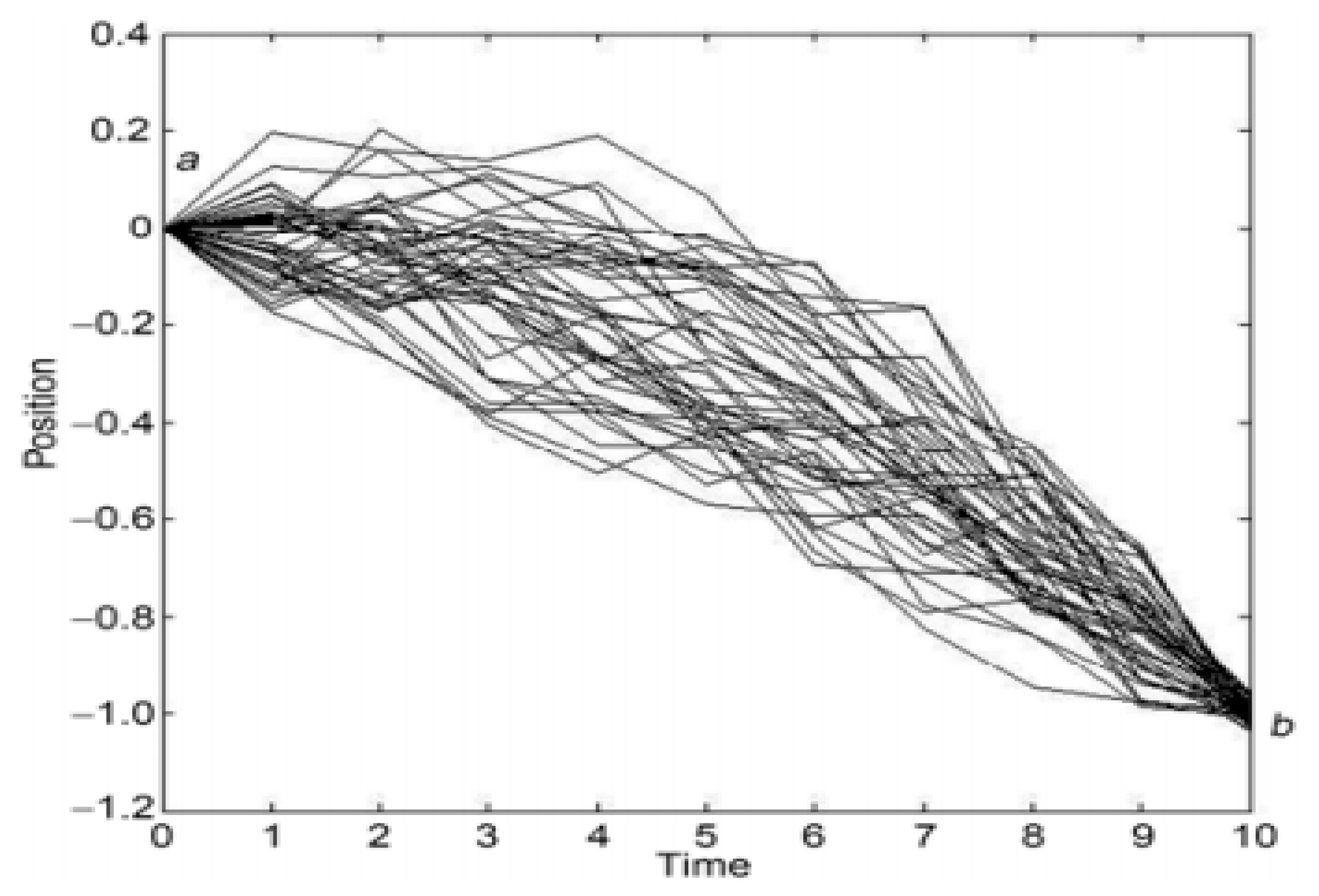
Brownian motion is an idealized approximation to actual random dynamics that has been extensively investigated over a long period time, but possibly still not thoroughly understood. Recently, Brownian, and random motion have been extended into the field of fractional Brownian motion, stochastic noise, and quantum random walks. Figure 4 shows a numerical simulation of paths (bundle) from point a to point b for particles in a constant force field such as weight. The time duration of the motion is $n=10$steps with the same unit time increment for each step. Each path is a sequence of positions $\{x_a, x_{1 },x_2, x_{n-1}, x_b\}$

The main original contributions of this paper are described below.

The rest of this paper is organised as follows: Section 1 lays out a brief introduction to Information geometry, IG and Generalized Brownian Motion , GBM. Section 2 presents preliminary definitions associated with (IG). In section 3, Ricci scalar,$\mathcal{R}$ and the $\alpha -\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e} \mathrm{R}\mathrm{i}\mathrm{e}\mathrm{m}\mathrm{a}\mathrm{n}\mathrm{n}\mathrm{i}\mathrm{a}\mathrm{n}$ Tensor, $\mathsf{\Pi }$ $-\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{a}\mathrm{l} \mathrm{c}\mathrm{u}\mathrm{r}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e} \mathrm{t}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{o}\mathrm{r},\mathrm{\beth }$ are calculated. In section 4, the Ricci Tensor, $\mathsf{{\rm Y}},$the $\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e} \mathrm{o}\mathrm{f} \mathrm{s}\mathrm{p}\mathrm{a}\mathrm{c}\mathrm{e} \mathrm{t}\mathrm{i}\mathrm{m}\mathrm{e}\left(\mathrm{e}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{i}\mathrm{n} \mathrm{t}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{o}\mathrm{r}\right)\mathrm{\wp }\mathsf{\alpha }\mathrm{n}\mathrm{d} \mathrm{s}\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{s} \mathrm{e}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{g}\mathrm{y} \mathrm{t}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{o}\mathrm{r},\mathsf{\Omega }$ are calculated. Concluded remarks and future work are given in section 5.

The scalar curvature(Ricci Scalar), $\mathcal{R}$ is the contraction of Ricci Tensor. The two-dimensional Ricci Scalar, $\mathcal{R}$ is twice as the Gaussian Curvature $K_G$ The Ricci scalar $\mathcal{R}$ has a meaning very similar to the Gaussian Curvature. If we imagine instead of taking a circle, taking a generalized $n-1$ sphere, i.e. the set of all points a geodesic distance$ϵ$ from a given starting point $x_0^{\zeta }$. We can calculate the area of this sphere in flat space, but in a curved space the area will deviate from the one we calculated by an amount proportional to the curvature. Thus, the Ricci Scalar is: Ricci scalar completely captures the curvature of the surface.

The equations of motion of a classical theory like General Relativity can be derived directly from a suitable action by using the Euler-Lagrange equations, leading to the well-known Einstein equations: where $G_{ij }$is the Curvature of Spacetime(Einstein tensor), $\wp$, ${ R}_{ij}^{\left(\alpha \right)}$is the Ricci tensor of the spacetime represented by the metric $g_{ij}$, $\mathcal{R}=R_{ij}^{\left(\alpha \right)}{g}^{ij}, i,j=\mathrm{1,2},3,\dots ,$is the Ricci scalar or scalar curvature,$\mathcal{g}$is the universal gravitational constant,$c_{light}$is the speed of light, and ${\varpi }_{ij}$ are the components of the stress-energy tensor,$\varpi$,describing generically the matter-energy distributions in the spacetime.

The curvature of the $n - 1$ dimmensional subspace orthogonal to the unit vector t is just negative two times the Einstein tensor fully contracted with the temporal vector${ t}^{\to }$. For general relativity, this means that once we choose a time direction, Einstein’s tensor tells us the scalar curvature of the corresponding spacial dimensions.

Theorem 1.1 The Ricci Scalar, $\mathcal{R}$ of the GBM Manifold is given by: ${\psi , \psi }_1 are the digamma and trigamm functions, respectively (c.f., \left[2\right])$Proof

The Gaussian Curvature $K_G$ of GBM Manifold (c.f., [2]) is given by:

Following (2.6), it holds that:

This proves our theorem.

In this section, $\mathsf{\alpha }-\mathrm{C}\mathrm{u}\mathrm{r}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{R}\mathrm{i}\mathrm{e}\mathrm{n}\mathrm{m}\mathrm{m}\mathrm{a}\mathrm{n}\mathrm{i}\mathrm{a}\mathrm{n}\mathrm{T}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{o}\mathrm{r},\mathsf{\Pi }$ is obtained. This unifies GBM manifold with Riemannian geometry, which will be used to devise the $\alpha -\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{a}\mathrm{l}\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{s}$ tensor, $\mathrm{\beth }$.

Theorem 3.2 The $\mathsf{\alpha }-\mathrm{C}\mathrm{u}\mathrm{r}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{R}\mathrm{i}\mathrm{e}\mathrm{n}\mathrm{m}\mathrm{m}\mathrm{a}\mathrm{n}\mathrm{i}\mathrm{a}\mathrm{n}\mathrm{T}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{o}\mathrm{r},\mathsf{\Pi }$ of the GBM Manifold is given by: 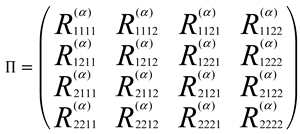where

))] (

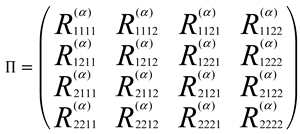
Where ${\psi }_2\left(z\right)=\frac{d}{dz}\left({\psi }_1\right)$

It is obtained that the Fisher Information Matrix of GBM Manifold, $\left[g_{ij}\right]$ (c.f., [1]) is determined by:

Moreover, the reader can check that the $\alpha -$ connections of the GBM manifold (c.f., [1]) given by

It can be verified that:

))]