Prerpints.org logo
Preprint
Communication

Diversity of the Japanese Gut Microbiome Analysis: Relative Approach Using Principal Component Analysis

Altmetrics

Downloads

312

Views

515

Comments

0

supplementary.docx (238.26KB )

Submitted:

11 March 2024

Posted:

11 March 2024

You are already at the latest version

Alerts
Abstract
A compositional data vector is a special type of multivariate observation in which the elements of the vector are non-negative and sum to a constant, usually taken to be unity. A compositional data does not have zero and only retains relative information. Furthermore, comparisons can only be made between compositional data of the same component. The relevant sample space is the standard simplex. A simplex space is a space that is a generalized form of a triangle. For compositional data, many of the operations defined in Euclidean space are meaningless. Microbiome analyzes have become popular in recent years. Operational Taxonomic Units (OTU) and Amplicon Sequence Variants (ASVs) used in microbiome analysis are one type of compositional data. The microbiome data are counts of different species within a sample and it is compositional. Although there is an order of bacterial abundance within a sample, there is no order of bacterial abundance between samples. Firmicutes and Bacteroidetes, the major phyla in the colon, have been observed in humans worldwide. Gut microbiome analyses often use the Firmicutes/Bacteroidetes ratio and principal coordinates analysis (PCoA). Alpha and beta diversities are used as indicators of bacterial flora diversity. However, misinformation is pervasive in the human microbiome literature and analysis. There is a lot of misunderstanding regarding compositional data and its analysis. An attempt was made to demonstrate how to analyze using the “National Institutes of Biomedical Innovation, Health and Nutrition (NIBIOHN JMD) (Public Data).” The results showed that PCoA did not work, and principal component analysis (PCA) was useful for analyzing the gut microbiome relative diversity.
Keywords: 
Subject: Biology and Life Sciences  -   Biology and Biotechnology

1. Introduction

Basis is a non-constrained data (counting data) [1,2,3,4,5]. Composition corresponds to the constrained data [1,2,3,4,5]. Compositional data is relatively normalized data. When considering the ratios of compositions, the coefficient of variation is affected by moments up to the fourth order of basis. The coefficient of variation of ratios is subject to change when the unchanging component is switched between the denominator and numerator [1]. Compositional data cannot be used to calculate sums, differences, products, or quotients [1,2,3,4,5]. When the constituent elements are not the same, the appearance patterns will be different, and the differences in each component cannot be compared using compositional data [1,2,3,4,5]. The correlation and rank correlation coefficients do not mean the correlation on compositional data [[2], Supplementary Materials]. The comparisons of the compositional components varied depending on the denominator size [1,2,3,4,5]. In other words, while the proportion is one for the whole, it is common to extract a portion and renormalize the whole to one with the data from that portion, resulting in an apparent change. Changes in percentages represent apparent changes in relative abundance [3,4,5]. A simple example of calculating percentages is that if one mixes 10% saline and 20% saline, the resulting concentration will be between 10% and 20%, depending on the amount added to each concentration. To determine whether a 10% saline solution or a 20% saline solution contains more salt, we need to know the total amount of saline solution. However, this argument cannot be made if the total quantity is unknown. This indicates that the 20% saline solution had a higher percentage of salt. The order of bacteria abundance among individuals cannot be determined by compositional data. Even if the relative abundance is low, the absolute abundance may be high.
Principal component analysis (PCA) and multidimensional scaling (MDS or principal coordinates analysis/PCoA) are often used for gut microbiome analyses [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]. PCA and PCoA are types of unsupervised machine learning. Use of these analyzes requires algebraic knowledge. A simplex is a generalization of a triangle or a tetrahedron [3,4,5]. PCA corresponds to the task of finding a specific Cartesian coordinate axis in a p-dimensional subspace within a n-dimensional vector space and synthesizing principal component vectors on that Cartesian coordinate axis. The ordinary PCA uses n subjects that are independent of each other as the coordinate axes of a n-dimensional vector space, and p types of observed items that are correlated with each other as the coordinate axes of a p-dimensional subspace. In the case of compositional data, it is a (p-1)-dimensional subspace [1]. PCA is a commonly used analysis to show relative relationships. In contrast, the multidimensional scaling method uses p observation items that are independent of each other as the coordinate axes of a p-dimensional vector space, and on subjects that are treated as correlated in terms of their similarity or distance to each other as the coordinate axes of a n-dimensional subspace. Considering these points, it is contradictory to apply PCA and multidimensional scaling to the same data at the same time. When constructing a positional relationship in Euclidean space from a distance matrix representing dissimilarity in multidimensional scaling, even the same compositional data are often plotted at different positions in Euclidean space. Furthermore, the distances commonly used in multidimensional scaling methods are the Bray-Curtis distance and the Jaccard distance, but these are only used in Euclidean space and cannot be used for compositional data in simplex space. PCoA is used when an order holds between samples, such as in a questionnaire. Therefore, PCoA cannot be applied to compositional data. For ordinary medical data involving intestinal flora, it is more reasonable to apply PCA rather than the multidimensional scaling construction method [24].
Firmicutes and Bacteroidetes, the major phyla in the colon, have been observed in humans worldwide. The five major colonic phyla in Japanese individuals were Firmicutes, Bacteroidetes, Actinobacteria, Proteobacteria, and Fusobacteria. Gut microbiome analysis is a field of information engineering. Moreover, in recent years, bacteriological studies have sometimes been conducted using the results from the gut microbiome analysis [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]. However, misinformation is pervasive in the human microbiome literature [6]. Operational taxonomic units (OTU) and Amplicon Sequence Variants (ASVs) are the results of clustering the 16S rRNA gene sequences at a certain cutoff value [7]. Many recent microbiome analyses have compared the proportions of compositional data. Many studies apply mathematical incorrect methods (multidimensional scaling, correlation coefficient and arithmetic means) for analyzing the gut microbiome [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]. Misinformation on microbiota analysis can cause great harm to bacteriology professionals.
Gut microbiome analyses often use the Firmicutes/Bacteroidetes (F/B) ratio [11,12,13,14,15]. Many studies have explored the relationship between the F/B ratio and the evaluation index[11,12,13,14,15]. The ratio is the same for both basis and composition. The F/B ratio is always the same when the results are given in OTU or in any subcomposition. Using the ratio of Bacteroidetes, the relative abundance of other bacteria was compared to that of Bacteroidetes in previous research [11,12,13,14,15]. However, most studies did not provide reasons for using the ratio of Bacteroidetes [11,12,13,14,15]. Moreover, many microbiota analyses have been performed assuming the same number of bacteria among individuals, with many standardized 10,000 OTU reads [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]. However, the assumption that the number of bacteria is the same among individuals is a severe condition that is not necessarily met. The denominator can be chosen arbitrarily for a ratio, as long as it's not zero. If the denominator with the smallest difference between individuals is selected, the ratio only requires consideration of the numerator's effect. A ratio analysis was not done since the same constituent components of the OTU data were little in this study. Therefore, the purpose of this study was to clarify the misconceptions regarding diversity of the Japanese gut microbiome by showing the difference between PCoA and PCA.

2. Materials and Methods

Datasets

The OTU dataset was extracted from the “NIBIOHN JMD (Public Data).” The normalization technique used was total-sum scaling. This study evaluated the fecal samples and metadata of community-dwelling Japanese volunteers from a cohort of the health- and nutrition-based cohort study conducted by the NIBIOHN, hereafter referred to as the NIBIOHN cohort [23]. In the NIBIOHN cohort, 1518 healthy Japanese adult volunteers were analyzed from October 2015 to October 2020 (age range: 19.5–80 years; males: 693; females: 825; 6 regions: Kanagawa, Atsugi; Niigata, Minamiuonuma; Osaka, Osaka; Tokyo, Shinjuku; Yamaguchi, Shunan; Yamanashi, Chuo) [23].

Procedure

All data was analyzed using R version 4.3.1 (2023-06-16 ucrt) or MANTA (Microbiota And pheNoType correlation Analysis platform) public version [23]. Vegan 2.6-4 package was used. PCoA and PCA were performed on the OTU Dataset from the “NIBIOHN JMD (Public Data).” Since compositional data is already normalized data, PCA was performed using sample variance without standardizing the data. MANTA public version's PCoA can use the Bray-Curtis distance, Jaccard distance and weighted UniFrac distance. Two PCoA charts were shown as nonmeaning figures of an index of the diversity. Scatter plots of principal component scores were shown as an index of relative diversity. The relationship between green tea intake and bacterial flora of genus level was investigated using principal component regression analysis. The information on green tea intake was adopted because it had fewer 0s than the others.

3. Results

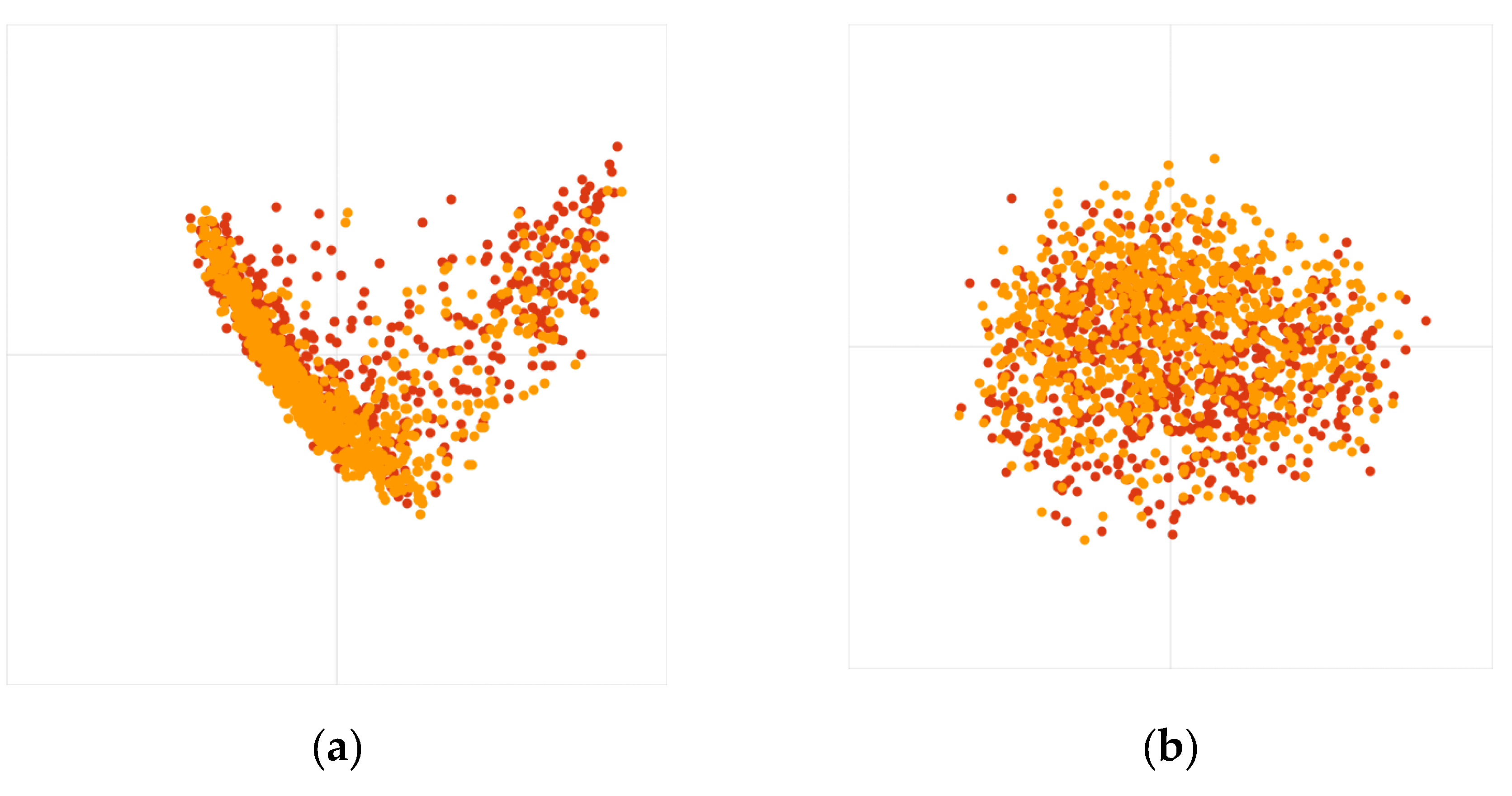
The PCoA results of OTU were shown in Figure 1. The contribution rate of principal coordinates 1 and 2 was less than 22% and 10%, respectively. This indicates that dimensionality reduction failed. Moreover, these results had no scientific meaning for the reasons mentioned above [[1,2,3,4,5], Supplementary Materials].
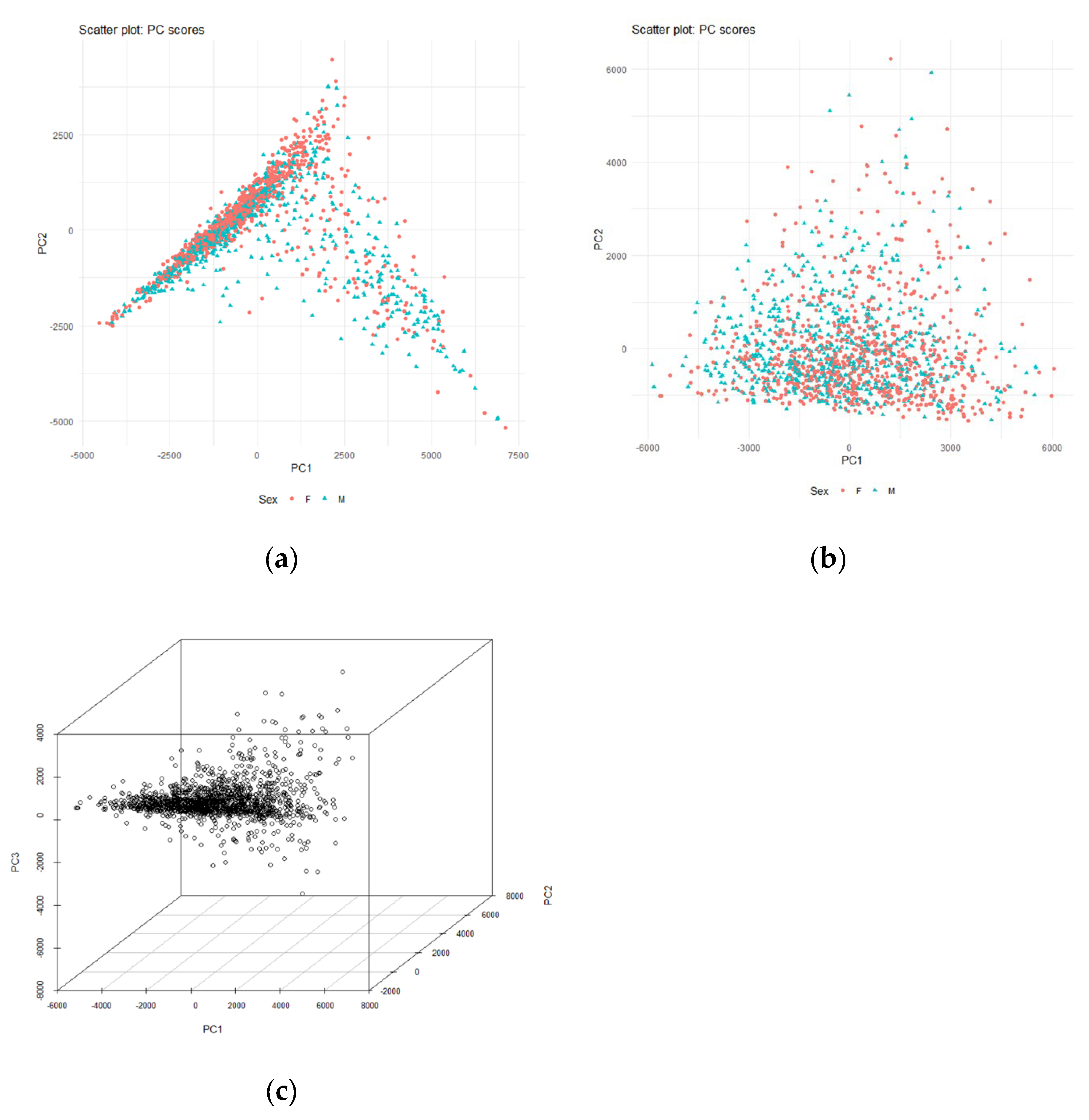
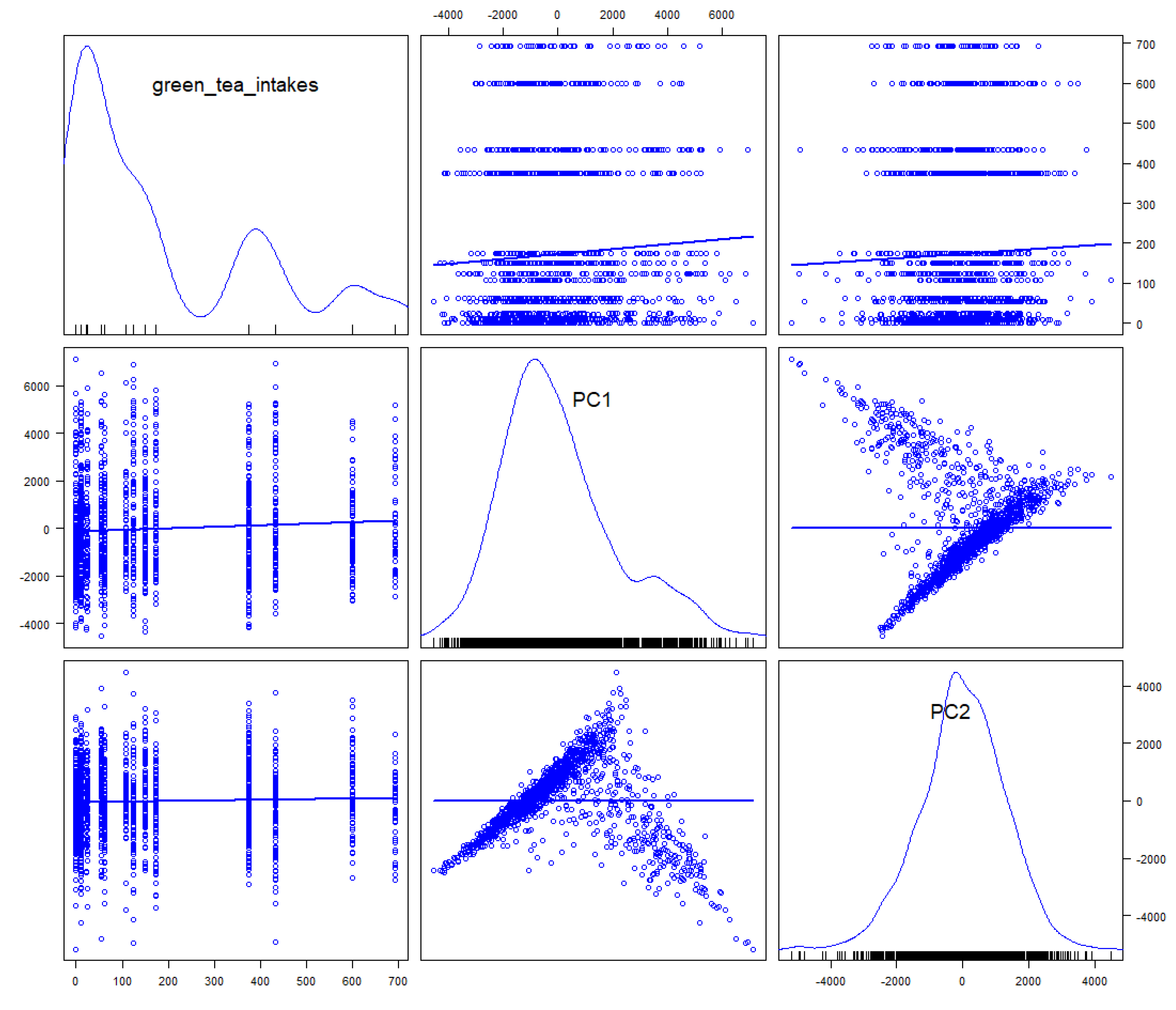
The PCA results of OTU were shown in Figure 2. Principal component scores were plotted in simplex space. The contribution rate of principal components 1 and 2 at the genus level was 66.3%. The contribution rate of principal components 1 and 2 at the class level was 81.0%. These plots summarize the results of a 100% stacked bar graph, thus indicating relative diversity. The adjusted R-squared of principal component regression analysis for green tea intakes was 0.00338 for PC1 and 0.0006333 for PC2, and no relationship was observed (Figure 3). The adjusted R-squared was small, so the fit of the regression model to the data was poor.

4. Discussion

PCoA failed to reduce the dimensionality of compositional information. However, PCA was able to reduce the dimensionality of compositional information. The analysis of beta and alpha diversity using multidimensional scaling was not good because it assumed no correlation between bacteria [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]. ANOSIM, ADONIS, and other analyses may result in small p-values and small values of R and R-squared values. Sometimes, the number of null distributions generated was small, but this only indicated little consistency between the numerical data values, statistical model, and null hypothesis, probably resulting from ignoring correlations between bacteria. On the other, PCA was better because it considered correlations among bacteria. However, the information possessed by compositional data limited PCA because only one composition had only enough information to add up to 100% of the composition [1,2,3,4,5]. A scatterplot of principal component scores was a summary of the 100% stacked bar graph. These scatterplots showed the relative diversity (Figure 2).
Analysis using principal component scores is a univariate analysis. It is necessary to select the classification level used for PCA depending on the number of subjects. As shown in Figure 3, there was no relative relationship. However, this was of little scientific significance as it explored the relationship to relative change. It is difficult to show a true relationship between bacterial flora and diet. Absolute changes rather than relative changes should be examined, but there are currently few methods for doing so [[1,2,3,4,5], Supplementary Materials]. Ratio analysis is effective in solving this problem, but the components that take the ratio must have the same absolute amount [[1], Supplementary Materials]. It is difficult to identify components whose absolute amounts is same, and there are not necessarily such kinds of components [[1], Supplementary Materials]. Analyzing relative information often only examines apparent changes. Therefore, the absolute relationship cannot be investigated in this study.
A limitation of this study was the research design. This was a study that collected data on bacterial composition between individuals, not from the same person. The components of the compositional data defined by Aitchison were positive values [3,4,5]. Since it is only possible to compare compositions of the same component, it is desirable to conduct research that examines changes over time within individuals. In other words, a desirable study design is to collect samples from the same person multiple times and compare changes in the microbiome. Technology has advanced rapidly in recent years. The new technology, Barcoding Bacteria for Identification and Quantification, enables to identify and quantify the individual constituent bacteria [25]. This would allow comparisons of absolute abundances.

5. Conclusions

Many studies apply mathematical incorrect methods (multidimensional scaling, correlation coefficient and arithmetic means) for analyzing the gut microbiome. PCA is recommended for compressing these dimensions. For analyzing the gut microbiome, it is desirable to study changes over time within an individual, form the same person. True compositional data that does not contain zero can use centered log-ratio transformation.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org. Table S1: Sample dataset on artificial composition, Table S2: Sample dataset on artificial basis, Table S3: Statistics of the sample data, Table S4: Sample dataset on artificial composition, Figure S1: Absolute variation and apparent variation of F, Figure S2(a): Absolute variation and apparent variation of G, Figure S2(b): The difference between absolute and apparent variation of G, Figure S3(a): Absolute variation and apparent variation of H, Figure S3(b): The difference between absolute and apparent variation of H. Figure S4: The results of principal coordinates analysis of the same data in Table S4.

Author Contributions

Conceptualization, T.I. and K.S..; methodology, T.I..; software, T.I..; validation, T.I., A.H. and Y.K.; formal analysis, T.I.; investigation, T.I.; resources, T.I.; data curation, T.I.; writing—original draft preparation, T.I.; writing—review and editing, T.I. and Y.K.; visualization, T.I.; supervision, T.I. and A.H.; project administration, T.I.; funding acquisition, K.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

This retrospective study procedures were performed in accordance with the principles of the Declaration of Helsinki.

Informed Consent Statement

This article does not disclose identifiable information of any of the participants in any form. Hence, consent for publication is not applicable in this case.

Data Availability Statement

The OTU data that support the findings of this study are accessible at https://microbiome.nibiohn.go.jp/jmd-public. (The authors accessed on 2023.07.03.)

Acknowledgments

The authors would like to thank Norio Sugimoto for suggesting the idea of using principal component analysis. He then explained to us the difference between principal component analysis and multidimensional scaling in an easy-to-understand manner.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Ohta, T.; Arai, H.; Noda, A. Identification of the unchanging reference component of compositional data from the properties of the coefficient of variation. Math. Geosci. 2011, 43, 421–434. [Google Scholar] [CrossRef]
  2. Pearson, K. Mathematical contributions to the theory of evolution: On a form of spurious correlation which may arise when indices are used in the measurement of organs. Proc. R. Soc. Lond. 1897, 60, 489–498. [Google Scholar] [CrossRef]
  3. Aitchison, J. The statistical analysis of compositional data. J. R. Stat. Soc. Series B (Methodol) 1982, 44, 139–160. [Google Scholar] [CrossRef]
  4. Aitchison, J.; Egozcue, J. The statistical analysis of geochemical compositions. Math. Geol. 1984, 16, 531–564. [Google Scholar] [CrossRef]
  5. Aitchison, J. Compositional data analysis: Where are we and where should we be heading? Math. Geol. 2005, 37, 829–850. [Google Scholar] [CrossRef]
  6. Walker, A. W.; Hoyles, L. Human microbiome myths and misconceptions. Nature Microbiology. 2023, 8(8), 1392–1396. [Google Scholar] [CrossRef] [PubMed]
  7. Mysara, M.; Vandamme, P.; Props, R.; Kerckhof, F.-M.; Leys, N.; Boon, N.; Raes, J.; Monsieurs, P. Reconciliation between operational taxonomic units and species boundaries. FEMS Microbiology Ecology 2017, 93, fix029. [Google Scholar] [CrossRef] [PubMed]
  8. Fan, Y.; Støving, R.K.; Berreira Ibraim, S.; Hyötyläinen, T.; Thirion, F.; Arora, T.; Lyu, L.; Stankevic, E.; Hansen, T.H.; Déchelotte, P.; et al. The gut microbiota contributes to the pathogenesis of anorexia nervosa in humans and mice. Nature Microbiology 2023, 8, 787–802. [Google Scholar] [CrossRef]
  9. Chen, X.; Hashimoto, D.; Ebata, K.; Takahashi, S.; Shimizu, Y.; Shinozaki, R.; Hasegawa, Y.; Kikuchi, R.; Senjo, H.; Yoneda, K.; et al. Reactive granulopoiesis depends on T-cell production of IL-17A and neutropenia-associated alteration of gut microbiota. Proceedings of the National Academy of Sciences 2022, 119, e2211230119. [Google Scholar] [CrossRef]
  10. Turnbaugh, P.J.; Ley, R.E.; Mahowald, M.A.; Magrini, V.; Mardis, E.R.; Gordon, J.I. An obesity-associated gut microbiome with increased capacity for energy harvest. Nature 2006, 444, 1027–1031. [Google Scholar] [CrossRef]
  11. Stojanov, S.; Berlec, A.; Štrukelj, B. The Influence of Probiotics on the Firmicutes/Bacteroidetes Ratio in the Treatment of Obesity and Inflammatory Bowel disease. Microorganisms 2020, 8. [Google Scholar] [CrossRef] [PubMed]
  12. Nakayama, J.; Yamamoto, A.; Palermo-Conde, L.A.; Higashi, K.; Sonomoto, K.; Tan, J.; Lee, Y.K. Impact of westernized diet on gut microbiota in children on Leyte island. Front. Microbiol. 2017, 14, 197. [Google Scholar] [CrossRef] [PubMed]
  13. An, J.; Kwon, H.; Kim, Y.J. The Firmicutes/Bacteroidetes Ratio as a Risk Factor of Breast Cancer. Journal of Clinical Medicine 2023, 12. [Google Scholar] [CrossRef] [PubMed]
  14. Takezawa, K.; Fujita, K.; Matsushita, M.; Motooka, D.; Hatano, K.; Banno, E.; Shimizu, N.; Takao, T.; Takada, S.; Okada, K.; et al. The Firmicutes/Bacteroidetes ratio of the human gut microbiota is associated with prostate enlargement. The Prostate 2021, 81, 1287–1293. [Google Scholar] [CrossRef]
  15. Jasirwan, C.O.M.; Muradi, A.; Hasan, I.; Simadibrata, M.; Rinaldi, I. Correlation of gut Firmicutes/Bacteroidetes ratio with fibrosis and steatosis stratified by body mass index in patients with non-alcoholic fatty liver disease. Biosci Microbiota Food Health 2021, 40, 50–58. [Google Scholar] [CrossRef] [PubMed]
  16. Park, S.H.; Kim, K.A.; Ahn, Y.T.; Jeong, J.J.; Huh, C.S.; Kim, D.H. Comparative analysis of gut microbiota in elderly people of urbanized towns and longevity villages. BMC Microbiol. 2015, 15, 1–5. [Google Scholar] [CrossRef] [PubMed]
  17. Park, J.; Kato, K.; Murakami, H.; Hosomi, K.; Tanisawa, K.; Nakagata, T.; Ohno, H.; Konishi, K.; Kawashima, H.; Chen, Y.A.; Mohsen, A.; Xiao, J.Z.; Odamaki, T.; Kunisawa, J.; Mizuguchi, K.; Miyachi, M. Comprehensive analysis of gut microbiota of a healthy population and covariates affecting microbial variation in two large Japanese cohorts. BMC Microbiol. 2021, 2, 151. [Google Scholar] [CrossRef] [PubMed]
  18. Maruyama, S.; Matsuoka, T.; Hosomi, K.; Park, J.; Nishimura, M.; Murakami, H.; Konishi, K.; Miyachi, M.; Kawashima, H.; Mizuguchi, K.; et al. Characteristic Gut Bacteria in High Barley Consuming Japanese Individuals without Hypertension. Microorganisms 2023, 11. [Google Scholar] [CrossRef]
  19. Matsuoka, T.; Hosomi, K.; Park, J.; Goto, Y.; Nishimura, M.; Maruyama, S.; Murakami, H.; Konishi, K.; Miyachi, M.; Kawashima, H.; et al. Relationships between barley consumption and gut microbiome characteristics in a healthy Japanese population: a cross-sectional study. BMC Nutrition 2022, 8, 23. [Google Scholar] [CrossRef]
  20. Naito, Y.; Takagi, T.; Inoue, R.; Kashiwagi, S.; Mizushima, K.; Tsuchiya, S.; Itoh, Y.; Okuda, K.; Tsujimoto, Y.; Adachi, A.; et al. Gut microbiota differences in elderly subjects between rural city Kyotango and urban city Kyoto: an age-gender-matched study. Journal of Clinical Biochemistry and Nutrition 2019, 65, 125–131. [Google Scholar] [CrossRef]
  21. Nishino, K.; Nishida, A.; Inoue, R.; Kawada, Y.; Ohno, M.; Sakai, S.; Inatomi, O.; Bamba, S.; Sugimoto, M.; Kawahara, M.; et al. Analysis of endoscopic brush samples identified mucosa-associated dysbiosis in inflammatory bowel disease. Journal of Gastroenterology 2018, 53, 95–106. [Google Scholar] [CrossRef] [PubMed]
  22. Takagi, T.; Naito, Y.; Inoue, R.; Kashiwagi, S.; Uchiyama, K.; Mizushima, K.; Tsuchiya, S.; Dohi, O.; Yoshida, N.; Kamada, K.; et al. Differences in gut microbiota associated with age, sex, and stool consistency in healthy Japanese subjects. Journal of Gastroenterology 2019, 54, 53–63. [Google Scholar] [CrossRef] [PubMed]
  23. Chen, Y.-A.; Park, J.; Natsume-Kitatani, Y.; Kawashima, H.; Mohsen, A.; Hosomi, K.; Tanisawa, K.; Ohno, H.; Konishi, K.; Murakami, H.; et al. MANTA, an integrative database and analysis platform that relates microbiome and phenotypic data. PLOS ONE 2020, 15, e0243609. [Google Scholar] [CrossRef] [PubMed]
  24. Mori, H.; Kato, T.; Ozawa, H.; Sakamoto, M.; Murakami, T.; Taylor, T.D.; Toyoda, A.; Ohkuma, M.; Kurokawa, K.; Ohno, H. Assessment of metagenomic workflows using a newly constructed human gut microbiome mock community. DNA Research 2023, 30, dsad010. [Google Scholar] [CrossRef]
  25. Jin, J.; Yamamoto, R.; Takeuchi, T.; Cui, G.; Miyauchi, E.; Hojo, N.; Ikuta, K.; Ohno, H.; Shiroguchi, K. High-throughput identification and quantification of single bacterial cells in the microbiota. Nature Communications 2022, 13, 863. [Google Scholar] [CrossRef]
Preprints 101080 g001
Figure 1. PCoA results were shown. The calculations based on the Bray-Curtis distance and Jaccard distance were represented by (a) and (b), respectively. All plots were in Euclidean space.
Figure 1. PCoA results were shown. The calculations based on the Bray-Curtis distance and Jaccard distance were represented by (a) and (b), respectively. All plots were in Euclidean space.
Preprints 101080 g001
Preprints 101080 g002
Figure 2. PCA results were shown. The genus level scatterplots were represented by (a), and the class level scatterplots were represented by (b) and (c).All plots were in simplex space.
Figure 2. PCA results were shown. The genus level scatterplots were represented by (a), and the class level scatterplots were represented by (b) and (c).All plots were in simplex space.
Preprints 101080 g002
Preprints 101080 g003
Figure 3. The scatterplots. The regression lines were nearly horizontal.
Figure 3. The scatterplots. The regression lines were nearly horizontal.
Preprints 101080 g003
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated