Prerpints.org logo
Preprint
Article

Characterizing Spatiotemporal Complex Patterns from Entropy Measures

Altmetrics

Downloads

176

Views

78

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

05 February 2024

Posted:

06 February 2024

You are already at the latest version

Alerts
Abstract
In addition to their importance in statistical thermodynamics, probabilistic entropy measurements are crucial for understanding and analyzing complex systems, with diverse applications in time series and one-dimensional profiles. However, extending these methods to two- and three-dimensional data still requires further development. In this study, we present a new method to classify spatiotemporal processes based on entropy measurements. To test and validate the method, we selected four classes of similar processes related to the evolution of random patterns: dynamic colored noises ((i)~white and (ii)~red); (iii)~weak turbulence from reaction-diffusion; (iv)~hydrodynamic fully developed turbulence, and (v)~plasma turbulence from MHD. Considering seven possible ways to measure entropy from a matrix, we present the method as a parameter space composed of the two best separating measures of the five selected classes. The results highlight better combined performance of Shannon Permutation Entropy ($S^p_H$) and a new approach based on Tsallis Spectral Permutation Entropy ($S^s_q$). Notably, our observations reveal the segregation of reaction terms in this $S^p_H \times S^s_q$ space, a result that identifies specific sectors for each class of dynamic process, and can be used to train machine learning models for automatic classification of complex spatiotemporal patterns.
Keywords: 
Subject: Physical Sciences  -   Fluids and Plasmas Physics

1. Introduction

The intricate relationship between probability and entropy is a cornerstone in information theory and statistical thermodynamics, providing a robust framework for analyzing a multitude of phenomena ranging from data transmission processes to the behavior of many physical systems. Entropy, derived from the probability distribution of the states of a process or system, can be interpreted as a quantitative measure of randomness or disorder, offering deep insights into the underlying dynamics of several complex systems (see, for instance, Refs. [2,7,12,23,24,25]).
From a thermodynamic perspective, the entropy concept is intimately tied to the statistical mechanics of microstates. The entropy, S, is defined by Boltzmann’s entropy equation, S = k B ln Ω , where k B is the Boltzmann constant and Ω represents the number of microstates. This relationship can be interpreted as the degree of disorder or randomness in a system’s microscopic configurations, drawing a direct connection between the macroscopic observable properties and the statistical behavior of microstates. Complementary, in the realm of information theory, entropy is fundamentally concerned with quantifying the expected level of “information,” “surprise,” or “uncertainty” in the potential outcomes of a system [3]. This quantification is intricately linked to the probability distribution of these outcomes. It essentially measures the average unpredictability or the requisite amount of information needed to describe a random event, thereby providing a metric for the efficiency of data transmission and encoding strategies. Therefore, the duality of the entropy interpretation works as a bridge between the abstract realm of information and the tangible world of the statistics of physical systems. It encapsulates the essence of entropy as a fundamental measure, providing a unifying lens through which the behavior of complex systems, whether in the context of information processing or thermodynamics, can be coherently understood and analyzed. This interdisciplinary approach not only deepens our understanding of individual phenomena but also reveals the underlying universality of the concepts of randomness and information across diverse scientific domains.
In the scenario described above, it is necessary to identify entropy measures that are effective in characterizing spatiotemporal patterns of complex processes typically observed or simulated in 2 D + 1 and 3 D + 1 : following the notation of the amplitude equation theory, where D corresponds to the spatial dimension in which the amplitude of a variable fluctuates over time. This need is justified by the great advances in the generation of Big Data in computational physics, with emphasis on Direct Numerical Simulation (DNS) of turbulence [17,18], ionized fluids [19,21,22,26,27], reactive-diffusive processes [14], to highlight a few.
Our main objective in this work is to present and evaluate the performance of a set of information entropy measurements, conjugated two by two, to characterize different classes of 3D structural patterns arising from nonlinear spatiotemporal processes. To this end, the article is organized as follows: the analytical methodology is presented in Section 2, and the data in Section 3. The results, in the context of a benchmark based on the generalization of the Silhouette Score, are presented and interpreted in Section 4. Our concluding remarks, with emphasis on pointing out the usability of the method in the context of data-driven science, are presented in the last section.

2. Methods

Various entropy metrics have been proposed in the literature, including spectral entropy, permutation entropy, and statistical complexity.
The process of defining a new metric typically involves two fundamental steps: (i) establishing the probability definition, and (ii) determining the entropic form. This framework allows for the generalization of any new metric by specifying these two steps1. In the following subSection 2.1 and Section 2.2, we present respectively the key techniques for defining probabilities and entropic forms. Subsequently, in subSection 2.3, we introduce a methodology to assess these metrics using criteria commonly applied to clustering techniques.

2.1. Probabilities

Probability is a concept that quantifies the likelihood of an event occurring. It is expressed as a numerical value between 0 and 1. Here, 0 signifies the complete impossibility of an event, while 1 denotes absolute certainty. Mathematically, if we consider a process with a finite number of possible outcomes, the probability Pr ( E ) of an event E is defined by the ratio:
Pr ( E ) = Number of favorable outcomes Total number of possible outcomes .
This definition is useful to gain insight of systems that produce discrete real-valued outcomes. In such a case, the histogram of proportions of observed events is the usual tool to estimate the underlying probability distribution of such outcomes.
Many systems produce continue-valued multidimensional outcomes, and the observer needs to define how to estimate a useful probability able to characterize their behavior. Approaches such as permutation and spectral analysis incorporate spatial locality and scale considerations to elucidate the occurrence of specific patterns.
In the permutation approach, local spatial differences (increase, decrease, or constancy) represent the states. New states can be generated by permuting the array elements. Thus, the probabilities account for the occurrences of those states. To extend this definition to multiple dimensions, a given array is flattened. Further details of this technique have been explored by Pessa ([5]).
Another methodology involves spectral analysis, wherein the probability is computed as the Power Spectrum Density (PSD) of the signal P ( ω ) , normalized accordingly. Since this approach considers the probability associated with a given frequency ω , it explores the scaling relation of the signal. For instance, white noise, characterized by equal power across all frequencies, represents a type of signal exhibiting maximum entropy. Whereas the red noise presents a higher PSD for lower frequencies, which represents a lower entropy value. This approach has been popularized in the literature to study time series [7,8,33]. The probabilities presented in this section describe the possible spatial states, while the subsequent subsection elaborates on the entropic characterization of this system.

2.2. Entropic Forms

Several entropy equations and generalizations have been proposed, such as the Boltzmann-Gibbs entropy (also known as Shannon entropy), Tsallis entropy, and Rényi entropy. The most general form is the Shannon entropy, expressed as:
S H = − ∑ i = 1 W p i log p i .
Here, p i is the probability of state i, which can also comprise complex numbers [10], and W is the size of the set of possible events. The value of S H depends on the distribution. Notably, S H is maximum when all the probabilities are equal, i.e., under the uniform distribution; in this case, S H = − log W , and minimum when p i is Dirac’s delta. To account for this maximum value, the normalized Shannon entropy is given by:
S H = − ∑ i = 1 W p i log p i log W .
Another significant entropic form is the Tsallis entropy, proposed as a generalization of Boltzmann-Gibbs entropy [1], with the equation:
S q = 1 − ∑ i = 1 W p i q q − 1 ,
where q is the entropic index or nonextensivity parameter, and plays a crucial role in determining the degree of nonextensivity in the Tsallis entropy.
It is important to explore a range of values for the parameter q to derive a metric distinct from Shannon entropy since lim q → 1 S q = S H . Therefore, we suggest exploring values for q in the range 1 < q < 5 and seek a relationship denoted by α , where log S q = α log q . This approach enables the examination of this generalization of S H .
A unique strategy to characterize complex non-linear systems has been the Gradient Pattern Analysis (GPA). This technique involves computing a set of metrics derived from the gradient lattice representation and the gradient moments, see Appendix A. Specifically, we highlight G 4 , which is determined as the Shannon entropy from the complex representation of the gradient lattice:
G 4 = ∑ j = 0 V A z j z ln z j z .
In the lattice context, the gradient signifies the local variation of amplitudes, computed as the spatial derivative at every embedding dimension. From these spatial derivatives, the complex representation:
z j = | v j | e i θ j ,
is formed, comprising both the modulus ( | v j | ) and phases ( θ j ). To obtain a probability, the complex notation is normalized by z = ∑ z j . For a in-depth review of this metric, please refer to [9,10]. Table 1 provides a summary of all combinations of entropic forms with associated probabilities, along with the GPA metric, that were examined in this study.
To assess the efficacy of each metric and explore the impact of various combinations of probability definitions with entropic forms, we introduce a criterion outlined in the subsequent section. This criterion is formulated with a focus on clustering the entropy measures of the dataset.

2.3. Silhouette Score and Generalized Silhouette Score

Non-supervised algorithms face unique challenges, a remarkable one is defining their efficiency. The silhouette score is a criterion for defining if a set has been well-clusterized [34]. Given an element x i in a cluster π k , this metric is computed as follows [11,12]:
s ( x i ) = b ( x i ) − a ( x i ) max b ( x i ) , a ( x i ) ,
where a ( x i ) is the average dissimilarity, that is the average distance of x i to all other elements in the cluster π k , and b ( x i ) is the average distance to elements of other clusters. The greater the s ( x i ) value, the better performance of the clustering algorithm because it has produced groups with low dissimilarity and large distances between clusters. This technique can be extended to feature extraction if one considers the individual datasets as the clusters π k . However, it is equally essential to account for the potential correlation between metrics, as metrics may inadvertently capture the same data aspects, which is undesirable. To mitigate this, we use the modulus of the Pearson correlation | r | to form the penalty term 1 − | r | as follows:
s ′ ( x i ) = 1 − | r | b ( x i ) − a ( x i ) max b ( x i ) , a ( x i ) ,
which we call the Generalized Silhouette Score (GSS).
After defining a group of entropy measurements and the tool (GSS), which allows determining the best pair of measurements to compose a 2D parameter space, we selected the data set to test and validate our methodological approach.

3. Data

Our main objective is to test the performance of a space composed of two entropy measures in which it is possible to distinguish different classes of complex spatiotemporal processes. For this first study, we chose turbulence-related processes and simulated dynamic colored noises.
We employ simulated data related to the following processes: (i) white noise; (ii) colored noise; (iii) weak turbulence; (iv) hydrodynamic turbulence; and (v) magnetohydrodynamic turbulence (MHD). The main reason for choosing these processes, except colored noise, is that they all present random-type patterns with underlying dynamic characteristics based on physical processes described by partial differential equations (diffusion, reaction and advection). Each was obtained from simulations identified in Table 2.
Based on the power law scaling algorithm technique [13], we created our noise simulator [15]. The data representing weak turbulence (also called chemical or reactive-diffusive turbulence) were obtained from the solution of the Ginzburg-Landau Complex Equation [14,16]. The hydrodynamic turbulence patterns were selected from the John Hopkins database (JHTDB) [20], and the MHD turbulence simulation was simulated using the PENCIL code [19]. Details regarding the simulations are provided in the supplementary material.
To test the approach based on entropy measurements, we selected a total of 25 snapshots representing the evolution of each chosen process. The snapshots were extracted from 3D simulations, taking as a criterion the analysis of the central slice of each hypercube, as the measurement techniques used to act on matrices within a two-dimensional approach.
Figure 1 shows representative snapshots of the respective spatiotemporal processes. These visualizations provide a compelling narrative of the dynamic behavior of each system, highlighting the wide variety of patterns that emerge through temporal dynamics in the phase space.
The numerical procedures and/or technical acquisition details related to the data shown in Figure 1 are available as supplementary material in the repository3, in the section entitled Data Simulations.

4. Results and Interpretation

The analyses in this study were conducted within 2D metric spaces, encompassing all possible entropy measure combinations. Based on the minimum information principle, this configuration offers advantages in terms of interpretability, considering the minimum set of parameters that can be addressed as labels in a possible machine learning interpretation. Our approach to measuring entropies from the data follows the following steps:
  • Input of a snapshot;
  • Pre-processing whose output is a 64 × 64 matrix with amplitude ranging from 0 to 255;
  • Generation of 3 matrix data outputs: 2D-histogram, 2D-Permutation and 2D-FFT Spectra
  • For each of the three domains, the entropy measures are calculated.
Given the definition of the three types of domains interpreted as probability (from histogram, permutation and spectrum), we have six entropy variations, as detailed in Section 2. To distinguish these metrics, we introduced superscripts denoted by h for histogram probability, p for permutation probability, and s for spectral probability. The GPA analysis yields another metric, resulting in 21 scores, as illustrated in Figure 2.
As a result, the most effective combination is the pair Spectral Tsallis Entropy ( S q s ) and Permutation Shannon Entropy ( S H p ). A visual representation of this space, accompanied by some snapshots, is presented in Figure 3. In this space, the metrics reveal a constant Permutation Shannon Entropy dynamical noise systems, that are solely distinguished by the Spectral Tsalllis Entropy, indicating the differences of scaling effects in pattern formation. Conversely, the distinct complex nonlinear characteristics and reaction terms observed in MHD simulations are more pronounced in Permutation Shannon Entropy, accentuating the diversity of localized patterns alongside the larger-scale ones.
The analysis of the entropy distribution is essential in a classification context, as it offers insights into the similarity between a new dataset and various models. However, carefully analysing the entropy metrics over time can highlight important aspects of the underlying physical processes. For instance, the transition from initial conditions to an oscillatory relaxation state is evident in Figure 4. This outcome aligns with expectations in the context of the CGL system, owing to the periodic nature of the reaction term. However, it is essential to highlight that in this introductory study, we avoided simulations with more complex regimes (such as relaxations) as the primary purpose here is to present a new method, and the objective here is not to use it to deepen the physical interpretation of each process.

5. Outlook

Based on the study and approach presented here, we defined a methodological pipeline for spatiotemporal characterization of simulated and/or observed complex processes (Figure 5). The method can be applied to identify and segregate different classes of processes, as well as to classify isolated patterns when necessary. In a context where measured and simulated data may exist, it also serves to validate models. Likewise, the pair of entropy measurements can also serve as a binomial label for training deep learning architectures for automatic classification.

6. Concluding Remarks

This work undertook a comprehensive analysis of entropy metrics and their application to complex extended non-linear systems. The study explored new approaches, including different entropy measures and a new generalized silhouette score for measure evaluation.
Through meticulous consideration of canonical datasets, distinct patterns have been characterized in terms of entropy metrics. The pivotal finding was the identification of the optimal pair: Spectral Tsallis Entropy ( S q s ) and Permutation Shannon Entropy ( S H p ), yielding superior outcomes in the generalized silhouette score. This combination showcased efficacy in distinguishing spatiotemporal dynamics coming from different classes of turbulent-like processes, including pure stochastic 2D 1 / f − k (colored) noise.
The new method contributes valuable insights into applying entropy probabilistic measures, providing a foundation for future studies in terms of extended complex system pattern formation characterization.
Initial work considering entropy measurements for training machine learning models is underway. In this context, it also includes a study of the computational complexity of the method for a benchmark with other measures and approaches that may emerge. This strategy is fundamental when we think about the presented method being applied in a data science context.
Finally, we carefully organize all the mathematical content and data used in this work in a GitHub repository4 to guarantee the reproducibility of this experiment.

Acknowledgments

R.R.R. thanks FAPESP under Grant No. 2021/15114-8 for partial financial support. L.O. Barauna and R.A.S was supported by the Federal Brazilian Agency-CAPES.

Appendix A. Gradient Pattern Analysis

Gradient Pattern Analysis (GPA) represents a paradigm shift in data analysis, focusing on the spatiotemporal dynamics of information rather than static values. This innovative approach emphasizes the examination of gradients within datasets—dynamic vectors that encode the rate of change—thereby revealing patterns and structures that are often obscured by traditional analytical methods.
From a mathematical perspective, GPA utilizes a series of gradient moments to quantify the smoothness and alignment of these vectors within the data lattice:
G 1 = N C − N V N V ,
G 2 = V A V 1 − ∑ i = 0 V A v i 2 ∑ i = 0 V A v i ,
G 3 = 1 2 V A V + 1 2 V A ∑ i = 0 i = V A u i . v i + 1 ,
and
1 − 1 G 4 = − ∑ i = 0 V A z i z ln z i z ,
were N C and N V are the connections in the Delaunay triangulation and the number of vertices; V A is the number of asymmetrical vectors, V is the total number of vectors in the lattice, and v i A is an asymmetrical vector; u i = ( cos ( ϕ i ) , sin ( ϕ i ) ) and z i = | v i | exp ( i θ i ) , where | v i | represents the modulus and θ i represents the phase and
z = ∑ i V A z i .
These moments provide a distinctive signature that characterizes the inherent patterns in the data, applicable across various domains. This versatility enables GPA’s application in diverse fields, ranging from time-series analysis in climatology to image recognition in computer vision.
One of the notable strengths of GPA is its capacity for efficient data compression. By discerning and eliminating redundant information while retaining the essential gradient characteristics, GPA achieves data compression without losing the dataset’s critical structural and dynamic properties. This aspect of GPA is particularly advantageous for storing, transmitting, and analysing large-scale datasets in numerous scientific and engineering disciplines. For a complete review see Refs. [9,10].

Appendix B. 2D-Permutation Entropy

Based on the concept of permutation entropy [29], two-dimensional multiscale sample entropy has been proposed as a new texture algorithm [30,31] and has therefore been used to evaluate the complexity of 2D patterns [32]. In a simplified way, the technique is based on the following steps:
  • Step 1: Get the coarse-grained image as an N × N matrix;
  • Step 2: Apply a window of size D × D to it;
  • Step 3: Do D ! reshape permutations to obtain the probabilities of each local pattern;
  • Step 4: Repeat the last procedure, scanning the entire matrix
  • Step 5: Apply as input the probability values to the chosen entropy formula.
In our application we use D = 9 .

References

  1. Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1998, 52, 479–487. [Google Scholar] [CrossRef]
  2. Tsallis, C. When may a system be referred to as complex? An entropic perspective. Frontiers in Complex Systems 2023, 1, 1–11. [Google Scholar] [CrossRef]
  3. Brissaud, J. The meanings of entropy. Entropy 2005, 7, 68–96. Available online: https://www.mdpi.com/1099-4300/7/1/68. [CrossRef]
  4. Lesne, A. Shannon entropy: a rigorous notion at the crossroads between probability, information theory, dynamical systems and statistical physics. Mathematical Structures in Computer Science 2014, 24, e240311. [Google Scholar] [CrossRef]
  5. Pessa, A.A.B.; Ribeiro, H.V. ordpy: A Python package for data analysis with permutation entropy and ordinal network methods. Chaos: An Interdisciplinary Journal of Nonlinear Science 2021, 31, 1–23. [Google Scholar] [CrossRef] [PubMed]
  6. Li, C.; Shang, P. Multiscale Tsallis permutation entropy analysis for complex physiological time series. Phys. A 2019, 523, 10–20. [Google Scholar] [CrossRef]
  7. Zhang, A.; Yang, B.; Huang, L. Feature Extraction of EEG Signals Using Power Spectral Entropy. In Proceedings of the International Conference on BioMedical Engineering and Informatics, Sanya, China, 27-30 May 2008. [Google Scholar]
  8. Xiong, P.Y.; Jahanshahi, H.; Alcarazc, R.; Chud, Y.M.; Gómez-Aguilar, J.F.; Alsaadi, F.E. Spectral Entropy Analysis and Synchronization of a Multi-Stable Fractional-Order Chaotic System using a Novel Neural Network-Based Chattering-Free Sliding Mode Technique. Chaos, Solitons & Fractals 2021, 144, 110576. [Google Scholar] [CrossRef]
  9. Rosa, R.R.; de Carvalho, R.R. and Sautter, R.A.; Barchi, P.H.; Stalder, D.H.; Moura, T.C.; Rembold, S.B.; Morell, D.R.F.; Ferreira, N.C. Gradient pattern analysis applied to galaxy morphology. MNRAS 2018, 477, L101–L105. [Google Scholar] [CrossRef]
  10. Ramos, F.M.; Rosa, R.R.; C. Rodrigues Neto; Zanandrea A. Generalized complex entropic form for gradient pattern analysis of spatio-temporal dynamics. Phys. A 2000, 283, 171–174. [Google Scholar] [CrossRef]
  11. Shutaywi, M.; Kachouie, N.N. Silhouette analysis for performance evaluation in machine learning with applications to clustering. Entropy 2021, 23, 759–776. [Google Scholar] [CrossRef]
  12. Abdullah, R.S.A.R.; Saleh, N.L.; Rahman, S.M.S. A; Zamri, N.S.; Rashid, N.E.A. Texture classification using spectral entropy of acoustic signal generated by a human echolocator. Entropy 2019, 21, 963–983. [Google Scholar] [CrossRef]
  13. Timmer, J.; Koenig, M. On generating power law noise. Astronomy and Astrophysics 1995, 300, 707. [Google Scholar]
  14. Lu, H.; Lü, S.J.; Zhang, M.J. Fourier spectral approximations to the dynamics of 3D fractional complex Ginzburg-Landau equation. Discrete and Continuous Dynamical Systems 2017, 37, 2539–2564. [Google Scholar] [CrossRef]
  15. Sautter, R. A. Gradient pattern analysis: enhancements and applications including the influence of noise on pattern formation. Doctoral Thesis, National Institute for Space Research, São José dos Campos, 2023. [Google Scholar]
  16. Sautter, R.A.; Rosa, R.R.; Pontes, J. Incremental Gradient Pattern Analysis of Stochastic Complex Ginzburg-Landau Dynamics. Phys. Rev. E 2023, ED12304. [Google Scholar] [CrossRef]
  17. Gotoh, T.; Kraichnan, R.H. Turbulence and Tsallis statistics. Physica D 2004, 193, 231–244. [Google Scholar] [CrossRef]
  18. Abdelsamie, A.; Janiga, G.; Thévenin, D. Spectral entropy as a flow state indicator. International Journal of Heat and Fluid Flow 2017, 68, 102–113. [Google Scholar] [CrossRef]
  19. Brandenburg, A.; et al. The Pencil Code, a modular MPI code for partial differential equations and particles: multipurpose and multiuser-maintained. J. Open Source Software 2021, arXiv:2009.082316, 2807. [Google Scholar]
  20. Li, Yi; Perlman, E.; Wan, M.; Yang,Y.; Meneveau, C.; Burns,R.; Chen, S.; Szalay, A.; Eyink, E. A public turbulence database cluster and applications to study Lagrangian evolution of velocity increments in turbulence. Journal of Turbulence 2008, 9:N31. [CrossRef]
  21. Mignone, A.; Bodo, G.; Massaglia, S.; Matsakos, T.; Tesileanu, O.; Zanni, C.; Ferrari, A. PLUTO: A numerical code for computational astrophysics. ApJS 2007, 170, 228–242. [Google Scholar] [CrossRef]
  22. Franci, L.; Hellinger, P.; Guarrasi, M.; Chen, C. H. K.; Papini, E.; Verdini, A.; Matteini, L.; Landi, S. Three-dimensional simulations of solar wind turbulence. Proceedings of IOP Conf. Series: Journal of Physics, Kuala Lumpur, Malaysia, 3-5 May 2017. [Google Scholar]
  23. Mattedi, A. P.; Ramos, F. M.; Rosa, R. R.; Mantegna, R. N. Value-at-risk and Tsallis statistics: risk analysis of the aerospace sector. Physica A: Statistical Mechanics and its Applications 2004, 344, 554–561. [Google Scholar] [CrossRef]
  24. Ramos, F. M.; Rosa, R. R.; Rodrigues Neto, C.; Bolzan, M. J. A.; Abren Sá, L. D. Nonextensive thermostatistics description of intermittency in turbulence and financial markets. Nonlinear Analysis: Theory, Methods & Applications 2001, 47, 3521–3530. [Google Scholar] [CrossRef]
  25. Ramos, F. M.; Bolzan, M. J. A.; Abreu Sá, L. D.; Rosa, R. R. Atmospheric turbulence within and above an Amazon forest. Physica D: Nonlinear Phenomena 2004, 193, 278–291. [Google Scholar] [CrossRef]
  26. Bolzan, M. J. A.; Sahai, Y.; Fagundes, P. R.; Rosa, R. R.; Ramos, F. M.; Abalde, J. R. Intermittency analysis of geomagnetic storm time-series observed in Brazil. Journal of Atmospheric and Solar-Terrestrial Physics 2005, 67, 1365–1372. [Google Scholar] [CrossRef]
  27. Veronese, T.B.; Rosa, R. R.; Bolzan, M. J. A.; Rocha Fernandes, F. C.; Sawant, H. S.; Karlicky, M. Fluctuation analysis of solar radio bursts associated with geoeffective X-class flares. Journal of Atmospheric and Solar-Terrestrial Physics 2011, 73, 1311–1316. [Google Scholar] [CrossRef]
  28. Ferreira da Silva, A.; Rosa, R. R.; Roman, L. S.; Veje, E.; Pepe, I. Characterization of asymmetric fragmentation patterns in SFM images of porous silicon. Solid State Communications 2000, 113, 703–708. [Google Scholar] [CrossRef]
  29. Bandt, C. , Pompe, B., 2002. Permutation entropy: a natural complexity measure for time series. Physical Review Letters 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
  30. Silva, L. , Duque, J., Felipe, J., Murta, L., Humeau-Heurtier, A., 2018. Twodimensional multiscale entropy analysis: Applications to image texture evaluation. Signal Processing 2018, 147, 224–232. [Google Scholar] [CrossRef]
  31. Humeau-Heurtier, A. , Omoto, A.C.M., Silva, L.E., 2018. Bi-dimensional multiscale entropy: Relation with discrete Fourier transform and biomedical application. Computers in Biology and Medicine 2018, 100, 36–40. [Google Scholar] [CrossRef]
  32. Morel, C.; HUmeau-Heurtier, A. Multiscale permutation entropy for two-dimensional patterns. Pattern Reg. Letters 2021, 150, 139–146. [Google Scholar] [CrossRef]
  33. Chagas, E., Queiroz-Oliveira. White Noise Test from Ordinal Patterns in the Entropy-Complexity Plane. International Statistical Review 2022, 90, 374–396. [Google Scholar] [CrossRef]
  34. Kaufman, L. & Rousseeuw, P. Finding Groups in Data: An Introduction to Cluster Analysis; Wiley & Sons, 2005. [Google Scholar] [CrossRef]
1
Code publicly available at https://github.com/rsautter/Eta
2
Our 3D simulator is public available at: https://github.com/rsautter/Noisy-Complex-Ginzburg-Landau
3
(https://github.com/rsautter/Eta/)
4
https://github.com/rsautter/Eta/
Preprints 98259 g001
Figure 1. Snapshots of the spatiotemporal evolution of each selected system class, listed in Table 2. Each row shows one of the simulations, rendered at time-steps that show a representative pattern dynamics: Dynamic White Noise (1st row), Random Red Noise (2nd row); Weak turbulence from the Reaction-Diffusion Complex Ginzburg-Landau Dynamics; Fully Developed Turbulence from JHTDB (4th row) and MHD turbulence from PENCIL.
Figure 1. Snapshots of the spatiotemporal evolution of each selected system class, listed in Table 2. Each row shows one of the simulations, rendered at time-steps that show a representative pattern dynamics: Dynamic White Noise (1st row), Random Red Noise (2nd row); Weak turbulence from the Reaction-Diffusion Complex Ginzburg-Landau Dynamics; Fully Developed Turbulence from JHTDB (4th row) and MHD turbulence from PENCIL.
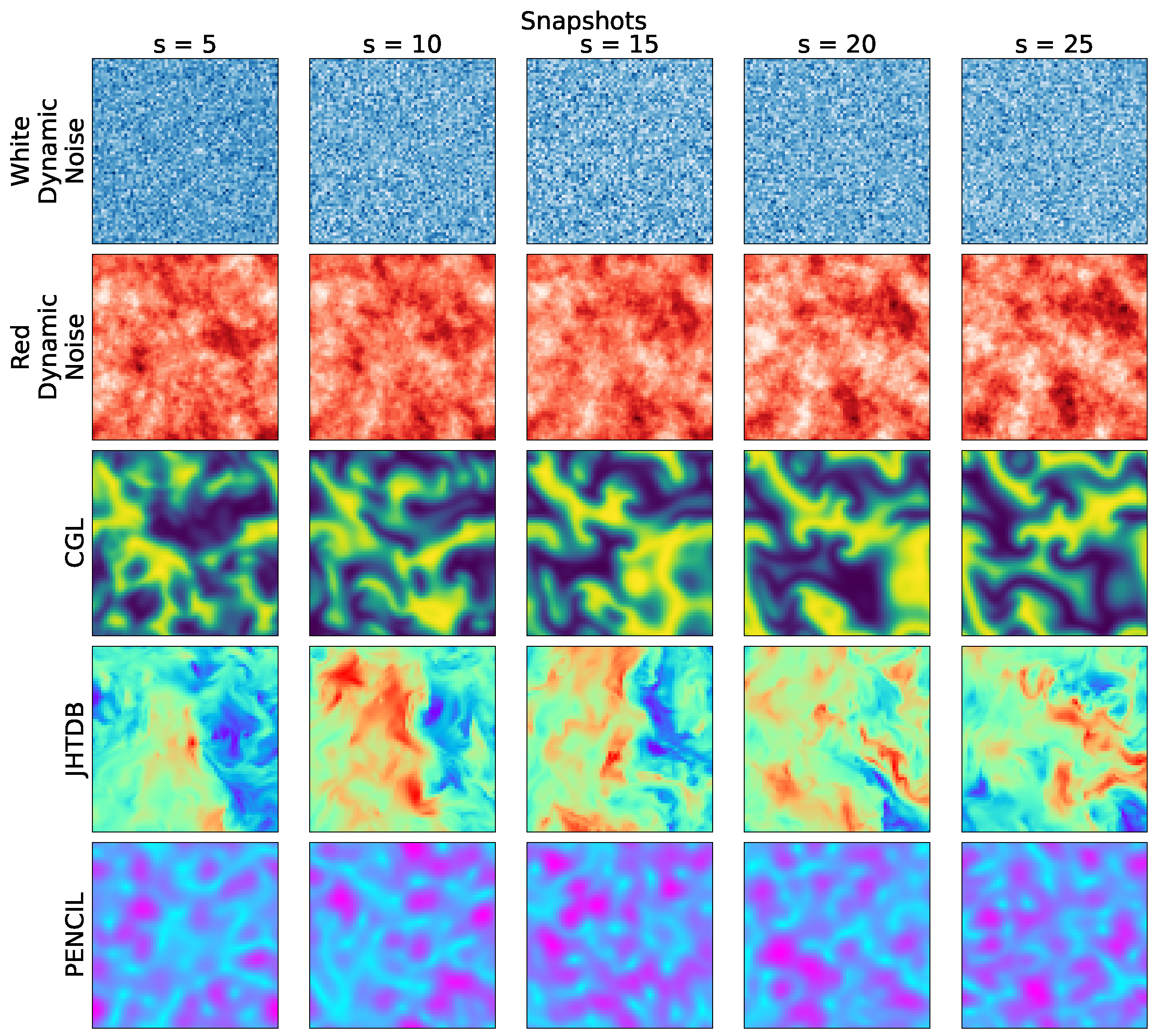
Preprints 98259 g001
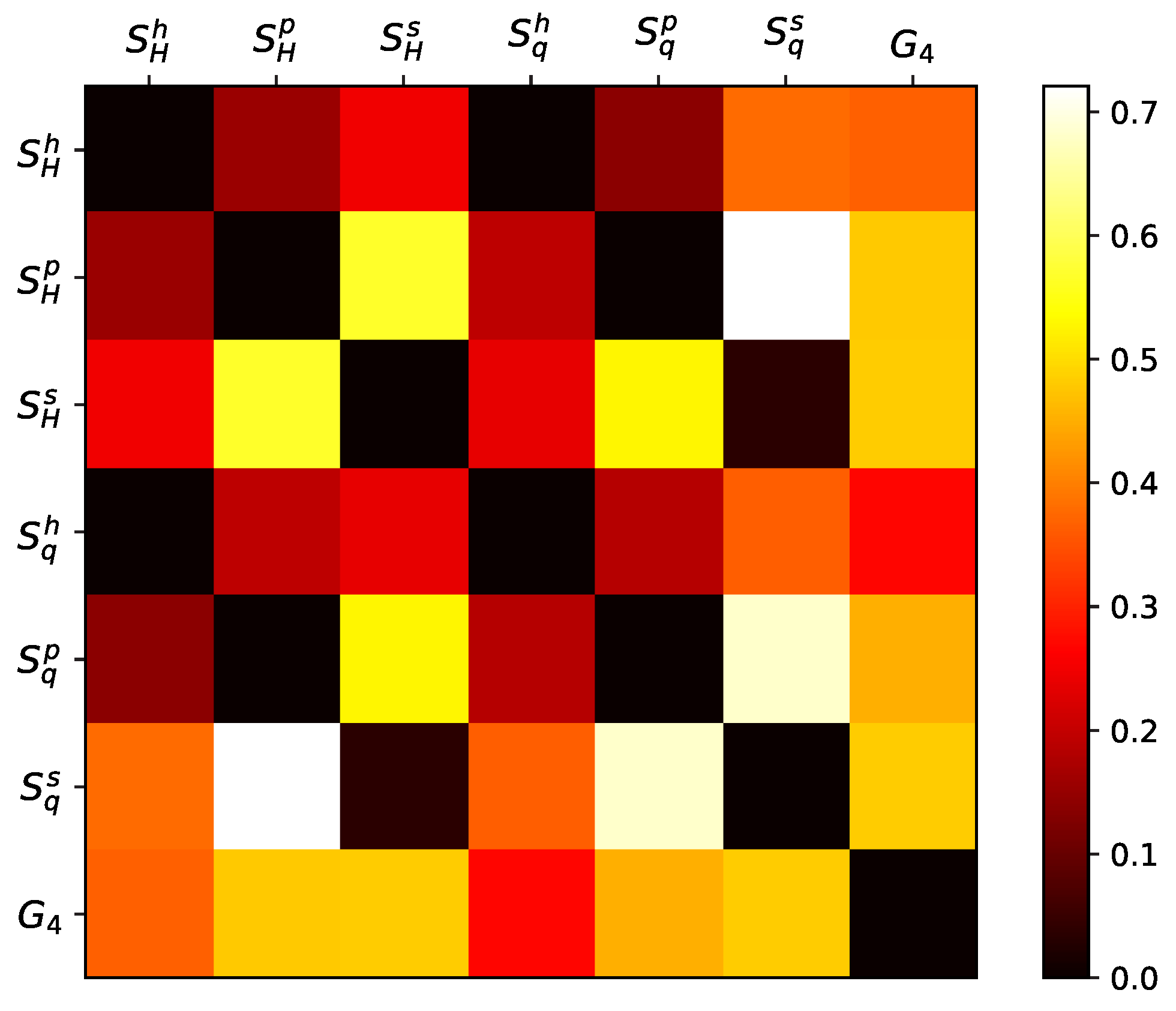
Preprints 98259 g002
Figure 2. Generalized Silhouette Score for all 2D metric combinations. Higher values on the heatmap indicate superior metric performance. The optimal result is achieved with the pairing of Spectral Tsallis Entropy and Permutation Shannon Entropy ( S q s x S H p ).
Figure 2. Generalized Silhouette Score for all 2D metric combinations. Higher values on the heatmap indicate superior metric performance. The optimal result is achieved with the pairing of Spectral Tsallis Entropy and Permutation Shannon Entropy ( S q s x S H p ).
Preprints 98259 g002
Preprints 98259 g003
Figure 3. Optimal outcomes achieved assessed through the generalized silhouette score criterion. The method achieves its best performance in the ( S q s x S H p ) parameter space.
Figure 3. Optimal outcomes achieved assessed through the generalized silhouette score criterion. The method achieves its best performance in the ( S q s x S H p ) parameter space.
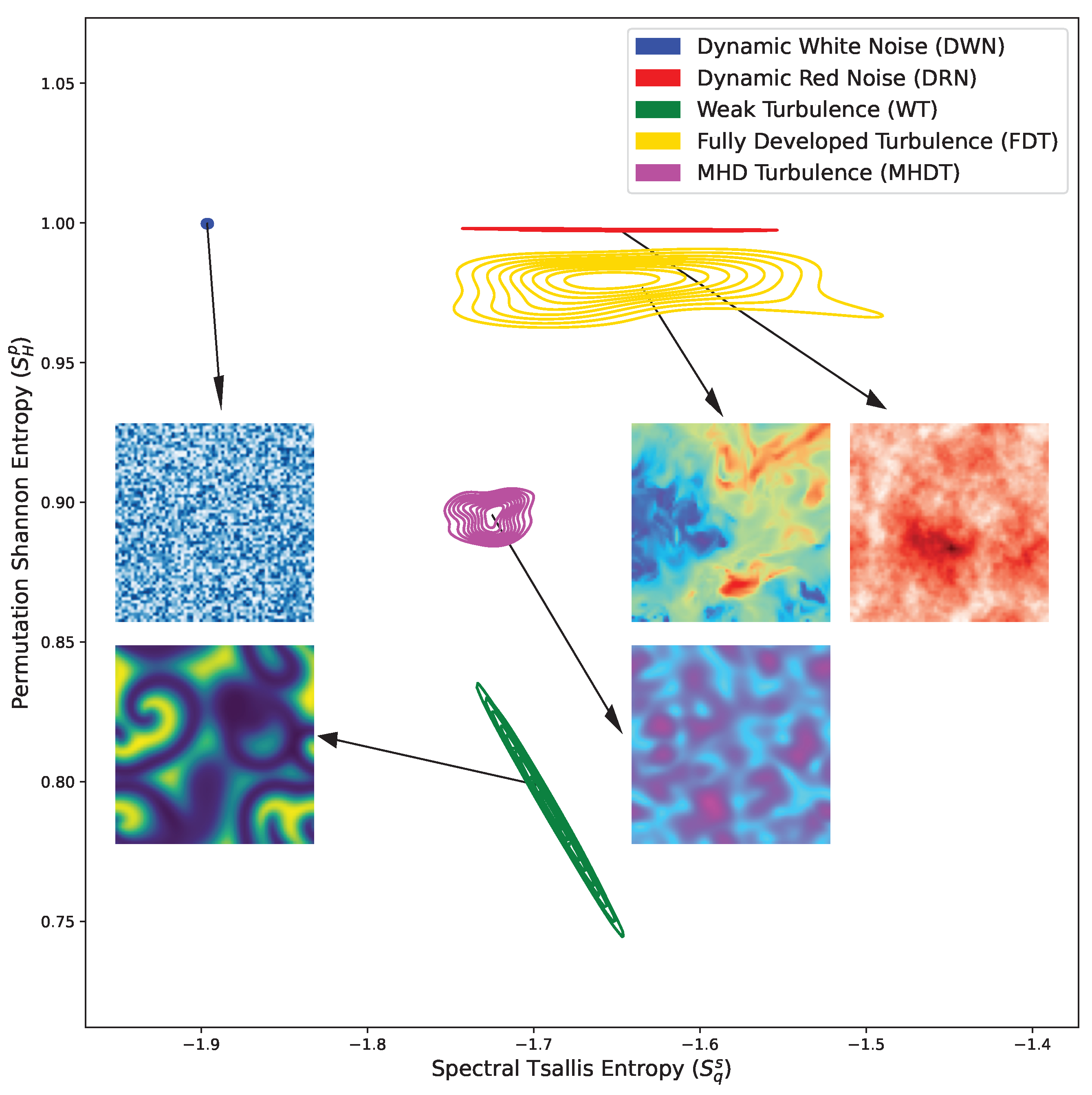
Preprints 98259 g003
Preprints 98259 g004
Figure 4. Best entropy set according to the generalized silhouette score (see Figure 2) for the 3D-CGL solution over time, where the oscillatory dynamic of the system is highlighted. The color indicates the snapshot, where 500 samples are presented.
Figure 4. Best entropy set according to the generalized silhouette score (see Figure 2) for the 3D-CGL solution over time, where the oscillatory dynamic of the system is highlighted. The color indicates the snapshot, where 500 samples are presented.
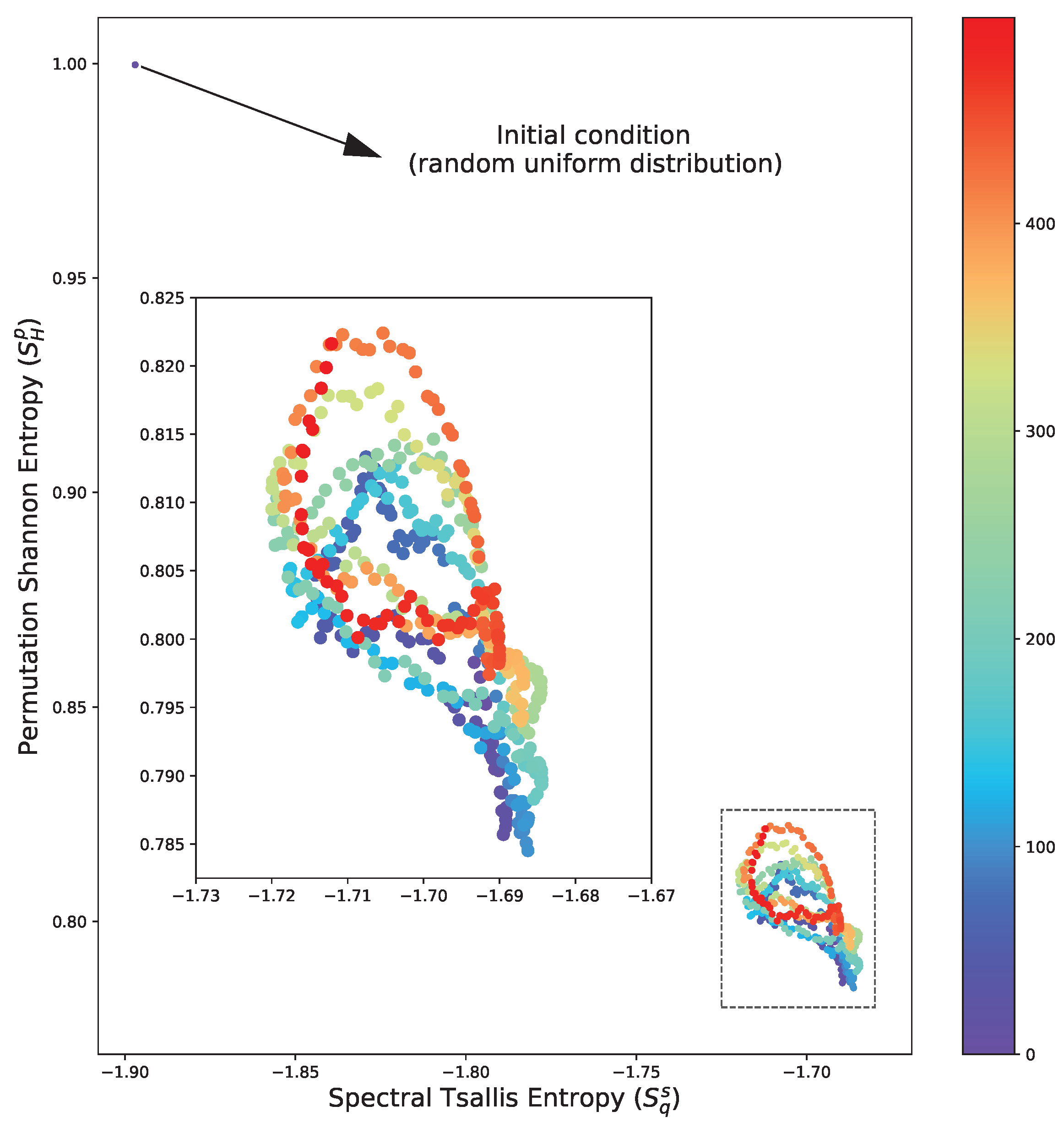
Preprints 98259 g004
Preprints 98259 g005
Figure 5. Pipeline of the method proposed in this study based on the best results we found: A sequence of snapshots from the simulation of a given process (in the 2 D + 1 or 3 D + 1 domains) are the input on which entropy measurements will be obtained. To calculate the respective permutation Shannon entropy values S H p , the permutation values are obtained (see Appendix 2). To calculate the Spectral Tsallis Entropy S q s , the respective spectra are obtained. From the calculated values, the parameter space is constructed where it is proposed to characterize the underlying process. The space also work for classifying isolated patterns, taking as reference distinct processes that have already been characterized.
Figure 5. Pipeline of the method proposed in this study based on the best results we found: A sequence of snapshots from the simulation of a given process (in the 2 D + 1 or 3 D + 1 domains) are the input on which entropy measurements will be obtained. To calculate the respective permutation Shannon entropy values S H p , the permutation values are obtained (see Appendix 2). To calculate the Spectral Tsallis Entropy S q s , the respective spectra are obtained. From the calculated values, the parameter space is constructed where it is proposed to characterize the underlying process. The space also work for classifying isolated patterns, taking as reference distinct processes that have already been characterized.
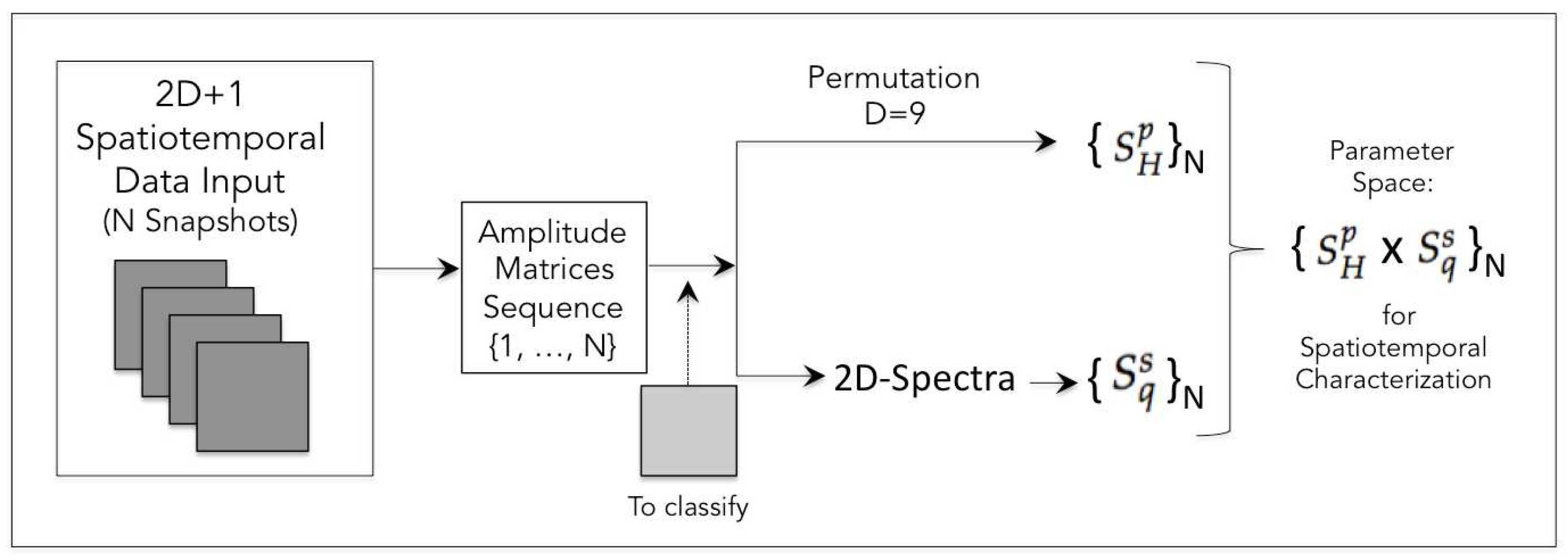
Preprints 98259 g005
Table 1. Entropy Measures.
Table 1. Entropy Measures.
Measure Probability Entropic Form Reference
S H h histogram Shannon, Equation (3) Lesne [4]
S H p permutation Shannon, Equation (3) Pessa [5]
S H s spectral Shannon, Equation (3) Abdelsamie [18], Abdullah [12]
S q h histogram Tsallis q-law, Equation (4)) Li [6]
S q p permutation Tsallis q-law, Equation (4)) Li [6]
S q s spectral Tsallis q-law, Equation (4) This paper
G 4 gradient Shannon*, Equation (5) Ramos [10]
Table 2. Datasets and references.
Table 2. Datasets and references.
Simulation Process Reference
White Dynamic Noise Spatiotemporal stochastic Timmer [13]
Red Dynamic Noise Spatiotemporal stochastic Timmer [13]
CGL2 Weak Turbulence Sautter [15], Sautter [16]
JHTDB Fully Developed Turbulence Brandenburg [19]
PENCIL MHD Turbulence Brandenburg [19]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated