Is Entropy a Force of Nature?

1. Introduction

After Arno Penzias (b. 1944) and Robert Wilson’s (b. 1936) discovery [1] of the cosmic microwave background (CMB), consensus among astronomers converged around the hot-big-bang concept of the Universe’s origin. The competing “static” or non-expanding Universe was conclusively excluded as a proper model. This discarded model left a legacy: “dark energy” Λ, a repulsive scalar field, which kept a static Universe from collapsing. Dark energy Λ was proposed [2] by no less of an intellect than Albert Einstein (1879-1955) himself, the greatest theoretical physicist who ever lived. For the next 33 years after Penzias and Wilson, Λ was kept in circulation but thought to have no value, as Edwin Hubble’s (1889-1953) linear distance-ladder model [3] was adequate to explain observed stellar movement within the uncertainties of the day. That changed in 1998. Two independent groups of astronomers, in a pair of tours de force [4,5,6,7], found deviance from the linear distance ladder. The same deviance. They populated Λ, giving rise to today’s “ΛCDM” model [8].

The ΛCDM model has been applied to the CMB’s tiny anisotropies to calculate the Hubble constant H₀ [9]. These results differ from the distance ladder [10,11,12,13,14,15]. Explanations have been proffered to resolve this tension [16,17,18,19,20,21,22,23,24,25,26]. Most but not all of these rely on Λ. One alternate, quintessence [27], having a time-dependent scalar field, has been proposed. Quintessence is, like Λ and the energy field first proposed by Peter Higgs (b. 1929)[28], held to exist in vacuo. Of these three only the Higgs field has an experimentally consistent in vacuo theoretical foundation, and to date neither Λ nor quintessence have been shown to have a clearly defined, energy-conservative source.

Attempts to treat the second law of thermodynamics within a Λ-containing Universe have arisen in numerous papers, many of which (2,000 and counting) cite an original publication [29] by Erik Verlinde (b. 1962). While Verlinde’s proposed entropic “screen” or end state has proven quite popular, it tends to indicate that at some point in time, Universal entropy reaches a final value with no further increase. Inconsistency with the second law remains in such treatments.

The present paper takes an approach to Universal expansion consistent with the second law by treating baryon content as the unbound gas it mostly is. The model that arises from this treatment is called the GCDM model, for gas-cold-dark-matter. The GCDM model does give a repulsive field, plasma kinetic energy, but this field bears little theoretical resemblance to a quintessent, Λ, or Higgs field. Its density is a miniscule fraction of Λ’s purported value, and its ultimate source is nuclear fusion in stars.

The difference between ΛCDM and GCDM is fairly easy to picture. The ΛCDM model treats the Universe as all accreted matter, like rocks all hurtling away from each other. Their mutual gravitational attraction isn’t enough to pull them back together. They slow down, but still keep getting further and further apart. Their separation is accelerated by Λ. The GCDM model treats the Universe as an infinitely massive gas. It has some rocks, we live on one of them. But mostly it’s a gas. The Universe has no boundary, so the gas is freely expanding. Gas free expansion carries a repulsive force: Thermal pressure. The attractive force of gravity from all kinds of mass can’t offset the gas’s thermal pressure. Extra force from nonthermal pressure accelerates the expansion.

Gas free expansion gives entropic gain. Herein I propose entropic gain as a force of Nature. When bound, it keeps a balloon inflated. When unbound, it propels rockets. It also pushes distant galaxies apart. The presently defined four forces of Nature cannot account for any of these behaviors. We can use the gas laws to express this force, more properly treating the Universe as an unbound gas and not as expanding accreted matter.

Einstein is widely considered as first among equals in the pantheon of great theoreticians. To this author, J. Willard Gibbs (1839-1903) is a close contender for the crown. It is only through both of these scholars’ teachings that we can properly understand Universal behavior.

2. The GIBBS EQUATION, BOUND AND UNBOUND

Since the Gibbs equation plays such a central role in the development of both ΛCDM and GCDM models, it’s important to understand the meaning of its terms, and its expression of the first two thermodynamic laws.

The first and second laws of thermodynamics were developed in the 19^th century by many authors and fully quantified by the early 20^th, notably by Gibbs.¹ The first law says that energy is neither created nor destroyed:

$$dE/dt=0$$

(1)

Where E is the total energy. Total energy is also called “internal energy”.² It’s the sum of all forms of energy in the Universe as a whole and in a sufficiently large homogenous and isotropic proxy sphere, generally accepted as not less than 200 megaparsecs (Mpc) or about 600 million light-years (ly) in observed diameter. A sphere this large is said to be “at scale”. Long ago, the Universe had a more uniform density, and “at scale” can refer to much smaller comoving volumes for those earlier times.

The second law of thermodynamics says that entropy always increases with time (regardless of scale):

$$dS/dt>0$$

(2)

An isoentropic process cannot occur in real time. You can slow entropy down in e.g. an insulated vessel, but you can’t stop it. At scale, dS/dt >> 0.

Equation (2) can’t be directly compared to (1) because they have different units. At scale, (2) can be directly compared to (1) by expression as gain E_S:

$$d\left(E_S\right)/dt>0$$

(3)

For a gas:

$$d\left(E_S\right)=d\left(TS\right)$$

(4)

In this paper, (3) and (4) refer to an unbound system: The Universe at scale. “System” usually means e.g. a bound vessel and its contents, for example, gas in a piston. Herein it also refers to a constant amount of gas at an instant in time, and more generally instant total energy, that isn’t bound. In a bound system, it’s common for d(TS)/dV < 0 and d(S)/dV > 0 if work is performed. However, for both the system and its surroundings combined, (3) is always true. At scale, system and surroundings are indistinguishable. They’re one and the same thing.

• When bound, a gas’s pressure P, volume V, temperature T, entropy S, and internal energy E are connected by the Gibbs equation:

  $$dE=TdS-PdV$$

  (5)

If the atomic nuclei aren’t fusing or fissioning, their rest mass doesn’t change, so bound internal energy change $dE$ is just the change in the atoms’ collective kinetic energy $d\left(U_i\right)$:

$$dE=d\left(U_i\right)$$

(6)

The term $U_i$ is also known as “thermal” energy. Practically, for a bound gas:

$$d\left(U_i\right)=TdS-PdV$$

(7)

In a vessel, we can say the gas’s mass doesn’t change, so its entropy change dS and heat flow dQ into the vessel from its (warmer) surroundings are related:

$$dQ=TdS$$

(8)

At a reequilibrium T₂ = T₁, all the heat flow ${{\displaystyle \int }}^{\text{}}dQ$ is converted to work ${{\displaystyle \iint }}^{\text{}}dPdV$. The vessel’s internal energy U_i (and PV) doesn’t change, but its entropy S and volume V have increased. If there’s no heat flow into the vessel, both U_i and PV drop as the gas converts thermal energy into work.

Unbound gases behave differently from bound gases: They freely expand ad infinitum. There is no reequilibrium. System and surroundings merge, so there is no heat flow, and no change in total energy. However, the thermal energy of the unbound gas does change. It drops without performing work as the atoms collide and repel each other:

$$d\left(U_i\right)=d\left(TS\right)=-d\left(PV\right)$$

(9)

Free expansion has kinetic energy which is different from random thermal atomic movement $U_i$. We will refer to the kinetic energy of free expansion as kinetic gain, termed E_k. Kinetic gain E_k is best understood by example. We can shoot a rifle in outer space, using either a blank cartridge or a live round.

With a live round, the gas performs work on the bullet until it exits the barrel. The bullet’s acceleration gives equal-and-opposite recoil. The astronaut holding the gun drifts backwards. The expanding gas’s entropy during recoil doesn’t increase much; most of the PV loss is work. Once the bullet leaves the barrel, the gas freely expands into outer space, and its E_k looks almost constant if we’re holding the gun. The atoms’ individual momentum tensors change relatively little as they move away from our astronaut. From the gas’s reference frame, it’s the gun and bullet that are moving away. The gas is roughly an expanding oblate spheroid of atoms with reduced internal energy $U_i$. These atoms can be subsumed in toto by an imaginary sphere around an atom close to the sphere’s center of gravity. The atoms’ outward (radial) kinetic energy in this sphere is 100% entropic E_k. The expanding sphere’s entropy dS and gain d(TS) continues to increase as the atoms move apart. Collisions approach zero. For an amount of mass this small, E_k doesn’t change after collisions end, and is irreversible when unbound, giving entropic force d(TS)/dr. Thermal energy $U_i\to 0$, as dS > 0, and the atoms’ E_k = d(TS) neither changes nor comprises $U_i$. This is further examined in Appendix A.

With a blank, there’s no bullet, and no work performed. The gas is freely expanding inside the barrel, again giving recoil more like a rocket’s thrust, but now the PV loss in the barrel is 100% kinetic gain E_k. Again, when we take away the gun, we get the subsuming sphere of gas, which is bigger without the bullet. A proper numeric description of this gas’s free expansion requires an extensive finite-element model. If the subsuming sphere maintains a uniform density as it expands, its conversion of thermal loss into kinetic gain is more simply described, and can be numerically expressed with just a spreadsheet (see Supplemental Material). At scale, gas is well approximated as uniformly dense and peppered with accreted matter: bullets, rocks, planets, stars, and galaxies, all of which can be kinetically connected to the expanding gas from which they formed (section 4.2).

An unbound sphere of gas at scale works internally against its own gravity. Its thermal loss is expressed with the unbound Gibbs equation:

$$d\left(U_i\right)-d\left(TS\right)+d\left(PV\right)=0$$

(10)

Where d(PV) is the classic bound expression of work. Since unbound d(PV) also comprises -d(TS), this may seem confusing, but a classic d(PV) in (10) aligns its meaning with the bound Gibbs equation (7), and (10) will be shown as an accurate expression of gas thermal behavior at scale.

For a freely expanding sphere of gas with uniform comoving density, its kinetic gain E_k is expressed as:

$$E_k=\frac{d\left(TS\right)}{dt}dt=\frac{d\left(TS\right)}{dV}dV=\frac{-d\left(PV\right)}{dV}dV=-P_{V^{\prime }}dV$$

(11)

Where $P_{V^{\prime }}=d\left(PV\right)/dV$ is the entropic pressure. With a rigid boundary, dV = 0 and $P_{V^{\prime }}=P$. At scale, $P_{V^{\prime }}$ is diminished by the gas’s internal gravity. Entropic $P_{V^{\prime }}$ and thermal P have different meanings for z < 9 (see Appendix D). Much of today’s $P_{V^{\prime }}$ cannot exist in a bound state. Although expressable, this extra kinetic gain’s theoretical origin is not well understood by the present author. Thermal P is well understood, and comprises about half of today’s total $P_{V^{\prime }}$.

Bound P keeps a balloon inflated. Unbound $P_{V^{\prime }}$ is pushing the Universe apart. We will now examine this at the time of last scattering.

3. Construction OF THE THERMAL MODEL AT z = 1089

3.1. Parameters

The thermal model, Eq. (37), expresses the unbound Gibbs equation (10) through a combination of equivalent mass and kinetic energy. We construct the thermal model at the time of last scattering, or more simply “last scatter”, with a finite difference method using the radius r of a sphere as the variable. A popular value of the cosmic redshift at last scatter is z = 1089 and we use this. A spreadsheet is used for the calculations. This is less satisfactory than an analytic derivation, but it does give solace in that expressions herein describe thermal loss ΔU_i precisely. It is only in the partition of ΔU_i between kinetic gain and gravity loss where error accrues. We treat the gas as a single species with a mean atomic weight Ж. The BBN estimate for baryons [30] gives a mass proportion of about 75% hydrogen : 25% helium, so Ж = 1.24 x 10^-3 kg/mol. Hydrogen was monatomic and nonrecombinant to diatomic form, absent catalysis through aggregation. Atomic collisions are all treated as elastic. The initial parameters for our model are given in Table 1 and were derived by the author from table 6 of Planck 2020 [9]. The baryon temperature T at z = 1089 will be set to 2971K, the CMB’s extrapolated value. From our chosen H₀ in Table 1, the baryon density ρ_b at last scatter was 5.46 x 10^-19 kg/m³. This is very low and we can easily treat the gas as ideal.

3.2. The Universe at the time of last scattering was Euclidean

The observed tiny wiggles [9], in the otherwise perfect Boltzmann³ distribution of the CMB, are telling. There is a metric, η_slip, found from the wiggles. It describes variance in the behavior of light between Einstein’s and Newton’s⁴ Universes at last scatter. If η_slip = 1, then there was no variance. The value of η_slip was found to be 1.004 ± 0.007. The text in [9] proclaims that such a value of η_slip justifies an assumption of minimal gravitational anisotropy. Gravitational stress tensors in Einstein’s field matrix vanish. This allows us to say that at last scatter, the entire instant Universe was effectively Euclidean.⁵ Thermal energy $U_i$ is nonrelativistic at 2971K, so atomic momentum tensors were Newtonian, which allows the gas laws to be applied to their collective behavior. The wiggles do indicate minor density variance, attributable in part to baryon acoustic oscillation, i.e. “sonic waves”. This variance may have been negligible back then, but these acoustic waves began to overlap within a colder and colder Universe, creating permanent regions of high gas density whose formation was abetted by the cold. Within these regions of higher density, acoustic resonance gave occasional antinodes that were dense enough to cause gravitational collapse into stars via a process first described by James Jeans (1877-1946) [31]. Treatment of baryon mass using all of general relativity becomes necessary after that, and we will accept without reservation the consistency of myriad observations of the behavior of energy in all its forms with the predictions of general relativity. That said, the Euclidian approximation at last scatter remains accurate. We can also treat the intergalactic medium (IGM) today as Euclidean. The Universe is widely regarded as mathematically “flat”. A flat Universe is Euclidean ad infinitum, and the IGM today comprises about 90% of the Universe’s volume. Accreted matter is only a local perturbation within this larger and much more massive volume. Progress of time in the IGM has been linear ever since last scatter. Its density was and is so low that negligible gravitational time dilation has occurred from then to now.

3.3. The thermal model at the time of last scattering

The thermal model is constructed using monatomic gas expressions found in many introductory engineering textbooks and Wikipedia. Most of the z values in the thermal model (9→1089) cover the dark age [31,32]. The effect of ionizing radiation on the thermal model at z ≥ 9 is practically nil.

3.3.1. Adiabatic energy release

Consider a comoving sphere of initial radius r₁ around a single atom of H₁, at 2971K and ρ_b = 5.46 x 10^-19 kg/m³. All the other atoms are surrounded by an r₁ sphere as well. The gas is monatomic, so:

$$U_i=\frac{3}{2}PV$$

(12)

There are two competing forces of Nature acting on this sphere: Repulsive entropic push, and attractive gravity pull. We are using a finite difference method, so we define an increment: $\frac{\left(r_2-r_1\right)}{r_1}=\frac{\mathsf{\Delta }r}{r}$, which must be kept below 10^-4 for most purposes to minimize the partition error. I use 10^-9, as low as the spreadsheet will tolerate. When the gas in the sphere expands, it must do so adiabatically, and there’s no void outside the sphere into which free expansion can occur. Under classic bound conditions, the sphere would then have to lose $U_i$ (through work). From (9) we can postulate that this adiabatic thermal loss occurs in our cosmic setting as well. For monatomic gases it is:

$$U_{i_1}-U_{i_2}=\Delta U_i=\frac{3}{2}{P}_1{V}_1\left({\left(\frac{V_2}{V_1}\right)}^{-\frac{2}{3}}-1\right)$$

(13)

Where the numeric subscripts refer to the before and after U_i and V values. Volumes V₁ and V₂ are readily found (4πr³/3). Thermal pressure P₁ is found from the ideal gas law:

$$P=\frac{\rho RT}{\text{Ж}}=\frac{MRT}{\text{Ж}V}=\frac{3MRT}{4\text{Ж}\pi r^3}$$

(14)

If work against gravity is negligible, there is no alternative to free expansion within the sphere that I can find, so the released energy (13) is 100% kinetic gain. The finite differential value ΔE_S is the increment kinetic gain $E_{k_{\mathsf{\Delta }r}}$:

$$E_{k_{\mathsf{\Delta }r}}=\Delta E_S=\underset{V_1}{\overset{V_2}{{\displaystyle \int }}}d\left(E_S\right)dV=\underset{V_1}{\overset{V_2}{{\displaystyle \int }}}d\left(TS\right)dV=\underset{V_1}{\overset{V_2}{{\displaystyle \int }}}\left(TdS+SdT\right)dV\approx \left(S_2-S_1\right)\left(T_2+\frac{1}{2}\left(T_1-T_2\right)\right)$$

(15)

The movement of any one atom is no longer entirely thermally random. It has outward radial momentum and kinetic energy E_k. Volume increase is strictly local to the sphere. In an infinitely large Universe, it all just gets less dense. The pressure gradient which drives this density decrease is temporal, not spatial.

3.3.2. Gravity loss

We now look at the gravitational potential energy U of the sphere:

$$U=\frac{\begin{array}{c}-3G{M^{\prime }}^2\end{array}}{5r}$$

(16)

Where G is the gravitational constant. The potential energy U must take into account the total mass $M^{\prime }$, not just the baryons’ thermal mass M. There’s evidence for the existence of cold dark matter (CDM) which is held to be about five times as abundant as baryon mass. Its only interaction with nucleons⁶, electrons, or light, is through gravity. CDM is herein treated as scalar in xyz. While it can move relative to accreted baryons like stars, all that occurs within the gravitationally bound network of galaxies known as the “cosmic web”, and within GCDM, does not affect H. A consistent description of CDM’s composition and origin is elusive [34]. Cold dark matter’s density evolution is presently treated nonrelativistically; we use this convention. Its density is kept constant with respect to the baryons. Both follow 1/r³, as expressed by the scale factor a:

$$a=\frac{r}{r_0}=\frac{1}{\left(z+1\right)}=\frac{1}{z^{\prime }}$$

(17)

where r₀ is the comoving radius of a sphere today, and z is the cosmic redshift:

$$z=\frac{{\lambda }_{ob}-{\lambda }_{em}}{{\lambda }_{em}}$$

(18)

Where λ_ob is the observed wavelength of light of known laboratory value, λ_em. There’s also relativistic CMB energy density ϵ_CMB, which at last scatter fully comprised photon density ϵ_λ. It follows 1/r⁴. The effect of these combined densities on H is expressed in the minimum flat-universe ΛCDM model by (19):

$$H_{\Lambda }=H_0\sqrt{{\Omega }_{\lambda }{a}^{-4}+{\Omega }_b{a}^{-3}+{\Omega }_c{a}^{-3}+{\Omega }_{\Lambda }}=H_0\sqrt{{ϵ}_{M^{\prime }}}$$

(19)

Where H_Λ is the ΛCDM Hubble parameter, and H₀ is today’s Hubble constant (z = 0), found with a telescope. The Ω values are energy density ratios $ϵ/{ϵ}_{M^{\prime }}$ at z = 0, and ${ϵ}_{M^{\prime }}$ is the total energy density, usually called the “critical energy density” ${ϵ}_{crit}$.

Our two models’ densities comove with a:

$$\frac{3H^2{c}^2}{8\pi G}={ϵ}_{crit}={ϵ}_{M^{\prime }}\ne {\rho }_{M^{\prime }}{c}^2$$

(20)

Where c is the speed of light. The reference density ${ϵ}_{M_0^{\text{'}}}$ is given from (20) at H = H₀.

In ΛCDM, ${ϵ}_{M^{\prime }}={ϵ}_{crit}$ is used. It includes repulsive dark energy ${\Omega }_{\Lambda }$. In GCDM, the total mass density ${\rho }_{M^{\prime }}$ is used. It differs from ${ϵ}_{crit}$ in that dark energy ${\Omega }_{\Lambda }$ isn’t included. Dark energy is considered an artifact of the fluid equation (Section 6.2). The baryon mass density ${\rho }_b$ at z = 0 is $\left({\Omega }_b{ϵ}_{M_0^{\text{'}}}/c^2\right)$. Proper total density ${\rho }_{M_0^{\text{'}}}$ and earlier ${\rho }_{M_z^{\text{'}}}$ values result, as shown below.

The Ω’s in ΛCDM always add up to one at any given a. These contributions to total mass are expressed within GCDM via a density multiplier $\mathrm{ɱ}$:

$$\mathrm{ɱ}=\frac{{\Omega }_{\lambda }{a}^{-4}+{\Omega }_b{a}^{-3}+{\Omega }_c{a}^{-3}}{{\Omega }_b{a}^{-3}}=\frac{{\Omega }_{\lambda }{a}^{-4}+{\Omega }_{\left(b+c\right)}{a}^{-3}}{{\Omega }_b{a}^{-3}}$$

(21)

The “$\mathrm{ɱ}$” term is dimensionless and expresses the ratio of total mass to baryon mass. It’s derived from dark-energy-containing Ω’s but does not depend on dark energy content.

The total mass $M^{\prime }$ of a sphere is:

$$M^{\prime }=M\mathrm{ɱ}=M\left(\frac{{\Omega }_{\lambda }{a}^{-4}+{\Omega }_{\left(b+c\right)}{a}^{-3}}{{\Omega }_b{a}^{-3}}\right)$$

(22)

Total mass $M^{\prime }$ = 6.313M at z = 0 and increases to $M^{\prime }$= 8.336M at z = 1089.

The energy lost to gravity upon incremental expansion of the sphere is:

$$\Delta U_r=U_1-U_2=\frac{\begin{array}{c}-3G{M^{\prime }}^2\end{array}}{5}\left(\frac{1}{r_1}-\frac{1}{r_2}\right)$$

(23)

Where $U_1$ and $U_2$ are the before and after gravitational potential energies, respectively.

• Atoms can freely expand without colliding. At scale they can perform work without colliding. When the atoms of a model sphere move away from the center, they are climbing out of a gravity well caused by the reduced density resulting from their movement, and E_k diminishes accordingly. It is this loss of radial kinetic energy to gravity which gives $\Delta U_r$.

3.3.3. Release equals loss: the adiabatic sphere

Combining (9), (10), (13), and (23) gives a finite expression of thermal loss → kinetic gain:

$$E_{k_{\mathsf{\Delta }r}}=\left(\frac{3}{2}\right)P_1{V}_1\left({\left(\frac{V_2}{V_1}\right)}^{-\frac{2}{3}}-1\right)-\frac{\begin{array}{c}3G{M^{\prime }}^2\end{array}}{5}\left(\frac{1}{r_1}-\frac{1}{r_2}\right)$$

(24)

A finite expression of conserved total energy is given by (25):

$$E_1-E_2=\left[\begin{array}{c}\left(M_b{c}^2+M_e{c}^2+M_c{c}^2+E_{CM{B}_1}+U_{i_1}+U_1\right)-\\ \left(M_b{c}^2 +M_e{c}^2+M_c{c}^2+E_{CM{B}_2}+\Delta E_{S_{\lambda }}+ U_{i_2}+U_2+ E_{k_{\mathsf{\Delta }r}} \right)\end{array}\right]=\Delta U_i+\Delta U_r-E_{k_{\mathsf{\Delta }r}}=0$$

(25)

Where E₁ and E₂ are the total energies of the before and after sphere. The CMB gain $\Delta E_{S_{\lambda }}=E_{CM{B}_1}-E_{CM{B}_2}$, discussed in section 6.3.2, is decoupled from E_k at z < 1089 and separately expressed. The nucleon rest mass M_b, electron mass M_e, and CDM mass M_c are unchanged at last scatter so their rest energies Mc² cancel. Eq. (25) is an expanded restatement of the unbound Gibbs equation (10), connected by $\Delta U_r= \Delta \left(PV\right)$ and $E_{k_{\mathsf{\Delta }r}}=\Delta \left(TS\right)$.

When $E_{k_{\mathsf{\Delta }r}}$→ 0 we get an adiabatic sphere. Thermal loss is completely taken up by gravity: $\Delta U_i=-\Delta U_r$. Energy is conserved within all of these spheres, and (1) is obeyed. The radius r_e is its adiabatic radius or endpoint, found by convergence of r around $-\Delta U_i/\Delta U_r$ = 1. If we use H₀ = 67.70 km/sec/Mpc, then at last scatter, r_e = 9.691 x 10¹⁶ m (about 10 ly). It’s very big. The sphere’s imaginary boundary is its adiabatic surface. In today’s variegated Universe, the adiabatic surface around a central atom isn’t always spherical due to e.g. anisotropic stress near the cosmic web. In these regions E_k behaves like thrust and must be expressed with entropic stress tensors not found within Einstein’s field equation matrix. Deep in today’s IGM, Einstein’s and Newton’s Universes closely converge, and the surfaces are near spherical. At last scatter, it’s all spheres.

For an adiabatic sphere, the postulate connecting classic to cosmic gas behavior is clearly seen. The thermal loss in the sphere just balances gravity, like a piston’s expansion just holding up a weight. The postulate holds for lesser, medium spheres, as their thermal loss creates kinetic gain (E_k > 0). These medium spheres aren’t adiabatic since kinetic energy is escaping from them.

The adiabatic sphere’s mass changes as it expands. We are following a specific amount of gas only instantly, at the differential limit. Over time we follow conserved energy.

The adiabatic sphere at the time of last scattering is a central reference from which both earlier and later values can be derived. We will call its radius the pure endpoint and assign it a term, $r_{e_{1090}}$. It can be calculated:⁷

$$r_{e_{1090}}=\frac{6.560754\ast {10}^{18}}{H_0}$$

(26)

Where H₀ is given in km/sec/Mpc.

3.3.4. The expanding adiabatic sphere

The adiabatic sphere contains medium spheres which all have E_k > 0. To determine how fast it is expanding, we have to figure out how fast these lesser spheres expand, and add up their combined radial speeds.

The finite kinetic gain $E_{k_{\mathsf{\Delta }r}}$ of a medium sphere gives its increment radial velocity $v_{s_{\Delta r}}$:

$$v_{s_{\Delta r}}=\sqrt{\frac{2E_{k_{\mathsf{\Delta }r}}}{M}}$$

(27)

Which is best visualized as each and every atom in the sphere moving away from the center at the same speed. Its instant or true velocity $v_s$ gives a true E_k, and vice versa:

$$v_s=\sqrt{\frac{2E_k}{M}}$$

(28)

Below a cutoff radius r_c (= 0.003r_e), loss to gravity is negligible, and all these small spheres give the same initial radial velocity v_i, developed in Appendix B:

$$v_i=\sqrt{\frac{2U_i}{M}}=\sqrt{\frac{3RT}{Ж}}=\sqrt{\frac{3\left(8.3145\right)\left(2971\right)}{\left(0.00123988\right)}}=7731 \mathrm{m}/\mathrm{s}$$

(29)

For a medium sphere, its increment and true velocities are connected by v_i:

$$v_s=\frac{v_{s_{\Delta r}}}{{\left(v_{s_{\Delta r}}\right)}_0}{v}_i$$

(30)

Where $v_{s_{\Delta r}}={\left(v_{s_{\Delta r}}\right)}_0$ for all r < r_c. A 10^-9 increment does a pretty good job of connecting (27) with (28) via (30). Larger increments can be used, to about $\frac{\mathsf{\Delta }r}{r}$ = 10^-4, but these are less accurate, since the partition error goes up.

The integral radial velocity v_e of the adiabatic sphere is the sum of its medium shells, plus the small core:

$$v_e=\left(v_i\right)\left(\frac{r_c}{r_e}\right)+{\sum }_{r_c}^{r_e}\left(\frac{r}{r_e}{v}_s\right)=0.79210v_i=K{v}_i$$

(31)

Which tells us how fast the sphere expands while conserving energy. The value of K is constant to the 5^th decimal place.⁸ It’s independent of any change in $M^{\prime }$, ρ, T, or Ж.

The kinetic gain of an instant sphere is:

$$E_k=\frac{M{\left(v_s\right)}^2}{2}$$

(32)

The integral kinetic gain of an adiabatic sphere, also termed E_k, is expressed with v_i and its thermal mass M_e:

$$E_k=\frac{M_e{K}^2{\left(v_i\right)}^2}{2}$$

(33)

Eq. (33) redefines E_k as its r-integral value at the endpoint, rather than its r-differential value (which is zero). This adiabatic redefinition of E_k properly connects it to the Gibbs meanings (7) and (10) through (11). Kinetic gain E_k only exists instantly, as it is continuously transformed into entropic gain d(TS).

A normalized plot, (v_s/v_i)² vs. (r/r_e) (Figure 1) shows thermal loss distribution within an instant sphere as a function of its radius. Its r-integral value at (r/r_e) = 1 is exactly 2/3 kinetic gain:⁹

$$\frac{2}{3}d\left(U_i\right)=E_k$$

(34)

Only 1/3 of an adiabatic sphere’s thermal loss is taken up by gravity:

$$\frac{1}{3}d\left(U_i\right)=-d\left(U_r\right)$$

(35)

Since the Universe at last scatter was Euclidean, we can construct a line of adiabatic spheres, connected at their tangent points. Anywhere along this line, for any two atoms separated by a distance r, their recession rate $v_r$ is:

$$v_r=K\frac{r}{r_e}{v}_i$$

(36)

Rearrangement gives the fundamental equation:

$$H_g=K\frac{v_i}{r_e}$$

(37)

Where $H_g=v_r/r$ is its atomic Hubble parameter. Eq. (37) is the thermal model. Deployment of (37) at varying T from 10K to 100,000K at z = 1089, or any other dark z value, gives the same H_g(z) to < 1ppm every time. The thermal model is zero-order in temperature. Its independence of thermal content is a bit ironic, isn’t it? The thermal model is also zero-order in Ж. A universe made of xenon atoms (0.131 kg/mole) at the same ρ returns 100.000% of our primordial mix’s H_g. The mass density ρ is the only independent variable in the thermal model. This makes possible its direct comparison with ΛCDM.

Although (37) conceals its underlying calculus, the thermal model is simply expressed, and its message is easy to understand: The Universe’s entropic pressure perpetually exceeds the attractive force of gravity. Anisotropic mass before last scatter was arguably equally negligible, so by suitable modification of v_i, r_e, and perhaps K, we can more properly understand Universal behavior at scale for its entire post-inflation history. The present paper truncates that history at z = 1089, which we further examine.

3.3.5. The Hubble tension

We now compare the thermal and ΛCDM models at the time of last scattering. Since the Hubble constant H₀ is used to get the total density, we must choose from a menu of H₀ estimates. Then we extrapolate today’s total density backwards in time with the scale factor to get the total density at last scatter, and use that density to calculate H₁₀₈₉ for each model. Most H₀ values derive from distance-ladder measurements of stars. There is another method which relies on the cosmic microwave background [9]. It uses the tiny variances in the CMB’s Boltzmann temperature to get an H value at last scatter. This H estimate includes baryon acoustic oscillation, a contribution from sonic effects. The last-scatter H is then extrapolated forward in time using ΛCDM to give H₀. If accurate, this method should give an estimate of H₀ fairly close to the distance ladder estimates. But it doesn’t. The distance ladder gives H₀ values around 74 km/sec/Mpc. Last-scatter extrapolation gives an H₀ of around 68 km/sec/Mpc. These values differ too much to be reconciled, and this discrepancy is known as the Hubble tension. There’s been a lot of speculation about the Hubble tension’s origin [16,17,18,19,20,21,22,23,24,25,26], much of which preserves ΛCDM as a proper method of extrapolation from last scatter to today. This author believes ΛCDM is inaccurate to begin with. The inaccuracy is pronounced at last scatter, as shown in Table 2.

All of Table 2’s calculations start with H₀ and are extrapolated backward in time to find H₁₀₈₉. The top two rows give the Hubble parameters with all energy included. The rows below that show what happens when we remove energy.

On the far-left column of Table 2 are estimates of H₀. The upper number in each set of rows, 67.70 km/sec/Mpc, is a CMB-derived value from [9]. The topmost row of the table recalculates its last-scatter H_Λ. The result is 5.045 x 10^-14 sec^-1 which presumably re-expresses the authors’ starting point; I couldn’t find it anywhere in their paper. The lower number, 74.40 km/sec/Mpc, is one of many distance-ladder estimates.

The second column converts km/sec/Mpc → (sec)^-1, which gives the proportionate increase in adiabatic sphere radius, per second. The next two columns give the Hubble parameters at last scatter for each model. The final three columns give H/H ratios for the four different input sets.

The ratio H₁₀₈₉/H₀ is constant for each pair of H₀’s. It’s always the same within any of the eight pairs shown in the table. Other H₀’s give the same result. The accuracy of this H₁₀₈₉/H₀ ratio depends on the accuracy of the model, and the accuracy of H₁₀₈₉ depends on both H₀ and the model. I believe the distance-ladder H₀ and the thermal model, in Einstein’s Universe, gives the best result: H₁₀₈₉ = 6.945 x 10^-14 sec^-1, or 2.14 million km/sec/Mpc.

The far-right column gives the relative values of the models at last scatter. When CMB energy is included in both models, GCDM gives a value that is 125% of ΛCDM in a single row. That tension increases to 138% if we compare H₁₀₈₉’s between the top two rows. When we remove CMB energy from GCDM, its value drops to 95% within a single row. This is because relativistic mass shrinks the adiabatic sphere, increases its baryon density, and increases H. When this mass is removed from the sphere, it gets larger and its baryon density drops, which reduces H. Density is covariant with entropy in a freely expanding gas, and an adiabatic sphere’s increase in density gives an increase in its entropic pressure. Entropic pressure is presently neglected by acoustic oscillation calculations. The below excerpt from Wikipedia is succinct:

“Without the photo-baryon pressure driving the system outwards, the only remaining force on the baryons was gravitational.”¹⁰

The above assertion does not account for entropic pressure. Gaseous baryons comprise this pressure. They are the force-carrying particles. Entropic force d(TS)/dr plausibly propels expansion at last scatter.

Acoustic oscillation is only a small part of the CMB picture. When it’s excluded from the Planck 2020 calculations [9], H₀ moves to 67.32 km/sec/Mpc, not a very large drop. Maybe inclusion of entropic force bolsters oscillation enough to bring H₁₀₈₉ up to 2.14 million km/sec/Mpc, maybe not. I can’t comment intelligently about that, or about how H₁₀₈₉ is derived from thermal variance in the CMB’s Boltzmann curve. It’s the ratio H₁₀₈₉/H₀ where the models’ predictions differ the most. They give different results at last scatter, and when acoustic oscillation is included, some of the variance credibly arises from entropic neglect. This author believes that all of the variance, and the Hubble tension, can be attributed to ΛCDM’s treatment of baryon mass as accreted rather than gaseous. This difference between the models is developed for z < 1089 in the next section.

4. Variance BETWEEN THE ΛCDM AND GCDM MODELS AT z = 1089 → 9

4.1. The thermal model in z’

The thermal model (37) can be expressed with the inverse scale factor $z^{\prime }$:

$$H_g=\frac{K}{r_{e_1}}\mathrm{ɱ}\text{'}\sqrt{\frac{3R{T}^{\prime }}{Ж}\frac{{\left(z_2^{\text{'}}\right)}^3}{z_1^{\text{'}}}}$$

(38)

Eq. (38) is developed in Appendix C. The term $T^{\prime }$ = 0.0025K is a constant, expressed in Kelvins.¹¹ The term ${\mathrm{ɱ}}^{\prime }$ expresses relative mass density, has a range of 0.757 ≤ ${\mathrm{ɱ}}^{\prime }$ ≤ 1, and is given by (39):

$${\mathrm{ɱ}}^{\prime }=\frac{{\mathrm{ɱ}}_{z_2^{\text{'}}}}{{\mathrm{ɱ}}_{z_1^{\text{'}}}}=\frac{\left({\Omega }_{\lambda }{\left(z_2^{\text{'}}\right)}^4+{\Omega }_{\left(b+c\right)}{\left(z_2^{\text{'}}\right)}^3\right){\left(z_1^{\text{'}}\right)}^3}{\left({\Omega }_{\lambda }{\left(z_1^{\text{'}}\right)}^4+{\Omega }_{\left(b+c\right)}{\left(z_1^{\text{'}}\right)}^3\right){\left(z_2^{\text{'}}\right)}^3}$$

(39)

The $\Omega$’s are given in Table 1. When $z_1^{\text{'}}$ = 1090, we get the pure thermal model:

$$H_g=\frac{K}{r_{e_{1090}}}{\mathrm{ɱ}}^{\prime }\sqrt{\frac{3R{T}^{\prime }}{Ж}\frac{{\left(z^{\prime }\right)}^3}{1090}}$$

(40)

Eq. (40) gives < 0.1 ppm deviance from (37)’s manually calculated $H_g$’s for all z = 0→1089 (see Supplemental Material). It’s exact for any input H₀ and is a perfect expression of gas thermal behavior at scale. We just need to find the pure endpoint from (26) to get thermal $H$ values at lower z from (40).

When we eliminate CMB energy from (40) we get Newton’s Universe. The term ${\mathrm{ɱ}}^{\prime }=1.000$ for all z, giving $H_g^{\text{'}}$:

$$H_g^{\text{'}}=\frac{K}{r_{e_{1090}}}\sqrt{\frac{3R{T}^{\prime }}{Ж}\frac{{\left(z^{\prime }\right)}^3}{1090}}$$

(41)

Here, the “pure endpoint” $r_{e_{1090}}$ is Newtonian. Eq. (41) also gives < 0.1 ppm deviance from (37). Since “$r_{e_{1090}}$” has increased, $H_g^{\text{'}}<H_g$.

• We can compare (41) with a modified ΛCDM $H_{\Lambda }^{\text{'}}$, where relativistic mass and dark energy have been removed:

  $$H_{\Lambda }^{\text{'}}=H_0\sqrt{{\Omega }_{\left(b+c\right)}{a}^{-3}}=H_0\sqrt{{\Omega }_{\left(b+c\right)}{\left(z^{\prime }\right)}^3}$$

  (42)

This is the Newtonian version of the Friedmann¹² equation. It describes the behavior of expanding rocks and CDM in a vacuum, in Newton’s Universe, at their comoving critical density. The thermal (41) and Friedmann (42) equations give an invariant $H_g^{\text{'}}/H_{\Lambda }^{\text{'}}=1.09$ for all z. We can bring $H_g^{\text{'}}/H_{\Lambda }^{\text{'}}$ down to 1.00 with an accretion term.

4.2. Mass accretion

Accretion is expressed with a mass partition ${\rho }^{*}$≤ 1, giving accreted thermal models. The mean gas density ${\rho }_g$ is divided by the mean baryon density ${\rho }_b$:

$${\rho }^{*}=\frac{{\rho }_g}{{\rho }_b}$$

(43)

The mass partition removes accreted mass, its kinetic energy, and its proportion of CDM mass from (24)’s endpoint calculation. CMB energy, if present, is unaffected. This twinned “Universe” is both unaccreted and has a lower baryon density, so it expands more slowly. We connect it with its denser, mass-partitioned twin through ${\rho }^{*}$:

$$H_{g^{*}}^{\text{'}}=\frac{K}{r_{e_{1090}}}\sqrt{\frac{3R{T}^{\prime }}{Ж}\frac{{\left(z^{\prime }\right)}^3{\rho }^{*}}{1090}}$$

(44)

The pure endpoint must be used for ${\rho }^{*}$ to be properly expressed as a second independent variable. Eq. (44) again gives <0.1 ppm deviance from its less-dense twin’s manually found values (which have larger endpoints). Since we use the pure endpoint, the accreted baryons aren’t really missing from (44). They’re coasting alongside the expanding gas from which they formed, and exhibit Friedmann behavior.

When ${\rho }^{*}$ = 0.8418, for the entire domain $z$ = 0 to 1089, the thermal and Friedmann equations give identical results:

$$\frac{H_{g^{*}}^{\text{'}}}{H_{\Lambda }^{\text{'}}}=\frac{\frac{K}{r_{e_{1090}}}\sqrt{\frac{3R{T}^{\prime }}{Ж}\frac{{\left(z^{\prime }\right)}^3{\rho }^{*}}{1090}}}{H_0\sqrt{{\Omega }_{\left(b+c\right)}{\left(z^{\prime }\right)}^3}}=1.000 \mathrm{for} \mathrm{all} z=0 \mathrm{to} 1089$$

(45)

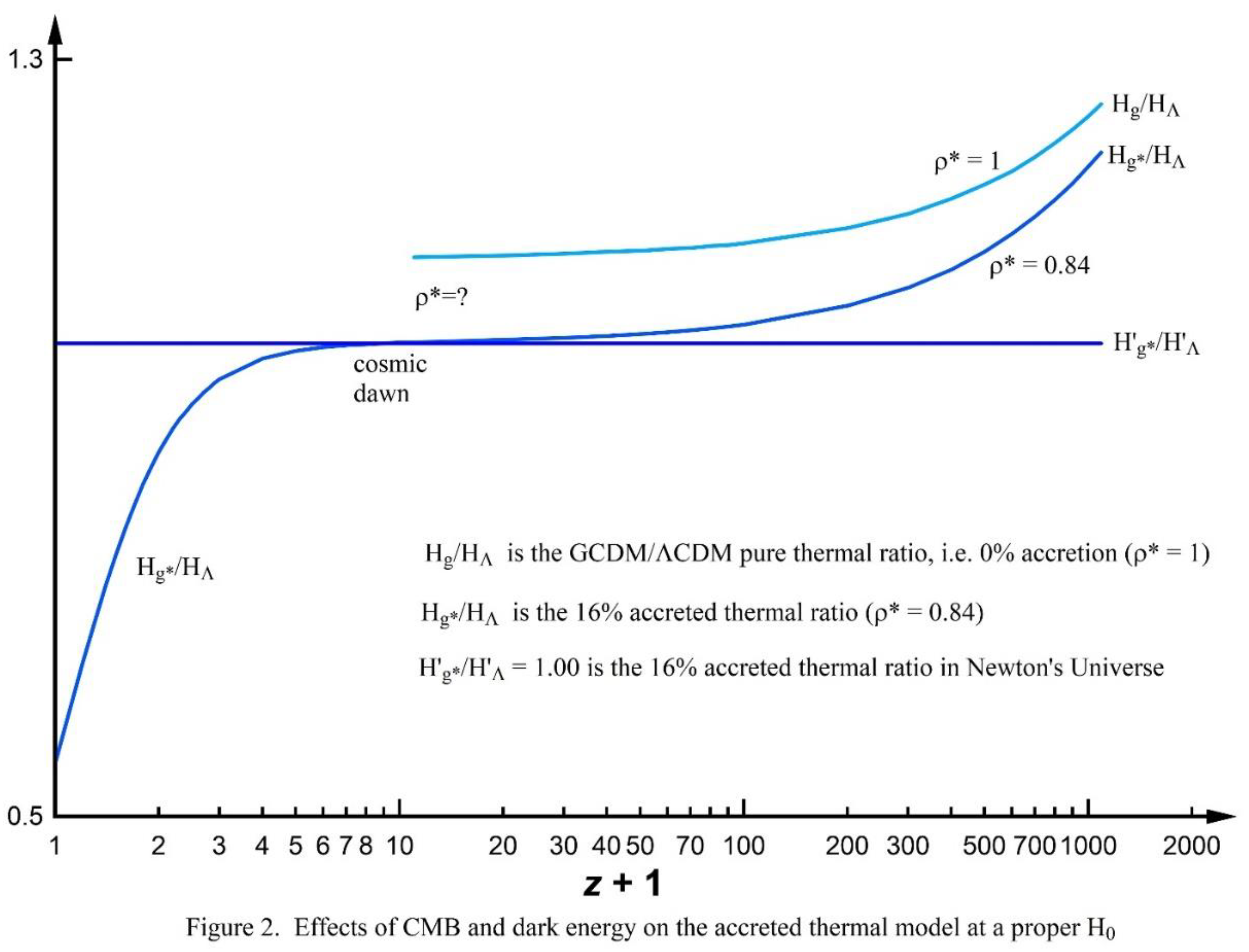
In other words, expanding rocks which are forever slowing to an eventual halt behave exactly a freely expanding gas forever pushing itself apart. The only thing the CMB does is increase the push, and that mostly happens way back near last scatter. The “rocks”, of course, are stars. In today’s intergalactic medium, entropic pressure makes its gas expand, separating the tendrils of the cosmic web. About 90% of our Universe’s present volume is occupied by this expanding gas, which contains 84% of all baryon mass. After around z = 9 or so, accretion into the cosmic web seems to have stabilized at 16% of the total. This 84/16 proportion probably hasn’t changed much since then; however, mass loss from nuclear fusion remains unaddressed.

Eqs. (41) – (45) deal with Newton’s Universe, where the CMB’s equivalent mass isn’t included. In Einstein’s Universe, they underestimate $H_g$. Also, CMB mass is unaffected by ${\rho }^{*}$.

• The thermal model in Einstein’s Universe, with accretion, is termed $H_{g^{*}}$:

  $$H_{g^{*}}=\frac{K}{r_{e_{1090}}}{\mathrm{ɱ}}^{\prime }\sqrt{\frac{3R{T}^{\prime }}{Ж}\frac{{\left(z^{\prime }\right)}^3{\rho }^{*}}{1090}}$$

  (46)

The pure endpoint $r_{e_{1090}}$ re-includes CMB energy. The ${\mathrm{ɱ}}^{\prime }$ term now includes ${\rho }^{*}$:

$${\mathrm{ɱ}}^{\prime }=\frac{\left(\frac{{\Omega }_{\lambda }{\left(z_2^{\text{'}}\right)}^4}{{\rho }^{*}}+{\Omega }_{\left(b+c\right)}{\left(z_2^{\text{'}}\right)}^3\right){\left(z_1^{\text{'}}\right)}^3}{\left({\Omega }_{\lambda }{\left(z_1^{\text{'}}\right)}^4+{\Omega }_{\left(b+c\right)}{\left(z_1^{\text{'}}\right)}^3\right){\left(z_2^{\text{'}}\right)}^3}$$

(47)

Where $z_1^{\text{'}}$ = 1090. For ${\rho }^{*}$ = 0.8418, its ${\mathrm{ɱ}}^{\prime }$ range is 0.757 ≤ ${\mathrm{ɱ}}^{\prime }$ ≤ 1.046. We again find that (46) gives < 1ppm deviance from the manually found values (37) for our input H₀’s (see Supplemental Material).

4.3. Progress of accretion at cosmic dawn

The term (1-${\rho }^{*}$) is the accretion parameter. It’s the fraction of (baryon + CDM) mass that is gravitationally bound: Stars, planets, black holes, bound gases, etc. At scale, these accreted baryons act like rocks and comprise the cosmic web of galaxies with all of its gravity-bound behavior. How did accretion evolve? We may be able to answer this question through observation of stars at cosmic dawn.

For z > 9, “dark” energy is minimal (Ω_Λ < 0.002), and ${\rho }^{*}$ (43) might be estimable from the H values of any luminous bodies we are fortunate enough to see. The accuracy of ${\rho }^{*}$ depends on a proper value of H₀ for which the range of distance-ladder estimates remains large. What we can do is determine if observed H/H_Λ values deviate upwards as we go back in time from z = 9→50 or so. This in turn depends on whether or not star formation and accretion are coevolving phenomena. If accretion ends before starlight begins, then ${\rho }^{*}$= 0.84 applies and the value of H/H_Λ will remain close to one. However, if accretion and starlight coevolve, then H/H_Λ > 1 may be significant enough to measure. For example, the newly found galaxy JADES-GS-z13-0 [35,36] has a spectroscopic redshift of 13.2, so Ω_Λ = 0.0007, a minimal dark energy value. If ${\rho }^{*}$ = 0.84 at this redshift then $H_{g^{*}}$/H_Λ = 1.002, not significant. If ${\rho }^{*}$ = 0.9 then $H_{g^{*}}$/H_Λ = 1.037 which if true ought to be detectable. The theoretical upper limit of $H_{g^{*}}$/H_Λ at z = 13.2 is 1.09, shown in Figure 2. These ratios don’t change in z for any H₀, but if H₀ = 67.70 km/sec/Mpc is in fact a low estimate then observed ratios using it should start high (H/H_Λ = 1.139 for ${\rho }^{*}$=0.9) and get higher as z increases (if the Universe coevolves). This author believes that star formation and accretion do coevolve, and I predict upwardly-trending deviance of H from H_Λ in the z > 9 domain now accessible from the James Webb space telescope. If we can get reliable luminosity-based distance estimates from these faint bodies, and can find the proper H₀, we should be able to follow the progress of accretion through (1-${\rho }^{*}$).

Figure 2 gives a complete picture of the thermal model over the entire domain z = 0 to 1089. There are two domains of variance, overlapping at cosmic dawn, where both dark and CMB energies aren’t large. For z > 9, predicted variances $H_{g^{*}}$/H lie somewhere in the area between the pure and accreted curves in Figure 2. For z < 9, the variance of $H_{g^{*}}$/H due to added repulsive force is clearly shown and discussed in section 5 below.

Two numbers are worthy of mention. The dark-matter-to-baryon ratio ${\Omega }_c/{\Omega }_b$ is 5.311. The accretion ratio ${\rho }_g/\left(1-{\rho }_g\right)$ for z < 9 is 5.321. These differ by less than half a percent. Is this just a coincidence, or is there a causal connection?

5. Suprathermal ENERGY

5.1. The suprathermal model, z = 9 to 0

None of the above expressions come any closer to explaining the source of the repulsive “dark energy” term Ω_Λ in the ΛCDM model. I propose that suprathermal kinetic energy in the IGM is responsible. It arises mostly from Compton¹³ scattering, reliant in turn on energetic photon flux $E_{\gamma }$. There are direct partial flux estimates available at the high end [37,38] but the process of connecting these and other sources to produce a definitive suprathermal model is an undertaking of considerable magnitude. The present paper is merely an introduction.

The suprathermal model is developed in Appendix D and expressed by (48):

$$H=H_{g^{*}}\sqrt{\left(1+\frac{U_{{\beta }_s}}{U_b}\right)}$$

(48)

Where $U_{{\beta }_s}$ is electron suprathermal energy in the adiabatic sphere, $U_b$ is nucleon thermal energy, and $U_{{\beta }_s}/U_b$ is the suprathermal ratio.

Eq. (48) presupposes thermal plasma, a safe bet for a reionized Universe. Accretion is presumed complete after z = 9 so we use ${\rho }^{*}$ = 0.84. The suprathermal ratio $U_{{\beta }_s}/U_b$ is, like $H_{g^{*}}$, zero-order in T,¹⁴ so (48) is completely temperature-independent. We fit the suprathermal model to the ΛCDM model by convergence of $U_{{\beta }_s}/U_b$ around H/H_Λ = 1 for each datum. These results are shown in Figure 3. A ln-ln line is found¹⁵ for z = 0→2, giving (49):

$$\frac{U_{{\beta }_s}}{U_b}=e^{\left(0.8045-2.9915ln\left(z^{\prime }\right)\right)}\approx \frac{2.2397}{{\left(z^{\prime }\right)}^3}$$

(49)

At z = 0, $U_{{\beta }_s}/U_b$ = 2.2397 gives H/H_Λ = 1; the regressed value is 2.236. This is close to the ratio ${\Omega }_{\Lambda }/\left({\Omega }_b+{\Omega }_c\right)$ in the ΛCDM model, 2.235, and a simple restatement of the source of “dark energy” repulsion. A modest deviance from linearity in the plot occurs above z = 2; these are shown in Figure 3 but not included in the regression. The line is still very good out to z = 4. At z = 5 there’s deviance and $U_{{\beta }_s}/U_b$ drops to 0.01. The crossover to $U_{{\beta }_s}$dominance is found at z = 0.309. Eq. (49) derives from ΛCDM and accordingly gives the suprathermal ratio as proportionate to ${\left(z^{\prime }\right)}^{-3}$.

Inserting (49) into (48) gives:

$$H=H_{g^{*}}\sqrt{\left(1+\frac{2.2397}{{\left(z^{\prime }\right)}^3}\right)}=H_{g^{*}}\sqrt{1+2.2397a^3}$$

(50)

Using the same data, a ln-ln regression of r_e vs. z’ gives (51):¹⁶

$$r_e=r_0{e}^{\left[0.00006-1.5006ln\left(z^{\prime }\right)\right]}\approx r_0{\left(z^{\prime }\right)}^{-\frac{3}{2}}$$

(51)

Where r₀ = r_e at z = 0. From (51) we see that the adiabatic volume V_e/V₀ varies as ${\left(z^{\prime }\right)}^{\frac{-9}{2}}$, not ${\left(z^{\prime }\right)}^{-3}$. A constant “dark energy density” expressed as $\left[U_{{\beta }_s}/U_b\right]/{\left(z^{\prime }\right)}^3$ might be accurate, but within GCDM, isn’t proper.

From (48) – (51) we arrive at an expression of H for z = 0 to 2:

$$H=H_{g_0^{*}}{\left(z^{\prime }\right)}^{\frac{3}{2}}\sqrt{1+\frac{2.2397}{{\left(z^{\prime }\right)}^3}}=H_{g_0^{*}}{a}^{-\frac{3}{2}}\sqrt{1+2.2397a^3}$$

(52)

When H₀ = 74.40 km/sec/Mpc, the thermal $H_{g_0^{*}}$ = 1.339 x 10^-18 sec^-1 (at z = 0). Eq. (52) gives 100.00%→99.90% of the ΛCDM value (19) for z = 0 to 2. The exponents in (49) – (51) are rounded to the nearest fraction. The rounding excises CMB density from r_e/r₀ (51), giving some of the observed -0.1% deviance at z = 2. When (50) is properly expressed with (46), the error drops considerably, only reaching 0.1% at z = 9. (see Supplemental Material).

From (26), (46), (47), and (50), a full expression of H can be given:

$$H=\frac{K{H}_0{\left(1090\right)}^3{a}^{1.5}\left(\frac{{\Omega }_{\lambda }}{{\rho }^{*}{a}^4}+\frac{{\Omega }_{\left(b+c\right)}}{a^3}\right)\sqrt{\frac{3RT\text{'}{\rho }^{*}}{1090Ж}\left(1+2.2397a^3\right)}}{\left(6.5608\ast {10}^{18}\right)\left({\Omega }_{\lambda }{\left(1090\right)}^4+{\Omega }_{\left(b+c\right)}{\left(1090\right)}^3\right)}$$

(53)

Which contains two independent variables: a (=1/[z+1]), and ρ* ≤ 1. For z < 9, ρ* = 0.84, and Eq. (53) agrees with ΛCDM (19) (±0.1%). For z > 9, ρ* rises, giving tension with (19). At z = 1089, ρ* = 1, and (53)/(19) = 1.25.

At z = 0, the models converge:

$$\frac{U_{{\beta }_s}}{\left(U_b+U_{{\beta }_s}\right)}={\Omega }_{\Lambda }=0.691$$

(54)

If we include thermal free electron energy $U_{{\beta }_t}$ in the denominator of (54), we get $\frac{U_{{\beta }_s}}{\left(U_b+U_{{\beta }_s}+U_{{\beta }_t}\right)}=$ 0.53, still more than half of all kinetic energy in the IGM today.

The suprathermal model gives a “pumped Universe” scenario. In a pumped Universe, the intergalactic medium is continually fed with suprathermal energy $U_{{\beta }_s}$. This energy persists and accumulates. Most of it comes from electrons which in turn derive their energy from photons produced by nuclear fusion within the cosmic web of galaxies. Compton scattering imparts kinetic energy to the electrons. Much of that energy is well above the nucleons’ thermal range given by the Boltzmann curve, so the Universe isn’t just getting hotter. Its kinetic energy is increasing above and beyond simple thermal heat. This adds a tremendous amount of entropic force d(TS)/dr.

We should be able to connect suprathermal energy generation with the small number of known sources which are capable of producing $E_{\gamma }$ photons: Type “O” stars and active galactic nuclei. Maybe additional scattering of free electrons by the lower-energy photons emitted by all stars today gives net addition enough to account for the “dark energy” effect. If $U_{{\beta }_s}$ persists indefinitely, then $d\left(U_{{\beta }_s}\right)/dt$ can be estimated from stellar photon flux and lookback. Those calculations involve several other assumptions not covered here and lie outside the scope of the present paper.

5.2. Origin of suprathermal electrons in the IGM

By z ≈ 6 the Universe was fully reionized, so Compton scattering from neutral IGM atoms isn’t a significant source of suprathermal energy after that. A second source is Compton scattering of free electrons in the IGM, which would taper off to a steady state if the energy profiles of the electrons and photons were to converge. Cosmic radiation $U_{b_s}$ from the web is a third source. The reader is asked to consider a fourth source, kinetic energy of electron escape from the web, as a present-day contributor to the IGM’s suprathermal content. Any resulting IGM charge buildup is presently untreated. This author estimates these electrostatic effects as minor compared to $U_{{\beta }_s}$.

5.3. Suprathermal effects on r_e and K

Suprathermal electrons do not behave like thermal baryons, and their kinetic gain hasn’t been properly addressed. Thermal free electrons are treated as a gas (appendix D) which seems proper, but I’m not so sure if it’s accurate. This author is unaware of any treatments involving electron kinetic gain. Electron thermal energy may partly comprise $U_{{\beta }_s}$. What we can say is that electron kinetic energy in general only minimally affects nucleon endpoint values. The presumption that v_e/v_i = K remains constant with added suprathermal energy is conjecture, but it appears to work well. For special effects, any relativistic mass increase would cause a decrease in r_e. The entropic partition (2/3) and K may also change with introduction of highly relativistic kinetic energy. I believe such changes in K and r_e aren’t large. Even if K/r_e is theoretically shown to change by as much as 1%, the suprathermal model still allows us to use known and conserved energy sources, in compliance with (1), to account for H.

6. Discussion: GCDM VERSUS ΛCDM

The ΛCDM model (19) is a benchmark, giving the most accurate empirical fit to date. It closely converges with the GCDM model at z = 0. The models have different theoretical foundations and their predictions diverge at last scatter.

The ΛCDM model combines three formulas:

1)

The Friedmann equation gives a relation between H and total energy density ${ϵ}_{M^{\prime }}$.

2)

The fluid equation adds a (kinetic) mass equivalence term “P” and describes covariant ( ${ϵ}_{M^{\prime }}+"P"$) vs. H.

3)

The equation of state divides “P” into three different constituents.

We use H(t) below. It’s connected to H(a) by lookback ${{\displaystyle \int }}^{\text{}}\left(dt/da\right)da$.

6.1. The Friedmann equation

The question of Universal curvature is historically important and extensively treated in modern introductory texts [39,40]. That debate is largely settled now. Most of us believe in a flat Universe, so the Friedmann equation can be simply expressed:

$$H=\sqrt{\frac{8\pi G{ϵ}_{M^{\prime }}}{3c^2}}$$

(55)

The Friedmann equation overlooks the fact that most Universal baryon mass is gaseous. Instead of the thermal model’s perpetual entropic pressure, we have ΛCDM’s rocks at a “miraculous” critical density. While the Friedmann equation (43) may not properly express entropic gain, it can be shown as identical to thermal behavior (45) through ρ*.

Friedmann employed Einstein’s field equation which makes no provision for entropic gain. Einstein invented the Λ force to offset gravity, as the Universe was thought to be static at the time, and he had to do something to prevent its collapse. Both Friedmann’s and Einstein’s entropic omissions were benign. It just didn’t occur to either author to include entropy. Einstein’s later doubts about Λ are well known [41].

6.2. The fluid and acceleration equations

The fluid equation is a different story. It actively excludes entropic gain. We start, as do the texts, with the bound Gibbs equation (5) which describes e.g. gas in a vessel:

$$dE=TdS-PdV$$

(5)

Over time, this is:

$$\frac{dE}{dt}=T\frac{dS}{dt}-P\frac{dV}{dt}$$

(56)

When applied to the unbound Universe, dE/dt = 0. We include rest mass equivalence E = Mc². Nuclear fusion. The unbound Gibbs equation (10) is now:

$$dE=d\left(M{c}^2\right)+d\left(U_i\right)+d\left(PV\right)-d\left(TS\right)=0$$

(57)

At last scatter there was no fusion, so M was unchanged, $d\left(M{c}^2\right)$ = 0, and (57) = (10). Photon energy from the CMB isn’t included here and is discussed in more detail below (section 6.3.2). It’s unimportant for now.

The fluid equation’s development continues with heat flow:

$$\frac{dQ}{dt}=T\frac{dS}{dt}$$

(58)

This relates thermal change dQ with the entropy change dS in a vessel. If there’s no vessel, we get the Universe. We will assume there’s no heat flow in or out of the Universe. This assumption gives rise to a philosophical discussion about the meaning of the first law vs. unbound thermal loss. We will sidestep that entire debate and can properly treat lost kinetic energy as entropic gain.

The second law (2) is clear about entropy: dS/dt > 0 always. At scale, we can get a rough estimate of gas dS/dt from the thermal model (37) at a constant T and P by setting dE/dt = 0 in (56). For H₀ = 74.40 km/sec/Mpc and z = 1089, this gives:

$${\left(\frac{\mathsf{\partial }S}{\mathsf{\partial }t}\right)}_{T,P}=\frac{4\pi r_e^{2}PK{v}_i}{T{M}_e}$$

(59)

= 106 (J/K)/sec/kg

The fluid equation sets Universal dS/dt = 0 despite the second law. Baryon mass is treated as a pressureless perfect fluid, called a “dust”, which is inconsistent with its actual existence as a gas having entropic pressure. Entropic gain is eliminated, and all energy change is isoentropic. Eq. (56) now looks like this:

$$PdV/dt=-dE/dt$$

(60)

Which describes gas in an adiabatic vessel. The term -dE/dt = -d(U_i)/dt describes its rate of thermal loss. Setting dS = 0 means that all the loss is reversibly stored, and in the unbound Universe, there’s only one place this author knows of to store it: work against gravity. I’ve shown that only a third of this thermal loss is stored that way. The remaining two-thirds vanishes, and requires entropic power d(TS)/dt to properly describe its fate. Entropic power gives over time an irreversible loss of thermal energy, and a reduction in density which acts as a thermodynamic repository or “sink”. If entropy is excised from the Gibbs equation, the lost thermal energy cannot be accounted for, giving inconsistency with (1).

There is another significant issue with the fluid equation which only became relevant after 1998. Internal energy change dE gets improperly redefined in the fluid equation’s development. It isn’t thermal anymore, it’s total, and now includes rest mass dE = d(Mc²). Eq. (60) is then used to treat the energy change of rest mass d(Mc²) as a thermal variable. Rest mass does not change thermally, it stays constant.¹⁷ From (1), dE/dt in (60) should be zero. Conflation of the dE terms can thus appear to create an enormous amount of what is fictitious repulsive energy from what is actually a much smaller amount of suprathermal energy. In this author’s opinion, that’s what happened when the distance ladder line was found to be a curve by the seminal observations of the two research groups who first published their findings in 1998 [4],[6]. They accounted for the distance-ladder curvature by populating Λ with fictitious negative mass. The reader may wish to consider the alternative, suprathermal energy, and the possibility that the source of Λ cannot be identified because it doesn’t exist.

Further development of the fluid equation is in the texts. The result is the same for both Einsteinian and Newtonian versions, which differ only by c². The Newtonian expression of the fluid equation is:

$$\frac{d\left("{\rho }_{M^{\prime }}"\right)}{dt}+3H\left("{\rho }_{M^{\prime }}"+"P"/c^2\right)=0$$

(61)

In (61), “${\rho }_{M^{\prime }}$” includes ${ϵ}_{\Lambda }/c^2$. The other terms in “P/c²” are equivalent mass density of energy not at rest, so if we exclude Λ, (61) is an attractive term. The energy density term “P” is thus also attractive and labelled as “pressure”:

$$\text{"}\mathrm{P}\text{"}=w_b{ϵ}_b+w_{\lambda }{ϵ}_{\lambda }+w_{\Lambda }{ϵ}_{\Lambda }$$

(62)

The w terms are dimensionless numbers whose values are expressed using a: w_b << 1, w_λ = 1/3, and w_Λ = -1. This definition of “pressure P” is known as the equation of state. It’s the third leg of ΛCDM and is discussed below. The equation of state inverts the meaning of pressure. Most of us think of positive pressure as repulsive, like in a balloon. Not here. Repulsive energy density $w_{\Lambda }{ϵ}_{\Lambda }$ in (62) is called “negative pressure”.

When we talk about the meaning of pressure, the Jeans model of star formation [30] is relevant. Both (62) and the Jeans model operate concurrently within any given volume. The Jeans model treats P as repulsive, an offset against gravitational collapse. The fluid and state equations treat “P” as attractive, which is inconsistent with the Jeans model. The GCDM model treats P as repulsive, which is consistent with the Jeans model’s treatment of P.

6.3. The equation of state

The equation of state (62) is combined with the Friedmann (55) and fluid (61) equations to complete the ΛCDM model (19).

6.3.1. Baryonic mass

Baryonic matter comprises stars, rocks, and helium balloons, and is treated by ΛCDM as 100% accreted and therefore 100% attractive. In GCDM, baryon mass is mostly repulsive, a gas. At last scatter, baryon mass was 100% gas. Presently, the repulsive/attractive ratio of baryon mass in the Universe is about 84:16, or 5¼:1.

The ΛCDM term $w_b{ϵ}_b$ is expressed as:

$$w_b{ϵ}_b\approx \left(\frac{kT}{\mu c^2}\right){ϵ}_b=\left(\frac{kT}{\mu c^2}\right)\left({\rho }_b{c}^2\right)=\frac{kT{\rho }_b}{\mu }$$

(63)

Where μ is the mean atomic mass and k is Boltzmann’s constant. Eq. (63) is simply thermal pressure. Its equivalent mass density, and suprathermal pressure, are both negligible compared to ΛCDM’s ϵ_crit, whose conflated term Ω_Λ and rest term Ω_(b+c) together comprise almost 100% of ϵ_crit today. In GCDM, there is no Ω_Λ, and Ω_(b+c) ≈ 0.9997. Although only an infinitesimal fraction of total energy today, entropic pressure $P_{V^{\prime }}$ is ample, and provides both thermal and suprathermal repulsive force.

6.3.2. Relativistic mass; entropy of a photon

Relativistic mass, expressed as $w_{\lambda }{ϵ}_{\lambda }$ in the ΛCDM model, is attractive in both models and arises from photon and neutrino energy.¹⁸ Its effect on the Hubble parameter at last scatter gives rise to the Hubble tension.

We now examine photon energy more closely. An expanding sphere of CMB light has an r^-4 dependence of energy density. Volume increases as r³, so there appears to be a 1/r loss of CMB energy upon expansion. During the dark age there was minimal CMB energy transfer to the IGM’s baryons [41]. Most of the CMB’s energy vanished; we get inconsistency with (1). I see no escape from this conundrum except to apply (3): CMB light yields gain through wavelength stretch Δλ. Any one CMB photon’s wavelength increases with time and their combined lost energy becomes entropic gain $\Delta E_{S_{\lambda }}$:

$$\Delta E_{S_{\lambda }}=E_{CM{B}_1}-E_{CM{B}_2}={\sum }_{{\lambda }_1\approx 0}^{\infty }{n}_{\lambda }hc\left(\frac{1}{{\lambda }_1}-\frac{1}{{\lambda }_2}\right)$$

(64)

where $E_{CM{B}_1}$ and $E_{CM{B}_2}$ are the before and after photon energies during the dark age, h is Planck’s¹⁹ constant, λ₁ and λ₂ are the before and after wavelengths of the stretched photon, and $n_{\lambda }$ is the number of photons at a wavelength λ₁. The distribution $n_{\lambda }$ vs. λ is observed in the CMB as a blackbody curve, which gives $n_{\lambda }$ vs. λ at earlier times.

The above analysis gives an individual photon’s entropy $S_{\lambda }$ as equal to Planck’s constant:

$$S_{\lambda }=h$$

(65)

Entropy is expressed as J/Hz rather than the more conventional J/K.²⁰ Unbound photon energy $E_{\lambda }$ is potentially 100% entropic, in that all of it is eventually lost to time. From (65), photons are isoentropic, so the second law as applied to them is expressed with gain d(E_S) rather than simple entropy increase dS. Gain d(E_S) is connected to E_k, hence volume. The rate of volume increase $d{V}_{\lambda }/dt$ of radial light in a model sphere is:

$$\frac{d{V}_{\lambda }}{dt}=\frac{4\pi c^3}{3}$$

(66)

which far outpaces nonrelativistic E_k.

Current treatment of CMB energy also begins isoentropically, again from the bound Gibbs equation (5) [39,40]. While the present paper concurs with isoentropic photon treatment, photon gain $\Delta E_{S_{\lambda }}$ is neglected, and light energy is purported to expand more slowly than baryonic matter. A different result might be found if $\Delta E_{S_{\lambda }}$ is included in an ab initio derivation.

Cosmic free electron gain resembles that of photons, as they both have wavelike character. Electron kinetic gain has yet to be properly expressed. Before last scatter, when z > 1089, free electrons coupled with photons. The coupling gives an increase in H. The present author believes that the thermal model (37) can be applied to give H over the entire domain a → 0. This interesting subject lies beyond the scope of the present paper.

6.3.3. Dark energy

The remaining term, $w_{\Lambda }{ϵ}_{\Lambda }$, describes repulsion. In the ΛCDM model, Λ is used to account for distance-ladder curvature, e.g. [4,5,6,7]. Its predominance, ϵ_Λ = 0.69ϵ_crit at z = 0, arises from the fluid equation’s isoentropic and variable total energy. The behavior described by w_Λϵ_Λ is herein proposed to arise instead from suprathermal pressure $P_{V_s^{\text{'}}}$ in the IGM, mostly carried by electrons. Electron and nucleon pressure does create a repulsive in toto scalar field, but its ${\Omega }_{U_i}$ is more than ten orders of magnitude smaller than ${\Omega }_{\Lambda }$, is variable, and can be locally nonscalar. A noncovariant Λ means a constant ϵ_Λ. This creates more and more energy as the Universe expands, which is inconsistent with (1). If (1) is obeyed, the field must have a conserved source. Suprathermal energy $U_{i_s}$ meets this requirement.

7. Concluding REMARKS

The present paper proposes a fundamental change in the way the Universe is viewed: As an unbound thermodynamic system in which a freely expanding gas has partly accreted into stars. The gas comprises a repulsive field, IGM kinetic energy, scalar in xyz at last scatter. It’s now locally variable in xyz but still behaves in toto as a time-variant scalar in the flat Universe we see. Thermal behavior is shown to be identical to the Friedmann equation’s predictions. Suprathermal behavior causes “dark energy” Λ. The GCDM model predicts variance from ΛCDM at cosmic dawn, and the Hubble tension at the time of last scattering.

This author has herein made the case that Λ is an artifact arising from inconsistency with the thermodynamic laws, and that kinetic density, rather than total density, is the primary metric through which H is properly expressed. While not the first to suggest that entropy is a force of Nature, I hope that the present paper will be persuasive enough to convince the reader.²¹