Secure and Fast Image Encryption Algorithm Based on Modified Logistic Map

In the past few decades, the transmission of data over an unsecure channel resulted in an increased rate of hacking. Therefore, the requirement to make multimedia data more secure is increasing day by day. Numerous algorithms are developed to improve efficiency and robustness. In this article, a novel and secure image encryption algorithm is presented. It is based on a modified chaotic logistic map (CLM) that provides the advantage of having less computational time to encrypt an input image. The encryption algorithm is based on Shannon’s idea of using substitution-permutation and one-time-pad network to achieve ideal secrecy. The CLM is used for substitution and permutation to improve randomness and increase dependency on the encryption key. Various statistical tests are conducted, such as Key Space Analysis, Complexity Analysis, Sensitivity Analysis, Strict Avalanche Criteria (SAC), Histogram Analysis, Entropy Analysis, Mean of Absolute Deviation (MAD) Analysis, Correlation Analysis, Contrast Analysis, and Homogeneity to give a comparative analysis of the proposed algorithm and verify its security. As a result of various statistical tests, it is evident that the proposed algorithm is more efficient and robust as compared to previous ones.

Keywords:

Subject: Computer Science and Mathematics - Computer Vision and Graphics

1. Introduction

In recent years, multimedia and communications industry have developed rapidly. Many large streams of multimedia data is transmitted over an insecure channel. As the rate of hacking increased with the passage of time, therefore, the security of the data must be increased day by day [1]. Numerous algorithms are developed in the world that are efficient and robust, but are still not sufficient to protect data. In addition, less computationally complex algorithms are required to cater the need to secure high speed data transmissions. A lossless, novel and secure image encryption algorithm based on the modified chaotic logistic map (CLM) that takes less computational time for encryption is presented in this research.

The CLM has many great features such as sensitive dependence on initial conditions, random orbit, pseudorandomness, good ergodicity, better cross-correlation properties, high efficiency, better mixing properties and large keyspace. These features makes CLM a potential candidate in quantum image encryption algorithms [2,3,4]. Therefore CLM is also quantum safe. CLM also has low computational cost and it takes less hardware and it is easy to implement [5]. It is verified that CLM provides high speed with low cost [6].

A good encryption scheme must have a substitution-permutation (SP) network as indicated by C. E. Shanon [7] to increase its security [8]. The pixel level substitution and permutation is used in the algorithm to save computation time and cost. Otherwise, if bit level substitution and permutation is used then the algorithm’s computation time and cost will increase eight times.

Permutation is the property used for the rearrangement of pixels in some pseudorandom order. It means that several pixels of the encrypted image are affected by just changing one pixel of the original image. Therefore, it hides any dependency between the input image and the encrypted image [9]. Any algorithm is more resistant to frequency analysis attacks by using permutation techniques. The permutation techniques are further classifieed into two categories, one is pixel level permutation and the second is bit level permutation. These permutations are achieved by employing various transforms [10,11], chaotic maps [12,13,14,15,16,17], cyclic shifts [18,19,20,21], hash functions [22], sorting techniques [15,23,24,25,26,27] and parallel computing [28]. Although, these transformational techniques based algorithms have many flaws, one of them is that they create high security but increases time complexity which further results in lengthy preprocessing and poor permutation performance. On the other hand, sorting based permutation techiniques gives the best permutation effect but the time complexity will be increased and memory cost will be high. if cyclic shift permutation techniques are utilized, they reduce the computational complexity and therefore reducing memory costs, but weaken the permutation effect. So, there is a need for a secure encryption algorithm which reduces the time complexity and memory cost but not at the cost of reduction in the security.

Substitution is used to obscure the connection between the corresponding pixels of the input image and the encrypted image. This property of substitution makes it ideal to hide the connection between the secret key and the encrypted image. Substitution is also subdivided into pixel level substitution [10,11,12,13,14,15,16,17,24,25,26,27,29,30,31,32] and bit level substitution [18,23,33,34]. In bit level substitution, the substitution can be lengthy and thus time consuming. Therefore in the proposed algorithm, pixel level substitution is used.

Image encryption can be lossy or lossless [35]. Various transformation techniques used for image encryption are lossy [10,11]. In the proposed algorithm, we employ CLM because of its high dependency towards initial conditions. Therefore, we achieved lossless encryption. A novel and secure image encryption algorithm based on CLM that requires less computational time to encrypt an original image is presented. Shannon’s idea of using substitution-permutation and one-time-pad network to achieve ideal secrecy is the backbone of this research [7].

The organization of rest of the paper is as follows: The proposed image encryption algorithm is presented in Section 2. The results alongwith statistical tests are presented in Section 3. The conclusion of the research is presented in Section 4.

2. Proposed Algorithm

The encryption process is divided into six stages. The block diagram is given in Figure 1. In the first stage, the permutations on the grayscale image is performed. The second stage involves the substitution of pixel intensities of the permuted grayscale image. The pixel intensities are then converted into binary bits in the third stage. In the fourth stage, the random binary bits are collected from the CLM. In the fifth stage, the binary bits from stage three and four are added using an “XOR” operation. In the last and final stage, the resultant bits are converted in to pixel intensities. The details of the six stages are presented as follows:

2.1. Permutation

The permutation process rearranges pixel intensities according to a sequence acquired from CLM. For example, if a permutation matrix [2, 4, 1, 3] obtained from CLM with population growth, is applied to numbers

2, 4, 1, 3

(Pixel intensities), the resultant sequence after permutation is

4, 3, 2, 1 .

In an image, all the input pixels are shuffled in a random manner. In the proposed algorithm, the new rows and columns of the substituted image are computed by using CLM and its population growth is a part of its key.

2.1.1. Chaotic Logistic Map

The logistic map was first introduced by Robert May [36]. The governing equation for the logistic map is:

b_{n + 1} = γ b_{n} (1 - b_{n})

(1)

where

γ

is the population growth of the logistic map. The proposed algorithm presents a unique combination of 256 numbers that are required. Therefore, through extensive testing, it is determined that the numbers from

[0, 255]

arranged in ascending order are permuted with the help of CLM. It is necessary for the population growth of the logistic map to be equal to

0.5, 1.5, 2.5, 3.5, 4.5, . . . .

. Only on these values, we can achieve a unique and random combination of

[0, 255]

numbers. Therefore, the equation is modified and can be written as:

b_{n + 1} = (γ + 0.5) b_{n} (1 - b_{n})

(2)

where

γ \in Z^{+}

is a set of positive integers in eq. 2. In this way, we permute the arrangement of rows and columns. Consider an image of Lena (

256 \times 256

). (The image and histogram are shown in the Figure 2.) Its permuted image and its histogram are shown in Figure 3. It is evident from both histograms (which are identical) that pixels are shuffled in such a manner that the permuted image is not depicting any resemblance with the original image.

2.2. Substitution

The substitution is a process in encryption, where the bits from the original message are substituted with pseudorandom bits. It is used to obscure the relationship between the pixels of input image and the corresponding pixels of the encrypted image [9]. Pixel intensities are used rather than bits to reduce computation time. Therefore, pixel intensities are substituted using enhanced version of CLM, which is explained in Section 2.1.1.

Example of this substitution is shown in Table 1 and Table 2.

The substituted pixels are shown in Table 2 with population growth at

5.5

of CLM

In comparison to Table 1 and Table 2, pixel intensity 1 is substituted to pixel intensity 245. The permuted image of Lena is shown in Figure 3, is substituted and its image and histogram are shown in Figure 4. The histogram is not similar to uniform distribution, therefore, binary bits are added in the form of one-time pad and it is explained in the latter sections.

2.3. Binary Form of the Image

The data of pixel intensities is now converted as sequence of binary bits of 8-tuple. The range of pixel intensities is from 0 to 255. The pixel intensities from Section 2.2 (each pixel intensity between 0 to 255 ) are now converted as sequence of binary bits of 8-tuple. In the latter section, it will be easier for us to add random binary bits in the pixel intensities to increase the randomness and consequently increasing the security of our proposed cryptosystem.

2.4. Bit Generation

It is a common misconception that one-time pad is breakable. It is contrary to that. If the key used in one-time pad is random and it is kept hidden from all possible hacks (attacks), then the only possible way to hack a one-time pad is only by brute force attack [37].

In this attack, all possible combinations are applied. For Example, if the key consists of 2-bits, then the possible combinations are

2^{2} = 4

. It means that for a two-bit key, hacker must enter the key four time. One of them is the actual key. In this way, brute force attack can occur. In general, if the key is

n - b i t s

long then the combinations will be

2^{n}

. C. E. Shannon [7] in his paper proves that ideal secrecy depends on the randomness of the key.

It is evident from the graph in Figure 5 that if we increase the number of bits then the number of combinations will also increase exponentially. Therefore, the hacker must have to enter more and more combinations, if the key gets longer. The pseudorandom orbit of chaotic logistic map is very high. The secret key space, a chaotic logistic map can offer is more than

2^{302}

[38]. The random binary bits are generated from the CLM.

2.5. XOR Operation

The binary of the pixel intensities and binary bits from CLM are added in the form of “XOR” operation. In the “XOR” operation same bits result in the output 0 and unlike bits give the output 1.

2.6. Conversion of Binary Bits to Encrypted Image

The resultant binary bits are then converted into pixel intensities. The acquired pixel intensities represent the encrypted image of Lena from the proposed algorithm. As an example, the substituted image of Lena shown in Figure 4 is then XORed. The encrypted image and its histogram are shown in Figure 6. The histogram is resembles uniform distribution, as shown in Figure 6.

3. Results

We perform numerous statistical tests on the proposed encryption algorithm. These statistical tests include: key space analysis, sensitivity analysis, strict avalanche criteria (SAC), histogram analysis, entropy analysis, mean of absolute deviation (MAD) analysis, correlation analysis, contrast analysis and homogeneity. The images used in the testing are taken from the University of Southern California - Signal and Image Processing Institute (USC - SIPI) database [39].

3.1. Keyspace Analysis

It is a well-known fact that a large key space is essential for an encryption algorithm to be resistant against brute force attack [40]. The proposed algorithm uses the key at four different stages. First, the key is broken into four parts. First two parts are used for permutation of the image. Its distinct combinations are

(256 \times 256)!

. The third part is used in the s-box for substitution. Its distinct combination are

256!

. The fourth part is used in obtaining the random bits from the CLM. It ranges from

[0, 1]

. Therefore, it accumulates a huge key space, resultantly increase the security of the encryption scheme.

3.2. Complexity Analysis

Complexity analysis is used to check how much memory and time is used to run a certain algorithm on a machine.

The permutation performance of the proposed algorithm is compared with some of the classical encryption algorithms as shown in Table 3. The proposed algorithm shows best performance.

3.3. Sensitivity Analysis

The initial conditions of any algorithm play a key role in its security. Therefore, the security of the algorithm is dependent over its initial conditions. For this, two common measures are used, [41,42], i.e., the number of pixels change rate (NoPCR) and unified average pixel changing intensity (UAPCI) are used.

3.3.1. Number of Pixel Change Rate (NoPCR)

It is used to check how a minute change in the input image can affect the output image. For this purpose, an input image is acquired, only one-bit change is performed in it. In image processing, one-bit change means one intensity change in pixel value. The original input image and the one-bit changed image are processed through the algorithm, two separate ciphered images are acquired. After that, the following relationship is applied to both of the images.

D (x, y) = \{\begin{matrix} 0, & if C_{x, y}^{1} = C_{x, y}^{2} \\ 1, & if C_{x, y}^{1} \neq C_{x, y}^{2} \end{matrix}

(3)

N o P C R = \frac{\sum_{x, y} D (x, y)}{B \times H} \times 100 %

(4)

where

$C^{1} =$ Cipher Image of Input Image
$C^{2} =$ Cipher Image of Input Image with one-bit change
$B =$ Breadth of the Image
$H =$ Height of the Image
x and y represents the positions of pixel in the horizontal and vertical direction respectively
In this manner, a percentage is computed to check how many pixels are change in both of the ciphered images i.e., between $C^{1}$ and $C^{2}$ . In this way, we are checking the security of our proposed algorithm. It is applied on various images, some of the results are given in Table 4.

In Table 4, it is evident that a one-bit change in the input image can result more than 99% change in the ciphered image.

3.3.2. Unified Average Pixel Changing Intensity (UAPCI)

In the previous subsection, the change in number of pixels is calculated for the entire image. In this subsection, we compute how much one pixel is changed according to its neighbouring pixel. A unified average value is computed for the whole image. First, two ciphered images are taken whose input image is changed in one-bit.

D (x, y) = \{\begin{matrix} 0, & if C_{x, y}^{1} = C_{x, y}^{2} \\ 1, & if C_{x, y}^{1} \neq C_{x, y}^{2} \end{matrix}

(5)

U A P C I = \frac{1}{B \times H} [\sum_{x, y} \frac{| C_{x, y}^{1} - C_{x, y}^{2} |}{255}] \times 100 %

(6)

where

$C^{1} =$ Cipher Image of Input Image
$C^{2} =$ Cipher Image of Input Image with one-bit change
$B =$ Breadth of the Image
$H =$ Height of the Image
x and y represents the positions of pixel in the horizontal and vertical direction respectively

In Table 5, UAPCI of various images with different image sizes along with one-bit change in input image are given. It is proved from the table that an average of 7% change is occurring from pixel to pixel if a one-bit change occurred in the input image. These two measures show us that our proposed algorithm is dependent on input image. If any hacker tries to change one-bit value in the system, it can easily be identified.

3.4. Strict Avalanche Criteria (SAC)

It is performed to check the algorithm’s dependency over its initial conditions. It is performed in such a manner that one bit in

" O "

creates more than 50% change in

" C "

. A function

g : Z_{2}^{n} \to Z_{2}^{m}

exhibits the avalanche effect if and only if

\sum_{x \in Z_{2}^{n}} w t (g (O) \oplus g (O \oplus C_{i}^{n})) = m 2^{n - 1}

(7)

\forall i \in [1, n]

where

$O =$ Original Image
$C =$ Cipher Image
$\oplus =$ Exclusive OR Operation
Eq. 7 depicts that if one input bit is changed then 50% of the output bits must change [43,44]. Therefore, strict avalanche criteria is applied on the proposed algorithm and it was found that almost 50% bits are inverted. Table 6 gives the comparison of SAC of various algorithms.

3.5. Histogram Analysis

It is performed to check whether the encrypted image represent any resemblance towards the original image or not. If the histogram of the image is equiprobable than it is hard for the attackers to know which original image was transmitted. Equal distribution gives no clue to the hackers and it increases the security of the algorithm. It is shown in Figure 7 and Figure 9 , the histogram is equally distributed. Therefore, it makes it hard for the hackers to retrieve the original message.

3.6. Entropy Analysis

Entropy gives us the measure of randomness and distortion within the gray values of the image. [46]. To achieve ideal distribution, then the entropy should be equal to 8 [47]. In this proposed algorithm, entropy of various images was found and it was close to 8. The entropy of various images are given in Table 7. In Table 8, entropy of the proposed algorithm is compared with AES [48] and one of its variation [48]. It is verified that the average entropy of the algorithm is better than AES and much closer to 8.

3.7. Mean of Absolute Deviation (MAD) Analysis

If the difference between the input image and the encrypted image is high. Then it is more difficult for the hackers and therefore, it gives us more security against them. MAD gives us the quantified value, that how much encrypted image is displaced from the input image [49,50]. MAD is determined to compute the difference between two images. MAD can be mathematically represented as:

M A D = \frac{1}{B \times H} \sum_{y = 1}^{L} \sum_{x = 1}^{L} | O_{x y} - C_{x y} |

(8)

where

$O_{x y} =$ pixels of original image at $(x, y)$ position,
$C_{x y} =$ pixels of the encrypted image at $(x, y)$ position,
$B =$ Breadth of Image
$H =$ Height of image.
MAD analysis of Various Images are performed, and the results are compiled in Table 9

3.8. Correlation Analysis

Correlation is the measure of dependency of one image on another. Every algorithm developer tries to reduce the dependency. It will be harder for any hacker to perform any kind of malicious activity. Therefore, it increases the algorithm’s security. It is computed by the following equation:

c o r r (O, C) = \frac{E ((O - μ_{o}) (C - μ_{c}))}{σ_{o} σ_{c}}

(9)

Where

$c o r r (O, C) =$ correlation between the original image and its encrypted image
$O =$ Original Image
$C =$ Cipher Image
$μ_{o} =$ mean of the original image
$μ_{c} =$ mean of the encrypted image
$E =$ Expected Value Operator
$σ_{o} =$ Standard Deviation of the original Image
$σ_{c} =$ Standard Deviation of the cipher Image
Table 10 gives the correlation between various original images and their cipher images. It’s evident from Table 10, that the correlation is less than 1%. Also in Table 11, correlation of AES and its variations are compared with our proposed algorithm. It was verified that the correlation of our proposed algorithm is less than 1%. Therefore, it shows that it will be hard for the hackers to determine the original image from the cipher image.

3.9. Contrast Analysis

It gives the user to identify the textures of two images. It allows the user to identify any resemblance of texture between two separate images [51,52]. If the texture of an original image and its encrypted has any closeness of texture between them, it computes contrast using eq.( 10). In this equation, it is clearly visible that a co-occurrence matrix is used to compute contrast value. It basically gives any kind of resemblance between any neighboring pixels of the same image. It is mathematically represented as:

C = \frac{\sum_{x, y} {| x - y |}^{2} p (x, y)}{B \times H}

(10)

Where

$p (x, y) =$ gray level co-occurrence matrix.
$B =$ Breadth of $p (x, y)$
$H =$ Height of $p (x, y)$
$x, y$ represents the location of elements within $p (x, y)$

In Table 12, it is evident that our proposed algorithm encrypt any two or more images and those encrypted images has the same contrast value. This shows that it will be harder for any hacker or intruder to comprise the security of our proposed algorithm.

3.10. Homogeneity

It measures the closeness of elements within a specified image. It tells how the neighboring elements of a pixel is related to another. This analysis is based on the distribution of any pixel with respect to its neighboring pixels. It gives the statistical distribution over the whole image.

The homogeneity can be determined using the following relation:

\sum_{x, y} \frac{p (x, y)}{1 + |x - y|}

(11)

Where

$p (x, y) =$ gray level co-occurrence matrix.
$x, y$ represents the location of elements within $p (x, y)$

In Table 3, the proposed algorithm is compared with [15,22,28] techniques, where it reduces space complexity by utilizing only two coefficients and taking minimum permutation time. Therefore, the proposed technique is time efficient and less complex as compared to the other techniques. It means, memory cost for the implementation of the proposed technique is reduced. In table 6, the SAC is compared with various established techniques, the ideal value of SAC is 50%. The proposed techniques gives 49% SAC. In table 8, the average entropy of various images is compared with AES and its variants [48]. The ideal entropy should be 8 for a 8-bit image. This means that the information of the input image is scattered evenly in encrypted image. The AES and its variants can only give entropy upto 7.96 The proposed technique gives 7.9952 entropy. It means, it is harder for the hacker to get scattered information from encrypted image. In table 11, the correlation of the proposed technique is with AES and its variants [48]. AES and its variants can provide 2% to 7% similarity between input and encrypted image. The proposed technique has reduced this similarity measure to 0.3% If we reduce the similarity measure, this proves, we are enhancing its security.

4. Conclusion

In this study, an image encryption algorithm is proposed, which is based on CLMs. The algorithm’s security is verified though various tests, which include key space analysis, complexity analysis, sensitivity analysis, strict avalanche criteria, histogram analysis, entropy analysis, mean of absolute deviation analysis, correlation analysis, contrast analysis and homogeneity. These tests have assured a high level of security in applied mathematical, cryptography and engineering applications. Researchers/practitioners can use the proposed encryption algorithm in different fields such as image encryption, data encryption, audio/video encryption etc.

Funding

This work got no funding from any source.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:

MAD	Mean of Absolute Deviation
SAC	strict avalanche criteria
NoPCR	Number of Pixel Change Rate
UAPCI	Unified Average Pixel Changing Intensity

References

Su, Z.; Zhang, G.; Jiang, J. Multimedia security: a survey of chaos-based encryption technology. Multimedia-A Multidisciplinary Approach to Complex Issues 2012.
Wu, W.; Wang, Q. Quantum image encryption based on Baker map and 2D logistic map. International Journal of Theoretical Physics 2022, 61, 64. [Google Scholar] [CrossRef]
Liu, X.; Xiao, D.; Liu, C. Three-level quantum image encryption based on Arnold transform and logistic map. Quantum Information Processing 2021, 20, 1–22. [Google Scholar] [CrossRef]
Hu, W.W.; Zhou, R.G.; Jiang, S.; Liu, X.; Luo, J. Quantum image encryption algorithm based on generalized Arnold transform and Logistic map. CCF Transactions on High Performance Computing 2020, 2, 228–253. [Google Scholar] [CrossRef]
Xu, J.; Li, P.; Yang, F.; Yan, H. High intensity image encryption scheme based on quantum logistic chaotic map and complex hyperchaotic system. IEEE Access 2019, 7, 167904–167918. [Google Scholar] [CrossRef]
Abd El-Latif, A.A.; Li, L.; Wang, N.; Han, Q.; Niu, X. A new approach to chaotic image encryption based on quantum chaotic system, exploiting color spaces. Signal Processing 2013, 93, 2986–3000. [Google Scholar] [CrossRef]
Shannon, C.E. Communication theory of secrecy systems. The Bell system technical journal 1949, 28, 656–715. [Google Scholar] [CrossRef]
Biryukov, A. Substitution–Permutation (SP) Network. In Encyclopedia of Cryptography and Security; van Tilborg, H.C.A., Jajodia, S., Eds.; Springer US: Boston, MA, 2011; p. 1268. [Google Scholar] [CrossRef]
Biyashev, R.G.; Kapalova, N.A.; Dyusenbayev, D.S.; Algazy, K.T.; Wojcik, W.; Smolarz, A. Development and analysis of symmetric encryption algorithm Qamal based on a substitution-permutation network. International Journal of Electronics and Telecommunications 2021, 67, 127–132. [Google Scholar] [CrossRef]
Ni, Z.; Kang, X.; Wang, L. A novel image encryption algorithm based on bit-level improved Arnold transform and hyper chaotic map. 2016 IEEE International Conference on Signal and Image Processing (ICSIP). IEEE, 2016, pp. 156–160.
Singh, P.; Yadav, A.; Singh, K. Phase image encryption in the fractional Hartley domain using Arnold transform and singular value decomposition. Optics and Lasers in Engineering 2017, 91, 187–195. [Google Scholar] [CrossRef]
Fu, C.; Chen, J.j.; Zou, H.; Meng, W.h.; Zhan, Y.f.; Yu, Y.w. A chaos-based digital image encryption scheme with an improved diffusion strategy. Optics express 2012, 20, 2363–2378. [Google Scholar] [CrossRef]
Zhang, Y.Q.; Wang, X.Y. Spatiotemporal chaos in mixed linear–nonlinear coupled logistic map lattice. Physica A: Statistical Mechanics and Its Applications 2014, 402, 104–118. [Google Scholar] [CrossRef]
Zhu, Z.l.; Zhang, W.; Wong, K.w.; Yu, H. A chaos-based symmetric image encryption scheme using a bit-level permutation. Information Sciences 2011, 181, 1171–1186. [Google Scholar] [CrossRef]
Hua, Z.; Zhou, Y. Image encryption using 2D Logistic-adjusted-Sine map. Information Sciences 2016, 339, 237–253. [Google Scholar] [CrossRef]
Liu, L.; Miao, S. An image encryption algorithm based on Baker map with varying parameter. Multimedia Tools and Applications 2017, 76, 16511–16527. [Google Scholar] [CrossRef]
Liu, W.; Sun, K.; Zhu, C. A fast image encryption algorithm based on chaotic map. Optics and Lasers in Engineering 2016, 84, 26–36. [Google Scholar] [CrossRef]
Chai, X.; Chen, Y.; Broyde, L. A novel chaos-based image encryption algorithm using DNA sequence operations. Optics and Lasers in engineering 2017, 88, 197–213. [Google Scholar] [CrossRef]
Wang, X.; Zhang, H.l. A novel image encryption algorithm based on genetic recombination and hyper-chaotic systems. Nonlinear Dynamics 2016, 83, 333–346. [Google Scholar] [CrossRef]
Wang, X.Y.; Zhang, Y.Q.; Bao, X.M. A novel chaotic image encryption scheme using DNA sequence operations. Optics and Lasers in Engineering 2015, 73, 53–61. [Google Scholar] [CrossRef]
Zhou, N.; Hu, Y.; Gong, L.; Li, G. Quantum image encryption scheme with iterative generalized Arnold transforms and quantum image cycle shift operations. Quantum Information Processing 2017, 16, 1–23. [Google Scholar] [CrossRef]
Wang, X.; Zhu, X.; Wu, X.; Zhang, Y. Image encryption algorithm based on multiple mixed hash functions and cyclic shift. Optics and Lasers in Engineering 2018, 107, 370–379. [Google Scholar] [CrossRef]
Kulsoom, A.; Xiao, D.; Abbas, S.A.; others. An efficient and noise resistive selective image encryption scheme for gray images based on chaotic maps and DNA complementary rules. Multimedia Tools and Applications 2016, 75, 1–23. [Google Scholar] [CrossRef]
Wang, L.; Song, H.; Liu, P. A novel hybrid color image encryption algorithm using two complex chaotic systems. Optics and Lasers in Engineering 2016, 77, 118–125. [Google Scholar] [CrossRef]
Wang, X.; Liu, C.; Xu, D.; Liu, C. Image encryption scheme using chaos and simulated annealing algorithm. Nonlinear Dynamics 2016, 84, 1417–1429. [Google Scholar] [CrossRef]
Wang, X.; Liu, C.; Zhang, H. An effective and fast image encryption algorithm based on Chaos and interweaving of ranks. Nonlinear Dynamics 2016, 84, 1595–1607. [Google Scholar] [CrossRef]
Wang, X.; Zhu, X.; Zhang, Y. An image encryption algorithm based on Josephus traversing and mixed chaotic map. IEEE Access 2018, 6, 23733–23746. [Google Scholar] [CrossRef]
Wang, X.; Feng, L.; Zhao, H. Fast image encryption algorithm based on parallel computing system. Information Sciences 2019, 486, 340–358. [Google Scholar] [CrossRef]
Jain, R.; Sharma, J. Symmetric color image encryption algorithm using fractional DRPM and chaotic baker map. 2016 IEEE International Conference on Recent Trends in Electronics, Information & Communication Technology (RTEICT). IEEE, 2016, pp. 1835–1840.
Wang, X.; Zhang, H.l. A color image encryption with heterogeneous bit-permutation and correlated chaos. Optics Communications 2015, 342, 51–60. [Google Scholar] [CrossRef]
Wu, X.; Wang, D.; Kurths, J.; Kan, H. A novel lossless color image encryption scheme using 2D DWT and 6D hyperchaotic system. Information Sciences 2016, 349, 137–153. [Google Scholar] [CrossRef]
Xu, L.; Li, Z.; Li, J.; Hua, W. A novel bit-level image encryption algorithm based on chaotic maps. Optics and Lasers in Engineering 2016, 78, 17–25. [Google Scholar] [CrossRef]
Liu, H.; Wang, X.; others. Image encryption using DNA complementary rule and chaotic maps. Applied Soft Computing 2012, 12, 1457–1466. [Google Scholar] [CrossRef]
Zhang, Y.Q.; Wang, X.Y.; Liu, J.; Chi, Z.L. An image encryption scheme based on the MLNCML system using DNA sequences. Optics and Lasers in Engineering 2016, 82, 95–103. [Google Scholar] [CrossRef]
Hussain, I.; Anees, A.; Al-Maadeed, T.A. A novel encryption algorithm using multiple semifield S-boxes based on permutation of symmetric group. Computational and Applied Mathematics 2023, 42, 80. [Google Scholar] [CrossRef]
May, R.M. Simple mathematical models with very complicated dynamics. The Theory of Chaotic Attractors 2004, 85–93. [Google Scholar]
Agrawal, V.; Agrawal, S.; Deshmukh, R. Analysis and review of encryption and decryption for secure communication. International Journal of scientific engineering and research 2014, 2, 2347–3878. [Google Scholar]
Riaz, M.; Ahmed, J.; Shah, R.A.; Hussain, A. Novel secure pseudorandom number generator based on duffing map. Wireless Personal Communications 2018, 99, 85–93. [Google Scholar] [CrossRef]
SIPI Image Database — sipi.usc.edu. http://sipi.usc.edu/database/database.php. [Accessed 19-September-2023].
Mishra, M.; Mankar, V. A Chaotic encryption algorithm: Robustness against Brute-force attack. In Advances in Computer Science, Engineering & Applications; Springer, 2012; pp. 169–179.
Kamat, V.G.; Sharma, M. Symmetric Image Encryption Algorithm Using 3D Rossler System. International Journal of Computer Science and Business Informatics 2014, 14. [Google Scholar]
Radwan, A.G.; AbdElHaleem, S.H.; Abd-El-Hafiz, S.K. Symmetric encryption algorithms using chaotic and non-chaotic generators: A review. Journal of advanced research 2016, 7, 193–208. [Google Scholar] [CrossRef]
Motara, Y.M.; Irwin, B. Sha-1 and the strict avalanche criterion. 2016 Information security for South Africa (ISSA). IEEE, 2016, pp. 35–40.
Mar, P.P.; Latt, K.M. New analysis methods on strict avalanche criterion of S-boxes. World Academy of Science, Engineering and Technology 2008, 48, 25. [Google Scholar]
Hussain, I.; Shah, T.; Gondal, M.A.; Wang, Y. Analyses of SKIPJACK S-box. World Appl. Sci. J 2011, 13, 2385–2388. [Google Scholar]
Zhen, P.; Zhao, G.; Min, L.; Jin, X. Chaos-based image encryption scheme combining DNA coding and entropy. Multimedia Tools and Applications 2016, 75, 6303–6319. [Google Scholar] [CrossRef]
Wu, Y.; Noonan, J.P.; Agaian, S. A novel information entropy based randomness test for image encryption. 2011 IEEE International Conference on Systems, Man, and Cybernetics. IEEE, 2011, pp. 2676–2680.
Zeghid, M.; Machhout, M.; Khriji, L.; Baganne, A.; Tourki, R. A modified AES based algorithm for image encryption. International Journal of Computer and Information Engineering 2007, 1, 745–750. [Google Scholar]
Högel, J.; Schmid, W.; Gaus, W. Robustness of the standard deviation and other measures of dispersion. Biometrical journal 1994, 36, 411–427. [Google Scholar] [CrossRef]
Mazumder, S.; Serfling, R. Bahadur representations for the median absolute deviation and its modifications. Statistics & probability letters 2009, 79, 1774–1783. [Google Scholar]
Pizolato Jr, J.C.; Neto, L.G. Phase-only optical encryption based on the zeroth-order phase-contrast technique. Optical Engineering 2009, 48, 098201. [Google Scholar]
Bibi, N.; Farwa, S.; Muhammad, N.; Jahngir, A.; Usman, M. A novel encryption scheme for high-contrast image data in the Fresnelet domain. PLoS One 2018, 13, e0194343. [Google Scholar] [CrossRef] [PubMed]

Figure 1. Encryption Model

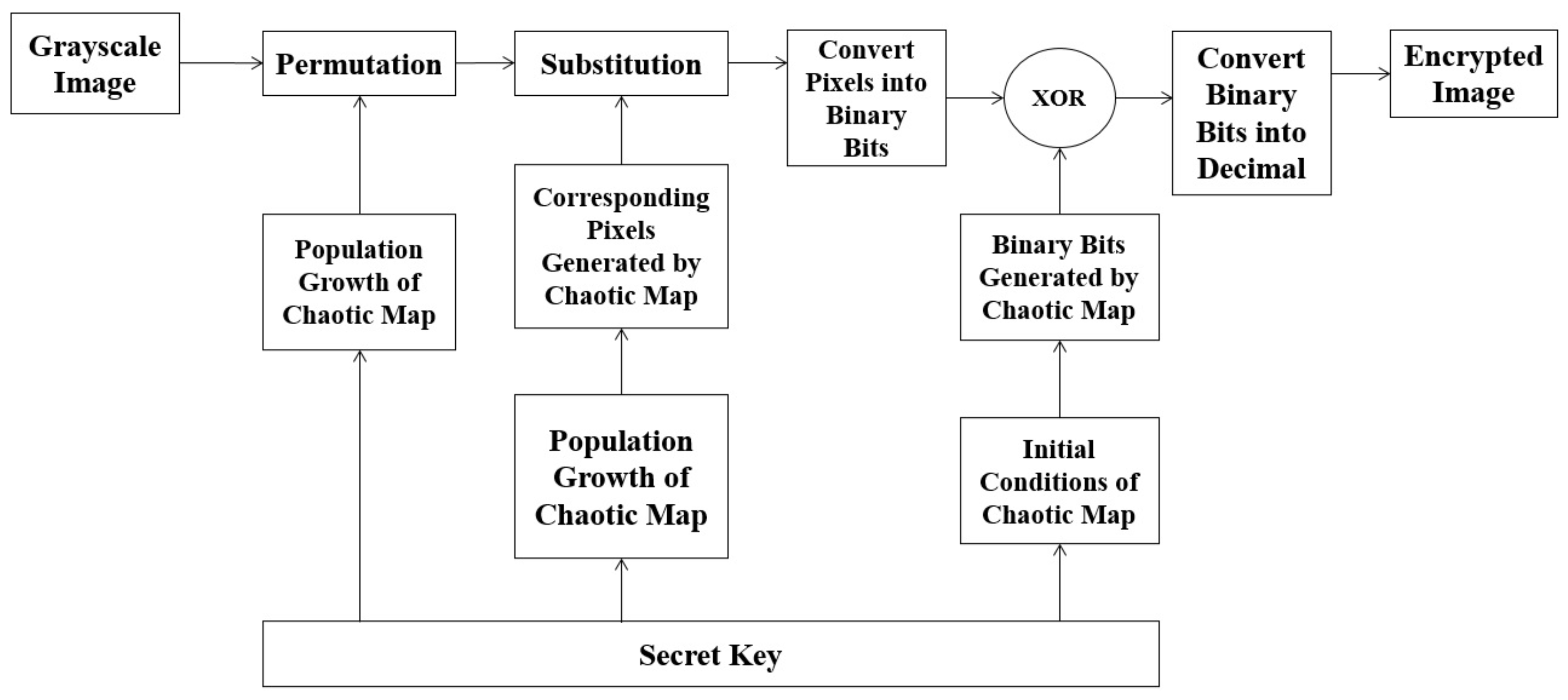
Figure 2. Lena Image and its Histogram

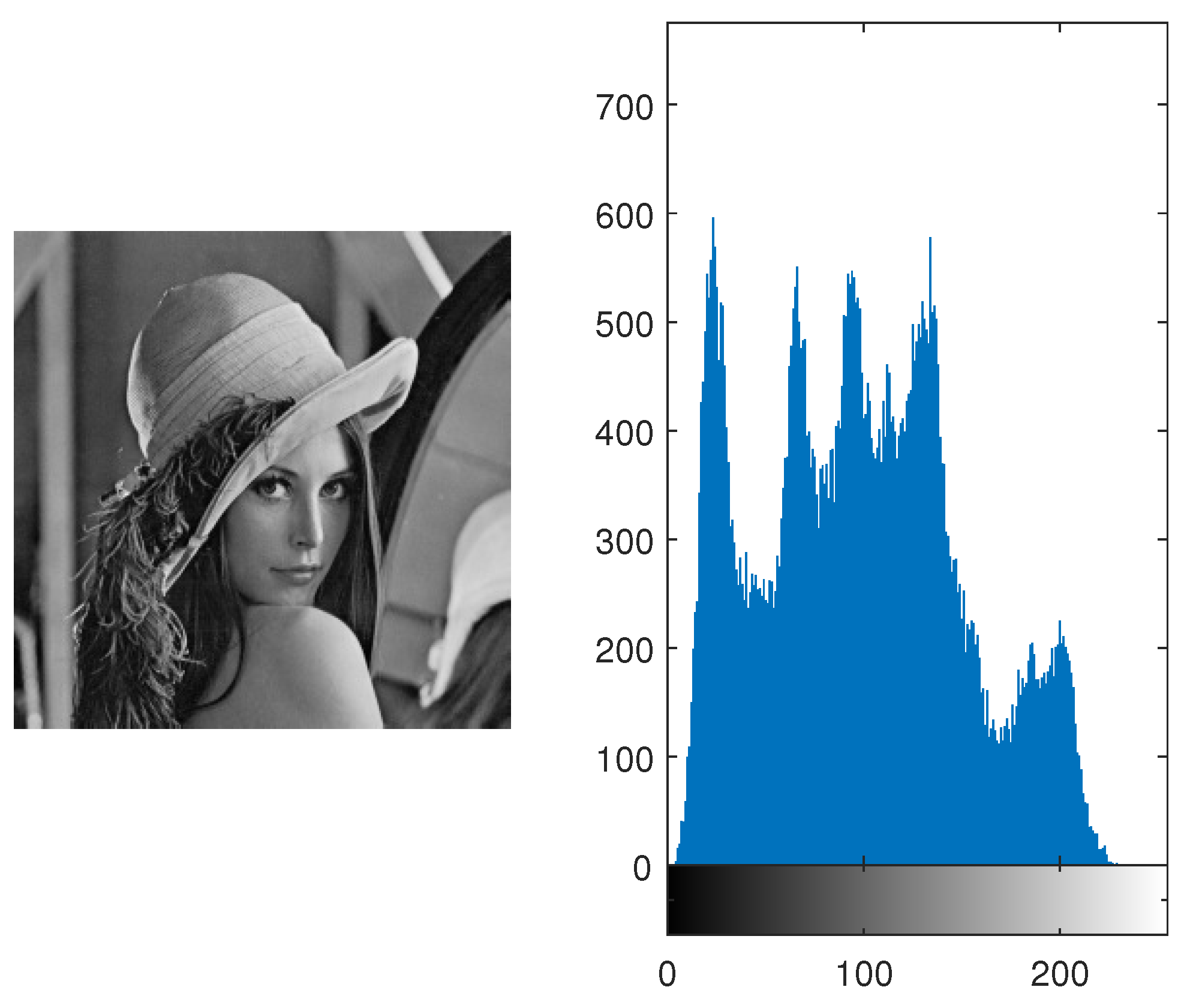
Figure 3. Permuted Image of Lena and its Histogram depicting that the substituted image do not resemble the original image

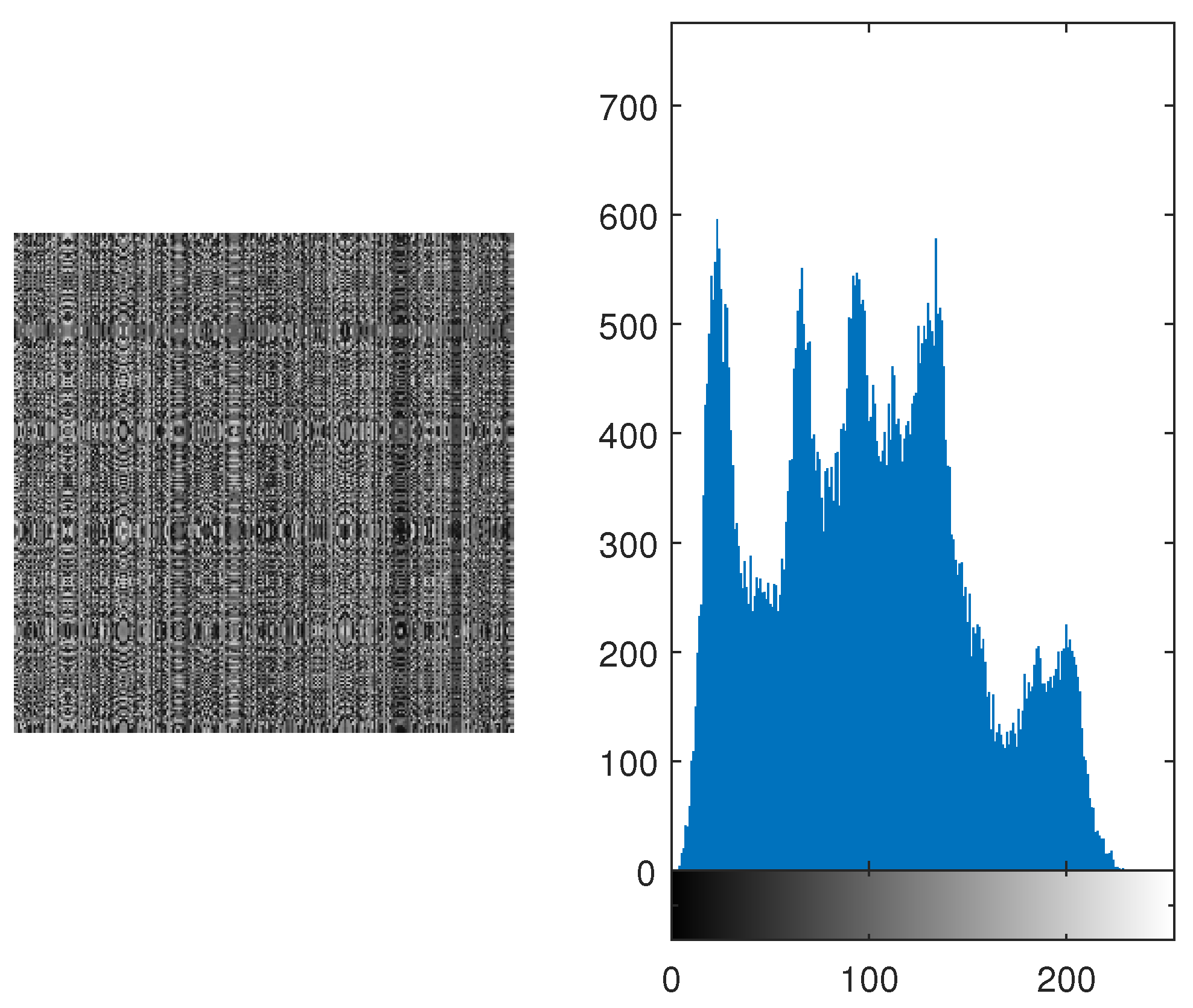
Figure 4. Substituted Image of Lena and its Histogram showing no information regarding original image

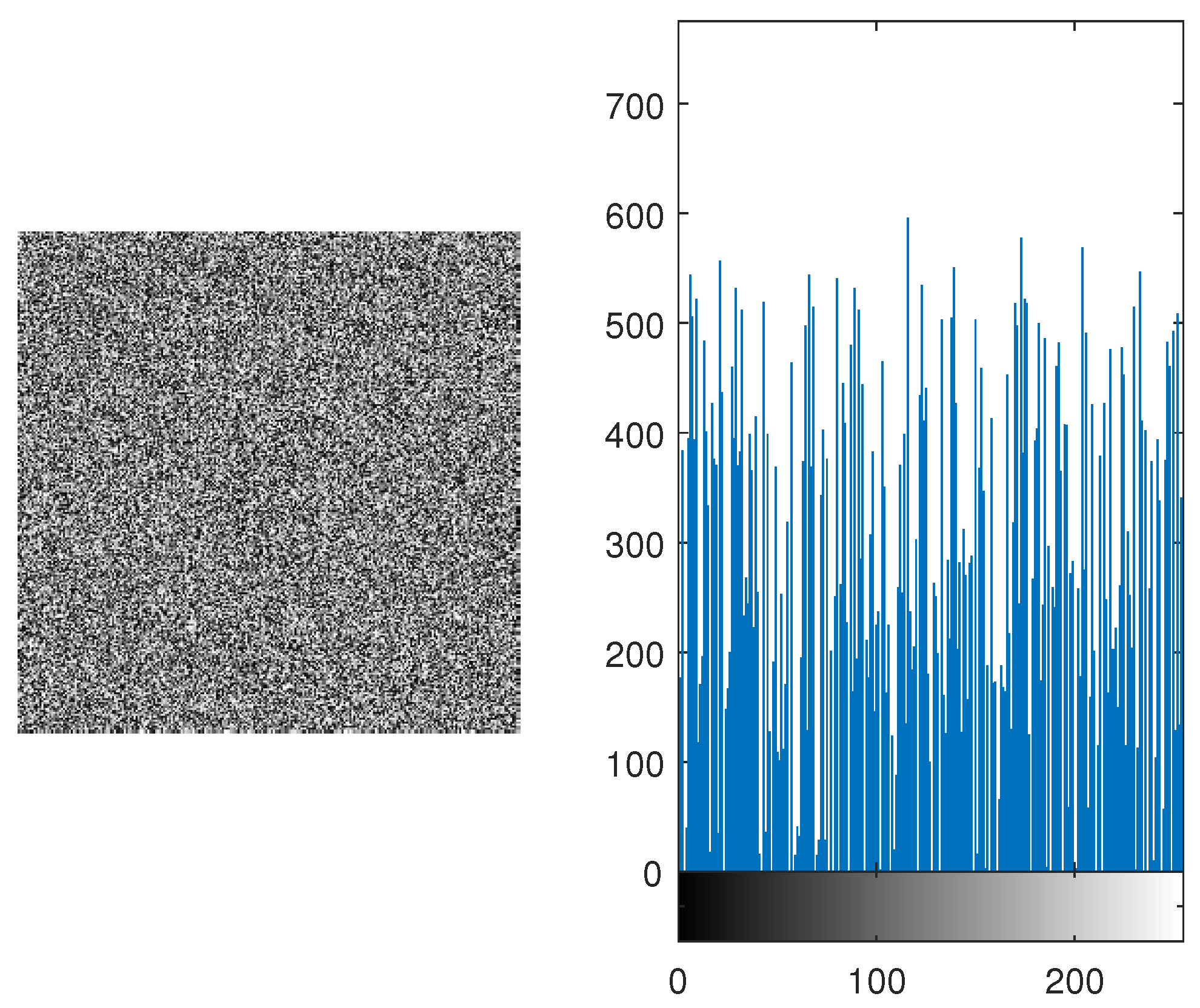
Figure 5. No . of Bits vs No. of Combinations Graph depicting exponential growth

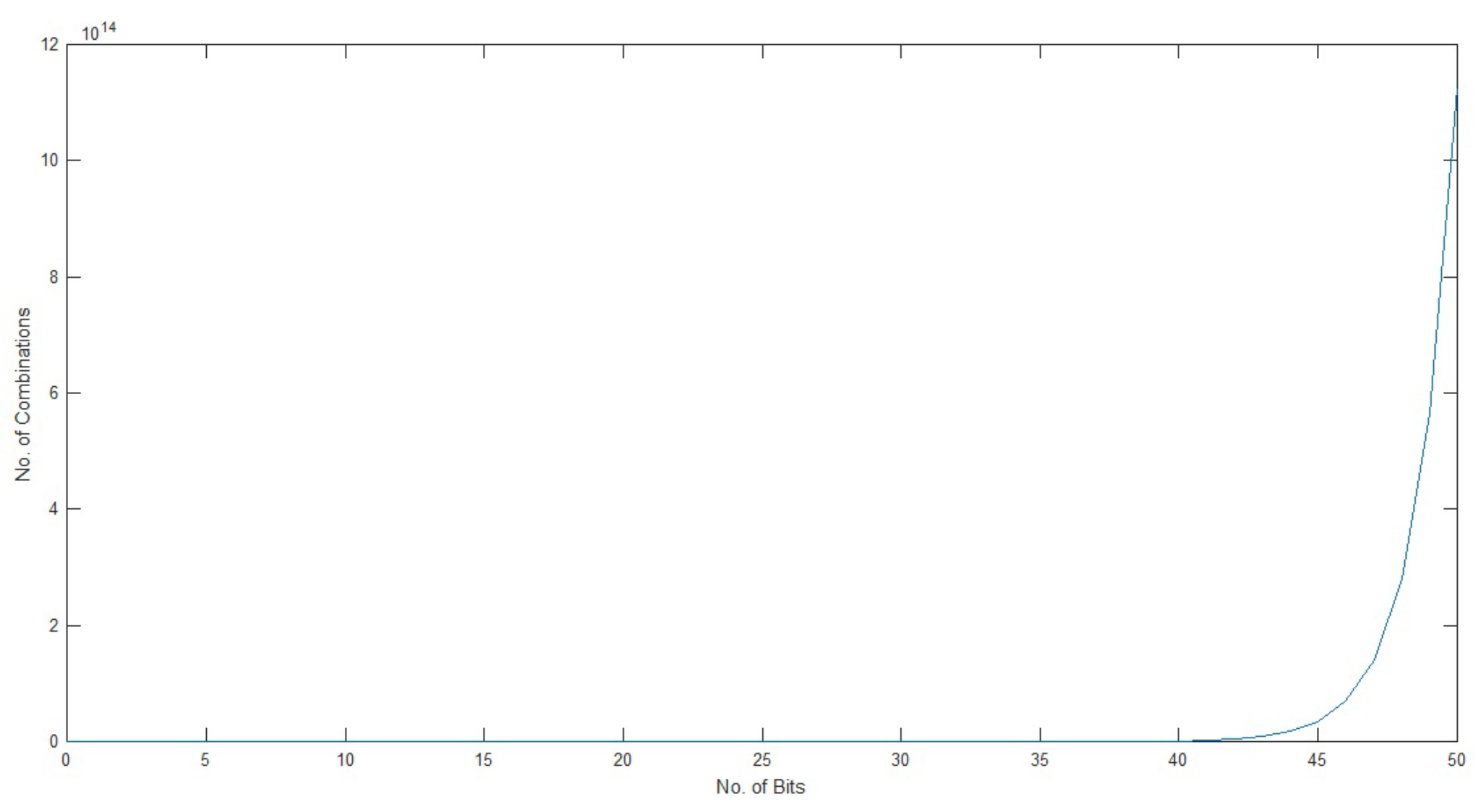
Figure 6. Encrypted Image and its Histogram

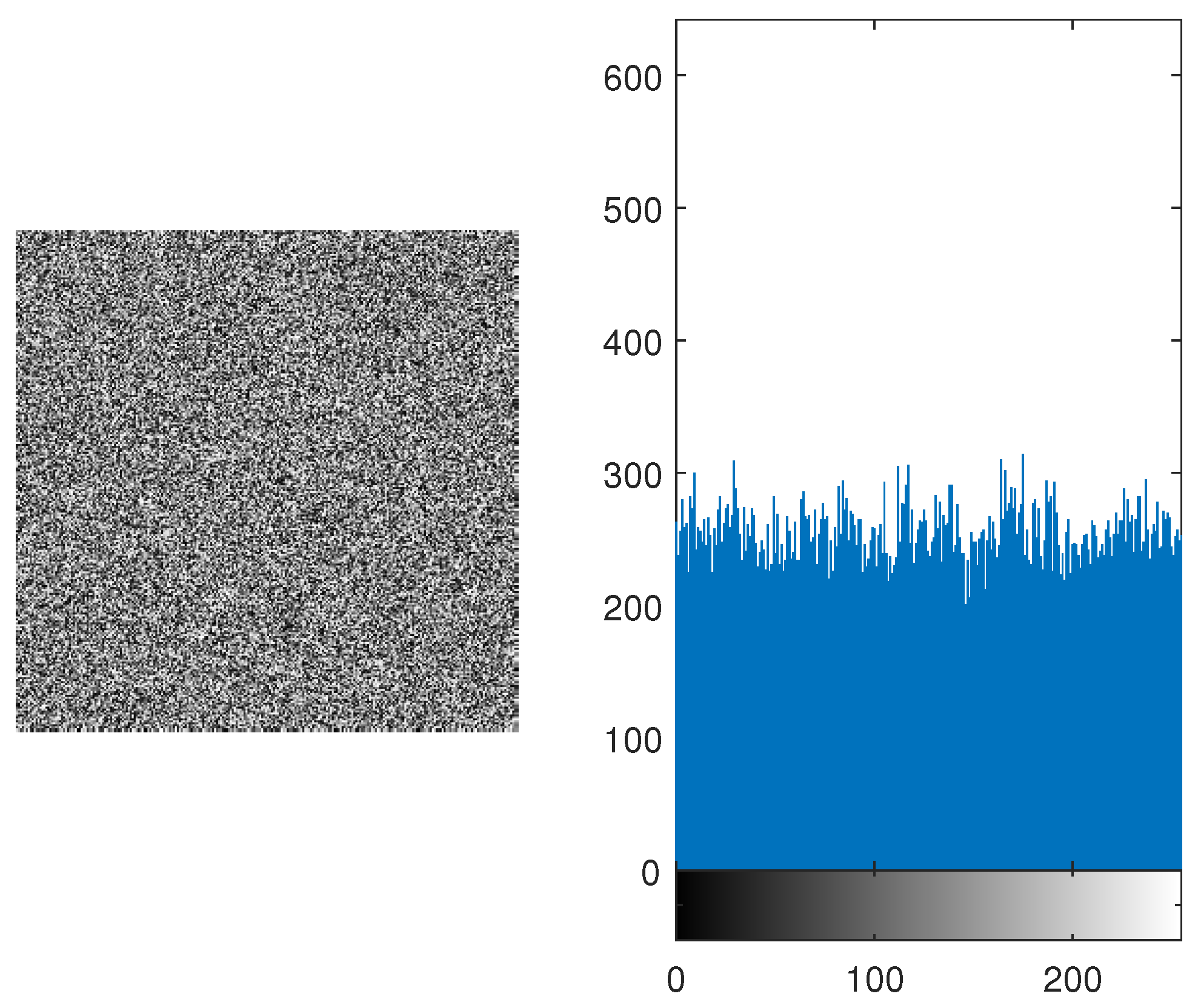
Figure 7. Encrypted Lena Image and its Histogram

Figure 8. Original Boat Image and its Histogram depicting various peaks in the pixel intensities

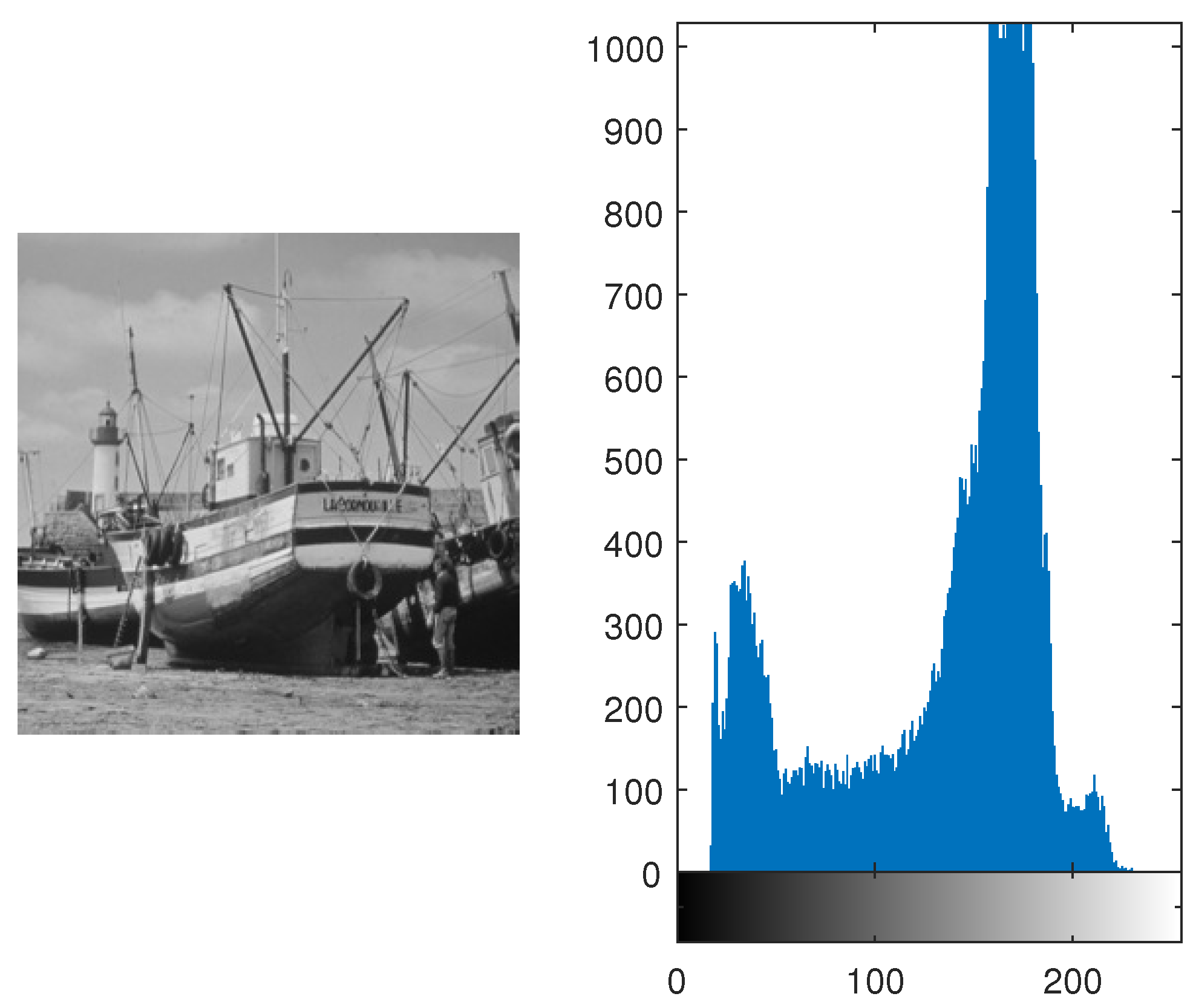
Figure 9. Encrypted Boat Image with Histogram showing that all pixels are almost uniformally distributed.

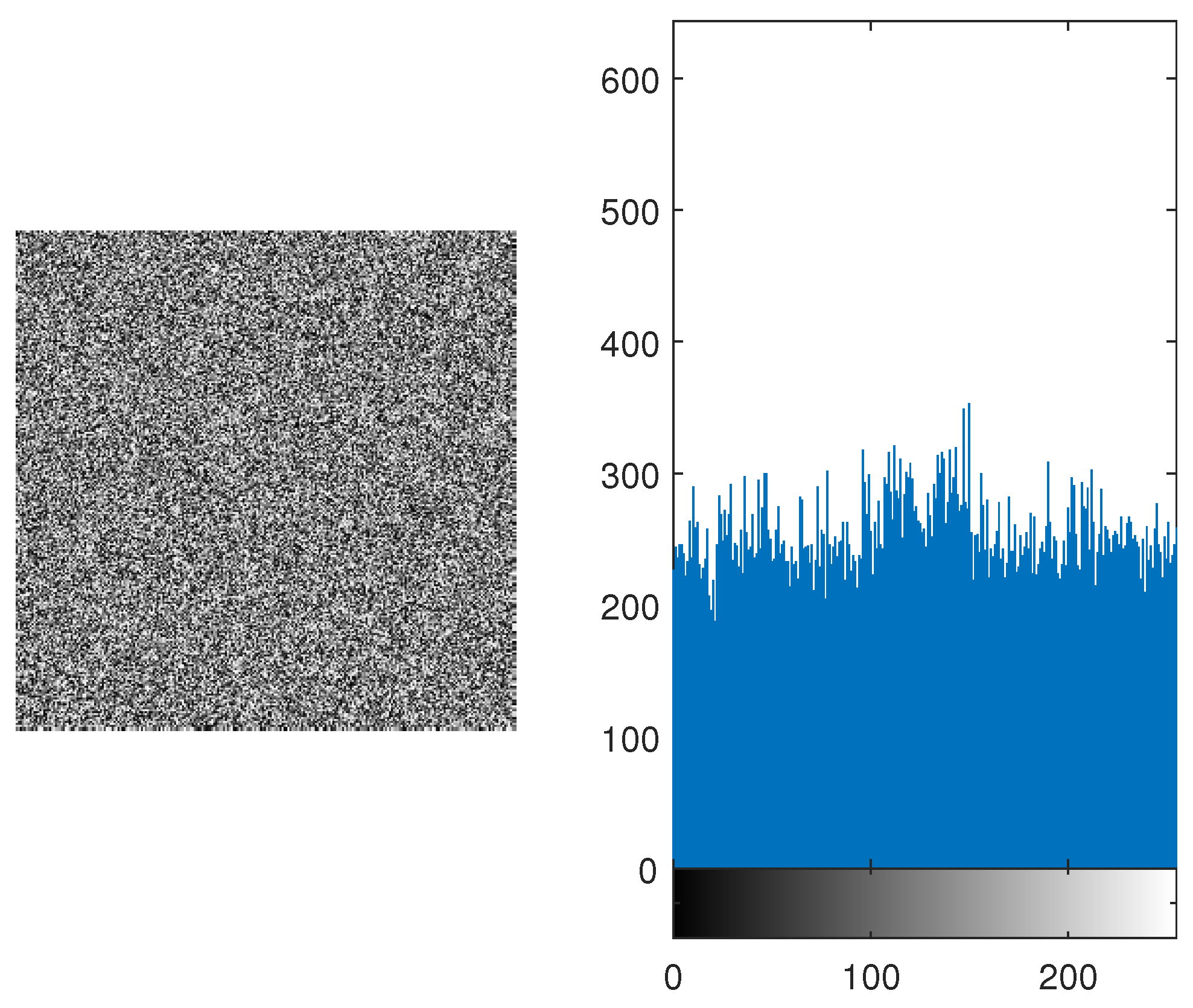
Table 1. Input Pixel Intensities for Substitution.

0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31
32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47
48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63
64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79
80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95
96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111
112	113	114	115	116	117	118	119	120	121	122	123	124	125	126	127
128	129	130	131	132	133	134	135	136	137	138	139	140	141	142	143
144	145	146	147	148	149	150	151	152	153	154	155	156	157	158	159
160	161	162	163	164	165	166	167	168	169	170	171	172	173	174	175
176	177	178	179	180	181	182	183	184	185	186	187	188	189	190	191
192	193	194	195	196	197	198	199	200	201	202	203	204	205	206	207
208	209	210	211	212	213	214	215	216	217	218	219	220	221	222	223
224	225	226	227	228	229	230	231	232	233	234	235	236	237	238	239
240	241	242	243	244	245	246	247	248	249	250	251	252	253	254	255

Table 2. Pixels arranged in random order based on CLM with population growth at

5.5

Table 2. Pixels arranged in random order based on CLM with population growth at

5.5

0	245	223	190	146	91	25	204	116	17	163	42	166	23	125	216
40	109	167	214	250	19	33	36	28	9	235	194	142	79	5	176
80	229	111	238	98	203	41	124	196	1	51	90	118	135	141	136
120	93	55	6	202	131	49	212	108	249	123	242	94	191	21	96
160	213	255	30	50	59	57	44	20	241	195	138	70	247	157	56
200	77	199	54	154	243	65	132	188	233	11	34	46	47	37	16
240	197	143	78	2	171	73	220	100	225	83	186	22	103	173	232
24	61	87	102	106	99	81	52	12	217	155	82	254	159	53	192
64	181	31	126	210	27	89	140	180	209	227	234	230	215	189	152
104	45	231	150	58	211	97	228	92	201	43	130	206	15	69	112
144	165	175	174	162	139	105	60	4	193	115	26	182	71	205	72
184	29	119	198	10	67	113	148	172	185	187	178	158	127	85	32
224	149	63	222	114	251	121	236	84	177	3	74	134	183	221	248
8	13	7	246	218	179	129	68	252	169	75	226	110	239	101	208
48	133	207	14	66	107	137	156	164	161	147	122	86	39	237	168
88	253	151	38	170	35	145	244	76	153	219	18	62	95	117	128

Table 3. Complexity Analysis of Different Permutation Algorithms with the Proposed Algorithm

Algorithms	Space Complexity	Permutation Time
		256 × 256	512 × 512	1024 × 1024
Proposed Algorithm	$O (m + n)$	1.5ms	6ms	18ms
Ref. [15]	$O (m \times n)$	20ms	80ms	330ms
Ref. [22]	$O (1)$	4ms	16ms	68ms
Ref. [28]	$O (m + n)$	2.5ms	10ms	42ms

Table 4. NoPCR

Image Name	NoPCR
Lena (256,256)	99.2282
Black Image (All zeros)	99.2282
Cameraman (256,256)	99.2282
Baboon (512,512)	99.4743
White Image (All ones)	99.2282
Peppers (512,512)	99.4742
Random Image [0 255]	99.2282
Barbara (512,512)	99.4743
Lena (512,512)	99.4804

Table 5. UAPCI

Image Name	UAPCI
Lena (256,256)	12.5527
Black Image (All zeros)	18.5472
Cameraman (256,256)	12.1591
Baboon (512,512)	7.2304
White Image (All ones)	6.5406
Peppers (512,512)	7.1747
Random Image [0 255]	12.5526
Barbara (512,512)	7.2447
Lena (512,512)	7.1499

Table 6. SAC Comparison of Various Algorithms

S - Boxes	SAC
Proposed S-box	0.491
AES [45]	0.504
APA [45]	0.5
Gray [45]	0.499
S8 AES [45]	0.504
Skipjack [45]	0.503
Xyi [45]	0.502
Prime [45]	0.516

Table 7. Entropy of Various Images

Image Name	Original Image	Cipher Image
Lena (256,256)	7.5683	7.9956
Lena (512,512)	7.4318	7.9956
Cameraman (256,256)	7.0097	7.9907
Black Image (All zeros)	0	7.6822
Barbara (512,512)	7.3925	7.9960
White Image (All ones)	0	7.6822
Peppers (512,512)	7.5700	7.9958
Random Image [0 255]	7.9951	7.9972
Baboon (512,512)	7.2288	7.9952

Table 8. Entropy of Various Algorithms

Algorithm	Entropy
Proposed Algorithm	7.9952
AES [48]	7.91
AES+A5/1 [48]	7.96

Table 9. MAD Analysis of Various Images

Image Name	MAD
Lena (256,256)	77.90740
Lena (512,512)	72.82140
Cameraman (256,256)	79.01410
Black Image (All zeros)	127.9119
Barbara (512,512)	72.60550
White Image (All ones)	127.0529
Peppers (512,512)	78.51690
Random Image [0 255]	85.23000
Baboon (512,512)	69.36040

Table 10. Correlation of Various Images

Image Name	Correlation Value
Lena (256,256)	0.0021
Black Image (All zeros)	NaN
Cameraman (256,256)	-0.0048
Baboon (512,512)	0.001
White Image (All ones)	NaN
Peppers (512,512)	-0.0027
Random Image [0 255]	-0.000542209
Barbara (512,512)	0.0016
Lena (512,512)	-0.0071

Table 11. Correlation of Various Algorithms

Algorithm	Correlation Between Various Algorithms
Proposed Algorithm	0.0028
AES [48]	0.072
AES+A5/1 [48]	0.067
AES+W7 [48]	0.025

Table 12. The Contrast of Various Images

Image Name	Original Image	Cipher Image
Lena (256,256)	235	255
Black Image (All zeros)	0	255
Baboon (512,512)	203	255
White Image (All ones)	0	255
Peppers(512,512)	228	255
Lena (512,512)	217	255
Random Image [0 255]	255	255
Barbara (512,512)	210	255
Cameraman (256,256)	246	255

Table 13. Homogeneity of Various Images

Image Name	Original Image	Cipher Image
Lena (256,256)	0.8573	0.3874
Black Image (All zeros)	0.9961	0.3828
Baboon (512,512)	0.7988	0.3872
White Image (All ones)	0.9961	0.4345
Peppers(512,512)	0.8946	0.3886
Random Image [0 255]	0.9961	0.4345
Barbara (512,512)	0.8560	0.3880
Cameraman (256,256)	0.8918	0.3907
Lena (512,512)	0.8813	0.3899

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31
32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47
48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63
64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79
80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95
96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111
112	113	114	115	116	117	118	119	120	121	122	123	124	125	126	127
128	129	130	131	132	133	134	135	136	137	138	139	140	141	142	143
144	145	146	147	148	149	150	151	152	153	154	155	156	157	158	159
160	161	162	163	164	165	166	167	168	169	170	171	172	173	174	175
176	177	178	179	180	181	182	183	184	185	186	187	188	189	190	191
192	193	194	195	196	197	198	199	200	201	202	203	204	205	206	207
208	209	210	211	212	213	214	215	216	217	218	219	220	221	222	223
224	225	226	227	228	229	230	231	232	233	234	235	236	237	238	239
240	241	242	243	244	245	246	247	248	249	250	251	252	253	254	255

0	245	223	190	146	91	25	204	116	17	163	42	166	23	125	216
40	109	167	214	250	19	33	36	28	9	235	194	142	79	5	176
80	229	111	238	98	203	41	124	196	1	51	90	118	135	141	136
120	93	55	6	202	131	49	212	108	249	123	242	94	191	21	96
160	213	255	30	50	59	57	44	20	241	195	138	70	247	157	56
200	77	199	54	154	243	65	132	188	233	11	34	46	47	37	16
240	197	143	78	2	171	73	220	100	225	83	186	22	103	173	232
24	61	87	102	106	99	81	52	12	217	155	82	254	159	53	192
64	181	31	126	210	27	89	140	180	209	227	234	230	215	189	152
104	45	231	150	58	211	97	228	92	201	43	130	206	15	69	112
144	165	175	174	162	139	105	60	4	193	115	26	182	71	205	72
184	29	119	198	10	67	113	148	172	185	187	178	158	127	85	32
224	149	63	222	114	251	121	236	84	177	3	74	134	183	221	248
8	13	7	246	218	179	129	68	252	169	75	226	110	239	101	208
48	133	207	14	66	107	137	156	164	161	147	122	86	39	237	168
88	253	151	38	170	35	145	244	76	153	219	18	62	95	117	128

0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31
32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47
48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63
64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79
80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95
96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111
112	113	114	115	116	117	118	119	120	121	122	123	124	125	126	127
128	129	130	131	132	133	134	135	136	137	138	139	140	141	142	143
144	145	146	147	148	149	150	151	152	153	154	155	156	157	158	159
160	161	162	163	164	165	166	167	168	169	170	171	172	173	174	175
176	177	178	179	180	181	182	183	184	185	186	187	188	189	190	191
192	193	194	195	196	197	198	199	200	201	202	203	204	205	206	207
208	209	210	211	212	213	214	215	216	217	218	219	220	221	222	223
224	225	226	227	228	229	230	231	232	233	234	235	236	237	238	239
240	241	242	243	244	245	246	247	248	249	250	251	252	253	254	255

0	245	223	190	146	91	25	204	116	17	163	42	166	23	125	216
40	109	167	214	250	19	33	36	28	9	235	194	142	79	5	176
80	229	111	238	98	203	41	124	196	1	51	90	118	135	141	136
120	93	55	6	202	131	49	212	108	249	123	242	94	191	21	96
160	213	255	30	50	59	57	44	20	241	195	138	70	247	157	56
200	77	199	54	154	243	65	132	188	233	11	34	46	47	37	16
240	197	143	78	2	171	73	220	100	225	83	186	22	103	173	232
24	61	87	102	106	99	81	52	12	217	155	82	254	159	53	192
64	181	31	126	210	27	89	140	180	209	227	234	230	215	189	152
104	45	231	150	58	211	97	228	92	201	43	130	206	15	69	112
144	165	175	174	162	139	105	60	4	193	115	26	182	71	205	72
184	29	119	198	10	67	113	148	172	185	187	178	158	127	85	32
224	149	63	222	114	251	121	236	84	177	3	74	134	183	221	248
8	13	7	246	218	179	129	68	252	169	75	226	110	239	101	208
48	133	207	14	66	107	137	156	164	161	147	122	86	39	237	168
88	253	151	38	170	35	145	244	76	153	219	18	62	95	117	128

Secure and Fast Image Encryption Algorithm Based on Modified Logistic Map

Abstract

1. Introduction

2. Proposed Algorithm

2.1. Permutation

2.1.1. Chaotic Logistic Map

2.2. Substitution

2.3. Binary Form of the Image

2.4. Bit Generation

2.5. XOR Operation

2.6. Conversion of Binary Bits to Encrypted Image

3. Results

3.1. Keyspace Analysis

3.2. Complexity Analysis

3.3. Sensitivity Analysis

3.3.1. Number of Pixel Change Rate (NoPCR)

3.3.2. Unified Average Pixel Changing Intensity (UAPCI)

3.4. Strict Avalanche Criteria (SAC)

3.5. Histogram Analysis

3.6. Entropy Analysis

3.7. Mean of Absolute Deviation (MAD) Analysis

3.8. Correlation Analysis

3.9. Contrast Analysis

3.10. Homogeneity

4. Conclusion

Funding

Conflicts of Interest

Abbreviations

References

MDPI Initiatives

Important Links

Subscribe

0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31
32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47
48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63
64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79
80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95
96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111
112	113	114	115	116	117	118	119	120	121	122	123	124	125	126	127
128	129	130	131	132	133	134	135	136	137	138	139	140	141	142	143
144	145	146	147	148	149	150	151	152	153	154	155	156	157	158	159
160	161	162	163	164	165	166	167	168	169	170	171	172	173	174	175
176	177	178	179	180	181	182	183	184	185	186	187	188	189	190	191
192	193	194	195	196	197	198	199	200	201	202	203	204	205	206	207
208	209	210	211	212	213	214	215	216	217	218	219	220	221	222	223
224	225	226	227	228	229	230	231	232	233	234	235	236	237	238	239
240	241	242	243	244	245	246	247	248	249	250	251	252	253	254	255

0	245	223	190	146	91	25	204	116	17	163	42	166	23	125	216
40	109	167	214	250	19	33	36	28	9	235	194	142	79	5	176
80	229	111	238	98	203	41	124	196	1	51	90	118	135	141	136
120	93	55	6	202	131	49	212	108	249	123	242	94	191	21	96
160	213	255	30	50	59	57	44	20	241	195	138	70	247	157	56
200	77	199	54	154	243	65	132	188	233	11	34	46	47	37	16
240	197	143	78	2	171	73	220	100	225	83	186	22	103	173	232
24	61	87	102	106	99	81	52	12	217	155	82	254	159	53	192
64	181	31	126	210	27	89	140	180	209	227	234	230	215	189	152
104	45	231	150	58	211	97	228	92	201	43	130	206	15	69	112
144	165	175	174	162	139	105	60	4	193	115	26	182	71	205	72
184	29	119	198	10	67	113	148	172	185	187	178	158	127	85	32
224	149	63	222	114	251	121	236	84	177	3	74	134	183	221	248
8	13	7	246	218	179	129	68	252	169	75	226	110	239	101	208
48	133	207	14	66	107	137	156	164	161	147	122	86	39	237	168
88	253	151	38	170	35	145	244	76	153	219	18	62	95	117	128