Prerpints.org logo
Preprint
Article

Effects of Heat Treatment on the Microstructure and Mechanical Properties of a Dual-Phase High-Entropy Alloy Fabricated via Selective Laser Melting

Altmetrics

Downloads

124

Views

39

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

06 February 2024

Posted:

07 February 2024

You are already at the latest version

Alerts
Abstract
To enhance the applicability of dual-phase high-entropy alloys (HEAs) like Fe32Cr33Ni29Al3Ti3, fabricated via selective laser melting (SLM), a focus on improving their mechanical properties is essential. As part of this effort, heat treatment was explored. This study compares the microstructure and mechanical properties of the as-printed sample with those cooled in water after undergoing heat treatment at temperatures ranging from 1000 to 1200 ℃ for 1 hour. Both pre- and post-treatment samples reveal a dual-phase microstructure comprising FCC and BCC phases. Although heat treatment led to a reduction in tensile and yield strength, it significantly increased ductility compared to the as-printed sample. This strength-ductility trade-off is related to changes in grain sizes with ultrafine grains enhancing strength and micron grains optimizing ductility, also the influence of the content of FCC/BCC phases and dislocation density. In particular, the sample heat-treated at 1000 °C for 1 hour and then water-cooled exhibited a better combination of strength and ductility, a yield strength of 790 MPa, and an elongation of 13%. This research offers innovative perspectives on crafting dual-phase HEA of Fe32Cr33Ni29Al3Ti3, allowing for tailorable microstructure and mechanical properties through a synergistic approach involving SLM and heat treatment.
Keywords: 
Subject: Chemistry and Materials Science  -   Metals, Alloys and Metallurgy

1. Introduction

The heightened interest in high-entropy alloys (HEAs) arises from their remarkable characteristics, making them well-suited for a diverse range of applications. [1,2]. Conventional methods for producing HEAs present various limitations, including the need for molds or postprocessing and restricted capabilities for intricate geometries [3,4]. Additive manufacturing (AM) provides a solution by directly constructing parts layer-by-layer. This enables the fabrication of sizable components with complex shapes and internal characteristics. [5,6]. In the realm of HEAs, different AM processes are being explored to meet modern industrial demands for intricate geometries. Particularly, SLM technology distinguishes itself among these additive manufacturing methods because of its precision and rapid cooling rate [7,8]. However, the as-printed samples often exhibit a significant amount of residual stress, which is detrimental to ductility. Therefore, post-heat treatment is commonly employed to alleviate the residual stress in as-printed samples and enhance ductility [8].
Zhu et al. [9] fabricated CoCrFeNiMn samples with a single FCC phase via SLM and heat-treated them at 900 °C for 1 hour in an Argon atmosphere, followed by furnace cooling. After heat treatment, although the yield strength decreases, the ductility increases. Fu et al. [10] also found this phenomenon when the as-printed CoCrFeNiMn samples were heat-treated at 900 °C for 1 hour and cooled in water. The microstructure, residual stress, and mechanical properties of the as-printed single FCC phase FeCoCrNi specimen and specimens heat-treated at 500 – 1300 °C for 2 hours were compared by Lin et al. [11]. With the elevation of the heat-treating temperature, the structural transformation of the specimen occurred, transitioning from an arrangement of all columnar grains to equiaxial grains characterized by numerous heat-treating twins. Simultaneously, the dislocation network, initially formed during the solidification process under significant shrinkage strain, underwent decomposition into dislocations. This led to a reduction in residual stress, yield strength, and hardness, accompanied by an increase in ductility and impact toughness.
In the research of as-printed dual-phase HEAs, Yang et al. [12] fabricated a dual-phase Ni30Co30Cr10Fe10Al18W1Mo1 HEA via SLM, and the samples were heat-treated at 900 °C for 2 hours followed by air cooling to alleviate the residual stress. An elongation exceeded 15% of the heat-treated samples was achieved from that of less than 1% of the as-printed samples. Vogiatzief et al. [13] heat-treated the as-printed Al0.9Cr0.9Fe2.1Ni2.1 HEA with dual-phase at 950 °C for 6 h in a furnace under an argon atmosphere, and furnace cooling was applied. After heat treatment, the elongation was improved to 20%, higher than that of the as-printed sample, which was about 15%. Zhang et al. [14] conducted an investigation into alterations in both microstructures and mechanical properties of AlCoCuFeNi HEA, which was fabricated via SLM followed by heat treatment at temperatures of 900 °C and 1000 °C for 10 hours. Results show that heat treatment decreased the microhardness and compressive yield strength, but increased the ductility significantly as compared to the as-printed sample. In particular, the sample heat-treated at 1000 °C exhibited a better compressive fracture strength of 1600 MPa, a yield strength of 744 MPa, and a strain of 13.1%. However, these studies did no systematic research on heat treatment of as-printed dual-phase HEAs because too less temperatures were chosen, and the heat treatment efficiency was not taken into consideration.
In this study, we selected an as-printed dual-phase Fe32Cr33Ni29Al3Ti3 HEA as a representative specimen to investigate the impact of various heat-treated temperatures on its mechanical properties. The as-printed dual-phase Fe32Cr33Ni29Al3Ti3 HEA fabricated in our preliminary work has a high yield strength exceeding 880 MPa, but a low elongation of less than 6% [15]. Thus, a post-heat treatment is necessary for as-printed samples to widen their applications. The heat-treated temperatures were set as 1000 °C, 1100 °C, or 1200 °C according to the research of Zhang et al. [14], and the heat-treated time was set as 1 hour to save time, and water cooling was chosen as the cooling method after heat treatment to prevent residues [16]. Air cooling was also tried on the as-printed samples at 900 °C for 1 hour. However, the elongation was even lower than that of the as-printed samples (seen in Supplementary Material Figure S1). Thus, water cooling was tried.

2. Material and methods

2.1. Samples preparation

Cube samples with dimensions of 10×10×10 mm and dog-bone-shaped samples featuring a gauge length of 25 mm, width of 5 mm, and thickness of 10 mm were fabricated using a laser power of 240 W, a scanning speed of 1000 mm/s, an interlayer scanning angle of 67°, a hatch spacing of 60 μm, and a layer thickness of 30 μm. Detailed information on the powder and SLM strategy can be found in the previous research [15]. All the as-printed samples were cut to a thickness of 2 mm by wire EDM for the subsequent heat treatment and tensile tests.
A furnace (SX2-5-12, LICHEN, Shanghai, China) was used for the post-heat treatment. The equipment has a heating power of 5 kW, the average heating rate is about 10 °C/min under 500 °C, and at a higher temperature above 500 °C, the heating rate will be lower due to the faster heat dissipation at the elevated temperatures. A set of heat-treated parameters was tried for experimental optimization, as shown in Table 1. All the samples were water-cooled after being kept at their corresponding temperature for one hour. The heat-treated samples were abbreviated as 1000W-1, 1100W-1, and 1200W-1, respectively, according to their heat-treated parameters.

2.2. Phase and microstructural characterization

The phase and microstructures on the X–Y plane of both as-printed and heat-treated samples were assessed through XRD (X-ray diffraction), SEM (scanning electron microscope), and EBSD (electron backscatter diffraction) techniques (detailed information of these test equipment and the test details can be found in the previous research [15]). The X-Y plane was chosen for characterization according to the research of Fu et al. [17] in which they characterized the X-Y plane of the as-printed and annealed CoCrFeMnNi HEA samples.
Initially, the samples underwent grinding with silicon carbide paper ranging from 400 to 1500 grit, then polishing using 0.05 μm alumina polishing fluid. In SEM analysis, electrolytic etching in a 5% HCL solution for approximately 1 minute was employed. EBSD analysis involved meticulous polishing for about 7 hours, employing an oxide suspension with 50 nm silica particles to effectively remove the deformation layer resulting from mechanical grinding. Subsequently, the sample surfaces underwent a thorough water rinse to eliminate the nano-silica particles. The step size for EBSD measurements was set at 0.06 μm for the as-printed sample and 0.18 μm for the 1000W-1, 1100W-1, and 1200W-1 samples, considering variations in grain size. High-angle grain boundaries (HAGBs) were defined as those with a grain boundary angle higher than 15°, while low-angle grain boundaries (LAGBs) had a grain boundary angle lower than 15°. The Aztec Crystal software was utilized for the analysis of the EBSD results.

2.3. Tensile test

Tensile tests were conducted on the dog-bone-shaped as-printed and heat-treated samples as the previous research did [15]. The dimensions of the dog-bone-shaped samples adhered to the specifications outlined in the ASTM standard E1820 [18].

3. Results

3.1. Phase and microstructure analysis

The XRD analysis of both the as-printed and heat-treated samples is depicted in Figure 1 (a) to verify the phase composition of FCC and BCC dual phases. A closer look at the magnified region in 2θ, ranging from 73.5° to 75.5° (Figure 1 (b)), clearly reveals that the 2θ angles of heat-treated samples are lower than those of the original as-printed sample, with the trend indicating that the higher the heat-treated temperature, the lower the 2θ angles.
Figure 2 illustrates SEM images of the X-Y plane for both the as-printed HEA and the heat-treated samples. In Figure 2 (a), the microstructure of the as-printed sample reveals the BCC phase enveloped by the FCC phase. Figure 2 (b) shows that the BCC particles of the 1000W-1 sample are larger than those in the as-printed sample. In Figure 2 (c) of the 1100W-1 sample, some of the BCC particles distribute at the FCC grain boundary and the other BCC particles distribute within the FCC grain. Figure 2 (d) shows that the BCC particles of the 1200W-1 sample are noticeably larger than those of other samples.
Additional examination of grain characteristics was performed through EBSD on the X-Y plane for both the as-printed and heat-treated samples, as shown in Figure 3. In Figure 3 (a), the inverse pole figure (IPF) map with grain boundaries of the as-printed HEA is presented, revealing numerous refined equiaxed grains. Figure 3 (b) shows that the grain size of the 1000W-1 sample is quite similar to that of the as-printed sample. In Figure 3 (c) and Figure 3 (d), the grains of 1100W-1 and 1200W-1 samples grow a lot when compared with those of as-printed or 1000W-1 samples, especially the 1200W-1 samples. The FCC phases of the as-printed sample show a more obvious orientation between <001> and <101>, while the heat-treated samples show a more obvious orientation of <101>. The BCC phases of the as-printed sample show a more obvious orientation <111>. In contrast, the BCC phases of the 1000W-1 and 1100W-1 samples show a more obvious orientation of <001>, and the BCC phases of the 1200W-1 sample show an orientation more similar to those of the as-printed sample than other samples.
Figure 4 depicts the phase distribution with grain boundaries of these samples. The BCC phases of the as-printed sample show a random distribution, as shown in Figure 4 (a). In Figure 4 (b), some of the BCC phases distribute along the HAGBs of FCC phases and the other BCC phases show a random distribution among the FCC phases. This phenomenon is more severe in Figure 4 (c) and (d) of the 1100W-1 and 1200W-1 samples. In Figure 4 (c) and (d), the average sizes of BCC phases of 1100W-1 or 1200W-1 samples are much larger than those in the 1000W-1 sample. Most of the BCC phases are distributed along the HAGBs and only a few small BCC phases are distributed within the FCC grains. In Figure 4 (b), (c), and (d), a lot of LAGBs are seen among the FCC grains.
Detailed information on the average phase sizes and their content and the content of HAGBs is shown in Table 2. μ B C C , μ H A G B s are the content of BCC phases and HAGBs, respectively. d F C C , d B C C are the average grain size of FCC and BCC phases, respectively. The content of BCC phases becomes less with the heat-treated temperature increases. Especially for the sample of 1200W-1, the content of BCC phases is only 13.4%, less than half of the as-printed sample. The average grain size of FCC phases first shows a little increase when comparing the 1000W-1 sample with the as-printed sample and then shows a drastic increase in the samples of 1100W-1 and 1200W-1. Especially for the sample of 1100W-1, the average grain size of FCC phases is 4.33 μm, which is more than 3.0 times larger than that of the 1000W-1 sample. The average size of the BCC size shows a stable increase after heat-treating at 1000 °C or 1100 °C for 1 hour and then cooled in water, but a drastic increase when heat-treated at 1200 °C for 1 hour and then cooled in water. The average grain size of the BCC phases in the 1200W-1 sample is 2.32 μm, which is about 1.8 times larger than the 1100W-1 sample and 4.1 times larger than that of the as-printed sample. The content of HAGBs suffers a drastic decrease from the as-printed sample to the 1000W-1 sample and a further decrease with the heat-treated temperature increased to 1100 °C. The 1200W-1 has a similar content of HAGBs as compared to the sample of 1100W-1.

3.2. Mechanical properties

Tensile tests were carried out at room temperature on as-printed and cooled HEA samples. The outcomes are illustrated in Figure 5, and comprehensive tensile test results for the HEA samples are provided in Table 3. The as-printed sample shows a high yield strength of 913 MPa and a high tensile strength of 1239 MPa. However, the elongation is quite low, about 4.0%. After heat-treating at 1000 °C for 1 hour and then water-cooled, the yield strength decreased to 790 MPa (about a 13.5% decrease from the as-printed sample) and the tensile strength decreased to 1115 MPa. However, the elongation increased to 13.0% (about 3.0 times higher than the as-printed sample). At a higher temperature heat-treated at 1100 °C for 1 hour, the yield strength decreased by 37.5% from the as-printed sample to about 571 MPa, and the elongation increased to 20.0%. Further higher temperature heat-treating at 1200 °C, the yield strength decreased to 430 MPa, and the elongation increased to 24.5%.
The fracture surface morphology is shown in Figure 6. Figure 6 (a) shows a brittle fracture of the as-printed sample with a polyhedron rocky shape. In Figure 6 (b), small dimples are seen on the fracture of the 1000W-1 sample, indicating a ductile fracture. In Figure 6 (c), large dimples are seen on the fracture of the 1100W-1 sample. Figure 6 (d) shows the fracture of the 1200W-1 sample, the dimples are the largest among all these samples. The heat-treated samples all show a ductile fracture, however, the as-printed sample shows a brittle fracture.

4. Discussions

4.1. Microstructure evolution

Figure 1 (b) clearly shows that the 2θ angles of heat-treated samples become lower than that of the as-printed sample, which proves that the lattice distortion inside the sample was alleviated during the heat-treating process. The as-printed sample underwent a rapid solidification during the SLM process layer by layer, the residual stress was very large inside the sample. Thus, the lattice distortion was serious inside the sample [12]. However, after being heated to a high temperature and kept for a long time, the dislocation network, originating from the solidification process subjected to substantial shrinkage strain, underwent decomposition into individual dislocations, and the lattice distortion inside the sample was alleviated [11].
The content of HAGBs suffers a drastic decrease from the as-printed sample to the heat-treated samples. This observation aligns well with the findings obtained from XRD analysis. HAGBs often have higher energy than LAGBs. A higher content of HAGBs means a severe lattice distortion [19,20]. A further decrease in the content of HAGBs happens when the heat-treating temperature increases to 1100 °C, which means a higher heat-treating temperature of 1100 °C is helpful to release the residual stress [11]. The 1200W-1 has a similar content of HAGBs as compared to the sample of 1100W-1, which means the residual stress has almost been released over a temperature of 1100 °C, so the content of HAGBs changes little. The heat-treating method has been used to alleviate the residual stress of as-printed samples in many reports [11,12].
The BCC phases get larger after heat treatment as shown in Figure 4 and Table 2. This is because when a material is heated to such high temperatures, the atoms within the grains diffuse and rearrange themselves to minimize their energy. This can result in the coalescence of smaller grains into larger ones, which would make the BCC phases appear larger. Ostwald [21] found the Ostwald ripening phenomenon, which shows smaller grains dissolve, and their material reprecipitates on the surface of larger grains. This can lead to the growth of larger BCC grains and a corresponding reduction in the number of smaller ones. The average grain size of BCC phases shows a stable increase after heat-treated at 1000 °C or 1100 °C for 1 hour and then cooled in water, but a drastic increase when heat-treated at 1200 °C for 1 hour and then cooled in water, which means that a higher heat-treated temperature is good for the growth of the BCC grain size.
The size of the FCC phase of the 1000W-1 sample is similar to that of the as-printed sample, as shown in Figure 4 and Table 2. The BCC phases with a small average size of 0.82 μm which are distributed along the FCC grain boundaries can pin grain boundaries. Thus, inhibiting the growth of FCC phases during heat treatment. However, after heat-treating at 1100 °C for 1 hour, the FCC phases become more than 3.0 times larger than those of the 1000W-1 sample. The BCC phases of the the1100W-1 sample have a large average size of 1.29 μm and the number of the BCC phases has decreased a lot when compared with as-printed or 1000W-1 samples, the pinning effect is weakened and the FCC phases of the 1100W-1 sample grow up to an average size of 4.33 μm. After heat-treating at a higher heat-treating temperature of 1200°C, the FCC phases grow up to 5.8 μm. Oikawa et al. [22] found the pinning effects of second-phase particles with an average size of 0.28 μm influencing the grain growth of ferrite in a Fe-0.1C alloy enriched with 5 ppm of boron (B). Li et al. [23] introduced a phase field model to explore how particle pinning influences the migration of grain boundaries in materials with stored energy variations along the grain boundaries. The outcomes indicated that reducing particle size and increasing particle area fraction could amplify the pinning effect.
The content of FCC phases increases and the content of BCC phases decreases with the increase in heat-treating temperature. At a certain temperature, the BCC phase will convert to the FCC phase, and the heat during heat treatment makes this happen. Panda et al. [24] heat-treated AlCoCrFeNi (prepared by arc melting, BCC + B2 structure) in the temperature range starting from 1073 K to 1373 K up to 10 hours. Results showed that the formation of the FCC phase was up to 30% ~ 35%. Indicating a long time at a high-temperature range will lead to the BCC phase transforming to the FCC phase.
During heat treatment, nucleation and growth of new phases can occur. HAGBs of the FCC phases provide sites for nucleation of the BCC phases because they often have higher energy. The large BCC phases may have nucleated along these boundaries due to favorable thermodynamic conditions and then grown as heat treatment continued. Zhang et al. [25] suggested a thermomechanical treatment method capable of adjusting the lamellar structure of duplex stainless steel to form an equiaxed matrix of austenite and ferrite. Their observations revealed a preference for alpha-martensite nucleation at the large-angle grain boundaries (HAGBs) between austenite grains. The small BCC phases that remained among the FCC phases represent that the phase transformation was less severe in these regions because these regions consist of LAGBs with lower energy than HAGBs.

4.2. Strengthening mechanism

The tailorable mechanical properties of Fe32Cr33Ni29Al3Ti3 fabricated via SLM before and after heat treatment can be explained by the following:
(1) The tailorable mechanical strength of Fe32Cr33Ni29Al3Ti3 fabricated via SLM before and after heat treatment is attributed to the tailorable grain size and the influence of dislocation density.
To investigate this trend, the primary mechanisms contributing to strengthening were examined as a combination of dislocation hardening and grain refinement [26]. This was succinctly expressed in the following equation:
Δ σ Y S = σ 0 + Δ σ g b + Δ σ d i s l
where σ Y S represents the yield strength of these samples, and Δ σ g b and Δ σ d i s l denote the strengthening contributions from grain boundaries and dislocations, respectively.
The lattice frictional strength of the present alloy, denoted as σ 0 , can be regarded as 267 MPa, according to (CoCrNi)94Al3Ti3 HEA reported by Zhao et al. [27]. The Δ σ g b can be regarded as [15]:
Δ σ g b = σ g b − σ 0 = σ 0 + K × d − 1 2 − σ 0 = K × d − 1 2 = μ F C C × k FCC × d FCC − 1 2 + μ B C C × k BCC × d BCC − 1 2
where d represents the average grain size, and K is a grain boundary strengthening coefficient. μ F C C is the content of FCC phase of each sample; μ B C C is the content of BCC phase of each sample, k FCC , k BCC are the strengthening coefficient of the FCC-FCC interface and the FCC-BCC interface, respectively; the coefficient k FCC and k BCC were considered as 275 MPa∙μm1/2 and 574 MPa∙μm1/2, respectively [28]. The value of kBCC is higher than k FCC because the BCC phase displays greater resistance to dislocations compared to the FCC phase [29]. d FCC and d BCC represent the average grain sizes of the FCC and BCC phases in each sample, respectively. The data in Table 2 was brough into Equation (2), and Δ σ g b is calculated to be 396 MPa, 332 MPa, 205 MPa, and 149 MPa for as-printed, 1000W-1, 1100W-1 and 1200W-1 samples, respectively.
In SLM-processed materials, the high dislocation density often plays a crucial role in achieving high strength levels [30]. The dislocation hardening effect can be described by the Taylor equation, which is expressed as follows [31,32]:
Δ σ d i s l = M α G b ρ 1 / 2 = μ F C C M F C C α F C C G F C C b F C C ρ F C C 1 / 2 + μ B C C M B C C α B C C G B C C b B C C ρ B C C 1 / 2
where M is the Taylor factor (3.09 and 2.71 for FCC and BCC materials, respectively), α is a constant (0.20 and 0.24 for FCC and BCC materials, respectively), G is the shear modulus (81 and 57 GPa for FCC and BCC materials, respectively), b is the Burgers vector (0.254 and 0.248 nm for FCC and BCC materials, respectively), and ρ is the dislocation density. The values of M , α , G , b were achieved from the research of Ren et al [32]. The dislocation density was calculated using the Williamson-Hall method based on XRD pattern (Figure 1) [33,34]. The measured values of ρ were shown in Table 4. These data were brought into Equation (3), Δ σ d i s l could be estimated to be 179 MPa, 133 MPa, 132 MPa and 125 MPa for as-printed, 1000W-1, 1100W-1 and 1200W-1 samples, respectively, as shown in Table 4.
Upon substituting each strengthening contribution into Equation (1), the predicted yield strengths are approximately 842 MPa, 732 MPa, 604 MPa, and 541 MPa for the as-printed, 1000W-1, 1100W-1, and 1200W-1 samples, respectively. These values demonstrate a satisfactory agreement with our experimental data, as depicted in Figure 7. The main cause of error between predicted yield strength and actual yield strength is that K (grain boundary strengthening coefficient) may differ in these samples. Huang et al. [35] found that the Hall-Petch slopes ( K values) slightly increased with offset strain. In this study, the strain shows a decrement with the increase of heat-treating temperature as the dislocation density becomes lower and lower. The value of K was supposed to be getting smaller and smaller with the increase of heat-treating temperature. But in calculation by Equation (2), it was set as the same. So actual yield strength was higher than the predicted yield strength in as-printed and 1000W-1 samples, and lower than the predicted yield strength in 1100W-1 and 1200W-1 samples.
(2) The tailorable ductility of Fe32Cr33Ni29Al3Ti3 fabricated via SLM before and after heat treatment is attributed to the tailorable grain size.
The average grain sizes of as-printed, 1000W-1, 1100W-1, and 1200W-1 samples are 0.69, 1.00, 1.94 and 3.70 μm, respectively. The grains of the as-printed sample are ultra-fine grains, with an average grain size of less than 1 μm. And the grains of other samples are micron grains. The relationship between elongation and the average grain sizes is shown in Figure 8.
The relationship between elongation and the average grain size fits well with the influence of grain size on elongation studied by other researchers [36,37]. The elongation increases with the average grain size increases. The samples with micron grains have an elongation higher than 10%. The as-printed sample shows a sharp decrease in elongation from the 1000W-1 sample because of its ultra-fine grains. When the grain size is less than 1.00 μm, the elongation decreases sharply [36].
The content of FCC and BCC phases is another factor that influenced the elongation of these samples. The higher content of the FCC phase is good for the ductility of a dual-phase sample [14]. As the heat-treating temperature increases, the content of the FCC phase also increases, contributing positively to ductility.

5. Conclusions

This study investigated different heat treatment parameters for the mechanical performance optimization of a HEA devoid of cobalt, characterized by a composition comprising Fe32Cr33Ni29Al3Ti3 fabricated via selective laser melting (SLM). Heat treatment decreased the yield strength, but increased the ductility significantly when compared with the as-printed sample. The as-printed sample with ultra-fine grains, higher content of BCC phases, and higher dislocation density showed higher strength and lower elongation. While, heat-treated samples with micron grains, lower content of BCC phases, and lower dislocation density showed lower strength and higher elongation. In particular, the sample heat-treated at 1000 °C for 1 hour and water-cooled exhibited a better combination of yield strength and ductility, a yield strength of 790 MPa, and an elongation of 13%. This study may have particular value in the post-heat treatment of dual-phase HEAs fabricated via SLM.

Acknowledgments

This work was financially supported by, the Natural Science Foundation of Guangdong Province (Grant No. 2023A1515011641), Key field research projects in Foshan City (Grant No. 2120001009232), Shenzhen Science and Technology Program (Grant No. GJHZ20220913143012022), the School-level scientific research project of Shenzhen Institute of Technology (Grant No. 2211017), Guangdong HUST Industrial Technology Research Institute, Guangdong Provincial Key Laboratory of Manufacturing Equipment Digitization (Grant No. 2020B1212060014), the Postdoctoral Science Foundation of China (Grant No. 2022M710503), the Natural Science Foundation Commission of Chongqing (Grant No. CSTB2022NSCQ-BHX0029), Guangdong Basic and Applied Basic Research (Grant No. 2019A1515110360).

Conflicts of Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

  1. Miracle, D.B.; Senkov, O.N. A critical review of high entropy alloys and related concepts. Acta Materia 2017, 122, 448–511. [Google Scholar] [CrossRef]
  2. Li, Z.; Pradeep, K.G.; Deng, Y.; Raabe, D.; Tasan, C.C. Metastable high-entropy dual-phase alloys overcome the strength–ductility trade-off. Nature 2016, 534, 227–230. [Google Scholar] [CrossRef] [PubMed]
  3. Huang, X.L.; Huang, L.P.; Peng, H.L.; Liu, Y.; Liu, B.; Li, S. Enhancing strength-ductility synergy in a casting non-equiatomic NiCoCr-based high-entropy alloy by Al and Ti combination addition. Scr. Mater. 2021, 203, 114046. [Google Scholar] [CrossRef]
  4. Xie, Y.; Liang, J.; Zhang, D.; Luo, Y.; Zhang, Z.; Liu, Y.; Wang, J. Sustaining strength–ductility synergy of CoCrFeNiMn high entropy alloy by a multilevel heterogeneity associated with nanoparticles. Scr. Mater. 2020, 187, 390–394. [Google Scholar] [CrossRef]
  5. Han, C.; Fang, Q.; Shi, Y.; Tor, S.B.; Chua, C.K.; Zhou, K. Recent Advances on High-Entropy Alloys for 3D Printing. Adv. Mater. 2020, 32, e1903855. [Google Scholar] [CrossRef] [PubMed]
  6. Li, R.; Niu, P.; Yuan, T.; Cao, P.; Chen, C.; Zhou, K. Selective laser melting of an equiatomic CoCrFeMnNi high-entropy alloy: Processability, non-equilibrium microstructure and mechanical property. J. Alloy. Compd. 2018, 746, 125–134. [Google Scholar] [CrossRef]
  7. Brif, Y.; Thomas, M.; Todd, I. The use of high-entropy alloys in additive manufacturing. Scr. Mater. 2015, 99, 93–96. [Google Scholar] [CrossRef]
  8. Moghaddam, A.O.; Shaburova, N.A.; Samodurova, M.N.; Abdollahzadeh, A.; Trofimov, E.A. Additive manufacturing of high entropy alloys: A practical review. J. Mater. Sci. Technol. 2020, 77, 131–162. [Google Scholar] [CrossRef]
  9. Zhu, Z.; Nguyen, Q.; Ng, F.; An, X.; Liao, X.; Liaw, P.; Nai, S.; Wei, J. Hierarchical microstructure and strengthening mechanisms of a CoCrFeNiMn high entropy alloy additively manufactured by selective laser melting. Scr. Mater. 2018, 154, 20–24. [Google Scholar] [CrossRef]
  10. Fu, Z.; Yang, B.; Gan, K.; Yan, D.; Li, Z.; Gou, G.; Chen, H.; Wang, Z. Improving the hydrogen embrittlement resistance of a selective laser melted high-entropy alloy via modifying the cellular structures. Corros. Sci. 2021, 190, 109695. [Google Scholar] [CrossRef]
  11. Lin, D.; Xu, L.; Jing, H.; Han, Y.; Zhao, L.; Minami, F. Effects of annealing on the structure and mechanical properties of FeCoCrNi high-entropy alloy fabricated via selective laser melting. Addit. Manuf. 2020, 32, 101058. [Google Scholar] [CrossRef]
  12. Yang, F.; Wang, L.; Wang, Z.; Wu, Q.; Zhou, K.; Lin, X.; Huang, W. Ultra strong and ductile eutectic high entropy alloy fabricated by selective laser melting. J. Mater. Sci. Technol. 2022, 106, 128–132. [Google Scholar] [CrossRef]
  13. Vogiatzief, D.; Evirgen, A.; Pedersen, M.; Hecht, U. Laser powder bed fusion of an Al-Cr-Fe-Ni high-entropy alloy produced by blending of pre-alloyed and elemental powder: Process parameters, microstructures, and mechanical properties. J. Alloys Compd 2022, 918, 165658. [Google Scholar]
  14. Zhang, M.; Zhou, X.; Wang, D.; Zhu, W.; Li, J.; Zhao, Y.F. AlCoCuFeNi high-entropy alloy with tailored microstructure and outstanding compressive properties fabricated via selective laser melting with heat treatment. MAT SCI ENG A-STRUCT 2019, 743, 773–784. [Google Scholar] [CrossRef]
  15. Tan, X.; Chen, D.; Xu, J.; Chen, H.; Peng, X.; Guo, L.; Xiao, H.; Zhang, Q. High strength Fe32Cr33Ni29Al3Ti3 manufactured by selective laser melting. J MATER RES TECHNOL 2023, 27, 3701–3711. [Google Scholar] [CrossRef]
  16. Miller, M.; Burke, M. An APFIM/AEM characterization of alloy X750. Appl. Surf. Sci. 1993, 67, 292–298. [Google Scholar] [CrossRef]
  17. Fu, Z.; Yang, B.; Gan, K.; Yan, D.; Li, Z.; Gou, G.; Chen, H.; Wang, Z. Improving the hydrogen embrittlement resistance of a selective laser melted high-entropy alloy via modifying the cellular structures. Corros. Sci. 2021, 190, 109695. [Google Scholar] [CrossRef]
  18. E08 Committee, E1820-11E2 Standard Test Methods for Measurement of Fracture Toughness, ASTM International, USA, 2011.
  19. Wang, L.; Kong, D.; Zhang, Y.; Xiao, L.; Lu, Y.; Chen, Z.; Zhang, Z.; Zou, J.; Zhu, T.; Han, X. Mechanically Driven Grain Boundary Formation in Nickel Nanowires. ACS Nano 2017, 11, 12500–12508. [Google Scholar] [CrossRef]
  20. Li, N.; Jia, C.-L.; Wang, Z.-W.; Wu, L.-H.; Ni, D.-R.; Li, Z.-K.; Fu, H.-M.; Xue, P.; Xiao, B.-L.; Ma, Z.-Y.; et al. Achieving a High-Strength CoCrFeNiCu High-Entropy Alloy with an Ultrafine-Grained Structure via Friction Stir Processing. Acta Met. Sin. (English Lett. 2020, 33, 947–956. [Google Scholar] [CrossRef]
  21. Dong, Y.; Zhang, D.; Li, D.; Jia, H.; Qin, W. Control of Ostwald ripening. Sci. China Mater. 2022, 66, 1249–1255. [Google Scholar] [CrossRef]
  22. Oikawa, T.; Enomoto, M. Pinning Effects on Grain Growth of Ferrite in an Fe-C-B Alloy. TETSU TO HAGANE-JOURNAL OF THE IRON AND STEEL INSTITUTE OF JAPAN 2011, 97, 584–591. [Google Scholar] [CrossRef]
  23. Li, K.; Shen, Y.; Li, D.Y.; Peng, Y.H. Phase Field Study of Second Phase Particles-Pinning on Strain Induced Grain Boundary Migration. Mater. Sci. Forum 2020, 993, 967–975. [Google Scholar] [CrossRef]
  24. Panda, J.P.; Arya, P.; Guruvidyathri, K.; Ravikirana; Murty, B. S. Studies on Kinetics of BCC to FCC Phase Transformation in AlCoCrFeNi Equiatomic High Entropy Alloy. Met. Mater. Trans. A 2021, 52, 1679–1688. [Google Scholar] [CrossRef]
  25. Zhang, X.; Mu, W.; Li, J. Microstructure evolution of TRIP-assisted lean duplex stainless steel 2101 during in-situ tensile test after a thermomechanical treatment. Mater. Sci. Eng. A 2022, 143037, 20. [Google Scholar] [CrossRef]
  26. Zhou, R.; Liu, Y.; Liu, B.; Li, J.; Fang, Q. Precipitation behavior of selective laser melted FeCoCrNiC0.05 high entropy alloy. Intermetallics 2018, 106, 20–25. [Google Scholar] [CrossRef]
  27. Zhao, Y.L.; Yang, T.; Tong, Y.; Wang, J.; Luan, J.H.; Jiao, Z.B.; Chen, D.; Yang, Y.; Hu, A.; Liu, C.T.; Kai, J.J. Heterogeneous precipitation behavior and stacking-fault-mediated deformation in a CoCrNi-based medium-entropy alloy. Acta Mater 2017, 138, 72–82. [Google Scholar] [CrossRef]
  28. Guo, Y.; Li, M.; Li, P.; Chen, C.; Zhan, Q.; Chang, Y.; Zhang, Y. Microstructure and mechanical properties of oxide dispersion strengthened FeCoNi concentrated solid solution alloys. J. Alloy. Compd. 2019, 820, 153104. [Google Scholar] [CrossRef]
  29. Mohanty, S.; Kothari, A.; Raghavan, R.; Sahu, V.K.; Gurao, N.P.; Sahu, K.K.; Dhindaw, B.K.; Zeng, L.; Xia, M.; Gollapudi, S. Microstructure and Mechanical Properties of High-Carbon-Containing Fe-Ni-Mn-Al-Cr High-Entropy Alloy: Effect of Thermomechanical Treatment. Front. Mater. 2022, 9, 915278. [Google Scholar] [CrossRef]
  30. Wang, Y.M.; Voisin, T.; Mckeown, T.; et al. Additively tailorable hierarchical stainless steels with high strength and ductility. Nat Mater 2018, 17, 63–70. [Google Scholar] [CrossRef]
  31. Yim, D.; Sathiyamoorthi, P.; Hong, S.J.; et al. Fabrication and mechanical properties of TiC reinforced CoCr-FeMnNi high-entropy alloy composite by water atomization and spark plasma sintering. J Alloys Compd 2019, 781, 389–396. [Google Scholar] [CrossRef]
  32. Ren, J.; Zhang, Y.; Zhao, D.; Chen, Y.; Guan, S.; Liu, Y.; Liu, L.; Peng, S.; Kong, F.; Poplawsky, J.D.; et al. Strong yet ductile nanolamellar high-entropy alloys by additive manufacturing. Nature 2022, 608, 62–68. [Google Scholar] [CrossRef] [PubMed]
  33. Williamson, G.K.; Smallman, R.E., III. Dislocation densities in some annealed and cold-worked metals from measurements on the X-ray debye-scherrer spectrum. Philos. Mag. 1956, 1, 34–46. [Google Scholar] [CrossRef]
  34. Williamson, G.K.; Hall, W.H. X-ray line broadening from filed aluminium and wolfram. Acta Metallurgica 1953, 1, 22–31. [Google Scholar] [CrossRef]
  35. Huang, T.; Shuai, L.; Wakeel, A.; Wu, G.; Hansen, N.; Huang, X. Strengthening mechanisms and Hall-Petch stress of ultrafine grained Al-0.3%Cu. Acta Mater. 2018, 156, 369–378. [Google Scholar] [CrossRef]
  36. Liu, H.; Shen, Y.; Ma, J.; Zheng, P.; Zhang, L. Grain Size Dependence of Uniform Elongation in Single-Phase FCC/BCC Metals. J. Mater. Eng. Perform. 2016, 25, 3599–3605. [Google Scholar] [CrossRef]
  37. Furui, M.; Iishiro, A.; Saji, S. Effect of grain size on the elongation for 3004 aluminum alloy. J. Jpn. Inst. Light Met. 2001, 51, 409–413. [Google Scholar] [CrossRef]
Preprints 98326 g001
Figure 1. (a) XRD patterns; (b) partial XRD patterns of the as-printed and heat-treated HEA samples with different heat-treated parameters.
Figure 1. (a) XRD patterns; (b) partial XRD patterns of the as-printed and heat-treated HEA samples with different heat-treated parameters.
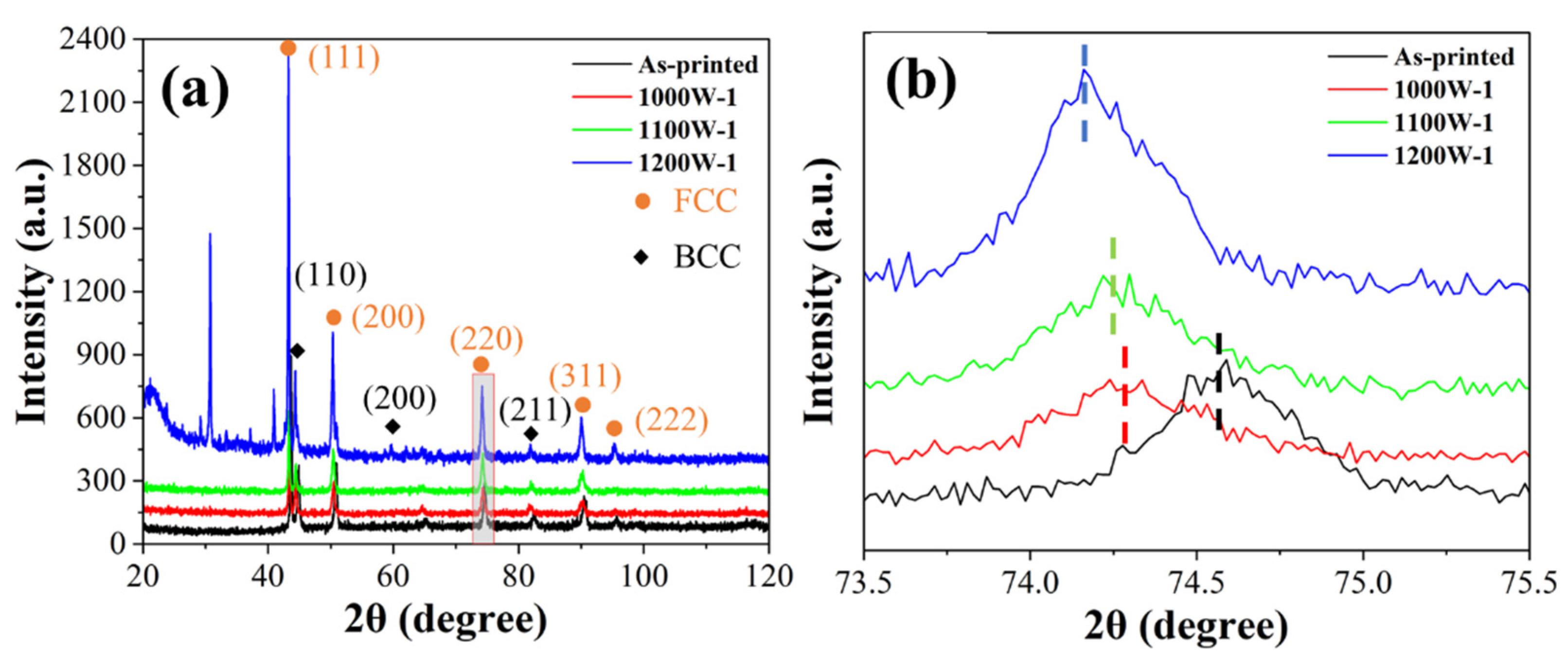
Preprints 98326 g001
Preprints 98326 g002
Figure 2. SEM microstructures of the X-Y plane of the as-printed HEA (a) and heat-treated samples: 1000W-1 (b); 1100W-1 (c); 1200W-1 (d).
Figure 2. SEM microstructures of the X-Y plane of the as-printed HEA (a) and heat-treated samples: 1000W-1 (b); 1100W-1 (c); 1200W-1 (d).
Preprints 98326 g002
Preprints 98326 g003
Figure 3. IPF map with grain boundary of the as-printed HEA (a) and heat-treated samples: 1000W-1 (b); 1100W-1 (c); 1200W-1 (d).
Figure 3. IPF map with grain boundary of the as-printed HEA (a) and heat-treated samples: 1000W-1 (b); 1100W-1 (c); 1200W-1 (d).
Preprints 98326 g003
Preprints 98326 g004
Figure 4. Phase distribution of the as-printed HEA (a) and heat-treated samples: 1000W-1 (b), 1100W-1 (c), 1200W-1 (d).
Figure 4. Phase distribution of the as-printed HEA (a) and heat-treated samples: 1000W-1 (b), 1100W-1 (c), 1200W-1 (d).
Preprints 98326 g004
Preprints 98326 g005
Figure 5. Tensile stress-strain curves at room temperature of as-printed and heat-treated HEA samples with different parameters.
Figure 5. Tensile stress-strain curves at room temperature of as-printed and heat-treated HEA samples with different parameters.
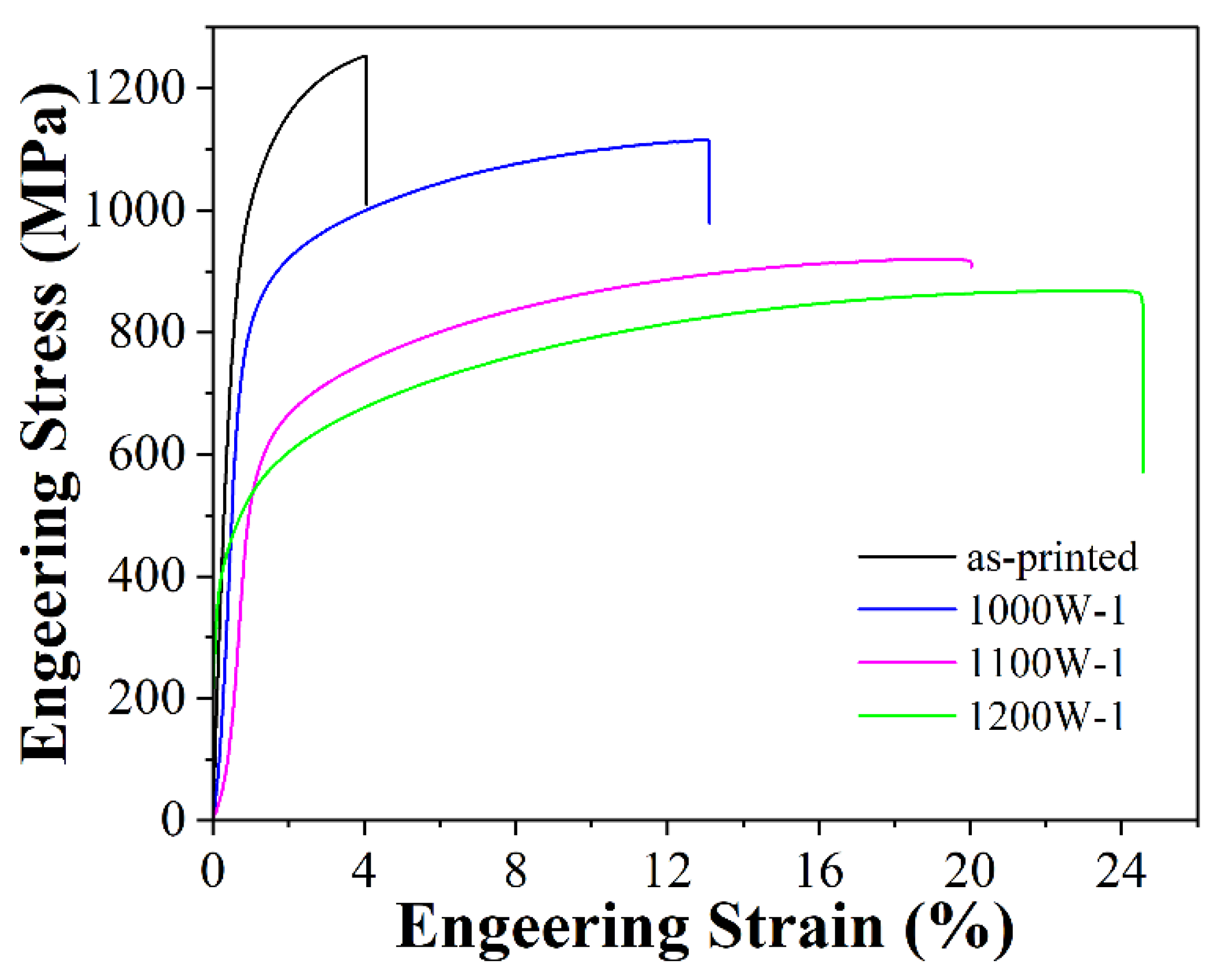
Preprints 98326 g005
Preprints 98326 g006
Figure 6. Fracture morphology of the as-printed HEA (a) and heat-treated samples: 1000W-1 (b), 1100W-1 (c), 1200W-1 (d).
Figure 6. Fracture morphology of the as-printed HEA (a) and heat-treated samples: 1000W-1 (b), 1100W-1 (c), 1200W-1 (d).
Preprints 98326 g006
Preprints 98326 g007
Figure 7. Strength contributions from different strengthening mechanisms of as-printed; 1000W-1; 1100W-1; and 1200W-1 samples.
Figure 7. Strength contributions from different strengthening mechanisms of as-printed; 1000W-1; 1100W-1; and 1200W-1 samples.
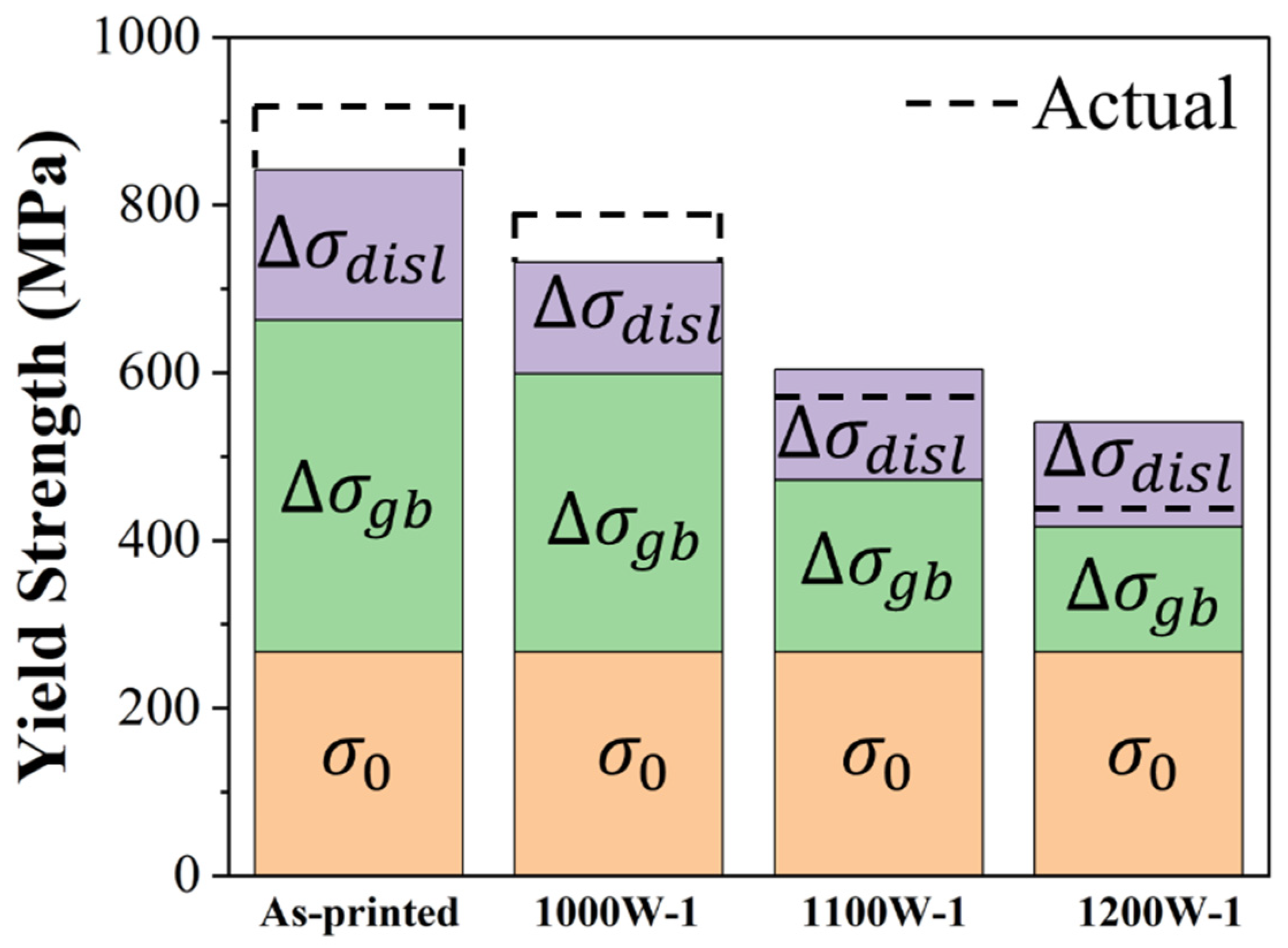
Preprints 98326 g007
Preprints 98326 g008
Figure 8. The relationship between elongation and grain sizes.
Figure 8. The relationship between elongation and grain sizes.
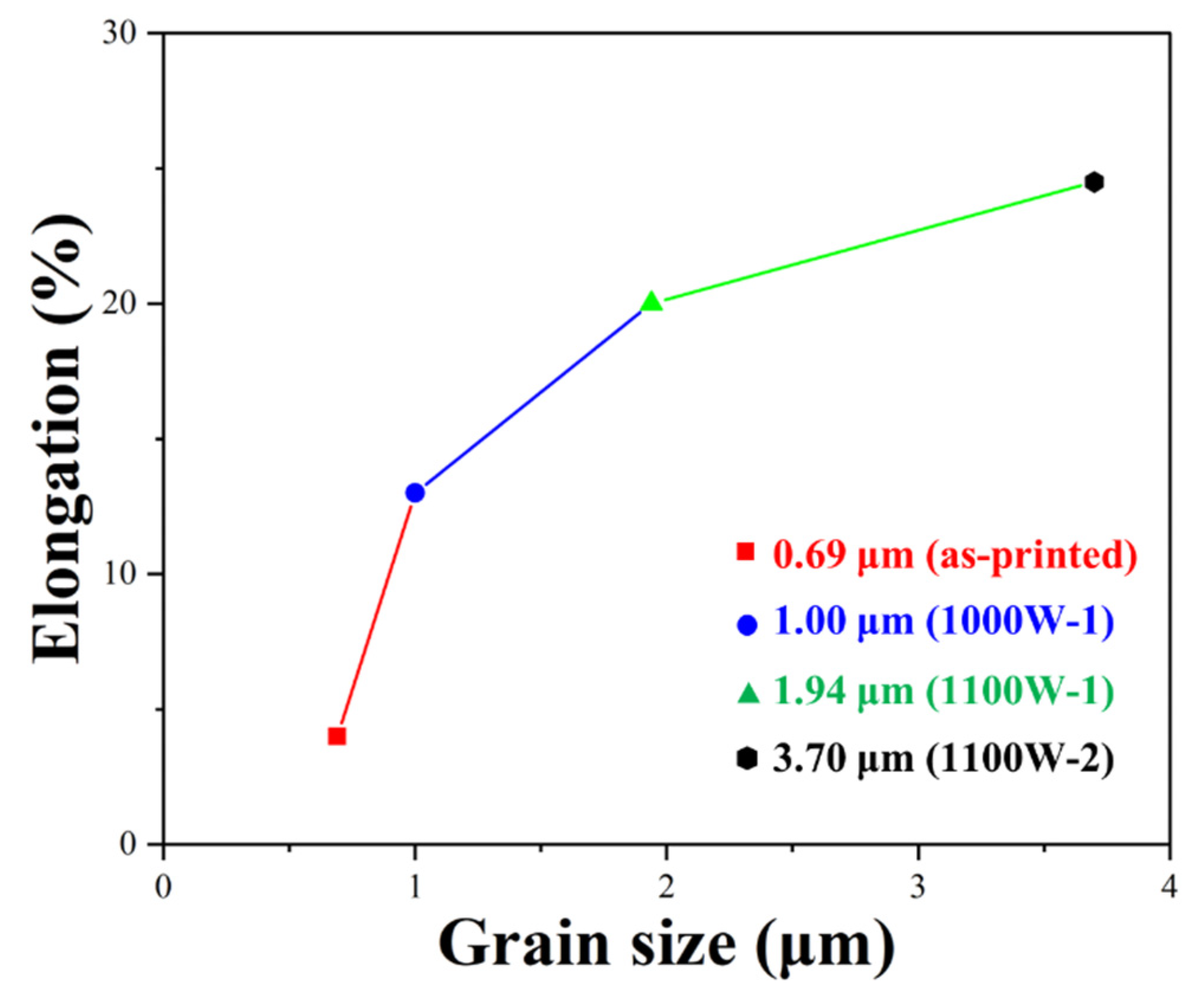
Preprints 98326 g008
Table 1. Heat-treated parameters after SLM.
Table 1. Heat-treated parameters after SLM.
Sample Temperature Heat preservation time Cooling method
1000W-1 1000 °C 1 hour Water-cooled
1100W-1 1100 °C 1 hour Water-cooled
1200W-1 1200 °C 1 hour Water-cooled
Table 2. The average phase sizes and their content and HAGB content.
Table 2. The average phase sizes and their content and HAGB content.
Sample μ B C C d F C C d B C C μ H A G B s
As-printed 28.1% 1.20 μm 0.56 μm 83.1%
1000W-1 23.6% 1.33 μm 0.82 μm 47.0%
1100W-1 19.6% 4.33 μm 1.29 μm 20.6%
1200W-1 13.4% 5.8 μm 2.32 μm 21.8%
Table 3. Mechanical properties of tensile tests.
Table 3. Mechanical properties of tensile tests.
Sample Yield strength (MPa) Tensile Strength (MPa) Elongation (%)
As-printed 913 1239 4.0
1000W-1 790 1115 13.0
1100W-1 571 920 20.0
1200W-1 430 868 24.5
Table 4. The dislocation density of FCC and BCC phases in each sample and the calculated Δ σ d i s l .
Table 4. The dislocation density of FCC and BCC phases in each sample and the calculated Δ σ d i s l .
Sample ρ F C C (×1014 m−2) ρ B C C (×1014 m−2) Δ σ d i s l   ( MPa )
As-printed 215 306 179
1000W-1 137 86 133
1100W-1 130 77 132
1200W-1 111 67 125
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated