Preprint
Review
The Critical Role of Networks to Describe Disease Spreading Dynamics in Social Systems: A Perspective
Altmetrics
Downloads
88
Views
25
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
06 February 2024
Posted:
07 February 2024
You are already at the latest version
Alerts
Abstract
This review underscores the critical significance of incorporating network perspectives in epidemiology. Classic compartmental models (CM) employed to describe epidemic spreading often fail to capture the intricacies of real disease dynamics. Rooted in the mean-field assumption, CM models oversimplify by assuming that every individual has the potential to "infect" any other, neglecting the inherent complexity of underlying network structures. Given that social interactions follow a networked pattern with specific links between individuals based on social behaviors, the amalgamation of classic CM and network science in epidemiology becomes essential for a more authentic portrayal of epidemic spreading. This review delves into noteworthy research studies that, from various perspectives, elucidate how the synergy between networks and CM can enhance the accuracy of epidemic descriptions. In conclusion, we explore research prospects aimed at further elevating the integration of networks within the realm of epidemiology, recognizing its pivotal role in refining our understanding of disease dynamics.
Keywords:
Subject: Physical Sciences - Theoretical Physics
1. Introduction
Classic compartmental models (CM) describing epidemic spreading assume that any individual in the infective compartment can “infect” any other in the susceptible compartment [1]. This assumption called the mean-field approximation, ignores the network effects in favor of analytical tractability [1]. However, social interactions do not randomly occur. They are structured along social links between specific individuals based on social interactions, e.g., love, friendship, work, etc. CMs, including explicit representations of network topologies, have been advocated as a necessary improvement of classical CMs since early 2000 [2,3].
In the last two decades, the research has recognized the importance of networks in epidemiology, and this has led to relevant contributions, such as the finding that the vaccination thresholds strongly depend on network topology [4], or that network community structure, i.e., the presence of groups of nodes/individuals strongly connected among them in real social networks, has a significant impact on disease dynamics [5].
Despite this evidence, during the COVID-19 pandemic crisis, CMs have mainly been used to predict the macroscopic dynamics of infections and deaths and to assess different policies to curb the pace of the person-to-person contagion dynamic [3]. For example, Ferguson et colleagues [6] ‘s famous study, which was the basis of the first containment measures to halt COVID-19 spreading, analyzed the epidemic dynamic using a simple Susceptible-Infectious-Recovered (SIR) model neglecting the social network topological structure. Kissler et al. [7] used an ordinary differential equation mathematical analysis adapted from a Susceptible-Exposed-Infectious-Recovered (SEIR) model to simulate the transmission of SARS-CoV-2 and the hospital care capacity of the United States.
Here, we comment on research manuscripts with classic, significant, or interesting insights explaining how coupling networks and CM may improve the description of epidemic spreading. Then, we discuss the research perspective for further enhancing network use in epidemiology.
2.1. Epidemic Spreading in Scale-Free Networks
About twenty years ago, Pastor-Satorras and Vespignani [8] published a classic research paper showing that scale-free (SF) networks unveil the absence of an epidemic threshold and the persistence of infections at whatever spreading rate the epidemic possesses. They perform large-scale simulations and analytical analyses by describing the spreading process with the Susceptible-Infected-Susceptible (SIS) compartmental model on SF networks. Formally, a scale-free network is a network presenting a power-law distribution of the node degree (number of direct neighbors to the node), i.e., the node degree distribution follows a decaying function of the form , with few nodes of a very large degree. In general terms, scale-free networks are characterized by the presence of large hubs (hyperconnected nodes) [9]. Simulating a SIS model on SF networks, for whatever spreading pace the authors set for the spreading dynamic, the epidemic can persist and infect a significant portion of network nodes [8]. This result emphasized to the scientific community the role of network topology in epidemic modeling and the importance of accounting for network structure in describing spreading in real complex networks. The authors outlined how these results are particularly important to model epidemic spreading on the Internet and the world-wide-web system, which are technological networks showing a typical scale-free connectivity [8].
2.2. Spreading, Node Clustering Coefficient, and Node Assortativity
CM assumes that epidemic transmission passes through interactions occurring randomly in groups, with all individuals potentially interacting with all other individuals at an equal rate [10]. However, social interactions among individuals do not occur randomly, and nodes in real social networks unveil preferential ways of connecting with other nodes, making non-random peculiar structural features [11,12]. Network science uses mathematical approaches to describe these structural features of real social networks.
The network clustering coefficient is an indicator that counts node triplets in the network. A triplet (or triangle) is a set of three nodes. A closed triplet is a full network of three nodes, i.e., a set of three nodes in which a link connects each node with the others. In other words, a triplet is three nodes connected by either two (open triplet) or three (closed triplet) links.
The ‘local clustering coefficient’ of node is defined as:
where is the number of closed triplets centered on node, and is the total number of triplets (both open and closed) centered on node [13]. The node clustering coefficient is also named node transitivity [12]. Node transitivity is related to the binary transitive relation in mathematics, stating that a set is transitive if, for all elements in , whenever relates to and to , then also relates to . Translating in network science terms, a network is transitive whether, for the connected node pairs and it is likely that nodes and are also connected.
Computing the triplets over the whole network, we can define the binary global clustering coefficient by generalizing Eq. 1:
where is the number of closed triplets, and is the total number of triplets (both open and closed) in the network [13].
Calculating the clustering coefficient is the simplest method to investigate the presence of node communities in the network, i.e., node communities are groups of nodes that are densely connected among them. The clustering coefficient evaluates the local group cohesiveness accounting for the fraction of connected neighbors, and for this, it evaluates the tendency of network nodes to form communities. In other words, it is a measure of the magnitude to which nodes tend to form strongly connected communities characterized by a higher density of links than the average probability of links randomly drawn among nodes [14,15]. Figure 1A depicts a toy model network with a lower clustering coefficient, and Figure 1B shows a network with a higher clustering coefficient.
Assortativity is a network structure indicator that evaluates to what extent nodes in a network associate with other nodes in the network, being of similar sort or being of opposing sort. Generally, the assortativity of a network is determined by the degree of the nodes in the network [16]. The notion of assortativity was introduced by Newman [17] and was widely used in network science for many different applications [16].
The node degree assortativity is defined as:
is the standard deviation of the excess degree distribution, is the fraction of links connecting nodes of degree and , and, are the excess degree of nodes of degree and . On other terms, degree assortativity is a measure of its degree correlation, describing how nodes in the network associate based on their number of connections. In Figure 1C we show a disassortative network in which higher degree nodes tend to be connected preferentially with lower degree nodes. On the opposite, in Figure 1D, we draw an assortative network in which nodes of higher degrees are connected preferentially with nodes of higher degrees, and, therefore, the nodes of lower degrees are more likely to relate to other lower-degree nodes. Social networks are typically thought to be distinct from other networks in being assortative (possessing positive degree correlations); well-connected individuals associate with other well-connected individuals, and less connected individuals associate with each other [18].
The node degree assortativity is an essential concept in the field of epidemiology since it can affect the spread of disease [19].
Badham and Stocker [19] investigate how node degree assortativity and clustering coefficient affect the spread of the SIR epidemic. They built model networks using an algorithm to tune node degree assortativity and clustering coefficient. To incorporate a real-world social network structure, the authors used a degree distribution based on the number of friends in a friendship social network of young children [20]. To evaluate the extent of the epidemic spreading, the authors account for the final size (as a proportion of nodes infected at the end of the simulation) and whether an epidemic occurred (at least 25 nodes ever become infected, representing at least some secondary infections).
They found that there is no consistent trend in epidemic proportion related to either the degree assortativity or the clustering coefficient. However, low epidemic occurrence is associated with a high value of either feature.
Further, the authors discovered that the final size of the epidemic decreases when the assortativity or clustering coefficient increases. This means that the final number of infected nodes would be lower if connected nodes/individuals are preferentially connected with nodes of similar degrees.
Based on their results, Badham and Stocker [19] stated that the structural properties identified by social network researchers are relevant for epidemiology, and systematic research is necessary to shed light on the potential size of the effect of the network epidemic spreading.
Volz et al. [21] conducted mathematical and numerical analyses of the SIR model investigating the effect of node clustering over the epidemic spreading entity on networks. They found that in most cases, node clustering is correlated with a lower final extent of the spreading, i.e., networks with a higher clustering presented a lower number of infected at the end of the SIR simulations. The finding of Volz et al. [21] corroborates the Badham and Stocker [2010] results by outlining the importance of considering the structural features of the networks when the aim is to predict the epidemic spreading. It is important for network interventions to halt epidemics, such as concerning the vaccination of individuals [22] or performing social distancing [23], to consider the extent of node clustering.
2.3. Spreading and Community Structure
Real social networks show marked patterns of community structure; that is, social networks present groups of nodes/individuals that are more connected among them [24]. In Figure 1E we depict a random network that does not present a community structure; at the opposite, in Figure 1F we show a network with a strong community structure. The presence of communities of individuals highly connected among them may change the epidemic spreading dynamics. Salathè and Jones [25] investigated the spread of disease in networks with community structure. They simulate SIR epidemic dynamics over both real and model networks. The authors assembled model networks with community structure by joining different subnetworks with randomly drawn edges. Then, they correlate the epidemic spreading pace with the modularity coefficient [26], which evaluates the magnitude of the community structure of the network.
The network modularity measures how good the division of two node communities is or how separated the different node communities are from each other [26].
The modularity indicator is defined as:
where is the total number of links in the network, is the element , of the adjacency matrix, equal to 1 if nodes and j are connected, and 0 otherwise, , and are the degrees of nodes and , respectively, , and are the modules (or community) of node and respectively, and is 1 if and 0 otherwise. The modularity represents the fraction of the links that fall within the given community minus the expected fraction if links are drowned at random. Positive indicates that the number of links within communities exceeds the randomly expected number by chance, the maximum possible value of is 1, nonzero values indicate deviations from randomness, and values around 0.3 or more usually indicate good divisions.
Salathè and Jones [25] found that community structure has a major impact on disease dynamics in a peculiar way; in networks with a strong community structure, an infected individual is more likely to infect members of the same community than members outside the community. Therefore, in a network with strong community structure, local outbreaks may extinguish before spreading to other communities.
Further, Salathè and Jones [25] investigated how individuals’ immunization (vaccination) curbs the epidemic’s spread. Vaccination corresponds to removing nodes or setting nodes in a recovered (not infectious) state [27,28,29]. Salathè and Jones [25] showed that networks with strong community structure, immunization interventions targeted at individuals bridging different communities are more effective than those simply targeting highly connected individuals [25]. These results have implications for the design of control strategies.
2.4. Effective Network Size (ENS)
Transposing the mean-field approach of the classic CM epidemic dynamics to a network model, one should use a “complete network” in which all nodes/individuals interact with each other.
In this spirit, McCabe and Nunn [10] compare the SI/SIR spreading pace of i) complete networks, ii) Erdos-Renyi (ER) random networks, and iii) real primate networks of the same size (number of nodes). The ER random network is a classic model for generating a random network with only two parameters, i.e., the number of nodes () and a fixed probability () for links being present or absent, independently of the other links.
The primate networks are empirically observed networks of social interactions among primates (Pan troglodytes), and they are valuable frameworks for investigating disease spreading in nature.
The authors use the ‘outbreak duration’, i.e., the number of days until the simulation ended, i.e., when all the individuals were recovered and/or infected, as a proxy of the spreading pace.
They find that outbreak durations of simulations on ER networks are more variable than those on complete networks, whereas they show similar mean durations of disease spread. This result indicates that including a simple structural feature, such as removing a fraction of the possible link/interactions, as passing from a complete network to an ER network, can increase the variability of the outbreak duration. On the other hand, real primate networks show a longer outbreak duration concerning a complete network, suggesting how the mean-field approach overestimates the spreading pace.
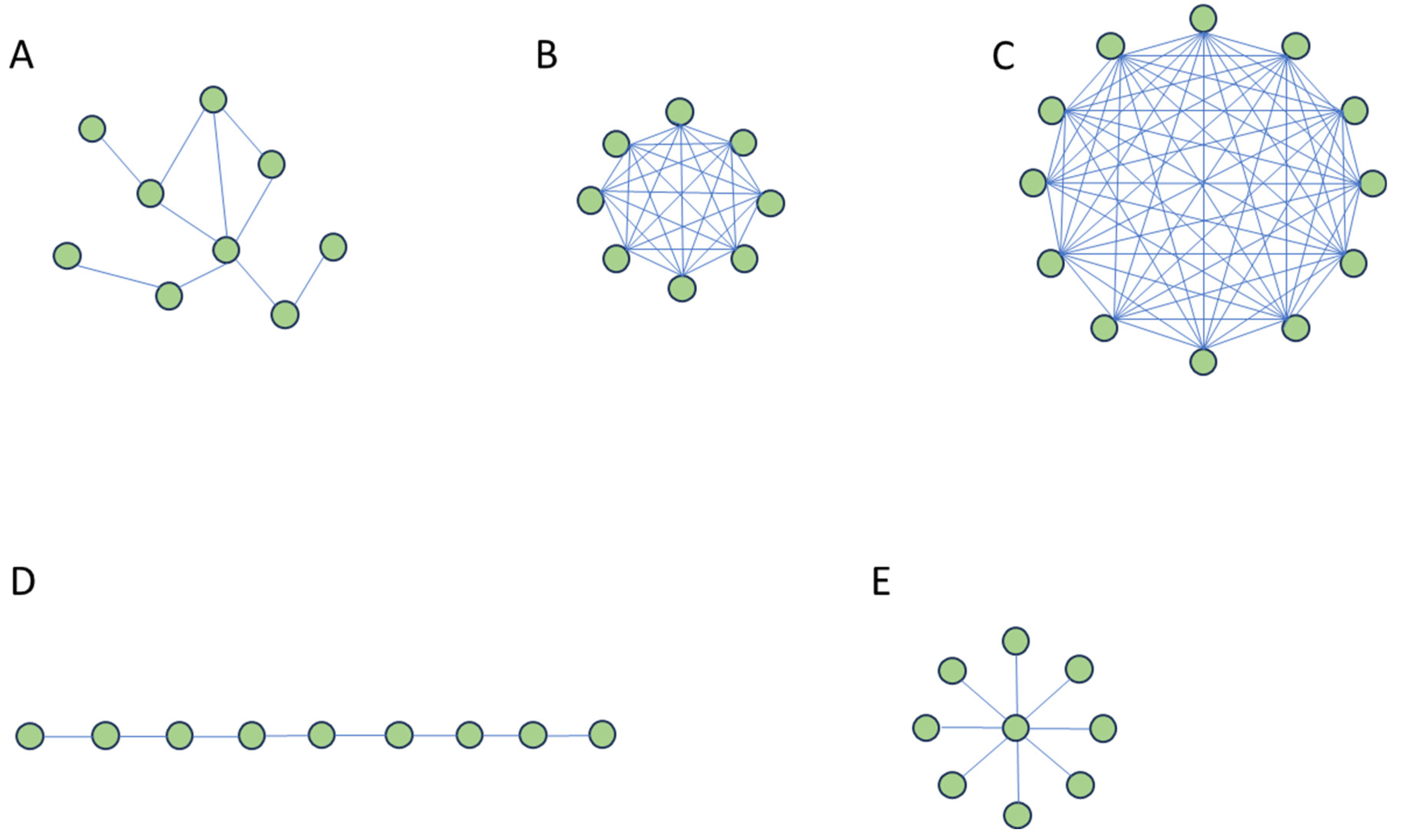
Bearing on these results, the authors propose a measure to account for such heterogeneity: ‘effective network size’ (ENS), which refers to the size of a complete network (i.e., unstructured, where all individuals interact with all others equally) that corresponds to the outbreak characteristics of a given heterogeneous, structured network. The ENS of real primate networks are always higher than their real network size, meaning that the CM models with infection probability parameter values of the real network will overestimate the pace of the epidemic spreading. In Figure 2 A-C we explain the rationale of the McCabe and Nunn [10] analyses.
The article has excellent merit in showing in a simple way how to assume the mean field interaction may produce an erroneous description of the disease spreading in real social networks.
2.5. The Case of the COVID-19 Spreading
A recent paper by Thurner et al. [1] adopts a network approach to investigate the spread of the COVID-19 epidemic. The authors point out that traditional CM epidemiological models cannot explain how the COVID-19 infection curves for many countries reveal a remarkable linear growth over extended periods. Using the salient real network features and a SIR model, the authors explain that linear growth can emerge naturally in real social networks. Traditional CM typically ignore the structure of real contact networks that are essential in the characteristic spreading dynamics of COVID-19.
The authors consider structural features of empirical social contact networks, including node degree heterogeneity (heterogeneity in the number of social links), the fact that people tend to live in small groups (families or communities), and bridge links connecting distant groups (such as that work and leisure links/relations). They show that in these realistic social network structures, a critical number of social contacts () exists for any given transmission rate, below which linear growth and low infection prevalence must occur.
Calibrating the SIR model to empirical estimates of the Covid-19 transmission rate and the number of days being individually contagious, the authors found ∼7.2, i.e., the node degree indicating the number of social contact links should be above 7.2 to produce a super linear epidemic growth. Realistic contact networks show a node degree of about five, and lockdown measures would reduce the social interactions to household size (∼2.5). Therefore, the real social contact networks may reproduce the empirical infection curves with significant precision without additional model assumptions or fine-tuning of parameters.
The probability of observing linear growth with standard CM is practically zero. For this, Thurner et al. [1] question the applicability of standard CM to describe the COVID-19 containment phase. Further, the effect of non-pharmaceutical interventions (NPIs), like national lockdowns, can be modeled with a remarkable degree of precision by coupling a proper network approach to standard epidemiological CM models.
2.6. Predict Epidemic Spreading in Real-World Social Networks
Bellingeri et al. [30] investigated the effect of the network structure on the spread of the epidemic. They simulate SIR spreading over a dataset of 50 real-world complex systems from different fields of science.
To model the effect of the network structure on the epidemic spreading, the authors considered 40 different network structure indexes (NSIs) to test which were the best predictors of the SIR model epidemic spreading. The NSIs covered the relevant network structural features, such as community structure, link density, node distance, node assortativity, etc.
They found that the ‘average node distance’, or a derived notion such as the “average normalized node closeness”, are the best predictors of the initial spreading pace. The ‘distance’ between nodes and is the minimum length of a path joining them, i.e., the minimum number of links to travel between the nodes. The average node distance for undirected networks is defined as:
The average node distance measures the mean number of links to travel along the shortest path among node pairs in the network [31]. The authors find that the higher , the lower the spreading pace.
Further, indexes of ‘topological complexity’ of the network that consider both the node degree and the node distance are the best predictors of both the epidemic peak’s value and the spreading’s final extent. The index, as the ratio of the average node degree (i.e., the average number of links per node) and the average node distance , was introduced in mathematical graph theory to evaluate the topological complexity of the network [32]. The index, which is a derivation of the index using the farness at the place of the node distance, produced the best fitting of the SIR epidemic peak and total number of infected individuals at the end of the epidemic.
Very important, Bellingeri et colleagues [30] research outlines that the most usual NSI evaluating the connectivity level of the network, such as the average node degree , returns a scarce prediction of the network spreading for all the three spreading indicators adopted in the study. Network structures with the same average node degree and, for this, the same connectivity level may show very different epidemic spreading paces (See Figure 2D and 2E).
The authors point out that most of the non-pharmaceutical interventions (NPIs) implemented to curb the SARS-Cov2 epidemic follow the rationale of reducing social interactions, which is equivalent to decreasing the number of social network links. Nonetheless, the Bellingeri et al. [30] study unveils that considering the distance among nodes is more important than focusing on their connectivity level to predict network spreading. These findings suggest that performing a reliable social network disease spreading model is necessary to account for the node distance. Therefore, implementing NPIs to space out the nodes/individuals, i.e., increasing the node distance in the network, would be a more effective strategy to halt the epidemic.
3. Discussion
Coupling classic CM and networks in epidemiology is fundamental to performing more realistic and more accurate epidemic spreading descriptions. Insights and findings from the studies we comment on here demonstrate that the sole use of CM to describe disease spreading may produce erroneous modeling of the disease dynamics. We outline how CM models may underestimate the real ‘outbreak duration’ [10], fail to fit the linear growth of the empirical disease spreading [1], and neglect the critical network structural features to forecast epidemic spreading [30]. We are then convinced that research needs to make significant efforts to enhance the use of network science in epidemiology.
CMs are simpler tools for describing disease spreading, and they require a reduced amount of empirical information. Building real social network structures is challenging for field research, requiring time, money, and sample efforts. For this reason, the classic CM models may hold an important role in urgent analyses to face a novel epidemic event. In fact, during the COVID-19 pandemic crisis, CMs have been largely used to predict the macroscopic dynamics of infections and deaths and to assess different NPIs aimed to contain the microscopic dynamics of person-to-person contagions [3]. However, CMs supporting policy decision-making in the COVID-19 crisis ignored the consequences of not properly considering social networks for intervention [3]. The lack of considering the network structure can be viewed as a lack of reality. As shown by Thurner and colleagues [33], considering structural features of empirical social contact networks, heterogeneity in the number of social links to the nodes/individuals, the presence of small people groups with denser connectivity, and bridge links connecting distant groups (such as that work and leisure links/relations), may unveil the linear growth of the Covid-19 epidemic.
Therefore, using networks in epidemiology must overcome the significant problem of collecting empirical data about social interactions among individuals. In the last few years, due to the need to face the Covid 19 pandemic, technological tools and several methods have been improved (or developed) to reconstruct social interaction networks. The new tools made available have allowed the building of social networks in numerous real environments of epidemic importance, such as schools, museums, and hospitals [34]. Among the essential tools to gather social contact interactions is the use of wearable proximity sensors to characterize social contact patterns [35,36,37], considering the mobility data to build contact networks for epidemic spreading [38], and using phone data to reconstruct the disease spreading network [39,40]. Using real-world networks seems promising because recent technological progress has made collecting massive amounts of social interaction data easier.
4. Conclusion
In conclusion, the integration of classic compartmental models (CM) with network science in epidemiology emerges as a crucial endeavour for a more accurate understanding of epidemic spreading dynamics. The studies discussed in this article underscore the limitations of relying solely on CMs, revealing instances where these models may inadequately capture real-world scenarios.
The investigation into epidemic spreading in scale-free networks, as exemplified by Pastor-Satorras and Vespignani’s [8] seminal work, highlighted the pivotal role of network topology in influencing disease dynamics. The interplay between spreading, node clustering coefficient, and node assortativity, as explored by Badham and Stocker [19], emphasized the importance of considering non-random structural features in social networks for more nuanced epidemic predictions.
Moreover, the examination of community structure by Salathè and Jones [25] demonstrated its significant impact on disease dynamics, showcasing the potential for targeted interventions within specific communities. The concept of Effective Network Size (ENS), as introduced by McCabe and Nunn [10], further highlighted the need to move beyond mean-field approaches, considering the heterogeneity inherent in real-world social networks.
Recent studies, such as those by Thurner et al. [33] and Bellingeri et al. [30], reinforced the critical role of network structure in predicting epidemic spreading, particularly in the context of the COVID-19 pandemic. The inadequacy of traditional CMs to explain the observed linear growth of infections in real social networks underscores the necessity of incorporating network features for more precise modeling of disease dynamics.
While CMs remain valuable for prompt analyses during novel epidemic events, the collective findings advocate for a paradigm shift towards leveraging technological tools and methodologies to gather empirical data on social interactions. The advancements in wearable proximity sensors, mobility data analysis, and phone data utilization offer promising avenues for reconstructing real-world networks, enhancing the reliability of social network disease spreading models.
In light of these insights, it is evident that the future of epidemiological modeling necessitates a more comprehensive integration of network science, ensuring that interventions and policy decisions accurately account for the intricate interplay between infectious diseases and the complex social structures in which they unfold.
Acknowledgments
This research is funded by Ecosister project, funded under the National Recovery and Resilience Plan (NRRP), Mission 4 Component 2 Investment 1.5 - Call for tender No. 3277 of 30/12/2021 of Italian Ministry of University and Research funded by the European Union – NextGenerationEU Award Number: Project code ECS00000033, Concession Decree No. 1052 of 23/06/2022 adopted by the Italian Ministry.
References
- Thurner, S.; Klimek, P.; Hanel, R. A Network-Based Explanation of Why Most COVID-19 Infection Curves Are Linear. [CrossRef]
- Keeling, M.J.; Eames, K.T.D. Networks and Epidemic Models. J R Soc Interface 2005, 2, 295–307. [Google Scholar] [CrossRef] [PubMed]
- Manzo, G. Complex Social Networks Are Missing in the Dominant COVID-19 Epidemic Models. Sociologica 2020, 14, 31–49. [Google Scholar] [CrossRef]
- Pastor-Satorras, R.; Castellano, C.; Van Mieghem, P.; Vespignani, A. Epidemic Processes in Complex Networks. Rev Mod Phys 2015, 87. [Google Scholar] [CrossRef]
- Salathé, M.; Jones, J.H. Dynamics and Control of Diseases in Networks with Community Structure. PLoS Comput Biol 2010, 6. [Google Scholar] [CrossRef] [PubMed]
- Ferguson, N.M.; Laydon, D.; Nedjati-Gilani, G.; Imai, N.; Ainslie, K.; Baguelin, M.; Bhatia, S.; Boonyasiri, A.; Cucunubá, Z.; Cuomo-Dannenburg, G.; et al. Of Non-Pharmaceutical Interventions (NPIs) to Reduce COVID-19 Mortality and Healthcare Demand. [CrossRef]
- Kissler, S.; Tedijanto, C.; Lipsitch, M.; Grad, Y. Social Distancing Strategies for Curbing the COVID-19 Epidemic Citation Terms of Use Share Your Story.
- Pastor-Satorras, R.; Vespignani, A. Epidemic Spreading in Scale-Free Networks. Phys Rev Lett 2001, 86, 3200–3203. [Google Scholar] [CrossRef]
- ka Albert, R.; szló Barabá si, A.-L. Statistical Mechanics of Complex Networks.
- McCabe, C.M.; Nunn, C.L. Effective Network Size Predicted from Simulations of Pathogen Outbreaks through Social Networks Provides a Novel Measure of Structure-Standardized Group Size. Front Vet Sci 2018, 5. [Google Scholar] [CrossRef] [PubMed]
- Borgatti, S.P.; Mehra, A.; Brass, D.J.; Labianca, G. Network Analysis in the Social Sciences. Science (1979) 2009, 323, 892–895. [Google Scholar] [CrossRef]
- Bellingeri, M.; Bevacqua, D.; Sartori, F.; Turchetto, M.; Scotognella, F.; Alfieri, R.; Nguyen, N.K.K.; Le, T.T.; Nguyen, Q.; Cassi, D. Considering Weights in Real Social Networks: A Review. Front Phys 2023, 11. [Google Scholar] [CrossRef]
- Opsahl, T.; Panzarasa, P. Clustering in Weighted Networks. Soc Networks 2009, 31, 155–163. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective Dynamics of “small-World” Networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Holland, P.W.; Leinhardt, S. Transitivity in Structural Models of Small Groups. Comparative Group Studies 1971, 2, 107–124. [Google Scholar] [CrossRef]
- Noldus, R.; Mieghem, P. Van Assortativity in Complex Networks. J Complex Netw 2014, 3, 507–542. [Google Scholar] [CrossRef]
- Newman, M.E.J. Mixing Patterns in Networks. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics 2003, 67, 13. [Google Scholar] [CrossRef] [PubMed]
- Fisher, D.; Silk, M.; Franks, D. The Perceived Assortativity of Social Networks: Methodological Problems and Solutions. In Trends in Social Network Analysis; 2017; pp. 1–19.
- Badham, J.; Stocker, R. The Impact of Network Clustering and Assortativity on Epidemic Behaviour. Theor Popul Biol 2010, 77, 71–75. [Google Scholar] [CrossRef] [PubMed]
- Rapoport, A.; Horvath, W.J. A Study of a Large Sociogram. Behavioral Science 2007, 6, 279–291. [Google Scholar] [CrossRef] [PubMed]
- Volz, E.M.; Miller, J.C.; Galvani, A.; Meyers, L. Effects of Heterogeneous and Clustered Contact Patterns on Infectious Disease Dynamics. PLoS Comput Biol 2011, 7. [Google Scholar] [CrossRef]
- Fransson, C.; Trapman, P. SIR Epidemics and Vaccination on Random Graphs with Clustering. J Math Biol 2019, 78, 2369–2398. [Google Scholar] [CrossRef]
- Bellingeri, M.; Turchetto, M.; Bevacqua, D.; Scotognella, F.; Alfieri, R.; Nguyen, Q.; Cassi, D. Modeling the Consequences of Social Distancing Over Epidemics Spreading in Complex Social Networks: From Link Removal Analysis to SARS-CoV-2 Prevention. Front Phys 2021, 9. [Google Scholar] [CrossRef]
- Kumpula, J.M.; Onnela, J.P.; Saramäki, J.; Kertész, J.; Kaski, K. Model of Community Emergence in Weighted Social Networks. Comput Phys Commun 2009, 180, 517–522. [Google Scholar] [CrossRef]
- Salathé, M.; Jones, J.H. Dynamics and Control of Diseases in Networks with Community Structure. PLoS Comput Biol 2010, 6. [Google Scholar] [CrossRef]
- Clauset, A.; Newman, M.E.J.; Moore, C. Finding Community Structure in Very Large Networks. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics 2004, 70, 6. [Google Scholar] [CrossRef]
- Sartori, F.; Turchetto, M.; Bellingeri, M.; Scotognella, F.; Alfieri, R.; Nguyen, N.K.K.; Le, T.T.; Nguyen, Q.; Cassi, D. A Comparison of Node Vaccination Strategies to Halt SIR Epidemic Spreading in Real-World Complex Networks. Sci Rep 2022, 12. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Zhao, D.W.; Wang, L.; Sun, G.Q.; Jin, Z. Immunity of Multiplex Networks via Acquaintance Vaccination. EPL 2015, 112. [Google Scholar] [CrossRef]
- Holme, P. Efficient Local Strategies for Vaccination and Network Attack. 2004. [Google Scholar]
- Bellingeri, M.; Bevacqua, D.; Turchetto, M.; Scotognella, F.; Alfieri, R.; Nguyen, N.K.K.; Le, T.T.; Nguyen, Q.; Cassi, D. Network Structure Indexes to Forecast Epidemic Spreading in Real-World Complex Networks. Front Phys 2022, 10. [Google Scholar] [CrossRef]
- Freeman, 1977.
- Bonchev, D.; Buck, G.A. QUANTITATIVE MEASURES OF NETWORK COMPLEXITY.
- Thurner, S.; Klimek, P.; Hanel, R. A Network-Based Explanation of Why Most COVID-19 Infection Curves Are Linear. [CrossRef]
- Firth, J.A.; Hellewell, J.; Klepac, P.; Kissler, S.; Jit, M.; Atkins, K.E.; Clifford, S.; Villabona-Arenas, C.J.; Meakin, S.R.; Diamond, C.; et al. Using a Real-World Network to Model Localized COVID-19 Control Strategies. Nat Med 2020, 26, 1616–1622. [Google Scholar] [CrossRef] [PubMed]
- Génois, M.; Barrat, A. Can Co-Location Be Used as a Proxy for Face-to-Face Contacts? EPJ Data Sci 2018, 7. [Google Scholar] [CrossRef]
- Vanhems, P.; Barrat, A.; Cattuto, C.; Pinton, J.F.; Khanafer, N.; Régis, C.; Kim, B. a.; Comte, B.; Voirin, N. Estimating Potential Infection Transmission Routes in Hospital Wards Using Wearable Proximity Sensors. PLoS One 2013, 8. [Google Scholar] [CrossRef]
- Ozella, L.; Paolotti, D.; Lichand, G.; Rodríguez, J.P.; Haenni, S.; Phuka, J.; Leal-Neto, O.B.; Cattuto, C. Using Wearable Proximity Sensors to Characterize Social Contact Patterns in a Village of Rural Malawi. EPJ Data Sci 2021, 10. [Google Scholar] [CrossRef]
- Klise, K.; Beyeler, W.; Finley, P.; Makvandi, M. Analysis of Mobility Data to Build Contact Networks for COVID-19. PLoS One 2021, 16. [Google Scholar] [CrossRef]
- Oliver, N.; Lepri, B.; Sterly, H.; Lambiotte, R.; Deletaille, S.; De Nadai, M.; Letouzé, E.; Salah, A.A.; Benjamins, R.; Cattuto, C.; et al. Mobile Phone Data for Informing Public Health Actions across the COVID-19 Pandemic Life Cycle; 2020; Vol. 6.
- Ciddio, M.; Mari, L.; Sokolow, S.H.; De Leo, G.A.; Casagrandi, R.; Gatto, M. The Spatial Spread of Schistosomiasis: A Multidimensional Network Model Applied to Saint-Louis Region, Senegal. Adv Water Resour 2017, 108, 406–415. [Google Scholar] [CrossRef]
Figure 1.
Node clustering. (A) toy model network with a lower clustering coefficient (one closed triple), vs. (B) network with higher clustering coefficient (four closed triplets). Links of closed triplets are in red. Node assortativity. (C) a disassortative network in which nodes of higher degree (more links) are connected preferentially with nodes of lower degree. (D) assortative network in which nodes of higher degree are connected preferentially with nodes of higher degree, and nodes of lower degree are connected preferentially with lower degree nodes. Network community structure. (E) Random network that does not present a community structure. (F) network with a strong community structure (node colour indicates nodes belonging to the same community); this network is composed of four clearly separated communities.
Figure 1.
Node clustering. (A) toy model network with a lower clustering coefficient (one closed triple), vs. (B) network with higher clustering coefficient (four closed triplets). Links of closed triplets are in red. Node assortativity. (C) a disassortative network in which nodes of higher degree (more links) are connected preferentially with nodes of lower degree. (D) assortative network in which nodes of higher degree are connected preferentially with nodes of higher degree, and nodes of lower degree are connected preferentially with lower degree nodes. Network community structure. (E) Random network that does not present a community structure. (F) network with a strong community structure (node colour indicates nodes belonging to the same community); this network is composed of four clearly separated communities.
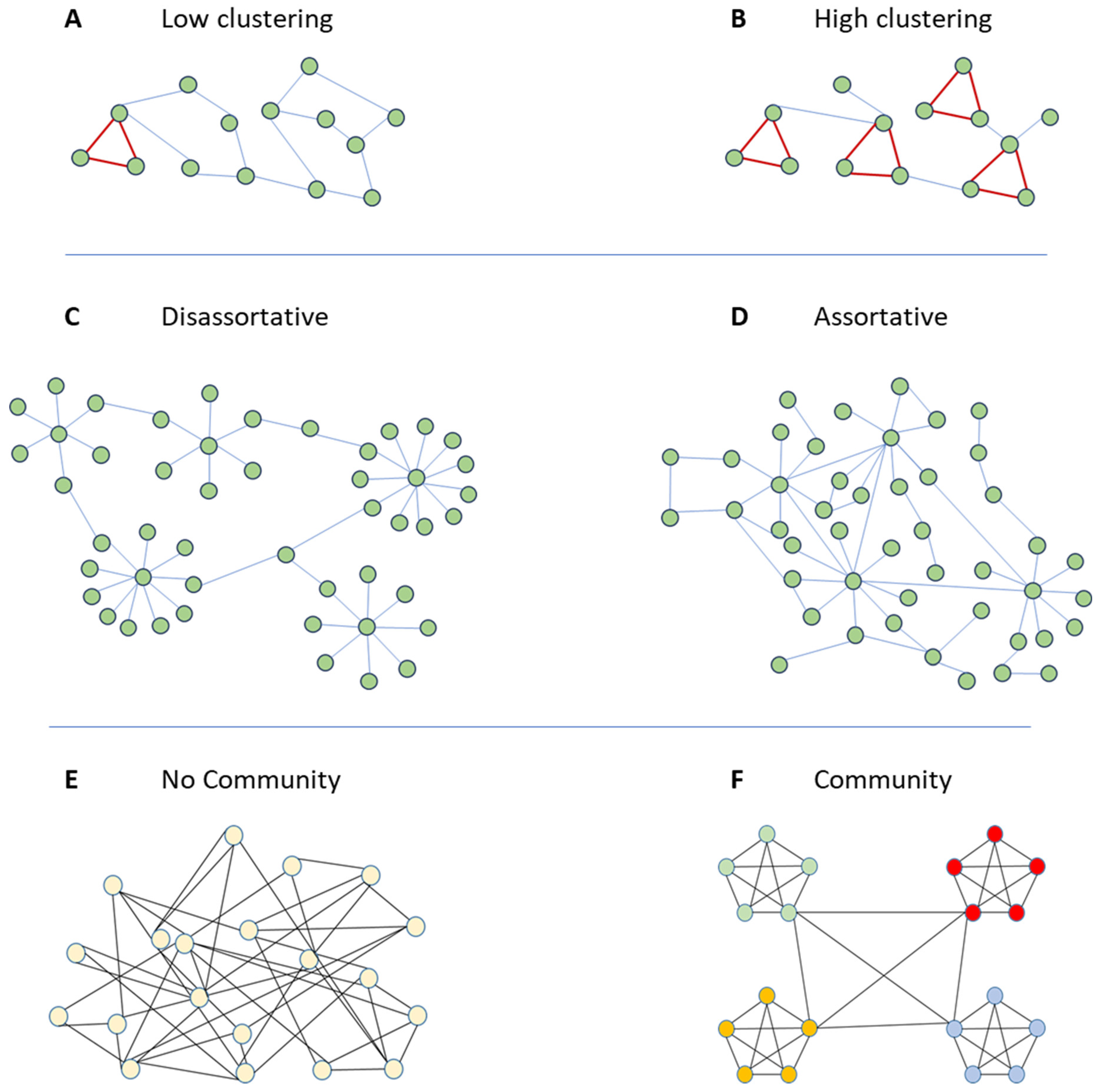
Figure 2.
The effective network size. (A) depicts a hypothetical real network over which a disease can spread; (B) the complete network underlying the mean-field approach at the base of the classic CMs, in which every node interacts with each other. Authors simulated epidemics spread via a type SIR model with the same infectious probability over the real (Figure 2A) and the complete network of the same size (Figure 2B). The complete network shows a higher pace of the disease spreading, resulting in a shorter outbreak duration. Starting from the real network in Figure 2A, to obtain a similar pace of the SIR spreading pace, measured by the outbreak duration, we must consider a complete network of larger size, such as the one depicted in Figure 2C. On the other hand, to produce the same spreading pace in the real (Figure 2A) and the corresponding mean field approach complete network (Figure 2B), we must assume different infection probabilities over the network links, decreasing the infection probability in the complete network. Assuming the complete network in Figure 2C as the complete network that corresponds to the outbreak characteristics of the real network in Figure 2A, its number of nodes is the ‘effective network size’ (ENS) of the real network in Figure 2A [10]. Node distance and the pace of the epidemic spreading. (D) the chain network of N=9 nodes; (E) the star network of =9 nodes. The two model networks have the same number of links , i.e., , and, for this, the same average node degree . The two network models are limit structures showing very different distances among nodes. The chain network is much longer than the star network (average node distance =1.8 for the star and =3.3 for the chain network). Consequently, the chain network will show a lower epidemic spreading pace.
Figure 2.
The effective network size. (A) depicts a hypothetical real network over which a disease can spread; (B) the complete network underlying the mean-field approach at the base of the classic CMs, in which every node interacts with each other. Authors simulated epidemics spread via a type SIR model with the same infectious probability over the real (Figure 2A) and the complete network of the same size (Figure 2B). The complete network shows a higher pace of the disease spreading, resulting in a shorter outbreak duration. Starting from the real network in Figure 2A, to obtain a similar pace of the SIR spreading pace, measured by the outbreak duration, we must consider a complete network of larger size, such as the one depicted in Figure 2C. On the other hand, to produce the same spreading pace in the real (Figure 2A) and the corresponding mean field approach complete network (Figure 2B), we must assume different infection probabilities over the network links, decreasing the infection probability in the complete network. Assuming the complete network in Figure 2C as the complete network that corresponds to the outbreak characteristics of the real network in Figure 2A, its number of nodes is the ‘effective network size’ (ENS) of the real network in Figure 2A [10]. Node distance and the pace of the epidemic spreading. (D) the chain network of N=9 nodes; (E) the star network of =9 nodes. The two model networks have the same number of links , i.e., , and, for this, the same average node degree . The two network models are limit structures showing very different distances among nodes. The chain network is much longer than the star network (average node distance =1.8 for the star and =3.3 for the chain network). Consequently, the chain network will show a lower epidemic spreading pace.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Dynamic Contact Networks in Confined Spaces: Synthesizing Micro-Level Encounter Patterns Through Human Mobility Models from Real-World Data
Diaoulé Diallo
et al.
,
2024
HIV Propagation in a Population Group Considering Infection in the Immune System Of Each Infected Individual
Sol de Amor Vásquez-Quintero
et al.
,
2021
Transportation, Germs, Culture: A Dynamic Graph Model of 2019-nCoV Spread
Xiaofei Yang
et al.
,
2020
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated








