Prerpints.org logo
Preprint
Review

A Guide for the Bioinformatic Analysis of Metabolomics Data

Altmetrics

Downloads

411

Views

420

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

07 February 2024

Posted:

08 February 2024

You are already at the latest version

Alerts
Abstract
Metabolites are at the end of the gene-transcript-protein-metabolism cascade. As such, metabo-lomics is the omic approach that offers the most direct correlation with phenotype. This allows that, where genomics, transcriptomics and proteomics fail to explain a trait, metabolomics might give an answer. Complex phenotypes, which are determined by the influence of multiple small effect alleles, are an example of these situations. Consequently, the interest in metabolomics has increased ex-ponentially in the last years. As a newer discipline, the metabolomics bioinformatics analysis pipe-lines are not as standardized as in the other omic approaches. In this review we synthesized the different steps that need to be carried out to obtain biological insight from the annotated metabolite abundance raw data. These steps were grouped in three different modules: preprocessing, statistical analyses and metabolic pathway enrichment. We included within each one of them the different state-of-the art procedures and tools that can be used depending on the characteristics of the study, providing details about the characteristics of each method has, as well as the issues the reader might encounter. Finally, we introduce genome scale metabolic modeling as a tool for obtaining pseu-do-metabolomic data in situations where its acquisition is difficult, being possible to analyze the resulting data with the modules of the described workflow.
Keywords: 
Subject: Biology and Life Sciences  -   Other

1. Introduction

Metabolism is the currency of the physiological processes of all living organisms. The biomass that forms all organisms is a product of metabolism, as well as the chemical reactions that ensure its energetic viability and maintenance. The metabolome encompasses all the small chemical compounds (metabolites) that are present in a biological system at a given moment [1]. These small compounds include sugars, amino acids, nucleic acids, lipids, fatty acids, phenolic compounds, and alkaloids. Due to metabolism being at the end of the gene-transcript-protein-metabolism cascade, the metabolome is the omic dataset that is closer to the phenotypic state of the organism under investigation [2]. This straightforward correlation facilitates that the study of metabolism may provide explanations to the mechanisms driving phenotypes where genomic, transcriptomic, or proteomic approaches cannot. One example of this are complex phenotypes, where the observed features are product of a high number of small-effect alleles, rather than few strong-effect mutations, which makes it difficult to stablish connections between, for example, genome and phenotype [3]. In the context of pathogenic microorganisms, the possibility of examining their physiological state in a particular moment can give insight of their virulence mechanisms. Some pathogens rely on the production of secondary metabolites to display increased virulence. For example, Pseudomonas aeruginosa produces rhamnolipids in order to form biofilms and swarm through surfaces, and the secretion of these compounds serves as a mean for reducing oxidative stress [4,5,6,7]. Other pathogens rewire their metabolic network to adjust to the stresses imposed by the infected host, diverting fluxes towards metabolic products that help to evade the immune response, serve as reserve resources against starving and protect against the host’s attacks. An example of this is Mycobacterium tuberculosis infection, which is characterized by a switch from carbohydrate to lipid use as a carbon source, an altered composition of the cell wall and an abrupt decrease of the growth rate [8,9,10]. These facts have contributed to an exponential increase of the interest in the application of metabolomic techniques in microbiological studies [11].
Metabolomic data is most frequently acquired with gas chromatography-mass spectrometry (GC-MS), followed closely by liquid chromatography-mass spectrometry (LC-MS) and nuclear magnetic resonance (NMR) [11,12]. GC-MS offers the advantages that the equipment is cheaper, easier to operate and less prone to maintenance issues. Additionally, retention times between runs are highly reproducible, being automated compound identification easier. Consequently, it is the gold standard for profiling primary metabolism [13,14]. An important drawback is that the sample needs to be volatilized prior to enter the chromatographic column, being necessary to derivatize non-volatile compounds, therefore existing the possibility of the degradation of compounds and the formation of new ones as a product of the heat [15]. On the contrary, LC-MS has the advantage that allows for the detection of more compounds than GC—MS, being able to acquire tens of thousands of features in a single run. The lack of methods to determine the metabolite identity of all detected ions is, however, a major limitation [11]. Other advantages are a high sensitivity and, as it does not need compound derivatization, sample preparation is easier, faster and cheaper [16]. The main drawback is that the chromatographic column does not behave exactly the same in separate runs, causing compound elution times to naturally drift between runs [17], implying extra steps for identifying the identity of the peaks. Among the advantages offered by NMR are that it allows in vivo measurements, can provide information about interaction of metabolites with macromolecules and has an easier workflow for performing isotope tracing than LC-MS or GC-MS, with the drawback of less sensitive measurements [18]. In the three cases, after the steps needed to be carried out to convert the raw spectra data to metabolite feature data [19,20], the outcome will be a table of peak areas where each row will constitute the analyzed samples and each column the features, in other words, the metabolites. These peak areas are proportional to the relative abundance of the metabolite within the sample.
To get biological insight from the raw peak areas several steps must be carried out, which can be summarized in preprocessing, unsupervised exploratory analyses, supervised analyses and pathway enrichment. In the preprocessing step, missing values need to be imputed and the unwanted experimental variability removed. Non-supervised approaches are usually used to explore the data, showing if there are differences between the experimental groups (for example phenotype or treatment) without informing the algorithm about what the group each sample belongs to. When there are many metabolomic differences strongly correlated to the target grouping unsupervised methods can be used to determine what are the features driving this difference. When this is not the case supervised approaches need to be used: information about the group of each sample is required by the algorithm, which determines what features are more strongly associated to the differences. The final step consists in, having the metabolites that are altered between the different groups, determine which are the metabolic pathways that appear to be perturbed. In this review we discuss the different state-of-the-art approaches that fall within each one of these three modules, detailing the particularities of each method and the issues that need to be considered. In the final section we will discuss alternative approaches for cases where the access to metabolomic data is difficult.

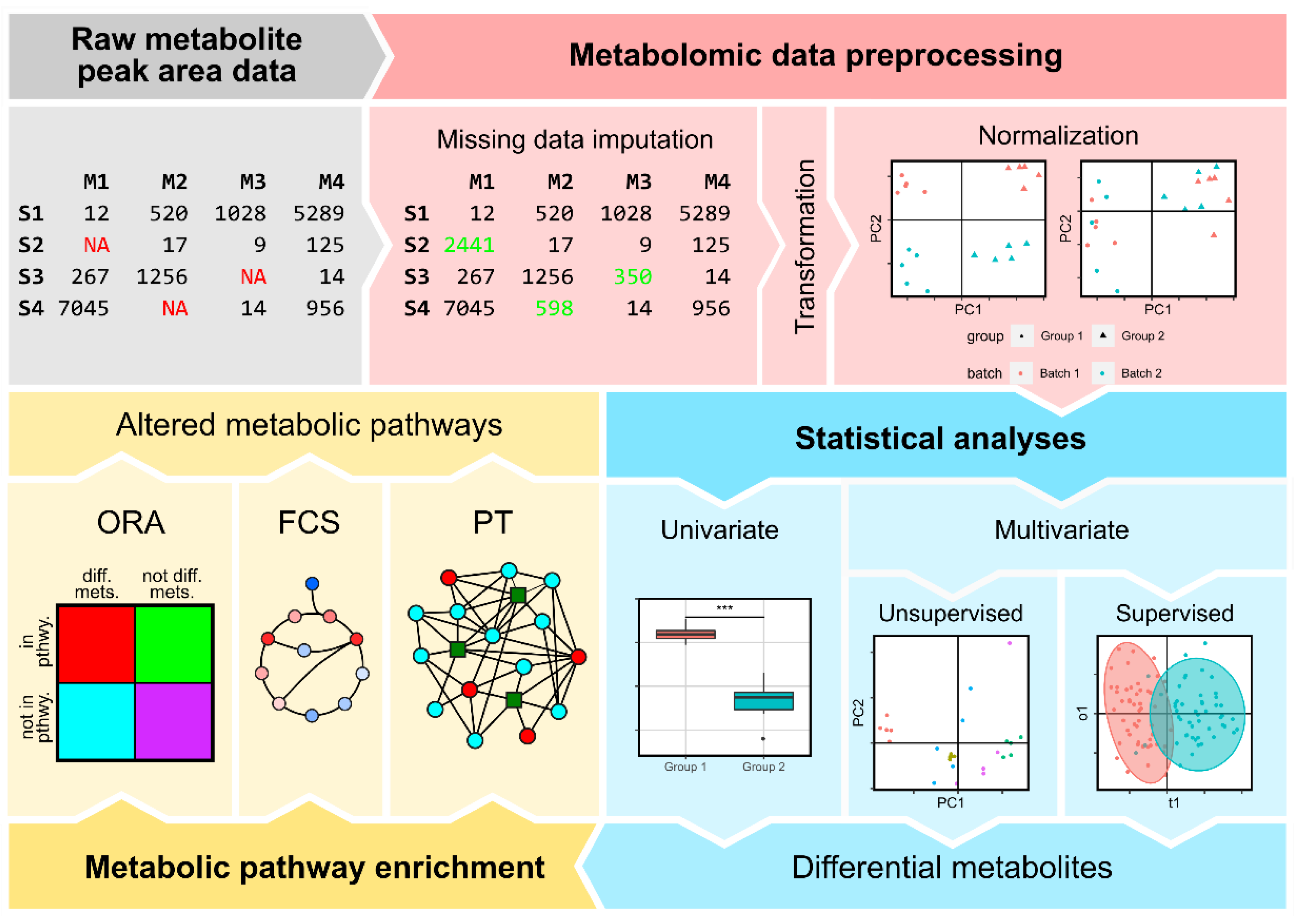
2. Data Preprocessing

Once metabolite extracts are analyzed with the chosen technique and the metabolite peaks are identified for each one of the samples, a metabolite table of peak areas will be generated, where rows and columns correspond to samples and metabolites, respectively. This table will present two issues: some metabolites will have missing values in some samples and there will be variability between batches introduced by technical errors. Regarding the missing values, it needs to be determined if these metabolites are truly absent in the sample or below the limit of detection, or there was some error in the metabolite detection or in the determination of the peak, and their abundances need to be inferred. This process is known as metabolite imputation. The handling of the technical variation introduced during sampling preparation and data acquisition is done in the normalization step.

2.1. Metabolite Imputation

Metabolomic data acquired with Mass Spectrometry (MS) have the drawback that present missing values at a proportion that can be as high as 20% and affect 80% of the detected metabolites [21]. These missing values can interfere in the statistical analyses done downstream, so an important step in the preprocessing step is to handle them with imputation [22]. The approaches for dealing with the missing values in metabolomics are borrowed from other omics disciplines, mostly transcriptomics. Before the imputation usually the variables with a high proportion of missing values are completely removed from the dataset. An example of this approach is the “80% rule”, where metabolites with more than the 20% of missing values are removed from the dataset [23]. The samples with more than the 80% of the variables missing are also filtered out.
After the prefiltering, there are different approaches to deal with missing values, some of them more sophisticated than others. They can be divided in three categories [24]. The simplest ones belong to single value imputation, which includes the imputation by the mean, by the median, by the minimum, by the minimum/2 or by zero. Imputation by the mean and the median of the non-missing values of a given variable assumes that the origin of the missing values is random, caused by errors during the sample preparation or detection. Conversely, imputation by the minimum, the minimum/2 and zero assume that the value is missing because it is below the limit of detection. Because of their approach, they do not determine the cause of each missing value observation. With an increasing complexity, we can find the imputation methods based on local structures. Some examples are random forest and k-nearest neighbors imputation [25,26,27]. These methods infer the imputed value based on the value of the same variable in other samples that are similar according to the rest of the variables, so it can at some level determine if the missing metabolite is in the limit of detection or was not detected because of some other issue. The third category encompasses the methods based on global structures, which infer missing values based on the “shape” of the vector space determined by the metabolomic matrix, being iteratively the missing values estimated until they converge. Among the different options there are methods based on Single Value Decomposition (SVD) [28], on Bayesian Principal Component Analysis (BPCA) [29] and on Probabilistic Principal Component Analysis (PPCA) [30].

2.2. Normalization

After missing value imputation an important step is to normalize metabolomic data in order to remove the technical variation that might have been introduced during the experimental procedure. The sources of this variation are diverse, being among them human error, differences in temperature or atmospheric conditions, and between- and within-instrument variation, among many other sources. When samples are acquired in short intervals of time the produced variation might or not have a large impact, but when samples are acquired in different batches is when batch effect arises: samples that have been ran in the same batch were subjected to the same technical variation conditions determined by the moment when the analysis was performed and, therefore, have common traits that are not related to the biological factors of interest [31]. In order to help to distinguish if the observed differences are due to true biological variation or batch effects and to facilitate its correction, it is important to evenly split the samples belonging to the different biological groups across different batches during the design of the experiment in the data acquisition step.
Compared to transcriptomics or proteomics, where commonly all the abundances are normalized to a single value (i.e., the total amount of transcripts or proteins in the sample, the mean, the median, or a value obtained based on a set of house-keeping features) [32,33,34,35], in metabolomics there is no standard method for dealing with non-biological variability [36,37]. Furthermore, the outcome of the experiment can vary greatly depending on the chosen normalization method [38]. Consequently, a good practice is to test different methods and compare their performance [39].

2.2.1. Normalization Methods

Normalization methods can be classified as pre-acquisition, or preventive, and post-acquisition, or curative [40]. Pre-acquisition methods consist in diluting the samples in order to force all of them to have the same global concentration, previously to sample preparation and analysis. In the case of microbial metabolomics, the most common approach is taking all the samples to the same optical density (OD, absorbance at 600 nm) before metabolite extraction [41]. For other cases some alternatives are normalizing to the total dry weight, to the number of cells or to the total DNA or protein quantity in the sample [36]. Post-acquisition methods are mathematical procedures that aim to remove the technical variation after the analytical process [36]. Differences in the performance between pre- and post-acquisition methods have been reported, with many post-acquisition methods failing to overcome non-linear variability [42]. However, even performing pre-acquisition normalization, differences in the analytic equipment conditions between runs can still produce variation during data acquisition that still need to be handled [43]. So, a combination of both approaches is advisable.
Before post-acquisition normalization it is also advisable to transform the data, as metabolite abundances tend to have a right skewed distribution [44]. Log-transformation is the most used approach but may become problematic when dealing with small values, because as they approximate to zero, log-transformation tends to minus infinite. An alternative to overcome this problem is the power transformation, which consists in raising the values to the power of a rational number, commonly 1/2 [45]. Other solution that allows to use log-transformation consists in adding a small number c to all the values before transformation to avoid having zeros.
Regarding post-acquisition methods, there are different alternatives. In this review we will cover a selection of them. As with missing value imputation, there are some normalization methods that are more sophisticated than others. The less sophisticated methods are inherited from transcriptomics and proteomics. These are the scaling normalization methods, which consist in subtracting to each sample a single value corresponding to that sample, let it be the mean, median or sum of all the peak intensity values for the given sample [46]. When the number of differential compounds is low, these methods can be efficient solutions. But they present the problem that on many occasions the increase of abundance of a particular group of metabolites is not accompanied by a decrease of another group (self-averaging property does not occur). So, if there are many differential compounds, normalizing to a single value obtained from the total peak values can introduce differences in some metabolites that are not actually there [47]. With an increased level of sophistication, there are the normalization methods that rely on the spiking of one or several quality control metabolites in the sample. These compounds are known as internal standards. Depending on if it is desired to capture only differences in instrumental variation, or also in extraction efficiency, the internal standards can be added just before running the analytical step, or before the metabolite extraction, respectively. The compounds used in the latter case are referred by some authors as surrogate standards. The compounds typically used as internal standards are isotopically labeled versions of known metabolites [48]. The simplest of the normalization methods within this family is based on a single standard and is simply referred as IS (internal standard) method [49]. Here the peak intensity of each metabolite in each sample is normalized to the peak intensity of the internal standard, either by dividing each metabolite by this value or by subtracting it from each metabolite peak intensity [46,49]. The main drawback of this method is the assumption that all the metabolites are affected equally by the technical variation, which might not be always appropriate as variation can be influenced by their chemical properties. Therefore, the chemical properties of the standard might introduce variation due to matrix specific effects [47]. A solution to these issues is to add more than one quality control metabolite. The simplest approach using several quality control metabolites is the retention index method (RI). Here standards with different retention times are added to the samples, normalizing each analyte to the quality control metabolite with the closest retention [23]. However, technical variation might arise from other sources than retention time. NOMIS (Normalization using Optimal selection of Multiple Internal Standards) aims to solve this issue by determining the covariance between the quality control metabolites and the analytes through multiple linear regression, for then removing this covariance from the analytes [47]. This way the standards that covariate more with each metabolite are given more weight in the normalization, effectively selecting the optimal standards for the normalization of the given analyte [47]. Despite this improvement, the internal standards could be still affected by cross-contribution, a phenomenon that is observed when different analytes co-elute in the chromatographic column, producing interference in the measurement [50]. Cross-contribution Compensating Multiple standard Normalization method (CCMN) overcomes this issue by performing the normalization in several steps [51]. First the variation introduced by the experimental design that is cross-contributed through the analytes to the standards is removed via multiple linear regression (MLR), for later using these cross-contribution free standard values for performing normalization [51]. Instead of using internal standards for normalization, another option is to use non-changing metabolites, which are present in the biological samples and therefore are exposed to technical variation but are uncorrelated to the biological factors of interest. RUV-2 (remove unwanted variation, 2-step) method uses this approach [43,52]. Here the unwanted component factors are estimated via single value decomposition (SVD) of the non-changing metabolite matrix, for later fitting a linear model to each metabolite using as explanatory variables both the factors of interest and the unwanted component factors [43,52]. These non-changing metabolites can be determined by statistical analysis or by determining which are the metabolites that correlate more with the standards (if included in the experiment) [43]. Non-changing metabolites have also been used with success with other normalization methods such as CCMN instead of internal standards [53]. Other category includes the methods based on quality control (QC) samples, which are analyzed before, after and scattered at regular intervals throughout each batch. These methods use the shifts between the measures of the QC sample to correct the values obtained from the test samples. A representative method of this class is quality control–based robust LOESS (locally estimated scatterplot smoothing) signal correction (QC- RLSC) [54]. These QC samples can be either pooled samples, obtained by combining small aliquotes of all the samples in the study, or commercially available QC samples made of combinations of different biofluids [54,55,56,57]. Pooled QC samples offer the advantage that contain the same metabolites that can be found in the individual samples, constituting the average of all the samples. The use of commercially available QC samples often implies metabolic information losses due to metabolites detected in the test samples but not in the QCs. Consequently, these metabolites will not be considered in downsream analyses. However, in long studies where sample preparation and data acquisition starts before the collection of all the samples, the use of commercially available QC samples might be necessary [54]. Finally, blank samples are another type of QC samples that, whether not directly related to normalization, are important in the assessment of the reproducibility of the analyses. These samples consist in either only solvent or the matrix of the sample, with optional internal standards spiked. Furthermore, the use of these samples allows to identify background compounds that should be excluded from downstream analyses [58]. The use of QC samples also serves for preparing the equipment for the analysis of the test samples, as the first few injections in a run tend to be poorly reproducible [54,59,60].
There are of course many more post-acquisition normalization methods than the ones covered here, but the aforementioned ones cover the different approaches used to handle technical variation. The scaling normalization methods can be easily implemented using any programming language such as R or Python, and are also included in NormalizeMets R package, as well as the methods based on internal standards and non-changing metabolites mentioned in this section [46].

2.2.2. Assessment of Post-Acquisition Normalization Effectivity

Each one of the post-acquisition methods mentioned here solves an increasing number of issues metabolomic data can present and, consequently, there is an increment of complexity as well. Depending on the experimental implementation, the use of some methods might be more appropriate than others, as in some cases using excessively complicated methods may be overkill. For example, in cases where the number of differential metabolites is small, such as in drug screening, scaling methods or IS method might be enough [50]. But in comparisons involving multiple differential metabolites, an increasing level of complexity is probably needed. Thus, it is recommended to test the performance of different methods to assess which is the one that best suits the dataset. There are different approaches to determine this, all of them complementary.
One approach is to evaluate the tightness of the replicates. A way of assessing this is by comparing the average distance of each sample to its replicates to the average distance of each sample to the samples that are not replicates. A good normalization method should minimize the distance between replicates while maximizing the distance between groups. So, a scatterplot showing the average within- and between- group distances in the x and y axis for each one of the tested normalization methods can easily show which of them is optimizing these distances. Tightness of replicates can also be determined by using silhouette statistic [61]. Silhouette can be computed for each one of the data points in each one of the datasets generated with the tested normalization methods, considering the cluster as the group of replicate samples. The best performing normalization method, in terms of tightness of replicates, will display a distribution of silhouettes with lower standard deviation and higher median. Another option is to use within and between relative log abundance (RLA) plots [43]. Within-group RLA plots are boxplots of groupwise standardized log metabolite abundances, obtained by subtracting the median of the log abundances of each metabolite in the replicated samples to each sample. Within-group RLA plots show the tightness of the replicates achieved by the normalization method: all the samples should have a median within-group relative abundance close to zero and low standard deviation. For obtaining across-group plots, the median log abundance of each metabolite across all the samples is subtracted to the log abundance of each metabolite in each one of the samples. The obtained boxplots show the variability between groups of replicates: replicates should not vary a lot, but differences between groups of replicates should be observed. If the within-group RLA plots show a big proportion of the samples having their medians different from zero it means that the normalization method is not removing the unwanted variation properly. If within-group RLA plots look as expected, but across-group RLA plots also show no difference between groups is a sign that the normalization method is removing the technical variation but also an important part of the biological variation [39]. Multivariate non-supervised approaches such as Principal component analysis (PCA) or hierarchical clustering analysis (HCA) can also be used to see if the samples aggregate according to their replicate structure or, instead, they group by batch. The results obtained with the unnormalized dataset and each one of the normalization methods can be compared to determine which of the methods yields tighter replicates and better removes batch effects [51].
Other approach for assessing the adequacy of the normalization method is, if there are metabolites that are known beforehand to be differential between the levels of the biological factor of interest (positive control metabolites), rank the statistically significative metabolites before and after normalization, and see if they are among the top significative after normalization, meaning that the biological variation has not been removed [62].
The normalization diagnostic procedures depicted in this section can be performed using R statistical software with its included plotting features, or alternatively with ggplot2 package. RLA plots can be obtained easily with NormalizeMets R package [46]. In Python SciPy and Matplotlib libraries can be used for this same purpose [63,64].

3. Statistical Analysis of Metabolomics Data

Once the metabolomic data has been normalized with the best performing method, different approaches can be used to answer the biological questions that have given origin to the performed study. Depending on the complexity of the question to be answered different approaches can be used.

3.1. Univariate Analyses

The most straightforward statistical methods to determine the metabolites associated with the biological factors of interest (phenotypes or experimental conditions applied to the biological samples) are univariate analyses. Here the values of a single variable (metabolite) are tested one at a time for significant association with the factors of interest [65]. Depending on the variables being categorical or quantitative, on the distribution of the data and, if the variables are categorical, on how many categories there are, the most appropriate test needs to be chosen. If both the factor (independent variables) and the response variables (metabolite abundances) are quantitative, simple regression should be used, using t-statistic (for regression coefficients) or F-statistic for determining the significance of the association. If the factors are categorical, some examples of univariate tests to be used when there are only two categories are Student’s t-test and Mann-Whitney U test, the first one used when the distribution of the metabolite abundance is normal, while the second one does not assume normality. Simple logistic regression can also be used in this context, determining the significance of the association by using a Wald test [66]. ANOVA and Kruskal-Wallis test are some of the options that can be used when there are more than two categories. ANOVA, as the t-test, assumes normal distribution, while Kruskal-Wallis test does not [65]. As we are dealing with multiple testing, being that metabolomics datasets normally have from tens to hundreds of metabolites, p-value correction will be necessary to compensate for the increasing probability of obtaining false positives [67].

3.2. Multivariate Analyses

In multivariate analyses, instead of testing the association of independent variables to response variables one by one, all of them are tested at the same time. In metabolomic experiments, metabolite abundances are measured outcomes and are not usually manipulated. Therefore, they have the role of dependent variables according to the experimental design (as was considered in univariate analysis). But metabolites are not independent entities because they are connected through the metabolic network. Therefore, we expect that the different phenotypes being compared or the adaptation to the experimental treatments may result from the coordinated change of multiple metabolites. By using metabolite abundances as independent variables in multivariate analyses it is possible to assess the relationships between the different variables, giving insight about their interaction in relation to a particular biological factor [68]. Another advantage is that multiple hypothesis-testing is avoided, as only one test is performed for all the variables. Multivariate analysis methods can be broadly divided into supervised and unsupervised, according to the information about the response biological variable being given to the method or not, respectively.

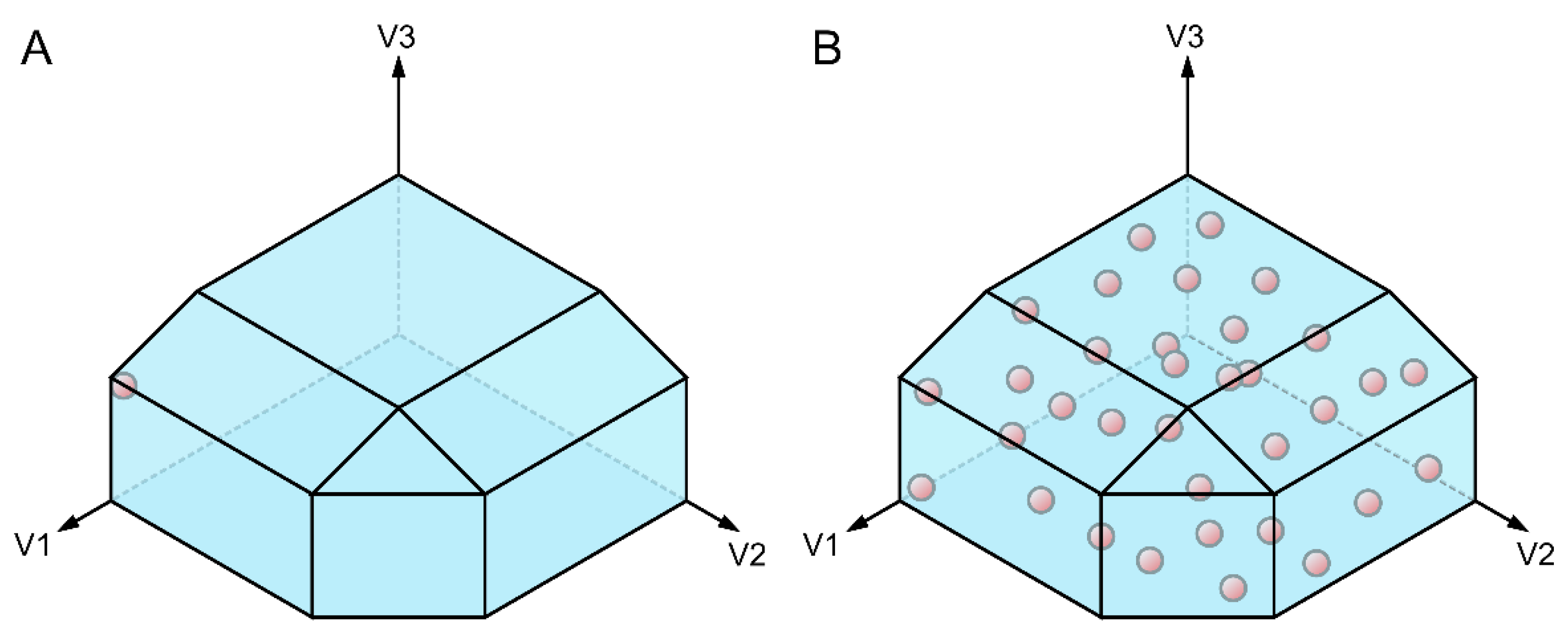
3.2.1. Non-Supervised Multivariate Analyses

Non-supervised multivariate analyses are a good way of visualizing the structure of the dataset. In metabolomics, the most used method within this category is principal component analysis (PCA). PCA rotates the data in the multidimensional space determined by the variables, bringing the data to a new coordinate system where the variance is maximized across its axis (the principal components). The typical graphical representation of the PCA is the score plot, which is a scatterplot of the sample values for the two first components, which contain most of the variance of the dataset. With this representation it is possible to see the clustering of the samples according to their metabolite abundances, which ideally would correspond to the biological factors of interest, if variation between the samples sharing the same phenotype is smaller enough compared to the variation between samples belonging to different biological groups [69]. It is also common to overlay vectors of the loadings of the represented principal components of some or all of the variables used in the PCA, as loadings reflect the contribution of each variable to the correspondent principal component. This combination is designated as biplot (Figure 1A). It is also common to represent the amount of variance included in the sorted principal components as a barplot (Scree plot, Figure 1B).
Another commonly used non-supervised multivariate approach is hierarchical clustering analysis (HCA). Here a determined distance metric, usually Euclidean distance, is obtained between pairs of samples and the samples are iteratively aggregated into clusters, according to a criterion determined by the linkage method. In metabolomics HCA is usually represented graphically in heatmaps, where metabolites are clustered vertically, and samples horizontally, resulting in a row dendrogram and a column dendrogram, usually containing the metabolites and the samples, respectively, and a tile plot in between where the colors reflect metabolite abundance (Figure 1C). With this visual representation it is possible to easily visualize groups of samples that have similar metabolic profiles, and groups of metabolites that have similar abundance patterns across groups of samples, which could reveal alterations in metabolic pathways correlated with sample grouping.
PCA score plot has the advantage that, as only two principal components are represented, which contain most of the variance of the variables, low correlated information is filtered out. Therefore, PCA plots usually give a cleaner representation of the groups. However, this can come as a disadvantage when there is biologically relevant information included in principal components other than the two represented in the score plot. In the HCA heatmap, on the other hand, all the information of the dataset is included, which makes it easier to visualize the influence of the variables over the sample aggregation but causes the grouping to be noisier. Another disadvantage of the HCA is that it will always output some grouping, despite the existence (or not) of any pattern. PCA score plot, on the contrary, would display in this situation a sparse cloud pattern, where all the samples appear distributed without any structure in the bidimensional space.
An approach to assess the stability of the observed grouping using HCA is consensus clustering, where several iterations of the clustering algorithm are performed, excluding a random number of samples on each round. This method needs previous indication of the number of groups (k) the samples are being clustered in. In order to determine what is the number of significant groups, different ks are tested and for each k a consensus matrix is obtained. This consensus matrix indicates for each pair of samples how many times they were clustered together divided by how many times they were selected together. Ideally this matrix would be composed by zeros and ones. By determining how far is the obtained consensus matrix from the ideal one the optimal number of clusters can be obtained. This can be done by comparing the CDF (Cumulative Distribution Function) curves of each k. The original metric used for this comparison is the delta K, which is the relative change in the area under the curve. However, the Proportion of Ambiguous clustering (PAC) has been shown to outperform delta K [70]. PAC quantifies the proportion of pairs of samples that fall in the middle segment of each CDF curve, which indicates that they cluster ambiguously. PAC is computed by substracting CDFk(u1) to CDFk(u2), being the u1 and u2 commonly used 0.1 and 0.9, respectively. With both metrics the ‘elbow’ method is the most commonly used to select the best k. This approach is, however, rather subjective, so different alternatives have been proposed in order to determine the number of significant clusters more objectively. An example is the M3C method, which computes a p-value based on a null distribution obtained by applying consenus clustering on random-generated datasets, which have the same feature correlation structure as the original dataset, but do not present clustering [71].
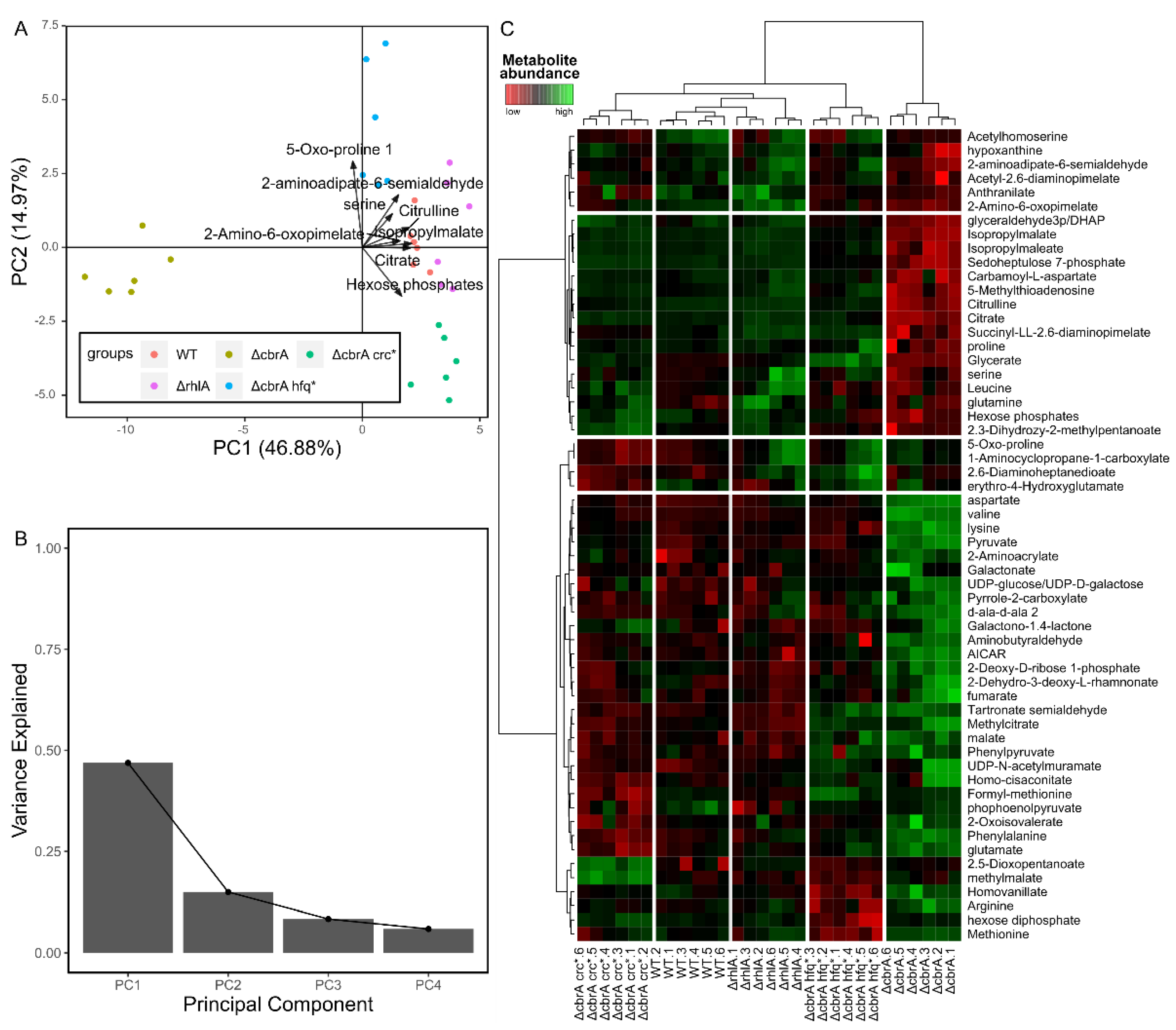
Preprints 98449 g001
Figure 1. Graphical outputs of a selection of unsupervised multivariate analyses. These plots were obtained using the metabolomic dataset included in the work by Boyle et al. from 2017 [72], obtained from different P. aeruginosa mutants. (A,B). Principal component analysis (PCA). A. PCA biplot, with the loadings of the top 8 metabolites that most contribute to the two first components overlayed. (B). Scree plot of the four first components, showing the variance of the data explained by them. (C). Heatmap of two hierarchical clustering analysis sample and metabolite-wise. The color gradient indicates metabolite abundance.
Figure 1. Graphical outputs of a selection of unsupervised multivariate analyses. These plots were obtained using the metabolomic dataset included in the work by Boyle et al. from 2017 [72], obtained from different P. aeruginosa mutants. (A,B). Principal component analysis (PCA). A. PCA biplot, with the loadings of the top 8 metabolites that most contribute to the two first components overlayed. (B). Scree plot of the four first components, showing the variance of the data explained by them. (C). Heatmap of two hierarchical clustering analysis sample and metabolite-wise. The color gradient indicates metabolite abundance.
Preprints 98449 g001
The unsupervised approaches described in this section can be applied easily both in R and Python programming languages. PCA and HCA can be computed using R’s base functions (prcomp() and hclust(), respectively), while in Python it is necessary to install scikit-learn library [73]. Both consensus clustering and M3C algorithm can be implemented in R using ConsensusClusterPlus and M3C packages, respectively [71,74]. Using these last two methods is, to our knowledge, more difficcult to do in Python, as there are just a couple of GitHub-released implementations of consensus clustering for python, and the authors of M3C method only released it as an R package.
Unsupervised multivariate approaches are usually used exploratively, with the aim of visualizing the underlying patterns hidden in the data. In cases where there is a great proportion of the total variance correlated with the studied phenotypic traits, unsupervised analysis can be sufficient for assessing what are the metabolic differences driving the separation. But if the data is structured but it is not possible to see a clear separation according to the biological factors, a supervised approach will be needed to determine if there are metabolic traits correlated with the phenotype, and to identify them.

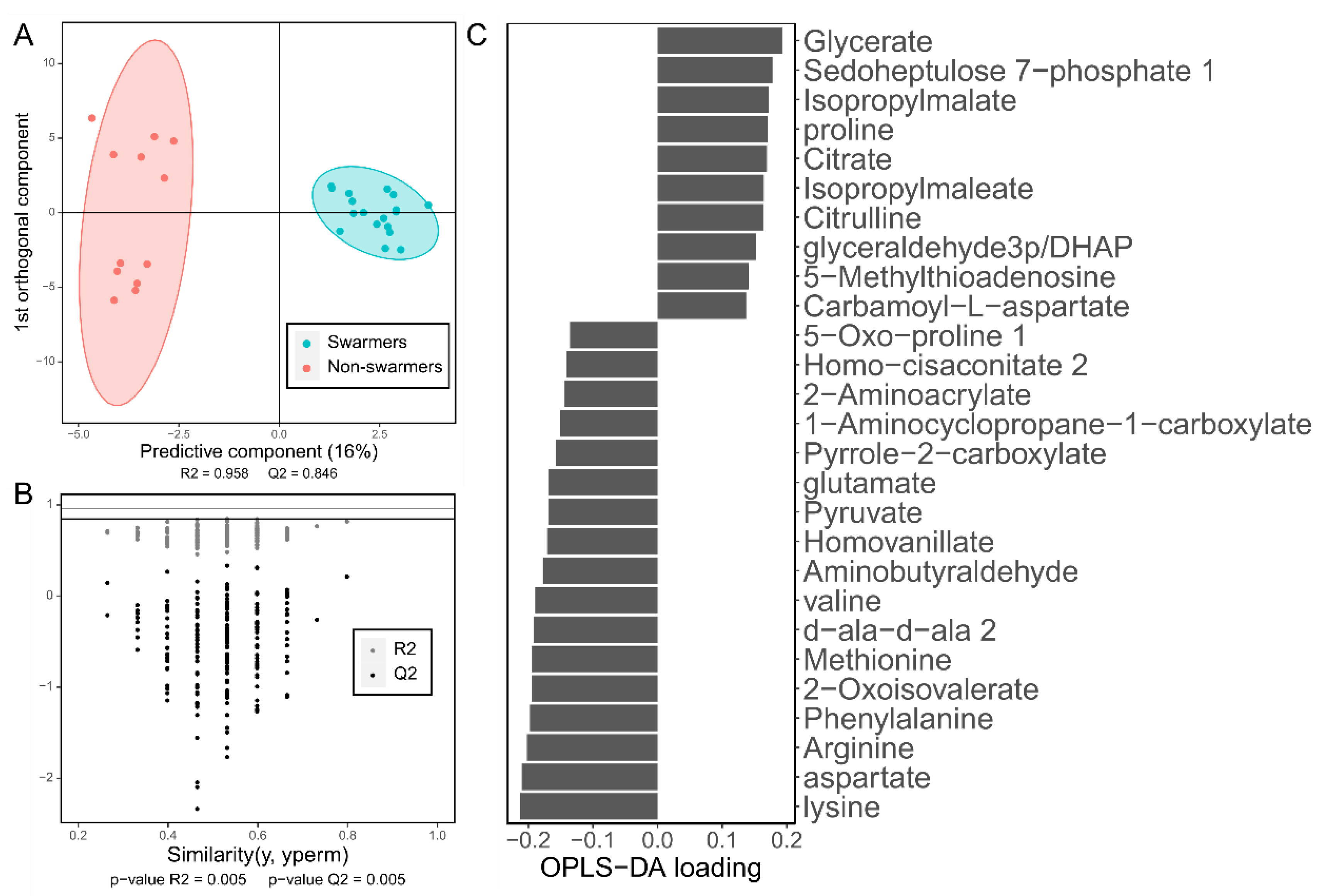
3.2.2. Supervised Multivariate Approaches

Supervised multivariate analysis methods are used to determine the strength of the correlation of the multiple variables with the phenotype of interest. Formally, univariate tests are supervised analyses, so many of the supervised multivariate analyses are univariate methods extended for multiple explanatory variables. Some examples of these methods are multiple linear regression (MLR), used when the phenotype to be explained is quantitative, or multiple logistic regression, used when the phenotype is categorical, with only two groups. Multinomial logistic regression can be used when there are more than two categories. For MLR the significance of the full model can be obtained by the p-value computed from the F-statistic, while the significance of the association of each one of the variables to the response is given by its t-statistic. Regarding logistic regression methods, as in simple logistic regression, the significance of each one of the variables is given by the Z-value obtained with a Wald test [66].
MLR and logistic regression work well when the predictor variables are uncorrelated, but when some of them are correlated (multicollinearity) they fail to explain their individual effects on the response variable. In metabolomic datasets, where typically there are a high number of predictors, and some of them are correlated because of their role in the same metabolic pathways, MLR might not be the best solution if the objective is to determine the association of the metabolite abundances to the phenotype. Partial least squares methods solve this problem, being widely used in metabolomics for this reason. These methods include Partial Least Squares (PLS), Partial Least Squares Discriminant Analysis (PLS-DA), Orthogonal Partial Least Squares (OPLS) and Orthogonal Partial Least Squares Discriminant Analysis (OPLS-DA) [75,76]. PLS solve the multicollinearity by reducing the dimension of the data, projecting the variables to a lower dimension space that maximizes the covariance with the response variable. OPLS goes one step further by separating the variability that is correlated to the response variable and the variability that is orthogonal to it, making easier the interpretation of the influence of each individual variable on the response variable, but not improving the overall model results. PLS-DA and OPLS-DA are versions of the methods intended to work with discrete binary response variables, but their foundations are the same as the ones of their continuous counterparts. The significance of the metabolites in the separation of the samples according to the response variable can be determined by the variable importance in projection (VIP). This statistic is defined as the weighted sum of squares of the PLS weight, reflecting the importance of the variable to the entire model [77]. The common threshold to consider a variable significant is VIP ≥ 1 [78,79,80].
The drawback of the PLS methods is that they are prone to overfitting. To solve this obstacle a good approach is to split the dataset in training and testing subsets and assess if the performance of the model in the testing set is significantly different than in the training set. R2 and Q2 can be used for this aim. R2, as in linear regression, indicates the proportion of the variation in the response explained by the model. Q2 refers to the R2 obtained with the testing set. If the model is not overfitting R2 should be high and Q2 should be slightly smaller than R2, but not very different. However, because of the time-consuming nature of metabolomics sample acquisition, the number of samples is not always high enough to be able to split the dataset and still have an appropriate number of samples. An alternative to this approach is to use label permutation and cross validation [81]. In cross validation the dataset is split into several sample subsets, the model is fitted to all the combined subsets except for one and is tested in the left-out subset. This process is repeated until all the subsets have been used as a testing set. This allows to have R2 and Q2 values while keeping all the samples for the analysis. In permutation test the responses variables are randomly permutated between samples, a model is fitted to the altered dataset and R2 and Q2 are computed, comparing the values to the ones of the actual model. If the model is overfitting, the permutated model might have a higher R2 or Q2 just by chance. Several permutation rounds are carried out, obtaining a p-value based on the proportion of R2 of permutated sets higher than the actual R2. Another p-value is obtained analogously for Q2. Some useful graphical representations for OPLS and OPLS-DA models are the score plot of the predictive and first orthogonal components (Figure 2A), the scatterplot of the R2 and Q2 values obtained before and after label permutation (Figure 2B) or the barplot of each metabolite’s loading for the predictor component (Figure 2C). These plots allow to visualize how well the model is separating the samples, if the model is statistically significant and the contribution of each metabolite to the separation of the samples according to the response variable, respectively.
Another multivariate supervised method useful in omics analysis is a random forest, which is less prone to overfitting in comparison with PLS methods. A random forest is based on the decision tree method. Decision trees iteratively select the variable that best splits the data in two subsets, according to a threshold that maximizes that separation (i.e., minimize the sum of the squared residuals)[82]. At the end the samples have been separated according to similar values of the response variable. They can be used with discrete or continuous response and predictor variables (although in metabolomics predictors will be always continuous). Decision trees that work with continuous response variables are denominated regression trees, while when the response variable is discrete, they are called classification trees [82]. Decision trees are very prone to overfitting, so random forests come as a solution to this problem [83]. In random forests, instead of fitting a single tree, an ensemble of trees is fitted to randomly generated subsets of the total samples, and a random subset of the total number of predictor variables (sample and variable bagging, respectively) with the aim of making each tree in the ensemble as uncorrelated to each other as possible [84,85]. The results of each tree are aggregated by either averaging (in case of regression trees) or majority vote (in the case of classification trees) for obtaining the global results [86]. The resulting model can be interrogated to obtain the importance of each variable in the prediction of the outcome by permuting the values of each variable and computing how much the accuracy of the resulting model decreases [83].
Linear and logistic regression models can be implemented using glm function in R, while for Python scikit learn library is the best option [73]. Multinomial logistic regression can be implemented in R using nnet R package [87], and some options for implementing the PLS methods described in this section are ropls and pls R packages [88,89], and scikit-learn library and pyopls module for Python [73,90]. Regarding random forests, they can be implemented in R using caret and randomForest R packages [91,92], and in Python with scikit-learn [73].

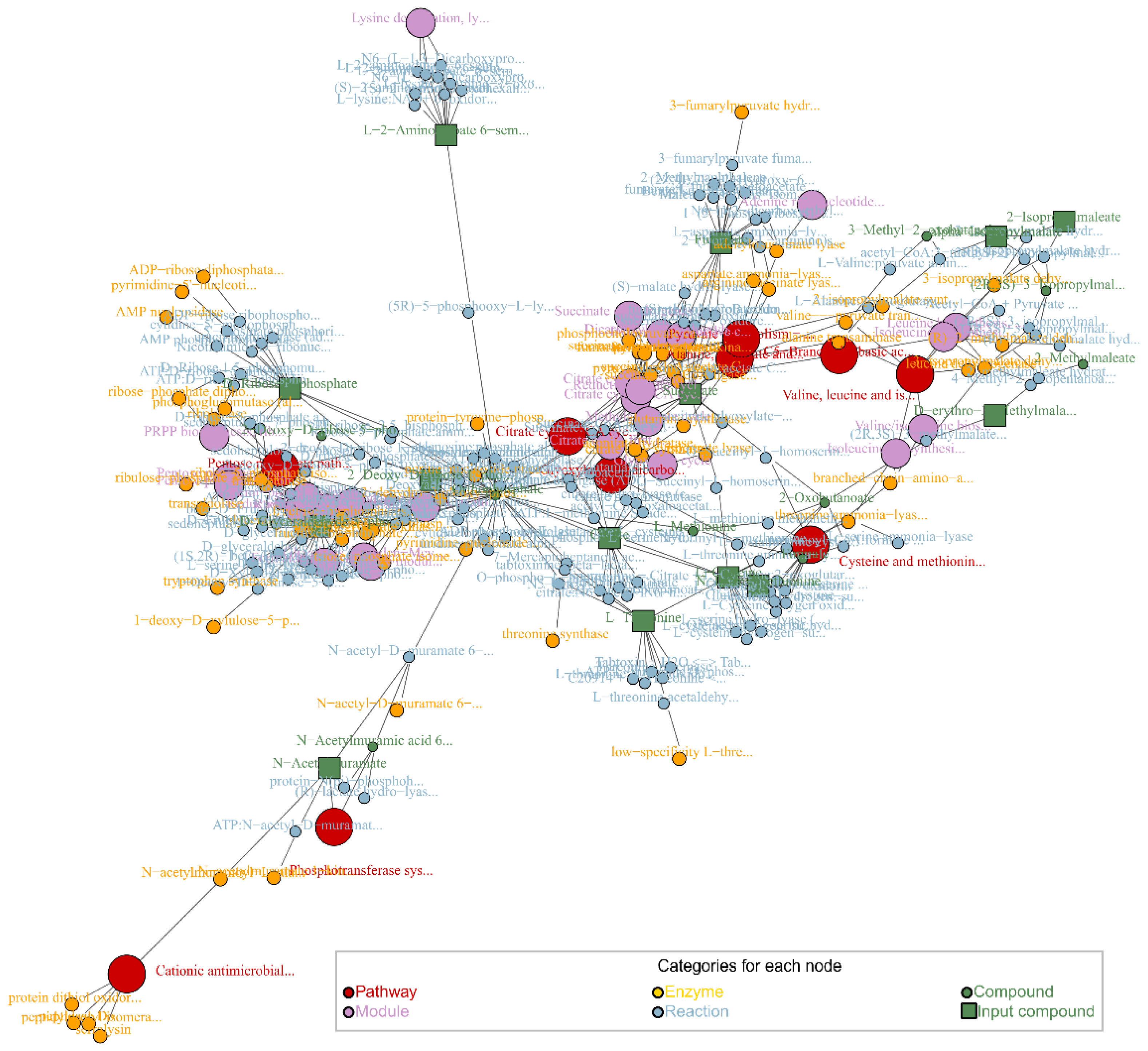
4. Metabolic Pathway Enrichment

Once the set of metabolites significatively associated with the phenotype(s) of interest is known, it is important to determine which are the metabolic subsystems that are more likely to be perturbed in order to gain biological insight. This process is known as metabolic pathway enrichment. Pathway enrichment methods, as other computational tools used in metabolomics, were inherited from transcriptomics and proteomics. The different metabolic pathway enrichment methods can be divided in three different groups: over-representation analysis (ORA), functional class scoring (FCS) and pathway topology (PT) [93].

4.1. Over-Representation Analysis (ORA)

ORA is the simplest approach for performing metabolic pathway enrichment. It relies on statistical tests that determine what metabolic pathways have more metabolites with significantly altered abundances than the ones that could be expected by chance. This is accomplished, for each metabolic pathway, by building a 2x2 table containing the number of statistically significant metabolites that are included in the pathway, as well as the number of statistically significant metabolites not included in it, the number of metabolites in the pathway that are not statistically significant and the number of metabolites not in the pathway that are not statistically significant. This table is used to determine if there is over-representation in the metabolic pathway, usually using tests based in hypergeometric, chi-square or binomial distributions [94].
Among ORA’s advantages are its simplicity, the ease of implementation and has its fast computation time. However, it also has several limitations, among them that it does not account for the actual metabolite abundances, instead cataloguing the metabolites as differential by applying a threshold to a determined statistic and discarding the ones that do not pass the threshold, therefore implying information loss. It also does not take into account the interactions of the metabolites within the metabolic network, which implies that alterations in anyone of the metabolites within a pathway have the same effect on it. It also considers metabolic pathways as independent isolated compartments, which is not the case [93].
ORA can be easily implemented directly in any programming language with statistical capabilities such as R or Python, and it is available as prebuilt functions in R packages such as clusterProfiler [95].

4.2. Functional Class Scoring (FCS)

FCS tries to improve the information loss limitation ORA implies by using the actual metabolite abundances of the whole dataset, without applying any statistic-based threshold. The hypothesis supporting this approach is that small but coordinated changes in several metabolites belonging to the same pathway can produce observable differences [93]. There are two types of FCS methods: univariate and multivariate FCS methods [96]. In univariate FCS methods a score is computed for each individual metabolite based on correlation with the studied biological factor, for later integrating them in a single score for each set of metabolites (metabolic pathway), while in multivariate FCS methods the score is directly computed for each pathway [96]. The pathway scores are tested for significance by using a null hypothesis either by permuting the phenotypes or the metabolites [93].
FCS methods do not solve all the ORA limitations, still considering each metabolic pathway as an independent unit and not considering the position of metabolites within the metabolic network.
MSEA, the metabolomics version of GSEA (an FCS univariate method intended to be used with transcriptomic data) [97], can be implemented in metaboAnalyst web server and the R package version metaboAnalystR [98,99]. mPLAGE, the metabolomics-adapted version of PLAGE (pathway level analysis of gene expression), is another FCS method that is implemented in Python within the PALS library, which is also available as a web application (https://pals.glasgowcompbio.org/app/) and as a standalone program [100,101].

4.3. Pathway Topology (PT)

PT methods take advantage of the fact that databases such as KEGG provide information about the interaction between different elements of the metabolic network, building a graph accounting for all the relationships, and using it for determining how likely it is that differences in abundances in given metabolites affect certain metabolic pathways. There are different approaches that take into account the metabolic network, each of them with its own limitations. Some examples of these methods are NetGSA, FELLA and DEGraph, which can be implemented in netgsa, FELLA and DEGraph R packages, respectively [102,103,104,105]. NetGSA uses a graph based on the interaction between the different elements of the metabolic network, which must be provided by the user as an adjacency matrix. With this network it calculates the influence of the concentration of each metabolite to the rest of them. It then uses this propagation to decompose the reads of the abundance of each metabolite in baseline level and propagated signal through its neighbors. With these values it then computes a statistic for each pathway to determine if the pathway is potentially perturbed [102]. FELLA retrieves a graph consisting of the interconnections between the different entries existing in KEGG database for a given organism for latter applying network propagation algorithms on it using as input differentially abundant metabolites, yielding a subnetwork of entries with a high probability of receiving propagated signals from the input metabolites, meaning that they are highly interconnected [104] (Figure 3). DEGraph compares two conditions by using the same interconnected graph, which can be downloaded from KEGG using DEGraph R package. It uses a Hotelling T2 test on a lower dimension space built from the graph to determine the significance of subnetworks (pathways) within the graph [105].

5. Generating Insight when Metabolomic Data Is Not Available: Genome-Scale Metabolic Models

There are some cases where the acquisition of intracellular metabolomics data is challenging, such as during infection of animal or cellular models with intracellular pathogens like Mycobacterium tuberculosis or Legionella pneumophilla [106]. In this situation the recovery of the bacteria from within the infected cells at sufficient biomass amounts without perturbing the metabolic state of the bacteria makes the obtention of metabolomic data virtually impossible. A suitable alternative to evaluate how differences of genomic content translate into distinct metabolic phenotypes can be the use of genome scale metabolic models (GEMs). GEMs are representations of the metabolic capabilities of an organism, based on its genomic content [107]. They have been used with success to predict the growth rate of an organism in a particular medium composition, gene essentiality, production of virulence factors or response to stresses in different microorganisms [108,109]. GEM reconstruction typically starts with the genome annotation of the organism to be modelled, from which the reactions that the organism is capable of catalyzing are inferred. With these reactions a draft metabolic network is automatically built, accounting for the constraints imposed by reaction stoichiometry. Later, further constraints based on experimental data are applied, such as compartmentalization of reactions and compounds, measured intake and secretion rates of metabolic compounds and biomass composition, integrated in a special reaction denominated biomass reaction, which represents the specific growth rate [110]. The obtained metabolic network will contain some gaps due to incompleteness and mistakes in the annotation and promiscuous enzymes that catalyze reactions that are not accounted for, which will need to be filled. This step is preferred to be carried out manually [111].
Once the metabolic network is complete, the rate of change of each metabolite concentration can be represented as:
d C d t = S v
Being C a vector of metabolite concentrations, S the stoichiometric matrix, with each row representing a metabolite and each column a reaction, being the matrix elements the stoichiometric coefficients of each metabolite relatively to each reaction (positive if the metabolite is produced, negative if it is consumed, zero if does not intervene in the reaction), and v the vector of reaction rates or fluxes [112]. As the metabolic reactions occur at a much shorter time scale than biomass growth, the system is assumed to be in stationary state, so:
0 = S v
This system of equations will be under-determined, as the number of reactions is higher than the number of metabolites for known metabolic networks. So, rather than giving a single solution of reaction fluxes for a particular medium composition, the GEM will delimit a multidimensional space containing all the metabolic states the model predicts to be possible in the specified conditions [110]. For obtaining particular solutions there are different approaches available. The first one is flux balance analysis (FBA), which consists in maximizing, or in some cases minimizing, at least one objective reaction [113]. Usually, objective reactions are biomass and/or ATP production maximization, and/or minimization of the total flux through the metabolic network [114,115]. With FBA a flux distribution in the edge of the solution space is obtained, under the assumption that a set of objective functions is at its maximum (Figure 4A). But in some situations, this assumption might not be adequate: in many natural environments, where nutrients are not abundant, the organisms prioritize global robustness against a wider range of stresses rather than in maximizing few objectives such as energy production or growth rate [114]. Some examples of this situation are M. tuberculosis macrophage infectious process, where bacteria diverts several resources to counteract the stresses imposed by the host [116], rhamnolipid production of Pseudomonas aeruginosa induced by high density bacterial population, where this microorganism secretes vast amounts of carbon-rich resources to the extracellular medium instead of using them for growth [117], or during adaptation to different temperatures in Arabidopsis thaliana, where this plant prioritizes the reallocation of metabolic resources to adapt to the new conditions [118]. In such situations a suitable alternative that allows to examine flux distributions without introducing any bias by the researchers is flux sampling. It consists in taking random samples of the solution space imposed by the model’s constraints (Figure 4B). If the number of samples is large enough it is possible to get an idea of the shape of the solution space [119], being then able to make comparisons between the sampled flux distributions of model versions reflecting different genotypes or conditions [106].
With GEMs and FBA and/or flux sampling it is possible to obtain a flux matrix for different genotypes or conditions, which can be considered as analogous to the imputed and normalized metabolite matrix obtained in Section 2. The statistical analyses and the pathway enrichment methods depicted in Section 3 and Section 4 can be used to determine, for example, what are the metabolic pathways more likely to be affected by genomic differences between different bacterial strains when intracellular metabolome data is not available [106].

6. Conclusions

Metabolomics is an emerging field with promising perspectives in several life-science disciplines [120]. As such, there is not a go-to procedure of how to deal with the computational analysis of these data as in other omic disciplines, for example in genomics or transcriptomics. In this review we managed to put together the most commonly applied approaches, suggesting a typical metabolomic bioinformatic workflow to be carried out after the raw data is acquired, either with LC-MS, GC-MS or NMR, and annotated. We divided the process in three main modules, namely data preprocessing, statistical analyses, and metabolic pathway enrichment, and displayed some of the most popular approaches for tackling these steps, indicating state-of-the-art tools that can be used by the reader for this aim. We schematized the steps to be performed in Figure 5. This workflow is intended to be used as a comprehensive guide, advancing the difficulties that can arise in each step of the bioinformatic analysis and highlighting the advantages of the presented methods, as well as their drawbacks. We introduced, as an alternative for the acquisition of intracellular metabolomics data in cases when it is not possible, the use of GEMs to generate metabolomic-like data that can be used to determine how differences at a genomic level can translate in metabolic discrepancies, taking into account the whole metabolic network [106]. If there is not available intracellular metabolomic data but it is possible to take measurements of the exchange compound rates of the extracellular metabolites, it is possible to further constrain these models, being possible to infer the metabolic phenotype across different environmental situations or individuals of the same species [118,121].

Author Contributions

G.S and F.R.P. conceptualized the review, G.S. performed the literature search and the data analysis, and wrote the original manuscript. G.S. and F.R.P. edited the manuscript.

Funding

G.S. is recipient of a fellowship from BioSys PhD programme PD65-2012 (Ref SFRH/BD/142899/2018) from FCT (Portugal). Work partially supported by UIDB/04046/2020 and UIDP/04046/2020 Research Unit grants from FCT, Portugal (to BioISI). The funders had no role in the preparation of the manuscript neither the decision to publish.

Institutional Review Board Statement

Not applicable

Informed Consent Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Oliver, S.G.; Winson, M.K.; Kell, D.B.; Baganz, F. Systematic Functional Analysis of the Yeast Genome. Trends Biotechnol. 1998, 16, 373–378. [Google Scholar] [CrossRef]
  2. Fiehn, O. Metabolomics – the Link between Genotypes and Phenotypes. Plant Mol. Biol. 2002, 48, 155–171. [Google Scholar] [CrossRef]
  3. Marian, A.J. Molecular Genetic Studies of Complex Phenotypes. Transl. Res. 2012, 159, 64–79. [Google Scholar] [CrossRef]
  4. Zulianello, L.; Canard, C.; Köhler, T.; Caille, D.; Lacroix, J.S.; Meda, P. Rhamnolipids Are Virulence Factors That Promote Early Infiltration of Primary Human Airway Epithelia by Pseudomonas Aeruginosa. Infect. Immun. 2006, 74, 3134–3147. [Google Scholar] [CrossRef]
  5. Davey, M.E.; Caiazza, N.C.; O’Toole, G.A. Rhamnolipid Surfactant Production Affects Biofilm Architecture in Pseudomonas Aeruginosa PAO1. J. Bacteriol. 2003, 185, 1027–1036. [Google Scholar] [CrossRef]
  6. Caiazza, N.C.; Shanks, R.M.Q.; O’Toole, G.A. Rhamnolipids Modulate Swarming Motility Patterns of Pseudomonas Aeruginosa. J. Bacteriol. 2005, 187, 7351–7361. [Google Scholar] [CrossRef] [PubMed]
  7. Sabra, W.; Kim, E.J.; Zeng, A.P. Physiological Responses of Pseudomonas Aeruginosa PAO1 to Oxidative Stress in Controlled Microaerobic and Aerobic Cultures. Microbiology 2002, 148, 3195–3202. [Google Scholar] [CrossRef]
  8. Mukhopadhyay, S.; Nair, S.; Ghosh, S. Pathogenesis in Tuberculosis: Transcriptomic Approaches to Unraveling Virulence Mechanisms and Finding New Drug Targets. FEMS Microbiol. Rev. 2012, 36, 463–485. [Google Scholar] [CrossRef] [PubMed]
  9. Galagan, J.E.; Minch, K.; Peterson, M.; Lyubetskaya, A.; Azizi, E.; Sweet, L.; Gomes, A.; Rustad, T.; Dolganov, G.; Glotova, I.; et al. The Mycobacterium Tuberculosis Regulatory Network and Hypoxia. Nature 2013, 499, 178–183. [Google Scholar] [CrossRef] [PubMed]
  10. Raghunandanan, S.; Jose, L.; Gopinath, V.; Kumar, R.A. Comparative Label-Free Lipidomic Analysis of Mycobacterium Tuberculosis during Dormancy and Reactivation. Sci. Rep. 2019, 9, 1–12. [Google Scholar] [CrossRef] [PubMed]
  11. Ye, D.; Li, X.; Shen, J.; Xia, X. Microbial Metabolomics: From Novel Technologies to Diversified Applications. TrAC - Trends Anal. Chem. 2022, 148, 116540. [Google Scholar] [CrossRef]
  12. Emwas, A.H.; Roy, R.; McKay, R.T.; Tenori, L.; Saccenti, E.; Nagana Gowda, G.A.; Raftery, D.; Alahmari, F.; Jaremko, L.; Jaremko, M.; et al. Nmr Spectroscopy for Metabolomics Research. Metabolites 2019, 9. [Google Scholar] [CrossRef]
  13. Lu, H.; Liang, Y.; Dunn, W.B.; Shen, H.; Kell, D.B. Comparative Evaluation of Software for Deconvolution of Metabolomics Data Based on GC-TOF-MS. TrAC - Trends Anal. Chem. 2008, 27, 215–227. [Google Scholar] [CrossRef]
  14. Oliver Fiehn Metabolomics by Gas Chromatography-Mass Spectrometry: The Combination of Targeted and Untargeted Profiling; 2017; Vol. 7; ISBN 0471142727.
  15. Perez, E.R.; Knapp, J.A.; Horn, C.K.; Stillman, S.L.; Evans, J.E.; Arfsten, D.P. Comparison of LC-MS-MS and GC-MS Analysis of Benzodiazepine Compounds Included in the Drug Demand Reduction Urinalysis Program. J. Anal. Toxicol. 2016, 40, 201–207. [Google Scholar] [CrossRef]
  16. Chen, C.; Gonzalez, F.J.; Idle, J.R. LC-MS-Based Metabolomics in Drug Metabolism. Drug Metab. Rev. 2007, 39, 581–597. [Google Scholar] [CrossRef]
  17. Johnson, C.H.; Ivanisevic, J.; Benton, H.P.; Siuzdak, G. Bioinformatics: The next Frontier of Metabolomics. Anal. Chem. 2015, 87, 147–156. [Google Scholar] [CrossRef]
  18. Edison, A.S.; Colonna, M.; Gouveia, G.J.; Holderman, N.R.; Judge, M.T.; Shen, X.; Zhang, S. NMR: Unique Strengths That Enhance Modern Metabolomics Research. Anal. Chem. 2021, 93, 478–499. [Google Scholar] [CrossRef]
  19. Karaman, I.; Climaco Pinto, R.; Graça, G. Metabolomics Data Preprocessing: From Raw Data to Features for Statistical Analysis. Compr. Anal. Chem. 2018, 82, 197–225. [Google Scholar] [CrossRef]
  20. Alonso, A.; Marsal, S.; Julià, A. Analytical Methods in Untargeted Metabolomics: State of the Art in 2015. Front. Bioeng. Biotechnol. 2015, 3, 1–23. [Google Scholar] [CrossRef] [PubMed]
  21. Hrydziuszko, O.; Viant, M.R. Missing Values in Mass Spectrometry Based Metabolomics: An Undervalued Step in the Data Processing Pipeline. Metabolomics 2012, 8, S161–S174. [Google Scholar] [CrossRef]
  22. Barnard, J.; Meng, X.L. Applications of Multiple Imputation in Medical Studies: From AIDS to NHANES. Stat. Methods Med. Res. 1999, 8, 17–36. [Google Scholar] [CrossRef]
  23. Bijlsma, S.; Bobeldijk, I.; Verheij, E.R.; Ramaker, R.; Kochhar, S.; Macdonald, I.A.; Van Ommen, B.; Smilde, A.K. Large-Scale Human Metabolomics Studies: A Strategy for Data (Pre-) Processing and Validation. Anal. Chem. 2006, 78, 567–574. [Google Scholar] [CrossRef]
  24. Kokla, M.; Virtanen, J.; Kolehmainen, M.; Paananen, J.; Hanhineva, K. Random Forest-Based Imputation Outperforms Other Methods for Imputing LC-MS Metabolomics Data: A Comparative Study. BMC Bioinformatics 2019, 20, 492. [Google Scholar] [CrossRef] [PubMed]
  25. Hong, S.; Lynn, H.S. Accuracy of Random-Forest-Based Imputation of Missing Data in the Presence of Non-Normality, Non-Linearity, and Interaction. BMC Med. Res. Methodol. 2020, 20, 1–12. [Google Scholar] [CrossRef] [PubMed]
  26. Hu, L.Y.; Huang, M.W.; Ke, S.W.; Tsai, C.F. The Distance Function Effect on K-Nearest Neighbor Classification for Medical Datasets. Springerplus 2016, 5. [Google Scholar] [CrossRef] [PubMed]
  27. Kim, H.; Golub, G.H.; Park, H. Missing Value Estimation for DNA Microarray Gene Expression Data: Local Least Squares Imputation. Bioinformatics 2005, 21, 187–198. [Google Scholar] [CrossRef] [PubMed]
  28. Troyanskaya, O.; Cantor, M.; Sherlock, G.; Brown, P.; Hastie, T.; Tibshirani, R.; Botstein, D.; Altman, R.B. Missing Value Estimation Methods for DNA Microarrays. Bioinformatics 2001, 17, 520–525. [Google Scholar] [CrossRef] [PubMed]
  29. Oba, S.; Sato, M.A.; Takemasa, I.; Monden, M.; Matsubara, K.I.; Ishii, S. A Bayesian Missing Value Estimation Method for Gene Expression Profile Data. Bioinformatics 2003, 19, 2088–2096. [Google Scholar] [CrossRef] [PubMed]
  30. Ilin, A.; Raiko, T. Practical Approaches to Principal Component Analysis in the Presence of Missing Values. J. Mach. Learn. Res. 2010, 11, 1957–2000. [Google Scholar]
  31. Leek, J.T.; Scharpf, R.B.; Bravo, H.C.; Simcha, D.; Langmead, B.; Johnson, W.E.; Geman, D.; Baggerly, K.; Irizarry, R.A. Tackling the Widespread and Critical Impact of Batch Effects in High-Throughput Data. Nat. Rev. Genet. 2010, 11, 733–739. [Google Scholar] [CrossRef]
  32. Marioni, J.C.; Mason, C.E.; Mane, S.M.; Stephens, M.; Gilad, Y. RNA-Seq: An Assessment of Technical Reproducibility and Comparison with Gene Expression Arrays. Genome Res. 2008, 18, 1509–1517. [Google Scholar] [CrossRef]
  33. Karpievitch, Y. V.; Dabney, A.R.; Smith, R.D. Normalization and Missing Value Imputation for Label-Free LC-MS Analysis. BMC Bioinformatics 2012, 13, S5. [Google Scholar] [CrossRef] [PubMed]
  34. Vandesompele, J.; De Preter, K.; Pattyn, F.; Poppe, B.; Van Roy, N.; De Paepe, A.; Speleman, F. Accurate Normalization of Real-Time Quantitative RT-PCR Data by Geometric Averaging of Multiple Internal Control Genes. Rock Mech. Rock Eng. 2002, 3, research0034.1–research0034.11. [Google Scholar] [CrossRef] [PubMed]
  35. Wiśniewski, J.R.; Mann, M. A Proteomics Approach to the Protein Normalization Problem: Selection of Unvarying Proteins for MS-Based Proteomics and Western Blotting. J. Proteome Res. 2016, 15, 2321–2326. [Google Scholar] [CrossRef]
  36. Wu, Y.; Li, L. Sample Normalization Methods in Quantitative Metabolomics. J. Chromatogr. A 2016, 1430, 80–95. [Google Scholar] [CrossRef]
  37. Chen, J.; Zhang, P.; Lv, M.; Guo, H.; Huang, Y.; Zhang, Z.; Xu, F. Influences of Normalization Method on Biomarker Discovery in Gas Chromatography-Mass Spectrometry-Based Untargeted Metabolomics: What Should Be Considered? Anal. Chem. 2017, 89, 5342–5348. [Google Scholar] [CrossRef]
  38. Temmerman, L.; De Livera, A.M.; Browne, J.B.; Sheedy, J.R.; Callahan, D.L.; Nahid, A.; De Souza, D.P.; Schoofs, L.; Tull, D.L.; McConville, M.J.; et al. Cross-Platform Urine Metabolomics of Experimental Hyperglycemia in Type 2 Diabetes. J. Diabetes Metab. 2012, S6:002. [Google Scholar] [CrossRef]
  39. De Livera, A.M.; Sysi-Aho, M.; Jacob, L.; Gagnon-Bartsch, J.A.; Castillo, S.; Simpson, J.A.; Speed, T.P. Statistical Methods for Handling Unwanted Variation in Metabolomics Data. Ann. Chem. 2015, 87, 3606–3615. [Google Scholar] [CrossRef]
  40. Edmands, W.M.B.; Ferrari, P.; Scalbert, A. Normalization to Specific Gravity Prior to Analysis Improves Information Recovery from High Resolution Mass Spectrometry Metabolomic Profiles of Human Urine. Anal. Chem. 2014, 86, 10925–10931. [Google Scholar] [CrossRef]
  41. Marcinowska, R.; Trygg, J.; Wolf-Watz, H.; Mortiz, T.; Surowiec, I. Optimization of a Sample Preparation Method for the Metabolomic Analysis of Clinically Relevant Bacteria. J. Microbiol. Methods 2011, 87, 24–31. [Google Scholar] [CrossRef]
  42. Chen, Y.; Shen, G.; Zhang, R.; He, J.; Zhang, Y.; Xu, J.; Yang, W.; Chen, X.; Song, Y.; Abliz, Z. Combination of Injection Volume Calibration by Creatinine and MS Signals’ Normalization to Overcome Urine Variability in LC-MS-Based Metabolomics Studies. Anal. Chem. 2013, 85, 7659–7665. [Google Scholar] [CrossRef]
  43. De Livera, A.M.; Dias, D.A.; De Souza, D.; Rupasinghe, T.; Pyke, J.; Tull, D.; Roessner, U.; McConville, M.; Speed, T.P. Normalizing and Integrating Metabolomics Data. Anal. Chem. 2012, 84, 10768–10776. [Google Scholar] [CrossRef]
  44. Antonelli, J.; Claggett, B.L.; Henglin, M.; Kim, A.; Ovsak, G.; Kim, N.; Deng, K.; Rao, K.; Tyagi, O.; Watrous, J.D.; et al. Statistical Workflow for Feature Selection in Human Metabolomics Data. Metabolites 2019, 9, 1–15. [Google Scholar] [CrossRef]
  45. van den Berg, R.A.; Hoefsloot, H.C.J.; Westerhuis, J.A.; Smilde, A.K.; van der Werf, M.J. Centering, Scaling, and Transformations: Improving the Biological Information Content of Metabolomics Data. BMC Genomics 2006, 7, 1–15. [Google Scholar] [CrossRef] [PubMed]
  46. De Livera, A.M.; Olshansky, G.; Simpson, J.A.; Creek, D.J. NormalizeMets: Assessing, Selecting and Implementing Statistical Methods for Normalizing Metabolomics Data. Metabolomics 2018, 5, 1–5. [Google Scholar] [CrossRef] [PubMed]
  47. Sysi-Aho, M.; Katajamaa, M.; Yetukuri, L.; Orešič, M. Normalization Method for Metabolomics Data Using Optimal Selection of Multiple Internal Standards. BMC Bioinformatics 2007, 8, 93. [Google Scholar] [CrossRef]
  48. Grocholska, P.; Bachor, R. Trends in the Hydrogen−deuterium Exchange at the Carbon Centers. Preparation of Internal Standards for Quantitative Analysis by Lc-Ms. Molecules 2021, 26, 2969. [Google Scholar] [CrossRef] [PubMed]
  49. Gullberg, J.; Jonsson, P.; Nordström, A.; Sjöström, M.; Moritz, T. Design of Experiments: An Efficient Strategy to Identify Factors Influencing Extraction and Derivatization of Arabidopsis Thaliana Samples in Metabolomic Studies with Gas Chromatography/Mass Spectrometry. Anal. Biochem. 2004, 331, 283–295. [Google Scholar] [CrossRef]
  50. Liu, R.H.; Lin, D.L.; Chang, W.-T.; Liu, C.; Tsay, W.-I.; Li, J.-H.; Kuo, T.-L. Isotopically Labeled Analogues for Drug Quantitation. Anal. Chem. 2002, 74, 618A–626A. [Google Scholar] [CrossRef]
  51. Redestig, H.; Fukushima, A.; Stenlund, H.; Moritz, T.; Arita, M.; Saito, K.; Kusano, M. Compensation for Systematic Cross-Contribution Improves Normalization of Mass Spectrometry Based Metabolomics Data. Anal. Chem. 2009, 81, 7974–7980. [Google Scholar] [CrossRef]
  52. Gagnon-Bartsch, J.A.; Speed, T.P. Using Control Genes to Correct for Unwanted Variation in Microarray Data. Biostatistics 2012, 13, 539–552. [Google Scholar] [CrossRef]
  53. Santamaria, G.; Liao, C.; Lindberg, C.; Chen, Y.; Wang, Z.; Rhee, K.; Pinto, F.; Yan, J.; Xavier, J.B. Evolution and Regulation of Microbial Secondary Metabolism. Elife 2022, 1–64. [Google Scholar] [CrossRef]
  54. Dunn, W.B.; Broadhurst, D.; Begley, P.; Zelena, E.; Francis-Mcintyre, S.; Anderson, N.; Brown, M.; Knowles, J.D.; Halsall, A.; Haselden, J.N.; et al. Procedures for Large-Scale Metabolic Profiling of Serum and Plasma Using Gas Chromatography and Liquid Chromatography Coupled to Mass Spectrometry. Nat. Protoc. 2011, 6, 1060–1083. [Google Scholar] [CrossRef]
  55. Sangster, T.; Major, H.; Plumb, R.; Wilson, A.J.; Wilson, I.D. A Pragmatic and Readily Implemented Quality Control Strategy for HPLC-MS and GC-MS-Based Metabonomic Analysis. Analyst 2006, 131, 1075–1078. [Google Scholar] [CrossRef]
  56. Gika, H.G.; Theodoridis, G.A.; Wingate, J.E.; Wilson, I.D. Within-Day Reproducibility of an HPLC-MS-Based Method for Metabonomic Analysis: Application to Human Urine. J. Proteome Res. 2007, 6, 3291–3303. [Google Scholar] [CrossRef]
  57. Broadhurst, D.; Goodacre, R.; Reinke, S.N.; Kuligowski, J.; Wilson, I.D.; Lewis, M.R.; Dunn, W.B. Guidelines and Considerations for the Use of System Suitability and Quality Control Samples in Mass Spectrometry Assays Applied in Untargeted Clinical Metabolomic Studies. Metabolomics 2018, 14, 1–17. [Google Scholar] [CrossRef]
  58. Schiffman, C.; Petrick, L.; Perttula, K.; Yano, Y.; Carlsson, H.; Whitehead, T.; Metayer, C.; Hayes, J.; Rappaport, S.; Dudoit, S. Filtering Procedures for Untargeted Lc-Ms Metabolomics Data. BMC Bioinformatics 2019, 20, 1–10. [Google Scholar] [CrossRef]
  59. Begley, P.; Francis-McIntyre, S.; Dunn, W.B.; Broadhurst, D.I.; Halsall, A.; Tseng, A.; Knowles, J.; HUSERMET Consortium; Goodacre, R. ; Kell, D.B. Development and Performance of a Gas Chromatography-Time-of-Flight Mass Spectrometry Analysis for Large-Scale Nontargeted Metabolomic Studies of Human Serum. anal 2009, 81, 7038–7046. [Google Scholar] [CrossRef]
  60. Zelena, E.; Dunn, W.B.; Broadhurst, D.; Francis-McIntyre, S.; Carroll, K.M.; Begley, P.; O’Hagan, S.; Knowles, J.D.; Halsall, A.; HUSERMET Consortium; et al. Development of a Robust and Repeatable UPLC-MS Method for the Long-Term Metabolomic Study of Human Serum. Anal. Chem. 2009, 81, 1357–1364. [Google Scholar] [CrossRef] [PubMed]
  61. Rousseeuw, P.J. Silhouettes: A Graphical Aid to the Interpretation and Validation of Cluster Analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
  62. De Livera, A.M.; Olshansky, M.; Speed, T.P. Statistical Analysis of Metabolomics Data. In Metabolomics Tools for Natural Product Discovery; 2013; pp. 291–307. [Google Scholar]
  63. Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. Author Correction: SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 352. [Google Scholar] [CrossRef] [PubMed]
  64. Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
  65. Sokal, R.R.; Rohlf, F.J. Biometry. The Principles and Practice of Statistics in Biological Research.; Third Edit.; W. H. Freeman and Company: New York, 1995. [Google Scholar]
  66. Bewick, V.; Cheek, L.; Ball, J. Statistics Review 14: Logistic Regression. Crit. Care 2005, 9, 112–118. [Google Scholar] [CrossRef] [PubMed]
  67. Broadhurst, D.I.; Kell, D.B. Statistical Strategies for Avoiding False Discoveries in Metabolomics and Related Experiments. Metabolomics 2006, 2, 171–196. [Google Scholar] [CrossRef]
  68. Saccenti, E.; Hoefsloot, H.C.J.; Smilde, A.K.; Westerhuis, J.A.; Hendriks, M.M.W.B. Reflections on Univariate and Multivariate Analysis of Metabolomics Data. Metabolomics 2014, 10, 361–374. [Google Scholar] [CrossRef]
  69. Worley, B.; Powers, R. Multivariate Analysis in Metabolomics. Curr. Metabolomics 2013, 1, 92–107. [Google Scholar] [CrossRef]
  70. Şenbabaoğlu, Y.; Michailidis, G.; Li, J.Z. Critical Limitations of Consensus Clustering in Class Discovery. Sci. Rep. 2014, 4, 6207. [Google Scholar] [CrossRef]
  71. John, C.R.; David, W.; Russ, D.; Goldmann, K.; Ehrenstein, M.; Pitzalis, C.; Lewis, M.; Barnes, M. M3C: Monte Carlo Reference-Based Consensus Clustering. Sci. Rep. 2020, 10, 1816. [Google Scholar] [CrossRef]
  72. Boyle, K.E.; Monaco, H.T.; Deforet, M.; Yan, J.; Wang, Z.; Rhee, K.; Xavier, J.B. Metabolism and the Evolution of Social Behavior. Mol. Biol. Evol. 2017, 34, 2367–2379. [Google Scholar] [CrossRef]
  73. Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar] [CrossRef]
  74. Wilkerson, M.D.; Hayes, D.N. ConsensusClusterPlus : A Class Discovery Tool with Confidence Assessments and Item Tracking. Bioinformatics 2010, 26, 1572–1573. [Google Scholar] [CrossRef]
  75. Wold, S.; Sjöström, M.; Eriksson, L. PLS-Regression: A Basic Tool of Chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
  76. Trygg, J.; Wold, S. Orthogonal Projections to Latent Structures (O-PLS). J. Chemom. 2002, 16, 119–128. [Google Scholar] [CrossRef]
  77. Mehmood, T.; Liland, K.H.; Snipen, L.; Sæbø, S. A Review of Variable Selection Methods in Partial Least Squares Regression. Chemom. Intell. Lab. Syst. 2012, 118, 62–69. [Google Scholar] [CrossRef]
  78. Rizvi, A.; Shankar, A.; Chatterjee, A.; More, T.H.; Bose, T.; Dutta, A.; Balakrishnan, K.; Madugulla, L.; Rapole, S.; Mande, S.S.; et al. Rewiring of Metabolic Network in Mycobacterium Tuberculosis during Adaptation to Different Stresses. Front. Microbiol. 2019, 10, 1–16. [Google Scholar] [CrossRef] [PubMed]
  79. Feng, Q.; Liu, Z.; Zhong, S.; Li, R.; Xia, H.; Jie, Z.; Wen, B.; Chen, X.; Yan, W.; Fan, Y.; et al. Integrated Metabolomics and Metagenomics Analysis of Plasma and Urine Identified Microbial Metabolites Associated with Coronary Heart Disease. Sci. Rep. 2016, 6, 1–14. [Google Scholar] [CrossRef] [PubMed]
  80. Ma, X.; Chi, Y.H.; Niu, M.; Zhu, Y.; Zhao, Y.L.; Chen, Z.; Wang, J.B.; Zhang, C.E.; Li, J.Y.; Wang, L.F.; et al. Metabolomics Coupled with Multivariate Data and Pathway Analysis on Potential Biomarkers in Cholestasis and Intervention Effect of Paeonia Lactiflora Pall. Front. Pharmacol. 2016, 7, 1–12. [Google Scholar] [CrossRef] [PubMed]
  81. Szymańska, E.; Saccenti, E.; Smilde, A.K.; Westerhuis, J.A. Double-Check: Validation of Diagnostic Statistics for PLS-DA Models in Metabolomics Studies. Metabolomics 2012, 8, 3–16. [Google Scholar] [CrossRef] [PubMed]
  82. Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Chapman & Hall/CRC, 1984; ISBN 0412048418. [Google Scholar]
  83. Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
  84. Breiman, L. Bagging Predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
  85. Amit, Y.; Geman, D. Shape Quantization and Recognition with Randomized Trees. Neural Comput. 1997, 9, 1545–1588. [Google Scholar] [CrossRef]
  86. Devroye, L.; Lugosi, G. Consistency of Random Forests and Other Averaging Classifiers. J. Mach. Learn. Res. 2008, 9, 2015–2033. [Google Scholar] [CrossRef]
  87. Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S; Fourth edi.; Springer: New York, 2002. [Google Scholar]
  88. Thévenot, E.A.; Roux, A.; Xu, Y.; Ezan, E.; Junot, C. Analysis of the Human Adult Urinary Metabolome Variations with Age, Body Mass Index, and Gender by Implementing a Comprehensive Workflow for Univariate and OPLS Statistical Analyses. J. Proteome Res. 2015, 14, 3322–3335. [Google Scholar] [CrossRef]
  89. Mevik, B.-H.; Wehrens, R. The Pls Package: Principal Component and Partial Least Squares Regression in R. J. Stat. Softw. 2007, 18. [Google Scholar] [CrossRef]
  90. BiRG - Wright State University Pyopls. Available online: https://pypi.org/project/pyopls/.
  91. Kuhn, M. Building Predictive Models in R Using the Caret Package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
  92. Liaw, A.; Wiener, M. Classification and Regression by RandomForest. R News 2002, 2, 18–22. [Google Scholar] [CrossRef]
  93. Khatri, P.; Sirota, M.; Butte, A.J. Ten Years of Pathway Analysis: Current Approaches and Outstanding Challenges. PLoS Comput. Biol. 2012, 8. [Google Scholar] [CrossRef]
  94. Goeman, J.J.; Bühlmann, P. Analyzing Gene Expression Data in Terms of Gene Sets: Methodological Issues. Bioinformatics 2007, 23, 980–987. [Google Scholar] [CrossRef] [PubMed]
  95. Yu, G.; Wang, L.G.; Han, Y.; He, Q.Y. ClusterProfiler: An R Package for Comparing Biological Themes among Gene Clusters. Omi. A J. Integr. Biol. 2012, 16, 284–287. [Google Scholar] [CrossRef]
  96. Maleki, F.; Ovens, K.; Hogan, D.J.; Kusalik, A.J. Gene Set Analysis: Challenges, Opportunities, and Future Research. Front. Genet. 2020, 11, 1–16. [Google Scholar] [CrossRef]
  97. Mootha, V.K.; Lindgren, C.M.; Eriksson, K.F.; Subramanian, A.; Sihag, S.; Lehar, J.; Puigserver, P.; Carlsson, E.; Ridderstråle, M.; Laurila, E.; et al. PGC-1α-Responsive Genes Involved in Oxidative Phosphorylation Are Coordinately Downregulated in Human Diabetes. Nat. Genet. 2003, 34, 267–273. [Google Scholar] [CrossRef]
  98. Pang, Z.; Chong, J.; Zhou, G.; De Lima Morais, D.A.; Chang, L.; Barrette, M.; Gauthier, C.; Jacques, P.É.; Li, S.; Xia, J. MetaboAnalyst 5.0: Narrowing the Gap between Raw Spectra and Functional Insights. Nucleic Acids Res. 2021, 49, W388–W396. [Google Scholar] [CrossRef]
  99. Pang, Z.; Chong, J.; Li, S.; Xia, J. MetaboAnalystR 3.0: Toward an Optimized Workflow for Global Metabolomics. Metabolites 2020, 10, 186. [Google Scholar] [CrossRef]
  100. Tomfohr, J.; Lu, J.; Kepler, T.B. Pathway Level Analysis of Gene Expression Using Singular Value Decomposition. BMC Bioinformatics 2005, 6, 1–11. [Google Scholar] [CrossRef]
  101. McLuskey, K.; Wandy, J.; Vincent, I.; Hooft, J.J.J. va. der; Rogers, S.; Burgess, K.; Daly, R. Ranking Metabolite Sets by Their Activity Levels. Metabolites 2021, 11, 103. [Google Scholar] [CrossRef] [PubMed]
  102. Shojaie, A.; Michailidis, G. Analysis of Gene Sets Based on the Underlying Regulatory Network. J. Comput. Biol. 2009, 16, 407–426. [Google Scholar] [CrossRef] [PubMed]
  103. Hellstern, M.; Ma, J.; Yue, K.; Shojaie, A. Netgsa: Fast Computation and Interactive Visualization for Topology-Based Pathway Enrichment Analysis. PLoS Comput. Biol. 2021, 17, e1008979. [Google Scholar] [CrossRef] [PubMed]
  104. Picart-Armada, S.; Fernández-Albert, F.; Vinaixa, M.; Yanes, O.; Perera-Lluna, A. FELLA: An R Package to Enrich Metabolomics Data. BMC Bioinformatics 2018, 19, 538–546. [Google Scholar] [CrossRef] [PubMed]
  105. Jacob, L.; Neuvial, P.; Dudoit, S. More Power via Graph-Structured Tests for Differential Expression of Gene Networks. Ann. Appl. Stat. 2012, 6, 561–600. [Google Scholar] [CrossRef]
  106. Santamaria, G.; Ruiz-Rodríguez, P.; Renau-Mínguez, C.; Pinto, F.R.; Coscollá, M. In Silico Exploration of Mycobacterium Tuberculosis Metabolic Networks Shows Host-Associated Convergent Fluxomic Phenotypes. Biomolecules 2022, 376. [Google Scholar] [CrossRef]
  107. Baart, G.J.; Martens, D.E. Genome-Scale Metabolic Models: Reconstruction and Analysis. In Neisseria meningiditis: Advanced Methods and Protocols; Christodoulides, M., Ed.; Humana Press, 2011; pp. 107–126. [Google Scholar]
  108. Santamaria, G.; Liao, C.; Wang, Z.; Rhee, K.; Pinto, F.; Yan, J.; Xavier, J.B. Evolution and Regulation of Microbial Secondary Metabolism. bioRxiv 2021, 1–64. [Google Scholar] [CrossRef]
  109. Bartell, J.A.; Blazier, A.S.; Yen, P.; Thøgersen, J.C.; Jelsbak, L.; Goldberg, J.B.; Papin, J.A. Reconstruction of the Metabolic Network of Pseudomonas Aeruginosa to Interrogate Virulence Factor Synthesis. Nat. Commun. 2017, 8. [Google Scholar] [CrossRef] [PubMed]
  110. Edwards, J.S.; Palsson, B.O. Systems Properties of the Haemophilus Influenzae Rd Metabolic Genbotype. Mol. Biol. 1999, 274, 17410–17416. [Google Scholar]
  111. Karp, P.D.; Weaver, D.; Latendresse, M. How Accurate Is Automated Gap Filling of Metabolic Models ? 2018, 1–11.
  112. Palsson, B.Ø. Systems Biology: Properties of Reconstructed Networks; Cambridge University Press: Cambridge, 2006; ISBN 9780521859035. [Google Scholar]
  113. Varma, A.; Palsson, B.Ø. Metabolic Flux Balancing: Basic Concepts, Scientific and Practical Use. Nat. Biotechnol. 1994, 12, 994–998. [Google Scholar] [CrossRef]
  114. Feist, A.M.; Palsson, B.Ø. The Biomass Objective Function. Curr. Opin. Microbiol. 2010, 13, 344–349. [Google Scholar] [CrossRef]
  115. Schuetz, R.; Kuepfer, L.; Sauer, U. Systematic Evaluation of Objective Functions for Predicting Intracellular Fluxes in Escherichia Coli. Mol. Syst. Biol. 2007, 3. [Google Scholar] [CrossRef] [PubMed]
  116. Piddington, D.L.; Kashkouli, A.; Buchmeier, N.A. Growth of Mycobacterium Tuberculosis in a Defined Medium Is Very Restricted by Acid PH and Mg 2 Levels Mycobacterium Tuberculosis Grows within the Phagocytic Vacuoles of Macrophages, Where It Encounters a Moderately Acidic and Possibly Nutrient-Restricted. Infect. Immun. 2000, 68, 4518–4522. [Google Scholar] [CrossRef] [PubMed]
  117. Boyle, K.E.; Monaco, H.; van Ditmarsch, D.; Deforet, M.; Xavier, J.B. Integration of Metabolic and Quorum Sensing Signals Governing the Decision to Cooperate in a Bacterial Social Trait. PLoS Comput. Biol. 2015, 11, 1–26. [Google Scholar] [CrossRef] [PubMed]
  118. Herrmann, H.A.; Dyson, B.C.; Vass, L.; Johnson, G.N.; Schwartz, J.M. Flux Sampling Is a Powerful Tool to Study Metabolism under Changing Environmental Conditions. npj Syst. Biol. Appl. 2019, 5, 32. [Google Scholar] [CrossRef]
  119. Wiback, S.J.; Famili, I.; Greenberg, H.J.; Palsson, B. Monte Carlo Sampling Can Be Used to Determine the Size and Shape of the Steady-State Flux Space. J. Theor. Biol. 2004, 228, 437–447. [Google Scholar] [CrossRef]
  120. Wishart, D.S. Emerging Applications of Metabolomics in Drug Discovery and Precision Medicine. Nat. Rev. Drug Discov. 2016, 15, 473–484. [Google Scholar] [CrossRef] [PubMed]
  121. Øyås, O.; Borrell, S.; Trauner, A.; Zimmermann, M.; Feldmann, J.; Liphardt, T.; Gagneux, S.; Stelling, J.; Sauer, U.; Zampieri, M. Model-Based Integration of Genomics and Metabolomics Reveals SNP Functionality in Mycobacterium Tuberculosis. Proc. Natl. Acad. Sci. U. S. A. 2020, 117, 8494–8502. [Google Scholar] [CrossRef] [PubMed]
Preprints 98449 g002
Figure 2. Plots obtained from an OPLS-DA model. The OPLS-DA model was fitted on the metabolomic dataset included in the study by Boyle et al. 2017 [72], classifying the Pseuromonas aeruginosa clinical isolates as swarmers and non-swarmers (a collective motility phenotype P. aeruginosa displays). (A). Score plot of the predictive component and the first orthogonal component. Swarmers are indicated in blue, and non-swarmers in red. At the bottom of the plot the R2 value of the predictive component and the Q2 obtained with cross-validation are indicated. (B). Scatterplot of the R2 and Q2 values obtained with a permutation test (n = 200). Actual R2 values are indicated in gray, while Q2 are indicated in black. The respective horizontal lines represent actual R2 and Q2. At the bottom are the p-values of R2 and Q2, which are the proportion of permutated values that are higher or equal than the actual values. The similarity between the response variable value and the permutated response variable is represented in the X axis. (C). Barplot of the loadings for the predictive component of the metabolites that were determined as statistically significant by the OPLS-DA model, by having a variable importance in the projection (VIP) higher or equal than 1. The metabolites with a negative loading are at higher abundance in non-swarmers, while the ones with a positive value are at higher abundance in swarmers.
Figure 2. Plots obtained from an OPLS-DA model. The OPLS-DA model was fitted on the metabolomic dataset included in the study by Boyle et al. 2017 [72], classifying the Pseuromonas aeruginosa clinical isolates as swarmers and non-swarmers (a collective motility phenotype P. aeruginosa displays). (A). Score plot of the predictive component and the first orthogonal component. Swarmers are indicated in blue, and non-swarmers in red. At the bottom of the plot the R2 value of the predictive component and the Q2 obtained with cross-validation are indicated. (B). Scatterplot of the R2 and Q2 values obtained with a permutation test (n = 200). Actual R2 values are indicated in gray, while Q2 are indicated in black. The respective horizontal lines represent actual R2 and Q2. At the bottom are the p-values of R2 and Q2, which are the proportion of permutated values that are higher or equal than the actual values. The similarity between the response variable value and the permutated response variable is represented in the X axis. (C). Barplot of the loadings for the predictive component of the metabolites that were determined as statistically significant by the OPLS-DA model, by having a variable importance in the projection (VIP) higher or equal than 1. The metabolites with a negative loading are at higher abundance in non-swarmers, while the ones with a positive value are at higher abundance in swarmers.
Preprints 98449 g002
Preprints 98449 g003
Figure 3. Example of pathway enrichment graph obtained by FELLA. The graph depicted here includes all the KEGG entries with a high probability of receiving propagated signal from the differential metabolites, represented as green squares. The category of each KEGG entry is represented with a color. These results can be printed out as a table of p-values too.
Figure 3. Example of pathway enrichment graph obtained by FELLA. The graph depicted here includes all the KEGG entries with a high probability of receiving propagated signal from the differential metabolites, represented as green squares. The category of each KEGG entry is represented with a color. These results can be printed out as a table of p-values too.
Preprints 98449 g003
Preprints 98449 g004
Figure 4. Graphical 3D representation of flux distribution obtention methods. The three axes represent the values of the three variables in our simplification: the flux for each of the three reactions. The constraints the model determines delimit the solution space, which is represented as the blue polyhedron. The red spheres represent a feasible solution of the solution space. (A). In flux balance analysis (FBA) the flux of an objective reaction is maximized, in this case V1, so the solution is at the edge of the solution space where V1 is maximized. (B). In flux sampling the solution space is randomly sampled a determined number of times. Therefore, each red sphere is a sampled flux distribution from the solution space.
Figure 4. Graphical 3D representation of flux distribution obtention methods. The three axes represent the values of the three variables in our simplification: the flux for each of the three reactions. The constraints the model determines delimit the solution space, which is represented as the blue polyhedron. The red spheres represent a feasible solution of the solution space. (A). In flux balance analysis (FBA) the flux of an objective reaction is maximized, in this case V1, so the solution is at the edge of the solution space where V1 is maximized. (B). In flux sampling the solution space is randomly sampled a determined number of times. Therefore, each red sphere is a sampled flux distribution from the solution space.
Preprints 98449 g004
Preprints 98449 g005
Figure 5. Overview of bioinformatic analysis of metabolomic data. Each one of the three modules in which we divided the process is indicated in a different color. The workflow starts with the annotated metabolite peak area data. The first module is preprocessing, where the initial step is missing value imputation. After this the data is transformed, if necessary, for later being normalized with the most appropriate method for the dataset. Once the data is pre-processed, we can perform statistical analysis, being possible to use one or several univariate or multivariate methods. Within this second category we can alternate between unsupervised and supervised approaches. The outcome of this step are the differential metabolites. Finally, the last module is metabolic pathway enrichment. Some approaches like ORA and some PT methods such as FELLA require lists of differential metabolites. In FCS and in other PT methods the normalized metabolite abundances can be used directly. The output of the metabolic pathway enrichment are the altered metabolic pathways. Abbreviations: ORA – over-representation analysis; FCS – functional class scoring; PT – pathway topology.
Figure 5. Overview of bioinformatic analysis of metabolomic data. Each one of the three modules in which we divided the process is indicated in a different color. The workflow starts with the annotated metabolite peak area data. The first module is preprocessing, where the initial step is missing value imputation. After this the data is transformed, if necessary, for later being normalized with the most appropriate method for the dataset. Once the data is pre-processed, we can perform statistical analysis, being possible to use one or several univariate or multivariate methods. Within this second category we can alternate between unsupervised and supervised approaches. The outcome of this step are the differential metabolites. Finally, the last module is metabolic pathway enrichment. Some approaches like ORA and some PT methods such as FELLA require lists of differential metabolites. In FCS and in other PT methods the normalized metabolite abundances can be used directly. The output of the metabolic pathway enrichment are the altered metabolic pathways. Abbreviations: ORA – over-representation analysis; FCS – functional class scoring; PT – pathway topology.
Preprints 98449 g005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated