Prerpints.org logo
Preprint
Article

Predicting Surface Roughness in Turning Complex-Tructured Workpieces Using Vibration Signal-Based Gaussian Process Regression

Altmetrics

Downloads

83

Views

16

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

07 February 2024

Posted:

08 February 2024

You are already at the latest version

Alerts
Abstract
Surface roughness prediction is a pivotal aspect of the manufacturing industry, as it directly influences product quality and process optimization. This study introduces a predictive model for surface roughness in the turning of complex-structured workpieces, utilizing Gaussian Process Regression (GPR) informed by vibration signals. The model captures parameters from both the time and frequency domains of the turning tool, encompassing the mean, median, standard deviation (STD), and root mean square (RMS) values. The signal is from the time to frequency domain is executed using Welch's method, complemented by time-frequency domain analysis employing three levels of Daubechies Wavelet Packet Transform (WPT). The selected features are then utilized as inputs for the GPR model to forecast surface roughness. Empirical evidence indicates that the GPR model can accurately predict the surface roughness of turned complex-structured workpieces. This predictive strategy has the potential to improve product quality, streamline manufacturing processes, and minimize waste within the industry.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

Surface roughness is a critical determinant of product quality, functionality, and reliability in the manufacturing industry. It quantifies the deviation of a workpiece's actual surface from its ideal form and is influenced by factors such as cutting parameters, tool geometry, material, and machining processes. The complexity of manufacturing intricate geometric parts often involves multiple steps, including boring, milling, roughing, and finishing, with surface roughness needing to meet assembly process specifications post-finishing. Achieving an optimal balance of surface roughness is essential, as it can be neither too low nor too high. Consequently, surface roughness is a vital metric for assessing product quality. Traditionally, quality assurance has relied on periodic sampling and manual inspection, which can lead to significant waste when surface roughness fails to meet standards. Thus, the development of a real-time, accurate surface roughness prediction method is imperative.
Previous research has investigated artificial intelligence (AI) approaches for predicting surface roughness in turning processes. Benardos and Vosniakos [1] found that AI methods outperformed traditional approaches, while Özel and Karpat [2] and Palanisamy and Shanmugasundaram [3] reported that artificial neural networks (ANNs) surpassed regression models and response surface methodologies.
Researchers have also refined input variables to enhance prediction accuracy. For example, in 2010, T. Reddy and C. Reddy [4] correlated acoustic emission (AE) with surface roughness, Marani et al. [5] evaluated feed rate and cutting speed in adaptive neuro-fuzzy inference systems (ANFIS), and Lin et al. [6] demonstrated that ANNs could improve prediction accuracy by incorporating vibration signals. Vasanth et al. [7] fused cutting force, tool wear, displacement of tool vibration and three cutting parameters to predict the roughness in ANN. Moreover, researchers have improved prediction accuracy by enhancing model capabilities. Pimenov et al. [8] found that random forests outperformed other models, while Badiger et al. [9] and Kong et al. [10] utilized ANNs and machine learning techniques to optimize cutting parameters and feature extraction,respectively. Su et al. [11] and Lu et al. [12] applied SVM and GPR, respectively, achieving promising results.
Despite these efforts, existing methods, which primarily rely on traditional statistics, SVM, and ANN, depend heavily on comprehensive training data. The complex machining environment, including the use of cutting coolants, often hinders the acquisition of real surface images, necessitating a reliable and accessible method for initial data collection.
Time domain signal processing methodologies, encompassing statistical functions and advanced techniques, have been extensively investigated for tool condition monitoring in turning processes. Siddhpura and Paurobally [13] conducted a review of flank wear prediction methods, while Elangovan [14] enhanced the selection of statistical features from vibration signals using principal component analysis (PCA), achieving a classification accuracy of 91.2% for flank wear. Aghdam et al. [15] employed the autoregressive moving average (ARMA) model to identify wear-sensitive features based on the dynamics of the tool-holder system, addressing the challenges of identifying random tool wear features in time domain analysis, as noted by Siddhpura and Paurobally [13], Nath [16], and Kuntoğlu et al. [17].
Frequency-domain analysis methods, such as FFT and PSD, have been explored by Fang et al. [18] and Plaza et al. [21]. Bhuiyan and Choudhury [19] utilized the root mean square (RMS) of vibration signals and frequency analysis to assess machine tools under various cutting conditions. Tangjitsitcharoen and Lohasiriwat [20] differentiated broken chip signals from tool wear using PSD of decomposed cutting force.
Time-frequency domain analysis, including STFT, WT, HHT, and EMD, is widely applied for machinery fault diagnosis. Scheffer and Heyns [22], Wang et al. [23,33,34], and Segreto et al. [24] applied wavelet analysis to classify tool wear, achieving high success rates. Gangadhar et al. [25] used the mean square value of DWT features from vibration signals to classify different worn conditions using a decision tree algorithm. Plaza and López [26,27] established criteria for WPT based on vibration and force signals, applying packet reduction criteria such as maximum energy and maximum entropy. Du et al. [28] combined WPT and WT features, re-extracted using the Relief-F algorithm, to predict tool wear with a mean absolute error of 0.01-0.03mm. Kong et al. [29] presented a predictive model for tool wear, integrating radial basis function-based principal component analysis and relevance vector machine, with features extracted from time-domain statistical functions, frequency domain parameters, and Daubechies WPT energy using Shannon entropy.
In contrast, the empirical mode decomposition (EMD) has seen limited application in turning tool condition monitoring (TCM). Babouri et al. [30] combined WT and EMD to detect tool wear, while Li et al. [31,32] utilized a meta-learning model based on a fully connected neural network, integrating time-domain statistical functions, frequency domain features, EMD, wavelet analysis, and STFT, achieving a mean absolute error of 0.01-0.03mm in predicting tool wear.
This paper proposes the use of Gaussian Process Regression (GPR) based on vibration signals to accurately predict surface roughness in turning complex-structured workpieces. GPR offers several advantages: it provides uncertainty estimates, is non-parametric and flexible, and has demonstrated higher accuracy and robustness compared to other methods. In turning processes, vibration signals, which are less affected by external noise and easier to install, are analyzed using GPR. This approach leverages the strengths of vibration signals to improve the prediction of surface roughness.
In turning processes, there are various types of signals that can be utilized as inputs for GPR when predicting surface roughness. These signals include commonly used ones such as acoustic emission and cutting force. However, these signals have limitations that can affect their accuracy and applicability in different scenarios. On the other hand, vibration signals possess several advantages. Firstly, vibration sensors can be easily installed without the need to damage the original structure of the machine tool. Secondly, vibration signals are less susceptible to external noise and disturbances, resulting in more reliable and accurate predictions of surface roughness. Therefore, in this paper, GPR is employed to analyze vibration signals from turning complex-structured workpieces.

2. Methodology

The proposed model comprises three primary components: signal acquisition, feature extraction, and surface roughness prediction. The signal acquisition module captures vibration signals in three orthogonal directions from the turning tool throughout the machining process. These signals undergo pre-processing to mitigate noise from extraneous sources. The feature extraction module then extracts parameters from the pre-processed signals, encompassing both time and frequency domains. Time-domain features are derived using statistical measures such as mean, maximum, median, standard deviation (STD), and root mean square (RMS). The frequency domain analysis is facilitated by Welch's method, which transforms the signals from the time domain to the frequency domain, and is further enhanced by a three-level Daubechies Wavelet Packet Transform (WPT). These features are subsequently utilized to construct the surface roughness prediction model.

2.1. Feature Extraction and Correlation

Feature extraction from vibration signals is a pivotal step in preprocessing, aimed at isolating pertinent information that enhances signal quality and processing efficiency. This process encompasses various methodologies, such as statistical characteristics, frequency domain features, time-frequency features, and nonlinear characteristics.
Statistical characteristics involve calculating the mean, variance, standard deviation, and peak values of the vibration signal, which reflect the average vibration level and tool fluctuation. Frequency domain features are derived through Fourier or wavelet transforms, capturing attributes like power spectral density, frequency components, and dominant frequencies, essential for analyzing the frequency composition and distribution of the tool's vibrations.
Welch's method, a prevalent frequency domain feature extraction technique, employs Fourier transform-based signal analysis. It segments the raw vibration data, x(n), into L overlapping subsegments, each containing M data points, resulting in a total of N=LM data points. The jth segment is represented as:
  X j n = x n + j M − M ,   0 ≤ n ≤ M ,     1 ≤ j ≤ L
Then a window function w(n) is added to each data segment, and the power spectrum of each segment is calculated. The power spectrum of the jth segment is:
I j w = 1 U ∑ n = 0 M − 1 x j n w n e − j e n 2
where U is the normalization factor:
U = 1 M ∑ n = 0 M − 1 w 2 n  
Assuming that the power spectra of each segment is approximately uncorre-lated, the power spectral estimate is given by:
P x x e j w = 1 L ∑ j = 1 L I j w
The Welch feature extraction method is employed to obtain frequency components and power spectral density, which are instrumental in analyzing the signal's frequency composition and distribution. This method enhances the accuracy of spectral estimation but may introduce information loss and estimation errors during signal segmentation and windowing. Consequently, careful parameter selection and optimization are essential, tailored to the specific application and data characteristics.
Time-frequency domain analysis, including short-time Fourier transform (STFT), wavelet transform (WT), Hilbert-Huang transform (HHT), and empirical mode decomposition (EMD), is extensively applied to nonstationary signals for machinery fault diagnosis. In the context of turning process tool condition monitoring (TCM), WT analysis is particularly prevalent due to its significant reduction in processing time and precise identification of specific frequency contributions.
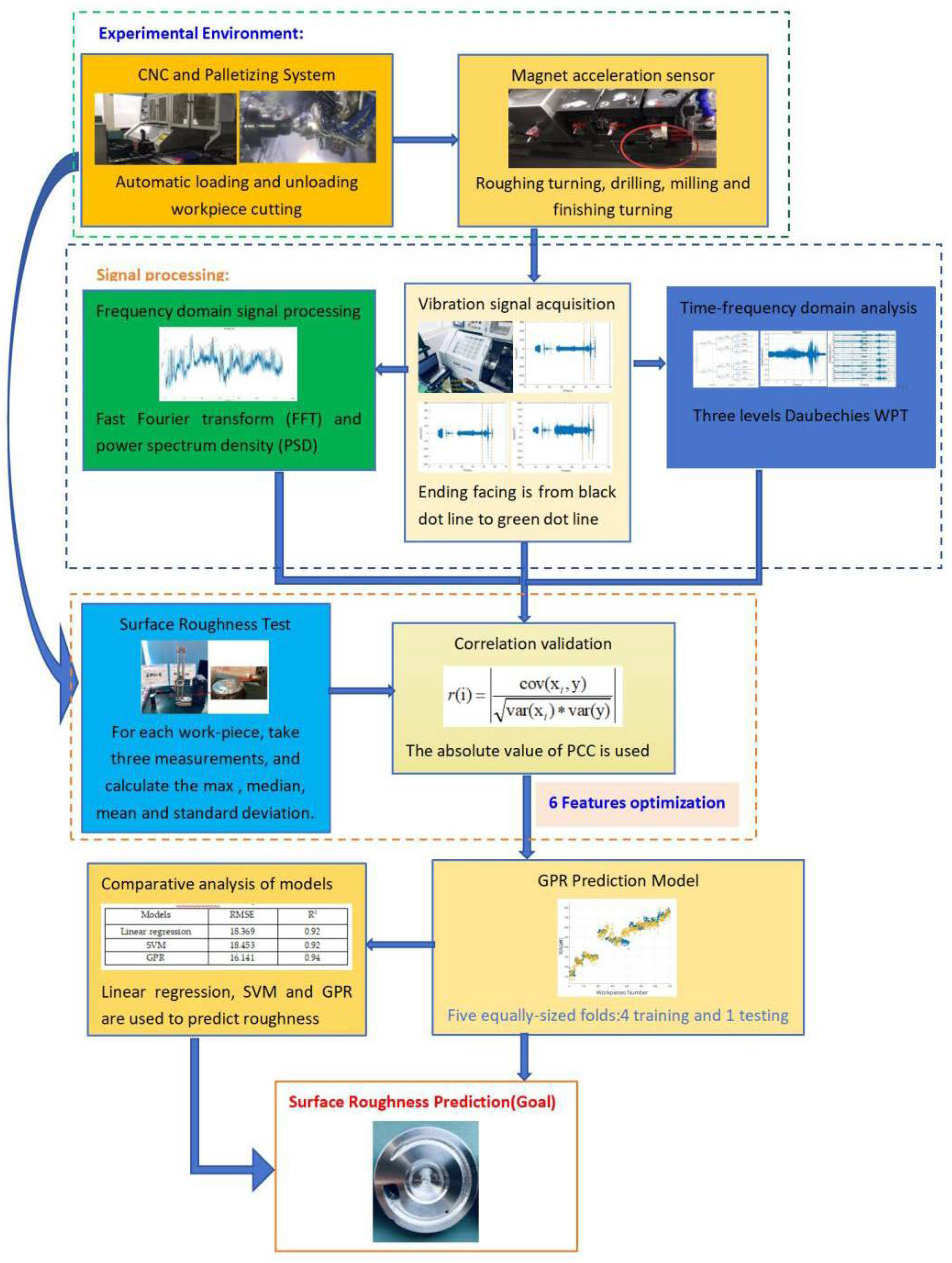
Preprints 98450 g001
Figure 1. Surface Roughness Prediction and Signal Processing Workflow.
Figure 1. Surface Roughness Prediction and Signal Processing Workflow.
Preprints 98450 g001
To assess the correlation between the statistical properties of time and frequency domain acceleration signals and roughness data, the Pearson correlation coefficient (PCC) is utilized. The PCC ranges from -1 to 1, with a value of 0 indicating no correlation. Negative values denote an inverse relationship, while positive values indicate a direct correlation. In this study, the absolute value of PCC is prioritized, as higher absolute values suggest stronger correlation features. The mathematical equation for PCC is as follows:
P C C i = c o v X i , R a v a r X × v a r R a
Here, X i is the i th variable, Ra is the roughness, var represents variance and cov represents covariance. The value of PCC i represents the correlation between X and Ra .

2.2. Gaussian Process Regression (GPR) Model

To predict surface roughness, a subset of relevant features is selected based on actual requirements and the nature of the problem. These features are then incorporated into a prediction model for tool wear degree, utilizing machine learning algorithms such as Support Vector Machine (SVM), decision trees, and neural networks for modeling and prediction.
Gaussian Process Regression (GPR) is a machine learning algorithm adept at modeling nonlinear relationships between inputs and outputs. It uses the chosen features from signal acquisition and feature extraction modules to predict surface roughness. The Gaussian process, represented by equation (2), is characterized by feature vectors that include parameters such as the time-domain maximum, average, median, and root mean square values.
f ~ G P m X ,   k X , X ′
The mean function, as described by equation (3), represents the expected value of the function.
m X = E f X
The covariance function, detailed in equation (4), is a critical component of the GPR model.
k X , X ′ = E f X − m X ′ f X ′ − m X ′
The kernel function of GPR, which combines a mean function and a covariance function, typically sets the mean function to zero. The rational quadratic kernel function, as shown in equation (5), is a common choice.
  k X , X ′ = σ 2 1 + X − X ′ 2 2 α s 2 − α
This function's parameters, including the scale factors σ, s, and the proportional mixed factor α, are optimized for the study. The rational quadratic kernel function can be interpreted as a sum of square exponential kernel functions with varying reduction lengths, and it reduces to a square exponential kernel under certain conditions. Its infinite differentiability ensures a smooth function, which is crucial for the GPR model. The optimal parameter solution is determined using an iterative conjugate gradient method.
In essence, a robust prediction model requires accurate signal collection, followed by the optimization and adjustment of feature extraction methods and parameters based on specific vibration signals and tool wear conditions. Additionally, the efficacy of feature extraction and model construction necessitates experimental validation.

3. Field Tests and Data Acquisition

3.1. Field Experiment Setup

The field experiments were conducted using a CNC machine, model SNC-A200, from Shanghai SYMA Machine Tool Technology Corporation, as depicted in Figure 2(a). Four types of tools were employed for the machining process: roughing turning, finishing turning, milling, and drilling. The focus of this study is on finishing turning, as it directly impacts surface roughness. The specific tool used is shown in Figure 2(b), and a sample of the finished workpiece with a complex structure is presented in Figure 2(c). Uniform cutting conditions were maintained for all workpieces, as detailed in Table 1. Figure 3 displays the magnetically attached acceleration sensor on the finishing turning tool.
To ensure high-quality signal preprocessing, several measures were implemented. Prior to collecting vibration signals, the machine tool was meticulously calibrated to eliminate external noise and other factors that could compromise the accuracy of the signals. This included the precise placement of the sensor on the machine tool, positioning it as close to the tool's head as possible, and adjusting the sensor's orientation to align with the actual working conditions. Furthermore, the sensor and tool were securely affixed using strong glue and a powerful magnet. After careful adjustment, the sensor position, as shown in Figure 3, was finalized.
During the experiment, vibration signals from 50 workpieces were recorded, along with their surface roughness measurements, over a period of cutting 1000 workpieces. An increase in the number of workpieces processed corresponded to an increase in surface roughness.

3.2. Description of Data

The correlation between the workpiece's surface roughness and the vibration signals during turning is presented below.

3.2.1. Roughness

The workpiece, constructed from ADC-6 aluminum alloy die casting, underwent surface roughness measurements at three distinct surface locations using the Surftest SJ-210 Surfagauge, as shown in Figure 4. The Surfagauge's stylus was employed to meticulously assess the workpiece's surface, with the Ra value representing the arithmetic mean of the roughness profile. The maximum permissible Ra value for this workpiece is established at 700 μm.
The roughness values are described as:
r j = [ r j 1 , r j 2 , r j 3 ]
The measured values are taken at three distinct positions on each workpiece. Similarly, the maximum, median, mean, and standard deviation (STD) roughness values are calculated from three separate measurements for each workpiece.
During the SYMA field test, No. 1 Tool was utilized for 62 days, during which it processed a total of 40,060 workpieces. Some of the workpieces exhibited roughness levels exceeding the specified tolerance of 600 µm. Owing to nightly downtime, the daily production ranged from 500 to 1600 workpieces, with acceleration data being collected from approximately 30 workpieces each day. No.2 tool was under same cutting parameters as No.1 tool. However, No.2 tool only cuts 29196 work-pieces that reaches the desired tolerance.

3.2.2. Vibration Data

The vibration sensor utilized is the CA-YD-3193 from Sinocera Piezotronics Inc., featuring a sample frequency of 25,600 Hz. The cutting process for a single workpiece encompasses loading (approximate time), rough turning, drilling, milling, finishing turning, and unloading, totaling an approximate cutting time of 50 seconds. Further details are provided in Table 2.

3.3. Vibration Signature

3.3.1. Time Domain Vibration for Cutting One Work-Piece

Vibration measurements were conducted using a triaxial accelerometer, with the measurement directions specified in Figure 3. Table 2 outlines the procedures in chronological order. Figure 5 presents the vibration signals along the X, Y, and Z axes, as indicated in Figure 5(a), (b), and (c), respectively. The Y-axis displays the highest acceleration values, followed by the X and Z axes. For this study, only the finishing turning process, which is most relevant to surface roughness, was selected. This is represented by the vibration signal between the two orange dashed lines in Figure 6.

3.3.2. Frequency Analysis of Finishing Turning Signals

Employing Welch's method, the power spectrum density of the finishing turning process was obtained and is depicted in Figure 6. The red circles in the figure denote the harmonic peaks of the signal. The fundamental frequency of the vibration was determined to be 53.3 Hz, corresponding to the CNC spindle speed of 3200 RPM.

4. Signal Processing and Features Optimization

4.1. Time Domain Analysis

The commonly utilized statistical functions in time domain analysis encompass a range of well-established metrics, such as mean, root mean square (RMS), standard deviation (STD), skewness, kurtosis, and crest factor. These functions are instrumental in characterizing the behavior of signals and identifying trends or anomalies within the data.
The time domain analysis involved the examination of signals from both ending facing and cylindrical turning processes, focusing on parameters such as mean, RMS, STD, skewness, kurtosis, and crest factor. The statistical properties were categorized into three distinct groups based on the production timeline: the first group spanned from the 2nd to the 17th day, with approximately 5000 workpieces produced; the second group from the 23rd to the 50th day; and the third group on the 62nd day. Over the 62-day sample period, the analysis revealed fluctuations in amplitude with minimal changes in skewness. The mean value, RMS, and STD decreased in the first group, while the second group showed an increase, and the crest factor and kurtosis exhibited a contrasting trend. The RMS and STD properties were notably similar.
Figure 7(a) presents roughness measurements from three different positions of the 30 workpieces for each day, with Figure 7(b) to (e) depicting the max, median, mean, and STD of these measurements. The roughness values fluctuate, with some abnormal peaks, but generally trend upwards over time. The roughness can be divided into three groups: the first from the 2nd to the 17th day, with values primarily between 350µm and 450µm; the second from the 23rd to the 50th day, with values around 450µm to 550µm; and the third on the 62nd day, with some workpieces exceeding the desired tolerance of 600µm.
The STD, as shown in Figure 7(b), occasionally highlighted discrepancies among the roughness measurements. Figure 8's heatmaps illustrate the PCCs between the time domain's statistical properties and roughness metrics. The mean value and kurtosis of the time domain in the X-axis (tangential direction) and Z-axis (feed direction) showed stronger correlations with the max, median, and mean of roughness, with PCC absolute values ranging from 0.70 to 0.79. The kurtosis of the time domain in the X-axis demonstrated the highest correlation with each statistical roughness, with a maximum PCC of 0.7969 for the mean roughness value.
In summary, the mean value of the time domain signals in the X-axis and Z-axis demonstrated consistent performance across both tools, suggesting their potential as relevant features for predicting roughness.

4.2. Frequency Domain Analysis

The Fast Fourier Transform (FFT) is a highly regarded and widely applied technique for processing signals in the frequency domain, harnessing the Fourier Transform (FT) to seamlessly transition signals from the time domain to the frequency domain. The FFT algorithm achieves this by performing a series of multiplications and additions, which markedly decreases the computational burden compared to the traditional DFT. This optimization significantly enhances the efficiency of the DFT computation by minimizing the number of complex operations required.
While the FT is fundamental to signal analysis, it faces a limitation due to its reliance on sinusoidal basis functions. This dependency can impede the precise determination of FT coefficients for non-stationary signals, which lack a constant frequency throughout their duration.
Power Spectral Density (PSD) quantifies the distribution of signal power across various frequency bands. Welch's method enhances PSD analysis by introducing window functions, which effectively mitigate the noise associated with finite data sets, providing a more precise depiction of the signal's power distribution across frequencies.
Figure 9 demonstrates the application of Welch's method to analyze the frequency domain of acceleration signals in three orthogonal directions, with a sample rate of 25600 Hz. The data is divided into 256 overlapping segments, each processed with a Hamming window. The PSD is depicted for the three axes—X, Y, and Z—represented in blue, red, and green, respectively. Typically, PSD increases with frequency, with distinct peaks observed around 3700 Hz for the X-axis (Figure 9a) and Z-axis (Figure 9c) in Group 1 and 3. The Y-axis (Figure 9b) for Group 2 exhibits the highest PSD at approximately 3700 Hz.
Figure 10 presents the Pearson Correlation Coefficients (PCCs) between the PSD of every 100 frequencies and the statistical roughness, aiding in the selection of relevant frequencies. The blue, red, yellow, and purple curves represent the max, mean, median, and STD of roughness, respectively. The largest PCCs in the X-axis are approximately 0.8446, 0.8674, and 0.8595 for the maximum values, mean values, and median values of roughness, respectively, at 3700 Hz (Figure 10a). Although these PCCs are not the highest in the Y-axis (Figure 10b) and Z-axis (Figure 10c), they still exhibit strong correlations, around 0.67 and 0.72, respectively. The PCCs for mean values, median, and max of roughness are similar, with the median roughness PCC slightly higher. The highest PCCs are around 0.7689 at 1300 Hz for the Y-axis and around 0.7562 at 3800 Hz for the Z-axis. Other significant PCCs are observed around 1200 Hz, 6500 Hz, and 12600 Hz for the X and Y axes. The STD of roughness is less related to the frequency domain.
Figure 11 also shows the comparison of PCCs between the frequency domain and roughness for Tool No.1 and No.2. The STD of roughness, which is less related to the frequency domain, is disregarded. The blue and red curves represent Tool No.1 and No.2, respectively. For No.2, the highest PCCs are around 0.8221 at 4700 Hz for the X-axis, 0.7749 at 8100 Hz for the Y-axis, and 0.8511 at 3100 Hz for the Z-axis. The PCCs between the frequency domain and max, mean value, and median of roughness for both tools exhibit similar trends in low frequencies across all three axes. The ranges from 3000 Hz to 4000 Hz generally exhibit steady high PCCs for both tools, especially in the X-axis. The PCCs between the frequency domain and roughness are consistently higher than 0.7 around 12600 Hz for both tools in the X-axis.
Table 3 summarizes the comparison of maximum PCCs for time and frequency domains for both tools. The frequency domain PCCs are superior to those of the time domain for both tools.
In summary, the correlation between the frequency domain and surface roughness outperforms that of the time domain, particularly in the frequency range around 12,600 Hz for the X-axis, where the PCC exceeds 0.7, indicating a strong correlation and suggesting these frequencies as promising features for analysis. While the peaks of PCCs in the frequency domain vary between the two tools, the trends in low frequencies are notably similar.

4.3. Wavelet Packet Transform

Wavelet analysis employs a set of mother wavelets, such as Haar, Daubechies, symlets, Morlets, and coiflets, to decompose signals into their constituent components. The three principal types of wavelet analysis are the continuous wavelet transform (CWT), discrete wavelet transform (DWT), and wavelet packet transform (WPT). A crucial distinction between the short-time Fourier transform (STFT) and wavelet analysis is that STFT breaks down signals into shorter segments using a window function for DFT computation, while wavelet analysis relies on mother wavelets in place of sinusoidal functions. The WPT extends the capabilities of DWT by providing further decomposition of the approximation and detail signals.
Figure 12 presents a three-level WPT decomposition, where the input signal (x) is initially processed by a low-pass filter to obtain the approximation coefficients (AL) and a high-pass filter to extract the detailed coefficients (DH). This process is recursively applied at subsequent levels.
Figure 13 provides an example of a workpiece's signal decomposition using a three-level Daubechies WPT. The original vibration signals for the X, Y, and Z axes are depicted in Figure 13(a), (c), and (e), respectively. The corresponding reconstructions of wavelet coefficients are shown in Figure 13(b), (d), and (f), where larger nodes represent higher-pass wavelet coefficients, indicating regions of greater frequency content.
The PSD results of reconstructed coefficient 3 (frequency range: 3200Hz to 4800Hz) are exemplified in Figure 14. Blue, red, and green represent Groups 1, 2, and 3, respectively, consistent with Section 4.1. Notably, there are clear peaks around 3700Hz in the X and Z axes for Group 3, similar to Figure 9.
Table 4 lists fifty-two mother wavelet families. Two sets of data are analyzed to determine the optimal performance of PCCs between the energy percentage of these wavelet coefficients and surface roughness, as shown in Figure 15(a) for Tool No.1 and (b) for Tool No.2. Stability-wise, levels L2 and L3 exhibit variability, and their PCCs are lower than other levels for both tools. The best mother wavelet for Tool No.1 is dmey at level L4 with a PCC of 0.8558 in Figure 15(a). For Tool No.2, the best mother wavelet is db18 at level L6 with a PCC of 0.9109 in Figure 15(b).
Figure 16 explores the effect of decomposition level (L) on the PCCs between the energy percentage of wavelet decomposition and the roughness of Tool No.1 in three directions. The highest PCC is 0.8558 at 8000Hz to 8800Hz in Y-axis level L4 in Figure 16(d). Low-pass coefficients of scale functions and high-pass coefficients of wavelet functions fail to filter signals correctly at L2 and L3. Changes in energy percentage at high frequencies are more relevant to roughness at L4, L5, L6, and L7. However, increasing decomposition levels does not improve PCCs, as L7's high-frequency PCC is lower than L5 and L6. There are no significant differences between L5, L6, and L7.
Figure 17 compares the PCCs between the energy of dmey decomposition level L6 and roughness for Tool No.1 and Tool No.2. The blue line represents Tool No.1, and the cyan line represents Tool No.2. PCCs decrease at lower frequencies after WPT in the X-axis, while they increase at higher frequencies. The frequency around 10000Hz in the X-axis is a common feature for both tools, with PCCs around 0.7.
WPT can enhance PCC performance at low and high frequencies, but important features may be filtered during signal decomposition. Increasing decomposition levels does not yield better results, as there are no significant differences between L5, L6, and L7. The best mother wavelet for both tools is dmey.

4.4. Results of GPR Predicts Roughness

To prevent overfitting due to a large number of features, six optimal features with high correlation to roughness were selected as inputs for the Gaussian Process Regression (GPR) model. The dataset was divided into five equally-sized folds, with four folds used for training and one for testing. This cross-validation process was repeated five times, rotating the folds, and the average performance of the model across all folds was calculated to determine the final evaluation model.
Figure 18 shows that the blue dots represent the surface roughness measurements obtained by the Surftest SJ-210 Surfagauge, while the yellow dots indicate the GPR predicted values. The model's predictions exhibit a strong correlation with the measured results, as demonstrated by an R-squared value of 0.96 and a root-mean-square error (RMSE) of 35 μm.

5. Discussion

The literature review indicates that research on linear regression, support vector machines (SVM), and Gaussian process regression (GPR) models has shown promising results. Consequently, this study undertakes a comparative analysis of these three models as detailed below.

5.1. Cross-Validation

Cross-validation is a robust technique for model training and validation, which involves partitioning the training data into two distinct subsets: one for actual training and the other for validation. In the context of k-fold cross-validation, k-1 subsets are designated for training, while the remaining subset serves as the validation set. This process is iterated k times, with each of the k subsets being used as the validation set once. In this thesis, a k-fold cross-validation with k set to 5 is employed.
The predictive accuracy of the models is assessed using two key metrics: the root mean square error (RMSE), which quantifies the magnitude of the prediction error, and the determination coefficient (R²), which measures the degree of correlation between the predicted and actual data.
For predicting surface roughness, linear regression, SVM, and GPR models are applied, utilizing features derived from the preceding sections. Table 5 presents the accuracy metrics for the No. 1 tool, with GPR emerging as the most accurate model, boasting the lowest RMSE (16.141) and the highest R² (0.94). The GPR model utilizes an exponential kernel function, and the results are visually depicted in Figure 19, where the red points represent the predicted roughness by GPR, contrasted with the green points representing the measured roughness.

5.2. Discussion

In this research, the feature set has been expanded to encompass both time and frequency domains, thereby enhancing the predictive precision of surface roughness estimation.
For the No. 2 tool, the analysis is conducted using the same input variables and models as for the No. 1 tool. The comparative results, as presented in Table 5, reveal that the GPR model, once again, outperforms others with the lowest RMSE (26.682) and the highest R² (0.83). The GPR's predictive performance is visually demonstrated in Figure 9, where the predicted roughness (red points) is juxtaposed with the measured roughness (green points). The reduced accuracy observed for the No. 2 tool is attributed to the lower Pearson correlation coefficients (PCCs) of the input variables, indicating a weaker correlation with the output variable.

6. Conclusions

This study presents a predictive model for surface roughness in the turning of complex-structured workpieces, employing Gaussian process regression (GPR) and vibration signals. The model incorporates parameters extracted from the time and frequency domains of vibration signals captured in three orthogonal directions from the cutting tool. These features are then utilized as inputs for GPR to forecast surface roughness. The experimental outcomes confirm that the model delivers precise predictions for surface roughness in complex turning operations. The model's utility extends to the optimization of cutting parameters, tool geometry, and material selection, enabling the attainment of desired surface finish within a turning system.
A significant advantage of this approach is its ability to accurately predict surface roughness for intricate workpieces without relying on intricate simulations or laborious physical measurements. This capability can streamline the quality control process in manufacturing, reducing both costs and time, and aiding manufacturers in refining their production methods to enhance surface quality and minimize waste.
Furthermore, the model's predictive capabilities can be harnessed for real-time surface roughness estimation during manufacturing. This real-time feedback allows manufacturers to dynamically adjust machining parameters, ensuring superior surface finish and a lower rate of defective products.

Author Contributions

conceptualization and methodology, Q.L.; software and validation, Q.L., M.Z.; formal analysis, Q.L., J.C. and M.Z.; investigation, Q.L.; resources, Q.L.; data curation, Q.L., M.Z.; writing —original draft preparation, Q.L., J.L. and M.Z.; writing —review and editing, Q.L.; visuali- zation; supervision, Q.L. and J.C.; project administration, Q.L. and J.L.; funding acquisition. All authors have read and agreed to the published version of the manuscript.

Funding

This work was funded by Wenzhou Basic Scientific Research Project (R20220048) and Wenzhou Major Science and Technology Innovation Project of China (ZF2022002).

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. P. G. Benardos and G. C. Vosniakos, Predicting surface roughness in machining: A review, Int. J. Mach. Tools Manuf., 2003(43), 833-844. [CrossRef]
  2. T. Özel and Y. Karpat, Predictive modeling of surface roughness and tool wear in hard turning using regression and neural networks, Int. J. Mach. Tools Manuf., 2005(45),467-479. [CrossRef]
  3. P. Palanisamy and S. Shanmugasundaram, Modelling of tool wear and surface roughness in hard turning using regression and artificial neural network, Int. J. Mach. Mach. Mater., 2008(48),76-94. [CrossRef]
  4. T. S. Reddy and C. E. Reddy, Real Time Monitoring of Surface Roughness by Acoustic Emissions in CNC Turning, J. Eng. Sci. Technol. Rev., 2010(3),111-115. [CrossRef]
  5. M. Marani, V. Songmene, M. Zeinali, J. Kouam, and Y. Zedan, Neuro-fuzzy predictive model for surface roughness and cutting force of machined Al–20 Mg2Si–2Cu metal matrix composite using additives, Neural Comput. Appl., 2020(32), 8115–8126. [CrossRef]
  6. Y. C. Lin, K. Da Wu, W. C. Shih, P. K. Hsu, and J. P. Hung, Prediction of surface roughness based on cutting parameters and machining vibration in end milling using regression method and artificial neural network, Appl. Sci., 2020(11), 3941. [CrossRef]
  7. X. A. Vasanth, P. S. Paul, and A. S. Varadarajan, A neural network model to predict surface roughness during turning of hardened SS410 steel, Int. J. Syst. Assur. Eng. Manag., 2020(11), 704–715. [CrossRef]
  8. D. Y. Pimenov, A. Bustillo, and T. Mikolajczyk, Artificial intelligence for automatic prediction of required surface roughness by monitoring wear on face mill teeth, J. Intell. Manuf., 2018(29), 1045–1061. [CrossRef]
  9. P. V. Badiger, V. Desai, M. R. Ramesh, B. K. Prajwala, and K. Raveendra, Cutting Forces, Surface Roughness and Tool Wear Quality Assessment Using ANN and PSO Approach During Machining of MDN431 with TiN/AlN-Coated Cutting Tool, Arab. J. Sci. Eng., 2019(44), 7465–7477. [CrossRef]
  10. D. Kong, J. Zhu, C. Duan, L. Lu, and D. Chen, Bayesian linear regression for surface roughness prediction, Mech. Syst. Signal Process., 2020(142),106770. [CrossRef]
  11. Y. Su, C. Li, G. Zhao, C. Li, and G. Zhao, Prediction models for specific energy consumption of machine tools and surface roughness based on cutting parameters and tool wear, Proc. Inst. Mech. Eng. Part B J. Eng. Manuf., 2021(235),943–957. [CrossRef]
  12. J. Lu et al., Effect of machining parameters on surface roughness for compacted graphite cast iron by analyzing covariance function of Gaussian process regression, Meas. J. Int. Meas. Confed., 2020(157),107578. [CrossRef]
  13. A. Siddhpura and R. Paurobally, A review of flank wear prediction methods for tool condition monitoring in a turning process, Int. J. Adv. Manuf. Technol., 2013(65),371-393. [CrossRef]
  14. M. Elangovan, N. R. Sakthivel, S. Saravanamurugan, B. B. Nair, and V. Sugumaran, Machine learning approach to the prediction of surface roughness using statistical features of vibration signal acquired in turning, Procedia Computer Science, 2015(50), 282–288. [CrossRef]
  15. B. H. Aghdam, M. Vahdati, and M. H. Sadeghi, Vibration-based estimation of tool major flank wear in a turning process using ARMA models, Int. J. Adv. Manuf. Technol., 2015(76), 1631–1642. [CrossRef]
  16. C. Nath, Integrated tool condition monitoring systems and their applications: A comprehensive review, Procedia Manufacturing, 2020(48), 852-863. [CrossRef]
  17. M. Kuntoğlu et al., A review of indirect tool condition monitoring systems and decision-making methods in turning: Critical analysis and trends, Sensors, 2021, 21(1), 108. [CrossRef]
  18. N. Fang, P. S. Pai, and S. Mosquea, Effect of tool edge wear on the cutting forces and vibrations in high-speed finish machining of Inconel 718: An experimental study and wavelet transform analysis, Int. J. Adv. Manuf. Technol., 2011(52), 65–77. [CrossRef]
  19. M. S. H. Bhuiyan and I. A. Choudhury, Investigation of tool wear and surface finish by analyzing vibration signals in turning ASSAB-705 steel, Mach. Sci. Technol., 2015(19), 236-261. [CrossRef]
  20. S. Tangjitsitcharoen and H. Lohasiriwat, Intelligent monitoring and prediction of tool wear in CNC turning by utilizing wavelet transform, Int. J. Adv. Manuf. Technol., 2018(99), 2219–2230. [CrossRef]
  21. E. García Plaza, P. J. Núñez López, and E. M. Beamud González, Efficiency of vibration signal feature extraction for surface finish monitoring in CNC machining, J. Manuf. Process., 2019(44), 145-157. [CrossRef]
  22. C. Scheffer and P. S. Heyns, Wear monitoring in turning operations using vibration and strain measurements, Mech. Syst. Signal Process., 2001(15), 1185-1202. [CrossRef]
  23. L. Wang, M. G. Mehrabi, and E. Kannatey-Asibu, Hidden Markov model-based tool wear monitoring in turning, J. Manuf. Sci. Eng. Trans. ASME, 2002, 124(3), 651-658. [CrossRef]
  24. T. Segreto, A. Caggiano, S. Karam, and R. Teti, Vibration sensor monitoring of nickel-titanium alloy turning for machinability evaluation, Sensors (Switzerland), 2017, 17(12), 2885. [CrossRef]
  25. N. Gangadhar, K. Vernekar, H. Kumar, and S. Narendranath, Fault diagnosis of single point cutting tool through discrete wavelet features of vibration signals using decision tree technique and multilayer perceptron, J. Vib. Eng. Technol., 2014(5), 1434-1441.
  26. E. García Plaza and P. J. Núñez López, Application of the wavelet packet transform to vibration signals for surface roughness monitoring in CNC turning operations, Mech. Syst. Signal Process., 2018(98), 902-919. [CrossRef]
  27. E. García Plaza and P. J. Núñez López, Analysis of cutting force signals by wavelet packet transform for surface roughness monitoring in CNC turning, Mech. Syst. Signal Process., 2018(98), 634-651. [CrossRef]
  28. M. Du, P. Wang, J. Wang, Z. Cheng, and S. Wang, “Intelligent Turning Tool Monitoring with Neural Network Adaptive Learning,” Complexity, 2019. [CrossRef]
  29. D. Kong, Y. Chen, N. Li, C. Duan, L. Lu, and D. Chen, Relevance vector machine for tool wear prediction, Mech. Syst. Signal Process., 2019(127), 573-594. [CrossRef]
  30. M. K. Babouri, N. Ouelaa, and A. Djebala, Experimental study of tool life transition and wear monitoring in turning operation using a hybrid method based on wavelet multi-resolution analysis and empirical mode decomposition, Int. J. Adv. Manuf. Technol., 2016(82), 2017–2028. [CrossRef]
  31. Y. Li, C. Liu, J. Hua, J. Gao, and P. Maropoulos, A novel method for accurately monitoring and predicting tool wear under varying cutting conditions based on meta-learning, CIRP Ann., 2019(68), 487-490. [CrossRef]
  32. Liu, J.; Huang, Y. Surface Roughness Prediction and Parameter Optimization for Turning Using Hybrid Intelligent Algorithms. Journal of Intelligent Manufacturing 2017, 28(7), 1625-1637.
  33. Zhang, L.; Wang, F.; & Jiang, S. Surface roughness prediction of turning based on extreme learning machine and wavelet packet decomposition. The International Journal of Advanced Manufacturing Technology 2019, 103(5-8), 2355-2367.
  34. Wang, Y.; & Zhang, J. Surface roughness prediction of turning based on machine learning method. The International Journal of Advanced Manufacturing Technology 2019,105(1-4), 113-123.
Preprints 98450 g002
Figure 2. (a) The CNC machine; (b) The finishing turning tool; (c) Workprice.
Figure 2. (a) The CNC machine; (b) The finishing turning tool; (c) Workprice.
Preprints 98450 g002
Preprints 98450 g003
Figure 3. Four machine tools with a magnet acceleration sensor.
Figure 3. Four machine tools with a magnet acceleration sensor.
Preprints 98450 g003
Preprints 98450 g004
Figure 4. Surfagauge measures roughness.
Figure 4. Surfagauge measures roughness.
Preprints 98450 g004
Preprints 98450 g005
Figure 5. Measured three axis acceleration of the tool when cutting one work-piece.
Figure 5. Measured three axis acceleration of the tool when cutting one work-piece.
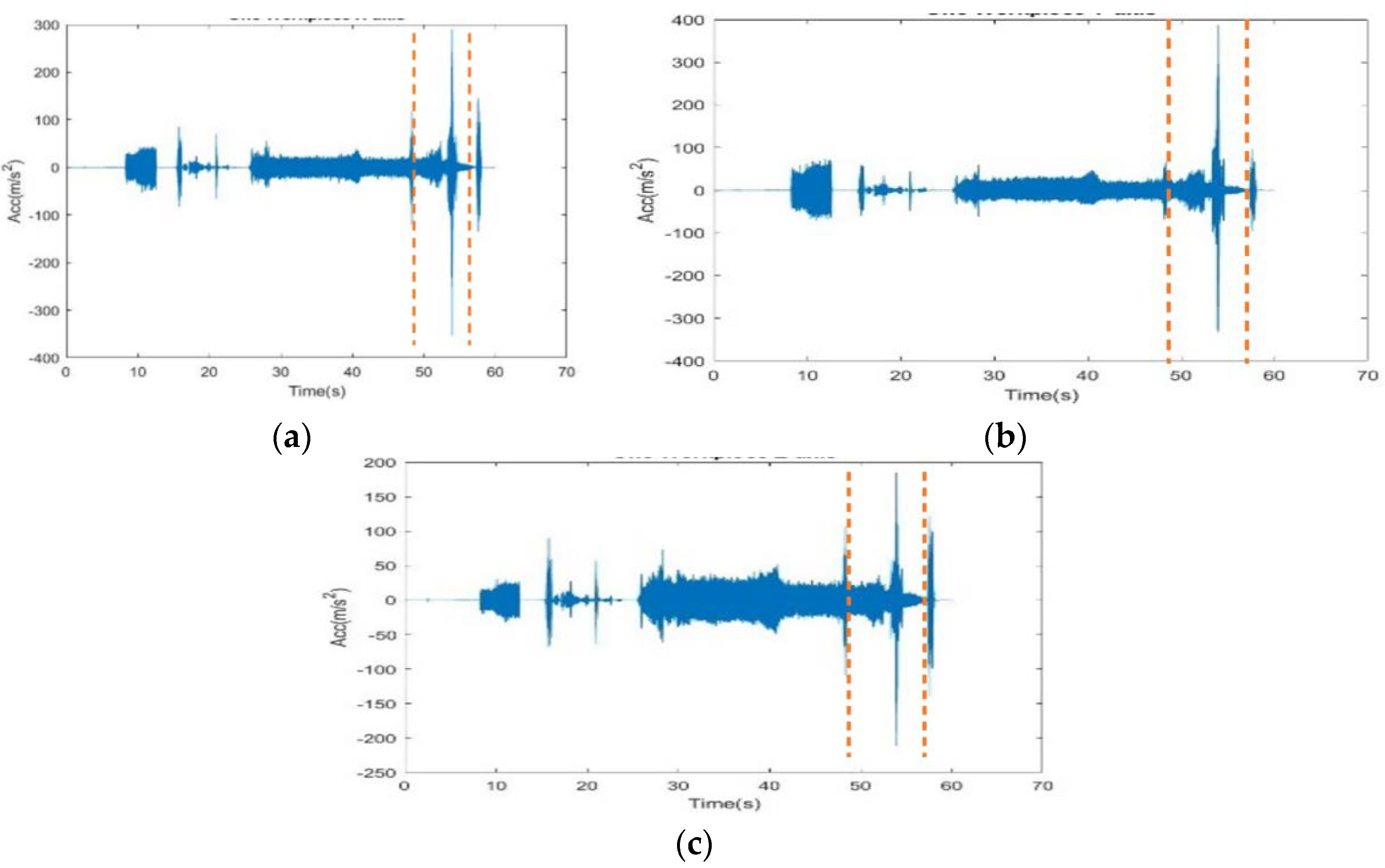
Preprints 98450 g005
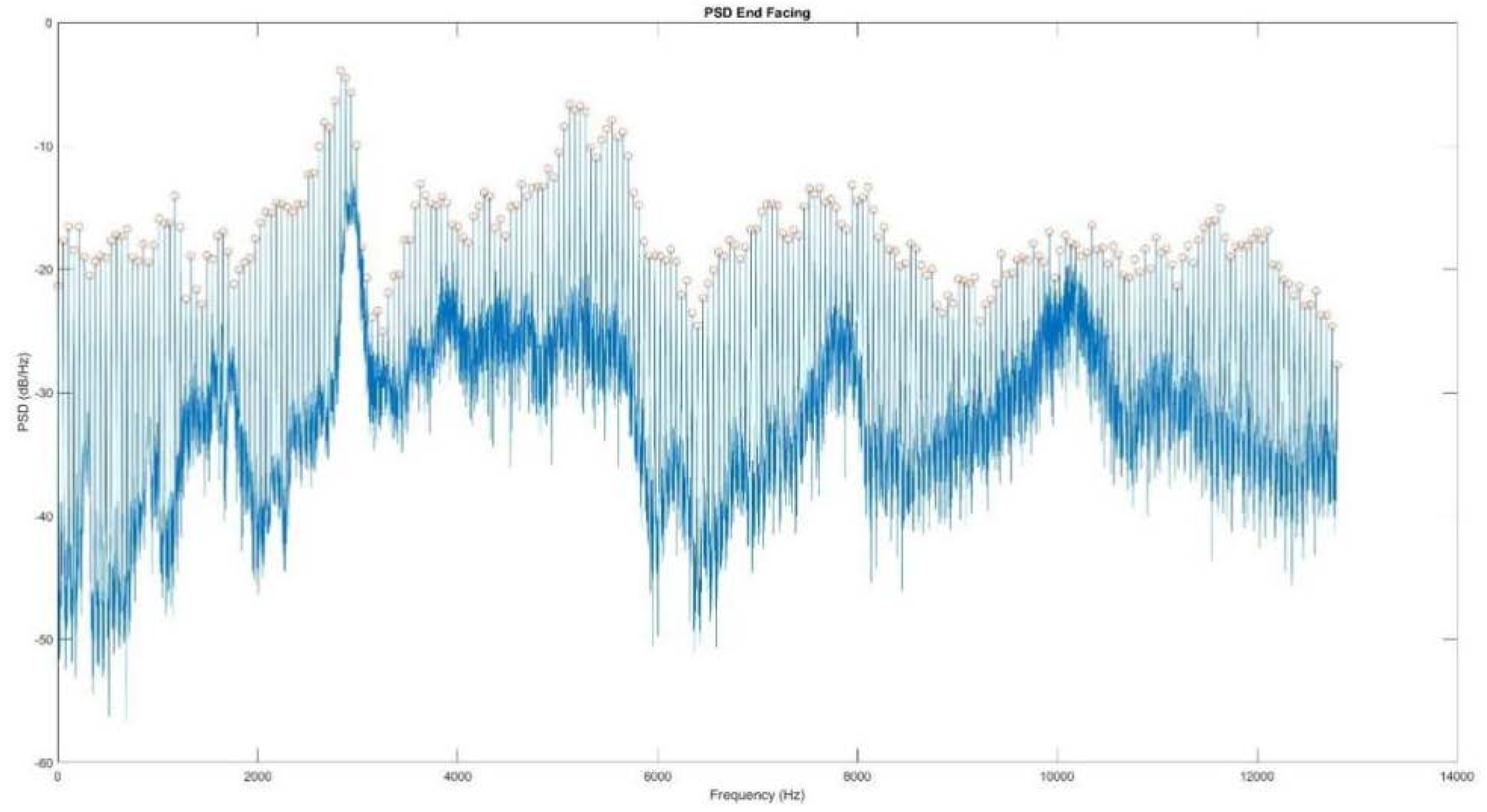
Preprints 98450 g006
Figure 6. Frequency analysis of finishing turning signals.
Figure 6. Frequency analysis of finishing turning signals.
Preprints 98450 g006
Preprints 98450 g007
Figure 7. (a)Three times of Ra; (b) Max of Ra; (c) Median of Ra; (d) Mean of Ra; (e) STD of Ra.
Figure 7. (a)Three times of Ra; (b) Max of Ra; (c) Median of Ra; (d) Mean of Ra; (e) STD of Ra.
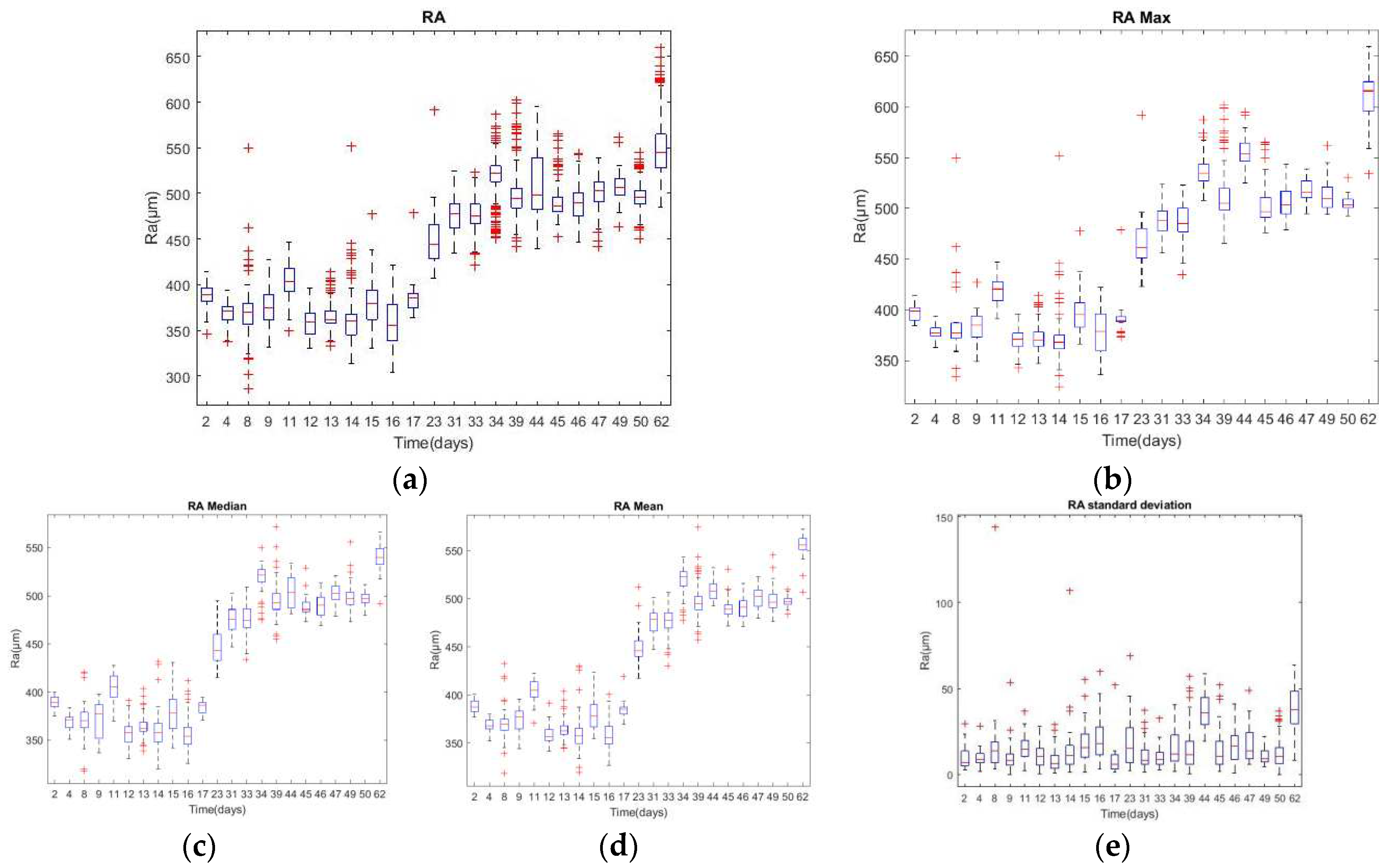
Preprints 98450 g007
Preprints 98450 g008
Figure 8. Correlations between statistical properties of time domain and roughness.
Figure 8. Correlations between statistical properties of time domain and roughness.
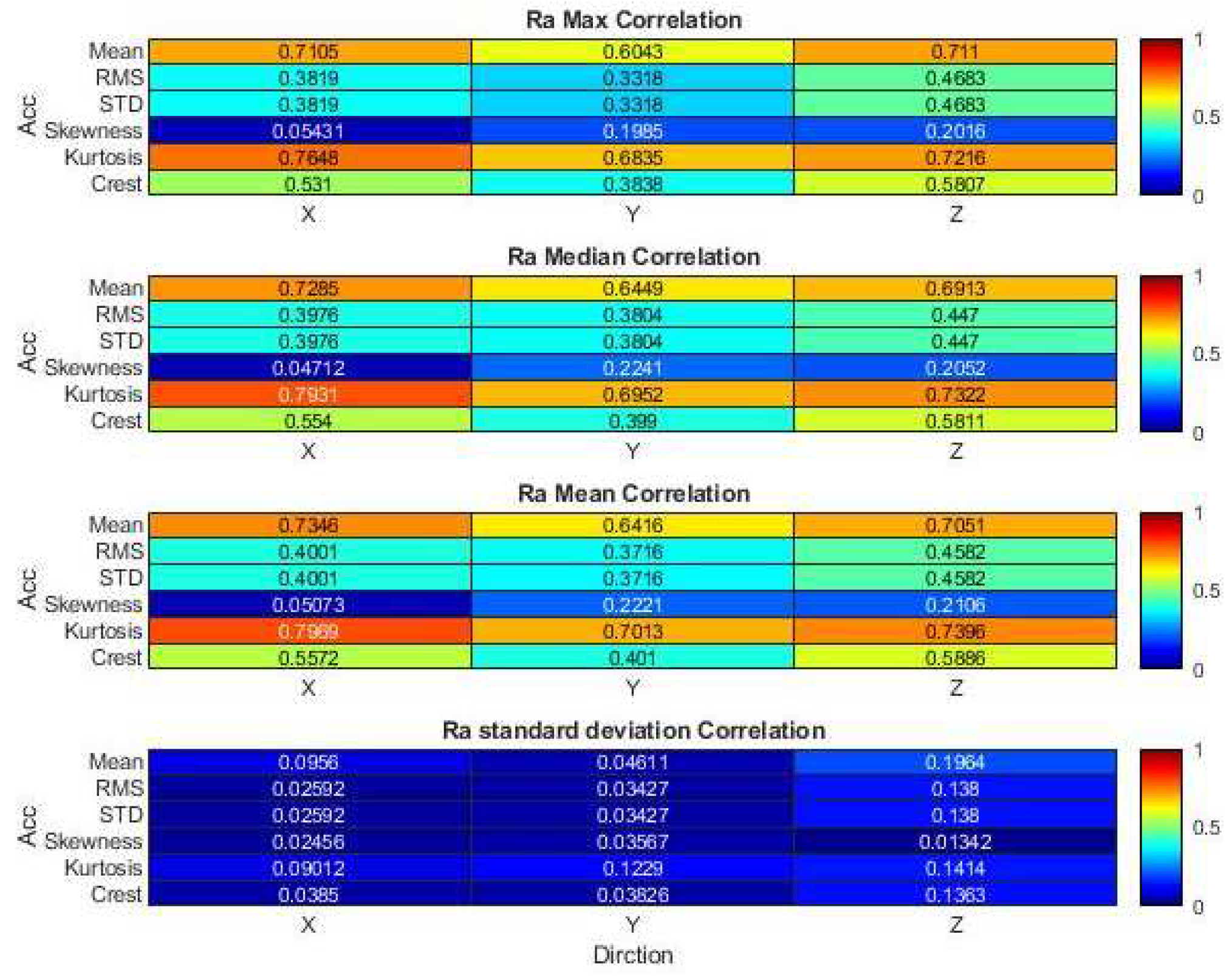
Preprints 98450 g008
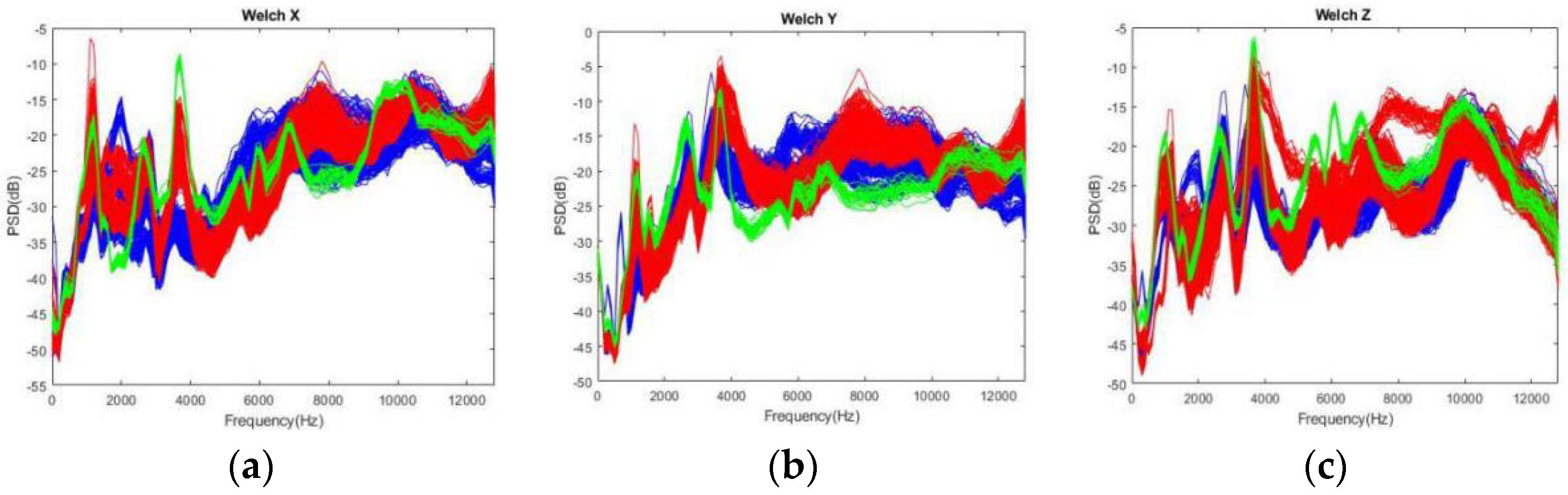
Preprints 98450 g009
Figure 9. Welch results (a) X-axial; (b) Y-axial; (c) Z-axial.
Figure 9. Welch results (a) X-axial; (b) Y-axial; (c) Z-axial.
Preprints 98450 g009
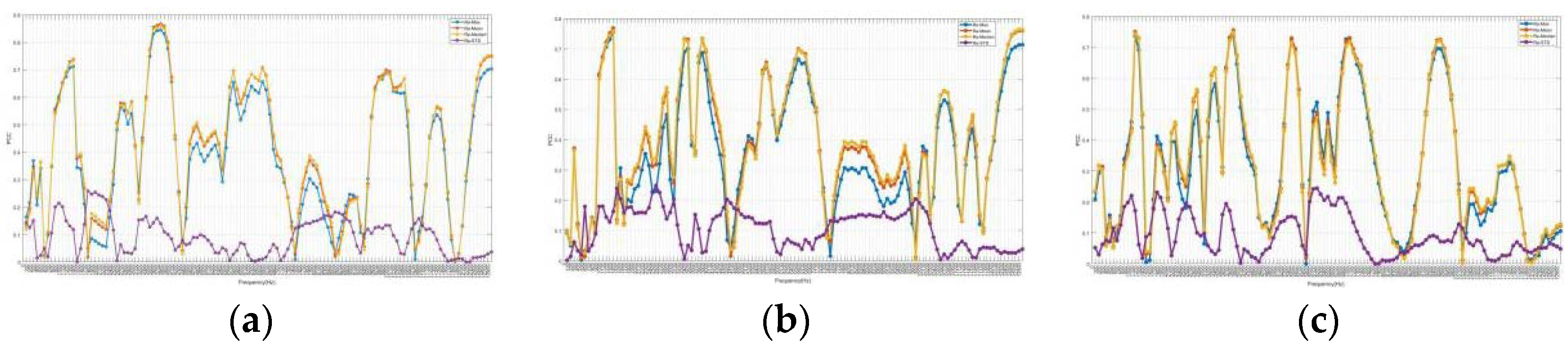
Preprints 98450 g010
Figure 10. Correlations between roughness and frequency domain (a)X-axial; (b)Y-axial; (c)Z-axial.
Figure 10. Correlations between roughness and frequency domain (a)X-axial; (b)Y-axial; (c)Z-axial.
Preprints 98450 g010
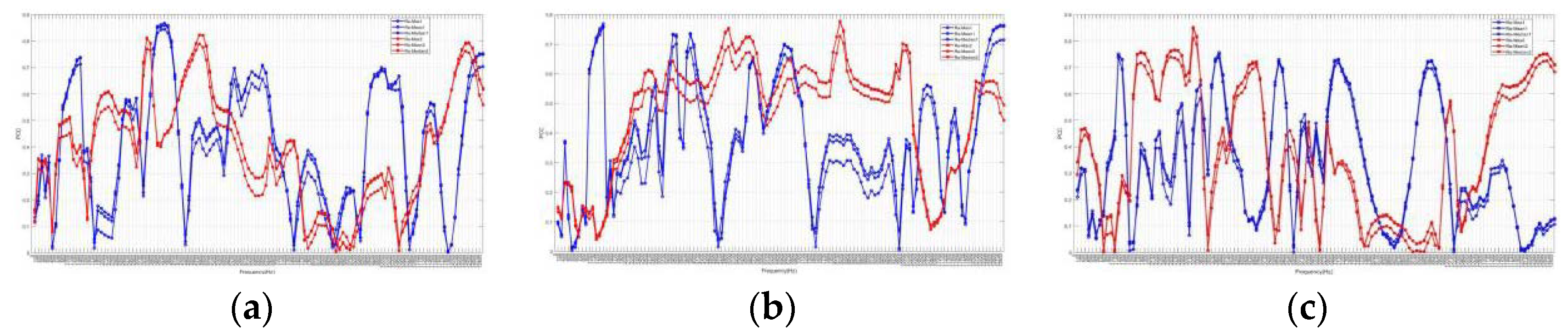
Preprints 98450 g011
Figure 11. Comparison PCCs of frequency domain and roughness for No.1 tool with No.2 tool (a)X-axial; (b)Y-axial; (c)Z-axial.
Figure 11. Comparison PCCs of frequency domain and roughness for No.1 tool with No.2 tool (a)X-axial; (b)Y-axial; (c)Z-axial.
Preprints 98450 g011
Preprints 98450 g012
Figure 12. WPT of three levels decomposition Measured vs predicted roughness by GPR.
Figure 12. WPT of three levels decomposition Measured vs predicted roughness by GPR.
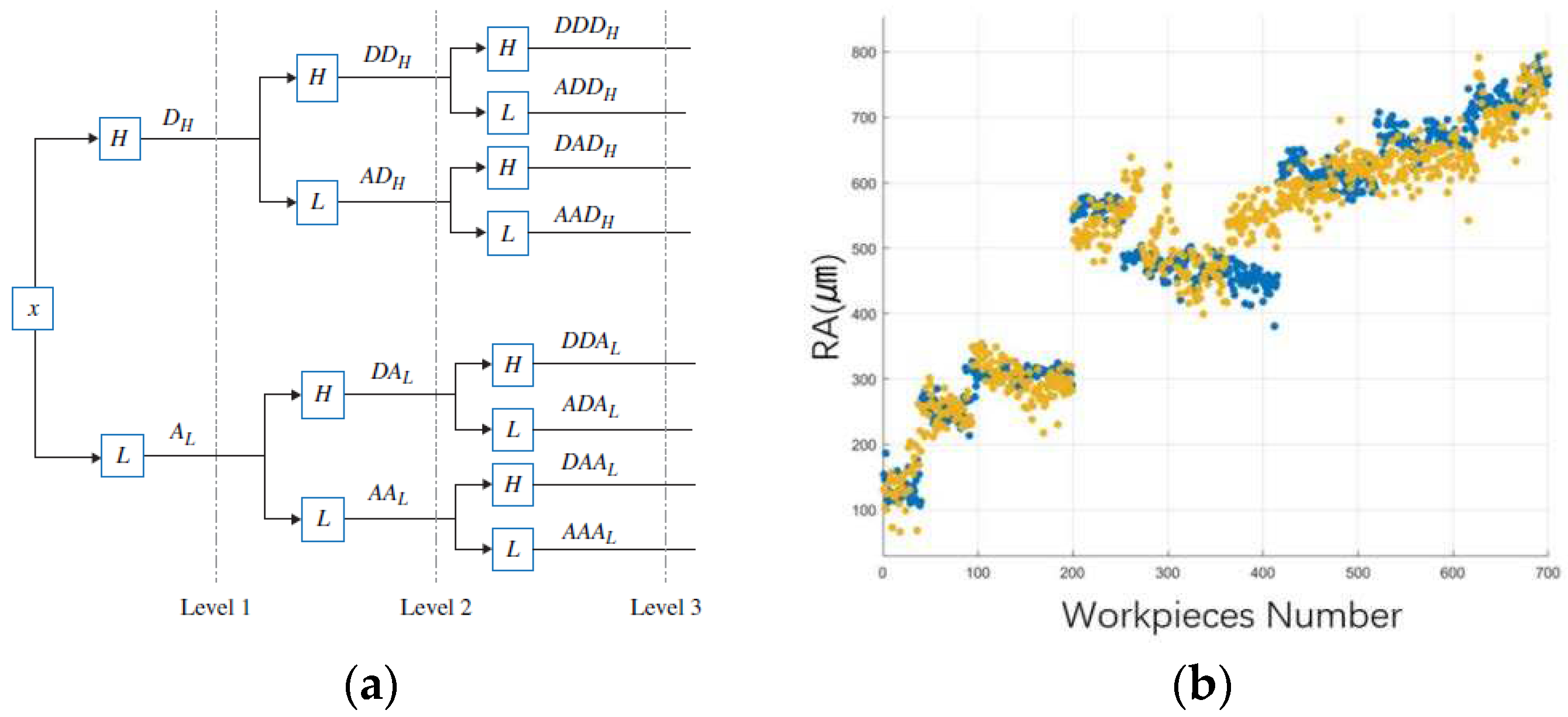
Preprints 98450 g012
Preprints 98450 g013
Figure 13. An example of the WPT of three levels decomposition.
Figure 13. An example of the WPT of three levels decomposition.
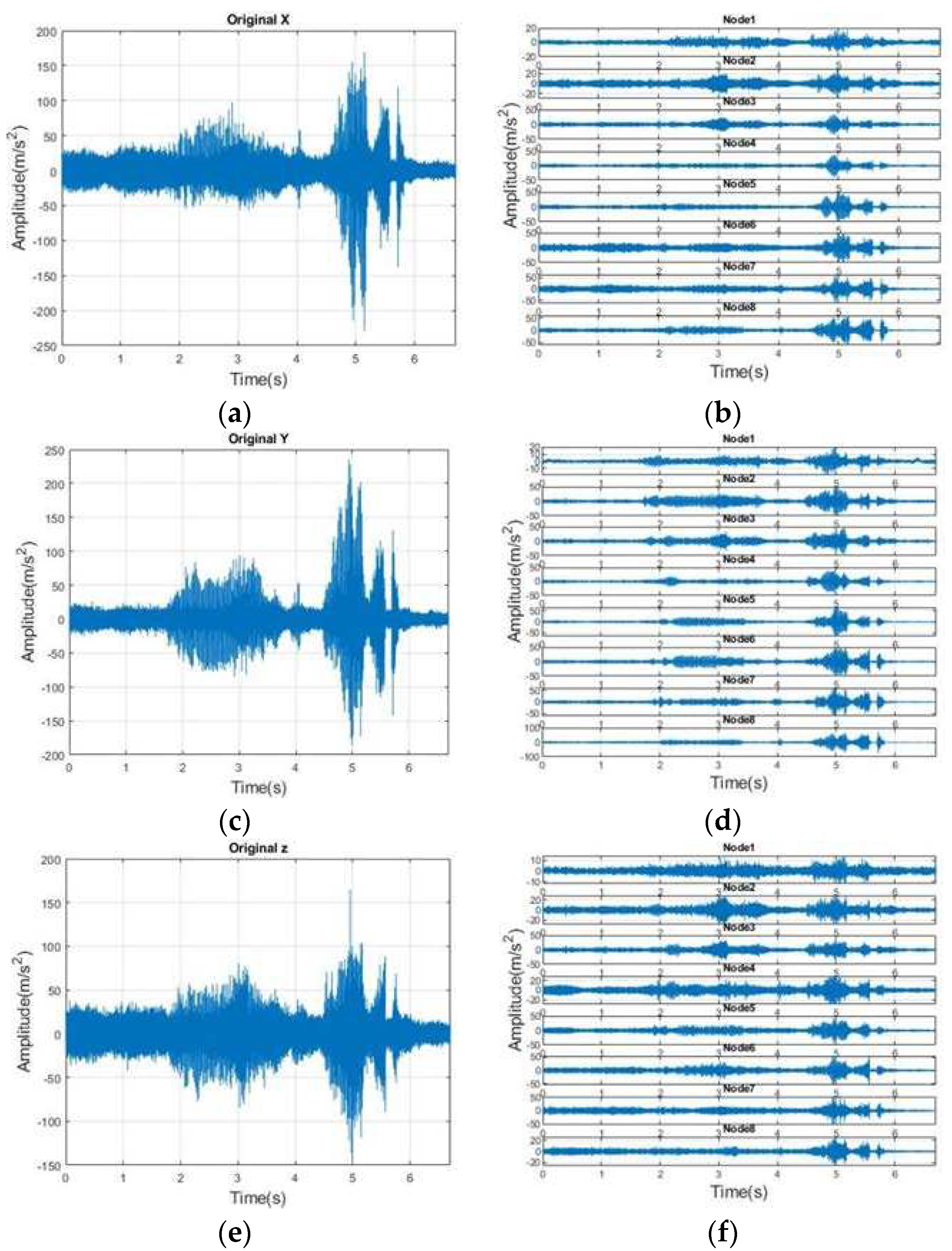
Preprints 98450 g013
Preprints 98450 g014
Figure 14. An example of PSDs of wavelet coefficient 3 .
Figure 14. An example of PSDs of wavelet coefficient 3 .
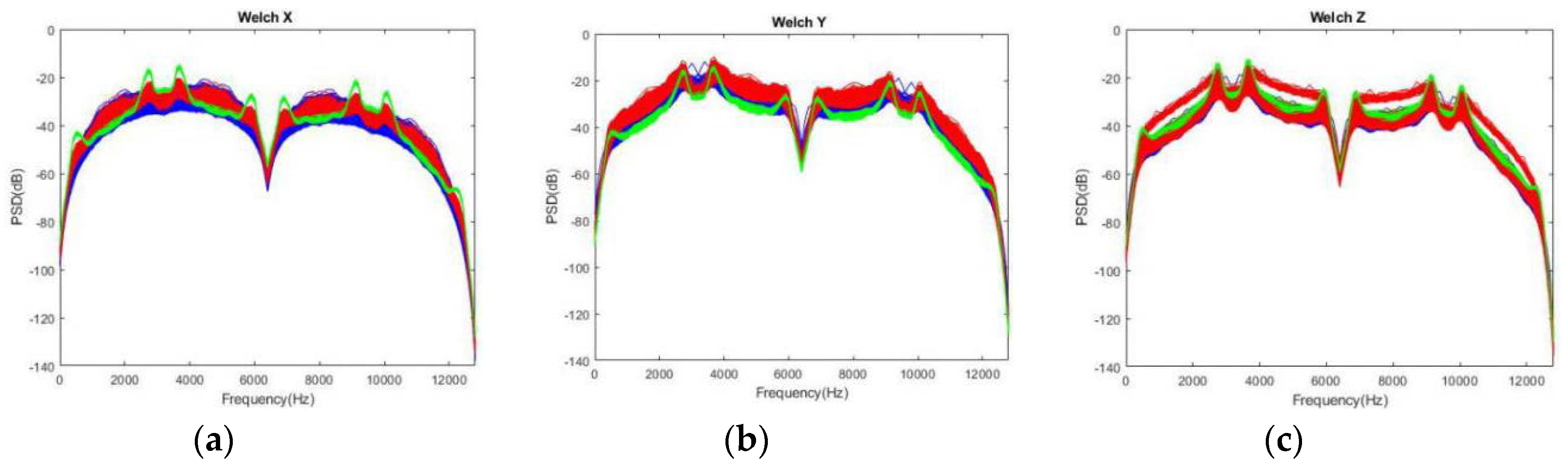
Preprints 98450 g014
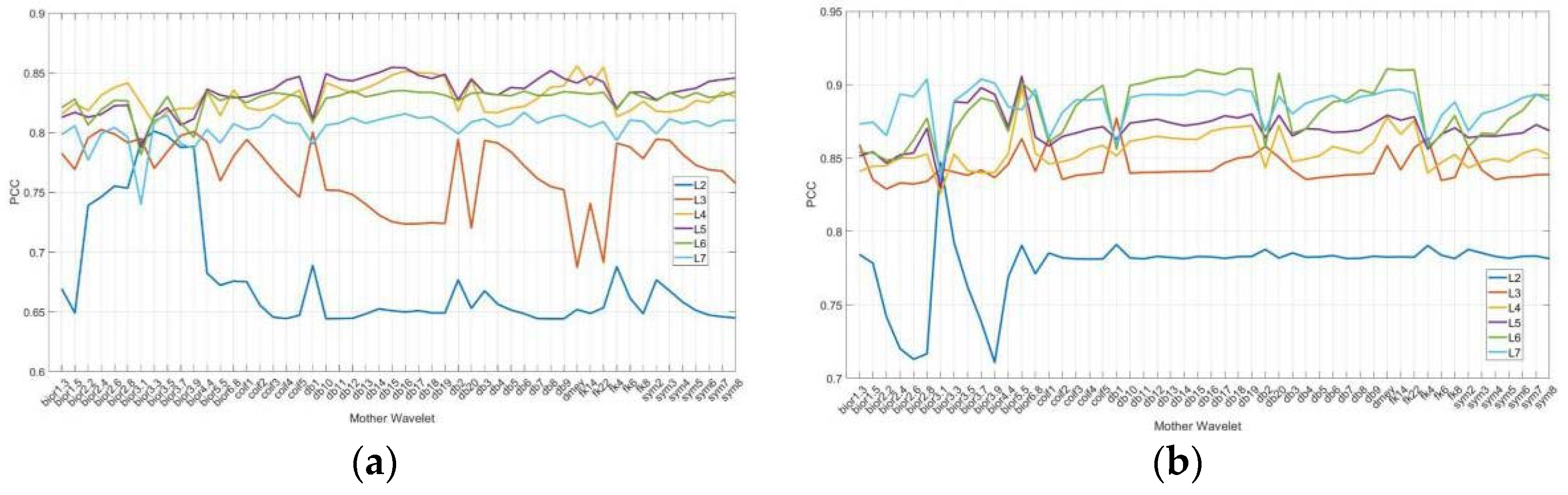
Preprints 98450 g015
Figure 15. PCCs between energy of each decomposition level (L) and roughness (a) No.1 tool; (b)No.2 tool.
Figure 15. PCCs between energy of each decomposition level (L) and roughness (a) No.1 tool; (b)No.2 tool.
Preprints 98450 g015
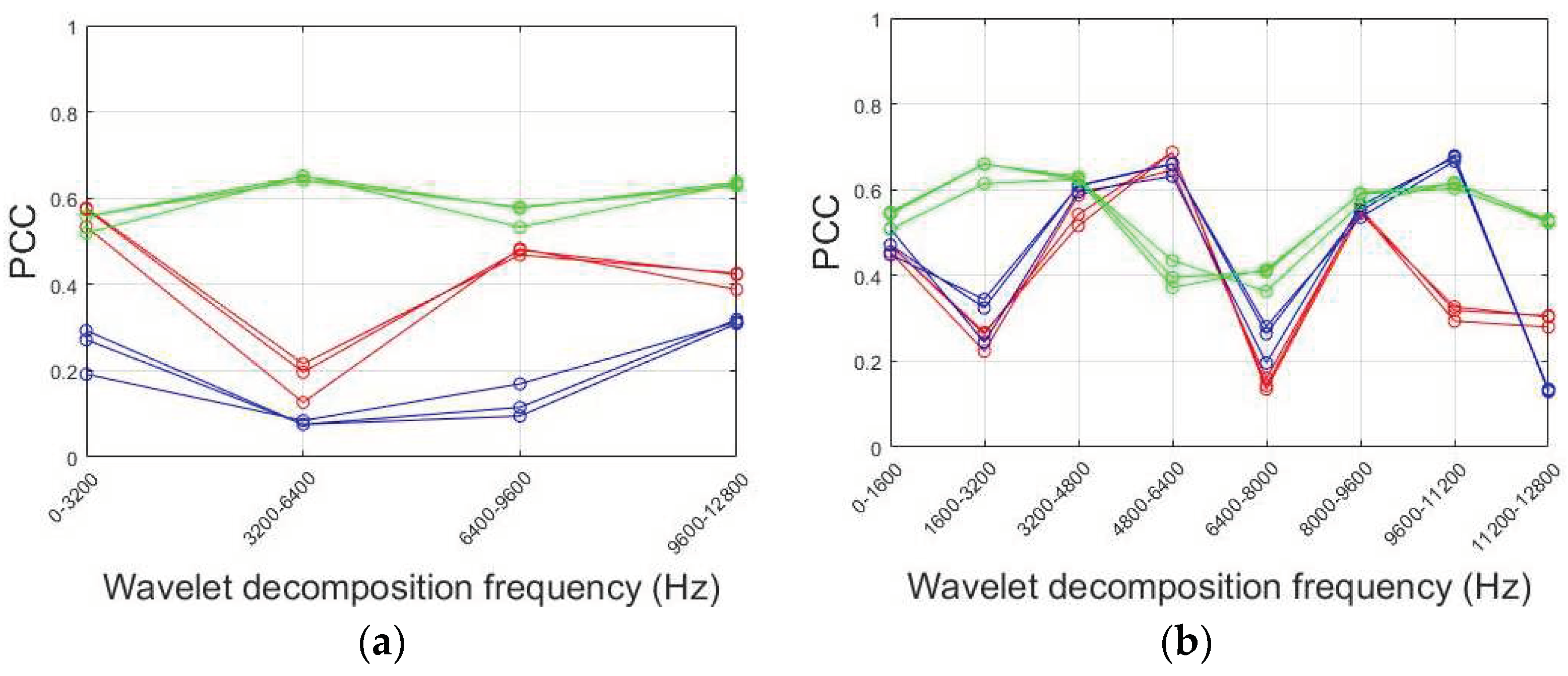
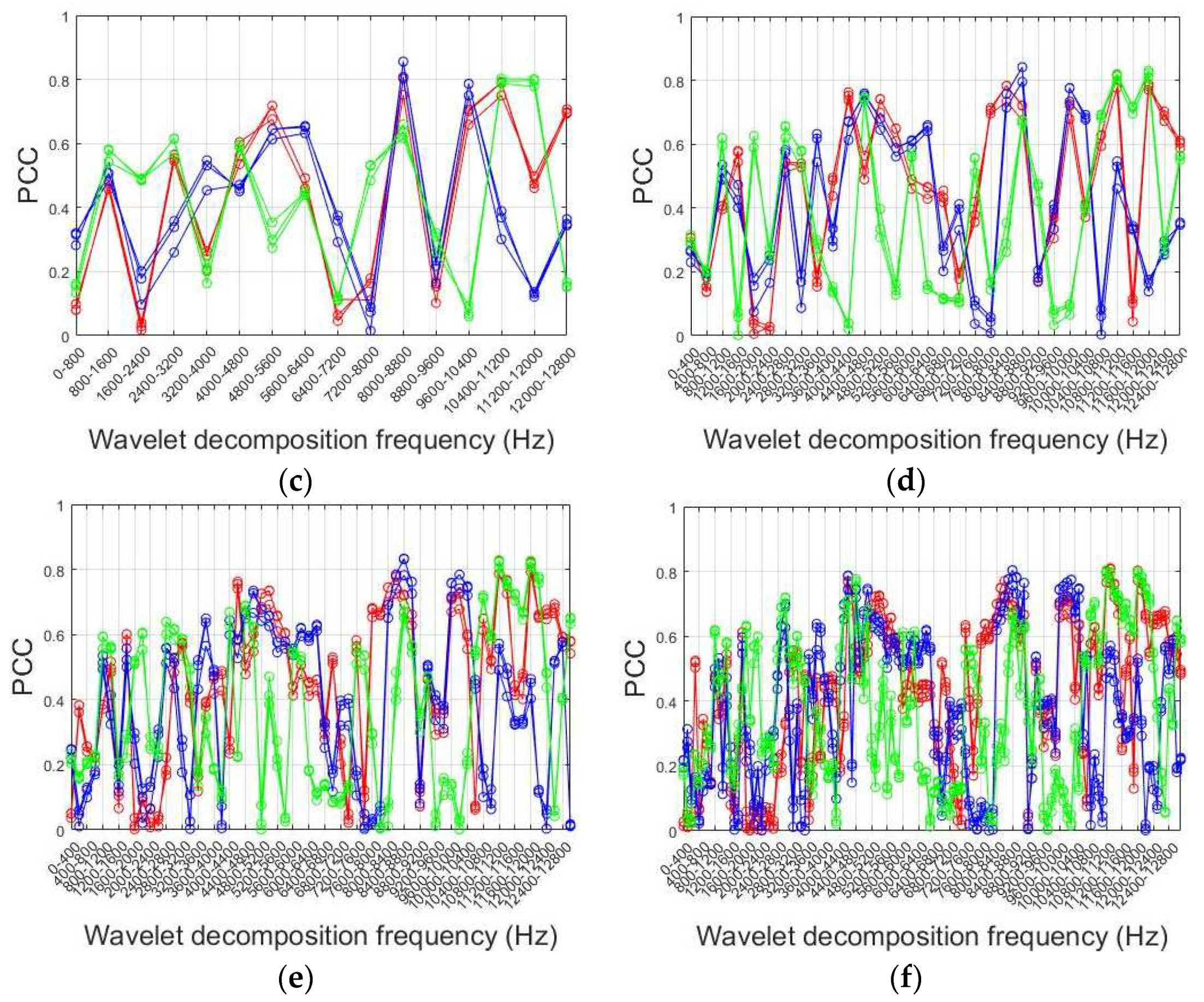
Preprints 98450 g016aPreprints 98450 g016b
Figure 16. PCCs between energy of each decomposition level (L) and roughness (a) L2; (b) L3; (c) L4; (d) L5; (e) L6; (f) L7.
Figure 16. PCCs between energy of each decomposition level (L) and roughness (a) L2; (b) L3; (c) L4; (d) L5; (e) L6; (f) L7.
Preprints 98450 g016aPreprints 98450 g016b
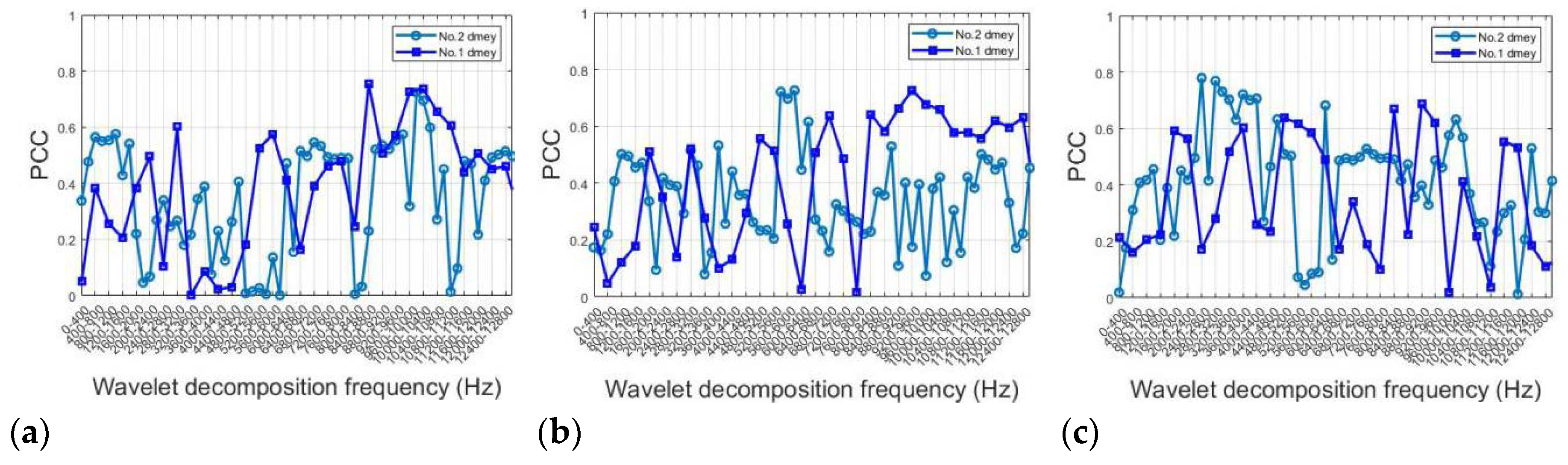
Preprints 98450 g017
Figure 17. PCCs between energy of dmey decomposition level (L6) and roughness for No.1 and No.2 tool.
Figure 17. PCCs between energy of dmey decomposition level (L6) and roughness for No.1 and No.2 tool.
Preprints 98450 g017
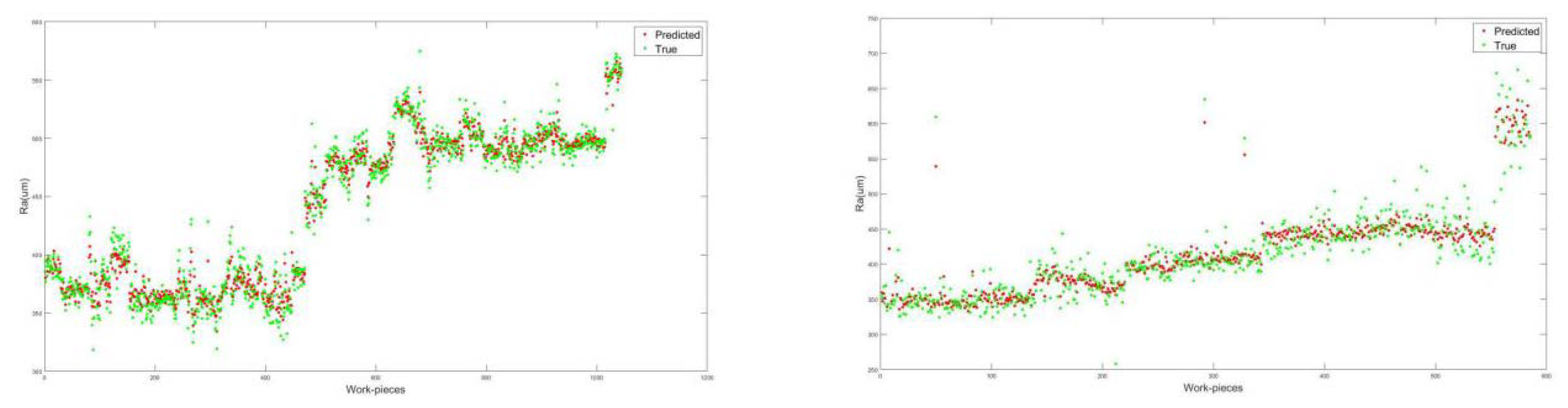
Preprints 98450 g018
Figure 19. GPR prediction results for No. 1 tool and No. 2 tool.
Figure 19. GPR prediction results for No. 1 tool and No. 2 tool.
Preprints 98450 g018
Table 1. SYMA CNC Cutting parameters.
Table 1. SYMA CNC Cutting parameters.
Cutting Parameters Data
Depth of cut 0.06(mm)
Spindle speed 3200(RPM)
Feed rate 0.06 (mm/rev)
Tool nose radius 0.6(mm)
Tool overhang length 13 (mm)
Cutting fluid With Coolant
Table 2. Approximate time duration of each step of cutting.
Table 2. Approximate time duration of each step of cutting.
1 8~12 Loading
2 15~16 Moving
3 16~20 Roughing
4 21~23 Drilling
5 23~25 Moving
6 25~47 Milling
7 47~48 Moving
8 48~53 Finishing Turning
9 53~58 Moving Back
Table 3. comparison two tools’ maximum values of PCCs.
Table 3. comparison two tools’ maximum values of PCCs.
Tool No. Domain Parameters X Y Z
1 Time PCC 0.7969 0.7013 0.7396
Property Kurtosis Kurtosis Kurtosis
Frequency PCC 0.8674 0.7689 0.7562
Frequency (Hz) 3700 1300 3800
2 Time PCC 0.8267 0.2708 0.7402
Property STD/RMS STD/RMS STD/RMS
Frequency PCC 0.8221 0.7749 0.8511
Frequency (Hz) 4700 8100 3100
Table 4. Fifty-two mother wavelets.
Table 4. Fifty-two mother wavelets.
Mother Wavelets Families Order
Daubechies db2, db3, db4, db5, db6, db7, db8, db9, db10, db11, db12,db13, db14, db15, db16, db17, db18, db19, db20
Haar Haar
Discrete Meyer dmey
Fejer-Korovkin filters fk4, fk6, fk8, fk14, fk22
Coiflets coif1,coif2, coif3, coif4, coif5
Symmlets sym2, sym3, sym4, sym5, sym6, sym7, sym8
Biorthogonal bior1.3, bior1.5, bior2.2, bior2.4, bior2.6, bior2.8, bior3.1, bior3.3, bior3.5, bior3.7, bior3.9, bior4.4, bior5.5, bior6.8.
Table 5. Prediction models’s accuracy.
Table 5. Prediction models’s accuracy.
Models Tool RMSE R2
Linear regression 1# 18.369 0.92
2# 28.19 0.81
SVM 1# 18.453 0.92
2# 27.779 0.81
GPR 1# 16.141 0.94
2# 26.682 0.83
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated