Prerpints.org logo
Preprint
Article

Trade Agreements and Financial Market Integration in Latin America and the US

Altmetrics

Downloads

112

Views

57

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

07 February 2024

Posted:

08 February 2024

You are already at the latest version

Alerts
Abstract
The primary objective of this study is to examine the extent of financial integration between Latin American and US financial markets, particularly in light of recent efforts to foster integration through trade agreements. Spanning from January 1, 1990, to December 31, 2019, the sample focuses on major market indices and key sectors. Financial integration is quantified using a DCC multivariate GARCH model, incorporating a smooth transition model, structural breaks, and regression-based approaches. Results indicate increased comovement with the US for main market indices in Argentina, Chile, Colombia, Mexico, and Peru, while Brazil shows a decrease. Similar trends are observed in sectoral analyses. The study also reveals heightened correlation post-trade agreements. Structural break analysis highlights significant shifts in dynamic correlations for countries with US free trade agreements. These findings support the argument of increased financial integration, bearing significance for portfolio diversification and international policy formulation.
Keywords: 
Subject: Business, Economics and Management  -   Finance

1. Introduction

Financial market integration has been a topic of great interest among academicians and practitioners as it directly impacts investments across the world. Financial integration among countries is significant in many aspects of financial economics. For policymakers, understanding the impact that other countries have on their financial market, hence the country’s economy is of utmost importance. For investors, well diversified portfolios are created under the idea that correlations are understood but if these correlations are changing over time, then portfolios should be adjusted based on the time-varying fluctuations on these correlations.
It is important to point out that financial market integration can be measured through several approaches. This investigation focused mainly on one specific measure, comovement, of financial markets. Previous literature has examined the level of comovement within developed countries (Berben and Jansen, 2005; Longin and Solnik, 1995; Eun and Shim, 1989; Rua and Nunes, 2009). The results support the argument that market integration is time-varying and that the degree of comovement among financial markets in developed countries is increasing. Most of these studies have focused on financial integration between major developed countries. However, financial market integration between emerging economies has not been examined as thoroughly as developed markets in recent time even though investors are flocking towards international investments seeking a higher degree of diversification. Forbes and Rigobon (2002) study comovement among international stock markets and find that correlation coefficients are conditional on the examined markets’ volatility. In addition, Bekeart and Harvey (1995) show that some Latin American equity markets tend to have a low correlation with the US while Johnson and Soenen (2003) show that Latin American markets comovement with the US is changing in different directions. Also, Fujii (2005) investigate the links between selected Asian and Latin American countries and find significant market connections between the examined Asian and Latin American markets.
Latin American countries have been working to integrate their main financial markets. These efforts have increased access to capital for both domestic and international firms. For example, the creation of the Mercado Integrado Latinoamericano (MILA) which is an integrated exchange that consists of four of the most relevant markets in the region (Chile, Colombia, Mexico, and Peru). With this new integration, stocks from all these countries can be traded by investors in any of the four markets in their original currency. Further, regional cooperation organizations like Latin American Integration Association (ALADI) or Mercosur (South American Common Market) have helped unite these countries in a wide range of factors. These efforts have also focused on aiding economies and financial markets to interact more closely within this region.
In addition, regional trading deals such as the North American Free Trade Agreement (NAFTA), which involves a direct free trade agreement between Canada, the US, and Mexico was established in 1994. This trade agreement included tariff reductions for a significant number of goods between these countries that were gradually reduced until 2008. In 2019, a new NAFTA deal is being prepared [1]. This was the initial free trade agreement between the US and any Latin American country. The US government has gradually increased trade and cooperation efforts with several countries in this region by creating trade agreements with a significant number of countries in Central and South America.
The US has put in place several bilateral trade agreements with countries in this region. For example, the US government has utilized three main types of trade agreements with countries in the Latin American region, which are: the Trade and Investment Framework Agreement (TIFA), Agreement on Trade and Economic Cooperation (ATEC), and bilateral Free Trade Agreements (FTA). A Trade and Investment Framework Agreement (TIFA) is considered a trade deal that creates a strategic framework to expand trade and resolve any disputes between countries. The Agreement on Trade and Economic Cooperation (ATEC) created between Brazil and the US is a specific agreement between these countries. The ATEC is a unique pact in the sense that it promotes bilateral trade and economic cooperation, but it is not a full free trade agreement. In essence, the agreement is very similar to a Trade and Investment Framework Agreement (TIFA), and it is perceived as a first step towards the creation of a future free trade agreement between both countries. These agreements tend to pave the way for bilateral free trade agreements with the US. A free trade agreement is a trade deal that diminishes barriers of imports and exports. Under a free trade agreement, goods and services can be exchanged across countries borders with minimal or no government tariffs, quotas, subsidies, or prohibitions. This type of trade pact is the strongest among the three different types the US has used within this region. Nonetheless, all the above-mentioned trade agreements intend to reduce trade and investment barriers, open markets and eliminate obstacles between these two countries over time.
Specifically in this region, the US has created 3 different free trade agreements. NAFTA includes three countries (the US, Mexico, and Canada) while the remaining deals are bilateral free trade agreements. The US has a bilateral free trade agreement with Chile, Colombia, and Peru. Moreover, The United States-Chile Free Trade Agreement (FTA) entered into force on January 1, 2004, but the deal was signed on March 6, 2003. The United States-Colombia Trade Promotion Agreement (FTA) was signed on November 22, 2006, but took about 6 years to get into force on May 15, 2012. From the bilateral free trade agreements, the Colombian pact took the longest to get implemented after the official signature between the countries. The United States-Peru Free Trade Agreement (FTA) entered into force on February 1, 2009, while it was initially agreed upon on April 12, 2006. On the other hand, the US has also instituted a TIFA and an ATEC with Argentina and Brazil, respectively. On March 18, 2011, the US and Brazil signed an Agreement on Trade and Economic Cooperation (ATEC) to strengthen trade and investment between the two nations. Finally, Argentina and the US signed a bilateral Trade and Investment Framework Agreement (TIFA) on March 23, 2016, to advance trade and market accessibility between both countries [2]. As a result, these trade agreements have strengthened the ties between the US and these 6 countries on a wide range of levels, sectors, and industries.
All these integration efforts have been of great importance considering the close geographical proximity between these countries. For instance, Bae, Elkhami, and Simutin (2019) state that most Latin American countries import heavily from the US. According to Bae et al. (2019), the US is the largest importer for all the Latin American countries examined in this paper, which shows these countries are deeply connected in a wide range of levels. According to Forbes and Chinn (2004), trade flows are one of the most relevant determinants of cross-country relations. Basnet and Sharma (2013) examine the integration in terms of macro variables (i.e., GDP, Investment, Trade, and Consumption) between the major Latin American countries and the study concludes that these countries are getting a higher degree of synchronization both in short and long terms. Consequently, the expectation is that the trade agreements are able to help these countries accelerate the integration among the studied stock markets.
Whether the degree of comovement has increased or decreased it is of great importance to closely examine these correlations to determine how to properly construct portfolios. Consequently, this study brings a contribution to the existing literature by examining the degree of financial integration, through market comovement, within the stock markets in Latin America as well as their degree of comovement with the American market. In addition, this investigation helps determine how these trade agreements affect financial market integration and if they have been a direct catalyst for a higher or lower degree of integration.
Finally, the main objectives of this paper are twofold. First, to research the level of financial market integration between the US and the main Latin American markets over time. Second, to explore if the different types of trade agreements between the US and these countries have impacted the comovement of these financial markets. The study concludes that the degree of comovement between the US and the main Latin American countries (Argentina, Brazil, Chile, Colombia, Mexico, and Peru) vary widely. Different sectors and industries are affected differently through the sample and the trade agreements seem to impact sectors that deal with physical products (basic materials, consumer goods, industrial, financial, and energy) more than the others. In terms of the main market indices, the results show that the integration with the American market index (S&P 500) has increased over time for all the countries except for Brazil which had a small reduction in correlation during the end of the sample period.
The rest of the study is organized as follows. Section 2 and Section 3 present the methodology and data, respectively. Section 4 reports empirical results. Section 5 offers concluding remarks of this study.

2. Methodology

To thoroughly research the correlations between the returns of the different stock markets, the paper investigates the dynamic conditional correlations between the American market index and sector indices with their Latin American counterparts. This approach will help us determine the level of comovement between the market index as well as different sector indices. In addition, a smooth transitional model in introduced do establish the changes in correlation over time while structural breaks on this correlation are implemented to determine if the signing and/or implementation of the trade agreements had a direct impact on these correlations. Finally, a regression-based approach is considered to study the degree of comovement before and after the sign and/or implementation of the trade agreements.
As previously mentioned, this paper focuses on one of the most used measure of financial integration, comovement between market indices. For asset return volatility, it is shown that large changes in returns in one period tend to be followed by large changes in the following periods. This is called volatility clustering which usually becomes more evident as the frequency of the data rises. The GARCH class models have proven to be successful in capturing volatility clustering. As shown in previous studies, GARCH models appear to properly account for the stochastic properties of stock returns and correlation, in other words, time-variation and persistence of the variables.
Taking these properties into account, this paper will follow the dynamic conditional correlation (DCC) approach proposed by Engle (2002). The dynamic conditional correlation model can determine how correlations among the examined countries have changed through the studied sample. Therefore, this model can measure comovement between the US and the Latin American financial markets. The DCC-GARCH model follows:
r t = µ t + ε t , ε t | I t − 1 → N ( 0 , H t )
where r t is a k × l vector that consists of the index return series for each market and H t is the conditional variance-covariance matrix of the return vector r t while ε t | I t − 1 accounts for the information set that considers all the information up to time t. Further, the conditional variance-covariance matrix can be expressed as follows:
H t = D t R t D t
and
D t = d i a g ( h 1 t ,   h 2 t )
where D t is the 2 × 2 diagonal matrix of time-varying standard deviations from the univariate GARCH models with h i t on the diagonal and R t is considered the time variant conditional correlation matrix. Thus, we first estimate the univariate volatility model for each market and the best one is selected using the Akaike Information Criterion (AIC). The considered models include the GARCH model proposed by Bollerslev (1986), EGARCH model proposed by Nelson (1991), TGARCH proposed by Zakoian (1994) and GJR-GARCH of Glosten et al. (1993). Consequently, the residuals of each are specific market are utilized to estimate the dynamic conditional correlation matrix R t .
The dynamic conditional correlation matrix R t is expected to change based on a GARCH process and follows:
R t = Q t * − 1 Q t Q t * − 1
In this case Q is the unconditional correlation matrix of the ε ’s and follows:
Q t = 1 − a − b Q ¯ + a ε t − 1 − 1 ε t − 1 ′ + b Q t − 1
The parameters a and b represent the effect of preceding shocks and former dynamic correlations. These estimates are obtained from the univariate GARCH estimations, and they satisfy a + b > 1 .
The bivariate conditional correlation coefficient ρ i j between two markets therefore follows the equation:
ρ i j = 1 − a − b Q ¯ + a ε t − 1 − 1 ε t − 1 ′ + b Q t − 1 1 − a − b Q i i ¯ + a ε i , t − 1 2 + b Q i i , t − 1 1 − a − b Q j j ¯ + a ε j , t − 1 2 + b Q j j , t − 1
In addition, to examine the effects of free trade agreements within the conditional correlations of the US and these Latin American countries. Therefore, the second approach is to use structural breaks within the dynamic conditional correlations between these countries’ indices. For this approach, two different structures were used. The first one tested for structural breaks for known dates which in this case will be the signing date and implementation or start date. The other structure lets the data determine the structural breaks and the idea is to establish the breaks and their location in a linear regression framework. Following Bai and Perron (2003) if we assume that the dynamic conditional correlations have m number of breaks ( b 1 … b m ), then we determine the date of any structural breaks by focusing on the breakpoints that minimize the following function:
b ^ 1 … b ^ m = a r g m i n b ^ 1 … b ^ m R S S b ^ 1 … b ^ m
where RSS is the residual sum of squares that results from the b regressions. These regressions that the following form:
y t = β x t T + ϵ t   ; ( t = 1 ,   2 ,   … , n )
In this case the y t is the estimated bivariate dynamic conditional correlation series at time t , x t is a vector of the observations of y t − 1 , β is the vector of regression coefficients and ϵ t is the error term which is assumed to be independent and identically distributed ( 0 , δ 2 ).
The null hypothesis states that there is no structural break while the alternative hypothesis that the regression coefficients vary over time. Therefore, if we reject the null then we conclude that the estimated structural break is statistically significant. The idea is to determine if a structural change occurred around the trade agreements.
Structural breaks assume that changes in comovement are instantaneous and readily visible. This might not always be the case considering that these markets can gradually integrate rather than at a determined point in time regardless of external shocks that impact integration. As a result, the structural breaks approach has several limitations that can be mitigated by using other methods. One of those methods is the smooth transition model. The idea behind the smooth transition model is to measure the changes in comovement in an extended period rather than at a specific moment in time. This long-term approach gives a better understanding of the movement between the examined markets as the models show the change in comovement over time.
In addition, other researchers have examined DCC-GARCH models with a smooth transition model to detect structure changes in the correlations (Chelley-Steeley, 2005; Berben and Jansen, 2005; Lin and Teräsvirta, 1994). However, a disadvantage of the smooth transition model is that it assumes a single transition period between two long-run means. This model specification can limit the number of structural changes in the correlation in our sample considering the sample covers an extensive amount of time. The smooth transition model is applied to bivariate equity market dynamic conditional correlations which have been obtained using the previously discussed dynamic conditional correlation (DCC-GARCH) model.
The logistic smooth transition regression model for the conditional correlations time series between the US and the Latin American countries, ρ i j , t estimated earlier can be expressed as:
ρ ^ i j 2 t = α + β S t γ , τ + ϵ t
where ϵ t is considered a stationary ( I 0 ) process with zero mean. Consequently, the smooth transition between the two examined indices is commanded by the log function S t γ , τ . This log function can then be formalized using the following equation:
S t γ , τ = 1 + exp ⁡ − γ t − τ N − 1 ; ( r > 1 )
where N is the size of the sample. Further, τ establishes the point in which the dynamic conditional correlation changed from pattern one to pattern two. In other words, τ determined the midpoint or the point of change between the dynamic conditional correlations. The midpoint essentially partitions the sample into a section before integration and section after the integration. Therefore, there is a before and an after in terms of average correlation. The a represents the mean of the section of the sample before the midpoint or old structure before integration while β determines the change in correlations of the sample after the midpoint or turning point as shown by the smooth transition model. Consequently, if β > 0 then we can conclude that the newer conditional correlation or the correlation after the midpoint has increased through the sample. On the other hands, if β < 0 it means that the newer conditional correlation or the correlation after the midpoint has decreased compared to initial section. As a result, the summation between a and β signifies the mean of the new regime. This method gives us an idea regarding the integration changes over time as well as after the trade agreement.
Although the smooth transition model is able to give us a better representation of the different regimes of correlation it is also important to note that this approach specifies one single midpoint that serves as the turning point between the changes in correlation. Considering the large time frame, the turning point could appear at any given point in our sample. To determine if dynamic conditional correlations have changed over time, a regression-based approach is taken into consideration. This approach follows:
y t = α 1 + δ 1 α 2 + ϵ t
where y t is the dynamic conditional correlations previously computed, δ is the dummy variable indicating the date after the signing or start date of the trade agreement between the US and the given Latin American country while α 1 is the constant and α 2 is the coefficient that determines the increase or decrease after the trade agreement. A positive α 2 indicates an increase in correlation after the trade agreement while a negative α 2 shows a decrease in correlation after the trade agreement. Finally, ϵ t represents the error term.

3. Data

The data used for this study was collected from DataStream. The most important stock exchange markets in Latin America were selected for this research. The selection is based on market capitalization and data availability and includes the following countries: Argentina, Brazil, Chile, Colombia, Mexico, and Peru. The market indices selected for the mentioned nations are: MERVAL for Argentina, IBOVESPA or B3 for Brazil, IPSA for Chile, COLCAP for Colombia, IPC for Mexico, and SPBLPGPT for Peru. On the other hand, the two main American market indices in the US were obtained (S&P500 and DJIA) [3].
In addition, for each country the main industry sectors were considered. Following the industry classification benchmark (ICB) used by the FTSE for sector and industry classification, the main industry sectors studied are basic materials, consumer discretionary, consumer staples, energy, financials, healthcare, industrials, real estate, technology, telecommunications, and utilities [4]. However, considering that the healthcare and technology sectors are not present in 4 out of the 7 countries those were not taken into consideration. Further, the real estate index is not available for Colombia while the energy index is not available for Mexico. The idea is to incorporate as many sectors as possible to research how each different sector comoves with the same sectors in the US. The more sectors incorporated the better one can understand the different changes in correlations with the US.
The data was selected for the period between January 1, 1990, and December 31, 2019. Although some countries only have available data slightly after the selected starting date, if that is the case, the earliest available data is used. From this data, the daily and weekly returns for each index and sector over the entire sample were computed. Moreover, the log daily and weekly returns were considered as well as the daily and weekly raw returns. The results are consistent but the weekly log returns were used in this study [5]. To eliminate any possible discrepancies with different currencies and to make the returns more comparable, the returns were calculated in U.S. Dollars. As a result, the weekly log returns in USD were used for the entire analysis.

4. Empirical Analysis

4.1. Preliminary Analysis and Time-Varying Estimation Models

Table 1 presents the summary statistics for every country sorted by industry. The summary statistics show huge variations in returns. Returns range from -25.80% to 86.40%. Also, the volatility of the market in terms of standard deviation of all indices is relatively high during the sample period. Standard deviations range from about 2.20% to 24.01%. In our sample, Colombia is the most vulnerable in terms of returns and standard deviations: it exhibits the highest and lowest returns, and the highest standard deviations among countries. Compared to other countries, the U.S. exhibit the lowest standard deviations and the second highest returns, which show the ideal market conditions.
Figure 1 shows a graphical representation of the returns on the main market indices for each country. A visual representation shows that the market indices for these countries are stationary [6]. In addition, we generate normality and autocorrelation tests for further analysis [7].
Billio, Donadelli, Paradiso, and Riedel (2015) show that unconditional correlations performed as well as more sophisticated financial integration measures proposed in the existing literature and even though many authors have shown that correlation is time varying, the unconditional correlation of each countries’ main market and sectors indices to determine each country’s pairwise correlation without considering the time-variance adjustments. This way one can establish if the correlations have drastically changed during the different time periods. Table 2 shows the correlations among the examined indices. At a first glance, we observe that there are no negative correlations which indicates that these countries up to a given extent move in the same direction. For the main market index, the highest correlations are between the Brazil and Mexico with 0.649, the US and Mexico with 0.617, Also, Brazil and the US with 0.574, and Brazil and Argentina with 0.538 exhibit strong positive correlations as well.
In addition, we report correlations between all countries sorted by industry [8]. We observe all correlations are positive and each country and industry exhibit different levels of connectedness. For example, the basic materials sector the highest correlation is between the US and Brazil with 0.640, for consumer services the US and Mexico share the strongest relation with 0.507 while for consumer goods the strongest pairwise correlation is between Chile and Brazil with 0.370. Brazil dominates the energy (and utilities) correlation with the US (and Chile) with correlations of 0.667 (and 0.491). Mexico dominates the correlation with the US in the industrials sector with 0.597.
Now that we have a sense of the pairwise correlations among the countries and their sectors, the univariate generalized autoregressive conditional heteroskedasticity (GARCH) model is considered since all the returns showed autocorrelation. The next step included the estimation of the univariate GARCH model and selecting the best model based on the Akaike Information Criterion (AIC) and Schwarz’s Bayesian Criterion (BIC) to determine the best GARCH model based on the estimation of each model. As previously stated, the best model was selected among the traditional GARCH, EGARCH, GJR-GARCH and TGARCH. The model with the lowest AIC (BIC) score will be selected since it shows the best fit.
According to the results in Table 3, GARCH (1,1) is the best model for 11 of the analyzed sectors’ returns. EGARCH (1,1) and GJR-GARCH (1,1) are present in 34 and 21 of studied sectors, respectively. Like EGARCH (1,1) and GJR-GARCH (1,1), TGARCH (1,1) also shows the presence of asymmetric effects on these sectors. This indicates that there exist significant asymmetric effects on time-series. For example, EGARCH (1,1) model predominates in Argentina, Brazil, Mexico, and the US. Also, GJR-GARCH (1,1) predominates within sectors, indicating that most countries and sectors react differently to good and/or bad news. Before moving to the conditional correlation approach, we generate normality tests for the residuals and the squared residuals of the models [9].
As previously stated, the DCC-GARCH model will be a bivariate model with the US market and US sectors being paired with their respective counterpart from the Latin American countries (Argentina, Brazil, Chile, Colombia, Mexico, and Peru). That is, the US will be paired with each Latin American country’s index to determine their comovement. The estimates of the dynamics on the conditional correlations are shown in Table 4. The coefficients among the different sectors and countries are quite similar. We observe that coefficients, a , are relatively small (with the except of a couple of the coefficients), indicating that conditional volatility does not change very rapidly. Coefficients, b , are much larger than coefficients, a , indicating gradual fluctuations over time. We confirm that the estimated coefficients a and b satisfy the stationary conditions for all the variance and covariance processes.
Table 5 presents the summary statistics of the bivariate conditional correlations between U.S. and each of the respective Latin American markets. It is important to notice that similar to the unconditional correlations we find that all the Latin American indices studied have an average positive correlation with the US indices. In terms of the market index, on average, Mexico has the highest conditional correlation with the US with 0.532, and Colombia has the lowest mean conditional correlation relative to the US with 0.182, indicating that Mexican market tends to comove with U.S. markets relatively more compared to the remaining Latin American countries. This is not surprising since Mexico has engaged in a free trade agreement with the US since 1994. Also, the geographical proximity to the US is significant for their strong comovement. On the other hand, Colombia has the lowest conditional correlation which should imply higher diversification gains to an American investor relative to the rest of Latin America nations. Moreover, the ranking shows that the countries more developed (Argentina, Brazil, and Mexico) within this group have a higher positive dynamic conditional correlation with the US than countries relatively less developed (Colombia and Peru). Lastly, we observe that countries more developed (Argentina, Brazil, and Mexico) tend to have a higher correlation with the US than countries relatively less developed (Colombia and Peru). These findings show where American investors can get portfolio diversification benefits with Latin American countries and their sectors as well [10].
The dynamic conditional correlation for the main market indices between the US and the examined countries can be seen in Figure 2. All graphs show 2 lines that denote the signing date of the trade agreement with the US while the second line shows the point in time in which the trade deal started and was implemented. A visual examination of the Argentina-US conditional correlation shows that conditional correlation has increased from the start of the sample (1990) and mostly increased through time. Some of the abrupt changes can be attributed to the several financial problems related to currency issues as well as default problems that Argentina has encountered in the last 15 years. Brazil has a very low correlation and large spikes on the beginning of the sample which coincide with the implementation of the Real as the nation’s currency (replacing the cruzeiro real). However, we observe that an upward trend and a significant increase in correlations, especially during the financial crisis and the years after that. For Chile, we observe that comovement was low at the beginning of the sample but gradually increased while the country started liberalizing its market. Colombia shows a low correlation with the US for the first 10 years but has a significant bump in correlation close to the signing of the bilateral free trade agreement with the US. After that considerable rise, the correlations seem to stabilize during the new range. In 2016, Colombia experienced high inflation and lowered GDP growth. This matches the movements shown in the graph of the dynamic conditional correlation. Mexico shows a different story than the rest of the countries. It seems that comovement between the US and Mexico has been significantly strong over most of the sample. However, the later part of the sample correlation between these countries suffers a significant downward trend for a short period. Although it does not involve any specific crisis or country specific turmoil, it does conform with the initial stages of negotiation of a new trade agreement. During this time, several negotiation talks failed to move the new agreement forward and talks of eliminating free trade between Mexico and the US were surfaced. After long negotiations occurred a new deal was signed, and the graphs shows the correlation bouncing back to previous values. Lastly, Peru has been a relatively small market in Latin America that has started growing in the last 10 years. The graph of the conditional correlation shows that comovement was relatively low and has a gradual trend towards a higher degree of comovement. The graphs for the remaining sector indices show similar effects to the ones shown on the main market indices.

4.2. Smooth Transition Model

The smooth transition model on the dynamic bivariate conditional correlation between the US and the examined Latin American countries was computed [11].
The results of the smooth transition estimation are shown in Table 6. The smooth transition model estimates the average correlation between two different regimes. The term α is the average correlation of the first (old) regime while β is the change in correlation on the second (new) regime. Consequently, α + β is an indicator of the average correlation on the second (new) regime. The term γ establishes the slope of the transition curve. The highest the values of γ the more drastic the change between the two correlations (old and new) regimes. Lastly, τ show the midpoint or turning point of the transition curve.
For the market index comovement between the US and Argentina, the first regime has an average correlation of 0.378 while the second regime has correlation of 0.472. This would be clear evidence that comovement has increased during the sample period. The midpoint was in mid-2003 and it shows a large γ which signifies a more abrupt change in correlations. On the other hand, Brazil shows an average correlation of 0.513 on the first part of the sample but the second regime reduces by 0.064, resulting in a decrease of comovement in the second regime. The market index in Chile shows a 0.358 correlation for the first regime while 0.024 for the second regime. For Colombia, the midpoint was on the earliest part of the sample in late 1995. The correlation regimes moved from 0.080 to 0.246. Mexico also shows a similar story with an old regime correlation of 0.512 and with a new correlation regime of 0.634. In this case the midpoint occurred in early 2001. Peru shows an old regime correlation of 0.261 while a new correlation regime of 0.474, which is the biggest increase in correlation among the main market indices. From all the countries’ main indices all increased their level of comovement with the US in the smooth transition approach except Brazil. We conclude that the degree of comovement mostly increased. In terms of all the different sectors across the Latin American countries, the results show that the majority of the indices exhibit an increase in correlation from the old regime to the new one, indicating that different countries and sectors have shifted differently over the entire sample but most of the countries show a significant increase.
Employing the smooth transition model, we observe that the comovement between the US and Latin American countries (except Brazil) has increased during the sample period. One downside of this model is that we only consider one midpoint of the entire sample of 30 years. To check robustness of the smooth transition model, we generate tests for a unit root on the residuals of the model [12]. We confirm that the smooth transition model is appropriate for the evaluated series.

4.3. Structural Breaks

The structural break analysis was divided into two main approaches. The first included testing known dates that includes considering if structural breaks are present during the signing date as well as during the established start date of the bilateral trade agreements. The second approach tested for unknown structural breaks. In Table 7 Panel A, we report results for the structural breaks around the signing and start dates of the dynamic conditional correlations show the presence of structural breaks in some of the main indices.
In Table 7, we report structural breaks with known dates (Panel A) and unknow dates (Panel B). Also, the regression analysis was taken to examine directly if the dynamic conditional correlation between these countries has changed after the signing and implementation of each trade agreement (Panel C).
Table 7. Structure Breaks and Regression Analysis.
Table 7. Structure Breaks and Regression Analysis.
Panel A. Structure Breaks - Known Dates
Country List Sign Date Start Date
Argentina and US 3.737 3.737
Brazil and US 3.841 3.841
Chile and US 5.621* 2.841
Colombia and US 5.833** 3.353
Mexico and US 6.602** 7.204**
Peru and US 6.577** 6.920**
Notes: *, **, and *** indicate a significant at the 90%, 95%, and 99% levels, respectively.
Panel B. Structure Breaks - Unknown Dates
Country List Number of Breakpoints Estimated Break Dates
Argentina and US 5 07-1994; 04-1999; 05-2006; 01-2011; 04-2016
Brazil and US 5 04-1998; 07-2002; 05-2006; 02-2011; 03-2016
Chile and US 5 01-1997; 06-2003;05-2006; 11-2010; 07-2015
Colombia and US 5 12-1997; 03-2002; 08-2006; 02-2011; 04-2015
Mexico and US 5 07-1996; 05-2011; 05-2006; 01-2011; 07-2015
Peru and US 5 07-1997; 07-2002; 04-2006; 05-2011; 08-2015
Notes: *, **, and *** indicate a significant at the 90%, 95%, and 99% levels, respectively.
Panel C. Regression Analysis
Country List Sign Date Start Date
Argentina and US 0.051*** 0.051***
Brazil and US -0.122*** -0.122***
Chile and US 0.118*** 0.115***
Colombia and US 0.212*** 0.135***
Mexico and US 0.202*** 0.225***
Peru and US 0.060*** 0.065***
Notes: *, **, and *** indicate a significant at the 90%, 95%, and 99% levels, respectively.
We observe structural breaks for Chile, Colombia, Mexico, and Peru while the other two (Argentina and Brazil) do not exhibit a structural break after the signing or start dates of their trade agreements. This coincides with the countries that have a stronger trade agreement with the US. It is important to recall that Colombia, Chile, Mexico, and Peru have a full bilateral free trade agreement while Argentina and Brazil have trade agreements that are not completely free trade agreements hence their strength is weaker relative to a full free trade agreement. Some specific sectors such as materials, consumer goods, financial, energy and industrial exhibit the highest number of structural breaks during the sign and start dates, indicating that such industries in Latin America tend to have a higher level of commercial connection with the US [13].
In addition, we report unknown structure breaks in Table 7 Panel B. Contrary to the known structural breaks, the unknown structural break approach used by Bai and Perron (2003) tests for a specified number of breaks in the bivariate dynamic conditional correlation. In this case, the unknown structural breaks were limited to 5 but would incorporate more than 5 if these breaks were present. The results of the unknown structural breaks show a very similar story to the one from the known structural breaks (signing and start dates). It is also important to consider that several unknown breaks are very close to the signing and start dates. Although the structural breaks are not on the exact same date, according to the data, there is a break present near that specific date. This can be attributed to the trade agreements considering there are significant or major events that could produce such a shock on the correlation between these countries in that given time. As mentioned previously and as shown by the analysis, the impact on the bivariate dynamic conditional correlation might not be shown immediately but through a more prolonged period of time. Therefore, the smooth transition model was considered to study how the correlations have changed over the sample period.
Lastly, to examine directly if the dynamic conditional correlation between these countries has changed after the signing and implementation of each trade agreement a regression approach was taken. The idea is to use the dynamic conditional correlation as the dependent variable, and an indicator variable determines the creation and implementation of the trade agreements. In Table 7 Panel C presents the coefficients of the model, and we observe that after the respective bilateral trade agreements between the US and Argentina, Chile, Colombia, Mexico, and Peru have increased comovement in the main market indices between these countries. Also, the US and Brazil dynamic conditional correlation shows a negative and significant coefficient that signifies that the comovement between the US and Brazil has fallen after the implementation of their trade agreement.

5. Conclusions

The main objective of this study was to empirically investigate if the comovement between main stock indices of Argentina, Brazil, Colombia, Chile, Mexico, and Peru have shown greater or lower comovement in relation to the US financial markets. We conclude that main market indices of Argentina, Chile, Colombia, Mexico, and Peru have increased their correlation with the main market index in the US after the respective bilateral trade agreements. In addition, the results indicate that the integration with the US market index has increased over time for all the countries except for Brazil which had a small reduction in correlation during the end of the sample period. The results of the smooth transition model also provide support to the previous claims.
The lower values and lack of structural breaks around Argentina and Brazil can be partly explained by the type of trade agreement. Considering that the agreements that Argentina and Brazil signed with the US are not full free trade agreements the impact on financial market integration seems lower. On the contrary, the countries that do have a free trade agreement (Chile, Colombia, Mexico, and Peru) with the US shown a higher number of structural breaks around the signing and implementation dates of these treaties. In addition, the regression-based approach shows the comovement between Latin American and the US financial markets.
The results show evidence that the financial market integration between these countries is varying consistently over time so close attention must be taken. The implication of the study for policy makers can be stated as, an increase in the level of correlations between Latin American and the US financial markets means that financial market disturbances in the US are more likely to be transmitted to these countries, which may have adverse consequences for the stability of the financial systems involved. On the other hand, a higher degree of comovement implies that optimal portfolios have changed as a result of the correlation variation hence investors will have to adjust their portfolios accordingly. The results support the idea that financial market integration in the region is increasing overall as well as the argument that the US has become more integrated with this region over time.

Notes

  • The new deal is now known as the USMCA (US-Mexico-Canada Agreement) and it was implemented in July 1, 2020. Although the new deal is within the scope of this research, it is out of the research sample and time frame.
  • Detailed information about the implementation and creation of each Trade Agreement is given in Appendix A.
  • The results shown in this study used the S&P500. DJIA was used and showed very similar results.
  • Appendix B shows the sectors with their respective industries as per the ICB-FTSE classification.
  • Although the results are similar, the weekly approach was used to accommodate for any potential biases regarding holidays, exchange operational days and time differences.
  • We conduct an Augmented-Dickey-Fuller (ADF) test and confirm that the given time-series are stationary.
  • We generate wilk-Shapiro (Normality) and Ljung-Box Q (Autocorrelation) tests. The results are available upon request.
  • When we report unconditional correlations of energy and real estate sectors, we exclude Mexico and Colombia, respectively, due to data unavailability.
  • Normality tests for residuals and squared residuals are available upon request.
  • Appendix C provides the summary statistics of the bivariate conditional correlations between US and each of the respective Latin American markets sorted by industry.
  • Appendix D provides ADF statistics before fitting the smooth transition model. We confirm that a smooth transition model can be used on dynamic conditional correlations.
  • The assumption behind the smooth transition model is that the residuals should be stationary to be a good fit for the data: An Augmented-Dickey Fuller test was conducted on the residuals and all the results show that the residuals are stationary. Appendix E provides all results.
  • In Table 7, we only report the results based on the market index between countries. Sectors information is reported separately and is available upon request.

References

  1. Bae, K.H.; Karolyi, G.A.; Stulz, R.M. A new approach to measuring financial contagion. Rev. Financ. Stud. 2003, 16, 717–763. [Google Scholar] [CrossRef]
  2. Bae, J.W.; Elkamhi, R.; Simutin, M. The best of both worlds: Accessing emerging economies via developed markets. J. Financ. 2019, 74, 2579–2617. [Google Scholar] [CrossRef]
  3. Bai, J.; Perron, P. Estimating and testing linear models with multiple structural changes. Econometrica 1998, 47–78. [Google Scholar] [CrossRef]
  4. Bai, J.; Perron, P. Computation and analysis of multiple structural change models. J. Appl. Econom. 2003, 18, 1–22. [Google Scholar] [CrossRef]
  5. Basnet, H.C.; Sharma, S.C. Economic Integration in Latin America. Journal of Economic Integration 2013, 551–579. [Google Scholar] [CrossRef]
  6. Bekaert, G.; Harvey, C.R. Time-varying world market integration. J. Financ. 1995, 50, 403–444. [Google Scholar]
  7. Berben, R.P.; Jansen, W.J. Comovement in international equity markets: A sectoral view. J. Int. Money Financ. 2005, 24, 832–857. [Google Scholar] [CrossRef]
  8. Bekaert, G.; Hodrick, R.J.; Zhang, X. International stock return comovements. J. Financ. 2009, 64, 2591–2626. [Google Scholar] [CrossRef]
  9. Billio, M.; Paradiso, A.; Donadelli, M.; Riedel, M. (2015). Measuring financial integration: lessons from the correlation. University Ca’Foscari of Venice, Dept. of Economics Working Paper Series No, 23.
  10. Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef]
  11. Boubaker, S.; Jouini, J.; Lahiani, A. Financial contagion between the US and selected developed and emerging countries: The case of the subprime crisis. Q. Rev. Econ. Financ. 2016, 61, 14–28. [Google Scholar] [CrossRef]
  12. Chelley-Steeley, P.L. Modeling equity market integration using smooth transition analysis: A study of Eastern European stock markets. J. Int. Money Financ. 2005, 24, 818–831. [Google Scholar] [CrossRef]
  13. Engle, R. Dynamic conditional correlation: A simple class of multivariate generalized autoregressive conditional heteroskedasticity models. J. Bus. Econ. Stat. 2002, 20, 339–350. [Google Scholar] [CrossRef]
  14. Eun, C.S.; Shim, S. International transmission of stock market movements. J. Financ. Quant. Anal. 1989, 24, 241–256. [Google Scholar] [CrossRef]
  15. Forbes, K.J.; Rigobon, R. No contagion, only interdependence: measuring stock market comovements. J. Financ. 2002, 57, 2223–2261. [Google Scholar] [CrossRef]
  16. Forbes, K.J.; Chinn, M.D. A decomposition of global linkages in financial markets over time. Rev. Econ. Stat. 2004, 86, 705–722. [Google Scholar] [CrossRef]
  17. Glosten, L.R.; Jagannathan, R.; Runkle, D.E. On the relation between the expected value and the volatility of the nominal excess return on stocks. J. Financ. 1993, 48, 1779–1801. [Google Scholar] [CrossRef]
  18. Goetzmann, W.N.; Li, L.; Rouwenhorst, K.G. Long-term global market correlations. De Nederlandsche Bank Working Paper Series No 2001, 98. [Google Scholar]
  19. Johnson, R.; Soenen, L. Economic integration and stock market comovement in the Americas. J. Multinatl. Financ. Manag. 2003, 13, 85–100. [Google Scholar] [CrossRef]
  20. Lahrech, A.; Sylwester, K. US and Latin American stock market linkages. J. Int. Money Financ. 2011, 30, 1341–1357. [Google Scholar] [CrossRef]
  21. Lin, C.F.J.; Teräsvirta, T. Testing the constancy of regression parameters against continuous structural change. J. Econom. 1994, 62, 211–228. [Google Scholar] [CrossRef]
  22. Longin, F.; Solnik, B. Is the correlation in international equity returns constant: 1960–1990? J. Int. Money Financ. 1995, 14, 3–26. [Google Scholar] [CrossRef]
  23. Mun, K.C. Volatility and correlation in international stock markets and the role of exchange rate fluctuations. J. Int. Financ. Mark. Inst. Money 2007, 17, 25–41. [Google Scholar] [CrossRef]
  24. Nelson, D.B. Conditional heteroskedasticity in asset returns: A new approach. Econometrica: Journal of the econometric society 1991, 347–370. [Google Scholar] [CrossRef]
  25. Pukthuanthong, K.; Roll, R. Global market integration: An alternative measure and its application. J. Financ. Econ. 2009, 94, 214–232. [Google Scholar] [CrossRef]
  26. Rua, A.; Nunes, L.C. International comovement of stock market returns: A wavelet analysis. J. Empir. Financ. 2009, 16, 632–639. [Google Scholar] [CrossRef]
  27. Zakoian, J.M. Threshold heteroskedastic models. J. Econ. Dyn. Control 1994, 18, 931–955. [Google Scholar] [CrossRef]
Preprints 98480 g001
Figure 1. exhibits returns of Latin American and the US market indices. This is based on weekly-based log returns sample data. The sample period is between January 1, 1990, and December 31, 2019.
Figure 1. exhibits returns of Latin American and the US market indices. This is based on weekly-based log returns sample data. The sample period is between January 1, 1990, and December 31, 2019.
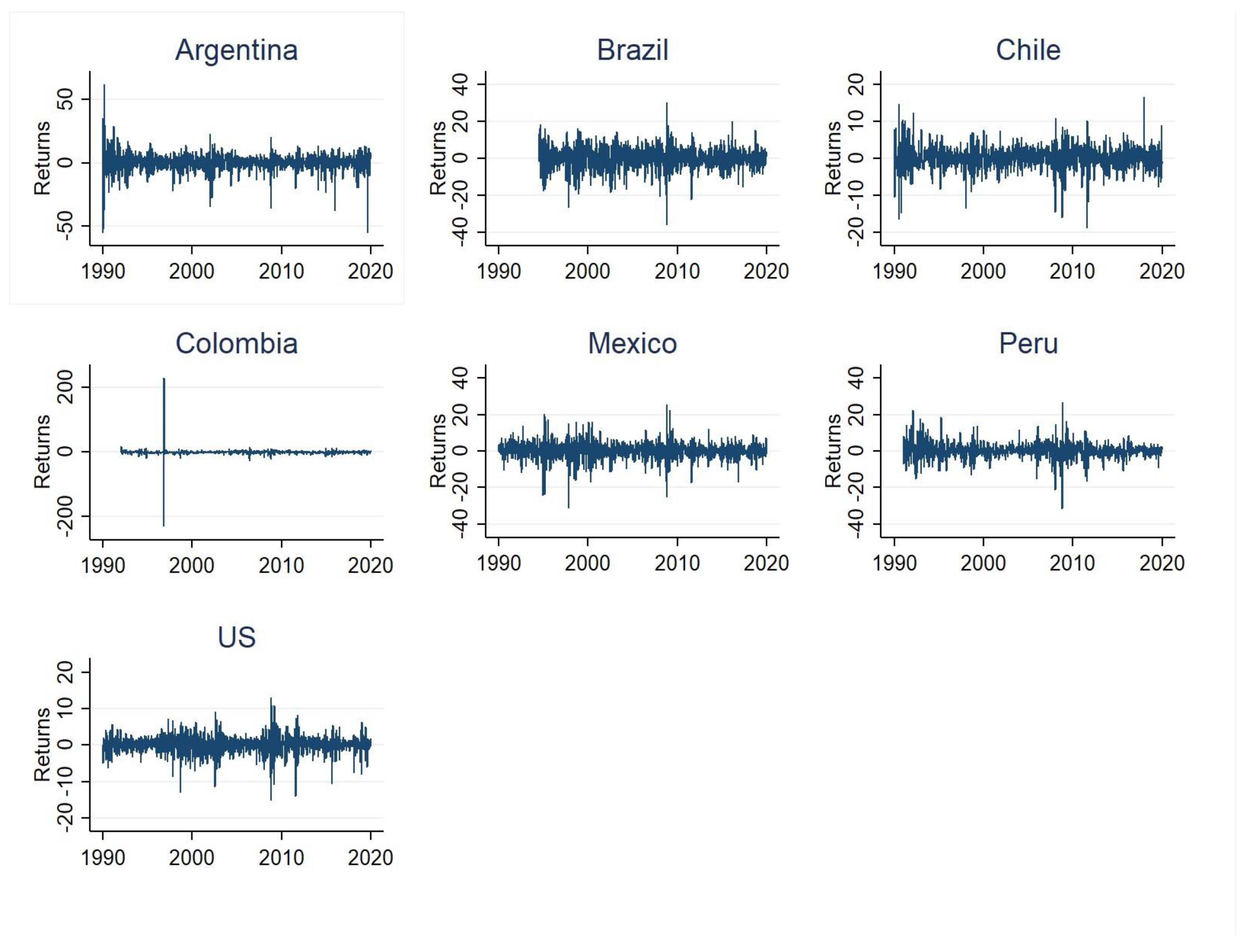
Preprints 98480 g001
Preprints 98480 g002aPreprints 98480 g002b
Figure 2. exhibits the dynamic conditional correlation for the main market indices between the US and the examined countries: Argentina, Brazil, Chile, Colombia, Mexico, and Peru. We also show (red) lines that denote the trade agreement signing date with the US. Two separate lines indicate that the signing date and implemented dates are different.
Figure 2. exhibits the dynamic conditional correlation for the main market indices between the US and the examined countries: Argentina, Brazil, Chile, Colombia, Mexico, and Peru. We also show (red) lines that denote the trade agreement signing date with the US. Two separate lines indicate that the signing date and implemented dates are different.
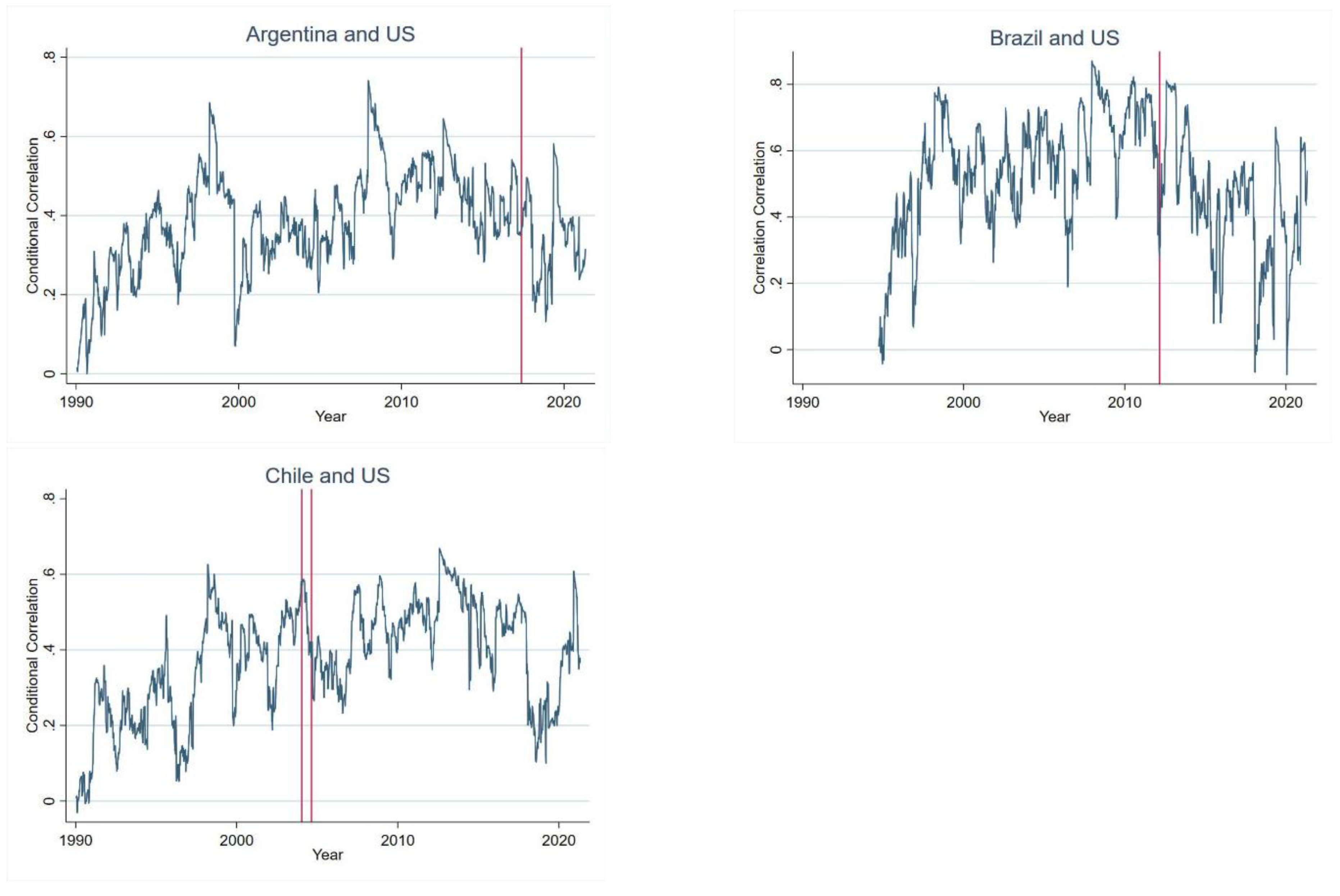
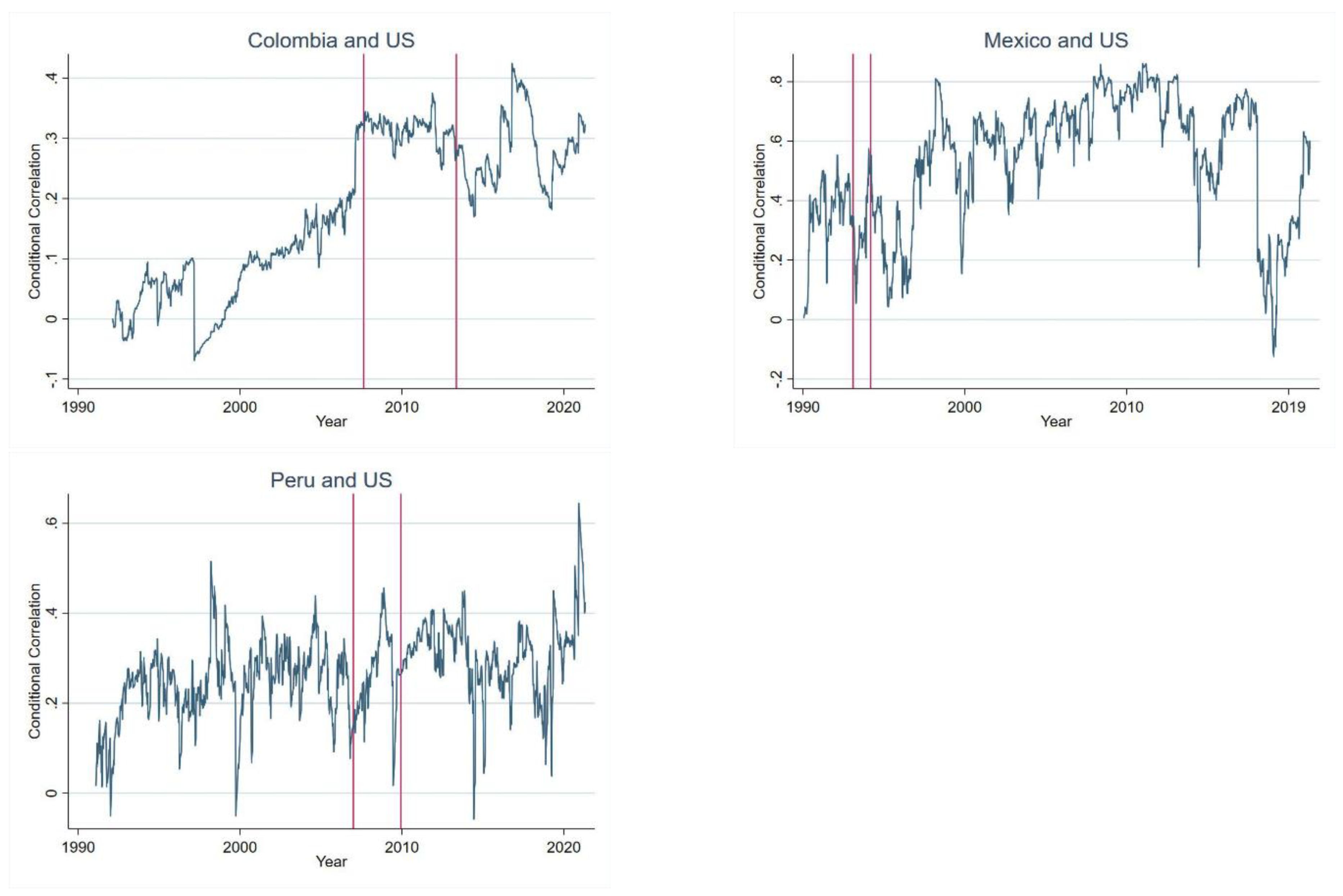
Preprints 98480 g002aPreprints 98480 g002b
Table 1. Summary Statistics.
Table 1. Summary Statistics.
Table 1 reports summary statistics for Latin American countries and the US. In our Latin American data, we have several Latin American countries including Argentina, Brazil, Chile, Colombia, Mexico, and Peru. We first collect daily financial data and then calculate weekly-based log returns and standard deviations sorted by industries. The sample data period is between January 1, 1990, and December 31, 2019.
Argentina Brazil Chile Colombia Mexico Peru US
Mean SD Mean SD Mean SD Mean SD Mean SD Mean SD Mean SD
Market Index 0.059 0.069 0.152 0.058 0.159 0.030 0.097 0.092 0.172 0.045 0.322 0.041 0.141 0.024
Basic Materials 0.047 0.070 0.068 0.055 0.126 0.038 0.199 0.099 0.222 0.050 0.087 0.038 0.119 0.034
Consumer Discretionary -0.136 0.079 0.149 0.049 0.135 0.041 -0.258 0.105 0.165 0.041 0.249 0.059 0.166 0.024
Consumer Goods 0.104 0.063 0.188 0.047 0.148 0.036 0.049 0.096 -0.115 0.054 0.111 0.034 0.158 0.021
Energy 0.024 0.073 0.170 0.068 0.115 0.042 -0.003 0.102 N/A N/A -0.199 0.069 0.099 0.031
Financials 0.054 0.064 0.129 0.054 0.177 0.034 0.063 0.092 0.187 0.048 0.187 0.024 0.142 0.032
Industrials 0.119 0.070 0.198 0.049 0.107 0.038 -0.087 0.056 0.051 0.049 -0.018 0.097 0.176 0.028
Real Estate -0.004 0.054 0.007 0.055 0.082 0.041 N/A N/A -0.022 0.035 0.072 0.020 0.104 0.032
Telecommunications -0.036 0.064 -0.006 0.053 0.064 0.043 0.024 0.054 0.209 0.048 -0.022 0.066 0.046 0.028
Utilities -0.086 0.058 0.007 0.055 0.155 0.035 0.864 0.240 0.108 0.041 0.092 0.029 0.084 0.022
Table 2. Unconditional Correlations of Main Market Indices and Sectors.
Table 2. Unconditional Correlations of Main Market Indices and Sectors.
Table 2 reports unconditional correlations of main market indices and sectors. When we report unconditional correlations of energy and real estate sectors, we exclude Mexico and Colombia, respectively, due to data unavailability. The sample data period is between January 1, 1990, and December 31, 2019.
Main Market Index Argentina Brazil Chile Colombia Mexico Peru US
Argentina 1.000
Brazil 0.538 1.000
Chile 0.468 0.598 1.000
Colombia 0.109 0.133 0.168 1.000
Mexico 0.508 0.649 0.536 0.142 1.000
Peru 0.403 0.514 0.526 0.162 0.472 1.000
US 0.432 0.574 0.498 0.156 0.617 0.408 1.000
Basic Materials Argentina Brazil Chile Colombia Mexico Peru US
Argentina 1.000
Brazil 0.365 1.000
Chile 0.322 0.559 1.000
Colombia 0.063 0.108 0.133 1.000
Mexico 0.362 0.629 0.477 0.111 1.000
Peru 0.219 0.416 0.370 0.092 0.444 1.000
US 0.333 0.640 0.503 0.112 0.605 0.394 1.000
Consumer Discretionary Argentina Brazil Chile Colombia Mexico Peru US
Argentina 1.000
Brazil 0.275 1.000
Chile 0.223 0.395 1.000
Colombia 0.046 0.092 0.059 1.000
Mexico 0.301 0.437 0.372 0.075 1.000
Peru 0.020 0.052 0.022 0.029 0.032 1.000
US 0.225 0.347 0.393 0.076 0.507 0.030 1.000
Consumer Staples Argentina Brazil Chile Colombia Mexico Peru US
Argentina 1.000
Brazil 0.326 1.000
Chile 0.307 0.370 1.000
Colombia 0.047 0.122 0.143 1.000
Mexico 0.303 0.303 0.269 0.110 1.000
Peru 0.108 0.149 0.147 0.006 0.107 1.000
US 0.233 0.302 0.305 0.123 0.270 0.072 1.000
Energy Argentina Brazil Chile Colombia Peru US
Argentina 1.000
Brazil 0.391 1.000
Chile 0.300 0.480 1.000
Colombia 0.294 0.530 0.431 1.000
Peru 0.159 0.296 0.279 0.302 1.000
US 0.417 0.667 0.507 0.528 0.334 1.000
Financials Argentina Brazil Chile Colombia Mexico Peru US
Argentina 1.000
Brazil 0.323 1.000
Chile 0.332 0.532 1.000
Colombia 0.239 0.451 0.482 1.000
Mexico 0.284 0.525 0.505 0.422 1.000
Peru 0.191 0.303 0.328 0.304 0.258 1.000
US 0.267 0.465 0.442 0.369 0.490 0.222 1.000
Industrials Argentina Brazil Chile Colombia Mexico Peru US
Argentina 1.000
Brazil 0.261 1.000
Chile 0.244 0.424 1.000
Colombia 0.158 0.332 0.251 1.000
Mexico 0.239 0.559 0.430 0.330 1.000
Peru 0.040 0.075 0.092 0.060 0.100 1.000
US 0.208 0.511 0.396 0.293 0.597 0.124 1.000
Real Estate Argentina Brazil Chile Mexico Peru US
Argentina 1.000
Brazil 0.294 1.000
Chile 0.150 0.385 1.000
Mexico 0.202 0.422 0.391 1.000
Peru 0.104 0.110 0.081 0.145 1.000
US 0.196 0.423 0.430 0.430 0.119 1.000
Telecommunications Argentina Brazil Chile Colombia Mexico Peru US
Argentina 1.000
Brazil 0.371 1.000
Chile 0.252 0.385 1.000
Colombia 0.753 0.254 0.222 1.000
Mexico 0.327 0.606 0.398 0.302 1.000
Peru 0.090 0.136 0.080 0.028 0.123 1.000
US 0.262 0.486 0.293 0.238 0.537 0.084 1.000
Utilities Argentina Brazil Chile Colombia Mexico Peru US
Argentina 1.000
Brazil 0.219 1.000
Chile 0.271 0.491 1.000
Colombia 0.110 0.451 0.472 1.000
Mexico 0.120 0.339 0.386 0.390 1.000
Peru 0.092 0.254 0.143 0.170 0.148 1.000
US 0.037 0.304 0.238 0.231 0.244 0.081 1.000
Table 3. Univariate GARCH Models.
Table 3. Univariate GARCH Models.
Table 3 reports traditional GARCH, EGARCH, GJR-GARCH, and TGARCH models and their parameters sorted by industry. The sample data period is between January 1, 1990, and December 31, 2019.
Argentina Model Selected ω θ Z δ
Main Index EGARCH 0.219*** -0.068*** 0.263*** 0.941***
Basic Materials GARCH 1.351*** 0.130*** N/A 0.843***
Consumer Discretionary EGARCH 0.256*** 0.019* 0.355*** 0.942***
Consumer Goods GJR-GARCH 1.861*** 0.162*** 0.087*** 0.758***
Energy EGARCH 0.273*** -0.061*** 0.326*** 0.930***
Financial EGARCH 0.140*** -0.021*** 0.232*** 0.965***
Industrials EGARCH 0.154*** -0.150* 0.352*** 0.963***
Real Estate GJR-GARCH 1.436*** 0.106*** -0.052*** 0.869***
Telecommunications EGARCH 0.432*** -0.098*** 0.250*** 0.885***
Utilities GJR-GARCH 0.565*** 0.086*** 0.065*** 0.880***
Brazil Model Selected ω θ Z δ
Main Index EGARCH 0.145*** -0.075*** 0.174*** 0.958***
Basic Materials EGARCH 0.102*** -0.063*** 0.198*** 0.970***
Consumer Discretionary EGACRH 0.227*** -0.065*** 0.178*** 0.929***
Consumer Goods GJR-GARCH 0.856*** 0.144*** -0.010*** 0.839***
Energy EGARCH 0.205*** -0.061*** 0.180*** 0.946***
Financial GJR-GARCH 26.370*** 0.352*** -0.327*** -0.093**
Industrials GJR-GARCH 1.082*** 0.126*** -0.076*** 0.861***
Real Estate EGACRH 0.084*** -0.056*** 0.139*** 0.976***
Telecommunications EGARCH 0.147*** -0.064*** 0.183*** 0.955***
Utilities EGARCH 0.084*** -0.056*** 0.139*** 0.976***
Chile Model Selected ω θ Z δ
Main Index GJR-GARCH 1.632*** 0.220*** 0.023*** N/A
Basic Materials GJR-GARCH 0.389*** 0.111*** -0.035*** 0.880***
Consumer Discretionary GARCH 3.285*** 0.156*** N/A 0.651**
Consumer Goods GJR-GARCH 0.199*** 0.115*** -0.047*** 0.897***
Energy GJR-GARCH 1.130*** 0.117*** -0.059*** 0.843***
Financial GJR-GARCH 0.302*** 0.137*** -0.091*** 0.890***
Industrials GJR-GARCH 0.268*** 0.135*** -0.045*** 0.877***
Real Estate EGARCH 0.196*** -0.028** 0.221*** 0.937***
Telecommunications GJR-GARCH 0.429*** 0.098*** -0.037*** 0.902***
Utilities EGARCH 0.112*** -0.044*** 0.212*** 0.954***
Colombia Model Selected ω θ Z δ
Main Index GARCH 49.422*** 0.072*** N/A -0.008*
Basic Materials GARCH -0.108*** -0.001*** N/A 1.000***
Consumer Discretionary GARCH 0.014*** -0.002*** N/A 1.003**
Consumer Goods TGARCH -0.008*** -0.005*** N/A 1.000***
Energy EGARCH 3.607*** 0.851*** 1.251*** 0.168***
Financial EGARCH 0.477*** -0.271*** -0.148*** 0.856***
Industrials EGARCH 0.068*** -0.045*** 0.200*** 0.982***
Telecommunications GJR-GARCH 11.067*** 0.175*** 0.212*** 0.383***
Utilities GARCH 0.010*** -0.001*** N/A 0.999***
Mexico Model Selected ω θ Z δ
Main Index EGARCH 0.167*** -0.113*** 0.220*** 0.943***
Basic Materials GJR-GARCH 1.108*** 0.128*** -0.063*** 0.854***
Consumer Discretionary EGARCH 0.127*** -0.071*** 0.216*** 0.955***
Consumer Goods EGARCH 0.210*** -0.173*** 0.328*** 0.942***
Financial EGARCH 0.110*** -0.096*** 0.213*** 0.966***
Industrials EGARCH 0.208*** -0.096*** 0.198*** 0.934***
Real Estate GARCH 2.180*** 0.088*** N/A 0.726***
Telecommunications EGARCH 0.169*** -0.084*** 0.198*** 0.947***
Utilities TGARCH N/A N/A N/A N/A
Peru Model Selected ω θ Z δ
Main Index GJR-GARCH 0.630*** 0.147*** 0.044*** 0.799***
Basic Materials EGARCH 0.113*** -0.048*** 0.214*** 0.959***
Consumer Discretionary GARCH 0.213*** 0.025*** N/A 0.970***
Consumer Goods GARCH 0.014*** 0.083*** N/A 0.935***
Energy GARCH 26.500*** 0.198*** N/A 0.257***
Financial EGARCH 0.116*** 0.003*** 0.364*** 0.944***
Industrials EGARCH 5.186*** 0.317*** -0.021*** -0.149***
Real Estate EGARCH 0.021*** -0.047*** 0.074*** 0.997***
Telecommunications GARCH 3.557*** 0.337*** N/A 0.703***
Utilities GJR-GARCH 0.224*** 0.095*** -0.062*** 0.906***
US Model Selected ω θ Z δ
Main Index EGARCH 0.117*** -0.163*** 0.236*** 0.924***
Basic Materials GJR-GARCH 0.317*** 0.130*** -0.087*** 0.880***
Consumer Discretionary EGARCH 0.132*** -0.156*** 0.260*** 0.917***
Consumer Goods EGARCH 0.086*** -0.126*** 0.201*** 0.935***
Energy EGARCH 0.111*** -0.099*** 0.201*** 0.950***
Financial GJR-GARCH 0.282*** 0.179*** -0.126*** 0.847***
Industrials EGARCH 0.108*** -0.139*** 0.183*** 0.942***
Real Estate GJR-GARCH 0.334*** 0.192*** -0.123*** 0.825***
Telecommunications GJR-GARCH 0.149*** 0.098*** -0.089*** 0.920***
Utilities EGARCH 0.076*** -0.041*** 0.254*** 0.952***
Notes: *, **, and *** indicate a significant at the 90%, 95%, and 99% levels, respectively.
Table 4. DCC GARCH Model - US and Latin American Countries.
Table 4. DCC GARCH Model - US and Latin American Countries.
Table 4 reports the estimates of DCC-GARCH model. In all six tables, US will be paired with each Latin American country’s index to determine their comovement.
Argentina and US a b Brazil and US a b
Market Index 0.032** 0.941*** Market Index 0.069 0.923***
Basic Materials 0.031** 0.948*** Basic Materials 0.067*** 0.931***
Consumer Discretionary 0.053** 0.829*** Consumer Discretionary 0.018*** 0.981***
Consumer Goods 0.023* 0.946*** Consumer Goods 0.043** 0.847***
Energy 0.029*** 0.949*** Energy 0.072*** 0.918***
Financials 0.029 0.925*** Financials 0.029** 0.975***
Industrials 0.007 0.971*** Industrials 0.063*** 0.935***
Real Estate 0.024** 0.958*** Real Estate 0.047* 0.880***
Telecommunications 0.029*** 0.937*** Telecommunications 0.053** 0.904***
Utilities 0.021* 0.948*** Utilities 0.035*** 0.955***
Peru and US a b Chile and US a b
Market Index 0.035 0.914** Market Index 0.034** 0.952***
Basic Materials 0.033* 0.966*** Basic Materials 0.054*** 0.944***
Consumer Discretionary 0.027** 0.965*** Consumer Discretionary 0.017*** 0.977***
Consumer Goods 0.009 0.126 Consumer Goods 0.047*** 0.921***
Energy 0.038* 0.911*** Energy 0.044* 0.946***
Financials 0.019** 0.978*** Financials 0.059*** 0.927**
Industrials 0.01 0.967*** Industrials 0.049*** 0.945***
Real Estate 0 0.991*** Real Estate 0.012* 0.984***
Telecommunications 0.001 0.994*** Telecommunications 0.037 0.527**
Utilities 0.003 0.986*** Utilities 0.029*** 0.958***
Colombia and US a b Mexico and US a b
Market Index 0.015*** 0.980*** Market Index 0.050*** 0.947***
Basic Materials 0.696*** 0.035 Basic Materials 0.058*** 0.938***
Consumer Discretionary 0.008 0.994*** Consumer Discretionary 0.044 0.934***
Consumer Goods 0.195 0.520** Consumer Goods 0.067* 0.918***
Energy 0.033** 0.964*** Financials 0.062*** 0.878**
Financials 0.265** 0.114 Industrials 0.064*** 0.935***
Industrials 0.053** 0.917*** Real Estate 0.098** 0.856***
Telecommunications 0.142** 0.189 Telecommunications 0.043*** 0.941***
Utilities 0.011* 0.975*** Utilities 0.005 0.982***
Notes: *, **, and *** indicate a significant at the 90%, 95%, and 99% levels, respectively.
Table 5. Summary Statistics of Bivariate Conditional Correlation.
Table 5. Summary Statistics of Bivariate Conditional Correlation.
Table 5 reports the summary statistics of bivariate conditional correlation. In Table 5, we only report the main market index. We separately report all sectors’ information in Appendix G.
Country List Mean Median Min Max SD
Argentina and US 0.382 0.380 -0.001 0.741 0.126
Brazil and US 0.514 0.528 -0.075 0.870 0.189
Chile and US 0.377 0.400 -0.029 0.669 0.146
Colombia and US 0.182 0.189 -0.069 0.424 0.126
Mexico and US 0.532 0.588 -0.124 0.861 0.213
Peru and US 0.267 0.273 -0.057 0.644 0.093
Table 6. The Estimated Smooth Transition Model.
Table 6. The Estimated Smooth Transition Model.
Table 6 presents the smooth transition model to estimate the average correlation between two different regimes.
Argentina and US α β γ T Midpoint
Market Index 0.378*** 0.094* 633*** 0.449*** Jun-03
Basic Materials 0.293*** 0.008 242*** 0.292*** Sep-98
Consumer Discretionary 0.193*** -0.084* 13.300 0.566*** Dec-06
Consumer Goods 0.240*** 0.011* 316.00 0.223*** Oct-96
Energy 0.341*** -0.024*** 581*** 0.467*** Jan-04
Financials 0.317*** -0.010* 434** 0.325*** Oct-99
Industrials 0.262*** -0.095 31.8** 0.476*** Apr-04
Real Estate 0.222*** 0.244*** 4.13*** 0.584*** Jul-07
Telecommunications 0.246*** 0.417 7.77** 0.889* Aug-16
Utilities 0.183*** 0.018*** 66.3*** 0.228*** Oct-96
Brazil and US α β γ T Midpoint
Market Index 0.513*** -0.064** 1116*** 0.554*** Jan-04
Basic Materials 0.536*** -0.010** 786*** 0.656*** Aug-09
Consumer Discretionary 0.318*** -0.624 111** 0.682*** Jun-10
Consumer Goods 0.277** 0.055 76.70 0.152*** May-95
Energy 0.492*** -0.006** 506 0.523*** Sep-05
Financials 0.339*** -0.015 98 0.272*** Mar-95
Industrials 0.402*** -0.014** 582 0.371*** Feb-01
Real Estate 0.323*** -0.077* 227 0.484*** Apr-99
Telecommunications 0.374*** -0.018* 21.9*** 0.305*** Feb-99
Utilities 0.184*** 0.114*** 355*** 0.052*** Jul-91
Chile and US α β γ T Midpoint
Market Index 0.358*** 0.024 51.3*** 0.262*** Nov-97
Basic Materials 0.04 0.348*** 116*** 0.142*** Mar-94
Consumer Discretionary 0.239*** 0.099** 149*** 0.019*** Aug-90
Consumer Goods 0.254*** 0.523*** 12.3*** 0.780*** May-13
Energy 0.199*** 0.060*** 125*** 0.025*** Oct-90
Financials 0.250*** 0.055 13.2*** 0.137* Jan-94
Industrials -0.059 0.319*** 434*** 0.173*** Apr-95
Real Estate 0.140*** 0.015*** 377*** 0.081*** May-92
Telecommunications 0.247*** -0.009*** 99.3*** 0.142*** Apr-94
Utilities 0.198*** 0.042*** 6.90*** 0.065* Dec-91
Colombia and US α β γ T Midpoint
Market Index 0.080*** 0.166** 21.2*** 0.211* Dec-95
Basic Materials 0.049** -0.739*** 8.62*** 0.805*** Feb-14
Consumer Discretionary 0.014* 0.069*** 21.9*** 0.006 Sep-91
Consumer Goods 0.120*** -0.034*** 213*** 0.265*** Dec-97
Energy 0.175*** 0.029* 674*** 0.119** Jul-93
Financials 0.108*** -0.379** 19*** 0.797*** Nov-13
Industrials 0.292*** 0.004* 812*** 0.241*** Mar-97
Telecommunications 0.226*** 0.071*** 26.0*** 0.506*** Jan-05
Utilities 0.115*** 0.216 9.14*** 0.508*** Mar-05
Mexico and US α β γ T Midpoint
Market Index 0.512*** 0.122* 277*** 0.375*** Mar-01
Basic Materials 0.348*** 0.144*** 151** 0.161** Oct-94
Consumer Discretionary 0.376*** 0.051 63 0.224*** Sep-96
Consumer Goods 0.157*** 0.131*** 502*** 0.040*** Mar-91
Financials 0.261*** 0.08 417*** 0.045*** Apr-91
Industrials -0.152 0.622*** 95*** 0.119*** Jul-93
Real Estate 0.334*** 0.057** 37.2*** 0.211*** Apr-96
Telecommunications 0.349*** 0.040** 39.9*** 0.298*** Nov-98
Utilities 0.192*** -0.344 15.8** 0.422* Aug-02
Peru and US α β γ T Midpoint
Market Index 0.261*** 0.213** 65.5*** 0.303*** Feb-99
Basic Materials 0.276*** 0.099*** 4.55** 0.328** Jul-98
Consumer Discretionary 0.219*** -0.139** 255*** 0.114*** May-93
Consumer Goods 0.102*** 0.012*** 84.2*** 0.235*** Jan-97
Energy 0.259*** 0.034 254*** 0.249*** Jul-96
Financials 0.142*** 0.066*** 12.5*** 0.471*** Feb-04
Industrials 0.144*** 0.495*** 13.3*** 0.552*** Jul-06
Real Estate 0.052*** 0.002 681*** 0.102** Dec-91
Telecommunications 0.074*** 0.016 516*** 0.086*** May-92
Utilities 0.109*** 0.318 6.69*** 0.776 Apr-14
Notes: *, **, and *** indicate a significant at the 90%, 95%, and 99% levels, respectively.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated