Investigating the Performance of Timex Intervals for Shoreline Edge Detection: A Sensitivity Analysis from a Low-Cost Coastal Monitoring System in Brandon Bay, Ireland

1. Introduction

Coastal zones are unique and dynamic environments of high economic and ecological importance, with approximately 31% of all coastal zones containing sandy beaches [1]. These are particularly dynamic and some of the most responsive environments on Earth. In order to get a better understanding of their dynamics, repeat topographic surveys have become an essential part of coastal zone research, coastal engineering applications, and coastal zone management. Indeed, survey data and their analysis are a valuable resource for quantifying long-term trends such as erosion and/or accretion of beaches [2]; [3]; [4], beach and dune response-recovery patterns due to storm events [5,6,7], impacts of engineering works [8,9], as well as identifying dynamic features such as beach cusps and nearshore bars [10,11,12]. The site-specific nature and variability of coastal response means that coastal monitoring programmes should, preferably, span years to decades and include local environmental factors (e.g., coastal morphology, sediment budget, rates of sea-level rise, nearshore- and swash dynamics) [13]. For many decades, the logistics (e.g., time, cost, travel) of field monitoring precluded our ability to collect high temporal resolution datasets but the advent of commercial, low-cost camera systems in coastal science has removed this obstacle.

In order to better understand and characterize the different coastal processes occurring in the nearshore and swash zones, longer datasets with higher spatial and temporal resolution are preferable. These can be obtained using indirect measurement/remote sensing techniques which were originally developed to facilitate the collection of data in the nearshore [14]. Remote sensing techniques provide an attractive alternative to direct measuring techniques, especially in difficult environments, extreme conditions, or to achieve high temporal resolutions. A range of indirect measuring techniques is already used in coastal areas, including active sensors, e.g., LiDAR [15,16] and RADAR [17], and passive sensors, e.g., time-lapse [10], video- [18,19], infrared cameras [20], and smartphones [21,22].

The conventional products that can be extracted from passive sensors are:

1) Snapshots: one-off pictures.

2) Time exposure or “Timex” images: the average of a large number of snapshots, typically 600 corresponding to 10 minutes at 1 Hz.

3) Time-variance or “variance” images: the standard deviation of snapshots (similar to Timex).

4) Time stack images: time evolution at a given transect, typically 10 minutes at 2 Hz.

These approaches have been used to monitor a broad number of coastal forms and nearshore processes including, but not limited to, extraction of beach and nearshore bathymetry [23,24], nearshore hydrodynamics [25,26], formation and displacement of sand bars [27,28,29] and beach face morphodynamics [30,31,32,33].

In addition, passive sensors such as time-lapse cameras and video cameras have been used to detect and delineate shoreline positions [34,35,36]. Identifying shoreline positions and their shift in response to hydrodynamics is essential to coastal scientists, engineers, and managers [37]. With data of where the current shoreline position is, where it has been in the past and being able to predict where it will be in the future, can inform coastal protection strategies [38]. It also provides the ability to calibrate and verify numerical models [39], assess sea-level change [40], and identify high-risk coastal zones [41]. Indeed, the detection of shorelines from processed video images has become a standard tool in nearshore studies [42], especially since the growth of the ARGUS system [43].

For most remotely sensed systems, the sensor is in a fixed location and collects oblique images of the nearshore. The fixed location of the sensor means that only the lens characteristics and ground control points (GCP) are required to create a georectified image [44]. From this, objective information can be subtracted from the oblique images (e.g., shoreline positions). The shoreline itself can be defined in optical images as the time-varying interface between ‘wet’ pixels, representing the ocean surface, and ‘dry’ pixels indicating beach sediments [45]. In order to identify shoreline positions from optical images, several approaches have been proposed: localised maxima in the image intensity (SLIM) [46]; pixel clustering based on HUE and intensity (PIC) [23]; divergence in RGB colour channels [22,47]; and machine learning techniques [48]. Each of these techniques manipulates the optical information in a slightly different manner to objectively define a proxy shoreline feature.

Finding a compromise between the optimum sampling rate and the time period over which to average the images remains an ongoing challenge in this research area. [45] and [49] found that the sampling interval of 1 Hz over 10 minutes has become a standard procedure but there has been no investigation into the performance of Timex images with different sampling rates. To the best of our knowledge, no analysis has been carried out to investigate the optimum interval of Timex images in coastal research applications. Such an investigation can benefit low-cost monitoring systems, as a potential increase in sampling intervals can dramatically improve current limitations on battery requirements and storage capacity.

A low-cost (circa €500) monitoring system (e.g., off-the-shelf time-lapse cameras) that can be rapidly deployed in the field and/or in remote areas can reduce the initial capital and current investment in monitoring systems and can lead to a fully autonomous system (e.g., no external power source or hardware). The internal batteries from off-the-shelf time-lapse cameras are often small and data is stored on SD cards. This makes them fully autonomous but also reduces the time period that they can sample at field sites.

This research aims to provide guidance for the identification of the optimum temporal resolution needed for processing Timex images for shoreline detection. To achieve this, two fully autonomous low-cost time-lapse cameras were deployed in Brandon Bay, Ireland. Timex images were created from high-resolution oblique imagery using different imaging intervals i.e., 1 s, 3 s, 5 s, 10 s, 20 s, and 30 s and shoreline positions were determined from the different Timex images. A sensitivity analysis was then conducted comparing the shoreline positions derived from the different Timex intervals. Section 2 of the paper presents the methodology used for the research including deployment and calibration of the cameras and image processing and analysis. The results of the sensitivity analysis are presented and discussed in Section 3 and conclusions are presented in Section 4.

2. Materials and Methods

Study Area

Two remote photogrammetry monitoring stations were deployed in Brandon Bay, a semi-enclosed bay on the northern side of the Dingle Peninsula (Co. Kerry) on the southwest coast of Ireland. The sandy shoreline extends approximately 12 km (Error! Reference source not found.) with sediment consisting of mainly well-sorted, medium-sized sand. There is an extensive dune system behind the dissipative beaches along the entire bay, commonly exceeding 10 m elevation for long tracts of the coastline. The monitoring period used in this study was 22 continuous days (8 February to 1 March 2022).

Figure 1. Location of study site on the west coast of Ireland with a satellite image of Brandon Bay and the datapoints used for extracting hydrodynamic data (from ESA - Sentinel 2).

Figure 1. Location of study site on the west coast of Ireland with a satellite image of Brandon Bay and the datapoints used for extracting hydrodynamic data (from ESA - Sentinel 2).

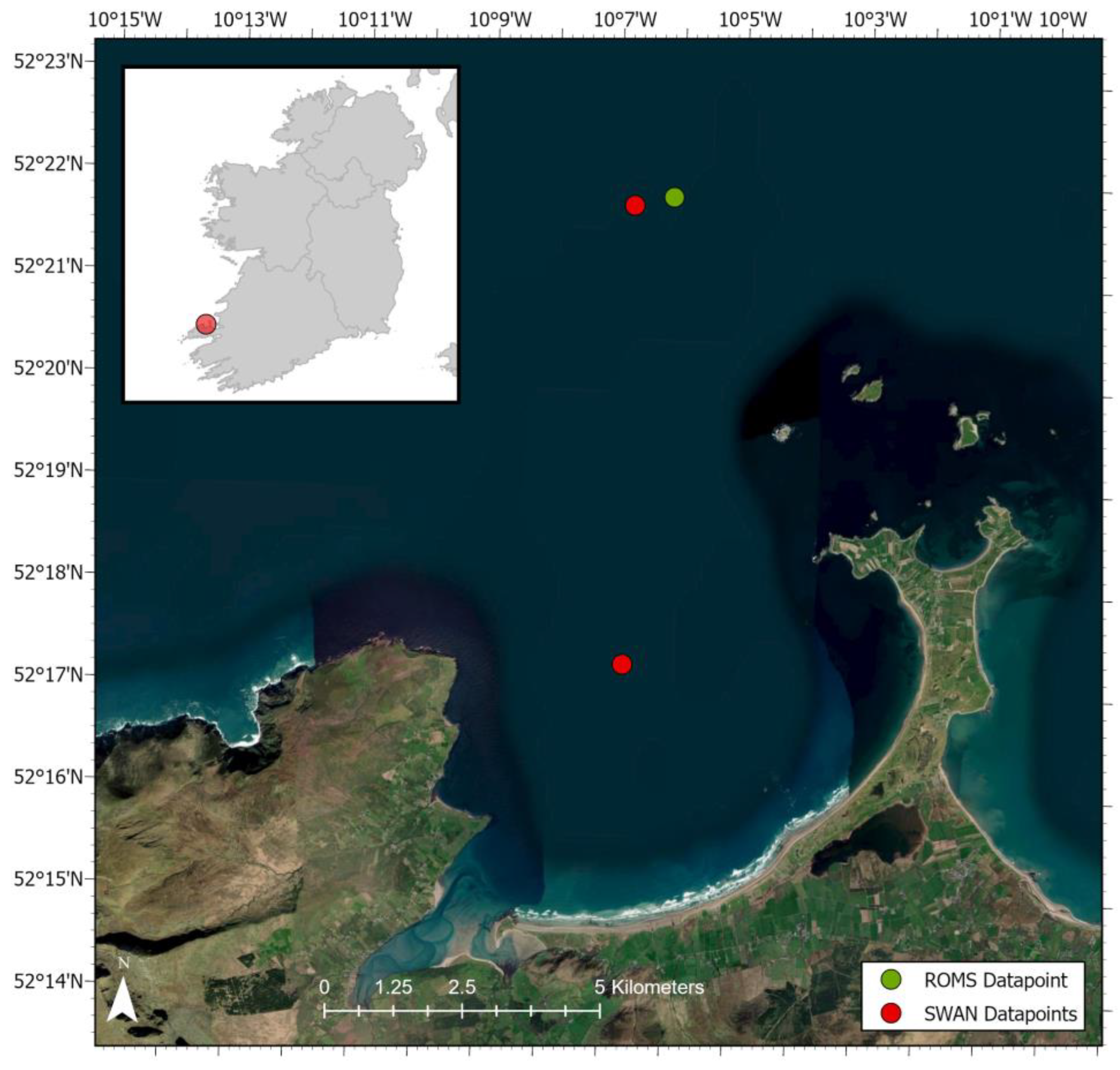
Statistical analysis of deep-water wave data between 2011 – 2022, available from the East Atlantic SWAN Wave Model Dataset [50], shows that the wave conditions in Brandon Bay are characterized by mean annual significant wave height H_s = 1.91 m, a mean annual peak wave period T_p = 10.95 s, and a mean annual wave direction of 275^o (W). The hydrodynamic characteristics of the area are dominated by semidiurnal tides, available from NEATL ROMS [51] and classifies Brandon Bay as a macrotidal beach (>4m).

Intertidal beach profiles obtained during the study indicate that the offshore slope is relatively even and regular with a gentle slope (tan β = 0.03/1.72^o). The beach slope varies from tan β = 0.02/1.14^o to tan β = 0.06/3.43^o, with a tendency to decrease towards the south of the bay. The medium grain size is d₅₀ = 250 μm [52], which classifies the beach as fine to medium sand, according to the Udden-Wentworth grade scale [53].

Hydrodynamics Monitoring Period

Due to energetic wave conditions observed during the monitoring period (i.e., 8 February 2022 until 1 March 2022) and the lack of in-situ measurements in the bay, it was decided to extract hydrodynamic conditions as close to the study site as possible from a coupled Regional Ocean Model System (ROMS) - Simulating Waves Nearshore (SWAN) model, with a horizontal resolution of the model grid of 0.025 degrees. Significant wave height, peak wave period, and wave direction were extracted in both shallow and deep water from SWAN datapoints, and tidal elevation from a ROMS datapoint (Error! Reference source not found.).

Over a period of approximately one week, a series of low-pressure systems resulted in the occurrence of three storms (i.e., Dudley, Eunice, and Franklin) and produced record-breaking wind gusts over Ireland which led to severe weather impacts. This is reflected in the hydrodynamic conditions in Brandon Bay during the monitoring period in February 2022 when significant wave height exceeded 4.5 m during storm Eunice (Error! Reference source not found.). During fair-weather conditions over this same time period, a range of lower energy conditions were observed over the neap-spring tide cycle. Significant wave heights were much lower, e.g., 0.6 m in early and late February.

Figure 2. Hydrodynamics during the monitoring period with in A) Tidal elevation, B) Significant wave height, C) Peak wave period, and D) Mean wave direction, from shallow water SWAN datapoint. Source: Marine Institute.

Figure 2. Hydrodynamics during the monitoring period with in A) Tidal elevation, B) Significant wave height, C) Peak wave period, and D) Mean wave direction, from shallow water SWAN datapoint. Source: Marine Institute.

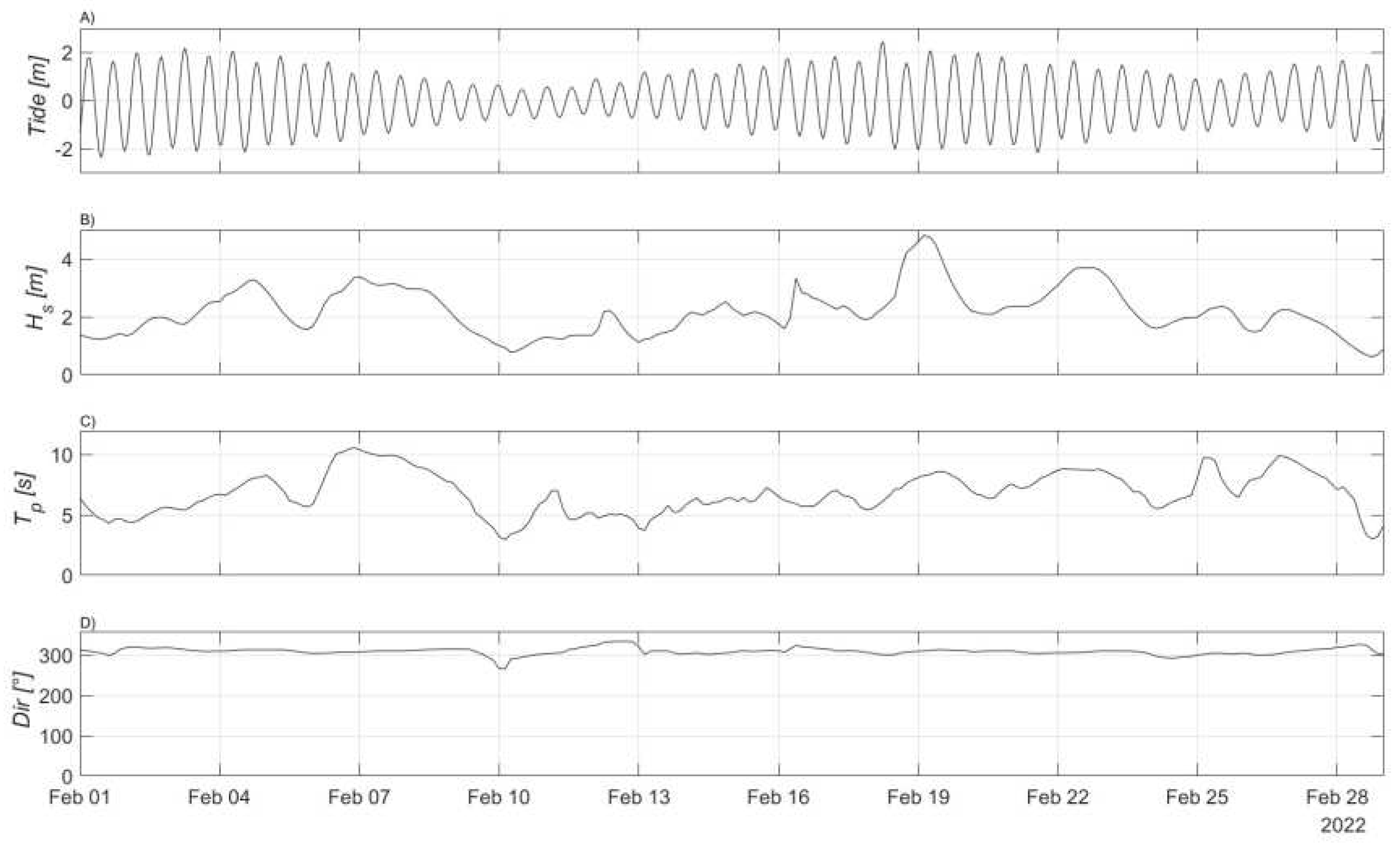
As such, the monitoring period provides an ideal scenario for the testing of the low-cost monitoring system as a wide range of conditions are observed with both low and extreme hydrodynamic events.

Monitoring System

Two monitoring stations were deployed along the bay, facing the beach face and nearshore (Error! Reference source not found. and Error! Reference source not found.). The cameras used were the Brinno TLC2000 (1920 x 1080-pixel resolution) (Error! Reference source not found.). They were mounted on wooden stakes approximately 1.5 m in height. The elevation of the centre of view for Camera 1 is approximately 11 m ITM and for Camera 2 is 14 m ITM. The fields of view (FoV) of the cameras cover alongshore lengths of 200 m and 250 m, respectively. The dataset for the analysis was acquired from 8 February 2022 until 1 March 2022 during daylight with an acquisition frequency of 1 Hz.

Table 1. Overview of the cameras deployed in Brandon Bay.

Site	Location ITM [m]		Camera Specifications				Elevation ITM [m]	FoV [m]
	Easting	Northing	Type	Resolution	Battery	SD Card
1	458967.02	613891.61	Brinno TLC 2000	1980 x 1080	16 x AA	128 GB	11	200
2	461425.81	617447.31					14	250

Table 1. Overview of the cameras deployed in Brandon Bay.

Site	Location ITM [m]		Camera Specifications				Elevation ITM [m]	FoV [m]
	Easting	Northing	Type	Resolution	Battery	SD Card
1	458967.02	613891.61	Brinno TLC 2000	1980 x 1080	16 x AA	128 GB	11	200
2	461425.81	617447.31					14	250

Figure 3. (a) Overview of Brandon Bay with the location of both cameras; (b) Detail of the Field of View of Camera 1; and (c) Detail of the Field of View of Camera 2, on a satellite image (from ESA – Sentinel 2).

Figure 3. (a) Overview of Brandon Bay with the location of both cameras; (b) Detail of the Field of View of Camera 1; and (c) Detail of the Field of View of Camera 2, on a satellite image (from ESA – Sentinel 2).

Figure 4. Photo of Brinno TLC2000 camera 1 deployed in the field.

Figure 4. Photo of Brinno TLC2000 camera 1 deployed in the field.

For this study, Timex images were generated on an hourly basis. The collected images from the timelapse camera can be found here: https://github.com/NuytsSiegmund/Shoreline_Timex.git. Standard transformation from image to world coordinates (image georectification) was conducted after applying lens distortion correction using the methodology described in [54], as well as camera calibration. Camera calibration is intended to identify the geometric characteristics of the image creation process and is an essential step here (in contrast to smartphones and other cameras that internally correct for radial distortion in image pre-processing) in order to perform analysis from camera applications. The camera that is deployed in the field is categorized on the basis of: 1) intrinsic parameters, which are the parameters necessary to link the pixel coordinates of an image point with the corresponding coordinates in the camera reference frame (e.g., focal length, size of pixels, radial distortion); and 2) extrinsic parameters, which are the parameters that define the location and orientation of the camera reference frame with respect to a known world reference frame (e.g., rotation, azimuth, tilt). As such, camera calibration allows one to determine an accurate relationship between a 3D point in the real world and its corresponding 2D projection in the image acquired by the calibrated camera. This was carried out with a chessboard pattern of known side lengths and requires the camera to observe the planar patterns at different orientations.

Image Georectification

Ground Control Points (GCPs) were used for georectification to get image planes relative to world coordinates. With the focus on the development of a low-cost, mobile system, road traffic cones were successfully utilised as GCPs, with a total of 10 temporary GCPs at each of the two sites (Error! Reference source not found.). In addition, as the beach is open to the public and well used, the use of permanent GCPs was not an option. The location of the traffic cones, at the centre of the base facing the cameras, was measured using a Trimble 10 VRS system in ITM.

Figure 5. Road traffic cones were placxed in the field and used as temporary GCPs.

Figure 5. Road traffic cones were placxed in the field and used as temporary GCPs.

An example of the image georectification at the Camera 2 site, including the location of the GCPs in the image, is presented in Error! Reference source not found.. The image georectification, and subsequent analyses, was done using MATLAB, with some of the scripts provided by the Coastal Imaging Network ([55]). These scripts were modified and adapted to the specific requirements and environmental settings of the study area. The scripts prominently call and highlight a series of sub-functions that implement fundamental photogrammetry calculations (e.g., intrinsic and extrinsic parameters). In order to adapt the scripts, camera calibration parameters were added, GCPs were imported with their responding geographic coordinates, and extrinsic parameters were obtained. An additional script was written to extract shoreline positions and rotate them to local coordinates.

Figure 6. Temporary GCPs used in the field (Camera 2).

Figure 6. Temporary GCPs used in the field (Camera 2).

Error! Reference source not found. shows the initial picture taken by the camera and the same image georectified. The RMSD error between the entered xy-coordinates of the GCPs and the xy-coordinates found, using the extrinsic solution with the distorted UV (UVd) coordinates, which denotes the axes of the 2D image pane, were 0.58 m and 0.78 m in the x-direction and y-direction, respectively, for Camera 1 and 0.54 m and 0.74 m for Camera 2.

Figure 7. a) Image taken by Camera 2, and b) the same image after georectification.

Figure 7. a) Image taken by Camera 2, and b) the same image after georectification.

Generating Timex Images

After georectification, Timex images were generated by processing still images to obtain a single time-averaged image. Images are captured at a 10-minute interval at 1 Hz, with little deviation from this standard procedure. Nevertheless, [56] and [57] both used an interval of 2 Hz over 10 minutes. [58] produced Timex images from 20 frames with a sampling interval of 0.5 Hz, although their approach was not focused on shoreline detection. Others have produced Timex images by averaging long-exposure images, e.g., 15 seconds over a detection interval of 10 minutes [59], and 5-minute time-exposure images at 10 minutes [19].

In order to provide guidance on the impact of the sampling interval on shoreline detection, Timex images were produced using MATLAB with different intervals ranging from 1 to 30 s over a 10-minute period (Error! Reference source not found.) and a sensitivity analysis was carried out comparing the shorelines detected for each interval.

Table 2. Overview of intervals analysed in this study.

Overview Intervals
Interval [s]	Time period [min]	Total Pictures	Memory Demand [MB]
1	10	600	93.3
3	10	200	31.2
5	10	120	18.7
10	10	60	9.5
20	10	30	4.8
30	10	20	3.2

Table 2. Overview of intervals analysed in this study.

Overview Intervals
Interval [s]	Time period [min]	Total Pictures	Memory Demand [MB]
1	10	600	93.3
3	10	200	31.2
5	10	120	18.7
10	10	60	9.5
20	10	30	4.8
30	10	20	3.2

As times of tidal elevation differ each day, the data was normalized in order to compare Timex images during tidal cycles. As such, the data was tidally adjusted, where “Hour 6” is always high tide, and “Hour 0” and “Hour 12” represent low tide. The xy-coordinates of each of the shorelines, detected by the MATLAB scripts, were analysed using RMSD and standard deviations (σ).

Shoreline Edge Detection

Scripts from the Coastal Imaging Research Network [55] were used for shoreline detection using the difference between red and blue colour channels [22]. On the georectified Timex images, transects were drawn alongshore from the swash zone to the back beach and dune (Error! Reference source not found.). The MATLAB script identified the transect with the highest difference between the red and blue channel, after which it locates a point at the peak of the difference, i.e., the shoreline edge.

Figure 8. Transects covering the swash zone in front of Camera 2 (From 26 February 2022) – Interval 1 second.

Figure 8. Transects covering the swash zone in front of Camera 2 (From 26 February 2022) – Interval 1 second.

In order to avoid bias by shoreline outliers (i.e., in the far-field of each image), only shoreline data within a distance of 200 m for Camera 1 and 250 m for Camera 2 alongshore from the camera position were considered. This distance was adopted based on previous studies with similar elevations above MSL [60] and visual inspection. The difference between the alongshore distances is considered due to the elevation difference between the two cameras (i.e., z = 11 m and 14 m). This series of operations generated a set of approximately 150 xy-data points for each image, i.e., one datapoint for each transect. For each of the accepted shorelines, RMSD values of the alongshore position was estimated, as well as the mean RMSD for all images and the standard deviation.

3. Results and Discussion

Shoreline Edge Detection

All Timex images were processed and the automatically extracted shoreline edges were manually checked in MATLAB, as the image-processing algorithm’s performance occasionally produced rogue measurements when precipitation or sea spray affected image quality or during storm/dark conditions when the contrast between sediment and water was too low to distinguish the shoreline edge. Consequently, these Timex images were excluded from the dataset, resulting in a total of 796 (out of 840) Timex images used in this analysis, from both cameras deployed in Brandon Bay (Error! Reference source not found.). Error! Reference source not found. shows an example of the shoreline edge detected by the MATLAB script on 26 February 2022 at high tide (2022-02-26T13:10:00) for the six different intervals (1 s, 3 s, 5 s, 10 s, 20 s, and 30 s).

Figure 9. Example of the shoreline edge at different intervals on 26 February 2022 at high tide, with the shoreline edge at a) 1 s, b) 3 s, c) 5 s, d) 10 s, e) 20 s, and f) 30 s. The x-axis is the alongshore distance from the camera in metres, and the y-axis the cross-shore distance from the camera in metres.

Figure 9. Example of the shoreline edge at different intervals on 26 February 2022 at high tide, with the shoreline edge at a) 1 s, b) 3 s, c) 5 s, d) 10 s, e) 20 s, and f) 30 s. The x-axis is the alongshore distance from the camera in metres, and the y-axis the cross-shore distance from the camera in metres.

From the transects in Error! Reference source not found., the RMSD is calculated between the transect resulting from a 1 s interval and the transects from the other intervals. The RMSD is defined by the distance between the different transects and consequently takes into account both x-direction and y-direction of the produced transects. Error! Reference source not found. provides an example of the shoreline edge detected from the MATLAB scripts and the resulting RMSD between two example transects (i.e., 1 s and 5 s as seen in Error! Reference source not found.). Here, the solid line represents the transect from the 1 s interval and the dashed line the transect from the 5 s interval on 26 February 2022 at high tide. The red shaded area is then the resulting RMSD between the two transects. In this particular example, the x-direction RMSD is 0.368 m, and the y-direction RMSD is 0.321 m.

Figure 10. Example of RMSD between shoreline edge detected on Timex with 1-second interval (Solid line) and 5-second interval (Dashed line) from 26 February 2022 at high tide. The red area represents the RMSD between both lines.

Figure 10. Example of RMSD between shoreline edge detected on Timex with 1-second interval (Solid line) and 5-second interval (Dashed line) from 26 February 2022 at high tide. The red area represents the RMSD between both lines.

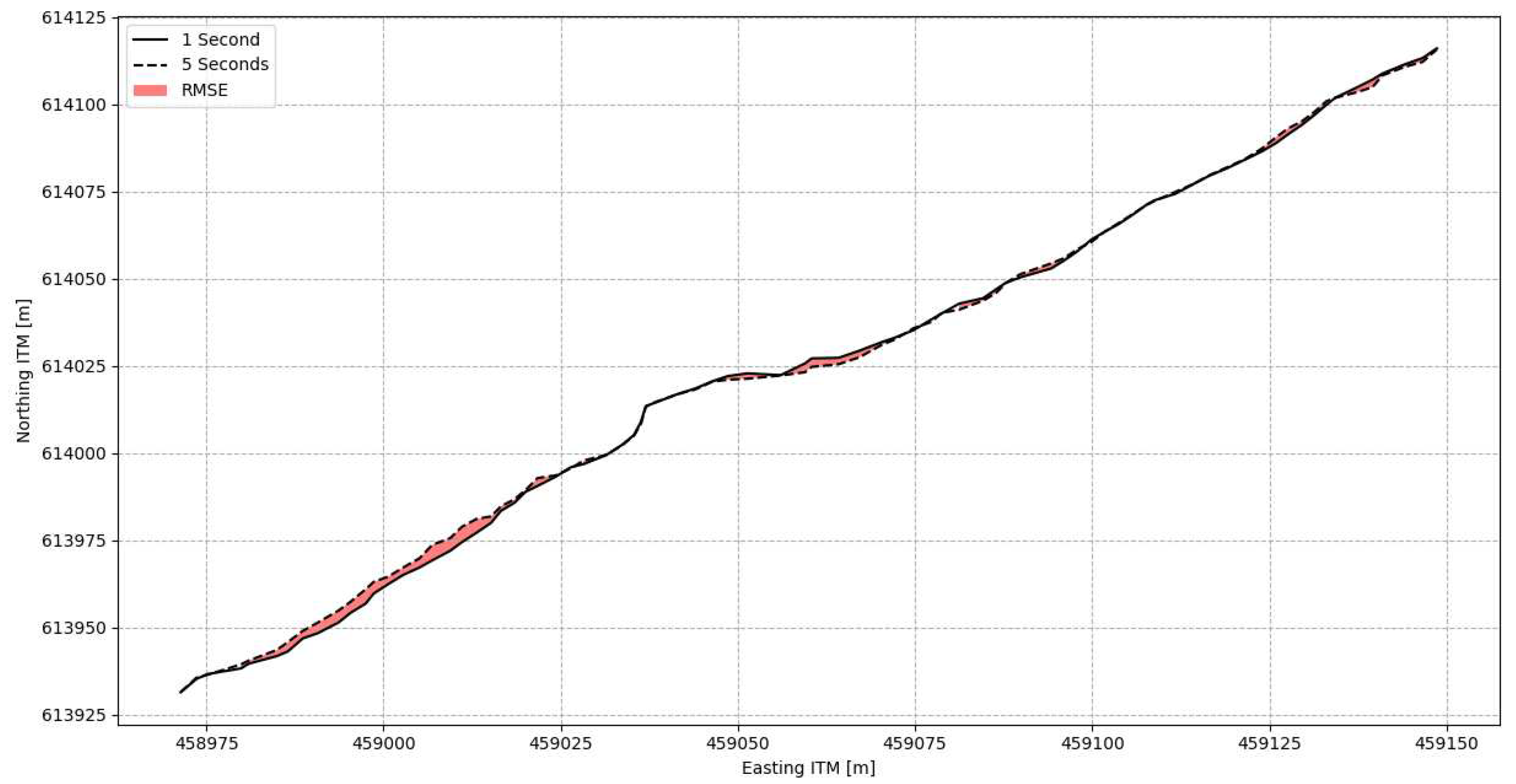
This analysis was carried out for all 796 Timex images and its result is shown in Error! Reference source not found.. Here, the overall RMSD (RMSD_mean) is shown of the shoreline edges derived from the sampling intervals of 3 s (i.e., 200 pictures, 5 s (120 pictures), 10 s (60 pictures), 20 s (30 pictures), and 30 s (20 pictures), compared to an interval of 1 s (600 pictures). The solid line represents RMSD_mean and the shaded area the standard deviation.

Table 3. Details on Timex images used for analysis.

Total number of accepted Timex images
Hour	Camera 1	Camera 2
0	12	12
1	12	36
2	24	24
3	24	36
4	24	42
5	36	42
6	36	42
7	36	42
8	36	38
9	36	42
10	36	32
11	24	36
12	12	24
Total	348	448

Table 3. Details on Timex images used for analysis.

Total number of accepted Timex images
Hour	Camera 1	Camera 2
0	12	12
1	12	36
2	24	24
3	24	36
4	24	42
5	36	42
6	36	42
7	36	42
8	36	38
9	36	42
10	36	32
11	24	36
12	12	24
Total	348	448

Figure 11. Mean RMSD (Solid blue line) and standard deviation (shaded areas) of all intervals compared to the 1-second interval of the different daylight hours, for (Top) Camera 1; and (Bottom) Camera 2, based on 796 Timex images.

Figure 11. Mean RMSD (Solid blue line) and standard deviation (shaded areas) of all intervals compared to the 1-second interval of the different daylight hours, for (Top) Camera 1; and (Bottom) Camera 2, based on 796 Timex images.

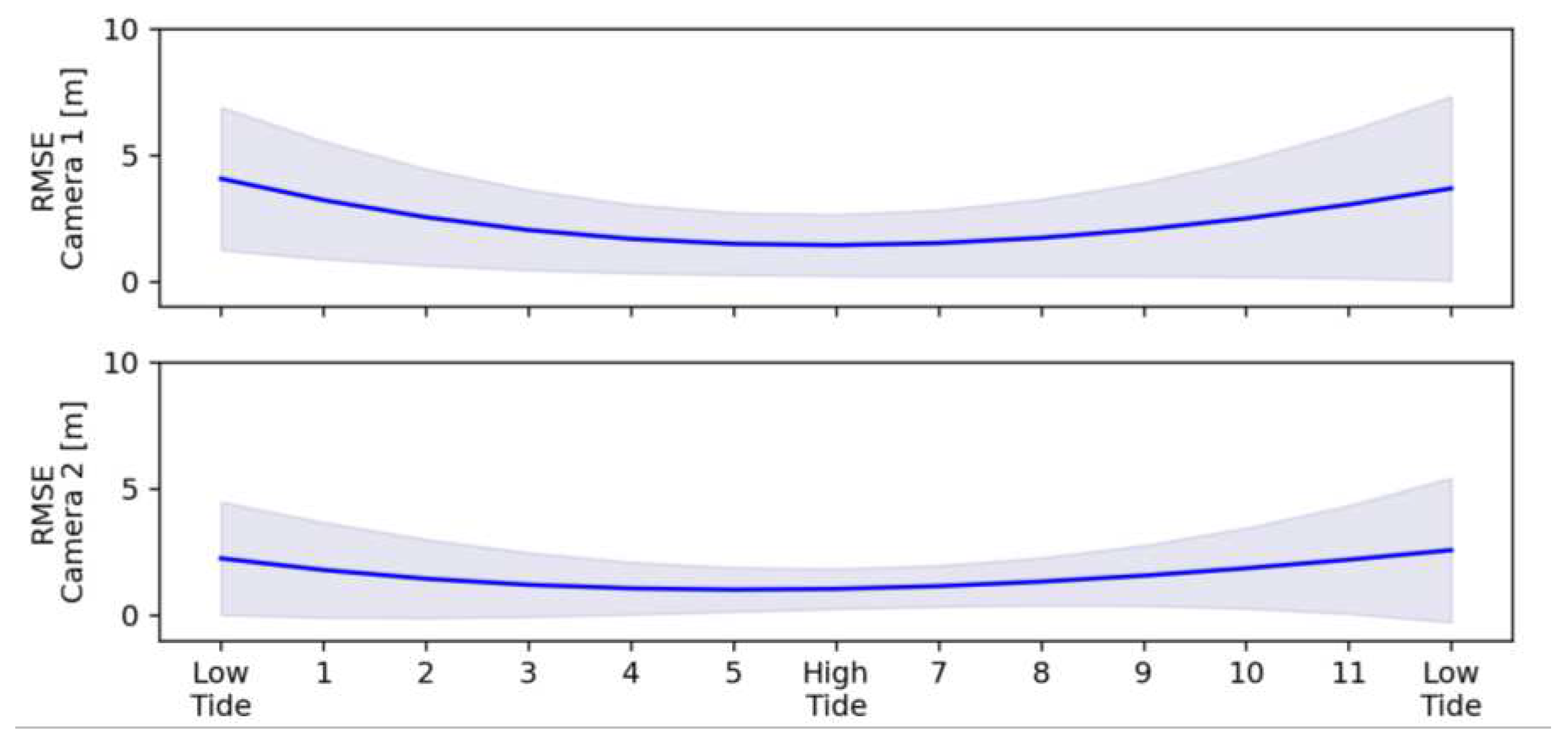
It is clear that the RMSD and standard deviation are lowest during high tide when the shoreline is closest to the camera position, thus resulting in less distortion and errors. Moreover, the RMSD for Camera 1 is clearly higher than for Camera 2; this is due to the higher elevation of Camera 2. In general, the higher the camera is positioned above mean sea level (MSL), the greater the FoV [22]. Indeed, there will be less noise in the shoreline detection due to the greater FoV.

In addition, the RMSD and standard deviation tend to be higher going from high tide to low tide, compared to the RMSD from low to high tide. Indeed, the average RMSD at low tide – “Hour 0” is RMSD_mean = 4.1 m, RMSD_mean = 1.4 m at “6”, and RMSD_mean = 3.7 m (with a higher standard deviation), and for camera 2: RMSD_mean = 2.3 m at “0”, RMSD_mean = 1.03 at “6”, and RMSD_mean = 2.6 m at “12”. This can be explained due to the dissipative nature of the beach; water and surface moisture remains on the beachface in the intertidal parts of the beach during receding tides, especially if prominent ridge and runnel systems are present, resulting in erroneous processing of the shoreline. Error! Reference source not found. shows a Timex image from 26 February 2022 at daylight hour “10” (Camera 1), clearly indicating that the shoreline edge detection will be impacted by the pools of water left behind by the receding tide.

Figure 12. Example of a) snapshot, and b) resulting Timex image during receding tides, showing remaining water on the beachface resulting in shoreline edge detection not representing the actual shoreline (from 26 February 2022 at 10h).

Figure 12. Example of a) snapshot, and b) resulting Timex image during receding tides, showing remaining water on the beachface resulting in shoreline edge detection not representing the actual shoreline (from 26 February 2022 at 10h).

Optimisation through intervals

In order to get additional insights into the impact of the image intervals on shoreline precision, the RMSD was extracted during high tide for both cameras, as the distortion and errors are the lowest during that time period (Error! Reference source not found.). This resulted in 78 shoreline positions (36 for Camera 1 and 42 for Camera 2) for RMSD analysis. Similar to before, the RMSD of shorelines detected using the larger time intervals were calculated relative to those detected from the 1-second interval images; these are shown in Figure 13.

Figure 13. Mean RMSD (Solid blue line) and standard deviation (shaded areas), for intervals of 3 seconds, 5 seconds, 10 seconds, 20 seconds, and 30 seconds, compared to 1-second interval, for (Top) Camera 1; and (Bottom) Camera 2.

Figure 13. Mean RMSD (Solid blue line) and standard deviation (shaded areas), for intervals of 3 seconds, 5 seconds, 10 seconds, 20 seconds, and 30 seconds, compared to 1-second interval, for (Top) Camera 1; and (Bottom) Camera 2.

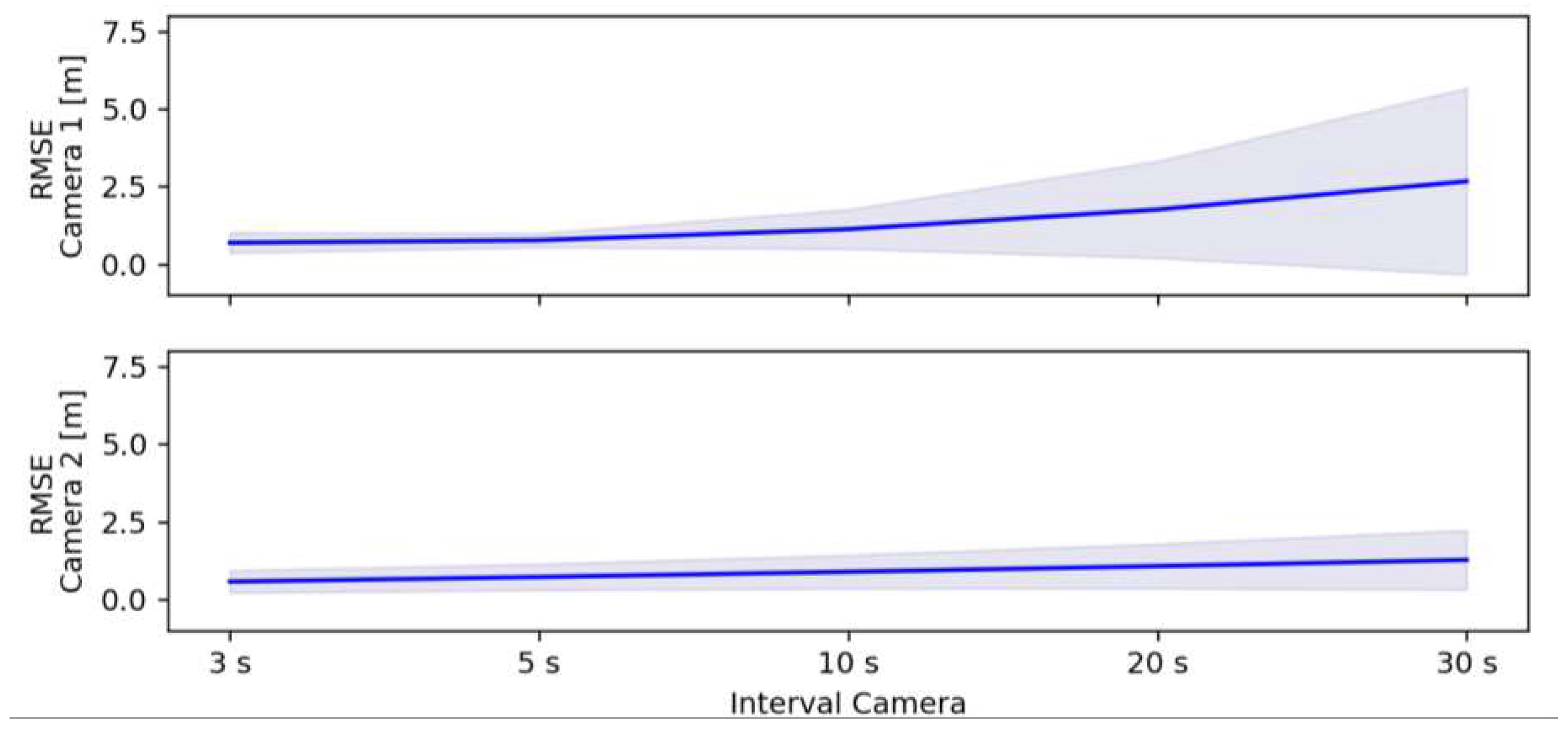
As expected, the precision decreases as the image time interval increases from 3 to 30 s. It is clear that Camera 2 (RMSD_range = 0.49 – 1.43 m, σ_range = 0.26 – 1.21) performs better than Camera 1 (RMSD_range = 0.64 – 3.62 m, σ_range = 0.14 – 4.56) producing lower mean RMSD and standard deviations (Camera 1: RMSD_mean = 1.4 m, σ_mean = 1.15; Camera 2: RMSD_mean = 0.9 m, σ_mean = 0.59) especially during the longer intervals (e.g., 20 and 30 s). The mean RMSD does not increase significantly, however, with the maximum mean RMSD for Camera 1 = 3.62 m and for Camera 2 = 1.43 m, both at an interval of 30 s. The RMSD shows that the detected shorelines for all time intervals were close to that of the 1-second interval, which is currently used as the standard in Timex image analysis. However, the shoreline is an ambiguous feature and always carries some uncertainties. Previous studies have shown that the feature identified as ‘shoreline’ varies among different methods (e.g., shorelines extracted using PIC method are sometimes shifted onshore [23], or the SLIM method can be erroneous for submerged positions [61]. Nevertheless, the RMSDs described in this study, for all intervals, are similar to RMSDs presented in other studies using similar analysis (Error! Reference source not found.); e.g., RMSD_mean = 0.93 m [62], RMSD_mean = 1.06 m [63], RMSD_mean = 1.41 m [59], RMSD_mean = 1.71 m [60], and RMSD_mean = 5.1 m [57]. As such, sampling intervals to produce Timex images can increase taking into consideration the influence of: 1) elevation of the camera; 2) battery life and memory; and 3) the particular application of the detected shorelines. These three considerations are discussed in the following sections.

Elevation of Camera

A higher elevation of the centre of the camera above MSL will increase the FoV and, consequently, the alongshore distance that can be analysed from the Timex images. Shorelines are two-dimensional features that inherently display greater dependence on the alongshore direction compared to the cross-shore direction. [22] already pointed out the dependency of elevation compared to the alongshore distance that can be analysed. As such, an increase in elevation above MSL will benefit the analysis that can be carried out.

Due to the local topography, the cameras positioned in this study have a low elevation above MSL (z < 15 m), which is substantially lower than other studies that report elevation of 20 m above MSL [63], up to 80 m [49] (Error! Reference source not found.). Nevertheless, this study shows that low elevations of the camera will still produce shoreline edges with an RMSD that is similar to other studies. In addition, this study shows that a ratio of xy/z = 15, with xy representing the alongshore distance analysed from the camera and z being the elevation of the centre of the camera above MSL, will lead to no substantial errors or adverse impacts. [43] showed that the principal loss of resolution with distance from the camera is the worsening of range resolution as pixel footprints stretch out. There is no easy fix for this technical challenge other than to use the maximum possible camera height or prioritize alongshore views that inherently have much smaller spatial gradients (compared with cross-shore views).

Table 4. Comparison of results with previous studies.

Comparison With Other Studies
Study	Camera Type	Sampling Rate	Method	Elevation Camera Above MSL [m]	FoV [m]	RMSD [m]
This study	Brinno TLC2000	10 min at 1 Hz	Red minus Blue channel	11 and 14	Camera 1 Alongshore: 200 Cross-shore: 200 Camera 2 Alongshore: 250 Cross-shore: 250	1.4 0.9
[49]	Surfcam	10 min at 5 Hz	Pixel Intensity	80	Alongshore: 800 Cross-shore: 400	/
[59]	/	10 min at 2 Hz	/	/	Alongshore: 100 Cross-shore: 16	1.41
[57]	ARGUS	10 min at 2 Hz	ASLIM method	43	Alongshore: 1500 Cross-shore:120	5.1
[62]	Bullet cameras	Averaged over short periods (30 s)	Color contrast between water and beach	11	Alongshore: 1340	0.93
[60]	Point Gray Blackfly 5 MP	900 video frames at 1.5 Hz	Four methods: - Max grayscale intensity - color channel divergence - pixel intensity clustering - Otsu method	15.9	Alongshore: 250 Cross-shore: 112	1.71
[63]	Mobotix M22	10 min at 1 Hz	ANN	20	Alongshore: 700 Cross-shore: 200	1.06

Table 4. Comparison of results with previous studies.

Comparison With Other Studies
Study	Camera Type	Sampling Rate	Method	Elevation Camera Above MSL [m]	FoV [m]	RMSD [m]
This study	Brinno TLC2000	10 min at 1 Hz	Red minus Blue channel	11 and 14	Camera 1 Alongshore: 200 Cross-shore: 200 Camera 2 Alongshore: 250 Cross-shore: 250	1.4 0.9
[49]	Surfcam	10 min at 5 Hz	Pixel Intensity	80	Alongshore: 800 Cross-shore: 400	/
[59]	/	10 min at 2 Hz	/	/	Alongshore: 100 Cross-shore: 16	1.41
[57]	ARGUS	10 min at 2 Hz	ASLIM method	43	Alongshore: 1500 Cross-shore:120	5.1
[62]	Bullet cameras	Averaged over short periods (30 s)	Color contrast between water and beach	11	Alongshore: 1340	0.93
[60]	Point Gray Blackfly 5 MP	900 video frames at 1.5 Hz	Four methods: - Max grayscale intensity - color channel divergence - pixel intensity clustering - Otsu method	15.9	Alongshore: 250 Cross-shore: 112	1.71
[63]	Mobotix M22	10 min at 1 Hz	ANN	20	Alongshore: 700 Cross-shore: 200	1.06

We acknowledge that the RMSD results reported for this study (Table 4) are based on comparing video-derived shorelines with themselves which inevitably should have greater precision than shorelines observed outside of the monitoring period when conditions have changed (e.g., changing light; changing elevation).

Battery life and memory requirements

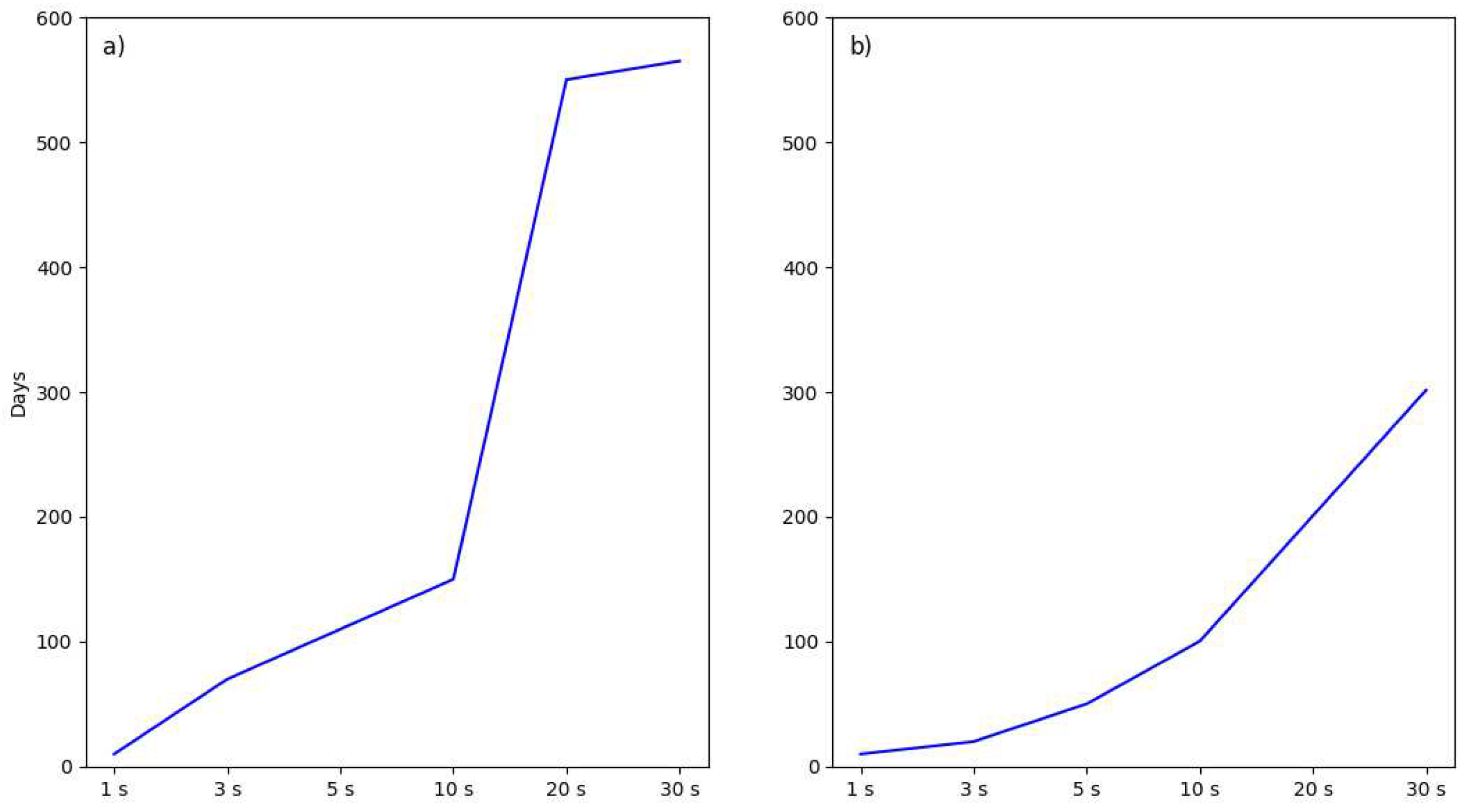
Due to the autonomous setup (e.g., no connection to power or other hardware) of a shoreline imaging system, battery life or memory (in the form of SD cards) can impose limitations on the system performance. The system used in this study can function with internal AA batteries or an external powerbank and has the option to use an SD card up to 128 GB capacity. Error! Reference source not found. shows how the operation time of the system is impacted by AA battery life and SD card memory depending on the imaging interval. When the imaging interval is set to 1 second, the maximum battery life is 10 days, which is the limiting factor in this setup as ten daylight hours will only produce 5 GB of data. As expected, the battery life increases when the imaging interval increases, and the time-lapse camera can last up to 550 days when set to sample every 30 seconds. The limiting factor then becomes the memory, i.e., the SD card capacity. For the maximum 128 GB card and a 30-second interval, the maximum capacity is reached after approximately 300 days.

Figure 14. a) Average battery life for the different intervals, and b) Average days that SD card can be used for the different intervals, from Brinno (2022).

Figure 14. a) Average battery life for the different intervals, and b) Average days that SD card can be used for the different intervals, from Brinno (2022).

Application of Timex images

For event scales (storm and other extreme events), often resulting in rapid changes in the beach and dune morphology, intervals of 1 second are generally preferred. Such intervals are necessary in order to delineate areas of preferred wave breaking in the surf zone [35,64] or rip currents [65], as well as to estimate intertidal and subtidal bathymetries [23] and also to produce time stack images [12,42]. Increasing the interval up to 30 seconds will potentially lead to erroneous analysis in these types of applications.

If long (seasonal to annual) time scales are considered for the application of the research, the analysis carried out here shows that low frequency processes (i.e., tidal cycles to years) can be analysed and assessed using an interval of up to 30 seconds, e.g., seasonal erosion and accretion trends, beach cusp evolution. Setting the interval to 30 seconds, compared to 1 second, proved to have a very limited impact on the precision but would significantly improve the autonomous operation time leading to no modification to the off the shelf cameras.

5. Conclusions

This research deployed two low-cost (~ €500) time-lapse cameras in Brandon Bay, Ireland in a remote area, overlooking a dissipative beach. The time-lapse cameras had a frequency interval of 1 s and image processing had been developed, aimed at extracting shoreline edge positions from oblique Timex images. The current standard for producing Timex images is averaging 600 pictures over a 10-minute period, with an interval of 1 s. However, there are no studies that investigate the precision of shoreline edge detection using Timex images with 1 s interval compared to other intervals. With the focus of deploying a fully autonomous, low-cost time-lapse camera in a remote area, increasing the interval over which Timex images are produced, an increase in interval can increase battery life and reduce memory constraints. As such, shoreline edge detection was carried out in MATLAB from Timex images produced from 1 s, 3 s, 5 s, 10 s, 20 s, and 30 s over a 10-minute period. Consequently, RMSD and standard deviations were calculated between the shoreline edges from a 1 s interval compared to the shoreline edges from the other intervals.

The results in this study showed that there is limited loss of the precision in shoreline edge detection when increasing the time-lapse interval from 1 s up to 30 s. In addition, the RMSDs in shoreline edges presented in this study are in a similar range to other studies, highlighting that the presented dataset is of sufficient precision to be used for coastal monitoring applications. Moreover, the sensitivity analysis carried out shows that battery life and memory do not necessarily need to be a limiting factor on autonomous operation time. Indeed, the system used in this study showed that autonomy can be increased from 10 days, using a 1 s imaging interval, to approximately 300 days if the interval is increased to 30 s, without having an adverse effect on the shoreline precision.

Overall, the analysis of the presented dataset from a low-cost monitoring system showed several advantages over existing techniques reported in similar remotely sensed approaches in coastal monitoring. Firstly, coastal monitoring systems do not necessarily require sophisticated hardware or sophisticated image processing techniques, making their applications easier to replicate. Secondly, the off-the-shelve time-lapse cameras used in this study can be easily and quickly deployed in the field, as well as in remote areas, while still producing outcomes similar to very expensive systems like ARGUS. Thirdly, while elevation above MSL is a limiting factor, this study shows that low elevations can produce meaningful insights into coastal processes. As such, the analysis outlined in this paper results in a better understanding of the setup of coastal imaging systems, which can improve the current methods available for coastal engineers and coastal managers.