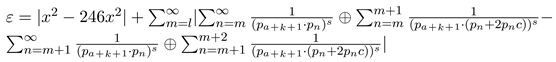Gocgen Approach for Zeta Function in Twin Primes

Preprint

Article

Gocgen Approach for Zeta Function in Twin Primes

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Ahmet F. Gocgen^*

This version is not peer-reviewed

Submitted:

08 February 2024

Posted:

09 February 2024

You are already at the latest version

Alerts

Abstract

I had previously developed an approach called Gocgen approach, which claimed to prove twin prime conjecture. In this paper, I processed the previously developed Gocgen approach with the zeta function and explained the relationship between the zeta function with some formulas to offer another perspective on the zeta function, and also created a new function that explains the Gocgen approach using the zeta function. Understanding the new function created will provide insight into the frequency of prime numbers.

Keywords:

Subject: Computer Science and Mathematics - Algebra and Number Theory

1. Introduction

Let

p_{n}

denote the n-th prime. Twin prime conjecture is conjectured that

\underset{n \to \infty}{lim inf} (p_{n + 1} - p_{n}) = 2 .

Lemmas

Lemma 1. According to Aysun and Gocgen [1]:

np+p gives all composite numbers where n is a positive natural numbers and p is a prime number.

Proof.

n p + p = p (n + 1)

. Then, according to fundamental theorem of arithmetic:

(n + 1 \in C) \oplus (n + 1 \in P)

Let

n + 1 \in C

n + 1 = p_{m} \times \dots \times p_{m + k}

Then,

p (n + 1) = p \times (p_{m} \times \dots \times p_{m + k})

Let

n + 1 \in P

n + 1 = p_{m}

Then,

p (n + 1) = p \times p_{m}

Lemma 2. According to Aysun and Gocgen [1].

2np+p gives all odd composite numbers where n is a positive natural numbers and p is an odd prime numbers.

Proof.

n p + p

gives odd composite numbers where p is a odd number and n is a even number. Then as already proved

n p + p

gives all composite numbers where n is a positive natural number and p is an prime number. Only possibility for odd composite just specified. Therefore,

n p + p

gives all odd composite numbers where p is a odd number and n is a even number. This equal to:

2 n p + p

gives all odd composite numbers where n is a positive natural numbers and p is an odd prime numbers.

Lemma 3. According to Rhafli [2]:

2 n p + p^{2}

gives all odd composite numbers where n is a natural numbers and p is a odd prime numbers.

Proof. with

n \in N

and p are all the primes except 2 which satisfy

p \leq \sqrt{N}

, the equation

2 n p + p^{2}

= all odd composite is true since if we divide it by p we get the trivial equation for odd numbers. For a given interval

I = [a, b]

one calculates the constant n and iterates to generates the odd composites included in the interval I.

Since the proofs of the following statements are dense and long, only the statements accepted as Lemma are given without citing any evidence, by citing articles directly related to the proof.

Lemma 4. According to Zhang, Maynard and Polymath project [3,4,5]:

\underset{n \to \infty}{lim inf} (p_{n + 1} - p_{n}) \leq 7 \times 10^{7},

\underset{n \to \infty}{lim inf} (p_{n + 1} - p_{n}) \leq 4680,

\underset{n \to \infty}{lim inf} (p_{n + 1} - p_{n}) \leq 246 .

Lemma 5. According to Gocgen [6]:

The expressions

6 n + p_{1} \times \dots \times p_{k} - 4

and

6 n + p_{1} \times \dots \times p_{k} - 2

produce composite numbers that cannot be divided by

p_{1} \dots p_{k}

primes, that is, cannot be expressed with

6 n + p_{1} \times \dots \times p_{k} - 6

6 n + p_{1} \times \dots \times p_{k} - 4, 6 n + p_{1} \times \dots \times p_{k} - 2 (s . group)

6 n + p_{1} \times \dots \times p_{k} + 2, 6 n + p_{1} \times \dots \times p_{k} + 4 (s + 1 . group)

Accordingly, let’s examine the possibilities in which at least one value in both groups is a composite, and let’s look at the gap that must remain between the composites forever after a certain number so that the twin primes are not infinite:

6 n + p_{1} \times \dots \times p_{k} - 4

and

6 n + p_{1} \times \dots \times p_{k} + 2

can be composite. Bounded of gaps: 6.

6 n + p_{1} \times \dots \times p_{k} - 4

and

6 n + p_{1} \times \dots \times p_{k} + 4

can be composite. Bounded of gaps: 8.

6 n + p_{1} \times \dots \times p_{k} - 2

and

6 n + p_{1} \times \dots \times p_{k} + 2

can be composite. Bounded of gaps: 4.

6 n + p_{1} \times \dots \times p_{k} - 2

and

6 n + p_{1} \times \dots \times p_{k} + 4

can be composite. Bounded of gaps: 6.

6 n + p_{1} \times \dots \times p_{k} - 4

6 n + p_{1} \times \dots \times p_{k} - 2

and

6 n + p_{1} \times \dots \times p_{k} + 2

6 n + p_{1} \times \dots \times p_{k} + 4

can be composite. Bounded of gaps: 2.

Then we can pose a new question as follows: Can the gaps between odd composite numbers that are not divisible by

p_{1}, \dots, p_{k}

be 6 and/or 8 and/or 4 and/or 2 forever after a certain number?

Therefore, the following question arises:

p \neq 2

c: composite numbers that cannot be divided by

p_{1}, \dots, p_{k}

\underset{n \to \infty}{lim inf} (c_{n + 1} - c_{n}) \geq 10 ?

For the difference between composite numbers that cannot be divided by

p_{1}, \dots, p_{k}

lim_{n \to 1} (c_{n + 1} - c_{n}) = ((p_{k + 2} \cdot p_{k + 1}) - p_{k + 1}^{2})

Since p is a prime number, and

\underset{n \to \infty}{lim inf} (p_{n + 1} - p_{n}) \leq 246

has been proven, the number of cases where

p_{k + 1}

and

p_{k + 2}

differ by 246 is infinite. Therefore (

p_{k + 1} = x

p_{k + 2} = x + 246

\underset{n \to \infty}{lim inf} (c_{n + 1} - c_{n}) = ((x + 246 \cdot x) - x^{2})

Let’s edit this expression:

\underset{n \to \infty}{lim inf} (c_{n + 1} - c_{n}) = (x^{2} + 246 x - x^{2})

\underset{n \to \infty}{lim inf} (c_{n + 1} - c_{n}) = (246 x)

When it is not forgotten that x is prime:

\underset{n \to \infty}{lim inf} (c_{n + 1} - c_{n}) \geq 10 .

Accordingly, the gap between odd composite numbers that cannot be divided by

p_{1}, \dots p_{k}

cannot be 6 and/or 8 and/or 4 and/or 2 forever after a certain number.

Therefore twin primes are infinite.

2. Theorems and Proofs

Let’s apply the same method to the zeta function as Marouane:

ζ (s) = 1 + \frac{1}{2^{s}} + \frac{1}{3^{s}} + \frac{1}{4^{s}} + \frac{1}{5^{s}} + \dots

\frac{1}{2^{s}} ζ (s) = \frac{1}{2^{s}} + \frac{1}{4^{s}} + \frac{1}{6^{s}} + \frac{1}{8^{s}} + \frac{1}{10^{s}} + \dots

(1 - \frac{1}{2^{s}}) ζ (s) = 1 + \frac{1}{3^{s}} + \frac{1}{5^{s}} + \frac{1}{7^{s}} + \frac{1}{9^{s}} + \frac{1}{11^{s}} + \dots

(1 - \frac{1}{2^{s}}) ζ (s) = 1 + \sum_{n = 1}^{\infty} \frac{1}{{(p_{n})}^{s}} + \sum_{n = 1}^{\infty} \frac{1}{{(p_{n} + 2 p_{n} c)}^{s}}

ζ (s) = {(1 - \frac{1}{2^{s}})}^{- 1} (1 + \sum_{n = 1}^{\infty} \frac{1}{{(p_{n})}^{s}} + \sum_{n = 1}^{\infty} \frac{1}{{(p_{n} + 2 p_{n} c)}^{s}})

To set the zeta function as divisible by a specific prime:

[p_{a} \cdot (1 - \frac{1}{2^{s}})] ζ (s) = p_{a} + \frac{1}{{(p_{a} \cdot 3)}^{s}} + \frac{1}{{(p_{a} \cdot 5)}^{s}} + \frac{1}{(p_{a} \cdot 7^{s})} + \dots

[p_{a} \cdot (1 - \frac{1}{2^{s}})] ζ (s) = p_{a} + \sum_{n = 1}^{\infty} \frac{1}{{(p_{a} \cdot p_{n})}^{s}} + \sum_{n = 1}^{\infty} \frac{1}{{(p_{a} \cdot (p_{n} + 2 p_{n} c))}^{s}}

ζ (s) = {[p_{a} \cdot (1 - \frac{1}{2^{s}})]}^{- 1} (p_{a} + \sum_{n = 1}^{\infty} \frac{1}{{(p_{a} \cdot p_{n})}^{s}} + \sum_{n = 1}^{\infty} \frac{1}{{(p_{a} \cdot (p_{n} + 2 p_{n} c))}^{s}})

To set the same operation to the zeta function as divisible by more than one prime:

[p_{a} \cdot p_{a + k} \cdot (1 - \frac{1}{2^{s}})] ζ (s) = p_{a} \cdot p_{a + k} + \frac{1}{{(p_{a} \cdot p_{a + k} \cdot 3)}^{s}} + \frac{1}{{(p_{a} \cdot p_{a + k} \cdot 5)}^{s}} + \frac{1}{(p_{a} \cdot p_{a + k} \cdot 7^{s})} + \dots

[p_{a} \cdot p_{a + k} \cdot (1 - \frac{1}{2^{s}})] ζ (s) = p_{a} \cdot p_{a + k} + \sum_{n = 1}^{\infty} \frac{1}{{(p_{a} \cdot p_{a + k} \cdot p_{n})}^{s}} + \sum_{n = 1}^{\infty} \frac{1}{{(p_{a} \cdot p_{a + k} \cdot (p_{n} + 2 p_{n} c))}^{s}}

ζ (s) = {[p_{a} \cdot p_{a + k} \cdot (1 - \frac{1}{2^{s}})]}^{- 1} (p_{a} \cdot p_{a + k} + \sum_{n = 1}^{\infty} \frac{1}{{(p_{a} \cdot p_{a + k} \cdot p_{n})}^{s}} + \sum_{n = 1}^{\infty} \frac{1}{{(p_{a} \cdot p_{a + k} \cdot (p_{n} + 2 p_{n} c))}^{s}})

For those divisible by both primes:

ζ (s) = {[p_{a} \cdot p_{a + k} \cdot (1 - \frac{1}{2^{s}})]}^{- 1} (p_{a} \cdot p_{a + k} + \sum_{n = 1}^{\infty} \frac{1}{{(p_{a} \cdot p_{a + k} \cdot p_{n})}^{s}} + \sum_{n = 1}^{\infty} \frac{1}{{(p_{a} \cdot p_{a + k} \cdot (p_{n} + 2 p_{n} c))}^{s}})

For those divisible only by the first prime:

{[p_{a} \cdot (1 - \frac{1}{2^{s}})]}^{- 1} (p_{a} + \sum_{n = 1}^{\infty} \frac{1}{{(p_{a} \cdot p_{n})}^{s}} + \sum_{n = 1}^{\infty} \frac{1}{{(p_{a} \cdot (p_{n} + 2 p_{n} c))}^{s}})

For those divisible only by the second prime:

{[p_{a + k} \cdot (1 - \frac{1}{2^{s}})]}^{- 1} (p_{a + k} + \sum_{n = 1}^{\infty} \frac{1}{{(p_{a + k} \cdot p_{n})}^{s}} + \sum_{n = 1}^{\infty} \frac{1}{{(p_{a + k} \cdot (p_{n} + 2 p_{n} c))}^{s}})

If we write the expression steady:

ζ (s) = {[p_{a} \cdot p_{a + k} \cdot (1 - \frac{1}{2^{s}})]}^{- 1} (p_{a} \cdot p_{a + k} + \sum_{n = 1}^{\infty} \frac{1}{{(p_{a} \cdot p_{a + k} \cdot p_{n})}^{s}} + \sum_{n = 1}^{\infty} \frac{1}{(p_{a} \cdot p_{a + k} \cdot p_{n} + 2 p_{n} c))^{s}})

{[p_{a} \cdot (1 - \frac{1}{2^{s}})]}^{- 1} (p_{a} + \sum_{n = 1}^{\infty} \frac{1}{{(p_{a} \cdot p_{n})}^{s}} + \sum_{n = 1}^{\infty} \frac{1}{{(p_{a} \cdot (p_{n} + 2 p_{n} c))}^{s}})

{[p_{a + k} \cdot (1 - \frac{1}{2^{s}})]}^{- 1} (p_{a + k} + \sum_{n = 1}^{\infty} \frac{1}{{(p_{a + k} \cdot p_{n})}^{s}} + \sum_{n = 1}^{\infty} \frac{1}{{(p_{a + k} \cdot (p_{n} + 2 p_{n} c))}^{s}})

For odd numbers that cannot be divided by the first and second prime (

p_{n}

must be greater then

p_{a + k + 1}

ζ (s) = {[p_{a + k + 1} \cdot (1 - \frac{1}{2^{s}})]}^{- 1} (p_{a + k + 1}^{2} + \frac{1}{{(p_{a + k + 1} \cdot p_{a + k + 2})}^{s}} + \sum_{n = 1}^{\infty} \frac{1}{{(p_{a + k + 1} \cdot p_{n})}^{s}} + \sum_{n = 1}^{\infty} \frac{1}{{(p_{a + k + 1} \cdot (p_{n} + 2 p_{n} c))}^{s}})

Now let’s rearrange this expression according to Lemma 4:

ζ (s) = {[p_{a + k + 1} \cdot (1 - \frac{1}{2^{s}})]}^{- 1} (x^{2} + \frac{1}{{(x \cdot 246 x)}^{s}} + \sum_{n = 1}^{\infty} \frac{1}{{(x \cdot p_{n})}^{s}} + \sum_{n = 1}^{\infty} \frac{1}{{(x \cdot (p_{n} + 2 p_{n} c))}^{s}})

In this regard, let’s create another function based on the zeta function to simplify our operations:

ε = x \times x + 246 x \times x + \sum_{n = 1}^{\infty} \frac{1}{{(p_{a + k + 1} \cdot p_{n})}^{s}} + \sum_{n = 1}^{\infty} \frac{1}{{(p_{a + k + 1} \cdot (p_{n} + 2 p_{n} c))}^{s}}

ε = x^{2} + 246 x^{2} + \sum_{n = 1}^{\infty} \frac{1}{{(p_{a + k + 1} \cdot p_{n})}^{s}} + \sum_{n = 1}^{\infty} \frac{1}{{(p_{a + k + 1} \cdot (p_{n} + 2 p_{n} c))}^{s}}

For the difference between odd numbers that are not divisible by the specified primes:

The first part to the right of the equation is the part where there is a 246x difference between the numbers that are not divisible by the specified primes. Considering that there are an infinite number of situations with 216 differences between them (Lemma 4), there will be a situation with a 216x difference between the only primes that cannot be divided into an infinite number of specified primes with different x values. This shows the infinity of twin primes, as in Lemma 5, based on the fact that the difference between odd numbers that cannot be divided by certain primes is greater than 10. In addition, by understanding the part on the second side of the equation, it is possible to obtain new information about the frequencies between primes.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Acknowledgments

I would like to express my endless gratitude to Marouane Rhafli for inspiring this work.

References

Aysun, E.; Gocgen, A.F. A Fundemental Study of Composite Numbers as a Different Perspective on Problems Related to Prime Numbers. International Journal of Pure and Applied Mathematics Research 2023, 3, 70–76. [Google Scholar] [CrossRef]
Rhafli, M. Sublinear Segmented Prime Sieve. Far East Journal at Mathematical Sciences 2019, 120, 147–159. [Google Scholar] [CrossRef]
Zhang, Y. Bounded Gaps Between Primes. Annals of Mathematics 2014, 179, 1121–1174. [Google Scholar] [CrossRef]
Polymath, D.H.J. The "bounded gaps between primes" Polymath project - a retrospective. arXiv 2014. [Google Scholar]
Hasanalizade, E. The Goldston-Pintz-Yıldırım sieve and some applications. KTH Royal Institute of Technology 2012. [Google Scholar]
Gocgen, A.F. Gocgen Approach for Bounded Gaps Between Odd Composite Numbers. Preprints 2024. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Gocgen Approach for Zeta Function in Twin Primes

Abstract

1. Introduction

2. Theorems and Proofs

Funding

Institutional Review Board Statement

Informed Consent Statement

Acknowledgments

References

MDPI Initiatives

Important Links

Subscribe