Submitted:
09 February 2024
Posted:
09 February 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Vertex Splittable Monomial Ideals
- (i)
- If u is a monomial and , or , then I is vertex splittable.
- (ii)
-
If there exists a variable and vertex splittable ideals andsuch that , and is the union of and , then I is vertex splittable. In this case, we say that is a vertex splitting of I and is a splitting vertex of I.
3. A Cohen-Macaulay Criterion
- (a)
- I is Cohen-Macaulay.
- (b)
- are Cohen-Macaulay and .
- (a)
- .
- (b)
- is Gorenstein if and only if I is a principal ideal.
- (c)
- is level if and only if and are level and .
- (d)
-
is pseudo-Gorenstein if and only if
- (i)
- either is pseudo-Gorenstein and , or
- (ii)
- is pseudo-Gorenstein and .
- (e)
- .
4. Families of Cohen-Macaulay Vertex Splittable Ideals
4.1. (Vector-Spread) Strongly Stable Ideals
4.2. Componentwise Polymatroidal Ideals
- (a)
- as monomial ideals of S.
- (b)
- is a componentwise polymatroidal ideal of S.
- (c)
- is a componentwise polymatroidal ideal of .
- (a)
- I is Cohen-Macaulay.
- (b)
- are Cohen-Macaulay componentwise polymatroidal ideals and .
- (a)
- a principal ideal,
- (b)
- a Veronese ideal, or
- (c)
- a squarefree Veronese ideal.
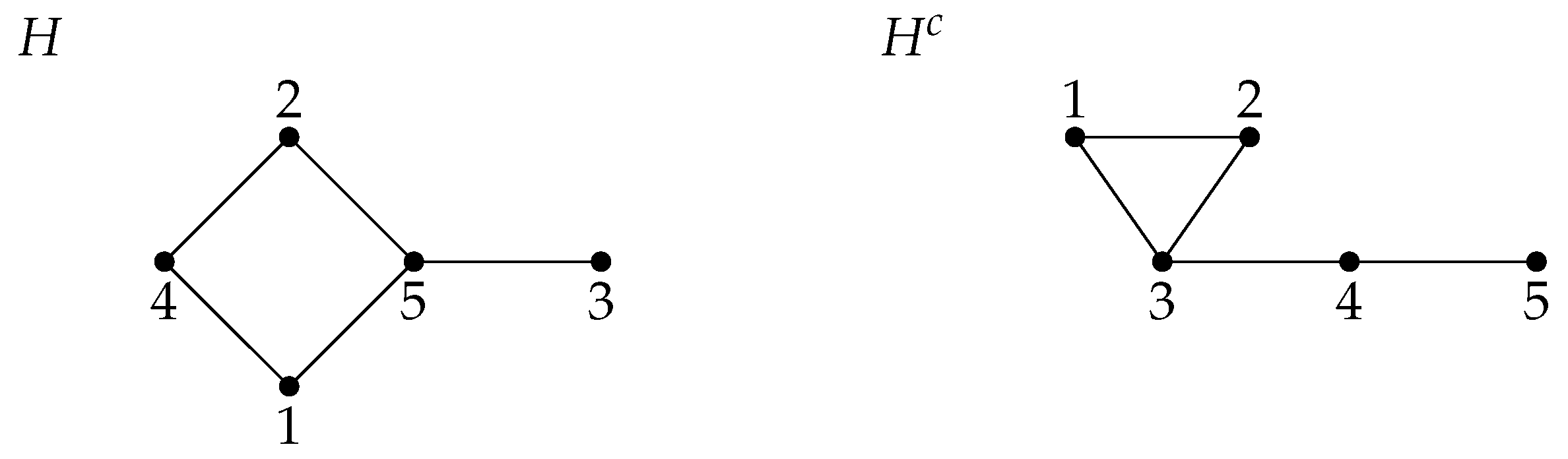
4.3. Bi-Cohen-Macaulay Graphs
- (a)
- G is a bi-Cohen-Macaulay graph.
- (b)
-
is a chordal graph with perfect elimination order andfor all such that .
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bandari, S.; Herzog, J. Monomial localizations and polymatroidal ideals. Eur. J. Combin. 2013, 34, 752–763. [Google Scholar] [CrossRef]
- Bruns, W; Herzog, J. Cohen–Macaulay rings, Cambridge University Press, 1998.
- Crupi, M.; Ficarra, A. Minimal resolutions of vector-spread Borel ideals. Analele Stiintifice ale Universitatii Ovidius Constanta, Seria Matematicat 2023, 31(2), 71–84.
- Crupi, M.; Ficarra, A. Very well–covered graphs by Betti splittings. J. Algebra 2023, 629, 76–108. [Google Scholar] [CrossRef]
- Crupi, M.; Ficarra, A. Very well-covered graphs via the Rees algebra. ArXiv 2023, arXiv:2305.01448v3. submitted. [Google Scholar]
- Deshpande, P.; Roy, A.; Singh, A.; Van Tuyl, A. Fröberg’s Theorem, vertex splittability and higher independence complexes. ArXiv, 2023; arXiv:2311.02430. [Google Scholar]
- Dirac, G. A On rigid circuit graphs. Abh. Math. Sem. Univ. Hamburg 1961, 38, 71–76. [Google Scholar] [CrossRef]
- Ene, V.; Herzog, J.; Hibi, T.; Saeedi Madani, S. Pseudo-Gorenstein and level Hibi rings. J. Algebra 2015, 431, 138–161. [Google Scholar] [CrossRef]
- Ficarra, A. Vector-spread monomial ideals and Eliahou–Kervaire type resolutions. J. Algebra 2023, 615, 170–204. [Google Scholar] [CrossRef]
- Ficarra, A. Shellability of componentwise discrete polymatroids. ArXiv, 2023; arxiv.org/abs/2312.13006, submitted. [Google Scholar]
- Ficarra, A. Simon’s conjecture and the v-number of monomial ideals. ArXiv, 2023; arXiv.org/abs/2309.09188, submitted. [Google Scholar]
- Francisco, C. A.; Ha, H. T.; Van Tuyl, A. Splittings of monomial ideals. Proc. Amer. Math. Soc. 2009, 137(10), 3271–3282. [Google Scholar] [CrossRef]
- Fröberg, R. On Stanley-Reisner rings. In Topics in algebra, Part 2 (Warsaw, 1988), Banach Center Publ., 26, Part 2, PWN, Warsaw, 1990, 57–70.
- Grayson, D.R.; Stillman, M.E. Macaulay2, a Software System for Research in Algebraic Geometry. Available online: http://www.math.uiuc.edu/Macaulay2 (accessed on 5 February 2024).
- Herzog, H.; Hibi, T. Discrete polymatroids. J. Algebraic Combin. 2002, 16, 239–268. [Google Scholar] [CrossRef]
- Herzog, H.; Hibi, T. Cohen-Macaulay polymatroidal ideals. European J. Combin. 2006, 27(4), 513–517. [Google Scholar] [CrossRef]
- Herzog, H.; Hibi, T. Monomial ideals; Graduate texts in Mathematics 260, Springer, 2011.
- Herzog, H.; Hibi, T.; Ohsugi, H. Binomial Ideals, 279; Graduate Texts in Mathematics, Springer, Cham, 2018.
- Herzog, J.; Rahimi, A. Bi-Cohen–Macaulay graphs. Electron. J. Combin. 2016, 23(1), #P1.11.
- Mafi, A.; Naderi, D.; Saremi, H. Vertex decomposability and weakly polymatroidal ideals. ArXiv, 2022; arxiv.org/abs/2201.06756. [Google Scholar]
- Moradi, S.; Khosh-Ahang, F. On vertex decomposable simplicial complexes and their Alexander duals. Math. Scand. 2016, 118(1), 43–56. [Google Scholar] [CrossRef]
- Moradi, S. Normal Rees algebras arising from vertex decomposable simplicial complexes. ArXiv, 2023; arxiv.org/abs/2311.15135. [Google Scholar]
- Villarreal, R. H. Monomial Algebras; Second Edition, Monographs and Research Notes in Mathematics, CRC Press, Boca Raton, FL, 2015.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).



