Preprint
Article
In an Eggshell: Baryonic Black Hole Universe with CMB Cycle for Gravity and Λ
Altmetrics
Downloads
166
Views
302
Comments
2
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
09 February 2024
Posted:
12 February 2024
You are already at the latest version
Alerts
Abstract
A persistent idea in cosmology is that the universe originated and then continued to evolve as a black hole. While the notion of a black hole universe has generally been framed within the standard cosmological model, the latter has had numerous problems related to dark matter, dark energy and other issues. To avoid such problems an alternative is proposed which omits cosmic expansion, dark matter and dark energy. The observable universe is cast instead as primarily a thin spherical shell of cold (~29 K) baryonic matter situated near the Hubble radius. This shell of plasma holds 95% of the observable universe’s mass, the remaining 5% existing in the interior galaxies and gas clouds. A key premise of the model is that spacetime is fundamentally photonic in nature. This allows photon energy to be transferred to spacetime in the Hubble redshift and to be transferred back to photons in a novel blueshift. These exchanges together drive a cosmic energy cycle for gravity and the cosmological constant, Λ. Photons of the cosmic microwave background originating in the plasma shell lose energy to ‘cooler’ regions of spacetime in interior zones via the Hubble redshift. This gives rise to gravity through the optical gravity approach. The depleted photons moving back towards the shell are then reenergized in ‘hotter’ spacetime regions via the Hubble blueshift. These photons eventually exert outward pressures on the shell which perfectly balance the inward forces of gravity, in this manner functioning as Einstein’s cosmological constant. The observable universe behaves as a closed system in thermodynamic equilibrium with constant energy and entropy and indeterminate age. Black holes are suggested to have analogous plasma shell structures and gravity/Λ cycles.
Keywords:
Subject: Physical Sciences - Astronomy and Astrophysics
1. Introduction
Recently there has been renewed interest in the idea that the observable universe arose and continues to exist as some form of black hole [1,2,3,4,5,6,7,8]. Proposals for a black hole universe have generally been premised on the Lambda cold dark matter (ΛCDM) consensus model of cosmology (expansion + dark matter + dark energy). The inclusion of dark matter and dark energy is necessary to allow a black hole universe with its Schwarzschild radius near the Hubble radius to attain the critical density needed to form a black hole. This density is the same as the ΛCDM critical density ρc, which requires just the same contributions from dark matter and dark energy [5].
Black hole universe models nonetheless face many problems. Due to the black hole mass-radius relationship, the radius of a black hole cannot increase without its mass increasing proportionately. It is unclear how mass growth through accretion could precisely balance the supposed radial increase of cosmic expansion. In addition, as initially described by Pathria [1], a black hole universe typically has a hybrid structure, with an external Schwarzschild metric enclosing an expanding Friedmann–Lemaître–Robertson–Walker internal metric. These two metrics may not match up in the way Pathria supposed [9,10]. While the interior metric might conceivably be replaced with a Schwarzschild metric, there is no consensus solution for such a metric [11].
Some mechanism is also needed to prevent a black hole universe from collapsing into a singularity. While various mechanisms have been suggested for achieving this in ordinary black holes [12,13,14,15,16,17,18,19,20,21,22,23,24], none of these seem immediately applicable to a black hole universe. Dark energy has been linked to possible expansion of black holes [25] and might similarly prevent cosmic collapse. Yet there has been negligible progress in identifying realistic candidates for either dark energy or dark matter over many decades. In addition, if cosmological expansion were abandoned in a black hole universe, the conceptual underpinnings for both dark matter and dark energy would also largely disappear.
A non-expanding black hole universe without dark matter and dark energy would be the very antithesis of the ΛCDM model. Such a universe at first seems impossible. Not only would there be no apparent mechanism to avoid singularity, but without dark matter and dark energy the observable universe would no longer have the mass density needed to enclose itself in a black hole [5].
Yet some black hole models do afford a clue as to where the additional baryonic mass required for a black hole universe could conceivably reside. Adapting Susskind’s 2D holographic representation of a black hole, these models include thin spherical shells [18,19,20]; black shells [21]; dark energy stars [22] and gravastars [23,24]. These thin-shell models collectively suggest that the missing mass for a black hole universe could reside in a thin shell of plasma located near the Hubble radius.
Pursuing this theme, we now propose a thin-shell black hole universe which is not expanding and possesses neither dark matter nor dark energy. Its mass is instead entirely baryonic, with 95% of it residing in a shell of cold (~ 29 K) plasma positioned near the Schwarzschild radius (also the Hubble radius, c/H0) and the remaining 5% in interior galaxies, gas and dust. The plasma shell is undetectable except through its influence on the cosmic microwave background (CMB). The CMB originates at the shell and also terminates there, its outward pressure holding the shell in place against gravity. The interactions between the CMB and the plasma shell dominate the model.
The absence of cosmic expansion will greatly simplify our model. The universe in this case need not have originated in an ultra-compact state, as in the ΛCDM model, but conceivably with galactic or even cosmic dimensions. Moreover, as the long-range gravitational forces between remote shell baryons would be extremely weak, it becomes permissible to use Newtonian gravity initially and thus avoid the many mathematical complexities of relativistic black hole, gravastar and black hole universe models. In this connection it should be recalled that the concept of ‘dark stars’ – large stars from which nothing can escape – predated general relativity by centuries.
The plasma shell design furthermore allows for strict energy conservation to be built into the model. The Hubble redshift removes enormous quantities of energy from the universe each second, primarily from the cosmic microwave background (CMB). Unlike the ΛCDM model, which allows for non-conservation of energy in this process, the present model can account for both the Hubble redshift and the fate of the lost photon energy. In cosmological models which omit expansion the Hubble redshift is typically ascribed to some ‘tired light’ mechanism, whereby photon energy is transformed to some other form. Tired light mechanisms, however, encounter two basic problems: the temperature-redshift relation in the CMB and the time dilation seen in Type 1a supernovae. They otherwise afford explanations for cosmological observations that match or improve upon those of the ΛCDM model [26,27].
The solutions to these problems in our model lie in a different conceptualization of spacetime: as being essentially photonic in nature. In previous work on gravitation and astro/geophysics spacetime was modeled as a network of graviton filaments interconnecting all particles, with the gravitons themselves having photonic structure. This arrangement allows masses to be pushed together by photons in a classic gravity mechanism [28,29]. The photonic model of spacetime will now be augmented using the paired-photon vacuum (PPV) scheme of Annila and coworkers, in which the gravitons within these filaments consist of overlapping photon pairs [30,31,32]. Such a photonic spacetime would be able to exchange energy with photons, such that CMB radiation undergoing the Hubble redshift still has the characteristics of blackbody radiation.
A key point that will be emphasized throughout is that the CMB temperatures measured at high redshifts record not only the temperatures at those distances as they existed long ago, but also the temperatures likely existing there today. The CMB closest to the plasma shell thus always has TCMB ~ 29 K in our model. This CMB has an energy density of u = 5.3 × 10−9 erg cm−3, similar to that of the cosmological constant Λ. This supports the notion that CMB photons rather than dark energy prevent singularity in the universe.
The Hubble constant H0 will also be reinterpreted as the fundamental recycling parameter describing the universe’s central functions. The Hubble time Ht = H0−1 thus no longer describes an ‘age of the universe’ but rather the basic cycle period of the universe. It corresponds roughly to the time required for a photon to travel from the shell to the centre of the observable universe, at which point the photon energy has been almost entirely degraded. This allows the Hubble radius to be defined as RU = cHt = c/H0, as it is in the ΛCDM model
From wave-particle duality it can be inferred that particles should also transfer energy and momentum to photonic spacetime via the Hubble redshift. While space does not permit development of this aspect here, in future work it will be connected to quantum physics and Modified Newtonian Dynamics (MOND). Of significance for the present discussion is that establishing a firm basis for the latter model would remove one of principal reasons for supposing the existence of dark matter.
The paper will be organized as follows. An overview of the model is given in Section 2. In Section 3 the problem of the TCMB-redshift relationship in tired light models is then reviewed. Our proposed solution is then given that spacetime is photonic in nature and that the Hubble redshift is actually a multiphotonic process, in which the CMB attempts to reach thermal equilibrium with spacetime. In Section 4 the Hubble blueshift of CMB photons will be examined in relation to shell stability and to the origin of the CMB and the cosmological constant Λ. The general CMB cycle for gravity and Λ is then presented in Section 5. In this section some CMB tests of the model are discussed, as well as some general implications for energy and entropy conservation in the model. Brief discussions of gravity and black holes are then given in Section 6 and Section 7, with some general conclusions lastly made in Section 8.
2. The Eggshell Universe
The basic model is shown in Figure 1. Superficially, the graphic resembles familiar depictions of the ΛCDM model, where the ‘shell’ corresponds to the surface of the primordial cosmic object. The universe in the ΛCDM model evolves inwardly from that surface, first with formation of particles of matter and radiation and later with stars and galaxies. The present model is entirely different from this. The density of baryons and CMB photons at various positions remains nearly constant over time, with only slow changes arising due to mass accretion. In the figure the network of graviton filaments, equated with spacetime, has its highest density nearest the shell and its lowest density near the centre, which is assumed to be close to our position in the Milky Way. The CMB energy density has this same distribution, its highest value found near the shell.
From the black hole mass-radius relationship, the observable universe has a mass M = RSc2/2G, where RS is the Schwarzschild radius. Since RS = RU = c/H0, we then have M = c3/2GH0 ≈ 9 × 1055 gm. Since almost all the mass is in the shell, the shell surface density is then ρA ≈ cH0/8πG ≈ 4 × 10−2 gm cm−2. Remarkably, this value is only about half that of the eggshell of a domestic chicken. To highlight this unusual cosmic feature, the plasma shell universe is termed the ‘eggshell universe’ (EU).
The thin-shell configuration affords a simple description of the metric in the interior space. From Birkhoff’s theorem the metric generated by the shell baryons alone would be flat and Minkowski. The gravitational potentials at different positions within the interior would be constant, such that the shell exerts no gravitational effects there. The interior galaxies, gas and dust comprising only 5% of the total mass would not significantly distort this flat interior metric. Unlike the gravitational potentials, however, the density of gravitational potential energy – or equivalently of spacetime in our model – would not be uniform at each point in the interior space. The density of photonic spacetime would be at its maximum value near the shell and at its minimum at the cosmic centre.
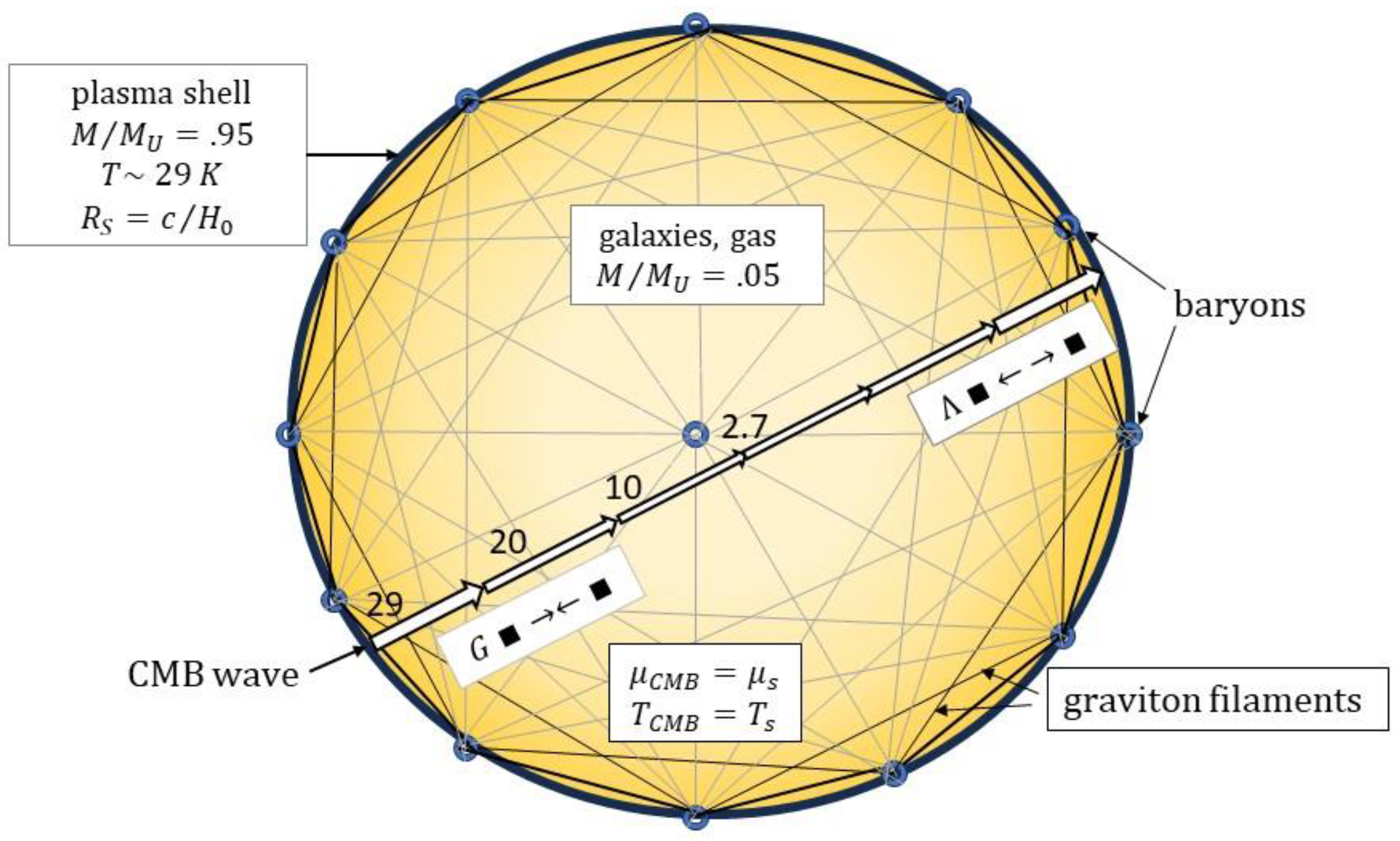
Figure 1.
Eggshell universe with CMB cycle for gravity and Λ. Representative shell baryons and one interior baryon are small blue circles. Graviton filaments of spacetime connecting baryons are shown as dark lines, with line thickness representing filament energy (. Concentric zones of uniform TCMB are shown with yellow shading, with darker shades indicating higher values. A CMB wave moving inwardly from the shell is redshifted by energy loss to spacetime filaments, causing masses to be attracted in gravity (■ →← ■). The weakened photons are then blueshifted by return transfer of energy from spacetime filaments as they head back towards the shell. This causes masses to be pushed apart, generating Λ (■ ←→ ■). At all positions the CMB temperature and energy density equals the spacetime temperature and density (indicated by ‘s’ subscripts). See text for full description.
Figure 1.
Eggshell universe with CMB cycle for gravity and Λ. Representative shell baryons and one interior baryon are small blue circles. Graviton filaments of spacetime connecting baryons are shown as dark lines, with line thickness representing filament energy (. Concentric zones of uniform TCMB are shown with yellow shading, with darker shades indicating higher values. A CMB wave moving inwardly from the shell is redshifted by energy loss to spacetime filaments, causing masses to be attracted in gravity (■ →← ■). The weakened photons are then blueshifted by return transfer of energy from spacetime filaments as they head back towards the shell. This causes masses to be pushed apart, generating Λ (■ ←→ ■). At all positions the CMB temperature and energy density equals the spacetime temperature and density (indicated by ‘s’ subscripts). See text for full description.

This density gradient is the key to cosmic
operation in the model. It enables energy exchanges between spacetime and CMB
photons which drive gravity and a CMB-based cosmological constant. In a vast cosmic
cycle CMB photons originating at the shell are redshifted as they move towards
the interior space. The lost photon momentum is transferred to the graviton
filaments connecting masses and then to the masses themselves, pushing them
together. Since the observable universe in our model has essentially fixed
energy, mass and volume, however, increasing spacetime curvature at one
position through gravitation of masses is necessarily balanced by spacetime
relaxation (and thus mass separation) elsewhere. By symmetry, the energy
released by spacetime in this way would be transferred back to photons. As
will be discussed in Section 4, abundant
evidence already exists for such an energy release in a variety of masses and
mass systems [28,29,33–35]. In the model CMB
photons that have been blueshifted in this manner eventually exert outward
pressure on the shell, thereby preventing its gravitational collapse and
performing the role of Λ in the Einsteinian sense
of a cosmological constant.
3. Photonic Spacetime
The eggshell universe has at its centre a
fundamentally different view of spacetime, one based on physicality rather than
geometry. This photonic spacetime allows for a new interpretation of the
Hubble redshift that can be grouped with tired light (TL) mechanisms. As noted
above, TL models have had difficulty in accounting for two problems that are
well addressed in the ΛCDM model: the linear TCMB-redshift
relation and the time dilation seen in supernovae. In other respects, however,
they perform just as well as the ΛCDM model or better [26].
Let us first consider the TCMB
problem in TL models (for a general discussion of the historical roles of the
CMB in cosmology see [36]). In the ΛCDM model
the CMB temperature Tz at a redshift z increases
according to the relationship
where T0 = 2.726 K is the average
CMB temperature today [37]. Here the CMB
photons originate from the surface of last scattering at the time of
recombination, with Tz ≈ 3,000 K and redshift z ≈
1100. Evidence in favour of Equation (1) is found with the presumed CMB
heating of atoms and molecules in remote gas clouds [38,39];
in the Sunyaev–Zeldovich (SZ) effect [40];
and with water molecules at the very high redshift of 6.34 [41].
The temperature-redshift relationship for the CMB
follows from some basic relations for a photon gas:
Here U is the total energy, V the
volume, u the energy density, P the pressure, T the
temperature, n the photon number density, r a constant and σ the
Stefan-Boltzmann constant. In a laboratory system a photon gas is in constant
contact with matter, such that equilibration between photons and baryons
maintains the blackbody spectrum appropriate for the system. In the ΛCDM
model, however, the CMB photons after leaving the surface of last scattering
are only able to retain their blackbody spectrum by virtue of cosmological
expansion. This allows the energy density and photon number of the CMB
to diminish in the correct manner.
Significant deviations from Equation (1) would be
possible indications of other processes at work, such as a decaying vacuum
energy density [42]. A net photon production
or destruction over time would give TCMB(z) (1 + z)(1 – β), with β ≠ 0. A
positive β would be consistent with net photon production until today, while β
< 0 would imply photon destruction. With no clear evidence thus far for a
non-zero β, however, a basic challenge for TL models lacking cosmic expansion
is thus how to retain the CMB blackbody signature over time. The CMB photon
energy would vary as (1 + z)−1, but the photon number density
would remain constant.
3.1. Spacetime as a Photon Gas
As in our earlier work on gravity, we model
spacetime as a network of graviton filaments linking all the particles of the
observable universe, with the graviton subunits themselves being photonic in
nature [28,29,33,34]. The photonic energy in
the graviton filaments connecting any two masses is assumed to be equal in
magnitude to the mutual gravitational potential energy of those masses. This
arrangement allows spacetime to be continuously updated at each point in space
by the masses embedded within it, as required in general relativity.
Information concerning a particle’s velocity or spin, for example, would be
continuously encoded and carried away from it by gravitons. Particles act
essentially as reprocessing centres for gravitons, converting gravitons with
older, outdated information originating from remote masses into newer ones
carrying updated information about local particles.
The paired photon vacuum (PPV) model of Annila and
coworkers can be integrated with this scheme (Figure
2) [30–32]. In the PPV model the
vacuum likewise consists of filaments of spin-2 gravitons, but with the latter
occurring as overlapping pairs of in-phase and antiphase spin-1 photons. In
their overlapping, double-stranded state, the photons do not exert
electromagnetic forces but still have energy density. When pushed into hotter
states, the photon pairs unwind and the now single-stranded, non-overlapping
photons (e.g., CMB photons) do exert electromagnetic forces. The
spectral density of the paired-photon vacuum in their model has the same form
as blackbody radiation (Figure 2).
From these considerations it is evident that such a
photonic spacetime might be treated as a quasi-photon gas similar to the CMB.
Like the CMB, it would have analogous values for energy density us,
pressure ps, temperature Ts and
photon number ns (where the subscripts ‘s’ denote
spacetime). Since the CMB contributes the largest energy component to
electromagnetic radiation fields, even in the local universe, the CMB and
spacetime pools at all locations would thus exchange energy primarily with each
other. This would tend to bring these two photon gases into thermal
equilibrium at each point in space, such that everywhere Ts= TCMB. A laboratory model for such a spacetime could
even exist in recent work showing that light pulses propagating in optical
fibers organize themselves in the manner of ordinary gases [43].
A spacetime with variable photon content can
account for the Hubble redshift, as well as the TCMB problem
and supernova time dilation in TL models. This is because spacetime would at
points in space be capable of exchanging energy with the CMB or other
electromagnetic waves directly, mediating their photon number in the process.
3.2. Hubble Redshift of CMB versus Stellar Photons
In our model the Hubble redshift is viewed as a
multiphotonic process operating on wave trains of photons. Stellar surfaces
have effective temperatures thousands of degrees higher than that of the CMB at
any point in the EU. This gives rise to a critical difference in how the
Hubble redshift would operate on CMB photons versus ordinary starlight.
Consider first the CMB photons. At their hottest
positions near the shell, we have TCMB = Tshell~ 29 K and u ~ 5 × 10−9 erg cm−3 (Figure 1). At their weakest position, possibly
near our location, the respective values could be 2.7 K and 4 × 10−13 erg
cm−3. As it moves towards the interior, an array of CMB photons
would transfer energy to spacetime packets it encounters along the way. The
photon wavelengths in the array would thus increase, while its values for u
and n would decrease: the Hubble redshift. As discussed in Sections 5 and 6, the energy and momentum lost
from the wave trains would be transferred to graviton filaments, setting them
in motion and pushing masses together in gravitation.
Conversely, an array of ‘cooler’ CMB photons moving
from the interior back towards the shell encounters regions of progressively
‘hotter’ and denser spacetime, with higher TCMB and Ts.
With equipartition of energy the CMB photon wavelengths would accordingly
diminish, while its values for u and n would increase: the Hubble
blueshift (Figure 1). This blueshift
comes at the expense of graviton energies within spacetime filaments, with
masses now being pushed apart and |U| thereby diminished. In this
picture, inwardly moving waves of CMB radiation would lose most of their energy
in the outermost regions of the EU, since graviton filaments are densest
there. This would be consistent with Equation (1).
In the case of starlight, however, there would only
be a Hubble redshift. A sunlike star has TEff ~ 6,000 K.
Its photon energies thus vastly exceed those of CMB photons at any point within
the EU. With the assumption that Ts = TCMB
at each point in space, equipartition of energy between starlight, spacetime
and the CMB thus results in a one-way Hubble redshift for starlight photons.
As will be discussed below,
mechanisms for gravity and Λ can then exploit the difference between the
energies of CMB photons entering or leaving a specific zone of space with those
of CMB photons that are characteristic of that zone. In
each specific zone of space the decrease in TCMB due
to the Hubble redshift is balanced by an increase arising from an analogous
Hubble blueshift. In a sense there would be two equal and opposite β terms in
operation, such that overall β = 0.
3.3. Supernova Time Dilation and Gravitational Time Dilation
The other main piece of evidence considered to
support the ΛCDM model rather than TL models is the observed time dilation in
supernovae [27]. In the ΛCDM model this time
dilation arises due to expansion of spacetime since the time of the stellar
explosion. The light curve of the distant supernova is stretched in the
observer’s frame by a factor (1 + z) compared to the supernova’s rest
frame [44].
A similar effect can be produced in the present
model. Consider a wave of radiation leaving the supernova. As with stellar
radiation generally, photon energy would flow unidirectionally in the Hubble
redshift from these photons to spacetime photons due to the large energy gap
between them. The photon number in the wave would again diminish in this
process, while the average photon wavelength would increase. The wave as a
whole would thus expand by a factor (1 + z), producing the same time
dilation effect as in ΛCDM model.
Gravitational time dilation in our model could have
an additional interpretation not available in general relativity. In the
latter theory the gravitational redshift and gravitational time dilation are
observed in a light source positioned relatively nearer to a mass than the
observer. Both effects arise because the observer’s clock runs faster than the
clock at the source’s position. Since only clocks are involved, photon energy
is conserved throughout its trajectory. In the photonic spacetime model the
light wave leaving the vicinity of a mass encounters regions with progressively
reduced spacetime density, since the array of graviton filaments attached to
the mass thins out with increasing separation from it. The energy gap with these
spacetime photons consequently increases and there is a progressively greater
flow of photon energy to spacetime. The photon number in the wave consequently
diminishes and the average photon wavelength again increases, again producing
time dilation in the wave.
This mechanism is also consistent with a simpler
Newtonian explanation. Observationally, it is hard to distinguish between the
explanation of the gravitational redshift in general relativity and the classic
Newtonian one, in which a photon loses energy climbing out of a gravitational
well. A theoretical problem exists in general relativity with the latter
interpretation, as there is no obvious candidate sink for the lost photon
energy. In the present model, however, there is such a sink: the graviton
filaments of spacetime. As discussed in Section
6, these energy losses are what give rise to gravity.
4. Origin of Λ, the CMB and Eggshell Structure
With spacetime modeled in this way
we next consider how the basic cosmic structure – a plasma shell enclosing a
CMB – could have arisen in the first place and thereafter have remained
stable. As was noted in
Section 2
, the plasma shell in the EU is stabilized against gravitational
collapse by the Hubble blueshift of CMB photons. The energy density of the CMB
thus constitutes a cosmological constant Λ in the Einsteinian sense. It does
not have a uniform value at each point in space, as Einstein’s constant does,
but instead increases from its minimum at the centre of the EU to its maximum
value at the shell, tracking the CMB energy density (
Figure 1
).
Λ is a direct result of gravitation in our model.
Since the energy of the graviton filaments of spacetime consists of real energy
quanta, the sum of their total energies within an EU of essentially fixed mass
and radius must have a finite value. This implies that the total quantity |U|
is approximately fixed also. When two particles approach each other in
gravitation, increasing their share of the total |U|, other spacetime
filaments must diminish in energy by amounts which offset this energy
increase. For symmetry with the Hubble redshift, wherein photon energy is
absorbed into spacetime filaments, the reverse process would be a transfer of
photon energy from spacetime to other photons, leading to a blueshift of the
latter.
The Hubble blueshift of graviton filaments in each
mass or system of masses would give rise to an effective ‘Λ luminosity’,
described by
where U is the internal gravitational
potential energy (conventionally negative). The term Λ luminosity replaces the
‘Hubble luminosity’ previously used to describe this process, in recognition of
its essential cosmic function. In those accounts it was suggested that the
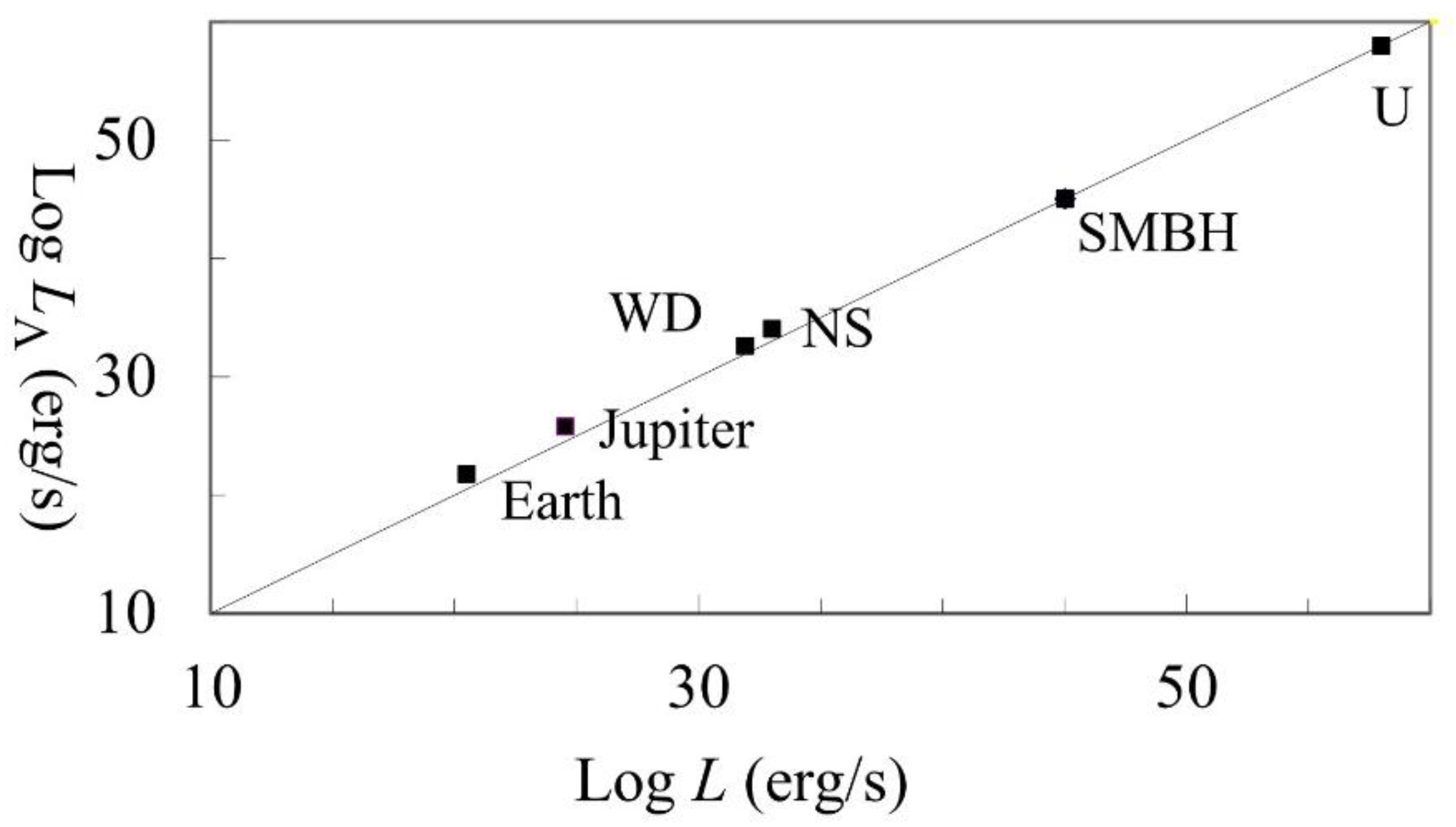
energy released through Equation (5) could account for the excess energy
releases seen in planets, white dwarfs, neutron stars and supermassive black
holes (SMBHs) (Figure 3) [33,34]. In geophysics it also forms the basis for
a different model of plate tectonics, in which the release of core energy
drives a slow expansion of the mantle [35].
Since the Λ luminosity of SMBHs would be mostly internally directed and thus
not observable externally, the observed luminosity may arise from that portion of the mass residing outside the Schwarzschild radius [34] .
The Hubble blueshift would give rise to repulsive Λ forces
between masses. For local systems, where the separation r is much less
than RU, these forces would be negligible in comparison to
the gravitational force. Supposing that the radiation released with the Λ luminosity is transported along the graviton filaments connecting
masses, the force arising in two masses separated by a distance r would
be
The factor c appears in the
denominator since a quantum of radiation with energy E has momentum E/c.
The gravitational and Λ forces come into balance, however, when r ≈ RS =
RU = c/H0, the radius of the baryon shell. As
a spherical shell of plasma, the internal gravitational potential energy of the
EU is
Since H0 = c/RU,
the Λ luminosity from Equation (5) is then
From the black hole mass-radius
relationship we have RS = RU = 2GM/c2.
Substituting for RU in Equation (8), we have
Since a photon with energy E has
momentum E/c, the sum of the forces associated with this power is
By comparison, the sum of all the
inwardly acting Newtonian forces on the particles of the shell is
Once again making the substitution
for RU, the magnitude in Equation (11) becomes equal to that
of Equation (10). The inward forces of attraction thus precisely balance the
outward forces of repulsion at the shell. It is the Λ
luminosity which thus ensures stability of the plasma shell against
gravitation. Any material entering the shell would tend to remain there
indefinitely. In Section 7 it is suggested that similar values for total power and total force
occur in all objects of the black hole class.
The power c5/4G
and force c4/4G have long attracted interest as a
possible maximum power and maximum force in the universe, possibly even
reflected in the field equations of general relativity [20,45–48] . The essentially
Newtonian model for gravity and Λ presented here may thus nonetheless connect
with general relativity through the EU Λ luminosity.
The so-called ‘Dyson luminosity’ would be just the Λ
luminosity of the observable universe.
4.1. Cosmic Microwave Background
We next consider the nature and
origin of the CMB and its role in stabilizing the plasma shell. As the EU is a
black hole, the radiation emitted from the shell would be entirely directed
inwards. Under equilibrium conditions the redirected bolometric luminosity
must be equal to the rate at which radiation returns to the shell as
blueshifted CMB photons. The effective shell temperature in this case can then
be estimated as
where σ is the Stefan-Boltzmann constant = 5.67 ×
10−5 erg cm−2 s−1 K−4. With LΛ = c 5 /4 G from Equation (5) and R U = c / H 0 , we find T shell = 29 K.
Near the shell the CMB would thus
have T CMB = 29 K and a corresponding energy density u = 5.3 × 10−9 erg cm−3.
By comparison, recent measurements from the Planck Collaboration for the ΛCDM
model give a strikingly similar vacuum energy density ρvac =
5.36 × 10−9 erg cm−3. Despite the different
assumptions used, this is consistent with the CMB energy functioning as the
cosmological constant Λ in the static Einsteinian sense.
Concerning the origin of the proto-CMB in an EU, it
might be supposed that it arose from gravitational energy released by a
collapsing baryon cloud, with this energy subsequently captured as photons
within the Schwarzschild radius (see [49] for
a similar scenario in the ΛCDM model). It is
unclear, however, whether enough energy could have been captured before
enclosure to generate the proto-CMB in this way.
It is suggested instead that the proto-CMB arose
through the action of the EU Λ luminosity. With its thin-shell structure, the
total gravitational potential energy of the EU is given by Equation (7). The
density of this gravitational energy would then be ug
= −U/V = GM2/(4/3πRU4).
From the black hole mass-radius relationship RS = 2GM/c2
and with RS = RU we then obtain a
gravitational energy density in the EU of
This density, expressed in terms of mass,
corresponds to half the cosmic critical density of the ΛCDM model, ρc
= 3H02/8πG. For H0 = 67
km s−1 Mpc−1 = 2.2 ×
10−18 s−1 gm−1, we find ug =
3.9 × 10−9 erg
cm−3.
We next apply the Λ luminosity to this gravitational
energy. From Equation (5) electromagnetic radiation would be produced
inside the EU per unit volume at the rate ug × H0.
Over one EU cycle period of Ht the quantity of
radiation generated per unit volume would then be ug ×
H0 × H0−1 = ug.
Assuming that this radiation is ultimately converted to CMB radiation with
density u, we would then have u = ug = 3.9 × 10−9 erg
cm−3. This would match the density of a uniform CMB throughout the
proto-EU with TCMB = 27 K. If TCMBvalues in the EU range from ~ 0 at the centre to ~ 29 at the shell, as
discussed below, then this value for u would not be unreasonable. Its
similarity to the value for Λ in the ΛCDM model is again suggestive of a link
between the CMB and Λ. After many cycles of duration H t
the Λ luminosity would eventually chiefly operate by
reenergizing CMB photons, thereby generating Λ.
As a further check on our general
approach, the rate of energy loss by spacetime via the Λ luminosity in the EU should equal the rate at which energy is
absorbed by it from CMB photons in the Hubble redshift. For the EU this
equality can be written as uVH0 = c5/4G.
This condition is once again satisfied for u = 3.9 × 10−9
erg cm−3 and for a uniform TCMB
~ 27 K, consistent with the other estimates given above.
While the hypothesis of cosmic
acceleration supported by dark energy is enshrined in the ΛCDM model, a number
of outstanding difficulties remain with it. For example, its energy density is
far below the amount predicted to exist from quantum field theory. There is
also a problem of timing, since the ratio ΩΛ/Ω, while adequate to
explain the supposed acceleration at this particular epoch, would be ever
changing in an expanding universe. Even within the ΛCDM model the requirement
for dark energy to account for cosmic acceleration can be removed if
gravitational time dilation were assumed to proceed in parallel with spacetime
expansion
[50]
.
As shown here, however, there is no need for dark energy at all if
the universe is not expanding and reenergized
CMB photons
play the role of cosmological constant.
4.2. Evolutionary Processes
Due to the mass-radius relationship of black holes,
a proto-EU of fixed mass could not have increased in size through cosmological
expansion while at the same time remaining a thin-shell black hole. Just as in
ordinary black holes, however, it could have grown by accretion, capturing dust
and gas at the rim until reaching its current size. Inside the proto-EU
smaller black holes could at all times also have formed and likewise have grown
through accretion. The oldest and largest of these would presumably be at
the very centre of the EU, perhaps near our position, while the youngest ones
would presumably be out at the rim. Some evidence already exists for such a
pattern of black hole growth over time [25].
In this case observations of star and galaxy formation out at the Hubble radius
could match predictions of the ΛCDM model, with these new galaxies and stars
having a ‘younger’ look. The general pattern would be one of successive
waves of black hole-like structures emanating from the centre of the observable
universe, engulfing extant structures encountered. Voids would arise with the
counterbalancing of the Λ luminosity and gravity, in a manner perhaps akin to
the forces operating in soap bubbles.
5. CMB Cycle for Gravity and Λ
In the EU model gravity arises from absorption of
photon energy by spacetime, while Λ results from the reverse process of release
of photon energy from spacetime. We now link these two processes more formally
to CMB photons in a cosmic cycle. In this context it is noteworthy that Carnot
cycles for the CMB have previously been discussed within the ΛCDM model
framework [51–53].
In Figure 1
the EU is shown as having concentric zones of space each having a uniform CMB
temperature. Let us take the outermost zone near the shell to have TCMB
~ 29 K and thus u ~ 5.3 × 10−9 erg cm−3.
This is 104 times that of the zone nearest our position, where TCMB
= 2.73 K and u = 4.2 × 10−13 erg cm−3. As the
CMB photons move inwards from the shell they lose energy and momentum to
spacetime filaments, leading to gravitational work being done. Gravitational
work here also refers unconventionally to masses being pushed together rather
than exclusively to them being forced apart. During this cooling phase the CMB
photon number and energy density in these inwardly moving waves diminish.
When the CMB photons reach the innermost points
along their trajectories, they have completed their gravitational work. The
photons then continue along on routes which ultimately take them back towards
the shell, passing through regions of higher spacetime density. Having already
been maximally ‘cooled’, these photons can now only gain energy back from
spacetime. As discussed above, the rate of energy gain here on the cosmic
level yields the Λ luminosity output, c5/4G. With the
release of energy spacetime curvature is relaxed and masses are pushed apart.
The validity of the temperature-distance
relationship for the CMB is only well established for redshifts less than z ~
3. The present model thus requires verification out to the Hubble distance RU.
Recent observations from the JSWT have up to this point not found galaxies with
redshifts larger than z ~ 17 [54]. If
these were the galaxies closest to the EU baryon shell, then applying the
relationship from Equation (1) would yield TCMB
~ 50 K near the shell. As discussed above, however, other considerations
favour a cooler shell with Tshell ~ 29 K.
5.1. Conservation of Energy and Entropy
The EU model has major implications regarding
energy and entropy conservation in the observable universe. Energy would not
be endlessly dissipated in the EU, as it is in the ΛCDM model. At each point
in space the energy density of CMB radiation u would be equal to that of
the photonic spacetime and thus also to the gravitational energy density there,
i.e., u = us ≡ ug. These
equalities would also hold for the EU as a whole. Energy would be conserved
under the Hubble redshift and gravitation, since the lost photon energy is
converted to spacetime energy, i.e., du/dt = − dus/dt.
With the action of the Λ luminosity spacetime energy reenergizes CMB photons,
such that on the cosmic scale the two pools of energy are always equal.
It is generally supposed, as originally by Kelvin,
that a gradual conversion of all the universe’s mechanical energy to thermal
energy would steadily increase the universe’s entropy, ultimately culminating
in a ‘heat death’ of the universe. If the universe’s temperature were to
become the same everywhere, there would be no temperature difference that could
be exploited to perform useful work. That concept is clearly negated in the EU
model. While kinetic and electromagnetic energy are steadily lost to photonic
spacetime, the lost energy goes into gravitation and thence to processes such
as star formation, which inject new photon energy into space. Nor would matter
fall into one heap as a singularity, since the energy stored in spacetime is
returned to CMB photons, in the process restoring Λ.
Unlike a Carnot cycle, there would be no net work
done and no increase in system entropy. The system, if it were acting in
complete isolation, would instead operate endlessly. The universe in this case
would more aptly be viewed as a perpetuum mobile, with all its energy
forms being interconvertible at rates proportional to H0.
This consideration potentially has significant philosophical and even political
ramifications, as a society no longer believing that the universe is doomed may
be more motivated to invest time and energy in securing long-term survival of
humans and Earth life [55].
5.2. CMB Tests of the Model
Measuring TCMB at different points in space potentially affords a method of testing
between the EU and ΛCDM models. Such measurements may not be feasible in the
regions that would be closest to the shell but could well be in the
central regions closer to us. If the Milky Way is not at the very centre of
the EU, for example, TCMB might drop further than 2.7 K,
conceivably reaching 0 K at the centre. In this connection, other asymmetries
in the CMB and in galaxy/quasar counts already lend support for such an offset
and to the notion that the cosmological principle may no longer be valid [56]. At the same time, searching for nearby anisotropies
in T CMB could be problematic. A CMB with TCMB
= 1 K, for example, would have an energy density only 2% that of the 2.7 K
CMB. Its peak wavelength could thus be obscured by other radiation known to
exist in that range.
A further possibility is that TCMB
cools to a minimal but non-zero temperature in the central region incorporating
our position. This could arise, for example, through the Λ luminosity that is
specific to galaxies and galaxy filaments, which we have not considered here.
Possessing only 5% of the EU mass, the Λ luminosity of this component from
Equation (5) would be lower than the EU total by a factor ~ 2.5 × 10−3.
Yet this small luminosity could still be enough to generate a temperature of a
few degrees K at the centre. This energy output could have a role in
preventing bulk aggregation of galactic matter, analogous to the role of the
CMB in generating Λ.
Further tests of the EU model would involve
reinterpretation of data from Planck and other CMB studies to search for
signatures of a cold plasma shell. Just as this data had previously been used
to characterize the dimensions of the primordial mass configuration in the ΛCDM model, it might likewise allow structural details of the
EU shell to be revealed, such as its thickness and whether or not it has a dual
or composite structure. The observed baryon structure inferred from CMB
observations already demonstrates that the shell would have to be formed of gas
and dust.
In an EU the many problems
connected to inflation in the ΛCDM model are notably avoided, as the cool glow
of a spherical baryonic shell alone suffices to account for the extreme
smoothness of the CMB. The concentration of the universe’s mass in the shell
also eliminates the need for dark matter to explain the CMB data.
6. Gravity from CMB Photons
The model of optical gravity is based on the
treatment of relativistic light deflection as a quasi-refraction of light in an
optical medium with a varying density gradient [57–64].
This optical analogy has been used in numerous studies of gravitational lensing
and simulation of black holes [65–67] and in
gravity models featuring spacetime as a material medium [68–71]. Within this context the possibility that
gravity arises from absorption of CMB photon energy in a photonic spacetime was
considered by the author [28]. The local CMB
of 2.7 K was found, however, to have insufficient energy to drive gravity and
in a later proposal gravity was powered instead by photons released in the Λ
luminosity [29].
The two approaches can be unified, however, with
the provision that the Λ luminosity reenergizes redshifted CMB photons and the
recognition that the hotter CMB in remote regions closer to the shell has
enough energy to drive gravity. In this case energy is essentially transferred
from inwardly moving, hotter CMB photons to cooler regions of spacetime due to
the Hubble redshift. That same energy is later returned to outwardly moving,
cooler CMB photons with the Hubble blueshift and Λ. Where the graviton
filaments around masses are evenly balanced no force from absorption of photon
energy occurs. Gravity only arises when the graviton filaments about masses
are unbalanced.
This can easily be shown as follows. With the
Hubble redshift photon energy and momentum are lost to filaments at the rates:
The linear absorption coefficient of light with the
Hubble redshift in TL models is given by α = 1/RU = H0/c
[29]. From this the mass absorption
coefficient h is obtained as
with units of cm2 gm−1. For H0= 67 km s−1 Mpc−1 = 2.2 × 10−18 s−1 gm−1 and ρ = ρc ≡
3H02/8πG = 8.7 × 10−30 gm cm−3, we have h = 8.5 cm2
gm−1. This large value reflects that absorption occurs mainly in
the extended filaments of spacetime connecting each particle to other masses
rather than in the particle centres. It is also consistent with gravity being
driven by CMB photons in the remotest and hottest parts of the EU, rather than
the weak local CMB [29]. The remote CMB
energy is vastly greater due to the higher CMB energy densities and volumes of
space.
The CMB radiation pressure conventionally is p =
u/3, which includes terms for the incident and emitted radiation. Since
the CMB photon energy absorbed by graviton filaments is only reradiated later,
where it generates Λ, the effective pressure on graviton filaments is just one
half this, i.e., p = u/6. Due to this remote CMB
pressure, a uniform force would be exerted isotropically on all bodies.
The force on an isolated mass M1 from any direction
would be
Since the impulses from CMB photons are symmetrical
from all parts of the sky, they cancel out and for M1 no
velocity boosts would occur.
Let us now introduce a second mass M2
at a distance d from M1, where d << RU.
Ordinarily, in a Le Sage-type mechanism, the inverse square relationship with
distance results from mutual flux shielding by the subatomic components of
matter. In optical gravity the shielding arises instead from mutual shielding
of the spacetime envelopes about masses, which can likewise be shown to have an
inverse square relationship. We then find that the solid angle that M2
effectively subtends at M1 is hM2/d2.
The force generated on M1 due to this missing momentum flux
is then
Accordance with Newton’s law is gained if we write
With the value obtained above for h, a
suitable value for G is obtained if u = 5.5 × 10−9 erg
cm−3. This corresponds to a uniform CMB with TCMB
~ 29 K, which is once again consistent with other values given above for the
outermost regions of the EU.
7. Black Holes
As emphasized at the
outset, the semi-Newtonian method that we have used in the present analysis on
the cosmic scale is not appropriate for the ultra-dense objects that have been
termed black holes or gravastars. These objects typically require full
relativistic treatment in general relativity. Relativistic models of black
holes and gravastars have become so densely convoluted, however, that we
nonetheless briefly consider whether the present approach can still yield any
useful clues as to the structures and processes of these objects.
We first consider non-rotating black holes.
Immediately it is seen that the Hubble constant is no longer a true constant in
these objects. Drawing from the basic relationship in the EU that H0
= c/RU, we would have for black holes, by
analogy,
The Hubble constant in each black hole would thus
be inversely proportional to RS. Since bh = Mbh/(4/3πRS3)and RS = 2GMbh/c2,
we would then have
and thus bh 1/RS2. Inserting
Equation (19) in Equation (20), we find that the expression for the black hole
density then becomes precisely analogous to that of the cosmic critical
density, i.e.,
Would G have a
constant value in all non-rotating black holes? Using the gravity model from
Section (6) we have from Equation (18) that G
uh2. From Section (4) we also
have a general equality u = ug,
with the expression for ug given in Equation (13). Assuming
that all non-rotating black holes have a thin-shell structure, we then have u
1/RS2. Since
by analogy from Equation (15) we have h = 1/(ρbhRS)
and from Equation (20) that ρbh 1/RS2, we then have h
RS. From this we find
that the expression for G in Equation (18) is invariant in black holes,
even though Hbh varies significantly.
With these relationships, we can
also follow the same sequence of steps that was used in Section (4) to
determine the cosmic Λ luminosity to find the
respective values for black holes. Remarkably, it is found for each black hole
that LΛ has the same maximal value, c5/4G,
regardless of the black hole mass. Black holes would thus all feature
the ‘maximum luminosity’ or ‘Dyson luminosity’ discussed in Section 4 [20,45–48] . The larger Hubble constant of a black hole would here reflect the
greater rate of photon recycling needed to prevent gravitational collapse into
a singularity.
The eggshell model can
again be roughly applied to estimate the characteristics of the internal
radiation of black holes. The equivalent blackbody radiation
inside a non-rotating, thin-shell SMBH, for example, would have a much higher
energy density than the CMB at any point in the EU, since u 1/RS2. Using the
same sequence of steps as in the EU model for Sagittarius A*,
where RS ≈ 1012 cm,
we would find Tshell ≈ 109 K. Its peak blackbody
wavelength would therefore be ~ 1 pm, in the gamma ray band. This radiation
would ordinarily be confined within the shell, but in certain situations could
conceivably give rise to the GRB-type phenomena that have been observed.
The situation would be quite different in rapidly rotating SMBHs, however, where photographic evidence and theoretical considerations related to the Kerr metric suggest that the spherical shell collapses to a torus.
On a larger scale, supposing that the EU itself resides in a still larger thin-shell black hole, the Hubble constant of the latter would be much smaller than H0 and its internal blackbody radiation much cooler than the CMB. Yet from the above considerations it can be inferred that G would once again remain unchanged.
8. Concluding Remarks
In this paper we have used some key concepts of black holes to construct a model of the observable universe termed the eggshell universe. Almost all the mass in this universe is concentrated in a thin membrane of cold plasma situated near the Hubble radius. This plasma shell anchors a CMB energy cycle linking gravity and Λ. The cycle requires a novel premise concerning spacetime: that it is photonic in nature and thus has the capacity to absorb and release photon energy and exchange it with the CMB. This permits the CMB to maintain its characteristic blackbody spectrum at all times, locations and temperatures. While patterned on thin-shell black hole and gravastar models, the EU model can potentially be used to reverse engineer these dense objects and assist in finding relativistic solutions for them.
A general consistency in our approach can be seen with two estimates for a shell temperature and outermost TCMB of ~ 29 K, one based on the Λ luminosity and one from the density of gravitational energy. There is also a requirement for an average energy of a 29 K CMB in the EU for gravity, a density which also remarkably matches the required value for Λ in the ΛCDM model. On the other hand, strict adherence to the observed temperature-redshift relationship in the CMB would seem to require a higher TCMB ~ 50 K near the shell.
While the eggshell black hole universe accounts for numerous observations that are problematic in the ΛCDM model, the central premises of the model still require additional theoretical and experimental support. It needs to be verified that spacetime indeed has photonic characteristics that enable it to exchange energy with photons, in such a way that the CMB retains its blackbody spectrum at all times and locations. The pathway to this verification is unclear.
The situation is more promising, however, with respect to the Λ luminosity. In this paper we have now linked the Λ luminosity to gravity, Λ and the basic structure of the cosmos. There is thus a pressing need to study and confirm the Λ luminosity in objects and mass systems on all scales. In this effort promising candidates for study might include such objects as brown dwarfs, planetary moons and icy asteroids – objects which might in some cases be free of other sources of internal heating. Theoretical support for a fundamental gravitational decay process might come from further geophysical evidence of expansion-related tectonic processes [35] or astrophysical evidence of a general secular increase in the orbits of moons and planets, as highlighted in some recent studies [72,73].
In addition to confirming the Λ luminosity, future work will focus on the analogous deceleration of particles in the EU frame that would arise from the Hubble redshift mechanism and linking this to MOND and to quantum physics generally. Photonic spacetime would after all be particularly well-suited to incorporate quantum entanglement, as all particles within the observable universe would be physically interconnected by filaments of photon-like gravitons.
Author Contributions
All contributions are by the author, ME.
Funding
There are no funding sources to report for this article.
Data Availability Statement
There are no data sets to be made available for this article.
Acknowledgments
I wish to thank Javier Viaña, Katherine O'Grady and Louis Marmet for valuable discussions.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Pathria RK. The universe as a black hole. Nature (1972) 240:298-299. [CrossRef]
- Zhang TX, Frederick C. Acceleration of black hole universe. Astrophys Space Sci (2014) 349:567–573. [CrossRef]
- Popławski N. Universe in a black hole in Einstein-Cartan gravity. Astrophys J (2016) 832:96. [CrossRef]
- Zhang TX. (2018) The principles and laws of black hole universe. J Mod Phys (2018) 9:1838-1865. [CrossRef]
- Lineweaver CH, Patel VM. All objects and some questions, Am J Phys (2023) 91:819-825. [CrossRef]
- Gaztañaga E. How the Big Bang ends up inside a black hole. Universe (2022) 8:257. [CrossRef]
- Stuckey WM. The observable universe inside a black hole. Am J Phys (1994) 62:788–795. [CrossRef]
- Seahra SS, Wesson PS. The universe as a five-dimensional black hole. Gen Relativ Gravit (2005) 37:1339–1347 (2005). [CrossRef]
- Knutsen H. The idea of the universe as a black hole revisited. Gravit Cosmol (2009) 15:273–277. [CrossRef]
- Khakshournia S. A note on Pathria’s model of the universe as a black hole. Gravit Cosmol (2010) 16:178–180. [CrossRef]
- Doran R, Lobo FSN, Crawford P. Interior of a Schwarzschild black hole revisited. Found Phys (2008) 38:160–187. [CrossRef]
- González-Díaz PF. The space-time metric inside a black hole. Lett Nuovo Cimento (1981) (1981) 32:161. [CrossRef]
- Poisson E, Israel W. Internal structure of black holes. Phys Rev D (1986) 41:1796-1809. [CrossRef]
- Bouhmadi-López M, Chen CY, Chew XY et al. Regular black hole interior spacetime supported by three-form field. Eur Phys J C (2021) 81:278. [CrossRef]
- Brahma S, Yeom D. Can a false vacuum bubble remove the singularity inside a black hole?. Eur Phys J C (2020) 80:713. [CrossRef]
- Habib Mazharimousavi S, Halilsoy M. Interpolation of Schwarzschild and de Sitter spacetimes by a cosmological fluid. Phys Scr (2021) 96:065208. [CrossRef]
- Roupas Z. Detectable universes inside regular black holes. Eur Phys J C (2022) 82:255. [CrossRef]
- Eiroa EF, Figueroa Aguirre G. Thin shells surrounding black holes in F(R) gravity. Eur Phys J C (2019) 79:171. [CrossRef]
- Luís Rosa J, Piçarra P. Existence and stability of relativistic fluid spheres supported by thin shells. Phys Rev D (2020) 102:064009. [CrossRef]
- Viaña J, O'Grady KL. If black holes are superficial. (2021). ⟨hal-03469571⟩.
- Danielsson UH, Giri S. Observational signatures from horizonless black shells imitating rotating black holes. J High Energ Phys (2018) 70. [CrossRef]
- Chapline G. Dark energy stars. (2005) https://arxiv.org/abs/astro-ph/0503200.
- Mazur PO, Mottola E. Gravitational condensate stars: An alternative to black holes. Universe (2023) 9:88. [CrossRef]
- Chirenti C, Rezzolla L. How to tell a gravastar from a black hole. Class Quantum Grav (2007) 24:4191. [CrossRef]
- Farrah D, Petty S, Croker KS, et al. A preferential growth channel for supermassive black holes in elliptical galaxies at z ≲ 2. Astrophys J (2023) 943:133.
- López-Corredoira M. Tests and problems of the standard model in cosmology. Found Phys (2017) 47:711–768. [CrossRef]
- López-Corredoira M, Marmet L. Alternative ideas in cosmology, Int J Mod Phys D (2022) 31:2230014. [CrossRef]
- Edwards MR. Gravity from refraction of CMB photons using the optical-mechanical analogy in general relativity. Astrophys Space Sci (2014) 351:401-406. [CrossRef]
- Edwards MR. Optical gravity in a graviton spacetime. Optik (2022) 260:169059. [CrossRef]
- Grahn P, Annila A, Kolehmainen E. On the carrier of inertia. AIP Advances (2018) 8:035028. [CrossRef]
- Annila A, Wikström M. Dark matter and dark energy denote the gravitation of the expanding universe. Front Phys (2022) 10:995977. [CrossRef]
- Annila A. What is everything made of? In Back to reality, a revision of the scientific worldview; Privus Press: New York, 2022; pp. 65–132.
- Edwards MR. Graviton decay without decreasing G: a possible cause of planetary heating, expansion and evolution. Ann Geophys (2006) 49:501-509.
- Edwards MR. Does the Hubble redshift flip photons and gravitons? Astrophys Space Sci (2012) 339:13-17. [CrossRef]
- Edwards MR. Deep mantle plumes and an increasing Earth radius. Geod Geodyn (2019) 10:173-17. [CrossRef]
- Ćirković MM, Perović S. Alternative explanations of the cosmic microwave background: A historical and an epistemological perspective. Stud Hist Philos Sci B: Stud Hist Philos Mod Phys (2018) 62: 1–18. [CrossRef]
- Fixsen DJ. The temperature of the cosmic microwave background. Astrophys J (2009) 707:916. [CrossRef]
- Noterdaeme P, Petitjean P, Srianand R, Ledoux C, López S. The evolution of the cosmic microwave background temperature: Measurements of TCMB at high redshift from carbon monoxide excitation. Astron Astrophys (2011) 526:L7. [CrossRef]
- Klimenko VV, Ivanchik AV. The measurements of the CMB temperature in diffuse interstellar medium of the Milky-Way and high redshift galaxies based on excitation of CI fine-structure and H2 rotational levels. J Phys: Conf Ser (2020) 1697:012013. [CrossRef]
- Li Y, Hincks AD, Amodeo S et al. Constraining cosmic microwave background temperature evolution with Sunyaev–Zel'Dovich galaxy clusters from the Atacama Cosmology Telescope. Astrophys J (2021) 922:136. [CrossRef]
- Riechers DA, Weiss A, Walter F, et al. Microwave background temperature at a redshift of 6.34 from H2O absorption. Nature (2022) 602:58–62. [CrossRef]
- Chluba J. Tests of the CMB temperature–redshift relation, CMB spectral distortions and why adiabatic photon production is hard. Month Not Royal Astron Soc (2014) 443:1881–1888. [CrossRef]
- Marques Muniz AL, Wu FO, Jung PS, Khajavikhan M, et al. Observation of photon-photon thermodynamic processes under negative optical temperature conditions. Science (2023) 379:1019-1023. [CrossRef]
- Leibundgut B, Schommer R, Phillips M, et al. Time dilation in the light curve of the distant type Ia supernova SN 1995K. Astrophys J (1996) 466:L21. [CrossRef]
- Schiller C. General relativity and cosmology derived from principle of maximum power or force. Int J Theor Phys (2005) 44:1629–1647 (2005). [CrossRef]
- Kenath A, Schiller C, Sivaram C. From maximum force to the field equations of general relativity and implications. Int J Mod Phys D (2022) 31:2242019. [CrossRef]
- Schiller C. From maximum force via the hoop conjecture to inverse square gravity. Gravit Cosmol (2022) 28:305–307. [CrossRef]
- Jowsey A, Visser M. Reconsidering maximum luminosity. Int J Mod Phys D (2021) 30:2142026. [CrossRef]
- Dinculescu A. On the energy density of the cosmic microwave background. Astrophys Space Sci (2007) 310:237–239. [CrossRef]
- Vavryčuk V. Cosmological redshift and cosmic time dilation in the FLRW metric. Front Phys (2022) 10:826188. [CrossRef]
- Lee MH. Carnot cycle for photon gas? Am J Phys (2001) 69:874–878. [CrossRef]
- Gonzalez-Ayala J, Perez-Oregon J, Cordero R, Angulo-Brown F. A possible cosmological application of some thermodynamic properties of the black body radiation in n-dimensional Euclidean spaces. Entropy (2015) 17:4563-4581.
- Pilot C. Modeling cosmic expansion, and possible inflation, as a thermodynamic heat engine. Zeit Naturforsch A (2019) 74:153-162. [CrossRef]
- Melia F. The cosmic timeline implied by the JWST high-redshift galaxies. Month Not Roy Astron Soc (2023) 521:L85–L89. [CrossRef]
- Edwards MR. Blueprint for forever: Securing human far futures with ectogenesis. Futures (2023) 146:103085. [CrossRef]
- Secrest NJ, von Hausegger S, Rameez M, Mohayaee R, Sarkar S. A challenge to the standard cosmological model. Astrophys J Lett (2022) 937:L31. [CrossRef]
- de Felice F. On the gravitational field acting as an optical medium. Gen Relativ Gravit (1971) 2:347-357. [CrossRef]
- Evans J, Rosenquist M. ‘F = ma’ optics. Am J Phys (1986) 54:876-883.
- Nandi KK, Islam A. On the optical–mechanical analogy in general relativity. Am J Phys (1995) 63:251-256. [CrossRef]
- Evans J, Nandi KK, Islam I. The optical–mechanical analogy in general relativity: New methods for the paths of light and of the planets. Am J Phys (1996) 64:1404-1415. [CrossRef]
- Alsing PM. The optical-mechanical analogy for stationary metrics in general relativity. Amer J Phys (1998) 66:779. [CrossRef]
- Puthoff HE, Davis EW, Maccone C. Levi–Civita effect in the polarizable vacuum (PV) representation of general relativity. Gen Relativ Gravit (2005) 37:483–489. [CrossRef]
- Feng G, Huang J. A geometric optics method for calculating light propagation in gravitational fields. Optik (2019) 194:163082. [CrossRef]
- Feng G, Huang J. An optical perspective on the theory of relativity - II: Gravitational deflection of light and Shapiro time delay. Optik (2020) 224:165685. [CrossRef]
- Ye X, Lin Q. Gravitational lensing analysed by the graded refractive index of a vacuum. J Opt A: Pure Appl Opt (2008) 10:075001. [CrossRef]
- Sheng C, Liu H, Wang Y, et al. Trapping light by mimicking gravitational lensing. Nature Photon (2013) 7:902–906. [CrossRef]
- Gupta RC, Pradhan A, Gupta S, et al. Refraction-based alternative explanation for: bending of light near a star, gravitational red/blueshift and black-hole. arXiv:1004.1467v2 [physics.gen-ph] (2015).
- Wilson HA. An electromagnetic theory of gravitation. Phys Rev (1921) 17:54-59. [CrossRef]
- Dicke RH. Gravitation without a principle of equivalence. Rev Mod Phys (1957) 29:363–376. [CrossRef]
- Yi YG. Optical approach to gravitational redshift. Astrophys Space Sci (2011) 336:347-355. [CrossRef]
- Sarazin X, Couchot F, Djannati-Ataï A, et al. Can the apparent expansion of the universe be attributed to an increasing vacuum refractive index? Eur Phys J C (2018) 78:444. [CrossRef]
- Křížek M, Gueorguiev VG, Maeder A. An alternative explanation of the orbital expansion of Titan and other bodies in the Solar System. Gravit Cosmol (2022) 28: 122–132. [CrossRef]
- Vavryčuk V. Gravitational orbits in the expanding Universe revisited. Front Astron Space Sci (2023) 10:1071743. [CrossRef]
Figure 2.
The paired-photon vacuum. Vacuum spectral density, u, sums up from numerous rays of photons (blue-red waves) with a spectrum of energies, εi, about the average energy, kBT. The paired photons cannot be seen as light but are sensed as inertia and gravitation through their coupling to matter. In contrast, the odd quanta (blue or red), distributed in-phase or antiphase among the paired rays, are seen as light and manifest as electromagnetism. Inset: The cumulative spectral density vs. energy (dashed line) (from Annila and Wikström [31]).
Figure 2.
The paired-photon vacuum. Vacuum spectral density, u, sums up from numerous rays of photons (blue-red waves) with a spectrum of energies, εi, about the average energy, kBT. The paired photons cannot be seen as light but are sensed as inertia and gravitation through their coupling to matter. In contrast, the odd quanta (blue or red), distributed in-phase or antiphase among the paired rays, are seen as light and manifest as electromagnetism. Inset: The cumulative spectral density vs. energy (dashed line) (from Annila and Wikström [31]).
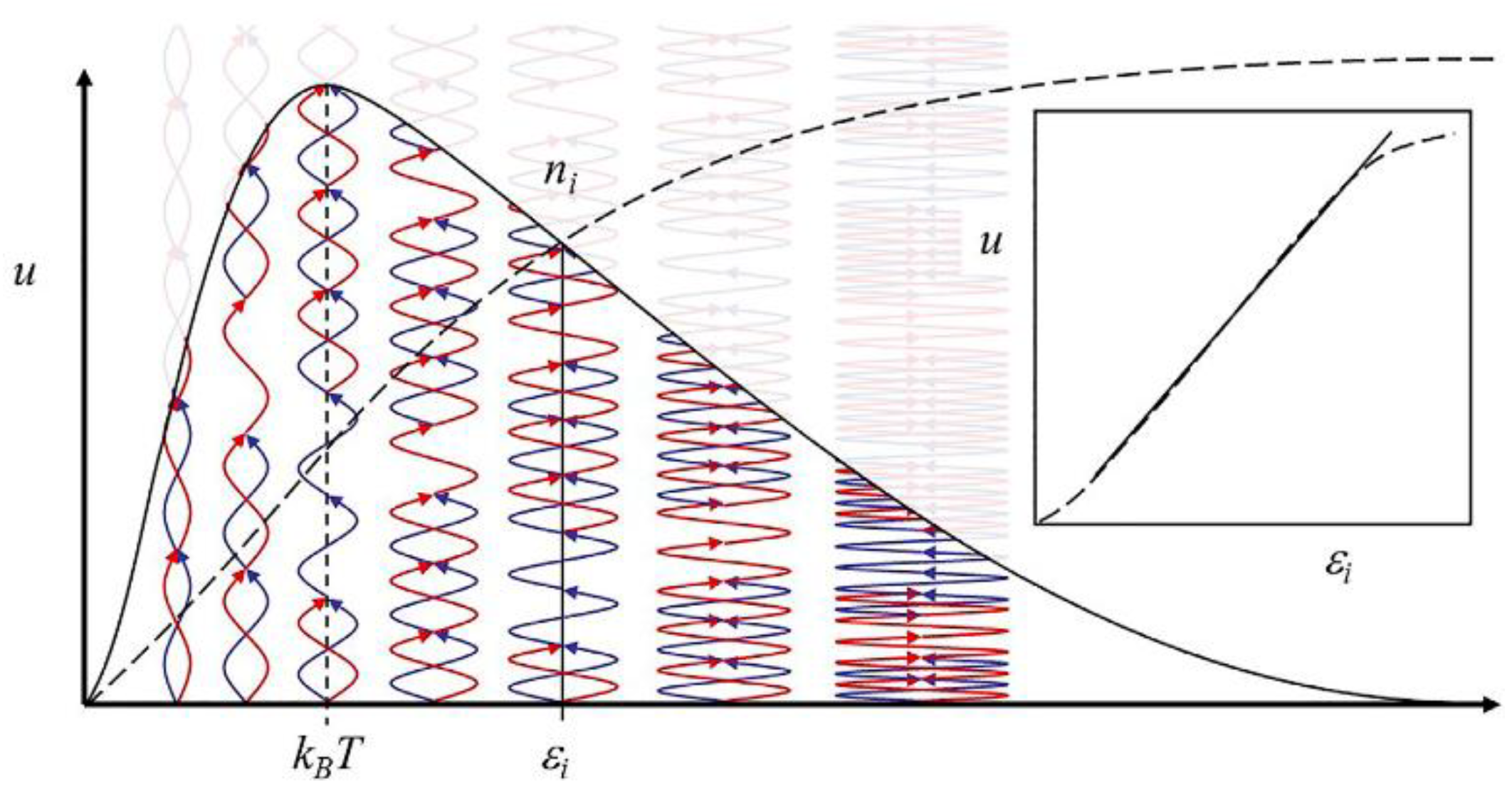
Figure 3.
Λ luminosity at many scales. On the horizontal axis are plotted the bolometric luminosities of representative white dwarfs (WD); neutron stars (NS); supermassive black holes (SMBH); the observable universe (U); and the excess heat emissions of Earth and Jupiter. Their respective Λ luminosities are on the vertical axis. The solid line is the 1:1 correspondence. The range of luminosities covers 35 orders of magnitude. Adapted from [34].
Figure 3.
Λ luminosity at many scales. On the horizontal axis are plotted the bolometric luminosities of representative white dwarfs (WD); neutron stars (NS); supermassive black holes (SMBH); the observable universe (U); and the excess heat emissions of Earth and Jupiter. Their respective Λ luminosities are on the vertical axis. The solid line is the 1:1 correspondence. The range of luminosities covers 35 orders of magnitude. Adapted from [34].
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





