1. Introduction

2. Materials and Methods

2.1. Existing Reference Systems

The TEE probe mechanism technically can be described as serially connected rigid links driven by a cable passed through the links. The cable goes around a pulley and is driven manually with rotation knobs known as “big” and “small” wheels. Figure 1 shows actual probes used in hospital for adult patients. The probes are of different types, namely T6210, X7-2t, and IPX-1 from Philips^®. All probes possess the same mechanical dimensions and exhibit similar bending when the wheels were rotated. This rotation causes the straight part at the tip to be located in desired poses. The fact that only the distal section of the probe is inserted in the patient body, as in Figure 1 (b), encouraging us to think of a soft robot of as a replacement. The proximal part of the tube, from the active part to the handle, is mechanically passive. The big wheel provides the anteflexion-retroflection, and the small wheel provides lateral bending.

Figure 1. The conventional system: (a) Philips^® TEE probes used for adult patients, (b) Example of application in surgery, (c) The distal section, and (d) Linkage coordinate systems.

Figure 1. The conventional system: (a) Philips^® TEE probes used for adult patients, (b) Example of application in surgery, (c) The distal section, and (d) Linkage coordinate systems.

The probe kinematic model can be constructed of two parts, where the first part maps the inputs which is the rotation of the wheels of the TEE probe [11] to the probe states (bending and flexing angles). The same pattern is used for the soft probe where the inputs (contraction of the McKibben actuators) are mapped to the segmental bending and rotations. The second part of the kinematic model relates the states to the tip position. The state-output relations can be used for workspace evaluation for the different probes. For the TEE probe, a model is considered to consist of some serially connected links as in Figure 1 (d), where X₈Y₈Z₈ is located at the tip and Z₈ is normal to the sensor. Each link rotates around the Z-axis of the previous link in ante flex-retroflex, and around the relevant Y-axis in the lateral bending. Mathematically, each coordinate i is obtained by rotating the previous system of angle ${\theta }_{zi}$ around Z_i-1, followed by a translation l_i (=length of the link) along the new coordinate, followed by a rotation ${\theta }_{yi}$ around the new Y-axis002E

$$T_i=Rotz({\theta }_{zi})Trans(l_i,0,0)Roty({\theta }_{yi})$$

(1)

Ignoring friction and extensibility of the cables, it can be supposed that the links have similar conditions, and so the links show equal rotations, i.e., ${\theta }_{zi}={\theta }_z$, ${\theta }_{yi}={\theta }_y$. A homogeneous transformation matrix, H, relates the tip position in frame 8 to its position vector in frame 0 as

$$H=T_1{T}_2{T}_3\dots T_8\begin{array}{ccc}& ,& \end{array}{\stackrel{\rightharpoonup }{P}}_{Tip}^0=H{\stackrel{\rightharpoonup }{P}}_{Tip}^8$$

(2)

The reachable work space is defined as the set of tip point positions ${\stackrel{\rightharpoonup }{P}}_{Tip}^0$ that can be reached by some choice of state vector, ${\stackrel{\rightharpoonup }{q}}_R$, within the set of admissible states $Q^{rigid}$

$$W^{rigid}=\left\{\left.{\stackrel{\rightharpoonup }{P}}_{Tip}^0\right|{\stackrel{\rightharpoonup }{q}}_R\in Q^{rigid}\right\}\subset {ℝ}^3$$

(3)

Where the state vector is described by constant curvature rule as ${\stackrel{\rightharpoonup }{q}}_R={\left[{\theta }_z,{\theta }_y\right]}^T$; and Q^rigid can be represented by the range of the angles obtained from measurements as

$$Q^{rigid}=\left\{\stackrel{\rightharpoonup }{q}\left|0<{\theta }_z<{18}^o,0<{\theta }_y<7^o\right.\right\}$$

(4)

Then, using (2) and (4) in (3), a set of reachable points is obtained, denoted as W^rigid. The next steps were to design and fabricate a soft robot, and to propose a method to match the input-outputs kinematics of the soft robot to that of the conventional system as described in the following subsections.

2.2. Biomimetic Concept

From a technical perspective, present endoscopes are bending beams with a rather stiff “body”, and a “neck” with under-actuated rotatory DoFs (Degrees of Freedom) around two orthogonal bending axes each. This principle biologically roughly mirrors a motion segment [20] of a vertebral column (without the rotatory DoF around the longitudinal axis, which leads to torsion of the spine), or a mechanically coupled (not independently movable) series of motion segments. The desirable extreme to optimize the versatility and adaptability of endoscope to changing moving paths is a continuum, which is actuated locally leading to a DoF of theoretically up to infinity. The more obvious biological paragon, which realizes this principle nearly perfectly, is obvious: the elephant’s trunk. Structures like that are in meso and micro scale at present technologically not realizable. Biomimetics in its technical part for present customer demands must find at present technologically realizable solutions, biomimetics is no one way from biology to engineering. One first at present realizable step in the wanted direction for endo devices may the (phylogenetically back-) step from the structure of the vertebral column (which very roughly transferred underlies the present constructions) to that of its historical precursor Chorda dorsalis as a biomimetic paragon, as illustrated in Figure 2.

Figure 2. Left: principle of conventional endoscopes. Bending is realized by a series of rigid bodies (forming “segments”), rotating around defined joint axes. Motion of all segments is coupled by application of the same force via a Bowden drive. Center: principle of bending a vertebrates’ spine. Comparable to the principle used in conventional endoscope, with the exception that rotation in all segments may be different, since forces are provided by intersegmental muscles. In the real animal, the rotation axis is slightly moving during motion, and additional longer muscles allow controlled coupled bending as well. Right: principle of Chorda dorsalis system in basic Chordates. The support structure is a compliant beam (in the natural paragon with changing geometry over length), which due to action of small muscles can be bent locally with different curvatures along the length. For reasons of clarity, motion is shown around one axis in one direction, in technology as in nature actuation in up to 3 rotational DoF in antagonistic manner may provide six overlaid rotational directions.

Figure 2. Left: principle of conventional endoscopes. Bending is realized by a series of rigid bodies (forming “segments”), rotating around defined joint axes. Motion of all segments is coupled by application of the same force via a Bowden drive. Center: principle of bending a vertebrates’ spine. Comparable to the principle used in conventional endoscope, with the exception that rotation in all segments may be different, since forces are provided by intersegmental muscles. In the real animal, the rotation axis is slightly moving during motion, and additional longer muscles allow controlled coupled bending as well. Right: principle of Chorda dorsalis system in basic Chordates. The support structure is a compliant beam (in the natural paragon with changing geometry over length), which due to action of small muscles can be bent locally with different curvatures along the length. For reasons of clarity, motion is shown around one axis in one direction, in technology as in nature actuation in up to 3 rotational DoF in antagonistic manner may provide six overlaid rotational directions.

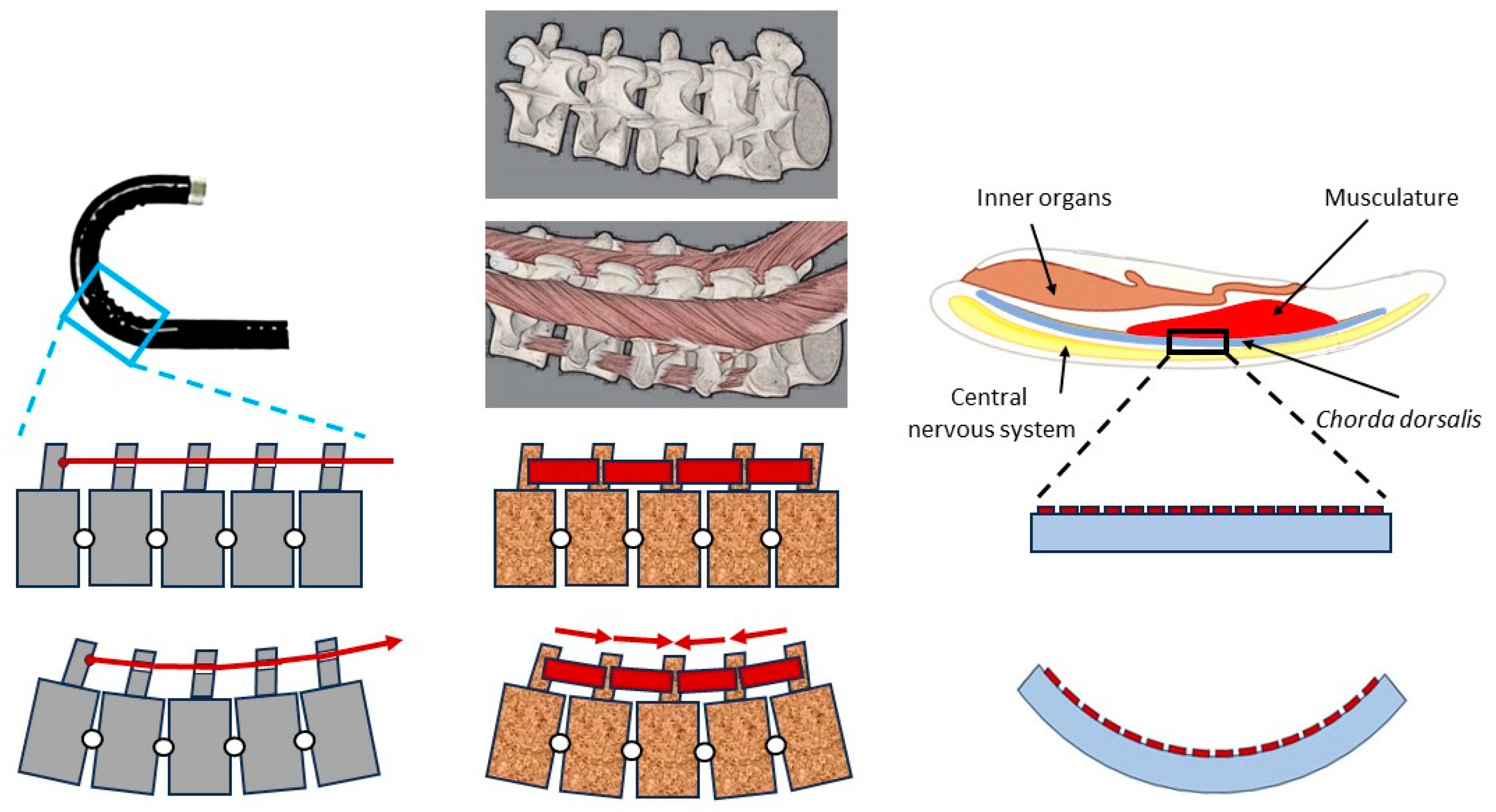
While the spine may be seen as a series of rigid segments, connected by “real” joints (diarthroses), actively moved by muscles bridging the gaps, Chorda dorsalis a continuous bending beam, to which local bending is imprinted by local muscle fibres. These allow the controlled application of bending moments and axial (compressive) forces. Transverse forces in a bending beam are coupled in a fixed manner to the bending moment around the transversal axis, thus they as well may be controlled in a coupled manner as 1 DoF.

The chorda is by no means a faulty construction, it has fulfilled its tasks for half a billion years and still fulfills them in recent animals. Beneath other factors, growing body masses and thus gravitational and inertial forces in combination with the utilization of torsional movements led to the evolution of the spinal column, which we as humans anthropocentrically consider to be the better solution. However, both the chorda and the spine are adapted to their respective tasks, and the chorda, with its lower load-bearing capacity but higher local bending, due to flexibility in combination with a monolithic structure when torsion is not required, corresponds better in its functional description to the requirements of an endoscope than a spine, so it is the more suitable biological paragon.

Derived from that (simplified) model of a chorda, we realized a demonstrator in meso scale with a, due to the lack of a yet not industrialized precise process at present feasible, very limited number of synergistic “muscle pairs” on a continuous flexible beam, which was formed by segments (technically: in modular design), which are rigidly coupled to resemble a monolithic structure.

2.3. Proposed Soft Mechanism

Design, and Prototyping

Dominantly, soft pneumatic actuators contain silicon rubbers as their main material, and generally make use of a sort of asymmetry, either via asymmetric cross-section or strengthening fibers, to yield a directed motion when pressurized air is exerted. A McKibben actuator is a type of pneumatic muscle that is attractive for biomedical applications [21], with advantages of similarity with biological muscles, reliable safety, and good performance. The actuator consists of a hollow cylinder soft tube, and a braided reinforcing net [22]. A method of fabrication of small-size McKibben actuators was proposed in [23]. Using a braider machine, like the machines used for producing braided strings, as described in [24], the actuators are manufactured in long lengths that can be cut to desired size. In this study, we proposed a multi-segment McKibben-based soft probe, schematically shown in Figure 3.

Figure 3. Design of the soft mechanism.

Figure 3. Design of the soft mechanism.

Each segment contains symmetrically to the midline two “muscles” or McKibben actuators of 1.3 mm diameter with equal lengths, a=25 mm. Table 1 represents the dimensions. Each actuator is connected to a pneumatic pressure source and controlled individually. To investigate feasibility of the proposed design, a prototype of the soft robot was fabricated. The main steps for prototyping are illustrated in Figure 4.

Table 1. Dimensions of the soft probe.

Table 1. Dimensions of the soft probe.

Parameter	Description	Amount (mm)
a	Length of actuators	25 ±1
b	Tip center position	27 ±0.1
c	Lateral distance	5±0.5
d	Lateral distance	8 ±0.5
e	Longitudinal distance	2 ±0.5
t	Core width	10 ±0.1

Figure 4. Prototyping the soft robot: (a) Vacuum of mixed material, (b) Molding, (c) Trimming, (d) Preparation of the muscles and pipes, (e) Adhesive curing, (f) The fabricated prototype.

Figure 4. Prototyping the soft robot: (a) Vacuum of mixed material, (b) Molding, (c) Trimming, (d) Preparation of the muscles and pipes, (e) Adhesive curing, (f) The fabricated prototype.

For mechanical modelling purpose, we consider a single segment of the soft robot as in Figure 5. Due to compliance, the resistance force of the soft beam (bending stiffness) is negligible. This means that the external load on the McKibben actuators is zero, and their length depends on the pneumatic pressure. Thus, the quasi-static geometry relations and equations are represented as a function of the actuators’ length.

Figure 5. Schematic representation of segmental bending.

Figure 5. Schematic representation of segmental bending.

First, the material of the core was mixed and processed by a vacuum pump for approximately one hour to reduce bubbles. The material was cast in an aluminum mold. Then, the McKibben actuators were connected to 0.5 mm pipes, and attached to the core. For more robust attachment, the same mixture of the material was used as the adhesive and was cured in an oven. The electronic hardware for control of valves includes an Arduino^® Mega and the interfacing circuits (using TBD62183AFNG) installed on the Arduino^® as in Figure 6.

Figure 6. The microcontroller system.

Figure 6. The microcontroller system.

The pneumatic control system includes 10 miniature 3/2 NC Solenoid valves working with 24V. The actual system is shown in Figure 7.

Figure 7. Final hardware setup.

Figure 7. Final hardware setup.

The valve control system was programmed with MATLAB^® and deployed on Arduino^®. An MPU 6050 as the tilt sensor was added to system at the tip of the robot. It was programmed just to measure angles, though the sensor has more capabilities like acceleration measurement. The McKibben muscles can be pressurized individually.

Modelization

Suppose the actuator with initial length $a_0$ is contracted to $a<a_0$ result in the bending of the soft beam. Let be $\tau =t_1/2+t_2$. Then for angle $\theta =\measuredangle AOH$ we have

$$a=2(R-\tau )\mathrm{Sin}(\theta )$$

(5)

Defining contraction rate, $\lambda =a/a_0$, for the actuator is

$$a=2\lambda \theta R$$

(6)

Combining (5) and (6) we get

$$2\tau \theta \mathrm{Sin}(\theta )+\lambda a_0\theta -a_0\mathrm{Sin}(\theta )=0$$

(7)

The nonlinear equation (7) can be solved for $\theta$. An approximation can be written in series form as follows

$$\frac{2\tau }{5!}{\theta }^6-\frac{a_0}{5!}{\theta }^5-\frac{2\tau }{3!}{\theta }^4+\frac{a_0}{3!}{\theta }^3+2\tau {\theta }^2+(\lambda -a_0){\theta }^{}=0+O({\theta }^7)$$

(8)

The length of the soft probe with three actuators is approximately equal to the TEE active part (and the two distal actuators are integrated for future use such as locomotion). For the three-segment model, the transformation matrix can be obtained by multiplying the transformation matrices of the segments, which in turn can be obtained in various ways. In this work, considering Figure 8, the coordinate system located at the tip is obtained by the following rotations and transformations of the base coordinate system. First, a rotation of ${\theta }_x$ around the current X axis, a transformation along the new X and Y axes to reach the tip point, O₁, and finally, a rotation of ${\theta }_z$ around the Z axis. In case the segment is not actuated, i.e., when the pressure is zero, the transformation matrix is given merely by a transformation along the X axis. The transformation matrix for segment 1 is represented by the double statement as follows.

Figure 8. The coordinates and kinematic representation.

Figure 8. The coordinates and kinematic representation.

$$T_1=\left\{\begin{array}{l}Rotx({\theta }_{x1})Trans(b_1,0,0)*\\ \hspace{1em}\hspace{1em}Trans(r_1.\sin ({\theta }_{z1}),r_1.[1-\cos ({\theta }_{z1})],0)Rotz({\theta }_{z1}),\hspace{1em}\left(\mathrm{actuated}\right)\\ Trans(a_{01},0,0)\hspace{1em}\hspace{1em}\hspace{1em}(\mathrm{not} \mathrm{actuated})\end{array}\right.$$

(9)

Similarly, for segments 2 and 3

$$T_2=\left\{\begin{array}{l}Rotx({\theta }_{x2})Trans(b_2,0,0)*\\ \hspace{1em}\hspace{1em}Trans(r_2.\sin ({\theta }_{z2}),r_2^{}.[1-\cos ({\theta }_{z2})],0)Rotz({\theta }_{z2}),\\ Trans(a_{02},0,0)\end{array}\right.$$

(10)

$$T_3=\left\{\begin{array}{l}Rotx({\theta }_{x3})Trans(b_3,0,0)*\\ \hspace{1em}\hspace{1em}Trans(r_3.\sin ({\theta }_{z3}),r_3^{}.[1-\cos ({\theta }_{z3})],0)Rotz({\theta }_{z3}),\\ Trans(a_{03},0,0)\end{array}\right.$$

(11)

Note that $a_{01}=a_{02}=a_{03}=a_0$ and $a_{0i}=r_i{\theta }_{zi}$. For the inactive part at the tip the transformation matrix is

$$T_4=Trans(b,0,0)$$

(12)

Finally, with the homogeneous transformation matrix H, the tip position in frame X₀Y₀Z₀, denoted as ${\stackrel{\rightharpoonup }{P}}_{TipS}^0$, can be obtained related to its local coordinates as

$$H_{1\to 4}=T_1{T}_2{T}_3{T}_4\begin{array}{ccc}& ,& \end{array}{\stackrel{\rightharpoonup }{P}}_{TipS}^0=H_{1\to 4}{\stackrel{\rightharpoonup }{P}}_{Tip}^4$$

(13)

The application of actuators in pairs makes it possible to rotate the bending plate, and so the term Rotx(.) appeared based on the following description. When the actuators at both sides are equally contracted, the probe will show retroflex without lateral bending. However, if any pair of the adjacent actuators are operated with different pressures, the bending plate will rotate along X axis as shown in Figure 9.

Figure 9. Rotation of the bending plate (a) equal contraction, (b) asymmetric bending, (c) The geometry.

Figure 9. Rotation of the bending plate (a) equal contraction, (b) asymmetric bending, (c) The geometry.

As long as the length of actuators denoted as A₁A₂ and B₁B₂ are equal to L₁, the Rotx(.) term in the equations is zero. Otherwise,

$$L=l+2\sin (\alpha ).r.(1-\cos (\phi ))$$

(14)

$$\begin{gathered} L_1=l+2\sin (\alpha ).r.(1-\cos ({\phi }_1)) \\ {L}_2=l+2\sin (\alpha ).r.(1-\cos ({\phi }_2)) \end{gathered}$$

(15)

$$L_1-L_2=2\sin (\alpha ).r.(\cos ({\phi }_2)-\cos ({\phi }_1))$$

(16)

Then, the rotation angle is obtained as follows.

$${\theta }_x=\theta =-0.5({\phi }_2-{\phi }_1)=-0.5\mathrm{Arccos}[(L_1-L_2)/2\sin (\alpha ).r]$$

(17)

The chosen state vector includes states of each segment that is the segmental bending angles. The soft probe is described with the following states

$$\begin{gathered} {\stackrel{\rightharpoonup }{q}}_S={\left[{\theta }_{x1},{\theta }_{z1},{\theta }_{x2},{\theta }_{z2},{\theta }_{x3},{\theta }_{z3}\right]}^T \\ {Q}^{SoRo}=\left\{{\stackrel{\rightharpoonup }{q}}_S\left|0<{\theta }_{xi}<{20}^o,0<{\theta }_{zi}<{50}^o\right.\right\} \end{gathered}$$

(18)

In comparison with the conventional probes, the soft robot has fundamental different structure and mechanics. While the conventional probe is a two DoF system with a 3D manifold workspace, the soft robot has six DoFs due to the six actuators on the active part. In fact, actuator redundancy is common in soft robots, but in most cases the actuators (e.g., chambers in multi-chamber robots) share a single pressurizing tube. We investigate a method to make use of the redundancy to map the soft robot trajectory and workspace on those of the rigid counterpart. The next subsection explains the method.

Control Method

Neural Networks (NNs) are extensively used for the modelling and control of soft robots [25,26,27] to alleviate the complexity of mathematical modelling, making use of the advances in data science. However, the literature mainly deals with the modelling or control of soft robots as individual or independent devices like conventional robots. In this section, an algorithm is proposed to provide kinematic similarity between a reference system and a soft robot. We propose an NN based on the Kohonen (aka SOM) network and a nearest neighbour search (NNS), to provide the required kinematic similarity. The method is an unsupervised machine-learning technique that represents a two-dimensional map of the data set. Similar tools such as the k-means and related algorithms operate without topology preservation. The training is based on competitive learning. First, the distance of the input data W^R to all current weight vectors W^SOM is measured. Then, the neuron with the most similarity to the weight vector is labelled as the best matching unit (BMU). One single neuron is assigned as the winning neuron for the input points. Then, neighbour neurons in the grid are moved towards the input points. For any node j the number of data points, having the node as their BMU is calculated and assigned as, n_j. Then the weights are updated as a function of the average of the distances of the n_j points from the node j, denoted as ${\overline{x}}_j$ with the following rule

$$W^{SOM}\left|{}_{node\hspace{1em}i}\right.=\frac{{\displaystyle \sum n_j{h}_{j,i}{\overline{x}}_j}}{{\displaystyle \sum n_j{h}_{j,i}}}$$

(19)

Where, h_j,i denotes a neighbourhood distance of winning node j to node i to spread the grid over the data set. The next task of the algorithm includes an NNS, which is a kind of proximity search. The points in the cloud of soft probe tip positions closest to the SOM nodes are labelled, and the corresponding states are recorded by the algorithm. The training algorithm, which contains the offline calculations, is given as Algorithm A (given in Appendix A) and is represented as the block diagram in Figure 10.

Figure 10. The training procedure.

Figure 10. The training procedure.

In the training algorithm, ${\phi }_1,{\phi }_2$ can be seen as inputs of the reference system, ${\delta }_1=({\phi }_1^{\max }-{\phi }_1^{\min })/N$,${\delta }_2=({\phi }_2^{\max }-{\phi }_2^{\min })/M$, and $N,M\in \mathbb{N}$. The set of admissible configuration angles is denoted as A. The subset $W^R\subset {ℝ}^3$ represents the workspace of the rigid system $\left|W^R\right|=NM$. The homogeneous transformation matrix is shown as $H^R$ and the tip position vector in the relevant local coordinate system is ${\mathsf{\Gamma }}^R$. The SOM network is constructed with a rectangular grid of size $N_{SOM}\times M_{SOM}$ and initial weights W^(PCA). The trained SOM weight matrix is represented as $W^{SOM}$. For the soft robot, the state vector is represented as $\mathsf{\Theta }$, and the set of all admissible states is shown by B. The soft robot tip points are obtained with the soft robot transformation matrix $H^S$ for all the n members of B.

For each ${\mathsf{\Gamma }}^{SOM}(i,j)\in W^{SOM}$ and all ${\mathsf{\Gamma }}^S(n)$, the index, m_ij, is found so that

$$\begin{array}{c}{‖{\mathsf{\Gamma }}^S(m_{ij})-{\mathsf{\Gamma }}^{SOM}(i,j)‖}_2\le \end{array}{‖{\mathsf{\Gamma }}^S(n)-{\mathsf{\Gamma }}^{SOM}(i,j)‖}_2$$

(20)

Finally, the modified network weights are saved as $W^{NET}$. The NN maps the reference input to the follower input so that the outputs meet at the representative points. Algorithm A is used for constructing and training the NN. Algorithm B (given in Appendix B) represents the way the trained system is implemented for control.

3. Results

Figure 11. Representation of the tip access points for the soft robot and the rigid probe.

Figure 11. Representation of the tip access points for the soft robot and the rigid probe.

3.1. Fabrication and Testing

An experimental verification was used to evaluate the prototype as the demonstrator. For this purpose, the pneumatic circuit as shown in Figure 12 was used with an input signal that consequently (with 10 s intervals) opens the valves of each segment was considered. The test was performed for three contraction ratios a/L (L=a₀). The measured values are the tip angles. For a smooth transition, each pneumatic valve was excited with a PWM signal. However, only at the final states, the values were read. The results are summarized in Table II and Figure 13. A calibration may be used to make up for the errors. Nevertheless, the small errors in this work are ignored. Note that all the five segments were used in this test, so the transformation matrices of the other segments were included. Employing the standard pneumatic equipment enables us to make use of established pneumatics and commercially available components. In this work, miniature 3/2 solenoid valves with spring return were used. Proper excitation combination of the valves provides different gestures in the robot as in Figure 14. Nevertheless, to have control over the pressure, more complex proportional valves are suggested.

Figure 12. The pneumatic circuit.

Figure 12. The pneumatic circuit.

Figure 13. Experiment of the prototype: (a) The input, (b) The response.

Figure 13. Experiment of the prototype: (a) The input, (b) The response.

Figure 14. Bending to different directions.

Figure 14. Bending to different directions.

Table 2. Numerical values.

Table 2. Numerical values.

a/a0		Tip angle (o )
80	Simulation	59.9	122.6	184.8	246.4	280
	Experiment	57	118	176	235	269
	Error 1	-4.8	-3.7	-4.8	-4.6	-3.9
85	Simulation	47.1	96.4	145.2	193.6	220
	Experiment	44	92	140	187	210
	Error	-6.6	-4.6	-3.6	-3.4	-4.5
90	Simulation	30	61.3	92.4	123.2	140
	Experiment	27	59	89	116	133
	Error	-10	-3.8	-3.7	-5.8	-5.0

¹Error=(Experiment-Simulation)/Simulation*100.

3.2. Training Results and Error Analysis

Generally, success of training depends on many factors and need to be shown with experiments (i.e., simulations). The result’s numerical values have some randomness and can be different in different runs. Normally, repetition of training is required to achieve a good result. One advantage of the SOM nets is that the network has some visual presentation that can be used to observe the results. If the training result is not sufficiently good, some nodes will appear outside of the data (the desired manifold in this work), or the nodes do not spread uniformly. In that case, the training can be repeated by refining the parameters. The trained network used in this work is represented in Figure 15. The neurons are represented as a square lattice as in Figure 15 (a), where the nodes represent neurons that are loaded with weights shown in Figure 15 (b). The result of NNS is shown in Figure 15 (c). In feedforward neural networks, an error number is calculated that can be used to indicate the training result. However, in the unsupervised NN, the error cannot be calculated by normal means. In fact, unsupervised learning has not defined error because there is no ideal data to calculate the error against it. Many SOM implementations do not even report an error and the literature does not provide an error calculation method. The worst distance from BMUs may be taken as the error, but such an index is used in the algorithm to stop the training when the learning is not improved more. In this work, the distance between the tip of the soft robot with that of the rigid probe model is considered as the error.

Figure 15. Topology of the trained network: (a) Lattice of neurons, (b) The SOM weights, (c) NNS nodes vs. the SOM weights.

Figure 15. Topology of the trained network: (a) Lattice of neurons, (b) The SOM weights, (c) NNS nodes vs. the SOM weights.

The error may be examined over the whole workspace. The NN algorithm was used to map the representative points of the workspace of the rigid probe, to the workspace of the controlled soft robot (as in Figure 16). The error was calculated by moving average represented in Figure 17, using MATLAB^® syntax:

avErr = tsmovavg(sqrt(e),’s’,15,2);

minimumDist =0.143 mm

maximumDist =18.0 mm

RMSE =4.36 mm

The RMSE value over the whole workspace is less than 5 mm. However, the maximum value shows a large error. The error can be reduced, for example, by increasing the resolution of the NN or the number of neurons, which in turn increases the size of weight matrices, complexity, and calculation time (and delay). However, the large errors appear mainly at the ends of the workspace where the probe is either close to the straight initial status or bent to maximum angles. These states are not important as they have no contribution to US imaging.

Figure 16. Comparison on the workspace.

Figure 16. Comparison on the workspace.

Figure 17. The corresponding error.

Figure 17. The corresponding error.

3.3. Case-Study Simulations

To examine the method in the trajectory following scenarios, two simulations are presented as case studies. In Figure 18, the desired trajectories are shown by the red line on the reference workspace manifold. The stars represent the weight of excited neurons, and the robot’s path is shown by the black line. The errors are shown in Figure 19 consequently. (Note that the examples presented here are essentially arbitrary, but we had some clues from medical experts regarding practical scenarios and the normalized flexing and bending during the scenarios were reconstructed as Figure 20 and used in the simulation.)

Figure 18. The simulation results.

Figure 18. The simulation results.

Figure 19. The trajectory errors.

Figure 19. The trajectory errors.

Figure 20. Description of the example scenarios.

Figure 20. Description of the example scenarios.

4. Discussion

5. Conclusions

References

1. Sayahkarajy, M. Mode shape analysis, modal linearization, and control of an elastic two-link manipulator based on the normal modes. Applied Mathematical Modelling 2018, 59, 546–570. [Google Scholar] [CrossRef]
2. Andrada, E.; Mämpel, J.; Schmidt, A.; Fischer, M.; Karguth, A.; Witte, H. From biomechanics of rats’inclined locomotion to a climbing robot. International Journal of Design Nature Ecodynamics 2013, 8, 192–212. [Google Scholar] [CrossRef]
3. Zhong, Y.; Hu, L.; Xu, Y. Recent advances in design and actuation of continuum robots for medical applications. In Proceedings of the Actuators; 2020; p. 142. [Google Scholar]
4. Sayahkarajy, M.; Witte, H. Soft medical robots and probes: Concise survey of current advances. Design, Construction, Maintenance 2023, 3, 263–278. [Google Scholar] [CrossRef]
5. Kondoyanni, M.; Loukatos, D.; Maraveas, C.; Drosos, C.; Arvanitis, K.G. Bio-Inspired robots and structures toward fostering the modernization of agriculture. Biomimetics 2022, 7, 69. [Google Scholar] [CrossRef]
6. Hahn, R.T.; Abraham, T.; Adams, M.S.; Bruce, C.J.; Glas, K.E.; Lang, R.M.; Reeves, S.T.; Shanewise, J.S.; Siu, S.C.; Stewart, W. Guidelines for performing a comprehensive transesophageal echocardiographic examination: recommendations from the American Society of Echocardiography and the Society of Cardiovascular Anesthesiologists. Journal of the American Society of Echocardiography 2013, 26, 921–964. [Google Scholar] [CrossRef] [PubMed]
7. Zhang, H.; Wang, J.; Guo, C. Tool frame calibration for robot-assisted ultrasonic testing. Sensors 2023, 23, 8820. [Google Scholar] [CrossRef] [PubMed]
8. Hidalgo, E.M.; Wright, L.; Isaksson, M.; Lambert, G.; Marwick, T.H. Current applications of robot-assisted ultrasound examination. Cardiovascular Imaging 2023, 16, 239–247. [Google Scholar] [CrossRef] [PubMed]
9. Wang, S.; Housden, J.; Bai, T.; Liu, H.; Back, J.; Singh, D.; Rhode, K.; Hou, Z.-G.; Wang, F.-Y. Robotic intra-operative ultrasound: virtual environments and parallel systems. IEEE/CAA Journal of Automatica Sinica 2021, 8, 1095–1106. [Google Scholar] [CrossRef]
10. Xie, Y.; Hou, X.; Wang, S. Design of a novel haptic joystick for the teleoperation of continuum-mechanism-based medical robots. Robotics 2023, 12, 52. [Google Scholar] [CrossRef]
11. Sayahkarajy, M.; Mohd Faudzi, A.A. Design of a mechatronic interface with compliant manipulator for robot assisted echocardiography. In Proceedings of the Journal of Physics, Conference Series, 2021; p. 012005.
12. Witte, H. The interplay of biomimetics and biomechatronics. Biomimetics 2022, 7, 96. [Google Scholar] [CrossRef] [PubMed]
13. Stano, G.; Percoco, G. Additive manufacturing aimed to soft robots fabrication: A review. Extreme Mechanics Letters 2021, 42, 101079. [Google Scholar] [CrossRef]
14. Lee, C.; Kim, M.; Kim, Y.J.; Hong, N.; Ryu, S.; Kim, H.J.; Kim, S. Soft robot review. International Journal of Control, Automation and Systems 2017, 15, 3–15. [Google Scholar] [CrossRef]
15. Faudzi, A.A.; Azmi, N.I.; Sayahkarajy, M.; Xuan, W.L.; Suzumori, K. Soft manipulator using thin McKibben actuator. In Proceedings of the 2018 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), 2018; pp. 334–339.
16. Conrad, S.; Teichmann, J.; Auth, P.; Knorr, N.; Ulrich, K.; Bellin, D.; Speck, T.; Tauber, F. 3D-printed digital pneumatic logic for the control of soft robotic actuators. Science Robotics 2024, 9, eadh4060. [Google Scholar] [CrossRef] [PubMed]
17. Duanmu, D.; Li, X.; Huang, W.; Hu, Y. Soft finger rehabilitation exoskeleton of biomimetic dragonfly abdominal ventral muscles: Center tendon pneumatic bellows actuator. Biomimetics 2023, 8, 614. [Google Scholar] [CrossRef]
18. Banerjee, H.; Tse, Z.T.H.; Ren, H. Soft robotics with compliance and adaptation for biomedical applications and forthcoming challenges. International Journal of Robotics and Automation 2018, 33. [Google Scholar] [CrossRef]
19. Zhang, Y.; Lu, M. A review of recent advancements in soft and flexible robots for medical applications. The International Journal of Computer Assisted Radiology and Surgery 2020, 16, e2096. [Google Scholar] [CrossRef]
20. Junghanns, H. Der Lumbosakralwinkel: Messungen an Röntgenbildern und frischen Präparaten. Deutsche Zeitschrift für Chirurgie 1929, 213, 322–340. [Google Scholar] [CrossRef]
21. Xiang, C.; Guo, J.; Chen, Y.; Hao, L.; Davis, S. Development of a SMA-fishing-line-McKibben bending actuator. IEEE Access 2018, 6, 27183–27189. [Google Scholar] [CrossRef]
22. Daerden, F.; Lefeber, D. Pneumatic artificial muscles: actuators for robotics and automation. European Journal of Mechanical and Environmental Engineering 2002, 47, 11–21. [Google Scholar]
23. De Volder, M.; Moers, A.; Reynaerts, D. Fabrication and control of miniature McKibben actuators. Sensors and Actuators A: Physical 2011, 166, 111–116. [Google Scholar] [CrossRef]
24. Tian, W.; Wakimoto, S.; Yamaguchi, D.; Kanda, T. Fabrication process for twisting artificial muscles by utilizing braiding technology and water-soluble fibers. IEEE Robotics Automation Letters 2024. [Google Scholar] [CrossRef]
25. Salem, M.E.; Wang, Q.; Xu, M.H. Application of neural network fitting for modeling the pneumatic networks bending soft actuator behavior. Engineering Research Express 2022. [Google Scholar] [CrossRef]
26. Kim, D.; Kim, S.-H.; Kim, T.; Kang, B.B.; Lee, M.; Park, W.; Ku, S.; Kim, D.; Kwon, J.; Lee, H. Review of machine learning methods in soft robotics. Plos one 2021, 16, e0246102. [Google Scholar] [CrossRef] [PubMed]
27. Li, Y.; Cao, Y.; Jia, F. A neural network based dynamic control method for soft pneumatic actuator with symmetrical chambers. In Proceedings of the Actuators, 2021; p. 112.