Snapshot Optimal Real-time Ride Sharing

Preprint

Article

Snapshot Optimal Real-time Ride Sharing

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Afzaal Hassan,Mark Wallace,

Irene Moser^*,Daniel Harabor

Afzaal Hassan,Mark Wallace,

Irene Moser^*,Daniel Harabor

This version is not peer-reviewed

Submitted:

14 February 2024

Posted:

14 February 2024

You are already at the latest version

Alerts

Abstract

Ridesharing effectively tackles urban mobility challenges by providing a service comparable to private vehicles while minimising resource usage. Our research primarily concentrates on dynamic ridesharing, which conventionally involves connecting drivers with passengers in need of transportation. The process of one-to-one matching presents a complex challenge, particularly when addressing it on a large scale, as the substantial number of potential matches make the attainment of a global optimum a challenging endeavour. This paper aims to address the absence of an optimal approach for dynamic ridesharing by refraining from conventional heuristic-based methods, commonly used to achieve timely solutions in large-scale ride-matching. We propose a novel approach that provides snapshot optimal solutions for various forms of one-to-one matching, ensuring they are generated within an acceptable timeframe for service providers. Additionally, we introduce and solve a new variant where the system itself provides the vehicles. The efficacy of our methodology is substantiated through experiments carried out with real-world data extracted from the openly available New York City taxicab dataset.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction

Traffic congestion is a global problem. While travel delays are the most visible consequence of congestion, the economic toll it exacts reaches billions of dollars [1]. To mitigate congestion costs, promoting shared private vehicles and mass public transport is beneficial. They are faster, cost-effective, and have a lower carbon footprint. However, limitations include less flexibility, constrained routes, variable service frequencies, and limited availability. This research aims to develop better algorithmic techniques for intelligent trip sharing. In this context, we introduce a novel algorithmic approach, SnapPair, that optimises participant pairing in a ride-sharing system. This adaptable approach can be applied in various settings and under different policies. We not only implement SnapPair in traditional role-based one-to-one matching scenarios, encompassing designated drivers and riders, but also in scenarios with flexible roles. Furthermore, we propose a new type of ride matching scheme that involves a fleet of autonomous vehicles (AVs) or human-driven cars providing on-demand door-to-door transportation. Passengers can request trips on the spot and centralized algorithms then schedule vehicles and combine trips to maximise efficiency. The system aims to reduce vehicle hours traveled (VHT), thereby mitigating congestion and associated costs. In this latter formulation, we assume the existence of a fleet operator responsible for providing the vehicles to serve all trips generated by SnapPair. These fleets can be operated by public or private entities, similar to UberPool or Lyft Shared Rides. The formulation envisions a future where car ownership becomes obsolete, and shared trips become the default mode of transportation for optimal vehicle utilisation.

We perform an experimental evaluation of SnapPair by applying it in an online fashion, which imitates the behaviour of commuters who book their journeys ad hoc in everyday life. New demand is included in the subsequent time window. Time windows are optimised at regular intervals.

We also devise and implement several matching policies that differ in their level of eagerness to commit to a match. Our experiments evaluate their performance using both classic role-based matching schemes and our new formulation.

Given the dynamic nature of link costs that can experience rapid fluctuations throughout the day, we have also taken an additional step by investigating an unconventional scenario where the matching algorithm itself performs the shortest path calculations.

2. Definitions

Rider: A participant in the ride sharing system wishing to be transported from their origin to their destination within an announced time frame.
Match: A pair of riders who share a vehicle on their trip.
Snapshot Optimality: Attaining an optimal solution to a pairwise matching problem with a fixed demand.

3. Previous Work

Peer to Peer ride matching offers shared journeys to the participants while maximising some global objective (usually savings in travel time) subject to participants’ spatio-temporal constraints [2]. There are multiple variants of this problem, some classifications are based on cardinality of matching (one-to-one, one-to-many, many-to-many) while others are based on roles the participants play (riders, drivers). These roles can be fixed or flexible [3].

One-to-One ride matching can be represented as a graph matching problem [3], where each participant is a node, potential matches are edges, and edge weight indicates the savings from the match. When roles are fixed, it becomes maximum weighted bipartite matching. If roles are flexible, it can be formulated as maximum weight matching in general graphs. In the past many polynomial time algorithms have been proposed to solve these problems optimally [4,5,6,7]. Recent studies with exact solutions [8,9], have attempted the matching problem at a very small scale with up to few hundred participants and a small number of locations.

Unlike in the above studies, real world ride sharing problems are large scale and dynamic in nature [2] and require solutions in close to real time. In their landmark survey a decade ago Agatz et al. [10] noted the lack of fast optimal solutions for large metropolitan areas. Since then, a substantial body of work has focused on developing fast solutions for real time large scale ride sharing systems, especially for the one-to-one version. To cater for the assumption of continuous travel requests, most studies are dynamic with a rolling time windows approach [11]. To reduce complexity, studies tend to publish methods to divide the problem into smaller subproblems. Shen et al. [12] partitioned the road network into grids and every participant can only be matched within their grid. Xu et al. [13] made use of ellipses to bound possible locations for matches to avoid removing the optimal solution during pruning, but this approach requires equal speed limits. A similar approach was taken by Masoud and Jayakrishnan [8]. Some approaches have used graph partitioning techniques. [11,14] The ride sharing problem has also been formulated as a linear program, but at times this has been applied to a reduced search space [11], while in other cases authors have used a time-out period to provide answers in time [15].

So far, no published approach has solved dynamic one-to-one matching for a large scale demand in time for an operating service. Tafreshian and Masoud [11] are the closest, but they take an impractially long time to compute an optimal matching. For example, when working with another instace of similar size from the same dataset that we have utilised, it takes them roughly six minutes to solve for one-to-one matching with flexible roles for a demand contained in a one-minute time window. To address this shortcoming, they have resorted to using graph partitioning heuristic to achieve real time solutions. Similarly, Lu et al. [16] recently proposed an exact methodology for addressing one-to-one matching with flexible roles. However, it is crucial to highlight that their approach achieves optimality only for very small instances. For problem instances involving 10 participants, the algorithm required only a few minutes for completion, whereas experiments with 35 participants took hours to solve. Consequently, the absence of an optimal approach for one-to-one matching that provides solutions within practical time frames is evident in the literature.

Furuhata et al. [17] postulate that an optimal approach to solve one-to-one matching at a large scale in an authentic setting would be a major breakthrough. In this paper, we propose and empirically test such an approach.

3.1. Contributions

In this paper we publish the following contributions:

A fully implemented and tested new algorithm, SnapPair that guarantees a snapshot optimal solution at each time point in a dynamic one-to-one matching problem. SnapPair is more than two orders of magnitude faster than the current state-of-the-art.
A novel formulation of the dynamic one-to-one matching problem, where riders and vehicles are independent. This new formulation is more complex due to an increased number of possible matches. We call this formulation FreeMatch. We consider this formulation timely and significant, particularly in light of research indicating that a higher number of individuals have reported issues with crowded vehicles since the pandemic, compared to the pre-pandemic period [18]. With FreeMatch, our objective is to establish a framework that optimally utilises smaller vehicles with a maximum capacity of two, enhancing the appeal of ridesharing, in the forever changed post pandemic world.
An extended algorithm including a rematching procedure that pairs both new riders and riders whose previous match has been dropped off, with the objective of optimising the use of vehicles available in the system.
Experiments successfully applying the algorithms to a problem of a size that is relevant to a fleet operator.

4. Methodology

4.1. Overview

One-to-one matching is a well established problem which involves participants bringing their own vehicles and can be viewed in two different versions. In the first version, certain individuals are designated as drivers and have vehicles, while others are riders in need of transportation. The second version assumes that all participants have vehicles, but the matching system determines which individuals will assume the role of driver or rider.

For FreeMatch every participant is a rider looking to be transported. Riders are paired when possible.

To identify potential matches for a rider, the system generates reachability graphs, which associate road network nodes with riders who can pass through the node without reaching their destination late, along with the time interval they can spend at each node. The riders associated with the start node of rider r are the potential matches for r.

4.2. Parameters and Variables

The road network is represented as a graph

G = (V, E)

where

E \subseteq V \times V

and where each edge

(i, j) \in E

has an associated and positive edge cost

e c_{i j}

which indicates travel time. Based on these times the system uses Dijkstra’s algorithm [19] to compute the shortest paths between all pairs of nodes

u, v

in the graph, and records the time

w (u, v)

. In our experiments we show this can either be done once in advance, or else repeatedly for all relevant pairs at the beginning of every iteration based on the current congestion-dependent edge costs.

R is the set of riders, and each rider

r \in R

has an origin

o_{r}

, destination

d_{r}

, earliest possible departure time

t_{r}^{e d}

and latest possible arrival time

t_{r}^{l a}

For each rider r, the system computes the earliest possible arrival time

t_{r}^{e a} = t_{r}^{e d} + w (o_{r}, d_{r})

A match

< j, k >

where j and k are riders, is feasible if j can pick up k, both riders depart after their earliest departure time and reach their destinations before their latest arrival time. If j is on the way to picking up k, then either j or k may have to wait at

o_{k}

until the other party is ready. Waiting times are permitted as long as both riders arrive at their destinations in time. For the sake of simplicity, the pick-up and drop-off are instantaneous and do not incur any delay. Formally, the route

r o u t e 1 (j, k) = < o_{j}, o_{k}, d_{k}, d_{j} >

is feasible for riders j and k if:

$m a x (t_{j}^{e d} + w (o_{j}, o_{k}), t_{k}^{e d}) + w (o_{k}, d_{k}) \leq t_{k}^{l a}$
and
$m a x (t_{j}^{e d} + w (o_{j}, o_{k}), t_{k}^{e d}) + w (o_{k}, d_{k}) + w (d_{k}, d_{j}) \leq t_{j}^{l a}$ .
The cost of this match is
$c o s t 1 (j, k) = w (o_{j}, o_{k}) + w (o_{k}, d_{k}) + w (d_{k}, d_{j})$
if $r o u t e 1 (j, k)$ is feasible and infinity otherwise.

The route

r o u t e 2 (j, k) = < o_{j}, o_{k}, d_{j}, d_{k} >

is feasible for riders j and k if

$m a x (t_{j}^{e d} + w (o_{j}, o_{k}), t_{k}^{e d}) + w (o_{k}, d_{j}) \leq t_{j}^{l a}$
and
$m a x (t_{j}^{e d} + w (o_{j}, o_{k}), t_{k}^{e d}) + w (o_{k}, d_{j}) + w (d_{j}, d_{k}) \leq t_{k}^{l a}$ .
Its cost is $c o s t 2 (j, k) = w (o_{j}, o_{k}) + w (o_{k}, d_{j}) + w (d_{j}, d_{k})$ if $r o u t e 2 (j, k)$ is feasible and infinity otherwise.

< j, k >

is a feasible match if

r o u t e 1 (j, k)

r o u t e 2 (j, k)

is feasible, and its cost is

$c o s t (j, k) = m i n (c o s t 1 (j, k), c o s t 2 (j, k))$

For an unmatched rider the cost is

$c o s t (r) = w (o_{r}, d_{r})$

We write F for the set of all feasible matches.

To minimise VHT (the vehicle hours travelled), the model can be formulated in terms of the variables M (set of matched pairs) and U (set of unmatched riders) as follows:

\begin{matrix} minimise & (\sum_{j \in U} c o s t (j) + \sum_{< j, k > \in M} c o s t (j, k)) \\ subject to & M \subset F \land U \subset R \\ R = U \cup ⋃_{< j, k > \in M} {j, k} \\ U \cap ⋃_{< j, k > \in M} {j, k} = Ø \\ \forall i, j, k, \in R : < i, j > \in M \to \\ (< j, k > \notin M \land (j \neq k \to < i, k > \notin M)) \end{matrix}

(1)

This model corresponds to both flexible roles and FreeMatch problems, where matched riders are picked up by a dedicated vehicle at their origin and taken to their destination using the shortest path. In FreeMatch, a vehicle is assumed to materialise instantly at the origin of its first rider and disappear when no longer needed, while in flexible roles version, vehicle is provided by one of the participants and stays with them.

The model is modified, below, to handle driver and passenger roles. With fixed role ride matching, the driver is responsible for initiating the trip and providing the vehicle for the passenger. For this variant riders are divided into a set of drivers D and a set of passengers P. A match

< j, k >

is now feasible only if

j \in D

and

k \in P

. Consequently it is computationally easier to generate the set F of feasible matches.

The model (1) to minimise VHT can be be modfied as below to cater for the fixed roles scenario.

\begin{matrix} minimise & (\sum_{j \in U} c o s t (j) + \sum_{< j, k > \in M} c o s t (j, k)) \\ subject to & M \subset F \land U \subset R \\ R = U \cup ⋃_{< j, k > \in M} {j, k} \\ U \cap ⋃_{< j, k > \in M} {j, k} = Ø \\ \forall i, k \in D \land \forall j, l \in P : < i, j > \in M \to \\ (< i, l > \notin M \land < k, j > \notin M) \end{matrix}

(2)

4.3. Reachability Graphs

Many existing ride-sharing studies use pruning mechanisms to speed up the matching of travellers. Approaches include use of grids [20,21] and geometric shapes [8,13]. These approaches are approximations and may miss candidates with longer journeys and faraway origins.

Here, we propose a pruning mechanism that preserves all possible matches. The reachability graph algorithm identifies and records the nodes that a rider r can reach without exceeding their deadline to reach their destination. Using the identified reachable nodes of each rider, the road graph is annotated with the arrival and departure times of the riders who can traverse each node of the road graph without missing their destination arrival deadline

t_{r}^{l a}

for

d_{r}

. This provides a fast mechanism to identify candidates for matches.

Algorithm 1 illustrates the simple procedure, which is called for each rider r. The network graph, the origin

o_{r}

, destination

d_{r}

, earliest departure time

t_{r}^{e d}

and latest arrival time

t_{r}^{l a}

are passed to the procedure. It starts the traversal of the road graph at

o_{r}

and examines the nodes in its immediate neighbourhood. For each node, we test whether the destination can be reached by the required time, given we have to travel to this node from

o_{r}

and reach

d_{r}

after departing from this node (line 5). If the node is included in the reachability graph, its children must also be examined. If a node does not qualify, we do not examine its neighbours. This renders the algorithm very efficient.

If a node is reachable, we store the information of the rider and their earliest arrival and latest departure with it. The time interval that can be spent on the current node is determined based on the time (cost) it takes to get to it

c (o_{r}, n)

added to the earliest possible departure

t_{r}^{e d}

. The end of the interval can be calculated by subtracting the time it takes to get from the current node to the destination node

c (n, d_{r})

(line 6). This method guarantees the preservation of the optimal solution within the search space, as any additional deviation would result in r failing to meet the deadline.

Algorithm 1: Creating a Reachability Graph

4.4. Construction of Match Graph

The construction of the match graph builds on the reachability graphs and road graph with annotated nodes indicating which riders can traverse at specific times. The goal is to compute all possible pairwise matches and store them as a graph, where every node represents a rider, every edge a possible match and the direction of the edge denotes the order of the pickup. This graph builds on similar approaches used in other studies [15,22].

Algorithm 2 initially builds the nodes of the match graph from the list of riders. Then for every rider r, it retrieves all riders passing through r’s origin

o_{r}

. This is a simple lookup operation as every node holds the list of trips passing through it along with the corresponding times (line 4). For establishing a possible match, the next step verifies which of the riders in these trips can either drop r to its destination or be dropped by r to their destination (line 6). Once a match has been established, it is added as an edge between the corresponding riders where the direction of the edge represents the order of pickup and the weight of the edge represents the savings this match will provide.

Algorithm 2: Creating the Match Graph

As we repeat these steps for every rider, all possible matches are found and stored. For every rider r’s turn, only those matches are found where r is being picked up. The other riders’ turns will take care of any such matches where r is doing the pick up.

4.5. Optimality

Our optimisation model has information on all potential rider pairings and all individual journeys, including their respective minimum costs. From this we argue that an optimal mathematical solver will select a combination of paired rides and solo journeys that ensures the lowest overall cost.

Lemma 1.

SnapPair records all possible pairings of riders.

Proof.

We show that if it is possible for

r 1

to give a ride to

r 2

then

r 2

appears in the list of matches for

r 1

For our road graph G we use Dijkstra’s algorithm [19] to compute the shortest paths between all pairs of nodes

u, v

in the graph, and to record the optimal time

w (u, v)

. Our reachability graph method records all possible nodes

r 1

can visit en route to

d_{r 1}

. This is determined by starting at

o_{r 1}

and expanding (a): all neighbours of all locations which can be reached with time

t_{r 1}^{e d} + w (o_{r}, n) + w (n, d_{r}) \leq t_{r 1}^{l a}

, with n denoting a node expanded during this traversal. By the correctness and completeness of Dijkstras algorithm, all locations L satisfying (a) are returned, the returned set includes all locations that can be reached by

r_{1}

en route to

d_{1}

. If rider

r 2

starts at any other location

n^{'} \notin L

, then

t_{r 1}^{e d} + w (o_{r}, n^{'}) + w (n^{'}, d_{r}) > t_{r 1}^{l a}

, then

r 1

arrives late and

r 1

cannot feasibly pick up

r 2

(i.e.,

r 2

does not appear in the list of matches for

r 1

). □

Lemma 2.

SnapPair records the minimum cost for each individual journey or potential pairing.

Proof.

For any possible pairing between two riders

r 1

and

r 2

, we show that our algorithm calculates the lowest cost journey for both riders to reach their destinations in time. Suppose rider

r 1

picks up another rider

r 2

. Once set L for

r 1

has been ascertained, SnapPair then checks for each possible rider

r 2

that starts at a location

n \in L

whether it is feasible for

r 1

to pick up

r 2

and if so at what cheapest cost. The cost is determined by the route chosen for the journey. For each potential match

〈 r 1, r 2 〉

three routes are possible

$r o u t e 1 (r 1, r 2) = 〈 o_{r 1}, o_{r 2}, d_{r 2}, d_{r 1} 〉$ having a cost of $c o s t_{r o u t e 1} (r 1, r 2) = w (o_{r 1}, o_{r 2}) + w (o_{r 2}, d_{r 2}) + w (d_{r 2}, d_{r 1})$
$r o u t e 2 (r 1, r 2) = 〈 o_{r 1}, o_{r 2}, d_{r 1}, d_{r 2} 〉$ having a cost of $c o s t_{r o u t e 2} (r 1, r 2) = w (o_{r 1}, o_{r 2}) + w (o_{r 2}, d_{r 1}) + w (d_{r 1}, d_{r 2})$ and only if $(d_{r 1} = o_{r 2})$
$r o u t e 3 (r 1, r 2) = 〈 o_{r 1}, d_{r 1}, o_{r 2}, d_{r 2} 〉$ having a cost of $c o s t_{r o u t e 3} (r 1, r 2) = w (o_{r 1}, d_{r 1}) + w (o_{r 2}, d_{r 2})$ .

The cost of

r o u t e 3

is equal to the cost of the two direct routes

r o u t e_{r 1} = 〈 o_{r 1}, d_{r 1} 〉

incurring

c o s t (r 1)

and

r o u t e_{r 2} = 〈 o_{r 2}, d_{r 2} 〉

with

c o s t (r 2)

, and is therefore subsumed by the solution in which

r 1

and

r 2

travel alone. For this reason it is not considered. If neither of

r o u t e 1 (r 1, r 2)

r o u t e 2 (r 1, r 2)

is feasible then

r 2

is not added to the list of possible riders for

r 1

to pick up. If either route is possible, then the corresponding cost is recorded, and the match

〈 r 1, r 2 〉

is included in the match graph. If both routes are possible, then the minimum cost for it, denoted as

c o s t (r 1, r 2) = m i n (c o s t_{r o u t e 1}, c o s t_{r o u t e 2})

along with shortest route is recorded. □

Theorem 1.

Computed solutions are globally optimal

Proof.

Lemma 1 and Lemma 2 establish that the mathematical optimiser is provided with every conceivable individual journey and pairing, each accompanied by its lowest cost. The model’s constraints guarantee that every rider is either chosen for a solo trip or included in a matched pairing. The optimiser returns such an arrangement that minimises costs, yielding the optimal solution. This solution is derived using a branch-and-bound approach, ensuring the return of an optimal combination, though it may entail exploring all potential combinations to achieve this guarantee. □

4.6. Dynamic Optimisation and Rematching

Dynamic optimisation handles new demand within a rolling time horizon. When new demand is introduced at time t, the system simulates the situation up to t, determining which existing riders can be considered for the optimisation iteration.

We introduce the notion of slack for riders, which is the difference between the latest arrival time and earliest possible arrival time. The slack for an unmatched rider is:

s l a c k_{r} = t_{r}^{l a} - t_{r}^{e a}

(3)

For each unmatched rider r, they can be reoptimised if:

$t - t_{r}^{e d} < s l a c k_{r}$ . In this case $t_{r}^{e d}$ is updated to t.

A vehicle, currently in transit with matched riders

〈 j, k 〉

, may cater for multiple matches if after dropping the first rider the remaining rider is matched again. Thus, for matched riders

〈 j, k 〉

in transit their departure location and earliest departure time are updated according to the current trip leg and position.

If the current leg ends at $d_{j}$ arriving there at time $t_{a r r}$ , then $o_{k}$ is updated to $d_{j}$ and $t_{k}^{e d}$ is updated to $t_{a r r}$ . Rider k is added to the set of drivers, D. Rider j is dropped from R.
If the current leg ends at $d_{k}$ arriving there at time $t_{a r r}$ , then $o_{j}$ is updated to $d_{k}$ and $t_{j}^{e d}$ is updated to $t_{a r r}$ . Rider j is added to the set of drivers, D. Rider k is dropped from R.

Riders may request a ride with advance notice of $τ$ minutes. $τ$ denotes how long before their earliest departure time $t_{r}^{e d}$ a rider r becomes known to the system.

The newly arrived riders are added to R. The earliest departure time and origin for in-transit riders is updated to the current time t and rider’s current location. Once participants in the iteration have been determined, the reachability and match graphs are reconstructed, enforcing the constraint that

\forall 〈 j, k 〉 \in R : k \in R_{t} \to 〈 j, k 〉 \notin F

where

R_{t}

denotes the riders in transit.

This implies that, for riders already in transit, a modification of the match graph construction outlined in Algorithm 2 is implemented. These riders are exempt from the need to seek potential candidates who can pick them up, as they are already in transit. So they are only considered for such matches where they will be doing the pick up.

For matching variants where participants provide vehicles, i.e., fixed roles and flexible roles, an additional constraint is enforced while constructing the match graph:

\begin{matrix} \forall 〈 j, k 〉 \in R : j \in R_{t} \land 〈 j, k 〉 \in F \to \\ r o u t e (j, k) = 〈 o_{j}, o_{k}, d_{k}, d_{j} 〉 \end{matrix}

This ensures that the vehicle stays with the participant which provided it. The constraint disallows routes such as

〈 o_{j}, o_{k}, d_{j}, d_{k} 〉

where the last person to be dropped off did not bring the vehicle in the first place. The optimal pairing of riders that minimises the total cost as in the model (1), accordingly results in snapshot optimal solution.

4.7. Eager and lazy optimisation

Regardless of the type of matching, practitioners can choose whether matched riders should leave immediately or wait in situ for as long as their schedule allows. This “lazy optimisation” opens the possibility of improving the match for better savings of VHT.

In case “eager optimisation” is chosen for a match

〈 j, k 〉

, the time of arrival at

o_{k}

t_{j}^{e d} + w (o_{j}, o_{k})

. Similarly the pair depart from

o_{k}

m a x (t_{j}^{e d} + w (o_{j}, o_{k}), t_{k}^{e d})

and arrive at the first drop off location by the shortest route.

However for lazy optimisation, the time of departure from

o_{j}

is the latest possible consistent with arriving at both destinations in time. For example on route

$r 1 (j, k) = 〈 o_{j}, o_{k}, d_{k}, d_{j} 〉$ the departure time from $o_{j}$ would be:

$t_{j}^{d e p} = m i n (t_{k}^{l a}, t_{j}^{l a} - w (d_{k}, d_{j})) - w (o_{k}, d_{k}) - w (o_{j}, o_{k})$

When reoptimising at time t, if

t < t_{j}^{d e p}

then

o_{j}

remains as before. However if

t > t_{j}^{d e p}

then the match

〈 j, k 〉

cannot be changed, so j and k are dropped from the set of riders R and begin their combined trip.

4.8. Dynamically changing edge costs

Traffic congestion varies during the day, causing pre-recorded costs for specific time periods to potentially become outdated. Thus, we also examine impact of link costs changing after each time window. Updating edge costs at each reoptimisation is slower, but it still provides optimal solutions within an acceptable timeframe for fleet operators. Dijkstra’s algorithm [19] is used for all shortest path calculations, whether the costs are precomputed or generated during the matching algorithm. While the majority of studies favour the first option, a few incorporate shortest path calculations within the matching algorithm. However, those studies tended to conduct matching on a smaller scale or relied on heuristics [21,23].

Beside recalculating all shortest paths, changing edge costs also requires recomputing the slacks for unmatched riders, and the predicted departure and arrival times for matched riders. For lazy optimisation, dynamically changing edge costs may, inevitably, cause some riders who started their trips as late as possible to arrive late. However for other riders, the changed edge costs result in reoptimisations that enable them to arrive on time. Naturally, if the edge costs increase, the total VHT also increases.

5. Experiments

5.1. Case Study

In our study, we use the New York City taxicab dataset [24] as a case study. This dataset is favoured for shared mobility studies due to its provision of GPS coordinates for requests instead of zones [25]. The road network in Manhattan, New York City, consists of 4484 nodes and 8839 edges. Unlike previous studies that employ designated pickup/drop-off points [11], SnapPair considers every node for pickup and drop-off. For edge costs, we compute free-flow travel times in seconds by dividing edge length by the maximum allowed speed, following similar methods in other research [26]. Our travel demand consists of 23,981 requests, covering the one-hour morning peak from 8-9 am on May 1, 2013, a working Wednesday. Under free-flow conditions, commuters traveling independently in their own vehicles would spend around 1800 hours in total transportation time. In our simulation, we introduce new demand every minute during a one-hour period. The notice period for all requests is set to one minute, mimicking the behavior of ride-hailing service users who request a ride when they need it. On average, each minute in the simulation includes around 400 new riders, with a maximum of 444 new riders occurring in any minute. All requests originate and terminate within Manhattan. Each request is assumed to have one rider, following assumptions in previous work [15]. Vehicle capacity is capped at two passengers in all experiments. For experimental evaluation of the system, first we apply SnapPair to the classic one-to-one matching scenario, and then to our new formulation called FreeMatch,with vehicles provided. We produce results for both online and offline settings with different slack levels, achieved by modifying riders’ latest arrival times. The resulting slack levels are percentages of the shortest rider journey. In offline experiment, we assume full advance knowledge of travel demand, a rarity in real-world situations. Yet, we follow prior research [27] to set a baseline optimum for our ride-sharing system. Additionally, we present the following matching policies and assess their impact on the system’s performance.

Eager departing without rematching: Following this approach, once the optimal set of matches for a specific time window is identified, they are immediately put into action. The initial riders in these matches begin their journey right away, the successfully matched riders are not subject to rematching, even if they become available after their match is dropped off. Unmatched riders, however, stay in the queue, awaiting future rounds of matching for as long as their deadlines allow.
Lazy departure without rematching: Matched participants delay committing to the first optimal match offer if it remains valid in the next iteration, allowing them to potentially be paired with someone else for greater system-wide savings. If waiting would invalidate the match, participants commit and depart. Riders are not rematched even if they become available after dropping the other rider in the match.
Eager departure with rematching: Under this policy, participants commit to the first optimal match presented but can be rematched after the first rider in the match is dropped off, potentially multiple times. Unmatched riders wait until their slack runs out before departing on their own, without being matched.
Lazy departure with rematching: Matched participants delay committing to a match as long as it remains valid in the next iteration. They can be rematched after the first match. Unmatched riders wait until their slack is fully utilised while waiting to be matched, and then depart on their own.

We ran the experiments on a Lenovo laptop with 16 GB RAM and a 1.80 GHz Processor. The implementation was carried out in Java using the JgraphT library [28] for graph representations. To solve the linear programming formulations, we used Minizinc [29] and Gurobi [30].

5.2. One-to-One Ride-matching with Fixed Roles

First, we solve the more established formulation where the roles of driver and passenger are fixed. Rematching is avoided to match the formulations in prior studies.

Table 1 shows the result of this matching approach. The slack column indicates how much extra time a traveller is prepared to spend on their trip as a percentage of the shortest travel time possible given origin and destination. The time column indicates the average time in milliseconds taken for optimising a time window, calculated as the average optimisation time of the 60 one-minute time windows given an hourly dataset, including the preoptimisation steps. Matches denote the number of matches made between pairs of travellers and VHT are the vehicle hours travelled.

Lazy departing leaves matched drivers waiting at their respective origins until their slack runs out. During this time, the pairs may be split up and matched again if this leads to greater savings than the original match. It is no surprise that the eager approach takes less time to optimise, as fewer riders remain for the next iteration. The VHT are nearly identical for both the lazy and eager approaches here. This similarity is primarily due to the comparable number of potential matches between the two approaches, especially at lower levels of slack. However, a significant difference emerges at 50% slack, where the eager policy results in an average of 443 potential matches per minute, while the lazy approach offers 688 potential matches every minute to choose from.

5.3. One-to-One Ride-matching with Flexible Roles

Table 2 and Table 3 present the results of the experiments that match travellers one-to-one assuming the one who starts the journey provides the vehicle (hence “flexible roles").

Table 2 shows the results of the algorithm that does not match a driver with a new passenger after they have dropped off the previous. Up to 30% slack, the optimisation of a time window takes less than a second for an average of over 400 travellers per time window. Although eager departing produces slightly (at most 1%) more matches, lazy departing provides better cost savings, suggesting that the quality of the matches is better. The differences between the gains in VHT is meager with up to 30% slack. Meaningful differences are only observed above 40% slack. Compared to fixed roles, the policy of flexible roles provides sometimes more than thrice the number of matches, at worst, one and half times the matches in the case of 50% slack. The VHT is between 3% and 12% shorter when compared to the flexible policy without rematching.

Table 3 shows the results of the algorithm that differs from Table 2 in that it rematches the drivers when they have dropped off the rider they were previously matched with. Rematching does not appear to affect the runtime, but it leads to significant (2 - 34 hours’) savings in VHT. Overall, rematching leads to a 3% increase in the number of matches at 50% slack when comparing the lazy option with rematching to the lazy option without rematching (9715 vs. 9451). This saves 34 hours of system travel time (1253 compared to 1287).

5.4. Ride Matching with Vehicles Provided (FreeMatch)

Table 4 and Table 5 contain the same result columns as Table 2 and Table 3, but assume that the vehicle is provided by the system rather than belonging to either traveller.

Assuming vehicle provision allows for more matches by permitting the same traveler starting and ending their journey first. On average, this results in 2.13 times the potential matches per iteration compared to the flexible roles version. Consequently, it is expected that both eager and lazy departure will have longer running times. A comparison of the run times in Table 4 (compared to Table 2) and Table 5 (compared to Table 3) illustrates this.

The assumption that vehicles appear when needed without the need to designate a driver leads to significant further savings in travel time. As a consequence, for 20% and 30% slack, the eager policy creates slightly more savings in travel times, suggesting that there are plenty of good options to choose from without reoptimising existing pairs of riders.

The best results - a VHT of 1226 - are achieved by allowing 50% slack and applying a lazy policy with rematching while the vehicle is provided as a service. The second best option only differs in the way the vehicle is provided. Requiring a driver, applying 50% slack and a lazy policy with rematching achieves a VHT that is 27 hours or 2% longer (1253 hours), whereas providing a vehicle but refraining from rematching takes 43 hours longer. The results suggest that the most significant contributors to the savings are 1. rematching, 2. providing a vehicle, and 3. lazy departure.

5.5. Comparison with Static Formulation

Dynamic, rolling time window approaches yield inferior results to static, offline approaches that have complete information. But, offline optimisation may not always be feasible in ridesharing due to last-minute travel decisions by riders. However, offline optimisation results can be used as a baseline. Figure 1 displays a comparison between a subset of policy combinations and 40% slack against the results of offline optimisation using the same dataset. All results apply the lazy departure approach and demonstrate small differences compared to the offline optimum across the four settings (left to right). For flexible roles, without rematching, the online formulation is only 7.18% costlier than the offline optimum. For the Vehicle as a service, no rematching this difference is 7.74%. For the flexible roles, with rematching this value is at 5.24%. For Vehicle as a service, with rematching online performance is only 5.23% far from the true optimum.

5.6. Impact of Shortest Path Calculations on the Matching Algorithm’s Performance

In the previous experiments, pre-stored shortest path calculations were used. This is a reasonable approach in real-world settings, where average travel times on urban roads during specific hours are predictable. However, we now consider a scenario where shortest path calculations are necessary due to unavailability of pre-stored link costs and the cost of each trip is predicted at the start using the current link cost information. For simulations, we increase the cost of half the links by 0.5% every minute. In this scenario, Reachability and Match graphs are constructed using a travel function that accounts for real-time travel time, rather than relying on initial shortest path calculations. Compared to the other experiments with an overall transport cost of 1800 hours, the altered link costs have resulted in an increase to 1928 hours.

Table 6 shows that even under these challenging conditions the matching algorithm performs well with the Eager policy. It would arguably be considered acceptable for real-life matching service providers, taking a maximum of 19.5 seconds to optimally match a minute’s worth of demand.

6. Conclusion

Matching drivers to riders in a ridesharing service presents a scalability challenge. Hence previous solutions have broken the problem into distinct regions, or reduced the number of pickup points, or used incomplete search methods. Having precomputed the shortest path cost between each pair of points in the ridesharing area, this paper presents an algorithm that links each rider to all their possible matches. Consequently, even when new ridesharing requests arise every minute, optimal pairings are computed in seconds. Indeed the computation time was so short that it was possible to recompute shortest paths dynamically at each time point and successfully handle dynamic link costs, still retaining optimality computed within 20 seconds. This highly efficient implementation has supported extensions to the basic ridesharing matching service, with experimental results showing their potential contribution to congestion reduction on our city streets. Firstly, if riders are flexible about using their own vehicle or riding as a passenger, savings increase by up to 12%. Secondly, if the “slack” time overhead for sharing increases from 10% to 50% the number of matches increases 5-fold, which reduces the total vehicle hours travelled (VHT) by 27%. Thirdly, if the vehicle used for transport is not linked to any of the passengers (using an automated vehicle for example), even with a limit of two occupants at any time, the same vehicle can match sets of up to 7 riders. In this case VHT cost is reduced by over a third for lower slack times. For 50% slack, however there is some additional reduction, but at most just 10% more.

Finally it was possible to compare two policies.

Eager or Lazy

either eagerly starting a trip as soon as a match is found, or lazily delaying the start in case the slack time enables the trip to be delayed until the next update of demands (after one minute), in case a better option comes up.
Rematching

when one of a pair of travellers has been dropped off, the remaining traveller can be paired again with a new traveller.

Among these improvements, the rematching approach has the most beneficial impact on the total hours travelled. Providing vehicles was the second most impactful measure. Our experiments showed significant benefits of larger slack times for all ridesharing variations studied. Automated vehicles also offer substantial advantages with low slack times. Additionally, lazy starting and rematching yield comparable benefits, with rematching showing slightly better vehicle hours travelled savings when using automated vehicles.

Author Contributions

Conceptualization, A.H., M.W., D.H and I.M.; methodology, A.H., M.W., D.H and I.M.; software, A.H.; validation, A.H.; formal analysis, A.H. M.W. and I.M.; investigation, A.H., M.W., D.H and I.M.; resources, A.H. M.W. and I.M.; data curation, A.H.; writing—original draft preparation, A.H., M.W., D.H and I.M.; supervision, M.W., I.M.; All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the Australian Government through the Australian Research Council’s Discovery Projects funding scheme (project DP190100013).

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Goodwin, P. The economic costs of road traffic congestion 2004.
Martins, L.d.C.; de la Torre, R.; Corlu, C.G.; Juan, A.A.; Masmoudi, M.A. Optimizing ride-sharing operations in smart sustainable cities: Challenges and the need for agile algorithms. Computers & Industrial Engineering 2021, 153, 107080. [Google Scholar]
Tafreshian, A.; Masoud, N.; Yin, Y. Frontiers in service science: Ride matching for peer-to-peer ride sharing: A review and future directions. Service Science 2020, 12, 44–60. [Google Scholar] [CrossRef]
Hopcroft, J.E.; Karp, R.M. An n^5/2 algorithm for maximum matchings in bipartite graphs. SIAM Journal on computing 1973, 2, 225–231. [Google Scholar] [CrossRef]
Fredman, M.L.; Tarjan, R.E. Fibonacci heaps and their uses in improved network optimization algorithms. Journal of the ACM (JACM) 1987, 34, 596–615. [Google Scholar] [CrossRef]
Edmonds, J. Maximum matching and a polyhedron with 0, 1-vertices. Journal of research of the National Bureau of Standards B 1965, 69, 55–56. [Google Scholar] [CrossRef]
Gabow, H.N.; Tarjan, R.E. Faster scaling algorithms for general graph matching problems. Journal of the ACM (JACM) 1991, 38, 815–853. [Google Scholar] [CrossRef]
Masoud, N.; Jayakrishnan, R. A real-time algorithm to solve the peer-to-peer ride-matching problem in a flexible ridesharing system. Transportation Research Part B: Methodological 2017, 106, 218–236. [Google Scholar] [CrossRef]
Chen, W.; Mes, M.; Schutten, M.; Quint, J. A ride-sharing problem with meeting points and return restrictions. Transportation science 2019, 53, 401–426. [Google Scholar] [CrossRef]
Agatz, N.; Erera, A.; Savelsbergh, M.; Wang, X. Optimization for dynamic ride-sharing: A review. European Journal of Operational Research 2012, 223, 295–303. [Google Scholar] [CrossRef]
Tafreshian, A.; Masoud, N. Trip-based graph partitioning in dynamic ridesharing. Transportation Research Part C: Emerging Technologies 2020, 114, 532–553. [Google Scholar] [CrossRef]
Shen, B.; Huang, Y.; Zhao, Y. Dynamic ridesharing. Sigspatial Special 2016, 7, 3–10. [Google Scholar] [CrossRef]
Xu, Y.; Qi, J.; Borovica-Gajic, R.; Kulik, L. Geoprune: Efficiently matching trips in ride-sharing through geometric properties. 32nd International Conference on Scientific and Statistical Database Management, 2020, pp. 1–12.
Pelzer, D.; Xiao, J.; Zehe, D.; Lees, M.H.; Knoll, A.C.; Aydt, H. A partition-based match making algorithm for dynamic ridesharing. IEEE Transactions on Intelligent Transportation Systems 2015, 16, 2587–2598. [Google Scholar] [CrossRef]
Alonso-Mora, J.; Samaranayake, S.; Wallar, A.; Frazzoli, E.; Rus, D. On-demand high-capacity ride-sharing via dynamic trip-vehicle assignment. Proceedings of the National Academy of Sciences 2017, 114, 462–467. [Google Scholar] [CrossRef]
Lu, W.; Quadrifoglio, L.; Lee, D.; Zeng, X. The ridesharing problem without predetermined drivers and riders: formulation and heuristic. Transportation Letters 2023, 15, 969–979. [Google Scholar] [CrossRef]
Furuhata, M.; Dessouky, M.; Ordóñez, F.; Brunet, M.E.; Wang, X.; Koenig, S. Ridesharing: The state-of-the-art and future directions. Transportation Research Part B: Methodological 2013, 57, 28–46. [Google Scholar] [CrossRef]
Jabbari, P.; MacKenzie, D. Ride sharing attitudes before and during the COVID-19 pandemic in the United States. Transport Findings. November 2020, 26. [Google Scholar] [CrossRef]
Dijkstra, E.W. A note on two problems in connexion with graphs. Numerische mathematik 1959, 1, 269–271. [Google Scholar] [CrossRef]
Ma, S.; Zheng, Y.; Wolfson, O. T-share: A large-scale dynamic taxi ridesharing service. 2013 IEEE 29th International Conference on Data Engineering (ICDE). IEEE, 2013, pp. 410–421.
Thangaraj, R.S.; Mukherjee, K.; Raravi, G.; Metrewar, A.; Annamaneni, N.; Chattopadhyay, K. Xhare-a-ride: A search optimized dynamic ride sharing system with approximation guarantee. 2017 IEEE 33rd International Conference on Data Engineering (ICDE). IEEE, 2017, pp. 1117–1128.
Santi, P.; Resta, G.; Szell, M.; Sobolevsky, S.; Strogatz, S.H.; Ratti, C. Quantifying the benefits of vehicle pooling with shareability networks. Proceedings of the National Academy of Sciences 2014, 111, 13290–13294. [Google Scholar] [CrossRef] [PubMed]
Ta, N.; Li, G.; Zhao, T.; Feng, J.; Ma, H.; Gong, Z. An efficient ride-sharing framework for maximizing shared route. IEEE Transactions on Knowledge and Data Engineering 2017, 30, 219–233. [Google Scholar] [CrossRef]
Donovan, B.; Work, D. New york city taxi trip data (2010-2013). Univ. Illinois Urbana-Champaign, Champaign, IL, USA, Tech. Rep 2014. [Google Scholar]
Qin, Z.T.; Zhu, H.; Ye, J. Reinforcement learning for ridesharing: An extended survey. Transportation Research Part C: Emerging Technologies 2022, 144, 103852. [Google Scholar] [CrossRef]
Mahéo, A.; Zhao, S.; Hassan, A.; Harabor, D.D.; Stuckey, P.J.; Wallace, M. Customised Shortest Paths Using a Distributed Reverse Oracle. Proceedings of the International Symposium on Combinatorial Search, 2021, Vol. 12, pp. 79–87.
Agatz, N.; Erera, A.L.; Savelsbergh, M.W.; Wang, X. Dynamic ride-sharing: A simulation study in metro Atlanta. Procedia-Social and Behavioral Sciences 2011, 17, 532–550. [Google Scholar] [CrossRef]
Michail, D.; Kinable, J.; Naveh, B.; Sichi, J.V. JGraphT–A Java Library for Graph Data Structures and Algorithms. ACM Trans. Math. Softw. 2020, 46. [Google Scholar] [CrossRef]
Nethercote, N.; Stuckey, P.J.; Becket, R.; Brand, S.; Duck, G.J.; Tack, G. MiniZinc: Towards a standard CP modelling language. International Conference on Principles and Practice of Constraint Programming. Springer, 2007, pp. 529–543.
Gurobi Optimization, LLC. Gurobi Optimizer Reference Manual, 2022.

Figure 1. Comparison with Static.

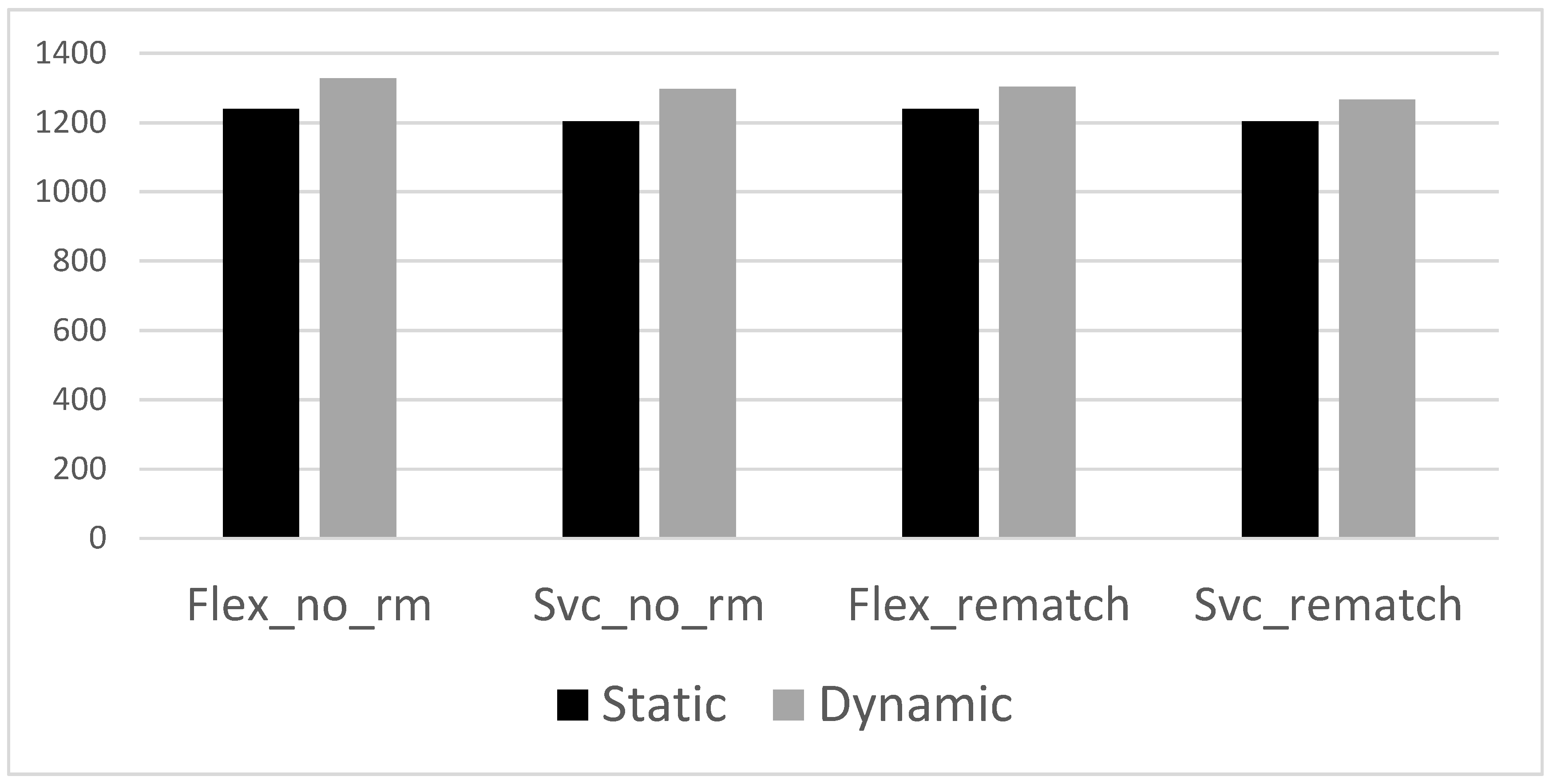
Table 1. Eager departure is compared to lazy departure, roles are fixed.

Slack	Time		Matches		VHT
	Eager	Lazy	Eager	Lazy	Eager	Lazy
10%	325	334	356	356	1781	1781
20%	372	388	1494	1494	1707	1707
30%	447	467	3151	3146	1607	1607
40%	554	642	4803	4774	1521	1521
50%	690	860	6132	6112	1464	1461

Table 2. Eager departure is compared to lazy departure, driver is decided after the match, no rematching after first drop-off.

Slack	Time		Matches		VHT
	Eager	Lazy	Eager	Lazy	Eager	Lazy
10%	371	397	1316	1316	1724	1724
20%	497	509	4112	4113	1547	1547
30%	708	751	6819	6803	1405	1404
40%	1016	1362	8501	8463	1337	1328
50%	1413	2985	9553	9451	1307	1287

Table 3. Eager departure is compared to lazy departure, driver is decided after the match, driver may be rematched after drop-off.

Slack	Time		Matches		VHT
	Eager	Lazy	Eager	Lazy	Eager	Lazy
10%	362	395	1321	1321	1722	1722
20%	470	478	4147	4146	1534	1535
30%	696	738	6953	6925	1389	1384
40%	1049	1373	8800	8661	1317	1304
50%	1518	2742	10016	9715	1287	1253

Table 4. Eager departure is compared to lazy departure, vehicle is provided and no rematching after first drop-off.

Slack	Time		Matches		VHT
	Eager	Lazy	Eager	Lazy	Eager	Lazy
10%	391	397	1929	1929	1692	1692
20%	587	612	5339	5245	1489	1494
30%	995	1134	7966	7743	1357	1361
40%	1621	2455	9420	9119	1300	1297
50%	2424	6067	10271	9764	1279	1269

Table 5. Eager departure is compared to lazy departure, vehicle is provided and remaining rider after first drop-off may be rematched.

Slack	Time		Matches		VHT
	Eager	Lazy	Eager	Lazy	Eager	Lazy
10%	390	394	1966	1966	1689	1689
20%	607	614	5594	5479	1474	1478
30%	1064	1181	8536	8221	1335	1339
40%	1819	2735	10338	9706	1274	1267
50%	2723	7147	11519	10529	1251	1226

Table 6. Eager departure is applied on changing link costs, vehicle is provided and remaining rider after first drop-off may be rematched. Shortest path calculations are performed within matching algorithm.

Slack	Time	Matches	VHT
30%	13044	6654	1499
40%	18118	9156	1357
50%	19575	10731	1293

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Snapshot Optimal Real-time Ride Sharing

Abstract

1. Introduction

2. Definitions

3. Previous Work

3.1. Contributions

4. Methodology

4.1. Overview

4.2. Parameters and Variables

4.3. Reachability Graphs

4.4. Construction of Match Graph

4.5. Optimality

4.6. Dynamic Optimisation and Rematching

4.7. Eager and lazy optimisation

4.8. Dynamically changing edge costs

5. Experiments

5.1. Case Study

5.2. One-to-One Ride-matching with Fixed Roles

5.3. One-to-One Ride-matching with Flexible Roles

5.4. Ride Matching with Vehicles Provided (FreeMatch)

5.5. Comparison with Static Formulation

5.6. Impact of Shortest Path Calculations on the Matching Algorithm’s Performance

6. Conclusion

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe