Prerpints.org logo
Preprint
Review

Research Progress on the Dynamic Stability of Dry Gas Seals

Altmetrics

Downloads

119

Views

21

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

14 February 2024

Posted:

18 February 2024

You are already at the latest version

Alerts
Abstract
With the application of high-precision, enormous rotating equipment and the addition of harsh working conditions, the advantages of dry gas sealing technology are increasingly obvious. Herein, research on the dynamic stability of dry gas seals is reviewed based on their operating mechanism. The influence of the dry gas seal structure, vibration response, and dynamic followability on the reliability of the shaft end sealing system of rotating machinery is the focus of current dry gas sealing technology. This work reviews the research history; analyzes the key coefficient of instability of the sealing system under external disturbances and the existing research on stability models; discusses the influence of starting and stopping characteristics, working conditions, and groove parameters on the stability of dry gas seals; and points out the shortcomings in the existing research. In addition, potential developments in dynamic stability are proposed, including improving model accuracy, improving experimental techniques, or applying intelligent control and optimization methods to enhance the dynamic stability of the sealing system. Finally, the development prospects for dry gas sealing technology in intelligent monitoring and wide temperature range adaptations are discussed, and theoretical guidance for improving the dry gas seal system is provided.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

With the rapid development of industrial technology, rotating machinery is also gradually moving toward extreme, intelligent, green, and cross development, and the long-term stable operation of the unit is a challenge for the development of quality equipment [1,2,3]. China called for the efficient use of energy, energy conservation, and emission reduction in the “14th Five-Year Plan.” Efficient sealing technology is an effective way to address this call in the industrial field. Current dry gas sealing technology has exposed various hidden dangers in practice (airflow excitation, thermal deformation, grinding, etc.). A variety of factors, such as severe vibration of the rotating shaft and installation deviations between the pairs of seals, can lead to instability of the sealing gas film. This instability results in friction and vibration failure and sudden leak increases, causing energy loss and environmental pollution [4]. Research shows that the reliability of equipment operation is directly determined by the sealing performance, and advanced and efficient sealing technology is the key to ensure the stability of rotating machinery operation [5]. Improving the shaft end sealing system of rotating machinery can effectively increase the efficiency of the whole machine by 4.2% [6]. 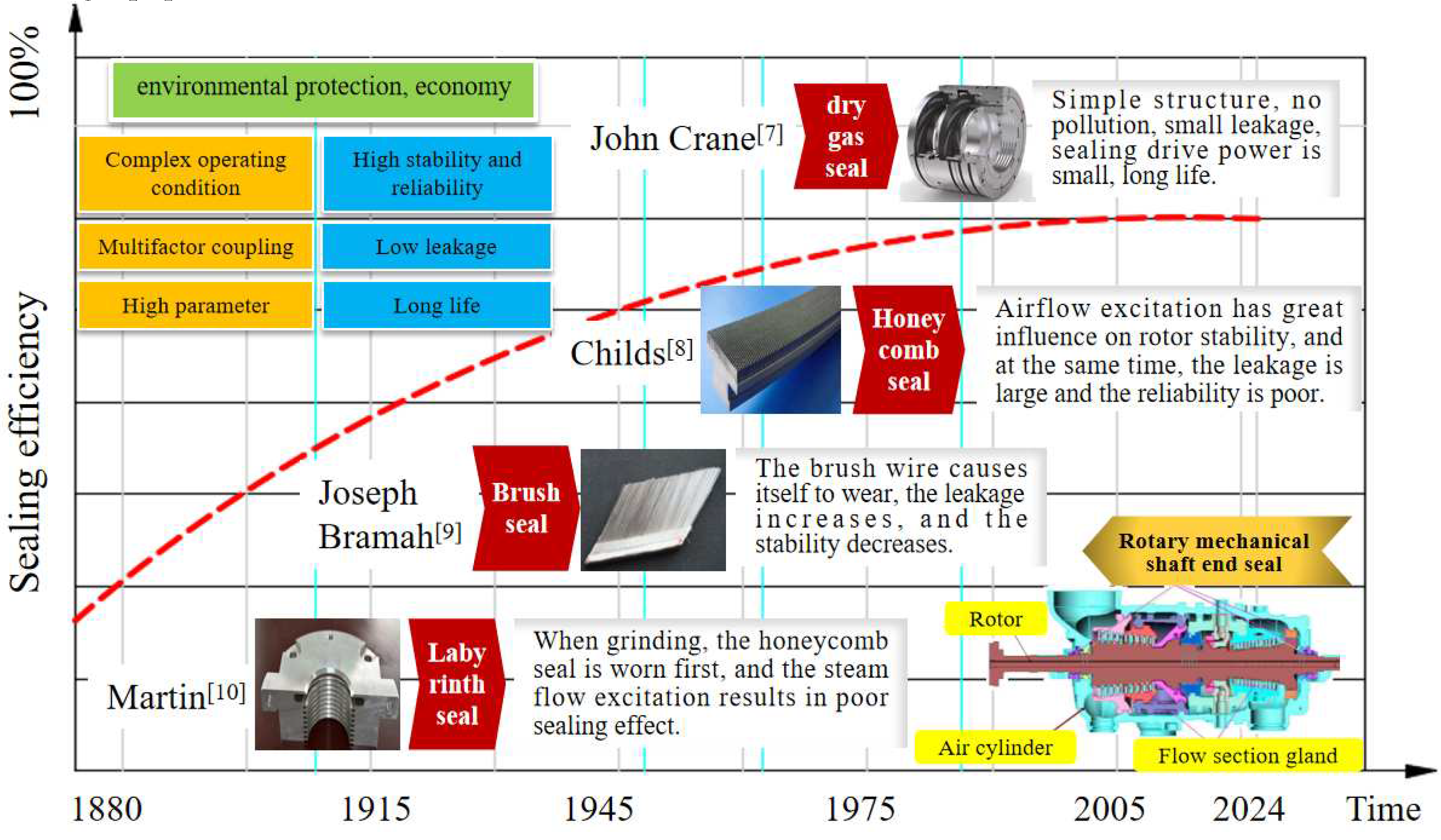Figure 1 shows several types of shaft end seals for rotating machinery.
Figure 1 also compares the sealing efficiency of these various shaft end seals for rotating machines. In increasing order of efficiency, the labyrinth seal generates airflow excitation, the brush seal’s wires wear easily, and the honeycomb seal has problems with friction and sparks. The dry gas seal has gradually become the standard shaft end seal for rotating machinery because of its good sealing performance and adaptability to high-pressure and high-speed conditions [10]. The characteristics of dry gas seals save energy, protect the environment, and improve production efficiency. High-precision and enormous rotating equipment operating in harsh working conditions have made the superiority of dry gas sealing technology increasingly valuable [11]. From the aspects of environmental protection, economy, energy conservation, and production efficiency, intelligent control units for extremely complex conditions are the trend in green development of rotary power plants. The sealing system is an important part of rotary equipment and the key to research. At present, although the dry gas seal has obvious advantages over the traditional shaft end seal, its stability under extreme working conditions is still poor. Therefore, further research to improve the long-term stability of the dry gas sealing system is important for the development of large-scale rotating equipment.

2. Dry Gas Seals

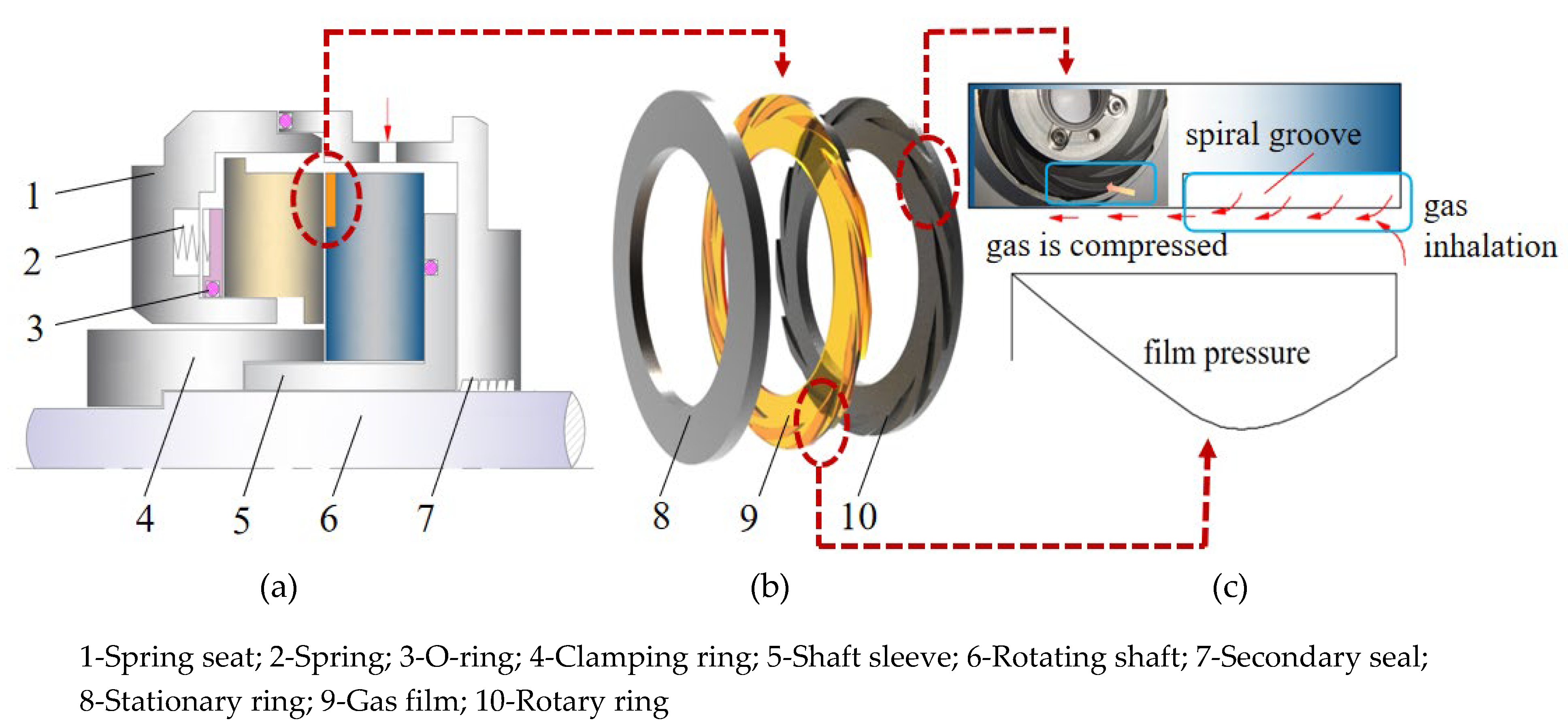
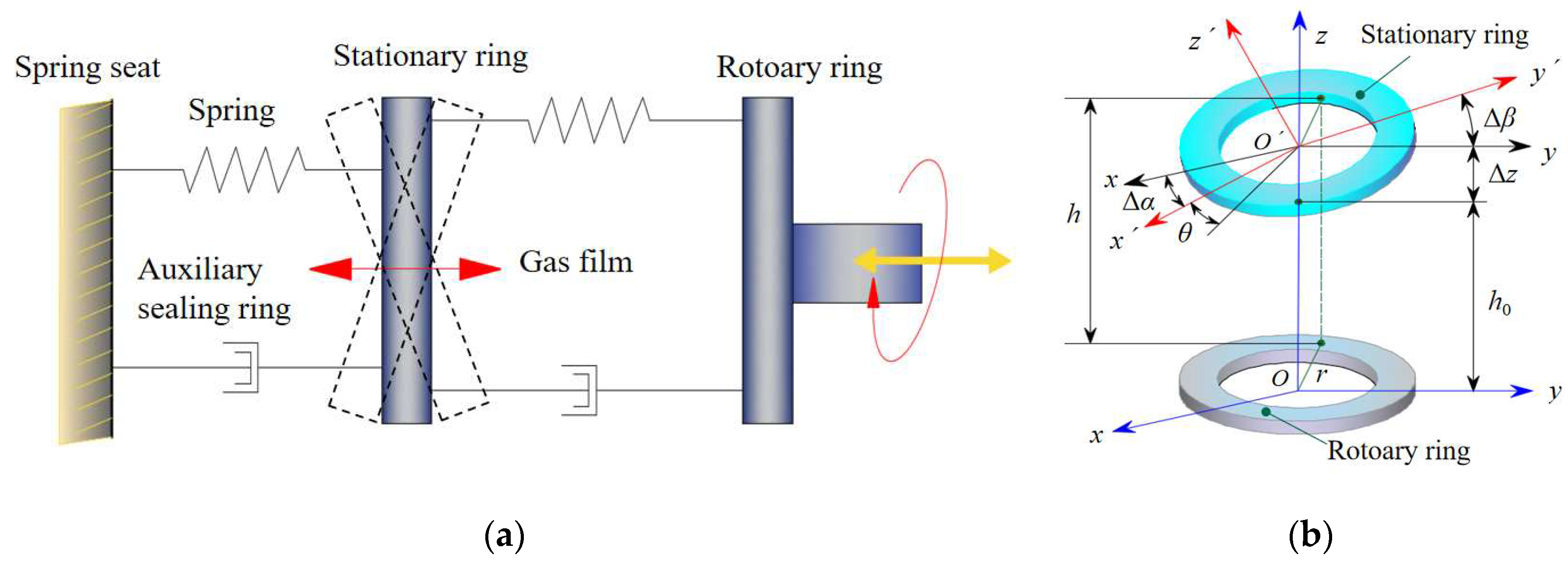
2.1. Structure and Working Principle of Dry Gas Seals

The structure of the dry gas seal is shown in Figure 2 [12,13,14], which primarily comprises the static ring seat, spring, sealing ring, pressing sleeve, shaft sleeve, rotating shaft, static ring, moving ring, and other parts. As can be seen from Figure 2(a), the static ring installed in the static ring seat is sealed by a sealing ring. The static ring moves freely along the axis under the guiding action of the static ring seat and the spring load. The moving ring is fixed on the rotating axis and rotates with the axis by the interference fit. To improve the dynamic-pressure effect of the seal, microgrooves are usually added to the surface of the moving ring. When the shaft rotates at a high speed, a gas film with high stiffness is formed between the sealing pairs, thus producing the sealing effect [15]. The structure of the sealing pairs is shown in Figure 2(b), and the spiral-groove structure of the end face of the moving ring is shown in Figure 2(c).

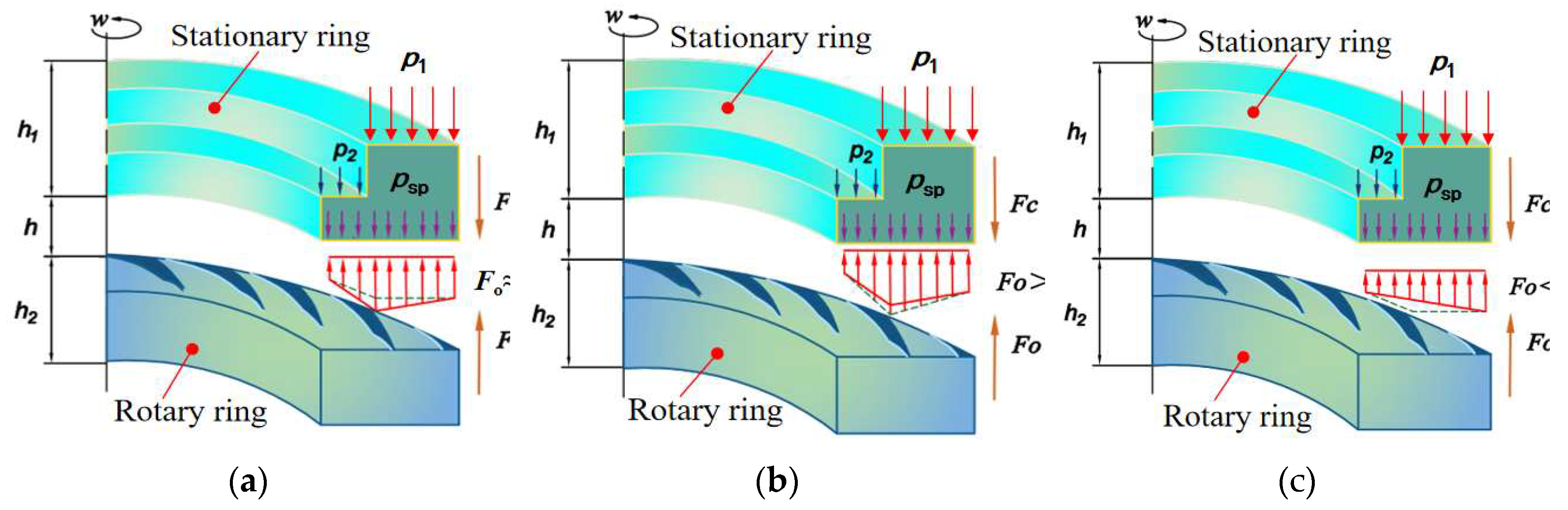
2.2. Dry Gas Seal Force Analysis

The dynamic balance of forces in the sealing system is essential to the stable operation of dry gas seals [16]. Figure 3 shows the force analysis of the dry gas seal structure, in which the opening force Fo is caused by the hydrodynamic pressure and hydrostatic pressure acting on the seal end face, while the closing force Fc comprises the spring force psp, medium pressure p1, and back pressure p2. The pressure distribution of the gas film when the seal is working normally is shown in Figure 3(a). Under normal operation, Fo ≈ Fc and a stable gas film with high rigidity forms between the sealing pairs. A change in seal clearance will change the dynamic balance. If the seal clearance decreases, so that Fo > Fc, it develops in the direction of equilibrium due to the unbalanced force of the seal pair, and the thickness of the gas film increases until the seal gap equilibrates. The pressure distribution of the gas film when clearance decreases is shown in Figure 3(b). When the gas film gap increases, the compression of the sealing gas decreases, and the dynamic-pressure effect weakens, leading to Fo < Fc. The gas film pressure distribution when clearance increases is shown in Figure 3(c). Therefore, in a certain range, the dry gas seal has an adaptive ability, which reduces the probability of friction between the sealing pairs.

3. Research on Dynamic Characteristics of the Dry Gas Seal

3.1. Dynamic Characteristic Coefficients

The dynamic characteristic coefficients of the dry gas seal are numerical values obtained by theoretical calculation or experimental measurement. The coefficients are used to evaluate the dynamic response and the stability of the seal system when the rotor changes rapidly. In dry gas sealing technology, the commonly used dynamic characteristic coefficients include the stiffness coefficient, damping coefficient, and inertia coefficient. The stiffness coefficient is a measure of the stiffness response of the dry gas seal to the numerical direction, indicating the elastic characteristics of the gas film. The higher the stiffness coefficient, the higher the seal stiffness, which means that the deformation or vibration of the seal has less influence on the thickness of the gas film. The damping coefficient is a measure of the damping response of the dry gas seal to the relative velocity, indicating the energy dissipation characteristics of the gas film. The larger the damping coefficient, the better the seal damping effect, which can effectively reduce vibration and shock. The inertia coefficient is a measure of the inertial response to acceleration, indicating the degree of reaction of the gas film to acceleration. The greater the inertia coefficient, the more obvious the inertial effect, which may lead to deformation and vibration. Therefore, research on the dynamic characteristic coefficients of the gas film in dry gas seals is the key evaluating the advantages and disadvantages of dry gas seal system designs [17]. Usually, researchers obtain the stiffness coefficient and damping coefficient of the gas film based on different theoretical calculation methods. Relevant motion equations are established to discuss the dynamic behavior of the gas film on the seal end face and to determine whether the sealing system will be unstable due to external interference. The dynamic performance of the lubricating gas film of the dry gas seal structure can then be analyzed [18].
Badykov R et al. [19] analyzed the axial vibration of the sealing system under different working conditions, obtained the influences of the elasticity of the gas film dynamic response and of the damping component on the dynamic characteristics of the dry gas seal, and calculated the relevant dynamic characteristic coefficients. Ding X et al. [20] established a calculation model for dynamic characteristic coefficients by using the PH linearization method, solved the relevant calculation using the Maple software, analyzed its dynamic stability, obtained the optimal stable spiral angle range, and verified the correctness of their model through experiments. Liu Y et al. [21] used the perturbation method to numerically solve for the damping coefficient and stiffness coefficient of the gas film on the end face of the seal and believed that the interaction between axial vibration and angular oscillation was small and could be ignored. Xu H et al. 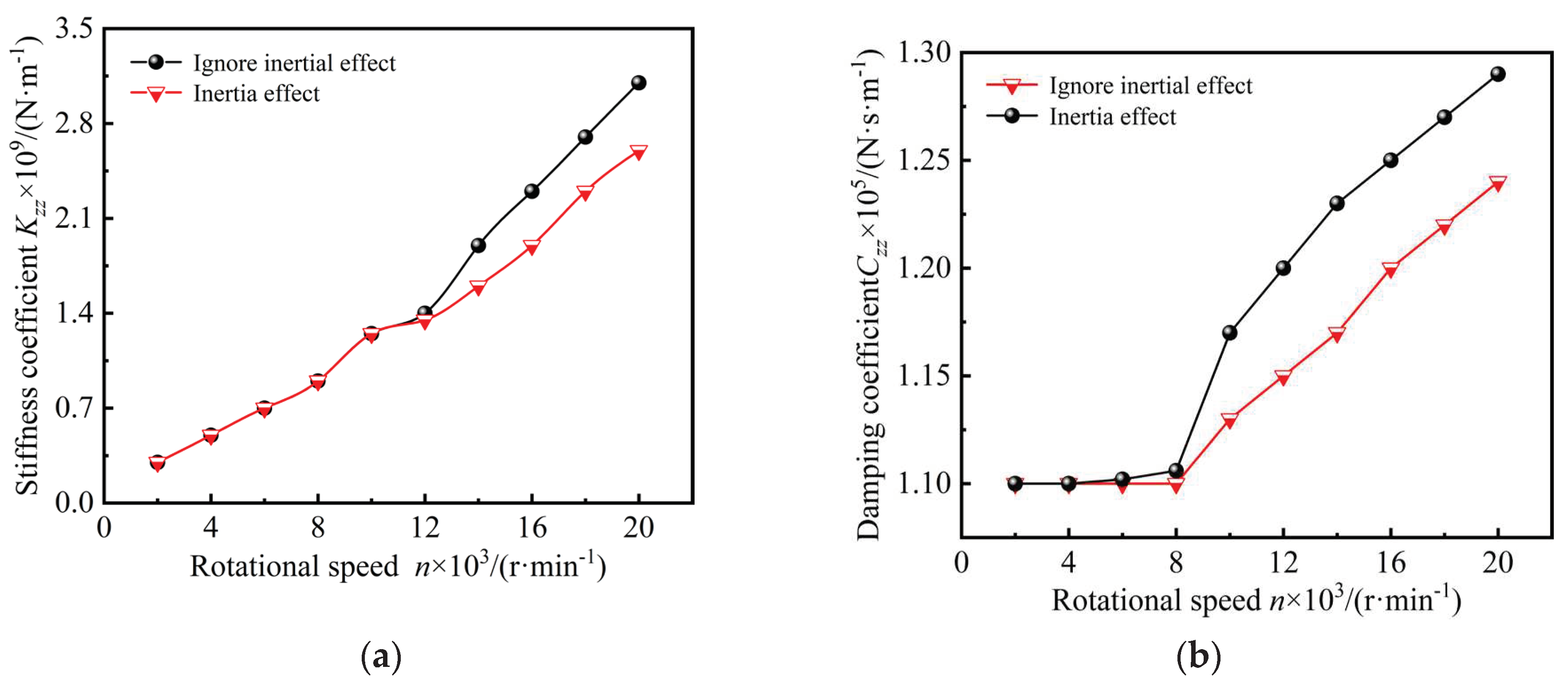[22] established a mathematical model under multiple effects and analyzed the influence of different parameters on the stiffness coefficient and damping coefficient through numerical examples. These research examples solve for the characteristic coefficients of each degree of freedom of the dry gas seal by analyzing the structural parameters and external excitation, and then evaluate the dynamic stability and reliability of the dry gas seal. In addition, the influence of inertia effects on the dynamic characteristic coefficients cannot be ignored. Yang Q et al. analyzed the dynamic characteristic coefficients of a supercritical carbon dioxide dry gas seal under inertia effects, and considered the changes of the dynamic characteristic coefficients. Figure 4 shows the influence of speed on the axial dynamic characteristic coefficient. Compared with ignoring the inertia effect, the axial dynamic characteristic coefficient is lower when the inertia effect is considered. With the increase of speed, the calculated differences of the axial damping coefficient and axial stiffness coefficient can reach 5.27% and 12.2%, respectively [23].
The application range of the dynamic characteristic coefficients of the dry gas seal depends on the structure and working condition of the seal. For high-speed rotating equipment such as shaft seals or turbines, the axial (or radial) dynamic characteristic coefficient is suitable for evaluating the stiffness and damping response of the dry gas seal in the axial (or radial) direction. The application range of the dynamic characteristic coefficients needs to be quantitatively evaluated and analyzed according to specific working conditions, medium properties, sealing structures, and other factors. Calculation errors of the dynamic characteristic coefficients are affected by many factors, including the accuracy of the calculation model, the calculated instability accuracy, and the choice of parameters. To accurately evaluate the dynamic characteristic coefficients of the dry gas seal, finite element analysis, experimental analysis, and numerical simulation are often used to obtain the calculation results. To improve the calculation accuracy, experiments can be repeated several times to minimize errors. In the process of numerical calculation, it is necessary to consider certain model assumptions and accuracy verifications. These methods can provide more reference for the optimization of dry gas seal structures and further improve the performance and stability of dry gas seals under complex working conditions.

3.2. Research on Methods of Stability Models

Both the dry gas seal and the gas dynamic-pressure bearing produce dynamic-pressure effects through gas compression, and there is a close relation between these parts. Many research methods for dry gas seals have been introduced and further developed from the field of gas dynamic-pressure bearings. Through the in-depth study of dynamic characteristics of dry gas seals, scholars use different research methods to solve for and analyze dry gas seal stability.
Faria M et al. [24] analyzed the influence of rotational speed on the dynamic characteristics of the dry gas seal. By calculating the characteristic parameters of the end-face gas film, the change behaviors of the dynamic characteristic coefficients of the gas film at high excitation frequency were analyzed. Sato Y et al. [25] used a visual method to study the performance of the end grooves of a bidirectional rotary seal structure, and compared with unidirectional grooves, its lubrication characteristics were reduced. Zirkelback N et al. [26] used the finite element method to solve the static and dynamic performance equations of the dry gas seal, compared the influence of the isothermal compressible fluid model on the seal performance, and obtained the axial stiffness coefficient and damping coefficient under the disturbance frequency. As the frequency increased, the axial stiffness coefficient and damping coefficient tended to be asymptotic values. Ruan B et al. [27] studied the dynamic characteristics of the dry gas seal with a semianalytical method. They analyzed the axial and angular modes by using dynamic coefficients related to frequency and found that the coupling forces and moment coefficients were zero and decoupled. Ding X et al. [28] used the iterative method and PH linearization method to solve the approximate equation of gas film stiffness. They concluded that under different working conditions, the gas film stiffness increased with increased groove depth, and the maximum value appeared near the bottom of the groove. Liu X et al. [29] analyzed the influence of geometric parameters on the dynamic coefficients of dry gas seals based on a semianalytical method, obtained reasonable value ranges of the seal end parameters by optimizing the structural parameters, and then proposed effective measures to improve the dynamic performance of the seal. Liu Y et al. [30] studied the influences of end-face structure parameters on the dynamic characteristics of dry gas seals through the particle swarm optimization (PSO) algorithm and projection tracking analysis method in the global optimization algorithm. Table 1 summarizes the existing commonly used research methods of stability models.
To sum up, the key aspects of dry gas seal stability model research methods are to improve the experimental accuracy, perfect the numerical calculation models, introduce accurate analysis methods, and consider the actual application conditions. The traditional dry gas seal stability model assumes that the system behavior is linear, and the improved models should consider the contact stiffness, vibration characteristics, etc., and then verify the accuracy of the models through experiments to further improve the applicability. The research of dry gas seal stability models involves many disciplines. Appropriate research methods can be selected according to specific problems and conditions, or a comprehensive application of multiple methods can be conducted. Regression analysis and statistical simulation can be used to evaluate the uncertainties in the sealing system, or the uncertainties can be measured through experimental verification.

3.3. Experimental Studies on the Dynamic Stability of Dry Gas Seals

Dry gas seal analyses usually include sealing performance, friction characteristics, thermal characteristics, and other aspects to determine its feasibility under actual working conditions. Assessment of the dynamic characteristics of dry gas seals is an important research field, which evaluates the dynamic performance and the design effects of the dry gas seal. The leakage rate, vibration behavior, temperature rise, and other parameters of the seal can be assessed by simulating actual operating conditions to evaluate the seal performance and optimize the design through specific characteristics. The stability of the dry gas seal is a measure of the ability of the seal to operate continuously and stably under certain conditions, which is important to ensure the safety and stability of the shaft end seal in rotating equipment. It is often necessary to establish an experimental test device to analyze the performance of the dry gas seal by controlling the pressure, temperature, speed, and other working conditions. Such analyses enable researchers to comprehensively and accurately evaluate the dry gas seal stability and optimize and improve its structure.
Rozova L et al. [38] developed a dry gas seal modeling program based on experimental research, to evaluate the stability under fluctuating working conditions. Kolomoets A et al. [39] conducted experiments to evaluate the dynamic stability of the dry gas seal system under a certain pressure and rotational speed and verified the correctness of the design parameters. Green I [40] conducted real-time monitoring and control of the seal’s dynamic behavior through experiments, and further explored the root cause of poor seal dynamic stability. Based on the Reynolds equation model, Lu J et al. [41] tested the stiffness of the gas film in the dry gas seal under the sliding effect using a new technology and found that the optimal spiral angle of the stiffness of the air-enhanced film was 76.8° and the groove depth was 1 × 10−5 m, and the average error of the experimental and theoretical calculations was <20%. He F et al. [42] conducted experimental research and verification on the gas film flow field at the end face of the dry gas seal under different working conditions and analyzed the influence of working condition fluctuations on the balance state of the gas film gap. Zou M et al. [43] numerically calculated the angular motion response of the moving ring under a certain angular deviation and monitored the angular displacement and angular motion trajectory of the sealing ring through experiments. Ding X et al. [44] conducted experimental research and comparative analyses on the performance parameters and stability of dry gas seals and obtained the dynamic characteristic coefficients under different speeds and pressures. Rozova and Kolomoets et al. verified the rationality of structural parameter design under different working conditions through experimental research. Based on their work, Fei and Xuexing et al. obtained the stability parameters through experimental research. However, due to the limitations of experimental methods and testing techniques, the parameters obtained are not ideal. The new technology adopted by Lu determined the gas film stiffness and corresponding slot parameters, The theoretical and experimental errors were within a certain range, which not only clarified the design parameters but also reduced the error range, which is helpful for future optimization.
In practical engineering applications, the dynamic operation of dry gas seals is complicated due to random factors such as external excitation disturbances, installation deviations, machining errors, and working condition fluctuations. Currently, there is a gap between the simplified theoretical calculation models of dry gas seal stability based on assumptions and the actual working conditions. This gap results in deviations between the data obtained through testing and the numerical simulation results. Although the existing experimental studies provide references for theoretical modeling and computational coordination optimization, further improvements are needed to achieve accurate measurements. Additionally, the working principle of the dry gas seal involves complex fluid thermodynamics and dynamics. To ensure the feasibility of modeling in theoretical analysis and apply it to experimental design and data analysis, it is necessary to continue to deeply explore its operating mechanism under different working conditions.
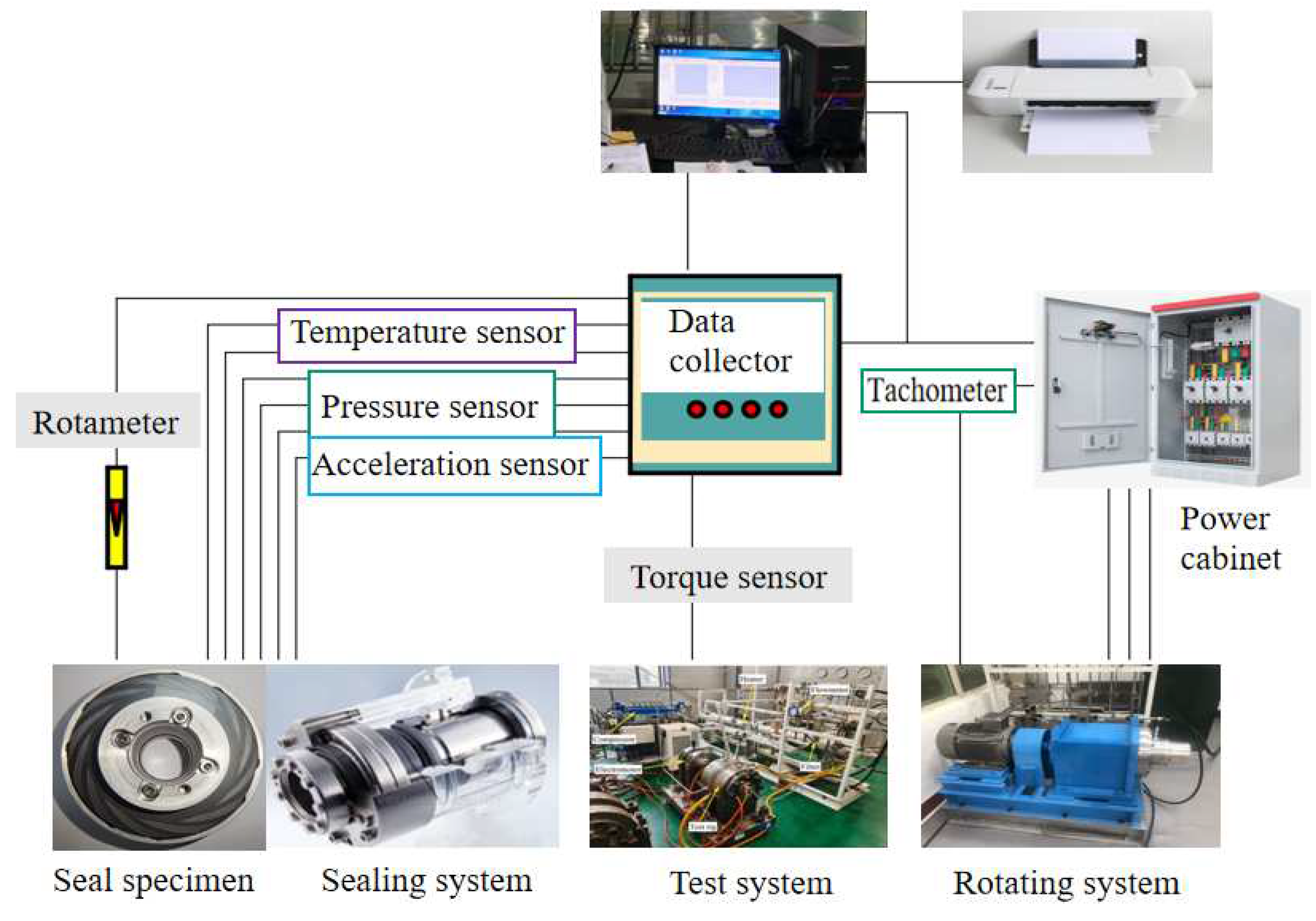
Experimental studies not only validate the theoretical calculations but also provide the basis for monitoring and control of the high-parameter sealing system. Experimentation is the most effective way to solve practical engineering and technological problems and evaluate parameters related to dynamic characteristics of dry gas seal within a certain range. The dry gas seal experimental device is shown in Figure 5. It comprises the seal system, gas path system, power system, and test system. However, with the development of science and technology and the increased demands of extremely complex working conditions, the current experimental research is still insufficient. The three main problems are as follows: (1) poor accuracy due to uncertainty: parts machining accuracy and installation deviations affect the measurement accuracy. (2) The experimental method needs to be improved: The accuracy and authenticity of monitoring data are difficult to verify due to the complex and changeable influencing factors in practical engineering applications and the measurement of the instability region needs to be further improved. (3) Monitoring system improvements: the influences of external excitations on experimental measurements and of the disturbances in experimental equipment signals on experimental accuracy need to be better understood.

3.4. Factors Affecting the Stability of Dry Gas Seals

3.4.1. Starting and Stopping Phases

The starting and stopping processes of dry gas seals are quick, but the sealing mechanism is complicated. During operation, the sealing system inevitably experiences a low-speed stage before the opening of the seal face when transitioning from the stopped state to the operating condition or from the operating rotation to shut down. At this time, the dynamic contact friction caused by external excitation affects the reliability and stability of the sealing system to a certain extent [45,46]. Industrial practice [47] demonstrates that wear failures in dry gas sealing devices occur during the startup and trial operation stages of sealing. Therefore, increasing the stiffness of the gas film improves the stability of dry gas seal operations.
The influence of starting and stopping conditions on the stability of the dry gas seal system was analyzed. To improve the starting stability of the seal system, Wang H et al. [48] analyzed changes in the opening force of the seal face by exploring the starting and stopping conditions of the dry gas seal. They designed a new seal face structure reduces the seal face contact frequency during the starting process. Gao K et al. [49] established a three-dimensional contact model based on the channel structure of the dry gas seal in the starting and stopping stages to study the friction characteristics and the friction thermodynamics of the end-face microtexture under dry friction conditions. Peng X et al. [50] established a dynamic-pressure opening performance analysis model for dry gas seal structures of three typical channels, compared and analyzed the influence of critical dynamic pressure on the opening performance of the seal, and numerically calculated the gas film pressure distribution behavior of the seal end face under different working conditions. Fan W et al. [51] used acoustic emission technology to analyze the stability of the actual startup process and divided the state evolution into the grinding contact stage, normal operation stage, transition stage, and failure stage according to changes in the test parameters. This method provides a comparative reference for exploring the starting and stopping characteristics of dry gas seals in the field of high parameters. Ding X et al. [52] used numerical calculations to analyze the friction characteristics in the unsteady state. They quantified the influences of friction heat caused by elastic deformation stress as well as temperature rise on the sealing performance, which provided a theoretical basis for the later optimization of structural parameter design. Sun X et al. [53] revealed the contact friction mechanical characteristics of the end face of the dry gas seal by analyzing the surface topography of the seal pair experimentally, determining the initial parameters of the contact model, and obtaining the change behavior of the starting parameters of the dry gas seal. Deng Q et al. [54] analyzed the influences of the gas effect and the gap inlet gas film temperature on the startup conditions under different groove parameters. They studied the variations of viscous shear heat during startup, providing certain theoretical references for the engineering design of dry gas seals under high-pressure conditions. Li S et al. 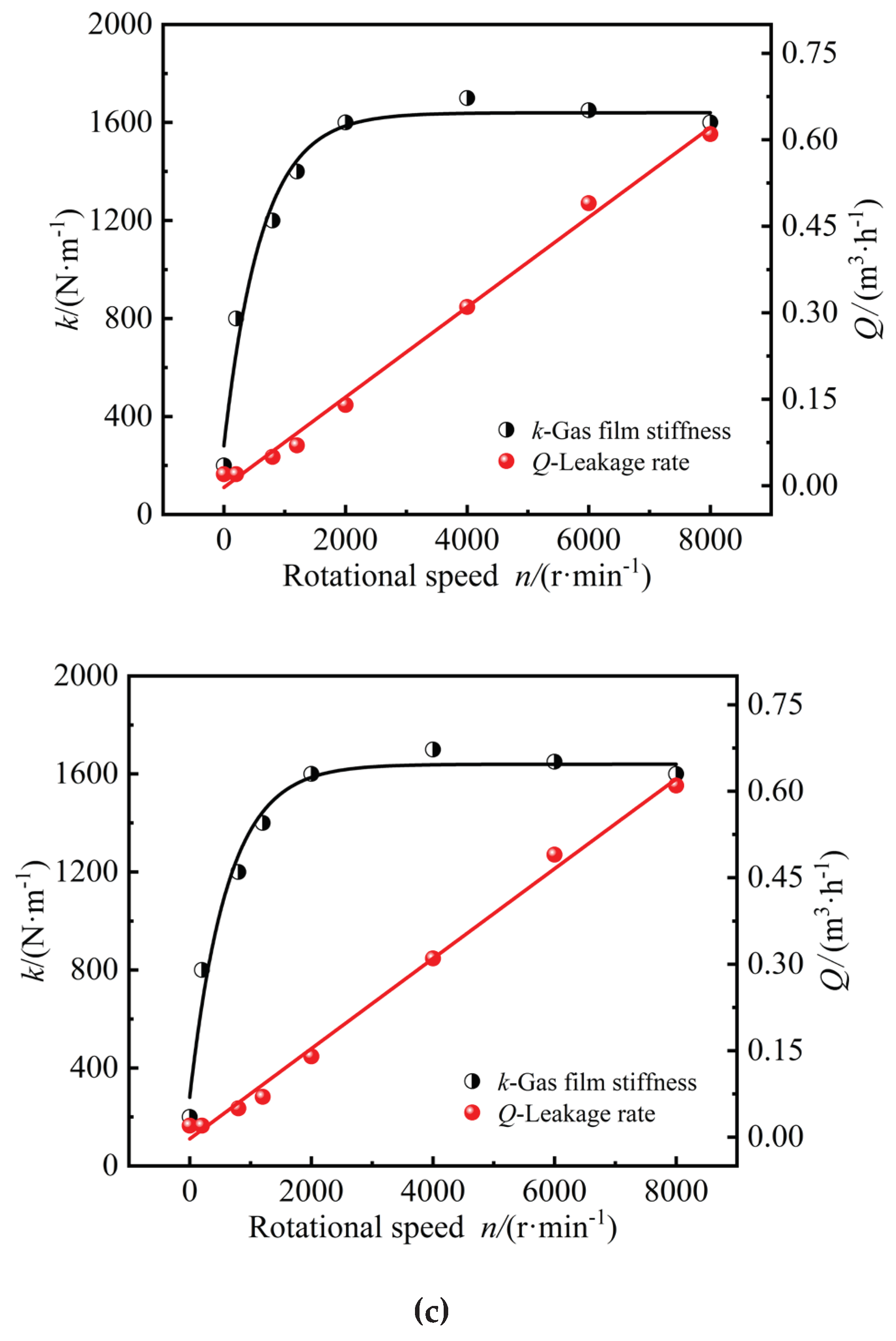[55] put forward the criterion of opening critical speed for analyzing the opening performance of the dry gas seal and analyzed the influence of starting conditions on the seal performance. The performance parameter changes during startup are shown in Figure 6. Figure 6(a) shows the curves for friction power consumption and frictional torque as the rotational speed increases before and after the critical speed. Figure 6(b) indicates that when the operating speed is lower than the critical speed, the seal end face is in contact and Fo < Fc. As speed increases, the dynamic-pressure effect increases sharply. The gas film thickness and opening force increase, and when the critical speed is reached, Fo ≈ Fc. Figure 6(c) demonstrates that the gas film stiffness increases sharply with the increase of dynamic-pressure effect, and then the curve stabilizes with the increasing gas film thickness. When the working speed is lower than the critical speed, the gas film thickness is unchanged, the leakage amount changes slightly, and the leakage amount increases with the increase of the speed.
In the described research, the various scholars analyzed the friction characteristics of the dry gas seal in the starting and stopping stages by numerical calculation, acoustic emission testing, and critical condition parameter discrimination. Friction and vibration in the starting and stopping stage have profound influences on the operating stability of the dry gas seal system and are the main causes of early seal failure. Considering the instantaneity and complexity of the dry gas sealing system during starting and stopping, it is necessary to explore more accurate and advanced analysis methods to develop efficient sealing technology.

3.4.2. Effects of Operating Parameters

Frequent friction failures of the dry gas seal end face in practical engineering applications have affected the normal operation of the dry gas seal [56]. Exploring the operating mechanism of the dry gas seal under fluctuating conditions is the basis for the development of efficient sealing technology.
Based on the Navier–Stokes equation, Wang H et al. [57] analyzed the characteristics of the flow field under different speeds and inlet pressures and concluded that increasing the positive pressure zone and decreasing the negative pressure zone increased the opening force of the seal end face and the stiffness of the film, thereby improving its stability. Kolomoets A et al. [58] experimentally determined the stability parameters of the dry gas seal under different working conditions, which provided a reference for the coordinated optimization of the seal face structure under fluctuating working conditions in the later stage. Hu H et al. [59] analyzed the influence of different speeds, pressures, and temperatures on the steady-state performance of the dry gas seal and on the leakage and friction power consumption. Chen W et al. [60] obtained the flow-field distribution behavior of the dry gas seal under different operating conditions using the finite difference method and calculated the steady-state performance parameters such as opening force and leakage rate. 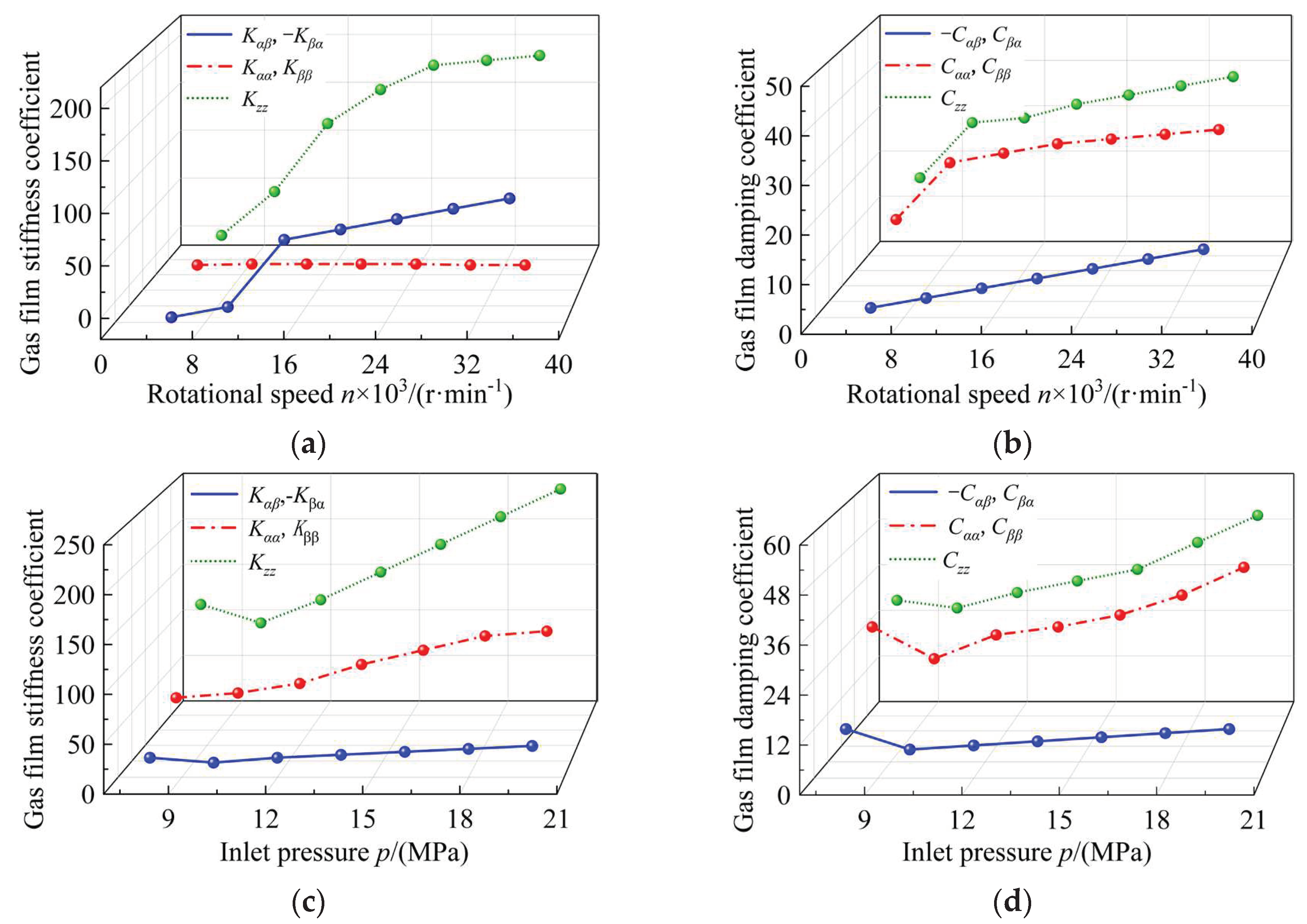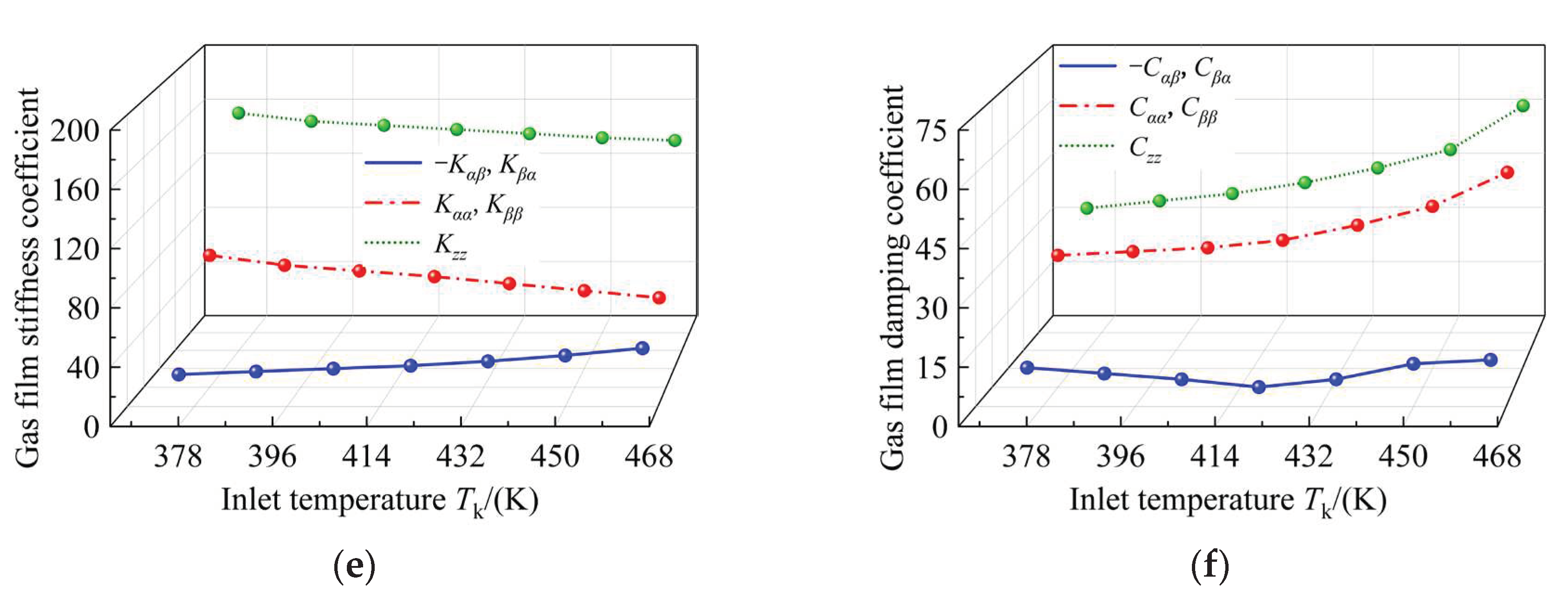Ran R [61] studied the effect of operating parameters on the dynamic characteristics of supercritical carbon dioxide dry gas seals. When the frequency ratio is 1, the changes in the calculated gas film stiffness coefficient and damping coefficient under different working conditions are shown in Figure 7. Figure 7(a) and (b) show that with the increase of rotational speed, the dynamic-stiffness coefficient and damping coefficient of the gas film tend to increase, which is caused by the enhancement of the dynamic-pressure effect. Figure 7(c) shows that the gas film stiffness coefficient increases linearly under different pressures and substantially changes near the critical point. Figure 7(d) shows that the higher the pressure, the greater the medium viscosity and the increase of the gas film resistance. Figure 7(e) shows that the gas film stiffness coefficient decreases at different temperatures, while the damping coefficient increases with the increase of temperature in Figure 7(f). As the temperature increases, the density of the medium decreases and it is easily compressed, which decreases the stiffness coefficient. Similarly, the medium viscosity increases with temperature, and the damping of the dissipation mechanism increases. The research described here shows that the working condition parameters are some of the main factors that affect the dynamic characteristics. Increasing the inlet pressure and the rotational speed will promote the stable operation of the dry gas seal system. Simultaneously, increasing the inlet temperature reduces the ability of the gas film to resist external disturbances, but the mechanism of stabilizing against external disturbances is improved. With increases of medium pressure and rotational speed, both gas film stiffness and gas film damping increase, and the stability is improved to a certain extent.

3.4.3. Influence of the Groove Structure

In the design of dry gas seals, changes in gas film thickness stability are considered. However, in actual production applications, changes in gas film thickness are often ignored to simplify design and reduce costs. In some application scenarios, the stability of the gas film thickness may not be a key issue, so the designer can decide whether to consider the changes of gas film thickness stability according to the actual needs. However, for some key applications such as high-speed rotating equipment, changes in the stability of the gas film thickness may have a serious impact on the safety and performance of the equipment. It is necessary to seriously consider the stability of the gas film thickness and act appropriately to solve the issue. The dynamic-pressure effect of the end surface fluid of the dry gas seal is closely related to the groove parameters. If the groove parameters are not designed properly, the gas pressure is easily destabilized or vibrated, which will affect the operation and service life of the sealing system. To improve the problem of poor stability caused by the weak dynamic-pressure effect of dry gas seals in actual operation, scholars optimized the structural parameters of the dry gas seal end face to meet the demand for gas film stiffness [62].
Zirkelback N et al. [63] studied the influence of the structural parameters of a spiral-groove dry gas seal on dynamic performance, calculated the optimization range of the structural parameters of the end face, and obtained a method to improve the stability of the dry gas seal system. Based on the narrow groove theory, Li Y et al. [64] compared and analyzed dry gas seal structures with an inner-ring groove and with a traditional dry gas seal structure and found that under low-speed and high-pressure conditions, the gas film stiffness of the dry gas seal structure with an inner-ring groove increases, and the difference is <5%. Kou G et al. [65] obtained the maximum steady-state stiffness coefficient of 1.3 and maximum dynamic-stiffness coefficient of 1.4 by improving the stability dynamic analysis of the dry gas seal groove structure. These values can provide references for the optimal design of the dry gas seal structure with low leakage and high stiffness under high-speed working conditions. Yu C et al. [66] designed and analyzed the channel structure of the dry gas seal under different working conditions and believed that a reasonably designed channel structure under high pressures and low speeds could improve the rigid-leakage ratio of the dry gas seal and the gas film stiffness of the seal end face. Huang L et al. [67] compared the stability performance parameters of the traditional spiral groove, spiral groove with an inner-ring groove, and en echelon spiral-groove dry gas seals and concluded that the en echelon spiral-groove dry gas seal has higher stability and better sealing performance than the traditional seal with a wider range of applications. Zirkelback N et al. developed a method to improve stability based on the spiral-groove sealing structure. By comparing and analyzing the dynamic characteristics of the optimized seal structure, Kou G et al. found that the stability was improved. In summary, the structural parameters of the end face have considerable influence on the stability of the dry gas seal. Reasonable structural design can improve the sealing stability and reduce the possibility of leakage. The specific structural parameter designs should be coordinated and optimized according to the actual engineering requirements, working conditions, and relevant experimental verifications.

4. Research Hotspots and Improvement Measures of Dry Gas Seal Stability

4.1. Vibration Response of the Dry Gas Seal System

With the development of rotating machinery for use in extreme conditions, the anti-interference ability of the dry gas sealing device is relatively poor. Most of the existing research is based on steady-state conditions. However, under extreme working conditions, the gas film stability of the sealing end face is easily damaged due to the intensification of shaft vibration. The sealing performance under steady working conditions does not well represent the actual situation. To further improve the reliability of the dry gas sealing device in actual operation, its dynamic behavior is beginning to attract notice. The end clearance and leakage of the dry gas seal fluctuate slightly and the change rate over time is small but their average values are constant; the seal is considered to be in a stable operating state [68]. The vibration response of the dry gas seal refers to the vibration phenomenon caused by an external disturbance or internal instability of the sealing system during operation. Specifically, when the dry gas sealing system is affected by an external disturbance or by internal instability factors, some parts of the system will have unstable vibrations, which are manifested in different forms, such as axial vibration and angular swing. Figure 8 shows a kinematic model of the dry gas seal. When the system is in normal operation, the moving ring and the static ring are not in contact, and there is an extremely thin gas film between the sealing pair. The gas film with certain damping and stiffness characteristics is regarded as a damper and spring structure. Under the synergistic action of the spring-damping structure of the dynamic ring, the dynamic ring responds to the angular and axial excitation, and the sealing ring response follows [69]. The vibration model of the gas film sealing ring is shown in Figure 8(a) [70], and the dynamic analysis model of the gas film is shown in Figure 8(b).
A. According to the axial vibration model of the gas film seal auxiliary system, the axial vibration equation is established:
m x   ″ + C g x ′ + ( K s + K g ) x = K g x d + C g x d ′ = K g b cos ω t − C g b ω sin ω t
B. For the two degrees of freedom angular disturbance of the static ring, the motion equation is established as:
{ J x α ¨ ∗ + [ d ∗ + d s e ∗ ] α ˙ ∗ + d ∗ β ∗ + [ k ∗ + k s p ∗ ] α ∗ + k ∗ β ∗ = 0 J y β ¨ ∗ + d ∗ α ˙ ∗ + [ d ∗ + d s e ∗ ] β ˙ ∗ + k ∗ α ∗ + [ k ∗ + k s p ∗ ] α ∗ = 0
C. The stability conditions of angular oscillation are set as follows
Angular vibration instability condition:
J ≥ J cr
Static ring vibration inertia:
J = 1 4 m ( r o 2 − r i 2 )
Angular vibration stability condition:
J < J cr
D. Judgment and analysis of angular instability:
The microclearance of the dry gas seal is affected by angular swing, which can easily increase the leakage or dry friction of the seal pair. Therefore, it is necessary to ensure the dynamic stability of the gas film between the seal pair. By solving the dynamic motion equation of the gas film and analyzing the relation between the critical moment of inertia (Jcr) and the helix angle (β), the instability range of the helix corner can be obtained, and the stability behavior of the angular swing of the sealing pair can be further analyzed. From the angular vibration instability condition (Eq. (3)), it is known that the swing inertia of the static ring J is greater than Jcr. Because J is small, the instability region is very narrow and only in the point region at Jcr = 0. 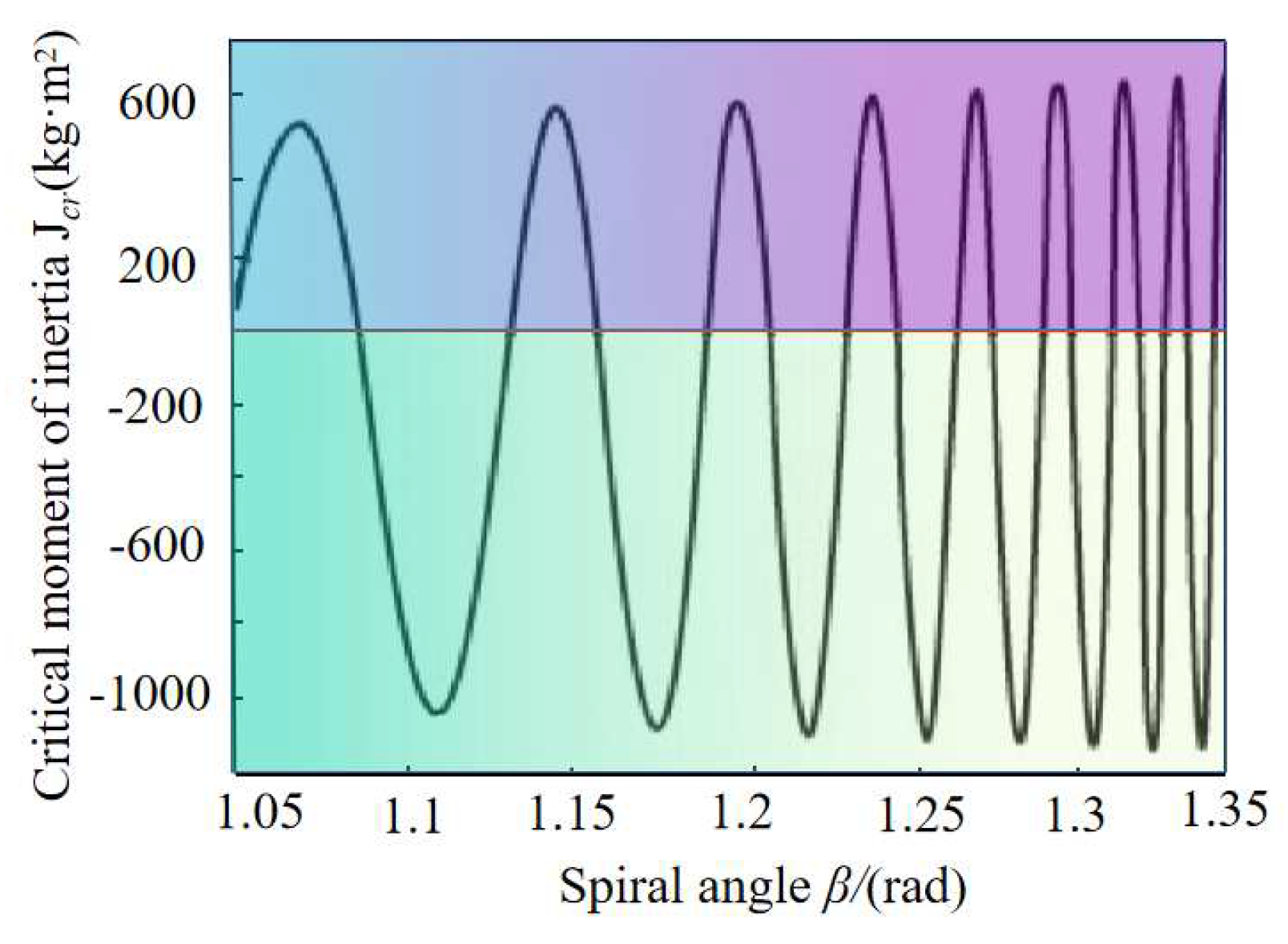Figure 9 shows the relation between Jcr and β. β has 16 instability point domains within the range of 60°~80°, and the specific instability region parameters are shown in Table 2. 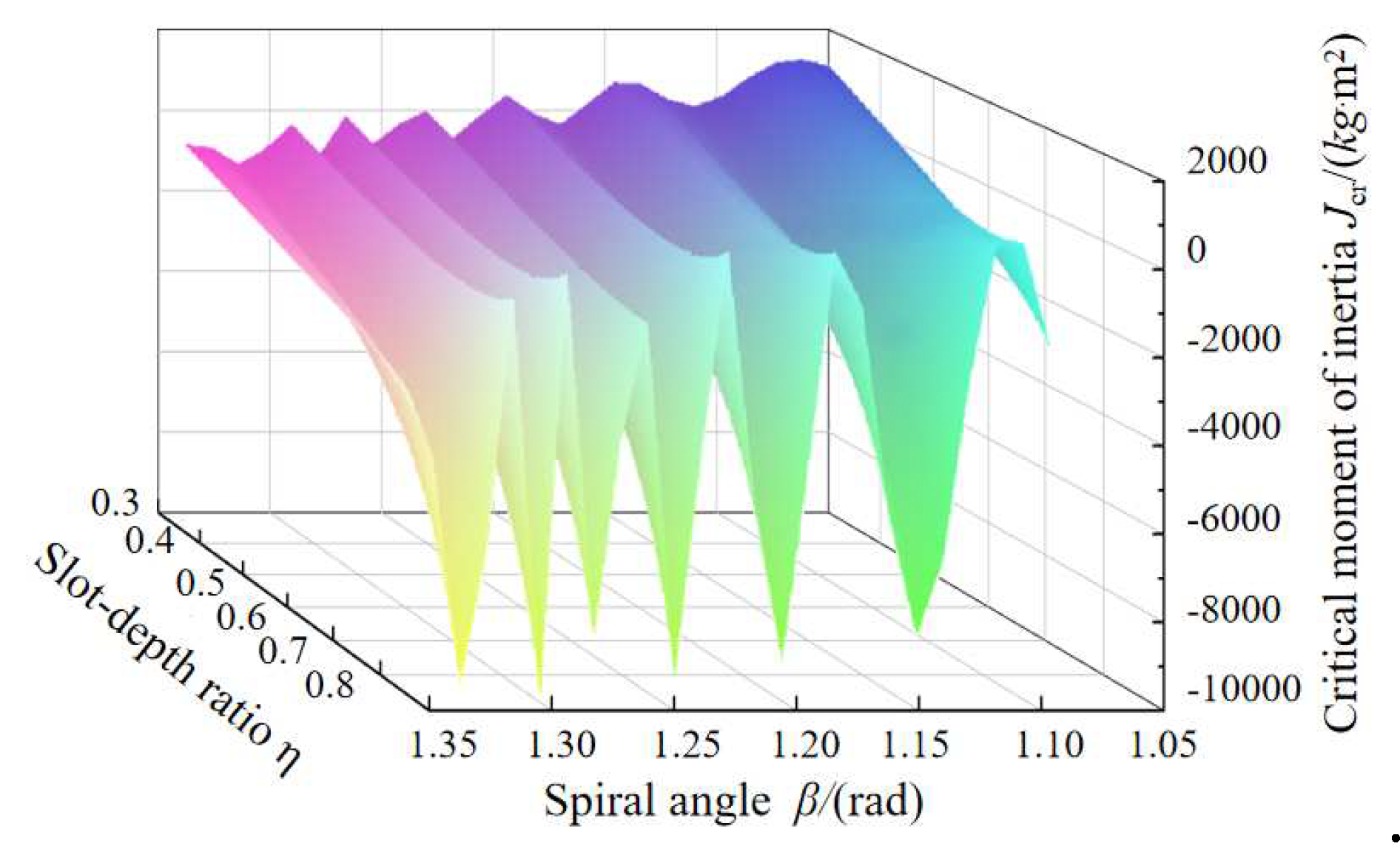Figure 10 shows the relations between Jcr, β, and slot depth ratio (η). The surficial changes in Figure 10 indicate that β has a major influence on Jcr, and the steady-state optimized β has a discontinuous stable region in the range of 60°~80° [71].
The instability region parameter ranges of the dry gas seal are judged by the angular swing stability condition. Based on the above research, Mingjun et al. [72] analyzed the dynamic stability of the dry gas seal system with the Floquet theory as the criterion for the stability of the angular swing, and obtained the influences of the spiral angle range and damping size of the system on the chaotic motion during stable operation. The effect of the axial-vibration response on the stability of the dry gas seal were also analyzed. Based on the Laplace transform, Teng L et al. [73] obtained the axial-vibration and forced-vibration-displacement responses of dry gas seals under different conditions and analyzed the influence of external factors and dynamic characteristic parameters on the axial vibration. Liu Y et al. [74] studied the dynamic characteristics of the gas film thickness stability in the dry gas sealing system based on numerical calculations. They analyzed the factors affecting the vibration response and stability under different working conditions by establishing axial vibration models of the dynamic and static rings. Ding X et al. [75] analyzed the dynamic stability of the dry gas seal based on the nonlinear vibration theory and microscale thermal dissipation deformation and obtained the stable operation ranges for the structural parameters of the end face of the seal pair. The bifurcation problem of the system is studied by solving the Floquet index method without external excitation. Zhang W et al. [76] analyzed the axial-vibration and angular-oscillation stability of the dry gas seal system in an impeller rotor system and obtained the influences of gas film stiffness and excitation force on axial vibration and angular oscillation.
Based on the research on dry gas seal stability models in Table 1 and the research described in this section, it is considered that the perturbation method and the Runge–Kutta method have high calculation accuracy and strong reliability and are the first choices for research algorithms to analyze the axial-vibration and angular-oscillation responses of the dry gas seal system. The effect of the dry gas seal vibration response on the normal operation and service life of rotating equipment is analyzed. When the equipment vibrates, the dry gas seal may leak or generate additional friction, which will affect the service performance of the equipment. In addition, the power consumption or torque of the dry gas seal increases with the rotating speed during operation, and the rotation speed and impact load response also have certain effects on the dynamic characteristics of the dry gas seal. Therefore, the vibration response of the sealing system should be minimized to ensure the normal operation.

4.2. Improving the Dynamic Followability and Reducing Film Thickness Disturbances

The thickness disturbance amplitude of the dry gas sealing film reflects the dynamic followability of sealing system. Most scholars calculate the dynamic-stiffness coefficient and damping coefficient to determine whether the sealing system is unstable due to self-induced vibration, and then evaluate the dynamic characteristics of the gas film. However, in addition to the influence of the gas film dynamic coefficients on the stability, the flexible installation form of the seal ring and the stiffness or damping characteristics of the elastic element or the auxiliary seal ring greatly affect the dynamic tracking of the seal device.
To further reduce the film thickness disturbance and improve the dynamic stability of the dry gas seal, Blasiak S et al. [77] compared and analyzed the dynamic followability of sealing devices with various groove types and learned that operating speed, groove structure, and elastic components would all affect the axial-vibration and angular-swing responses of the sealing system. Based on the above research, a test device was designed to compensate for the dislocation of the flexible mounting ring and automatically control the height of radial clearance. Su H et al. [78] calculated the dynamic characteristics of the gas film on the end face of the bidirectional dry gas seal, and then analyzed the influence of the gas film thickness on its stability. By improving the dynamic followability, the film thickness disturbance is reduced, and the operating stability is further improved. Green I et al. [79] coupled the Reynolds equation and motion equation to study the transient motion behavior of the film thickness disturbance and the static ring flexible installation. They conducted a structural coordination optimization, and finally obtained a reasonable clearance structure that was conducive to the dynamic followability of the seal ring. Hu S et al. [80] analyzed the dynamic performance of dry gas seals under different disturbance conditions and the influence of auxiliary sealing rings. They concluded that the gas film force between the dynamic and static sealing rings indirectly alleviates the interaction between axial vibration and angular oscillation, and effectively weakens the transient vibration caused by disturbance. Shang H et al. [81] studied three typical dry gas seal structures under different film thickness disturbances and believed that when the gap film thickness amplitude of the seal pair was severe, the average values of the sealing performance parameters were slightly higher than the steady-state values, and the calculation errors were large. The typical spiral-groove dry gas seal is less affected by nonlinear factors and is in good agreement with the actual changes. 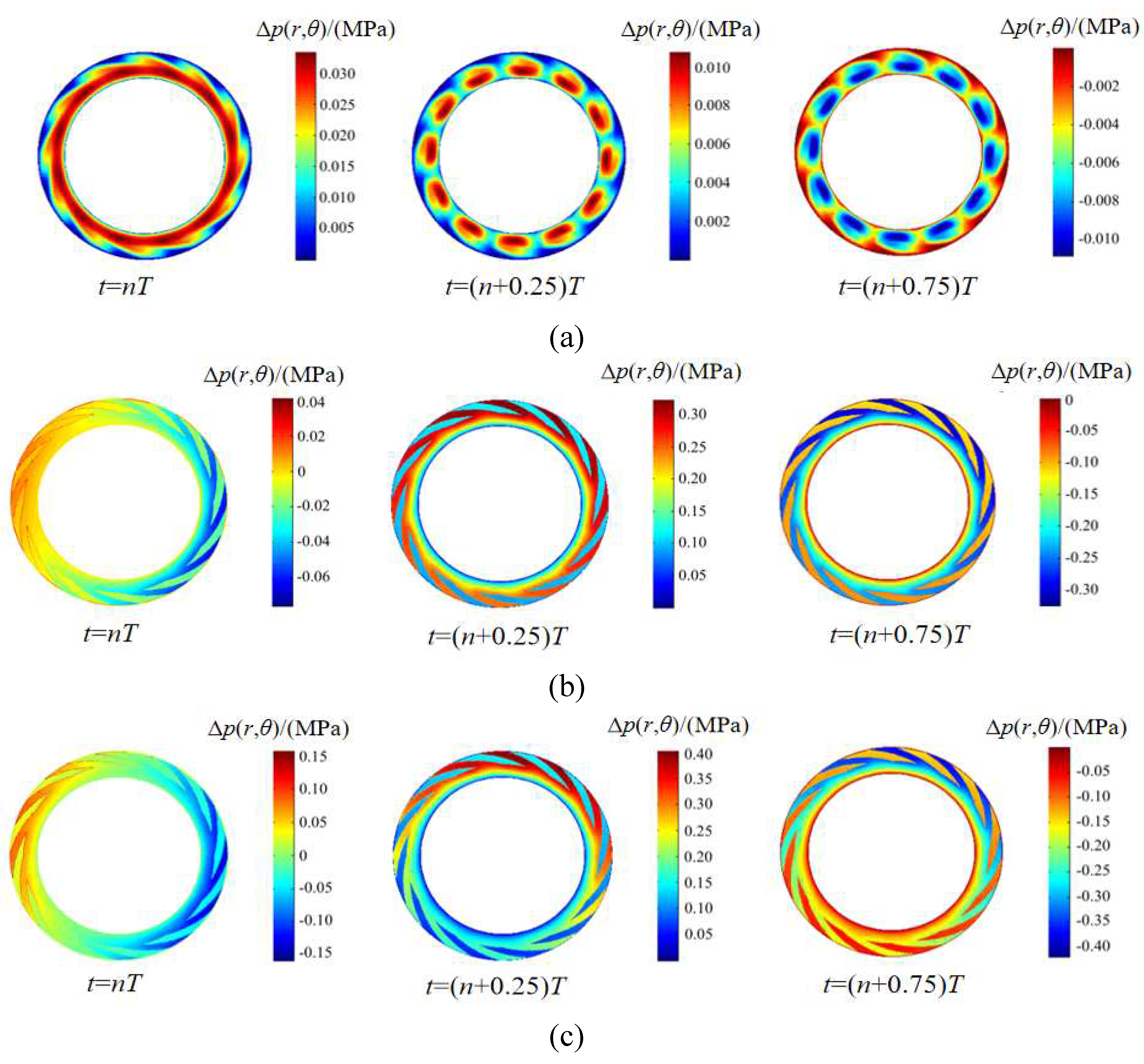Figure 11 [82] shows the transient disturbance distribution of dry gas seal film pressure. Figure 11(a)–(c) show the film pressure distribution cloud maps on the seal end face at various times during the rotation period when the film pressure disturbance Δp(r, θ) is generated at the angular excitation amplitudes of Ar = 0 μrad, Ar = 100 μrad and Ar = 300 μrad respectively. The cloud images show that the membrane pressure disturbance is obvious when the excitation amplitude is greater than 0. The main reason is that the wedge gap formed between the sealing pairs after the angular excitation affects the dynamic and static pressures. The greater the excitation, the greater the nonuniform membrane pressure disturbance. By comparing the film pressure disturbance Δp(r, θ) at different times with the same amplitude, it is found that the wedge-shaped gap at a certain angle severely disturbs the gas film, and the amplitude is also affected by the axial film thickness disturbance, which indicates that the film pressure of the dry gas seal is affected by the interaction between the wedge-shaped gap and the axial disturbance.
The stability of dry gas seal is improved by increasing the dynamic stiffness of the dry gas seal system or considering compensation measures to offset the disturbance of the film thickness. To solve the problem of frequent failure caused by the insufficient disturbance capacity of the dry gas sealing system under extreme operating conditions, two actions can be taken: (1) coordinate and optimize the structural design parameters. Reasonable structural design and layout result in a small low-frequency disturbance amplitude, which is conducive to maintaining the stability of the seal end face. (2) Improve dynamic followability and use active control technology, such as a vibration suppression device or adaptive adjustment, to adjust the sealing system in real time. By improving the sealing environment, reducing external excitation interference, or using dynamic balancing technology to balance the rotating parts of the equipment, the problem of film thickness disturbance can be alleviated, and the dynamic stability of the dry gas sealing system can be improved.

5. Conclusions

The dynamic characteristics and stability of dry gas seals are reviewed and summarized in this work. To ensure the excellent dynamic characteristics of the dry gas sealing system, structural design and performance analyses have been conducted to determine the best structural design parameters by considering the influencing factors under multiple effects. The stability of the dry gas seal is crucial for the reliability and safety of the rotating equipment; if not optimized and controlled, it will easily lead to friction and wear, leakage, and even failure of the seal end face. This review highlights the importance of the stiffness and damping coefficients of the gas film for evaluating dynamic stability as well as the effectiveness of experimental research in model verification. The research methods of stability models provide a theoretical basis for comprehensively characterizing the nonlinear dynamic behavior of dry gas seals. In addition, the effects of starting and stopping characteristics, working parameters, and groove parameters on the flow characteristics of the dry gas seal have been analyzed. Finally, the influence of vibration responses on dynamic stability and reliability is discussed. Although the dry gas sealing system has been studied from the aspects of operating mechanism, research methods, dynamic characteristics, vibration response, etc., the following problems remain to be solved in terms of dynamic stability:
(1) The coupling effect between multiple factors has been ignored, and the sealing performance in the actual environment is comprehensively affected by various factors such as gas dynamics, heat conduction, and fluid mechanics. The current theoretical models tend to treat these factors independently, ignoring the interactions and coupling effects among them, resulting in incomplete descriptions and predictions of dry gas sealing behavior.
(2) The experimental data is affected by calculation errors, working conditions, and external interference, which can easily lead to inaccuracies. Concurrently, there are differences in experimental methods and complex conditions, resulting in some errors in experimental results.
(3) The dynamic vibration response relies on numerical simulation and theoretical derivation and lacks unified standard mathematical models and evaluation methods to predict the dynamic behavior and nonlinear effects of dry gas seals, resulting in limitations of research results.

6. Development Trend

Dry gas sealing technology has a wide range of applications in industrial and manufacturing fields, especially in high-speed rotating equipment and high sealing requirements. With the progress and innovation of science and technology, additional developments are expected in terms of improving efficiency, expanding applications, increasing reliability, and reducing costs.
(1) A remote intelligent control system is used to monitor and adjust the working status of the sealing system in real time, and regular predictive maintenance is conducted to describe the stable operating status of the dry gas sealing system in a more timely and accurate manner and improve its operational reliability.
(2) Exploration can be conducted on the application of new materials and coating technologies to adapt to extreme working environments such as high or low temperature or pressure. Strengthen the coordinated optimization to further reduce the gap leakage, reduce energy consumption and environmental pollution, improve the service cycle of the dry gas sealing system. Further study the advanced sealing technology for stable operation in a wide temperature and pressure range.
(3) There are corrosion and wear challenges in some industrial environments, which can easily lead to the deterioration of the dry gas seal performance. Future development can focus on more wear-resistant and corrosion-resistant materials to expand the application range of dry gas seals.
(4) Lubrication plays a key role in sealing performance and friction loss. The use of advanced lubrication technology, such as nanoscale lubricants or frictionless lubrication technology, can effectively reduce energy consumption and leakage.

Author Contributions

Conceptualization, L.Z. and X.D.; methodology, L.Z.; validation, L.Z., and X.D.; formal analysis, L.Z.; investigation, S.Z.; resources, S.W.; data curation, X.D.; writing—original draft preparation, L.Z.; writing—review and editing, L.Z.; visualization, S.W.; supervision, S.Z.; project administration, J.D.; funding acquisition, L.Z. All authors have read and agreed to the published version of the manuscript.

Funding

The research was supported by the National Natural Science Foundation of China (No. 51565029) and Ningbo Major Special Project (No. 2020Z112).

Acknowledgments

All the authors would like to support the result the results of this study are included within the manuscript.

Conflicts of Interest

The authors declare that the research was conducted in the absence of any commerical or financial relationships that could be construed as a potnetial conflict of interest.

Nomenclature

Ar angular excitation amplitude, μrad
cxx, cyx angular principal dynamic damping and angular cross damping, N·s/rad
czz axial dynamic damping, N·s/m
Cαα, Cαβ, Cββ dimensionless damping coefficient
Fc, Fo closing force, opening force, N
h, ho transient gas film thickness, equilibrium gas film thickness, μm
J, Jcr static ring swing inertia, critical moment of inertia, kg·m2
kxx, kyx angular principal dynamic stiffness and angular cross stiffness, N·m/rad
kzz axial dynamic stiffness, N/m
Kαα, Kαβ, Kββ dimensionless stiffness coefficient
n rotational speed, r/min
p, p1, p2, psp inlet pressure, medium pressure, back pressure and spring pressure, MPa
Q leakage, m3/h
r, ri, ro the radius of any point on the moving ring, inner radius and outer radius, mm
t time, s
Tf frictional torque, N·m
Tk Inlet temperature, K
Wf frictional power consumption, W
x, y, z x axis, y axis and z axis
α, β helix angle and helix angle, rad
η slot-depth ratio
ω moving ring angular velocity, rad/s
Δp film pressure disturbance, MPa
Δα, Δβ, Δz perturbation displacement in the x, y, z direction

References

  1. He, X.; Wang, H.; Li, R.; Sun, H.; Chen, H.; Li, C.; Ge, G. Thermo-Conversion of a Physical Energy Storage System with High-Energy Density: Combination of Thermal Energy Storage and Gas-Steam Combined Cycle. J. Energy. 2022, 239, 122325. [Google Scholar] [CrossRef]
  2. Fan, Z.; Friedmann S, J. Low-Carbon Production of Iron And Steel: Technology Options, Economic Assessment, and Policy. J. Joule. 2021, 5, 829–862. [Google Scholar] [CrossRef]
  3. Wang, Z.; Duan, L. Thermoeconomic Optimization of Steam Pressure of Heat Recovery Steam Generator in Combined Cycle Gas Turbine under Different Operation Strategies. J. Energies 2021, 14, 4991. [Google Scholar] [CrossRef]
  4. Yang, Z.; Luo, D.; Huang, D. Research on a Transonic Supercritical Carbon Dioxide Centrifugal Turbine. J. Journal of Nuclear Engineering and Radiation Science 2019, 5, 041202. [Google Scholar] [CrossRef]
  5. Zhou, D.; Wei, T.; Huang, D.; Liang, M.; Zhang, H.; Weng, S.; Jiang, P.J. Journal of Pressure Vessel Technology 2021, 143, 031702. [CrossRef]
  6. Mayhew, E.; Bill, R.; Voorhees, W. Military Engine Seal Development-Potential for Dual Use. 30th Joint Propulsion Conference and Exhibit. 1994. [Google Scholar]
  7. Atkinson, S. Service Centre Helps John Crane to Repair and Test Dry Gas Seals Locally Within Qatar. J. Sealing Technology. 2019, 6, 5. [Google Scholar] [CrossRef]
  8. Childs, D.; Elrod, D.; Hale, K. Annular Honeycomb Seals: Test Results for Leakage and Rotordynamic Coefficients; Comparisons to Labyrinth and Smooth Configurations. J. Tribol. 1989, 111, 293–300. [Google Scholar] [CrossRef]
  9. Raben, M.; Friedrichs, J.; Helmis, T.; Flegler, J. Brush Seals Used in Steam Environments-Chronological Wear Development and the Impact of Different Seal Designs. J. Journal of Engineering for Gas Turbines and Power 2016, 138, 051901. [Google Scholar] [CrossRef]
  10. Li, G.; Zhang, Q.; Lei, Z.; Huang, E.; Wu, H.; Xu, G. Leakage Performance of Labyrinth Seal For Oil Sealing of Aero-Engine. Propulsion and Power Research 2019, 8, 13–22. [Google Scholar] [CrossRef]
  11. Laxander, A.; Fesl, A.; Hellmig, B. Development and Testing of Dry Gas Seals for Turbomachinery in Multiphase CO2 Applications. European Supercritical CO2 Conference 2019, 1–11. [Google Scholar]
  12. Cao, H.; Liu, Y.; Lin, C. Failure Analysis and Transformation of Hydrogen Compressor Dry Gas Seal. J. Applied Mechanics & Materials 2013, 331, 98–101. [Google Scholar]
  13. Deng, Q.; Song, P.; Xu, H.; Mao, W.; Sun, X. Analysis on the Startup Characteristics of CO2 Dry Gas Seal Based on the F-K Slip Flow Model at High Pressure. J. Advances in Mechanical Engineering. 2023, 15, 1–13. [Google Scholar] [CrossRef]
  14. Jin, Z.; Li, S.; Cai, J.; Zhang, Q. Optimizing on Hydrostatic Structural Parameters for Regulatable Dry Gas Seal Based on Central Composite Design Test. J. Industrial Lubrication and Tribology. 2016, 68, 99–105. [Google Scholar] [CrossRef]
  15. Saxena, M. Dry Gas Seals and Support Systems: Benefits and Options. J. Hydrocarbon Processing 2003, 82, 37–41. [Google Scholar]
  16. Chen, W.; Song, P.; Xu, H.; Sun, X. Study on Startup Process of Carbon Dioxide with Impurities Lubricating Dry Gas Seal. J. Lubrication Engineering 2022, 47, 1–9. [Google Scholar]
  17. Su, H.; Rahmani, R.; Rahnejat, H. Performance Evaluation of Bidiectional Dry Gas Seals with Evaluation of Bidirectional Dry Gas Seals With Special Groove Geometry. J. Tribology Transactions 2017, 60, 58–69. [Google Scholar] [CrossRef]
  18. Xu, H.; Yue, Y.; Song, P.; Mao, W.; Deng, Q.; Sun, X. Analysis on the Dynamic Characteristics of Spiral Groove Dry Gas Seal Based on the Gas Film Adaptive Adjustment Model. J. Industrial Lubrication and Tribology 2023, 75, 406–414. [Google Scholar] [CrossRef]
  19. Badykov, R.; Falaleev, S. Advanced Dynamic Model Development of Dry Gas Seal. J. Procedia engineering. 2017, 176, 344–354. [Google Scholar] [CrossRef]
  20. Ding, X.; Pu, J.; Han, M.; Zhang, W.; Yu, S. Calculation and Analysis of Gas Film Stiffness in the Spiral Groove Gas Seal Based on the Second Order Slip Boundary. J. Journal of mechanical engineering 2011, 47, 119–124. [Google Scholar] [CrossRef]
  21. Liu, Y.; Xu, W.; Wang, Z.; Shen, X. Dynamic Coefficients for Gas Film Face Seal. J. Tsinghua Univ. (Sci. & Technol.) 2002, 42, 185–189. [Google Scholar]
  22. Xu, H.; Song, P.; Mao, W.; Deng, Q. Dynamic Characteristics of Spiral Groove Dry Gas Seals with Consideration of Hydrogen Real Gas and Choked Flow Effects. J. CIESC Journal 2017, 68, 4675–4684. [Google Scholar]
  23. Yang, Q.; Sun, X.; Hao, M.; Mei, B.; Li, Z.; Ren, B. Study on Dynamic Characteristics of Supercritical Carbon Dioxide Dry Gas Seal Considering Inertia Effect. J. Lubrication Engineering 2022, 47, 44–52. [Google Scholar]
  24. Faria, M. Finite Element Analysis of the Misalignment Effects on The Dynamic Force Coefficients of Spiral Groove Gas Face Seals. J. JSME International Journal Series C 2004, 47, 289–296. [Google Scholar] [CrossRef]
  25. Sato, Y.; Ochiai, M. Flow Visualization of Non-Contacting Mechanical Seals with Bidirectional Rotation. Journal of Physics: Conference Series. IOP Publishing 2022, 2217, 012–028. [Google Scholar] [CrossRef]
  26. Zirkelback, N.; Andrés, L. Effect of Frequency Excitation on Force Coefficients of Spiral Groove Gas Seals. J. Journal of Tribology Transactions of the ASME. 1999, 121, 853–861. [Google Scholar] [CrossRef]
  27. Ruan, B. A Semi-Analytical Solution to the Dynamic Tracking of Non-Contacting Gas Face Seals. Journal of Tribology 2002, 124, 196–202. [Google Scholar] [CrossRef]
  28. Ding, X.; Liu, Y.; Chen, Z.; Wu, H.; Yan, F. Research on Flow Characteristics of Micro-Gas Film In the Spiral Groove Dry-Gas Seal under the Thermo-Elastic Deformation Considering the Thermal Dissipation. J. Engineering mechanics 2014, 31, 237–243. [Google Scholar]
  29. Liu, X.; Xu, C.; Huang, W. Analysis and Parametric Design of the Dynamics of a Dry Gas Seal for Extreme Operating Conditions Using a Semi-Analytical Method. J. Tsinghua Univ. (Sci. & Technol.) 2014, 54, 223–228. [Google Scholar]
  30. Liu, Y.; Liu, Q.; Yin, M.; Yin, G. Dynamic Feature Optimization of Dry Gas Seal Based on Particle Swarm Optimization and Projection Pursuit. J. Advanced Engineering Sciences 2019, 51, 248–255. [Google Scholar]
  31. Chen, Y.; Jiang, J.; Peng, X. Gas Film Disturbance Characteristics Analysis of High-Speed and High-Pressure Dry Gas Seal. Chinese Journal of MechanicalEngineering 2016, 29, 1226–1233. [Google Scholar] [CrossRef]
  32. Elrod, H.; Mccabe, J.; Chu, T. Determination of Gas-Bearing Stability By Response to a Step-Jump. J. Journal of Tribology 1967, 89, 493–498. [Google Scholar] [CrossRef]
  33. Ding, X.; Wang, Y.; Zhang, W.; Yu, S.; Du, Z. A Stability Analysis for Lubricating Gaseous Film of Spiral Grooved Gas Seals Subjected to Angular Eddy Motion. J. Journal of Beijing University of Chemical Technology. 2008, 35, 82–86. [Google Scholar]
  34. Zhang, W.; Yu, S.; Ding, X.; Han, M.; Du, Z. Stability Analysis and Vibratory Response of Angular Wobbly In The System of Dry Gas Seal. J. Journal of Vibration and Shock 2011, 30, 96–99. [Google Scholar]
  35. Wang, Y.; Zhou, X.; Wang, D.; Zhou, Y.; Cao, B.; Yang, X. Analysis Stability Factor of Dry Gas Seal Based On Fault Tree. J. Mechanical Engineering & Automation 2017, 28–30. [Google Scholar]
  36. Miller, B.; Green, I. Numerical Techniques for Computing Rotordynamic Properties of Mechanical Gas Face Seals. J. Journal of Tribology 2002, 124, 1–9. [Google Scholar] [CrossRef]
  37. Liu, Y.; Liu, Q.; Yin, M.; Yin, G. Dynamic Analysis and Structure Optimization of a Floating Ring System In Dry Gas Seal. Journal of Advanced Mechanical Design, Systems, and Manufacturing 2018, 12, 1–18. [Google Scholar] [CrossRef]
  38. Rozova, L.; Martynenko, G. Information technology in the modeling of dry gas seal for centrifugal compressors. 2020.
  39. Kolomoets, A.; Dotsenko, V. Experimental Investigation of Dry Gas-Dynamic Seals Used for Gas-Compressor Unit. Procedia Engineering 2012, 39, 379–386. [Google Scholar] [CrossRef]
  40. Green, I. Real-Time Monitoring and Control of Mechanical Face-Seal Dynamic Behavior. Sealing Technology 2001, 96, 6–11. [Google Scholar] [CrossRef]
  41. Lu, J. Theoretical Analysis and Experiment On Gas Film Stiffness with Slip Flow In a Spiral-Grooved Dry Gas Seal. J. Industrial Lubrication and Tribology 2021, 73, 1226–1236. [Google Scholar] [CrossRef]
  42. He, F.; Kang, Z. Experimental Study On Gas Film Flow Field of Dry Gas Seal End Face. Technology & Development of Chemical Industry 2019, 48, 42–47. [Google Scholar]
  43. Zou, M.; Dayan, J.; Green, I. Dynamic Simulation and Monitoring of a Non-Contacting Flexibly Mounted Rotor Mechanical Face Seal. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science 2000, 214, 1195–1206. [Google Scholar] [CrossRef]
  44. Ding, X.; Lu, J. Theoretical Analysis and Experiment On Gas Film Temperature In a Spiral Groove Dry Gas Seal Under High Speed and Pressure. International Journal of Heat and Mass Transfer 2016, 96, 438–450. [Google Scholar] [CrossRef]
  45. Hu, F.; He, Q.; Huang, W.; Yin, Y.; Wen, X.; Liu, Y.; Wang, Y. Face grooves for state monitoring in dry gas seals. Tribology International 2023, 189, 108950. [Google Scholar] [CrossRef]
  46. Kröger, M.; Neubauer, M.; Popp, K. Experimental Investigation on the Avoidance of Self-Excited Vibrations. Philosophical Transactions. Series A, Mathematical, Physical, and Engineering Sciences 2008, 366, 785–810. [Google Scholar] [CrossRef]
  47. Huang, W.; Lin, Y.; Liu, Y.; Gao, Z.; Wang, Y. Face Rub-Impact Monitoring of a Dry Gas Seal Using Acoustic Emission. J. Tribology Letters 2013, 52, 253–259. [Google Scholar] [CrossRef]
  48. Wang, H.; Chen, C.; Huang, Z.; Wang, X. Research on Start-Up Process of Dry Gas Seal. Lubrication engineering 2006, 1, 14–16, 19. [Google Scholar]
  49. Gao, K.; Mutellip, A.; Zhang, Z. Study on Friction Thermodynamics of the microstructure of Dry Gas Seal Interface during the Start-Stop Phase. J. Lubrication Engineering 2021, 46, 68–74. [Google Scholar]
  50. Peng, X.; Liu, K.; Bai, S.; Li, J.; Sheng, S. Dynamic Opening Characteristics of Dry Gas Seals with Typical Types of Spiral Grooves. CIESC J. 2013, 64, 326–333. [Google Scholar]
  51. Fan, W.; Huang, W.; Liu, Y.; Yin, Y.; Liu, X.; Wang, Y. State Evolution of Dry Gas Seal During Repeated Start-Stop Operation Usingacoustic-Emission Method. J. Tribology Transactions 2020, 63, 173–181. [Google Scholar] [CrossRef]
  52. Ding, X.; Wang, W.; Jin, H.; Zhao, H. A Numerical Simulation Study of Frictional Characteristics of Seal Faces on the Starting and Stopping Process of a Dry Gas Seal. J. Journal of petrochemical universities 2017, 30, 91–96. [Google Scholar]
  53. Sun, X.; Song, P.; Mao, W.; Deng, Q.; Xu, H.; Chen, W. Analysis of Dynamic Contact Characteristics of Dry Gas Seal During Start-Up and Stop Considering Seal Ring Material Properties and Surface Morphology. CIESC J. 2021, 72, 4279–4291. [Google Scholar]
  54. Deng, Q.; Song, P.; Hu, X.; Hu, X.; Xu, H.; Sun, X.; Mao, W. Startup Performance of Dry Gas Seals with Different Types of Grooves Considering the Slip Flow Effect. In International Workshop of Advanced Manufacturing and Automation; Springer: Singapore, 2022; pp. 578–586. [Google Scholar]
  55. Li, S.; Song, W.; Zhang, Q.; Cai, J.; Gao, J. Opening Characteristics of Dry Gas Seal. CIESC J. 2011, 62, 766–772. [Google Scholar]
  56. Fairuz, Z.; Jahn, I.; Abdul-Rahman, R. The Effect of Convection Area on the Deformation of Dry Gas Seal Operating with Supercritical CO2. Tribology International 2019, 137, 349–365. [Google Scholar] [CrossRef]
  57. Wang, H.; Chen, C.; Wang, J. Numerical Simulation of Face Flow Field for Dry Gas Seal. J. Journal of Southwest Jiaotong University 2007, 42, 568–573. [Google Scholar]
  58. Kolomoets, A.; Dotsenko, V. Experimental Investigation Dry Gas-Dynamic Seals Used for Gas-Compressor Unit. Procedia Engineering 2012, 39, 379–386. [Google Scholar] [CrossRef]
  59. Hu, H.; Ling, L.; Yu, X.; Song, H.; Qian, J. Simulation Analysis on Sealing Performance of Supernal Parameters Supercritical Carbon Dioxide Dry Gas Seal. J. Process Equipment & Piping 2022, 59, 62–68. [Google Scholar]
  60. Chen, W.; Song, P.; Xu, H.; Song, X. Calculation of Physical Parameters and Analysis of Temperature Fields of CO2 with Impurities Dry Gas Seal at Operating Points. J. Advanced Engineering Sciences 2023, 55, 265–278. [Google Scholar]
  61. Yan, R.; Chen, H.; Zhang, W.; Hong, X.; Bao, X. Calculation and Verification of Flow Field in Supercritical Carbon Dioxide Dry Gas Seal Based on Turbulent Adiabatic Flow Model. Tribology International 2022, 165, 107275. [Google Scholar] [CrossRef]
  62. Laxander, A.; Fesl, A.; Hellmig, B. Development and Testing of Dry Gas Seals for Turbomachinery in Multiphase CO2 Applications. 3rd European Supercritical CO2 Conference. 2019; 1–11. [Google Scholar]
  63. Zirkelback, N. Parametric Study of Spiral Groove Gas Face Seals. J. Tribology Transactions 2000, 43, 337–343. [Google Scholar] [CrossRef]
  64. Li, Y.; Song, P.; Xu, H. Performance Analyses of the Spiral Groove Dry Gas Seal with Inner Annular Groove. Applied Mechanics and Materials 2013, 420, 51–55. [Google Scholar] [CrossRef]
  65. Kou, G.; Li, X.; Wang, Y.; Lin, M.; Tan, C.; Mou, M. Steady Performance and Dynamic Characteristics of a Superellipse Groove Dry Gas Seal at a High-Speed Condition. J. Industrial Lubrication and Tribology 2020, 72, 789–796. [Google Scholar] [CrossRef]
  66. Yu, C.; Jiang, J.; Zhao, W.; Li, J.; Peng, X.; Wang, Y. Geometrical Model of Surface Groove Based on Microsegment Combination for Dry Gas Seal and Its Parameter Influence. CIESC J. 2021, 72, 5294–5309. [Google Scholar]
  67. Huang, L.; Peng, X.; Bai, S.; Li, J.; Sheng, S. Comparison Study on Performance of Three Types of Dry Gas Seal with Different Grooves. J. Fluid Machinery 2010, 38, 14–17. [Google Scholar]
  68. Zhu, W.; Wang, H.; Zhou, S.; Chen, X. Research on Face Fluid Field and Seal Performance of T-Shape Groove Dry Gas Seal. 2009 Second International Conference on Intelligent Computation Technology and Automation IEEE 2009, 2, 902–906. [Google Scholar]
  69. Wang, Y.; Hu, Q.; Xiao, Y.; Huang, G.; Zhu, Y.; Ge, Y. Turbulence Effect and Suppression Mechanism of Dry Gas Seal at Ultra-High Speeds. Acta Aeronautica et Astronautica Sinica 2019, 40, 111–120. [Google Scholar]
  70. Zhang, W.; Xi, X.; Li, S. Analysis on the Angular Wobble of a Dry Gas Seal System with Thermal Dissipation. Journal of Vibration and Shock 2018, 37, 30–37+50. [Google Scholar]
  71. Liu, K.; Liu, Z.; Khan, A.; Chen, L.; Zhao, M. Effects of the Inclination Angles of DLC End Face Micro-Texture on the Tribological Properties of Dry Gas Seal Rings. J. Surface Topography: Metrology and Properties 2021, 9, 045014. [Google Scholar] [CrossRef]
  72. Han, M.; Li, F.; Wang, W.; Ding, X.; Ma, L. Nonlinear Stability and Chaotic Motion of Angulation Sway of Dry Gas Seal in case of Its Thermal Deformation. J. Journal of Lanzhou university of technology 2019, 45, 166–171. [Google Scholar]
  73. Teng, L.; Jiang, J.; Peng, X.; Li, J.; Zheng, S. Study on Angular Free Vibration Stability and Parameters Influence of Dry Gas Seal Based on the Characteristic Equation. J. Shock and Vibration 2022, 41, 148–160. [Google Scholar] [CrossRef]
  74. Liu, Y.; Yin, G.; Du, J.; Zhang, Z. Research of Axial Vibration of Dry Gas Seal System with Spiral Groove. Journal of Sichuan University (Engineering Science Edition) 2016, 48(S2), 155–160. [Google Scholar]
  75. Ding, X.; Lu, J.; Liu, Y.; Zhang, Y. Stability Analysis on Axial Vibration of Dry Gas Seal System under the Thermo-Elastic Deformation Considering the Thermal Dissipation. J. Journal of Vibration Engneering 2016, 29, 78–86. [Google Scholar]
  76. Zhang, W.; Xue, J.; Li, J.; Ding, X. Axial Vibration Dynamic Stability Analysis of Rotor-Bearing-Dry Gas Sealing System. J. Lubrication Engineering 2019, 44, 9–16. [Google Scholar]
  77. Blasiak, S.; Laski, P.; Takosoglu, J. Parametric Analysis of Heat Transfer in Non-Contacting Face Seals. J. International Journal of Heat and Mass Transfer 2013, 57, 22–31. [Google Scholar] [CrossRef]
  78. Su, H.; Rahmani, R.; Rahnejat, H. Performance Evaluation of Bidirectional Dry Gas Seals with Special Groove Geometry. J. Tribology Transactions 2017, 60, 58–69. [Google Scholar] [CrossRef]
  79. Green, I.; Barnsby. A Parametric Analysis of the Transient Forced Response of Noncontacting Coned-Face Gas Seals. Journal of Tribology 2002, 124, 151–157. [Google Scholar] [CrossRef]
  80. Hu, S.; Huang, W.; Liu, X.; Wang, Y. Transient Response Analysis of Spiral Groove Gas Face Seals under Pressure-Drop Fluctuation. J. Fluid Machinery 2017, 45, 22–27. [Google Scholar]
  81. Shang, H.; Chen, Y.; Li, X.; Wang, B.; Li, Y.; Peng, X. Study on the Influence of Nonlinear Effect on Performance of Dry Gas Seal under Film Thickness Disturbance. CIESC J. 2021, 72, 2213–2222. [Google Scholar]
  82. Chen, Y.; Jiang, J.; Peng, X. Dynamic Characteristics and Transient Sealing Performance Analysis of Hyperelliptic Curve Groove Dry Gas Seals. J. Tribology International 2017, 116, 217–228. [Google Scholar] [CrossRef]
Preprints 98936 g001
Figure 1. Rotary mechanical shaft end seal forms [7,8,9,10].
Figure 1. Rotary mechanical shaft end seal forms [7,8,9,10].
Preprints 98936 g001
Preprints 98936 g002
Figure 2. Structure and working principle of dry gas seals: (a) Dry gas seal structure; (b) Seal pairs; (c) Working principle of hydrodynamic pressure.
Figure 2. Structure and working principle of dry gas seals: (a) Dry gas seal structure; (b) Seal pairs; (c) Working principle of hydrodynamic pressure.
Preprints 98936 g002
Preprints 98936 g003
Figure 3. Dry gas seal force analysis: (a) Gas film pressure distribution during normal operation; (b) Gas film pressure distribution when clearance decreases; (c) Gas film pressure distribution when clearance increases.
Figure 3. Dry gas seal force analysis: (a) Gas film pressure distribution during normal operation; (b) Gas film pressure distribution when clearance decreases; (c) Gas film pressure distribution when clearance increases.
Preprints 98936 g003
Preprints 98936 g004
Figure 4. Effect of rotational speed on axial dynamic characteristic coefficient: (a) Influence of axial dynamic stiffness coefficient; (b) Influence of axial dynamic damping coefficient.
Figure 4. Effect of rotational speed on axial dynamic characteristic coefficient: (a) Influence of axial dynamic stiffness coefficient; (b) Influence of axial dynamic damping coefficient.
Preprints 98936 g004
Preprints 98936 g005
Figure 5. Dry gas seal test bench.
Figure 5. Dry gas seal test bench.
Preprints 98936 g005
Preprints 98936 g006aPreprints 98936 g006b
Figure 6. Changes in performance parameters during startup: (a) Friction power consumption and frictional torque during starting process; (b) Opening force and gas film thickness during starting process; (c) Gas film stiffness and leakage rate during start-up.
Figure 6. Changes in performance parameters during startup: (a) Friction power consumption and frictional torque during starting process; (b) Opening force and gas film thickness during starting process; (c) Gas film stiffness and leakage rate during start-up.
Preprints 98936 g006aPreprints 98936 g006b
Preprints 98936 g007aPreprints 98936 g007b
Figure 7. Dynamic characteristic coefficients of the gas film under different working conditions: (a) Stiffness coefficient at different speeds; (b) Damping coefficient at different speeds; (c) Stiffness coefficients at different inlet pressures; (d) Damping coefficients at different inlet pressures; (e) Stiffness coefficients at different inlet temperatures; (f) Damping coefficients at different inlet temperatures.
Figure 7. Dynamic characteristic coefficients of the gas film under different working conditions: (a) Stiffness coefficient at different speeds; (b) Damping coefficient at different speeds; (c) Stiffness coefficients at different inlet pressures; (d) Damping coefficients at different inlet pressures; (e) Stiffness coefficients at different inlet temperatures; (f) Damping coefficients at different inlet temperatures.
Preprints 98936 g007aPreprints 98936 g007b
Preprints 98936 g008
Figure 8. Kinematic model of the dry gas seal [70] : (a) Sealing ring vibration model; (b) Gas film dynamic analysis model.
Figure 8. Kinematic model of the dry gas seal [70] : (a) Sealing ring vibration model; (b) Gas film dynamic analysis model.
Preprints 98936 g008
Preprints 98936 g009
Figure 9. Jcr – β relationship diagram.
Figure 9. Jcr – β relationship diagram.
Preprints 98936 g009
Preprints 98936 g010
Figure 10. Jcr–β–η relationship diagram.
Figure 10. Jcr–β–η relationship diagram.
Preprints 98936 g010
Preprints 98936 g011
Figure 11. Transient disturbance distribution of membrane pressure [82] : (a) Ar=0μrad membrane pressure cloud image; (b)Ar=100μrad membrane pressure cloud image; (c)Ar=300μrad membrane pressure cloud image.
Figure 11. Transient disturbance distribution of membrane pressure [82] : (a) Ar=0μrad membrane pressure cloud image; (b)Ar=100μrad membrane pressure cloud image; (c)Ar=300μrad membrane pressure cloud image.
Preprints 98936 g011
Table 1. Existing research on stability models [31,32,33,34,35,36,37].
Table 1. Existing research on stability models [31,32,33,34,35,36,37].
Stability model methods Advantage Shortcoming Scope of application
Perturbation method[31] The calculation speed is fast, and the complex physical systems can be solved more accurately The uncertainty is limited by the small perturbation hypothesis Suitable for systems with sufficiently small perturbations A computational method for characterizing gas film characteristics
Step-by-step method[32] Parallelizes the iterative process to speed up calculations The convergence is unstable, and there may be cases of nonconvergence for some problems It is especially effective for solving nonlinear problems and optimization problems
PH linearization method[33] It has good convergence when the initial solution is close to the real solution The choice of initial solution is closely related to convergence Suitable for local analysis of the system
Runge-kutta method[34] It has high numerical stability and accuracy When solving large-scale problems, it consumes more computing resources Reliable and accurate numerical solutions are provided in cases where high numerical accuracy is required A method for solving equations of motion
Fault tree analysis method[35] It provides a means to evaluate the reliability of the system and helps to identify the main factors leading to system failure As a static analysis method, the influence of dynamic behavior and interaction of the system cannot be considered It can be used to identify system weaknesses, optimize design, develop security policies and control risks Methods for evaluating the reliability of sealing systems
Analytical method[36] Relatively simple problems and specific types of equations can be solved quickly, saving calculation time For complex problems and nonlinear problems, analytical solutions may not be obtained It is widely used to solve wave equations, heat conduction equations, electrostatics or electromagnetism problems The sealing linear motion differential equation is established by using the characteristics of the gas film
Particle swarm optimization(PSO) and projection tracking analysis[37] Simple and easy to understand and implement, without complex mathematical derivation and optimization skills In some cases, PSO may be trapped in the local optimal solution, and it cannot find the global optimal solution In the case of large a problem space and high complexity, it performs well and can find good approximate solutions Multiobjective optimization algorithm
Table 2. Spiral angle instability point ranges.
Table 2. Spiral angle instability point ranges.
Spiral angle range Instability point range
60° ~ 70° 62.47° ~ 62.49° 65.51° ~ 65.53° 67.28° ~ 67.30° 69.34° ~ 69.36°
70° ~ 80° 70.72° ~ 70.74° 72.27° ~ 72.29° 73.24° ~ 73.26° 74.39° ~ 74.41°
75.25° ~ 75.27° 76.16° ~ 76.18° 76.85° ~ 76.87° 77.60° ~ 77.62°
78.05° ~ 78.07° 78.69° ~ 78.71° 79.14° ~ 79.16° 79.60° ~ 79.62°
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated