Prerpints.org logo
Preprint
Review

Thermodynamic Insights into Symmetry-Breaking: Exploring Energy Dissipation across Diverse Scales

This is a preprint, it has not been peer-reviewed.

Submitted:

31 January 2024

Posted:

16 February 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
Symmetry-breaking is a phenomenon that is observed in various contexts, from the early universe to complex organisms, and is considered a key puzzle in understanding the emergence of life. The presence of enantiomeric amino acids and proteins highlights its critical role. However, the origin of symmetry-breaking has yet to be comprehensively explained, particularly from an energetic standpoint. This article explores a novel approach by considering energy dissipation, specifically lost free energy, as a crucial factor in elucidating symmetry-breaking. Through a thorough thermodynamic analysis applicable to enantiomeric systems at various scales, from elementary particles to aggregated matter like crystals, we present experimental findings that establish a direct correlation between non-equilibrium free energy and energy dissipation during formation processes. Results emphasize the pivotal role of energy dissipation not only as an outcome but as the trigger for symmetry-breaking. This insight suggests that understanding the origins of complex systems, from cells to living beings and the universe itself, requires a lens focused on non-equilibrium processes, ultimately facilitating the formation of non-racemic systems.
Keywords: 
  -  

1. Introduction

Symmetry-breaking stands as a foundational concept that extends beyond subatomic and quantum scales, finding applications across diverse scientific disciplines. In particle physics, it sheds light on the origin of mass and particle formation [1,2], while in condensed matter physics, it elucidates material behavior and phase transitions [3,4]. In cosmology, symmetry-breaking contributes to understanding the distribution of matter and the formation of large-scale structures in the universe [5]. Additionally, in biology, symmetry-breaking plays a fundamental role in embryonic development, giving rise to complex and asymmetric structures [6,7,8]. This versatile concept serves as a unifying principle, connecting phenomena from the subatomic to the cosmic and from the quantum to the classical, highlighting its significance in explaining the emergence of patterns, structures, and asymmetry in the natural world.
At subatomic scales, fundamental forces orchestrate a symmetrical dance among particles. However, this balance is disrupted as specific particles gain mass through the Higgs mechanism, marking a subtle yet profound form of symmetry-breaking in the subatomic domain [9]. At the molecular scale, the realm of chirality and enantiomerism illustrates symmetry-breaking in biomolecular structures. The prevalence of specific handedness in biological molecules, such as amino acids and DNA, underscores the fundamental role of asymmetry in the foundations of life. Unravelling the origin of this chiral bias remains an intriguing puzzle, interwoven with inquiries into the prebiotic conditions that shaped the essential building blocks of life [10].
Ascending to larger scales, the process of crystal formation stands as a macroscopic manifestation of symmetry-breaking. As atoms intricately organize into structured arrays, the resulting crystalline structures showcase distinctive symmetries that diverge from the theoretically perfect arrangement dictated by fundamental atomic interactions. This departure accentuates the influence of diverse factors, encompassing temperature gradients, pressure variations, and the presence of impurities, all of which collectively contribute to shaping the ultimate symmetry exhibited by these materials [11].
Transcending the limits of the molecular and atomic domains, the impact of symmetry-breaking resonates across astrophysical scales. The very fabric of the universe carries the echoes of symmetry-breaking occurrences during its early stages. With the formation of galaxies, stars, and planets, the once uniform nature of the cosmos transforms into a complex tapestry of structures, eloquently mirroring the indelible imprint left by primordial asymmetries.[5].
Delving into the phenomenon of symmetry-breaking across diverse scales and scientific domains holds the promise of unraveling fundamental principles that govern our surroundings and shed light on the origins of the cosmos and life itself. Fluctuations and symmetry-breaking, deeply embedded since the inception of space and time, emerge as a recurring theme with profound consequences. Central to this exploration is the phenomenon of energy dissipation through entropy production, which serves to illuminate the complexities of symmetry-breaking. Our inquiry critically reexamines the interplay between energy dissipation and symmetry-breaking across various scales, aiming to unveil profound insights into the emergence of asymmetry in the physical universe. Concentrating on aggregated matter systems, including crystals and self-assembled structures, We examine how fluctuations, non-equilibrium processes, and energy dissipation shape patterns of symmetry-breaking.

2. Symmetry breaking across Scales

2.1. Subatomic World

Since its inception, the universe has served as a testament to the absence of inherent symmetry. A pivotal moment during the birth of the cosmos witnessed the emergence of consequential asymmetry, tipping the scales in favor of the formation of a slightly greater amount of matter than antimatter. This event has played a profound role in shaping the characteristics of our known universe [1,2]. Known as broken symmetry in particle physics, this phenomenon is well-established at the subatomic level. Yet, a compelling question emerges: does symmetry-breaking confine itself to this minuscule scale? The answer unravels as we delve into the pivotal role of symmetry-breaking in comprehending the origins of life, where dissipation assumes a significant role. [12].
In quantum field theory, spontaneous symmetry breaking involves the field interacting with itself, resulting in an energy landscape, as depicted in Figure 1. This landscape prompts the field to minimize its energy by rolling downhill. In this process, the field acquires a nonzero strength and randomly selects a direction in a two-dimensional "phase space," thereby breaking the initial symmetry. This symmetry-breaking gives rise to the emergence of distinct particles, with oscillations within the trough corresponding to massless particles (Goldstone bosons), and oscillations spanning the trough and ascending indicating the existence of massive particles.
In the Higgs mechanism, massless Goldstone bosons combine with other force-carrying particles, imparting mass to them. The Higgs boson becomes a massive particle resulting from jiggling uphill in the energy landscape [9]. Additionally, it is worth noting that Figure 1 has significant importance, as this energy landscape can be observed at various scales and in different processes [13,14], as discussed in the following subsections. It also highlights the possibility of finding more "particles" in one stable state than in the other, even when both states have equal energy.
Within the realm of spontaneous symmetry breaking and the Higgs mechanism, the interplay among quantum fields holds profound implications for the properties of particles. Specifically, the gravitational induction of chirality flips in fermions, notably in the presence of right-handed neutrinos and left-handed antineutrinos, introduces a mechanism for these particles to gain mass upon interacting with Higgs bosons. The perturbatively induced self-gravity effects, potentially more pronounced for antineutrinos, result in prolonged trapping in flight for right-handed antineutrinos compared to left-handed neutrinos, contributing to a matter-antimatter asymmetry. While this asymmetry is exceedingly subtle, it offers a plausible explanation for the observed prevalence of matter over antimatter, thereby providing insights into the existence of our universe[15]. As initially highlighted by Sakharov [16], an essential prerequisite for baryogenesis, the process that leads to the generation of baryon asymmetry favouring a higher proportion of matter over antimatter in the early universe, is the out-of-equilibrium condition.

2.2. Molecular Level

Symmetry-breaking and enantiomers are two interrelated concepts found in molecular and crystalline structures. Symmetry-breaking occurs when a system loses or alters its symmetrical properties, leading to an asymmetrical or distorted state[17]. This phenomenon can take place at different scales, affecting the overall structure and properties of the system. Enantiomers, on the other hand, are mirror-image molecules that cannot be superimposed onto each other, as depicted in Figure 2(a). Enantiomers introduce a form of intrinsic asymmetry at the molecular level due to their distinct handedness. Although symmetry-breaking can occur in the macroscopic arrangement of molecules or crystals, enantiomers are unique in embodying molecular-level chirality, which results in different physical and chemical properties. In essence, symmetry-breaking is a comprehensive concept that encompasses various forms of asymmetry, as seen in the disproportion of enantiomers in a solution (Figure 2(b)) and the disproportion of chiral proteins (Figure 3). Enantiomers, on the other hand, specifically highlight the unique chiral properties of mirror-image molecules.
At the boundary between chemistry and quantum physics, fundamental symmetry-breaking helps us understand how molecular structures and enantiomers emerge [10]. This asymmetry, known as homochirality, is reflected in the prevalence of L-form amino acids in proteins and D-form sugars in DNA/RNA. However, the reasons behind this inherent disparity are still an open question, leading researchers to explore the factors that trigger symmetry-breaking. At equilibrium, the free energy change Δ r G required for the formation of possible enantiomers is practically the same, resulting in weak or no chiral symmetry breaking. However, experimental evidence shows that forces such as polarized light, shear, temperature gradients, and others can either hinder the formation or enhance the decomposition of one enantiomer over the other [19,20,21,22,23,24]. This observation is of particular significance in the origin of life, especially considering the likely extreme and non-equilibrium environments during prebiotic conditions [25,26].
Free energy change consists of reversible and irreversible contributions:
Δ G = Δ r G + Δ i G
The reversible free energy change depends on the state variables whereas the irreversible free energy change, Δ i G = T Σ , is given through the total entropy produced Σ in the process, defined as:
Σ = ∫ 0 ∞ σ ( t ) d t
where σ is the entropy production rate. At the molecular scale, energy-release processes primarily involve the formation and breaking of chemical bonds and hydrogen bonds. These events may be driven by differences in free energy between the initial and final states. Additionally, external factors like temperature gradients or stress can influence chemical reactions and phase transitions. At this level, we can quantify the probability ρ ( γ , t ) of observing the system in a specific configuration γ = [ γ 1 , . . . , γ i , . . . , γ n ] at time t [27], where γ i represents an internal coordinate associated with the i-th process. The conservation of probability is elucidated by the conservation law
∂ ρ ∂ t + v . ∇ γ ρ = − ∇ γ · J
in which J is the probability current associated to the n processes taking place in the system, v the fluid velocity field and ∇ γ is the gradient operator along γ -space.
On the other hand, in a system in which there is momentum and heat transport, the entropy production rate can be expressed as[27,28,29]
σ ( t ) = − 1 T ∫ γ ∫ r J · ∇ γ μ + J q · ∇ r T + Π : ∇ r v d γ d r
where J q is the heat flux, Π the viscous pressure tensor and ∇ r the gradient operator in the euclidean space.
The expression for the current of the i-th process then results from the linear coupling with the conjugate thermodynamic forces:
J i = − L i i T ∂ μ ∂ γ i − 1 T L ̲ q i · ∇ r T − 1 T L ̲ ̲ v i : ∇ r v
in which we have made the assumption that the process occurs on a surface, allowing the coupling of processes that originally exhibit different tensorial orders. The coefficients L i i , L ̲ q i and L ̲ ̲ v i form the Onsager coefficients’ matrix .

2.3. Enantiomeric Crystals

Enantiomeric crystals, highlighting the profound influence of molecular chirality on crystal symmetry, are encountered across diverse scientific disciplines. A striking illustration is evident in the pharmaceutical field, where enantiomeric crystals of drug compounds can exhibit markedly distinct pharmacological activities [30]. The thalidomide case serves as a noteworthy example, where one enantiomer led to severe birth defects, while the other demonstrated safe sedative properties [31]. Enantiomeric crystals also find applications in materials science due to their unique optical properties. The chirality of meso-crystals has recently emerged as a prominent and dynamic topic in nanoresearch. Significant exploration and study of the unique and intriguing properties of chiral meso-crystals underscore their relevance in both fundamental research and potential applications [32,33,34].
The diverse proportions of enantiomeric crystals can be understood by applying thermodynamic principles [35]. To illustrate this, it is essential to calculate the free energy change of the process. This computation is crucial for revealing the probability linked to the observation of a specific structural configuration
p ∝ exp − Δ G k B T
In scenarios where only two potential enantiomers are involved, the deviation from the equilibrium distribution can be characterized by χ , defined as χ = 2 p − 1 . From this parameter, we can calculate the enantiomeric excess percentage
% e . e . = χ * 100 %
The D and L enantiomeric configurations of chiral crystals exhibit specular macro- and micromorphologies and possess opposite directions of optical rotation. Secondary nucleation and Viedma ripening are two well-known and complementary mechanisms that explain chiral symmetry breaking [20,36,37]. In addition, the presence of an enantiomeric excess has also been attributed to differences in activation energies between the enantiomers, leading to different rates of formation [26,38]. These variations in the nucleation stage, proposed by both secondary nucleation and Viedma ripening mechanisms, are influenced by shear rates affecting crystal and nuclei formation, which could be related to variations in activation energies during the nucleation stage. Therefore, non-equilibrium conditions during the crystallisation play a crucial role [39,40,41], determining the symmetry-breaking phenomenon and not only the initial conditions, as illustrated in Figure 4.
Experiments consisting of evaporating the solvent to obtain NaClO3 crystals [20], performed by stirring the sample, revealed a significant disproportion in the concentrations of both enantiomeric crystals of NaClO3. In a recent study, it was found that the energy dissipation rate of the phase change T σ c h and heat transfer T σ T determines the enantiomeric excess percentage in the case of enantiomeric crystals of NaClO3 [35]:
T σ p h ( y , t ) = − ( r ˙ L Δ z L + r ˙ D Δ z D )
T σ T ( y , t ) = κ T ∂ T ∂ y 2
r ˙ L and r ˙ D are the nucleation rates of both enantiomers whereas Δ z L and Δ z D are the driving force (fugacity difference between liquid and solid state). Moreover, κ is the thermal conductivity of the system and T is the temperature. In this case, the activation energy E a in the formation of the nuclei differs between enantiomers, and the difference ( Δ E a ) is proportional to the energy dissipated per salt mole in the process, i.e., Δ E a = Δ i G = T Σ .
In Figure 5, the anticipated behavior of the energy dissipation rate ( T σ ), energy dissipated per solid salt mol ( T Σ / n s ), and the enantiomeric excess percentage ( % e . e . ) is presented over time. The figure delineates these behaviors under distinct cooling conditions (depicted by red and blue lines) and various initial concentrations of dissolved salt (continuous and dashed lines). These specified conditions exert influence over the energy dissipation, consequently impacting the symmetry-breaking observed in the enantiomeric excess. Notice that as the energy dissipation reaches higher peaks, there is a corresponding increase in the energy dissipated per mole of salt, leading to a higher enantiomeric excess.

2.4. Mesoscopic Domain

The concept of symmetry-breaking is responsible for creating homochirality, a phenomenon that is present across different levels of existence and fields. The explanation for the emergence of biological chirality can be found in the homochirality of chemical and physical systems. The directed and selective self-assembly of components, combined with the dissipation of energy and auto-catalytic networks, drives self-organization. [42,43,44,45,46,47]. This intersection of physical chemistry and biology witnesses the spontaneous emergence of self-assembled and self-organized structures driven by the dissipation of energy [14,43,44,48]. Lately, there has been a lot of thought given to whether the dissipation of energy can help explain why symmetry is broken. The focus of this inquiry is to better understand how homochiral structures (enantiomers) come to be, as they are the precursors to self-organized structures.
Enantiomeric structures can be elucidated as formations stemming from non-equilibrium self-assembly (NESA) processes, where the fundamental components consist of chiral molecules or chiral building blocks, as illustrated in Figure 6. A conceptual framework for comprehending out-of-equilibrium crystallization through non-equilibrium self-assembly (NESA) processes has been previously proposed [49]. At this level, enantiomers can be more than two, also termed polymorphs. In a steady state, a system with more than two enantiomers can emerge due to the interplay of self-assembly and symmetry-breaking. The probability for the η configuration is [14]
p ( η ) = p ( η 0 ) e − β Δ G ( η )
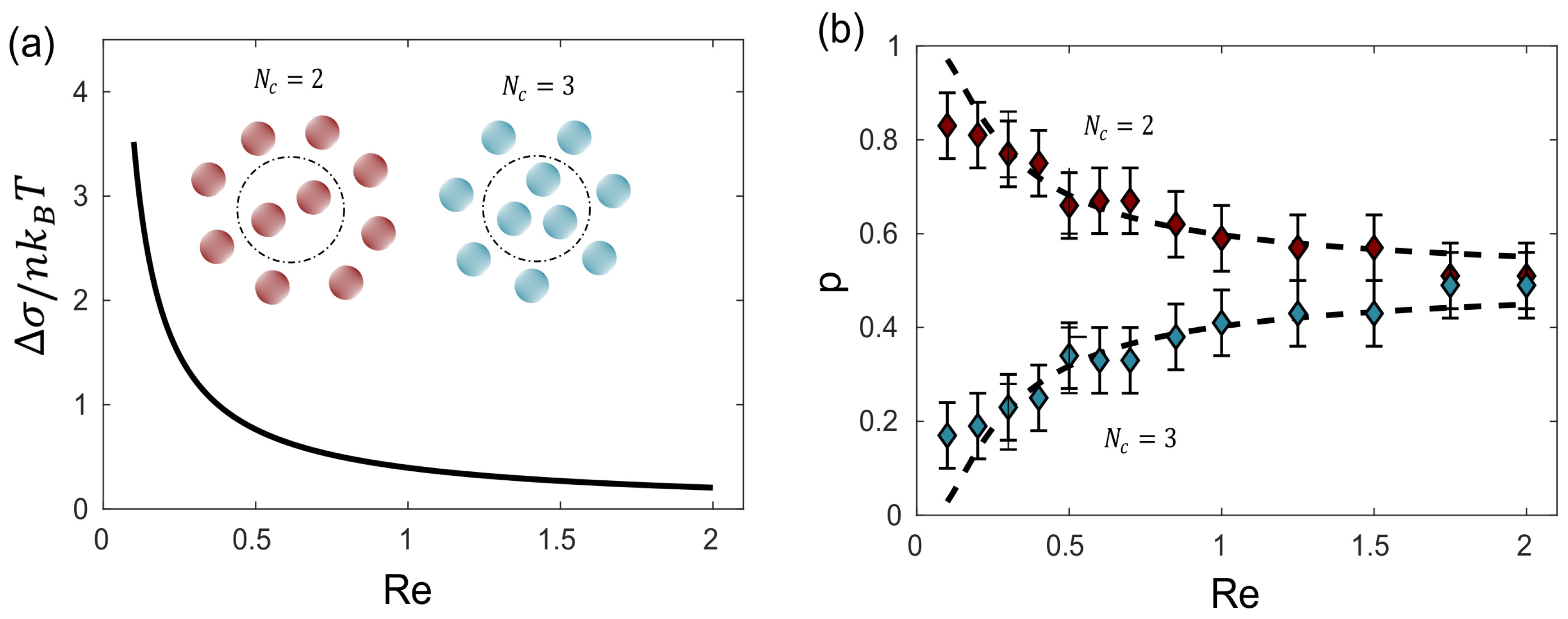
In the case of the steady-state magneto-hydrodynamic self-assembly, two enantiomers (polymorphs) can arise. In that case, a set of small magnetic particles suspended on a liquid–air interface under the influence of a magnetic field generated by a rotating magnet [50], which can be controlled to contain different Reynolds numbers. The movement of the particles perturbs the fluid’s state of rest giving rise to the formation of a hydrodynamic pattern which in turn induces the assembly of the particles that orbit around the axis of the magnet (inset Figure 7). The energy supplied by the rotating magnet is dissipated in the fluid due to its viscous nature. The entropy production for a configuration N c is given by:
σ ( N c ) = − 1 T ∫ v : Π d r
where the velocity field v and the tensor Pi depend on the particle configuration in the system N c . It was proven that the probability of observation is given by the entropy production rate:
p ( N c = 2 ) p ( N c = 3 ) = exp ( − β ( T Δ σ ) )
in which σ is the entropy production rate per molecule of moving fluid around the particles and Δ σ = σ ( N c = 2 ) − σ ( N c = 3 ) .

2.5. Living Organisms

Living organisms are complex, self-organized structures [44] composed of chiral molecules, entities that inherently exhibit asymmetry [51,52].
The simplicity of left-right asymmetry offers a basis for meaningful comparisons across different organisms. Exploring how this asymmetry varies, is inherited, and operates at the molecular level provides surprising insights into the evolution of development [53,54]. Firstly, this type of asymmetry often arises from non-inherited traits as much as from genetic mutations, suggesting a reciprocal relationship where traits can influence genes over time. Conditions and diet [55], along with dissipation, as seen in studied self-organized structures [44], may play crucial roles. Secondly, the development of left-sided preference in hearts varies widely among animals. This developmental process might have been borrowed from an older asymmetrical organ system in chordates [55]. Hence, external conditions, initial chiral or asymmetric structures, genes, and mutations collectively influence the likelihood of encountering, for instance, a left-sided heart. This raises the question: Can we analyze symmetry-breaking in organisms by studying dissipation under the usual conditions they face? This mirrors the approach taken in understanding cancer evolution, where carcinogenic tissues are viewed as self-organized structures [56].
Handedness, one of the most extensively studied asymmetries in human motor behavior, refers to the preference for using one hand over the other. This inclination is universally observed and consistent among Homo sapiens. Remarkably, across all human cultures, approximately 90% of individuals favor their right hand, while the remaining 10% exhibit a preference for their left hand [57]. Notably, other socially intelligent mammals do not display such a consistent handedness pattern at the species or population level. This lateralization in hand use is indicative of underlying asymmetry in cerebral structure, and the evolution of handedness appears to be linked to other lateralized abilities such as footedness, earedness, and eyedness. This intricate interplay of brain, hand, and speech forms an adaptive complex that is characteristic of our species [58,59].
Various theories, including genetic, environmental, social, and behavioural perspectives, have been proposed to comprehend the symmetry-breaking observed in the dominant hand; however, consensus remains elusive in the literature [60]. A compelling question arises: Can we integrate these diverse theories within the realm of the mind and consciousness, especially considering that energy emerges as a common variable? The processes unfolding—from individual neuronal interactions and biochemical reactions facilitating thoughts or cascades of thoughts to the intelligence enabling communication and communal life—undoubtedly involve changes in energy and energy flows. Could future theories explore the notion that more efficient energy flows or considerations of energy dissipation, the loss of energy, and information might shed light on understanding handedness, similar to phenomena observed at the molecular and mesoscopic scales?

3. Discussion and Conclusions

The exploration of symmetry-breaking and its connection to energy dissipation traverses various scales, providing profound insights into the fundamental principles governing a myriad of phenomena. Starting from the cosmic scale, the birth of the universe marked a crucial asymmetry, resulting in the dominance of matter over antimatter. This broken symmetry, firmly established in particle physics at the subatomic level, continues to exert its influence on the emergence of life, particularly evident in the homochirality of biomolecules.
A pivotal proposition has arisen regarding the significance of energy dissipation in elucidating symmetry-breaking. The dissipation of energy through entropy production has emerged as a consistent and compelling phenomenon, influencing the system’s free energy and leading to the establishment of an effective free energy potential. This concept underwent thorough exploration across diverse scales, ranging from elemental particles to aggregated matter systems like crystals.
The inquiry extended to human-scale observations, unveiling an inherent connection between our perception of asymmetry and our chiral nature. Biological chirality, manifest in cellular processes and psychological aspects, underwent scrutiny in the context of self-assembly, auto-catalytic networks, and energy dissipation at the intersection of physical chemistry and biology.
Symmetry-breaking has proven instrumental in crystallography, shedding light on how external conditions and non-equilibrium processes govern deviations from perfect arrangements and symmetric properties during crystal formation. Enantiomeric crystals, formed through dissipation-driven symmetry-breaking, vividly illustrate the transformation from achiral compounds to distinct L- and D-crystals.
The discussion converged on the overarching theme of exploring symmetry-breaking across scales, with a particular focus on aggregated matter systems such as crystals and self-assembled structures. The intricate interplay of fluctuations, non-equilibrium processes, and energy dissipation emerged as pivotal factors shaping the patterns of symmetry-breaking.
In essence, this discussion delves into the coherence of symmetry-breaking phenomena across different scales and disciplines, revealing a common thread in the dissipation of energy. From the cosmic to the molecular scale, the exploration of this relationship provides valuable insights into the fundamental principles governing the emergence of asymmetry in the physical universe.

Author Contributions

All authors have contributed equally. All authors have read and agreed to the published version of the manuscript.

Funding

The authors are grateful for the financial support of MICIU (Spanish Government) under grant No. PID2021-126570NB-I00.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Smith, A. Speed read: The Importance of Asymmetry., 2008. Last accessed Wed. 10 Nov 2021.
  2. Kolb, E.W.; Wolfram, S. Spontaneous symmetry breaking and the expansion rate of the early universe. The Astrophysical Journal 1980, 239, 428–432. [Google Scholar] [CrossRef]
  3. Ideue, T.; Iwasa, Y. Symmetry Breaking and Nonlinear Electric Transport in van der Waals Nanostructures. Annual Review of Condensed Matter Physics 2021, 12, 201–223. [Google Scholar] [CrossRef]
  4. Fischer, M.H.; Sigrist, M.; Agterberg, D.F.; Yanase, Y. Superconductivity and Local Inversion-Symmetry Breaking. Annual Review of Condensed Matter Physics 2023, 14, 153–172. [Google Scholar] [CrossRef]
  5. Evans, N.; Morris, T.R.; Scott, M. Translational symmetry breaking in field theories and the cosmological constant. Phys. Rev. D 2016, 93, 025019. [Google Scholar] [CrossRef]
  6. Zhang, H.T.; Hiiragi, T. Symmetry Breaking in the Mammalian Embryo. Annual Review of Cell and Developmental Biology 2018, 34, 405–426. [Google Scholar] [CrossRef] [PubMed]
  7. Inagaki, N.; Toriyama, M.; Sakumura, Y. Systems biology of symmetry breaking during neuronal polarity formation. Developmental Neurobiology 2011, 71, 584–593. [Google Scholar] [CrossRef] [PubMed]
  8. Korenić, A.; Perović, S.; Ćirković, M.M.; Miquel, P.A. Symmetry breaking and functional incompleteness in biological systems. Progress in Biophysics and Molecular Biology 2020, 150, 1–12. [Google Scholar] [CrossRef]
  9. Cho, A. Spontaneous Symmetry Breaking Decanted. Science 2012, 337, 1289–1289. [Google Scholar] [CrossRef] [PubMed]
  10. Ribó, J.M. Chirality: The Backbone of Chemistry as a Natural Science. Symmetry 2020, 12. [Google Scholar] [CrossRef]
  11. Kondepudi, D.K.; Asakura, K. Chiral Autocatalysis, Spontaneous Symmetry Breaking, and Stochastic Behavior. Accounts of Chemical Research 2001, 34, 946–954. [Google Scholar] [CrossRef]
  12. Laguna, P.; Zurek, W.H. Critical dynamics of symmetry breaking: Quenches, dissipation, and cosmology. Phys. Rev. D 1998, 58, 085021. [Google Scholar] [CrossRef]
  13. Heylighen, F. Entanglement, symmetry breaking and collapse: correspondences between quantum and self-organizing dynamics. Foundations of Science 2023, 28, 85–107. [Google Scholar] [CrossRef]
  14. Arango-Restrepo, A.; Barragán, D.; Rubi, J.M. A Criterion for the Formation of Nonequilibrium Self-Assembled Structures. The Journal of Physical Chemistry B 2021, 125, 1838–1845. [Google Scholar] [CrossRef]
  15. Maes, S.H. More Matter Than Antimatter, All Falling Down 2020.
  16. Shakarov, A. Symmetry Violation, C-Asymmetry and Baryonic Asymmetry of the Universe. Pisma Zh.Eksp.Teor.Fiz. 1967, 5, 32–35. [Google Scholar]
  17. Castellani, E.; Dardashti, R. Symmetry breaking. In The Routledge Companion to Philosophy of Physics; Routledge, 2021; pp. 620–631. [Google Scholar]
  18. Ousaka, N.; MacLachlan, M.J.; Akine, S. Stapling strategy for slowing helicity interconversion of α-helical peptides and isolating chiral auxiliary-free one-handed forms. Nat Commun 2023, 14, 6834. [Google Scholar] [CrossRef]
  19. Garay, A. Origin and role of optical isomery in life. Nature 1968, 219, 338–340. [Google Scholar] [CrossRef] [PubMed]
  20. Kondepudi, D.K.; Kaufman, R.J.; Singh, N. Chiral symmetry breaking in sodium chlorate crystallizaton. Science 1990, 250, 975–976. [Google Scholar] [CrossRef] [PubMed]
  21. Niinomi, H.; Sugiyama, T.; Tagawa, M.; Harada, S.; Ujihara, T.; Uda, S.; Miyamoto, K.; Omatsu, T. In Situ Observation of Chiral Symmetry Breaking in NaClO3 Chiral Crystallization Realized by Thermoplasmonic Micro-Stirring. Crystal Growth & Design 2018, 18, 4230–4239. [Google Scholar] [CrossRef]
  22. Ribó, J.M.; Crusats, J.; El-Hachemi, Z.; Moyano, A.; Blanco, C.; Hochberg, D. Spontaneous Mirror Symmetry Breaking in the Limited Enantioselective Autocatalysis Model: Abyssal Hydrothermal Vents as Scenario for the Emergence of Chirality in Prebiotic Chemistry. Astrobiology 2013, 13, 132–142. [Google Scholar] [CrossRef] [PubMed]
  23. Buhse, T.; Cruz, J.M.; Noble-Terán, M.E.; Hochberg, D.; Ribó, J.M.; Crusats, J.; Micheau, J.C. Spontaneous Deracemizations. Chemical Reviews 2021, 121, 2147–2229. [Google Scholar] [CrossRef] [PubMed]
  24. Szurgot, M. Crystallization and Materials Science of Modern Artificial and Natural Crystals; InTech: Rijeka, Croatia, 2012; chapter Parity Violation in Unstirred Crystallization from Achiral Solutions. [Google Scholar]
  25. Plasson, R.; Kondepudi, D.K.; Bersini, H.; Commeyras, A.; Asakura, K. Emergence of homochirality in far-from-equilibrium systems: Mechanisms and role in prebiotic chemistry. Chirality 2007, 19, 589–600. [Google Scholar] [CrossRef] [PubMed]
  26. Ribó, J.M.; Hochberg, D.; Crusats, J.; El-Hachemi, Z.; Moyano, A. Spontaneous mirror symmetry breaking and origin of biological homochirality. Journal of The Royal Society Interface 2017, 14, 20170699. [Google Scholar] [CrossRef]
  27. Reguera, D.; Rubi, J.; Vilar, J. The Mesoscopic Dynamics of Thermodynamic Systems. J. Phys. Chem. B 2005, 109, 21502–21515. [Google Scholar] [CrossRef]
  28. Pérez-Madrid, A.; Rubí, J.; Mazur, P. Brownian motion in the presence of a temperature gradient. Physica A: Statistical Mechanics and its Applications 1994, 212, 231–238. [Google Scholar] [CrossRef]
  29. De Groot, S.R.; Mazur, P. Non-equilibrium thermodynamics; Courier Corporation, 2013. [Google Scholar]
  30. Nunez, M.C.; Garcia-Rubino, M.E.; Conejo-Garcia, A.; Cruz-Lopez, O.; Kimatrai, M.; Gallo, M.A.; Espinosa, A.; Campos, J.M. Homochiral Drugs: A Demanding Tendency of the Pharmaceutical Industry. Current Medicinal Chemistry 2009, 16, 2064–2074. [Google Scholar] [CrossRef] [PubMed]
  31. Rajkumar, S.V. Thalidomide: tragic past and promising future. Mayo Clinic Proceedings. Elsevier, 2004, Vol. 79, pp. 899–903. [CrossRef]
  32. Xia, Y.; Zhou, Y.; Tang, Z. Chiral inorganic nanoparticles: origin, optical properties and bioapplications. Nanoscale 2011, 3, 1374–1382. [Google Scholar] [CrossRef] [PubMed]
  33. Takanabe, A.; Tanaka, M.; Johmoto, K.; Uekusa, H.; Mori, T.; Koshima, H.; Asahi, T. Optical Activity and Optical Anisotropy in Photomechanical Crystals of Chiral Salicylidenephenylethylamines. Journal of the American Chemical Society 2016, 138, 15066–15077. [Google Scholar] [CrossRef] [PubMed]
  34. Döring, A.; Ushakova, E.; Rogach, A.L. Chiral carbon dots: synthesis, optical properties, and emerging applications. Light: Science & Applications 2022, 11, 75. [Google Scholar]
  35. Arango-Restrepo, A.; Arteaga, O.; Barragán, D.; Rubi, J.M. Chiral symmetry breaking induced by energy dissipation. Phys. Chem. Chem. Phys. 2023, 25, 9238–9248. [Google Scholar] [CrossRef] [PubMed]
  36. Viedma, C. Chiral Symmetry Breaking During Crystallization: Complete Chiral Purity Induced by Nonlinear Autocatalysis and Recycling. Phys. Rev. Lett. 2005, 94, 065504. [Google Scholar] [CrossRef]
  37. Sögütoglu, L.C.; Steendam, R.R.; Meekes, H.; Vlieg, E.; Rutjes, F.P. Viedma ripening: a reliable crystallisation method to reach single chirality. Chemical Society Reviews 2015, 44, 6723–6732. [Google Scholar] [CrossRef] [PubMed]
  38. Rekharsky, M.; Inoue, Y. Chiral Recognition Thermodynamics of β-Cyclodextrin:The Thermodynamic Origin of Enantioselectivity and the Enthalpy-Entropy Compensation Effect. Journal of the American Chemical Society 2000, 122, 4418–4435. [Google Scholar] [CrossRef]
  39. Santamaría-Holek, I.; Gadomski, A.; Rubí, J.M. Controlling protein crystal growth rate by means of temperature. Journal of Physics: Condensed Matter 2011, 23, 235101. [Google Scholar] [CrossRef]
  40. Gadomski, A. Kinetic–thermodynamic effects accompanying model protein-like aggregation: The wave-like limit and beyond it. Physica A: Statistical Mechanics and its Applications 2007, 373, 43–57. [Google Scholar] [CrossRef]
  41. Gadomski, A.; Siódmiak, J. A Kinetic Model of Protein Crystal Growth in Mass Convection Regime. Crystal Research and Technology 2002, 37, 281–291. [Google Scholar] [CrossRef]
  42. Kauffman, S.A.; others. The origins of order: Self-organization and selection in evolution; Oxford University Press, USA, 1993. 1993. [CrossRef]
  43. Tena-Solsona, M.; Wanzke, C.; Riess, B.; Bausch, A.R.; Boekhoven, J. Self-selection of dissipative assemblies driven by primitive chemical reaction networks. Nature communications 2018, 9, 1–8. [Google Scholar] [CrossRef] [PubMed]
  44. Arango-Restrepo, A.; Barragán, D.; Rubi, J.M. Self-assembling outside equilibrium: emergence of structures mediated by dissipation. Phys. Chem. Chem. Phys. 2019, 21, 17475–17493. [Google Scholar] [CrossRef]
  45. van Ravensteijn, B.G.; Voets, I.K.; Kegel, W.K.; Eelkema, R. Out-of-equilibrium colloidal assembly driven by chemical reaction networks. Langmuir 2020, 36, 10639–10656. [Google Scholar] [CrossRef]
  46. Hochberg, D.; Ribó, J.M. Entropic Analysis of Mirror Symmetry Breaking in Chiral Hypercycles. Life 2019, 9. [Google Scholar] [CrossRef]
  47. Ribó, J.M.; Hochberg, D. Spontaneous mirror symmetry breaking: An entropy production survey of the racemate instability and the emergence of stable scalemic stationary states. Physical Chemistry Chemical Physics 2020, 22, 14013–14025. [Google Scholar] [CrossRef]
  48. Arango-Restrepo, A.; Rubi, J.M.; Barragán, D. The Role of Energy and Matter Dissipation in Determining the Architecture of Self-Assembled Structures. The Journal of Physical Chemistry B 2019, 123, 5902–5908. [Google Scholar] [CrossRef] [PubMed]
  49. Arango-Restrepo, A.; Barragán, D.; Rubi, J.M. Variations in activation energy and nuclei size during nucleation explain chiral symmetry breaking. Phys. Chem. Chem. Phys. 2023, 25, 29032–29041. [Google Scholar] [CrossRef] [PubMed]
  50. Tretiakov, K.V.; Bishop, K.J.M.; Grzybowski, B.a. The dependence between forces and dissipation rates mediating dynamic self-assembly. Soft Matter 2009, 5, 1279. [Google Scholar] [CrossRef]
  51. Frank, F. On spontaneous asymmetric synthesis. Biochimica et Biophysica Acta 1953, 11, 459–463. [Google Scholar] [CrossRef] [PubMed]
  52. Kuhn, H. Origin of life - Symmetry breaking in the universe: Emergence of homochirality. Current Opinion in Colloid & Interface Science 2008, 13, 3–11, Molecular Recognition and Chirality in Amphiphilic Assemblies. [Google Scholar] [CrossRef]
  53. Shubin, N.; Tabin, C.; Carroll, S. Fossils, genes and the evolution of animal limbs. Nature 1997, 388, 639–648. [Google Scholar] [CrossRef] [PubMed]
  54. Arthur, W. The emerging conceptual framework of evolutionary developmental biology. Nature 2002, 415, 757–764. [Google Scholar] [CrossRef] [PubMed]
  55. Palmer, A.R. Symmetry Breaking and the Evolution of Development. Science 2004, 306, 828–833. [Google Scholar] [CrossRef] [PubMed]
  56. Arango-Restrepo, A.; Rubi, J. Predicting cancer stages from tissue energy dissipation. Scientific Reports 2023, 13, 15894. [Google Scholar] [CrossRef] [PubMed]
  57. Marchant, L.F.; McGrew, W.C.; Eibl-Eibesfeldt, I. Is human handedness universal? Ethological analyses from three traditional cultures. Ethology 1995, 101, 239–258. [Google Scholar] [CrossRef]
  58. Corballis, M.C. Laterality and human evolution. Psychological review 1989, 96, 492. [Google Scholar] [CrossRef] [PubMed]
  59. Corballis, M.C. From mouth to hand: gesture, speech, and the evolution of right-handedness. Behavioral and brain sciences 2003, 26, 199–208. [Google Scholar] [CrossRef] [PubMed]
  60. Marcori, A.J.; Okazaki, V.H.A. A historical, systematic review of handedness origins. Laterality 2020, 25, 87–108. [Google Scholar] [CrossRef] [PubMed]
Preprints 97794 g001
Figure 1. Energy landscapes before and after symmetry-breaking: On the left, a symmetric energy landscape where particles (red dots) are uniformly localized in a single state. On the right, an asymmetric landscape follows symmetry-breaking, where particles tend to occupy one of the available states.
Figure 1. Energy landscapes before and after symmetry-breaking: On the left, a symmetric energy landscape where particles (red dots) are uniformly localized in a single state. On the right, an asymmetric landscape follows symmetry-breaking, where particles tend to occupy one of the available states.
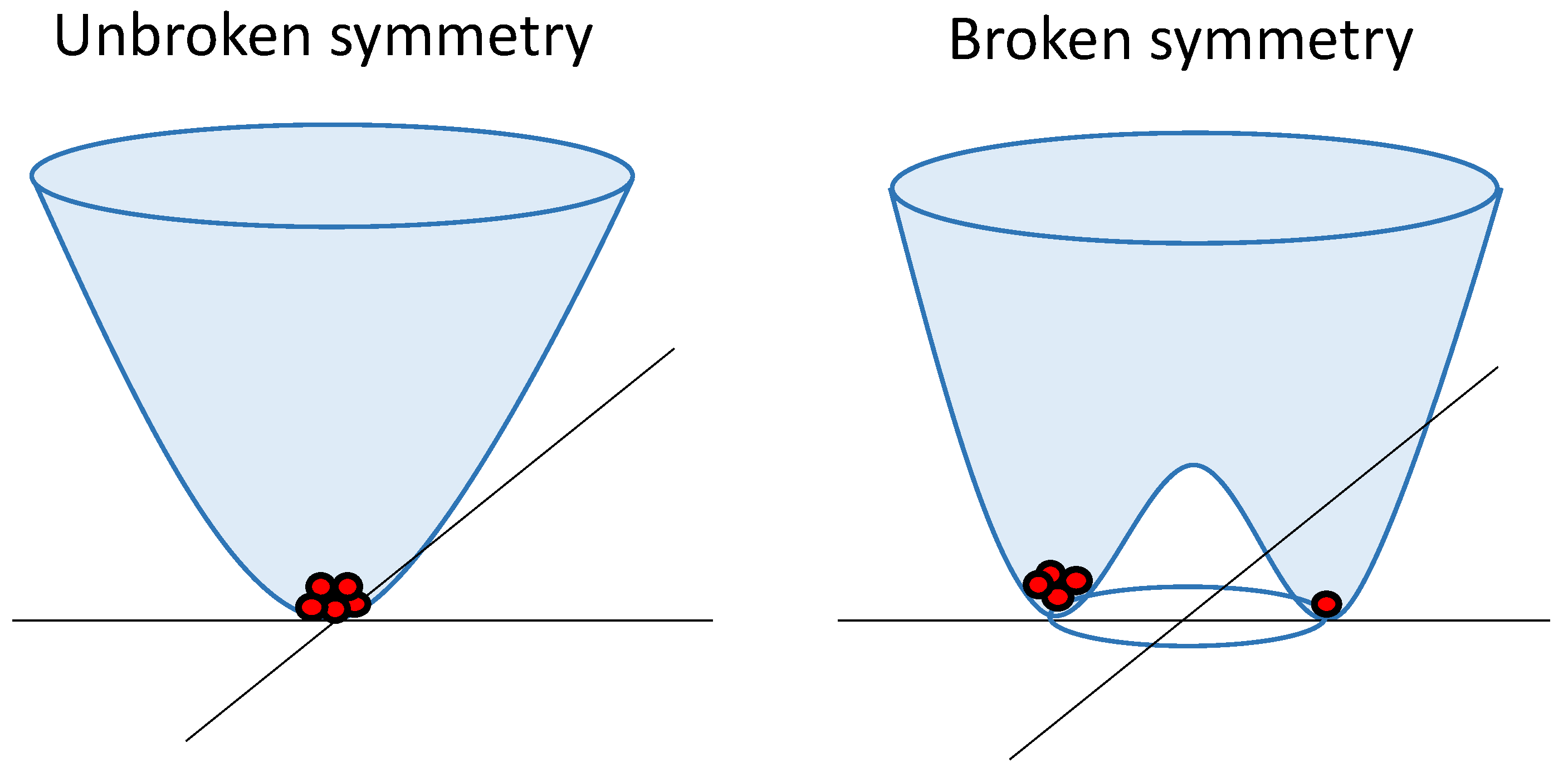
Preprints 97794 g001
Preprints 97794 g002
Figure 2. Chiral amino acids: a) Enantiomers: Chiral amino acids are non-superposable onto their mirror images due to the inability to align the four unique groups on the chiral carbon precisely, even with reorientation in three spatial dimensions. b) Symmetry-breaking in a solution of amino acids results in a non-racemic mixture, indicating a disproportion between the two possible enantiomers (chiral amino acids).
Figure 2. Chiral amino acids: a) Enantiomers: Chiral amino acids are non-superposable onto their mirror images due to the inability to align the four unique groups on the chiral carbon precisely, even with reorientation in three spatial dimensions. b) Symmetry-breaking in a solution of amino acids results in a non-racemic mixture, indicating a disproportion between the two possible enantiomers (chiral amino acids).
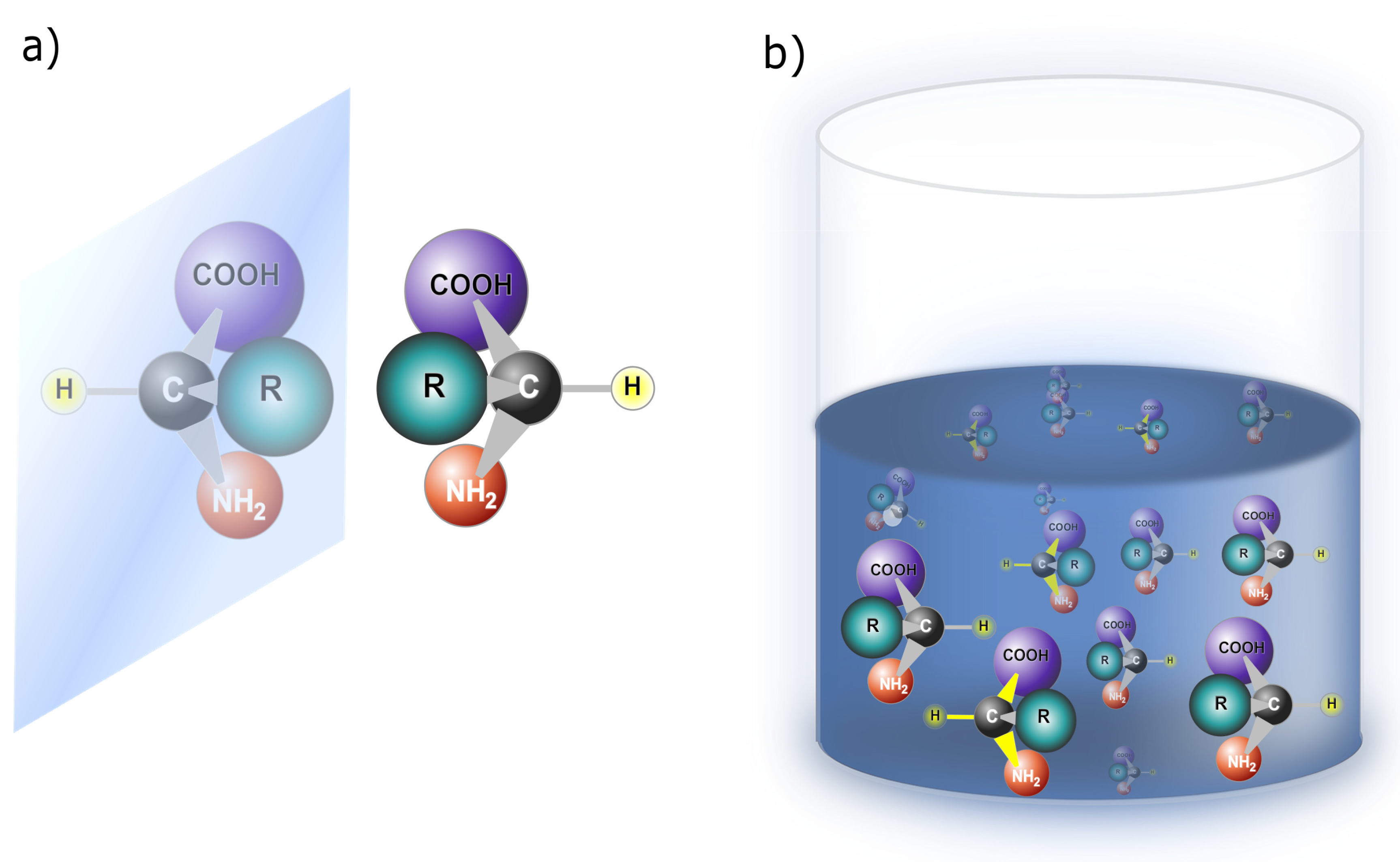
Preprints 97794 g002
Preprints 97794 g003
Figure 3. Chiral proteins: Despite being constructed from achiral amino acids, proteins can display mirror images owing to the configuration of the α -helix. Recent studies, such as those by [18], reveal that the population disproportion of protein enantiomers can be controlled.
Figure 3. Chiral proteins: Despite being constructed from achiral amino acids, proteins can display mirror images owing to the configuration of the α -helix. Recent studies, such as those by [18], reveal that the population disproportion of protein enantiomers can be controlled.
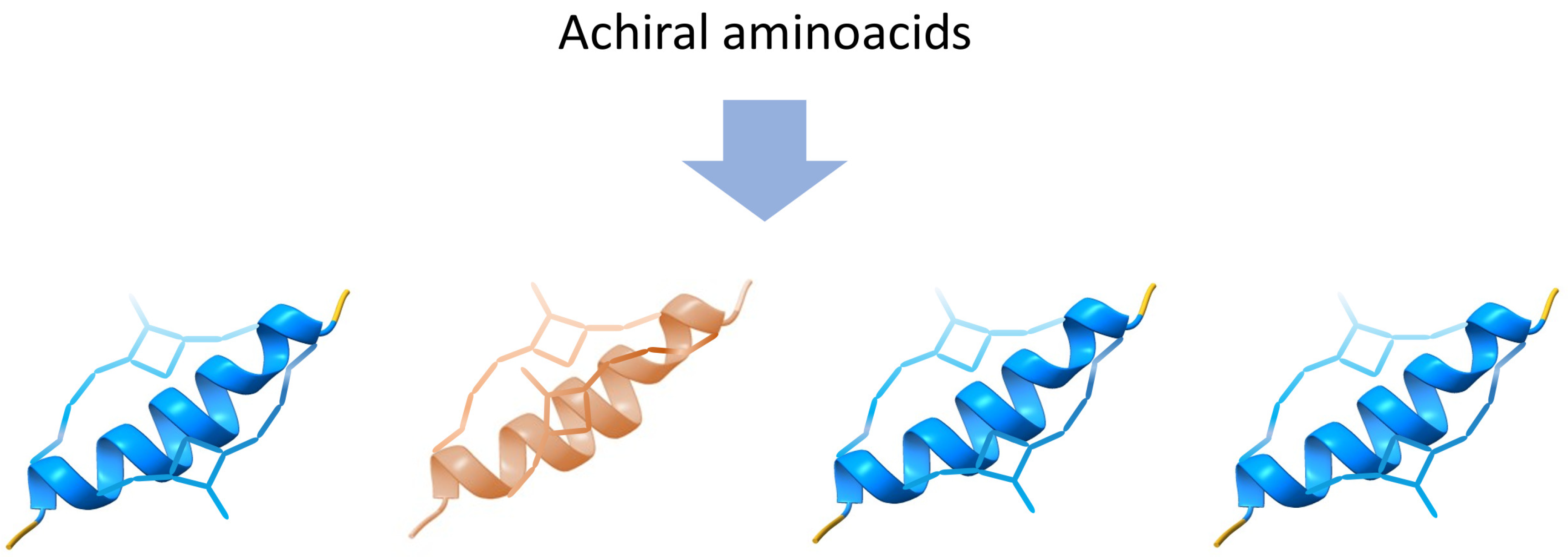
Preprints 97794 g003
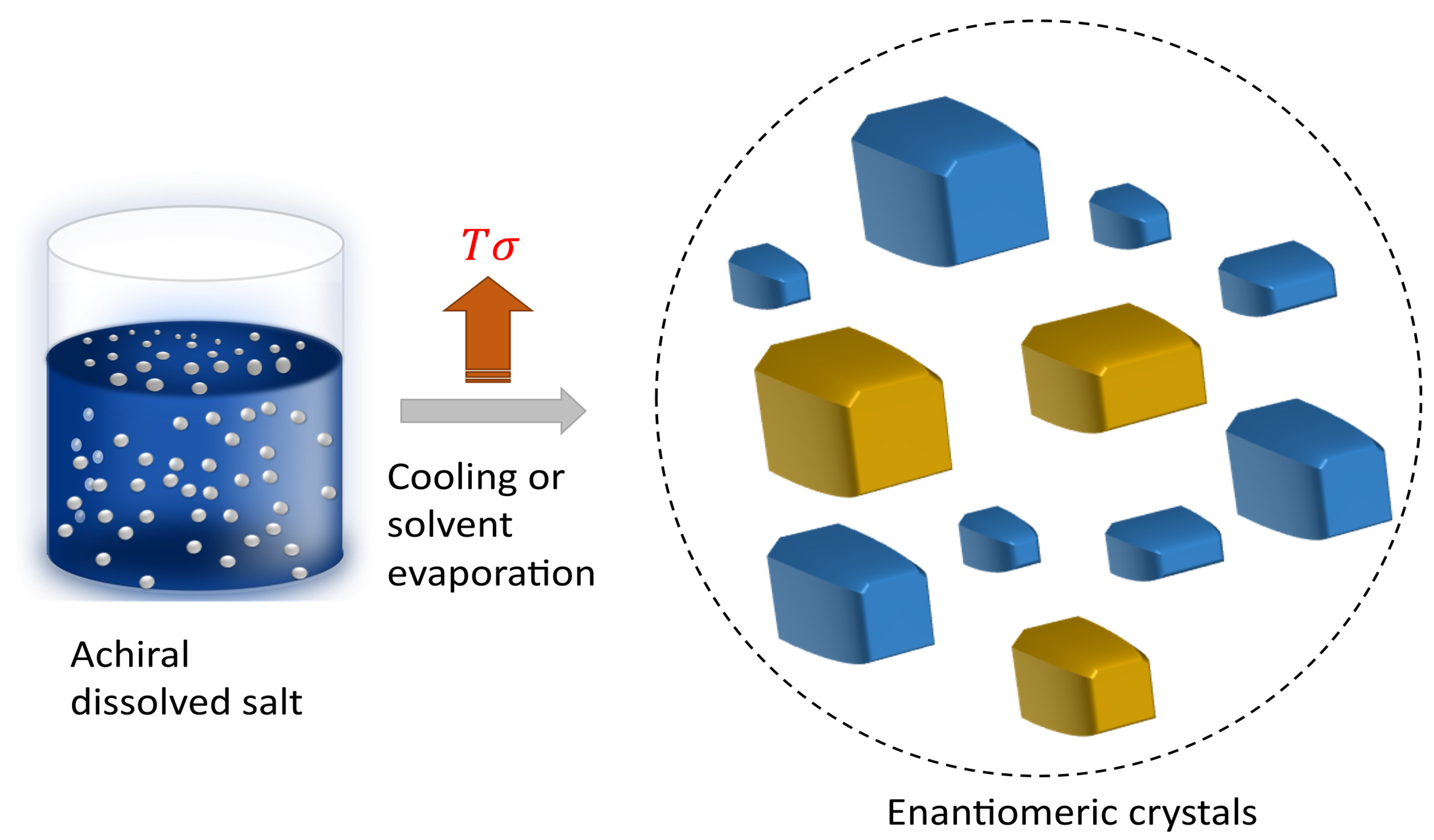
Preprints 97794 g004
Figure 4. Enantiomeric crystals and symmetry-breaking: The genesis of L- and D-crystals (depicted by blue and yellow cubes), in different ratios, originates from achiral compounds (illustrated as white dots). Symmetry-breaking occurs as driving forces, namely temperature gradients and local oversaturation, emerge during the system’s cooling or the solvent’s evaporation, leading to irreversible energy dissipation T σ .
Figure 4. Enantiomeric crystals and symmetry-breaking: The genesis of L- and D-crystals (depicted by blue and yellow cubes), in different ratios, originates from achiral compounds (illustrated as white dots). Symmetry-breaking occurs as driving forces, namely temperature gradients and local oversaturation, emerge during the system’s cooling or the solvent’s evaporation, leading to irreversible energy dissipation T σ .
Preprints 97794 g004
Preprints 97794 g005
Figure 5. Non-equilibrium thermodynamic data on symmetry breaking [35]: Formation of enantiomeric crystals under varied cooling conditions and salt concentrations. The left plot illustrates the total energy dissipated per mol of solid salt over time, with the inset depicting the energy dissipation rate. The right plot shows the enantiomeric excess as a function of time. Red lines represent high salt concentration, while blue lines denote the lowest salt concentration permitting crystal formation. Dotted lines signify enhanced cooling, while continuous lines depict natural (slower) cooling.
Figure 5. Non-equilibrium thermodynamic data on symmetry breaking [35]: Formation of enantiomeric crystals under varied cooling conditions and salt concentrations. The left plot illustrates the total energy dissipated per mol of solid salt over time, with the inset depicting the energy dissipation rate. The right plot shows the enantiomeric excess as a function of time. Red lines represent high salt concentration, while blue lines denote the lowest salt concentration permitting crystal formation. Dotted lines signify enhanced cooling, while continuous lines depict natural (slower) cooling.
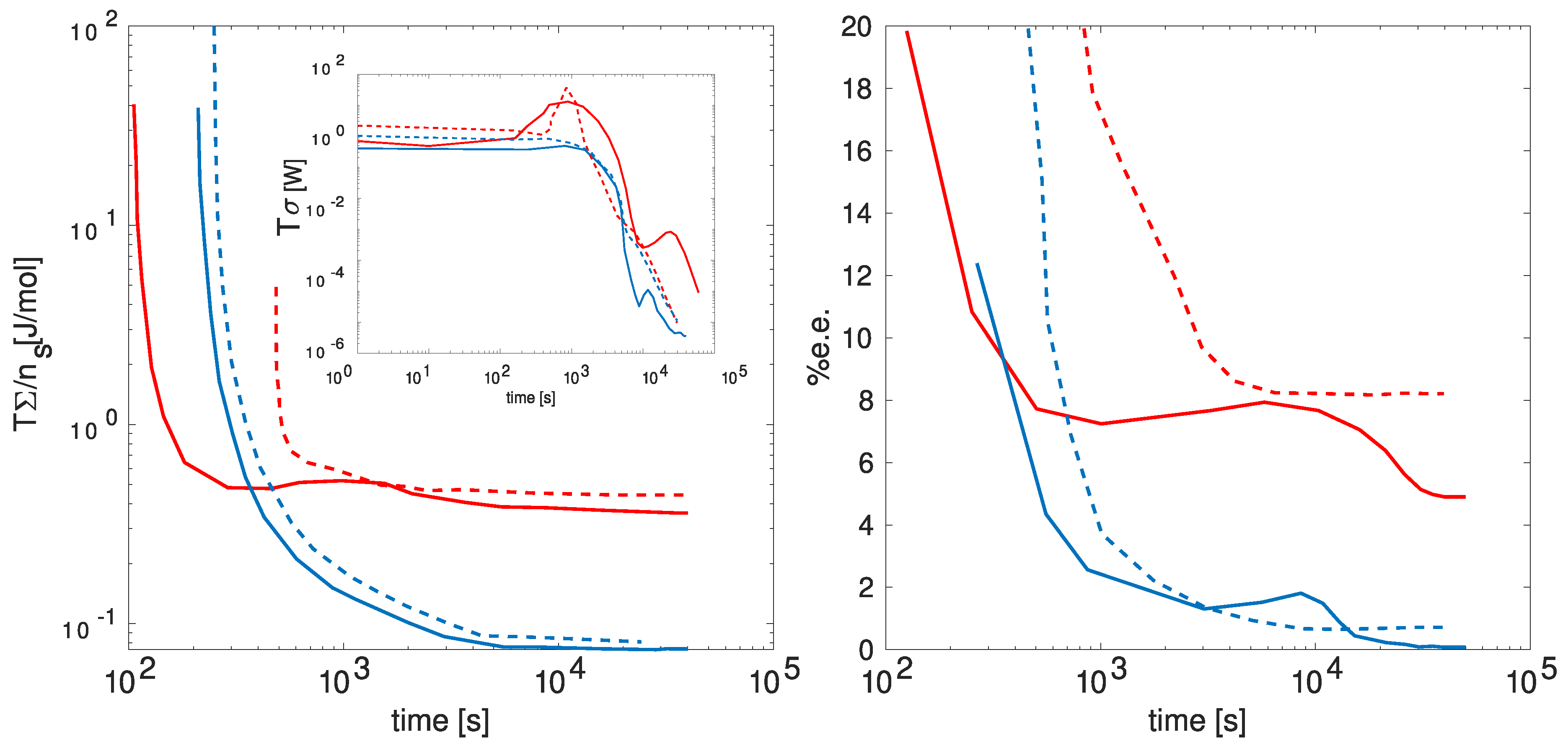
Preprints 97794 g005
Preprints 97794 g006
Figure 6. Polymorphic meso-structures derived from self-assembled chiral building blocks: Symmetry is disrupted as equiprobable meso-structures, possessing identical energy, emerge in varying proportions due to dissipative-driven self-assembly processes. It’s noteworthy that the self-assembly can yield more than one polymorph, representing distinct enantiomeric structures.
Figure 6. Polymorphic meso-structures derived from self-assembled chiral building blocks: Symmetry is disrupted as equiprobable meso-structures, possessing identical energy, emerge in varying proportions due to dissipative-driven self-assembly processes. It’s noteworthy that the self-assembly can yield more than one polymorph, representing distinct enantiomeric structures.
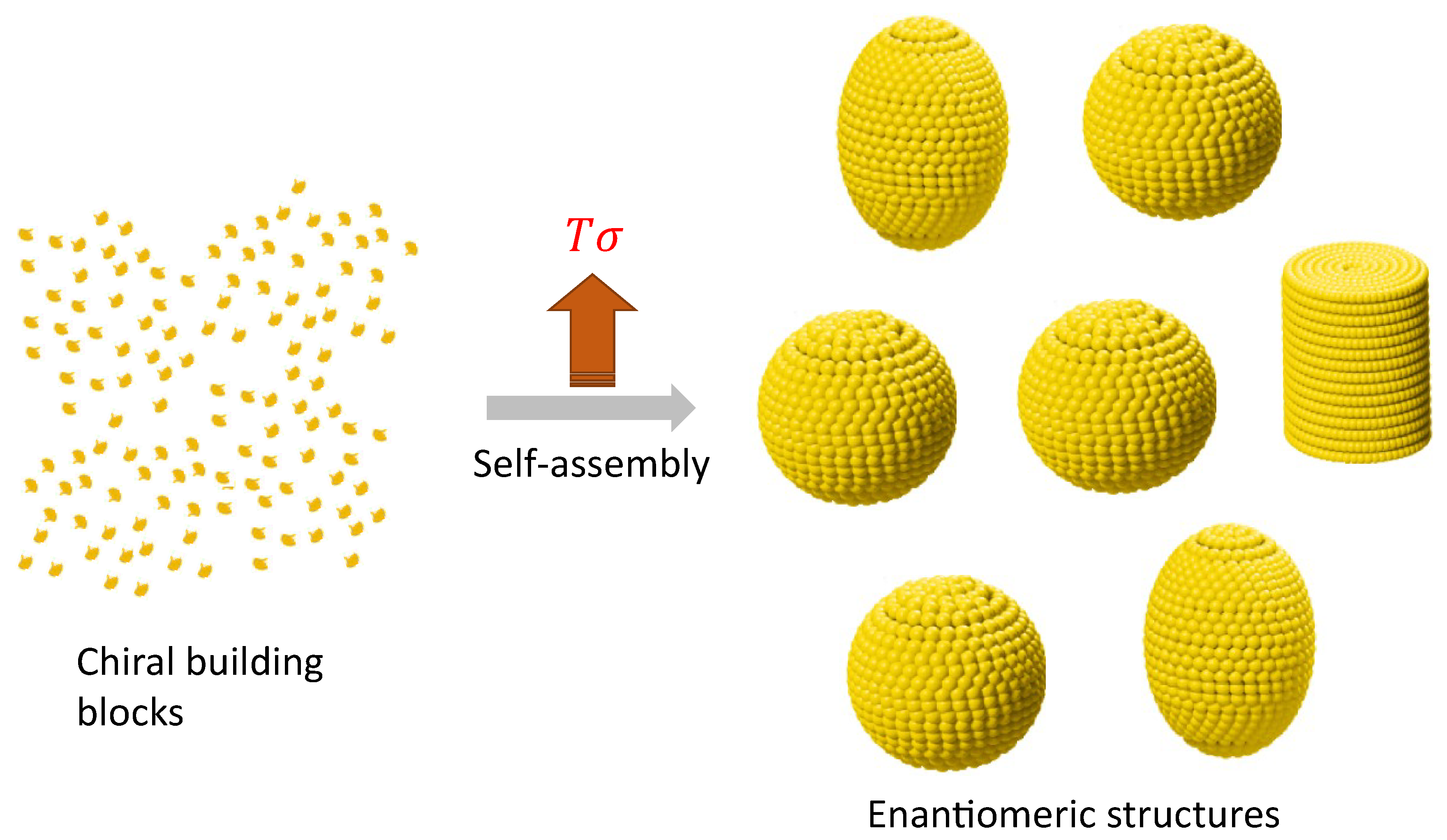
Preprints 97794 g006
Preprints 97794 g007
Figure 7. Magneto-hydrodynamic self-assembled polymorphs: The structure manifests two potential configurations, N c = 2 and N c = 3 , distinguished by the number of central particles. The left plot illustrates the difference in entropy production rate between both polymorphs as a function of the Reynolds number, while the right plot showcases the probability of observing both polymorphs in relation to the Reynolds number. Experimental results are denoted by dots, and dashed lines represent the estimated probability derived from theory, considering energy dissipation as the primary variable.
Figure 7. Magneto-hydrodynamic self-assembled polymorphs: The structure manifests two potential configurations, N c = 2 and N c = 3 , distinguished by the number of central particles. The left plot illustrates the difference in entropy production rate between both polymorphs as a function of the Reynolds number, while the right plot showcases the probability of observing both polymorphs in relation to the Reynolds number. Experimental results are denoted by dots, and dashed lines represent the estimated probability derived from theory, considering energy dissipation as the primary variable.
Preprints 97794 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated