Prerpints.org logo
Preprint
Article

Elastic Critical Buckling Coefficients for Oblique Plates of Steel Structures under Biaxial Normal Stress

Altmetrics

Downloads

89

Views

17

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

15 February 2024

Posted:

15 February 2024

You are already at the latest version

Alerts
Abstract
In steel structures, oblique thin steel plates serve as panel zones in structures spanning large spaces (e.g., warehouses and gymnasiums). Considerable research has been conducted on the shear buckling of panels due to seismic loads acting on a structure. Conversely, under snow or wind loads, the panel zone may experience compressive and tensile stresses simultaneously from two directions. Considering the economic preference for thin steel plates, evaluating the elastic critical local buckling stresses in the panel zone under biaxial normal stress may provide essential information to structural engineers. In this study, an elastic buckling analysis based on the energy method is performed to clarify the impact of panel geometry and boundary conditions on the elastic local buckling stresses of oblique panel zones. As confirmed, the buckling stresses derived from the energy method could simulate the local buckling stresses with accuracy comparable to that of finite element analysis, and an engineer-friendly design formula was proposed. Finally, we determined the correlation of the buckling stresses under biaxial stresses and presented a method for evaluating this correlation. Engineers can utilize the provided design equations to more efficiently and accurately calculate buckling loads, facilitating safer and more economical design of structures with oblique plates.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

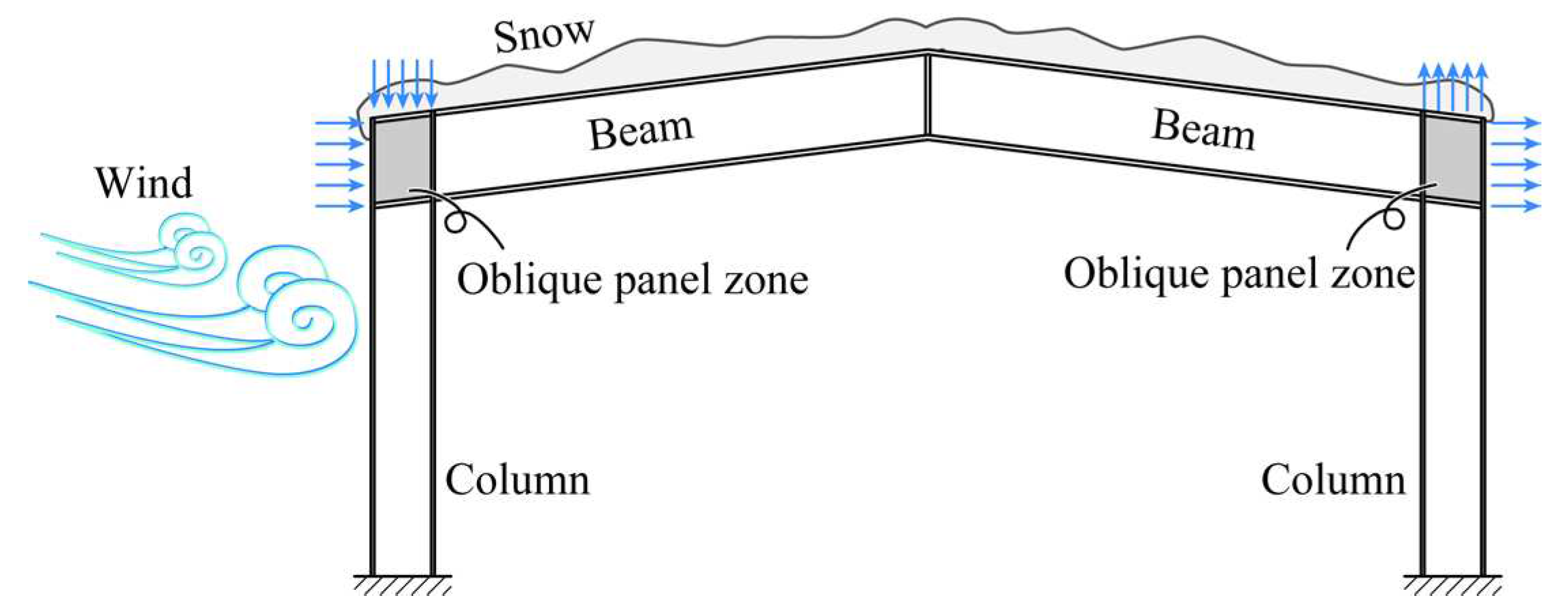
Parallelogram-shaped (oblique) thin steel plates are frequently integrated into diverse structures such as swept-wing aircraft, ships, and bridge plate girders. In structural steel buildings, oblique thin steel plates function as panel zones within structures encompassing large spaces such as warehouses and gymnasiums, contingent on a roof slope of approximately 30° [1], as illustrated in Figure 1. When a horizontal load, such as an earthquake load, acts on a structure, the moment acting on the column is transferred to the beam through the panel zone; consequently, the stress acting on the panel zone is dominated by shear stress [1,2]. Therefore, several studies have investigated the effect of shear stress on shear buckling in the panel zone [3,4,5,6,7].
In contrast, under snow or wind loads, the panel zone may be subjected to both compressive and tensile stresses simultaneously from two directions. Given the recent trend toward utilizing thinner steel plates for economic advantages, assessing the elastic critical local buckling stress in the panel zone under biaxial normal stresses is imperative for providing essential design information to structural engineers. Nonetheless, the elastic critical local buckling stress of oblique plates, even under the basic stress state of uniform compressive stresses, remains poorly understood, in stark contrast to the well-explored domain of elastic critical local buckling issues of rectangular shapes. Clarifying this discrepancy is vital for a comprehensive understanding of the behavior of oblique plates under compressive stress.
The energy method is a promising theoretical approach for determining the local buckling loads of flat plates. Research on the critical local buckling load of rectangular plates employing the energy method has been conducted. Timoshenko [8] provided an analysis of the elastic critical buckling stress of simply supported rectangular plates under uniform normal stresses using this method. In his study, Timoshenko considered not only uniaxial stress but also biaxial normal stresses, presenting correlated functions for rectangular plates under simply supported conditions subjected to biaxial stresses.
Araghi et al. [9] introduced interaction curves and a methodology for predicting the post-buckling behavior of orthotropic rectangular plates under biaxial stresses, utilizing an energy method for precise buckling load predictions. Wang et al. [10] developed a differential quadrature method to solve the elastic local buckling load of rectangular plates under biaxial compressive point loads. The stress distribution in a plate element subjected to a point load is nonuniform, making it difficult to accurately determine its buckling load. However, the method presented by Wang et al. can accurately reproduce the stress distribution and calculate the buckling load, even when the boundary conditions are varied.
Research on the local buckling of oblique plates has also utilized the energy method for addressing local instability issues. Wittrick [11] investigated the elastic local buckling stress of clamped supported oblique plates under uniform compression along longitudinal edges, offering an early solution to the buckling problem of oblique plates with a formula for uniaxial compression-induced local buckling stress [8]. Durvasula [12] explored buckling stresses of simply supported oblique plates under uniaxial compression, employing the Rayleigh-Ritz method to formulate a matrix equation for computing buckling coefficients, and providing charts for these coefficients under uniform compressive and shear stresses.
Kennedy et al. [13] applied an energy method to assess the elastic local buckling stress in simply supported orthotropic and isotropic oblique plates under uniaxial compressive forces, demonstrating that an increase in the oblique angle elevates the buckling stress and offering a chart for engineering design applications. Mizusawa et al. [14,15] examined the buckling stress of oblique plates with mixed boundary conditions through the spline element method, noting an increase in elastic local buckling stress with the oblique angle. Despite numerous studies [16,17,18,19,20] on the local buckling load of oblique plates, few have theoretically examined these loads under biaxial stresses. Moreover, a straightforward design equation for quantitatively evaluating the elastic local buckling stress under uniaxial compression, without necessitating complex calculations, has yet to be introduced.
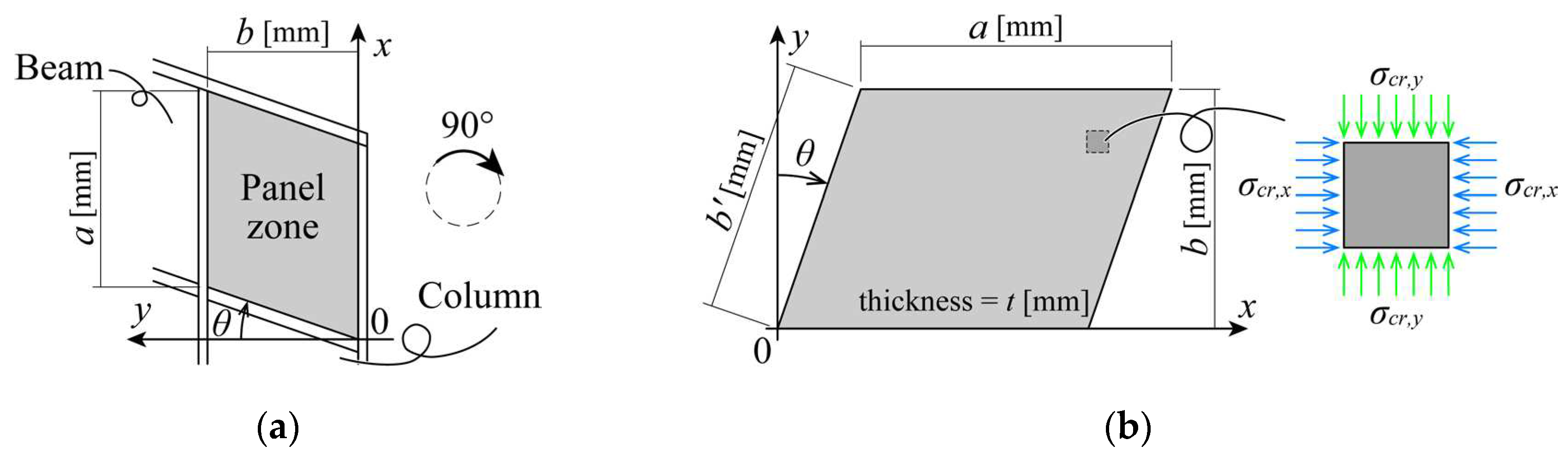
To address this issue, the current study endeavors to clarify the impacts of panel geometry, boundary conditions, and load conditions on the elastic local buckling stresses of oblique panel zones, as depicted in Figure 2, through an elastic buckling analysis utilizing the energy method. Section 2 introduces a distinctive displacement function that replicates local buckling deformation under uniform uniaxial and biaxial normal stresses, alongside a description of an energy method informed by Timoshenko's plate buckling theory [8]. In Section 3, the study examines the influence of the oblique shape and boundary conditions on the elastic local buckling coefficient, specifically for scenarios where the normal stress, as shown in Figure 2, independently impacts the oblique plate.
Because design equations for the buckling coefficient of oblique plates subjected to uniaxial stress have not been presented in prior research, this study proposes design equations derived from theoretical analysis results. In Section 4, we delve into biaxial normal stresses and generate correlation curves for each boundary condition, offering structural engineers reference data for designing steel structures, including panel zones of moment frames under biaxial stress and plate girders of bridges under distributed vertical loads and axial forces in the horizontal direction.

2. Elastic Local Buckling of Oblique Plates under Uniform Uniaxial Normal Stress

2.1. Outline of Theoretical Analysis Modeling

Utilizing an energy method grounded in Timoshenko's plate buckling theory [8], this study investigates the elastic local buckling stress of an oblique plate under an ideal uniaxial uniform normal stress. The theoretical analysis model and the coordinate system, outlined in Figure 2, employ a Cartesian coordinate system for straightforward stress management. The theoretical model, illustrated in Figure 2(b), represents an oblique plate, with the panel zone in the moment frame depicted in Figure 2(a) rotated by 90° to align with theoretical models from previous studies. The dimensions of the theoretical model include length a, height b, and a uniform thickness t, with θ indicating the oblique angle.
This research considers oblique angles ranging from 0° to 30° to reflect practical applications. σcr,x represents the critical normal stress acting parallel to the longitudinal direction, and σcr,y signifies the critical normal stress acting perpendicular to the longitudinal direction. The boundary conditions are defined as simply clamped-supported for all four edges.
The displacement function w, utilized in the theoretical model, aligns with the method previously employed by the authors for determining the buckling coefficients of oblique plates under uniform shear stress [7]. The displacement function w for simply supported oblique plates is expressed by Equation (1).
w = ∑ m = 1 M ∑ n = 1 N c m n sin ⁡ m π x + y tan ⁡ θ a sin ⁡ n π y b .
Displacement function w for clamped supported oblique plates is expressed as Equation (2).
w = ∑ m = 1 M ∑ n = 1 N c m n sin ⁡ π x + y tan ⁡ θ a sin ⁡ m π x + y tan ⁡ θ a sin ⁡ π y b sin ⁡ n π y b ,
where m and n are natural numbers representing the number of terms in the series and represent the number of half-wavelengths in the parallel and perpendicular directions, respectively. cmn is an undetermined coefficient. Both displacement functions w for the oblique plates were expressed using a Fourier series and satisfied the boundary conditions on the edges. The out-of-plane displacements of all the edges of the oblique plate defined by both displacement functions were zero (w = 0). Since the rotation of the simply supported edges are allow to rotate, and the displacement function (1) is defined so that it can express the rotation of simply supported edges (∂w/∂x ≠ 0, ∂w/∂y ≠ 0). Conversely, the displacement function (2) is defined so that it can express the non-rotation of clamped supported edges (∂w/∂x = 0, ∂w/∂y = 0).

2.2. Outline of Theoretical Analysis Modeling

According to Timoshenko's plate buckling theory [8], the strain energy of an oblique plate ΔU can be expressed as follows:
∆ U = D 2 ∬ A   𝜕 2 w 𝜕 x 2 2 + 𝜕 2 w 𝜕 y 2 2 + 2 ν 𝜕 2 w 𝜕 x 2 𝜕 2 w 𝜕 y 2 + 2 1 − ν 𝜕 2 w 𝜕 x 𝜕 y 2 d x d y ,
where A is the integral range enclosed by the plate, and D denotes the flexural rigidity of the plate and can be expressed as
D = E t 3 12 1 − ν 2 ,
where E denotes the modulus of elasticity, ν denotes the Poisson's ratio. As shown in Figure 2(b), the works ΔTx, ΔTy done by uniform normal stresses parallel and perpendicular to the longitudinal edges can be written as follows, respectively.
∆ T x = σ c r , x t 2 ∬ A   𝜕 w 𝜕 x 2 d x d y = k x σ 0 t 2 ∬ A   𝜕 w 𝜕 x 2 d x d y ,
∆ T y = σ c r , y t 2 ∬ A   𝜕 w 𝜕 y 2 d x d y = k y σ 0 t 2 ∬ A   𝜕 w 𝜕 y 2 d x d y ,
σ 0 = π 2 E t 2 12 1 − ν 2 b 2 .
Here, kx, ky are the buckling coefficients, respectively, and σ0 is defined as the base stress in this study. Assuming that the strain energy is equal to the work done by the uniform normal stress parallel to the longitudinal edges, the potential energy Πx obtained by performing an integral calculation can be expressed as follows:
Π x = ∆ U + ∆ T x = 0 .
Based on the principle of minimum potential energy, the buckling condition equation [Equation (9)] can be obtained by differentiating Equation (8) with respect to the auxiliary variable cmn as follows:
𝜕 Π x 𝜕 c m n = 𝜕 ∆ U + k x σ 0 · 𝜕 ∆ T x 0 𝜕 c m n = 0   m = 1 ,   2 ,   3 ,   ⋯ ,   M ;   n = 1 ,   2,3 ,   ⋯ , N ,
c m n T = c 11 c 12 ⋯ c 1 N c 21 ⋯ c M 1 c M 2 ⋯ c M N .
Equation (10) was used to simplify the expression for the buckling condition in Equation (9). The following buckling conditions can be obtained by differentiating Equation (8) using all auxiliary variables cmn and formulating a system of linear equations:
B + k x σ 0 C c m n = 0 ,
c m n T = c 11 c 12 ⋯ c 1 N c 21 ⋯ c M 1 c M 2 ⋯ c M N ,
where B denotes a matrix composed of Equation (3), C indicates a matrix composed of Equation (5), and {cmn} represents a coefficient matrix expressed by Equation (12). The elastic local buckling stress parallel to the longitudinal direction σcr,x = kxσ0 can be obtained by determining the lowest eigenvalues when Equation (11) has nontrivial solutions, i.e., when {cmn} in Equation (11) has a non-{0} solution. Equations (8)–(11) detail the elastic local buckling stress induced by normal stress parallel to the longitudinal direction, whereas the elastic local buckling stress owing to normal stress perpendicular to the longitudinal direction was ascertained using an analogous procedure. The buckling displacements corresponding to the elastic local buckling stresses in each direction were identified as eigenvectors associated with the eigenvalues.

2.3. Finite Element Model for Validation of Energy Methods

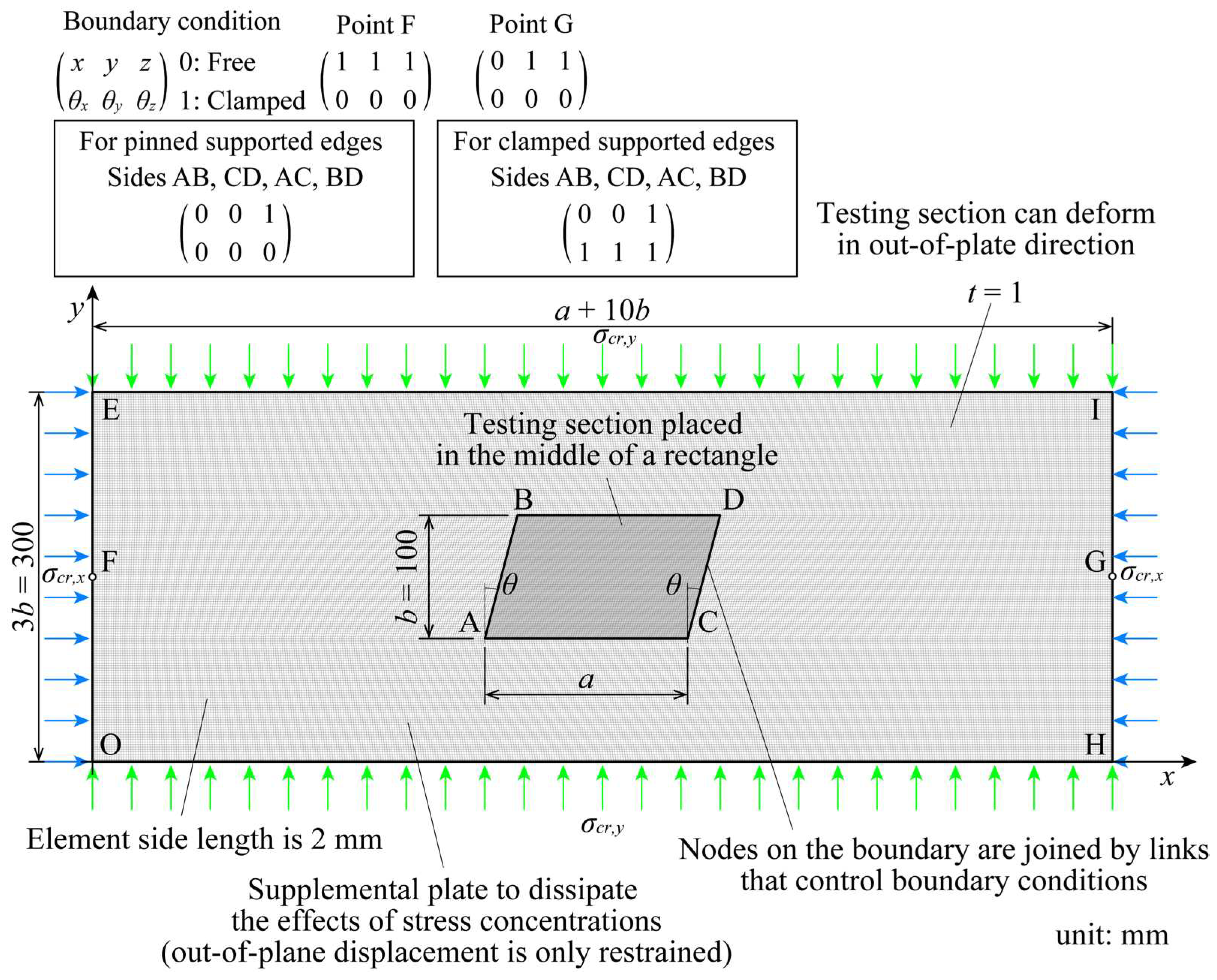
Buckling eigenvalue analysis employing the finite element method (FEM) precisely determines the elastic local buckling loads of an oblique plate under compressive stresses. This analysis is conducted using FEM to validate the outcomes of the eigenvalue analysis based on the energy method detailed in the preceding section.
The finite element (FE) software MSC Marc version 2022 [21,22] was utilized to develop a numerical model of the oblique plates, as illustrated in Figure 3. The FE model employed Element 139 (four-node shell elements with six degrees of freedom per node, accommodating translations and rotations about three reference axes) [22], which is suitable for analyzing thin-shell structures. A mesh size of 2 × 2 mm was selected, guided by a convergence study, to ensure precision. Regarding material properties, the modulus of elasticity, E, was set to 205 GPa and Poisson's ratio ν was set to 0.3. The FE model had a rectangular shape and was composed of a testing section and auxiliary plates to apply only a uniform uniaxial normal stress to the oblique plates.
The out-of-plane displacement of the auxiliary plate was constrained, permitting only the test section to undergo out-of-plane deformation, thereby localizing buckling deformation to the test section. The test section and auxiliary plates were interconnected using RBE2 links, facilitating stress transfer and enabling modifiable boundary conditions. In modeling the test section, both simple and clamped supported boundary conditions were examined, with RBE2 link boundary conditions adjusted accordingly [22].
For the simply supported model, rotational degrees of freedom at all edges of the oblique plate were released, whereas in the clamped-supported model, these were fixed. Uniaxial normal stresses were applied to the nodes along the rectangular edges to generate a uniform shear stress in the testing section. The analytical variables included height, b, fixed at 100 mm thickness, t, fixed at 1.0, and aspect ratio, a/b, varying in the range 0.5–10.
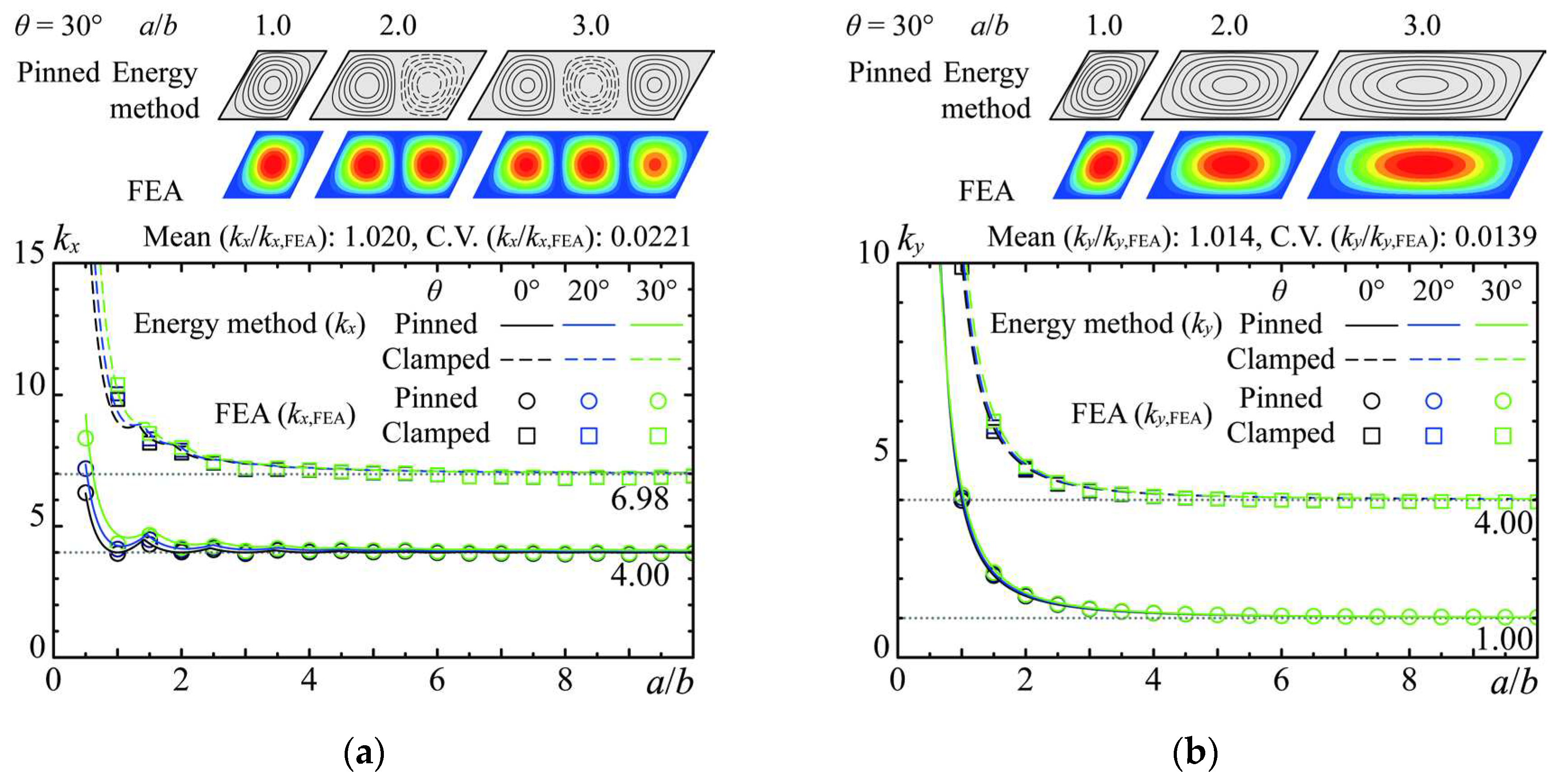
Figure 4 presents a graphical comparison between the theoretical results (kx, ky) derived from the energy method and the finite element analysis (FEA) results (kx,FEA, ky,FEA), including the buckling modes at θ = 30°, as determined by both theoretical and FEA methods. The buckling stresses were converted into buckling coefficients, emphasizing that the precision of these coefficients calculated via the energy method hinges on the displacement function's ability to replicate buckling displacement. Consequently, the parameters m and n of the Fourier series defined in Equations (1) and (2) were set to 40 times the aspect ratio a/b such that the elastic buckling load could be accurately calculated.
The congruence between the theoretical buckling coefficients and modes with the FEA outcomes across various oblique angles, normal stress directions, and boundary conditions was notable. The average ratios of the theoretical to FEA results (kx/kx,FEA, ky/ky,FEA) were 1.020 and 1.014, respectively, with standard deviations of 0.0221 and 0.0139, indicating the capability of the theoretical model to simulate local buckling stress with almost the same accuracy as the FEA.

2.4. Comparison with Buckling Coefficients of Previous Studies

Table 1 compares the buckling coefficients under uniaxial normal stresses parallel and perpendicular to the longitudinal direction, as reported in this and prior research. An exemplar outcome for an oblique angle θ = 30° is highlighted. Although previous investigations calculated the buckling coefficient based on the height b′ along the diagonal edge illustrated in Figure 1, Table 1 recalibrates it to a buckling coefficient based on the height b orthogonal to the longitudinal direction, adhering to the definition adopted in this study. As reported in Table 1, this research uniquely examines the buckling coefficients for both normal stress directions under simple and clamped supports. Anderson [23] reported a heightened buckling coefficient relative to other studies and FEA results, attributed to his examination of an infinitely continuous parallelogram in longitudinal and transverse directions, thereby increasing the buckling coefficient due to constraints from adjacent parallelograms.
Kennedy's [13] findings revealed a lower buckling coefficient compared to FEA results, possibly induced by the coordinate system aligned with the edge of the oblique plate, which differs from the Cartesian coordinate system defined in this study. This difference in coordinate systems may have affected the results of the buckling coefficient calculations. Although Durvasula [12] adopted a coordinate system along the edge of the plate, the displacement function did not completely satisfy the boundary conditions of the oblique plate, resulting in a comparatively higher buckling coefficient against FEA results.

3. Elastic Local Buckling of Oblique Plate under Uniaxial Normal Stress

3.1. Influence of Geometries and Boundary Conditions on Elastic Local Buckling

The effects of the geometries, such as the aspect ratio a/b and oblique angle θ, and boundary conditions of the oblique plates on the buckling coefficients kx, ky were examined under uniaxial normal stress using the developed energy method. For the material properties in this investigation, the modulus of elasticity, E, was set to 205 GPa and Poisson's ratio ν was set to 0.3.
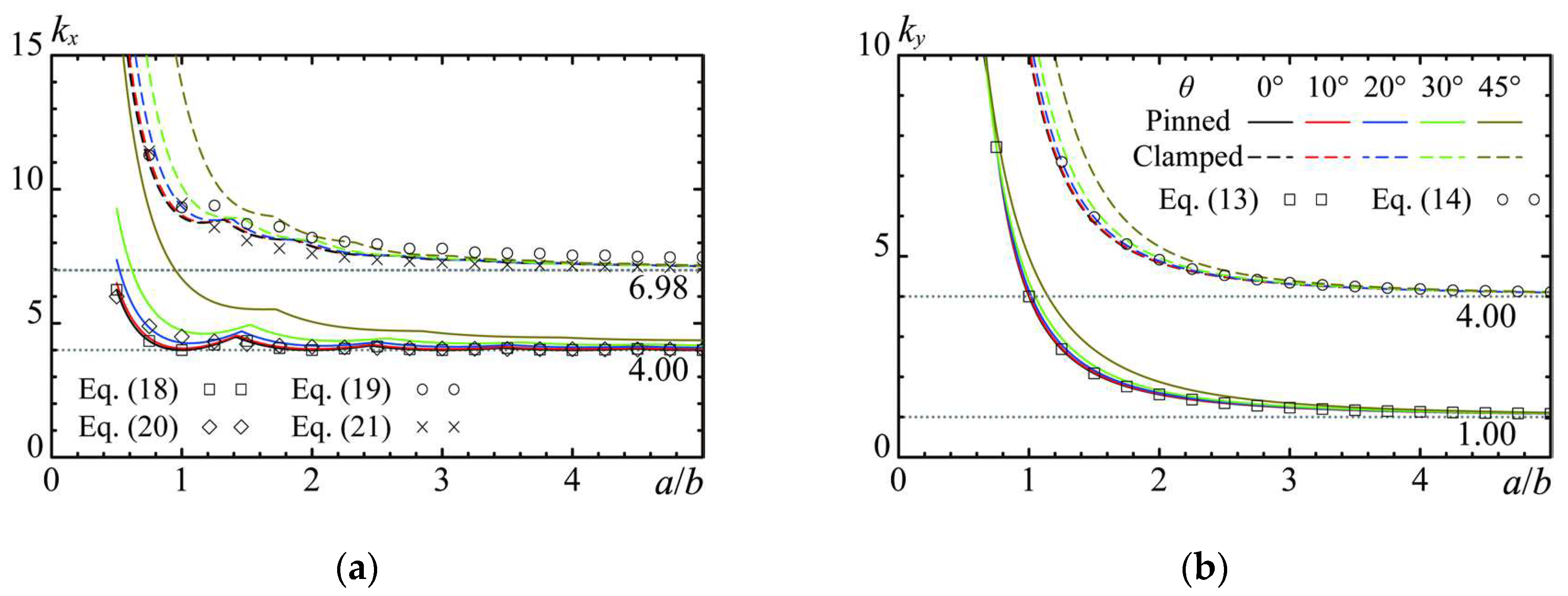
Figure 5 illustrates the influence of geometries on the elastic local buckling stresses, differentiated by various line types corresponding to the boundary conditions. Consistent with prior research [11,12,13], the buckling coefficient exhibits a marginal increase with the augmentation of the oblique angle. The impact of the oblique angle is less pronounced when normal stress is applied perpendicular to the longitudinal direction compared to its application parallel to this direction. These observations align with the buckling modes derived as eigenvectors through the energy method, as depicted in Figure 6.
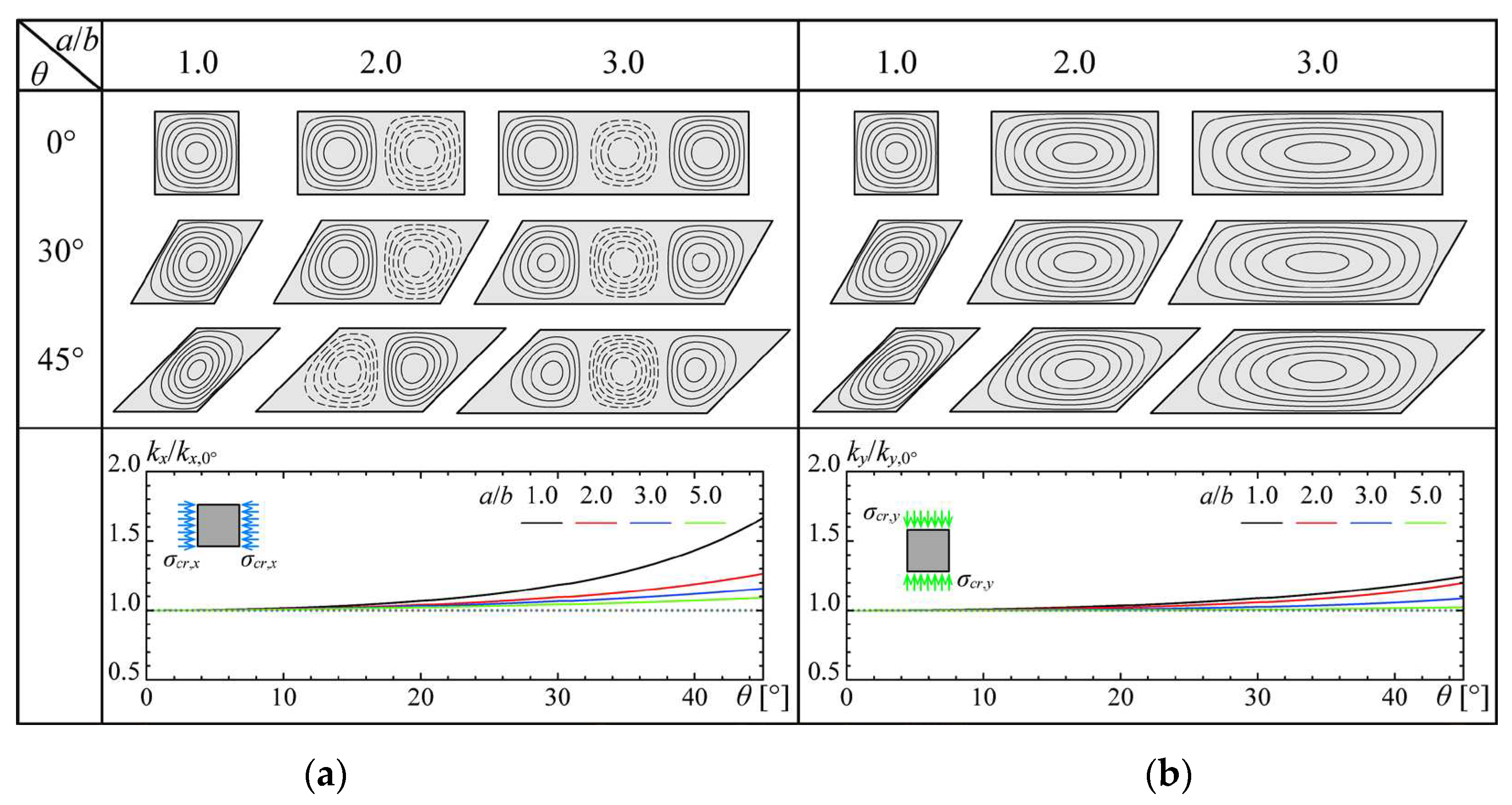
Furthermore, Figure 6 demonstrates the effects of the oblique angle on the buckling coefficients, normalized to the coefficients at an oblique angle of 0° (kx,0°, ky,0°). Regarding the effect of oblique angle, the displacement and wavelength of the buckling mode exhibit negligible variation with changes in the aspect ratio within the examined range up to 30°, suggesting the buckling coefficients remain substantially constant. However, at an oblique angle of 45°, buckling displacement becomes less probable near the acute angle, and the span of buckling waveforms narrows, leading to a reduction in the buckling half-wavelength and an increment in the buckling coefficient. In scenarios where normal stress acts perpendicular to the longitudinal direction, the buckling mode remains largely unchanged across various oblique angles, indicating a minimal effect of the oblique angle on the buckling coefficient under these stress conditions. The buckling coefficient for oblique plates stabilizes at a specific value at an aspect ratio of 5.0, with this convergence value being identical to that of the rectangular plates under analogous boundary and loading conditions.

3.2. Deviation of Design Equations for Oblique Plates under Uniaxial Normal Stress

In Section 3.1, the exploration of the buckling coefficient for an oblique plate under uniaxial normal stress is conducted through the energy method. Although this method facilitates accurate calculation of the buckling coefficient, the numerical computation involved necessitates the determination of the eigenvalues of the matrix, rendering the process computationally intensive. Wittrick [11] and Durvasula [12] similarly introduced methodologies for formulating the determinant elements to ascertain the buckling coefficient for oblique plates, which involved elaborate calculations and eigenvalue determination. Drawing from the findings of the current study employing the energy method, this section devises engineer-friendly design equations that are both accurate and exempt from the need for complex numerical computations.
As illustrated in Figure 5, predicting the variation in the buckling coefficient proved more straightforward when normal stress was applied perpendicular to the longitudinal direction of the oblique plate, compared to parallel application. Consequently, design equations were initially developed for scenarios where stress acts perpendicular to the longitudinal direction. Figure 6 reveals that under such stress conditions, the oblique plate exhibits a single-wave buckling pattern. Based on these results, substituting 1 for m and n and 0° for θ in Equations (1) and (2), and following the calculation process described in Section 2.2, equations for the buckling coefficients of simply and clamped supported rectangular plates can be obtained, respectively.
For simply supported rectangular plates:
k y , p , 0 ° = b a 2 b a + a b 2 .
For clamped supported rectangular plates:
k y , c , 0 ° = 4 b a 2 b a + a b 2 − 4 3 ,
where ky,p,0° and ky,c,0° denote the buckling coefficients for simply supported and clamped-supported rectangular plates under normal stress perpendicular to the longitudinal direction, accurately reflect the variation in buckling coefficients with plate length, as depicted in Figure 5(b). This study introduces practical design equations for the buckling coefficients of oblique plates, incorporating the influence of the oblique angle θ in Equations (13) and (14). This approach benefits from the observation that the convergence values of the buckling coefficients for oblique plates align with those for rectangular plates, facilitating a unified and simplified calculation framework.
For simply supported oblique plates:
k y , p = b y a 2 b y a + a b y 2 .
For clamped supported oblique plates:
k y , c = 4 b y a 2 b y a + a b y 2 − 4 3 ,
where ky,p and ky,c are the buckling coefficients of the simply supported and clamped-supported oblique plates, respectively, under normal stress perpendicular to the longitudinal direction. by represents the assumed plate width for a simplified estimation of the buckling coefficient and is defined by Equation (17).
b y = b cos ⁡ θ 3 .
When a normal stress acts on the rectangular plate parallel to the longitudinal direction, multiple buckling waves occur in the longitudinal direction. Thus, the buckling coefficients can be derived by substituting 1 for n and 0° for θ into Equations (1), (2).
For simply supported rectangular plates:
k x , p , 0 ° = m i n m b a + a m b 2 m = 1 ,   2 ,   3 ,   ⋯ .
For clamped supported rectangular plates:
k x , c , 0 ° = m i n 8 3 1 + m 2 3 8 b a 2 4 m 2 + 1 + m 2 2 + 2 a b 2 + 1 + m 2 m = 1 ,   2 ,   3 ,   ⋯ ,
where kx,p,0° and kx,c,0° denote the buckling coefficients of the simply supported and clamped-supported rectangular plates under normal stress perpendicular to the longitudinal direction, respectively. m signifies the number of buckling half-waves along the longitudinal direction and is a natural number. For a simply supported rectangular plate, Equation (18) accurately captures the variation in the buckling coefficient as it fluctuates with the number of buckling half-waves in the longitudinal direction, as demonstrated in Figure 5(a). Conversely, Equation (19) for a clamped-supported rectangular plate approximates the buckling coefficient within about 5% accuracy because the actual buckling displacement is less accurately represented with a displacement function when n = 1.
Additionally, adopting the plate width from simplified estimations as in Equations (15) and (16) and substituting for b in Equations (18) and (19) proved inadequate for accurately estimating the buckling coefficient, which changes with length a. Consequently, this study formulated design Equations (20) and (21), leveraging the observation that the convergence value of the buckling coefficient for oblique plates aligns with the minimum value for rectangular plates.
For simply supported oblique plates:
k x , p = 4.00 + 0.50 b x , p a 2 ,
For clamped supported oblique plates:
k x , c = 6.98 + 2.50 b x , c a 2 ,
where kx,p and kx,c indicate the buckling coefficients of the simply supported and clamped-supported oblique plates, respectively, under a normal stress parallel to the longitudinal direction. bx,p and bx,c denote the assumed plate widths used to calculate the buckling coefficients and are defined by Equations (22) and (23).
b x , p = b cos ⁡ 2 θ 3 .
b x , c = b cos ⁡ θ .
As depicted in Figure 5(a), substituting θ = 0° into the design equation and treating it as the equation for a rectangular plate reveals that it does not accommodate fluctuations in the buckling coefficient with variations in the number of buckling half-waves. Nonetheless, the design Equations (20) and (21) are capable of approximately estimating the variations in the buckling coefficient with increases in length. However, design Equation (20) for simply supported plates falls short of being conservative for oblique plates with an aspect ratio of 2.0 or less, necessitating caution in its application under such conditions.

3.3. Validation of Proposed Design Equations

The design equations derived in the previous section were validated by comparing them with analytical results based on FEM. The FE model used in the validity test is the same as that shown in Figure 3. The range of oblique angle θ to be verified is from 0° to 45°, and the range of aspect ratio a/b is from 1.0 to 3.0, which is the range where the buckling coefficient is not convergent.
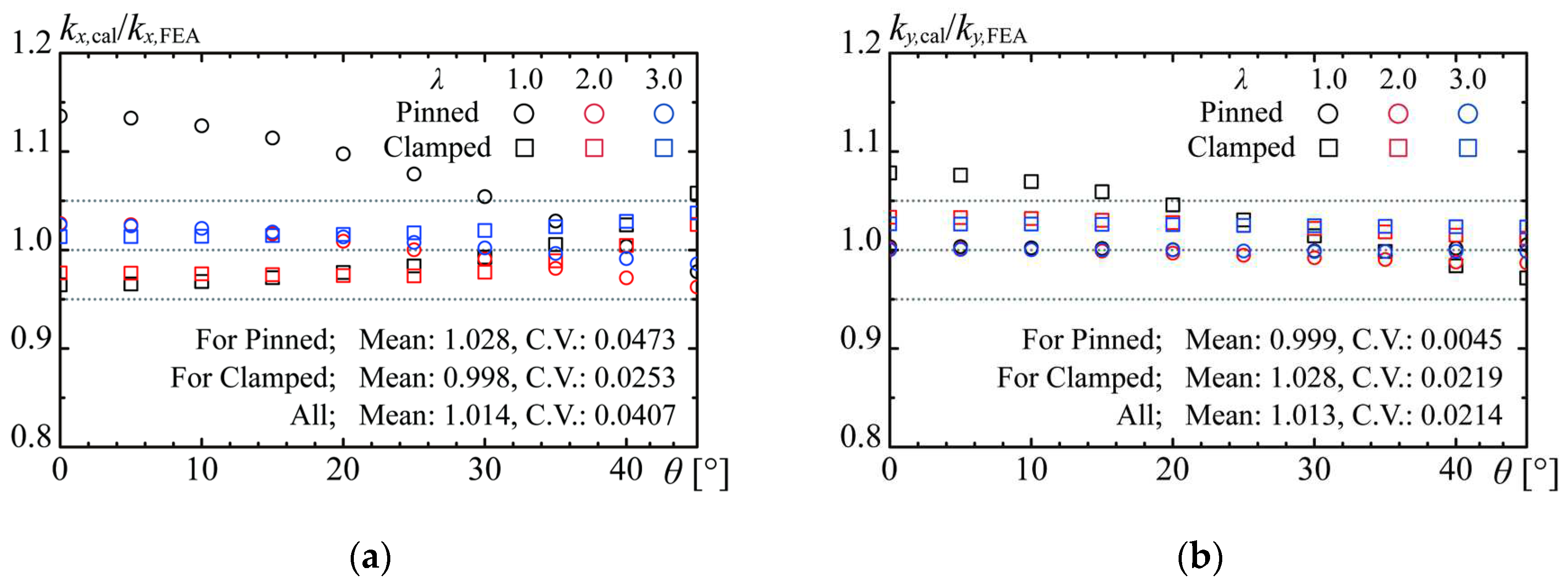
A comparison of the buckling coefficients for the oblique plate under uniaxial normal stress obtained using the proposed design equations is shown in Figure 7. The mean and standard deviation of the buckling coefficients predicted based on the proposed design equations for the stress acting in the longitudinal direction with respect to the FEA results were 1.014 and 0.0407, respectively. Note, as mentioned before, that the design equations developed by the approximation do not match the change in the buckling coefficient with the change in the number of buckling half-waves when a simply supported oblique plate is subjected to stress parallel to the longitudinal direction. Therefore, design equation (20) does not yield conservative results when the aspect ratio is as low as 1.0. Therefore, a conservative design can be achieved by setting the buckling coefficient to 4.0 [2,8,24], which is the minimum value for simply supported plates when stresses act parallel to the longitudinal direction on simply supported oblique plates with oblique angles of 30° or less.

4. Elastic Local Buckling of Oblique Plate under Biaxial Normal Stresses

The preceding sections explored the elastic local buckling of oblique plates under uniaxial normal stress via the energy method. It acknowledges the possibility of biaxial normal compressive stresses impacting oblique thin steel plates utilized in aircraft, ships, and structural steel buildings, or scenarios where normal compressive stress acts in one direction and normal tensile stress in the opposite. Thus, the study verified the elastic local buckling load and buckling mode for oblique plates under normal stresses from two axes employing the energy method.
The potential energy Πxy for oblique plates under biaxial uniform normal stresses can be expressed by using Equations (3), (5), and (6).
Π x y = ∆ U + α ∆ T x + β ∆ T y = 0 ,
where α and β are coefficients indicating the stress ratio from two axes, with positive values signifying compressive stress and negative values indicating tensile stress. Consequently, as buckling does not ensue when both coefficients are negative, this investigation focuses on scenarios where both coefficients exceed −1, and at least one coefficient is positive. The buckling conditions under biaxial normal stresses are derived by differentiating Equation (24) with all auxiliary variables cmn and formulating a system of linear equations as follows:
B + α k x , 0 σ 0 C + β k y , 0 σ 0 D c m n = 0 ,
where D denotes a matrix composed of Equation (6), and kx,0 and ky,0 denote the buckling coefficients for uniaxial compression with stresses parallel or perpendicular to the longitudinal direction, respectively, i.e., β is necessarily zero when α equals one, and vice versa.
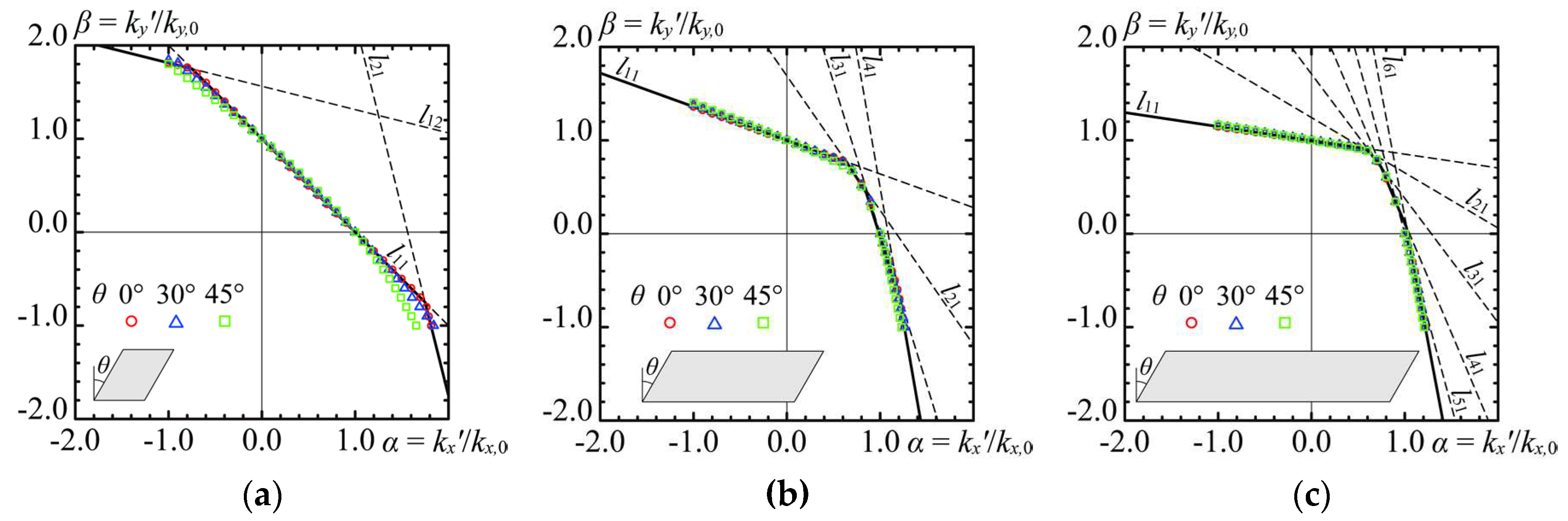
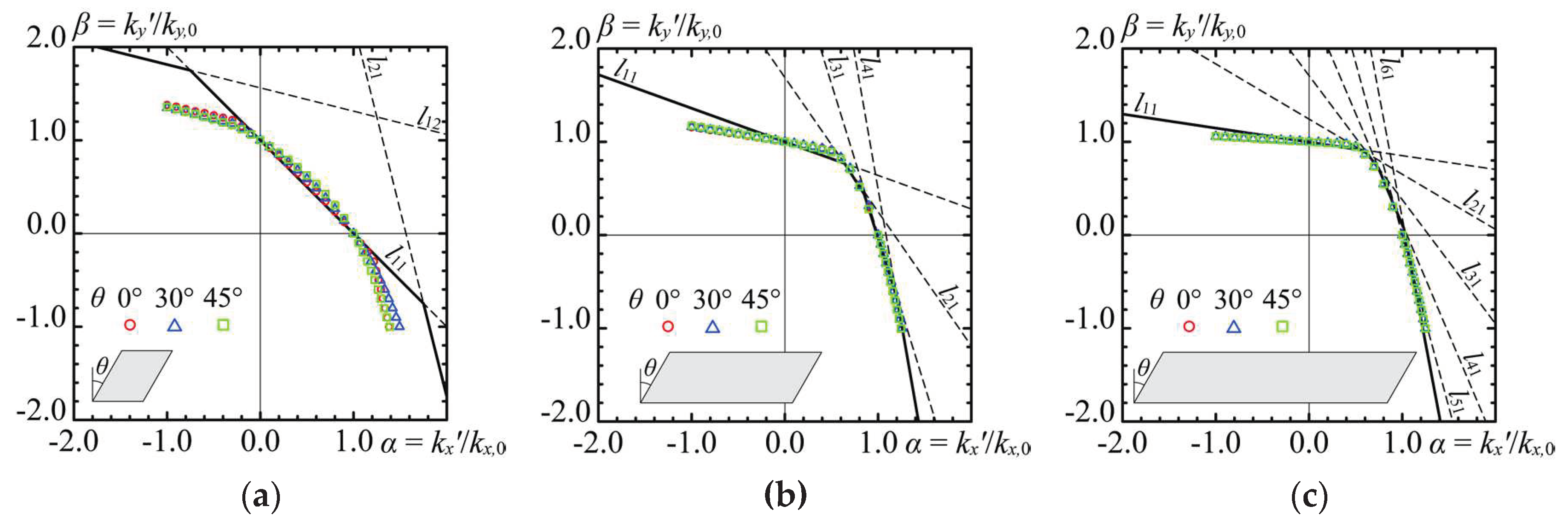
Figure 8 and Figure 9 illustrate the correlation curves for the buckling coefficient of the oblique plate under biaxial stress across various boundary conditions. kx' and ky' denote the buckling coefficients under biaxial stress conditions for stresses parallel or perpendicular to the longitudinal direction, respectively. The findings are represented by distinct color plots, showcasing examples for θ at 0, 30, and 45°.
The influence of boundary conditions on the correlation curves is minimal at lower aspect ratios (1.0), while the general trend remains unaffected by boundary conditions. Similarly, the correlation curve is largely uninfluenced by the oblique angle θ, especially the range where the aspect ratio is greater than 3.0.
Timoshenko [8] derived a relationship for the buckling stress of a simply supported rectangle under biaxial stress, as expressed in Equation (26):
σ x ' m 2 + σ y ' n 2 a 2 b 2 = π 2 D a 2 t m 2 + n 2 a 2 b 2 2 ,
where σx' and σy' denote the critical stresses at which local buckling occurs in the oblique plate under biaxial stress, and m and n denote the number of half wavelength in parallel and perpendicular to the longitudinal directions. Converting the critical stress in Equation (26) to a buckling coefficient yields Equation (27).
k y ' = − m 2 b 2 n 2 a 2 k x ' + b 2 n 2 a 2 m 2 + n 2 a 2 b 2 2 = l m n ,
As expressed in Equation (27), the buckling coefficient ky' for a simply supported rectangular plate subjected to biaxial stress is expressed as a linear expression of kx’. We define lmn as a straight line that varies with the number of half-wavelengths m and n and the aspect ratio a/b. For example, the line l31, substituting 3 for m and 1 for n, is denoted as in Equation (28).
l 31 = k y ' = − 3 2 b 2 1 2 a 2 k x ' + b 2 1 2 a 2 3 2 + 1 2 a 2 b 2 2 . .
In Figure 8, results derived by substituting various integers for m and n into Equation (27) are denoted by black dashed lines, with scenarios yielding the lowest buckling coefficient highlighted by thick solid lines. The influence of the oblique angle on the buckling coefficient for oblique plates is minimal, allowing for precise evaluation using the buckling correlation function established by Timoshenko for simply supported rectangular plates. Similarly, Figure 9 employs the Timoshenko correlation function to assess buckling coefficient correlations for clamped-supported oblique plates. At an aspect ratio of 1.0, this function tends to overestimate the buckling coefficient when either of the biaxial stresses is tensile. However, for larger aspect ratios, Timoshenko's correlation function for simply supported rectangles effectively estimates the buckling coefficient for oblique plates under biaxial stress.

5. Conclusions

This study presents a comprehensive analysis of the elastic local buckling loads of simply supported and clamped-supported oblique plates utilizing the energy method. Buckling displacement functions for an oblique plate within the Cartesian coordinate system were introduced. Furthermore, engineer-friendly design equations for determining the elastic local buckling coefficients of oblique plates were proposed. The main conclusions of this investigation are summarized as follows:
  • The critical buckling stress for oblique plates under uniaxial stress was calculated through an energy method that employs the Cartesian coordinate system for displacement function derivation, contrasting with previous studies that used the coordinate system aligned with oblique edges. The accuracy of the proposed method is corroborated by comparison with buckling eigenvalue results from FEA, demonstrating superior precision over prior literature.
  • We derived design equations to facilitate the simplification of buckling load calculations for stresses acting parallel or perpendicular to the longitudinal direction. Comparisons with FEA results validate the adequacy of these equations, enabling engineers to efficiently compute buckling loads for panel zones.
  • The impact of the oblique angle on the buckling stress for oblique plates under biaxial stress was determined to be insignificant. Based on this insight, the buckling stress correlation function for rectangular plates under biaxial stress, as proposed by Timoshenko, is applicable for estimating the buckling stress of oblique plates.

Author Contributions

Conceptualization, K. Mitsui and K. Ikarashi; methodology, K. Mitsui and K. Ikarashi; software, K. Mitsui and K. Sada; validation, K. Mitsui; formal analysis, K. Mitsui; investigation, K. Mitsui; resources, K. Mitsui and K. Sada; data curation, K. Mitsui and K. Sada; writing—original draft preparation, K. Mitsui; writing—review and editing, K. Mitsui and K. Ikarashi; visualization, K. Mitsui and K. Sada; supervision, K. Mitsui and K. Ikarashi; project administration, K. Mitsui and K. Ikarashi; funding acquisition, K. Mitsui and K. Ikarashi. All the authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by KAKENHI, grant number No. 20K14868, and KAKENHI, grant number No. 20H02294.

Data Availability Statement

All information and data are given in the text completely.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Architectural Institute of Japan (AIJ). AIJ Recommendations for Design of Connections in Steel Structures; Architectural Institute of Japan: Tokyo, Japan, 2021; pp. 225–258.
  2. American Institute of Steel Construction (AISC). Seismic Provisions for Structural Steel Buildings; American Institute of Steel Construction: Chicago, Illinois, USA, 2016; pp. 9.1-103– 9.1-105.
  3. Wittrick, W.H. Buckling of oblique plates with clamped edges under uniform shear. The Aeronautical Quarterly. 1954, 5, 1, 39–51. [CrossRef]
  4. Cook, I.T.; Rockey, K.C. Shear buckling of clamped and simply-supported infinitely long plates reinforced by transverse stiffeners. The Aeronautical Quarterly. 1962, 13, 1, 41–70. [CrossRef]
  5. Cook, I.T.; Rockey, K.C. Shear buckling of rectangular plates with mixed boundary conditions. The Aeronautical Quarterly. 1962, 14, 4, 349–356. [CrossRef]
  6. Ikarashi, K.; Utsuki, Y.; Mitsui, K. Elastic Shear buckling strength of L-shaped beam-to-column joint panels composed with I-shaped members. J Strct Const Eng (Trans of AIJ) 2020, 85, 771, 759–769, https://doi.org/10.3130/aijs.85.759. (In Japanese).
  7. Mitsui, K.; Ikarashi, K. Elastic shear buckling coefficients for oblique plates. Mathematical Problems in Engineering 2022, 2022, 9532380. [Google Scholar] [CrossRef]
  8. Timoshenko, S.P.; Gere, J.M. Theory of elastic stability, 2nd ed.; McGraw-Hill Book Co., Inc.: New York, New York, USA, 1959; pp. 319–439. [Google Scholar]
  9. Araghi, S.N.; Shanmugam, N.E. Strength of biaxially loaded orthotropic plates. Thin-Walled Structures 2012, 53, 40–47. [Google Scholar] [CrossRef]
  10. Wang, X.; Wang, Y. Buckling analysis of thin rectangular plates under uniaxial or biaxial compressive point loads by the differential quadrature method. Int J Mech Sci 2015, 101, 38–48. [Google Scholar] [CrossRef]
  11. Wittrick, W.H. Buckling of oblique plates with clamped edges under uniform compression. The Aeronautical Quarterly. 1953, 4, 2, 151–163. [CrossRef]
  12. Durvasula, S. Buckling of Simply Supported Skew Plates. J Eng Mech. 1971, 97, 3, 967–979. [CrossRef]
  13. Kennedy, J.B.; Prabhakara, M.K. Buckling of simply supported orthotropic skew plates. The Aeronautical Quarterly. 1978, 29, 3, 161–174. [CrossRef]
  14. Mizusawa, T.; Kajita, T.; Naruoka, M. Analysis of skew plate problems with various constraints. J sound and vibration. 1980, 73, 4, 575–584. [CrossRef]
  15. Mizusawa, T.; Leonard, J.W. Vibration and buckling of plates with mixed boundary conditions. Eng Strct. 1990, 12, 4, 285–290. [CrossRef]
  16. Wittrick, W.H. On the buckling of oblique plates in shear: An examination of the critical shear stresses in 45-degree parallelogram plates. Aircraft Engineering and Aerospace Technology 1956, 28, 25–27. [Google Scholar] [CrossRef]
  17. Iguchi, S. Iguchi, S. Eine Lösung für die Berechnung der biegsamen rechteckigen Platten. Report Julius Springer, Berlin, Germany, 1933. [CrossRef]
  18. Yoshimura, Y.; Iwata, K. Buckling of simply supported oblique plates. J Appl Mech. 1963, 30, 3, 363–366. [CrossRef]
  19. Ashton, J.E. Stability of clamped skew plates under combined loads. J Appl Mech. 1969, 36, 1, 139–140. [CrossRef]
  20. Lotfi, S.; Azhari, M.; Heidarpour, A. Inelastic initial local buckling of skew thin thickness-tapered plates with and without intermediate supports using the isoparametric spline finite strip method. Thin-Walled Structures. 2011, 49, 11, 1475–1482. [CrossRef]
  21. MSC Software: Marc 2022 Feature Pack 1, Volume A: Theory and User Information, USA, 2023.
  22. MSC Software: Marc 2022 Feature Pack 1, Volume B: Element Library, USA, 2023.
  23. Anderson, R.A. Charts giving Critical Compressive Stress of Continuous Flat Sheet Divided into Parallelogram-shaped Panels. National Advisory Committee for Aeronautics (NACA), Washington, D.C, USA, 1951.
  24. Architectural Institute of Japan (AIJ). Recommendations for Stability Design of Steel Structures; Architectural Institute of Japan: Tokyo, Japan, 2018; pp. 180–228. [Google Scholar]
Preprints 98964 g001
Figure 1. Stress state on panel zones varying with multiple loads.
Figure 1. Stress state on panel zones varying with multiple loads.
Preprints 98964 g001
Preprints 98964 g002
Figure 2. Oblique plates under uniform biaxial normal stresses and its geometry: (a) Panel zone in moment frame; (b) Theoretical analysis model.
Figure 2. Oblique plates under uniform biaxial normal stresses and its geometry: (a) Panel zone in moment frame; (b) Theoretical analysis model.
Preprints 98964 g002
Preprints 98964 g003
Figure 3. Overview of FE model for oblique plates under normal stress.
Figure 3. Overview of FE model for oblique plates under normal stress.
Preprints 98964 g003
Preprints 98964 g004
Figure 4. Graphical comparisons between present theoretical and FEA results and buckling modes under uniaxial compression where θ = 30°: (a) Under stress parallel to longitudinal direction; (b) Under stress perpendicular to longitudinal direction.
Figure 4. Graphical comparisons between present theoretical and FEA results and buckling modes under uniaxial compression where θ = 30°: (a) Under stress parallel to longitudinal direction; (b) Under stress perpendicular to longitudinal direction.
Preprints 98964 g004
Preprints 98964 g005
Figure 5. Effect of geometries on the local buckling load: (a) Under stress parallel to longitudinal direction; (b) Under stress perpendicular to longitudinal direction.
Figure 5. Effect of geometries on the local buckling load: (a) Under stress parallel to longitudinal direction; (b) Under stress perpendicular to longitudinal direction.
Preprints 98964 g005
Preprints 98964 g006
Figure 6. Effect of geometries on the local buckling modes with simply supported condition: (a) Under stress parallel to longitudinal direction; (b) Under stress perpendicular to longitudinal direction.
Figure 6. Effect of geometries on the local buckling modes with simply supported condition: (a) Under stress parallel to longitudinal direction; (b) Under stress perpendicular to longitudinal direction.
Preprints 98964 g006
Preprints 98964 g007
Figure 7. Comparison between FEA results and calculations based on the proposed design equations: (a) Stress parallel to longitudinal direction; (b) Stress parallel to longitudinal direction.
Figure 7. Comparison between FEA results and calculations based on the proposed design equations: (a) Stress parallel to longitudinal direction; (b) Stress parallel to longitudinal direction.
Preprints 98964 g007
Preprints 98964 g008
Figure 8. Correlation curve of buckling coefficient for simply supported condition: (a) a/b = 1.0; (b) a/b = 3.0; (c) a/b = 5.0.
Figure 8. Correlation curve of buckling coefficient for simply supported condition: (a) a/b = 1.0; (b) a/b = 3.0; (c) a/b = 5.0.
Preprints 98964 g008
Preprints 98964 g009
Figure 9. Correlation curve of buckling coefficient for clamped supported condition: (a) a/b = 1.0; (b) a/b = 3.0; (c) a/b = 5.0.
Figure 9. Correlation curve of buckling coefficient for clamped supported condition: (a) a/b = 1.0; (b) a/b = 3.0; (c) a/b = 5.0.
Preprints 98964 g009
Table 1. Comparisons with buckling coefficients where θ = 30°.
Table 1. Comparisons with buckling coefficients where θ = 30°.
Stress directions Boundary conditions Aspect ratio a/b
0.5 1.0 1.5 2.0 3.0
σcr,x Pinned Present study 8.82 4.64 4.91 4.38 4.27
FEA 8.35 4.33 4.66 4.18 4.05
Durvasula [12] 7.80 4.81 4.78 4.52 –
Kennedy [13] 7.20 4.15 4.19 3.90 –
Anderson [23] 9.60 6.62 6.26 5.21 –
Clamped Present study 29.22 10.45 8.85 8.09 7.42
FEA 25.95 10.39 8.53 7.99 7.21
Wittrick [11] – 10.23 – – –
σcr,y Pinned Present study 16.82 4.36 2.28 1.66 1.27
FEA 16.87 4.13 2.16 1.59 1.24
Durvasula [12] 13.80 4.00 1.98 1.51 –
Kennedy [13] 12.53 3.07 1.76 1.40 –
Clamped Present study 38.28 11.41 6.19 4.96 4.33
FEA 35.11 10.84 6.00 4.85 4.25
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated