Prerpints.org logo
Preprint
Article

A Study of {10–12} Twinning Activity Associated with Stress State in Mg-3Al-1Zn Alloy during Compression

Altmetrics

Downloads

76

Views

16

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

16 February 2024

Posted:

16 February 2024

You are already at the latest version

Alerts
Abstract
An eight-sided prism sample, obtained from a hot-rolled AZ31 magnesium alloy sheet, was compressed at room temperature along the transverse direction to investigate the influence of local strain on twinning behavior using electron backscatter diffraction (EBSD) measurements. The octagonal surface of the sample was divided into distinct regions based on hardness distribution and metallographic observations. The EBSD maps of different areas show significant variations, suggesting that these areas experienced different local strain conditions. The EBSD measurements provided detailed data from three distinct regions, with the strain state known in two regions and uncertain in the third. The combined analysis of the Schmid factor (SF) and the strain compatibility factor (m') was employed to study twin variant selection. The comparison of twinning behavior in different regions showed that the strain compatibility factor offered a more comprehensive explanation for the observed twinning pattern in the region with local shear strain.
Keywords: 
Subject: Chemistry and Materials Science  -   Materials Science and Technology

1. Introduction

The occurrence of {10-12} twinning is widely acknowledged for its significant impact on plastic deformation at room temperature [1,2,3]. Moreover, the incidence of {10-12} twinning is closely related to the initial crystal orientations and the loading path [4,5,6,7,8,9,10,11]. Theoretically, Mg alloy has six equivalent {10-12} twin variants within each grain. Several studies have investigated variant selection using a Schmid factor criterion [12,13,14]. The previous study by Hong et al. [12] indicated that the activation of {10-12} twinning depended on strain paths, and the selection mechanism of the six variants was governed by the Schmid factor (SF) criterion. Song et al. [13] suggested that variant selection in twinned grains generally follows the Schmid factor criterion. Various non-Schmid phenomena have been recorded, attributed to the different local stress from externally applied stress [15,16,17]. Lou et al. [18] suggested that non-Schmid behavior in certain grains is linked to local stress variations near the grain boundary, resulting from strain accommodation between grains.
Several recent publications [13,19,20,21,22,23,24] aim to understand the strain accommodation needed for twinning to spread across grain boundaries. The quantification of strain accommodation can be assessed using a geometric compatibility factor, m'=cos(Ψ)×cos(κ), where Ψ and κ represent the angles between the normal of the twinning plane and the twinning shear direction of adjacent grains, respectively. Guo et al. [25] conducted a thorough analysis of the SF criterion and local strain accommodation to study the variant selection of {10-12} twinning. The researchers found that stress concentration relief happened through transfer across grain boundaries and the formation of new twinning. Zhang et al. [26] also studied cross-grain boundary contraction paired twins (CTW), and found that the formation of CTW was influenced by the twinning shear compatibility across grain boundaries, characterized by a high m' value. The statistical results showed that macro stress near the grain boundary significantly influenced the stress state, leading to twinning initiation. The presence of non-Schmid twin variants indicates that strain compatibility in neighboring grains significantly influences variant selection.
Currently, few studies have examined the impact of the local strain state on twinning variant selection [27,28,29]. Huang et al. [28] analyzed twinning variant selection behavior in different local strain areas and observed the complexity of twinning behaviors. In regions with significant shear strain, the presence of twin variants can be explained by the Schmid factor criterion, which involves assessing the local stress state as a pure shear model. The impact of local strain on the strain compatibility of cross-boundary twin pairs is not yet fully understood.
The primary aim of this study is to investigate how local strain affects twinning behavior in Mg-3Al-1Zn alloy under compression, with a focus on {10-12} twinning. The Schmid factor, strain compatibility factor, and twinning strain tensor are calculated using the results of electron backscattered diffraction (EBSD) to study the selection of twinning variants.

2. Materials and Methods

The study used a commercial hot-rolled AZ31 (Mg-3%Al-1%Zn) magnesium alloy sheet. The observation shows that the material exhibits a strong {0001} basal texture and a twin-free equiaxed grain structure, with an average grain size of ~35μm, as shown in Figure 1. An eight-sided prism with bottom sides and edge sides measuring 8mm each, obtained from the as-received material. The compression test was conducted using a CMT5504 testing machine, with the loading direction (LD) aligned parallel to the transverse direction (TD) at a strain rate of 0.01s-1 and a final strain of 3.9%. The hardness was measured at 0.5mm intervals along lines a-e, and texture observations were made in areas A-D after the compression (see Figure 2b). Electrolytic polishing involves immersing the material in a Struers ACII electrolyte solution and applying a 20 V at a temperature of -5 °C for 90 seconds. EBSD analyses were performed using a Zeiss Supra 55 FEG-SEM with an HKL Channel 5 EBSD system.

3. Results

3.1. Distribution of the Hardness Values

The distribution of hardness values along the five lines is shown in Figure 3. Only a quarter of the octagonal surface was measured. The decrease in hardness values from line a to line e is evident. The hardness values decrease as the tested position moves away from the center for each line. The phenomenon may be due to work hardening. The variation in hardness at different positions suggests non-uniformity in the local strain state, which could affect twinning activation.

3.2. Microstructure after Uniaxial Compression

To investigate the effect of local strain, the octagonal surface corroded by a picric acid solution was divided into nine areas labeled as letters (a–i). The microstructure displays well-defined and aligned twin lamellae, primarily showing {10-12} extension twinning, as shown in Figure 4. Furthermore, the grains at the center have significantly decreased in size compared to those in other areas. The twinning volume fraction is highest in the center areas (b,e,h), followed by the corner areas (a,c,g,i), and then the side areas (d,f). In relation to the distribution of hardness values shows that the localized strain in the central area exceeds that of other regions, making the activation of {10-12} extension twinning more readily in the central area than in other regions.

3.3. Microstructure and Texture Differences in Different Regions

In order to enhance the clarity of the twinning structures, EBSD maps are shown in Figure 5. Twinning is significantly present in regions A, C, and D, while region B shows minimal to no twinning. Region B was located outside the directly compressed area, which hindered twinning activation due to the low normal strain. In contrast, region A and region D experienced direct compression from the force, resulting in normal strain with minimal local shear strain. Region C experienced both normal and shear strain. In boundary structure maps, red lines represent {10-12} extension twinning boundaries. From the {0001} pole figures, it is evident that the matrix orientations are centrally distributed around the ND, while the variant orientations rotate after compression. The distinction is based on the different orientations of variants in region A and region D, which rotate around the TD (y), while variant orientations in region C deviate by approximately 45° between the TD (y) and RD (x), referred to as the xy-direction for ease of reference.

3.4. SF Ratio Distribution

The Schmid factors for twinning were calculated using the equation SF=cos(λ)×cos(φ), where λ(φ) represents the angle between the loading direction and the normal to the twinning plane. A total of 97 grains containing 123 twin variants in region A, 102 grains containing 129 twin variants in region C, and 143 grains containing 191 twin variants in region D were selected for detailed analysis of twin variant selection behavior using the SF criterion. For each grain analyzed, the SFs for all 6 potential twin variants, based on the grain matrix orientation, were calculated as the ratio of SF (SFratio). This quantity is defined as the ratio of the SF of the activated twin variant to the highest SF of the twin variant. A higher SFratio value (up to 1) indicates a smaller difference in resolved shear stress between the activated and most heavily stressed variants.
Figure 6 illustrates the distribution of SFratio values for regions A, C, and D. In region A (Figure 6a), about 45% of the variants exhibit the highest SF (SFratio=1), while approximately 35% of the other variants have the second highest SF (0.8<SFratio<1). In region D (Figure 6b), the variants with the highest SF, while approximately 40% have the second highest SF. In both regions, at least 80% of twinning behavior meets the Schmid factor criterion, with the highest or second highest SF. In contrast to regions A and D, where the normal stress is aligned along the y-direction, region C experiences both normal and shear stresses, leading to an indeterminate stress state. Huang et al. [28] also reported a similar situation and suggested a pure shear model similar to the rolling model. Therefore, it is possible to create a stress state model that combines tension and compression, as shown in Figure 6c. The SF values can be recalculated using the equation SF=(cosλ1×cosφ1-cosλ2×cosφ2)/2, where λ1 (φ1) represents the angle between the tensile stress direction and the twinning plane normal (twinning plane), and λ2 (φ2) represents the angle between the compressed stress direction and the twinning plane normal. The distribution of SFratio values for region C under this stress state (Figure 6d). The data suggests that around 20% of twin variants exhibit the highest SF values, while over 60% show the second highest SF values. Approximately 80% of twin variants exhibit the highest or second highest SF for region C in total.

3.5. Strain Tensor Distribution

In order to investigate the relationship between the activated twin variants and the local strain state, the strain tensors of all the activated twin variants were calculated using the method described by Luo et al. [22]. The average strain tensor component values for the three regions undergoing 4% deformation are shown in Table 1. The negative and positive values represent compressed and tensile strain resulting from twinning formed along the force direction. The mean values of the ɛyy components in region A and region D are -0.0448 and -0.0393, respectively. The absolute values are both around 4%, consistent with the sample's deformation when compressed in the transverse direction (y-direction). In contrast, region C exhibits average values of -0.0204, -0.0215, and -0.0312 for the ɛxx, ɛxy, and ɛyy components, respectively, suggesting compression along the y-direction with 4% deformation.
The detailed results are illustrated in Figure 7. A wide dispersion of the ɛxx components is observed for the activated twin variants in three regions, with values ranging from -0.07 to 0.07. In region A (Figure 7a–c), the sum of all ɛxx components approaches zero because approximately half of the twin variants have negative ɛxx components and the other half have positive ɛxx components. The same conclusion applies to the ɛxy elements. Nevertheless, the ɛyy component exhibits negativity, suggesting the existence of multiple half-twin variants with a negative ɛyy component. This suggests that most twinning results in compression along the y-direction. A similar situation can be observed in region D (Figure 7g–i).
The strain tensor components ɛxx, ɛxy and ɛyy for the twin variants observed in region C are shown in Figure 7d, 7e and 7f, respectively. The three components of the strain tensor show significant variations, ranging from -0.07 to 0.03. The total of all ɛxx elements is negative, aligning with the ɛyy elements, indicating strain accommodation from activated twin variants in the x and y directions. The components of ɛxy mainly show negative values, indicating that most activated twin variants effectively accommodate overall strain in response to local deformation conditions in the xy-direction.

4. Discussion

The strain compatibility factor for twinning across a grain boundary was calculated by the equation m' = cos(Ψ) × cos(κ), as previously mentioned. The lamella connecting two adjacent grains is termed as paired twins, while the lamella connecting three neighboring grains is referred to as twin chains. The accurate prediction of the activated twin variant in deformed Mg alloy using only the SF or the m' can be quite challenging. A comprehensive analysis of the Schmid factor and strain compatibility factor is used to study the selection behavior of twin variants in the presence of inhomogeneous local strain.
Figure 8 illustrates the distribution of rank, value, and ratio of m' for the three regions. A comprehensive analysis of twin variant selection behavior was conducted, involving 49 twin variants in region A, 62 twin variants in region C, and 55 twin variants in region D. This analysis employed the strain compatibility factor and involved classifying the variants into paired twins and twin chains for statistical analysis. There is little variation in the rank of m' across the three regions. The occurrence of the twin variant with a rank of 1 for paired twins is over 70%, whereas that for twin chains exceeds 80%. Over 80% of twin variants in both paired twins and twin chains exhibit high m' values (>0.6). The phenomenon is observed in all three regions. m' ratio is calculated as the m' of the activated paired twins divided by the highest m' of the paired twins, where a value of 1 indicating the highest m' value. The results of the m' ratio closely resemble those of the m' rank, with minimal variation observed across the three regions. The percentage of the twin variant with an m' ratio of 1 for paired twins is over 70%, while for twin chains, it exceeds 80%, resulting in a combined total of approximately 80%. The analysis using the strain compatibility factor may not be affected by the direction of the force. The selection behavior of most of the {10-12} twinning variants is influenced by the strain compatibility factor in scenarios with inhomogeneous local strain.
Figure 9a illustrates a twin chain across three neighboring grains in region A. Twinning Th1 and Th2 intersect each other in grain Mh. Twinning occurs with Ti in grain Mi and Tj in grain Mj. The twin variants, connected at grain boundaries, form a twin chain denoted as Th1-Ti-Tj. The spectral characteristics of six potential twin variants of the parent grain Mh, Mi, and Mj are depicted in Figure 9b. V1-V6 represent the six equivalent variations of {10-12} extension twinning. The data suggests that variants Th1, Ti, and Tj all exhibit the second highest SF. The distribution of the strain compatibility factor m' for the twin chain is displayed in Figure 9c. The strain compatibility factor m' exhibits its highest value of 0.966 between Ti and Th1, and also records the highest value of 0.937 between Ti and Tj. The strain tensors for the grain Mh, Mi, and Mj are illustrated in Figure 9d. For Mh, the value of the y-direction (loading direction) is negative, and the magnitudes are significantly greater than zero, similar to the calculated results for Mi and Mj. The activation of the twin chain is essential for facilitating compressed deformation in the force direction, influenced by a combination of the Schmid factor criterion and strain accommodation.
Figure 10a illustrates two different paired twins located in neighboring grains within region A. In grain Mp, Tp1 and Tp1' exhibit the same type of twin variant, characterized by parallel lamellae, while Tp1 and Tp2 represent different twin variants. The twinning of To and Tq corresponds to the activated twin variant in grains Mo and Mq, respectively. The variants associated with grain boundaries form twin chains Tp1-To and Tp1'-Tq. As shown in Figure 10b, twinning To and Tq exhibit the second highest SF, while Tp1 (Tp1') only has the fourth highest SF. This suggests that Tp1 (Tp1') may not be solely governed by the Schmid factor criterion. Figure 10c shows that the strain compatibility factor m' is highest between Tp1 and To (0.967), and also highest between Tp1' and Tq (0.645). Figure 10d illustrates the strain tensors of grains Mo, Mp, and Mq, indicating that the paired twins undergo compression in the y-direction. The two paired twins exhibit a high m' rank, suggesting that strain compatibility significantly influences the behavior of neighboring grains. Conversely, a variant with a low SF rank suggests that the formation of paired twins is driven by strain accommodation rather than adherence to the Schmid factor criterion.
Figure 11a illustrates a twin chain Tk1-Tl-Tn1 spanning three adjacent grains in region C. In this study, the distribution of SF ratio calculated by the pure shear model for region C, only marginally satisfies the Schmid factor criterion. The SF values are significantly lower than 0.5 (Figure 11b). The twinning of Tk1, Tl, and Tn1 can be identified as variants V1, V5, and V5, respectively. The results indicate that the activation of twin variants in region C is not influenced by the Schmid factor criterion. Figure 11c illustrates that the strain compatibility factor m' is highest between Tl and Tk1 (0.801), and also highest between Tl and Tn1 (0.895). This twin chain activation indicates the effect of strain accommodation, which is independent of the force direction. Figure 11d illustrates the strain tensors of grains Mk, Ml, and Mn, indicating that the twin chain experiences compressed deformation in the xy-direction. Consequently, the twin variant possessing the highest m' rank is favored for activation in the form of the twin chain within grain boundaries to release the local stress concentration.
Figure 12a illustrates a twin chain Tr1-Ts1-Tt across three adjacent grains in region C. Similar to the twin chain Tk1-Tl-Tn1, the SF values of variants Tr1, Ts1, and Tt are all significantly less than 0.5. These can be identified as variants V4, V4, and V1, respectively, as shown in Figure 12b. Figure 12c illustrates that the strain compatibility factor m' between Ts1 and Tt is the highest (0.823), whereas the factor between Ts1 and Tr1 is the second lowest (-0.001). This observation suggests that the activated twin chain does not conform to the law of strain accommodation. The strain tensors of grains Mr, Ms, and Mt indicate that the twin chain experiences compressed deformation in the y-direction rather than the xy-direction, as shown in Figure 12d. This indicates that the generation of certain paired twins cannot be explained by the strain compatibility factor.
The above observation suggests that variants with high strain compatibility may prefer activation and eventually form paired twins or twin chains to reduce stress concentration. In certain regions with non-uniform local strain, there are instances that cannot be explained by the strain compatibility factor law and Schmid factor criterion.

5. Conclusions

EBSD was used to investigate the {10-12} extension twinning during the compression of AZ31 Mg alloy with a strong basal texture along the transverse direction. The geometry of the sample, in the form of an eight-sided prism, leads to the generation of inhomogeneous local strain in different regions after compression. The mechanism of twin variants selection was investigated through a comprehensive analysis of the Schmid factor and strain compatibility factor. The main conclusions can be summarized as follows:
(1)
Under inhomogeneous deformation, the stress, strain, and microstructure of the compressed AZ31 magnesium alloy sample exhibit significant variations across different regions.
(2)
In regions under uniaxial compression with minimal shear strain, the Schmid factor criterion can predict over 80% of observed twin variants. In regions where shear strain cannot be ignored, the behavior of twin variant selection can be effectively explained using a pure shear model.
(3)
In regions with local shear strain, the strain compatibility factor is more appropriate than the Schmid factor for analyzing the effect of local strain on the selection behavior of twin variants.

Author Contributions

Conceptualization, B.W.; methodology, B. L. and J.Y.; formal analysis, W.W.; investigation, B.L., J.Y. and W.W.; resources, L.D.; data curation, L.X.; writing—original draft preparation, B.L. and J.Y.; writing—review and editing, L.D.; visualization, L.X.; supervision, B.W.; funding acquisition, B.W. All authors have read and agreed to the published version of the manuscript.

Funding

This work was financially supported by the Natural Science Foundation of Fujian Province of China (Grant No. 2020J01352), and the Quanzhou City Science & Technology Program of China (Grant No. 2021C027R).

Data Availability Statement

The data that support the findings of this study are available on request from the corresponding author, bswang@fzu.edu.cn, upon reasonable request.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Barnett, M.R. Twinning and the ductility of magnesium alloys: Part I: "Tension" twins. Materials Science and Engineering: A 2007, 464, 1–7. [Google Scholar] [CrossRef]
  2. Barnett, M.R. Twinning and the ductility of magnesium alloys: Part II. "Contraction" twins. Materials Science and Engineering: A 2007, 464, 8–16. [Google Scholar] [CrossRef]
  3. Malik, A.; Wang, Y.; Nazeer, F.; Khan, M.A.; Ali, T.; Ain, Q.T. Effect of pre-straining on twinning, texture and mechanical behavior of magnesium alloys A-review. J Mater Res Technol 2020, 9, 14478–14499. [Google Scholar] [CrossRef]
  4. Jiang, L.; Jonas, J.J.; Mishra, R.K.; Luo, A.A.; Sachdev, A.K.; Godet, S. Twinning and texture development in two Mg alloys subjected to loading along three different strain paths. Acta Materialia 2007, 55, 3899–3910. [Google Scholar] [CrossRef]
  5. Brown, D.W.; Almer, J.D.; Clausen, B.; Mosbrucker, P.L.; Sisneros, T.A.; Vogel, S.C. Twinning and de-twinning in beryllium during strain path changes. Materials Science and Engineering: A 2013, 559, 29–39. [Google Scholar] [CrossRef]
  6. Park, S.H.; Hong, S.-G.; Lee, J.H.; Huh, Y.-H. Texture evolution of rolled Mg–3Al–1Zn alloy undergoing a {10-12} twinning dominant strain path change. Journal of Alloys and Compounds 2015, 646, 573–579. [Google Scholar] [CrossRef]
  7. Hou, D.W.; Li, Q.Z.; Wen, H.M. Study of reversible motion of {10 (1)over-bar 2} tensile twin boundaries in a magnesium alloy during strain path changes. Mater. Lett. 2018, 231, 84–86. [Google Scholar] [CrossRef]
  8. Wang, B.; Xin, R.; Huang, G.; Liu, Q. Effect of crystal orientation on the mechanical properties and strain hardening behavior of magnesium alloy AZ31 during uniaxial compression. Materials Science and Engineering: A 2012, 534, 588–593. [Google Scholar] [CrossRef]
  9. Hou, M.J.; Zhang, H.; Fan, J.F.; Zhang, Q.; Wang, L.F.; Dong, H.B.; Xu, B.S. Microstructure evolution and deformation behaviors of AZ31 Mg alloy with different grain orientation during uniaxial compression. Journal of Alloys and Compounds 2018, 741, 514–526. [Google Scholar] [CrossRef]
  10. Jiang, J.; Godfrey, A.; Liu, W.; Liu, Q. Microtexture evolution via deformation twinning and slip during compression of magnesium alloy AZ31. Materials Science and Engineering: A 2008, 483-484, 576-579. https://doi.org/10.1016/j.msea.2006.07.175. [CrossRef]
  11. Zhou, L.; Yan, R.; He, Z.; Wang, Z.; Wang, F.; Wei, Z.; Mao, P.; Liu, Z. Quasi-in situ observation of extension twinning of AZ31 magnesium alloy under co-directional dynamic compression. Journal of Alloys and Compounds 2023, 969. [Google Scholar] [CrossRef]
  12. Hong, S.-G.; Park, S.H.; Lee, C.S. Role of {10–12} twinning characteristics in the deformation behavior of a polycrystalline magnesium alloy. Acta Materialia 2010, 58, 5873–5885. [Google Scholar] [CrossRef]
  13. Song, B.; Xin, R.; Liang, Y.; Chen, G.; Liu, Q. Twinning characteristic and variant selection in compression of a pre-side-rolled Mg alloy sheet. Materials Science and Engineering: A 2014, 614, 106–115. [Google Scholar] [CrossRef]
  14. Luo, J.R.; Godfrey, A.; Liu, W.; Liu, Q. Twinning behavior of a strongly basal textured AZ31 Mg alloy during warm rolling. Acta Materialia 2012, 60, 1986–1998. [Google Scholar] [CrossRef]
  15. Barnett, M.; Keshavarz, Z.; Beer, A.; Ma, X. Non-Schmid behaviour during secondary twinning in a polycrystalline magnesium alloy. Acta materialia 2008, 56, 5–15. [Google Scholar] [CrossRef]
  16. Jonas, J.J.; Mu, S.; Al-Samman, T.; Gottstein, G.; Jiang, L.; Martin, Ė. The role of strain accommodation during the variant selection of primary twins in magnesium. Acta Materialia 2011, 59, 2046–2056. [Google Scholar] [CrossRef]
  17. Xin, R.; Ding, C.; Guo, C.; Liu, Q. Crystallographic analysis on the activation of multiple twins in rolled AZ31 Mg alloy sheets during uniaxial and plane strain compression. Materials Science & Engineering A 2015, 652, 42–50. [Google Scholar] [CrossRef]
  18. Lou, C.; Zhang, X.Y.; Ren, Y. Non-Schmid-based {10-12} twinning behavior in polycrystalline magnesium alloy. Mater Charact 2015, 107, 249–254. [Google Scholar] [CrossRef]
  19. Liu, X.; Zhu, B.; Huang, G.; Li, L.; Xie, C.; Tang, C. Initiation and strain compatibility of connected extension twins in AZ31 magnesium alloy at high temperature. Mater Charact 2016, 122, 197–205. [Google Scholar] [CrossRef]
  20. Xin, R.; Guo, C.; Xu, Z.; Liu, G.; Huang, X.; Liu, Q. Characteristics of long {10-12} twin bands in sheet rolling of a magnesium alloy. Scripta Materialia 2014, 74, 96–99. [Google Scholar] [CrossRef]
  21. Shi, Z.Z. Secondary twin variant selection in Mg alloy after a strain-path change. Journal of Alloys & Compounds 2017, 696, 510–515. [Google Scholar] [CrossRef]
  22. Vasilev, E.; Knezevic, M. Experimental characterization of voids and surrounding microstructures developed under tension of Mg, Mg-3Zn, and Ti: A statistical study. Materials Science and Engineering a-Structural Materials Properties Microstructure and Processing 2023, 862. [CrossRef]
  23. Yaddanapudi, K.; Kumar, M.A.; Wang, J.; Wang, X.; Rupert, T.J.; Lavernia, E.J.; Schoenung, J.M.; Beyerlein, I.J.; Mahajan, S. Local hardening and asymmetric twin growth by twin-twin interactions in a Mg alloy. Journal of Magnesium and Alloys 2023, 11, 176–191. [Google Scholar] [CrossRef]
  24. Paramatmuni, C.; Zheng, Z.; Rainforth, W.M.; Dunne, F.P.E. Twin nucleation and variant selection in Mg alloys: An integrated crystal plasticity modelling and experimental approach. International Journal of Plasticity 2020, 135. [Google Scholar] [CrossRef]
  25. Guo, C.; Xin, R.; Ding, C.; Song, B.; Liu, Q. Understanding of variant selection and twin patterns in compressed Mg alloy sheets via combined analysis of Schmid factor and strain compatibility factor. Materials Science and Engineering: A 2014, 609, 92–101. [Google Scholar] [CrossRef]
  26. Shi, Z.Z.; Liu, X.F. Characteristics of cross grain boundary contraction twin pairs and bands in a deformed Mg alloy. Journal of Alloys & Compounds 2017, 692, 274–279. [Google Scholar] [CrossRef]
  27. Yoshida, Y.; Shibano, J.-i.; Ogura, M.; Saito, K.; Kajiwara, K. Localized shear deformation in magnesium alloy by four-point bending. Materials Science and Engineering a-Structural Materials Properties Microstructure and Processing 2020, 793. [CrossRef]
  28. Huang, H.T.; Godfrey, A.; Zheng, J.P.; Liu, W. Influence of local strain on twinning behavior during compression of AZ31 magnesium alloy. Materials Science and Engineering a-Structural Materials Properties Microstructure and Processing 2015, 640, 330–337. [Google Scholar] [CrossRef]
  29. Chang, Y.; Tian, J.; Deng, J.-f.; Zhou, Y.; Wang, X.; Liang, W.; Shi, Q.-x. Local twinning behavior of ZK61m magnesium alloy sheet under multiaxial stress during drawing-pressing with Erichsen test machine. Journal of Alloys and Compounds 2023, 968. [Google Scholar] [CrossRef]
Preprints 99035 g001
Figure 1. The as-received AZ31 Mg alloy sheet: (a) Orientation map and (b) {0001} pole figure.
Figure 1. The as-received AZ31 Mg alloy sheet: (a) Orientation map and (b) {0001} pole figure.
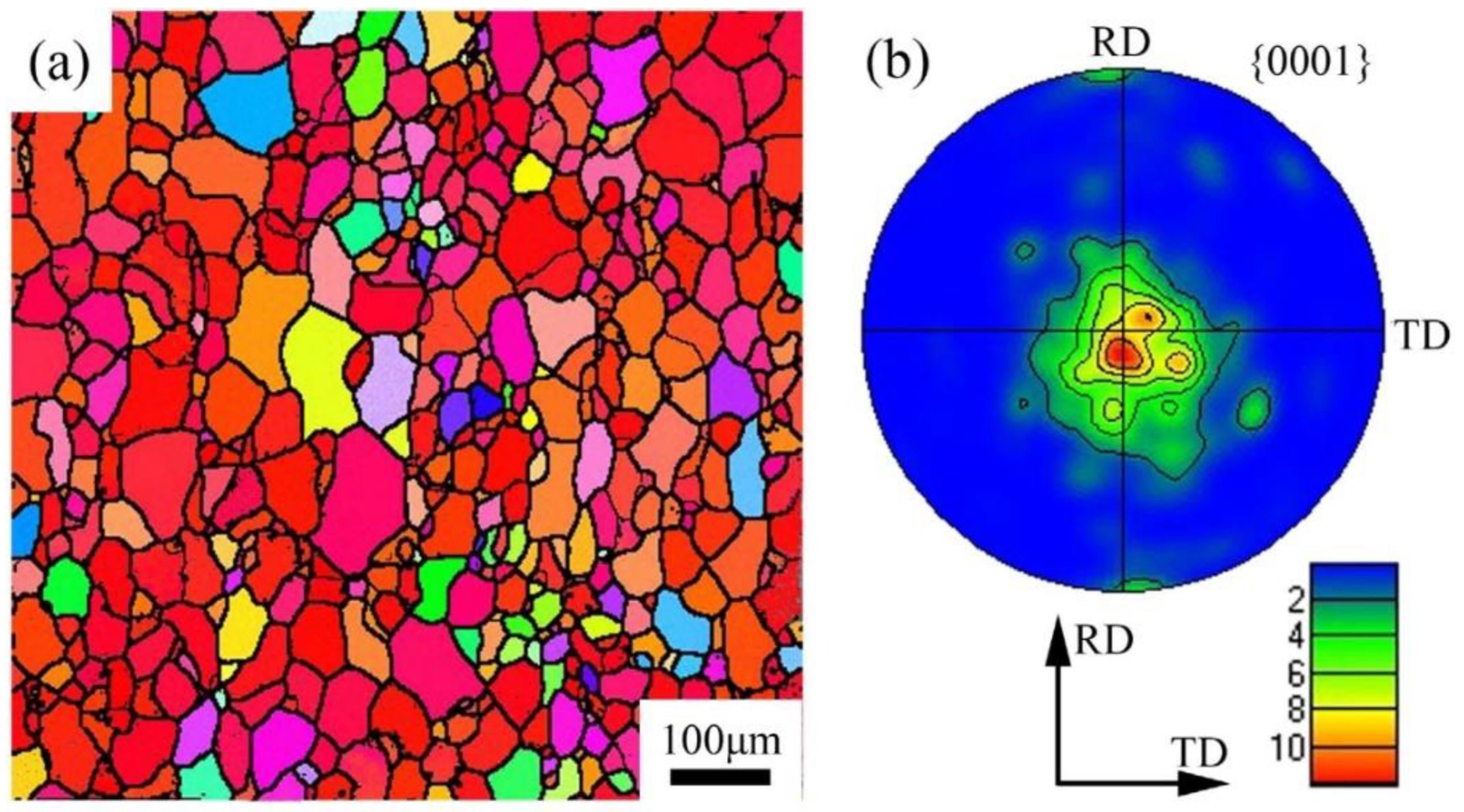
Preprints 99035 g001
Preprints 99035 g002
Figure 2. (a) Schematic illustration of the sample (RD, TD and ND represent the rolling, transverse and normal directions of the rolled sheet, respectively. LD represents the loading directions). The lengths of both the bottom and edge sides are each 8 mm. (b) Schematic illustration of hardness test and texture observation.
Figure 2. (a) Schematic illustration of the sample (RD, TD and ND represent the rolling, transverse and normal directions of the rolled sheet, respectively. LD represents the loading directions). The lengths of both the bottom and edge sides are each 8 mm. (b) Schematic illustration of hardness test and texture observation.
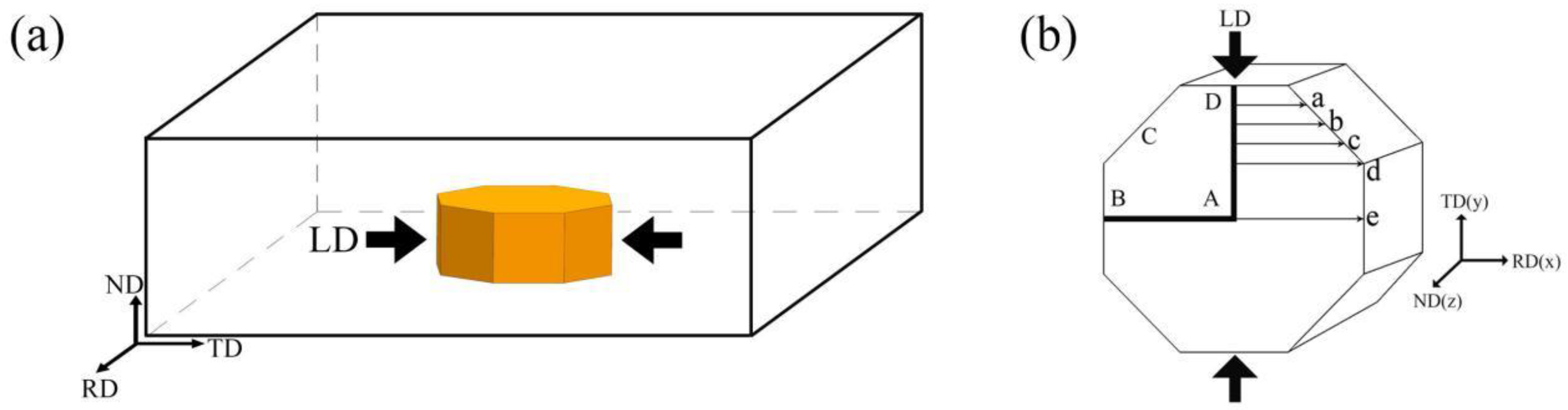
Preprints 99035 g002
Preprints 99035 g003
Figure 3. Hardness values were measured along lines of the eight-sided prism sample following compression.
Figure 3. Hardness values were measured along lines of the eight-sided prism sample following compression.
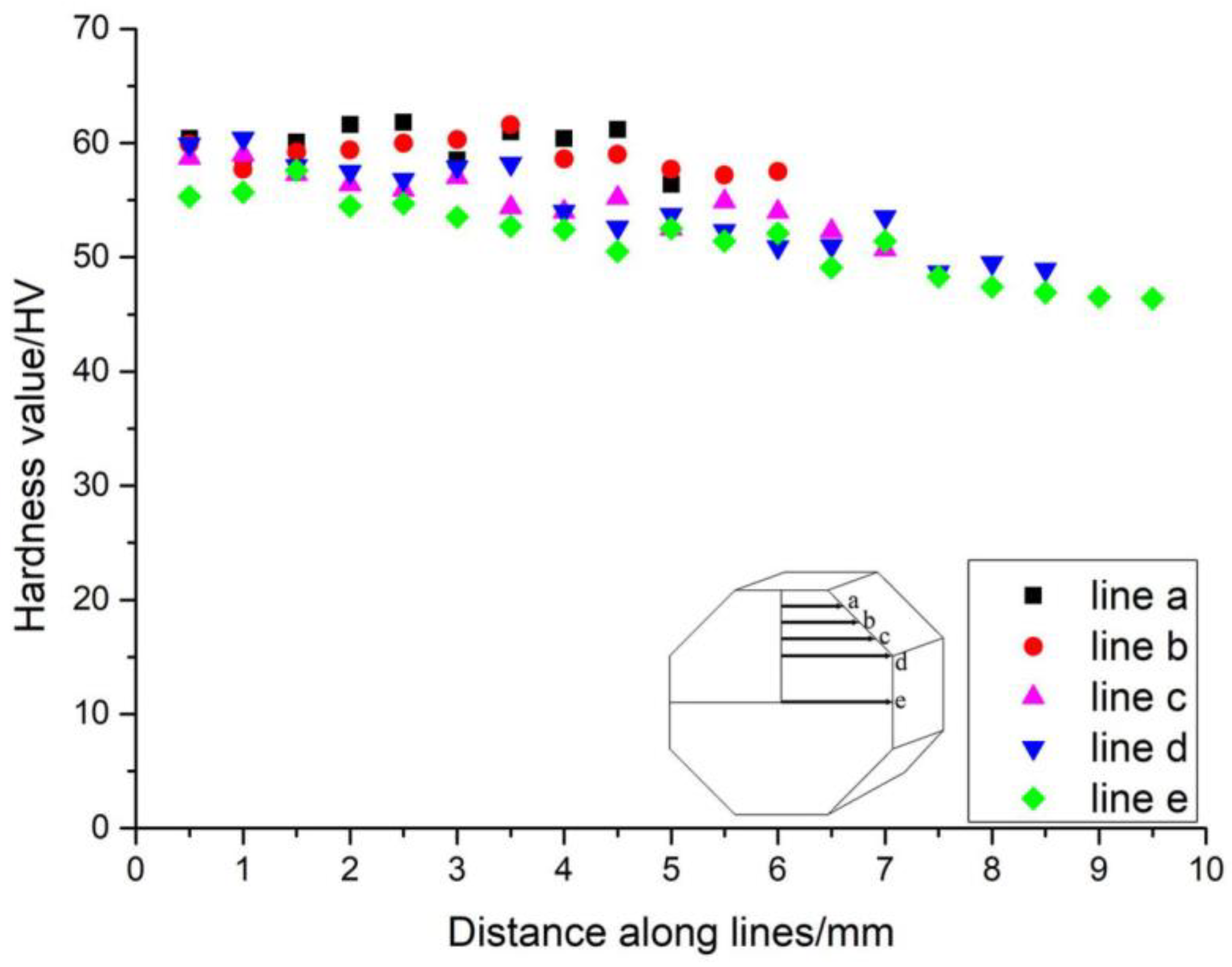
Preprints 99035 g003
Preprints 99035 g004
Figure 4. Optical micrographs at different areas of the sample after ɛ=3.9% compression at room temperature.
Figure 4. Optical micrographs at different areas of the sample after ɛ=3.9% compression at room temperature.
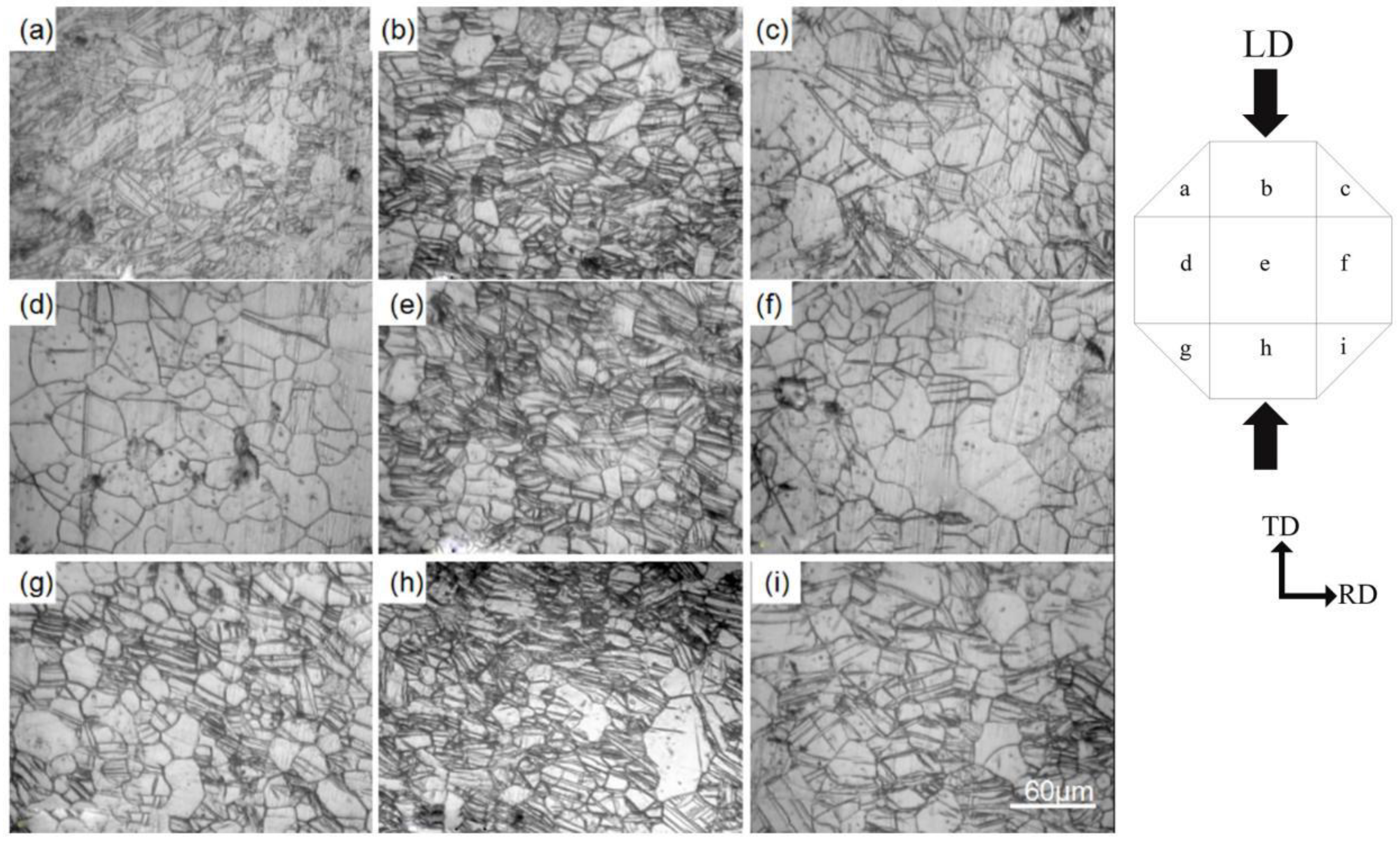
Preprints 99035 g004
Preprints 99035 g005
Figure 5. Orientation image maps, grain boundaries maps and {0001} pole figures of four regions: (a) region A; (b) region B; (c) region C; (d) region D.
Figure 5. Orientation image maps, grain boundaries maps and {0001} pole figures of four regions: (a) region A; (b) region B; (c) region C; (d) region D.
Preprints 99035 g005
Preprints 99035 g006
Figure 6. Frequency of twin variants displayed in terms of SFratio using an assumption of uniaxial loading: (a) region A and (b) region D. Results for region C using an assumption of pure shear, modeled as a combination of tension and compression (c) are shown in (d).
Figure 6. Frequency of twin variants displayed in terms of SFratio using an assumption of uniaxial loading: (a) region A and (b) region D. Results for region C using an assumption of pure shear, modeled as a combination of tension and compression (c) are shown in (d).
Preprints 99035 g006
Preprints 99035 g007
Figure 7. Distribution of calculated strain tensor components (ɛxx, ɛxy, ɛyy) of the observed twin variants for regions A, C and D: (a–c) region A; (d–f) region C; (g–i) region D.
Figure 7. Distribution of calculated strain tensor components (ɛxx, ɛxy, ɛyy) of the observed twin variants for regions A, C and D: (a–c) region A; (d–f) region C; (g–i) region D.
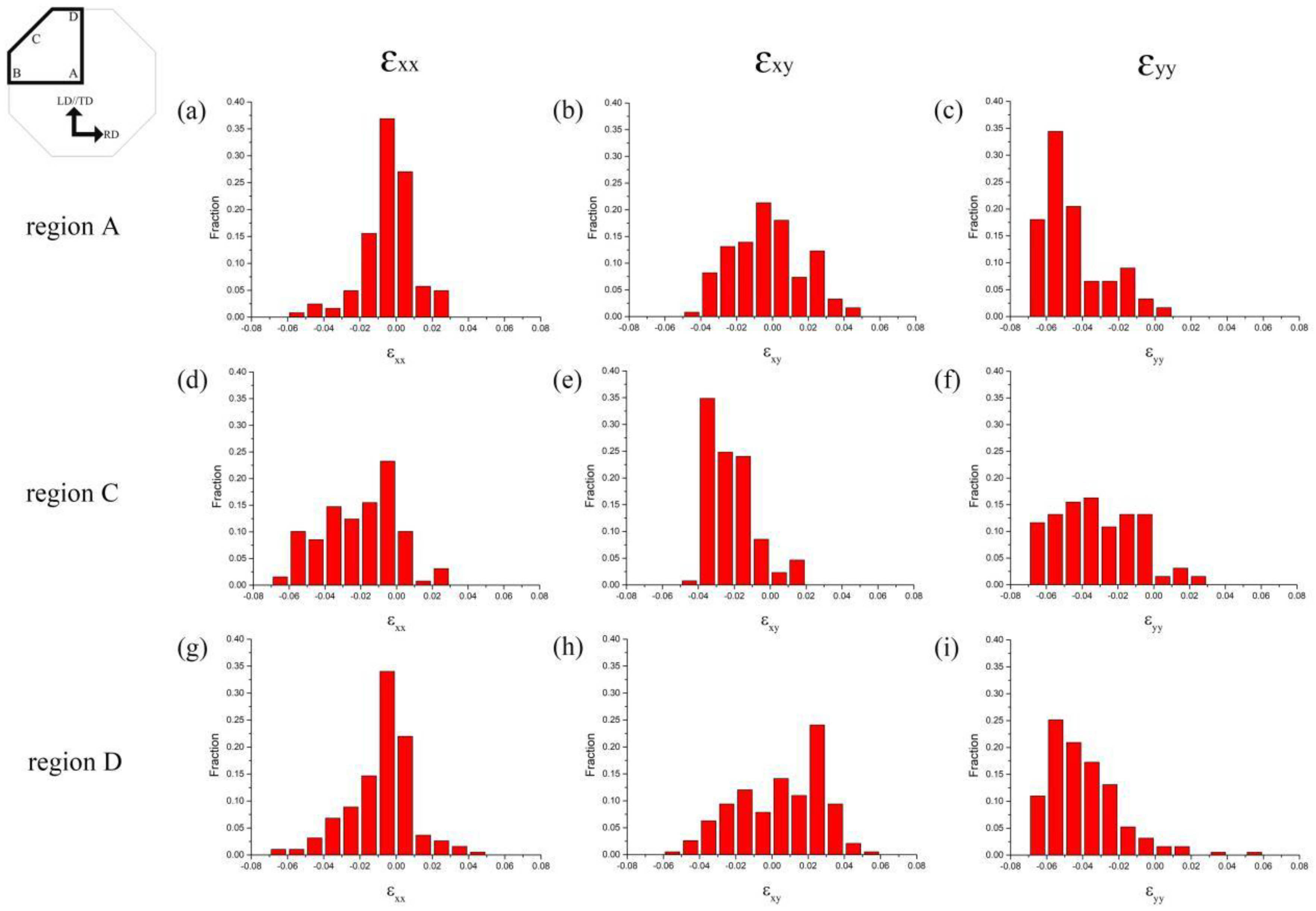
Preprints 99035 g007
Preprints 99035 g008
Figure 8. Distribution of m' rank, m' value and m' ratio of the observed paired twins (a,d,g), twin chains (b,e,h) and all twin variants (c,f,i) for the three regions.
Figure 8. Distribution of m' rank, m' value and m' ratio of the observed paired twins (a,d,g), twin chains (b,e,h) and all twin variants (c,f,i) for the three regions.
Preprints 99035 g008
Preprints 99035 g009
Figure 9. Analysis of twin chain across three neighboring grains which follow Schmid factor law and strain compatibility factor law for region A: (a) EBSD map; (b) Schmid factor distribution figure; (c) m' distribution figure; (d) strain tensors for twin variants.
Figure 9. Analysis of twin chain across three neighboring grains which follow Schmid factor law and strain compatibility factor law for region A: (a) EBSD map; (b) Schmid factor distribution figure; (c) m' distribution figure; (d) strain tensors for twin variants.
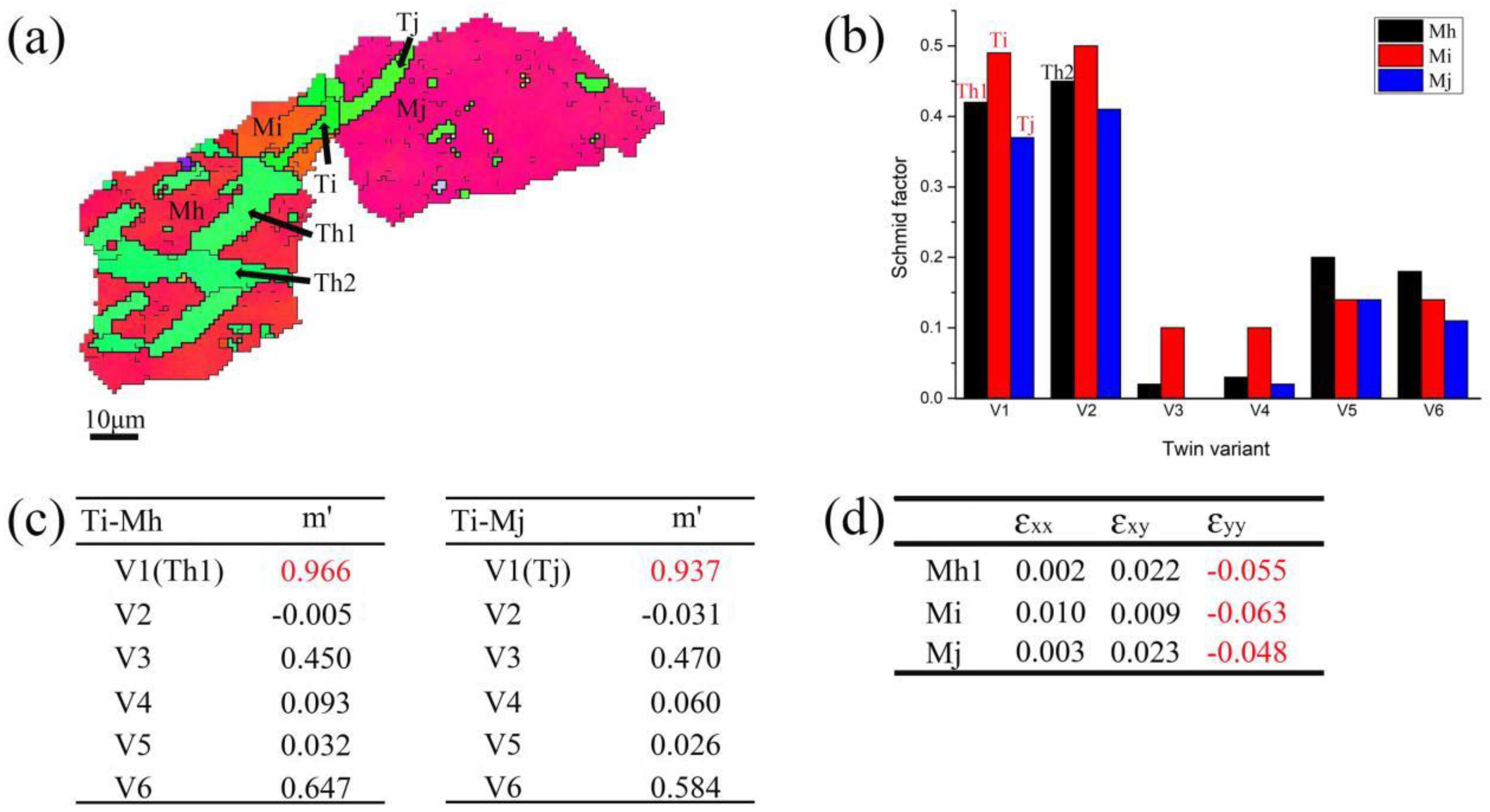
Preprints 99035 g009
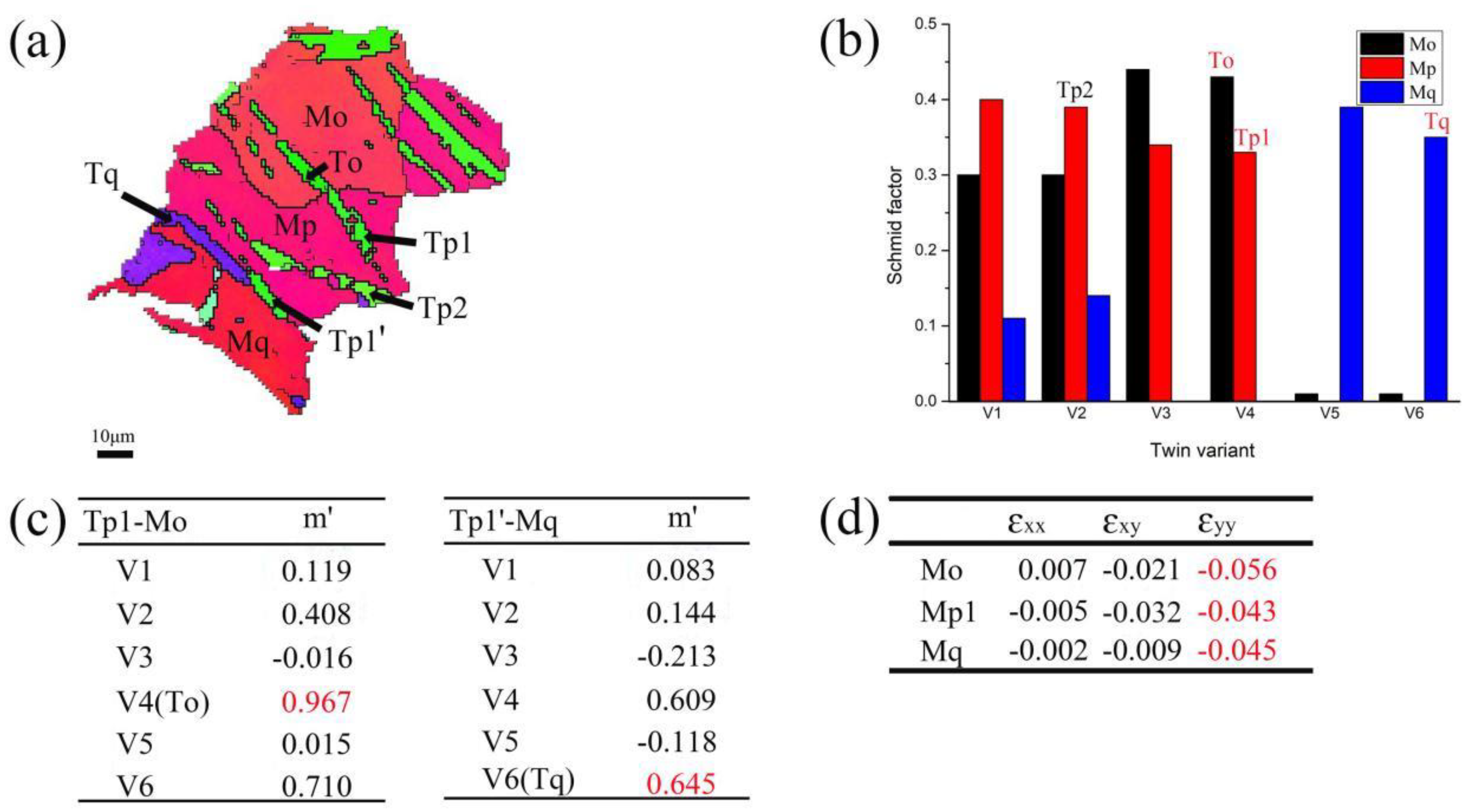
Preprints 99035 g010
Figure 10. Analysis of the cross-boundary twins which don't follow Schmid factor law but follow strain compatibility factor law for region A: (a) EBSD map; (b) Schmid factor distribution figure; (c) m' distribution figure; (d) strain tensors for twin variants.
Figure 10. Analysis of the cross-boundary twins which don't follow Schmid factor law but follow strain compatibility factor law for region A: (a) EBSD map; (b) Schmid factor distribution figure; (c) m' distribution figure; (d) strain tensors for twin variants.
Preprints 99035 g010
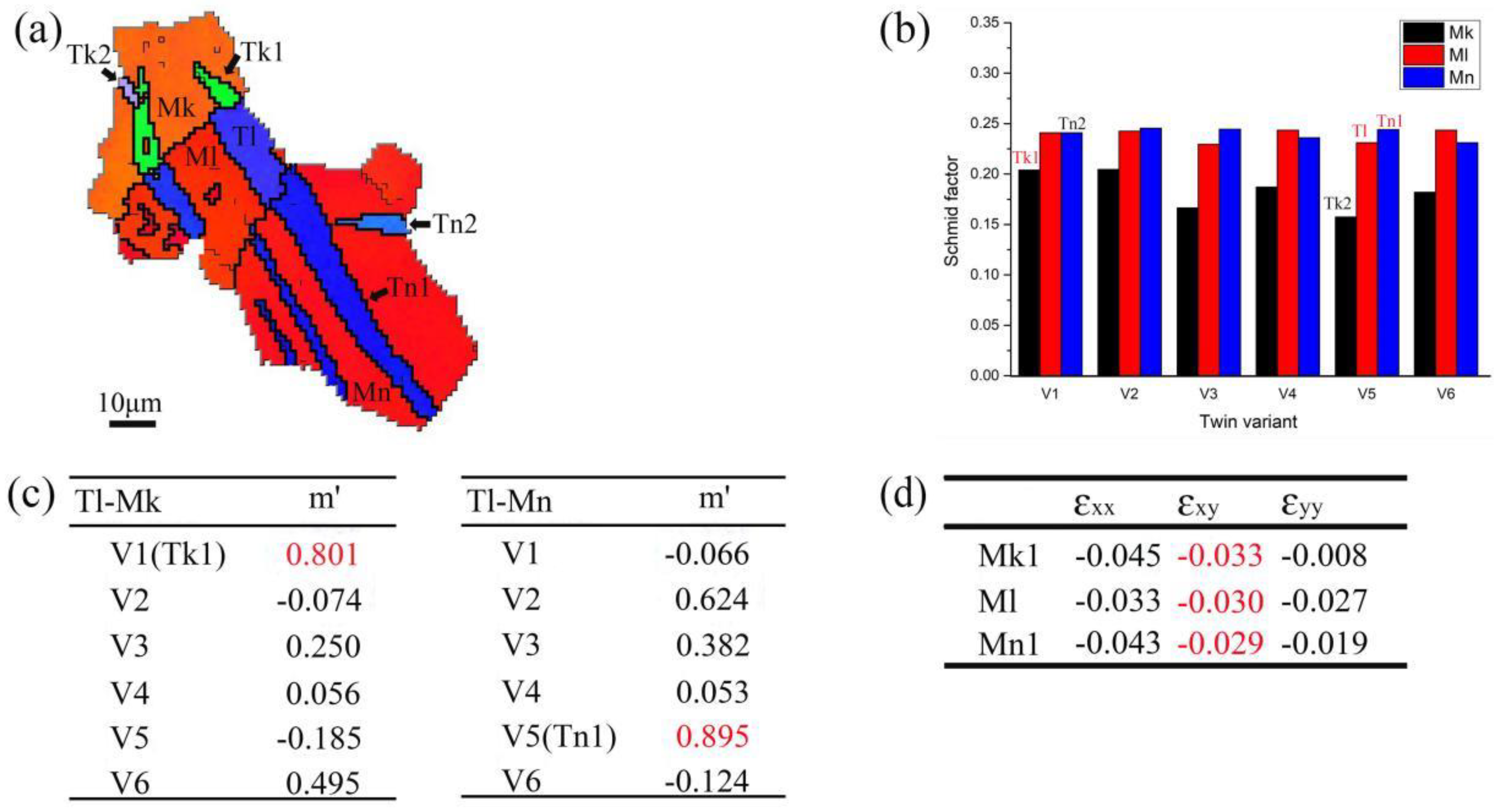
Preprints 99035 g011
Figure 11. Analysis of twin chain across three neighboring grains which follow strain compatibility factor law for region C: (a) EBSD map; (b) Schmid factor distribution figure; (c) m' distribution figure; (d) strain tensors for twin variants.
Figure 11. Analysis of twin chain across three neighboring grains which follow strain compatibility factor law for region C: (a) EBSD map; (b) Schmid factor distribution figure; (c) m' distribution figure; (d) strain tensors for twin variants.
Preprints 99035 g011
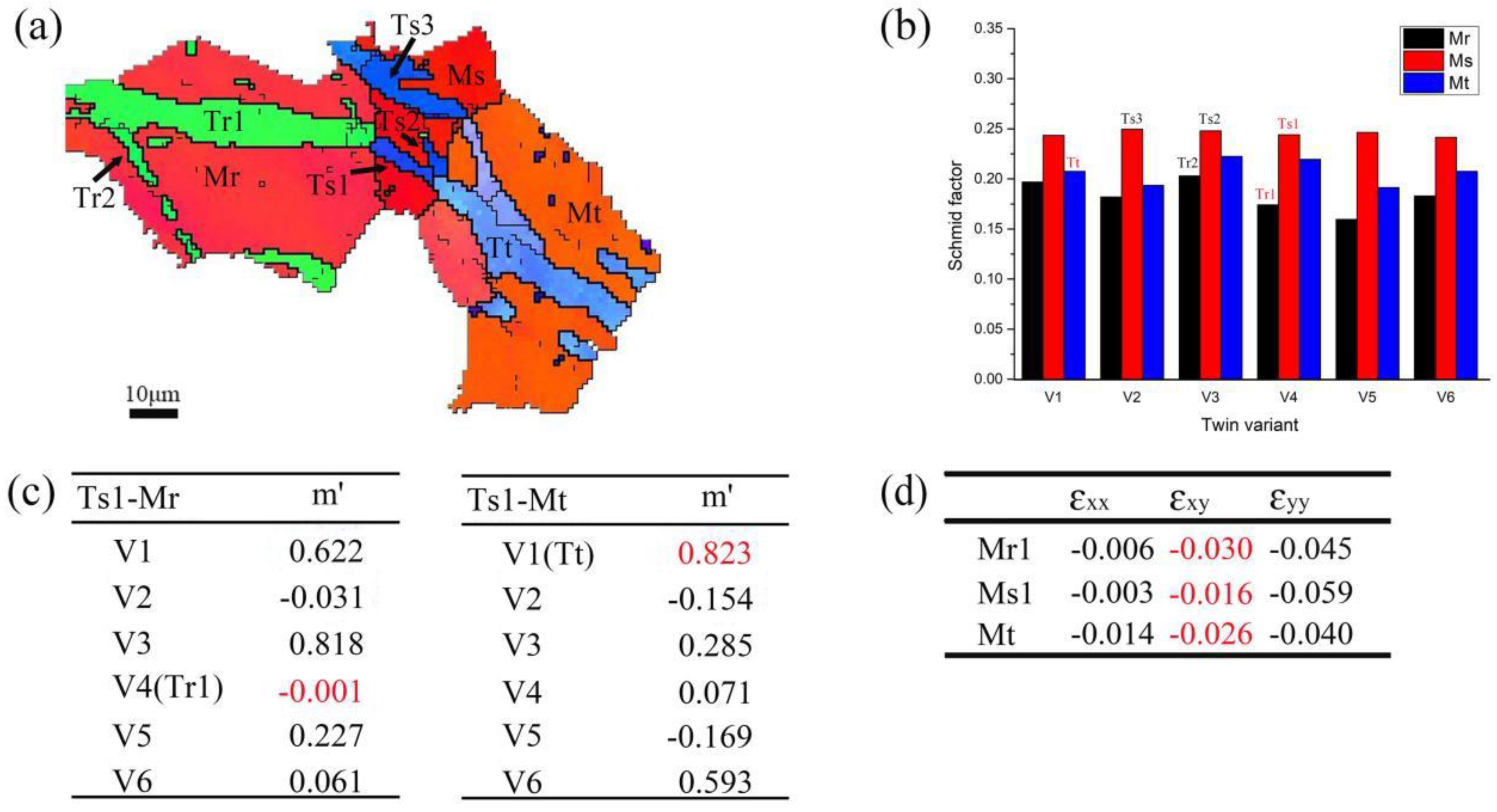
Preprints 99035 g012
Figure 12. Analysis of twin chain across three neighboring grains which doesn't follow strain compatibility factor law for region C: (a) EBSD map; (b) Schmid factor distribution figure; (c) m' distribution figure; (d) strain tensors for twin variants.
Figure 12. Analysis of twin chain across three neighboring grains which doesn't follow strain compatibility factor law for region C: (a) EBSD map; (b) Schmid factor distribution figure; (c) m' distribution figure; (d) strain tensors for twin variants.
Preprints 99035 g012
Table 1. Average values of strain tensor components for the respective regions.
Table 1. Average values of strain tensor components for the respective regions.
Ɛxx Ɛxy Ɛyy
region A -0.0031 -0.0029 -0.0448
region C -0.0204 -0.0215 -0.0312
region D -0.0073 0.0048 -0.0393
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated